принцип, теорема и примеры решения задач
Задание. Решить СЛАУ методом Гаусса.
Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент равнялся 1 (это мы делаем для упрощения вычислений):
Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей — три первых:
Все элементы третьей строки делим на два (или, что тоже самое, умножаем на ):
Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:
От третьей строки отнимаем вторую, умноженную на 3:
Умножив третью строку на , получаем:
Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент , для этого от второй строки отнимем третью:
Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:
Полученной матрице соответствует система
или
Ответ.
Метод Гаусса (оптимизация) — Википедия
Материал из Википедии — свободной энциклопедии
Метод Гаусса[1] — прямой метод решения задач многомерной оптимизации.
Пусть необходимо найти минимум действительнозначной функции f(x→)→minx→∈Rn{\displaystyle f({\vec {x}})\to \min _{{\vec {x}}\in \mathbb {R} ^{n}}}, а x→0{\displaystyle {\vec {x}}_{0}} — начальное приближение.
Суть метода заключается в том, чтобы на каждой итерации по очереди минимизировать функцию вдоль каждой из координат, то есть:
- x→0k+1=x→k{\displaystyle {\vec {x}}_{0}^{k+1}={\vec {x}}_{k}}
- x→0k+1=x→k{\displaystyle {\vec {x}}_{0}^{k+1}={\vec {x}}_{k}}
- {x→1k+1=x→0k+1+λ1e→1,λ1=argminλf(x→0k+1+λ1e→1)…x→nk+1=x→n−1k+1+λne→n,λn=argminλf(x→n−1k+1+λne→n){\displaystyle \left\{{\begin{array}{rl}{\vec {x}}_{1}^{k+1}={\vec {x}}_{0}^{k+1}+\lambda _{1}{\vec {e}}_{1},&\lambda _{1}=\arg \min _{\lambda }f({\vec {x}}_{0}^{k+1}+\lambda _{1}{\vec {e}}_{1})\\\ldots &\\{\vec {x}}_{n}^{k+1}={\vec {x}}_{n-1}^{k+1}+\lambda _{n}{\vec {e}}_{n},&\lambda _{n}=\arg \min _{\lambda }f({\vec {x}}_{n-1}^{k+1}+\lambda _{n}{\vec {e}}_{n})\end{array}}\right.},
где e→1,…,e→n{\displaystyle {\vec {e}}_{1},\ldots ,{\vec {e}}_{n}} — ортонормированный базис в рассматриваемом пространстве.
Таким образом метод как бы «поднимется» по координатам, используя на шагах одной итерации для вычисления следующей координаты точки приближения все предыдущие значения координат, вычисленные на той же итерации, в этом и состоит схожесть с одноимённым методом решения СЛАУ.
При завершении итерации, точка, полученная на последнем шаге этой итерации, берётся в качестве следующего приближения:
- x→k+1=x→nk+1{\displaystyle {\vec {x}}_{k+1}={\vec {x}}_{n}^{k+1}}.
Процедура продолжается до тех пор, пока не будет достигнута заданная точность ε{\displaystyle \varepsilon }, то есть пока:
- ||x→k+1−x→k||<ε{\displaystyle ||{\vec {x}}_{k+1}-{\vec {x}}_{k}||<\varepsilon }.
Улучшением данного метода является метод покоординатного спуска Гаусса — Зейделя.
- Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
- Максимов Ю.А.,Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
3.2 Метод исключения Гаусса. Схема единственного деления
Основная идея метода исключений Гаусса состоит в том, что система уравнений (3.1) приводится к эквивалентной ей системе с верхней треугольной матрицей (прямой ход исключений), а затем неизвестные вычисляются последовательной подстановкой (обратный ход исключений).
Рассмотрим сначала простейший метод исключения Гаусса, называемый схемой единственного деления.
Прямой ход состоит из n — 1 шагов. На первом шаге исключается переменная x1 из всех уравнений, кроме первого. Для этого нужно из второго, третьего, …, n-го уравнений вычесть первое, умноженное на величину
m = , i = 2, 3, …, n. (3.4)
При этом коэффициенты при x1 обратятся в нуль во всех уравнениях, кроме первого.
Введем обозначения:
a = aij — ma1j , b= bi — mb1. (3.5)
Легко убедиться, что для всех уравнений, начиная со второго, a= 0, i = 2, 3, …, n. Преобразованная система запишется в виде:
a11x1 + a12
x2 + a13x3 + … + a1nxn = b1ax2 + ax3 + … + axn = b
a x2 + ax3 + … + axn = b (3.6)
ax2 + ax3 + … + axn = b
Все уравнения (3.6), кроме первого, образуют систему (n — 1)-го порядка. Применяя к ней ту же процедуру, мы можем исключить из третьего, четвертого, …, n-го уравнений переменную x2. Точно так же исключаем переменную x3 из последних n — 3 уравнений.
На некотором k-ом шаге в предположении, что главный элемент k-ого шага a0, переменная xk исключается с помощью формул:
m = ,
b= b — mb, i, j = k + 1, k + 2, …, n. (3.7)
Индекс k принимает значения 1, 2, …, n — 1.
При k = n — 1 получим треугольную систему:
a11x1 + a12 x2 + a13x3 + … + a1nxn = b1
ax2 + ax3 + …+ axn = b
ax3 + …+ axn = b (3.8)
axn = b
с треугольной матрицей An.
Приведение системы (3.1) к треугольному виду (3.8) составляет прямой ход метода Гаусса.
При использовании метода Гаусса нет необходимости в предварительном обосновании существования и единственности решения (т. е. доказательства, что det A 0). Если на k-ом шаге все элементы a (i = k, k + 1, …, n) окажутся равными нулю, то система (3.1) не имеет единственного решения.
Обратный ход состоит в вычислении переменных. Из последнего уравнения (3.8) определяем xn... Подставляя его в предпоследнее уравнение, находим xn-1, и т. д. Общие формулы имеют вид:
xn = ,
xk = (b- a xk+1— a xk+2 — … — a xn), k = n — 1, n — 2, …, 1 (3.9)
Трудоемкость метода.
Для реализации
метода исключения Гаусса требуется
примерно 2/3n3 операций для прямого хода и n2 операций для обратного хода. Таким
образом, общее количество операций
составляет примерно 2/3n3 + n
Пример 3.1.
Применим метод исключения Гаусса по схеме единственного деления для решения системы уравнений:
2.0x1 + 1.0x2 — 0.1x3 + 1.0x4 = 2.7
0.4x1 + 0.5x2 + 4.0x3 — 8.5x4 = 21.9
0.3x1 — 1.0x2 + 1.0x3 + 5.2x4 = — 3.9 (3.10)
1.0x1 + 0.2x2 + 2.5x3 — 1.0x4 = 9.9
Будем делать округление чисел до четырех знаков после десятичной точки.
Прямой ход. 1-ый шаг. Вычислим множители:
m = = = 0.2; m = = = 0.15; m = = = 0.5.
Вычитая из второго, третьего и четвертого уравнений системы (3.10) первое уравнение, умноженное соответственно на m, m, m, получим новую систему:
2.0x1 + 1.0x2 — 0.1x3 + 1.0x4 = 2.7
0.3x2 + 4.02x3 — 8.70x4 = 21.36
-1.15x2 + 1.015x3 + 5.05x4 = — 4.305 (3. 11)
— 0.30x2 + 2.55x3 — 1.50x4 = 8.55
2-ой шаг. Вычислим множители:
m = = = — 3.83333; m = = = -1.0.
Вычитая из третьего и четвертого уравнений системы (3.11) второе уравнение, умноженное соответственно на
2.0x1 + 1.0x2 — 0.1x3 + 1.0x4 = 2.7
0.3x2 + 4.02x3 — 8.70x4 = 21.36
16. 425x3 — 28.300x4 = 77.575 (3.12)
6.570x3 — 10.200x4 = 29.910
3-ий шаг. Вычислим множитель:
m = = = 0.4.
Вычитая из четвертого уравнения системы (3.12) третье, умноженное на m, приведем систему к треугольному виду:
2.0x1 + 1.0x2 — 0.1x3 + 1.0x4 = 2.7
0.3x 2 + 4.02x3 — 8.70x4 = 21.36
16. 425x3 — 28.300x4 = 77.575 (3.13)
1.12x4 = -1.12
Обратный ход. Из последнего уравнения системы (3.13) находим x4 = 1.000. Подставляя значение x4 в третье уравнение, получим x3 = 2.000. Подставляя найденные значения x4 и x3 во второе уравнение, найдем x2 = 3.000. Наконец, из первого уравнения, подставив в него найденные значения x4, x3 и x2, вычислим x1 = -1.000.
Итак система (3.10) имеет следующее решение:
x1
Метод Гаусса-Жордана (единичная матрица) (метод полного исключения)
Схема Гаусса-Жордана или метод полного исключения, заключается в одновременном исключении (Жордановом исключении) какого либо переменного из всех уравнений системы, кроме одного. Его удобно реализовать на ЭВМ, учитывая ограниченность на их памяти, так как схема вычислений не требует выполнения обратного хода.
На первом шаге
этого метода выберем ведущий элемент 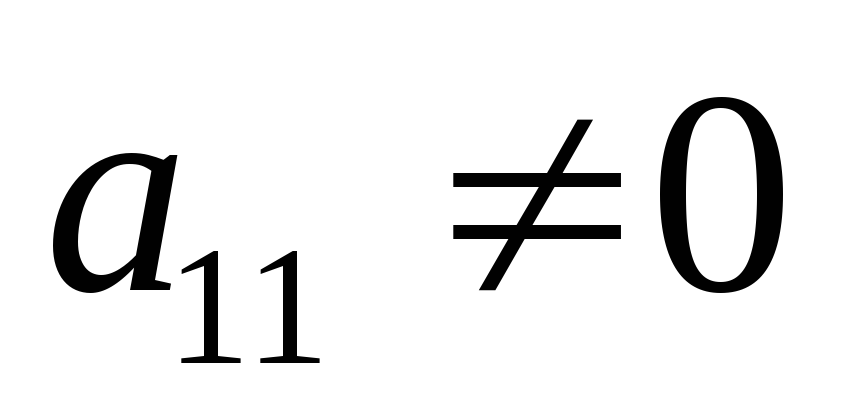 (перестановкой уравнений системы можно
добиться того, что
(перестановкой уравнений системы можно
добиться того, что будет наибольшим по модулю коэффициентом
при
будет наибольшим по модулю коэффициентом
при
 ,
во всех остальных уравнениях исключим
,
во всех остальных уравнениях исключим ,
то есть сведем расширенную матрицы
системы к виду
,
то есть сведем расширенную матрицы
системы к виду 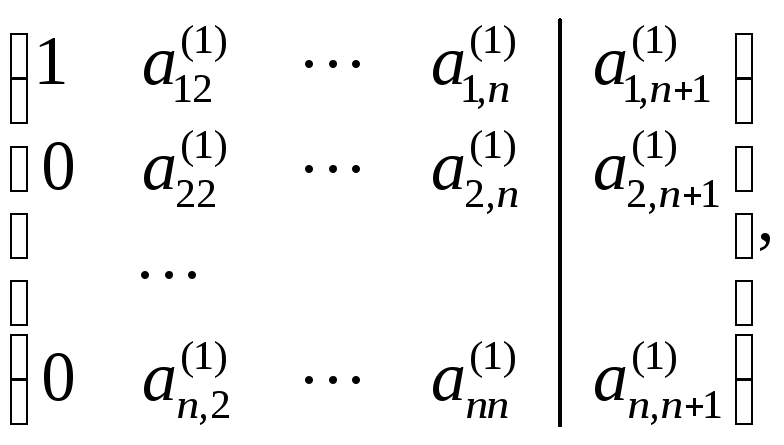
где
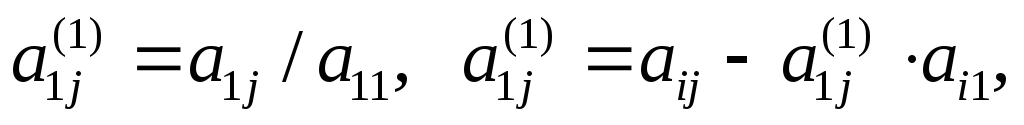
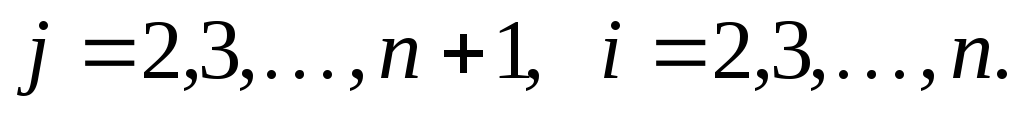
во втором шаге
выберем ведущий элемент (можно
сделать перестановку строк 2,…,n таким
образом чтобы он был наибольшим по
модулю). Разделим второе уравнение на
(можно
сделать перестановку строк 2,…,n таким
образом чтобы он был наибольшим по
модулю). Разделим второе уравнение на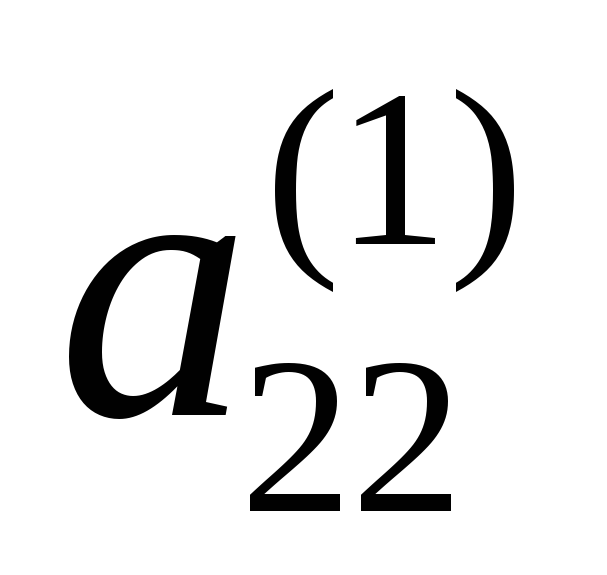
 из всех уравнений кроме второго.
из всех уравнений кроме второго. 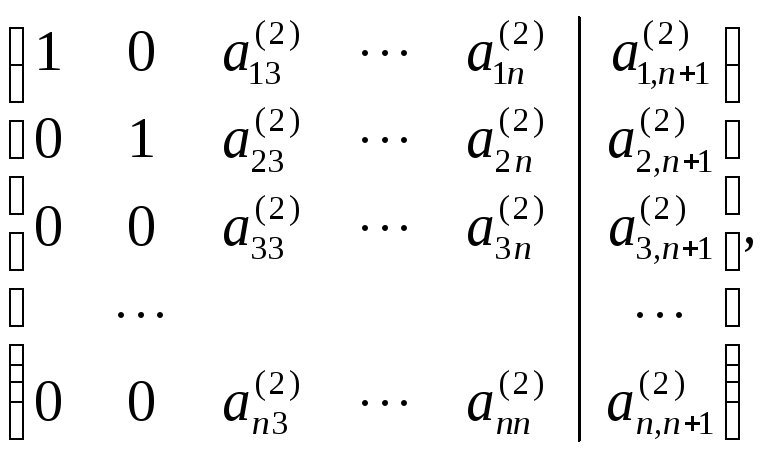
где

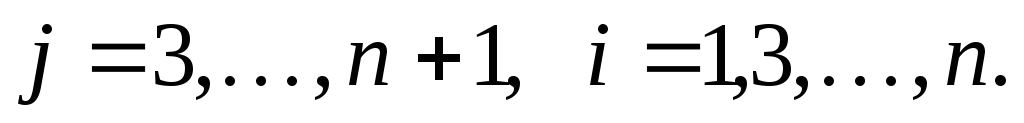
После n шагов получим матрицу

и численное значение неизвестных

Контроль вычислений можно осуществлять также, как и в схеме единственного деления, используя контрольные суммы.
Вычисление определителя и обратной матрицы метода Гаусса
В прямом ходе метода Гаусса над элементами матрицы А производятся элементарные преобразования, которые не изменяют определитель матрицы, кроме операции деления на ведущий элемент. Матрица преобразуется к треугольному виду с единичными диагональными элементами, ее определитель равен единице. Если в прямом ходе строки матрицы не переставляются то знак определителя не изменяется. Таким образом определитель не вырожденной матрицы системы равен произведению ведущих элементов в прямом ходе исключения Гаусса
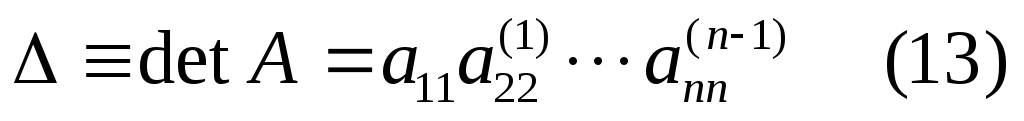 .
.
Для его вычисления прямой ход метода Гаусса , как и при решении системы, только без преобразований вектора b. При решении линейной системы определитель можно вычислить попутно.
Если применяется
метод исключения с выбором главного
элемента, то в (13) необходимо добавить
множитель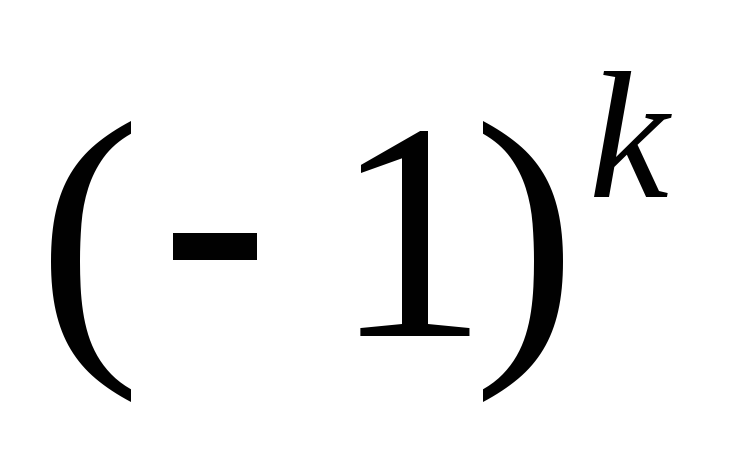 ,
гдек – количество перестановок строк и
столбцов.
,
гдек – количество перестановок строк и
столбцов.
Все вычислительные
схемы метода Гаусса позволяют осуществлять
одновременное решение систем линейных
уравнений с различными правыми частями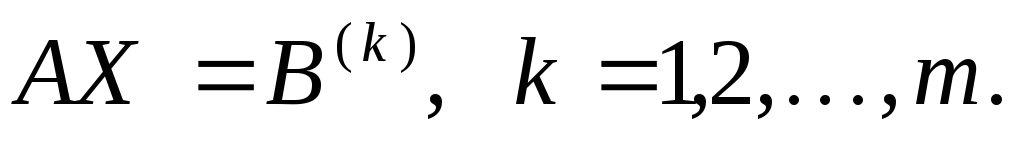 При этом количество вычислений
увеличивается на преобразование новых
столбцов правых частей, что дает
значительную экономию времени счета.
При этом количество вычислений
увеличивается на преобразование новых
столбцов правых частей, что дает
значительную экономию времени счета.
В частности если
вместо столбцов 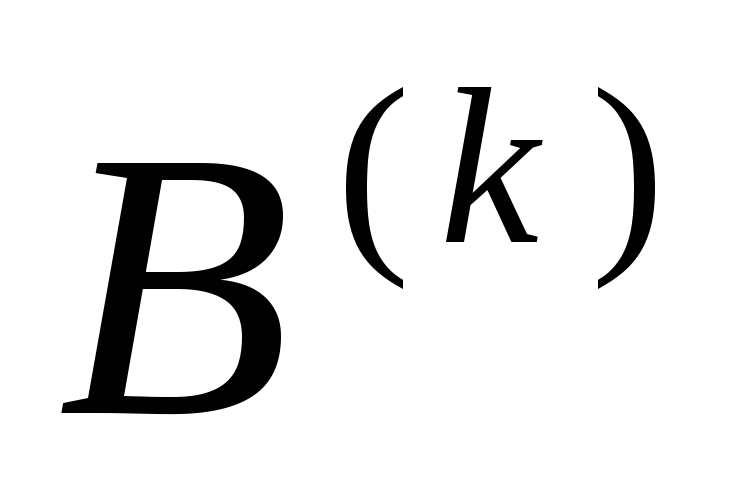 выбирать столбцы единичной матрицы
порядкаn:
выбирать столбцы единичной матрицы
порядкаn:
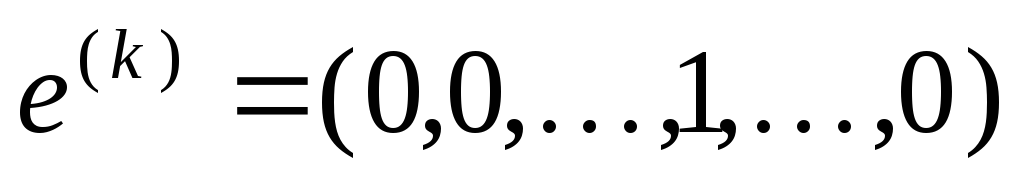
(1 на к-ом
месте, остальные элементы – нули), к=1.2
, …, n, то
решение 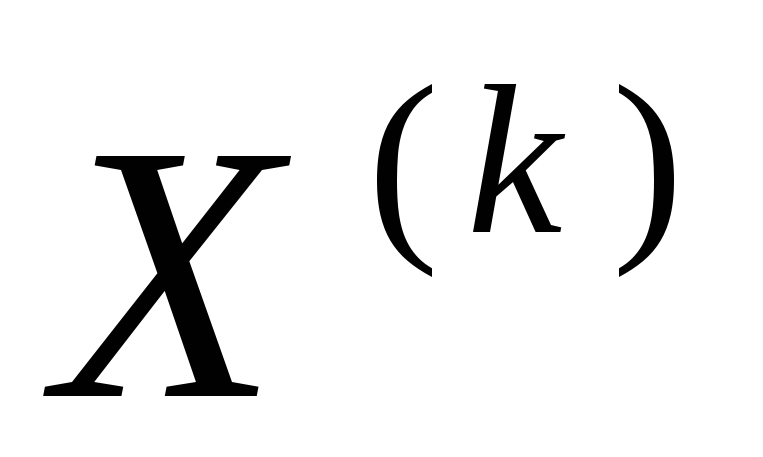 системы
системы будетк-м
столбцом обратной матрицы
будетк-м
столбцом обратной матрицы 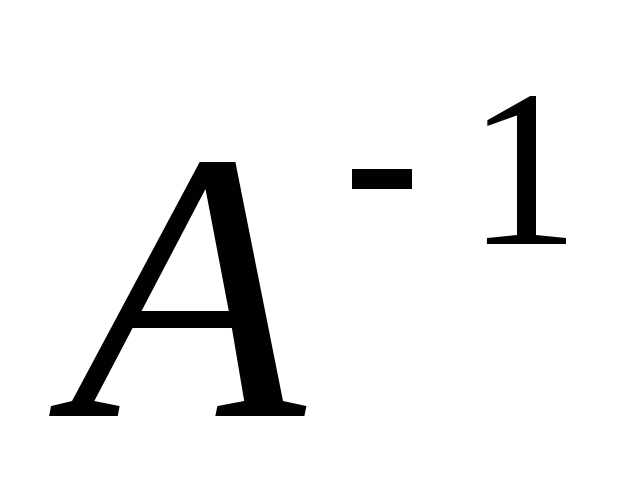 .
.
Таким образом для вычисления обратной матрицы требуется решить одновременно n систем уравнений с n неизвестными. Проводим последовательные исключения неизвестных в расширенной матрице
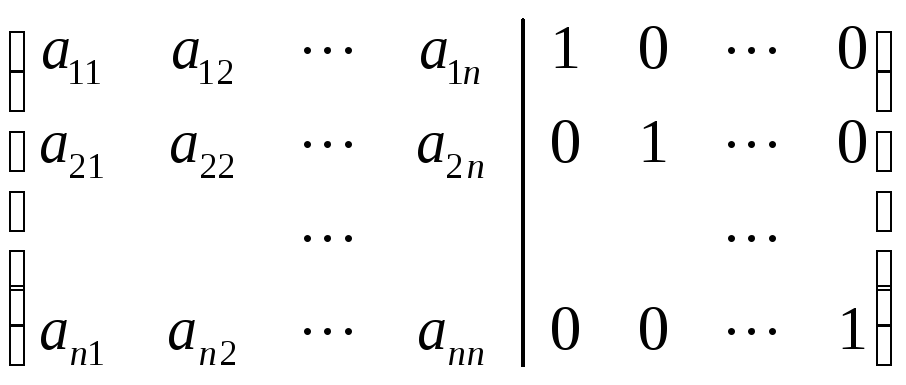 ~после n шагов
~после n шагов
~ .
.
Справа получим элементы обратной матрицы
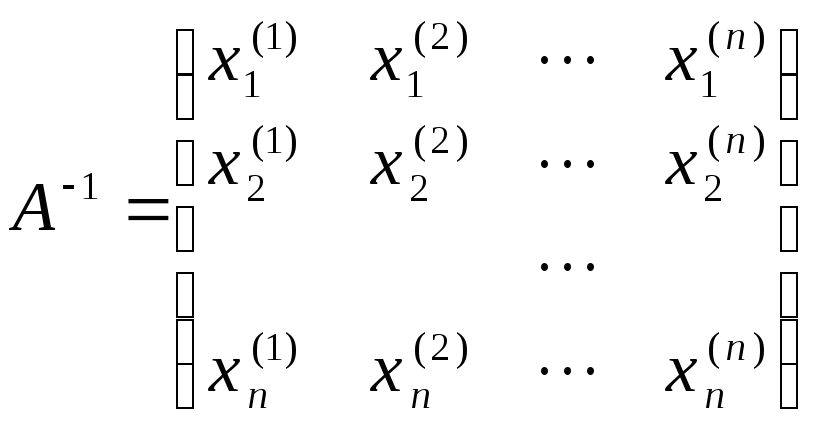 .
.
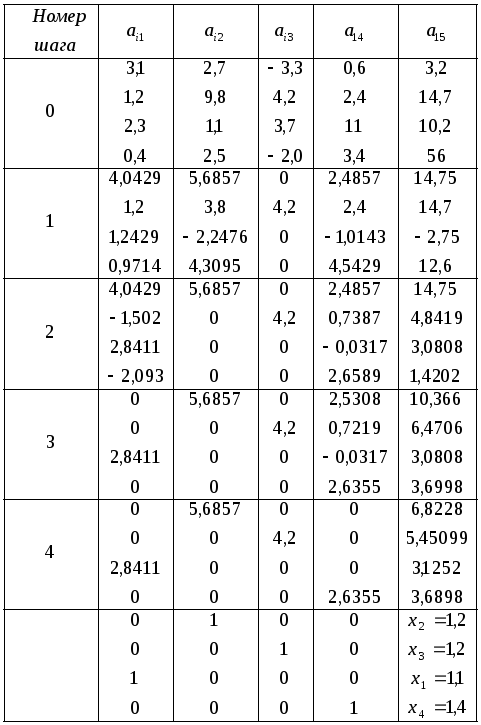
Пример. Решить систему
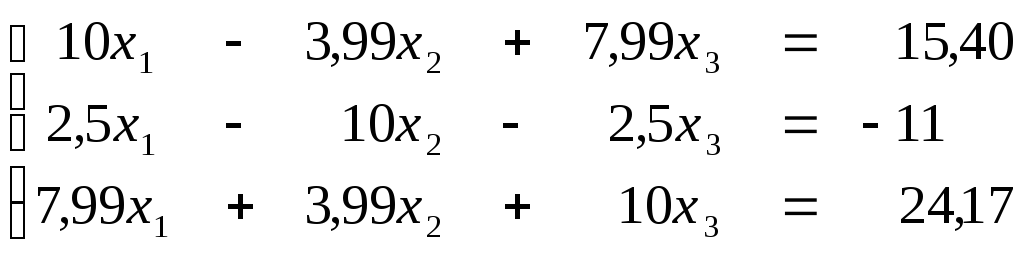
методом Жордана-Гаусса.
Ответ,,.
Пример. Решить методом Гаусса-Жордана с выбором главного элемента системы
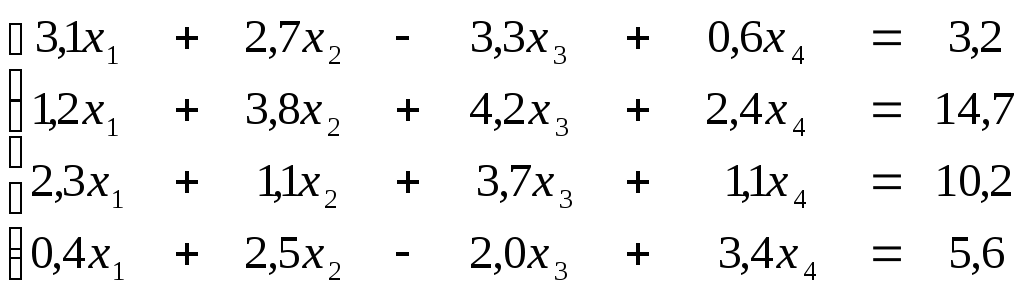
Ответ
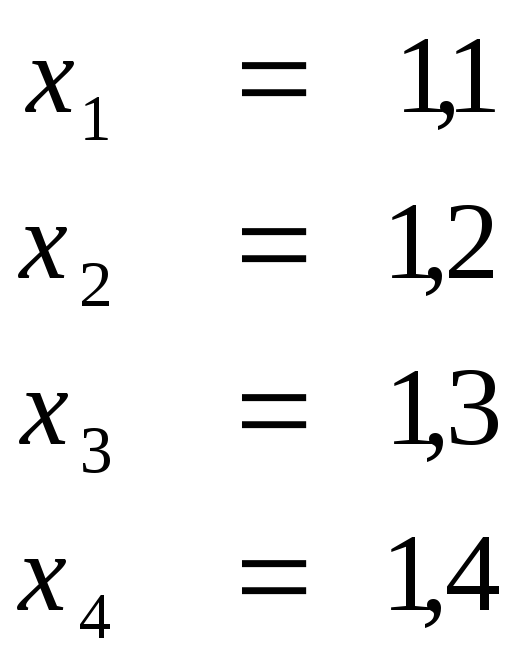 .
.
Определитель равен 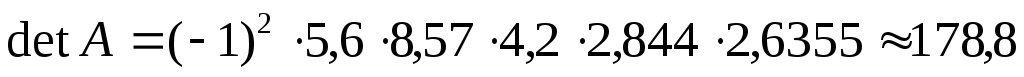 .
.
Метод прогонки
Большинство технических задач сводится к решению систем линейных алгебраических уравнений, в которых матрицы содержат много нулевых элементов, а ненулевые элементы расположены по специальной структуре, например, ленточные квазитреуголные матрицы.
Задачи построения интерполяционных сплайнов, разностные методы решения краевых задач для дифференциальных уравнений сходится к решению системы алгебраических уравнений с трехдиагональной матрицей А. В матрице А все элементы не лежащие на главной диагонали и двух соседних диагоналях равны нулю. Такие системы можно записать

Выбор наибольшего элемента при исключении неизвестных методом Гаусса в таких системах делать нельзя, поскольку перестановка строк разрушает структуру матрицы. Наиболее часто к решению систем с трехдиагональной матрицей применяют метод прогонки, который является частным случаем метода Гаусса.
Прямой ход метода
прогонки заключается в исключении
элементов  в системе (25). Так как
в системе (25). Так как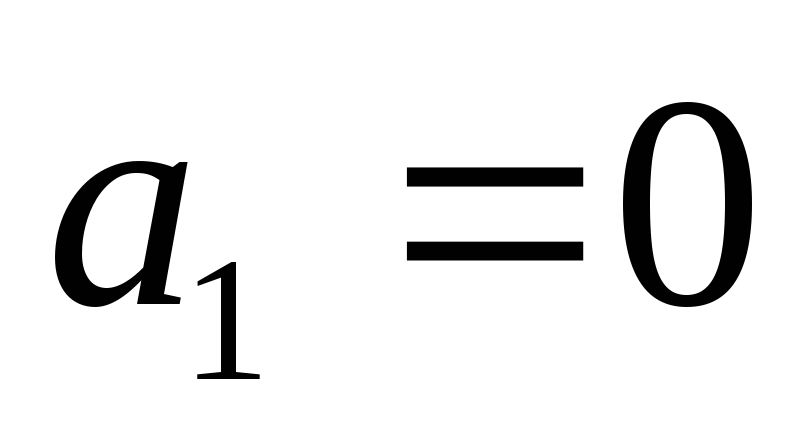 ,
то первое уравнение системы имеет вид
,
то первое уравнение системы имеет вид
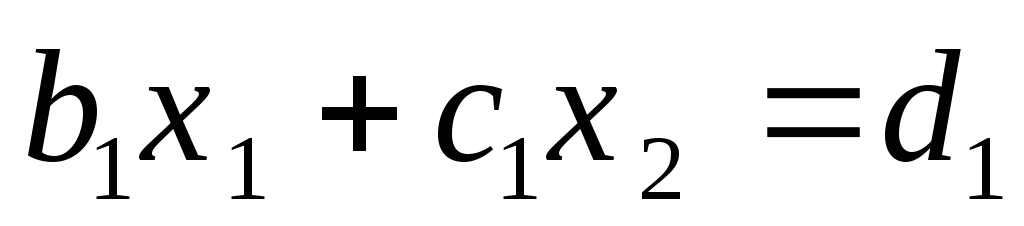 .
.
Выразим 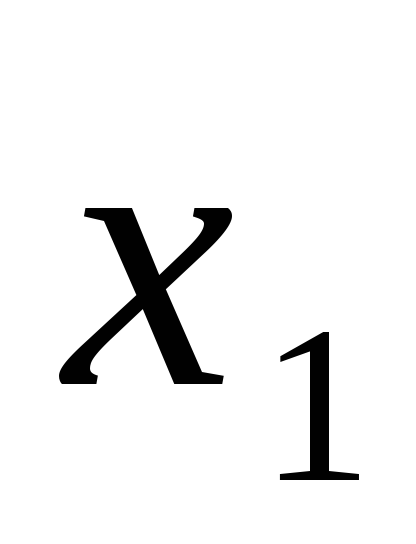 через
через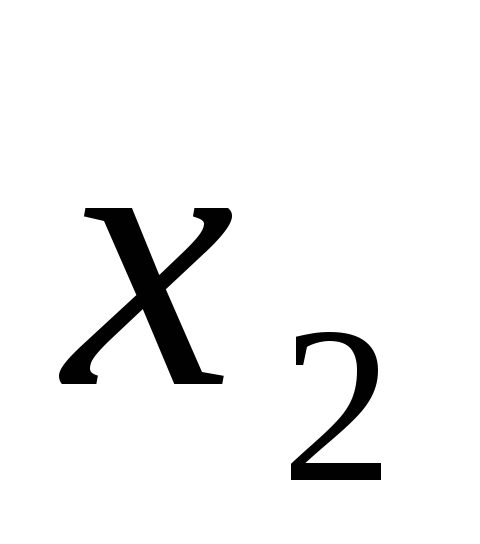 :
: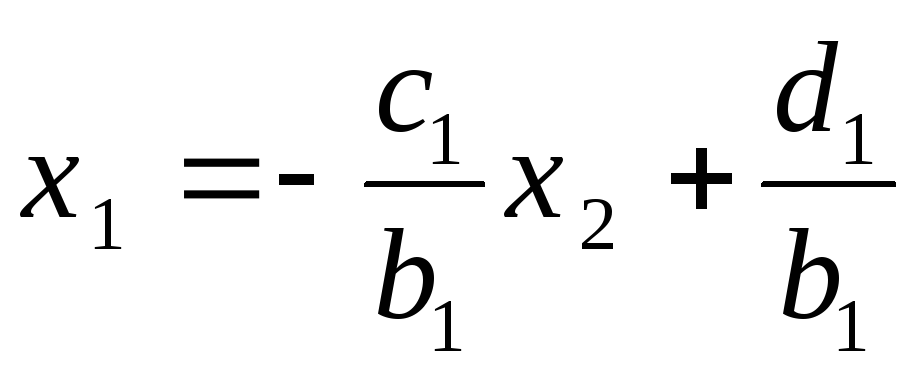 и подставим во второе уравнение системы,
получим уравнение связывающее
и подставим во второе уравнение системы,
получим уравнение связывающее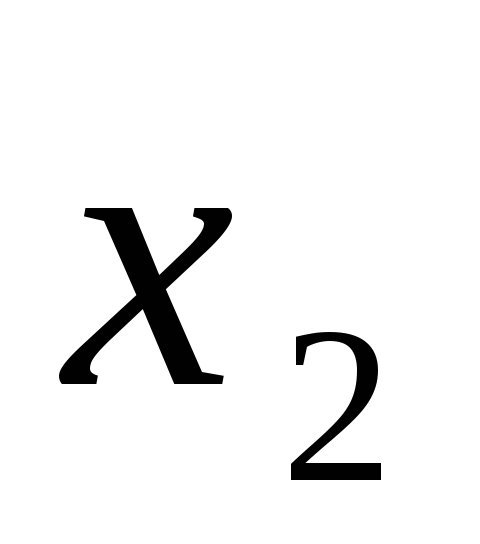 и
и и так далее. Пусть уже получено соотношение
и так далее. Пусть уже получено соотношение

Понизим в (26) индекс
на единицу и подставим значение  вi-е
уравнение системы (25)
вi-е
уравнение системы (25)
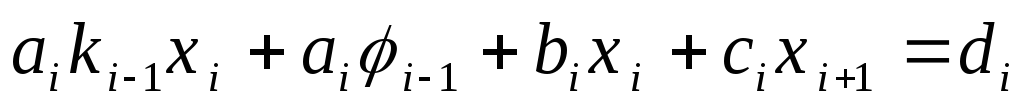 .
.
Отсюда
 .
.
Сравнивая это
выражение с (26) получим рекуррентные
формулы для вычисления 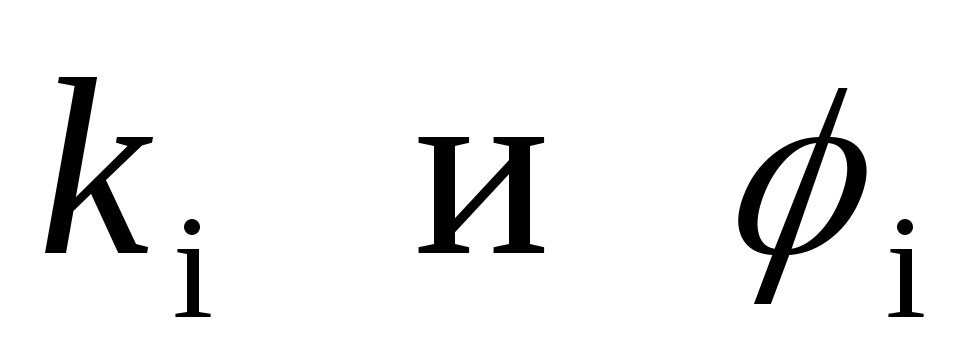 в прямом ходе:
в прямом ходе:
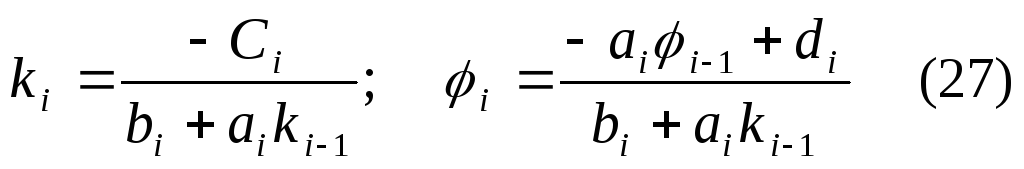 .
.
Учитывая, что 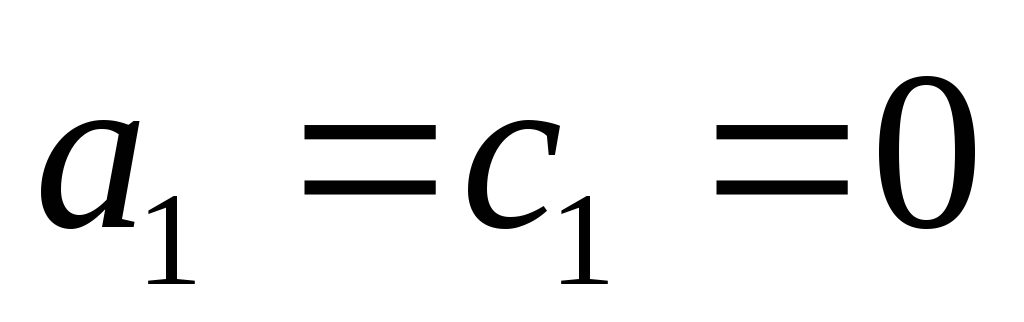 ,
полагаем
,
полагаем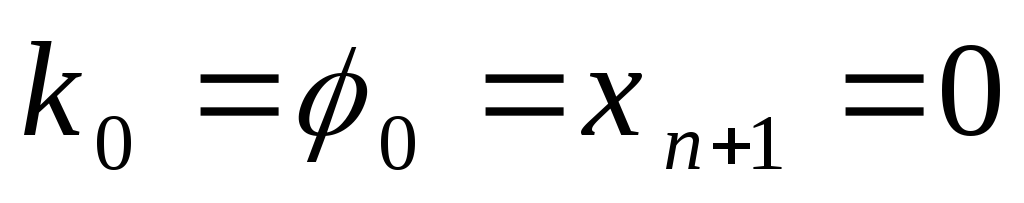 .
Обратный ход осуществляется по (26).
.
Обратный ход осуществляется по (26).
Почти во всех
задачах, приводящих к решению системы
(25) с трехдиагональной матрицей,
обеспечивается условие преобладания
диагональных элементов 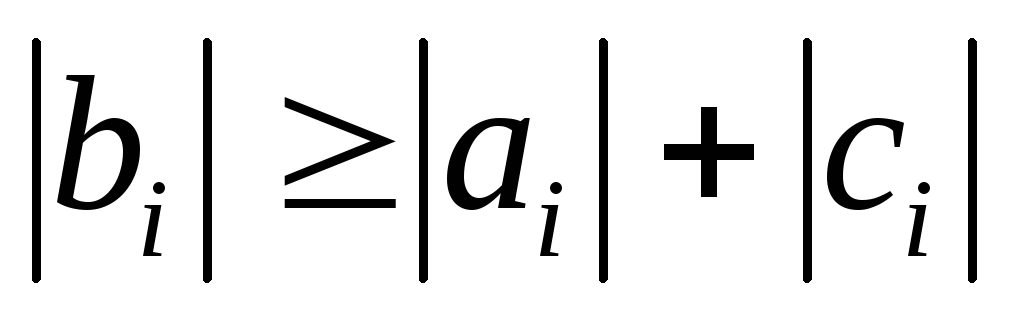 .
.
Это обеспечивает существование единичного решения и достаточно хорошую устойчивость метода прогонки относительно