7 класс. Алгебра. Системы двух уравнений с двумя переменными. — Способы решения систем уравнений с двумя неизвестными.
Комментарии преподавателяМетод подстановки.
Существует несколько методов решения систем. Один из них метод подстановки. Рассмотрим пример.
Пример 1:
Суть метода подстановки заключается в том, что в одном из уравнений нужно выразить одну переменную через вторую и подставить полученное выражение во второе уравнение.
В данном случае удобно выразить х во втором уравнении:
Подставим полученное выражение в первое уравнение:
Преобразуем первое уравнение:
,
,
,
Подставим полученное значение во второе уравнение:
, ,
Получаем следующее решение системы:
Пример 2:
В данном случае некоторая сложность заключается в том, что исходную систему нужно преобразовать, чтобы была возможность удобно и без ошибок применить метод подстановки. Для этого умножим оба уравнения на шесть:
Выразим у из первого уравнения:
Подставим полученное выражение во второе уравнение и выполним преобразования:
, ,
,
Подставим полученное значение в первое уравнение:
Получаем единственное решение системы, пара чисел:
Вывод:
на данном уроке мы ознакомились с понятием системы двух линейных уравнений с двумя неизвестными и одним из методов ее решения – способом подстановки. Мы решили примеры для понимания и закрепления данной техники.
Источник конспекта: http://interneturok. ru/ru/school/algebra/7-klass/glava-3-sistema-dvuh-lineynyh-uravneniy-s-dvumya-peremennymi/osnovnye-ponyatiya-metod-podstanovki?konspekt&chapter_id=10
ru/ru/school/algebra/7-klass/glava-3-sistema-dvuh-lineynyh-uravneniy-s-dvumya-peremennymi/osnovnye-ponyatiya-metod-podstanovki?konspekt&chapter_id=10
Метод алгебраического сложения, как и метод подстановки, заключается в том, что изначально из двух уравнений с двумя переменными нужно получить одно уравнение с одной переменной. Рассмотрим метод алгебраического сложения на примере:
Пример 1:
Задана система двух линейных уравнений с двумя неизвестными, и нужно найти такую пару х и у, чтобы при подстановке ее в уравнения получились верные числовые равенства.
Несложно заметить, что в первом уравнении у стоит с минусом, а во втором – с плюсом, и если сложить эти уравнения, то у уничтожится, и мы получим одно уравнение с одной неизвестной:
+
Получаем:
Найдем значение х:
,
Подставим значение х во второе уравнение и найдем у:
Ответ: (2,4; 2,2)
Обратим внимание на то, что мы рассматриваем метод алгебраического сложения, значит, уравнения можно не только складывать, но и вычитать. Рассмотрим пример:
Пример
При сложении уравнений получим:
,
Попробуем вычесть уравнения, причем, вычтем первое из второго:
,
Ответ: (5,5; 0,5)
Вывод:
на данном уроке мы рассмотрели новый метод решения систем двух линейных уравнений – метод алгебраического сложения. Мы решили несколько примеров для закрепления данной техники.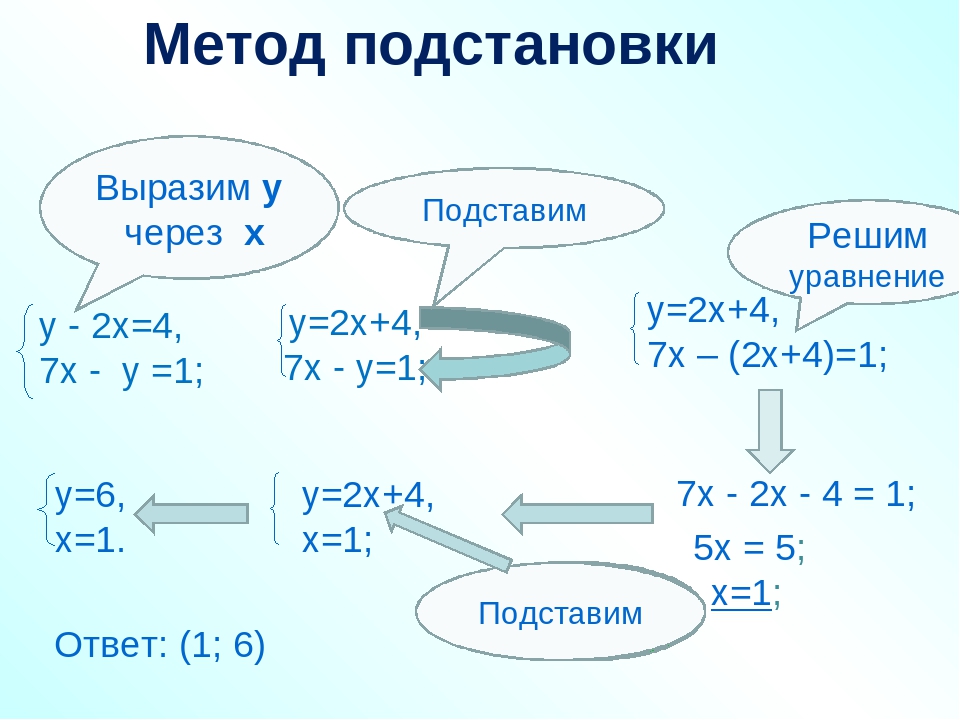
- Способ заключается в построении графика каждого уравнения, входящего в данную систему, в одной координатной плоскости и нахождении точки пересечения этих графиков. Координаты этой точки (x; y) и будут являться решением данной системы уравнений.
- Если прямые, являющиеся графиками уравнений системы, пересекаются, то система уравнений имеет единственное решение.
- Если прямые, являющиеся графиками уравнений системы, параллельны, то система уравнений не имеет решений.
- Если прямые, являющиеся графиками уравнений системы, совпадают, то система уравнений имеет бесконечное множество решений.
Примеры. Решить графическим способом систему уравнений.
Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений
Прямую y=2x-3 провели через точки (0; -3) и (2; 1).
Прямую y=x+1 провели через точки (0; 1) и (2; 3).
Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.
Ответ: (4; 5).
Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.
Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).
Наши прямые пересеклись в точке В(-2; 5).
Ответ: (-2; 5).
Источники конспекта: http://interneturok.
http://www.mathematics-repetition.com/6-klass-mathematics/6-9-1-reshenie-sistem-lineynh-uravneniy-grafitcheskim-sposobom.html
Источник видео: https://www.youtube.com/watch?v=VltC62A-Tt4
Конспект урока: Решение системы двух линейных уравнений методом подстановки.
Тема урока: Решение системы двух линейных уравнений методом подстановки.
Предмет: математика Класс: 7
Тип урока: урок «закрепления» нового знания
— Деятельностная: формирование у учащихся навыков решения системы уравнений методом подстановки, простейших преобразований линейных уравнений;
— Содержательная:
— Воспитательная: формирование общекультурных нравственных и морально-этических норм и способов поведения при работе в парах, фронтально; создание в коллективе атмосферы товарищества.
Ожидаемый результат:
-научить решать системы линейных уравнений с двумя переменными методом подстановки
-приобрести умения участвовать в диалоге, высказывать своё мнение, строить умозаключения, делать выводы.
Оборудование: интерактивная доска, презентация, задачник, раздатка, рабочая тетрадь.
ХОД УРОКА
|
№ п/п |
Этап урока |
Деятельность учителя |
Деятельность учащихся |
|
1. |
Самоопределение к коррекционной деятельности |
1) Знания, по какой теме вы получили на прошлых уроках? 2) Как вы думаете, какую цель поставим на этом уроке? |
1) Решают кроссворд, формулируют тему урока 2) Повторить и закрепить алгоритм решения систем уравнений методом подстановки. 3) Проверяют задания. |
|
2.
3. |
Актуализация знаний и умений
Работают самостоятельно по вариантам с проверкой по эталону. |
Фронтальная устная работа
2) Задания:
3) Расскажите алгоритм решения системы уравнений методом подстановки
2. №12.3 ( а, б) №12.9 (а,б)
2. В тетрадях записать самостоятельная работа № 1.
3. По истечении времени ???. Зафиксируйте полученные результаты, без исправления ошибок. Правильный результат «+», неправильный «-». |
Дают ответы
Записать ответ: (х; у) .
Выходят к доске 4 ученика (по 2 чел. одновременно каждый номер)
2. Выполняют самостоятельную работу.
3. Фиксируют полученные результаты знаками «+» (правильно) и «-» (неправильно).
|
|
3. |
Зарядка для глаз |
Следим за точкой глазами Закрыли глаза на 5секуд. Наши глазки отдохнули , продолжаем работать) |
|
|
4. |
Локализация затруднений |
1. Учащиеся, допустившие ошибки, анализируют решение по образцу, фиксируют места затруднений и определяют способы действий. Учащиеся, получившие верные ответы, также выполняют проверку решений по образцу, исключая ситуацию, когда ответ случайно верный, а решение – нет. Если ошибок нет – выполняют под в) из данной карточки.
|
1.
|
|
5 |
Построение проекта преодоления затруднений |
Определите, какие способы действий вам необходимо научиться правильно применять. |
В тетрадях, учебнике находят соответствующие способы действий, получают консультацию учителя и учащихся, выполнивших задание правильно. (КАК ЭТО ОРГАНИЗОВАТЬ ЛУЧШЕ???) Проверяют и находят ошибки, если не удается справиться самому, поднимают руку и учитель объясняет на месте. |
|
6. |
Самостоятельная работа по уровням сложности |
1. В тетрадях записать самостоятельная работа № 2. 2. Выполнить самостоятельную работу. |
1. Записывают самостоятельная работа № 2. 2. Выполняют соответствующие задания и сдают работы.
|
|
7. |
Включение в систему знаний и повторения |
|
Проговаривают алгоритм решения системы уравнений с двумя переменными методом подстановки |
|
8. |
Постановка домашнего задания |
№12.3(г), № 12.9(б) №12.15(а) (стр.43)
|
Записывают задание в дневниках. |
|
9 |
Рефлексия деятельности |
Учащимся предлагается рисунок (у каждого на парте приготовлена заготовка), на котором нужно отметить свое место положение для данного урока, т.е.:
|
Фиксируют степень усвоения материала, отмечая свое место положение в усвоении материала. Поднимите руку, кто себя определил на вершину горы? Кто на подъеме? (нужно закрепить дома) Кто у подножья горы? (остаться после уроков для отработки).
|
|
10 |
Оценки за работу на уроке |
|
Всем спасибо за урок , было приятно с вами работать) |
Конспект урока по алгебре «Решение систем уравнения способом подстановки и алгебраического сложения» 7 класс
Конспект коррекционно-развивающего урока алгебры в 7 классе.
Тип урока: закрепление знаний и умений.
Базовый учебник: Ш. А. Алимов Алгебра 7 класс.
Класс: коррекционный класс VII вида (12 обучающихся).
Тема урока: Решение систем уравнения способом подстановки и алгебраического сложения.
Цель урока: создание условий для обобщения знаний и закрепления навыков решения систем уравнений.
Задачи урока:
Образовательная – повторить алгоритм решения систем линейных уравнений методом подстановки и алгебраического сложения; закрепить умение решать системы линейных уравнений изученными способами.

Развивающая – продолжить развивать грамотность математического письма, внимание, память, логическое мышление, умение слушать и способность к рефлексии собственной деятельности.
Воспитательная – воспитывать умение доводить до конца начатую работу.
Коррекционная – коррекция устных вычислительных навыков, слухового восприятия и тренировка устойчивости внимания.
Ход урока
Организационный момент (создание условий для успешной совместной деятельности).
— Я сегодня пришла на урок с хорошим настроением. А у кого настроение плохое? Вы его умножьте на 0. Что получилось? Всё плохое исчезло. С этой «весёлой нотки» начинаем наш урок.
Сообщение темы и постановка учебной задачи урока.
— Знания, по какой теме вы получили на прошлых уроках?
— Какие способы решения систем линейных уравнений, вы знаете?
— Как вы думаете, какую цель поставим на этом уроке?
— Откройте тетради, запишите число и тему урока.
Устный счёт.
— Ребята, скажите, пожалуйста, какие устройства придумали люди для быстрого счёта?
— Представьте, что все электронно-вычислительные машины сломались, а нам надо срочно посчитать.
— Как мы будем считать, если нет ничего под рукой?
— Без устного счёта не сдвинется с места любая работа.
Дети по цепочки устно решают примеры.
— 3,2 – 5,8 = 1 — =
0,8 – 6 = — 23 =
— 0,25 • 40 = 7,2 : 0,1 =
— 6 + 6 = =
Дима моет 4 тарелки за тоже время, что и 6 чашек. Что он моет быстрее – тарелку или чашку?
Что он моет быстрее – тарелку или чашку?
— Теперь я проверю, насколько внимательно вы изучаете математику.
— Я буду говорить слова, а вы должны определить, если это математическое понятие, вы показываете зелёную карточку, в остальных случаях красную.
Слова: медиана, уравнение, приставка, диффузия, пропорция, вулкан, род, хорда, молекула, ордината.
Закрепление изученного материала (на данном этапе урока используется технология дифференцированного обучения).
— Решите систему линейных уравнений способом подстановки и алгебраическим сложением.
Двое обучающихся с подробным комментированием решают на школьной доске, предложенную систему линейных уравнений. При решении используют опорную (печатную) схему с алгоритмом выполнения действий.
Трое учеников, которые нуждаются в направляющей помощи со стороны учителя, решают индивидуальное задание.
Карточка №1
Решить уравнение: 21 – 2(3 – 4х) = 3 – 2х
Карточка №2
Вычислить:
— 4,8 – 5,2 = — 8 : 0,2 =
3,4 – 9 = — 8 + 8 =
0 – (- 6) = — 1,7 + 0,7 =
Карточка №3
Вычислить:
5 • 0,32 + 1,7 = : =
— = ( — 0,3) • 5 – 3 =
Физкультминутка – комплекс упражнений на общее развитие организма.
— Представьте себе, прямоугольник, у которого длина 3 см, а ширина 2 см.
— Сожмите кисти рук столько раз, чему равна площадь этого прямоугольника.
— Присядьте столько раз, чему равен периметр этого прямоугольника.
— Сделайте столько наклонов вниз туловищем, чему равна площадь квадрата со стороной 2 см.
Самостоятельная работа по вариантам (самоконтроль).
Двое обучающихся решают систему линейных уравнений на обратной стороне школьной доски.
Вариант 1
Вариант 2
Коллективная проверка индивидуальной работы.
Подведение итогов урока. Рефлексия.
— Какими способами, можно решить систему линейных уравнений?
— Какой способ является более простым и рациональным?
— Теперь с помощью листа самооценки оцените свою учебную деятельность на уроке.
Обучающиеся по кругу в устной форме заканчивают, на выбор одну из предложенных фраз из листа самооценки.
Лист самооценки
Сегодня я узнал…
У меня получилось…
Мне было интересно…
Было трудно…
Теперь я умею…
Постановка домашнего задания (дифференцированный подход)
«3» — №635 (чётные)
«4» и «5» — самостоятельно составить систему линейных уравнений и решить её.
Конспект урока по теме «Решение систем уравнений» 7 класс.
Решение систем уравнений.
PPTX / 81.94 Кб
Конспект урока алгебры 7 класс:
«Решение систем линейных уравнений»
Мартынова Вера Аркадьевна, учитель математики
ГОУ РК «РЦО» г. Сыктывкара
Сыктывкара
Тип урока: Урок закрепления новых знаний и способов деятельности
Тема | РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ. | |||
Цель урока | обеспечить закрепление знаний и способов деятельности, создание условий для формирования умений решать системы линейных уравнений с двумя переменными способом подстановки; | |||
Задачи | содействовать развитию познавательной активности, навыков самооценки и самопроверки, умения работать в группе, брать на себя ответственность, за решение систем уравнений, развивать коммуникативную компетенцию и математическую речь через работу в группах. | |||
УУД | ЛичностныеУУД: способствовать развитию критического мышления, Регулятивные УУД: умения работать в паре, группе, брать на себя ответственность; навыков саморегуляции через самооценку и взаимооценку , рефлексию, Коммуникативные УУД: для развития коммуникативной компетенции и математической речи через работу в группах,. Познавательные УУД: содействовать развитию познавательной активности, навыков самооценки и самопроверки. | |||
Планируемые результаты | Предметные: Знать алгоритм решения систем уравнений подстановкой. Уметь решать системы уравнений. | |||
Основные понятия | Системы уравнений, решение систем уравнений. | |||
Межпредметные связи |
| |||
Ресурсы: основные дополнительные |
| |||
Формы урока | Ф — фронтальная, И – индивидуальная, Г – групповая | |||
Технология | Системно –деятельностный подход. | |||
Дидактическая | Деятельность | Деятельность | ||
Мотивация
| Тема урока. | Работа с выходом на тему. Ф | ||
Актуализация опорных знаний и умений
| Выполняют устные упражнения. | Ф. Устные задания. 1.Является ли пара чисел решением системы? 2. Выразите переменные Х через У, и У через Х
| ||
Организация деятельности учащихся по использованию знаний в стандартных и измененных ситуациях
| Работа в группах. | Г. И. Организация работы в группах | ||
Контроль и самоконтроль
| С одной стороны букв, с обратной — ответ решенной системы уравнения. . Получили слово. КВАШИОРКОР. Питание и здоровье. Белки, аминокислоты, жиры, углеводы, витамины. Белок необходим для мышечной работы, успешного обучения, для поддержания нормального иммунитета. Школьнику требуется ежедневно около 70 – 90 г. белка. Для этого необходимо съедать примерно 100 – 200г. мяса, 30 – 50г. рыбы, 400 – 500г. молока или кисломолочных продуктов, 30 – 40г. творога, 5 – 10г. сыра. Дефицит белков ведет к задержке роста, снижению устойчивости к инфекциям, малокровию. Квашиоркор – заболевание развивается в случае белкового голодания Разгадывают кроссворд. По горизонтали: 1. График линейного уравнения с 2 переменными. 2. Уравнения с 2 переменными, имеющие одни и те же решения. 3. Один из способов решения систем линейных уравнений. По вертикали: 4. Множество всех точек плоскости, координаты которых являются решениями уравнения с 2 переменными. 5. 6. Пара значений переменных, обращающая уравнение с 2 переменными в верное равенство. 7. Французский математик, который ввел и разработал
| Ф. Презентация, Вспомним теоретический материал по теме, разгадав кроссворд. Решение кроссворда на экране. Какое слово вы не разгадали «СЛОЖЕНИЕ». Решение методом сложения, мы будем решать на следующем уроке.
| ||
Коррекция
|
| Рефлексия.
| ||
Дополнительный материал:
а. б. в.
( -2; -3) ( 2; 5) (4,5; 2,5)
Задания.
1. 2. 3.
4. 5. 6.
7. 8. 9.
10. 11. 12.
а. б. в.
Ответы:
1. 2. 3.
(8; — 1) (2; — 1) (3;3)
4. 5. 6.
(-3;-3) ( 4; 1) (2; 7)
7. 8. 9.
(1;6) ( -8; 0) (2; 2)
10. 11. 12.
(1; 2) (3; -1) (16; 22)
а. б. в.
б. в.
( -2; -3) ( 2; 5) (4,5; 2,5)
Устные упражнения. 1. Является ли решением системы пара чисел: (-1;1), (2;-1), (6;2,5)?
2. Выразите:
а) Х через У.
б) У через Х.
1. Х + У = 2
2. Х + 3 У = 10
3. 2 Х + 7 У = 8
4. 6 Х — 5 У = 4
Самоанализ урока.
Тема: «Решение систем линейных уравнений»
Цель: закрепление знаний и способов деятельности, создание условий для формирования умений решать системы линейных уравнений с двумя переменными способом подстановки.
Задачи: содействовать развитию познавательной активности, навыков самооценки и самопроверки, умения работать в группе, брать на себя ответственность, за решение систем уравнений, развивать коммуникативную компетенцию и математическую речь через работу в группах.
Урок закрепления новых знаний и способов деятельности, с использованием системно – деятельностного подхода в обучении, его дополняла презентация и повторение теоретического материала, через решение кроссворда. Для активизации познавательной деятельности учащихся и занесения правильных ответов на системы уравнений, использовано зашифрованное слово КВАШИОРКОР. Для каждой группы — свои задания, только совместная работа поможет найти верный ответ. При повторении теоретической части, разгадан кроссворд. И слово «сложение» в кроссворде, при решении систем методом сложения ещё не изучена — это выход на тему следующего урока. Проведена самооценка и взаимооценка, рефлексия, записав своё имя для точек в 1 четверть координатной плоскости (Тема урока понятна), 2 – Недостаточно усвоил(а), и в нижнюю полуплоскость — Не понял(а) тему урока. Все имена были в верхней полуплоскости.
Все имена были в верхней полуплоскости.
На уроке достигнута поставленная цель. Считаю, что большинство учащихся научились решать системы методом подстановки, узнали смысл разгаданного слова, получили информацию о здоровом питании. Содержание, методы и формы организации учебного процесса соответствовали поставленной цели.
На уроке была организована работа учащихся в группах. Для активизации познавательной деятельности учащихся и занесения правильных ответов на системы уравнений учитель использовала зашифрованное слово КВАШИОРКОР. Учащиеся узнали о распространении, причинах возникновения, симптомах и лечении этого редкого заболевания. Через решение математического кроссворда учащиеся повторили теоретический материал. Также на уроке была проведена физкультминутка с использованием видеоролика проекта «Инфоурок». При подведении итогов урока учащиеся проводили самооценку и взаимооценку своей деятельности с использованием координатной плоскости.
Цель урока была достигнута. Большинство учащихся научились решать системы методом подстановки, узнали значение разгаданного слова, получили информацию о здоровом питании.
Алгебра, 7 класс «системы линейных уравнений и способы их решения»
Слайды и текст этой онлайн презентации
Слайд 1
Алгебра, 7 класс «Системы линейных уравнений и способы их решения»
Слайд 2
Знаете ли вы?
1. Какую математическую модель называют линейным уравнением с двумя переменными?
2. Что является решением системы уравнений с двумя переменными?
3. Что значит решить систему уравнений?
Слайд 3
Способы решения систем уравнений
1. Графический способ.
2. Способ подстановки.
3. Способ сложения.
Слайд 4
Алгоритм решения системы уравнений графическим способом
Слайд 5
Решить систему уравнений
Рассмотрим первое уравнение
Выразим из этого уравнения y через x .
Для построения графика найдем две точки.
Слайд 6
Построим график
Слайд 7
Рассмотрим второе уравнение
Выразим из этого уравнения y через x .
Слайд 8
Построим график второй функции
Слайд 9
Найдем координаты точки пересечения прямых
Слайд 10
Координаты точки пересечения прямых ― это решение системы
В этом случае говорят, что система решена графически
Слайд 11
Три случая взаимного расположения двух прямых
1. Прямые пересекаются.
То есть имеют одну общую точку.
Тогда система уравнений имеет единственное решение.
Например, как в рассмотренной системе
Слайд 12
Три случая взаимного расположения двух прямых
2. Прямые параллельны.
То есть не имеют общих точек.
Тогда система уравнений решений не имеет.
Например:
Слайд 13
Три случая взаимного расположения двух прямых
3. Прямые совпадают.
Например:
Тогда система уравнений имеет бесконечно много решений.
Слайд 14
Но
при графическом способе решения системы уравнений обычно получается приближенное решение
Слайд 15
Алгоритм решения системы уравнений способом подстановки
Слайд 16
Способ подстановки
Этот способ удобен тогда, когда хотя бы один из коэффициентов при x или y равен 1 или -1.
Дана система уравнений
Рассмотрим каждое уравнение в отдельности.
1) Выразим одно из неизвестных через другое неизвестное из любого уравнения.
Слайд 17
Способ подстановки
Вернемся в систему:
2) Полученное для y выражение подставим вместо данной неизвестной во второе уравнение.
Получилось уравнение с одной неизвестной
Слайд 18
Способ подстановки
3) Решаем уравнение с одной неизвестной:
Возвращаемся к системе:
Слайд 19
Способ подстановки
Возвращаемся к системе:
4) Подставим найденное значение x в первое уравнение и найдем вторую неизвестную
Запишем ответ.
Ответ:
Слайд 20
Алгоритм решения системы уравнений способом сложения
Слайд 21
Способ сложения
Задача 1. Решить систему уравнений
В тех случаях, когда в обоих линейных уравнениях системы при каком-либо из неизвестных коэффициентами являются противоположные числа, удобно применять способ алгебраического сложения уравнений.
Слайд 22
Способ сложения
Сложим эти равенства почленно. В результате получим тоже верное равенство
+
Слайд 23
Способ сложения
Вернемся в систему, записав одно из исходных уравнений и полученное значение x.
Подставим найденное значение x во второе уравнение, найдем вторую неизвестную.
Тогда пара чисел (5; 4) и будет решением системы.
Ответ:
Слайд 24
Способ сложения
Задача 2. Решить систему уравнений
1) Выберем неизвестную (например x).
уравняем коэффициенты умножением на соответствующие числа.
2) Вычтем одно уравнение из другого.
3) Решим полученное уравнение с одним неизвестным
Слайд 25
Способ сложения
4) Вернемся в систему, записав одно из исходных уравнений и полученное значение y
5) Подставим найденное значение y в первое уравнение, найдем вторую неизвестную.
Тогда пара чисел (-3; 1) и будет решением системы.
Ответ:
Слайд 26
Решите следующие системы уравнений:
Слайд 27
Урок закончен.
Спасибо за внимание.
Системы уравнений. Способы решения систем уравнений
Система уравнений — это группа уравнений, в которых одни и те же неизвестные обозначают одни те же числа. Чтобы показать, что уравнения рассматриваются как система, слева от них ставится фигурная скобка:
| x — 4y = 2 | |
| 3x — 2y = 16 |
Решить систему уравнений — это значит, найти общие решения для всех уравнений системы или убедиться, что решения нет.
Чтобы решить систему уравнений, нужно исключить одно неизвестное, то есть из двух уравнений с двумя неизвестными составить одно уравнение с одним неизвестным. Исключить одно из неизвестных можно тремя способами: подстановкой, сравнением, сложением или вычитанием.
Способ подстановки
Чтобы решить систему уравнений способом подстановки, нужно в одном из уравнений выразить одно неизвестное через другое и результат подставить в другое уравнение, которое после этого будет содержать только одно неизвестное. Затем находим значение этого неизвестного и подставляем его в первое уравнение, после этого находим значение второго неизвестного.
Рассмотрим решение системы уравнений:
| x — 4y = 2 | |
| 3x — 2y = 16 |
Сначала найдём, чему равен x в первом уравнении. Для этого перенесём все члены уравнения, не содержащие неизвестное x, в правую часть:
x — 4y = 2;
x = 2 + 4y.
Так как x, на основании определения системы уравнений, имеет такое же значение и во втором уравнении, то подставляем его значение во второе уравнение и получаем уравнение с одним неизвестным:
| 3x | — 2y = 16; |
| 3(2 + 4y) | — 2y = 16. |
Решаем полученное уравнение, чтобы найти, чему равен y. Как решать уравнения с одним неизвестным, вы можете посмотреть в соответствующей теме.
| 3(2 + 4y) — 2y = 16; |
| 6 + 12y — 2y = 16; |
| 6 + 10y = 16; |
| 10y = 16 — 6; |
| 10y = 10; |
| y = 10 : 10; |
| y = 1. |
Мы определили что y = 1. Теперь, для нахождения численного значения x, подставим значение y в преобразованное первое уравнение, где мы ранее нашли, какому выражению равен x:
x = 2 + 4y = 2 + 4 · 1 = 2 + 4 = 6.
Ответ: x = 6, y = 1.
Способ сравнения
Способ сравнения — это частный случай подстановки. Чтобы решить систему уравнений способом сравнения, нужно в обоих уравнениях найти, какому выражению будет равно одно и то же неизвестное и приравнять полученные выражения друг к другу. Получившееся в результате уравнение позволяет узнать значение одного неизвестного. С помощью этого значения затем вычисляется значение второго неизвестного.
Например, для решение системы:
| x — 4y = 2 | |
| 3x — 2y = 16 |
найдём в обоих уравнениях, чему равен y (можно сделать и наоборот — найти, чему равен x):
| x — 4y = 2 | 3x — 2y = 16 |
| -4y = 2 — x | -2y = 16 — 3x |
| y = (2 — x) : — 4 | y = (16 — 3x) : -2 |
Составляем из полученных выражений уравнение:
Решаем уравнение, чтобы узнать значение x:
| ||||||
| 2 — x = 32 — 6x | ||||||
| —x + 6x = 32 — 2 | ||||||
| 5x = 30 | ||||||
| x = 30 : 5 | ||||||
| x = 6 |
Теперь подставляем значение x в первое или второе уравнение системы и находим значение y:
| x — 4y = 2 | 3x — 2y = 16 |
| 6 — 4y = 2 | 3 · 6 — 2y = 16 |
| -4y = 2 — 6 | -2y = 16 — 18 |
| -4y = -4 | -2y = -2 |
| y = 1 | y = 1 |
Ответ: x = 6, y = 1.
Способ сложения или вычитания
Чтобы решить систему уравнений способом сложения, нужно составить из двух уравнений одно, сложив левые и правые части, при этом одно из неизвестных должно быть исключено из полученного уравнения. Неизвестное можно исключить, уравняв при нём коэффициенты в обоих уравнениях.
Рассмотрим систему:
| x — 4y = 2 | |
| 3x — 2y = 16 |
Уравняем коэффициенты при неизвестном y, умножив все члены второго уравнения на -2:
(3x — 2y) · -2 = 16 · -2
-6x + 4y = -32
Получим:
| x — 4y = 2 | |
| -6x + 4y = -32 |
Теперь сложим по частям оба уравнения, чтобы получить уравнение с одним неизвестным:
| + | x — 4y = 2 |
| -6x + 4y = -32 | |
| -5x = -30 |
Находим значение x (x = 6). Теперь, подставив значение x в любое уравнение системы, найдём y = 1.
Если уравнять коэффициенты у x, то, для исключения этого неизвестного, нужно было бы вычесть одно уравнение из другого.
Уравняем коэффициенты при неизвестном x, умножив все члены первого уравнения на 3:
(x — 4y) · 3 = 2 · 3
3x — 12y = 6
Получим:
| 3x — 12y = 6 | |
| 3x — 2y = 16 |
Теперь вычтем по частям второе уравнение из первого, чтобы получить уравнение с одним неизвестным:
| — | 3x — 12y = 6 |
| 3x — 2y = 16 | |
| -10y = -10 |
Находим значение y (y = 1). Теперь, подставив значение y в любое уравнение системы, найдём x = 6:
Теперь, подставив значение y в любое уравнение системы, найдём x = 6:
| 3x — 2y = 16 |
| 3x — 2 · 1 = 16 |
| 3x — 2 = 16 |
| 3x = 16 + 2 |
| 3x = 18 |
| x = 18 : 3 |
| x = 6 |
Ответ: x = 6, y = 1.
Для решения системы уравнений, рассмотренной выше, был использован способ сложения, который основан на следующем свойстве:
Любое уравнение системы можно заменить на уравнение, получаемое путём сложения (или вычитания) уравнений, входящих в систему. При этом получается система уравнений, имеющая те же решения, что и исходная.
«Решение систем уравнений способом подстановки» конспект урока алгебры 8 класс.
Управление образования администрации муниципального образования «Вельский муниципальный район»
Муниципальное бюджетное общеобразовательное учреждение
«Средняя школа №92 г. Вельска»
«Решение систем уравнений способом подстановки»
конспект урока алгебры 8 класс.
г. Вельск
2016 г.
СОДЕРЖАНИЕ
1. Введение. 3
2. Основная часть. 4
3. Заключение. 10
4. Список литературы. 10
5. Приложения. 11
Введение.
В данной методической разработке представлен конспект урока по алгебре в 8 классе по теме «Решение систем уравнений способом подстановки». Этот материал будет интересен учителям математики по применению проблемно-деятельностного подхода.
Актуальность этой методической разработки состоит в том, что представленный урок математики разработан с элементами ФГОС. Выбранная тема урока, важный материал для обучающихся 8 класса, так как прочные знания по этой теме помогут решить данное задание при сдаче ОГЭ, а также для решения задач различной тематики и сложности. В данной методической разработке показан урок «открытия» нового знания.
Выбранная тема урока, важный материал для обучающихся 8 класса, так как прочные знания по этой теме помогут решить данное задание при сдаче ОГЭ, а также для решения задач различной тематики и сложности. В данной методической разработке показан урок «открытия» нового знания.
Структура урока «открытия» нового знания (первый из трех в данной теме)
1)этап мотивации (самоопределения) к учебной деятельности;
2) этап актуализации и пробного учебного действия;
3) этап создания проблемной ситуации и выхода из затруднения;
4) этап построения проекта выхода из затруднения, изучение нового;
5) этап первичного закрепления с проговариванием во внешней речи;
6) этап включения в систему знаний и повторения;
7) этап рефлексии учебной деятельности на уроке.
Цель: формировать представление о системе уравнений; познакомить обучающихся со способом подстановки его применением при решении системы уравнения.
Задачи:
Научить в реальной ситуации использовать способ подстановки;
Учить слушать вступать в диалог, участвовать в коллективном обсуждении проблем.
Развивать умение обрабатывать информацию, формировать коммуникативную компетенцию, контроль и оценка процесса и результатов деятельности.
Техническое оборудование: Компьютер, проектор, учебник «Алгебра» для 8 класса под редакцией Г.Ф.Дорофеева. Издательство Москва «Просвещение» 2009год., электронная презентация.
Основная часть
Технологическая карта урока алгебры в 8 классе по теме «Решение систем уравнений способом подстановки»
Этапы урока | Задачи этапа | Деятельность учителя | Деятельность учащихся | УУД |
1. | Создать благоприятный психологический настрой на работу | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. | Включаются в деловой ритм урока. | Личностные: самоопределение. Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. |
2. Вводная беседа. | Актуализация опорных знаний и способов действий. | Новые знания будет трудно осваивать без умения быстро и верно решать уравнения и системы уравнений, а также знаний теории. (Приложение1, Слайд 1) а) Что является решением уравнения с двумя переменными? б)Что значит решить систему уравнений? в) Какими способами можно решить систему уравнений? г) Что является решением системы уравнений? Устная работа по презентации. 1). Является ли пара чисел (3;1) решением уравнения:(Приложение1, Слайд 2) 2) В данных уравнениях выразите переменную у через х: (Приложение1, Слайд 3) 3) 1. Выясните, является ли пара чисел (–1; 1) решением системы уравнений: (Приложение1, Слайд 4) Повторяем алгоритмы решения систем уравнений методом алгебраического сложения. 1).Назовите этапы метода алгебраического сложения, если имеются противоположные коэффициенты 2)Назовите этапы метода алгебраического сложения, если нет противоположных коэффициентов 3). Решите системы уравнений (устно) (Приложение1, Слайд 5) | Отвечают на вопросы учителя, выполняют устные задания. | Коммуникативные: развитие устной научной речи, умение слушать и говорить. Познавательные: анализ и разделение алгоритма на два случая. |
3.Целеполагание и мотивация | Обеспечение мотивации учения детьми, принятие ими целей урока. | На доске записаны две системы линейных уравнений. К доске выходят по очереди 2 ученика и решают совместно с классом системы уравнений, (Приложение 4). Ответить на вопрос: — какими способами можно решить систему уравнений? — А можно ли решить систему уравнений б) другим способом, не выполняя построения графика? — А как решить систему уравнений используя умения выражать одну переменную через другую? (Приложение1, Слайд 6) — Как этот способ можно назвать? -Какая цель нашего урока сегодня? -Чему должны научиться на уроке? Это и будут наши цели на урок. Запишите тему урока « Способ подстановки» (Приложение2,Слайд 7) | Решают системы Обобщают знания о методах решения систем уравнений. Выясняют, что можно использовать другой способ решения систем уравнений. Способ подстановки. Цель урока: Решение систем уравнений способом подстановки. | Регулятивные: целеполагание. Коммуникативные: постановка вопросов. Познавательные: самостоятельное выделение-формулирование цели урока. |
4. Изучение нового материала. | Работа над алгоритмом решения системы уравнений способом подстановки. | Работа над алгоритмом решения системы уравнений способом подстановки.( Приложение2, Слайд 8,9). Алгоритм в учебнике стр. 176 Пример решения системы уравнения. (Приложение2, Слайд 10). | Учащиеся работают с учебником. | Познавательные: применение новых знаний на практике. |
5. Первичное закрепление. | Обучение применению алгоритма. | Устная работа: 1. Определите, из какого уравнения системы и какую переменную удобнее выразить. (Приложение2, Слайд 11) Давайте решим систему уравнений б) новым способом – подстановкой ( Приложение 4). Оба способа дают один и тот же результат. | Определяют какую переменную удобнее выразить. Делают вывод- системы уравнений можно решать разными способами. | Познавательные: применение новых знаний на практике, умение делать выводы о способах решения систем уравнений. |
6. Включение новых знаний в систему учебных действий. | Выявление качества и уровня усвоения знаний и способов действий, а также выявление недостатков в знаниях и способах действий. | Решают из учебника № 650 (а,в,д), № 651(а,в,д), (Приложение 5) , № 652(а,в) (Приложение 6). Учащиеся выходят решать к доске, комментируя применение алгоритма. | На местах самостоятельное решение в тетради с проверкой. | Коммуникативные: контроль, коррекция, оценка действий. |
7. Подведение итогов урока. | Дать качественную оценку работы класса и отдельных учащихся | -Какими способами можно решить систему уравнений? -Расскажите алгоритм решения системы уравнений способом подстановки. -Каким способом больше нравиться решать системы уравнений? (Приложение2, Слайд 12) | Правильно выбирать способ решения систем уравнений. | Регулятивные: оценка-осознание уровня и качества усвоения; контроль |
8. Информация о домашнем задании. | Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания. | № 650 (б,г), № 651(б,г),№ 652(б,г), с 175-176 (Приложение3, Слайд 13) | ||
9. Рефлексия | Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации их собственной деятельности и взаимодействия с учителем и другими детьми в классе. | Закончите предложение: Мне на уроке понравилось…. Мне показалось сложным… Я бы еще хотел выполнить… Главным результатом считаю… | Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли и эмоции; Познавательные: рефлексия. |
ЗАКЛЮЧЕНИЕ
Данная методическая разработка была посвящена уроку «открытия» новых знаний по алгебре в 8 классе. Урок был проведен для учителей школы в рамках методической недели.
Задача учителя активизировать деятельность каждого учащегося, создать ситуации для их творческой активности в процессе обучения. Использование новых технологий не только оживляет и разнообразит учебный процесс, но и открывает большие возможности для расширения образовательных рамок, несомненно, несет в себе огромный мотивационный потенциал и способствует принципам индивидуализации обучения.
Из проделанной работы можно сделать следующие общие выводы: для повышения интереса к математике необходимо применять различные технологии, а правильная организация работы по математике и подбор материала поможет созданию эмоционального настроения учащихся по решению учебных задач урока, и тем самым обеспечить прочные и осознанные знания изучаемого материала.
Литература
Учебник «Алгебра» для 8 класса под редакцией Г.Ф.Дорофеева. Издательство Москва «Просвещение» 2009год.
Дидактические материалы по алгебре для 8 класса к учебнику алгебры 8 класс под редакцией Г.Ф.Дорофеева.
Образовательные порталы интернета.
Приложение 4
Решение систем уравнений способом сложения.
а) домножим первое уравнение на 2
(-) вычтем из второго уравнения первое
х=3, найдем у, подставив 3 вместо х в первое уравнение
3·4+6у=9
6у=-3
у=-
Ответ: ( -3;-0. 5)
5)
б)
13х=26
х=2 10·2+5у=10
5у=-10
у=-2
Ответ: (2; -2).
Решим эту же систему уравнений способом подстановки.
выразим из второго уравнения у=2-2х.
Подставим вместо у, выражение у=2-2х в первое уравнение.
3х-5(2-2х)=16
3х-10+10х=16
13х=26
Х=2
Найдем у. у=2-2·2= -2
Ответ :(2; -2)
Приложение 5
Решают из учебника № 650 (а,в,д), № 652(а,в,д).
в) д)
3х+2х=5 у=2 2b+3b+=-15 z-4+2z=14
5х=5 5b=-15 3z=18
х=1 b=-3, a=-3 z=6, y=6-4, y=2
Ответ: (1;2) Ответ: (-3;-3) Ответ:(2;6).
№ 651(а,в,д),
а) в)
у=21-х у=21-8 х=2у+5 х=2·(-0,5)+5
21-х-х=3 у=3 3(2у+5)+4у=10 х=4
-2х=-18 6у+15+4у=10
х=9 10у=-5
Ответ:(9;3) у=-0,5
Ответ: (4;-0,5)
д)
u=1-2v u=1-4
3(1-2v)+5v=1 u=-3
3-6v+5v=1
-v=-2
v=2
Ответ: (-3;2)
Приложение 6.
№ 652(а,в)
Решите систему уравнений, применив любой из известных вам способов:
Подстановка:
а)
n=8-2m n=8-10
3m+4(8-2m)=7 n=-2
3m+32-8m=7
-5m=-25
m=5
Ответ: (-5;2)
Сложение:
в) 5·(-47) + 2b=15
-235+2b=15
a=-47 2b=250
b=125
Ответ:(-47; 125)
Алгебраические методы решения систем
Цели обучения
- Используйте метод замены
- Решите систему уравнений, используя метод подстановки.
- Распознавать системы уравнений, не имеющие решения или бесконечное количество решений
- Используйте метод исключения без умножения
- Решите систему уравнений, когда умножение не требуется для исключения переменной
- Используйте метод исключения с умножением
- Использование умножения в сочетании с методом исключения для решения системы линейных уравнений
- Распознавать, когда решение системы линейных уравнений подразумевает, что существует бесконечное число решений
Решите систему уравнений методом подстановки
В последних парах разделов мы проверили, что упорядоченные пары являются решениями систем, и использовали графики, чтобы классифицировать, сколько решений имеет система двух линейных уравнений. Что, если нам не дана точка пересечения или она не очевидна из графика? Можем ли мы еще найти решение этой системы? Конечно, можно, используя алгебру!
Что, если нам не дана точка пересечения или она не очевидна из графика? Можем ли мы еще найти решение этой системы? Конечно, можно, используя алгебру!
В этом разделе мы изучим метод подстановки для нахождения решения системы линейных уравнений с двумя переменными. На протяжении всего курса мы использовали подстановку по-разному, например, когда использовали формулы для вычисления площади треугольника и простого процента. Мы подставили значения, которые мы знали, в формулу, чтобы найти значения, которые мы не знали.Идея аналогична применительно к системам решения, в этом процессе всего несколько этапов. Сначала вы решите одну переменную, а затем подставите это выражение в другое уравнение. Давайте начнем с примера, чтобы понять, что это значит.
Пример
Найдите значение x для этой системы.
Уравнение A: [латекс] 4x + 3y = −14 [/ латекс]
Уравнение B: [латекс] y = 2 [/ латекс]
Показать решение Задачу просит решить для x .Уравнение B дает вам значение y , [latex] y = 2 [/ latex], поэтому вы можете подставить 2 в уравнение A для y.[латекс] \ begin {array} {r} 4x + 3y = −14 \\ y = 2 \, \, \, \, \, \, \, \ end {array} [/ latex]
Подставьте [латекс] y = 2 [/ латекс] в уравнение A.
[латекс] 4x + 3 \ влево (2 \ вправо) = — 14 [/ латекс]
Упростите и решите уравнение для x.
[латекс] \ begin {array} {r} 4x + 6 = −14 \\ 4x = −20 \ x = −5 \, \, \, \ end {array} [/ latex]
Ответ
[латекс] x = −5 [/ латекс]
Вы можете заменить значение переменной, даже если это выражение.Вот пример.
Пример
Решите для x и y .
Уравнение A: [латекс] y + x = 3 [/ латекс]
Уравнение B: [латекс] x = y + 5 [/ латекс]
Показать решение Цель метода подстановки — переписать одно из уравнений в терминах одной переменной. Уравнение B говорит нам, что [латекс] x = y + 5 [/ latex], поэтому имеет смысл заменить [latex] y + 5 [/ latex] в уравнение A для x .
[латекс] \ begin {массив} {l} y + x = 3 \\ x = y + 5 \ end {array} [/ latex]
Подставьте [латекс] y + 5 [/ латекс] в уравнение A для x .
[латекс] \ begin {array} {r} y + x = 3 \\ y + \ left (y + 5 \ right) = 3 \ end {array} [/ latex]
Упростите и решите уравнение для y.
[латекс] \ begin {array} {r} 2y + 5 = \, \, \, \, 3 \\\ подчеркивание {−5 \, \, \, \, \, — 5} \\ 2y = — 2 \\ y = −1 \ end {array} [/ latex]
Теперь найдите x , подставив это значение для y в любое уравнение, и решите для x . Здесь мы будем использовать уравнение A.
[латекс] \ begin {array} {r} y + x = 3 \\ — 1 + x = 3 \\\ подчеркивание {+1 \, \, \, \, \, \, \, \, \, +1} \\ x = 4 \ end {array} [/ latex]
Наконец, проверьте решение [latex] x = 4 [/ latex], [latex] y = −1 [/ latex], подставив эти значения в каждое из исходных уравнений.
[латекс] \ begin {массив} {r} y + x = 3 \\ — 1 + 4 = 3 \\ 3 = 3 \\\ text {TRUE} \ end {array} [/ latex]
[латекс] \ begin {массив} {l} x = y + 5 \\ 4 = −1 + 5 \\ 4 = 4 \\\ text {TRUE} \ end {array} [/ latex]
Ответ
[латекс] x = 4 [/ латекс] и [латекс] y = -1 [/ латекс]
Решение — [латекс] (4, -1) [/ латекс].
Помните, решение системы уравнений должно быть решением каждого из уравнений внутри системы. Упорядоченная пара [latex] (4, −1) [/ latex] действительно работает для обоих уравнений, поэтому вы знаете, что это также решение системы.
Давайте посмотрим на другой пример, замена которого включает свойство распределения.
Пример
Решите для x и y .
[латекс] \ begin {array} {l} y = 3x + 6 \\ — 2x + 4y = 4 \ end {array} [/ latex]
Показать решение Выберите уравнение для замены.Первое уравнение говорит вам, как выразить y через x , поэтому имеет смысл подставить 3 x + 6 во второе уравнение для y .
[латекс] \ begin {array} {l} y = 3x + 6 \\ — 2x + 4y = 4 \ end {array} [/ latex]
Подставьте [латекс] 3x + 6 [/ latex] вместо y во второе уравнение.
[латекс] \ begin {array} {r} −2x + 4y = 4 \\ — 2x + 4 \ left (3x + 6 \ right) = 4 \ end {array} [/ latex]
Упростите и решите уравнение для x.
[латекс] \ begin {array} {r} −2x + 12x + 24 = 4 \, \, \, \, \, \, \, \\ 10x + 24 = 4 \, \, \, \, \ , \, \, \\\ подчеркивание {−24 \, \, — 24 \, \, \, \,} \\ 10x = −20 \\ x = −2 \, \, \, \ end {array} [/ латекс]
Чтобы найти y , замените это значение на x обратно в одно из исходных уравнений.
[латекс] \ begin {array} {l} y = 3x + 6 \\ y = 3 \ left (−2 \ right) +6 \\ y = −6 + 6 \\ y = 0 \ end {array} [/ латекс]
Проверьте решение [латекс] x = −2 [/ latex], [latex] y = 0 [/ latex], подставив их в каждое из исходных уравнений.
[латекс] \ begin {array} {l} y = 3x + 6 \\ 0 = 3 \ left (−2 \ right) +6 \\ 0 = −6 + 6 \\ 0 = 0 \\\ text { ИСТИНА} \ end {array} [/ latex]
[латекс] \ begin {array} {r} −2x + 4y = 4 \\ — 2 \ left (-2 \ right) +4 \ left (0 \ right) = 4 \\ 4 + 0 = 4 \\ 4 = 4 \\\ текст {ИСТИНА} \ end {array} [/ latex]
Ответ
[латекс] x = -2 [/ латекс] и [латекс] y = 0 [/ латекс]
Решение: (−2, 0).
В приведенных выше примерах одно из уравнений уже было дано нам в терминах переменной x или y . Это позволило нам быстро подставить это значение в другое уравнение и найти одно из неизвестных.
Иногда вам, возможно, придется сначала переписать одно из уравнений в терминах одной из переменных, прежде чем вы сможете произвести замену. В приведенном ниже примере вам сначала нужно изолировать одну из переменных, прежде чем вы сможете заменить ее в другое уравнение.
Пример
Решите для x и y .
[латекс] \ begin {array} {r} 2x + 3y = 22 \\ 3x + y = 19 \ end {array} [/ latex]
Показать решение Выберите уравнение для замены. Второе уравнение, [латекс] 3x + y = 19 [/ latex], может быть легко переписан в терминах y , поэтому имеет смысл начать с этого.
[латекс] \ begin {массив} 2x + 3y = 22 \\ 3x + y = 19 \ end {array} [/ latex]
Перепишите [латекс] 3x + y = 19 [/ latex] в виде y .
[латекс] \ begin {array} 3x + y = 19 \\ y = 19–3x \ end {array} [/ latex]
Замените [латекс] 19–3x [/ латекс] на y в другом уравнении.
[латекс] \ begin {array} {r} 2x + 3y = 22 \\ 2x + 3 (19–3x) = 22 \ end {array} [/ latex]
Упростите и решите уравнение для x.
[латекс] \ begin {array} {r} 2x + 57–9x = 22 \, \, \, \, \\ — 7x + 57 = 22 \, \, \, \, \\ — 7x = −35 \\ x = 5 \, \, \, \, \, \, \, \ end {array} [/ latex]
Подставьте [latex] x = 5 [/ latex] обратно в одно из исходных уравнений, чтобы найти y.
[латекс] \ begin {array} {r} 3x + y = 19 \, \, \, \, \, \, \, \, \, \, \, \, \\ 3 \ left (5 \ right ) + y = 19 \, \, \, \, \, \, \, \, \, \, \, \, \\ 15 + y = 19 \, \, \, \, \, \, \, \, \, \, \, \, \\ y = 19−15 \\ y = 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ end {array} [/ latex]
Проверьте оба решения, подставив их в каждое из исходных уравнений.
[латекс] \ begin {array} {r} 2x + 3y = 22 \\ 2 (5) +3 \ left (4 \ right) = 22 \\ 10 + 12 = 22 \\ 22 = 22 \\\ текст {ИСТИНА} \\\\ 3x + y = 19 \\ 3 \ left (5 \ right) + 4 = 19 \\ 19 = 19 \\\ text {TRUE} \ end {array} [/ latex]
Ответ
[латекс] x = 5 [/ латекс] и [латекс] y = 4 [/ латекс]
Решение (5, 4).
В следующем видео вам будет показан пример решения системы двух уравнений с использованием метода подстановки.
Если бы вы выбрали другое уравнение для начала в предыдущем примере, вы все равно смогли бы найти то же решение. Это действительно вопрос предпочтений, потому что иногда решение для переменной приводит к необходимости работать с дробями. По мере того, как вы приобретете больше опыта в алгебре, вы сможете предвидеть, какой выбор приведет к более желаемым результатам.
По мере того, как вы приобретете больше опыта в алгебре, вы сможете предвидеть, какой выбор приведет к более желаемым результатам.
Распознавать системы уравнений, не имеющие решения или бесконечное число решений
Когда мы изучили методы решения линейных уравнений с одной переменной, мы обнаружили, что некоторые уравнения не имеют решений, а другие имеют бесконечное количество решений. Мы снова увидели это поведение, когда начали описывать решения систем уравнений с двумя переменными.
Вспомните этот пример из модуля 1 для решения линейных уравнений с одной переменной:
Решите для x .[латекс] 12 + 2x – 8 = 7x + 5–5x [/ латекс]
[латекс] \ displaystyle \ begin {array} {l} 12 + 2x-8 = 7x + 5-5x \\\, \, \, \, \, \, \, \, \, \, \, \ , \, \, 2x + 4 = 2x + 5 \ end {array} [/ latex]
[латекс] \ begin {array} {l} \, \, \, \, \, \, \, \, \, \, \, \, 2x + 4 = 2x + 5 \\\, \, \ , \, \, \, \, \, \ underline {-2x \, \, \, \, \, \, \, \, \, \, — 2x \, \, \, \, \, \, \, \,} \\\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ , \, \, 4 = \, 5 \ end {array} [/ latex]
Это ложное утверждение подразумевает, что не существует решений этого уравнения. Таким же образом вы можете увидеть такой результат, когда используете метод подстановки, чтобы найти решение системы линейных уравнений с двумя переменными.В следующем примере вы увидите пример системы двух уравнений, не имеющей решения.
Пример
Решите для x и y .
[латекс] \ begin {array} {l} y = 5x + 4 \\ 10x − 2y = 4 \ end {array} [/ latex]
Показать решение Поскольку первое уравнение [латекс] y = 5x + 4 [/ latex], вы можете заменить [latex] 5x + 4 [/ latex] на y во втором уравнении.[латекс] \ begin {array} {r} y = 5x + 4 \\ 10x − 2y = 4 \, \, \, \, \, \, \, \, \, \, \, \, \\ 10x – 2 \ left (5x + 4 \ right) = 4 \, \, \, \, \, \, \, \, \, \, \, \, \ end {array} [/ latex]
Разверните выражение слева.
[латекс] 10x – 10x – 8 = 4 [/ латекс]
Объедините похожие члены в левой части уравнения.
[латекс] 10x – 10x = 0 [/ latex], поэтому у вас остается [latex] −8 = 4 [/ latex].
[латекс] \ begin {array} {r} 0–8 = 4 \\ — 8 = 4 \ end {array} [/ latex]
Ответ
Утверждение [latex] −8 = 4 [/ latex] неверно, поэтому решения нет.
Вы получаете ложное утверждение [латекс] −8 = 4 [/ латекс]. Что это значит? График этой системы проливает свет на то, что происходит.
Прямые параллельны, они никогда не пересекаются, и у этой системы линейных уравнений нет решения. Обратите внимание, что результат [latex] −8 = 4 [/ latex] — это , а не как решение. Это просто ложное утверждение, и оно указывает на то, что не существует решения .
Мы также видели линейные уравнения с одной переменной и системы уравнений с двумя переменными, которые имеют бесконечное количество решений. В следующем примере вы увидите, что происходит, когда вы применяете метод подстановки к системе с бесконечным числом решений.
Пример
Решите относительно x и y.
[латекс] \ begin {массив} {l} \, \, \, y = −0,5x \\ 9y = −4,5x \ end {array} [/ latex]
Показать решениеПодставляя -0,5 x вместо y во втором уравнении, вы получаете следующее:
[латекс] \ begin {array} {r} 9y = −4.5x \\ 9 (−0.5x) = — 4.5 \, \, \, \\ — 4.5x = −4.5x \ end {array} [/ латекс]
На этот раз вы получите верное утверждение: [латекс] −4,5x = −4,5x [/ латекс]. Но что означает такой ответ? Опять же, построение графиков может помочь вам разобраться в этой системе.
Эта система состоит из двух уравнений, которые представляют одну и ту же линию; две линии коллинеарны. Каждая точка на линии будет решением системы, и поэтому метод подстановки дает верное утверждение. В этом случае существует бесконечное количество решений.
В следующем видео вы увидите пример решения системы, имеющей бесконечное количество решений.
В следующем видео вы увидите пример решения системы уравнений, не имеющей решений.
Решите систему уравнений методом исключения
Метод исключения для решения систем линейных уравнений использует добавочное свойство равенства. Вы можете добавить одно и то же значение к каждой стороне уравнения, чтобы исключить один из переменных членов. В этом методе вам может потребоваться, а может и не потребоваться сначала умножить члены в одном уравнении на число. Сначала мы рассмотрим примеры, в которых умножение не требуется для использования метода исключения.В следующем разделе вы увидите примеры использования умножения после того, как познакомитесь с идеей метода исключения.
С помощью этого метода легче показать, чем рассказать, поэтому давайте сразу же рассмотрим несколько примеров.
Если сложить два уравнения,
[латекс] x – y = −6 [/ latex] и [latex] x + y = 8 [/ latex] вместе, посмотрите, что произойдет.
[латекс] \ displaystyle \ begin {array} {l} \, \, \, \, \, xy = \, — 6 \\\ подчеркивание {+ \, x + y = \, \, \, 8} \\\, 2x + 0 \, = \, \, \, \, 2 \ end {array} [/ latex]
Вы исключили член y , и это уравнение можно решить, используя методы решения уравнений с одной переменной.
Давайте посмотрим, как эта система решается методом исключения.
Пример
Используйте устранение, чтобы решить систему.
[латекс] \ begin {array} {r} x – y = −6 \\ x + y = \, \, \, \, 8 \ end {array} [/ latex]
Показать решение Добавьте уравнения.[латекс] \ displaystyle \ begin {array} {r} xy = \, \, — 6 \\ + \ underline {\, \, x + y = \, \, \, \, \, 8} \\ \, \, \, \, \, \, 2x \, \, \, \, \, = \, \, \, \, \, \, 2 \ end {array} [/ latex]
Решите для x .
[латекс] \ begin {array} {r} 2x = 2 \\ x = 1 \ end {array} [/ latex]
Подставьте [latex] x = 1 [/ latex] в одно из исходных уравнений и решите относительно y .
[латекс] \ begin {array} {l} x + y = 8 \\ 1 + y = 8 \\\, \, \, \, \, \, \, \, \, \, y = 8– 1 \\\, \, \, \, \, \, \, \, \, \, y = 7 \ end {array} [/ latex]
Обязательно проверьте свой ответ в обоих уравнениях!
[латекс] \ begin {array} {r} x – y = −6 \\ 1–7 = −6 \\ — 6 = −6 \\\ text {TRUE} \\\\ x + y = 8 \ \ 1 + 7 = 8 \\ 8 = 8 \\\ текст {ИСТИНА} \ end {array} [/ latex]
Ответы проверяют.
Ответ
Решение (1, 7).
К сожалению, не все системы справляются с этим легко. Как насчет такой системы, как [латекс] 2x + y = 12 [/ latex] и [latex] −3x + y = 2 [/ latex].Если вы сложите эти два уравнения вместе, никакие переменные не будут исключены.
[латекс] \ displaystyle \ begin {array} {l} \, \, \, \, 2x + y = 12 \\\ подчеркивание {-3x + y = \, \, \, 2} \\ — x + 2y = 14 \ end {array} [/ latex]
Но вы хотите исключить переменную. Итак, давайте добавим противоположность одного из уравнений к другому уравнению. Это означает умножение каждого члена в одном из уравнений на -1, чтобы знак каждого члена был противоположным.
[латекс] \ begin {array} {l} \, \, \, \, 2x + \, \, y \, = 12 \ rightarrow2x + y = 12 \ rightarrow2x + y = 12 \\ — 3x + \, \, y \, = 2 \ rightarrow− \ left (−3x + y \ right) = — (2) \ rightarrow3x – y = −2 \\\, \, \, \, 5x + 0y = 10 \ end {array} [/ латекс]
Вы удалили переменную y , и теперь проблема может быть решена.
В следующем видео описывается аналогичная проблема, при которой можно исключить одну переменную, сложив два уравнения вместе.
Осторожность! Когда вы добавляете противоположность одного целого уравнения к другому, не забудьте изменить знак КАЖДОГО члена с обеих сторон уравнения.
 Это очень распространенная ошибка.
Это очень распространенная ошибка.Пример
Используйте устранение, чтобы решить систему.
[латекс] \ begin {array} {r} 2x + y = 12 \\ — 3x + y = 2 \, \, \, \ end {array} [/ latex]
Показать решение Вы можете исключить переменную y , добавив противоположность одного из уравнений к другому уравнению.[латекс] \ begin {array} {r} 2x + y = 12 \\ — 3x + y = 2 \, \, \, \ end {array} [/ latex]
Перепишите второе уравнение как противоположное.
Доп. Решите для x .
[латекс] \ begin {array} {r} 2x + y = 12 \, \\ 3x – y = −2 \\ 5x = 10 \, \\ x = 2 \, \, \, \, \ end { array} [/ latex]
Подставьте [latex] y = 2 [/ latex] в одно из исходных уравнений и решите относительно y .
[латекс] \ begin {array} {r} 2 \ left (2 \ right) + y = 12 \\ 4 + y = 12 \\ y = 8 \, \, \, \ end {array} [/ latex ]
Обязательно проверьте свой ответ в обоих уравнениях!
[латекс] \ begin {array} {r} 2x + y = 12 \\ 2 \ left (2 \ right) + 8 = 12 \\ 4 + 8 = 12 \\ 12 = 12 \\\ text {TRUE} \\\\ — 3x + y = 2 \\ — 3 \ left (2 \ right) + 8 = 2 \\ — 6 + 8 = 2 \\ 2 = 2 \\\ текст {ИСТИНА} \ end {array} [/ латекс]
Ответы проверяют.
Ответ
Решение (2, 8).
Ниже приведены еще два примера, показывающих, как решать линейные системы уравнений с использованием исключения.
Пример
Используйте устранение, чтобы решить систему.
[латекс] \ begin {array} {r} −2x + 3y = −1 \\ 2x + 5y = \, 25 \ end {array} [/ latex]
Показать решение Обратите внимание на коэффициенты каждой переменной в каждом уравнении. Если вы сложите эти два уравнения, член x будет удален, поскольку [latex] −2x + 2x = 0 [/ latex].[латекс] \ begin {array} {r} −2x + 3y = −1 \\ 2x + 5y = \, 25 \ end {array} [/ latex]
Сложите и решите для и .
[латекс] \ begin {array} {r} −2x + 3y = −1 \\ 2x + 5y = 25 \, \\ 8y = 24 \, \\ y = 3 \, \, \, \, \ end {array} [/ latex]
Подставьте [латекс] y = 3 [/ latex] в одно из исходных уравнений.
[латекс] \ begin {array} {r} 2x + 5y = 25 \\ 2x + 5 \ left (3 \ right) = 25 \\ 2x + 15 = 25 \\ 2x = 10 \\ x = 5 \, \, \, \ end {array} [/ latex]
Проверить решения.
[латекс] \ begin {array} {r} −2x + 3y = −1 \\ — 2 \ left (5 \ right) +3 \ left (3 \ right) = — 1 \\ — 10 + 9 = — 1 \\ — 1 = −1 \\\ текст {ИСТИНА} \\\\ 2x + 5y = 25 \\ 2 \ left (5 \ right) +5 \ left (3 \ right) = 25 \\ 10 + 15 = 25 \\ 25 = 25 \\\ текст {ИСТИНА} \ end {array} [/ latex]
Ответы проверяют.
Ответ
Решение (5, 3).
Пример
Используйте исключения, чтобы найти x и y.
[латекс] \ begin {array} {r} 4x + 2y = 14 \\ 5x + 2y = 16 \ end {array} [/ latex]
Показать решение Обратите внимание на коэффициенты каждой переменной в каждом уравнении. Вам нужно будет добавить противоположное одному из уравнений, чтобы исключить переменную y , так как [latex] 2y + 2y = 4y [/ latex], но [latex] 2y + \ left (−2y \ right) = 0 [ /латекс].[латекс] \ begin {array} {r} 4x + 2y = 14 \\ 5x + 2y = 16 \ end {array} [/ latex]
Замените одно из уравнений на противоположное, сложите и решите для x .
[латекс] \ begin {array} {r} 4x + 2y = 14 \, \, \, \, \\ — 5x – 2y = −16 \\ — x = −2 \, \, \, \\ x = 2 \, \, \, \, \, \, \, \ end {array} [/ latex]
Подставьте [latex] x = 2 [/ latex] в одно из исходных уравнений и решите относительно y .
[латекс] \ begin {array} {r} 4x + 2y = 14 \\ 4 \ left (2 \ right) + 2y = 14 \\ 8 + 2y = 14 \\ 2y = 6 \, \, \, \ \ y = 3 \, \, \, \ end {array} [/ latex]
Ответ
Решение (2, 3).
Проверьте последний пример — подставьте (2, 3) в оба уравнения. Получается два верных утверждения: 14 = 14 и 16 = 16!
Обратите внимание, что вы могли бы использовать противоположное первому уравнению, а не второе уравнение, и получить тот же результат.
Распознавать системы, у которых нет решения или бесконечное количество решений
Как и в случае с методом подстановки, метод исключения иногда удаляет как v ariables, и вы получаете либо истинное, либо ложное утверждение. Напомним, ложное утверждение означает, что решения нет.
Напомним, ложное утверждение означает, что решения нет.
Давайте посмотрим на пример.
Пример
Решите для x и y.
[латекс] \ begin {массив} {r} -x – y = -4 \\ x + y = 2 \, \, \, \, \ end {array} [/ latex]
Показать решение Добавьте уравнения, чтобы исключить член x .[латекс] \ begin {array} {r} -x – y = -4 \\\ underline {x + y = 2 \, \, \,} \\ 0 = −2 \ end {array} [/ latex ]
Ответ
Нет решения.
Построение этих линий показывает, что они являются параллельными линиями и, как таковые, не имеют общих точек, подтверждая отсутствие решения.
Если обе переменные исключены и вы остаетесь с истинным утверждением, это означает, что существует бесконечное количество упорядоченных пар, которые удовлетворяют обоим уравнениям. По сути, уравнения — это одна и та же линия.
Пример
Решите для x и y .
[латекс] \ begin {array} {r} x + y = 2 \, \, \, \, \\ — x − y = -2 \ end {array} [/ latex]
Показать решение Добавьте уравнения, чтобы исключить член x .[латекс] \ begin {array} {r} x + y = 2 \, \, \, \, \\\ underline {-x − y = -2} \\ 0 = 0 \, \, \, \ , \, \ end {array} [/ latex]
Ответ
Существует бесконечное количество решений.
Построение графика этих двух уравнений поможет проиллюстрировать, что происходит.
На следующем видео система уравнений, не имеющая решений, решается методом исключения.
Решите систему уравнений, когда необходимо умножение, чтобы исключить переменную
Многократное добавление уравнений или добавление противоположности одного из уравнений не приведет к удалению переменной. Посмотрите на систему ниже.
[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} [/ latex]
Если вы сложите приведенные выше уравнения или сложите противоположное одному из уравнений, вы получите уравнение, в котором по-прежнему есть две переменные. Итак, давайте теперь сначала воспользуемся свойством умножения равенства. Вы можете умножить обе части одного уравнения на число, которое позволит вам исключить ту же переменную из другого уравнения.
Итак, давайте теперь сначала воспользуемся свойством умножения равенства. Вы можете умножить обе части одного уравнения на число, которое позволит вам исключить ту же переменную из другого уравнения.
Мы делаем это с умножением. Обратите внимание, что первое уравнение содержит член 4 y , а второе уравнение содержит член y . Если вы умножите второе уравнение на −4, когда вы сложите оба уравнения, переменные y в сумме дадут 0.
В следующем примере показаны все шаги по поиску решения этой системы.
Пример
Решите для x и y .
Уравнение A: [латекс] 3x + 4y = 52 [/ латекс]
Уравнение B: [латекс] 5x + y = 30 [/ латекс]
Показать решение Ищите термины, которые можно исключить. В уравнениях нет членов размером x или y с одинаковыми коэффициентами.[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} [/ latex]
Умножьте второе уравнение на [латекс] −4 [/ латекс], чтобы получить одинаковый коэффициент.
[латекс] \ begin {array} {l} \, \, \, \, \, \, \, \, \, 3x + 4y = 52 \\ — 4 \ left (5x + y \ right) = — 4 \ влево (30 \ вправо) \ end {array} [/ latex]
Перепишите систему и добавьте уравнения.
[латекс] \ begin {array} {r} 3x + 4y = 52 \, \, \, \, \, \, \, \\ — 20x – 4y = −120 \ end {array} [/ latex]
Решите для x .
[латекс] \ begin {array} {l} −17x = -68 \\\, \, \, \, \, \, \, \, \, \, \, x = 4 \ end {array} [/ latex ]
Подставьте [latex] x = 4 [/ latex] в одно из исходных уравнений, чтобы найти y .
[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 3 \ left (4 \ right) + 4y = 52 \\ 12 + 4y = 52 \\ 4y = 40 \\ y = 10 \ end {array} [/ latex]
Проверьте свой ответ.
[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 3 \ left (4 \ right) +4 \ left (10 \ right) = 52 \\ 12 + 40 = 52 \\ 52 = 52 \\\ текст {ИСТИНА} \\\\ 5x + y = 30 \\ 5 \ влево (4 \ вправо) + 10 = 30 \\ 20 + 10 = 30 \\ 30 = 30 \\\ текст {ИСТИНА} \ конец {array} [/ latex]
Ответы проверяют.
Ответ
Решение (4, 10).
Осторожность! Когда вы используете умножение для исключения переменной, вы должны умножить КАЖДЫЙ член в уравнении на выбранное вами число.Забыть умножить каждый член — распространенная ошибка.Есть и другие способы решить эту систему. Вместо умножения одного уравнения, чтобы исключить переменную при добавлении уравнений, вы могли бы умножить и оба уравнений на разные числа.
На этот раз удалим переменную x . Умножьте уравнение A на 5 и уравнение B на [латекс] -3 [/ латекс].
Пример
Решите относительно x и y .
[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} [/ latex]
Показать решение Ищите термины, которые можно исключить.В уравнениях нет членов размером x или y с одним и тем же коэффициентом.[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} [/ latex]
Чтобы использовать метод исключения, вы должны создать переменные с одинаковым коэффициентом — тогда вы можете их исключить. Умножьте верхнее уравнение на 5.
[латекс] \ begin {array} {r} 5 \ left (3x + 4y \ right) = 5 \ left (52 \ right) \\ 5x + y = 30 \, \, \, \, \, \, \, \, \, \, \, \, \\ 15x + 20y = 260 \, \, \, \, \, \, \\ 5x + y = 30 \, \, \, \, \, \, \, \, \, \ end {array} [/ latex]
Теперь умножьте нижнее уравнение на −3.
[латекс] \ begin {array} {r} 15x + 20y = 260 \, \, \, \, \, \, \, \, \\ — 3 (5x + y) = — 3 (30) \\ 15x + 20y = 260 \, \, \, \, \, \, \, \, \\ — 15x – 3y = −90 \, \, \, \, \, \, \, \ end {array} [ / латекс]
Затем сложите уравнения и решите относительно y .
[латекс] \ begin {array} {r} 15x + 20y = 260 \\ — 15x – 3y = \, — 90 \\ 17y = 170 \\ y = \, \, \, 10 \ end {array} [ / латекс]
Подставьте [latex] y = 10 [/ latex] в одно из исходных уравнений, чтобы найти x .
[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 3x + 4 \ left (10 \ right) = 52 \\ 3x + 40 = 52 \\ 3x = 12 \\ x = 4 \, \, \, \ end {array} [/ latex]
Вы пришли к тому же решению, что и раньше.
Ответ
Решение (4, 10).
Эти уравнения были умножены на 5 и [латекс] −3 [/ латекс] соответственно, потому что это дало вам члены, которые в сумме дают 0. Не забудьте умножить все члены уравнения.
В следующем видео вы увидите пример использования метода исключения для решения системы уравнений.
Можно использовать метод исключения с умножением и получить результат, который не указывает никаких решений или бесконечно много решений, точно так же, как с другими методами, которые мы изучили для поиска решений систем.В следующем примере вы увидите систему, которая имеет бесконечно много решений.
Пример
Решите для x и y .
Уравнение A: [латекс] x-3y = -2 [/ латекс]
Уравнение B: [латекс] -2x + 6y = 4 [/ латекс]
Показать решение Ищите термины, которые можно исключить. В уравнениях нет членов размером x или y с одинаковыми коэффициентами.[латекс] \ begin {array} {r} x-3y = -2 \\ — 2x + 6y = 4 \ end {array} [/ latex]
Умножьте первое уравнение на [латекс] 2 [/ латекс] так, чтобы члены x исключались.
[латекс] \ begin {array} {l} \, \, \, \, \, \, \, \, \, 2 \ left (x-3y \ right) = 2 \ left (-2 \ right) \\ — 2x + 6y = 4 \ end {array} [/ latex]
Перепишите систему и добавьте уравнения.
[латекс] \ begin {array} {r} 2x-6y = -4 \\ — 2x + 6y = 4 \\ 0x + 0y = 0 \\\, \, \, \, \, \, \, \ , 0 = 0 \ end {array} [/ latex]
Вам знакомо такое решение? Это представляет собой решение всех действительных чисел для линейных уравнений, и это представляет то же самое, когда вы получаете такой результат с системами. Если мы решим оба этих уравнения относительно y, вы увидите, что это одно и то же уравнение.
Решите уравнение A относительно y:
[латекс] \ begin {array} {r} x-3y = -2 \\ — 3y = -x-2 \\ y = \ frac {1} {3} x + \ frac {2} {3} \ end {array} [/ latex]
Решите уравнение B относительно y:
[латекс] \ begin {array} -2x + 6y = 4 \\ 6y = 2x + 4 \\ y = \ frac {2} {6} x + \ frac {4} {6} \ end {array} [/ латекс]
Уменьшите дроби, разделив числитель и знаменатель обеих дробей на 2:
[латекс] y = \ frac {1} {3} + \ frac {2} {3} [/ latex]
Оба уравнения одинаковы, если записаны в форме пересечения наклона, и поэтому набором решений для системы являются все действительные числа.
Ответ
Решение: x и y могут быть действительными числами.
В следующем видео метод исключения используется для решения системы уравнений. Обратите внимание, что сначала нужно умножить одно из уравнений на отрицательное. Кроме того, у этой системы есть бесконечное количество решений.
Сводка
Метод подстановки — это один из способов решения систем уравнений. Чтобы использовать метод подстановки, используйте одно уравнение, чтобы найти выражение для одной из переменных в терминах другой переменной.Затем замените это выражение этой переменной во втором уравнении. Затем вы можете решить это уравнение, поскольку теперь оно будет иметь только одну переменную. Решение с использованием метода подстановки даст один из трех результатов: одно значение для каждой переменной в системе (с указанием одного решения), неверное утверждение (с указанием отсутствия решений) или истинное утверждение (с указанием бесконечного числа решений).
Объединение уравнений — мощный инструмент для решения системы уравнений.Сложение или вычитание двух уравнений для исключения общей переменной называется методом исключения (или добавления). Как только одна переменная исключена, становится намного проще найти другую.
Умножение можно использовать для настройки соответствующих членов в уравнениях перед их объединением, чтобы помочь в поиске решения системы. При использовании метода умножения важно умножить все члены с обеих сторон уравнения, а не только один член, который вы пытаетесь исключить.
Системы линейных уравнений
Линейное уравнение — это уравнение для линии .
Линейное уравнение не всегда имеет вид y = 3,5 — 0,5x ,
Это также может быть как y = 0,5 (7 — x)
Или как y + 0,5x = 3,5
Или как y + 0,5x — 3,5 = 0 и более.
(Примечание: все это одно и то же линейное уравнение!)
A Система линейных уравнений — это когда у нас есть два или более линейных уравнения , работающих вместе.
Пример: Вот два линейных уравнения:
Вместе они представляют собой систему линейных уравнений.
Можете ли вы сами определить значения x и y ? (Просто попробуйте, поиграйте с ними немного.)
Попробуем построить и решить реальный пример:
Пример: вы против лошади
Это гонка!
Вы можете бегать 0,2 км каждую минуту.
Лошадь может бежать 0.5 км каждую минуту. Но оседлать лошадь нужно за 6 минут.
Как далеко вы можете уйти, прежде чем лошадь вас поймает?
Мы можем составить два уравнения ( d = расстояние в км, t = время в минутах)
- Вы бежите со скоростью 0,2 км каждую минуту, поэтому d = 0,2t
- Лошадь бежит со скоростью 0,5 км в минуту, но мы берем на ее время 6: d = 0,5 (t − 6)
Итак, у нас есть система уравнений ( линейных ):
Решаем на графике:
Вы видите, как лошадь стартует через 6 минут, а потом бежит быстрее?
Кажется, тебя поймают через 10 минут… ты всего в 2 км.
В следующий раз беги быстрее.
Итак, теперь вы знаете, что такое система линейных уравнений.
Давайте продолжим узнавать о них больше ….
Решение
Существует множество способов решения линейных уравнений!
Давайте посмотрим на другой пример:
Пример: Решите эти два уравнения:
На этом графике показаны два уравнения:
Наша задача — найти место пересечения двух линий.
Ну, мы видим, где они пересекаются, так что это уже решено графически.
А теперь давайте решим это с помощью алгебры!
Хммм . .. как это решить? Способов может быть много! В этом случае в обоих уравнениях есть «y», поэтому давайте попробуем вычесть все второе уравнение из первого:
.. как это решить? Способов может быть много! В этом случае в обоих уравнениях есть «y», поэтому давайте попробуем вычесть все второе уравнение из первого:
x + y — (−3x + y) = 6-2
Теперь упростим:
х + у + 3х — у = 6-2
4x = 4
х = 1
Итак, теперь мы знаем, что линии пересекаются в точке x = 1 .
И мы можем найти совпадающее значение y , используя любое из двух исходных уравнений (потому что мы знаем, что они имеют одинаковое значение при x = 1). Воспользуемся первым (второй можете попробовать сами):
х + у = 6
1 + у = 6
г = 5
И решение:
x = 1 и y = 5
И график показывает, что мы правы!
Линейные уравнения
В линейных уравнениях допускаются только простые переменные. Нет x 2 , y 3 , √x и т. Д. :
Линейное против нелинейного
Размеры
| A Linear Equation может быть в 2 измерениях … (например, x и y ) | ||
| … или в 3-х измерениях … (он делает самолет) | ||
| … или 4 размера … | ||
| … или больше! |
Общие переменные
Чтобы уравнения «работали вместе», они разделяют одну или несколько переменных:
Система уравнений состоит из двух или более уравнений в одной или нескольких переменных
Множество переменных
Таким образом, Система уравнений может иметь многих, уравнений и , много переменных.
Пример: 3 уравнения с 3 переменными
| 2x | + | y | – | 2z | = | 3 |
| x | – | y | – | z | = | 0 |
| x | + | y | + | 3z | = | 12 |
Может быть любая комбинация:
- 2 уравнения с 3 переменными,
- 6 уравнений с 4 переменными,
- 9000 уравнений с 567 переменными,
- и др.

Решения
Когда количество уравнений равно , то же , что и количество переменных, , вероятно, будет решением. Не гарантировано, но вероятно.
На самом деле возможны только три случая:
- Нет раствор
- Одно решение
- Бесконечно много решений
Когда нет решения , уравнения называются «несовместимыми» .
Один или бесконечно много решений называются «согласованными»
Вот диаграмма для 2 уравнений с 2 переменными :
Независимая
«Независимый» означает, что каждое уравнение дает новую информацию.
В противном случае они «Зависимые» .
Также называется «линейная независимость» и «линейная зависимость»
Пример:
Эти уравнения — «Зависимые» , потому что они на самом деле являются тем же уравнением , только умноженным на 2.
Итак, второе уравнение не дало новой информации .
Где верны уравнения
Уловка состоит в том, чтобы найти, где все уравнений истинны одновременно .
Верно? Что это значит?
Пример: вы против лошади
Линия «ты» истинна по всей ее длине (но больше нигде).
В любом месте этой строки d равно 0.2т
- при t = 5 и d = 1 уравнение истинно (d = 0,2t? Да, поскольку 1 = 0,2 × 5 верно)
- при t = 5 и d = 3 уравнение не соответствует действительности (верно ли d = 0,2t? Нет, поскольку 3 = 0,2 × 5 неверно )
Точно так же линия «лошади» верна на всем протяжении (но больше нигде).
Но только в точке, где они пересекают (при t = 10, d = 2), они оба истинны .
Значит, они должны быть правдой одновременно . ..
..
… поэтому некоторые люди называют их «Одновременные линейные уравнения»
Решить с помощью алгебры
Для их решения принято использовать алгебру.
Вот пример «Лошади», решенный с помощью алгебры:
Пример: вы против лошади
Система уравнений:
В данном случае кажется проще всего установить равными друг другу:
d = 0.2т = 0,5 (т − 6)
Начать с : 0,2t = 0,5 (t — 6)
Расширить 0,5 (t − 6) : 0,2t = 0,5t — 3
Вычтем 0,5t с обеих сторон: −0,3t = −3
Разделите обе стороны на −0,3 : t = −3 / −0,3 = 10 минут
Теперь мы знаем , когда вас поймают!
Зная t , мы можем вычислить d : d = 0,2t = 0,2 × 10 = 2 км
И наше решение:
t = 10 минут и d = 2 км
Алгебра и графики
Зачем использовать алгебру, если графики настолько просты? Потому что:
Более двух переменных невозможно решить с помощью простого графика.
Итак, алгебра приходит на помощь двумя популярными методами:
- Решение заменой
- Решение методом исключения
Мы увидим каждую с примерами по 2 переменным и 3 переменным. Вот и …
Решение заменой
Это шаги:
- Напишите одно из уравнений в стиле «переменная = …»
- Заменить (т.е. заменить) эту переменную в другое уравнение (а).
- Решите другое уравнение (я)
- (при необходимости повторить)
Вот пример с 2 уравнениями с 2 переменными :
Пример:
Мы можем начать с любого уравнения и любой переменной .
Давайте использовать второе уравнение и переменную «y» (это выглядит как простейшее уравнение).
Напишите одно из уравнений в стиле «переменная =». .. «:
.. «:
Мы можем вычесть x из обеих частей x + y = 8, чтобы получить y = 8 — x . Теперь наши уравнения выглядят так:
Теперь замените «y» на «8 — x» в другом уравнении:
- 3x + 2 (8 — x) = 19
- у = 8 — х
Решите, используя обычные методы алгебры:
Развернуть 2 (8 − x) :
- 3x + 16 — 2x = 19
- у = 8 — х
Тогда 3x − 2x = x :
И на последок 19−16 = 3
Теперь мы знаем, что такое x , мы можем поместить его в уравнение y = 8 — x :
И ответ:
х = 3
у = 5
Примечание: поскольку — это решение, уравнения «непротиворечивы»
Проверка: почему бы вам не проверить, работают ли x = 3 и y = 5 в обоих уравнениях?
Решение подстановкой: 3 уравнения с 3 переменными
ОК! Давайте перейдем к более длинному примеру : 3 уравнения с 3 переменными .
Это не сложно, сделать … просто нужно много времени !
Пример:
- х + г = 6
- г — 3у = 7
- 2x + y + 3z = 15
Мы должны аккуратно выровнять переменные, иначе мы потеряем из виду, что делаем:
| x | + | z | = | 6 | |||||
| – | 3 года | + | z | = | 7 | ||||
| 2x | + | y | + | 3z | = | 15 |
WeI может начать с любого уравнения и любой переменной. Воспользуемся первым уравнением и переменной «x».
Воспользуемся первым уравнением и переменной «x».
Напишите одно из уравнений в стиле «переменная = …»:
| x | = | 6 — я | |||||||
| – | 3 года | + | z | = | 7 | ||||
| 2x | + | y | + | 3z | = | 15 | |||
Теперь замените «x» на «6 — z» в других уравнениях:
(К счастью, есть только одно уравнение с x в нем)
| х | = | 6 — z | ||||||||
| – | 3 года | + | z | = | 7 | |||||
| 2 (6-z) | + | y | + | 3z | = | 15 | ||||
Решите, используя обычные методы алгебры:
2 (6 − z) + y + 3z = 15 упрощается до y + z = 3 :
| x | = | 6 — z | |||||||
| – | 3 года | + | z | = | 7 | ||||
| y | + | z | = | 3 | |||||
Хорошо. Мы добились некоторого прогресса, но пока не достигли этого.
Мы добились некоторого прогресса, но пока не достигли этого.
Теперь повторите процесс , но только для последних 2 уравнений.
Напишите одно из уравнений в стиле «переменная = …»:
Выберем последнее уравнение и переменную z:
| x | = | 6 — z | |||||||
| – | 3 года | + | z | = | 7 | ||||
| z | = | 3 — х лет | |||||||
Теперь замените «z» на «3 — y» в другом уравнении:
| x | = | 6 — z | |||||||
| – | 3 года | + | 3 — х лет | = | 7 | ||||
| z | = | 3-й год | |||||||
Решите, используя обычные методы алгебры:
−3y + (3 − y) = 7 упрощается до −4y = 4 , или, другими словами, y = −1
| x | = | 6 — z | |||||||
| y | = | -1 | |||||||
| z | = | 3-й год | |||||||
Почти готово!
Зная, что y = −1 , мы можем вычислить, что z = 3 − y = 4 :
| x | = | 6 — z | |||||||
| y | = | -1 | |||||||
| z | = | 4 | |||||||
И зная, что z = 4 , мы можем вычислить, что x = 6 − z = 2 :
| x | = | 2 | |||||||
| y | = | -1 | |||||||
| z | = | 4 |
И ответ:
х = 2
у = -1
г = 4
Проверить: пожалуйста, проверьте это сами.
Мы можем использовать этот метод для 4 или более уравнений и переменных … просто повторяйте одни и те же шаги снова и снова, пока не решите проблему.
Вывод: Замена работает хорошо, но требует много времени.
Решение методом исключения
Устранение может быть быстрее … но должно быть аккуратным.
«Устранить» означает удалить : этот метод работает путем удаления переменных до тех пор, пока не останется только одна.
По идее, мы можем спокойно :
- умножить уравнение на константу (кроме нуля),
- прибавить (или вычесть) уравнение к другому уравнению
Как в этих примерах:
ПОЧЕМУ мы можем складывать уравнения друг в друга?
Представьте себе два действительно простых уравнения:
х — 5 = 3
5 = 5
Мы можем добавить «5 = 5» к «x — 5 = 3»:
х — 5 + 5 = 3 + 5
х = 8
Попробуйте сами, но используйте 5 = 3 + 2 в качестве второго уравнения
Он по-прежнему будет работать нормально, потому что обе стороны равны (для этого нужен знак =!).
Мы также можем поменять местами уравнения, чтобы первое могло стать вторым и т. Д., Если это поможет.
Хорошо, время для полного примера. Давайте использовать 2 уравнения с 2 переменными, пример из предыдущего:
Пример:
Очень важно, чтобы все было в порядке:
| 3x | + | 2 года | = | 19 | |||
| x | + | y | = | 8 |
Сейчас… наша цель — исключить переменную из уравнения.
Сначала мы видим, что есть «2y» и «y», так что давайте поработаем над этим.
Умножьте второе уравнение на 2:
| 3x | + | 2 года | = | 19 | |||
| 2 x | + | 2 y | = | 16 |
Вычтем второе уравнение из первого уравнения:
| x | = | 3 | |||||
| 2x | + | 2 года | = | 16 |
Ура! Теперь мы знаем, что такое x!
Затем мы видим, что во втором уравнении есть «2x», поэтому давайте уменьшим его вдвое, а затем вычтем «x»:
Умножьте второе уравнение на ½ (т.е.е. разделить на 2):
| x | = | 3 | |||||
| x | + | y | = | 8 |
Вычтем первое уравнение из второго уравнения:
| x | = | 3 | |||||
| y | = | 5 |
Готово!
И ответ:
x = 3 и y = 5
А вот график:
Синяя линия — это место, где 3x + 2y = 19 истинно
Красная линия — это место, где x + y = 8 верно
При x = 3, y = 5 (где линии пересекаются) они равны , оба значения истинны. Это и есть ответ.
Это и есть ответ.
Вот еще пример:
Пример:
- 2х — у = 4
- 6x — 3y = 3
Разложите аккуратно:
| 2x | – | y | = | 4 | |||
| 6x | – | 3 года | = | 3 |
Умножьте первое уравнение на 3:
| 6x | – | 3 года | = | 12 | |||
| 6x | – | 3 года | = | 3 |
Вычтем второе уравнение из первого уравнения:
| 0 | – | 0 | = | 9 | |||
| 6x | – | 3 года | = | 3 |
0-0 = 9 ???
Что здесь происходит?
Все просто, решения нет.
| На самом деле это параллельные линии: |
И напоследок:
Пример:
- 2х — у = 4
- 6x — 3y = 12
Аккуратно:
| 2x | – | y | = | 4 | |||
| 6x | – | 3 года | = | 12 |
Умножьте первое уравнение на 3:
| 6x | – | 3 года | = | 12 | |||
| 6x | – | 3 года | = | 12 |
Вычтем второе уравнение из первого уравнения:
| 0 | – | 0 | = | 0 | |||
| 6x | – | 3 года | = | 3 |
0 — 0 = 0
Ну, это на самом деле ИСТИНА! Ноль действительно равен нулю. ..
..
… это потому, что на самом деле это одно и то же уравнение …
… значит существует бесконечное количество решений
| Это та же строка: |
Итак, теперь мы рассмотрели пример каждого из трех возможных случаев:
- Нет раствор
- Одно решение
- Бесконечно много решений
Решение методом исключения: 3 уравнения с 3 переменными
Прежде чем мы начнем со следующего примера, давайте рассмотрим улучшенный способ решения задач.
Следуйте этому методу, и мы уменьшим вероятность ошибки.
Прежде всего удалите переменные в порядке :
- Сначала исключить x с (из уравнений 2 и 3, по порядку)
- , затем исключите y (из уравнения 3)
Вот как мы их устраняем:
У нас есть «форма треугольника»:
Теперь начните снизу и вернитесь к (так называемая «обратная подстановка»)
(введите z , чтобы найти y , затем z и y , чтобы найти x ):
И решаемся:
ТАКЖЕ, мы обнаружим, что проще выполнить примерно вычислений в уме или на бумаге для заметок, чем всегда работать в рамках системы уравнений:
Пример:
- х + у + г = 6
- 2y + 5z = −4
- 2x + 5y — z = 27
Аккуратно написано:
| x | + | y | + | z | = | 6 | |||
| 2 года | + | 5z | = | −4 | |||||
| 2x | + | 5лет | – | z | = | 27 |
Сначала удалите x из 2-го и 3-го уравнения.
Во втором уравнении нет x … переходите к третьему уравнению:
Вычтите 2 раза 1-е уравнение из 3-го уравнения (просто сделайте это в уме или на бумаге для заметок):
И получаем:
| x | + | y | + | z | = | 6 | |||
| 2 года | + | 5z | = | −4 | |||||
| 3 года | – | 3z | = | 15 |
Затем удалите y из 3-го уравнения.
Мы, , могли бы вычесть 1½ раза 2-е уравнение из 3-го уравнения (потому что 1½ раза 2 равно 3) …
… но мы можем избежать дробей , если мы:
- умножьте 3-е уравнение на 2 и
- умножьте 2-е уравнение на 3
и , затем выполняют вычитание … вот так:
И в итоге получаем:
| x | + | y | + | z | = | 6 | |||
| 2 года | + | 5z | = | −4 | |||||
| z | = | -2 |
Теперь у нас есть «треугольник»!
Теперь вернемся снова вверх «с обратной заменой»:
Мы знаем z , поэтому 2y + 5z = −4 становится 2y − 10 = −4 , затем 2y = 6 , поэтому y = 3 :
| x | + | y | + | z | = | 6 | |||
| y | = | 3 | |||||||
| z | = | −2 |
Тогда x + y + z = 6 становится x + 3−2 = 6 , поэтому x = 6−3 + 2 = 5
| x | = | 5 | |||||||
| y | = | 3 | |||||||
| z | = | −2 |
И ответ:
x = 5
y = 3
z = −2
Проверить: проверьте сами.
Общий совет
Как только вы привыкнете к методу исключения, он станет проще, чем замена, потому что вы просто выполняете шаги, и ответы появляются.
Но иногда замена может дать более быстрый результат.
- Замена часто проще для небольших случаев (например, 2 уравнения, а иногда и 3 уравнения)
- Устранение проще для больших ящиков
И всегда полезно сначала просмотреть уравнения, чтобы увидеть, есть ли простой ярлык… так что опыт помогает.
5.2 Решение систем уравнений подстановкой — элементарная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Решите систему уравнений заменой
- Решите приложения систем уравнений заменой
Будьте готовы 5,4
Прежде чем начать, пройдите тест на готовность.
Упростим −5 (3 − x) −5 (3 − x).
Если вы пропустили эту проблему, просмотрите Пример 1.136.
Будьте готовы 5.5
Упростим 4−2 (n + 5) 4−2 (n + 5).
Если вы пропустили эту проблему, просмотрите Пример 1.123.
Будьте готовы 5,6
Решить для гг. 8y − 8 = 32−2y8y − 8 = 32−2y
Если вы пропустили эту проблему, просмотрите Пример 2.34.
Будьте готовы 5,7
Решить относительно xx. 3x − 9y = −33x − 9y = −3
Если вы пропустили эту проблему, просмотрите Пример 2.65.
Решение систем линейных уравнений с помощью графиков — хороший способ визуализировать типы решений, которые могут возникнуть. Однако во многих случаях решение системы с помощью построения графиков неудобно или неточно. Если графики выходят за пределы небольшой сетки с x и y , оба между -10 и 10, построение линий может быть громоздким. И если решения системы не являются целыми числами, может быть трудно точно прочитать их значения с графика.
В этом разделе мы будем решать системы линейных уравнений методом подстановки.
Решите систему уравнений подстановкой
Мы будем использовать ту же систему, которую мы использовали вначале для построения графиков.
{2x + y = 7x − 2y = 6 {2x + y = 7x − 2y = 6Сначала мы решим одно из уравнений для x или y . Мы можем выбрать любое уравнение и решить любую переменную, но мы постараемся сделать выбор, который упростит работу.
Затем мы подставляем это выражение в другое уравнение. В результате получается уравнение с одной переменной — и мы знаем, как его решить!
После того, как мы найдем значение одной переменной, мы подставим это значение в одно из исходных уравнений и решим для другой переменной.Наконец, мы проверяем наше решение и убеждаемся, что оно соответствует обоим уравнениям.
Теперь мы выполним все эти шаги в примере 5.13.
Пример 5.13
Как решить систему уравнений подстановкой
Решите систему подстановкой. {2x + y = 7x − 2y = 6 {2x + y = 7x − 2y = 6
Попробовать 5.25
Решите систему подстановкой. {−2x + y = −11x + 3y = 9 {−2x + y = −11x + 3y = 9
Попробовать 5.26
Решите систему подстановкой.{x + 3y = 104x + y = 18 {x + 3y = 104x + y = 18
How To
Решите систему уравнений путем подстановки.
- Шаг 1. Решите одно из уравнений для любой переменной.
- Шаг 2. Подставьте выражение из шага 1 в другое уравнение.
- Шаг 3. Решите полученное уравнение.
- Шаг 4. Подставьте решение шага 3 в одно из исходных уравнений, чтобы найти другую переменную.
- Шаг 5. Запишите решение в виде упорядоченной пары.
- Шаг 6. Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.

Если одно из уравнений системы задано в форме углового пересечения, шаг 1 уже выполнен! Мы увидим это в примере 5.14.
Пример 5.14
Решите систему подстановкой.
{x + y = −1y = x + 5 {x + y = −1y = x + 5
Решение
Второе уравнение уже решено для y . Мы заменим выражение на в первом уравнении.
Попробовать 5.27
Решите систему подстановкой. {x + y = 6y = 3x − 2 {x + y = 6y = 3x − 2
Попробовать 5.28
Решите систему подстановкой. {2x − y = 1y = −3x − 6 {2x − y = 1y = −3x − 6
Если уравнения представлены в стандартной форме, нам нужно будет начать с решения для одной из переменных. В следующем примере мы решим первое уравнение относительно y .
Пример 5.15
Решите систему подстановкой. {3x + y = 52x + 4y = −10 {3x + y = 52x + 4y = −10
Решение
Нам нужно решить одно уравнение для одной переменной.Затем мы подставим это выражение в другое уравнение.
Попробовать 5.29
Решите систему подстановкой. {4x + y = 23x + 2y = −1 {4x + y = 23x + 2y = −1
Попробовать 5,30
Решите систему подстановкой. {−x + y = 44x − y = 2 {−x + y = 44x − y = 2
В примере 5.15 проще всего было решить для y в первом уравнении, потому что оно имело коэффициент 1. В примере 5.16 будет легче решить для x .
Пример 5.16
Решите систему подстановкой. {x − 2y = −23x + 2y = 34 {x − 2y = −23x + 2y = 34
Решение
Мы решим первое уравнение относительно xx, а затем подставим выражение во второе уравнение.
Попробовать 5,31
Решите систему подстановкой. {x − 5y = 134x − 3y = 1 {x − 5y = 134x − 3y = 1
Попробовать 5,32
Решите систему подстановкой. {x − 6y = −62x − 4y = 4 {x − 6y = −62x − 4y = 4
{x − 6y = −62x − 4y = 4 {x − 6y = −62x − 4y = 4
Когда оба уравнения уже решены для одной и той же переменной, их легко заменить!
Пример 5.17
Решите систему подстановкой. {y = −2x + 5y = 12x {y = −2x + 5y = 12x
Решение
Поскольку оба уравнения решаются относительно y , мы можем подставить одно в другое.
Попробовать 5,33
Решите систему подстановкой. {y = 3x − 16y = 13x {y = 3x − 16y = 13x
Попробовать 5,34
Решите систему подстановкой. {y = −x + 10y = 14x {y = −x + 10y = 14x
Будьте очень осторожны со знаками в следующем примере.
Пример 5.18
Решите систему подстановкой. {4x + 2y = 46x − y = 8 {4x + 2y = 46x − y = 8
Решение
Нам нужно решить одно уравнение для одной переменной. Решим первое уравнение относительно y .
Попробовать 5,35
Решите систему подстановкой. {x − 4y = −4−3x + 4y = 0 {x − 4y = −4−3x + 4y = 0
Попробовать 5,36
Решите систему подстановкой. {4x − y = 02x − 3y = 5 {4x − y = 02x − 3y = 5
В примере 5.19 потребуется немного больше работы, чтобы решить одно уравнение для x или y .
Пример 5.19
Решите систему подстановкой. {4x − 3y = 615y − 20x = −30 {4x − 3y = 615y − 20x = −30
Решение
Нам нужно решить одно уравнение для одной переменной. Решим первое уравнение относительно x .
Поскольку 0 = 0 — истинное утверждение, система согласована. Уравнения зависимы. Графики этих двух уравнений дадут одну и ту же линию.У системы бесконечно много решений.
Попробовать 5,37
Решите систему подстановкой. {2x − 3y = 12−12y + 8x = 48 {2x − 3y = 12−12y + 8x = 48
Попробовать 5,38
Решите систему подстановкой.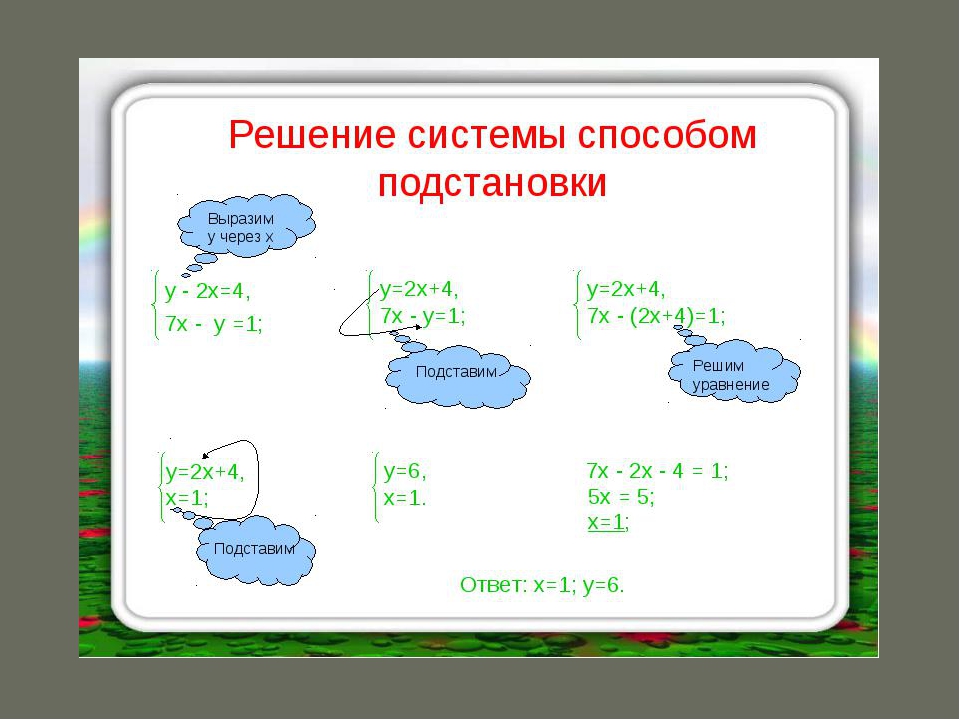 {5x + 2y = 12−4y − 10x = −24 {5x + 2y = 12−4y − 10x = −24
{5x + 2y = 12−4y − 10x = −24 {5x + 2y = 12−4y − 10x = −24
Вернитесь к уравнениям в Примере 5.19. Есть ли способ распознать, что это одна линия?
Давайте посмотрим, что происходит в следующем примере.
Пример 5.20
Решите систему подстановкой.{5x − 2y = −10y = 52x {5x − 2y = −10y = 52x
Решение
Второе уравнение уже решено относительно y , поэтому мы можем заменить y в первом уравнении.
| Замените x на y в первом уравнении. | |
| Замените y на 52x.52x. | |
| Решите относительно x . | |
Поскольку 0 = −10 — ложное утверждение, уравнения несовместимы.Графики двух уравнений будут параллельными линиями. В системе нет решений.
Попробовать 5,39
Решите систему подстановкой. {3x + 2y = 9y = −32x + 1 {3x + 2y = 9y = −32x + 1
Попробовать 5,40
Решите систему подстановкой. {5x − 3y = 2y = 53x − 4 {5x − 3y = 2y = 53x − 4
Решите приложения систем уравнений подстановкой
Мы скопируем сюда стратегию решения задач, которую мы использовали в разделе «Решение систем уравнений с помощью построения графиков» для решения систем уравнений.Теперь, когда мы знаем, как решать системы с помощью подстановки, это то, что мы сделаем на шаге 5.
How To
Как использовать стратегию решения задач для систем линейных уравнений.

- Шаг 1. Прочтите о проблеме. Убедитесь, что все слова и идеи понятны.
- Шаг 2. Определите то, что мы ищем.
- Шаг 3. Назовите то, что мы ищем. Выберите переменные для представления этих величин.
- Шаг 4. Переведите в систему уравнений.
- Шаг 5. Решите систему уравнений, используя хорошие методы алгебры.
- Шаг 6. Проверьте ответ в проблеме и убедитесь, что он имеет смысл.
- Шаг 7. Ответьте на вопрос полным предложением.
Некоторым людям проще создать текстовые задачи с двумя переменными, чем с одной переменной. Выбирать имена переменных проще, когда все, что вам нужно сделать, это написать две буквы.Подумайте об этом в следующем примере — как бы вы сделали это с помощью только одной переменной?
Пример 5.21
Сумма двух чисел равна нулю. Одно число на девять меньше другого. Найдите числа.
Попробовать 5,41
Сумма двух чисел равна 10. Одно число на 4 меньше другого. Найдите числа.
Попробовать 5,42
Сумма двух чисел равна −6. Одно число на 10 меньше другого. Найдите числа.
В Примере 5.22 воспользуемся формулой для периметра прямоугольника: P = 2 L + 2 W .
Пример 5.22
Периметр прямоугольника равен 88. Длина в пять раз больше ширины в два раза. Найдите длину и ширину.
Попробовать 5,43
Периметр прямоугольника равен 40. Длина на 4 раза больше ширины. Найдите длину и ширину прямоугольника.
Попробовать 5,44
Периметр прямоугольника 58.Длина в 5 раз больше ширины более чем в три раза. Найдите длину и ширину прямоугольника.
Найдите длину и ширину прямоугольника.
Для примера 5.23 нам нужно помнить, что сумма углов треугольника равна 180 градусам, а у прямоугольного треугольника один угол 90 градусов.
Пример 5.23
Размер одного из малых углов прямоугольного треугольника в десять раз больше размера другого малого угла. Найдите размеры обоих углов.
Решение
Нарисуем и обозначим фигуру.
Попробовать 5,45
Размер одного из малых углов прямоугольного треугольника в 2 раза больше, чем в 3 раза больше другого малого угла. Найдите размер обоих углов.
Попробовать 5,46
Размер одного из малых углов прямоугольного треугольника на 18 меньше, чем удвоение размера другого малого угла. Найдите размер обоих углов.
Пример 5.24
Хизер предложили два варианта заработной платы тренера в спортзале.Вариант А платит ей 25 000 долларов плюс 15 долларов за каждую тренировку. Вариант Б платит ей 10 000 + 40 долларов за каждую тренировку. Сколько тренингов уравняло бы варианты заработной платы?
Попробовать 5,47
Джеральдин предложили вакансии в двух страховых компаниях. Первая компания выплачивает заработную плату в размере 12 000 долларов плюс комиссия в размере 100 долларов за каждый проданный полис. Второй платит зарплату в размере 20 000 долларов плюс комиссию в размере 50 долларов за каждый проданный полис. Сколько полисов необходимо продать, чтобы общая сумма выплат была такой же?
Попробовать 5.48
Кеннет в настоящее время продает костюмы для компании А с зарплатой 22 000 долларов плюс 10 долларов комиссионных за каждый проданный костюм. Компания B предлагает ему должность с окладом в 28000 долларов плюс комиссия в размере 4 долларов за каждый проданный костюм. Сколько костюмов нужно продать Кеннету, чтобы варианты были равны?
Раздел 5.2 Упражнения
Практика ведет к совершенству
Решите систему уравнений подстановкой
В следующих упражнениях решите системы уравнений путем подстановки.
{2x + y = −43x − 2y = −6 {2x + y = −43x − 2y = −6
72.{2x + y = −23x − y = 7 {2x + y = −23x − y = 7
73.{x − 2y = −52x − 3y = −4 {x − 2y = −52x − 3y = −4
74.{x − 3y = −92x + 5y = 4 {x − 3y = −92x + 5y = 4
75.{5x − 2y = −6y = 3x + 3 {5x − 2y = −6y = 3x + 3
76.{−2x + 2y = 6y = −3x + 1 {−2x + 2y = 6y = −3x + 1
77.{2x + 3y = 3y = −x + 3 {2x + 3y = 3y = −x + 3
78.{2x + 5y = −14y = −2x + 2 {2x + 5y = −14y = −2x + 2
79.{2x + 5y = 1y = 13x − 2 {2x + 5y = 1y = 13x − 2
80.{3x + 4y = 1y = −25x + 2 {3x + 4y = 1y = −25x + 2
81.{3x − 2y = 6y = 23x + 2 {3x − 2y = 6y = 23x + 2
82.{−3x − 5y = 3y = 12x − 5 {−3x − 5y = 3y = 12x − 5
83.{2x + y = 10 − x + y = −5 {2x + y = 10 − x + y = −5
84.{−2x + y = 10 − x + 2y = 16 {−2x + y = 10 − x + 2y = 16
85.{3x + y = 1−4x + y = 15 {3x + y = 1−4x + y = 15
86.{x + y = 02x + 3y = −4 {x + y = 02x + 3y = −4
87.{x + 3y = 13x + 5y = −5 {x + 3y = 13x + 5y = −5
88.{x + 2y = −12x + 3y = 1 {x + 2y = −12x + 3y = 1
89.{2x + y = 5x − 2y = −15 {2x + y = 5x − 2y = −15
90.{4x + y = 10x − 2y = −20 {4x + y = 10x − 2y = −20
91.{y = −2x − 1y = −13x + 4 {y = −2x − 1y = −13x + 4
92.{y = x − 6y = −32x + 4 {y = x − 6y = −32x + 4
93.{y = 2x − 8y = 35x + 6 {y = 2x − 8y = 35x + 6
94.{y = −x − 1y = x + 7 {y = −x − 1y = x + 7
95.{4x + 2y = 88x − y = 1 {4x + 2y = 88x − y = 1
96.{−x − 12y = −12x − 8y = −6 {−x − 12y = −12x − 8y = −6
97.{15x + 2y = 6−5x + 2y = −4 {15x + 2y = 6−5x + 2y = −4
98.{2x − 15y = 712x + 2y = −4 {2x − 15y = 712x + 2y = −4
99.{y = 3x6x − 2y = 0 {y = 3x6x − 2y = 0
100.{x = 2y4x − 8y = 0 {x = 2y4x − 8y = 0
101.{2x + 16y = 8 − x − 8y = −4 {2x + 16y = 8 − x − 8y = −4
102.
{15x + 4y = 6−30x − 8y = −12 {15x + 4y = 6−30x − 8y = −12
103.{y = −4x4x + y = 1 {y = −4x4x + y = 1
104.{y = −14xx + 4y = 8 {y = −14xx + 4y = 8
105.{y = 78x + 4−7x + 8y = 6 {y = 78x + 4−7x + 8y = 6
106.{y = −23x + 52x + 3y = 11 {y = −23x + 52x + 3y = 11
Решите приложения систем уравнений подстановкой
В следующих упражнениях переведите в систему уравнений и решите.
107.Сумма двух чисел равна 15. Одно число на 3 меньше другого. Найдите числа.
108.Сумма двух чисел равна 30. Одно число на 4 меньше другого. Найдите числа.
109.Сумма двух чисел равна −26. Одно число на 12 меньше другого. Найдите числа.
110.Периметр прямоугольника равен 50. Длина на 5 больше ширины. Найдите длину и ширину.
111.Периметр прямоугольника равен 60. Длина на 10 больше ширины.Найдите длину и ширину.
112.Периметр прямоугольника равен 58. Длина в 5 раз больше ширины в 5 раз. Найдите длину и ширину.
113.Периметр прямоугольника равен 84. Длина в 10 раз больше ширины более чем в три раза. Найдите длину и ширину.
114.Размер одного из малых углов прямоугольного треугольника в 14 раз больше размера другого малого угла более чем в 3 раза. Найдите размер обоих углов.
115.Размер одного из малых углов прямоугольного треугольника в 26 раз больше, чем в 3 раза больше другого малого угла.Найдите размер обоих углов.
116.Размер одного из малых углов прямоугольного треугольника на 15 меньше, чем удвоение размера другого малого угла. Найдите размер обоих углов.
117.Размер одного из малых углов прямоугольного треугольника на 45 меньше, чем удвоение размера другого малого угла. Найдите размер обоих углов.
118. Maxim предложили вакансии два автосалона. Первая компания платит зарплату в размере 10 000 долларов плюс комиссионные в размере 1 000 долларов за каждую проданную машину. Второй платит зарплату в размере 20 000 долларов плюс комиссионные в размере 500 долларов за каждую проданную машину. Сколько автомобилей нужно продать, чтобы общая сумма была такой же?
Второй платит зарплату в размере 20 000 долларов плюс комиссионные в размере 500 долларов за каждую проданную машину. Сколько автомобилей нужно продать, чтобы общая сумма была такой же?
Джеки предложили должности две кабельные компании. Первая компания платит зарплату в размере 14 000 долларов плюс комиссию в размере 100 долларов за каждый проданный пакет кабеля. Второй платит зарплату в размере 20 000 долларов плюс комиссию в размере 25 долларов за каждый проданный пакет кабеля. Сколько пакетов кабеля нужно продать, чтобы общая сумма была такой же?
120.Амара в настоящее время продает телевизоры для компании А с зарплатой 17 000 долларов плюс комиссия 100 долларов за каждый проданный телевизор. Компания B предлагает ей должность с окладом в 29 000 долларов плюс 20 долларов комиссионных за каждый проданный телевизор. Какие телевизоры нужно будет продавать Amara, чтобы возможности были равными?
121.Mitchell в настоящее время продает печи компании А с зарплатой в 12 000 долларов плюс 150 долларов комиссионных за каждую проданную печь. Компания B предлагает ему должность с зарплатой в размере 24 000 долларов плюс комиссия в размере 50 долларов за каждую проданную печь.Сколько печей нужно продать Митчеллу, чтобы варианты были равны?
Повседневная математика
122.Когда Глория провела 15 минут на эллиптическом тренажере, а затем 30 минут выполняла круговые тренировки, ее фитнес-приложение показало, что она сожгла 435 калорий. Когда она потратила 30 минут на эллиптический тренажер и 40 минут на круговые тренировки, она сожгла 690 калорий. Решите систему {15e + 30c = 43530e + 40c = 690 {15e + 30c = 43530e + 40c = 690 для ee, количество калорий, которые она сжигает за каждую минуту на эллиптическом тренажере, и cc, количество калорий, которые она сжигает для каждую минуту круговой тренировки.
123. Стефани выехала из Риверсайда, Калифорния, на своем автодоме на север по межштатной автомагистрали 15 в сторону Солт-Лейк-Сити со скоростью 56 миль в час. Через полчаса Тина выехала из Риверсайда на своей машине по тому же маршруту, что и Стефани, со скоростью 70 миль в час. Решите систему {56s = 70ts = t + 12 {56s = 70ts = t + 12.
Через полчаса Тина выехала из Риверсайда на своей машине по тому же маршруту, что и Стефани, со скоростью 70 миль в час. Решите систему {56s = 70ts = t + 12 {56s = 70ts = t + 12.
- ⓐ, чтобы узнать, сколько времени потребуется Тине, чтобы догнать Стефани.
- ⓑ какова стоимость ss, количество часов, которое Стефани проехала, прежде чем Тина ее догонит?
Письменные упражнения
124. Решите систему уравнений
{x + y = 10x − y = 6 {x + y = 10x − y = 6
ⓐ по графику. Ⓑ заменой. Ⓒ Какой метод вы предпочитаете? Почему?
125. Решите систему уравнений
{3x + y = 12x = y − 8 {3x + y = 12x = y − 8 с помощью подстановки и объясните все свои шаги словами.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что вы сделаете, изучив этот контрольный список, чтобы стать уверенным в достижении всех целей?
5.2: Решение систем уравнений с помощью замены
Решение систем линейных уравнений с помощью построения графиков — хороший способ визуализировать типы решений, которые могут возникнуть. Однако во многих случаях решение системы с помощью построения графиков неудобно или неточно. Если графики выходят за пределы небольшой сетки с x и y , оба между -10 и 10, построение линий может быть громоздким. И если решения системы не являются целыми числами, может быть трудно точно прочитать их значения с графика.
В этом разделе мы будем решать системы линейных уравнений методом подстановки.
Решите систему уравнений подстановкой
Мы будем использовать ту же систему, которую мы использовали вначале для построения графиков.
\ (\ left \ {\ begin {array} {l} {2 x + y = 7} \\ {x-2 y = 6} \ end {array} \ right. \)
Сначала мы решим одно из уравнений для x или y . Мы можем выбрать любое уравнение и решить любую переменную, но мы постараемся сделать выбор, который упростит работу.
Мы можем выбрать любое уравнение и решить любую переменную, но мы постараемся сделать выбор, который упростит работу.
Затем мы подставляем это выражение в другое уравнение. В результате получается уравнение с одной переменной — и мы знаем, как его решить!
После того, как мы найдем значение одной переменной, мы подставим это значение в одно из исходных уравнений и решим для другой переменной. Наконец, мы проверяем наше решение и убеждаемся, что оно соответствует обоим уравнениям.
Теперь мы выполним все эти шаги в упражнении \ (\ PageIndex {1} \).
Упражнение \ (\ PageIndex {2} \)
Решите систему подстановкой.\ (\ left \ {\ begin {array} {l} {- 2 x + y = -11} \\ {x + 3 y = 9} \ end {array} \ right. \)
- Ответ
(6,1)
Упражнение \ (\ PageIndex {3} \)
Решите систему подстановкой. \ (\ left \ {\ begin {array} {l} {x + 3 y = 10} \\ {4 x + y = 18} \ end {array} \ right. \)
- Ответ
(4,2)
Решите систему уравнений подстановкой.
- Решите одно из уравнений для любой переменной.
- Подставьте выражение из шага 1 в другое уравнение.
- Решите полученное уравнение.
- Подставьте решение шага 3 в одно из исходных уравнений, чтобы найти другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
Если одно из уравнений системы задано в форме углового пересечения, шаг 1 уже выполнен! Мы увидим это в упражнении \ (\ PageIndex {4} \).
Упражнение \ (\ PageIndex {4} \)
Решите систему подстановкой. \ (\ left \ {\ begin {array} {l} {x + y = -1} \\ {y = x + 5} \ end {array} \ right. \)
- Ответ
Второе уравнение уже решено для y .
 Мы заменим выражение на в первом уравнении.
Мы заменим выражение на в первом уравнении.
Упражнение \ (\ PageIndex {5} \)
Решите систему подстановкой. \ (\ left \ {\ begin {array} {l} {x + y = 6} \\ {y = 3 x-2} \ end {array} \ right.\)
- Ответ
(2,4)
Упражнение \ (\ PageIndex {6} \)
Решите систему подстановкой. \ (\ left \ {\ begin {array} {l} {2 x-y = 1} \\ {y = -3 x-6} \ end {array} \ right. \)
- Ответ
(-1, -3)
Если уравнения представлены в стандартной форме, нам нужно будет начать с решения для одной из переменных. В следующем примере мы решим первое уравнение относительно y .
Упражнение \ (\ PageIndex {7} \)
Решите систему подстановкой. \ (\ left \ {\ begin {array} {l} {3 x + y = 5} \\ {2 x + 4 y = -10} \ end {array} \ right. \)
- Ответ
Нам нужно решить одно уравнение для одной переменной. Затем мы подставим это выражение в другое уравнение.
Упражнение \ (\ PageIndex {8} \)
Решите систему подстановкой. \ (\ left \ {\ begin {array} {l} {4 x + y = 2} \\ {3 x + 2 y = -1} \ end {array} \ right.\)
- Ответ
(1, −2)
Упражнение \ (\ PageIndex {9} \)
Решите систему подстановкой. \ (\ left \ {\ begin {array} {l} {- x + y = 4} \\ {4 x-y = 2} \ end {array} \ right. \)
- Ответ
(2,6)
В упражнении \ (\ PageIndex {7} \) было проще всего решить для и в первом уравнении, потому что оно имело коэффициент 1.В упражнении \ (\ PageIndex {10} \) будет легче найти x .
Упражнение \ (\ PageIndex {10} \)
Решите систему подстановкой. \ (\ left \ {\ begin {array} {l} {x-2 y = -2} \\ {3 x + 2 y = 34} \ end {array} \ right. \)
\ (\ left \ {\ begin {array} {l} {x-2 y = -2} \\ {3 x + 2 y = 34} \ end {array} \ right. \)
- Ответ
Мы решим первое уравнение относительно xx, а затем подставим выражение во второе уравнение.
Упражнение \ (\ PageIndex {11} \)
Решите систему подстановкой.\ (\ left \ {\ begin {array} {l} {x-5 y = 13} \\ {4 x-3 y = 1} \ end {array} \ right. \)
- Ответ
(-2, -3)
Упражнение \ (\ PageIndex {12} \)
Решите систему подстановкой. \ (\ left \ {\ begin {array} {l} {x-6 y = -6} \\ {2 x-4 y = 4} \ end {array} \ right. \)
- Ответ
(6,2)
Когда оба уравнения уже решены для одной и той же переменной, их легко заменить!
Упражнение \ (\ PageIndex {13} \)
Решите систему подстановкой.\ (\ left \ {\ begin {array} {l} {y = -2 x + 5} \\ {y = \ frac {1} {2} x} \ end {array} \ right. \)
- Ответ
Поскольку оба уравнения решаются относительно y , мы можем подставить одно в другое.
Упражнение \ (\ PageIndex {14} \)
Решите систему подстановкой. \ (\ left \ {\ begin {array} {l} {y = 3 x-16} \\ {y = \ frac {1} {3} x} \ end {array} \ right. \)
- Ответ
(6,2)
Упражнение \ (\ PageIndex {15} \)
Решите систему подстановкой.\ (\ left \ {\ begin {array} {l} {y = -x + 10} \\ {y = \ frac {1} {4} x} \ end {array} \ right. \)
- Ответ
(8,2)
Будьте очень осторожны со знаками в следующем примере.
Упражнение \ (\ PageIndex {16} \)
Решите систему подстановкой. \ (\ left \ {\ begin {array} {l} {4 x + 2 y = 4} \\ {6 x-y = 8} \ end {array} \ right. \)
\)
- Ответ
Нам нужно решить одно уравнение для одной переменной.Решим первое уравнение относительно y .
Упражнение \ (\ PageIndex {17} \)
Решите систему подстановкой. \ (\ left \ {\ begin {array} {l} {x-4 y = -4} \\ {-3 x + 4 y = 0} \ end {array} \ right. \)
- Ответ
\ ((2, \ frac {3} {2}) \)
Упражнение \ (\ PageIndex {18} \)
Решите систему подстановкой. \ (\ left \ {\ begin {array} {l} {4 x-y = 0} \\ {2 x-3 y = 5} \ end {array} \ right.\)
- Ответ
\ ((- \ frac {1} {2}, — 2) \)
В примере потребуется немного больше работы, чтобы решить одно уравнение для x или y .
Упражнение \ (\ PageIndex {19} \)
Решите систему подстановкой. \ (\ left \ {\ begin {array} {l} {4 x-3 y = 6} \\ {15 y-20 x = -30} \ end {array} \ right. \)
- Ответ
Нам нужно решить одно уравнение для одной переменной.Решим первое уравнение относительно x .
Поскольку 0 = 0 — истинное утверждение, система непротиворечива. Уравнения зависимы. Графики этих двух уравнений дадут одну и ту же линию. У системы бесконечно много решений.
Упражнение \ (\ PageIndex {20} \)
Решите систему подстановкой. \ (\ left \ {\ begin {array} {l} {2 x-3 y = 12} \\ {-12 y + 8 x = 48} \ end {array} \ right. \)
- Ответ
бесконечно много решений
Упражнение \ (\ PageIndex {21} \)
Решите систему подстановкой.\ (\ left \ {\ begin {array} {l} {5 x + 2 y = 12} \\ {-4 y-10 x = -24} \ end {array} \ right.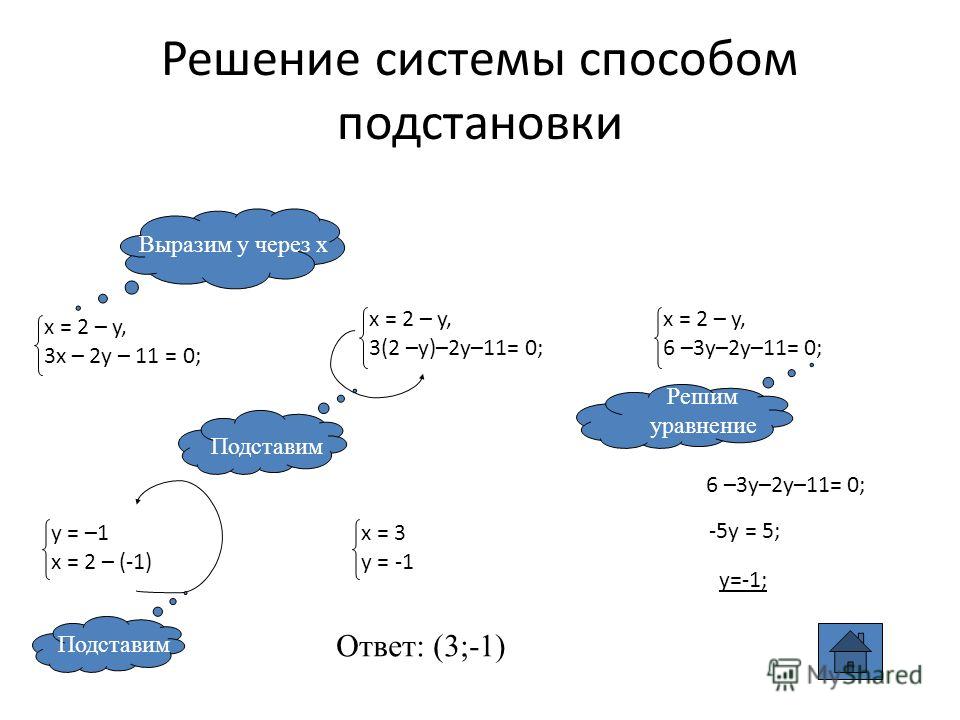 \)
\)
- Ответ
бесконечно много решений
Вернитесь к уравнениям в упражнении \ (\ PageIndex {22} \). Есть ли способ распознать, что это одна линия?
Давайте посмотрим, что происходит в следующем примере.
Упражнение \ (\ PageIndex {22} \)
Решите систему подстановкой. \ (\ left \ {\ begin {array} {l} {5 x-2 y = -10} \\ {y = \ frac {5} {2} x} \ end {array} \ right.\)
- Ответ
Второе уравнение уже решено относительно y , поэтому мы можем заменить y в первом уравнении.
Поскольку 0 = −10 — ложное утверждение, уравнения несовместимы. Графики двух уравнений будут параллельными линиями. В системе нет решений.Замените x на y в первом уравнении. Замените y на \ (\ frac {5} {2} x \). Решите относительно x .
Упражнение \ (\ PageIndex {23} \)
Решите систему подстановкой. \ (\ left \ {\ begin {array} {l} {3 x + 2 y = 9} \\ {y = — \ frac {3} {2} x + 1} \ end {array} \ right. \ )
\ )
- Ответ
нет решения
Упражнение \ (\ PageIndex {24} \)
Решите систему подстановкой.\ (\ left \ {\ begin {array} {l} {5 x-3 y = 2} \\ {y = \ frac {5} {3} x-4} \ end {array} \ right. \)
- Ответ
нет решения
Решите приложения систем уравнений подстановкой
Мы скопируем здесь стратегию решения проблем, которую мы использовали в разделе Решение систем уравнений с помощью графического представления для решения систем уравнений. Теперь, когда мы знаем, как решать системы с помощью подстановки, это то, что мы сделаем на шаге 5.
КАК ИСПОЛЬЗОВАТЬ СТРАТЕГИЮ РЕШЕНИЯ ЗАДАЧ ДЛЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ.
- Прочтите проблему. Убедитесь, что все слова и идеи понятны.
- Определите то, что мы ищем.
- Имя то, что мы ищем. Выберите переменные для представления этих величин.
- Переведите в систему уравнений.
- Решите систему уравнений, используя хорошие методы алгебры.
- Проверьте ответ в задаче и убедитесь, что он имеет смысл.
- Ответьте на вопрос полным предложением.
Некоторым людям проще создать текстовые задачи с двумя переменными, чем с одной переменной. Выбирать имена переменных проще, когда все, что вам нужно сделать, это написать две буквы. Подумайте об этом в следующем примере — как бы вы сделали это с помощью только одной переменной?
Упражнение \ (\ PageIndex {25} \)
Сумма двух чисел равна нулю.Одно число на девять меньше другого. Найдите числа.
- Ответ
Упражнение \ (\ PageIndex {26} \)
Сумма двух чисел равна 10. Одно число на 4 меньше другого. Найдите числа.
Одно число на 4 меньше другого. Найдите числа.
- Ответ
Цифры 3 и 7.
Упражнение \ (\ PageIndex {27} \)
Сумма двух чисел равна −6. Одно число на 10 меньше другого.Найдите числа.
- Ответ
Цифры 2 и −8.
В упражнении \ (\ PageIndex {28} \) мы будем использовать формулу для периметра прямоугольника: P = 2 L + 2 W .
Упражнение \ (\ PageIndex {28} \)
Добавьте сюда текст упражнения.
- Ответ
Упражнение \ (\ PageIndex {29} \)
Периметр прямоугольника равен 40.Длина в 4 раза больше ширины. Найдите длину и ширину прямоугольника.
- Ответ
Длина 12, ширина 8.
Упражнение \ (\ PageIndex {30} \)
Периметр прямоугольника равен 58. Длина в 5 раз больше ширины в 5 раз. Найдите длину и ширину прямоугольника.
- Ответ
Длина 23, ширина 6.
Для упражнения \ (\ PageIndex {31} \) нам нужно помнить, что сумма углов треугольника равна 180 градусам, а у прямоугольного треугольника один угол 90 градусов.
Упражнение \ (\ PageIndex {31} \)
Размер одного из малых углов прямоугольного треугольника в десять раз больше размера другого малого угла. Найдите размеры обоих углов.
- Ответ
Нарисуем и обозначим фигуру.
Упражнение \ (\ PageIndex {32} \)
Размер одного из малых углов прямоугольного треугольника в 2 раза больше, чем в 3 раза больше другого малого угла. Найдите размер обоих углов.
- Ответ
Размеры углов 22 градуса и 68 градусов.

Упражнение \ (\ PageIndex {33} \)
Размер одного из малых углов прямоугольного треугольника на 18 меньше, чем удвоение размера другого малого угла.Найдите размер обоих углов.
- Ответ
Углы 36 и 54 градуса.
Упражнение \ (\ PageIndex {34} \)
Хизер предложили два варианта заработной платы тренера в спортзале. Вариант А платит ей 25 000 долларов плюс 15 долларов за каждую тренировку. Вариант Б платит ей 10 000 + 40 долларов за каждую тренировку. Сколько тренингов уравняло бы варианты заработной платы?
- Ответ
Упражнение \ (\ PageIndex {35} \)
Джеральдин предложили вакансии в двух страховых компаниях.Первая компания выплачивает заработную плату в размере 12 000 долларов плюс комиссия в размере 100 долларов за каждый проданный полис. Второй платит зарплату в размере 20 000 долларов плюс комиссию в размере 50 долларов за каждый проданный полис. Сколько полисов необходимо продать, чтобы общая сумма выплат была такой же?
- Ответ
Потребуется продать 160 полисов, чтобы общая сумма выплат была такой же.
Упражнение \ (\ PageIndex {36} \)
Кеннет в настоящее время продает костюмы для компании А с зарплатой 22 000 долларов плюс 10 долларов комиссионных за каждый проданный костюм.Компания B предлагает ему должность с окладом в 28000 долларов плюс комиссия в размере 4 долларов за каждый проданный костюм. Сколько костюмов нужно продать Кеннету, чтобы варианты были равны?
- Ответ
Кеннету нужно будет продать 1000 костюмов.
Примечание
Воспользуйтесь этими онлайн-ресурсами, чтобы получить дополнительные инструкции и попрактиковаться в решении систем уравнений путем подстановки.
Решение системных уравнений | Уравнения и неравенства
\ (- 10 х = -1 \) и \ (- 4 х + 10 у = -9 \).
Решить относительно \ (x \):
\ begin {align *} — 10х = -1 \\ \ поэтому x = \ frac {1} {10} \ end {выровнять *}Подставьте значение \ (x \) во второе уравнение и решите относительно \ (y \):
\ begin {align *} -4x + 10y & = -9 \\ -4 \ left (\ frac {1} {10} \ right) + 10y & = -9 \\ \ frac {-4} {10} + 10y & = -9 \\ 100л & = -90 + 4 \\ y & = \ frac {-86} {100} \\ & = \ frac {-43} {50} \ end {выровнять *}Следовательно, \ (x = \ frac {1} {10} \ text {и} y = — \ frac {43} {50} \).
\ (3x — 14y = 0 \) и \ (x — 4y + 1 = 0 \)
Запишите \ (x \) через \ (y \):
\ begin {align *} 3х — 14лет & = 0 \\ 3х & = 14л \\ x & = \ frac {14} {3} y \ end {выровнять *}Подставьте значение \ (x \) во второе уравнение:
\ begin {align *} х — 4у + 1 & = 0 \\ \ frac {14} {3} y — 4y + 1 & = 0 \\ 14лет — 12лет + 3 & = 0 \\ 2у & = -3 \\ y & = — \ frac {3} {2} \ end {выровнять *}Подставить значение \ (y \) обратно в первое уравнение:
\ begin {align *} x & = \ frac {14 \ left (- \ frac {3} {2} \ right)} {3} \\ & = -7 \ end {выровнять *}Следовательно, \ (x = -7 \ text {и} y = — \ frac {3} {2} \).
\ (x + y = 8 \) и \ (3x + 2y = 21 \)
Запишите \ (x \) через \ (y \):
\ begin {align *} х + у & = 8 \\ х & = 8 — у \ end {выровнять *}Подставьте значение \ (x \) во второе уравнение:
\ begin {align *} 3х + 2у & = 21 \\ 3 (8 — у) + 2у & = 21 \\ 24 — 3л + 2у & = 21 \\ y & = 3 \ end {выровнять *}Подставить значение \ (y \) обратно в первое уравнение:
\ [x = 5 \]Следовательно, \ (x = 5 \ text {и} y = 3 \).
\ (y = 2x + 1 \) и \ (x + 2y + 3 = 0 \)
Запишите \ (y \) через \ (x \):
\ [y = 2x + 1 \]Подставьте значение \ (y \) во второе уравнение:
\ begin {align *} х + 2у + 3 & = 0 \\ х + 2 (2х + 1) + 3 & = 0 \\ х + 4х + 2 + 3 & = 0 \\ 5x & = -5 \\ х & = -1 \ end {выровнять *}Подставить значение \ (x \) обратно в первое уравнение:
\ begin {align *} у & = 2 (-1) + 1 \\ & = -1 \ end {выровнять *}Следовательно, \ (x = -1 \ text {и} y = -1 \).
\ (5x-4y = 69 \) и \ (2x + 3y = 23 \)
Сделайте \ (x \) объектом первого уравнения:
\ begin {align *} 5х-4л & = 69 \\ 5х & = 69 + 4у \\ x & = \ frac {69 + 4y} {5} \ end {выровнять *}Подставьте значение \ (x \) во второе уравнение:
\ begin {align *} 2х + 3у & = 23 \\ 2 \ left (\ frac {69 + 4y} {5} \ right) + 3y & = 23 \\ 2 (69 + 4у) +3 (5) у & = 23 (5) \\ 138 + 8л + 15л & = 115 \\ 23лет & = -23 \\ \ поэтому y & = -1 \ end {выровнять *}Подставить значение \ (y \) обратно в первое уравнение:
\ begin {align *} x & = \ frac {69 + 4y} {5} \\ & = \ frac {69 + 4 (-1)} {5} \\ & = 13 \ end {выровнять *}Следовательно, \ (x = 13 \ text {и} y = -1 \).
\ (x + 3y = 26 \) и \ (5x + 4y = 75 \)
Сделайте \ (x \) объектом первого уравнения:
\ begin {align *} х + 3у & = 26 \\ x & = 26 — 3 года \ end {выровнять *}Подставьте значение \ (x \) во второе уравнение:
\ begin {align *} 5х + 4у & = 75 \\ 5 (26 — 3л) + 4л & = 75 \\ 130 — 15л + 4л & = 75 \\ -11лет & = -55 \\ \ поэтому y & = 5 \ end {выровнять *}Подставить значение \ (y \) обратно в первое уравнение:
\ begin {align *} х & = 26 — 3г \\ & = 26 — 3 (5) \\ & = 11 \ end {выровнять *}Следовательно, \ (x = 11 \ text {и} y = 5 \).
\ (3x — 4y = 19 \) и \ (2x — 8y = 2 \)
Если мы умножим первое уравнение на 2, то коэффициент при \ (y \) будет одинаковым в обоих уравнениях:
\ begin {align *} 3х — 4л & = 19 \\ 3 (2) х — 4 (2) у & = 19 (2) \\ 6x — 8 лет & = 38 \ end {выровнять *}Теперь мы можем вычесть второе уравнение из первого:
\ [\ begin {array} {cccc} & 6x — 8лет & = & 38 \\ — & (2x — 8y & = & 2) \\ \ hline & 4x + 0 & = & 36 \ конец {массив} \]Решить относительно \ (x \):
\ begin {align *} \ поэтому x & = \ frac {36} {4} \\ & = 9 \ end {выровнять *}Подставьте значение \ (x \) в первое уравнение и решите относительно \ (y \):
\ begin {align *} 3х-4л & = 19 \\ 3 (9) -4y & = 19 \\ \ поэтому y & = \ frac {19-3 (9)} {- 4} \\ & = 2 \ end {выровнять *}Следовательно, \ (x = 9 \ text {и} y = 2 \).
\ (\ dfrac {a} {2} + b = 4 \) и \ (\ dfrac {a} {4} — \ dfrac {b} {4} = 1 \)
Сделайте \ (a \) предметом первого уравнения:
\ begin {align *} \ frac {a} {2} + b & = 4 \\ а + 2b & = 8 \\ а & = 8 — 2b \ end {выровнять *}Подставьте значение \ (a \) во второе уравнение:
\ begin {align *} \ frac {a} {4} — \ frac {b} {4} & = 1 \\ а — б & = 4 \\ 8 — 2б — б & = 4 \\ 3b & = 4 \\ b & = \ frac {4} {3} \ end {выровнять *}Подставить значение \ (b \) обратно в первое уравнение:
\ begin {align *} a & = 8 — 2 \ left (\ frac {4} {3} \ right) \\ & = \ frac {16} {3} \ end {выровнять *}Следовательно, \ (a = \ frac {16} {3} \ text {и} b = \ frac {4} {3} \).
\ (- 10x + y = -1 \) и \ (- 10x — 2y = 5 \)
Если мы вычтем второе уравнение из первого, то мы сможем решить для \ (y \):
\ [\ begin {array} {cccc} & -10x + y & = & -1 \\ — & (-10x — 2y & = & 5) \\ \ hline & 0 + 3г & = & -6 \ конец {массив} \]Решить относительно \ (y \):
\ begin {align *} 3г & = -6 \\ \ поэтому y & = -2 \ end {выровнять *}Подставьте значение \ (y \) в первое уравнение и решите относительно \ (x \):
\ begin {align *} -10x + y & = -1 \\ -10x — 2 & = -1 \\ -10x & = 1 \\ x & = \ frac {1} {- 10} \ end {выровнять *}Следовательно, \ (x = \ frac {-1} {10} \ text {и} y = -2 \).
\ (- 10 x — 10 y = -2 \) и \ (2 x + 3 y = 2 \)
Сделайте \ (x \) объектом первого уравнения:
\ begin {align *} — 10 х — 10 у = -2 \\ 5х + 5у & = 1 \\ 5x & = 1 — 5л \\ \ поэтому x = -y + \ frac {1} {5} \ end {выровнять *}Подставьте значение \ (x \) во второе уравнение и решите относительно \ (y \):
\ begin {align *} 2х + 3у & = 2 \\ 2 \ left (-y + \ frac {1} {5} \ right) + 3y & = 2 \\ -2y + \ frac {2} {5} + 3y & = 2 \\ y & = \ frac {8} {5} \ end {выровнять *}Подставьте значение \ (y \) в первое уравнение:
\ begin {align *} 5х + 5у & = 1 \\ 5x + 5 \ влево (\ frac {8} {5} \ right) & = 1 \\ 5х + 8 & = 1 \\ 5x & = -7 \\ x & = \ frac {-7} {5} \ end {выровнять *}Следовательно, \ (x = — \ frac {7} {5} \ text {и} y = \ frac {8} {5} \).
\ (\ dfrac {1} {x} + \ dfrac {1} {y} = 3 \) и \ (\ dfrac {1} {x} — \ dfrac {1} {y} = 11 \)
Переставьте оба уравнения, умножив на \ (xy \):
\ begin {align *} \ frac {1} {x} + \ frac {1} {y} & = 3 \\ у + х & = 3xy \\\\ \ frac {1} {x} — \ frac {1} {y} & = 11 \\ у — х & = 11xy \ end {выровнять *}Сложите два уравнения вместе:
\ [\ begin {array} {cccc} & y + x & = & 3xy \\ + & (у — х & = & 11xy) \\ \ hline & 2y + 0 & = & 14xy \ конец {массив} \]Решить относительно \ (x \):
\ begin {align *} 2y & = 14xy \\ у & = 7xy \\ 1 & = 7x \\ х & = \ гидроразрыв {1} {7} \ end {выровнять *}Подставить значение \ (x \) обратно в первое уравнение:
\ begin {align *} y + \ frac {1} {7} & = 3 \ left (\ frac {1} {7} \ right) y \\ 7у + 1 & = 3у \\ 4г & = -1 \\ y & = — \ frac {1} {4} \ end {выровнять *}Следовательно, \ (x = \ frac {1} {7} \ text {и} y = — \ frac {1} {4} \).2 + 1 \\ 0 & = 0 \ end {выровнять *}
Поскольку это верно для всех \ (x \) в действительных числах, \ (x \) может быть любым действительным числом.
Посмотрите, что происходит с \ (y \), когда \ (x \) очень маленький или очень большой:
Наименьшее значение \ (x \) может быть равно 0. Когда \ (x = 0 \), \ (y = 2- \ frac {3} {2} = \ frac {1} {2} \).2 & = 3 — ab \ end {выровнять *}
Обратите внимание, что это то же самое, что и второе уравнение
\ (a \) и \ (b \) могут быть любыми действительными числами, кроме \ (\ text {0} \).
Узнайте, как решать задачи со словами
После того, как вы закончите этот урок, просмотрите все наши уроки предварительной алгебры и практические задачи.После того, как вы закончите этот урок, просмотрите все наши уроки Алгебры 1 и попрактикуйтесь.
Решение проблем со словами
Чтобы решить проблему со словами с помощью системы уравнений, важно:
— Определите, чего мы не знаем
— Объявите переменные
— Используйте предложения для создания уравнений
Пример того, как это сделать:
Мэри и Хосе купили растения в одном магазине. Мэри потратила 188 долларов на 7 вишневых деревьев и 11 кустов роз. Хосе потратил 236 долларов на 13 вишневых деревьев и 11 кустов роз.Найдите стоимость одного вишневого дерева и стоимость одного куста роз.
Стоимость вишневого дерева:
Стоимость куста роз:
7 вишневых деревьев и 11 кустов роз = 188 долларов США
Значения y взаимно компенсируются, так что теперь у вас остается только x- значения и действительные числа.
Затем вы подставляете свое значение x в исходное уравнение, чтобы найти значение y.
Стоимость вишневого дерева: 8 долларов
Стоимость куста розы: 12 долларов
Примеры задач со словами — система уравнений
Пример 1
Три кофе и кекс стоят в общей сложности долларов.Два кофе и четыре кекса стоят в общей сложности долларов. Какова индивидуальная цена за один кофе и один кекс?
Давайте решим эту проблему, выполнив следующие действия.
1. Чего мы не знаем:
Стоимость одного кофе
Стоимость одного кекса
2. Объявите переменные:
Стоимость одного кофе =
Стоимость одного кекса =
3. Используйте предложения для составления уравнений.
Три кофе и кекс стоят в общей сложности долларов.
Два кофе и четыре кекса стоят в общей сложности долларов.
Теперь у нас есть система уравнений:
Давайте решим одну из переменных в одном из уравнений, а затем воспользуемся этим для замены в другое.
Теперь решите значение, используя первое уравнение.
Давайте решим значение, подставив значение в нижнее уравнение.
Распределить по каждому члену внутри круглых скобок
Объединить похожие термины
Теперь давайте вычленим с обеих сторон.
Затем разделите обе стороны на,
И у нас получится
Затем давайте подставим значение в одно уравнение, чтобы получить значение.
Стоимость одного кофе =
Стоимость одного кекса =
Пример 2
Старшие классы средней школы А арендовали и наполнили фургоны и автобусы учениками. Средняя школа B арендовала и наполнила фургоны и автобусы учениками. В каждом фургоне было столько же студентов, сколько в автобусах. Найдите количество учеников в каждом фургоне и в каждом автобусе.
Давайте решим эту проблему, выполнив следующие действия.
1. Чего мы не знаем:
Студенты в каждом фургоне
Студенты в каждом автобусе
2. Объявите переменные:
Студенты в каждом фургоне =
Студенты в каждом автобусе =
3. Используйте предложения создавать уравнения.
Средняя школа А арендовала и заправила 8 микроавтобусов и 8 автобусов с 240 учениками.
Средняя школа B арендовала и заполнила 4 фургона и 1 автобус 54 учениками.
Теперь у нас есть система уравнений:
Давайте решим одну из переменных в одном из уравнений, а затем воспользуемся этим для замены в другое.
Теперь решите значение, используя второе уравнение.
Давайте решим значение, подставив значение в нижнее уравнение.
Распределить по каждому члену внутри круглых скобок
Объединить похожие термины
Теперь давайте вычленим с обеих сторон.
Затем разделите обе стороны на,
И у нас получится
Затем давайте подставим значение в одно уравнение, чтобы получить значение.
Студенты в каждом фургоне =
Студенты в каждом автобусе =
Стенограмма видеоурока
Чтобы решить словесную задачу с помощью системы уравнений, важно:
1.Определите, чего мы не знаем
2. Объявите переменные.
3. Используйте предложения для создания уравнений.
Приведем пример:
Мэри и Хосе купили растения в одном магазине. Мэри потратила на вишни и кусты роз. Хосе тратил на вишневые деревья и кусты роз. Найдите стоимость одного вишневого дерева и стоимость одного куста роз.
Давайте решим эту проблему, выполнив шаги, описанные выше.
1. Чего мы не знаем:
стоимость вишневого дерева
стоимость куста розы
2.Объявите переменные:
стоимость вишневого дерева:
стоимость куста розы:
3. Используйте предложения для создания уравнений.
Для Мэри:
вишневых деревьев и розовых кустов
Для Хосе:
вишневых деревьев и розовых кустов
Теперь у нас есть система уравнений
Мы можем решить эту проблему путем замены, исключения или доля.
Поскольку значение одинаково для обоих уравнений, давайте проведем процесс исключения.
Во-первых, давайте умножим первое уравнение на
Здесь у нас будет уравнение с отрицанием
Давайте теперь выполним процесс исключения
У нас будет
Затем давайте изолируем, разделив обе части на
Теперь у нас есть
Помните, наша объявленная переменная?
Стоимость вишневого дерева:
Начиная с
Теперь мы можем сказать, что
Стоимость вишневого дерева:
Теперь давайте решим значение, получив одно уравнение и подставив значение.
Давайте воспользуемся первым уравнением, чтобы подставить
Давайте вычленим обе части уравнения
Затем разделим на
И мы получим
Теперь мы знаем, что стоимость куста розы составляет.
Решение одновременных уравнений: метод подстановки и метод сложения | Справочник по алгебре
Что такое одновременные уравнения и системы уравнений?
Термины системы уравнений и системы уравнений относятся к условиям, при которых две или более неизвестных переменных связаны друг с другом посредством равного количества уравнений.
Пример:
Для этой системы уравнений существует только одна комбинация значений для x и y, которая удовлетворяет обоим.
Любое уравнение, рассматриваемое по отдельности, имеет бесконечное количество допустимых (x, y) решений, но вместе существует только одно. На графике это условие становится очевидным:
Каждая линия на самом деле представляет собой континуум точек, представляющих возможные пары решений x и y для каждого уравнения.
Каждое уравнение в отдельности имеет бесконечное количество упорядоченных парных (x, y) решений. Есть только одна точка, где две линейные функции x + y = 24 и 2x — y = -6 пересекаются (где одно из многих их независимых решений работает для обоих уравнений), и это где x равно значению 6, а y равно 18.
Однако обычно построение графиков не очень эффективный способ определения одновременного набора решений для двух или более уравнений. Это особенно непрактично для систем из трех и более переменных.
В системе с тремя переменными, например, решение будет найдено путем пересечения трех плоскостей в трехмерном координатном пространстве — сценарий, который нелегко представить.
Решение одновременных уравнений методом подстановки
Существует несколько алгебраических методов решения одновременных уравнений.
Возможно, самый простой для понимания — это метод замены на .
Возьмем, к примеру, нашу задачу с двумя переменными:
В методе подстановки мы манипулируем одним из уравнений таким образом, чтобы одна переменная определялась в терминах другой:
Затем мы берем это новое определение одной переменной и заменяем его на ту же переменную в другом уравнении.
В этом случае мы берем определение y, равное 24 — x, и подставляем его вместо члена y, найденного в другом уравнении:
Теперь, когда у нас есть уравнение с одной переменной (x), мы можем решить его, используя «обычные» алгебраические методы:
Теперь, когда x известен, мы можем подставить это значение в любое из исходных уравнений и получить значение для y.
Или, чтобы сэкономить некоторую работу, мы можем вставить это значение (6) в уравнение, которое мы только что сгенерировали, чтобы определить y через x, поскольку оно уже находится в форме для решения для y:
Применение метода подстановки к системам из трех или более переменных включает аналогичный шаблон, только с дополнительным объемом работы.
Это обычно верно для любого метода решения: количество шагов, необходимых для получения решения, быстро увеличивается с каждой дополнительной переменной в системе.
Чтобы решить для трех неизвестных переменных, нам нужно как минимум три уравнения. Рассмотрим этот пример:
Поскольку первое уравнение имеет простейшие коэффициенты (1, -1 и 1 для x, y и z соответственно), кажется логичным использовать его для разработки определения одной переменной в терминах двух других.
Решите относительно x через y и z:
Теперь мы можем заменить это определение x, где x появляется в двух других уравнениях:
Приведение этих двух уравнений к их простейшей форме:
На данный момент наши усилия привели к сокращению системы с трех переменных в трех уравнениях до двух переменных в двух уравнениях.
Теперь мы можем снова применить технику подстановки к двум уравнениям 4y — z = 4 и -3y + 4z = 36, чтобы решить для y или z.Во-первых, я манипулирую первым уравнением, чтобы определить z через y:
Затем мы заменим это определение z на y, где мы видим z в другом уравнении:
Теперь, когда y — известное значение, мы можем подставить его в уравнение, определяющее z через y, и получить число для z:
Теперь, когда значения y и z известны, мы можем подставить их в уравнение, в котором мы определили x через y и z, чтобы получить значение x:
В заключение, мы нашли для x, y и z значения 2, 4 и 12 соответственно, которые удовлетворяют всем трем уравнениям.
Решение одновременных уравнений с использованием метода сложения
Хотя метод замены может быть самым простым для понимания на концептуальном уровне, нам доступны и другие методы решения.
Одним из таких методов является так называемый метод сложения и , при котором уравнения складываются друг с другом с целью исключения переменных членов.
Давайте возьмем нашу систему с двумя переменными, использованную для демонстрации метода подстановки:
Одно из наиболее часто используемых правил алгебры состоит в том, что вы можете выполнять любые арифметические операции с уравнением, если вы делаете это одинаково для обеих сторон .
Что касается сложения, это означает, что мы можем добавить любую величину, которую пожелаем, к обеим сторонам уравнения — при условии, что это то же самое количество — без изменения истинности уравнения.
У нас есть возможность сложить соответствующие части уравнений вместе, чтобы сформировать новое уравнение.
Поскольку каждое уравнение является выражением равенства (одна и та же величина по обе стороны от знака =), добавление левой части одного уравнения к левой части другого уравнения действительно до тех пор, пока мы складываем два правые части уравнений вместе.
В нашем примере набора уравнений, например, мы можем добавить x + y к 2x — y, а также сложить 24 и -6 вместе, чтобы сформировать новое уравнение.
Какая польза от этого для нас? Изучите, что произойдет, когда мы сделаем это с нашим примером набора уравнений:
Поскольку верхнее уравнение содержало положительный член y, в то время как нижнее уравнение содержало отрицательный член y, эти два члена компенсировали друг друга в процессе сложения, не оставляя члена y в сумме.
У нас осталось новое уравнение, но с единственной неизвестной переменной x! Это позволяет нам легко найти значение x:
Если у нас есть известное значение x, конечно, определение значения y — это простой вопрос подстановки (замены x числом 6) в одно из исходных уравнений.
В этом примере метод сложения уравнений хорошо сработал для создания уравнения с одной неизвестной переменной.
А как насчет примера, когда все не так просто? Рассмотрим следующий набор уравнений:
Мы могли бы сложить эти два уравнения вместе — это вполне допустимая алгебраическая операция — но это не принесет нам пользы для получения значений для x и y:
Полученное уравнение по-прежнему содержит две неизвестные переменные, как и исходные уравнения, поэтому мы не продвинемся дальше в поиске решения.
Однако что, если бы мы могли манипулировать одним из уравнений так, чтобы получить отрицательный член, который при добавлении аннулировал бы соответствующий член в другом уравнении?
Затем система сведется к одному уравнению с единственной неизвестной переменной, как в последнем (случайном) примере.
Если бы мы могли только превратить член y в нижнем уравнении в член — 2y, чтобы при сложении двух уравнений оба члена y в уравнениях уравнялись бы, оставив нам только член x, это принесло бы нам ближе к решению.
К счастью, это сделать несложно. Если мы умножим каждый член нижнего уравнения на -2, получится результат, который мы ищем:
Теперь мы можем добавить это новое уравнение к исходному, верхнему уравнению:
Решая относительно x, получаем значение 3:
Подставляя это новое найденное значение для x в одно из исходных уравнений, значение y легко определяется:
Использование этого метода решения в системе с тремя переменными немного сложнее.
Как и в случае подстановки, вы должны использовать этот метод, чтобы уменьшить систему из трех уравнений с тремя переменными до двух уравнений с двумя переменными, а затем применить его снова, чтобы получить одно уравнение с одной неизвестной переменной.
Для демонстрации я воспользуюсь системой уравнений с тремя переменными из раздела о заменах:
Поскольку верхнее уравнение имеет значения коэффициента, равные 1 для каждой переменной, это уравнение будет простым для обработки и использования в качестве инструмента отмены.
Например, если мы хотим отменить 3-кратный член из среднего уравнения, все, что нам нужно сделать, это взять верхнее уравнение, умножить каждый из его членов на -3, а затем добавить его к среднему уравнению следующим образом:
Мы можем избавить нижнее уравнение от его члена -5x таким же образом: возьмите исходное верхнее уравнение, умножьте каждый из его членов на 5, затем добавьте это модифицированное уравнение к нижнему уравнению, оставив новое уравнение только с y и z термины:
На данный момент у нас есть два уравнения с теми же двумя неизвестными переменными, y и z:
При осмотре должно быть очевидно, что член -z верхнего уравнения может быть использован для отмены члена 4z в нижнем уравнении, если только мы умножим каждый член верхнего уравнения на 4 и сложим два уравнения вместе:
Взяв новое уравнение 13y = 52 и решив относительно y (разделив обе части на 13), мы получим значение 4 для y.
Подстановка этого значения 4 вместо y в любое из уравнений с двумя переменными позволяет нам решить относительно z.
Подстановка обоих значений y и z в любое из исходных уравнений с тремя переменными позволяет нам решить относительно x.
Окончательный результат (я избавлю вас от алгебраических шагов, поскольку вы уже должны быть с ними знакомы!) Состоит в том, что x = 2, y = 4 и z = 12.
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
.


 Работа с задачником
Работа с задачником

 Анализируют решения по образцу, фиксируют места затруднений и определяют способы действий.
Анализируют решения по образцу, фиксируют места затруднений и определяют способы действий.




 Решить 4 системы, найти ответ и расшифровать слово. Решение одной системы оформить на доске. Каждый контролирует человека справа и выставит ему оценку за урок.
Решить 4 системы, найти ответ и расшифровать слово. Решение одной системы оформить на доске. Каждый контролирует человека справа и выставит ему оценку за урок. Один из способов решения систем линейных уравнений.
Один из способов решения систем линейных уравнений.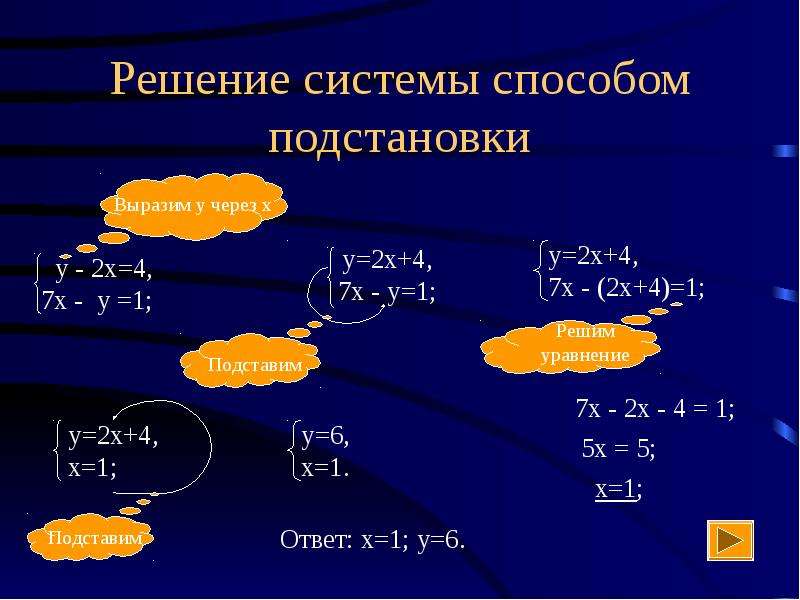 Организационный момент
Организационный момент
 Сравните ответы.
Сравните ответы.


 Мы заменим выражение на в первом уравнении.
Мы заменим выражение на в первом уравнении.