21. Расстояние от точки до прямой на плоскости (вывод).
Вывод формулы расстояния от точки до прямой
Вариант 1
Пусть на плоскости дана прямая l : ax + by + c = 0 и точка M1(x1;y1), не принадлежащая этой прямой. Найдем расстояние от точки до прямой. Под расстоянием ρ от точки M1 до прямой l понимают длину отрезка M0 M1⏊l.
Для определения расстояния удобно использовать единичный вектор, коллинеарный нормальному вектору прямой.
Пояснение: поскольку точка M0 лежит в на прямой l, то ее координаты должны удовлетворять уравнению данной прямой, т.е. ax0 + by
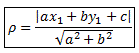Вариант
2 Если
задана точка М(х0,
у0),
то расстояние до прямой Ах + Ву + С =0
определяется как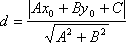 
.
Доказательство. Пусть точка М1(х1,
у1)
– основание перпендикуляра, опущенного
из точки М на заданную прямую. Тогда
расстояние между точками М и М1:
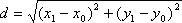(1)
Координаты x1 и у1 могут быть найдены как решение системы
уравнений: 
Второе
уравнение системы – это уравнение
прямой, проходящей через заданную точку
М0 перпендикулярно заданной прямой. Если
преобразовать первое уравнение системы
к виду: A(x – x 0)
+ B(y – y0)
+ Ax0 + By0 + C = 0, то, решая, получим: 
Подставляя
эти выражения в уравнение (1), находим:
.
Теорема доказана.
22. Условия параллельности и перпендикулярности прямых на плоскости (вывод).
1) Если прямые R1 и R2 параллельны, то φ = 0. Тогда tg φ = 0 и из формулы (7) имеем k2 — k1 = 0 или k2 = k1. Таким образом, условием параллельности двух прямых на плоскости является равенство их угловых коэффициентов.
2)
Если прямые R1 и R2 перпендикулярны,
то φ = 
.
Так как φ = φ2 – φ1 ,
то
φ2 =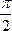 
+
φ1)
= ctg φ1 = —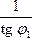 
,
т.е.
k2 = — 
.
(8)
Таким образом, условие перпендикулярности двух прямых состоит в том, что их угловые коэффициенты обратны по величине и противоположны по знаку.
23. Уравнение плоскости. Нормальное уравнение плоскости (вывод). Геометрический смысл коэффициентов.
Получение
уравнения плоскости 
в
нормальном виде представляет интерес
даже с формальной точки зрения: как
развитие аналитических моделей
геометрических фигур при переходе от
двумерного пространства к 3-мерному. С
другой стороны, от нормального уравнения
плоскости мы ожидаем расширения наших
возможностей при решении более сложных
геометрических задач.
Пусть точка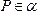
.
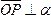Пусть
единичный векторсовпадает
по направлению с вектором
.
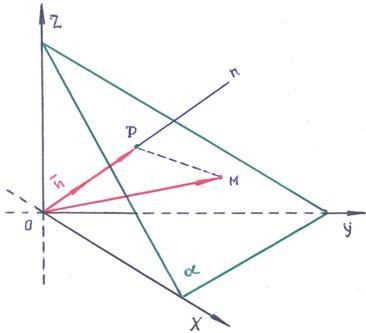
Известно,
что любой вектор можно представить как: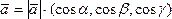
,
где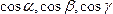
–
направляющие косинусы вектора
.
Учитывая: 
=1,
представим вектор
.
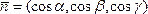Отметим
на плоскости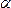
произвольную
точку:
=
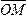=. Используя
заданные условия и принятые обозначения,
запишем (используя скалярное произведение
векторов и формулу для вычисления
проекции вектора 
на
направление
):
=
=
=×
=
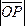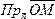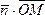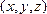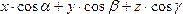, откуда
получаем: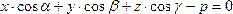 
.
(1)
Уравнение (1) называют нормальным уравнением плоскости. Если уравнение (1) рассматривать как общее уравнение плоскости, то, как легко заметить, нормальный вектор этой плоскости единичный.
Отнесёмся
к выражению: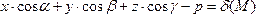 
формально.
Учитывая способ получения нормального
уравнения (1), нетрудно догадаться, что
для всех точек пространства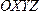
величина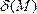
=0.
А что будет происходить с величиной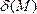
,
если
выбирать произвольные точки пространства? Пусть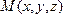 
–
произвольная точка пространства и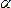
–
некоторая
плоскость пространства. Пусть точка
,
причём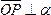
.
Пусть
единичный вектор
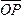и
представлен в виде: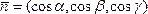
. Найдём
проекцию точки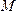 
на
направление
:
обозначим
проекцию как точку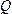
.
В
таком случае длина отрезка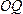
равна
расстоянию точки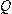
от
начала координат
=
+.
При
получении нормального уравнения
плоскости было показано, что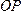
=.
Тогда: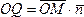
=
,
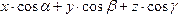после
чего можем записать: 
=
–
=
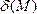. Итак,
геометрический смысл величины 
–отклонение произвольной точки 
пространства
от плоскости
,
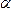причём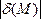
=
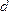–расстояние этой точки до этой плоскости.
Возникает
вопрос: почему для нахождения расстояния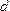 
потребовался
модуль
а)
если точки 
и
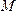располагаются
по разные стороны от плоскости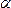
,
то
>0;
б)
если точки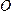 
и
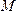располагаются
по одну сторону от плоскости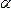
,
то
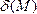<0.
Ещё
раз отметим, что величина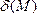 
–
это расстояние произвольной точки
пространства до заданной плоскости,
причёмсо
знаком!
Знак отражает процесс проектирования
вектора 
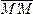на
направление вектора
,
а
именно:
=
.
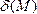Так
как вектор
единичный,
то получаем длину отрезка: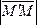
=
=
,
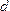измеренную
при помощи единичного вектора
.
Если
уравнение плоскости задано в общем
виде: 
,
то
его можнонормировать,
то есть привести к записи (1). Это делают
так:
1).
Умножим общее уравнение плоскости на
число 
:
.
(2)
2).
Пусть получили тождество: 
.
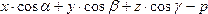Тогда
необходимо: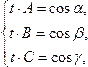
→
;
→
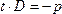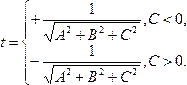(3)Замечания:
1). В результате нормализации вектор
нормали плоскости преобразован в
единичный вектор: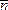 
=
→
=
,
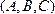причем
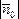=1.
2).
Смысл правил выбора знака величины t в преобразованиях (3), будет установлен
при рассмотрении задачи вычисления отклонения произвольной точки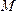 
от
заданной плоскости
.Замечание:
При решении задачи «Пересекает ли
отрезок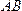 
плоскость
»
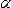достаточно подставить координаты этих
точек в заданное уравнение плоскости
(не обязательно нормированное!), чтобы
установить: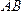
пересекает
плоскость, если вычисленные значения
правой части уравнения плоскости имеют
разные знаки;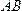
не
пересекает плоскость, если знаки
совпадают.
1.
Рассмотрим вектор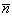 
с
проекциями на координатные оси,
соответственно равнымиA, B и C,
т. е.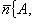 
.
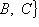2.
Возьмем на плоскости Ax + By + Cz + D = 0 две произвольные точки M(x1, y1, z1)
и N(x2, y2, z2)
и рассмотрим вектор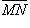 
.
Этот вектор лежит в плоскостиAx + By + Cz + D = 0. Его проекции на координатные оси
соответственно равны x2 — x1, y2 — y1, z2 — z1 и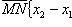 
.
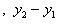
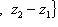3. Так как точки M и N лежат в плоскости Ax + By + Cz + D = 0, то имеют место равенства
Ax1 + By1 + Cz1 + D = 0
и
Ax2 + By2 + Cz2 + D = 0.
Вычитая первое уравнение из второго, получим
A(x2 — x1) + B(y2 — y1) + C(z2 — z1) = 0. (1)
Скалярное
произведение вектора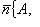 
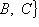на
вектор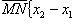
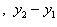
равно
A(x2 — x1) + B(y2 — y1) + C(z2 — z1).
Так
как на основании (1) это скалярное
произведение равно нулю, то вектор 
перпендикулярен
вектору
,
а тем самым и той плоскости, в которой
лежит этот вектор, т. е. вектор
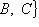перпендикулярен
плоскостиAx + By + Cz + D = 0.
Геометрическое значение коэффициентов A, B и C в общем уравнении плоскости Ax + By + Cz + D = 0 состоит в том, что они являются проекциями на координатные оси Ox, Oy, Oz вектора, перпендикулярного этой плоскости.
studfile.net
Определение расстояния от точки до плоскости
Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на плоскость, и в начертательной геометрии определяется графически согласно следующему алгоритму.
Алгоритм построения
- Плоскость переводят в проецирующее положение с помощью методов преобразования ортогональных проекций.
- Из точки на плоскость опускают перпендикуляр и находят его длину. Направление проекции перпендикуляра определяется на основании теоремы о проецировании прямого угла.
Задача № 1
Рассмотрим, как реализуется составленный нами алгоритм на практике. На рисунке ниже представлены графические построения, необходимые для определения расстояния между точкой N и плоскостью α, заданной треугольником ABC.
Ход решения
- Через вершину B» треугольника A»B»C» проводим проекцию h» горизонтали h. По линиям связи находим h’.
- Переводим ABC в проецирующее положение. Для этого перпендикулярно h вводим новую фронтальную плоскость П4. Проецируем на неё точку N и треугольник ABC.
- Из точки N»1 проводим N»1M»1 ⊥ A»1C»1. Длина отрезка N»1M»1 – искомое расстояние между плоскостью треугольника ABC и точкой N.
Задача № 2
Требуется определить величину расстояния между точкой K и плоскостью β, заданной следами. В отличие от предыдущей задачи здесь нет необходимости проводить линию уровня, так как её роль выполняет проекция h0β.
Ход решения
- Переводим плоскость β в проецирующее положение. Для этого перпендикулярно следу h0β вводим дополнительную фронтальную плоскость П4. На прямой f0β берем произвольную точку E, определяем её проекции E», E’ и E»1. Через E»1 и X0α1 проводим прямую f0β1, которая является следом плоскости β на П4. По линии связи определяем проекцию K»1 точки K.
- Из K»1 проводим перпендикуляр K»1M»1 в направлении прямой f0β1. Длина отрезка K»1M»1 – величина искомого расстояния от K до β.
Если требуется перевести отрезок KM в исходную систему плоскостей, то это делается с помощью обратных преобразований, как показано на следующем рисунке.
Похожие задачи:
ngeometry.ru
Графическое определение расстояния от точки до прямой
Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на прямую. В начертательной геометрии она определяется графическим путем по приведенному ниже алгоритму.
Алгоритм
- Прямую переводят в положение, в котором она будет параллельна какой-либо плоскости проекции. Для этого применяют методы преобразования ортогональных проекций.
- Из точки проводят перпендикуляр к прямой. В основе данного построения лежит теорема о проецировании прямого угла.
- Длина перпендикуляра определяется путем преобразования его проекций или с использованием способа прямоугольного треугольника.
Пример
На следующем рисунке представлен комплексный чертеж точки M и прямой b, заданной отрезком CD. Требуется найти расстояние между ними.
Решение
Согласно нашему алгоритму, первое, что необходимо сделать, это перевести прямую в положение, параллельное плоскости проекции. При этом важно понимать, что после проведенных преобразований фактическое расстояние между точкой и прямой не должно измениться. Именно поэтому здесь удобно использовать метод замены плоскостей, который не предполагает перемещение фигур в пространстве.
Результаты первого этапа построений показаны ниже. На рисунке видно, как параллельно b введена дополнительная фронтальная плоскость П4. В новой системе (П1, П4) точки C»1, D»1, M»1 находятся на том же удалении от оси X1, что и C», D», M» от оси X.
Выполняя вторую часть алгоритма, из M»1 опускаем перпендикуляр M»1N»1 на прямую b»1, поскольку прямой угол MND между b и MN проецируется на плоскость П4 в натуральную величину. По линии связи определяем положение точки N’ и проводим проекцию M’N’ отрезка MN.
На заключительном этапе нужно определить величину отрезка MN по его проекциям M’N’ и M»1N»1. Для этого строим прямоугольный треугольник M»1N»1N0, у которого катет N»1N0 равен разности (YM1 – YN1) удаления точек M’ и N’ от оси X1. Длина гипотенузы M»1N0 треугольника M»1N»1N0 соответствует искомому расстоянию от M до b.
Второй способ решения
- Параллельно CD вводим новую фронтальную плоскость П4. Она пересекает П1 по оси X1, причем X1∥C’D’. В соответствии с методом замены плоскостей определяем проекции точек C»1, D»1 и M»1, как это изображено на рисунке.
- Перпендикулярно C»1D»1 строим дополнительную горизонтальную плоскость П5, на которую прямая b проецируется в точку C’2 = b’2.
- Величина расстояния между точкой M и прямой b определяется длиной отрезка M’2C’2, обозначенного красным цветом.
Похожие задачи:
ngeometry.ru
Расстояние от точки до прямой онлайн
С помощю этого онлайн калькулятора можно найти расстояние от точки до прямой. Дается подробное решение с пояснениями. Для вычисления расстояния от точки до прямой, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точки и элементы уравнения в ячейки и нажимайте на кнопку «Решить».
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние от точки до прямой − теория, примеры и решения
Рассмотрим эту задачу в двухмерном и трехмерном пространствах.
1. Расстояние от точки до прямой на плоскости
Пусть в двухмерном пространстве задана точка M0(x0, y0) и прямая L:
где q=(m,p) направляющий вектор прямой L.
Найдем расстояние от точки M0 до прямой (1)(Рис.1).
Алгоритм нахождения расстояния от точки M0 до прямой L содержит следующие шаги:
- построить прямую L1, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение прямых L и L1(точка M1)
- найти найти расстояние между точками M0 и M1.
Уравнение прямой, проходящей через точку M0(x0, y0) имеет следующий вид:
где n=(A,B) нормальный вектор прямой L1.
Как видно из рисунка Рис.1, для того, чтобы прямая L1 была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n прямой L1, поэтому в качестве нормального вектора прямой L1 достаточно взять направляющий вектор прямой L. Тогда уравнение прямой L1, представленной уравнением (2) можно записать так:
Откроем скобки
Для нахождения точки пересечения прямых L и L1, которая и будет проекцией точки M0 на прямую L, можно решить систему из двух уравнений (1) и (3) с двумя неизвестными x и y. Выражая неизвестную x из одного уравнения и подставляя в другое уравнение получим координаты точки M1(x1, y1).
Найдем точку пересечения прямых L и L1 другим методом.
Выведем параметрическое уравнение прямой (1):
Подставим значения x и y в (4):
Мы нашли такое значение t=t’, при котором координаты x и y точки на прямой L удовлетворяют уравнению прямой L1(4). Следовательно, подставляя значение t’ в (5) получим координаты проекции точки M0 на прямую L:
где x1=mt’+x’, y1=pt’+y’.
Далее находим расстояние между точками M0 и M1 используя формулу:
Пример 1. Найти расстояние от точки M0(−6, 2) до прямой
Решение.
Направляющий вектор прямой (8) имеет вид:
Т.е. m=2, p=−1. Из уравнения прямой (8) видно, что она проходит через точку M’ (x’, y’)=(1, 7)(в этом легко убедится − подставляя эти значения в (8) получим тождество 0=0), т.е. x’=1, y’=7. Подставим значения m, p, x0, y0, x’, y’ в (6):
Подставляя значение t в (5), получим:
Вычислим расстояние между точками M0(-6, 2) и M1
Упростим и решим:
Ответ:
Расстояние от точки M0(-6, 2) до прямой (8) :
2. Расстояние от точки до прямой в пространстве
Пусть в трехмерном пространстве задана точка M0(x0, y0, z0) и прямая L:
где q=(m, p, l) направляющий вектор прямой L.
Найдем расстояние от точки M0 до прямой (9)(Рис.2).
Алгоритм нахождения расстояния от точки до прямой L содержит следующие шаги:
- построить плоскость α, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение плоскости α и прямой L(точка M1)
- найти расстояние между точками M0 и M1.
Уравнение плоскости, проходящей через точку M0(x0, y0, z0) имеет следующий вид:
где n=(A,B,C) нормальный вектор плоскости α.
Как видно из рисунка Рис.2, для того, чтобы плоскость α была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n плоскости α, поэтому в качестве нормального вектора плоскости α достаточно взять направляющий вектор прямой L. Тогда уравнение плоскости α, представленной уравнением (10) можно записать так:
Откроем скобки
Для нахождения точки пересечения плоскости α и прямой L, которая и будет проекцией точки M0 на прямую L, выведем параметрическое уравнение прямой (9):
Подставим значения x и y в (11):
Мы нашли такое значение t=t’, при котором координаты x,y и z точки на прямой L удовлетворяют уравнению плоскости (11). Следовательно, подставляя значение t’ в (12) получим координаты проекции точки M0 на прямую L:
где x1=mt’+x’, y1=pt’+y’, z1=lt’+z’.
Далее вычисляем расстояние между точками M0 и M1 используя формулу
которое является расстоянием между точкой M0 и прямой (9).
Пример 2. Найти расстояние от точки M0(1, 2, 1) до прямой
Решение.
Направляющий вектор прямой (15) имеет вид:
Т.е. m=2, p=4, l=−6. Из уравнения прямой (15) видно, что она проходит через точку M’ (x’, y’, z’)=(4, 3, 1)(в этом легко убедится − подставляя эти значения в (15) получим тождество 0=0=0), т.е. x’=4, y’=3, z’=1. Подставим значения m, p, l x0, y0, z0 x’, y’, z’ в (13):
Подставляя значение t=t’ в (12), получим координаты точки M1:
Далее, используя формулу (14) вычисляем расстояние от точки M0 до прямой (15):
Упростим и решим:
Ответ:
Расстояние от точки M0(1, 2, 1) до прямой (15) :
matworld.ru
| 1. | В кубе , ребра которого равны , найдите расстояние от точки B до плоскости . На данной плоскости выбираем прямую , перпендикулярно которой проводим две пересекающиеся прямые АС и АВ. Прямые АС , АВ и данная точка В лежат в одной плоскости . Плоскости и перпендикулярны по признаку перпендикулярности плоскостей (). Из точки В опускаем перпендикуляр ВО на линию пересечения этих плоскостей – АС. ВО -искомое расстояние. Ответ: ВО=1. |
|
| 2. | В кубе , ребра которого равны , найдите расстояние от точки B до плоскости . На данной плоскости выбираем прямую CD, перпендикулярно которой проводим две пересекающиеся прямые и. Прямые, и точка В лежат в плоскости . Плоскости и перпендикулярны по признаку перпендикулярности плоскостей (). Из точки В опускаем перпендикуляр ВО на линию пересечения этих плоскостей – . ВО – искомое расстояние. Ответ: ВО=1. |
|
| 3. | В единичном кубе найдите расстояние от точки В до плоскости . На данной плоскости выбираем прямую АС , перпендикулярно которой проводим две пересекающиеся прямые и . Прямые , и точка B лежат в одной плоскости . Плоскости иперпендикулярны по признаку перпендикулярности плоскостей (). Из точки В опускаем перпендикуляр ВК на линию пересечения этих плоскостей – . ВК – искомое расстояние. Ответ: . |
|
| 4. | В единичном кубе найти расстояние от точки В до. На данной плоскостивыбираем прямую АС, перпендикулярно которой проводим две пересекающиеся прямые ВD и D1O. Прямые BD, D1O и точка B лежат в одной плоскости . Плоскости и перпендикулярны по признаку перпендикулярности плоскостей () . Из точки B опускаем перпендикуляр ВК на линию пересечения этих плоскостей – . ВК – искомое расстояние. :; . Ответ:. |
|
| 5. | В единичном кубе найти расстояние от точки В до плоскости. На данной плоскостивыбираем прямую , перпендикулярно которой проводим две пересекающиеся прямыеи . Прямые , и точка В лежат в одной плоскости . Плоскости и перпендикулярны по признаку перпендикулярности плоскостей (). Из точки В опускаем перпендикуляр ВК на линию пересечения этих плоскостей – . Длина ВК – это искомое расстояние. : Ответ: . |
|
| 6. | В единичном кубе найти расстояние от точки В
до плоскости. Это тот случай, когда нужно сместить точку В по прямой DB параллельной (по признаку параллельности прямой и плоскости. BD параллельно ). На данной плоскости выбираем прямую ,перпендикулярно которой проводим две пересекающиеся прямые и. Прямые ,и точка О лежат в одной плоскости. Плоскости и перпендикулярны по признаку перпендикулярности плоскостей (). Из точки О опускаем перпендикуляр ОК на линию пересечения этих плоскостей – . Длина ОК и есть искомое расстояние. Ответ: . |
|
| 7. | В единичном тетраэдре DABC найдите расстояние от точки C до плоскости ADB. Проведем плоскость, проходящую через данную точку С и перпендикулярную плоскости ADB . Для этого в плоскоcти ADB выберем прямую АВ и к ней проведем две перпендикулярные прямые, образующие плоскость проходящую через точку С и перпендикулярную плоскости ADB по признаку перпендикулярности плоскостей. Одна прямая СК – высота треугольника АВС, вторая – DК, перпендикулярная АВ по теореме о трех перпендикулярах. В треугольнике DКС опустим перпендикуляр СТ на линию пересечения этих плоскостей DК . Длина СТ искомое расстояние. Ответ: |
|
| 8. | В единичном тетраэдре DABC точка Е-середина DC. Найдите расстояние от точки D до плоскости АВЕ. Треугольники ADC и BDC равносторонние, поэтому высоты этих треугольников AЕ и BЕ, опущенные на общую сторону DC имеют общее основание Е. DE перпендикулярна AЕ и BЕ, поэтому DE перпендикулярна плоскости ABE по признаку перпендикулярности прямой и плоскости. DE является расстоянием от точки D до плоскости ABE. Ответ: DE =0,5. |
|
| 9. | В правильной четырехугольной пирамиде SABCD, все ребра которой равнынайдите расстояние от точки B до плоскости SDC. Для определения искомого расстояния нужно через точку В провести плоскость перпендикулярную плоскости SDC. В данной задаче удобнее определить искомое расстояние от точки К, лежащей на прямой АВ параллельной плоскости SDC и являющейся серединой ребра АВ. Через точку К проводим плоскость перпендикулярную плоскости SDC . Для этого проведем прямую КМ перпендикулярную DC и прямую SM перпендикулярную DM . SM перпендикулярна DM по теореме о трех перпендикулярах. Получили плоскость KSM перпендикулярную плоскости SDC . Из точки К опускаем перпендикуляр КТ на линию пересечения плоскостей SM. Длина КТ есть искомое расстояние. Ответ: |
|
10. |
В правильной четырехугольной пирамиде найти расстояние от точки D до плоскости SKM, где К и М – середины ребер АВ и ВС соответственно. Необходимо через точку D провести плоскость перпендикулярную данной SKM. Для этого на плоскости KMS выбираем прямую КМ, перпендикулярно которой проводим две пересекающиеся прямые BD и SN. Прямые BD, SN и данная точка D лежат в одной плоскости SND. Плоскость SND перпендикулярна данной SKM по признаку перпендикулярности плоскостей (). Из точки А в плоскости SND опускаем перпендикуляр DP на линию пересечения плоскостей SN. Длина DP – искомое расстояние. Ответ: |
|
| 11. | В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точка К – середина ребра SA. Найти расстояние от точки C до плоскости KDB. Необходимо провести плоскость перпендикулярную DKB и проходящую через точку С. Для этого на плоскости DKB выбираем прямую DB и перпендикулярно ей проводим две пересекающиеся прямые АС и КО. следовательно. Из точки С опускаем перпендикуляр CN на линию пересечения плоскостей DBK и SCA KO. Длина CN – искомое расстояние. Ответ: |
|
urok.1sept.ru
Расстояние от точки до плоскости онлайн
С помощю этого онлайн калькулятора можно найти расстояние от точки до заданной плоскости. Дается подробное решение с пояснениями. Для вычисления расстояния от точки до плоскости введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние от точки до плоскости − теория, примеры и решения
Для нахождения расстояния от точки M0 до плоскости α, необходимо найти расстояние от точки M0 до проекции точки M0 на плоскость α:
Нахождение расстояния от точки до плоскости содержит следующие шаги:
- построение прямой L, проходящей через точку M0 и перпендикулярной плоскости α.
- нахождение точки M1 пересечения плоскости α с прямой L(Рис.1).
- вычисление расстояния между точками M0 и M1.
1. Общее уравнение плоскости имеет вид:
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M0(x0, y0, z0) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .
Таким образом, уравнение прямой, проходящей через точку M0(x0, y0, z0) и ортогональной плоскости (1) имеет следующий вид:
Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее
Выразим переменные x, y, z через рараметр t.
2. Найдем точку пересечения прямой (4) с плоскостью (1). Для этого нужно найти такой параметр t, при котором точка M(x, y, z) принадлежит плоскости (1). Поэтому подставим значения x,y,z из выражения (4) в (1) и решим относительно t.
Подставляя значение параметра t в выражения (4), находим проекцию M1(x1, y1, z1) точки M0 на плоскость (1).
3. Найдем, наконец, расстояние от точки M0 до плоскости (1). Очевидно, что расстояние от точки M0 до плоскости (1) − это расстояние от точки M0 до точки M1. А это расстояние вычисляется так:
Учитывая значение параметра t, имеем:
Пример 1. Найти расстояние от точки M0(2, -1, -9/31) до плоскости
Решение.
Нормальный вектор плоскости имеет вид:
т.е. A=5, B=1, C=2.
Координаты точки M0: x0=2, y0=−1, z0=−9/31.
Подставляя координаты точки M0 и нормального вектора плоскости в (5), получим:
Из выражений (4) находим:
Проекцией точки M0(2, -1, -9/31) на плоскость (7) является точка:
Вычислим расстояние между точками M0 и M1:
Упростим:
Ответ:
Расстояние от точки M0(2, -1, -9/31) до плоскости (7):
matworld.ru
Расстояние от точки до прямой на плоскости Википедия
Расстояние от точки до прямой на плоскости — это кратчайшее расстояние от точки до прямой в евклидовой геометрии. Расстояние равно длине отрезка, который соединяет точку с прямой и перпендикулярен прямой. Формула вычисления расстояния может быть получена и выражена несколькими способами.
Знание наименьшего расстояния от точки до прямой может быть полезно во многих случаях, например, для поиска кратчайшего пути для выхода на дорогу, определение разброса графа, и подобное. В регрессии Деминга, процедуре линейного сглаживания, если зависимые и независимые переменные имеют одну и ту же дисперсию, регрессия сводится к ортогональной регрессии, в которой степень приближения измеряется для каждой точки как расстояние от точки до регрессионной прямой.
Декартова система координат[ | ]
Прямая задана уравнением[ | ]
Когда прямая на плоскости задана уравнением ax + by + c = 0, где a, b и c — такие вещественные константы, что a и b не равны нулю одновременно, и расстояние от прямой до точки (x0,y0) равно [1]
- distance(ax+by+c=0,(x0,y0))=|ax0+by0+c|a2+b2.{\displaystyle \operatorname {distance} (ax+by+c=0,(x_{0},y_{0}))={\frac {|ax_{0}+by_{0}+c|}{\sqrt {a^{2}+b^{2}}}}.}
Точка на прямой, наиболее близкая к (x0,y0), имеет координаты [2]
- x=b(bx0−ay0)−aca2+b2{\displaystyle x={\frac {b(bx_{0}-ay_{0})-ac}{a^{2}+b^{2}}}} и y=a(−bx0+ay0)−bca2+b2.
ru-wiki.ru