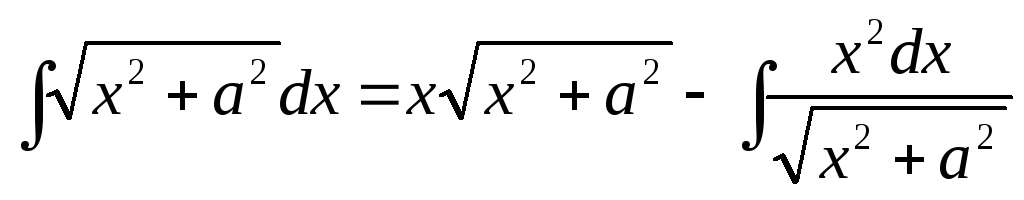Основные методы интегрирования
1. Непосредственное интегрирование
Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.
Пример 1. Найти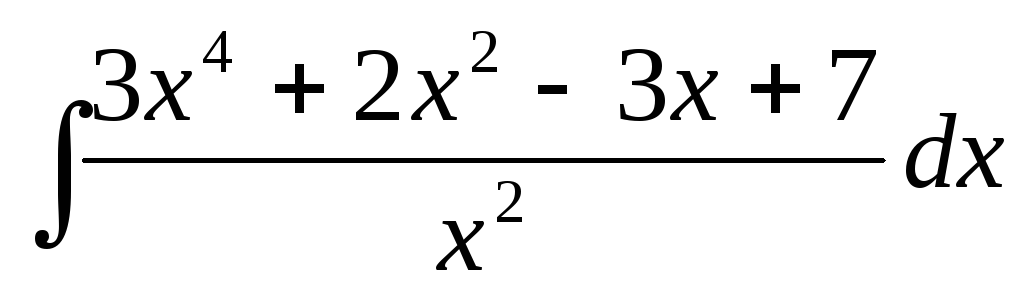 .
.
Разделив числитель на знаменатель, получим:
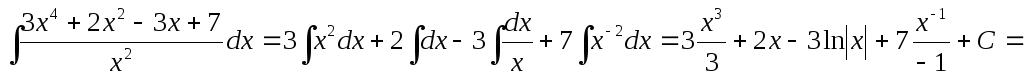 =
=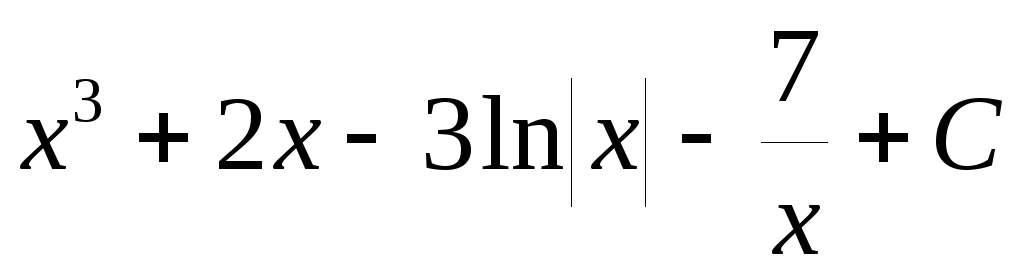 .
.
Отметим, что нет надобности после каждого слагаемого ставить произвольную постоянную, потому что их сумма есть также произвольная постоянная, которую мы пишем в конце.
Пример 2.Найти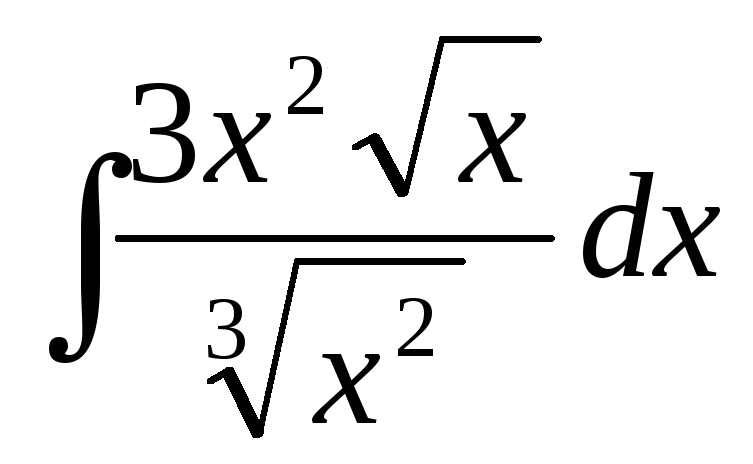 .
.
Преобразуем подынтегральную функцию следующим образом:
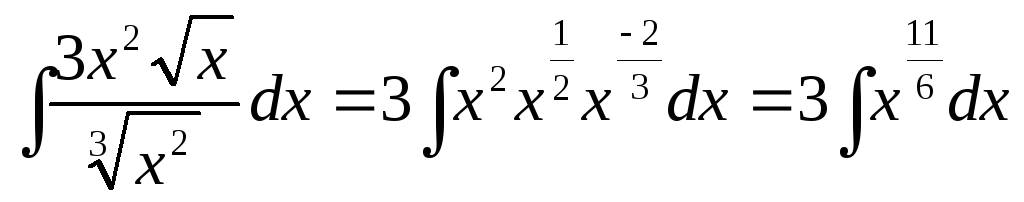 .
.
Применив табличный интеграл 1, получим:
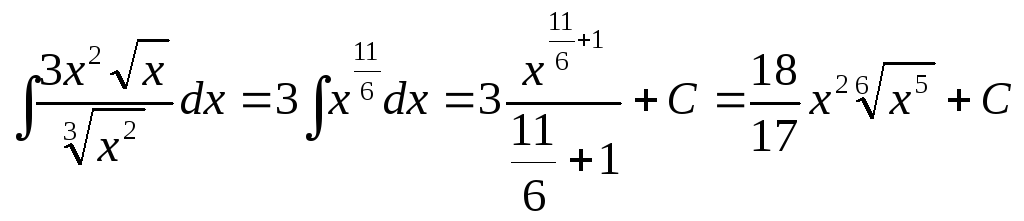 .
.
Пример 3.
 .
.
Пример 4.
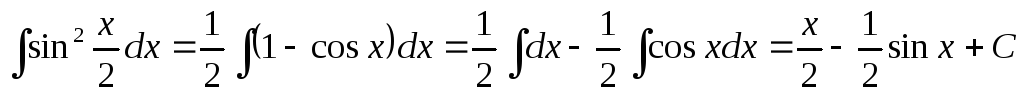 .
.
Пример 5.
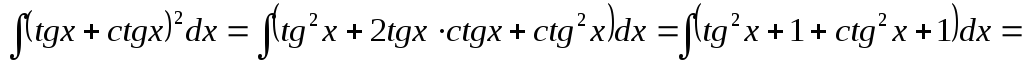
=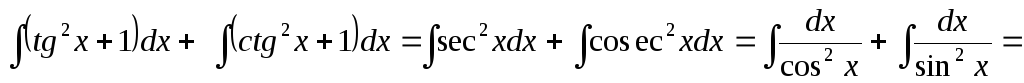
=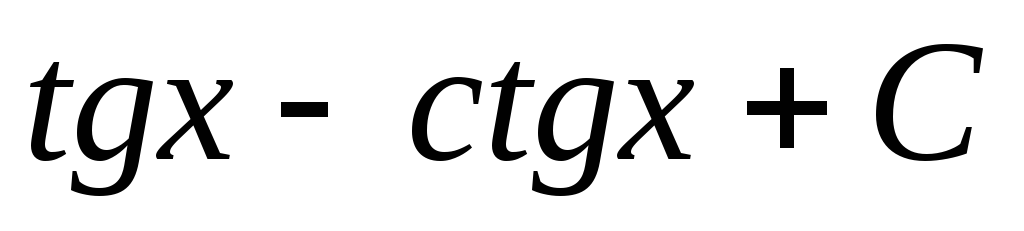 .
.
В некоторых случаях нахождение интегралов упрощается применением искусственных приемов.
Пример 6.Найти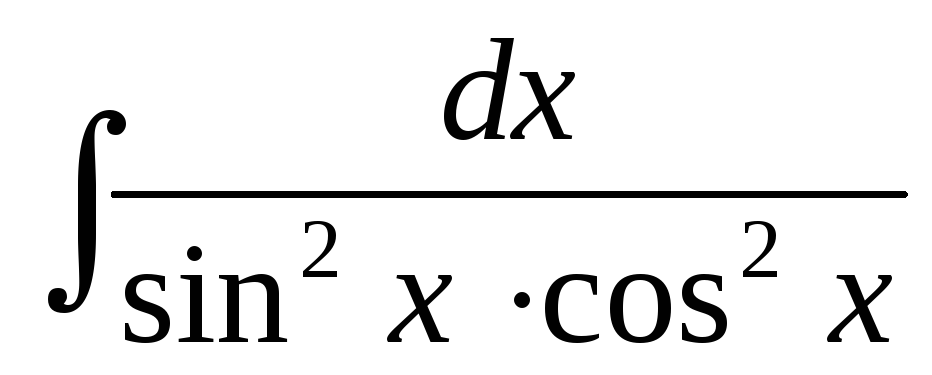 .
.
Умножив подынтегральное выражение
на 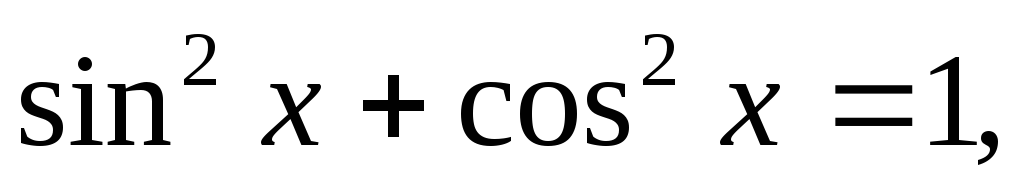 находим
находим
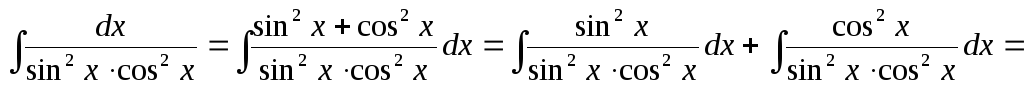
=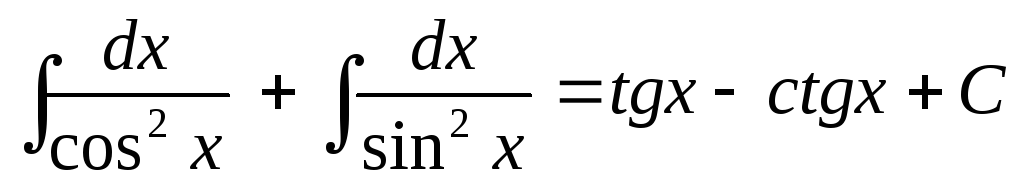 .
.
Пример 7.
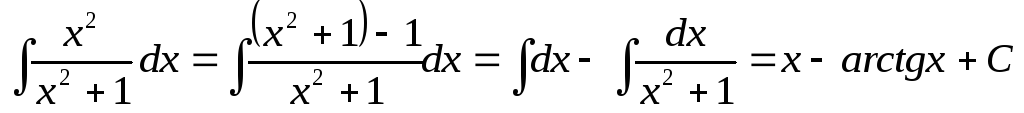 .
.Пример 8.
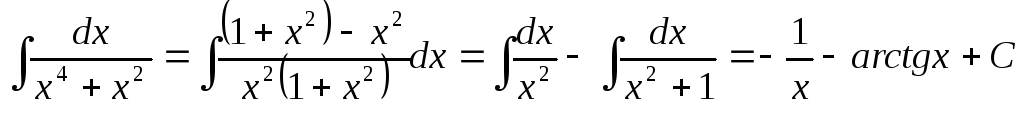 .
.
2. Интегрирование методом замены переменной
Вычислить заданный интеграл непосредственным интегрированием удается далеко не всегда, а иногда это связано с большими трудностями. В этих случаях применяют другие приемы. Одним из наиболее эффективных является метод замены переменной. Сущность его заключается в том, что путем введения новой переменной интегрирования удается свести заданный интеграл к новому, который сравнительно легко берется непосредственно. Существуют два варианта этого метода.
а) Метод подведения функции под знак дифференциала
По определению дифференциала функции 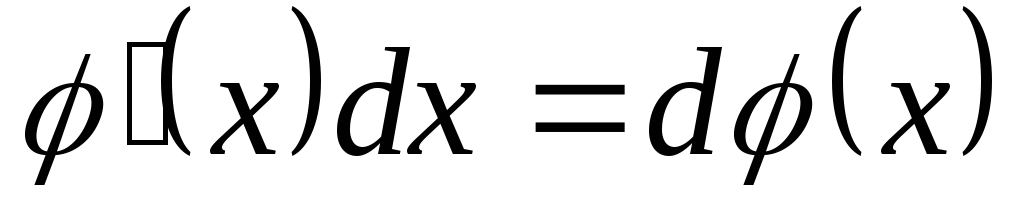 .
.
 под
знак дифференциала».
под
знак дифференциала».Теорема об инвариантности формул интегрирования
Всякая формула интегрирования сохраняет свой вид при подстановке вместо независимой переменной любой дифференцируемой функции от нее, т.е., если
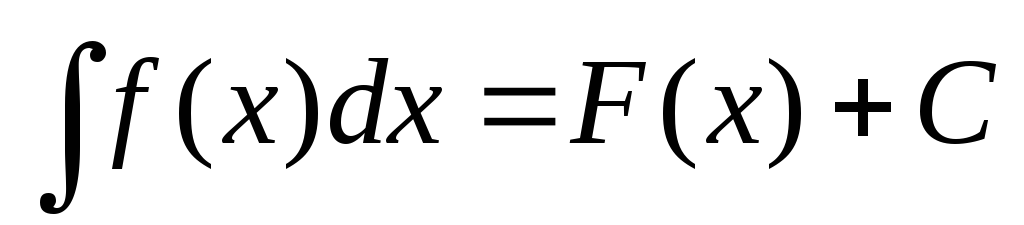 , то и
, то и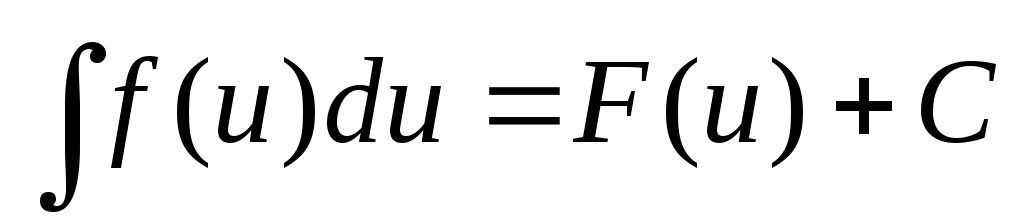 ,
,
где 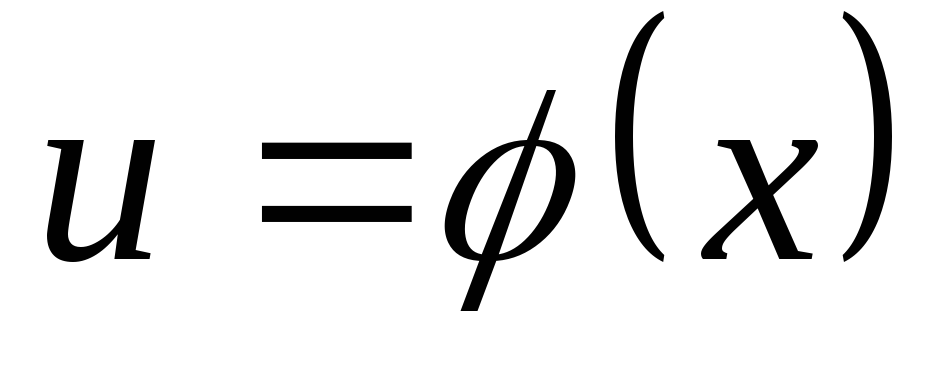 — любая дифференцируемая функция отx.
Ее значения должны принадлежать
интервалу, в котором функция
— любая дифференцируемая функция отx.
Ее значения должны принадлежать
интервалу, в котором функция определена и непрерывна.
определена и непрерывна.
Доказательство:
Из того, что 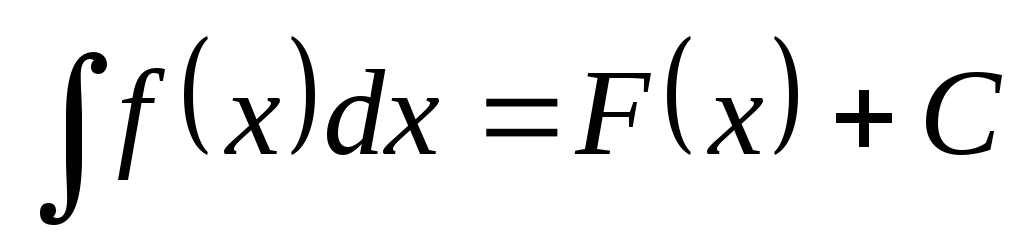 ,
следует
,
следует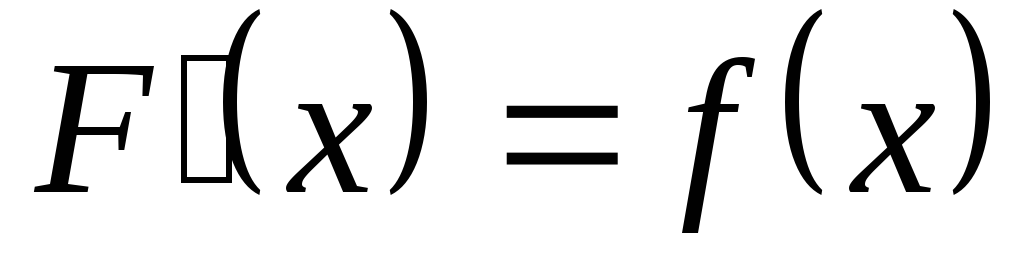 .
Возьмем теперь функцию
.
Возьмем теперь функцию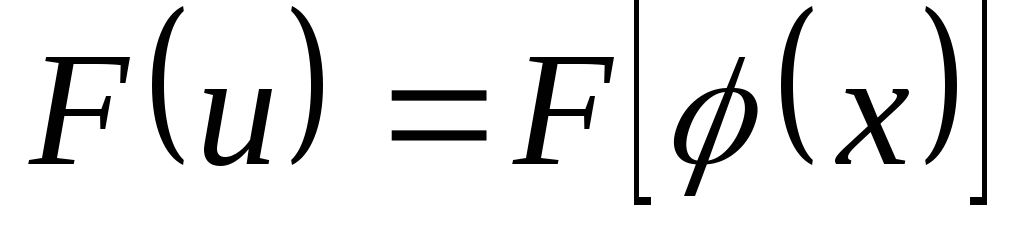 .
Для ее дифференциала в силу свойства
инвариантности формы первого дифференциала
функцииимеем
.
Для ее дифференциала в силу свойства
инвариантности формы первого дифференциала
функцииимеем
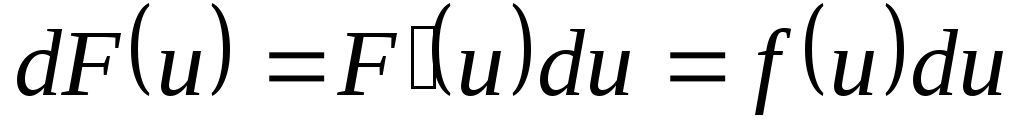 .
.
Отсюда 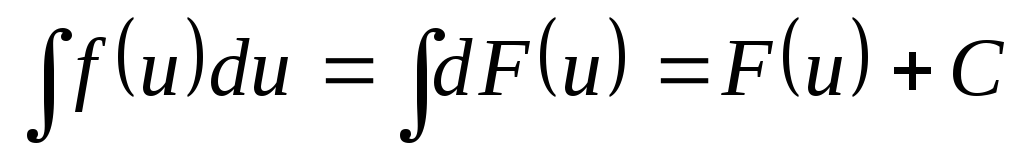 .
.
Пусть требуется вычислить интеграл 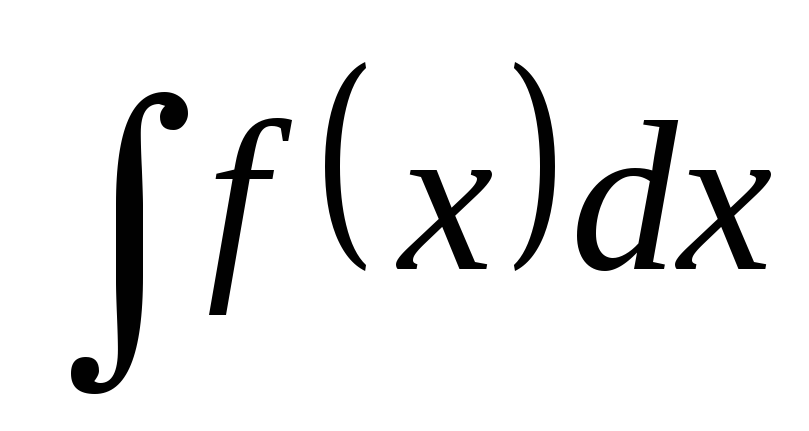 .
Предположим, что существуют дифференцируемая
функция
.
Предположим, что существуют дифференцируемая
функция
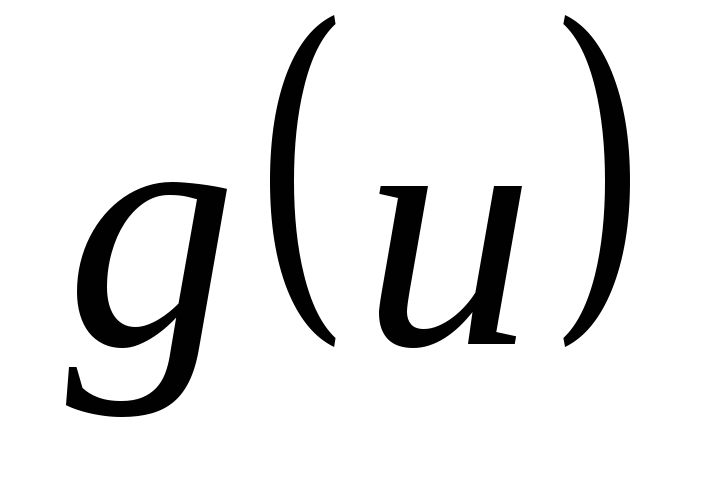 такие, что подынтегральное выражение
такие, что подынтегральное выражение 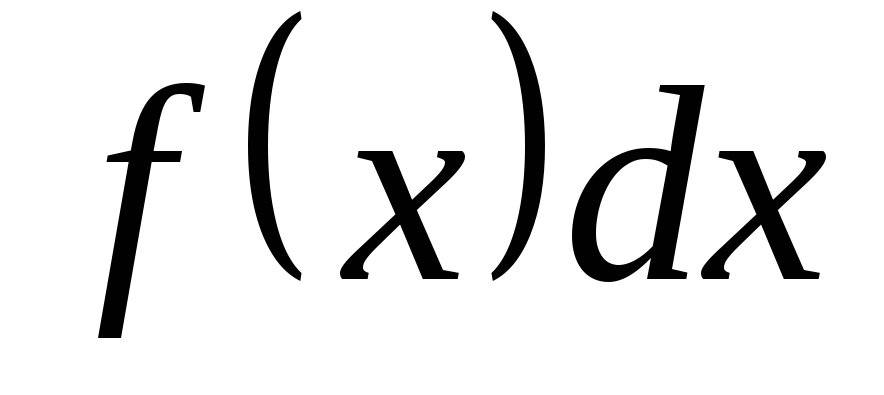 может быть записано в виде
может быть записано в виде
| (1) |
Тогда
| (2) |
т.е.
вычисление интеграла 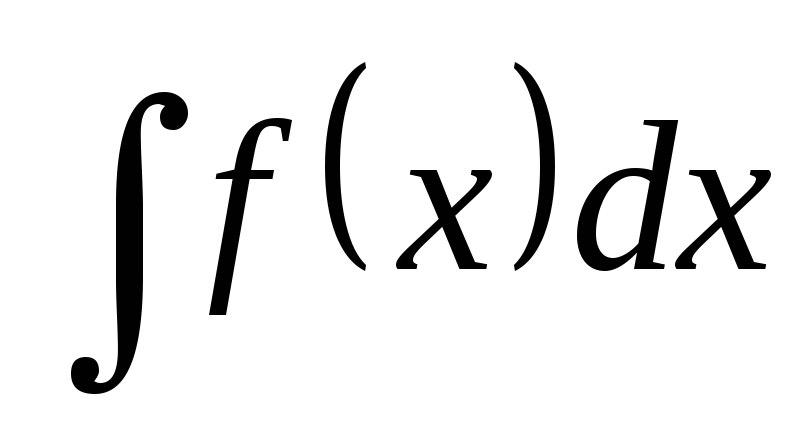 сводится к вычислению интеграла
сводится к вычислению интеграла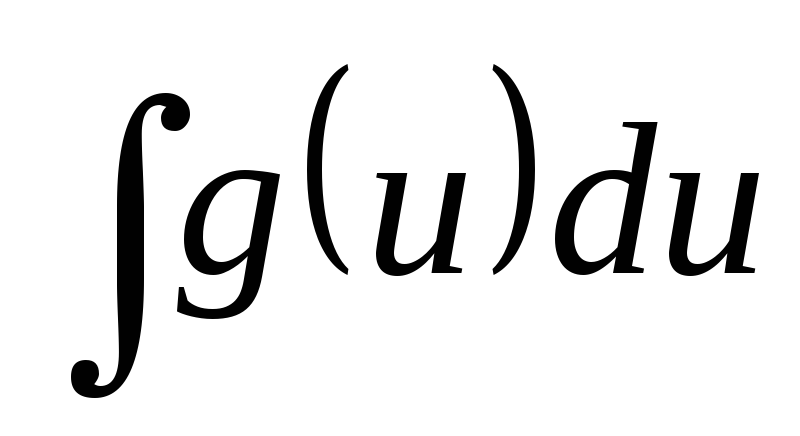
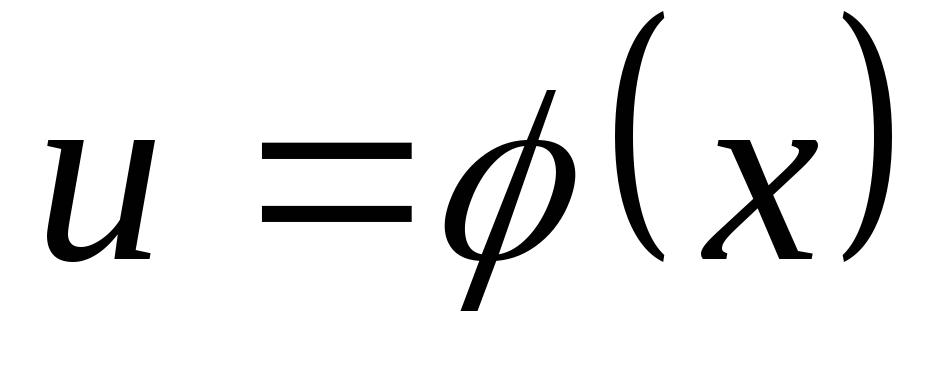 .
.Пример
1. 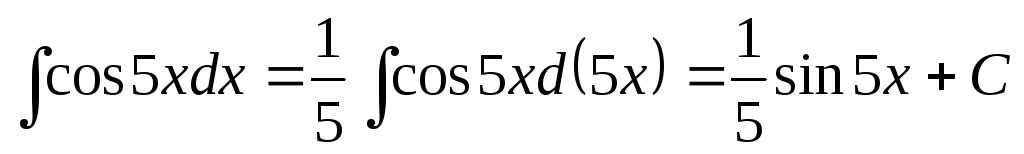 .
.
Пример
2.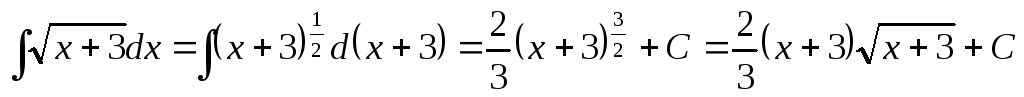 .
.
Пример
3.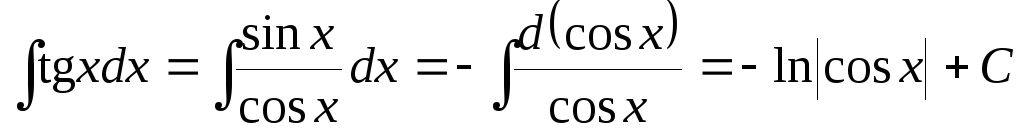 .
.
Пример
4.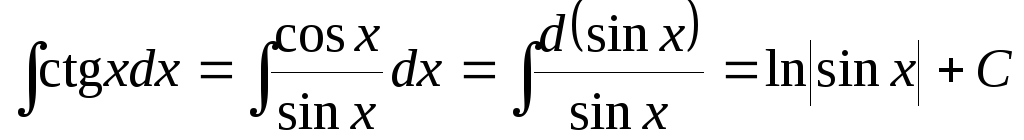 .
.
Пример
5.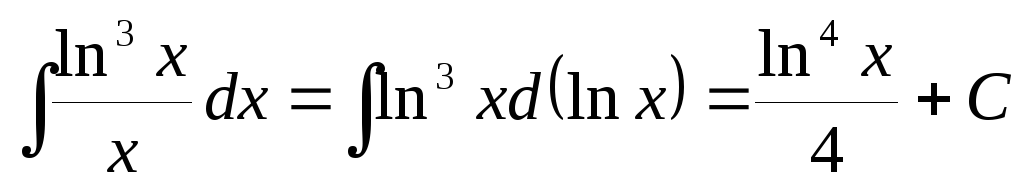 .
.
Пример
6.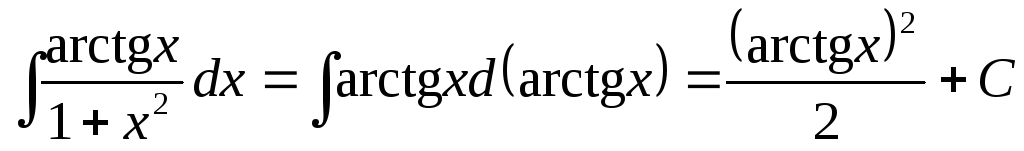 .
.
Пример
7.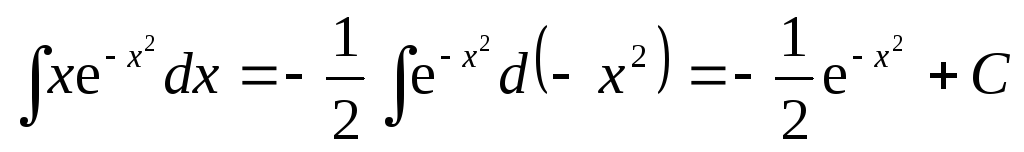
Пример
8.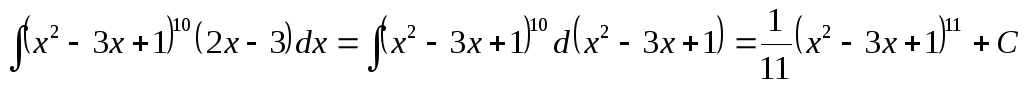 .
.
Пример
9.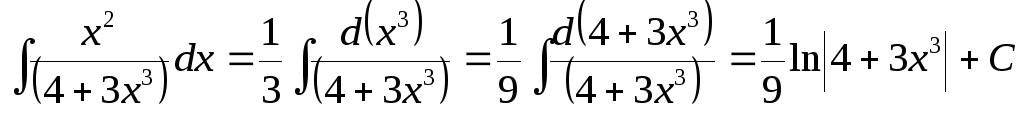 .
.
Пример
10.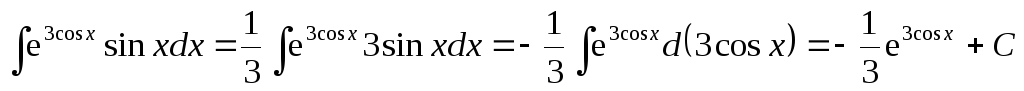 .
.
Пример 11.
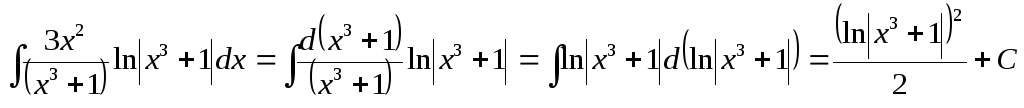 .
.
Приведем далее примеры вычисления интегралов, которые нам понадобятся в теории интегрирования рациональных дробей.
Пример
12.НайтиI=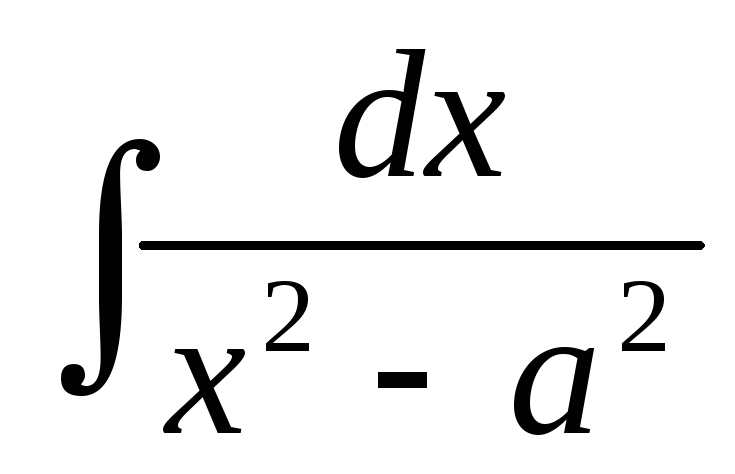 (0).
(0).
Представим подынтегральную функцию в виде:
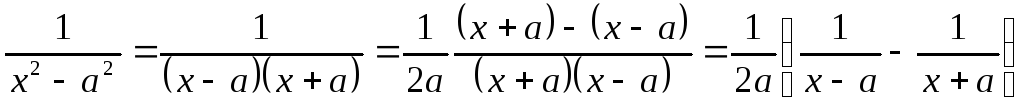 .
.
Следовательно,
I=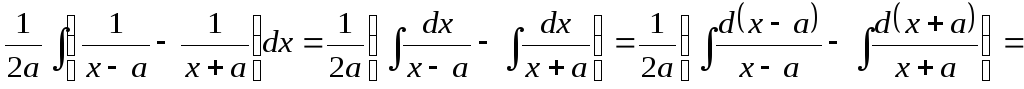
=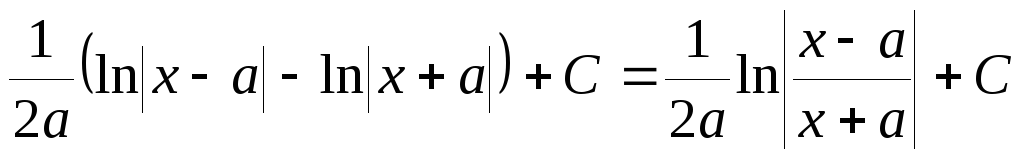 .
.
Таким образом, 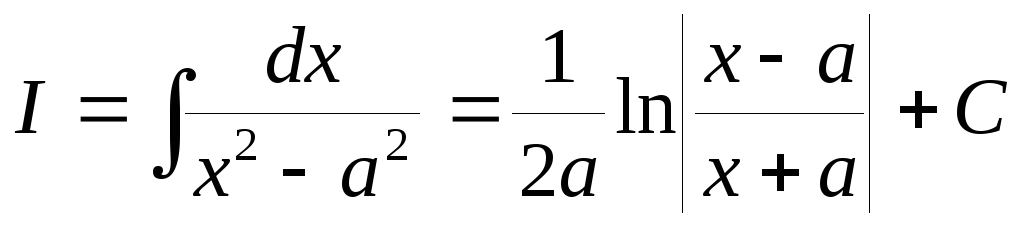 .
.
Пример
12а. НайтиI=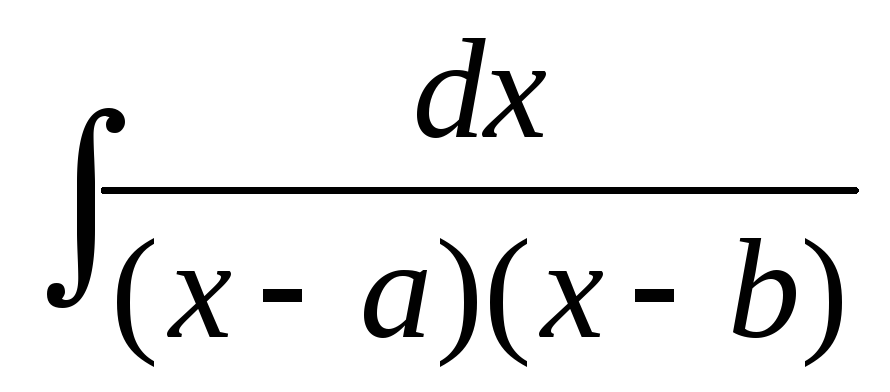 ,
, 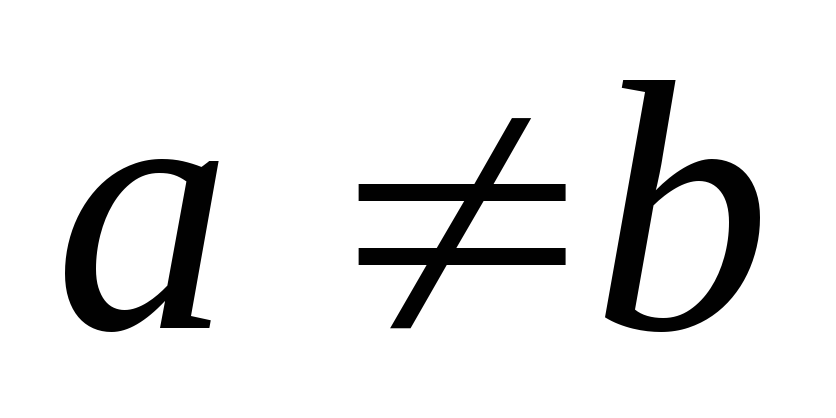 .
.
Так как 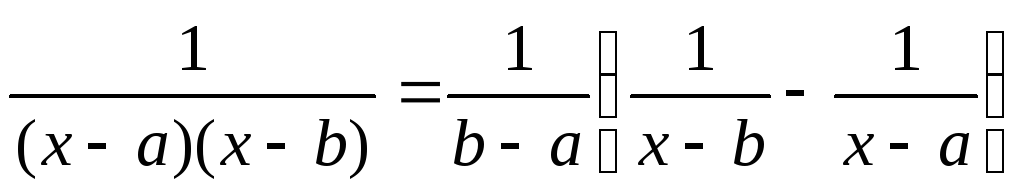 ,
,
следовательно I=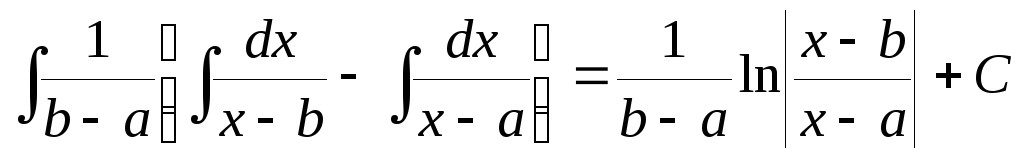 .
.
Пример 13.Найти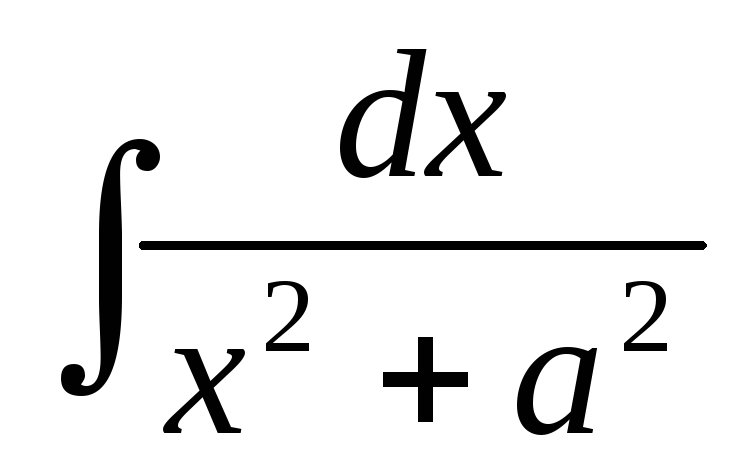
Для
того, чтобы свести этот интеграл к
табличному, разделим числитель и
знаменатель подынтегрального выражения
на 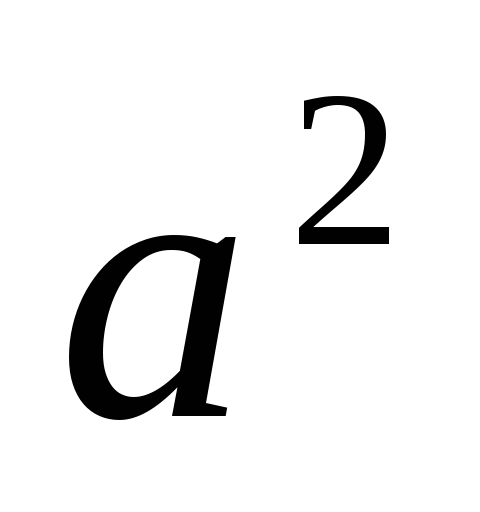 :
:
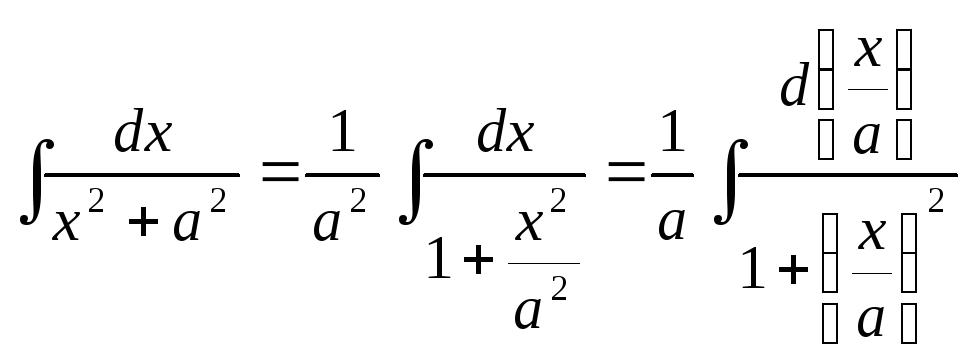 .
.
Мы подвели постоянный множитель 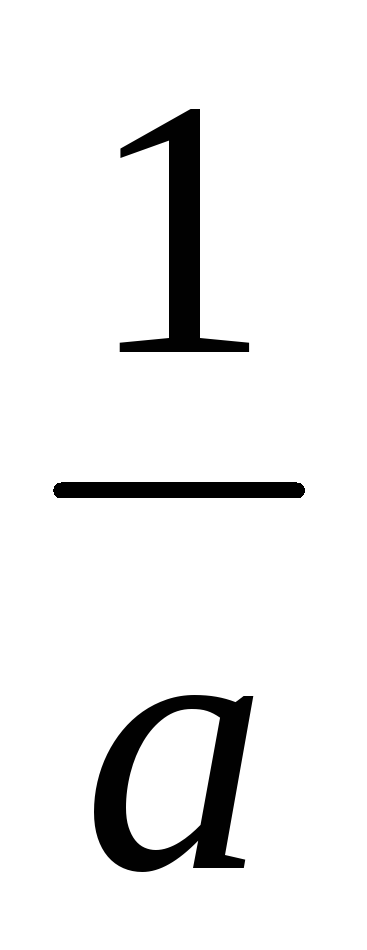 под знак дифференциала. Рассматривая
под знак дифференциала. Рассматривая как новую переменную, получим:
как новую переменную, получим:
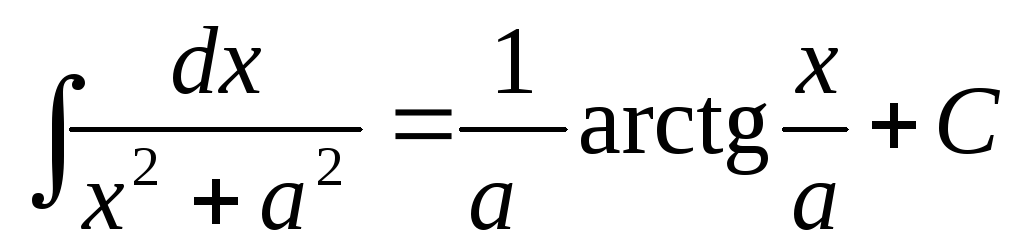 .
.
Вычислим также интеграл, который имеет важное значение при интегрировании иррациональных функций.
Пример 14.
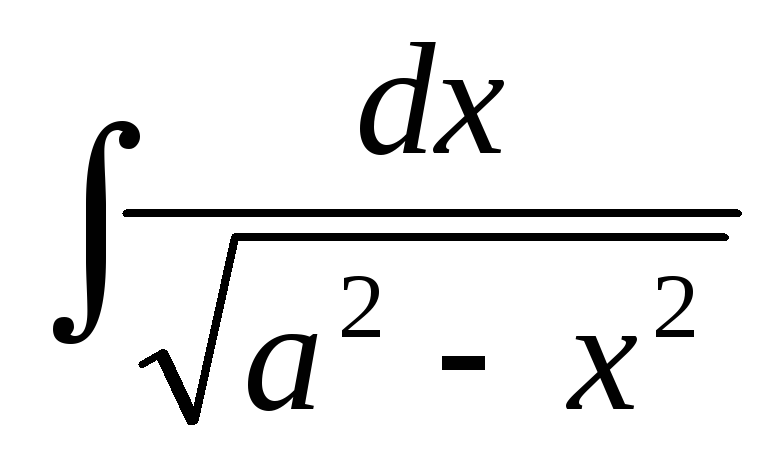 (ха,а0).
(ха,а0). Имеем 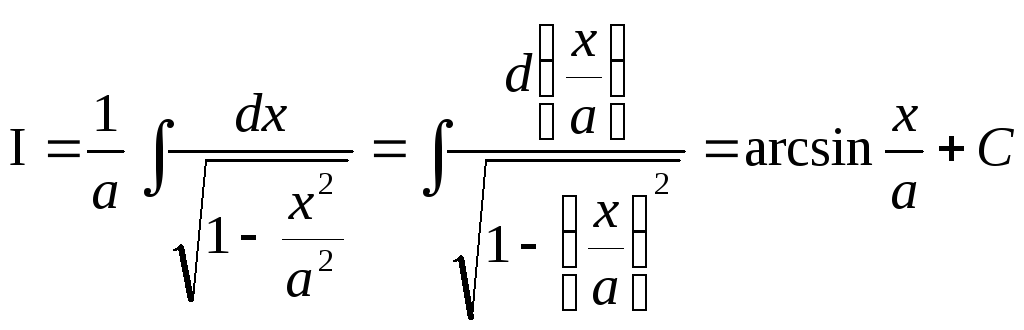 .
.
Итак, 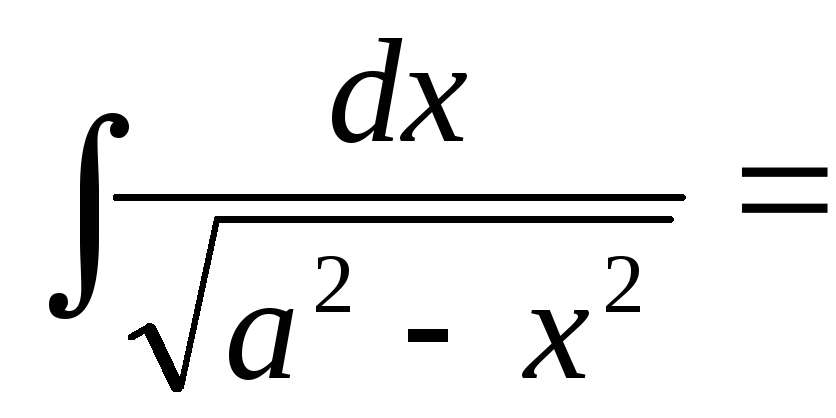
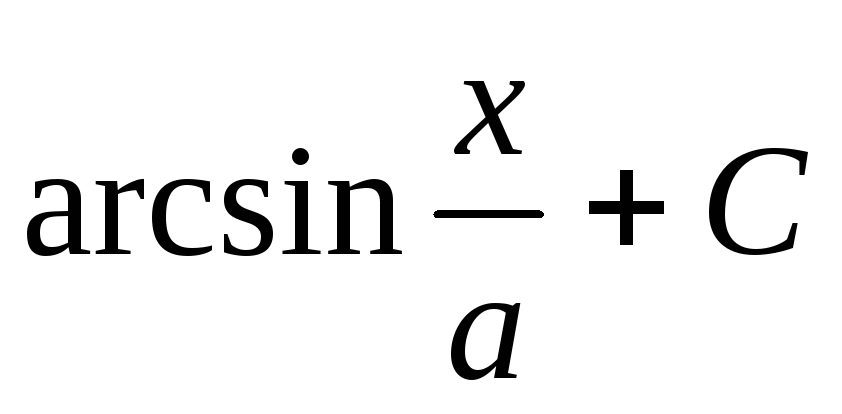 (ха,а0).
(ха,а0).
Представленные примеры иллюстрируют важность умения приводить данное
дифференциальное
выражение 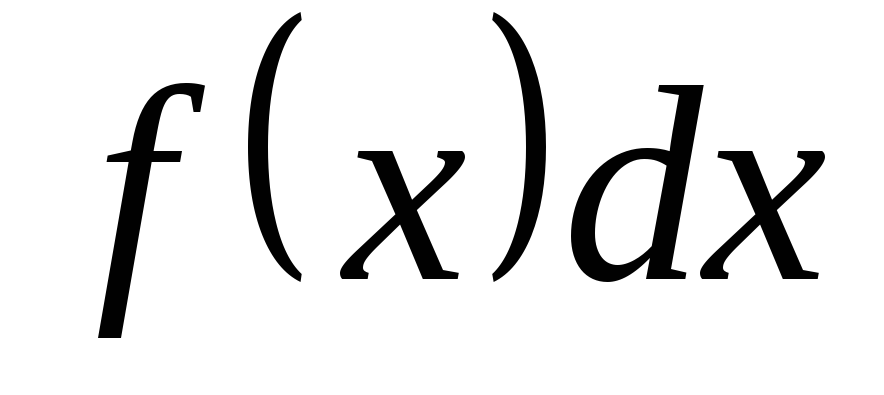 к виду
к виду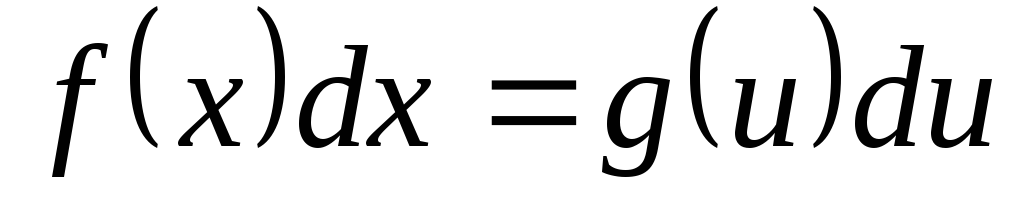 ,
где
,
где есть некоторая функция отxиg– функция более простая для интегрирования,
чемf.
есть некоторая функция отxиg– функция более простая для интегрирования,
чемf.
В этих примерах были проведены преобразования дифференциала, такие как
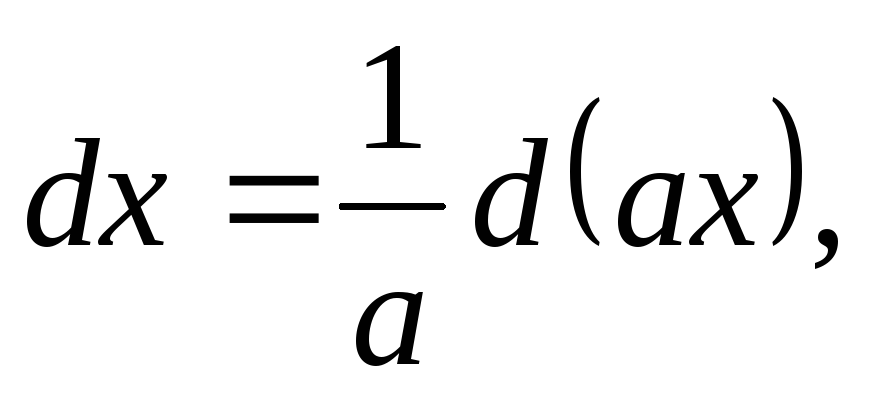
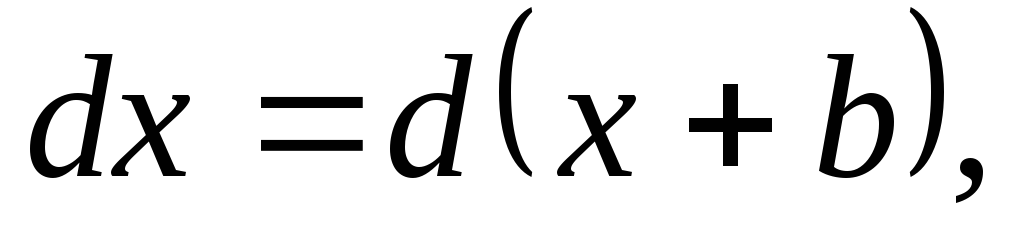 гдеb– постоянная
величина
гдеb– постоянная
величина
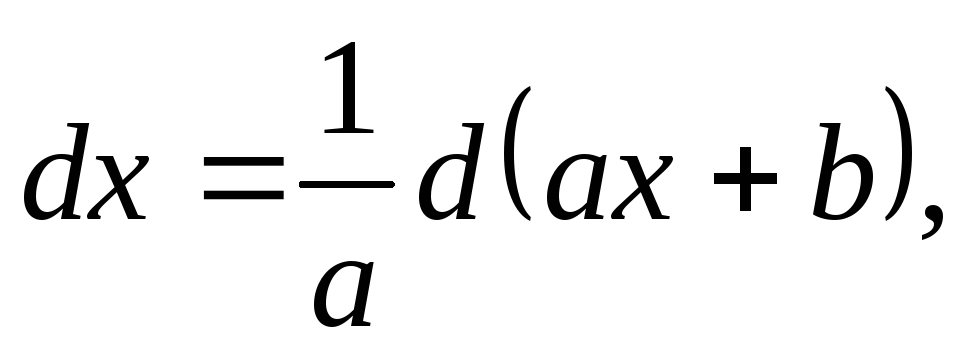
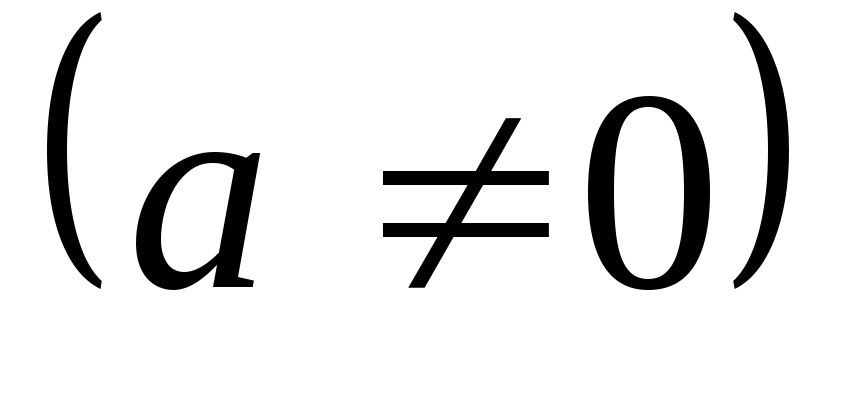
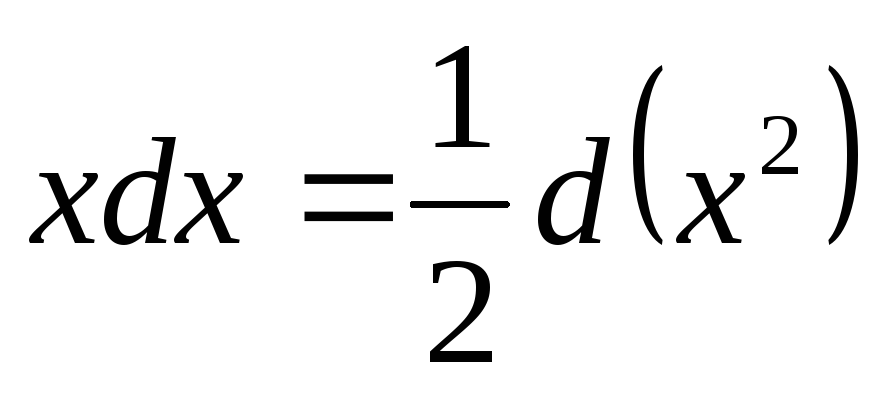 ,
,
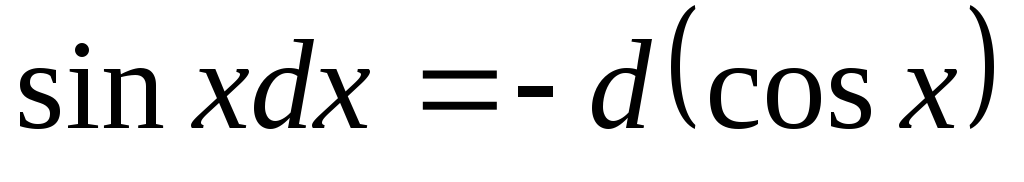 ,
,
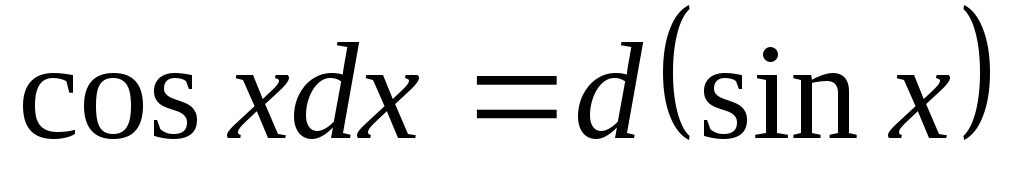 ,
,
часто используемые при нахождении интегралов.
В таблице основных интегралов предполагалось, что xесть независимая переменная. Однако, эта таблица, как следует из изложенного выше, полностью сохраняет свое значение, если подxпонимать любую непрерывно дифференцируемую функцию от независимой переменной. Обобщим ряд формул таблицы основных интегралов.
3а.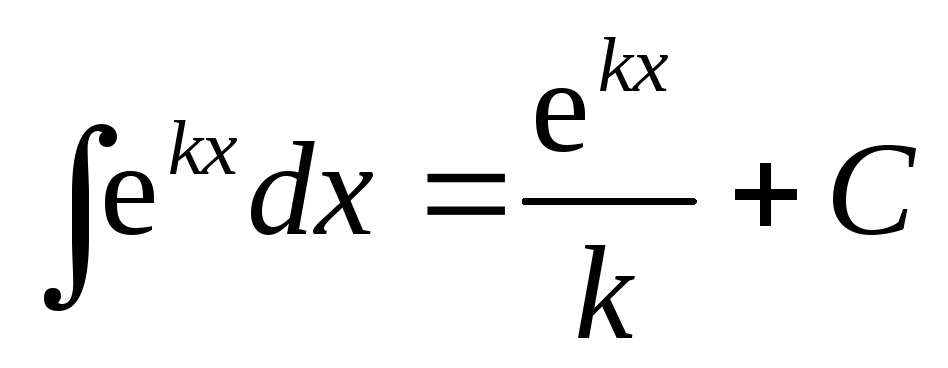 .
.
4.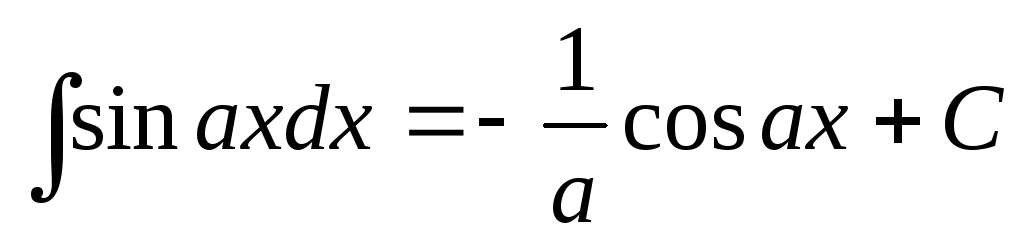 .
.
5.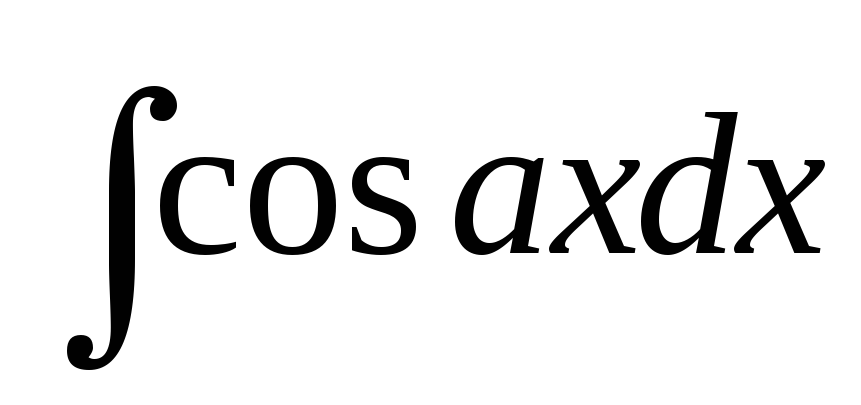 =
=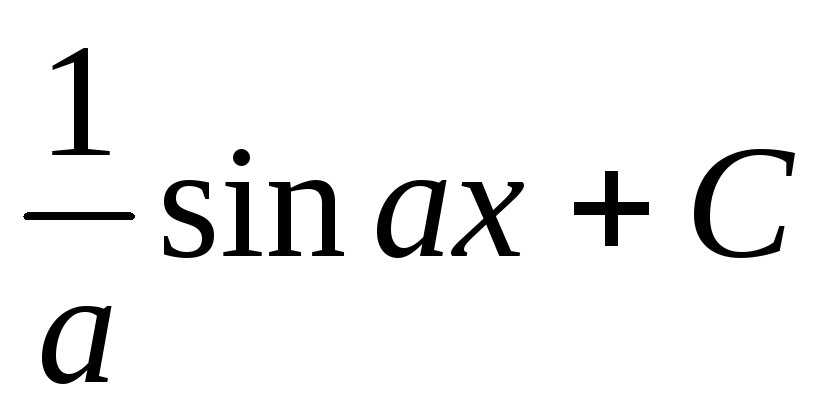 .
.
6.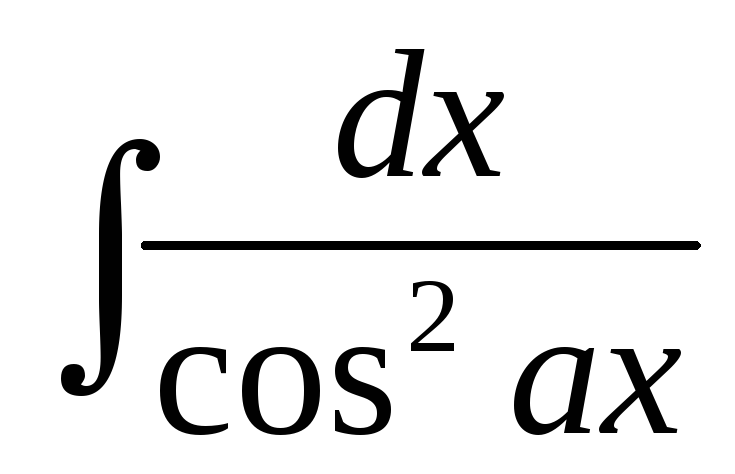
 =
= 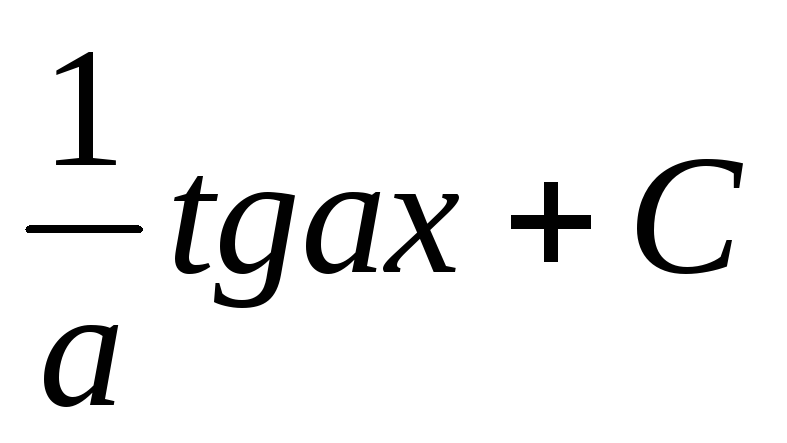 .
.
7.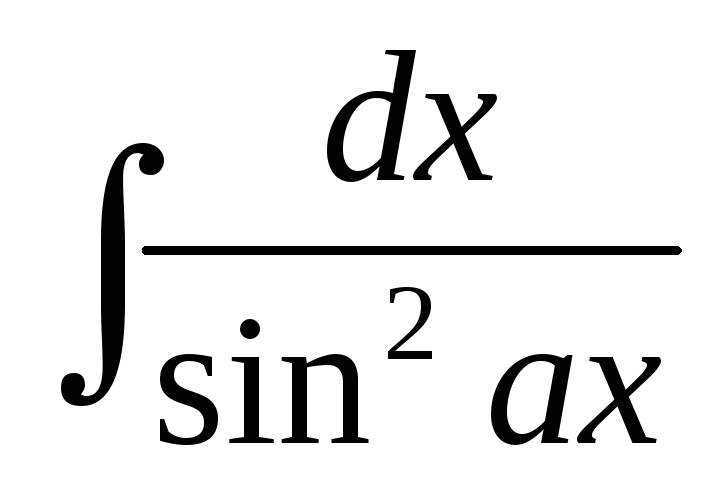 =
= 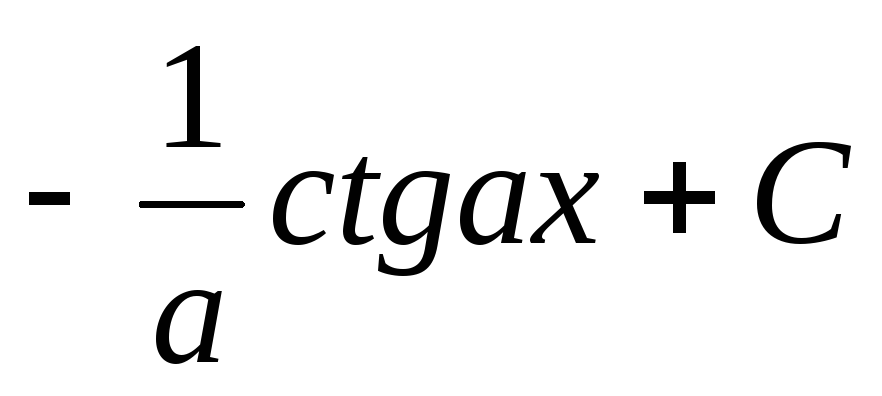 .
.
8. 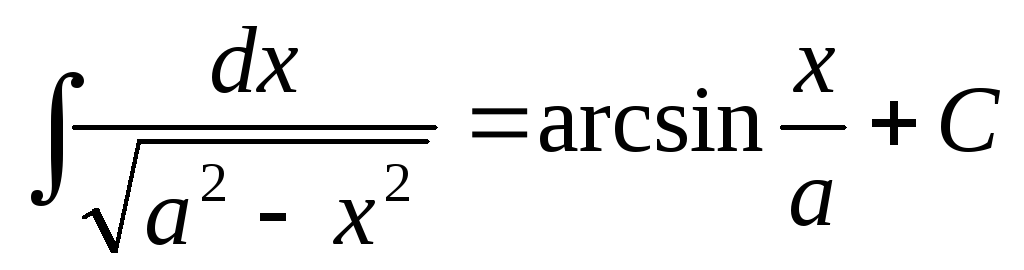 (ха,а0).
(ха,а0).
9. 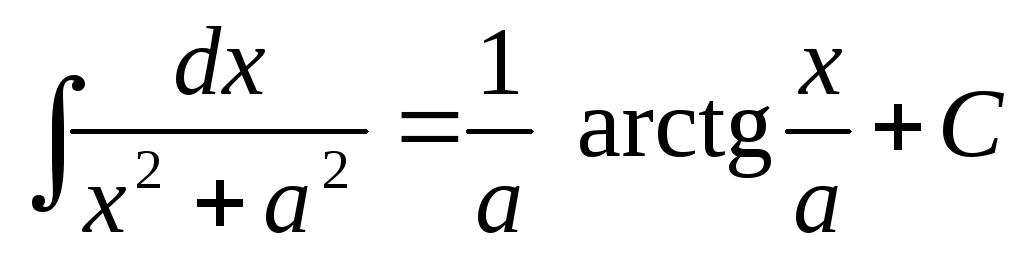 (а0).
(а0).
Операция подведения функции 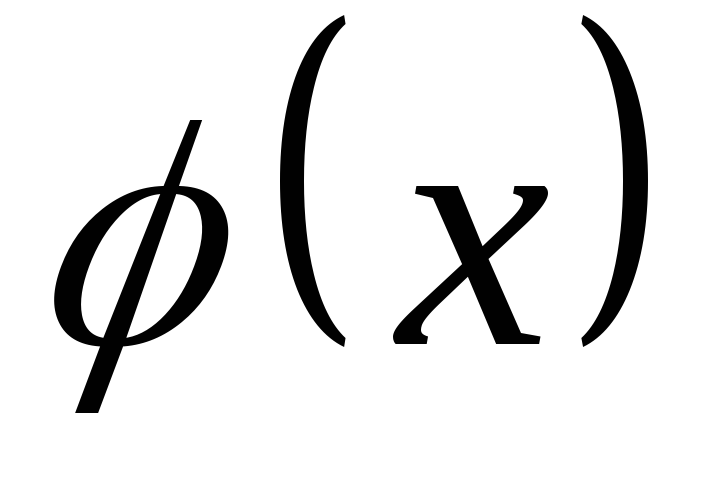 под знак дифференциала эквивалентна
замене переменнойхна новую переменную
под знак дифференциала эквивалентна
замене переменнойхна новую переменную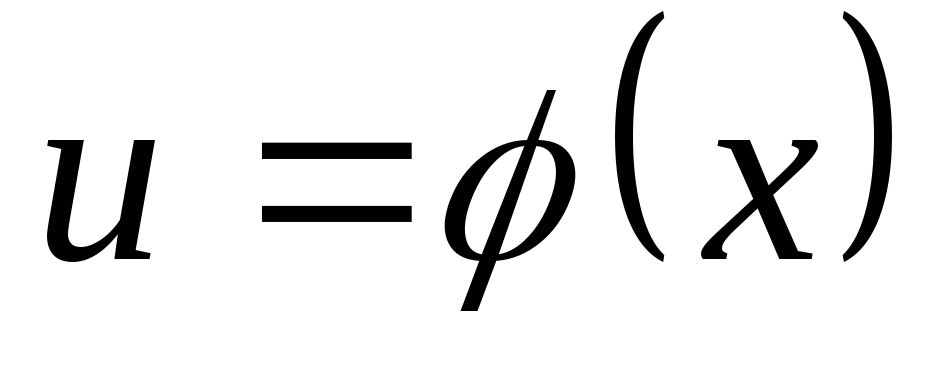 .
Нижеследующие примеры иллюстрируют
это положение.
.
Нижеследующие примеры иллюстрируют
это положение.
Пример
15.НайтиI=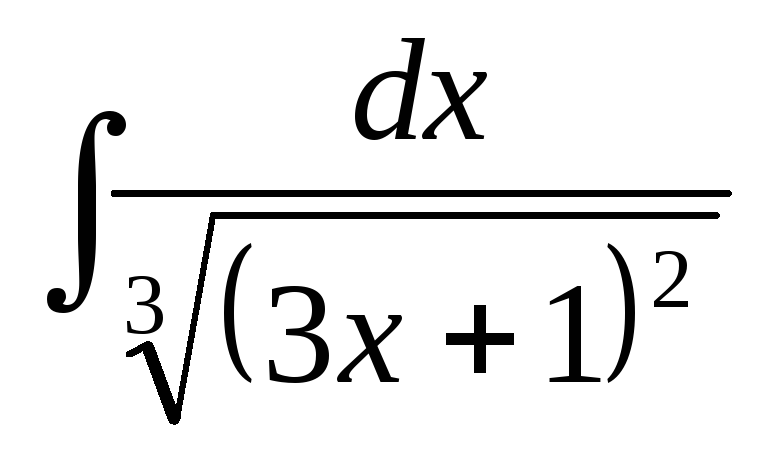 .
.
Произведем замену переменной по формуле 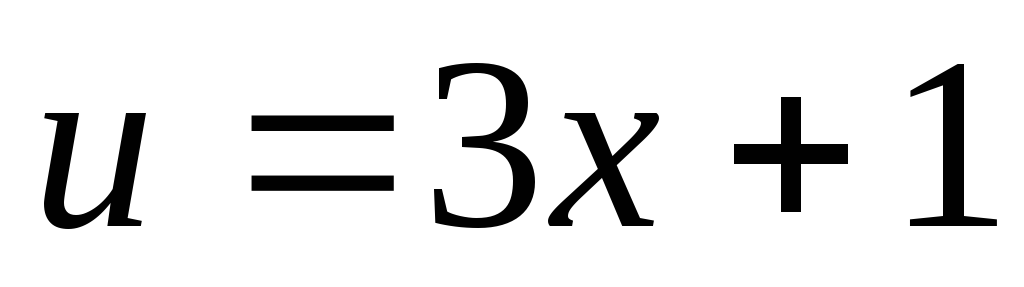 ,
тогда
,
тогда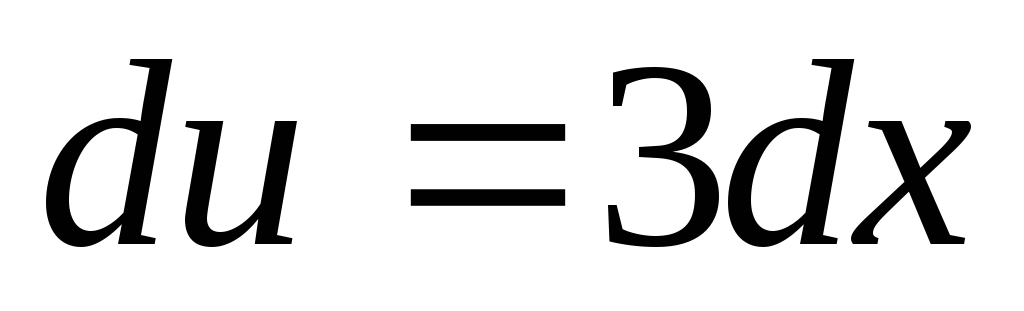 ,
т.е.
,
т.е.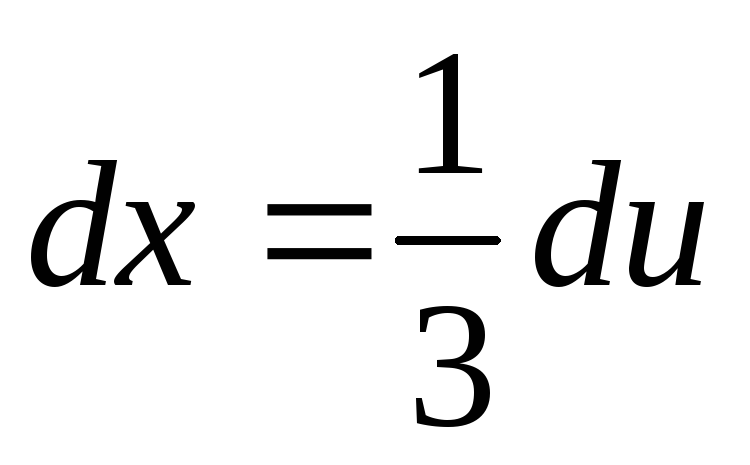 иI=
иI=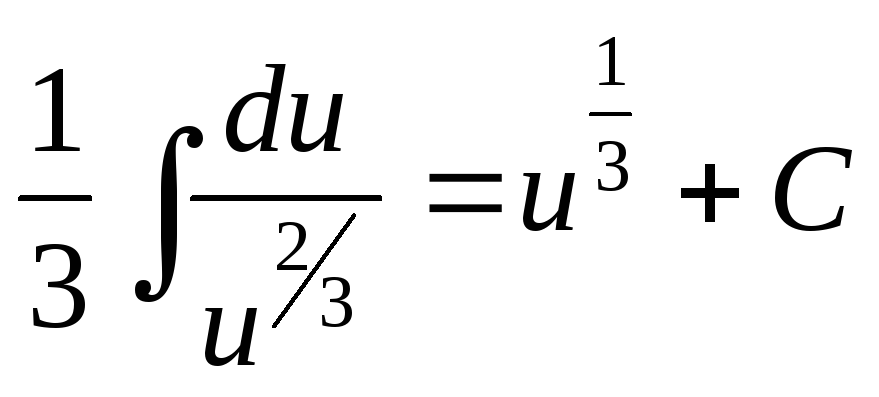 .
.
Заменив uего выражением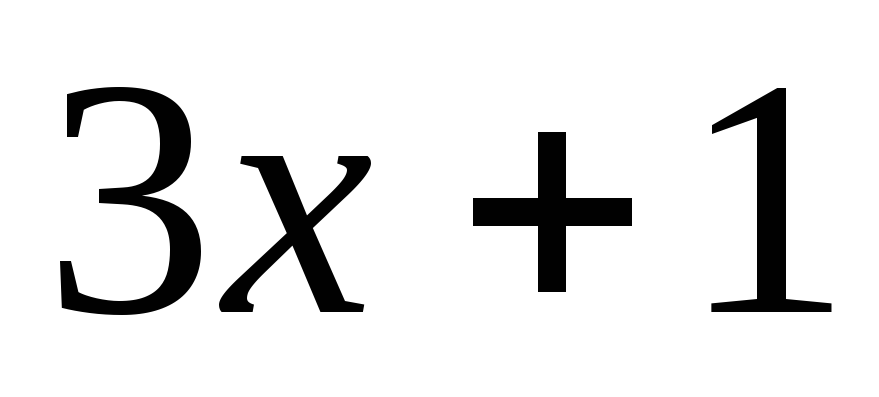 ,
окончательно получим
,
окончательно получим
I=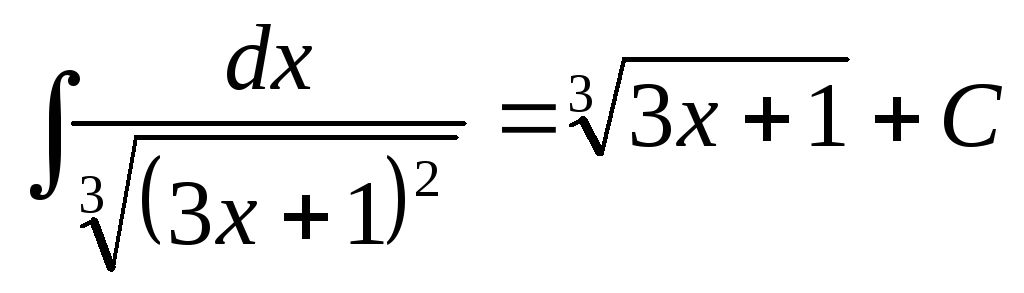 .
.
Выполненное преобразование эквивалентно
подведению под знак дифференциала
функции 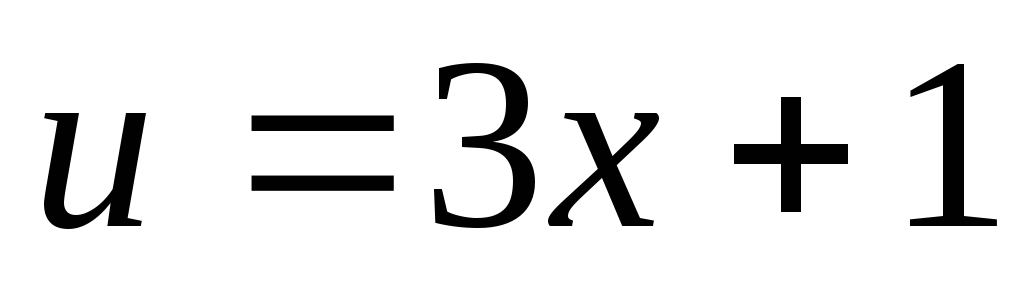 .
.
Пример 16.Найти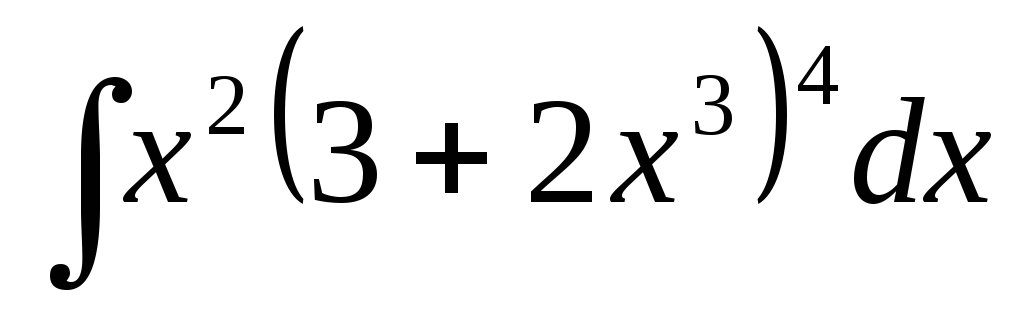 .
.
Положим 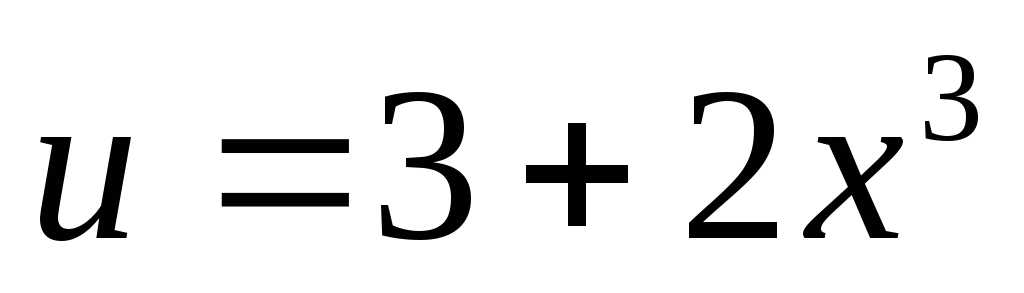 ,
тогда
,
тогда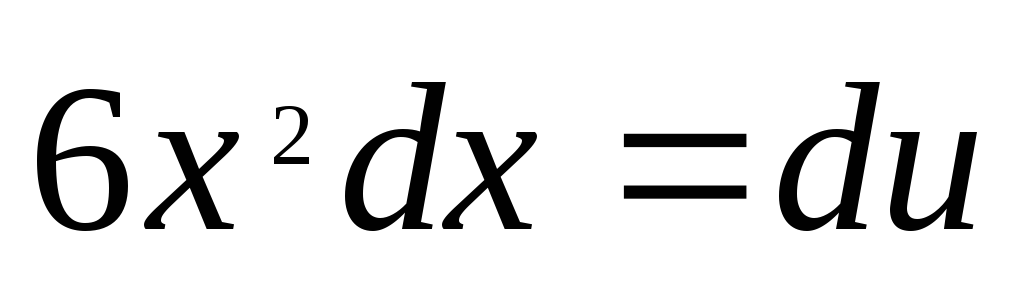 ,
откуда
,
откуда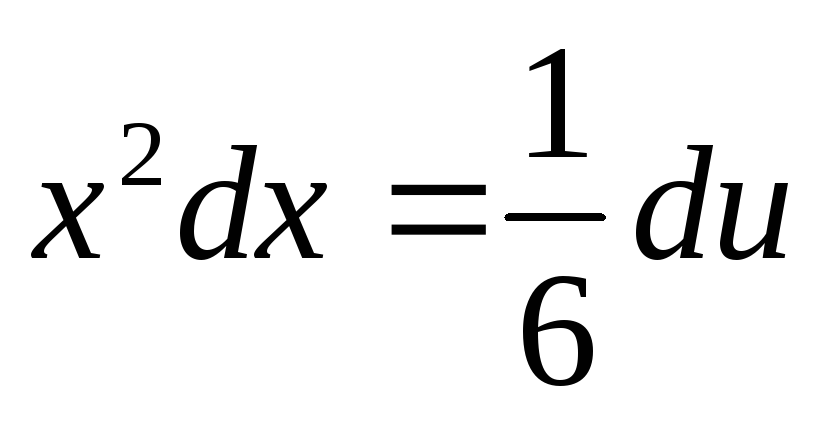 .
Следовательно,
.
Следовательно,
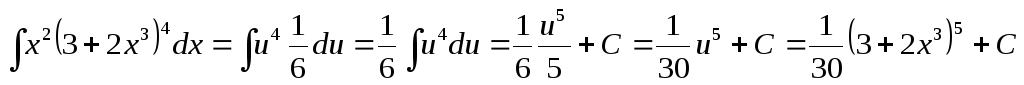 .
.
Пример 17.Найти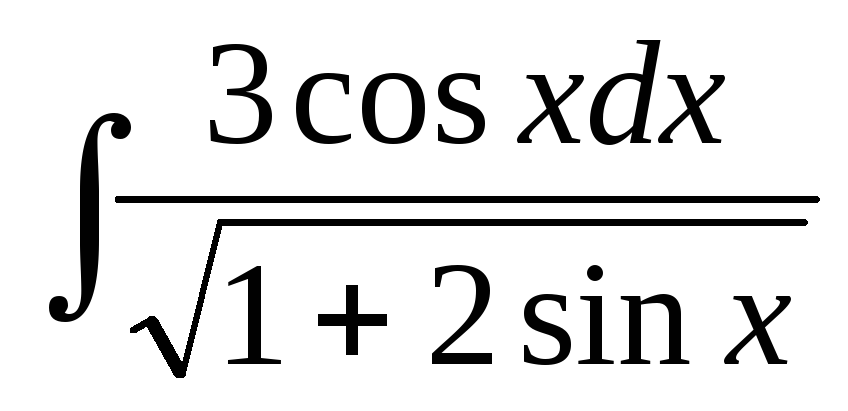 .
.
Пусть 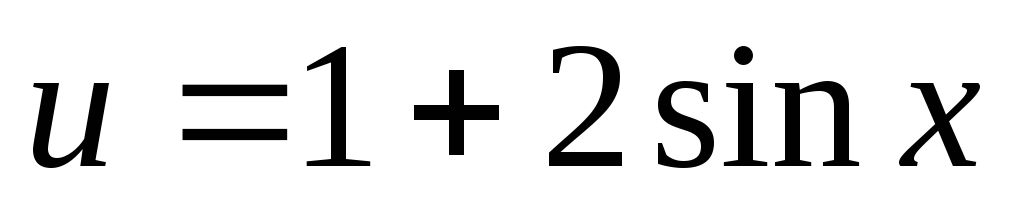 ,
тогда
,
тогда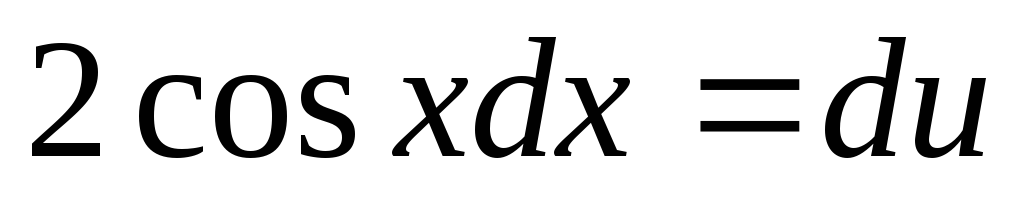 ,
или
,
или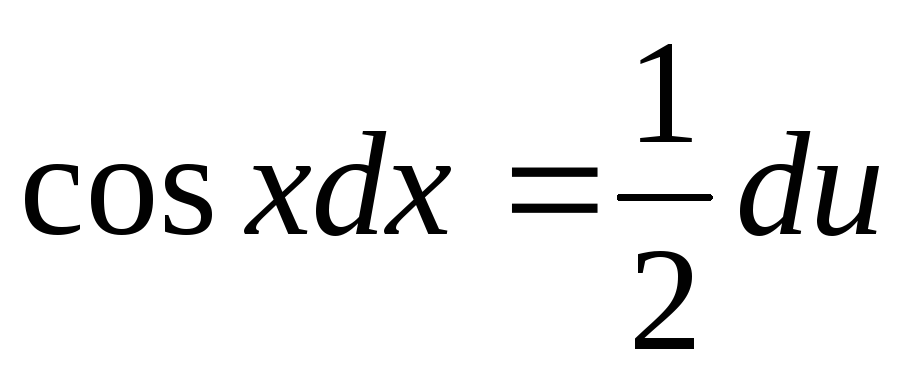 .
Следовательно,
.
Следовательно,
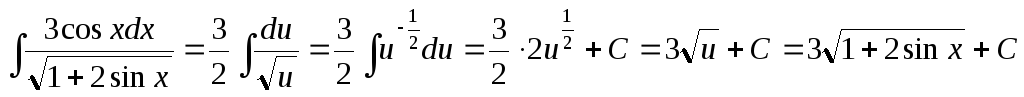 .
.
В заключение отметим, что разные способы интегрирования одной и той же функции иногда приводят к функциям, различным по своему виду. Это кажущееся противоречие можно устранить, если показать, что разность между полученными функциями есть постоянная величина (см. теорему, доказанную на лекции 1).
Примеры:
а) 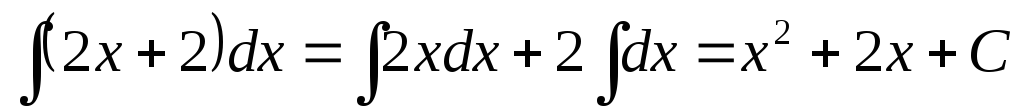 .
.
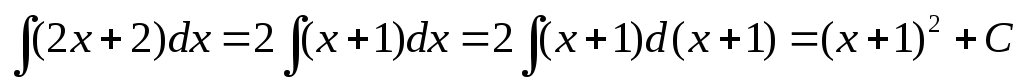 .
.
Результаты отличаются на постоянную величину, и, значит, оба ответа верны.
б) I=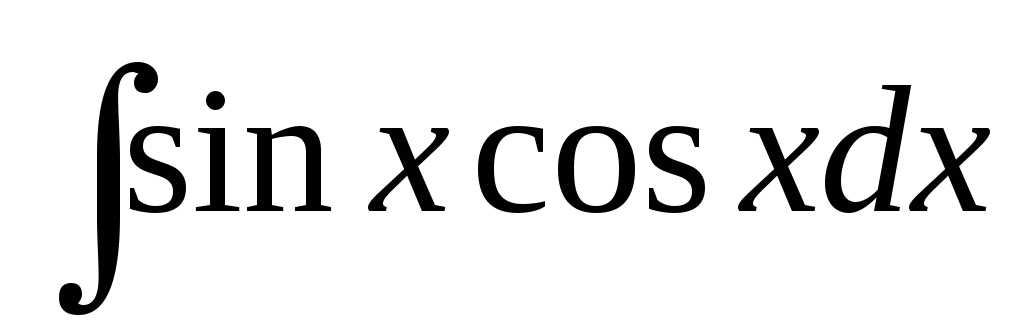 .
.
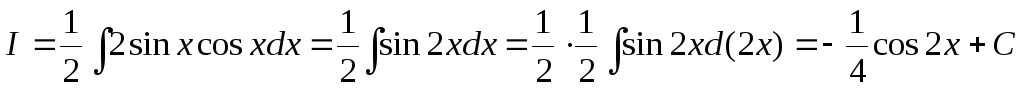 .
.
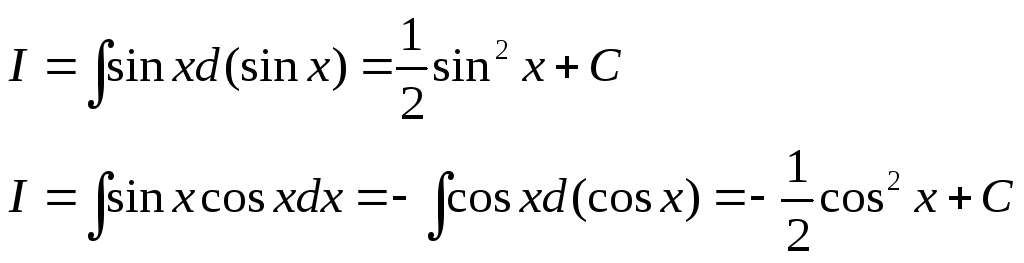
Легко убедиться, что любые из ответов отличаются друг от друга только на постоянную величину.
б) Метод подстановки (метод введения новой переменной)
Пусть интеграл 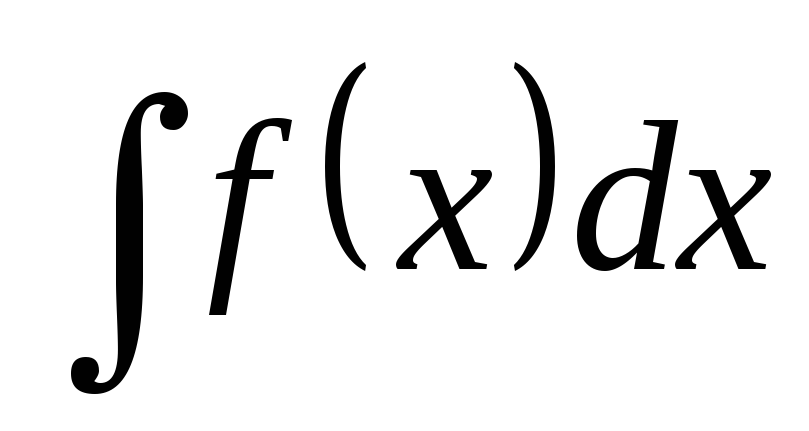 (
(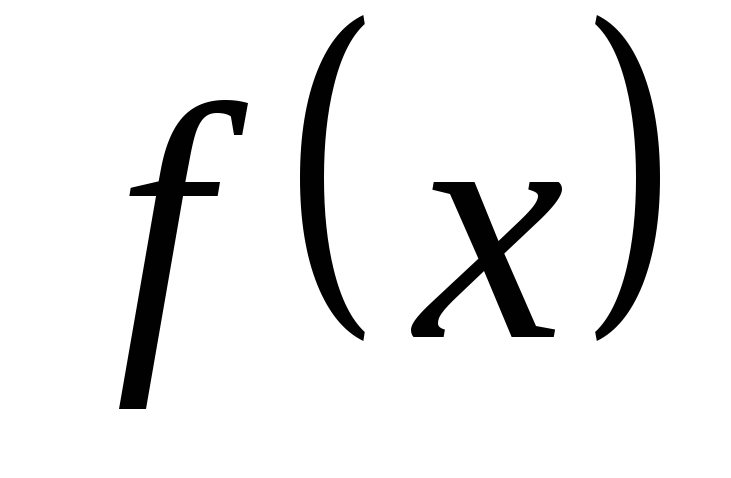 — непрерывна) не может быть непосредственно
преобразован к виду табличного. Сделаем
подстановку,
где
— непрерывна) не может быть непосредственно
преобразован к виду табличного. Сделаем
подстановку,
где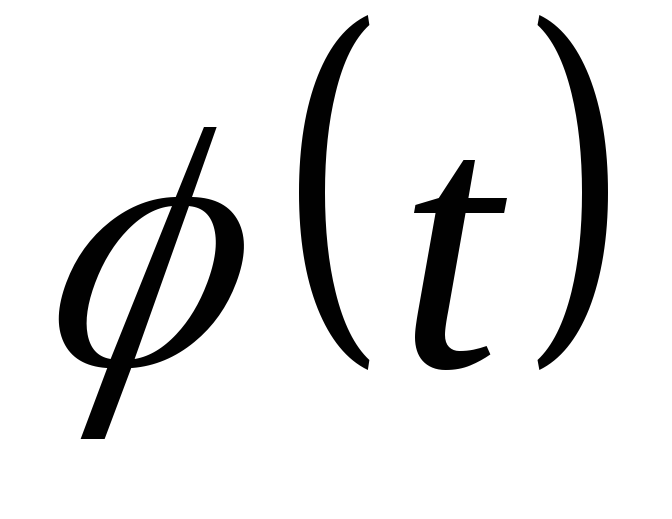 — функция, имеющая непрерывную производную.
Тогда
— функция, имеющая непрерывную производную.
Тогда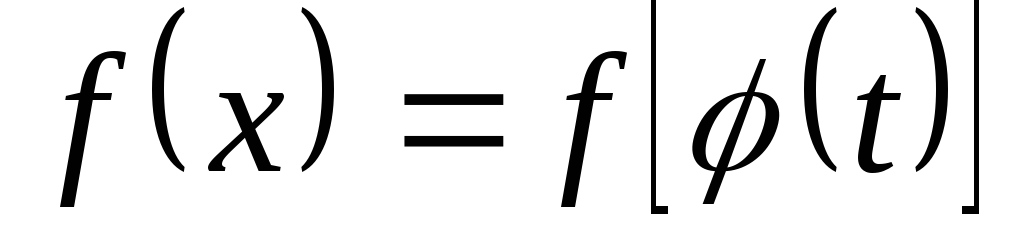 ,
,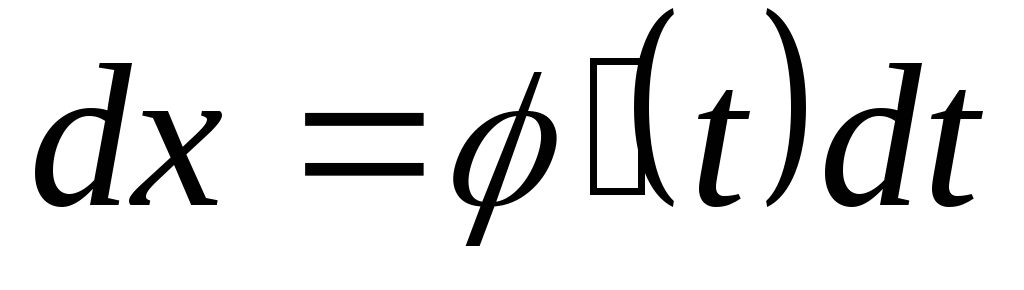 и
и
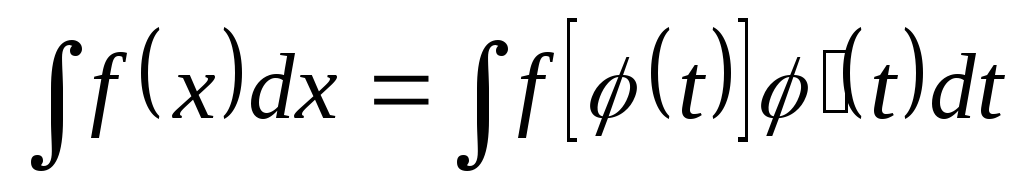 .
(3)
.
(3)
Формула (3) называется формулой замены переменной в неопределенном интеграле.
Как правильно выбрать подстановку? Это достигается практикой в интегрировании. Но можно установить ряд общих правил и некоторых приемов для частных случаев интегрирования.
Правило интегрирования способом подстановки состоит в следующем.
Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно).
Определяют, какую часть подынтегральной функции заменить новой переменной, и записывают эту замену.
Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.
Производят замену под интегралом.
Находят полученный интеграл.
Производят обратную замену, т.е. переходят к старой переменной.
Проиллюстрируем правило примерами.
Пример
18.Найти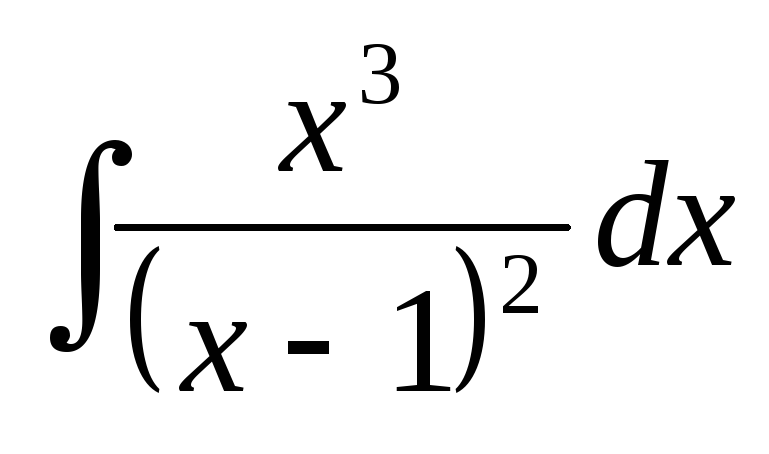 .
.
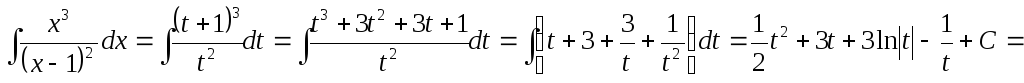
= 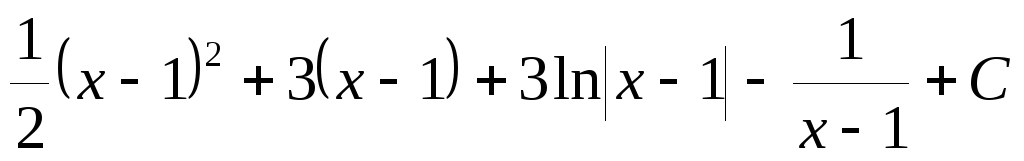 .
.
Пример
19.Найти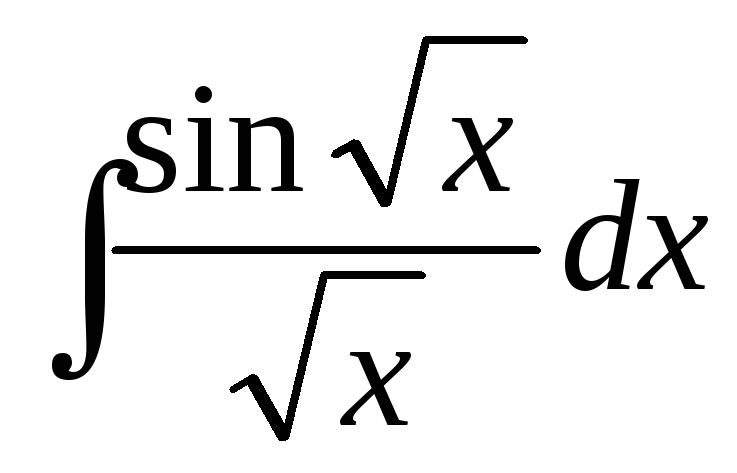 .
.
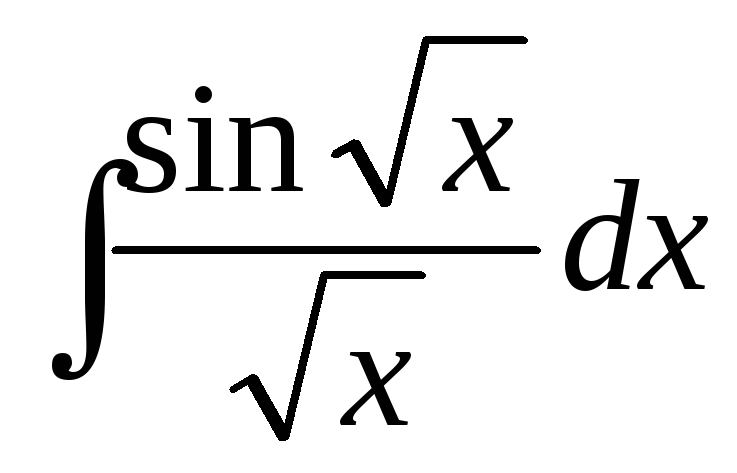 =
=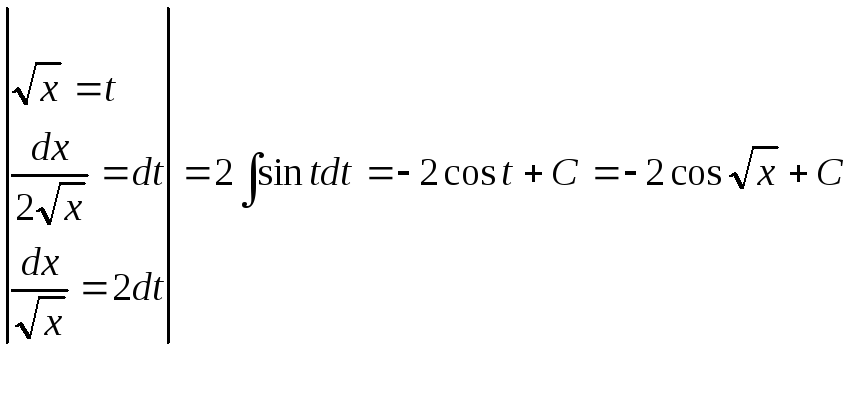 .
.
Этот интеграл найдем подведением 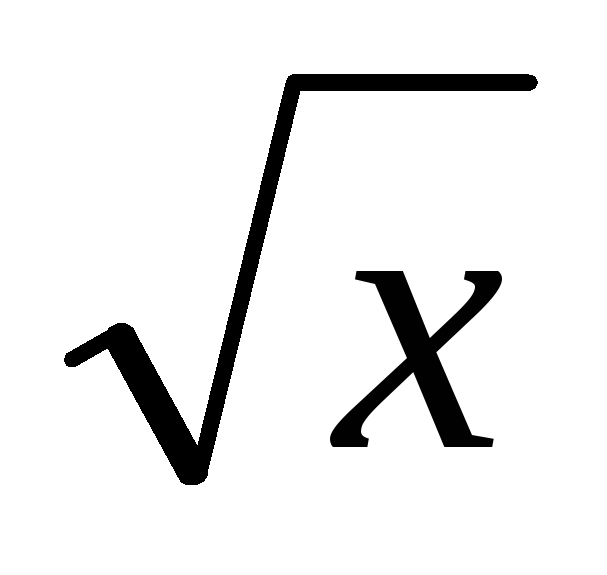 под
знак дифференциала.
под
знак дифференциала.
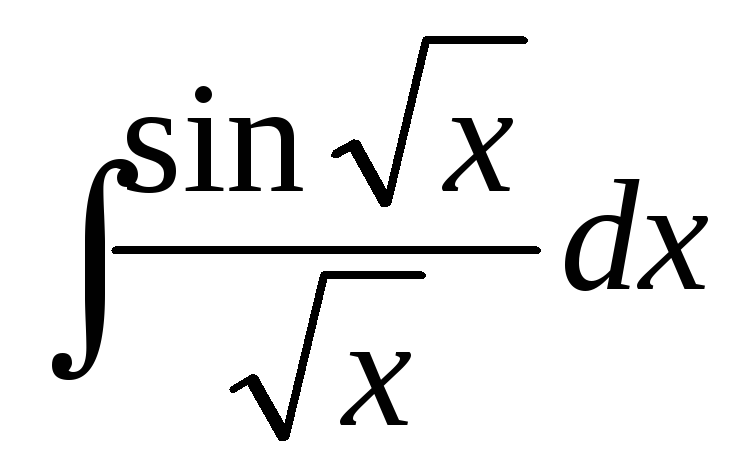 =
=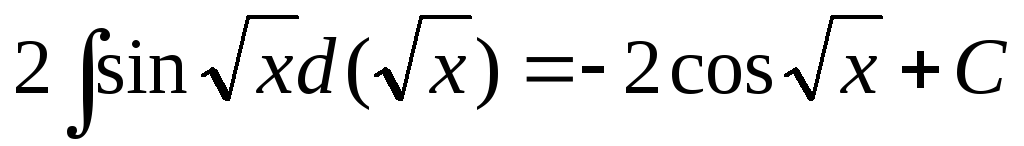 .
.
Пример 20.Найти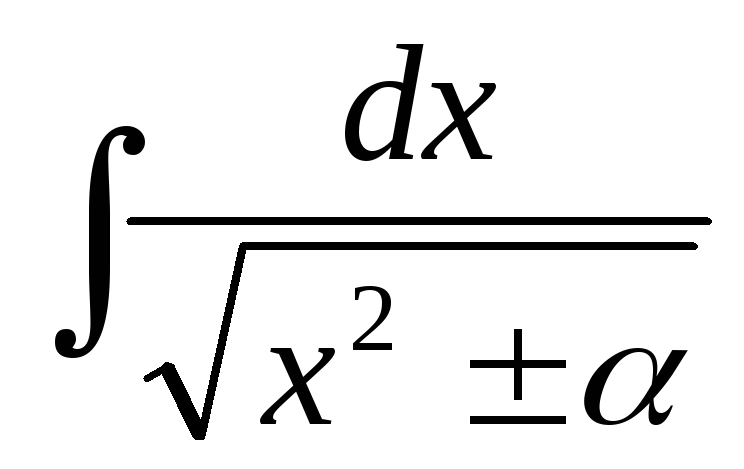 (
(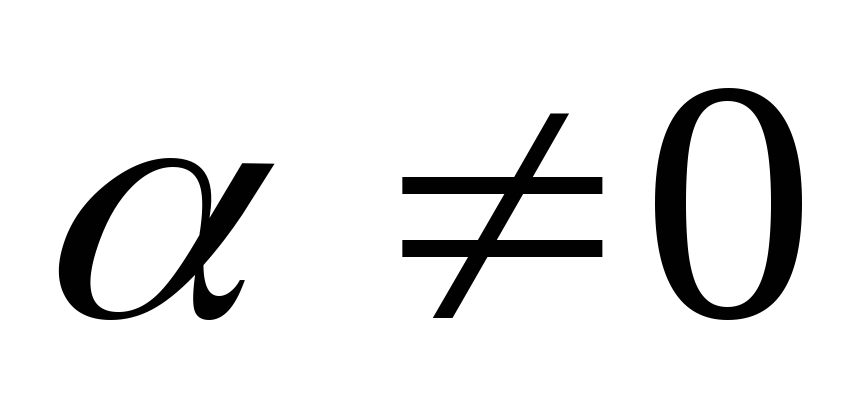 ).
).
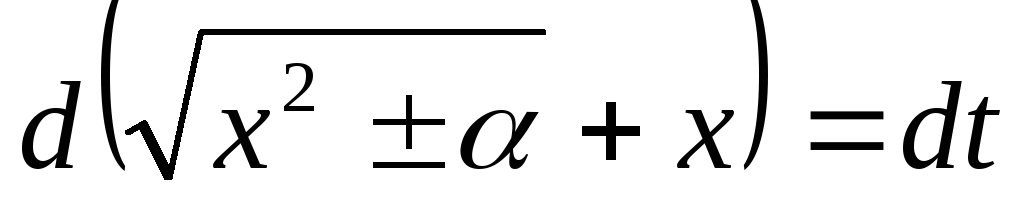 ,
т.е.
,
т.е.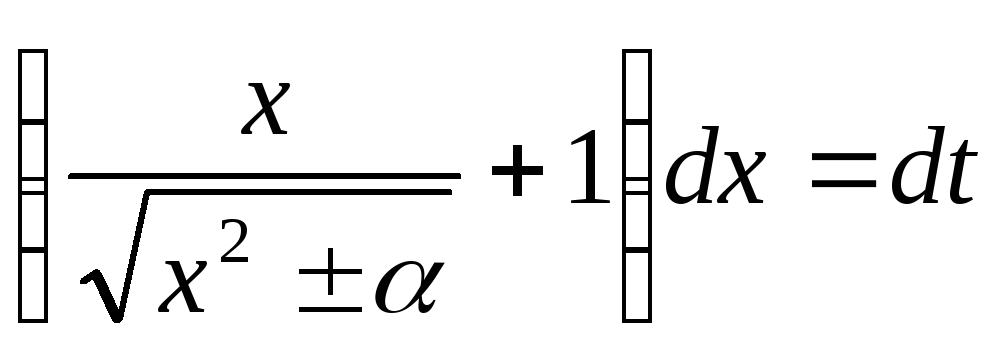 ,
или
,
или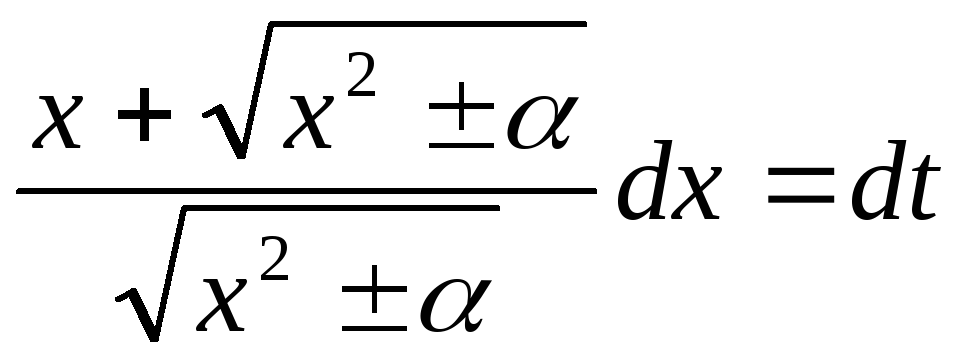 .
Отсюда
.
Отсюда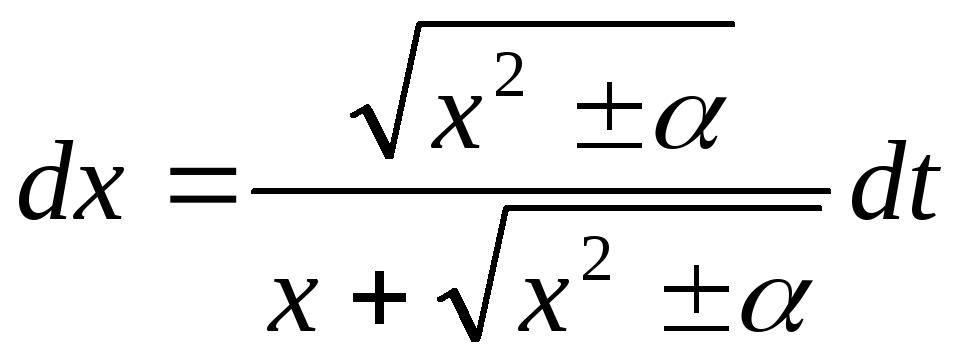 ,
т.е.
,
т.е.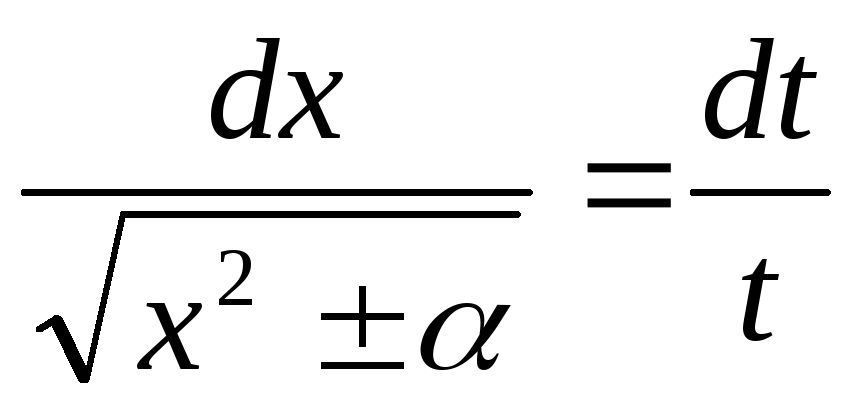 .
.
Таким образом, имеем 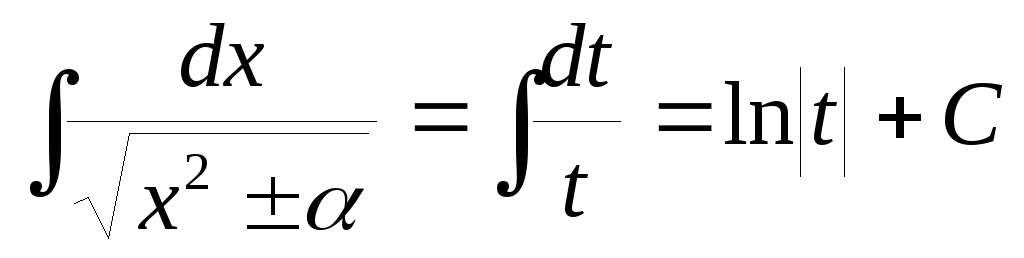 .
Заменяя
.
Заменяя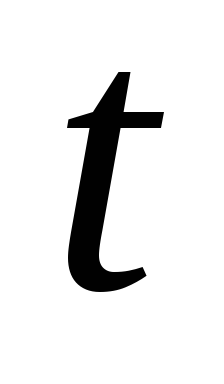 его выражением черезx, окончательно
находим интеграл, играющий важную роль
в интегрировании иррациональных функций:
его выражением черезx, окончательно
находим интеграл, играющий важную роль
в интегрировании иррациональных функций: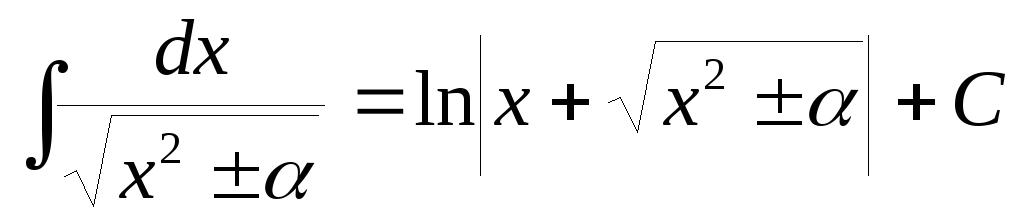 (
(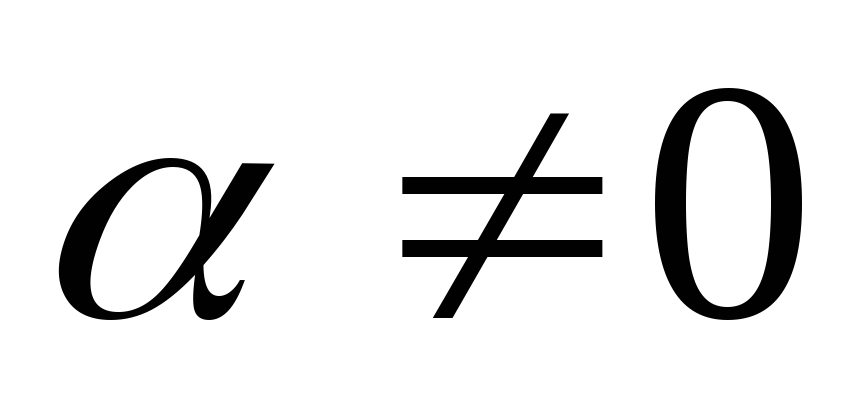 ).
).
Студенты прозвали этот интеграл «длинным логарифмом».
Иногда вместо подстановки 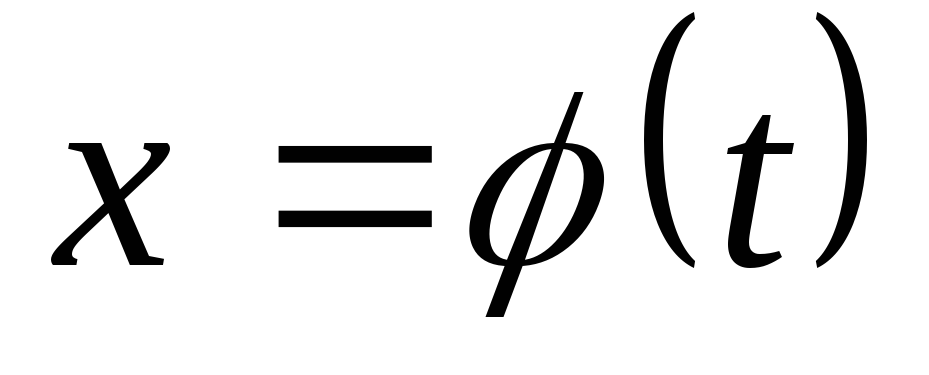 лучше выполнять замену переменной вида
лучше выполнять замену переменной вида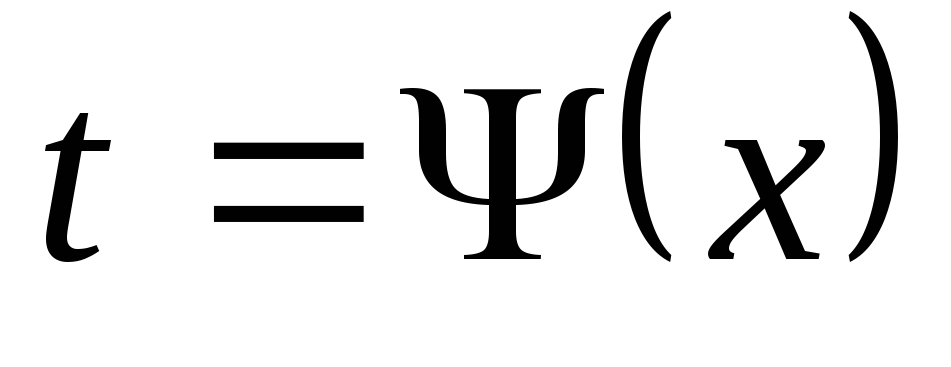 .
.
Пример 21.Найти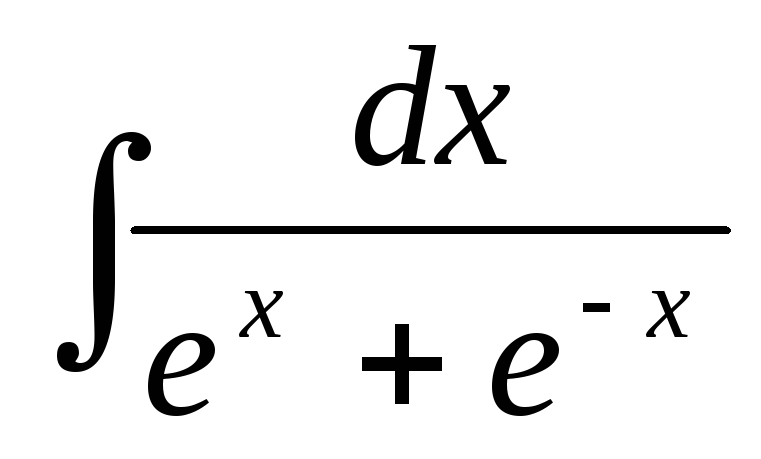 .
.
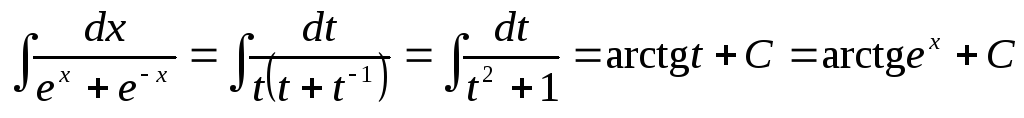 .
.
Пример 22.Найти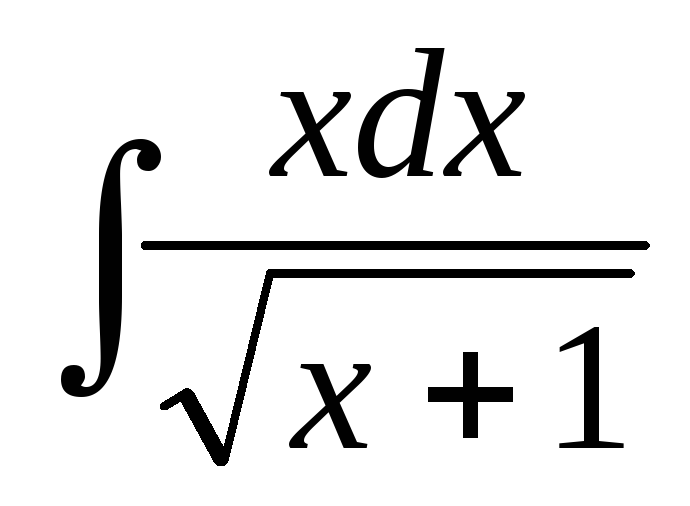 .
.
Воспользуемся подстановкой 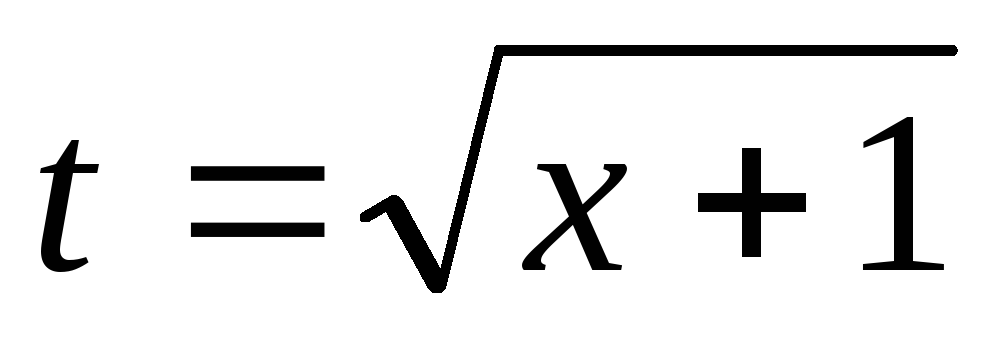 .
Тогда
.
Тогда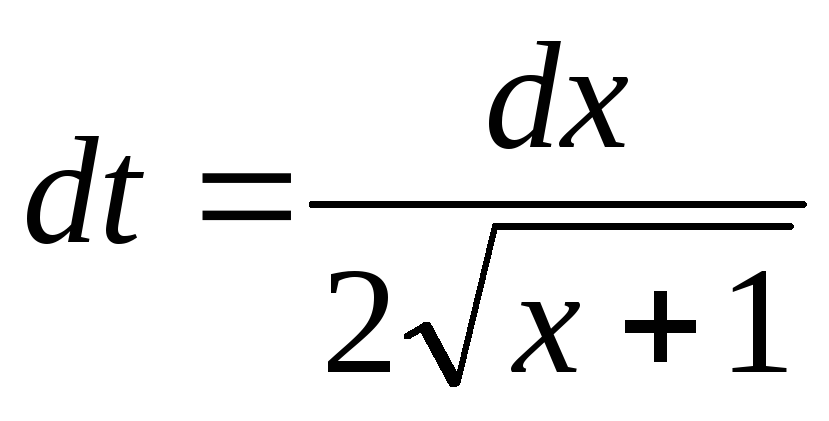 ,
,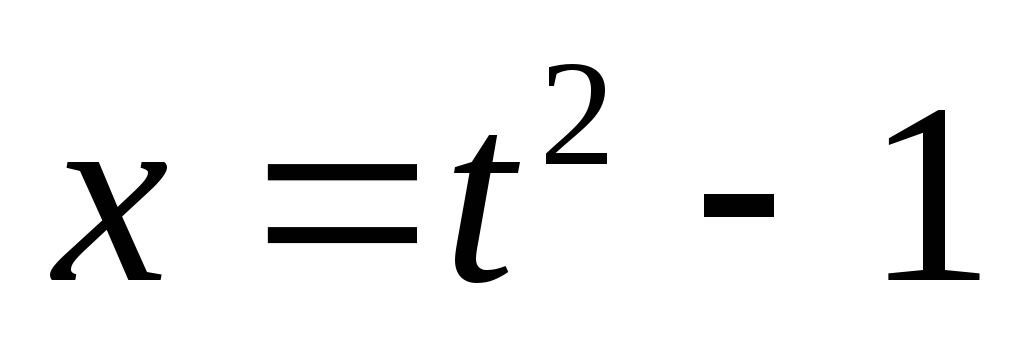 ,
,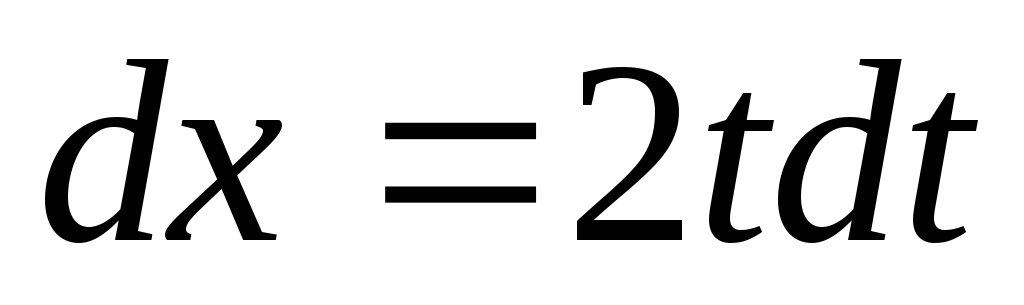 .
.
Следовательно, 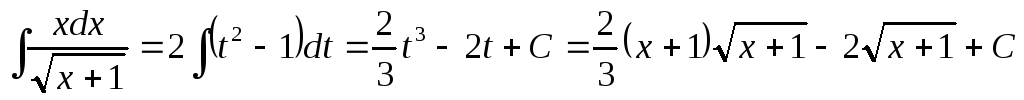 .
.
В ряде случаев нахождение интеграла основывается на использовании методов непосредственного интегрирования и подведения функций под знак дифференциала одновременно (см. пример 12).
Проиллюстрируем этот комбинированный подход к вычислению интеграла, играющего важную роль при интегрировании тригонометрических функций.
Пример 23.Найти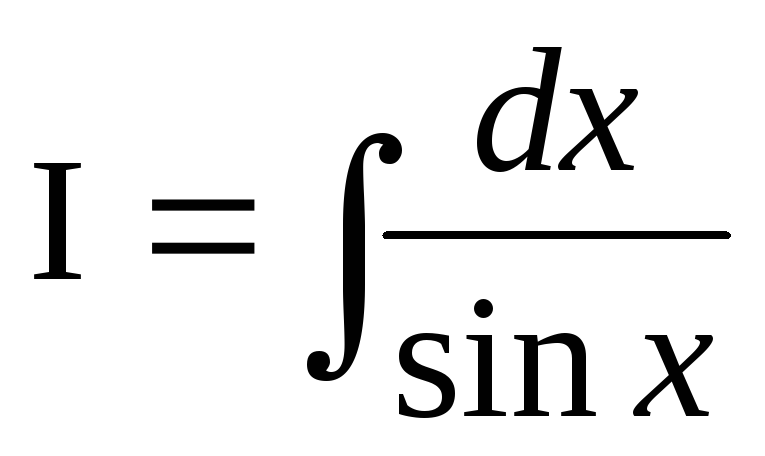 .
.
Имеем

=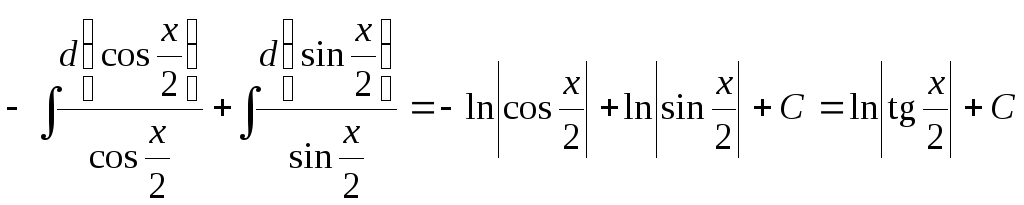 .
.
Итак, 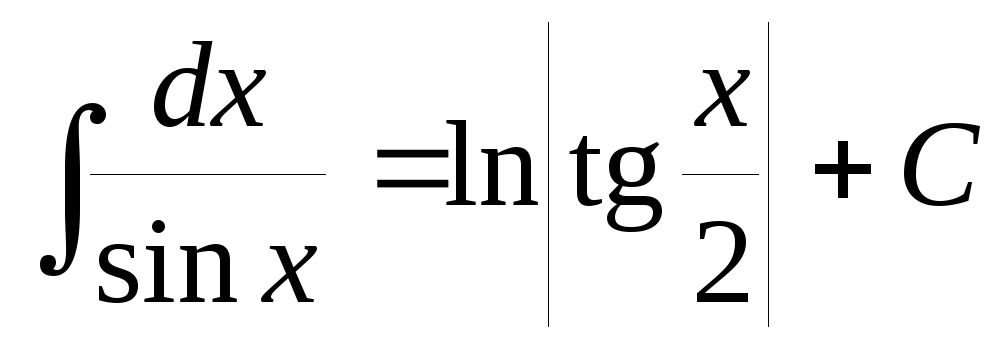 .
.
Другой подход к вычислению этого интеграла:
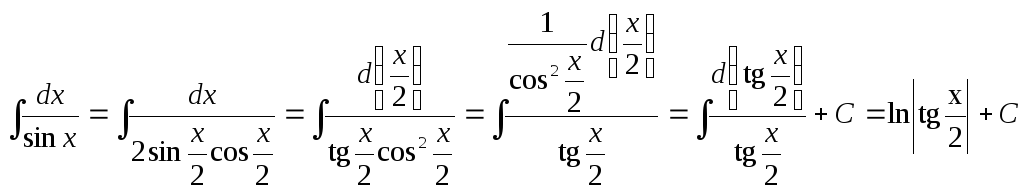 .
.
Пример 24.Найти.
Заметим, что удачный выбор подстановки обычно представляет трудности. Для их преодоления необходимо овладеть техникой дифференцирования и хорошо знать табличные интегралы.
Лекция 3.
studfile.net
6.5. Методы интегрирования
Интегрирование является значительно более сложным действием, чем дифференцирование, поскольку для отыскания первообразных нет таких универсальных правил и формул, как в дифференциальном исчислении.
Методы интегрирования сводятся к указанию ряда приемов, приводящих данный интеграл к табличному. К наиболее важным методам интегрирования относятся: непосредственное интегрирование, замена переменной (метод подстановки) и интегрирование по частям.
Метод непосредственного интегрирования
Интегрирование, основанное на прямом использовании таблицы интегралов и свойств неопределенного интеграла, называется непосредственным интегрированием.
При непосредственном интегрировании могут представиться три случая.
I. Интеграл находят непосредственно по соответствующему табличному интегралу.
Примеры
1) 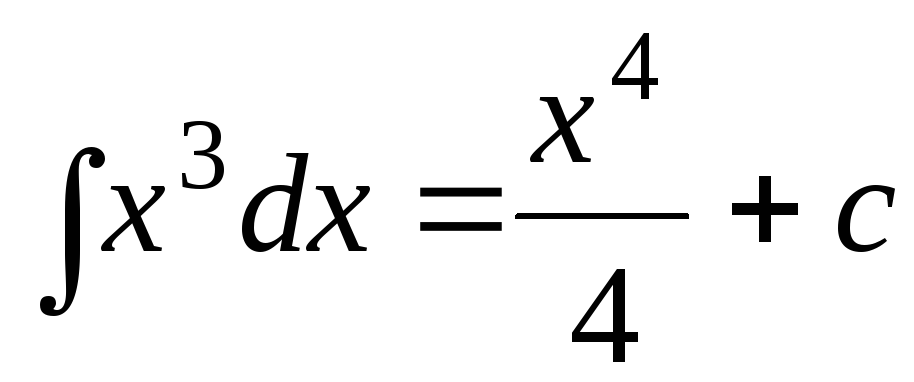 ;
;
2) 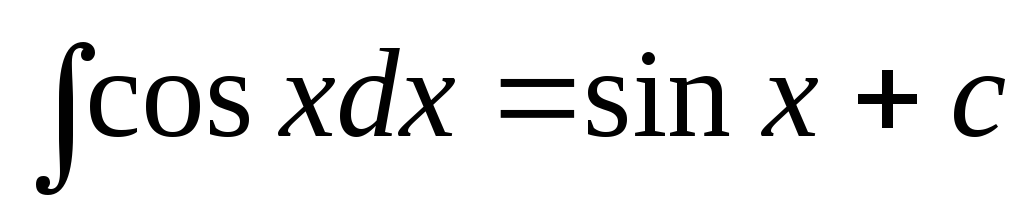 ;
;
II. Интеграл приводится к одному или нескольким табличным интегралам в результате применения свойств неопределенного интеграла.
Примеры
1. 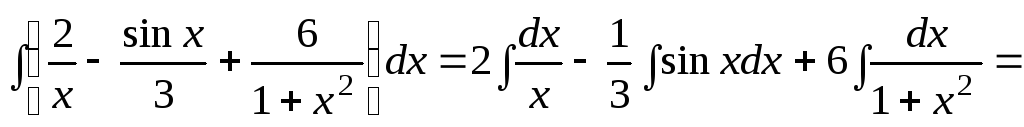
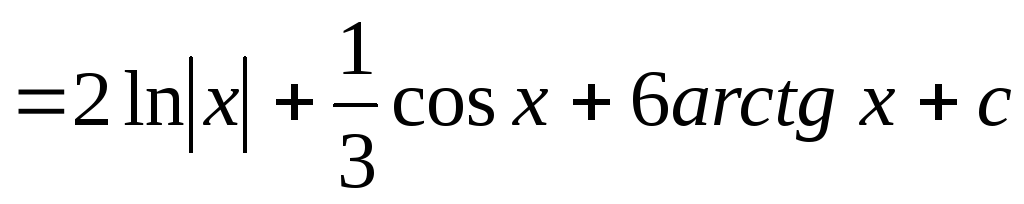 ;
;
2. 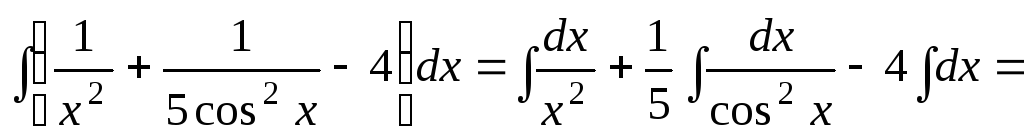
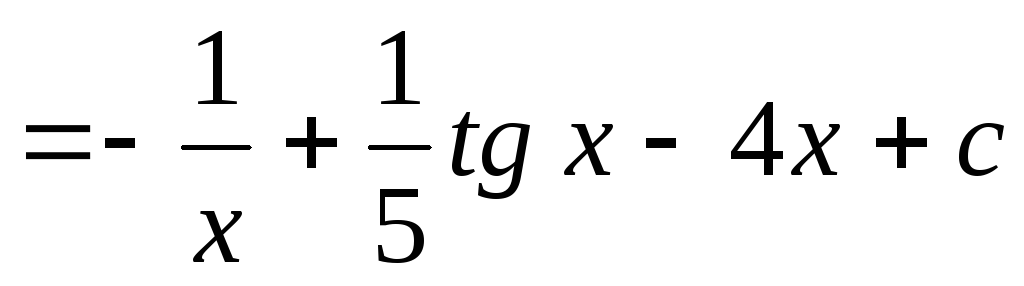 .
.
III. Интеграл приводится к одному или нескольким табличным интегралам в результате элементарных тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла.
Примеры
1. 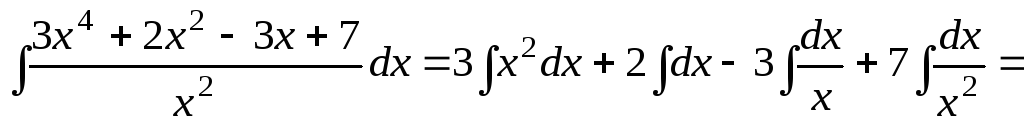
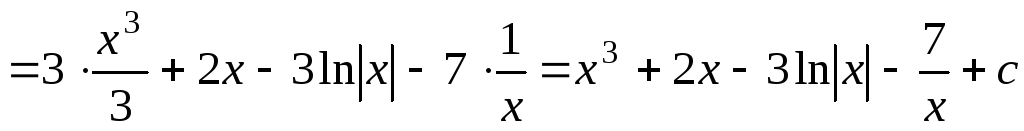 ;
;
2. 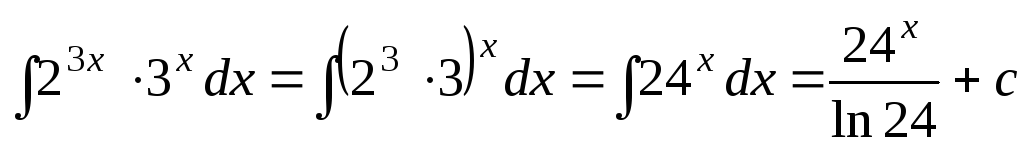 ;
;
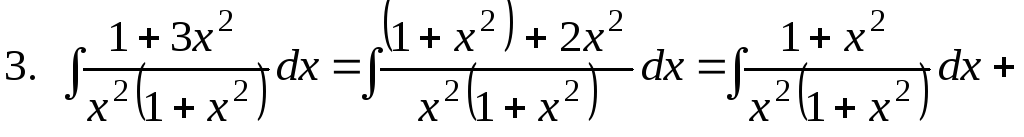
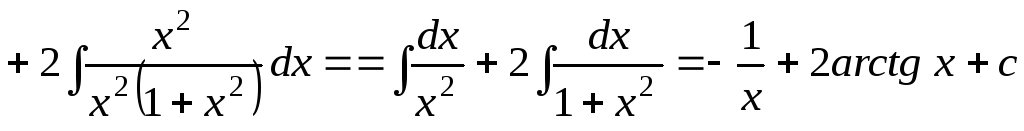 ;
;
4.
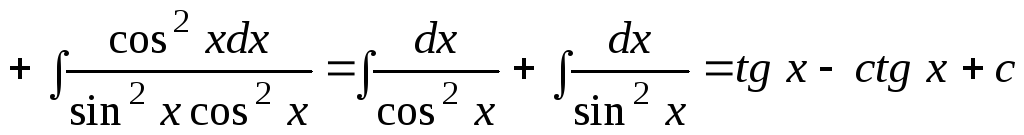 .
.
Метод интегрирования подстановкой (замена переменной)
Сущность метода заключается в том, что путем введения новой переменной интегрирования (т.е. подстановки) удается свести заданный интеграл к новому интегралу, который является табличным или легко находится другим способом. Общих методов подбора подстановок не существует. Рассмотрим некоторые варианты подстановок.
Линейные подстановки
При сведении данного интеграла к табличному часто используются преобразования дифференциала (операция «подведения под знак дифференциала»).
I. Под знак дифференциала, стоящего в интеграле, можно ввести любое постоянное слагаемое.
При любой постоянной а будет
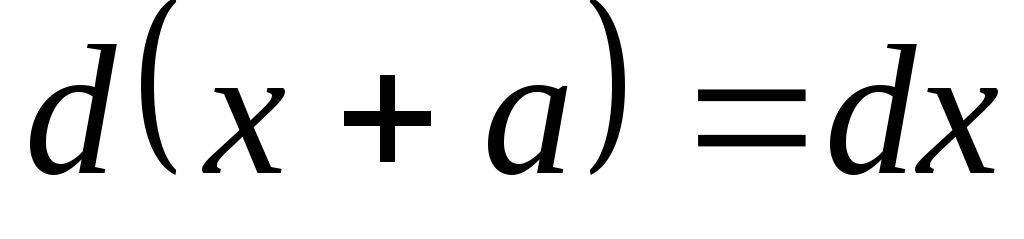 .
.
Поэтому
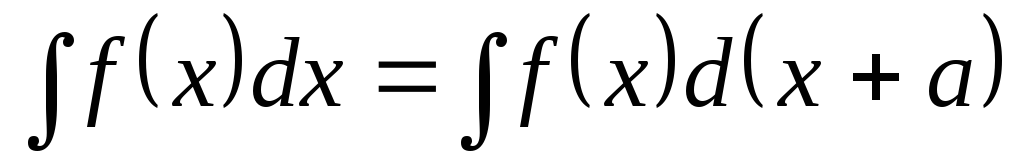 .
.
Примеры
1.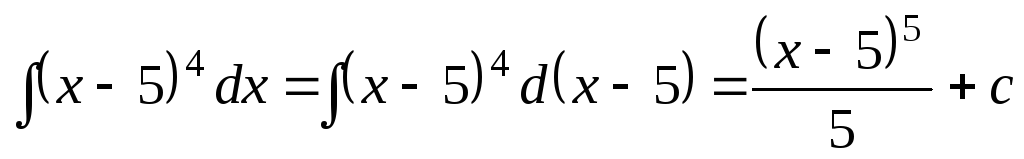 ;
;
2. 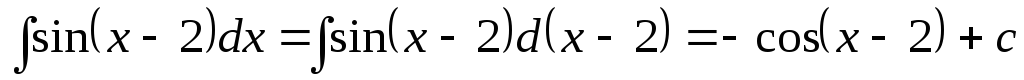 ;
;
3. 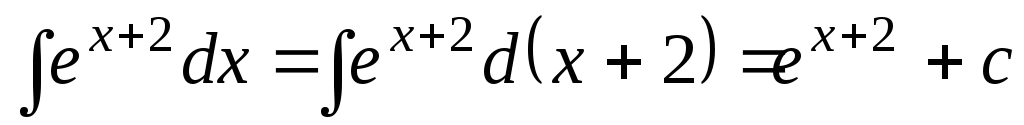 .
.
II. Под знак дифференциала, стоящего в интеграле, можно ввести любой постоянный множитель, разделив на него интеграл.
Известно, если а − постоянно, то
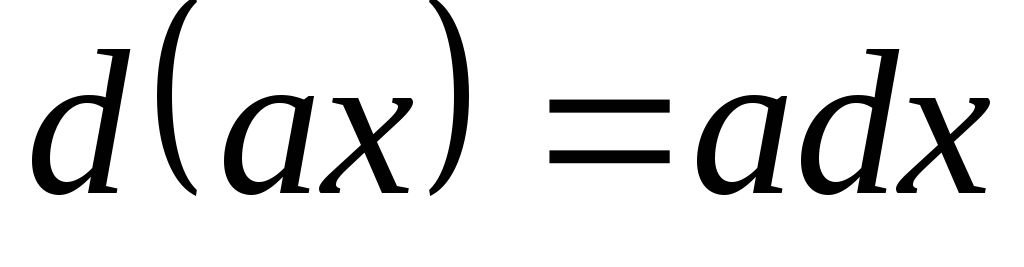 .
.
Тогда
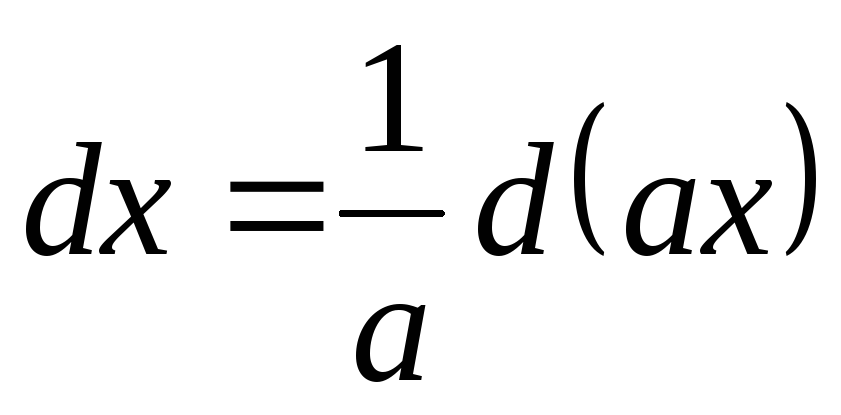 .
.
Поэтому
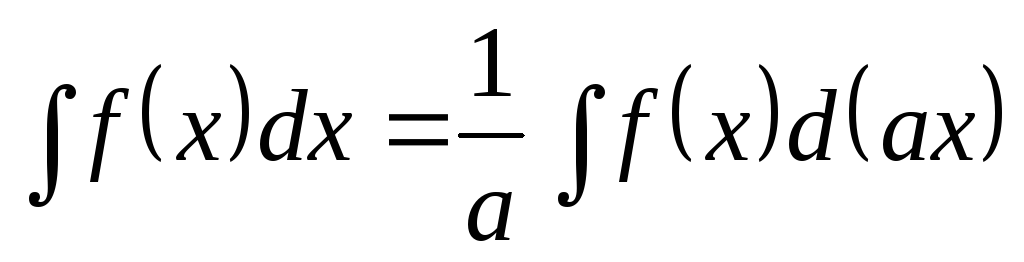 .
.
Примеры
1. 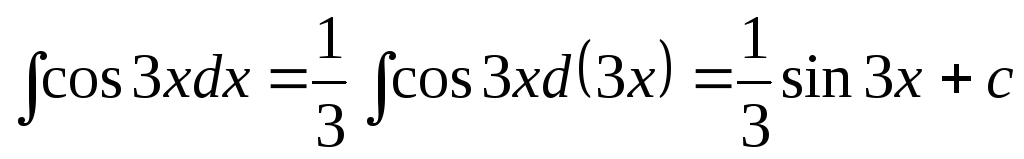 ;
;
2. 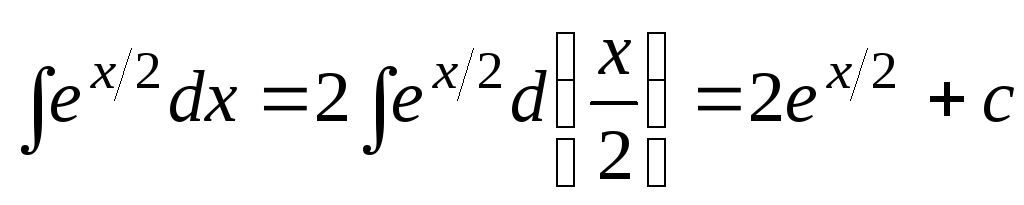 ;
;
3. 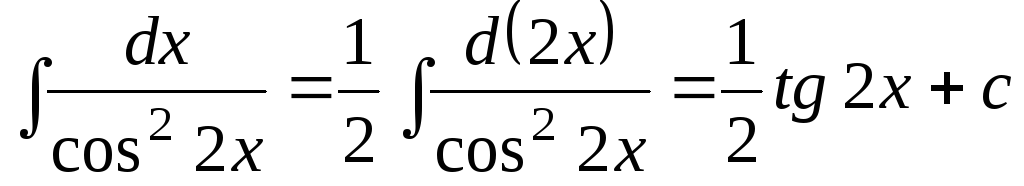 .
.
В некоторых случаях применяют оба приема вместе:
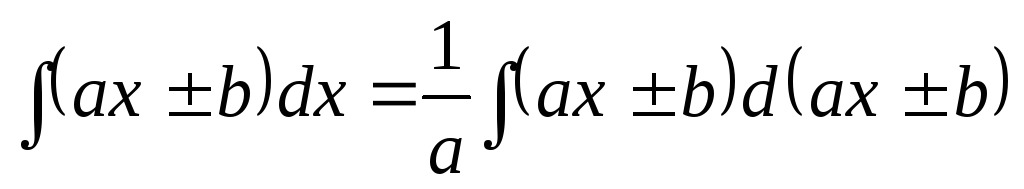 ,
,
где а и b − постоянные.
Примеры
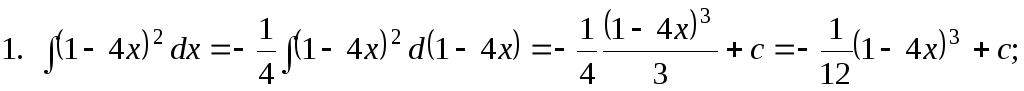
2. 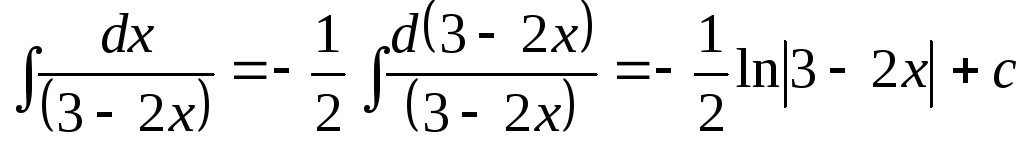 ;
;
3. 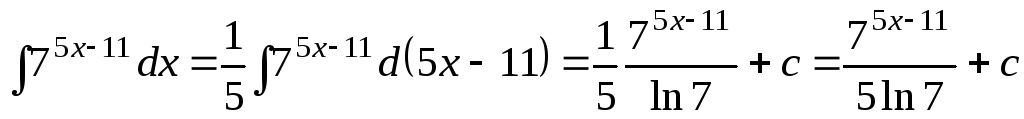 .
.
Подстановка вида 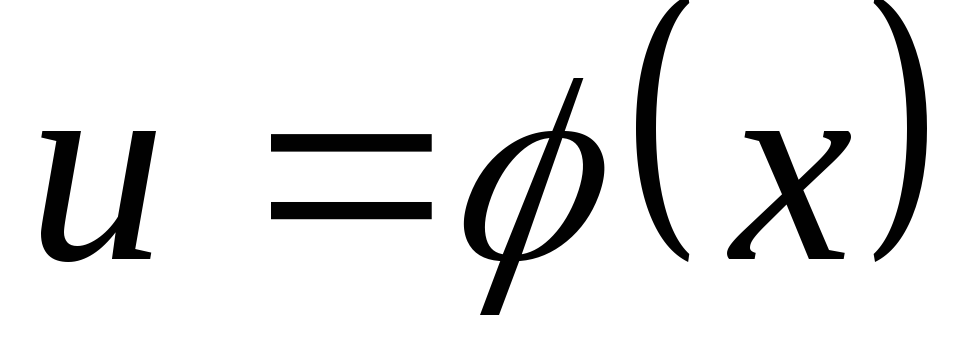
Если под знаком интеграла стоит сложная функция, умноженная на производную от внутренней функции, т.е. интеграл имеет вид:
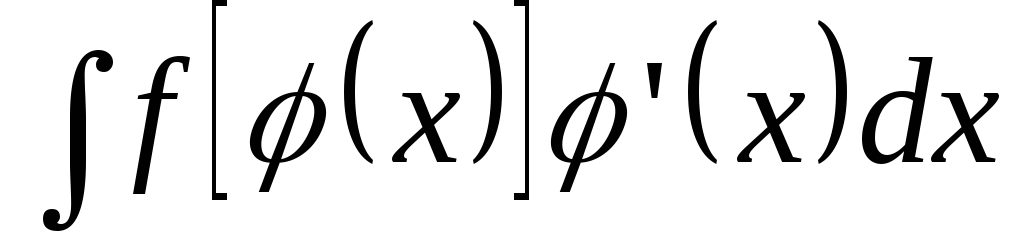 ,
,
то этот интеграл
можно упростить, если заменить внутреннюю
функцию новой переменной 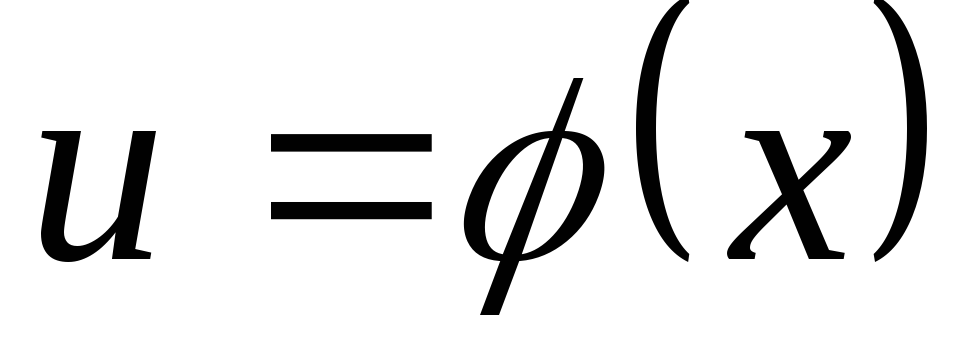 .
.
Тогда получим
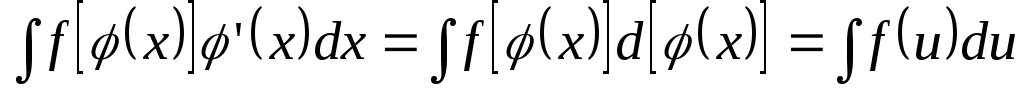 .
.
В данном случае
была применена операция «подведения
под знак дифференциала» (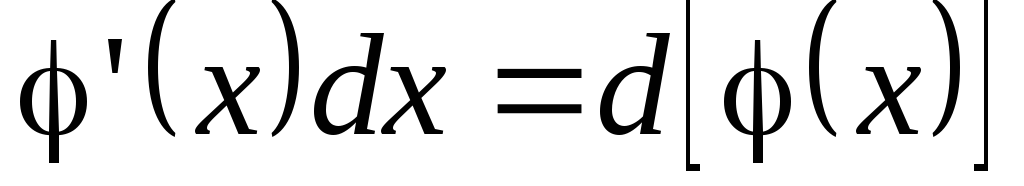 ).
).
Для применения
подстановки 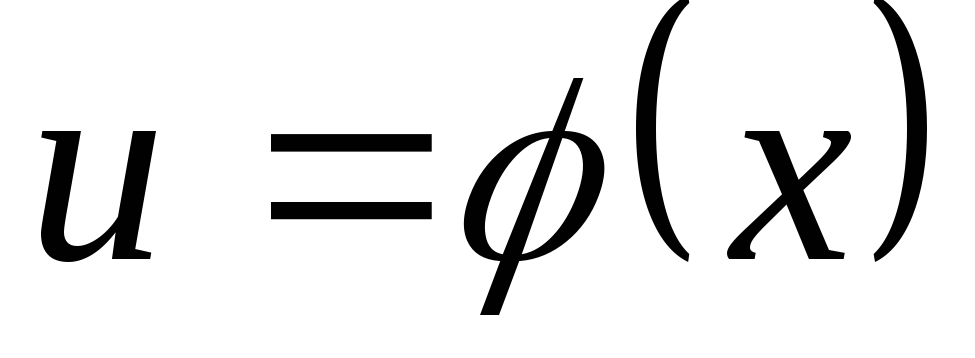 существует следующее правило.
существует следующее правило.
Правило.
Чтобы найти интеграл 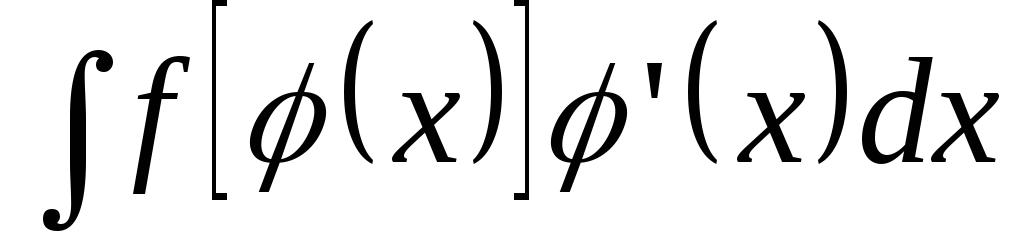 ,
надо
,
надо
1) переписать интеграл в виде
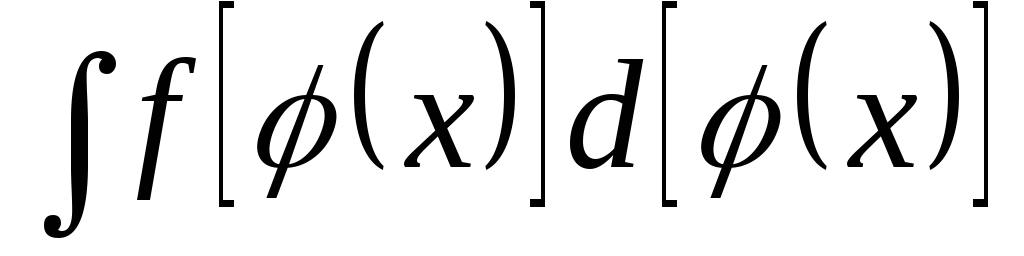 ;
;
2) сделать замену 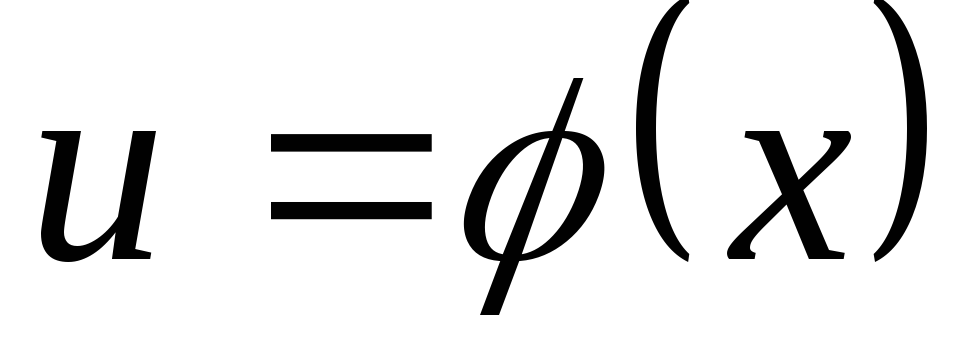 ,
что приведет к интегралу
,
что приведет к интегралу
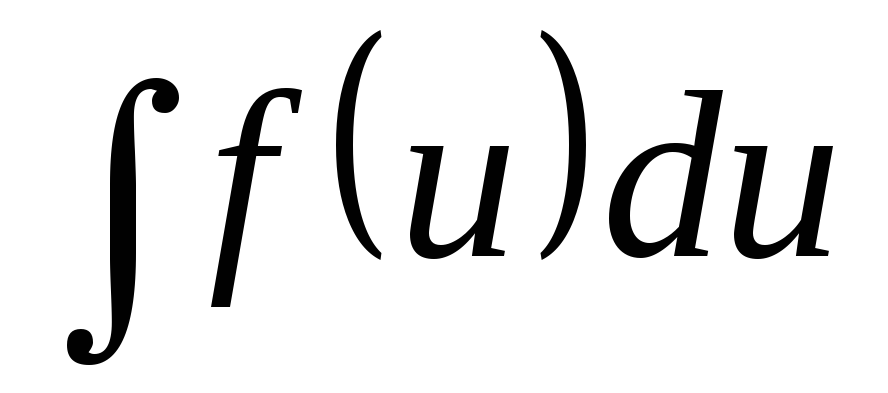 ;
;
3) найти последний интеграл;
4) в полученном
ответе произвести обратную замену u на 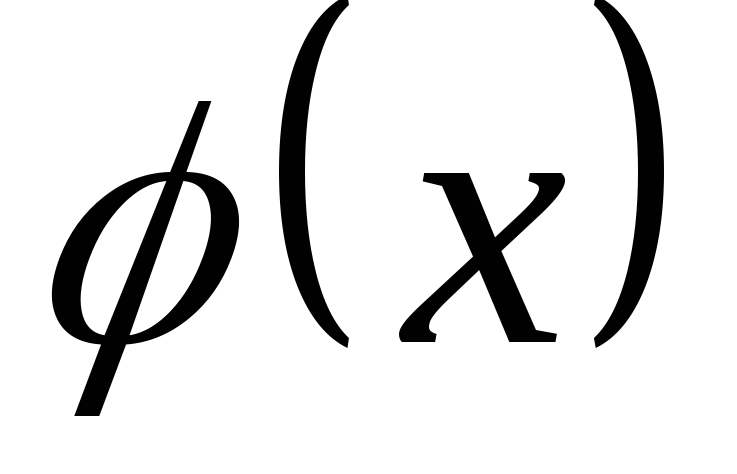 .
.
Примеры
1. 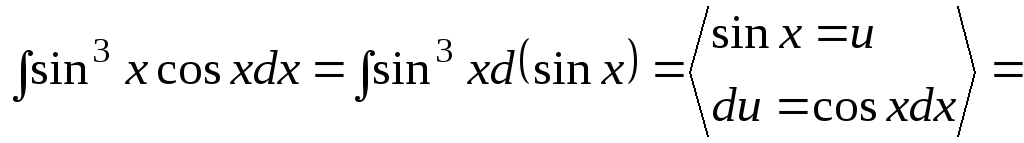
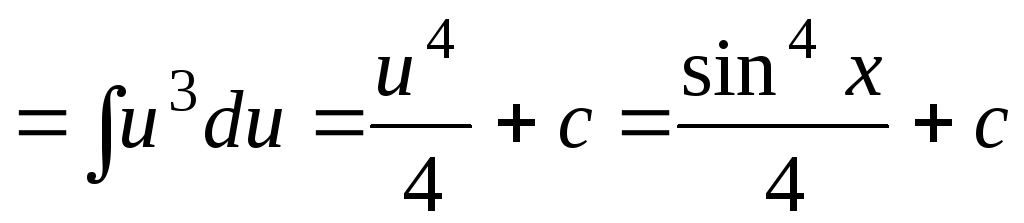 ;
;
2. 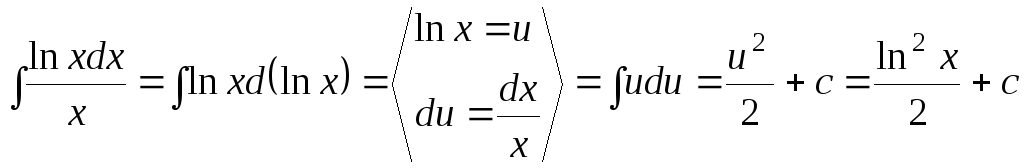 ;
;
3. 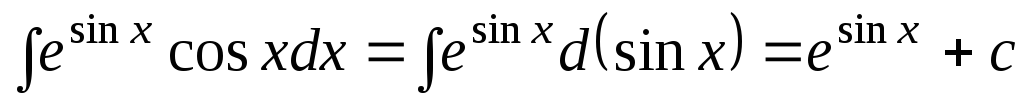 ;
;
4. 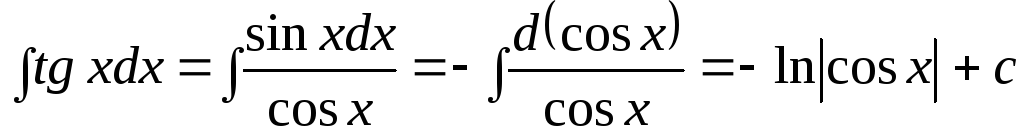 .
.
Подстановка вида
Пусть требуется найти интеграл
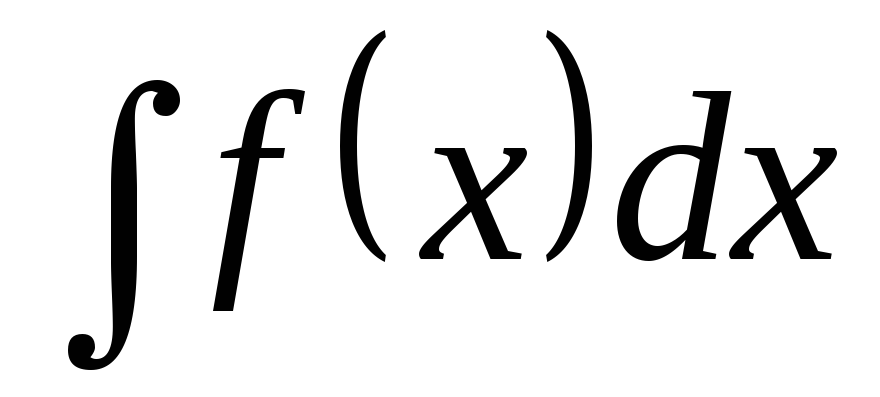 .
.
Иногда бывает
целесообразно при вычислении такого
интеграла, в котором независимой
переменой является х,
сделать подстановку 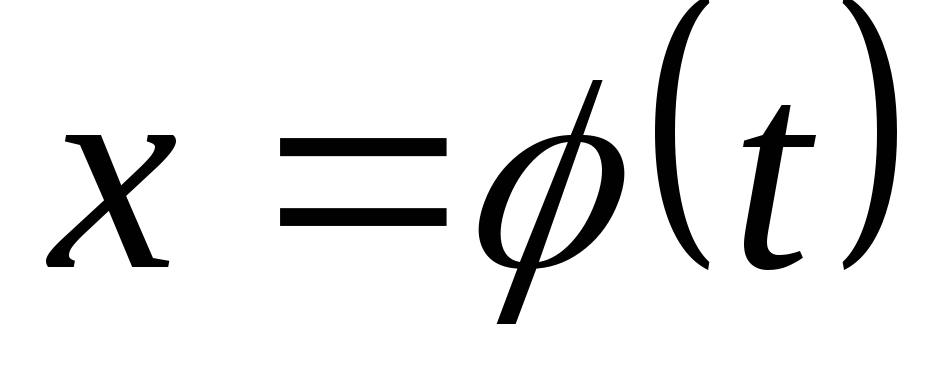 .
Преобразуя подынтегральное выражение
путем подстановки, имеем
.
Преобразуя подынтегральное выражение
путем подстановки, имеем
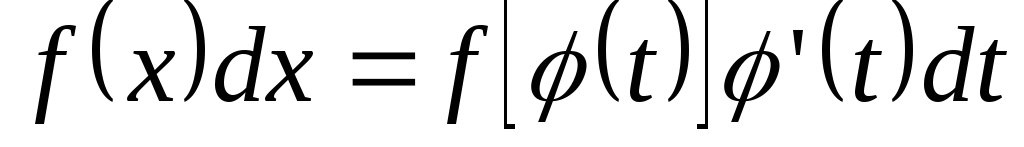 ,
,
так как 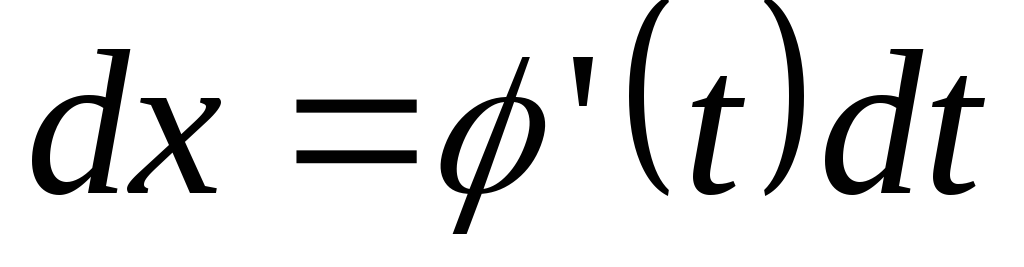 .
.
В результате
получаем формулу интегрирования
подстановкой 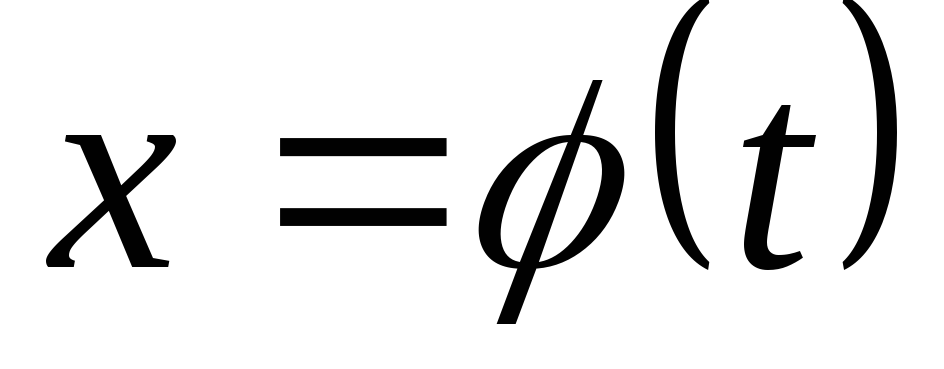 :
:
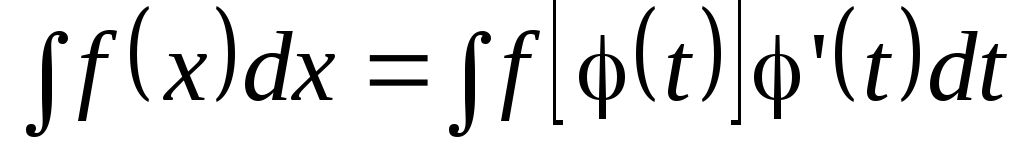 .
.
Замечание.
Функция 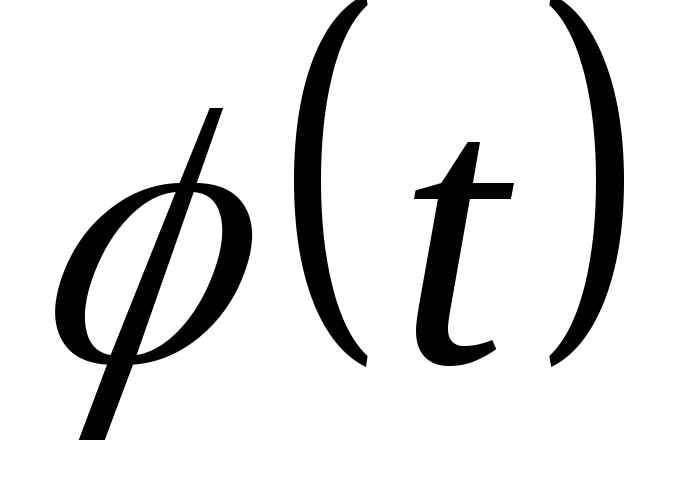 выбирается так, чтобы интеграл в правой
части равенства был более простым, чем
первоначальный.
выбирается так, чтобы интеграл в правой
части равенства был более простым, чем
первоначальный.
Сформулируем правило подстановки.
Правило.
Чтобы найти интеграл 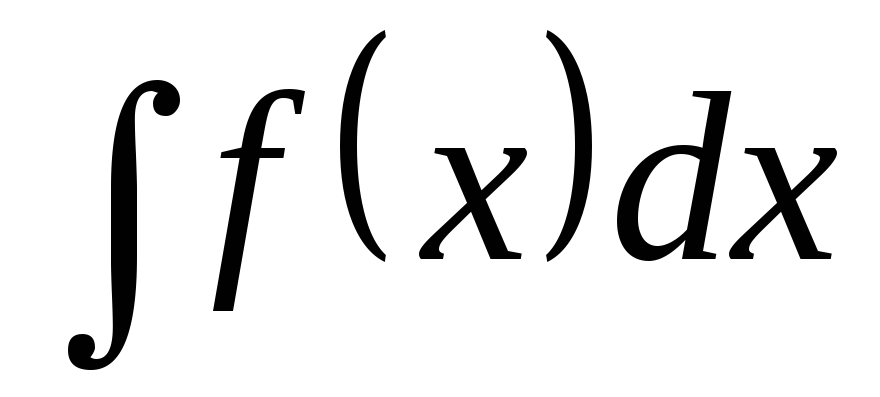 ,
надо
,
надо
1) перейти к новой
переменной t,
связанной с х выражением 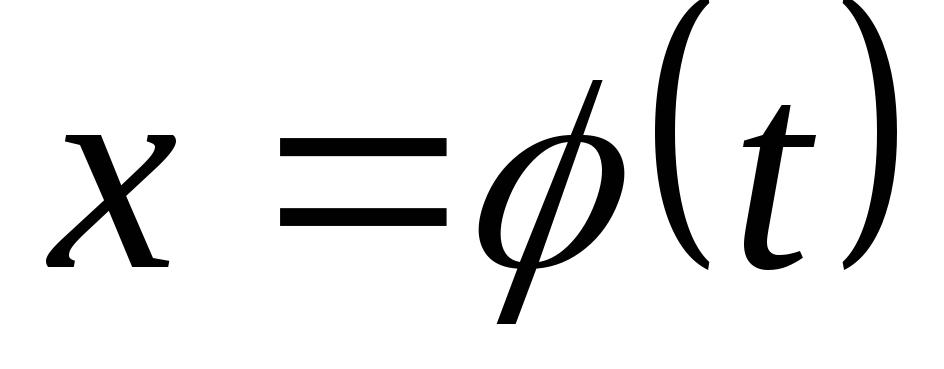 ;
;
2) выразить через t все подынтегральное выражение 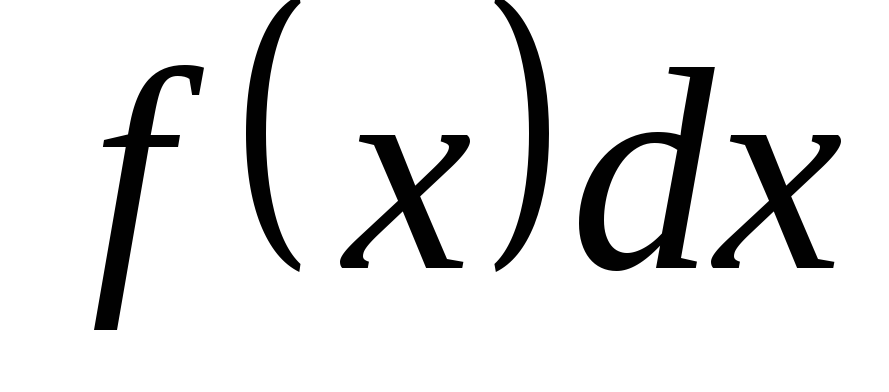 :
:
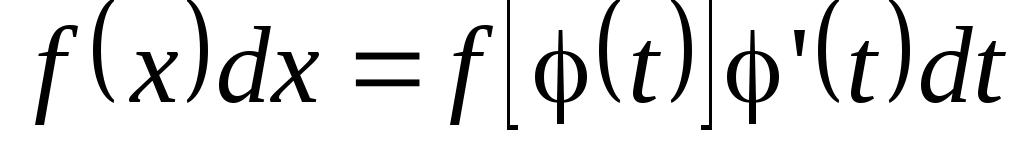 ;
;
3) найти новый интеграл:
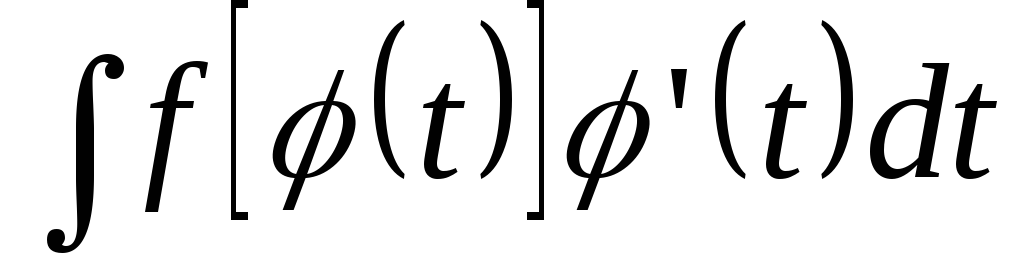 ;
;
4) в полученном
ответе произвести обратную замену 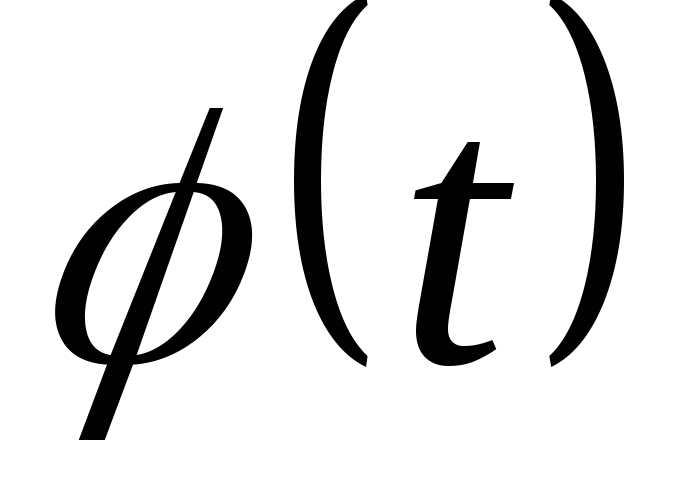 нах.
нах.
studfile.net
§2. Методы вычисления определенных интегралов
Так как формула Ньютона–Лейбница сводит задачу вычисления определенного интеграла от непрерывной функции к нахождению первообразной, то все основные методы вычисления неопределенных интегралов переносятся и на задачу вычисления определенных интегралов. Сформулируем эти методы с учетом специфики определенных интегралов.
1. Непосредственное интегрирование
Типовой пример
Вычислить
определенный интеграл 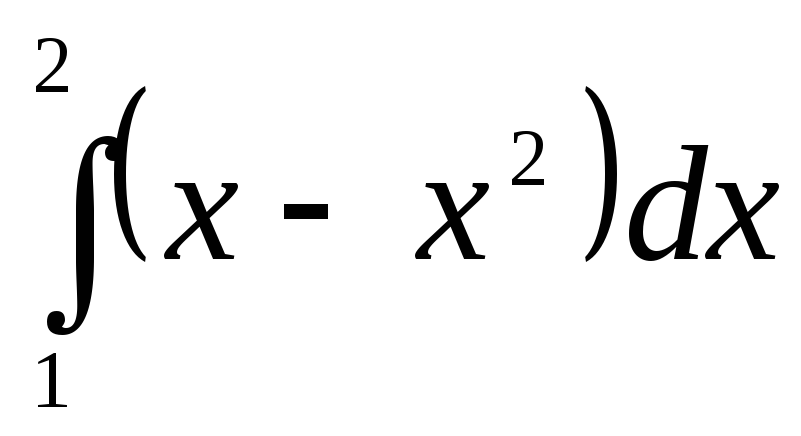 .
.
►Используя формулу Ньютона–Лейбница, получим:
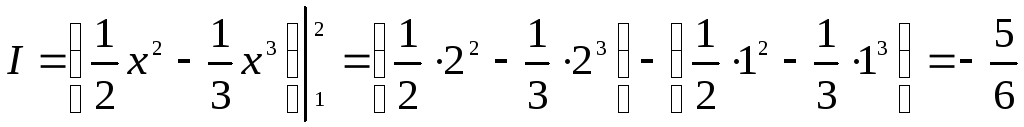 .◄
.◄
2. Замена переменной в определённом интеграле
ТЕОРЕМА
Пусть:
 ,
,  ;
; для
для  ;
; .
.
Тогда 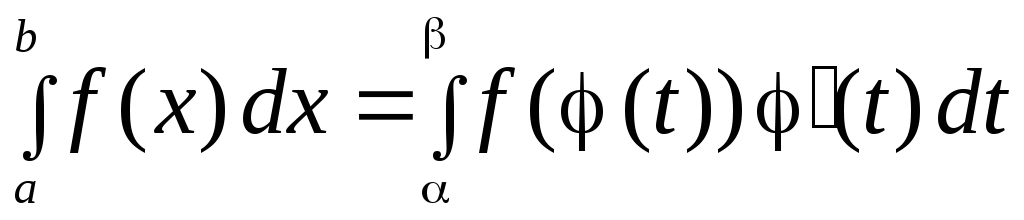 .
.
При решении задач нельзя забывать о том, что при переходе к новой переменной надо обязательно вычислить новые пределы интеграла.
Типовые примеры
Вычислить интегралы.
1. 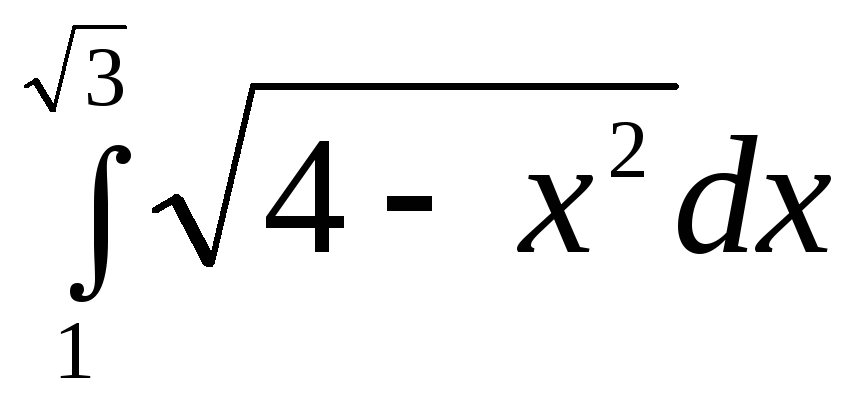 .
.
►
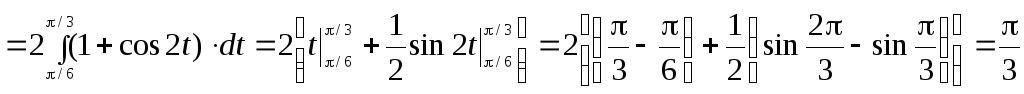 .◄
.◄
2. 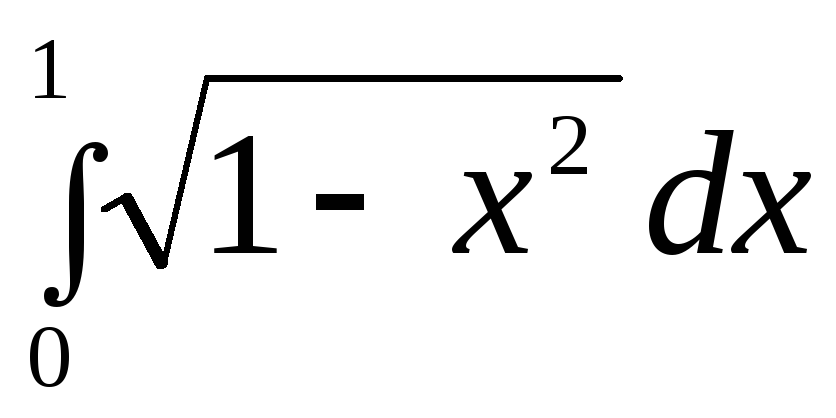 .
.
►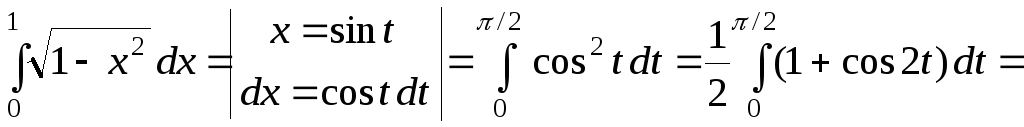
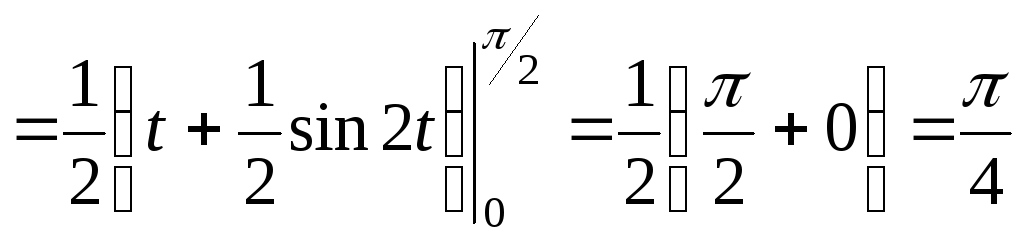 .◄
.◄
3. 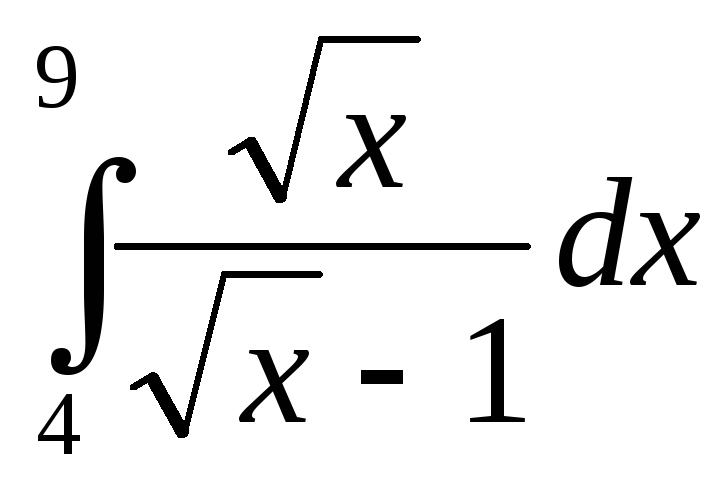 .
.
►Воспользуемся формулой замены переменной в определенном интеграле:
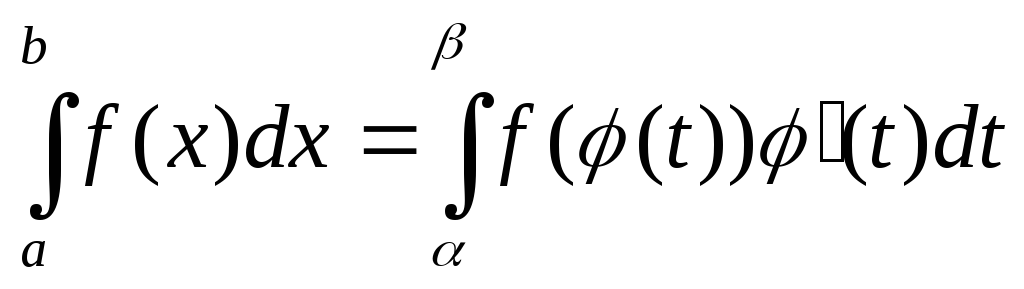
и
применим подстановку 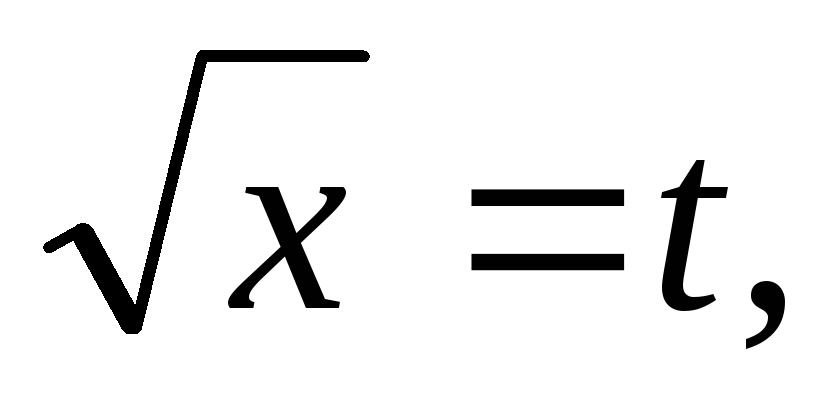 т.е.x = t².
Определим новый промежуток интегрирования: х = 4 при t = 2; х
= 9 при t = 3. Следовательно,
т.е.x = t².
Определим новый промежуток интегрирования: х = 4 при t = 2; х
= 9 при t = 3. Следовательно,
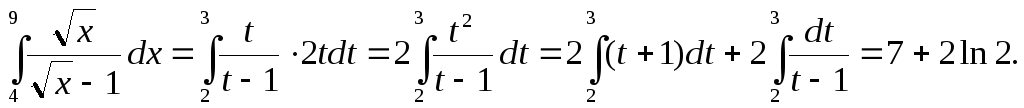 ◄
◄
3. Формула интегрирования по частям для определённого интеграла
ТЕОРЕМА
Пусть 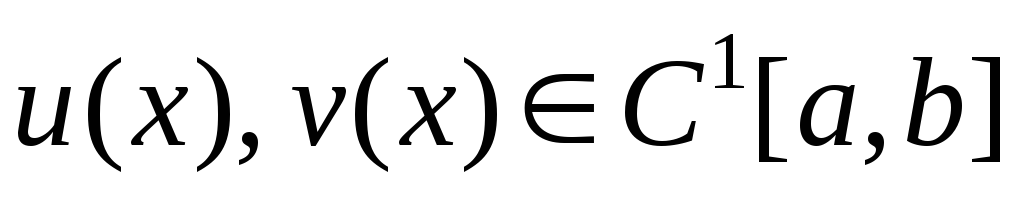 .Тогда
.Тогда
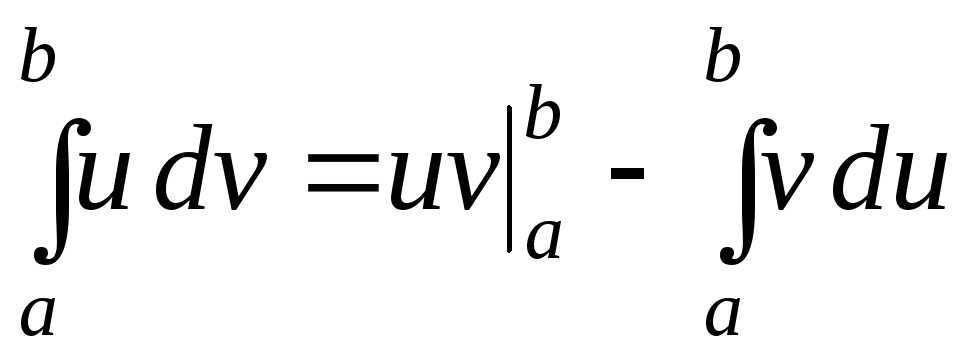 .
.
Типовые примеры
Вычислить интегралы.
1. 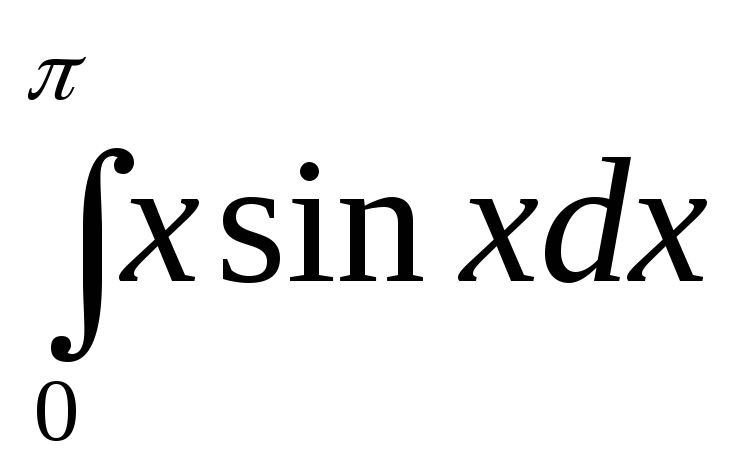 .
.
►Воспользуемся формулой интегрирования по частям в определенном интеграле. Имеем
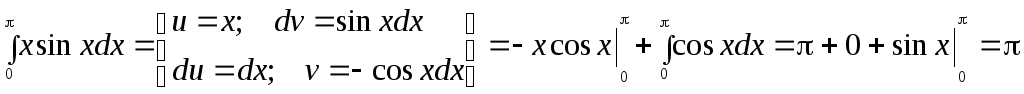 .
◄
.
◄
2. 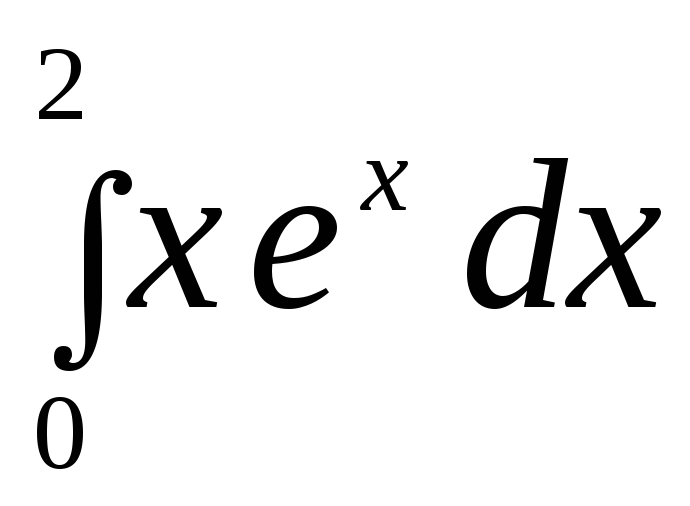 .
.
►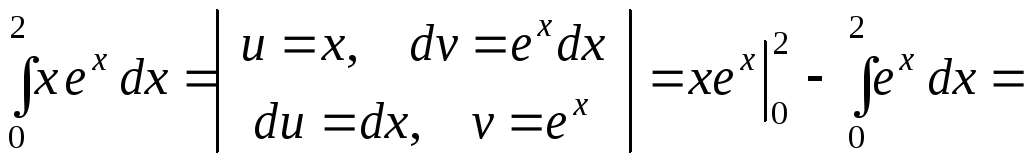
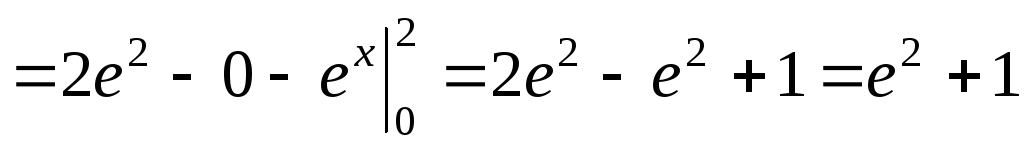 .◄
.◄
3. 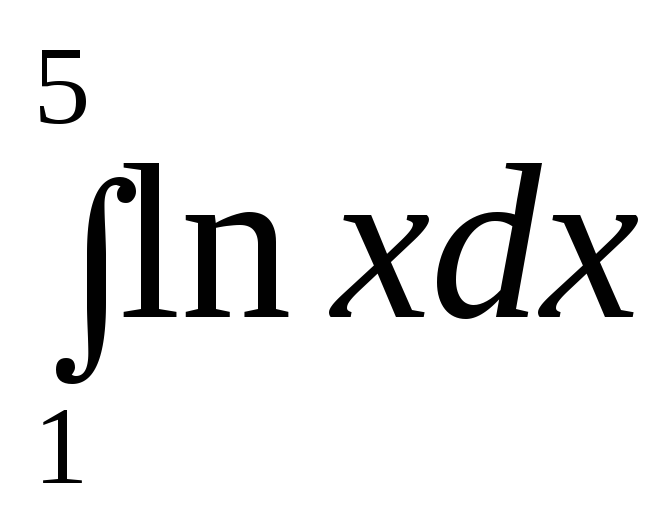 .
.
►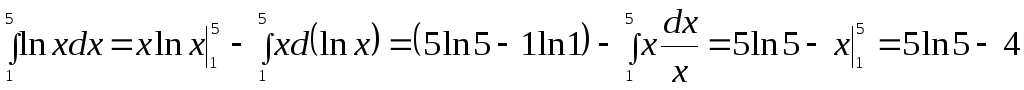 .◄
.◄
§3. Геометрические приложения определенного интеграла
1. Площадь плоской области
1.1. Декартовы координаты
Если 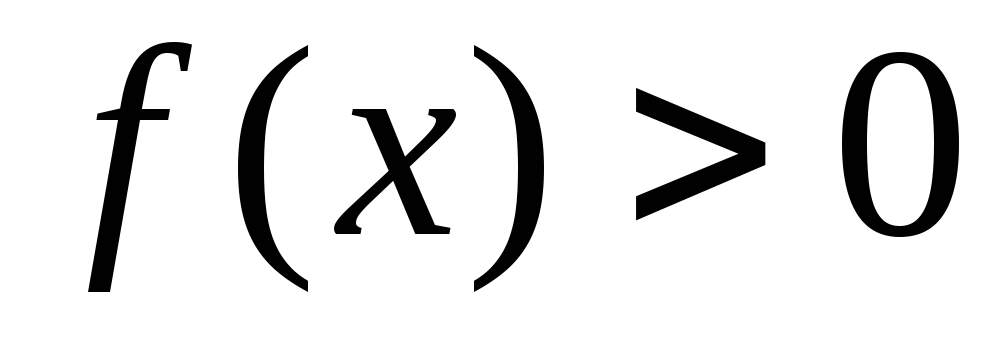 на отрезке
на отрезке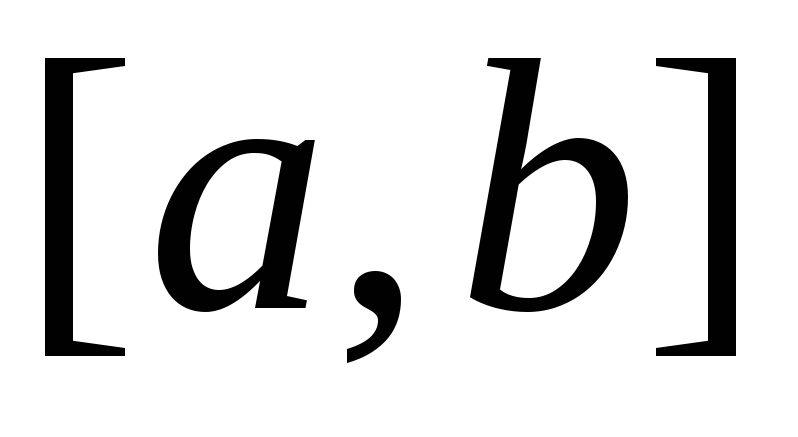 ,
то
,
то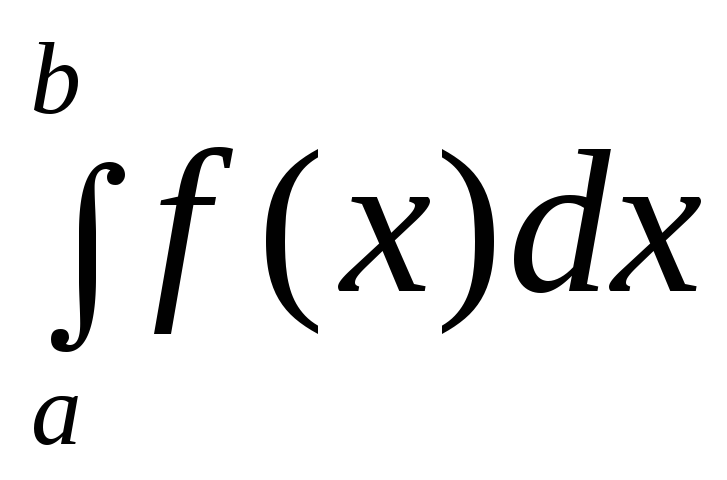 равен площади криволинейной трапеции
равен площади криволинейной трапеции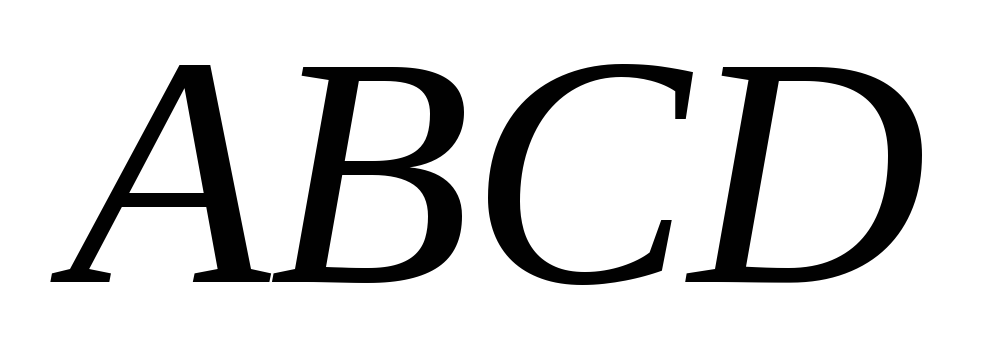 ,
ограниченной снизу отрезком
,
ограниченной снизу отрезком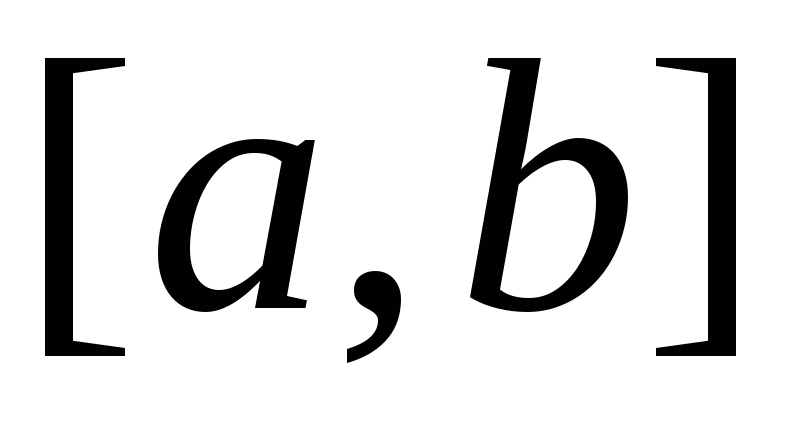 ,
слева и справа – прямыми
,
слева и справа – прямыми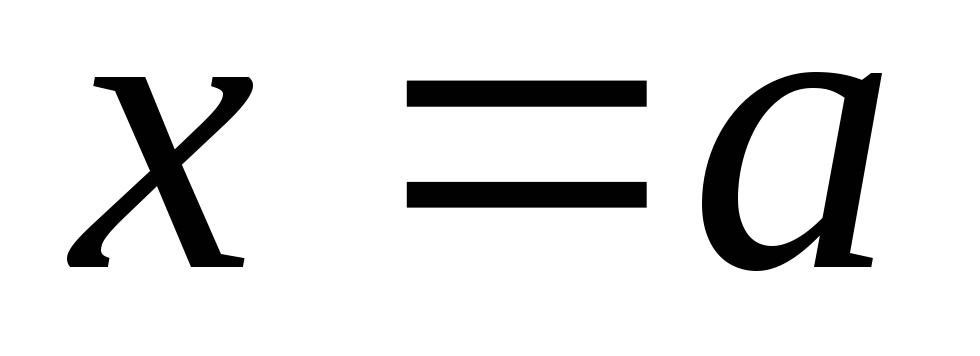 и
и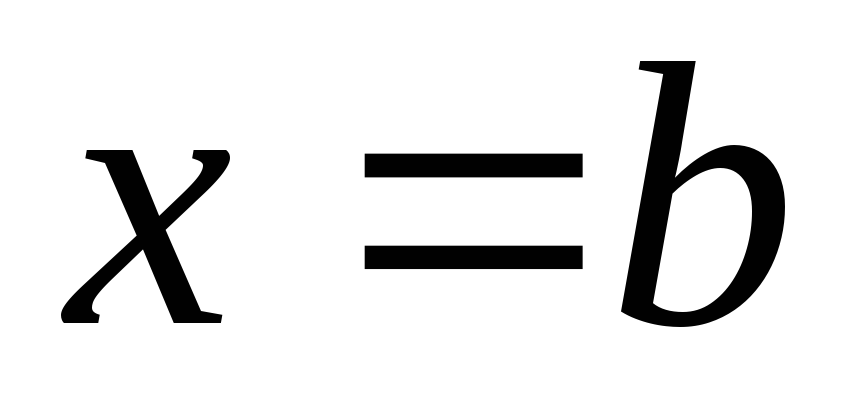 ,
сверху – функцией
,
сверху – функцией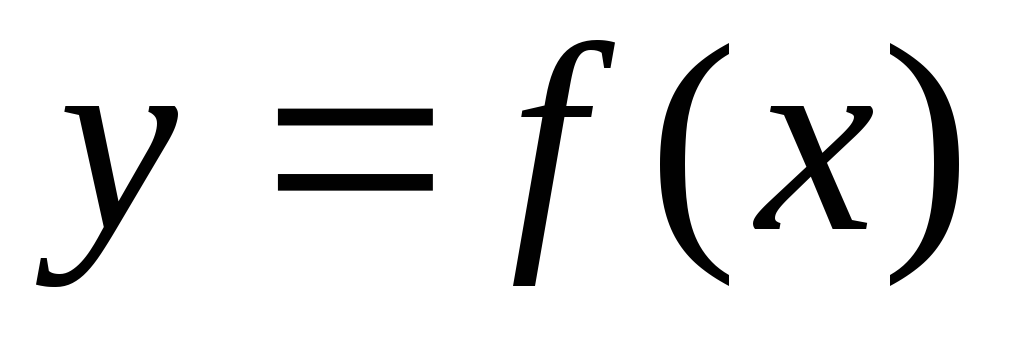 .
Следствие: если фигура ограничена сверху
кривой
.
Следствие: если фигура ограничена сверху
кривой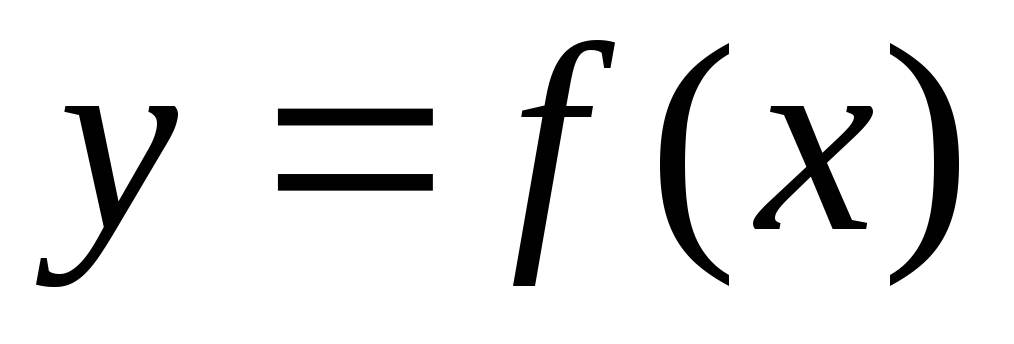 ,
снизу – кривой
,
снизу – кривой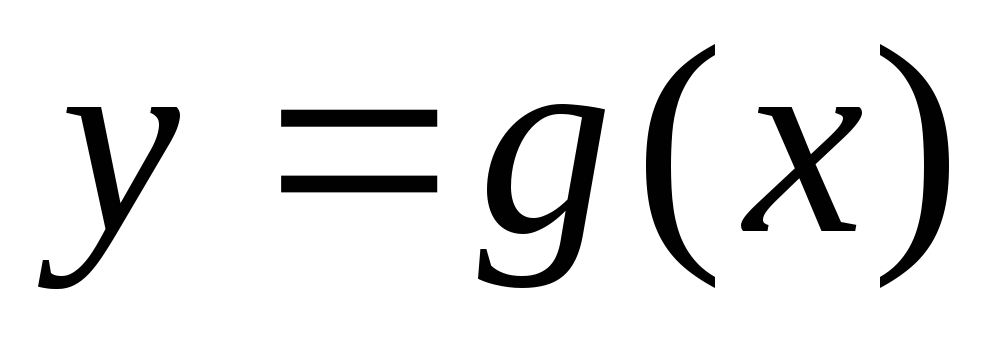 ,
слева и справа – отрезками прямых
,
слева и справа – отрезками прямых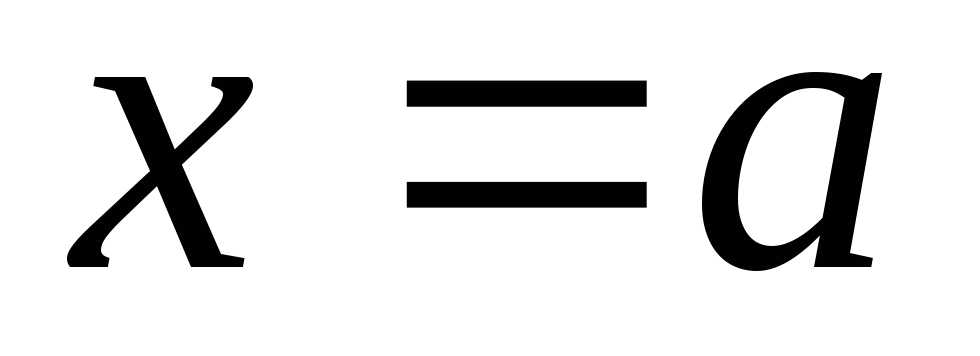 и
и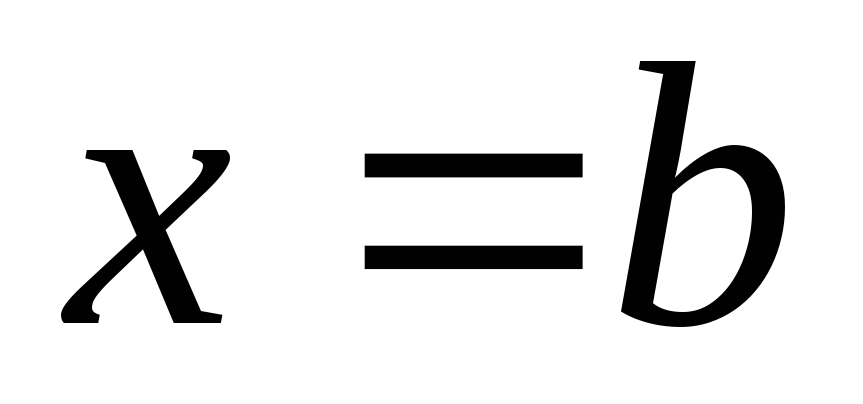 ,
то её площадь равна
,
то её площадь равна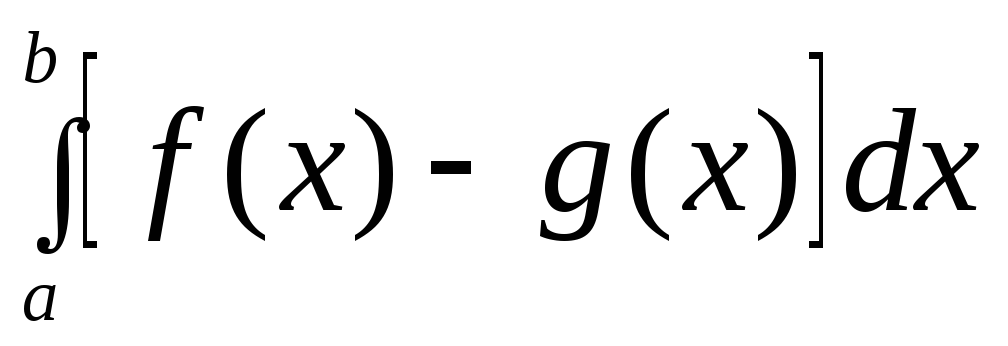 .
.
Т иповые
примеры
иповые
примеры
1)
Найти площадь области  ,
ограниченной кривыми
,
ограниченной кривыми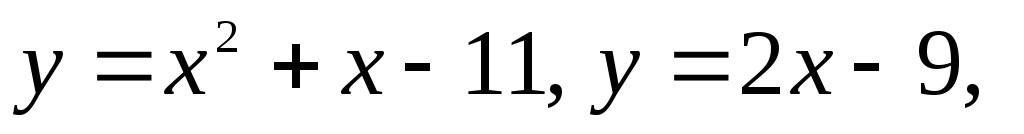 при
условии, что
при
условии, что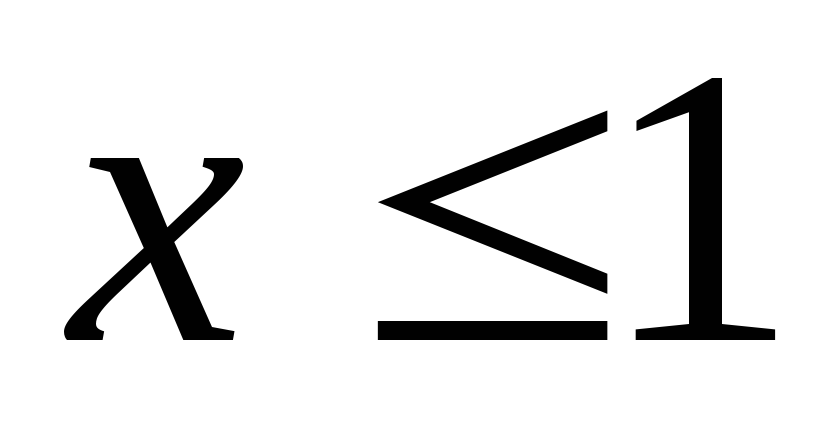 (дальше мы будем писать так:
(дальше мы будем писать так: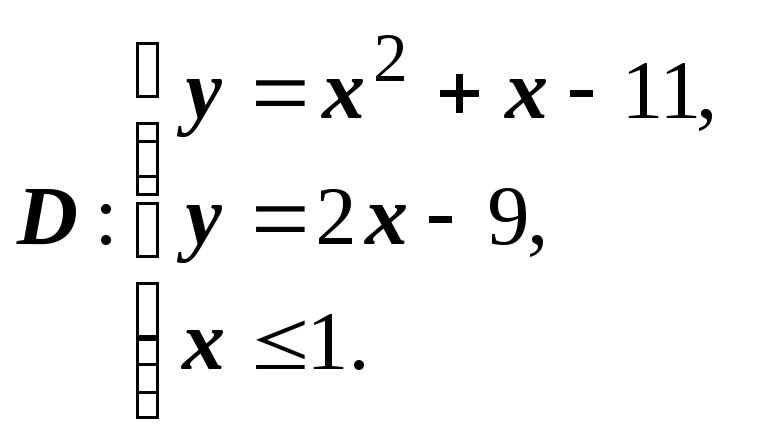 ).
).
►При
решении таких задач следует обязательно
изобразить исследуемый геометрический
объект. Для определения нижнего предела
интегрирования надо найти точку
пересечения кривых, уравнение 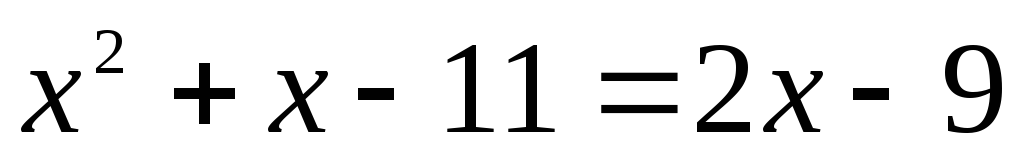 имеет два корня:
имеет два корня: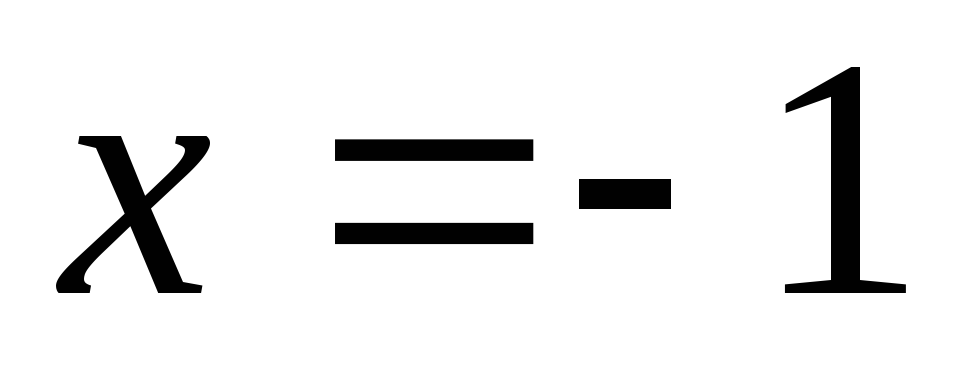 и
и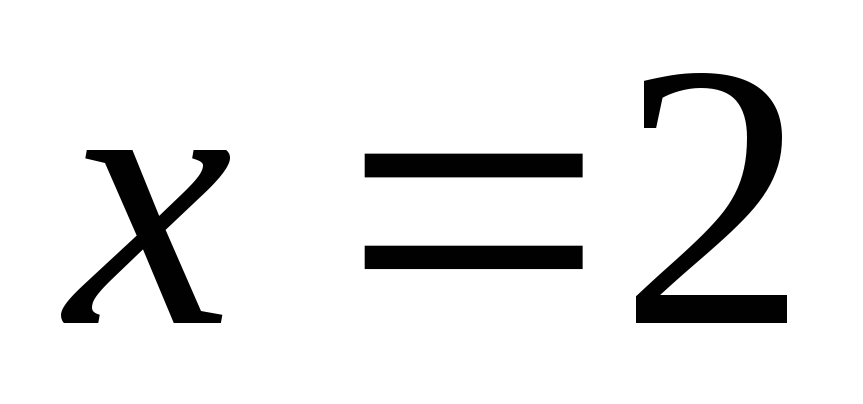 ;
;
Подходящий
корень – 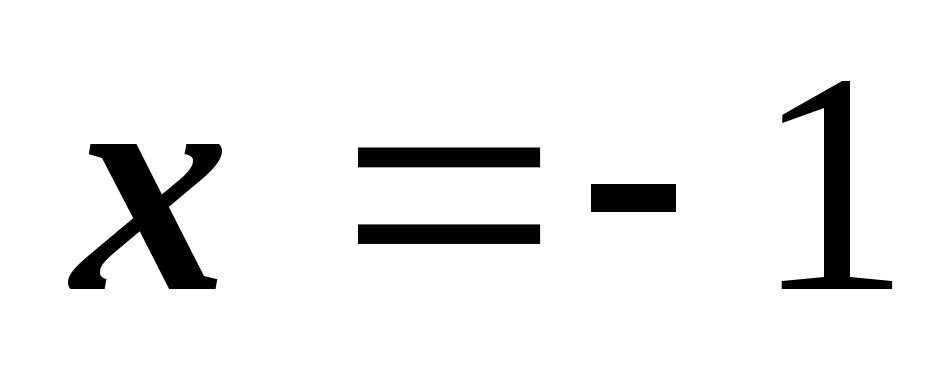 .
Область ограничена сверху параболой,
снизу – прямой, справа – прямой
.
Область ограничена сверху параболой,
снизу – прямой, справа – прямой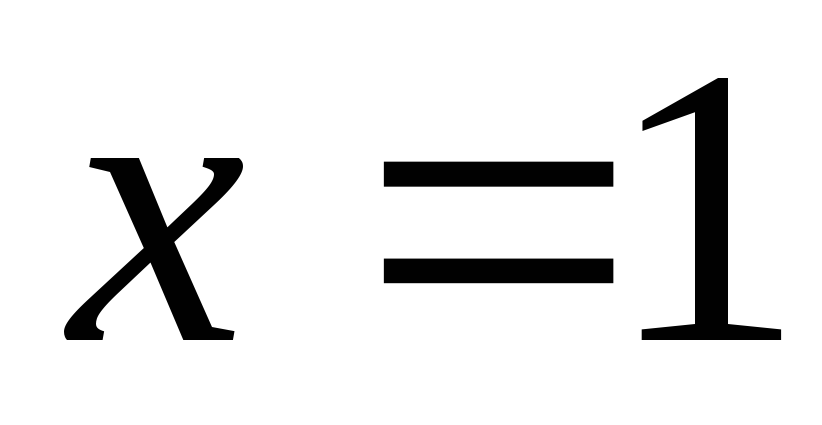 ,
крайняя левая точка –
,
крайняя левая точка –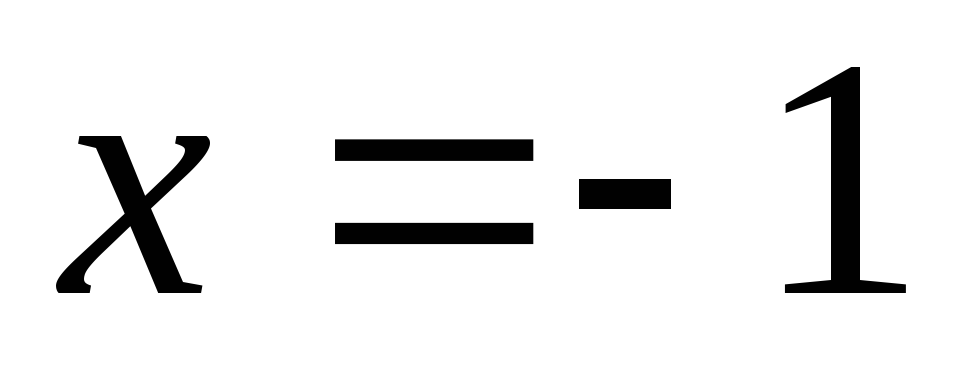 ,
поэтому
,
поэтому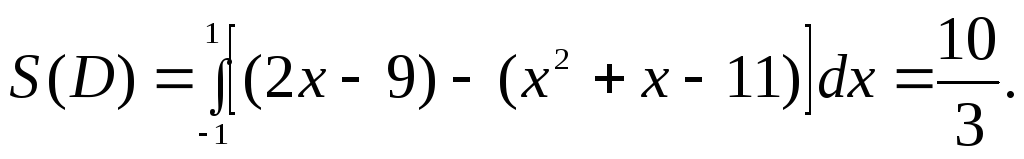 Если
область имеет более сложную структуру,
её следует разбить на простые части. ◄
Если
область имеет более сложную структуру,
её следует разбить на простые части. ◄
2)
Вычислить площадь фигуры, ограниченной
графиками функций 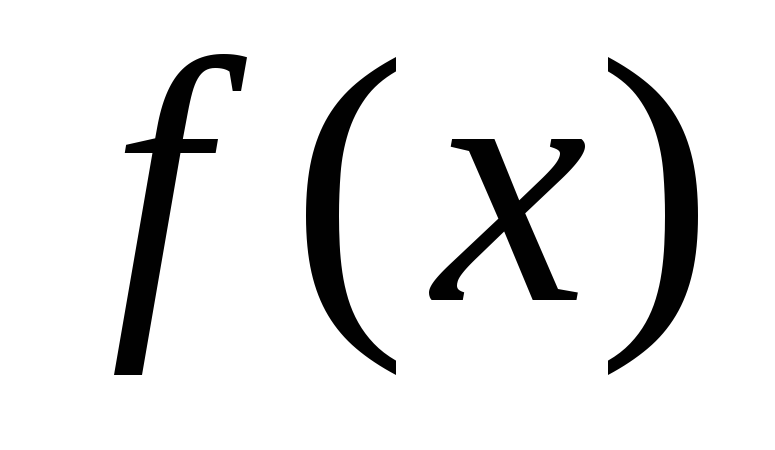 и
и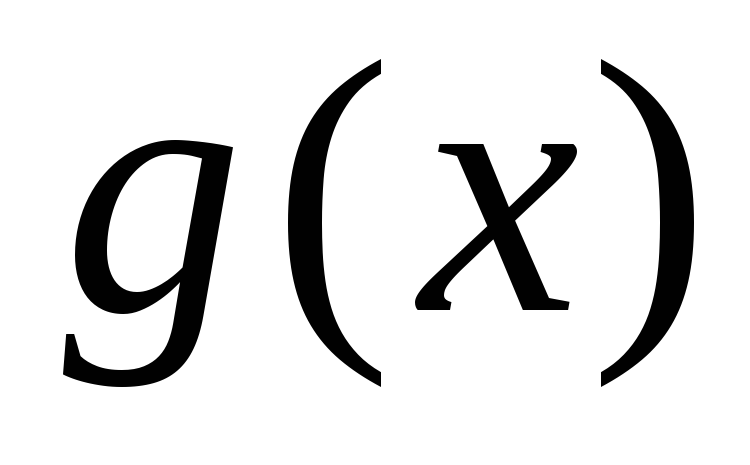 :
:
►Построим
графики функций и найдем их точки
пересечения. Точки пересечения: 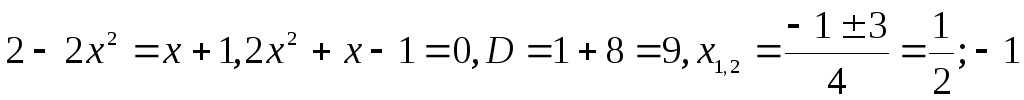 .Площадь
фигуры, ограниченной линиями находится
по формуле:
.Площадь
фигуры, ограниченной линиями находится
по формуле:
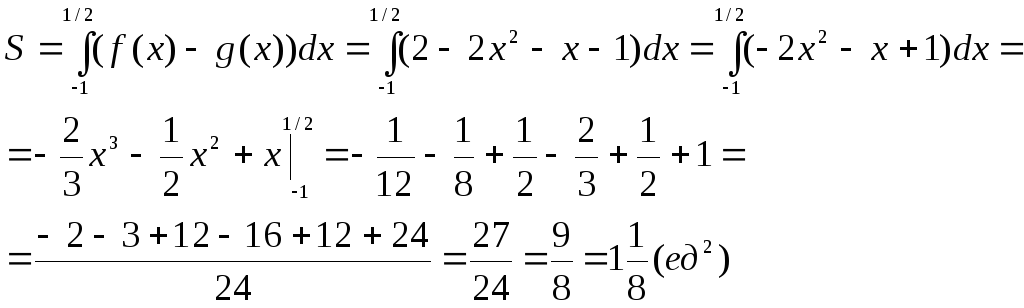
 ◄
◄
3)
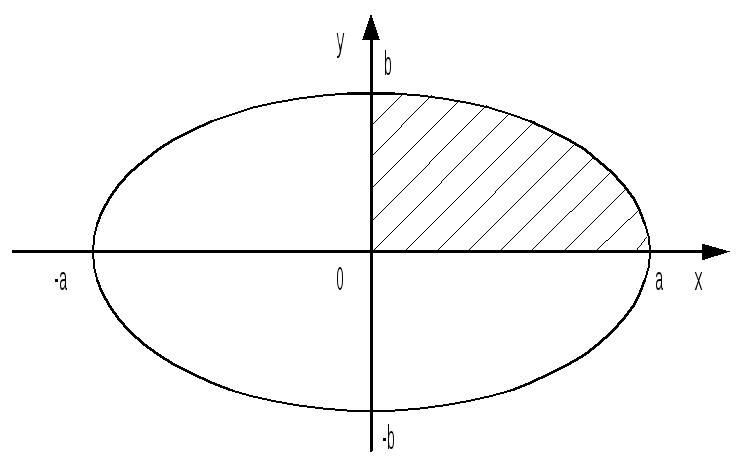
Найти площадь фигуры, ограниченной
эллипсом 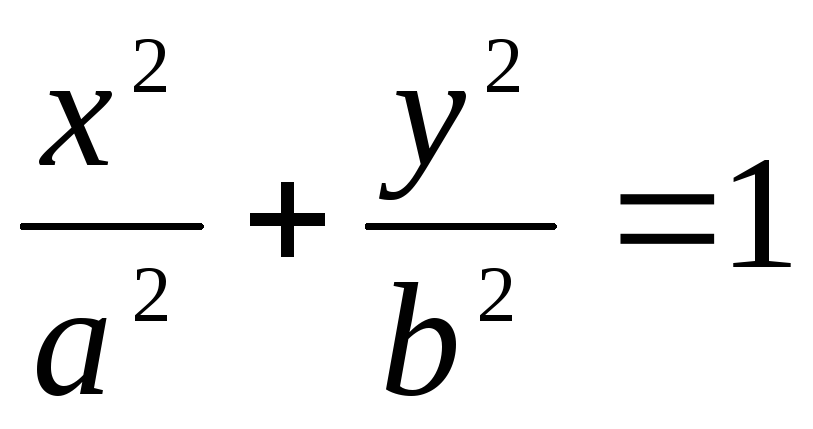 .
.
►Эллипс
имеет две оси симметрии: координатные
оси 0х и 0у. Поэтому площадь S
фигуры равна учетверённой площади S1 части (D1)
фигуры, расположенной в первой четверти
(заштриховано). Фигура (D1)
ограничена сверху линией 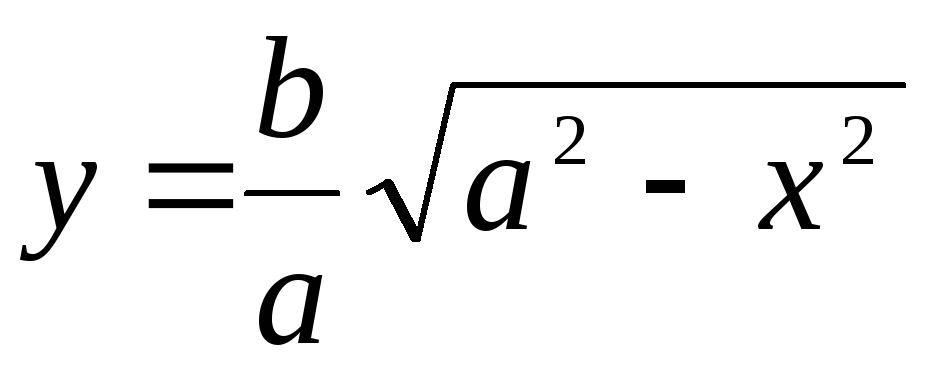 , снизу – осью 0х, слева – осью 0у. Поэтому
, снизу – осью 0х, слева – осью 0у. Поэтому
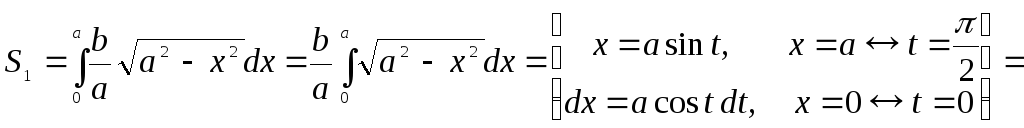
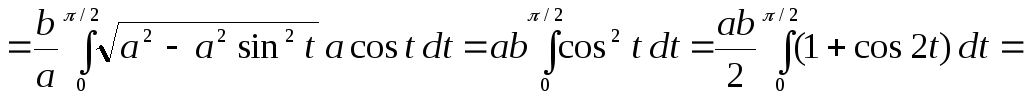
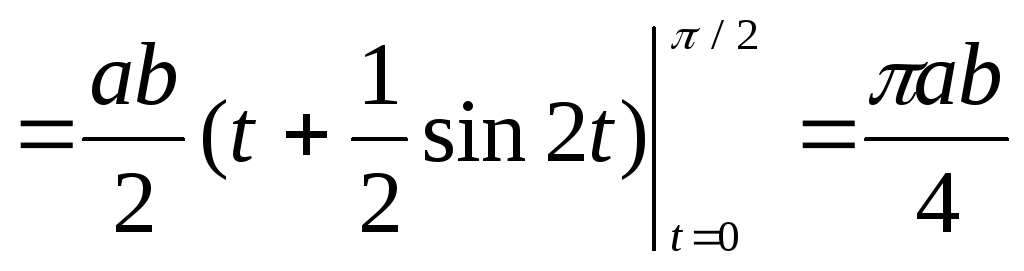 .
Отсюда находим S
= 4S1 = ab.
◄
.
Отсюда находим S
= 4S1 = ab.
◄
1.2. Область задана в полярных координатах
Если
область  – сектор, ограниченный лучами
– сектор, ограниченный лучами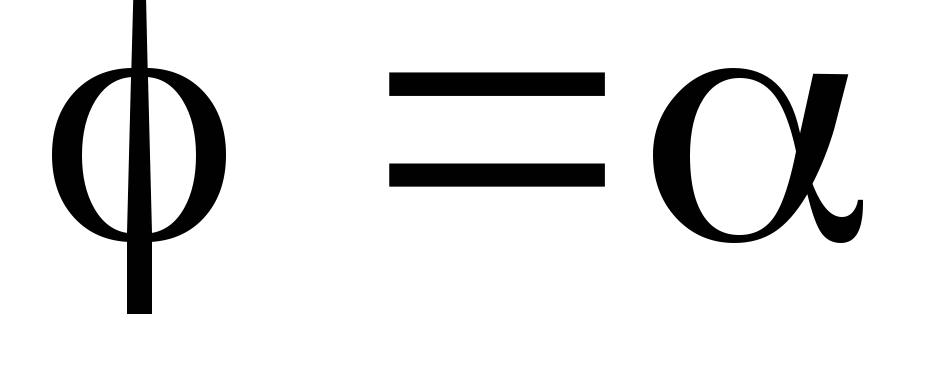 ,
,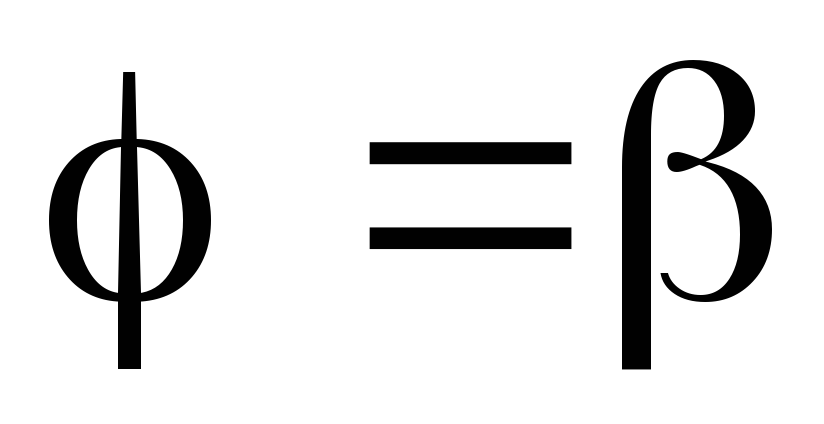 и кривой
и кривой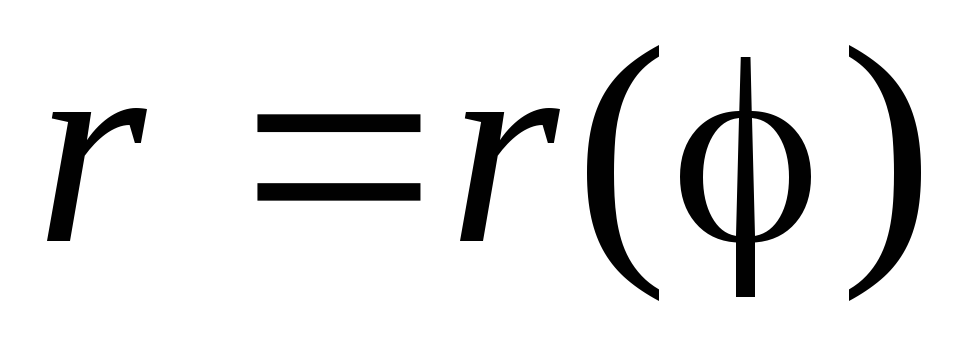 .
В Этом случае
.
В Этом случае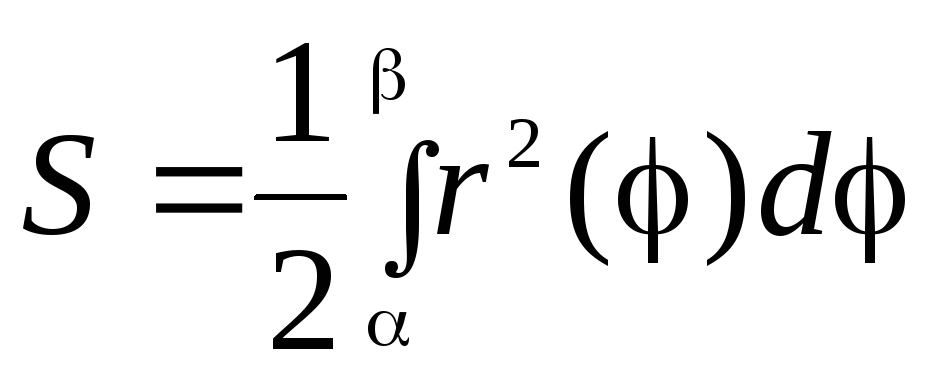 .
.
Типовые примеры
1.
Найти площадь, ограниченную лемнискатой 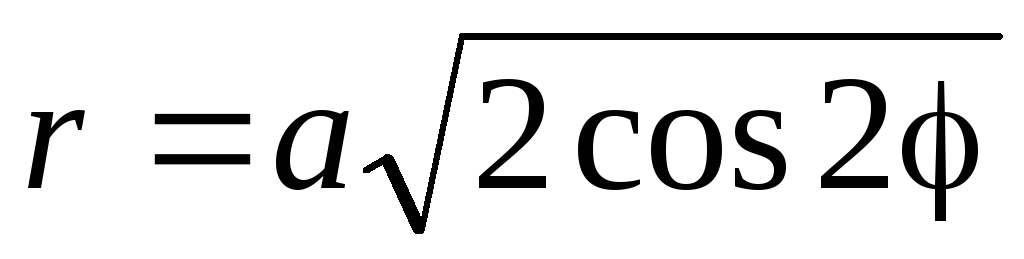 .
.
►Т очки
лемнискаты расположены в секторах
очки
лемнискаты расположены в секторах и
и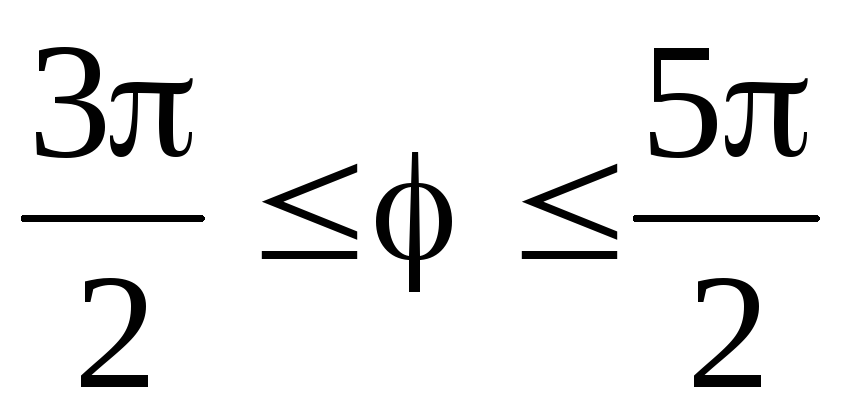 ;
кроме того, при решении таких задаче
целесообразно использовать симметрию
фигуры, поэтому мы найдём площадь части,
расположенной в секторе
;
кроме того, при решении таких задаче
целесообразно использовать симметрию
фигуры, поэтому мы найдём площадь части,
расположенной в секторе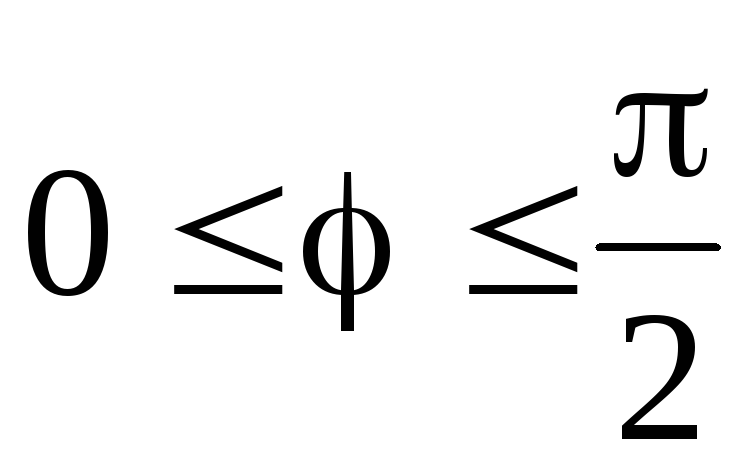 и учетверим её:
и учетверим её:
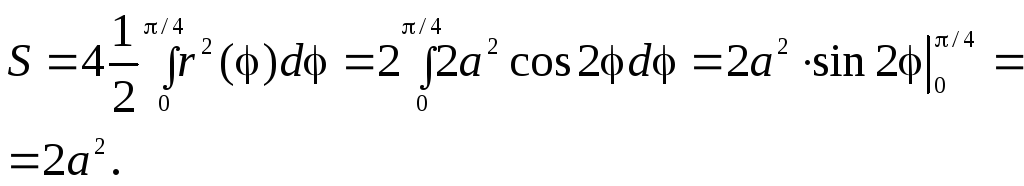 ◄
◄
2. Найти площадь, лежащую внутри кардиоиды 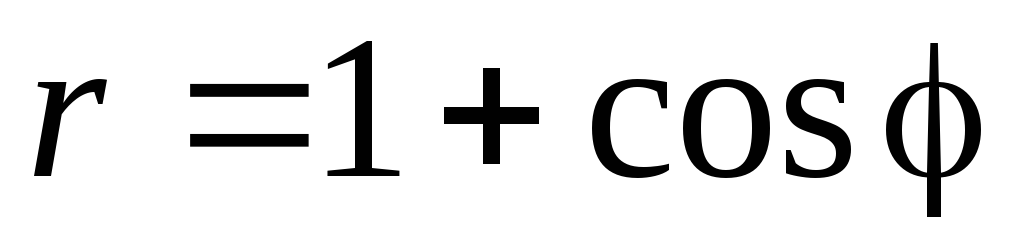 вне окружности
вне окружности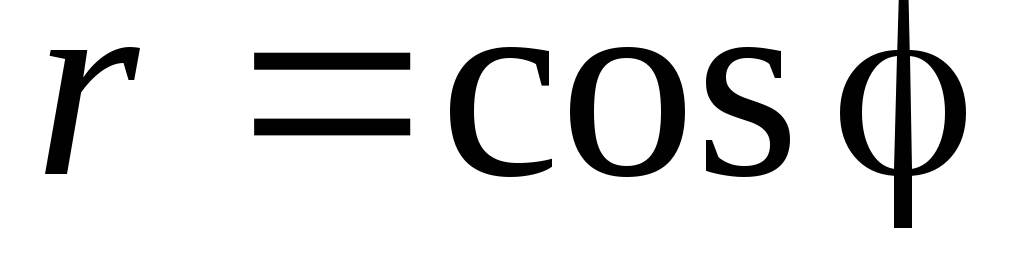 .
.
►Найдём
разность площадей, лежащих внутри
кардиоиды и окружности. Для верхней
части кардиоиды  ;
для верхней части окружности
;
для верхней части окружности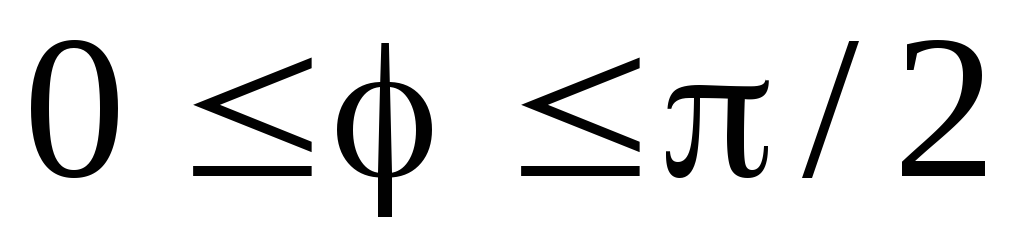 ,
поэтому
,
поэтому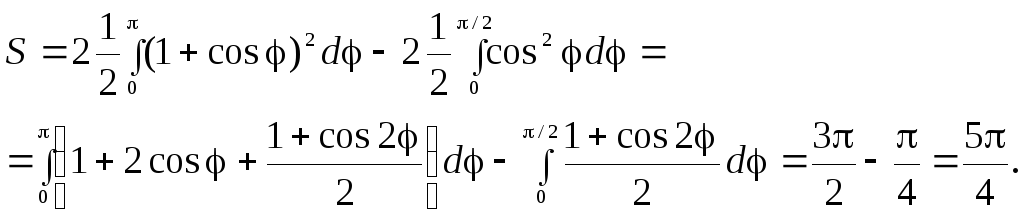 ◄
◄
1.3.
Область ограничена кривыми, заданными
параметрически Если кривая, ограничивающая криволинейную
трапецию  задана в параметрическом виде
задана в параметрическом виде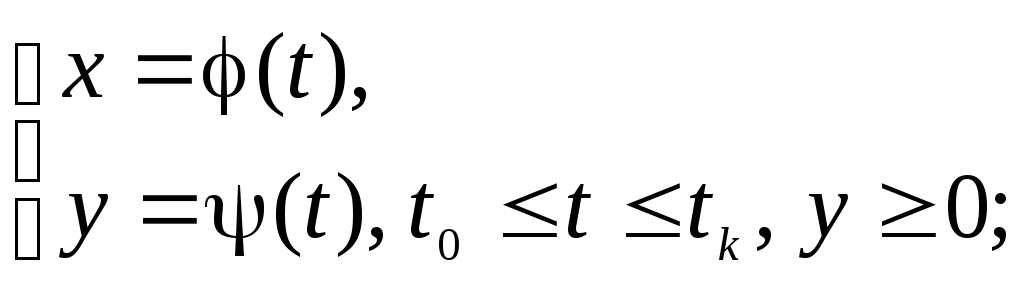
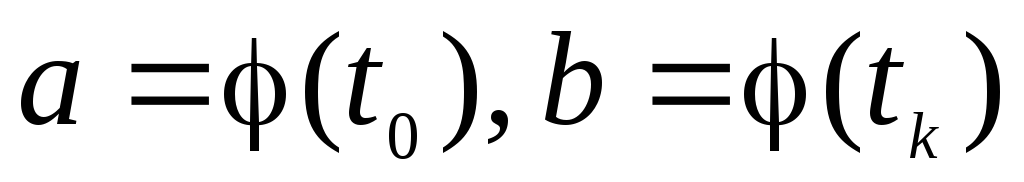 ,
то переход в интеграле
,
то переход в интеграле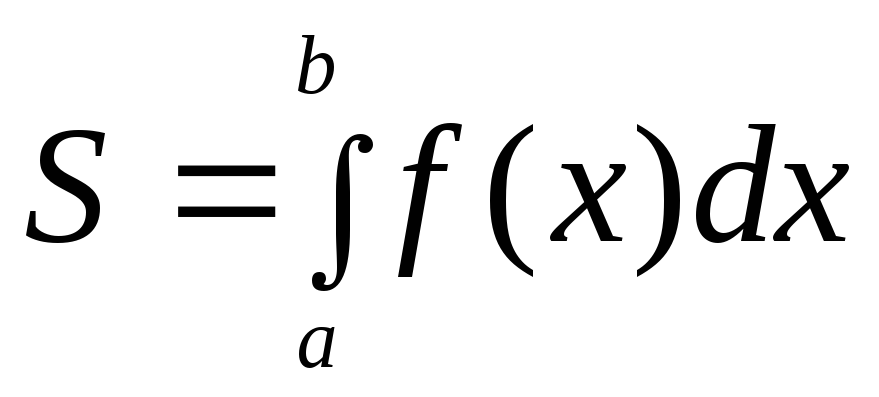 к переменной
к переменной приводит к формуле
приводит к формуле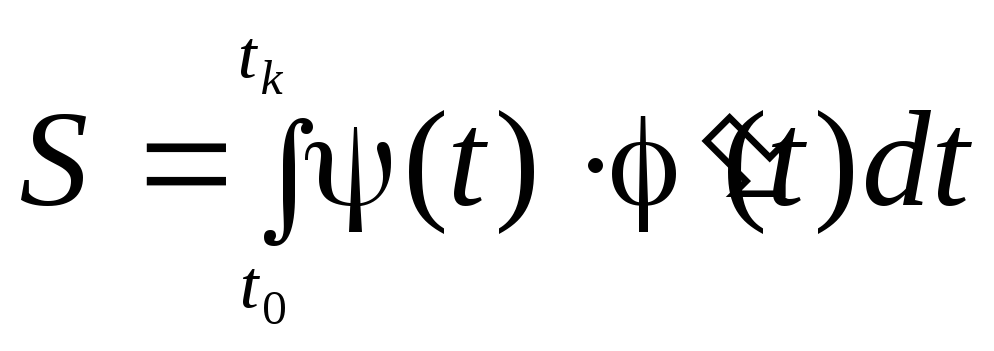 .
.
Типовой пример
Найти
площадь, ограниченную астроидой 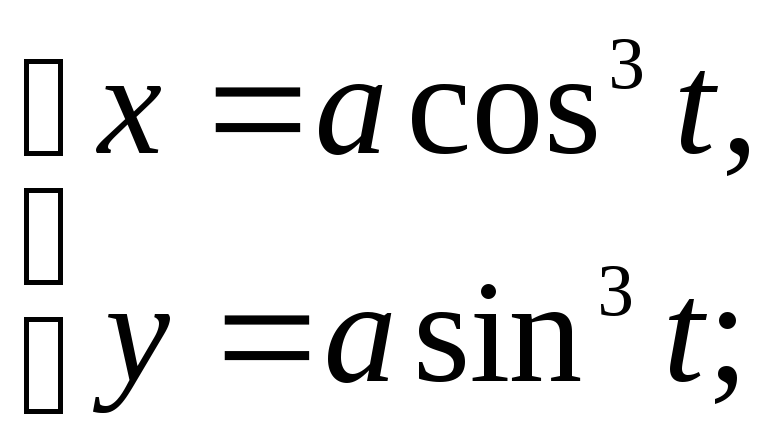 (
(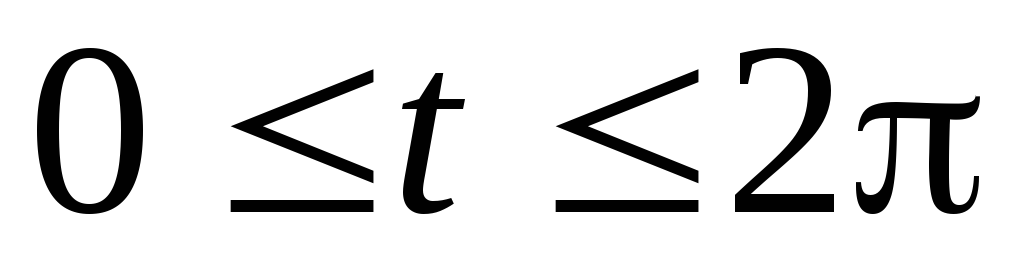 ).
).
►Используем
симметрию фигуры. Мы найдём площадь
части фигуры, расположенной в первом
квадранте (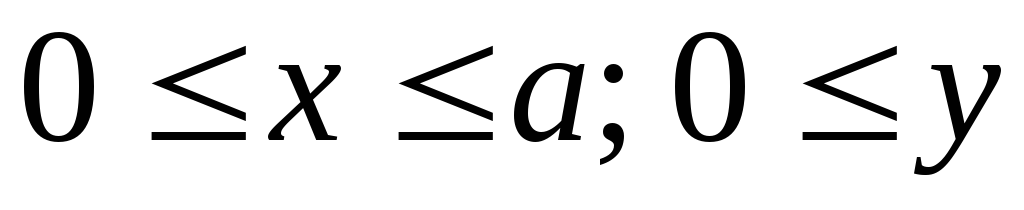 ),
и учетверим её. Точка
),
и учетверим её. Точка получается при
получается при ,
точка
,
точка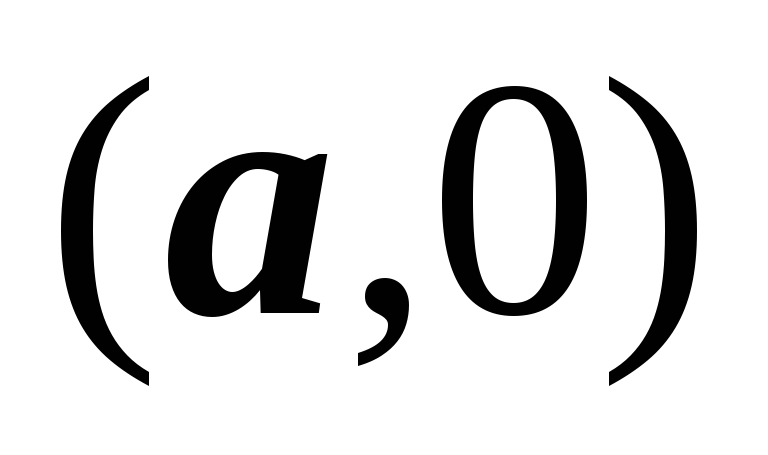 – при
– при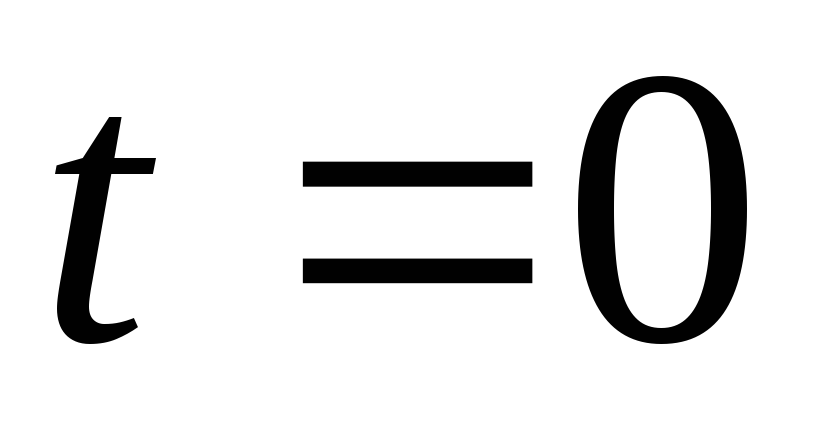 ,
поэтому
,
поэтому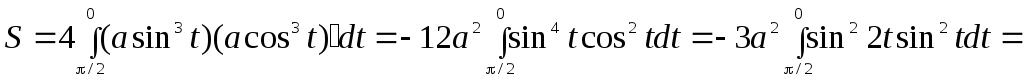
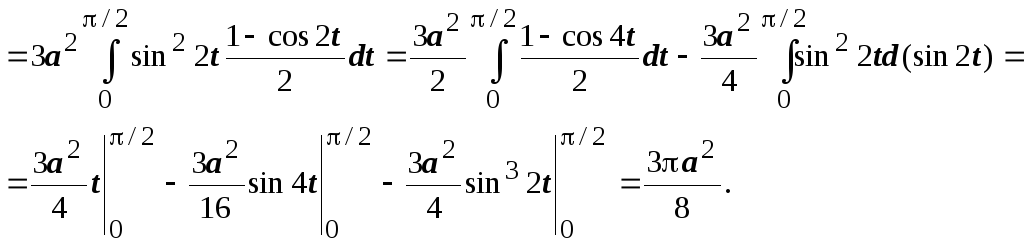 ◄
◄
studfile.net
3. Метод интегрирования по частям
Пусть 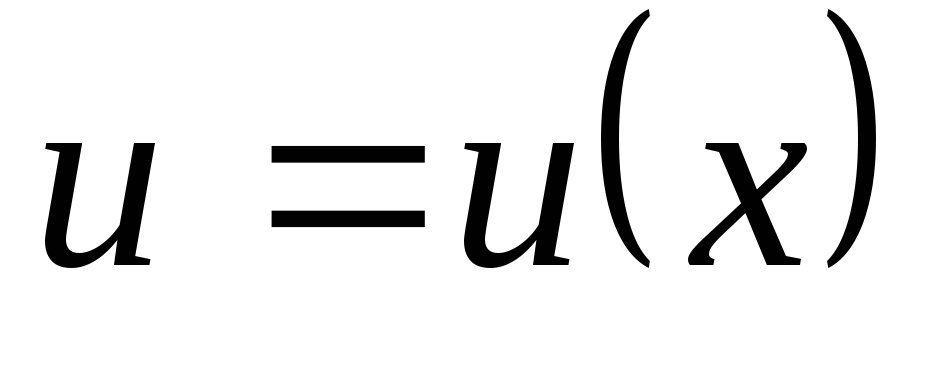 и
и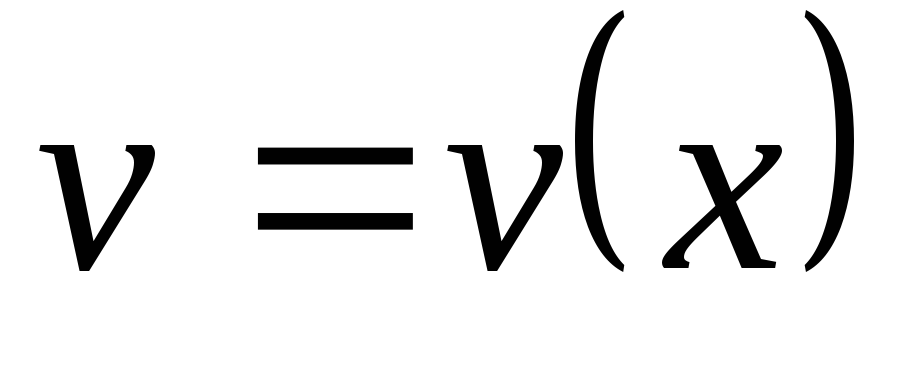 — непрерывно дифференцируемые функции.
На основании формулы дифференциала
произведения имеем
— непрерывно дифференцируемые функции.
На основании формулы дифференциала
произведения имеем
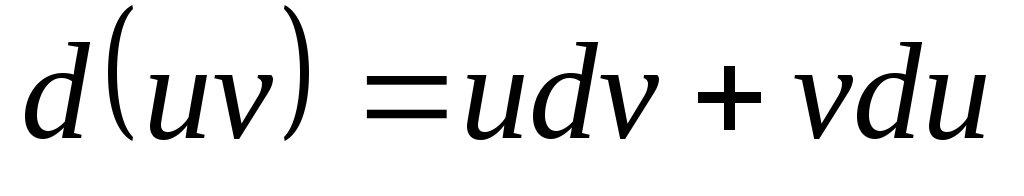 .
.
Отсюда
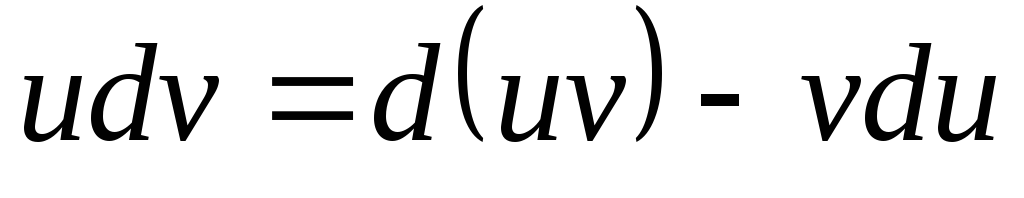 .
.
Интегрируя, получим:
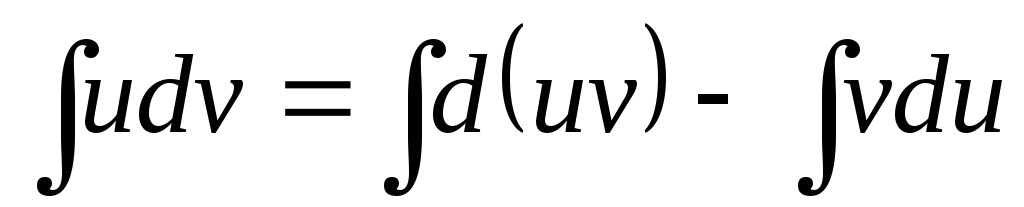 или окончательно
или окончательно
| (4) |
Формула (4) называется формулой интегрирования по частям.
Выведенная формула показывает, что
интеграл 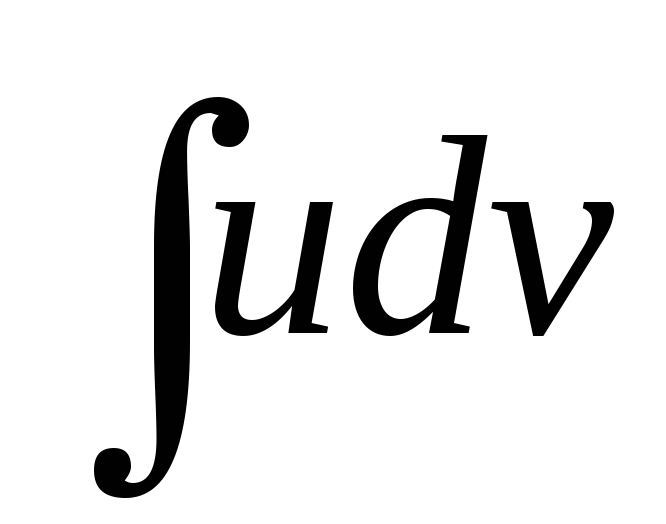 приводится к интегралу
приводится к интегралу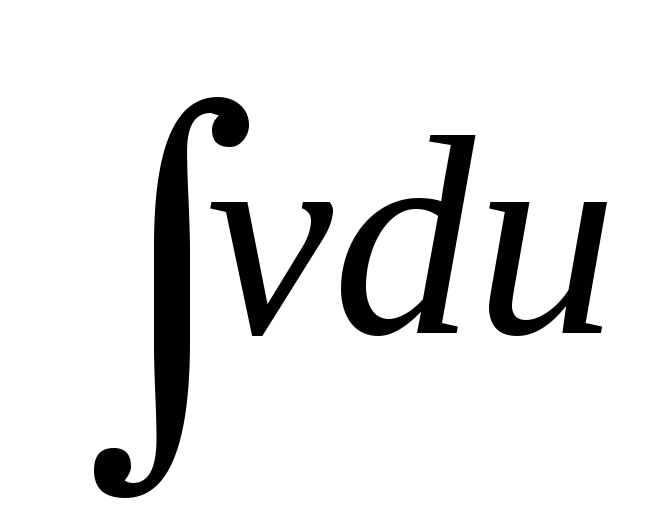 ,
который может оказаться более простым,
чем исходный, или даже табличным. Сущность
метода интегрирования по частям вполне
соответствует его названию. Дело в том,
что при вычислении интеграла этим
методом подынтегральное выражение
,
который может оказаться более простым,
чем исходный, или даже табличным. Сущность
метода интегрирования по частям вполне
соответствует его названию. Дело в том,
что при вычислении интеграла этим
методом подынтегральное выражение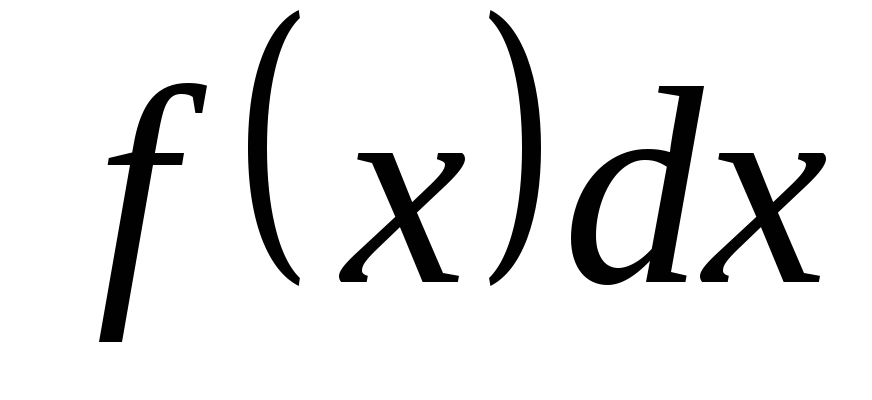 представляется в виде произведения
множителейuиdv. При этом dx обязательно входит в dv. В результате получается, что заданный
интеграл находится по частям: сначала
находим
представляется в виде произведения
множителейuиdv. При этом dx обязательно входит в dv. В результате получается, что заданный
интеграл находится по частям: сначала
находим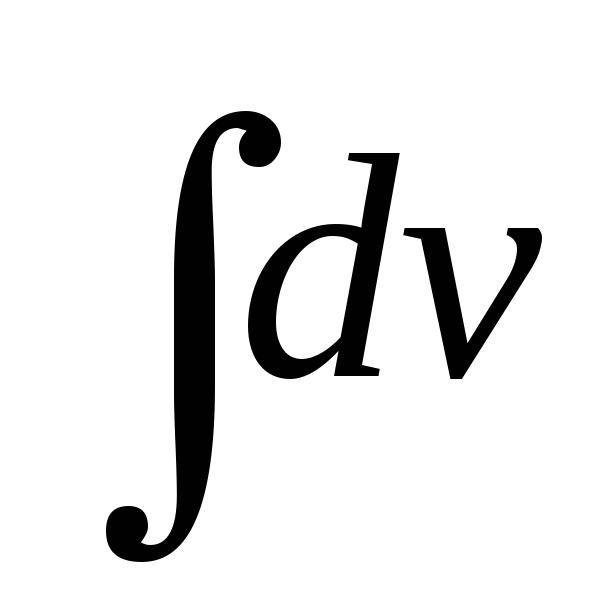 ,
а затем
,
а затем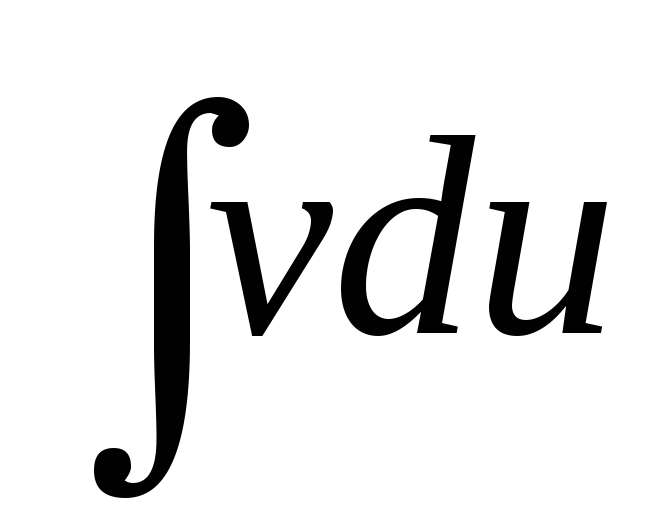 .
.
Пример 1.
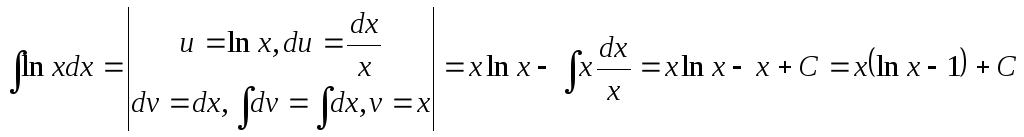 .
.
В представленном примере, как и в дальнейших, вертикальными черточками отделены вспомогательные записи. Отметим также, что в качестве vможно взять любую функцию видаx+C,гдеС– постоянная. Мы взялиv=x, т.е.С=0.
Пример
2. 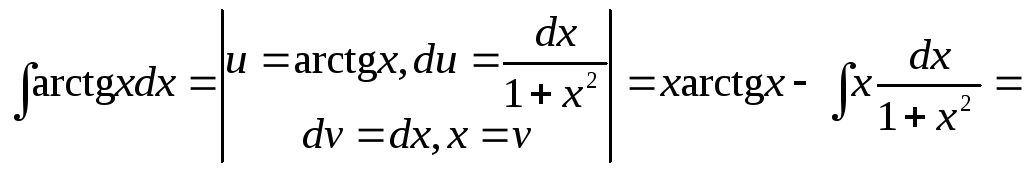
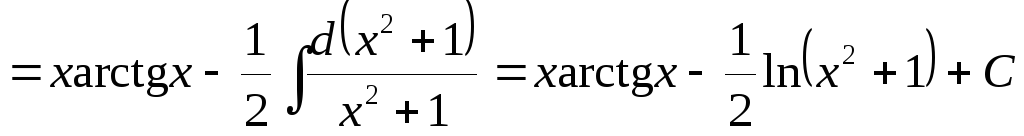 .
.
Пример 3.
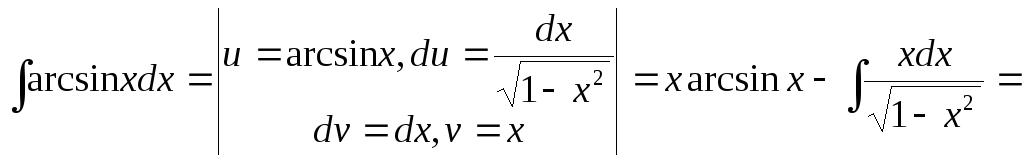
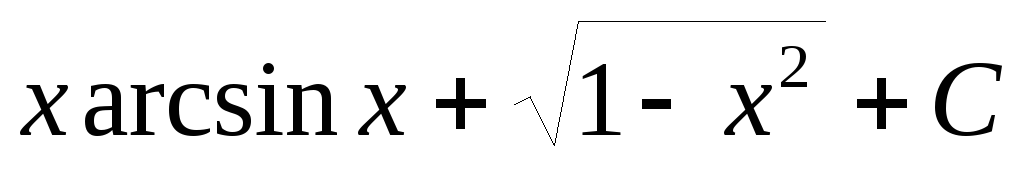 .
.
Пример 4.
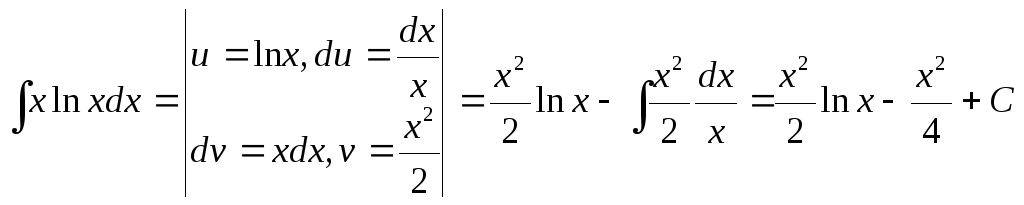 .
.
Иногда для вычисления интеграла формулу интегрирования по частям приходится применять несколько раз.
Пример 5.
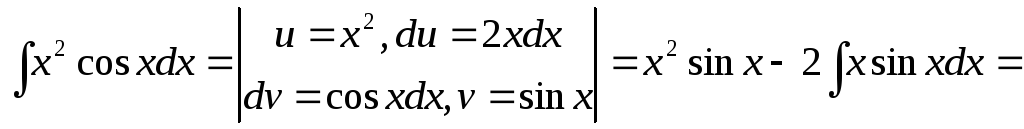
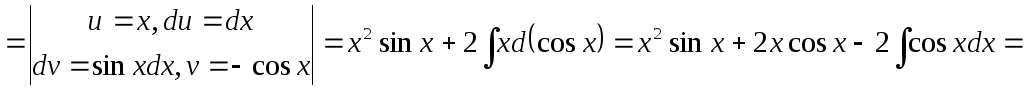
 .
.
Таким образом, интеграл 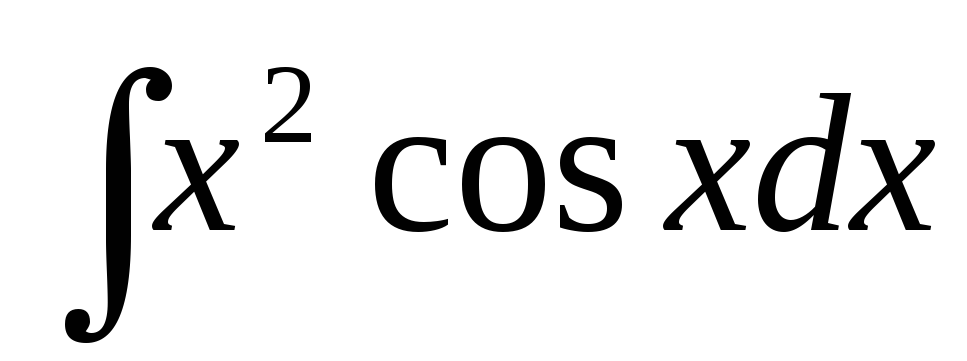 вычислен двукратным интегрированием
по частям.
вычислен двукратным интегрированием
по частям.
Пример 6.

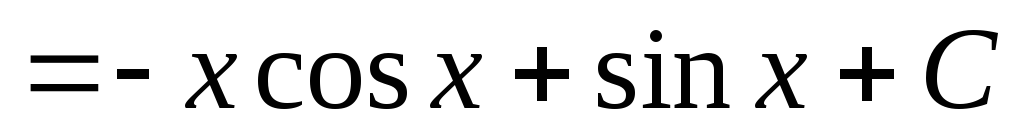 .
.
Если бы выражение u и dv мы выбрали иначе, т.е. 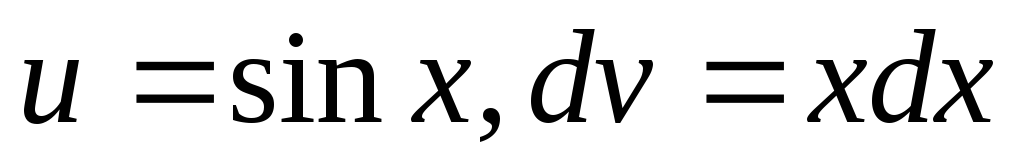 ,
то получили бы
,
то получили бы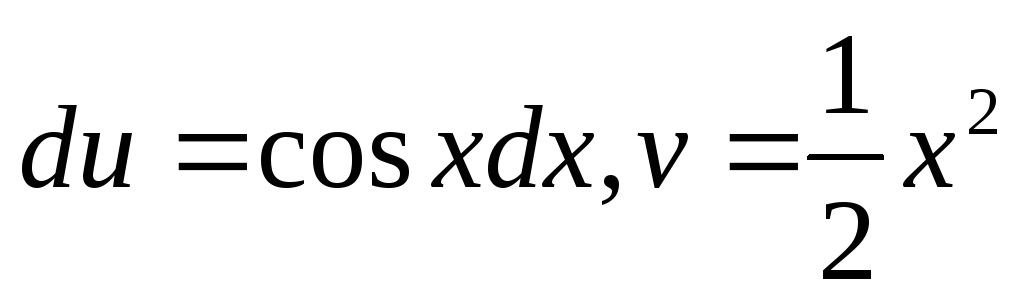 ,
откуда
,
откуда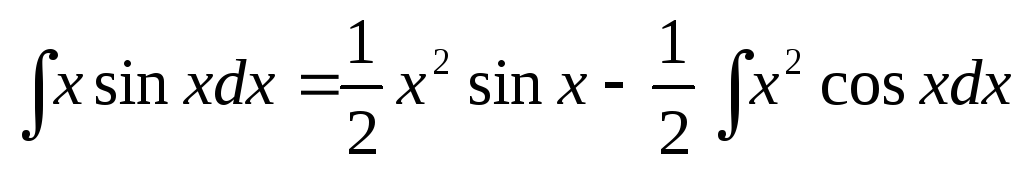 ,
и пришли бы к интегралу более сложному,
чем исходный, т.к. степень сомножителя
при тригонометрической функции повысилась
на единицу.
,
и пришли бы к интегралу более сложному,
чем исходный, т.к. степень сомножителя
при тригонометрической функции повысилась
на единицу.
Приведенный пример показывает, что при вычислении интегралов методом интегрирования по частям главным является разумное разбиение подынтегрального выражения на множители uиdv. Общих установок по этому вопросу не имеется. Однако, для некоторых типов интегралов сделать это возможно.
а) В интегралах вида
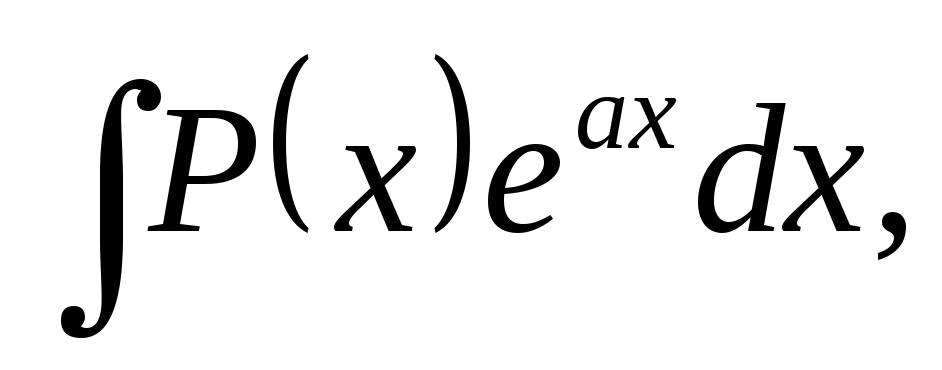
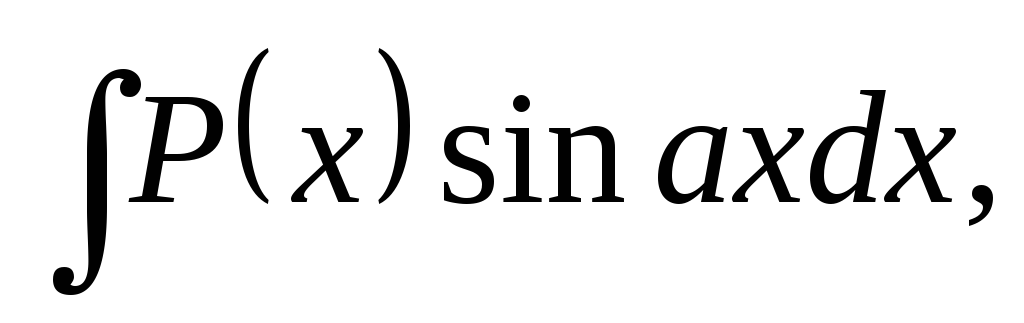
где P(х) – многочлен относительно x, а –
некоторое число, полагают u=P(x), а остальные сомножители за 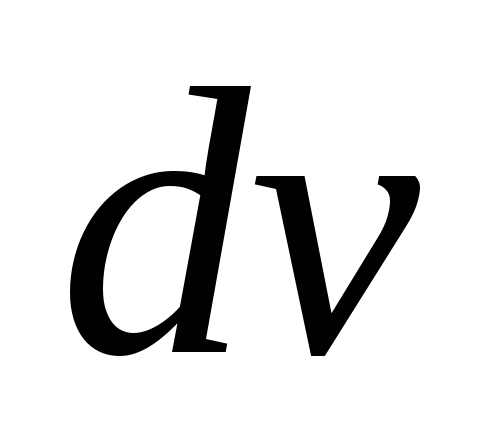 .
.
Пример 7. Найти 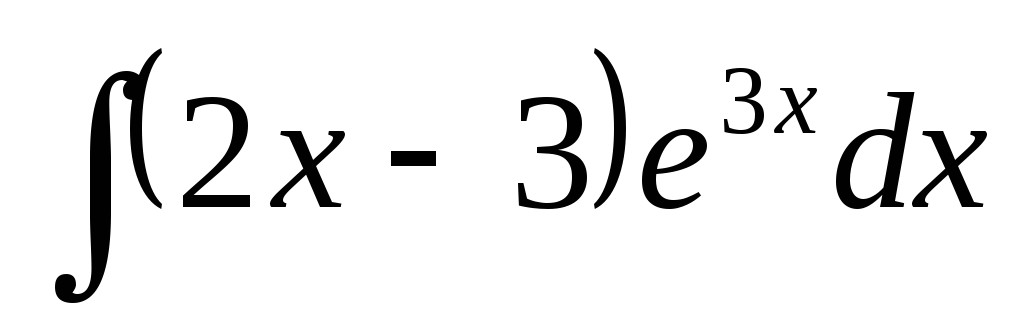 .
.
Положим 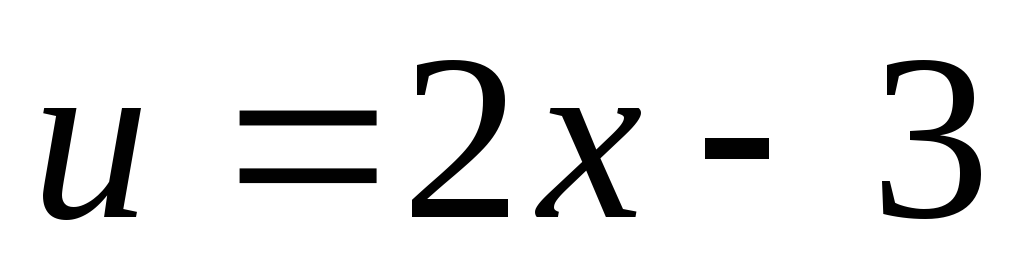 ,
,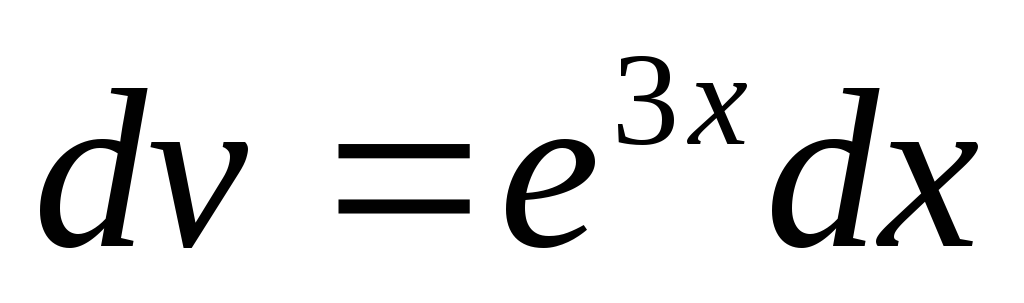 ,
тогда
,
тогда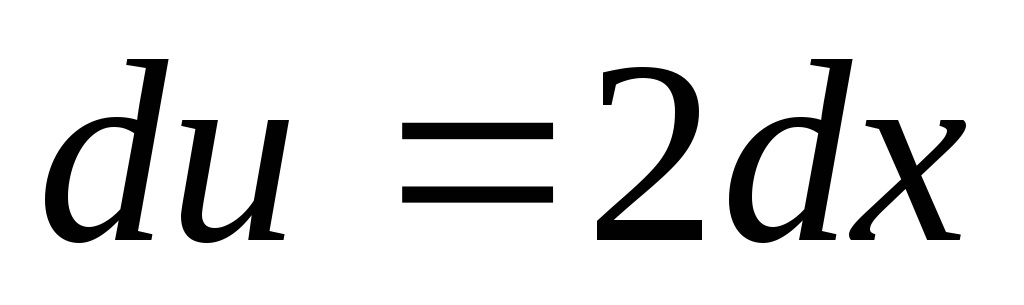 ,
,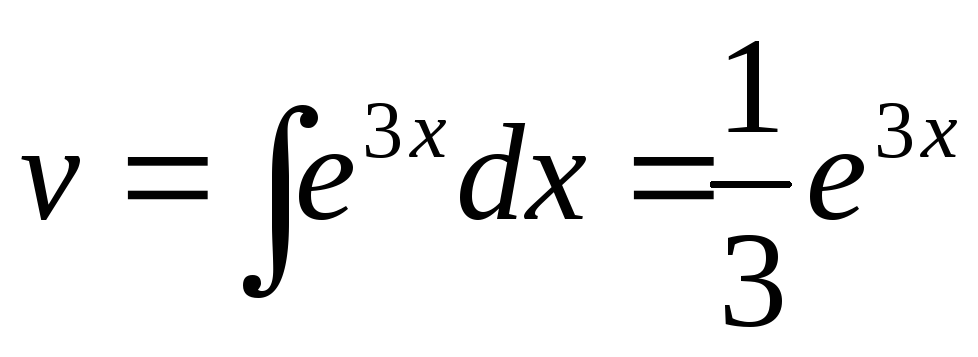 .
Следовательно,
.
Следовательно,
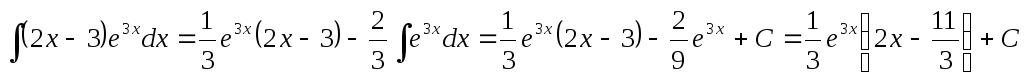
б) В интегралах вида
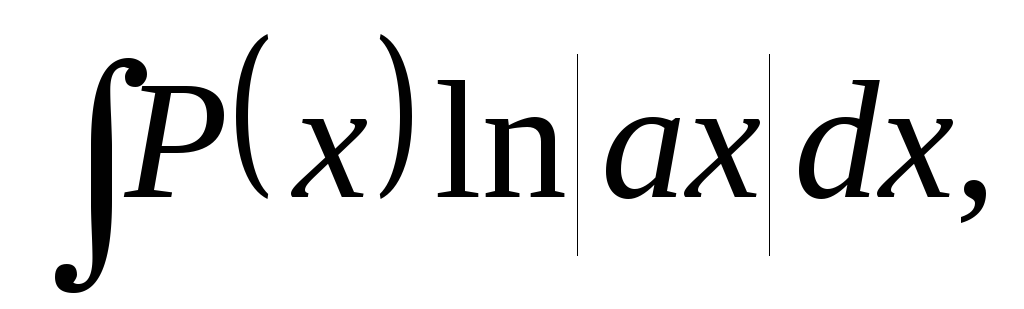
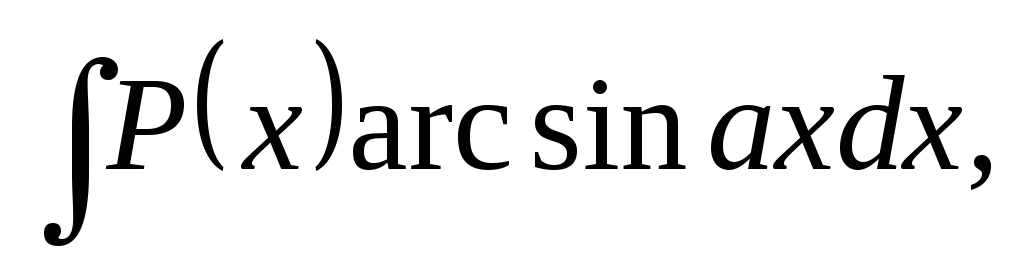
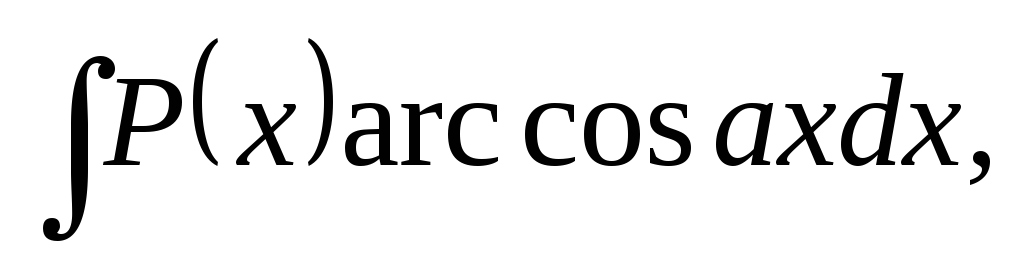
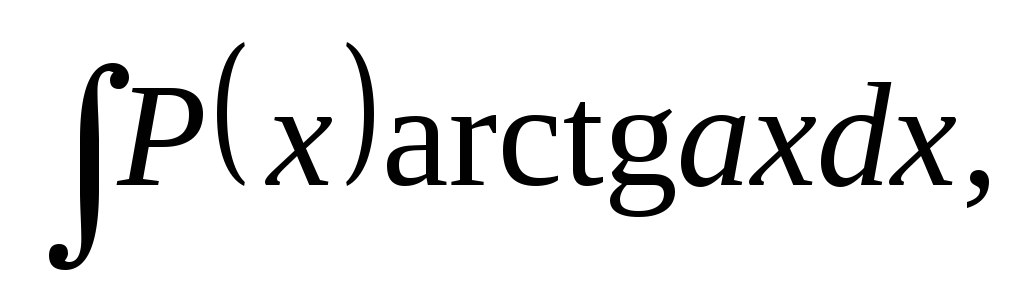
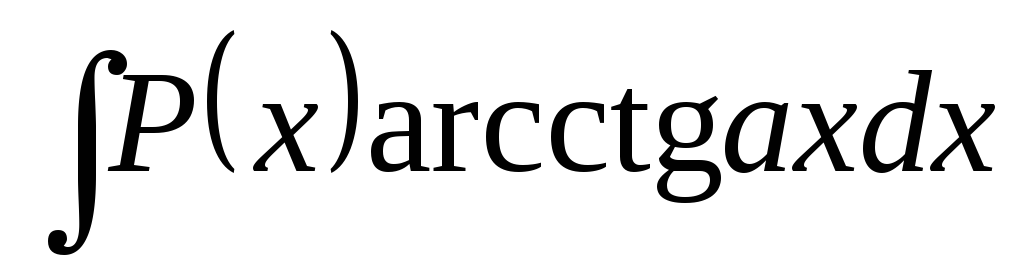
полагают 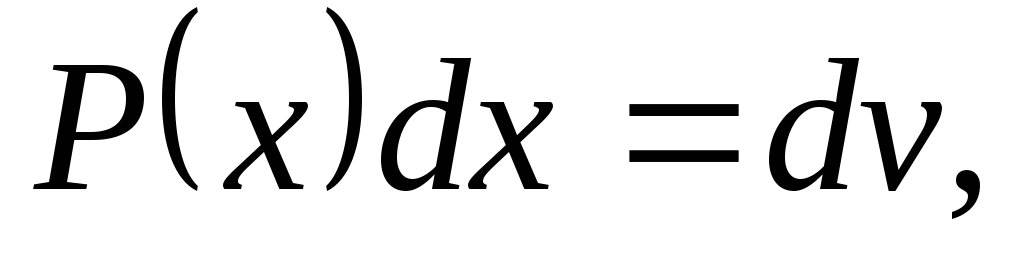 а
остальные сомножители – заu.
а
остальные сомножители – заu.
Пример 8. Найти 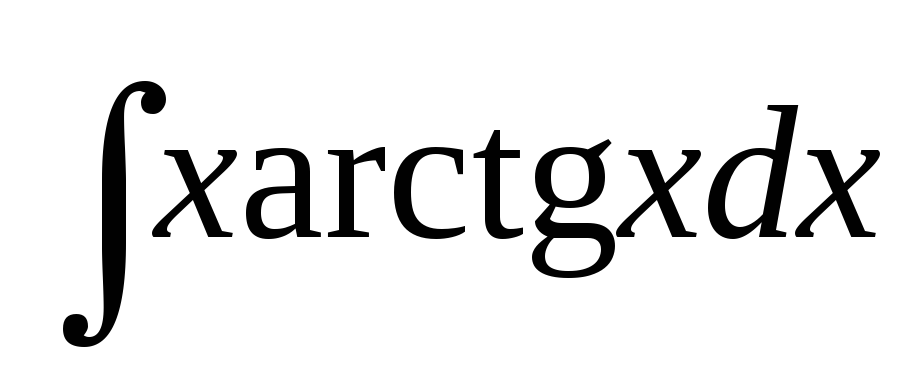 .
.
Положим
 ,
, ,
тогда
,
тогда ,
, .
.
Следовательно, 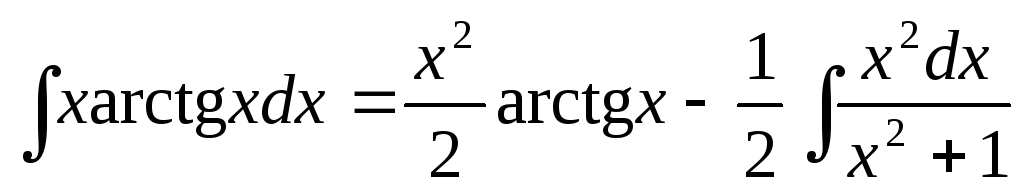 .
.
Вычислим отдельно последний интеграл:
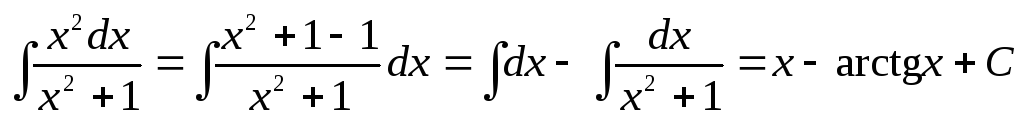 .
.
Итак, 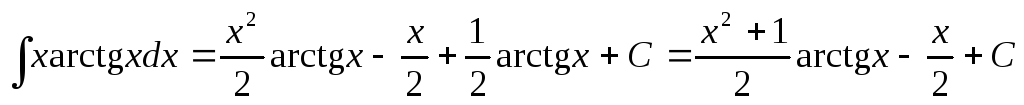 .
.
Отметим, что на практике важно научиться применять формулу (4), не выписывая по возможности в стороне выражения для функций u и v.
Так, решение приведенного примера может быть представлено в виде:
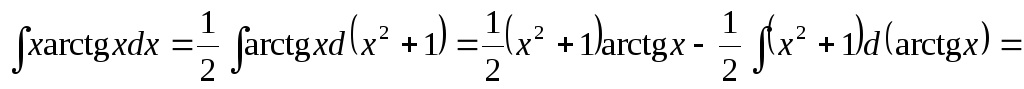
=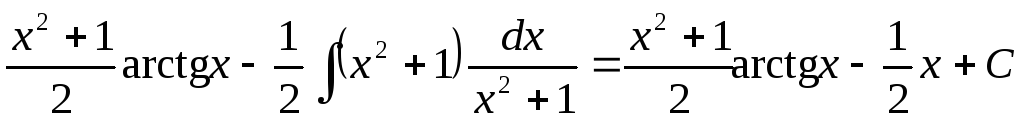 .
.
Возвращение к исходному интегралу
Формула интегрирования
по частям применима и для нахождения
интегралов вида 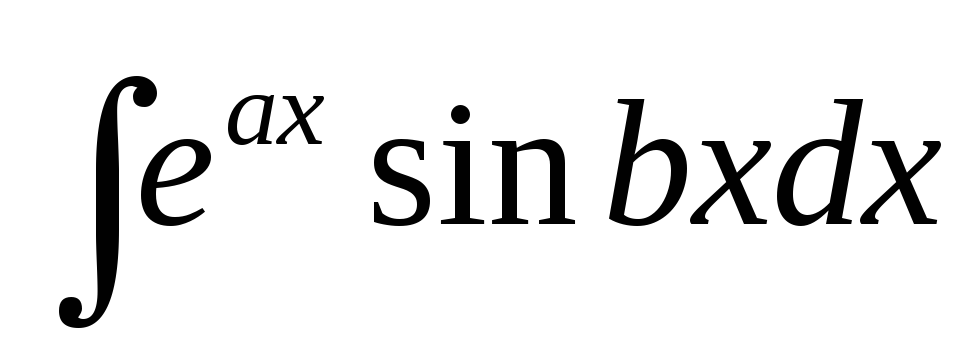 и
и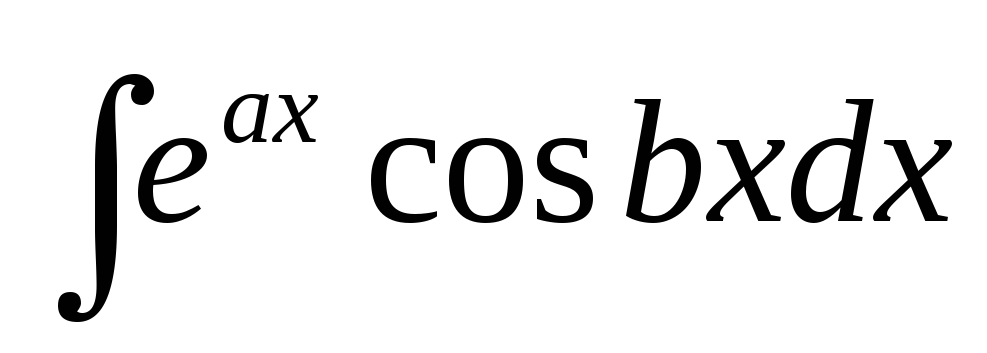 ,
гдеа и b – числа. При
нахождении этих интегралов она применяется
последовательно два раза, причем оба
раза за u выбирается либо показательная функция,
либо тригонометрическая. После
двукратного интегрирования по частям
получается линейное уравнение относительно
искомого интеграла.
,
гдеа и b – числа. При
нахождении этих интегралов она применяется
последовательно два раза, причем оба
раза за u выбирается либо показательная функция,
либо тригонометрическая. После
двукратного интегрирования по частям
получается линейное уравнение относительно
искомого интеграла.
Пример 9. Найти I
=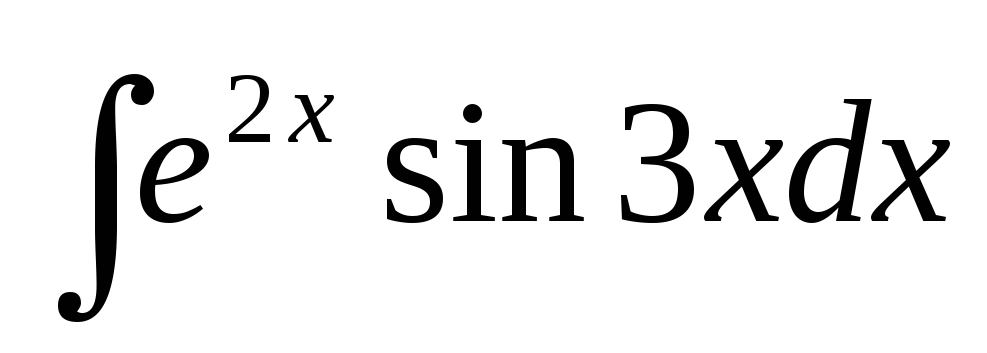 .
.
Положим 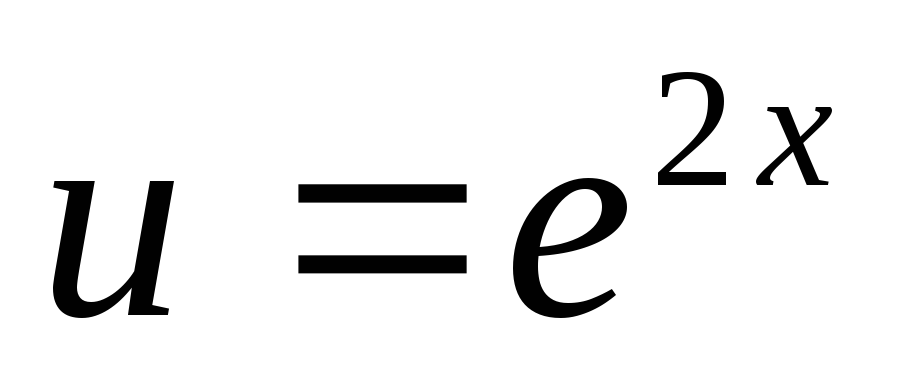 ,
,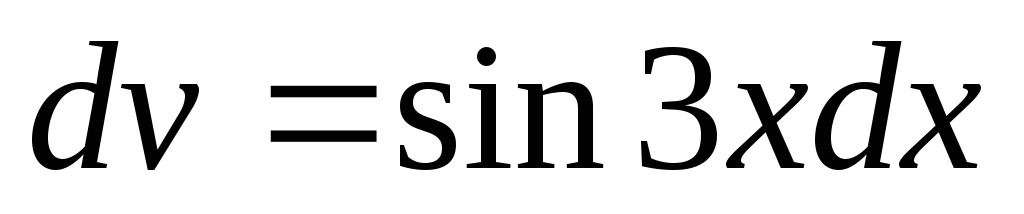 .
Тогда
.
Тогда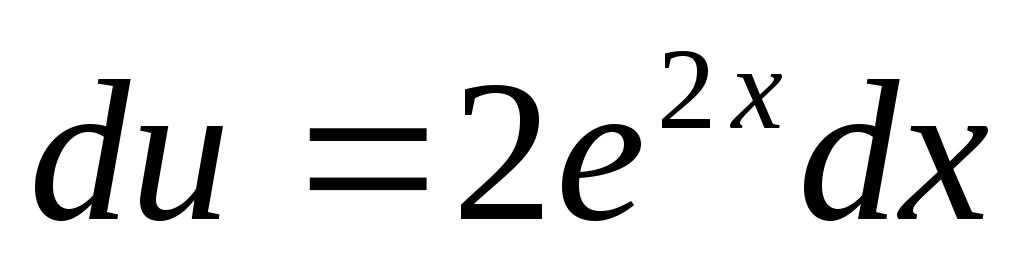 ,
,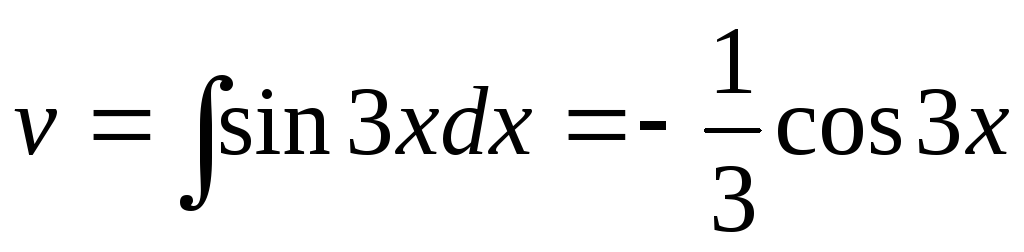 .
.
Следовательно,
I
=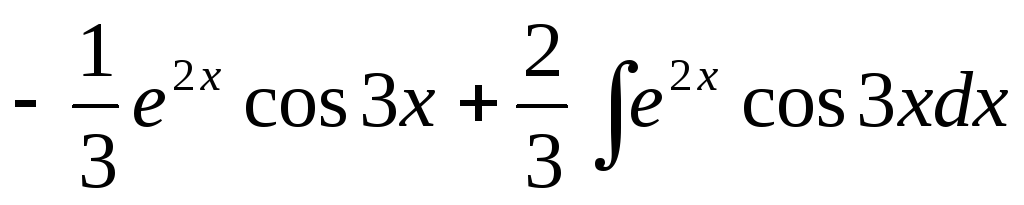 .
.
Для вычисления
интеграла  снова
применим интегрирование по частям.
Положим
снова
применим интегрирование по частям.
Положим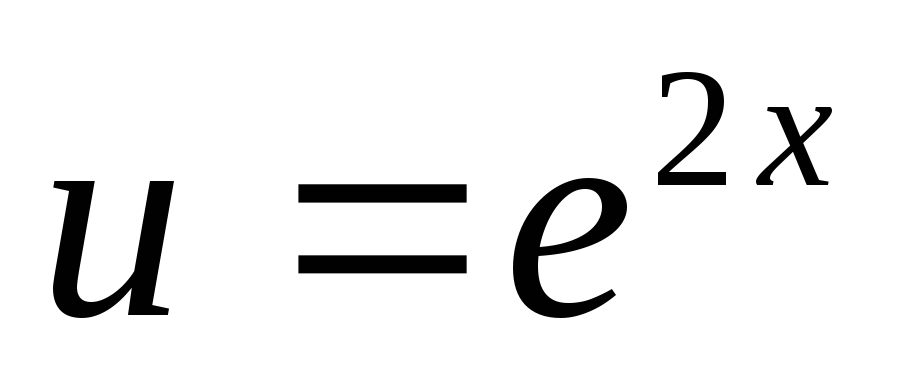 ,
,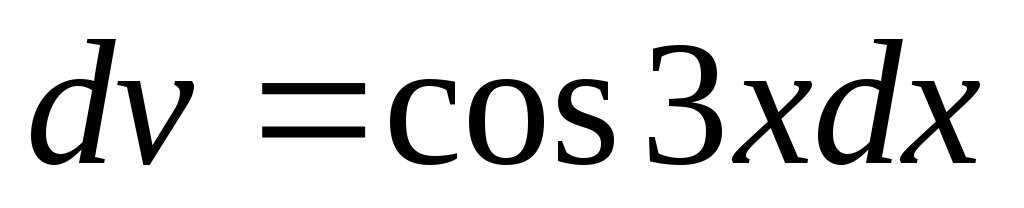 .
Тогда
.
Тогда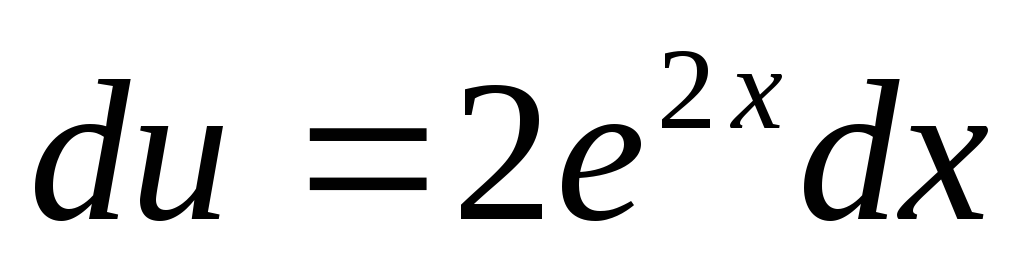 ,
,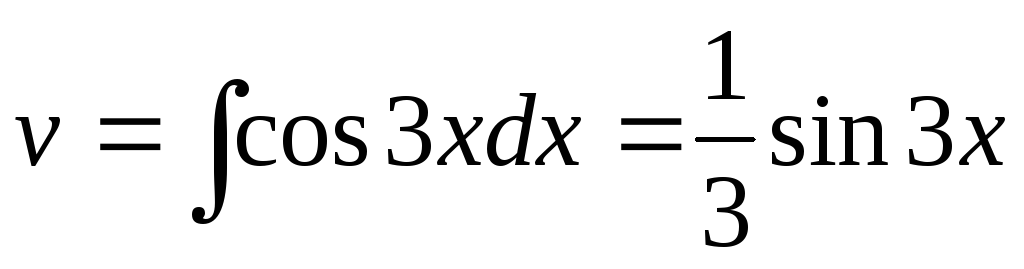 .
.
Таким образом,
I=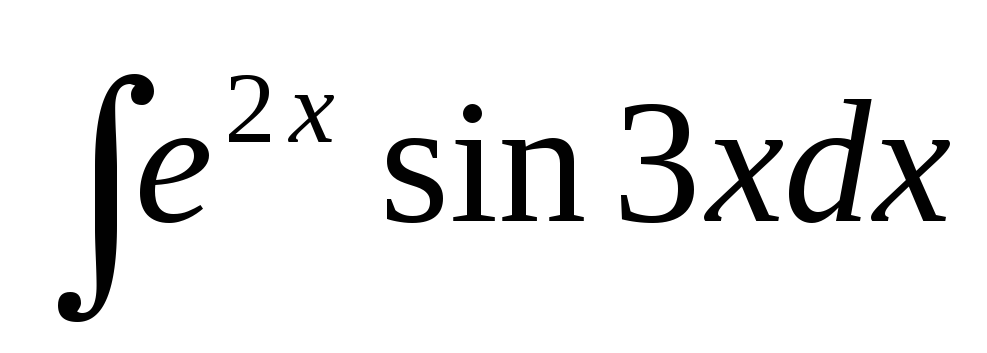 =
=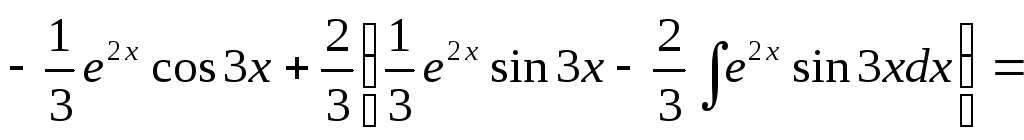
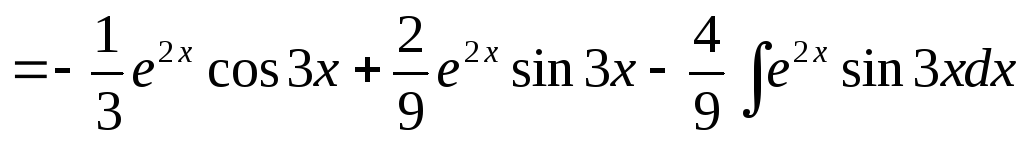 .
.
Так как в правой части стоит искомый интеграл, то, перенося его в левую часть, получим:
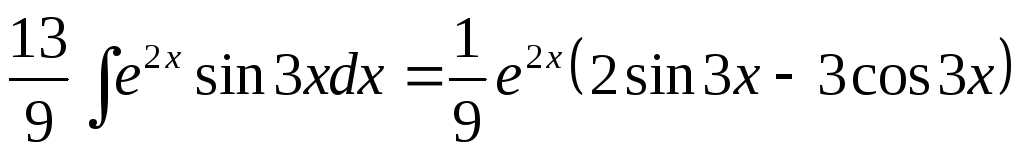 .
.
Отсюда получаем окончательный результат:
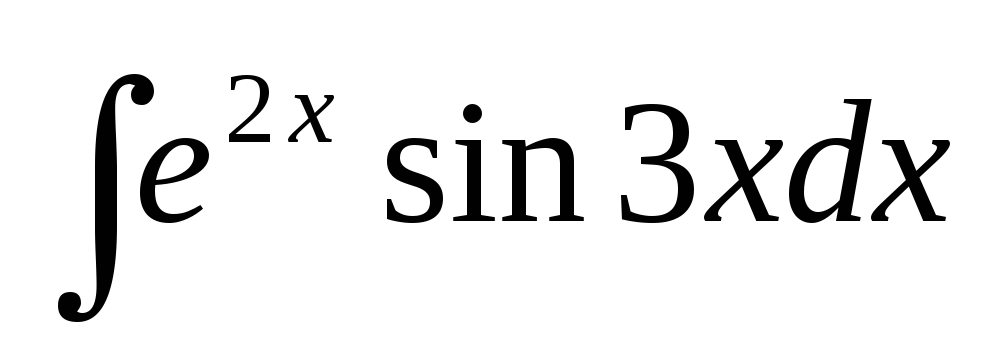 =
=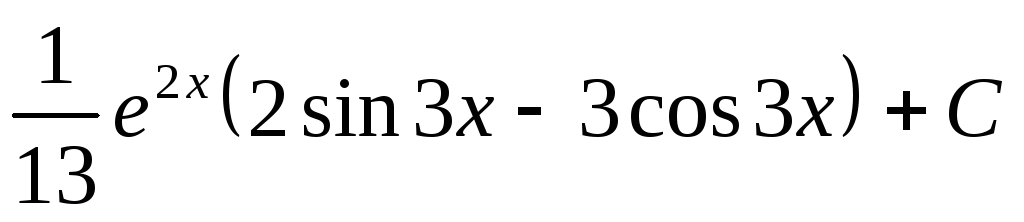 .
.
Применим изложенный метод к вычислению еще двух, часто используемых в приложении, интегралов.
Пример
10. Найти
I
=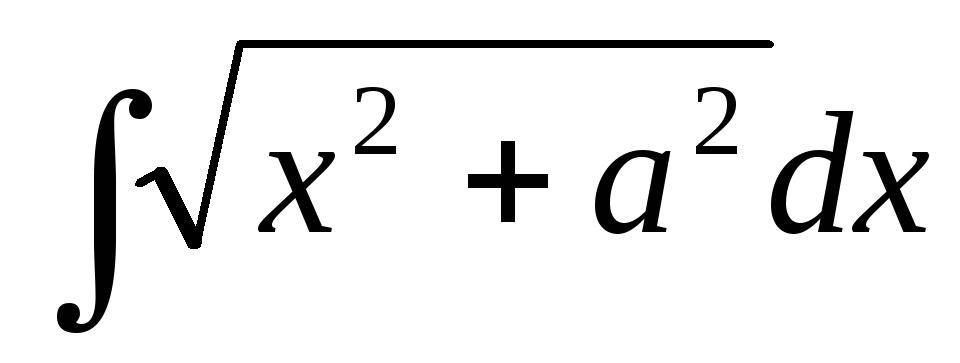 .
.
Положим 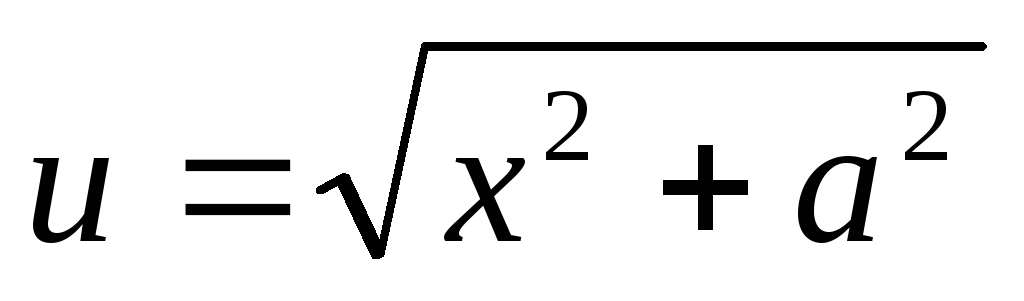 ,
,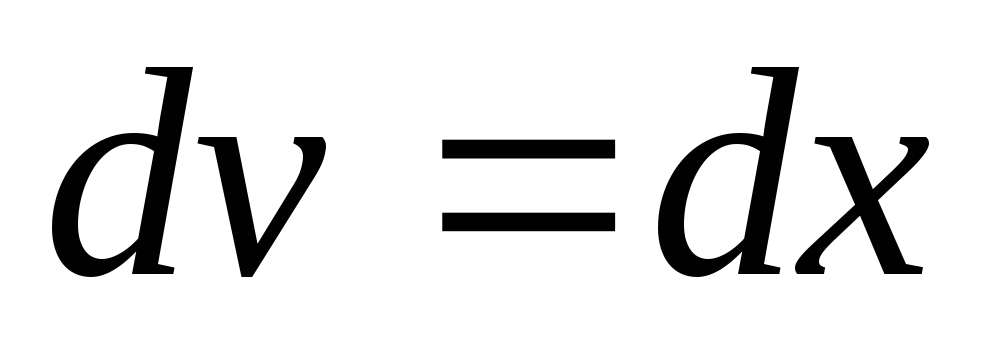 .
Тогда
.
Тогда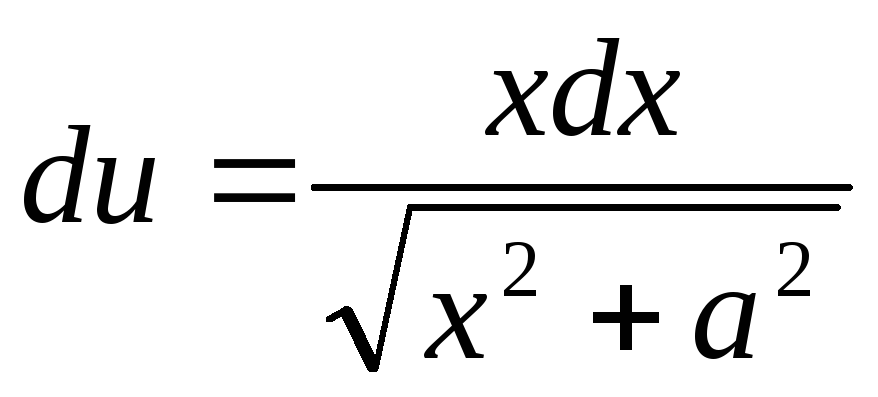 ,
,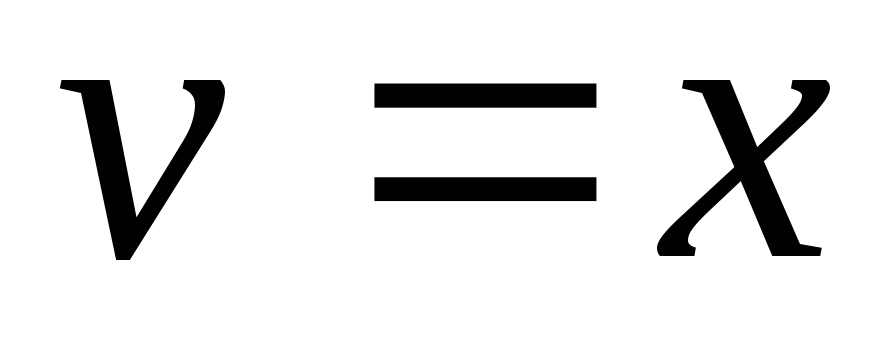 .
Следовательно,
.
Следовательно,
| (*) |
Так
как 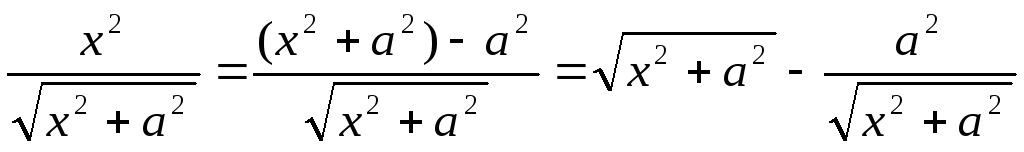 ,
то
,
то
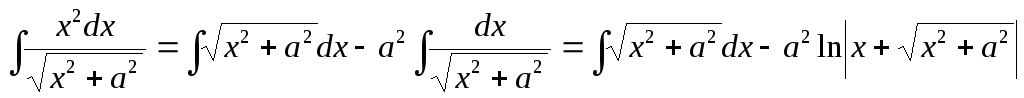
(см. лекция 2, п.2б, пример 20).
Подставив полученное выражение в равенство (*), будем иметь
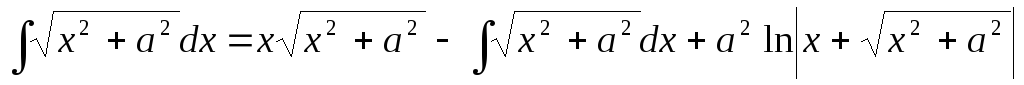 .
.
Таким
образом, 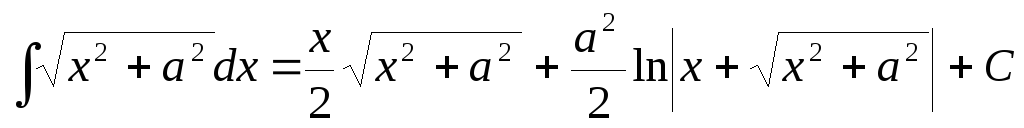 .
.
Пример
11. Найти 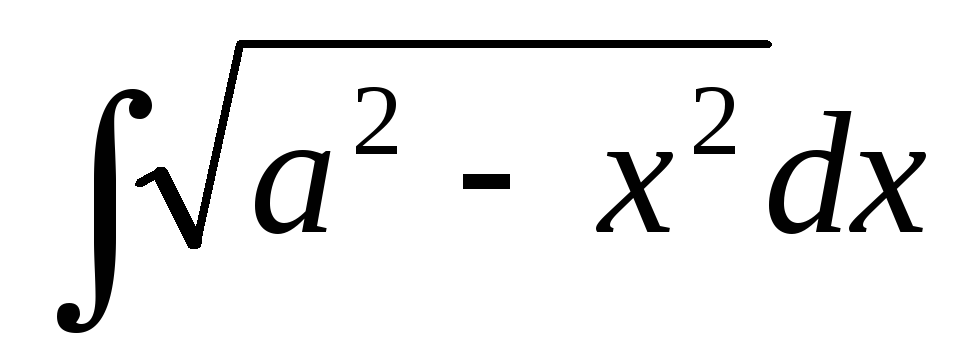 ,(а0)
,(а0)
Положим 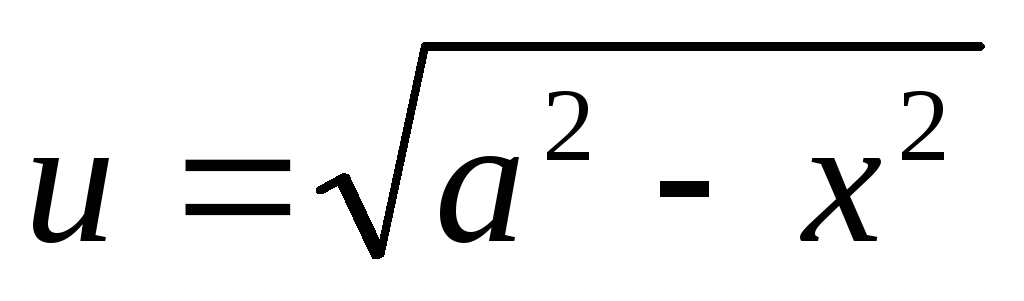 ,
,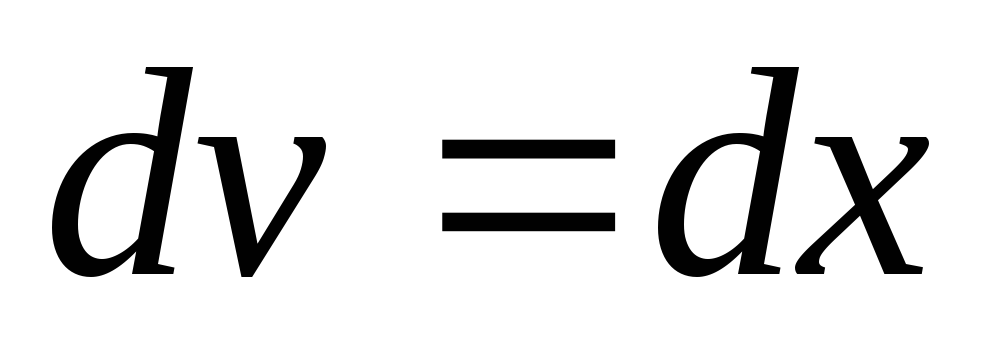 ,
откуда
,
откуда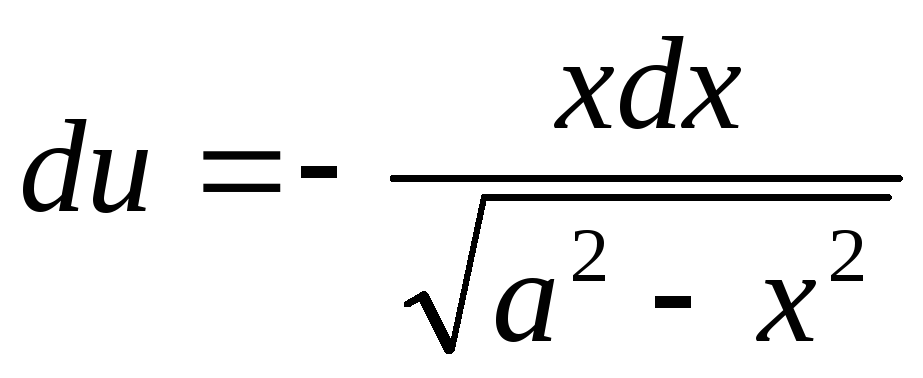 ,
,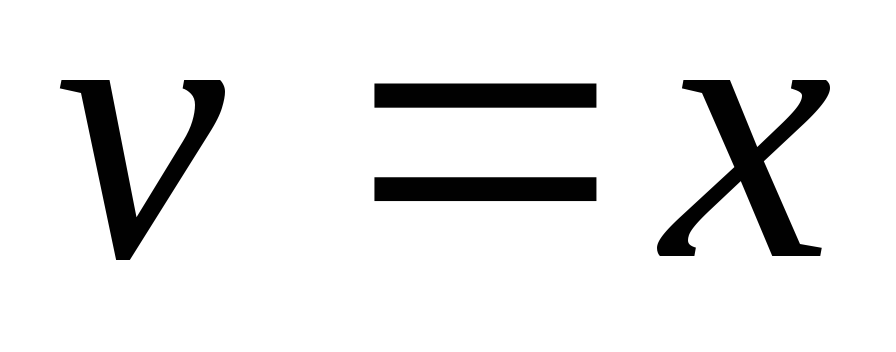 .
Следовательно,
.
Следовательно,
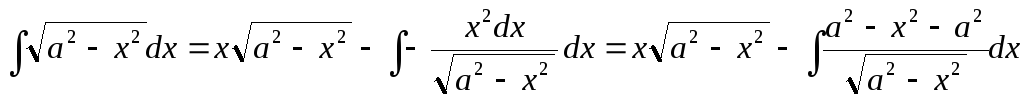 ,
,
или 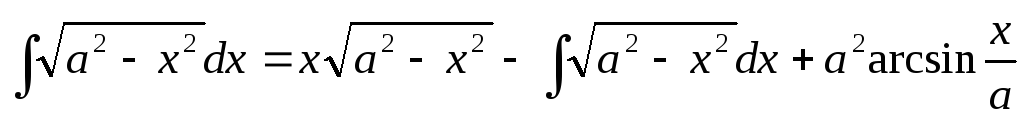 .
.
Отсюда получаем: 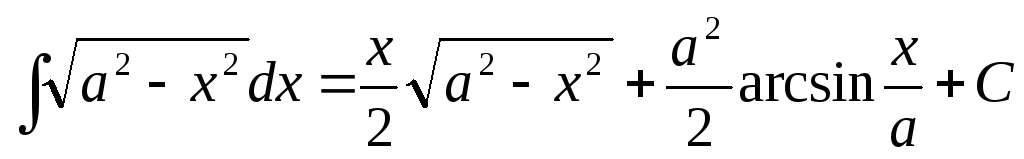 .
.
studfile.net
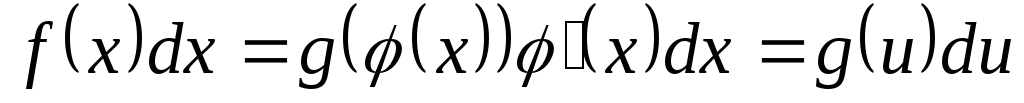 .
.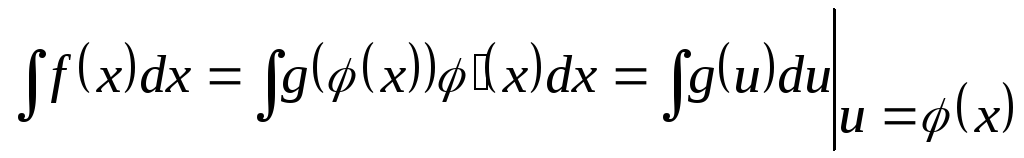 ,
,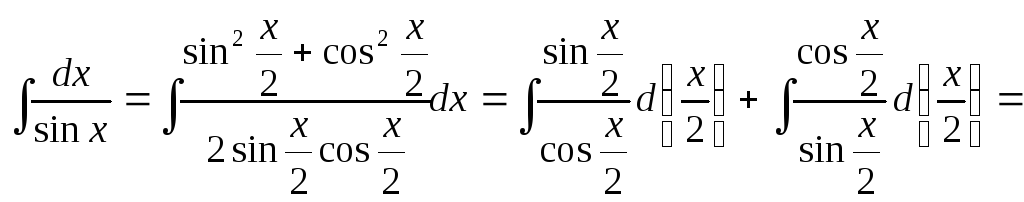
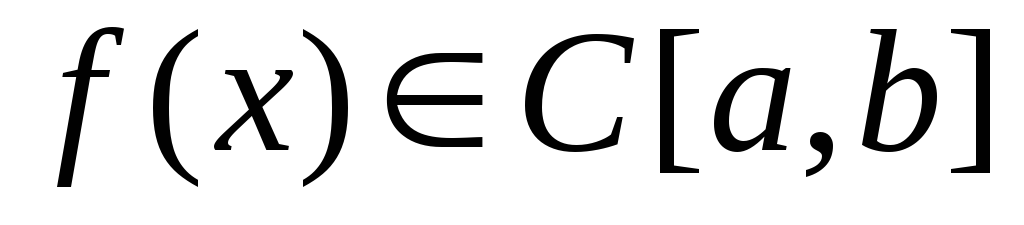 ,
, 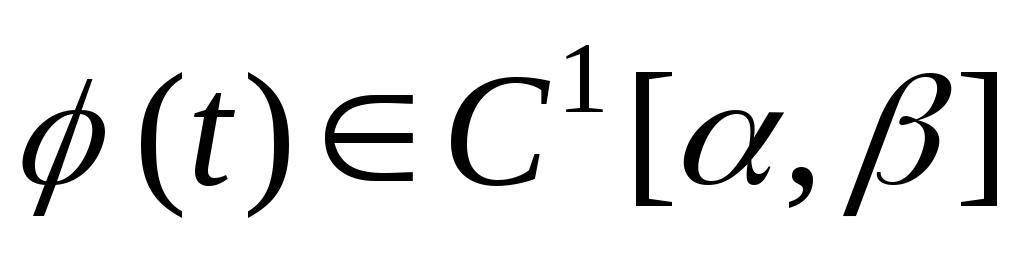 ;
;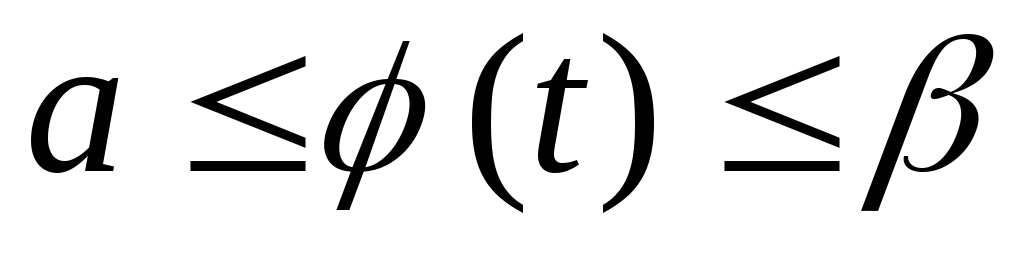 для
для 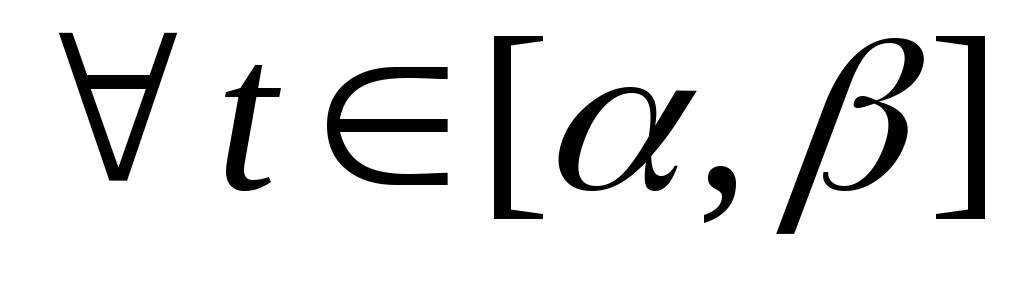 ;
;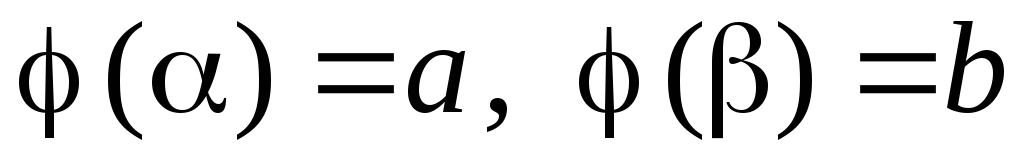 .
.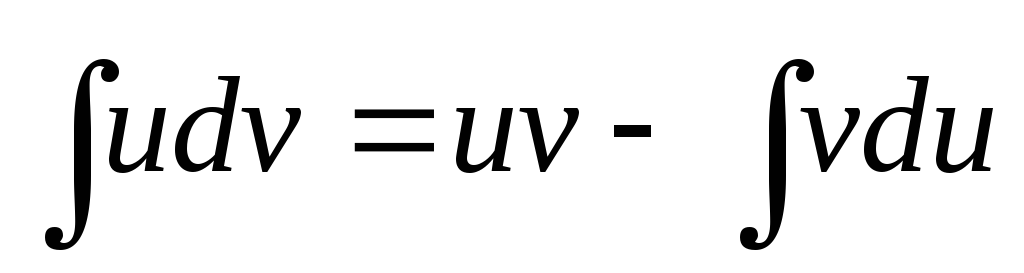 .
.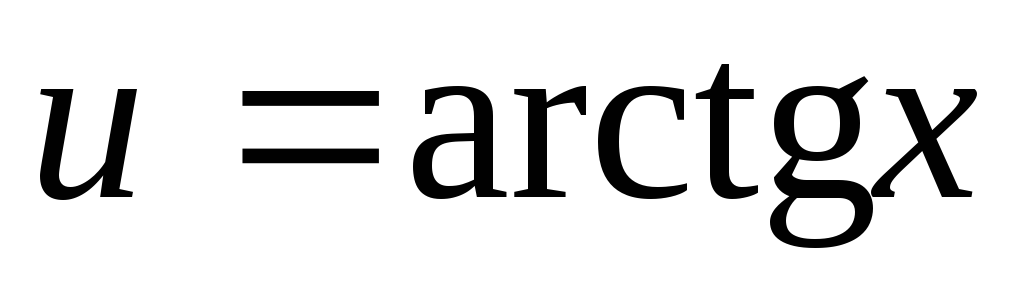 ,
,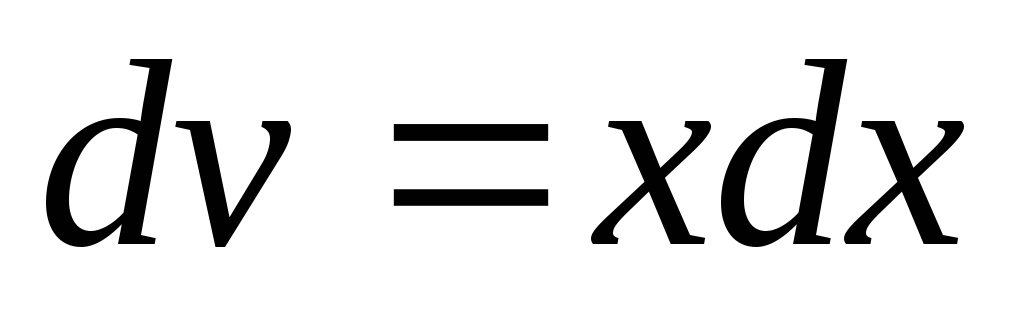 ,
тогда
,
тогда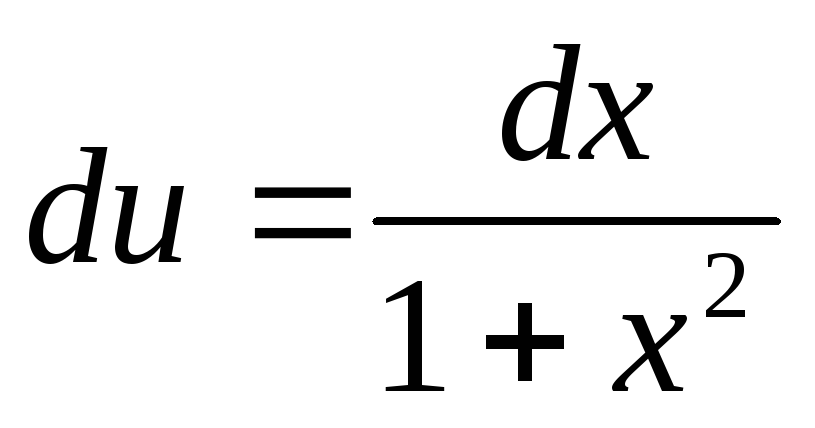 ,
,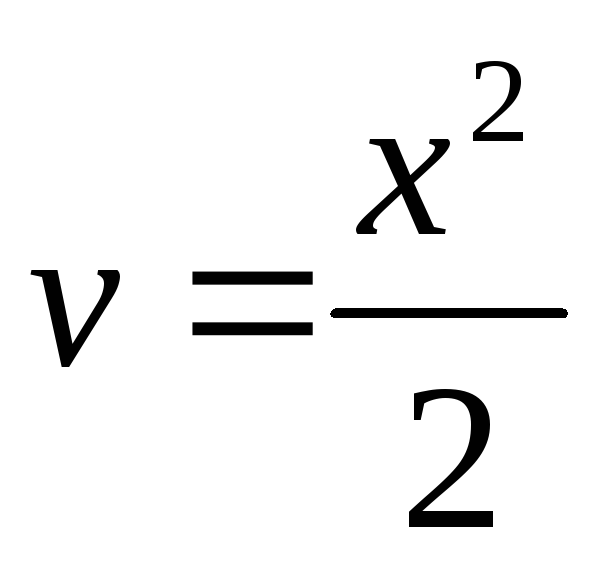 .
.