Элективный курс для 10 класса по математике (профильный уровень) «Абсолютная величина(модуль)»

Программа элективного курса

Практикум по решению задач по математике

«Абсолютная величина (модуль)»

Пояснительная записка

В соответствии с образовательной программой ОУ РП данный элективный курс ориентирован на учащихся 10 классов и рассчитан на овладение содержанием материала курса с изучением математики на профильном уровне. Ведется за счет школьного компонента и рассчитан на 36 часов — 1 час в неделю (на основании учебного плана МБОУ СОШ №2, утверждённого приказом директора №01-42 от 01 сентября 2015 года, приказом директора №01-63 от 01 сентября 2016 года).

Программа является обучающей и содержит:

• пояснительную записку;

• цели курса;

• задачи курса;

• требования к уровню усвоения учебного материала;

• содержание курса;

• тематическое планирование;

• темы творческих работ;

• литературу.

Понятие абсолютной величины (модуля) является одной из важнейших характеристик числа как в области действительных, так и в области комплексных чисел. Это понятие широко применяется не только в различных разделах школьного курса математики, но и в курсах высшей математики, физики и технических наук, изучаемых в вузах. Например, в теории приближенных вычислений используются понятия абсолютной и относительной погрешностей приближенного числа. В механике и геометрии изучаются понятия вектора и его длины (модуля вектора). В математическом анализе понятие абсолютной величины числа содержится в определениях таких основных понятий, как предел, ограниченная функция и др. Задачи, связанные с абсолютными величинами, часто встречаются на математических олимпиадах, на сдаче ЕГЭ.

Программой школьного курса математики не предусмотрены обобщение и систематизация знаний о модулях, их свойствах, полученных учащимися за весь период обучения. Это и позволит сделать элективный курс «Абсолютная величина (модуль)» эффективным при обучении учащихся.

Курс позволит школьникам систематизировать, расширить и укрепить знания, связанные с абсолютной величиной, подготовиться для дальнейшего изучения тем, использующих это понятие, научиться решать разнообразные задачи различной сложности, способствует выработке и закреплению навыков работы на компьютере.

Учителю курс поможет наиболее качественно подготовить учащихся к математическим олимпиадам и сдаче ЕГЭ.

Программа элективного курса предполагает знакомство с теорией и практикой рассматриваемых вопросов и рассчитана на 36 часов (14 часов лекций и 22 часа практических занятий).

Содержание курса состоит из семи разделов, включая введение и итоговое занятие. В зависимости от уровня подготовки учащихся, уровня сложности изучаемого материала и восприятия его школьниками, можно взять для изучения не все темы, увеличив при этом количество часов на изучение других.

Программа содержит темы творческих работ и список литературы по предложенным темам.

В процессе изучения данного курса предполагается использование различных методов активизации познавательной деятельности школьников, а также различных форм организации их самостоятельной работы.

Результатом освоения программы курса является представление школьниками творческих индивидуальных или групповых работ на итоговом занятии.

Оценка качества знаний элективного курса производится по пятибалльной системе.

Цели курса:

• обобщение и систематизация, расширение и углубление знаний по теме «Абсолютная величина»; обретение практических навыков выполнения заданий с модулем; повышение уровня математической подготовки школьников.

Задачи курса:

• вооружить учащихся системой знаний по теме: «Абсолютная величина»;

• сформировать навыки применения данных знаний при решении разнообразных задач различной сложности;

• подготовить учащихся к ЕГЭ;

• сформировать навыки самостоятельной работы, работы в малых группах;

• сформировать навыки работы со справочной литературой, с компьютером;

• сформировать умения и навыки исследовательской работы;

• способствовать развитию алгоритмического мышления учащихся;

• способствовать формированию познавательного интереса к математике.

Требования к уровню усвоения учебного материала

  В результате изучения программы элективного курса «Абсолютная величина (модуль)» учащиеся получают возможность

знать и понимать:

• определение абсолютной величины действительного числа;

• основные операции и свойства абсолютной величины;

• правила построения графиков уравнений (в т.ч. функций), содержащих знак абсолютной величины;

• алгоритмы решения уравнений, неравенств, систем уравнений и неравенств, содержащих переменную под знаком модуля.

Уметь:

• применять определение, свойства абсолютной величины действительного числа к решению конкретных задач;

• читать и строить графики функций, аналитическое выражение которых содержит знак абсолютной величины;

• решать уравнения, неравенства, системы уравнений и неравенств, содержащих переменную под знаком модуля.

 

Содержание элективного курса

(1 ч в неделю, всего 36 ч)

  1. Введение (1 ч)

Цели и задачи элективного курса. Вопросы, рассматриваемые в курсе и его структура. Знакомство с литературой, темами творческих работ. Требования, предъявляемые к участникам курса. Аукцион «Что я знаю об абсолютной величине?».

  2. Абсолютная величина действительного числа а (3 ч)

Абсолютная величина действительного числа а. Модули противоположных чисел. Геометрическая интерпретация понятия модуля а. Модуль суммы и модуль разности конечного числа действительных чисел. Модуль разности модулей двух чисел. Модуль произведения и модуль частного. Операции над абсолютными величинами. Упрощение выражений, содержащих переменную под знаком модуля. Применение свойств модуля при решении олимпиадных задач.

  3. Графики уравнений (в т.ч. функций), аналитическое выражение которых содержит знак абсолютной величины (8 ч)

Применение компьютерной программы «Advanced Grapher» при построении графиков функций, аналитическое выражение которых содержит знак модуля. Правила и алгоритмы построения графиков уравнений, аналитическое выражение которых содержит знак модуля. Графики уравнений:

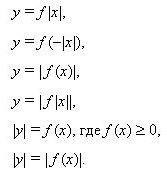
Графики некоторых простейших функций, заданных явно и неявно, аналитическое выражение которых содержит знак модуля. Графики уравнений (в т.ч. функций), аналитическое выражение которых содержит знак абсолютной величины в олимпиадных заданиях.

  4. Уравнения, содержащие абсолютные величины (11 ч)

Основные методы решения уравнений с модулем. Раскрытие модуля по определению, переход от исходного уравнения к равносильной системе, возведение в квадрат обеих частей уравнения, метод интервалов, графический метод, использование свойств абсолютной величины. Уравнения вида:

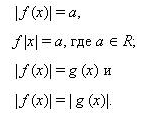
Метод замены переменных при решении уравнений, содержащих абсолютные величины. Метод интервалов при решении уравнений, содержащих абсолютные величины. Уравнения вида:

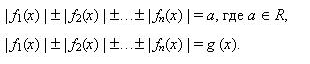
Способ последовательного раскрытия модуля при решении уравнений, содержащих «модуль в модуле». Графическое решение уравнений, содержащих абсолютные величины. Использование свойств абсолютной величины при решении уравнений. Уравнения с параметрами, содержащие абсолютные величины. Защита решенных олимпиадных заданий.

  5. Неравенства, содержащие абсолютные величины (9 ч)

Неравенства с одним неизвестным. Основные методы решения неравенств с модулем. Неравенства вида:

Неравенства вида:

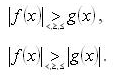
Метод интервалов при решении неравенств, содержащих знак модуля. Неравенства с параметрами, содержащие абсолютные величины. Неравенства с двумя переменными.

  6. Системы уравнений и неравенств, содержащие абсолютные величины (3 ч)

  7. Итоговое занятие (1 ч)

Учебно-тематическое планирование

п /п

Название

разделов и тем

Количество часов

Форма

проведения

Образовательный

продукт

всего

теории

практики

1.

Введение. Понятие модуля

1

1

аукцион знаний

анкета, записи

2.

Абсолютная величина действительного числа а

3

1

2

 

2.1.

Свойства модулей. Основные теоремы

1

1

лекция

опорный конспект

2.2.

Операции над абсолютными величинами

1

 

1

тренинг

с применением ПК

распечатка решений

2.3.

Упрощение выражений, содержащих переменную под знаком модуля

1

 

1

практикум

решенные задания

3.

Графики уравнений, аналитическое выражение которых содержит знак абсолютной величины

8

3 

5

 

3.1.

Применение компьютерной программы «Advanced Grapher» при построении графиков функций, аналитическое выражение которых содержит знак модуля

2

1 

1

исследовательская работа

с применением ПК

распечатка

построенных

графиков

3.2.

Правила и алгоритмы построения графиков (в т.ч. функций), аналитическое выражение которых содержит знак модуля

2

1 

1

семинар-практикум

памятка с правилами и алгоритмами

построений

3.3.

Графики уравнений

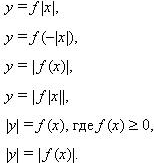
3

1

2

тренинг

выполненные

построения

3.4.

Графики некоторых простейших функций, заданных явно и неявно, аналитическое выражение которых содержит знак модуля

1

1

мастерская

рефераты,

опорный конспект,

выполненные

построения

4.

Уравнения, содержащие абсолютные величины

11

4

7

 

4.1.

Основные методы решения уравнений с модулем

1

1

 

лекция

конспект,

алгоритмы

4.2.

Уравнения вида

3

1

2

практикум

решенные задания

4.3.

Метод замены переменных при решении уравнений, содержащих абсолютные величины

1

 

1

практикум

памятка,

решенные задания

4.4.

Метод интервалов при решении уравнений, содержащих абсолютные величины. Уравнения вида

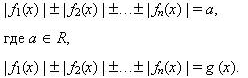
2

  1

1

семинар-практикум

реферат, памятка,

опорный конспект,

решенные задания

4.5.

Способ последовательного раскрытия модуля при решении уравнений, содержащих «модуль в модуле»

2

1 

1

практикум

реферат, памятка,

опорный конспект,

решенные задания

4.6.

Графическое решение уравнений, содержащих абсолютные величины

2

 

2

тренинг

с применением ПК

распечатка

решений

5 .

Неравенства, содержащие абсолютные величины

9

4

5

 

5.1.

Неравенства с одним неизвестным. Основные методы решения неравенств с модулем

2

1

  1

лекция

конспект

5.2.

Основные методы решения неравенств с модулем

2

1

  1

семинар

реферат,

алгоритмы решений

5.3.

Неравенства вида

2

1 

1

практикум

решенные задания

5.4.

Неравенства вида

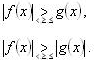
3

1 

2

практикум

решенные задания

6.

Системы уравнений и неравенств, содержащие абсолютные величины

3

1 

2

практикум

схемы решений,

решенные задания

7.

Итоговое занятие

1

1

семинар

защита творческих работ

Итого:

36

14

22

Темы творческих работ:

1. Применение модуля в механике и векторной алгебре.

2. Модуль в определении предела.

3. Погрешности.

4. Проект памятки правил и алгоритмов построения графиков уравнений (в т.ч. функций), аналитическое выражение которых содержит знак модуля.

5. Изготовление игры «Математическое лото» по теме «Графики уравнений, аналитическое выражение которых содержит знак модуля».

6. Проект опорных сигналов по способам решения уравнений и неравенств с модулем.

7. Простейшие функции, заданные явно и неявно, аналитическое выражение которых содержит знак модуля, и их графики.

Учебно-методическое обеспечение курса

Основная литература:

1. Башмаков М.И. Уравнения и неравенства. – М.: ВЗМШ при МГУ, 1983.

2. Виленкин Н.Я. и др. Алгебра и математический анализ. 11 кл. – М.: Просвещение, 1993.

3. Гайдуков И.И. Абсолютная величина. – М.: Просвещение, 1968.

4. Галицкий М.Л. и др. Сборник задач по алгебре 8 – 9 кл. – М.: Просвещение, 1995.

5. Говоров В.М. и др. Сборник конкурсных задач по математике.– М.: Просвещение, 1983.

6. Горнштейн П.И. и др. Задачи с параметрами. – М.: Илекса, Харьков: Гимназия, 2003.

Дополнительная литература:

1. Колесникова С.И. Математика. Интенсивный курс подготовки к Единому Государственному экзамену. М.: Айрис-пресс, 2004.

2. Мерзляк А.Г. и др. Алгебраический тренажер. – М.: Илекса, 2001.

3. Мордкович А.Г. Алгебра. 8 кл. – М.: Мнемозина, 2000.

4. Нешков К.И. и др. Множества. Отношения. Числа. Величины. – М.: Просвещение, 1978.

5. Никольская И.Л. Факультативный курс по математике. – М.: Просвещение, 1995.

6. Олехник С.Н. и др. Уравнения и неравенства. Нестандартные методы решения. 10 – 11 кл. – М.: Дрофа, 1995.

7. Шарыгин И.Ф. Факультативный курс по математике 10 – 11 кл. – М.: Просвещение, 1989.

8. Ястребинецкий Г.А. Задачи с параметрами. – М.: Просвещение, 1986.

Элективный курс по математике (10 класс) на тему: Контрольные работы по спецкурсу для 10 класса «Уравнения и неравенства с модулем»

КИМы  по  спецкурсу  для  10   КЛАССА

Всего  контрольных  работ – 6.

Контрольные  работы  полностью  соответствуют  плану  спецкурсу.

КОНТРОЛЬНАЯ  РАБОТА  № 1  по  теме  «Модуль  числа.  Уравнения,  содержащие  модуль» 

Контрольная  работа  №  1   состоят из  4   заданий  в  три  варианта.

На  оценку  «5»  —  необходимо  выполнить  верно  4  заданий;

На  оценку  «4»  —  необходимо  выполнить  верно  4 заданий;

На  оценку  «3»  —  необходимо  выполнить  верно  3  заданий;

2) Цели

1.Проверить   знания,  умения  их  применять  для  выполнения  учащимися:

а)  упрощения  иррациональных  выражений,  б)  построения  графиков  функций;

 в) решения  уравнений.

2.Проверка   уровня  сформированности   навыка   решения   различных  заданий

   по  изученным темам.  

   

3. Формировать  вычислительные  навыки  учащихся.

Текст  контрольной  работы  №  1.  

 Вариант  1.

       1.Найти  значение  выражения:  

а)  ∙ ;    б)     ;                          

 в)  -.

       2.Упростите  выражение:  а)  ;  б)    ;   в)  .

      3.Построить  график  функции:  а)  у = ;  б)  у = 2.  в)  у = х2 — 4 +3.

       4. Решите  уравнение:  а) = 1;   б)   — =9;  в)  + = 6.

Вариант  2.

1. Найти  значение  выражения:  

а)  ∙ ;    б)     ;                          

 в)  -.

       2.Упростите  выражение:  а)  ;  б)    ;   в)  .

      3.Построить  график  функции:  а)  у = ;  б)  у = 2.  в)  у = х2 — 6 + 5.

       4. Решите  уравнение:  а) = 1;   б)   — =9;  в)  + = 6.

С/ р    Неравенства с модулем

1. Неравенства вида «Модуль меньше функции»

1) . |2x + 3| x +7 ;   2). |x²+ 5x| 3). |x2 + 2x -3| + 3(x +1)

4). |x2 + 2x – 7|x ;   5). |x2 — x -1|x + 2 ;   6). |x2 — 4x – 4|x2 — 4 ;

7). |x3 — 2x -4|x — 4 .

2. Неравенства вида «Модуль больше функции»

1). |3x +1| > 5 — 4x ;   2). |x2 + 2x -3|> x ;   3). |2×2 — 9x +15|> 20 ;

4). |x2 — x -6 |>x +3;   5). |x2 -8x + 2|- x2 > 2x + 2 .

КОНТРОЛЬНАЯ  РАБОТА  № 2  по  теме  «Неравенства,  содержащие  модуль».

 

Контрольная  работа  №  2   состоят из  4   заданий  в  два  варианта.

На  оценку  «5»  —  необходимо  выполнить  верно  4  заданий;

На  оценку  «4»  —  необходимо  выполнить  верно  4  заданий;

На  оценку  «3»  —  необходимо  выполнить  верно  3 заданий;

2) Цели

1.Проверить   знания,  умения  их  применять  для  выполнения  учащимися:

а)  упрощения  иррациональных  выражений,  б)  построения  графиков  функций;

 в) решения  уравнений.

2.Проверка   уровня  сформированности   навыка   решения   различных  заданий

   по  изученным темам.  

   

3. Формировать  вычислительные  навыки  учащихся.

Текст  контрольной  работы  №  2.  

 Вариант  1.

1.Решить  неравенства  по  определению: а) ;  б)   

 2.Решите  неравенство  ;

 3. При  каких  значениях   х  выражение | |x| -3x + 5|  больше  3.

 4. Найдите  целые  решения  неравенства  ,  решив  его  методом  интервалов.

Вариант  2.

1.Решить  неравенства: а) ;  б)  .

2. Решите  неравенство  ;

3. При  каких  значениях   х  выражение | |x| + 3x — 5|  меньше  3.

4. Найдите  целые  решения  неравенства:,  решив  его  методом  интервалов.

КОНТРОЛЬНАЯ  РАБОТА  № 3  по  теме  «Решение  уравнений»

 

Контрольная  работа  №  3   состоят из  4   заданий  в  три  варианта.

На  оценку  «5»  —  необходимо  выполнить  верно  4  заданий;

На  оценку  «4»  —  необходимо  выполнить  верно  3  заданий;

На  оценку  «3»  —  необходимо  выполнить  верно  3 заданий;

2) Цели

1.Проверить   знания,  умения  их  применять  для  выполнения  учащимися:  

а) решения  уравнений:  иррациональных,  показательных,  логарифмических,

     тригонометрических;

б) нахождения  частных  решений  тригонометрических  уравнений.

2.Проверка   уровня  сформированности   навыка   решения   различных  заданий

   по  изученным темам.  

   

3. Формировать  вычислительные  навыки  учащихся.

Текст  контрольной  работы  №  3.  

 Вариант  1

1.Решите  уравнения: а) ;  б) ;  в)  .

2.Найдите  наибольший  корень  уравнения:  а) ;  

   б) ;  в)  .

3.Найдите  корни  уравнения:  а) 2lg x = lg (6 – x)2;   б)  lоg4 (x2 -15х ) = 2;

  в) 2lоg2(-х)  = 1 + lоg2 (х + 4).

4.Решите  уравнений:  a)  2cos (x- ;   б)  sin2x — .

  б)  Найдите  сумму  корней  уравнения  (sin x + cos x)2 = 1 + sin x∙ cos x,  принадлежащие  

       отрезку  .

Вариант  2

1.Решите  уравнения: а) ;  б) ;

 в)  .

2.Найдите  наибольший  корень  уравнения:  а) ;  

   б) ;  в)  .

3.Найдите  корни  уравнения:  а) 2lg x = lg (4 – x)2;   б)  lоg3 (x2 — 6х ) = 3;

  в) 2lоg3(-х)  = 2 + lоg3 (х — 2).

4.Решите  уравнений:  a)  2 sin (x — ;   б) cos2 x — .

  б)  Найдите  сумму  корней  уравнения  sin4 x — cos 4х = sin2 x — 1,  принадлежащие  

       отрезку  .

КОНТРОЛЬНАЯ  РАБОТА  №  4  по  теме   «Общие  методы  решения  уравнений».

Контрольная  работа  №  4   состоят из  4   заданий  в  три  варианта.

На  оценку  «5»  —  необходимо  выполнить  верно  4  заданий;

На  оценку  «4»  —  необходимо  выполнить  верно  4  заданий;

На  оценку  «3»  —  необходимо  выполнить  верно  3 заданий;

2) Цели

1.Проверить   знания,  умения  их  применять  для  выполнения  учащимися:  

а) решения  уравнений:  иррациональных,  показательных,  логарифмических,

     тригонометрических,  используя  общие  методы  решения  уравненийю

б) нахождения  частных  решений  тригонометрических  уравнений.

2.Проверка   уровня  сформированности   навыка   решения   различных  заданий

   по  изученным темам.  

   

3. Формировать  вычислительные  навыки  учащихся.

Текст  контрольной  работы  по  теме   «Общие  методы  решения  

Вариант  1

      1.Решите  уравнение:  а)  25∙;  б) х2 + х + 2 + ;

         в)  4.

2.Найдите  количество  корней  уравнения:  а)  ;

б)  41-х + 4х = 5,  в)  3⋅4х -5∙6х + 2⋅9х = 0.

      3.Решите  уравнения:  а)  lоg( х — 1 ) ∙ lоgх  = lоgх  

        б)  lоg х + lоgх  = 0;  в)  lоg(4 х ) — lоgх  — 2= 0.

      4. Решите  уравнение  а)  sin 3x – sin x = 0; в) 1+ cos 4x = cos  2x;

             и  найдите  его  корни  принадлежащие  промежутку  .

Вариант  2

      1.Решите  уравнение:  а) х2∙;  б) х2 — х +;

в) .

2.Найдите  количество  корней  уравнения:  а)  ;

б)  2х – 22-х = 3,  в)  3⋅25х — 8∙15х + 5⋅9х = 0.

      3.Решите  уравнения:  а)  lоgх = lоg ( х + 1 ) ∙ lоgх ;

        б)  lоgх — lоgх  = 0;  в)  lоg(2 х ) +3 lоgх  + 3= 0.

      4. Решите  уравнение  а)  cos 3x + cos x = 0;  в) 1- cos 4x = sin 2x;

           и  найдите  его  корни  принадлежащие  промежутку  .

       

КОНТРОЛЬНАЯ  РАБОТА  №  5  по  теме   «Неравенства».

Контрольная  работа  №  5   состоят из  4   заданий  в  три  варианта.

На  оценку  «5»  —  необходимо  выполнить  верно  4  заданий;

На  оценку  «4»  —  необходимо  выполнить  верно  4  заданий;

На  оценку  «3»  —  необходимо  выполнить  верно  3 заданий;

2) Цели

1.Проверить   знания,  умения  их  применять  для  выполнения  учащимися:  

а) решения  уравнений:  иррациональных,  показательных,  логарифмических,

     тригонометрических,  используя  общие  методы  решения  уравненийю

б) нахождения  частных  решений  тригонометрических  уравнений.

2.Проверка   уровня  сформированности   навыка   решения   различных  заданий

   по  изученным темам.  

   3. Формировать  вычислительные  навыки  учащихся.

Текст  контрольной  работы  по  теме   «Неравенства».

 Вариант  1

1.Решите  рациональное  неравенство:  а) 3х2 – 2х – 8 > 0;  б) ;

     в) .

2.Решите  показательное  уравнение:  а) 0,2;  б)  3х+1 ∙9х-0,5 ;

    в)  32х – 9х-1 + 27> 51.

3. решите  логарифмическое  уравнение :  а)  lоg(1 — 2х)

   б)  lоg0,5 (1 + 2х) > -1;  в)  lоg0,5 (х2 – 5х + 6) > -1.

4.  Решите  неравенство  методом  интервалов: а)  ;  б)  ;

     в) (х2 – 9) ∙ lоg0,5 х

     Вариант  2

    1. Решите  рациональное  неравенство:  а)  2х2 – 3х – 9 ;

     в)

 2.Решите  показательное  уравнение:  а) 0,5;  б)  2х-1 ∙4х+0,5 ;

    в)  22х – 4х-1 + 814.

3. Решите  логарифмическое  уравнение :  а)  lоg (1 -3х)

   б)  lоg0,5 (1 — 2х) > -2;  в)  lоg0,5 (х2 – 7х + 12) > -1.

4.  Решите  неравенство  методом  интервалов: а)  ;  б)  ;

     в) (х2 – 16) ∙ lоg0,2 х > 0.

КОНТРОЛЬНАЯ  РАБОТА  №  6   по  теме   «Решение  заданий  к  ЕГЭ».

Контрольная  работа  №  6   состоят из  5   заданий  в  три  варианта.

На  оценку  «5»  —  необходимо  выполнить  верно  5  заданий;

На  оценку  «4»  —  необходимо  выполнить  верно  5  заданий;

На  оценку  «3»  —  необходимо  выполнить  верно  5 заданий;

2) Цели

1.Проверить   знания,  умения  их  применять  для  выполнения  учащимися:  

а) решения  уравнений:  иррациональных,  показательных,  логарифмических,

     тригонометрических,  используя  общие  методы  решения  уравнений

 б) решения  неравенств:  рациональных,  показательных,  логарифмических,

      используя   методы  решения  неравенств.

в) нахождения  частных  решений   уравнений, неравенств

2.Проверка   уровня  сформированности   навыка   решения   различных  заданий

   по  изученным темам.  

   

3. Формировать  вычислительные  навыки  учащихся.

Текст  контрольной  работы  №  6  будет  составлен  на  основании  сборника для  подготовки  к  ЕГЭ  за 2019г.

Элективный курс по алгебре (10 класс) на тему: Алгебра модуля

Элективный курс

«Алгебра модуля»

Составлен учителем математики

средней школы №2 города Сосенский

Калужской области Козельского района

                                                     Муравьёвой Ириной Дмитриевной

2015 год

Аннотация

Данный элективный курс составлен для получения математических знаний по теме «Модули» учащимися школ, интересующихся математикой и желающими овладеть прочными знаниями при подготовке к единому и конкурсному экзаменам. Курс рассчитан на год (34 часа) и может служить дополнительным к теме в основной школе и в профильных классах средней школы.

---

Пояснительная записка.

Модули – одна из важных тем математики, которая нашла широкое практическое применение, как на едином экзамене, так и на конкурсных экзаменах.

В школьной программе данному выбору посвящены темы в 6-ом классе, а также включены отдельные задания в старших классах общеобразовательных школ, что явно недостаточно для прочного усвоения данного понятия и овладения навыками при решении заданий.

При выполнение программы реализуются следующие задачи:

1.Конкретизировать понятие модуля числа, рассмотреть различные методы решения уравнений и неравенств с модулем, основанные на его определении, свойствах и графической интерпретации.

 2.Уделить внимание вопросам приложения модуля к преобразованиям корней.

3.Организовать практическую направленность курса, показать полное решение заданий, иллюстрирующих тот или иной метод.

4.Подготовить учащихся к обучению в классах с математической направленностью, способствовать более полному и глубокому усвоению таких базовых понятий математике, как предел и производная.

5.Подготовить учащихся к сдаче единого экзамена, так как многие задания экзамена предполагают умение оперировать с модулем.

6.Готовить учащихся к сдаче конкурсного экзамена по математике.

Главная цель данного элективного курса посвящена  систематическому  изложению учебного материала, связанного с понятием модуля числа и аспектами его применения.

---

 Содержание курса (34 часа)

Тема 1: Определение модуля числа и его применение при решении уравнений (1 час).

Цели: 1.Познавательная: Конкретизировать понятие модуля, как расстояние от начала отсчета до точки, изображающей это число на координатной прямой. Провести аналогию между терминами «модуль» и «абсолютная величина».

Ввести аналогичную запись определения:

    а, если а•0

                                  |а|=        0, если а=0

        -а, если а•0

   

2.Учебная: Учить раскрывать модуль и решать уравнения на основе определения модуля.

Тема 2: Основные свойства модуля. Применение свойств модуля при решение уравнений и неравенств (2 часа).

Цели: 1.Познавательная: Ввести десять основных свойств модуля с доказательством некоторых из них и рассмотрением этих свойств на конкретных примерах.

2.Учебная: Учить применять свойства модуля при решении уравнений и неравенств.

Тема 3: Построение графиков функций, содержащих выражения под знаком модуля (3 часа).

Цели: 1.Познавательная: Систематизировать умения учащихся в построение графиков функции.

2.Учебная: Учить строить графики различных функций с модулем:

y=|f (x)|,   y=f (|x|),   y=|f (|x|)|,   |y|=|f (x)|,   y=|f (x)|+|g (x)|

Тема 4: Решение уравнений с модулем вида |f(x)| и также уравнений высших степеней, решаемых способом подстановки (1час).

Цели: 1.Познавательная: Познакомить учащихся с классификацией различных видов уравнений и способами их решения.

2.Учебная: Учить решать уравнения и неравенства методами, основанными на определение модуля, а также уравнения, решаемые подстановкой.

Тема 5: Решение уравнений с модулем, связанных с приёмами раскрытия модуля по определению (1 час).

Цели: 1.Познавательная: Показать способы решения уравнения с модулем вида

|f (x)|=a, a ≥ 0 переходом к совокупности:

 f (x) =a

f (x) =-a

конкретизировать представление о совокупности.

2.Учебная: учить решать уравнения данного типа и правильно записывать ответ.

Тема 6: Решение уравнений с модулем вида |f (x)|=g (x) (2 часа)

Цели: 1.Познавательная: Решение уравнений вида |f (x)|=g (x) путём равносильного перехода к системе:

           f (x) =g (x)

           f (x) =-g (x)

           (x) ≥0

 

Появление посторонних корней при решение уравнений.

2.Учебная: Учить выбирать рациональные пути решения уравнений подобного типа.

---

Тема 7: Метод интервалов решения уравнений, содержащих модуль

(2 часа)

Цель: 1.Познавательная: Доказать теорему о модуле «Если на интервале (а, в) функция f (x) непрерывна и не обращается в ноль, то она на этом интервале сохраняет знак». Алгоритм решения подобных уравнений.

2.Учебная: Учить решать уравнений, содержащие переменные с несколькими знаками модуля, совершенствовать умения в решение уравнений на промежутках. Учить применять на практике теорему о модуле.

Тема 8: Решение неравенств вида |x|•a; |x|•a посредством равносильных переходов (1 час).

Цель: 1.Познавательная: Доказать на основе определения модуля, что при любом а неравенство |x|•a равносильно системе неравенств:

x•a

x•-a,

а неравенство |x|•a равносильно совокупности неравенств:

x•-a

x•-a

2.Учебная: Учить применять эти теоремы при решение неравенств.

Тема 9: Решение дробно-рациональных уравнений и неравенств, содержащих выражение под знаком модуля (2 часа).

Цель: 1.Познавательная: Решение уравнений и неравенств, содержащих дробное выражение под знаком модуля.

2.Учебная: Закрепить навыки решения разными методами. Совершенствование метода интервалов при решение неравенств.

Тема 10: Решение неравенств вида |f (x)|•|g (x)| и | f (x)|• |g (x)| (1 час).

Цель: 1.Познавательная: Объяснение способов решения неравенств вида

|f (x)|•|g (x)| и | g (x)|• |g (x)| путём равносильного перехода к неравенствам вида f 2(x)• g2(x) и g2(x)• g2(x).

2.Учебная: Совершенствование навыков при решение неравенств, в том числе неравенств квадратных и более высоких степеней.

Тема 11: Решение уравнений и неравенств с модулем на координатной прямой (2 часа).

Цель: 1.Познавательная: Рассмотреть вопрос о расстоянии между двумя точками

   А (х1) и В (х2) координатной прямой, вывести формулу, согласно которой АВ=|х2-х1|. Учить использовать эту формулу при решение уравнений и неравенств вида |х-а|=в, |х-а|=|х-в|, |х-а|•в, |х-а|•|х-в|, |х-а|•|х-в|, а также уравнения и неравенства к ним сводимые.

2.Учебная: Развивать умение при решение уравнений и неравенств данного вида.

Тема 12: Решение различных видов тригонометрических уравнений и неравенств, содержащих переменные под знаком модуля (2 часа).

Цель: 1.Познавательная: Способствовать развитию познавательных интересов  

учащихся к данному вопросу и к математике в целом путём рассмотрения конкретных примеров заданий конкурсного экзамена.

2.Учебная: Совершенствование решения тригонометрических уравнений. Рассмотрение уравнений, содержащих под знаком абсолютной величины различные тригонометрические функции и тригонометрические выражения.

Тема 13: Решение тригонометрических неравенств, содержащих модуль, с помощью графика (2 часа).

Цель: 1.Познавательная: Показать использование графиков тригонометрических

функций для решения тригонометрических неравенств вида |cos x|≥|sin x|,

|sin x|≤|cos x| и т.д., а также рассмотреть способы решения тригонометрических неравенств с использованием единичной окружности.

2.Учебная: Учить искать рациональные пути решения поставленных задач. Совершенствовать навыки построения графиков тригонометрических функций, умения решать неравенства.

Тема 14: Модуль и преобразования корней (2 часа).

Цель: 1.Познавательная: Конкретизировать понятие арифметического корня.

2.Учебная: Учить преобразовывать выражения с использованием тождества:

√а2=|а|.

Тема 15: Модуль и иррациональные уравнения (2 часа).

Цель: 1.Познавательная: Знакомство учащихся с уравнениями, содержащими  

переменную под знаком радикала.

2.Учебная: Учить использовать модуль при решении иррациональных уравнений.

Тема 16: Единый экзамен и задания с модулем (3 часа).

Цель: 1.Познавательная: Повысить интерес к теме модуля, совершенствовать математические навыки путём рассмотрения конкретных заданий из материалов единого экзамена.

2.Учебная: Учить решать и правильно оформлять задания из уровня С.

Тема 17: Модуль и конкурсный экзамен (3 часа).

Цель: 1.Познавательная: Обобщить полученные знания по теме «Алгебра модуля» при решении заданий конкурсных экзаменов ведущих вузов.

2.Учебная: Совершенствование навыков решения заданий конкурсных экзаменов.

Тема 18: Контрольная работа (2 часа).

Цель: Выяснить эффективность занятий курса, уровень усвоения полученных знаний учащимися при выполнении контрольной работы.

---

Календарно-тематическое планирование.

N п/п	Тема	кол-во часов	тип урока	содержание урока
1	Определение модуля числа и его применение при решении уравнений	1	лекция	Сообщение учителя, беседа с учениками.
2	Основные свойства модуля. Применение свойств модуля при решение уравнений и неравенств	2	лекция, практикум	Лекция учителя, практическая работа по решению уравнений и неравенств.
3	Построение графиков функций, содержащих выражения под знаком модуля	3	семинарские уроки	Сообщение учащихся о разновидностях графиков с модулем и способах их построения. Обобщение учителя. Практическая работа по классификации графиков.
4	Решение уравнений с модулем вида |f(x)| и также уравнений высших степеней, решаемых способом подстановки	1	практикум	Сообщение учителя о способах решения уравнений. Практическая работа учащихся.
5	Решение уравнений с модулем, связанных с приёмами раскрытия модуля по определению	1	практикум	Презентация учителя. Работа в паре по решению уравнений.
6	Решение уравнений с модулем вида |f (x)|=g (x)	2	Урок «Интел — лектуальная игра»	Обобщающее закрепление двух способов решения уравнений. Работа учащихся по группам. Организация игры «Счастливый случай».
7	Метод интервалов решения уравнений, содержащих модуль	2	практикум	Беседа с учащимися. Практическая работа с учащимися.
8	Решение неравенств вида |x|•a; |x|•a посредством равносильных переходов	1	практикум	Самостоятельная работа учащихся в паре с использованием необходимых опорных карточек и справочных таблиц с последующим обсуждением результатов.

9	Решение дробно-рациональных уравнений и неравенств, содержащих выражение под знаком модуля	2	практикум	Урок-турнир. Практическая работа учащихся в двух командах, проверка результатов жюри и объявление результатов конкурса.
10	Решение неравенств вида |f (x)|•|g (x)| и | f (x)|• |g (x)|	1	практикум	Практическая работа учащихся с использованием слайдов и необходимых комментариев учителя.
11	Решение уравнений и неравенств с модулем на координатной прямой	2	лекция- -практикум	Объяснения учителя. Наглядная интерпретация метода с помощью координатной прямой. Практическая работа учащихся.
12	Решение различных видов тригонометрических уравнений и неравенств, содержащих переменные под знаком модуля	2	семинарские занятия	Выступления учеников с предварительной их подготовкой и прослушиванием о различных способах решения уравнений и неравенств. Организация практической работы учеников с консультациями подготовленных учеников или учителя.
13	Решение тригонометрических неравенств, содержащих модуль, с помощью графика	2	лекция- -практикум	Лекция учителя. Практическая работа учащихся.
14	Модуль и преобразования корней	2	семинарские занятия	Выступления подготовленных учащихся. Затем практическое использование полученных знаний.
15	Модуль и иррациональные уравнения	2	лекция- -практикум	Лекция учителя. Практическая работа учащихся.

---

16	Единый экзамен и задания с модулем	3	уроки обобщения знаний	Организация обстановки экзамена, с последующим обсуждением результатов.
17	Модуль и конкурсный экзамен	3	уроки обобщения знаний	Совместная работа учителя и учащихся по решению заданий экзамена.
18	Контрольная работа	2	урок-зачёт	Организация контрольной работы по теме. Зачётное занятие.

Итого: 34 часа

Уравнения и неравенства с модулем. Графики функций — §1. Свойства модуля. Уравнения с модулем — ЗФТШ, МФТИ

Напомним определение модуля числа:

\[ |a| = \left\{ \begin{aligned} a \text{, если } & a \ge 0, \\ -a \text{, если } & a < 0 \end{aligned} \right.  \]

Отметим следующие свойства модуля, вытекающие непосредственно из определения.

1○1^\bigcirc. |a|≥0.|a| \ge 0.            

2○2^\bigcirc. |a|≥a.|a|\ge a.          

3○3^\bigcirc. |ab|=|a|·|b|.|ab| = |a|\cdot|b|.          

4○4^\bigcirc. ab=|a||b|.\left| \dfrac{a}{b} \right| = \dfrac{|a|}{|b|}.        

5○5^\bigcirc. |-a|=|a|.|-a|=|a|.      

6○6^\bigcirc. |a2|=|a|2=a2.|a^2| = |a|^2 = a^2.

7○7^\bigcirc. |a+b|≤|a|+|b||a+b| \le |a| + |b| (здесь равенство достигается, когда числа `a` и `b` одного знака или одно из них равно нулю; если же числа `a` и `b` разных знаков, то выполняется строгое неравенство).

8○8^\bigcirc. |a-b|≥||a|-|b||.|a-b| \ge ||a|-|b||.

9○9^\bigcirc. |a||a| — это расстояние от точки `a` на числовой оси до точки `0`.

10○10^\bigcirc. |a-b||a-b| — это расстояние между точками `a` и `b` на числовой оси.

11○11^\bigcirc. a2=|a|.\sqrt{a^2} = |a|.

Докажем свойство 7○7^\bigcirc. Остальные свойства проверьте самостоятельно. Поскольку обе части неравенства неотрицательны, возведение их в квадрат является равносильным преобразованием. Получаем 

\[|a+b|^2 \le (|a| + |b|)^2 \Leftrightarrow a^2 + 2ab + b^2 \le |a|^2 + 2|a| \cdot |b| + |b|^2 \Leftrightarrow ab \le |ab|.\]

Последнее неравенство верно (свойство 2○2^\bigcirc). Заметим, что оно обращается в равенство, когда числа aa и bb одного знака (или одно из них равно нулю).

Перейдём к уравнениям с модулем. В простейших случаях можно воспользоваться свойством модуля 10○10^\bigcirc.

Решите уравнение:

a) |x-2|=5;|x-2| = 5;          б) |2x-1|=-1|2x-1| = -1         в) |x-2|=|x+6||x-2| = |x+6|

a) |x-2||x-2| — это расстояние между точками `x` и `2` на число вой прямой (свойство 10○10^\bigcirc). Поэтому уравнение можно прочитать так: точка `x` удалена от точки `2` на расстояние `5`. Иначе говоря, мы ищем точки, удалённые от точки `2` на расстояние `5`. Ясно, что это точки `-3` и `7`. Записать решение короче всего так:

\[|x-2| = 5\Leftrightarrow \left[ \begin{aligned} x-2 &= 5, \\ x-2 &= -5 \end{aligned} \right.  \Leftrightarrow \left[ \begin{aligned} x &= 7, \\ x &= -3 \end{aligned} \right. .\]

`x=-3`; `x=7`.

б) Левая часть уравнения неотрицательна (свойство 1○1^\bigcirc). Поэтому уравнение не имеет решений.

нет решений.

в) Задачу можно сформулировать так: расстояние от точки `x` до точки `2` равно расстоянию от точки `x` до точки `(– 6)`, то есть мы ищем точку на прямой, равноудалённую от точек `2` и `(– 6)`. Ясно, что это середина отрезка, соединяющего эти точки, т. е. `x = -2`. 

Покажем ещё один способ решения: 

\[|x-2| = |x+6|\Leftrightarrow (x-2)^2 = (x+6)^2\Leftrightarrow x = -2 \]

Если уравнение имеет более сложный вид, то, как правило, приходится раскрывать модуль по определению. Для этого отмечаем на числовой прямой точку (точки), в которых выражения, находящиеся под модулем, обращаются в ноль. Эти точки делят прямую на несколько промежутков, на каждом из которых знаки подмодульных выражений фиксированы, поэтому можно раскрыть модули. Рассмотрим пример. 

Решите уравнение: |x+1|+11= |2x+11|+|1-x||x+1| +11 =\ |2x+11| + |1-x|.

Отметим на числовой прямой точки x=-1, x= -112, x=1.x = -1, \; x = \ -\dfrac{11}{2}, \; x = 1.. Получаем `3` точки, которые разбивают числовую прямую на `4` интервала. Раскрываем модули на каждом из этих интервалов (см. рис. 1).

Рассмотрим 4 случая:

а) x≤-112.x \le -\dfrac{11}{2}. Тогда:

\[-(x+1) + 11 = -(2x+11) + (1-x) \Leftrightarrow x = -10.\]

Убеждаемся, что x=-10x =-10 удовлетворяет условию x≤-112x \le — \dfrac{11}{2}, поэтому x=-10x =-10 является решением данного уравнения.

б) -112<x<-1-\dfrac{11}{2} . Тогда:

\[-(x+1) + 11 = (2x+11) + (1-x) \Leftrightarrow x = -1.\]

Однако x=-1x =-1 не удовлетворяет условию -112<x<-1-\dfrac{11}{2} , поэтому x=-1x =-1  не подходит.

в) -1≤x≤1-1 \le x \le 1. Тогда:

\[(x+1) + 11 = (2x+11) + (1-x) \Leftrightarrow 12 = 12.\]

Получилось верное равенство, поэтому все `x`, удовлетворяющие условию -1≤x≤1-1 \le x \le 1 являются решениями.

г) x>1x>1. Тогда:

\[(x+1) + 11 = (2x+11) — (1-x) \Leftrightarrow x = 1.\]

Условие x>1x >1 не выполнено, поэтому данный корень не подходит.

Объединяем полученные решения и получаем x∈{-10}∪[-1; 1]x \in \{-10\} \cup [-1; \; 1] .

x∈{-10}∪[-1; 1]x \in \{-10\} \cup [-1; \; 1] .

1) При таком методе решения необходимо проверять принадлежат ли найденные корни рассматриваемому в данный момент промежутку – иначе можно получить неверный ответ.

2) Точки, в которых выражения под модулями обращаются в ноль, можно включать в любой из двух промежутков, для которых они являются границами. Например, если бы в случае б) мы взяли -112<x≤-1-\dfrac{11}{2}  то число x=-1x =-1 попало бы в промежуток. В случае в) мы бы рассматривали -1<x≤1-1 и здесь корня x=-1x = -1 мы бы не получили. При этом объединение всех решений было бы тем же самым.

Модуль числа | Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия

Модуль числа и уравнения с модулем — тема особенная, прямо-таки заколдованная 🙂 Она совсем не сложная, просто в школе её редко объясняют нормально. В результате без специальной подготовки почти никто из школьников не может дать правильное определение модуля и тем более решить уравнение с модулем. И эту картину мы наблюдаем на протяжении многих лет.

Поэтому осваивайте тему «Уравнения и неравенства с модулем» по нашим статьям и на наших занятиях! Вы сумеете обойти множество конкурентов на ЕГЭ, олимпиадах и вступительных экзаменах.

Модуль числа называют ещё абсолютной величиной этого числа. Попросту говоря, при взятии модуля нужно отбросить от числа его знак. В записи положительного числа и так нет. никакого знака, поэтому модуль положительного числа равен ему самому. Например,  Модуль нуля равен нулю. А модуль отрицательного числа равен противоположному ему положительному
(без знака!). Например,

Обратите внимание: модуль числа всегда неотрицателен:

Определение модуля

Вот оно:

От большинства известных из школы определений оно отличается лишь одним: в нём есть выбор. Есть условие. И в зависимости от этого условия мы раскрываем модуль либо так, либо иначе.

Так же, как в информатике — в разветвляющихся алгоритмах с применением условных операторов. Как, вообще-то, и в жизни: сдал ЕГЭ на минимальный балл — можешь подавать документы в ВУЗ. Не сдал на минимальный балл — можешь идти в армию 🙂

Таким образом, если под знаком модуля стоит выражение, зависящее от переменной, мы раскрываем модуль по определению. Например,

В некоторых случаях модуль раскрывается однозначно. Например,  так как выражение под знаком модуля неотрицательно при любых x и y. Или:  так так как выражение под модулем неположительно при любых z.

Геометрическая интерпретация модуля

Нарисуем числовую прямую. Модуль числа — это расстояние от нуля до данного числа. Например, То есть расстояние от точки −5 до нуля равно 5.
Эта геометрическая интерпретация очень полезна для решения уравнений и неравенств с модулем.

Рассмотрим простейшее уравнение . Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно трём. Это точки 3 и −3. Значит, у уравнения  есть два решения: x = 3 и x = −3.

Вообще, если имеются два числа a и b, то равно расстоянию между ними на числовой прямой.
(В связи с этим нередко встречается обозначение длины отрезка AB, то есть расстояния от точки A до точки B.)

Ясно, что (расстояние от точки a до точки b равно расстоянию от точки b до точки a).

Решим уравнение . Эту запись можно прочитать так: расстояние от точки x до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.

Мы видим, что наше уравнение имеет два решения: −1 и 7. Мы решили его самым простым способом — без использования определения модуля.

Перейдём к неравенствам. Решим неравенство .

Эту запись можно прочитать так: «расстояние от точки x до точки −7 меньше четырёх». Отмечаем на числовой прямой точки, удовлетворяющие этому условию.

Ответ: (-11; -3).

Другой пример. Решим неравенство |10 − x| ≥ 7.

Расстояние от точки 10 до точки x больше или равно семи. Отметим эти точки на числовой прямой.
Ответ:

График функции 

Этот график надо знать обязательно. Для имеем y = x. Для имеем y = −x. В результате получаем:
С помощью этого графика также можно решать уравнения и неравенства.

Корень из квадрата

Нередко в задачах ЕГЭ требуется вычислить , где – некоторое число или выражение. Не забывайте, что 

Действительно, по определению арифметического квадратного корня — это такое неотрицательное число, квадрат которого равен . Оно равно при и при , т. е. как раз .

Примеры заданий ЕГЭ

1. Найдите значение выражения при .
Заметим, что при . Следовательно, значение нашего выражения равно: .

2. Найдите значение выражения при .

Действуем аналогично:

В следующей статье мы рассмотрим более сложные уравнения и неравенства с модулем.

Читайте также: Уравнения с модулем

Презентация к уроку по алгебре (10 класс) по теме: Презентация к уроку «Графики уравнений,содержащих модули».Разработка урока.

Слайд 1

Тема урока : «Графики уравнений, содержащих модули». Учитель: Видмонт Татьяна Константиновна МБОУ СОШ №15 город Ростов-на-Дону

Слайд 2

х 2 — у = 2 ху = — 6 х 2 +у 2 = 16 х+2у = 4 2у-5 = 0

Слайд 3

Когда в «стандартные» уравнения прямых, парабол, гипербол включают знак модуля, их графики становятся необычными и даже красивыми. Чтобы научиться строить такие графики: надо владеть приемами построения базовых фигур; твердо знать и понимать определение модуля числа .

Слайд 4

Повторение понятия модуля числа.

Слайд 5

Если х ; Если х х, если х х , если х -х, если х Построение графика функции у=│х│ В результате имеем дело с кусочным заданием зависимости. у =

Слайд 6

Кусочный Геометрические преобразования Сдвиг Приемы построения графиков уравнений с модулями.

Слайд 7

Строим параболу у = х 2 — 4. Часть параболы, расположенную ниже оси х, нужно заменить линией, ей симметричной относительно оси х, т.е. геометрическое преобразование. Задание 1. Построить график функции у=│х 2 — 4│. Используем прием геометрического преобразования. Алгоритм построения.

Слайд 8

Построим параболу у=х 2 -2х и обведем ту ее часть, которая соответствует неотрицательным значениям х, то есть часть, расположенную правее оси у. В той же координатной плоскости построим параболу у=х 2 + 2х и обведем ту ее часть, которая соответствует отрицательным значениям х, то есть часть, расположенную левее оси у. Итак, мы имеем дело с кусочным заданием зависимости. Построить график функции у = х 2 -2 |х|. Используем прием кусочного построения. Если х≥0, то у = х 2 -2х; Если х

Слайд 9

Находим корни каждого выражения, стоящего под знаком модуля: 2х-4=0 , х=2. 6+3х=0, х=-2. Разобьем ось х на три промежутка: х -2; 2) -2 ; 3) х -5х-2, х х+10, -2 ; 5х+2,х у = Построить график функции у=│2х-4│+│6+3х│. Используем прием кусочного построения. х y=- (2x – 4) – ( 6x + 3x)=-5x- 2 -2 y=- ( 2x -4 )+ (6x + 3x) = x + 10 х у=2х-4+6+3х=5х+2. Итак, мы имеем дело с кусочным заданием зависимости.

Слайд 10

Строим график уравнения у = │х│ . х Сдвигаем его по оси х на 4 единицы вправо и по оси у на 2 единицы вниз.. Часть графика, расположенную ниже оси х, отображаем симметрично относительно оси х. Построить график функции у=││х-4│-2│. При построении этого графика удобно использовать способ сдвига вдоль осей координат. 0 у 1 -1 4 0 у х х 0 у -2

Слайд 11

Строим график уравнения у=│х│. Построить график функции у=│││х│-2│-2│. При построении этого графика удобно использовать способ сдвига вдоль осей координат. Алгоритм построения. Сдвинем построенный график на 2 ед. вниз.

Слайд 12

Сдвигаем построенный график на 2 единицы вниз. Часть графика, расположенную ниже оси х отображаем симметрично относительно оси х. Часть графика, расположенного ниже оси х, отобразим симметрично относительно этой оси.

Слайд 13

Каждой группе построить график одной функции. Задания для самостоятельной работы. 1)у=│2х-4│; 2)у =│9-х 2 │; 3)у =│х 2 -5х+6│; 4)у=│3-0,5х 2 │; 5)у=│х 2 -4│+3; 6)у=│х│-2х ; 7) у=х 2 + 3│х│.

Слайд 14

Заполнить таблицы. Графики Установите соответствие между графиками функций и формулами, которые их задают. Знаю определение модуля числа. Владею приемами построения базовых фигур. Знаю свойства этих функций. Умею сопоставлять уравнения с графиками функций. Умею строить кусочные функции. Умею строить графики функций. Знаю способы построения графиков уравнений с модулями.

Рабочая программа по алгебре (10 класс) на тему: Программа элективного курса «Уравнения и неравенства с модулем»

Муниципальное бюджетное общеобразовательное учреждение «Лицей №14»

Нижнекамского муниципального района Республики Татарстан

(МБОУ «Лицей №14» НМР РТ)

РАССМОТРЕНО ШМО учителей математики, физики и информатики (протокол от 02.06.2018 № 7)

СОГЛАСОВАНО Заместитель директора по УР МБОУ «Лицей №14» _________  Г.Р. Хаматова 24.08.2018

УТВЕРЖДАЮ Директор МБОУ «Лицей № 14» ___________ О.О.Пустоплеснова 29.08.2018

ПРОГРАММА

элективного курса

«Уравнения и неравенства с модулем»

для   10 Ю класса

Акимовой Альбины Тимуровны,

учителя   первой   квалификационной  категории

г. Нижнекамск

2018 год

ПОЯСНИТЕЛЬНАЯ  ЗАПИСКА

  Элективный курс посвящен изучению методов решения уравнений и неравенств с модулем и своим содержанием привлекает внимание учащихся 10 классов, которым  интересна математика.

Предлагаемый курс является развитием системы ранее приобретенных программных знаний, его цель – создать целостное представление о теме и значительно расширить спектр задач. Содержание  курса не  дублирует базовый курс, оно дополнено элементами, которые могут быть использованы для подготовки выпускников к  успешной сдаче выпускников ЕГЭ и вступительных экзаменов в ВУЗы страны.   Данный курс  расширяет  и углубляет изучение  тем базовых общеобразовательных программ по математике, дает возможность познакомиться учащимся с интересными, «нестандартными» методами, которые позволяют более эффективно решать широкий класс заданий, содержащих модуль,   и повышает  вероятность того, что выпускник  успешно и осознанно сделает свой выбор будущей специальности, связанной с математикой. В практике преподавания математике в средней общеобразовательной школе и других учебных заведениях понятие абсолютной величины числа встречается неоднократно, а задания на решение уравнений и неравенств, содержащих модуль или приводящиеся к модулям,  являются одними из высокооцениваемых  на ЕГЭ и вступительных экзаменах.

Данный курс предполагает компактное и четкое изложение теории вопроса, решение типовых задач, самостоятельную работу. Программа курса включает углубление отдельных базовых,  общеобразовательных программ по математике, а также  изучение некоторых тем, выходящих за их рамки,  не нарушая целостности базовой программы.

ЦЕЛИ ЭЛЕКТИВНОГО КУРСА:

• пробуждение и развитие устойчивого интереса к математике, повышение математической культуры учащихся;
• знакомство учащихся с методами решения различных по формулировке нестандартных задач;
• привитие навыков употребления функционально-графического метода при решении задач;
• расширение и углубление знаний по математике по программному материалу;
• подготовка учащихся к продолжению образования в вузе.
• формировать у учащихся умения и навыки по решению задач с параметрами, сводящихся к исследованию линейных и квадратных уравнений, неравенств для подготовки к экзамену в новой форме и к обучению в старшем звене;
• обеспечить условия для самостоятельной творческой работы;
• формировать исследовательский подход в решении задач;

ЗАДАЧИ КУРСА

• создать ориентационную и мотивационную основы у выпускников для осознанного выбора профессии физико-математического и экономического профилей;  
• углубить знания учащихся по предмету;
• систематизировать, обобщить знания учащихся о ранее приобретенных программных знаний по теме «Модуль числа», открыть учащимся новые приемы решения уравнений и неравенств с модулем;
• расширить математические представления о приемах и методах решения задач с модулями; выявить и развивать их математические способности;
• развивать логическую культуру и математическое мышление учащихся;
• повысить уровень понимания и практической подготовки учащихся в вопросах преобразования выражений, содержащих модуль, решения уравнений и неравенств с модулем, построения графиков функций, содержащих модуль;
• формирование у учащихся устойчивого интереса к предмету;
• помочь овладеть рядом технических и интеллектуальных умений на уровне свободного их использования;
• помочь ученику оценить свой потенциал с точки зрения образовательных перспектив;
• подготовить к экзамену.

ТРЕБОВАНИЯ К УРОВНЮ УСВОЕНИЯ УЧЕБНОГО МАТЕРИАЛА

В результате изучения программы элективного курса учащиеся получают возможность знать/понимать: 

• определение абсолютной величины (модуля) действительного числа, её геометрическую интерпретацию;
• основные операции и свойства абсолютной величины;
• правила построения графиков функций, содержащих знак абсолютной величины;
• алгоритмы решения линейных и квадратных уравнений и неравенств, содержащих переменную под знаком модуля.
• определение уравнения (неравенства) с модулем;
• что означает решить уравнение (неравенство) с модулем;

• правила решения неравенств, метод интервалов

      должны уметь:

• решать рациональные неравенства и их системы;
• использовать метод интервалов при решении неравенств;
• применять определение, свойства абсолютной величины числа при решении заданий с модулями и при преобразовании выражений с модулем;
• решать уравнения и неравенства, содержащих переменную под знаком модуля;
• уметь строить графики функций, содержащих модуль.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К ОРГАНИЗАЦИИ УЧЕБНОГО ПРОЦЕССА

В процессе освоения курса предусматриваются разные формы занятий: лекции, семинары, практикумы, компьютерное исследование и др. Отработка и закрепление основных умений и навыков осуществляется при выполнении практических заданий. Формирование важнейших умений и навыков происходит на фоне развития умственной деятельности, так как школьники учатся анализировать, замечать существенное, подмечать общее и делать обобщения, переносить известные приемы в нестандартные ситуации, находить пути их решения.

Уделяется внимание развитию речи: учащимся предлагается объяснять свои действия, вслух высказывать свою точку зрения, ссылаться на известные правила, факты, высказывать догадки, предлагать способы решения, задавать вопросы, публично выступать. Проектная и исследовательская деятельность учащихся позволяет удовлетворять их индивидуальные потребности и интересы, выявлять их индивидуальные возможности, т.е. максимально индивидуализировать обучение.

Преподавание курса строится как изучение вопросов, не предусмотренных программой основного курса.

Для эффективной реализации курса необходимо использовать разнообразные формы, методы и приёмы обучения, делая особый упор на развитие самостоятельности, познавательного интереса и творческой активности учащихся. Для этой цели проводят уроки:

          1) лекции;

          2) уроки консультации;

          3) самостоятельные работы;

          4) тестовые самостоятельные работы;

          5) зачеты;

          6) итоговые контрольные работы.

Итоговой формой контроля, подводящей изучение курса к логическому завершению, предполагается написание зачетной работы, реферата, проекта (создание презентации).

Важным достоинством предлагаемой программы, является:

• научность изложения материала, обогащение историческими сведениями,
• межпредметные связи (математика + информатика),
• доступность для восприятия учащимися,
• возможность организации занятий с элементами исследования,
• развитие абстрактного мышления, простор для творческой деятельности учащихся.

УЧЕБНО – ТЕМАТИЧЕСКИЙ ПЛАН

№	Наименование тем курса	Всего часов	В том числе:			Форма контроля
			лекции	практика	семинары
1	Неравенства	3	1	2	—	Самостоятельная работа
2	Модуль числа. Решение уравнений с модулем.	11	3	8	1	Самостоятельная работа
3	Решение неравенств с модулем	6	3	3	—	Самостоятельная работа
4	Функция. Графики функций, содержащих модуль	9	3	6	1	Домашняя работа с элементами  исследовательской деятельности
5	Решение задач ЕГЭ	6	1	5	1	Зачетная работа
ИТОГО		35	11	24	3

СОДЕРЖАНИЕ КУРСА

Тема 1. Неравенства.

Решение   линейных, квадратных, рациональных неравенств и их систем. Метод интервалов.

Тема 2. Модуль числа. Решение уравнений с модулем.

Определение  модуля и его основные теоремы. Геометрическая интерпретация модуля числа. Операции над абсолютными величинами.  Упрощение выражений, содержащих  переменную под знаком абсолютной величины.

Решение простейших уравнений вида ,и решение уравнений, содержащих не менее двух выражений под знаком модуля. Основные методы решения уравнений с модулем: раскрытие модуля по определению, переход от исходного уравнения к равносильной системе, возведение обеих частей уравнения   в квадрат, метод  введения новой переменной, метод последовательного раскрытия модуля при решении уравнений, содержащих « модуль в модуле».

Тема 3. Решение неравенств с модулем.

Решение неравенств вида ,. Решение неравенств, содержащих не менее двух выражений под знаком модуля. Метод интервалов.

Тема 4.Функция. Графики функций, содержащих модуль.

Свойства и графики элементарных функций. Преобразования графиков функций. Функция  и ее график. Функция  и ее график. Графический способ  решения уравнений и неравенств с модулем.

Тема 5. Решение задач ЕГЭ.

ЛИТЕРАТУРА ДЛЯ УЧАЩИХСЯ.

1.А.Г. Мордкович. Алгебра и начала анализа.10-11кл. Учебник. Задачник.Мнемозина.2005г.

2.АверьяновД.И., Алтынов П.И., Баврин Н.Н.. Математика: большой  справочник для школьников и поступающих в вузы. Москва: Дрофа, 2006г.

3.Учебно-тренировочные тесты ЕГЭ под редакцией Ф.Ф. Лысенко. Ростов-на-Дону. Издательство «Легион», 2012.

5. Тестовые контрольные задания по алгебре и началам анализа. Семенко Е.А., Фоменко М.В., Белай Е.Н., Ларкин Г.Н.Краснодар. 2006 г.

6.Шарыгин И.Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 класса средней школы: М., 1989 г.

ЛИТЕРАТУРА   ДЛЯ УЧИТЕЛЯ.

1. И. И. Гайдуков. Абсолютная величина. Просвещение.1968 г.
2.  П.Ф. Севрюков, А.Н. Смоляков. Уравнения и неравенства с модулями и методика их решения. Москва. Ставрополь. 2005 г.
3. А.Г. Цыпкин, А.И. Пинский. Справочник по методам решения задач по математике. Москва «Наука». Главная редакция физико-математической литературы, 2004 г.
4. Еженедельная учебно-методическая газета «Математика». Издательский дом «Первое сентября». 2010-2012 г.
5. Литвиненко В.Н., Мордкович А.Г.. Практикум по элементарной математике. Алгебра. Тригонометрия. Москва. «Просвещение».2005 г.
6. М.А. Галицкий, М.М. Мошкович., С.И. Шварцбурд. Углубленное изучение курса алгебры и математического анализа. Москва.  «Просвещение».2006 г.
7. А.В. Столин. Комплексные упражнения по математике с решениями 7-11 классы. Харьков. ИМП «Рубикон»,2006 г.
8. Обощающее повторение курса алгебры и начала анализа,  Части 1-3. под редакцией  Е.А. Семенко. Краснодар. 2006-2007.

---

КАЛЕНДАРНО – ТЕМАТИЧЕСКИЙ ПЛАН ЗАНЯТИЙ

№	Тема урока, тип урока	Кол-во часов	Виды учебной деятельности	Виды контроля, контрольно-измерительные материалы	Планируемые результаты освоения материала
	1. Неравенства	3
	Введение в курс. Решение рациональных неравенств. УОНМ	1	Фронтальная работа.	Фронтальный опрос	Знать алгоритм решения рациональных неравенств. Уметь решать рациональные неравенства.	01.09
	Решение систем рациональных неравенств. УОНМ, УПЗУ	1	Индивидуальная работа по карточкам.	Взаимоконтроль	Знать алгоритм решения систем рациональных неравенств. Уметь решать системы неравенств.	08.09
	Решение рациональных неравенств и их систем. Закрепление изученного материала. УПЗУ, КУ	1	Практикум по решению задач.	Тематический контроль	Закрепить ЗУН решения рац. неравенств и их систем.	15.09
	2.Модуль числа. Решение уравнений с модулем.	11
	Определение модуля. УОНМ	1	Фронтальная работа.	Самоконтроль	Знать определение модуля. Уметь вычислять модуль.	22.09
	Определение модуля и его основные теоремы. УПЗУ, КУ	1	Индивидуальная работа по карточкам.	Групповой контроль	Знать основные теоремы, связанные с модулем. Уметь использовать их в решении задач.	29.09
	Решение простейших уравнений вида   =a. УОНМ	1	Практикум по решению задач.	Взаимоконтроль	Знать алгоритм решения и уметь решать простейшие уравнения вида  =a.	06.10
	Решение простейших уравнений с модулем. УПЗУ	1	Фронтальная работа.	Индивидуальный контроль	Закрепить знания и навыки решения уравнений.	13.10
	Решение простейших уравнений вида =g(x). УОНМ	1	Работа в парах.	Фронтальный опрос	Знать алгоритм решения и уметь решать простейшие уравнения вида  =g(x).	20.10
	Упражнение в решении уравнений вида =g(x). УПЗУ	1	Практикум по решению задач.	Самоконтроль	Закрепить знания и навыки решения уравнений.	27.10
	Решение уравнений, содержащих не менее двух выражений под знаком модуля. УПЗУ	1	Индивидуальная работа по карточкам.	Взаимоконтроль	Систематизировать ЗУН решения уравнений, содержащих не менее двух выражений под знаком модуля.	10.11
	Решение уравнений, содержащих не менее двух выражений под знаком модуля. УПЗУ	1	Фронтальная работа.	Тематический контроль	Закрепить знания и навыки решения уравнений,  содержащих не менее двух выражений под знаком модуля.	17.11
	Закрепление изученного материала. Решение уравнений. КУ	1	Практикум по решению задач.	Тематический контроль	Закрепить знания и навыки решения уравнений.	24.11
	Упражнение в решении уравнений с модулем.	1	Индивидуальная работа.	Взаимоконтроль	Закрепить знания и навыки решения уравнений.	01.12
	Обобщение по теме «Модуль числа. Решение уравнений с модулем»	1	Практикум по решению задач.	Индивидуальный контроль	Систематизировать ЗУН решения уравнений.	08.12
	3.Решение неравенств с модулем	6		Фронтальный опрос
	Решение простейших неравенств вида	1	Фронтальная работа.	Групповой контроль	Знать алгоритм решения и уметь решать простейшие неравенства вида	15.12
	Упражнение в решении простейших неравенств вида	1	Работа в парах.	Тематический контроль	Знать алгоритм решения и уметь решать простейшие неравенства вида	22.12
	Решение простейших неравенств вида	1	Индивидуальная работа по карточкам.	Самоконтроль	Знать алгоритм решения и уметь решать простейшие неравенства вида	12.01
	Упражнение в решении  простейших неравенств вида	1	Практикум по решению задач.	Взаимоконтроль	Знать алгоритм решения и уметь решать простейшие неравенства вида	19.01
	Решение неравенств, содержащих не менее двух выражений под знаком модуля	1	Фронтальная работа.	Самоконтроль	Закрепить знания и навыки решения неравенств.	26.01
	Обобщение изученного материала по теме «Решение неравенств с модулем»	1	Индивидуальная работа по карточкам.	Тематический контроль	Систематизировать ЗУН решения уравнений, содержащих не менее двух выражений под знаком модуля.	02.02
	4.Функция. Графики функций, содержащих модуль	9
	Свойства и графики элементарных функций.	1	Фронтальная работа.	Индивидуальный контроль	Знать свойства элементарных функций. Уметь строить графики элементарных функций	09.02
	Преобразования графиков функций.	1	Работа в парах.	Тематический контроль	Развить знания и умения преобразовывать графики функций.	16.02
	Функция  и ее график	1	Индивидуальная работа по карточкам.	Взаимоконтроль	Знать свойства функции. Уметь строить ее график.	23.02
	Построение графиков функции	1	Работа в парах.	Индивидуальный контроль	Закрепить знания и умения построения графиков функции .	04.03
	Функция  и ее график	1	Фронтальная работа.	Фронтальный опрос	Знать свойства функции . Уметь строить ее график.	09.03
	Построение графиков функции	1	Индивидуальная работа по карточкам.	Групповой контроль,  индивидуальный контроль	Закрепить знания и умения построения графиков функции .	16.03
	Графический способ  решения уравнений с модулем	1	Индивидуальная работа.	Индивидуальный контроль	Знать алгоритм графического способа решения уравнений с модулем. Уметь решать уравнения с модулем.	23.03
	Графический способ  решения неравенств с модулем	1	Фронтальная работа.	Самоконтроль Фронтальный опрос	Знать алгоритм графического способа решения неравенств с модулем. Уметь решать уравнения с модулем.	06.04
	Графический способ  решения уравнений и неравенств с модулем	1	Работа в парах.	Групповой контроль	Знать алгоритм графического способа решения уравнений и неравенств с модулем. Уметь решать уравнения и неравенства с модулем.	13.04
	5.Решение задач ЕГЭ	6
	Алгоритмы решения заданий повышенного и высокого уровня с модулями	1	Индивидуальная работа.	Взаимоконтроль	Знать алгоритмы решения заданий повышенного и высокого уровня с модулями, развивать умения их решать.	20.04
	Решение заданий ЕГЭ	1	Фронтальная работа.	Тематический контроль	Развитие умения решать задания с модулем	27.04
	Решение заданий ЕГЭ	1	Индивидуальная работа по карточкам.	Фронтальный опрос	Развитие умения решать	04.05
	Решение заданий ЕГЭ	1	Фронтальная работа.	Групповой контроль	Развитие умения решать с модулем	11.05
	Решение заданий ЕГЭ	1	Работа в парах.	Индивидуальный контроль	Развитие умения решать с модулем	18.05
	Обобщение и систематизация знаний	1	Фронтальная работа.	Фронтальный опрос	Развитие умения решать с модулем	25.05

---