Модуль сдвига — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 мая 2017; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 мая 2017; проверки требует 1 правка.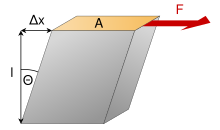 Сдвиговая деформация
Сдвиговая деформацияМодуль сдвига — физическая величина, характеризующая способность материала сопротивляться сдвиговой деформации. Является вторым параметром Ламе (μ{\textstyle \mu }). Модуль сдвига определяется следующим соотношением:
- G=τxyγxy=F/AΔx/I=FIAΔx,{\displaystyle G={\frac {\tau _{xy}}{\gamma _{xy}}}={\frac {F/A}{\Delta x/I}}={\frac {FI}{A\Delta x}},}
где
- τxy=F/A{\displaystyle \tau _{xy}=F/A} — касательное напряжение;
- A{\displaystyle A} — площадь, на которую действует сила;
- γxy=Δx/I=tgθ{\displaystyle \gamma _{xy}=\Delta x/I=\operatorname {tg} \theta } — сдвиговая деформация;
- Δx{\displaystyle \Delta x} — смещение;
- I{\displaystyle I} — начальная длина.
В международной системе единиц (СИ) модуль сдвига измеряется в паскалях (на практике —- в гигапаскалях).
Модуль сдвига — одна из нескольких величин, характеризующих упругие свойства материала. Все они возникают в обобщённом законе Гука:
- модуль Юнга описывает поведение материала при одноосном растяжении,
- объёмный модуль упругости описывает поведение материала при всестороннем сжатии,
- модуль сдвига описывает отклик материала на сдвиговую нагрузку.
У однородного изотропного материала модуль сдвига связан с модулем Юнга через коэффициент Пуассона:
G=E2(1+ν),{\displaystyle G={\frac {E}{2(1+\nu )}},}
где ν{\displaystyle \nu } — значение коэффициента Пуассона для данного материала.
В однородных изотропных средах существует два типа упругих волн: продольные волны и поперечные волны. Скорости продольной (cp){\displaystyle (c_{p})} и поперечной(cs){\displaystyle (c_{s})} волн зависят от модуля сдвига:
cp=2G(1−ν)ρ(1−2ν),cs=Gρ{\displaystyle c_{p}={\sqrt {\frac {2G(1-\nu )}{\rho (1-2\nu )}}},\qquad \qquad c_{s}={\sqrt {\frac {G}{\rho }}}}
где
- G — модуль сдвига
- ν{\displaystyle \nu } — коэффициент Пуассона
- ρ{\displaystyle \rho } — плотность материала.
- ↑ 1 2 3 4 Беляев Н.М. Сопротивление материалов.. — Москва: Наука, 1965.
Модуль комплексного числа — это… Что такое Модуль комплексного числа?
- Модуль комплексного числа
Модуль комплексного числа
 .
.
Модуль комплексного числа z обычно обозначается | z | или r.Пусть
 и
и  — вещественные числа такие, что комплексное число
— вещественные числа такие, что комплексное число  (обычные обозначения). Тогда
(обычные обозначения). Тогда
Wikimedia Foundation. 2010.
- Модули Perl
- Модуль центрифуг
Смотреть что такое «Модуль комплексного числа» в других словарях:
модуль комплексного числа
— kompleksinio skaičiaus modulis statusas T sritis fizika atitikmenys: angl. modulus of complex number vok. Betrag der komplexen Zahl, m rus. модуль комплексного числа, m pranc. module du nombre complexe, m … Fizikos terminų žodynasМОДУЛЬ — (modulus) Величина числа с точки зрения его расстояния от 0. Модуль, или абсолютное значение реального числа х (обозначается |х|), является разностью между х и 0 независимо от знака. Следовательно, если х>0, то |х|=х и если х <0, то |х|=–х … Экономический словарь
МОДУЛЬ — комплексного числа см. Абсолютная величина. Модуль перехода от системы логарифмов при основании a к системе при основании b есть число 1/logab … Большой Энциклопедический словарь
Модуль числа — Абсолютная величина или модуль вещественного или комплексного числа x есть расстояние от x до начала координат. Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… … Википедия
Модуль (в математике) — Модуль в математике, 1) М. (или абсолютная величина) комплексного числа z = х + iy есть число ═(корень берётся со знаком плюс). При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… … Большая советская энциклопедия
МОДУЛЬ — (в математике) мера для сравнения однородных величин и для выражения одной из них помощью другой; м. выражается числом. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907. МОДУЛЬ (лат.). 1) число, которым множатся… … Словарь иностранных слов русского языка
МОДУЛЬ (в математике) — МОДУЛЬ комплексного числа, см. Абсолютная величина (см. АБСОЛЮТНАЯ ВЕЛИЧИНА). Модуль перехода от системы логарифмов при основании a к системе при основании b есть число 1/logab … Энциклопедический словарь
Модуль — I Модуль (от лат. modulus мера) в архитектуре, условная единица, принимаемая для координации размеров частей здания или комплекса. В архитектуре разных народов в зависимости от особенностей строительной техники и композиции зданий за М.… … Большая советская энциклопедия
модуль — я; м. [от лат. modulus мера] 1. чего. Спец. Величина, характеризующая какое л. свойство твёрдого тела. М. сжатия. М. упругости. 2. Матем. Действительное число, абсолютная величина отрицательного или положительного числа. М. комплексного числа. М … Энциклопедический словарь
МОДУЛЬ — числовая характеристика какого либо математич. объекта. Обычно значение М. неотрицательное действительное число элемент , обладающий нек рыми характеристич. свойствами, обусловленными свойствами множества рассматриваемых объектов. Понятие М.… … Математическая энциклопедия
Модуль расстояния — Википедия
Материал из Википедии — свободной энциклопедии
Модуль расстояния — способ выражения расстояний, часто используемый в астрономии.
Модуль расстояния μ=m−M{\displaystyle \mu =m-M} показывает разность между видимой звёздной величиной m{\displaystyle m} (в идеальном случае, с внесёнными поправками за межзвёздное поглощение) и абсолютной звёздной величиной M{\displaystyle M} астрономического объекта. Модуль расстояния связан с расстоянием до объекта, выраженным в парсеках, соотношениями
- log10(d)=1+μ5{\displaystyle \log _{10}(d)=1+{\frac {\mu }{5}}},
- μ=5log10(d)−5{\displaystyle \mu =5\log _{10}(d)-5}.
Данное определение удобно, поскольку наблюдаемая яркость источника света связана с расстоянием по закону обратных квадратов (источник, находящийся вдвое дальше, кажется в четыре раза менее ярким), а также поскольку светимости объектов зачастую выражают в звёздных величинах.
Абсолютную звёздную величину M{\displaystyle M} определяют как видимую звёздную величину объекта при расположении его на расстоянии 10 пк. Предположим, что источник света имеет яркость L(d){\displaystyle L(d)} при наблюдении с расстояния d{\displaystyle d} пк и яркость L(10){\displaystyle L(10)} при наблюдении с расстояния 10 пк. Закон обратных квадратов в данном случае примет вид
- L(d)=L(10)(d10)2{\displaystyle L(d)={\frac {L(10)}{({\frac {d}{10}})^{2}}}}.
Разность видимой и абсолютной звёздных величин может быть выражена в виде
- m−M=−2.5log10L(d)+2.5log10L(10){\displaystyle m-M=-2.5\log _{10}L(d)+2.5\log _{10}L(10)}.
Выражение для модуля расстояния примет вид
- μ=5log10(d)−5=5log10(d10){\displaystyle \mu =5\log _{10}(d)-5=5\log _{10}\left({\frac {d}{10}}\right)}.
Расстояние d{\displaystyle d} (в парсеках) может быть выражено через модуль расстояния как
- d=10μ5+1{\displaystyle d=10^{{\frac {\mu }{5}}+1}}.
Неопределенность расстояния в парсеках δd{\displaystyle \delta d} можно выразить через неопределённость модуля расстояния δμ{\displaystyle \delta \mu } по формуле[1]
- δd=0.2ln(10)100.2μ+1δμ=0.461d δμ{\displaystyle \delta d=0.2\ln(10)10^{0.2\mu +1}\delta \mu =0.461d\ \delta \mu }.
Расстояние не является единственной величиной, определяющей разность между абсолютной и видимой звёздными величинами. Поглощение света также является важным фактором, и в некоторых случаях может иметь решающее значение (например, в случае направления на центр Галактики).
Следовательно, необходимо различать модуль расстояния без внесённой поправки за поглощение света (значение модуля расстояния в данном случае приводит к завышенной оценке расстояния до источника) и скорректированный за поглощение света модуль расстояния. В первом случае величина называется визуальным модулем расстояния, (m−M)v{\displaystyle {(m-M)}_{v}}, во втором случае — истинным модулем расстояния, (m−M)0{\displaystyle {(m-M)}_{0}}.
Визуальный модуль расстояния вычисляется как разность между наблюдаемой видимой звёздной величиной и некоторой теоретической оценкой абсолютной звёздной величины. Определение истинного модуля расстояния требует оценки коэффициента межзвёздного поглощения.
Модуль расстояния используется при выражении расстояния до других галактик в относительно близкой части Вселенной. Например, Большое Магелланово Облако имеет модуль расстояния 18.5[2], Туманность Андромеды — 24.5[3] , галактика NGC 4548 в скоплении Девы имеет модуль расстояния 31.0[4]. В случае БМО данное значение модуля расстояния означает, что сверхновая SN 1987A, имевшая видимую звёздную величину 2.8 в максимуме блеска, обладала абсолютной звёздной величиной -15.7.
Использование модулей расстояния упрощает вычисление звёздных величин. Например, звезда солнечного типа (M=5{\displaystyle M=5}) в Туманности Андромеды (μ=24.4{\displaystyle \mu =24.4}) будет иметь видимую звёздную величину m=5+24.4=29.4{\displaystyle m=5+24.4=29.4} и её можно будет с трудом наблюдать на телескопе Хаббл, имеющем предельную звёздную величину около 30[1].
- ↑ J. R. Taylor. An introduction to Error Analysis (неопр.). — Mill Valley, California: University Science Books, 1982. — ISBN 0-935702-07-5.
- ↑ D. R. Alvez. A review of the distance and structure of the Large Magellanic Cloud (англ.) // New Astronomy Reviews : journal. — 2004. — Vol. 48, no. 9. — P. 659—665. — DOI:10.1016/j.newar.2004.03.001. — Bibcode: 2004NewAR..48..659A. — arXiv:astro-ph/0310673.
- ↑ I. Ribas, C. Jordi, F. Vilardell, E. L. Fitzpatrick, R. W. Hilditch, E. F. Guinan. First Determination of the Distance and Fundamental Properties of an Eclipsing Binary in the Andromeda Galaxy (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2005. — Vol. 635, no. 1. — P. L37—L40. — DOI:10.1086/499161. — Bibcode: 2005ApJ…635L..37R. — arXiv:astro-ph/0511045.
- ↑ J. A. Graham, L. Ferrarese, W. L. Freedman, R. C. Kennicutt Jr., J. R. Mould, A. Saha, P. B. Stetson, B. F. Madore, F. Bresolin, H. C. Ford, B. K. Gibson, M. Han, J. G. Hoessel, J. Huchra, S. M. Hughes, G. D. Illingworth, D. D. Kelson, L. Macri, R. Phelps, S. Sakai, N. A. Silbermann, A. Turner. The Hubble Space Telescope Key Project on the Extragalactic Distance Scale. XX. The Discovery of Cepheids in the Virgo Cluster Galaxy NGC 4548 (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1999. — Vol. 516, no. 2. — P. 626—646. — DOI:10.1086/307151. — Bibcode: 1999ApJ…516..626G.
Длина модуля — Википедия
Материал из Википедии — свободной энциклопедии
Длина модуля — способ измерения «размера» модуля, обобщающий понятие размерности векторного пространства. Длина определяется как максимальная длина цепочки вложенных подмодулей.
Пусть M — (левый или правый) модуль над кольцом R. Мы говорим что длина цепочки его подмодулей вида
- N0⊊N1⊊⋯⊊Nn{\displaystyle N_{0}\subsetneq N_{1}\subsetneq \cdots \subsetneq N_{n}}
равна n, то есть считаем число строгих включений, а не число подмодулей. Длина модуля M — это наибольшая длина цепочки среди всех цепочек его подмодулей. Если наибольшей длины цепочки не существует, длина M равна бесконечности.
- Единственный модуль длины 0 — нулевой модуль. Модули длины 1 называются простыми.
- Для конечномерного векторного пространства длина совпадает с размерностью.
- Длина циклической группы Z/nZ{\displaystyle \mathbb {Z} /n\mathbb {Z} } равна числу множителей в разложении n на простые.
Модуль имеет конечную длину тогда и только тогда, когда он является артиновым и нётеровым.
Пусть
- 0→L→M→N→0{\displaystyle 0\rightarrow L\rightarrow M\rightarrow N\rightarrow 0}
является короткой точной последовательностью модулей. В этом случае M имеет конечную длину тогда и только тогда, когда L и N имеют конечную длину, причем длина M равна сумме их длин. В частности, длина прямой суммы модулей равна сумме длин компонент.
Принцип максимума модуля — Википедия
Материал из Википедии — свободной энциклопедии
Если f{\displaystyle f} голоморфна в некоторой области G⊂Cn{\displaystyle G\subset \mathbb {C} ^{n}} и существует точка z0∈G{\displaystyle z_{0}\in G} такая, что во всей области G{\displaystyle G} выполняется неравенство |f(z0)|⩾|f(z)|{\displaystyle |f(z_{0})|\geqslant |f(z)|}, то f(z)≡const{\displaystyle f(z)\equiv \mathrm {const} }.
Другими словами, модуль аналитической функции, отличной от константы, не может иметь локальных максимумов внутри области G{\displaystyle G}.
(Здесь используется обычный принцип максимума модуля для функций ef(z){\displaystyle e^{f(z)}} и eif(z){\displaystyle e^{if(z)}}, а также равенство |ef(z)|=eRef(z){\displaystyle \left|e^{f(z)}\right|=e^{\mathrm {Re} \,f(z)}}.)
- Пусть K⊂Cn{\displaystyle K\subset \mathbb {C} ^{n}} — компактное подмножество. Для всякой функции f{\displaystyle f}, непрерывной на K{\displaystyle K} и аналитичной внутри K{\displaystyle K}, выполнено равенство:
- ‖f‖K=‖f‖∂K.{\displaystyle \|f\|_{K}=\|f\|_{\partial K}.}
Если последовательность таких функций равномерно сходится на границе компакта K{\displaystyle K}, тогда она сходится равномерно на всём K{\displaystyle K}.
Комплексное число — Википедия
Запросы «Re», «Im» и «Мнимая величина» перенаправляются сюда; см. также другие значения терминов Re, Im и Мнимая величина.
Иерархия чисел
Ко́мпле́ксные чи́сла (от лат. complex — совокупный, тесно связанный[1]; о двойном ударении см. примечание[K 1]) — числа вида a+bi{\displaystyle a+bi}, где a,b{\displaystyle a,b} — вещественные числа, i{\displaystyle i} — мнимая единица[2], то есть число, для которого выполняется равенство: i2=−1.{\displaystyle i^{2}=-1.} Множество комплексных чисел обычно обозначается символом C.{\displaystyle \mathbb {C} .} Вещественные числа можно рассматривать как частный случай комплексных, они имеют вид a+0i{\displaystyle a+0i}. Главное свойство C{\displaystyle \mathbb {C} } — в нём выполняется основная теорема алгебры, то есть любой многочлен n{\displaystyle n}-й степени (n⩾1{\displaystyle n\geqslant 1}) имеет n{\displaystyle n} корней. Доказано[⇨], что система комплексных чисел логически непротиворечива[K 2].
Так же как и для вещественных чисел, для комплексных чисел определены операции сложения, вычитания[⇨], умножения[⇨] и деления[⇨]. Однако многие свойства комплексных чисел отличаются от свойств вещественных чисел; например, нельзя указать, какое из двух комплексных чисел больше или меньше[⇨]. Удобно представлять комплексные числа a+bi{\displaystyle a+bi} точками на комплексной плоскости[⇨]; например, для изображения сопряжённых чисел используется операция отражения относительно горизонтальной оси[⇨]. Альтернативное представление комплексного числа в тригонометрической записи оказалось полезным для вычисления степеней и корней[⇨]. Функции комплексного аргумента изучаются в комплексном анализе[⇨].
Первоначально идея о необходимости использования комплексных чисел возникла в результате формального решения кубических уравнений, при котором в формуле Кардано под знаком квадратного корня получалось отрицательное число[3]. Большой вклад в исследование комплексных чисел внесли такие математики, как Эйлер, который ввёл общепризнанное обозначение i{\displaystyle i} для мнимой единицы, Декарт, Гаусс[⇨]. Сам термин «комплексное число» ввёл в науку Гаусс в 1831 году[1].
Свойства комплексных чисел и функций нашли широкое применение для решения многих практических задач в различных областях математики, физики и техники: в обработке сигналов, теории управления, электромагнетизме, теории колебаний, теории упругости и многих других[4][⇨]. Преобразования комплексной плоскости оказались полезны в картографии и гидродинамике. Современная физика полагается на описание мира с помощью квантовой механики, которая опирается на систему комплексных чисел.
Известно также несколько обобщений комплексных чисел — например, кватернионы[⇨].
Связанные определения[править | править код]
Всякое комплексное число z=a+bi{\displaystyle z=a+bi} состоит из двух компонентов[5]:
Противоположным для комплексного числа z=a+bi{\displaystyle z=a+bi} является число −z=−a−bi.{\displaystyle -z=-a-bi.} Например, для числа 1−2i{\displaystyle 1-2i} противоположным будет число −1+2i.{\displaystyle -1+2i.}
Четыре арифметические операции для комплексных чисел имеют те же свойства, что и аналогичные операции с вещественными числами. В отличие от последних, комплексные числа нельзя сравнивать на больше/меньше; доказано, что нет способа распространить порядок, заданный для вещественных чисел, на все комплексные так, чтобы порядок был согласован с арифметическими операциями (например, чтобы из a<b{\displaystyle a<b} вытекало a+c<b+c{\displaystyle a+c<b+c}). Однако комплексные числа можно сравнивать на равно/не равно)[5]:
- a+bi=c+di{\displaystyle a+bi=c+di} означает, что a=c{\displaystyle a=c} и b=d{\displaystyle b=d} (два комплексных числа равны между собой тогда и только тогда, когда равны их вещественные и мнимые части).
Сложение и вычитание[править | править код]
Определение сложения и вычитания комплексных чисел[5]:
- (a+bi)+(c+di)=(a+c)+(b+d)i,{\displaystyle \left(a+bi\right)+\left(c+di\right)=\left(a+c\right)+\left(b+d\right)i,}
- (a+bi)−(c+di)=(a−c)+(b−d)i.{\displaystyle \left(a+bi\right)-\left(c+di\right)=\left(a-c\right)+\left(b-d\right)i.}
Следующая таблица[5] показывает основные свойства сложения для любых комплексных u,v,w.{\displaystyle u,v,w.}
Умножение[править | править код]
Определим произведение[5] комплексных чисел a+bi{\displaystyle a+bi} и c+di{\displaystyle c+di}:
- (a+bi)⋅(c+di)=ac+bci+adi+bdi2=(ac+bdi2)+(bc+ad)i=(ac−bd)+(bc+ad)i{\displaystyle (a+bi)\cdot (c+di)=ac+bci+adi+bdi^{2}=(ac+bdi^{2})+(bc+ad)i=(ac-bd)+(bc+ad)i}.
Следующая таблица[5] показывает основные свойства умножения для любых комплексных u,v,w{\displaystyle u,v,w}.
Правила для степеней мнимой единицы:
- i2=−1;i3=−i;i4=1;i5=i{\displaystyle i^{2}=-1;\;i^{3}=-i;\;i^{4}=1;i^{5}=i} и т. д.
Деление[править | править код]
Комплексное число z¯=x−iy{\displaystyle {\bar {z}}=x-iy} называется сопряжённым к комплексному числу z=x+iy{\displaystyle z=x+iy} (см. подробнее ниже).
Для каждого комплексного числа a+bi{\displaystyle a+bi}, кроме нуля, можно найти обратное к нему[8] комплексное число 1a+bi{\displaystyle {\frac {1}{a+bi}}}. Для этого умножим числитель и знаменатель дроби на число a−bi{\displaystyle a-bi}, комплексно сопряжённое знаменателю
- 1a+bi=a−bi(a+bi)(a−bi)=a−bia2+b2=aa2+b2−ba2+b2i.{\displaystyle {\frac {1}{a+bi}}={\frac {a-bi}{(a+bi)(a-bi)}}={\frac {a-bi}{a^{2}+b^{2}}}={\frac {a}{a^{2}+b^{2}}}-{\frac {b}{a^{2}+b^{2}}}i.}
Определим результат деления[5] комплексного числа a+bi{\displaystyle a+bi} на ненулевое число c+di{\displaystyle c+di}:
- a+bic+di=(a+bi)(c−di)(c+di)(c−di)=ac+bdc2+d2+(bc−adc2+d2)i.{\displaystyle {\frac {a+bi}{c+di}}={\frac {\left(a+bi\right)\left(c-di\right)}{\left(c+di\right)\left(c-di\right)}}={\frac {ac+bd}{c^{2}+d^{2}}}+\left({\frac {bc-ad}{c^{2}+d^{2}}}\right)i.}
Как и для вещественных чисел, деление можно заменить умножением делимого на число, обратное к делителю.
Другие операции[править | править код]
Для комплексных чисел определены также извлечение корня, возведение в степень и логарифмирование.
Основные отличия комплексных чисел от вещественных[править | править код]
Уже упоминалось, что комплексные числа нельзя сравнивать на больше-меньше. Другое отличие: любой многочлен с вещественными или комплексными коэффициентами имеет, с учётом кратности, столько корней (вообще говоря, комплексных), какова его степень (основная теорема алгебры)[9].
В системе вещественных чисел из отрицательного числа нельзя извлечь корень чётной степени. Для комплексных чисел возможно извлечение корня из любого числа любой степени, однако результат неоднозначен — комплексный корень n{\displaystyle n}-й степени из ненулевого числа имеет n{\displaystyle n} различных комплексных значений[10]. См., например, корни из единицы.
Дополнительные отличия имеют функции комплексного переменного[⇨]..
Замечания о выражении √−1[править | править код]
Заметим, что число i{\displaystyle i} не является единственным числом, квадрат которого равен −1{\displaystyle -1}. Число −i{\displaystyle -i} также обладает этим свойством.
Следует также заметить, что выражение −1{\displaystyle {\sqrt {-1}}}, ранее часто использовавшееся вместо i{\displaystyle i}, не вполне корректно, так как арифметический корень определяется только для неотрицательных чисел. Во избежание ошибок, выражение с квадратными корнями из отрицательных величин в настоящее время принято записывать как 5+i3{\displaystyle 5+i{\sqrt {3}}}, а не 5+−3{\displaystyle 5+{\sqrt {-3}}}, несмотря на то, что даже в XIX веке второй вариант записи считался допустимым[11].
Пример возможной ошибки при неосторожном использовании устаревшей записи:
- −3⋅−3=(−3)⋅(−3)=(−3)2=9=3{\displaystyle {\sqrt {-3}}\cdot {\sqrt {-3}}={\sqrt {\left(-3\right)\cdot \left(-3\right)}}={\sqrt {\left(-3\right)^{2}}}={\sqrt {9}}=3}.
При использовании современной записи такой ошибки не возникло бы:
- (i3)⋅(i3)=(i⋅3)2=i2⋅(3)2=−3.{\displaystyle \left(i{\sqrt {3}}\right)\cdot \left(i{\sqrt {3}}\right)=\left(i\cdot {\sqrt {3}}\right)^{2}=i^{2}\cdot \left({\sqrt {3}}\right)^{2}=-3.}
Комплексная плоскость[править | править код]
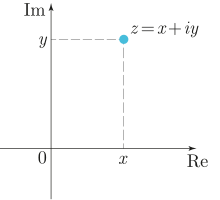 Геометрическое представление комплексного числа
Геометрическое представление комплексного числаКомплексные числа можно представить на плоскости с прямоугольной системой координат: числу z=x+iy{\displaystyle z=x+iy} соответствует точка плоскости с координатами {x,y}{\displaystyle \left\{x,y\right\}} (а также радиус-вектор, соединяющий начало координат с этой точкой). Такая плоскость называется комплексной. Вещественные числа на ней расположены на горизонтальной оси, мнимая единица изображается единицей на вертикальной оси; по этой причине горизонтальная и вертикальная оси называются соответственно вещественной и мнимой осями[12].
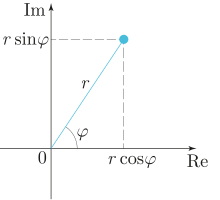 Модуль r{\displaystyle r} и аргумент φ{\displaystyle \varphi } комплексного числа
Модуль r{\displaystyle r} и аргумент φ{\displaystyle \varphi } комплексного числаБывает удобно рассматривать на комплексной плоскости также полярную систему координат (см. рисунок справа), в которой координатами точки являются расстояние r{\displaystyle r} до начала координат (модуль[⇨]) и угол φ{\displaystyle \varphi } радиус-вектора точки с горизонтальной осью (аргумент[⇨]).
В этом представлении сумма комплексных чисел соответствует векторной сумме соответствующих радиус-векторов, а вычитанию чисел соответствует вычитание радиус-векторов. При перемножении комплексных чисел их модули перемножаются, а аргументы складываются. Если модуль второго сомножителя равен 1, то умножение на него соответствует повороту радиус-вектора первого числа на угол, равный аргументу второго числа[13]. Этот факт объясняет широкое использование комплексного представления в теории колебаний, где вместо терминов «модуль» и «аргумент» используются термины «амплитуда» и «фаза»[14].
Пример: умножение на i{\displaystyle i} поворачивает радиус-вектор числа на прямой угол в положительном направлении, а после умножения на −i{\displaystyle -i} радиус-вектор поворачивается на прямой угол в отрицательном направлении.
Модуль[править | править код]
Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же самое, расстояние от точки комплексной плоскости до начала координат). Модуль комплексного числа z=x+iy{\displaystyle z=x+iy}
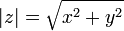 .
.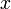 и
и 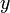 — вещественные числа такие, что комплексное число
— вещественные числа такие, что комплексное число 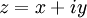 (обычные обозначения). Тогда
(обычные обозначения). Тогда