Модуль числа | Фізика — легко!
Противоположные числа – это числа, которые отличаются друг от друга только знаком. Выражение –а обозначает, что это число противоположное числу а.
Например, 7 и – 7;
41 и – 41 и т.д.
Число 0 противоположно самому себе!
То есть, для того, чтобы показать противоположность чисел в математике используют знак « – ».
Приписав знак « – » перед положительным числом 5, мы получим отрицательное число – 5.
Приписав знак « – » перед отрицательным числом – 5, мы получим противоположное ему положительное число 5, то есть – (–5) = 5.
– (–а) = а
На координатной прямой точки, у которых противоположные координаты, расположены на одинаковом расстоянии от начала отсчёта.
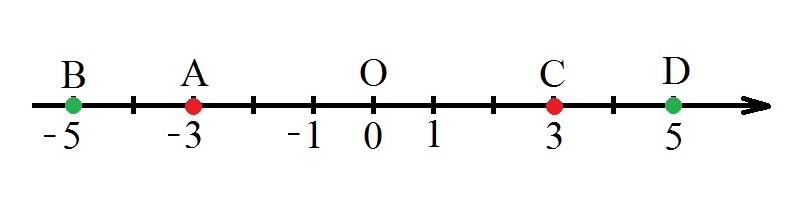
AO = OC
BO = OD
Модуль числа
Модуль числа – это расстояние (в единичных отрезках) от начала отсчёта до точки, которая изображает это число на координатной прямой.
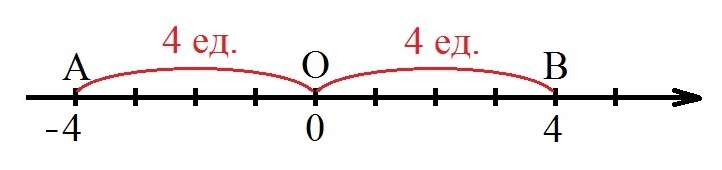
Точки А(– 4) и В (4) отдалены от начала отсчёта на 4 единичных отрезков, а числа – 4 и 4 имеют одинаковые модули, равные 4.
Модуль числа а обозначают | а |
Так как модуль – это расстояние, а расстояние не может быть отрицательным, то модуль числа не может быть отрицательным числом!!!
Модулем положительного числа и нуля является тоже самое число, а модулем отрицательного числа – противоположное ему число:
| а | = а, если а ≥ 0 (если а – неотрицательное число)
| а | = – а, если а < 0 (если а – отрицательное число)
Выводы
Свойства модуля числа:
- Модуль числа не может быть отрицательным. Модуль числа всегда или положительное число или равен 0.
| 4| = 4
| 0 | = 0
|– 4| = 4
- Противоположные числа имеют равные модули.
| – а | = | а | = а
Пример, | – 12 | = | 12 | = 12
Решение уравнений (примеры)
1. – x = 7
вместо – x и 7 напишем противоположные им числа, используя знак «–»
–(– x) = – 7
воспользуемся правилом, что – (–а) = а получим
x = – 7
2. – x = – 10
–(– x) = –(– 10)
x = 10
3. x = –(– 32)
x = 32
4. | x | = 4
x = 4 или x = – 4
Ответ: 4; – 4
5. | x | = 0
x = 0
Ответ: 0
6. | y | = – 8
модуль не может быть отрицательным числом, а значит данное уравнение не имеет решения
Ответ: нет корней
7. | – x | = 12
вспомним второе свойство модуля, что | – а | = | а | = а, тогда
| x | = 12
x = 12 или x = – 12
Ответ: 12; – 12
8. | y | – 2 = 12
подобные уравнения решаются как простые уравнения, только с учётом модуля
| y | = 12 + 2
| y | = 14
y = 14 или y = – 14
Ответ: 14; – 14
9. 10 – 2| x | = 4
2| x | = 10 – 4
2| x | = 6
| x | = 6 : 2
| x | = 3
x = 3 или x = – 3
Ответ: 3; – 3
То есть при решении уравнений, содержащих модуль мы получим три вида ответа:
два корня (если под знаком модуля положительное число), один корень (если под знаком модуля 0)
нет корней (если под знаком модуля отрицательное число).
Решение простейших неравенств, содержащих модуль
В 5 классе мы решали примеры с простейшими неравенствами. Линейные неравенства бывают строгие и нестрогие.
Строгие неравенства – это неравенства со знаками больше (>) или меньше (<).
x > a; x < a;
Нестрогие неравенства – это неравенства со знаками больше либо равно (≥) или меньше либо равно (≤).
x ≥ a; x ≤ a.
Примеры
1. Найдите все натуральные значения x, при которых является правильным неравенство x < 9
Решение.
Данное неравенство будет правильным при таких значениях x: 1; 2; 3; 4; 5; 6; 7; 8.
Ответ: х = {1; 2; 3; 4; 5; 6; 7; 8} – натуральные решения данного неравенства.
Примечание:
Число 0 не является решением этого неравества, так как 0 не является натуральным числом;
2. Какое наименьшее натуральное значение а удовлетворяет неравенство а > 12?
Решение.
Поскольку неравенство строгое, то число 13 является наименьшим натуральным значением а, которое удовлетворяет данному неравенству.
Ответ: 13
3. Какое наименьшее натуральное значение а удовлетворяет неравенство а ≥ 12?
Решение.
Поскольку неравенство нестрогое, то число 12 является наименьшим натуральным значением а, которое удовлетворяет данному неравенству.
Ответ: 12.
4. Найдите все натуральные значения x, при которых является правильным неравенство 2 < x < 9
Решение.
Неравенство двойное (читают как «х больше от 2, но меньше от 9»), строгое, поэтому 3; 4; 5; 6; 7; 8 – натуральные решения данного двойного неравенства.
Ответ: х = {3; 4; 5; 6; 7; 8}
5. Найдите все натуральные значения x, при которых является правильным неравенство 2 < x ≤ 9.
Решение.
3; 4; 5; 6; 7; 8; 9 – натуральные решения данного двойного неравенства.
Ответ: х = {3; 4; 5; 6; 7; 8; 9}
6. Найти все целые числа, которые удовлетворяют неравенству| x | < 5.
Решение.
| x | < 5 (читаем как «расстояние от начала отсчёта до точки изображающей х меньше 5»).
Неравенство | x | < 5 эквивалентно (может быть также записано) –5 < x < 5. Неравенство двойное, строгое, поэтому данное неравенство будет правильным при таких значениях x: –4; –3; –2; –1; 0; 1; 2; 3; 4.
Ответ:
7. Найти все целые числа, которые удовлетворяют неравенству| x | ≤ 5.
Решение.
Неравенство | x | ≤ 5 эквивалентно –5 ≤ x ≤ 5. Неравенство двойное, нестрогое, поэтому числа –5 и 5 войдут в множество чисел, при которых данное неравенство будет правильным. Таким образом, данное неравенство будет правильным при таких значениях x: –5; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5.
Ответ: х = {–5; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5}
8. Найти все целые числа, которые удовлетворяют неравенству | x | > 2 и обозначте их на координатной прямой.
Решение.
Неравенство | x | > 2 эквивалентно x < – 2 или x > 2. Обозначим на координатной прямой точки, координаты которых удовлетворяют данному неравенству
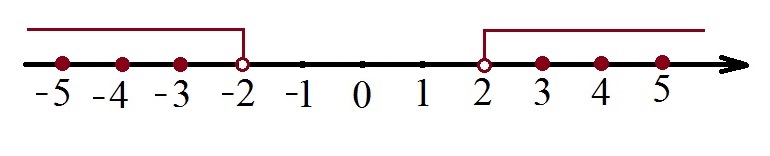
Ответ: х = {…–5; –4; –3; 3; 4; 5…}
9. Найти все целые числа, которые удовлетворяют неравенству | x | ≥ 2 и обозначте их на координатной прямой.
Решение.
Неравенство | x | ≥ 2 эквивалентно x ≤ – 2 или x ≥ 2. Обозначим на координатной прямой точки, координаты которых удовлетворяют данному неравенству
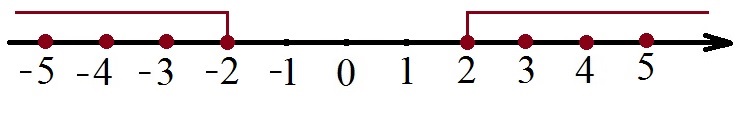
Поскольку неравенство нестрогое, то числа – 2 и 2 входят в множество целых чисел, при которых данное неравенство будет правильным. А на координатной прямой эти точки обозначаем в виде закрашенной точки.
Ответ: х = {…–5; –4; –3; –2; 2; 3; 4; 5…}
Решение.
Рассмотрим сначала левую часть неравенства. Она означает, что расстояние от начала отсчёта до точек меньше 1. Рассмотрим правую часть неравенства: расстояние от начала отсчёта до этих же точек меньше или равно 3.
Построим эти точки на координатной прямой:
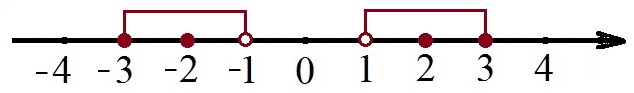
1 и – 1 не входят в множество целых чисел, которые удовлетворяют неравенству, потому что неравенство строгое.
3 и – 3 входят в множество целых чисел, которые удовлетворяют неравенству, потому что неравенство нестрогое.
Ответ: х = {–3; –2; 2; 3}
Модуль отрицательного числа | Математика
Модуль числа a — это расстояние в единичных отрезках на координатной прямой от начала отсчёта до точки с координатой a.
Расстояние от начала отсчёта — точки О с координатой 0 — до точки с отрицательной координатой -а равно а.
-а и а — противоположные числа.
Таким образом, модуль отрицательного числа равен противоположному ему числу.
В формулах принято записывать модуль отрицательного числа так: |а|, где а<0,
(а не |-а|).
Таким образом,
Примеры.
Так как модуль отрицательного числа равен противоположному ему числу, то
Светлана МихайловнаПоложительные и отрицательные числа
Простейшие уравнения с модулем | Математика
Рассмотрим простейшие уравнения с модулем вида «модуль x равен числу». Их решение опирается на определение модуля. Количество корней такого уравнения зависит от знака числа, стоящего в правой части.
Если модуль икса равен положительному числу, уравнение имеет два корня, которые являются противоположными числами:
Уравнения вида «модуль x равен отрицательному числу» не имеют корней, поскольку модуль не может быть отрицательным числом:
Примеры простейших уравнений с модулем.
Светлана МихайловнаУравнения в 6 классе
чему равен модуль положительного числа; отрицательного числа? чему равен модуль нуля?
Модуль положительного числа всегда равен самому числу, а отрицательного число умножить на -1 (то есть убрать минус перед числом) , нуля нулю.
положительному и нулюположительного этому же числу, отрицательного — этому числу с +
модуль — это расстояние в чистом виде, и всё равно, в какую сторону от нуля ты сделал эти 2 шага: +2 или -2, расстояние прошёл =2, поэтому модуль- всегда положительное число модуль 0 = 0
0=0 а любое отртцательное число меньше 0 и положытельного при сравнивание двух отрицательных чисел больше то число которое ближе к нуль например если мы сравниваем -5 и -6 то большее -5
если ты видишь это то ты задавал вопрос три года назад
всегда положительному
положительное-самому себе отрицательное-положительному 0 равен 0
Положительному, нолю.
самой стыдно, но забыла что делать с числом в модуле?
если число под модулем положительное то равно самому себе
Умножай дели вычитай не оброшяй внимания на знаки.. .
Если отрицательное число в модуле, то без модуля оно положительное
модуль положительного числа — есть само число, а модуль отрицательного числа, есть число ему противоположное … например : /x-7/,если X>0, то /x-7/=x-7 если X<0, то /x-7/=7-х
Если в модуле отрицательное число, то без модуля будет положительное. Из модуля всегда положительное!
Модулем рационального числа называют расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.
Скажу кратко, если число в модуле, то оно в любом случае будет положительным. Пример: |x|=|x| |-x|=|x|