Электронный учебник по физике: все темы школьной программы

 

Физика — одна из основных наук естествознания. Изучение физики в школе начинается с 7 класса и продолжается до конца обучения в школе. К этому времени у школьников уже должен быть сформирован должный математический аппарат, необходимый для изучения курса физики.

• Школьная программа по физике состоит из нескольких больших разделов: механика, электродинамика, колебания и волны оптика, квантовая физика, молекулярная физика и тепловые явления.

Темы школьной физики

В 7 классе идет поверхностное ознакомление и введение в курс физики. Рассматриваются основные физические понятия, изучается строение веществ, а также сила давления, с которой различные вещества действуют на другие. Кроме того изучаются законы Паскаля и Архимеда.

В 8 классе изучаются различные физические явления. Даются начальные сведения, о магнитном поле и явления, при которых оно возникает. Изучается постоянный электрический ток и основные законы оптики. Отдельно разбираются различные агрегатные состояния вещества и процессы, происходящие при переходе вещества из одного состояния в другое. 

9 класс посвящен основным законам движения тел и взаимодействия их между собой. Рассматриваются основные понятия механических колебаний и волн. Отдельно разбирается тема звука и звуковых волны. Изучается основы теории электромагнитного поля и электромагнитные волны. Кроме того происходит знакомство с элементами ядерной физики и изучается строение атома и атомного ядра.

В 10 классе начинается углубленное изучение механики (кинематики и динамики) и законов сохранения. Рассматриваются основные виды механических сил. Происходит углубленное изучение тепловых явлений, изучается молекулярно-кинетическая теория и основные законы термодинамики. Повторяются и систематизируются основы электродинамики: электростатика, законы постоянного электрического тока и электрический ток в различных средах. 

11 класс посвящен изучению магнитного поля и явления электромагнитной индукции. Подробно изучаются различные виды колебаний и волн: механические и электромагнитные. Происходит углубление знаний из раздела оптики. Рассматриваются элементы теории относительности и квантовая физика.

• Ниже идет список классов с 7 по 11. Каждый класс содержит темы по физике, которые написаны нашими репетиторами. Данные материалы могут использоваться как учениками и их родителями, так и школьными учителями и репетиторами.

 

Все материалы разбиты по классам:

Физика 7 классФизика 8 классФизика 9 классФизика 10 классФизика 11 класс

Нужна помощь в учебе?

Все неприличные комментарии будут удаляться.

www.nado5.ru

Начальная физика — 7-8 класс

Начальная физика — 7-8 класс

Физика природы  для начинающих

Вот еще забавное световое явление. Станьте по пояс в воде спиной к солнцу,  пустите перед собой  побольше  мелких брызг, и вы увидите яркую радугу, получающуюся при преломлении лучей солнца в капельках воды совершенно так же, как  настоящая радуга получается в каплях дождя ……… читать

В чем секреты лампы накаливания и энергосберегающей лампы?

Основной элемент энергосберегающей лампы — изогнутая трубка-колба, запаянная с двух концов. Изнутри ее стенки покрыты светящимся составом — люминофором.
На противоположных концах этой колбы находятся электроды. В колбу закачаны пары ртути, а также так называемые инертные газы аргон и неон ……… читать

Что может давление? — начинающим физикам

Вытекая, например, из трубы со скоростью около 100 метров в секунду, водяная струя становится упругой, как хорошая сталь. Её даже невозможно перерубить и саблей. Сталь не может рассечь струю воды ……… читать

Совсем просто о знаменитом маятнике Фуко. Познай на опыте!

Можно  проделать  дома интересный опыт. Сядьте  на вращающийся компьютерный стул.  Привяжите  к стулу  какой-нибудь  нитяной маятник  (грузик на нити). Раскачайте маятник.  Запомните,  в какой плоскости он начал колебаться ……… читать

Какой бывает радуга? — начинающим физикам

Первая радуга, внутренняя, всегда ярче второй, внешней. У второй радуги цвета полос располагаются в обратном порядке — верхняя часть дуги имеет фиолетовую окраску, а нижняя — красную. Так как при двойном отражении в капле теряется больше света, яркость второй радуги всегда меньше, и она выглядит бледнее. Небо между радугами всегда более тёмное, чем другие участки неба ……… читать

Ода силам тяготения. Нас тянут, и мы притягиваем!

Загородиться от гравитационных сил невозможно. Для всемирного тяготения нет преград. Гравитационное взаимодействие свободно передается через любые тела, экранов  для гравитации не существует. Гравитационные силы вездесущи и всепроникающи ……… читать

Агрегатные состояния – физика облаков для начинающих

Днем происходит процесс, обратный утреннему. Облака опускаются в более плотный слой атмосферы,  сжимаются, нагреваются и «тают». «И в тверди пламенной и чистой  лениво тают облака…» (Тютчев). На обычном, разговорном языке и на языке поэзии «тают». Точнее было  бы  сказать— «испаряются» ……… читать

Механические колебания и волны — физика волн  для начинающих

  Обратите внимание, как мелкая рябь, не искажаясь, налагается на изгибы крупных волн.  
В такую поучительную картину переплетающихся волн  любили всматриваться  Леонардо да-Винчи и Гельмгольц.   Здесь наглядно представляется  нашему глазу  то, что в случае звуковых волн,  пересекающихся в  воздухе, открывается лишь умственно  глазу  математика ……… читать

Смачивание и поверхностное натяжение – «мокрая» физика для начинающих

Зачерпните ложечкой мелкие пузырьки воздуха, выплывшие  из сахара на поверхности чая. Вглядитесь, как эти пузырьки   в неполной ложке прилипают к краям, а в переполненной  «с верхом» собираются к средине выпуклой поверхности ……… читать

Теплоизоляция у животных – «теплая» физика для начинающих

Распушив шерсть, перья, животные образуют воздушную подушку с высокими теплоизоляционными свойствами. Несмотря на то что у китов, тюленей, моржей  голая шкура  толщиной около  2-3 мм, они часами плавают в ледяной воде.   Их подкожный толстый слой жира хорошо задерживает утечку тепла. У императорского пингвина  жир составляет  10-15 кг  при общей массе около  35 кг. ……… читать

Испарение. О чем не пишут в учебниках — физика для начинающих

Одно многолетнее  растение из Северной Америки давно обратили на себя внимание, оно плоское, как лист гербария. Концы и профиль вертикальных листовых пластинок обращены к северу и югу, совсем как у магнитной иглы, а широкие стороны смотрят на запад и на восток. Это направление сохраняется растением прерий постоянно. Охотники  привыкли ориентироваться по этому растению и назвали его растением-компасом ……… читать

Физика у воды — тепловые явления   для начинающих

Вот убедительная  иллюстрация малой теплопроводности воды.  Правда, лучи солнца проникают до дна реки, но ведь верхние слои воды   поглощают самую энергичную, самую греющую часть лучей (инфракрасные и красные   лучи). Посмотрите на солнце из-под воды, каким тусклым, желто-зеленым оно  представляется. ……… читать

Механизмы у растений — физика природы для начинающих

Во влажных   лесных  оврагах  можно   найти  растение с замечательным   приспособлением  для разбрасывания семян. Это — бальзамин  «не тронь меня». Под нежными  зелеными листьями висят его полупрозрачные, нежные плоды. Нажмите пальцами  кончик плода, стенки лопнут, скрутившись упругими завитками, и брызнут в   стороны зрелыми семенами ……… читать

Физика на  закате – оптика для начинающих

Вы видите не круглый диск, а заметно сплюснутый сверху и  снизу.
От  преломления лучей в земной атмосфере («астрономическая рефракция») все небесные  тела кажутся несколько более приподнятыми над горизонтом, чем на самом деле.  Эта приподнятость тем сильнее, чем ближе наблюдаемая точка к горизонту.  ……… читать

Энергия Солнца – физика энергий для начинающих

Как углекислый газ,  получившийся от горения угля, да и тот, который выдыхаете вы, снова может образовать  запас энергии? Не зря зеленые насаждения называют «легкими» нашей планеты. Растения поглощают  из воздуха углекислый газ. Смотрите, как тянется к солнцу  каждая ветка дерева, как каждый листочек силится захватить побольше горячих лучей.  В этих зеленых листьях идет энергичная работа хитрого химического процесса ……… читать

 

class-fizik.ru

Физика, 7 класс: уроки, тесты, задания

Введение

1. Введение. Макро- и микромир. Числа со степенью 10

2. Наблюдения, опыты, измерения, гипотеза, эксперимент

3. Физические величины. Международная система единиц

Движение и взаимодействие тел

1. Механическое движение. Траектория и путь

2. Скорость. Неравномерное движение. Средняя скорость

3. Инерция

4. Взаимодействие тел. Масса тела. Единицы массы. Измерение массы тела на весах

5. Плотность вещества. Расчёт массы и объёма тела по его плотности

6. Сила. Сила тяжести

7. Свободное падение. Вес тела

8. Измерение силы с помощью динамометра

9. Деформации тел. Сила упругости. Закон Гука

10. Взаимодействие тел. Сила трения

Работа и мощность. Энергия

1. Механическая работа

2. Мощность

3. Рычаг. Простые механизмы

4. Блок

5. Коэффициент полезного действия

6. Энергия

Строение вещества

1. Строение вещества. Молекулы и атомы

2. Диффузия

3. Притяжение и отталкивание молекул. Смачивание и капиллярность

4. Агрегатные состояния вещества

Давление твёрдых тел, жидкостей и газов

1. Давление и сила давления. Единицы измерения

2. Давление твёрдых тел. Способы уменьшения и увеличения давления

3. Давление газа. Применение сжатого воздуха

4. Атмосферное давление и его измерение. Опыт Торричелли

5. Давление в жидкости. Закон Паскаля

6. Гидростатическое давление. Давление на дне морей и океанов

7. Сообщающиеся сосуды. Водопровод. Шлюзы

8. Гидравлический пресс. Насосы

9. Закон Архимеда

10. Действие жидкости на погружённое в неё тело. Плавание тел

11. Выталкивающая сила в газах. Воздухоплавание

Класс заполнен на 100 %

www.yaklass.ru

Физическое шоу «Физика вокруг нас»

Это итоговое занятие всегда провожу в рамках недели естественно — научных дисциплин. В этом году она проходила в апреле и была приурочена ко Дню Космонавтики. Обучающиеся 7-хклассов в течение всего года на занятиях по внеурочной деятельности готовят это мероприятие, а затем проводят его для ребят начальной школы и обучающихся 5-6 классов. Это очень познавательно для всех! После проведения занятия у ребят наблюдается увеличение интереса к проведению экспериментов. Они начинают больше читать, интересуются научными опытами.

Цели:

• расширение кругозора детей, их знаний по окружающему их миру, развитие познавательного интереса к изучению законов природы.
• развитие наблюдательности, внимания, мышления обучающихся начальной и средней школы.

Задачи:

• обучать детей умению проводить эксперименты с подручными материалами;
• развивать у детей внимание и интерес, эмоциональную отзывчивость;
• формировать у детей элементарные представления о законах природы;

Форма проведения: физическое интерактивное шоу

Целевая аудитория: учащиеся начальной школы, учащиеся средней школы.

Оборудование: воздушные шары, деревянная линейка, 3-х литровая банка, вода, пластиковые бутылки, одноразовые стаканы, трубочки для коктейля, банка из-под кофе, лампа накаливания, стеклянная палочка, мука, шелковая ткань, нитки, скотч.

ТСО: компьютер, проектор.

Ход мероприятия

1. Звучит музыка (фанфары с отсчетом времени, на экране слайд 1 «Физика вокруг нас»).

Ребята выходят из-за кулис или лаборантской.

2. Слайд 2. (музыка «минус» «Нам песня строить и жить помогает»).

Ребята поют песню.

Проникнуть в тайну тел могут дети,
Лишь только надо законы узнать.
Молекул, атомов много на свете,
Но мы сумеем секрет их разгадать.
Мы смело с физикой в ногу шагаем.
Нам помогают законы ее:
По траектории путь вычисляем,
Тела отсчета узнаем легко.

Ньютон открыл нам закон тяготенья –
Теперь мы «тяжесть» и «вес» различим.
Где польза есть, а где вред в силе тренья,
Легко на практике это применим.
Мы ставим опыт, познать чтоб явленье,
И изучаем наследье всех стран:
Как Торричелли измерил давленье,
Как Архимед дал нам выход в океан.

Формы энергии мы изучили,
Умеем мощность, работу искать,
Мы в песне физики курс повторили,
Чтоб отвечать на «четыре» и на «пять»!

1-й ученик. Вы находитесь в кабинете физики. И я вас понимаю, так хочется познакомиться с физикой поскорее! Ведь вы уже слышали, что эта замечательная наука нужна всем: токарю и водолазу, врачу и шоферу, космонавту и пахарю, ученому и клоуну!

Но оказывается, физика — это не только научные книги и сложные приборы, не только огромные лаборатории. Физика – это еще и фокусы, показанные в кругу друзей, это смешные истории и забавные игрушки-самоделки.

И когда ты начнешь изучать физику в школе, эта чудесная наука уже не покажется тебе такой загадочной и мудрой.

Ты скажешь ей как старой знакомой:

– Здравствуй, физика!

Сегодня ребята из 7 класса покажут вам занимательные опыты по физике, которые вы можете повторить самостоятельно.

1-й ученик и 2-й ученик

Диалог. (3 слайд)

— А вы знаете, что такое инерция? Я слышу ответ: «Нет». На самом деле, вы знакомы с ней очень давно!

— Вы никогда не задумывались, что с инерцией встречаетесь каждый день.

— Вспомни, ты бежишь, а ноги за что-то запнулись. Ноги остановились, а ты сам летишь вперед, пока не упадешь на землю.

Коль мы споткнулись – не беда,
Ведь знаем наперед,
Что будем падать мы всегда
Запомните: вперед!

— А бывает и наоборот! Стоит автобус на месте, а потом резко трогается. Автобус уже поехал, а пассажиры еще сидят неподвижно. От этого все откидываются назад.

Сейчас мы покажем вам два опыта, которые демонстрируют явление инерции.

Опыт 1. (слайд 4, а)

 Если медленно двигать лист, то стакан будет двигаться за листом, если выдернуть лист быстро, то стакан останется стоять на своем месте благодаря инерции, так как движение резкое, оно не успевает передаться и стакан сохранит свое состояние покоя.

— Ребята, кто хочет попробовать провести опыт?

Можно пригласить 3-4 человек. Они по очереди проводят опыт.

Опыт 2. (слайд 4,б)

Поместим картонку на стакан. Положим монетку на картон по центру. Щелкнем по картонке пальцем.

Картонка быстро движется вперед, а монетка падает в стакан. У вас возникает вопрос: «Почему монета не двигается вместе с открыткой?»

Монета и картонка находились без движения благодаря инерции. Инерция – это свойство предмета не менять свое состояние покоя или движения. При резком выбивании картонки из-под монеты время взаимодействия указанных тел мало, поэтому небольшое трение не может сообщить монете скорость в горизонтальном направлении. Когда мы щелкнули по картонке пальцем, она соскользнула под неподвижно лежащей монетой, и монета упала под влиянием силы тяжести в стакан.

Можно пригласить 3-4 человек. Они по очереди проводят опыт.

3-й ученик (слайд 5)

Земля – третья планета от Солнца. Родители и учителя в школе, наверное, рассказывали, что нам очень повезло! Земля – пока единственная планета в солнечной системе, обладающая атмосферой, содержащей кислород, жидкие океаны на поверхности и жизнь. Ребята, а вы знаете, что такое атмосфера? Это воздух, который окружает Землю. Слой воздуха, превышает 100 км. Основная масса атмосферы сосредоточено в нижнем слое высотой около 15 км от поверхности Земли. Воздух удерживается вблизи земной поверхности благодаря притяжению Земли. Если бы Земля не притягивала воздух, то он рассеялся бы в окружающем Землю пространстве. Этот воздух давит на нас и на все, тела находящиеся вокруг нас.

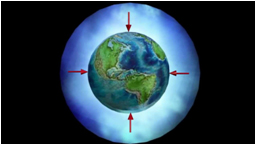
Опыт 3

И сейчас я покажу опыты со стаканом. Как вы считаете, может ли обыкновенный лист бумаги выдержать стакан воды? Я докажу сейчас, что это возможно. Я наливаю воду до половины, кладу сверху листок бумаги. Придерживая бумаге ладонью, опрокидываю стакан. И вот: отнимаю ладонь, а бумажка по-прежнему будет надежно закрывать стакан, и ни одна капля воды не выльется! Вы спросите: «Почему такое возможно?» Это возможно благодаря атмосферному давлению. Именно атмосфера давит на листок снизу и удерживает его. Давление атмосферного воздуха на бумажку больше давления воды на нее изнутри.

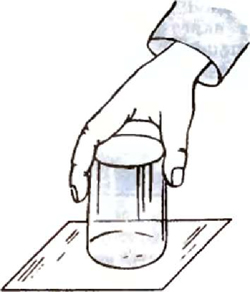
— Кто поможет мне продемонстрировать этот опыт?

Можно пригласить 1-2 учащихся.

Опыт 4 (Диалог 3-го и 4-го ученик)

У меня есть друг, Даня. Я люблю иногда подшутить над ним. Сейчас покажу вам опыт «Напои друга».

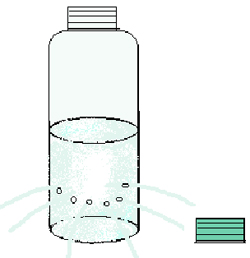
— Эй, Даня, иди сюда. Не хочешь попить?

— Хочу. Сегодня пил только с утра.

Даня отворачивает пробку. Из дырочек начинает вытекать вода.

— Даша, ну, ты опять со своими шуточками!

— Даня, ты же знаешь, что я очень люблю физику.

— А почему вода не вытекает из бутылки, ведь там же дырочки?

— А это всё проделки атмосферного давления. Это происходит потому, что на дырочки снаружи действует атмосферное давление. И оно больше, чем давление столба воды в бутылке. Когда мы откручиваем пробку, то на дырочки и внутри бутылки кроме жидкости действует атмосферное давление.

(Слайд 6 «Проявление действия атмосферного давления»)

Оно нам помогает пить, набирать лекарство в шприц, ставить банки, когда мы простудились. Оно помогает держать мыльницу с помощью присоски.

— А у тебя ещё есть опыты с атмосферным давлением?

— Нет. Но у Ани в запасе найдется ещё один.

— Аня, иди к нам.

Кто хочет попробовать «попить» из такой бутылочки?

Опыт 5. 5-й ученик (Слайд 6)

Я продемонстрирую вам еще один опыт. Как вы думаете, ребята, может ли вот такой шарик пролезть в банку?

Как это сделать?

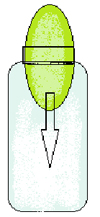
Для этого нам понадобятся чайник с кипятком, трехлитровая банка, воздушный шарик, наполненный водой так, чтобы он немного перекрывал горлышко банки.

Необходимо обдать банку кипятком.

ВНИМАНИЕ! Ребята, когда вы будете повторять этот опыт дома, обратитесь за помощью к старшим. Вы можете обжечься. Поэтому лучше, если вам помогут родители.

После того, как вы нагрели банку, её нужно закрыть воздушным шариком, заполненным водой. Что будет происходить? Воздух в банке нагревается и расширяется, часть его выходит из банки. В этот момент мы закрываем горло шариком. Затем воздух в банке охлаждается. Давление там падает. Возникает разница в давлениях снаружи и внутри банки. Под действием атмосферного давления шарик втягивается в банку.

Переключается на слайд 7 с Гермионой. Звучит музыка из фильма о Гарри Поттере.

Выходит Девочка, облаченная в мантию.

6-й ученик. Где живее электричество? Вы, конечно, знаете, где оно живет: в проводах, подвешенных на высоких мачтах, в комнатной электропроводке и ещё в батарейке от карманного фонаря. Но все это электричество домашнее, ручное. Человек его изловил и заставил работать. Оно накаляет электроплитку и утюг. Сияет в лампочке. Гудит в электродвигателях. Да мало ли что ещё может делать электричество!

Ну а есть ли на свете электричество дикое, неприрученное? – спросите вы. Да есть. Оно вспыхивает ослепительным зигзагом в грозовых тучах. Оно светится на мачтах кораблей в душные тропические ночи. Но оно есть не только в облаках и не только под тропиками. Тихое, незаметное, оно живет всюду. Ты часто держишь его в руках и сам не знаешь об этом. Но его можно обнаружить.

Опыт 6.

Вы читали про Гарри Поттера? Вы помните, с помощью чего он делал свои чудеса? Конечно, вы догадались. С помощью волшебной палочки. И у нас в кабинете физики такая имеется. Для опыта нам понадобится стеклянная палочка, лист бумаги или полиэтиленовый пакет, метровая деревянная линейка, бутылка.

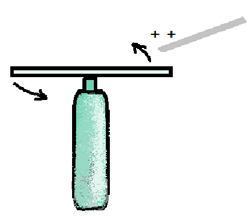
Я заставлю линейку вращаться, не прикасаясь к ней!

Как у меня это получилось? Ответ прост. Это опять электричество! Палочка наэлектризовалась, и к ней притянется абсолютно любое нейтральное тело. Скажу вам по секрету: «Замените палочку пластмассовой расческой, а метровую линейку – обыкновенной, и такой же опыт вы можете показать своим родителям и друзьям дома».

Кто хочет попробовать?

Можно пригласить 3-4 человек. Они по очереди проводят опыт.

Опыт 7

Натрем шарик пакетом и «повесим» на стену. Вы видите, шарик спокойно висит на стене. Наэлектризованный шарик будет долго висеть в таком положении. Притяжение шарика к стене вызвано электричеством.

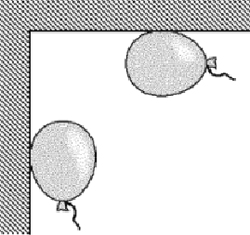
Кто пожертвует ради науки своими прическами? Приглашаются ребята. Натирают о волосы воздушные шарики и «подвешивают» их на стенку.

Если потереть два предмета, сделанные из разных материалов, то они наэлектризуются. Возьмем второй шарик, так же наэлектризуем его. Поднесем его к муке. Мука облепит шарик и он окажется покрытый инеем.

Можно пригласить 3-4 человек. Они по очереди проводят опыт.

Опыт 8. Опыт с лампочкой (Слайд 8)

5-й ученик. Может ли обычная стеклянная лампочка выдержать вес взрослого человека? Да, это возможно.

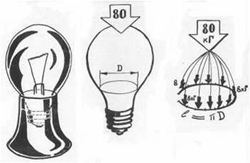
Лампочка вставлена в стеклянную банку из-под кофе. Теперь она может выдержать не только ваш вес, ребята, но и вес взрослого человека, если на нее аккуратно встать ногой.

В этом случае вес человека распределяется по длине окружности в месте соприкосновения лампы с горлышком банки. На единицу длины окружности приходится небольшая сила.

Эксперимент показывает, что обычная лампочка может выдержать вес до 120 кг. Однако, если на обуви окажется небольшая песчинка, то лампочка разрушается при малейшей нагрузке.

— Давайте попробуем постоять на лампочке. Кто станет сейчас юным экспериментатором? Приглашаются несколько учащихся.

1-й ученик Опыт 9. (Слайд 9)

Ребята, а я продемонстрирую опыт с воздушными шарами.

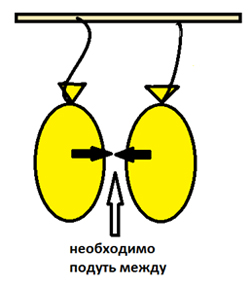
Если мы подуем между шарами, то на первый взгляд шары должны отлететь друг от друга. Но такого не происходит. Наоборот, шары притянутся друг к другу. Это происходит из-за того, что давление в струе меньше, чем атмосферное.

Кто умеет хорошо дуть? Приглашаются несколько учащихся.

5-й ученик (Слайд 10). Трудно придумать игрушку проще воздушного шарика. Еще труднее найти нехитрой резиновой оболочке какое-нибудь практическое применение. Надутый шарик можно использовать в различных летающих моделях. Энергия сжатого воздуха, который выходит из шарика, создает реактивную силу. Равная ей сила противодействия толкает резиновую оболочку вперед. Из этого нетрудно сделать вывод: воздушный шарик — это простейший реактивный двигатель.

По принципу реактивного движения передвигаются некоторые представители животного мира, например кальмары и осьминоги. Периодически выбрасывая вбираемую в себя воду, они способны развивать скорость 60-70 км/ч.

(Слайд 11) Основоположником теории космических полетов является выдающийся русский Ученый Константин Эдуардович Циолковский. Он разработал теорию реактивного движения. Благодаря ему сейчас космонавты летают на многоступенчатых ракетах.

Сегодня 12 апреля – День Космонавтики. И это выступление мы посвящаем тем замечательным людям, благодаря которым полеты в космос стали не мечтой, а реальностью!

Сегодня мы запустим свою ракету. Для этого нам необходим шарик, трубочка для коктейля, липкая лента и шелковая нить.

Давайте превратим шарик в модель простейшей ракеты.

(Слайд 12) Опыт 10. Запуск ракеты

3. Завершение вечера

3-й ученик. Сегодня мы подготовили для вас занимательные опыты, которые вы можете повторить дома. Для их проведения не потребуется дорогостоящего оборудования. Все необходимое вы сможете найти у себя дома. Проведя опыты, вы совершите увлекательное путешествие в мир науки – физики. Может быть, это станет первым шагом по дороге научного познания. Давайте скажем большое спасибо ребятам, учащимся 7 класса, которые подготовили для вас это маленькое шоу.

rosuchebnik.ru

«Азы физики». Главы из книги

Предисловие

0.1 Для кого написана эта книга *

Эта книга посвящена основам («азам») физики — науки о природе (по-гречески фиcис (φυσις) — природа). В XXI веке основой физики является так называемая стандартная модель элементарных частиц, из которых по законам теории относительности и квантовой теории построено всё сущее.

К сожалению, существующие введения в эти науки из-за их математической сложности недоступны не только школьникам, но и большинству преподавателей физики.

Эта маленькая книжечка — попытка максимально просто и кратко изложить основы теории относительности (с её главной константой c) и квантовой механики (с её главной константой ħ). Я отчётливо понимаю, что не могу написать её так, чтобы она была понятна человеку, не знающему физики. Поэтому книжка адресована прежде всего профессиональным физикам (особенно молодым) в надежде на то, что кто-то из них использует изложенные в ней идеи при написании простых курсов современной физики и научно-популярных книг и статей.

В отличие от научно-популярных книг, эта книга широко использует математические формулы. Но в отличие от формул в университетских учебниках, формулы, отобранные для этой книги, настолько просты, что для их понимания достаточно знания элементарной математики в объёме средней школы. Поэтому я уверен, что многие страницы книги будут понятны даже подросткам^{(соответствующие разделы помечены знаком *) и помогут тем из них, кто интересуется физикой, постепенно расширять свой научный кругозор. Для этого книга снабжена подробным указателем. Разумеется, из-за своего маленького формата путеводитель не может заменить учебника.}

При очень больших скоростях поступательного движения, близких к скорости света c, и очень малых величинах, характеризующих вращательное и колебательное движение, близких к кванту Планка ħ, элементарные частицы материи обладают совершенно необычными свойствами. Но именно необычность их свойств делает окружающий нас мир таким, каков он есть.

Одно из самых лучших научных описаний мира, основанных на теории относительности и квантовой механике, содержится в фундаментальных монографиях Вайнберга [1], [2], [3]. Чтобы рассказать о самом существенном в этих науках, мне пришлось отбирать не только самые простые формулы, но и отказаться от упоминания многих сложных понятий, разъяснению которых посвящены эти и многие другие курсы современной физики.

0.2 О содержании отдельных глав

В теории относительности фундаментальным является соотношение между энергией E, импульсом p и массой m свободной частицы. Как подробно разъясняется в главе 4, это соотношение позволяет с единой точки зрения понимать как свойства безмассовых частиц света — фотонов, так и свойства массивных частиц (масса которых отлична от нуля), например, электронов. Согласно квантовой механике, все частицы одного сорта, например, все электроны во вселенной, абсолютно тождественны.

Соответсвенно должны быть одинаковы их массы.

К сожалению, широко распространённое в научно-популярной литературе уравнение E = mc², интерпретируемое как зависимость массы частицы m от её скорости v, даёт ложное представление о том, что такое масса.

Закрепляется это ложное представление тем, что массу называют массой покоя и обозначают m₀, что разрывает связь между теорией относительности и механикой Ньютона, являющейся предельным случаем теории относительности при малых скоростях.

Фундаментальную роль в устройстве природы играет спин (т. е. собственный угловой момент) частицы. Как объясняется в главе 5, величину спина обычно выражают в единицах ħ. Частицы, спин которых равен целому числу ħ, называются бозонами. Частицы, спин которых равен полуцелому числу ħ, называются фермионами. Поведение частиц в системе, состоящей из двух или большего числа фермионов радикально не похоже на поведение частиц в системе, состоящей из двух или большего числа бозонов.

Как рассказано в главе 9, свойства атомов в Периодической системе элементов определяются тем, что спин электрона равен ½ħ.

Спин фотона равен 1ħ. Электроны взаимодействуют друг с другом и с другими электрически заряженными частицами, обмениваясь фотонами. (Теория взаимодействия фотонов с электронами называется квантовой электродинамикой (КЭД). КЭД является наиболее совершенной теорией, проверенной на опыте с точностью до десяти значащих цифр.) Аналогично, обмен гравитонами — безмассовыми частицами со спином 2ħ — объясняет гравитацию.

В отличие от изложения большинства учебников по квантовой механике, в основу нашего изложения положено не сравнительно сложное понятие волновой функции физической системы (например, атома), а гораздо более простое понятие элементарного квантового состояния этой системы (например, уровня атома), которое характеризуется значениями нескольких квантовых чисел. Смотрите главу 5.

Как показано в главе 6, это позволяет ввести амплитуду перехода между двумя квантовыми состояниями.

Квадрат модуля амплитуды определяет вероятность перехода (распада возбуждённого состояния атома с испусканием фотона) для ансамбля одинаковых состояний.

При этом распад конкретного атома — процесс абсолютно случайный, и момент времени, когда произойдёт этот распад, в принципе предсказан быть не может. Такой подход устраняет многие трудности интерпретации квантовой механики, связанные с проблемой измерения (редукции волновой функции).

С другой стороны, он даёт возможность выделить те квантовые аспекты, которые не связаны с процедурой измерения, и тем самым выйти за рамки представлений о квантовой механике как о науке, только связывающей результаты измерений.

Ещё одно отличие этой книги заключается в том, что в ней обычное гравитационное взаимодействие рассматривается как квантовый процесс обмена гравитонами.

Константа Ньютона G_N вместе с константами ħ и c определяет так называемую массу Планка m_P = (ħc/G_N)^1/2 ≈ 2,2·10^–5 грамм. Теория, описывающая гравитационное взаимодействие при энергиях порядка m_Pc², пока не построена, но при всех доступных опыту энергиях правильность описания гравитации как обмена гравитонами подтверждается опытом. Смотрите главу 16.

0.3 Два маяка *

Я пишу эту книгу в надежде, что даже частичное знакомство с ней будет полезно молодым людям и поможет им найти своё место в этом быстро меняющемся и во многом очень непонятном мире. Моя основная мысль заключается в том, что истина существует и к ней можно подойти гораздо ближе, чем это кажется многим. В физике есть несколько незыблемых и простых истин, доступных всем думающим людям. Эти истины добыты человечеством при изучении природы в основном в течение последних ста лет.

На первый взгляд, наука так разрослась, разветвилась и специализировалась, что усвоить её основы неспециалисту , стремящемуся понять, как устроен мир, невозможно.

Стремительное развитие интернета обрушивает на нас небывалые потоки информации и дезинформации. Разобраться в них нельзя, если не усвоить физический смысл констант c и ħ. Эти две мировые константы, как две путеводные звезды, помогут Вам найти свой путь к пониманию природы. Выбор именно этих самых фундаментальных констант природы в качестве научных маяков позволит Вам постепенно находить единомышленников и устанавливать критерии истины в конкретных ситуациях.

Ньютон сравнивал себя с мальчиком, стоящим на берегу океана непознанного. С тех пор физика неизмеримо выросла, и область познанного стала огромной. Некоторые современные учёные считают, что область непознанного стала меньше области познанного. Не знаю, так ли это, но считаю очень важным отделить то, что твёрдо установлено, от того, что лишь кажется правдоподобным.

Необходимо отделять хорошо установленные и понятые явления и свойства (такие, например, как свойства атомов и их ядер или основные свойства Солнечной системы) от гораздо более сложных вопросов (таких, как возникновение Вселенной или поведение гравитационного взаимодействия на планковской шкале, где оно сильнее всех других взаимодействий). Такие теории как механика Ньютона, электродинамика Максвелла, квантовая механика, теория относительности, будут справедливыми всегда. Здесь возможны лишь такие прояснения, которые не меняют основных математических соотношений между физическими величинами, но уточняют область применимости этих соотношений и обосновывают выбор входящих в них величин. В отличие от этого, слишком далёкие теоретические экстраполяции могут не подтвердиться дальнейшими измерениями.

Глава 1. Основы основ

1.1 Об интуиции *

Цель этой книги — на ста с чем-то страницах объяснить, каким образом современная физика элементарных частиц позволяет понять, как устроен окружающий нас мир. В основе всего мироздания лежат две мировые константы: максимальная скорость прямолинейного и равномерного перемещения c и минимальный квант вращательного и колебательного движения ħ. Слова «прямолинейное равномерное» наводят на мысль о неограниченном, бесконечном движении в пространстве и о линейности времени (философия Запада). Вращение говорит нам о цикличности времени и ограниченности, финитности движения (философия Востока).

Я буду говорить не о философии, а о том, как физики количественно описывают свои наблюдения и опыты, опираясь на интуицию. Основная трудность современной физики заключается в том, что понятия максимальной скорости и минимального кванта для тех, кто не занимается фундаментальной физикой, крайне антиинтуитивны.

1.2 Пространство и время *

Наше пространство трёхмерно: любой наблюдатель может представить себе систему координат — три взаимно ортогональных оси: сзади-вперёд (x), слева-направо (y), снизу-вверх (z).Себя наблюдатель обычно помещает в начало координат.

Пусть наблюдатель следит за движущейся частицей.

Положение частицы в момент времени t он характеризует радиус-вектором r с его тремя координатами: x; y; z.

Систему координат плюс время t называют системой отсчёта. Все точки в пространстве и времени равноправны: пространство и время однородны. Кроме того, пространство изотропно: тройку осей можно ориентировать произвольным образом. При этом модуль радиус-вектора не меняется: r ≡ |r| = const.

1.3 Материя и вещество *

Любое изменение в движении или поведении частицы — это акт проявления элементарных (т. е. самых маленьких и неделимых) частиц материи. Мы начнём с трёх элементарных частиц материи: фотона γ, электрона e и протона p. Выясним сначала, как в результате их взаимодействия появляется простейший атом водорода. Затем рассмотрим другие атомы и, постепенно углубляясь, познакомимся с остальными элементарными частицами.

До сих пор в литературе нет единой точки зрения на то, что называть веществом, а что материей. Многие авторы называют материальными частицами только те частицы, у которых есть масса. Достаточно вспомнить термин «материальная точка» который широко используется многими авторами (см. например книгу Вайнберга [1]), когда речь идёт о «массивных точках» — телах, размерами которых в той или иной задаче можно пренебречь.

Фотоны для этих авторов — это частицы не материи, а радиации. Вопрос о том, что как называть, постепенно решится. Пока же я буду называть все частицы, включая фотоны, частицами материи. А веществом буду называть атомы и всё, что построено из них.

1.4 Движение *

Движение — это перемещение частицы в пространстве.

Если движение поступательное (т. е. равномерное и прямолинейное), то скорость v перемещения определяется формулой v = r/t, где r — пройденный путь, а t — время, затраченное на него. Определение скорости в случае произвольного движения будет дано немного позднее.

Глава 2. Единицы

2.1 Стандарты *

Всякое измерение есть сравнение того, что измеряют, с известным стандартом. Те общепринятые стандарты, с которыми происходит сравнение, называют единицами.

2.2 Окружность и углы *

Углы измеряют в градусах (минутах и секундах) или в радианах. Угловой градус (1°) – это угол, под которым из центра окружности видна дуга, равная длине окружности, делённой на 360 частей. Угловая минута: 1′ = 1°/60.

Угловая секунда: 1» = 1’/60. Как известно, отношение длины окружности к её радиусу равно 2π , где π ≈ 3,14.

Один радиан =360°/2π ≈ 57° — это угол, отвечающий дуге, длина которой равна радиусу.

2.3 Единицы времени и длины *

Измерение времени производится сравнением с известными периодическими процессами. Исторически единицы времени связаны с суточным вращением Земли. Одни сутки = 24 часа. Один час = 60 минут. Одна минута = 60 секунд. Хотя в одном часе, как и в одном угловом градусе, содержится 60 минут и 3600 секунд, но на этом сходство между угловыми и временными единицами заканчивается.

Измерение расстояния производится сравнением с известным эталоном длины. За единицу длины обычно принимают один метр.

Глава 3. Минимум математики

3.1 Царица, служанка и барьер *

Говорят, что математика является царицей и служанкой всех естественных наук. Она же является и мощным барьером при знакомстве с этими науками. Именно поэтому в научно-популярных книгах и статьях принято не пользоваться математическими обозначениями. Мне кажется, что объяснить современную физику без математики невозможно. Я постараюсь обойтись минимумом математических знаний. Но этот минимум необходим.

3.2 Четыре действия школьной математики и мнимая единица *

Для понимания законов природы нам понадобятся два типа арифметических действий: 1) сложение/вычитание, 2) умножение/деление, и два типа алгебраических действий: 3) возведение в степень, и 4) логарифмирование. Послед нее нам понадобится не скоро. Также необходимым будет понятие мнимой единицы i = √(–1) и комплексного числа.

3.3 Степени десяти *

При изучении природы мы постоянно сталкиваемся с очень большими или очень маленькими числами, которые удобно изображать с помощью степеней десяти. Так, скорость света равна 3·10⁵ км/с = 3·10⁸ м/с, а размер атома порядка 10^–10 м. В отличие от авторов научно-популярных книг, я не буду использовать выражения типа «тысячные миллионные доли», а буду писать 10^–9.

3.4 Префиксы степеней десяти

Многие физические термины включают в себя следующие префиксы:

Русская приставка	Десятичный множитель	Международное обозначение	Русская приставка	Десятичный множитель	Международное обозначение
Дека	101	da	Деци	10–1	d
Гекто	102	h	Санти	10–2	c
Кило	103	k	Милли	10–3	m
Мега	106	M	Микро	10–6	μ
Гига	109	G	Нано	10–9	n
Тера	1012	T	Пико	10–12	p
Пета	1015	P	Фемто	10–15	f
Экза	1018	E	Атто	10–18	a
Зетта	1021	Z	Зепто	10–21	z
Йотта	1024	Y	Йокто	10–24	y

3.5 Дифференцирование и интегрирование

При произвольном движении скорость движения определяется как производная от расстояния по времени: v = dr/dt: Величина dt означает достаточно маленькую («бесконечно малую») разность между двумя очень близкими моментами времени. Аналогичный смысл имеет dr — это разность между двумя близкими точками в пространстве. При этом бесконечно малое расстояние между двумя точками в пространстве делится на бесконечно малый промежуток времени, давая в результате конечную скорость движения. Эта операция называется дифференцированием. Интегрирование является операцией, обратной дифференцированию: r = ∫vdt. Пока эти операции нам не понадобятся. Читателю, как знакомому с понятиями дифференцирования и интегрирования, так и не знакомому с ними, очень полезно время от времени заглядывать в замечательную книгу Якова Борисовича Зельдовича [4].

3.6 Матрицы

Ещё при изучении квантовой механики нам придётся познакомиться с матрицами. Особо важную роль играют матрицы Паули и матрицы Дирака.

Глава 27. Заключительные замечания

27.1 «Солнце всходит и заходит» *

Недавние опросы населения в России и США обнаружили, что многие люди в обеих странах считают, что не только Луна, но и Солнце вращаются вокруг Земли. То, что Солнце всходит и заходит (вращается вокруг нас) это не ошибка, это поверхностная правда, которая во многом справедлива и для многих людей достаточна. Для человека, никогда не совершавшего далёких путешествий, во многом достаточно представление, что Земля плоская. Тот, кто совершил межконтинентальный перелёт, мог убедиться, что Земля — шар, но по-прежнему может считать, что Солнце является её спутником. Но есть и более глубокая правда: Земля — шар, Луна — меньший шар, который вращается вокруг Земли, и вместе они вращаются вокруг Солнца.

В повседневной жизни можно обходиться поверхностными правдами. Но это совершенно недопустимо при преподавании современной астрономии и физики. Когда профессор убеждает своих студентов, что в Большом Адронном Коллайдере масса протона возрастает в тысячи раз, он не проповедует поверхностную правду о каждодневной жизни, а закладывает ложные понятия, основанные на пресловутой формуле E = mc², в представления своих студентов об основах теории относительности (см. книгу [25] и статью [26]).

27.2 О преподавании физики *

Современная техника, квантовая и релятивистская, наглядно демонстрирует, что в основе своей квантовой и релятивистской является сама природа. Это — основной урок ХХ века. Всё большее число людей сознаёт, что мы живём в эпоху квантовой и релятивистской цивилизации. Поэтому простой взгляд на мир, не противоречащий современной физике, должен быть доступен максимальному числу людей с самого раннего возраста, даже тем , кто никогда не станет физиком. Только так можно будет избежать глобальной катастрофы.

27.3 О трагической судьбе SSC *

В последние десятилетия ХХ века стало ясно, что основной нерешённой задачей физики высоких энергий является исследование хиггсовского сектора Стандартной модели. В регулярно публикуемом «Обзоре свойств частиц» в 1990 году можно было прочесть на стр III.12 о планах физического пуска трёх протон-протонных коллайдеров: 1) Ускорительно-накопительного комплекса UNK (3 ТэВ, 1995?), 2) Большого адронного коллайдера LHC (8 ТэВ, 1996?), 3) Сверхпроводящего суперколлайдера SSC (20 ТэВ, 1999), которым предстояло решить эту задачу. У двух первых из них даты пуска сопровождались вопросительными знаками. У третьего — Сверхпроводящего суперколлайдера SSC, который должен был иметь самую высокую энергию — 20 ТэВ в каждом пучке, вопросительного знака не было. Строительство тоннеля для этого коллайдера — кольца диаметром 87 км — шло полным ходом у городка Ваксахачи вблизи Далласа. Если бы этот проект был осуществлён, Стандартная модель элементарных частиц, возможно, перестала бы быть моделью, а стала бы законченной теорией. А может быть, что ещё интересней, было бы обнаружено существование «новой физики», не укладывающейся в рамки стандартной модели. Но в 1993 году конгресс США при обсуждении бюджета на 1994 год отправил на дно этот строившийся флагман физики высоких энергий, что нанесло сильнейший удар по развитию физики элементарных частиц (см. письмо Клинтона [22], так и не получившее статуса пресс-релиза Белого дома). В автобиографии Клинтона [23] обсуждение бюджета описано, но SSC не упоминается. Зато в 2011 году он посвятил заключительную часть своей лекции в Давосе SSC (LHC) (см. [24]).

За пару лет до закрытия SSC в России были прерваны работы по строительству Ускорительно-накопительного комплекса УНК, в котором должны были сталкиваться протонные пучки с энергией 3 ТэВ. Из Тэвных машин долгие годы (1985–2011) успешно работал лишь Тэватрон в США. В нём сталкивались пучки протонов и антипротонов с энергией 1 ТэВ.

27.4 LHC и перспективы *

Как сказано выше (в главе об электрослабой модели), сейчас поиски хиггсов ведутся на Большом адронном коллайдере LHC. Пока обнаружить хиггсы не удалось.

Возможно, что в ближайшем будущем их удастся найти на LHC. Это конечно будет триумфом электрослабой модели. Но в известном смысле гораздо интереснее будет, если на LHC будет доказано, что хиггсов с массами легче 1 ТэВ не существует. Это означало бы, что W- и Z-бозоны при энергиях существенно выше, чем 1 ТэВ, взаимодействуют по-настоящему сильно, и описать их поведение в рамках теории возмущений нельзя. Для экспериментального исследования таких взаимодействий понадобился бы коллайдер масштаба SSC или ещё большей энергии. В существующей электрослабой модели, основанной на теории возмущений, существует около двух дюжин параметров, численные значения которых мы объяснить (т. е. вычислить) не можем. Возможно это удастся сделать, если выйти за рамки теории возмущений.

27.5 О сути и истине в науке *

Мне кажется, что большинство людей не понимает сути современной науки не потому, что эта суть непостижима.

Конечно понять хоть что-нибудь до конца нельзя. Но иметь правильное представление о природе можно и нужно. Если отобрать в современной физике главные идеи, то можно объяснить ученику, как устроен окружающий его мир.

К сожалению, профессорам трудно договориться между собой о том, какие идеи в физике являются главными.

Меня поражает неспособность многих профессиональных физиков признать, что в специальной теории относительности масса не зависит от скорости, и терпимость тех из них, кто не сомневается в том, масса не зависит от скорости, к тому, чтобы их детей и внуков продолжали учить, что масса зависит от скорости.

Ещё больше меня поражает почти всеобщее восприятие квантовой механики как науки, сквозь призму которой наш мир выглядит призрачно зыбким. А ведь именно благодаря квантовой механике он так прочно устроен.

Мне кажется предвзятым отношение многих физиков к вопросу о гравитации и гравитонах. Сегодня очень модно (см. Например [27], [28]) объяснять всё — от свойств элементарных частиц до фазовых переходов — с помощью чёрных дыр и суперструн. Возможно, что со временем такая Теория Всего (TOE — Theory of Everything) и будет создана, но пока в ней ещё слишком много недоделанного [29] и не существует экспериментальных данных, подтверждающих справедливость ТОЕ. Так что не с изучения этой недостроенной теории должен начинать своё знакомство с физикой школьник.

А вот начинать его с твёрдо установленных основных констант природы — скорости c и кванта ħ — не только можно, но и нужно. Именно законы, содержащие эти константы, объясняют основные явления природы.

Очень важно понимание того, что истина существует, даже если нам не дано постичь окончательную истину. Что задача науки — стремиться к истине, всё более приближаясь к ней.

elementy.ru

Глава 2. Постигаем основы физики – FIZI4KA

В этой главе …

• Концепции физики и почему они так важны
• Учимся измерять (и решать уравнения)
• Оцениваем значимость и ошибку величин
• Освежаем свои знания алгебры и тригонометрии

Представьте себе, что вы бьетесь над решением почти неразрешимой физической задачи и пытаетесь найти подход к ней. Задача очень сложна и многим так и не поддалась. Внезапно в результате озарения все становится предельно ясным.

“Ну конечно, — говорите вы, — это же элементарно! Мяч в максимальной точке поднимется на высоту 9,8 м”.

Глядя на правильное решение задачи, преподаватель одобрительно кивнет головой, а вы, окрыленные успехом, с удвоенной силой приметесь за решение следующей задачи.

В физике, как и в любой другой области деятельности, заслуженный успех и слава достаются только в результате упорного труда. Не бойтесь работы, ведь цель оправдывает средства. По окончании чтения этого курса вы настолько овладеете предметом, что сможете решать те задачи, которые прежде казались вам просто неразрешимыми.

Эта глава начинается с описания некоторых базовых сведений и навыков, которые потребуются для освоения следующих глав. В ней описываются способы научных измерений, научные обозначения, базовые сведения по алгебре и тригонометрии, а также правила оценки значимости величин и точности полученных результатов. Полагаясь на эти твердые и незыблемые сведения, вы сможете овладеть всем другим материалом в этом курсе.

Не бойтесь, это всего лишь физика

Многих от слова “физика” бросает в дрожь. Легко прийти в ужас, если представить себе физику, как нечто совершенно чуждое с высосанными из пальца абстрактными числами и правилами. Однако истина заключается в том, что физика призвана помочь нам понять реальный мир. Погружение в физику — это увлекательное путешествие, которое совершает человечество в попытке понять устройство мира.

Хотя может показаться справедливым и обратное утверждение, но нет никакой загадки в целях и методах физики: физика просто моделирует мир. Идея заключается в том, чтобы создать мысленные модели, описывающие поведение мира: как бруски скользят по наклонной плоскости, как образуются и светят звезды, как черные дыры захватывают свет, что происходит при столкновении автомобилей и т.п. В момент создания модели она совсем не содержит чисел, а только описывает самую суть явления. Например, звезда образуется из этого слоя, потом из того слоя, дальше возникает реакция, за ней другая и — бац, вот вам новая звезда!

По мере совершенствования модели ее описание становится количественным, и именно с этого момента изучения физики у учеников и студентов возникает большинство проблем. С изучением физики было бы меньше проблем, если бы можно было просто сказать: “Тележка, скатываясь по наклонной плоскости, движется все быстрее и быстрее”. Но для полного физического описания этого явления недостаточно сказать, что тележка движется быстрее, нужно сказать, насколько именно быстрее движется тележка.

Суть физики заключается в следующем: сделать наблюдение, создать модель для имитации явления, добавить математическое описание и — все! В таком случае вы сможете предсказывать развитие событий в реальном мире. Математика нужна, чтобы занять более уверенную позицию в реальном физическом мире и чтобы помочь в исследовании принципов и причин такого явления.

Учитесь у гения: не отгораживайтесь математикой от физики

Ричард Фейнман, лауреат Нобелевской премии по физике 1965 года “За фундаментальные работы по квантовой электродинамике, имевшие глубокие последствия для физики элементарных частиц*, в 1950-1960 годах заработал уникальную репутацию среди физиков. Свой метод исследования он объяснял так: нужно мысленно “на пальцах” описать задачу с указанием аналогии из реальной жизни, тогда как другие стремились сразу перейти к математическому описанию. Когда ему встречалась очень длинная теория с подозрительным результатом, он стремился найти какое-то физическое явление, которое можно было бы объяснить этой теорией. Если в своих размышлениях он достигал точки, в которой ему становилось очевидно несоответствие предлагаемой теории и факта реального мира, он сразу же заявлял: “Это не верно, проблема в том-то и том-то”. Он всегда оказывался прав, что озадачивало многих его коллег и буквально лишало их дара речи. Многие современники считали и считают его настоящим гением. Хотели бы стать супергением? Поступайте так же: не дайте математике запугать вас и скрыть от вас физику.

Всегда имейте в виду, что реальный мир находится на первом месте, а математика — на втором. Для успешного решения физической задачи важно не утонуть в математических выкладках и сохранить глобальное видение явления, чтобы удержать контроль над ситуацией. После обучения физике студентов колледжа в течение многих лет я столкнулся с одной из самых крупных проблем в изучении физики: студенты часто напрочь запуганы математикой.

А теперь зададимся одним из наиболее важных вопросов: для чего вам нужна физика? Если вы хотите продолжить свою карьеру в физике или смежной области, то ответ прост: вам нужно знать физику для “ежедневного применения”. Но даже если вы не планируете карьеру физика, вы все еще можете извлечь достаточно много пользы от овладения этим предметом. Многие сведения из вводного курса физики можно применять на практике. Но еще более важным преимуществом овладения физикой является не ее применение на практике, а приобретенные навыки решения задач. Решение физических задач учит вас настойчивости, умению учитывать все варианты решения и выбирать наиболее оптимальный, а также поиску простейшего метода решения.

Измеряем окружающий мир и делаем предсказания

Физики прекрасно умеют измерять и предсказывать явления реального мира. В конце концов, именно потому физика оказалась такой жизнеспособной. Измерение является начальной точкой, на основе которой создается модель явления и делаются предсказания. Множество мер предусмотрено для измерения длины, веса, времени и т.д. Овладение искусством измерения величин является залогом успешного изучения физики.

Для достижения согласия в измерениях физики и математики сгруппировали меры в системы единиц измерения. Наиболее распространенными являются система СГС (сантиметр-грамм-секунда) и СИ (система интернациональная). Например, в табл. 2.1 показаны основные единицы измерения в системе СГС. (Пока не стоит напрягаться и запоминать эти единицы, поскольку мы вернемся к ним позже.)

В табл. 2.2 перечислены основные единицы измерения в системе СИ и их сокращения.

Никогда не смешивайте единицы из разных систем

Поскольку в разных системах используются разные единицы длины, то в зависимости от используемой системы можно получать разные численные значения. Например, для измерения глубины плавательного бассейна можно использовать систему СИ, с помощью которой ответ будет выражен в метрах; в системе СГС она будет представлена в сантиметрах, а в еще менее популярной системе — в дюймах.

Предположим, однако, что вам нужно узнать давление воды на дне бассейна. Измеряем глубину бассейна и подставляем найденное значение в формулу давления (см. главы 14 и 15). Однако в этом месте нужно обратить пристальное внимание на используемую систему единиц измерения.

Всегда помните, что в процессе решения задачи нужно использовать одну и ту же систему единиц измерения. Если вы начали решать задачу с помощью системы СИ, то придерживайтесь ее до конца. Иначе вместо правильного ответа вы получите бессмысленную смесь разных величин, поскольку в таком случае вы фактически приравниваете величины, измеренные с помощью разных мерок. Эта ситуация подобна ошибке кулинара, когда, читая рецепт, вместо двух ложек муки он использует два стакана.

В течение многих лет мне приходилось видеть, как студенты ошибочно смешивали величины, полученные с помощью разных систем измерения, и не могли понять причину неправильного решения. Конечно, их намерения были совершенно благородны, идеи прекрасны, выводы уравнений безупречны, а численные значения в ответах получались неверными. Например, в ответе для величины ускорения приведено значение 15, а студент получил 1500. Оказывается, в ответе используется система СИ и ответ дан в метрах на секунду в квадрате, а студент решал задачу с помощью системы СГС и получил правильный ответ, но выраженный в сантиметрах на секунду в квадрате. Численный ответ получился другим именно из-за использования другой системы единиц измерения.

От метров к дюймам и обратно: преобразуем значения из разных единиц измерения

Физики используют разные системы измерения для записи измеренных значений. Но как преобразовать эти значения при переходе от одной системы к другой? При решении физических задач часто приходится иметь дело с величинами, выраженными в разных системах: одни величины могут быть измерены в метрах, другие — в сантиметрах, а третьи — даже в дюймах. Не пугайтесь. Нужно просто научиться их преобразовывать из одной системы в другую. Как проще всего это сделать? Используйте коэффициенты преобразования! Рассмотрим следующую задачу.

Допустим, что за 3 дня вы преодолели расстояние 4680 миль. Впечатляет. Подсчитаем среднюю скорость движения. Как показано в главе 3, в физике скорость определяется так же, как и в жизни: нужно пройденное расстояние поделить на время. Итак, с помощью приведенной ниже формулы получим конечный результат:

Полученный ответ выражен в нестандартных единицах измерения. Обычно для скорости используют другие единицы, например мили в час (в США), а потому нам придется преобразовать полученный ответ в более понятные единицы.

Для преобразования величин из одной системы единиц измерения в другую нужно использовать коэффициенты преобразования. Коэффициент преобразования — это значение, после умножения на которое все нежелательные единицы измерения устраняются, а остаются только нужные.

В предыдущем примере результат получен в милях в день и записан как миль/день. Для вычисления количества миль в час нужно использовать коэффициент преобразования, который позволит исключить дни и оставить часы, т.е. нужно умножить на величину “количество дней в час” (дней/час) и таким образом избавиться от дней:

Коэффициентом преобразования в данном случае является количество дней в час. После подстановки всех значений, упрощения полученного выражения и умножения на коэффициент преобразования получим следующее выражение:

Слова “секунда” (или “метр”) можно рассматривать как некие переменные \( x \)или ​\( y \)​, которые исключают друг друга из соотношения, если встречаются одновременно в числителе и знаменателе.

Если числа затуманивают голову, взгляните на единицы измерения

Хотите узнать об одной хитрости, которую применяют учителя при решении задач по физике? Внимательно следите за единицами измерения! Мне приходилось тысячи раз решать задачи “лицом к лицу” со студентами, и я убедился в том, что преподаватели всегда пользуются этим трюком.

Допустим, что нужно определить скорость по заданному расстоянию и времени. Эта задача решается практически мгновенно, потому что всем известно, что расстояние (например, выраженное в метрах), деленное на время (например, выраженное в секундах), дает скорость (выраженную в метрах в секунду).

Однако в более сложных задачах может быть гораздо больше величин, например масса, расстояние, время и т.д. В таких случаях приходится вылавливать в формулировке задачи численные значения и единицы измерения. Как определить количество энергии? Как показано в главе 10, единица энергии выражается как единица массы, умноженная на квадрат единицы длины и деленная на квадрат единицы времени. Если вы сможете легко выделить величины и их единицы измерения, то сможете не запутаться и представить их в решении.

На самом деле единицы измерения — это наши друзья. Они упрощают нам жизнь, в общем, и путь к решению, в частности. Потому если вы чувствуете, что “погрязли» в числах, то проверьте используемые единицы измерения.

Обратите внимание, что в сутках 24 часа, т.е. коэффициент преобразования равен 1/24. Потому преобразование единиц измерения (дней на часы) происходит при умножении величины 1560 миль/день на этот коэффициент преобразования.

При исключении дней во время умножения отношений получается следующий ответ:

Итак, средняя скорость равна 65 милям в час, что достаточно быстро, если ехать с такой средней скоростью на протяжении 3 суток!

Совсем не обязательно использовать коэффициент преобразования. Если инстинктивно вам понятно, что для преобразования единицы измерения “миль в день” в единицу “миль в час” нужно поделить числовое значение на 24, то нечего такой огород городить. Но если вы все же пребываете в сомнениях, то лучше все-таки найти и использовать все нужные коэффициенты преобразования. Лучше пройти этот длинный путь преобразования единиц измерения, чем поспешить и людей насмешить. Мне довольно часто встречались студенты, которые умели успешно решать задачи, но не справлялись с такими преобразованиями.

Преобразование суток в часы выполняется легко и просто, поскольку всем известно, что в сутках содержится 24 часа. Однако не все преобразования единиц измерения столь очевидны. Далеко не всем хорошо известны системы единиц СГС и СИ. Потому всегда полезно иметь под рукой табличку преобразований единиц из одной системы в другую, как, например, табл. 2.3. (Расшифровка приведенных здесь сокращений приводится в табл. 2.1 и 2.2.)

Поскольку разница между величинами в двух этих системах практически всегда кратна степеням 10, то преобразование величин выполняется достаточно просто. Например, если шар падает с высоты 5 метров, но вам нужно выразить расстояние в сантиметрах, то для этого достаточно умножить результат на отношение 100 сантиметров/1 метр:

А как преобразовать величины в единицы измерения Английской системы мер на основе фута-фунта-дюйма (foot-pound-inch — FPI)? Нет проблем. Все необходимые сведения о таких преобразованиях приведены в шпаргалке. Держите ее под рукой при чтении этой книги или при решении задач.

Исключаем нули: представляем числа в экспоненциальном виде

Физики часто мысленно погружаются в самые темные глубины и отправляются в самые далекие дали, а потому вынуждены использовать чудовищно большие или малые величины. Например, расстояние от Солнца до Плутона приблизительно равно 5 890 000 000 000 метрам. Что делать с таким огромным количеством метров и нулей? Физики для более удобной работы с такими очень большими или очень малыми величинами используют экспоненциальное представление чисел. В этом представлении нули выражаются в степенях 10. Чтобы определить степень, нужно подсчитать все цифры справа налево до первой цифры (первая цифра будет находиться перед запятой в итоговом экспоненциальном представлении). Итак, расстояние от Солнца до Плутона можно выразить следующим образом:

Экспоненциальное представление чисел также используется для записи очень маленьких значений, где степень имеет отрицательный знак. В таком случае нужно подсчитать количество цифр слева направо от десятичной запятой до места после первой ненулевой цифры (опять первая ненулевая цифра будет находиться перед запятой в итоговом экспоненциальном представлении):

Если число больше 10, то в экспоненциальном представлении оно будет иметь положительную степень, а если меньше 1, то — отрицательную. Как видите, операции с очень большими или малыми числами в экспоненциальном представлении выполняются гораздо проще. Именно поэтому во многих калькуляторах встроена возможность такого представления чисел.

Проверяем точность измерений

Точность имеет огромную важность для измерения и анализа физических параметров. Нельзя считать, что измерение стало более точным, если к измеренной величине необоснованно добавить дополнительное количество значащих цифр. Кроме того, всегда следует указывать оценку ошибки измерения с помощью знака ±. В следующих разделах более подробно описываются указания точности измерения физических величин.

Определяем значащие цифры

В измеренной величине значащими цифрами считаются те, которые были фактически получены в ходе измерения. Так, например, если после измерения ученые сообщили, что ракета прошла расстояние 10,0 за 7,00 секунд, то в результате этих измерений получено по три значащие цифры.

Чтобы определить скорость ракеты, эти данные можно ввести в калькулятор и после деления 10,0 на 7,00 получить, казалось бы, очень точный результат: 1,428571429. Но это совсем не так: если после измерения расстояния и времени для них получено всего по три значащие цифры, то в результате манипуляций с числами точность измерений не может возрасти до десяти значащих цифр. Ведь после измерения расстояния с помощью линейки с миллиметровыми делениями нельзя утверждать, что результат получен с точностью до нескольких микрон.

В примере с ракетой получено только по три значащие цифры, потому величина скорости равна 1,43, а не 1,428571429. Если записать больше цифр, то в таком случае будет сделано ничем необоснованное заявление о повышенной точности измерений, которой не было на самом деле.

При округлении числа нужно учитывать следующее простое правило. Если цифра справа от округляемой цифры больше или равна 5, то округление выполняется в сторону увеличения, а если эта цифра меньше 5, то округление выполняется в сторону уменьшения. Например, число 1,428 округляется до 1,43, а число 1,42 — до 1,4.

А что если в результате двух измерений ракета преодолела 10,0 метров за 7,0 секунд? Одно число имеет три, а другое — две значащих цифры. В таком случае нужно учитывать перечисленные ниже правила округления чисел с разным количеством значащих цифр.

• При умножении или делении чисел результат будет иметь то же количество значащих цифр, что и исходное число с наименьшим количеством значащих цифр.

В примере с ракетой, где нужно поделить расстояние на время, результат будет иметь только две значащие цифры, т.е. правильный ответ равен 1,4 м/с.

• При сложении или вычитании чисел нужно расположить их в столбик и выровнять по положению десятичной запятой в числах; самая последняя значащая цифра в результате будет соответствовать самой правой значащей цифре в том столбце, в котором все числа в столбике имеют значащие цифры.

Например, при сложении чисел 3,6, 14 и 6,33 получим:

Здесь нужно округлить результат до целого числа, поскольку число 14 не имеет значащих цифр после десятичной запятой, т.е. до 24.

По соглашению нули, используемые доя заполнения пустых мест до или после десятичной запятой, не считаются значащими цифрами. Например, по умолчанию число 3600 имеет только две значащие цифры. Но если некая величина измерена с высокой точностью и действительно равна 3600, то для подчеркивания точности измерения ее иногда приводят с указанием знака, отделяющего целую часть числа от десятичной дроби 3600,0.

Оцениваем точность

Физики при записи результатов измерений не всегда полагаются только на значащие цифры, и иногда можно встретить следующую запись:

Символ ± обозначает оценку физика возможной ошибки измерения. Физик сообщает таким образом, что действительное значение измеряемой величины находится в промежутке от 5,36+0,05 (т.е. 5,41) до 5,36-0,05 (т.е. 5,31) метров. (Это не значит, что именно настолько измеренное значение отличается от “истинного”. Это просто оценка точности измерения, т.е. насколько надежно это измерение.)

Определяем размер ±

С недавних пор символ ± стал чрезвычайно популярным, и его можно встретить даже в объявлениях о продаже недвижимости, например “продается 35± акров”. Иногда даже публикуются объявления о продаже ±35 акров. Значит ли это, что в итоге вы можете приобрести участок площадью в диапазоне от «-35 до +35 акров? Что значит приобрести -15 акров? Может быть, то, что после приобретения такого участка вы будете должны 15 акров?

Вспоминаем алгебру

В физике используется довольно много уравнений, и чтобы умело работать с ними, нужно овладеть основными приемами манипулирования частями уравнения. Сейчас самое время напомнить некоторые основные сведения из курса алгебры.

Следующее уравнение выражает расстояние ​\( s \)​, которое проходит объект с ускорением ​\( a \)​ за время ​\( t \)​:

Допустим, что нужно определить ускорение по известному времени движения и пройденному расстоянию. Манипулируя отдельными членами уравнения, получим следующее соотношение:

Для получения такого соотношения для ​\( a \)​ нужно обе стороны предыдущего выражения умножить на 2 и поделить на ​\( t^2 \)​.

А что если нужно найти время \( t \)? С помощью несложных манипуляций с переменными и числами получим следующее соотношение:

Нужно ли запоминать все эти три варианта одного уравнения? Конечно же, нет. Достаточно запомнить только один вариант, который связывает эти три величины (расстояние, ускорение и время), а потом извлекать из него соотношение для нужной переменной. (В шпаргалке приводится несколько основных соотношений, которые следует помнить.)

Немного тригонометрии

Кроме базовых сведений из алгебры для решения физических задач необходимо также иметь некоторые сведения из тригонометрии, например о синусе, косинусе, тангенсе. Для этого нужно запомнить простые соотношения на основе прямоугольного треугольника, который показан на рис. 2.1 во всей своей красе.

Для определения тригонометрических величин с помощью треугольника на рис. 2.1 нужно поделить длину одной стороны на длину другой, как показано ниже:

Эти простые соотношения пригодятся нам при изучении векторов в главе 4 и при решении многих задач по физике.

Зная величину одного острого угла и длину одной стороны этого треугольника, можно найти величину другого угла и длины двух других сторон. Ниже приводится несколько примеров, которые по мере изучения курса станут для вас просто родными, но которые вовсе не нужно запоминать наизусть. Если вы знаете предшествующие соотношения для синуса, косинуса и тангенса, то вы сможете легко вывести приведенные ниже соотношения:

Помните, что можно пойти и в “обратную сторону”, т.е. вычислить обратные функции для синуса (\( sin^{-1} \), или \( arcsin \)), косинуса (​\( cos^{-1} \)​, или ​\( arccos \)​) или тангенса (\( tan^{-1} \), или ​\( arctg \)​). Вот как они определяются:

(Строго говоря, обратной синусу функцией является функция “арксинус”, или \( arcsin(x) \), обратной косинусу — “арккосинус”, или \( arccos(x) \), обратной тангенсу — “арктангенс”, или ​\( arctg(x) \)​. Обозначения \( sin^{-1}(x) \), \( cos^{-1}(x) \) и \( tg^{-1}(x) \) часто используются в иностранной литературе для обозначения функций “арксинус”, “арккосинус” и “арктангенс”, но их не рекомендуется употреблять, чтобы не путать с функциями ​\( 1/sin(x) \)​, \( 1/cos(x) \) и \( 1/tg(x) \). — Примеч. ред.)

Глава 2. Постигаем основы физики

5 (100%) 6 votes

fizi4ka.ru