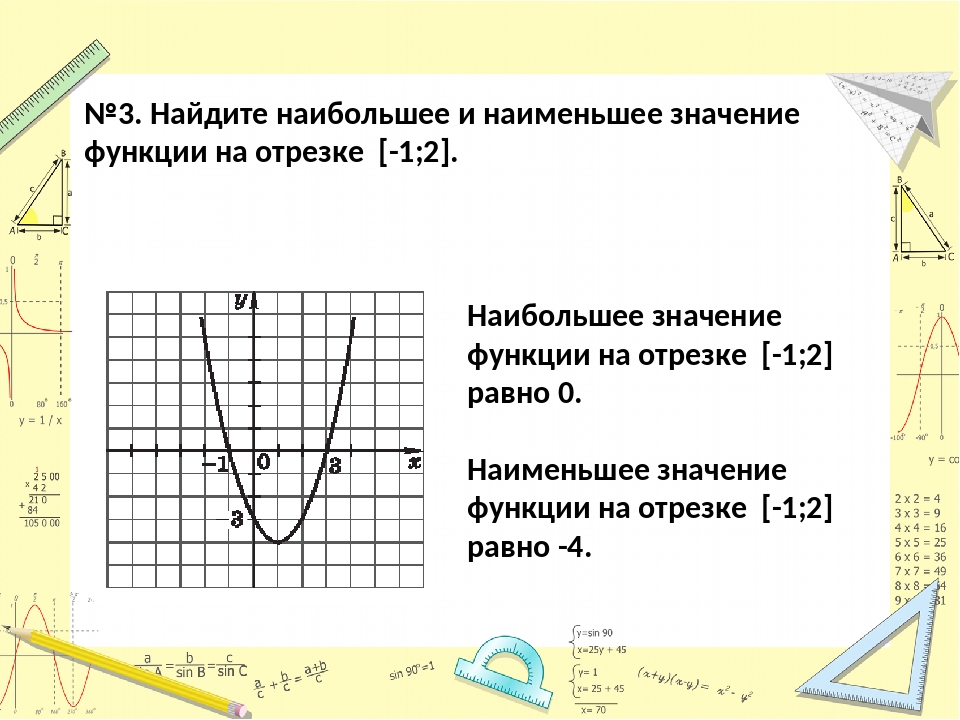
Как найти наибольшее значение функции y. Наибольшее и наименьшее значение функции
Пусть функция $z=f(x,y)$ определена и непрерывна в некоторой ограниченной замкнутой области $D$. Пусть в этой области заданная функция имеет конечные частные производные первого порядка (за исключением, быть может, конечного количества точек). Чтобы найти наибольшее и наименьшее значения функции двух переменных в данной замкнутой области требуется выполнить три шага простого алгоритма.
Алгоритм поиска наибольшего и наименьшего значений функции $z=f(x,y)$ в замкнутой области $D$.
- Найти критические точки функции $z=f(x,y)$, принадлежащие области $D$. Вычислить значения функции в критических точках.
- Исследовать поведение функции $z=f(x,y)$ на границе области $D$, найдя точки возможного наибольшего и наименьшего значений. Вычислить значения функции в полученных точках.
- Из значений функции, полученных в предыдущих двух пунктах, выбрать наибольшее и наименьшее.
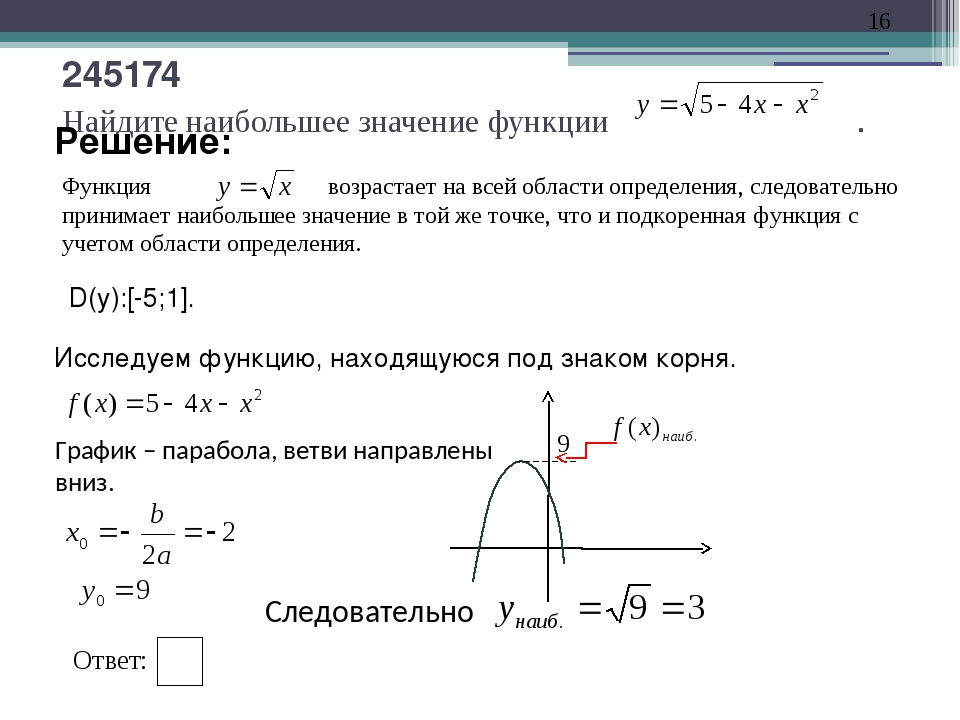
 2-4x$ в замкнутой области, ограниченной линиями $x=3$, $y=0$ и $y=x+1$.
2-4x$ в замкнутой области, ограниченной линиями $x=3$, $y=0$ и $y=x+1$.Будем следовать указанному выше , но для начала разберёмся с чертежом заданной области, которую обозначим буквой $D$. Нам заданы уравнения трёх прямых, кои эту область ограничивают. Прямая $x=3$ проходит через точку $(3;0)$ параллельно оси ординат (оси Oy). Прямая $y=0$ — это уравнение оси абсцисс (оси Ox). Ну, а для построения прямой $y=x+1$ найдём две точки, через которые и проведём данную прямую. Можно, конечно, подставить вместо $x$ парочку произвольных значений. Например, подставляя $x=10$, получим: $y=x+1=10+1=11$. Мы нашли точку $(10;11)$, лежащую на прямой $y=x+1$. Однако лучше отыщем те точки, в которых прямая $y=x+1$ пересекается с линиями $x=3$ и $y=0$. Почему это лучше? Потому, что мы одним выстрелом уложим пару зайцев: получим две точки для построения прямой $y=x+1$ и заодно выясним, в каких точках эта прямая пересекает иные линии, ограничивающие заданную область. Прямая $y=x+1$ пересекает прямую $x=3$ в точке $(3;4)$, а прямую $y=0$ — в точке $(-1;0)$.

Как были получены точки $(3;4)$ и $(-1;0)$? показать\скрыть
Начнём с точки пересечения прямых $y=x+1$ и $x=3$. Координаты искомой точки принадлежат и первой, и второй прямой, поэтому для нахождения неизвестных координат нужно решить систему уравнений:
$$ \left \{ \begin{aligned} & y=x+1;\\ & x=3. \end{aligned} \right. $$
Решение такой системы тривиально: подставляя $x=3$ в первое уравнение будем иметь: $y=3+1=4$. Точка $(3;4)$ и есть искомая точка пересечения прямых $y=x+1$ и $x=3$.
Теперь отыщем точку пересечения прямых $y=x+1$ и $y=0$. Вновь составим и решим систему уравнений:
$$ \left \{ \begin{aligned} & y=x+1;\\ & y=0. \end{aligned} \right. $$
Подставляя $y=0$ в первое уравнение, получим: $0=x+1$, $x=-1$. Точка $(-1;0)$ и есть искомая точка пересечения прямых $y=x+1$ и $y=0$ (оси абсцисс).
Всё готово для построения чертежа, который будет иметь такой вид:
Вопрос примечания кажется очевидным, ведь всё видно по рисунку.
 Однако стоит помнить, что рисунок не может служить доказательством. Рисунок — лишь иллюстрация для наглядности.
Однако стоит помнить, что рисунок не может служить доказательством. Рисунок — лишь иллюстрация для наглядности.Наша область была задана с помощью уравнений прямых, которые её ограничивают. Очевидно, что эти прямые определяют треугольник, не так ли? Или не совсем очевидно? А может, нам задана иная область, ограниченная теми же прямыми:
Конечно, в условии сказано, что область замкнута, поэтому показанный рисунок неверен. Но чтобы избегать подобных двусмысленностей, области лучше задавать неравенствами. Нас интересует часть плоскости, расположенная под прямой $y=x+1$? Ок, значит, $y ≤ x+1$. Наша область должна располагаться над прямой $y=0$? Отлично, значит $y ≥ 0$. Кстати, два последних неравенства легко объединяются в одно: $0 ≤ y ≤ x+1$.
$$ \left \{ \begin{aligned} & 0 ≤ y ≤ x+1;\\ & x ≤ 3. \end{aligned} \right. $$
Эти неравенства и задают область $D$, причём задают её однозначно, не допуская никаких двусмысленностей. Но как это поможет нам в том вопросе, что указан в начале примечания? Ещё как поможет:) Нам нужно проверить, принадлежит ли точка $M_1(1;1)$ области $D$.
 2-12\cdot(-3)+16\cdot 4=125.
\end{aligned}
2-12\cdot(-3)+16\cdot 4=125.
\end{aligned}На следует выбрать наибольшее и наименьшее значения из тех, что мы получили на первом и втором шагах. Но в данном случае выбор невелик:) Имеем:
$$ z_{min}=-75; \; z_{max}=125. $$
Ответ : $z_{min}=-75; \; z_{max}=125$.
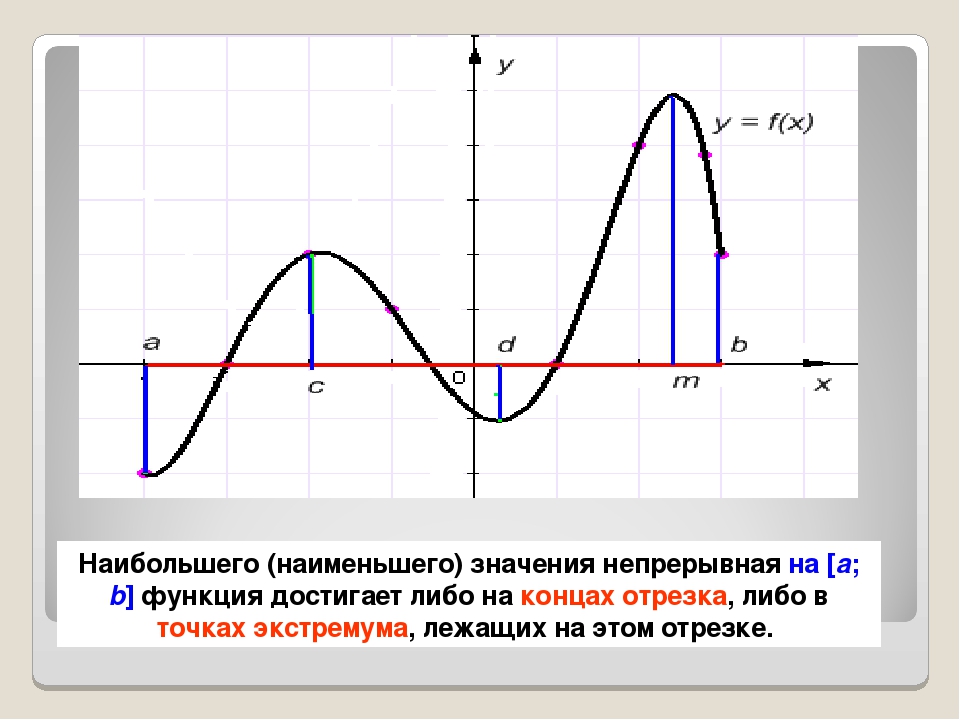
Процесс поиска наименьшего и наибольшего значения функции на отрезке напоминает увлекательный облёт объекта (графика функции) на вертолёте с обстрелом из дальнобойной пушки определённых точек и выбором из этих точек совсем особенных точек для контрольных выстрелов. Точки выбираются определённым образом и по определённым правилам. По каким правилам? Об этом мы далее и поговорим.
Если функция y = f (x ) непрерывна на отрезке [a , b ] , то она достигает на этом отрезке наименьшего и наибольшего значений . Это может произойти либо в точках экстремума , либо на концах отрезка. Поэтому для нахождения наименьшего и наибольшего значений функции , непрерывной на отрезке [a , b ] , нужно вычислить её значения во всех критических точках и на концах отрезка, а затем выбрать из них наименьшее и наибольшее.

Пусть, например, требуется определить наибольшее значение функции f (x ) на отрезке [a , b ] . Для этого следует найти все её критические точки, лежащие на [a
, b ] .Критической точкой называется точка, в которой функция определена , а её производная либо равна нулю, либо не существует. Затем следует вычислить значения функции в критических точках. И, наконец, следует сравнить между собой по величине значения функции в критических точках и на концах отрезка (f (a ) и f (b ) ). Наибольшее из этих чисел и будет наибольшим значением функции на отрезке [a , b ] .
Аналогично решаются и задачи на нахождение наименьших значений функции .
Ищем наименьшее и наибольшее значения функции вместе
Пример 1. Найти наименьшее и наибольшее значения функции на отрезке [-1, 2] .
Решение. Находим производную данной функции .
 Приравняем производную нулю ()
и получим две критические точки: и
. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на
концах отрезка и в точке ,
так как точка не
принадлежит отрезку [-1, 2]
. Эти значения функции — следующие: ,
,
. Из этого следует, что
Приравняем производную нулю ()
и получим две критические точки: и
. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на
концах отрезка и в точке ,
так как точка не
принадлежит отрезку [-1, 2]
. Эти значения функции — следующие: ,
,
. Из этого следует, что Если функция непрерывна в некотором промежутке и этот промежуток не является отрезком (а является, например, интервалом; разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок), то среди значений функции может и не быть наименьшего и наибольшего. Так, например, функция, изображённая на рисунке ниже, непрерывна на ]-∞, +∞[ и не имеет наибольшего значения.
Однако для любого промежутка (закрытого, открытого или бесконечного) справедливо следующее свойство непрерывных функций.

Пример 4. Найти наименьшее и наибольшее значения функции на отрезке [-1, 3] .
Решение. Находим производную данной функции как производную частного:
.
Приравниваем производную нулю, что даёт нам одну критическую точку: . Она принадлежит отрезку [-1, 3] . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:
Сравниваем эти значения. Вывод: , равного -5/13, в точке и наибольшего значения , равного 1, в точке .
Продолжаем искать наименьшее и наибольшее значения функции вместе
Есть преподаватели, которые по теме нахождения наименьшего и наибольшего значений функции не дают студентам для решения примеры сложнее только что рассмотренных, то есть таких, в которых функция — многочлен либо дробь, числитель и знаменатель которой — многочлены. Но мы не ограничимся такими примерами, поскольку среди преподавателей бывают любители заставить студентов думать по полной (таблице производных).

Пример 6. Найти наименьшее и наибольшее значения функции на отрезке .
Решение. Находим производную данной функции как производную произведения :
Приравниваем производную нулю, что даёт одну критическую точку: . Она принадлежит отрезку . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:
Результат всех действий: функция достигает наименьшего значения , равного 0, в точке и в точке и наибольшего значения , равного e ² , в точке .
Пример 7. Найти наименьшее и наибольшее значения функции на отрезке .
Решение. Находим производную данной функции:
Приравниваем производную нулю:
Единственная критическая точку принадлежит отрезку . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:
Вывод: функция достигает наименьшего значения , равного , в точке и наибольшего значения , равного , в точке .

В прикладных экстремальных задачах нахождение наименьшего (наибольшего) значений функции, как правило, сводится к нахождению минимума (максимума). Но больший практический интерес имеют не сами минимумы или максимумы, а те значения аргумента, при которых они достигаются. При решении прикладных задач возникает дополнительная трудность — составление функций, описывающих рассматриваемое явление или процесс.
Пример 8. Резервуар ёмкостью 4 , имеющий форму параллелепипеда с квадратным основанием и открытый сверху, нужно вылудить оловом. Каковы должны быть размеры резервуара, чтобы на его покрытие ушло наименьшее количество материала?
Решение. Пусть x — сторона основания, h — высота резервуара, S — площадь его поверхности без крышки, V — его объём. Площадь поверхности резервуара выражается формулой , т.е. является функцией двух переменных . Чтобы выразить S как функцию одной переменной, воспользуемся тем, что , откуда . Подставив найденное выражение h в формулу для S :
Исследуем эту функцию на экстремум.
 Она определена и дифференцируема всюду в
]0, +∞[
, причём
Она определена и дифференцируема всюду в
]0, +∞[
, причём.
Приравниваем производную нулю () и находим критическую точку . Кроме того, при производная не существует, но это значение не входит в область определения и поэтому не может быть точкой экстремума. Итак, — единственная критическая точка. Проверим её на наличие экстремума, используя второй достаточный признак. Найдём вторую производную . При вторая производная больше нуля (). Значит, при функция достигает минимума . Поскольку этот минимум — единственный экстремум данной функции, он и является её наименьшим значением . Итак, сторона основания резервуара должна быть равна 2 м, а его высота .
Пример 9. Из пункта A , находящегося на линии железной дороги, в пункт С , отстоящий от неё на расстоянии l , должны переправляться грузы. Стоимость провоза весовой единицы на единицу расстояния по железной дороге равна , а по шоссе она равна . К какой точке М линии железной дороги следует провести шоссе, чтобы транспортировка груза из А в С была наиболее экономичной (участок АВ железной дороги предполагается прямолинейным)?
Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.

Чтобы найти наибольшее или наименьшее значение функции необходимо:
- Проверить, какие стационарные точки входят в заданный отрезок.
- Вычислить значение функции на концах отрезка и в стационарных точках из п.3
- Выбрать из полученных результатов наибольшее или наименьшее значение.
Чтобы найти точки максимума или минимума необходимо:
- Найти производную функции $f»(х)$
- Найти стационарные точки, решив уравнение $f»(х)=0$
- Разложить производную функции на множители.
- Начертить координатную прямую, расставить на ней стационарные точки и определить знаки производной в полученных интервалах, пользуясь записью п.3.
- Найти точки максимума или минимума по правилу: если в точке производная меняет знак с плюса на минус, то это будет точка максимума (если с минуса на плюс, то это будет точка минимума). На практике удобно использовать изображение стрелок на промежутках: на промежутке, где производная положительна, стрелка рисуется вверх и наоборот.
 2}$
2}$4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции
$f(g(x))′=f′(g(x))∙g′(x)$
$f′(x)=cos′(5x)∙(5x)′= — sin(5x)∙5= -5sin(5x)$
Найдите точку минимума функции $y=2x-ln(x+11)+4$
1. Найдем ОДЗ функции: $х+11>0; х>-11$
2. Найдем производную функции $y»=2-{1}/{x+11}={2x+22-1}/{x+11}={2x+21}/{x+11}$
3. Найдем стационарные точки, приравняв производную к нулю
${2x+21}/{x+11}=0$
Дробь равна нулю если числитель равен нулю, а знаменатель не равен нулю
$2x+21=0; x≠-11$
4. Начертим координатную прямую, расставим на ней стационарные точки и определим знаки производной в полученных интервалах. Для этого подставим в производную любое число из крайней правой области, например, нуль.
$y»(0)={2∙0+21}/{0+11}={21}/{11}>0$
5. В точке минимума производная меняет знак с минуса на плюс, следовательно, точка $-10,5$ — это точка минимума.
Ответ: $-10,5$
Найдите наибольшее значение функции $y=6x^5-90x^3-5$ на отрезке $[-5;1]$
1.
 2=0 ; х-3=0; х+3=0$
2=0 ; х-3=0; х+3=0$$х=0;х=3;х=-3$
3. Выберем стационарные точки, которые принадлежат заданному отрезку $[-5;1]$
Нам подходят стационарные точки $х=0$ и $х=-3$
4. Вычислим значение функции на концах отрезка и в стационарных точках из п.3
С помощью данного сервиса можно найти наибольшее и наименьшее значение функции одной переменной f(x) с оформлением решения в Word . Если же задана функция f(x,y) , следовательно, необходимо найти экстремум функции двух переменных . Также можно найти интервалы возрастания и убывания функции .
Правила ввода функций :
Необходимое условие экстремума функции одной переменной
Уравнение f» 0 (x *) = 0 — это необходимое условие экстремума функции одной переменной, т.е. в точке x * первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x с, в которых функция не возрастает и не убывает.Достаточное условие экстремума функции одной переменной
Пусть f 0 (x) дважды дифференцируемая по x , принадлежащему множеству D . Если в точке x * выполняется условие:
Если в точке x * выполняется условие:F» 0 (x *) = 0
f»» 0 (x *) > 0То точка x * является точкой локального (глобального) минимума функции.
Если в точке x * выполняется условие:
F» 0 (x *) = 0
f»» 0 (x *)То точка x * — локальный (глобальный) максимум.
Пример №1 . Найти наибольшее и наименьшее значения функции: на отрезке .
Решение.
Критическая точка одна x 1 = 2 (f’(x)=0). Эта точка принадлежит отрезку . (Точка x=0 не является критической, так как 0∉).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)= 5 / 2 , f(3)=3 8 / 81
Ответ: f min = 5 / 2 при x=2; f max =9 при x=1Пример №2 . С помощью производных высших порядков найти экстремум функции y=x-2sin(x) .
Решение.
Находим производную функции: y’=1-2cos(x) . Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=± π / 3 +2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x= π / 3 +2πk, k∈Z – точки минимума функции; , значит x=- π / 3 +2πk, k∈Z – точки максимума функции.
Пример №3 . Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0 , то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x 0 или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.СХОЖИЕ СТАТЬИ
Полезное
Реклама
Новое
По графику производной найти наибольшее значение функции
Рассмотрим задания, в которых дан график производной функции и требуется найти, в какой точке данного отрезка эта функция принимает наибольшее значение.

№1
На рисунке изображён график производной функции f(x), определённой на интервале (-14;8). В какой точке отрезка [-11;-8] функция f(x) принимает наибольшее значение?
Решение:
Выделяем отрезок [-11;-8].
На этом отрезке производная f'(x) принимает положительные значения.
Следовательно, функция f(x) на этом отрезке возрастает, то есть бо́льшему значению аргумента соответствует бо́льшее значение функции:
x1,x2 ∈[-11;-8], x2>x1, ⇒ f(x2)>f(x1).
Поэтому наибольшее значение функция f(x) на отрезке принимает при наибольшем значении аргумента, то есть на правом конце отрезка, при x=-8.
Ответ: -8.
№2
На рисунке изображён график производной функции f(x), определённой на интервале (-7;9). В какой точке отрезка [4;8] функция f(x) принимает наибольшее значение?
Решение:
Выделяем отрезок [4;8].
Так как этом отрезке производная f'(x)<o, то функция f(x) на [4;8] убывает, то есть бо́льшему значению аргумента соответствует меньшее значение функции:
x1,x2 ∈[4;8], x2>x1, ⇒ f(x2)<f(x1).

Поэтому наибольшее значение f(x) принимает в этом случае при наименьшем значении аргумента, то есть на левом конце отрезка, при x=4.
Ответ: 4.
№3
Функция y=f(x) определена на промежутке (-5;9). На рисунке изображён график её производной. Найти абсциссу точки, в которой функция y=f(x) принимает наибольшее значение.
Решение:
В точке с абсциссой x=6 производная меняет знак с плюса на минус.
Следовательно, x=6 — точка максимума.
Производная f'(x) существует на всём интервале (-5;9), следовательно, функция f(x) непрерывна на (-5;9).
Если непрерывная функция f(x) имеет на заданном интервале (a;b) только одну точку экстремума xo и это точка максимума, то на (a;b) функция принимает своё наибольшее значение в точке xo.
Таким образом, функция f(x) на интервале (-5;9) принимает наибольшее значение в точке x=6.
Ответ: 6.
№4
Функция y=f(x) определена и непрерывна на отрезке [-1;9].
 На рисунке изображён график её производной. Найти точку xo, в которой функция принимает наибольшее значение, если f(-1)≥f(9).
На рисунке изображён график её производной. Найти точку xo, в которой функция принимает наибольшее значение, если f(-1)≥f(9).Решение:
На промежутках (-1;3) и (8;9) производная f'(x)>0, поэтому на этих промежутках функция f(x) возрастает.
На промежутке (3;9) производная f'(x)<0, поэтому на (3;9) функция f(x) убывает.
Так как функция определена и непрерывна на отрезке [-1;9], то точки -1, 3, 8 и 9 можно включать в промежутки монотонности.
Следовательно, на отрезках [-1;3] и [8;9] функция f(x) возрастает, на отрезке [3;8] — убывает.
На промежутках возрастания наибольшее значение функция принимает на правом конце отрезка. На [-1;3] наибольшее значение f(x) принимает в точке x=3 (точке максимума), на [8;9] — в точке x=9.
Так как на [-1;3] f(x) возрастает, то f(3)>f(-1). По условию, f(-1)≥f(9), значит f(3)>f(9).
Таким образом, наибольшее значение функции f(x) принимает в точке x=3.
Ответ: 3.
Наибольшее и наименьшее значения функции двух переменных в замкнутой области
Задача 1
Найти наибольшее и наименьшее значение в области , ограниченной заданными линиями.

Решение
Область показана на рисунке:
Найдем стационарные точки:
Частные производные:
Приравняем найденные частные производные к нулю и решим систему уравнений:
Области принадлежит точка
Исследуем функцию на границах области :
при :
Приравниваем производную к нулю:
Находим значения функции:
При
Приравниваем производную к нулю:
Находим значения функции:
при
Приравниваем производную к нулю:
Находим значения функции:
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
TelegramЯ буду работать с вами, над вашей проблемой, пока она не решится.

Сопоставляя полученные значения, получаем:
Задача 2
Найти наименьшее и наибольшее значения функции в указанной области. Сделать чертеж области.
в круге
Решение
Область показана на рисунке:
Найдем стационарные точки:
Стационарных точек функция не имеет
Исследуем функцию на границах области:
при
Приравниваем производную к нулю:
Значение в найденной точке:
Находим значения функции:
при
Приравниваем производную к нулю:
Значение в найденной точке:
Находим значения функции:
Сопоставляя полученные значения, находим:
в точке
в точке
Найти наименьшее и наибольшее значение в диапазоне в Excel — Учебники по Excel
Предположим, у нас есть таблица Excel с тремя столбцами: годовой оклад, сумма кредита и срок кредита.

В этой таблице не так много строк, и если кто-то захочет, чтобы мы назвали ему наименьшее число в каждом столбце, мы, вероятно, могли бы просто пойти и найти эти ячейки «невооруженным глазом».
Однако уже одно это кажется большой работой. А теперь представьте, что наш стол стал еще больше.К счастью, есть несколько способов найти нужные нам значения. В данном случае наименьшее и наибольшее число.
Наименьшее и наибольшее число с фильтром
Первый вариант заключается в том, что мы выбираем первые три столбца в нашей первой строке (тот, который содержит имена наших столбцов), переходим на вкладку Данные , затем на подвкладку Сортировка и фильтрация и затем нажимаем Фильтр :
Мы заметим, что наши ячейки в первой строке теперь имеют выпадающий список.
Если мы выберем кнопку раскрывающегося списка в ячейке A1 , мы заметим несколько вариантов в нашем распоряжении:
Мы можем сразу понять, что у нас есть два искомых варианта:
- Сортировать от наименьшего к наибольшему
- Сортировать от наибольшего к наименьшему
Если мы выберем первый вариант, то заметим, что наш первый столбец теперь упорядочен от наименьшей годовой зарплаты к наибольшей.

Логически, так как мы выбрали раскрывающийся список только из столбца A это столбец, из которого были упорядочены эти значения.
Теперь мы знаем самое высокое и самое низкое значение. Мы можем сделать то же самое и для других столбцов.
Наименьшее и наибольшее число с условным форматированием
Еще один способ найти наибольшее и наименьшее значение — это параметр Data Bars в условном форматировании.
Мы выберем столбец B , а затем перейдем к Условное форматирование >> Панели данных , а затем выберем первый вариант в Градиентная заливка .
Ячейки в столбце B теперь будут заполняться автоматически, при этом наименьшее значение будет наименее заполненным синим цветом, а наибольшее значение будет полностью окрашено.
Этот вариант очень удобен, когда мы работаем с небольшим набором данных или хотим показать наши данные с помощью более качественной графики, но довольно сложно найти наименьшее и наибольшее значения таким образом при работе с большим набором данных.
 данные.
данные.Наименьшее и наибольшее число с функциями
Самый простой способ найти наименьшее и наибольшее значения в нашем диапазоне — использовать функции.Предположим, что мы хотим найти наименьшее значение в нашем столбце C (срок кредита).
Мы перейдем к одной ячейке ниже нашей последней заполненной ячейки в столбце (в нашем случае ячейка C21 ).
Также проще перейти к последней ячейке в нашем диапазоне. Мы просто нажимаем CTRL + стрелка вниз , и Excel направляет нас к последней ячейке в нашем диапазоне.
После того, как мы нашли нашу ячейку, мы перейдем на вкладку Главная , на подвкладку Редактирование , щелкните стрелку рядом с Автосумма, нажмите Min (вычисляет наименьшее значение) или Max (вычисляет наибольшее значение ), а затем нажмите ENTER .
Если мы нажмем Min , нам автоматически будет представлена функция, которую Excel подготовил для нас:
Как видим, с нашей функцией все в порядке.
 Мы нажмем ENTER , а затем нам будет представлен результат, который в данном случае является числом 18.
Мы нажмем ENTER , а затем нам будет представлен результат, который в данном случае является числом 18.Чтобы найти наибольшее значение, мы должны изменить нашу функцию с MIN на MAX .
Наименьшее и наибольшее число с VBA
Поскольку мы не решили вопрос наименьшего и наибольшего значения в столбце B , сделаем это с помощью кода VBA.Для этого мы определим ячейку E1 как Наименьшую сумму кредита t и ячейку F1 как Наибольшую сумму кредита .
Мы введем наименьшее значение столбца B в ячейку E2 и наибольшее значение столбца B в ячейку F2 .
Наш код VBA будет следующим:
Sub Return_lowest_number() Dim ws As рабочий лист Установите ws = Рабочие листы («Ссудная таблица») вс.Range("E2") = Application. WorksheetFunction.Min(ws.Range("B2:B20"))
Конечный переходник
WorksheetFunction.Min(ws.Range("B2:B20"))
Конечный переходник В первой части кода мы объявляем переменную. Dim — это сокращение от «размерность», и мы используем его, когда хотим объявить переменную, которая будет запомнена и может быть использована позже в нашем коде.
В нашем примере мы создаем переменную ws , которая будет определена как рабочий лист.
На следующем шаге мы устанавливаем нашу переменную для ссылки на наш рабочий лист. Наш рабочий лист называется Loan table, поэтому мы установим нашу переменную ws равной этому имени.
Наконец, мы вызываем нашу переменную, а затем ставим точку («.»), что позволит нам вызывать определенную ячейку из нашего рабочего листа. На этом этапе мы определяем ячейку, в которую мы хотим ввести данные, а затем определяем сами данные. Наша нужная ячейка — ячейка E2 .
Мы хотим, чтобы наша ячейка E2 была равна минимальному значению диапазона в столбце B .
 С другой стороны уравнения, мы сначала вызываем наше приложение , чтобы мы могли также вызвать функцию рабочего листа .Затем мы вызываем функцию Min , чтобы вернуть минимальное значение нашего диапазона.
С другой стороны уравнения, мы сначала вызываем наше приложение , чтобы мы могли также вызвать функцию рабочего листа .Затем мы вызываем функцию Min , чтобы вернуть минимальное значение нашего диапазона.Затем мы хотим определить наш диапазон. Наш диапазон, очевидно, будет расположен на нашем листе, и мы вызываем нашу переменную для листа, а затем вызываем диапазон наших данных, который равен B2:B20 .
Когда мы запустим наш код с F5 , мы получим результат в ячейке E2 следующим образом:
Чтобы вернуть наибольшее значение, т. е. наибольшую сумму кредита, мы должны внести некоторые коррективы в наш код.Мы создадим еще один код под нашим первым, и он будет выглядеть так:
.Sub Return_largest_number() Dim ws As рабочий лист Установите ws = Рабочие листы («Ссудная таблица») ws.Range("F2") = Application.WorksheetFunction. Max(ws.Range("B2:B20"))
Конечный переходник
Max(ws.Range("B2:B20"))
Конечный переходник Как видно, мы изменили имя нашего кода, теперь оно Return_largest_number .
Затем мы изменили выходной диапазон, изменив ссылку на ячейку («F2») в нашем коде.
Наш диапазон остался прежним (B2:B20), хотя мы могли бы изменить его, если бы захотели.
Наконец, мы изменили нашу функцию с Min на Max.
Наша таблица выглядит так:
Просмотры сообщений: 115
Программа на Python для поиска наибольшего и наименьшего числа в списке
Напишите программу на Python для нахождения наибольшего и наименьшего числа в списке с практическим примером.
Программа на Python для поиска наибольшего и наименьшего числа в списке Пример 1
Эта программа на Python позволяет пользователю вводить длину списка.Затем мы использовали For Loop , чтобы добавить числа в список. Здесь функции min и max в Python возвращают наименьшее и наибольшее число или минимальное и максимальное значения в списке.

# Программа Python для поиска наибольшего и наименьшего числа в списке НумСписок = [] Number = int(input("Пожалуйста, введите общее количество элементов списка: ")) для i в диапазоне (1, число + 1): value = int(input("Пожалуйста, введите значение элемента %d: "%i)) NumList.append(значение) print("Самый маленький элемент в этом списке: ", min(NumList)) print("Самый большой элемент в этом списке: ", max(NumList))вывод наибольшего и наименьшего числа в списке Python
Пожалуйста, введите общее количество элементов списка: 5 Пожалуйста, введите значение 1 элемента: 50 Пожалуйста, введите значение 2 элемента: 45 Пожалуйста, введите значение 3 элемента: 33 Пожалуйста, введите значение 4 элемента: 78 Пожалуйста, введите значение элемента 5: 66 Самый маленький элемент в этом списке: 33 Самый большой элемент в этом списке: 78Программа Python для поиска наибольшего и наименьшего числа в списке Пример 2
Функция сортировки Python сортирует элементы списка в порядке возрастания.
 Затем мы используем индексную позицию 0 для печати первого элемента и последнюю индексную позицию для печати последнего элемента в списке.
Затем мы используем индексную позицию 0 для печати первого элемента и последнюю индексную позицию для печати последнего элемента в списке.# Программа Python для поиска наибольшего и наименьшего числа в списке НумСписок = [] Number = int(input("Пожалуйста, введите общее количество элементов списка: ")) для i в диапазоне (1, число + 1): value = int(input("Пожалуйста, введите значение элемента %d: "%i)) NumList.append(значение) NumList.sort() print("Самый маленький элемент в этом списке: ", NumList[0]) print("Самый большой элемент в этом списке: ", NumList[Number - 1])Программа Python для поиска наибольшего и наименьшего числа в списке Пример 3
В этой программе мы не используем никаких встроенных такие функции, как sort, max или min.
# Программа Python для поиска наибольшего и наименьшего числа в списке НумСписок = [] Number = int(input("Пожалуйста, введите общее количество элементов списка: ")) для i в диапазоне (1, число + 1): value = int(input("Пожалуйста, введите значение элемента %d: "%i)) NumList. append(значение)
наименьший = наибольший = NumList[0]
для j в диапазоне (1, число):
если (наименьший > NumList[j]):
наименьший = NumList[j]
минимальная_позиция = j
если (самый большой < NumList[j]):
наибольший = NumList[j]
макс_позиция = j
print("Самый маленький элемент в этом списке: ", самый маленький)
print("Позиция индекса наименьшего элемента в этом списке: ", min_position)
print("Самый большой элемент в этом списке: ", самый большой)
print("Индексная позиция самого большого элемента в этом списке: ", max_position)
append(значение)
наименьший = наибольший = NumList[0]
для j в диапазоне (1, число):
если (наименьший > NumList[j]):
наименьший = NumList[j]
минимальная_позиция = j
если (самый большой < NumList[j]):
наибольший = NumList[j]
макс_позиция = j
print("Самый маленький элемент в этом списке: ", самый маленький)
print("Позиция индекса наименьшего элемента в этом списке: ", min_position)
print("Самый большой элемент в этом списке: ", самый большой)
print("Индексная позиция самого большого элемента в этом списке: ", max_position) вывод наибольшего и наименьшего номера списка Python
Пожалуйста, введите общее количество элементов списка: 5 Пожалуйста, введите значение 1 элемента: 40 Пожалуйста, введите значение 2 элемента: 60 Пожалуйста, введите значение 3 элемента: 20 Пожалуйста, введите значение 4 элемента: 11 Пожалуйста, введите значение элемента 5: 50 Самый маленький элемент в этом списке: 11 Позиция индекса наименьшего элемента в этом списке: 3 Самый большой элемент в этом списке: 60 Индексная позиция наибольшего элемента в этом списке: 1Из приведенной выше программы Python для поиска наибольшего и наименьшего числа в выходном списке список вставленных пользователем значений:
NumList[5] = {40, 60, 20, 11, 50}
наименьший = наибольший = NumList[0] = 40Первая итерация — для 1 в диапазоне (1, 5) — условие истинно
Итак, он начинает выполнять оператор If внутри цикла до тех пор, пока условие не будет выполнено.
If (наименьший > NumList[j]) внутри цикла For имеет значение False, поскольку (40 > 60)
наименьший = 40
position = 1 40 < 60)
наибольшая = 60
позиция = 1Вторая итерация: для 2 в диапазоне (1, 5) — условие верно
Если (40 > 20) — условие истинно
наименьшая = 20
позиция = 2If (60 < 20) — условие False
наибольшее = 60 ==> без изменений
Position = 1 ==> без измененийТретья итерация: для 3 в диапазоне (1, 5) — условие истинно
If (20 > 11) – Условие Истинно
наименьшее = 11
Позиция = 3Если (60 < 11) – Условие Ложь
наибольшее = 60
Позиция = 1Четвертая итерация: для 4 в диапазоне (1, 5) – Условие истинно
Если (11 > 50) – Условие False
наименьшее = 11
Позиция = 3Если (60 < 11) – Условие False
наибольшее = 60
Позиция = 1Пятая итерация: для 5 in range(1, 5) – Condition is False
Таким образом, он выходит из цикла.
Alteryx для пользователей Excel: Найдите x наименьшее/наибольшее число в столбце
Возможно, вы уже знаете, как использовать функции MIN() и MAX() для поиска наименьшего и наибольшего значений в списке. Но что, если вам нужно второе по величине число или 3-е по величине число в списке?
В Excel есть функция для этого. Используя функцию =МАЛЕНЬКИЙ, вы должны указать диапазон данных, за которым следует 'x' наименьшее число, которое вы хотите найти. В приведенном ниже примере мы находим второе наименьшее значение в списке:
Точно так же, если вы хотите найти наибольшее значение 'x' в списке, вы должны использовать функцию =НАИБОЛЬШИЙ.Здесь мы используем функцию =НАИБОЛЬШИЙ, чтобы найти 3-е по величине значение в нашем списке:
Давайте посмотрим, как мы делаем то же самое, используя Alteryx. Мы начнем с того же массива чисел, используя инструмент ввода текста:
Мы хотим найти второе наименьшее значение в списке.
 Начнем с сортировки списка в порядке возрастания. Затем мы назначаем идентификатор записи каждой строке данных. Отфильтруйте, чтобы выбрать идентификатор записи = 2, и используйте инструмент выбора, чтобы удалить поле идентификатора записи (нам это не нужно в нашем конечном результате), и это оставит нас с нашим ответом «6».
Начнем с сортировки списка в порядке возрастания. Затем мы назначаем идентификатор записи каждой строке данных. Отфильтруйте, чтобы выбрать идентификатор записи = 2, и используйте инструмент выбора, чтобы удалить поле идентификатора записи (нам это не нужно в нашем конечном результате), и это оставит нас с нашим ответом «6».Чтобы найти 3-е по величине значение в списке, мы просто меняем порядок сортировки на убывающий и фильтруем, выбирая запись id = 3:
Наш результат — «13», так что все в порядке.
Мы воспроизвели в Alteryx функции Excel =МАЛЕНЬКИЙ и =БОЛЬШОЙ. Но давайте добавим пару наворотов в наш рабочий процесс и сделаем его приложением. Это дает пользователю возможность решить, хотят ли они выбрать наименьшее или наибольшее значение из нашего списка, а также каким будет значение «x».Начните с переноса Drop Down Tool на холст.
Введите текст или вопрос для отображения («Вернуть наименьшее/наибольшее значение:»).
 В разделе «Список значений» мы выберем «Установить значения вручную» и в разделе «Свойства» введите:
В разделе «Список значений» мы выберем «Установить значения вручную» и в разделе «Свойства» введите:Наименьшее значение: по возрастанию
Наибольшее значение: по убыванию
Соедините раскрывающийся список с молнией в верхней части инструмента сортировки. Автоматически инструмент действия будет вставлен между инструментами раскрывающегося списка и сортировки.
В окне конфигурации действия выберите @order - value = "По возрастанию".
Поместите другой раскрывающийся список на холст и введите тест или вопрос для отображения («Введите N-е наименьшее/наибольшее значение:»):
Соедините раскрывающийся инструмент с Инструмент фильтра. Инструмент действия будет автоматически вставлен между раскрывающимся списком и инструментами фильтра:
Обратите внимание, что выражение в инструменте фильтра настроено на отправку идентификатора записи = 1 на выходную сторону «T» (истина) инструмента. В окне конфигурации действия выберите «Выражение — значение = «[RecordID] = 1» и введите «1» в поле «Заменить определенную строку:», расположенном в нижней части окна конфигурации.

Необязательно: добавьте инструмент выходных данных в конец рабочего процесса, чтобы можно было отобразить результаты. В этом примере мы будем экспортировать результаты во временный HTML-файл:
Итак, полный рабочий процесс/приложение выглядит следующим образом:
Давайте запустим приложение. В главном меню справа от значка запуска нажмите на палочку:
Появится окно с раскрывающимися меню, которые вы настроили с помощью инструментов раскрывающегося списка.Давайте найдем второе наименьшее число в нашем столбце чисел:
Нажмите «Готово», и появится окно «Результаты приложения». Нажмите «ОК»:
Наши временные HTML-файлы возвращают правильное значение 6.
Теперь у вас есть приложение, с помощью которого другие пользователи могут легко и быстро выбирать наименьшее или наибольшее значение «x» в списке чисел. Чтобы узнать больше о приложениях и инструментах интерфейса в целом, см.
 здесь.
здесь.Урок № 69. Получение K-го наибольшего или K-го наименьшего
Если вы хотите получить наименьшее или наибольшее число из массива, используйте функции MAX и MIN.Но если вы хотите получить K-й наибольший или K-й наименьший, то для получения результата есть еще две функции. Это БОЛЬШОЙ и МАЛЕНЬКИЙ . Функция БОЛЬШОЙ
Функция НАИБОЛЬШИЙ возвращает K-е по величине значение (числовое) в массиве. Синтаксис этой функции:
k – Целое число, указывающее k-ю позицию.Функция МАЛЕНЬКИЙ
Функция МАЛЕНЬКИЙ возвращает K-е наименьшее значение (числовое) в массиве.Синтаксис этой функции SMALL (массив, k) массив – Массив, из которого вы хотите найти k-е наименьшее значение.
k – целое число, указывающее k-ю позицию.Теперь давайте рассмотрим пример БОЛЬШОЙ.
Здесь у меня есть несколько значений в столбце C, и я хочу получить 2-е, 5-е, 4-е по величине значение.
Итак, я поместил эту формулу
БОЛЬШОЙ($C$2:$C$15,2)
БОЛЬШОЙ($C$2:$C$15,5)
БОЛЬШОЙ($C$2:$C$15,4) )
чтобы узнать 2-е, 5-е, 4-е наибольшее значениеТочно так же я поставил эту формулу
МАЛЕНЬКИЙ ($ C $ 2: $ C $ 15,2)
МАЛЕНЬКИЙ ($ C $ 2: $ C $ 15,5)
МАЛЕНЬКИЙ ($ C $ 2: $ C $ 15,4) )
, чтобы узнать 2-е, 5-е, 4-е наименьшее значение.Теперь у меня есть таблица с некоторыми буквами в столбце B и некоторыми значениями в столбце C. Что делать, если мне нужно найти соответствующие значения в столбце B, которые соответствуют K-му наибольшему значению в столбце C.
Тогда я просто сделал комбинацию ИНДЕКС, ПОИСКПОЗ и БОЛЬШОЙ .
Поместив эту формулу
=ИНДЕКС($B$2:$B$15,ПОИСКПОЗ(НАИБОЛЬШИЙ($C$2:$C$15,2),$C$2:$C$15,0))
=ИНДЕКС( $B$2:$B$15,ПОИСКПОЗ(БОЛЬШОЙ($C$2:$C$15,5),$C$2:$C$15,0))=ИНДЕКС($B$2:$B$15,ПОИСКПОЗ(БОЛЬШОЙ($C$2:$C$15,4),$C$2:$C$15,0))
Связанные видеоуроки:
youtube.com/embed/rDVDjndB6Bs" frameborder="0" allowfullscreen="allowfullscreen"/>R макс. и мин. Функция
В этой статье вы узнаете, как использовать min и max в R.Я собираюсь объяснить обе функции в одном руководстве, поскольку синтаксис R этих двух функций абсолютно одинаков.
Базовый синтаксис R:
Функция R max возвращает максимальное значение вектора или столбца.
Функция R min возвращает минимальное значение вектора или столбца.Базовый код R для функций max и min показан выше. В следующем руководстве по R я покажу вам восемь примеров применения max и min в языке программирования R.
Давайте углубимся в это…
Пример 1: Применить max и min к вектору в R
Самое простое использование max и min — это их применение к числовому вектору.
 Давайте сначала создадим пример вектора:
Давайте сначала создадим пример вектора:x1 <- c(4, 1, - 50, 20, 8) # Создать пример вектора
x1 <- c(4, 1, - 50, 20, 8) # Создать пример вектора
Наш примерный вектор состоит из пяти чисел, хранящихся в объекте данных x1.Теперь давайте вычислим максимум и минимум этого вектора.
Максимум можно вычислить с помощью следующего R-кода:
max(x1) # Применить max к вектору # 20
max(x1) # Применить max к вектору № 20
Как вы видите в консоли RStudio, максимум нашего вектора равен 20.
Тот же код работает для функции min:
min(x1) # Применить min к вектору # -50
min(x1) # Применить min к вектору #-50
Минимальное значение нашего вектора — 50.
Кстати: я также записал видео, содержащее примеры 1 и 2 этого урока. Видеоурок можно посмотреть здесь:
Чтобы воспроизвести это видео, примите файлы cookie YouTube.
 Принимая это, вы получаете доступ к контенту с YouTube, службы, предоставляемой внешней третьей стороной.
Принимая это, вы получаете доступ к контенту с YouTube, службы, предоставляемой внешней третьей стороной.Политика конфиденциальности YouTube
Если вы примете это уведомление, ваш выбор будет сохранен, и страница обновится.
Принять контент YouTube
Как вы видели в видео, могут возникнуть сложности, когда у нас есть значения NA.Вы можете найти код второго примера видео в следующем…
Пример 2: Вектор со значением NA
Проблема может возникнуть, если ваши данные содержат значения NA (т.е. отсутствующие данные). Для второго примера давайте добавим недостающие данные в вектор нашего примера:
.x2 <- c(x1, NA) # Создать пример вектора с NA x2 # Печать вектора в консоль RStudio # 4 1 -50 20 8 NA
x2 <- c(x1, NA) # Создать пример вектора с NA x2 # Печать вектора в консоль RStudio # 4 1 -50 20 8 NA
Наш новый пример вектора выглядит точно так же, как в примере 1, но на этот раз со значением NA в конце.
 Давайте посмотрим, что произойдет, если мы применим max и min как раньше:
Давайте посмотрим, что произойдет, если мы применим max и min как раньше:max(x2) # max возвращает NA # NA
max(x2) # max возвращает NA №
Функция max возвращает NA…
min(x2) # min также возвращает NA # NA
min(x2) # min также возвращает NA №
… и функция min делает то же самое.
Но не волнуйтесь, есть простое решение! Просто укажите параметр na.rm = TRUE в функциях max и min:
max(x2, na.rm = TRUE) # Укажите na.rm = TRUE # 20
max(x2, na.rm = TRUE) # Укажите na.rm = TRUE № 20
Как видите, при использовании na.rm = TRUE мы получаем тот же максимум…
min(x2, na.rm = TRUE) # Укажите na.РМ = ИСТИНА # -50
мин(x2, na.rm = TRUE) # Укажите na.rm = TRUE #-50
… и минимум как в примере 1.
Отлично!
Но что, если мы хотим применить max и min к столбцу фрейма данных? Вы уже догадались, это то, что я собираюсь показать вам дальше.

Пример 3: max() и min() столбца
В следующем примере я буду использовать набор данных mtcars. Данные могут быть загружены с помощью следующего кода R:
data("mtcars") # Загрузить данные mtcars в RStudiodata("mtcars") # Загрузить данные mtcars в RStudio
Давайте посмотрим на данные:
head(mtcars) # Первые 6 строк кадра данных mtcars
head(mtcars) # Первые 6 рядов кадра данных mtcars
Таблица 1: Данные mtcars в качестве примера данных.кадр для приложения max() и min().
Каждая строка набора данных mtcars состоит из одного автомобиля, а столбцы данных содержат разную информацию о каждом автомобиле (mpg = мили на галлон, cyl = цилиндр и т. д.).
Если мы хотим вычислить максимум и минимум одного столбца, мы можем применить алгоритмы максимума и минимума к этому столбцу с именем данных, знаком $ и именем столбца.
 Сделаем это на практике:
Сделаем это на практике:max(mtcars$mpg) # Вычислить максимальное количество миль на галлон столбца № 33.9
max(mtcars$mpg) # Вычислить максимальное количество миль на галлон столбца № 33.9
То же самое для мин:
min(mtcars$mpg) # Вычислить максимальное количество миль на галлон столбца # 10.4
min(mtcars$mpg) # Вычислить максимальное значение столбца mpg # 10.4
Максимальное значение столбца mpg кадра данных mtcars составляет 33,9, а минимальное — 10,4.
Давайте автоматизируем этот код...
Пример 4: максимумы и минимумы по всем столбцам
Вас могут заинтересовать максимумы и минимумы всех столбцов вашей матрицы данных.Конечно, вы можете применить функции max и min R к каждому из столбцов по одному. Однако функция sapply обеспечивает гораздо более плавный и автоматизированный способ вычисления всех максимумов и минимумов с помощью одной строки кода.

Максимумы по всем столбцам можно вычислить следующим образом…
sapply(mtcars, max) # Вычислить максимальное количество всех столбцов # mpg cyl disp hp drat wt qsec vs am gear carb № 33.900 8.000 472.000 335.000 4.930 5.424 22.900 1.000 1.000 5.000 8.000
sapply(mtcars, max) # Вычисление максимума всех столбцов # mpg cyl disp hp drat wt qsec vs am gear carb # 33.900 8.000 472.000 335.000 4.930 5.424 22.900 1.000 1.000 5.000 8.000
… и минимумы по всем столбцам можно вычислить следующим образом:
sapply(mtcars, min) # Вычислить минимум всех столбцов # mpg cyl disp hp drat wt qsec vs am gear carb № 10.400 4.000 71.100 52.000 2.760 1.513 14.500 0.000 0.000 3.000 1.000
sapply(mtcars, min) # Вычисление минимума всех столбцов # mpg cyl disp hp drat wt qsec vs am gear carb # 10.400 4.000 71.100 52.000 2.760 1.513 14.500 0.000 0.000 3.000 1.000
Так что, если вам не нужен ни один столбец.
 Вы хотите знать максимум и минимум всего набора данных? Так и быть…
Вы хотите знать максимум и минимум всего набора данных? Так и быть…Пример 5: Глобальный максимум и минимум фрейма данных
Вычисление глобального максимума и минимума таблицы данных довольно просто.Просто примените max и min, как мы делали в предыдущих примерах, но на этот раз вставьте имя всего фрейма данных между скобками:
.max(mtcars) # Применить алгоритм max ко всему data.frame # 472
max(mtcars) # Применить алгоритм max ко всему data.frame № 472
Глобальный максимум mtcars 472…
min(mtcars) # Применить алгоритм min ко всем данным.Рамка # 0
min(mtcars) # Применить алгоритм min ко всему data.frame # 0
…и глобальный минимум равен нулю.
Кстати, если сравнить эти результаты с результатами Примера 4, то можно увидеть, что глобальный максимум 472 находится в столбце disp , а глобальный минимум ноль как в vs , так и в .

Пример 6: макс. и мин. между двумя столбцами
Еще одна ситуация, когда макс и мин могут быть полезны, — это когда вы хотите узнать макс и мин между двумя столбцами или векторами.
Предположим, что мы хотим узнать максимальное и минимальное значение столбцов mpg и cyl. Мы можем рассчитать это с помощью следующих кодов R для макс…
max(c(mtcars$mpg, mtcars$cyl)) # Максимум между двумя столбцами/векторами # 33.9
max(c(mtcars$mpg, mtcars$cyl)) # Максимум между двумя столбцами/векторами № 33.9
… и со следующей строкой команды для min:
min(c(mtcars$mpg, mtcars$cyl)) # Минимум между двумя столбцами/векторами # 4
min(c(mtcars$mpg, mtcars$cyl)) # Минимум между двумя столбцами/векторами № 4
OK выглядит хорошо.Думаю, для столбцов этого достаточно, а как насчет максимумов и минимумов строк?
Пример 7: максимум и минимум строки
Конечно, обычно max и min применяются к столбцам.
 Но иногда может быть полезно знать максимум или минимум строки. Мы можем вычислить это с помощью следующего кода R:
Но иногда может быть полезно знать максимум или минимум строки. Мы можем вычислить это с помощью следующего кода R:max(mtcars[5,]) # Вычислить максимум одной строки # 360
max(mtcars[5,]) # Вычислить максимум одной строки № 360
Максимум пятой строки 360…
min(mtcars[5,]) # Вычислить минимум одной строки # 0
min(mtcars[5,]) # Вычислить минимум одной строки # 0
… и минимум равен нулю.
Примечание. Вы можете заменить цифру 5 любым номером строки.
Вы думаете, что доказали гибкость min и max? Дождитесь следующего примера...
Пример 8: Максимум и минимум строки символов
Максимум и минимум полезны для чисел и все, правильно?
Нет, это неправильно!
Мы также можем использовать max и min для определения минимума или максимума строк в алфавитном порядке. Мы можем сделать это, просто вставив вектор символов (или столбец, или строку) между скобками функций max и min.

Как и в предыдущих примерах, давайте начнем с некоторых примеров данных:
x_char <- c("hello", # Создать вектор символов "Р хороший", "максимальные и минимальные функции потрясающие", "aaaaaa")x_char <- c("hello", # Создать вектор символов "Р хороший", "максимальные и минимальные функции потрясающие", "аааааа")
Наш пример вектора содержит несколько случайных слов и фраз.Если мы хотим проверить, какая из этих строк является последней в алфавите, мы можем применить функцию max…
max(x_char) # Применить max к вектору символов # "R is nice"
max(x_char) # Применить max к вектору символов # "Р хороший"
…и если мы хотим проверить, какая строка является первой в алфавитном порядке, мы можем использовать функцию R min…
min(x_char) # Применить min к вектору символов # aaaaaa
min(x_char) # Применить min к вектору символов # аааааа
Очевидно, в этой группе строк аааааа.

Видео: макс, мин и аналогичные функции
В этом уроке я показал вам несколько способов использования max и min для нахождения максимального и минимального значений в R. Однако существует множество функций R, которые можно использовать аналогичным образом. Если вы хотите узнать об этом больше, я могу порекомендовать следующее видео канала BIO-RESEARCH на YouTube.
Чтобы воспроизвести это видео, примите файлы cookie YouTube. Принимая это, вы получаете доступ к контенту с YouTube, службы, предоставляемой внешней третьей стороной.
Политика конфиденциальности YouTube
Если вы примете это уведомление, ваш выбор будет сохранен, и страница обновится.
Принять контент YouTube
Дополнительное чтение
/* Добавьте свои собственные переопределения стиля формы MailChimp в таблицу стилей вашего сайта или в этот блок стилей.
Мы рекомендуем переместить этот блок и предыдущую ссылку CSS в HEAD вашего HTML-файла. */
*/
]]>Excel MIN и MAX Примеры функций и видео
Найдите самое низкое и самое высокое значение с помощью функций MIN и MAX.Используйте с функцией ЕСЛИ для создания формул МИН. ЕСЛИ и МАКС. ЕСЛИ или используйте МИН. ЕСЛИ и МАКС. ЕСЛИ в Excel 365.
МИН. и МАКС. функции
Чтобы увидеть краткий обзор того, как вы можете создавать свои собственные формулы MIN, MAX, MIN, IF и MAX, если, вы можете посмотреть это короткое видео.
МИН Функция
Чтобы найти наименьшее значение в диапазоне ячеек, используйте функцию МИН. Например, эта формула найдет наименьшее значение в ячейках h3:h27
.=МИН(ч3:ч27)
МАКС. функция
Чтобы найти наибольшее значение в диапазоне ячеек, используйте функцию МАКС.Например, эта формула найдет наибольшее значение в ячейках h3:h27
.=МАКС(ч3:ч27)
МИН.
 и МАКС. с критериями
и МАКС. с критериямиВ Excel 2019 или Excel для Office 365 вы можете использовать функции MINIFS и MAXIFS, показанные ниже, чтобы найти минимальное значение на основе одного или нескольких критериев.
Для более ранних версий Excel используйте формулу МИН ЕСЛИ или функцию МАКСИМСЛИ, показанную ниже.
Функция МИНИФС
Используйте функцию MINIFS, чтобы найти наименьшее число на основе одного или нескольких критериев.
MINIFS имеет 3 обязательных аргумента:
- min_range : Диапазон, в котором находится минимальное значение
- range1 : Первый диапазон для проверки критерия
- критерии1 : Первый критерий
MINIFS — один критерий
Например, эта формула (для Excel 365) находит минимальное количество для названия продукта в ячейке B6.

- =MINIFS(tblProdCust[Qty], tblProdCust[Product], B4#)
В ячейке B4 есть формула разлива для создания уникального списка продуктов. В формуле MINIFS есть оператор сброса (#) в конце этой ссылки на ячейку — B4# — поэтому результаты MINIFS также переносятся вниз.
Excel 2019 : формулы переноса недоступны в Excel 2019. В этой версии обратитесь к ячейке B4 без оператора сброса и вручную скопируйте формулу вниз.
- =MINIFS(tblProdCust[Qty], tblProdCust[Product], B4 )
MINIFS — два критерия
Чтобы использовать два или более критериев с MINIFS, используйте необязательные аргументы для дополнительных диапазонов критериев и критериев.
Например, эта формула (для Excel 365) находит минимальное количество для клиента, выбранного в ячейке C3, и название продукта в ячейке B6.

- =MINIFS(tblProdCust[Qty], tblProdCust[Product], B6#, tblProdCust[Cust], $C$3)
В ячейке B6 есть формула разлива для создания уникального списка продуктов.Формула MINIFS относится к той ячейке с оператором разлива — B6# — поэтому результаты MINIFS тоже разливаются вниз.
Excel 2019 : формулы переноса недоступны в Excel 2019. В этой версии обратитесь к ячейке B6 без оператора сброса и вручную скопируйте формулу вниз.
- =MINIFS(tblProdCust[Qty], tblProdCust[Product], B6, tblProdCust[Cust], $C$3)
Функция МАКСИФС
В Excel 2019 или Excel для Office 365 вы можете использовать функцию МАКСИФМН, чтобы найти максимальное значение на основе одного или нескольких критериев.Для более ранних версий Excel используйте функцию MAXIFS, показанную ниже.
MAXIFS имеет 3 обязательных аргумента:
- max_range : Диапазон, в котором находится максимальное значение
- range1 : Первый диапазон для проверки критерия
- критерии1 : Первый критерий
MAXIFS — один критерий
Например, эта формула (для Excel 365) находит максимальное количество для названия продукта в ячейке B6.

- =MAXIFS(tblProdCust[Qty], tblProdCust[Product], B4#)
В ячейке B6 есть формула разлива для создания уникального списка продуктов. В формуле MAXIFS есть оператор сброса (#) в конце этой ссылки на ячейку — B4# — поэтому результаты MAXIFS также переносятся вниз.
Excel 2019 : формулы переноса недоступны в Excel 2019. В этой версии обратитесь к ячейке B4 без оператора сброса и вручную скопируйте формулу вниз.
- =MAXIFS(tblProdCust[Qty], tblProdCust[Product], B4)
MAXIFS — два критерия
Чтобы использовать два или более критериев с MAXIFS, используйте необязательные аргументы для дополнительных диапазонов критериев и критериев.
Например, эта формула (для Excel 365) находит максимальное количество для клиента, выбранного в ячейке C3, и название продукта в ячейке B6.

- =MAXIFS(tblProdCust[Qty], tblProdCust[Product], B6#, tblProdCust[Cust], $C$3)
В ячейке B6 есть формула разлива для создания уникального списка продуктов.Формула MAXIFS относится к той ячейке с оператором разлива — B6# — поэтому результаты MAXIFS также разливаются вниз.
Excel 2019 : формулы переноса недоступны в Excel 2019. В этой версии обратитесь к ячейке B6 без оператора сброса и вручную скопируйте формулу вниз.
- =MAXIFS(tblProdCust[Qty], tblProdCust[Product], B6, tblProdCust[Cust], $C$3)
МИН. ЕСЛИ Формула
Хотя в Excel есть функции СУММЕСЛИ и СЧЁТЕСЛИ, не является функцией MINIF.Чтобы создать свой собственный MINIF, вы можете комбинировать Функции МИН и ЕСЛИ в формуле массива.
В этом примере мы найдем наименьшее значение для определенного продукта.
 в списке продаж с несколькими продуктами. Формула будет введена
в ячейке D2, затем копируется в D5.
в списке продаж с несколькими продуктами. Формула будет введена
в ячейке D2, затем копируется в D5.Сначала введите функции МИН и ЕСЛИ и их открывающие скобки:
Затем выберите названия продуктов в списке продаж и нажмите клавишу F4. ключ, чтобы заблокировать ссылку.
Введите знак равенства и щелкните ячейку с критериями названия продукта. Эта ссылка не будет заблокирована.
Введите запятую, затем выберите ячейки количества в списке продаж. Нажмите клавишу F4, чтобы заблокировать эту ссылку.
- = МИН(ЕСЛИ($G$2:$G$17=C2,$H$2:$H$17
Чтобы закончить формулу, введите две закрывающие скобки, а затем нажмите Ctrl+Shift+Enter для массива-введите формулу.
- = МИН(ЕСЛИ($G$2:$G$17=C2,$H$2:$H$17))
В формуле в строке формул, показанной выше, вы можете видеть, что фигурные скобки были автоматически добавлены в начале и в конце формула, потому что она была введена массивом.

Если вы не видите эти фигурные скобки, значит, вы нажали Enter, а не Ctrl + Shift + Enter. Чтобы исправить это, щелкните где-нибудь в формуле бар и нажмите Ctrl + Shift + Enter.
Затем скопируйте формулу вниз, в строки ниже, чтобы увидеть минимум для каждого из продуктов.
МАКС. ЕСЛИ Формула
Хотя в Excel есть функции СУММЕСЛИ и СЧЁТЕСЛИ, не является функцией MAXIF. Чтобы создать свой собственный MAXIF, вы можете комбинировать Функции MAX и IF в формуле массива.
В этом примере мы найдем наибольшее значение для определенного продукта. в списке продаж с несколькими продуктами.
Сначала введите функции MAX и IF и их открывающие скобки:
Затем выберите названия продуктов в списке продаж и нажмите клавишу F4. ключ, чтобы заблокировать ссылку.

Введите знак равенства и щелкните ячейку с критериями названия продукта. Эта ссылка не будет заблокирована.
Введите запятую, затем выберите ячейки количества в списке продаж. Нажмите клавишу F4, чтобы заблокировать эту ссылку.
- =МАКС(ЕСЛИ($G$2:$G$17=C2,$H$2:$H$17
Чтобы закончить формулу, введите две закрывающие скобки, а затем нажмите Ctrl+Shift+Enter для массива-введите формулу.
- =МАКС(ЕСЛИ($G$2:$G$17=C2,$H$2:$H$17))
В формуле в строке формул, показанной выше, вы можете видеть, что фигурные скобки были автоматически добавлены в начале и в конце формула, потому что она была введена массивом.
Если вы не видите эти фигурные скобки, значит, вы нажали Enter, а не Ctrl + Shift + Enter.
 Чтобы исправить это, щелкните где-нибудь в формуле
бар и нажмите Ctrl + Shift + Enter.
Чтобы исправить это, щелкните где-нибудь в формуле
бар и нажмите Ctrl + Shift + Enter.Затем скопируйте формулу вниз, в строки ниже, чтобы увидеть минимум для каждого из продуктов.
МАКС. ЕСЛИ с несколькими критериями
В предыдущем примере мы нашли максимальное количество для определенного продукта, поэтому критерий был только один — название продукта.
Вы также можете использовать метод MAX IF с несколькими критериями, включение в формулу дополнительных функций ЕСЛИ. Например, если данные включают имя клиента, мы могли бы найти наибольшее количество для каждого продукта, для конкретного клиента.
Имя клиента вводится в ячейку D1 . В ячейках C4:C7 перечислены названия продуктов.
Введите следующую формулу в ячейку D4 и введите ее в виде массива, нажав Ctrl+Shift+Ввод.
 Затем скопируйте формулу в ячейку D7.
Затем скопируйте формулу в ячейку D7.- =МАКС(ЕСЛИ($H$2:$H$17=C4,ЕСЛИ($I$2:$I$17=$D$1,$J$2:$J$17)))
- Формула проверяет столбец H на наличие названий продуктов, соответствующих записи в ячейке С4.
- Затем он проверяет столбец I на наличие имен клиентов, совпадающих с именем в ячейке D1.
- Для этих строк находит наибольшее количество в столбце J.
Получить последнюю цену продукта
Если у вас есть список цен и дат продуктов, вы можете использовать формулу, чтобы найти последнюю дату ценообразования для определенного продукта:
Затем используйте СУММЕСЛИМН или СУММПРОИЗВ, чтобы получить цену этого продукта, в эту дату.
Последняя цена с функцией MAXIFS
В Excel 2019 или Excel для Office 365 вы можете использовать эту формулу MAXIFS, чтобы найти последнюю цену.

В этом примере есть таблица цен с продуктом, клиентом, датой и ценой.
В решении можно использовать две формулы: одну для нахождения самой последней цены, а другую для нахождения цены на эту дату.
Эта формула в C4 возвращает последнюю дату для выбранного продукта и клиента:
- =MAXIFS(tblPrice[Дата], tblPrice[Продукт], A4, tblPrice[Cust], B4)
Далее эта формула в ячейке D4 возвращает цену на эту дату, а также выбранный продукт и клиента:
- =СУММЕСЛИМН(Ценатаблицы[Цена],Ценатаблицы[Продукт],A4,Ценатаблицы[Заказ],B4,Ценатаблицы[Дата],C4)
Или используйте эту универсальную формулу в ячейке D6 , чтобы найти цену на последнюю дату:
- =СУММЕСЛИМН(Ценатаблицы[Цена],Ценатаблицы[Продукт],A4,Ценатаблицы[Заказ],B4,Ценатаблицы[Дата],МАКСИФМ(Ценатаблицы[Дата],Ценатаблицы[Продукт],A4,Ценатаблицы[ЦенаЗаказ],B4 ))
Последняя цена с формулой MAX/IF
В этом примере есть прайс-лист с продуктом, датой и ценой.

Чтобы найти самую последнюю цену на конкретный продукт, начните с использования MAX и ЕСЛИ, чтобы получить последнюю дату для этого продукта. Название продукта -- Ручки -- вводится в ячейку A12.
Чтобы найти последнюю дату ценообразования для этого продукта, введите следующее формулу в ячейке B12 и нажмите Ctrl + Shift + Введите :
- =МАКС(ЕСЛИ($A$2:$A$9=A12, $B$2:$B$9))
Затем, чтобы найти цену на этот продукт на эту дату, введите следующие СУММЕСЛИМН формула в ячейке C12:
- =СУММЕСЛИМН($C$2:$C$9, $A$2:$A$9,A12, $B$2:$B$9,B12)
Функция СУММЕСЛИМН доступна в Excel 2007 и более поздних версиях.Для более ранних версий Excel вы можете использовать функцию СУММПРОИЗВ. функция:
- =СУММПРОИЗВ(($A$2:$A$9=A12) *($B$2:$B$9=B12) *($C$2:$C$9))
MIN IF и MAX IF со сводной таблицей
При наличии некоторых данных простой способ найти наименьшее и наибольшее значения для определенного элемента — использовать сводную таблицу.
 Он автоматически создает список всех элементов, и вы можете отображать суммы как минимум или максимум.
Он автоматически создает список всех элементов, и вы можете отображать суммы как минимум или максимум.В этом видео показаны шаги, а под видео есть письменные инструкции.
Сводная таблица MIN IF и MAX IF
На приведенном ниже снимке экрана поле TotalPrice дважды добавлено в область значений. В одном столбце сводная функция сводного поля была изменена на MIN, а в другом — на MAX.
Из этой сводной таблицы можно быстро увидеть минимальную и максимальную суммы в зависимости от названия продукта.Например:
- MIN IF Отруби - 48,62
- MAX IF Крендели с солью — 97,65
Сводная таблица MINIFS и MAXIFS
С помощью сводной таблицы вы также можете видеть минимальное и максимальное количество на основе нескольких критериев, таких как новые функции Excel MINIFS и MAXIFS. Например:
- МИНИФС Восток, Барс - 20
- MAXIFS West, Закуски - 114
Извлечь MIN и MAX из сводной таблицы
Если вам нужно использовать значения Min и Max из сводной таблицы в других формулах, используйте функцию GetPivotData.
 В этом видео показано, как использовать функцию GetPivotData, а под видео есть письменные инструкции.
В этом видео показано, как использовать функцию GetPivotData, а под видео есть письменные инструкции.Получить MINIFS и MAXIFS с помощью GETPIVOTDATA
Чтобы извлечь значения из сводной таблицы, используйте функцию GetPivotData. В этом примере вы можете выбрать название региона в ячейке A4 и название категории в ячейке B4.
Эта формула находится в ячейке C4, чтобы получить минимальное количество для выбранного региона и категории:
- =GETPIVOTDATA("Минимальное количество",$A$7, "Регион",A4,"Категория",B4)
Эта формула находится в ячейке D4, чтобы получить максимальное количество для выбранного региона и категории:
- =GETPIVOTDATA("Максимальное количество",$A$7, "Регион",A4,"Категория",B4)
Получить образцы файлов
- Все версии Excel : Чтобы увидеть формулы MIN и MAX, вы можете загрузить
Пример файла MIN и MAX.
 Заархивированный файл имеет формат Excel xlsx и не содержит макросов.
Заархивированный файл имеет формат Excel xlsx и не содержит макросов. - Excel 365 или 2019 : чтобы увидеть формулы MAXIFS и MINIFS, вы можете загрузить образец файла MINIFS и MAXIFS. Заархивированный файл имеет формат Excel xlsx и не содержит макросов.
- Сводная таблица МИН. ЕСЛИ и МАКС. ЕСЛИ : Чтобы увидеть примеры МИН. ЕСЛИ и МАКС. Заархивированный файл имеет формат Excel xlsx и не содержит макросов.
Другие уроки
Список функций
Список совпадающих элементов
АГРЕГАТ
СРЕДНЕЕ
ВЫБЕРИТЕ
ИНДЕКС / ПОИСКПОЗ
ТЕКСТ
Python max() и min() — поиск максимума и минимума в списке или массиве
Примеры Python для поиска наибольшего (или наименьшего) элемента в коллекции (например, списке, наборе или массиве) сопоставимых элементов с использованием max( ) и методов min() .

1. Функция Python max()
max()функция используется для –- Вычисление максимального значения, переданного в ее аргументе.
- Максимальное лексикографическое значение, если в качестве аргументов передаются строки.
1.1. Найти наибольшее целое число в массиве
>>> числа = [1, 8, 2, 23, 7, -4, 18, 23, 42, 37, 2] >>> макс(числа) 42 #Максимальное значение в массиве
1.2. Найти самую большую строку в массиве
>>> blogName = ["как","чтобы","делать","в","java"] >>> макс(имя_блога) 'to' # Наибольшее значение в массиве
1.3. Найдите максимальный ключ или значение
Немного сложная структура.
>>> цены = { «как»: 45,23, 'до': 612,78, «делать»: 205,55, «в»: 37,20, «Ява»: 10,75 } >>> макс( цены.значения() ) 612,78 >>> макс( цены.ключи() ) #или макс( цены ). По умолчанию это ключи(). 'к'2.
 Функция Python min()
Функция Python min()Эта функция используется для –
- вычисления минимума значений, переданных в ее аргументе.
- лексикографически наименьшее значение, если в качестве аргументов передаются строки.
2.1. Найти наименьшее целое число в массиве
>>> числа = [1, 8, 2, 23, 7, -4, 18, 23, 42, 37, 2] >>> мин(числа) -4 #Минимальное значение в массиве
2.2. Найти наименьшую строку в массиве
>>> blogName = ["как","чтобы","делать","в","java"] >>> мин(имя_блога) 'do' #наименьшее значение в массиве
2.3. Найти минимальный ключ или значение
Немного сложная структура.
>>> цены = { «как»: 45,23, «к»: 612.78, «делать»: 205,55, «в»: 37,20, «Ява»: 10,75 } >>> мин(цены.значения()) 10,75 >>> мин( цены.ключи() ) #или мин( цены ). По умолчанию это ключи(). 'делать'Счастливого обучения!!
Дайте нам знать, если вам понравился пост.

 2-4x$ в замкнутой области, ограниченной линиями $x=3$, $y=0$ и $y=x+1$.
2-4x$ в замкнутой области, ограниченной линиями $x=3$, $y=0$ и $y=x+1$.
 Однако стоит помнить, что рисунок не может служить доказательством. Рисунок — лишь иллюстрация для наглядности.
Однако стоит помнить, что рисунок не может служить доказательством. Рисунок — лишь иллюстрация для наглядности. 2-12\cdot(-3)+16\cdot 4=125.
\end{aligned}
2-12\cdot(-3)+16\cdot 4=125.
\end{aligned}
 Приравняем производную нулю ()
и получим две критические точки: и
. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на
концах отрезка и в точке ,
так как точка не
принадлежит отрезку [-1, 2]
. Эти значения функции — следующие: ,
,
. Из этого следует, что
Приравняем производную нулю ()
и получим две критические точки: и
. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на
концах отрезка и в точке ,
так как точка не
принадлежит отрезку [-1, 2]
. Эти значения функции — следующие: ,
,
. Из этого следует, что 


 Она определена и дифференцируема всюду в
]0, +∞[
, причём
Она определена и дифференцируема всюду в
]0, +∞[
, причём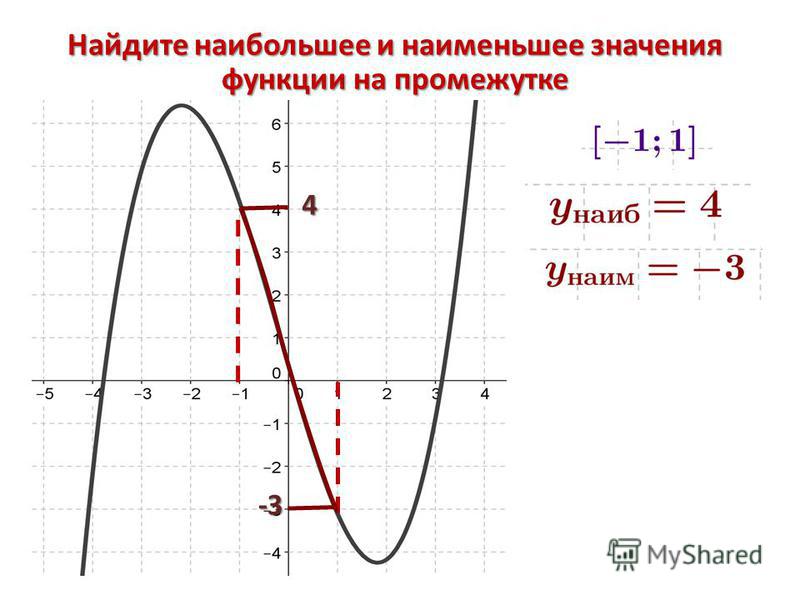
 2}$
2}$ 2=0 ; х-3=0; х+3=0$
2=0 ; х-3=0; х+3=0$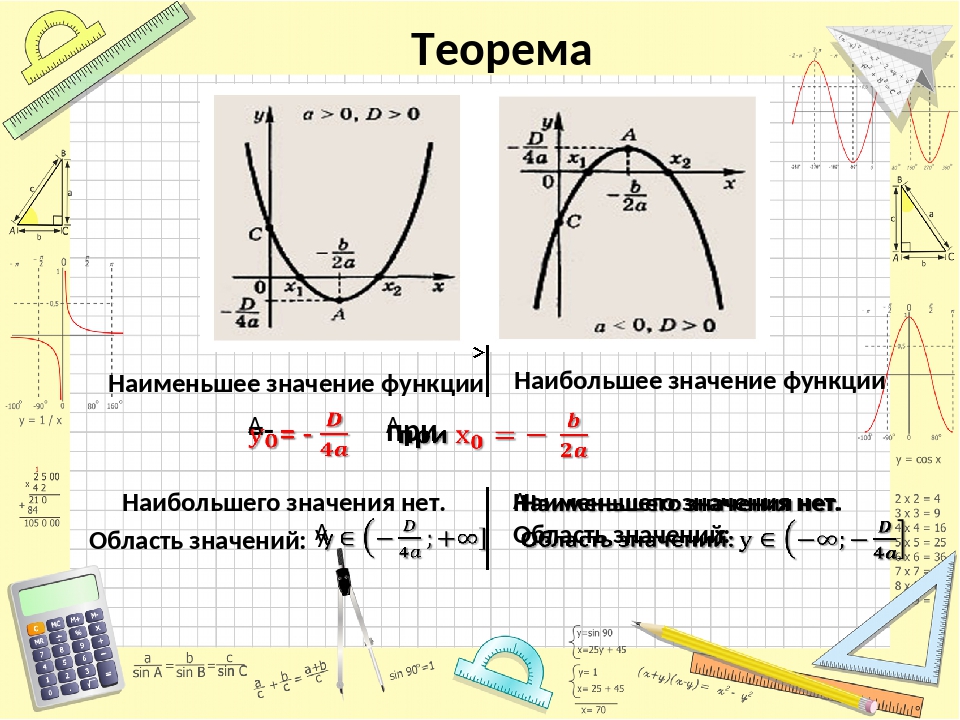 Если в точке x * выполняется условие:
Если в точке x * выполняется условие: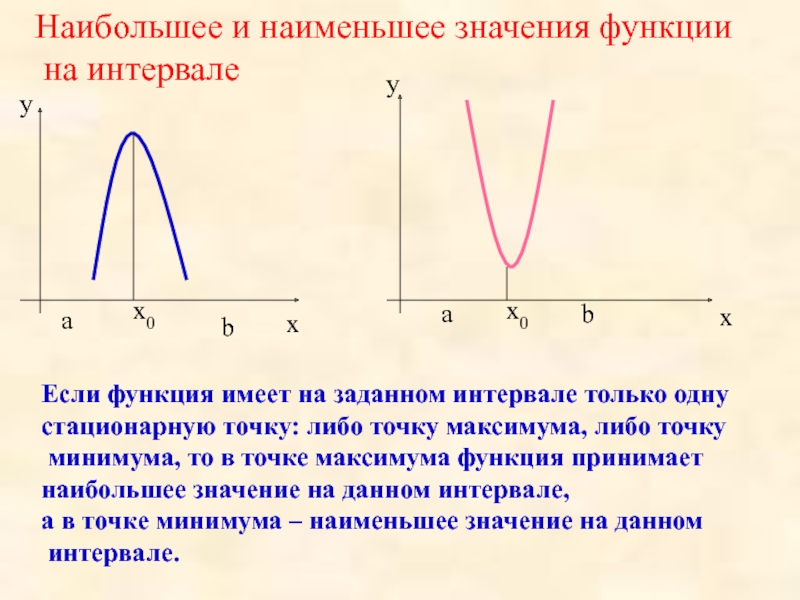


 На рисунке изображён график её производной. Найти точку xo, в которой функция принимает наибольшее значение, если f(-1)≥f(9).
На рисунке изображён график её производной. Найти точку xo, в которой функция принимает наибольшее значение, если f(-1)≥f(9).



 данные.
данные. Мы нажмем ENTER , а затем нам будет представлен результат, который в данном случае является числом 18.
Мы нажмем ENTER , а затем нам будет представлен результат, который в данном случае является числом 18. WorksheetFunction.Min(ws.Range("B2:B20"))
Конечный переходник
WorksheetFunction.Min(ws.Range("B2:B20"))
Конечный переходник  С другой стороны уравнения, мы сначала вызываем наше приложение , чтобы мы могли также вызвать функцию рабочего листа .Затем мы вызываем функцию Min , чтобы вернуть минимальное значение нашего диапазона.
С другой стороны уравнения, мы сначала вызываем наше приложение , чтобы мы могли также вызвать функцию рабочего листа .Затем мы вызываем функцию Min , чтобы вернуть минимальное значение нашего диапазона. Max(ws.Range("B2:B20"))
Конечный переходник
Max(ws.Range("B2:B20"))
Конечный переходник 
 Затем мы используем индексную позицию 0 для печати первого элемента и последнюю индексную позицию для печати последнего элемента в списке.
Затем мы используем индексную позицию 0 для печати первого элемента и последнюю индексную позицию для печати последнего элемента в списке. append(значение)
наименьший = наибольший = NumList[0]
для j в диапазоне (1, число):
если (наименьший > NumList[j]):
наименьший = NumList[j]
минимальная_позиция = j
если (самый большой < NumList[j]):
наибольший = NumList[j]
макс_позиция = j
print("Самый маленький элемент в этом списке: ", самый маленький)
print("Позиция индекса наименьшего элемента в этом списке: ", min_position)
print("Самый большой элемент в этом списке: ", самый большой)
print("Индексная позиция самого большого элемента в этом списке: ", max_position)
append(значение)
наименьший = наибольший = NumList[0]
для j в диапазоне (1, число):
если (наименьший > NumList[j]):
наименьший = NumList[j]
минимальная_позиция = j
если (самый большой < NumList[j]):
наибольший = NumList[j]
макс_позиция = j
print("Самый маленький элемент в этом списке: ", самый маленький)
print("Позиция индекса наименьшего элемента в этом списке: ", min_position)
print("Самый большой элемент в этом списке: ", самый большой)
print("Индексная позиция самого большого элемента в этом списке: ", max_position) 

 Начнем с сортировки списка в порядке возрастания. Затем мы назначаем идентификатор записи каждой строке данных. Отфильтруйте, чтобы выбрать идентификатор записи = 2, и используйте инструмент выбора, чтобы удалить поле идентификатора записи (нам это не нужно в нашем конечном результате), и это оставит нас с нашим ответом «6».
Начнем с сортировки списка в порядке возрастания. Затем мы назначаем идентификатор записи каждой строке данных. Отфильтруйте, чтобы выбрать идентификатор записи = 2, и используйте инструмент выбора, чтобы удалить поле идентификатора записи (нам это не нужно в нашем конечном результате), и это оставит нас с нашим ответом «6». В разделе «Список значений» мы выберем «Установить значения вручную» и в разделе «Свойства» введите:
В разделе «Список значений» мы выберем «Установить значения вручную» и в разделе «Свойства» введите:
 здесь.
здесь.
 Давайте сначала создадим пример вектора:
Давайте сначала создадим пример вектора: Принимая это, вы получаете доступ к контенту с YouTube, службы, предоставляемой внешней третьей стороной.
Принимая это, вы получаете доступ к контенту с YouTube, службы, предоставляемой внешней третьей стороной. Давайте посмотрим, что произойдет, если мы применим max и min как раньше:
Давайте посмотрим, что произойдет, если мы применим max и min как раньше:
 Сделаем это на практике:
Сделаем это на практике:
 Вы хотите знать максимум и минимум всего набора данных? Так и быть…
Вы хотите знать максимум и минимум всего набора данных? Так и быть…
 Но иногда может быть полезно знать максимум или минимум строки. Мы можем вычислить это с помощью следующего кода R:
Но иногда может быть полезно знать максимум или минимум строки. Мы можем вычислить это с помощью следующего кода R:

 */
*/  и МАКС. с критериями
и МАКС. с критериями



 в списке продаж с несколькими продуктами. Формула будет введена
в ячейке D2, затем копируется в D5.
в списке продаж с несколькими продуктами. Формула будет введена
в ячейке D2, затем копируется в D5.

 Чтобы исправить это, щелкните где-нибудь в формуле
бар и нажмите Ctrl + Shift + Enter.
Чтобы исправить это, щелкните где-нибудь в формуле
бар и нажмите Ctrl + Shift + Enter. Затем скопируйте формулу в ячейку D7.
Затем скопируйте формулу в ячейку D7.

 Он автоматически создает список всех элементов, и вы можете отображать суммы как минимум или максимум.
Он автоматически создает список всех элементов, и вы можете отображать суммы как минимум или максимум. В этом видео показано, как использовать функцию GetPivotData, а под видео есть письменные инструкции.
В этом видео показано, как использовать функцию GetPivotData, а под видео есть письменные инструкции. Заархивированный файл имеет формат Excel xlsx и не содержит макросов.
Заархивированный файл имеет формат Excel xlsx и не содержит макросов.
 Функция Python min()
Функция Python min()