Наибольшее и наименьшее значение функции, формулы и примеры
Если функция $y=f(x)$ определена и непрерывна на отрезке $[a ; b]$ , то она на этом отрезке достигает своих наибольшего и наименьшего значений. Если свое наибольшее значение $M$ функция $f(x)$ принимает в точке $x_{0} \in[a ; b]$, то $M=f\left(x_{0}\right)$ будет локальным максимумом функции $f(x)$, так как в этом случае существует окрестность точки $x_{0}$, такая, что $f(x) \leq f\left(x_{0}\right)$ .
Однако свое наибольшее значение $M$ функция
$f(x)$ может принимать и на концах отрезка
$[a ; b]$ . Поэтому, чтобы найти наибольшее значение
$M$ непрерывной на отрезке
$[a ; b]$ функции
$f(x)$, надо найти все максимумы функции на интервале
$(a ; b)$ и значения
$f(x)$ на концах отрезка
$[a ; b]$, то есть
$f(a)$ и
$f(b)$, и выбрать среди них наибольшее. Вместо исследования
на максимум можно ограничиться нахождением значений функции в критических точках.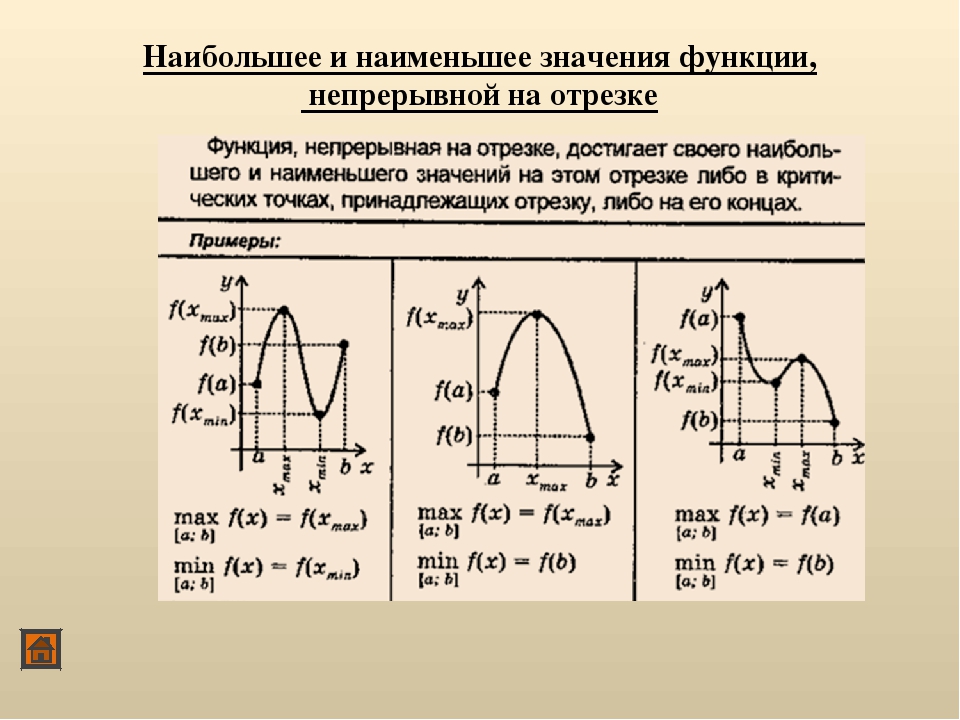
Из полученных значений нам надо оставить лишь те, которые принадлежат заданному промежутку $[0 ; 5]$ . Оба значения лежат в этом промежутке.
Находим значения функции в полученных стационарных точках из промежутка и на концах промежутка:
$y(0)=4 ; \quad y\left(\frac{1}{3}\right)=\frac{106}{27} \approx 3,92 ; y(5)=454$
Таким образом,
Ответ.
Читать дальше: выпуклость функции, точки перегиба.
Слишком сложно?
Наибольшее и наименьшее значение функции, непрерывной на отрезке не по зубам? Тебе ответит эксперт через 10 минут!
Урок 17. наибольшее и наименьшее значения функций — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №17. Наибольшее и наименьшее значения функции.
Перечень вопросов, рассматриваемых в теме
1) Нахождение наибольшего и наименьшего значения функции,
2)Определение алгоритма нахождения наибольшего и наименьшего значений функции на отрезке,
3) Рассмотреть прикладные задачи на нахождение наибольшего и наименьшего значений
Глоссарий по теме
Алгоритм нахождения наибольшего и наименьшего значений функции y = f(x) на отрезке [a; b]:
- Найти область определения функции D(f).

- Найти производную f‘ (x).
- Найти стационарные и критические точки функции, принадлежащие интервалу (a; b).
- Найти f(a), f(b) и значения функции в стационарных точках, принадлежащих интервалу (а; b).
- Среди полученных значений выбрать наибольшее и наименьшее.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Нахождение наибольшего и наименьшего значений функции на отрезке.
- Если функция непрерывна на отрезке, то она достигает на нем своего наибольшего и своего наименьшего значения.

- Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
- Если наибольшее (наименьшее) значение функции достигается внутри отрезка, то только в стационарной или критической точке.
Алгоритм нахождения наибольшего и наименьшего значений функции y = f(x) на отрезке [a; b]:
- Найти производную f‘ (x) стационарные и критические точки функции, принадлежащие интервалу (a; b).
- Найти f(a), f(b) и значения функции в стационарных точках, принадлежащих интервалу (а; b)и среди полученных значений выбрать наибольшее и наименьшее
Примеры и разбор решения заданий тренировочного модуля
№1.Найти наибольшее и наименьшее значения функции f (x) = 2x3 – 9x2 + 12x – 2 на отрезке [0; 3]
Решение. Действуем в соответствии с алгоритмом.
1) D(f) = (-∞; +∞).
2) f (x) = 6x2 – 18x + 12
3) Стационарные точки: х = 1; х = 2.
4) f(0) = -2
f(3) = 7
f(1) = 3
f(2) = 2
5) fнаим. =f(0) = -2
=f(0) = -2
fнаиб.=f(3) = 7.
Ответ: fнаим= -2
fнаиб.= 7.
№2.Найдите два положительных числа, сумма которых равна 16, а произведение наибольшее.
Решение.
Пусть первое число равно х,
Тогда второе число —
Следовательно,
Произведение этих чисел равно х(16 – х).
Составим функцию:
f(x) = x(16 – x)
x = 8 – единственная стационарная точка на интервале (0; 16), она является точкой максимума.
Следовательно, в этой точке функция F(x) = x(16 – x) принимает наибольшее значение.
Следовательно, два положительных числа, сумма которых равна 16, а произведение наибольшее, это 8 и 8.
Ответ: 8 и 8
Наибольшее и наименьшее значение функции.
В этой статье я расскажу о том, как применять умение находить производную сложной функции к исследованию функции: к нахождению ее наибольшего или наименьшего значения. А затем мы решим несколько задач из Задания В15 из Открытого банка заданий для подготовки к ЕГЭ по математике.
Как обычно, сначала вспомним теорию.
В начале любого исследования функции находим ее область определения.
Чтобы найти наибольшее или наименьшее значение функции , нужно исследовать, на каких промежутках функция возрастает, и на каких убывает.
Для этого надо найти производную функции и исследовать ее промежутки знакопостоянства, то есть промежутки, на которых производная сохраняет знак.
Промежутки, на которых производная функции положительна, являются промежутками возрастания функции.
Промежутки, на которых производная функции отрицательна, являются промежутками убывания функции.
1. Решим задание В15 (№ 245184)
Найдите наибольшее значение функции
Для его решения будем следовать такому алгоритму:
а) Найдем область определения функции
б) Найдем производную функции .
в) Приравняем ее к нулю.
г) Найдем промежутки знакопостоянства функции.
д) Найдем точку, в которой функция принимает наибольшее значение.
е) Найдем значение функции в этой точке.
Подробное решение этого задания я рассказываю в ВИДЕОУРОКЕ:
Вероятно, Ваш браузер не поддерживается. Чтобы использовать тренажёр «Час ЕГЭ», попробуйте скачатьFirefox
2. Решим задание В15 (№282862)
Найдите наибольшее значение функции на отрезке [1;3]
а) Найдем область определения функции . Эта функция определена при любом действительном значении
б) Найдем производную функции . Для этого удобно правую часть уравнения функции преобразовать в многочлен. Можно, конечно, использовать формулу для нахождения производной произведения, но в этом случае, мне кажется, что это нецелесообразно.
в) Приравняем производную к нулю:
,
г) Исследуем знаки производной:
Мы исследуем поведение функции на отрезке [1;3]:
Очевидно, что наибольшее значение на отрезке [1,3] функция принимает в точке максимума, при х=2. Найдем значение функции в этой точке:
Найдем значение функции в этой точке:
Ответ: 5
3. Решим задание В15 (№245180):
Найдите наибольшее значение функции
a) Найдем область определения функции . Выражение, стоящее под знаком логарифма должно быть больше нуля: . Пока на этом остановимся, решим неравенство, если в этом возникнет необходимость в процессе решения.
а) Найдем производную функции :
В таблице производных найдем производную логарифмической функции:
Для производной сложной функции эта формула выглядит так:
Выясним промежутки знакопостоянства выражения
Воспользуемся методом интервалов.
1. , , т.к. , поэтому это число не влияет на знак неравенства.
2. Т.к по область определения исходной функции , следовательно знаменатель дроби всегда больще нуля и дробь меняет знак только в нуле числителя.
3. Числитель равен нулю при . Проверим, принадлежит ли ОДЗ функции. Для этого проверим, выполняется ли условие при .
,
значит, точка принадлежит ОДЗ функции
Исследуем знак производной справа и слева от точки :
Мы видим, что наибольшее значение функция принимает в точке . Теперь найдем значение функции при :
Ответ: 4
Замечание 1. Заметим, что в этой задаче мы не находили область определения функции: мы только зафиксировали ограничения и проверили, принадлежит ли точка, в которой производная равна нулю области определения функции. В данной задаче этого оказалось достаточно. Однако, так бывает не всегда. Это зависит от задачи.
Замечание 2. При исследовании поведения сложной функции можно пользоваться таким правилом:- если внешняя функция сложной функции возрастающая, то функция принимает наибольшее значение в той же точке, в которой внутренняя функция принимает наибольшее значение. Это следует из определения возрастающей функции: функция возрастает на промежутке I, если большему значению аргумента из этого промежутка соответствует большее значение функции.

- если внешняя функция сложной функции убывающая, то функция принимает наибольшее значение в той же точке, в которой внутренняя функция принимает наименьшее значение. Это следует из определения убывающей функции: функция убывает на промежутке I, если большему значению аргумента из этого промежутка соответствует меньшее значение функции
В нашем примере внешняя функция — возрастает на всей области определения. Под знаком логарифма стоит выражение — квадратный трехчлен, который при отрицательном старшем коэффициенте принимает наибольшее значение в точке . Далее подставляем это значение х в уравнение функции и находим ее наибольшее значение.
И.В. Фельдман, репетитор по математике.
Как выделить наименьшее и наибольшее значение в Excel цветом
В процессе подготовки разного рода ранжирования или анализа показателей успешности, очень удобно если выделить цветом наилучший или наихудший результат. Как выделить максимальное значение в Excel цветом? Здесь существенно поможет условное форматирование. Преимуществом такого подхода является сохранение работоспособности автоматического выделения цветом лучших/худших показателей даже при добавлении или удалении данных из таблицы.
Преимуществом такого подхода является сохранение работоспособности автоматического выделения цветом лучших/худших показателей даже при добавлении или удалении данных из таблицы.
Как выделить цветом максимальное значение в Excel
Для примера возьмем таблицу расходов:
Чтобы молниеносно выделить наибольшие и наименьшие расходы делаем следующее:
- Выделите диапазон с расходами B2:B10 и выберите инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Создать правило».
- Выберите: «Использовать формулу для определения форматируемых ячеек».
- В поле ввода введите формулу: =МАКС($B$2:$B$10)=B2
- Нажмите на кнопку «Формат», чтобы выделить максимальное значение в столбце Excel. Для этого в появившемся окне «Формат ячеек» на вкладке «Заливка» выберите желаемый цвет заливки для ячеек. Например, зеленый. И нажмите ОК на всех открытых окнах.
В результате мы выделили цветом ячейку с максимальным числовым значением.
Как выбрать минимальное значение в Excel
Чтобы выделить цветом минимальное значение в Excel, повторите весь порядок действий, описанных выше. Только вместо функции МАКС, должна быть функция МИН. Данная функция позволяет выбрать наименьшее значение в таблице Excel. А вместо зеленого цвета заливки выберите красный цвет.
Только вместо функции МАКС, должна быть функция МИН. Данная функция позволяет выбрать наименьшее значение в таблице Excel. А вместо зеленого цвета заливки выберите красный цвет.
К одному и тому же диапазону должно быть применено 2 правила условного форматирования. Чтобы проверить выберите инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Управление правилами»
Финальный эффект применения двух правил условного форматирования для выделения цветом наибольшего и наименьшего значения столбца B (Расходы):
Принцип действий обоих правил одинаковый. Они отличаются только функциями =МАКС() и =МИН(). Более того аргументы функций идентичны. Первая функция =МАКС() ищет в несменяемом диапазоне с абсолютными ссылками $B$2:$B$10 максимальное значение. После функции стоит оператор сравнения с изменяемой текущей ячейкой которая имеет относительную ссылку начиная от B2. Правило условного форматирования читает данную формулу так: если число больше всех, то выделить цветом. Как только совпадает максимальное число (которое возвращает функция МАКС) со значением текущей ячейки, формула возвращает логическое значение ИСТИНА и сразу же применяется формат со соответствующим цветом заливки. Так же срабатывает правило для умного форматирования ячеек столбца и с функцией МИН.
Так же срабатывает правило для умного форматирования ячеек столбца и с функцией МИН.
Выделение цветом трех наименьших значений подряд
В разных ситуациях полезно применяется автоматическое выделение цветом трех ячеек с наименьшими значениями. Условное форматирование со соответственными формулами прекрасно справляется с данной задачей. Таблица с данными для примера:
Усложним немного задачу. Ячейка с наименьшим значением должна автоматически получить красный цвет заливки. Следующая ячейка с вторым наименьшим значением получит цвет заливки оранжевый. А третье наименьшее значение – желтый.
Чтобы добиться данного эффекта следует выполнить следующие действия:
- Выделите диапазон ячеек B2:B9 и выберите инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Создать правило»-«Использовать формулу для определения форматируемых ячеек».
- В поле ввода введите формулу: =НАИМЕНЬШИЙ($B$2:$B$9;1)=B2 и нажмите на кнопку «Формат», чтобы задать красный цвет заливки для ячейки.
 И нажмите ОК на всех открытых окнах.
И нажмите ОК на всех открытых окнах. - Не снимая выделения с диапазона B2:B9 сразу же создаем второе правило условного форматирования. Снова выберите инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Создать правило»-«Использовать формулу для определения форматируемых ячеек».
- В поле ввода введите формулу: =НАИМЕНЬШИЙ($B$2:$B$9;2)=B2 и нажмите на кнопку «Формат», чтобы задать оранжевый цвет заливки для ячейки. И нажмите ОК на всех окнах.
- Создайте третье правило. А в поле ввода введите формулу: =НАИМЕНЬШИЙ($B$2:$B$9;3)=B2 и нажмите на кнопку «Формат», чтобы задать желтый цвет заливки для ячейки. ОК на всех окнах.
- К одному и тому же диапазону должно быть применено 3 правила условного форматирования. Чтобы проверить выберите инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Управление правилами».
Три наименьшие значения автоматически выделились разными цветами.
Внимание! Если просматриваемый диапазон содержит несколько одинаковых минимальных значений все они будут выделены цветом.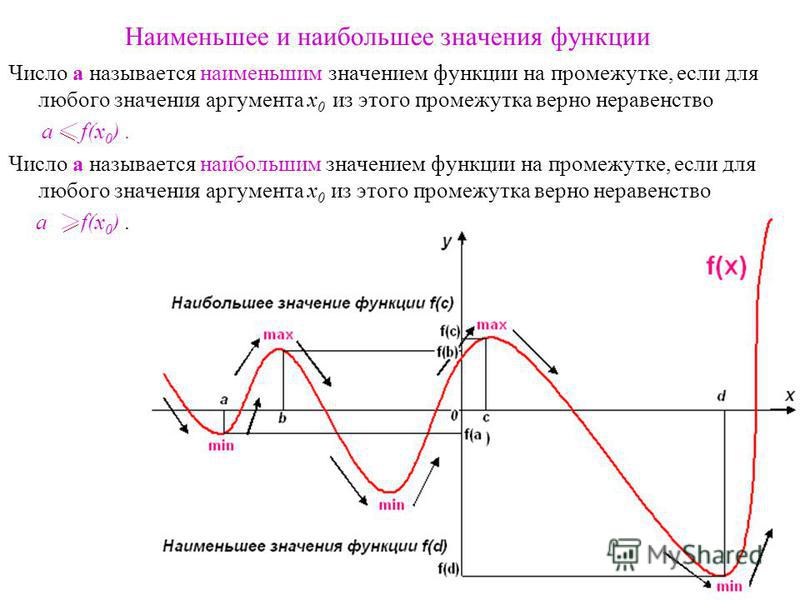
Аналогичным способом можно выделять цветом наибольшие значения. Просто изменить в формуле функцию НАИМЕНЬШИЙ на НАИБОЛЬШИЙ. Например: =НАИБОЛЬШИЙ($B$2:$B$9;3)=B2
Функция наименьший и наибольший в Excel
Функция =НАИМЕНЬШИЙ() ищет в заданном (в первом аргументе) диапазоне очередное наименьшее значение. Очередь указана во втором аргументе функции. То есть если во втором аргументе мы указали число 3, значит функция возвращает третье по очереди наименьшее значение заданного диапазона $B$2:$B$9. Если результат вычисления функции равен текущей ячейке значит к ней присваивается соответственный формат (цвет заливки). Важно отметить что в формуле для просмотра диапазона мы используем абсолютные адреса ссылки, а после оператора сравнения =B2 – относительные, так как значение функции сравнивается с каждой ячейкой выделенного диапазона. А функция НАИБОЛЬШИЙ работает обратно пропорционально.
Полезный совет! Если нет необходимости разбивать 3 наименьших значения на разные цвета, тогда необязательно создавать 3 правила условного форматирования для одного и того же диапазона.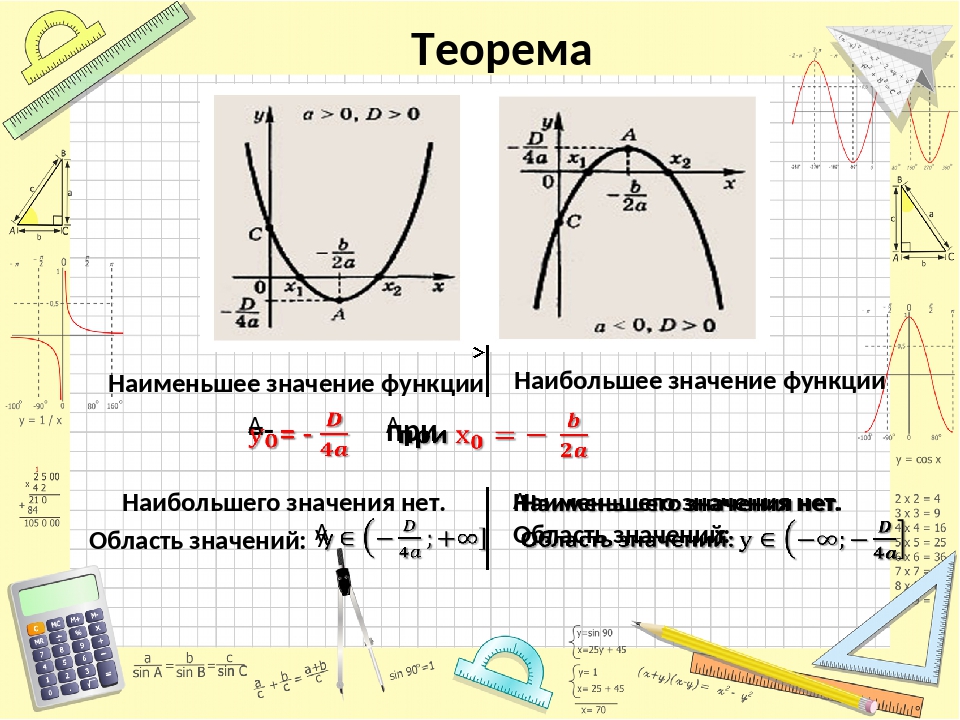 Достаточно просто немного изменить формулу добавив всего один символ оператора: =НАИМЕНЬШИЙ($B$2:$B$9;3)>=B2. То есть – больше или равно.
Достаточно просто немного изменить формулу добавив всего один символ оператора: =НАИМЕНЬШИЙ($B$2:$B$9;3)>=B2. То есть – больше или равно.
Все описанные способы хороши тем, что при изменении значений в ячейках они все равно будут работать автоматически.
Поиск наименьшего или наибольшего числа в диапазоне
Предположим, вы хотите узнать, у кого самый маленький показатель погрешности в производственной цехе или самая большая заработная плата в вашем отделе. Существует несколько способов вычисления наименьшего или наибольшего числа в диапазоне.
Если ячейки находятся в соединимой строке или столбце
-
Вы можете выбрать ячейку снизу или справа от чисел, для которых нужно найти наименьшее число.
-
На вкладке Главная в группе Редактирование щелкните стрелку рядом с кнопкой , выберите min (вычисляет наименьшее) или Max (вычисляет наибольшее) и нажмите клавишу ВВОД.

Если ячейки не находятся в подрядной строке или столбце
Для этого используйте функции МИН, МАКС, МАЛЫЙ или БОЛЬШОЙ.
Пример
Скопируйте следующие данные на пустой лист.
|
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
НАИБОЛЬШИЙ
MAX
MIN
НАИМЕНЬШИЙ
Наибольшее значение выражения
Чтобы найти наибольшее значение тригонометрического выражения, во многих случаях достаточно знать область значений синуса, косинуса, тангенса, котангенса и свойства неравенств.
Примеры.
Найти наибольшее значение выражения:
Решение:
Область допустимых значений данного выражения — вся числовая прямая:
ОДЗ: α∈(-∞; ∞).
Область значений косинуса — промежуток [-1;1]. Для оценки значений удобнее использовать двойное неравенство:
Умножаем неравенство почленно на 7. При умножении на положительное число знаки неравенства не изменяются:
Затем прибавляем почленно 5:
Таким образом, наибольшее значением выражения равно 12 (наименьшее — -2, область значений — [-2:12]).
Решение: ОДЗ: φ∈ (-∞; ∞).
Область значений синуса — промежуток [-1;1] или
При умножении на отрицательное число знаки неравенства меняются на противоположные:
Перепишем в порядке возрастания
Прибавляем почленно 4
Наибольшее значение выражения равно 7 (наименьшее — 1, область значений — [1;7]).
Решение: ОДЗ: х∈ (-∞; ∞).
Наибольшее значение выражения равно 10 (наименьшее — 8, область значений — [8;10]).
(Замечание. Если предварительно преобразовать данное выражение:
то можно упростить его оценку, поскольку в этом случае не нужно умножать неравенство на отрицательное число).
Решение: Дробь имеет смысл, если знаменатель отличен от нуля, поэтому ОДЗ: sinα≠0. Удобнее всего работать с ОДЗ на единичной окружности: точки α=0 и α=П, в которых sinα обращается в нуль, выкалываем:
Теперь можно упростить выражение, сократив его
Осталось оценить полученное выражение.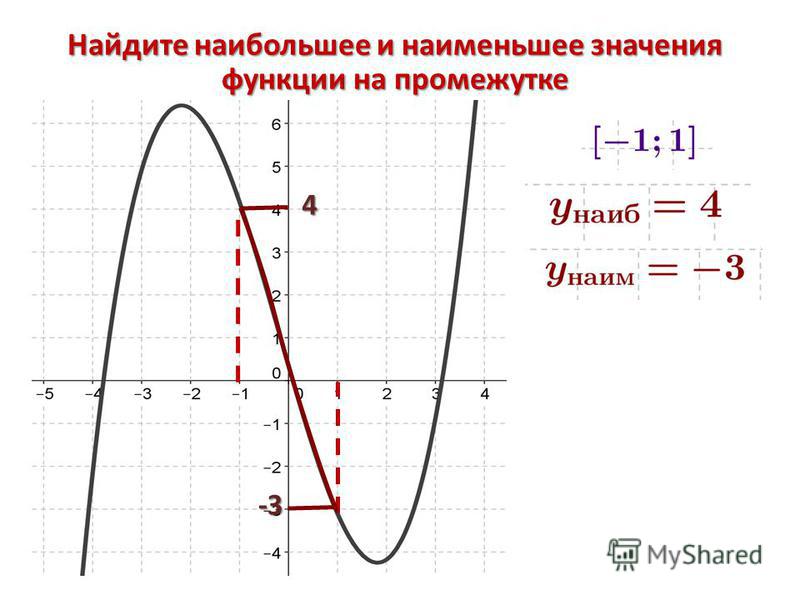
Однако, с учетом ОДЗ, имеем:
(cosα=1 при α=0, cosα=-1 при α=П).
Выражение не принимает ни наибольшего, ни наименьшего значений (область значений выражения — (8;10)).
В следующий раз продолжим рассматривать выражения с дробями, позже — выражения вида a∙sinα+b∙cosα.
Наибольшее и наименьшее значение функции теория. Исследование графика функции. Квадратичная функция записана через координаты вершины параболы
На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
Обычно мы определяем эти значения в рамках некоторого интервала x , который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [ a ; b ] , так и открытый интервал (a ; b) , (a ; b ] , [ a ; b) , бесконечный интервал (a ; b) , (a ; b ] , [ a ; b) либо бесконечный промежуток — ∞ ; a , (- ∞ ; a ] , [ a ; + ∞) , (- ∞ ; + ∞) .
В этом материале мы расскажем, как вычисляется наибольшее и наименьшее значение явно заданной функции с одной переменной y=f(x) y = f (x) .
Основные определения
Начнем, как всегда, с формулировки основных определений.
Определение 1
Наибольшее значение функции y = f (x) на некотором промежутке x – это значение m a x y = f (x 0) x ∈ X , которое при любом значении x x ∈ X , x ≠ x 0 делает справедливым неравенство f (x) ≤ f (x 0) .
Определение 2
Наименьшее значение функции y = f (x) на некотором промежутке x – это значение m i n x ∈ X y = f (x 0) , которое при любом значении x ∈ X , x ≠ x 0 делает справедливым неравенство f(X f (x) ≥ f (x 0) .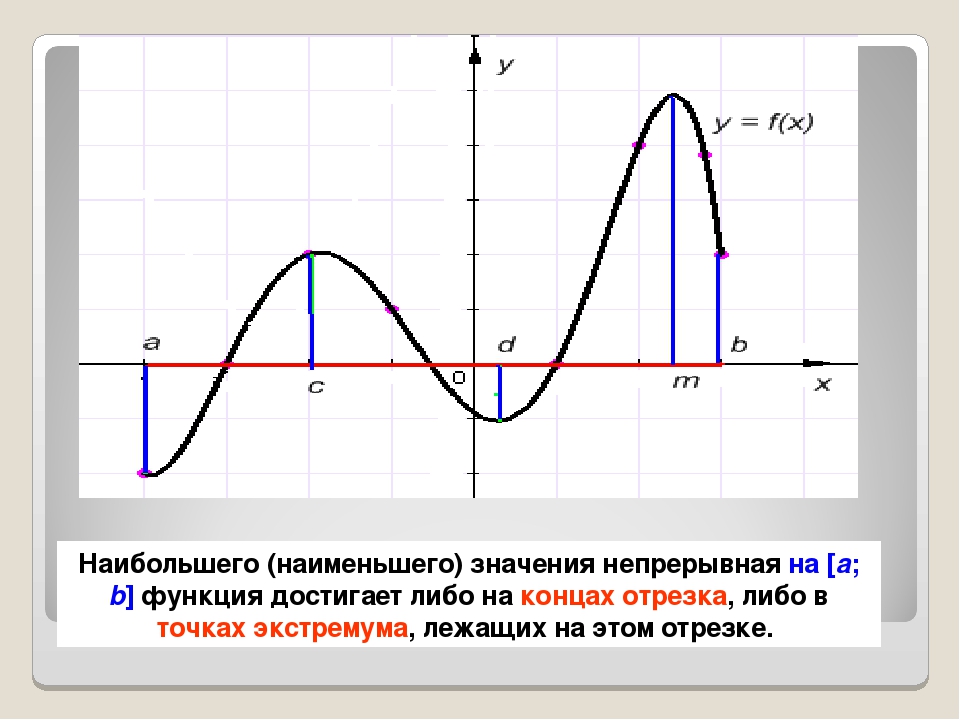
Данные определения являются достаточно очевидными. Еще проще можно сказать так: наибольшее значение функции – это ее самое большое значение на известном интервале при абсциссе x 0 , а наименьшее – это самое маленькое принимаемое значение на том же интервале при x 0 .
Определение 3
Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0 .
Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.
Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.
Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы может определить наибольшее или наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с бесконечным интервалом. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.
Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.
Более понятными эти моменты станут после изображения на графиках:
Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения (m a x y и m i n y) в стационарных точках, расположенных на отрезке [ — 6 ; 6 ] .
Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [ 1 ; 6 ] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.
На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [ — 3 ; 2 ] . Они соответствуют наибольшему и наименьшему значению заданной функции.
Теперь посмотрим на четвертый рисунок. В нем функция принимает m a x y (наибольшее значение) и m i n y (наименьшее значение) в стационарных точках на открытом интервале (- 6 ; 6) .
Если мы возьмем интервал [ 1 ; 6) , то можно сказать, что наименьшее значение функции на нем будет достигнуто в стационарной точке. Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x , равном 6 , если бы x = 6 принадлежала интервалу. Именно этот случай нарисован на графике 5 .
На графике 6 наименьшее значение данная функция приобретает в правой границе интервала (- 3 ; 2 ] , а о наибольшем значении мы не можем сделать определенных выводов.
На рисунке 7 мы видим, что функция будет иметь m a x y в стационарной точке, имеющей абсциссу, равную 1 . Наименьшего значения функция достигнет на границе интервала с правой стороны. На минус бесконечности значения функции будут асимптотически приближаться к y = 3 .
Если мы возьмем интервал x ∈ 2 ; + ∞ , то увидим, что заданная функция не будет принимать на нем ни наименьшего, ни наибольшего значения. Если x стремится к 2 , то значения функции будут стремиться к минус бесконечности, поскольку прямая x = 2 – это вертикальная асимптота. Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y = 3 . Именно этот случай изображен на рисунке 8 .
Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y = 3 . Именно этот случай изображен на рисунке 8 .
В этом пункте мы приведем последовательность действий, которую нужно выполнить для нахождения наибольшего или наименьшего значения функции на некотором отрезке.
- Для начала найдем область определения функции. Проверим, входит ли в нее заданный в условии отрезок.
- Теперь вычислим точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего их можно встретить у функций, аргумент которых записан под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом.
- Далее выясним, какие стационарные точки попадут в заданный отрезок. Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.

- Определим, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычисляем значения для x = a и x = b .
- 5. У нас получился ряд значений функции, из которых теперь нужно выбрать самое больше и самое маленькое. Это и будут наибольшее и наименьшее значения функции, которые нам нужно найти.
Посмотрим, как правильно применить этот алгоритм при решении задач.
Пример 1
Условие: задана функция y = x 3 + 4 x 2 . Определите ее наибольшее и наименьшее значение на отрезках [ 1 ; 4 ] и [ — 4 ; — 1 ] .
Решение:
Начнем с нахождения области определения данной функции. В этом случае ей будет множество всех действительных чисел, кроме 0 . Иными словами, D (y) : x ∈ (- ∞ ; 0) ∪ 0 ; + ∞ . Оба отрезка, заданных в условии, будут находиться внутри области определения.
Теперь вычисляем производную функции согласно правилу дифференцирования дроби:
y » = x 3 + 4 x 2 » = x 3 + 4 » · x 2 — x 3 + 4 · x 2 » x 4 = = 3 x 2 · x 2 — (x 3 — 4) · 2 x x 4 = x 3 — 8 x 3
Мы узнали, что производная функции будет существовать во всех точках отрезков [ 1 ; 4 ] и [ — 4 ; — 1 ] .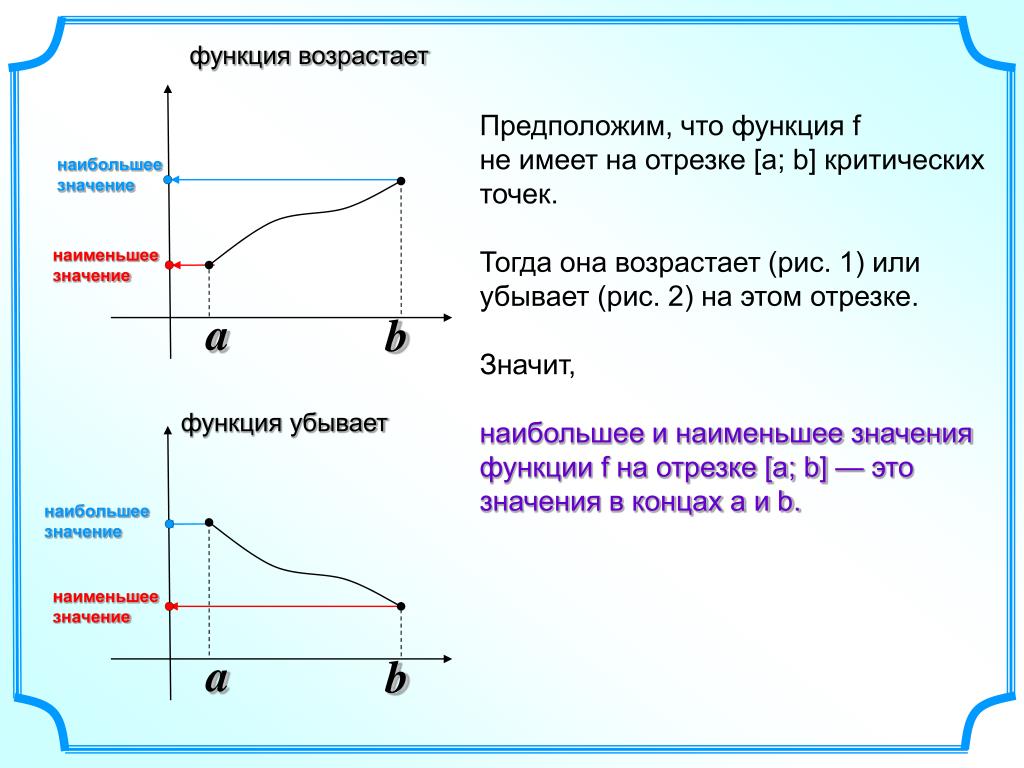
Теперь нам надо определить стационарные точки функции. Сделаем это с помощью уравнения x 3 — 8 x 3 = 0 . У него есть только один действительный корень, равный 2 . Он будет стационарной точкой функции и попадет в первый отрезок [ 1 ; 4 ] .
Вычислим значения функции на концах первого отрезка и в данной точке, т.е. для x = 1 , x = 2 и x = 4:
y (1) = 1 3 + 4 1 2 = 5 y (2) = 2 3 + 4 2 2 = 3 y (4) = 4 3 + 4 4 2 = 4 1 4
Мы получили, что наибольшее значение функции m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 будет достигнуто при x = 1 , а наименьшее m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 – при x = 2 .
Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:
y (- 1) = (- 1) 3 + 4 (- 1) 2 = 3
Значит, m a x y x ∈ [ — 4 ; — 1 ] = y (- 1) = 3 , m i n y x ∈ [ — 4 ; — 1 ] = y (- 4) = — 3 3 4 .
Ответ: Для отрезка [ 1 ; 4 ] — m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 , m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 , для отрезка [ — 4 ; — 1 ] — m a x y x ∈ [ — 4 ; — 1 ] = y (- 1) = 3 , m i n y x ∈ [ — 4 ; — 1 ] = y (- 4) = — 3 3 4 .
См. на рисунке:
Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
- Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
- Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
- Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0 , решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям.
 Их определяет вид интервала.
Их определяет вид интервала.
- Если интервал имеет вид [ a ; b) , то нам надо вычислить значение функции в точке x = a и односторонний предел lim x → b — 0 f (x) .
- Если интервал имеет вид (a ; b ] , то нам надо вычислить значение функции в точке x = b и односторонний предел lim x → a + 0 f (x) .
- Если интервал имеет вид (a ; b) , то нам надо вычислить односторонние пределы lim x → b — 0 f (x) , lim x → a + 0 f (x) .
- Если интервал имеет вид [ a ; + ∞) , то надо вычислить значение в точке x = a и предел на плюс бесконечности lim x → + ∞ f (x) .
- Если интервал выглядит как (- ∞ ; b ] , вычисляем значение в точке x = b и предел на минус бесконечности lim x → — ∞ f (x) .
- Если — ∞ ; b , то считаем односторонний предел lim x → b — 0 f (x) и предел на минус бесконечности lim x → — ∞ f (x)
- Если же — ∞ ; + ∞ , то считаем пределы на минус и плюс бесконечности lim x → + ∞ f (x) , lim x → — ∞ f (x) .
- В конце нужно сделать вывод на основе полученных значений функции и пределов.
 Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4 — 8 в первой части материала.
Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4 — 8 в первой части материала.
Условие: дана функция y = 3 e 1 x 2 + x — 6 — 4 . Вычислите ее наибольшее и наименьшее значение в интервалах — ∞ ; — 4 , — ∞ ; — 3 , (- 3 ; 1 ] , (- 3 ; 2) , [ 1 ; 2) , 2 ; + ∞ , [ 4 ; + ∞) .
Решение
Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в 0:
x 2 + x — 6 = 0 D = 1 2 — 4 · 1 · (- 6) = 25 x 1 = — 1 — 5 2 = — 3 x 2 = — 1 + 5 2 = 2 ⇒ D (y) : x ∈ (- ∞ ; — 3) ∪ (- 3 ; 2) ∪ (2 ; + ∞)
Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.
Теперь выполним дифференцирование функции и получим:
y » = 3 e 1 x 2 + x — 6 — 4 » = 3 · e 1 x 2 + x — 6 » = 3 · e 1 x 2 + x — 6 · 1 x 2 + x — 6 » = = 3 · e 1 x 2 + x — 6 · 1 » · x 2 + x — 6 — 1 · x 2 + x — 6 » (x 2 + x — 6) 2 = — 3 · (2 x + 1) · e 1 x 2 + x — 6 x 2 + x — 6 2
Следовательно, производные функции существуют на всей области ее определения.
Перейдем к нахождению стационарных точек. Производная функции обращается в 0 при x = — 1 2 . Это стационарная точка, которая находится в интервалах (- 3 ; 1 ] и (- 3 ; 2) .
Вычислим значение функции при x = — 4 для промежутка (- ∞ ; — 4 ] , а также предел на минус бесконечности:
y (- 4) = 3 e 1 (- 4) 2 + (- 4) — 6 — 4 = 3 e 1 6 — 4 ≈ — 0 . 456 lim x → — ∞ 3 e 1 x 2 + x — 6 = 3 e 0 — 4 = — 1
Поскольку 3 e 1 6 — 4 > — 1 , значит, m a x y x ∈ (- ∞ ; — 4 ] = y (- 4) = 3 e 1 6 — 4 . Это не дает нам возможности однозначно определить наименьшее значение функции. Мы можем только сделать вывод, что внизу есть ограничение — 1 , поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.
Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы. Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к — 3 с левой стороны, мы получим только интервал значений:
lim x → — 3 — 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 — 0 3 e 1 (x + 3) (x — 3) — 4 = 3 e 1 (- 3 — 0 + 3) (- 3 — 0 — 2) — 4 = = 3 e 1 (+ 0) — 4 = 3 e + ∞ — 4 = + ∞ lim x → — ∞ 3 e 1 x 2 + x — 6 — 4 = 3 e 0 — 4 = — 1
Значит, значения функции будут расположены в интервале — 1 ; + ∞
Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке x = — 1 2 , если x = 1 . Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к — 3 с правой стороны:
y — 1 2 = 3 e 1 — 1 2 2 + — 1 2 — 6 — 4 = 3 e 4 25 — 4 ≈ — 1 . 444 y (1) = 3 e 1 1 2 + 1 — 6 — 4 ≈ — 1 . 644 lim x → — 3 + 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 + 0 3 e 1 (x + 3) (x — 2) — 4 = 3 e 1 — 3 + 0 + 3 (- 3 + 0 — 2) — 4 = = 3 e 1 (- 0) — 4 = 3 e — ∞ — 4 = 3 · 0 — 4 = — 4
У нас получилось, что наибольшее значение функция примет в стационарной точке m a x y x ∈ (3 ; 1 ] = y — 1 2 = 3 e — 4 25 — 4 .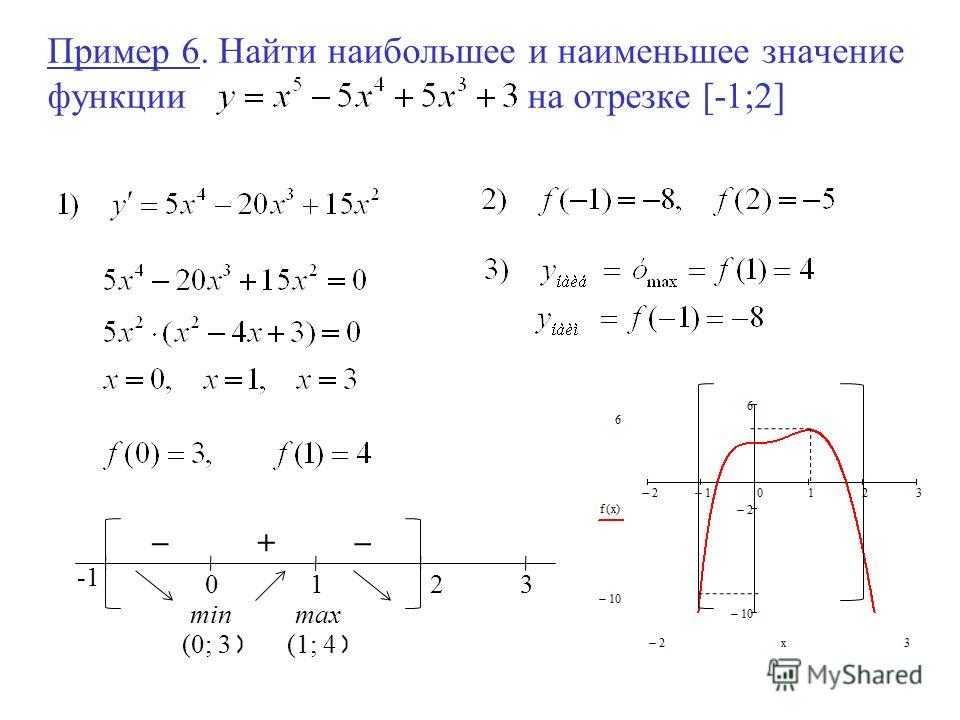 Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до — 4 .
Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до — 4 .
Для интервала (- 3 ; 2) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:
y — 1 2 = 3 e 1 — 1 2 2 + — 1 2 — 6 — 4 = 3 e — 4 25 — 4 ≈ — 1 . 444 lim x → — 3 + 0 3 e 1 x 2 + x — 6 — 4 = — 4 lim x → 2 — 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 + 0 3 e 1 (x + 3) (x — 2) — 4 = 3 e 1 (2 — 0 + 3) (2 — 0 — 2) — 4 = = 3 e 1 — 0 — 4 = 3 e — ∞ — 4 = 3 · 0 — 4 = — 4
Значит, m a x y x ∈ (- 3 ; 2) = y — 1 2 = 3 e — 4 25 — 4 , а наименьшее значение определить невозможно, и значения функции ограничены снизу числом — 4 .
Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [ 1 ; 2) наибольшее значение функция примет при x = 1 , а найти наименьшее невозможно.
На промежутке (2 ; + ∞) функция не достигнет ни наибольшего, ни наименьшего значения, т. е. она будет принимать значения из промежутка — 1 ; + ∞ .
е. она будет принимать значения из промежутка — 1 ; + ∞ .
lim x → 2 + 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 + 0 3 e 1 (x + 3) (x — 2) — 4 = 3 e 1 (2 + 0 + 3) (2 + 0 — 2) — 4 = = 3 e 1 (+ 0) — 4 = 3 e + ∞ — 4 = + ∞ lim x → + ∞ 3 e 1 x 2 + x — 6 — 4 = 3 e 0 — 4 = — 1
Вычислив, чему будет равно значение функции при x = 4 , выясним, что m a x y x ∈ [ 4 ; + ∞) = y (4) = 3 e 1 14 — 4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y = — 1 .
Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.
Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.
Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:
- область определения функции
- область значений функции
- нули функции
- промежутки возрастания и убывания
- точки максимума и минимума
- наибольшее и наименьшее значение функции на отрезке.
Уточним терминологию:
Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось .
Ось ординат — вертикальная ось, или ось .
Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается .
Другими словами, мы сами выбираем , подставляем в формулу функции и получаем .
Область определения функции — множество тех (и только тех) значений аргумента , при которых функция существует.
Обозначается: или .
На нашем рисунке область определения функции — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.
Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок — от самого нижнего до самого верхнего значения .
Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки и .
Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .
Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.
Функция возрастает
Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.
Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Для убывающей функции большему значению соответствует меньшее значение . График идет вправо и вниз.
На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .
Определим, что такое точки максимума и минимума функции .
Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше , чем в соседних. Это локальный «холмик» на графике.
На нашем рисунке — точка максимума.
Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».
На нашем рисунке — точка минимума.
Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и на нашем графике не может быть точкой минимума.
Точки максимума и минимума вместе называются точками экстремума функции . В нашем случае это и .
А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что минимум функции — это ее значение в точке минимума.
Аналогично, максимум нашей функции равен . Он достигается в точке .
Можно сказать, что экстремумы функции равны и .
Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.
В нашем случае наименьшее значение функции на отрезке равно и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно . Оно достигается в левом конце отрезка.
Оно достигается в левом конце отрезка.
В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.
Иногда в задачах B15 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ.
В этом случае работают другие приемы, один из которых — монотонность .
Функция f (x ) называется монотонно возрастающей на отрезке , если для любых точек x 1 и x 2 этого отрезка выполняется следующее:
x 1 x 1 ) x 2 ).
Функция f (x ) называется монотонно убывающей на отрезке , если для любых точек x 1 и x 2 этого отрезка выполняется следующее:
x 1 x 1 ) > f (x 2 ).
Другими словами, для возрастающей функции чем больше x
, тем больше f
(x
). Для убывающей функции все наоборот: чем больше x
, тем меньше f
(x
).
Например, логарифм монотонно возрастает, если основание a > 1, и монотонно убывает, если 0 0.
f (x ) = log a x (a > 0; a ≠ 1; x > 0)
Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:
Показательная функция ведет себя аналогично логарифму: растет при a > 1 и убывает при 0 0:
f (x ) = a x (a > 0)
Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.
Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, из-за которого становится тяжело считать производную. Что при этом происходит — сейчас разберем.
Координаты вершины параболы
Чаще всего аргумент функции заменяется на квадратный трехчлен вида y = ax 2 + bx + c . Его график — стандартная парабола, в которой нас интересуют:
- Ветви параболы — могут уходить вверх (при a > 0) или вниз (a
- Вершина параболы — точка экстремума квадратичной функции, в которой эта функция принимает свое наименьшее (для a > 0) или наибольшее (a
Наибольший интерес представляет именно вершина параболы , абсцисса которой рассчитывается по формуле:
Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее точка x
0 тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:
Но если исходная функция монотонна, для нее точка x
0 тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:
Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно искать x 0 для квадратного трехчлена, а на функцию — забить.
Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:
- Отрезок в условии задачи отсутствует. Следовательно, вычислять f (a ) и f (b ) не требуется. Остается рассмотреть лишь точки экстремума;
- Но таких точек всего одна — это вершина параболы x 0 , координаты которой вычисляются буквально устно и без всяких производных.
Таким образом, решение задачи резко упрощается и сводится всего к двум шагам:
- Выписать уравнение параболы y = ax 2 + bx + c и найти ее вершину по формуле: x 0 = −b /2a ;
- Найти значение исходной функции в этой точке: f
(x
0).
 Если никаких дополнительных условий нет, это и будет ответом.
Если никаких дополнительных условий нет, это и будет ответом.
На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.
Рассмотрим настоящие задачи из пробного ЕГЭ по математике — именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B15 становятся почти устными.
Под корнем стоит квадратичная функция y = x 2 + 6x + 13. График этой функции − парабола ветвями вверх, поскольку коэффициент a = 1 > 0.
Вершина параболы:
x 0 = −b /(2a ) = −6/(2 · 1) = −6/2 = −3
Поскольку ветви параболы направлены вверх, в точке x 0 = −3 функция y = x 2 + 6x + 13 принимает наименьшее значение.
Корень монотонно возрастает, значит x 0 — точка минимума всей функции. Имеем:
Задача. Найдите наименьшее значение функции:
y = log 2 (x 2 + 2x + 9)
Под логарифмом снова квадратичная функция: y
= x
2 + 2x
+ 9.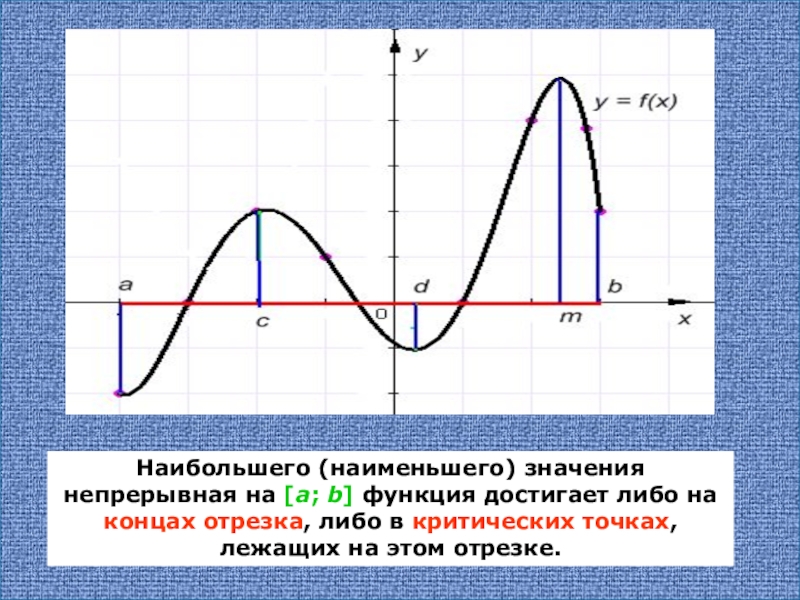 График — парабола ветвями вверх, т.к. a
= 1 > 0.
График — парабола ветвями вверх, т.к. a
= 1 > 0.
Вершина параболы:
x 0 = −b /(2a ) = −2/(2 · 1) = −2/2 = −1
Итак, в точке x 0 = −1 квадратичная функция принимает наименьшее значение. Но функция y = log 2 x — монотонная, поэтому:
y min = y (−1) = log 2 ((−1) 2 + 2 · (−1) + 9) = … = log 2 8 = 3
В показателе стоит квадратичная функция y = 1 − 4x − x 2 . Перепишем ее в нормальном виде: y = −x 2 − 4x + 1.
Очевидно, что график этой функции — парабола, ветви вниз (a = −1
x 0 = −b /(2a ) = −(−4)/(2 · (−1)) = 4/(−2) = −2
Исходная функция — показательная, она монотонна, поэтому наибольшее значение будет в найденной точке x 0 = −2:
Внимательный читатель наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.
Следствия из области определения функции
Иногда для решения задачи B15 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка , а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:
Искомое значение может лежать на конце отрезка , а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:
Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби — никогда. Посмотрим, как это работает на конкретных примерах:
Задача. Найдите наибольшее значение функции:
Под корнем снова квадратичная функция: y = 3 − 2x − x 2 . Ее график — парабола, но ветви вниз, поскольку a = −1
Выписываем область допустимых значений (ОДЗ):
3 − 2x − x 2 ≥ 0 ⇒ x 2 + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒ x ∈ [−3; 1]
Теперь найдем вершину параболы:
x 0 = −b /(2a ) = −(−2)/(2 · (−1)) = 2/(−2) = −1
Точка x 0 = −1 принадлежит отрезку ОДЗ — и это хорошо. Теперь считаем значение функции в точке x 0 , а также на концах ОДЗ:
y (−3) = y (1) = 0
Итак, получили числа 2 и 0. Нас просят найти наибольшее — это число 2.
Нас просят найти наибольшее — это число 2.
Задача. Найдите наименьшее значение функции:
y = log 0,5 (6x − x 2 − 5)
Внутри логарифма стоит квадратичная функция y = 6x − x 2 − 5. Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:
6x − x 2 − 5 > 0 ⇒ x 2 − 6x + 5
Обратите внимание: неравенство строгое, поэтому концы не принадлежат ОДЗ. Этим логарифм отличается от корня, где концы отрезка нас вполне устраивают.
Ищем вершину параболы:
x 0 = −b /(2a ) = −6/(2 · (−1)) = −6/(−2) = 3
Вершина параболы подходит по ОДЗ: x 0 = 3 ∈ (1; 5). Но поскольку концы отрезка нас не интересуют, считаем значение функции только в точке x 0:
y min = y (3) = log 0,5 (6 · 3 − 3 2 − 5) = log 0,5 (18 − 9 − 5) = log 0,5 4 = −2
\(\blacktriangleright\)
Для того, чтобы найти наибольшее/наименьшее значение функции на отрезке \(\)
, необходимо схематично изобразить график функции на этом отрезке. 2 + 1}} = 0\qquad\Leftrightarrow\qquad x = 0\,.\]
Производная существует при любом \(x\)
.
2 + 1}} = 0\qquad\Leftrightarrow\qquad x = 0\,.\]
Производная существует при любом \(x\)
.
2) Найдём промежутки знакопостоянства \(y»\) :
3) Найдём промежутки знакопостоянства \(y»\) на рассматриваемом отрезке \([-1; 1]\) :
4) Эскиз графика на отрезке \([-1; 1]\) :
Таким образом, наибольшего на \([-1; 1]\) значения функция достигает в \(x = -1\) или в \(x = 1\) . Сравним значения функции в этих точках.
\ Итого: \(2\) – наибольшее значение функции \(y\) на \([-1; 1]\) .
Ответ: 2
Задание 3 #2356
Уровень задания: Равен ЕГЭ
Найдите наименьшее значение функции \(y = \cos 2x\) на отрезке \(\) .
ОДЗ: \(x\) – произвольный.
1) \
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\)
или не существует): \[-2\cdot \sin 2x = 0\qquad\Leftrightarrow\qquad 2x = \pi n, n\in\mathbb{Z}\qquad\Leftrightarrow\qquad x = \dfrac{\pi n}{2}, n\in\mathbb{Z}\,. 2 — 12x + 36 + 2\ln 2)}\)
.
2 — 12x + 36 + 2\ln 2)}\)
.
С практической точки зрения наибольший интерес представляет использование производной для нахождения наибольшего и наименьшего значения функции. С чем это связано? Максимизация прибыли, минимизация издержек, определение оптимальной загрузки оборудования… Другими словами, во многих сферах жизни приходится решать задачи оптимизации каких-либо параметров. А это и есть задачи на нахождение наибольшего и наименьшего значения функции.
Следует отметить, что наибольшее и наименьшее значение функции обычно ищется на некотором интервале X , который является или всей областью определения функции или частью области определения. Сам интервал X может быть отрезком , открытым интервалом , бесконечным промежутком .
В этой статье мы будем говорить о нахождении наибольшего и наименьшего значений явно заданной функции одной переменной y=f(x) .
Навигация по странице.
Наибольшее и наименьшее значение функции — определения, иллюстрации.
Кратко остановимся на основных определениях.
Наибольшим значением функции , что для любого справедливо неравенство .
Наименьшим значением функции y=f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .
Эти определения интуитивно понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на рассматриваемом интервале при абсциссе .
Стационарные точки – это значения аргумента, при которых производная функции обращается в ноль.
Для чего нам стационарные точки при нахождении наибольшего и наименьшего значений? Ответ на этот вопрос дает теорема Ферма. Из этой теоремы следует, что если дифференцируемая функция имеет экстремум (локальный минимум или локальный максимум) в некоторой точке, то эта точка является стационарной. Таким образом, функция часто принимает свое наибольшее (наименьшее) значение на промежутке X в одной из стационарных точек из этого промежутка.
Также часто наибольшее и наименьшее значение функция может принимать в точках, в которых не существует первая производная этой функции, а сама функция определена.
Сразу ответим на один из самых распространенных вопросов по этой теме:»Всегда ли можно определить наибольшее (наименьшее) значение функции»? Нет, не всегда. Иногда границы промежутка X совпадают с границами области определения функции или интервал X бесконечен. А некоторые функции на бесконечности и на границах области определения могут принимать как бесконечно большие так и бесконечно малые значения. В этих случаях ничего нельзя сказать о наибольшем и наименьшем значении функции.
Для наглядности дадим графическую иллюстрацию. Посмотрите на рисунки – и многое прояснится.
На отрезке
На первом рисунке функция принимает наибольшее (max y ) и наименьшее (min y ) значения в стационарных точках, находящихся внутри отрезка [-6;6] .
Рассмотрим случай, изображенный на втором рисунке. Изменим отрезок на
. В этом примере наименьшее значение функции достигается в стационарной точке, а наибольшее — в точке с абсциссой, соответствующей правой границе интервала.
На рисунке №3 граничные точки отрезка [-3;2] являются абсциссами точек, соответствующих наибольшему и наименьшему значению функции.
На открытом интервале
На четвертом рисунке функция принимает наибольшее (max y ) и наименьшее (min y ) значения в стационарных точках, находящихся внутри открытого интервала (-6;6) .
На интервале , о наибольшем значении никаких выводов сделать нельзя.
На бесконечности
В примере, представленном на седьмом рисунке, функция принимает наибольшее значение (max y ) в стационарной точке с абсциссой x=1 , а наименьшее значение (min y ) достигается на правой границе интервала. На минус бесконечности значения функции асимптотически приближаются к y=3 .
На интервале функция не достигает ни наименьшего, ни наибольшего значения. При стремлении к x=2
справа значения функции стремятся к минус бесконечности (прямая x=2
является вертикальной асимптотой), а при стремлении абсциссы к плюс бесконечности, значения функции асимптотически приближаются к y=3
. Графическая иллюстрация этого примера приведена на рисунке №8.
Графическая иллюстрация этого примера приведена на рисунке №8.
Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на отрезке .
Запишем алгоритм, позволяющий находить наибольшее и наименьшее значение функции на отрезке.
- Находим область определения функции и проверяем, содержится ли в ней весь отрезок .
- Находим все точки, в которых не существует первая производная и которые содержатся в отрезке (обычно такие точки встечаются у функций с аргументом под знаком модуля и у степенных функций с дробно-рациональным показателем). Если таких точек нет, то переходим к следующему пункту.
- Определяем все стационарные точки, попадающие в отрезок . Для этого, приравниваем ее к нулю, решаем полученное уравнение и выбираем подходящие корни. Если стационарных точек нет или ни одна из них не попадает в отрезок, то переходим к следующему пункту.
- Вычисляем значения функции в отобранных стационарных точках (если такие имеются), в точках, в которых не существует первая производная (если такие имеются), а также при x=a
и x=b
.

- Из полученных значений функции выбираем наибольшее и наименьшее — они и будут искомыми наибольшим и наименьшим значениями функции соответственно.
Разберем алгоритм при решении примера на нахождение наибольшего и наименьшего значения функции на отрезке.
Пример.
Найти наибольшее и наименьшее значение функции
- на отрезке ;
- на отрезке [-4;-1] .
Решение.
Областью определения функции является все множество действительных чисел, за исключением нуля, то есть . Оба отрезка попадают в область определения.
Находим производную функции по :
Очевидно, производная функции существует во всех точках отрезков и [-4;-1] .
Стационарные точки определим из уравнения . Единственным действительным корнем является x=2 . Эта стационарная точка попадает в первый отрезок .
Для первого случая вычисляем значения функции на концах отрезка и в стационарной точке, то есть при x=1
, x=2
и x=4
:
Следовательно, наибольшее значение функции достигается при x=1
, а наименьшее значение – при x=2
.
Для второго случая вычисляем значения функции лишь на концах отрезка [-4;-1]
(так как он не содержит ни одной стационарной точки):
Решение.
Начнем с области определения функции. Квадратный трехчлен в знаменателе дроби не должен обращаться в ноль:
Легко проверить, что все интервалы из условия задачи принадлежат области определения функции.
Продифференцируем функцию:
Очевидно, производная существует на всей области определения функции.
Найдем стационарные точки. Производная обращается в ноль при . Эта стационарная точка попадает в интервалы (-3;1] и (-3;2) .
А теперь можно сопоставить полученные в каждом пункте результаты с графиком функции. Синими пунктирными линиями обозначены асимптоты.
На этом можно закончить с нахождением наибольшего и наименьшего значения функции. Алгоритмы, разобранные в этой статье, позволяют получить результаты при минимуме действий. Однако бывает полезно сначала определить промежутки возрастания и убывания функции и только после этого делать выводы о наибольшем и наименьшем значении функции на каком-либо интервале. Это дает более ясную картину и строгое обоснование результатов.
Это дает более ясную картину и строгое обоснование результатов.
Вычислите наименьшее или наибольшее число в диапазоне
Допустим, вы хотите выяснить, у кого наименьшая частота ошибок в производственном цикле на заводе или наибольшая зарплата в вашем отделе. Есть несколько способов вычислить наименьшее или наибольшее число в диапазоне.
Если ячейки находятся в непрерывной строке или столбце
Выберите ячейку ниже или справа от чисел, для которых вы хотите найти наименьшее число.
На вкладке Home в группе Editing щелкните стрелку рядом с AutoSum , щелкните Min (вычисляет наименьшее) или Max (вычисляет наибольшее), а затем нажмите клавишу ВВОД.
Если ячейки не находятся в непрерывной строке или столбце
Для выполнения этой задачи используйте функции MIN, MAX, SMALL или LARGE.
Пример
Скопируйте следующие данные на пустой лист.
|
Нужна дополнительная помощь?
Вы всегда можете спросить эксперта в сообществе специалистов по Excel или получить поддержку в сообществе Answers.
См. Также
БОЛЬШОЙ
МАКСИМУМ
MIN
МАЛЕНЬКИЙ
ФункцияНАИБОЛЬШИЙ
В этой статье описаны синтаксис формулы и использование функции НАИБОЛЬШИЙ в Microsoft Excel.
Описание
Возвращает k-е наибольшее значение в наборе данных. Вы можете использовать эту функцию, чтобы выбрать значение на основе его относительного положения. Например, вы можете использовать LARGE, чтобы получить наивысшее, второе или третье место.
Синтаксис
БОЛЬШОЙ (массив, k)
Аргументы функции НАИБОЛЬШИЙ:
Массив Обязательный.Массив или диапазон данных, для которых вы хотите определить k-е наибольшее значение.

K Обязательно. Позиция (начиная с наибольшего) в массиве или диапазоне ячеек возвращаемых данных.
Примечания
Если массив пуст, НАИБОЛЬШИЙ возвращает # ЧИСЛО! значение ошибки.
Если k ≤ 0 или если k больше количества точек данных, НАИБОЛЬШИЙ возвращает # ЧИСЛО! значение ошибки.
Если n — количество точек данных в диапазоне, то НАИБОЛЬШИЙ (массив, 1) возвращает наибольшее значение, а НАИБОЛЬШИЙ (массив, n) возвращает наименьшее значение.
Пример
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите Enter. При необходимости вы можете настроить ширину столбца, чтобы увидеть все данные.
Данные | Данные | |
|---|---|---|
3 | 4 | |
5 | 2 | |
3 | 4 | |
5 | 6 | |
4 | 7 | |
Формула | Описание | Результат |
= БОЛЬШОЙ (A2: B6,3) | 3-е по величине число среди чисел выше | 5 |
= БОЛЬШОЙ (A2: B6,7) | 7-е по величине число среди чисел выше | 4 |
функция МАЛЕНЬКИЙ
В этой статье описаны синтаксис формулы и использование функции МАЛЕНЬКИЙ в Microsoft Excel.
Описание
Возвращает k-е наименьшее значение в наборе данных. Используйте эту функцию для возврата значений с определенным относительным положением в наборе данных.
Синтаксис
МАЛЫЙ (массив, k)
Аргументы функции МАЛЕНЬКИЙ:
Массив Обязательный.Массив или диапазон числовых данных, для которых вы хотите определить k-е наименьшее значение.
K Обязательно. Позиция (начиная с наименьшей) в массиве или диапазоне возвращаемых данных.
Примечания
Если массив пуст, НАИМЕНЬШИЙ возвращает # ЧИСЛО! значение ошибки.
Если k ≤ 0 или если k превышает количество точек данных, НАИМЕНЬШИЙ возвращает # ЧИСЛО! значение ошибки.

Если n — количество точек данных в массиве, МАЛЕНЬКИЙ (массив, 1) равен наименьшему значению, а МАЛЕНЬКИЙ (массив, n) равен наибольшему значению.
Пример
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите Enter. При необходимости вы можете настроить ширину столбца, чтобы увидеть все данные.
Данные 1 | Данные 2 | |
|---|---|---|
3 | 1 | |
4 | 4 | |
5 | 8 | |
2 | 3 | |
3 | 7 | |
4 | 12 | |
6 | 54 | |
4 | 8 | |
7 | 23 | |
Формула | Описание (результат) | Результат |
= МАЛЕНЬКИЙ (A2: A10,4) | 4-е наименьшее число в первом столбце (4) | 4 |
= МАЛЕНЬКИЙ (B2: B10,2) | 2-е наименьшее число во втором столбце (3) | 3 |
Найдите наименьшие / наибольшие значения для строк или столбцов с условным форматированием в Excel: Chris Menard Training
Опубликовано: 04. 08.2019
08.2019Вы можете найти самые низкие или самые высокие значения для строк или столбцов в Excel с помощью условного форматирования.Вам нужно будет использовать либо функцию MIN, которая находит наименьшее значение, либо функцию MAX, которая находит наибольшее значение.
Найти наименьшее значение по строкам
- Выберите свой ассортимент
- Убедитесь, что вы находитесь на вкладке Home Tab.
- Щелкните Conditoinal Formatting, , затем New Rule.
- Нажмите Используйте формулу, чтобы определить, какие ячейки нужно форматировать.
- Введите = B2 = MIN ($ B2: $ E2) , затем щелкните Формат — Fill tab — выберите цвет.
- Нажмите ОК .
Чтобы найти наименьшее значение по столбцам
- Выберите свой ассортимент
- Убедитесь, что вы находитесь на вкладке Home Tab.

- Щелкните Conditoinal Formatting, , затем New Rule.
- Нажмите Используйте формулу, чтобы определить, какие ячейки нужно форматировать.
- Введите = B2 = MIN (B $ 2: B $ 5) , затем щелкните Format — Fill tab — выберите цвет.
- Нажмите ОК .
Видео на YouTube Криса Менара
Другие видео по условному форматированию
Условное форматирование с датами
Все, что угодно, более 30 дней на желтом фоне и все, что старше 60 дней, на зеленом фоне. Вы будете использовать функцию СЕГОДНЯ в Excel с условным форматированием.
Условное форматирование с функцией И
Чтобы использовать условное форматирование на основе двух условий в Excel, используйте функцию И.
= AND ($ E2 = «CA», $ F2 = «Google Ads»), чтобы найти людей в CA, которые нашли вас через Google Ads.
Плейлист Криса Менара в Excel на YouTube
Вот более 175 обучающих видео по Excel. Не стесняйтесь подписаться на мой канал на YouTube.
Крис Менард
Крис Менард — старший специалист по обучению в SurePoint Technologies.Крис имеет сертификат по Excel, Word, PowerPoint и Outlook. У Menard есть канал YouTube с другими 600 технологическими видеороликами, охватывающими Excel, Word, Zoom, Teams, Outlook, Gmail, Календарь Google и другие ресурсы, которые очень оценили более 7 миллионов зрителей. Благодаря сертификации и опыту работы Криса с Microsoft, Крис гордится тем, что является членом команды разработчиков Microsoft. Членство в команде разработчиков Microsoft означает, что многие из его видео доступны на канале Microsoft 365 на YouTube и на сайтах поддержки Microsoft.
Категории
Пожалуйста, включите JavaScript, чтобы просматривать комментарии от Disqus.
Статистика: Описание данных
Статистика: Описание данныхОпределения
- Статистика
- Характеристика или мера, полученная на основе образца
- Параметр
- Характеристика или мера, полученная от популяции
- Среднее
- Сумма всех значений, разделенная на количество значений.Это может быть популяция среднее (обозначено мю) или выборочное среднее (обозначено полосой x)
- Медиана
- Средняя точка данных после ранжирования (сортировка по возрастанию). Есть как много чисел ниже медианы, как и выше медианы.
- Режим
- Самый частый номер
- Перекосное распределение
- Большинство значений лежат вместе на одной стороне с очень немногими значениями (хвост) для
Обратная сторона. В положительно скошенном распределении хвост направлен вправо, а среднее значение равно
больше медианы.При отрицательно скошенном распределении хвост находится влево, а
среднее значение меньше медианы.

- Симметричное распределение
- Значения данных равномерно распределены по обе стороны от среднего. В симметричном распределения, среднее — это медиана.
- Средневзвешенное значение
- Среднее значение, когда каждое значение умножается на его вес и суммируется. Эта сумма делится по сумме весов.
- Средние частоты
- Среднее наибольшее и наименьшее значения.(Макс. + Мин.) / 2
- Диапазон
- Разница между наибольшим и наименьшим значениями. Макс — Мин
- Разница в численности населения
- Среднее квадратов расстояний от среднего по генеральной совокупности. Это сумма квадраты отклонений от среднего, деленные на размер популяции. Единицы на дисперсии — единицы населения в квадрате.
- Вариант выборки
- Несмещенная оценка дисперсии генеральной совокупности.Вместо деления на численность населения,
сумма квадратов отклонений от выборочного среднего делится на единицу меньше
чем размер выборки.
 Единицы дисперсии — это единицы населения в квадрате.
Единицы дисперсии — это единицы населения в квадрате. - Стандартное отклонение
- Квадратный корень из дисперсии. Стандартное отклонение совокупности — это квадратный корень из дисперсия генеральной совокупности и стандартное отклонение выборки — это квадратный корень из выборочная дисперсия. Стандартное отклонение выборки не является объективной оценкой для стандартное отклонение населения.Единицы стандартного отклонения такие же, как у единиц населения / выборки.
- Коэффициент вариации
- Стандартное отклонение, деленное на среднее значение, выраженное в процентах. Мы не будем работать с коэффициентом вариации в этом курсе.
- Теорема Чебышева
- Доля значений, попадающих в пределы k стандартных отклонений среднего, не менее где k> 1. Теорема Чебышева применима к любому распределению независимо от его формы.
- Эмпирическое или нормальное правило
- Действительно только при распределении в форме колокола (нормальное).
 Примерно 68% находится в пределах
1 стандартное отклонение среднего; 95% в пределах 2 стандартных отклонений; и 99,7% в пределах 3
стандартные отклонения среднего.
Примерно 68% находится в пределах
1 стандартное отклонение среднего; 95% в пределах 2 стандартных отклонений; и 99,7% в пределах 3
стандартные отклонения среднего. - Стандартный балл или Z-балл
- Значение, полученное путем вычитания среднего и деления на стандартное отклонение. Когда все значения преобразованы в их стандартные баллы, новое среднее (для Z) будет ноль, а стандартное отклонение будет равно единице.
- Процентиль
- Процент населения, находящегося ниже этого значения. Данные должны быть ранжированы найти процентили.
- Квартиль
- 25-й, 50-й или 75-й процентили. 50-й процентиль также называется медианой.
- Дециль
- 10-й, 20-й, 30-й, 40-й, 50-й, 60-й, 70-й, 80-й или 90-й процентили.
- Петля нижняя
- Медиана нижней половины чисел (до медианы включительно).В
нижний шарнир — это первый квартиль, если не получается остаток при делении размера выборки на
четыре — 3.

- Петля верхняя
- Медиана верхней половины чисел (включая медиану). Верхний шарнир 3-й квартиль, если остаток при делении размера выборки на четыре не равен 3.
- График коробок и усов (коробчатая диаграмма)
- Графическое представление минимального значения, нижнего шарнира, медианы, верхнего шарнира и максимум. Некоторые учебники и калькулятор TI-82 определяют пять значений как минимум, первый квартиль, медиана, третий квартиль и максимум.
- Сводка по пяти числам
- Минимальное значение, нижний шарнир, медиана, верхний шарнир и максимум.
- Межквартильный диапазон (IQR)
- Разница между 3-м и 1-м квартилями.
- выброс
- Чрезвычайно высокое или низкое значение по сравнению с остальными значениями.
- Мягкие выбросы
- Значения, которые лежат в 1,5–3,0 раза ниже межквартильного диапазона ниже 1-го
Квартиль или выше 3-го квартиля.Обратите внимание, что в некоторых текстах вместо квартилей используются петли.

- Экстремальные выбросы
- Значения, которые лежат более чем в 3,0 раза межквартильного размаха ниже 1-го квартиля или выше 3-го квартиля. Обратите внимание, что в некоторых текстах вместо квартилей используются петли.
Содержание
Как выделить наибольшее или наименьшее значение в Google Таблицах (простой способ)
Не хочется читать? Посмотрите наш видеоурок:
При работе с данными в Google Таблицах вам может потребоваться выделить наивысшее значение (максимальное значение) или наименьшее значение (минимальное значение) в наборе данных.
И вы можете легко сделать это с помощью условного форматирования. Это простой способ применить формат к ячейке на основе ее значения.
В этом руководстве я покажу вам, как использовать условное форматирование, чтобы выделить наивысшее значение (максимальное значение), выделить наименьшее значение (минимальное значение), а также выделить 3 верхних и 3 нижних значения в наборе данных.
Итак, приступим!
Подчеркните высшую ценность в Google Таблицах
Предположим, у меня есть набор данных с именами учащихся и их оценками по предмету, и я хочу выделить самый высокий результат в этом наборе данных.
Вот как это можно сделать с помощью условного форматирования:
- Выберите диапазон с оценками
- Выберите пункт «Формат» в меню.
- Щелкните условное форматирование
- Убедитесь, что на открывшейся панели «Правила условного формата» выбран «Одноцветный».
- Убедитесь, что диапазон правильный (если нет, вы можете изменить его здесь)
- В раскрывающемся меню «Правила формата» выберите «Пользовательская формула».
- Введите в поле следующую формулу:
= B2 = МАКС ($ B $ 2: $ B $ 21)
- Укажите цвет, которым вы хотите выделить ячейку (я выберу зеленый цвет по умолчанию)
Вышеупомянутые шаги выделят ячейку с наибольшим значением.
Как это работает?
В условном форматировании можно использовать настраиваемую формулу, которая возвращает ИСТИНА или ЛОЖЬ.
Условное форматирование просматривает каждую ячейку в указанном диапазоне и анализирует значение этой ячейки, используя указанную вами формулу.
Если результатом формулы является ИСТИНА, то условное форматирование будет применять указанный формат, а если результатом формулы является ЛОЖЬ, то условное форматирование ничего не даст.
В нашем примере выше он просматривает каждую ячейку и анализирует результат, а также проверяет, равен ли он максимальному количеству очков в списке. Только ячейка с максимальным количеством очков вернет ИСТИНА, а все остальные ячейки вернут ЛОЖЬ.
Вот почему только ячейка с максимальным значением выделяется зеленым цветом (это был формат, который мы указали при условном форматировании).
Если есть несколько ячеек с максимальным значением, все эти ячейки будут выделены.
Выделите самую низкую ценность в Google Таблицах
Так же, как я выделил самое высокое значение в наборе данных, я могу также выделить самое низкое значение в данных.
Все, что для этого нужно, — это небольшая настройка формулы.
Предположим, у вас есть набор данных, показанный ниже, и вы хотите выделить самый низкий балл в столбце B.
Ниже приведены шаги для этого:
- Выберите диапазон с оценками
- Выберите пункт «Формат» в меню.
- Щелкните условное форматирование
- Убедитесь, что на открывшейся панели «Правила условного формата» выбран «Одноцветный».
- Убедитесь, что диапазон правильный (если нет, вы можете изменить его здесь)
- В раскрывающемся меню «Правила формата» выберите «Пользовательская формула».
- Введите в поле следующую формулу:
= B2 = MIN ($ B $ 2: $ B $ 21) - Укажите цвет, которым вы хотите выделить ячейку.В данном случае я выберу красный оттенок цвета .

Вышеупомянутые шаги выделят ячейку с наименьшим (минимальным) значением.
Это снова работает так же, как я объяснил в предыдущем разделе, где условное форматирование проходит через каждую ячейку и проверяет значение этой ячейки на соответствие формуле.
Только ячейка с минимальным значением вернет ИСТИНА для этой формулы и будет выделена, а все остальные ячейки останутся нетронутыми
Выделите 3 верхних или 3 последних значения в Google Таблицах
Теперь предположим, что вместо выделения самого высокого или самого низкого значения вы хотите выделить 3 верхних или 3 нижних значения.
Процесс и логика остаются прежними.
Все, что вам нужно сделать, это настроить формулу таким образом, чтобы она возвращала ИСТИНА для трех верхних значений (или трех нижних значений) и выделяла эти ячейки в указанном формате.
Предположим, у вас есть набор данных, показанный ниже, и вы хотите выделить три лучших результата в этих данных.
Ниже приведены шаги для этого:
- Выберите диапазон с оценками
- Выберите пункт «Формат» в меню.
- Щелкните условное форматирование
- Убедитесь, что на открывшейся панели «Правила условного формата» выбран «Одноцветный».
- Убедитесь, что диапазон правильный (если нет, вы можете изменить его здесь)
- В раскрывающемся меню «Правила формата» выберите «Пользовательская формула».
- Введите в поле следующую формулу:
= B2> = БОЛЬШОЙ (2 $ B $: 21,3 $ B $)
- Укажите цвет, которым вы хотите выделить ячейку (я выберу зеленый цвет по умолчанию)
Вышеупомянутые шаги позволят выделить три наивысших результата в столбце B.
Формула НАИБОЛЬШИЙ позволяет нам получить N-е по величине значение. Например, вы можете использовать его для получения второго по величине значения или третьего по величине значения в наборе данных.
В нашем примере, поскольку мы хотим выделить три верхних значения, я использовал большую формулу, чтобы дать мне третий по величине результат.
Формула теперь просто проверяет каждую ячейку и проверяет, больше ли значение третьего по величине значения или нет. Если это так, то условное форматирование выделяет ячейки, в противном случае оно остается неизменным.
Если вы хотите выделить 3 наименьших результата, вы можете использовать формулу ниже в шаге 7:
= B2 <= МАЛЕНЬКИЙ ($ B $ 2: $ B $ 21,3)
И если вы хотите выделить три верхних и три нижних оценки, вам нужно дважды применить условное форматирование с формулами НАИБОЛЬШИЙ и МАЛЕНЬКИЙ.
И убедитесь, что форматирование другое (например, зеленый цвет для трех верхних значений и оранжевый или желтый цвет для трех нижних).
Выделить всю строку с наибольшим / наименьшим значением
В примерах, рассмотренных до сих пор, мы выделили только те ячейки, которые имеют оценки.
А что, если вы хотите выделить всю запись вместе с именем ученика.
Это легко сделать, немного изменив формулу условного форматирования.
Предположим, у вас есть набор данных, показанный ниже, и вы хотите выделить запись с наивысшим баллом в этих данных.
Ниже приведены шаги для этого:
- Выберите весь набор данных ( A2: B21 в этом примере )
- Выберите пункт «Формат» в меню.
- Щелкните условное форматирование
- Убедитесь, что на открывшейся панели «Правила условного формата» выбран «Одноцветный».
- Убедитесь, что диапазон правильный (если нет, вы можете изменить его здесь)
- В раскрывающемся меню «Правила формата» выберите «Пользовательская формула».
- Введите в поле следующую формулу:
= $ B2 = MAX ($ B $ 2: $ B $ 21)
Вышеупомянутые шаги выделят всю запись для ученика, который набрал наибольшее количество баллов.
Как работает эта формула?
Хотя эта формула работает так же, как и остальные, описанные выше, есть одно небольшое отличие, которое вам необходимо понять.
= $ B2 = MAX ($ B $ 2: $ B $ 21)
В приведенной выше формуле вместо B2 я использовал $ B2. Это называется смешанной ссылкой.
Ниже приведены три типа справочников, которые можно использовать в Google Таблицах:
- B2 - это относительная ссылка, не имеющая знака $
- B $ 2 / $ B2 - это смешанные ссылки, у которых есть один $ (либо перед буквой столбца, либо перед номером строки)
- $ B $ 2 - это абсолютная ссылка, в которой перед буквой столбца и номером строки стоит знак доллара.
В приведенном выше примере мы использовали $ B2, который является смешанной ссылкой.
Это означает, что, хотя условное форматирование анализирует все ячейки в каждой строке при переходе к ячейке A2, оно будет использовать следующую формулу, чтобы проверить, возвращает ли она истинное или ложное значение:
= $ B2 = MAX ($ B $ 2: $ B $ 21)
И когда он переходит к B2, он снова использует ту же формулу выше.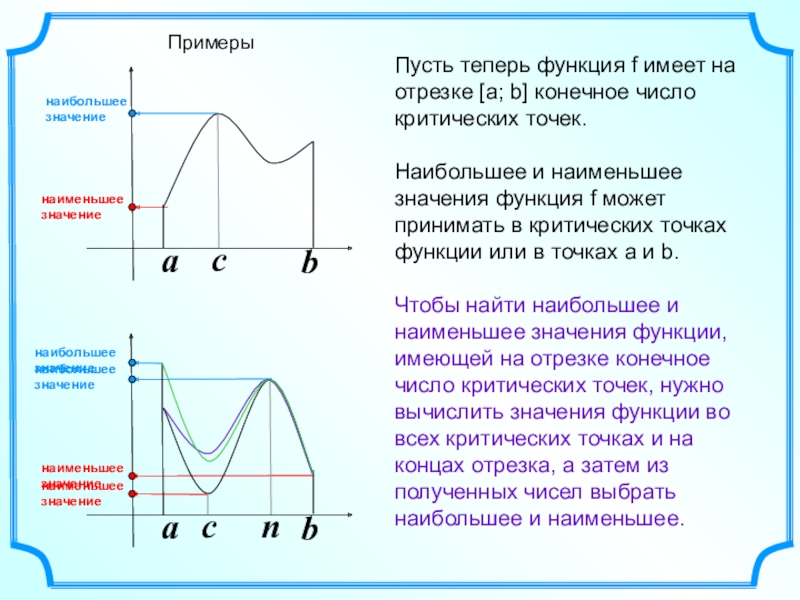
Теперь, когда он переходит в ячейку A3, он использует следующую формулу:
= $ B3 = MAX ($ B $ 2: $ B $ 21)
, и когда он переходит в ячейку B3, он снова использует приведенную выше формулу.
Добавив знак доллара перед буквой столбца, мы гарантируем, что даже когда ячейки в столбце анализируются, формула все еще ссылается на значение в столбце B.Это сделано потому, что даже если имя нужно выделить, нам все равно нужно проанализировать оценку этого человека.
Вот как вы можете использовать простые формулы условного форматирования, чтобы выделить наивысшее или наименьшее значение в наборе данных (или верхние N или нижние N значений).
Надеюсь, это руководство было для вас полезным.
Другие руководства по Google Таблицам, которые могут вам также понравиться:
Как выделить наибольшее и наименьшее значение в каждой строке или столбце в Excel
Этот пост расскажет, как выделить наивысшее значение в каждой строке или столбце в Excel. Как выделить наименьшее значение в каждой строке и столбце с помощью функции условного форматирования.
Как выделить наименьшее значение в каждой строке и столбце с помощью функции условного форматирования.
Выделить наибольшее значение в каждой строке
Предполагается, что у вас есть список данных в диапазоне A1: D7, и вы хотите выделить все самые высокие значения в каждой строке или выделить все самые низкие значения в каждой строке. Как этого добиться. Для достижения результата необходимо использовать функцию условного форматирования. Просто выполните следующие шаги:
# 1 выберите диапазон ячеек, в котором вы хотите выделить самые высокие значения в каждой строке.
# 2 перейдите на вкладку HOME , щелкните команду Условное форматирование в группе Стили . Затем выберите Новое правило из раскрывающегося списка меню. Появится диалоговое окно New Formatting Rule .
# 3 select Используйте формулу, чтобы определить, какие ячейки нужно форматировать в поле списка Выберите тип правила и введите следующую формулу в значениях формата , где эта формула истинна текстовое поле.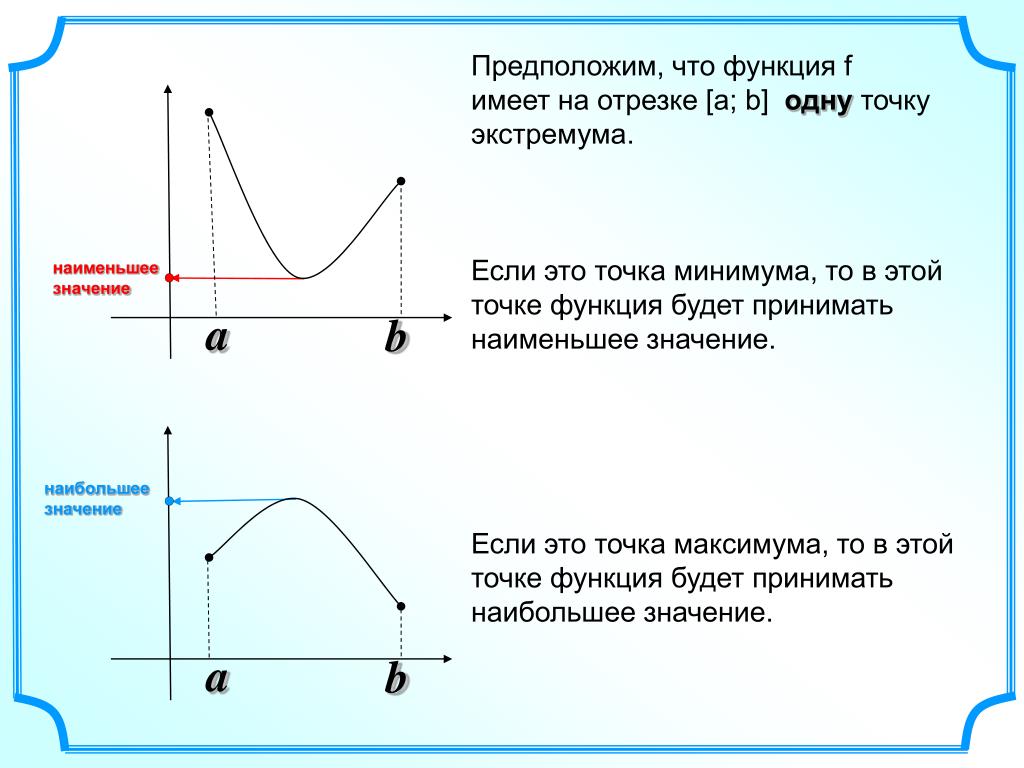 Затем нажмите кнопку Формат .
Затем нажмите кнопку Формат .
= B2 = МАКС ($ B2: $ D2)
# 4 переключитесь на Заполните вкладку , выберите нужный цвет фона. Нажмите кнопку Ok .
# 5 нажмите кнопку Ok . Было выделено самое высокое значение в каждой строке.
Выделить наименьшее значение в каждой строке
Если вы хотите выделить наименьшее значение в каждой строке таблицы, вам просто нужно повторить вышеуказанные шаги, просто используйте вместо нее следующую формулу.
= B2 = MIN ($ B2: $ D2)
Выделить наибольшее значение в каждом столбце
Если вы хотите выделить наибольшее значение в одном столбце, вы можете повторить вышеуказанные шаги, а затем использовать следующую формулу:
= B2 = MAX (2 млрд долларов: 7 млрд долларов)
Выделите наименьшее значение в каждом столбце
Если вы хотите выделить наибольшее значение в одном столбце, вы можете повторить вышеуказанные шаги, а затем использовать следующую формулу:
= B2 = MIN (2 B $: 7 B $)
Видео: выделение максимального и минимального значений в каждой строке или столбце
youtube.com/embed/PpmVqloIUUY" frameborder="0" allowfullscreen="allowfullscreen"/>
Связанные функции
- Функция МИН в Excel
Функция МИН в Excel возвращает наименьшее числовое значение из предоставленных вами чисел.Или возвращает наименьшее значение в массиве. Функция MIN является встроенной функцией в Microsoft Excel и относится к категории статистических функций. Синтаксис функции MIN следующий: = MIN (num1, [num2,… numn ])…. - Функция МАКС в Excel
Функция МАКС в Excel возвращает наибольшее числовое значение из указанных вами чисел. Или возвращает наибольшее значение в массиве. = МАКС (число1, [число2,… число])…
- Функция МИН в Excel
Похожие сообщения
Как отобразить отрицательное значение времени в Excel
В этом посте вы узнаете, как отображать отрицательное значение времени в Excel.
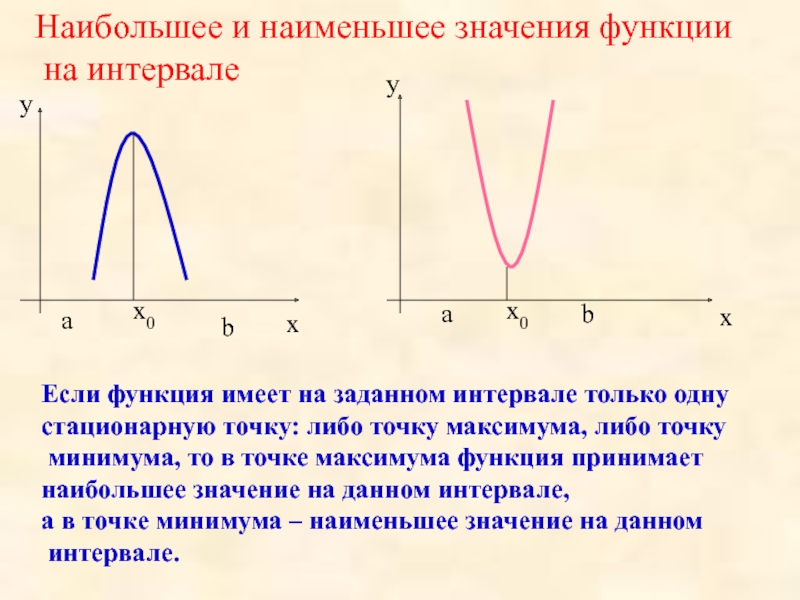

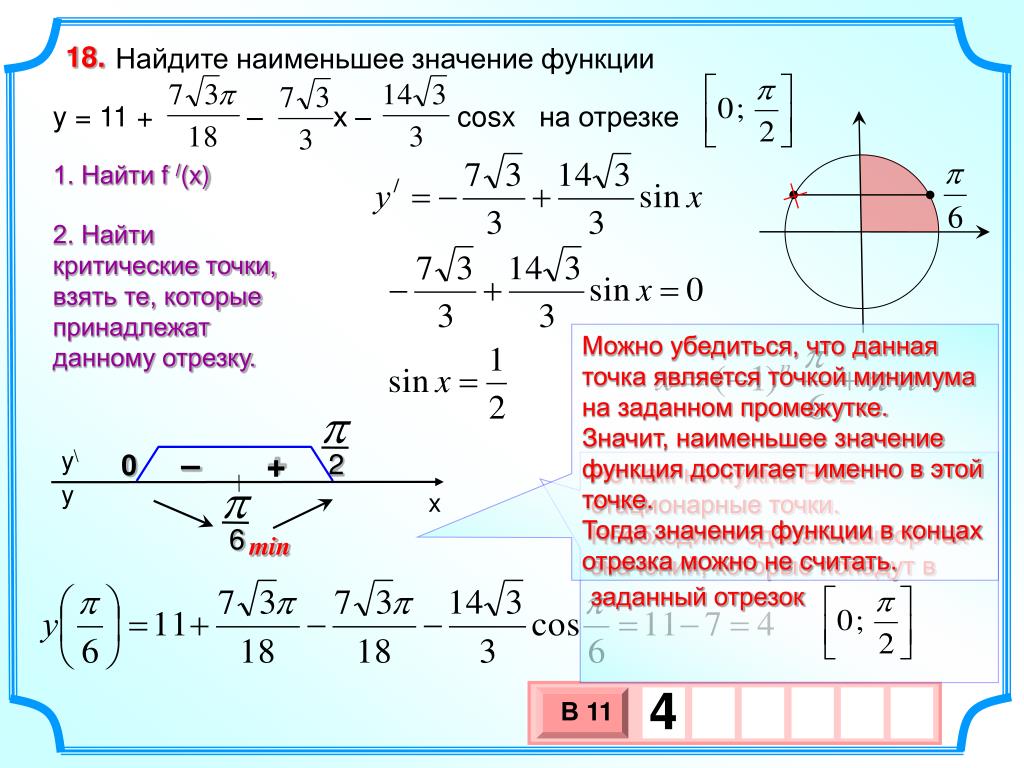 И нажмите ОК на всех открытых окнах.
И нажмите ОК на всех открытых окнах.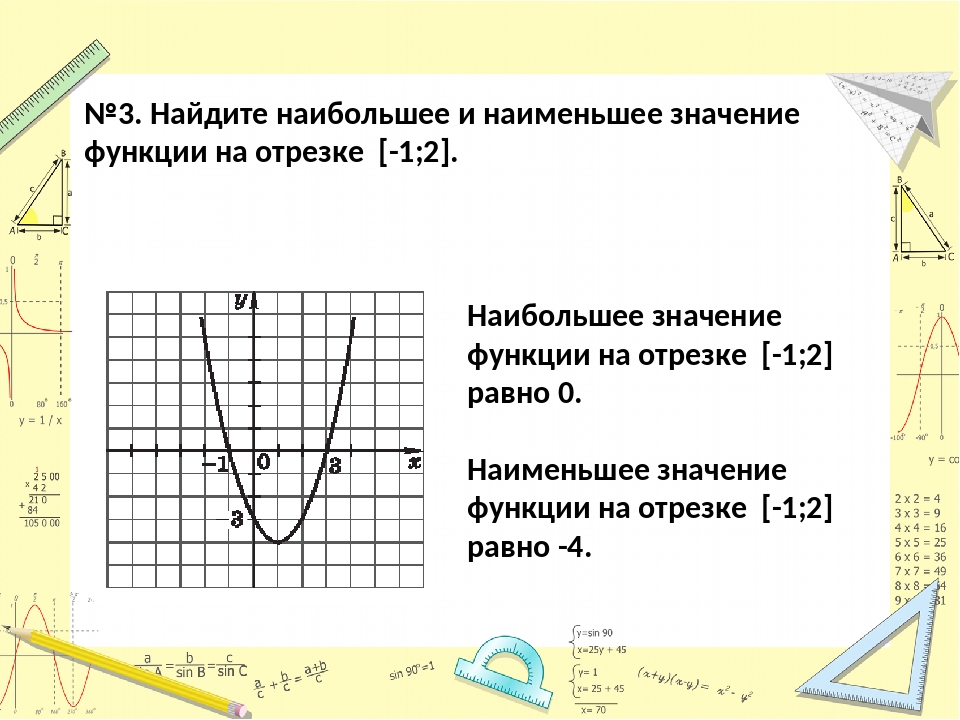

 Их определяет вид интервала.
Их определяет вид интервала. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4 — 8 в первой части материала.
Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4 — 8 в первой части материала. Если никаких дополнительных условий нет, это и будет ответом.
Если никаких дополнительных условий нет, это и будет ответом.




 Единицы дисперсии — это единицы населения в квадрате.
Единицы дисперсии — это единицы населения в квадрате. Примерно 68% находится в пределах
1 стандартное отклонение среднего; 95% в пределах 2 стандартных отклонений; и 99,7% в пределах 3
стандартные отклонения среднего.
Примерно 68% находится в пределах
1 стандартное отклонение среднего; 95% в пределах 2 стандартных отклонений; и 99,7% в пределах 3
стандартные отклонения среднего.
