Как найти наибольшее и наименьшее значения функции на отрезке.
Как найти наибольшее и наименьшее значения функции на отрезке?
Для этого мы следуем известному алгоритму:
1. Находим ОДЗ функции.
2. Находим производную функции
3. Приравниваем производную к нулю
4. Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции:
Если на промежутке I производная функции , то функция возрастает на этом промежутке.
Если на промежутке I производная функции , то функция убывает на этом промежутке.
5. Находим точки максимума и минимума функции.
В точке максимума функции производная меняет знак с «+» на «-«.
В точке минимума функции производная меняет знак с «-» на «+».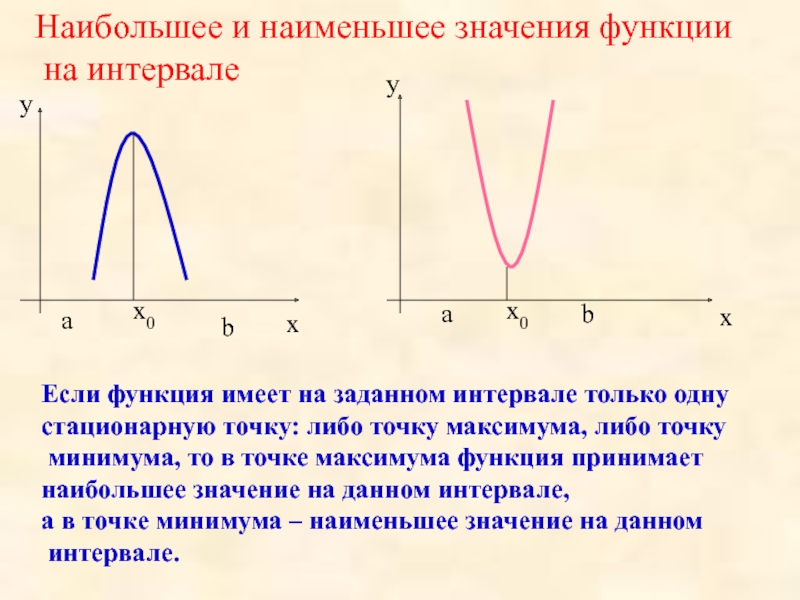
6. Находим значение функции в концах отрезка,
- затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции
- или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции
Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.
Рассмотрим функцию . График этой функции выглядит так:
В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.
1. Рассмотрим функцию на отрезке
Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка: , а наименьшее — в левом: .
2. Рассмотрим функцию на отрезке
Очевидно, что наибольшее значение функция принимает в точке максимума , а наименьшее — в одном из концов отрезка, то есть надо найти значения и и выбрать из них наименьшее.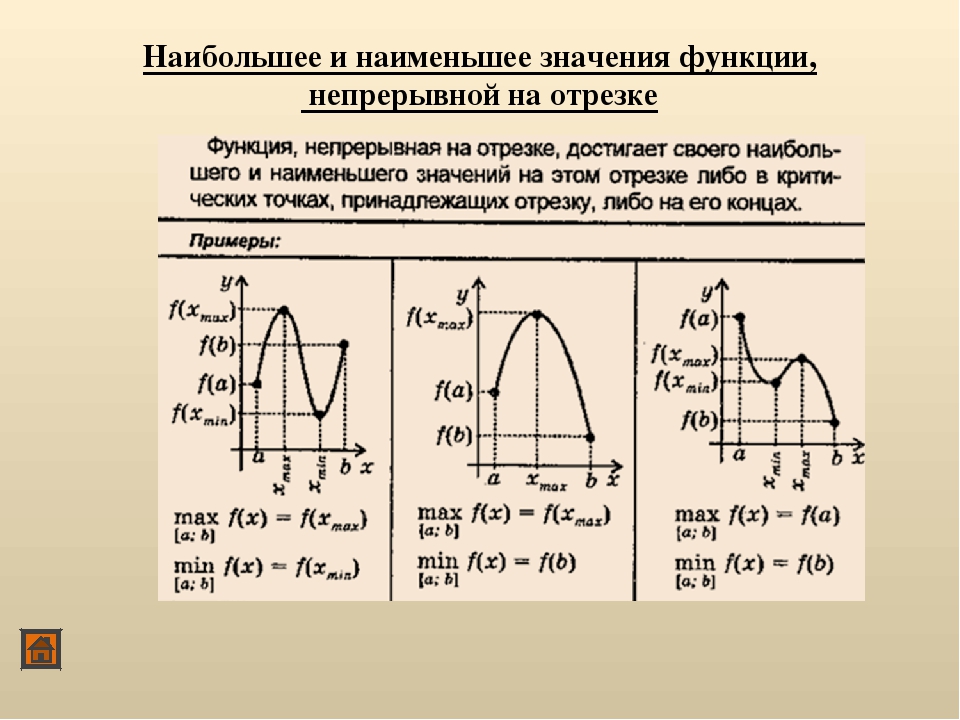
3. Если мы рассмотрим функцию на отрезке , то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то есть и .
Чтобы найти наименьшее значение функции, нам нужно будет сравнить значения функции в точке минимума и в левом конце отрезка, то есть и .
Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:
1. ОДЗ функции — множество действительных чисел.
2.
3. , если или
Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание — убывание, можно схематично изобразить ее график:
Рассмотрим несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике
1. Задание B15 (№ 26695)
Найдите наибольшее значение функции на отрезке .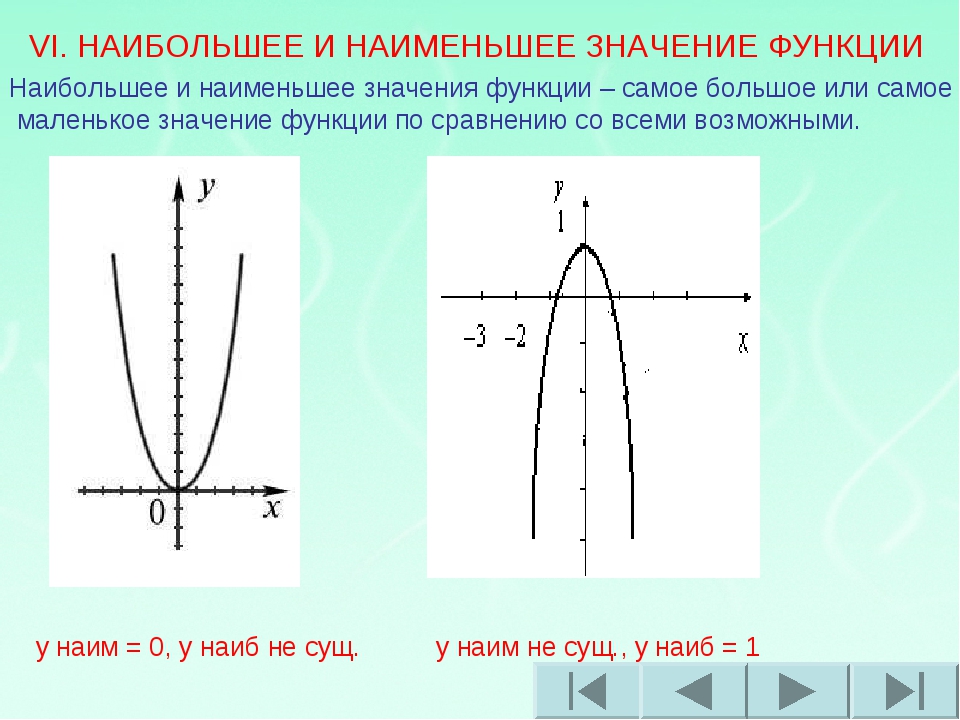
1. Функция определена при всех действительных значениях х
2.
3.
Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.
y(0)=5
Ответ: 5.
2. Задание B15 (№ 26702)
Найдите наибольшее значение функции на отрезке [].
1. ОДЗ функции
2.
Производная равна нулю при , однако, в этих точках она не меняет знак:
, следовательно, , значит, , то есть производная при всех допустимых значених х неотрицательна, следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, при .
Чтобы стало очевидно, почему производная не меняет знак, преобразуем выражение для производной следующим образом:
у(0)=5
Ответ: 5.
3. Задание B15 (№ 26708)
Задание B15 (№ 26708)
Найдите наименьшее значение функции на отрезке [].
1. ОДЗ функции :
2.
3.
,
Расположим корни этого уравнения на тригонометрической окружности.
Промежутку принадлежат два числа: и
Расставим знаки. Для этого определим знак производной в точке х=0: . При переходе через точки и производная меняет знак.
Изобразим смену знаков производной функции на координатной прямой:
Очевидно, что точка является точкой минимума ( в ней производная меняет знак с «-» на «+»), и чтобы найти наименьшее значение функции на отрезке , нужно сравнить значения функции в точке минимума и в левом конце отрезка, .
Схитрим: так как результат должен быть целым числом, или конечной десятичной дробью, а таковым на является, следовательно подставим в уравнение функции
Ответ: -1
Вероятно, Ваш браузер не поддерживается. Попробуйте скачатьFirefox
И.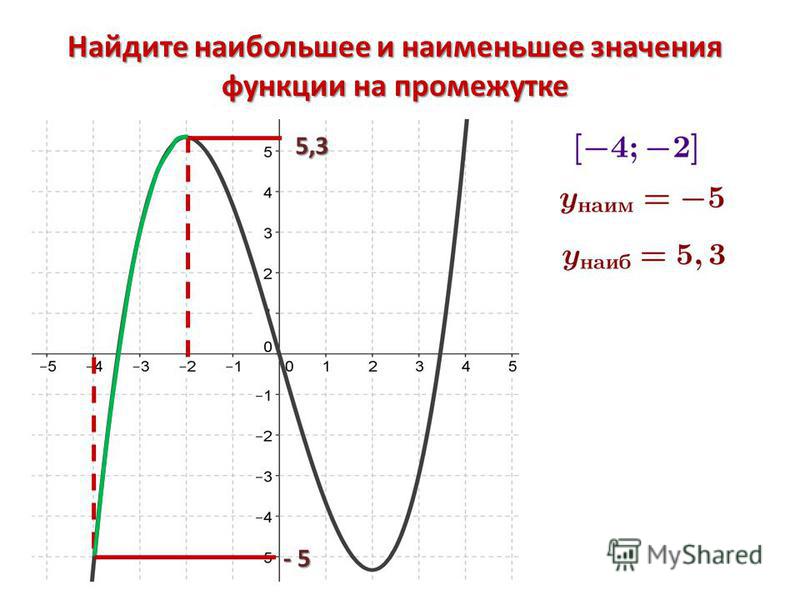 В. Фельдман, репетитор по математике.
В. Фельдман, репетитор по математике.
Значит найти наименьшее значение функции. Наибольшее и наименьшее значение функции на отрезке
С практической точки зрения наибольший интерес представляет использование производной для нахождения наибольшего и наименьшего значения функции. С чем это связано? Максимизация прибыли, минимизация издержек, определение оптимальной загрузки оборудования… Другими словами, во многих сферах жизни приходится решать задачи оптимизации каких-либо параметров. А это и есть задачи на нахождение наибольшего и наименьшего значения функции.
Следует отметить, что наибольшее и наименьшее значение функции обычно ищется на некотором интервале X , который является или всей областью определения функции или частью области определения. Сам интервал X может быть отрезком , открытым интервалом , бесконечным промежутком .
В этой статье мы будем говорить о нахождении наибольшего и наименьшего значений явно заданной функции одной переменной y=f(x)
.
Навигация по странице.
Наибольшее и наименьшее значение функции — определения, иллюстрации.
Кратко остановимся на основных определениях.
Наибольшим значением функции , что для любого справедливо неравенство .
Наименьшим значением функции
Эти определения интуитивно понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на рассматриваемом интервале при абсциссе .
Стационарные точки – это значения аргумента, при которых производная функции обращается в ноль.
Для чего нам стационарные точки при нахождении наибольшего и наименьшего значений? Ответ на этот вопрос дает теорема Ферма. Из этой теоремы следует, что если дифференцируемая функция имеет экстремум (локальный минимум или локальный максимум) в некоторой точке, то эта точка является стационарной. Таким образом, функция часто принимает свое наибольшее (наименьшее) значение на промежутке X
в одной из стационарных точек из этого промежутка.
Также часто наибольшее и наименьшее значение функция может принимать в точках, в которых не существует первая производная этой функции, а сама функция определена.
Сразу ответим на один из самых распространенных вопросов по этой теме:»Всегда ли можно определить наибольшее (наименьшее) значение функции»? Нет, не всегда. Иногда границы промежутка X совпадают с границами области определения функции или интервал X бесконечен. А некоторые функции на бесконечности и на границах области определения могут принимать как бесконечно большие так и бесконечно малые значения. В этих случаях ничего нельзя сказать о наибольшем и наименьшем значении функции.
Для наглядности дадим графическую иллюстрацию. Посмотрите на рисунки – и многое прояснится.
На отрезке
На первом рисунке функция принимает наибольшее (max y ) и наименьшее (min y ) значения в стационарных точках, находящихся внутри отрезка [-6;6] .
Рассмотрим случай, изображенный на втором рисунке.
На рисунке №3 граничные точки отрезка [-3;2] являются абсциссами точек, соответствующих наибольшему и наименьшему значению функции.
На открытом интервале
На четвертом рисунке функция принимает наибольшее (max y ) и наименьшее (min y ) значения в стационарных точках, находящихся внутри открытого интервала (-6;6) .
На интервале , о наибольшем значении никаких выводов сделать нельзя.
На бесконечности
В примере, представленном на седьмом рисунке, функция принимает наибольшее значение (max y ) в стационарной точке с абсциссой x=1 , а наименьшее значение (min y ) достигается на правой границе интервала. На минус бесконечности значения функции асимптотически приближаются к y=3 .
На интервале функция не достигает ни наименьшего, ни наибольшего значения.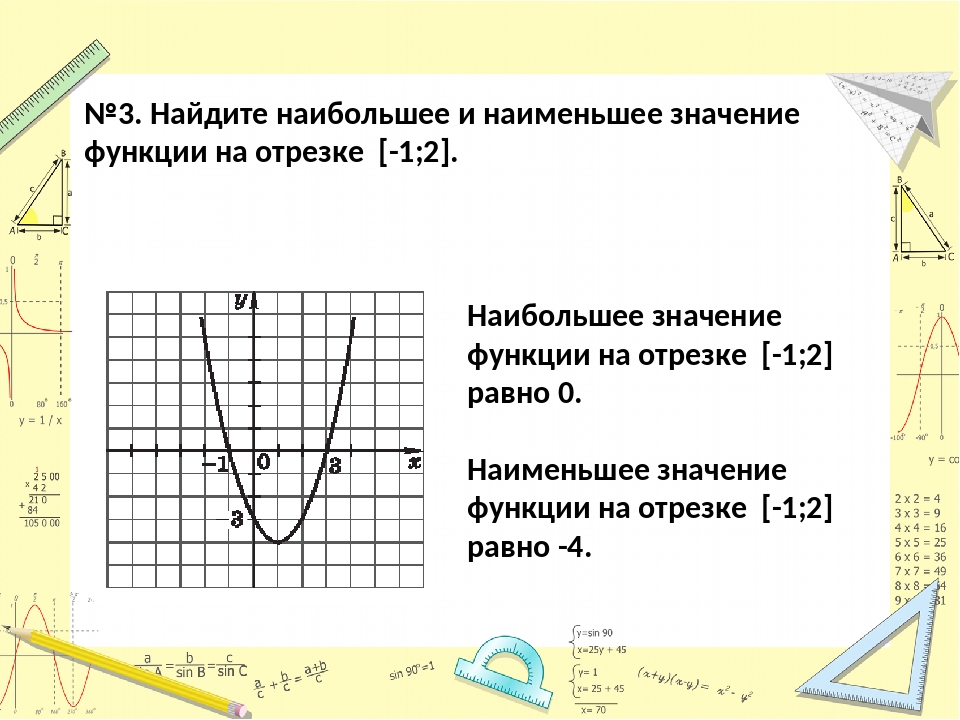 При стремлении к x=2
справа значения функции стремятся к минус бесконечности (прямая x=2
является вертикальной асимптотой), а при стремлении абсциссы к плюс бесконечности, значения функции асимптотически приближаются к y=3
. Графическая иллюстрация этого примера приведена на рисунке №8.
При стремлении к x=2
справа значения функции стремятся к минус бесконечности (прямая x=2
является вертикальной асимптотой), а при стремлении абсциссы к плюс бесконечности, значения функции асимптотически приближаются к y=3
. Графическая иллюстрация этого примера приведена на рисунке №8.
Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на отрезке .
Запишем алгоритм, позволяющий находить наибольшее и наименьшее значение функции на отрезке.
- Находим область определения функции и проверяем, содержится ли в ней весь отрезок .
- Находим все точки, в которых не существует первая производная и которые содержатся в отрезке (обычно такие точки встечаются у функций с аргументом под знаком модуля и у степенных функций с дробно-рациональным показателем). Если таких точек нет, то переходим к следующему пункту.
- Определяем все стационарные точки, попадающие в отрезок
. Для этого, приравниваем ее к нулю, решаем полученное уравнение и выбираем подходящие корни.
 Если стационарных точек нет или ни одна из них не попадает в отрезок, то переходим к следующему пункту.
Если стационарных точек нет или ни одна из них не попадает в отрезок, то переходим к следующему пункту. - Вычисляем значения функции в отобранных стационарных точках (если такие имеются), в точках, в которых не существует первая производная (если такие имеются), а также при x=a и x=b .
- Из полученных значений функции выбираем наибольшее и наименьшее — они и будут искомыми наибольшим и наименьшим значениями функции соответственно.
Разберем алгоритм при решении примера на нахождение наибольшего и наименьшего значения функции на отрезке.
Пример.
Найти наибольшее и наименьшее значение функции
- на отрезке ;
- на отрезке [-4;-1] .
Решение.
Областью определения функции является все множество действительных чисел, за исключением нуля, то есть . Оба отрезка попадают в область определения.
Находим производную функции по :
Очевидно, производная функции существует во всех точках отрезков
и [-4;-1]
.
Стационарные точки определим из уравнения . Единственным действительным корнем является x=2 . Эта стационарная точка попадает в первый отрезок .
Для первого случая вычисляем значения функции на концах отрезка и в стационарной точке, то есть при x=1
, x=2
и x=4
:
Следовательно, наибольшее значение функции достигается при x=1 , а наименьшее значение – при x=2 .
Для второго случая вычисляем значения функции лишь на концах отрезка [-4;-1]
(так как он не содержит ни одной стационарной точки):
Стандартный алгоритм решения таких заданий предполагает после нахождения нулей функции, определение знаков производной на интервалах. Затем вычисление значений в найденных точках максимума (или минимума) и на границе интервала, в зависимости от того какой вопрос стоит в условии.
Советую поступать немного по-другому. Почему? Писал об этом .
Предлагаю решать такие задания следующим образом:
1. Находим производную.
2.Находим нули производной.
3. Определяем какие из них принадлежат данному интервалу.
4. Вычисляем значения функции на границах интервала и точках п.3.
5. Делаем вывод (отвечаем на поставленный вопрос).
В ходе решения представленных примеров подробно не рассмотрено решение квадратных уравнений, это вы должны уметь делать. Так же должны знать .
Рассмотрим примеры:
77422. Найдите наибольшее значение функции у=х 3 –3х+4 на отрезке [–2;0].
Найдем нули производной:
Указанному в условии интервалу принадлежит точка х = –1.
Вычисляем значения функции в точках –2, –1 и 0:
Наибольшее значение функции равно 6.
Ответ: 6
77425. Найдите наименьшее значение функции у = х 3 – 3х 2 + 2 на отрезке .
Найдём производную заданной функции:
Найдем нули производной:
Указанному в условии интервалу принадлежит точка х = 2.
Вычисляем значения функции в точках 1, 2 и 4:
Наименьшее значение функции равно –2.
Ответ: –2
77426. Найдите наибольшее значение функции у = х 3 – 6х 2 на отрезке [–3;3].
Найдём производную заданной функции:
Найдем нули производной:
Указанному в условии интервалу принадлежит точка х = 0.
Вычисляем значения функции в точках –3, 0 и 3:
Наименьшее значение функции равно 0.
Ответ: 0
77429. Найдите наименьшее значение функции у = х 3 – 2х 2 + х +3 на отрезке .
Найдём производную заданной функции:
3х 2 – 4х + 1 = 0
Получим корни: х 1 = 1 х 1 = 1/3.
Указанному в условии интервалу принадлежит только х = 1.
Найдём значения функции в точках 1 и 4:
Получили, что наименьшее значение функции равно 3.
Ответ: 3
77430. Найдите наибольшее значение функции у = х 3 + 2х 2 + х + 3 на отрезке [– 4; –1].
Найдём производную заданной функции:
Найдем нули производной, решаем квадратное уравнение:
3х 2 + 4х + 1 = 0
Получим корни:
Указанному в условии интервалу принадлежит корень х = –1.
Находим значения функции в точках –4, –1, –1/3 и 1:
Получили, что наибольшее значение функции равно 3.
Ответ: 3
77433. Найдите наименьшее значение функции у = х 3 – х 2 – 40х +3 на отрезке .
Найдём производную заданной функции:
Найдем нули производной, решаем квадратное уравнение:
3х 2 – 2х – 40 = 0
Получим корни:
Указанному в условии интервалу принадлежит корень х = 4.
Находим значения функции в точках 0 и 4:
Получили, что наименьшее значение функции равно –109.
Ответ: –109
Рассмотрим способ определения наибольшего и наименьшего значения функций без производной. Этот подход можно использовать, если с определением производной у вас большие проблемы. Принцип простой – в функцию подставляем все целые значения из интервала (дело в том, что во всех подобных прототипах ответом является целое число).
77437. Найдите наименьшее значение функции у=7+12х–х 3 на отрезке [–2;2].
Подставляем точки от –2 до 2: Посмотреть решение
77434. Найдите наибольшее значение функции у=х 3 + 2х 2 – 4х + 4 на отрезке [–2;0].
На этом всё. Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Миниатюрная и довольно простая задача из разряда тех, которые служат спасательным кругом плавающему студенту. На природе сонное царство середины июля, поэтому самое время устроиться с ноутбуком на пляже. Ранним утром заиграл солнечный зайчик теории, чтобы в скором времени сфокусироваться на практике, которая, несмотря на заявленную лёгкость, содержит осколки стекла в песке. В этой связи рекомендую добросовестно рассмотреть немногочисленные примеры этой странички. Для решения практических заданий необходимо уметь находить производные и понимать материал статьи Интервалы монотонности и экстремумы функции .
Сначала коротко о главном. На уроке о непрерывности функции я приводил определение непрерывности в точке и непрерывности на интервале. Образцово-показательное поведение функции на отрезке формулируется похожим образом. Функция непрерывна на отрезке если:
Образцово-показательное поведение функции на отрезке формулируется похожим образом. Функция непрерывна на отрезке если:
1) она непрерывна на интервале ;
2) непрерывна в точке справа и в точке слева .
Во втором пункте речь зашла о так называемой односторонней непрерывности функции в точке. Существует несколько подходов к её определению, но я буду придерживаться начатой ранее линии:
Функция непрерывна в точке справа , если она определена в данной точке и её правосторонний предел совпадает со значением функции в данной точке: . Она же непрерывна в точке слева , если определена в данной точке и её левосторонний предел равен значению в этой точке:
Представьте, что зелёные точки – это гвозди, на которых закреплена волшебная резинка:
Мысленно возьмите красную линию в руки. Очевидно, что как бы далеко мы не растягивали график вверх и вниз (вдоль оси ), функция всё равно останется ограниченной – изгородь сверху, изгородь снизу, и наше изделие пасётся в загоне.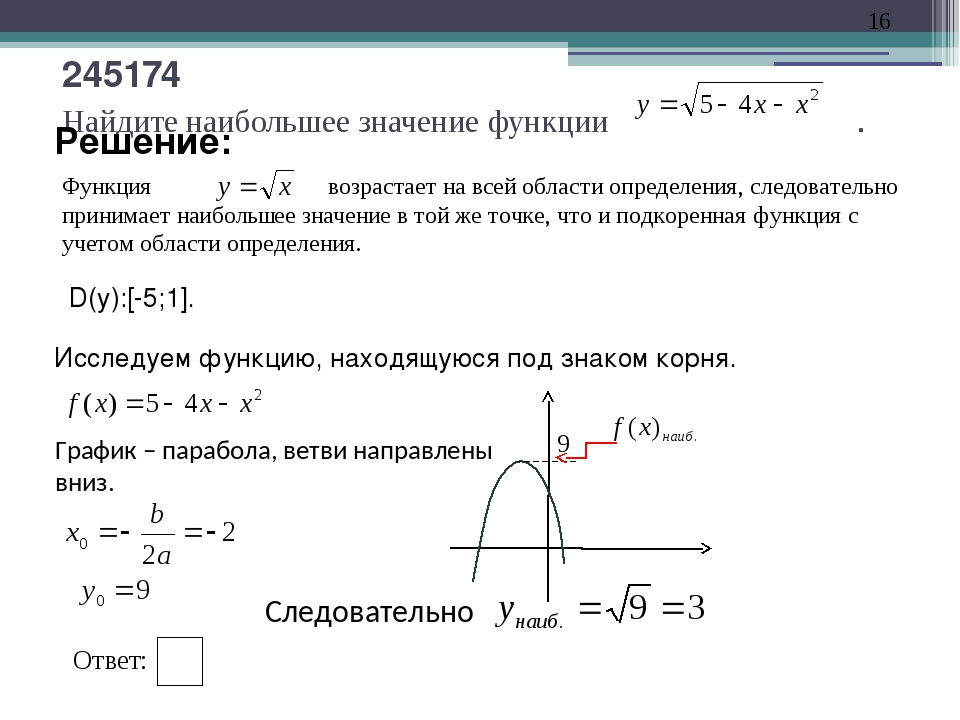 Таким образом, непрерывная на отрезке функция ограничена на нём . В курсе матанализа этот вроде бы простой факт констатируется и строго доказывается первой теоремой Вейерштрасса. …Многих раздражает, что в математике нудно обосновываются элементарные утверждения, однако в этом есть важный смысл. Предположим, некий житель махрового средневековья вытягивал график в небо за пределы видимости вот это вставляло. До изобретения телескопа ограниченность функции в космосе была вовсе не очевидна! Действительно, откуда вы знаете, что нас ждёт за горизонтом? Ведь когда-то и Земля считалась плоской, поэтому сегодня даже обыденная телепортация требует доказательства =)
Таким образом, непрерывная на отрезке функция ограничена на нём . В курсе матанализа этот вроде бы простой факт констатируется и строго доказывается первой теоремой Вейерштрасса. …Многих раздражает, что в математике нудно обосновываются элементарные утверждения, однако в этом есть важный смысл. Предположим, некий житель махрового средневековья вытягивал график в небо за пределы видимости вот это вставляло. До изобретения телескопа ограниченность функции в космосе была вовсе не очевидна! Действительно, откуда вы знаете, что нас ждёт за горизонтом? Ведь когда-то и Земля считалась плоской, поэтому сегодня даже обыденная телепортация требует доказательства =)
Согласно второй теореме Вейерштрасса , непрерывная на отрезке функция достигает своей точной верхней грани и своей точной нижней грани .
Число также называют максимальным значением функции на отрезке и обозначают через , а число – минимальным значением функции на отрезке с пометкой .
В нашем случае:
Примечание : в теории распространены записи .
Грубо говоря, наибольшее значение находится там, где самая высокая точка графика, а наименьшее – где самая низкая точка.
Важно! Как уже заострялось внимание в статье об экстремумах функции , наибольшее значение функции и наименьшее значение функции – НЕ ТО ЖЕ САМОЕ , что максимум функции и минимум функции . Так, в рассматриваемом примере число является минимумом функции, но не минимальным значением.
Кстати, а что происходит вне отрезка ? Да хоть потоп, в контексте рассматриваемой задачи это нас совершенно не интересует. Задание предполагает лишь нахождение двух чисел и всё!
Более того, решение чисто аналитическое, следовательно, чертежа делать не надо !
Алгоритм лежит на поверхности и напрашивается из приведённого рисунка:
1) Находим значения функции в критических точках , которые принадлежат данному отрезку .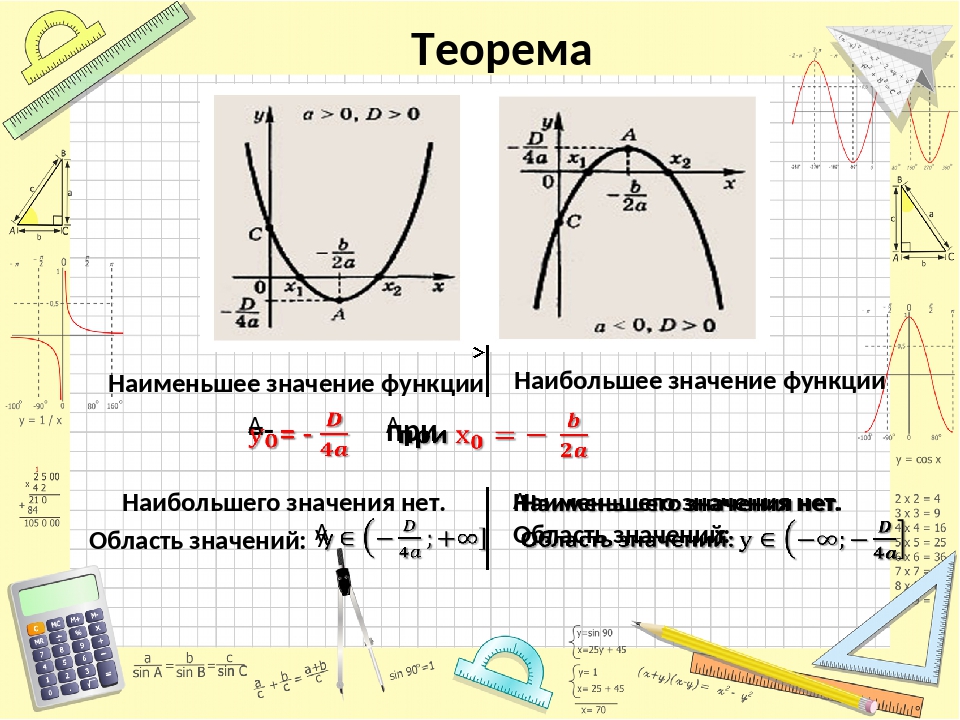
Ловите ещё одну плюшку: здесь отпадает необходимость проверять достаточное условие экстремума, поскольку, как только что было показано, наличие минимума или максимума ещё не гарантирует , что там минимальное или максимальное значение. Демонстрационная функция достигает максимума и волей судьбы это же число является наибольшим значением функции на отрезке . Но, понятно, такое совпадение имеет место далеко не всегда.
Итак, на первом шаге быстрее и проще вычислить значения функции в критических точках, принадлежащих отрезку, не заморачиваясь есть в них экстремумы или нет.
2) Вычисляем значения функции на концах отрезка.
3) Среди найденных в 1-м и 2-м пунктах значений функции выбираем самое маленькое и самое большое число, записываем ответ.
Садимся на берег синего моря и бьём пятками по мелководью:
Пример 1
Найти наибольшее и наименьшее значения функции на отрезке
Решение :
1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:
Вычислим значение функции во второй критической точке:
2) Вычислим значения функции на концах отрезка:
3) «Жирные» результаты получены с экспонентами и логарифмами, что существенно затрудняет их сравнение.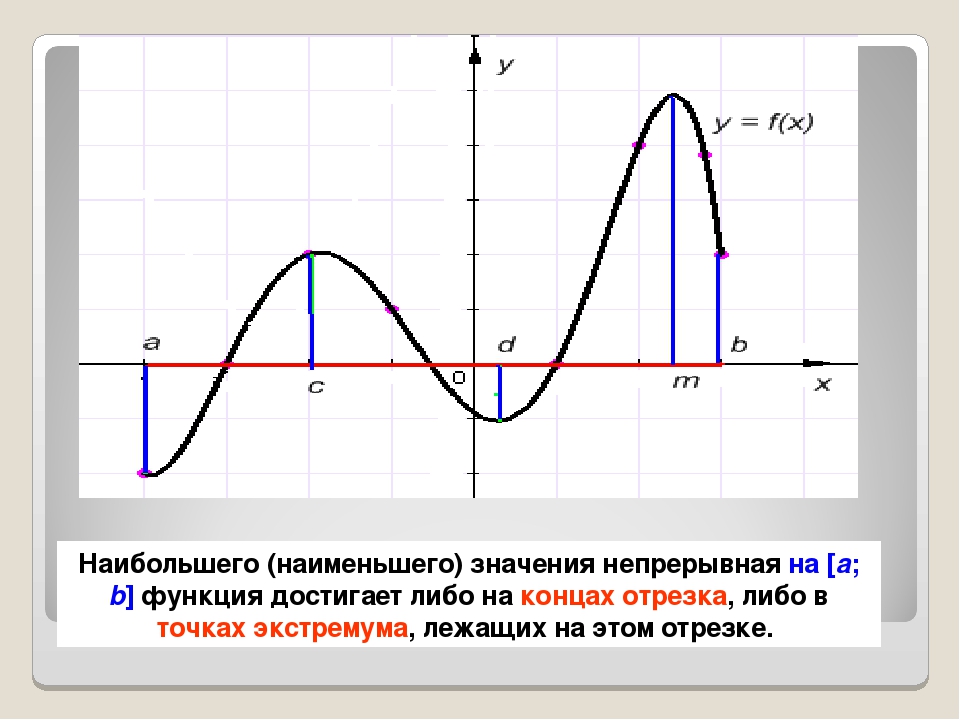 По сей причине вооружимся калькулятором либо Экселем и вычислим приближённые значения, не забывая, что :
По сей причине вооружимся калькулятором либо Экселем и вычислим приближённые значения, не забывая, что :
Вот теперь всё понятно.
Ответ :
Дробно-рациональный экземпляр для самостоятельного решения:
Пример 6
Найти максимальное и минимальное значения функции на отрезке
Урок на тему: «Нахождение наибольшего и наименьшего значения непрерывной функции на отрезке»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Решаем задачи по геометрии. Интерактивные задания на построение в пространстве
Что будем изучать:
1. Нахождение наибольшего и наименьшего значения по графику функции.2. Нахождение наибольшего и наименьшего значения с помощью производной.
3. Алгоритм поиска наибольшего и наименьшего значения непрерывной функции y=f(x) на отрезке .
4. Наибольшее и наименьшее значение функции на незамкнутом интервале.
5. Примеры.
Нахождение наибольшего и наименьшего значения по графику функции
Ребята, мы с вами находили наибольшее и наименьшее значения функции и раньше. Мы смотрели на график функции и делали вывод, где функция достигает наибольшего значения, а где — наименьшего.
Давайте повторим:
По графику нашей функции видно, что наибольшее значение достигается в точке x= 1, оно равно 2. Наименьшее значение достигается в точке x= -1, и оно равно -2. Данным способом довольно просто находить наибольшие и наименьшие значения, но не всегда существует возможность построить график функции.
Нахождение наибольшего и наименьшего значения с помощью производной
Ребята, а как вы думаете, как с помощью производной можно найти наибольшее и наименьшее значение?
Ответ можно найти в теме экстремумы функции. Там мы с вами находили точки максимума и минимума, не правда ли термины похожи. Однако, путать наибольшее и наименьшее значение с максимум и минимум функции нельзя, это разные понятия.
Там мы с вами находили точки максимума и минимума, не правда ли термины похожи. Однако, путать наибольшее и наименьшее значение с максимум и минимум функции нельзя, это разные понятия.
Итак, давайте введем правила:
а) Если функция непрерывна на отрезке, то она достигает своего наибольшего и наименьшего значения на этом отрезке.
б) Наибольшего и наименьшего значения функция может достигать как на концах отрезках, так и внутри него.
Давайте рассмотрим этот пункт подробнее.
На рисунке а функция достигает своего наибольшего и наименьшего значения на концах отрезках .
На рисунке б функция достигает своего наибольшего и наименьшего значения внутри отрезка .
На рисунке в точка минимума находится внутри отрезка, а точка максимума — на конце отрезка, в точке b.
в) Если наибольшее и наименьшее значение достигается внутри отрезка, то только в стационарных или критических точках.
Алгоритм поиска наибольшего и наименьшего значения непрерывной функции y= f(x) на отрезке
- Найти производную f»(x).
 3}{3}$ + 2x 2 + 4x — 5 на отрезке
3}{3}$ + 2x 2 + 4x — 5 на отрезке
а) [-9;-1], б) [-3;3], в) .
Решение: Найдем производную: y»= x 2 + 4x + 4.
Производная существует на всей области определения, тогда нам надо найти стационарные точке.
y»= 0, при x= -2.
Дальнейшие расчеты проведем для требуемых отрезков.
а) Найдем значения функции на концах отрезка и в стационарной точки.
Тогда y наим. = -122, при x= -9; y наиб. = y = -7$\frac{1}{3}$, при x= -1.
б) Найдем значения функции на концах отрезка и в стационарной точке. Наибольшее и наименьшее значение достигается на концах отрезка.
Тогда y наим. = -8, при x= -3, y наиб. = 34, при x= 3.
в) Стационарная точка не попадает на наш отрезок, найдем значения на концах отрезка.
Тогда y наим. = 34, при x= 3, y наиб. = 436, при x= 9.Пример
Найти наибольшее и наименьшее значение функции y= x 2 — 3x + 5 + |1-x| на отрезке .
Решение: Раскроем модуль и преобразуем нашу функцию:
y= x 2 — 3x + 5 + 1 — x, при x ≤ 1.
y= x 2 — 3x + 5 — 1 + x, при x ≥ 1. 2 + 3}$ на луче: , б) , в) [-4;7].
2 + 3}$ на луче: , б) , в) [-4;7].
б) Найти наибольшее и наименьшее значение функции y= x 2 — 6x + 8 + |x — 2| на отрезке [-1;5].
в) Найти наибольшее и наименьшее значение функции y= $-2x-\frac{1}{2x}$ на луче (0;+∞).Наименьшее значение функции по графику производной
Рассмотрим примеры, в которых дан график производной и требуется определить, в какой точке данного отрезка функция принимает наименьшее значение.
№1
На рисунке изображён график производной функции f(x), определённой на интервале (-10;8). В какой точке отрезка [-8;-1] функция f(x) принимает наименьшее значение?
Решение:
Выделяем отрезок [-8;-1].
На этом отрезке производная f'(x) принимает положительные значения.
Значит, на [-8;-1] функция f(x) возрастает, то есть бо́льшему значению аргумента соответствует бо́льшее значение функции:
x1,x2 ∈[-8;-1], x2>x1, ⇒ f(x2)>f(x1).

Следовательно, наименьшее значение f(x) принимает при наименьшем значении аргумента, то есть на левом конце отрезка, при x=-8.
Ответ: -8.
№2
На рисунке изображён график производной функции f(x), определённой на интервале (-6;8). В какой точке отрезка [-3;6] функция f(x) принимает наименьшее значение?
Решение:
Выделяем отрезок [-3;6].
На этом отрезке f'(x)<0, поэтому f(x) убывает, то есть бо́льшему значению аргумента соответствует меньшее значение функции:
x1,x2 ∈[-3;6], x2>x1, ⇒ f(x2)<f(x1).
Поэтому наименьшее значение функция f(x) в этом случае принимает при наибольшем значении аргумента, то есть на правом конце отрезка, при x=6.
Ответ: 6.
№3
Функция y=f(x) определена на промежутке (-9;6). На рисунке изображён график её производной. Найти абсциссу точки, в которой функция y=f(x) принимает наименьшее значение.

Решение:
В точке с абсциссой x=2 производная меняет знак с минуса на плюс.
Значит, x=2 — точка минимума.
Производная f'(x) существует на всём интервале (-9;6), следовательно, функция f(x) на (-9;6) непрерывна.
Если непрерывная функция f(x) имеет на заданном интервале (a;b) только одну точку экстремума xo и это точка минимума, то на (a;b) функция принимает своё наименьшее значение в точке xo.
Таким образом, наименьшее значение функция f(x) принимает в точке с абсциссой x=2.
Ответ: 2.
№4
Функция y=f(x) определена и непрерывна на отрезке [-4;9]. На рисунке изображён график её производной. Найти точку xo, в которой функция принимает наименьшее значение, если f(9)≤f(-4).
Решение:
На промежутках (-4;-3) и (2;9) производная f'(x) принимает положительные значения, поэтому функция f(x) на этих промежутках возрастает.
На промежутке (-3;2) производная f'(x)<0, поэтому функция f(x) убывает.

Так как функция определена и непрерывна на отрезке [-4;9], то точки -4, -3, 2 и 9 можно включить в промежутки монотонности.
Следовательно, функция f(x) возрастает на промежутках [-4;-3] и [2;9] и убывает на [-3;2].
На промежутках возрастания своё наименьшее значение функция принимает на левом конце отрезка. На отрезке [2;9] наименьшее значение f(x) принимает в точке x=2 (точке минимума), на [-4;-3] — в точке x=-4.
Так как на [2;9] функция f(x) возрастает, то f(2)<f(9).
По условию, f(9)≤f(-4). Значит, f(2)<f(-4).
Таким образом, наименьшее значение функция f(x) принимает в точке x=2.
Ответ: 2.
Урок на тему «Наибольшее и наименьшее значение функции»
Урок на тему «Наибольшее и наименьшее значение функции»
Цели урока.
Образовательные: дать определение наибольшего и наименьшего значений, выявить, в каких точках области определения функция может иметь наибольшее и наименьшее значение, составить алгоритм отыскания наибольшего и наименьшего значений.

Развивающие: совершенствование умений по применению приемов мышления, овладение содержанием и структурой поисковой работы.
Воспитательные: умение высказывать и аргументировать свою точку зрения, воспитывать работу в команде.
Структура урока.
I. Актуализация знаний.
Мобилизующее начало
Фронтальный опрос по теме «Исследование функции на монотонность и экстремумы» с целью актуализации знаний
Самостоятельная работа по теме «Исследование функции на монотонность и экстремумы» с целью проверки усвоения темы
Беседа с целью мотивации изучения новой темы, постановка цели и задач урока
II. Формирование новых знаний и способов действия.
Фронтальная исследовательская работа поискового характера с целью определения, при каком значении аргумента функция может принимать наибольшее или наименьшее значение
Обсуждение результатов исследовательской работы и их обобщение с целью определения того, как аналитическими средствами можно найти точки, в которых функция принимает наибольшее или наименьшее значение.

Беседа с целью составления алгоритма для отыскания наибольшего и наименьшего значений
III. Применение знаний, умений и навыков.
Решение задач с целью усвоения алгоритма на материализованном уровне
Подведение итогов урока, постановка домашнего задания
Ход урока.
I. Актуализация знаний.
Мобилизующее начало(1 мин.)
Фронтальный опрос по теме «Исследование функции на монотонность и экстремумы» с целью актуализации знаний
Здравствуйте.
Давайте с вами вспомним, что мы изучали на протяжении последних уроков? (Экстремумы функции) Какие точки мы назвали точками максимума, минимума? (точкой максимума называется такая точка, в которой функция принимает наибольшее значение в окрестности этой точки. Точкой минимума называется такая точка, в которой функция принимает наименьшее значение в окрестности этой точки).
И конечно же давайте вспомним алгоритм исследования функции на монотонность и экстремумы:
Найти производную функции f`(x)
Найти стационарные и критические точки: f`(x)=0, f`(x) – не существует.

Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках
Записать точки экстремума, опираясь на следующее правило: при переходе через критическую(стационарную) точку производная меняет знак с плюса на минус – точка максимума, производная меняет знак с минуса на плюс – точка минимума.
Самостоятельная работа по теме «Исследование функции на монотонность и экстремумы» с целью проверки усвоения темы
Чтобы проверить, как хорошо вы усвоили данную тему, напишем небольшую самостоятельную работу, в которой требуется исследовать функцию на монотонность и экстремумы, а также по графику производной функции определить промежутки возрастания (убывания) и указать точки экстремума.
Самостоятельная работа.
1 вариант
1.Исследовать функцию на монотонность и экстремумы:
2. На рисунке изображен график производной функции f(x), определенной на интервале (-∞;+ ∞).
 Укажите точки максимума функции, а также промежутки убывания функции.
Укажите точки максимума функции, а также промежутки убывания функции.2 вариант
1.Исследовать функцию на монотонность и экстремумы:
2. На рисунке изображен график производной функции f(x), определенной на интервале (-∞;+ ∞). Укажите точки минимума функции, а также промежутки возрастания функции.
Беседа с целью мотивации изучения новой темы, постановка цели и задач урока
Ребята, посмотрите на график и назовите наибольшее и наименьшее значение функции. ( наибольшее значение = 7, наименьшее значение = -3)
Все правильно. Как видите, определить наибольшее и наименьшее значение функции по ее графику нам не составило труда. Но нам может быть не дан график, а дано аналитическое задание функции, график которой нам будет сложно построить. Нам снова совершенно необходимо найти способ определения наиб. и наим. значения функции не строя график.
Для того, чтобы выяснить, в каких точках области определения функция может принимать наибольшее и наименьшее значение, воспользуемся тем, что мы умеем это делать по графику функции.

Для этого рассмотрим следующие графики:
— Посмотрите на первый график и скажите, в каких точках функция принимает свое наибольшее и наименьшее значение?(наибольшее в точке с, а наименьшее в точке b)
— А чем являются эти точки?(точка с – точка максимума функции, точка b – точка минимума функции)
— Посмотрите на второй график и скажите, в каких точках функция принимает свое наибольшее и наименьшее значение?(наибольшее в точке d, а наименьшее в точке а)
— А чем являются эти точки?(эти точки – концы области определения функции)
— Посмотрите на третий график и скажите, в каких точках функция принимает свое наибольшее и наименьшее значение?(наибольшее в точке b, а наименьшее в точке а)
— А чем являются эти точки?(точка b – это точка максимума функции, точка а – граница области определения функции)
— Всё верно. Мы рассмотрели различные примеры функций, заданных графически. Давайте сделаем вывод, в каких точках области определения функция может иметь наибольшее и наименьшее значения.
 ( в точках экстремума или на концах отрезка, являющимся областью определения функции)
( в точках экстремума или на концах отрезка, являющимся областью определения функции)— Как вы думаете, как аналитическими средствами можно найти наибольшее или наименьшее значение функции, опираясь на тот вывод, который мы сделали?(найти значение функции в точках экстремума и на концах отрезка, являющимся областью определения функции)
— Достаточно ли нам знаний, чтобы это сделать?(да, найти значение функции в точке экстремума – значит найти экстремум функции, а это мы уже умеем делать по алгоритму)
— А что значит найти значение функции на концах отрезка, являющимся областью определения функции? (для этого нужно подставить граничные значения области определения в функцию)
— Да, верно! Мы нашли значения функции в точках экстремума и на концах промежутка, как теперь найти наибольшее или наименьшее значение функции? (все полученные значения нужно сравнить: большее число – это будет наибольшее значение функции, меньшее число – наименьшее значение функции)
— Вы правильно рассуждали, давайте теперь составим алгоритм для отыскания наибольшего и наименьшего значения функции:
Алгоритм отыскания наибольшего и наименьшего значения функции:
Найти критические (и стационарные) точки функции на области определения функции.

Найти значения функции в критических точках и на концах отрезка, являющимся областью определения функции
Выбрать из полученных значений наибольшее и наименьшее, если они существуют
Елена Игоревна, мы специально рассмотрели случай, когда обл. опр-я ф-ции отрезок, а случай с интервалом рассмотрим на примере специально подобранной задачи.
Решение задач с целью усвоения алгоритма на материализованном уровне.
— Теперь применим этот алгоритм при решении задач. Он перед вами, поэтому при решении задач проговариваем каждый пункт и выполняем четко его шаги.
Задание:
Найти наибольшее и наименьшее значения функции: на отрезке [0,2]
Решение:
Если останется время, то решаем аналогичные задания.
Подведение итогов урока, постановка домашнего задания
– Сегодня на уроке мы с вами научились находить наибольшее и наименьшее значения функции, составили алгоритм для их отыскания.

Давайте его ещё раз повторим:
1. Найти критические (и стационарные) точки функции на области определения функции.
2.Найти значения функции в критических точках и на концах отрезка, являющимся областью определения функции
3.Выбрать из полученных значений наибольшее и наименьшее, если они существуют
Домашнее задание аналогично тому, что решали на уроке.
Наибольшее и наименьшее значение функции. Алгебра
Дата публикации: .
Что будем изучать:
1. Нахождение наибольшего и наименьшего значения по графику функции.
2. Нахождение наибольшего и наименьшего значения с помощью производной.
3. Алгоритм поиска наибольшего и наименьшего значения непрерывной функции y=f(x) на отрезке [a;b].
4. Наибольшее и наименьшее значение функции на незамкнутом интервале.
5. Примеры.Нахождение наибольшего и наименьшего значения по графику функции
Ребята, мы с вами находили наибольшее и наименьшее значения функции и раньше.
 Мы смотрели на график функции и делали вывод, где функция достигает наибольшего значения, а где — наименьшего.
Мы смотрели на график функции и делали вывод, где функция достигает наибольшего значения, а где — наименьшего.
Давайте повторим:По графику нашей функции видно, что наибольшее значение достигается в точке x= 1, оно равно 2. Наименьшее значение достигается в точке x= -1, и оно равно -2. Данным способом довольно просто находить наибольшие и наименьшие значения, но не всегда существует возможность построить график функции.
Нахождение наибольшего и наименьшего значения с помощью производной
Ребята, а как вы думаете, как с помощью производной можно найти наибольшее и наименьшее значение?
Ответ можно найти в теме экстремумы функции. Там мы с вами находили точки максимума и минимума, не правда ли термины похожи. Однако, путать наибольшее и наименьшее значение с максимум и минимум функции нельзя, это разные понятия.Итак, давайте введем правила:
а) Если функция непрерывна на отрезке, то она достигает своего наибольшего и наименьшего значения на этом отрезке.
б) Наибольшего и наименьшего значения функция может достигать как на концах отрезках, так и внутри него. Давайте рассмотрим этот пункт подробнее.
На рисунке а функция достигает своего наибольшего и наименьшего значения на концах отрезках [a;b].
На рисунке б функция достигает своего наибольшего и наименьшего значения внутри отрезка [a;b]. На рисунке в точка минимума находится внутри отрезка, а точка максимума — на конце отрезка, в точке b.
в) Если наибольшее и наименьшее значение достигается внутри отрезка, то только в стационарных или критических точках.Алгоритм поиска наибольшего и наименьшего значения непрерывной функции y= f(x) на отрезке [a;b]
- Найти производную f'(x).
- Найти стационарные и критические точки внутри отрезка [a;b].
- Вычислить значение функции в стационарных и критических точках, а так же в f(a) и f(b). Выбрать наименьшее и наибольшее значения, это и будут точки наименьшего и наибольшего значения функции.
 3}{3}$ + 2x2 + 4x — 5 на отрезке
3}{3}$ + 2x2 + 4x — 5 на отрезке
а) [-9;-1], б) [-3;3], в) [3;9].
Решение: Найдем производную: y’= x2 + 4x + 4.
Производная существует на всей области определения, тогда нам надо найти стационарные точке.
y’= 0, при x= -2.
Дальнейшие расчеты проведем для требуемых отрезков.
а) Найдем значения функции на концах отрезка и в стационарной точки.
Тогда yнаим.= -122, при x= -9; yнаиб.= y = -7$\frac{1}{3}$, при x= -1.
б) Найдем значения функции на концах отрезка и в стационарной точке. Наибольшее и наименьшее значение достигается на концах отрезка.
Тогда yнаим.= -8, при x= -3, yнаиб.= 34, при x= 3.
в) Стационарная точка не попадает на наш отрезок, найдем значения на концах отрезка.
Тогда yнаим.= 34, при x= 3, yнаиб.= 436, при x= 9.Пример
Найти наибольшее и наименьшее значение функции y= x2 — 3x + 5 + |1-x| на отрезке [0;4].
Решение: Раскроем модуль и преобразуем нашу функцию:
y= x2 — 3x + 5 + 1 — x, при x ≤ 1. 2 + 3}$= $\frac{3√3}{6}$= $\frac{√3}{2}$.
2 + 3}$= $\frac{3√3}{6}$= $\frac{√3}{2}$.Ответ: yнаиб.= $\frac{√3}{2}$.
Задачи для самостоятельного решения
а) Найти наибольшее и наименьшее значение функции y= x4 — 3x3 + 2x2 — 9x + 1
на отрезке а) [-3;1], б) [2;5], в) [-4;7].
б) Найти наибольшее и наименьшее значение функции y= x2 — 6x + 8 + |x — 2| на отрезке [-1;5].
в) Найти наибольшее и наименьшее значение функции y= $-2x-\frac{1}{2x}$ на луче (0;+∞).Наибольшее и наименьшее значения функции. Сложная функция
Открытый банк заданий по математике http://mathege.ru:8080/or/ege/Main.action
СЛОЖНАЯ ФУНКЦИЯ – функция, представленная как композиция
нескольких функций. Сложная функция – функция от функции.
(
)
Сложная функция u v (x) представлена в виде цепочки простых
функций. v (x) – промежуточный аргумент, x – независимая переменная.
Здесь у нас две функции – u и v, причем функция v, образно говоря,
вложена в функцию u. Функция такого вида (когда одна функция вложена в
Функция такого вида (когда одна функция вложена в
другую) и называется сложной функцией.
Производная сложной функции равна произведению производной данной
функции по промежуточному аргументу на производную промежуточного
аргумента по независимому аргументу. Это правило (цепное правило)
распространяется на сложные функции с двумя, тремя и т. д.
промежуточными аргументами:
[ u (v (x))] /= u /(v (x ))
/ /
u
v
[ ( )] = u (v) v /
v /(x)
В этой записи я «сэкономила» независимый
аргумент «х».
Чтобы найти производную сложной функции, нужно
1. Определить, какая функция является внешней и найти по таблице
производных соответствующую производную.
2. Определить промежуточный аргумент.
В этой процедуре наибольшие затруднения вызывает нахождение
внешней функции. Для этого используется простой алгоритм:
а. Запишите формулу функции.
б. Представьте, что вам нужно вычислить значение функции при каком-то
значении х. Для этого вы подставляете это значение х в уравнение
Для этого вы подставляете это значение х в уравнение
функции и производите арифметические действия. То действие, которое
вы делаете последним и есть внешняя функция.
В композиции может быть и больше двух функций:
у / = f / ( f1 ( f2 ( f3 ( f4 ( x))))) f1 / ( f2 ( f3 ( f4 ( x)))) f2 / ( f3 ( f4 ( x))) f3 / ( f4 ( x)) f4 / ( x)
Функция квадратного корня
у = 5 4х х2
Функция промежуточного аргумента – квадратичная функция
Показательная функция
у=2
х 2 2 х 5
Функция промежуточного аргумента – квадратичная функция
Логарифмическая функция
(
)
у = log 5 4 2 x x 2 3
Функция промежуточного аргумента – квадратичная функция
Степенная функция
у = sin 4 x
Функция промежуточного аргумента – тригонометрическая функция sinx
1. Найдите наименьшее значение функции y = e2x – 6ex + 3 на
отрезке [1; 2]
4– 6e2+ 3
2 – 6e + 3;
y(2)
=
e
1)
y(1)
=
e
Значения функции в
концах отрезка.
– 6ex + 0 = 2ex(ex – 3)
[ u v)] /= u /(v) v / (e2x)/ = e2x (2x)/ = e2x 2 >0
= 2e2x
2) y / =
(
(ex)/
=
ex
(kx)/ = k
0
r
log b(e=) r=log
2e (eab
– 3) = 0
e
1) производная
a
для внешней функции:
x
x /
x
x
ex – 3 = 0
Наименьшее
2) умножим
значение
на производную
(kx)/ =1 k
функция
промежуточного
будет принимать
аргумента:
в
x= ln
e
ln
3
Найдем критические точки,
точке минимума.
Проверим, принадлежит ли
которые принадлежат Можно сэкономить на
x = ln3 [1; 2]
х=ln3 промежутку [1; 2]
заданному отрезку.
вычислениях значений
ln 3отрезка.
2
функции в1концах
(С)/ = 0
ln e ln 3 ln e
\
2
y
e 3 e верно
y
e 2,7
2
Найдем значение
функции в критической
точке.
2 ln 3
у(ln 3) = e
logaa = 1
–
+
ln3
min
6eln3 3 = 9 6 3 3 = 6
x
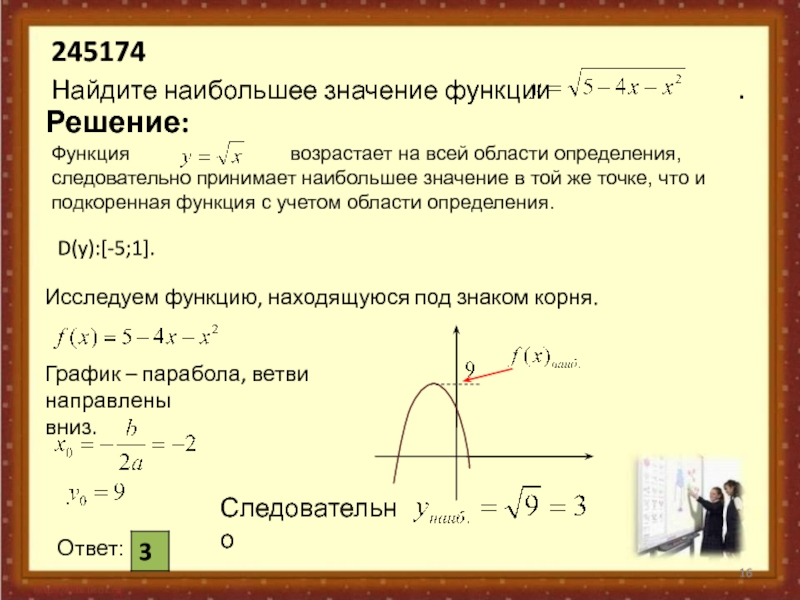
2. Найдите наибольшее значение функции у =
Найдите наибольшее значение функции у =
D(y): 5 – 4х – х2
f /(g (x)) = f /(g (x)) g /(x)
/
( х) =
у =
2 х
Вычислим производную, используя
формулу для вычисления
производной сложной функции.
Найдем критические точки,
которые принадлежат D(у).
1
/
1
=
2 5 4х х2
1
2 5 4х х2
x=–2
(
0
)
5 4х х2 / =
2(2 х )
=( 4 2 х)
2 5 4х х2
D(y)
y\
y
Наибольшее значение
функция примет в точке
максимума.
у ( 2)
5 4х х2
–
+
-2
max
x
= 5 4 ( 2) ( 2) 2 = 5 8 4 = 9 = 3
В 14
3
3
10 х
х
При решении некоторых заданий на вычисление наибольшего и
наименьшего значений функции можно найти ответ и без
вычисления производной.
Сложная функция f (g(x)) представлена в виде цепочки простых
функций.
Где g(x) – промежуточный аргумент, квадратичная функция
g(x) = ax2 +bx + c
Если внешняя функция является монотонно возрастающей на всей области
определения. Значит, наибольшее значение она будет иметь, когда функция
Значит, наибольшее значение она будет иметь, когда функция
промежуточного аргумента, т.е. квадратичная функция будет иметь
наибольшее значение.
А наименьшее значение она будет иметь, когда функция промежуточного
аргумента, т.е. квадратичная функция будет иметь наименьшее значение.
Рассмотрим примеры.
2 способ
2. Найдите наибольшее значение функции у =
Решим задание без вычисления производной.
5 4х х2
D(y): 5 – 4х – х2
0
Функция квадратного корня монотонно возрастает на всей области
определения. Значит, наибольшее значение она будет иметь, когда функция
промежуточного аргумента, т.е. квадратичная функция – х2 – 4х + 5 будет
иметь наибольшее значение.
Старший коэффициент квадратного трехчлена равен – 1
параболы направлены вниз. И наибольшее значение квадратичная функция
будет иметь в вершине.
х0 = b
2a
х0 = -4
D(y)
2*(-1) = -2
Итак, наибольшее значение функция квадратного корня примет, когда
промежуточная квадратичная функция примет наибольшее значение, т. е. в
е. в
точке х = – 2. Вычислим его:
у ( 2) = 5 4 ( 2) ( 2) 2 = 5 8 4 = 9 = 3
В 14
3
3
10 х
х
3. Найдите наименьшее значение функции у =
D(y): х2– 6х +13
f /(g (x)) = f /(g (x)) g /(x)
/
( х) =
1
у =
Вычислим производную, используя
формулу для вычисления
производной сложной функции.
Найдем критические точки,
которые принадлежат D(у).
0
)
х 2 6 х 13 / =
2 х 2 6 х 13
1
2( х 3)
=
=
(2х 26)
2
2 х 6 х 13 2 х 6 х 13
x=3
D(y)
–
y\
y
Наименьшее значение
функция примет в точке
минимума.
у (3)
(
1
/
2 х
х 2 6 х 13
+
3
min
x
= 32 6 3 13 = 9 18 13 = 4 = 2
В 14
2
3
10 х
х
2 способ
3. Найдите наименьшее значение функции у =
Решим задание без вычисления производной.
х 2 6 х 13
D(y): х2– 6х +13
0
Функция квадратного корня монотонно возрастает на всей области
определения. Значит, наименьшее значение она будет иметь, когда функция
Значит, наименьшее значение она будет иметь, когда функция
промежуточного аргумента, т.е. квадратичная функция х2 – 6х + 13 будет
иметь наименьшее значение.
Старший коэффициент квадратного трехчлена равен +1> 0, значит, ветви
параболы направлены вверх. И наименьшее значение квадратичная
функция будет иметь в вершине.
х0 = b
2a
х0 = -6
2· 1
= 3 D(y)
Итак, наименьшее значение функция квадратного корня примет, когда
промежуточная квадратичная функция примет наименьшее значение, т.е. в
точке х = 3. Вычислим его:
у (3) = 32 6 3 13 = 9 18 13 = 4 = 2
В 14
2
3
10 х
х
4. Найдите наименьшее значение функции
f /(g (x)) = f /(g (x)) g /(x)
(a )
х
/
= a х ln a
у =2
/
х 2 2 х 5
Вычислим производную, используя
формулу для вычисления
производной сложной функции.
у=2
D(y): x R
(
)
ln 2 x 2 2 x 5 / =
=2
х 2 2 х 5
ln 2 (2 x 2)
x = — 1 D(y)
Найдем критические точки,
которые принадлежат D(у).
–
y\
y
Наименьшее значение
функция примет в точке
минимума.
х 2 2 х 5
+
-1
min
( 1) 2 2 ( 1) 5
у( 1) = 2
В 14
x
= 21 2 5 = 24 = 16
1 6
3
10 х
х
2 способ
4. Найдите наименьшее значение функции
Решим задание без вычисления производной.
х 2 2 х 5
у=2
D(y): x R
Показательная функция с основанием 2>1 монотонно возрастает на всей
области определения. Значит, наименьшее значение она будет иметь, когда
функция промежуточного аргумента, т.е. квадратичная функция х2 + 2х + 5
будет иметь наименьшее значение.
Старший коэффициент квадратного трехчлена равен +1> 0, значит, ветви
параболы направлены вверх. И наименьшее значение квадратичная
функция будет иметь в вершине.
х0 = 2
2* 1
х0 = b
2a
= – 1 D(y)
Итак, наименьшее значение показательная функция примет, когда
промежуточная квадратичная функция примет наименьшее значение, т. е. в
е. в
точке х = – 1. Вычислим его:
( 1) 2 2 ( 1) 5
1 2 5
4
у( 1) = 2
=2
В 14
1 6
=2
3
10 х
х
= 16
7 6 х х 2
у =3
D(y): x R
5. Найдите наибольшее значение функции
f /(g (x)) = f /(g (x)) g /(x)
(a )
х
/
= a х ln a
7 6 х х 2
у =3
/
Вычислим производную, используя
формулу для вычисления
производной сложной функции.
)
7 6 х х 2
=3
ln 3 ( 6 2 х )
x = — 3 D(y)
Найдем критические точки,
которые принадлежат D(у).
y\
y
Наибольшее значение
функция примет в точке
максимума.
у( 3)
(
ln 3 7 6 х x 2 / =
–
+
-3
max
7 6 ( 3) ( 3) 2
=3
В 14
=3
9
x
7 18 9
3
10 х
=3
х
2
=9
2 способ
5. Найдите наибольшее значение функции
Решим задание без вычисления производной.
7 6 х х 2
у =3
D(y): x R
Показательная функция с основанием 3>1 монотонно возрастает на всей
области определения. Значит, наибольшее значение она будет иметь, когда
Значит, наибольшее значение она будет иметь, когда
функция промежуточного аргумента, т.е. квадратичная функция – х2 – 6х – 7
будет иметь наибольшее значение.
Старший коэффициент квадратного трехчлена равен – 1
параболы направлены вниз. И набольшее значение квадратичная функция
будет иметь в вершине.
х0 = b
2a
х0 = — 6
D(y)
2· (-1) = – 3
Итак, наибольшее значение показательная функция примет, когда
промежуточная квадратичная функция примет наибольшее значение, т.е. в
точке х = – 3. Вычислим его:
2
у( 3) = 3 7 6 ( 3) ( 3) = 3 7 18 9 = 32 = 9
В 14
9
3
10 х
х
6. Найдите наибольшее значение функции
(
)
у = log 5 4 2 x x 2 3
Решим задание без
вычисления производной.
D(y): 4 – 2х – х2
0
Логарифмическая функция с основанием 5 является монотонно
возрастающей на всей области определения. Значит, наибольшее значение
она будет иметь, когда функция промежуточного аргумента, т. е.
е.
квадратичная функция 4 – 2х – х2 будет иметь наибольшее значение.
Старший коэффициент квадратного трехчлена равен –1
параболы направлены вниз. И наибольшее значение квадратичная функция
будет иметь в вершине.
х0 = -2 = -1
2(-1)
х0 = b
2a
(
1
)
у( 1) = log 5 4 2 ( 1) ( 1) 3 = log 5 (4 2 1) 3 = log 5 5 3
2
=4
В 14
4
3
10 х
х
7. Найдите наименьшее значение функции
(
)
у = log 3 x 2 6 х 10 2
Решим задание без
вычисления производной.
D(y): х2 – 6х + 10 0
Логарифмическая функция с основанием 3 является монотонно
возрастающей на всей области определения. Значит, наименьшее значение
она будет иметь, когда функция промежуточного аргумента, т.е.
квадратичная функция х2 – 6х + 10 будет иметь наименьшее значение.
Старший коэффициент квадратного трехчлена равен +1>0, значит, ветви
параболы направлены вверх. И наименьшее значение квадратичная
функция будет иметь в вершине.
х0 = b
2a
(
х0 = -6 = 3
2·1
0
)
у (3) = log 3 32 6 3 10 2 = log 3 (9 18 10) 2 = log 3 1 2 = 2
В 14
2
3
10 х
хКак найти наибольшее значение функции по графику. Как найти наибольшее и наименьшее значение функции на интервале
Процесс поиска наименьшего и наибольшего значения функции на отрезке напоминает увлекательный облёт объекта (графика функции) на вертолёте с обстрелом из дальнобойной пушки определённых точек и выбором из этих точек совсем особенных точек для контрольных выстрелов. Точки выбираются определённым образом и по определённым правилам. По каким правилам? Об этом мы далее и поговорим.
Если функция y = f (x ) непрерывна на отрезке [a , b ] , то она достигает на этом отрезке наименьшего и наибольшего значений . Это может произойти либо в точках экстремума , либо на концах отрезка. Поэтому для нахождения наименьшего и наибольшего значений функции , непрерывной на отрезке [a , b ] , нужно вычислить её значения во всех критических точках и на концах отрезка, а затем выбрать из них наименьшее и наибольшее.

Пусть, например, требуется определить наибольшее значение функции f (x ) на отрезке [a , b ] . Для этого следует найти все её критические точки, лежащие на [a , b ] .
Критической точкой называется точка, в которой функция определена , а её производная либо равна нулю, либо не существует. Затем следует вычислить значения функции в критических точках. И, наконец, следует сравнить между собой по величине значения функции в критических точках и на концах отрезка (f (a ) и f (b ) ). Наибольшее из этих чисел и будет наибольшим значением функции на отрезке [a , b ] .
Аналогично решаются и задачи на нахождение наименьших значений функции .
Ищем наименьшее и наибольшее значения функции вместе
Пример 1. Найти наименьшее и наибольшее значения функции на отрезке [-1, 2] .
Решение. Находим производную данной функции .
 Приравняем производную нулю ()
и получим две критические точки: и
. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на
концах отрезка и в точке ,
так как точка не
принадлежит отрезку [-1, 2]
. Эти значения функции — следующие: ,
,
. Из этого следует, что наименьшее значение функции (на графике ниже обозначено красным), равное -7, достигается на правом конце отрезка — в точке
, а наибольшее (тоже
красное на графике), равно 9,
— в критической точке .
Приравняем производную нулю ()
и получим две критические точки: и
. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на
концах отрезка и в точке ,
так как точка не
принадлежит отрезку [-1, 2]
. Эти значения функции — следующие: ,
,
. Из этого следует, что наименьшее значение функции (на графике ниже обозначено красным), равное -7, достигается на правом конце отрезка — в точке
, а наибольшее (тоже
красное на графике), равно 9,
— в критической точке .Если функция непрерывна в некотором промежутке и этот промежуток не является отрезком (а является, например, интервалом; разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок), то среди значений функции может и не быть наименьшего и наибольшего. Так, например, функция, изображённая на рисунке ниже, непрерывна на ]-∞, +∞[ и не имеет наибольшего значения.
Однако для любого промежутка (закрытого, открытого или бесконечного) справедливо следующее свойство непрерывных функций.

Пример 4. Найти наименьшее и наибольшее значения функции на отрезке [-1, 3] .
Решение. Находим производную данной функции как производную частного:
.
Приравниваем производную нулю, что даёт нам одну критическую точку: . Она принадлежит отрезку [-1, 3] . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:
Сравниваем эти значения. Вывод: , равного -5/13, в точке и наибольшего значения , равного 1, в точке .
Продолжаем искать наименьшее и наибольшее значения функции вместе
Есть преподаватели, которые по теме нахождения наименьшего и наибольшего значений функции не дают студентам для решения примеры сложнее только что рассмотренных, то есть таких, в которых функция — многочлен либо дробь, числитель и знаменатель которой — многочлены. Но мы не ограничимся такими примерами, поскольку среди преподавателей бывают любители заставить студентов думать по полной (таблице производных).
 Поэтому в ход пойдут логарифм и тригонометрическая функция.
Поэтому в ход пойдут логарифм и тригонометрическая функция.Пример 6. Найти наименьшее и наибольшее значения функции на отрезке .
Решение. Находим производную данной функции как производную произведения :
Приравниваем производную нулю, что даёт одну критическую точку: . Она принадлежит отрезку . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:
Результат всех действий: функция достигает наименьшего значения , равного 0, в точке и в точке и наибольшего значения , равного e ² , в точке .
Пример 7. Найти наименьшее и наибольшее значения функции на отрезке .
Решение. Находим производную данной функции:
Приравниваем производную нулю:
Единственная критическая точку принадлежит отрезку . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:
Вывод: функция достигает наименьшего значения , равного , в точке и наибольшего значения , равного , в точке .

В прикладных экстремальных задачах нахождение наименьшего (наибольшего) значений функции, как правило, сводится к нахождению минимума (максимума). Но больший практический интерес имеют не сами минимумы или максимумы, а те значения аргумента, при которых они достигаются. При решении прикладных задач возникает дополнительная трудность — составление функций, описывающих рассматриваемое явление или процесс.
Пример 8. Резервуар ёмкостью 4 , имеющий форму параллелепипеда с квадратным основанием и открытый сверху, нужно вылудить оловом. Каковы должны быть размеры резервуара, чтобы на его покрытие ушло наименьшее количество материала?
Решение. Пусть x — сторона основания, h — высота резервуара, S — площадь его поверхности без крышки, V — его объём. Площадь поверхности резервуара выражается формулой , т.е. является функцией двух переменных . Чтобы выразить S как функцию одной переменной, воспользуемся тем, что , откуда . Подставив найденное выражение h в формулу для S :
Исследуем эту функцию на экстремум.
 Она определена и дифференцируема всюду в
]0, +∞[
, причём
Она определена и дифференцируема всюду в
]0, +∞[
, причём.
Приравниваем производную нулю () и находим критическую точку . Кроме того, при производная не существует, но это значение не входит в область определения и поэтому не может быть точкой экстремума. Итак, — единственная критическая точка. Проверим её на наличие экстремума, используя второй достаточный признак. Найдём вторую производную . При вторая производная больше нуля (). Значит, при функция достигает минимума . Поскольку этот минимум — единственный экстремум данной функции, он и является её наименьшим значением . Итак, сторона основания резервуара должна быть равна 2 м, а его высота .
Пример 9. Из пункта A , находящегося на линии железной дороги, в пункт С , отстоящий от неё на расстоянии l , должны переправляться грузы. Стоимость провоза весовой единицы на единицу расстояния по железной дороге равна , а по шоссе она равна . К какой точке М линии железной дороги следует провести шоссе, чтобы транспортировка груза из А в С была наиболее экономичной (участок АВ железной дороги предполагается прямолинейным)?
Пусть функция $z=f(x,y)$ определена и непрерывна в некоторой ограниченной замкнутой области $D$.
 Пусть в этой области заданная функция имеет конечные частные производные первого порядка (за исключением, быть может, конечного количества точек). Чтобы найти наибольшее и наименьшее значения функции двух переменных в данной замкнутой области требуется выполнить три шага простого алгоритма.
Пусть в этой области заданная функция имеет конечные частные производные первого порядка (за исключением, быть может, конечного количества точек). Чтобы найти наибольшее и наименьшее значения функции двух переменных в данной замкнутой области требуется выполнить три шага простого алгоритма.Алгоритм поиска наибольшего и наименьшего значений функции $z=f(x,y)$ в замкнутой области $D$.
- Найти критические точки функции $z=f(x,y)$, принадлежащие области $D$. Вычислить значения функции в критических точках.
- Исследовать поведение функции $z=f(x,y)$ на границе области $D$, найдя точки возможного наибольшего и наименьшего значений. Вычислить значения функции в полученных точках.
- Из значений функции, полученных в предыдущих двух пунктах, выбрать наибольшее и наименьшее.
Что такое критические точки? показать\скрыть
Под критическими точками подразумевают такие точки, в которых обе частные производные первого порядка равны нулю (т.
 2-4x$ в замкнутой области, ограниченной линиями $x=3$, $y=0$ и $y=x+1$.
2-4x$ в замкнутой области, ограниченной линиями $x=3$, $y=0$ и $y=x+1$.Будем следовать указанному выше , но для начала разберёмся с чертежом заданной области, которую обозначим буквой $D$. Нам заданы уравнения трёх прямых, кои эту область ограничивают. Прямая $x=3$ проходит через точку $(3;0)$ параллельно оси ординат (оси Oy). Прямая $y=0$ — это уравнение оси абсцисс (оси Ox). Ну, а для построения прямой $y=x+1$ найдём две точки, через которые и проведём данную прямую. Можно, конечно, подставить вместо $x$ парочку произвольных значений. Например, подставляя $x=10$, получим: $y=x+1=10+1=11$. Мы нашли точку $(10;11)$, лежащую на прямой $y=x+1$. Однако лучше отыщем те точки, в которых прямая $y=x+1$ пересекается с линиями $x=3$ и $y=0$. Почему это лучше? Потому, что мы одним выстрелом уложим пару зайцев: получим две точки для построения прямой $y=x+1$ и заодно выясним, в каких точках эта прямая пересекает иные линии, ограничивающие заданную область. Прямая $y=x+1$ пересекает прямую $x=3$ в точке $(3;4)$, а прямую $y=0$ — в точке $(-1;0)$.
 Дабы не загромождать ход решения вспомогательными пояснениями, то вопрос о получении этих двух точек вынесу в примечание.
Дабы не загромождать ход решения вспомогательными пояснениями, то вопрос о получении этих двух точек вынесу в примечание.Как были получены точки $(3;4)$ и $(-1;0)$? показать\скрыть
Начнём с точки пересечения прямых $y=x+1$ и $x=3$. Координаты искомой точки принадлежат и первой, и второй прямой, поэтому для нахождения неизвестных координат нужно решить систему уравнений:
$$ \left \{ \begin{aligned} & y=x+1;\\ & x=3. \end{aligned} \right. $$
Решение такой системы тривиально: подставляя $x=3$ в первое уравнение будем иметь: $y=3+1=4$. Точка $(3;4)$ и есть искомая точка пересечения прямых $y=x+1$ и $x=3$.
Теперь отыщем точку пересечения прямых $y=x+1$ и $y=0$. Вновь составим и решим систему уравнений:
$$ \left \{ \begin{aligned} & y=x+1;\\ & y=0. \end{aligned} \right. $$
Подставляя $y=0$ в первое уравнение, получим: $0=x+1$, $x=-1$. Точка $(-1;0)$ и есть искомая точка пересечения прямых $y=x+1$ и $y=0$ (оси абсцисс).
Всё готово для построения чертежа, который будет иметь такой вид:
Вопрос примечания кажется очевидным, ведь всё видно по рисунку.
 Однако стоит помнить, что рисунок не может служить доказательством. Рисунок — лишь иллюстрация для наглядности.
Однако стоит помнить, что рисунок не может служить доказательством. Рисунок — лишь иллюстрация для наглядности.Наша область была задана с помощью уравнений прямых, которые её ограничивают. Очевидно, что эти прямые определяют треугольник, не так ли? Или не совсем очевидно? А может, нам задана иная область, ограниченная теми же прямыми:
Конечно, в условии сказано, что область замкнута, поэтому показанный рисунок неверен. Но чтобы избегать подобных двусмысленностей, области лучше задавать неравенствами. Нас интересует часть плоскости, расположенная под прямой $y=x+1$? Ок, значит, $y ≤ x+1$. Наша область должна располагаться над прямой $y=0$? Отлично, значит $y ≥ 0$. Кстати, два последних неравенства легко объединяются в одно: $0 ≤ y ≤ x+1$.
$$ \left \{ \begin{aligned} & 0 ≤ y ≤ x+1;\\ & x ≤ 3. \end{aligned} \right. $$
Эти неравенства и задают область $D$, причём задают её однозначно, не допуская никаких двусмысленностей. Но как это поможет нам в том вопросе, что указан в начале примечания? Ещё как поможет:) Нам нужно проверить, принадлежит ли точка $M_1(1;1)$ области $D$.
 2-12\cdot(-3)+16\cdot 4=125.
\end{aligned}
2-12\cdot(-3)+16\cdot 4=125.
\end{aligned}На следует выбрать наибольшее и наименьшее значения из тех, что мы получили на первом и втором шагах. Но в данном случае выбор невелик:) Имеем:
$$ z_{min}=-75; \; z_{max}=125. $$
Ответ : $z_{min}=-75; \; z_{max}=125$.
Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.
Чтобы найти наибольшее или наименьшее значение функции необходимо:
- Проверить, какие стационарные точки входят в заданный отрезок.
- Вычислить значение функции на концах отрезка и в стационарных точках из п.3
- Выбрать из полученных результатов наибольшее или наименьшее значение.
Чтобы найти точки максимума или минимума необходимо:
- Найти производную функции $f»(х)$
- Найти стационарные точки, решив уравнение $f»(х)=0$
- Разложить производную функции на множители.
- Начертить координатную прямую, расставить на ней стационарные точки и определить знаки производной в полученных интервалах, пользуясь записью п.
 2}$
2}$4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции
$f(g(x))′=f′(g(x))∙g′(x)$
$f′(x)=cos′(5x)∙(5x)′= — sin(5x)∙5= -5sin(5x)$
Найдите точку минимума функции $y=2x-ln(x+11)+4$
1. Найдем ОДЗ функции: $х+11>0; х>-11$
2. Найдем производную функции $y»=2-{1}/{x+11}={2x+22-1}/{x+11}={2x+21}/{x+11}$
3. Найдем стационарные точки, приравняв производную к нулю
${2x+21}/{x+11}=0$
Дробь равна нулю если числитель равен нулю, а знаменатель не равен нулю
$2x+21=0; x≠-11$
4. Начертим координатную прямую, расставим на ней стационарные точки и определим знаки производной в полученных интервалах. Для этого подставим в производную любое число из крайней правой области, например, нуль.
$y»(0)={2∙0+21}/{0+11}={21}/{11}>0$
5. В точке минимума производная меняет знак с минуса на плюс, следовательно, точка $-10,5$ — это точка минимума.
Ответ: $-10,5$
Найдите наибольшее значение функции $y=6x^5-90x^3-5$ на отрезке $[-5;1]$
1.
 2=0 ; х-3=0; х+3=0$
2=0 ; х-3=0; х+3=0$$х=0;х=3;х=-3$
3. Выберем стационарные точки, которые принадлежат заданному отрезку $[-5;1]$
Нам подходят стационарные точки $х=0$ и $х=-3$
4. Вычислим значение функции на концах отрезка и в стационарных точках из п.3
Постановка задачи 2:Дана функция , определенная и непрерывная на некотором промежутке . Требуется найти наибольшее (наименьшее) значение функции на этом промежутке.
Теоретические основы.
Теорема (Вторая теорема Вейерштрасса):Если функция определена и непрерывна в замкнутом промежутке , то она достигает в этом промежутке своих наибольшего и наименьшего значений.
Функция может достигать своих наибольших и наименьших значений либо на внутренних точках промежутка, либо на его границах. Проиллюстрируем все возможные варианты.
Пояснение:
1) Функция достигает своего наибольшего значения на левой границе промежутка в точке , а своего наименьшего значения на правой границе промежутка в точке .
2) Функция достигает своего наибольшего значения в точке (это точка максимума) , а своего наименьшего значения на правой границе промежутка в точке .
3) Функция достигает своего наибольшего значения на левой границе промежутка в точке , а своего наименьшего значения в точке (это точка минимума).
4) Функция постоянна на промежутке, т.е. она достигает своего минимального и максимального значения в любой точке промежутка, причем минимальное и максимальное значения равны между собой.
5) Функция достигает своего наибольшего значения в точке , а своего наименьшего значения точке (несмотря на то, что функция имеет на этом промежутке как максимум, так и минимум).
6) Функция достигает своего наибольшего значения в точке (это точка максимума), а своего наименьшего значения в точке (это точка минимума).
Замечание:«Максимум» и «максимальное значение» — разные вещи. Это следует из определения максимума и интуитивного понимания словосочетания «максимальное значение».

Алгоритм решения задачи 2.
4) Выбрать из полученных значений наибольшее (наименьшее) и записать ответ.
Пример 4:
Определить наибольшее и наименьшее значение функции на отрезке .
Решение:
1) Найти производную функции .
2) Найти стационарные точки (и точки, подозрительные на экстремум), решив уравнение . Обратить внимание на точки, в которых не существует двусторонней конечной производной.
3) Вычислить значения функции в стационарных точках и на границах интервала.4) Выбрать из полученных значений наибольшее (наименьшее) и записать ответ.
Функция на этом отрезке достигает своего наибольшего значения в точке с координатами .
Функция на этом отрезке достигает своего наименьшего значения в точке с координатами .
В правильность вычислений можно убедиться, взглянув на график исследуемой функции.
Замечание: Наибольшего значения функция достигает в точке максимума, а наименьшего – на границе отрезка.
Частный случай.
Предположим, требуется найти максимально и минимальное значение некоторой функции на отрезке. После выполнение первого пункта алгоритма, т.е. вычисления производной, становится ясно, что, например, она принимает только отрицательные значения на всем рассматриваемом отрезке. Помним, что если производная отрицательна, то функция убывает. Получили, что на всем отрезке функция убывает. Эта ситуация отображена на графике № 1 в начале статьи.
На отрезке функция убывает, т.е. точек экстремумов у нее нет. Из картинки видно, что наименьшее значение функция примет на правой границе отрезка, а наибольшее значение — на левой. если же производная на отрезке всюду положительна, то функция возрастает. Наименьшее значение — на левой границе отрезка, наибольшее — на правой.
Минимальные значения: определение и концепция — видео и стенограмма урока
Как определить минимальное значение
Существует три метода определения минимального значения квадратного уравнения.
МАЛЕНЬКАЯ функция 2 / 4 а .2 + k и член a положителен, тогда минимальным значением будет значение k . Поиск минимума имеет практическое применение в науке, технике и других областях.
2 / 4 а .2 + k и член a положителен, тогда минимальным значением будет значение k . Поиск минимума имеет практическое применение в науке, технике и других областях.— примеры, примеры, как использовать в Excel
Что такое МАЛЕНЬКАЯ функция?
Функция МАЛЕНЬКАЯ относится к категории статистических функций Excel. ФункцииСписок наиболее важных функций Excel для финансовых аналитиков. Эта шпаргалка охватывает 100 функций, которые критически важно знать аналитику Excel.Он будет возвращать числовые значения в зависимости от их позиции в списке, ранжированные по значению. По сути, он вычисляет и возвращает k наименьшее значение в наборе данных.
В финансовом анализе функция МАЛЕНЬКИЙ может быть полезна для поиска наименьшего значения в заданном наборе значений. Например, если всем продавцам дана одна и та же цель, мы можем узнать, кто из них достиг этой цели в кратчайшие сроки для данного года.
Формула
= МАЛЕНЬКИЙ (массив, k)
Функция МАЛЕНЬКИЙ использует следующие аргументы:
- Массив (обязательный аргумент) — это массив или диапазон числовых данных, для которых мы хотим найти k наименьшее значение.

- K (обязательный аргумент) — это наименьшее значение из данного массива.
Как использовать функцию МАЛЕНЬКИЙ в Excel?
Чтобы понять использование функции МАЛЕНЬКИЙ, давайте рассмотрим несколько примеров:
Пример
Предположим, нам даны следующие данные о нескольких бегунах, а также их время начала и окончания:
Мы можем использовать функцию МАЛЕНЬКИЙ, чтобы получить n-е наименьшее значение из набора данных, то есть первое, второе или третье время в гонке.
Формула, которая будет использоваться для определения победителя:
Формула, которая будет использоваться для поиска первого участника, занявшего второе место, будет:
Формула, которая будет использоваться при поиске второго участника, занявшего второе место, будет:
Мы получим следующие результаты:
Что нужно помнить о МАЛЕНЬКОЙ функции
- #NUM! ошибка — Возникает, когда:
- Заданный массив пуст; или
- Заданное значение k меньше 1 или больше количества значений в данном массиве.

- #VALUE! ошибка — возникает, если заданное k не является числовым.
- Если n — количество точек данных в массиве, МАЛЕНЬКИЙ (массив, 1) равняется наименьшему значению, а МАЛЕНЬКИЙ (массив, n) равняется наибольшему значению.
- Иногда функция МАЛЕНЬКИЙ возвращает неправильное значение или # ЧИСЛО! ошибка, даже если предоставленное значение k находится между 1 и количеством значений в предоставленном массиве. Это произойдет, когда мы предоставим текстовые значения или текстовые представления чисел в предоставленном массиве.Функция игнорирует текстовые значения. Следовательно, эта проблема может возникнуть, если значения в предоставленном массиве являются текстовыми представлениями чисел, а не фактическими значениями. Мы можем решить эту проблему, преобразовав все значения массива в числовые значения.
Щелкните здесь, чтобы загрузить образец файла Excel
Дополнительные ресурсы
Спасибо за чтение руководства CFI по функции Excel SMALL.
 Потратив время на изучение и освоение этих функций, вы значительно ускорите свое финансовое моделирование.Чтобы узнать больше, ознакомьтесь с этими дополнительными ресурсами CFI:
Потратив время на изучение и освоение этих функций, вы значительно ускорите свое финансовое моделирование.Чтобы узнать больше, ознакомьтесь с этими дополнительными ресурсами CFI:- Формулы Excel для FinanceExcel for Finance Это руководство по Excel для финансов научит 10 основных формул и функций, которые вы должны знать, чтобы стать отличным финансовым аналитиком в Excel.
- Расширенный курс Excel
- Расширенные формулы и функции Excel Расширенные формулы Excel, которые необходимо знатьЭти сложные формулы Excel очень важно знать и выведут ваши навыки финансового анализа на новый уровень. Загрузите нашу бесплатную электронную книгу Excel!
- Ярлыки Excel для Windows и MacExcel Ярлыки ПК MacExcel Ярлыки — Список наиболее важных и распространенных ярлыков MS Excel для пользователей ПК и Mac, специалистов в области финансов и бухгалтерского учета.Сочетания клавиш ускоряют ваши навыки моделирования и экономят время. Изучите редактирование, форматирование, навигацию, ленту, специальную вставку, манипулирование данными, редактирование формул и ячеек и другие короткие статьи
Calculus I — Minimum and Maximum Values
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана ( i.
 е. вы, вероятно, разговариваете по мобильному телефону). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, разговариваете по мобильному телефону). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.Раздел 4-3: Минимальные и максимальные значения
Многие из наших приложений в этой главе вращаются вокруг минимального и максимального значений функции.Хотя все мы можем визуализировать минимальные и максимальные значения функции, мы хотим быть более конкретными в нашей работе. В частности, мы хотим различать два типа минимальных и максимальных значений. Следующее определение дает типы минимальных и / или максимальных значений, которые мы будем рассматривать.
Определение
- Мы говорим, что \ (f \ left (x \ right) \) имеет абсолютный (или глобальный) максимум в \ (x = c \), если \ (f \ left (x \ right) \ le f \ left (c \ right) \) для каждого \ (x \) в области, над которой мы работаем.

- Мы говорим, что \ (f \ left (x \ right) \) имеет относительный (или локальный) максимум в точке \ (x = c \), если \ (f \ left (x \ right) \ le f \ left (c \ right) \) для каждого \ (x \) в некотором открытом интервале вокруг \ (x = c \).
- Мы говорим, что \ (f \ left (x \ right) \) имеет абсолютный (или глобальный) минимум в \ (x = c \), если \ (f \ left (x \ right) \ ge f \ left (c \ right) \) для каждого \ (x \) в области, над которой мы работаем.
- Мы говорим, что \ (f \ left (x \ right) \) имеет относительный (или локальный) минимум в точке \ (x = c \), если \ (f \ left (x \ right) \ ge f \ left (c \ right) \) для каждого \ (x \) в некотором открытом интервале вокруг \ (x = c \).
Обратите внимание: когда мы говорим «открытый интервал вокруг \ (x = c \)», мы имеем в виду, что мы можем найти некоторый интервал \ (\ left ({a, b} \ right) \), не включая концы, такой, что \ (а <с <Ь \).
 Или, другими словами, \ (c \) будет содержаться где-то внутри интервала и не будет ни одной из конечных точек.
Или, другими словами, \ (c \) будет содержаться где-то внутри интервала и не будет ни одной из конечных точек.Кроме того, мы будем совместно называть точки минимума и максимума функции экстремумами функции. Таким образом, относительные экстремумы будут относиться к относительным минимумам и максимумам, а абсолютные экстремумы относятся к абсолютным минимумам и максимумам.
Теперь давайте поговорим немного о тонкой разнице между абсолютным и относительным в приведенном выше определении.
У нас будет абсолютный максимум (или минимум) в \ (x = c \) при условии, что \ (f \ left (c \ right) \) будет наибольшим (или наименьшим) значением, которое функция когда-либо будет принимать в области, которая мы работаем. Кроме того, когда мы говорим «домен, над которым мы работаем», это просто означает диапазон \ (x \), который мы выбрали для работы с данной проблемой.Могут быть и другие значения \ (x \), которые мы действительно можем подключить к функции, но по какой-то причине исключили их.

Относительный максимум или минимум немного отличается. Все, что требуется для точки, чтобы быть относительным максимумом или минимумом, — это чтобы эта точка была максимумом или минимумом в некотором интервале \ (x \) вокруг \ (x = c \). Могут быть большие или меньшие значения функции в каком-то другом месте, но относительно \ (x = c \) или локально для \ (x = c \), \ (f \ left (c \ right) \) равно больше или меньше, чем все другие значения функции, которые находятся рядом с ним.
Также обратите внимание, что для того, чтобы точка была относительным экстремумом, мы должны иметь возможность смотреть на значения функций по обе стороны от \ (x = c \), чтобы увидеть, действительно ли это максимум или минимум в этой точке. Это означает, что относительные экстремумы не возникают в конечных точках области. Они могут возникать только внутри домена.
На самом деле, по предыдущему пункту ведутся споры. Некоторые люди действительно считают, что относительные экстремумы могут возникать в конечных точках области.
 Однако в этом классе мы будем использовать определение, в котором говорится, что они не могут возникать в конечных точках домена.Это будет обсуждаться более подробно в конце раздела, когда мы позаботимся о соответствующем факте.
Однако в этом классе мы будем использовать определение, в котором говорится, что они не могут возникать в конечных точках домена.Это будет обсуждаться более подробно в конце раздела, когда мы позаботимся о соответствующем факте.Обычно легче понять определения, взглянув на график.
Для функции, показанной на этом графике, у нас есть относительные максимумы в \ (x = b \) и \ (x = d \). Обе эти точки являются относительными максимумами, поскольку они находятся внутри показанной области и являются самой большой точкой на графике в некотором интервале вокруг этой точки.У нас также есть относительный минимум в точке \ (x = c \), поскольку эта точка находится внутри области и является самой низкой точкой на графике в интервале вокруг нее. Крайняя правая конечная точка \ (x = e \) не будет относительным минимумом, поскольку это конечная точка.
Функция будет иметь абсолютный максимум в точке \ (x = d \) и абсолютный минимум в точке \ (x = a \).
 Эти две точки являются наибольшим и наименьшим из возможных для функции. Мы также можем заметить, что абсолютные экстремумы для функции будут возникать либо в конечных точках области, либо в относительных экстремумах.2} \ hspace {0,25 дюйма} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{- 1,2} \ right] \]
Показать решение
Эти две точки являются наибольшим и наименьшим из возможных для функции. Мы также можем заметить, что абсолютные экстремумы для функции будут возникать либо в конечных точках области, либо в относительных экстремумах.2} \ hspace {0,25 дюйма} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{- 1,2} \ right] \]
Показать решениеТак как эту функцию достаточно просто построить график, давайте сделаем это. Однако нам нужен только график на интервале \ (\ left [{- 1,2} \ right] \). Вот график,
Обратите внимание, что мы использовали точки в конце графика, чтобы напомнить нам, что график заканчивается в этих точках.
Теперь мы можем идентифицировать экстремумы на графике.Похоже, у нас есть относительный и абсолютный минимум ноль в точке \ (x = 0 \) и абсолютный максимум четыре в точке \ (x = 2 \). Обратите внимание, что \ (x = — 1 \) не является относительным максимумом, поскольку он находится в конечной точке интервала.

Эта функция не имеет относительных максимумов.
Как мы видели в предыдущем примере, функции не обязательно должны иметь относительные экстремумы. Функция вполне может не иметь относительного максимума и / или относительного минимума.2} \ hspace {0,25 дюйма} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{- 2,2} \ right] \] Показать решение
Вот график этой функции.
В этом случае у нас все еще есть относительный и абсолютный минимум нуля в точке \ (x = 0 \). У нас также есть абсолютный максимум — четыре человека. Однако, в отличие от первого примера, это произойдет в двух точках, \ (x = — 2 \) и \ (x = 2 \).
Опять же, функция не имеет относительных максимумов.2} \] Показать решение
В данном случае мы не указали домен, поэтому предполагаем, что мы возьмем максимально возможный домен. Для этой функции это означает все действительные числа.
 Вот график.
Вот график.В этом случае график не перестает расти ни на одном конце, поэтому для этой функции нет никаких максимумов. Независимо от того, какую точку мы выберем на графике, с обеих сторон будут точки как больше, так и меньше, поэтому у нас не может быть никаких максимумов (любого рода, относительных или абсолютных) на графике.3} \ hspace {0,25 дюйма} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{- 2,2} \ right] \] Показать решение
Вот график этой функции.
Эта функция имеет абсолютный максимум восемь при \ (x = 2 \) и абсолютный минимум отрицательный восемь при \ (x = — 2 \). У этой функции нет относительных экстремумов.
Итак, функция не обязана иметь относительные экстремумы, как показано в этом примере.
Пример 5 Определите абсолютные и относительные экстремумы для следующей функции.3} \] Показать решениеОпять же, на этот раз мы не ограничиваем домен, поэтому вот график.

В этом случае функция не имеет ни относительных, ни абсолютных экстремумов.
Как мы видели в предыдущем примере, функции не обязательно должны иметь какие-либо экстремумы, относительные или абсолютные.
Пример 6 Определите абсолютные и относительные экстремумы для следующей функции.\ [е \ влево (х \ вправо) = \ соз \ влево (х \ вправо) \] Показать решениеМы не ограничивали домен для этой функции. Вот график.
Косинус имеет экстремумы (относительные и абсолютные), которые встречаются во многих точках. Косинус имеет как относительный, так и абсолютный максимум 1 при
. \ [x = \ ldots — 4 \ pi, \, — 2 \ pi, \, \, 0, \, \, 2 \ pi, \, \, 4 \ pi, \ ldots \]Косинус также имеет как относительные, так и абсолютные минимумы -1 на уровне
. \ [x = \ ldots — 3 \ pi, \, — \ pi, \, \, \ pi, \, \, 3 \ pi, \ ldots \]Как показал этот пример, на самом деле у графика могут быть экстремумы, возникающие в большом количестве (в данном случае бесконечном) точках.

Мы проработали довольно много примеров, и мы можем использовать эти примеры, чтобы увидеть хороший факт об абсолютных экстремумах. Прежде всего, заметим, что все перечисленные выше функции были непрерывными. Затем обратите внимание, что каждый раз, когда мы ограничивали область закрытым интервалом (, т.е. интервал содержит его конечные точки), мы получали абсолютные максимумы и абсолютные минимумы. Наконец, только в одном из трех примеров, в которых мы не ограничивали область, мы получили как абсолютный максимум, так и абсолютный минимум.
Эти наблюдения приводят нас к следующей теореме.
Теорема об экстремальном значении
Предположим, что \ (f \ left (x \ right) \) непрерывно на интервале \ (\ left [{a, b} \ right] \), тогда есть два числа \ (a \ le c, d \ le b \), так что \ (f \ left (c \ right) \) является абсолютным максимумом для функции, а \ (f \ left (d \ right) \) является абсолютным минимумом для функции.

Итак, если у нас есть непрерывная функция на интервале \ (\ left [{a, b} \ right] \), то мы гарантированно имеем как абсолютный максимум, так и абсолютный минимум для функции где-то в интервале.Теорема не говорит нам, где они возникнут или будут ли они встречаться более одного раза, но, по крайней мере, она говорит нам, что они где-то существуют. Иногда все, что нам нужно знать, это то, что они действительно существуют.
Эта теорема ничего не говорит об абсолютных экстремумах, если мы не работаем с интервалом. Выше мы видели примеры функций, у которых были как абсолютные экстремумы, так и один абсолютный экстремум, и не было абсолютных экстремумов, когда мы не ограничивались интервалом.
Требование непрерывности функции также необходимо для использования теоремы.2}}} \ hspace {0,25 дюйма} {\ mbox {on}} \ hspace {0,25 дюйма} [- 1,1] \]
Вот график.
Эта функция не является непрерывной в точке \ (x = 0 \), поскольку мы приближаемся к нулю, функция приближается к бесконечности.
 2}}}} \ hspace {0.25 дюймов} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{\ frac {1} {2}, 1} \ right] \]
2}}}} \ hspace {0.25 дюймов} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{\ frac {1} {2}, 1} \ right] \]функция теперь будет иметь оба абсолютных экстремума. Мы можем столкнуться с проблемами только в том случае, если интервал содержит точку разрыва. Если нет, то теорема верна.
Мы также должны указать, что тот факт, что функция не является непрерывной в точке, не означает, что у нее не будет обоих абсолютных экстремумов в интервале, содержащем эту точку. Ниже приведен график функции, которая не является непрерывной в точке данного интервала, но имеет оба абсолютных экстремума.
Этот график не является непрерывным в точке \ (x = c \), но он имеет как абсолютный максимум (\ (x = b \)), так и абсолютный минимум (\ (x = c \)). Также обратите внимание, что в этом случае один из абсолютных экстремумов произошел в точке разрыва, но это не обязательно. Абсолютный минимум мог просто быть в другой конечной точке или в какой-то другой точке внутри региона.
. Дело в том, что этот график не является непрерывным и все же имеет оба абсолютных экстремума
Дело в том, что этот график не является непрерывным и все же имеет оба абсолютных экстремумаСмысл всего этого в том, что нам нужно быть осторожными и использовать теорему об экстремальном значении только при выполнении условий теоремы и не неправильно интерпретировать результаты, если условия не выполняются.
Чтобы использовать теорему об экстремальном значении, у нас должен быть интервал, который включает в себя его конечные точки, часто называемый закрытым интервалом, и функция должна быть непрерывной на этом интервале. Если у нас нет замкнутого интервала и / или функция не является непрерывной на интервале, тогда функция может иметь или не иметь абсолютных экстремумов.
Нам нужно обсудить одну последнюю тему в этом разделе, прежде чем перейти к первому важному применению производной, которое мы собираемся рассмотреть в этой главе.
Теорема Ферма
Если \ (f \ left (x \ right) \) имеет относительные экстремумы в \ (x = c \) и существует \ (f ‘\ left (c \ right) \), то \ (x = c \) есть критическая точка \ (f \ left (x \ right) \).
 3} \ hпространство {0.2} \]
3} \ hпространство {0.2} \]Ясно, что \ (x = 0 \) является критической точкой. Однако мы видели в предыдущем примере, что эта функция не имеет каких-либо относительных экстремумов. Итак, критические точки не обязательно должны быть относительными экстремумами.
Также заметьте, что эта теорема ничего не говорит об абсолютных экстремумах. Абсолютные экстремумы могут быть, а могут и не быть критической точкой.
Прежде чем мы покинем этот раздел, нам нужно обсудить пару вопросов.
Во-первых, теорема Ферма работает только для критических точек, в которых \ (f ‘\ left (c \ right) = 0 \).Однако это не означает, что относительных экстремумов не будет в критических точках, где не существует производной. Чтобы убедиться в этом, рассмотрим \ (f \ left (x \ right) = \ left | x \ right | \). Эта функция явно имеет относительный минимум в точке \ (x = 0 \), и все же в предыдущем разделе мы показали на примере, что \ (f ‘\ left (0 \ right) \) не существует.

Все это означает, что если мы хотим определить местонахождение относительных экстремумов, все, что нам действительно нужно сделать, это посмотреть на критические точки, поскольку это места, где могут существовать относительные экстремумы.
Наконец, напомним, что в начале раздела мы заявили, что относительных экстремумов не будет в конечных точках рассматриваемого нами интервала. Причина этого в том, что если мы позволим относительным экстремумам возникать там, это вполне может (и фактически в большинстве случаев) нарушить теорему Ферма. Нет причин ожидать, что конечные точки интервалов будут критическими точками любого типа. Следовательно, мы не допускаем существования относительных экстремумов на концах интервалов.
Как использовать функцию МИН в Microsoft Excel
В этом руководстве объясняется, как использовать функцию MIN в Microsoft Excel 2007–2019, найти наименьшее значение по условию и выделить нижнее число в вашем диапазоне.

Сегодня вы узнаете, как использовать простую, но очень важную функцию МИН в Excel. Вы увидите способы получить наименьшее число без нулей, абсолютный минимум и наименьшее значение на основе некоторых критериев. Кроме того, я покажу вам шаги, чтобы выделить наименьшую ячейку, и расскажу, что делать, если ваши функции MIN возвращают ошибку вместо результата.
Ну что ж, приступим. 🙂
ФункцияМИН — синтаксис и примеры использования в Excel
Функция MIN проверяет диапазон данных и возвращает наименьшее значение в наборе.Его синтаксис следующий:
МИН (число1, [число2],…)
число1, [число2],… — это ряд значений, из которых вы хотите получить минимум. Число1 является обязательным, а [число2] и следующие — необязательными.
В одной функции допускается до 255 аргументов. Аргументами могут быть числа, ячейки, массивы ссылок и диапазоны. Однако такие аргументы, как логические значения, текст, пустые ячейки, игнорируются.

Примеры использования формулы MIN
MIN — одна из самых простых в применении функций.Позвольте мне доказать вам это:
Пример 1. Поиск наименьшего значения
Допустим, у вас есть фрукты. Ваша задача — проверить, не заканчиваются ли они. Есть несколько способов попасть:
Случай 1: Введите каждую цифру из столбца «Кол-во на складе»:
= МИН (366, 476, 398, 982, 354, 534, 408)Случай 2. Поочередно ссылаться на ячейки из столбца «Кол-во»:
= МИН (B2, B3, B4, B5, B6, B7, B8)Случай 3: Или просто укажите весь диапазон:
= МИН (B2: B8)Случай 4. В качестве альтернативы вы можете создать именованный диапазон и использовать его вместо прямых ссылок:
= МИН (количество на складе)Пример 2.Ищем самую раннюю дату
Представьте, что у вас запланировано несколько поставок и вы хотите быть готовы к самой предстоящей.
 Как узнать самую раннюю дату в Excel? Легкий! Используйте MIN, следуя той же логике из примера 1:
Как узнать самую раннюю дату в Excel? Легкий! Используйте MIN, следуя той же логике из примера 1:Примените формулу и выберите даты, напрямую указав диапазон:
= МИН (B2: B8)Или именованный диапазон:
= МИН (дата поставки)Пример 3.Получение абсолютного минимума
Предположим, что у вас есть диапазон данных, и вам нужно определить не просто самый низкий, а абсолютный минимум. Один только MIN не сможет справиться с этим, поскольку он просто вернет наименьшее число. Здесь вам понадобится вспомогательная функция, которая может преобразовывать все отрицательные числа в положительные.
Здесь есть готовое решение? Вопрос был риторический, в Excel есть решение любой задачи. Если у вас есть сомнения, просто просмотрите наш блог.:)
Но вернемся к нашей задаче. Готовое решение для этого конкретного случая называется функцией ABS, которая возвращает абсолютное значение указанных вами чисел.
 Таким образом, комбинация функций MIN и ABS сделает свое дело. Просто введите следующую формулу в любую пустую ячейку:
Таким образом, комбинация функций MIN и ABS сделает свое дело. Просто введите следующую формулу в любую пустую ячейку:
Примечание! Вы обратили внимание на фигурные скобки вокруг функции? Это признак того, что это формула массива и ее нужно вводить с помощью Ctrl + Shift + Enter, а не только Enter.Вы можете узнать больше о формулах массива и их использовании здесь.{= MIN (ABS (A1: E12))}Как найти наименьшее значение без нулей
Кажется, вы знаете все о том, как найти минимум? Не торопитесь с выводами, еще есть чему поучиться. Например, как определить наименьшее ненулевое значение? Любые идеи? Не обманывайте и не гуглите, просто продолжайте читать;)
Дело в том, что MIN работает не только с положительными и отрицательными числами, но и с нулями. Если вы не хотите, чтобы нули были таким минимумом, вам понадобится помощь функции ЕСЛИ.Как только вы добавите ограничение, согласно которому ваш диапазон должен быть больше нуля, ожидаемый результат не заставит вас ждать.
 Вот пример формулы, которая возвращает нижнее значение на основе некоторого условия:
Вот пример формулы, которая возвращает нижнее значение на основе некоторого условия:{= МИН (ЕСЛИ (B2: B15> 0, B2: B15))}Вы, наверное, обратили внимание на фигурные скобки вокруг формулы массива. Просто помните, что вы не вводите их вручную. Они появляются, когда вы нажимаете Ctrl + Shift + Enter на клавиатуре.
Нахождение минимума на основе условия
Предположим, вам нужно найти в списке наименьший объем продаж определенного фрукта.Другими словами, ваша задача — определить минимум по каким-то критериям. В Excel условия обычно приводят к использованию функции ЕСЛИ. Все, что вам нужно сделать, это создать идеальную комбинацию MIN и IF для решения этой задачи:
{= МИН (ЕСЛИ (A2: A15 = D2, B2: B15))}Нажмите Ctrl + Shift + Enter, чтобы функция массива работала и наслаждалась.
Выглядит довольно просто, правда? И как вы определите самую маленькую фигуру на основе 2 или более условий? Как определить минимум по нескольким критериям? Может быть, есть более легкая формула? Пожалуйста, проверьте эту статью, чтобы узнать это.
 😉
😉Выделите наименьшее число в Excel
А что, если вам не нужно возвращать самую маленькую цифру, но вы хотите найти ее в своей таблице? Самый простой способ направить взгляд на эту ячейку — выделить ее. И самый простой способ сделать это — применить условное форматирование. Это даже проще, чем писать функции:
- Создайте новое правило условного форматирования, щелкнув Условное форматирование -> Новое правило
- Когда откроется диалоговое окно Новое правило форматирования , выберите тип правила «Форматировать только значения с верхним или нижним рангом»
- Поскольку задача состоит в том, чтобы выделить одну и единственную наименьшую цифру, выберите в раскрывающемся списке опцию Нижний и установите 1 в качестве количества ячеек для выделения.
Но что делать, если в вашей таблице снова ноль? Как игнорировать нули при выделении наименьшего числа? Не беспокойтесь, здесь тоже есть хитрость:
- Создайте новое правило условного форматирования, выбрав параметр «Использовать формулу, чтобы определить, какие ячейки нужно форматировать».

- Введите следующую формулу в значениях формата , где эта формула верна Поле :
= B2 = MIN (IF ($ B $ 2: $ B $ 15> 0, $ B $ 2: $ B $ 15))Где B2 — это первая ячейка диапазона, чтобы выделить наименьшее число в - Задайте цвет ( Правка правила форматирования -> Формат… -> Заливка ) и нажмите ОК.
- Наслаждайтесь 🙂
Почему не работает моя функция MIN?
В идеальном мире все формулы работали бы как шарм и возвращали бы правильные результаты, как только вы нажмете Enter. Но в мире, в котором мы живем, бывает, что функции возвращают ошибку вместо нужного нам результата. Не беспокойтесь, сама ошибка всегда намекает на ее возможную причину. Вам просто нужно внимательнее присмотреться к своим функциям.
Исправление ошибки #VALUE в MIN
Как правило, вы получаете # ЗНАЧЕНИЕ! сообщение об ошибке, когда хотя бы один из аргументов, используемых в формуле, неверен.Что касается MIN, это может произойти, когда один из них поврежден, например.
 что-то не так с данными, на которые ссылается формула.
что-то не так с данными, на которые ссылается формула.Например, #VALUE! может появиться, если один из его аргументов является ячейкой с ошибкой или в его ссылке есть опечатка.
Что может вызвать ошибку # ЧИСЛО! ошибка?
Excel показывает # ЧИСЛО! ошибка, когда невозможно вычислить вашу формулу. Обычно это происходит, когда числовое значение слишком велико или мало для отображения. Допустимые числа — от -2.2251E-308 и 2.2251E-308. Если один из ваших аргументов выходит за рамки этой области, вы увидите # ЧИСЛО! ошибка.
Я получаю # DIV / 0! ошибка, что делать?
Крепление # DIV / 0! легко. Не делите на ноль! 🙂 Без шуток, это единственное решение этой проблемы. Проверьте, есть ли ячейка с # DIV / 0! в своем диапазоне данных исправьте это, и формула сразу же вернет результат.
Ищете самую маленькую цифру, но получаете # ИМЯ? ошибка?
# ИМЯ? означает, что Excel не может распознать формулу или ее аргументы.
 Наиболее вероятная причина такого результата — опечатка. Вы можете неправильно написать функцию или указать неверные аргументы. Более того, текстовое представление чисел тоже вызовет эту ошибку.
Наиболее вероятная причина такого результата — опечатка. Вы можете неправильно написать функцию или указать неверные аргументы. Более того, текстовое представление чисел тоже вызовет эту ошибку. Другая возможная причина этой проблемы находится в именованном диапазоне. Итак, если вы укажете несуществующий диапазон или в нем есть опечатка, вы увидите # ИМЯ? в том месте, где вы ожидаете появления вашего результата.
Это способы найти минимум с помощью функции Excel MIN .Для вас я рассмотрел различные подходы к обнаружению самого низкого значения и определения абсолютного минимума. Вы можете считать эту шпаргалку своей шпаргалкой и использовать ее всякий раз, когда вам нужно получить наименьшее число в зависимости от условия, а также предотвратить и исправить возможные ошибки.
На сегодня все. Спасибо, что прочитали это руководство! Не стесняйтесь делиться своими мыслями и вопросами в комментариях, я буду рад получить от вас обратную связь! 🙂
Вас также может заинтересовать
5.
 1 Максима и Минима
1 Максима и МинимаТочка локального максимума на функции является точка $ (x, y) $ на графике функции, координата $ y $ которой равна больше, чем все другие координаты $ y $ на графике в точках «близких» к » $ (x, y) $. Точнее, $ (x, f (x)) $ является локальным максимумом, если существует — интервал $ (a, b) $ с $ локальной точкой минимума если он имеет локально наименьшую координату $ y $. Снова точнее: $ (x, f (x)) $ является локальным минимумом, если существует — интервал $ (a, b) $ с $ a локальным экстремумом является либо локальным минимумом, либо локальным максимумом.
Точки локального максимума и минимума весьма различимы на графике функции, и поэтому полезны для понимания формы график. Во многих прикладных задачах мы хотим найти самые большие или наименьшее значение, достигаемое функцией (например, мы можем захотеть найти минимальную стоимость, при которой может быть выполнено какое-либо задание) и так определение максимальных и минимальных точек будет полезно для применения проблемы тоже.
 Некоторые примеры локальных точек максимума и минимума
показаны на рисунке 5.1.1.
Некоторые примеры локальных точек максимума и минимума
показаны на рисунке 5.1.1.Рисунок 5.1.1. Некоторые точки локального максимума ($ A $) и точки минимума ($ B $).
Если $ (x, f (x)) $ — это точка, в которой $ f (x) $ достигает локального максимума или минимума, и если производная $ f $ существует в $ x $, то граф имеет касательная линия и касательная линия должны быть горизонтальными. Это достаточно важно, чтобы сформулировать его как теорему, хотя мы не будем его доказывать.
Теорема 5.1.1 (теорема Ферма) Если $ f (x) $ имеет локальный экстремум при $ x = a $ и $ f $ дифференцируема в $ a $, тогда $ f ‘(a) = 0 $.$ \ qed $
Таким образом, единственный точки, в которых функция может иметь локальный максимум или минимум, являются точки, в которых производная равна нулю, как на левом графике в рисунок 5.1.1, или производная не определена, как на правом графике. Любое значение $ x $, для которого $ f ‘(x) $ равно нулю или не определено, называется критическое значение для $ f $, и точка $ (x, f (x)) $ на кривой называется критическая точка за $ f $.
 При поиске локальных точек максимума и минимума вы, вероятно,
сделать два вида ошибок: вы можете забыть, что максимум или минимум
может возникнуть там, где производная не существует, поэтому забудьте проверить
существует ли производная везде.2 $, и $ f ‘(0) = 0 $, но нет ни максимума, ни
минимум на уровне $ (0,0) $.
При поиске локальных точек максимума и минимума вы, вероятно,
сделать два вида ошибок: вы можете забыть, что максимум или минимум
может возникнуть там, где производная не существует, поэтому забудьте проверить
существует ли производная везде.2 $, и $ f ‘(0) = 0 $, но нет ни максимума, ни
минимум на уровне $ (0,0) $.Рисунок 5.1.2. Нет ни максимума, ни минимума, даже если производная равна нулю.
Поскольку производная равна нулю или не определена как в локальном максимуме, так и в точки локального минимума, нам нужен способ определить, какие из них на самом деле происходит. Большинство элементарный подход, но тот, который часто бывает утомительным или трудным, заключается в непосредственно проверить, находится ли $ y $ «рядом» с потенциалом максимум или минимум выше или ниже координаты $ y $ в точке представляет интерес.Конечно, «около» точки слишком много точек. чтобы проверить, но небольшая мысль показывает, что нам нужно проверить только два, при условии, что мы знать, что $ f $ непрерывно (напомним, это означает, что график $ f $ не имеет скачков и разрывов).

Предположим, например, что мы определили три точки, в которых $ f ‘$ равен нулю или не существует: $ \ ds (x_1, y_1) $, $ \ ds (x_2, y_2) $, $ \ ds (x_3, y_3) $, и $ \ ds x_15.1.3). Предположим, что мы вычисляем значение $ f (a) $ для $ \ ds x_1f (x_2) $? Нет: если бы были, график пошел бы вверх от $ (a, f (a)) $ в $ (b, f (b)) $, затем вниз до $ \ ds (x_2, f (x_2)) $ и где-то в между ними будет локальная точка максимума.(Это не очевидно; это результат теоремы о крайнем значении, теорема 6.1.2.) Но на этом локальном максимуме точка, производная от $ f $ была бы равна нулю или не существовала бы, но мы уже известно, что производная равна нулю или не существует только в $ \ ds x_1 $, $ \ ds x_2 $ и $ \ ds x_3 $. В результате одно вычисление говорит нам, что $ \ ds (x_2, f (x_2)) $ имеет наибольшую координату $ y $ любой точки на график около $ \ ds x_2 $ и слева от $ \ ds x_2 $. Мы можем сделать то же самое тест справа. Если мы обнаружим, что по обе стороны от $ \ ds x_2 $ значения меньше, то должен быть локальный максимум в $ \ ds (x_2, f (x_2)) $; если мы обнаруживаем, что по обе стороны от $ \ ds x_2 $ значения больше, то есть должен быть локальным минимумом в $ \ ds (x_2, f (x_2)) $; если мы найдем по одному из каждого, тогда нет ни локального максимума, ни минимума в $ \ ds x_2 $.

Рисунок 5.1.3. Тестирование на максимум или минимум.
Не всегда легко вычислить значение функции в конкретный момент. Задача облегчается наличием калькуляторы и компьютеры, но у них есть свои недостатки — они не всегда позволяют различать очень близкие значения вместе. Тем не менее, поскольку этот метод концептуально прост и иногда легко выполнить, вы всегда должны учитывать это.
Пример 5.2-1 $. Это определяется всюду и равен нулю в $ \ ds x = \ pm \ sqrt {3} / 3 $. Глядя сначала на $ \ ds x = \ sqrt {3} / 3 $, мы видим, что $ \ ds f (\ sqrt {3} / 3) = — 2 \ sqrt {3} / 9 $. Сейчас мы тестируем две точки по обе стороны от $ \ ds x = \ sqrt {3} / 3 $, убедившись, что ни один из них не находится дальше, чем ближайшее критическое значение; поскольку $ \ ds \ sqrt {3} -2 \ sqrt {3} / 9 $ и $ \ ds f (1) = 0> -2 \ sqrt {3} / 9 $, должен быть локальный минимум в $ \ ds x = \ sqrt {3} / 3 $. Для $ \ ds x = — \ sqrt {3} / 3 $ мы видим, что $ \ ds f (- \ sqrt {3} / 3) = 2 \ sqrt {3} / 9 $.
 На этот раз мы можем использовать $ x = 0 $ и $ x = -1 $,
и находим, что $ \ ds f (-1) = f (0) = 0
На этот раз мы можем использовать $ x = 0 $ и $ x = -1 $,
и находим, что $ \ ds f (-1) = f (0) = 0Конечно, этот пример очень упрощен благодаря нашему выбору точек для test, а именно $ x = -1 $, $ 0 $, $ 1 $.Мы могли бы использовать другие значения, например $ -5 / 4 $, $ 1/3 $ и $ 3/4 $, но это сделало бы вычисления значительно утомительнее.
Пример 5.1.3 Найдите все локальные точки максимума и минимума для $ е (х) = \ грех х + \ соз х $. Производная равна $ f ‘(x) = \ cos x- \ sin x $. Это всегда определен и равен нулю всякий раз, когда $ \ cos x = \ sin x $. Напоминая, что $ \ cos x $ и $ \ sin x $ — координаты $ x $ и $ y $ точек на единичный круг, мы видим, что $ \ cos x = \ sin x $, когда $ x $ равен $ \ pi / 4 $, $ \ pi / 4 \ pm \ pi $, $ \ pi / 4 \ pm2 \ pi $, $ \ pi / 4 \ pm3 \ pi $ и т. д.Поскольку оба синуса и косинус имеют период $ 2 \ pi $, нам нужно только определить статус из $ x = \ pi / 4 $ и $ x = 5 \ pi / 4 $. Мы можем использовать $ 0 $ и $ \ pi / 2 $ для проверки критическое значение $ x = \ pi / 4 $.
 Получаем, что $ \ ds f (\ pi / 4) = \ sqrt {2} $, $ \ ds f (0) = 1
Получаем, что $ \ ds f (\ pi / 4) = \ sqrt {2} $, $ \ ds f (0) = 1Мы используем $ \ pi $ и $ 2 \ pi $ для проверки критического значения $ x = 5 \ pi / 4 $. В соответствующие значения: $ \ ds f (5 \ pi / 4) = — \ sqrt2 $, $ \ ds f (\ pi) = — 1> — \ sqrt2 $, $ \ ds f (2 \ pi) = 1> — \ sqrt2 $, поэтому существует локальный минимум в $ x = 5 \ pi / 4 $, $ 5 \ pi / 4 \ pm2 \ pi $, $ 5 \ pi / 4 \ pm4 \ pi $ и т. Д. Более лаконично, есть локальные минимумы в $ 5 \ pi / 4 \ pm 2k \ pi $ для каждое целое число $ k $.2 & $ x \ neq 0 $ \ cr} $ (отвечать)
Пример 5.1.13 Для любого действительного числа $ x $ существует уникальное целое число $ n $ такое, что $ n \ leq x
Пример 5.1.14 Объясните, почему функция $ f (x) = 1 / x $ не имеет локального максимумы или минимумы.
Пример 5.1.15 Сколько критических точек может иметь квадратичная полиномиальная функция? (отвечать)
Пример 5.1.16 Докажите, что кубический многочлен может иметь не более двух критических точки.
 Приведите примеры, показывающие, что кубический многочлен может иметь нуль,
одна или две критические точки.3 + cx + 1 $, где $ c $
является константой. Сколько и каких видов локальных крайностей существует?
Ваш ответ должен зависеть от значения $ c $, то есть разного
значения $ c $ дадут разные ответы.
Приведите примеры, показывающие, что кубический многочлен может иметь нуль,
одна или две критические точки.3 + cx + 1 $, где $ c $
является константой. Сколько и каких видов локальных крайностей существует?
Ваш ответ должен зависеть от значения $ c $, то есть разного
значения $ c $ дадут разные ответы.MIN, функция Excel — найти наименьшее число
В этом руководстве показано, как использовать функцию Excel MIN в Excel для вычисления наименьшего числа.
Обзор функций MIN
Функция MIN Вычисляет наименьшее число.
Чтобы использовать функцию минимального рабочего листа Excel, выберите ячейку и введите:
(обратите внимание, как появляются входные данные формулы)
Функция MIN Синтаксис и входные данные:
массив — массив чисел.
Как использовать функцию MINФункция MIN возвращает наименьшее значение из диапазона значений. Это полная противоположность функции MAX.

Давайте воспользуемся функцией MIN, чтобы найти самую низкую цену на учебник.
Пустые ячейки или ячейки с текстомФункция MIN игнорирует пустые ячейки или ячейки, содержащие нечисловые значения.
МИН ДатаПоскольку Excel хранит дату в виде серийных номеров, мы можем использовать функцию MIN, чтобы найти минимальную дату.
ВПР И МИН.В нашем примере выше мы использовали функцию MIN, чтобы определить самую низкую цену учебника. Мы можем использовать функцию ВПР, чтобы найти самый дешевый учебник, используя следующую формулу.
= ВПР (МИН (A2: A9), A2: B9, 2, 0)
Обратите внимание, как функция MIN вычисляет самую низкую цену учебника и возвращает это значение в функцию VLOOKUP. После этого функция ВПР возвращает учебник, связанный с самой низкой ценой, путем поиска во втором столбце (обозначенном цифрой «2» в нашей формуле) таблицы.

Примечание. Для работы функции ВПР цены на учебники должны быть помещены в первый столбец.
Функция MINIFSMINIFS Функция возвращает минимальное значение из набора значений, применяя одно или несколько условий. Допустим, мы хотим найти учебник по самой низкой цене, который был продан.
= MINIFS (C2: C9, B2: B9, «Продано»)
Обратите внимание, как формула ищет статус «Продано» из B2: B9 и создает подмножество цены учебника. Затем минимальное значение рассчитывается только на основе соответствующего набора данных — проданных учебников.
Чтобы узнать больше о том, как работает функция MINIFS, прочитайте наше руководство по MAXIFS и MINIFS.
Примечание. Функция MINIFS доступна только в Excel 2019 или Excel 365. Если у вас более старая версия Excel, вы можете использовать функцию массива для создания собственного MIN IF.
MIN IFЕсли вы используете старые версии Excel, вы можете комбинировать функцию IF с функцией MIN с помощью функции массива.
 Взяв тот же пример, что и выше, используйте формулу:
Взяв тот же пример, что и выше, используйте формулу:= МИН (ЕСЛИ (B2: B9 = «Продано», C2: C9))
Примечание. При построении функций массива после создания формулы необходимо нажимать CTRL + SHIFT + ENTER, а не просто ENTER.
Вы заметите, как появляются фигурные скобки. Вы не можете просто вручную ввести фигурные скобки; вы должны использовать CTRL + SHIFT + ENTER.
Функция IF помогает сузить диапазон данных, а функция MIN вычисляет минимальное значение из этого подмножества. Таким образом можно рассчитать цену самого дешевого проданного текста.
Примечание. В приведенной выше формуле используются абсолютные ссылки (знаки $) для блокировки ссылок на ячейки при копировании формул.Если вы не знакомы с этим, прочтите наше справочное руководство по Excel
Функция MIN в Google ТаблицахФункция МИН работает в Google Таблицах точно так же, как и в Excel.

Дополнительные примечания
Функция MIN возвращает наименьшее число в серии. Логические значения (ИСТИНА и ЛОЖЬ) и числа, хранящиеся в виде текста, не учитываются. Вместо этого для подсчета логических значений и чисел, хранящихся в виде текста, используйте MINA.
MIN Примеры в VBA
Вы также можете использовать функцию MIN в VBA. Введите:
application.worksheetfunction.min (number1, number2)
Для аргументов функции (массив и т. Д.) Вы можете либо ввести их непосредственно в функцию, либо определить переменные, которые будут использоваться вместо них.Предполагая, что у нас есть следующий диапазон
, мы можем получить минимальное число в диапазоне A1: D5 с помощью следующего оператора VBA
Рабочий листМин. (Диапазон («A1: D5»))
Что вернет 14, так как это наименьшее число в этом диапазоне
Функция MIN также может принимать таблицу в качестве параметра, поэтому следующий оператор также действителен при условии, что в нашем рабочем листе есть таблица с именем «Таблица1»
Рабочий лист Функция.
 Мин (Диапазон («Таблица1»))
Мин (Диапазон («Таблица1»))Мы также можем использовать функцию MIN, напрямую вводя числа в качестве параметров, как в следующем примере
Рабочий листМин. (1, 2, 3, 4, 5, 6, 7, 8, 9)
, который вернет 1 в результате
Вернуться к списку всех функций в Excel
Как с помощью графических функций найти относительный минимум на интервале
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т.
 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
.
- Массив (обязательный аргумент) — это массив или диапазон числовых данных, для которых мы хотим найти k наименьшее значение.
 Если стационарных точек нет или ни одна из них не попадает в отрезок, то переходим к следующему пункту.
Если стационарных точек нет или ни одна из них не попадает в отрезок, то переходим к следующему пункту. Находим нули производной.
Находим нули производной.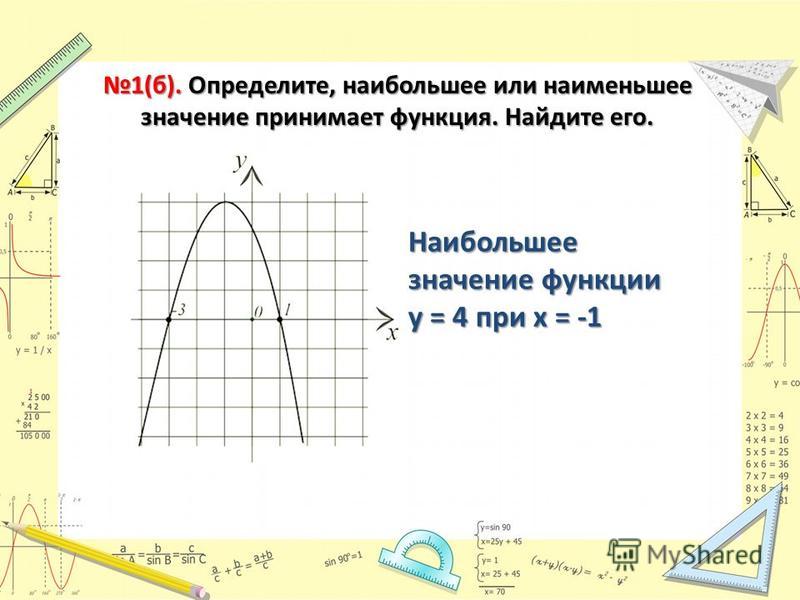 3}{3}$ + 2x 2 + 4x — 5 на отрезке
3}{3}$ + 2x 2 + 4x — 5 на отрезке  2 + 3}$ на луче: , б) , в) [-4;7].
2 + 3}$ на луче: , б) , в) [-4;7].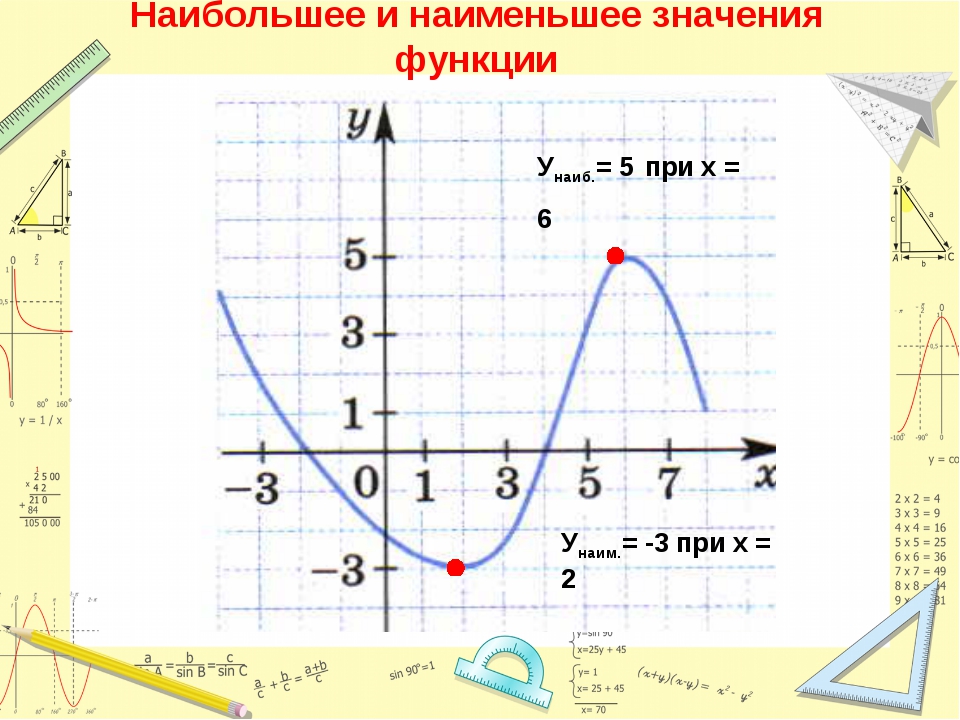
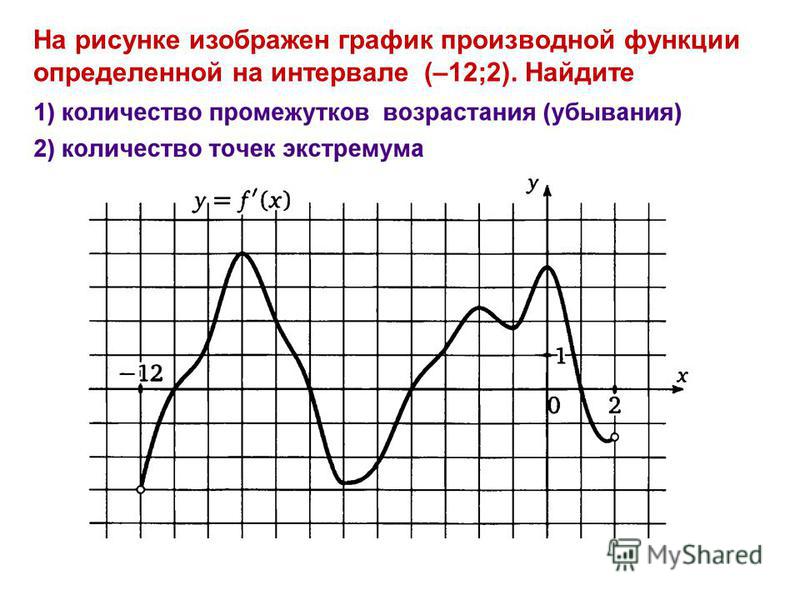




 Укажите точки максимума функции, а также промежутки убывания функции.
Укажите точки максимума функции, а также промежутки убывания функции.
 ( в точках экстремума или на концах отрезка, являющимся областью определения функции)
( в точках экстремума или на концах отрезка, являющимся областью определения функции)

 Мы смотрели на график функции и делали вывод, где функция достигает наибольшего значения, а где — наименьшего.
Мы смотрели на график функции и делали вывод, где функция достигает наибольшего значения, а где — наименьшего.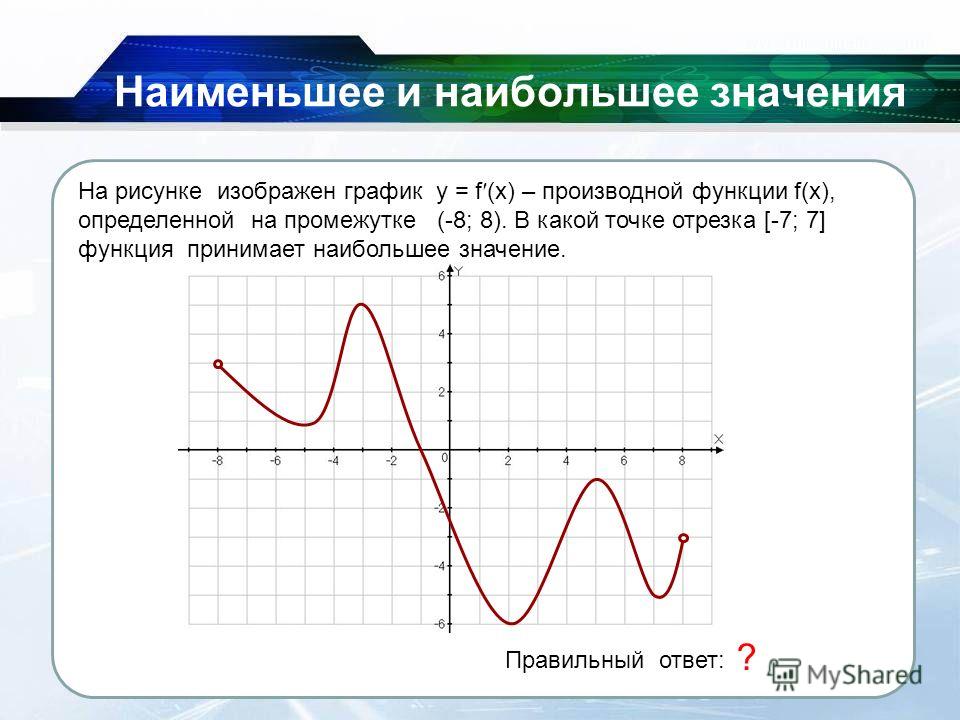
 3}{3}$ + 2x2 + 4x — 5 на отрезке
3}{3}$ + 2x2 + 4x — 5 на отрезке  2 + 3}$= $\frac{3√3}{6}$= $\frac{√3}{2}$.
2 + 3}$= $\frac{3√3}{6}$= $\frac{√3}{2}$. Функция такого вида (когда одна функция вложена в
Функция такого вида (когда одна функция вложена в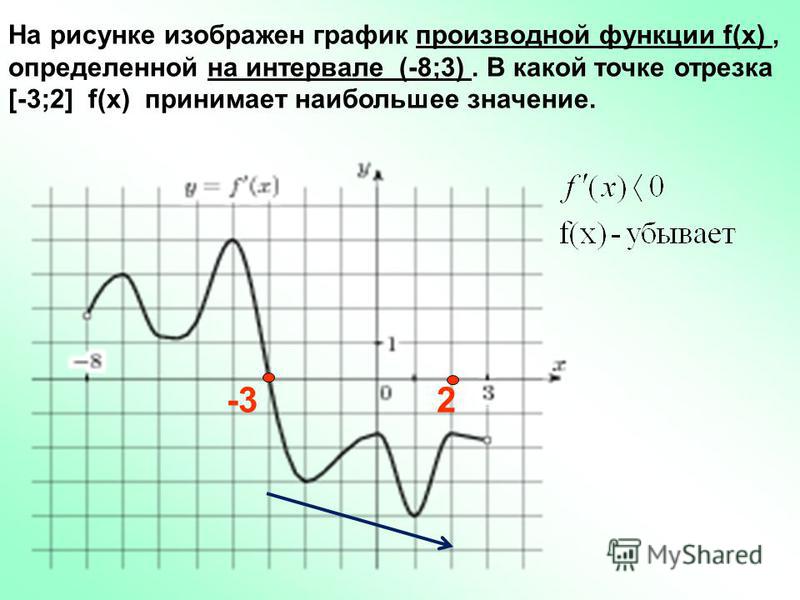 Для этого вы подставляете это значение х в уравнение
Для этого вы подставляете это значение х в уравнение
 Найдите наибольшее значение функции у =
Найдите наибольшее значение функции у = Значит, наибольшее значение она будет иметь, когда функция
Значит, наибольшее значение она будет иметь, когда функция е. в
е. в Значит, наименьшее значение она будет иметь, когда функция
Значит, наименьшее значение она будет иметь, когда функция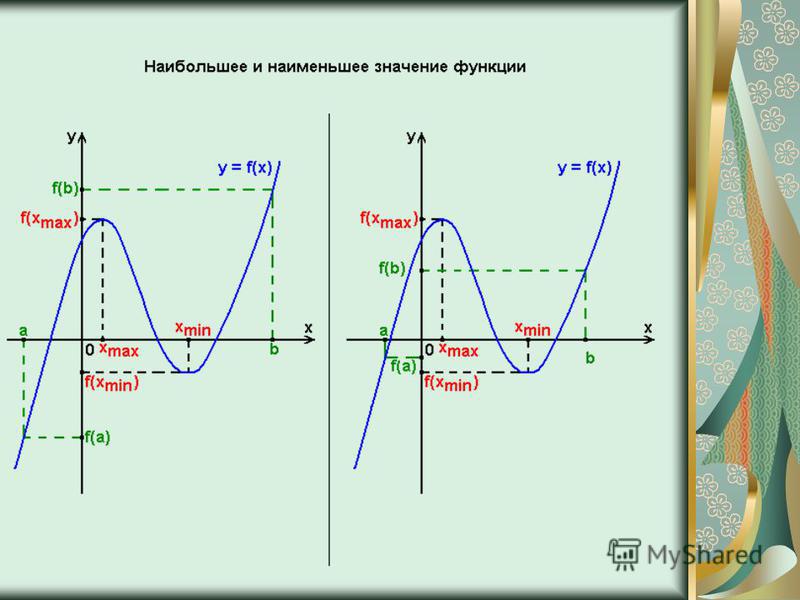
 е. в
е. в Значит, наибольшее значение она будет иметь, когда
Значит, наибольшее значение она будет иметь, когда е.
е.

 Приравняем производную нулю ()
и получим две критические точки: и
. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на
концах отрезка и в точке ,
так как точка не
принадлежит отрезку [-1, 2]
. Эти значения функции — следующие: ,
,
. Из этого следует, что наименьшее значение функции (на графике ниже обозначено красным), равное -7, достигается на правом конце отрезка — в точке
, а наибольшее (тоже
красное на графике), равно 9,
— в критической точке .
Приравняем производную нулю ()
и получим две критические точки: и
. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на
концах отрезка и в точке ,
так как точка не
принадлежит отрезку [-1, 2]
. Эти значения функции — следующие: ,
,
. Из этого следует, что наименьшее значение функции (на графике ниже обозначено красным), равное -7, достигается на правом конце отрезка — в точке
, а наибольшее (тоже
красное на графике), равно 9,
— в критической точке .
 Поэтому в ход пойдут логарифм и тригонометрическая функция.
Поэтому в ход пойдут логарифм и тригонометрическая функция.
 Она определена и дифференцируема всюду в
]0, +∞[
, причём
Она определена и дифференцируема всюду в
]0, +∞[
, причём Пусть в этой области заданная функция имеет конечные частные производные первого порядка (за исключением, быть может, конечного количества точек). Чтобы найти наибольшее и наименьшее значения функции двух переменных в данной замкнутой области требуется выполнить три шага простого алгоритма.
Пусть в этой области заданная функция имеет конечные частные производные первого порядка (за исключением, быть может, конечного количества точек). Чтобы найти наибольшее и наименьшее значения функции двух переменных в данной замкнутой области требуется выполнить три шага простого алгоритма. 2-4x$ в замкнутой области, ограниченной линиями $x=3$, $y=0$ и $y=x+1$.
2-4x$ в замкнутой области, ограниченной линиями $x=3$, $y=0$ и $y=x+1$. Дабы не загромождать ход решения вспомогательными пояснениями, то вопрос о получении этих двух точек вынесу в примечание.
Дабы не загромождать ход решения вспомогательными пояснениями, то вопрос о получении этих двух точек вынесу в примечание. Однако стоит помнить, что рисунок не может служить доказательством. Рисунок — лишь иллюстрация для наглядности.
Однако стоит помнить, что рисунок не может служить доказательством. Рисунок — лишь иллюстрация для наглядности.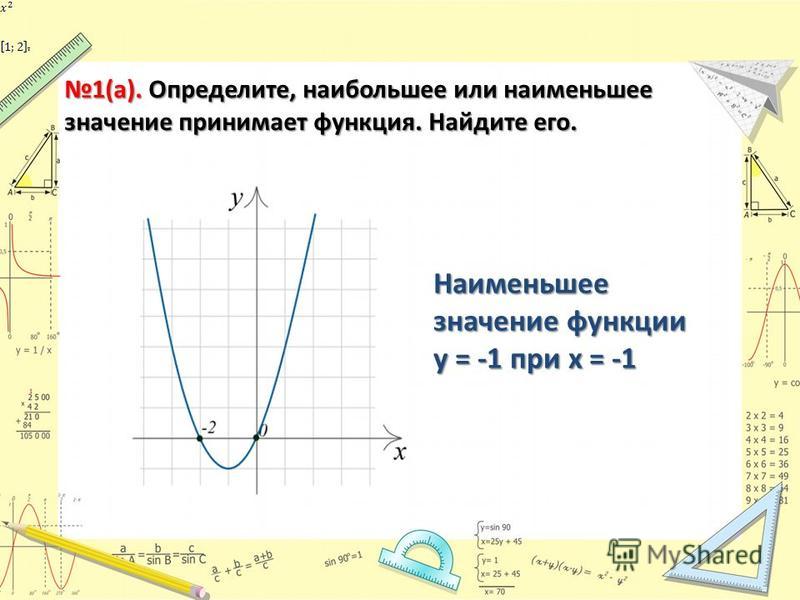 2-12\cdot(-3)+16\cdot 4=125.
\end{aligned}
2-12\cdot(-3)+16\cdot 4=125.
\end{aligned} 2}$
2}$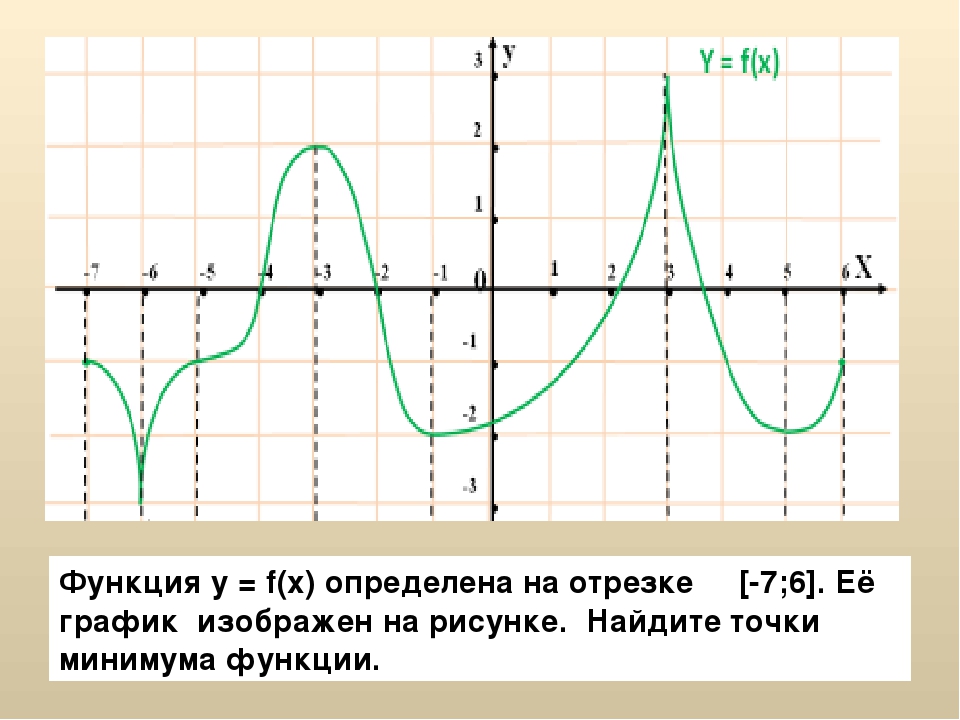 2=0 ; х-3=0; х+3=0$
2=0 ; х-3=0; х+3=0$


 2 / 4 а .2 + k и член a положителен, тогда минимальным значением будет значение k . Поиск минимума имеет практическое применение в науке, технике и других областях.
2 / 4 а .2 + k и член a положителен, тогда минимальным значением будет значение k . Поиск минимума имеет практическое применение в науке, технике и других областях.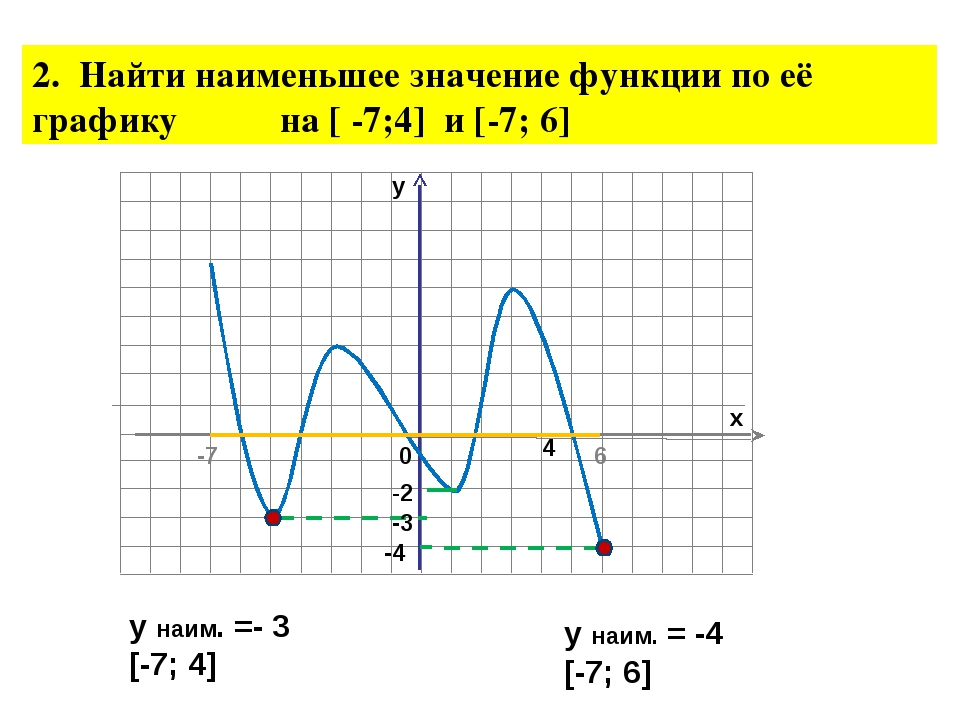

 Потратив время на изучение и освоение этих функций, вы значительно ускорите свое финансовое моделирование.Чтобы узнать больше, ознакомьтесь с этими дополнительными ресурсами CFI:
Потратив время на изучение и освоение этих функций, вы значительно ускорите свое финансовое моделирование.Чтобы узнать больше, ознакомьтесь с этими дополнительными ресурсами CFI: е. вы, вероятно, разговариваете по мобильному телефону). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, разговариваете по мобильному телефону). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
 Или, другими словами, \ (c \) будет содержаться где-то внутри интервала и не будет ни одной из конечных точек.
Или, другими словами, \ (c \) будет содержаться где-то внутри интервала и не будет ни одной из конечных точек.
 Однако в этом классе мы будем использовать определение, в котором говорится, что они не могут возникать в конечных точках домена.Это будет обсуждаться более подробно в конце раздела, когда мы позаботимся о соответствующем факте.
Однако в этом классе мы будем использовать определение, в котором говорится, что они не могут возникать в конечных точках домена.Это будет обсуждаться более подробно в конце раздела, когда мы позаботимся о соответствующем факте.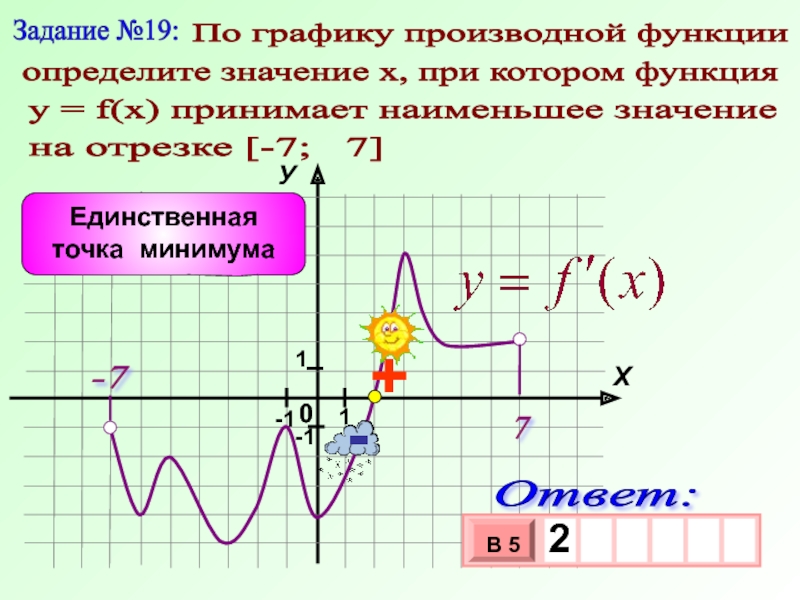 Эти две точки являются наибольшим и наименьшим из возможных для функции. Мы также можем заметить, что абсолютные экстремумы для функции будут возникать либо в конечных точках области, либо в относительных экстремумах.2} \ hspace {0,25 дюйма} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{- 1,2} \ right] \]
Показать решение
Эти две точки являются наибольшим и наименьшим из возможных для функции. Мы также можем заметить, что абсолютные экстремумы для функции будут возникать либо в конечных точках области, либо в относительных экстремумах.2} \ hspace {0,25 дюйма} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{- 1,2} \ right] \]
Показать решение
 Вот график.
Вот график.


 2}}}} \ hspace {0.25 дюймов} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{\ frac {1} {2}, 1} \ right] \]
2}}}} \ hspace {0.25 дюймов} {\ mbox {on}} \ hspace {0,25 дюйма} \ left [{\ frac {1} {2}, 1} \ right] \] Дело в том, что этот график не является непрерывным и все же имеет оба абсолютных экстремума
Дело в том, что этот график не является непрерывным и все же имеет оба абсолютных экстремума 3} \ hпространство {0.2} \]
3} \ hпространство {0.2} \]

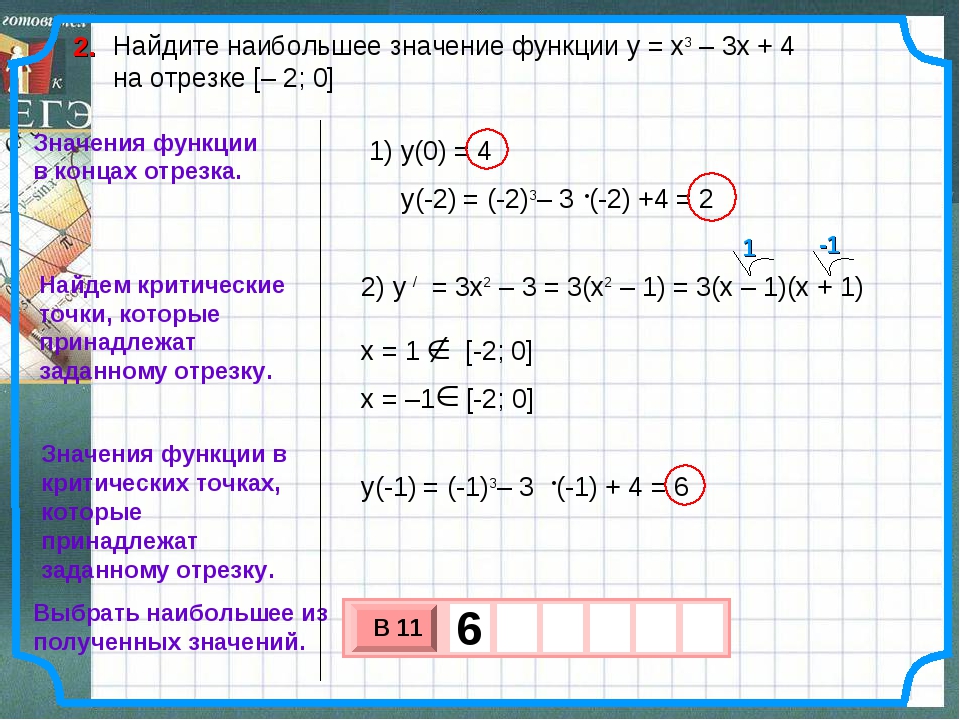
 Как узнать самую раннюю дату в Excel? Легкий! Используйте MIN, следуя той же логике из примера 1:
Как узнать самую раннюю дату в Excel? Легкий! Используйте MIN, следуя той же логике из примера 1: Таким образом, комбинация функций MIN и ABS сделает свое дело. Просто введите следующую формулу в любую пустую ячейку:
Таким образом, комбинация функций MIN и ABS сделает свое дело. Просто введите следующую формулу в любую пустую ячейку: Вот пример формулы, которая возвращает нижнее значение на основе некоторого условия:
Вот пример формулы, которая возвращает нижнее значение на основе некоторого условия: 😉
😉
 что-то не так с данными, на которые ссылается формула.
что-то не так с данными, на которые ссылается формула. Наиболее вероятная причина такого результата — опечатка. Вы можете неправильно написать функцию или указать неверные аргументы. Более того, текстовое представление чисел тоже вызовет эту ошибку.
Наиболее вероятная причина такого результата — опечатка. Вы можете неправильно написать функцию или указать неверные аргументы. Более того, текстовое представление чисел тоже вызовет эту ошибку.  1 Максима и Минима
1 Максима и Минима Некоторые примеры локальных точек максимума и минимума
показаны на рисунке 5.1.1.
Некоторые примеры локальных точек максимума и минимума
показаны на рисунке 5.1.1. При поиске локальных точек максимума и минимума вы, вероятно,
сделать два вида ошибок: вы можете забыть, что максимум или минимум
может возникнуть там, где производная не существует, поэтому забудьте проверить
существует ли производная везде.2 $, и $ f ‘(0) = 0 $, но нет ни максимума, ни
минимум на уровне $ (0,0) $.
При поиске локальных точек максимума и минимума вы, вероятно,
сделать два вида ошибок: вы можете забыть, что максимум или минимум
может возникнуть там, где производная не существует, поэтому забудьте проверить
существует ли производная везде.2 $, и $ f ‘(0) = 0 $, но нет ни максимума, ни
минимум на уровне $ (0,0) $.

 На этот раз мы можем использовать $ x = 0 $ и $ x = -1 $,
и находим, что $ \ ds f (-1) = f (0) = 0
На этот раз мы можем использовать $ x = 0 $ и $ x = -1 $,
и находим, что $ \ ds f (-1) = f (0) = 0 Получаем, что $ \ ds f (\ pi / 4) = \ sqrt {2} $, $ \ ds f (0) = 1
Получаем, что $ \ ds f (\ pi / 4) = \ sqrt {2} $, $ \ ds f (0) = 1 Приведите примеры, показывающие, что кубический многочлен может иметь нуль,
одна или две критические точки.3 + cx + 1 $, где $ c $
является константой. Сколько и каких видов локальных крайностей существует?
Ваш ответ должен зависеть от значения $ c $, то есть разного
значения $ c $ дадут разные ответы.
Приведите примеры, показывающие, что кубический многочлен может иметь нуль,
одна или две критические точки.3 + cx + 1 $, где $ c $
является константой. Сколько и каких видов локальных крайностей существует?
Ваш ответ должен зависеть от значения $ c $, то есть разного
значения $ c $ дадут разные ответы.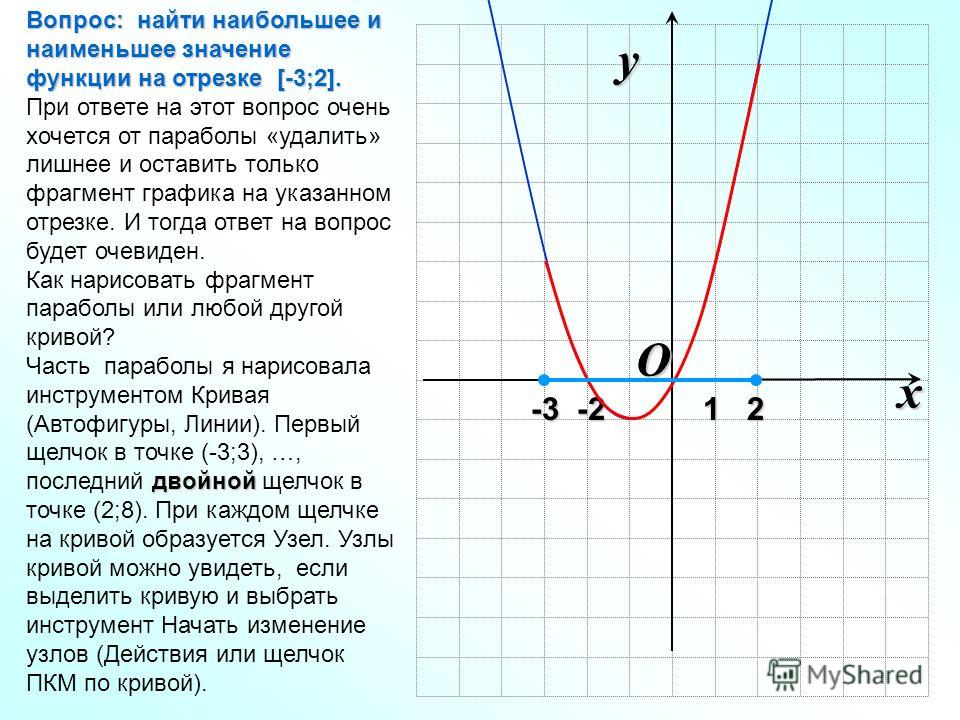

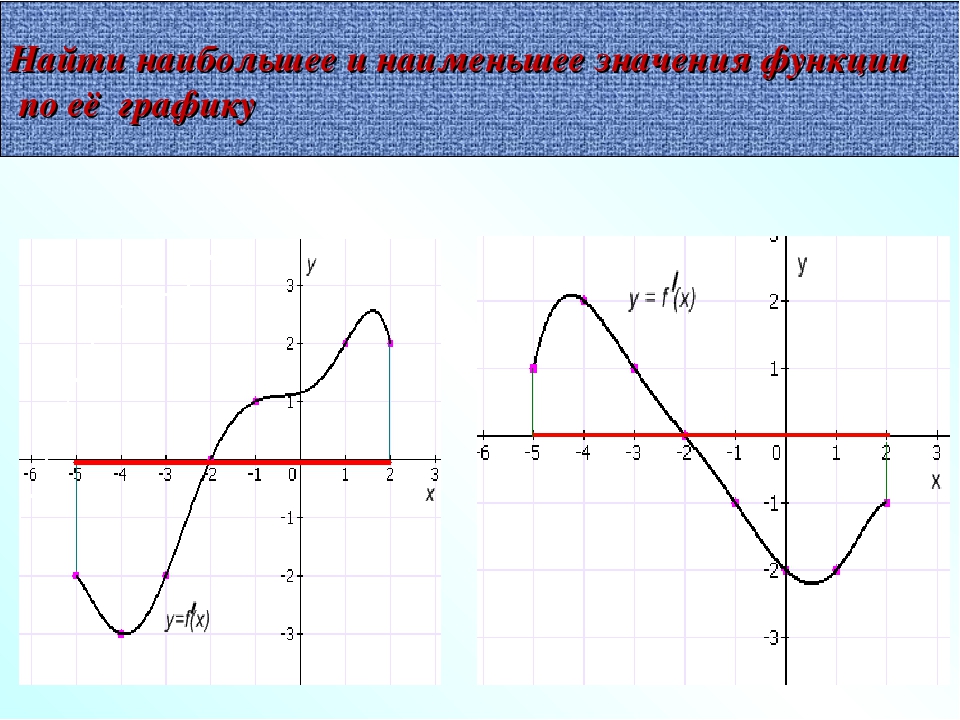 Взяв тот же пример, что и выше, используйте формулу:
Взяв тот же пример, что и выше, используйте формулу:
 Мин (Диапазон («Таблица1»))
Мин (Диапазон («Таблица1»))
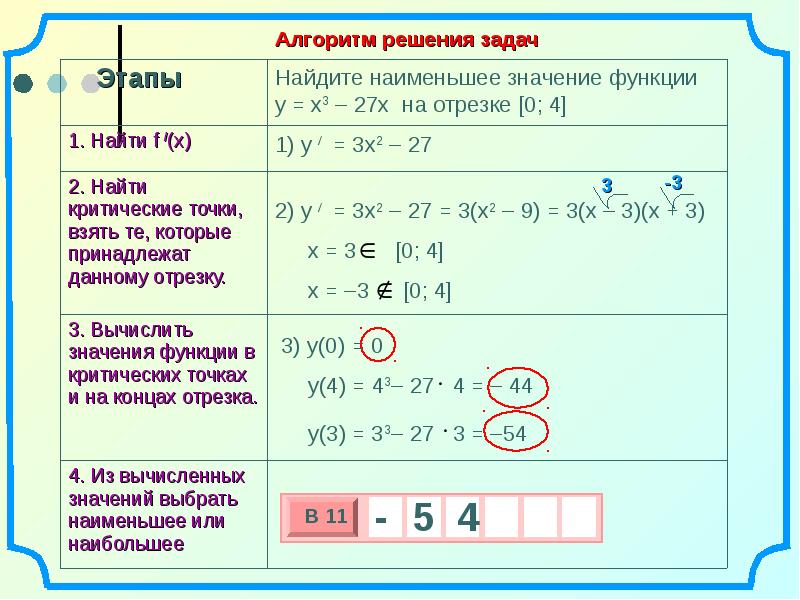 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.