Решение показательных уравнений

Показательные уравнения – это уравнения вида

где

x -неизвестный показатель степени,

a и b– некоторые числа.

Примеры показательного уравнения:

А уравнения:

уже не будут являться показательными.

 

Рассмотрим примеры решения показательных уравнений:

Пример 1.
Найдите корень уравнения:

Приведем степени к одинаковому основанию, чтобы воспользоваться свойством степени с действительным показателем

 

Тогда можно будет убрать основание степени и перейти к равенству показателей.

Преобразуем левую часть уравнения:

Далее используем свойство степени 

Преобразуем правую часть уравнения:

Используем свойство степени 

Ответ: 4,5.

Пример 2.
Решите неравенство:

Разделим обе части уравнения на 

Замена:

Обратная замена:

Число обращается в 1, если его показатель равен 0

Ответ: x=0.

 

Пример 3.

Решите уравнение и найдите корни на заданном промежутке:

Приводим все слагаемые к одинаковому основанию:

Замена:

Ищем корни уравнения, путём подбора кратных свободному члену:

 – подходит, т.к. равенство выполняется.
 – подходит, т.к. равенство выполняется.
– подходит, т.к. равенство выполняется.
– не подходит, т.к. равенство не выполняется.

Обратная замена:

1) 

Число обращается в 1, если его показатель равен 0

2)

Не подходит, т.к. 

3)

Логарифмируем обе части по основанию 2:

Правая часть равна 1, т.к.

Показатель степени встаёт перед выражение, т.к. 

Отсюда:

 

Пример 4.

Решите уравнение:

Замена: , тогда

Обратная замена:

1 уравнение:

если основания чисел равны, то их показатели будут равны, то

2 уравнение:

Логарифмируем обе части по основанию 2:

Показатель степени встаёт перед выражение, т.к. 

Левая часть равна 2x, т.к. 

Отсюда:

 

Пример 5.

Решите уравнение:

Преобразуем левую часть:

Перемножаем степени по формуле: 

Упростим:  по формуле: 

Представим  в виде :

Замена:

Переведём дробь в неправильную:

Вычисляем корень из дискриминанта:

a₂ -не подходит, т.к. а не принимает отрицательные значения

Обратная замена:

Приводим к общему основанию:

Если 

Ответ: x=20.

Пример 6.

Решите уравнение:

О.Д.З.

Преобразуем левую часть по формуле: 

Замена:

Вычисляем корень из дискриминанта:

a₂-не подходит, т.к. а не принимает отрицательные значения

Приводим к общему основанию:

Если 

Возводим в квадрат обе части:

Ответ: x=9.

Автор статьи: Дьяков Александр Дмитриевич

Редакторы статьи: Гаврилина Анна Викторовна, Агеева Любовь Александровна

www.teslalab.ru

Показательные уравнения

    Показательные уравнения. Как известно — в состав ЕГЭ входят простые уравнения. Некоторые мы уже рассмотрели – это логарифмические, тригонометрические, рациональные. Здесь представлены показательные уравнения.

В недавней статье мы поработали с показательными выражениями, посмотрите, будет полезно. Сами уравнения решаются просто и быстро. Требуется лишь знать свойства показателей степени и…  Об этом далее.

Перечислим свойства показателей степени:

Нулевая степень любого числа равна единице.

Далее:

Следствие из данного свойства:

Ещё немного теории.

Показательным уравнением называется уравнение содержащее переменную в показателе, то есть  это уравнение вида:

f(x)  выражение, которое содержит переменную

Методы решения показательных уравнений

1. В результате преобразований уравнение можно привести к виду:

Тогда применяем свойство:

2. При получении уравнения вида  a ^f(x) = b  используется определение логарифма, получим:

3. В результате преобразований можно получить уравнение вида:

Применяется логарифмирование:

Далее применяем свойство логарифма степени:

Выражаем и находим х.

В задачах вариантов ЕГЭ достаточно будет использовать первый способ.

То есть, необходимо представить левую и правую части в виде степеней с одинаковым основанием, а далее приравниваем показатели и решаем обычное линейное уравнение.

Рассмотрим уравнения:

Найдите корень уравнения 4^1–2х = 64.

Необходимо сделать так, чтобы в левой и правой частях были показательные выражения с одним основанием. 64 мы можем представить как 4 в степени 3. Получим:

4^1–2х = 4³

Основания равны, можем приравнять показатели:

1 – 2х = 3

– 2х = 2

х =  – 1

Проверка:

4^1–2(–1) = 64

4¹⁺² = 64

4³ = 64

64 = 64

Ответ: –1

Найдите корень уравнения 3^х–18 = 1/9.

Известно, что

Значит  3^х-18 = 3^-2

Основания равны, можем приравнять показатели:

х – 18 = – 2

х = 16

Проверка:

3^16–18 = 1/9

3^–2 = 1/9

1/9 = 1/9

Ответ: 16

Найдите корень уравнения:

Представим дробь 1/64 как  одну четвёртую в третьей степени:

Теперь можем приравнять показатели:

2х – 19 = 3

2х = 22

х = 11

Проверка:

Ответ: 11

Найдите корень уравнения:

Представим 1/3 как  3^–1, а 9 как 3 в квадрате, получим:

(3^–1)^8–2х = 3²

3^{–1∙(8–2х)} = 3²

3^–8+2х = 3²

Теперь можем приравнять показатели:

 – 8+2х = 2

2х = 10

х = 5

Проверка:

Ответ: 5

26654. Найдите корень уравнения:

Решение:

Ответ: 8,75

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Что хочется отметить обсобо!!!

Как бы  вы не были уверены в правильности решения — ОБЯЗАТЕЛЬНО делайте проверку.

Ещё теория (чуть-чуть):

Самое простейшее показательное уравнение:

При данных условиях уравнение всегда имеет решение, при том единственное.

Действительно, при а > 1 показательная функция монотонно возрастает, а при 0 < а < 1 — монотонно убывает. В любом случае, она принимает каждое своё значение ровно один раз (видно по графику):

А вот если b < 0, то уравнение не имеет решений, ведь показательная функция может принимать только положительные значения.

Действительно, в какую бы степень мы не возвели положительное число a, мы никак не можем получить число отрицательное.

Любое показательное уравнение после соответствующих преобразований сводится к реше­нию одного или нескольких простейших.В данной рубрике мы ещё рассмотрим решение некоторых уравнений, не пропустите! На этом всё. Успеха вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Методы решения уравнений высших степеней

Методы решения уравнений высших степеней.

I) Решение уравнений с помощью деления в столбик.

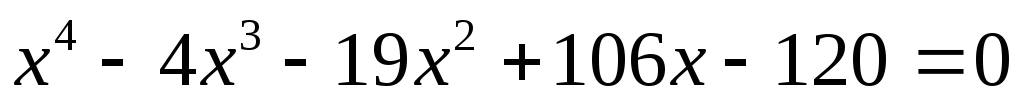
Очевидно — корень уравнения

Очевидно 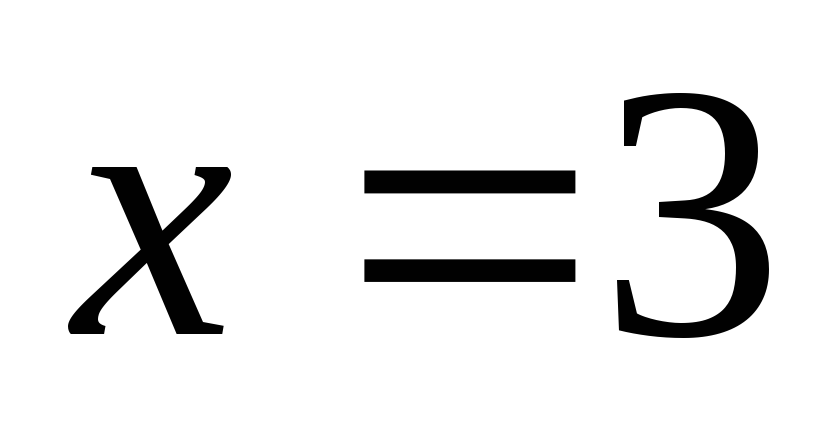— корень уравнения

Ответ: -5;2;3;4

II) Возвратные уравнения и к ним сводящиеся.

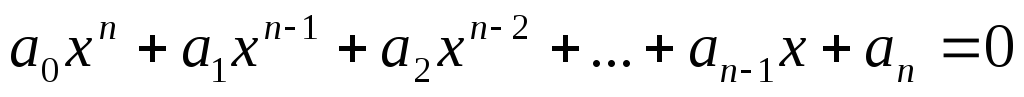
Уравнение называется возвратным, если в нем коэффициенты равноудаленные от концов совпадают, т.е. , ,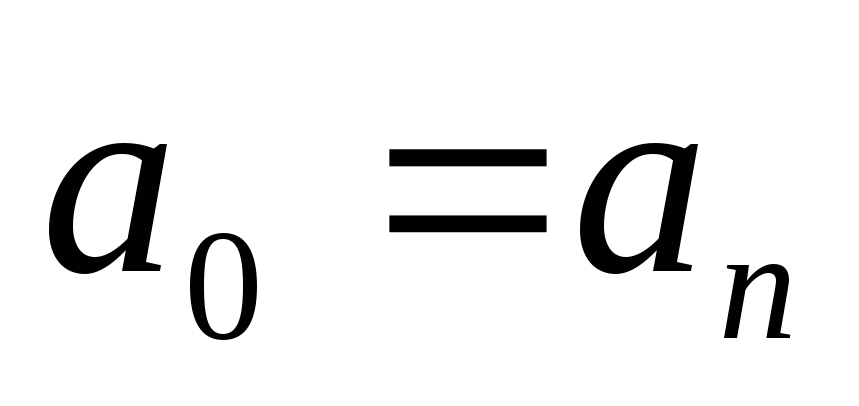

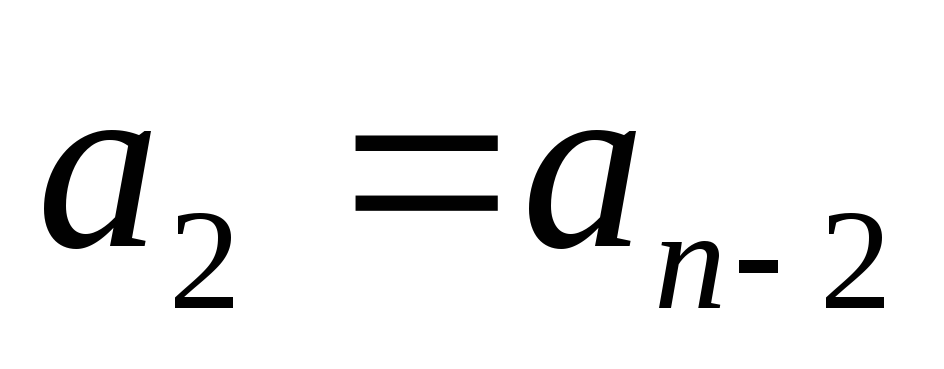
1) Возвратные уравнения четной степени.

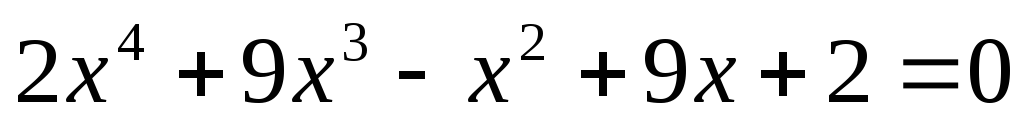
т.к. 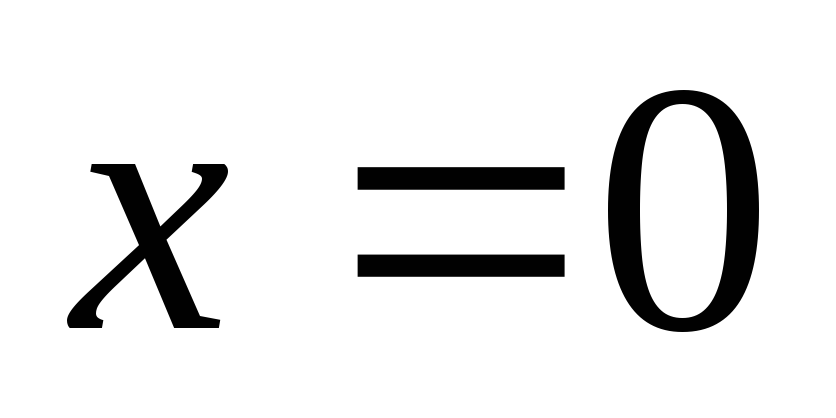— не является корнем уравнения, то разделим обе части уравнения на

.

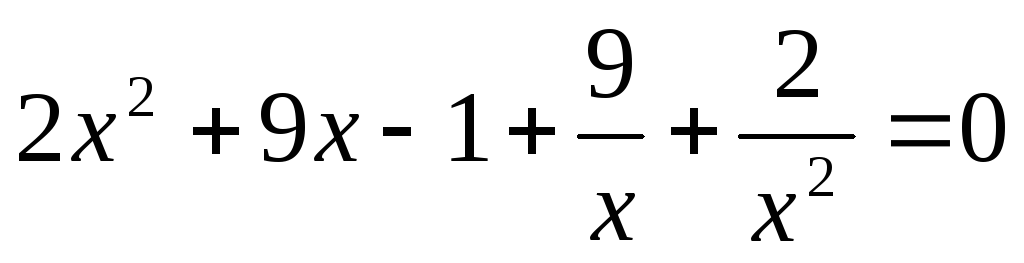
Введем замену.

Пусть 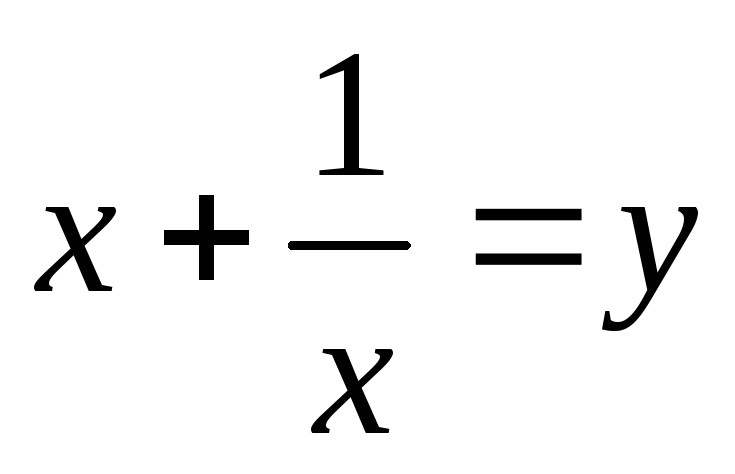, , получим

;

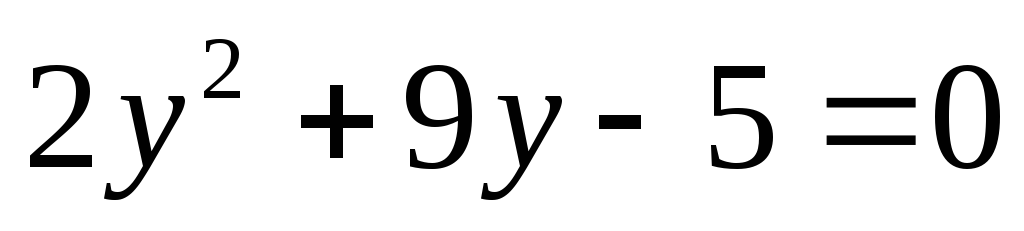
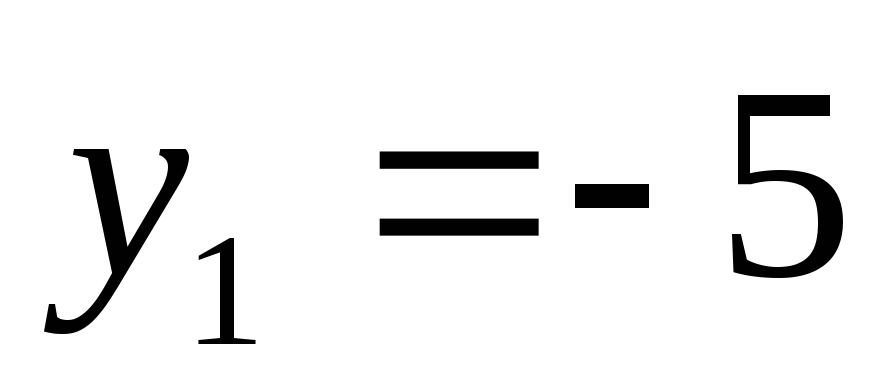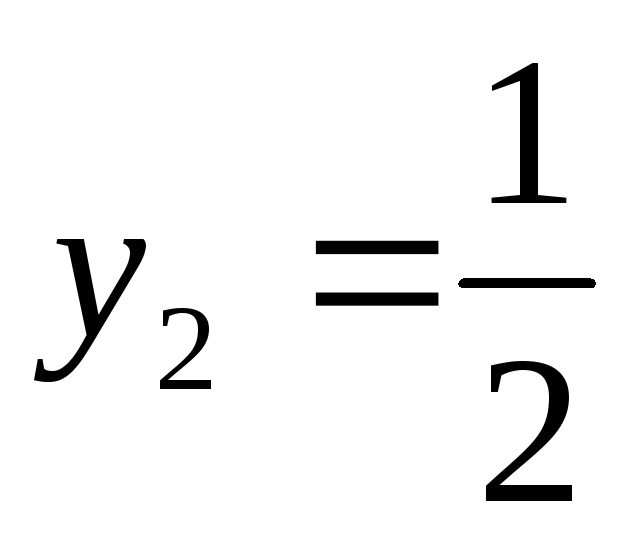
Вернемся к замене.

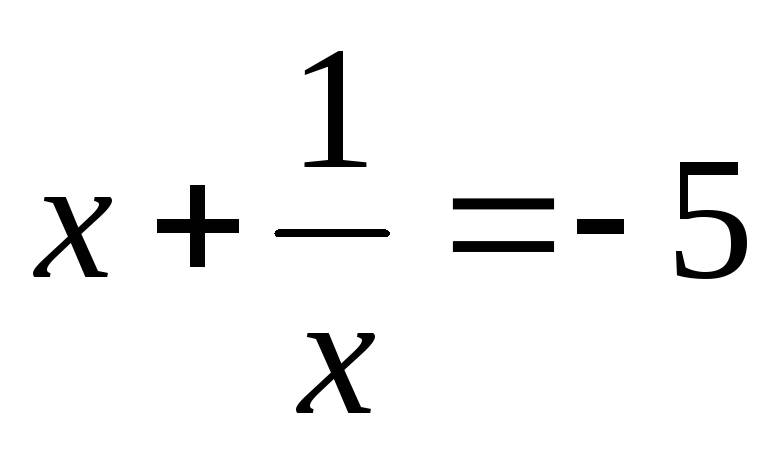или

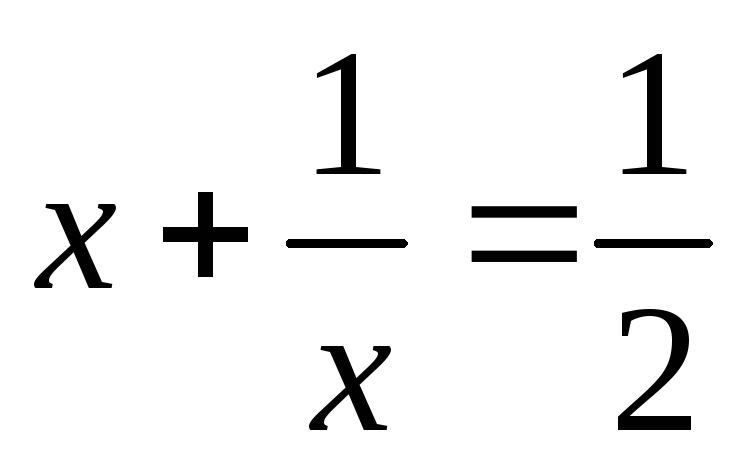
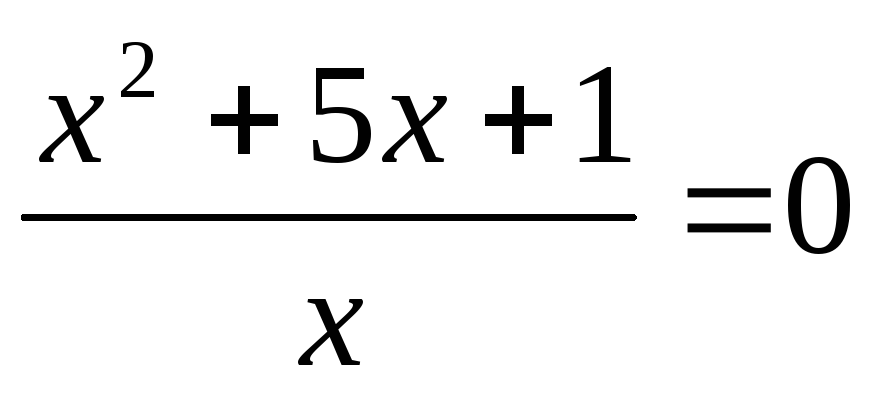
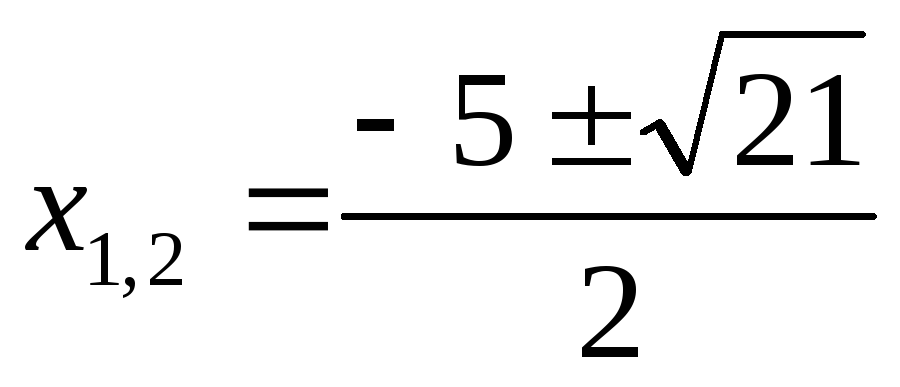корней нет

Ответ:

2) Возвратные уравнения нечетной степени.

Любое возвратное уравнение нечетной степени сводится к квадратному уравнению четной степени, т.к у любого возвратного ур–ия нечетной степени один из корней всегда равен –1

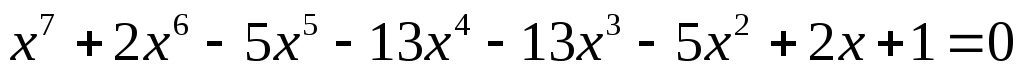
Очевидно — корень уравнения.

или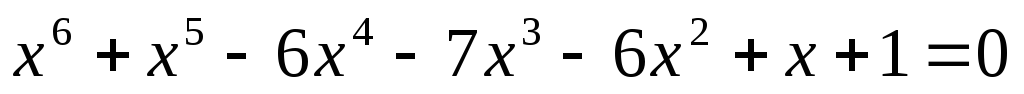

т.к 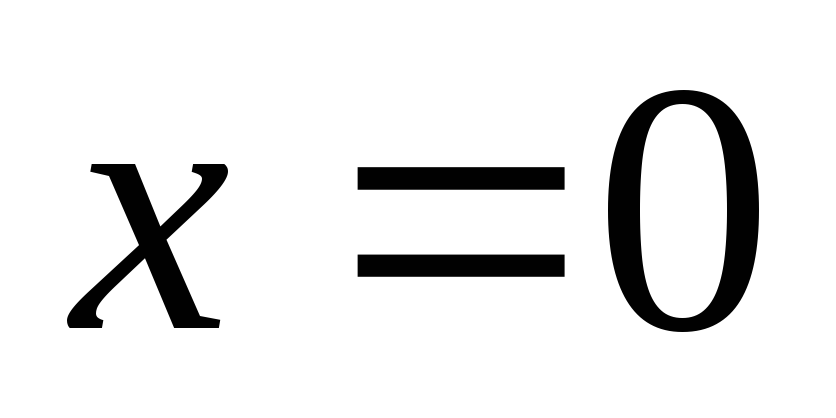— не является корнем уравнения, то разделим обе части

уравнения на

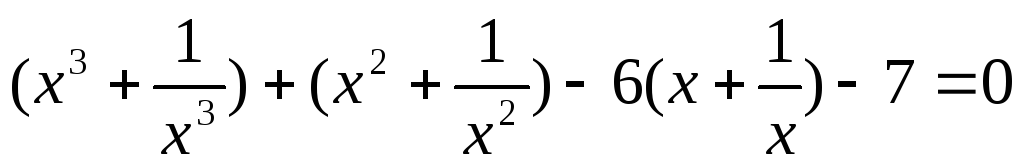
Введем замену.

Пусть 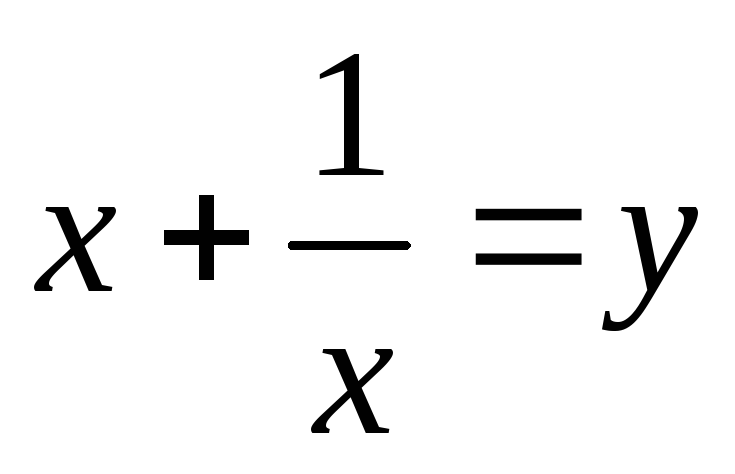, , 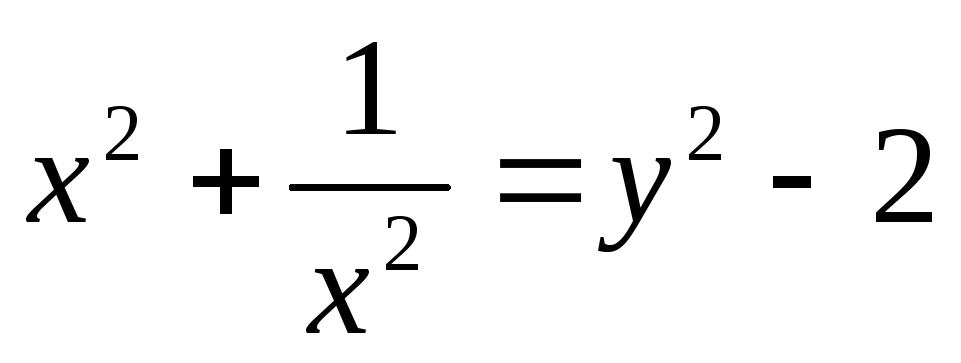, 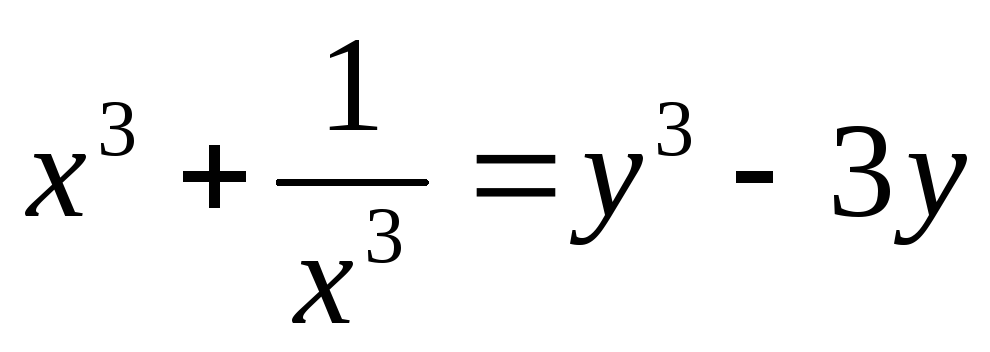получим

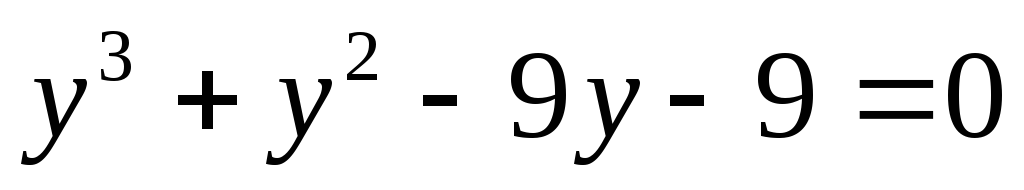
или или

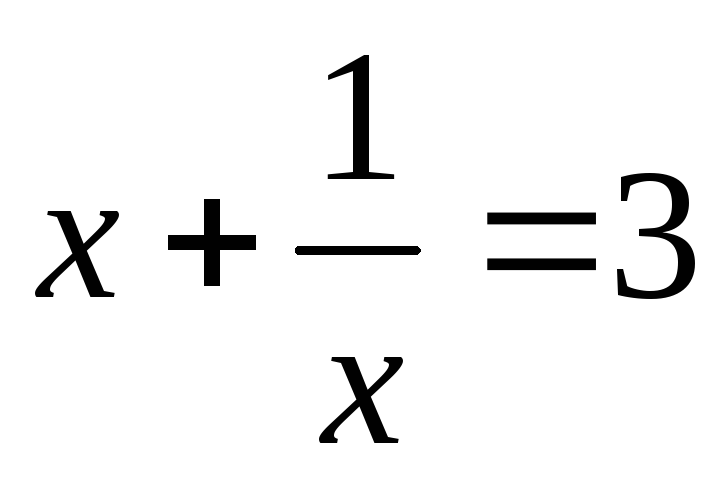
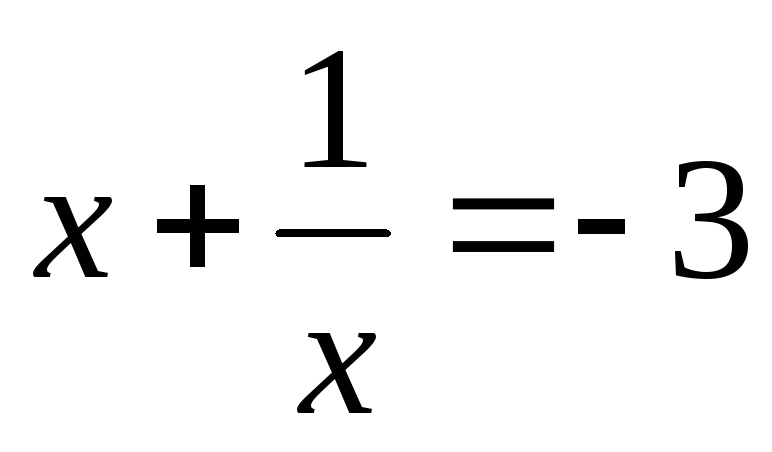
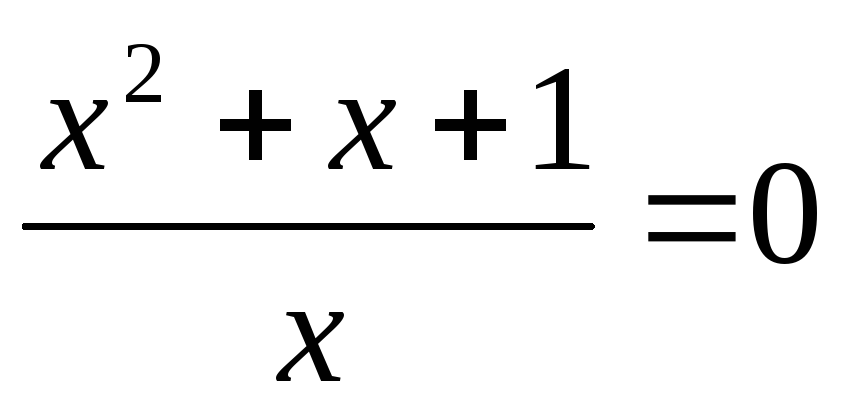
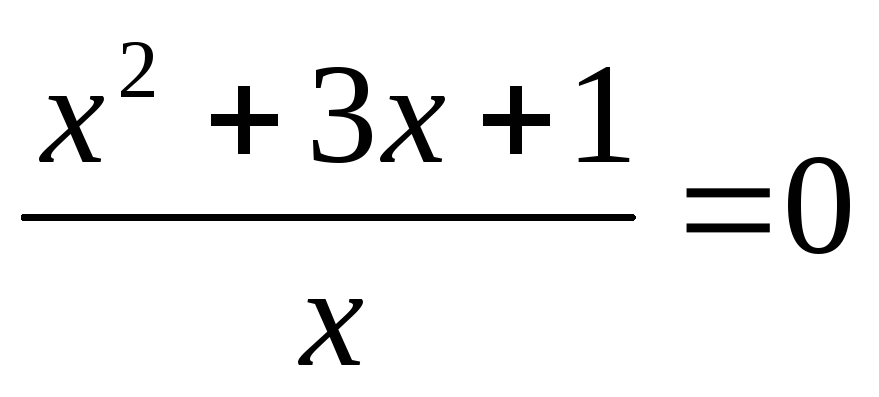
корней нет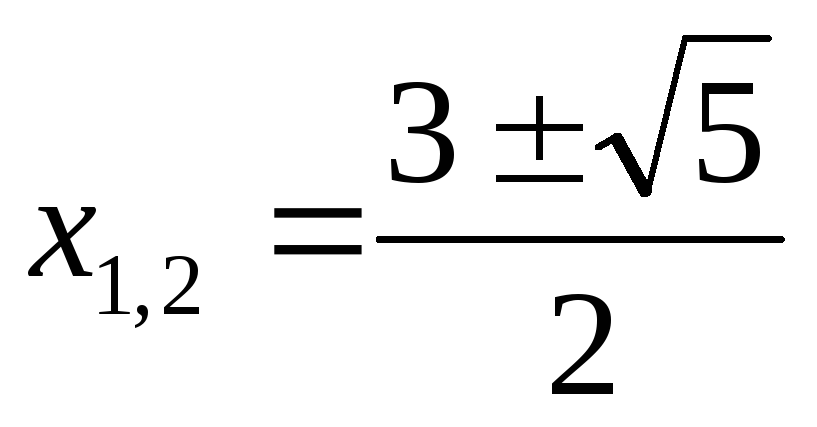

Ответ: , ,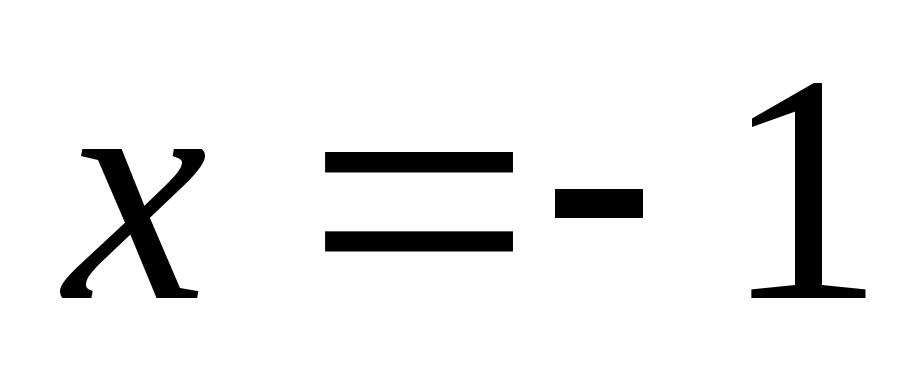

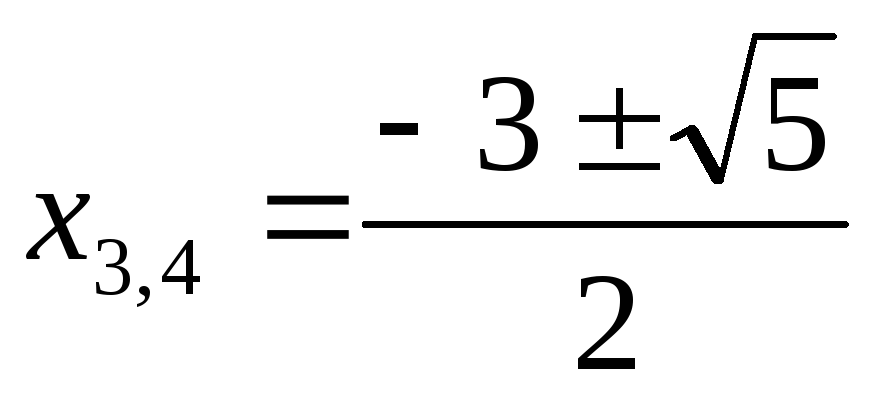
III) Уравнения вида, где решаются как возвратные.

IV) Замена переменных по явным признакам.

V) В следующих уравнениях используется “идея однородности”.

Пример №1

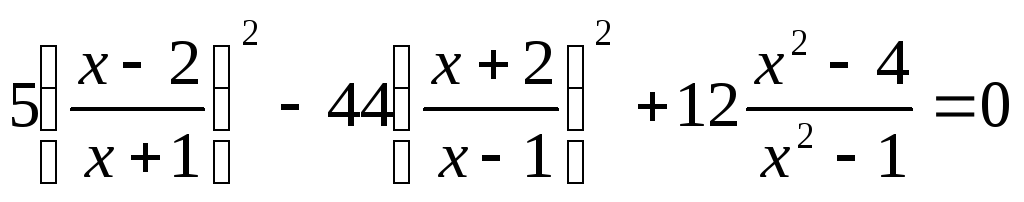
Введем замену.

Пусть 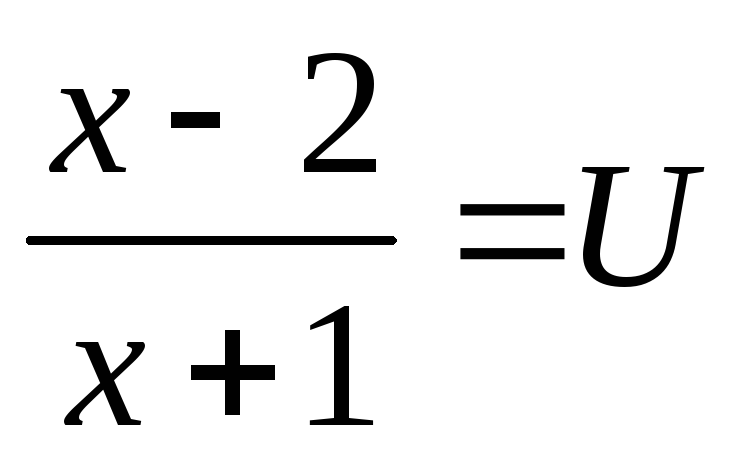, , тогда

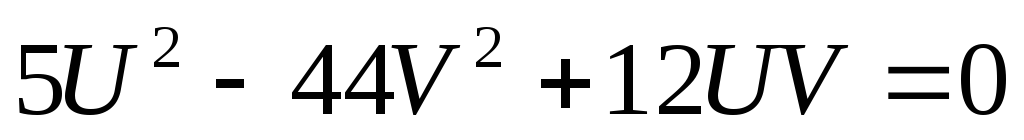
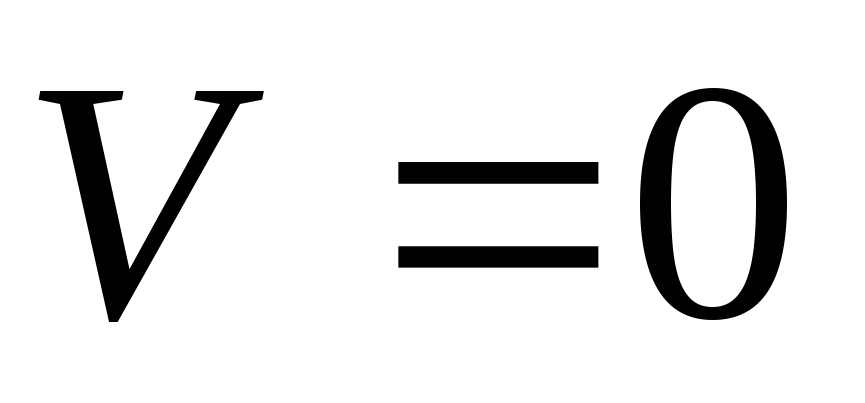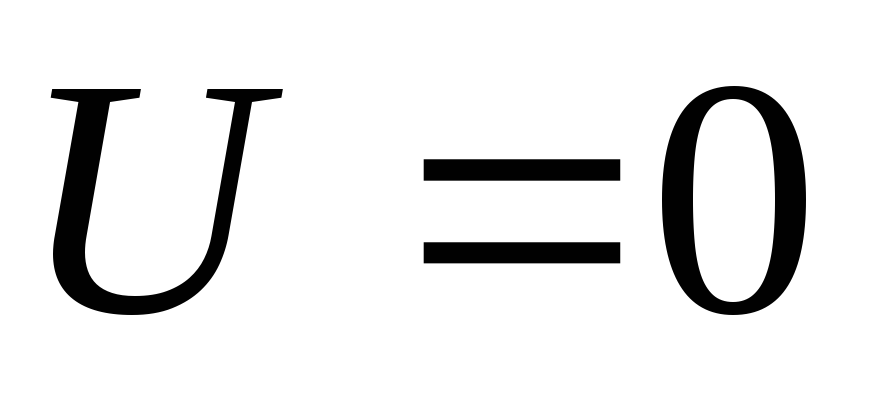1) если , тогда , тогда

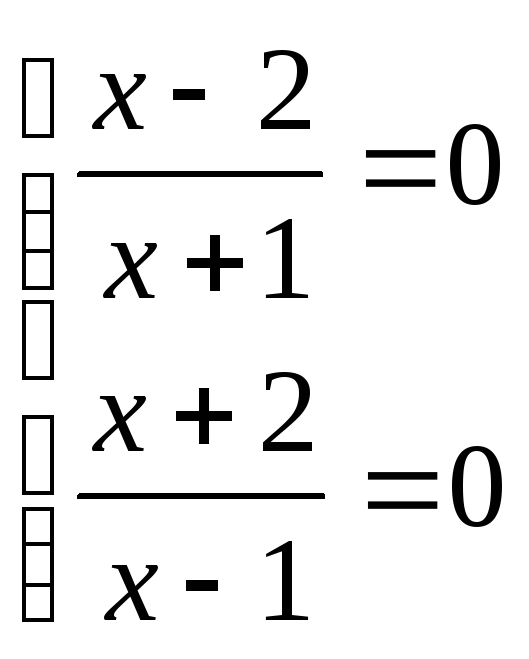
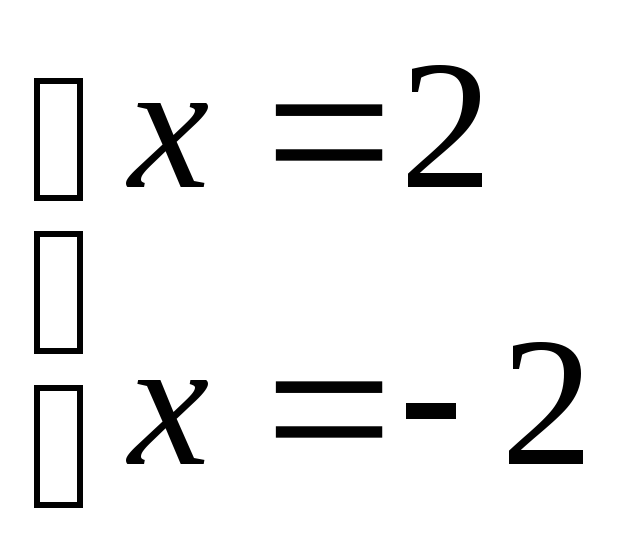решений нет

2) Разделим обе части уравнения на 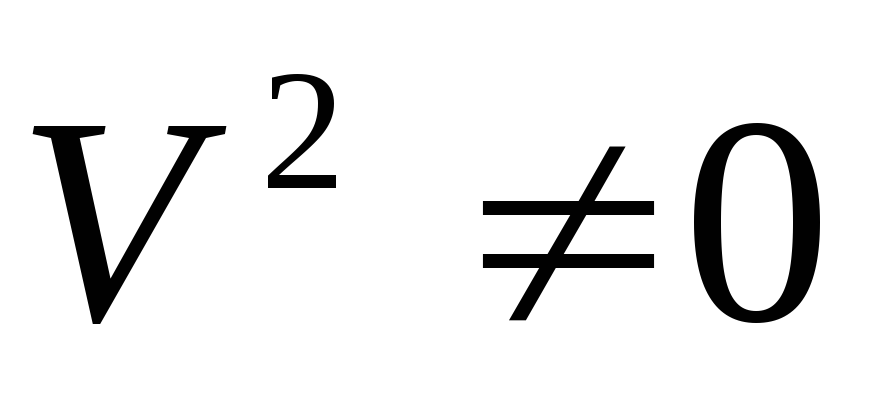, получим

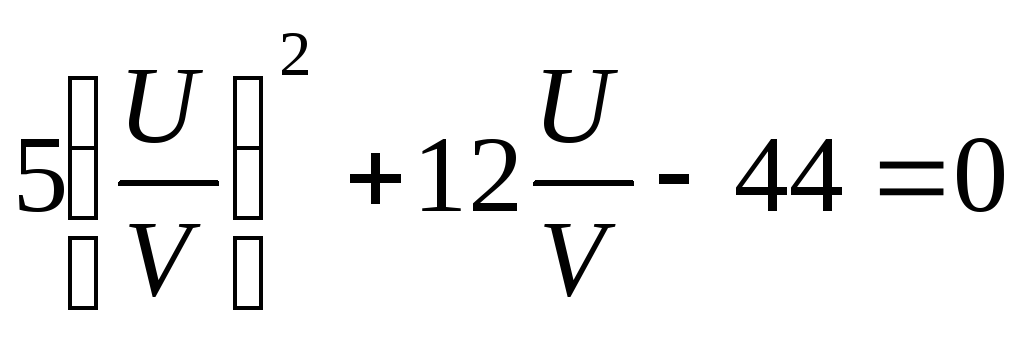
Решим последнее уравнение, как квадратное относительно , получим

;

;

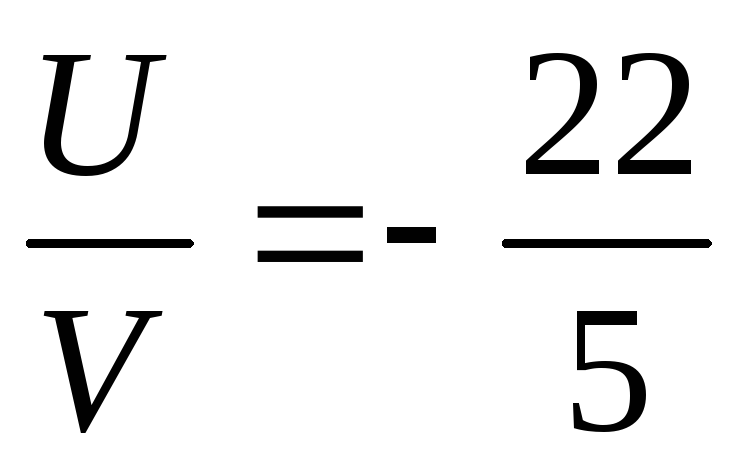
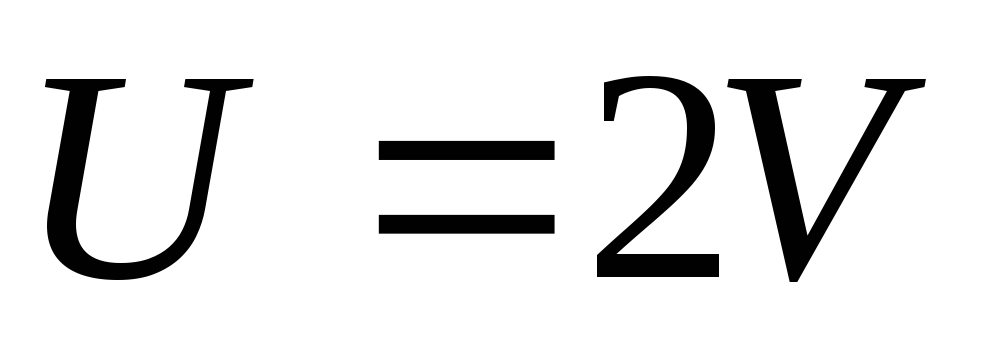Вернемся к замене.

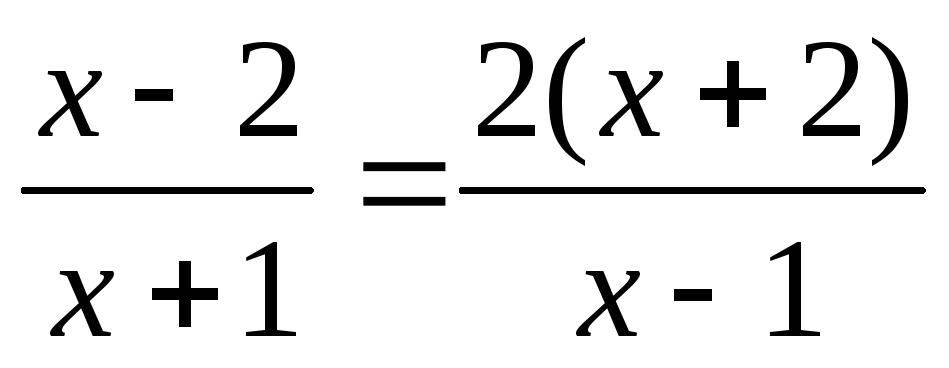или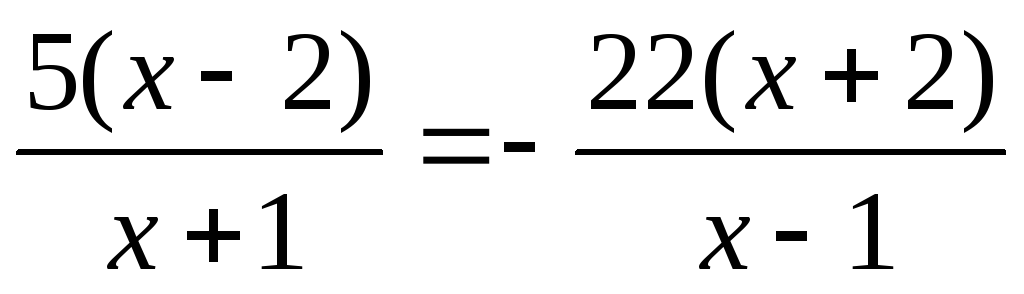

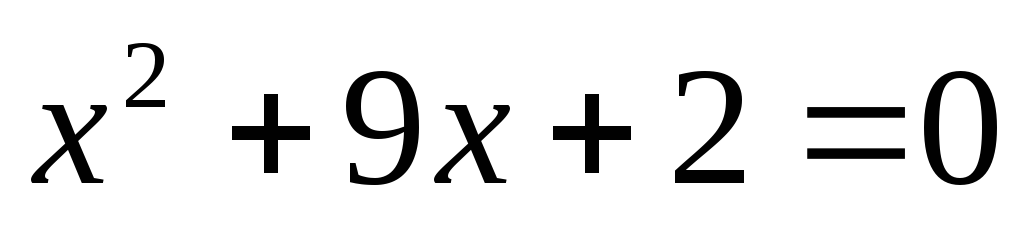
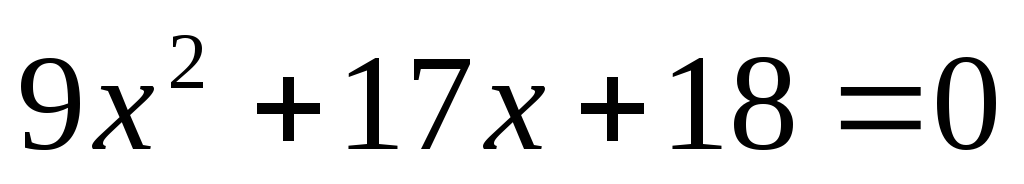корней нет

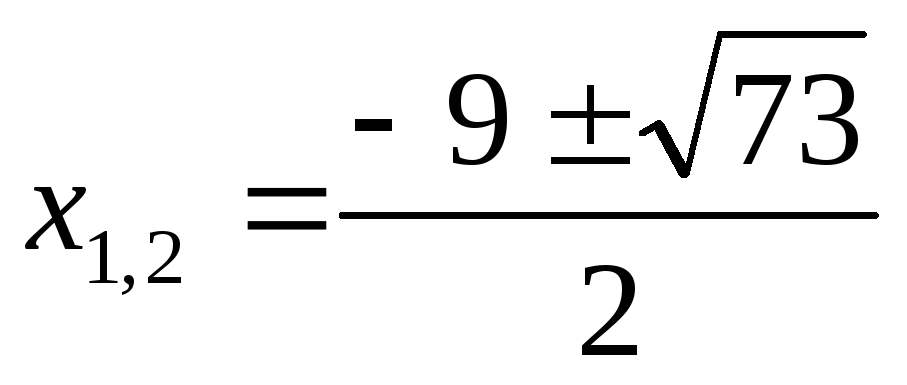
Ответ:

Пример №2.

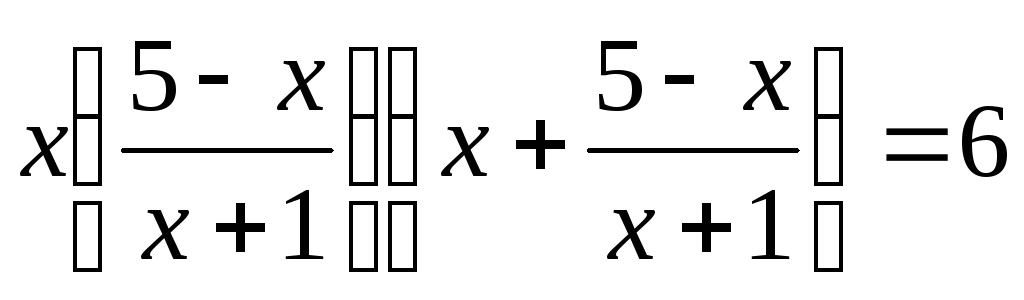
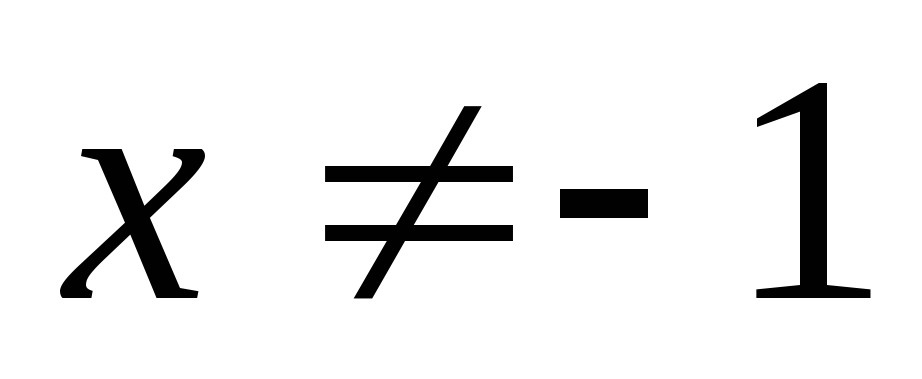
Пусть 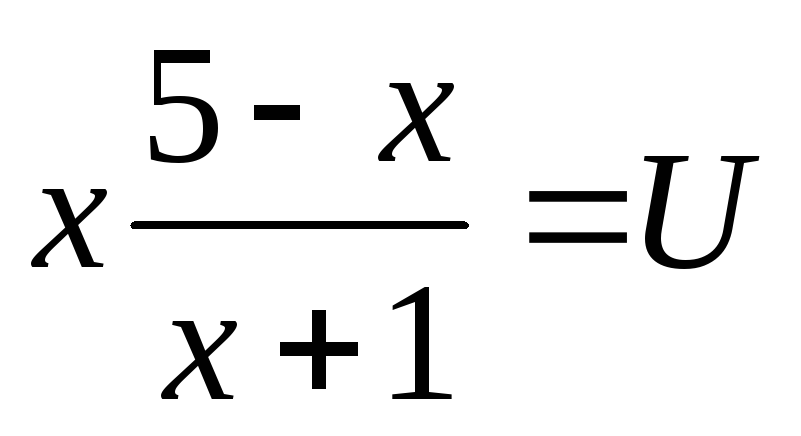, , 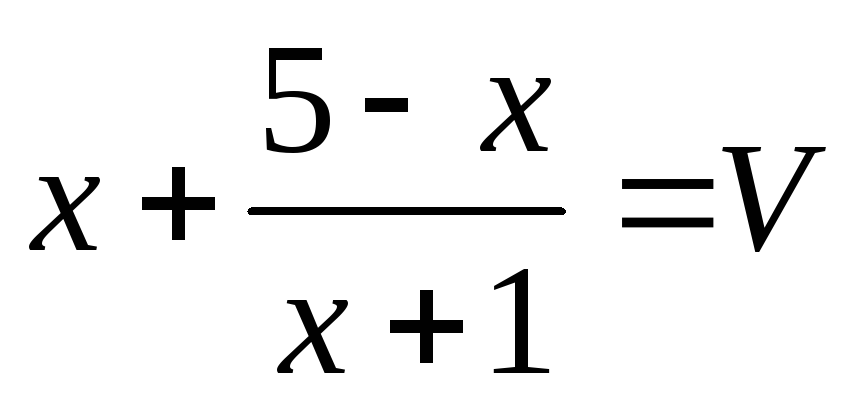тогда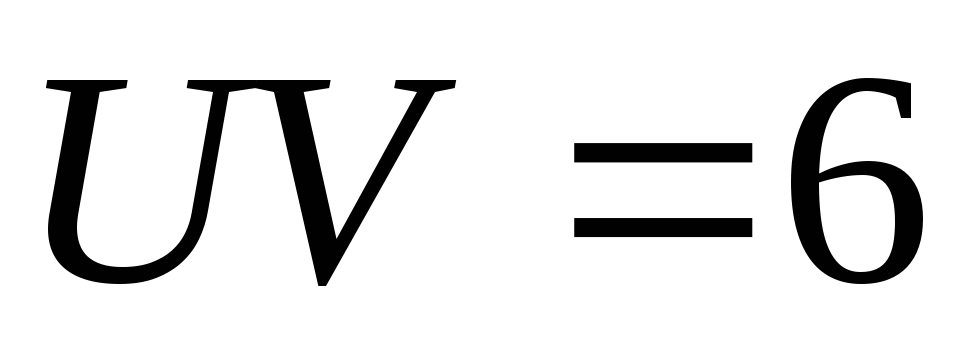

Найдем

Составим систему:

Решая систему подстановкой, получим

или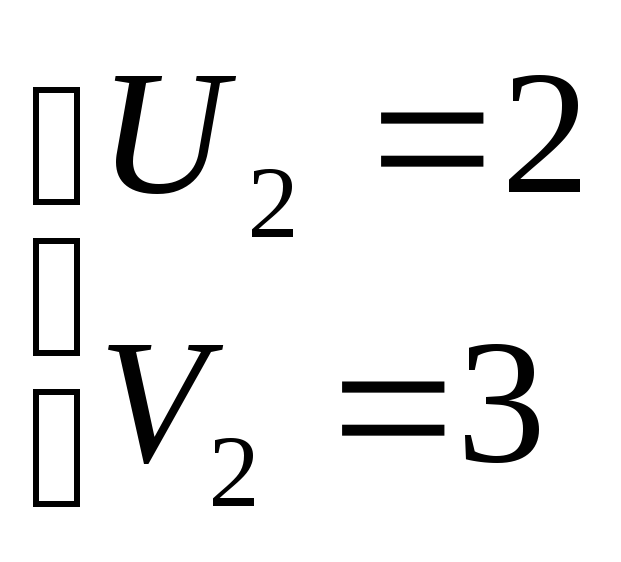

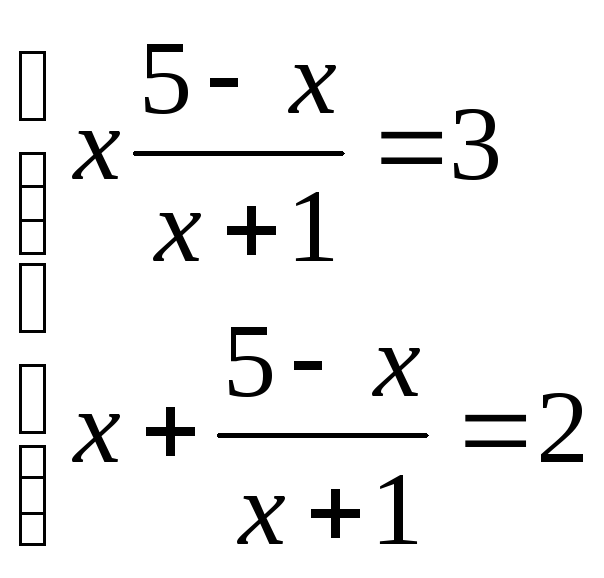
корней нет ;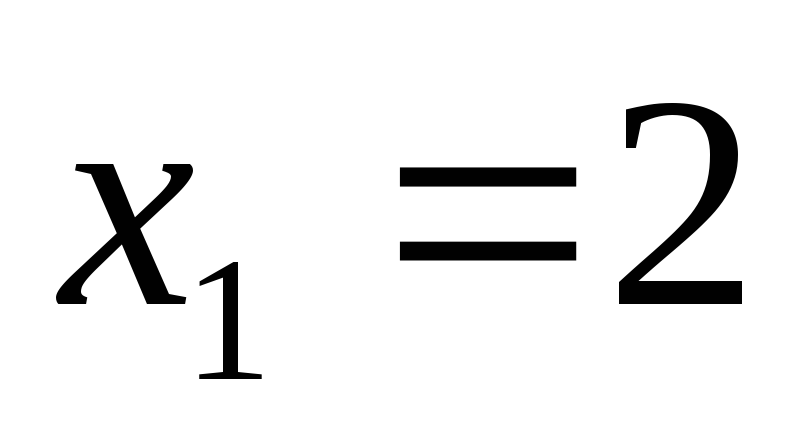

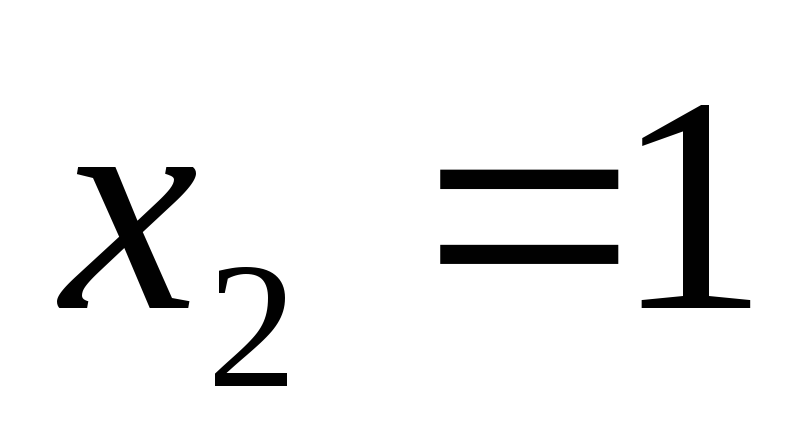
Ответ: ;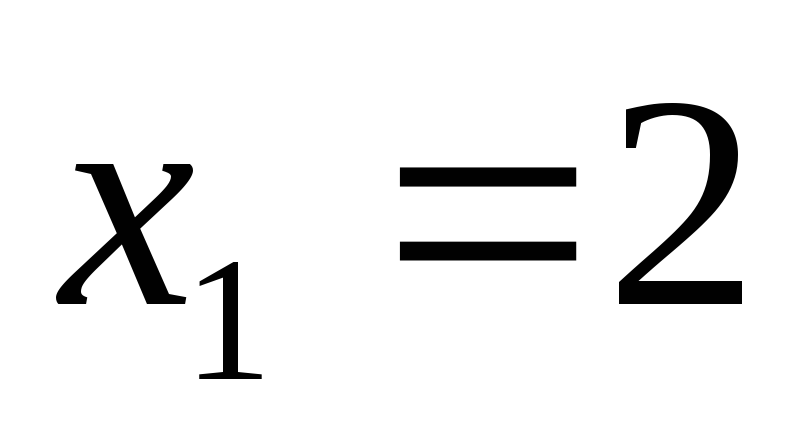

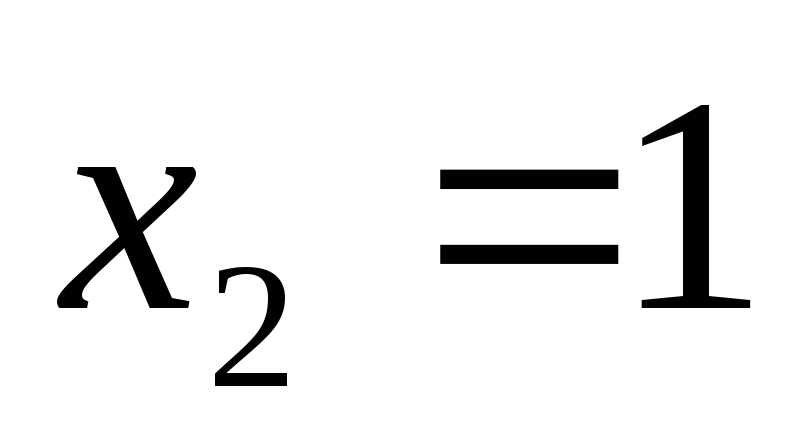
Пример №3.

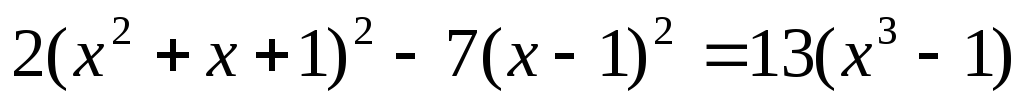
— не является корнем уравнения

Разделим обе части уравнения на 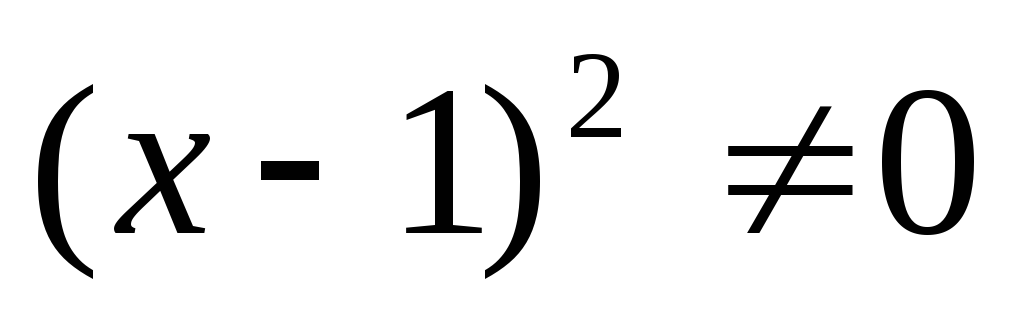, получим

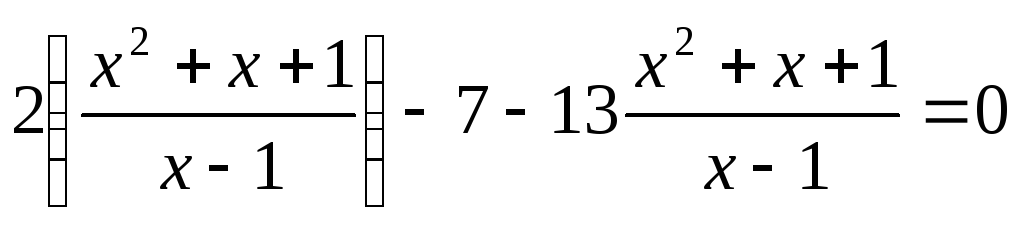
Введем замену.

Пусть 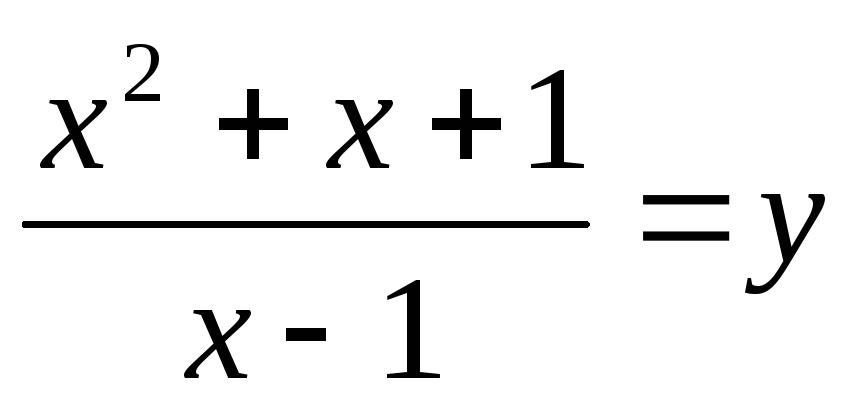, тогда

;

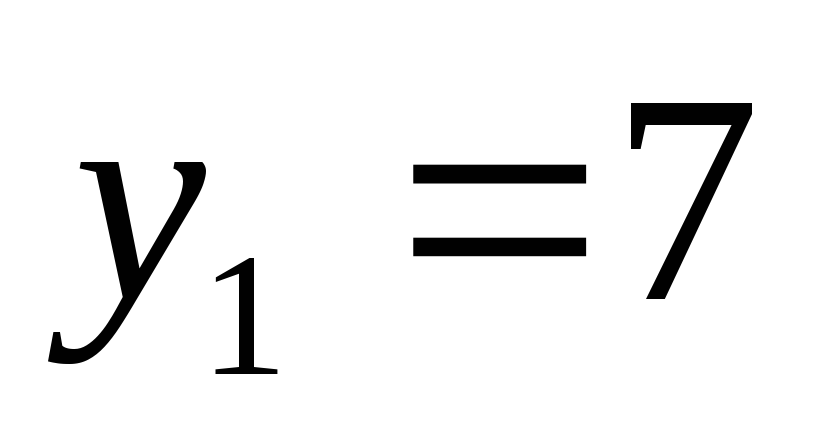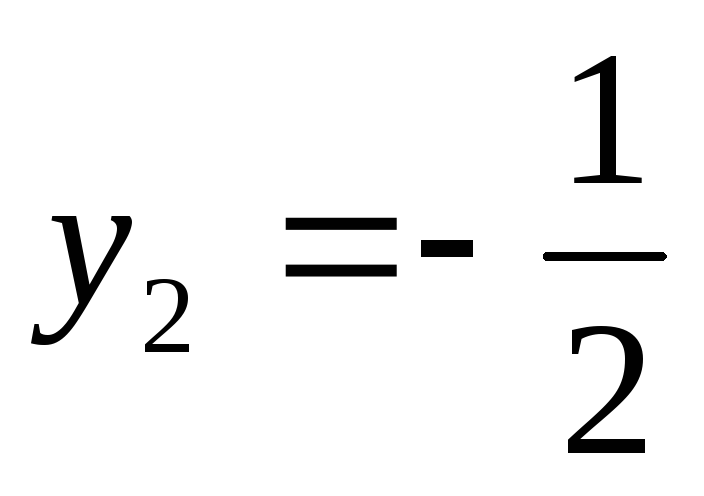
или

; ;

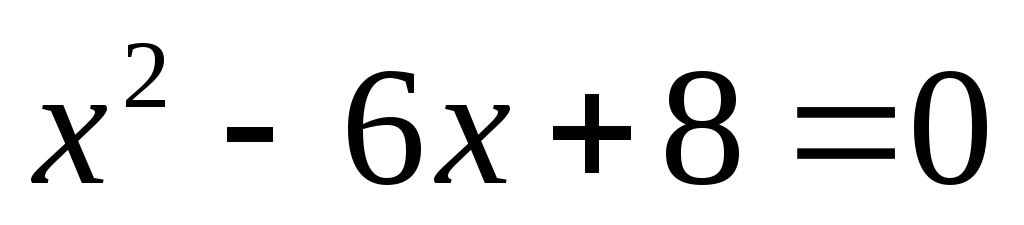
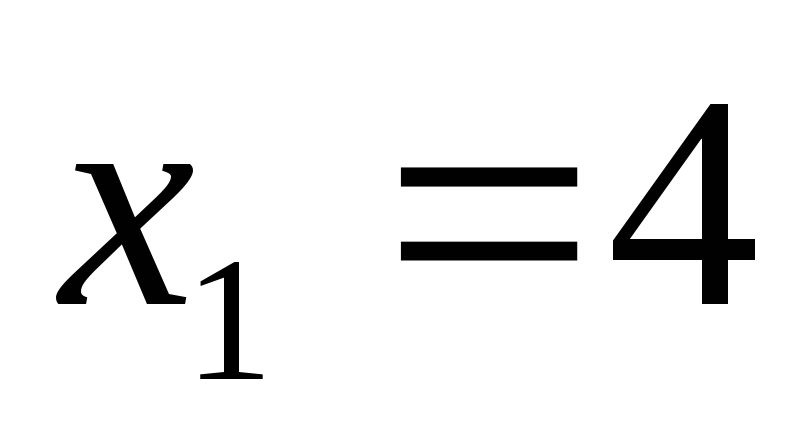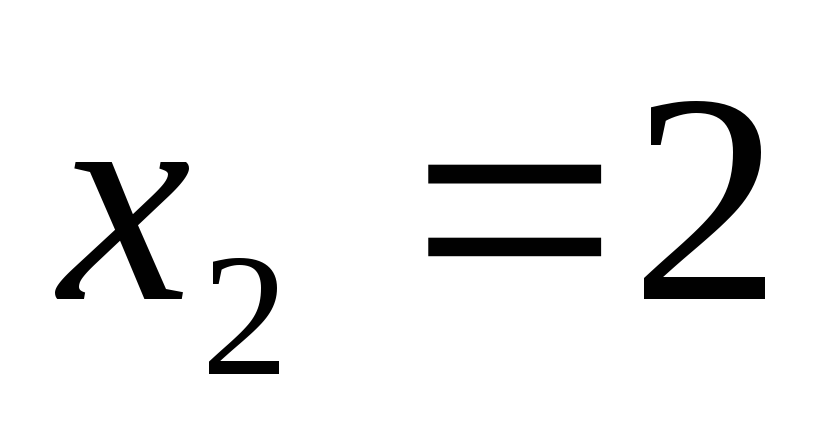
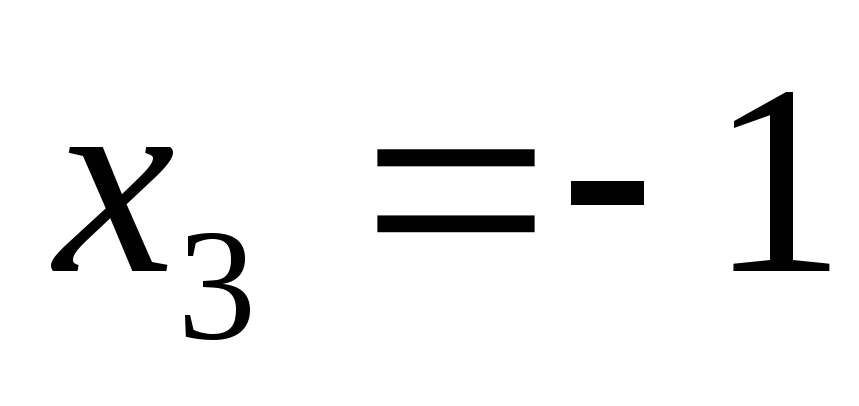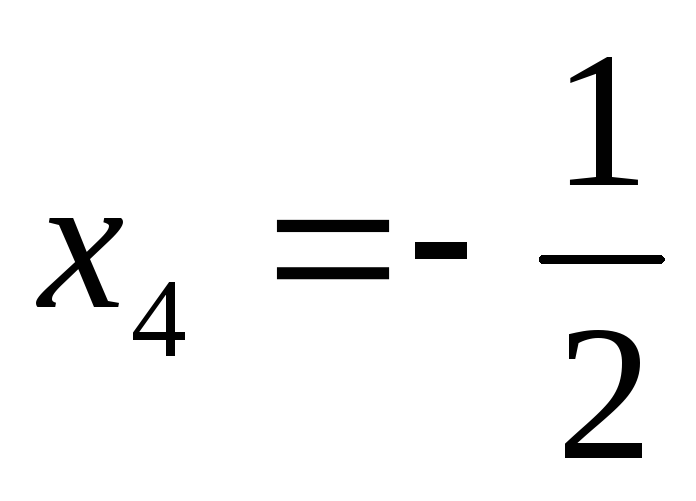
Ответ: ; ; ;

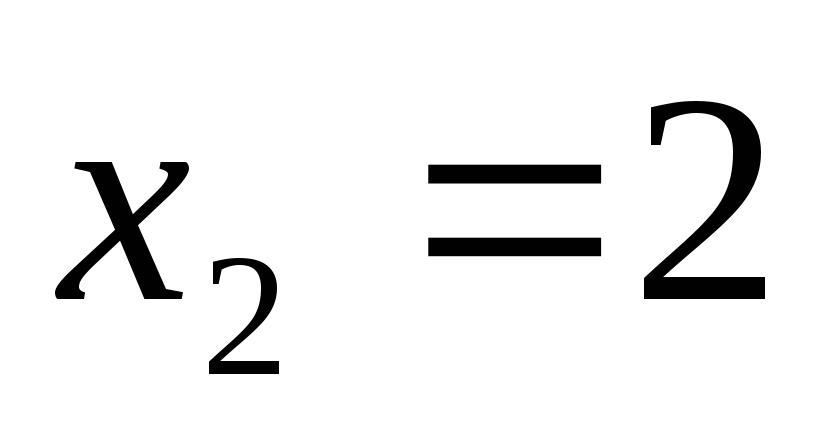VI) Уравнения вида, где эффективно решать перемножением и , а затем делать замену.

VII) В уравнениях вида 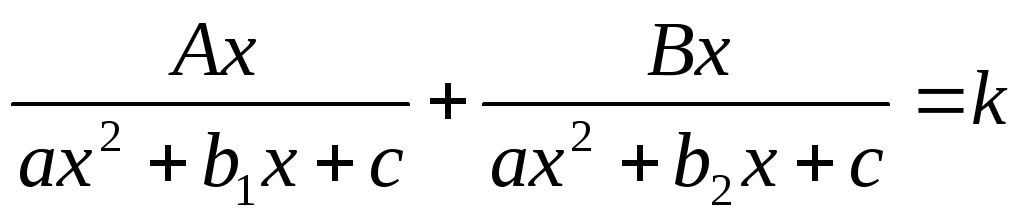и в уравнениях к ним сводящимся, в знаменателях обоих дробей необходимо вынести х за скобки и сделать замену.

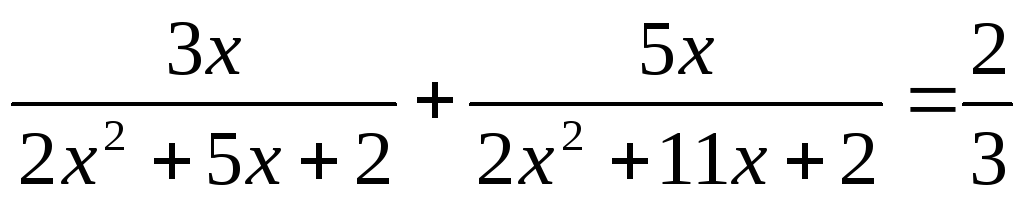(1)

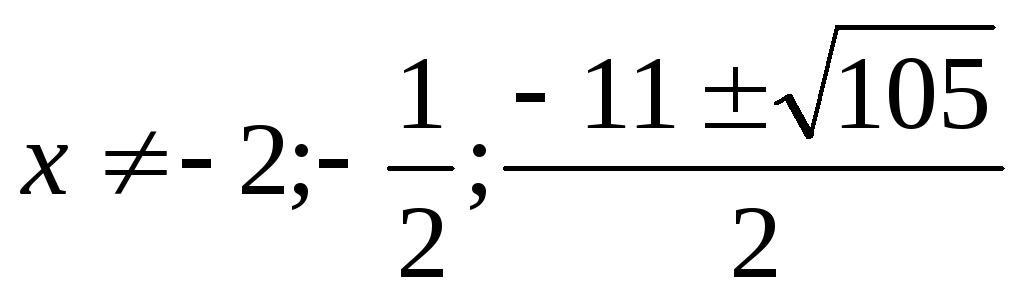
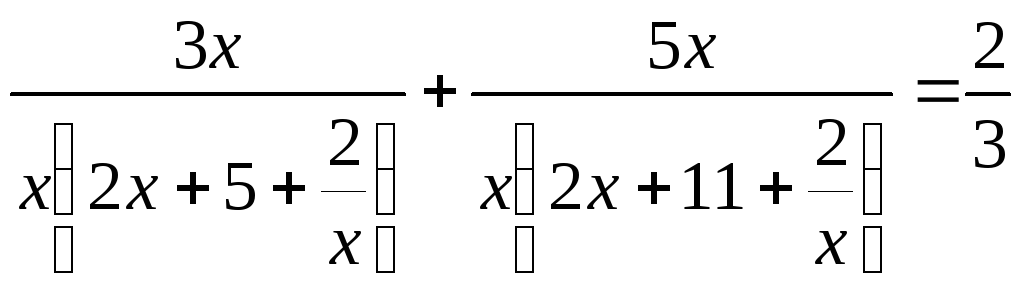(2)

При переходе 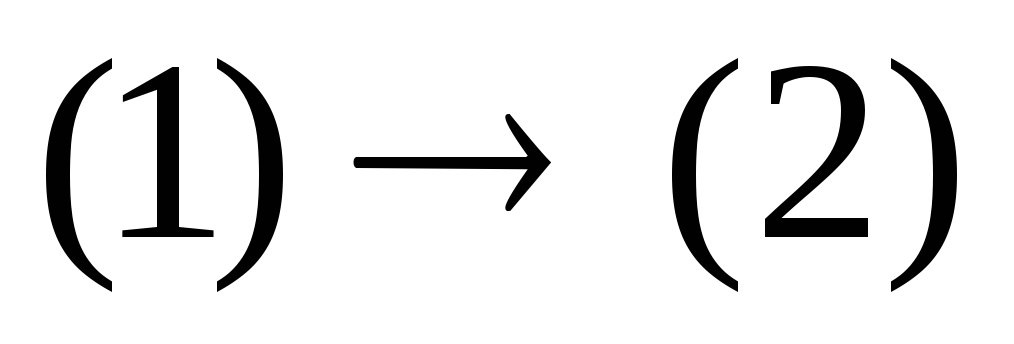область определения уравнения сузилась на 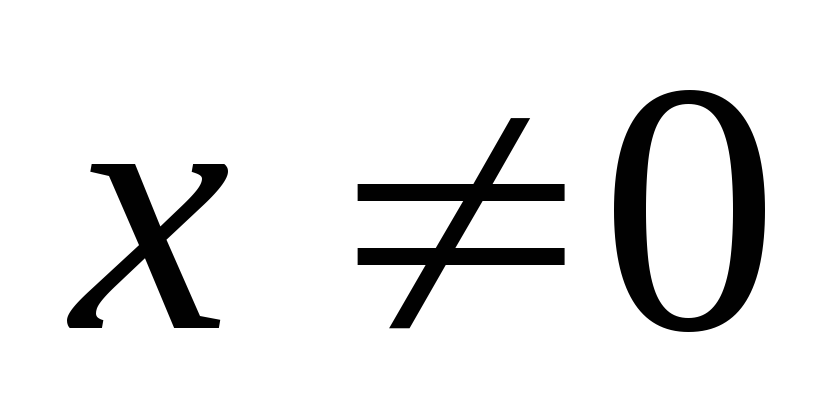. Проверим, является ли 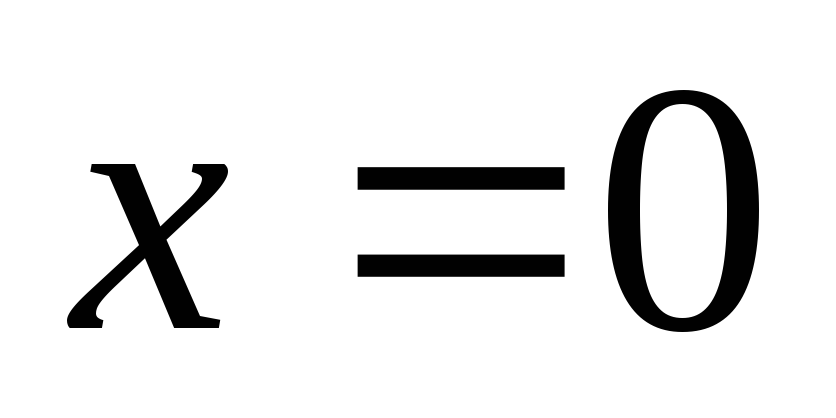корнем уравнения. Не является.

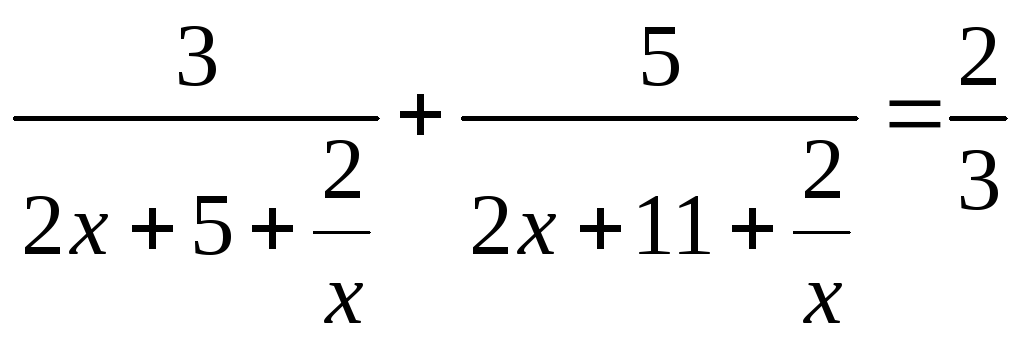
Введем замену.

Пусть 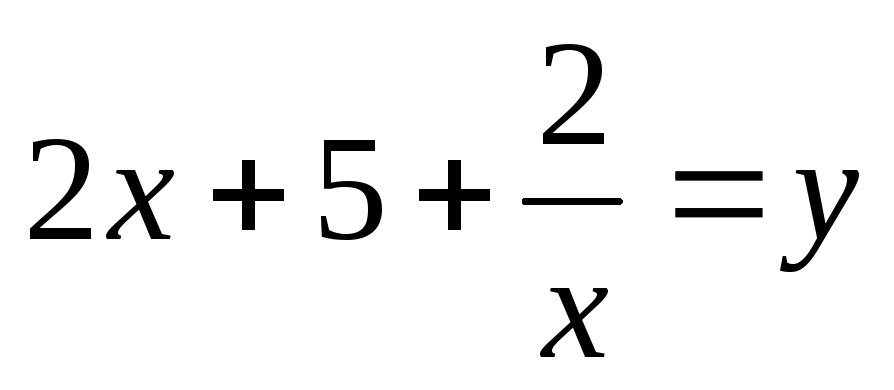, , 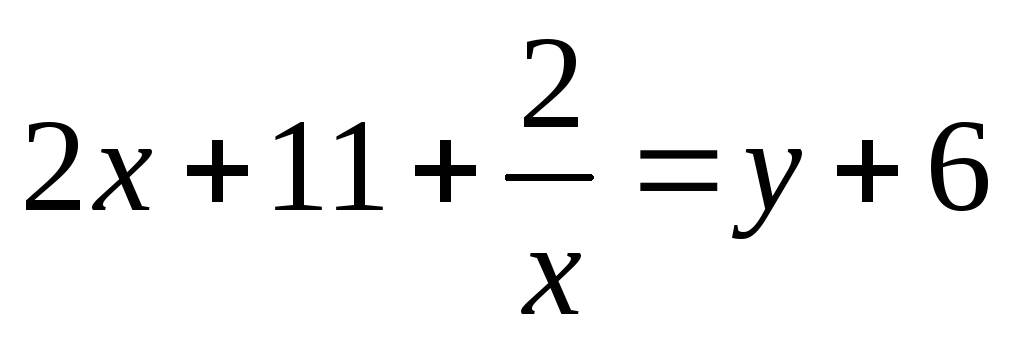тогда

;

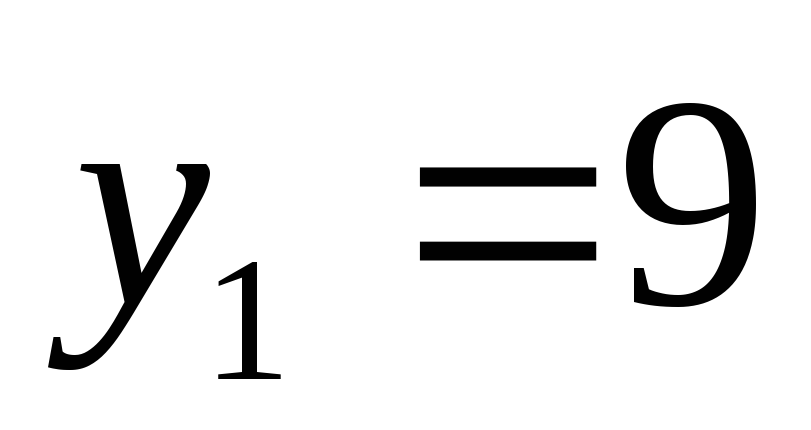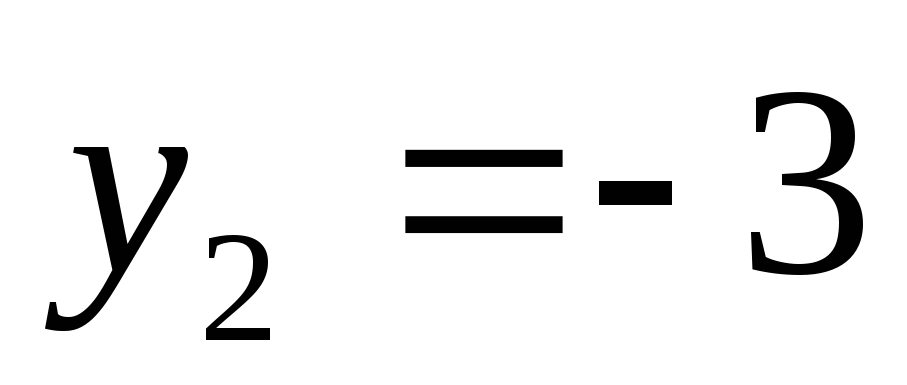
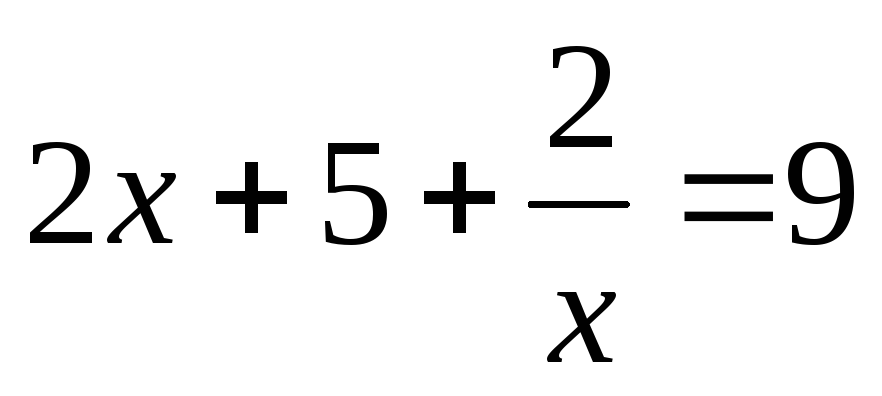или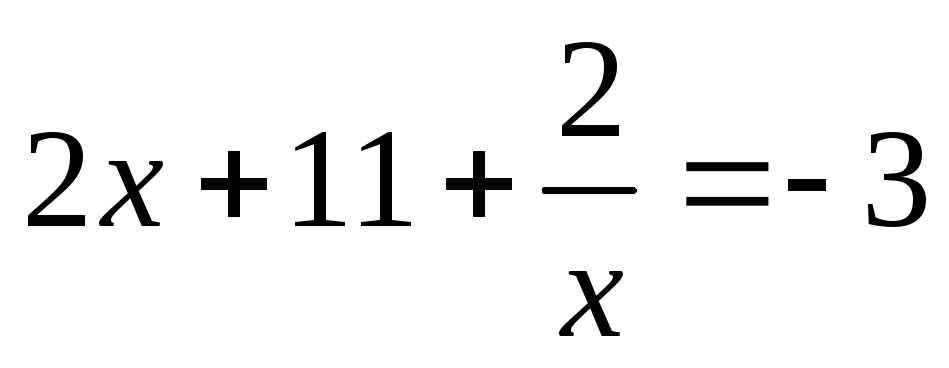

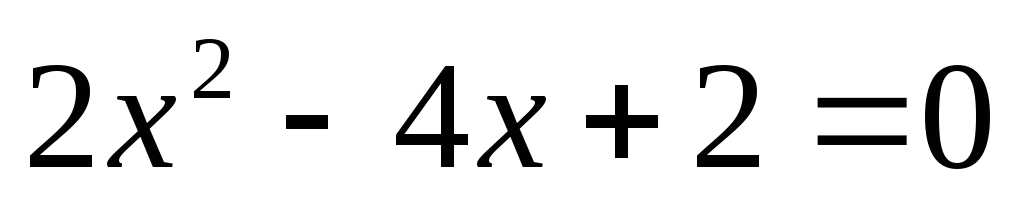
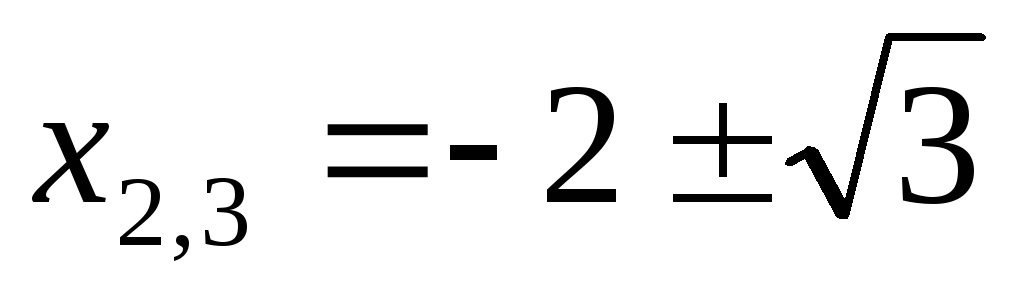
Ответ: ;

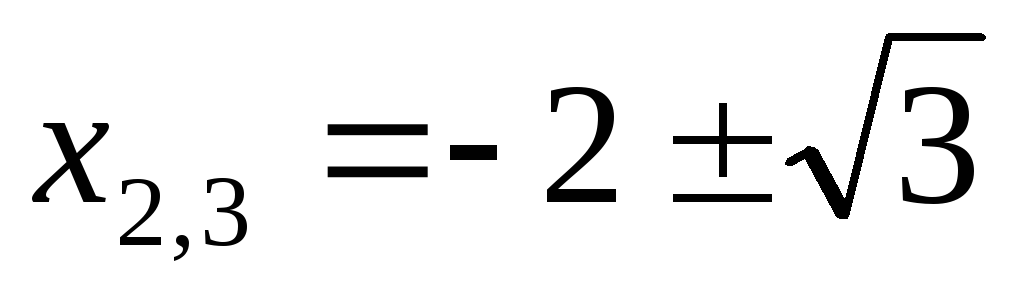
VIII) В уравнениях вида 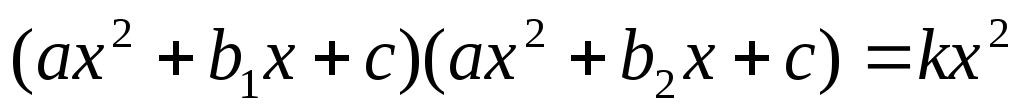обе части уравнения делятся на

— не является корнем уравнения. Разделим на , получим

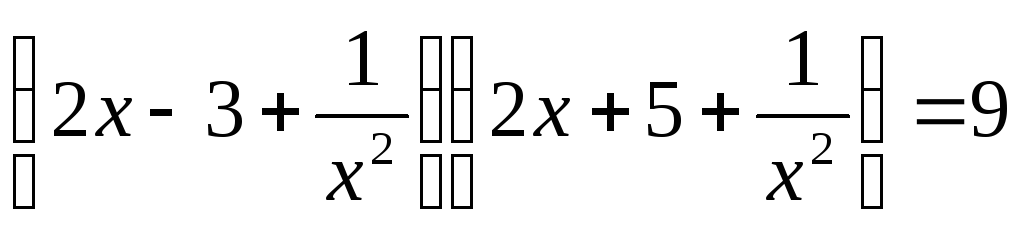
Введем замену.

Пусть ; 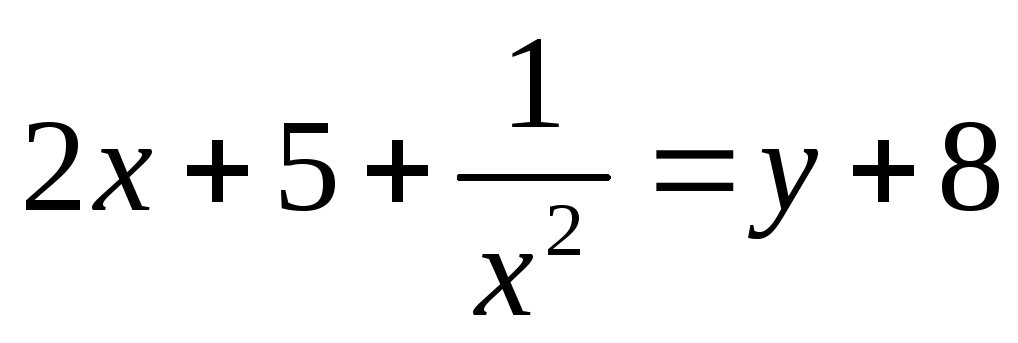, тогда

;

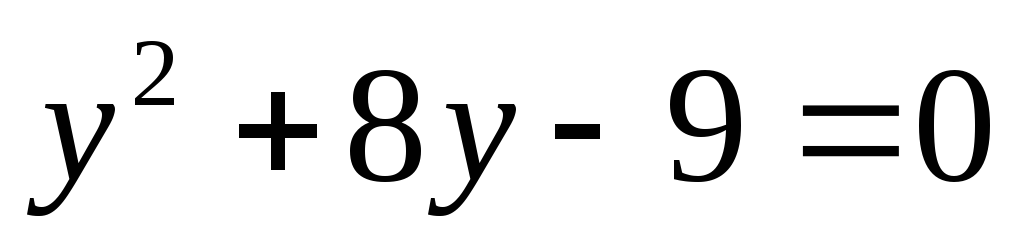
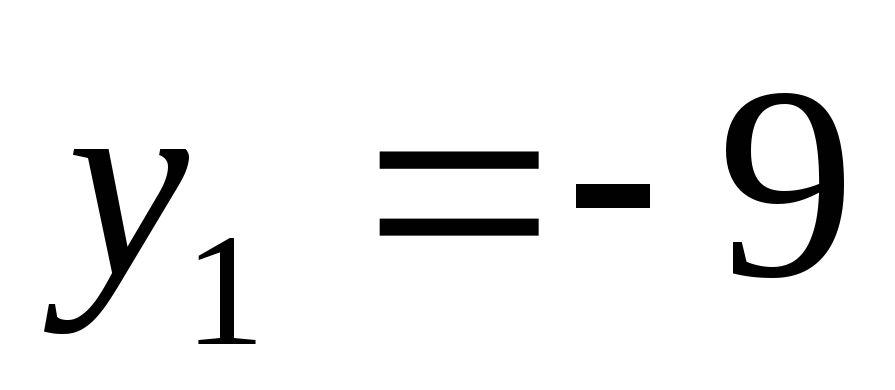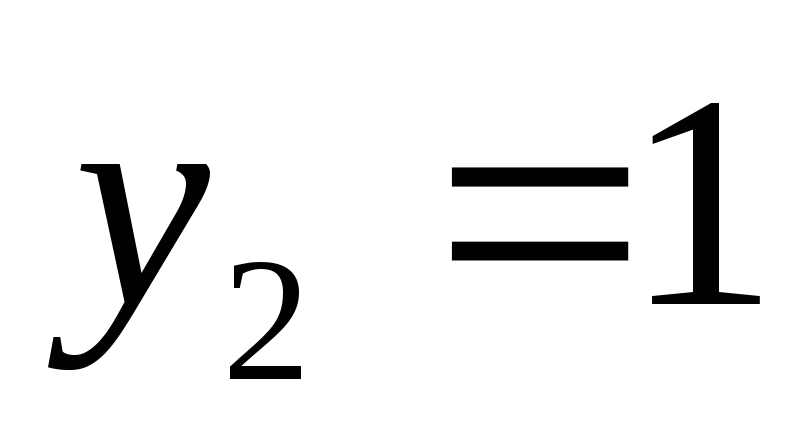
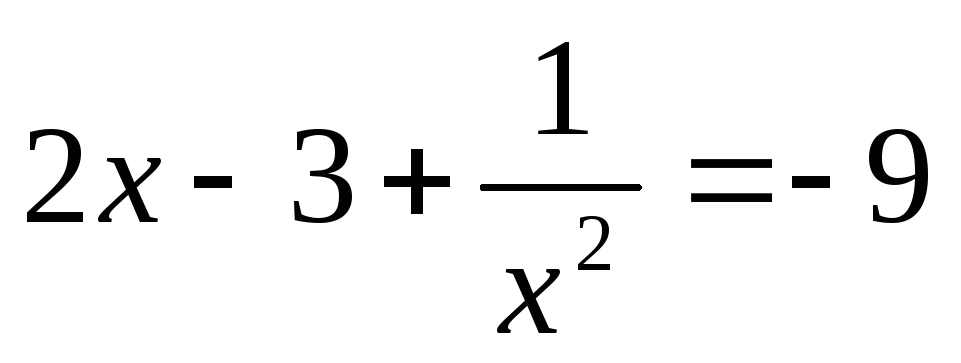или

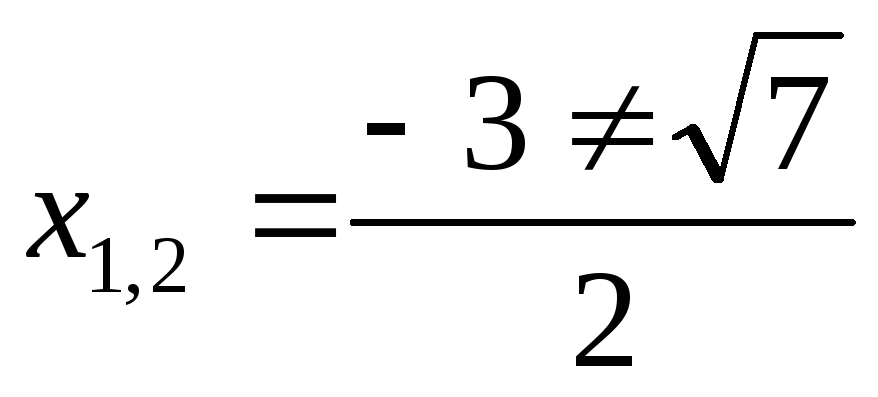
Ответ: ;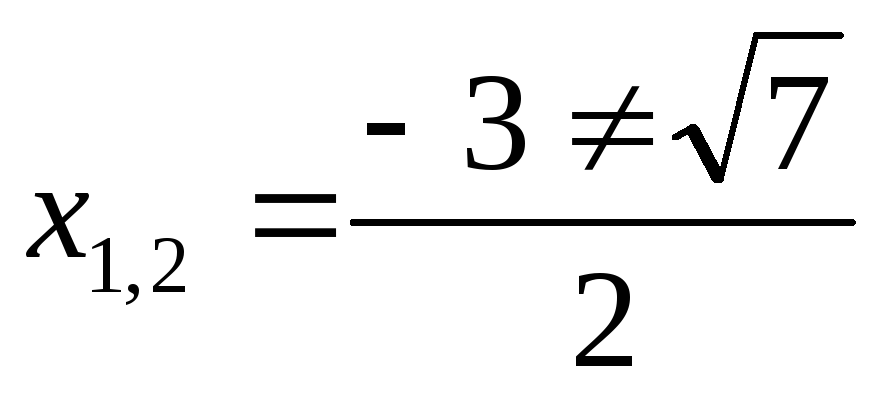

IX) Выделение полного квадрата.

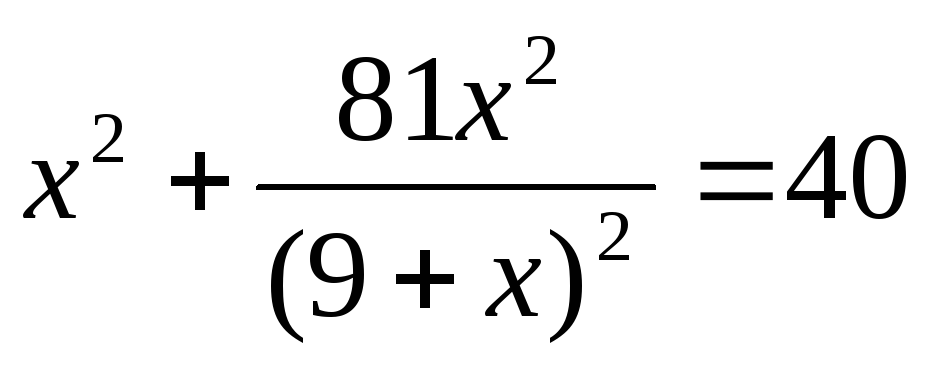
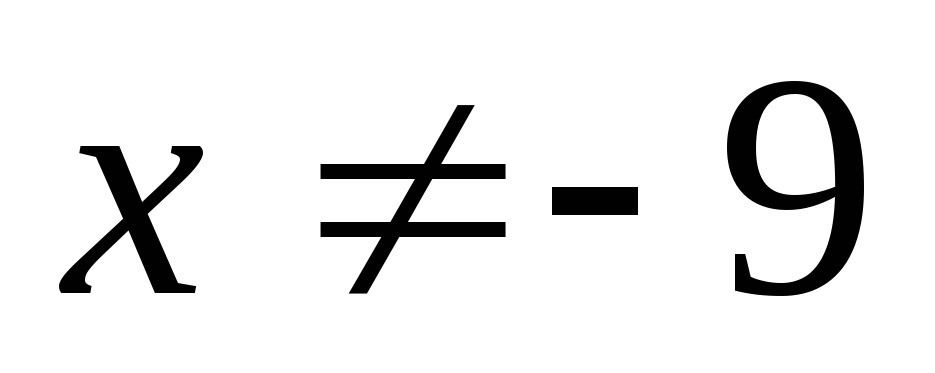
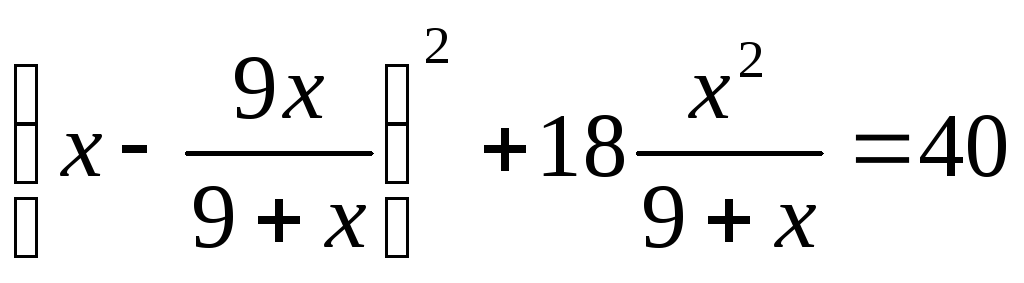
Введем замену.

Пусть 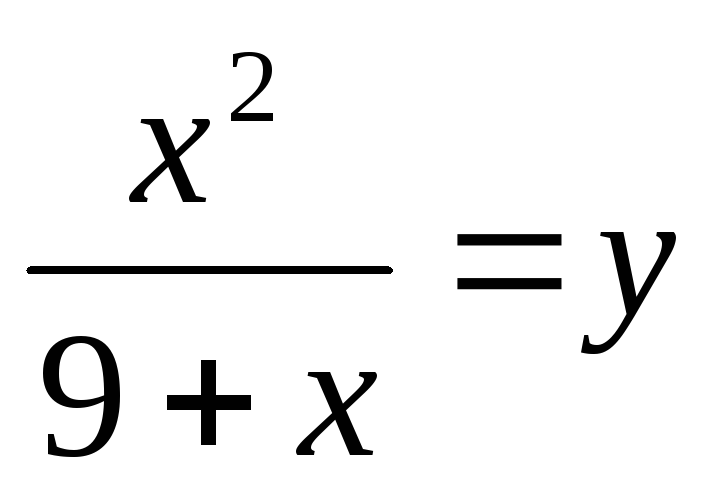, тогда

;

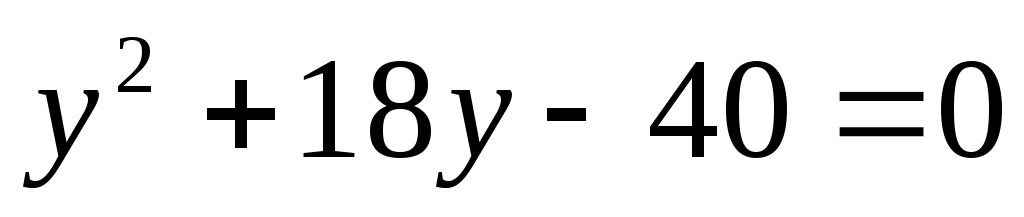
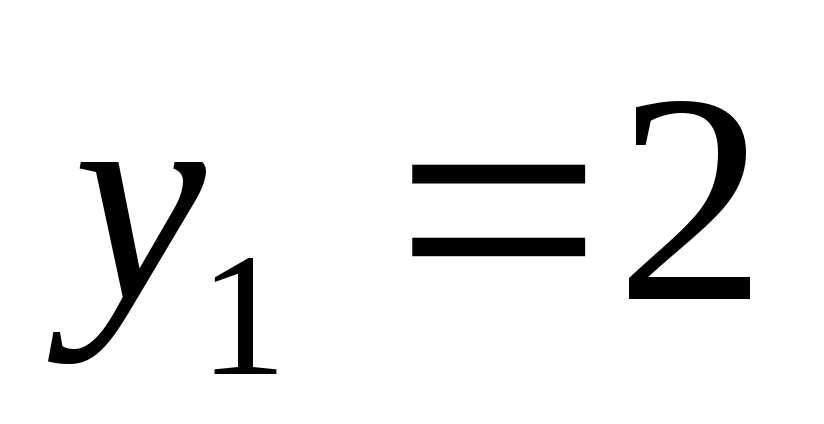Вернемся к замене.

или

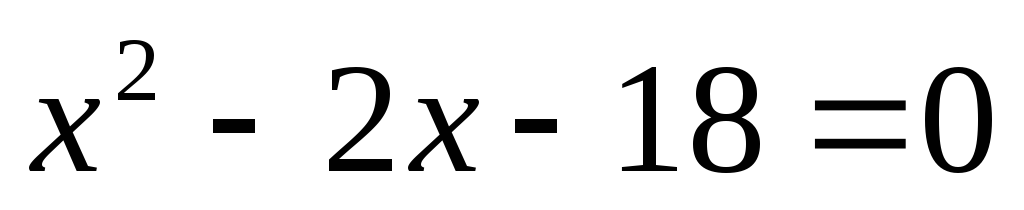
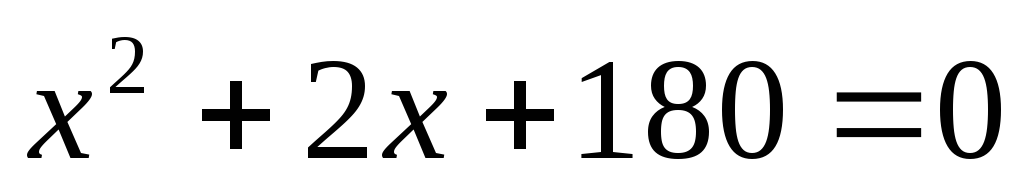
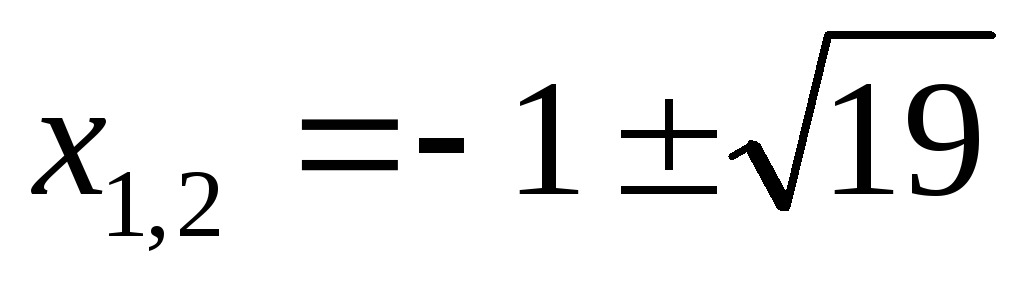корней нет

Ответ: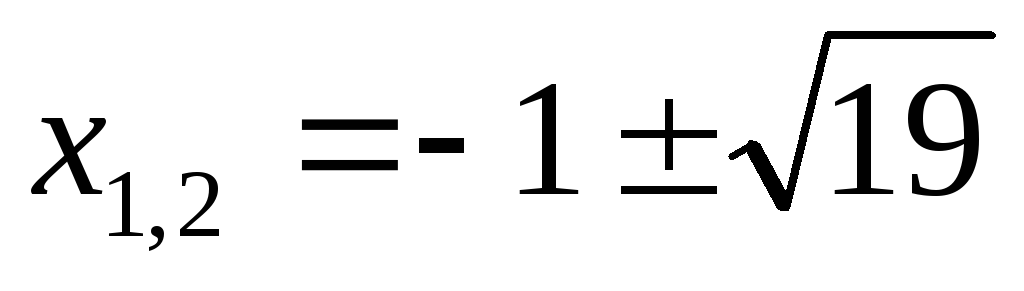

X) Решение уравнений с помощью формулы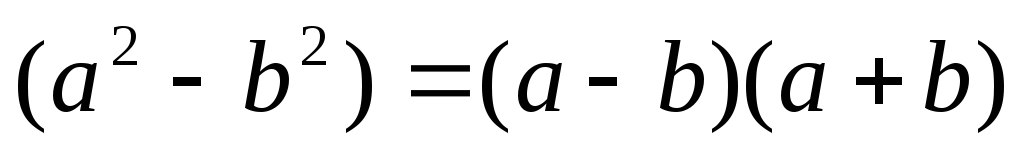

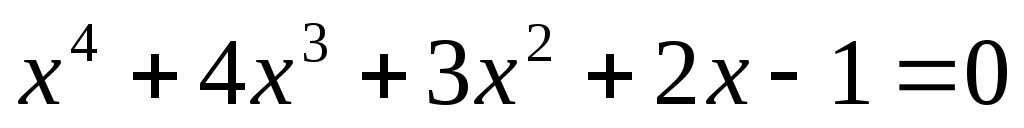
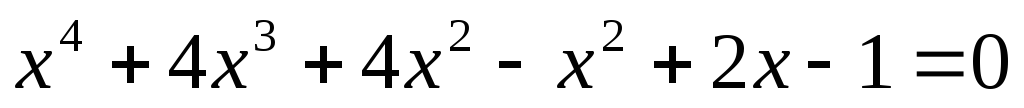
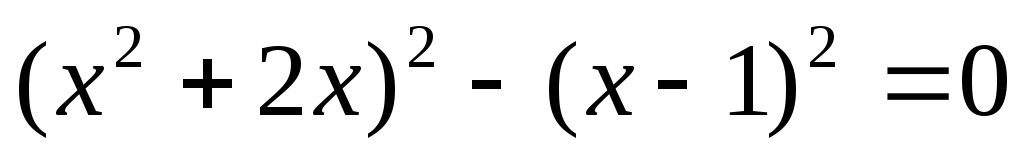
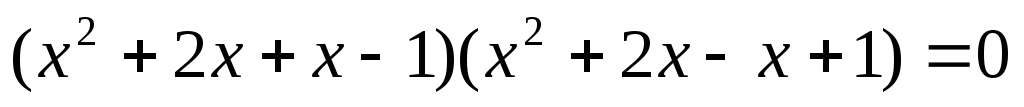
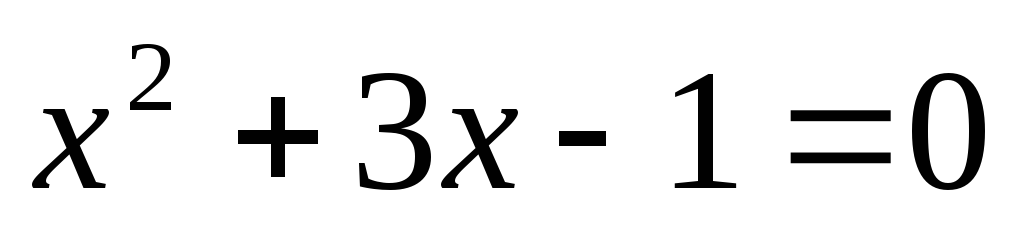или

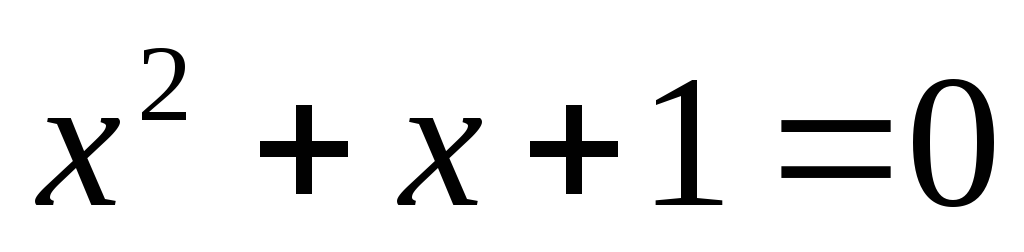
корней нет

XI) Уравнения вида 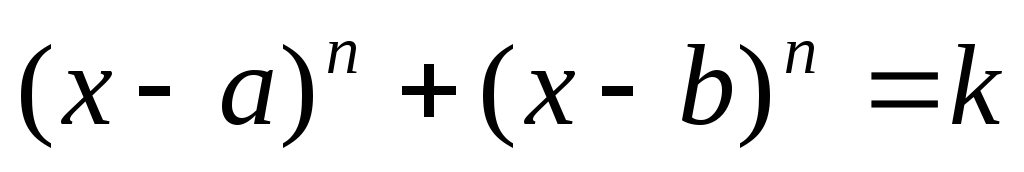и к ним сводящиеся решаются при помощи замены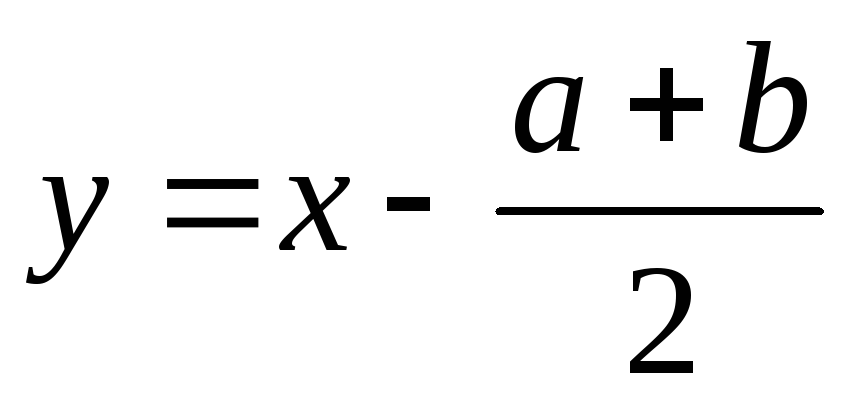

Введем замену.

Пусть 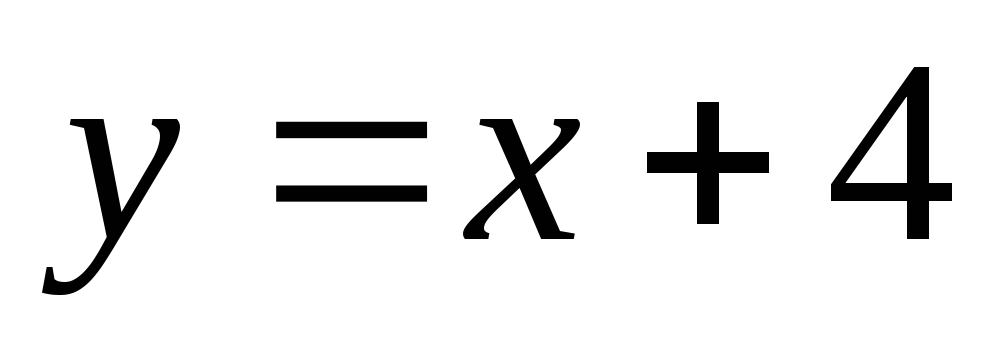, тогда

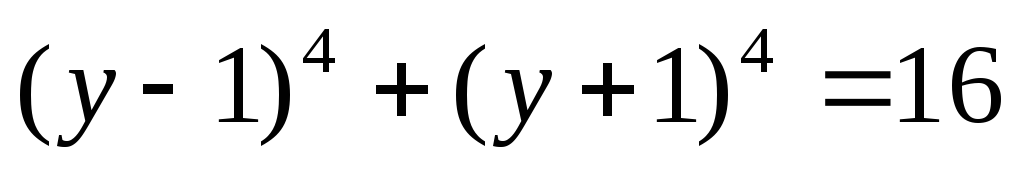
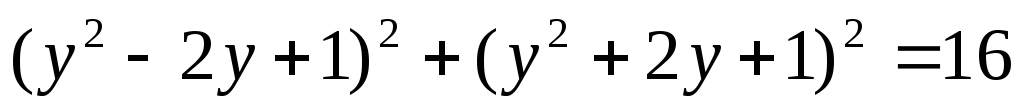
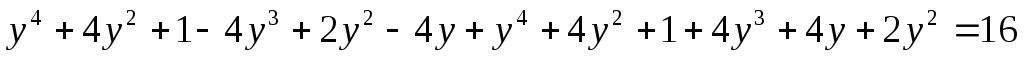
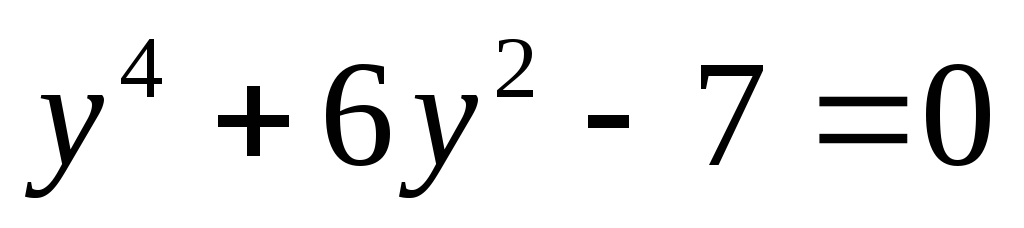
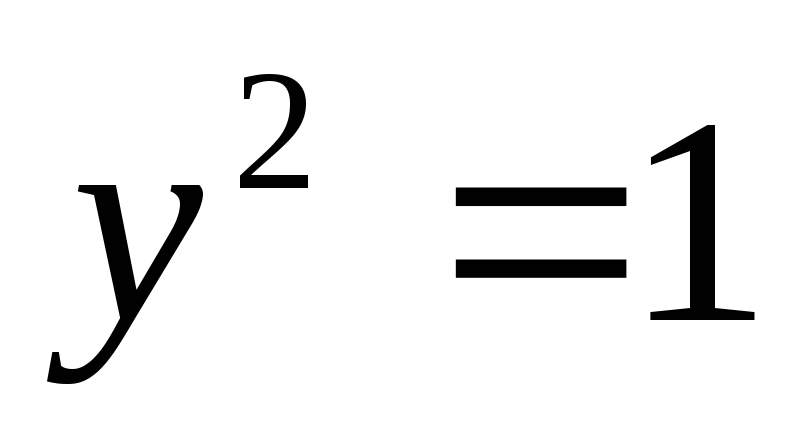или 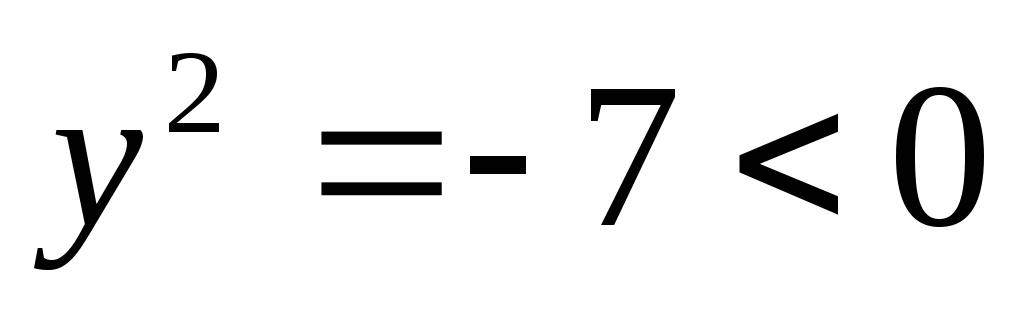корней нет

;

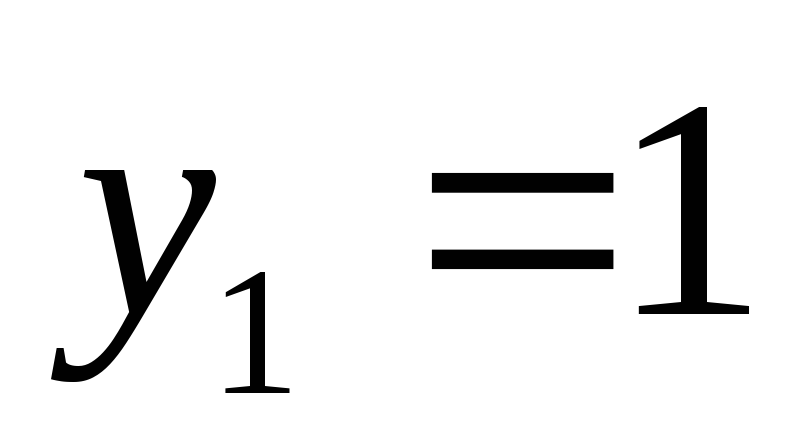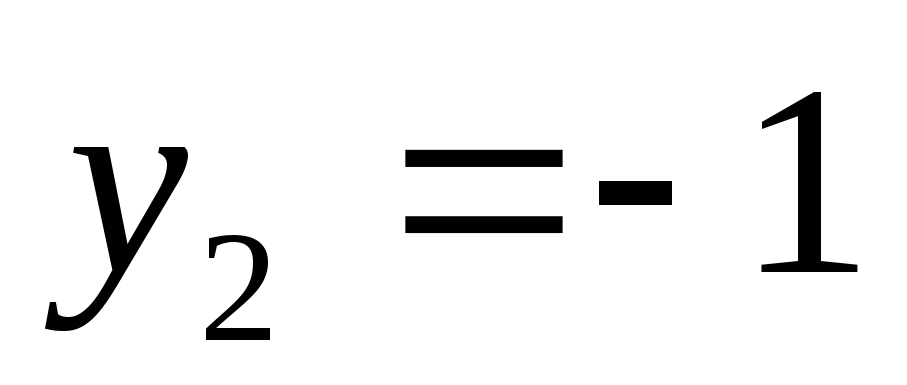
Вернемся к замене.

или

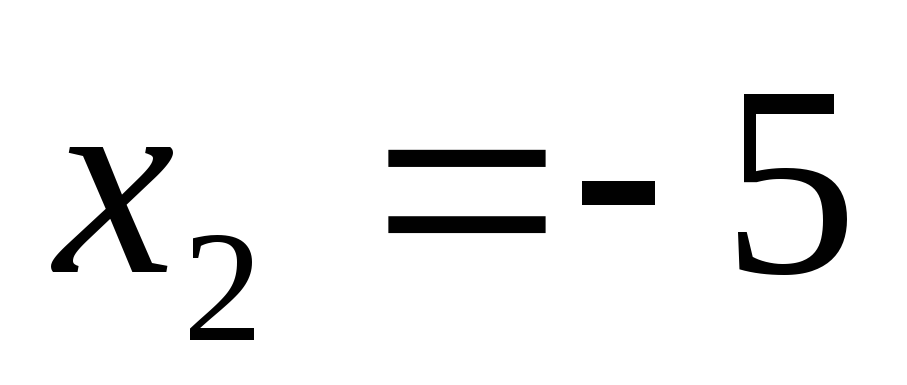
Ответ: ;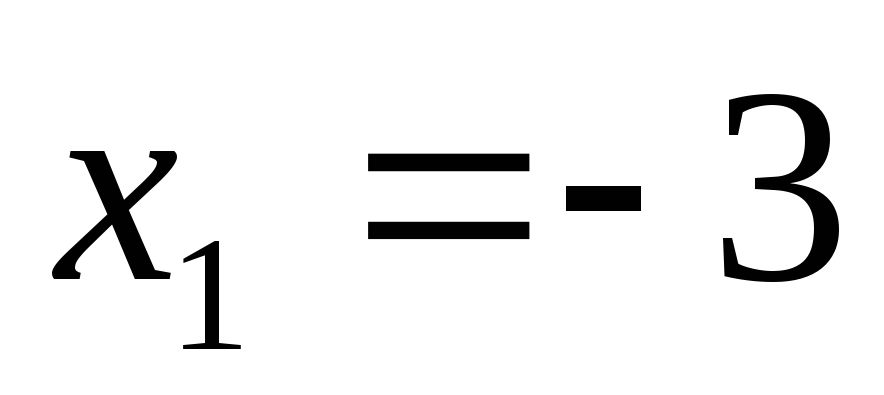

XII) Решение уравнений относительно коэффициентов.

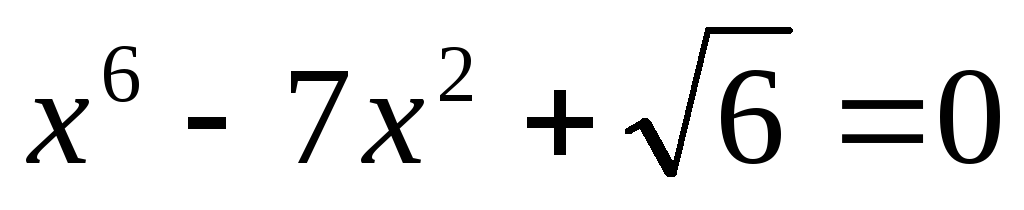
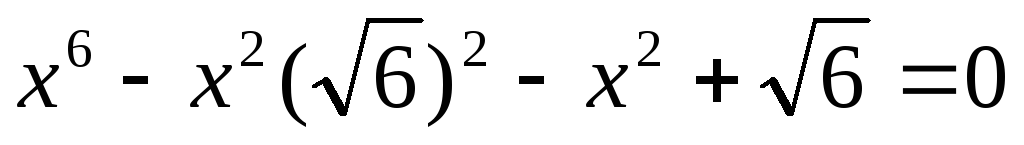
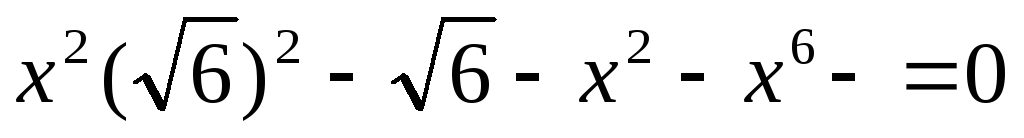
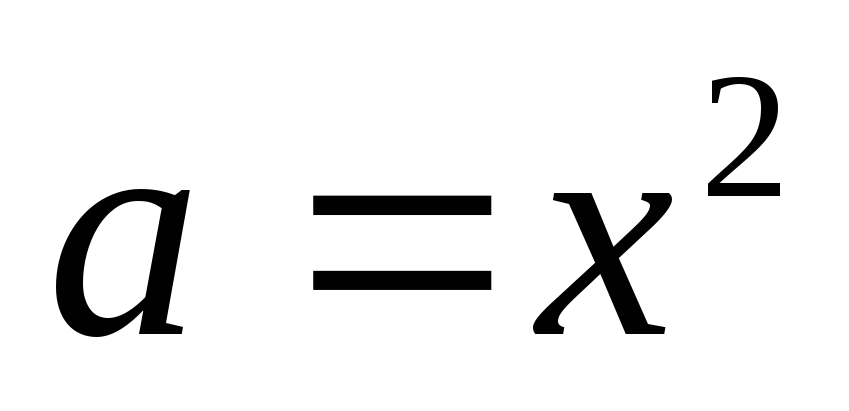
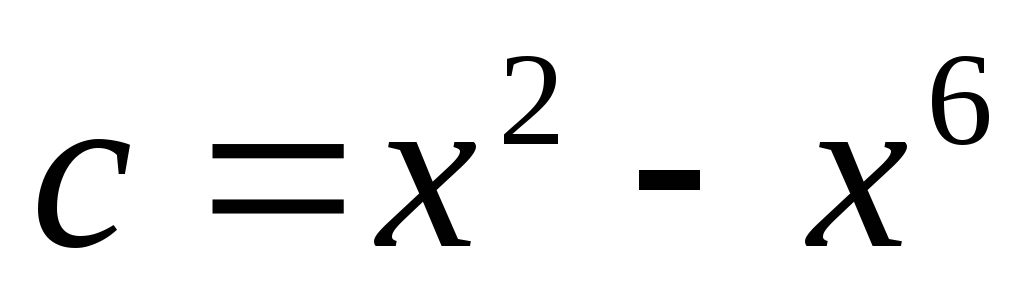
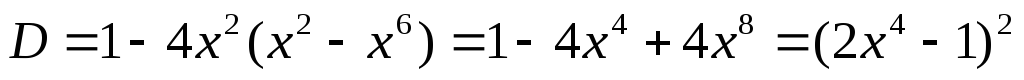
или

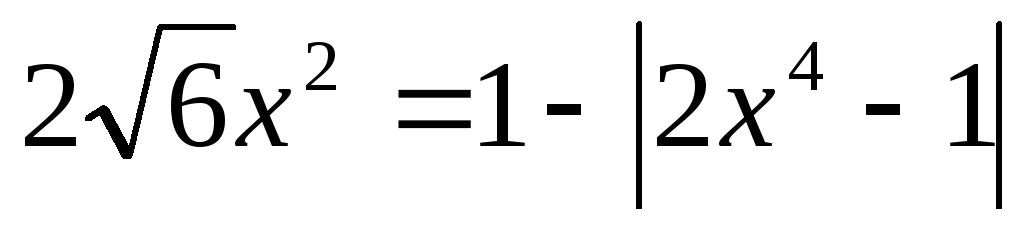
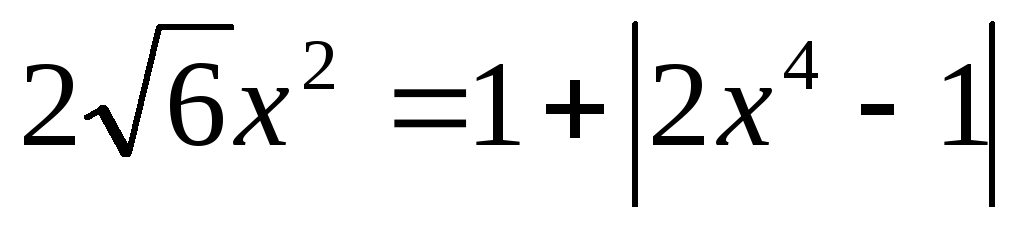
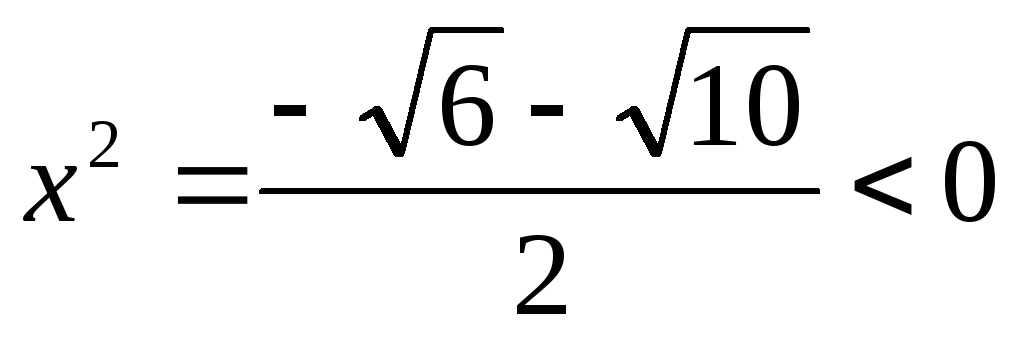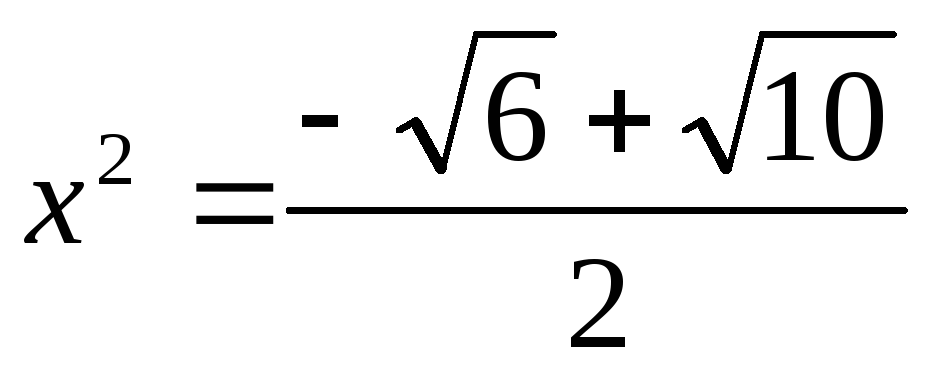
; — посторонний корень

корней нет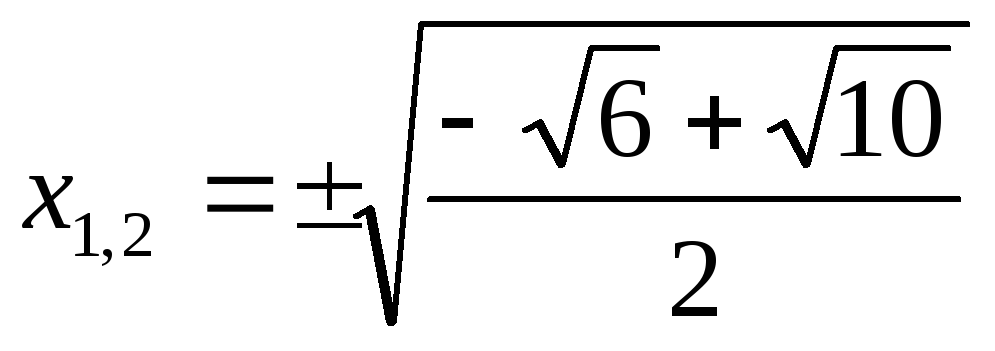

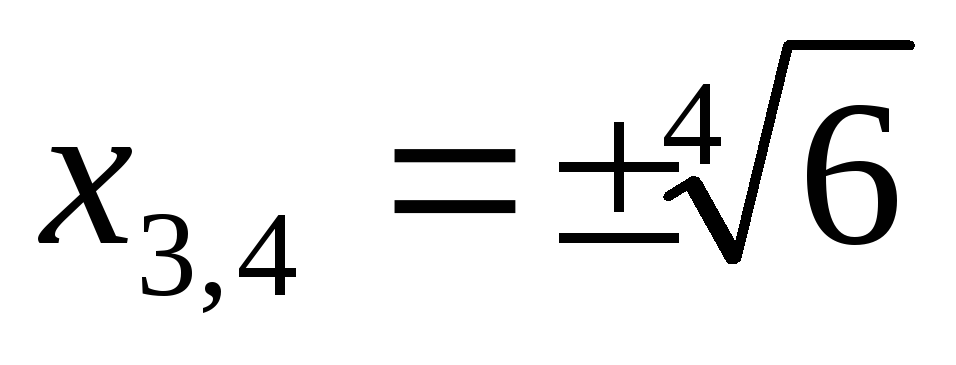
Ответ: ;

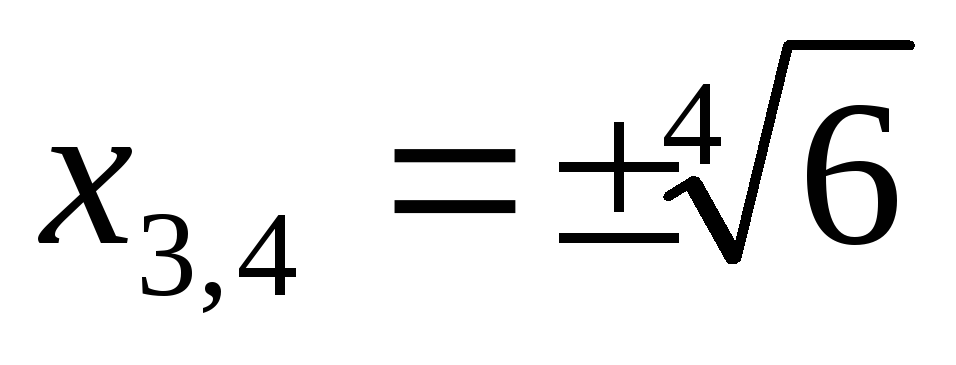
XIII) Метод разложения на простейшие дроби.

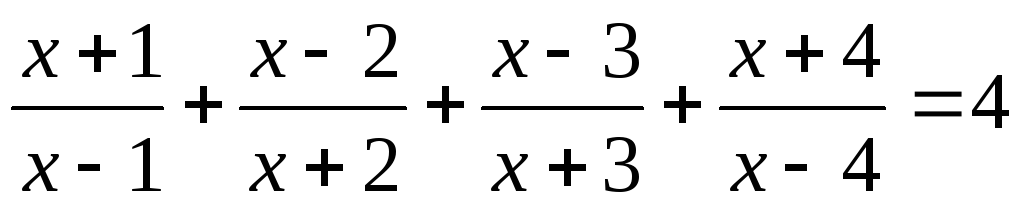
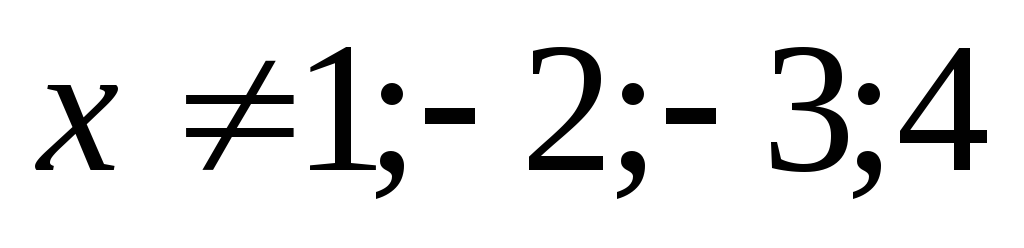
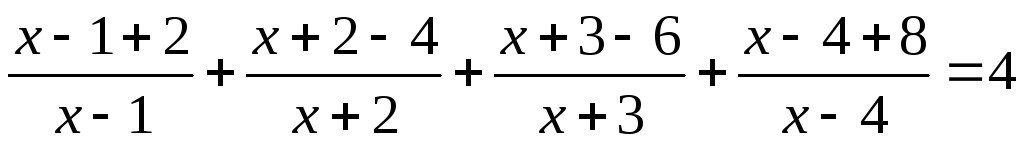
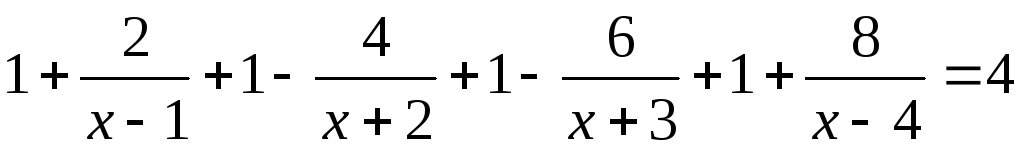
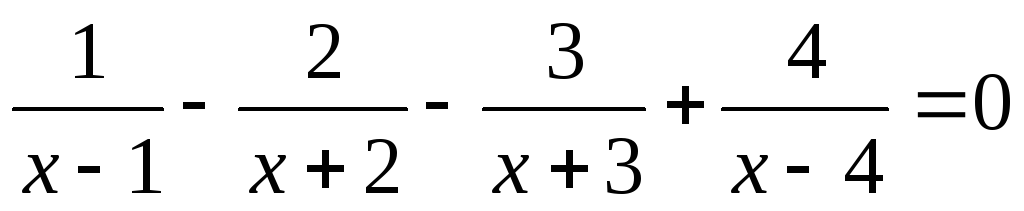
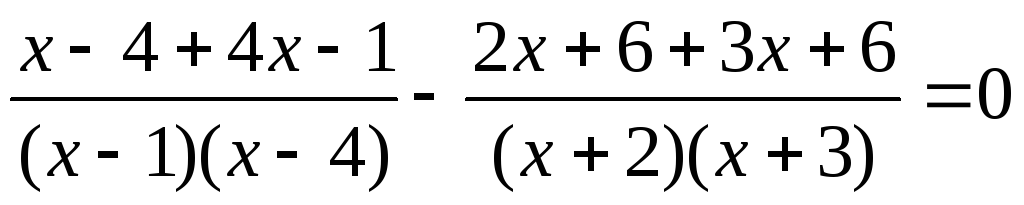
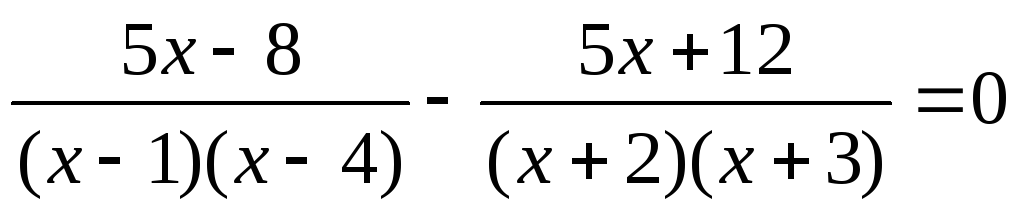
Ответ: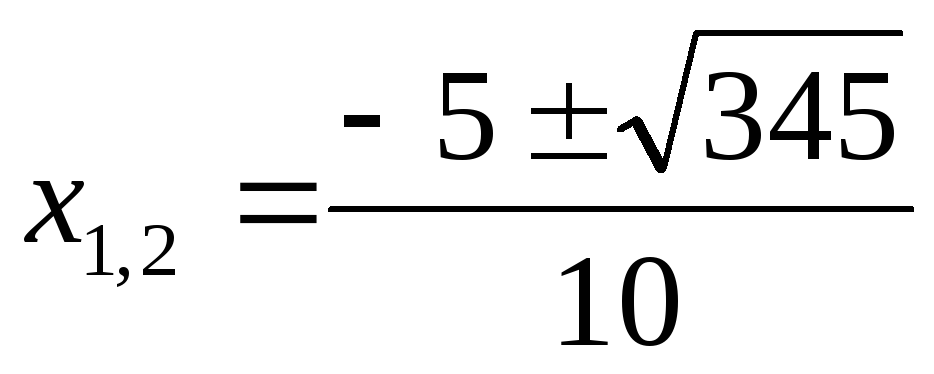

studfile.net

11.3.2. Решение простейших показательных уравнений   математика-повторение

Уравнения, содержащие переменную в показателе степени, называются показательными уравнениями.

Простейшие показательные уравнения — это уравнения вида: a^x=a^y. Отсюда следует равенство: х=у. В самом деле, степени с одинаковыми основаниями могут быть равными только в том случае, если равны показатели этих степеней.

Примеры.

Решить уравнение:

1) 5^x=125.  Представим число 125 в виде степени числа 5:

5^x=5³; Степени равны, их основания равны, значит, и показатели степеней будут равны:

x=3.

2) 4^x=32. Представим левую и правую части в виде степеней с основанием 2:

(2²)^x=2⁵; используем формулу возведения степени в степень: (a^x)^y=a^xy  

2^2x=2⁵;

2x=5  |:2

x=2,5.

 3) 3^2x-1=81. Число 81 представим в виде степени числа 3:

3^2x-1=3⁴;  приравняем показатели степеней с одинаковыми основаниями:

2x-1=4;  решаем простейшее линейное уравнение:

2x=4+1;

2x=5  |:2;

x=2,5.

 

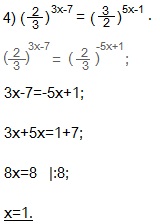
К правой части применяем формулу: (a/b)^-x=(b/a)^x. Получим равенство степеней с одинаковыми основаниями.

Приравниваем показатели степеней и находим х из полученного линейного уравнения.

 

 

 

 

 

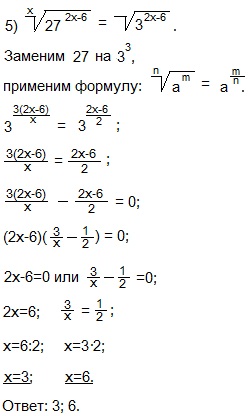
Приравняем показатели степеней с одинаковыми основаниями.

Переносим степень из правой части уравнения в левую.

Вынесли общий множитель (2х-6) за скобки. Произведение двух или нескольких множителей равно нулю, если один из множителей равен нулю, а другие при этом значении не теряют смысла. Содержимое каждой из скобок приравниваем к нулю и решаем простейшие уравнения.

 

6) 7∙5^x-5^x+1=2∙5³.

Показатели степеней складываются, если степени перемножаются ( a^x∙a^y=a^x+y ), поэтому:

7∙5^x-5^x∙5¹=2∙5³;

5^x(7-5)=2∙5³;  вынесли общий множитель за скобки.

5^x∙2=2∙5³     |:2

5^x=5³;  отсюда следует:

x=3.

7) 3^x+2+4∙3^x+1=21.  Применим формулу: a^x+y=a^x∙a^y  (При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают):

3^x∙3²+4∙3^x∙3¹=21; вынесем общий множитель за скобки:

3^x(9+12)=21;

3^x∙21=21  |:21

3^x=1; число 1 можно представлять в виде нулевой степени с любым основанием.

3^x=3⁰;

x=0.

5^1+2x+5^2x+3=650.  Решаем аналогично.

5¹∙5^2x+5^2x∙5³=650;

5^2x(5+125)=650;

5^2x∙130=650   |:130

5^2x=5; приравняем показатели равных степеней с основаниями 5.

2x=1  |:2

x=0,5.

 

Запись имеет метки: показательные уравнения

www.mathematics-repetition.com

49. Показательные уравнения, показательно-степенные уравнения

Показательным уравнением называется уравнение, которое содержит неизвестную величину в показателе степени при постоянном основании A (A > 0).

Типы показательных уравнений и способы их решения

Всюду далее F(X), G(X) – некоторые выражения с неизвестной величиной X.

I тип: уравнение вида

где (6.2)

Имеет решение, если B > 0. Его решают логарифмированием по основанию A:

Тогда

(6.3)

Решение уравнения (6.3) производят соответственно типу этого уравнения.

II тип: Уравнение вида

где (6.4)

По свойству равенства степеней равносильно уравнению

Последнее уравнение решают в зависимости от его типа.

III тип: уравнение вида

(6.5)

Где F – некоторое выражение относительно

Производят замену переменной и решают уравнение F(Y) = 0.

Если – корни уравнения, то после возвращения к старой переменной решение уравнения (6.5) сводится к решению равносильной ему совокупности уравнений

IV тип: уравнения, решаемые графическим методом.

Для таких уравнений строят соответствующие графики для левой и правой частей уравнения. Определяют, для каких значений X графики имеют общую ординату. Используют также иные функциональные свойства, в частности, монотонность функции (возрастание, убывание).

Показательно-степенным уравнением называется уравнение, в котором неизвестная величина содержится и в основании степени, и в показателе. Такие уравнения принято решать при условии, что основания степени положительны (ОДЗ уравнения).

Типы показательно-степенных уравнений

И способы их решения

Всюду далее F(X), G(X), H(X) – Некоторые выражения с неизвестной X, F(X) > 0.

I тип: уравнение вида

(6.6)

Решение уравнения (6.6) на ОДЗ сводится к решению совокупности

II тип: уравнение вида

(6.7)

Решение уравнения (6.7) на ОДЗ сводится к решению совокупности

Пример 1. Решить уравнение

Решение. 1-й способ. Имеем уравнение I типа (формула (6.2)). Решаем логарифмированием по основанию 3. Получаем:

т. е.

Приходим к линейному уравнению

Откуда

2-й способ. Преобразуем правую часть при помощи основного логарифмического тождества:

Получили уравнение II типа (формула (6.4)), которое решаем по свойству равенства степеней:

Пришли к ответу:

Пример 2. Решить уравнение

Решение. Выполним необходимые преобразования, сведем показательные выражения к одному и тому же основанию 3:

По свойству степеней:

Получаем ответ: Х = 0.

Пример 3. Решить уравнение

Решение. Преобразуем уравнение

Имеем квадратное уравнение относительно 2Х. Решаем при помощи замены Получаем:

Корнями последнего уравнения являются значения

Возвращаясь к неизвестной X, имеем совокупность:

Первое уравнение совокупности решений не имеет. Решаем второе уравнение:

т. е.

Получили ответ: Х = 3.

Пример 4. Решить уравнение

Решение. Выполним необходимые преобразования:

Имеем однородное уравнение. Разделим обе части уравнения на 92Х (92Х ¹ 0). Получим:

Т. е. получили квадратное уравнение относительно Вводим замену Тогда

Откуда

Возвращаемся к старой переменной:

Получили ответ:

Пример 5. Решить уравнение

Решение. 1-й способ. Подбором убеждаемся, что Х = 2– корень уравнения. Функции (т. е. ) и монотонно возрастают (рис. 6.12). Они имеют единственную общую точку.

Рис. 6.12

2-й способ. Разделим обе части уравнения на 2Х. Получим:

или

Заменим Получим

При Х = 2 получим основное тригонометрическое тождество, т. е. Х = 2 является корнем исходного уравнения.

Получили ответ: Х = 2.

Пример 6. Решить уравнение

Решение. ОДЗ: X = 2, 3, …, N, … .

Перепишем уравнение в виде

Разделим обе части уравнения на (так как ). Получим:

Вводим замену

Получаем квадратное уравнение откуда

Возвращаемся к старой переменной:

Но ни один из корней не подходит по ОДЗ. Следовательно, уравнение корней не имеет.

Пример 7. Решить уравнение

Решение. ОДЗ: X ¹ 2.

Решением является совокупность

Корень X = 2 не подходит по ОДЗ.

Получили ответ: X = 1, X = 3.

< Предыдущая		Следующая >

matica.org.ua