Найти расстояние от этой точки до координатных плоскостей: а) координатных плоскостей; б) осей координат. — Детская игровая комната «Волшебный лес»

Posted on 25.03.197011.06.2021 by alexxlab

Содержание

определение и примеры нахождения, расстояние между точкой и плоскостью

Данная статья рассказывает об определении расстояния от точки до плоскости. произведем разбор методом координат, который позволит находить расстояние от заданной точки трехмерного пространства. Для закрепления рассмотрим примеры нескольких задач.

Расстояние от точки до плоскости – определение

Расстояние от точки до плоскости находится посредством известного расстояния от точки до точки, где одна из них заданная, а другая – проекция на заданную плоскость.

Когда в пространстве задается точка М1 с плоскостью χ, то через точку можно провести перпендикулярную плоскости прямую. Н1 является общей точкой их пересечения. Отсюда получаем, что отрезок М1Н1 – это перпендикуляр, который провели из точки М1 к плоскости χ, где точка Н1 – основание перпендикуляра.

Определение 1

Расстоянием от точки до плоскости называют расстояние от заданной точки к основанию перпендикуляра, который провели из заданной точки к заданной плоскости.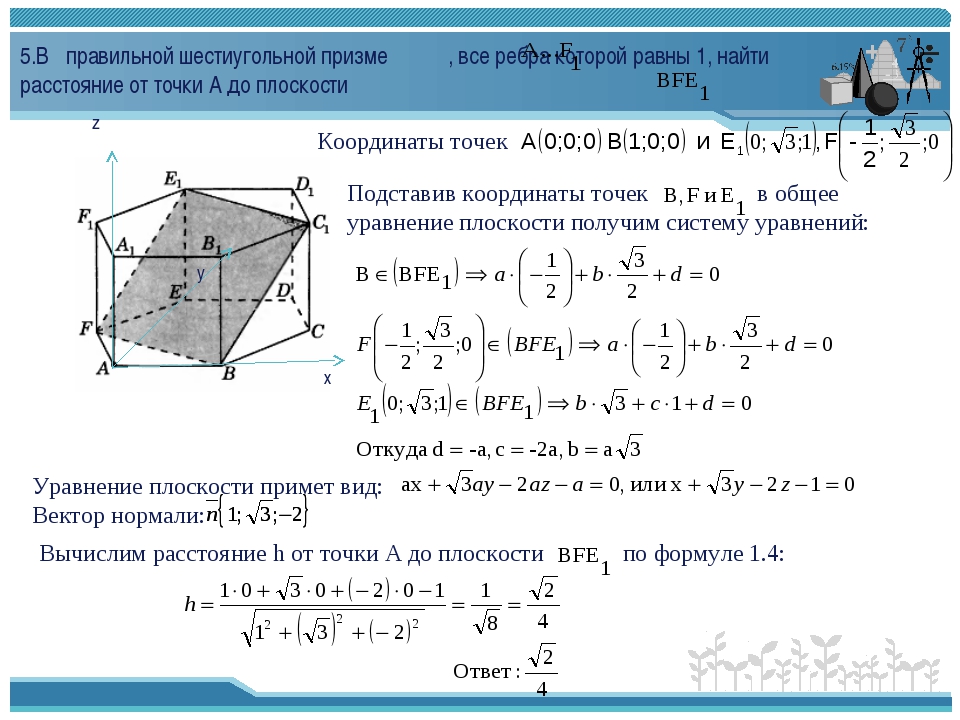

Определение может быть записано разными формулировками.

Определение 2

Расстоянием от точки до плоскости называют длину перпендикуляра, который провели из заданной точки к заданной плоскости.

Расстояние от точки М1 к плоскости χ определяется так: расстояние от точки М1 до плоскости χ будет являться наименьшим от заданной точки до любой точки плоскости. Если точка Н2 располагается в плоскости χ и не равна точке Н2, тогда получаем прямоугольный треугольник вида М2h2h3, который является прямоугольным, где имеется катет М2h2, М2h3 – гипотенуза. Значит, отсюда следует, что M1h2<M1h3. Тогда отрезок М2h2считается наклонной, которая проводится из точки М1 до плоскости χ. Мы имеем, что перпендикуляр, проведенный из заданной точки к плоскости, меньше наклонной, которую проводят из точки к заданной плоскости. Рассмотрим этот случай на рисунке, приведенном ниже.

Расстояние от точки до плоскости – теория, примеры, решения

Существует ряд геометрических задач, решения которых должны содержать расстояние от точки до плоскости. Способы выявления этого могут быть разными. Для разрешения применяют теорему Пифагора или подобия треугольников. Когда по условию необходимо рассчитать расстояние от точки до плоскости, заданные в прямоугольной системе координат трехмерного пространства, решают методом координат. Данный пункт рассматривает этот метод.

По условию задачи имеем, что задана точка трехмерного пространства с координатами M1(x1, y1, z1) с плоскостью χ, необходимо определить расстояние от М1 к плоскости χ. Для решения применяется несколько способов решения.

Первый способ

Данный способ основывается на нахождении расстояния от точки до плоскости при помощи координат точки Н1, которые являются основанием перпендикуляра из точки М1_{к плоскости χ. Далее необходимо вычислить расстояние между М1 и Н1.}

Для решения задачи вторым способом применяют нормальное уравнение заданной плоскости.

Второй способ

По условию имеем, что Н1 является основанием перпендикуляра, который опустили из точки М1 на плоскость χ. Тогда определяем координаты (x2, y2, z2) точки Н1. Искомое расстояние от М1 к плоскости χ находится по формуле M1h2=(x2-x1)2+(y2-y1)2+(z2-z1)2, где M1(x1, y1, z1) и h2(x2, y2, z2). Для решения необходимо узнать координаты точки Н1.

Имеем, что Н1 является точкой пересечения плоскости χ с прямой a, которая проходит через точку М1, расположенную перпендикулярно плоскости χ. Отсюда следует, что необходимо составление уравнения прямой, проходящей через заданную точку перпендикулярно к заданной плоскости. Именно тогда сможем определить координаты точки Н1. Необходимо произвести вычисление координат точки пересечения прямой и плоскости.

Алгоритм нахождения расстояния от точки с координатами M1(x1, y1, z1) к плоскости χ:

Определение 3

составить уравнение прямой а, проходящей через точку М1 и одновременно
перпендикулярной к плоскости χ;
найти и вычислить координаты (x2, y2, z2) точки Н1, являющимися точками
пересечения прямой a с плоскостью χ;
вычислить расстояние от М1 до χ, используя формулу M1h2=(x2-x1)2+(y2-y1)2+z2-z12.

Третий способ

В заданной прямоугольной системе координат Охуz имеется плоскость χ, тогда получаем нормальное уравнение плоскости вида cos α· x+cos β·y+cos γ·z-p=0. Отсюда получаем, что расстояние M1h2 с точкой M1(x1, y1, z1) , проведенной на плоскость χ, вычисляемое по формуле M1h2=cos α· x+cos β·y+cos γ·z-p. Эта формула справедлива, так как это установлено благодаря теореме.

Теорема

Если задана точка M1(x1, y1, z1) в трехмерном пространстве, имеющая нормальное уравнение плоскости χ вида cos α· x+cos β·y+cos γ·z-p=0, тогда вычисление расстояния от точки до плоскости M1h2 производится из формулы M1h2=cos α· x+cos β·y+cos γ·z-p, так как x=x1, y=y1, z=z1.

Доказательство

Доказательство теоремы сводится к нахождению расстояния от точки до прямой. Отсюда получаем, что расстояние от M1 до плоскости χ — это и есть модуль разности числовой проекции радиус-вектора M1 с расстоянием от начала координат к плоскости χ. Тогда получаем выражение M1h2=npn→OM→-p. Нормальный вектор плоскости χ имеет вид n→=cos α, cos β, cos γ, а его длина равняется единице, npn→OM→ — числовая проекция вектора OM→=(x1, y1, z1) по направлению, определяемым вектором n→.

Применим формулу вычисления скалярных векторов. Тогда получаем выражение для нахождения вектора вида n→, OM→=n→·npn→OM→=1·npn→OM→=npn→OM→, так как n→=cos α, cos β, cos γ·z и OM→=(x1, y1, z1). Координатная форма записи примет вид n→, OM→=cos α· x1+cos β·y1+cos γ·z1, тогда M1h2=npn→OM→-p=cos α· x1+cos β·y1+cos γ·z1-p. Теорема доказана.

Отсюда получаем, что расстояние от точки M1(x1, y1, z1) к плоскости χ вычисляется при помощи подстановки в левую часть нормального уравнения плоскости cos α· x+cos β·y+cos γ·z-p=0 вместо х, у, z координаты x1, y1 и z1 ,относящиеся к точке М1, взяв абсолютную величину полученного значения.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Рассмотрим примеры нахождения расстояния от точки с координатами до заданной плоскости.

Пример 1

Вычислить расстояние от точки с координатами M1(5, -3, 10) к плоскости 2x-y+5z-3=0.

Решение

Решим задачу двумя способами.

Первый способ начнется с вычисления направляющего вектора прямой a. По условию имеем, что заданное уравнение 2x-y+5z-3=0 является уравнением плоскости общего вида, а n→=(2, -1, 5) является нормальным вектором заданной плоскости. Его применяют в качестве направляющего вектора прямой a, которая перпендикулярна относительно заданной плоскости. Следует записать каноническое уравнение прямой в пространстве, проходящее через M1(5, -3, 10) с направляющим вектором с координатами 2, -1, 5.

Уравнение получит вид x-52=y-(-3)-1=z-105⇔x-52=y+3-1=z-105.

Следует определить точки пересечения. Для этого нежно объединить уравнения в систему для перехода от канонического к уравнениям двух пересекающихся прямых. Данную точку примем за Н1. Получим, что

x-52=y+3-1=z-105⇔-1·(x-5)=2·(y+3)5·(x-5)=2·(z-10)5·(y+3)=-1·(z-10)⇔⇔x+2y+1=05x-2z-5=05y+z+5=0⇔x+2y+1=05x-2z-5=0

После чего необходимо разрешить систему

x+2y+1=05x-2z-5=02x-y+5z-3=0⇔x+2y=15x-2z=52x-y+5z=3

Обратимся к правилу решения системы по Гауссу:

120-150-252-153~120-10-10-2100-555~120-10-10-2100060⇒⇒z=06=0, y=-110·10+2·z=-1, x=-1-2·y=1

Получаем, что h2(1, -1, 0).

Производим вычисления расстояния от заданной точки до плоскости. Берем точки M1(5, -3, 10) и h2(1, -1, 0) и получаем

M1h2=(1-5)2+(-1-(-3))2+(0-10)2=230

Второй способ решения заключается в том, чтобы для начала привести заданное уравнение 2x-y+5z-3=0 к нормальному виду. Определяем нормирующий множитель и получаем 122+(-1)2+52=130. Отсюда выводим уравнение плоскости 230·x-130·y+530·z-330=0. Вычисление левой части уравнения производится посредствам подстановки x=5, y=-3, z=10, причем нужно взять расстояние от M1(5, -3, 10) до 2x-y+5z-3=0 по модулю. Получаем выражение:

M1h2=230·5-130·-3+530·10-330=6030=230

Ответ: 230.

Когда плоскость χ задается одним из способов раздела способы задания плоскости, тогда нужно для начала получить уравнение плоскости χ и вычислять искомое расстояние при помощи любого метода.

Пример 2

В трехмерном пространстве задаются точки с координатами M1(5, -3, 10), A(0, 2, 1), B(2, 6, 1), C(4, 0, -1). Вычислить расстяние от М1 к плоскости АВС.

Решение

Для начала необходимо записать уравнение плоскости, проходящее через заданные три точки с координатами M1(5, -3, 10), A(0, 2, 1), B(2, 6, 1), C(4, 0, -1).

Получим:

x-0y-2z-12-06-21-14-00-2-1-1=0⇔xy-2z-12404-2-2=0⇔⇔-8x+4y-20z+12=0⇔2x-y+5z-3=0

Отсюда следует, что задача имеет аналогичное предыдущему решение. Значит, расстояние от точки М1 к плоскости АВС имеет значение 230.

Ответ: 230.

Нахождение расстояния от заданной точки на плоскости или к плоскости, которым они параллельны, удобнее, применив формулу M1h2=cos α·x1+cos β·y1+cos γ·z1-p. Отсюда получим, что нормальные уравнения плоскостей получают в несколько действий.

Пример 3

Найти расстояние от заданной точки с координатами M1(-3, 2, -7) к координатной плоскости Охуz и плоскости, заданной уравнением 2y-5=0.

Решение

Координатная плоскость Оуz соответствует уравнению вида х=0. Для плоскости Оуz оно является нормальным. Поэтому необходимо подставить в левую часть выражения значения х=-3 и взять модуль значения расстояния от точки с координатами M1(-3, 2, -7) к плоскости. Получаем значение, равное -3=3.

После преобразования нормальное уравнение плоскости 2y-5=0 получит вид y-52=0. Тогда можно найти искомое расстояние от точки с координатами M1(-3, 2, -7) к плоскости2y-5=0. Подставив и вычислив, получаем 2-52=52-2.

Ответ: Искомое расстояние от M1(-3, 2, -7) до Оуz имеет значение 3, а до 2y-5=0 имеет значение 52-2.

Контрольная работа №1 Вариант 1 (геометрия 11) Найдите координаты вектора , если А(5 -1 3), В(2 -2 4). Даны векторы и . Найдите . 3. Изобразите систему координат Охуz и постройте точку B(-2 -3 4). Найдите расстояние от этой точки до координатных плоскостей.

3. Изобразите систему координат Охуz и постройте точку А(1; -2; -4). Найдите расстояние от этой точки до координатных плоскостей.
4. Вершины 13 EMBED Equation.3 1415 АВС имеют координаты А(-2;0;1), В(-1;2;3), С(8;-4;9). Найдите координаты вектора ВМ, если ВМ – медиана 13 EMBED Equation.3 1415АВС.
5. Даны точки А (-1; 5; 3), В (7; -1; 3), С (3; -2; 6). Докажите, что 13 EMBED Equation.3 1415АВС прямоугольный.
—————————————————————————————

Контрольная работа №1 Вариант 2
(геометрия 11)
Найдите координаты вектора 13 EMBED Equation.3 1415, если С(6; 3; -2), D(2; 4; -5).
Даны векторы 13 EMBED Equation.3 1415 и 13 EMBED Equation.3 1415. Найдите 13 EMBED Equation.3 1415.
3. Изобразите систему координат Охуz и постройте точку B(-2; -3; 4). Найдите расстояние от этой точки до координатных плоскостей.
4. Вершины 13 EMBED Equation. 3 1415 АВС имеют координаты А(-1; 2; 3), В(1; 0; 4), С(3;-2; 1). Найдите координаты вектора АМ, если АМ – медиана 13 EMBED Equation.3 1415АВС.
5. Даны точки А (-1; 5; 3), В (-1; 3; 9), С (3; -2; 6). Докажите, что 13 EMBED Equation.3 1415АВС прямоугольный.

——————————————————————————————————————

Контрольная работа №1 Вариант 1
(геометрия 11)
Найдите координаты вектора 13 EMBED Equation.3 1415, если А(5; -1; 3), В(2; -2; 4).
Даны векторы 13 EMBED Equation.3 1415 и 13 EMBED Equation.3 1415. Найдите 13 EMBED Equation.3 1415.
3. Изобразите систему координат Охуz и постройте точку А(1; -2; -4). Найдите расстояние от этой точки до координатных плоскостей.
4. Вершины 13 EMBED Equation.3 1415 АВС имеют координаты А(-2;0;1), В(-1;2;3), С(8;-4;9). Найдите координаты вектора ВМ, если ВМ – медиана 13 EMBED Equation.3 1415АВС.
5. Даны точки А (-1; 5; 3), В (7; -1; 3), С (3; -2; 6). Докажите, что 13 EMBED Equation.3 1415АВС прямоугольный.
————————————————————————————-

Контрольная работа №1 Вариант 2
(геометрия 11)
Найдите координаты вектора 13 EMBED Equation.3 1415, если С(6; 3; -2), D(2; 4; -5).
Даны векторы 13 EMBED Equation.3 1415 и 13 EMBED Equation.3 1415. Найдите 13 EMBED Equation.3 1415.
3. Изобразите систему координат Охуz и постройте точку B(-2; -3; 4). Найдите расстояние от этой точки до координатных плоскостей.
4. Вершины 13 EMBED Equation.3 1415 АВС имеют координаты А(-1; 2; 3), В(1; 0; 4), С(3;-2; 1). Найдите координаты вектора АМ, если АМ – медиана 13 EMBED Equation.3 1415АВС.
5. Даны точки А (-1; 5; 3), В (-1; 3; 9), С (3; -2; 6). Докажите, что 13 EMBED Equation.3 1415АВС прямоугольный.

Приложенные файлы

5042185
Размер файла: 51 kB Загрузок: 0

Декартова система координат: основные понятия и примеры

Если вы находитесь в некоторой нулевой точке и размышляете над тем, сколько единиц расстояния нужно пройти строго вперёд, а затем — строго вправо, чтобы оказаться в некоторой другой точке, то вы уже пользуетесь прямоугольной декартовой системой координат на плоскости. А если точка находится выше плоскости, на которой вы стоите, и к вашим расчётам добавляется подъём к точке по лестнице строго вверх также на определённое число единиц расстояния, то вы уже пользуетесь прямоугольной декартовой системой координат в пространстве.

Упорядоченная система двух или трёх пересекающихся перпендикулярных друг другу осей с общим началом отсчёта (началом координат) и общей единицей длины называется прямоугольной декартовой системой координат.

С именем французского математика Рене Декарта (1596-1662) связывают прежде всего такую систему координат, в которой на всех осях отсчитывается общая единица длины и оси являются прямыми. Помимо прямоугольной существует общая декартова система координат (аффинная система координат). Она может включать и не обязательно перпендикулярные оси. Если же оси перпендикулярны, то система координат является прямоугольной.

Прямоугольная декартова система координат на плоскости имеет две оси, а прямоугольная декартова система координат в пространстве — три оси. Каждая точка на плоскости или в пространстве определяется упорядоченным набором координат — чисел в соответствии единице длины системы координат.

Заметим, что, как следует из определения, существует декартова система координат и на прямой, то есть в одном измерении. Введение декартовых координат на прямой представляет собой один из способов, с помощью которого любой точке прямой ставится в соответствие вполне определённое вещественное число, то есть координата.

Метод координат, возникший в работах Рене Декарта, ознаменовал собой революционную перестройку всей математики. Появилась возможность истолковывать алгебраические уравнения (или неравенства) в виде геометрических образов (графиков) и, наоборот, искать решение геометрических задач с помощью аналитических формул, систем уравнений. Так, неравенство z < 3 геометрически означает полупространство, лежащее ниже плоскости, параллельной координатной плоскости xOy и находящейся выше этой плоскости на 3 единицы.

С помощью декартовой системы координат принадлежность точки заданной кривой соответствует тому, что числа x и y удовлетворяют некоторому уравнению. Так, координаты точки окружности с центром в заданной точке (a; b) удовлетворяют уравнению (x — a)² + (y — b)² = R².

Две перпендикулярные оси на плоскости с общим началом и одинаковой масштабной единицей образуют декартову прямоугольную систему координат на плоскости. Одна из этих осей называется осью Ox, или осью абсцисс, другую — осью Oy, или осью ординат. Эти оси называются также координатными осями. Обозначим через Mx и My соответственно проекции произвольной точки М на оси Ox и Oy. Как получить проекции? Проведём через точку М прямую, перпендикулярную оси Ox. Эта прямая пересекает ось Ox в точке Mx. Проведём через точку М прямую, перпендикулярную оси Oy. Эта прямая пересекает ось Oy в точке My. Это показано на рисунке ниже.

Декартовыми прямоугольными координатами x и y точки М будем называть соответственно величины направленных отрезков OMx и OMy. Величины этих направленных отрезков рассчитываются соответственно как x = x0 — 0 и y = y0 — 0. Декартовы координаты x и y точки М называются соответственно её абсциссой и ординатой. Тот факт, что точка М имеет координаты x и y, обозначается так: M(x, y).

Координатные оси разбивают плоскость на четыре квадранта, нумерация которых показана на рисунке ниже. На нём же указана расстановка знаков координат точек в зависимости от их расположения в том или ином квадранте.

Помимо декартовых прямоугольных координат на плоскости часто рассматривается также полярная система координат. О способе перехода от одной системы координат к другой — в уроке полярная система координат.

Декартовы координаты в пространстве вводятся в полной аналогии с декартовыми координатами на плоскости.

Три взаимно перпендикулярные оси в пространстве (координатные оси) с общим началом O и одинаковой масштабной единицей образуют декартову прямоугольную систему координат в пространстве.

Одну из указанных осей называют осью Ox, или осью абсцисс, другую — осью Oy, или осью ординат, третью — осью Oz, или осью аппликат. Пусть Mx, My Mz — проекции произвольной точки М пространства на оси Ox, Oy и Oz соответственно.

Проведём через точку М плоскость, перпендикулярную оси Ox. Эта плоскость пересекает ось Ox в точке Mx. Проведём через точку М плоскость, перпендикулярную оси Oy. Эта плоскость пересекает ось Oy в точке My. Проведём через точку М плоскость, перпендикулярную оси Oz. Эта плоскость пересекает ось Oz в точке Mz.

Декартовыми прямоугольными координатами x, y и z точки М будем называть соответственно величины направленных отрезков OMx, OMy и OMz. Величины этих направленных отрезков рассчитываются соответственно как x = x0 — 0, y = y0 — 0 и z = z0 — 0.

Декартовы координаты x, y и z точки М называются соответственно её абсциссой, ординатой и аппликатой.

Попарно взятые координатные оси располагаются в координатных плоскостях xOy, yOz и zOx.

Пример 1. В декартовой системе координат на плоскости даны точки

A(2; -3);

B(3; -1);

C(-5; 1).

Найти координаты проекций этих точек на ось абсцисс.

Решение. Как следует из теоретической части этого урока, проекция точки на ось абсцисс расположена на самой оси абсцисс, то есть оси Ox, а следовательно имеет абсциссу, равную абсциссе самой точки, и ординату (координату на оси Oy, которую ось абсцисс пересекает в точке 0), равную нулю. Итак получаем следующие координаты данных точек на ось абсцисс:

Ax(2; 0);

Bx(3; 0);

Cx(-5; 0).

Пример 2. В декартовой системе координат на плоскости даны точки

A(-3; 2);

B(-5; 1);

C(3; -2).

Найти координаты проекций этих точек на ось ординат.

Решение. Как следует из теоретической части этого урока, проекция точки на ось ординат расположена на самой оси ординат, то есть оси Oy, а следовательно имеет ординату, равную ординате самой точки, и абсциссу (координату на оси Ox, которую ось ординат пересекает в точке 0), равную нулю. Итак получаем следующие координаты данных точек на ось ординат:

Ay(0; 2);

By(0; 1);

Cy(0; -2).

Пример 3. В декартовой системе координат на плоскости даны точки

A(2; 3);

B(-3; 2);

C(-1; -1).

Найти координаты точек, симметричных этим точкам относительно оси Ox.

Решение. Поворачиваем на 180 градусов вокруг оси Ox направленный отрезок, идущий от оси Ox до данной точки. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно оси Ox, будет иметь такую же абсциссу, что и данная точка, и ординату, равную по абсолютной величине ординате данной точки, и противоположную ей по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно оси Ox:

A’(2; -3);

B’(-3; -2);

C’(-1; 1).

Пример 4. Определить, в каких квадрантах (четвертях, рисунок с квадрантами — в конце параграфа «Прямоугольная декартова система координат на плоскости») может быть расположена точка M(x; y), если

1) xy > 0;

2) xy < 0;

3) x − y = 0;

4) x + y = 0;

5) x + y > 0;

6) x + y < 0;

7) x − y > 0;

8) x − y < 0.

Правильное решение и ответ.

Пример 5. В декартовой системе координат на плоскости даны точки

A(-2; 5);

B(3; -5);

C(a; b).

Найти координаты точек, симметричных этим точкам относительно оси Oy.

Правильное решение и ответ.

Пример 6. В декартовой системе координат на плоскости даны точки

A(-1; 2);

B(3; -1);

C(-2; -2).

Найти координаты точек, симметричных этим точкам относительно оси Oy.

Решение. Поворачиваем на 180 градусов вокруг оси Oy направленный отрезок, идущий от оси Oy до данной точки. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно оси Oy, будет иметь такую же ординату, что и данная точка, и абсциссу, равную по абсолютной величине абсциссе данной точки, и противоположную ей по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно оси Oy:

A’(1; 2);

B’(-3; -1);

C’(2; -2).

Пример 7. В декартовой системе координат на плоскости даны точки

A(3; 3);

B(2; -4);

C(-2; 1).

Найти координаты точек, симметричных этим точкам относительно начала координат.

Решение. Поворачиваем на 180 градусов вокруг начала координат направленный отрезок, идущий от начала координат к данной точке. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно начала координат, будет иметь абсциссу и ординату, равные по абсолютной величине абсциссе и ординате данной точки, но противоположные им по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно начала координат:

A’(-3; -3);

B’(-2; 4);

C(2; -1).

Пример 8. В декартовой системе координат в пространстве даны точки

A(4; 3; 5);

B(-3; 2; 1);

C(2; -3; 0).

Найти координаты проекций этих точек:

1) на плоскость Oxy;

2) на плоскость Oxz;

3) на плоскость Oyz;

4) на ось абсцисс;

5) на ось ординат;

6) на ось апликат.

Решение.

1) Проекция точки на плоскость Oxy расположена на самой этой плоскости, а следовательно имеет абсциссу и ординату, равные абсциссе и ординате данной точки, и апликату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxy:

Axy(4; 3; 0);

Bxy(-3; 2; 0);

Cxy(2; -3; 0).

2) Проекция точки на плоскость Oxz расположена на самой этой плоскости, а следовательно имеет абсциссу и апликату, равные абсциссе и апликате данной точки, и ординату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxz:

Axz(4; 0; 5);

Bxz(-3; 0; 1);

Cxz(2; 0; 0).

3) Проекция точки на плоскость Oyz расположена на самой этой плоскости, а следовательно имеет ординату и апликату, равные ординате и апликате данной точки, и абсциссу, равную нулю. Итак получаем следующие координаты проекций данных точек на Oyz:

Ayz(0; 3; 5);

Byz(0; 2; 1);

Cyz(0; -3; 0).

4) Как следует из теоретической части этого урока, проекция точки на ось абсцисс расположена на самой оси абсцисс, то есть оси Ox, а следовательно имеет абсциссу, равную абсциссе самой точки, а ордината и апликата проекции равны нулю (поскольку оси ординат и апликат пересекают ось абсцисс в точке 0). Получаем следующие координаты проекций данных точек на ось абсцисс:

Ax(4; 0; 0);

Bx(-3; 0; 0);

Cx(2; 0; 0).

5) Проекция точки на ось ординат расположена на самой оси ординат, то есть оси Oy, а следовательно имеет ординату, равную ординате самой точки, а абсцисса и апликата проекции равны нулю (поскольку оси абсцисс и апликат пересекают ось ординат в точке 0). Получаем следующие координаты проекций данных точек на ось ординат:

Ay(0; 3; 0);

By(0; 2; 0);

Cy(0; -3; 0).

6) Проекция точки на ось апликат расположена на самой оси апликат, то есть оси Oz, а следовательно имеет апликату, равную апликате самой точки, а абсцисса и ордината проекции равны нулю (поскольку оси абсцисс и ординат пересекают ось апликат в точке 0). Получаем следующие координаты проекций данных точек на ось апликат:

Az(0; 0; 5);

Bz(0; 0; 1);

Cz(0; 0; 0).

Пример 9. В декартовой системе координат в пространстве даны точки

A(2; 3; 1);

B(5; -3; 2);

C(-3; 2; -1).

Найти координаты точек, симметричных этим точкам относительно:

1) плоскости Oxy;

2) плоскости Oxz;

3) плоскости Oyz;

4) оси абсцисс;

5) оси ординат;

6) оси апликат;

7) начала координат.

Решение.

1) «Продвигаем» точку по другую сторону оси Oxy на то же расстояние. По рисунку, отображающему координатное пространство, видим, что точка, симметричная данной относительно оси Oxy, будет иметь абсциссу и ординату, равные абсциссе и ординате данной точки, и апликату, равную по величине апликате данной точки, но противоположную ей по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно плоскости Oxy:

A’(2; 3; -1);

B’(5; -3; -2);

C’(-3; 2; 1).

2) «Продвигаем» точку по другую сторону оси Oxz на то же расстояние. По рисунку, отображающему координатное пространство, видим, что точка, симметричная данной относительно оси Oxz, будет иметь абсциссу и апликату, равные абсциссе и апликате данной точки, и ординату, равную по величине ординате данной точки, но противоположную ей по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно плоскости Oxz:

A’(2; -3; 1);

B’(5; 3; 2);

C’(-3; -2; -1).

3) «Продвигаем» точку по другую сторону оси Oyz на то же расстояние. По рисунку, отображающему координатное пространство, видим, что точка, симметричная данной относительно оси Oyz, будет иметь ординату и апликату, равные ординате и апликате данной точки, и абсциссу, равную по величине абсциссе данной точки, но противоположную ей по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно плоскости Oyz:

A’(-2; 3; 1);

B’(-5; -3; 2);

C’(3; 2; -1).

По аналогии с симметричными точками на плоскости и точками пространства, симметричными данным относительно плоскостей, замечаем, что в случае симметрии относительно некоторой оси декартовой системы координат в пространстве, координата на оси, относительно которой задана симметрия, сохранит свой знак, а координаты на двух других осях будут теми же по абсолютной величине, что и координаты данной точки, но противоположными по знаку.

4) Свой знак сохранит абсцисса, а ордината и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси абсцисс:

A’(2; -3; -1);

B’(5; 3; -2);

C’(-3; -2; 1).

5) Свой знак сохранит ордината, а абсцисса и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси ординат:

A’(-2; 3; -1);

B’(-5; -3; -2);

C’(3; 2; 1).

6) Свой знак сохранит апликата, а абсцисса и ордината поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси апликат:

A’(-2; -3; 1);

B’(-5; 3; 2);

C’(3; -2; -1).

7) По аналогии с симметрии в случае с точками на плоскости, в случае симметрии относительно начала координат все координаты точки, симметричной данной, будут равными по абсолютной величине координатам данной точки, но противоположными им по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно начала координат:

A’(-2; -3; -1);

B’(-5; 3; -2);

C’(3; -2; 1).

Поделиться с друзьями

Весь блок «Аналитическая геометрия»

Векторы
Плоскость
Прямая на плоскости

Плоскости координатные — Энциклопедия по машиностроению XXL

Геометрические образы в пространстве ориентируются также и относительно системы трех взаимно перпендикулярных координатных плоскостей. Линии пересечения этих плоскостей — координатные оси — показаны на рис. 16. [c.22]

Входящая в соотношения (5.10) и (5.11) величина р считается постоянной. При изменении параметра р происходит вращение вектора Э в плоскости координатных единичных векторов (ё,, ёз). Полагая, например, р = 0, получаем [c.87]

Между моментами инерции твёрдого тела относительно координатных плоскостей, координатный осей и начала координат существуют зависимости. [c.47]

Ось перпендикулярна к чему (к прямой, к плоскости…), параллельна чему (осям…), пересекает что (плоскость, координатную ось…), проходит, расположена как (перпендикулярно…), описывает что (поверхность…), делит что (расстояние на отрезки…), (не) проходит через что (точку, центр тяжести, центр масс…), является чем (главной осью…), находится где (на расстоянии…). [c.55]

Пусть даны координатные оси х, у, сила Р, приложенная в точке А и расположенная в плоскости координатных осей (рис. 2.3). [c.23]

Запишем моменты сил данной системы относительно оси у. Для того чтобы легче представить, чему равен момент силы относительно оси, следует мысленно перенести силу вдоль линии действия до положения, когда точка приложения силы окажется в плоскости координатных осей (сила Г/ на рис. 8.2) [c.67]

Центр давления. Выше были определены сила давления жидкости на плоскую стенку и направление этой силы. Определим теперь точку D ее приложения (см. рис. 1.16). Эта точка лежит в плоскости стенки, т. е. в плоскости координатных осей xOz а поэтому необходимо определить только две ее координаты Xd и г . Определим сначала координату г . [c.52]

Гаусс, однако, стал на путь исследования поверхности при параметрическом ее задании и тем положил начало современной ди-ференциальной геометрии. Каждая пара значений параметров и V таким образом определяет точки на поверхности в этом смысле параметры и можно рассматривать как своеобразные координаты точки поверхности это и есть гауссовы координаты . Если возьмем плоскость в трехмерном пространстве и в ней установим систему декартовых координат, то таковые, конечно, можно будет рассматривать как гауссовы координаты этой плоскости. Координатными линиями при этом будут служить параллельные прямые. Но вообще координаты линии (т. е. линии, на которых тот или иной параметр сохранит постоянное значение) будут кривыми гауссовы координаты суть криволинейные координаты на поверхности. [c.380]

Пример 1 (Материальная точка движется по плоскости). Координатное пространство — сама эта плоскость. [c.42]

Уравнения (6.37)—(6.38) можно рассматривать в плоскости координатных осей s—Мд, как параметрические уравнения динамической характеристики машинного агрегата. В рассматриваемом случае динамическая характеристика представляет собой эллипс с центром не в начале координат и осями, повернутыми на некоторый угол. Размеры эллипса и угол наклона центральных осей к осям координат, определяются частотой нагружения и отношением постоянных времени у,.. [c.39]

Граничными кривыми, разделяющими области существования корней в плоскости координатных осей а, р, будут [c.68]

Для изучения геометрии резца вводятся следующие условные плоскости (рис. 1.5). Основная плоскость Д — это координатная плоскость, проведенная через рассматриваемую точку режущей кромки перпендикулярно направлению скорости главного движения резания в этой точке. У резцов с прямоугольным поперечным сечением за основную плоскость принимается плоскость, параллельная его опорной поверхности, т. е. его установочной базе. Плоскость резания Р — координатная плоскость, касательная к режущей кромке в рассматриваемой точке и перпендикулярная основной плоскости. Главная секущая плоскость — координатная плоскость, перпендикулярная линии пересечения основной плоскости и плоскости резания. [c.8]

В частном случае декартовых координат координатными поверхностями являются три взаимно перпендикулярные плоскости координатными кривыми являются три взаимно перпендикулярные прямые. [c.549]

Анализируя скорость какого-либо простого движения, можно представлять ее как векторную сумму двух или более составляющих скорости. Например, шарик движется по горизонтальной плоскости координатные оси х и у лежат в этой плоскости. Вектор скорости о имеет в некоторый момент совершенно определенное направление относительно координатных осей х и у, которое определяется углом а между направлениями скорости и оси X. Можно найти величину и направление вектора скорости, если указаны проекции вектора скорости вдоль координатных осей х и у. Можно считать, что вектор V слагается из двух векторов (рис. 17), один из которых направлен по оси X, другой — по оси у [c.37]

Пусть прямолинейная образующая пересекается с плоскостью координатных осей в точке N, принадлежащей меридиональному сечению. [c.133]

Входящую в эти соотношения величину 3 будем считать постоянной при изменении параметра /3 происходит вращение вектора э э] ) в плоскости координатных векторов (ех, 62). [c.177]

Детекторами распада служили либо калориметры из чередующихся топких слоев металла и плоскостей координатных датчиков, либо водяные черепковские счетчики. [c.211]

Основная плоскость — координатная плоскость, проведенная через рассматриваемую точку режущей кромки перпендикулярно направлению скорости [c.8]

На рис. 7 показано проецирование на некоторую аксонометрическую плоскость координатной системы, на всех осях которой отложены равные отрезки ОА = ОВ = ОС. [c.12]

Главная секущая плоскость — координатная плоскость, перпендикулярная линии пересечения основной плоскости и плоскости резания (рис. 2.5). [c.66]

В данном случае плоскости координатных осей совпадают, по направлению с главными кривизнами. Именно, согласно уравнению (7.23) кривизны Б направлении осей х и у составляют [c.102]

Итак, П2 — это а) плоскость координатных направлений X, 2 или плоскость, где можно показать относительное положение точек в этих координатных направлениях б) плоскость, показывающая движения над , под и левее , правее .. [c.18]

П1, будучи плоскостью координатных направлений х, у, очевидно, будет перпендикулярна П2 (рис. 9а, б). Относительно плоскости 2 можем сказать, что это плоскость координатных направлений ж, у или плоскость, показывающая движения левее , правее и перед , за , например, точка С перед точкой В на 15 мм, точка С за точкой А на 5 мм. [c.18]

Основные плоскости комплексного чертежа — это плоскости координатных направлений или плоскости, показывающие соответствующие координатные направления. Так, например, П2 можно считать плоскостью координатных направлений х та. г, П1 — плоскостью координатных направлений х, у. [c.123]

На рисунке 1306 построены проекции окружностей, лежащих в плоскостях координатных направлении х и у. Построение окружностей в плоскостях х, г ъ у, г аналогично. [c.128]

А — расстояние между плоскостями М В, которое при практических расчетах заменяется расстоянием между наружной поверхностью коробки 6 (см. фиг. 1) и плоскостью координатной сетки [c.354]

А — расстояние между плоскостями М и й — длина стороны квадрата координатной сетки и I — расстояние между фотопластинкой и плоскостью координатной сетки. [c.155]

Пусть теперь плоская волна падает под произвольным углом на границу полупространства или на плоскость раздела сред с разными свойствами. При исследовании процесса отражения целесообразно совместить с этой плоскостью координатную плоскость, например, х, у. Тогда, если фронт волны составляет с плоскостью раздела угол а (О а я), вместо координаты х в выражение (32.2) будет входить X = X sin а — г os а (ось у параллельна линии пересечения фронта волны с плоскостью раздела, см. рис. 22). [c.185]

Плоскость координатная степени k 149 [c.253]

Центральные силы. Силы называются центральными,, если они проходят через неподвижную точку О, которая при этом называется центром, сил. Под действием центральных сил точка описывает кривую, лежащую в некоторой плоскости, проходящей через центр сил О. Примем плоскость траектории за плоскость координатных осей х, у с началом в центре сил О. Центральную снлу будем считать положительной, если она отталкивающая, и отрицательной, если она притягивающая. Для движения под действием центральных сил, зависящих от расстояния г движущейся точки до центра О, имеют место два первых интеграла — интеграл площадей и интеграл живой силы, потому что момент центральных сил относительно центра сил всегда равен нулю, а зависящие от г центральные силы всегда допускают силовую функцию. [c.103]

Если мы будем изменять размеры звеньев механизма г, I и d с таким расчетом, чтобы сохранить углы фр б и ф -о , а вместе с тем коэффициент к, то при этих условиях шарниры А, О и А в плоскости координатных осей х и у будут перемещаться по вполне определенным кривым (рис. 167), которые мы обозначим через ЕА, f oi и Га . Знание этих геометрических мест позволяет данный механизм заменить другим при сохранении коэффициента к и параметров R и фкда. Для выявления упомянутых геометрических мест, которые потом положим в основу проектирования четырехзвенного шарнирного механизма, предположим, что механизм уже спроектирован и известен его базовый треугольник В 0[c.108]

Основная плоскость — координатная плоскость, проведенная через рассматриваемую точку режущей кромки перпендикулярно направлению скорости гМвного или результирующего движения резания в этой точке. Плоскость резания Р — координатная плоскость, касательная к поверхности резания и проходящая через главную режущую кромку резца. Главная секущая плоскость — координатная — плоскость, перпендикулярная линии пересечения основной плоскости и плоскости резания. Рабочая плоскость Р — плоскость, в которой расположены направления скоростей движения резания и движения подачи. [c.445]

Случай Я-поляризации (рис. 124, в, г, кривые которого построены соответственно в областях 1, 1) и 1, 2) на разрезах в плоскости х, б, отмеченных на рис. 121,6 отрезками прямых) дает пример еще более явного различия между влиянием поглощения в неидеальных диэлектриках в зависимости от добротности эффекта полного незеркального отражения. В области [1,1 энергетические потери не превышают 0,7 %, достигая в области 1,2 значений порядка 33 %. Таким образом, геометрические места точек, соответствующих режиму полного незеркального отражения, в областях 1,М , М=, 2,. .., для решеток волноводного типа образуют непрерывные линии на плоскостях х, б (аналогичный вывод справедлив для любой плоскости, координатная система которой определяется произвольной парой независимо изменяющихся параметров). В областях 7V, М) с N > 2, N режимам незеркального отражения с уровнем концентрации не ниже заданного соответствуют лишь отдельные острова в плоскости изменения любых двух независимых параметров. В областях с одинаковым N при возрастании М увеличивается и количество таких островов. Существует возможность достижения практически полного незеркального отражения на одной из гармоник в отдельных точках. При практическом использовании решеток с диэлектрическим заполнением в режиме полного автоколлима- [c.180]

Для равновесия системы еил, расположенных как угодно в пространстве, необходимо и достаточно, чтобы порознь равнялись яулю суммы проекций всех сил на шждую шз трех произвольно выбранных, но не лежащих в одной плоскости координатных осхй, и суммы моментов всех сил относительно каждой из трех таких осей. [c.130]

НИИ координатного угла не следует упускать из вида наличия внутренних связей между координатными плоскостями. Координатная плоскость XOZ должна быть перпендикулярна плоскости XOY, положение которой уже определено тремя внешними связями, а плоскость YOZ—перпендикулярна плоскостям XOY и XOZ. Таким образом, положение каждой координатной плоскости в пространстве определяется тремя связями XOY — тремя внешними связями, XOZ—двумя внешними и одной внутренней, YOZ—одной внешней и двумя внутренними. Это справедливо в отношении координатных плоскостей любой системы O XiYiZ , связываемой со станком или инструментом. [c.636]

Указанием трех точек определить секущую плоскость. Первая из указанных точек связанная с сюсущей плоскостью ПСК, задает начало (0,0,0),, вторая — направление оси X, третья — направление оси Y. Можно использовать задание секущей плоскости координатными плоскостями (XY, YZ, XZ).. [c.358]

Проведем через напряженную точку А (рис. 3.1) три плоскости, параллельные плоскостям координат. Для того чтобы иметь возможность обозначить на чертеже напряжения, действующие на точку в этих плоскостях, построим параллелепипед, ребра которого примем бесконечно малыми, неограниченно приближающимися к точке. Тогда на гранях такого элементарного параллелепипеда, проходящих через точку А, можно изобразить векторы напряжений, действующих на точку в трех взаимно перпендикулярных плоскостях (координатных площадках). При этом напряжение в каждой площадке разложим на три одно нормальное и два касательных, которые направим параллельно осям координат. Таким образом, всего будет три ормальных и шесть касательных напряжений. [c.72]

§ 26. Расстояние от точки до плоскости в координатах

§ 26.Расстояние от точки до плоскости в координатах

Напомним, что расстояние от данной точки M0 до плоскости α равно длине перпендикуляра M0M1_{(M1∈ α), опущенного из точки M0 на плоскость α (рис. 228).}

Проведём через точку M0(x0; y0; z0), не лежащую на плоскости α, прямую h, перпендикулярную α. Так как вектор нормали плоскости α является направляющим вектором прямой h, то для поиска координат x1, y1, z1 точки M1 пересечения прямой h и плоскости α достаточно, как и в предыдущем параграфе, решить систему уравнений относительно параметра t:

Решением этой системы является

t0 = = ,

что позволяет нам найти искомые координаты точки пересечения прямой h и плоскости α:

Тогда находим длину отрезка M0M1, равную искомому расстоянию d от точки M0 до плоскости α:

d = | M0M1 | =

= =

= |t0| =

= •=

= .

Если точка M0 лежит на данной плоскости, то

Ax0 + By0 + Cz0 + D = 0

и искомое расстояние равно нулю, что также следует из полученной формулы

d = .

Расстояние от начала координат O(0; 0; 0) до плоскости α равно

Приведём ещё один способ рассуждений.

Расстояние от точки M0 до плоскости α обозначим: d = | M0; α | = | M0M1|, где точка M1 — основание перпендикуляра, опущенного из точки M0 на плоскость α (см. рис. 228).

Пусть в системе координат Oxyz плоскость α задана уравнением

Ax + By + Cz + D = 0,(1)

точки M0 и M1 имеют координаты: M0(x0; y0; z0), M1(x1; y1; z1).

Заметим, что

M1 ∈ α ⇒ Ax1 + By1 + Cz1 + D = 0.(2)

Вектор (x0 – x1; y0 – y1; z0 – z1) и вектор нормали (A; B; C) плоскости α коллинеарны, так как каждый из них перпендикулярен плоскости α, поэтому

• = | |•| |•(±1) = ±d•| |;

(+1, если ↑↑ ; – 1, если ↑↓ ).

Тогда

|M0; α | = d = | | = = .

Раскроем в числителе скобки и, пользуясь соотношением (2), заменим выражение –Ax1 – By1 – Cz1 числом D. Получаем

d = .(3)

Сравните два приведённых способа рассуждений и выберите для себя наиболее понятный.

ЗадаЧа 7.182. Найти расстояние от точки K(1; –2; 3) до плоскости 3x + 2y – 6z + 5 = 0.

Решение. Находим координаты вектора нормали плоскости: (3; 2; –6). Тогда

d = = = 2.

Ответ: 2.

ЗадаЧа 7.183. Найти множество точек, равноудалённых от плоскостей 2x + 2y – z – 3 = 0 и 3x + 4y + 12z – 13 = 0.

Решение. Пусть точка M(x; y; z) равноудалена от данных плоскостей, тогда

= , т. е.

= .

Данное уравнение распадается на совокупность двух уравнений

= ,

или = – .

После упрощения получим уравнения двух плоскостей

17x + 14y – 49z = 0 и 35x + 38y + 23z – 78 = 0.

Подумайте, почему эти плоскости получились взаимно перпендикулярными и как они связаны с данными в задаче плоскостями.

Задания для работы с интернет-ресурсами

1. Вы можете найти в Интернете дополнительный материал по темам «Декартова прямоугольная система координат в пространстве», «Координаты вектора», «Условие параллельности двух векторов в координатах», «Скалярное произведение векторов в координатах», «Условие перпендикулярности двух векторов в координатах», «Проекция вектора на ось в координатах».

2. Найдите и изучите дополнительные материалы и презентации по темам: «Простейшие задачи стереометрии в координатах», «Уравнения и неравенства, задающие множества точек в пространстве», «Уравнение сферы и неравенство шара».

3. Найдите и выпишите знакомые и незнакомые формулы по теме «Плоскость в пространстве в координатах».

4. Найдите и выпишите знакомые и незнакомые формулы по темам «Прямая в координатах», «Взаимное расположение прямой и плоскости в координатах».

5. Набрав в поисковой системе слова «Прямая и плоскость в пространстве», «Параллельность прямой и плоскости», вы увидите, как можно использовать векторы и координаты при изучении вопросов параллельности прямой и плоскости.

6. Посмотрите статьи по теме «Аналитическая геометрия». Этот раздел математики вы будете изучать в высших учебных заведениях, но многими формулами и приёмами координатного метода изучения свойств геометрических фигур вы владеете уже сейчас. Попытайтесь узнать об этом ещё больше.

Вопросы для самооценки

1. Оцените результаты изучения этой главы. Довольны ли вы ими?

2. Что нового вы узнали в этой главе?

3. Как могут пригодиться вам эти знания в повседневной жизни?

4. Какие задания в этой главе были для вас самыми трудными? Почему?

5. Использовали ли вы при выполнении заданий дополнительные источники: справочники, пособия, интернет-ресурсы?

6. Обращались ли вы за помощью к одноклассникам, родителям, учителю?

Определить расстояние от точки m до плоскости. Расстояние от точки до плоскости онлайн. Вывод формулы для координатного метода поиска расстояния от точки до плоскости в пространстве

Рассмотрим в пространстве некоторую плоскость π и произвольную точку M 0 . Выберем для плоскости единичный нормальный вектор n с началом в некоторой точке М 1 ∈ π, и пусть р(М 0 ,π) — расстояние от точки М 0 до плоскости π. Тогда (рис. 5.5)

р(М 0 ,π) = | пр n M 1 M 0 | = |nM 1 M 0 |, (5.8)

так как |n| = 1.

Если плоскость π задана в прямоугольной системе координат своим общим уравнением Ax + By + Cz + D = 0, то ее нормальным вектором является вектор с координатами {A; B; C} и в качестве единичного нормального вектора можно выбрать

Пусть (x 0 ; y 0 ; z 0) и (x 1 ; y 1 ; z 1) координаты точек M 0 и M 1 . Тогда выполнено равенство Ax 1 + By 1 + Cz 1 + D = 0, так как точка M 1 принадлежит плоскости, и можно найти координаты вектора M 1 M 0 : M 1 M 0 = {x 0 -x 1 ; y 0 -y 1 ; z 0 -z 1 }. Записывая скалярное произведение nM 1 M 0 в координатной форме и преобразуя (5.8), получаем

поскольку Ax 1 + By 1 + Cz 1 = — D. Итак, чтобы вычислить расстояние от точки до плоскости нужно подставить координаты точки в общее уравнение плоскости, а затем абсолютную величину результата разделить на нормирующий множитель, равный длине соответствующего нормального вектора.

Плоскость в пространстве задана уравнением 3x-4y+2z+5=0, найдите расстояние от нее до точки M(3;-2;6).
Дано:
$$ x_0 = 3, \quad y_0 = -2, \quad z_0 = 6 $$
$$ A = 3, \quad B = -4, \quad C = 2, \quad D = 5 $$
Решение:
Для решения задачи воспользуемся формулой для нахождения расстояния от точки до плоскости, которое равно длине перпендикуляра, опущенного из этой точки на плоскость:
$$ p = {| A \cdot x_0 + B \cdot y_0 + C \cdot z_0 + D|} \over \sqrt{(A^2 + B^2 + C^2)} $$
где A, B, C, D – коэффициенты уравнения плоскости, а x0, y0, z0 – координаты точки.2) } } = 0,85 $$
Ответ:

Когда в пространстве задается точка М 1 с плоскостью χ , то через точку можно провести перпендикулярную плоскости прямую. Н 1 является общей точкой их пересечения. Отсюда получаем, что отрезок М 1 Н 1 – это перпендикуляр,который провели из точки М 1 к плоскости χ , где точка Н 1 – основание перпендикуляра.

Определение 1

Называют расстояние от заданной точки к основанию перпендикуляра, который провели из заданной точки к заданной плоскости.

Определение может быть записано разными формулировками.

Определение 2

Расстояние от точки М 1 к плоскости χ определяется так: расстояние от точки М 1 до плоскости χ будет являться наименьшим от заданной точки до любой точки плоскости. Если точка Н 2 располагается в плоскости χ и не равна точке Н 2 , тогда получаем прямоугольный треугольник вида М 2 H 1 H 2 , который является прямоугольным, где имеется катет М 2 H 1 , М 2 H 2 – гипотенуза. Значит, отсюда следует, что M 1 H 1 считается наклонной, которая проводится из точки М 1 до плоскости χ . Мы имеем, что перпендикуляр, проведенный из заданной точки к плоскости, меньше наклонной, которую проводят из точки к заданной плоскости. Рассмотрим этот случай на рисунке, приведенном ниже.

Расстояние от точки до плоскости – теория, примеры, решения

По условию задачи имеем, что задана точка трехмерного пространства с координатами M 1 (x 1 , y 1 , z 1) с плоскостью χ , необходимо определить расстояние от М 1 к плоскости χ . Для решения применяется несколько способов решения.

Первый способ

Данный способ основывается на нахождении расстояния от точки до плоскости при помощи координат точки Н 1 , которые являются основанием перпендикуляра из точки М 1 к плоскости χ . Далее необходимо вычислить расстояние между М 1 и Н 1 .

Для решения задачи вторым способом применяют нормальное уравнение заданной плоскости.

Второй способ

По условию имеем, что Н 1 является основанием перпендикуляра, который опустили из точки М 1 на плоскость χ . Тогда определяем координаты (x 2 , y 2 , z 2) точки Н 1 . Искомое расстояние от М 1 к плоскости χ находится по формуле M 1 H 1 = (x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2 , где M 1 (x 1 , y 1 , z 1) и H 1 (x 2 , y 2 , z 2) . Для решения необходимо узнать координаты точки Н 1 .

Имеем, что Н 1 является точкой пересечения плоскости χ с прямой a , которая проходит через точку М 1 , расположенную перпендикулярно плоскости χ . Отсюда следует, что необходимо составление уравнения прямой, проходящей через заданную точку перпендикулярно к заданной плоскости. Именно тогда сможем определить координаты точки Н 1 . Необходимо произвести вычисление координат точки пересечения прямой и плоскости.

Алгоритм нахождения расстояния от точки с координатами M 1 (x 1 , y 1 , z 1) к плоскости χ :

Определение 3

составить уравнение прямой а, проходящей через точку М 1 и одновременно
перпендикулярной к плоскости χ ;
найти и вычислить координаты (x 2 , y 2 , z 2) точки Н 1 , являющимися точками
пересечения прямой a с плоскостью χ ;
вычислить расстояние от М 1 до χ , используя формулу M 1 H 1 = (x 2 — x 1) 2 + (y 2 — y 1) 2 + z 2 — z 1 2 .

Третий способ

В заданной прямоугольной системе координат О х у z имеется плоскость χ , тогда получаем нормальное уравнение плоскости вида cos α · x + cos β · y + cos γ · z — p = 0 . Отсюда получаем, что расстояние M 1 H 1 с точкой M 1 (x 1 , y 1 , z 1) , проведенной на плоскость χ , вычисляемое по формуле M 1 H 1 = cos α · x + cos β · y + cos γ · z — p . Эта формула справедлива, так как это установлено благодаря теореме.

Теорема

Если задана точка M 1 (x 1 , y 1 , z 1) в трехмерном пространстве, имеющая нормальное уравнение плоскости χ вида cos α · x + cos β · y + cos γ · z — p = 0 , тогда вычисление расстояния от точки до плоскости M 1 H 1 производится из формулы M 1 H 1 = cos α · x + cos β · y + cos γ · z — p , так как x = x 1 , y = y 1 , z = z 1 .

Доказательство

Доказательство теоремы сводится к нахождению расстояния от точки до прямой. Отсюда получаем, что расстояние от M 1 до плоскости χ — это и есть модуль разности числовой проекции радиус-вектора M 1 с расстоянием от начала координат к плоскости χ . Тогда получаем выражение M 1 H 1 = n p n → O M → — p . Нормальный вектор плоскости χ имеет вид n → = cos α , cos β , cos γ , а его длина равняется единице, n p n → O M → — числовая проекция вектора O M → = (x 1 , y 1 , z 1) по направлению, определяемым вектором n → .

Применим формулу вычисления скалярных векторов. Тогда получаем выражение для нахождения вектора вида n → , O M → = n → · n p n → O M → = 1 · n p n → O M → = n p n → O M → , так как n → = cos α , cos β , cos γ · z и O M → = (x 1 , y 1 , z 1) . Координатная форма записи примет вид n → , O M → = cos α · x 1 + cos β · y 1 + cos γ · z 1 , тогда M 1 H 1 = n p n → O M → — p = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p . Теорема доказана.

Отсюда получаем, что расстояние от точки M 1 (x 1 , y 1 , z 1) к плоскости χ вычисляется при помощи подстановки в левую часть нормального уравнения плоскости cos α · x + cos β · y + cos γ · z — p = 0 вместо х, у, z координаты x 1 , y 1 и z 1 ,относящиеся к точке М 1 , взяв абсолютную величину полученного значения.

Рассмотрим примеры нахождения расстояния от точки с координатами до заданной плоскости.

Пример 1

Вычислить расстояние от точки с координатами M 1 (5 , — 3 , 10) к плоскости 2 x — y + 5 z — 3 = 0 .

Решение

Решим задачу двумя способами.

Первый способ начнется с вычисления направляющего вектора прямой a . По условию имеем, что заданное уравнение 2 x — y + 5 z — 3 = 0 является уравнением плоскости общего вида, а n → = (2 , — 1 , 5) является нормальным вектором заданной плоскости. Его применяют в качестве направляющего вектора прямой a , которая перпендикулярна относительно заданной плоскости. Следует записать каноническое уравнение прямой в пространстве, проходящее через M 1 (5 , — 3 , 10) с направляющим вектором с координатами 2 , — 1 , 5 .

Уравнение получит вид x — 5 2 = y — (- 3) — 1 = z — 10 5 ⇔ x — 5 2 = y + 3 — 1 = z — 10 5 .

x — 5 2 = y + 3 — 1 = z — 10 5 ⇔ — 1 · (x — 5) = 2 · (y + 3) 5 · (x — 5) = 2 · (z — 10) 5 · (y + 3) = — 1 · (z — 10) ⇔ ⇔ x + 2 y + 1 = 0 5 x — 2 z — 5 = 0 5 y + z + 5 = 0 ⇔ x + 2 y + 1 = 0 5 x — 2 z — 5 = 0

После чего необходимо разрешить систему

x + 2 y + 1 = 0 5 x — 2 z — 5 = 0 2 x — y + 5 z — 3 = 0 ⇔ x + 2 y = 1 5 x — 2 z = 5 2 x — y + 5 z = 3

Обратимся к правилу решения системы по Гауссу:

1 2 0 — 1 5 0 — 2 5 2 — 1 5 3 ~ 1 2 0 — 1 0 — 10 — 2 10 0 — 5 5 5 ~ 1 2 0 — 1 0 — 10 — 2 10 0 0 6 0 ⇒ ⇒ z = 0 6 = 0 , y = — 1 10 · 10 + 2 · z = — 1 , x = — 1 — 2 · y = 1

Получаем, что H 1 (1 , — 1 , 0) .

Производим вычисления расстояния от заданной точки до плоскости. Берем точки M 1 (5 , — 3 , 10) и H 1 (1 , — 1 , 0) и получаем

M 1 H 1 = (1 — 5) 2 + (- 1 — (- 3)) 2 + (0 — 10) 2 = 2 30

Второй способ решения заключается в том, чтобы для начала привести заданное уравнение 2 x — y + 5 z — 3 = 0 к нормальному виду. Определяем нормирующий множитель и получаем 1 2 2 + (- 1) 2 + 5 2 = 1 30 . Отсюда выводим уравнение плоскости 2 30 · x — 1 30 · y + 5 30 · z — 3 30 = 0 . Вычисление левой части уравнения производится посредствам подстановки x = 5 , y = — 3 , z = 10 , причем нужно взять расстояние от M 1 (5 , — 3 , 10) до 2 x — y + 5 z — 3 = 0 по модулю. Получаем выражение:

M 1 H 1 = 2 30 · 5 — 1 30 · — 3 + 5 30 · 10 — 3 30 = 60 30 = 2 30

Ответ: 2 30 .

Пример 2

В трехмерном пространстве задаются точки с координатами M 1 (5 , — 3 , 10) , A (0 , 2 , 1) , B (2 , 6 , 1) , C (4 , 0 , — 1) . Вычислить расстяние от М 1 к плоскости А В С.

Решение

Для начала необходимо записать уравнение плоскости, проходящее через заданные три точки с координатами M 1 (5 , — 3 , 10) , A (0 , 2 , 1) , B (2 , 6 , 1) , C (4 , 0 , — 1) .

x — 0 y — 2 z — 1 2 — 0 6 — 2 1 — 1 4 — 0 0 — 2 — 1 — 1 = 0 ⇔ x y — 2 z — 1 2 4 0 4 — 2 — 2 = 0 ⇔ ⇔ — 8 x + 4 y — 20 z + 12 = 0 ⇔ 2 x — y + 5 z — 3 = 0

Отсюда следует, что задача имеет аналогичное предыдущему решение. Значит, расстояние от точки М 1 к плоскости А В С имеет значение 2 30 .

Ответ: 2 30 .

Нахождение расстояния от заданной точки на плоскости или к плоскости, которым они параллельны, удобнее, применив формулу M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p . Отсюда получим, что нормальные уравнения плоскостей получают в несколько действий.

Пример 3

Найти расстояние от заданной точки с координатами M 1 (- 3 , 2 , — 7) к координатной плоскости О х у z и плоскости, заданной уравнением 2 y — 5 = 0 .

Решение

Координатная плоскость О у z соответствует уравнению вида х = 0 . Для плоскости О у z оно является нормальным. Поэтому необходимо подставить в левую часть выражения значения х = — 3 и взять модуль значения расстояния от точки с координатами M 1 (- 3 , 2 , — 7) к плоскости. Получаем значение, равное — 3 = 3 .

После преобразования нормальное уравнение плоскости 2 y — 5 = 0 получит вид y — 5 2 = 0 . Тогда можно найти искомое расстояние от точки с координатами M 1 (- 3 , 2 , — 7) к плоскости 2 y — 5 = 0 . Подставив и вычислив, получаем 2 — 5 2 = 5 2 — 2 .

Ответ: Искомое расстояние от M 1 (- 3 , 2 , — 7) до О у z имеет значение 3 , а до 2 y — 5 = 0 имеет значение 5 2 — 2 .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Пусть существует плоскость . Проведем нормаль
через начало координат О. Пусть заданы
– углы, образованные нормальюс осями координат.
. Пусть– длина отрезка нормали
до пересечения с плоскостью. Считая известными направляющие косинусы нормали, выведем уравнение плоскости.

Пусть
) – произвольная точка плоскости. Вектор единичной нормали имеет координаты. Найдем проекцию вектора
на нормаль.

Поскольку точка М принадлежит плоскости, то

Это и есть уравнение заданной плоскости, называющееся нормальным .

Расстояние от точки до плоскости

Пусть дана плоскость ,М *
– точка пространства,d – её расстояние от плоскости.

Определение. Отклонением точки М* от плоскости называется число (+ d ), если M * лежит по ту сторону от плоскости, куда указывает положительное направление нормали , и число (-d ), если точка расположена по другую сторону плоскости:

Теорема . Пусть плоскость с единичной нормальюзадана нормальным уравнением:

Пусть М *
– точка пространства Отклонение т.M * от плоскости задаётся выражением

Доказательство. Проекцию т.
* на нормаль обозначимQ . Отклонение точки М* от плоскости равно

Правило. Чтобы найти отклонение т. M * от плоскости, нужно в нормальное уравнение плоскости подставить координаты т. M * . Расстояние от точки до плоскости равно .

Приведение общего уравнения плоскости к нормальному виду

Пусть одна и та же плоскость задана двумя уравнениями:

Общее уравнение,

Нормальное уравнение.

Поскольку оба уравнения задают одну плоскость, их коэффициенты пропорциональны:

Первые три равенства возведем в квадрат и сложим:

Отсюда найдем – нормирующий множитель:

. (10)

Умножив общее уравнение плоскости на нормирующий множитель, получим нормальное уравнение плоскости:

Примеры задач на тему «Плоскость».

Пример 1. Составить уравнение плоскости , проходящей через заданную точку
(2,1,-1) и параллельной плоскости.

Решение . Нормаль к плоскости :
. Поскольку плоскости параллельны, то нормальявляется и нормалью к искомой плоскости. Используя уравнение плоскости, проходящей через заданную точку (3), получим для плоскостиуравнение:

Ответ:

Пример 2. Основанием перпендикуляра, опущенного из начала координат на плоскость , является точка
. Найти уравнение плоскости.

Решение . Вектор
является нормалью к плоскости. ТочкаМ 0 принадлежит плоскости. Можно воспользоваться уравнением плоскости, проходящей через заданную точку (3):

Ответ:

Пример 3. Построить плоскость , проходящую через точки

и перпендикулярную плоскости :.

Следовательно, чтобы некоторая точка М (x , y , z ) принадлежала плоскости , необходимо, чтобы три вектора
были компланарны:

=0.

Осталось раскрыть определитель и привести полученное выражение к виду общего уравнения (1).

Пример 4. Плоскость задана общим уравнением:

Найти отклонение точки
от заданной плоскости.

Решение . Приведем уравнение плоскости к нормальному виду.

Подставим в полученное нормальное уравнение координаты точки М* .

Ответ:
.

Пример 5. Пересекает ли плоскость отрезок.

Решение . Чтобы отрезок АВ пересекал плоскость, отклонения иот плоскостидолжны иметь разные знаки:

Пример 6. Пересечение трех плоскостей в одной точке.

Система имеет единственное решение, следовательно, три плоскости имеют одну общую точку.

Пример 7. Нахождение биссектрис двугранного угла, образованного двумя заданными плоскостями.

Пусть и- отклонение некоторой точки
от первой и второй плоскостей.

На одной из биссектральных плоскостей (отвечающей тому углу, в котором лежит начало координат) эти отклонения равны по модулю и знаку, а на другой – равны по модулю и противоположны по знаку.

Это уравнение первой биссектральной плоскости.

Это уравнение второй биссектральной плоскости.

Пример 8. Определение местоположения двух данных точек иотносительно двугранных углов, образованных данными плоскостями.

Пусть
. Определить: в одном, в смежных или в вертикальных углах находятся точкии.

а). Если илежат по одну сторону оти от, то они лежат в одном двугранном углу.

б). Если илежат по одну сторону оти по разные от, то они лежат в смежных углах.

в). Если илежат по разные стороны оти, то они лежат в вертикальных углах.

Системы координат 3

Линии на плоскости 8

Линии первого порядка. Прямые на плоскости. 10

Угол между прямыми 12

Общее уравнение прямой 13

Неполное уравнение первой степени 14

Уравнение прямой “в отрезках” 14

Совместное исследование уравнений двух прямых 15

Нормаль к прямой 15

Угол между двумя прямыми 16

Каноническое уравнение прямой 16

Параметрические уравнения прямой 17

Нормальное (нормированное) уравнение прямой 18

Расстояние от точки до прямой 19

Уравнение пучка прямых 20

Примеры задач на тему «прямая на плоскости» 22

Векторное произведение векторов 24

Свойства векторного произведения 24

Геометрические свойства 24

Алгебраические свойства 25

Выражение векторного произведения через координаты сомножителей 26

Смешанное произведение трёх векторов 28

Геометрический смысл смешанного произведения 28

Выражение смешанного произведения через координаты векторов 29

Примеры решения задач

, Конкурс «Презентация к уроку»

Класс: 11

Презентация к уроку

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели:

обобщение и систематизация знаний и умений учащихся;
развитие умений анализировать, сравнивать, делать выводы.

Оборудование:

мультимедийный проектор;
компьютер;
листы с текстами задач

ХОД ЗАНЯТИЯ

I. Организационный момент

II. Этап актуализации знаний (слайд 2)

Повторяем как определяется расстояние от точки до плоскости

III. Лекция (cлайды 3-15)

На занятии мы рассмотрим различные способы нахождения расстояния от точки до плоскости.

Первый метод: поэтапно-вычислительный

Расстояние от точки М до плоскости α:
– равно расстоянию до плоскости α от произвольной точки Р, лежащей на прямой a, которая проходит через точку М и параллельна плоскости α;
– равно расстоянию до плоскости α от произвольной точки Р, лежащей на плоскости β, которая проходит через точку М и параллельна плоскости α.

Решим следующие задачи:

№1. В кубе А…D 1 найти расстояние от точки С 1 до плоскости АВ 1 С.

Осталось вычислить значение длины отрезка О 1 Н.

№2. В правильной шестиугольной призме А…F 1 , все ребра которой равны 1, найдите расстояние от точки А до плоскости DEA 1 .

Следующий метод: метод объемов .

Если объем пирамиды АВСМ равен V, то расстояние от точки М до плоскости α, содержащей ∆АВС вычисляется по формуле ρ(М; α) = ρ(М; АВС) =
При решении задач мы используем равенство объемов одной фигуры, выраженные двумя различными способами.

Решим следующую задачу:

№3. Ребро AD пирамиды DABC перпендикулярно плоскости основания АВС. Найдите расстояние от А до плоскости, проходящей через середины ребер АВ, АС и АD, если.

При решении задач координатным методом расстояние от точки М до плоскости α можно вычислить по формуле ρ(М; α) = , где М(х 0 ; у 0 ; z 0), а плоскость задана уравнением ax + by + cz + d = 0

Решим следующую задачу:

№4. В единичном кубе A…D 1 найдите расстояние от точки А 1 до плоскости ВDC 1 .

Введем систему координат с началом в точке А, ось у пройдет по ребру АВ, ось х – по ребру АD, ось z – по ребру АА 1 . Тогда координаты точек В (0; 1; 0) D (1; 0; 0;) C 1 (1; 1; 1)
Составим уравнение плоскости, проходящей через точки В, D, C 1 .

Тогда – dx – dy + dz + d = 0 x + y – z – 1= 0. Следовательно, ρ =

Следующий метод, который можно использовать при решении задач данного типа – метод опорных задач.

Применение данного метода состоит в применении известных опорных задач, которые формулируются как теоремы.

Решим следующую задачу:

№5. В единичном кубе А…D 1 найдите расстояние от точки D 1 до плоскости АВ 1 С.

Рассмотрим применение векторного метода.

№6. В единичном кубе А…D 1 найдите расстояние от точки А 1 до плоскости ВDС 1 .

Итак, мы рассмотрели различные способы, которые можно использовать при решении данного типа задач. Выбор того или иного метода зависит от конкретной задачи и ваших предпочтений.

IV. Работа в группах

Попробуйте решить задачу разными способами.

№1. Ребро куба А…D 1 равно . Найдите расстояние от вершины С до плоскости BDC 1 .

№2. В правильном тетраэдре АВСD с ребром найдите расстояние от точки А до плоскости BDC

№3. В правильной треугольной призме АВСА 1 В 1 С 1 все ребра которой равны 1, найдите расстояние от А до плоскости ВСА 1 .

№4. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от А до плоскости SCD.

V. Итог урока, домашнее задание, рефлексия

Решение задач с использованием координатных плоскостей Текст научной статьи по специальности «Математика»

Заключение

Представлена методика оптимизации АСЭС, использующей ВИЭ и АБ. На основании описанной методики реализована математическая модель АСЭС. Разработанная модель позволяет решать задачи оптимизации, а именно, нахождение оптимального соотношения генерирующих мощностей, выбора оптимального единичного типоразмера оборудования, выбора установленных мощностей вспомогательного оборудования.

Литература

1. Возобновляемая энергетика в децентрализованном электроснабжении: монография / Б. В. Лукутин, О. А. Суржикова, Е. Б. Шандарова. -М.:Энергоатомиздат, 2008. — 231 с.

2. Rodolfo Dufo-Lopez, Jose L. Bernal-Agustin, Jose M. Yusta-Loyo, Jose A. Dominguez-Navarro, Ignacio J. Ramirez-Rosado, Juan Lujano, Ismael Aso / Multi-objective optimization minimizing cost and life cycle emissions of stand-alone PV-wind-diesel systems with batteries storage/Applied Energy / 2011 / том 88 / стр. 4033 -4041.

3. Tremblay O., Dessaint L. / Experimental validation of a battery dynamic model for EV application / World Electric Vehicle Journal / № 3 / 2009 / с. 1-10.

4. Erkan Dursun, Osman Kilic / Comparative evaluation of different power management strategies of a stand-alone PV/Wind/PEMFC hybrid power system/ International Journal of Electrical Power & Energy Systems / 2012 / том 34 / стр. 81-89.

5. Salas V., Alonso-Abella M., Chenlo F., Olias E. / Analysis of the maximum power point tracking in the photovoltaic grid inverters of 5kW / Renewable Energy / 2009 / том 37 / стр. 2366-2372.

Solving problems using coordinate planes Raximov N. (Republic of Uzbekistan) Решение задач с использованием координатных плоскостей Рахимов Н. Н. (Республика Узбекистан)

Рахимов Насриддин Номозович /Raximov Nasriddin — заведующий кафедрой, кафедра математики и информатики, академический лицей № 2, Самаркандский государственный университет, г. Самарканд, Республика Узбекистан

Аннотация: в статье показано решение некоторых задач с использованием координатных плоскостей Декарта./3 координаты векторов Ь(х; у). Тогда будет а(3;0) и Л- Ь(2;2л/3). Из условия перпендикулярности двух векторов:

а — Ь = 0

а — Ь = 6 + 4Л +12Л = 0

л = — 3 8

2-задача. Внутри прямоугольника расположена точка М. Расстояние из этой точки до трех вершин прямоугольника соответственно равно т, п, к, требуется найти расстояние до четвертой вершины.

Решение

По координатам плоскости построим прямоугольник со сторонами а и Ь (рисунок 2).

Рис. 2.

Из условия задачи |АМ|=т, |ВМ|=п, |СМ|=к. Надо найдем 7=|БМ|=? По формуле расстояние между двух точек будет

2,2 2 х + у = т

х2 + (у-Ь)2 = п2 (х-а)2 + (у-Ь)2 = к2

Вычтем от первого уравнение вторые, из него слагаем третье: (х-а)2+у2=т2-п2+к2.(х — 7)2 + 32 . Наименьшее значение этой суммы равно расстоянию от точки А'(3;-2) до точки В (7; 3). В самом деле, если А'(3;-2) — точка, симметричная точке А относительно оси Ох, то АМ + МВ = А’М + МВ, но последняя сумма минимальна, когда точки А’, М и В лежат на одной прямой. Значит, ответ

А В| = д/(7 — 3)2 +(3 + 2)2 =74! [1, с. 55-64].

4-задача. Дано три окружности w3 соответственно с радиусом 1, 2, и 3. Они

касаются друг с другом внешним образом. Эти окружности образуют треугольник. Найдите радиус вписанной окружности — W4 этого треугольника. Решение

Длина отрезков между центрами окружности V2, w3 , равны 3, 4, 5. Поэтому при построении треугольника эти отрезки составляет прямоугольные треугольники. Рисуем график координат плоскости по условию:

о а А X

Рис. 4.

Здесь, точки О, А и В — центры окружности V2, w3 . Искомый радиус г, а центр окружности W4 равен Б (а; Ь). Из рисунка будет ОБ=1+г, АБ=2+г, ВБ=3+г. Значит, напишем следующие системы уравнений:

(1 + г)2 = а2 + Ъ2 (2 + г )2 =(3 — а)2 + Ъ2 (3 + г)2 = а2 +(4 — Ъ)2

От этой системы происходит уравнение 23г2 + 132г — 36 = 0. Решим это

уравнение, найдем радиус окружности w4 , г = — [3, а 62-64].

5-задача. По дороге едут четверо: один на автомобиле, второй на мотоцикле, третий на мопеде, четвертый на велосипеде. Каждый едет со своей постоянной скоростью. Едущий на автомобиле догнал мопед в 12 ч, встретился с велосипедистом в 14 ч, а с мотоциклистом в 16 ч. Мотоциклист встретил мопед в 17 ч. и догнал велосипедиста в 18 ч. В котором часу велосипедист встретил мопед? Решение

Рис. 5.

Изобразим все перемещения в координатах t — время и х — расстояние (рисунок 5). Мы видим, что АК=КМ, т. е. AN и PK являются медианами АЛМР.

Поэтому ЛQ = — ЛЫ, и в проекции на ось t получаем

t* —12 = 2(17 —12) . отсюда t* = — = 151.

3 3 3

Ответ: Велосипедист встретил мопед в 1520 часов [2, с. 21].

Литература

1. Генкин Г. 3. Геометрические решения негеометрических задач. Москва «Просвещение» 2007. 75 с.

2. Яковлев Г. Н., Купцов Л. П. и др. Всероссийские математические олимпиады школьников. Москва, Издательство «Просвещение», 1992 г., 383 с.

3. Научный журнал «Физика, математика и информатика», 5/2010. Ташкент. [с. 62-64].

The distribution of the «non — trivial zeroes» of Riemann’s Zeta-function (Part 2) Kulshaeva T. (Russian Federation) Распределение нетривиальных нулей дзета-функции Римана (Часть 2) Кульшаева Т. В. (Российская Федерация)

Кульшаева Татьяна Вячеславовна /Kulshaeva Tatyana — независимый исследователь,

г. Саратов

Abstract: In this paper I’ll try to prove that distribution of Prime numbers is described by

the following Zeta function: H_1 n (s = a =1/2), which attached to the formula,

detecting the complex number z=x+iy.

Аннотация: При выполнении этой работы я постараюсь доказать, что распределение простых чисел может быть описано при помощи дзета-функции:

°° 1 н-1 п

M_1 » (s = а =1/2), которая привязывается к формуле, отражающей комплексное число.

Keywords: millennium problems, Riemann hypothesis. Ключевые слова: проблемы тысячелетия, гипотеза Римана.

Practical part

The decision of the Riemann hypothesis is very difficult because no one knows exactly the wording of the task. I have found a lot of interesting works, among which I was interested in three works [1, 2, 3]. The official version indicates that the exponent is a complex number.

, where s=l/2+it [4]

In my work [5], it’s showed that the distribution of Prime numbers can be described with

the help of the Zeta — function of Riemann «-1 n (s = с =1/2), and «it» — the

second addend, added to and deducted from «ns».

To verify this fact, I apply the theorem of Sturm, which change a little.

Калькулятор расстояний

Калькуляторы, представленные ниже, можно использовать для определения расстояния между двумя точками на двухмерной плоскости или трехмерном пространстве. Их также можно использовать для определения расстояния между двумя парами широты и долготы или двумя выбранными точками на карте.

2D-калькулятор расстояния

Используйте этот калькулятор, чтобы найти расстояние между двумя точками на 2D-координатной плоскости.

Трехмерный калькулятор расстояний

Используйте этот калькулятор, чтобы найти расстояние между двумя точками в трехмерном координатном пространстве.

Расстояние по широте и долготе

Используйте этот калькулятор, чтобы найти кратчайшее расстояние (большой круг / воздушное расстояние) между двумя точками на поверхности Земли.

Расстояние на карте

Щелкните карту ниже, чтобы установить две точки на карте и найти кратчайшее расстояние (большой круг / воздушное расстояние) между ними. После создания маркер (маркеры) можно переместить, щелкнув и удерживая, а затем перетащив их.

‘; calcResult + = »; } else if (markerCount> 0) { calcResult + = ‘

Point 1: [‘ + lat1 + ‘,’ + lon1 + ‘]

Установите другой маркер на карте, чтобы рассчитать расстояние.

‘; }еще{ calcResult + = ‘

Установите два маркера на карте, чтобы рассчитать расстояние между ними.

‘; } calcResult + = »; gObj («mapresult»). innerHTML = calcResult; }

Расстояние в системе координат

Расстояние в двухмерной координатной плоскости:

Расстояние между двумя точками на двухмерной координатной плоскости можно найти с помощью следующей формулы расстояния

d = √ (x ₂ — x ₁) ² + (y ₂ — y ₁) ²

, где (x ₁, y ₁) и (x ₂, y ₂) — координаты двух задействованных точек.Порядок точек не имеет значения для формулы, если выбранные точки совпадают. Например, учитывая две точки (1, 5) и (3, 2), либо 3, либо 1 могут быть обозначены как x ₁ или x ₂, если используются соответствующие значения y:

Использование (1, 5) как (x ₁, y ₁) и (3, 2) как (x ₂, y ₂):

d =	√ (3-1) ² + (2-5) ²
=	√2 ² + (-3) ²
=	√4 + 9
=	√13

Использование (3, 2) как (x ₁, y ₁) и (1, 5) как (x ₂, y ₂):

d =	√ (1-3) ² + (5-2) ²
=	√ (-2) ² + 3 ²
=	√4 + 9
=	√13

В любом случае результат один и тот же.

Расстояние в трехмерном координатном пространстве:

Расстояние между двумя точками на трехмерной координатной плоскости можно найти с помощью следующей формулы расстояния

d = √ (x ₂ — x ₁) ² + (y ₂ — y ₁) ² + (z ₂ — z ₁) ²

, где (x ₁, y ₁, z ₁) и (x ₂, y ₂, z ₂) — это трехмерные координаты двух задействованных точек.Как и в случае двухмерной версии формулы, не имеет значения, какая из двух точек обозначена (x ₁, y ₁, z ₁) или (x ₂, y ₂, z ₂ ), если в формуле используются соответствующие точки. Учитывая две точки (1, 3, 7) и (2, 4, 8), расстояние между точками можно найти следующим образом:

d =	√ (2-1) ² + (4-3) ² + (8-7) ²
=	√1 ² + 1 ² + 1 ²
=	√3

Расстояние между двумя точками на поверхности Земли

Есть несколько способов найти расстояние между двумя точками на поверхности Земли.Ниже приведены две общие формулы.

Формула Хаверсина:

Формула гаверсинуса может использоваться, чтобы найти расстояние между двумя точками на сфере, учитывая их широту и долготу:

В формуле гаверсинуса d — это расстояние между двумя точками вдоль большого круга, r — радиус сферы, & directphi; ₁ и & Stratocaster; ₂ — это широты двух точек, а λ ₁ и λ ₂ — долготы двух точек, все в радианах.

Формула гаверсинуса работает, находя расстояние по большому кругу между точками широты и долготы на сфере, которое можно использовать для аппроксимации расстояния на Земле (поскольку оно в основном сферическое). Большой круг (также ортодромия) сферы — это самый большой круг, который можно нарисовать на любой данной сфере. Он образован пересечением плоскости и сферы через центральную точку сферы. Расстояние по дуге большого круга — это кратчайшее расстояние между двумя точками на поверхности сферы.

Результаты с использованием формулы гаверсинуса могут иметь погрешность до 0,5%, поскольку Земля не является идеальной сферой, а представляет собой эллипсоид с радиусом 6 378 км (3963 мили) на экваторе и радиусом 6 357 км (3950 миль). у столба. Из-за этого формула Ламберта (формула эллипсоидальной поверхности) более точно аппроксимирует поверхность Земли, чем формула гаверсинуса (формула сферической поверхности).

Формула Ламберта:

Формула Ламберта (формула, используемая вычислителями выше) — это метод, используемый для вычисления кратчайшего расстояния по поверхности эллипсоида.Когда он используется для аппроксимации Земли и расчета расстояния на поверхности Земли, он имеет точность порядка 10 метров на тысячи километров, что более точно, чем формула гаверсинуса.

Формула Ламберта выглядит следующим образом:

, где a — экваториальный радиус эллипсоида (в данном случае Земли), σ — центральный угол в радианах между точками широты и долготы (найденный с использованием такого метода, как формула гаверсинуса), f — сглаживание Земля, а также X и Y развернуты ниже.

Где P = (β ₁ + β ₂) / 2 и Q = (β ₂ — β ₁) / 2

В приведенных выше выражениях β ₁ и β ₁ представляют собой приведенные широты с использованием следующего уравнения:

загар (β) = (1 — f) загар (& Straightphi;)

, где & Straightphi; широта точки.

Обратите внимание, что ни формула гаверсинуса, ни формула Ламберта не обеспечивают точное расстояние, потому что невозможно учесть все неровности на поверхности Земли.

Координатная плоскость

Координатная плоскость — это двумерная плоскость, образованная пересечением оси x и оси y. Его можно использовать для поиска точек на плоскости. На рисунке ниже показана координатная плоскость, определяющая пять точек: A, B, C, D и E.

Координатная плоскость также может называться декартовой координатной плоскостью, поскольку она используется как часть декартовой системы координат.

Свойства координатной плоскости

Координатная плоскость характеризуется несколькими свойствами.

ось x и ось y

Координатная плоскость образована пересечением горизонтальной числовой линии, называемой осью x, и вертикальной числовой линии, называемой осью y. Две оси (множественное число для оси) пересекаются по вертикали в точке, называемой началом координатной плоскости.

Сетка часто рисуется на координатной плоскости, чтобы упростить поиск точки. Сетка — это набор равномерно расположенных горизонтальных и вертикальных линий. Сетка на координатной плоскости выше показана светло-серыми отрезками линий.

Квадранты и заказанные пары

Местоположение точки задается упорядоченной парой чисел (x ₁, y ₁). Первое число в паре называется координатой x. Он представляет положение точки на оси x. Точно так же второе число представляет положение точки на оси y и соответственно называется координатой y.

Оси также делят координатную плоскость на четыре области, называемые квадрантами, как показано на координатной плоскости выше.

Определение точки на координатной плоскости

Начать с начала координат при нахождении точки на координатной плоскости. Считайте в положительном (вправо) или отрицательном (влево) направлении по оси x, чтобы определить горизонтальное положение точки. Считайте в положительном (вверх) или отрицательном (вниз) направлении по оси Y, чтобы определить вертикальное положение точки, как показано на рисунке ниже.

Две точки, одна в квадранте I и одна в квадранте III, показаны на рисунке выше.

Пример:

Запишите упорядоченные пары для точек A, B и C, показанных на координатной плоскости ниже.

Начиная с происхождения:

Для точки A переместитесь на 2 единицы влево, чтобы получить x-координату -2. Поскольку вертикального расстояния для перемещения нет, координата y равна 0. Упорядоченная пара для точки A равна (-2, 0).

Для точки B переместитесь на 4 единицы вправо, чтобы получить координату x, равную 4, затем переместитесь на 3 единицы вниз, чтобы получить координату y, равную -3. Упорядоченная пара для точки B — (4, -3).

Для точки C переместитесь на 3 единицы вправо, чтобы получить координату x, равную 3, затем переместитесь на 5 единиц, чтобы получить координату y, равную 5. Упорядоченная пара для точки C для (3, 5).

Построение набора решений в координатной плоскости

График уравнения, записанного в терминах x и y в координатной плоскости, представляет собой набор точек (x, y), который представляет набор решений уравнения.

Например, три решения (их бесконечно много) для y = 2x-1 показаны ниже.

x	y = 2x — 1	(x, y)
-2	y = 2 (-2) — 1 = -5	(-2, -5)
0	y = 2 (0) — 1 = -1	(0, -1)
2	y = 2 (2) — 1 = 3	(2, 3)

График набора решений показан в координатной плоскости ниже.

График содержит три точки, определенные выше. Любая точка на графике линии является частью набора решений для y = 2x — 1.Например, (3, 5) — это еще одна точка на линии, и ее включение дает:

5 = 2 (3) — 1

5 = 5 — истинное утверждение, поэтому (3, 5) — решение для y = 2x — 1.

Знаете ли вы?

Сегодня используется много других систем координат. Одна из них — Глобальная система позиционирования (GPS), система, которая позволяет вам определять ваше местоположение в любой точке Земли в любое время, независимо от погоды.

Прямоугольная система координат

Точка, которая делит пополам отрезок прямой, образованный двумя точками (x1, y1) и (x2, y2), называется средней точкой. Если две точки (x1, y1) и (x2, y2), Средняя точка — это упорядоченная пара, заданная формулой (x1 + x22, y1 + y22).и определяется по следующей формуле:

Средняя точка — это упорядоченная пара, образованная путем нахождения среднего значения x и среднего значения y данных точек.

Пример 8: Вычислите среднюю точку между (-1, -2) и (7, 4).

Решение: Сначала вычислите среднее значение x — и y — значений данных точек.

Затем сформируйте среднюю точку в виде упорядоченной пары, используя усредненные координаты.

Чтобы убедиться, что это действительно средняя точка, вычислите расстояние между двумя заданными точками и убедитесь, что результат равен сумме двух равных расстояний от конечных точек до этой средней точки. Эта проверка предоставляется читателю в качестве упражнения.

Попробуй! Найдите середину между (−6, 5) и (6, −11).

Тематические упражнения

Часть A: Заказанные пары

Укажите координаты точек A , B , C , D и E .

Изобразите данный набор упорядоченных пар.

7. {(−4, 5), (−1, 1), (−3, −2), (5, −1)}

8. {(−15, −10), (−5, 10), (15, 10), (5, −10)}

9. {(−2, 5), (10, 0), (2, −5), (6, −10)}

10. {(−8, 3), (−4, 6), (0, −6), (6, 9)}

11. {(−10, 5), (20, −10), (30, 15), (50, 0)}

12. {(−53, −12), (- 13, 12), (23, −1), (53, 1)}

13. {(-35, -43), (25, 43), (1, -23), (0, 1)}

14.{(−3,5, 0), (−1,5, 2), (0, 1,5), (2,5, −1,5)}

15. {(-0,8, 0,2), (-0,2, -0,4), (0, -1), (0,6, -0,4)}

16. {(-1,2, -1,2), (-0,3, -0,3), (0, 0), (0,6, 0,6), (1,2, 1,2)}

Укажите квадрант, в котором находится данная точка.

17. (−3, 2)

18. (5, 7)

19. (−12, −15)

20. (7, −8)

21. (-3,8, 4.6)

22. (17,3, 1,9)

23. (−18, −58)

24. (34, −14)

25. x> 0 и y <0

26. x <0 и y <0

27. x <0 и y> 0

28. x> 0 и y> 0

Средняя цена галлона обычного неэтилированного бензина в городах США представлена на следующем линейном графике. Используйте график, чтобы ответить на следующие вопросы.

Источник: Бюро статистики труда.

29. Какова была средняя цена галлона неэтилированного бензина в 2004 году?

30. Какова была средняя цена галлона неэтилированного бензина в 1976 году?

31. В какие годы средняя цена галлона неэтилированного бензина составляла 1,20 доллара США?

32. Насколько выросла цена галлона бензина с 1980 по 2008 год?

33.На сколько процентов увеличилась цена галлона неэтилированного бензина с 1976 по 1980 год?

34. Каков процент увеличения цены галлона неэтилированного бензина с 2000 по 2008 год?

Средняя цена на универсальную белую муку в городах США с 1980 по 2008 год представлена на следующем линейном графике. Используйте график, чтобы ответить на следующие вопросы.

Источник: Бюро статистики труда.

35. Какова была средняя цена за фунт универсальной белой муки в 2000 году?

36. Какова была средняя цена за фунт универсальной белой муки в 2008 году?

37. В каком году мука стоила в среднем 0,25 доллара за фунт?

38. В какие годы цена на муку составляла в среднем 0,20 доллара за фунт?

39. Каков процент увеличения производства муки с 2000 по 2008 год?

40.Каков процент увеличения муки с 1992 по 2000 год?

Используя следующие данные, создайте линейный график.

41. Процент от общего числа выпускников средней школы, поступивших в колледж.

Год	В процентах
1969	36%
1979	40%
1989	47%
1999	42%

Источник: Сборник статистики образования.

42. Средняя дневная температура в мае в градусах Фаренгейта.

Экзамен	Температура
8:00	60
12:00	72
16:00	75
20:00	67
12:00	60
4:00	55

Вычислите площадь формы, образованной соединением следующего набора вершин.

43. {(0, 0), (0, 3), (5, 0), (5, 3)}

44. {(−1, −1), (−1, 1), (1, −1), (1, 1)}

45. {(−2, −1), (−2, 3), (5, 3), (5, −1)}

46. {(−5, −4), (−5, 5), (3, 5), (3, −4)}

47. {(0, 0), (4, 0), (2, 2)}

48. {(−2, −2), (2, −2), (0, 2)}

49. {(0, 0), (0, 6), (3, 4)}

50. {(−2, 0), (5, 0), (3, −3)}

Часть B: Формула расстояния

Рассчитайте расстояние между заданными двумя точками.

51. (−5, 3) и (−1, 6)

52. (6, −2) и (−2, 4)

53. (0, 0) и (5, 12)

54. (−6, −8) и (0, 0)

55. (−7, 8) и (5, −1)

56. (-1, -2) и (9, 22)

57. (−1, 2) и (−7/2, −4)

58. (−12, 13) и (52, −113)

59. (−13, 23) и (1, −13)

60. (12, −34) и (32, 14)

61.(1, 2) и (4, 3)

62. (2, −4) и (−3, −2)

63. (-1, 5) и (1, -3)

64. (1, −7) и (5, −1)

65. (−7, −3) и (−1, 6)

66. (0, 1) и (1, 0)

67. (-0,2, -0,2) и (1,8, 1,8)

68. (1,2, −3,3) и (2,2, −1,7)

Для каждой задачи покажите, что три точки образуют прямоугольный треугольник.

69.(−3, −2), (0, −2) и (0, 4)

70. (7, 12), (7, −13) и (−5, −4)

71. (-1,4, 0,2), (1, 2) и (1, -3)

72. (2, -1), (-1, 2) и (6, 3)

73. (−5, 2), (−1, −2) и (−2, 5)

74. (1, −2), (2, 3) и (−3, 4)

Равнобедренные треугольники имеют две стороны равной длины. Для каждой задачи покажите, что следующие точки образуют равнобедренный треугольник.

75.(1, 6), (−1, 1) и (3, 1)

76. (−6, −2), (−3, −5) и (−9, −5)

77. (−3, 0), (0, 3) и (3, 0)

78. (0, -1), (0, 1) и (1, 0)

Вычислите площадь и периметр треугольников, образованных следующим набором вершин.

79. {(−4, −5), (−4, 3), (2, 3)}

80. {(−1, 1), (3, 1), (3, −2)}

81. {(−3, 1), (−3, 5), (1, 5)}

82.{(−3, −1), (−3, 7), (1, −1)}

Часть C: Формула средней точки

Найдите середину между заданными двумя точками.

83. (−1, 6) и (−7, −2)

84. (8, 0) и (4, −3)

85. (−10, 0) и (10, 0)

86. (−3, −6) и (−3, 6)

87. (−10, 5) и (14, −5)

88. (0, 1) и (2, 2)

89. (5, −3) и (4, −5)

90.(0, 0) и (1, 1)

91. (-1, -1) и (4, 4)

92. (3, −5) и (3, 5)

93. (−12, −13) и (32, 73)

94. (34, −23) и (18, −12)

95. (53, 14) и (−16, −32)

96. (−15, −52) и (710, −14)

97. Дан прямоугольный треугольник, образованный вершинами (0, 0), (6, 0) и (6, 8), покажите, что середины сторон образуют прямоугольный треугольник.

98. Для равнобедренного треугольника, образованного вершинами (−10, −12), (0, 12) и (10, −12), покажите, что середины сторон также образуют равнобедренный треугольник.

99. Вычислите площадь треугольника, образованного вершинами (−4, −3), (−1, 1) и (2, −3). (Подсказка: вершины образуют равнобедренный треугольник.)

100. Вычислите площадь треугольника, образованного вершинами (−2, 1), (4, 1) и (1, −5).

Часть D. Темы дискуссионной доски

101.Изучите и обсудите жизнь и вклад в математику Рене Декарта.

102. Изучите и обсудите историю прямоугольного треугольника и теоремы Пифагора.

103. Что такое тройка Пифагора? Приведите несколько примеров.

104. Объясните, почему нельзя использовать линейку для вычисления расстояния на графике.

105. Как разделить отрезок пополам с помощью циркуля и линейки?

Уклон, середина, параллельность и расстояние в координатной плоскости — видео и стенограмма урока

Различные размеры

1.Наклон

Наклон , примененный к координатной сетке XY, является мерой того, насколько изменяется значение y по сравнению с тем, насколько быстро изменяется значение x . Чтобы найти наклон между двумя точками на координатной сетке, разделите изменение значений y на изменение значений x .

Многие четырехугольники требуют, чтобы две стороны и диагонали были перпендикулярны. Вы можете найти наклон каждого сегмента линии, чтобы определить, перпендикулярны ли сегменты линии.Два отрезка линии будут перпендикулярными, если наклон этих отрезков обратный.

2. Параллельность

Если две линии, нарисованные на координатной сетке, никогда не пересекаются, то эти линии на параллельны друг другу. Два отрезка параллельны, если отрезки никогда не пересекаются. Чтобы проверить, параллельны ли два отрезка геометрической фигуры, найдите наклон обоих отрезков. Два параллельных отрезка имеют одинаковый наклон.

3. Средняя точка

Если у вас есть две точки, расположенные на координатной сетке XY, вы можете найти среднюю точку между двумя точками. Средняя точка — это точка, которая находится на равном расстоянии от обеих точек и лежит на отрезке линии, соединяющей две точки. Вы найдете среднюю точку, сложив два значения x вместе и разделив на 2, затем сложив два значения y вместе и разделив на 2. Если у вас диаметр круга; вы можете найти центр круга, найдя середину конечных точек диаметра.

4. Расстояние

Расстояние между двумя точками на координатной сетке можно найти с помощью формулы расстояния. Формула расстояния основана на теореме Пифагора. Теорема Пифагора утверждает, что сумма квадратов двух катетов равна квадрату гипотенузы.

Чтобы найти расстояние между двумя точками с помощью формулы расстояния, найдите разницу между двумя значениями x и двумя значениями y .Возведите каждую разницу в квадрат и затем возьмите их сумму. Найдите квадратный корень из суммы квадратов разностей. Когда геометрические фигуры рисуются на координатной сетке, вам часто приходится определять длину стороны фигуры. Если сторона проходит по диагонали, формула расстояния позволяет найти длину.

Пример 1

Точки A (1,5), B (4,1), C (9,6), D (6,10) являются вершинами четырехугольника.

Является ли этот четырехугольник ABCD параллелограммом?

У параллелограммов два набора параллельных сторон.Наклон AD равен 1, наклон DC равен -4/3, наклон BC равен 1, а наклон AB равен -4/3. AD и BC параллельны. DC и AB параллельны. Два набора параллельных линий. Четырехугольник ABCD — параллелограмм.

Четырехугольник ABCD — это прямоугольник?

Прямоугольники имеют два набора параллельных сторон, и стороны образуют прямые углы.

Мы уже доказали, что стороны параллельны. Если два отрезка прямых перпендикулярны (образуют прямые углы), у них будет отрицательный обратный наклон.Наклон DC и AB составляет -4/3. Наклон другого набора сторон должен был бы составлять 3/4, если бы они были перпендикулярны. Четырехугольник ABCD не является прямоугольником.

Пример 2

AB — диаметр окружности. A — это точка (7,10), а B — (13,20).

Какой центр круга?

Центр круга будет средней точкой диаметра. ((7 + 13) / 2, (10 + 20) / 2). (10,15) — центр круга.

Пример 3

Обратно в Нью-Йорк.Если вы хотите узнать, сколько кварталов вы прошли по Бродвею, вам нужно будет использовать формулу расстояния. Например, сколько кварталов от 59-й улицы и 8-й авеню до 72-й улицы и 10-й авеню проходит вдоль Бродвея?

Найдите расстояние между точками (59,8) и (72,10). Формула расстояния заставит нас найти квадратный корень из суммы квадрата 13 и 2. 169 + 4 = 173. Квадратный корень 173 равен 13,2. Расстояние по Бродвею — 13,2 квартала.

Резюме урока

Давайте уделим несколько минут тому, чтобы повторить то, что мы узнали в этом уроке.Когда фигуры нарисованы на геометрической плоскости, они обладают такими свойствами, как наклон, расстояние и средняя точка. Мы узнали, что наклон , когда он применяется к координатной сетке XY, является мерой того, насколько изменяется значение y по сравнению с тем, насколько быстро изменяется значение x . Средняя точка — это точка, которая находится на равном расстоянии от обеих точек и лежит на отрезке линии, соединяющей две точки. А расстояние находится с помощью формулы расстояния.

Чтобы найти наклон, найдите разницу между двумя значениями y и разделите ее на разницу между двумя значениями x . Средняя точка получается путем взятия среднего из двух значений x и среднего из двух значений y . Формула расстояния, которую мы упомянули секунду назад, основана на теореме Пифагора , которая гласит, что сумма квадратов двух катетов равна квадрату гипотенузы. Чтобы найти расстояние между двумя точками, найдите разницу между двумя значениями y и разницу между двумя значениями x .Возведите оба числа в квадрат, сложите квадраты вместе и извлеките квадратный корень из общей суммы.

7.3.4: Расстояния на координатной плоскости

Давайте исследуем расстояние на координатной плоскости.

Упражнение \ (\ PageIndex {3} \): определение расстояний на координатной плоскости

Обозначьте каждую точку ее координатами.
Найдите расстояние между каждой из следующих пар точек.
1. Точка \ (B \) и \ (C \)
2. Точка \ (D \) и \ (B \)
3. Точка \ (D \) и \ (E \)
Какая из точек равна 5 единицам от \ ((- 1.5, -3) \)?
Какая из точек равна 2 единицам от \ ((0,5, -4,5) \)?
Постройте точку, которая находится на расстоянии 2,5 единиц от \ (A \) и 9 единиц от \ (E \). Обозначьте эту точку \ (F \) и запишите ее координаты.

Вы готовы к большему?

Прия говорит: «Есть ровно четыре точки на расстоянии 3 единиц от \ ((- 5,0) \)». Лин говорит: «Я думаю, что есть множество точек, которые находятся на расстоянии 3 единиц от \ ((- 5,0) \)».

Вы согласны с одним из них? Объясните свои рассуждения.

Сводка

Точки \ (A = (5,2), B = (- 5,2), C = (- 5, -2), \) и \ (D = (5, -2) \) показаны на самолет. Обратите внимание, что все они имеют почти одинаковые координаты, за исключением разных знаков. Все они находятся на одинаковом расстоянии от каждой оси, но находятся в разных квадрантах.

Рисунок \ (\ PageIndex {1} \)

Обратите внимание, что вертикальное расстояние между точками \ (A \) и \ (D \) составляет 4 единицы, потому что точка \ (A \) находится на 2 единицы выше горизонтальной оси, а точка \ (D \) на 2 единицы ниже горизонтальной оси.Горизонтальное расстояние между точками \ (A \) и \ (B \) составляет 10 единиц, потому что точка \ (B \) находится на 5 единиц слева от вертикальной оси, а точка \ (A \) — на 5 единиц вправо. вертикальной оси.

По знакам координат всегда можно определить, в каком квадранте находится точка.

Таблица \ (\ PageIndex {1} \)
\ (х \)	\ (г \)	квадрант
положительный	положительный	I
отрицательный	положительный	II
отрицательный	отрицательный	III
положительный	отрицательный	IV

Рисунок \ (\ PageIndex {2} \)

В общем:

Если две точки имеют противоположные координаты \ (x \) (например, 5 и -5), они находятся на одинаковом расстоянии от вертикальной оси, но одна находится слева, а другая — справа.
Если две точки имеют противоположные координаты \ (y \) (например, 2 и -2), они находятся на одинаковом расстоянии от горизонтальной оси, но одна находится выше, а другая ниже.

Когда две точки имеют одинаковое значение для первой или второй координаты, мы можем найти расстояние между ними, вычитая разные координаты. Например, рассмотрим \ ((1,3) \) и \ ((5,3) \):

Рисунок \ (\ PageIndex {3} \)

У них одинаковая \ (y \) — координата. Если мы вычтем \ (x \) — координаты, мы получим \ (5-1 = 4 \).Эти точки находятся на расстоянии 4 единиц друг от друга.

Как выполнять вычисления с использованием точек на графике [Видео и практика]

Расчеты с использованием точек на графике

Здравствуйте и добро пожаловать в это видео о расчетах с использованием точек на координатной плоскости !

Итак, во-первых, давайте вспомним, что одномерная числовая линия представляет собой представление всех действительных чисел, которое бесконечно простирается как в положительном, так и в отрицательном направлениях и выглядит примерно так:

Когда две числовые линии пересекаются справа угол в их координатах 0 формируется двумерная координатная плоскость, которая обычно выглядит примерно так:

Обычно горизонтальная ось называется осью x , а вертикальная ось называется y — ось.Точка пересечения осей называется исходной точкой . Давайте нарисуем точку на координатной плоскости.

Местоположение точки A задается как горизонтальный компонент ( x ) и вертикальный компонент ( y ) и записывается как \ ((x, y) \). Из исходной точки, чтобы добраться до точки A , мы должны отсчитать 2 единицы вправо и 3 единицы вверх. Итак, координаты Точки A равны \ ((2,3) \). Точно так же координаты начала координат равны \ ((0,0) \).

Так как координатная плоскость состоит из числовых линий, их можно просматривать «увеличенными» или «уменьшенными» настолько, насколько это необходимо для передачи данных или истории. Например, ось x здесь была «увеличена»:

Из-за масштаба оси x координаты точки B следующие: \ ((\ frac {1} {2}, 3) \).

При этом ось x была увеличена, а ось y уменьшена:

Из-за масштабов осей координаты точки C равны \ (( 0. 2} \)

.2} \)

\ (D = \ sqrt {0,36 + 422,500} \)

\ (D = \ sqrt {422,500,36} \)

\ (D≈650 \)

Используя координаты точек на координатной плоскости, мы также можем вычислить координаты точки, которая находится точно посередине между двумя точками, которая называется средней точкой.

Формула для определения координат средней точки выглядит следующим образом:

\ (M = (\ frac {x_1 + x_2} {2}, \ frac {y_1 + y_2} {2}) \)

На словах это легко запомнить как «(среднее значение x , среднее значение x )».

Как мы видели ранее, расстояние между точками A и D составляет 6. Половина этого расстояния составляет 3. Поскольку точки A и D лежат на одной линии сетки, средняя точка будет лежать там. а также в координатах \ ((- 1, 3) \).

Мы можем проверить это с помощью формулы:

\ (M = (\ frac {x_1 + x_2} {2}, \ frac {y_1 + y_2} {2}) \)

\ (M = (\ frac {-4 + 2} {2}, \ frac {3 + 3} {2}) \)

\ (M = (\ frac {-2} {2}, \ frac {6} {2}) \)

\ (М = (- 1,3) \)

Хотя мы всегда можем вычислить половину расстояния между двумя точками, это не скажет нам координаты средней точки в этом примере, как это делает формула:

\ (M = (\ frac {x_1 + x_2} {2}, \ frac {y_1 + y_2} {2}) \)

\ (M = (\ frac {\ frac {1} {2} + \ frac {3} {2}} {2}, \ frac {3 + (- 6)} {2}) \)

\ (M = (\ frac {2} {2}, \ frac {-3} {2}) \)

\ (M = (1, — \ frac {3} {2}) \)

Для построения графика нам нужно оценить местоположение \ (- \ frac {3} {2} \).

Ранее мы оценивали координаты точки F как \ ((- 0.4, -350) \). Давайте воспользуемся формулой для оценки средней точки между точками C и F :

\ (M = (\ frac {x_1 + x_2} {2}, \ frac {y_1 + y_2} {2}) \)

\ (M≈ (\ frac {0,2 + (- 0,4)} {2}, \ frac {-350 + 300} {2}) \)

\ (M≈ (\ frac {-0.2} {2}, \ frac {-50} {2}) \)

\ (M≈ (-0,1, -25) \)

Для построения графика нам нужно оценить местоположение -25.

Я надеюсь, что это видео помогло вам понять, как выполнять вычисления с использованием точек на координатной плоскости! Спасибо за просмотр и удачной учебы!

Координатная плоскость — формула средней точки и расстояния

Координатная плоскость

Координатная плоскость — это двумерная числовая линия, в которой каждая точка однозначно определяется парой числовых координат.Он содержит две вертикальные линии, называемые осью , .

Кроме того, горизонтальная линия называется осью $ x $ , а вертикальная линия — осью $ y $ . Их пересечение называется точкой начала отсчета .

Координата — это упорядоченная пара, которая сообщает нам местоположение точки, которую она представляет. Первое число в упорядоченной паре говорит нам, как далеко находится точка от исходной точки на оси $ x $.Точно так же другое число говорит нам, как далеко находится точка от исходной точки на оси $ y $.

Координаты исходной точки: $ (0, 0) $.

Обе оси имеют положительную сторону и отрицательную сторону . Отрицательная сторона оси $ x $ находится слева от исходной точки, а положительная — справа. Точно так же отрицательная сторона оси $ y $ расположена ниже исходной точки, а положительная — вверху.

Кроме того, две оси делят плоскость на четыре секции, которые называются квадрантами . Квадранты помечены римскими цифрами , начиная с положительной стороны оси $ x $ и заканчивая против часовой стрелки .

Точки на координатной плоскости

Все точки в первом квадранте имеют обе координаты положительные, во втором квадранте все координаты $ x $ отрицательны, а координаты $ y $ положительны, в третьем обе координаты отрицательны, а в четвертом координаты $ x $ равны положительные и отрицательные координаты $ y $.

Например, $ A (1,1) $ — точка в первом квадранте, $ B (-3,2) $ — во втором квадранте, $ C (-4, -4) $ — в третьем квадранте и $ D (5, -2) $ в четвертом.

Как определить координаты конкретных точек, находящихся в координатной плоскости?

Координата $ x $ определяется путем проведения линии через $ A $, перпендикулярной оси $ x $, а координата $ y $ определяется путем проведения линии через $ A $, перпендикулярной оси $ y $.

Кроме того, вертикальная линия пересекает ось $ x $ в $ 2 $ и горизонтальную ось $ y $ в $ 3 $.В результате $ x $ -координата $ A $ равна $ 2 $, а $ y $ -координата $ A $ равна $ 3 $. Впоследствии это записывается как: $ A (2, 3) $.

Формула средней точки

Как мы можем вычислить точную середину отрезка $ AB $, если, например, $ A (2, 4) $ и $ B (-4, 2) $?

Средняя точка сегмента находится на полпути между двумя конечными точками сегмента. То есть его координата $ x $ находится на полпути между координатами $ x $ конечных точек, а его координата $ y $ находится на полпути между координатами $ y $ конечных точек.

Следовательно, если мы хотим вычислить среднюю точку, мы просто добавляем модули координат $ x $ и делим на 2. После этого мы делаем то же самое для координат $ y $.

Далее, в нашем примере: $$ \ frac {-4 + 2} {2} = -1, \ frac {4 + 2} {2} = 3. $$

Точнее точная формула:

$ \ M = \ left (\ frac {x_1 + x_2} {2}, \ frac {y_1 + y_2} {2} \ right) $

, где $ x_1 $ и $ y_1 $ — координаты первой точки, а $ x_2 $ и $ y_2 $ — второй.

Формула расстояния

Расстояние между точками $ A $ и $ B $ отмечено модулем : $ | AB | $ . Кроме того, он представляет собой наименьшей длины от одной точки до другой.

Например, если $ A (-2, 2), B (4, -2) $ и $ C (4, 2) $, то расстояние между $ A $ и $ C $ легко определить, так как их $ y $ координаты совпадают. Поэтому все, что вам нужно сделать, это добавить длину слева к правой.Другими словами, $ | AC | = 2 + 4 = 6 $.

Аналогично, $ C $ и $ B $ имеют общую координату $ x $, поэтому: $ | CB | = 2 + 2 = 4 $.

Но что делать с расстоянием между $ A $ и $ B $? Как вы уже заметили, треугольник $ ABC $ прямоугольный. Кроме того, расстояние между $ A $ и $ B $ равно длине его гипотенузы. Таким образом, теперь мы знаем, что можем легко вычислить желаемое расстояние с помощью теоремы Пифагора.2} = \ sqrt {4} = 2

долл. США
Параллельные линии в координатной плоскости
Наклон линии — это число, которое описывает крутизны линии или насколько она отклонена от оси $ x $. Обычно мы обозначаем его $ m $.
Кроме того, если угол наклона двух прямых равен , тогда прямые параллельны .
Кроме того, мы можем рассчитать наклон по формуле:
$ m = \ frac {y_2 — y_1} {x_2 — x_1}, $
, где $ T_ {1} = (x_1, y_1) $ и $ T_ {2} = (x_2, y_2) $ — произвольные точки данной прямой.
Пример 2:
Если $ A \ left (-4, 5 \ right) $ и $ B \ left (\ frac {2} {3}, 4 \ right) $, вычислить наклон прямой $ AB $.
Решение:
$ m = \ frac {y_2 — y_1} {x_2 — x_1} = \ frac {4 — 5} {\ frac {2} {3} — (-4)} = \ frac {-1} {\ frac { 14} {3}} = — \ frac {3} {14}
долл. США
В итоге, наклон этой прямой равен $ — \ frac {3} {14} $.
Пример 3:
Вычислить наклон заданной линии.
Решение:
Вы просто выбираете любые две точки, через которые проходит линия. Например, мы можем выбрать $ (- 2, 0) $ и $ (0, 1) $. В итоге получаем
$ m = \ frac {y_2 — y_1} {x_2 — x_1} = \ frac {1 — 0} {0 — (-2)} = \ frac {1} {2}. $
Пример 4:
Если первая строка содержит точки $ A (2, 4) $ и $ B (3, 2) $, а вторая строка содержит точки $ C (4,8) $ и $ D (6, 4) $, то эти строки являются параллельно?
Решение:
$ m_1 = \ frac {y_2 — y_1} {x_2 — x_1} = \ frac {2 — 4} {3 — 2} = \ frac {2 — 4} {3 — 2} = -2 $
Аналогично
$ m_2 = \ frac {y_2 — y_1} {x_2 — x_1} = \ frac {4-8} {6-4} = \ frac {-4} {2} = -2.$
Следовательно, их наклоны равны, поэтому мы заключаем, что линии параллельны.
Листы координатной плоскости
Параллельные прямые и поперечные
Назовите связь (647,5 KiB, 997 совпадений)
Найдите значение x (809,9 KiB, 1283 совпадений)
Найдите недостающий угол (767,1 KiB, 984 совпадений)
Найдите угол и отсутствующее значение (840.6 KiB, 1218 обращений)
Найдите значение, зная 2 параметра (755,1 KiB, 766 обращений)
Точки на координатной плоскости
Найдите квадрант (2,4 МБ, 1006 обращений)
Точки Plote (2,5 МБ, 1015 обращений)
Найдите координаты каждой точки (2,1 МБ, 1007 обращений)
Формула средней точки
Целые числа (207,6 КиБ, 1102 совпадений)
Десятичные числа (211.

определение и примеры нахождения, расстояние между точкой и плоскостью

Расстояние от точки до плоскости – определение

Расстояние от точки до плоскости – теория, примеры, решения

Декартова система координат: основные понятия и примеры

Плоскости координатные — Энциклопедия по машиностроению XXL

§ 26. Расстояние от точки до плоскости в координатах

Расстояние от точки до плоскости – теория, примеры, решения

Расстояние от точки до плоскости

Приведение общего уравнения плоскости к нормальному виду

Примеры задач на тему «Плоскость».

Презентация к уроку

Решение задач с использованием координатных плоскостей Текст научной статьи по специальности «Математика»

Калькулятор расстояний

2D-калькулятор расстояния

Трехмерный калькулятор расстояний

Расстояние по широте и долготе

Расстояние на карте

Расстояние в системе координат

Расстояние между двумя точками на поверхности Земли

Координатная плоскость

Свойства координатной плоскости

ось x и ось y

Квадранты и заказанные пары

Определение точки на координатной плоскости

Построение набора решений в координатной плоскости

Знаете ли вы?

Прямоугольная система координат

Тематические упражнения

Уклон, середина, параллельность и расстояние в координатной плоскости — видео и стенограмма урока

Различные размеры

1.Наклон

2. Параллельность

3. Средняя точка

4. Расстояние

Пример 1

Пример 2

Пример 3

Резюме урока

7.3.4: Расстояния на координатной плоскости

Сводка

Как выполнять вычисления с использованием точек на графике [Видео и практика]

Расчеты с использованием точек на графике

Координатная плоскость — формула средней точки и расстояния

Координатная плоскость

Точки на координатной плоскости

Формула средней точки

Формула расстояния

Параллельные линии в координатной плоскости

Листы координатной плоскости

Добавить комментарий Отменить ответ