Неравенство Коши — Буняковского — Википедия
Материал из Википедии — свободной энциклопедии
Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в евклидовом или гильбертовом пространстве. Это неравенство эквивалентно неравенству треугольника для нормы.
Неравенство Коши — Буняковского иногда, особенно в иностранной литературе, называют неравенством Шварца и неравенством Коши — Буняковского — Шварца («неравенство КБШ»), хотя работы Шварца на эту тему появились только спустя 25 лет после работ Буняковского[1]. Конечномерный случай этого неравенства называется неравенством Коши и был доказан Коши в 1821 году.
Формулировка
Пусть дано линейное пространство L{\displaystyle L} со скалярным произведением ⟨x,y⟩{\displaystyle \langle x,\;y\rangle }. Пусть ‖x‖{\displaystyle \|x\|} — норма, порождённая скалярным произведением, то есть ‖x‖≡⟨x,x⟩,∀x∈L{\displaystyle \|x\|\equiv {\sqrt {\langle x,\;x\rangle }},\;\forall x\in L}. Тогда для любых x,y∈L{\displaystyle x,\;y\in L} имеем:
- |⟨x,y⟩|⩽‖x‖⋅‖y‖,{\displaystyle |\langle x,\;y\rangle |\leqslant \|x\|\cdot \|y\|,}
причём равенство достигается тогда и только тогда, когда векторы x{\displaystyle x} и y{\displaystyle y} пропорциональны (коллинеарны).
Комментарии
В конечномерном случае можно заметить, что ‖x‖2‖y‖2−⟨x,y⟩2=S(x,y)2{\displaystyle \|x\|^{2}\|y\|^{2}-\langle x,\;y\rangle ^{2}=S(x,\;y)^{2}}, где S(x,y){\displaystyle S(x,\;y)} — площадь параллелограмма, натянутого на векторы x{\displaystyle x} и y{\displaystyle y}.
В общем случае:
- ‖x‖2−⟨x,y⟩2‖y‖2=‖x−⟨x,y⟩‖y‖2y‖2.{\displaystyle \|x\|^{2}-{\frac {\langle x,\;y\rangle ^{2}}{\|y\|^{2}}}=\left\|x-{\frac {\langle x,\;y\rangle }{\|y\|^{2}}}y\right\|^{2}.}
Примеры
- Важным частным случаем, часто использующимся в теории чисел, является случай, когда один из векторов полностью состоит из единиц:
- (∑i=1nai)2≤(∑i=1n1)∑i=1nai2=n∑i=1nai2{\displaystyle \left({\sum \limits _{i=1}^{n}{a_{i}}}\right)^{2}\leq \left({\sum \limits _{i=1}^{n}{1}}\right)\sum \limits _{i=1}^{n}{{a_{i}}^{2}}=n\sum \limits _{i=1}^{n}{{a_{i}}^{2}}}
- |∑k=1∞xky¯k|2⩽(∑k=1∞|xk|2)⋅(∑k=1∞|yk|2),{\displaystyle \left|\sum \limits _{k=1}^{\infty }x_{k}{\bar {y}}_{k}\right|^{2}\leqslant \left(\sum _{k=1}^{\infty }|x_{k}|^{2}\right)\cdot \left(\sum _{k=1}^{\infty }|y_{k}|^{2}\right),}
где y¯k{\displaystyle {\bar {y}}_{k}} обозначает комплексное сопряжение yk{\displaystyle y_{k}}.
- |∫Xf(x)g(x)¯μ(dx)|2⩽(∫X|f(x)|2μ(dx))⋅(∫X|g(x)|2μ(dx)).{\displaystyle \left|\int \limits _{X}f(x){\overline {g(x)}}\,\mu (dx)\right|^{2}\leqslant \left(\int \limits _{X}\left|f(x)\right|^{2}\,\mu (dx)\right)\cdot \left(\int \limits _{X}\left|g(x)\right|^{2}\,\mu (dx)\right).}
- В пространстве случайных величин с конечным вторым моментом L2(Ω,F,P){\displaystyle L^{2}(\Omega ,\;{\mathcal {F}},\;\mathbb {P} )} неравенство Коши — Буняковского имеет вид:
- cov2(X,Y)⩽D[X]⋅D[Y],{\displaystyle \mathrm {cov} ^{2}(X,\;Y)\leqslant \mathrm {D} [X]\cdot \mathrm {D} [Y],}
- где cov{\displaystyle \mathrm {cov} } обозначает ковариацию, а D{\displaystyle \mathrm {D} } — дисперсию.
- Для двух независимых случайных величин ξ{\displaystyle \xi } и η{\displaystyle \eta } неравенство Коши — Буняковского имеет вид:
- M[η⋅ξ]2⩽M[η2⋅ξ2]=Mη2⋅Mξ2.{\displaystyle \mathbf {M} \left[\eta \cdot \xi \right]^{2}\leqslant \mathbf {M} \left[\eta ^{2}\cdot \xi ^{2}\right]=\mathbf {M} \eta ^{2}\cdot \mathbf {M} \xi ^{2}.}
Доказательство
- Если ⟨x,y⟩∈R,{\displaystyle \langle x,y\rangle \in \mathbb {R} ,} то ∀λ∈R{\displaystyle \forall \lambda \in \mathbb {R} } верно следующее
- 0⩽⟨λx+y,λx+y⟩=λ2⟨x,x⟩+2λ⟨x,y⟩+⟨y,y⟩.{\displaystyle 0\leqslant \langle \lambda x+y,\;\lambda x+y\rangle =\lambda ^{2}\langle x,\;x\rangle +2\lambda \langle x,\;y\rangle +\langle y,\;y\rangle .}
Значит, дискриминант многочлена λ2⟨x,x⟩+2λ⟨x,y⟩+⟨y,y⟩{\displaystyle \lambda ^{2}\langle x,\;x\rangle +2\lambda \langle x,\;y\rangle +\langle y,\;y\rangle } неположительный, то есть
- D=4(⟨x,y⟩)2−4⟨x,x⟩⟨y,y⟩⩽0.{\displaystyle D=4(\langle x,\;y\rangle )^{2}-4\langle x,\;x\rangle \langle y,\;y\rangle \leqslant 0.}
Следовательно,
- |⟨x,y⟩|⩽‖x‖⋅‖y‖.{\displaystyle |\langle x,\;y\rangle |\leqslant \|x\|\cdot \|y\|.}
- Если Im⟨x,y⟩≠0,{\displaystyle \operatorname {Im} \langle x,y\rangle \neq 0,} то представим скалярное произведение в тригонометрическом виде ⟨x,y⟩=reiϕ.{\displaystyle \langle x,y\rangle =re^{i\phi }.}
Определим вектор z=e−iϕx.{\displaystyle z=e^{-i\phi }x.} Тогда
- ⟨z,y⟩=e−iϕ⟨x,y⟩=r=|⟨x,y⟩|∈R{\displaystyle \langle z,y\rangle =e^{-i\phi }\langle x,y\rangle =r=\left|\langle x,y\rangle \right|\in \mathbb {R} } и
- ⟨z,z⟩=e−iϕ⟨x,e−iϕx⟩=e−iϕeiϕ⟨x,x⟩=⟨x,x⟩.{\displaystyle \langle z,z\rangle =e^{-i\phi }\langle x,e^{-i\phi }x\rangle =e^{-i\phi }e^{i\phi }\langle x,x\rangle =\langle x,x\rangle .}
К скалярному произведению ⟨z,y⟩∈R{\displaystyle \langle z,y\rangle \in \mathbb {R} } применим результат первого пункта доказательства.
- |⟨x,y⟩|=r=⟨z,y⟩⩽‖z‖⋅‖y‖=‖x‖⋅‖y‖.{\displaystyle \left|\langle x,y\rangle \right|=r=\langle z,y\rangle \leqslant \|z\|\cdot \|y\|=\|x\|\cdot \|y\|.}
Примечания
- ↑ Bounjakowsky W. «Mémoires de l’Académie des sciences de St-Pétersbourg. 7 série», 1859, t. 1, № 9.
Буняковского неравенство — это… Что такое Буняковского неравенство?
- Буняковского неравенство
одно из важнейших неравенств математического анализа, утверждающее, что
 установлено В. Я. Буняковским (См. Буняковский). Это неравенство аналогично элементарному алгебраическому Коши неравенству (См. Коши неравенство):
установлено В. Я. Буняковским (См. Буняковский). Это неравенство аналогично элементарному алгебраическому Коши неравенству (См. Коши неравенство):
 и может быть получено из последнего посредством перехода к пределу. Нередко в математической литературе Б. н. ошибочно называется неравенством Шварца — по имени Г. А. Шварца. Однако В. Я. Буняковский опубликовал свою работу о неравенствах ещё в 1859, тогда как в работах Шварца то же неравенство появляется не ранее 1884 (без ссылок на Буняковского).
и может быть получено из последнего посредством перехода к пределу. Нередко в математической литературе Б. н. ошибочно называется неравенством Шварца — по имени Г. А. Шварца. Однако В. Я. Буняковский опубликовал свою работу о неравенствах ещё в 1859, тогда как в работах Шварца то же неравенство появляется не ранее 1884 (без ссылок на Буняковского).Лит.: Bounjakowsky W., Sur quelques inégalités concernant les intégrates ordinaires et les intégrates aux différences finies (Lu ie 29 avril 1859), «Mémoires de l’Académie des sciences de St.-Pétersbourg. 7 série», 1859, t. 1, № 9.
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Буняковский Виктор Яковлевич
- Буолкалах
Смотреть что такое «Буняковского неравенство» в других словарях:
Буняковского неравенство
— Неравенство Коши Буняковского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Неравенство Коши Буняковского… … ВикипедияБУНЯКОВСКОГО НЕРАВЕНСТВО — неравенство математич. анализа; для функций j(x).и g(x), интегрируемых с квадратом, установлено В. Я. Буняковским [1]. Это неравенство аналогично алгебраич. неравенству Коши: Иногда Б. н. наз. неравенством Шварца (по имени Г. А. Шварца; Н. A.… … Математическая энциклопедия
Неравенство Коши — Буняковского — Неравенство Коши Буняковского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Неравенство Коши … … Википедия
Неравенство Коши — Неравенство Коши Буняковского связывает норму и скалярное произведение векторов в евклидовом пространстве. Это неравенство эквивалентно неравенству треугольника для нормы. Неравенство Коши Буняковского иногда, особенно в иностранной… … Википедия
Неравенство Буняковского — Неравенство Коши Буняковского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Неравенство Коши Буняковского… … Википедия
Неравенство Коши-Буняковского — связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Неравенство Коши Буняковского иногда, особенно в иностранной… … Википедия
Неравенство Коши—Буняковского — связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Неравенство Коши Буняковского иногда, особенно в иностранной… … Википедия
Неравенство Шварца — Неравенство Коши Буняковского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Неравенство Коши Буняковского… … Википедия
Неравенство Гёльдера — в функциональном анализе и смежных дисциплинах это фундаментальное свойство пространств . Содержание 1 Формулировка 2 Доказательство … Википедия
Неравенство Гельдера — Неравенство Гёльдера в функциональном анализе и смежных дисциплинах это фундаментальное свойство пространств Lp. Содержание 1 Формулировка 2 Частные случаи 2.1 Неравен … Википедия
Буняковского неравенство Википедия
Неравенство Коши — Буняковского иногда, особенно в иностранной литературе, называют неравенством Шварца и неравенством Коши — Буняковского — Шварца, хотя работы Шварца на эту тему появились только спустя 25 лет после работ Буняковского[1]. Конечномерный случай этого неравенства называется неравенством Коши и был доказан Коши в 1821 году.
Формулировка[ | ]
Пусть дано линейное пространство L{\displaystyle L} со скалярным произведением ⟨x,y⟩{\displaystyle \langle x,\;y\rangle }. Пусть ‖x‖{\displaystyle \|x\|} — норма, порождённая скалярным произведением, то есть ‖x‖≡⟨x,x⟩,∀x∈L{\displaystyle \|x\|\equiv {\sqrt {\langle x,\;x\rangle }},\;\forall x\in L}. Тогда для любых x,y∈L{\displaystyle x,\;y\in L} имеем:
- |⟨x,y⟩|⩽‖x‖⋅‖y‖,{\displaystyle |\langle x,\;y\rangle |\leqslant \|x\|\cdot \|y\|,}
причём равенство достигается тогда и только тогда, когда векторы x{\displaystyle x} и y{\displaystyle y} пропорциональны (коллинеарны).
Комментарии[ | ]
В конечномерном случае можно заметить, что
Неравенство Буняковского Википедия
Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в евклидовом или гильбертовом пространстве. Это неравенство эквивалентно неравенству треугольника для нормы.
Неравенство Коши — Буняковского иногда, особенно в иностранной литературе, называют неравенством Шварца и неравенством Коши — Буняковского — Шварца, хотя работы Шварца на эту тему появились только спустя 25 лет после работ Буняковского[1]. Конечномерный случай этого неравенства называется неравенством Коши и был доказан Коши в 1821 году.
Формулировка[ | ]
Пусть дано линейное пространство L{\displaystyle L} со скалярным произведением ⟨x,y⟩{\displaystyle \langle x,\;y\rangle }. Пусть ‖x‖{\displaystyle \|x\|} — норма, порождённая скалярным произведением, то есть ‖x‖≡⟨x,x⟩,∀x∈L{\displaystyle \|x\|\equiv {\sqrt {\langle x,\;x\rangle }},\;\forall x\in L}. Тогда для любых x,y∈L{\displaystyle x,\;y\in L} имеем:
- |⟨x,y⟩|⩽‖x‖⋅‖y‖,{\displaystyle |\langle x,\;y\rangle |\leqslant \|x\|\cdot \|y\|,}
причём равенство достигается тогда и только тогда, когда векторы x{\displaystyle x} и y{\displaystyle y} пропорциональны (коллинеарны).
Комментарии[ | ]
В конечномерном случае можно заметить, что
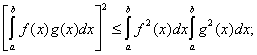 установлено В. Я. Буняковским (См. Буняковский). Это неравенство аналогично элементарному алгебраическому Коши неравенству (См. Коши неравенство):
установлено В. Я. Буняковским (См. Буняковский). Это неравенство аналогично элементарному алгебраическому Коши неравенству (См. Коши неравенство):
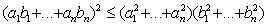 и может быть получено из последнего посредством перехода к пределу. Нередко в математической литературе Б. н. ошибочно называется неравенством Шварца — по имени Г. А. Шварца. Однако В. Я. Буняковский опубликовал свою работу о неравенствах ещё в 1859, тогда как в работах Шварца то же неравенство появляется не ранее 1884 (без ссылок на Буняковского).
и может быть получено из последнего посредством перехода к пределу. Нередко в математической литературе Б. н. ошибочно называется неравенством Шварца — по имени Г. А. Шварца. Однако В. Я. Буняковский опубликовал свою работу о неравенствах ещё в 1859, тогда как в работах Шварца то же неравенство появляется не ранее 1884 (без ссылок на Буняковского).