2. Несобственные интегралы
Несобственный интеграл
Определенный интеграл как предел интегральной суммы
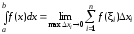
может существовать (т.е. иметь определенное конечное значение) лишь при выполнении условий
отрезок интегрирования [a; b] конечный;
подынтегральная функция
 непрерывная (или хотя бы кусочно-непрерывная)
и, следовательно, ограниченная на этом
отрезке.
непрерывная (или хотя бы кусочно-непрерывная)
и, следовательно, ограниченная на этом
отрезке.
Если хотя бы одно из этих условий нарушено, то определение теряет смысл. Действительно, в случае бесконечного отрезка, например [
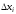 ,
которая к тому же с увеличением количества
отрезков стремилась бы к нулю. В случае
же неограниченной в некоторой точке с[a; b]
нарушается требование произвольного
выбора точки
,
которая к тому же с увеличением количества
отрезков стремилась бы к нулю. В случае
же неограниченной в некоторой точке с[a; b]
нарушается требование произвольного
выбора точки 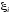 на частичных отрезках – нельзя выбрать
на частичных отрезках – нельзя выбрать 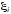 =с,
поскольку значение функции в этой точке
не определено. Однако и для этих случаев
можно обобщить понятие определенного
интеграла, введя еще один предельный
переход. Интегралы по бесконечным
промежуткам и от разрывных (неограниченных)
функций называют несобственными.
=с,
поскольку значение функции в этой точке
не определено. Однако и для этих случаев
можно обобщить понятие определенного
интеграла, введя еще один предельный
переход. Интегралы по бесконечным
промежуткам и от разрывных (неограниченных)
функций называют несобственными.Определение.
Пусть
функция 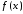
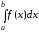 для любого b > a.
Предел вида
для любого b > a.
Предел вида 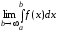 называют несобственным
интегралом первого
рода (или
несобственным интегралом по бесконечному
промежутку) и обозначают
называют несобственным
интегралом первого
рода (или
несобственным интегралом по бесконечному
промежутку) и обозначают 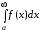 .
. Таким
образом, по определению, 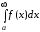 =
= .
.
Если
предел справа существует и конечен, то
несобственный интеграл 
Аналогично
можно ввести понятие несобственного
интеграла от функции 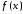 по промежутку (–; b]:
по промежутку (–; b]:
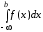 =
= .
.
А
несобственный интеграл от функции  по промежутку (–;
+)
определяется как сумма введенных выше
интегралов:
по промежутку (–;
+)
определяется как сумма введенных выше
интегралов:
 =
=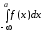
 ,
,где а – произвольная точка. Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно из слагаемых.
 С
геометрической точки зрения, интеграл
С
геометрической точки зрения, интеграл  ,
,  ,
определяет численное значение площади
бесконечной криволинейной трапеции,
ограниченной сверху графиком функции
,
определяет численное значение площади
бесконечной криволинейной трапеции,
ограниченной сверху графиком функции 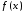 ,
слева – прямой
,
слева – прямой 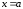 ,
снизу – осью ОХ. Сходимость интеграла
означает существование конечной площади
такой трапеции и равенство ее пределу
площади криволинейной трапеции с
подвижной правой стенкой
,
снизу – осью ОХ. Сходимость интеграла
означает существование конечной площади
такой трапеции и равенство ее пределу
площади криволинейной трапеции с
подвижной правой стенкой 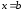
На случай интеграла с бесконечным пределом можно обобщить и формулу Ньютона-Лейбница:
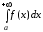 =
=  =
F(+)
– F(a),
=
F(+)
– F(a),
где
F(+)
= 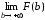 .
Если этот предел существует, то интеграл
сходится, в противном случае – расходится.
.
Если этот предел существует, то интеграл
сходится, в противном случае – расходится.
Мы рассмотрели обобщение понятия определенного интеграла на случай бесконечного промежутка.
Рассмотрим теперь обобщение для случая неограниченной функции.
Определение
Пусть
функция  определена на промежутке [a; b),
неограниченна в некоторой окрестности
точки b,
и непрерывна на любом отрезке
определена на промежутке [a; b),
неограниченна в некоторой окрестности
точки b,
и непрерывна на любом отрезке 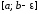 ,
где >0
(и, следовательно, интегрируема на этом
отрезке, т.е.
,
где >0
(и, следовательно, интегрируема на этом
отрезке, т.е.  существует). Предел вида
существует). Предел вида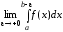 называется несобственным
интегралом второго рода (или несобственным интегралом от
неограниченной функции) и обозначается
называется несобственным
интегралом второго рода (или несобственным интегралом от
неограниченной функции) и обозначается  .
.
Таким образом, несобственный интеграл от неограниченной в точке
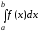 =
=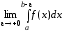 .
.
Если предел справа существует и конечен, то интеграл называется сходящимся. Если конечного предела не существует, то несобственный интеграл называется расходящимся.
Аналогично
можно определить несобственный интеграл
от функции 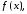 имеющей бесконечный разрыв в точке а:
имеющей бесконечный разрыв в точке а:
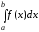 =
=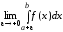 .
.
Если
функция 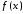
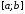 ,
то несобственный интеграл определяется
следующим образом
,
то несобственный интеграл определяется
следующим образом =
=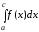 +
+ 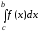 =
=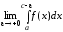 +
+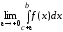 .
.
Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно слагаемое.
 С
геометрической точки зрения, несобственный
интеграл от неограниченной функции
также характеризует площадь неограниченной
криволинейной трапеции:
С
геометрической точки зрения, несобственный
интеграл от неограниченной функции
также характеризует площадь неограниченной
криволинейной трапеции:
Поскольку несобственный интеграл выводится путем предельного перехода из определенного интеграла, то все свойства определенного интеграла могут быть перенесены (с соответствующими уточнениями) на несобственные интеграла первого и второго рода.
Во многих задачах, приводящих к несобственным интегралам, не обязательно знать, чему равен этот интеграл, достаточно лишь убедиться в его сходимости или расходимости. Для этого используют признаки сходимости. Признаки сходимости несобственных интегралов:
1) Признак сравнения.
Пусть
для всех х
 .
Тогда, если
.
Тогда, если 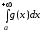
 ,
причем
,
причем 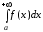
 .
Если
.
Если 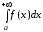 расходится, то расходится и
расходится, то расходится и  .
.2)
Если сходится 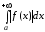 ,
то сходится и
,
то сходится и 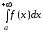 (последний интеграл в этом случае
называется абсолютно
сходящимся).
(последний интеграл в этом случае
называется абсолютно
сходящимся).
Признаки сходимости и расходимости несобственных интегралов от неограниченных функций аналогичны сформулированным выше.
Примеры решения задач.
Пример 1.
Вычислить несобственный интеграл или установить его расходимость:
а) 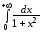 ;
б)
;
б) 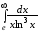 ;
в)
;
в)
г) 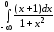 ; д).
; д).
Решение.
а) По определению имеем:
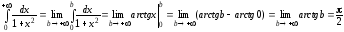 ,
,
Следовательно,
данный интеграл сходится и равен 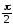 .
.
б) Аналогично
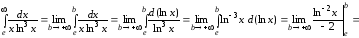
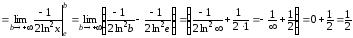 .
.
Следовательно,
данный интеграл сходится и равен 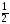 .
.
в)
По определению 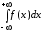 =
=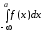 +
+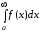 ,
причем, а – произвольное число. Положим в нашем
случае
,
причем, а – произвольное число. Положим в нашем
случае 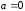 ,
тогда получим:
,
тогда получим:
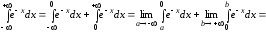

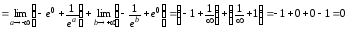 .
.
Данный интеграл сходится.
г) 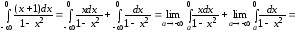

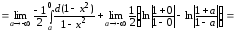
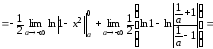


Значит, данный интеграл расходится.
д)
Рассмотрим .
Чтобы найти первообразную подынтегральной
функции, необходимо применить метод
интегрирования по частям. Тогда получим:
.
Чтобы найти первообразную подынтегральной
функции, необходимо применить метод
интегрирования по частям. Тогда получим:

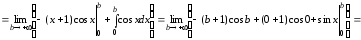

Поскольку
ни 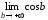 ,
ни
,
ни не существуют, то не существует и
не существуют, то не существует и
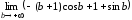 .
.
Следовательно, данный интеграл расходится.
Пример 2.
Исследовать
сходимость интеграла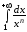 в зависимости от п.
в зависимости от п.
Решение.
При 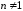 имеем:
имеем:
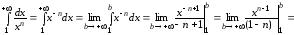
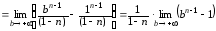 .
.
Если  ,
то
,
то  и
и 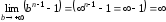 .
Следовательно, интеграл расходится.
.
Следовательно, интеграл расходится.
Если 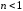 ,
то
,
то  ,
а
,
а 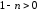 ,
тогда
,
тогда
 ,
,
 =
= 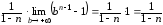 ,
,
Следовательно, интеграл сходится.
Если 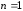 ,
то
,
то
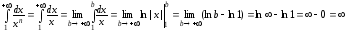 ,
,
следовательно, интеграл расходится.
Таким образом, 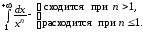
Пример 3.
Вычислить несобственный интеграл или установить его расходимость:
а) 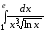 ;
б)
;
б)  ;
в)
;
в) 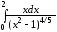 .
.
Решение.
а) Интеграл 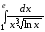 является несобственным интегралом
второго рода, поскольку подынтегральная
функция
является несобственным интегралом
второго рода, поскольку подынтегральная
функция  не ограничена в точке
не ограничена в точке 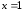
 .
Тогда, по определению,
.
Тогда, по определению,

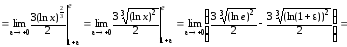
 .
.
Интеграл сходится и равен 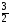 .
.
б) Рассмотрим .
Здесь также подынтегральная функция
не ограничена в точке
.
Здесь также подынтегральная функция
не ограничена в точке 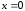 .
Поэтому, данный интеграл – несобственный
второго рода и по определению,
.
Поэтому, данный интеграл – несобственный
второго рода и по определению,
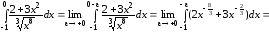

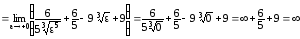 .
.
Следовательно, интеграл расходится.
в) Рассмотрим 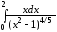 .
Подынтегральная функция
.
Подынтегральная функция 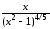 терпит бесконечный разрыв в двух точках:
терпит бесконечный разрыв в двух точках:  и
и  ,
первая из которых принадлежит промежутку
интегрирования
,
первая из которых принадлежит промежутку
интегрирования  .
Следовательно, данный интеграл –
несобственный второго рода. Тогда, по
определению
.
Следовательно, данный интеграл –
несобственный второго рода. Тогда, по
определению

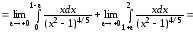

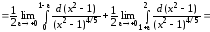

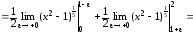
=
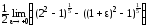 =
=

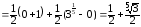 .
.
Следовательно, интеграл
сходится и равен 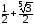 .
.
Несобственные интегралы первого и второго рода. Решение задач по высшей математике
Понятие несобственного интеграла является обобщением понятия определенного интеграла на случай, когда либо промежуток интегрирования бесконечен (интеграл имеет бесконечные пределы интегрирования), либо подынтегральная функция в некоторых точках обращается в бесконечность.
Рассмотрим несобственные интегралы первого рода.
Если функция определена на промежутке и при любом существует определенный интеграл
то можно рассматривать
этот предел и называют несобственным интегралом от функции на промежутке . Его обозначают
примем, если предел конечен, то говорят, что несобственный интеграл сходится, а функция интегрируема на промежутке ; если же предел бесконечен или вовсе не существует, то говорят, что несобственный интеграл расходится, а функция не интегрируема на .
Таким образом, по определению, если существует
то
Подобным образом определяются несобственные интегралы и для других бесконечных промежутков:
Так как несобственные интегралы с бесконечными пределами получаются предельным переходом из соответствующих определенных (собственных) интегралов, то на первые переносятся все те свойства последних, которые сохраняются при этом предельном переходе.
Перейдем теперь к рассмотрению несобственного интеграла от неограниченной функции (несобственного интеграла второго рода). Пусть функция определена на отрезке , за исключением точки , в окрестности которой она не ограничена. Если существует определенный интеграл
при любом , то можно рассматривать
Этот предел называется несобственным интегралом второго рода на от неограниченной на нем функции и обозначается
При этом, если предел существует и конечен, то несобственный интеграл называется сходящимся, а неограниченная функция – интегрируемой на . Если же предел бесконечен или вовсе не существует, то несобственный интеграл называется расходящимся, а функция – не интегрируемой на .
Аналогично определяется несобственный интеграл для случая, когда функция определена на отрезке , за исключением точки , в окрестности которой она не ограничена.
В случае, если точка разрыва функции – точка – лежит между точками и и несобственные интегралы на отрезках и существуют, то считают, то
Несобственные интегралы, зависящие от параметра. Равномерная сходимость
Решение.
\(\vartriangle\) Пусть \(y \geq \delta > 0\). Тогда оба интеграла сходятся равномерно по параметру \(y\) на \([\delta, +\infty)\) в силу признака Дирихле: функции \(\cos xy\) и \(\sin xy\) имеют ограниченные первообразные, а функции \(\displaystyle\frac{1}{1+x^{2}}\) и \(\displaystyle\frac{x}{1+x^{2}}\) стремятся к нулю при \(x \rightarrow +\infty\), причем
$$
\frac{d}{dx} \left(\frac{1}{1+x^{2}}\right) = -\frac{2x}{(1+x^{2})^{2}} \leq 0,\quad \frac{d}{dx} \left(\frac{x}{1+x^{2}}\right) = \frac{1-x^{2}}{(1+x^{2})^{2}} \leq 0\nonumber
$$
при \(x \geq 1\).
Дифференцируя \(I_{1}(y)\) по параметру, получаем
$$
\frac{dI_{1}(y)}{dy} = -\int\limits_{0}^{+\infty} \frac{x\sin xy}{1+x^{2}}\ dx = -I_{2}(y),\ \delta \leq y < +\infty.\label{ref26}
$$
Дифференцирование по параметру законно, так как интеграл \(I_{2}(y)\) сходится равномерно по параметру \(y\) при \(y \in [\delta, +\infty)\). Чтобы найти производную \(I_{2}(y)\), заметим, что при \(y \geq \delta > 0\)
$$
I_{2}(y) = \int\limits_{0}^{+\infty} \frac{x\sin xy}{1+x^{2}}\ dx = \int\limits_{0}^{+\infty} \left(\frac{1}{x}-\frac{1}{x(1+x^{2})}\right) \sin xy\ dx =\\= \int\limits_{0}^{+\infty} \frac{\sin xy}{x}\ dx-\int\limits_{0}^{+\infty} \frac{x\sin xy}{x(1+x^{2})}\ dx =\\= \int\limits_{0}^{+\infty} \frac{\sin t}{t}\ dt-\int\limits_{0}^{+\infty} \frac{x\sin xy}{(1+x^{2})x}\ dx = \frac{\pi}{2}-\int\limits_{0}^{+\infty} \frac{x\sin xy}{(1+x^{2})x}\ dx.\nonumber
$$
Применяя теорему 6, получаем
$$
\frac{dI_{2}(y)}{dy} = -\int\limits_{0}^{+\infty} \frac{\cos xy}{1+x^{2}}\ dx = -I_{1}(y),\ y \in [\delta, +\infty).\label{ref27}
$$
Из формул \eqref{ref26} и \eqref{ref27} следует, что при \(y \in [\delta, +\infty)\)
$$
I’_{1}(y) = -I_{2}(y),\ I’_{2}(y) = -I_{1}(y),\ I″_{1}(y)-I_{1}(y) = 0.\label{ref28}
$$
Решая это дифференциальное уравнение, получаем
$$
I_{1}(y) = C_{1}e^{-y}+C_{2}e^{y}\ \mbox{при}\ y \in [\delta, +\infty),\label{ref29}
$$
где \(C_{1}\) и \(C2\) — произвольные постоянные.
Покажем, что \(C_{2} = 0\). Так как
$$
|I_{1}(y)| = \left|\int\limits_{0}^{+\infty} \frac{\cos xy}{1+x^{2}}\ dx\right| \leq \int\limits_{0}^{+\infty} \frac{|\cos xy|}{1+x^{2}}\ dx \leq \int\limits_{0}^{+\infty} \frac{dx}{1+x^{2}} = \frac{\pi}{2},\nonumber
$$
то \(I_{1}(y)\) есть ограниченная функция на \([\delta, +\infty)\). Так как \(e^{y}\) — неограниченная функция на \([\delta, +\infty)\), то в формуле \eqref{ref29} нужно принять \(C_{2} = 0\).
Итак,
$$
I_{1}(y) = C_{1}e^{-y},\ I_{2}(y) = -I’_{1}(y) = C_{1}e^{-y}\ \mbox{при}\ y \in [\delta, +\infty).\label{ref30}
$$
Так как \(\delta\) — произвольное положительное число, то из \eqref{ref30} следует, что
$$
I_{1}(y) = C_{1}e^{-y} = I_{2}(y)\ \mbox{при}\ y > 0.\label{ref31}
$$
Замечая, что интеграл Лапласа \(I_{1}(y)\) есть четная функция на \((-\infty, +\infty)\), а интеграл \(I_{2}(y)\) есть нечетная функция на \((-\infty, +\infty)\), перепишем равенство \eqref{ref31} в следующем виде:
$$
I_{1}(y) = C_{1}e^{-|y|},\ I_{2}(y) = C_{1}\ \operatorname{sign}\ ye^{-|y|}\ \mbox{при}\ y \neq 0.\label{ref32}
$$
Для определения произвольной постоянной \(C_{1}\) воспользуемся тем, что интеграл Лапласа \(I_{1}(y)\) сходится равномерно по параметру \(y\) на \((-\infty, +\infty)\) (пример 3). Поэтому \(I_{1}(y)\) есть непрерывная функция в точке \(y = 0\). Следовательно,
$$
\frac{\pi}{2} = \int\limits_{0}^{+\infty} \frac{dx}{1+x^{2}} = I_{1}(0) = \lim_{y \rightarrow +0} I_{1}(y) = \lim_{y \rightarrow +0} C_{1}e^{-y} = C_{1}.\nonumber
$$
Теперь формулы \eqref{ref32} дают, что при любом \(y \in \boldsymbol{R}\)
$$
\int\limits_{0}^{+\infty} \frac{\cos xy}{1+x^{2}}\ dx = \frac{\pi}{2}e^{-|y|},\\ \int\limits_{0}^{+\infty} \frac{x\sin xy}{1+x^{2}}\ dx = \frac{\pi}{2}\ \operatorname{sign}\ ye^{-|y|}.\label{ref33}
$$
То, что формулы \eqref{ref33} справедливы при \(y = 0\), проверяется непосредственно. \(\blacktriangle\)
При рассмотрении определенного интеграла как предела интегральных сумм предполагалось, что подынтегральная функция ограничена на конечном отрезке интегрирования. Данное Определение определенного интеграла не имеет смысла, если не выполняется хотя бы одно из этих условий. Нельзя разбить бесконечный интеграл на конечное число отрезков конечной длины. Если подынтегральная функция неограниченна, то интегральная функция не имеет предела. Тем не менее возможно обобщить понятие предела и на эти случаи, с чем и связано понятие несобственного интеграла.
Интегралы с бесконечными пределами интегрирования
Определение
Пусть функция определена на промежутке и интегрируема на любом отрезке , , так что интеграл
Имеет смысл. Предел этого интеграла при называется Несобственным интегралом первого рода и обозначается
. | (7.15.1) |
В том случае, если этот предел конечен, говорят, что несобственный интеграл сходится, а функцию называют интегрируемой на бесконечном промежутке ; если же предел в формуле (7.15.1) бесконечен или не существует, то говорят, что несобственный интеграл расходится.
Аналогичным образом вводится понятие несобственного интеграла по промежутку :
. | (7.15.2) |
Наконец, несобственный интеграл с двумя бесконечными пределами можно определить как сумму несобственных интегралов (7.15.1) и (7.15.2):
, | (7.15.3) |
Где с – любое число.
Геометрический смысл несобственного интеграла первого рода основан на геометрической интерпретации определенного интеграла на отрезке : это площадь бесконечной области, ограниченной сверху неотрицательной функцией , снизу – осью Ох, слева – прямой (см. Рис.1). Такая же интерпретация имеет место и для несобственных интегралов (7.15.2) и (7.15.3).
Рассмотрим несколько примеров несобственных интегралов первого рода.
Пример
,
Но предела функции при не существует, т. е. данный интеграл расходится.
Пример
,
Рис. 7.15.1
Т. е. данный интеграл сходится.
Пример
.
Конечный предел существует – значит исходный интеграл сходится.
Пример
.
Интегралы от неограниченных функций
Рассмотрим функцию , определенную на промежутке , но неограниченную на нем. Для определенности положим, что ограничена и интегрируема на любом отрезке , , но не ограничена в любой окрестности точки или на промежутке . В таком случае точка называется особой точкой.
Определение
Предел интеграла при Называется несобственным интегралом второго рода и обозначается
. | (7.15.4) |
Если этот предел конечный, то говорят, что интеграл (7.15.4) существует или сходится, а функцию называют интегрируемой на промежутке ; если же предела нет или он бесконечен, то говорят, что интеграл (7.15.4) расходится.
Аналогично, если особой точкой является точка , то несобственный интеграл второго рода определяется как
. | (7.15.5) |
Если функция неограниченна в окрестности некоторой внутренней точки , то определению полагают, что
. | (7.15.6) |
Наконец, если и – особые точки, т. е. функция ограничена и интегрируема на интервале , то несобственный интеграл второго рода определяется в виде суммы
,
Где с – произвольная точка на , а несобственные интегралы второго рода в правой части этого равенства определяются по формулам (23.1.4) и (23.1.5).
Рассмотрим несколько примеров на вычисление несобственных интегралов второго рода.
Пример
,
Т. е. данный интеграл сходится.
Пример
Найти интеграл, учитывая, что особыми являются точки 1 и–1.
Следовательно, данный несобственный интеграл второго рода сходится.
Пример
.
Предел равен , поэтому интеграл расходится.
Признаки сходимости несобственных интегралов
Теорема (признак сравнения несобственных интегралов)
Пусть функции и непрерывны на промежутке и удовлетворяют на нем условию . Тогда из сходимости интеграла следует сходимость интеграла и наоборот, из Расходимости интеграла следует Расходимость интеграла .
Замечание
Аналогичный признак сравнения справедлив и для несобственных интегралов второго рода.
Рассмотрим примеры использования признака сравнения несобственных интегралов.
Пример
.
Сравним подынтегральную функцию в этом интеграле с функцией . Очевидно, что . Интеграл сходится, следовательно, в силу признака сравнения сходится и данный интеграл.
Пример
.
Сравним подынтегральную функцию в этом интеграле с функцией . Очевидно, что . Поскольку интеграл сходится, то сходится и исходный интеграл.
Теорема (признак Абеля–Дирихле)
Пусть функция непрерывна и имеет ограниченную первообразную на промежутке , а функция имеет непрерывную производную на этом промежутке, не возрастает и стремится к нулю при . Тогда несобственный интеграл
(7.15.7) |
Сходится.
Рассмотрим примеры использования признака Абеля – Дирихле сходимости несобственных интегралов.
Пример
.
Если принять в качестве , а в качестве , то легко убедиться, что все требования, накладываемые на функции, выполнены, т. е. данный интеграл сходится.
83.1. Упражнения
Вычислить интегралы:
Интегрирование методом подстановки:
5. | 6. | ||
7. | 8. | ||
9. | 10. | ||
11. | 12. |
Интегралы вида
Интегралы вида
Интегрирование по частям:
Применить тригонометрические подстановки в следующих примерах:
Интегрирование рациональных дробей:
Интегрирование иррациональных функций:
Интегралы вида
Интегрирование тригонометрических функций:
Пользуясь формулой Ньютона—Лейбница, вычислить определенные интегралы:
Вычислить значения нижеследующих интегралов, применяя указанные подстановки:
49. | 50. |
Вычислить следующие несобственные интегралы:
| < Предыдущая | Следующая > |
|---|
несобственные интегралы 1 и 2 рода — Высшая математика
Несобственные интегралы 1 и 2 рода.
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий.
Область интегрирования является бесконечной. Например, является бесконечным интервалом
.
Функция является неограниченной в окрестности некоторых точек области интегрирования.
Если интервал конечный, и функция интегрируема по Риману, то значение несобственного интеграла совпадает с значением определённого интеграла.
Несобственные интегралы I рода
Пусть определена и непрерывна на интервале и. Тогда:
- Если , то используется обозначение и интеграл называется несобственным интегралом Римана первого рода. В этом случае
называется сходящимся.
- Если не существует конечного ( или ), то интеграл
называется расходящимся к , или просто расходящимся.
Пусть определена и непрерывна на множестве от и
. Тогда:
- Если , то используется обозначение и интеграл называется несобственным интегралом Римана первого рода. В этом случае
называется сходящимся.
- Если не существует конечного ( или ), то интеграл
называется расходящимся к , или просто расходящимся.
Если функция определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:
, где с — произвольное число.
Геометрический смысл несобственного интеграла I рода
Несобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции.
Примеры
Несобственные интегралы II рода
Пусть определена на , терпит бесконечный разрыв в точке x=a и
. Тогда:
Если , то используется обозначение и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
Если или , то обозначение сохраняется, а
называется расходящимся к , или просто расходящимся.
Пусть определена на , терпит бесконечный разрыв при x=b и
. Тогда:
Если , то используется обозначение и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
Если или , то обозначение сохраняется, а
называется расходящимся к , или просто расходящимся.
Абсолютная сходимость
Интеграл называется абсолютно сходящимся, если
сходится. Если интеграл сходится абсолютно, то он сходится.
Условная сходимость
Интеграл называется условно сходящимся, если сходится, а
расходится.
Пример 1. Вычислить интеграл:
Положим z = e ix, тогда cos x = (z + z — 1)/2. Вычислим dz = d(e ix), откуда dx = (dz)/(iz), а исходный интеграл запишется в виде:
Так как при |a|<1, подинтегральная функция внутри круга
имеет один полюс первого порядка в точке z = a.
Поскольку будем иметь
Пример 2.1. Вычислить интеграл:
Рассмотрим функцию
Она является аналитической функцией, имеющей полюсы второго порядка в точках и в бесконечности имеет нуль второго порядка.
Согласно формуле (1.1) имеем
Пример 2.2. Вычислить интеграл:
Используя результаты вычисления интеграла в примере 2.1 (обозначив его
как I 1 ), вычислим данный интеграл:
Источники использованной информации:
https://ru.wikipedia.org/wiki/Несобственный_интеграл
http://www.mathprofi.ru/nesobstvennye_integraly.html
http://www.exponenta.ru/educat/class/courses/tfkp/theme11/example.asp
Несобственные кратные интегралы
Исчерпывающие последовательности множеств.
Пусть \(G\) есть область в \(\boldsymbol{R}^{m}\). Последовательность открытых измеримых по Жордану множеств \(\{G_{n}\}\) будем называть исчерпывающей множество \(G\), если \(G = \displaystyle\bigcup_{i=1}^{\infty}G_{n}\) и \(\overline{G}_{n} \subset G_{n + 1}\), \(n = 1, 2, \ldots\).
Лемма 1.
Если \(\{G_{n}\}\) и \(\{G’_{n}\}\) есть последовательности, исчерпывающие область \(G \subset \boldsymbol{R}^{m}\), то для любого номера \(n\) найдется номер \(k(n)\) такой, что \(\overline{G}_{n} \subset G’_{k(n)}\).
Доказательство.
\(\circ\) Пусть для некоторого множества \(G_{N}\) не существует такого номера \(k\), что \(\overline{G}_{N} \subset G’_{k}\). Тогда найдется точка \(x_{1} \in \overline{G}_{N}\) такая, что \(x_{1} \notin G’_{1}\), найдется точка \(x_{2} \in \overline{G}_{N}\) такая, что \(x_{2} \notin G’_{2}\). Продолжая эти рассуждения, построим последовательность точек \(\{x_{k}\}\) такую, что \(x_{k} \in \overline{G}_{N}\), \(x_{k} \notin G’_{k}\). Так как измеримое по Жордану множество \(\overline{G}_{N}\) ограничено, то из последовательности \(x_{k}\) можно в силу теоремы Больцано-Вейерштрасса выделить сходящуюся подпоследовательность. Без ограничения общности можно считать, что и последовательность \(x_{k}\) сходится, то есть \(\displaystyle\lim_{k \rightarrow \infty} x_{k} = x_{0}\). В силу замкнутости множества \(\overline{G}_{N}\) точка \(x_{0} \in \overline{G}_{N} \subset G_{N + 1} \subset G\).
Так как последовательность множеств \(\{G’_{k}\}\) исчерпывает множество \(G\), то найдется такой номер \(r\), что \(x_{0} \in G’_{r}\). Открытое множество \(G’_{r}\) есть окрестность точки \(x_{0}\). Поэтому в \(G’_{r}\) лежит бесконечное множество членов последовательности \(\{x_{k}\}\). Следовательно, найдется в этом бесконечном множестве точка \(x_{s}\) с номером \(s \geq r\). Тогда \(x_{s} \in G’_{r} \subset G’_{s}\), так как при \(r < s\) и \(G’_{r} \subset G’_{s}\). Но по построению \(x_{s} \notin G’_{s}\). Полученное противоречие доказывает, что для любого \(n\) существует номер \(k(n)\) такой, что \(G_{n} \subset G’_{k(n)}\). \(\bullet\)
Несобственные интегралы от неотрицательных функций.
Определение.
Пусть функция \(f(x)\) непрерывна и неотрицательна в области \(G \subset \boldsymbol{R}^{m}\), а последовательность множеств \(\{G_{n}\}\) исчерпывает множество \(G\). Предел
$$
\lim_{n \rightarrow \infty} \int\limits_{G_{n}} f(x)\ dx\label{ref1}
$$
называют несобственным интегралом от функции \(f(x)\) по множеству \(G\). Несобственный интеграл обозначается символом \(\displaystyle\int\limits_{G} f(x)\ dx\).
Будем говорить, что несобственный интеграл \(\int\limits_{G} f(x)\ dx\) сходится, если предел \eqref{ref1} конечен, и что несобственный интеграл расходится, если предел \eqref{ref1} равен \(+\infty\).
Теорема 1.
Определение несобственного интеграла от непрерывной неотрицательной в области \(G\) функции корректно: предел \eqref{ref1} для любой исчерпывающей область \(G\) последовательности множеств \(\{G_{n}\}\) существует и не зависит от выбора исчерпывающей последовательности.
Доказательство.
\(\circ\) Пусть \(\{G_{n}\}\) и \(\{G’_{n}\}\) — две исчерпывающие последовательности. Так как \(\overline{G}_{n} \subset G_{n + 1} \subset G\) и \(\overline{G}’_{n} \subset G’_{n + 1} \subset G\), а на множестве \(G\) функция \(f(x)\) неотрицательна и непрерывна, то функция \(f(x)\) неотрицательна и непрерывна на любых множествах \(\overline{G}_{n}\) и \(\overline{G}’_{n}\), \(n = 1, 2, \ldots\) Поэтому интегралы \(\displaystyle\int\limits_{G_{n}} f(x)\ dx\) и \(\displaystyle\int\limits_{G’_{n}} f(x)\ dx\) существуют и числовые последовательности \(\alpha_{n} = \displaystyle\int\limits_{G_{n}} f(x)\ dx\) и \(\beta_{n} = \displaystyle\int\limits_{G’_{n}} f(x)\ dx\) являются монотонно возрастающими. Монотонно возрастающая числовая последовательность всегда имеет конечный или бесконечный предел.Пусть \(\alpha = \displaystyle\lim_{n \rightarrow \infty} \alpha_{n}\) и \(\beta = \displaystyle\lim_{n \rightarrow \infty} \beta_{n}\).
В силу леммы 1 для любого \(n\) найдется такой номер \(k(n)\), что \(G_{n} \subset G’_{k(n)}\). Так как \(f(x) \geq 0\), то
$$
\alpha_{n} = \int\limits_{G_{n}} f(x)\ dx \leq \int\limits_{G’_{k(n)}} f(x)\ dx = \beta_{k(n)} \leq \lim_{k \rightarrow \infty} \beta_{k} = \beta.\nonumber
$$
Переходя к пределу при \(n \rightarrow \infty\), получаем, что \(\alpha \leq \beta\). Аналогично доказывается, что \(\beta \leq \alpha\). Поэтому \(\alpha = \beta\). \(\bullet\)
Пример 1.Интеграл
$$
\int\limits_{0 < x^{2} + y^{2} < R^{2}} \frac{dx\ dy}{(x^{2} + y^{2})^{\alpha}}\label{ref2}
$$
сходится при \(\alpha < 1\) и расходится при \(\alpha \geq 1\).
\(\vartriangle\) Положим
$$
G = \{(x, y): 0 < x^{2} + y^{2} < R^{2}\},\ G_{n} = \left\{(x, y): \frac{R^{2}}{n^{2}} < x^{2} + y^{2} < R^{2}\right\}.\nonumber
$$
Тогда последовательность колец \(G_{n}\) образует исчерпывающую последовательность для круга \(G\). Переходя к полярным координатам, получаем
$$
\iint\limits_G \frac{dx\ dy}{(x^{2} + y^{2})^{\alpha}} = \lim_{n \rightarrow \infty} \iint\limits_{G_{n}} \frac{dx\ dy}{(x^{2} + y^{2})^{\alpha}} = \lim_{n \rightarrow \infty} \int\limits_{0}^{2\pi} d\varphi \int\limits_{R/n}^{R} \frac{r\ dr}{r^{2\alpha}} =\\=\lim_{n \rightarrow \infty} 2\pi \int\limits_{R/n}^{R} r^{1 — 2\alpha}dr = 2\pi \int\limits_{0}^{R} r^{1 — 2\alpha}dr.\nonumber
$$
Таким образом, несобственный интеграл \eqref{ref2} сходится в том и только том случае, когда сходится несобственный интеграл
$$
\int\limits_{0}^{R} r^{1 — 2\alpha}dr,\nonumber
$$
то есть при \(1 — 2\alpha > -1\) или \(\alpha < 1\). \(\blacktriangle\)
Несобственные интегралы от знакопеременных функций.
Пусть функция \(f(x)\) непрерывна в области \(G \subset \boldsymbol{R}^{m}\), \(m \geq 2\). Будем говорить, что функция \(f(x)\) интегрируема по области \(G\) в несобственном смысле, если сходятся интегралы \(\displaystyle\int\limits_{G_{n}} f^{+}(x)\ dx\) и \(\displaystyle\int\limits_{G_{n}} f^{-}(x)\ dx\) от неотрицательных функций \(f^{+} = \displaystyle\frac{1}{2}(|f| + f)\) и \(f^{-} = \displaystyle\frac{1}{2}(|f| — f)\). Несобственным интегралом \(\displaystyle\int\limits_{G} f(x)\ dx\) в этом случае будем называть число
$$
\int\limits_{G} f(x)\ dx = \int\limits_{G} f^{+}(x)\ dx — \int\limits_{} f^{-}(x)\ dx.\label{ref3}
$$
В определении \eqref{ref3} не случайно оговорено, что \(m \geq 2\). При \(m = 1\) это определение не совпадает с определением несобственного интеграла (§ 38) \(\displaystyle\int\limits_{a}^{b} f(x)\ dx\) (с особой точкой \(b\)) как предела \(\displaystyle\lim_{\xi \rightarrow b — 0} \int\limits_{a}^{\xi} f(x)\ dx\). Функции, интегрируемые на интервале \((a, b)\), могут оказаться неинтегрируемыми в смысле определения \eqref{ref3}. Проще всего в этом убедиться, заметив, что функция \(f(x)\) интегрируема в смысле определения \eqref{ref3} в том и только том случае, когда интегрируем ее модуль, так что определение \eqref{ref3} не допускает существования условно сходящихся интегралов. Для функций одной переменной сохраним определение данное ранее, а для функций двух и большего числа переменных будем использовать определение \eqref{ref3}.
Можно показать, что функция \(f(x)\) интегрируема в несобственном смысле на множестве \(G \subset \boldsymbol{R}^{m}\), где \(m \geq 2\), в том и только том случае, когда для любой исчерпывающей множество \(G\) последовательности \(\{G_{n}\}\) существует конечный предел \(\displaystyle\lim_{n \rightarrow \infty} \iint\limits_{G_{n}} f(x)\ dx\), не зависящий от выбора исчерпывающей последовательности \(\{G_{n}\}\).
 непрерывная (или хотя бы кусочно-непрерывная)
и, следовательно, ограниченная на этом
отрезке.
непрерывная (или хотя бы кусочно-непрерывная)
и, следовательно, ограниченная на этом
отрезке.