кружок по математике 5 класс
кружок по математике 5 класс
- Подробности
- Категория: Материалы МО естественно-научного цикла
- Опубликовано 02.11.2016 22:09
Пояснительная записка.
Математика — это орудие для размышления, в ее арсенале имеется большое количество задач, которые на протяжении тысячелетий способствовали формированию мышления людей, умению решать нестандартные задачи, с честью выходить из затруднительных положений.
Математика — это язык, на котором говорят не только наука и техника, математика – это язык человеческой цивилизации. Она практически проникла во все сферы человеческой жизни. Современное производство, компьютеризация общества, внедрение современных информационных технологий требует математической грамотности. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемый математикой.
Кружок предназначен для учащихся 5 класса.
Кружок направлен на развитие логического мышления учащегося, на умение создавать математические модели практических задач, на расширение математического кругозора учащихся.
Целями данного кружка являются:
— Создание условий для самореализации учащихся в процессе учебной деятельности.
— Развитие математических, интеллектуальных способностей учащихся, обобщенных умственных умений.
-Знакомство с историей математики и известными математиками
Для достижения поставленных целей в процессе обучения решаются следующие задачи:
— Помочь овладеть конкретными математическими знаниями, необходимыми для применения в практической деятельности.
— Формировать у учащихся устойчивый интерес к математике.
— Формировать представление о математике как части общечеловеческой культуры, понимание значимости математики для общественного прогресса.
— Развивать математические способности.
— Развивать качества мышления, характерные для математической деятельности.
— Развивать умение переводить различные задачи на язык математики.
— Подготовить к сознательному усвоению систематического курса алгебры и геометрии.
— развивать находчивость, сообразительность, умение логично рассуждать.
В результате изучения курса учащиеся будут уметь:
— Решать основные виды логических задач. Знать способы решения популярных логических задач. Познакомятся с историей математики и известными математиками.
Программа составлена на основе новых ФГОС по математике.
Календарно-тематический план изучения кружка
«За страницами учебника » 5 класс
|
№ |
Содержание
|
Кол-во часов
|
Дата |
факт |
|
|
|
Как люди научились считать
|
2 |
|
|
|
|
1 |
Арифметика каменного века.
|
1 |
12.09 |
|
|
|
2 |
Абак и пальцевый счет |
1 |
26.09 |
|
|
|
|
Развитие арифметики и алгебры |
2 |
|
|
|
|
3 |
Открытие нуля. Что такое квадриллион. |
1 |
3. |
|
|
|
4 |
Всегда ли дважды два-четыре?
|
1 |
17.10 |
|
|
|
|
Из науки о числах |
3 |
|
|
|
|
5 |
Любопытные свойства натуральных чисел
|
1 |
14.11 |
|
|
|
6 |
Некоторые приемы быстрого счета
|
1 |
28. |
|
|
|
7 |
Числовые фокусы |
1 |
5.12 |
|
|
|
|
Математические игры
|
3 |
|
|
|
|
8 |
Числовые головоломки |
1 |
19.12 |
|
|
|
9 |
Башня из колец |
1 |
16. |
|
|
|
10 |
Игра в 15 |
1 |
30.01 |
|
|
|
|
Решение задач |
8 |
|
|
|
|
11 |
Решение логических задач с помощью таблиц
|
|
6.02 |
|
|
|
12 |
Решение логических задач с помощью графов
|
|
20. |
|
|
|
13 |
Решение задач на взвешивание
|
|
6.03 |
|
|
|
14 |
Решение задач на переливание |
|
20.03 |
|
|
|
15 |
Решение задач с конца |
|
3.04 |
|
|
|
16 |
Задачи на разрезание |
|
17. |
|
|
|
17 |
Упражнения со спичками |
|
24.04 |
|
|
|
18 |
Числовые ребусы |
|
8.05 |
|
|
|
19 |
Итоговое занятие |
|
15.05 |
|
|
|
|
|
|
|
|
|
Литература:
1. Н.А. Козловская. Нестандартные занятия по развитию логического и комбинаторного мышления. 5-6 кл., Москва: ЭНАС, 2007 Г.
Н.А. Козловская. Нестандартные занятия по развитию логического и комбинаторного мышления. 5-6 кл., Москва: ЭНАС, 2007 Г.
2. Кострикина Н.П. Задачи повышенной трудности в курсе математики 4 – 5 классов. Москва «Просвещение», 1986
3. И.Я. Депман, Н.Я. Виленкин За страницами учебника математики, Москва, просвещение, 1989 г.
4. Е.И.Игнатьев В царстве смекалки, Москва Наука,1979 г.
5. О.С. Шейнина, Г.М.Соловьева Математика. Занятия школьного кружка, Москва, Издательство НЦ ЭНАС, 2004
6. Перельман Я.И. Математические рассказы и головоломки. Домодедово. ВАП-VAP, 1994.
Муниципальное образовательное бюджетное учреждение
«Саха гимназия»
Утверждаю: Рассмотрено на заседании НМС
Зам директора по ВР: ____________________________
__________________
Программа кружка
«За страницами учебника»
на 2013-2014 учебный год
Руководитель — учитель математики Бандерова Т. Г.
Г.
Количество часов за год – 19ч
Программа факультативного курса «Решение нестандартных задач»
Муниципальное бюджетное общеобразовательное учреждение
Касплянская средняя школа
Смоленского района Смоленской области
РАБОЧАЯ ПРОГРАММА
факультатива «Решение нестандартных задач»
Класс 5
Учитель Богачева О.В.
Количество часов всего 34; в неделю 1 час
Планируемые результаты освоения курса «Решение нестандартных задач»
В результате факультативных занятий учащиеся должны:
расширить и углубить знания, получаемые на уроках математики;
овладеть новыми способами и методами решения трудных задач;
принимать участие в проведении математических конкурсов, викторин, олимпиад;
осознавать значимость проводимой работы, свою причастность к научной деятельности: возможность делать самостоятельные открытия, проводить исследования.
Личностные результаты
Чувство гордости за свою Родину, российский народ и историю России;
Осознание роли своей страны в мировом развитии, уважительное отношение к семейным ценностям, бережное отношение к окружающему миру.
Целостное восприятие окружающего мира.
Развитую мотивацию учебной деятельности и личностного смысла учения, заинтересованность в приобретении и расширении знаний и способов действий, творческий подход к выполнению заданий.
Рефлексивную самооценку, умение анализировать свои действия и управлять ими.
Навыки сотрудничества со взрослыми и сверстниками.
Установку на ЗОЖ, наличие мотивации к творческому труду, к работе на результат.
Метапредметные результаты
Способность принимать и сохранять цели и задачи учебной деятельности, находить средства и способы её осуществления.
Овладение способами выполнения заданий творческого и поискового характера.
Умения планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями её выполнения, определять наиболее эффективные способы достижения результата.
Способность использовать знаково-символические средства представления информации для создания моделей изучаемых объектов и процессов, схем решения учебно-познавательных и практических задач.
Использование речевых средств и средств информационных и коммуникационных технологий для решения коммуникативных и познавательных задач.
Овладение логическими действиями сравнения, анализа, синтеза, обобщения, классификации по родовидовым признакам, установления
аналогий и причинно-следственных связей, построения рассуждений, отнесения к известным понятиям.
Готовность слушать собеседника и вести диалог; готовность признать возможность существования различных точек зрения и права каждого иметь свою; излагать своё мнение и аргументировать свою точку зрения.
Определение общей цели и путей её достижения: умение договариваться о распределении функций и ролей в совместной деятельности, осуществлять взаимный контроль в совместной деятельности, адекватно оценивать собственное поведение и поведение окружающих.
Овладение начальными сведениями о сущности и особенностях объектов и процессов в соответствии с содержанием учебного предмета «математика».
Овладение базовыми предметными и межпредметными понятиями, отражающими существенные связи и отношения между объектами и процессами.
Предметные результаты
Использование приобретённых математических знаний для описания и объяснения окружающих предметов, процессов, явлений, а также для оценки их количественных и пространственных отношений.
Умения выполнять устно и письменно арифметические действия с числами и числовыми выражениями, решать текстовые задачи, выполнять и строить алгоритмы и стратегии в игре, исследовать, распознавать и изображать геометрические фигуры, работать с таблицами, схемами, графиками и диаграммами, цепочками, представлять, анализировать и интерпретировать данные.
Приобретение первоначальных навыков работы на компьютере (набирать текст на клавиатуре, работать с меню, находить информацию по заданной теме, распечатывать её на принтере).
Содержание курса
1. Решение текстовых задач различных типов.
Занимательные задачи на сообразительность и внимательность.
Задачи на переливание.
Задачи на планирование действий.
Логические задачи. Применение таблиц и графов при решении логических задач.
Дележи при затруднительных обстоятельствах.
Переправы и разъезды.
Задачи на дроби и проценты.
2. Задачи с геометрическим содержанием.
Упражнения со спичками.
Упражнения с куском бумаги (складывание, разрезание).
Периметр и площадь.
Равновеликие фигуры.
3. Приемы рационализации вычислений.
Свойства чисел. Свойства арифметических действий.
Числовые ребусы. Арифметические фокусы и софизмы.
Арифметические фокусы и софизмы.
Числовые суеверия.
4. Теория множеств и комбинаторика.
Множества. Подмножества.
Диаграммы Эйлера.
Решение комбинаторных задач.
5. История развития математики. Исторические задачи.
Цифра и число. Цифры у разных народов. Задачи на нумерацию.
Метрическая система мер.
Старые русские меры.
Магницкий и его «Арифметика». Старинные русские задачи.
Форма организации занятий
Основной является классно-урочная форма занятий.
Предусматривается работа с учетом запросов и индивидуальных наклонностей ученика.
Изучение теоретического материала сочетается с практической работой:
решение нестандартных задач, задач повышенного уровня трудности;
проведение исторических экскурсов, математических игр и фокусов;
разработка конкурсов, викторин, сценариев;
оформление математической газеты.
коллективные и индивидуальные математические проекты.
Методика работы предполагает применение различных технологий (игровых, дифференцированного обучения, УДЕ) и методов обучения.
Календарно – тематическое планирование занятий
факультативного курса по математике
«Решение нестандартных задач»
5 класс
№ занятия в году | Дата | Тема, содержание | № темы |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | Введение. Числовые ребусы. Угадывание чисел. Задачи на переливание. Задачи на планирование действий. Задачи с геометрическим содержанием. Упражнения со спичками. Логические задачи. Решение логических задач с помощью графов. Решение комбинаторных задач с помощью графов. Цифра и число. Цифры у разных народов. Задачи на нумерацию. Метрическая система мер. Старые русские меры. Магницкий и его «Арифметика». Старинные русские задачи. Из истории дробей. Свойства чисел. Свойства арифметических действий. Приемы быстрого счета. Числовые суеверия. Арифметические фокусы и софизмы. Упражнения с куском бумаги (складывание, разрезание). Периметр и площадь. Равновеликие фигуры. Геометрические фокусы и софизмы. Множества. Подмножества. Диаграммы Эйлера. Решение комбинаторных задач. Задачи на дроби и проценты. Задачи на совместную работу. Дележи при затруднительных обстоятельствах. Переправы и разъезды. Задачи на движение. Задачи на движение по воде. Геометрия вокруг нас (конкурс) Итоги года Состязание эрудитов. | 1 3 1 1 2 2 1 1 4 5 1 5 5 5 5 5 3 3 3 3 2 2 2 4 4 4 1 1 1 1 1 1 2 1 |
В современном обществе возрастает значимость качества математического образования. Правильное изучение математики приводит не только к умению считать, но и к умению логически мыслить, исследовать, конструировать, представлять себе сложные объекты, развивать познавательные виды деятельности, осваивать новые идеи, самостоятельно находить решения. Очень важно, что на занятиях основное внимание уделяется не заучиванию готовых определений, формул и методов, а пониманию материала. Под руководством учителя ребенок учится сам находить решения задач, а новые знания теории помогают ему в этом. В процессе занятий формируются и развиваются не только умения и навыки по математике, но и умение слушать, понимать, проверять свои и чужие действия, делать выводы, находить и исправлять ошибки, решать нестандартные задачи. Также происходит процесс развития интереса детей к математике и её приложениям в различных отраслях человеческой деятельности, формируется позитивная мотивация к занятиям и воспитывается стремление к сотрудничеству во время работы. Необходимо, чтобы учащийся мог проявить свои способности в разнообразных сферах деятельности, поэтому важный аспект – создание условий для такого развития и самореализации ребенка. Программа рассчитана на 40.5 часов (по 1.5 часа в неделю). Актуальность программы обусловлена тем, что в настоящее время увеличение умственной нагрузки на уроках математики заставляет задуматься над тем, как охранить у школьников интерес к изучаемому материалу, поддержать активность на протяжении всего занятия. В связи с этим ведутся поиски новых эффективных методов обучения и таких методических приемов, которые активизировали бы мышление обучающихся, стимулировали бы их самостоятельность в приобретении знаний. Имеется большое количество задач, для решения которых используют арифметические способы мышления, что позволяет развивать логику, интуицию и речь. Часть задач требует не долгих вычислений, а ясного взгляда и сосредоточенности, что развивает внимательность, смекалку, здравый смысл, способствует общему развитию детей. Важное место в программе отведено знакомству, правилам проведения, подготовке к участию и разбору задач различных математических соревнований, проводимых в Москве и России: интернет-карусели, турниру Архимеда, Матпразднику, конкурсу Кенгуру и устной математической олимпиаде. Очень важно правильно подготовить детей к участию в этих конкурсах, объяснив особенности и правила их проведения и специфику предлагаемых задач. Цели и задачи программы
Ожидаемый результат
Учебный план
Содержание изучаемого курса
Литература
|
Аттестационная работа. Программа факультативного курса «Занимательные и нестандартные задачи по математике». (5 класс)
1. Аттестационная работа
Слушателя курсов повышения квалификации попрограмме:
«Проектная и исследовательская деятельность как
способ формирования метапредметных результатов
обучения в условиях реализации ФГОС»
Яковлевой Ирины Викторовны
Фамилия,
Фамилия, имя,
имя, отчество
отчество
ЧОУ школа «Таланъ» г.
 Новосибирск
НовосибирскОбразовательное
Образовательное учреждение,
учреждение, район
район
На тему:
программа факультативного курса
«Занимательные и нестандартные задачи по математике»
для обучающихся 5 класса
1
2. Краткая характеристика жанра работы
Внеурочная деятельность необходимое условиедля
гармоничного развития личности. Поэтому она является одним
из приоритетных направлений в современном образовании.
Одним из направлений внеурочной деятельности по ФГОС
является
общеинтеллектуальное.
Общеинтеллектуальное
направление
базируется
на
организацию научно-познавательной и проектной деятельности
обучающихся.
Внеурочная познавательная деятельность школьников может
быть организована в форме факультативов, кружков
познавательной
направленности,
научного
общества
обучающихся,
интеллектуальных
клубов,
библиотечных
вечеров, дидактических театров, познавательных экскурсий,
олимпиад, викторин и т.
 п.
п.Поэтому в качестве итоговой работы предлагаю разработку
рабочей программы факультативного курса «Занимательные и
нестандартные задачи по математике».
2
3. Краткая характеристика образовательного учреждения
Я работаю в ЧОУ школа «Таланъ» г. Новосибирска,которая была основана в 1993 году.
Школа «Таланъ» — школа полного дня, реализующая
образовательные программы, разработанные на основе
ФКГОС и ФГОС, кроме этого реализуются
предпрофильная и мультипрофильная модели обучения.
Школа осуществляет широкий спектр внеурочной деятельности. Это и
предметные факультативы (для учащихся 1-7 класса), элективные курсы по
индивидуальным учебным планам (для учащихся 8-11 классов), театральная
студия, студия ИЗО, кружок мягкой игрушки, шахматная секция, баскетбольная
секция, ЛФК, бассейн (выездной). Осуществляется психолого- логопедическое
сопровождение.
В нашей школе созданы условия для научно- исследовательской
деятельности учащихся.
 Одним из итогов данной деятельности является
Одним из итогов данной деятельности являетсявыступление ребят в первой декаде февраля на традиционной научно3
практической конференции «Талановские чтения».
Целью курса является создание условий и содействие в формирование
устойчивого интереса учащихся к математике через
развитие
математического и логического мышления при решении нестандартных
задач.
Задачи факультативного курса определены следующие:
• привитие интереса к изучению предмета;
• расширение и углубление знаний по предмету; формирование
пространственного воображения и графической культуры;
• развитие математического кругозора, логического и творческого
мышления, исследовательских умений учащихся;
• знакомство с различными типами задач как классических, так и
нестандартных;
• практика решения олимпиадных заданий; приобретение опыта
коммуникативной, творческой деятельности;
• формирование у учащихся таких необходимых для дальнейшей успешной
учебы качеств, как упорство в достижении цели, трудолюбие,
любознательность,
аккуратность,
внимательность,
чувство
ответственности, культура личности;
• выявление одаренных детей.

4
Программа содержит материал, как занимательного
характера, так и дополняющий, расширяющий программу
общеобразовательной школы по математике. В программе
уделяется внимание истории математики, рассказами,
связанными с математикой, геометрическому материалу,
развитию пространственного воображения, выполнению
самостоятельных заданий творческого характера, изучению
различных арифметических методов решения задач метод
решения.
Программа факультатива «Занимательные
и
нестандартные задачи по математике» рассчитана на 1 час в
неделю; 35 часов в год.
Обучение будет, осуществляется в виде теоретических и
практических занятий для учащихся. В ходе занятий ребята
будут выполнять практические работы, готовить выступления,
проекты, примут участие в конкурсных программах.
5
Программа курса содержит темы:
Занимательная арифметика (9 часов): запись цифр и чисел
других народов,
числа- великаны и числа- малютки,
головоломки, числовые ребусы, составление выражений.

Геометрические задачи (9 часов): рисование фигур на
клетчатой бумаге, задачи на разрезание и переклеивание,
пентамино, геометрия в пространстве, построение фигур
одним росчерком карандаша, простейшие графы.
Логические задачи (9 часов): задачи, решаемые с конца,
чётность, принцип Дирихле, логические задачи, задачи на
переливания, задачи взвешивания, задачи на движение.
Занимательные задачи (8 часов): математические фокусы,
математические ребусы, лабиринты, софизмы.
6
Каждый блок будет заканчиваться защитой проектов.
Планируемые темы проектов:
Календарь: от древних времен до наших дней
Из истории происхождения математических действий
Обозначение чисел у разных народов
Древние меры длины.
Единицы измерения длины в разных странах и в разное
время.
Математические головоломки и кроссворды
Угадывание чисел
Загадочные фигуры пентамино
Число и числовая мистика.
Числовые забавы
Старинные русские меры длины в народных пословицах и
поговорках
7
При оценивание проектов будет использоваться самооценка
и взаимооценка учащегося по следующим критериям:
• оформление (соответствие содержанию, иллюстрации и т.
 д.)
д.)• содержание (глубина раскрытия темы, творческий подход)
• защита (выразительность, умение отвечать на вопросы,
соблюдение регламента)
8
Использование современных технологий позволяет
сочетать все режимы работы: индивидуальный, парный,
групповой, коллективный.
Кроме того, эффективности организации курса
способствует использование различных форм занятий:
эвристическая беседа, практикум, интеллектуальная игра,
дискуссия, творческая работа и проектная работа.
9
10. Планируемые результаты изучения курса
Планируемые результаты изучения курсаПредполагается, что знакомство учащихся с нестандартными
(как по формулировке, так и по решению) задачами будет
способствовать повышению их успеваемости на уроках
математики и развитию у них интереса к предмету.
Личностные результаты
• ориентация в системе требований при обучении математике;
• позитивное, эмоциональное восприятие математических
объектов, рассуждений, решений задач, рассматриваемых
проблем.

Ученик получит возможность для формирования:
• выраженной устойчивой учебно-познавательной мотивации и
интереса к изучению математики;
• умение выбирать желаемый уровень математических
результатов;
• адекватной позитивной самооценки и Я-концепции.
10
11. Метапредметные результаты
Метапредметные результатыРегулятивные универсальные учебные действия
Ученик научится:
• совместному с учителем целеполаганию в математической
деятельности;
• анализировать условие задачи;
• действовать в соответствии с предложенным алгоритмом,
составлять несложные алгоритмы вычислений и построений;
• применять приемы самоконтроля при решении математических
задач;
• оценивать правильность выполнения действия и вносить
необходимые коррективы на основе имеющихся шаблонов.
Ученик получит возможность научиться:
• видеть различные стратегии решения задач, осознанно выбирать
способ решения;
• основам саморегуляции в математической деятельности в форме
осознанного управления своим поведением и деятельностью,
направленной на достижение поставленных целей.

11
Коммуникативные универсальные учебные действия
Ученик научится:
• строить речевые конструкции с использованием изученной
терминологии и символики, понимать смысл поставленной
задачи, осуществлять перевод с естественного языка на
математический и наоборот;
• осуществлять контроль, коррекцию, оценку действий
партнёра, уметь убеждать.
Ученик получит возможность научиться:
• задавать вопросы, необходимые для организации
собственной деятельности взаимодействия с другими;
• устанавливать и сравнивать разные точки зрения, прежде
чем принимать решения и делать выбор;
• отображать в речи (описание, объяснение) содержание
совершаемых действий
12
Познавательные универсальные учебные действия
Ученик научится:
• анализировать
и
осмысливать
тексты
задач,
переформулировать их условия моделировать условие с
помощью схем, рисунков, таблиц, реальных предметов,
строить логическую цепочку рассуждений;
• формулировать
простейшие
свойства
изучаемых
математических объектов;
• с помощью учителя анализировать, систематизировать,
классифицировать изучаемые математические объекты.

Ученик получит возможность научиться:
• осуществлять выбор наиболее эффективных способов
решения задач в зависимости от конкретных условий.
13
Итогом
реализации
программы
факультатива
«Занимательные и нестандартные задачи по математике»
могут служить: успешные выступления учеников в
общешкольных
олимпиадах,
международной
математической
игре-конкурсе
«Кенгуру»,
создание
предпосылок для успешного выступления обучающихся на
олимпиадах всех уровней, участие в школьной научнопрактической конференции.
14
15. Перспективы развития исследовательской/проектной деятельности в профессиональной деятельности .
Математика – наука экспериментальная.В
математической
деятельности
существенна
исследовательская
составляющая. Поэтому проектную и
исследовательскую работы я в обязательном порядке включу как
в учебный процесс, так и внеурочную деятельность. Ведь это
лучший путь познания от действия к мысли, входе которого идет
формирование творческих, познавательных способностей
обучающихся.

Человек может стать умным тремя путями:
путём подражания- это самый лёгкий путь,
путём опыта – это самый трудный путь
и путём размышления – это самый благородный путь.
Китайская пословица 15
Центр довузовской подготовки ТТИ ЮФУ
Школа детского творческого развития «Радуга» — одна из форм реализации дополнительного образования. Основные задачи Школы детского творческого развития «Радуга» — повышение уровня знаний элементарной математики, физики, информатики, русского и английского языков в рамках школьной программы и изучение этих предметов за «пределами стандарта». Изучение предмета «за пределами стандарта» дает настоящее (качественное) образование, формирует логическое мышление, развивает творческие и интеллектуальные качества личности.
Одним из важнейших факторов развития личностных и творческих качеств ребенка является помещение его в соответствующую среду. Приходя в нашу школу, ребенок попадает в коллектив единомышленников, где желание узнать больше не осмеивается сверстниками, где всячески приветствуется творческое любопытство, где нет культа «оценки», где появляется здоровый азарт и блеск в глазах детей.
Главная цель нашей школы — заинтересовать школьника. Увлеченный ребенок может невероятно много.
Занятия проходят по адресу: Чехова, 22, корпус «А» Южного федерального университет в г.Таганроге.
Оформить документы в Школу детского творческого развития «Радуга» можно уже сейчас. Запись проводится по адресу: ул. Чехова, 24, к.16. При себе необходимо иметь паспорт и ИНН родителя, свидетельство о рождении или паспорт (при его наличии) и ИНН обучающегося, две фотографии 3х4.
Групповые занятия проходят по воскресеньям. Длительность занятия – 60 минут.
Математика 2-8 класс
Учимся решать математические задачи, развиваем логику и умение рассуждать, узнаём множество интересных фактов и мира математики; развиваем логическое и абстрактное мышление, учимся решать нестандартные задачи и применять математику в реальной жизни.
Физика 6-8 класс
Научим понимать смысл физических явлений и решать задачи: от простых до нестандартных.
Информатика
«Основы работы с компьютером» 2-5 классы
рассматриваем основы, необходимые для работы на компьютере: изучение ОС, обработка файлов, основы работы в Internet.
«Работа с графикой» 4-7 классы
рассматриваем вопросы, связанные с компьютерной графикой, начиная от способов хранения и заканчивая продвинутыми способами редактирования фотографий.
«Анимация» 6-8 классы
знакомим с понятием компьютерной анимации, способами создания классической и автоматической анимации, учим создавать собственные проекты.
«3d-моделирование» 7-8 классы
рассматриваем основы работы с трёхмерной графикой,
от правил оформления до создания трёхмерных моделей реальных объектов.
«Программирование» 5-8 классы
алгоритмы, блок-схемы, лексика и синтаксис, методы программирования, понятие сайта, программирование в сети,…
«Web-программирование» 5-8 классы
Изучаем сеть Internet, учим работать с файлами в сети, разбираем понятие сайта и основы его работы.
Русский язык 2-8 класс
В занимательной форме знакомимся с разными языковыми явлениями, учимся грамотно писать, формируем круг чтения.
Английский язык 2-8 класс
Учим грамотно строить предложения, обогащаем словарный запас, тренируем навыки беседы и многое другое.
Рабочая программа «Решение нестандартных задач по математике. Подготовка к олимпиаде» для 5 класса
Программа «Решение нестандартных задач по математике.
Подготовка к олимпиаде» для 5 класса
Программа «Решение нестандартных задач по математике. Подготовка к олимпиаде» разработана с учётом Федерального государственного образовательного стандарта основного общего образования1, Концепции духовно-нравственного развития и воспитания личности гражданина России2, примерной программы по математике основного общего образования3, Положения о рабочей программе учителя, учебного плана МАОУ «СОШ №99», с учетом программы внеурочной деятельности для начальной и основной школы (Информатика. Математика. Программы внеурочной деятельности для начальной и основной школы: 3 – 6 классы. / М. С. Цветкова, О. Б. Богомолова. – М.: БИНОМ. Лаборатория знаний, 2013.)
Математика. Программы внеурочной деятельности для начальной и основной школы: 3 – 6 классы. / М. С. Цветкова, О. Б. Богомолова. – М.: БИНОМ. Лаборатория знаний, 2013.)
Программа включает следующие разделы: пояснительную записку, общую характеристику учебного предмета, описание места учебного предмета в учебном плане, результаты изучения курса (личностные, межпредметные и предметные), содержание курса, тематическое планирование с определением основных видов учебной деятельности обучающихся и описание материально-технического обеспечения образовательного процесса.
Пояснительная записка
Обучение математике является важнейшей составляющей основного общего образования и призвано развивать логическое мышление и математическую интуицию учащихся, обеспечить овладение учащимися умениями в решении различных практических и межпредметных задач. Математика входит в предметную область «Математика и информатика». Основной целью учебного курса является обучение решению нестандартных задач по математике. Курс также закладывает пропедевтику наиболее значимых тем курса математики и позволяет успешно готовиться к участию в олимпиадах по предмету. Достижение перечисленных целей предполагает решение следующих задач:
Курс также закладывает пропедевтику наиболее значимых тем курса математики и позволяет успешно готовиться к участию в олимпиадах по предмету. Достижение перечисленных целей предполагает решение следующих задач:
обеспечить уровневую дифференциацию в ходе обучения;
формировать устойчивый интерес учащихся к предмету;
создать условия формирования у учащихся способности к организации своей учебной деятельности посредством освоения личностных, познавательных, регулятивных и коммуникативных универсальных учебных действий;
создать условия для освоения в ходе изучения математики специфических видов деятельности, таких как построение математических моделей, выполнение инструментальных вычислений, овладение символическим языком предмета и др.;
формировать умения представлять информацию в зависимости от поставленных задач в виде таблицы, схемы, графика, диаграммы, использовать компьютерные программы, Интернет при её обработке;
воспитывать отношение к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.

Содержание курса строится на основе системно-деятельностного подхода.
Программа предназначена для организации внеурочной деятельности по нескольким взаимосвязанным направлениям развития личности, таким как общеинтеллектуальное, общекультурное и социальное.
Общая характеристика курса
Одной из особенностей творческой личности является устойчивое умение (превращенное в привычку) находить лучшее решение проблемы (творчество). Это относится к любым задачам.
Множество нестандартных задач для учащихся основной школы сконцентрировано в математике. В различных математических книгах, посвященных олимпиадным задачам, дается обзор с решениями и без них, в ряде случаев разбирается методика решения. Однако сам мыслительный процесс нахождения решения задачи, как правило, не отражается. И у учителя возникает вопрос, как «додуматься» до решения задачи. Другой не менее важный вопрос, на который необходимо обращать внимание при обучении решению нестандартных задач, – каковы составляющие мыслительного процесса от «прочтения» задачи до ее решения?
Научить решать нестандартные задачи – интересная, но и достаточно непростая работа, которая предполагает применение знаний по педагогике, методике, психологии, личного творчества и многого другого. Решение нестандартных задач соотносится с творчеством личности. Поэтому чем больше учтено существенных элементов, входящих в процесс творчества, тем успешнее будет достигнута цель.
Решение нестандартных задач соотносится с творчеством личности. Поэтому чем больше учтено существенных элементов, входящих в процесс творчества, тем успешнее будет достигнута цель.
Для достижения указанной цели, прежде всего, необходимо познакомиться с идеями и механизмом, лежащими в основе творчества, необходимого для решения нестандартных задач, получить представление о новом подходе к обучению и познакомиться с методикой достижения значимых результатов. А далее на примере достаточно большого числа олимпиадных задач разобрать различные приемы решений, для которых вычленены и обобщены их особенности.
Так, прослеживая связь творческого процесса и процесса решения нестандартной задачи, рассматриваются компоненты творчества: научные знания, творческое мышление, умения творческой работы, а также такие качества, без которых немыслимо творчество: анализ, синтез и умение предвидеть (т.е. прогнозировать, экстраполировать имеющиеся знания на еще непознанную ситуацию).
Большое внимание необходимо уделять возрастным особенностям восприятия учебного материала учащимися, а также принципам организации занятий по развитию творческого мышления при решении нестандартных и олимпиадных задач у учащихся пятых классов.
В программе учитывается взаимосвязь репродуктивной и проблемной формы обучения, коллективной и самостоятельной работы. Используются активные и интерактивные формы учебного сотрудничества: «учитель-ученик», парная и групповая работа, что в свою очередь так же влияет на формирование УУД.
Практическое выполнение программы предполагает выполнение обучающимися конкретных видов УД: творческих работ, проверочных работ, диктантов (выборочный, творческий, графический).
Курс завершается демонстрацией творческой работы и/или защитой проекта.
Описание места курса в учебном плане
Курс «Решение нестандартных задач. Подготовка к олимпиаде» реализуется за счет плана внеурочной деятельности для 5-х классов на 2015-2016 учебный год МБОУ «СОШ № 47» . Используется время, отведенное на внеурочную деятельность. Форма реализации курса – кружок. Программа курса общим объемом 35 часов изучается в течение года. Изучение данного курса является пропедевтикой к изучению курса математики старшей школы.
Подготовка к олимпиаде» реализуется за счет плана внеурочной деятельности для 5-х классов на 2015-2016 учебный год МБОУ «СОШ № 47» . Используется время, отведенное на внеурочную деятельность. Форма реализации курса – кружок. Программа курса общим объемом 35 часов изучается в течение года. Изучение данного курса является пропедевтикой к изучению курса математики старшей школы.
Личностные, метапредметные и предметные результаты
освоения конкретного учебного курса
В результате изучения всех без исключения предметов основной школы получат дальнейшее развитие личностные, регулятивные, коммуникативные и познавательные универсальные учебные действия, учебная (общая и предметная) и общепользовательская ИКТ-компетентность обучающихся, составляющие психолого-педагогическую и инструментальную основы формирования способности и готовности к освоению систематических знаний, их самостоятельному пополнению, переносу и интеграции; способности к сотрудничеству и коммуникации, решению личностно и социально значимых проблем и воплощению решений в практику; способности к самоорганизации, саморегуляции и рефлексии.
В ходе изучения курса в основном формируются и получают развитие метапредметные результаты, такие как:
умение самостоятельно планировать пути достижения целей, в том числе альтернативные, и осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;
умение оценивать правильность выполнения учебной задачи, собственные возможности ее решения;
умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач;
владение основами самоконтроля, самооценки, принятия решений и осуществления осознанного выбора в учебной и познавательной деятельности;
умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками; работать индивидуально и в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; формулировать, аргументировать и отстаивать свое мнение;
формирование и развитие компетентности в области использования ИКТ-компетенции.

Вместе с тем вносится существенный вклад в развитие личностных результатов, таких как:
формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, осознанному выбору и построению дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений, с учетом устойчивых познавательных интересов, а также на основе формирования уважительного отношения к труду, развития опыта участия в социально значимом труде;
формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками, детьми старшего и младшего возраста, взрослыми в процессе образовательной, общественно полезной, учебно-исследовательской, творческой и других видов деятельности.
В части развития предметных результатов наибольшее влияние изучения курса оказывает:
на овладение простейшими способами представления и анализа статистических данных; формирование представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о простейших вероятностных моделях; развитие умений извлекать информацию, представленную в таблицах, на диаграммах, графиках, описывать и анализировать массивы числовых данных с помощью подходящих статистических характеристик, использовать понимание вероятностных свойств окружающих явлений при принятии решений;
формирование умений формализации и структурирования информации, умения выбирать способ представления данных в соответствии с поставленной задачей – таблицы, схемы, графики, диаграммы, с использованием соответствующих программных средств обработки данных;
формирование навыков и умений безопасного и целесообразного поведения при работе с компьютерными программами и в Интернете, умения соблюдать нормы информационной этики и права.

Содержание учебного курса
Содержание учебного курса представлено подборкой нестандартных задач по арифметике, геометрии и логике для 5-х классов. Для дальнейшего использования учебного курса список задач по указанным темам расширяется и усложняется содержание заданий за счет работы с аналитическими задачами, задачами на комбинаторику, теорию множеств и т.д.
Арифметика. Методы устного счета. Признаки делимости. Числовые ребусы. Проценты. Числовые неравенства и оценки. Дроби.
Геометрия. Задачи на разрезание, перекладывание и построение фигур. Вычисление площадей фигур разбиением на части и дополнением.
Логика. Логические таблицы. Переливания. Взвешивания. Решения «с конца». Популярные и классические логические задачи.
Примерное тематическое планирование
Тематическое планирование реализует один из возможных подходов к распределению изучаемого материала. Оно не носит обязательного характера и не исключает возможностей иного распределения содержания. В примерном тематическом планировании разделы основного содержания разбиты на темы в порядке их изучения. Особенностью примерного тематического планирования является то, что в нём содержится описание возможных видов деятельности учащихся в процессе усвоения соответствующего содержания, направленных на достижение поставленных целей обучения. Это помогает учителю реализовать системно-деятельностный подход в обучении, организовать разнообразную учебную деятельность, отвечающую современным психолого-педагогическим взглядам, на использование современных технологий.
Оно не носит обязательного характера и не исключает возможностей иного распределения содержания. В примерном тематическом планировании разделы основного содержания разбиты на темы в порядке их изучения. Особенностью примерного тематического планирования является то, что в нём содержится описание возможных видов деятельности учащихся в процессе усвоения соответствующего содержания, направленных на достижение поставленных целей обучения. Это помогает учителю реализовать системно-деятельностный подход в обучении, организовать разнообразную учебную деятельность, отвечающую современным психолого-педагогическим взглядам, на использование современных технологий.
Тематическое планирование курса
«Решение нестандартных задач по математике. Подготовка к олимпиаде» для 5 класса
Учебная тема | Количество часов | Характеристика основных видов деятельности ученика (на уровне учебных действий) |
Арифметика | 15 | Фронтальная работа с классом, работа у доски и в тетрадях, индивидуальная работа (карточки-задания), математический диктант с последующей взаимопроверкой, текущий тестовый контроль. Применять основные приемы устного счета; применять признаки делимости при решении задач; применять различные алгоритмы решения числовых ребусов; рассмотреть различные задачи на проценты и схемы их решения; применять свойства числовых неравенств и оценки при решении нестандартных заданий; применять изученный теоретический материал при выполнении учебных заданий и в жизни. |
Геометрия | 5 | Фронтальная работа по решению задач, работа в парах, в группах, индивидуальная работа (карточки-задания), творческий проект, практическая работа, защита проекта. Решать различные типы задач на разрезание, перекладывание и построение фигур; решать нестандартными способами задачи на вычисление площадей фигур; применять симметрию, неравенство треугольника при решении различных задач; применять изученный теоретический материал при выполнении учебных заданий и в жизни. |
Логика | 15 | Фронтальная работа с классом, индивидуальная работа (карточки-задания), работа с дополнительной литературой, работа с конспектом, создание и защита презентации. Решать различные типы логических задач с помощью таблиц, матричным способом; познакомиться с принципом Дирихле и научиться применять его к решению задач; применять изученный теоретический материал при выполнении учебных заданий и в жизни. |
Учебно-методическое и материально-техническое обеспечение
образовательного процесса
Учебное и учебно-методическое обеспечение:
таблицы по математике для 5 класса;
таблицы выдающихся математиков;
доска магнитная с координатной сеткой:
комплект классных чертежных инструментов: линейка, транспортир, угольник(30, 60), угольник (45, 45), циркуль;
комплекты демонстрационных планиметрических и стереометрических тел.

Материально-техническое обеспечение:
Литература для учителя
1. Жильцова, О. А. Организация исследовательской и проектной деятельности школьников: дистанционная поддержка педагогических инноваций при подготовке школьников к деятельности в сфере науки и высоких технологий. — М. : Просвещение, 2015. – 40с. ISBN: 978-5-98594-528-7
2. Поливанова, К. А. Проектная деятельность школьников. — М. : Просвещение, 2011. – 192с. ISBN: 978-5-0902-0813-0
3. Дрозина, В. В., Дильман, В. Л. Механизм творчества решения нестандартных задач. — М. : БИНОМ. Лаборатория знаний, 2008. – 250 с. ISBN: 978-5-94774-733-1
4. Цветкова, М. С. Информатика. Математика. Программы внеурочной деятельности для начальной и основной школы: 3 – 6 классы / М.С. Цветкова, О.Б. Богомолова. — М. : БИНОМ. Лаборатория знаний, 2015. – 128с. ISBN: 978-5-9963-1891-9
Литература для учащихся
1. Дрозина, В. В., Дильман, В. Л. Механизм творчества решения нестандартных задач. — М. : БИНОМ. Лаборатория знаний, 2008. – 250 с. ISBN: 978-5-94774-733-1
Дрозина, В. В., Дильман, В. Л. Механизм творчества решения нестандартных задач. — М. : БИНОМ. Лаборатория знаний, 2008. – 250 с. ISBN: 978-5-94774-733-1
Планируемые результаты изучения учебного курса
В результате изучения курса «Решение нестандартных задач по математике. Подготовка к олимпиаде» 5 класса учащиеся
Научатся:
в сфере предметных результатов
основным приемам устного счета;
применять признаки делимости при решении задач;
применять различные алгоритмы решения числовых ребусов;
решать различные типы задач на разрезание, перекладывание и построение фигур;
уметь применять симметрию, неравенство треугольника при решении различных задач;
применять принцип Дирихле к решению задач;
в сфере метапредметных результатов:
формировать коммуникативные действия, направленные на структурирование информации по данной теме;
организовывать и планировать учебное сотрудничество с учителем и одноклассниками;
осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;
учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве;
аргументировать свою точку зрения, спорить и отстаивать свою позицию не враждебным для оппонентов образом;
задавать вопросы, необходимые для организации собственной деятельности и сотрудничества с партнером;
адекватно самостоятельно оценивать правильность выполнения действий и вносить необходимые коррективы в исполнение, как в конце действия, так и по ходу его реализации;
давать определение понятиям;
осуществлять взаимный контроль и оказывать в сотрудничестве необходимую взаимопомощь;
устанавливать и сравнивать разные точки зрения, прежде чем принимать решение и делать выбор;
сравнивать способ действия и его результат с заданным эталоном с целью обнаружения отклонений от эталона и внесения необходимых коррективов;
находить и формулировать учебную проблему, составлять план выполнения работы;
объяснять явления, процессы, связи и отношения, выявляемые в ходе исследования;
в сфере личностных результатов
проявлять устойчивый интерес к творческой деятельности;
проявлять креативные способности;
применять элементы анализа, творческой инициативности и активности;
выполнять творческие задания;
сотрудничать с взрослыми и сверстниками;
Получат возможность научиться:
в сфере предметных результатов
решать различные задачи на проценты и схемы их решения;
применять свойства числовых неравенств и оценки при решении нестандартных заданий;
решать нестандартными способами задачи на вычисление площадей фигур;
решать различные типы логических задач с помощью таблиц, матричным способом;
в сфере метапредметных результатов
с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации;
самостоятельно анализировать условия достижения цели на основе учета выделенных учителем ориентиров действия в новом материале;
самостоятельно контролировать свое время и управлять им;
создавать и преобразовывать модели и схемы для решения задач;
осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;
планировать пути достижения целей;
применять основы реализации проектно-исследовательской деятельности;
устанавливать причинно-следственные связи;
развивать умение обмениваться знаниями между одноклассниками для принятия эффективных совместных решений;
осознавать уровень и качество усвоения знаний и умений;
в сфере личностных результатов
делать осознанный выбор наиболее эффективного способа решения;
применять элементы самоанализа и самоконтроля;
применять элементы индивидуальной и коллективной исследовательской деятельности;
составлять алгоритм выполнения задания.

1 Федеральный государственный образовательный стандарт основного общего образования / Министерство образования и науки РФ.— М. : Просвещение, 2011. (Стандарты второго поколения.) Приказ Министерства образования и науки РФ от 17.12.2010. № 1897.
2 Данилюк А. Я., Кондаков А.М., Тишков В. А. Концепция духовно-нравственного развития и воспитания личности гражданина России. — М.: Просвещение, 2010. (Стандарты второго поколения.).
3 Примерные программы по учебным предметам. Математика. 5-9 классы: проект. — М. : Просвещение, 2010. (Стандарты второго поколения.).
Олимпиадные задачи по математике 5 класс . Ассорти от репетитора
Продолжаю публиковать занимательные и логические задачи по математике для 5 класса из своей личной коллекции. Источники разные. Некоторые экземпляры я составляю сам, кое-что беру со вступительных экзаменов в сильные школы, в такие, например, как Курчатовская школа, 179 школа, лицей Втора Школа. Примерно половину задач приносят сами ученики с различных очных и заочных туров.
Примерно половину задач приносят сами ученики с различных очных и заочных туров.
Для интеллектуального развития ребенка и поддержания его интереса к предмету олимпиадные задачи — важный и незаменимый учебный инструмент репетитора по математике. Каждый пришедший ко мне ученик, ориентированный на математику, в обязательном порядке получает свою порцию подобного материала, предварительно прошедшего жесткий отбор на предмет пригодности для конкретного возраста, класса и текущей школьной программы.
Репетитор по математике, сваливающий на ученика подряд все попавшиеся ему на глаза нестандартные задачки, как правило, пожинает плоды своего непрофессионализма в виде хаоса в голове воспитанника. Я гарантирую Вам правильную качественную работу, полностью исключая подобную халтуру.
Олимпиадные задачи по математике — 5 класс
1) На круговую трассу вышли 47 машинок и одновременно стартовали. Скорость первой 48км/ч, второй 49 км/ч, у третьей 50 км/ч и так далее. трасса однополосная и когда одна машинка обгоняет другую через круг, то обе сталкиваясь слетают с трассы в кювет. В конце гонки на трассе осталась одна единственная машинка. Какова ее скорость?
В конце гонки на трассе осталась одна единственная машинка. Какова ее скорость?
2) Петя занумеровал все ребра прямоугольного параллелепипеда числами от 1 до 12. Затем у каждой вершины нашел сумму номеров выходящих из нее ребер. Могли ли все 8 сумм оказаться равными?
3) Егора поставил в ряд 5 клеток с хомячками. В каждой из них сидит хотя бы один хомяк. Егор называет хомячков соседними, если они живут либо в соседних клетках, либо в одной клетке. Выяснилось, что каждый хомяк имеет либо 7, либо 3 соседа. сколько хомячков оказалось в центральной клетке?
4) В поселке 250 домов. В некоторых из них сделаны по одному камину, в половине остальных сделаны по 2 камина, а в остальных домах вообще нет каминов. Сколько всего каминов в поселке?
5) В тетради у Димы — математика записаны числа 1; 2; 3; 4; 5. Каждую секунду Дима прибавляет одно из чисел на 3 или на 5. Через какое наименьшее время он сможет сделать все 5 чисел равными?
6) В сказочном городе живут 27 гномов. Каждый из них сделал по подарку ровно 13 другим гномам. Докажите, что найдутся три гнома А, В и С, такие, что А подарил подарок гному В, гном В подарил подарок гному С, а С подарил подарок гному А.
Каждый из них сделал по подарку ровно 13 другим гномам. Докажите, что найдутся три гнома А, В и С, такие, что А подарил подарок гному В, гном В подарил подарок гному С, а С подарил подарок гному А.
7) У Пети есть чашечные весы и 3 гирьки весом 3г, 4 г и 5 г, внешне не отличимые друг от друга. Когда он взвешивает гирьки на весах на одну из чаш запрыгивает маленький кузнечик — невидимка с весом в 1г. Петя хочет за 2 взвешивания распознать хотя бы одну гирьку. Как ему это сделать?
8) Нарисуйте на листе бумаги треугольник, круг и квадрат, чтобы листочек распался на 22 части, если его разрезать по всем нарисованным линиям. Посмотреть решение репетитора по математике
Жду Вас у себя в Строгино на олимпиадных занятиях. Проведу качественную подготовку любую в математическую школу и помогу по ходу учебы в ней.
С уважением, Колпаков А.Н. Репетитор по математике.
Метки: Занимательный репетитор по математике, Олимпиадные задачи по математике, Ученикам
нестандартных измерений {Наше секретное оружие!}
Нестандартные измерения Занятия помогают детям действительно научиться измерять. Но это нужно делать правильно, иначе ваши дети не поймут! Читайте дальше, чтобы получить наше секретное оружие для обучения нестандартным измерениям.
Но это нужно делать правильно, иначе ваши дети не поймут! Читайте дальше, чтобы получить наше секретное оружие для обучения нестандартным измерениям.
Прежде чем дети познакомятся со стандартными измерениями с помощью линеек и рулеток, они должны понять, что такое измерения. Чтобы развить глубокое понимание измерения и навыки, необходимые для правильного измерения, дети должны научиться измерять, используя нестандартные единицы измерения.
К сожалению, нестандартные измерения часто преподаются плохо или вообще упускаются! Чаще всего многие нестандартные действия по измерению на самом деле связаны со счетом, а не с измерением.
Продолжайте читать, чтобы узнать, как дети могут измерять предметы, не используя линейки, рулетки или весы. Мы также расскажем вам о нашем секретном оружии для обучения нестандартным измерениям… «Беспорядок» — необходимый элемент набора, который поможет вам обучать измерению.
В конце поста также есть удобная БЕСПЛАТНАЯ шпаргалка по измерениям, которую можно распечатать. Идеально подходит для вашего набора инструментов для обучения счету!
Идеально подходит для вашего набора инструментов для обучения счету!
*Этот пост содержит партнерские ссылки. Это не влияет на ваш опыт покупки, но A Plus Teaching Resources может получать небольшую комиссию за рекомендацию о вашей покупке.
Связанная запись: Как преподавать стандартные измерения
В чем разница между стандартными и нестандартными измерениями?
Нестандартное измерение
Нестандартные измерения — это способ познакомить детей дошкольного возраста, детского сада, приемных или первоклассников с измерениями с использованием нестандартных единиц.Это включает в себя выяснение того, насколько большой, тяжелый, длинный и т. д. что-то есть, и как два или более объектов сравниваются (ПРЯМОЕ СРАВНЕНИЕ) друг с другом.
Стандартное измерение
Стандарт измерения вводится для учащихся средних и старших классов. Их учат стандартным единицам измерения, таким как метры и сантиметры, дюймы и футы. Стандартное измерение более сложное, потому что оно включает в себя формулы или преобразование между единицами измерения, чтобы узнать, насколько большим, маленьким, длинным и т. д. является что-то.(КОСВЕННОЕ СРАВНЕНИЕ).
Стандартное измерение более сложное, потому что оно включает в себя формулы или преобразование между единицами измерения, чтобы узнать, насколько большим, маленьким, длинным и т. д. является что-то.(КОСВЕННОЕ СРАВНЕНИЕ).
Также требуются навыки и понимание в использовании измерительных инструментов и инструментов, в частности умение читать и интерпретировать шкалу на инструментах.
В этом посте мы сосредоточимся на НЕСТАНДАРТНЫХ измерениях. Вы можете прочитать о стандартных измерениях в нашем соответствующем посте.
Печатные измерения
Станьте VIP-членом и получите все в нашем магазине ПЛЮС 20 НОВЫХ ресурсов в месяц всего за 3 доллара.08!!! Нажмите на изображение, чтобы узнать больше…
Является ли нестандартное измерение РЕАЛЬНЫМ измерением?
Процесс измерения очень сложен и требует много размышлений, действий и шагов, если вы хотите правильно и точно измерить объект. Знакомство детей с действиями по измерению с использованием нестандартных единиц, если все сделано правильно, выделяет эти шаги и дает им возможность «ПРОИЗВОДИТЬ» измерения. Нестандартные измерения — это основа НАСТОЯЩИХ измерений, без них дети не понимают важности:
Знакомство детей с действиями по измерению с использованием нестандартных единиц, если все сделано правильно, выделяет эти шаги и дает им возможность «ПРОИЗВОДИТЬ» измерения. Нестандартные измерения — это основа НАСТОЯЩИХ измерений, без них дети не понимают важности:
- Начальные точки
- Стандартные блоки
- Единообразные повторяющиеся единицы для измерения и сравнения объектов
- Без пропусков и перекрытий
- Сколько единиц было использовано, говорит о том, насколько «большим» является что-то
Итак, что я имею в виду под измерением «DO»? Я имею в виду, что если вы попросите ученика выяснить, что из них самое большое, самое длинное, самое высокое, самое тяжелое….книга, стол, ножка… смогли бы они это сделать?
Ну, конечно, вы, наверное, скажете! Но спросите себя, какую часть «Измерения» они выполнили сами, а какую — вы? И под эшафотом я имею в виду, дети сами принимали важные решения об измерениях или вы давали им все ответы? Они решили:
- Какие части объекта необходимо измерить?
- Какой «нестандартный» инструмент выбрать для измерения с помощью
- Будут ли они использовать один и тот же отряд снова и снова?
- Как обращаться с частями юнита?
- Знаешь меру?
- Говорить и общаться, используя правильные слова измерения?
Итак, если вы попросите детей узнать, как долго в книге используются кубики unifix, сколько на самом деле измерили дети? Сосредоточен ли этот тип измерительной деятельности на «СЧИТАНИИ СКОЛЬКО» кубиков длиной, книги или измерения?
САМАЯ важная вещь в обучении нестандартным измерениям заключается в том, что задача измерения является задачей ИЗМЕРЕНИЯ, которая дает детям возможность узнать, что вам нужно «ДЕЛАТЬ», если вы хотите измерить объект. (ПОМНИТЕ ЭТО!)
(ПОМНИТЕ ЭТО!)
Информирование родителей о нестандартных измерениях
Вам может быть интересно, как и вашим родителям и ученикам… Почему учеников заставляют измерять предметы с помощью ручек, палочек, веревки, чего угодно, кроме линейки?
Использование нестандартных измерений (прямое измерение) помогает учащимся понять процесс измерения. Уроки и занятия, которые позволяют детям научиться измерять с помощью нестандартных измерительных инструментов (поп-стиков, универсальных фиксирующих кубиков или шариков), позволяют им сосредоточиться на том, как измерять и определять, какой предмет тяжелее, легче, длиннее, короче и т. д.без считывания шкал на стандартных измерительных инструментах.
Эти процессы являются важной основой для измерения и помогают учащимся понять, что такое измерение, прежде чем они перейдут к следующему шагу измерения объектов с использованием стандартных единиц.
Планирование уроков нестандартных измерений
Отличным ресурсом, который мы использовали для планирования нашей нестандартной деятельности по измерению, являются книги по измерениям «Первые шаги». Эти книги основаны на исследованиях и определяют, что следует включить в планы уроков и мероприятия по измерению.Это мой ресурс, который помогает мне понять, какие процессы нужно изучать детям. Для обучения нестандартным измерениям это 3 фазы, которые необходимо использовать для обучения всем атрибутам измерения:
Эти книги основаны на исследованиях и определяют, что следует включить в планы уроков и мероприятия по измерению.Это мой ресурс, который помогает мне понять, какие процессы нужно изучать детям. Для обучения нестандартным измерениям это 3 фазы, которые необходимо использовать для обучения всем атрибутам измерения:
- длина
- район
- том
- емкость
- масса
Уроки и блоки должны давать возможность исследовать ключевые идеи:
- Измерение чего-либо означает, сколько определенного атрибута оно имеет.
- Прибор, который мы выбираем для представления единицы, должен хорошо соответствовать тому, что мы измеряем, и должен легко повторяться
- Наш выбор атрибута и единицы измерения зависит от того, что мы пытаемся измерить и почему
- Для последовательного измерения нам нужно использовать наш инструмент таким образом, чтобы он хорошо соответствовал измеряемому объекту
Получите доступ к БЕСПЛАТНО онлайн-книгам «Первые шаги по обучению математике» здесь.
Фаза 1: определение атрибута
В центре внимания – Разработка концепции атрибута, отличие его от других атрибутов и получение интуитивного понимания свойств.
Деятельность будет включать возможность:
- Выучить язык измерения
(как далеко, как долго, высокий, короткий, широкий, расстояние вокруг дерева, длина…) - Сравнивать предметы по признаку
(какая змея длиннее, кто выше, какой дом дальше, сортировать ручки по длине…) - Сравните с другими атрибутами
(этот ящик длиннее, а тот ящик больше; он выше, но я старше) - Использовать неформальные единицы
(это 5 гигантских шагов до окна, этот стол длиной в 12 книг…)
Этап 2: Обучение измерению
Измерьте сколько (количество), используйте формальные единицы, оцените измерения.
- Переход от неформальных единиц к формальным единицам
(создайте «линейку» для неформальной единицы (например, длину палочки для поп-музыки, обсудите значение согласованной единицы, сделайте собственную линейку в сантиметрах…) - Изготовление и использование упрощенных «инструментов», подчеркивающих ключевые особенности
(линейки с маркировкой только в сантиметрах, однострелочные часы, маркировка кувшина «чашками»…) - Измеряйте объекты различными способами
(правильное использование линейки, рулетки, колесика…) - Получение набора личных ориентиров, которые можно использовать для оценки
(мой размах рук около 15 см; мой рост около 130 см…)
Этап 3: Обучение вычислениям
Преобразование из одних единиц в другие, вычисление, вместо прямого измерения.
- Формулы, полученные из первых принципов, а не только заученные
(периметр прямоугольника = 2 × длина + 2 × ширина, длина окружности = 2 r) - Преобразование между единицами измерения основано на принципах пропорционального рассуждения
(нарисуйте двойную числовую прямую, чтобы увидеть, что 3,2 км = 3200 м и т. д.)
Нестандартные единицы измерения
Грязная математическая коробка
Чтобы эффективно обучать нестандартным измерениям, вам понадобится «грязная» измерительная коробка.Это коробка, наполненная всякими нестандартными измерительными инструментами.
Используя «грязную» коробку для измерения предметов, дети узнают, что измерение — это не просто численное окончательное измерение. Они узнают, что измерение также касается:
- выбор правильного инструмента для работы
- выбор единой повторяющейся единицы
- , используя единицу таким же образом без пробелов или перекрытий, чтобы узнать, насколько что-то велико.

Процесс нестандартного измерения выдвигает на первый план некоторые важные идеи измерения, и учащиеся должны освоить весь спектр навыков, чтобы стать компетентными, прежде чем они начнут использовать масштабированные измерительные инструменты.
Что включить в грязный ящик для измерений
При измерении учащиеся должны самостоятельно выбрать правильный инструмент для работы, а не должны измерять стол с помощью палочек. Предоставив учащимся «коробку с беспорядком для измерений» и спросив их: «Какой длины стол?» или «Какой самый большой?» вы позволяете своим детям демонстрировать и использовать свои навыки измерения, чтобы «ДЕЛАТЬ» измерения!
В нашу «беспорядочную» коробку мы включили ряд предметов для измерения всех характеристик, а не только длины, поэтому учащимся действительно нужно было решить, какой измерительный инструмент подходит для работы.Мы включили:
- штифты
- шерсть, резинка, нитки
- спички
- клейкая лента
- пластиковые стаканчики для питья
- сломанные линейки
- палочки для поп-музыки
- блю так
- ватные палочки
- шарики
- сломанные линейки (подробности об этом см.
 в соответствующем посте!)
в соответствующем посте!)
Есть так много предметов, которые вы можете включить, но убедитесь, что коробка с оборудованием НЕ ГРЯЗНА, и предметы не должны быть рассортированы или организованы каким-либо образом.Если вы упорядочиваете и сортируете беспорядочные элементы коробки, то на самом деле вы сортируете их по единообразным повторяющимся единицам. Это подталкивает учащегося и побуждает его выбрать повторяющуюся однородную единицу, а не осознает важность этого самостоятельно.
Вы можете подумать, что дети инстинктивно знают, чем измерять длину, ширину, массу и т. д., но это не так… Это было недавно доказано, когда я попросил 4-классников измерить их парты. Их попросили выяснить, насколько велик их стол и у кого самый большой стол? Достаточно просто, верно?
У каждой группы на столах стояла ЗАГРЯЗНЕННАЯ ИЗМЕРИТЕЛЬНАЯ КОРОБКА, содержащая различные предметы, веревки, палочки для поп-музыки, сломанные линейки, пластиковые стаканчики, блутак, спички, клейкую ленту, резинки, прищепки, мелки, карандаши, ватные палочки и т. д.. Пока мы стояли и смотрели на детей, мы с коллегами не могли поверить в то, что видели.
д.. Пока мы стояли и смотрели на детей, мы с коллегами не могли поверить в то, что видели.
Как дети измеряли с помощью грязной коробки
Поведение групп четко определило, чему нам нужно учить, Группа:
- Стояли, смотрели и отстранялись, ожидая, потому что они просто не могли пройти мимо «практического» подхода и не понимали концепции измерения
- Попросил линейку,
- Решил использовать bluetac и растянул его на столе.Когда он щелкнул, они положили удила в руки на край стола и проигнорировали тот факт, что им не хватило .
- Использовали смесь предметов, мелок, палочку для поп-музыки и резинку, и выложили их встык по столу очень наклонной линией, а когда они дошли до конца и не имели маленького предмета, просто проигнорировали зазор.
- Многократно использовали один и тот же предмет, но измеряли расстояние между пальцами каждый раз, когда перемещали инструмент
- Группа, которая использовала МРАМОР для измерения длины!!!!!!!!
Итак, теперь вы видите важность того, чтобы учащиеся могли выбирать свои собственные инструменты для измерения из «беспорядочного» поля. Если бы мы просто дали им линейки или палочки для попкорна, мы бы не определили области их потребностей. Попробуйте это в своем классе и дайте нам знать, что получится!
Если бы мы просто дали им линейки или палочки для попкорна, мы бы не определили области их потребностей. Попробуйте это в своем классе и дайте нам знать, что получится!
Вы пытаетесь быть лучшим учителем, которым можете быть, но чувствуете себя подавленным и ВЫГОРЕННЫМ из-за бесконечного списка дел? Что ж, теперь есть способ сбалансировать работу и личную жизнь и вернуть РАДОСТЬ преподаванию, не делая ВСЕ это самостоятельно! Â Нажмите на изображение сейчас и присоединитесь к тысячам учителей, которые победили выгорание и снова обрели РАДОСТЬ в обучении!
Обучение ресурсам измерения
Чтобы помочь определить, какие уровни года чему учат в измерении, я создал Шпаргалку по измерению.Это помогает преподавателям установить связь между тем, что должно преподаваться на каждом уровне года, конкретными концепциями и стандартами достижений. Существует также удобная страница разъяснения терминологии измерения, чтобы помочь с общим пониманием обучения измерению.
И наконец…
Измерение сложно даже для взрослых. Сколько раз вы недооценивали что-то, и когда вы получили это мотыгой или доставили, это не подходит !!! Так что дайте своим ученикам время, необходимое им для изучения измерения и искусства измерения!
Сколько раз вы недооценивали что-то, и когда вы получили это мотыгой или доставили, это не подходит !!! Так что дайте своим ученикам время, необходимое им для изучения измерения и искусства измерения!
Похожие посты для обучения измерению
Задача модерации измерений
Детские книги для обучения измерению
Распознавание номеров
Сенсорная корзина с радужным рисом
PSST! Если вы хотите сэкономить время и $$$ на учебных ресурсах, присоединяйтесь к нашему VIP-клубу! Получите мгновенный доступ
ко ВСЕМ нашим ПЛАТНЫМ и БЕСПЛАТНЫМ ресурсам, а также более 20 новых мероприятий каждую неделю! Нажмите на изображение ниже, чтобы узнать больше…
(PDF) ЗАДАЧИ ПРИ РЕШЕНИИ НЕСТАНДАРТНЫХ МАТЕМАТИЧЕСКИХ ЗАДАЧ
• стандартные математические учебные задачи – где для решения используются известные формулы, правила или процедуры (алгоритмы)
• нестандартные (проблемные) учебные задачи – где известны методов и алгоритмов недостаточно
для их решения.
В общем, нестандартные задачи и задачи в математическом образовании представляют собой нетрадиционную
тему, которая направлена на развитие логического и комбинаторного мышления учащихся, развитие у них
восприятия пространственных отношений и указание на удобство использования, игривость и интересность по математике, а
поощряют учеников получать удовольствие от математических открытий. [3]
Решение нестандартных задач и задач представляет собой способность человека использовать
когнитивные процессы для решения реальных межпредметных ситуаций, в которых решение не сразу
очевидно.Такие задания ориентированы на оценку навыков, а не знаний, и, кроме взаимосвязей
по разным предметам, они также делают акцент на связи между школьной программой и реальными
ситуациями, с которыми ученики сталкиваются в повседневной жизни. [4] Кроме того, эти задания ставятся в ситуациях, когда
обычно не входят в учебную программу и обычно не встречаются в школьных учебниках.
Разделение решения задачи на несколько шагов можно считать подходящей основой для
анализа мыслительного процесса ученика.Различаем [5]:
а) подход к проблеме — задача воздействует на сознание ученика. Он знает о задаче
и решает, решать ее или нет. В случае положительного решения следует следующий шаг,
б) понимание задачи — учащийся находит соответствующие данные и связи между ними. Он
понимает, что дано и что мы ищем. Однако степень понимания может быть
разной — ученик может неправильно «понимать» задачу, неправильно понимать или интерпретировать
информацию,
в) математизация — ученик формулирует задачу на языке математики .Индивидуальные
количественные данные и отношения между известными и неизвестными элементами задачи
записываются формальным (математическим) языком или с помощью рисунков, графиков и других
представлений,
г) расчет — учащийся вычисляет математически сформулированную задачу и находит определенные данные,
которые он считает результатом решения задачи,
д) интерпретация — учащийся формулирует результат в контексте вопроса задачи, словесно как
словесный ответ на вопрос задачи или по-другому,
е) смысловой тест — ученик проверяет, соответствует ли результат контексту задания
и/или действительности. При положительном ответе решение заканчивается, в отрицательном случае следует исправление,
При положительном ответе решение заканчивается, в отрицательном случае следует исправление,
г) исправление — учащийся ищет ошибку, находит ее и формулирует новый ответ.
Более детальное рассмотрение решений задач учащимися позволяет не только обнаружить и идентифицировать
типичных используемых приемов (стратегий) решения, но и выявить «особые» показатели
учащихся. У учителей этот анализ вызывает такие вопросы, как: Какие трудности могут возникнуть при понимании продуктов учеников? Какие интерпретации возможны? Какие неожиданные трудности
возникли (в смысле
отклонение от собственного опыта учителя на сегодняшний день или от данных, опубликованных в литературе)?
Нестандартные задачи и задачи в математическом образовании
означают задачи не столько сложные, сколько необычные (как по вводу, так и по способу решения) и пригодные также для исследовательской деятельности учащихся.
При решении таких задач следует уважать и ценить индивидуальные решения учеников, если
решения правильные и соответствующим образом (например, дополнительные вопросы) исправлять неверные или неточные действия учеников
. Также комплексные задачи из практической жизни имеют нестандартный
Также комплексные задачи из практической жизни имеют нестандартный
характер, в котором взаимосвязаны разные области математики. При решении практических задач мы используем
конкретный опыт школьников из повседневной жизни, а также из разных областей их интересов (спорт,
техника, природа, искусство и др.), которые повышают мотивационную ценность заданий. [6]
Это означает, что нестандартные задачи часто носят дивергентный характер, а также множество естественно дивергентных
ситуаций, которые ученики решают в практической жизни – от построения отношений, решения школьных или рабочих
задач до повседневных задач, таких как одевание, свободное время и т. д. В отличие от этого конвергентные задачи доминируют в
математическом образовании (90-95% в традиционных учебниках). [7] Эти расходящиеся задачи требуют мышления
, которое не приводит к одному ответу, а требует генерирования как можно большего числа предложений, альтернатив или
возможных стратегий. И наоборот, решение конвергентных задач требует мыслительных процессов, которые
И наоборот, решение конвергентных задач требует мыслительных процессов, которые
Решение нестандартных задач по математике
Что такое решение нестандартных задач?Решение нестандартных задач, также называемое творческим решением проблем, требует определенной степени творчества или оригинальности. Нестандартные проблемы обычно не имеют сразу очевидной стратегии их решения. Часто эти проблемы можно решить несколькими способами и с помощью различных стратегий.Так же, как и вычислительные упражнения (например, деление в большую сторону), решение нестандартных задач должно преподаваться учащимся в явном виде.
Почему решение нестандартных задач всегда будет не входить в мои инструкции:
- Готовит учащихся к решению реальных задач. В реальных проблемах нет предписанных шагов по их решению. Люди должны мыслить творчески и логически, чтобы решить их.
- Это дает учащимся подарок на выбор. Я использую слово «подарок», однако для многих студентов этот аспект очень важен.
 Они привыкли, что им говорят, что и как делать. Это буквально калечит учащихся, когда приходит время решать задачу, которая не следует заученному алгоритму. Что касается нестандартных задач, учащиеся должны выбрать, как они будут их решать. Со временем они учатся доверять себе, чтобы определить подходящие стратегии для использования и решения этих проблем с уверенностью.
Они привыкли, что им говорят, что и как делать. Это буквально калечит учащихся, когда приходит время решать задачу, которая не следует заученному алгоритму. Что касается нестандартных задач, учащиеся должны выбрать, как они будут их решать. Со временем они учатся доверять себе, чтобы определить подходящие стратегии для использования и решения этих проблем с уверенностью. - Как упоминалось выше, это укрепляет уверенность учащихся. Учащиеся вскоре понимают, что могут самостоятельно выбирать подходящую стратегию (или стратегии) и успешно ее применять.
- Он дает ученикам здоровую дозу «борьбы». Я полностью за преподавание на уровне обучения студентов. Тем не менее, я твердо верю, что студенты также должны иногда чувствовать себя немного некомфортно, даже разочарованно. Нестандартное решение проблем расстроит некоторых ваших учеников, особенно поначалу. Не сдавайся! Поговорите со своими учениками о том, что они чувствуют. Обеспечьте соответствующую поддержку, необходимую, чтобы помочь им справиться с этой проблемой.
 Со временем ваши ученики поразят вас своими способностями.
Со временем ваши ученики поразят вас своими способностями. - Это весело!!! Я говорю это не только потому, что я помешан на математике. Это действительно весело, и вашим ученикам понравится это разнообразие, которое оно предлагает. Даже мои ученики, которые не дают правильного ответа, получают удовольствие от процесса.
- Развивает коммуникативные навыки учащихся. Студенты должны задокументировать и объяснить стратегии, которые они используют.
- Это для ВСЕХ. Я никогда не резервировал эти занятия для своих «более успевающих» учеников. На самом деле, многие учащиеся, которые боролись с вычислительными концепциями , РАЗВИВАЛИСЬ, решая нестандартные задачи.
Шаги для нестандартного решения проблем:
Есть четыре широко используемых шага, которые должны быть смоделированы для ваших студентов, чтобы дать им основу при работе с этими проблемами.
- Понять
- План
- Выполнить
- Обзор
Обучающие приложения:
У вас есть несколько вариантов того, как вы можете представить эти
проблемы своим ученикам.
- Вся группа: Вы можете спроектировать проблему для всего класса. для просмотра с помощью ЖК-дисплея или диапроектора. Учащиеся могут работать на доске или просто использовать бумагу и карандаш для решать проблему. Работа может быть выполнена самостоятельно, или вы можете предложить учащимся работать вместе в парах или небольшими группами. группы. В последнем варианте я бы требовать, чтобы все учащиеся записывали работу на своей доске или бумага. Этот вариант всей группы может следовать с несколькими студентами, представляющими свой план решения проблемы; это хорошая возможность для класса увидеть несколько стратегий, которые можно использовать для решить ту же проблему.
- Самостоятельная работа: учащиеся могут подготовить свою задачу в любое время, когда им нужно работать независимо (т. е. быстрые финишеры, центровые, утренняя работа и др.)
- Совместное обучение:
Объедините учащихся в пары для совместной работы над проблемой. Это ценный вариант, поскольку он добавляет
учебные преимущества общения и сотрудничества в процессе.

Презентация:
И последнее, что следует учитывать: в дополнение к вышеупомянутым приложениям, подумайте о том, как бы вы хотели, чтобы ваши ученики делились или представляли свои работай.Это важный компонент для ряд причин:- Выдерживает учащиеся несут ответственность за свою работу.
- Обеспечивает студенты с важной возможностью объяснить решение своих проблем процессы.
- Позволяет другим учащимся, чтобы увидеть различные способы решения проблемы.
- Обеспечивает студенты, у которых есть «время проявить себя», когда они представляют свою работу другим.
- Они могут представляют свою работу всему классу, в основном проводя собственные «мысли вслух», аналогично тому, что делал учитель, когда он/она непосредственно моделировал процесс в классе.
- Они могут
представить свою работу другому студенту или небольшой группе студентов.

- Они могут подарить свою работу родителям или старшему брату или сестре.
- Они могут представить свою работу на онлайн-форуме (например, Edmodo и т. д.), организованном учитель.
Приведенные выше задачи взяты из моих Brain Power Math Books .Если ваши дети «голодны» по больше, проверьте их!
Учебник по математике для изучающих английский язык
Мой отец дал мне одну долларовую купюру
Потому что я его самый умный сын,
И я обменял ее на две блестящие монетки
Потому что два больше, чем один!— Отрывок из книги Шела Сильверстайна «Умный»
Будучи студентом, у меня были проблемы с математикой. Я не понимал, почему это было так естественно для некоторых студентов, но не для меня. Однако, оглядываясь назад, я понимаю, что у меня было преимущество, о котором я даже не догадывался — я понимал язык, на котором написаны задачи, даже если не понимал, как их решать! Хотя легко предположить, что многие изучающие английский язык (ELL) будут преуспевать в математике, потому что математика является «универсальным языком» и учащиеся могут иметь предыдущий образовательный опыт, включающий математические инструкции, это предположение может ввести преподавателей в заблуждение.
Когда я разговаривал с учителями и проводил исследования для этой статьи, стало совершенно ясно, что очень важно убедиться, что учащиеся понимают математический словарь и имеют широкие возможности для его использования. Решение текстовых задач, следование инструкциям, понимание и правильное использование математической лексики — все эти навыки требуют владения языком, которое иногда превосходит наши ожидания. Мы склонны думать о математике как о предмете, который не требует сильного владения языком.В действительности, однако, математическое мышление и решение задач тесно связаны с языком и зависят от твердого понимания базовой математической лексики (Dale & Cuevas, 1992; Jarret, 1999).
Для многих педагогов задача объединения обучения языку и математике является относительно новой. Учителей ELL, которые ранее не преподавали предметные области, теперь просят вести или поддерживать обучение в классе математики, и многие учителя математики, которые не считают себя инструкторами по языку, теперь несут ответственность за обеспечение эффективного обучения математике для ELL.
Учитель математики средней школы Хиллари Хансен узнала, насколько большую роль играет язык в обучении математике, когда в прошлом году она преподавала свой первый базовый курс математики для ELL. Ей так хотелось дать ученикам хорошую основу, в которой они нуждались, но она чувствовала, что не может достучаться до учеников или вовлечь их в свои уроки, и к концу года она была измотана и расстроена.
Тем летом у нее была возможность присоединиться к когорте округа Sheltered Instruction Observation Protocol (SIOP), чтобы получить профессиональное развитие и поддержку для удовлетворения потребностей ELL в предметных классах.Она узнала о важности овладения языком, накопления фоновых знаний, повышения языковой продуктивности учащихся и явного обучения академическому языку. Она начала этот учебный год с нового набора инструментов и более глубокого понимания учебных пособий, необходимых ELL для изучения содержания, одновременно изучая английский язык. Я рад сообщить, что, хотя Хиллари все еще испытывает трудности и очень усердно работает, этот год был намного более успешным для нее и ее учеников.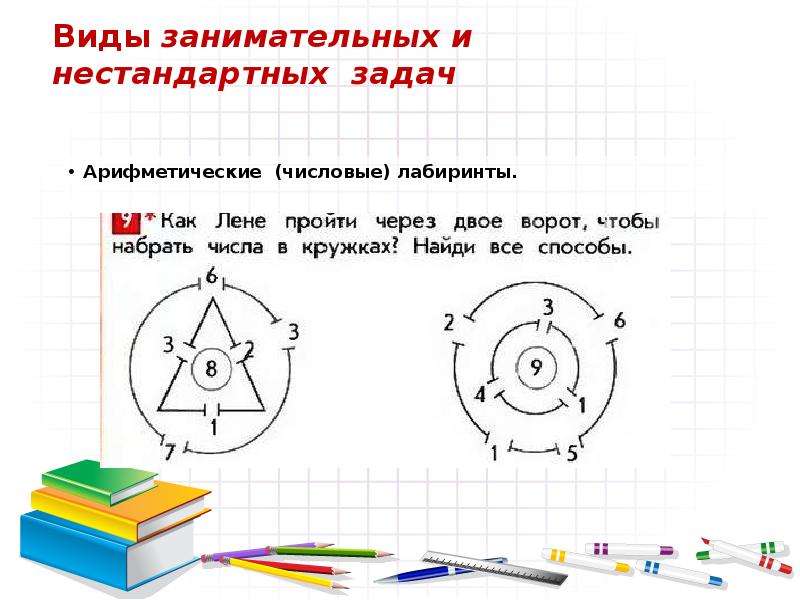
В результате более эффективного обучения ее ученики:
- лучше понимают содержание и вместе работают над поиском творческих способов изучения
- больше обсуждают математику и знают, как использовать учебные пособия, которые есть у учителя
- легко разбираются в математике и задают вопросы, чтобы получить необходимую им помощь.
Хиллари считает, что дает им основу, необходимую не только для понимания математических концепций, но и для успешного взаимодействия в математическом классе, чтобы продолжить изучение более сложных концепций.
Ниже приведены некоторые стратегии, которые Хиллари и некоторые другие учителя, с которыми я разговаривал, сочли полезными в этом году и которые они рекомендуют в качестве передового опыта при обучении математике учащихся ELL.
Важность обучения академической лексике
Обучение словарному запасу необходимо для эффективного обучения математике. Он включает не только обучение математическим терминам, таким как «проценты» или «десятичные числа», но также включает понимание разницы между математическим определением слова и другими определениями этого слова.
Следующий пример, использованный в презентации д-ром Джудит Мошкович из Калифорнийского университета в Санта-Круз, показывает, почему словарный запас должен быть введен в контексте содержания (Moschkovich, 2008):
задача, ученику предлагается «найти x». Студент, очевидно, знал значение слова «найти», потому что он «нашел» его на странице и обвел. Ученик даже оставил на странице заметку, чтобы помочь учителю найти потерянный «x».Студент понял значение слова «найти» в одном контексте, но не в соответствующем математическом контексте.
Недавно я помогала учителю математики проводить закрытый урок и с удивлением обнаружила, что в нем есть слова, которые я не понимаю. Мое незнание слов мешало мне решить математическую задачу и дало мне более глубокое сочувствие к ELL, которые так же борются со словарным запасом и пониманием математических заданий. Ниже приведен список советов по явному преподаванию математической академической лексики:
- Продемонстрируйте, что лексика может иметь несколько значений.
 Помогите учащимся понять различные значения таких слов, как «стол» и «четверть», а также как правильно их использовать в математическом контексте.
Помогите учащимся понять различные значения таких слов, как «стол» и «четверть», а также как правильно их использовать в математическом контексте. - Поощряйте студентов предлагать двуязычную поддержку друг другу. Учащиеся лучше поймут материал, если объяснят его другому учащемуся, а новому учащемуся будет полезно услышать объяснение на своем родном языке. (Проверьте горячие ссылки для получения списка двуязычных переводов математической лексики на нескольких языках).
- Визуальные подсказки, графические представления, жесты, реалии и изображения. Предложите учащимся поработать с объектами и изображениями, чтобы овладеть словарным запасом. Если предметов недостаточно для каждого учащегося, используйте манипулятивные изображения на надписях или развесьте по всему классу и продемонстрируйте словарный запас перед учащимися. Например, Хиллари создала стену математических слов, состоящую из трех частей: ключевой словарь, определения «своими словами» и различные способы изображения функции.
 Например, умножение обозначается следующими символами: x, * и ( ).
Например, умножение обозначается следующими символами: x, * и ( ). - Определите ключевые фразы или новую лексику для предварительного обучения. Эта стратегия поможет учащимся решить, какую математическую функцию им следует применить. Пример: «больше чем» означает «добавить». (См. горячие ссылки для получения дополнительных ссылок на математический словарь.)
Важность чтения и понимания письменных математических задач
Письменные задачи представляют собой уникальную проблему как для учащихся ELL, так и для учителей.В книге «Чтение и понимание письменных математических задач» Бренда Крик-Моралес пишет: «Задачи со словами в математике часто представляют собой проблему, потому что они требуют, чтобы учащиеся прочитали и поняли текст задачи, определили вопрос, на который нужно ответить, и, наконец, создали и решить числовое уравнение — ELL, которые получили формальное образование в своих странах, как правило, не имеют математических трудностей; следовательно, их трудности начинаются, когда они сталкиваются со словесными задачами на втором языке, которым они еще не овладели» (Бернардо, 2005).
Учитель Сяо-линь Инь-Крофт столкнулась с этим явлением в своем классе двуязычных китайских учеников в Сан-Франциско. Она разработала очень творческий способ использования базовых знаний своих учеников по математике в качестве трамплина для изучения других языков. Она делает это, ускоряя обучение математике в начале учебного года, а затем опираясь на то, что учащиеся изучили по математике в чтении и других предметных областях. В статье «Наведение мостов для будущего» в Colorín Colorado «От всего сердца» Сяолинь объясняет свою стратегию:
Сначала мы читаем математические задачи; Я демонстрирую процесс логического мышления при переводе слов в картинки и, наконец, в числовые предложения.Вскоре они начинают объяснять свои мысли после прочтения сложных словесных задач, включающих несколько шагов. Они поправляют друг друга и спорят о том, какие числовые предложения им следует использовать, чтобы получить правильные окончательные результаты. По мере того как они оттачивают свои математические навыки, я использую их энтузиазм, чтобы научить их извлекать самую важную информацию из текстов и продвигать их к устной речи и беглости чтения, которые им необходимы для понимания и обсуждения более сложных текстов.
Даже если вы не ускоряете обучение математике, существует ряд способов помочь учащимся справиться со словесными задачами.Крик-Моралес предлагает предложения в ранее упомянутой статье, такие как подробное обучение ключевой лексике, ежедневная практика решения проблем, многократное чтение слова «проблема» вместе всем классом и практические действия, такие как движение, эксперименты или рисование для помочь учащимся понять проблему. По мере того, как учащиеся лучше знакомятся с математической лексикой, им будет легче решать задачи.
Важность накопления базовых знаний
Как напоминает нам вступительная цитата из стихотворения Шела Сильверстайна, базовые знания играют решающую роль на уроках математики! Моя коллега Хиллари обнаружила, что иногда ее ученики «терялись» в задаче просто потому, что не понимали контекста.Ниже приведены некоторые советы, которые помогут в формировании фоновых знаний учащихся.
- Изменить лингвистическую сложность языка и перефразировать математические задачи.
 Учащиеся лучше поймут задачу, если она будет изложена более короткими предложениями и на понятном им языке.
Учащиеся лучше поймут задачу, если она будет изложена более короткими предложениями и на понятном им языке. - Помогите учащимся вычеркнуть ненужную лексику в текстовых задачах. Это позволяет учащимся сосредоточиться на необходимой математической функции. Например, одна проблема, с которой столкнулись ученики Хиллари, касалась «школьного собрания».» Несмотря на то, что значение этой фразы не имело значения при решении математической задачи, учащиеся не знали, что это неважно, и отсутствие понимания способствовало их замешательству. Постарайтесь закрепить понятия примерами, которые учащиеся могут изобразить и обсудить с учащимися в этой ситуации.Например, если вам нужно покрасить комнату, вам нужно знать, какая площадь будет покрыта, чтобы вы знали, сколько краски нужно купить.Ищите знакомые идеи или реквизиты, которые можно использовать для привлечения учащихся, такие как рецепты, новости об экономике или обсуждение личных привычек в отношении расходов.

- Целенаправленно используйте манипуляции. Это важно на всех уровнях обучения. Хиллари обнаружила, что математические кубики очень полезны, когда учащиеся представляют числа в задачах, а затем манипулируют кубиками, чтобы получить ответ. Она использовала кубики и термины «горячие» и «холодные» числа при обучении концепции отрицательных чисел.Студенты использовали красные кубики как «горячие» или положительные числа, а синие кубики как «холодные» или отрицательные числа. Когда учащиеся раскладывали количество представленных горячих и холодных кубиков, они могли легко увидеть, будет ли ответ положительным или отрицательным числом, на какой цвет приходится больше всего кубиков. Такая задача, как -2 + 1 = -1, будет выглядеть так: затем учащийся убирает пары кубиков — один красный, один синий — до тех пор, пока он больше не сможет удалять блоки. Остальные блоки представляют собой ответ.
Важность повышения языковой продуктивности учащихся в предметной области
Когда я работал с учителями предметной области в моем округе над разработкой уроков и мероприятий Shelted Instruction для улучшения обучения ELL, я сказал им: «Если учащийся не говорит этого в вашем классе, они никогда не скажут этого. Это немного драматично, но в какой-то степени это правда. Когда учащиеся изучают новую лексику, возможность использовать ее должна быть представлена в классе, потому что учащиеся вряд ли будут пробовать ее самостоятельно — особенно такие академические слова, как «параллелограмм». или «функция»!
Это немного драматично, но в какой-то степени это правда. Когда учащиеся изучают новую лексику, возможность использовать ее должна быть представлена в классе, потому что учащиеся вряд ли будут пробовать ее самостоятельно — особенно такие академические слова, как «параллелограмм». или «функция»!
Вот несколько советов, как улучшить взаимодействие между учащимися с помощью академического языка в классе математики:
- Предложите учащимся перевести символы в слова и написать предложение. Хиллари использовала эту стратегию, чтобы проверить понимание учащимися задач до их решения.Например, 3x + 4 = 16 будет записано: «Три раза X плюс четыре равно шестнадцати». Это помогает учащимся обработать операции, связанные с вопросом, и дает им возможность продумать, как его решить. Это также дает учащимся возможность ознакомиться с важными словарными словами.
- Создайте «рамку предложения» и разместите ее на доске. Напишите формат предложения, который вы хотели бы, чтобы учащиеся использовали в обсуждении, а затем привлеките их к ответственности за его использование.
 Например, «Ответ равен _______ градусам, потому что это треугольник _________».
Например, «Ответ равен _______ градусам, потому что это треугольник _________». - Предложите учащимся поделиться стратегиями решения проблем. Для этого нужно задать простой вопрос, например: «Кто-нибудь еще получил ответ другим способом?» Затем дайте учащимся достаточно времени для ожидания, чтобы они могли обдумать, чем их процесс решения задач был похож или отличался от предложенного
- Позвольте учащимся обсудить, как они думают о математике Это способ перенаправить урок от учителя — к ученику к ученику к ученику.Например, студент может задать вопрос: «Откуда вы знаете, что это за треугольник?» Вместо того, чтобы учитель отвечал, подходил к доске и указывал на имена и разные треугольники, учитель может просто спросить: «У кого-нибудь есть ответ? Или: «Кто-нибудь хочет предложить помощь Марио?» Позвольте учащимся поделиться своими впечатлениями. подумайте о математической концепции и любых советах, которые они могут дать для запоминания информации.
 Дневник можно начать с простых подсказок, таких как: «Одна вещь, которую я сегодня узнал…» «Одна вещь, которую я до сих пор не понимаю…» «Один из способов получить необходимую мне помощь…» «Ответ на эту проблему таков: …» Написание ответа на задачу — очень важный навык, который нужно развивать, потому что многие тесты штата по математике требуют сконструированного ответа на вопросы.
Дневник можно начать с простых подсказок, таких как: «Одна вещь, которую я сегодня узнал…» «Одна вещь, которую я до сих пор не понимаю…» «Один из способов получить необходимую мне помощь…» «Ответ на эту проблему таков: …» Написание ответа на задачу — очень важный навык, который нужно развивать, потому что многие тесты штата по математике требуют сконструированного ответа на вопросы. - Предложите учащимся создать свои собственные математические задачи. Это может быть увлекательным занятием, если учащиеся создают задачу, аналогичную той, которую вы использовали в классе, и обмениваются задачами с партнером.Создавая проблему и проверяя ответ, они укрепляют собственное обучение.
Использование технологий
Технологии также могут быть мощным инструментом обучения математике для ELL. Вот несколько идей, как вы можете поиграть с технологиями на уроке математики:
- Найдите образовательные ресурсы, которые сопровождают технологические инструменты и программы вашей школы.
 Для учителей могут быть доступны онлайновые программы или программы. Для учителей, у которых в классе есть электронная доска, есть много ресурсов, доступных по ссылкам, к которым можно легко получить доступ и принести в класс.
Для учителей могут быть доступны онлайновые программы или программы. Для учителей, у которых в классе есть электронная доска, есть много ресурсов, доступных по ссылкам, к которым можно легко получить доступ и принести в класс. - Ищите интерактивные игры, которые дают учащимся возможность попрактиковаться в математических навыках. На Nintendo DS есть образовательная игра Brain Age, которая не зависит от языка. Игра обеспечивает отличную математическую подготовку для чисел и отслеживает результаты, показывая прогресс ученика с течением времени.
- Узнайте, что доступно онлайн. Vital NY (Видеопреподавание и обучение для преподавателей штата Нью-Йорк) на сайте Teachers’ Domain предлагает онлайн-библиотеку бесплатных медиа-ресурсов от лучших представителей общественного телевидения.Ресурсы домена учителей включают в себя видео- и аудиосегменты, интерактивные Flash-материалы, изображения, документы, планы уроков для учителей и мероприятия, ориентированные на учащихся.
 (Требуется бесплатная регистрация.)
(Требуется бесплатная регистрация.) - Если учащиеся используют графический калькулятор, убедитесь, что они научились им пользоваться. В зависимости от подготовки и предшествующего образовательного опыта учащиеся могут не знать, как пользоваться калькулятором, а также с некоторыми более сложными моделями, например, с графическим калькулятором. Дайте учащимся возможность попрактиковаться в решении задач на своих калькуляторах после того, как вы ознакомитесь с различными функциями.Texas Instruments предлагает многочисленные занятия и руководства по продуктам в своих учебных материалах.
Даже если поначалу это дается нелегко, есть способы заинтересовать ELL математикой. Учитывая их языковые навыки и потребности при планировании обучения математике (и помогая своим коллегам делать то же самое), вы сделаете важные шаги, помогая учащимся овладеть математическими понятиями и навыками — и кто знает? Ваши ученики могут стать экономистами нового поколения, учеными-ракетчиками и учителями математики, которые только и ждут необходимых им инструментов!
Примечание. Я хотел бы поблагодарить моих коллег из Миннесоты, Хиллари Хансен из старшей школы Бернсвилля и Ким Олсон из начальной школы Хидден-Вэлли, а также Сяо-линь Инь-Крофт из Сан-Франциско за предоставление многих полезных советы по обучению математике в этой статье.Вдохновляет знать, что есть талантливые, творческие учителя, которые всегда находят лучшие способы преподавания и готовы делиться знаниями.
Я хотел бы поблагодарить моих коллег из Миннесоты, Хиллари Хансен из старшей школы Бернсвилля и Ким Олсон из начальной школы Хидден-Вэлли, а также Сяо-линь Инь-Крофт из Сан-Франциско за предоставление многих полезных советы по обучению математике в этой статье.Вдохновляет знать, что есть талантливые, творческие учителя, которые всегда находят лучшие способы преподавания и готовы делиться знаниями.
Горячие ссылки
Common Core Math и ELL: сообщения в блоге
Эти сообщения из нашего блога Common Core посвящены ресурсам, которые можно использовать в инструкциях по математике Common Core для ELL.
EngageNY: Common Core and Math
Веб-сайт EngageNY содержит материалы, посвященные примерам учебных программ, стандартам математической практики и другие материалы для профессионального развития.
Discovery Education: Puzzlemaker
Puzzlemaker — это бесплатный инструмент для создания головоломок для учителей, учащихся и родителей, в котором пользователи могут создавать и распечатывать индивидуальные головоломки с поиском слов, крест-накрест, математические головоломки и многое другое, используя свои собственные списки слов.
Кэтрин Сноу: Word Generation
Новый веб-сайт Кэтрин Сноу предоставляет информацию и ресурсы для преподавателей, которые хотели бы узнать больше о Word Generation и о том, как это реализовано. Включает ссылки на исчерпывающий список академических слов, которые учащиеся должны освоить, чтобы понять учебный контент.
Математические таблицы Дейва: англо-испанский словарь
Список слов английского математического словаря с испанским эквивалентом.
Учителя PBS: уроки математики
Учителя PBS предлагают базу данных мультимедийных уроков математики и заданий, которые можно искать по классам или темам.
Учебные занятия SMART Notebook
Просматривайте учебные занятия и материалы для классов с помощью программного обеспечения SMART Notebook. Выберите страну или регион и выполните поиск по стандартам учебной программы, предмету и уровню класса.
Colorín Colorado Веб-трансляция: Учащиеся, изучающие английский язык в средних и старших классах
В этой веб-трансляции с участием доктора Деборы Шорт обсуждаются эффективные учебные стратегии для обучения учащихся, изучающих английский язык, в средних и старших классах, такие как модель SIOP.
Перевод задач
Это отличный сайт для учителей начальных классов, так как он содержит список ключевых слов, которые вы можете научить ELL искать, когда они читают задачи.Также включены полезные идеи и приемы, чтобы лучше подготовить учащихся к пониманию письменных математических задач.
5280 Math
Math Pickle
mathpickle.com содержит коллекцию глубоких, открытых и сложных (некоторые из них нерешенных!) математических задач для учащихся всех возрастов, доступных для поиска по классам, в том числе множество для самых маленьких учеников. Каждая задача была найдена или создана профессиональным математиком и удобно укладывается в временные рамки 45-60 минут.
богатая математика
богатая математика.org содержит обширную коллекцию увлекательных математических задач с возможностью поиска по возрасту и концепции. Существует много поддержки для учителей, и студенты могут представить решения для возможной публикации в Интернете.
Головоломки Кен-Кен
Головоломки Кен-Кен похожи на судоку, но с математическим уклоном. Головоломки развивают не только вычислительные способности, но и навыки решения задач, чувство числа и более глубокое понимание свойств чисел. Этот веб-сайт будет генерировать для вас головоломки кен-кен на основе вашего выбора уровня обучения, математических операций, размера сетки и уровня сложности.
Головоломки Zukei
Головоломки Zukei включают в себя поиск геометрических фигур, спрятанных в сетках или точках. Основное внимание уделяется рассуждениям о свойствах двумерных фигур. Головоломки бывают всех уровней сложности. Вы и учащиеся также можете легко создавать свои собственные.
Exploding Dots
Exploding Dots Джеймса Тэнтона штурмом покорили мир математики за последние пару лет. Используя простую визуальную модель, учащиеся изучают разрядность, сложение, вычитание, умножение, деление и многое другое в различных базовых системах.
Академия Зверей
Академия Зверей — это полная учебная программа по математике для одаренных и продвинутых учащихся 2–5 классов. (Я бы не рекомендовал ее другим учащимся.) за материалы для одаренных учащихся средних школ. Основное внимание уделяется решению проблем и глубокому концептуальному пониманию. Сообщается, что скоро появится онлайн-версия программы.
(Я бы не рекомендовал ее другим учащимся.) за материалы для одаренных учащихся средних школ. Основное внимание уделяется решению проблем и глубокому концептуальному пониманию. Сообщается, что скоро появится онлайн-версия программы.
Project M2
Созданный теми же людьми, которые разработали Project M3 для учащихся старших классов, Project M2 «содержит восемь разделов учебной программы, предназначенных для классов K-2, чтобы стимулировать исследования и вовлекать учащихся в критическое мышление, решение проблем и коммуникативные действия…[с] акцентом на «углубленную» математику с использованием научно-исследовательских практик и стандартов в математическом образовании и дошкольном образовании.
Project M3
Эта серия книг от Кендалла Ханта хорошо известна в США благодаря тому, что она предлагает основанную на исследованиях глубокую и сложную учебную программу по математике для продвинутых учащихся. Каждый модуль поставляется с обширной поддержкой преподавателей, и вы можете использовать проекты в качестве учебных единиц или в качестве дополнения. Единственные минусы: материалы довольно дорогие и требуют от преподавателей изрядного времени на подготовку.
Единственные минусы: материалы довольно дорогие и требуют от преподавателей изрядного времени на подготовку.
10 способов помочь ELL добиться успеха в математике
Когда дело доходит до изучения математики, перед изучающими английский язык (ELL) стоит уникальная задача. В отличие от большинства англоговорящих учащихся, перед ELL стоит задача одновременного изучения второго языка и содержания. Вопреки распространенному мнению, язык играет решающую роль не только в чтении и письме, но и в изучении математики. Перед вами как учителем стоит задача сделать уроки математики понятными и обеспечить, чтобы учащиеся владели языком, позволяющим понимать инструкции и выражать свое понимание математических понятий устно и письменно.Наша группа экспертов делится десятью способами научить ELL их ABC и их 123.
1 Создание словарных банков.
Таблицы, содержащие ключевые слова и фразы из математического словаря, являются полезным справочным материалом для ELL при обсуждении или написании своего математического мышления, особенно если слова сопровождаются иллюстрациями.
2 Используйте манипуляции.
Манипуляторы — важные инструменты, которые делают математический контент понятным. Они дают учащимся способы построения физических моделей абстрактных математических идей; они укрепляют доверие студентов, давая им возможность проверить и подтвердить свои рассуждения; они полезны для решения проблем; и они делают изучение математики интересным и приятным.
3. Изменить время разговора учителя и время ожидания.
Важно дать всем учащимся, особенно изучающим английский язык, время для обработки вопросов и формулирования ответов. Говорите медленно и используйте четкую артикуляцию. Уменьшите количество разговоров учителя и используйте разные слова для одной и той же идеи. Преувеличивайте интонацию и делайте больший акцент на важных новых концепциях или вопросах. Задав вопрос, подождите несколько минут, прежде чем позвать волонтера. Также поможет запись вопроса на доске.
4. Вызовите невербальные ответы, такие как большой палец вверх или вниз.
Невербальные ответы помогут вам проверить понимание, не требуя от учащихся воспроизведения языка. ELL могут принять участие и показать, что они понимают концепцию, или согласны или не согласны с идеей, без необходимости говорить. Это особенно важно для студентов, чье понимание английского выше, чем их способность говорить на этом языке.
5. Используйте рамки предложений.
Математические рамки предложений служат множеству целей. Они обеспечивают поддержку, необходимую изучающим английский язык для полноценного участия в математических дискуссиях; они контекстуализируют и придают смысл словарному запасу; они обеспечивают структуру для практики и расширения навыков английского языка; и они помогают студентам использовать словарный запас, который они изучают, в грамматически правильных и полных предложениях. После достаточной практики использования фреймов для выражения своего математического мышления учащиеся будут готовы использовать фреймы для письма.
Например, следующие рамки помогают учащимся с разным уровнем владения языком в обсуждении многоугольников.
Начальный уровень
Это не полигон . Это/имеет кривых .
Средний уровень
Это не полигон , потому что он имеет кривых , а открыт .
Продвинутый уровень
Эта фигура имеет четыре прямые стороны , четыре вершины и замкнута ; следовательно, это полигон .
6. Составьте вопросы и подсказки для разных уровней владения языком.
Опрос студентов позволяет им раскрыть то, что они узнали. Ответы на вопросы позволяют учащимся проверить, подтвердить или изменить свое собственное понимание. Ни одна из этих целей не может быть достигнута, если запросы не структурированы таким образом, чтобы учащиеся могли дать ответ. Вот несколько примеров вопросов и подсказок, используемых для поддержки учащихся с разным уровнем владения языком.
Начальный уровень
Изучающие английский язык не всегда могут ответить на заданные им вопросы, особенно когда вопросы открытые.Обеспечьте поддержку и улучшите участие учащихся с более низким уровнем владения английским языком, используя подсказку, требующую физической реакции, например «Покажи мне кружок» или «Дотронься до большего числа».
Вы также можете задать вопрос, требующий ответа «да» или «нет»: «Одно число больше другого?»
Задавая вопросы с кратким ответом, встраивайте ответ в вопрос для дополнительной поддержки: «Это треугольник или круг?» или «Линия горизонтальная или вертикальная?» или «Должны ли мы добавить или вычесть?»
Средний и продвинутый уровни
Учащимся со средним и продвинутым уровнями владения языком требуется меньшая поддержка, чтобы понимать вопросы и отвечать на них, но тщательно составленные запросы могут улучшить качество их ответов и их английского языка.Например, вместо того, чтобы спрашивать учащегося среднего уровня: «Как вы решили задачу?» можно сформулировать вопрос так: «Что вы сделали в первую очередь, во вторую и в третью, чтобы решить проблему?» Такого рода вопросы моделируют структуру хорошо продуманного ответа: «Во-первых, я складываю блоки по десять штук. Во-вторых, я считаю по десяткам. В-третьих, я добавляю оставшиеся блоки». Сравните это с ответом, который, скорее всего, вытекает из первого вопроса: «Я их посчитал».
Во-вторых, я считаю по десяткам. В-третьих, я добавляю оставшиеся блоки». Сравните это с ответом, который, скорее всего, вытекает из первого вопроса: «Я их посчитал».
Учащиеся с продвинутой беглостью могут отвечать на вопросы и подсказки, которые являются еще более открытыми, например: «Опишите мне шаги, которые вы использовали для решения проблемы, и объясните, как вы их использовали.»
7. Используйте подсказки для поддержки ответов учащихся.
Подсказки могут помочь изучающим английский язык начать работу при ответе на вопрос. Например, начните со слов: «Вы догадались, что…» или «Это многоугольник, потому что…» или «Сначала вы положили шестиугольник на стол, а потом…». ответ, они с большей вероятностью последуют вашему примеру и ответят с уверенностью.
8. Учитывайте языковые и математические навыки при группировании учащихся.
Бывают случаи, когда имеет смысл объединять учеников с одинаковыми способностями в математике, особенно когда все эти ученики борются с одной и той же концепцией или навыком. Однако в большинстве случаев учащиеся получают пользу от работы в группах, участники которых имеют разный уровень знаний по математике. Студентам также полезно работать в группах, участники которых имеют разный уровень владения английским языком. Однако важно следить за разговорами учащихся, чтобы у всех учащихся была возможность участвовать в математических беседах.
Однако в большинстве случаев учащиеся получают пользу от работы в группах, участники которых имеют разный уровень знаний по математике. Студентам также полезно работать в группах, участники которых имеют разный уровень владения английским языком. Однако важно следить за разговорами учащихся, чтобы у всех учащихся была возможность участвовать в математических беседах.
9. Используйте разговор с партнером.
Для разговора с партнером задайте вопрос, а затем дайте учащимся минуту или две, чтобы выразить свои мысли словами с ближайшим соседом. Разговор с партнером позволяет большему количеству учащихся участвовать в обсуждениях в классе и устраняет давление, возникающее при выступлении в одиночку перед большой группой. Это также способствует позитивному сотрудничеству с коллегами; когда студенты что-то решают вместе, между ними строится доверие.
10.Попросите учащихся ответить хором.
Когда учащиеся повторяют слово или фразу, они знакомятся с новым словарным запасом и служат образцом для правильного произношения, синтаксиса и грамматики.
Советы учителю
Инструктор читатели делятся тем, что им больше всего подходит.
«Чем больше вы используете сильную иллюстрированную и манипулятивную поддержку, тем легче ELL изучать математику. На самом деле, даже те, кто говорит на английском как на родном языке, получают большую пользу от манипуляций и рисунков.Немногие учащиеся эффективно понимают математический язык без визуального опыта.» -Lin Cazares
«Показывайте и рассказывайте, когда это возможно, посредством демонстрации, ролевых игр и моделирования. Используйте картинки и видео во время изучения словарного запаса и понятий. Наконец, обратитесь за помощью, если вам это нужно! В вашем округе и/или школе должен быть специалист, обученный помогать вам!» — Дженифер Л. Мур
«Поднимите учеников и активизируйте их. Они по своей природе очень кинестетичны; они хлопают в ладоши, когда учатся считать пятерками и десятками, отправляются на «охоту за числами», гуляя и обыскивая комнату, или патрулируют школу, чтобы определить геометрические фигуры. » -Nanette Avery
» -Nanette Avery
«Небольшие группы позволяют учащимся ELL чувствовать себя более комфортно и уверенно. Им нравится общаться со сверстниками, а не задавать вопросы перед всем классом. Кроме того, перемещение по комнате позволяет мне остановиться и сосредоточиться на их потребностях.» -Sarah Wilson
«Предоставьте ELL возможность работать индивидуально, чтобы они могли прогрессировать в своем собственном темпе. Во время сложного урока вы можете сказать что-то вроде: «Выполните как можно больше вопросов 5 за 10 минут» или «Выберите вопрос, с которого вы хотите начать».'» -Dorit Sasson
«Связать концепцию с личным опытом студента в прошлом; таким образом у них будет больше шансов понять преподаваемую информацию. Попробуйте ввести понятие, связав его с чем-то из их страны. Например, у меня есть ученица, приехавшая из Голландии, и я всегда спрашиваю ее, как называется определенное слово на голландском языке». имеют отношение к недавнему уроку.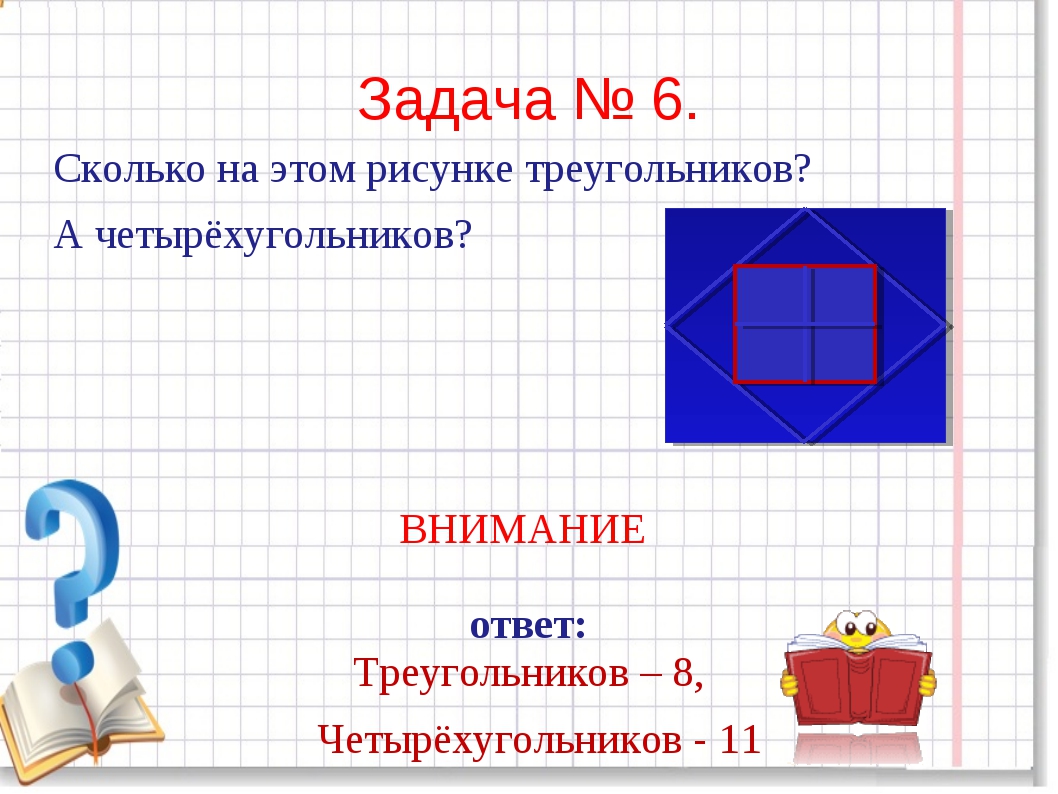 Я читаю их записи и отвечаю на них и поддерживаю.» -Нанетт Эйвери
Я читаю их записи и отвечаю на них и поддерживаю.» -Нанетт Эйвери
О книге:
Эти стратегии воплощены в жизнь в новом ресурсе Math Solutions, широко используемом педагогами по подготовке учителей K-5: Поддержка изучающих английский язык на уроках математики: мультимедийный профессиональный учебный ресурс (Bresser et al., 2009). Этот инструмент был разработан для учителей обычных или обычных классов с одним или несколькими учащимися ELL и включает в себя три основных компонента: DVD с изображением учителей и учащихся в действии, серию из двух книг для классов K-2 и 3-5, а также руководство ведущего. руководство по поддержке внедрения эффективных стратегий.Посмотрите видеоклипы авторов, использующих стратегии ELL с учащимися, и найдите дополнительные ресурсы для ELL в Интернете по адресу www.mathsolutions.com/ELL.
Познакомьтесь с экспертами
Кристин Уиллиг , президент и главный исполнительный директор Math Solutions, 25 лет проработала на руководящих должностях в сфере образования.
Расти Брессер читает лекции и руководит обучением учителей в Калифорнийском университете в Сан-Диего (UCSD).
Кэти Меланезе — почетный учитель-резидент (двуязычная начальная школа) в UCSD.
Кристин Сфар, , администратор по поддержке новых учителей в школьном округе Союза Кахон-Вэлли в Сан-Диего.
Кэролин Фелюкс — директор по образованию Math Solutions.
Математические задания для 5-го класса — бесплатные развлечения для пятиклассников — JumpStart
Если вы ищете увлекательные математические задания для пятиклассников, вы попали по адресу! Math Blaster содержит обширную коллекцию бесплатных математических заданий, рабочих листов и задач для детей.Проверьте их сейчас!
Умножение коробок для яиц
Ваш пятиклассник уже должен освоиться с умножением, но нет ничего плохого в том, чтобы научить его умножать числа в уме. Попробуйте эту веселую групповую игру! Увидеть больше
Попробуйте эту веселую групповую игру! Увидеть больше
В поисках углов
Пятиклассники, изучающие геометрию, иногда могут быть сбиты с толку странной новой лексикой и определениями. Протяните руку помощи своему ребенку с помощью этого веселого урока по углам.Увидеть больше
Карты, кости и проценты
Используйте образовательную ценность карт, игральных костей и калькуляторов, чтобы дать пятиклассникам возможность попрактиковаться в математических навыках. Увидеть больше
Увесистая математика
Дайте своему пятикласснику возможность попрактиковаться в своих навыках оценки, когда вся семья соберется на Рождество или День Благодарения. Увидеть больше
Экспоненты упрощенные
Как насчет использования карточных игр, чтобы помочь вашему ребенку понять показатели? Этот веселый урок для детей, посвященный играм и показам, покажет вам, как это сделать.Увидеть больше
Игральные карты вероятности
Познакомить ребенка с карточными играми — отличный способ отточить его математические способности. Вот забавная карточная игра, которая также служит уроком вероятности и статистики.Подробнее
Вот забавная карточная игра, которая также служит уроком вероятности и статистики.Подробнее
Дробная кратность
Эквивалентные дроби могут быть проблемой, если вы не поняли концепцию должным образом. Вот увлекательное занятие, которое поможет вашему ребенку понять, что такое обыкновенные и эквивалентные дроби. Увидеть больше
Гонка за общим знаменателем
Если вашему ребенку трудно усвоить понятие дробей, игра «Гонка с общим знаменателем» может быть именно тем, что ему нужно! Увидеть больше
Математика купонов
«Математика купонов» — это простая и увлекательная игра, с помощью которой вы можете научить своего пятиклассника базовым математическим навыкам.Увидеть больше
Охота за простыми числами
«Охота за простыми числами» — увлекательное математическое задание, которое поможет ему понять простые и составные числа. Увидеть больше
Эквиваленты обучения с игральными картами
С помощью этой забавной версии классической карточной игры ваш пятиклассник получит четкое представление об основных эквивалентах. Увидеть больше
Увидеть больше
Факторы с друзьями
В «Факторы с друзьями» дети работают в парах, чтобы найти множители двух чисел по отдельности, а затем сравнить ответы, чтобы найти НОК.Увидеть больше
Фактор Цветы
В этом бесплатном математическом задании дети соревнуются друг с другом, чтобы рассортировать цветы в правильные горшки.Подробнее
GCF и LCM с диаграммами Венна
Используйте это бесплатное математическое задание, чтобы помочь своим детям понять, как работает диаграмма Венна, а затем научить их находить GCF и LCM двух чисел с помощью диаграммы Венна. Подробнее
GCF Бинго
GCF Bingo — это простая разновидность игры «Бинго», которая позволяет большой группе детей попрактиковаться в нахождении GCF двух чисел.Увидеть больше
Кольцо GCF
Перенесите урок математики на улицу с этим увлекательным математическим заданием. «Ring the GCF» — это простая игра, которая идеально подходит для увлекательной практики GCF.Подробнее
«Ring the GCF» — это простая игра, которая идеально подходит для увлекательной практики GCF.Подробнее
Гигантская конфета
Превратите свой урок пропорций в веселый и захватывающий урок рисования с помощью этой распечатываемой игры с пропорциями «Гигантская конфета». Увидеть больше
Сколько пакетов с сахаром
«Сколько сахарных пакетов» — интересное задание, в котором исследуется, сколько сахара содержится в обычных продуктах нездоровой пищи.Увидеть больше
Если бы у меня был сверхскоростной поезд
«Если бы я владел сверхскоростным поездом» — это забавное задание, в котором рассказывается, каково это — передвигаться по городу на сверхскоростном поезде. Увидеть больше
Цена правильная
Это бесплатное математическое задание демонстрирует важность использования пропорций для определения фактической цены предметов, а не просто просмотра общей стоимости пакета. Увидеть больше
Куклы в натуральную величину
Узнайте, как бы выглядели ваши куклы, если бы они стали такими же высокими, как вы, с помощью этого веселого задания «Куклы в натуральную величину». Увидеть больше
Увидеть больше
Вы знаете алгебру?
Знакомство с алгеброй как с языком и демонстрация учащимся того, как ее понимать и использовать, — отличный способ повысить их уважение и любовь к предмету. Увидеть больше
Двойное отрицание
Помогите шестиклассникам запомнить правила сложения и умножения положительных и отрицательных чисел с помощью этого задания по алгебре, которое можно распечатать. Подробнее
Это война
It’s War — это бумажная и карандашная игра в стиле «Морской бой» с забавным алгебраическим уклоном.Увидеть больше
Уравнения быстрой стрельбы
«Быстрые уравнения» — это бесплатное задание по алгебре, которое дает шестиклассникам много практики в выполнении основных математических операций с целыми числами. Подробнее
Квадратные корни с помощью Пифагора
Покажите учащимся, как можно использовать теорему Пифагора для вычисления приблизительного квадратного корня из различных чисел. Подробнее
Подробнее
Алгебра телевизионного времени
«Алгебра TV Time» — это веселое и бесплатное занятие по алгебре, которое побуждает учащихся 5-го класса изучать и узнавать больше об алгебре и алгебраических уравнениях.Увидеть больше
Странствующий математический бафф
«Путешествие по математике» — это веселое и бесплатное математическое задание для 5-го класса. Сделайте это частью своих путешествий, чтобы научить своих детей быстро рассчитывать расстояние, скорость и время. Увидеть больше
Нет страха перед дробью
«Без страха перед дробью» — это бесплатное задание с дробями для пятого класса, которое можно распечатать и знакомит пятиклассников с этой важной математической концепцией, одновременно занимая их веселой игрой! Увидеть больше
Развивайте свой график
«Увеличь свой график» — это бесплатное задание по графикам для 5-го класса, которое можно распечатать.Это увлекательное занятие научит пятиклассников рисованию и построению графиков! Увидеть больше
Поедание десятичных дробей
«Поедание десятичных знаков» — увлекательное занятие по десятичным числам для пятиклассников. Получите это бесплатное задание, которое можно распечатать, чтобы помочь своим детям узнать о десятичных дробях, развлекаясь! Увидеть больше
Получите это бесплатное задание, которое можно распечатать, чтобы помочь своим детям узнать о десятичных дробях, развлекаясь! Увидеть больше
Характеристики твердых тел
«Характеристики твердых тел» — отличный рабочий лист, который позволяет учащимся исследовать и манипулировать основными твердыми формами в их трехмерных формах, прежде чем обсуждать их характеристики.Увидеть больше
Кошка и Крыса
«Кот и крыса» — классный рабочий лист по геометрии, который показывает детям, как спроектировать собственный лабиринт, используя только сетку и кальку! Увидеть больше
Додекаэдр Десятичные дроби
Научите детей расставлять значения с помощью нашей веселой игры «Десятичные числа додекаэдра»! Эта игра со спичками — отличный способ привлечь детей и сделать их экспертами в этой теме. Увидеть больше
Потрясающие танграмы
«Потрясающие танграмы» — это простое математическое задание с формами, которое наверняка вызовет интерес у самых маленьких! Увидеть больше
Вокруг Света
«Вокруг света» — это забавная математическая тетрадь, которая заставит учащихся путешествовать по миру и обратно за долю времени, которое потребовалось Филеасу Фоггу. Увидеть больше
Увидеть больше
Утки подряд
Ducks in a Row — увлекательная игра, похожая на бинго. Учащиеся должны решить задачи на десятичное умножение и покрыть продукты на своих досках маркерами уток. Увидеть больше
Верхний счетчик
Top Spinner — это игра на умножение, которую можно адаптировать к уровню навыков разных учащихся. Младшие школьники могут играть в простую версию, а старшие или более опытные ученики могут играть в сложную версию.Увидеть больше
Бесплатные математические задания для пятиклассников
Математика 5-го класса включает широкий спектр тем, таких как определение наибольшего общего делителя или наименьшего общего кратного чисел; сложение, вычитание и умножение десятичных дробей и дробей; расчет площади и периметра; измерение углов; и больше!
Хотя некоторые из этих тем относительно легко понять, другие могут оказаться более сложными. Чтобы побудить детей получать удовольствие от изучения предмета и заниматься математикой, рекомендуется вовлечь их в увлекательные математические занятия.
 Числа начинают получать имена. Первые цифры.
Числа начинают получать имена. Первые цифры.  10
10 11
11 01
01 02
02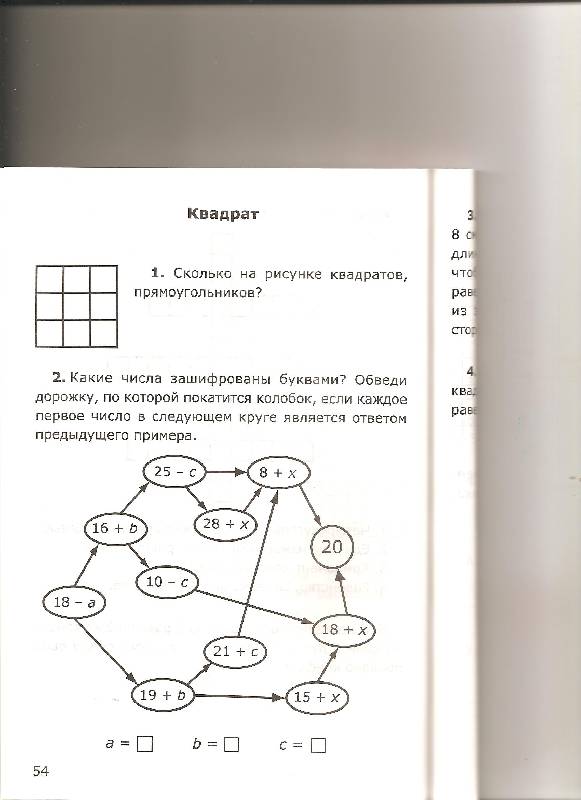 04
04 Занимательные задачи на сообразительность и внимательность.
Занимательные задачи на сообразительность и внимательность.
 Основой его высокого уровня является математическая грамотность подрастающего поколения. Поэтому обеспечение ею школьников – важная задача. Программа направлена на развитие математических способностей и формирование различных типов мышления.
Основой его высокого уровня является математическая грамотность подрастающего поколения. Поэтому обеспечение ею школьников – важная задача. Программа направлена на развитие математических способностей и формирование различных типов мышления. 
 Нестандартные задачи и разные способы их решения способствуют развитию мышления и познавательного интереса. Практические задания подобраны таким образом, что постепенно и неоднократно повторяясь, осознаются и запоминаются основные принципы и методы решения задач, дети учатся анализировать и задавать правильные вопросы. Большое внимание уделяется геометрии, конструированию, моделированию и исследованию. Учебные занятия позволяют формировать интеллектуальное, научное и творческое мышления.
Нестандартные задачи и разные способы их решения способствуют развитию мышления и познавательного интереса. Практические задания подобраны таким образом, что постепенно и неоднократно повторяясь, осознаются и запоминаются основные принципы и методы решения задач, дети учатся анализировать и задавать правильные вопросы. Большое внимание уделяется геометрии, конструированию, моделированию и исследованию. Учебные занятия позволяют формировать интеллектуальное, научное и творческое мышления.
 5
5 5
5 5
5 5
5 5
5

 И. Занимательные задачи и опыты. – М.: Книжный клуб Книговек, 2015. – 496 с.: ил.
И. Занимательные задачи и опыты. – М.: Книжный клуб Книговек, 2015. – 496 с.: ил.







 в соответствующем посте!)
в соответствующем посте!) Они привыкли, что им говорят, что и как делать. Это буквально калечит учащихся, когда приходит время решать задачу, которая не следует заученному алгоритму. Что касается нестандартных задач, учащиеся должны выбрать, как они будут их решать. Со временем они учатся доверять себе, чтобы определить подходящие стратегии для использования и решения этих проблем с уверенностью.
Они привыкли, что им говорят, что и как делать. Это буквально калечит учащихся, когда приходит время решать задачу, которая не следует заученному алгоритму. Что касается нестандартных задач, учащиеся должны выбрать, как они будут их решать. Со временем они учатся доверять себе, чтобы определить подходящие стратегии для использования и решения этих проблем с уверенностью. Со временем ваши ученики поразят вас своими способностями.
Со временем ваши ученики поразят вас своими способностями.

 Помогите учащимся понять различные значения таких слов, как «стол» и «четверть», а также как правильно их использовать в математическом контексте.
Помогите учащимся понять различные значения таких слов, как «стол» и «четверть», а также как правильно их использовать в математическом контексте. Например, умножение обозначается следующими символами: x, * и ( ).
Например, умножение обозначается следующими символами: x, * и ( ).
 Учащиеся лучше поймут задачу, если она будет изложена более короткими предложениями и на понятном им языке.
Учащиеся лучше поймут задачу, если она будет изложена более короткими предложениями и на понятном им языке.
 Например, «Ответ равен _______ градусам, потому что это треугольник _________».
Например, «Ответ равен _______ градусам, потому что это треугольник _________». Дневник можно начать с простых подсказок, таких как: «Одна вещь, которую я сегодня узнал…» «Одна вещь, которую я до сих пор не понимаю…» «Один из способов получить необходимую мне помощь…» «Ответ на эту проблему таков: …» Написание ответа на задачу — очень важный навык, который нужно развивать, потому что многие тесты штата по математике требуют сконструированного ответа на вопросы.
Дневник можно начать с простых подсказок, таких как: «Одна вещь, которую я сегодня узнал…» «Одна вещь, которую я до сих пор не понимаю…» «Один из способов получить необходимую мне помощь…» «Ответ на эту проблему таков: …» Написание ответа на задачу — очень важный навык, который нужно развивать, потому что многие тесты штата по математике требуют сконструированного ответа на вопросы. Для учителей могут быть доступны онлайновые программы или программы. Для учителей, у которых в классе есть электронная доска, есть много ресурсов, доступных по ссылкам, к которым можно легко получить доступ и принести в класс.
Для учителей могут быть доступны онлайновые программы или программы. Для учителей, у которых в классе есть электронная доска, есть много ресурсов, доступных по ссылкам, к которым можно легко получить доступ и принести в класс. (Требуется бесплатная регистрация.)
(Требуется бесплатная регистрация.)