Как найти площадь фигуры ограниченной кривыми линиями
В одном из предыдущих постов, посвященных применению интегрального исчисления, уже обсуждался вопрос Как найти площадь плоской фигуры в Wolfram|Alpha.И было сказано, что запрос area between, который
в Wolfram|Alpha служит для вычисления площадей плоских фигур при помощи интегралов, срабатывает корректно лишь в некоторых относительно простых случаях. А для решения более сложных задач можно обратится к «ручному» способу — пошаговой процедуре вычисления площади плоской фигуры при помощи интеграла. То есть, на первом шаге определяем пределы интегрирования, а затем, используя найденные пределы, вычисляем определенный интеграл — площадь фигуры. Как это сделать практически, описано в упомянутом выше посте.
Однако, для решения большинства прикладных задач, особенно для не математиков, этот «ручной» способ не очень-то удобен. Поэтому Wolfram|Alpha предлагает и другие способы как найти площадь фигуры ограниченной двумя кривыми.
Наконец, если нужно вычислить площадь, ограниченную замкнутой кривой, например, площадь внутри эллипса, используйте для этого запрос area inside:
Таким образом, для вычисления площадей плоских фигур, ограниченных кривыми линиями, Wolfram|Alpha использует такие запросы: area between, area between … domain … и area inside.
Калькулятор онлайн.Вичісліть певний інтеграл (площа криволінійної трапеції). Як знайти площу криволінійної трапеції
Тема: Обчислення площі плоскої фігури за допомогою певного інтеграла
Завдання: вивчити визначення та формули знаходження площі криволінійної трапеції;
розглянути різні випадки знаходження площі криволінійної трапеції;
Вміти обчислювати площу криволінійної трапеції.
план:
Криволінійна трапеція.
Формули обчислення площі криволінійної трапеції.
криволінійної трапецієюназивається фігура, яка обмежена графіком безперервної, неотрицательной функції f (x) на проміжку, відрізками прямих x = a і x = b, а також відрізком осі абсцис між точками a і b.
Зображення криволінійних трапецій:
Тепер перейдемо до можливих варіантів розташування фігур, площа яких треба обчислити на координатної площині.
першим буде найпростіший варіант (перший малюнок), звичайна криволинейная трапеція, Як у визначенні. Тут нічого не треба придумувати просто беремо інтеграл від aдо bвід функції f (x). Знайдемо інтеграл — будемо знати і площа даної трапеції.
під другому варіанті наша фігура буде обмежена не віссю абсцис, а інший функцією g (x). Тому, що б знайти площу
 І шукана площа фігури CEFD, Буде різниця між першим і другим площами криволінійної трапеції. Оскільки межі інтегрування тут однакові, то це все можна записати під одним інтегралом (дивіться формули під малюнком) все залежить від складності функцій, в якому випадку простіше буде знайти інтеграл.
І шукана площа фігури CEFD, Буде різниця між першим і другим площами криволінійної трапеції. Оскільки межі інтегрування тут однакові, то це все можна записати під одним інтегралом (дивіться формули під малюнком) все залежить від складності функцій, в якому випадку простіше буде знайти інтеграл.
третій дуже схожий до першого, але тільки наша трапеція розміщена, чи не над віссю абсцис, А під нею. Тому тут треба брати таке саме невід’ємне, тільки зі знаком мінус, тому що значення інтеграла буде негативним, а значення площі має бути позитивне. Якщо замість функції f (x)взяти функцію -f (x), То її графік буде такою ж просто симетрично відображений щодо осі абсцис.
І четвертийваріант, коли частина нашої фігури знаходиться над віссю абсцис, а частина під нею. Тому нам треба спочатку знайти площу фігури AEFB, Як в першому варіанті, а потім площу фігури ABCD, Як в третьому варіанті і потім скласти їх. У підсумку ми отримаємо площу фігури DEFC. Оскільки межі інтегрування тут однакові, то це все можна записати під одним інтегралом (дивіться формули під малюнком) все залежить від складності функцій, в якому випадку простіше буде знайти інтеграл.
У підсумку ми отримаємо площу фігури DEFC. Оскільки межі інтегрування тут однакові, то це все можна записати під одним інтегралом (дивіться формули під малюнком) все залежить від складності функцій, в якому випадку простіше буде знайти інтеграл.
Питання для самоперевірки:
Яка фігура називається криволінійної трапецією?
Як знайти площу криволінійної трапеції?
Переходимо до розгляду додатків інтегрального числення. На цьому уроці ми розберемо типову і найбільш поширену задачу — як за допомогою певного інтеграла обчислити площу плоскої фігури. Нарешті шукають сенс у вищій математиці — нехай знайдуть його. Мало чи. Доведеться ось в житті наближати дачну ділянку елементарними функціями і знаходити його площа за допомогою певного інтеграла.
Для успішного освоєння матеріалу, необхідно:
1) Розбиратися в невизначеному інтегралі хоча б на середньому рівні. Таким чином, чайникам для початку слід ознайомитися з уроком Чи не.
2) Вміти застосовувати формулу Ньютона-Лейбніца і обчислювати визначений інтеграл. Налагодити теплі дружні стосунки з певними інтегралами можна на сторінці Визначений інтеграл. приклади рішень.
Насправді, для того щоб знаходити площа фігури не треба так вже й багато знань по невизначеному і певного інтеграла. Завдання «обчислити площу за допомогою певного інтеграла» завжди передбачає побудову креслення, Тому набагато більш актуальним питанням будуть ваші знання і навички побудови креслень. У зв’язку з цим корисно освіжити в пам’яті графіки основних елементарних функцій, а, як мінімум, вміти будувати пряму, параболу і гіперболу. Зробити це можна (багатьом — потрібно) за допомогою методичного матеріалу та статті про геометричні перетвореннях графіків.
Власне, з завданням знаходження площі за допомогою визначеного інтеграла всі знайомі ще зі школи, і ми мало підемо вперед від шкільної програми. Цієї статті взагалі могло б і не бути, але справа в тому, що завдання зустрічається в 99 випадків з 100, коли студент страждає від ненависної вишки з захопленням освоює курс вищої математики.
Матеріали даного практикуму викладені просто, докладно і з мінімумом теорії.
Почнемо з криволінійної трапеції.
криволінійної трапецієюназивається плоска фігура, обмежена віссю, прямими, і графіком безперервної на відрізку функції, яка не змінює знак на цьому проміжку. Нехай дана фігура розташована
тоді площа криволінійної трапеції чисельно дорівнює визначеному інтегралу. У будь-якого певного інтеграла (який існує) є дуже хороший геометричний сенс. На уроці Визначений інтеграл. приклади рішенья говорив, що визначений інтеграл — це число. А зараз прийшла пора констатувати ще один корисний факт. З точки зору геометрії визначений інтеграл — це ПЛОЩА.
Тобто, певного інтеграла (якщо він існує) геометрично відповідає площа деякої фігури. Наприклад, розглянемо певний інтеграл. Підінтегральна функція задає на площині криву, розташовану вище осі (бажаючі можуть виконати креслення), а сам певний інтеграл чисельно дорівнює площі відповідної криволінійної трапеції.
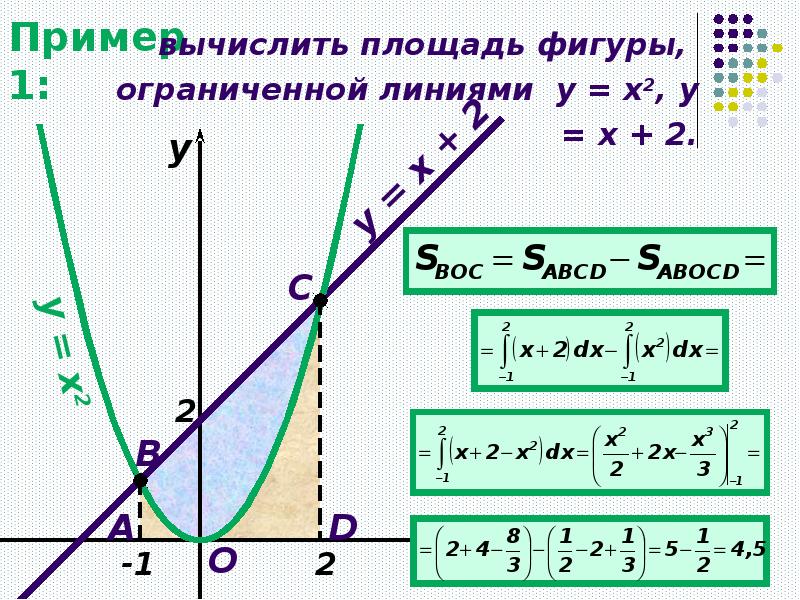
приклад 1
Це типова формулювання завдання. Перший і найважливіший момент рішення — побудова креслення
. Причому, креслення необхідно побудувати ПРАВИЛЬНО.При побудові креслення я рекомендую наступний порядок: спочаткукраще побудувати всі прямі (якщо вони є) і тільки потім— параболи, гіперболи, графіки інших функцій. Графіки функцій вигідніше будувати поточечно, З технікою поточечного побудови можна ознайомитися в довідковому матеріалі Графіки і властивості елементарних функцій. Там же можна знайти дуже корисний стосовно нашого уроку матеріал — як швидко побудувати параболу.
У цьому завданню рішення може виглядати так.
Виконаємо креслення (зверніть увагу, що рівняння задає вісь):
Штрихована криволинейную трапецію я не буду, тут очевидно, про яку площі йдеться. Рішення триває так:
На відрізку графік функції розташований над віссю, Тому:
відповідь:
У кого виникли труднощі з обчисленням певного інтеграла і застосуванням формули Ньютона-Лейбніца , Зверніться до лекції
 приклади рішень.
приклади рішень.Після того, як завдання виконано, завжди корисно поглянути на креслення і прикинути, чи реальний вийшов відповідь. В даному випадку «на око» підраховуємо кількість клітинок в кресленні — ну, приблизно 9 набереться, схоже на правду. Цілком зрозуміло, що якби у нас вийшов, скажімо, відповідь: 20 квадратних одиниць, то, очевидно, що десь допущена помилка — в розглянуту фігуру 20 клітинок явно не вміщається, від сили десяток. Якщо відповідь вийшов негативним, то завдання теж вирішено некоректно.
приклад 2
Обчислити площу фігури, обмеженої лініями,, і віссю
Це приклад для самостійного рішення. Повне рішення і відповідь в кінці уроку.
Що робити, якщо криволинейная трапеція розташована під віссю?
приклад 3
Обчислити площу фігури, обмеженої лініями, і координатними осями.
Рішення: Виконаємо креслення:
Якщо криволінійна трапеція розташована під віссю(Або, принаймні, Не вищеданої осі), то її площа можна знайти за формулою:
В даному випадку:
Увага! Не слід плутати два типи завдань:
1) Якщо Вам запропоновано вирішити просто певний інтеграл без всякого геометричного сенсу, то він може бути негативним.
2) Якщо Вам запропоновано знайти площу фігури за допомогою певного інтеграла, то площа завжди позитивна! Саме тому в тільки що розглянутої формулою фігурує мінус.
На практиці найчастіше фігура розташована і в верхній і в нижній півплощині, а тому, від найпростіших шкільних задачок переходимо до більш змістовним прикладів.
приклад 4
Знайти площу плоскої фігури, обмеженої лініями,.
Рішення: Спочатку потрібно виконати креслення. Взагалі кажучи, при побудові креслення в задачах на площу нас найбільше цікавлять точки перетину ліній. Знайдемо точки перетину параболи і прямої. Це можна зробити двома способами. Перший спосіб — аналітичний. Вирішуємо рівняння:
Значить, нижня межа інтегрування, верхня межа інтегрування.
Цим способом краще, по можливості, не користуватися.
Набагато вигідніше і швидше побудувати лінії поточечно, при цьому межі інтегрування з’ясовуються як би «самі собою». Техніка поточечного побудови для різних графіків докладно розглянута в довідці Графіки і властивості елементарних функцій. Проте, аналітичний спосіб знаходження меж все-таки доводиться іноді застосовувати, якщо, наприклад, графік досить великий, або поточені побудова не виявило меж інтегрування (вони можуть бути дробовими або ірраціональними). І такий приклад, ми теж розглянемо.
Проте, аналітичний спосіб знаходження меж все-таки доводиться іноді застосовувати, якщо, наприклад, графік досить великий, або поточені побудова не виявило меж інтегрування (вони можуть бути дробовими або ірраціональними). І такий приклад, ми теж розглянемо.
Повертаємося до нашого завдання: раціональніше спочатку побудувати пряму і тільки потім параболу. Виконаємо креслення:
Повторюся, що при поточечной побудові межі інтегрування найчастіше з’ясовуються «автоматом».
А тепер робоча формула: Якщо на відрізку деяка безперервна функція більше або дорівнюєдеякої неперервної функції, то площа фігури, обмеженої графіками даних функцій і прямими,, можна знайти за формулою:
Тут вже не треба думати, де розташована фігура — над віссю або під віссю, і, грубо кажучи, важливо, який графік ВИЩЕ(Щодо іншого графіка), а який — НИЖЧЕ.
У розглянутому прикладі очевидно, що на відрізку парабола розташовується вище прямої, а тому з необхідно відняти
Завершення рішення може виглядати так:
Шукана фігура обмежена параболою зверху і прямий знизу.
На відрізку, за відповідною формулою:
відповідь:
Насправді шкільна формула для площі криволінійної трапеції в нижній півплощині (див. Простенький приклад №3) — окремий випадок формули . Оскільки вісь задається рівнянням, а графік функції розташований Не вищеосі, то
А зараз кілька прикладів для самостійного рішення
приклад 5
приклад 6
Знайти площу фігури, обмеженої лініями,.
В ході вирішення задач на обчислення площі за допомогою визначеного інтеграла іноді трапляється кумедний казус. Креслення виконано правильно, розрахунки — правильно, але через неуважність … знайдена площа не тієї фігури, Саме так кілька разів лажа ваш покірний слуга. Ось реальний випадок з життя:
приклад 7
Обчислити площу фігури, обмеженої лініями,,,.
Рішення: Спочатку виконаємо креслення:
… Ех, креслення хреновенький вийшов, але начебто все розбірливо.
Фігура, площа якої нам потрібно знайти, заштрихована синім кольором(Уважно дивіться на умова — чим обмежена фігура!). Але на практиці через неуважність нерідко виникає «глюк», що потрібно знайти площу фігури, яка заштрихована зеленим кольором!
Але на практиці через неуважність нерідко виникає «глюк», що потрібно знайти площу фігури, яка заштрихована зеленим кольором!
Цей приклад ще корисний і тим, що в ньому площу фігури вважається за допомогою двох визначених інтегралів. дійсно:
1) На відрізку над віссю розташований графік прямої;
2) На відрізку над віссю розташований графік гіперболи.
Цілком очевидно, що площі можна (і потрібно) приплюсувати, тому:
відповідь:
Переходимо до ще одного змістовного завданням.
приклад 8
Обчислити площу фігури, обмеженої лініями,
Уявімо рівняння в «шкільному» вигляді, і виконаємо поточечной креслення:
З креслення видно, що верхня межа у нас «хороший»:.
Але чому дорівнює нижня межа ?! Зрозуміло, що це не ціле число, але яке? Може бути ? Але де гарантія, що креслення виконаний з ідеальною точністю, цілком може виявитися що. Або корінь. А якщо ми взагалі неправильно побудували графік?
У таких випадках доводиться витрачати додатковий час і уточнювати межі інтегрування аналітично.
Знайдемо точки перетину прямої і параболи.
Для цього вирішуємо рівняння:
,
Дійсно,.
Подальше рішення тривіально, головне, не заплутатися в підстановках і знаках, обчислення тут не найпростіші.
на відрізку , За відповідною формулою:
відповідь:
Ну, і на закінчення уроку, розглянемо два завдання складніше.
приклад 9
Обчислити площу фігури, обмеженої лініями,,
Рішення: Зобразимо цю фігуру на кресленні.
Блін, забув графік підписати, а переробляти картинку, вибачте, не Хотц. Чи не креслярський, коротше, сьогодні день =)
Для поточечного побудови необхідно знати зовнішній вигляд синусоїди (і взагалі корисно знати графіки всіх елементарних функцій), А також деякі значення синуса, їх можна знайти в тригонометричної таблиці. У ряді випадків (як в цьому) допускається побудова схематичного креслення, на якому принципово правильно повинні бути відображені графіки і межі інтегрування. (2) $).
(2) $).
Розглянемо криволінійну трапецію, обмежену віссю Ох, кривої y = f (x) і двома прямими: х = а і х = Ь (рис. 85). Візьмемо довільне значення х (тільки не а й не Ь). Дамо йому приріст h = dx і розглянемо смужку, обмежену прямими АВ і CD, віссю Ох і дугою BD, що належить даної кривої. Цю смужку будемо називати елементарною смужкою. Площа елементарної смужки відрізняється від площі прямокутника ACQB на криволінійний трикутник BQD, а площа останнього менше площі прямокутника BQDM зі сторонами BQ = = h = dx) QD = Ay і площею, яка дорівнює hAy = Ay dx. Зі зменшенням боку h сторона Ду також зменшується і одночасно з h прагне до нуля. Тому площа BQDM є нескінченно малою другого порядку. Площа елементарної смужки є приріст площі, а площа прямокутника ACQB, рівна АВ-АС == / (х) dx> є диференціал площі. Отже, саму площу знайдемо, інтегруючи її диференціал. В межах даної фігури незалежне змінне л: змінюється від а до b, тому шукана площа 5 буде дорівнює 5 = \ f (x) dx. (I) Приклад 1. віссю Ох на одному пе-х періоді (рис. 88). Попередні рас-рис судження дозволяють припустити, що площа вийде в чотири рази більше, ніж в ін. 2. Однак, провівши обчислення, отримаємо «я Г, * я S — \ sin х dx = [- cos х] 0 = = — cos 2л — (- cos 0) = — 1 + 1 = 0. Цей результат вимагає роз’яснень. Для з’ясування суті справи обчислюємо ще площа, обмежену тієї ж синусоїдою у = sin л: і віссю Ох в межах від л до 2га. Застосовуючи формулу (I), отримуємо 2л $ 2л sin хdx = [- cosх] л = -cos 2а ~) -с05я = — 1-1 = -2. я Таким чином, бачимо, що ця площа вийшла негативною. Порівнюючи її з площею, обчисленої в ін. 3, отримуємо, що їх абсолютні величини однакові, а знаки різні. Якщо застосувати властивість V (див. Гл. XI, § 4), то отримаємо 2л я 2л J sin xdx = J sin * dx [sin x dx = 2 + (- 2) = 0То, що вийшло в цьому прикладі, не є випадковістю. Завжди площа, розташована нижче осі Ох, за умови, що незалежне змінне змінюється зліва направо, виходить при обчисленні за допомогою інтегралів негативною.
віссю Ох на одному пе-х періоді (рис. 88). Попередні рас-рис судження дозволяють припустити, що площа вийде в чотири рази більше, ніж в ін. 2. Однак, провівши обчислення, отримаємо «я Г, * я S — \ sin х dx = [- cos х] 0 = = — cos 2л — (- cos 0) = — 1 + 1 = 0. Цей результат вимагає роз’яснень. Для з’ясування суті справи обчислюємо ще площа, обмежену тієї ж синусоїдою у = sin л: і віссю Ох в межах від л до 2га. Застосовуючи формулу (I), отримуємо 2л $ 2л sin хdx = [- cosх] л = -cos 2а ~) -с05я = — 1-1 = -2. я Таким чином, бачимо, що ця площа вийшла негативною. Порівнюючи її з площею, обчисленої в ін. 3, отримуємо, що їх абсолютні величини однакові, а знаки різні. Якщо застосувати властивість V (див. Гл. XI, § 4), то отримаємо 2л я 2л J sin xdx = J sin * dx [sin x dx = 2 + (- 2) = 0То, що вийшло в цьому прикладі, не є випадковістю. Завжди площа, розташована нижче осі Ох, за умови, що незалежне змінне змінюється зліва направо, виходить при обчисленні за допомогою інтегралів негативною. х = [Заміна:
х = [Заміна:
] =
Значить, невласний інтеграл збігається і його значення дорівнює.
Обчислити невласний інтеграл за допомогою граничних теорем. Певний інтеграл онлайн
Невласні інтеграли першого роду: поширення поняття певного інтеграла на випадки інтегралів з нескінченним верхнім або нижніми межами інтегрування, або обидва межі інтегрування нескінченні.
Невласні інтеграли другого роду: поширення поняття певного інтеграла на випадки інтегралів від необмежених функцій, підінтегральна функція в кінцевому числі точок кінцевого відрізка інтегрування не існує, звертаючись в нескінченність.
Для порівняння. При введенні поняття певного інтеграла передбачалося, що функція f(x) Неперервна на відрізку [ a, b], А відрізок інтегрування є кінцевим, тобто обмежений числами, а не нескінченністю. Деякі завдання призводять до необхідності відмовитися від цих обмежень. Так з’являються невласні інтеграли.
Геометричний сенс невласного інтеграла з’ясовується досить просто. У разі, коли графік функції y = f(x) знаходиться вище осі Ox , Певний інтеграл виражає площу криволінійної трапеції, обмеженої кривою y = f(x) , Віссю абсцис і ординат x = a , x = b . У свою чергу невласний інтеграл виражає площу необмеженої (нескінченної) криволінійної трапеції, укладеної між лініями y = f(x) (На малюнку нижче — червоного кольору), x = a і віссю абсцис.
Аналогічним чином визначаються невласні інтеграли і для інших нескінченних інтервалів:
Площа нескінченної криволінійної трапеції може бути кінцевим числом і в цьому випадку невласний інтеграл називається збіжним. Площа може бути і нескінченністю і в цьому випадку невласний інтеграл називається розбіжним.
Використання межі інтеграла замість самого невласного інтеграла. Для того, щоб обчислити невласний інтеграл, потрібно використовувати межа певного інтеграла.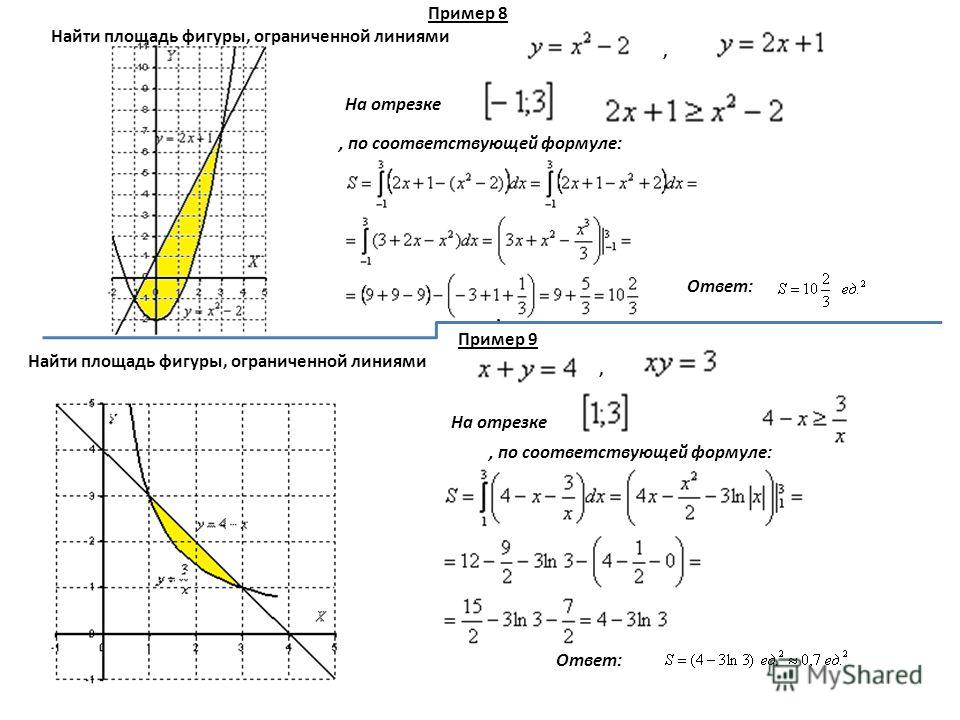 Якщо ця межа існує і кінцевий (чине дорівнює нескінченності), то невласний інтеграл називається збіжним, а в іншому випадку — розбіжним. До чого прагне змінна під знаком межі, залежить від того, маємо ми справу з невласних інтегралом першого роду або другого роду. Дізнаємося про це зараз же.
Якщо ця межа існує і кінцевий (чине дорівнює нескінченності), то невласний інтеграл називається збіжним, а в іншому випадку — розбіжним. До чого прагне змінна під знаком межі, залежить від того, маємо ми справу з невласних інтегралом першого роду або другого роду. Дізнаємося про це зараз же.
Невласні інтеграли першого роду — з нескінченними межами і їх збіжність
Невласні інтеграли з нескінченним верхньою межею
Отже, запис невласного інтеграла як відрізняється від звичайного певного інтеграла тим, що верхня межа інтегрування нескінченний.
Визначення. Невласних інтегралом з нескінченним верхньою межею інтегрування від неперервної функції f(x) на проміжку від a до ∞ називається межа інтеграла цієї функції з верхньою межею інтегрування b і нижньою межею інтегрування a за умови, що верхня межа інтегрування необмежено зростає, Тобто
.
Якщо ця межа існує і дорівнює деякому числу, а не нескінченності, то невласний інтеграл називається збіжним, А число, якому дорівнює межа, приймається за його значення.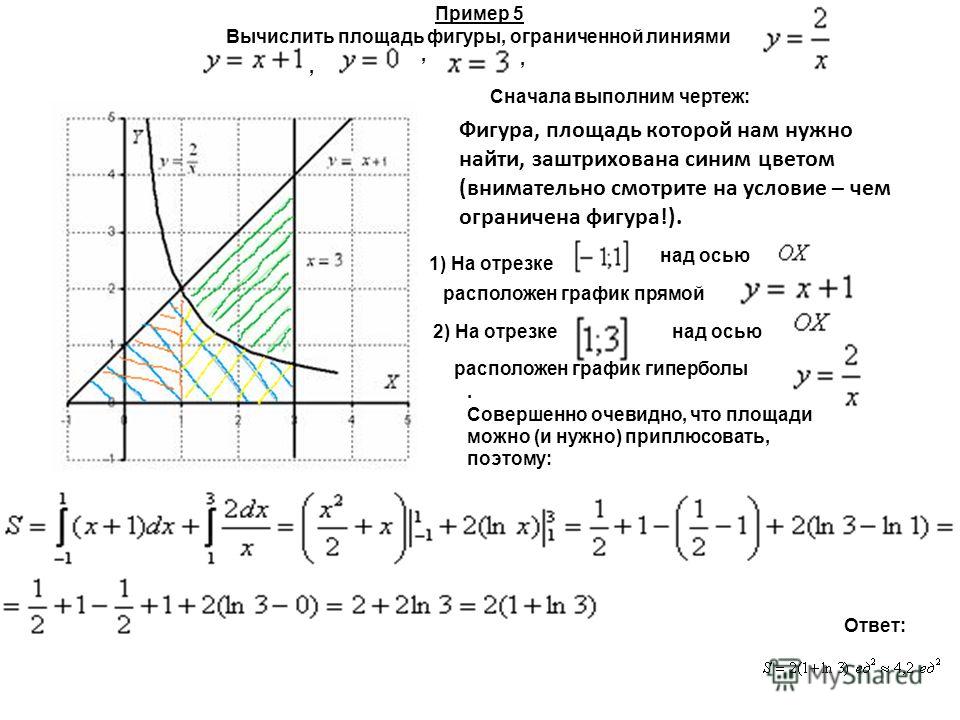 В іншому випадку невласний інтеграл називається розбіжним і йому не приписується ніякого значення.
В іншому випадку невласний інтеграл називається розбіжним і йому не приписується ніякого значення.
Приклад 1. Обчислити невласний інтеграл (Якщо він сходиться).
Рішення. На підставі визначення невласного інтеграла знаходимо
Так як межа існує і дорівнює 1, то і даний невласний інтеграл сходиться і дорівнює 1.
У наступному прикладі подинтегральная функція майже як в прикладі 1, тільки ступінь ікси — НЕ двійка, а буква альфа, а завдання полягає в дослідженні невласного інтеграла на збіжність. Тобто має бути відповісти на питання: при яких значеннях альфи даний невласний інтеграл сходиться, а при яких розходиться?
Приклад 2. Дослідити на збіжність невласний інтеграл (Нижня межа інтегрування більше нуля).
Рішення. Припустимо спочатку, що, тоді
В отриманому виразі перейдемо до межі при:
Неважко бачити, що межа в правій частині існує і дорівнює нулю, коли, тобто, і не існує, коли, тобто.
У першому випадку, тобто при має місце. Якщо то і не існує.
Висновок нашого дослідження наступний: даний невласний інтеграл сходиться при і розходиться при.
Застосовуючи до досліджуваного виду невласного інтеграла формулу Ньютона-Лейбніца , Можна вивести таку дуже схожу на неї формулу:
.
Це узагальнена формула Ньютона-Лейбніца.
Приклад 3. Обчислити невласний інтеграл (Якщо він сходиться).
Межа цього інтеграла існує:
Другий інтеграл, що становить суму, яка має вихідний інтеграл:
Межа цього інтеграла також існує:
.
Знаходимо суму двох інтегралів, що є і значенням вихідного невласного інтеграла з двома нескінченними межами:
Невласні інтеграли другого роду — від необмежених функцій і їх збіжність
нехай функція f(x) задана на відрізку від a до b і необмежена на ньому. Припустимо, що функція звертається в нескінченність в точці b , В той час як у всіх інших точках відрізка вона неперервна.
Визначення. Невласних інтегралом функції f(x) на відрізку від a до b називається межа інтеграла цієї функції з верхньою межею інтегрування c , Якщо при прагненні c до b функція необмежено зростає, а в точці x = b функція не визначена, Тобто
.
Якщо ця межа існує, то невласний інтеграл другого роду називається збіжним, в іншому випадку — розбіжним.
Використовуючи формулу Ньютона-Лейбніца, виводимо.
Ви ще тут? \u003d) Ні, я нікого не намагався залякати, просто тема невласних інтегралів — дуже хороша ілюстрація того, як важливо не запускати вищу математику і інші точні науки. Для освоєння уроку на сайті все є — в докладної і доступній формі, було б бажання ….
Отже, почнемо-с. Образно кажучи, невласний інтеграл — це «просунутий» певний інтеграл, і насправді складнощів з ними не так вже й багато, до того ж у невласного інтеграла є дуже хороший геометричний сенс.
Що значить обчислити невласний інтеграл?
Обчислити невласний інтеграл — це значить, знайти ЧИСЛО(Точно так само, як в певному інтегралі), або довести, що він розходиться (Тобто, отримати в результаті нескінченність замість числа).
Невласні інтеграли бувають двох видів.
Невласний інтеграл з нескінченним межею (ами) інтегруванняІноді такий невласний інтеграл називають невласних інтегралом першого роду. В загалом вигляді невласний інтеграл з нескінченним межею найчастіше виглядає так:. У чому його відмінність від певного інтеграла? У верхній межі. Він нескінченний:.
Рідше зустрічаються інтеграли з нескінченним нижньою межею або з двома нескінченними межами:, і їх ми розглянемо пізніше — коли увійдете до смаку 🙂
Ну а зараз розберемо найпопулярніший випадок. У переважній більшості прикладів подинтегральная функція неперервна на проміжку, і цей важливий факт слід перевіряти в першу чергу! Бо якщо є розриви, тобто додаткові нюанси. Для визначеності припустимо, що і тоді типова криволинейная трапеція буде виглядати так:
Для визначеності припустимо, що і тоді типова криволинейная трапеція буде виглядати так:
Зверніть увагу, що вона нескінченна (не обмежена праворуч), і невласний інтеграл чисельно дорівнює її площі. При цьому можливі наступні варіанти:
1) Перша думка, яка приходить в голову: «раз фігура нескінченна, то », Іншими словами, площа теж нескінченна. Так можливо. У цьому випадку говорять, що невласний інтеграл розходиться.
2) але. Як це не парадоксально прозвучить, площа нескінченної фігури може дорівнювати … кінцевого числа! Наприклад:. Чи може так бути? Запросто. У другому випадку невласний інтеграл сходиться.
3) Про третьому варіанті трохи пізніше.
В яких випадках невласний інтеграл розходиться, а в якому сходиться? Це залежить від підінтегральної функції, і конкретні приклади ми дуже скоро розглянемо.
А що буде, якщо нескінченна криволинейная трапеція розташована нижче осі? В цьому випадку, невласний інтеграл (Розходиться) або дорівнює кінцевому негативного числа.
Таким чином, невласний інтеграл може бути негативним.
Важливо!Коли Вам для вирішення запропонований БУДЬ невласний інтеграл, то, взагалі кажучи, ні про яку площі мови не йде і креслення будувати не потрібно. Геометричний сенс невласного інтеграла я розповів тільки для того, щоб легше було зрозуміти матеріал.
Коль скоро, невласний інтеграл дуже схожий на певний інтеграл, то згадаємо формулу Ньютона-Лейбніца: . Насправді формула застосовна і до невласних інтегралів, тільки її треба трохи модифікувати. В чому різниця? У нескінченному верхній межі інтегрування:. Напевно, багато хто здогадався, що це вже пахне застосуванням теорії меж, і формула запишеться так: .
У чому відмінність від певного інтеграла? Так ні в чому особливому! Як і в певному інтегралі, потрібно вміти знаходити первісну функцію (невизначений інтеграл), вміти застосовувати формулу Ньютона-Лейбніца. Єдине, що додалося — це обчислення межі. У кого з ними погано, вивчіть урок Межі функцій. приклади рішеньБо краще пізно, ніж в армії.
приклади рішеньБо краще пізно, ніж в армії.
Розглянемо два класичних приклади:
приклад 1
Для наочності я побудую креслення, хоча, ще раз підкреслюю, на практиці будувати креслення в даному завданні не потрібно.
Підінтегральна функція неперервна на полуінтервале, значить, все нормально і невласний інтеграл можна обчислити «штатним» методом.
Застосування нашої формули і рішення задачі виглядає так:
Тобто, невласний інтеграл розходиться, і площа заштрихованої криволінійної трапеції дорівнює нескінченності.
У розглянутому прикладі у нас найпростіший табличний інтеграл і така ж техніка застосування формули Ньютона-Лейбніца, як в певному інтегралі. Але застосуються ця формула під знаком межі. Замість звичної букви «динамічної» змінної виступає буква «бе». Це не повинно бентежити або ставити в глухий кут, тому що будь-яка буква нічим не гірше стандартного «ікси».
Якщо Вам не зрозуміло чому при, то це дуже погано, або Ви не розумієте найпростіші межі (і взагалі не розумієте, що таке межа), або не знаєте, як виглядає графік логарифмічною функції.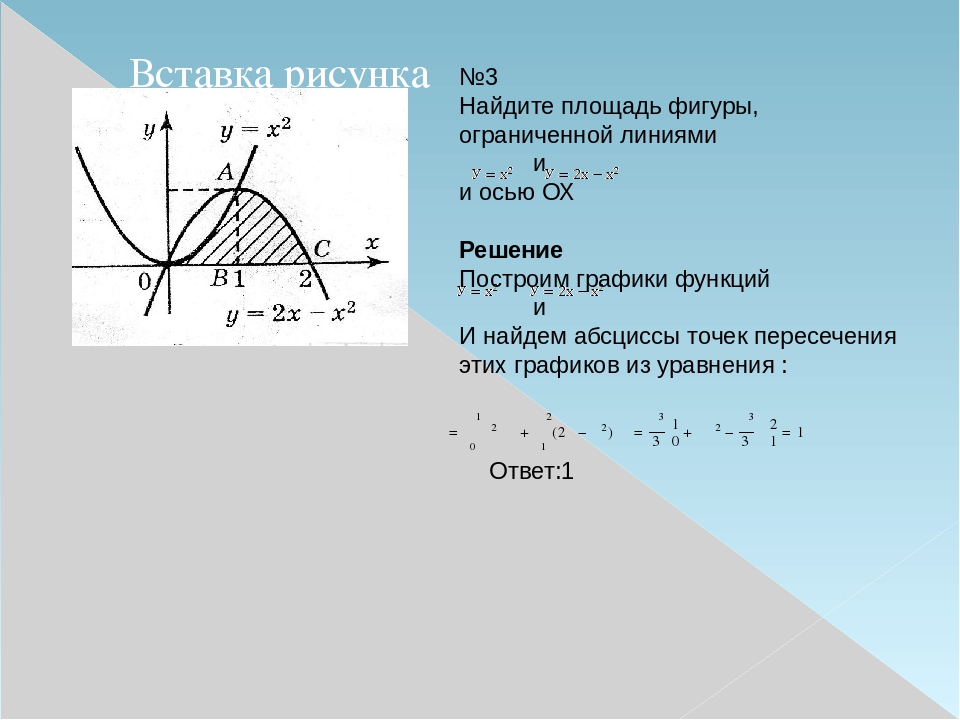 У другому випадку відвідайте урок Графіки і властивості елементарних функцій.
У другому випадку відвідайте урок Графіки і властивості елементарних функцій.
При вирішенні невласних інтегралів дуже важливо знати, як виглядають графіки основних елементарних функцій!
чистове оформлення завдання має виглядати приблизно так:
“
! При оформленні прикладу завжди перериваємо рішення, і вказуємо, що відбувається з підінтегральної функцією – неперервна вона на проміжку інтегрування чи ні. Цим ми ідентифікуємо тип невласного інтеграла і обгрунтовуємо подальші дії.
приклад 2
Обчислити невласний інтеграл або встановити його розбіжність.
Виконаємо креслення:
По-перше, помічаємо наступне: підінтегральна функція неперервна на полуінтервале. Гуд. Вирішуємо за допомогою формули :
(1) Беремо найпростіший інтеграл від статечної функції (Цей окремий випадок є в багатьох таблицях). Мінус краще відразу винести за знак межі, щоб він не плутався під ногами в подальших обчисленнях.
(2) Підставляємо верхній і нижній межі за формулою Ньютона-Лейбніца.
(3) Вказуємо, що при (Господа, це вже давно потрібно розуміти) і спрощуємо відповідь.
Ось тут площа нескінченної криволінійної трапеції дорівнює кінцевому числу! Неймовірно, але факт.
Чистове оформлення прикладу має виглядати приблизно так:
“
Підінтегральна функція неперервна на
“
Що робити, якщо вам зустрінеться інтеграл зразок — з точкою розриву на інтервалі інтегрування? Це говорить про те, що в прикладі помилка (найвірогідніше), Або про просунутому рівні навчання. В останньому випадку, в силу властивості адитивності, Слід розглянути два невласних інтеграла на проміжках і і потім розібратися з сумою.
Іноді внаслідок помилки або умислу невласного інтеграла може зовсім не існувати, Так, наприклад, якщо в знаменник вищевказаного інтеграла поставити квадратний корінь з «ікс», то частина проміжку інтегрування взагалі не увійде в область визначення підінтегральної функції.
Більш того, невласного інтеграла може не існувати навіть при всьому «видимому благополуччі». Класичний приклад:. Незважаючи на визначеність і безперервність косинуса, такого невласного інтеграла не існує! Чому? Все дуже просто, тому що:
— не існує відповідного межі.
І такі приклади нехай рідко, але зустрічаються на практиці! Таким чином, крім збіжності і розбіжність, є ще й третій результат рішення з повноправним відповіддю: «невласного інтеграла не існує».
Слід також зазначити, що суворе визначення невласного інтеграла дається саме через межу, і бажаючі можуть ознайомитися з ним в навчальній літературі. Ну а ми продовжуємо практичне заняття і переходимо до більш змістовним завданням:
приклад 3
Обчислити невласний інтеграл або встановити його розбіжність.
Спочатку спробуємо знайти первісну функцію (невизначений інтеграл). Якщо нам не вдасться цього зробити, то невласний інтеграл ми, природно, теж не вирішимо.
На який із табличних інтегралів схожа подинтегральная функція? Нагадує вона арктангенс: .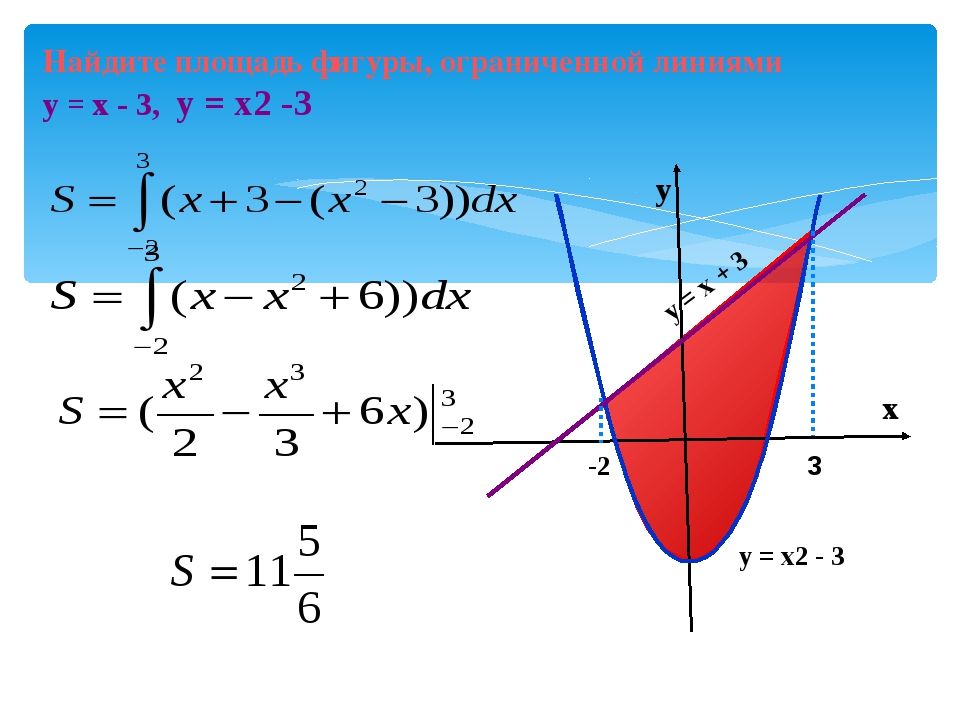 З цих міркувань напрошується думка, що непогано б в знаменнику отримати квадрат. Робиться це шляхом заміни.
З цих міркувань напрошується думка, що непогано б в знаменнику отримати квадрат. Робиться це шляхом заміни.
Проведемо заміну:
Невизначений інтеграл знайдений, константу в даному випадку додавати не має сенсу.
На чернетці завжди корисно виконати перевірку, тобто продифференцировать отриманий результат:
Отримано вихідна подинтегральная функція, значить, невизначений інтеграл знайдений правильно.
Тепер знаходимо невласний інтеграл:
(1) Записуємо рішення відповідно до формули . Константу краще відразу винести за знак межі, щоб вона не заважала в подальших обчисленнях.
(2) Підставляємо верхній і нижній межі відповідно до формули Ньютона-Лейбніца. чому при? Дивіться графік арктангенса в уже неодноразово рекомендованої статті.
(3) Отримуємо остаточну відповідь. Той факт, що корисно знати напам’ять.
Просунуті студенти можуть не знаходити окремо невизначений інтеграл, і не використовувати метод заміни, а використовувати метод підведення функції під знак диференціала і вирішувати невласний інтеграл «відразу». У цьому випадку рішення повинно виглядати приблизно так:
У цьому випадку рішення повинно виглядати приблизно так:
“
Підінтегральна функція неперервна на.
“
приклад 4
Обчислити невласний інтеграл або встановити його розбіжність.
! це типовий приклад, І схожі інтеграли зустрічаються дуже часто. Добре його опрацювати! Первісна функція тут знаходиться методом виділення повного квадрата, більш детально з методом можна ознайомитися на уроці Інтегрування деяких дробів.
приклад 5
Обчислити невласний інтеграл або встановити його розбіжність.
Цей інтеграл можна вирішити детально, тобто спочатку знайти невизначений інтеграл, провівши заміну змінної. А можна вирішити «відразу» — підведенням функції під знак диференціала. У кого яка математична підготовка.
повні рішення і відповіді в кінці уроку.
Приклади рішень невласних інтегралів з нескінченним нижньою межею інтегрування можна подивитися на сторінці Ефективні методи вирішення невласних інтегралів. Там же розібраний випадок, коли обидва межі інтегрування нескінченні.
Там же розібраний випадок, коли обидва межі інтегрування нескінченні.
або невласні інтегралами другого роду. Невласні інтеграли другого роду підступно «шифруються» під звичайний певний інтеграл і виглядають точно так же: Але, на відміну від певного інтеграла, підінтегральна функція терпить нескінченний розрив (не існує): 1) в точці, 2) або в точці, 3) або в обох точках відразу, 4) або навіть на відрізку інтегрування. Ми розглянемо перші два випадки, для випадків 3-4 в кінці статті є посилання на додатковий урок.
Відразу приклад, щоб було зрозуміло:. Начебто це певний інтеграл. Але насправді — це невласний інтеграл другого роду, якщо ми підставимо в підінтегральної функції значення нижньої межі, то знаменник у нас звертається в нуль, тобто підінтегральної функції просто не існує в цій точці!
Взагалі при аналізі невласного інтеграла завжди потрібно підставляти в підінтегральної функції обидва межі інтегрування.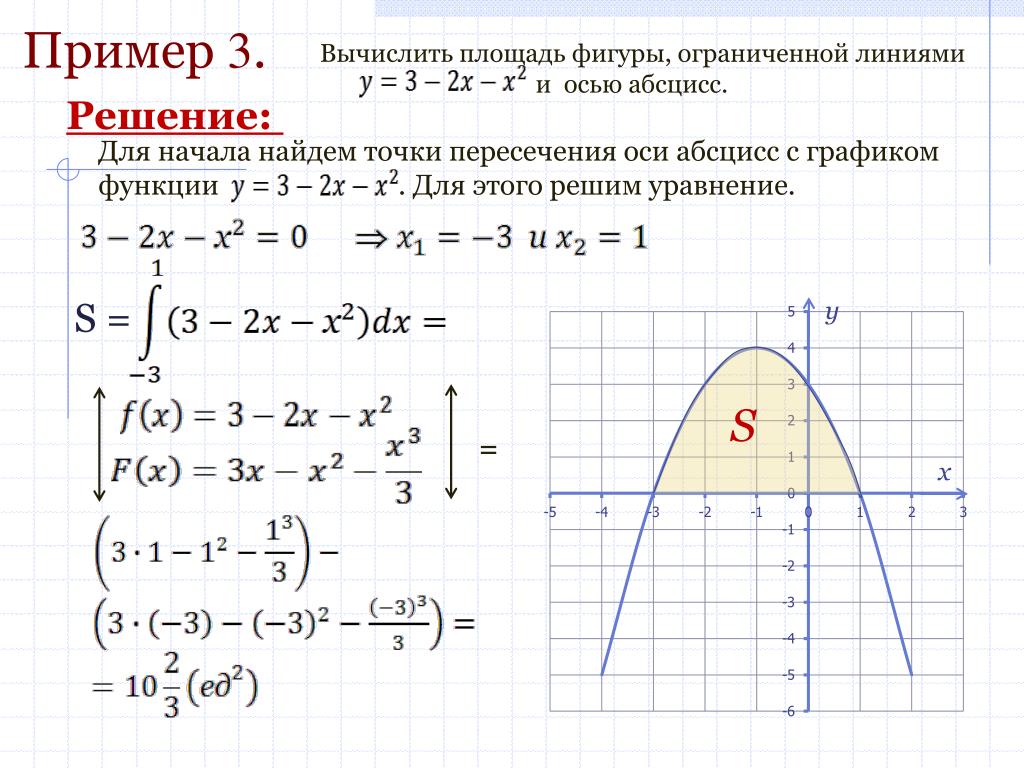 У зв’язку з цим перевіримо і верхня межа: . Тут все добре.
У зв’язку з цим перевіримо і верхня межа: . Тут все добре.
Криволінійна трапеція для розглянутої різновиди невласного інтеграла принципово виглядає так:
Тут майже все так само, як в інтеграл першого роду.
Наш інтеграл чисельно дорівнює площі заштрихованої криволінійної трапеції, яка не обмежена зверху. При цьому можуть бути два варіанти *: невласний інтеграл розходиться (площа нескінченна) або невласний інтеграл дорівнює кінцевому числу (тобто, площа нескінченної фігури — кінцева!).
* за замовчуванням звично вважаємо, що невласний інтеграл існує
Залишилося тільки модифікувати формулу Ньютона-Лейбніца. Вона теж модифікується за допомогою межі, але межа прагне вже не до нескінченності, а до значення праворуч. Легко простежити за кресленням: по осі ми повинні нескінченно близько наблизитися до точки розриву справа.
Подивимося, як це реалізується на практиці.
приклад 6
Обчислити невласний інтеграл або встановити його розбіжність.
Підінтегральна функція терпить нескінченний розрив в точці (не забуваємо усно або на чернетці перевірити, чи все нормально з верхньою межею!)
Спочатку обчислимо невизначений інтеграл:
заміна:
У кого виникли труднощі із заміною, зверніться до уроку Метод заміни в невизначеному інтегралі.
Обчислимо невласний інтеграл:
(1) Що тут нового? За технікою рішення практично нічого. Єдине, що змінилося, це запис під значком межі:. Добавка позначає, що ми прагнемо до значення праворуч (що логічно — див. Графік). Така межа в теорії меж називають одностороннім межею. В даному випадку у нас правобічний межа.
(2) Підставляємо верхню і нижню межу по формулі Ньютона Лейбніца.
(3) Розбираємося з прі. Як визначити, куди прагне вираз? Грубо кажучи, в нього потрібно просто підставити значення, підставляємо три чверті і вказуємо, що. Причісуємо відповідь.
В даному випадку невласний інтеграл дорівнює негативному числу. В цьому ніякого криміналу немає, просто відповідна криволінійна трапеція розташована під віссю.
В цьому ніякого криміналу немає, просто відповідна криволінійна трапеція розташована під віссю.
А зараз два приклади для самостійного рішення.
приклад 7
Обчислити невласний інтеграл або встановити його розбіжність.
приклад 8
Обчислити невласний інтеграл або встановити його розбіжність.
Якщо підінтегральної функції не існує в точці
Нескінченна криволинейная трапеція для такого невласного інтеграла принципово виглядає наступним чином.
Певні інтеграли онлайн на сайт для закріплення студентами та школярами пройденого матеріалу. І тренування своїх практичних навичок. Повноцінне рішення певних інтегралів онлайн для вас в лічені миті допоможе визначити всі етапи процесу .. Інтеграли онлайн — певний інтеграл онлайн. Певні інтеграли онлайн на сайт для повноцінного закріплення студентами та школярами пройденого матеріалу і тренування своїх практичних навичок. Повноцінне рішення певних інтегралів онлайн для вас в лічені миті допоможе визначити всі етапи процесу .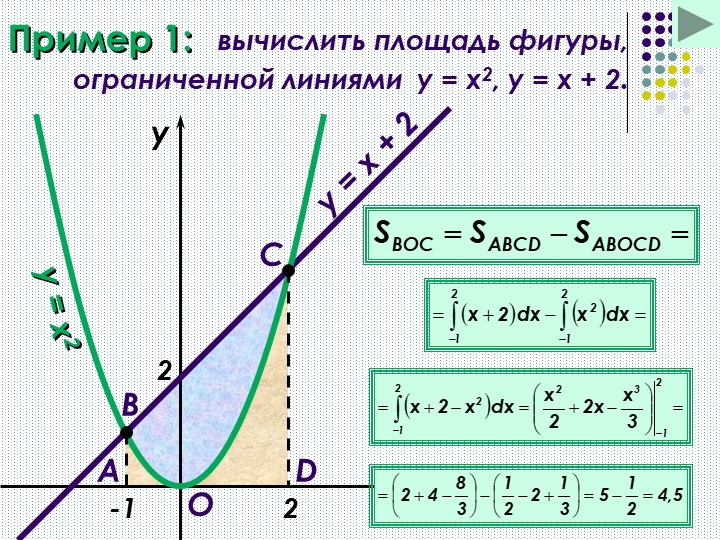 . Інтеграли онлайн — певний інтеграл онлайн. Для нас певний інтеграл онлайн взяти не видається чимось понад природним, вивчивши дану тему по книзі видатних авторів. Величезне їм спасибі і висловлюємо респект цим особистостям. Допоможе визначити певний інтеграл онлайн сервіс по обчисленню таких завдань за дві секунди. Тільки вкажіть правильні дані і все буде Good! Всякий певний інтеграл як рішення задачі підвищить грамотність студентів. Про це мріє кожен лінивець, і ми не виняток, визнаємо це чесно. Якщо все-таки вийде обчислити визначений інтеграл онлайн з рішенням безкоштовно, то, будь ласка, залиште свій E сайт усім бажаючим ним скористатися. Як то кажуть, поділишся корисною посиланням — і тебе віддячать гарні люди за даром. Дуже цікавим буде питання розбору завдання, в якій певний інтеграл буде калькулятор вирішувати самостійно, а не за рахунок витрати вашого дорогоцінного часу. На те вони і машини, щоб орати на людей. Однак рішення певних інтегралів онлайн не всякому сайту по зубах, і це легко перевірити, а саме, досить взяти складний приклад і спробувати вирішити його за допомогою кожного такого сервісу.
. Інтеграли онлайн — певний інтеграл онлайн. Для нас певний інтеграл онлайн взяти не видається чимось понад природним, вивчивши дану тему по книзі видатних авторів. Величезне їм спасибі і висловлюємо респект цим особистостям. Допоможе визначити певний інтеграл онлайн сервіс по обчисленню таких завдань за дві секунди. Тільки вкажіть правильні дані і все буде Good! Всякий певний інтеграл як рішення задачі підвищить грамотність студентів. Про це мріє кожен лінивець, і ми не виняток, визнаємо це чесно. Якщо все-таки вийде обчислити визначений інтеграл онлайн з рішенням безкоштовно, то, будь ласка, залиште свій E сайт усім бажаючим ним скористатися. Як то кажуть, поділишся корисною посиланням — і тебе віддячать гарні люди за даром. Дуже цікавим буде питання розбору завдання, в якій певний інтеграл буде калькулятор вирішувати самостійно, а не за рахунок витрати вашого дорогоцінного часу. На те вони і машини, щоб орати на людей. Однак рішення певних інтегралів онлайн не всякому сайту по зубах, і це легко перевірити, а саме, досить взяти складний приклад і спробувати вирішити його за допомогою кожного такого сервісу.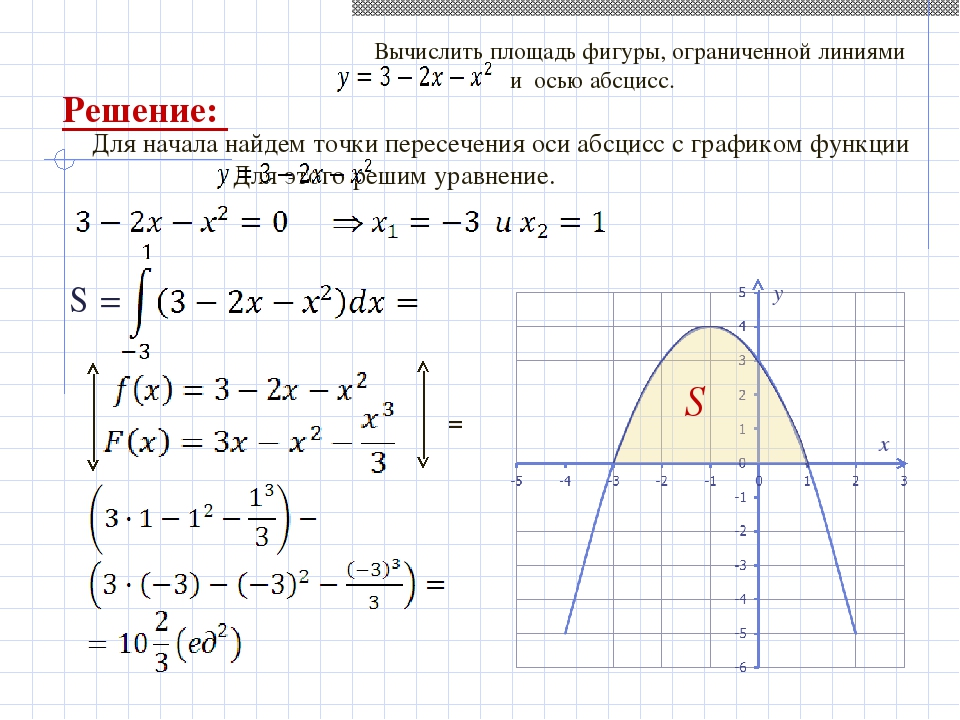 Ви відчуєте різницю на власній шкурі. Найчастіше знайти певний інтеграл онлайн без прикладених зусиль стане досить складно і безглуздо буде виглядати ваша відповідь на фоні загальної картини уявлення результату. Краще б спочатку пройти курс молодого бійця. Будь-яке рішення невласних інтегралів онлайн зводиться спочатку до обчислення невизначеного, а потім через теорію меж обчислити як правило односторонні межі від отриманих виразів підперті межами A і B. Розглянувши вказаний вами певний інтеграл онлайн з докладним рішенням, ми зробили висновок, що ви помилилися на п’ятому кроці, а саме при використанні формули заміни змінної Чебишева. Будьте дуже уважні в подальшому вирішенні. Якщо ваш певний інтеграл онлайн калькулятор не зміг взяти з першого разу, то в першу чергу варто перевірити ще раз написані дані у відповідні форми на сайті. Переконайтеся, що все гаразд і вперед, Go-Go! Для кожного студента перешкодою є обчислення невласних інтегралів онлайн при самому препода, так як це або іспит, або колоквіум, або просто контрольна робота на парі .
Ви відчуєте різницю на власній шкурі. Найчастіше знайти певний інтеграл онлайн без прикладених зусиль стане досить складно і безглуздо буде виглядати ваша відповідь на фоні загальної картини уявлення результату. Краще б спочатку пройти курс молодого бійця. Будь-яке рішення невласних інтегралів онлайн зводиться спочатку до обчислення невизначеного, а потім через теорію меж обчислити як правило односторонні межі від отриманих виразів підперті межами A і B. Розглянувши вказаний вами певний інтеграл онлайн з докладним рішенням, ми зробили висновок, що ви помилилися на п’ятому кроці, а саме при використанні формули заміни змінної Чебишева. Будьте дуже уважні в подальшому вирішенні. Якщо ваш певний інтеграл онлайн калькулятор не зміг взяти з першого разу, то в першу чергу варто перевірити ще раз написані дані у відповідні форми на сайті. Переконайтеся, що все гаразд і вперед, Go-Go! Для кожного студента перешкодою є обчислення невласних інтегралів онлайн при самому препода, так як це або іспит, або колоквіум, або просто контрольна робота на парі .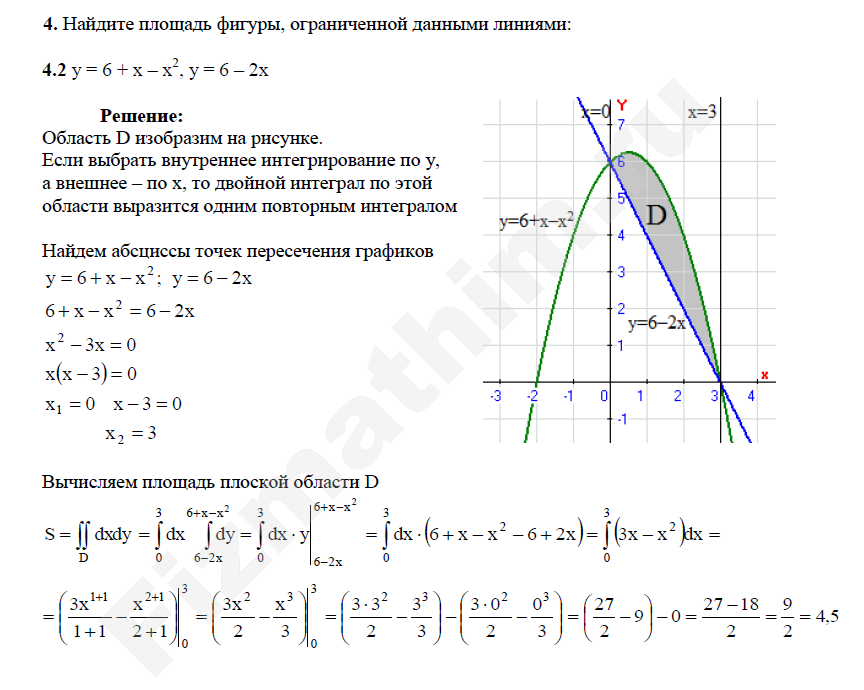 . Як тільки заданий невласний інтеграл онлайн калькулятор буде у вашому розпорядженні, то відразу вбивайте задану функцію, Підставляйте задані межі інтегрування і натискайте на кнопку Рішення, після цього вам буде доступний повноцінний розгорнуту відповідь. І все-таки добре, коли є такий чудовий сайт як сайт, тому що він і безкоштовний, і простий в користуванні, також містить дуже багато розділів. якими студенти користуються повсякденно, один з них як раз є певний інтеграл онлайн з рішенням в повному вигляді. У цьому ж розділі можна обчислити невласний інтеграл онлайн з докладним рішенням для подальших застосувань відповіді як в інституті, так і в інженерних роботах. Здавалося б, всім визначити певний інтеграл онлайн справа нехитра, якщо заздалегідь вирішити такий приклад без верхньої і нижньої межі, тобто не інтеграл Лейбніца, а невизначений інтеграл. Але тут ми з вами не згодні категорично, так як на перший погляд це може здатися саме так, проте є істотна різниця, давайте розберемо все по поличках.
. Як тільки заданий невласний інтеграл онлайн калькулятор буде у вашому розпорядженні, то відразу вбивайте задану функцію, Підставляйте задані межі інтегрування і натискайте на кнопку Рішення, після цього вам буде доступний повноцінний розгорнуту відповідь. І все-таки добре, коли є такий чудовий сайт як сайт, тому що він і безкоштовний, і простий в користуванні, також містить дуже багато розділів. якими студенти користуються повсякденно, один з них як раз є певний інтеграл онлайн з рішенням в повному вигляді. У цьому ж розділі можна обчислити невласний інтеграл онлайн з докладним рішенням для подальших застосувань відповіді як в інституті, так і в інженерних роботах. Здавалося б, всім визначити певний інтеграл онлайн справа нехитра, якщо заздалегідь вирішити такий приклад без верхньої і нижньої межі, тобто не інтеграл Лейбніца, а невизначений інтеграл. Але тут ми з вами не згодні категорично, так як на перший погляд це може здатися саме так, проте є істотна різниця, давайте розберемо все по поличках. Такий певний інтеграл рішення дає не в явному вигляді, а в наслідок перетворення виразу в граничне значення. Іншими словами, потрібно спочатку вирішити інтеграл з підстановкою символьних значень кордонів, а потім обчислити межа або на нескінченності, або в певній точці. Звідси обчислити визначений інтеграл онлайн з рішенням безкоштовно означає ні що інше як уявлення точного рішення по формулі Ньютона-Лейбніца. Якщо ж розглядати наш певний інтеграл калькулятор допоможе його підрахувати за кілька секунд прямо на ваших очах. Такий поспіх потрібна всім бажаючим якнайшвидше впоратися із завданням і звільнитися для особистих справ. Не варто шукати в інтернеті сайти, на яких попросять вас реєструватися, потім поповнити гроші на баланс і все заради того, щоб який-небудь розумник готував рішення певних інтегралів нібито онлайн. Запам’ятайте адресу Math34 — це безкоштовний сервіс для вирішення безлічі математичних задач, в тому ж числі ми допоможемо знайти певний інтеграл онлайн, і щоб в цьому переконатися, просимо перевірити наше твердження на конкретних прикладах.
Такий певний інтеграл рішення дає не в явному вигляді, а в наслідок перетворення виразу в граничне значення. Іншими словами, потрібно спочатку вирішити інтеграл з підстановкою символьних значень кордонів, а потім обчислити межа або на нескінченності, або в певній точці. Звідси обчислити визначений інтеграл онлайн з рішенням безкоштовно означає ні що інше як уявлення точного рішення по формулі Ньютона-Лейбніца. Якщо ж розглядати наш певний інтеграл калькулятор допоможе його підрахувати за кілька секунд прямо на ваших очах. Такий поспіх потрібна всім бажаючим якнайшвидше впоратися із завданням і звільнитися для особистих справ. Не варто шукати в інтернеті сайти, на яких попросять вас реєструватися, потім поповнити гроші на баланс і все заради того, щоб який-небудь розумник готував рішення певних інтегралів нібито онлайн. Запам’ятайте адресу Math34 — це безкоштовний сервіс для вирішення безлічі математичних задач, в тому ж числі ми допоможемо знайти певний інтеграл онлайн, і щоб в цьому переконатися, просимо перевірити наше твердження на конкретних прикладах. Введіть підінтегральної функції в відповідне поле, потім вкажіть або нескінченні граничні значення (в це випадку буде вирахувано і отримано рішення невласних інтегралів онлайн), або задайте свої числові або символьні кордону і певний інтеграл онлайн з докладним рішенням виведеться на сторінці після натискання на кнопку «Рішення «. Чи неправда — це дуже просто, не вимагає від вас зайвих дій, безкоштовно, що найголовніше, і в той же час результативно. Ви можете самостійно скористатися сервісом, щоб певний інтеграл онлайн калькулятор приніс вам максимум користі, і ви б отримали комфортний стан, не напружуючись на складність всіх обчислювальних процесів, дозвольте нам зробити все за вас і продемонструвати всю міць комп’ютерних технологій сучасного світу. Якщо занурюватися в нетрі найскладніших формул і обчислення невласних інтегралів онлайн вивчити самостійно, то це похвально, і ви можете претендувати на можливість написання кандидатської роботи, однак повернемося до реалій студентського життя.
Введіть підінтегральної функції в відповідне поле, потім вкажіть або нескінченні граничні значення (в це випадку буде вирахувано і отримано рішення невласних інтегралів онлайн), або задайте свої числові або символьні кордону і певний інтеграл онлайн з докладним рішенням виведеться на сторінці після натискання на кнопку «Рішення «. Чи неправда — це дуже просто, не вимагає від вас зайвих дій, безкоштовно, що найголовніше, і в той же час результативно. Ви можете самостійно скористатися сервісом, щоб певний інтеграл онлайн калькулятор приніс вам максимум користі, і ви б отримали комфортний стан, не напружуючись на складність всіх обчислювальних процесів, дозвольте нам зробити все за вас і продемонструвати всю міць комп’ютерних технологій сучасного світу. Якщо занурюватися в нетрі найскладніших формул і обчислення невласних інтегралів онлайн вивчити самостійно, то це похвально, і ви можете претендувати на можливість написання кандидатської роботи, однак повернемося до реалій студентського життя. А хто такий студент? В першу чергу — це молода людина, енергійний і життєрадісний, який бажає встигнути відпочити і зробити домашку! Тому ми подбали про учнів, які намагаються відшукати на просторах глобальної мережі невласний інтеграл онлайн калькулятор, і ось він до вашої уваги — сайт — найкорисніша для молоді решалка в режимі онлайн. До речі наш сервіс хоч і підноситься як помічник студентам і школярам, \u200b\u200bале він в повній мірі підійде будь-якому інженеру, тому що нам під силу будь-які типи завдань і їх рішення представляється в професійному форматі. Наприклад, певний інтеграл онлайн з рішенням в повному вигляді ми пропонуємо по етапах, тобто кожному логічного блоку (підзадачі) відводиться окрема запис з усіма викладками по ходу процесу спільного рішення. Це звичайно ж спрощує сприйняття багатоетапних послідовних розкладок, і тим самим є перевагою проекту сайт перед аналогічними сервісами по знаходженню невласний інтеграл онлайн з докладним рішенням.
А хто такий студент? В першу чергу — це молода людина, енергійний і життєрадісний, який бажає встигнути відпочити і зробити домашку! Тому ми подбали про учнів, які намагаються відшукати на просторах глобальної мережі невласний інтеграл онлайн калькулятор, і ось він до вашої уваги — сайт — найкорисніша для молоді решалка в режимі онлайн. До речі наш сервіс хоч і підноситься як помічник студентам і школярам, \u200b\u200bале він в повній мірі підійде будь-якому інженеру, тому що нам під силу будь-які типи завдань і їх рішення представляється в професійному форматі. Наприклад, певний інтеграл онлайн з рішенням в повному вигляді ми пропонуємо по етапах, тобто кожному логічного блоку (підзадачі) відводиться окрема запис з усіма викладками по ходу процесу спільного рішення. Це звичайно ж спрощує сприйняття багатоетапних послідовних розкладок, і тим самим є перевагою проекту сайт перед аналогічними сервісами по знаходженню невласний інтеграл онлайн з докладним рішенням.
Визначений інтеграл
\\ [I \u003d \\ int_a ^ bf (x) dx \\]
був побудований в припущенні, що числа $ a, \\, b $ кінцеві і $ f (x) $ — безперервна функція. 3 + 1). \\]
3 + 1). \\]
Як визначити площу трикутника формула. Як обчислити площу трикутника. Загальні формули для обчислення площі трикутника
визначення трикутника
трикутник — це геометрична фігура, яка утворюється в результаті перетину трьох відрізків, кінці яких не лежать на одній прямій. У будь-якого трикутника є три сторони, три вершини і три кути.
Онлайн-калькулятор
трикутники бувають різних видів. Наприклад, існує рівносторонній трикутник (той, у якого всі сторони рівні), рівнобедрений (в ньому рівні дві сторони) і прямокутний (в якому один з кутів прямий, т. Е. Дорівнює 90 градусам).
Площа трикутника можна знайти різними способами в залежності від того, які елементи фігури відомі за умовою завдання, будь то кути, довжини, або ж взагалі радіуси кіл, пов’язаних з трикутником. Розглянемо кожен спосіб окремо з прикладами.
Формула площі трикутника по підставі і висоті
S \u003d 1 2 ⋅ a ⋅ h S \u003d \\ frac (1) (2) \\ cdot a \\ cdot hS \u003d2 1 ⋅ a ⋅h,
A a a — підстава трикутника;
h h h — висота трикутника, проведена до цієї підстави a.
Знайти площу трикутника, якщо відома довжина його заснування, що дорівнює 10 (см.) І висота, проведена до цього підстави, що дорівнює 5 (див.).
Рішення
A \u003d 10 a \u003d 10 a \u003d1
0
h \u003d 5 h \u003d 5 h \u003d5
Підставляємо в формулу для площі і отримуємо:
S \u003d 1 2 ⋅ 10 ⋅ 5 \u003d 25 S \u003d \\ frac (1) (2) \\ cdot10 \\ cdot 5 \u003d 25S \u003d2 1 ⋅ 1
0
⋅ 5
= 2
5 (Див. Кв.)
відповідь: 25 (см. Кв.)
Формула площі трикутника за довжинами всіх сторін
S \u003d p ⋅ (p — a) ⋅ (p — b) ⋅ (p — c) S \u003d \\ sqrt (p \\ cdot (p-a) \\ cdot (p-b) \\ cdot (p-c))S \u003dp ⋅ (p — a) ⋅ (p — b) ⋅ (p — c) ,
A, b, c a, b, c a, b, c — довжини сторін трикутника;
p p p — половина суми всіх сторін трикутника (тобто, половина периметра трикутника):
P \u003d 1 2 (a + b + c) p \u003d \\ frac (1) (2) (a + b + c)p \u003d2 1 (A +b +c)
Ця формула називається формулою Герона. (\\ circ))) \u003d 50 \\ cdot \\ frac ( 1) (2 \\ sqrt (3)) \\ approx14.4S \u003d2 1
0
2 ⋅ sin (3 0
∘ +
3
0
∘ ) sin 3
0
∘ sin 3
0
∘ = 5
0
⋅ 2
3 1 ≈ 1
4
.
4 (Див. Кв.)
(\\ circ))) \u003d 50 \\ cdot \\ frac ( 1) (2 \\ sqrt (3)) \\ approx14.4S \u003d2 1
0
2 ⋅ sin (3 0
∘ +
3
0
∘ ) sin 3
0
∘ sin 3
0
∘ = 5
0
⋅ 2
3 1 ≈ 1
4
.
4 (Див. Кв.)
відповідь: 14.4 (див. Кв.)
Формула площі трикутника за трьома сторонами і радіусу описаного кола
S \u003d a ⋅ b ⋅ c 4 R S \u003d \\ frac (a \\ cdot b \\ cdot c) (4R)S \u003d4 Ra ⋅ b ⋅ c ,
A, b, c a, b, c a, b, c — сторони трикутника;
R R R — радіус описаного кола навколо трикутника.
Числа візьмемо з другої нашої задачі і додамо до них радіус R R R окружності. Нехай він буде дорівнює 10 (см.).
Рішення
A \u003d 3 a \u003d 3 a \u003d3
b \u003d 4 b \u003d 4 b \u003d4
c \u003d 5 c \u003d 5 c \u003d5
R \u003d 10 R \u003d 10 R \u003d1
0
S \u003d 3 ⋅ 4 ⋅ 5 4 ⋅ 10 \u003d 60 40 \u003d 1.5 S \u003d \\ frac (3 \\ cdot 4 \\ cdot 5) (4 \\ cdot 10) \u003d \\ frac (60) (40) \u003d 1.5S \u003d4
⋅
1
0 3
⋅
4
⋅
5 = 4
0 6
0
=
1
. 5
(Див. Кв.)
5
(Див. Кв.)
відповідь: 1.5 (см.кв.)
Формула площі трикутника за трьома сторонами і радіусу вписаного кола
S \u003d p ⋅ r S \u003d p \\ cdot rS= p⋅ r,
p pp — половина периметра трикутника:
p \u003d a + b + c 2 p \u003d \\ frac (a + b + c) (2)p= 2 a+ b+ c ,
a, b, c a, b, ca,
b,
c — сторони трикутника;
r rr — радіус вписаного в трикутник кола.
Нехай радіус вписаного кола дорівнює 2 (див.). Довжини сторін візьмемо з попереднього завдання.
Рішення
a \u003d 3 a \u003d 3a=
3
b \u003d 4 b \u003d 4b=
4
c \u003d 5 c \u003d 5c=
5
r \u003d 2 r \u003d 2r=
2
p \u003d 3 + 4 + 5 2 \u003d 6 p \u003d \\ frac (3 + 4 + 5) (2) \u003d 6p= 2 3 + 4 + 5 = 6
S \u003d 6 ⋅ 2 \u003d 12 S \u003d 6 \\ cdot 2 \u003d 12S= 6 ⋅ 2 = 1 2 (Див. Кв.)
відповідь: 12 (см. Кв.)
Формула площі трикутника за двома сторонами і кутом між ними
S \u003d 1 2 ⋅ b ⋅ c ⋅ sin \u2061 (α) S \u003d \\ frac (1) (2) \\ cdot b \\ cdot c \\ cdot \\ sin (\\ alpha)S= 2 1 ⋅ b⋅ c⋅ sin(α ) ,
b, c b, cb, c — сторони трикутника;
α \\ alphaα
— кут між сторонами b bb і c cc. (\\ circ)) \u003d 7.5S=
2 1
⋅
5
⋅
6
⋅
sin(3
0
∘
)
=
7
.
5
(Див. Кв.)
(\\ circ)) \u003d 7.5S=
2 1
⋅
5
⋅
6
⋅
sin(3
0
∘
)
=
7
.
5
(Див. Кв.)
відповідь: 7.5 (див. Кв.)
Площа геометричної фігури — чисельна характеристика геометричної фігури показує розмір цієї фігури (частини поверхні, обмеженої замкнутим контуром даної фігури). Величина площі виражається числом полягають в неї квадратних одиниць.
Формули площі трикутника
- Формула площі трикутника по стороні і висоті
Площа трикутника дорівнює половині твори довжини сторони трикутника на довжину проведеної до цієї сторони висоти - Формула площі трикутника за трьома сторонами і радіусу описаного кола
- Формула площі трикутника за трьома сторонами і радіусу вписаного кола
Площа трикутника дорівнює добутку напівпериметр трикутника на радіус вписаного кола. де S — площа трикутника,
— довжини сторін трикутника,
— висота трикутника,
— кут між сторонами і,
— радіус вписаного кола,
R — радіус описаного кола,
Формули площі квадрата
- Формула площі квадрата по довжині боку
Площа квадрата дорівнює квадрату довжини його сторони.
- Формула площі квадрата по довжині діагоналі
Площа квадрата дорівнює половині квадрата довжини його діагоналі. де S — Площа квадрата,
— довжина сторони квадрата,
— довжина діагоналі квадрата.
Формула площі прямокутника
- Площа прямокутника дорівнює добутку довжин двох його суміжних сторін
де S — Площа прямокутника,
— довжини сторін прямокутника.
Формули площі паралелограма
- Формула площі паралелограма по довжині боку і висоті
Площа паралелограма - Формула площі паралелограма за двома сторонами і кутом між ними
Площа паралелограма дорівнює добутку довжин його сторін помноженому на синус кута між ними.a · b · sin α
де S — Площа паралелограма,
— довжини сторін паралелограма,
— довжина висоти паралелограма,
— кут між сторонами паралелограма.
Формули площі ромба
- Формула площі ромба по довжині боку і висоті
Площа ромба дорівнює добутку довжини його сторони і довжини опущеною на цю сторону висоти.
- Формула площі ромба по довжині боку і розі
Площа ромба дорівнює добутку квадрата довжини його сторони і синуса кута між сторонами ромба. - Формула площі ромба по довжинах його діагоналей
Площа ромба дорівнює половині добутку довжин його діагоналей. де S — Площа ромба,
— довжина сторони ромба,
— довжина висоти ромба,
— кут між сторонами ромба,
1, 2 — довжини діагоналей.
Формули площі трапеції
- Формула Герона для трапеції
Де S — Площа трапеції,
— довжини основ трапеції,
— довжини бічних сторін трапеції,
Трикутник — добре знайома всім фігура. І це, незважаючи на багату різноманітність його форм. Прямокутний, рівносторонній, гострокутний, рівнобедрений, тупоугольние. Кожен з них чимось відрізняється. Але для будь-якого потрібно дізнаватися площа трикутника.
Загальні для всіх трикутників формули, в яких використовуються довжини сторін або висот
Позначення, прийняті в них: сторони — а, в, с; висоти на відповідні сторони н а, н в, н с.
1. Площа трикутника обчислюється, як твір ½, сторони і висоти, опущеної на неї. S \u003d ½ * а * н а. Аналогічно слід записати формули для двох інших сторін.
2. Формула Герона, в якій фігурує напівпериметр (його прийнято позначати маленькою літерою р, на відміну від повного периметра). Напівпериметр необхідно порахувати так: скласти всі сторони і розділити їх на 2. Формула напівпериметр: р \u003d (а + в + с) / 2. Тоді рівність для площі фігури виглядає так: S \u003d √ (р * (р — а) * ( р — в) * (р — с)).
3. Якщо не хочеться використовувати напівпериметр, то стане в нагоді така формула, в якій присутні тільки довжини сторін: S \u003d ¼ * √ ((а + в + с) * (в + с — а) * (а + с — в) * (а + в — с)). Вона кілька довше попередньою, але виручить, якщо забулося, як знаходити напівпериметр.
Загальні формули, в яких фігурують кути трикутника
Позначення, які потрібні для прочитання формул: α, β, γ — кути. Вони лежать навпроти сторін а, в, с, відповідно.
1. По ній половина твори двох сторін і синуса кута між ними дорівнює площі трикутника. Тобто: S \u003d ½ а * в * sin γ. Подібним чином слід записати формули для двох інших випадків.
Тобто: S \u003d ½ а * в * sin γ. Подібним чином слід записати формули для двох інших випадків.
2. Площа трикутника можна обчислити по одній стороні і трьом відомим кутах. S \u003d (а 2 * sin β * sin γ) / (2 sin α).
3. Існує ще формула з однієї відомої стороною і двома прилеглими до неї кутами. Вона виглядає таким чином: S \u003d з 2 / (2 (ctg α + ctg β)).
Дві останні формули не є найпростішими. Запам’ятати їх досить складно.
Загальні формули для ситуації, коли відомі радіуси вписаних або описаних кіл
Додаткові позначення: r, R — радіуси. Перший використовується для радіуса вписаного кола. Другий — для описаної.
1. Перша формула, по якій обчислюється площа трикутника, пов’язана з напівпериметр. S \u003d р * r. По-іншому її можна записати так: S \u003d ½ r * (а + в + с).
2. У другому випадку потрібно перемножити всі сторони трикутника і розділити їх на учетверенное радіус описаного кола. У буквеному вираженні це виглядає так: S \u003d (а * в * с) / (4R).
3. Третя ситуація дозволяє обійтися без знання сторін, але будуть потрібні значення всіх трьох кутів. S \u003d 2 R 2 * sin α * sin β * sin γ.
Окремий випадок: прямокутний трикутник
Це найпростіша ситуація, оскільки потрібне знання лише довжини обох катетів. Вони позначаються латинськими буквами а і в. Площа прямокутного трикутника дорівнює половині площі добудованого до нього прямокутника.
Математично це виглядає так: S \u003d ½ а * в. Вона запам’ятовується найпростіше. Тому що виглядає, як формула для площі прямокутника, тільки з’являється ще дріб, що позначає половину.
Окремий випадок: трикутник
Оскільки у нього дві сторони рівні, то деякі формули для його площі виглядають дещо спрощеними. Наприклад, формула Герона, за якою обчислюється площа рівнобедреного трикутника, Приймає наступний вигляд:
S \u003d ½ в √ ((a + ½ в) * (a — ½ в)).
Якщо її перетворити, то вона стане коротшим. В такому випадку формула Герона для рівнобедреного трикутника записується так:
S \u003d ¼ в √ (4 * a 2 — b 2).
Трохи простіше, ніж для довільного трикутника, виглядає формула площі, якщо відомі бічні сторони і кут між ними. S \u003d ½ a 2 * sin β.
Окремий випадок: рівносторонній трикутник
Зазвичай в задачах про нього відома сторона або її можна будь-яким чином дізнатися. Тоді формула, по якій знаходиться площа такого трикутника, виглядає наступним чином:
S \u003d (а 2 √3) / 4.
Задачі на знаходження площі, якщо трикутник зображений на картатій папері
Найпростішою є ситуація, коли прямокутний трикутник накреслений так, що його катети збігаються з лініями паперу. Тоді потрібно просто порахувати число клітинок, що укладаються в катети. Потім перемножити їх і розділити на два.
Коли трикутник гострокутний або тупоугольние, його потрібно домалювати до прямокутника. Тоді в вийшла фігурі буде 3 трикутника. Один — той що дан в завданні. А два інших — допоміжні і прямокутні. Визначити площі двох останніх потрібно за описаним вище способом. Потім порахувати площу прямокутника і відняти від нього ті, що обчислені для допоміжних. Площа трикутника визначена.
Площа трикутника визначена.
Набагато складніше виявляється ситуація, в якій жодна зі сторін трикутника не збігається з лініями паперу. Тоді його потрібно вписати в прямокутник так, щоб вершини вихідної фігури лежали на його сторонах. В цьому випадку допоміжних прямокутних трикутників буде три.
Приклад завдання на формулу Герона
Умова. У деякого трикутника відомі боку. Вони рівні 3, 5 і 6 см. Необхідно дізнатися його площу.
Тепер можна обчислювати площу трикутника за вказаною вище формулою. Під квадратним коренем виявляється твір чотирьох чисел: 7, 4, 2 і 1. Тобто площа дорівнює √ (4 * 14) \u003d 2 √ (14).
Якщо не потрібна велика точність, то можна витягти квадратний корінь з 14. Він дорівнює 3,74. Тоді площа буде дорівнює 7,48.
Відповідь. S \u003d 2 √14 см 2 або 7,48 см 2.
Приклад завдання з прямокутним трикутником
Умова. Один катет прямокутного трикутника більше, ніж другий на 31 см. Потрібно дізнатися їх довжини, якщо площа трикутника дорівнює 180 см 2.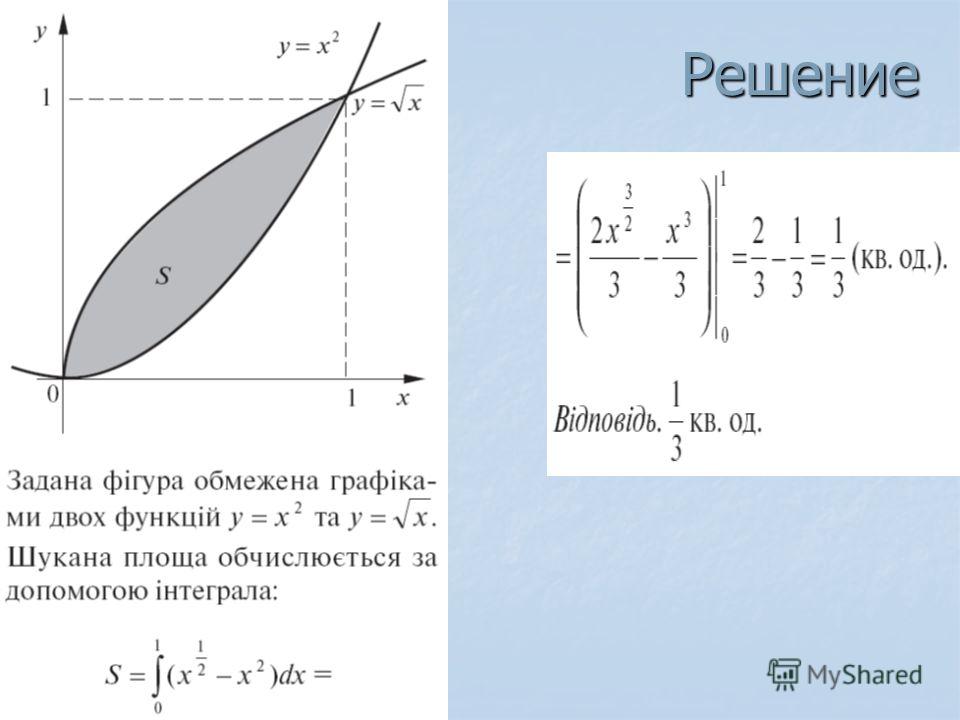
Рішення. Доведеться вирішити систему з двох рівнянь. Перша пов’язана з площею. Друге — з відношенням катетів, яке дано в завданні.
180 \u003d ½ а * в;
а \u003d в + 31.
Спочатку значення «а» потрібно підставити в перше рівняння. Вийде: 180 \u003d ½ (в + 31) * в. У ньому тільки одна невідома величина, тому його легко вирішити. Після розкриття дужок виходить квадратне рівняння: в 2 + 31 в — 360 \u003d 0. Воно дає два значення для «в»: 9 і — 40. друге число не підходить в якості відповіді, так як довжина сторони трикутника не може бути негативною величиною.
Залишилося обчислити другий катет: додати до отриманого числа 31. Виходить 40. Це шукані в задачі величини.
Відповідь. Катети трикутника рівні 9 і 40 см.
Завдання на знаходження сторони через площу, сторону і кут трикутника
Умова. Площа деякого трикутника 60 см 2. Необхідно обчислити одну з його сторін, якщо друга сторона дорівнює 15 см, а кут між ними дорівнює 30º.
Рішення. Виходячи з прийнятих позначень, шукана сторона «а», відома «в», заданий кут «γ». Тоді формула площі можна переписати так:
Тоді формула площі можна переписати так:
60 \u003d ½ а * 15 * sin 30º. Тут синус 30 градусів дорівнює 0,5.
Після перетворень «а» виявляється рівним 60 / (0,5 * 0,5 * 15). Тобто 16.
Відповідь. Шукана сторона дорівнює 16 см.
Завдання про квадраті, вписанном в прямокутний трикутник
Умова. Вершина квадрата зі стороною 24 см збігається з прямим кутом трикутника. Дві інші лежать на катетах. Третя належить гіпотенузі. Довжина одного з катетів дорівнює 42 см. Чому дорівнює площа прямокутного трикутника?
Рішення. Розглянемо два прямокутних трикутника. Перший — заданий в завданні. Другий — спирається на відомий катет вихідного трикутника. Вони подібні, так як мають загальний кут і утворені паралельними прямими.
Тоді відносини їх катетів дорівнюють. Катети меншого трикутника рівні 24 см (сторона квадрата) і 18 см (заданий катет 42 см відняти сторону квадрата 24 см). Відповідні катети великого трикутника — 42 см і х см. Саме цей «х» потрібен для того, щоб обчислити площу трикутника.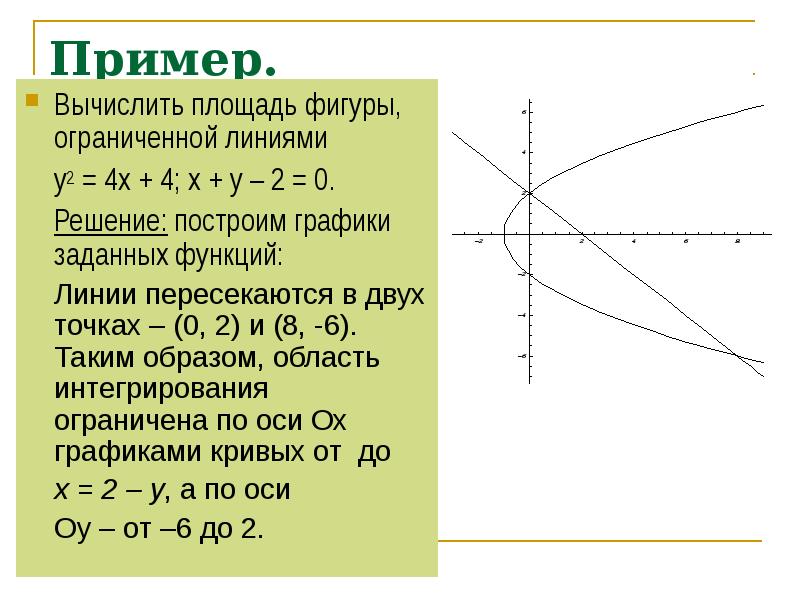
18/42 \u003d 24 / х, тобто х \u003d 24 * 42/18 \u003d 56 (см).
Тоді площа дорівнює добутку 56 і 42, розділеному на два, тобто 1176 см 2.
Відповідь. Шукана площа дорівнює 1176 см 2.
Щоб визначити площу трикутника, можна користуватися різними формулами. З усіх способів найлегший і часто вживаний — це множення висоти на довжину підстави з наступним розподілом отриманого результату на два. Однак даний метод далеко не єдиний. Нижче ви зможете прочитати, як знайти площу трикутника, використовуючи різні формули.
Окремо ми розглянемо способи обчислення площі специфічних видів трикутника — прямокутного, рівнобедреного і рівностороннього. Кожну формулу ми супроводжуємо коротким поясненням, яке допоможе вам зрозуміти її суть.
Універсальні способи знаходження площі трикутника
У наведених нижче формулах використовуються спеціальні позначення. Ми розшифруємо кожне з них:
- a, b, c — довжини трьох сторін розглянутої нами фігури;
- r — радіус кола, яка може бути вписана в наш трикутник;
- R — радіус тієї окружності, яка може бути описана навколо нього;
- α — величина кута, утвореного сторонами b і с;
- β — величина кута між a і c;
- γ — величина кута, утвореного сторонами а і b;
- h — висота нашого трикутника, опущена з кута α на сторону а;
- p — половина суми сторін a, b і с.

Логічно зрозуміло, чому можна знаходити площа трикутника цим способом. Трикутник легко добудовується до паралелограма, в якому одна сторона трикутника буде виконувати роль діагоналі. Площа паралелограма знаходиться множенням довжини однієї з його сторін на значення висоти, проведеної до неї. Діагональ розділяє цей умовний паралелограм на 2 однакових трикутника. Отже, цілком очевидно, що площа нашого вихідного трикутника має дорівнювати половині площі цього допоміжного паралелограма.
S \u003d ½ a · b · sin γ
Відповідно до цієї формули, площа трикутника знаходиться множенням довжин двох його сторін, тобто а і b, на синус утвореного ними кута. Ця формула логічно виводиться з попередньої. Якщо опустити висоту з кута β на сторону b, то, згідно з властивостями прямокутного трикутника, при множенні довжини сторони a на синус кута γ отримуємо висоту трикутника, тобто h.
Площа розглянутої фігури знаходимо шляхом множення половини радіусу кола, яку в нього можна вписати, на його периметр. Іншими словами, знаходимо твір напівпериметр на радіус згаданої окружності.
Іншими словами, знаходимо твір напівпериметр на радіус згаданої окружності.
S \u003d a · b · с / 4R
Згідно цій формулі, необхідну нам величину можна знайти шляхом поділу праці сторін фігури на 4 радіусу кола, навколо неї описаної.
Ці формули універсальні, так як дають можливість визначити площу будь-якого трикутника (різнобічного, рівнобедреного, рівностороннього, прямокутного). Можна це зробити і за допомогою більш складних обчислень, на яких ми детально зупинятися не будемо.
Площі трикутників зі специфічними властивостями
Як знайти площу прямокутного трикутника? Особливістю цієї фігури є те, що дві її сторони одночасно є її висотами. Якщо а і b є катетами, а з стає гипотенузой, то площа знаходимо так:
Як знайти площу рівнобедреного трикутника? У ньому дві сторони з довжиною а й одна сторона з довжиною b. Отже, його площа визначити можна шляхом ділення на 2 твори квадрата сторони а на синус кута γ.
Як знайти площу рівностороннього трикутника? У ньому довжина всіх сторін дорівнює а, а величина всіх кутів — α. Його висота дорівнює половині твори довжини сторони а на корінь квадратний з 3. Щоб знайти площу правильного трикутника, потрібно квадрат сторони а помножити на корінь квадратний з 3 і розділити на 4.
Його висота дорівнює половині твори довжини сторони а на корінь квадратний з 3. Щоб знайти площу правильного трикутника, потрібно квадрат сторони а помножити на корінь квадратний з 3 і розділити на 4.
поняття площі
Поняття площі будь-якої геометричної фігури, зокрема трикутника, будемо пов’язувати з такою фігурою, як квадрат. За одиницю площі будь-якої геометричної фігури будемо приймати площа квадрата, сторона якого дорівнює одиниці. Для повноти, згадаємо дві основні властивості для поняття площ геометричних фігур.
Властивість 1:якщо геометричні фігури рівні, то значення їх площ є рівними.
Властивість 2: Будь-яка фігура може бути розбита на кілька фігур. Причому площа первісної фігури дорівнює сумі значень площ всіх складових її фігур.
Розглянемо приклад.
приклад 1
Очевидно, що одна зі сторін трикутника є діагоналлю прямокутника, у якого одна сторона має довжину $ 5 $ (так як $ 5 $ клітин), а друга $ 6 $ (так як $ 6 $ клітин). Отже, площа цього трикутника буде дорівнювати половині такого прямокутника. Площа прямокутника дорівнює
Отже, площа цього трикутника буде дорівнювати половині такого прямокутника. Площа прямокутника дорівнює
Тоді площа трикутника дорівнює
Відповідь: $ 15 $.
Далі розглянемо кілька методів для знаходження площ трикутників, а саме за допомогою висоти і підстави, за допомогою формули Герона і площа рівностороннього трикутника.
Як знайти площу трикутника через висоту і підстава
теорема 1
Площа трикутника можна знайти як половину твору довжини сторони, на висоту, проведену до цієї сторони.
Математично це виглядає наступним чином
$ S \u003d \\ frac (1) (2) αh $
де $ a $ — довжина сторони, $ h $ — висота, проведена до неї.
Доведення.
Розглянемо трикутник $ ABC $, в якому $ AC \u003d α $. До цієї стороні проведена висота $ BH $, яка дорівнює $ h $. Добудуємо його до квадрата $ AXYC $ як на малюнку 2.
Площа прямокутника $ AXBH $ дорівнює $ h \\ cdot AH $, а прямокутника $ HBYC $ дорівнює $ h \\ cdot HC $. тоді
тоді
$ S_ABH \u003d \\ frac (1) (2) h \\ cdot AH $, $ S_CBH \u003d \\ frac (1) (2) h \\ cdot HC $
Отже, шукана площа трикутника, по властивості 2, дорівнює
$ S \u003d S_ABH + S_CBH \u003d \\ frac (1) (2) h \\ cdot AH + \\ frac (1) (2) h \\ cdot HC \u003d \\ frac (1) (2) h \\ cdot (AH + HC) \u003d \\ Теорема доведена.
приклад 2
Знайти площу трикутника на малюнку нижче, якщо клітина має площу, рівну одиниці
Підстава цього трикутника дорівнює $ 9 $ (так як $ 9 $ становить $ 9 $ клітин). Висота також дорівнює $ 9 $. Тоді, по теоремі 1, отримаємо
$ S \u003d \\ frac (1) (2) \\ cdot 9 \\ cdot 9 \u003d 40,5 $
Відповідь: $ 40,5 $.
Формула Герона
теорема 2
Якщо нам дано три сторони трикутника $ α $, $ β $ і $ γ $, то його площа можна знайти в такий спосіб
$ S \u003d \\ sqrt (ρ (ρ-α) (ρ-β) (ρ-γ)) $
тут $ ρ $ означає напівпериметр цього трикутника.
розглянемо наступний малюнок:
Доведення.
По теоремі Піфагора з трикутника $ ABH $ отримаємо
З трикутника $ CBH $, по теоремі Піфагора, маємо
$ H ^ 2 \u003d α ^ 2 (β-x) ^ 2 $
$ H ^ 2 \u003d α ^ 2-β ^ 2 + 2βx-x ^ 2 $
З цих двох співвідношень отримуємо рівність
$ Γ ^ 2-x ^ 2 \u003d α ^ 2-β ^ 2 + 2βx-x ^ 2 $
$ X \u003d \\ frac (γ ^ 2-α ^ 2 + β ^ 2) (2β) $
$ H ^ 2 \u003d γ ^ 2 — (\\ frac (γ ^ 2-α ^ 2 + β ^ 2) (2β)) ^ 2 $
$ H ^ 2 \u003d \\ frac ((α ^ 2 (γ-β) ^ 2) ((γ + β) ^ 2-α ^ 2)) (4β ^ 2) $
$ H ^ 2 \u003d \\ frac ((α-γ + β) (α + γ-β) (γ + β-α) (γ + β + α)) (4β ^ 2) $
Так як $ ρ \u003d \\ frac (α + β + γ) (2) $, то $ α + β + γ \u003d 2ρ $, значить
$ H ^ 2 \u003d \\ frac (2ρ (2ρ-2γ) (2ρ-2β) (2ρ-2α)) (4β ^ 2) $
$ H ^ 2 \u003d \\ frac (4ρ (ρ-α) (ρ-β) (ρ-γ)) (β ^ 2) $
$ H \u003d \\ sqrt (\\ frac (4ρ (ρ-α) (ρ-β) (ρ-γ)) (β ^ 2)) $
$ H \u003d \\ frac (2) (β) \\ sqrt (ρ (ρ-α) (ρ-β) (ρ-γ)) $
По теоремі 1, отримаємо
$ S \u003d \\ frac (1) (2) βh \u003d \\ frac (β) (2) \\ cdot \\ frac (2) (β) \\ sqrt (ρ (ρ-α) (ρ-β) (ρ-γ) ) \u003d \\ sqrt (ρ (ρ-α) (ρ-β) (ρ-γ)) $
Статті по темі:
Ходовая часть.
 Обзоры. Топливная система. Шины и диски. Салон. Двигатель Ходовая часть. Обзоры. Топливная система. Шины и диски. Салон. Двигатель
Обзоры. Топливная система. Шины и диски. Салон. Двигатель Ходовая часть. Обзоры. Топливная система. Шины и диски. Салон. Двигатель- Конспект занятия по обучению грамоте детей старшего дошкольного возраста «Звук и буква Ц» Знакомство со звуком ц в подготовительной группе
- К чему снится крыша по соннику К чему снится строить крышу дома
- Кубинские генералы расстрелянные ф кастро
- Евреи в правительстве рф
- Сирия Большой котел для игил
- Значение слова, традиции, кушанье
- Рождество Христово: дата, рождественские традиции, Сочельник Православный сочельник
- Боевая магия стихий, заклинания и обучение Обучение боевой магии древних славян
- Управление — Беседы — Дополнительное чтение — Приложения — Ликбез
- Образец приказа о служебном расследовании в отношении работника
- Фактически отработанное время
- Служебное расследование в отношении работника
- Трудовой кодекс РФ о применении труда несовершеннолетних
- Переход на эффективный контракт (образец приказа)
- Конвенция МОТ об инспекции труда в промышленности и торговле (рус
- О контрактной службе и ее руководителе
- Цитаты из романа в стихах «Евгений Онегин» А
- Характеристика Молчалина в комедии “Горе от ума” Грибоедова, описание характера героя Лицемерие в произведении горе от ума
- Речевая характеристика Молчалина («Горе от ума»)
- Антуан де Сент-Экзюпери: биография, фото и интересные факты Биография де сент экзюпери краткая
- Антуан де сент-экзюпери, краткая биография Сообщение о писателе антуан де сент экзюпери
- Сочинение город калинов и его обитатели в пьесе островского гроза
- А зори здесь тихие (повесть)
- Натали: биография, личная жизнь, семья, муж, дети — фото Кто такая натали
- Кто отец наргиз закировой
- Личная жизнь адель Сын певицы Адель – Анджело
- Андрей губин — биография, информация, личная жизнь
- Опубликовано интервью с живущей в россии матерью джамалы
- Сколько лет криду сейчас в
- Биография CC Catch.
 Биография C.C.Catch Юность и молодость будущей певицы
Биография C.C.Catch Юность и молодость будущей певицы - Звезда «Голоса» Елена Максимова наслаждается медовым месяцем на Багамах
- Соня Мармеладова — главный женский образ в романе «Преступление и наказание Ее даже нельзя было назвать и хорошенькой
- Сравнение Обломова и Штольца (ЕГЭ по русскому) Критерии для сравнения обломова и штольца
- Михаил александрович шолохов, краткая биография
- Как нарисовать валентинку: идеальные способы для начинающих и не только Идеи поделок для украшения дома
- Гадкий утенок поэтапно карандашом
- Жилищная лотерея — проверка выигрыша
- Правила «Жилищной лотереи
- Певец русской природы – Михаил Пришвин
- Группа кватро концерты. Истории успеха. Рождение и полет «Кватро»
Калькулятор площади между двумя кривыми
Следуйте простым указаниям, чтобы найти площадь между двумя кривыми, расположенными вдоль линий
- Если у нас есть две кривые P: y = f(x), Q: y = g(x)
- Получить точки пересечения кривой, подставив значения одного уравнения в другое и сделав это уравнение только одной переменной.

- Решите это уравнение и найдите точки пересечения.
- Нарисуйте график для заданных кривых и точек пересечения.
- Тогда площадь будет равна A = ∫ x2 x1 [f(x)-g(x)]dx
- Подставьте значения в приведенную выше формулу.
- Решите интегрирование и замените значения, чтобы получить результат.
Пример
Вопрос: Вычислите площадь области, ограниченной кривыми y 2 + 4x – y = 0 и прямой y = x?
Решение:
Даны уравнения: y 2 + 4x – y = 0, y=x
г 2 + 4х – у = 0
Прибавьте y и вычтите y 2 с обеих сторон.
у 2 + 4х – у + у — у 2 = у — у 2
4x = у — у 2
Разделить на 4 с обеих сторон
х = у — у 2 /4
Используя другое уравнение y = x в уравнении кривой будет
г 2 +4г-г = 0
г 2 +3г = 0
у(у+3) = 0
г = 0 или -3
В соответствии со значениями y мы получаем x = 0 или -3. Таким образом, точками пересечения являются P(-3,-3) и Q(0,0).
Таким образом, точками пересечения являются P(-3,-3) и Q(0,0).
График для системы будет:
На графике кривая справа — f(y), а кривая слева — g(y).
f(y) = y — y 2 /4
г(у) = у
Площадь A = ∫ x2 x1 [f(x)-g(x)]dx
А = ∫ 3 0 [(у — у 2 /4)-у]дд
= ∫ 3 0 ((-y 2 -3y)/4)dy
= [ — у 3 /4*3 — 3/4 * у 2 /2] 3 0
= — [(0+0) — (- 3 3 /4*3 — 3/4 * 3 2 /2)
= — (-27/12 + 3/4 * 9/2)
= 27/24
Площадь, определяемая определенным интегралом, равна -27/24.
Независимо от того, является ли это векторным произведением векторов, площадью между кривыми, площадью или периметром любой фигуры, вы можете рассчитать ее с помощью бесплатных инструментов, предоставленных на сайте Onlinecalculator. guru
guru
Калькулятор площади между двумя кривыми
В контексте математики мы часто использовали интегральное исчисление, чтобы найти площадь под кривой. Точно так же верно и то, что мы можем найти площадь между двумя кривыми. Для этого воспользуемся понятием определенных интегралов.Однако калькулятор площади между двумя кривыми поможет вам выполнить эти вычисления гораздо проще.
Площадь между двумя кривыми формула:Как мы уже говорили ранее, мы будем использовать понятия определенных интегралов, чтобы найти площадь между двумя кривыми. Помимо важного применения определенных интегралов, эти задачи также дают представление о природе двух задействованных кривых.
Итак, формула для расчета площади между двумя кривыми выглядит так:
A = [f(x)–g(x)]dx,
Где f(x) — уравнение одной кривой, а g( x) — уравнение другой кривой, а
x1 и x2 — граничные значения x (в данном случае).
Калькулятор площади между двумя кривыми: Калькулятор площади между двумя кривыми — это онлайн-инструмент, который эффективно вычисляет площадь между двумя кривыми.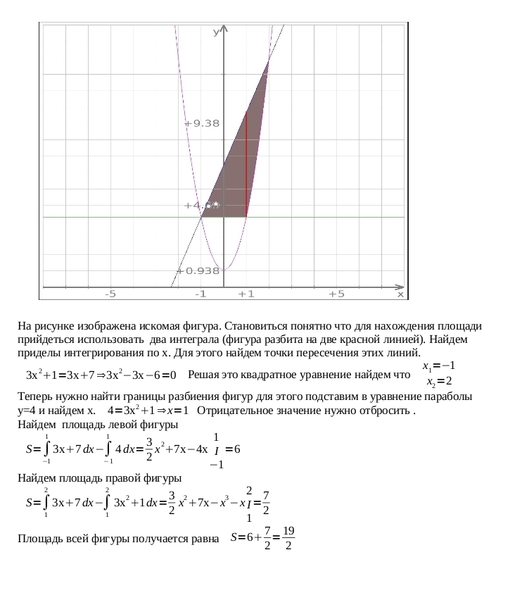
Поскольку нахождение площади между двумя кривыми является важным применением интегрального исчисления, мы можем использовать этот калькулятор по многим причинам.
- Калькулятор дает очень точные результаты.
- Также легко доступен калькулятор площади между двумя кривыми.
- Кроме того, он совсем не требует много времени по сравнению с
методом, основанным на ручке и бумаге.
- Также вам не нужно знать площадь между кривыми
Формула для использования калькулятора площади между двумя кривыми.
Калькулятор площади между двумя кривыми с шагами:Вычислить площадь между двумя кривыми достаточно просто, зная точки их пересечения. Кроме того, точки пересечения двух кривых называются нижней и верхней границами.
В заключение, он существует между двумя точками, он вычисляется путем вычисления определенного интеграла между двумя точками.
Расчет площади между двумя кривыми
y= f(x) между x= a и x= b
y= f(x) между пределами a и b (b должно быть больше a).
Для получения правильных результатов выполните следующие действия.
- Во-первых, напишите первую функцию в предоставленном вам месте. Собственно, это уравнение первой кривой.
- Во-вторых, напишите вторую функцию в отведенном для вас месте. Собственно, это и есть уравнение второй кривой.
- В-третьих, укажите левую и правую границы функций. Левая и правая границы — это не что иное, как точки пересечения двух кривых.
- Наконец, нажмите кнопку «Отправить». В окне вывода будет отображаться результат соответственно.
Есть несколько условных обозначений, которые необходимо учитывать.
Это:
- Верхняя кривая/функция на графике – f(x).
- Нижняя кривая/функция на графике — это g(x).
- Мы присвоим положительные знаки области над осью Y.
- Мы присвоим отрицательные знаки области под осью Y.
Площадь между двумя кривыми вычисляется с помощью интегрирования.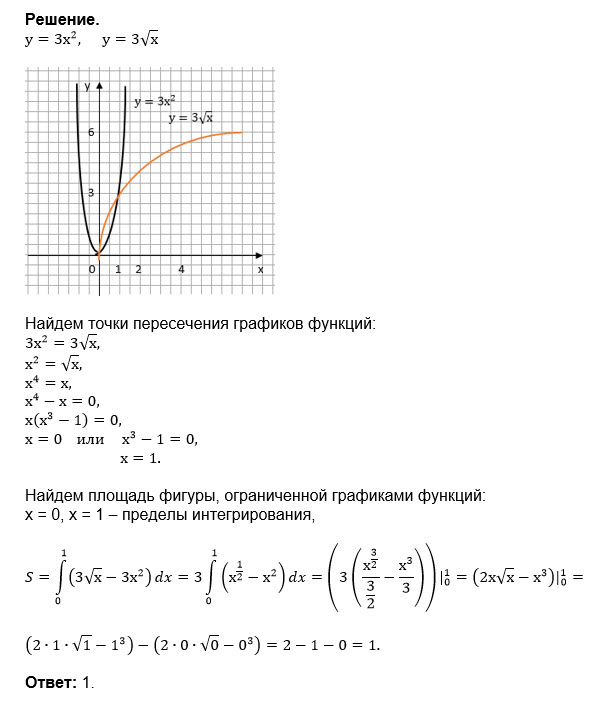 Теперь мы объясним основную концепцию этого приложения. На самом деле область, которая лежит в области пересечения двух кривых, разбита на тонкие прямоугольные полосы.
Теперь мы объясним основную концепцию этого приложения. На самом деле область, которая лежит в области пересечения двух кривых, разбита на тонкие прямоугольные полосы.
Теперь сложите отдельные области этих тонких полос, чтобы найти общую площадь этой области.
Предположим, что ширина этих прямоугольных полос равна ‘dx’.
Таким образом, вычислите площадь этой зоны как A = [f(x)–g(x)]dx
Аналогично, площадь между двумя кривыми также можно найти по оси y.
Однако мы обсудим это в следующем разделе.
Калькулятор площади двух кривых относительно оси Y:Вы также можете найти площадь между двумя кривыми вдоль оси Y.
На самом деле найти его проще.
Когда уравнение кривой выражается через y, площадь
между кривыми может быть рассчитана по оси y.
Теперь разделите область внутри границ на тонкие горизонтальные полосы. В этом случае
добавьте площади горизонтальных полос, чтобы вычислить общую площадь
этой области.
Предположим, что f(y) и g(y) непрерывны на [c,d], тогда
A = [f(y)–g(y)] dy.
Область между двумя полярными кривымиПолярная кривая представляет собой фигуру, построенную с использованием полярной системы координат.Полярные кривые определяются точками, которые находятся на переменном расстоянии от начала координат (полюса) в зависимости от угла, измеренного от положительной оси x. Существует пять классических полярных кривых: кардиоиды, лиманоны, лемнискаты, кривые розы и спирали Архимеда.
Однако выполните следующие шаги, чтобы найти площадь между двумя полярными кривыми:
Во-первых, найдите точки пересечения, если вы не знаете интервал.
Во-вторых, графическое изображение кривых также очень важно.2) dθ
, где [α,β] — интервал, определяющий площадь,
, где r o — внешняя кривая, и,
, где r I — внутренняя кривая.
Калькулятор площади между двумя кривыми desmos Калькулятор площади между двумя кривыми (полярный) также очень легко доступен онлайн.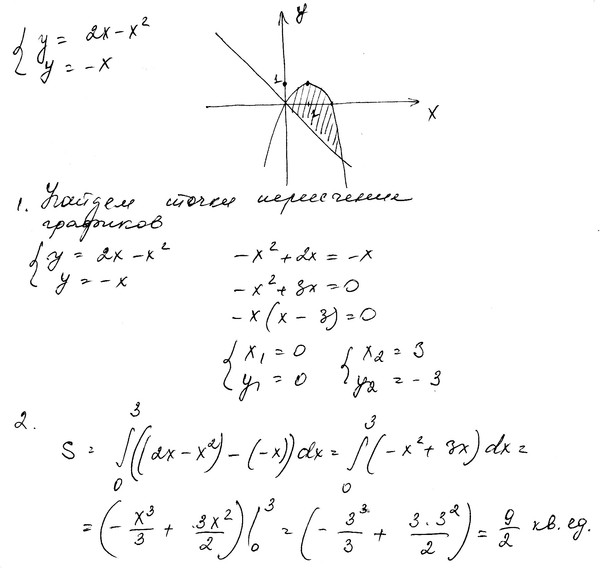
На самом деле вам не нужно запоминать формулу для вычисления площади между двумя полярными кривыми.2 dθ
На графике n1 — это количество зеленых секций, которые необходимо завершить или свести на нет, чтобы получить желаемую область.
Кроме того, n 2 — это количество синих секций, которые необходимо завершить или свести на нет, чтобы получить желаемую область. Таким образом, после ввода этой информации в поле вывода отображается результат.
калькулятор
Калькулятор площади между двумя кривыми symbolabЭто еще один онлайн-калькулятор, который используется для нахождения площади между двумя кривыми.Этот калькулятор в основном простой способ интегрировать функции. На самом деле все, что вам нужно сделать, это выбрать знак интеграции. Затем вы можете написать требуемую функцию в соответствующем поле.
Наконец ответ отображается автоматически.
Также мы предоставляем вам ссылку для доступа к этому калькулятору:
калькулятор символов
Калькулятор площади между двумя кривыми mathway Этот калькулятор от Mathway поможет вам найти площадь между двумя кривыми всего за долю из нескольких секунд.
Во-первых, рассмотрим два уравнения для двух кривых.
Сначала решите подстановкой, чтобы найти пересечение между кривыми.
Затем исключите равные части каждого уравнения и объедините их.
Решением системы является полный набор упорядоченных пар, являющихся действительными решениями.
Площадь области между кривыми определяется как интеграл верхней кривой минус интеграл нижней кривой по каждой области. Области определяются точками пересечения кривых.
Однако это можно сделать алгебраически или графически.
Вы можете ввести любую проблему в отведенное место. Затем этот калькулятор отобразит результат вместе с подробным объяснением всех включенных шагов.
Здесь мы предоставляем вам ссылку для доступа к этому калькулятору Mathway:
mathway
Калькулятор объема площади между двумя кривыми: Теперь вы знаете, как легко вычислить площадь между двумя кривыми.Теперь мы можем приступить к нахождению объема площади между двумя кривыми.
Для расчета этого вы можете легко использовать калькулятор «объем площади между двумя кривыми». Этот калькулятор доступен онлайн. Вам просто нужно подставить уравнения двух кривых и граничных точек, которые ограничивают область между ними. Затем автоматически отображается ответ.
Далее, этот калькулятор еще называют Калькулятор объема тела вращения.
Мы также прикрепляем ссылку для этого Объем тела вращения Калькулятор представлен символом:
Площадь между задачами двух кривых: Пример 1:Найдите площадь между кривыми y=0 и y = 3 ( – x).
Когда мы рисуем область, мы видим, что кривые пересекаются друг с другом, так что верхняя и нижняя части меняются местами. Следовательно, мы разобьем интеграл на два интеграла:
Таким образом, график теперь выглядит так:
[3 ( – x) – 0] dx + [0 – 3 ( – x)] dx
Или, ( 3 / 4 * – 3/2 ) проинтегрировано по [-1 до 0] – (3/4 * – 3/2 ) проинтегрировано по [0 до 1].
Или, (- 3/4 + 3/2) – (3/4 – 3/2) = 3/2.
Таким образом, площадь между этими двумя кривыми составляет 3/2 единицы.3] в определенном интервале от -1 до +1.
Или, [2 – (2/3)] – [- 2 – (2/3)] = 8/3.
Таким образом, площадь между двумя кривыми составляет 8/3 единиц.
Пример 3:Теперь воспользуемся этим понятием в контексте решения экономической задачи.
Пусть y=f(x) — функция спроса на продукт, а y=g(x) — функция предложения. Затем мы определяем точку равновесия как пересечение двух кривых. Излишек потребителя определяется площадью выше равновесного значения и ниже кривой спроса, а излишек производителя определяется площадью ниже равновесного значения и выше кривой предложения.х и у = 2х +3.
Площадь между двумя кривыми: 1. Кривая Лоренца: . Его также можно использовать для отображения распределения активов (общее богатство, а не доход). Экономисты считают его мерой социального неравенства.
Экономисты считают его мерой социального неравенства.
Однако Макс О. Лоренц разработал его в 1905 году для представления неравенства в распределении богатства.
На этом рисунке
Кривая Лоренца L(x) по сравнению с диагональной линией, которая представляет идеальное равенство доходов. Область А представляет собой разницу между идеальным равенством доходов и фактическим распределением доходов. Экспериментально, чем больше A, тем более неравномерно распределение доходов.
2. Излишек потребителя и излишек производителя: Излишек потребителя – это разница между общей суммой, которую потребители готовы и могут заплатить за товар или услугу (обозначается кривой спроса), и общей суммой сумма, которую они фактически платят (т.д., фактическая рыночная цена товара). Таким образом, уровень потребительского излишка показан площадью ниже кривой спроса и выше линии господствующей рыночной цены, как показано на рисунке.
Напротив, излишек производителя представляет собой разницу между общей суммой, которую получают производители товара, и минимальной суммой, которую они были бы готовы принять за этот товар (синяя заливка).
Таким образом, понятие площади под кривыми/площади между двумя кривыми важно для расчетов излишка потребителя и производителя.
Площадь между двумя кривыми с помощью EXCEL:Чтобы найти площадь между двумя кривыми с помощью EXCEL, выполните следующие действия:
- вашу таблицу Excel.
- Измените параметры команды ЛИНЕЙН, чтобы отразить расположение ваших данных для одного из графиков. Например, если ваши y-данные находятся в ячейках A1:A8, а ваши x-данные находятся в ячейках B1:B8, тогда функция будет читать ЛИНЕЙН(A1:A8, B1:B8, ИСТИНА, ЛОЖЬ).
- Нажмите «Ввод», чтобы получить уравнение для первого набора данных.
- Введите «ЛИНЕЙН(yrange, xrange, TRUE, FALSE)» во вторую пустую ячейку электронной таблицы Excel.

- Измените параметры команды ЛИНЕЙН, чтобы отразить расположение фактических данных для второго графика. Например, если данные y для вашего второго графика находятся в ячейках C1:C8, а ваши данные x находятся в ячейках D1:D8, тогда функция будет читать ЛИНЕЙН(C1:C8, D1:D8, ИСТИНА, ЛОЖЬ).
- Теперь нажмите «Enter», чтобы получить уравнение для второго набора данных.
- Затем вычислите определенный интеграл для двух уравнений. Вам потребуется знание исчисления для этой части. Существуют онлайн-калькуляторы для вычисления определенных интегралов. Например, многие сайты предлагают онлайн-калькуляторы определенных интегралов. Мы также предоставили один в нашей статье.
- Рассчитайте площадь под первой кривой, используя определенный интеграл.
- Рассчитайте площадь под второй кривой, используя определенный интеграл.
- Вычтите шаг 9 из шага 8, чтобы найти площадь между двумя кривыми.
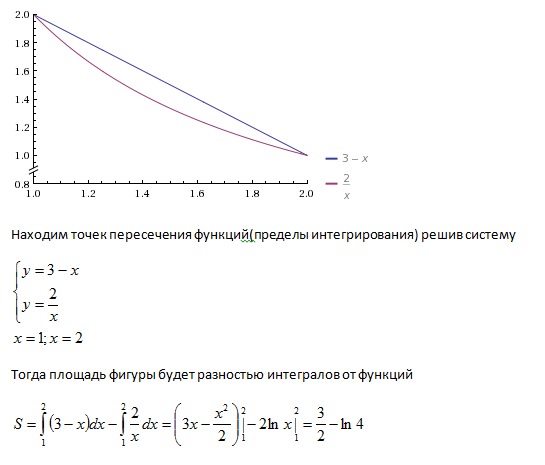 Может ли площадь между двумя кривыми быть отрицательной при использовании калькулятора?
Может ли площадь между двумя кривыми быть отрицательной при использовании калькулятора? Ответ : Нет, результат вычисления площади между двумя кривыми никогда не может быть отрицательным. Однако типичный метод решения в этом случае состоит в том, чтобы рассматривать каждую часть отдельно, интегрируя (верхняя функция) – (нижняя функция) для каждой части, чтобы гарантировать положительный (неотрицательный) результат.По определению, «Площадь между двумя графиками» положительна независимо от того, где в плоскости она находится.
2. Что означает площадь между двумя кривыми, полученными калькулятором?Ответ : Значение, полученное из калькулятора площади между двумя кривыми, дает нам площадь общей области, занимаемой между двумя кривыми в координатной плоскости.
3. Какова концепция нахождения площади между двумя кривыми? Ответ : Площадь под кривой между двумя точками можно найти, выполнив определенный интеграл между двумя точками.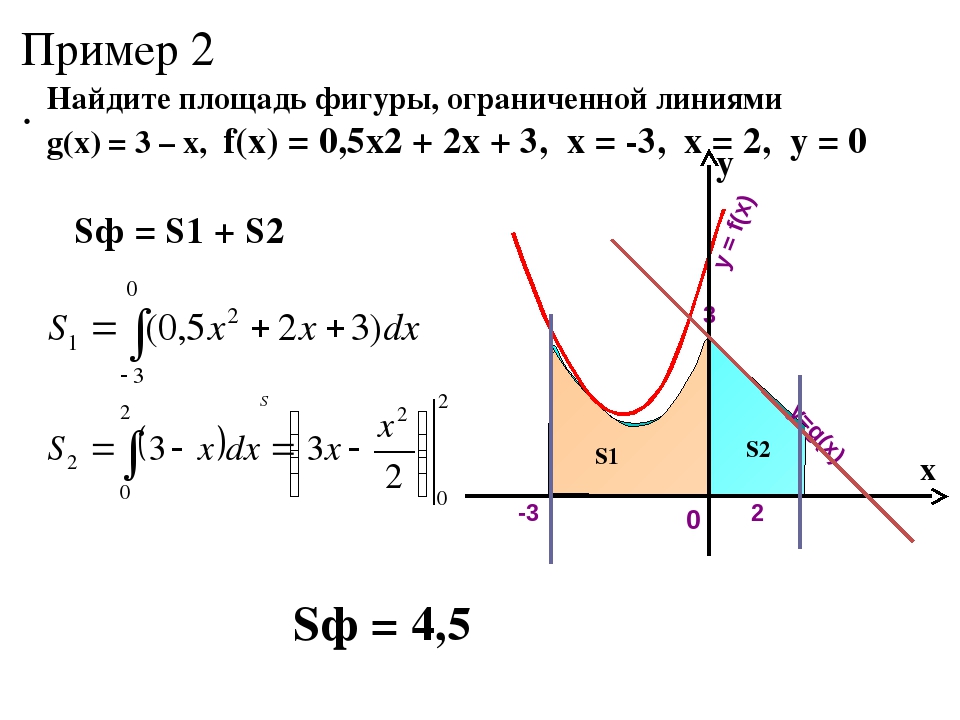 Таким образом, чтобы найти площадь под кривой y = f(x) между x = a и x = b, проинтегрируйте y = f(x) между пределами a и b.
Таким образом, чтобы найти площадь под кривой y = f(x) между x = a и x = b, проинтегрируйте y = f(x) между пределами a и b.
Ответ : Если вы не хотите использовать метод графика для нахождения площади между двумя кривыми, вы можете просто поместить функцию в калькулятор области между двумя кривыми. Основная идея состоит в том, чтобы вычислить определенный интеграл от a до b. Вам нужно найти абсолютное значение функции в точке «а» и вычесть его из абсолютного значения функции в точке «b».
5. Какой первый шаг к нахождению площади между двумя кривыми?Ответ : Всякий раз, когда вам нужно найти площадь между двумя кривыми, первым шагом, который вы должны рассмотреть для решения проблемы, является ее графическое изображение. Кроме того, это значительно упрощает процесс решения.
При правильном построении необходимых кривых точку пересечения становится легче найти. Даже становится ясной форма области в середине и граничные точки, ограничивающие эту область.Таким образом, в целом весь процесс становится очень простым, и вы можете вычислить площадь между двумя заданными кривыми, не сталкиваясь с какими-либо трудностями.
Даже становится ясной форма области в середине и граничные точки, ограничивающие эту область.Таким образом, в целом весь процесс становится очень простым, и вы можете вычислить площадь между двумя заданными кривыми, не сталкиваясь с какими-либо трудностями.
Ответ : Да, можно получить площадь между этими двумя функциями либо по горизонтальной, либо по вертикальной оси. Во-первых, мы должны нарисовать график для двух кривых.Затем разделите область между двумя кривыми либо на тонкие горизонтальные полосы, либо на тонкие вертикальные полосы. Наконец, вы можете продолжить, используя процесс, который мы проиллюстрировали в нашей статье выше.
Калькулятор площади между двумя кривыми
Калькулятор площади между двумя кривыми вычисляет площадь, занимаемую между двумя кривыми, с помощью бесплатного онлайн-инструмента.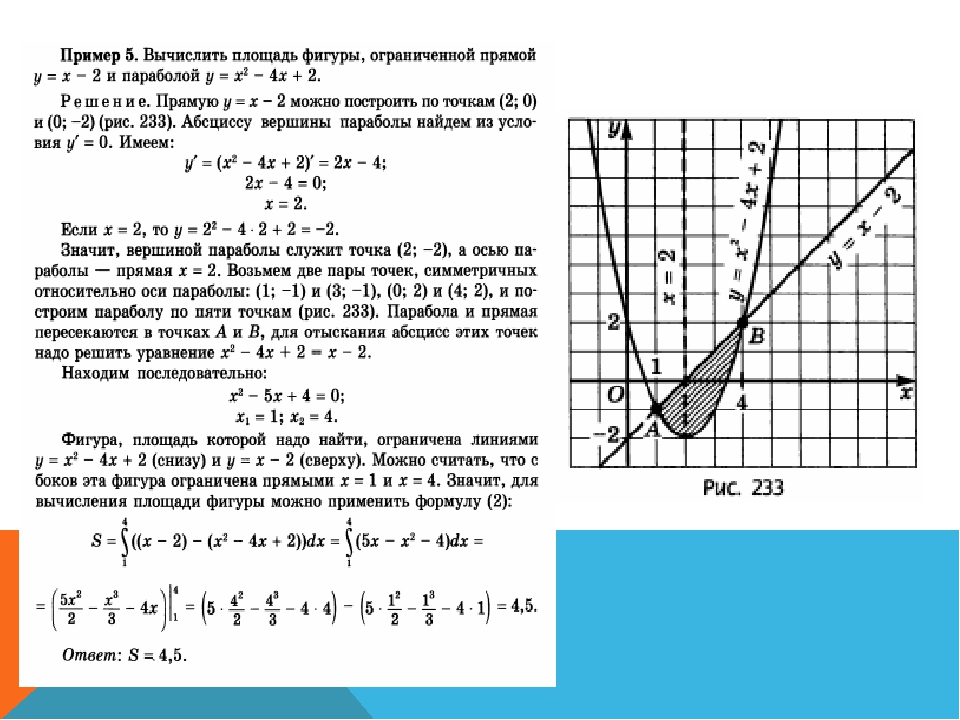 Он прост в использовании и отображает результаты за считанные секунды благодаря онлайн-калькулятору STUDYQUERIES между двумя кривыми.
Он прост в использовании и отображает результаты за считанные секунды благодаря онлайн-калькулятору STUDYQUERIES между двумя кривыми.
Чтобы использовать калькулятор площади между двумя кривыми, выполните следующие действия:
- Шаг 1: Введите меньшую функцию, большую функцию и предельные значения в заданных полях ввода
- Шаг 2: Чтобы рассчитать площадь, нажмите кнопку «Рассчитать площадь»
- Шаг 3: Наконец, в новом окне вы увидите область между этими двумя кривыми
Калькулятор площади между двумя кривымиОбласть между двумя кривыми
Необходимо интегрировать две кривые, чтобы найти площадь между ними.С помощью интегрирования мы научились находить площадь под кривой. Точно так же мы можем найти площадь между двумя пересекающимися кривыми, используя интегрирование. В данном пространстве это будет область, расположенная между двумя линейными или нелинейными кривыми.
В данном пространстве это будет область, расположенная между двумя линейными или нелинейными кривыми.
Также можно легко найти составную площадь между двумя кривыми, изменив формулы, используемые для нахождения площади под двумя кривыми с помощью интегрирования. Пожалуйста, читайте дальше для дальнейшего обсуждения этого вопроса.
Область между двумя кривыми ВведениеИнтегральное исчисление можно использовать для вычисления площади между двумя кривыми, которые находятся между двумя пересекающимися кривыми.Когда мы знаем уравнение двух кривых и точки их пересечения, мы можем использовать интегрирование, чтобы найти площадь под двумя кривыми.
Площадь между двумя кривыми ВведениеСогласно изображению у нас есть две функции, f(x) и g(x), и нам нужно найти площадь между этими двумя кривыми. Используя интегрирование, мы можем легко вычислить площадь заштрихованной области. Мы обсудим, как рассчитать эту площадь в следующем разделе.
Площадь между двумя кривыми Формула Нам нужно разделить площадь на множество тонких прямоугольных полос, параллельных оси y, начиная с x = a до x = b, чтобы найти приблизительную площадь между двумя кривыми путем интегрирования площадей этих тонких полос. Прямоугольные полоски будут иметь ширину «dx» и высоту f(x) – g(x).
Прямоугольные полоски будут иметь ширину «dx» и высоту f(x) – g(x).
В результате мы можем вычислить площадь треугольника, используя интегрирование в пределах a и b. Площадь между двумя кривыми равна dx(f(x) – g(x)). Формула для f(x) и g(x) непрерывна на [a, b], и мы имеем g(x) < f(x) для всех x в [a, b].
Формула площади между двумя кривымиОбщие соглашения по площади между двумя кривыми
- Верхняя функция на графике, т.е.е. тот, у которого больше значение y для данного x, называется f (x).
- Нижняя функция на графике, то есть функция с меньшим значением y для данного x, называется g(x).
- Две разные области на графике могут иметь разные верхние и нижние функции. В таких случаях важно рассчитывать площадь отдельно.
- Положительные знаки назначаются области над осью Y.
- Области под осью Y присваивается отрицательный знак.
Кривая, уравнение которой выражается через y, может быть рассчитана путем вычисления площади между двумя кривыми относительно оси y.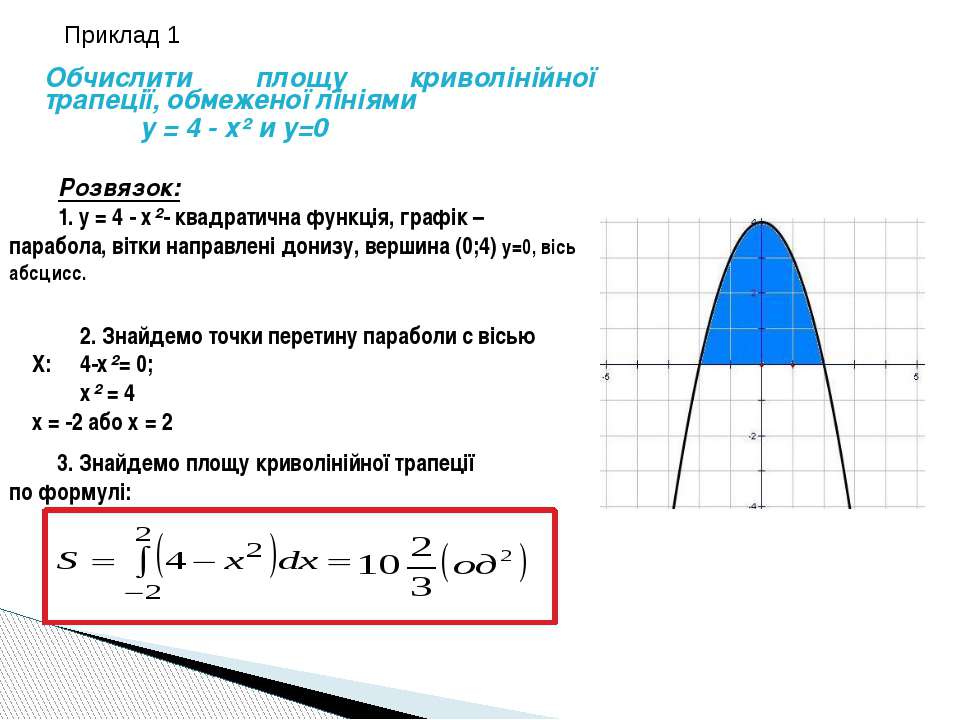 Вычислить площадь по оси Y проще, чем вычислить площадь по оси X.
Вычислить площадь по оси Y проще, чем вычислить площадь по оси X.
Применяя интегрирование, мы складываем площади горизонтальных полос, чтобы определить площадь сечения между двумя кривыми путем деления заданного прямоугольника на горизонтальные полосы между пределами.Предположим, что f(y) и g(y) непрерывны на [c, d] и g(y) < f(y) для всех y в [c, d], тогда
Площадь между двумя кривыми относительно YОбщие соглашения по площади между двумя кривыми относительно Y
- Предположим, что f(y) — правильная функция на графике, то есть та, которая имеет наибольшее значение x для данного y
- На графике левая функция — это функция с меньшим значением x для заданного y, известная как g(y).
- Если на графике есть разные области, будут применяться разные функции.Если на графике есть разные области, для каждой из них следует рассчитывать отдельные области.
- Прямо на оси x области присваивается положительный знак.

- Знак минус добавляется к области слева от оси x.
Приведенные выше формулы приведут к некорректному расчету площадей между двумя составными кривыми, пересекающимися друг с другом.
Площадь между двумя составными кривыми ДиаграммаМы рассчитали отдельные площади между кривыми между различными частями кривых в каждой части кривых, показанных на изображении.Если f(x) и g(x) непрерывны в интервалах [a,b], то площадь между кривыми будет:
Площадь между двумя составными кривыми Площадь между двумя полярными кривыми Кроме того, там, где встречаются две полярные кривые, мы можем вычислить их площадь с помощью интегрального исчисления. Когда у нас есть две кривые, координаты которых заданы не в прямоугольных, а в полярных координатах, мы используем этот метод. Чтобы решить эту проблему, мы всегда можем преобразовать полярные координаты в прямоугольные координаты, однако этот метод снижает сложность задачи.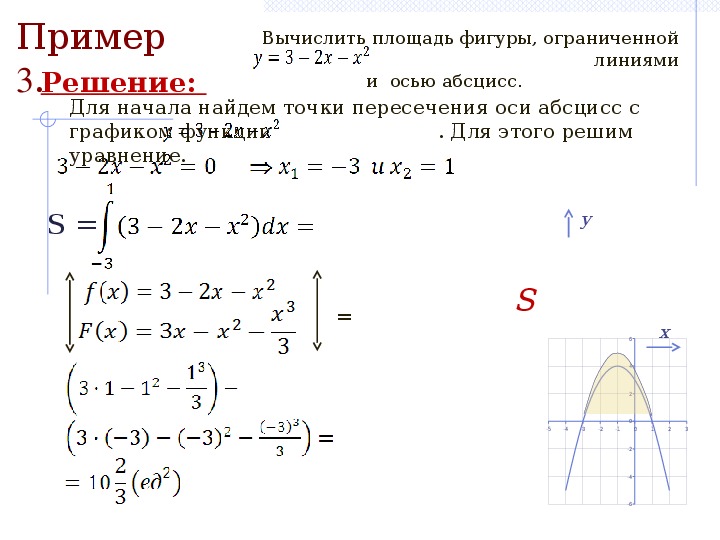
Допустим, у нас есть две полярные кривые r0 = f(θ) и ri = g(θ), как показано на рисунке, и мы хотим найти площадь, заключенную между этими двумя кривыми, такую, что α ≤ θ ≤ β, где [α, β] — ограниченная область. Следовательно, площадь между кривыми будет:
Площадь между двумя полярными кривыми Площадь между двумя кривыми Проблемы и решенияТеперь давайте решим несколько вопросов, чтобы узнать, как использовать общую формулу с необходимыми соглашениями!
Площадь между двумя кривыми, пример 1Площадь между двумя кривыми, пример 2 Часто задаваемые вопросы о площади между двумя кривымиЧто представляет площадь между двумя кривыми?
Затем вы сможете определить смещение между начальным и конечным положениями частиц, рассчитав площади между двумя графиками.
Всегда ли площадь между двумя кривыми положительна?
И, наконец, площадь между двумя кривыми всегда имеет положительное значение, в отличие от площади под кривой, которую мы изучали в предыдущей главе.
Какой первый шаг к нахождению площади между двумя кривыми?
Сначала вы возьмете интегралы обеих кривых. После того, как вы взяли интегралы обеих кривых, решите их обычным образом. Наконец, вы вычтете интеграл кривой выше на графике из интеграла кривой ниже на графике.
Как вы используете интеграцию для поиска областей?
Выполнив определенный интеграл между двумя точками, вы можете найти площадь под кривой между двумя точками. Используя предел между a и b, проинтегрируйте y = f(x) между a и b, чтобы найти площадь под кривой y = f(x). Отрицательные значения будут отображаться для областей ниже оси x и положительные значения для областей выше оси x.
Почему две кривые положительные?
При решении задач такого типа к каждой части подходят индивидуально, интегрируя (верхнюю функцию) и (нижнюю функцию), чтобы гарантировать положительный (неотрицательный) результат для каждой части.«Площадь между двумя графиками» по определению положительна независимо от того, где она находится на плоскости.
Как найти площадь между двумя кривыми в Excel?
- Введите «ЛИНЕЙН(yдиапазон, диапазон, ИСТИНА, ЛОЖЬ)» в пустую ячейку электронной таблицы Excel.
- Измените параметры команды ЛИНЕЙН, чтобы отразить расположение ваших данных для одного из графиков.
- Нажмите «Ввод», чтобы получить уравнение для первого набора данных.
Может ли площадь между двумя кривыми быть отрицательной?
Определенный интеграл может быть отрицательным.Когда вся площадь в пределах интервала находится ниже оси X, но все еще выше кривой, результат отрицательный.
Как найти площадь вертикального среза?
Площадь между двумя кривыми с использованием вертикальных срезов A = ∫ a b ( g ( x ) − f ( x ) ) dx.
Почтовая навигация
Расчет объемов с использованием тройных интегралов
Объем твердого тела \(U\) в декартовых координатах \(xyz\) равен
\[V = \iiint\limits_U {dxdydz} .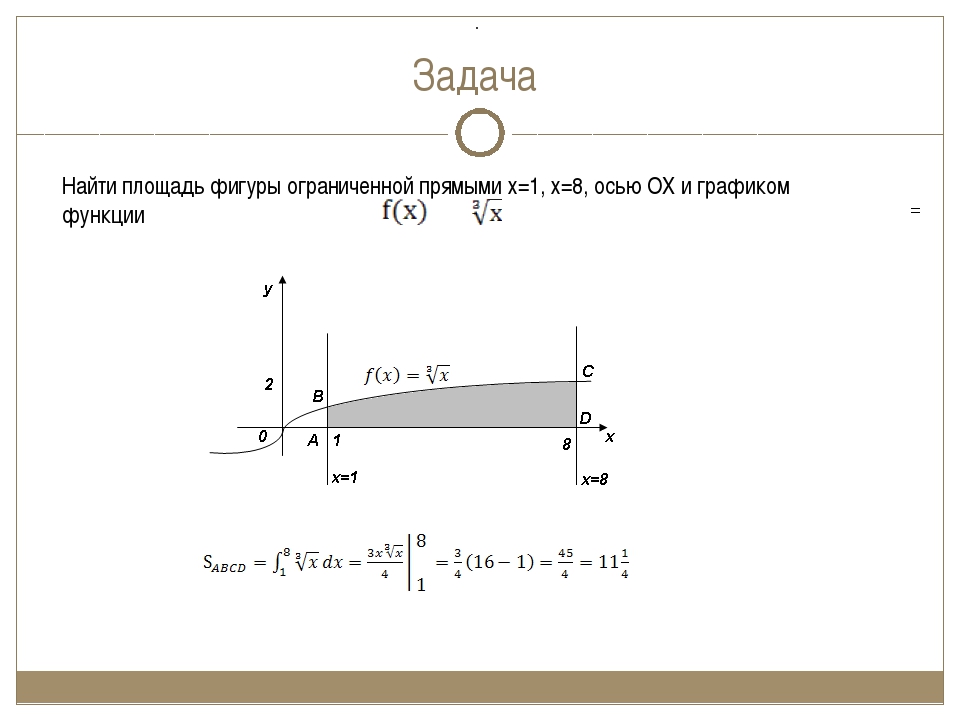 2}.\]
2}.\]
Пример 3
Найдите объем тетраэдра, ограниченного плоскостями, проходящими через точки \(A\left( {1,0,0} \right),\) \(B\left( {0,2,0} \right) ,\) \(C\left( {0,0,3} \right)\) и координатные плоскости \(Oxy,\) \(Oxz,\) \(Oyz\) \(\left({\text {Рисунок }2}\справа).\)
Пример 4
Найдите объем тетраэдра, ограниченного плоскостями
\[х + у + г = 5, х = 0, у = 0, г = 0\]
(рис. \(4\)).
Пример 1.3}}}{3}.\]
В результате получаем известное выражение для объема шара радиуса \(R.\)
Пример 3.
Найдите объем тетраэдра, ограниченного плоскостями, проходящими через точки \(A\left( {1,0,0} \right),\) \(B\left( {0,2,0} \right) ,\) \(C\left( {0,0,3} \right)\) и координатные плоскости \(Oxy,\) \(Oxz,\) \(Oyz\) \(\left({\text {Рисунок }2}\справа).\)
Раствор.
Уравнение прямой \(AB\) в плоскости \(xy\) (рис. \(3\)) записывается в виде \(y = 2 — 2x.\) Переменная \(x\) находится здесь в интервале \(0 \le x \le 1,\), а переменная \(y\) находится в интервале \(0 \le y \le 2 — 2x.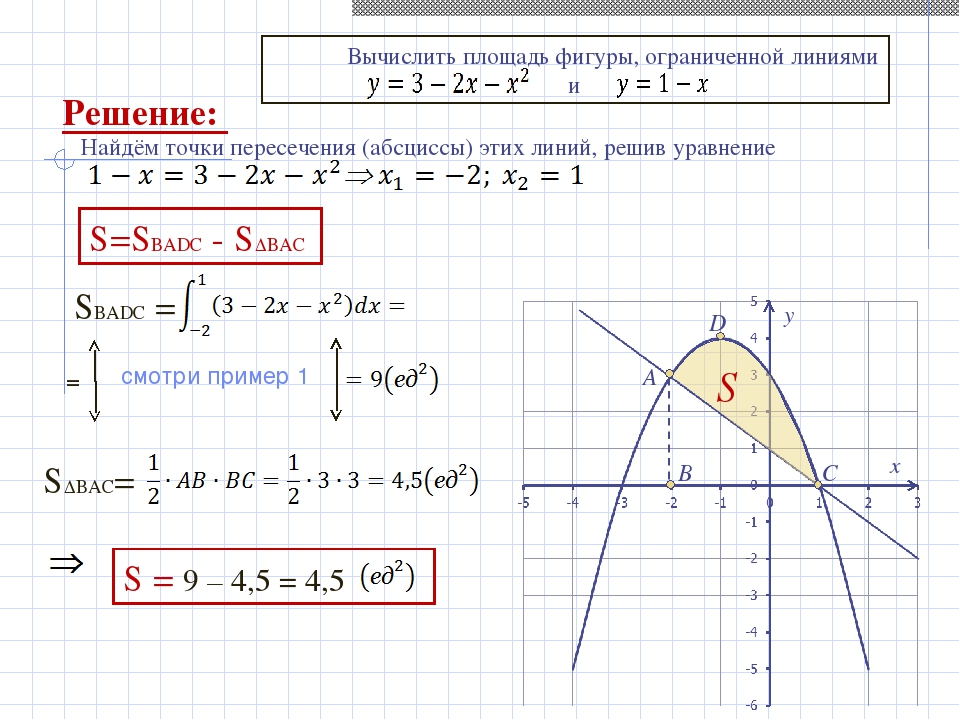 \)
\)
Запишем уравнение плоскости \(ABC\) в виде отрезка. Поскольку плоскость \(ABC\) пересекает отрезки \(1, 2,\) и \(3,\) соответственно, на \(x-,\) \(y-,\) и \(z- \)оси, то ее уравнение можно записать в виде
\[\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1.\]
В общем случае уравнение плоскости \(ABC\) записывается как
\[6x + 3y + 2z = 6\;\;\text{or}\;\; z = 3 — 3x — \frac{3}{2}y.3}}}{3}} \справа) = 1.\]
Пример 4.
Найдите объем тетраэдра, ограниченного плоскостями
\[х + у + г = 5, х = 0, у = 0, г = 0\]
(рис. \(4\)).
Раствор.
Уравнение плоскости \(x + y + z = 5\) можно переписать в виде
\[г = 5 — х — у.\]
Установив \(z = 0,\), мы получим
\[5 — х — у = 0\;\;\текст{или}\;\;у = 5 — х.\]
Следовательно, область интегрирования \(D\) в плоскости \(xy\) ограничена прямой линией \(y = 5 — x\), как показано на рисунке \(5.5} \справа]
= \frac{1}{2}\left( {125 — 5 \cdot 25 + \frac{{125}}{3}} \right)
= \frac{{125}}{6}. \]
\]
Дополнительные проблемы см. на стр. 2.
Узнайте все о коробке
Быстрый! Мне нужна помощь с: Выберите элемент справки по математике … Исчисление, Исчисление производных, Исчисление интеграции, Правило частного, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Расчет с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование длины, Преобразование массы, Преобразование мощности, Преобразование скорости, Преобразование температуры , Анализ объемных данных, Поиск среднего анализа данных, Поиск стандартного отклонения Анализ данных, Гистограммы Десятичные числа, Преобразование в дробь Электричество, Стоимость факторинга, Целые коэффициенты, Наибольшие общие коэффициенты, Наименьшие общие дроби, Добавление дробей, Сравнение дробей, Преобразование дробей, Преобразование в десятичные дроби, Разделение дробей, Умножение дробей, Сокращение дробей, ВычитаниеДроби, Что это такоеГеометрия, КоробкиГеометрия, КругиГеометрия, ЦилиндрыГеометрия, ПрямоугольникиГеометрия, Прямоугольные треугольникиГеометрия, СферыГеометрия, КвадратыГрафика, ЛинииГрафика, Любая функцияГрафика, КругиГрафика hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x,y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Уравнение из точки и наклонных линий, Уравнение из наклона и y-intLines, Уравнение из двух точек, Кредит, График платежей, Лотерея , Нахождение коэффициентовМатематика, Практика полиномовМатематика, Практика Основыметрической системы, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменнымиЧислами, Деление чисел, Умножение чисел, Сравнение чисел в ряду, Числовые числа в ряду, Размещение значений чисел, Произношение чисел, Округление чисел, Вычитание парабол, Вычисление полиномов, Вычитание полиномов, Сложение КвадратМногочлены, РазделениеМногочленов, Разложение на множители КвадратовМногочлены, Разложение на множители ТрехчленовМногочлены, Факторизация с помощью GCFМногочлены, УмножениеМногочленов, Возведение в степеньПрактика, Математические задачиПропорции, Что они собой представляютКвадратные уравнения, Квадратное F ormulaКвадратные уравнения, Решить с помощью разложения на множителиРадикалы, Другие корниРадикалы, Соотношения квадратных корней, Каковы ониВыход на пенсию, Сбережение для продажной цены, РасчетНаучная запись, ПреобразованиеНаучная запись, ДелениеНаучная запись, Умножение фигур, ПрямоугольникиУпрощение, Упрощение чего-либо, ЭкспонентыУпрощение, Как терминыУпрощение, ПродуктыВремя, Выражение тригонометрии , Прямоугольные треугольникиWindchill, Фигура
Как рассчитать длину окружности и площадь круга
Ключевые термины
o Обведите
o Равноудаленный
o Радиус
o Диаметр
o Окружность
o Пи ( π )
Цели
o Определите некоторые основные части круга, такие как радиус и диаметр
o Вычислить длину окружности
o Вычислить площадь круга
В этой статье мы рассмотрим геометрическую фигуру, которая не состоит из прямых отрезков, а имеет изогнутую форму: круг.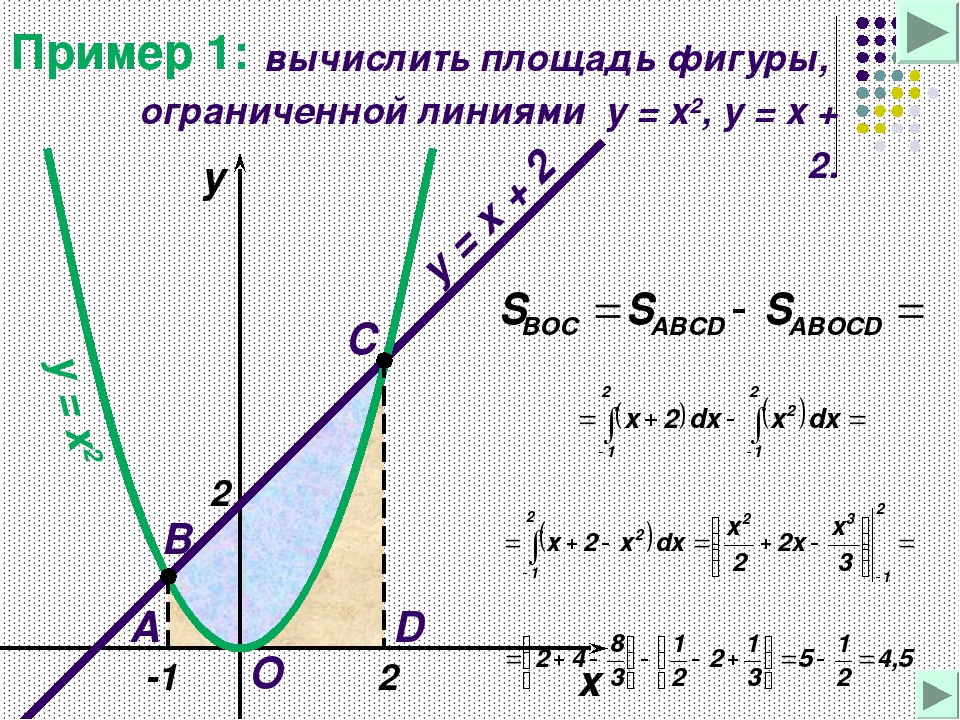 Мы применим то, что знаем об алгебре, к изучению окружностей и тем самым определим некоторые свойства этих фигур.
Мы применим то, что знаем об алгебре, к изучению окружностей и тем самым определим некоторые свойства этих фигур.
Знакомство с кругами
Представьте себе точку P , имеющую определенное местоположение; затем представьте себе все возможные точки, которые находятся на некотором фиксированном расстоянии r от точки P. Некоторые из этих точек показаны ниже. Если бы мы начертили все (бесконечное число) точек, находящихся на расстоянии r от P, , мы получили бы круг, который показан ниже сплошной линией.
Таким образом, окружность — это просто набор всех точек , равноудаленных (т. е. находящихся на одинаковом расстоянии) от центральной точки ( P в приведенном выше примере). Расстояние r от центра круга до самого круга называется радиусом ; удвоенный радиус (2 r ) называется диаметром . Радиус и диаметр показаны ниже.
Радиус и диаметр показаны ниже.
Окружность круга
Как и в случае с треугольниками и прямоугольниками, мы можем попытаться вывести формулы для площади и «периметра» круга.В отличие от треугольников, прямоугольников и других подобных фигур, расстояние вокруг внешней стороны круга называется окружностью , а не периметром — однако концепция, по сути, та же самая. Однако вычисление длины окружности не так просто, как вычисление периметра прямоугольника или треугольника. Учитывая, что объект в реальной жизни имеет форму круга, один из подходов может заключаться в том, чтобы обернуть нить ровно один раз вокруг объекта, а затем выпрямить нить и измерить ее длину.Такой процесс проиллюстрирован ниже.
Очевидно, что по мере увеличения диаметра (или радиуса) окружности окружность становится больше, а значит, и длина окружности тоже увеличивается.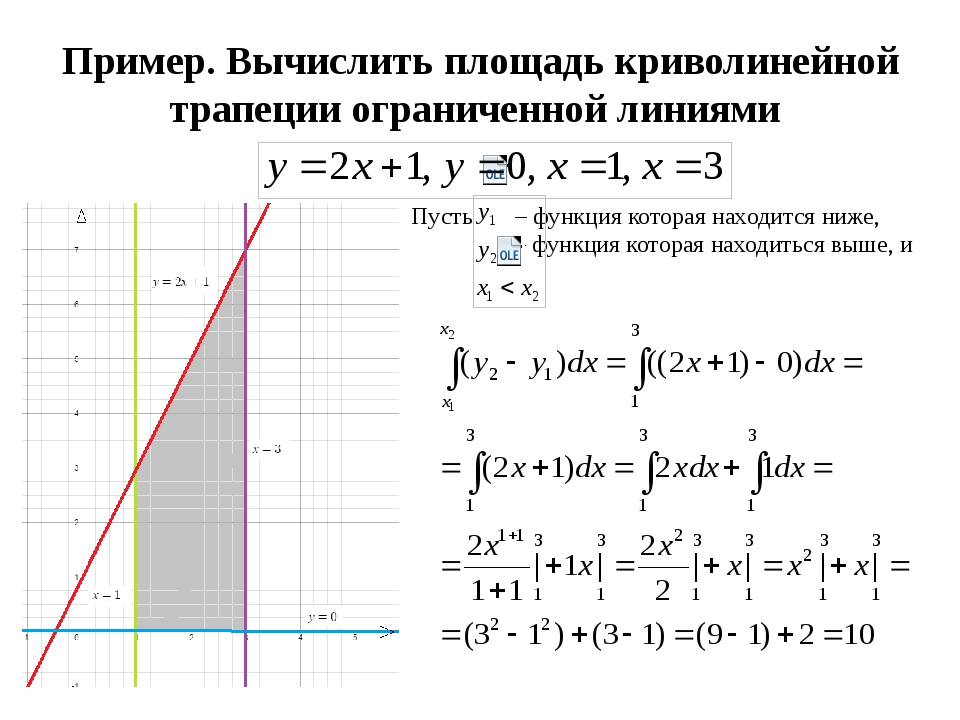 Мы приходим к мысли, что, таким образом, существует некоторая связь между окружностью и диаметром. Оказывается, если мы измерим длину окружности и диаметр любого круга, мы всегда обнаружим, что длина окружности чуть больше, чем в три раза превышает диаметр.Два примерных круга ниже иллюстрируют эту точку, где D — это диаметр, а C — длина окружности каждого круга.
Мы приходим к мысли, что, таким образом, существует некоторая связь между окружностью и диаметром. Оказывается, если мы измерим длину окружности и диаметр любого круга, мы всегда обнаружим, что длина окружности чуть больше, чем в три раза превышает диаметр.Два примерных круга ниже иллюстрируют эту точку, где D — это диаметр, а C — длина окружности каждого круга.
Опять же, в каждом случае длина окружности чуть более чем в три раза превышает диаметр окружности. Если мы разделим длину окружности любого круга на его диаметр, мы получим постоянное число. Эта константа, которую мы обозначаем греческим символом π ( пи ), приблизительно равна 3.141593. Точное значение π неизвестно, и есть подозрение, что пи — иррациональное число (неповторяющееся десятичное число, поэтому его нельзя выразить в виде дроби с целым числителем и целым знаменателем). Запишем упомянутое выше соотношение: частное длины окружности ( C ) разделить на диаметр ( D ) есть постоянное число π.
Мы можем получить выражение для длины окружности через диаметр, умножив обе части вышеприведенного выражения на D, , тем самым выделив C.
Поскольку диаметр в два раза больше радиуса (другими словами, D = 2 r ), мы можем заменить D на 2 r в приведенном выше выражении.
Таким образом, мы можем вычислить длину окружности, если знаем радиус окружности (или, следовательно, ее диаметр).Для большинства расчетов, требующих десятичного ответа, часто бывает достаточно оценки π как 3,14. Например, если круг имеет радиус 3 метра, то его окружность C будет следующей.
Приведенный выше ответ является точным (хотя он записан с помощью символа π ). Если нам нужен приблизительный числовой ответ, мы можем оценить π как 3.14. Тогда
Если нам нужен приблизительный числовой ответ, мы можем оценить π как 3.14. Тогда
Символ ≈ просто означает «приблизительно равно».
Практическая задача : Круг имеет радиус 15 дюймов. Какова его окружность?
Решение : Давайте начнем с рисования диаграммы ситуации. Этот подход может быть очень полезен, особенно в ситуациях, связанных с кругами, где радиус и диаметр можно легко спутать.
Поскольку нам дан радиус, мы должны либо вычислить длину окружности ( C ), используя выражение в терминах радиуса, либо мы должны преобразовать радиус в диаметр (удвоенный радиус) и использовать выражение в терминах диаметр. Для простоты мы будем использовать первый подход.
Этот результат является точным. Если нам нужен приблизительный десятичный результат, мы можем использовать π ≈ 3.14.
Если нам нужен приблизительный десятичный результат, мы можем использовать π ≈ 3.14.
Площадь круга
Как вычисление длины окружности сложнее, чем вычисление треугольника или прямоугольника, так и вычисление площади. Давайте попробуем получить оценку площади круга, нарисовав круг внутри квадрата, как показано ниже. Площадь круга заштрихована.
Нарисуем вертикальный диаметр и горизонтальный диаметр в круге; мы обозначим эти диаметры как имеющие длину D. Обратите внимание, что по сравнению с квадратом, квадрат также должен иметь длину сторон D .
Мы знаем, что квадрат (который является прямоугольником, длина и ширина которого равны) со стороной длины D имеет следующую площадь A квадрат (обратите внимание, что мы добавляем нижний индекс, чтобы определить эту площадь как площадь квадрат-мы добавим аналогичный индекс в случае площади круга):
Поскольку круг диаметром D , очевидно, имеет меньшую площадь, чем квадрат со сторонами D, , мы знаем, что площадь круга должна быть меньше D 2 . Посмотрев, мы можем догадаться, что площадь круга составляет примерно три четверти площади квадрата. Таким образом,
Посмотрев, мы можем догадаться, что площадь круга составляет примерно три четверти площади квадрата. Таким образом,
Как оказалось, это предположение близко к реальному результату. С помощью более сложной математики, выходящей за рамки учебника, можно показать, что площадь круга точно равна:
.
Обратите внимание, что снова появляется число π .Давайте теперь сравним этот точный результат с нашим предположением выше. Мы просто изменим выражение, имея в виду, что радиус ( r ) равен половине диаметра ( D ) — другими словами, D = 2 r.
С Д = 2 р, потом
Подставим это значение r в выражение для площади круга; мы должны сделать замену дважды. Тогда мы можем несколько упростить выражение.
Тогда мы можем несколько упростить выражение.
Так как π примерно равно 3,14, то
Таким образом, наша догадка была очень близка к реальной площади!
Практическая задача : Круг имеет диаметр 6 сантиметров.Какова его площадь?
Решение : Обратите внимание, что указан диаметр , а не радиус. Таким образом, если мы хотим использовать выражение для площади через радиус, мы должны преобразовать диаметр в радиус (просто разделив диаметр пополам).
Теперь мы можем вычислить площадь по следующей формуле.
Опять же, этот ответ 9 квадратных сантиметров является точным. Но,
Но,
Это приблизительный результат, но его будет достаточно во многих случаях.
Практическая задача : Окружность имеет длину 8 π футов.Какова его площадь?
Решение : Мы узнали, что длина окружности тесно связана с радиусом (и диаметром). Таким образом, используя это известное значение длины окружности, мы можем вычислить радиус и использовать его для нахождения площади. Во-первых, давайте решим выражение для длины окружности, чтобы получить радиус.
Хотим выделить р; мы можем использовать тот же подход, что и при решении линейных уравнений.
Теперь, когда мы знаем радиус круга, мы можем вычислить его площадь.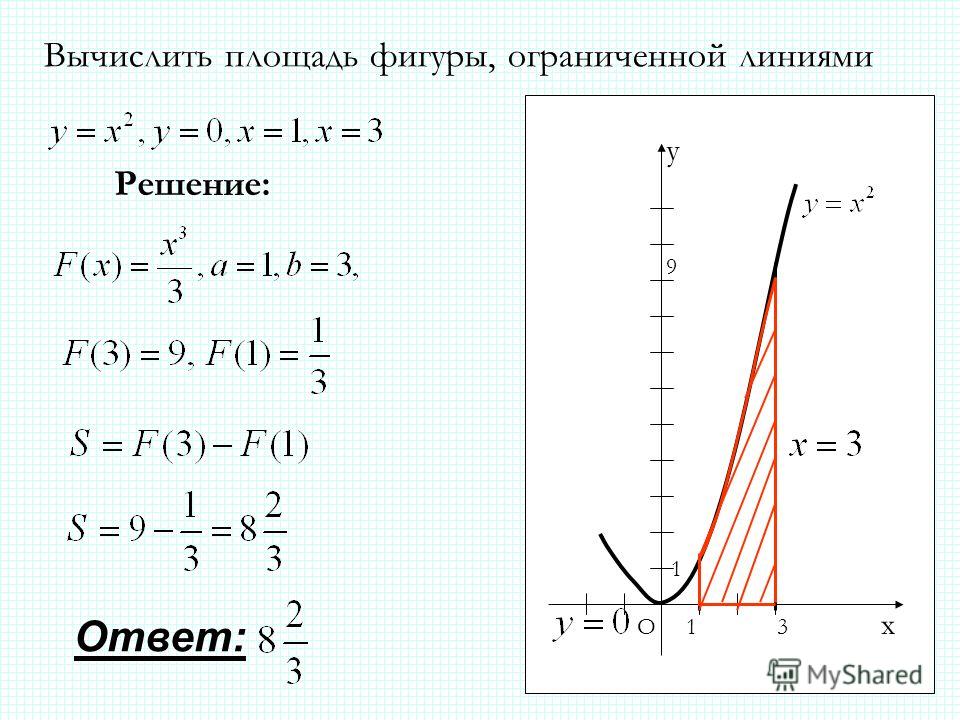
или
Размер ячейки, площадь поверхности и объем
Размер ячейки, площадь поверхности и объем Размер ячейки: масштабирование ПроблемыПочему клетки такие маленькие? Ответ на этот вопрос имеет столько же делать с математикой как с биологией.Представьте, что клетка имеет форму примерно куб.
По мере увеличения размера клетки отношение площади ее поверхности к объему изменения. Площадь поверхности и объем рассчитываются, как показано на рисунок ниже:
площадь стороны равна длина x ширина . Мы можем записать это как A=L*W , а когда стороны одинаковой длины, мы можем написать A=L 2
Поскольку у куба шесть сторон, давайте также рассчитаем площадь поверхности всей внешней части ячейки как 6 * L 2
объем куба равен длине x ширине x высоте , или V=L*W*H , и когда стороны имеют одинаковую длину, мы можем написать V=L 3
Вот где становится интересно.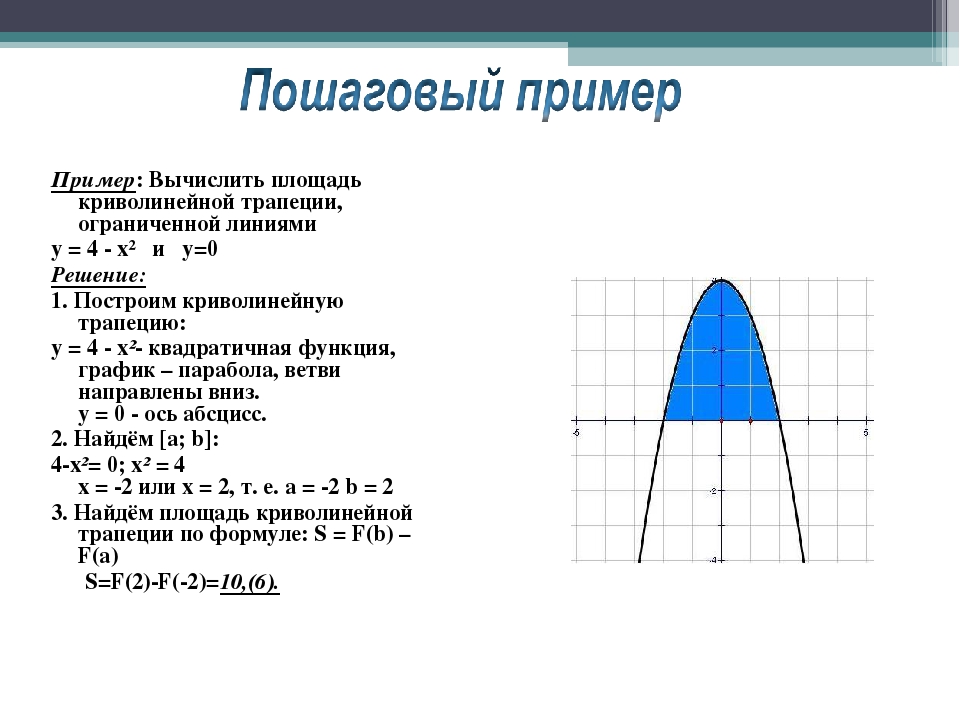 Поскольку мы продолжаем удваивать переменную L , от 1 до 2, от 4 до 8, площадь поверхности и объем не увеличиваются с одинаковой скоростью.
Поскольку мы продолжаем удваивать переменную L , от 1 до 2, от 4 до 8, площадь поверхности и объем не увеличиваются с одинаковой скоростью.
Вопросы :
1. Перечислите некоторые вещества, проникающие через клеточную мембрану:
я. ___________________ ii. ___________________ III. ___________________2. Почему важно, чтобы клетка имела большую площадь поверхности относительно его объема? (Другими словами, высокая площадь поверхности до соотношение объемов ?)
3.Представьте, что длина стороны ячейки может быть любого размера. Рассчитайте, что произойдет с отношением площади поверхности к объему, если клетка растет. Единицы здесь могут быть ничего, так как мы просто гипотезы.
| Размер ячейки | Длина стороны Л | Площадь поверхности 6л 2 | Том л 3 | Соотношение SA:V 6л 2 / л 3 |
| Маленькая ячейка | 0.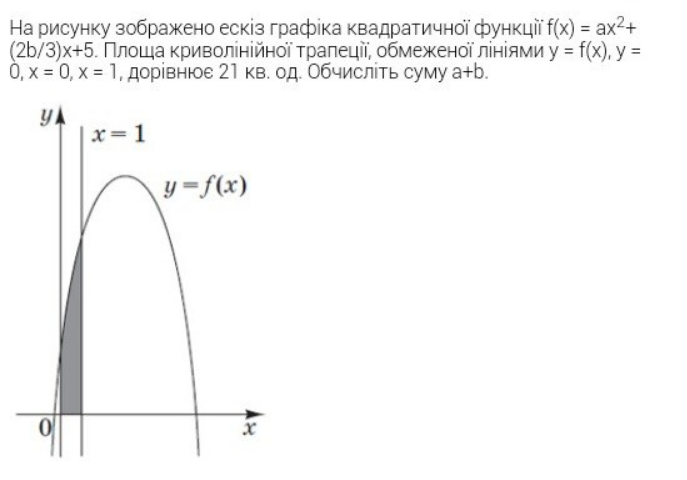 5 5 | 6 ( 0,5 ) 2 = 1,5 | ( 0,5 ) 3 = 0,125 | 1,5 ÷ 0,125 = 12 |
| 1 | 6 ( 1 ) 2 = 6 | ( 1 ) 3 = 1 | 6 ÷ 1 = 6 | |
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 10 | ||||
| 25 | ||||
| 50 | ||||
| Большая ячейка | 100 |
4.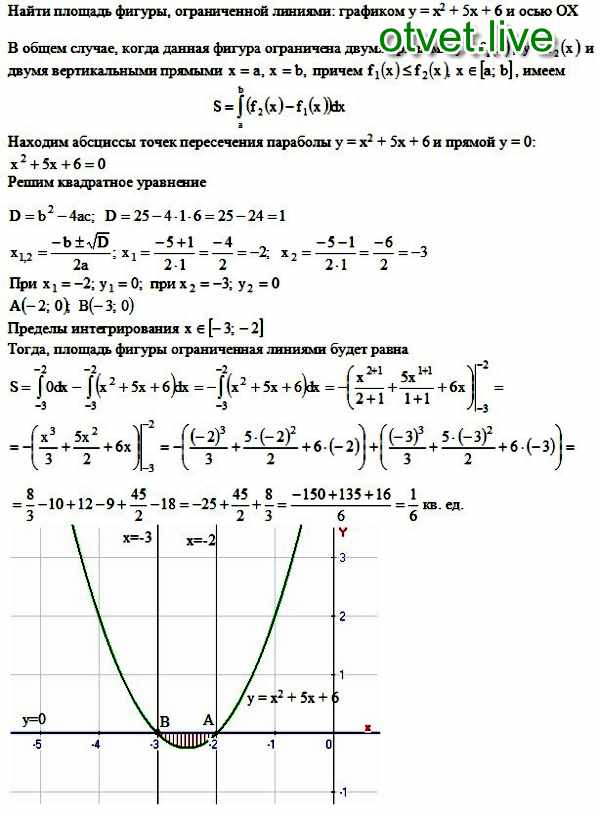 Создайте свой собственный график x-y с помощью Create-A-Graph или Excel, где x — площадь поверхности, а y — объем, и подставьте диапазон значений. Что происходит с отношением площади поверхности к объему при увеличении размера клетки? (Если бы площадь поверхности и объем увеличивались с одинаковой скоростью, линия была бы диагональной с наклоном 1.) Что на самом деле происходит при малых размерах? В промежуточных размерах? В больших размерах? Загрузите электронную таблицу Excel, в которой я сделал свои расчеты и создал эти графики: Surface_area_volume_graph.xlsx.
Создайте свой собственный график x-y с помощью Create-A-Graph или Excel, где x — площадь поверхности, а y — объем, и подставьте диапазон значений. Что происходит с отношением площади поверхности к объему при увеличении размера клетки? (Если бы площадь поверхности и объем увеличивались с одинаковой скоростью, линия была бы диагональной с наклоном 1.) Что на самом деле происходит при малых размерах? В промежуточных размерах? В больших размерах? Загрузите электронную таблицу Excel, в которой я сделал свои расчеты и создал эти графики: Surface_area_volume_graph.xlsx.
Рис. 2: Длина стороны клетки в зависимости от отношения площади поверхности к объему. По мере уменьшения размера ячейки до нуля отношение SA:V приближается к бесконечности.
5.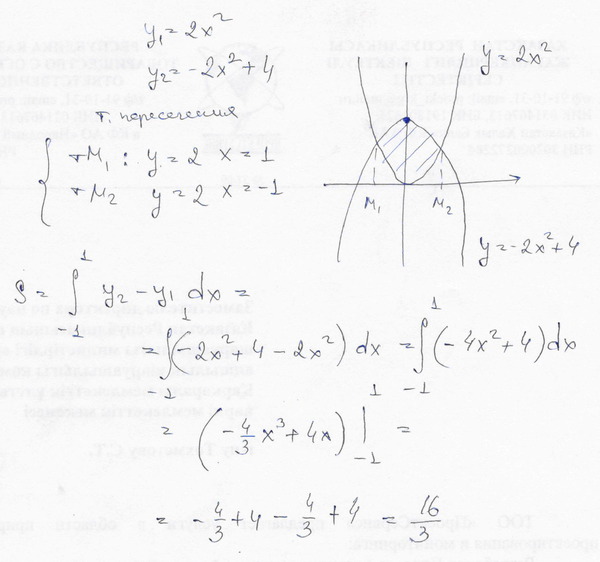 Поскольку транспорт материалов в клетку и из нее возможен только
происходит на поверхности клетки, что происходит, когда клетки становятся больше? Как это накладывает ограничение на размер ячейки?
Поскольку транспорт материалов в клетку и из нее возможен только
происходит на поверхности клетки, что происходит, когда клетки становятся больше? Как это накладывает ограничение на размер ячейки?
6.Таким образом масштабируются не только клетки. Целые животные тоже. Изучение размера тела в связи с анатомией, физиологией и поведением называется аллометрией. Для гомеотермных (животных, которые пытаются поддерживать постоянную температуру тела) необходимо производить тепло по мере его потери в окружающую среду, чтобы поддерживать равновесие. Если потеря тепла происходит только на открытых поверхностях, что бы вы предсказали относительно скорости метаболизма на единицу ткани тела крупного животного по сравнению с маленьким?
7.Возьмите то, что вы знаете об отношении площади поверхности к объему, и попробуйте
чтобы объяснить следующий график, который известен как «кривая мыши к слону». Предположим, что скорость метаболизма связана с теплотой
производство и что все эти животные пытаются сохранить свое
тела нагреваются в одинаковых условиях окружающей среды. Обратите внимание, например
что слон имеет массу (и объем) более чем в 1000 раз больше
мыши, в то время как скорость ее метаболизма (и теплопродукция) всего лишь
примерно в 100 раз больше, чем у мыши.Другими словами, «Почему слон может больше нагреваться?
эффективно (на единицу массы), чем мышь?»
Обратите внимание, например
что слон имеет массу (и объем) более чем в 1000 раз больше
мыши, в то время как скорость ее метаболизма (и теплопродукция) всего лишь
примерно в 100 раз больше, чем у мыши.Другими словами, «Почему слон может больше нагреваться?
эффективно (на единицу массы), чем мышь?»
Кривая Броуди (1945) от мыши к слону
8. «Правило Аллена» предсказывает, что эндотермические животные (те, которые регулируют температуру своего тела внутренне) с одинаковым объемом тела должны иметь различную площадь поверхности, предназначенную либо для помощи, либо для препятствия рассеиванию тепла, в зависимости от температуры их окружения. Объясните со ссылкой на площадь поверхности и объем.(Подумайте о необходимости сохранения тепла в холодном климате или о теплоотдаче в жарком климате и сделайте прогноз о типах телосложения.)
9. «Правило Бергмана» гласит, что среди видов животных, имеющих
глобальное распространение, размер взрослого тела, как правило, самый большой в
полярные районы, средние в умеренном климате и наименьшие в тропическом
те. Хотя есть исключения, в целом это так. Почему
должно быть так?
Хотя есть исключения, в целом это так. Почему
должно быть так?
10. Контрольный вопрос: В одном из моих любимых старых фильмов о монстрах Их , гигантские муравьи атакуют город.К сожалению, могло никогда не случится. Невероятная сила муравья зависит от его небольшой размер. Увеличьте его даже до человеческого размера, и он рухнет под собственным весом на этих тощих ножках. Объем (и поэтому вес) масштабируется до степени 3, а площадь поверхности (и размер) масштабируйте до степени 2. Создайте график, показывающий, почему гигантский муравей не может разрушить город, а вместо этого рухнет под собственным весом.
11. Контрольный вопрос: Как показано эмпирически на графике Броуди, мощность пропорциональна массе в степени 0.734, примерно 3/4, однако отношение площади поверхности к объему предсказывает значение только 2/3 или 0,67. Животные в реальном мире работают лучше, чем ожидалось, но животные в реальном мире не полностью полагаются на площадь поверхности для обогрева, охлаждения, газообмена и т.



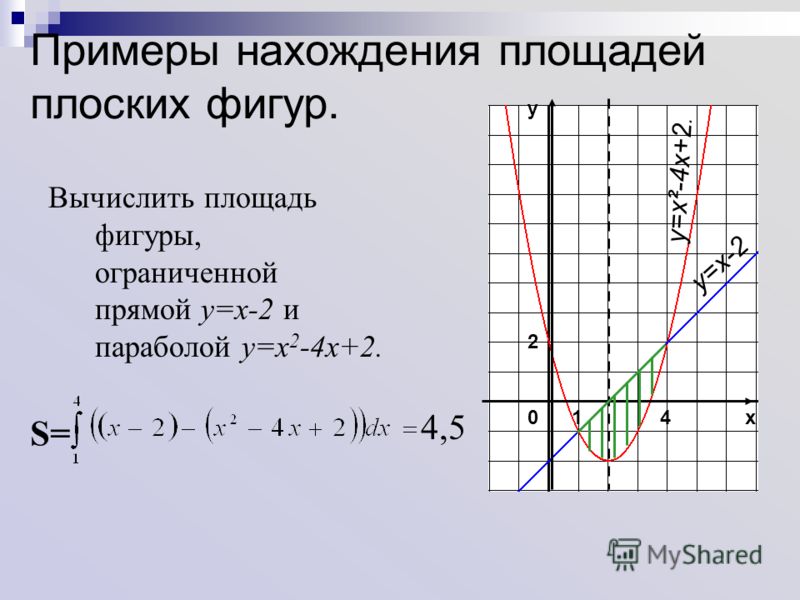 Биография C.C.Catch Юность и молодость будущей певицы
Биография C.C.Catch Юность и молодость будущей певицы

