Вычислить площадь фигуры ограниченной линиями

Для того, чтобы вычислить площадь фигуры, которая ограничена указанными линиями, полезно сначала начертить графики заданных функций и определить какими функциями она ограничена сверху, снизу и на каком отрезке по оси Ох. Затем уже используют формулу нахождения площади фигуры:

   

Удобнее этот вопрос изучать на примерах.

Пример.
Найдем площадь фигуры, которая ограничена линиями , , , .

Решение.
Из условия видно, что площадь фигуры нужно найти на промежутке (на это указывают функции и ).

При построении графика функций определим, что сверху фигура будет ограничена функцией , а снизу — функцией .

Подставим полученные данные в формулу:

   

   

   

   

Ответ.  кв. ед.

Встречаются случаи, когда отрезок, на котором нужно вычислить площадь фигуры, явно не задан. В таком случае сначала находят этот отрезок, а затем вычисляют определенный интеграл.

Пример.
Вычислить площадь фигуры, которая ограничена линиями и .

Решение.
Найдем точки пересечения данных функций. Для этого составим уравнение:

   

   

   

   

Запишем определенный интеграл для нахождения площади заданной фигуры:

   

   

 

   

Ответ.  кв. ед.

ru.solverbook.com

как найти площадь фигуры ограниченной линиями заданными параметрически — 11 Августа 2013 — Примеры решений задач

Если кривая задана параметрическими уравнениями

 

то площадь криволинейной трапеции, ограниченной этой кривой, прямыми  x=a, x=b и отрезком [a,b]оси Ox, выражается формулой

 

 

Пример. Найти площадь фигуры ограниченной одной аркой циклоиды
x=3(t-sint), y=3(1-cost), 0≤t≤2π и осью Ox.

Решение.

Шаг 1. Выполним построение графика функции заданной параметрически с помощью калькулятора

Вводим функцию и границы параметра, как указано в примере, нажимаем «Ok», получаем построение графика.

Шаг 2. Находим производную x'(t)

x'(t)=(3(t-sint))’=3(1-cost)

Выполнить дифференцирование  можно с помощью калькулятора

Шаг 3. По формуле

  , подставляем значения, имеем

Ответ:  S=27π

Проверить вычисление площади фигуры ограниченной параметрически заданной кривой можно с помощью калькулятора

Замечание: в калькулятор вводим не саму функцию x(t) , а ее производную!

www.reshim.su

Площа фігури обмеженої кривими в прямокутних координатах

Площа фігури між двома кривими в прямокутних координатах визначається інтегралом
від різниці кривих, де одна з них завжди приймає не менші значення ніж інша , а також криві неперервні. Межі інтегрування — прямі x₁=a, x₂=b — обмежують фігуру, (a<b найчастіше це точки перетину заданих кривих).
Даний цикл задач в першу чергу підійде студентам мех-мату Львівського національного університету імені Івана Франка для проходження практикуму з математичного аналізу. Студенти інших ВУЗів можуть набиратися практики на таких інтегралах, та вивчати методику обчислення.
Наведені пояснення навчать Вас обчислювати типові завдання з наступних тем:

Перший номер в прикладах відповідає номеру основного завдання зі збірника М. В. Заболоцький, Фединяк С.І., Філевич П.В. «Практикум з математичного аналізу» (поруч стоїть номер зі збірника Б. П. Демидовича).
Для запам’ятовування основних моментів схема інтегрування та знаходження площ з прикладу в приклад буде повторюватися. По можливості самі розв’язки будуть проілюстровані підінтегральними кривими.

 

Приклад 2.81 ( 2397). Знайти площу фігури, обмеженої кривими, заданими в прямокутних координатах ax=y², ay=x²,(a>0).

Обчислення: Запишемо графіки функцій, що обмежують шукану площу фігури: На графіку вони матимуть наступний вигляд

Площу між кривими і потрібно знайти. Як правило, Вам рідко буде відомо сам графік, тому в завданнях де не задано області на якій знаходити площу в першу чергу необхідно знайти точки перетину кривих.
Знайдемо межі інтегрування, тобто точки абсцис перетину заданих функцій y₁(x)=y₂(x):

Як бачите такою умовою є умова рівності функцій.
З останнього рівняння отримаємо дві точки x₁=0, x₂=a. Далі, коли Ви не бачите графіка функцій необхідно встановити котра з кривих приймає більші значення. Це потрібно лише для того, щоб з першого разу отримати позитивне значення площі фігури. Оскільки площа завжди додатна, а інтеграл може приймати довільні значення, то без перевірки наступної умови для знаходження площі інтеграл потрібно брати за модулем.
Вибираємо довільну точку з відрізку інтегрування [0;a] і переконуємося у правильності нерівності , тобто перевіряємо котра з кривих приймає вищі значення . Як відзначалося ви

yukhym.com

Обчислення площ і об’ємів за допомогою визначеного інтеграла

Площа криволінійної трапеції

Площа криволінійної трапеції, обмеженої графіком неперервної додатної на відрізку функції віссю і прямими і дорівнює

 

Приклад.Обчислити площу фігури, обмеженої лініями

Зображуючи ці лінії, одержуємо криволінійну трапецію

 

 

Площа фігури обмеженої графіками двох функцій і прямими і

Якщо на заданому відрізку неперервні функції і

мають ту властивість, що для всіх то

 

 

Приклад.Обчислити площу фігури, обмеженої лініями

Зобразимо задані лінії і абсциси їх точок перетину.

Абсциси точок перетину:

Тоді за формулою

 

 

Обєми тіл

У загальному випадку

Якщо тіло вміщено між двома перпендикулярними до осі площинами, що проходять через точки і то

де — площа перерізу тіла площиною, що проходить через точку

і перпендикулярна до осі

 

 

Для тіла обертання

Якщо тіло одержано в результаті обертання навколо осі криволінійної трапеції, яка обмежена графіком неперервної і невідємної функції на відрізку і прямими

і то

 

 

cubens.com

Площа плоскої фігури. Застосування інтеграла до обчислення площі плоскої фігури.

Автор: admin | Дата: 22.02.2015 | Переглядів : 13,881 | Коментарів немає 

За геометричним тлумаченням визначного інтегралу, площа криволінійної трапеції

, яка обмежена кривою , лініями і , та віссю , обчислюється за формулою .

Криволінійна трапеція

Якщо плоска фігура обмежена лініями і , то для обчислення площі такої фігури, на першому кроці, необхідно знайти точки перетину кривих і . Ці точки є границями інтегрування.

Плоска фігура

Після цього, шукана площа плоскої фігури може бути знайдена як різниця між площами криволінійних трапецій, обмежених лініями і , тобто:

Знаходження площі плоскої фігури — приклад:

Обчислити площу фігури, обмежену лініями та . Для цього, в першу чергу, скориставшись графічним методу, визначемо межі інтегрування. Нагадаємо, що графічний метод зводиться до побудови графіків обох функцій та візуального визначення точок, де вони перетинаються.

Визначення точок перетину кривих

Отже, згідно побудованого графіка межі інтегрування

рівні і . Далі, використовуючи будь-який з відомих чисельних методів обчислення визначених інтегралів, наприклад методом прямокутників, знаходимо площі криволінійних трапецій. Для цього, проміжок інтегрування розбиваємо на рівних частин, після чого, на кожному відрізку задані функції замінюють на пряму лінію, паралельну до осі абсцис, і таким чином, значення визначених інтегралів замінюють на суму площ прямокутників, кожна з яких, може бути обчислена за флормулою .

Процес обчислення визначених інтегралів від функцій  та  на проміжку , міститься в наступній таблиці:

Обчислювальний процес методу прямокутників

Далі, скориставшись формулою (2) знаходимо наближене значення площі плоскої фігури: .

Блок-схема алгоритму обчислення площі плоскої фігури:

www.mathros.net.ua

Площа фігури в полярних координатах

Площа S криволінійного сектора, обмеженого неперервною кривою r=r(f) і двома променями f=f₁ і f=f₂, де f₁< f₂ дорівнює половині визначеного інтегралу від квадрату радіуса кривої, проінтегрованого в межах зміни кута
Задачі взяті із програми практикуму для студентів мех-мату Львівського національного університету імені Івана Франка. Студенти всіх ВУЗ-ів України можуть набиратися практики на таких інтегралах, та вивчати методику обчислення площі фігури у полярній системі координат.
Наведені пояснення навчать Вас обчислювати типові завдання з наступних тем:

Перший номер в прикладах відповідає номеру основного завдання зі збірника М. В. Заболоцький, Фединяк С.І., Філевич П.В. «Практикум з математичного аналізу» (поруч стоїть номер зі збірника Б. П. Демидовича).
Для запам’ятовування основних моментів схема інтегрування та знаходження площ з прикладу в приклад буде повторюватися. По можливості самі розв’язки будуть проілюстровані графіками досліджуваних кривих.

Знайти площі фігур, обмежених кривими, заданими в полярних координатах

Приклад 2.106 (2418) Обчислити площу фігури, обмеженої кривими r²=a²*cos(2f) (лемніската Бернуллі).
Обчислення: Лемніската Бернуллі – геометричне місце точок, добуток відстаней від яких до двох фіксованих точок (фокусів) залишається постійним і дорівнює квадрату половини відстані між фокусами.
Запишемо підінтегральну функцію: r²=a²*cos(2f) (відома за умовою).
Знайдемо межі інтегрування: Задана крива замкнена, симетрична відносно прямих r*cos(f)=0 і r*sin(f)=0.
Наведемо графік лемніскати Бернуллі

Оскільки задана функція осями координат ділиться на чотири рівні частини і досягає своїх критичних значень при f₁=0 (r=a) і f₂=p/4 (r=0) , то площу фігури обчислимо для однієї частини лемніскати, а результат помножимо на 4.
Знайдемо площу фігури інтегруванням по куту

Площа вимірюється в одиницях квадратних, проте в цьому та наступних прикладах розмірності наводити не будемо, хоча про них пам’ятаємо.

Приклад 2.107 (2419) Знайти площу фігури, обмеженої кривими r=a*(1+cos(f)) – кардіоїда.
Обчислення: Кардіоїда – плоска лінія, яка описується фіксованою точкою кола, що котиться по нерухомому колі з таким же радіусом a.
Записуємо підінтегральну функцію: r²=a²*(1+cos(f))².
Знаходимо межі інтегрування: Задана крива замкнена, симетрична відносно прямої r*sin(f)=0.
Оскільки задана функція осями координат ділиться на дві рівні частини і досягає своїх критичних значень при f₁=0 (r=2a) і f₂=p (r=0) , то площу фігури обчислимо для половини кардіоїди, а результат помножимо на 2. Графік кардіоїди має вигляд

Обчислимо площу фігури, що обмежена заданою кривою:

Приклад 2.108 (2420) Знайти площу фігури, обмеженої кривою r=a*sin(f) -трилисник.
Обчислення: Підносимо до квадрату, щоб отримати підінтегральну функцію: r²=a²*sin²(f).
Графік трилисника в полярній системі координат

Встановимо межі інтегрування: Оскільки заданий графік функції ділиться на шість рівних частин (півпелюсток) і досягає своїх критичних значень при f₁=0 (r=0) і f₂=p/6 (r=a/2), то площу фігури обчислимо для однієї частини фігури, а результат помножимо на 6.
Знаходимо площу фігури інтегруванням по куту

Отримали просту для обчислень формулу площі трилисника S=Pi*a²/4.

Приклад 2.109 ( 2421) Обчислити п

yukhym.com

3.2.5. Геометричні застосування визначеного інтеграла

Основними геометричними застосуваннями визначеного інтеграла є: обчислення площі плоскої фігури, обчислення об’ємів тіл обертання навколо осей координат і обчислення довжини дуги плоскої кривої.

Обчислення площ плоских фігур у декартових координатах

Площа плоскої фігури, обмеженої неперервною на відрізку кривою , віссю , а також вертикальними прямими і (площа криволінійної трапеції – Рис. 12), визначається за формулою:

.

Якщо графік функції розташовано нижче осі (Рис. 13), то площа фігури визначається за формулою:

.

Площа фігури, обмеженої кривими і , прямими і, за умови, що (Рис. 14), визначається за формулою:

.

Зауваження: Якщо плоска фігура має складну форму, то прямими, паралельними осі , її варто розбити на частині таким чином, щоб можна було застосовувати вже відомі формули.

Приклад 43.

Обчислити площу фігур, обмежених лініями:

а) ; б).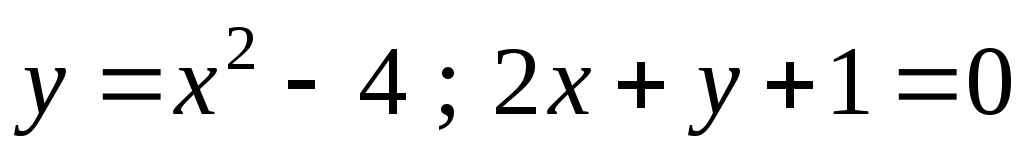

Розв’язок.

а)

Фігура обмежена віссю 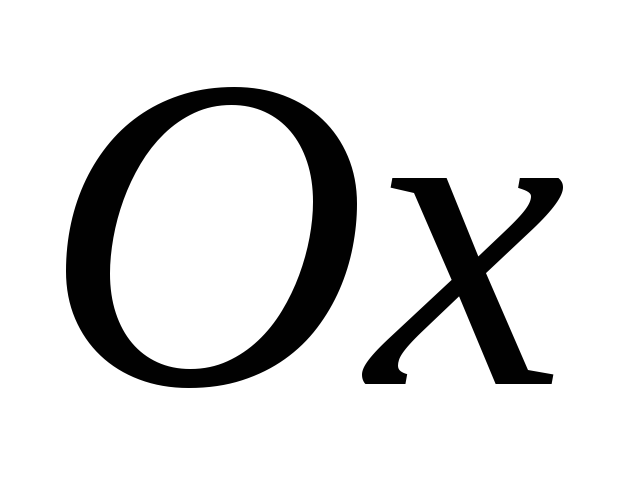() і параболою на відрізку .

Побудуємо параболу. Знайдемо точки перетину параболи з віссю . Для цього дорівняємо :

; ;;.

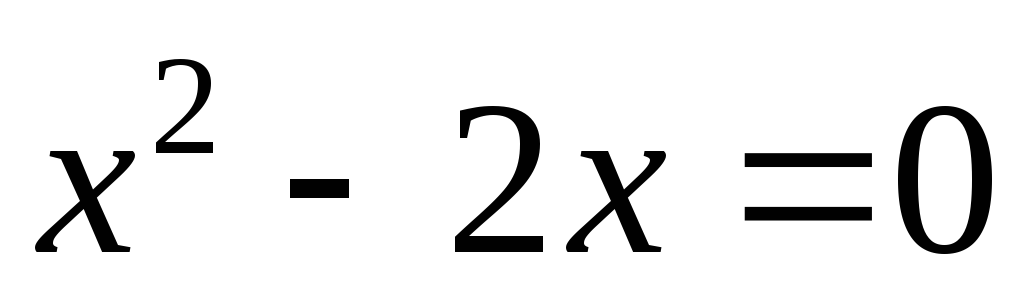Знайдемо координати вершини параболи:

,

.

Парабола має вершину в точці з координатами 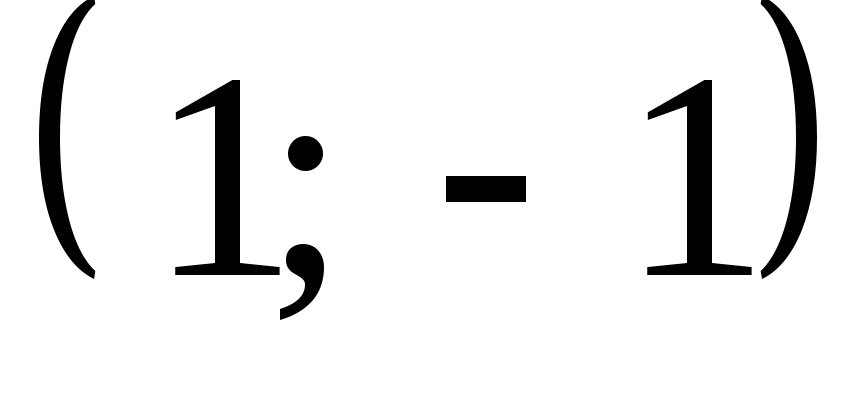і гілки її спрямовано вгору.

Фігура, обмежена заданими лініями зображена на рис. 15.

Площа шуканої фігури дорівнює сумі площ двох криволінійних трапецій:

.

Знайдемо площу:

(од.²)

(од.²)

Тоді площа заданої плоскої фігури дорівнює:

(од.²).

б)

Фігура обмежена параболою і прямою .

Побудуємо дані параболу і пряму (рис. 16).

Знайдемо межі інтегрування, тобто точки перетину прямої і параболи. Для цього розв’яжемо систему, складену з рівнянь цих ліній:

; ;

;

;

;

.

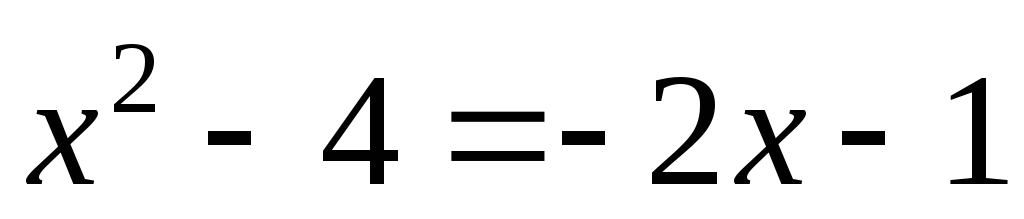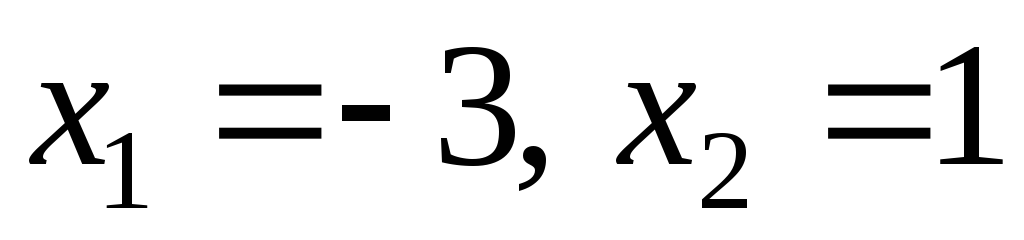Отже, парабола і пряма перетинаються в точках з абсцисами 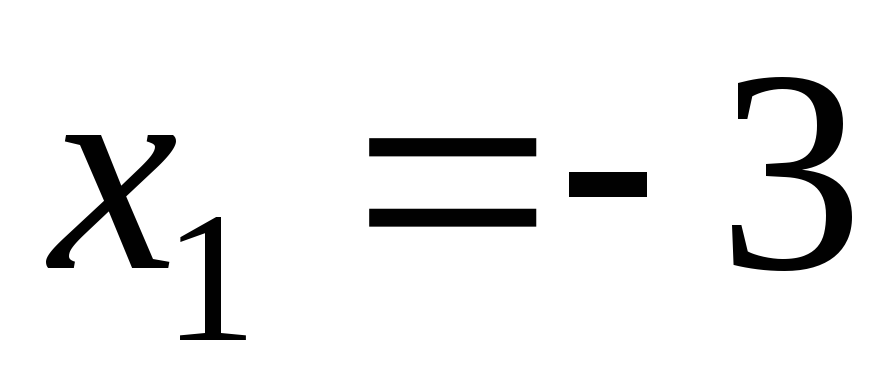і.

Площу фігури визначаємо за формулою:

,

де лінією є пряма(обмежує фігуру зверху), алінією є парабола (обмежує фігуру знизу).

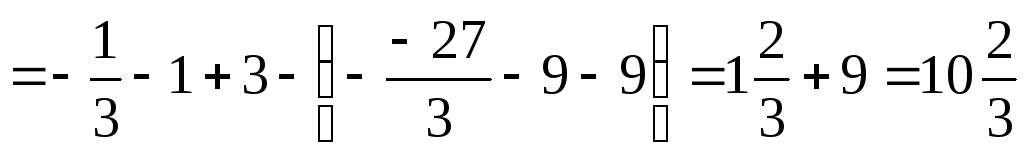(од.²).

Обчислення об’єму тіла обертання

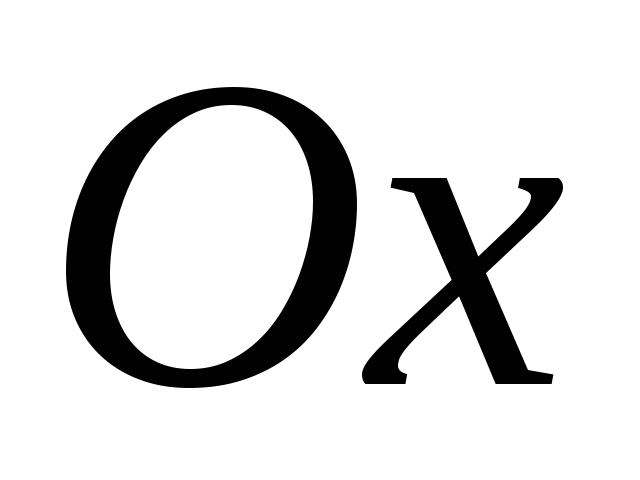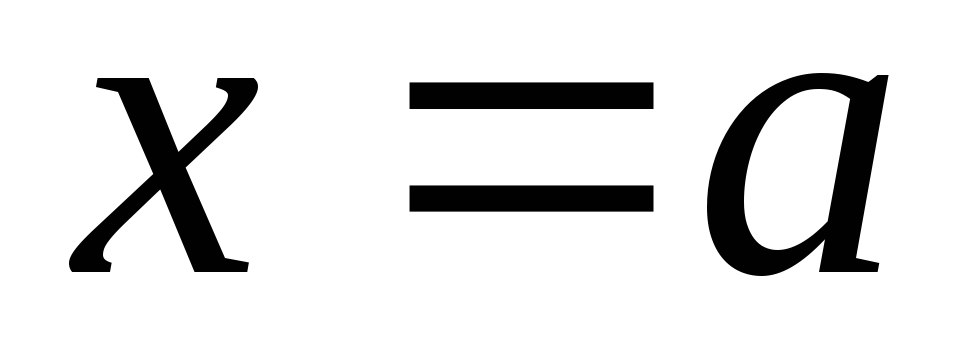Тілом обертання навколо осі Ох називається фігура, отримана від обертання навколо осі криволінійної трапеції, обмеженої графіком неперервної на відрізку кривої і прямими , і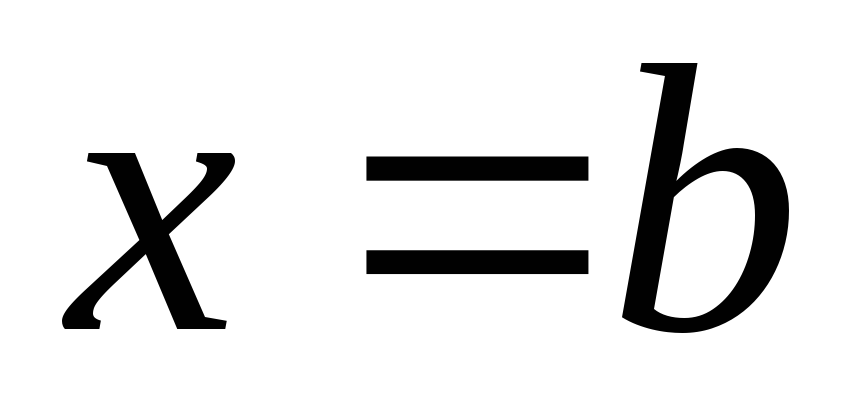 (Рис.17).

Об’єм тіла обертання навколо осі визначається за формулою:

.

Тілом обертання навколо осі 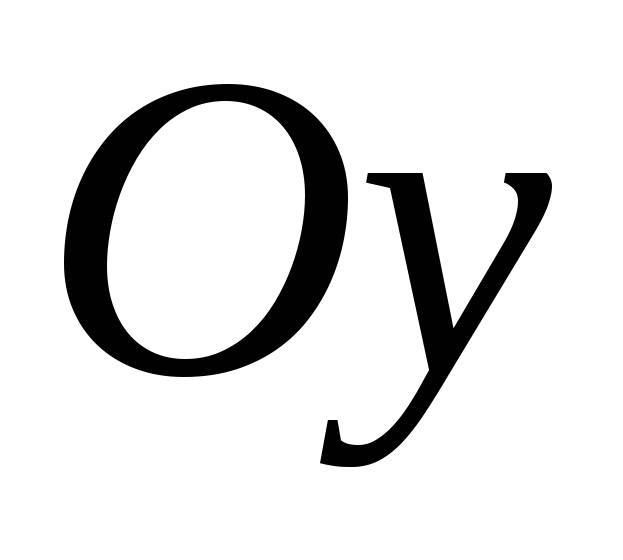називається фігура, отримана від обертання навколо осі криволінійної трапеції, обмеженої графіком неперервної на відрізку кривої 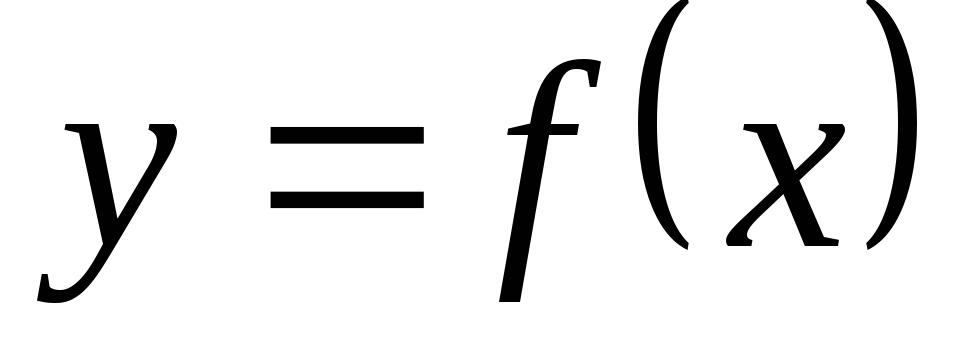і прямими , і (рис.18).

Об’єм тіла обертання навколо осі визначається за формулою:

.

Приклад 44.

Обчислити об’єм тіла обертання.

а) Обчислити об’єм тіла утвореного обертанням навколо осі фігури, обмеженої лініями .

Розв’язок.

Побудуємо плоску фігуру, обмежену параболою (гілки спрямовані вправо)і вертикальними прямими , а також тіло, утворене обертанням навколо осі цієї плоскої фігури (рис. 19).

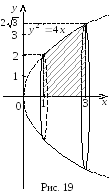
Визначимо об’єм тіла обертання, підставивши функцію у формулу для знаходження об’єму тіла обертання навколо осі :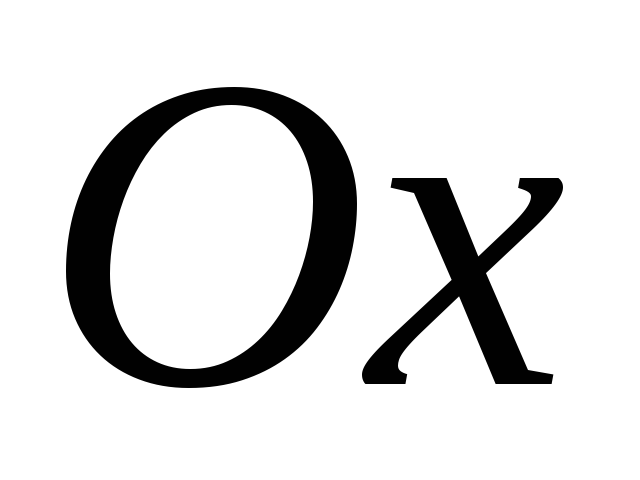

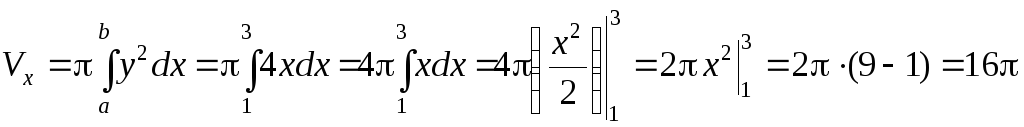(од.³⁾.

б) Обчислити об’єм тіла, утвореного обертанням навколо осі фігури, обмеженої лініями .

Рішення.

Побудуємо плоску фігуру, обмежену гіперболою і горизонтальними прямими , а також тіло, утворене обертанням навколо осі 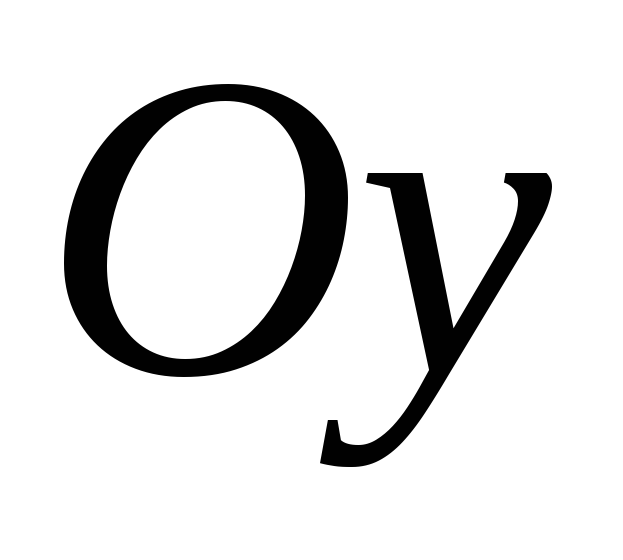цієї плоскої фігури (рис. 20).

Визначимо об’єм тіла обертання, підставивши функцію у формулу для знаходження об’єму тіла обертання навколо осі :

(од.³⁾.

studfile.net