параллельный перенос (сдвиг), отображение, растяжение, сжатие, отражение. Курсы по математике
Тестирование онлайн
Преобразование графиков
Параллельный перенос
График функции y=f(x)+B получается параллельным переносом графика функции y=f(x) в положительном направлении вдоль оси Оу на расстояние В, если В>0 и в отрицательном направлении вдоль оси Оу, если B.
График функции y=f(x+b) получается параллельным переносом графика функции y=f(x) в положительном направлении вдоль оси Оx на расстояние b, если b и в отрицательном направлении вдоль оси Оx, если b>0.
Отображение
График функции y=-f(x) получается симметричным отображением графика y=f(x) относительно оси Ох.
График функции y=f(-x) получается симметричным отображением графика y=f(x) относительно оси Оу.
Деформация (растяжение и сжатие) графика
График функции y=Af(x), получается растяжением графика y=f(x) вдоль оси Оу от оси Ох в A раз при A>1 или сжатием вдоль оси Оу к оси Ох в раз при

График функции y=f(ax), получается сжатием графика y=f(x) вдоль оси Ох к оси Оу в а раз при а>1 или растяжением вдоль оси Ох к оси Оу в раз при а.
Отражение
График функции получается из графика функции y=f(x) следующим образом: часть графика функции y=f(x), лежащая над осью Ох и на оси, остается без изменений, а часть графика, лежащая под осью Ох, отражается симметрично относительно оси Ох на верхнюю полуплоскость.
График функции получается из графика функции y=f(x) следующим образом: часть графика функции y=f(x), соответствующая неотрицательным значениям аргумента , остается без изменений, а отрицательным значениям аргумента будет соответствовать график, полученный путем симметричного относительно оси Оy отображения части графика, оставленной без изменений.
Примеры
Урок на тему «Построение графиков функций путем преобразования»
Презентация на тему: Построение графиков функций путем преобразования
Цели урока:
Повторить способы преобразования графиков функций.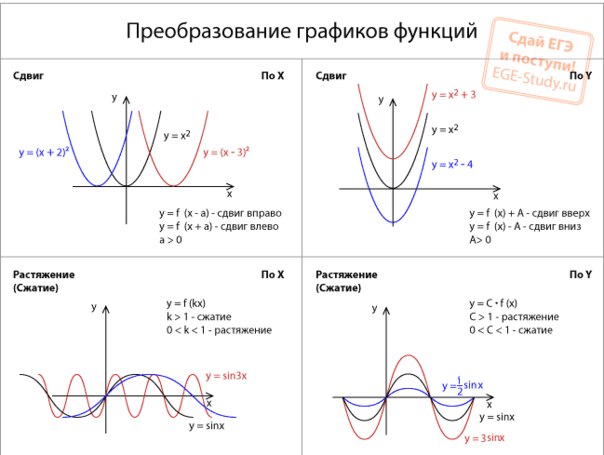
Проверить знания учащихся.
Преобразования:
1. y = f(x – a)
2. y = f(x) + b
3. y = — f(x)
4. y = f(-x) 5. y = kf(x), где k>0
6. y = f(kx), где k>0
7. y = |f(x)|
8. y = f(|x|)
Запишите уравнение параболы с координатами вершины (x0 ;y)
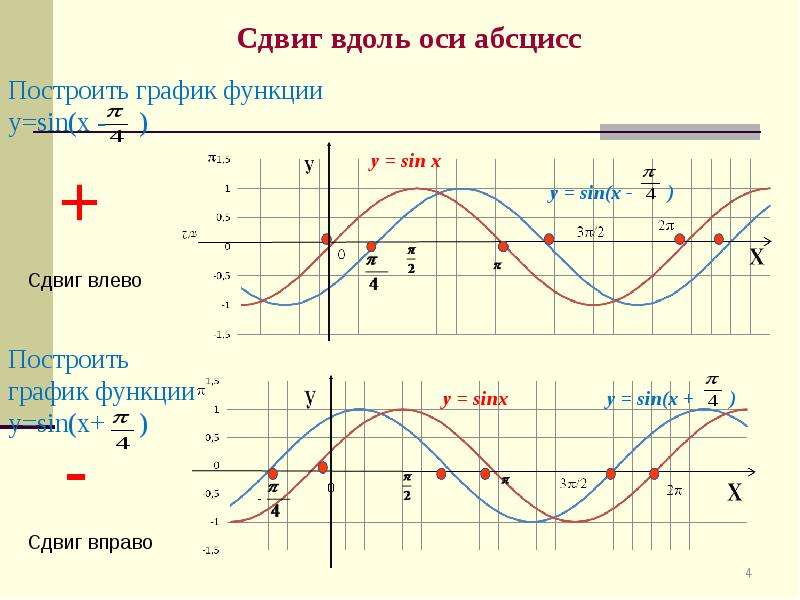
Параллельный перенос (сдвиг). Рассмотрим параллельный перенос вдоль оси абсцисс. Пусть дан график функции y = f(x). Как по отношению к нему будет расположен график функции y = f(x – a), a>0 ?
График функции y = f (x — a), a > 0, получается из графика функции y = f(x) сдвигом (переносом) вдоль оси Ох на а единиц вправо.
Ясно, что если а<0, то график функции y = f (x — a) получается из графика функции y = f(x) сдвигом (переносом) вдоль оси Ох на а единиц влево.
Пример 1. График функции получается из графика функции сдвигом (переносом) вдоль оси Ох на 4 единицы влево.
График функции получается из графика функции сдвигом (переносом) вдоль оси Ох на 4 единицы влево.
Пример 2. График функции получается из графика функции сдвигом (переносом) вдоль оси Ох на 2 единицы вправо.
Рассмотрим теперь параллельный перенос вдоль оси ординат. В этом случае график функции y = f(x) + b получается из графика функции y=f(x) при b > 0 смещением на b единиц вверх, а при b < 0 – на |b| единиц вниз.
Пример 3. Чтобы построить график функции , сначала строим график функции , а затем сдвигаем его вниз на единицу.
Пример 4. Чтобы построить график функции , сначала строим график функции , а затем сдвигаем его вверх на единицу. Тест
Тест. Вопрос 1. График функции (зеленый) получен из графика функции с помощью параллельного переноса. Выберите соответствующую формулу.
Вопрос 2. График функции (зеленый) получен из графика функции с помощью параллельного переноса. Выберите соответствующую формулу.
График функции (зеленый) получен из графика функции с помощью параллельного переноса. Выберите соответствующую формулу.
Вопрос 3. График функции получен из данного с помощью параллельного переноса и симметричного отображения относительно прямой Ох. Напишите соответствующую формулу.
2. Деформация (растяжение и сжатие) графика. График функции у = f(ω·x), ω>0, получается из графика функции у = f(x), «сжатием» к оси у в ω раз при ω>1 и «растяжением» от оси у в раз при 0<ω<1. График функции у = k·f(x), k>0, получается из графика функции у = f(x), «растяжением» от оси х в k раз при k>1 и «сжатием» к оси х в раз при 0< k<1.
Пример 5. График функции y =sin 2x получается из графика функций y = sin x «сжатием» к оси у в 2 раза.
Пример 6. График функции получается из графика функции «растяжением» от оси у в 2 раза.
Пример 7. График функции y = 2·f(x) получается из графика функции y = f(x) «растяжением» от оси х в 2 раза.
Пример 8. График функции получается из графика функции «сжатием» к оси х в 2 раза.
3. Отражение. График функции получается зеркальным отражением графика функции относительно оси х.
График функции получается зеркальным отражением графика функции относительно оси у.
График функции получается из графика функции следующим образом:
а) Часть графика, лежащую над осью x, оставляем без изменения;
б) Часть графика, лежащую под осью x, отражаем симметрично относительно оси x. Таким образом, ниже оси Ox графика нет.
;
– четная функция, ее график получится отражением ветви при x≥0 графика функции симметрично относительно оси Оу.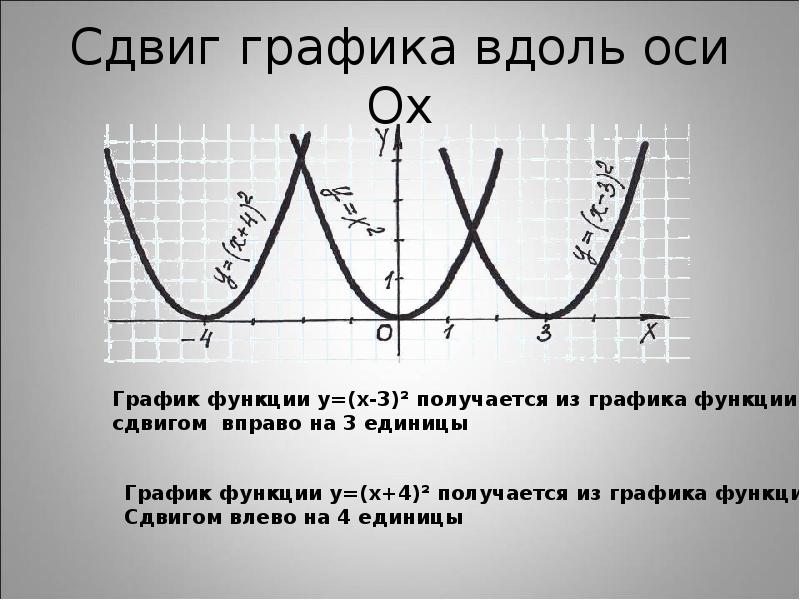 Ветвь графика при х < 0 пропадает.
Ветвь графика при х < 0 пропадает.
Замечание. Нетрудно показать, что если периодическая функция с периодом , то функция , , является периодической с периодом. В самом деле, так как функция имеет период , то при любом x выполняется равенство . Положим ; тогда для любого х получим
и, следовательно, функция имеет период . Например, функция имеет период , а функция — период .
Список использованной литературы:
1. Бахтина Т. П. «Таблетки» и «компрессы» при построении графиков. // Математика в школе. 2000. № 8.
2. Игудисман О. С. Математика на устном экзамене. Пособие для поступающих в вузы с повышенными требованиями по математике. ─ М: «Московский Лицей», 1997.
3. Райхмист Р. Б. Графики функций: задачи и упражнения. ─ М: Школа-Пресс, 1997. — 384с. (Cерия «ШАНС» — «Школа Абитуриента: Научись Сам»).
Построение графиков функций путем преобразования
PPT / 659. 5 Кб
5 Кб
растяжение и сжатие, параллельный перенос, общее уравнение синусоиды, тангенцоиды
Общие принципы преобразования графиков функций изучались нами в главе 8, (см. §47, §48, §50 справочника для 8 класса). В этом параграфе мы рассмотрим особенности тригонометрических функций при использовании этих преобразований.
п.1. Растяжение и сжатие графиков тригонометрических функций по оси
OXОбщие принципы растяжения и сжатия графиков по оси OX:
При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(px),\ \ p\gt 1 $$ график второй функции сжимается в p раз по оси OX по сравнению с графиком первой функции.
При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(\frac{x}{p}),\ \ p\gt 1 $$ график второй функции растягивается в p раз по оси OX по сравнению с графиком первой функции.
Эти принципы справедливы и для тригонометрических функций.
Тригонометрические функции являются периодическими: синус и косинус с периодом 2π, тангенс и котангенс – с периодом π.
При сравнении двух тригонометрических функций $$ y_1=f(x),\ \ y_2=f(px),\ \ p\gt 1 $$ период второй функции уменьшается в p раз: $$ T_2=\frac{T_1}{p} $$
При сравнении двух тригонометрических функций $$ y_1=f(x),\ \ y_2=f(\frac{x}{p}),\ \ p\gt 1 $$ период второй функции увеличивается в p раз: $$ T_2=pT_1 $$
Например:Построим в одной системе координат три графика: $$ f(x)=sinx,\ \ g(x)=sin2x,\ \ h(x)=sin\frac{x}{2} $$
Период колебаний функции \(g(x)=sin2x\) в 2 раза меньше: \(T_g=\frac{2\pi}{2}=\pi\).
Период колебаний функции \(h(x)=sin\frac{x}{2}\) в 2 раза больше: \(T_h=2\cdot 2\pi=4\pi\).
п.2. Растяжение и сжатие графиков тригонометрических функций по оси
OYОбщие принципы растяжения и сжатия графиков по оси OY:
При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=Af(x),\ \ A\gt 1 $$ график второй функции растягивается в A раз по оси OY по сравнению с графиком первой функции.
Общий принцип сжатия графиков:
При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=\frac{1}{A}f(x),\ \ A\gt 1 $$ график второй функции сжимается в A раз по оси OY по сравнению с графиком первой функции.
Эти принципы справедливы и для тригонометрических функций.
Т.к. для графиков синуса и косинуса (синусоиды) характерна амплитуда колебаний, то также говорят, что:
- умножение на параметр \(A\gt 1\) увеличивает амплитуду колебаний в \(A\) раз;
- деление на параметр \(A\gt 1\) уменьшает амплитуду колебаний в \(A\) раз.
1) Построим в одной системе координат три графика: $$ f(x)=cosx,\ \ g(x)=2cosx,\ \ h(x)=\frac{1}{2}cosx $$
Умножение на \(A=2\) увеличивает амплитуду колебаний в 2 раза.
Область значений функции \(g(x)=2cosx:\ y\in[-2;2]\). График растягивается по оси OY.
Деление на \(A=2\) уменьшает амплитуду колебаний в 2 раза. Область значений функции \(h(x)=\frac12 cosx:\ y\in\left[-\frac12; \frac12\right]\).
2) Теперь построим $$ f(x)=tgx,\ \ g(x)=2tgx,\ \ h(x)=\frac{1}{2}tgx $$
В этом случае хорошей иллюстрацией растяжения по оси OY при умножении и сжатия по оси OY при делении на \(A=2\) служит поведение функции при \(x=\frac\pi4\). $$ f\left(\frac\pi4\right)=tg\left(\frac\pi4\right)=1,\ \ g\left(\frac\pi4\right)=2tg\left(\frac\pi4\right)=2,\ \ h\left(\frac\pi4\right)=\frac12 tg\left(\frac\pi4\right)=\frac12 $$ Аналогично – для любого другого значения аргумента x.
п.3. Параллельный перенос графиков тригонометрических функций по оси
OXОбщие принципы переноса по оси OX:
При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(x+a),\ \ a\gt 0 $$ график второй функции смещается влево на a по оси OX по сравнению с графиком первой функции.
При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(x-a),\ \ a\gt 0 $$ график второй функции смещается вправо на a по оси OX по сравнению с графиком первой функции.
Эти принципы справедливы и для тригонометрических функций.
При этом параметр x называют начальной фазой колебаний.
При сравнении двух тригонометрических функций \(y_1=f(x)\) и \(y_2=f(x\pm a)\) говорят, что у второй функции сдвиг по фазе равен \(\pm a\).
1) Построим в одной системе координат три графика: $$ f(x)=sinx,\ \ g(x)=sin\left(x+\frac\pi4\right),\ \ h(x)=sin\left(x-\frac\pi4\right) $$
Функция \(g(x)=sin\left(x+\frac\pi4\right)\) сдвинута на \(\frac\pi4\) влево по сравнению с \(f(x)\)
Функция \(h(x)=sin\left(x-\frac\pi4\right)\) сдвинута на \(\frac\pi4\) вправо по сравнению с \(f(x)\)
п.4. Параллельный перенос графиков тригонометрических функций по оси
OYОбщие принципы переноса по оси OY:
При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(x)+a,\ \ a\gt 0 $$ график второй функции смещается вверх на
При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(x)-a,\ \ a\gt 0 $$ график второй функции смещается вниз на a по оси OY по сравнению с графиком первой функции.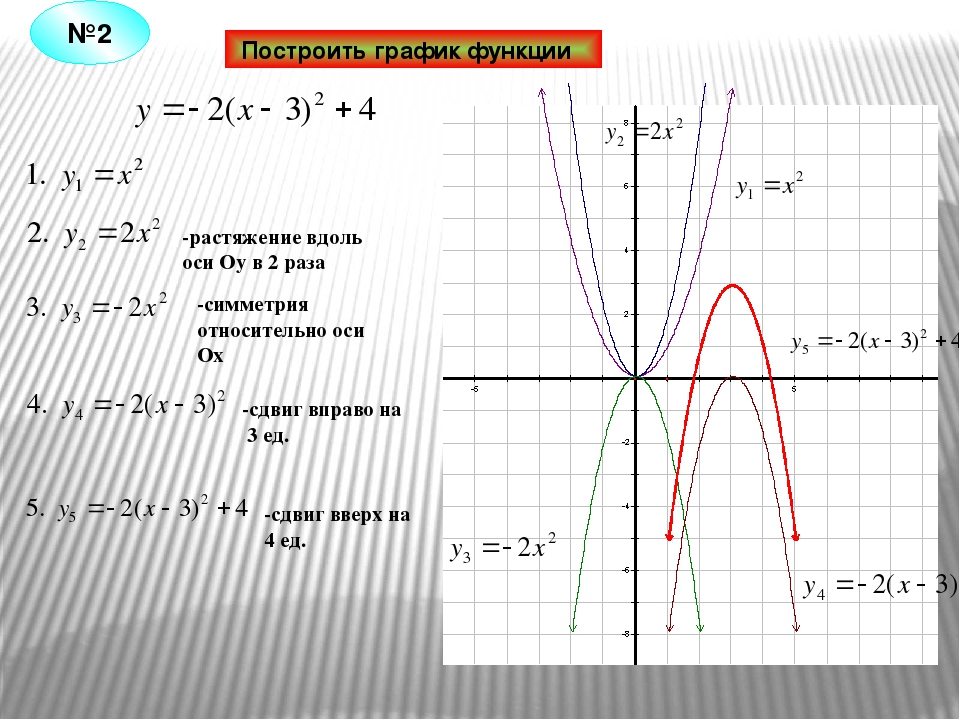
Эти принципы справедливы и для тригонометрических функций.
Например:1) Построим в одной системе координат три графика: $$ f(x)=sinx,\ \ g(x)=sinx+1,\ \ h(x)=sinx-1 $$
Функция \(g(x)=sinx+1\) сдвинута на 1 вверх по сравнению c \(f(x)\)
Функция \(h(x)=sinx-1\) сдвинута на 1 вниз по сравнению с \(f(x)\)
п.5. Общее уравнение синусоиды
Синусоида – плоская кривая, которая задается в прямоугольной системе координат уравнением: $$ y(x)=Asin(cx+d)+B $$ где
A — амплитуда, характеризует растяжение графика по оси OY
B – вертикальный сдвиг, характеризует сдвиг графика по оси OY (вверх/вниз)
c — циклическая частота, характеризует период колебаний и растяжение графика по оси OX
d- начальная фаза, характеризует сдвиг графика по оси OX(влево/вправо)
График \(y(x)=Acos(cx+d)+B\) также называют синусоидой. Термин «косинусоида» употребляется относительно редко.
Поскольку график косинуса получается из графика синуса сдвигом по фазе на π/2 влево, вводить термин «косинусоида» излишне.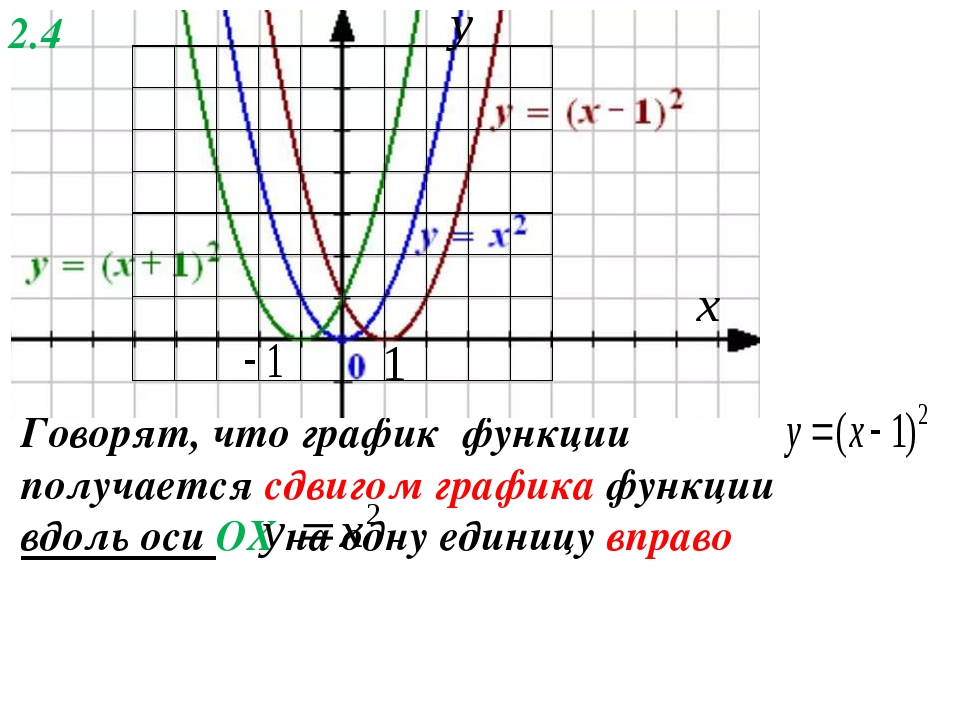
Построим график \(g(x)=3sin\left(2x+\frac\pi2\right)-1\)
По сравнению с \(f(x)=sinx\):
- \(A=3\) — график растянут по оси OY в 3 раза
- \(c=2\) — период меньше в 2 раза T=π, график сжат в 2 раза по оси OX
- \(d=\frac\pi2\) – начальная фаза положительная, график сдвинут на \(\frac{\pi}{2\cdot 2}=\frac\pi4\) влево
- \(B=-1\) — график сдвинут по оси
п.6. Общее уравнение тангенцоиды
Tангенцоидa – плоская кривая, которая задается в прямоугольной системе координат уравнением: $$ y(x)=Atg(cx+d)+B $$ где
A — амплитуда, характеризует растяжение графика по оси OY
B – вертикальный сдвиг, характеризует сдвиг графика по оси OY (вверх/вниз)
c — циклическая частота, характеризует период колебаний и растяжение графика по оси OX
d- начальная фаза, характеризует сдвиг графика по оси OX(влево/вправо)
График \(y(x)=Actg(cx+d)+B\) также называют тангенцоидой.
Построим график \(g(x)=\frac12 tg\left(\frac{x}{2}-\frac\pi3\right)+1\)
По сравнению с \(f(x)=tgx\):
- \(A=\frac12\) — график сжат по оси OY в 2 раза
- \(c=\frac12\) — период больше в 2 раза T=2π, расстояние между асимптотами 2π, график растянут в 2 раза по оси OX
- \(d=-\frac\pi3\) – начальная фаза отрицательная, график сдвинут на \(\frac{\pi}{3\cdot 1/2}=\frac{2\pi}{4}\) вправо
- \(B=1\) — график сдвинут по оси OY на 1 вверх
п.7. Примеры
Пример 1.Постройте в одной системе координат графики: $$ f(x)=sinx,\ \ g(x)=-sinx,\ \ h(x)=cosx $$ Найдите сдвиг по фазе для \(g(x)\) и \(h(x)\) в сравнении с \(f(x)\).
Сдвиг по фазе удобно определять по главной арке синусоиды.
Для \(f(x)=sinx\) главная арка определена на отрезке \(0\leq x\leq \pi\)
Для \(g(x)=-sinx\) главная арка определена на отрезке \(-\pi\leq x\leq 0\), т.е. сдвинута на π влево от \(f(x)\).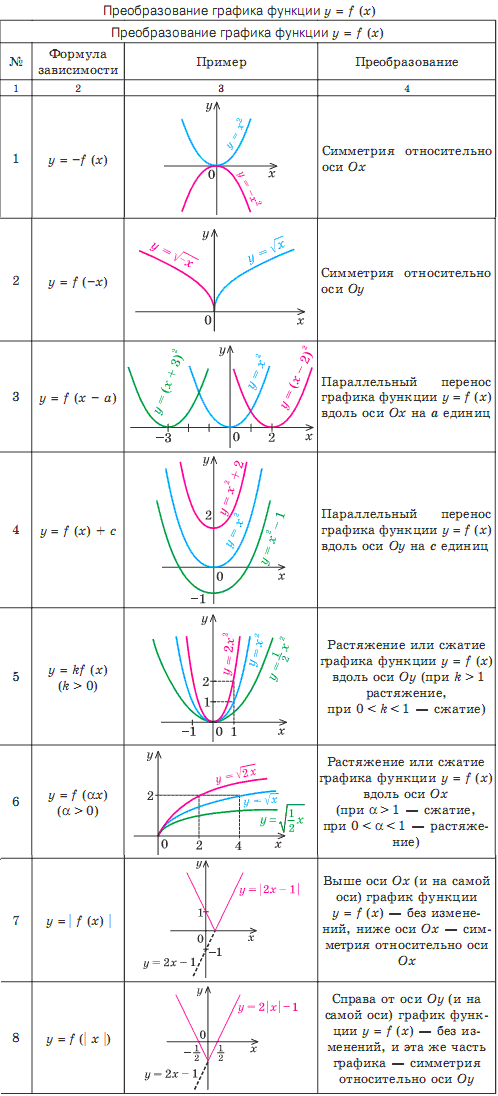 Это означает, что: $$ f(x)=g(x+\pi),\ \ sinx=-sin(x+\pi) $$ Для \(h(x)=cosx\) главная арка определена на отрезке \(-\frac\pi2\leq x\leq \frac\pi2\), т.е. сдвинута на \(\frac\pi2\) влево от \(f(x)\). Это означает, что: $$ f(x)=h\left(x+\frac\pi2\right),\ \ sinx=cos\left(x+\frac\pi2\right) $$
Это означает, что: $$ f(x)=g(x+\pi),\ \ sinx=-sin(x+\pi) $$ Для \(h(x)=cosx\) главная арка определена на отрезке \(-\frac\pi2\leq x\leq \frac\pi2\), т.е. сдвинута на \(\frac\pi2\) влево от \(f(x)\). Это означает, что: $$ f(x)=h\left(x+\frac\pi2\right),\ \ sinx=cos\left(x+\frac\pi2\right) $$
Пример 2. Найдите наименьшие положительные периоды функций:
a) \(y=sin5x\)
Период синуса \(2\pi\) уменьшается в 5 раз. Получаем: \(T=\frac{2\pi}{5}\)
б) \(y=cos\pi x\)
Период косинуса \(2\pi\) уменьшается в \(\pi\) раз. Получаем: \(T=\frac{2\pi}{\pi}=2\)
в) \(y=tg\frac{x}{4}\)
Период тангенса \(\pi\) увеличивается в 4 раза. Получаем: \(T=4\pi\)
г) \(y=tg\left(2x+\frac{\pi}{3}\right)\)
Период тангенса \(\pi\) уменьшается в 2 раза. Получаем: \(T=\frac\pi2\)
Пример 3. Используя правила преобразования графиков функций, постройте график $$ f(x)=2ctg\left(3x+\frac\pi6\right) $$ По сравнению с \(g(x)=tgx\):
- \(A=2\) — график растянут по оси OY в 2 раза
- \(c=3\) — период меньше в 3 раза \(T=\frac\pi3\), расстояние между асимптотами \(\frac\pi3\), график сжат в 3 раза по оси OX
- \(d=-\frac\pi6\) – начальная фаза положительная, график сдвинут на \(\frac{\pi}{6\cdot 3}=\frac{\pi}{18}\) влево
Расположение нулей: $$ tg\left(3x+\frac\pi6\right)=0\Rightarrow 3x+\frac\pi6=\pi k\Rightarrow 3x=-\frac\pi6+\pi k\Rightarrow x =-\frac{\pi}{18}+\frac{\pi k}{3} $$ Вертикального сдвига нет, нули расположены на оси OX.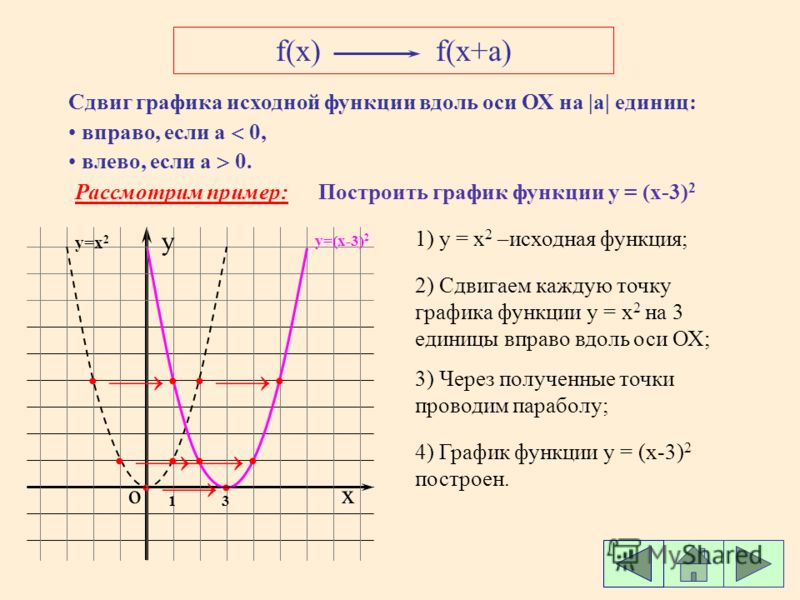
Расположение асимптот: $$ 3x+\frac\pi6\ne\frac\pi2+\pi k\Rightarrow 3x\ne\frac\pi3+\pi k\Rightarrow x\ne\frac\pi9+\frac{\pi k}{3} $$ Пересечение главной ветви с осью OY: \(x=0,\ y=2tg\frac\pi6=\frac{2}{\sqrt{3}}\)
С учетом периода \(\frac\pi3\) получаем семейство дополнительных точек для построения графика \(\left(\frac{\pi k}{3}; \frac{2}{\sqrt{3}}\right)\).
Пример 4. Определите графически, сколько корней имеет уравнение на отрезке: a) \(sinx=sin2x\) при \(0\leq x\leq 3\pi\)
Ответ: 7 корней
б) \(cos\frac{x}{2}=cos2x\) при \(-2\pi\leq x\leq 2\pi\)
Ответ: 7 корней
Урок 4. свойства и график функции y=sinx — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №4. Свойства и график функции .
Перечень вопросов, рассматриваемых в теме
Глоссарий по теме
Синусоидой называется множество точек плоскости, которое в некоторой системе координат является графиком функции , где a≠0.
Число │a│ называется амплитудой.
Основная литература:
Колягин М.В. Ткачева Ю.М., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. М.: Просвещение, 2010.–336 с.
Дополнительная литература:
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс]. – Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
На прошлом уроке мы говорили о свойствах графика косинуса:
1) область определения функции – множество R всех действительных чисел;
2) Множество значений функции – отрезок [–1;1];
3) Функция косинуса периодическая, ;
4) Функция чётная;
5) Функция принимает:
- значение, равное 0, при ;
- наименьшее значение, равное –1, при
;
- наибольшее значение, равное 1, при ;
6) Функция
- возрастает на отрезке и на отрезках, получаемых сдвигами этого интервала на .

Давайте сравним их со свойствами графика синуса, а для начала определим следующие моменты:
- При движении точки до первой четверти ордината увеличивается;
- При движении точки по второй четверти ордината постепенно уменьшается;
- Функция возрастает на отрезке и убывает на отрезке .
Свойства функции :
1) D(y) =R;
2) E (y) =[–1;1];
3) Период функции равен ;
4) Функция чётная/нечётная;
5) Функция принимает:
6) Функция
- возрастает на отрезке и на отрезках, получаемых сдвигами этого отрезка на ;
- убывает на отрезке и на отрезках, получаемых сдвигами этого отрезка на .
Изменяя амплитуду и значение аргумента функции синуса график ведет себя следующим образом (рис.1)
Рис. 1 – графики синуса
Сдвиг графика влево/вправо вдоль оси абсцисс
Если к аргументу функции добавляется постоянная, то происходит сдвиг (параллельный перенос) графика вдоль оси Ох.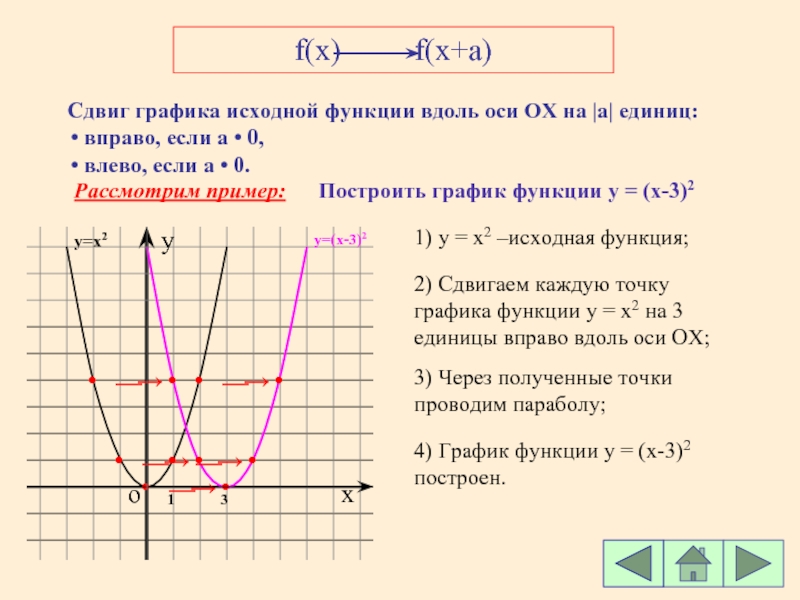
Правило:
1) чтобы построить график функции , нужно сдвинуть график вдоль оси Ох на b единиц влево;
2) чтобы построить график функции , нужно график сдвинуть вдоль оси ОХ на b единиц вправо.
Теоретический материал для самостоятельного изучения
Актуализация знаний
1. На следующие утверждения нужно ответить верно/неверно.
1) Тригонометрическая функция определена на всей числовой прямой.
2) График нечетной функции можно построить с помощью преобразования симметрии относительно оси Оу.
3) График тригонометрической функции можно построить, используя одну главную полуволну.
Ответ: верно, неверно, верно.
2. Вспомним, что мы уже знаем о функции , ответив на вопросы:
1) Какие значения может принимать переменная х. Какова область определения этой функции?
2) В каком промежутке заключены значения выражения . Назови наибольшее и наименьшее значения функции .
3) Функция синуса чётная или нечётная?
Ответ:1) 𝑥∈𝑅; 2) [–1;1]; 𝑦𝑚𝑎𝑥=3, 𝑦𝑚𝑖𝑛=–3; 3) чётная;
Примеры и разборы решения заданий тренировочного модуля:
Пример 1.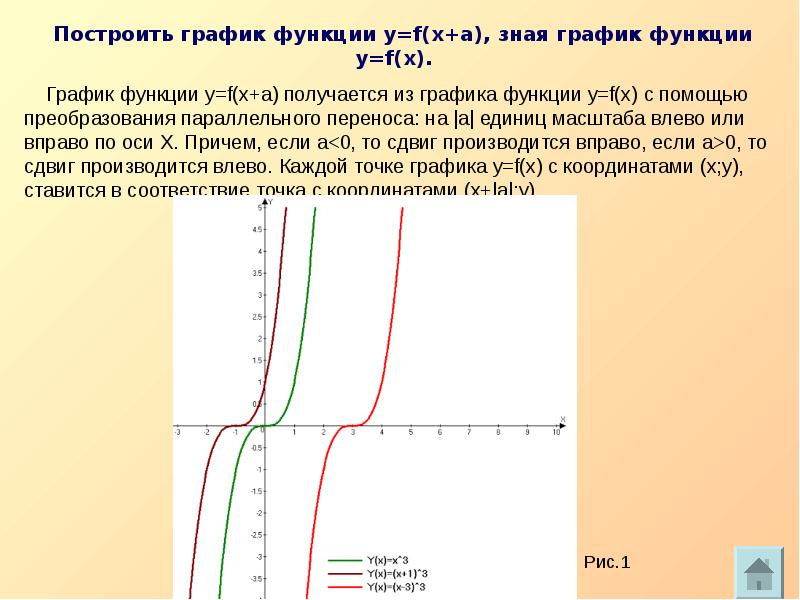 Найдем все корни уравнения , принадлежащие отрезку .
Найдем все корни уравнения , принадлежащие отрезку .
Построим графики функций и (рис. 6)
Рис. 7 – графики функций и .
Графики пересекаются в четырёх точках, абсциссы которых являются корнями уравнения . На выбранном отрезке от корни уравнения симметричны: и . Из рисунка видно, что симметричность корней объясняется периодичностью функции: аналогично для
Ответ: ; .
Пример 2.Найти все решения неравенства , принадлежащие отрезку .
Из рисунка 7 видно, что график функции лежит выше графика функции на промежутках и и
Ответ: , ,
Конспект урока по Алгебре «Построение графика квадратичной функции с использованием сдвигов по осям координат» 8 класс
МБОУ Чистопольская СОШ
Урок алгебры в 8 классе.
Тема «Построение графика квадратичной функции с использованием сдвигов по осям координат».
(открытый урок в рамках месячника методической работы по теме «Современный урок» с применением элементов системно-деятельностного метода обучения)
Автор: ТиховаЮ. К.
К.
учитель математики
МБОУ Чистопольской СОШ
20 февраля 2013 год
Цели урока:
Образовательные:
Развивающие:
развивать математическую зоркость и математическую речь, умение сравнивать, выделять характерные признаки, классифицировать;
Воспитательные:
формировать навыки сотрудничества, организации работы в группе, повышение мотивации изучения математики.
Задачи урока:
повторить основной материал, связанный с квадратичной функцией;
продолжить отработку и закрепление навыка построения графиков квадратичных функций с помощью таблицы;
создать условия (подвести) для учащихся к открытию ими алгоритмов построения графиков функций;
выявить уровень усвоения алгоритмов;
выработка компетенций:
1) общеобразовательных:
-умения самостоятельно и мотивированно организовывать свою познавательную деятельность;
-умения использовать элементы причинно-следственного анализа, определять существенные характеристики изучаемого объекта;
-умения оценивать и корректировать своё поведение в окружающей среде, выполнять требования в практической деятельности.
2) предметно-ориентированных:
-развивать познавательные интересы в процессе самостоятельного приобретения математических знаний;
-воспитывать убежденность в позитивной роли математики в жизни современного общества.
Формы работы на уроке:
Оборудование урока:
интерактивная доска;
карточки-задания;
карточки-шаблоны;
буклеты.
Планируемые результаты обучения:
Обучаемый должен знать:
Определение квадратичной функции, график квадратичной функции и его элементы, алгоритм построения графика с использованием сдвигов по осям координат.
Обучаемый должен уметь:
Узнавать квадратичную функцию, определять направление ветвей параболы по старшему коэффициенту, строить график функции у=х2, строить график квадратичной функции, определяя направление и величину сдвига по формуле.
Личностные:
Стараться ясно, точно, грамотно излагать свои мысли в устной речи; понимать смысл поставленной задачи; учиться контролировать процесс и результат учебной математической деятельности.
Метапредметные:
Видеть математические объекты «квадратичную функцию», «параболу» в окружающей жизни; формулировать гипотезы при решении математических задач; применять индуктивные и дедуктивные способы рассуждений.
План урока.
1. Организационный момент.
2. Мотивация (просмотр презентации) + стихотворение.
3. Актуализация знаний:
Задание 1. Из данных функций выбрать те, которые являются квадратичными (соединить стрелками или вычеркнуть).
Задание 2. Из графиков функций, выбрать те, которые являются графиками квадратичной функции.
Задание 3. Назвать основные элементы параболы.
Задание 4. Определить направление ветвей
параболы по формуле, задающей функцию.
4. Работа в группах.
Работа в группах.
Группа 1 (учащиеся, имеющие низкий уровень математической
подготовки)
Группы 2 и 3 (учащиеся, имеющие средний и хороший уровень
математической подготовки)
5. Анализ полученных результатов (презентация).
6. Систематизация полученных результатов: заполнение сводной
таблицы, оформление результатов в виде буклета.
7. Домашнее задание.
8. Первичный контроль (самостоятельная работа) с последующей
проверкой.
9. Рефлексия.
Ход урока.
1. Организационный момент:
Начать урок я хочу словами Конфуция о трёх путях ведущих к знаниям…..
Перед человеком к разуму три пути: путь размышления – это самый благородный путь, путь подражания – это самый лёгкий; путь личного опыта – это самый тяжёлый.
Я думаю, каждый из вас уже определил для себя свой путь к знанию и уровень, на котором вы будете сегодня работать.
Итак начнем.
На уроке можно ошибаться, сомневаться, консультироваться.
Если вам что-то непонятно помните: «Я всегда рядом».
2. Мотивация:
Сегодня мы с вами продолжим изучение одной из основных видов функций в курсе алгебры – квадратичной.
— Сформулируйте определение квадратичной функции (функция вида …..)
— Как называется график квадратичной функции? (парабола).
И сейчас мне бы хотелось обратить ваше внимание на то, что квадратичная функция и её график являются не только алгебраическими понятиями, а реально существуют вокруг нас (презентация).
Параболу можно встретить везде и не только в объектах, созданных человеком, как, например, в фонтанах, но и в самой природе, где не касалась рука человека: в виде горных хребтов, морских заливов и в другом большом количестве знакомых нам объектов.
Термин парабола не только математический, но и литературный.
Парабола — термин, обозначающий близкую притче жанровую разновидность в драме и прозе XX века.
Послушайте отрывок из стихотворения, его автор Михаил Зимогляд:
Отдохнуть не пора бы ли, щелкнув автопилот?
Я по жизни параболе совершаю полет.
Ввысь однажды отправленный, катапультой-судьбой,
подымался не плавно я, а летел, как шальной.
Под холодными звездами знаний клад отыскал.
Что людьми было создано, словно губка, впитал.
Испытал наслаждение от житейских страстей.
Только в небо движение становилось трудней.
Подо мной даль бескрайняя. Ах, какой чудный миг!
И восторг осознания — я вершины достиг!
Но недолго парение продолжалось, и вот,
незаметно в падение превратился полет.,,,
Жизнь острижена наголо, смято время в комок.
Вниз уходит парабола, приближая мой срок.
Ведь кривой той симметрия — скоротечности знак.
И Творца геометрию не отменишь никак.
На какой ординате я, кувыркаясь, лечу?
Не имею понятия, одного лишь хочу,
разглядеть с облегчением, камнем падая вниз,
точку пересечения на оси, что абсцисс.
Что сравнивает автор с изучаемой нами кривой?
3. Актуализация знаний.
А теперь повторим основные моменты, связанные с квадратичной функцией, которые нам сегодня пригодятся:
Задание 1.
Из данных функций выбрать те, которые являются квадратичными (соединить стрелками или вычеркнуть).
Задание 2.
Из графиков функций, выбрать те, которые являются графиками квадратичной функции.
Задание 3.
Назвать основные элементы параболы.
Задание 4. Определить направление ветвей параболы:
по формуле, задающей функцию.
4. Работа в группах.
Повторив основной материал, перейдем к главной части урока. На предыдущем уроке вы установили зависимость между внешним видом параболы и коэффициентом перед икс в квадрате. Сегодня вы попытаетесь установить зависимость между расположением параболы в системе координат и добавлением в формулу, задающую функцию, чисел в виде слагаемых.
Сначала вы установите эти зависимости при выполнении практических заданий на построение графиков функций с помощью заполнения таблиц значений, а затем после обобщения полученных результатов, попробуете сформулировать алгоритмы построения графиков без применения таблиц, а только пользуясь шаблоном параболы у=х2.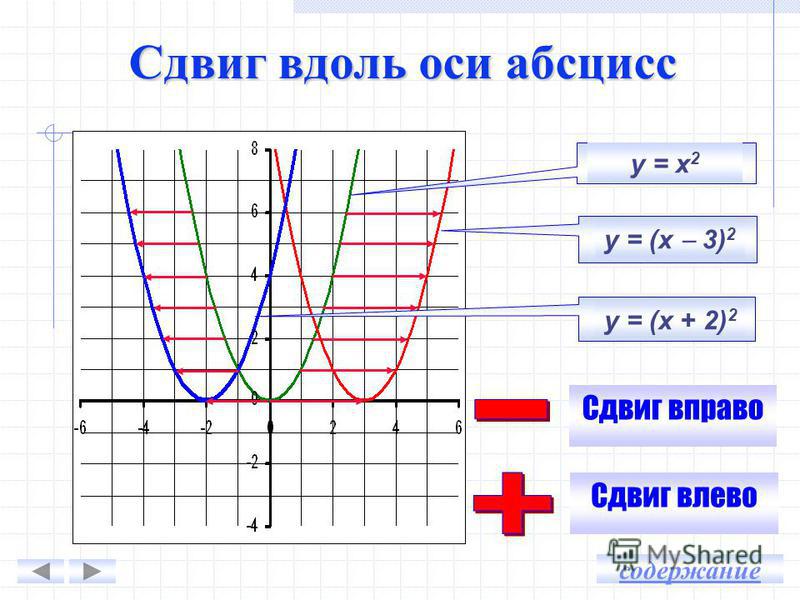
Каждая группа начинает работу по заданиям из желтого конверта. Внимательно ознакомьтесь с заданиями и выполняйте их в указанном порядке.
Разъяснить задания каждой группе.
Задание группе 1.
ШАГ 2. Сравните полученные графики с графиком функции у = х2 | ШАГ 3. Заполните пропуски: (укажите направление и число) | |
1) у = х2 – 4 2) у = х2 + 2 3) у = (х + 2)2 4) у = (х – 3)2 5) у = (х -2)2 + 1 6) у = (х + 3)2 -2 | Парабола графика 1) может быть получена из параболы у = х2 сдвигом ………………… по оси ………… на ……… единичных отрезка. Парабола графика 2) может быть получена из параболы у = х2 сдвигом ………………… по оси …………… на …… единичных отрезка. Парабола графика 3) может быть получена из параболы у = х2 сдвигом ………………… по оси ………… на ……… единичных отрезка. Парабола графика 4) может быть получена из параболы у = х2 сдвигом ………………… по оси …………… на …… единичных отрезка. Парабола графика 5) может быть получена из параболы у = х2 сдвигом ………………… по оси ………… на ……… единичных отрезка и по оси ………. на …….. единичных отрезка. Парабола графика 6) может быть получена из параболы у = х2 сдвигом ………………… по оси …………… на …… единичных отрезка и по оси ………. на ………. единичных отрезка. |
Задания для 2 и 3 групп.
Цель: Сформулировать алгоритмы построения графиков квадратичных функций с использованием шаблона
Задания:
1. Построить графики функций:
Построить графики функций:
2. Сравните расположение каждого графика с графиком функции .
3. Результаты сравнения занесите в таблицу:
Направление сдвига | Ось (оси) сдвига | На сколько единиц | |
4. По результатам сравнения разбейте функции на 3 группы:
2 группа | 3 группа | |
5. Сформулируйте алгоритмы построения графиков с помощью шаблона.
5. Анализ результатов.
Приступим к анализу полученных вами результатов и проверке выполненных вами построений (по слайдам презентации).
Слово участникам первой группы: анализ функций 1 группы;
Слово участника второй группы: анализ функций второй группы;
Слово участникам третьей группы: анализ функций третьей группы.
Анализ результатов проведен, можем переходить к формулировке правил построения графиков (заполнение таблицы).
6. Систематизация полученных результатов: заполнение сводной таблицы, оформление результатов в виде буклета.
Таблица выводится на интерактивной доске. Все элементы таблицы-результата перемешаны. Задача ученика правильно переместить содержимое клеток по своим местам.
Результаты, проведенной работы, в форме этой таблицы раздаются ученикам в виде буклетов.
Физкультминутка.
Пока тему изучали деточки мои устали разрешаю детям встать,
Потянуться и параболу с положительным коэффициентом показать.
А теперь коэффициент отрицательный… Коэффициент 5…
Коэффициент 1/5… Садитесь.
7. Домашнее задание.
В дневниках: составить 6 квадратичных функций, графики которых вы построите с помощью шаблона параболы у=х2.
8. Самостоятельная работа.
Итогом вашей работы будет выполнение самостоятельной работы, тексты которой вы можете взять в зеленых конвертах.
Вариант 2 | |||||||||||||||||||||
Номер задания | 1 | 2 | 3 | 4 | 5 | 6 | Оценка | Номер задания | 1 | 2 | 3 | 4 | 5 | 6 | Оценка | ||||||
Вариант ответа | Вариант ответа | ||||||||||||||||||||
Укажите для каждой функции ее график 1. 2. у = х2 — 4 4. у = (х + 4)26. у = (х + 4)2 – 2 | Укажите для каждой функции ее график 1. у = х2 – 1 3. у = (х – 1)25. у = (х – 2)2 – 2 2. у = х2 + 1 4. у = (х + 3)26. у = (х — 2 )2 + 1 | ||||||||||||||||||||
Поменяйтесь заданием с соседом по парте, который проверит вашу работу и сравнит результаты с правильными ответами на доске.
Д | Б | Г | А | Е | В | |
2 | В | Д | Б | Г | А | Е |
Оцените работу товарища: без ошибок — 5
1 ошибка – 4, 2 ошибки — 3. (собрать листки).
(собрать листки).
Оценивание работы учащихся на уроке.
9. Рефлексия.
Закончите любое предложение из предложенных:
На уроке я узнал(а)…
На уроке понял…
На уроке научился…
Мне понравилось…
Мне было интересно…
Лучше всего у меня получилось…
Основные трудности у меня были…
Я хочу закончить наш урок словами французского писателя Эмиля Золя: «Весь смысл жизни заключается в бесконечном завоевании неизвестного, в вечном усилии познать больше».
Графики тригонометрических функций
Графики синуса и косинуса
График функции изображен на рисунке 1.
Рис. 1
График функции изображен на рисунке 2.
Рис. 2
Кривая, описывающая функцию синуса, называется синусоидой, а косинуса – косинусоидой.
График функции можно получить из графика функции сдвигом последнего влево на . Аналогично, график функции можно получить из графика функции сдвигом последнего вправо на .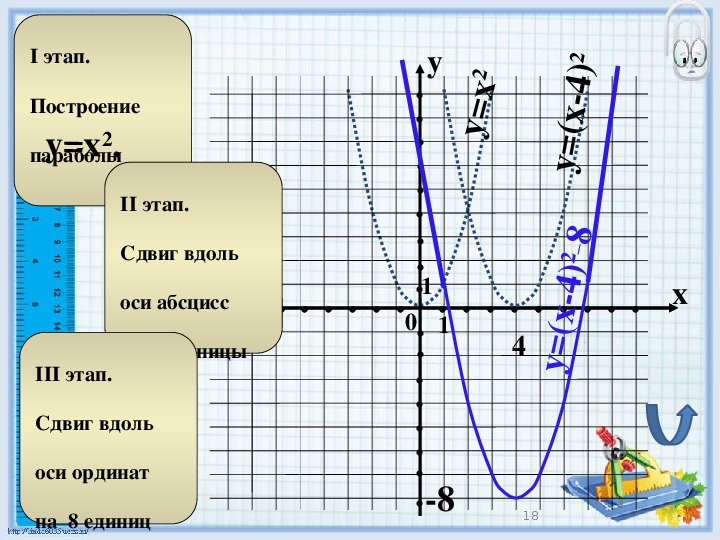
Графики тангенса и котангенса
График функции изображен на рисунке 3. Кривая, задающая функцию тангенса, называется тангенсоидой.
Рис. 3
График функции изображен на рисунке 4.
Рис. 4
Примеры решения задач
ПРИМЕР 1| Задание | Построить график функции |
| Решение | Искомый график получается из графика функции в результате параллельного переноса вдоль оси абсцисс вправо на (рис. 5).
Рис. 5 |
| Задание | Построить график функции |
| Решение | Искомый график получается из графика функции в результате параллельного переноса вдоль оси ординат вверх на 1 (рис. 6) .
Рис. 6 |
| Задание | Построить график функции |
| Решение | Искомый график получается из графика функции растяжением последнего вдоль оси ординат в три раза (увеличением расстояния от каждой точки графика до оси абсцисс в три раза) (рис. 7). 7).
Рис. 7 |
| Задание | Построить график функции |
| Решение | Заданный график построим с помощью элементарных преобразований графика функции . Осуществив параллельный перенос графика функции вдоль оси абсцисс влево на , получим (рис. 8)
Рис. 8 Затем, отразив график функции симметрично относительно оси абсцисс, получим искомый график (рис. 9). Рис. 9 |
Простейшие тригонометрические уравнения
Тригонометрические функции числового аргумента
Свойства тригонометрических функций
Упрощение тригонометрических выражений
Косинус суммы
|
Примеры моделей 1. Иллюстрации 2. Манипулятивные модели 3.  Конструктивные задания Конструктивные задания4. Задания с проверкой 5. В роли учителя 6. Виртуальные эксперименты |
3. Конструктивные задания3.1. Построения циркулем и линейкойВажнейшим классом учебных заданий, формируемых при помощи «Математического конструктора», являются задачи на конструирование с помощью предоставляемого ученику набора виртуальных инструментов. В частности, любая «классическая» школьная задача на построение циркулем и линейкой может быть представлена в интерактивной компьютерной форме. Причем как на итоговом чертеже, так и на всех промежуточных фазах решения важную роль играет возможность проверки правильности построения вариацией данных – когда кажущийся «правильным» чертеж рассыпается при деформировании исходных объектов, если он был создан лишь визуально похожим рисованием, а не геометрически корректным построением. 3.2. Настройка панели инструментов«Математический конструктор» позволяет настраивать набор инструментов на панели каждой модели-задания индивидуально, что дает возможность формировать задания с точно подобранными интерфейсными возможностями. Это позволяет, во-первых, облегчить интерфейс модели, не перегружая его ненужными в данном задании инструментами, а во-вторых, создавать новые задачи за счет изменения набора используемых инструментов. В геометрии рассматривают, например, построения одной линейкой или одним циркулем. Компьютер существенно расширяет спектр таких задач. Так, рассмотренная выше простая задача становится вполне содержательной, если попробовать решать ее одной линейкой. 3.3. 3D-построенияВ заданиях на построение можно разнообразить не только инструменты, но и «рабочее поле». 3.4. Преобразования графиковОтдельное место среди конструктивных заданий занимают задания на построение графиков функций. «Математический конструктор» позволяет строить графики функций, задаваемых аналитически (с помощью специального редактора формул). Можно строить и кривые, заданные уравнениями вида F(x, y) = 0, а также кривые, заданные параметрически. В школьном курсе большое внимание уделяется построению графиков с помощью преобразований: искомый график получается из некоторого стандартного сдвигами, растяжениями, симметриями.
|
|
Графические триггерные функции: фазовый сдвиг
Пурпурная математика
Единственная часть графика, которую мы еще не нарисовали, это фазовые сдвиги. Следующий пример включает этот аспект.
График двух периодов по
г ( x ) = sin (π x + π/2) + 3
Амплитида этого графика будет такой же, как и для обычных синусоидальных волн, потому что на синусе умножается «понятная» 1.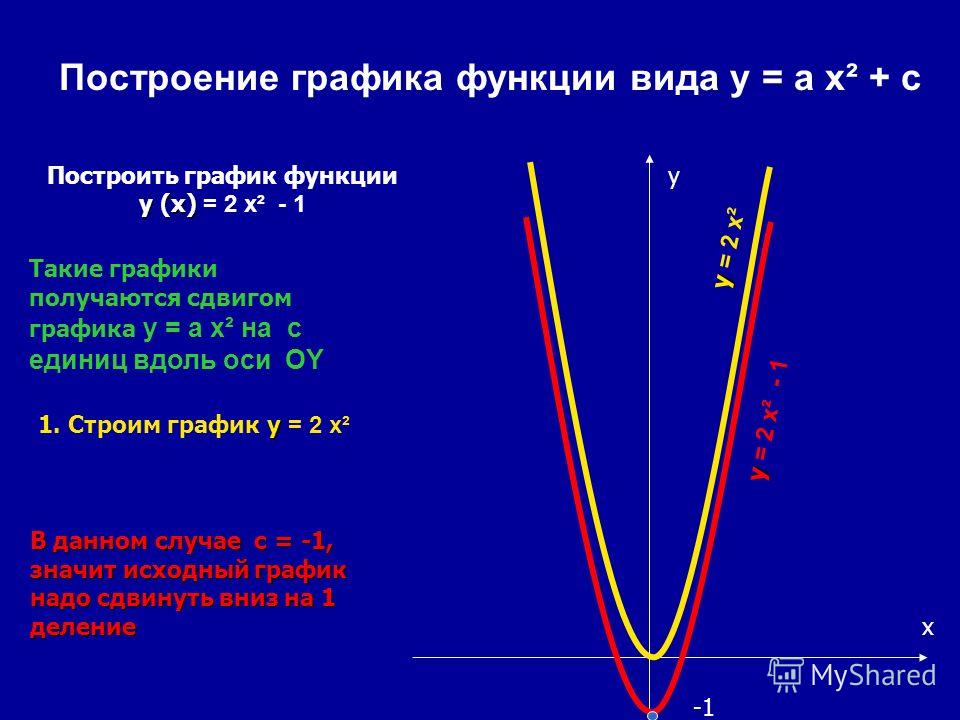
Но средняя линия графика будет на y = 3 вместо y = 0 (то есть на оси x ) из-за «+3» в конце функции.
MathHelp.com
Обычный период синусоиды равен 2π, но переменная в этой функции умножается на π; при делении период этой конкретной функции будет
(2π)/(π) = 2.Поскольку мне нужно отобразить «по крайней мере два периода» этой функции, мне нужно, чтобы моя ось x имела ширину не менее четырех единиц. Теперь новая часть графика: фазовый сдвиг. Заглянув внутрь аргумента, я вижу, что на переменную что-то умножается, а также что-то к ней прибавляется. Чтобы вычислить фактический фазовый сдвиг, мне придется вынести множитель π на переменную. Факторы аргумента как
Заглянув внутрь аргумента, я вижу, что на переменную что-то умножается, а также что-то к ней прибавляется. Чтобы вычислить фактический фазовый сдвиг, мне придется вынести множитель π на переменную. Факторы аргумента как
Начну с обычного графика:
Я знаю, что этот график имеет вертикальное смещение вверх на три единицы. Но вместо того, чтобы сместить синусоиду на три единицы вверх, я добавлю место под моим текущим графиком, сдвину горизонтальную ось на три единицы вниз, а затем перенумерую ось y :
.Выше тот же график; все, что я действительно сделал, это переместил ось x вниз на три единицы, перерисовал и переименовал ее, а затем перенумеровал ось y .Я не трогал синусоиду на графике, нарисованную синим цветом.
Обычный период синусоиды изменяется от 0 до 2π; этот идет от 0 до 2, поэтому я перенумерую ось x :
Все, что я сделал на приведенном выше графике, это перенумеровал оси x с π, 2π, 3π и 4π на 1, 2, 3 и 4 соответственно. Я не коснулся своей синей линии на графике.
Я не коснулся своей синей линии на графике.
Из вычислений фазового сдвига я знаю, что график сдвинут влево на
1/2, поэтому я сдвину ось y вправо на 1/2 и перенумерую x -ось снова.Это последняя часть вычислений, так что это мой окончательный график:Все, что я сделал, чтобы получить последний график выше, это стер существующую ось y , перерисовал ее на полединицы вправо, а затем стер и переписал метки на оси x , снова на полединицы вправо. право. Я никогда не трогал свой график с синей линией.
Вы понимаете, почему я использовал карандаш и много стирал, когда рисовал?
Мой лучший совет относительно построения этих графиков — практика, практика, практика.Вы же не хотите замерзнуть или получить «мозговой пук» на тесте, и это довольно просто, как только вы это прочувствуете. Так что продолжайте строить дополнительные графики, пока не почувствуете себя комфортно и уверенно в своих навыках.
Так что продолжайте строить дополнительные графики, пока не почувствуете себя комфортно и уверенно в своих навыках.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в определении амплитуды, периода и сдвига фазы. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, выбрав «Найти амплитуду, период и фазовый сдвиг» из списка вариантов, чтобы сравнить свой ответ с ответом Mathway.(Вы также можете выбрать «График».)
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway, где можно приобрести членство.)
URL-адрес: https://www.purplemath.com/modules/grphtrig3.htm
Горизонтальные и вертикальные сдвиги линейных функций — видео и стенограмма урока
Вертикальные смещения
Прежде всего, поговорим о вертикальных смещениях , или смещениях по оси Y. Это преобразования, которые перемещают функцию вверх или вниз по оси Y, не изменяя ничего в ней.
Это преобразования, которые перемещают функцию вверх или вниз по оси Y, не изменяя ничего в ней.
Когда вы сдвигаете функцию по вертикали, вы получаете новую функцию с тем же наклоном, но с другой точкой пересечения по оси Y. В уравнении
y = m x + b
, которое является уравнением для линейной функции, это представлено изменением b .
Для примера возьмем две функции:
Функция 1: y = 2 x + 1
Функция 2: y = 2 x + 3
Функция 2 за исключением того, что она будет смещена на 2 единицы вверх по оси Y, поэтому точка пересечения по оси Y функции 2 будет равна y = 3 вместо y = 1.
На каждую единицу, добавляемую к b , функция перемещается на 1 единицу вверх по оси y . На каждую 1, которую вы вычитаете из b , функция будет двигаться вниз на 1 единицу.
Горизонтальные сдвиги
Но что, если вам не нужен вертикальный сдвиг? Что делать, если вы хотите горизонтальное смещение?
Горизонтальное смещение — это смещение по оси x. Вместо перемещения вверх и вниз функция перемещается влево и вправо. Результатом каждого движения является новая функция с тем же наклоном, но перемещенная в другую точку на оси x.Если вы хотите выразить это в уравнении линии, это немного сложнее, чем вертикальные сдвиги. Чтобы произошел горизонтальный сдвиг, вы ничего не добавляете и не вычитаете из b . Вместо этого вы добавляете или вычитаете значение x перед тем, как умножить на наклон.
Вместо перемещения вверх и вниз функция перемещается влево и вправо. Результатом каждого движения является новая функция с тем же наклоном, но перемещенная в другую точку на оси x.Если вы хотите выразить это в уравнении линии, это немного сложнее, чем вертикальные сдвиги. Чтобы произошел горизонтальный сдвиг, вы ничего не добавляете и не вычитаете из b . Вместо этого вы добавляете или вычитаете значение x перед тем, как умножить на наклон.
Если у вас есть исходная функция
f( x ) = 2 x + 5
, то вы сдвинете ее по горизонтали, изменив значение x, например, f( x ) = 2( х + 1) + 5.Вместо умножения x на 2 вы теперь умножаете ( x + 1) на 2.
Добавление 1 к значению x сдвигает функцию влево на 1 единицу, а вычитание 1 из значения x сдвигает функцию вправо на 1 единицу.
Но подождите одну горячую секунду! Взгляните на это уравнение еще раз. Если вы умножите уравнение горизонтального сдвига, а затем объедините одинаковые члены, вы получите… вертикальный сдвиг? Какие? И если вы начертите эти две линии, горизонтальное и вертикальное смещение будет выглядеть одинаково! Что тут происходит?
Это специальное свойство только линейных функций. Подумайте о том, как умножение на 1 и деление на 1 дает один и тот же ответ. Это не значит, что умножение и деление — одно и то же, просто число 1 — особый случай.
Подумайте о том, как умножение на 1 и деление на 1 дает один и тот же ответ. Это не значит, что умножение и деление — одно и то же, просто число 1 — особый случай.
Горизонтальные сдвиги к линейной функции также могут быть записаны как вертикальные сдвиги, но будьте осторожны: обратите внимание, что (в этом примере) горизонтальный сдвиг на 1 единицу эквивалентен вертикальному сдвигу на 2 единицы, потому что изменение y- перехват равен 2. Вы можете записать сдвиг по горизонтали как сдвиг по вертикали, но вы не можете просто использовать одно и то же число и на этом закончить; вам нужно все перемножить и выяснить, какой сдвиг по вертикали соответствует данному смещению по горизонтали.
Когда вы доберетесь до нелинейных функций, вы увидите, что графики выглядят по-разному, и тогда важно понять разницу между горизонтальными и вертикальными сдвигами. А пока просто изучите концепцию и попрактикуйтесь в линейных функциях, чтобы числа были простыми, и вы сможете без проблем перейти к нелинейным функциям, когда придет время.
Итоги урока
В этом уроке вы узнали о сдвигах по горизонтали и вертикали в линейных функциях.
Вертикальный сдвиг — это движение вверх или вниз по оси Y, представленное изменением значения точки пересечения с Y.
Горизонтальное смещение — это движение влево или вправо по оси x, а в уравнении функции — это изменение значения x до умножения на наклон.
Для линейных функций сдвиги по горизонтали также могут быть записаны как сдвиги по вертикали, хотя изменение на x не всегда совпадает с изменением точки пересечения по оси y.Но это не означает, что сдвиги по горизонтали и по вертикали — одно и то же; они начнут выглядеть совсем по-другому, как только вы перейдете к нелинейным функциям, и важно понимать, что это разные концепции.
Горизонтальные и вертикальные сдвиги линейных функций Обзор
| Линейные функции | функции, в которых график представляет собой прямую линию |
| Смена | преобразование, которое перемещает функцию в другое место на графике без изменения ее основной формы |
| Вертикальные смещения | преобразования, которые перемещают функцию вверх или вниз по оси Y, не изменяя ничего в ней |
| Горизонтальное смещение | сдвиг по оси x; вместо перемещения вверх и вниз функция перемещается влево и вправо |
Результаты обучения
Обратитесь к этому уроку, чтобы узнать или заново изучить информацию о горизонтальных и вертикальных сдвигах линейных функций, затем:
- Описать линейные функции
- Распознать значение смены
- Контрастные сдвиги по вертикали и горизонтали
Формула E рисует правила Gen4 с водородным переключением рекламируется .
Новые правила вступят в силу в сезоне 2022–2023 годов, и, пока проводятся частные испытания от конструктора автомобилей Spark Racing Technology, весной команды получат новую технику.
За этим последует фейслифтинг автомобиля и технологии для набора правил Gen3 Evo.
Но правила Gen4 уже находятся на рассмотрении, и новые производители будут приглашены для «мозгового штурма» своих концепций будущего направления Формулы E.
Говоря с Motorsport.tv, соучредитель чемпионата Алехандро Агаг рассказал: «Gen3 уже потрясающий.
«Но мы только собираемся начать думать о Gen4, который появится через пять лет. Мы должны начать обсуждение сейчас.
«Мы, конечно, пригласим OEM-производителей и производителей, которые сейчас с нами.
«Но мы также расширим группу, чтобы пригласить всех производителей к мозговому штурму с очень непредвзятым мнением о том, как должно выглядеть Gen4.
«Там все открыто. Может произойти все, что угодно.”
В рамках этого открытого подхода Формула E рассмотрит возможность использования технологии водородных топливных элементов для питания электродвигателей.
Агаг продолжил: «Водород находится в рамках лицензии Формулы E от FIA [предполагаемый эксклюзивный 25-летний договор о правах на гонки только на электрических одноместных автомобилях].
«Есть два способа использования водорода, один из них — сжигать водород, что очень неэффективно, но некоторые люди работают над тем, чтобы сделать его более эффективным.
«Другой способ, который мы бы использовали, — это водородный топливный элемент, который в основном производит электричество, которое затем приводит в действие электродвигатель.
«Поэтому, как только эти технологии станут широко доступными и будут работать на гоночном уровне, мы обязательно займемся ими».
Микаэла Ахлин-Коттулински, Кевин Хансен, JBXE Extreme-E Team, бои с Молли Тейлор, Йоханом Кристофферссоном, Rosberg X Racing
Фото: Colin McMaster / Motorsport Images Extreme E для зарядки девяти внедорожников Odyssey 21 E-SUV на месте каждой гонки.
В 2020 году технический партнер Mercedes, компания HWA, выступила одним из основателей объявления о концепции HYRAZE League — серии спортивных автомобилей с водородным двигателем, которые планируется запустить с автомобилями мощностью 800 л. с. в 2023 году. большую техническую свободу, хотя в Формуле E будет установлен предел затрат производителей в размере 25 миллионов евро на два сезона подряд, который вступит в силу 1 октября 2022 года.
с. в 2023 году. большую техническую свободу, хотя в Формуле E будет установлен предел затрат производителей в размере 25 миллионов евро на два сезона подряд, который вступит в силу 1 октября 2022 года.
Агаг сказал: «Вы должны предоставить такую свободу, чтобы производители могли разрабатывать технологии и иметь причина, почему нужно участвовать в чемпионате.
«Баланс — это ключ.
«[Но] чем больше свободы вы даете, тем больше денег командам приходится тратить, а через некоторое время у них заканчиваются деньги, и они покидают чемпионат».
Читайте также:Помогите отобразить изменение результатов теста с течением времени: rstats
Привет,
Мне нужна помощь с построением графика изменения результатов теста с течением времени.
Постараюсь свести детали к необходимому минимуму. У меня практически нет гибкости с типом диаграммы, так как сообщество несколько зациклено на этой визуализации. ),
time_1 = sample(0:20, 7, replace = T),
time_2 = sample(0:20, 7, replace = T)
) %>% pivot_longer(cols = c(time_1, time_2))
хотел бы соединить края групп линиями, чтобы выделить изменение категорий с течением времени. Я надеюсь достичь этого конечного результата.
Я надеюсь достичь этого конечного результата.
Мой вопрос: как построить соединительные линии?
Спасибо
Редактировать:
Найдено:
Найдено Решение:
Библиотека (Tidyverse)
Samble_Data <- Tibble (
RUS = C (0: 6),
Time_1 = образец ( 0:20, 7, заменить = T),
time_2 = Sample(0:20, 7, заменить = T)
) %>% pivot_longer(cols = c(time_1, time_2))
bar_plot <- sample_data %>%
ggplot(aes(value, name, fill = res))+
geom_bar(stat = "identity", width = 0.6) # установить ширину, чтобы получить точные координаты y и yend ниже.
for (i in min(sample_data$res):max(sample_data$res)){
bar_plot <- bar_plot + geom_segment(aes(
x% sample_data %>) = !!i & name == "time_1") %>% pull(value) %>% sum(),
xend = sample_data %>% filter(res<= !!i & name == "time_2 ") %>% pull(value) %>% sum(),
y = 1. 3,
3,
ing = 2 - 0.3
))
}
Bar_plot
Решение было в безвкусном количестве переменных I с помощью Bang-Bang (!!) для AES (! ) для работы, которая цитирует аргументы ist.
https://ggplot2.tidyverse.org/reference/aes.html
График роста, Moose Knuckles перетасовывает исполнительную команду » стратегия
Исполнительный председатель Moose Knuckles становится генеральным директором, поскольку соучредители берут на себя новые роли Через несколько месяцев после того, как Виктор Луис был назначен исполнительным председателем монреальской компании Moose Knuckles, он взял на себя расширенную роль генерального директора бренда верхней одежды класса люкс.В результате перестановки соучредители и бывшие со-генеральные директора Ноа Стерн и Аял Твик становятся директором по маркетингу и директором по продукту соответственно.
Луис был назначен исполнительным председателем в июне после «значительных инвестиций» в компанию, в результате которых он стал операционным партнером вместе с ведущим институциональным инвестором Moose Knuckles, Cathay Capital. Бывший генеральный директор Tapestry Inc. (компании, которой принадлежат Coach, Kate Spade и Stuart Weitzman), Луис также был президентом и главным исполнительным директором Coach Japan и занимал руководящие должности в Moet-Hennessy Louis Vuitton и Baccarat.
В заявлении Twik говорится, что смена руководства позволит ему сосредоточиться на «культуре вождения, создании бренда и привлечении потребителей». И Стерн сказал, что он сможет уделять больше времени дизайну продукта, поскольку Moose Knuckles расширяет свой ассортимент в другие сезоны.
Оба лидера сохранили за собой места в совете директоров и соответствующие доли в компании.
За последние пять лет Moose Knuckles продемонстрировала годовой рост, выражающийся двузначными числами. Только в прошлом году объем прямых продаж потребителю увеличился почти трехзначным числом, а в Китае он вырос в 12 раз, несмотря на проблемы, связанные с пандемией.
Только в прошлом году объем прямых продаж потребителю увеличился почти трехзначным числом, а в Китае он вырос в 12 раз, несмотря на проблемы, связанные с пандемией.
По состоянию на июнь компания управляла 11 обычными магазинами, в том числе тремя в Китае, и планировала открыть еще десять магазинов к концу 2022 года. до 35 магазинов и всплывающих окон, а также продолжает инвестировать в свое предложение электронной коммерции.
Пункт назначения Британская Колумбия укрепляет планы преемственности генерального директораПосле года работы на этой должности Ричард Поргес официально стал президентом и главным исполнительным директором B.провинциальная туристическая ассоциация C.
Борхес изначально был назначен у руля Destination B.C. на временной основе после назначения бывшего исполнительного директора Марши Уолден генеральным директором своего национального партнера Destination Canada в августе 2020 года.
Уолден, присоединившийся к Destination B. C. в 2013 году был ее первым постоянным президентом и генеральным директором.
C. в 2013 году был ее первым постоянным президентом и генеральным директором.
Борхеса последовал за глобальным поиском, в ходе которого были рассмотрены сотни потенциальных кандидатов.
До того, как стать исполняющим обязанности президента и главного исполнительного директора, он был вице-президентом по корпоративному развитию Destination B.C. На этой должности он возглавлял отделы корпоративных коммуникаций, исследований и аналитики, управления персоналом и корпоративных услуг.
Литературный атлас: сюжеты англоязычных романов в Уэльсе
Сводка
Кейт ищет смысл в истории, оглядываясь назад на первые годы развития промышленности в долине.Джудит больше сосредоточена на настоящем, хотя вряд ли ее устраивает жизнь в дачном поселке или роль домохозяйки при неинтересном муже. Джек убегает от своего недавнего прошлого в Англии, но не хочет возвращаться домой. Сначала он поселился в двух долинах к востоку от своего родного города, найдя временную работу на сталелитейном заводе горячей прокатки. В конце концов он встречается со своим старым школьным другом в рабочих душевых и ложах с Китом и Джудом. О, это наблюдатель. Ритуал в его жесткой приверженности привычкам, он также обиженный посторонний, играет важную роль в разоблачении романа Джуда и Джека.Решения Джуда в конечном итоге сигнализируют о независимости, в то время как Джек и Кит должны решить, остаться ли им или покинуть город перед постиндустриальным будущим.
Сначала он поселился в двух долинах к востоку от своего родного города, найдя временную работу на сталелитейном заводе горячей прокатки. В конце концов он встречается со своим старым школьным другом в рабочих душевых и ложах с Китом и Джудом. О, это наблюдатель. Ритуал в его жесткой приверженности привычкам, он также обиженный посторонний, играет важную роль в разоблачении романа Джуда и Джека.Решения Джуда в конечном итоге сигнализируют о независимости, в то время как Джек и Кит должны решить, остаться ли им или покинуть город перед постиндустриальным будущим.
Главные герои
Роман рассказывается с точки зрения четырех персонажей – Кита, Джудит, Джека и О. Кит женат на Джудит. Он сталевар и краевед-любитель. Джудит коротает время домохозяйкой и в конце концов заводит роман с Джеком, который стал их жильцом. Джек вырос в Тредегаре, но жил в Англии.Он устраивается на сталелитейный завод, который постепенно закрывается. О — персонаж, который остается на периферии, топчется на месте в рутине и повторении. Он живет со своей матерью и не вписывается в культуру мачо сталелитейного завода, но внимательно наблюдает за другими.
Он живет со своей матерью и не вписывается в культуру мачо сталелитейного завода, но внимательно наблюдает за другими.
Повествование переключается между точками зрения четырех персонажей, иногда пересматривая одно и то же событие с разных точек зрения. Эффект состоит в том, чтобы нарушить возможность единой авторитетной позиции.
Настройка
Действие романа происходит на безымянном сталелитейном заводе и в соседних долинах, где живут рабочие. Хотя города не названы, действие романа происходит в основном в родном для автора Тредегаре и соседней Эббв-Вейл, где когда-то располагался один из крупнейших сталелитейных заводов в Европе.
Ключевые достопримечательности, такие как завод Sirhowy Iron Works, часы, которые стоят в центре круга в Тредегаре, и кладбище холеры над городом, подробно описаны в Shifts .
Более подробную информацию об истории Тредегара можно найти в этих видеороликах:
Сюжетные линии
Есть три сюжетные линии Shifts для изучения:
- Кит наносит на карту Железный город
- Возвращение Джека
- Перспектива Джудит
Shifts впервые опубликовано издательством Seren Books в 1988 г. Copyright © Christopher Meredith. Все права защищены. Никакая часть, включая материалы, используемые в этом Литературном атласе, не может быть воспроизведена, сохранена в поисковой системе, передана или размещена в Интернете в любое время любыми средствами, электронными, механическими, фотокопированием, записью или иным образом без предварительного письменного разрешения правообладатель.
Copyright © Christopher Meredith. Все права защищены. Никакая часть, включая материалы, используемые в этом Литературном атласе, не может быть воспроизведена, сохранена в поисковой системе, передана или размещена в Интернете в любое время любыми средствами, электронными, механическими, фотокопированием, записью или иным образом без предварительного письменного разрешения правообладатель.
построение графика смещения поселения с использованием металлоискателей. Резюме
Интернет-археол. 42. Халденби и Ричардс. Великая армия викингов и ее наследие: планирование смены поселения с использованием обнаруженных металлом находок. РезюмеДэйв Халденби и Джулиан Д. Ричардс
1. Независимый исследователь, металлоискатель и волонтер в Музее Халла и Ист-Райдинга.
2. Кафедра археологии, Королевское поместье, Йоркский университет, YO1 7EP, Великобритания. Джулиан.Ричардс@Йорк.ac.uk
Процитируйте это как : Haldenby, D. and Richards, JD 2016 Великая армия викингов и ее наследие: построение графика перемещения поселений с использованием обнаруженных металлом находок, Internet Archeology 42. https://doi.org/10.11141/ia.42.3
https://doi.org/10.11141/ia.42.3
Резюме
Исследование англо-скандинавского поселения на ферме Берроу-Хаус, Коттам, Восточный Йоркшир, в 1993–1995 годах было новаторским сотрудничеством между археологами и металлоискателями и привело к выявлению новой формы англо-скандинавской фермы.Это было также одно из первых исследований, когда-либо проводившихся на «производственном участке», названном так из-за большого количества раннесредневековых металлических изделий, обнаруженных с помощью металлодетекторов. Проект стал важной демонстрацией последствий реорганизации земельной собственности после скандинавского заселения Нортумбрии. Раскопки показали, что за отказом от английской ограды типа «Баттервик» в конце 9 века последовало строительство новой англо-скандинавской усадьбы примерно в 100 м к северу, усиленной рисунком, наблюдаемым в горизонтальной стратиграфии датированных металлических конструкций. получено в результате обнаружения металлов (Richards 1999a; 2001a).
Впоследствии поиски металла на этом участке продолжились, и количество артефактов увеличилось почти вдвое. Это привело к дальнейшим прорывам в интерпретации хронологического и пространственного развития поселения, а также к некоторым существенным изменениям в типологии и датировке раннесредневековых артефактов, что имело важные последствия для хронологии периода. Это позволяет сделать некоторые важные новые выводы о развитии поселений в Коттаме, выявляя изменяющуюся функцию поселений, а также их местонахождение:
- Есть две фазы английской деятельности, с переходом от центра поместья 8-го/9-го веков к рынку 9-го века, что повторяет аналогичные переходы, зарегистрированные в Скандинавии в таких местах, как Тиссё.Впервые такая конфигурация была обнаружена в Англии, и она проливает важный новый свет на природу «продуктивных участков».
- Есть также две фазы деятельности викингов, с начальной фазой грабежей, вероятно, связанной с действиями Великой армии викингов до основания англо-скандинавской фермы.
 Это запечатлел момент критического перехода в поведении викингов в Англии от набегов к поселенческой деятельности. Кроме того, впервые в сельской местности была обнаружена деятельность группы викингов.
Это запечатлел момент критического перехода в поведении викингов в Англии от набегов к поселенческой деятельности. Кроме того, впервые в сельской местности была обнаружена деятельность группы викингов.
Кроме того, наш проект демонстрирует, что детальное картографирование поверхностных находок, собранных с помощью металлоискателя, в настоящее время возведено в ранг основного метода исторического исследования и имеет гораздо больший потенциал, чем предполагалось до сих пор.
Одна из первых публикаций проекта Cottam (Richards 2001a) сама по себе была ранним экспериментом по публикации данных со связанной интерпретацией и архивом. Развитие электронных средств массовой информации в настоящее время позволяет все более изощренное представление данных, включая новые средства визуализации.Здесь использование Интернет-археологии показывает весь потенциал новых процедур. Интерактивная карта позволяет другим проверять наши гипотезы и самостоятельно анализировать данные. Кроме того, пересмотренная база данных находок вместе с новыми фотографиями многих раннесредневековых артефактов размещена в Службе археологических данных (Haldenby and Richards 2016).
Кроме того, пересмотренная база данных находок вместе с новыми фотографиями многих раннесредневековых артефактов размещена в Службе археологических данных (Haldenby and Richards 2016).
Перейти к содержанию статьи.
Характеристики
- Ключевые слова: англо-саксонский, англо-скандинавский, раннесредневековый, викинг, артефакты, поселение, ландшафт, металлоискатель
- Создание цифрового архива и этой публикации было щедро поддержано кафедрой археологии Йоркского университета.
В этой статье исследуются способы развития коммуникации археологии для различных аудиторий, что является одной из целей проекта NEARCH в рамках программы ЕС «Культура».
СЛЕДУЮЩИЙ РЕЗЮМЕ СОДЕРЖАНИЕ ПРОБЛЕМА ДОМОЙ
.

 у = х2 + 1 3. у = (х – 3)25. у = (х – 4)2 – 2
у = х2 + 1 3. у = (х – 3)25. у = (х – 4)2 – 2 Выполнив построение, ученик имеет возможность исследовать условия существования решения и зависимость числа решений от данных задачи.
Выполнив построение, ученик имеет возможность исследовать условия существования решения и зависимость числа решений от данных задачи. Особенно интересны в этом смысле построения на изображениях стереометрических фигур. Эти изображения снабжены механизмом, позволяющим изменять ракурс – вращать данную фигуру. Таким образом, по ходу работы ученик имеет возможность как бы выйти в пространство. Задания, которые при этом можно ставить, весьма разнообразны; в частности, большую популярность среди учителей завоевали задачи этого типа на построение сечений многогранников.
Особенно интересны в этом смысле построения на изображениях стереометрических фигур. Эти изображения снабжены механизмом, позволяющим изменять ракурс – вращать данную фигуру. Таким образом, по ходу работы ученик имеет возможность как бы выйти в пространство. Задания, которые при этом можно ставить, весьма разнообразны; в частности, большую популярность среди учителей завоевали задачи этого типа на построение сечений многогранников. Для таких преобразований в «Математическом конструкторе» предусмотрены специальные команды. Приводимое задание построено на их использовании.
Для таких преобразований в «Математическом конструкторе» предусмотрены специальные команды. Приводимое задание построено на их использовании.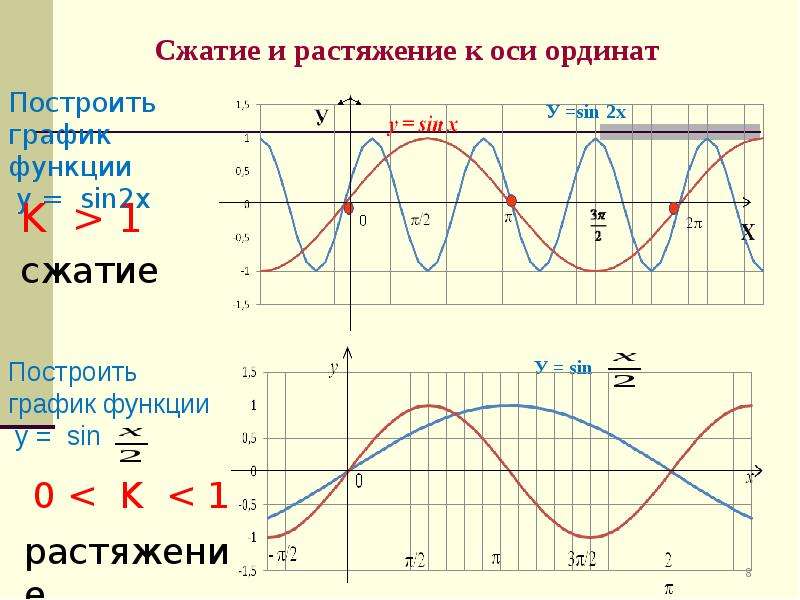 Это запечатлел момент критического перехода в поведении викингов в Англии от набегов к поселенческой деятельности. Кроме того, впервые в сельской местности была обнаружена деятельность группы викингов.
Это запечатлел момент критического перехода в поведении викингов в Англии от набегов к поселенческой деятельности. Кроме того, впервые в сельской местности была обнаружена деятельность группы викингов.