Область определения функции

Каждая функция имеет свою собственную область определения. Целью этого материала является объяснение этого понятия и описание способов ее вычисления. Сначала мы введем основное определение, а потом на конкретных примерах покажем, как выглядит область определения основных элементарных функций (степенной, постоянной и др.) Разбирать случаи с более сложными функциями мы пока не будем.

В рамках данной статьи мы рассмотрим область определения функций, включающих в себя только одну переменную.

Понятие и обозначение области определения функции

Самое простое определение этого понятия дается в учебниках тогда, когда впервые вводится понятие функции как таковой. На этом этапе термином «область определения» обозначают множество всех возможных значений аргумента.

По мере углубления знаний о функциях определение сужается и усложняется. Так, в одном из учебников можно встретить следующую формулировку:

Определение 1

Числовая функция с областью определения

D – это соответствие значений переменной x некоторому числу y, которое находится в зависимых отношениях с x.

Используя это определение, охарактеризуем нужное нам понятие более четко:

Определение 2

Областью определения функции называется множество значений аргумента, на котором можно задать эту функцию.

Теперь рассмотрим, как правильно обозначать ее на письме. Ранее мы договорились, что для записи самих функций будем использовать маленькие латинские буквы, например, g, f и др. Чтобы указать на наличие функциональной зависимости, используется запись вида y=f(x). Таким образом, функция f представляет собой некоторое правило, согласно которому каждому значению переменной x можно поставить в соответствие значение другой переменной y, которая находится в зависимых отношениях от x.

Пример 1

Возьмем для примера функцию y=x2^. Можно записать ее как f(x)=x2.  Это функция возведения в квадрат, которая ставит в соответствие каждому значению переменной

x=x0 некоторое значение y=x02^. Так, если мы возьмем число 3

Область определения функции — Википедия

Область определения  — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.

Если на множестве X{\displaystyle X} задана функция, которая отображает множество X{\displaystyle X} в другое множество, то множество X{\displaystyle X} называется областью определения или областью задания функции.

Более формально, если задана функция f{\displaystyle f}, которая отображает множество X{\displaystyle X} в Y{\displaystyle Y}, то есть: f:X→Y{\displaystyle f\colon X\to Y}, то множество X{\displaystyle X} называется областью определения^[1] или областью задания^[2] функции f{\displaystyle f} и обозначается D(f){\displaystyle D(f)} или domf{\displaystyle \mathrm {dom} \,f} (от англ. domain — «область»).

Иногда рассматриваются и функции, определённые на подмножестве D{\displaystyle D} некоторого множества X{\displaystyle X}. В этом случае множество X{\displaystyle X} называется

областью отправления функции f{\displaystyle f}^[3].

Наиболее наглядные примеры областей определения доставляют числовые функции. Мера и функционал также доставляют важные в приложениях виды областей определения.

Числовые функции[править | править код]

Числовые функции — это функции, относящиеся к следующим двум классам:

• вещественнозначные функции вещественного переменного — это функции вида f:R→R{\displaystyle f\colon \mathbb {R} \to \mathbb {R} };
• а также комплекснозначные функции комплексного переменного вида f:C→C{\displaystyle f\colon \mathbb {C} \to \mathbb {C} },

где R{\displaystyle \mathbb {R} } и C{\displaystyle \mathbb {C} } — множества вещественных и комплексных чисел соответственно.

Тождественное отображение[править | править код]

Область определения функции f(x)=x{\displaystyle f(x)=x} совпадает с областью отправления (R{\displaystyle \mathbb {R} } или C{\displaystyle \mathbb {C} }).

Гармоническая функция[править | править код]

Область определения функции f(x)=1/x{\displaystyle f(x)=1/x} представляет собой комплексную плоскость без нуля:

domf=C∖{0}{\displaystyle \mathrm {dom} \,f=\mathbb {C} \setminus \{0\}},

поскольку формула не задаёт значение функции в нуле каким-нибудь числом, что требуется в формулировке понятия функции. Область отправления представляет собой всю комплексную плоскость.

Дробно-рациональные функции[править | править код]

Область определения функции вида

f(x)=a0+a1x+⋯+amxmb0+b1x+⋯+bnxn{\displaystyle f(x)={\frac {a_{0}+a_{1}x+\dots +a_{m}x^{m}}{b_{0}+b_{1}x+\dots +b_{n}x^{n}}}}

представляет собой вещественную прямую или комплексную плоскость за исключением конечного числа точек, которые являются решениями уравнения

b0+b1x+⋯+bnxn=0{\displaystyle b_{0}+b_{1}x+\dots +b_{n}x^{n}=0}.

Эти точки называются полюсами функции f{\displaystyle f}.

Так, например, f(x)=2xx2−4{\displaystyle f(x)={\frac {2x}{x^{2}-4}}} определен на всех точках, где знаменатель не обращается в ноль, то есть, где x2−4≠0{\displaystyle x^{2}-4\neq 0}. Таким образом domf{\displaystyle \mathrm {dom} \,f} является множеством всех действительных (или комплексных) чисел кроме 2 и -2.

Мера[править | править код]

Если каждая точка области определения функции — это некоторое множество, например, подмножество заданного множества, то говорят, задана функция множества.

Мера — пример такой функции, где в качестве области определения функции (меры) выступает некоторая совокупность подмножеств заданного множества, являющееся, например, кольцом или полукольцом множеств.

Например, определённый интеграл представляет собой функцию ориентированного промежутка.

Функционал[править | править код]

Пусть F={f∣f:X→R}{\displaystyle \mathbb {F} =\{f\mid f\colon X\to \mathbb {R} \}} — семейство отображений из множества X{\displaystyle X} в множество R{\displaystyle \mathbb {R} }. Тогда можно определить отображение вида F:F→R{\displaystyle F\colon \mathbb {F} \to \mathbb {R} }. Такое отображение называется функционалом.

Если, например, фиксировать некоторую точку x0∈ X{\displaystyle x_{0}\in ~X}, то можно определить функцию F(f)=f(x0){\displaystyle F(f)=f(x_{0})}, которая принимает в «точке» f{\displaystyle f} то же значение, что и сама функция f{\displaystyle f} в точке x0{\displaystyle x_{0}}.

• Функция, математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
• Клейн Ф. Общее понятие функции. В кн.: Элементарная математика с точки зрения высшей. Т.1. М.-Л., 1933
• И. А. Лавров, Л. Л. Максимова. Часть I. Теория множеств // Задачи по теории множеств, математической логике и теории алгоритмов. — 3-е изд.. — М.: Физматлит, 1995. — С. 13 — 21. — 256 с. — ISBN 5-02-014844-X.
• А. Н. Колмогоров, С. В. Фомин. Глава 1.. Элементы теории множеств // Элементы теории функций и функционального анализа. — 3-е изд.. — М.: Наука, 1972. — С. 14 — 18. — 256 с.
• Дж. Л. Келли. Глава 0. Предварительные сведения // Общая топология. — 2-е изд.. — М.: Наука, 1981. — С. 19 — 27. — 423 с.
• В. А. Зорич. Глава I. Некоторые общематематические понятия и обозначения. § 3. Функция // Математический анализ, часть I. — М.: Наука, 1981. — С. 23 — 36. — 544 с.
• Г. Е. Шилов. Глава 2. Элементы теории множеств. § 2.8. Общее понятие функции. График // Математический анализ (функции одного переменного). — М.: Наука, 1969. — С. 65 — 69. — 528 с.
• А. Н. Колмогоров. «Что такое функция» // «Квант». — М.: «Наука», 1970. — Вып. 1. — С. 27-36. — ISSN 0130-2221.

Область определения функции, теория и примеры

1) Функцию можно представить в виде разности двух функций

   

Функция является многочленом и её областью определения есть множество всех действительных чисел .

Функция является дробно-рациональной. Найдем значения , которые обнуляют знаменатель

   

Таким образом, область определения функции находится из системы

   

2) Для нахождения области определения решим неравенство

   

Разложим на множители левую часть этого неравенства. Для этого решим уравнение . По теореме Виета: , отсюда . Таким образом, неравенство примет вид

   

Обозначим найденные корни на числовой оси и определим знак неравенства на полученных интервалах.

Таким образом, .

3) Функция представляет собой дробно-рациональную функцию, в числителе которой многочлен. Область определения многочлена есть множество действительных чисел . В знаменателе корень, область его определения находим из системы

   

Таким образом, .

Область определения функции

Сегодня потренируемся в отыскании области определения выражения и функции.

Когда отыскивают область определения функции, то часто она совпадает с областью определения выражения, задающего функцию: такая область определения называется естественной. Но бывает и так, что условия задачи накладывают особые ограничения: например, естественная область определения функции от (-8) до 8, но аргумент этой функции – время (или вес). Понятно тогда, что время (как и вес) не может быть отрицательной величиной и тогда естественная область определения  такой функции сужается до промежутка (0; 8).
При отыскании области определения функции надо помнить о следующих ограничениях:
1. При извлечении корня четной степени подкоренное выражение обязано быть неотрицательным (что не запрещает ему быть равным нулю). 2. Знаменатель дроби не может быть равным нулю. 3. Выражение, стоящее под знаком логарифма, не может быть отрицательным или равняться нулю. 4. Выражение, стоящее под знаком арксинуса или арккосинуса, не может превышать 1 по модулю
Также надо помнить, что область определения всегда нужно искать для исходной функции, до каких-либо преобразований.

Например, функции  и  имеют разные области определения: для первой это – вся числовая ось, а вторая не определена в точке 0. То же относится к функциям  и  –  у первой область определения – также вся числовая ось, а у второй – [)

1. Найдите область определения выражения:

Перепишем выражение:

Так как выражение стоит под корнем четной степени, значение его не должно быть отрицательным:

Дробь положительна, если числитель и знаменатель ее одновременно положительны или отрицательны. У нас в числителе положительное число, поэтому знаменатель неотрицателен. Кроме того, знаменатель не может быть равен нулю, поэтому неравенство становится таким:

Получили квадратное неравенство. Находим корни квадратного уравнения, чтобы выяснить точки перемены знака:




Наносим полученные точки на координатную прямую и расставляем знаки. Так как  (старший член) – со знаком «плюс», то ветви параболы направлены вверх, на самом правом отрезке ставим знак «плюс», а далее знаки меняются. Точки выкалываем, поскольку неравенство строгое:

Ответ: – круглые скобки показывают, что концы интервалов не входят в ответ.
2. Найдите область определения выражения:

Так как выражение стоит под корнем четной степени, значение его не должно быть отрицательным:

Получили квадратное неравенство. Находим корни квадратного уравнения, чтобы выяснить точки перемены знака:

Наносим полученные точки на координатную прямую и расставляем знаки. Так как  (старший член) в исходном неравенстве – со знаком «минус», то ветви параболы направлены вниз, на самом правом отрезке ставим знак «минус», а далее знаки меняются. Точки закрашиваем, поскольку неравенство нестрогое.
Ответ: – квадратные скобки показывают, что концы отрезка  входят в ответ.

3. Найдите область определения функции:

Очевидно, что область определения функции будет совпадать с областью определения выражения  – ищем естественную  область определения функции.  Данное выражение имеет смысл только при – задача сводится к решению этого неравенства. Определяем точки перемены знака:


Изображаем полученные точки на числовой оси, ставим знаки:

Точки закрашены, концы интервалов входят в решение. Тогда область определения функции: (] [)
4. Найдите область определения функции:
Очевидно, что область определения функции будет совпадать с областью определения выражения  – ищем естественную  область определения функции.  Данное выражение имеет смысл только при ; – задача сводится к решению системы неравенств. Определяем точки перемены знака:

Изображаем полученные точки на числовой оси:

Решение системы неравенств:  
Область определения функции: [ )
5. Найдите область определения функции:
Очевидно, что область определения функции будет совпадать с областью определения выражения
– ищем естественную  область определения функции.  Данное выражение имеет смысл только при – задача сводится к решению неравенства.
Рассмотрим два случая:


Решение:
Или


Решение:

Область определения функции: [)
6. Найти область определения функции:

Решение:

Ответ:

7. Найти область определения функции:
Решение:






Ответ:
8. Найти область определения функции:

Решение:


Ответ:

Как найти область определения функции

Чтобы находить области определения распространённых функций, на этом уроке порешаем уравнения и неравенства с одной переменной.

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

А что же такое область определения функции? Взглянем на график функции на рисунке. Каждой точке графика функции соответствует определённое значение «икса» — аргумента функции и определённое значение «игрека» — самой функции. От аргумента — «икса» — вычисляется «игрек» — значения функции. Область определения функции — это множества всех значений «икса», для которых существует, то есть может быть вычислен «игрек» — значение функции. Иначе говоря, множество значений аргумента, на котором «функция работает». Большая часть функций задаётся формулами. Поэтому область определения функции — это также наибольшее множество, на котором формула имеет смысл.

На рисунке изображён график функции . Знаменатель дроби не может быть равен нулю, так как на нуль делить нельзя. Поэтому, приравнивая знаменатель нулю, получаем значение, не входящее в область определения функции: 1. А область определения функции — это все значения «икса» от минус бесконечности до единицы и от единицы до плюс бесконечности. Это хорошо видно на графике

Пример 0. Как найти область определения функции игрек равен квадратному корню из икса минус пять (подкоренное выражение икс минус пять) ()? Нужно всего лишь решить неравенство

x — 5 ≥ 0,

так как для того, чтобы мы получили действительное значение игрека, подкоренное выражение должно быть больше или равно нулю. Получаем решение: область определения функции — все значения икса больше или равно пяти (или икс принадлежит промежутку от пяти включительно до плюс бесконечности).

На чертеже сверху — фрагмент числовой оси. На ней область опредения рассмотренной функции заштрихована, при этом в «плюсовом» направлении штриховка продолжается бесконечно вместе с самой осью.

Постоянная (константа) определена при любых действительных значениях x, следовательно, данная функция определена на всём множестве R действительных чисел. Это можно записать и так: областью определения данной функции является вся числовая прямая ]- ∞; + ∞[.

Пример 1. Найти область определения функции y = 2.

Решение. Область определения функции не указана, значит, в силу выше приведённого определения имеется в виду естественная область определения. Выражение f(x) = 2 определено при любых действительных значениях x, следовательно, данная функция определена на всём множестве R действительных чисел.

Поэтому на чертеже сверху числовая прямая заштрихована на всём протяжении от минус бесконечности до плюс бесконечности.

В случае, когда функция задана формулой 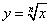и n — натуральное число:

Пример 2. Найти область определения функции .

Решение. Как следует из определения, корень чётной степени имеет смысл, если подкоренное выражение неотрицательно, то есть, если — 1 ≤ x ≤ 1. Следовательно, область определения данной функции — [- 1; 1].

Заштрихованная область числовой прямой на чертеже сверху — это область определения данной функции.

Область определения степенной функции с целым показателем степени

В случае, когда функция задана формулой :

если a — положительное, то областью определения функции является множество всех действительных чисел, то есть ]- ∞; + ∞[;

если a — отрицательное, то областью определения функции является множество ]- ∞; 0[ ∪ ]0 ;+ ∞[, то есть вся числовая прямая за исключением нуля.

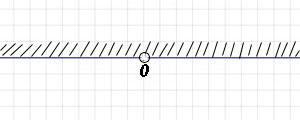
На соответствующем чертеже сверху вся числовая прямая заштрихована, а точка, соответствующая нулю, выколота (она не входит в область определения функции).

Пример 3. Найти область определения функции .

Решение. Первое слагаемое целой степенью икса, равной 3, а степень икса во втором слагаемом можно представить в виде единицы — так же целого числа. Следовательно, область определения данной функции — вся числовая прямая, то есть ]- ∞; + ∞[.

Область определения степенной функции с дробным показателем степени

В случае, когда функция задана формулой :

если — положительное, то областью определения функции является множество [0; + ∞[;

если — отрицательное, то областью определения функции является множество ]0; + ∞[.

Пример 4. Найти область определения функции .

Решение. Оба слагаемых в выражении функции — степенные функции с положительными дробными показателями степеней. Следовательно, область определения данной функции — множество [0; + ∞[.

На чертеже сверху заштрихована часть числовой прямой от нуля (включительно) и больше, причём штриховка продолжается вместе с самой прямой до плюс бесконечности.

Пример 5. Найти область определения функции

.

Решение. Дробный показатель степени данной степенной функции — отрицательный. Поэтому решим строгое неравенство, когда квадратный трёхчлен в скобках строго больше нуля::

.

Дикриминант получился отрицательный. Следовательно сопряжённое неравенству квадратное уравнение не имеет корней. А это значит, что квадратный трёхчлен ни при каких значениях «икса» не равен нулю. Таким образом, область определения данной функции — вся числовая ось, или, что то же самое — множество R действительных чисел, или, что то же самое — ]- ∞; + ∞[.

Область определения показательной функции

В случае, когда функция задана формулой , областью определения функции является вся числовая прямая, то есть ]- ∞; + ∞[.

Область определения логарифмической функции

Логарифмическая функция определена при условии, если её аргумент положителен, то есть, областью её определения является множество ]0; + ∞[.

Найти область определения функции самостоятельно, а затем посмотреть решение

---

Область определения функции y = cos(x) — так же множество R действительных чисел.

Область определения функции y = tg(x) — множество R действительных чисел, кроме чисел .

Область определения функции y = ctg(x) — множество R действительных чисел, кроме чисел .

Пример 8. Найти область определения функции

.

Решение. Внешняя функция — десятичный логарифм и на область её определения распространяются условия области определения логарифмической функции вообще. То есть, её аргумент должен быть положительным. Аргумент здесь — синус «икса». Поворачивая воображаемый циркуль по окружности, видим, что условие sin x > 0 нарушается при «иксе» равным нулю, «пи», два, умноженном на «пи» и вообще равным произведению числа «пи» и любого чётного или нечётного целого числа.

Таким образом, область определения данной функции задаётся выражением

,

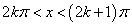где k — целое число.

Область определения обратных тригонометрических функций

Область определения функции y = arcsin(x) — множество [-1; 1].

Область определения функции y = arccos(x) — так же множество [-1; 1].

Область определения функции y = arctg(x) — множество R действительных чисел.

Область определения функции y = arcctg(x) — так же множество R действительных чисел.

Пример 9. Найти область определения функции .

Решение. Решим неравенство:

Таким образом, получаем область определения данной функции — отрезок [- 4; 4].

Пример 10. Найти область определения функции .

Решение. Решим два неравенства:

Решение первого неравенства:

Решение второго неравенства:

Таким образом, получаем область определения данной функции — отрезок [0; 1].

Если функция задана дробным выражением, в котором переменная находится в знаменателе дроби, то областью определения функции является множество R действительных чисел, кроме таких x, при которых знаменатель дроби обращается в нуль.

Пример 11. Найти область определения функции .

Решение. Решая равенство нулю знаменателя дроби, находим область определения данной функции — множество ]- ∞; — 2[ ∪ ]- 2 ;+ ∞[.

Пример 12. Найти область определения функции .

Решение. Решим уравнение:

Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 1[ ∪ ]1 ;+ ∞[.

Пример 13. Найти область определения функции .

Решение. Область определения первого слагаемого — данной функции — множество R действительных чисел, второго слагаемого — все действительные числа, кроме -2 и 2 (получили, решая равенство нулю знаменателя, как в предыдущем примере). В этом случае область определения функции должна удовлетворять условиями определения обоих слагаемых. Следовательно, область определения данной функции — все x, кроме -2 и 2.

Пример 14. Найти область определения функции .

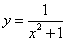Решение. Решим уравнение:

Уравнение не имеет действительных корней. Но функция определена только на действительных числах. Таким образом, получаем область определения данной функции — вся числовая прямая или, что то же самое — множество R действительных чисел или, что то же самое — ]- ∞; + ∞[.

То есть, какое бы число мы не подставляли вместо «икса», знаменатель никогда не будет равен нулю.

Пример 15. Найти область определения функции .

Решение. Решим уравнение:

Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 0[ ∪ ]0 ; 1[ ∪ ]1 ;+ ∞[.

Пример 16. Найти область определения функции .

Решение. Кроме того, что знаменатель не может быть равным нулю, ещё и выражение под корнем не может быть отрицательным. Сначала решим уравнение:

График квадратичной функции под корнем представляет собой параболу, ветви которой направлены вверх. Как следует из решения квадратного уравнения, парабола пересекает ось Ox в точках 1 и 2. Между этими точками линия параболы находится ниже оси Ox, следовательно значения квадратичной функции между этими точками отрицательное. Таким образом, исходная функция не определена на отрезке [1; 2].

Найти область определения функции самостоятельно, а затем посмотреть решение

---

Если функция задана формулой вида y = kx + b, то область определения функции — множество R действительных чисел.

Весь раздел «Исследование функций»