Функция обратной пропорциональности и её свойства

I. Обратной пропорциональностью называется функция, заданная формулой где k ≠ 0.

Графиком обратной пропорциональности является гипербола, расположенная в I и III четверти, если k>0; во II и IV четверти, если k<0.

Свойства обратной пропорциональности:  
1) Область определения функции — множество всех действительных чисел, кроме нуля:

 D(y)=(−; 0)(0; +).

2) Область значений функции – множество всех действительных чисел, кроме нуля:

Е(y)=(−; 0)(0; +).
3) , Функция   является нечётной, её график симметричен относительно начала координат, т.е. точки (0;0).
4) При k > 0 функция убывает, а при k < 0 возрастает на всей области определения.

Для точного построения графика, например, функции , возьмём несколько значений х и для каждого вычислим значение у.

Так как график функции симметричен относительно начала координат, то точки в III четверти будут иметь противоположные координаты.

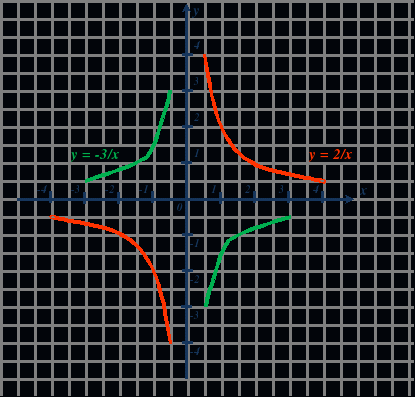
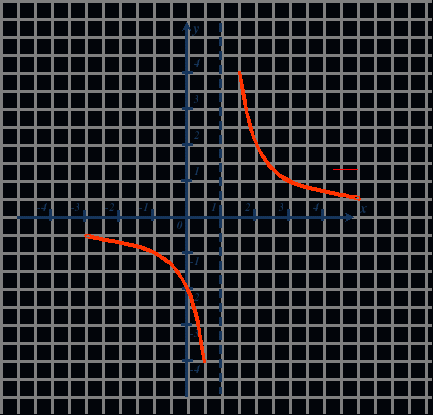
II. Обратная пропорциональность где k ≠ 0.

Графиком данной функции является гипербола, которая получается из графика функции смещением вдоль оси Ох на т единиц вправо, если т > 0, и влево, если т < 0. Чтобы построить график этой функции, проводим дополнительную прямую х = т, параллельную оси Оу, затем строим график функции относительно получившихся осей.

Свойства:  
1) Область определения функции — множество всех действительных чисел, кроме х = т:

 D(y)=(−; т)(т; +).

2) Область значений функции – множество всех действительных чисел, кроме нуля:

Е(y)=(−; 0)(0; +).
3) , значит, функция не является ни чётной, ни нечётной, её график не симметричен относительно оси Оу. и не симметричен относительно начала координат.
4) При k > 0 функция убывает, а при k < 0 возрастает на всей области определения.

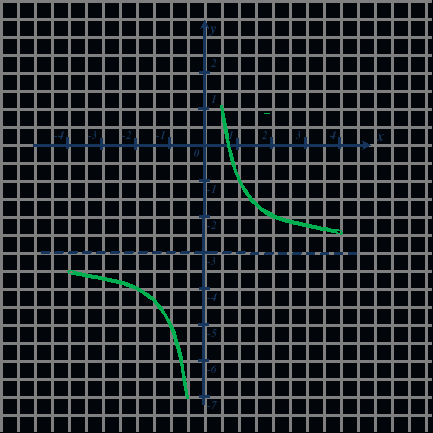
III. Обратная пропорциональность где k ≠ 0.

Графиком данной функции является гипербола, которая получается из графика функции смещением вдоль оси Оу на п единиц вверх, если п > 0, и вниз, если п < 0. Чтобы построить график этой функции, проводим дополнительную прямую у = п, параллельную оси Ох, затем строим график функции относительно получившихся осей.

Свойства:  
1) Область определения функции — множество всех действительных чисел, кроме нуля:

 D(y)=(−; 0)(0; +).

2) Область значений функции – множество всех действительных чисел, кроме у = п:

Е(y)=(−; п)(п; +).
3) , значит, функция не является ни чётной, ни нечётной, её график не симметричен относительно оси Оу. и не симметричен относительно начала координат.
4) При k > 0 функция убывает, а при k < 0 возрастает на всей области определения.

IV. Обратная пропорциональность где k ≠ 0.

Графиком данной функции является гипербола, которая получается из графика функции смещением вдоль оси Ох на т единиц вправо, если т > 0, и влево, если т < 0, и вдоль оси Оу на п единиц вверх, если п > 0, и вниз, если п < 0. Чтобы построить график этой функции, проводим дополнительные прямые х = т, параллельную оси Оу , и у = п, параллельную оси Ох, затем строим график функции относительно получившихся осей.

Свойства:  
1) Область определения функции — множество всех действительных чисел, кроме х = т:

 D(y)=(−; т)(т; +).

2) Область значений функции – множество всех действительных чисел, кроме у = п:

Е(y)=(−; п)(п; +).
3) , значит, функция не является ни чётной, ни нечётной, её график не симметричен относительно оси Оу. и не симметричен относительно начала координат.
4) При k > 0 функция убывает, а при k < 0 возрастает на всей области определения.

infourok.ru

Обратная пропорциональность

Представим, что у нас есть тело, движущееся равномерно от города А к городу В. Время, которое наше тело затрачивает на прохождение указанного пути зависит от скорости движения. Предположим, что расстояние между А и В равно 120 м, v – это скорость движения (м/с), а t – это время движения (с). Тогда получим, что
t = 120/v.

Подставим вместо v несколько значений и получим t:

если v = 5, то t = 120/5 = 24; если v = 10, то t = 120/10 = 12;
если v = 20, то t = 120/20 = 6.

Получается, что каждому значению переменной v (v > 0) соответствует единственное значение t. Формулой t = 120/v, где v > 0, задается функция.

Обратной пропорциональностью называется функция, которую можно задать формулой вида у = k/х, где k – не равное нулю число.

Относительно переменной у говорится, что она обратно пропорциональна переменной х.

Т.к. выражение k/х при любом значении х, кроме 0, имеет смысл, то областью определения функции, задаваемой формулой у = k/х, может служить множество всех чисел, отличных от нуля, или какое-нибудь его подмножество.

Из формулы у = k/х следует, что ху = k. Верно и обратное: если ху = k (k ≠ 0), то у = k/х. Логично, что, чтобы выяснить, является ли обратной пропорциональностью функция х – у, необходимо сравнить произведения ху для всех соответственных значений х и у. Если эти произведения равны одному и тому же числу k

, где k ≠ 0, то функция f является обратной пропорциональностью.

Определим, является ли обратной пропорциональностью функция m – n, заданная значениями:

если m = 1, то n = 15;
если m = 2, то n = 7,5;
если m = 3, то n = 5;
если m = 5, то n = 3;
если m = 6, то n = 2,5;
если m = 10, то n = 1,5;
если m = 15, то n = 1.

Для каждой пары (m; n) соответственных значений m и n найдем произведение mn:

если m = 1, n = 15, то mn = 15;
если m = 2, n = 7,5, то mn = 15;
если m = 3, n = 5, то mn = 15;
если m = 5, n = 3, то mn = 15;
если m = 6, n = 2,5, то mn = 15;
если m = 10, n = 1,5, то mn = 15;
если m = 15, n = 1, то mn = 15.

В результате получаем, что найденные произведения равны одному и тому же числу

15. Следовательно, функция f – обратная пропорциональность.

Решим задачу.

Пусть а – основание прямоугольника (см), b – его высота (см). Если площадь прямоугольника остается постоянной, то с изменением длины его основания должна изменяться и его высота. Является ли зависимость переменной b от переменной а обратной пропорциональностью?

Для любой пары соответственных значений переменных а и b произведение аb равно одному и тому же числу, выражающему площадь прямоугольника в см². Следовательно, зависимость b от а – обратная пропорциональность.

Вернемся к примеру с равномерным движением тела из города А в город В. Возьмем два произвольных значения переменной v: v₁ = 5 и v₂ = 6. Тогда соответствующие им значения переменной

t: t₁ = 24 и t₂ = 20.

Найдем частное v₁/v₂и частное t₁/t₂:

v₁/v₂ = 5/6;     t₁/t₂ = 6/5.

Отметим, что частное v₁/v₂ равно числу, обратному частному t₁/t₂. К такому же выводу мы придем, если выберем иные значения переменных.

Т.о., если функция х → у – обратная пропорциональность и (х₁; у₁), (х₂; у₂) – пары соответственных значений переменных х и у, то х₁/х₂ = у₂/у₁.

Докажем это. Из формулы у = k/х имеем, что у₁ = k/х₁, у₂ = k/х₂, причем у₁ ≠ 0, у₂ ≠ 0. Отсюда

у₂

/у₁ = (k/х₂) / (k/х₁) = (k/х₂) ∙ ( х₁/ k) = х₁/х₂.

Если значения переменных х и у – это положительные числа, то рассмотренное свойство обратной пропорциональности можно определить так:

с увеличением значения х в несколько раз соответствующее значение у уменьшается во столько же раз; аналогично: с уменьшением значения х в несколько раз соответствующее значение у увеличивается во столько же раз.

Применим установленное свойство к решению задач.

Задача.

Велосипедист, двигаясь со скоростью 10 км/ч, проехал расстояние от города А до города В за 6 ч. Сколько времени затратит велосипедист на обратный путь, если будет двигаться со скоростью 12 км/ч?

Решение.

Пусть на обратный путь велосипедист затратит х ч. Т.к. время, необходимое для прохождения одного и того же расстояния, обратно пропорционально скорости движения, то х/6 = 10/12. Отсюда 12х = 60, х = 5.

Ответ: велосипедисту понадобится 5 ч.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

22)Прямая и обратная пропорциональность

Две взаимно зависимые величины называются пропорциональными, если отношение их величин остается неизменным. С увеличением (уменьшением) одной величины в несколько раз другая величина увеличивается (уменьшается) во столько же раз.

Определение. Частное величин, составляющих пропорцию, называется коэффициентом пропорциональности. Коэффициент пропорциональности обозначается маленькой латинской буквой k.

Правило. Если две величины связаны между собой так, что увеличение (уменьшение) одной пропорционально (во столько же раз) увеличивает (уменьшает) и другую величину, то такие величины прямо пропорциональны.

Схематически прямую пропорциональность можно записать гак: «больше — больше» или «меньше — меньше». Примерами прямой пропорциональности служит зависимость скорости от пройденного пути, стоимости от веса товара.

Правило. Если две величины связаны между собой так, что увеличение (уменьшение) одной пропорционально (во столько же раз) уменьшает (увеличивает) и другую величину, то такие величины обратно пропорциональны.

Схематически обратную пропорциональность можно записать так: «больше — меньше» или «меньше — больше». Пример обратной пропорциональности: грузоподъемность одной машины и количество машин при перевозке одинакового объема груза.

23. Квадратичная функция и её свойства

Квадратичной функцией называется функция. которую можнозадать формулой вида y = ax2 + bx + c, где x – независимая переменная, a, b и с – некоторые числа, причем а 0. График – парабола. Свойства:

1) Областью определения функции является множество всех действительных чисел, т.е.

2) Множеством значений функции является промежуток

3) Значение функции y=0 является наименьшим, а наибольшего значения функция не имеет.

4) Функция является четной, график симметричен относительно оси Оу.

5) Функция непериодическая.

6)Парабола имеет с осями координат единственную общую точку (0;0) — начало координат.

7) Значение аргумента x=0 является нулем функции.

8) На промежутке функция убывающая, а на промежутке — возрастающая.

9) Функция принимает положительные значения на множестве , т.е. все точки параболы, кроме начала координат.

24. Основные элементарные функции и их графики

Пропорциональные величины. Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением:

y = k x ,где k — постоянная величина ( коэффициент пропорциональности ).

2.Линейная функция. Если переменные y и x связаны уравнением 1-ой степени:

A x + B y = C ,

3.Обратная пропорциональность. y = k / x где k — постоянная величина.

График обратной пропорциональности – гипербола

4. Квадратичная функция. Это функция: y = ax 2 + bx + c, где a, b, c — постоянные, a не равна 0. График — квадратная парабола.

5. Степенная функция. Это функция: y = axn, где a, n – постоянные. Её график — прямая линия, параллельная оси Х, исключая начало координат

6.Показательная функция. Функция y = ax

7. Логарифмическая функция. Функция y = log a x,

8.Тригонометрические функции. При построении тригонометрических функций мы используем радианную меру измерения углов. Тогда функция y = sin x представляется графиком ( рис.19 ). Эта кривая называется синусоидой.

9.Обратные тригонометрические функции. Графики, полученные поворотом графиков тригонометрических функций вокруг биссектрисы 1-го координатного угла.

studfile.net

Функция обратной пропорциональности и её свойства

I. Обратной пропорциональностью называется функция, заданная формулой где k ≠ 0.

Графиком обратной пропорциональности является гипербола, расположенная в I и III четверти, если k0; во II и IV четверти, если k

Свойства обратной пропорциональности:  
1) Область определения функции — множество всех действительных чисел, кроме нуля:

 D(y)=(−; 0)(0; +).

2) Область значений функции – множество всех действительных чисел, кроме нуля:

Е(y)=(−; 0)(0; +).
3) , Функция   является нечётной, её график симметричен относительно начала координат, т.е. точки (0;0).
4) При k  0 функция убывает, а при k 

Для точного построения графика, например, функции , возьмём несколько значений х и для каждого вычислим значение у.

х	0,5	1	2	4
у	4	2	1	0,5

Так как график функции симметричен относительно начала координат, то точки в III четверти будут иметь противоположные координаты.

II. Обратная пропорциональность где k ≠ 0.

Графиком данной функции является гипербола, которая получается из графика функции смещением вдоль оси Ох на т единиц вправо, если т 0, и влево, если т х = т, параллельную оси Оу, затем строим график функции относительно получившихся осей.

Свойства:  
1) Область определения функции — множество всех действительных чисел, кроме х = т:

 D(y)=(−; т)(т; +).

2) Область значений функции – множество всех действительных чисел, кроме нуля:

Е(y)=(−; 0)(0; +).
3) , значит, функция не является ни чётной, ни нечётной, её график не симметричен относительно оси Оу. и не симметричен относительно начала координат.
4) При k  0 функция убывает, а при k 

III. Обратная пропорциональность где k ≠ 0.

Графиком данной функции является гипербола, которая получается из графика функции смещением вдоль оси Оу на п единиц вверх, если п 0, и вниз, если п у = п, параллельную оси Ох, затем строим график функции относительно получившихся осей.

Свойства:  
1) Область определения функции — множество всех действительных чисел, кроме нуля:

 D(y)=(−; 0)(0; +).

2) Область значений функции – множество всех действительных чисел, кроме у = п:

Е(y)=(−; п)(п; +).
3) , значит, функция не является ни чётной, ни нечётной, её график не симметричен относительно оси Оу. и не симметричен относительно начала координат.
4) При k  0 функция убывает, а при k 

IV. Обратная пропорциональность где k ≠ 0.

Графиком данной функции является гипербола, которая получается из графика функции смещением вдоль оси Ох на т единиц вправо, если т 0, и влево, если т Оу на п единиц вверх, если п 0, и вниз, если п х = т, параллельную оси Оу , и у = п, параллельную оси Ох, затем строим график функции относительно получившихся осей.

Свойства:  
1) Область определения функции — множество всех действительных чисел, кроме х = т:

 D(y)=(−; т)(т; +).

2) Область значений функции – множество всех действительных чисел, кроме у = п:

Е(y)=(−; п)(п; +).
3) , значит, функция не является ни чётной, ни нечётной, её график не симметричен относительно оси Оу. и не симметричен относительно начала координат.
4) При k  0 функция убывает, а при k 

multiurok.ru

Урок «Обратная пропорциональность», алгебра 8 класс

Общеобразовательная школа І-ІІІ ступеней №1

отдела образования города Кировское

Урок по теме: «Функция у = k/x, ее свойства и график»

Алгебра, 8 класс

Разработала учитель высшей категории

Зуева Л.В.

Кировское 2015

Тема урока: Функция у = k/x, ее свойства и график

Цели урока:

• Образовательные: повторить определения: функции, прямо пропорциональной и обратно пропорциональной зависимостей, линейной функции, прямой пропорциональности; закрепить знания учащихся о определение и основные свойства функции у=k/x и ее графика.

• Развивающие: выработать стали умение построения графика функции y= k/x опираясь на свойства функции; дополнить знания учащихся о сфере применения свойств функции, представление о графический способ решения уравнений с одной переменной. Совершенствовать умения логически мыслить и выражать свои мысли вслух; стимулировать познавательную деятельность учащихся постановкой проблемного задания, оценкой и поощрением; способствовать развитию находчивости, сообразительности.

• Воспитательные: воспитывать у учащихся стремление к совершенствованию своих знаний; интерес к предмету, культуру математического вещания.

Оборудование:

проектор, компьютер; .

Презентация к уроку (смотреть в Зале компьютерных презентаций).

Эпиграф.

Первое условие, которого надо придерживаться в математике,— это быть точным, второе — быть ясным и, насколько возможно, простым.

Л. Карно

I. Организационный момент.

II. Конкретизация темы и цели урока:

Дорогие дети и уважаемые коллеги! Тема нашего урока «Функция у=k/x , ее свойства и график»

Дети, давайте определим с вами цель и задачи нашего урока.

Сегодняшний урок и домашнее задание, которое мы сейчас запишем, дадут вам возможность еще лучше усвоить материал, подготовиться к тематической контрольной работе. Поэтому сегодня нужно быть очень внимательными и старательными.

Запишите домашнее задание. Повторить §8 стр. 43, решить №184(построить график функции, определить по графику значения х, соответствующие данным значениям у), №186 (решить графически уравнение)

III. Актуализация опорных знаний.

Мотивация.

Весь реальный мир состоит из множества тел. Эти тела в любой момент времени взаимодействуют друг с другом на различных уровнях: химическом, физическом, информационном и т.д. (демонстрируется слайд) Например, на уроках физики Вы изучаете “зависимость силы тока от сопротивления”, “зависимость давления газа от объема”; из жизни мы знаем о “ зависимость радиуса колеса и число совершаемых им оборотов на определенном отрезке пути” и с этой зависимостью мы встречаемся на уроках математики и т.д. Умение анализировать эти взаимодействия или зависимость сделает Вас успешными в своей деятельности!

А сейчас мы повторим, что уже знаем об этих зависимостях.

Вопросы к классу:

• Что называется функцией?

• Какая зависимость называется прямо пропорциональной? Обратно пропорциональной?

• Какие функции вам известны?

• Дайте их определения.

• Что является графиками этих функций?

• Что является областью определения функции?

• Что является областью значений функции?

• Как называют фигуру, которая является графиком обратной пропорциональности?

• В каких четвертях расположен график функции у=k/x , если к>0, к<0?

Проверка домашнего задания.

№185

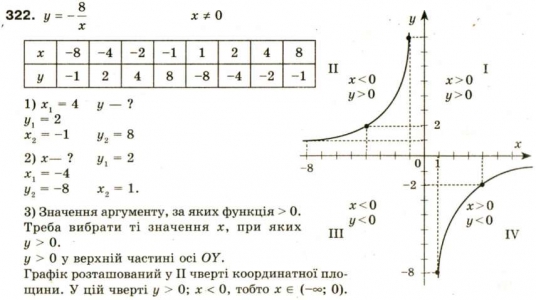
Если х=4, то у= -2;

Если х=-1, то у=8.

Если в=2, то х= -4;

Если у=-8, то х=1.

в>0, если х<0

№183

2. Повторение изученного материала.

1. Как называются функции, задаваемые формулами:

а) у=2х+3; б) у = -1/2х+4; в) у=2х; г) у =-3х; д) у = х²?

2. Что является их графиком? Как он расположен? Укажите область определения и область значения каждой из этих функций.

3. На рисунке изображен график функции у = f(x) на отрезке [- 3; 2].

• Укажите наибольшее значение функции.

• Найдите промежуток, в котором функция принимает отрицательные значения.

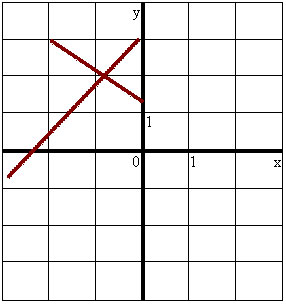
3. Задание для группы «Исследователи»

Разобрать пример.

По аналогии выполнить №186(б).

Ждем от вас результатов.

4. Решение упражнений

№190

Закрепление теоретического материала.

Итак, сегодня мы продолжаем изучать функцию у =k/x .

Обратной пропорциональностью называется функция, которую можно задавать формулой вида у=k/x.

где у – зависимая переменная

х – независимая переменная

К – не равное нулю число.

— Областью определения функции является множество всех чисел, отличных от нуля.

— Областью значений функции является множество всех чисел, отличных от нуля.

Поскольку выражение у =k/x имеет смысл при всех х не равных 0.

В явлениях природы, в человеческой деятельности часто встречается обратно пропорциональная зависимость между двумя величинами.

4. Историческая справка (демонстрируется слайд ).

5. Исследование функции на примере зависимости у=12/х.

Построение графика функции (самостоятельно)

Исследование функции ( работа в парах).

• определите область определения функции;

• определите область значения функции;

• определите точку разрыва функции

(Ученики выполняют задания в парах, после выполнения самопроверка (слайд ))

Проведем анализ графика (демонстрируется слайд 14).

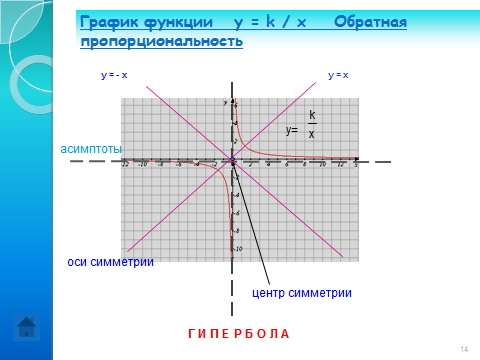
Графиком функции является гипербола.

Гипербола состоит из двух ветвей.

Посмотрите на график и скажите, пересекает ли он прямую ОХ? (Нет) ОУ? (Нет). Эти прямые называются асимптоты графика.

Посмотрите на график и скажите, имеет ли гипербола центр симметрии? (Точка (0;0)) Ось симметрии? (Прямые у = х ; у = — х)

(Учащихся выполняют задания в парах, после выполнения самопроверка (слайд 13)).

Что произошло с графиком функции, при изменении коэффициента?

Вернемся к графикам, которые вы получили.

На какие две группы можно разделить эти графики, чем отличаются эти группы?

(Эти группы располагаются в разных четвертях)

— От чего зависит расположение графиков? (Расположение графика зависит от знака коэффициента обратной пропорциональности)

Самостоятельная работа учебного характера (демонстрируется слайд ).

Результат работы группы «Исследователи»

Выступление группы

Алгоритм графического решения уравнения у=k/x и у=k₁x+b.

1. Построить в одной системе координат графики функций

у=k/x и у=k₁x+b.

2. Найти все точки пересечения построенных графиков.

3. Найти по рисунку абсциссы найденных точек пересечения графиков.

4. Записать ответ.

Вопрос: Скажите, вы встречали где-нибудь это слово раньше? (Один из способов создания художественного образа — это гипербола, то есть преувеличение.

Гипербола очень часто использовалась в устном народном творчестве: сказках, былинах, песнях. Так в былине «Илья Муромец и Соловей-разбойник» для яркой характеристика образа Соловья-разбойника, изображения его силы использована такая гипербола:

засвистел тут Соловей по-соловьиной,

Закричал, собака, по-звериному,

зашипел, проклятый, по-змеиному,

Так все травушки-муравушки уплетали,

Все лазурные цветочки осыпались,

А люди вблизи-все мертвы лежат.

(демонстрируются слайды 18,19, 20).

Итог урока.

(Устно). Слайд 18.

infourok.ru