Обратная задача — Википедия
Материал из Википедии — свободной энциклопедии
Обратная задача — тип задач, часто возникающий во многих разделах науки, когда значения параметров модели должны быть получены из наблюдаемых данных.
Примеры обратных задач можно найти в следующих областях: геофизика, астрономия, медицинская визуализация, компьютерная томография, дистанционное зондирование Земли, спектральный анализ, теория рассеяния и задачи по неразрушающему контролю.
Обратные задачи являются некорректно поставленными задачами. Из трёх условий корректно поставленной задачи (существование решения, единственность решения и его устойчивость) в обратных задачах наиболее часто нарушается последнее. В функциональном анализе обратная задача представляется в виде отображения между метрическими пространствами. Обратные задачи обычно формулируются в бесконечномерных пространствах, но ограничение на конечность измерений и целесообразность вычисления конечного числа неизвестных параметров приводят к изменению задачи в дискретной форме. В этом случае используют метод регуляризации для того, чтобы избежать переобучения.
Линейная обратная задача может быть описана в следующем виде:
- d=G(m){\displaystyle \ d=G(m)},
где G{\displaystyle G} — линейный оператор, описывающий явные отношения между данными и параметрами модели, и представляющий собой физическую систему. В случае дискретной линейной обратной задачи, описывающей линейную систему, d{\displaystyle d} и m{\displaystyle m} являются векторами, что позволяет использовать следующее представление задачи:
- d=Gm{\displaystyle \ d=Gm},
где G{\displaystyle G} является матрицей.
Примеры[править | править код]
Примером линейной обратной задачи служит интегральное уравнение Фредгольма первого порядка.
- d(x)=∫abg(x,y)m(y)dy{\displaystyle d(x)=\int \limits _{a}^{b}g(x,y)\,m(y)\,dy}
Для существенно гладкого g{\displaystyle g} определённый выше оператор является компактным на таких банаховых пространствах, как Пространства Lp{\displaystyle L^{p}}. Даже если отображение является взаимно однозначным, обратная функция не будет непрерывной. Таким образом, даже маленькие ошибки в данных d{\displaystyle d} будут сильно увеличены в решении m{\displaystyle m}. В этом отношении обратная задача по определению m{\displaystyle m} из измеренных данных d{\displaystyle d} будет являться некорректной.
Для получения численного решения необходимо аппроксимировать интеграл с помощью численного интегрирования и дискретных данных. Результирующая система линейных уравнений будет некорректно поставленной задачей.
Преобразование Радона также является примером линейной обратной задачи.
В нелинейных обратных задачах ставятся более сложные отношения между данными и моделью, которые описываются уравнением:
- d=G(m).{\displaystyle \ d=G(m).}
Здесь G{\displaystyle G} представляет собой нелинейный оператор, который не может быть приведён к виду линейного отображения, переводящего m{\displaystyle m} в данные. Линейные обратные задачи были полностью решены с теоретической точки зрения в конце XIX века, из нелинейных до 1970 года был решён только один класс задач — задача обратного рассеяния. Существенный вклад внесла российская математическая школа (Крейн, Гельфанд, Левитан).
- Гольцман Ф. М. Статистические модели интерпретации. — М., Наука, 1971. — 323 c.
Обратные задачи / Задачи / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Задачи
- Обратные задачи
В обратной задаче одна из искомых величин становится известной, а одна из данных величин становится неизвестной.
Прямая задача:
У Тани было 3 зелёных шарика и 2 красных. Сколько всего шариков было у Тани?
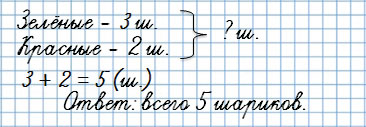
Первая обратная задача:
У Тани было 5 шариков, 3 шарика были зелёными, а остальные красные. Сколько красных шариков было у Тани?

Ты видишь, что известная величина — красные шарики — стала неизвестной.
А неизвестная величина — общее количество шариков — стало известной.
Вторая обратная задача:
У Тани было 5 шариков, 2 шарика были красными, а остальные зелёные. Сколько зелёных шариков было у Тани?
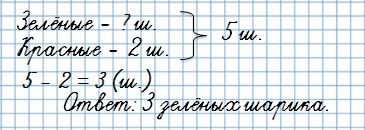
Ты видишь, что известная величина — зелёные шарики — стала неизвестной.
А неизвестная величина — общее количество шариков — стало известной.
ТАКИЕ ЗАДАЧИ НАЗЫВАЮТСЯ ОБРАТНЫМИ.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Задачи на движение
Цена. Количество. Стоимость
Скорость, время, расстояние
Задачи
Правило встречается в следующих упражнениях:
2 класс
Страница 57, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 72, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Задание 25, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 8. Вариант 1. № 3, Моро, Волкова, Проверочные работы
Страница 52, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 81, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 89, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 91, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 94, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 106, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
3 класс
Страница 19, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 20, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 38, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 64, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 10, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 29, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 30, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 71, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 6, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 21, Моро, Волкова, Рабочая тетрадь, 2 часть
4 класс
Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 11, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 76, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 87, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 49, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 68, Моро, Волкова, Рабочая тетрадь, 1 часть
© budu5.com, 2020
Пользовательское соглашение
Copyright
Урок 10. задачи, обратные данной — Математика — 2 класс
Математика, 2 класс
Урок № 10. Задачи, обратные данной
Перечень вопросов, рассматриваемых в теме:
- Что такое задачи, обратные данной?
- Как составлять и решать обратные задачи?
Глоссарий по теме:
Задачи, обратные данной — считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.26, 27
2. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017, с. 16, 17
3. Математика. Рабочая тетрадь. 2 кл. 1 часть: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.-с.31
Теоретический материал для самостоятельного изучения
Решим три задачи.
Составим по рисунку первую задачу.

В классе 10 девочек и 8 мальчиков. Сколько всего детей в классе?
Составим схематический рисунок.

Решим задачу:
10 + 8 = 18 (д.)
Ответ: 18 детей в классе.
Составим вторую задачу.

В классе 18 детей. Девочек 10, остальные-мальчики. Сколько мальчиков в классе?

Решим задачу:
18 – 10 = 8 (м.)
Ответ: 8 мальчиков в классе.
Составим третью задачу.

В классе 18 детей. Мальчиков 8, остальные — девочки. Сколько девочек в классе?

Решим задачу:
18 – 8 = 10 (д.)
Ответ: 10 девочек в классе.
Посмотрим еще раз на схемы к каждой задаче. Обратим внимание на то, что во всех задачах одинаковый сюжет, но то, о чем спрашивается в первой задаче стало известным во второй и третьей задачах, а узнать во второй задаче, сколько мальчиков и в третьей задаче сколько девочек в классе надо то, что известно в первой задаче.
Задачи, в которых известно то, о чем спрашивается в первой задаче и надо узнать то, что в первой задаче известно, называют обратными первой.
Сделаем вывод: задачи, обратные данной — считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
Тренировочные задания.
1.
Кате подарили 8 воздушных шариков красного и синего цвета. Красных шариков было 5. Сколько синих шариков у Кати?
Варианты ответов:
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
2. У Кати было 8 шариков. 3 шарика она подарила. Сколько шариков осталось у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
Правильные варианты:
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
2 . Восстановите пропуски в задачах.
1.В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в ________?
2. В июне ____ дней. Из них 10 дней были пасмурными. Сколько______ дней было в июне?
3. В июне 30 дней. Ясными были ____ дней. Сколько ____ дней было в июне?
Варианты ответов:
30, 20, ясных, пасмурных, июне
Правильный вариант:
1. В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в июне?
2. В июне 30 дней. Из них 10 дней были пасмурными. Сколько ясных дней было в июне?
3. В июне 30 дней. Ясными были 20 дней. Сколько пасмурных дней было в июне?
Обратная задача — это… Что такое Обратная задача?
Обратная задача — тип задач, часто возникающий во многих разделах науки, когда значения параметров модели должны быть получены из наблюдаемых данных.
Примеры обратных задач можно найти в следующих областях: геофизика, астрономия, медицинская визуализация, компьютерная томография, дистанционное зондирование Земли, спектральный анализ и задачи по неразрушающему контролю.
Обратные задачи являются некорректно поставленными задачами. Из трёх условий корректно поставленной задачи (существование решения, единственность решения и его устойчивость) в обратных задачах наиболее часто нарушается последнее. В функциональном анализе обратная задача представляется в виде отображения между метрическими пространствами. Обратные задачи обычно формулируются в бесконечномерных пространствах, но ограничение на конечность измерений и целесообразность вычисления конечного числа неизвестных параметров приводят к изменению задачи в дискретной форме. В этом случае используют метод регуляризации для того, чтобы избежать переобучения.
Линейная обратная задача
Линейная обратная задача может быть описана в следующем виде:
- ,
где — линейный оператор, описывающий явные отношения между данными и параметрами модели, и представляющий собой физическую систему. В случае дискретной линейной обратной задачи, описывающей линейную систему, и являются векторами, что позволяет использовать следующее представление задачи:
- ,
где является матрицей.
Примеры
Примером линейной обратной задачи служит интегральное уравнение Фредгольма первого порядка.
Для существенно гладкого определённый выше оператор является компактным на таких банаховых пространствах, как Пространства . Даже если отображение является взаимно однозначным, обратная функция не будет непрерывной. Таким образом, даже маленькие ошибки в данных будут сильно увеличены в решении . В этом отношении обратная задача по определению из измеренных данных будет являться некорректной.
Для получения численного решения необходимо аппроксимировать интеграл с помощью численного интегрирования и дискретных данных. Результирующая система линейных уравнений будет некорректно поставленной задачей.
Преобразование Радона также является примером линейной обратной задачи.
Нелинейная обратная задача
В нелинейных обратных задачах ставятся более сложные отношения между данными и моделью, которые описываются уравнением:
Здесь представляет собой нелинейный оператор, который не может быть приведён к виду линейного отображения, переводящего в данные. Линейные обратные задачи были полностью решены с теоретической точки зрения в конце XIX века, из нелинейных до 1970 года был решён только один класс задач — задача обратного рассеяния. Существенный вклад внесла российская математическая школа (Крейн, Гельфанд, Левитан).
Ссылки
Международные научные журналы
Что такое обратная задача ???
это когда дан ответ, а найти нужно задачу :))))
В обратной задаче ранее неизвестная величина становится известной, а та, что была известной-становится неизвестной. Например: У Маши было 8 конфет, 3 конфеты она съела. Сколько конфет у неё осталось? Это прямая задача. К ней можно составить две обратные. 1. Маша съела 3 конфеты и у неё осталось ещё 5 конфет. Сколько конфет у неё было? 2.У маши было 8 конфет. После того, как она несколько конфет съела, у неё осталось 5 конфет. Сколько конфет Маша съела?
Прямая задача — это теленка превратить в фарш. А обратная — это фарш провернуть обратно в теленка. В этой шутке есть доля шутки. Скажем, на входе измерительного канала (датчика) физическая величина Х, а на выходе Y — как правило электрический сигнал. Его точность определяется погрешностью, вносимой датчиком. Записать отображение Х в Y можно так: X = A(X) + v, где А — оператор отображения, а v — ошибка измерительного канала. Так вот, обратная задача возникает, например при калибровке, когда надо оцифровать все множество Y, каждому его элементу y поставить в соответствие точное значение х из множества X. То есть решить задачу Х* = А*(Y +v). Где Х* — искомая оценка входной величины, А* — оператор обратного преобразования, обычно записываемый как А с верхним индексом «-1». Очевидно, v входит внутрь оператора обратного преобразования и бывает сильно нарушает условия корректности математической процедуры. Поэтому обратная задача как правило считается некорректной. Много серьезных математиков — Тихонов, Адамар, Бакушинский и др. предлагали методы снижения фактора некорректности, однако проблема остро стоит по сей день и будет оставаться актуальной всегда.
как я ребенку обьясню что там на входе измерительного канала и как из фарша получить теленка?
аааааааааамммммммм
помогите решить 2 обратные задачи Ученики собрали с одной яблони 5 ведер ябло а с другой яблони 3
Чёёёёё вы чё обратная задача это ваапще другоееееее
да ты прова обратная задача я сейчас приведу пример в вазе лежат 5 барано миши взял 4 баранки и осталось не ивесно сколько баранок осталось в вазе а вот обратная например в вазе не извесно сколько было а сколько он взял извесно и сколько осталось тоже извесно ясно тебе или нет
Обратная задача — тип задач, часто возникающий во многих разделах науки, когда значения параметров модели должны быть получены из наблюдаемых данных. ..Из трёх условий корректно поставленной задачи (существование решения, единственность решения и его устойчивость) в обратных задачах наиболее часто нарушается последнее.
Конспект урока «Обратные задачи» — начальные классы, уроки

Составила и провела
учитель начальных классов
Хмель Л.В.
ГУО «Гимназия №1 г. Копыля имени Н. В. Ромашко»
Тема: Обратная задача
Цели и задачи урока: знакомство детей с новым математическим понятием: «обратные задачи», установление связи между прямой и обратной задачей; совершенствовать вычислительные навыки, развивать внимание, логическое мышление, математическую речь; воспитывать чувство ответственности за свое здоровье; прививать гигиенические навыки.
Ход урока
I. Организационный момент.
Психологический настрой.
– Сегодня я приглашаю вас в увлекательное путешествие по математическому лесу. Наше путешествие будет идти под девизом, который написан на слайде. Прочитаем его.
Чтоб водить корабли.
Чтобы лётчиком стать
Надо прежде всего
Математику знать.
И на свете нет профессии,
Вы смекайте-ка
Где бы нам не пригодилась
Математика.
– Это девиз нашего урока. Как вы его понимаете? (Чтобы стать хорошим летчиком капитаном, надо хорошо учиться. Преодолевать трудности, стараться самим добывать знания.)
– С каким настроением вы пришли на урок – покажите при помощи сигналов на «Светофорчике».
– Ну, что вперед за знаниями.
II. Актуализация опорных знаний.
Первая наша остановка «Соображай-ка»
1. Индивидуальная работа у доски (на местах работа в парах)
Закрепление знаний состава числа.
– Посмотрите, какие чудесные математические ёлочки. Как вы думаете, какое задание я вам хочу предложить? (приложение )
У вас на столах есть карточки с математическими ёлочками
– Каждая пара веточек даёт в сумме число на макушке, числа на веточках могут быть однозначные и двузначные.
(У доски 3 ученика – вписывают числа в круги.
Самостоятельная работа на местах в парах.)
– Кто согласен, покажите зелёный сигнал «Светофора», а кто не согласен – красный.
– С какой целью выполняли это задание? (повторили состав числа, способы получения чисел 7, 11, 15).
2. Устный счёт
– На поляне растут математические грибы. Эти грибочки необычные они волшебные. Посмотрите, какие числа записаны на шляпках грибов, поставьте их в порядке убывания (уменьшения) и вы узнаете, какое слово спряталось на грибочках
Ответ: 55, 50, 45, 35, 25, 15.
– Что вы знаете о задаче? Назовите основные части задачи (условие, вопрос, решение, ответ).
III. Гимнастика для глаз.
Остановка «Глазково»
Рисуй глазами треугольник
Рисуй глазами треугольник.
Теперь его переверни Вершиной вниз.
И вновь глазами ты по периметру веди.
Рисуй восьмерку вертикально.
Ты головою не крути,
А лишь глазами осторожно ты вдоль по линиям води.
И на бочок ее клади.
Теперь следи горизонтально,
И в центре ты остановись.
Зажмурься крепко, не ленись.
Глаза открываем мы наконец.
Зарядка окончилась. Ты молодец!
(Дети представляют внешний вид геометрических фигур.)
IV. Постановка темы и цели урока).
– Посмотрите, сегодня к нам на урок снова пришел Учёный Математик
– Как вы думаете, зачем он к нам пришёл? Что-то он не весёлый. Может быть что-нибудь случилось? (У Математика в руках листочек с буквами).
– Оказывается, Математик так спешил к нам, что пока бежал у него по листочку все буквы рассыпались. Поможем Математику расшифровать слово? Поставьте буквы в порядке возрастания их высоты и узнаете слово.
— Какое слово получилось? (Обратные). (Приложение )
– Итак, чем мы будем сегодня заниматься на уроке? (Решать обратные задачи).
– А обратные задачи, это какие?
– Попробуёте сформулировать цель урока? (Узнать о том, что такое обратные задачи и научиться их решать).
Остановка «Задачкино»
Задачи на доске (схемы краткой записи для заполнения учащимися(Приложене).
– Прочитайте тексты. Это одна и та же задача? В чём сходство? О чем говориться в задаче? (О листочках). В чём отличие?
- На землю с деревьев упало 5 дубовых и 6 кленовых листочков. Сколько всего на земле листочков?
- В лесу листопад. На землю с деревьев упало 11 листочков. Кленовых было 6. Сколько на земле дубовых листочков?
- В лесу листопад. На землю с деревьев упало 11 листочков. Из них было 5 дубовых. Сколько на земле кленовых листочков?
– Прочитайте первую задачу. О чем говориться в задаче? (Дубовых – 5 л., кленовых – 6 л., не знаем сколько всего на земле листочков).
– Впишите самостоятельно на карточках данные, которые известны и неизвестны в задаче.

– Решите задачу №1.
– Прочитайте вторую задачу. О чем говориться в задаче? (О кленовых и дубовых листочках, сколько упало листочков на землю).
– Чем задача похожа на предыдущую и чем отличается от неё? (В обеих задачах речь идёт о кленовых и дубовых листочках, и в той, и другой
– Запишите кратко условие.

– Решите задачу №2.
– Что вы можете сказать о решениях этих задач?
– Прочитайте третью задачу. Как изменилось ее условие? (Известно, сколько всего упало кленовых и дубовых листочков, и на земле кленовых листочков. Не знаем, сколько дубовых.)
– Что надо узнать? Запишите задачу кратко.

– Решите задачу №3.
– Внимательно посмотрите на условия этих трех задач. Что вы о них можете сказать? (Они похожи.)
– Что одинаково? (Данные, числа.) — Чем отличаются?
– Внимательно посмотрите на решения задач. Что одинаково? (Числа.) — Чем отличаются? (Действиями:1) +; 2) -; 3) -.)
– Как назовем вторую и третью задачи? (Обратные первой.)
– Конечно, это обратные задачи.
– В какой форме мы записали задачи? (в форме краткой записи).
– Кто может поделиться с Математиком о том, как понял, что такое обратная задача? (Задачи, в которых объект (число) и результат меняются местами (известное становится не известным, а неизвестное известным), называются обратными первой).
– Какую цель ставили? (узнать, что такое обратные задачи)
– Какой получили результат? (мы выяснили, что такое обратная задача и решили их).
– Что ещё нового мы узнали? В каком виде можно оформить кратко задачу? (схематический рисунок).
– Проверили мы наши предположения? Математик говорит, что вы молодцы.
V. Работа по теме урока
– Откройте учебник на стр. 39, № 3.
Остановка «Речная»
– Откройте тетрадь и запишите номер задания № 3.
— Измерь длины отрезков. Составьте задачу по схеме.
( краткое условие на доске)
– Решение и ответ задачи запишите самостоятельно.
– Составьте обратные задачи (устно). (Коллективное составление с комментированием).
1 вариант: решает задачу с вопросом: Сколько см 1 отрезок?
2 вариант: решает задачу с вопросом: Сколько см 2 отрезок?
Самостоятельная работа. Фронтальная проверка.
– Кому было легко решать задачи, покажите зелёный сигнал «Светофора».
– Кто затруднялся при работе с этим заданием, покажите жёлтый сигнал.
– С какой целью выполняли это упражнение из учебника? (закрепили умение решать задачи, учились устно составлять и решать обратные задачи).
VI. Остановка «Отдыхайкино»
Раз, два — хлопок в ладоши
Раз, два — хлопок в ладоши,
А потом на каждый счет.
Раз, два, три, четыре –
Руки выше, плечи шире.
Раз, два, три, четыре, пять,
Надо нам присесть и встать.
Руки вытянуть пошире.
Раз, два, три, четыре, пять.
Наклониться — три, четыре,
И на месте поскакать.
На носки, затем на пятки.
Лень отбросить и опять.
Сесть за парту, взять тетрадку,
Выражения решать.
VII. Работа над пройденным материалом
Остановка «Узнайкино»
- № 2 с.38
VIII. Домашнее задание
С.39 № 6
IX. Рефлексия учебной деятельности
– Вспомните девиз нашего путешествия.
Чтоб водить корабли.
Чтобы лётчиком стать
Надо прежде всего
Математику знать.
И на свете нет профессии,
Вы смекайте-ка
Где бы нам не пригодилась
Математика.
– Мы сегодня с вами хорошо поработали, и я считаю, что из вас должны получиться хорошие и летчики и капитаны и вы сможете для себя выбрать любую другую нужную профессию. Математические знания важны для всех сфер деятельности.
– Посмотрите, как смотрит на нас Математик. Он улыбается.
– Что нового вы узнали на уроке? Чему научились?
– Какие задачи называются обратными?
– Кто испытывал трудности при работе?
– Какие? Что нужно сделать, чтобы их устранить?
– Оцените свою работу на уроке при помощи «Светофорчика».
– Молодцы! Спасибо за работу на уроке. Наш помощник Учёный Математик благодарит вас и вручает «медальки» за работу на уроке в виде цветных кленовых и дубовых листочков: зелёный – активно работал на уроке, жёлтый – хорошо работал, красный – работал на уроке, но нужна ещё помощь.
Задачи, обратные данной
- Вот незадача… Точнее, задача…
- Минус, к тебе можно зайти?
- Да, Плюс, заходи.
- Здравствуй, Минус. Ты чем это так расстроен?
- Понимаешь, наша царица-Математика задала мне задачу. А получилась прямо какая-то незадача. Я не понимаю, что мне делать. Может быть, ты мне поможешь разобраться?
- Конечно! Все, что в моих силах. Ну рассказывай!
- Вот прочитай задачу.
- На болото царевны-лягушки прилетело 8 стрел. Из них 5 стрел прилетели из тридевятого царства, а остальные — из тридесятого государства. Сколько стрел прилетело из тридесятого государства?
Ну и что же здесь трудного? Совсем простенькая задача!
- Задачка-то простенькая. Но царица-Математика приказала мне составить к этой задаче какие-то обратные. Я понимаю, что можно куда-нибудь пойти, а потом вернуться обратно. Или кому-нибудь что-то подарить, а потом потребовать эту вещь обратно. Но вот что такое обратные задачи…
- Ну, Минус, я от тебя такого не ожидал. Ничего себе — сначала подарить, а потом потребовать подарок обратно. То, что ты кому-то подарил, тебе уже не принадлежит. Это не твоя вещь, так что обратно ты требовать ее не имеешь право.
- Да ладно, я это знаю. Я просто неудачно пошутил. Давай все-таки поговорим про задачи, обратные данной.
- Для того, чтобы ты понял, что такое задачи, обратные данной, надо составить краткое условие к задаче. О чем говорится в задаче.
- О том, что на болото царевны-лягушки прилетели стрелы.
- Значит, задача про стрелы. Давай еще раз прочитаем задачу, найдем в ней числа и выделим главные, опорные слова, которые помогут составить краткое условие. Читай первое предложение.
- На болото царевны-лягушки прилетело восемь стрел.
- Так и пишем:
Читай дальше
- Из них 5 стрел прилетело из тридевятого царства. Но это тоже прилетело.
- Да…надо подумать… А-а, восемь — это всего прилетело, а пять — из тридевятого царства.
Читаем дальше.
- А остальные — из тридесятого государства. Остальные — это неизвестно сколько.
Читаю дальше: сколько стрел прилетело из тридесятого государства?
- Нам надо узнать, сколько стрел прилетело из тридесятого государства. Получается вот такая запись.
Ну, теперь давай решим эту задачу.
- Задачка-то простая, для первоклашек. Нам надо узнать ту часть всех стрел, которые прилетели из тридесятого государства. Это мы будем находить, конечно, с моим любимым знаком — минусом.
Ну вот, задача решена. А где же обратные задачи?
- А теперь давай посмотрим еще раз на краткое условие задачи. В ней было известно, сколько всего стрел прилетело и сколько прилетело из тридевятого царства. А узнать надо было, сколько прилетело из тридесятого государства. Теперь мы и это знаем.
А вот чтобы составить задачи, обратные данной, надо изменить условие задачи так, чтобы то, что в первой задаче было известным, в обратной задаче, наоборот, становилось неизвестным. А то, что было неизвестным, становилось известным.
Давай составим новую задачу, в которой неизвестным будет второе число — количество стрел, которые прилетели из тридевятого царства:
Задача: На болото царевны-лягушки прилетело 8 стрел. Из них 3 стрелы прилетели из тридесятого государства, а остальные — из тридевятого царства. Сколько стрел прилетело из тридевятого царства?
- Ну, и эту задачку решить очень легко. Опять известно, сколько всего стрел, и известна та часть стрел, которую прислали из тридесятого государства. А узнать надо ту часть стрел, которая прилетела из тридевятого царства. Часть, как обычно, находим вычитанием. Я, Минус, на посту. Получили:
Отлично! Спасибо, Плюсик! Ты, как всегда, меня выручаешь!
- Не спиши, Минус! Ведь мы составили только одну задачу, обратную данной. Но в задаче есть еще одно число, которое ни разу пока не было неизвестным.
- Ну да, не было неизвестным общее количество стрел.
- Записываем:
- На болото царевны-лягушки прилетело несколько стрел. Из них 5 стрел прилетело из тридевятого царства, 3 стрелы — из тридесятого государства. Сколько всего стрел прилетело царевне-лягушке?
В этой задаче известна часть стрел, прилетевшая из тридевятого царства. И та часть стрел, которая прилетела из тридесятого государства. Надо узнать, сколько всего стрел прилетело.
Э-э, да мне в этой задаче делать нечего. Твоя очередь, Плюс.
- Конечно, эта задача решается со знаком плюс, ведь известны части, а надо узнать целое, т.е., сколько всего. Получаем:
- Ничего себе! Была одна задача, а стало три!
- Ну, Минус, ты понял, что такое обратная задача?
- Кажется понял. В задачах, обратных данной, каждое число по очереди становится неизвестным.
- А сейчас без моей помощи попробуй составить такие обратные задачи. Вот тебе задача. Слушай:
Петя играл в боулинг. 7 раз он сбивал кегли, а 3 раза промахнулся. Сколько всего раз бросал шар Петя?
- Так, составляю краткое условие:
А можно слово всего я напишу не снизу, а объединю две строчки фигурной скобкой?
- Конечно, так даже понятнее будет.
- Ой-ёй-ёй, Плюс, здесь нужен ты, ведь надо узнать, сколько всего.
- Хорошо, получим:
- Теперь составляю обратные задачи.
В первой задаче неизвестным будет число удачных бросков, когда Петя сбивал кегли, а остальные числа будут известны.
Вот в этой задаче уже нужен я, Минус, так как надо узнать только часть брошенных шаров. Получаем:
А еще одна задача нужна?
- Да, конечно. В задаче три данных, значит и задач должно быть три — одна прямая и две обратных.
- Так-так. Еще неизвестным не было количество промахов. Изменяю краткое условие:
И опять здесь надо узнать часть бросков, поэтому задачу надо решать вычитанием. Получим:
- Молодец, Минус! Так как мы составляем обратные задачи?
- В задачах, обратных данной, по очереди каждое данное становится неизвестным. А еще я заметил, что обратные задачи являются проверкой первой задачи.
- Абсолютно верно. И не забудь, обычно задач столько, сколько данных в задаче, включая неизвестное.
- Теперь я все понял. Пойду доложу царице-Математике о том, что ее задание выполнено. Спасибо, Плюсик! Пока.
- До свидания, Минус! Удачи!