Точка (геометрия) — Википедия

У этого термина существуют и другие значения, см. Точка. Точки в двумерном евклидовом пространстве (обозначены красным цветом) Точка P и её координаты в трёхмерной системе координат (с осью Х, направленной к читателю)

То́чка — одно из фундаментальных понятий математики, абстрактный объект в пространстве, не имеющий никаких измеримых характеристик (нульмерный объект).

В евклидовой геометрии точка — это неопределяемое понятие, на котором строится геометрия, то есть точка не может быть определена в терминах ранее определённых объектов. Иными словами, точка определяется только некоторыми свойствами, называемыми аксиомами, которым она должна удовлетворять. В частности, геометрические точки не имеют никакой длины, площади, объёма или какой-либо другой размерной характеристики. Распространённым толкованием является то, что понятие точки предназначено для обозначения понятия уникального местоположения в евклидовом пространстве

[1].

Физический смысл точки — материальная точка.

Евклид первой аксиомой в своих «Началах» определил точку как «объект, не имеющий частей». В современной аксиоматике евклидовой геометрии точка является первичным понятием, задаваемым лишь перечнем его свойств — аксиомами.

В выбранной системе координат любую точку двумерного евклидова пространства можно представить как упорядоченную пару (x; y) действительных чисел. Аналогично, точку n-мерного евклидова пространства (а также векторного или аффинного пространства) можно представить как кортеж (a₁, a₂, … , a_n) из n чисел.

Многие объекты в евклидовой геометрии состоят из бесконечного набора точек, которые соответствуют определённым аксиомам. Например, прямая — это бесконечное множество точек вида L={(a1,a2,…an)|a1c1+a2c2+…ancn=d}{\displaystyle \scriptstyle {L=\lbrace (a_{1},a_{2},…a_{n})|a_{1}c_{1}+a_{2}c_{2}+…a_{n}c_{n}=d\rbrace }}, где

c₁ … c_n и d — константы, а n — размерность пространства. Существуют аналогичные конструкции, которые определяют плоскость, отрезок и другие связанные понятия. Сегмент прямой, состоящий только из одной точки, называется вырожденным отрезком.

В дополнение к определению точек и объектов, связанных с точками, Евклид также постулировал ключевую идею, что любые две точки могут быть соединены прямой линией. Это позволило построить почти все геометрические понятия, известные в то время. Однако постулат Евклида о точках не был ни полным, ни окончательным, и содержал также положения, которые не следовали непосредственно из его аксиом, такие как упорядочение точек на линии или существование определённых точек. Некоторые современные расширения системы Евклида устраняют эти противоречия.

Во всех общих определениях размерности точка является 0-мерным объектом, но при этом описывается по-разному в различных концепциях размерности.

Векторное пространство[править | править код]

Размерность векторного пространства — это максимальный размер линейно независимого подмножества. В векторном пространстве, состоящем из одной точки (которая должна быть нулевым вектором 0), линейно независимое подмножество отсутствует. Нулевой вектор сам по себе не является линейно независимым, поскольку существует нетривиальная линейная комбинация, делающая его нулевым: 1⋅0=0{\displaystyle 1\cdot \mathbf {0} =\mathbf {0} }.

Топологическая размерность[править | править код]

Топологическая размерность топологического пространства X определяется как минимальное значение n, так что каждое конечное открытое покрытие A{\displaystyle {\mathcal {A}}} из X допускает конечное открытое покрытие B{\displaystyle {\mathcal {B}}} из X, которое уточняет A{\displaystyle {\mathcal {A}}}, в котором ни одна точка не включена в более чем n + 1 элементов. Если такого минимального n не существует, говорят, что пространство имеет бесконечную размерность покрытия.

Точка является нульмерной по отношению к размерности покрытия, потому что каждое открытое покрытие пространства имеет уточнение, состоящее из одного открытого множества.

Хаусдорфова размерность[править | править код]

Пусть X метрическое пространство. Если S ⊂ X и d ∈ [0, ∞), то множество Хаусдорфа в d-мерном пространстве S является инфимумом множества чисел δ ≥ 0, для которого существует некоторый (проиндексированный) набор метрик {B(xi,ri):i∈I}{\displaystyle \{B(x_{i},r_{i}):i\in I\}}, покрывающий S с r_i > 0 для каждого i ∈ I, удовлетворяющего ∑i∈Irid<δ{\displaystyle \sum _{i\in I}r_{i}^{d}<\delta }.

Хаусдорфова размерность метрического пространства X определяется как

dimH⁡(X):=inf{d≥0:CHd(X)=0}.{\displaystyle \operatorname {dim} _{\operatorname {H} }(X):=\inf\{d\geq 0:C_{H}^{d}(X)=0\}.}.

Точка имеет размерность Хаусдорфа 0, потому что она может быть покрыта одной сферой произвольно малого радиуса.

Понятие точки является фундаментальным в большинстве направлений геометрии и топологии, но существуют математические концепции, в принципе отказывающиеся от понятия точки, например, некоммутативная геометрия^[en] и Pointless topology (русскоязычного эквивалента термина пока не существует). В этих подходах «пространство без точек» определяется не как множество, а через некоторую структуру (соответственно алгебраическую или логическую), которая выглядит как хорошо известное функциональное пространство на множестве: алгебра непрерывных отображений или алгебра множеств соответственно. Точнее, такие структуры обобщают известные пространства функций таким образом, что операция «принять значение в этой точке» может быть не определена. Исследования таких структур содержатся в некоторых трудах А. Н. Уайтхеда.

Точечная масса и дельта-функция Дирака[править | править код]

Для ряда теорий в физике и математике полезно использование такого абстрактного объекта, как точка, которая имеет ненулевую массу или заряд (это особенно распространено в классической электродинамике, где электроны представляются как точки с ненулевым зарядом). Дельта-функция Дирака, или δ-функция, не является функцией вещественной переменной, а определяется как обобщённая функция: непрерывный линейный функционал на пространстве дифференцируемых функций, и не равна нулю только в точке x=0{\displaystyle x=0}, где она обращается в бесконечность таким образом, чтобы её интеграл по любой окрестности x=0{\displaystyle x=0} был равен 1.^[2][3][4]. Физическая интерпретация дельта-функции представляет собой идеализированную точечную массу или точечный заряд^[5]. Эта функция введена английским физиком-теоретиком Полем Дираком. В процессе обработки сигналов её часто называют единичным импульсным символом (или функцией)^[6]. Дискретным аналогом δ-функции Дирака является символ Кронекера, который обычно определяется в конечной области и принимает значения 0 и 1.

1. ↑ Ohmer, Merlin M. Elementary Geometry for Teachers (неопр.). — Reading: Addison-Wesley, 1969. — С. 34—37.
2. ↑ Dirac, 1958, §15 The δ function, p. 58
3. ↑ Gel’fand & Shilov, 1968, Volume I, §§1.1, 1.3
4. ↑ Schwartz, 1950, p. 3
5. ↑ Arfken & Weber, 2000, p. 84
6. ↑ Bracewell, 1986, Chapter 5

• Clarke, Bowman, 1985, «Individuals and Points,» Notre Dame Journal of Formal Logic 26: 61-75.
• De Laguna, T., 1922, «Point, line and surface as sets of solids, » The Journal of Philosophy 19: 449-61.
• Gerla, G., 1995, «Pointless Geometries» in Buekenhout, F., Kantor, W. eds., Handbook of incidence geometry: buildings and foundations. North-Holland: 1015-31.
• Whitehead, A. N., 1919. An Enquiry Concerning the Principles of Natural Knowledge. Cambridge Univ. Press. 2nd ed., 1925.
• Whitehead, A. N., 1920. The Concept of Nature. Cambridge Univ. Press. 2004 paperback, Prometheus Books. Being the 1919 Tarner Lectures delivered at Trinity College.
• Whitehead, A. N., 1979 (1929). Process and Reality. Free Press.

ru.wikipedia.org

Материальная точка — Википедия

Материал из Википедии — свободной энциклопедии

Материа́льная то́чка (частица)  — обладающее массой тело, размерами, формой, вращением и внутренней структурой которого можно пренебречь в условиях исследуемой задачи. Является простейшей физической моделью в механике. Положение материальной точки в пространстве определяется как положение геометрической точки^[1][2].

В классической механике масса материальной точки полагается постоянной во времени и не зависящей от каких-либо особенностей её движения и взаимодействия с другими телами^[3][4][5][6].

При аксиоматическом подходе к построению классической механики в качестве одной из аксиом принимается следующее^[7]:

Материальная точка — геометрическая точка, которой поставлен в соответствие скаляр, называемый массой: (r,m){\displaystyle (\mathbf {r} ,m)}, r{\displaystyle \mathbf {r} } — вектор в евклидовом пространстве, отнесённом к какой-либо декартовой системе координат. Масса полагается постоянной, не зависящей ни от положения точки в пространстве, ни от времени.

Если тело участвует только в прямолинейном движении, то для определения его положения достаточно одной координатной оси.

Применимость модели материальной точки к конкретному телу зависит не столько от размеров самого тела, сколько от условий его движения. В частности, в соответствии с теоремой о движении центра масс системы, при поступательном движении любое твёрдое тело можно считать материальной точкой, положение которой совпадает с центром масс тела.

Масса, положение, скорость и некоторые другие физические свойства^[8] материальной точки в каждый конкретный момент времени полностью определяют её поведение.

Механическая энергия может быть запасена материальной точкой лишь в виде кинетической энергии её движения в пространстве и (или) потенциальной энергии взаимодействия с полем. Это автоматически означает неспособность материальной точки к деформациям (материальной точкой может быть названо лишь абсолютно твёрдое тело) и вращению вокруг собственной оси и изменениям направления этой оси в пространстве. Вместе с этим модель, описывающая движение тела как движение материальной точки, при котором изменяются её расстояние от некоторого мгновенного центра поворота и два угла Эйлера (задающие направление линии «центр — точка»), чрезвычайно широко используется во многих разделах механики.

Свободные и несвободные материальные точки[править | править код]

Материальная точка, движение которой в пространстве не ограничено какими-либо механическими связями, называется свободной. Примерами свободных материальных точек являются искусственный спутник Земли на околоземной орбите и летящий самолет (если пренебречь их вращениями).

Материальная точка, свобода перемещения которой ограничена наложенными связями, называется несвободной. Примером несвободной материальной точки является движущийся по рельсам трамвай (если пренебречь его формой и размерами).

Ограниченность сферы применения понятия о материальной точке видна из такого примера: в разреженном газе при высокой температуре размер каждой молекулы очень мал по сравнению с типичным расстоянием между молекулами. Казалось бы, им можно пренебречь и считать молекулу материальной точкой. Однако это не всегда так: колебания и вращения молекулы — важный резервуар «внутренней энергии» молекулы, «ёмкость» которого определяется размерами молекулы, её структурой и химическими свойствами. В хорошем приближении как материальную точку можно иногда рассматривать одноатомную молекулу (инертные газы, пары́ металлов и др.), но даже у таких молекул при достаточно высокой температуре наблюдается возбуждение электронных оболочек за счёт соударений молекул, с последующим высвечиванием.

1. ↑ Материальная точка — Статья в Физической энциклопедии.
2. ↑ Курс физики. Трофимова Т. И. М.: Высш. шк., 2001, изд. 7-е.
3. ↑ «Дополнительной характеристикой (по сравнению с геометрическими характеристиками) материальной точки является скалярная величина m — масса материальной точки, которая, вообще говоря, может быть как постоянной, так и переменной величиной. … В классической ньютоновской механике материальная точка обычно моделируется геометрической точкой с присущей ей постоянной массой) являющейся мерой её инерции.» с. 137 Седов Л. И., Цыпкин А. Г. Основы макроскопических теорий гравитации и электромагнетизма. М: Наука, 1989.
4. ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
5. ↑ Голубев Ю. Ф. Основы теоретической механики. — М.: МГУ, 2000. — С. 160. — 720 с. — ISBN 5-211-04244-1. «Аксиома 3.3.1. Масса материальной точки сохраняет своё значение не только во времени, но и при любых взаимодействиях материальной точки с другими материальными точками независимо от их числа и от природы взаимодействий».
6. ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 287. — 416 с. — ISBN 5-06-003117-9. «В классической механике масса каждой точки или частицы системы считается при движении величиной постоянной».
7. ↑ Журавлёв В. Ф. Основы теоретической механики. — М.: Физматлит, 2008. — С. 9. — 304 с. — ISBN 978-5-9221-0907-9.
8. ↑ Материальная точка также может иметь заряд (подробнее см. Электродинамика).

ru.wikipedia.org

Критическая точка (математика) — Википедия

Критической точкой дифференцируемой функции f:Rn→R{\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} } называется точка, в которой её дифференциал обращается в нуль. Это условие эквивалентно тому, что в данной точке все частные производные первого порядка обращаются в нуль, геометрически оно означает, что касательная гиперплоскость к графику функции горизонтальна. В простейшем случае n=1 это значит, что производная f′{\displaystyle f’} в данной точке равна нулю. Это условие является необходимым (но не достаточным) для того, чтобы внутренняя точка области могла быть точкой локального минимума или максимума дифференцируемой функции^[1].

Понятие критической точки допускает обобщение на случай дифференцируемых отображений f:Rn→Rm{\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} ^{m}}, и на случай дифференцируемых отображений произвольных многообразий f:Nn→Mm{\displaystyle f:N^{n}\to M^{m}}. В этом случае определение критической точки состоит в том, что ранг матрицы Якоби отображения f{\displaystyle f} в ней меньше максимально возможного значения, равного min{n,m}{\displaystyle \min\{n,m\}}.

Критические точки функций и отображений играют важную роль в таких областях математики, как дифференциальные уравнения, вариационное исчисление, теория устойчивости, а также в механике и физике. Исследование критических точек гладких отображений составляет один из главных вопросов теории катастроф. Понятие критической точки обобщается также на случай функционалов, определенных на бесконечномерных функциональных пространствах. Поиск критических точек таких функционалов является важной частью вариационного исчисления. Критические точки функционалов (которые, в свою очередь, являются функциями) называются экстремалями.

Критической (или особой или стационарной) точкой непрерывно дифференцируемого отображения f:Rn→Rm{\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} ^{m}} называется такая точка x0∈Rn{\displaystyle x_{0}\in \mathbb {R} ^{n}}, в которой дифференциал этого отображения f∗=∂f∂x{\displaystyle f_{*}={\frac {\partial f}{\partial x}}} является вырожденным линейным преобразованием соответствующих касательных пространств Tx0Rn{\displaystyle T_{x_{0}}\mathbb {R} ^{n}} и Tf(x0)Rm{\displaystyle T_{f(x_{0})}\mathbb {R} ^{m}}, то есть размерность образа преобразования f∗(x0){\displaystyle f_{*}(x_{0})} меньше min{n,m}{\displaystyle \min\{n,m\}}^[2]. В координатной записи при n=m{\displaystyle n=m} это означает что якобиан — определитель матрицы Якоби отображения f{\displaystyle f}, составленной из всех частных производных ∂fj∂xi{\displaystyle {\frac {\partial f_{j}}{\partial x_{i}}}} — обращается в точке x0{\displaystyle x_{0}} в нуль^[2]. Пространства Rn{\displaystyle \mathbb {R} ^{n}} и Rm{\displaystyle \mathbb {R} ^{m}} в этом определении могут быть заменены на многообразия Nn{\displaystyle N^{n}} и Mm{\displaystyle M^{m}} таких же размерностей.

Значение отображения в критической точке называется его критическим значением. Согласно теореме Сарда^[3], множество критических значений любого достаточно гладкого отображения f:Rn→Rm{\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} ^{m}} имеет нулевую меру Лебега (хотя критических точек при этом может быть сколько угодно, например, для тождественного отображения любая точка является критической).

Если в окрестности точки x0∈Rn{\displaystyle x_{0}\in \mathbb {R} ^{n}} ранг непрерывно дифференцируемого отображения f:Rn→Rm{\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} ^{m}} равен одному и тому же числу r{\displaystyle r}, то в окрестности этой точки x0{\displaystyle x_{0}} существуют локальные координаты (x1,…,xn){\displaystyle (x_{1},\ldots ,x_{n})} с центром в x0{\displaystyle x_{0}}, а в окрестности её образа — точки y0=f(x0){\displaystyle y_{0}=f(x_{0})} — существуют локальные координаты (y1,…,ym){\displaystyle (y_{1},\ldots ,y_{m})} с центром в y0{\displaystyle y_{0}}, такие, что в них отображение f{\displaystyle f} задается соотношениями^[4][5]:

y1=x1, …, yr=xr, yr+1=0, …, ym=0.{\displaystyle y_{1}=x_{1},\ \ldots ,\ y_{r}=x_{r},\ y_{r+1}=0,\ \ldots ,\ y_{m}=0.}

В частности, если r=n=m{\displaystyle r=n=m}, то существуют локальные координаты (x1,…,xn){\displaystyle (x_{1},\ldots ,x_{n})} с центром в x0{\displaystyle x_{0}} и локальные координаты (y1,…,yn){\displaystyle (y_{1},\ldots ,y_{n})} с центром в y0{\displaystyle y_{0}}, такие, что в них отображение f{\displaystyle f} является тождественным.

В случае m=1{\displaystyle m=1} данное определение означает, что градиент ∇f=(fx1′,…,fxn′){\displaystyle \nabla f=(f’_{x_{1}},\ldots ,f’_{x_{n}})} в данной точке обращается в нуль.

Предположим, что функция f:Rn→R{\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} } имеет класс гладкости не ниже C3{\displaystyle C^{3}}. Критическая точка функции f называется невырожденной, если в ней гессиан |∂2f∂x2|{\displaystyle {\Bigl |}{\frac {\partial ^{2}f}{\partial x^{2}}}{\Bigr |}} отличен от нуля. В окрестности невырожденной критической точки существуют координаты, в которых функция f имеет квадратичную нормальную форму (лемма Морса)^[6].

Естественным обобщение леммы Морса для вырожденных критических точек является теорема Тужрона: в окрестности вырожденной критической точки функции f, дифференцируемой бесконечное число раз (C∞{\displaystyle C^{\infty }}) конечной кратности μ{\displaystyle \mu } существует система координат, в которой гладкая функция f(x){\displaystyle f(x)} имеет вид многочлена Pμ+1(x){\displaystyle P_{\mu +1}(x)} степени μ+1{\displaystyle \mu +1} (в качестве Pμ+1(x){\displaystyle P_{\mu +1}(x)} можно взять многочлен Тейлора функции f(x){\displaystyle f(x)} в точке 0{\displaystyle 0} в исходных координатах)^[7][8].

При m=1{\displaystyle m=1} имеет смысл вопрос о максимуме и минимуме функции. Согласно известному утверждению математического анализа, непрерывно дифференцируемая функция f{\displaystyle f}, определенная во всем пространстве Rn{\displaystyle \mathbb {R} ^{n}} или в его открытом подмножестве, может достигать локального максимума (минимума) только в критических точках, причем если точка невырождена, то матрица (∂2f∂x2)=(∂2f∂xi∂xj),{\displaystyle {\Bigl (}{\frac {\partial ^{2}f}{\partial x^{2}}}{\Bigr )}={\Bigl (}{\frac {\partial ^{2}f}{\partial x_{i}\partial x_{j}}}{\Bigr )},} i,j=1,…,n,{\displaystyle i,j=1,\ldots ,n,} в ней должна быть отрицательно (положительно) определённой. Последнее является также достаточным условием локального максимума (соответственно, минимума)^[1].

В случае n=m=2 мы имеем отображение f плоскости на плоскость (или двумерного многообразия на другое двумерное многообразие). Предположим, что отображение f дифференцируемо бесконечное число раз (C∞{\displaystyle C^{\infty }}). В этом случае типичные критические точки отображения f суть те, в которых определитель матрицы Якоби равен нулю, но её ранг равен 1, и следовательно, дифференциал отображения f в таких точках имеет одномерное ядро kerf∗{\displaystyle \ker \,f_{*}}. Вторым условием типичности является то, что в окрестности рассматриваемой точки на плоскости-прообразе множество критических точек образует регулярную кривую S, и почти во всех точках кривой S ядро kerf∗{\displaystyle \ker \,f_{*}} не касается S, а точки, где это не так, изолированы и в них касание имеет первый порядок. Критические точки первого типа называются точками складки, а второго типа — точками сборки. Складки и сборки являются единственными типами особенностей отображений плоскости на плоскость, устойчивыми относительно малых возмущений: при малом возмущении точки складки и сборки лишь немного перемещаются вместе с деформацией кривой S, но не исчезают, не вырождаются и не рассыпаются на другие особенности.

Складка и сборка реализуются как особенности проектирования гладкой поверхности на плоскость.

Теорема Уитни. Если x0{\displaystyle x_{0}} — точка складки или точка сборки, то её окрестности существуют локальные координаты (x1,x2){\displaystyle (x_{1},x_{2})} с центром в x0{\displaystyle x_{0}}, а в окрестности её образа y0{\displaystyle y_{0}} — локальные координаты (y1,y2){\displaystyle (y_{1},y_{2})} с центром в y0{\displaystyle y_{0}}, такие, что в них отображение f{\displaystyle f} задается соотношениями

• y1=x12,  y2=x2    {\displaystyle y_{1}=x_{1}^{2},\ \ y_{2}=x_{2}\ \ \ \ } (складка),

• y1=x13+x1x2,  y2=x2    {\displaystyle y_{1}=x_{1}^{3}+x_{1}x_{2},\ \ y_{2}=x_{2}\ \ \ \ } (сборка).

Эта теорема была доказана Хасслером Уитни в 1955 г.^[9] и стала одним из первых результатов теории катастроф^[10]. Современный вариант доказательства этой теоремы, основанный на применении более поздних результатах теории особенностей дифференцируемых отображений, приведен, например, в ^[11].

Теорема Уитни показывает, что складка и сборка реализуются как особенности проектирования гладкой поверхности, заданной в пространстве (x1,x2,y1)=0{\displaystyle (x_{1},x_{2},y_{1})=0} уравнением F(x1,x2,y1)=0{\displaystyle F(x_{1},x_{2},y_{1})=0}, на плоскость (x2,y1){\displaystyle (x_{2},y_{1})} (горизонтальная плоскость на рисунке) вдоль оси x1{\displaystyle x_{1}} (вертикальная ось на рисунке). В нормальных координатах из теоремы Уитни, функция F=x12−y1{\displaystyle F=x_{1}^{2}-y_{1}} для складки и F=x13+x1x2−y1{\displaystyle F=x_{1}^{3}+x_{1}x_{2}-y_{1}} для сборки. Множество критических точек (кривая S на поверхности F=0) изображена красной линией, а её образ на плоскости-образе изображён пурпурным цветом. В случае сборки образ кривой S имеет особенность, называемую каспом (или точкой возврата).

• Арнольд В. И., Варченко А. Н., Гусейн-Заде С. М. Особенности дифференцируемых отображений, — Любое издание.
• Зорич В. А. Математический анализ, — Любое издание.
• Брёкер Т., Ландер Л. Дифференцируемые ростки и катастрофы, — Любое издание.
• Н. Г. Павлова, А. О. Ремизов. Гладкие функции, формальные ряды и теоремы Уитни. Матем. обр., 2016, № 3(79), 49–65.
• Н. Г. Павлова, А. О. Ремизов. Гладкие функции, формальные ряды и теоремы Уитни (окончание). Матем. обр., 2017, № 3(83), 13–27.

1. ↑ ^{1 2} Зорич В. А. Математический анализ, том 1 — Любое издание, гл. VIII.
2. ↑ ^{1 2} Зорич В. А. Математический анализ, том 1 — Любое издание, гл. VIII, пар. 4.
3. ↑ Арнольд В. И., Варченко А. Н., Гусейн-Заде С. М. Особенности дифференцируемых отображений, параграф 2.
4. ↑ Зорич В. А. Математический анализ, том 1 — Любое издание, гл. VIII, пар. 6 (теорема о ранге).
5. ↑ Брёкер Т., Ландер Л. Дифференцируемые ростки и катастрофы, — Любое издание.
6. ↑ Зорич В. А. Математический анализ, том 1 — Любое издание, гл. VIII, пар. 6.
7. ↑ Арнольд В. И., Варченко А. Н., Гусейн-Заде С. М. Особенности дифференцируемых отображений.
8. ↑ Самойленко А. М. Об эквивалентности гладкой функции полиному Тэйлора в окрестности критической точки конечного типа, — Функц. анализ и его прил., 2:4 (1968), стр. 63-69.
9. ↑ Whitney H. On Singularities of Mappings of Euclidean Spaces. I. Mappings of the Plane into the Plane. Annals of Mathematics, Second Series, 62:3 (1955), 374–410.
10. ↑ Арнольд В. И., Варченко А. Н., Гусейн-Заде С. М. Особенности дифференцируемых отображений, параграф 1.
11. ↑ Н. Г. Павлова, А. О. Ремизов. Гладкие функции, формальные ряды и теоремы Уитни (окончание). Математическое образование, 2017, № 3(83), 13–27.

ru.wikipedia.org

Предельная точка — Википедия

Материал из Википедии — свободной энциклопедии

Преде́льная то́чка множества в общей топологии — это такая точка, любая проколотая окрестность которой пересекается с этим множеством.

Точка x{\displaystyle x} называется предельной точкой подмножества A{\displaystyle A} в топологическом пространстве X{\displaystyle X}, если всякая проколотая окрестность точки x{\displaystyle x} имеет с A{\displaystyle A} непустое пересечение.

Точка x{\displaystyle x} называется точкой накопления подмножества A{\displaystyle A}, если всякая окрестность точки x{\displaystyle x} имеет с A{\displaystyle A} бесконечное число общих точек. Для T₁-пространств (то есть пространств, у которых все точки (одноточечные множества) замкнуты) понятия предельная точка и точка накопления равносильны.

Точка x{\displaystyle x} называется точкой конденсации подмножества A{\displaystyle A}, если всякая окрестность точки x{\displaystyle x} содержит несчетное множество точек A{\displaystyle A}.

Точка x{\displaystyle x} называется точкой полного накопления подмножества A{\displaystyle A}, если для всякой окрестности U{\displaystyle U} точки x{\displaystyle x} мощность пересечения U∩A{\displaystyle U\cap A} равна мощности множества A{\displaystyle A}.

• Таким образом, все точки прикосновения любого множества A⊂X{\displaystyle A\subset X} (т.е. точки замыкания A¯{\displaystyle {\bar {A}}}) делятся на два вида: предельные и изолированные точки A{\displaystyle A}. Вторые составляют подмножество A{\displaystyle A}, первые же могут как принадлежать, так и не принадлежать ему.

• Совокупность всех предельных точек множества A{\displaystyle A} называется его произво́дным мно́жеством и обозначается A′{\displaystyle A’}. Все предельные точки множества входят в его замыкание A¯{\displaystyle {\bar {A}}}. Более того, справедливо равенство: A¯=A∪A′{\displaystyle {\bar {A}}=A\cup A’}, из которого легко получается следующий критерий замкнутости подмножеств: Множество A замкнуто тогда и только тогда, когда содержит все свои предельные точки.

• Если x{\displaystyle x} — предельная точка множества A{\displaystyle A}, то существует направление точек из A{\displaystyle A}, сходящееся к x{\displaystyle x}.

• Топологическое пространство X{\displaystyle X} счётно компактно тогда и только тогда, когда в нём всякое бесконечное подмножество имеет хотя бы одну строгую предельную точку в X{\displaystyle X}. Всякий компакт счётно компактен. Для метрических пространств верно и обратное (критерий компактности метрического пространства): метрическое пространство компактно тогда и только тогда, когда оно счётно компактно.

(В частности, поскольку отрезок прямой компактен, то он счётно компактен. Следовательно, всякое бесконечное ограниченное подмножество прямой имеет хотя бы одну предельную точку.)

Предельная точка числового множества[править | править код]

В частности, предельной точкой числового множества, имеющего бесконечное число элементов, называется точка числовой прямой, в любой окрестности которой содержится бесконечно много элементов этого множества. Также можно считать предельной точкой такого множества −∞{\displaystyle -\infty }, если из некоторых его элементов можно составить бесконечно большую последовательность с попарно различными отрицательными элементами. Если же можно составить бесконечно большую последовательность с попарно различными положительными элементами, то можно считать предельной точкой +∞{\displaystyle +\infty }^[1].

Верхняя предельная точка числового множества — это наибольшая из его предельных точек.

Нижняя предельная точка числового множества — это наименьшая из его предельных точек.

Свойства[править | править код]

• У любого ограниченного числового множества, имеющего бесконечное число элементов, существуют и верхняя, и нижняя предельные точки (в множестве вещественных чисел). Если добавить в множество вещественных чисел −∞{\displaystyle -\infty } и +∞{\displaystyle +\infty }, то в получившемся множестве предельные точки имеют вообще все числовые множества с бесконечным числом элементов.

• Из элементов любого ограниченного числового множества, имеющего бесконечное число элементов, можно выделить сходящуюся последовательность, элементы которой попарно различны.

Предельная точка числовой последовательности[править | править код]

Предельная точка последовательности — это точка, в любой окрестности которой содержится бесконечно много элементов этой последовательности^[1].

x{\displaystyle x} — предельная точка последовательности {xn}n=1∞⇔{\displaystyle \left\{x_{n}\right\}_{n=1}^{\infty }\Leftrightarrow }

⇔∀ε>0 ∃X⊆N:|X|=ℵ0∧∀i∈X:|xi−x|<ε{\displaystyle \Leftrightarrow \forall \varepsilon >0~\exists X\subseteq \mathbb {N} \colon \left|X\right|=\aleph _{0}\land \forall i\in X\colon \left|x_{i}-x\right|<\varepsilon }

Наибольшая предельная точка последовательности называется её верхним пределом, а наименьшая предельная точка — нижним пределом.

Иногда во множество возможных предельных точек включают «−∞{\displaystyle -\infty }» и «+∞{\displaystyle +\infty }». Так, если из последовательности можно выделить бесконечно большую подпоследовательность, все элементы которой отрицательны, то говорят, что «−∞{\displaystyle -\infty }» является предельной точкой этой последовательности. Если же из последовательности можно выделить бесконечно большую подпоследовательность с исключительно положительными элементами, то говорят, что «+∞{\displaystyle +\infty }» является её предельной точкой^[1]. При этом, разумеется, у последовательности могут быть и другие предельные точки.

Свойства[править | править код]

Примеры[править | править код]

Пусть {xα}α∈A{\displaystyle \left\{x_{\alpha }\right\}_{\alpha \in \mathrm {A} }} — направление элементов топологического пространства X{\displaystyle X}. Тогда x{\displaystyle x} называется предельной точкой направления, если для любой окрестности U{\displaystyle U} точки x{\displaystyle x} и для любого α∈A{\displaystyle \alpha \in \mathrm {A} } найдется индекс β∈A{\displaystyle \beta \in \mathrm {A} } такой что β⩾α{\displaystyle \beta \geqslant \alpha } и xβ∈U{\displaystyle x_{\beta }\in U}

Свойства[править | править код]

• Точка является предельной точкой направления тогда и только тогда, когда существует поднаправление, сходящееся к этой точке.
  • В частности, точка является предельной точкой последовательности тогда и только тогда, когда существует поднаправление, сходящееся к этой точке.
  • Если каждая точка топологического пространства обладает счетной базой, то в предыдущем пункте можно говорить о подпоследовательностях.

Примеры[править | править код]

Пусть A=[0,1){\displaystyle A=[0,1)} — направлено по возрастанию. У направления {α}α∈A{\displaystyle \left\{\alpha \right\}_{\alpha \in A}} существует единственная предельная точка 1{\displaystyle {1}} в топологическом пространстве [0,1]{\displaystyle [0,1]}.

1. ↑ ^{1 2 3} В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 3. Теория пределов // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 92 — 105. — 672 с. — ISBN 5-482-00445-7.

ru.wikipedia.org

Седловая точка — Википедия

Материал из Википедии — свободной энциклопедии

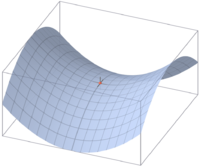Седловая точка функции z=x²-y² (обозначена красным) Седловая точка на карте высот (центр «восьмерки» образованной изолиниями)

Седловая точка в математическом анализе — такая точка из области определения функции, которая является стационарной для данной функции, однако не является её локальным экстремумом. В такой точке, если рассматривается функция двух переменных, образованная графиком функции поверхность обычно напоминает по форме седло или горный перевал — выпуклая в одном направлении и вогнутая в другом. На карте высот седловая точка может быть в общем случае обнаружена в месте пересечения изолиний. Например, два холма, между которыми находится высокий перевал, образуют седловую точку в вершине этого перевала: на карте высот это будет выглядеть как центр «восьмерки», образованной соответствующими изолиниями.

Седловая точка в математическом анализе[править | править код]

Проверить, является ли данная стационарная точка функции F(x,y) двух переменных седловой, можно, вычислив матрицу Гессе функции в этой точке: если гессиан будет неопределенной квадратичной формой, то данная точка — седловая. Например, составив матрицу Гессе функции z=x2−y2{\displaystyle z=x^{2}-y^{2}} в стационарной точке (0,0){\displaystyle (0,0)} получим матрицу:

[200−2]{\displaystyle {\begin{bmatrix}2&0\\0&-2\\\end{bmatrix}}}

которая является неопределенной. Поэтому, точка (0,0){\displaystyle (0,0)} данной функции — седловая. Однако вышеприведенный критерий предоставляет только достаточное условие наличия седловой точки. Например, (0,0){\displaystyle (0,0)} является седловой точкой функции z=x4−y4{\displaystyle z=x^{4}-y^{4}}, но матрица Гессе в данном случае будет нулевой матрицей, которую, по определению, нельзя назвать неопределенной.

В общем случае, седловой точкой гладкой функции (график которой изображает кривую, поверхность или гиперповерхность) называется такая стационарная точка, в окрестности которой данная кривая/поверхность/гиперповерхность не лежит полностью по одну сторону касательного пространства в данной точке.

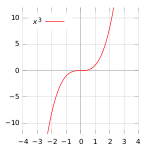График y = x³ с седловой точкой в 0

В случае функции одной переменной, седловая точка — такая точка, которая одновременно является и стационарной точкой, и точкой перегиба (точка перегиба не является локальным экстремумом).

• Gray, Lawrence F.; Flanigan, Francis J.; Kazdan, Jerry L. & Frank, David H (1990), Calculus two: linear and nonlinear functions, Berlin: Springer-Verlag, с. page 375, ISBN 0-387-97388-5 
• Гильберт Д., Кон-Фоссен С., Наглядная геометрия. — URSS, Пер. с нем., Изд.5, 2010. 344
• von Petersdorff, Tobias (2006), «Critical Points of Autonomous Systems», Differential Equations for Scientists and Engineers (Math 246 lecture notes), <http://www.wam.umd.edu/~petersd/stab.html>. Проверено 12 ноября 2009.  Архивная копия от 3 января 2007 на Wayback Machine
• Widder, D. V. (1989), Advanced calculus, New York: Dover Publications, с. page 128, ISBN 0-486-66103-2 

ru.wikipedia.org

Точка перегиба — Википедия

Точка перегиба — точка плоской кривой, в которой её ориентированная кривизна меняет знак. Если кривая является графиком функции, то в этой точке выпуклая часть функции отделяется от вогнутой (то есть вторая производная функции меняет знак).

Точка (простого) перегиба регулярной кривой — это такая точка этой кривой, в которой касательная к кривой имеет с ней соприкосновение второго порядка и разбивает кривую, то есть точки кривой, лежащие в некоторой окрестности данной точки по разные стороны от этой точки, лежат также по разные стороны от касательной^[1][2]. Если кривая 2-регулярна, то условие заменяется на следующее: ориентированная кривизна кривой при переходе через точку перегиба изменяет знак. Точкой высшего (вырожденного) перегиба кривой называется такая её точка, касательная к кривой в которой имеет с ней соприкосновение, порядок которого не ниже трёх, и касательная разбивает кривую^[1].

Условие смены знака ориентированной кривизны не равносильно разбиению кривой на вогнутую и выпуклую часть. Так, в случае точки возврата кривая может не иметь касательной. Для исключения этого вышеприведённых определениях требуется регулярность кривой. Более интересный случай — функция y=x5(1+sin2⁡1x){\displaystyle y=x^{5}(1+\sin ^{2}{\frac {1}{x}})} при x≠0,y=0{\displaystyle x\neq 0,y=0} при x=0{\displaystyle x=0}, которая в точке 0 касается оси x и пересекает её, но меняет знак вблизи нуля бесконечное число раз; здесь даже существует вторая непрерывная производная^[3]. Для исключения такого случая требуют, чтобы функция имела изолированный экстремум (см. ниже).

Точка кривой называется точкой распрямления, если кривизна кривой в этой точке равна нулю^[4]. Иногда точку распрямления кривой, не являющуюся точкой перегиба этой кривой, называют параболической точкой распрямления^[1].

Дифференцируемая функция имеет точку перегиба (x, f(x)) тогда и только тогда, когда её первая производная, f′, имеет изолированный экстремум в точке x (это не то же самое, что f имеет экстремум в этой точке). То есть в некоторой окрестности точки x имеется одна и только одна точка, в которой f′ имеет (локальный) минимум или максимум. Если все экстремумы функции f′ изолированы, то точка перегиба — это точка на графике f, в которой касательная пересекает кривую^[5][6].

Высшей (вырожденной) вершиной регулярной кривой называется такая её точка, в которой соприкасающаяся окружность имеет с ней касание, порядок которого выше третьего^[1].

Восходящая точка перегиба — это точка перегиба, где производная имеет локальный минимум, и нисходящая точка перегиба— это точка перегиба, где производная имеет локальный максимум.

Для алгебраической кривой несингулярная точка является точкой перегиба тогда и только тогда, когда кратность точки пересечения касательной с кривой нечётна и больше двух^[7].

Точка перегиба m{\displaystyle m} однозначно характеризуется двумя свойствами:

• в точке m{\displaystyle m} кривая имеет единственную касательную,
• в достаточно малой окрестности точки m{\displaystyle m} кривая расположена внутри одной пары противоположных углов, образуемых касательной и нормалью.

Если кривая задана как график дифференцируемой функции f{\displaystyle f}, точка перегиба является точкой экстремума для f′{\displaystyle f’}.

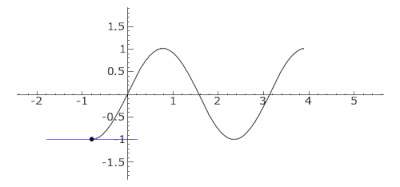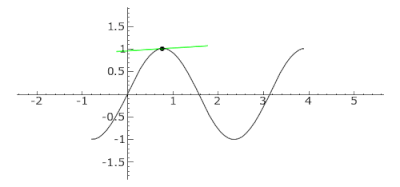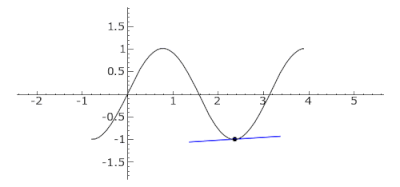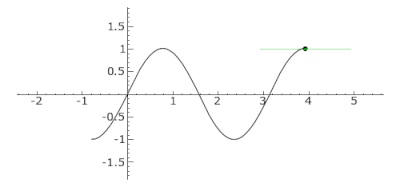График функции f(x) = sin(2x) from −π/4 to 5π/4. Заметьте, вторая производная функции f равна f″(x) = −4sin(2x). Касательная отражена синим цветом, где кривая выпукла (выше касательной), зелёным, где кривая вогнута (под касательной), и красным цветом в точках перегиба 0, π/2 и π

Если x является точкой перегиба для f, то вторая производная, f″(x), равна нулю, если существует, но это условие не является достаточным. Требуется, чтобы наименьший порядок ненулевой производной (выше второй) был нечётным (третья, пятая и т. д. производные). Если наименьший порядок ненулевой производной чётен, точка не является точкой перегиба, а является параболической точкой распрямления ^[8]. В алгебраической геометрии, однако, как точки перегиба, так и точки спрямления обычно называют точками перегиба.

Определение предполагает, что f имеет ненулевую производную более высокого порядка по x, которая не обязательно существует. Но если таковая существует, из определения следует, что знак f′(x) постоянен по обеим сторонам от x в окрестности точки x.

Достаточное условие точки перегиба:

1) Достаточным условием точки перегиба является:

Если f(x) k раз непрерывно дифференцируема в некоторой окрестности точки x, где k нечётно и k ≥ 3, f⁽ⁿ⁾(x₀)=0 для n = 2,…,k — 1 и f^(k)(x₀) ≠ 0, то x₀ является точкой перегиба f(x).

2) Другое достаточное условие требует, чтобы f″(x+ε){\displaystyle f»(x+\varepsilon )} и f″(x−ε){\displaystyle f»(x-\varepsilon )} имели разные знаки в окрестности точки x при условии, что в данной точке существует касательная^[2].

Точки перегиба можно классифицировать согласно производной f′(x).

• если f′(x) равно нулю, точка является стационарной точкой перегиба
• если f′(x) не равно нулю, точка является нестационарной точкой перегиба

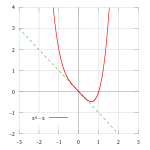y = x⁴ — x имеет вторую производную в точке (0,0), но она не является точкой перегиба, поскольку четвёртая производная является первым ненулевым порядком производной (третья производная равна нулю).

Примером седловой точки является точка (0,0) графика y = x³. Касательной служит ось x и она разделяет график в этой точке.

Нестационарные точки перегиба можно продемонстрировать графиком функции y = x³, если его чуть повернуть относительно начала координат. Касательная в начале координат всё ещё делит график на две части, но градиент не равен нулю.

Некоторые функции меняют выпуклость/вогнутость в некоторой точке, но не имеют в этой точке перегиба. Вместо этого они могут менять кривизну при переходе вертикальной асимптоты или в точке разрыва. Возьмём, например, функцию 2x²/(x² — 1). Она выпукла при |x| > 1 и вогнута при |x| < 1. Однако у этой функции нет точки перегиба, поскольку 1 и −1 не принадлежат области определения функции.

1. ↑ ^{1 2 3 4} Шикин, 1997, с. 39.
2. ↑ ^{1 2} Bronshtein, Semendyayev, 2005, с. 231.
3. ↑ Фихтенгольц, 2001, с. 305.
4. ↑ Шикин, 1997, с. 27.
5. ↑ Фихтенгольц, 2001, с. 294—305.
6. ↑ Кудрявцев, 1981, с. 190—195.
7. ↑ Point of inflection (неопр.). encyclopediaofmath.org.
8. ↑ Рашевский, 1950, с. 18—19.

• Е.В. Шикин, М.М. Франк-Каменецкий. Кривые на плоскости и в пространстве (справочник). — Москва: «ФАЗИС», 1997. — ISBN 5-7036-0027-8, ББК 22.15.
• I.N. Bronshtein, K.A. Semendyayev, G. Musiol, H. Muehlig. Handbook of Mathematics. — 5. — Berlin, Heidelberg, New York: Springer, 2005. — ISBN 978-3-540-72121-5.
• Л. Д. Кудрявцев. Гл. 1. Дифференциальное исчисление функций одного переменного // Математический анализ. — Москва: «Высшая школа», 1981. — Т. 1. — С. 190—195.
• Г. М. Фихтенгольц. Гл. IV. Исследование функций с помощью производных // Курс дифференциального и интегрального исчисления. — 8-е. — М.: ФИЗМАТЛИТ, 2001. — Т. 1. — ISBN 5-9221-0156-0.
• П. К. Рашевский. Курс дифференциальной геометрии. — Москва, Ленинград: Государственное издательство техническо-теоретической литературы, 1950.
• Weisstein, Eric W. Inflection Point (англ.) на сайте Wolfram MathWorld.
• Hazewinkel, Michiel, ed. (2001), «Point of inflection», Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 

ru.wikipedia.org

Геометрическое место точек — Википедия

Материал из Википедии — свободной энциклопедии

Геометри́ческое ме́сто то́чек (ГМТ) — фигура речи в математике, употребляемая для определения геометрической фигуры как множества точек, обладающих некоторым свойством.

• Серединный перпендикуляр к отрезку есть геометрическое место точек, равноудалённых от концов отрезка.
• Окружность есть геометрическое место точек, равноудалённых от данной точки, называемой центром окружности.
• Парабола есть геометрическое место точек, равноудалённых от точки (называемой фокусом) и прямой (называемой директрисой).
• Биссектриса есть геометрическое место точек, равноудаленных от сторон угла и лежащих внутри него.
• Окружность есть геометрическое место точек, из которых данный отрезок виден под прямым углом. Ещё одно определение — геометрическое место точек, отношение расстояния от которых до двух данных точек постоянно и не равно 1 (иначе это серединный перпендикуляр), см. окружность Аполлония.

В общем случае, геометрическое место точек формулируется параметрическим предикатом, аргументом которого является точка данного линейного пространства. Параметры предиката могут носить различный тип. Предикат называется детерминантом геометрического места точек. Параметры предиката называются дифференциалами геометрического места точек (не путать с дифференциалом в анализе).

Роль дифференциалов во введении видовых различий в фигуру. Количество дифференциалов может быть любым; дифференциалов может и вовсе не быть.

Если заданы детерминант P(M,a,b,c,…){\displaystyle P(M,\;a,\;b,\;c,\;\ldots )}, где M{\displaystyle M} — точка, a,b,c,…{\displaystyle a,\;b,\;c,\;\ldots } — дифференциалы, то искомую фигуру A{\displaystyle A} задают в виде: «A{\displaystyle A} — геометрическое место точек M{\displaystyle M}, таких, что P(M,a,b,c,…){\displaystyle P(M,\;a,\;b,\;c,\;\ldots )}». Далее обычно указывается роль дифференциалов, им даются названия применительно к данной конкретной фигуре. Под собственно фигурой понимают совокупность (множество) точек M{\displaystyle M}, для которых для каждого конкретного набора значений a,b,c,…{\displaystyle a,\;b,\;c,\;\ldots } высказывание P(M,a,b,c,…){\displaystyle P(M,\;a,\;b,\;c,\;\ldots )} обращается в тождество. Каждый конкретный набор значений дифференциалов определяет отдельную фигуру, каждую из которых и всех их в совокупности именуют названием фигуры, которая задаётся через ГМТ.

В словесной формулировке предикативное высказывание озвучивают литературно, то есть с привлечением различного рода оборотов и т. д. с целью благозвучия. Иногда, в случае простых детерминантов, вообще обходятся без буквенных обозначений.

Пример: параболу зададим как множество всех таких точек M{\displaystyle M}, что расстояние от M{\displaystyle M} до точки F{\displaystyle F} равно расстоянию от M{\displaystyle M} до прямой l{\displaystyle l}. Тогда дифференциалы параболы — F{\displaystyle F} и l{\displaystyle l}; детерминант — предикат P(M,F,l)=(ρ(M,F)=ρl(M,l)){\displaystyle P(M,\;F,\;l)=(\rho (M,\;F)=\rho _{l}(M,\;l))}, где ρ{\displaystyle \rho } — расстояние между двумя точками (метрика), ρl{\displaystyle \rho _{l}} — расстояние от точки до прямой. И говорят: «Парабола — геометрическое место точек M{\displaystyle M}, равноудалённых от точки F{\displaystyle F} и прямой l{\displaystyle l}. Точку F{\displaystyle F} называют фокусом параболы, а прямую l{\displaystyle l} — директрисой».

ru.wikipedia.org