Основные свойства функций. Справочник репетитора по математике
Данная страница справочника представляет собой виртуальную шпаргалку по математике для учеников и методическое справочное пособие для репетиторов. Тема «свойства функций», адаптированное для разных уровней учащихся 8-9класов. В нем перечислены определения основных понятий и свойств, виды функций, термины и обозначения, принятые в математике. Репетитору по математике показаны образцы рисунков, которые должны остаться в теради ученика. Информация изложена как на строгом и формальном математическом языке (для среднего и сильного ученика), так на простом (бытовом) уровне, доступном для понимания широкому кругу посетителей сайта. Каждый такой перевод с математического языка на русский отмечен одним из следующих указателей: «пояснение репетитора по математике», «редакция репетитора по математике» или «уточнение репетитора по математике». В этих — переводах вы встретите несколько моих собственных уникальных дополнений и комментариев к классическим фомулировкам, которые я использую на занятиях со слабым учеником.
Определение функции: функцией или функциональной зависимостью называется такое соответствие f (x) при котором числу x из множества X сопоставляется некоторое единственное число из множества Y.
Редакция репетитора по математике: функцией называется закон или правило, по которому можно найти число y (значение какой-нибудь величины), если известно число x (значение какой-нибудь другой величины).
При этом букву x называют независимой переменной (или аргументом), а букву y — зависимой переменной. Число, которое подставляется вместо x, называется значением переменной (или значением аргумента), а число y, которому оно соответствует, называется значением функции.
График функции — множество точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Пояснение репетитора по математике Графиком функции называется линия на координатной плоскости, каждая точка которой имеет следующие координаты: первая (абсцисса) — это значение аргумента x , а вторая (ордината) — найденное для этого икса значение функции y.
Свойства функции:
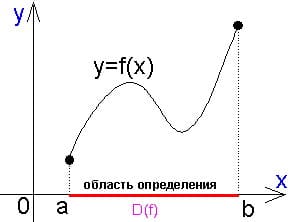
1) Что такое область определения функции? Область определения функции (О.О.Ф) — это множество всех значений переменной x, которые имеют соответствующие им значения функции.
Редакция репетитора по математике: область определения — множество значений переменной x, у которых можно найти y.
Обозначения области определения Для обозначения области определения используются следующие знаки: 
Как найти область определения по графику? Область определения — это промежутки на оси Ох, над которыми (или под которыми) имеются части графика.
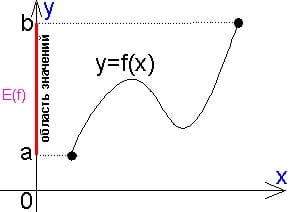
2) Что такое область значений функции? Областью значений функции (О.З.Ф) называется множество всех ее значений.
Редакция репетитора по математике:областью значений функции можно назвать часть оси ОY, состоящую из игреков, у которых есть соответствующие им иксы.
Как найти область значений по графику?: область значений функции — это промежутки на оси OY, слева или справа от которых (в горизонтальной полоске) находятся части графика.
3) Возрастание и убывание функции.
Какая функция называется возрастающей?Функция 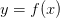 называется возрастающей, если для любой пары значений аргументов
называется возрастающей, если для любой пары значений аргументов 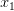 и
и 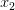 из неравенства
из неравенства 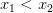
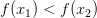 .
.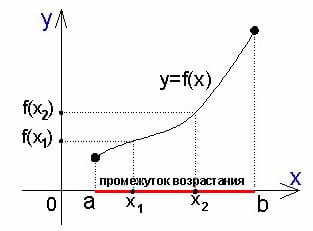
Редакция репетитора по математике: Функцию можно назвать возрастающей на промежутке, если, большему из любых двух взятых из него чисел всегда соответствует большее значение функции. Для графика это будет означать то, что при движении по нему карандашом слева направо карандаш будет подниматься вверх.
Какая функция называется убывающей? Функция 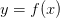
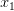 и
и 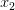 из неравенства
из неравенства 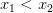 следует неравенство
следует неравенствоПромежуток отрицательного знака — это множество тех значений переменной х, у которых соответствующие значения функции меньше нуля (y).
Как найти все такие промежутки по графику? Определите промежутки оси ОХ, у которых соответствующие кусочки графика ниже оси Ох.
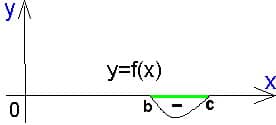
Как их найти без графика? Составьте и решите неравенство f (x) Оформление:  , если
, если 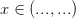
5) Нули функции:Число a называется нулем функции, если соответствующее ему значение функции равно нулю, то есть f (a)=0.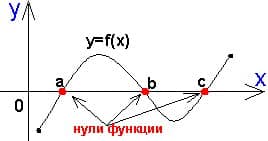
Редакция репетитора по математике: нулями функции называются такие числа х, у которых соответствующие игреки равны нулю.
Как найти нули функции без графика? Составьте и решите уравнение f (x)=0, то есть приравняйте аналитическое выражение функции (правую часть ее записи) к нулю.
Как найти по графику? Определите абсциссы точек пересечения графика с осью Ох.
Оформление: 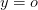 , если
, если 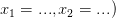
7) Четность и нечетность функции
а) Четность. Функция называется четной, если ее область определения симметрична относительно нуля и для любого
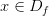 верно равенство
верно равенство  .
.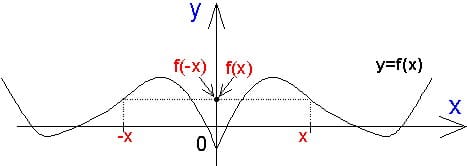
Редакция репетитора по математике:функция называется четной, если любым двум противоположным значениям аргумента соответствуют равные значения функции.
Уточнение репетитора по математике: равенство 
Как определить четность функции по графику?График четной функции должен быть симметричен оси Оу.
Пояснения репетитора по математике: симметрия графика означает то, что он состоит из двух частей, одна из которых является зеркальным отражением другой.
8) Нечетность. Функция называется нечетной, если ее область определения симметрична относительно нуля и для любого 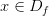 верно равенство
верно равенство 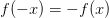

Редакция репетитора по математике:функция называется нечетной, если любым двум противоположным значениям аргумента соответствуют противоположные значения функции.
Уточнение репетитора по математике: равенство  можно получить только тогда, когда функция имеет симметричную область определения, поэтому проверку этой симметричности при решении задач часто опускают.
можно получить только тогда, когда функция имеет симметричную область определения, поэтому проверку этой симметричности при решении задач часто опускают.
Как определить нечетность функции по графику?График нечетной функции должен быть симметричен началу координат, Пояснения репетитора по математике: симметрия означает то, что если какая-то точка лежит на графике, то и симметричная ей точка (с противоположными координатами) тоже должна лежать на графике.
9) Наименьшее и наибольшее значение функции.
Число a называется наименьшим значением функции на промежутке, если для любого значения аргумента 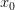 из этого промежутка верно неравенство
из этого промежутка верно неравенство 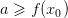 .
.
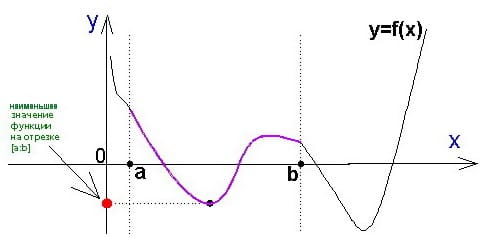
Число a называется наибольшим значением функции на промежутке, если для любого значения аргумента 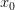 из этого промежутка верно неравенство
из этого промежутка верно неравенство  .
.
Материалы для подготовки к ГИА по математике, 9 класс.
Колпаков Александр Николаевич, репетитор по математике, профессиональный репетитор и методист. Москва, Строгино.
Метки: Справочник репетитора
ankolpakov.ru
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Понятие функции. Основные свойства функций. Область определения и значения. Четность и нечетность. Периодичность, нули функции, промежутки знакопостоянства, монотонность (возрастание, убывание), экстремумы (максимумы, минимумы), асимптоты Поделиться:
| |||||||||||||||
dpva.ru
Свойства функций
На прошлом уроке мы с вами изучили понятие функция. Изучили её график и научились находить область определения и область значений функции.

Свойства функций:
· нули функции;
· промежутки знакопостоянства функции;
· промежутки монотонности функции.
Нули функции
Определение:
Нулями функции называют такие значения аргумента, при которых функция равна нулю.

В данном случае функция задана графически и мы определили нули функции по графику. Так же нули функции можно находить по формуле, с помощью которой задана функция.

Решив уравнение, мы найдём те значения х, при которых функция равна нулю.
Стоит обратить внимание на то, что не каждая функция имеет нули.

График не пересекает ось икс ни в одной точке.

Промежутки знакопостоянства функции
Определение:
Промежутки знакопостоянства функции — это такие промежутки из области определения, на которых данная функция принимает значения только одного знака, либо положительные, либо отрицательные.

Функция принимает положительные значения:

И отрицательные значения:

Запишите промежутки знакопостоянства функции:

Положительные и отрицательные значения функции:

Промежутки монотонности функции
Определение:
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.


Определение:
Функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.


Определение:
Промежутками монотонности называют такие промежутки из области определения, на которых функция либо возрастает, либо убывает.

Опишем свойства функции:

Графиком является прямая, поэтому для построения достаточно двух точек:

Найдём значения функции:

Областью определения и областью значений будет множество всех действительных чисел. Ведь х и у могут быть любыми числами.

Найдём нули функции:

Запишем промежутки знакопостоянства:

Запишем промежутки монотонности:

videouroki.net
Показательная функция, ее свойства и график. Начальные сведения
Ранее мы изучали различные функции. Например, линейная функция 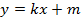 описывает прямолинейное движение. Квадратичная функция
описывает прямолинейное движение. Квадратичная функция  описывает равноускоренное движение.
описывает равноускоренное движение.
Теперь рассмотрим новую функцию, показательную – в ней основание степени постоянное число, а показатель изменяется: 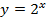 ;
;  ;
;  .
.
Пример
Масса 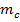 радиоактивного вещества в момент времени
радиоактивного вещества в момент времени 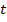 равна:
равна:
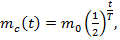 где
где  – начальная масса образца;
– начальная масса образца; 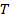 – период полураспада.
– период полураспада.
Здесь мы видим, что основание степени постоянная величина, а показатель – переменная.
Скорость роста показательной функции иллюстрируется примерами с шахматами.
Мы изучаем показательную функцию 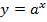 ,
,  ,
, 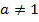 , ее график называется экспонентой (рис. 1):
, ее график называется экспонентой (рис. 1):
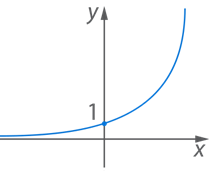
Рис. 1. Экспонента
Построить конкретную экспоненту, например 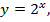 по точкам достаточно сложно, так как даже при
по точкам достаточно сложно, так как даже при 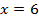 значение функции уже очень велико и элементарно не хватает листа бумаги, а при
значение функции уже очень велико и элементарно не хватает листа бумаги, а при 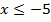 значения слишком малы и график почти сливается с осью
значения слишком малы и график почти сливается с осью  , очевидно, что с ростом аргумента данная функция резко возрастает, а с уменьшением – стремительно приближается к нулю, но не достигает его.
, очевидно, что с ростом аргумента данная функция резко возрастает, а с уменьшением – стремительно приближается к нулю, но не достигает его.
Так, при стремлении аргумента к бесконечности растет не только функция, но и скорость ее роста.
Задача о зернах на шахматной доске
По легенде мудрый изобретатель шахмат попросил у правителя награду: положить на первую клетку 1 зерно пшеницы, на вторую 2 зерна, то есть в два раза больше, на третью 4 и так далее, соответственно, на последнюю 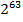 . Сколько зерна попросил мудрец?
. Сколько зерна попросил мудрец?
Решение
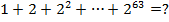
Данное выражение вычислить затруднительно. Даже число 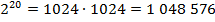 , что уже является очень большим числом.
, что уже является очень большим числом.
То есть если собрать зерна с первых 19 клеток, получится примерно один миллион зерен, что примерно помещается в литровом пакете от молока.
Но уже начиная со второй половины доски рост числа зерен столь стремителен, что их общее количество трудно представить.
Формально количество требуемых зерен есть геометрическая прогрессия:
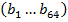 ;
; 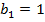 ;
; 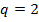
Найдем ее сумму:
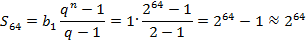
Такое число зерен просто огромно. Подсчитано, что это количество зерен превышает в 1800 раз мировой урожай пшеницы за 2008–2009 аграрный год, а он составил 686 млн тонн пшеницы.
Ответ: 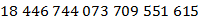 .
.
Можно представить, сколь малым является число 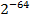 .
.
Определение
Показательной называется функция вида 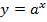 ,
,  ;
; 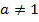 .
.
Основание показательной функции существенно влияет на ее график.
Рассмотрим семейство экспонент 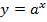 ,
,  ;
; 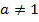 .
.
Все экспоненты проходят через точку 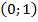 , так как
, так как 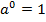 для любого
для любого 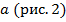 :
:

Рис. 2. Фиксированная точка всех экспонент
Рассмотрим случай, когда 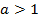 . В этом случае функция возрастает, но скорость роста зависит от основания степени. Рассмотрим это на примере функций
. В этом случае функция возрастает, но скорость роста зависит от основания степени. Рассмотрим это на примере функций 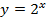 ;
;  ;
; 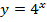 . Составим таблицы и постоим графики (рис. 3).
. Составим таблицы и постоим графики (рис. 3).
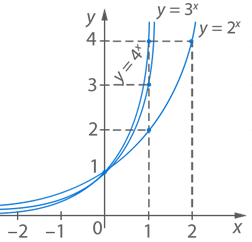
Рис. 3. Графики функций 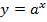 ,
, 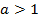
Так, при 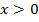 :
:  и при
и при 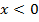 :
: 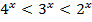 .
.
Пусть 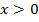 . Тогда
. Тогда 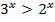 .
.
Доказательство
Обе части неравенства неотрицательны, поделим на 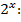
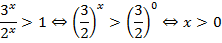
Получено верное выражение, значит, и исходное выражение верно.
Пусть 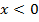 . Тогда
. Тогда 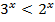 .
.
Доказательство
Обе части неравенства неотрицательны, поделим на 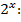
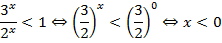
Получено верное выражение, значит, и исходное выражение верно.
Рассмотрим случай, когда 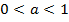 . В этом случае функция убывает, но скорость зависит от основания степени. Рассмотрим это на примере функций
. В этом случае функция убывает, но скорость зависит от основания степени. Рассмотрим это на примере функций 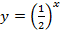 ;
;  ;
; 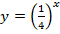 .
.
Отметим: 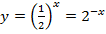 ;
; 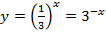 ;
; 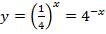 .
.
Используем тот факт, что кривые  и
и 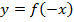 симметричны относительно оси
симметричны относительно оси  :
:
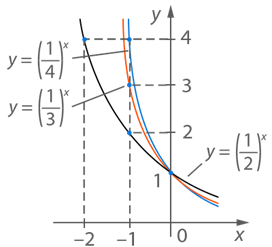
Рис. 4. Графики функций 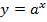 ,
, 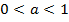
Так, чем меньше основание степени, тем быстрее рост функции, при стремлении 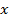 к минус бесконечности при отрицательных
к минус бесконечности при отрицательных 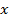 :
:
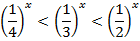
Если же 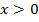 и стремится к плюс бесконечности, имеем:
и стремится к плюс бесконечности, имеем:

Теперь рассмотрим область определения показательной функции. Для начала ограничимся множествами целых, а затем рациональных чисел.
Пример
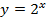 ,
, 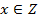
Графиком будем множество точек вида 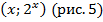 .
.
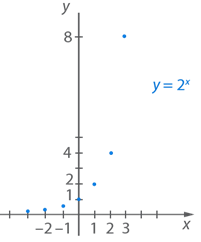
Рис. 5. График функции  ,
, 
1. Данная функция монотонно возрастает, то есть большему значению аргумента соответствует большее значение функции: 
Докажем этот факт. Обе части неравенства неотрицательны, разделим его на  :
:

Получено истинное выражение, значит, и предположение было верным.
2. При  функция резко возрастает; при стремлении аргумента к минус бесконечности функция стремительно приближается к нулю, не достигая его.
функция резко возрастает; при стремлении аргумента к минус бесконечности функция стремительно приближается к нулю, не достигая его.
3. Рассмотрим множество значений функции: это все числа вида 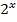 ,
,  .
.
4. Функция не ограничена сверху, но ограничена снизу нулем.
5. Функция не имеет ни наименьшего, ни наибольшего значения.
Пример
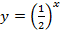 ,
, 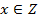
Графиком будем множество точек вида 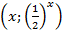 . График изображен на рисунке 6 синим цветом. Его можно получить по точкам, а можно отобразить график функции
. График изображен на рисунке 6 синим цветом. Его можно получить по точкам, а можно отобразить график функции 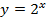 относительно оси ординат.
относительно оси ординат.
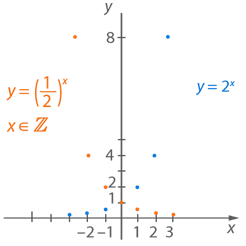
Рис. 6. График функции 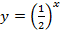 ,
, 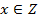
1. При возрастании аргумента от минус до плюс бесконечности функция убывает от бесконечности до нуля, но нуля не достигает.
2. Рассмотрим множество значений функции: это все числа вида 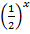 ,
, 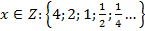 .
.
3. Отметим, что функция не ограничена сверху, но ограничена снизу нулем.
4. Функция не имеет ни наименьшего, ни наибольшего значения.
Пример
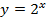 ,
, 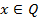
Найти значение функции при 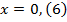 .
.
Решение
Переведем периодичную дробь в обыкновенную.
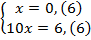
Вычтем из второго выражения первое:
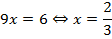
Требуется вычислить: 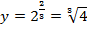 .
.
Так, мы можем вычислить значение показательной функции для любого рационального числа. Графиком функции 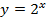 ,
, 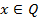 будет множество точек вида
будет множество точек вида  , но эти точки так близко расположены, что нарисовать такой график невозможно.
, но эти точки так близко расположены, что нарисовать такой график невозможно.
Свойства данной функции аналогичны свойствам той же функции, когда аргумент принимал целочисленные значения.
Теперь рассмотрим функцию 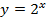 ,
,  .
.
Вспомним, что 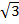 – это такое иррациональное число, квадрат которого равен трем. Его нельзя представить в виде обыкновенной дроби.
– это такое иррациональное число, квадрат которого равен трем. Его нельзя представить в виде обыкновенной дроби. 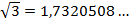
Число 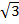
interneturok.ru
Показательная функция, ее свойства. Простейшие показательные уравнения
Рассмотрим основное определение.
Определение:
Функцию вида 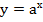 , где
, где 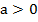 и
и  называют показательной функцией.
называют показательной функцией.
Например: 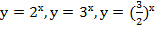 и т. д.
и т. д.
Рассмотрим первый случай, когда основание степени больше единицы: 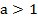 :
:
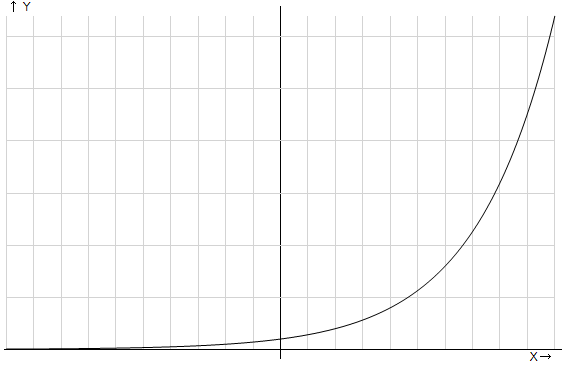
Рис. 1. График показательной функции, основание степени больше единицы
Основные свойства данного семейства функций:
Область определения: 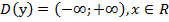 ;
;
Область значений: 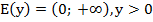 ;
;
Функция возрастает, т. е. большему значению аргумента соответствует большее значение функции;
Если аргумент стремится к минус бесконечности, функция стремится к нулю, если аргумент стремится к плюс бесконечности функция стремится также к плюс бесконечности.
Рассмотрим второй случай, когда основание степени меньше единицы  :
:
Например: 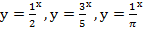 и т. д.
и т. д.
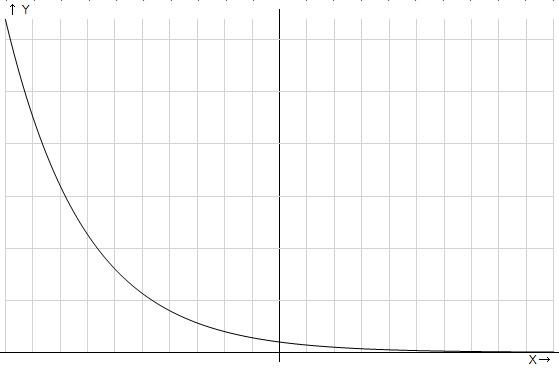
Рис. 2. График показательной функции, основание степени меньше единицы
Свойства данного семейства функций:
Область определения: 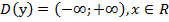 ;
;
Область значений: 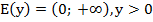 ;
;
Функция убывает, т. е. большему значению аргумента соответствует меньшее значение функции;
Если аргумент стремится к минус бесконечности, функция стремится к плюс бесконечности, если аргумент стремится к плюс бесконечности функция стремится к нулю.
Решение показательных уравнений и неравенств основывается на свойствах показательной функции.
Пример 1 – решить уравнение:
а) 
Ответ:  , т. к. показательная функция принимает строго положительные значения.
, т. к. показательная функция принимает строго положительные значения.
б) 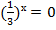
Ответ:  , т. к. показательная функция принимает строго положительные значения.
, т. к. показательная функция принимает строго положительные значения.
Пример 2 – решить неравенство:
а) 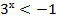
Ответ:  , т. к. показательная функция принимает строго положительные значения.
, т. к. показательная функция принимает строго положительные значения.
б) 
Ответ:  , т. к. показательная функция принимает строго положительные значения.
, т. к. показательная функция принимает строго положительные значения.
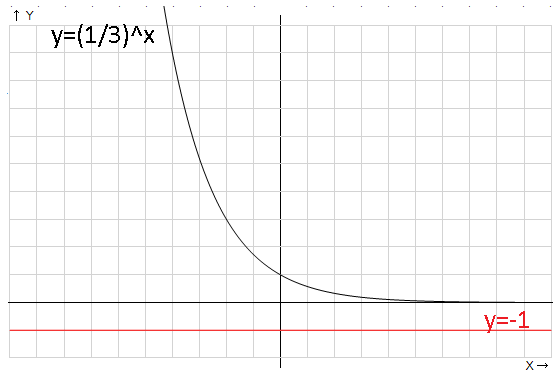
Рис. 3. Иллюстрация к примеру 2.б
Рассмотрим простейшие уравнения и неравенства.
Пример 3:
а) 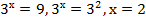 (рисунок 4)
(рисунок 4)
б) 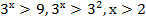 , т. к. функция монотонно возрастает на всей области определения (рисунок 4)
, т. к. функция монотонно возрастает на всей области определения (рисунок 4)
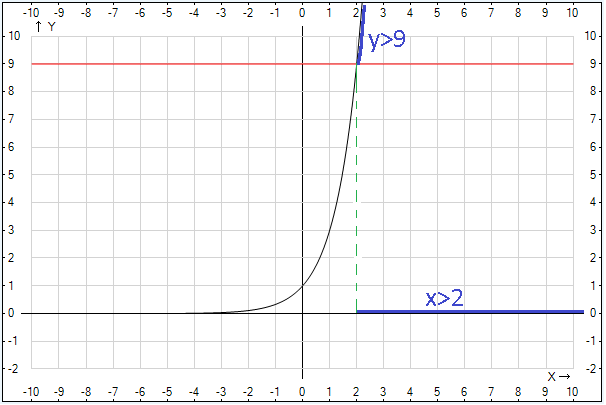
Рис. 4. Иллюстрация к примеру 3
Рассмотрим простейшие показательные уравнения в общем виде.

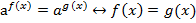
Равенство показателей степени при равных основаниях обусловлено свойством показательной функции, а именно ее монотонностью. Это означает, что каждое свое значение функция приобретает при единственном значении аргумента.
Таким образом, получаем методику решения показательных уравнений:
Уравнять основания степеней;
Приравнять показатели степеней;
Например:
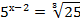
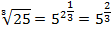
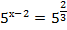
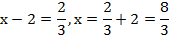
Пример 4 – решить уравнения:
а) 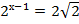
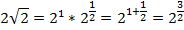
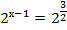
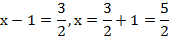
б) 


Итак, мы рассмотрели показательную функцию, ее график и свойства, научились решать простейшие показательные уравнения и неравенства, рассмотрели простейшие показательные уравнения в общем виде. В следующем уроке мы рассмотрим решение показательных неравенств.
Список литературы
- Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
- Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Mathematics-repetition.com (Источник).
- Terver.ru (Источник).
- Egesdam.ru (Источник).
Домашнее задание
1. Алгебра и начала анализа, 10–11 класс (А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын) 1990, № 446, 453, 460, 461;
2. Решить неравенство:
а) 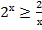 ; б)
; б) 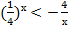 ; в)
; в) 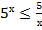 ; г)
; г) 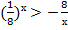 ;
;
3. Решить уравнение:
а) 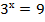 ; б)
; б)  ; в)
; в) 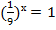 ; г)
; г)  ;
;
interneturok.ru
Математика
36
Раздел «Математический анализ»
Модуль 1. дифференциальное исчисление функции одной переменной
Содержание
Тема 1. Функции одной переменной, свойства и графики
Определение функций одной переменной.
Способы задания функций одной переменной.
Элементарные функции.
Основные свойства функций.
Преобразования графиков функций
Тема 2. Предел и непрерывность функции одной переменной
Предел функции в точке и на бесконечности.
Основные свойства пределов.
Бесконечно малые и бесконечно большие функции.
Раскрытие неопределенностей
 ,
, .
.Первый и второй замечательные пределы
Эквивалентные бесконечно малые функции
Непрерывность функции, точки разрыва
Свойства функций, непрерывных на отрезке.
Тема 3. Производные и дифференциалы. Экстремумы функции одной переменной
Определение производной.
Геометрический и экономический смысл производной.
Основные правила дифференцирования.
Таблица основных формул дифференцирования.
Производные высших порядков.
Вычисление пределов с помощью производных.
Дифференциал функции.
Свойства дифференциала функции.
Применение дифференциала к приближенным вычислениям.
Дифференциалы высших порядков
Монотонность функции.
Экстремумы (максимумы и минимумы) функции.
Наименьшее и наибольшее значения непрерывной функции на отрезке.
Модуль 1. Дифференциальное исчисление функции одной переменной
Тема 1. Функции одной переменной, свойства и графики
Содержание
Определение функций одной переменной.
Способы задания функций одной переменной.
Элементарные функции.
Основные свойства функций.
Преобразования графиков функций.
Понятие функции применяется не только в математике, но и в других областях знаний. В философии функция (лат. function – исполнение) – обязанность, круг деятельности1.
Функцией в общественных науках обычно называют предназначение, роль какого-либо элемента в социальной системе, или, иными словами, определенного вида работу, которая требуется от него в интересах системы в целом.
В менеджменте функция означает исполнение, совершенствование, служебную обязанность, назначение, роль. В широком смысле «функция» — это устойчивый вид деятельности, то, что обязан выполнять сотрудник независимо от своего желания.
1. Определение функций одной переменной
Дадим определение функции одной переменной.
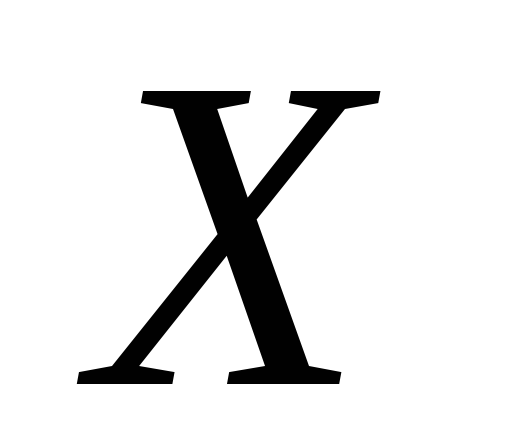


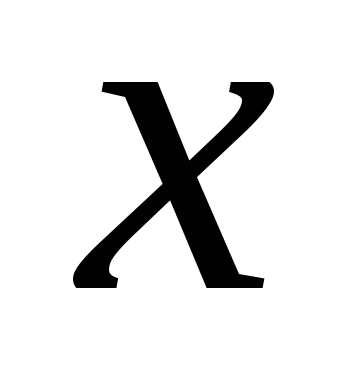

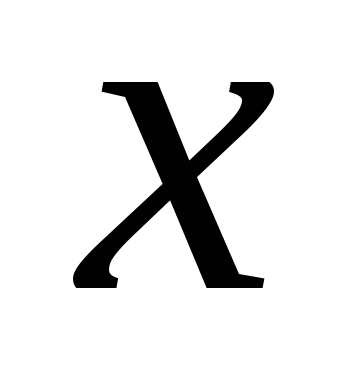
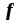


Рис. 1 – Математическое определение функции
Пример 1. 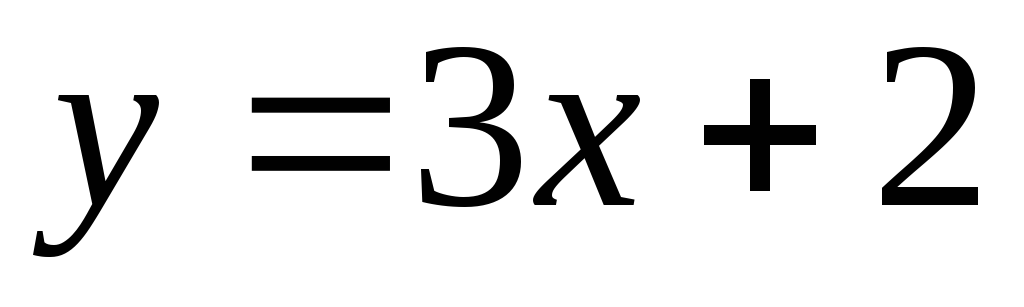 ,
область определения
,
область определения .
.
Пример 2. 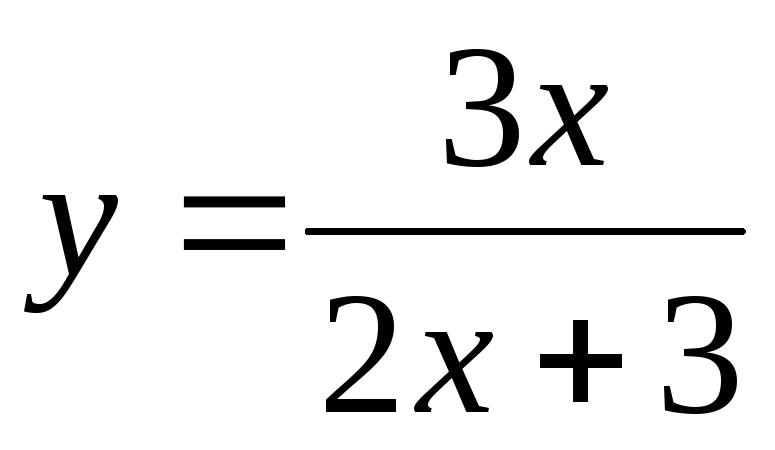 ,область
определения
,область
определения  .
.
Пример 3. 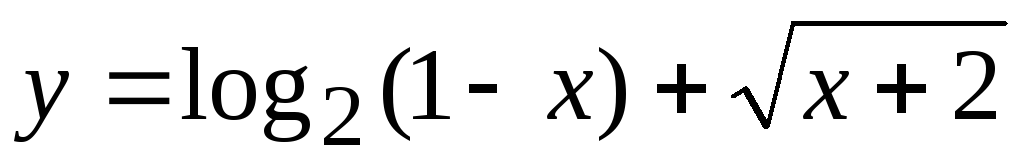 .
.
Решение.
Так как  ,
то ее область определения
,
то ее область определения ,
где
,
где ,
а
,
а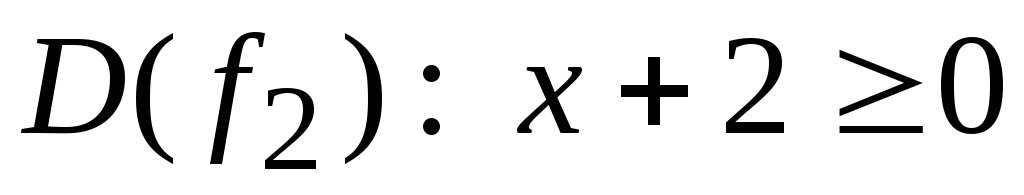 .
.
Тогда 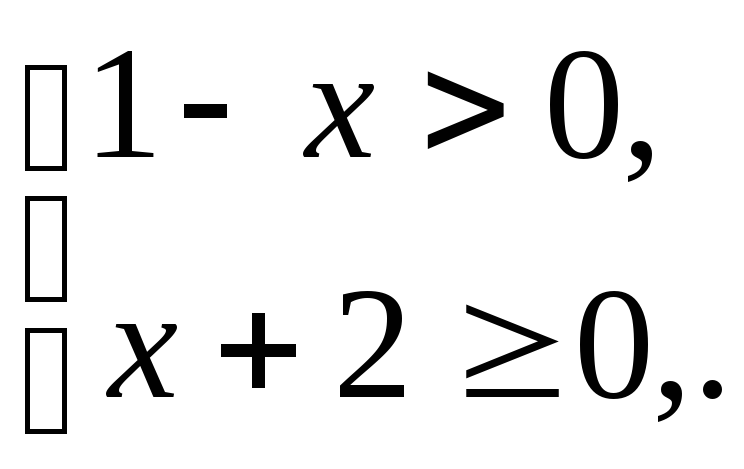

 .
.
Основными способами задания функций являются аналитический, табличный, графический. Существует и другие способы задания функций — алгоритмический, с помощью программы на ЭВМ.
Аналитический способ задания функции – имеется формула, указывающая, какие действия нужно произвести над аргументами, чтобы получить значение функции. Аналитический способ может быть явным и неявным.
Функция задана явно, если она задана:
одной формулой, разрешенной относительно зависимой переменной (например, у =
 или
или ),
или
),
илиразными формулами на определенных числовых промежутках (кусочно-аналитическое задание функции): например,
 или
или
Пример 4. Вычислить значения функции  при
при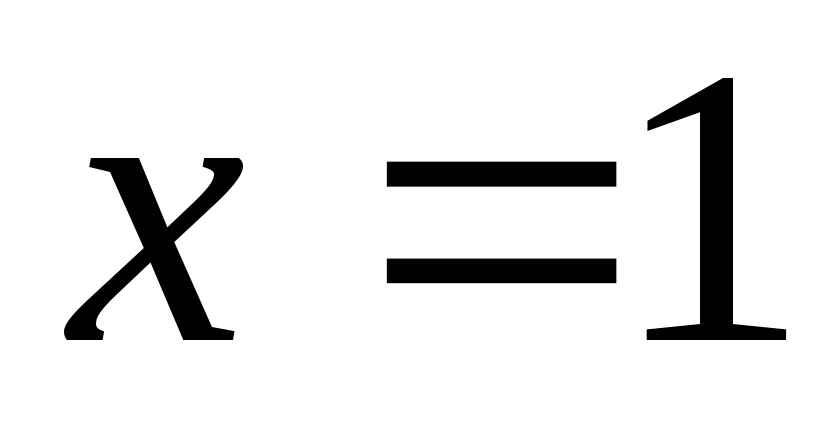 ,
,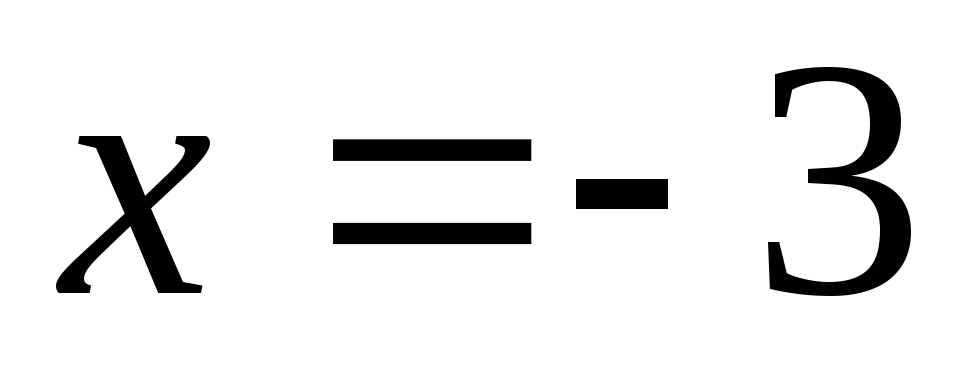 ,
,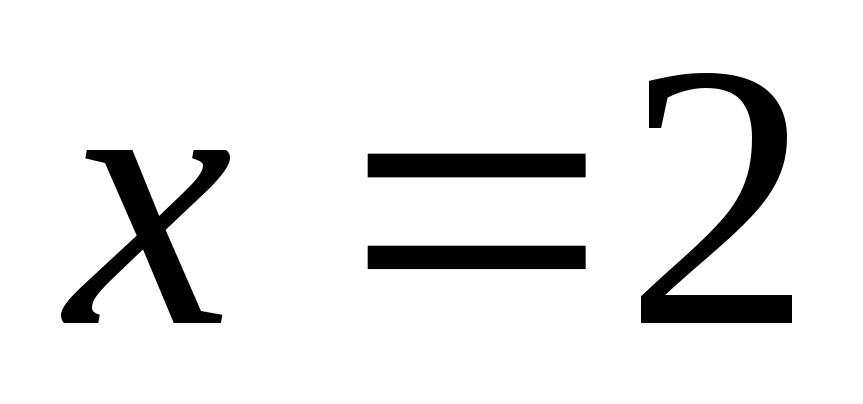 .
.
Решение.
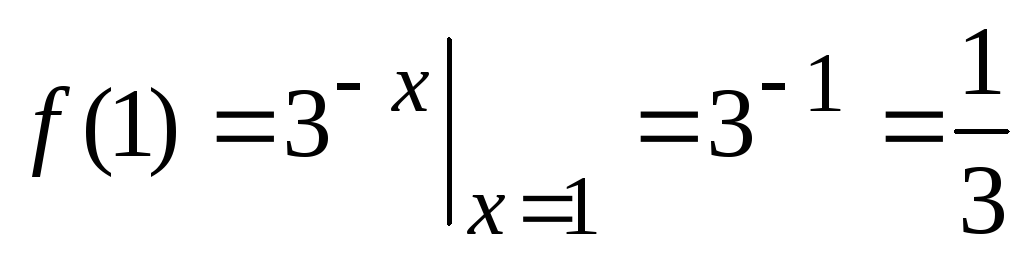 ;
;  ;
;
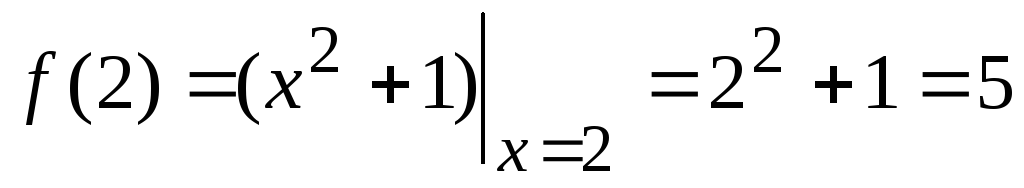 .
.
Функция одной или
двух переменных называется неявной,
если она задана уравнением, не разрешенной
относительно зависимой переменной.
Например, 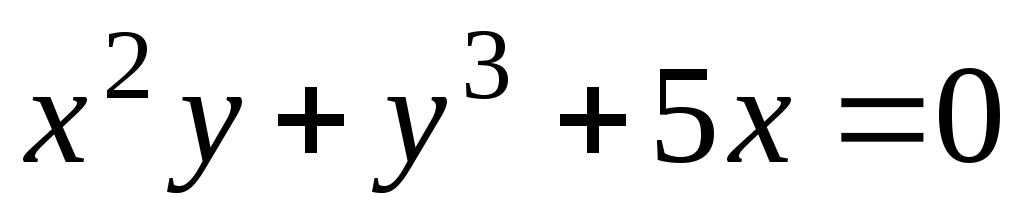 ,
или
,
или 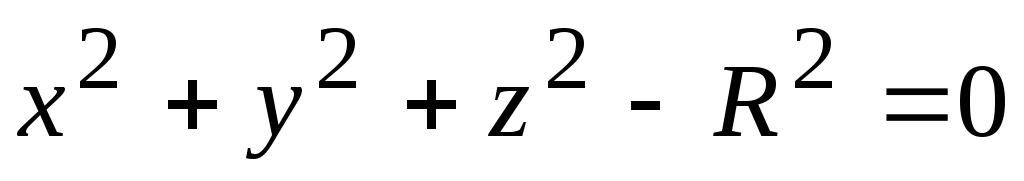 .
.
Табличный способ задания функции — с помощью таблицы, в которой указаны значения аргументов и соответствующие им значения зависимой переменной. Например, таблицы Брадиса.
Достоинством табличного способа является то, что по таблице можно непосредственно найти значение функции для имеющихся в таблице значений аргумента, а недостатком – отсутствие значений функции для промежуточных значений аргумента.
Таблица функции одной переменной
Для функции одной переменной:
Графиком функции
 называется множество точек плоскости
ХОУ, координаты которых связаны
соотношением
называется множество точек плоскости
ХОУ, координаты которых связаны
соотношением .
Равенство
.
Равенство называетсяуравнением этого графика.
называетсяуравнением этого графика.
Отличительной
чертой любого графика функции  является то, что каждая прямая
является то, что каждая прямая (для
(для из области определения), параллельная
оси ординат
из области определения), параллельная
оси ординат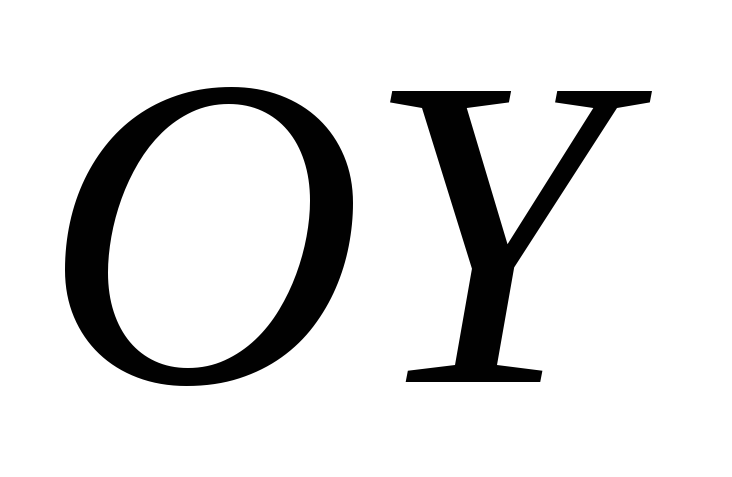 ,
пересекает график вединственной точке.
,
пересекает график вединственной точке.
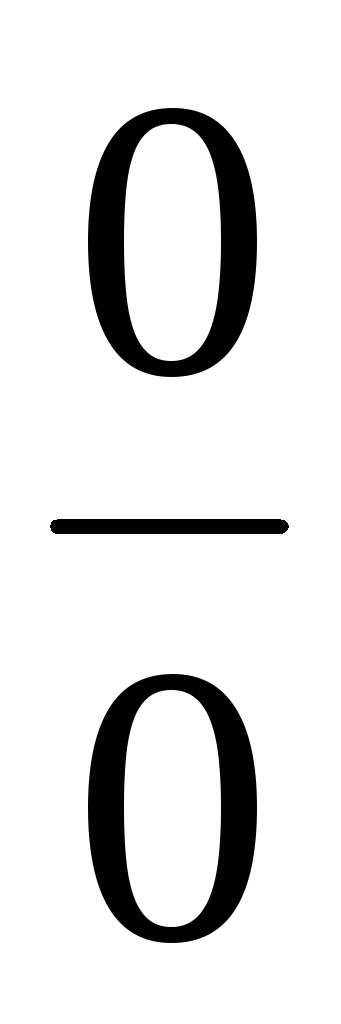
Пример 5. Функция «абсолютная
величина  »:
»:
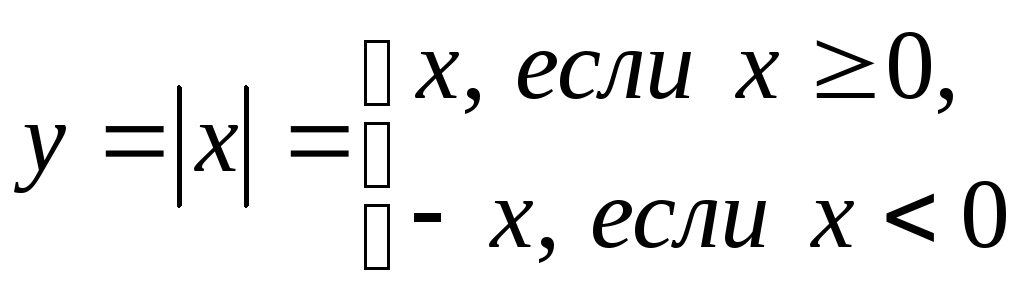 .
.
Функция задана с
помощью двух функций на разных числовых
промежутках. Поэтому график функции
«склеен» из двух графиков – графика  на промежутке
на промежутке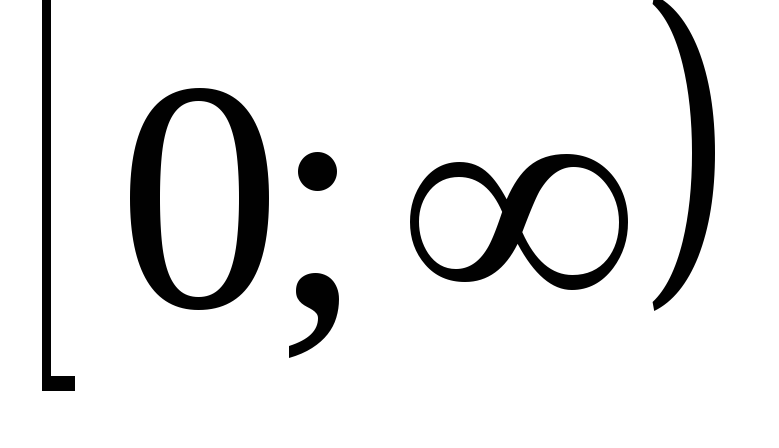 и графика
и графика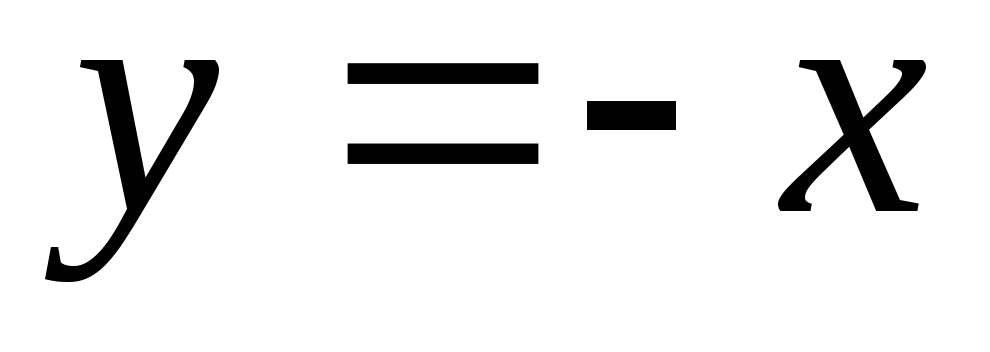 на промежутке
на промежутке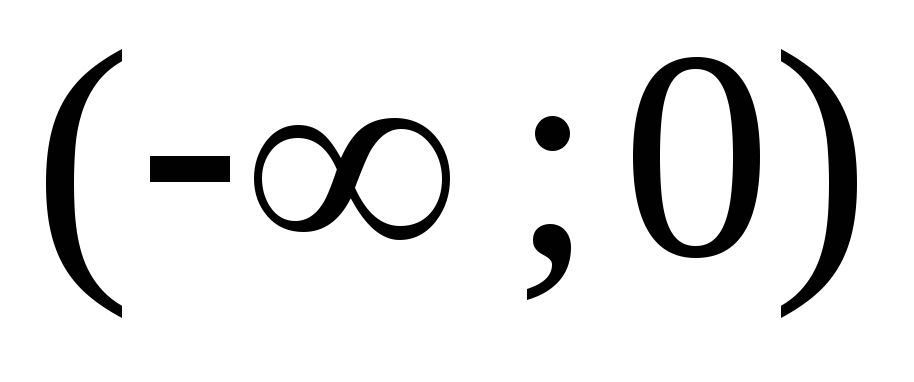 .
.


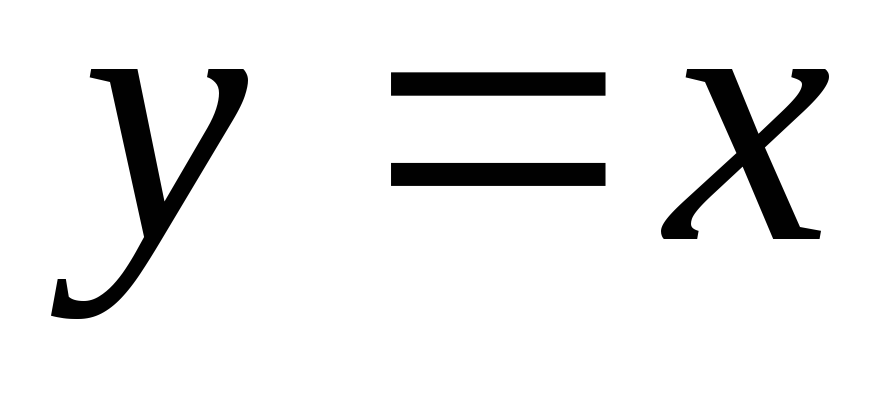
studfile.net
Квадратичная функция, парабола, график, свойства: нули, вершина, ось симметрии, промежутки возрастания, убывания. Тесты
Тестирование онлайн
Квадратичная функция
Определение. График
Квадратичной (квадратной) функцией называется функция вида
где a, b, с — числа.
Графиком квадратичной функции является парабола.
Парабола имеет вершину, ось, проведенная через вершину и параллельная оси Оу, делит параболу на две симметричные части. Вершиной параболы называется точка
Если коэффициент а>0, то ветви параболы направлены вверх, если a, то ветви параболы направлены вниз.
Свойства квадратичной функции y=x2
1) Областью определения функции является множество всех действительных чисел, т.е.
2) Множеством значений функции является промежуток
3) Значение функции y=0 является наименьшим, а наибольшего значения функция не имеет.
4) Функция является четной, график симметричен относительно оси Оу.
5) Функция непериодическая.
6)Парабола имеет с осями координат единственную общую точку (0;0) — начало координат.
7) Значение аргумента x=0 является нулем функции.
8) На промежутке функция убывающая, а на промежутке — возрастающая.
9) Функция принимает положительные значения на множестве , т.е. все точки параболы, кроме начала координат.
Преобразование параболы
Функция y=x2 — частный случай квадратичной функции.
Квадратичную функцию всегда можно привести у виду , а затем построить параболу с помощью ее геометрических преобразований.
Для построения параболы необходимо:
1) Найти координаты вершины
2) Построить ось симметрии, проанализировать куда направлены ветви параболы
3) Найти точки пересечения параболы с осью Ox (нули), если они есть, решив уравнение
4) Найти точку пересечения с осью Оу, решив уравнение
fizmat.by
 ,
, .
.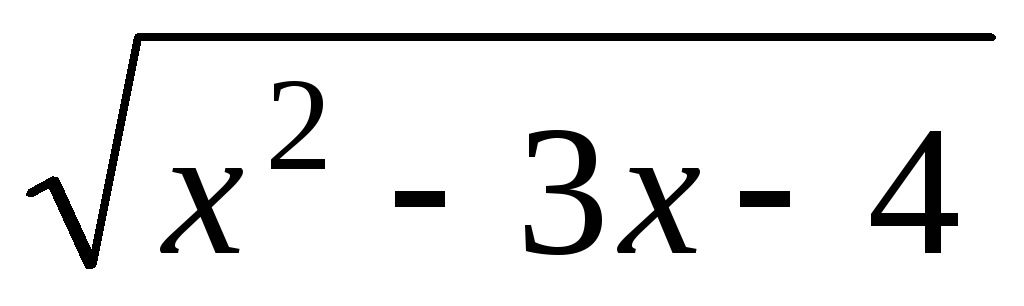 или
или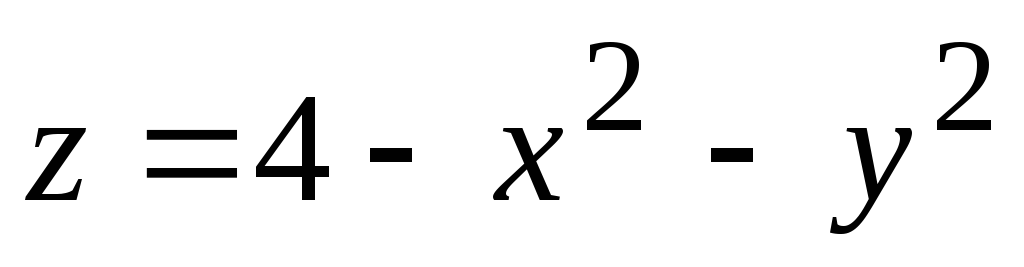 ),
или
),
или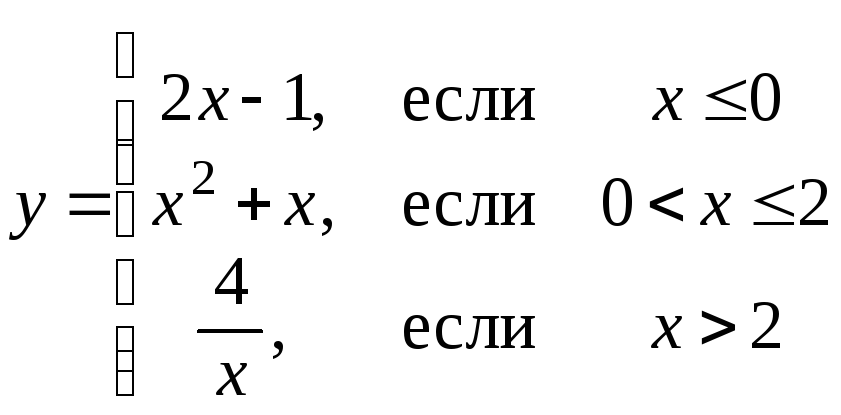 или
или
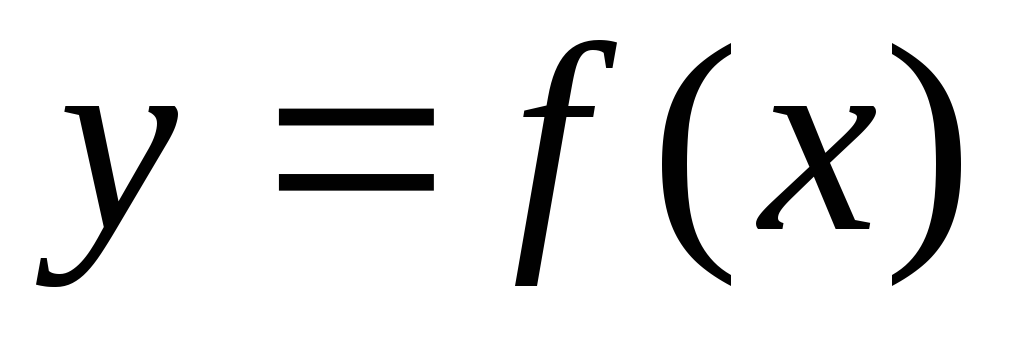 называется множество точек плоскости
ХОУ, координаты которых связаны
соотношением
называется множество точек плоскости
ХОУ, координаты которых связаны
соотношением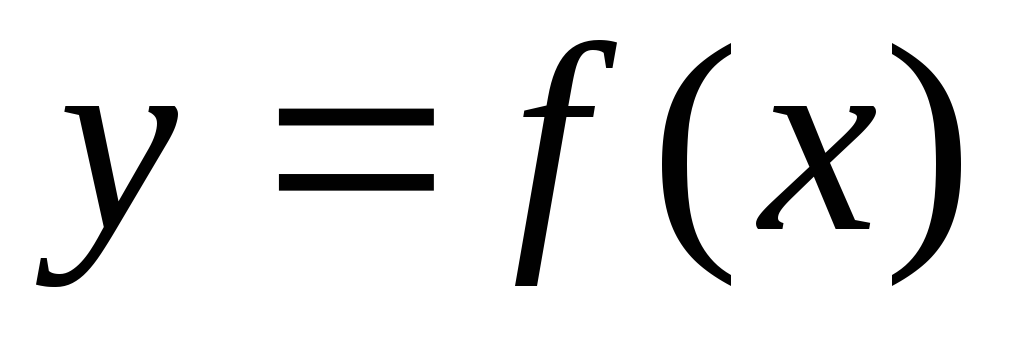 .
Равенство
.
Равенство называетсяуравнением этого графика.
называетсяуравнением этого графика.