Величина угла градусная мера. Градусная мера угла. Определение. Радианная мера угла
Основные понятия
В рамках вопроса измерения углов, в данном разделе рассмотрим несколько понятий, относящихся к начальным геометрическим сведениям:
- угол;
- развёрнутый и неразвёрнутый угол;
- градус, минута и секунда;
- градусная мера угла;
- прямой, острый и тупой углы.
Углом называют такую геометрическую фигуру, которая представляет собой точку (вершину) и исходящие из неё два луча (стороны). Угол называют развёрнутым, если оба луча лежат на одной прямой.
Благодаря градусной мере угла можно произвести измерение углов. Измерение углов проводится аналогично измерению отрезков. Так же, как и при измерении отрезков, при измерении углов используется специальная единица измерения. Чаще всего это градус.
Определение 1
Градус — это единица измерения. В геометрии он представляет собой угол, с которым сравнивают другие углы.
В данной статье мы раскрыли полностью вопрос о градусной мере угла и как измерять углы.
Лекция: Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
Мерой угла называют величину, на которую отклоняется некоторый луч относительно первоначального положения.
Мера угла может измеряться двумя величинами: градусами и радианами, отсюда и название единиц – градусная и радианная мера угла.
Градусная мера угла
Градусная мера дает возможность оценить, какое количество градусов, минут или секунд помещается в тот или иной угол.
Расчет углов в градусах производится с точки зрения того, что полный поворот луча – это 360°. Половина поворота 180° — развернутый угол, четверть – 90° — прямой угол и т.д.
Радианная мера угла
А теперь давайте же разберемся, что такое радианная мера угла. Как известно из физики, существуют дополнительные единицы. Например, для измерения температуры основной единицей являются Кельвины, а дополнительной градусы Цельсия.
Для определения радианной меры угла используют окружность. Считается, что радианная мера – это длина дуги окружности, описанная центральным углом.
Напомним, что центральный угол – это угол, вершина которого находится в центре окружности, а лучи опираются на некоторую дугу.
Итак, угол в 1 рад имеет градусную меру в 57,3°. Радианная мера угла описывается либо натуральными числами, или же с использованием числа π ≈ 3,14.
Для геометрии удобнее использовать градусную меру угла, однако для тригонометрии используют радианную меру.
Градусная мера угла – это положительное число, показывающее сколько раз градус и его части укладываются в угле.
У слова «угол» есть разные толкования. В геометрии углом называют часть плоскости, ограниченную двумя лучами, которые выходят из одной точки, так называемой вершины. Когда рассматриваются прямые, острые и развёрнутые углы, имеются ввиду именно геометрические углы.
Когда рассматриваются прямые, острые и развёрнутые углы, имеются ввиду именно геометрические углы.
Как и любые геометрические фигуры, углы можно сравнивать. В области геометрии описать, что один угол большего или меньшего размера по сравнению с другим, сегодня несложно.
За единицу измерения углов взят градус – 1/180 часть развернутого угла.
У каждого угла есть градусная мера, больше нуля. Развёрнутый угол соответствует 180 градусам. Градусная мера угла ровна сумме всех градусных мер углов, на которые можно разбить исходный угол лучами.
От любого луча к заданной плоскости можно отложить угол с градусной мерой не более 180 градусов. Мера плоского угла, являющаяся частью полуплоскости – это градусная мера угла, имеющая аналогичные стороны. Меру плоскости угла, в составе которого находится полуплоскость, обозначают числом 360 – ?, где? является градусной мерой дополнительного плоского угла.
Прямой угол всегда равен 90 градусам, тупой – менее 180 градусам, но более 90, острый – не превышает 90 градусов.
Кроме градусной меры угла существует радианная. В планиметрии длину дуги окружности обозначают как L, радиус – r, а соответствующему центральному углу досталось обозначение – ?.. Соотношение этих параметров выглядит так: ? = L/r.
Как найти градусную меру угла?
Для многих в школе геометрия — это настоящее испытание. Одной из базовых геометрических фигур является угол. Под этим понятием подразумевают два луча, которые берут начало в одной точке. Для измерения значения (величины) угла используют градусы или радианы. Как найти градусную меру угла, вы узнаете из нашей статьи.
Виды углов
Допустим, у нас есть угол. Если мы его разложим в прямую, тогда его величина будет равняться 180 градусам. Такой угол называют развернутым, а одним градусом считают 1/180 его часть.
Кроме развернутого угла различают еще острые (меньше 90 градусов), тупые (больше 90 градусов) и прямые (равные 90 градусам) углы. Эти термины используют для характеристики величины градусной меры угла.
Измерение угла
Величину угла измеряют с помощью транспортира. Это специальный прибор, на котором полукруг уже разбит на 180 частей. Приложите транспортир к углу так, чтобы одна из сторон угла совпадала с нижней частью транспортира. Второй луч должен пересекать дугу транспортира. Если этого не происходит, уберите транспортир и с помощью линейки удлините луч. Если угол «открывается» вправо от вершины, считывают его значение по верхней шкале, если влево — по нижней.
В системе СИ принято измерять величину угла в радианах, а не в градусах. В развернутом угле помещается всего 3,14 радиана, поэтому эта величина неудобна и на практике почти не применяется. Именно поэтому необходимо знать, как перевести радианы в градусы. Для этого существует формула:
- Градусы = радианы/π х 180
Например, величина угла равняется 1,6 радиана. Переводим в градусы: 1,6/3,14 * 180 = 92
Свойства углов
Теперь вы знаете, как измерять и пересчитывать градусные меры углов. {\circ}]\).
{\circ}]\).
Определение градусной меры дуги окружности
Градусной мерой дуги окружности называется градусная мера соответствующего ей центрального угла (т. е. центрального угла, который высекает эту дугу на окружности).
$$ \overset{\smile}{AB}=\angle AOB $$
Определение вписанного угла
Угол называется вписанным в окружность, если его вершина лежит на окружности, а стороны пересекают окружность. Говорят, что вписанный угол опирается на дугу, которую он вместе со своей внутренней областью высекает на окружности.
Вписанный угол \(ACB\) опирается на дугу \(AB\).
Теорема о вписанном угле
Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается, и равна половине градусной меры соответствующего этой дуге центрального угла.
$$ \alpha=\frac{1}{2}\beta=\frac{1}{2}\overset{\smile}{AB} $$
Угол, опирающийся на диаметр
Угол, вписанный в окружность, прямой, тогда и только тогда, когда он опирается на диаметр. {\circ} \Rightarrow ABCD\) – вписанный
{\circ} \Rightarrow ABCD\) – вписанный
Угол, образованный хордами
Градусная мера каждого из вертикальных углов, образованных двумя пересекающимися хордами, равна полусумме градусных мер дуг, которые эти углы высекают на окружности.
$$ \alpha=\frac{1}{2}\left(\overset{\smile}{AB}+\overset{\smile}{CD}\right) $$
Угол, образованный касательной и хордой
Градусная мера угла, образованного касательной к окружности и хордой с концом в точке касания, равна половине градусной меры дуги окружности, заключённой внутри этого угла.
$$ \alpha=\frac{1}{2}\overset{\smile}{AB} $$
Угол с вершиной на окружности
Пусть вершина угла принадлежит окружности, а одна из его сторон и продолжение другой стороны пересекают окружность. Тогда градусная мера этого угла равна полусумме градусных мер дуг, которые он вместе с вертикальным ему углом высекают на окружности.
$$ \alpha=\frac{1}{2}\left(\overset{\smile}{AB}+\overset{\smile}{BC}\right) $$
Угол с вершиной в круге
Градусная мера угла, вершина которого принадлежит кругу, равна полусумме градусных мер дуг, которые этот угол вместе с вертикальным ему высекает на окружности.
\( \alpha=\frac{1}{2} ( \)дуга\(_1\) + дуга\(_2 )\)
Угол, образованный секущими
Градусная мера угла, образованного двумя секущими к окружности, равна полуразности градусных мер дуг, которые он высекает на окружности.
$$ \alpha=\frac{1}{2}\left(\overset{\smile}{AB}-\overset{\smile}{CD}\right) $$
Угол, образованный касательными
Градусная мера угла, образованного двумя касательными к окружности, равна полуразности градусных мер дуг, на которые точки касания делят окружность.
$$ \alpha=\frac{1}{2}\left(\overset{\smile}{ACB}-\overset{\smile}{ADB}\right) $$
Угол, образованный касательной и секущей
Градусная мера угла, образованного касательной и секущей к окружности, равна полуразности градусных мер дуг, которые этот угол высекает на окружности.
$$ \alpha=\frac{1}{2}\left(\overset{\smile}{AB}-\overset{\smile}{BC}\right) $$
Признак касания прямой и окружности
Градусная мера угла, образованного касательной и секущей к окружности, равна полуразности градусных мер дуг, которые этот угол высекает на окружности.
$$ \alpha=\frac{1}{2}\left(\overset{\smile}{AB}-\overset{\smile}{BC}\right) $$
Угол с вершиной вне круга
Если вершина угла лежит вне круга, а каждая сторона пересекает круг или касается его, то градусная мера этого угла равна полуразности градусных мер дуг, которые он высекает на окружности.
\( \alpha=\frac{1}{2} ( \)дуга\(_1\) – дуга\(_2 )\)
Измерение углов. Транспортир
Цели:
- Образовательная: сформировать представление о градусе, как единице измерения угла, познакомить со структурой транспортира, научить измерять градусную меру угла с применением транспортира.
- Развивающая: любознательность, самостоятельность, целеустремленность, развитие креативного мышления.
- Воспитательная: интерес к предмету, уважение к одноклассникам, взаимопомощь.
Оборудование урока:
- Интерактивный комплекс.

- Презентация.
- Транспортир пластмассовый, классный.
- Учебники, письменные принадлежности, транспортиры.
Ход урока
- Организационная часть.
- Повторение материала предыдущего урока по теме «Угол. Типы углов».
- Определение темы и целей урока.
- Изучение материала по теме урока.
- Решение примеров по изученной теме урока.
- Закрепление материала.
- Домашнее задание.
1.
Повторение материала предыдущего урока по теме «Угол. Типы углов»Задание 1. На интерактивной модели построить острый угол. Назвать угол, записать обозначение угла, указать его тип (слайд 3).
Задание 2. На интерактивной модели построить тупой угол. Назвать угол, записать обозначение угла, указать его тип (слайд 3).
Задание 3. Учитель на интерактивной модели строит составные углы (слайд 3). Ученики называют углы, типы углов, записывают обозначение созданных углов, сравнивают углы.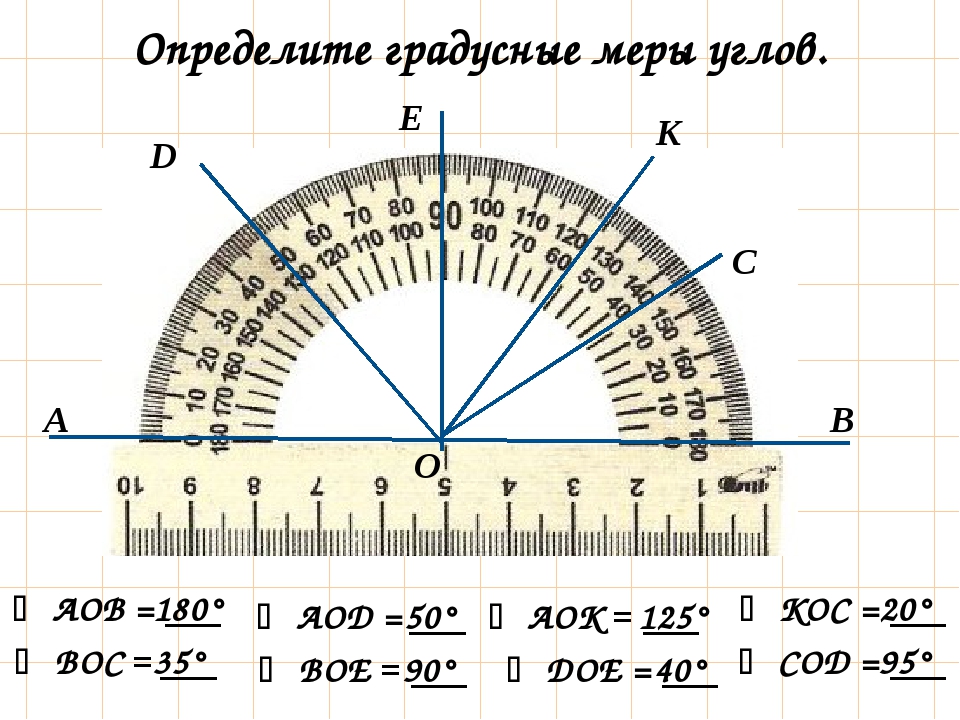
Задание 4. На интерактивной модели построить все углы (слайд 3). Назвать углы, указать типы углов, записать обозначения углов, сравнить углы. Сколько углов построено на рисунке?
2. Запись темы в тетрадь, определение целей урока3. Изучение темы урокаУчитель: Ребята! Сегодня на уроке, мы с вами научимся применять транспортир, для определения градусной меры угла.
Обратите внимание! На слайде показаны применяемые для измерения углов три вида транспортиров: полукруговые (1, 2, 3), круговой (4), геодезический (5).
Какие транспортиры есть в вашем инструментарии, и какой имеется в классе для измерения и построения углов?
Ответы учеников.
Учитель: Рассмотрим структуру транспортира, его составные части. Обратите внимание на слайд 5 нашей презентации. Анимированные стрелки показывают не только расположение двух угломерных шкал транспортира, но и направление определения градусной меры угла от начального значения – 00, внешней или внутренней шкалы, до конечного значения 1800 по каждой из угломерных шкал.
(При необходимости анимацию данного слайда можно повторить несколько раз).
Учитель: Сколько существует угломерных шкал?
Ответы учеников.
Учитель: Возьмите свои транспортиры, рассмотрите их и найдите угломерные шкалы на своих транспортирах и место расположения начального значения – нуль, каждой шкалы и конечное значение этих шкал.
Ученики рассматривают свои транспортиры, находят и показывают учителю результат свой работы.
Учитель: На слайде № 6 презентации показано расположение центра транспортира и его обозначение. Центр транспортира может обозначаться черточкой, окружностью, концентрическими окружностями, отверстием.
Вы легко сможете найти и показать центр своих транспортиров.
Ученики показывают центр своих транспортиров.
Учитель: А сейчас познакомимся с единицей измерения углов – градусом. Обратите внимание, шкала транспортира штрихами поделена на 180 долей (слайд 7).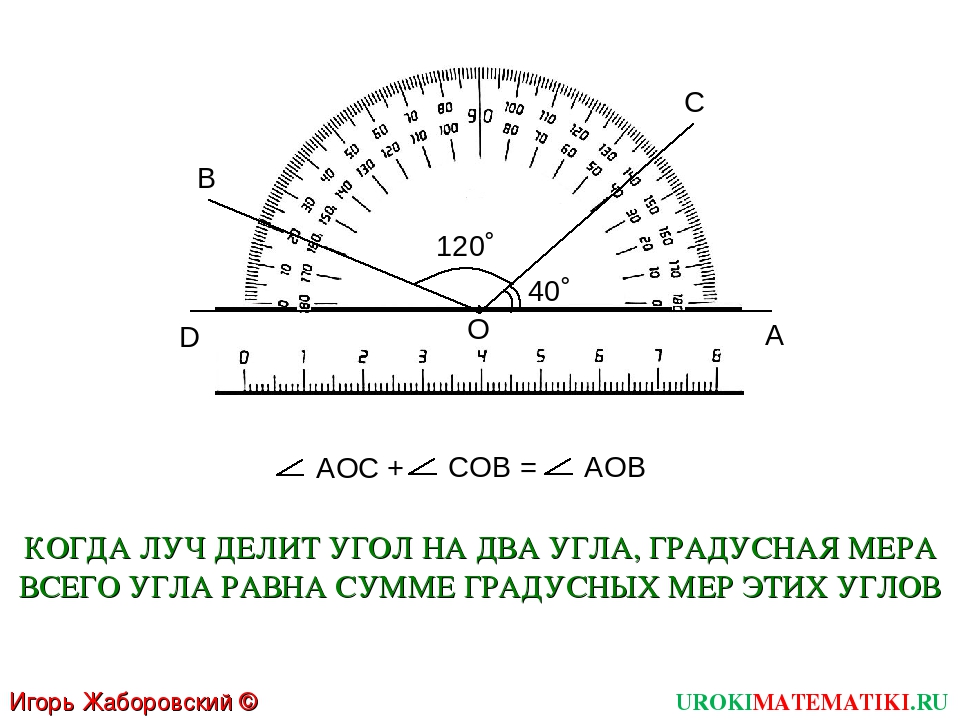 Расстояние между двумя соседними штрихами, которые показаны анимацией и есть 1/180 доля развернутого угла. Лучи, проведенные из центра полуокружности через эти штрихи, образуют 180 углов, каждый из которых равен 1 доли от 180. Таким образом, градусом называют 1/180 долю развернутого угла. Градусная мера развернутого угла равна 180 градусам.
Расстояние между двумя соседними штрихами, которые показаны анимацией и есть 1/180 доля развернутого угла. Лучи, проведенные из центра полуокружности через эти штрихи, образуют 180 углов, каждый из которых равен 1 доли от 180. Таким образом, градусом называют 1/180 долю развернутого угла. Градусная мера развернутого угла равна 180 градусам.
Учитель: Скажите, что такое градус?
Ученики отвечают.
Учитель: На сколько долей поделена шкала транспортира?
Ученики отвечают.
Учитель: Сколько углов можно провести через каждые два соседних штриха шкалы транспортира?
Ученики отвечают.
Учитель: Обратите внимание на то, каким символом обозначают градус. (слайд 8).
Учитель: А сейчас я прошу записать значения углов: 25 градусов, 107 градусов, 64 градуса (слайд 9).
Некоторые ученики делают записи на доске.
Затем, ученики называют градусные меры, которые записали на доске и те, которые представлены на слайде 8 презентации.
Учитель смотрит и проверяет записи учеников.
Учитель: На транспортире, кроме делений в 1 градус, есть деления по 5 градусов (слайд 10).
Посмотрите на свои транспортиры и найдите деления по 5 градусов.
Ученики находят и показывают эти деления.
Учитель: На транспортире есть и более крупные деления – по 10 градусов. (Слайд 11).
Найдите эти деления на своих транспортирах.
Ученики находят и показывают эти деления.
Учитель: А сейчас познакомимся с тем, как правильно записывать обозначение углов и их значение (слайд 12). Обратите внимание на то, что вершина О угла АОВ находится в центре полуокружности. Луч ОА проходит через нулевую отметку (начало отсчета), а луч ОВ проходит через отметку 110 градусов. Записывают значение угла так, как показано на слайде 12.
Обратите внимание! У вас есть карточки №K-1 – K-6. На этих карточках запишите значение каждого угла.
Ученики записывают обозначение углов с их градусной мерой.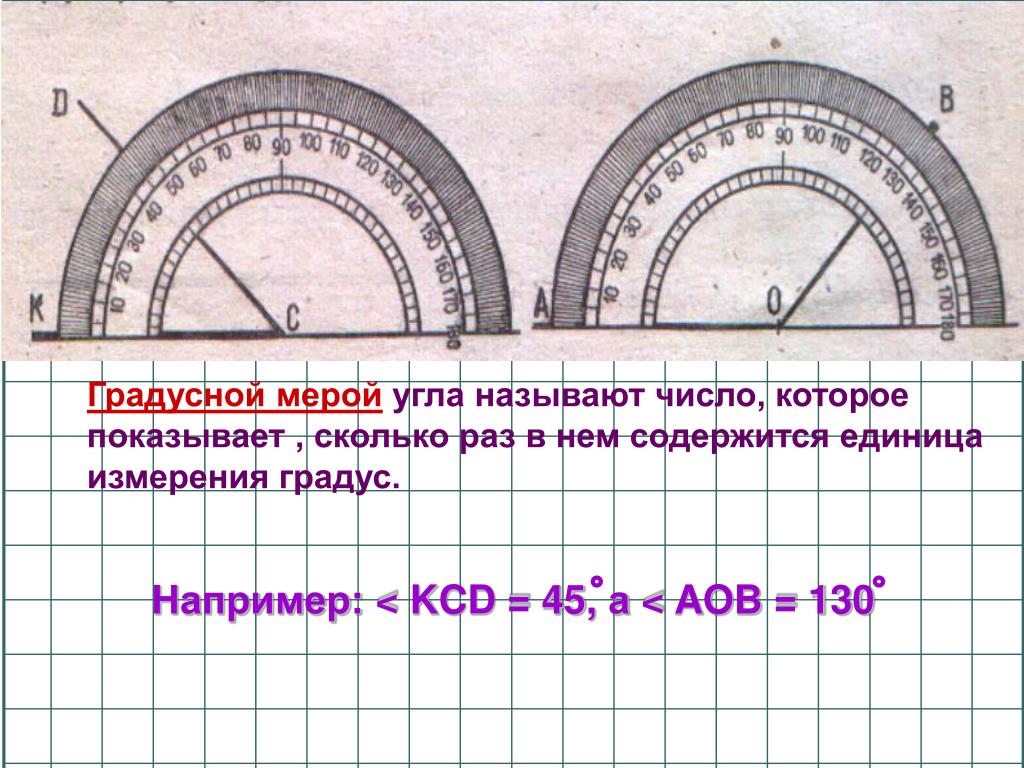 Затем показывают результаты выполненной работы.
Затем показывают результаты выполненной работы.
Называют углы и их градусные меры. Во время такой работы, углы можно показать с использованием документ-камеры или со слайда презентации.
Учитель: Вспомним, что представляет собой Развернутый угол (слайд 13).
Ученики дают определение Развернутого угла.
Учитель: Обратите внимание, что градусная мера развернутого угла равна 180 градусам.
Учитель: А какой угол называют прямым? (Слайд 14).
Ученики проговаривают определение прямого угла.
Учитель: Обратите внимание на то, что градусная мера прямого угла равна 90 градусов.
Покажите те карточки, где показаны прямые углы.
Ученики показывают карточки с прямыми углами.
Учитель: Как и все геометрические фигуры, углы сравниваются с помощью наложения. Поэтому с помощью следующих слайдов презентации сравним углы и выясним, какие углы равны между собой, а какие углы не равны, а также определим градусную меру углов (слайды 15-19).
Ученики смотрят, сравнивают, определяют градусную меру углов.
Учитель: Ребята! У вас есть карточки №U-1, U-2. Измерьте транспортиром углы и найдите среди них равные между собой углы.
Ученики измеряют и находят равные углы.
Учитель: Сейчас мы применяли транспортир для измерения углов, но его можно применять и для построения углов. (Слайд 20) Построим угол 50 градусов, одной стороной которого служит луч OB.
Учитель по анимированному слайду объясняет алгоритм построения угла (слайд 20). При необходимости анимацию данного слайда можно повторить.
Учитель: Ребята! Расскажите алгоритм построения угла.
Ученики рассказывают алгоритм построения угла.
Учитель: Закрепим алгоритм построения угла. (Слайд 21).
Ученики рассказывают алгоритм, проверяют свои ответы с действиями, которые показаны на слайде.
Учитель: Обратите внимание на углы, которые называют острыми (слайд 22). Как вы думаете, почему эти углы называют острыми углами?
Как вы думаете, почему эти углы называют острыми углами?
Ученики отвечают на вопрос, используя слайд презентации, на котором показано, что все острые углы меньше 90 градусов.
Учитель: За основу построений острых углов была выбрана внутренняя шкала транспортира.
Учитель: Если за основу построений углов также принять внутреннюю шкалу транспортира, то следующие углы, которые показаны на слайде 23, будут называться тупыми углами?
Ученики смотрят на слайд, отвечают на вопрос.
Учитель: Почему эти углы называют тупыми углами?
Ученики отвечают.
Учитель: А теперь познакомимся с острыми и тупыми углами, но за основу построений примем внешнюю шкалу транспортира.
Учитель: Какие углы называются острыми углами? (Слайд 24).
Ученики отвечают на вопрос.
Учитель: Обратите внимание, что сейчас мы рассматриваем углы относительно внешней шкалы транспортира.
Учитель: Как называются углы, представленные на слайде 25? Объясните, почему их так называют.
Ученики дают ответ на поставленный вопрос.
Учитель: На слайде 26 будут последовательно показаны углы. Ваша задача, записать в тетрадь градусные меры углов, назвать угол и его градусную меру, указать его тип и шкалу, относительно которой определяли градусные меры углов.
Ученики дают ответы по слайду 26 презентации, результаты ответов записывают в тетрадь.
Учитель: На слайде 27 будут последовательно показаны углы. Задача состоит в том, что вызываемый к доске ученик должен своим транспортиром измерить угол и записать на доске результат измерений, указать тип угла. Остальные ученики наблюдают за правильностью выполняемых измерений и делают записи в тетрадях.
Учитель: Разберем решение №1653 (а), которое представлено на слайде 28.
- Начнем с углов, которые равны между собой (слайд 28). ∠AOC =∠COB=90o.

- (ЩЛКМ. Слайд 28). По условию задачи ∠AOC > ∠COB в три раза. Т.е. ∠AOC состоит из трех углов СОВ.
- (ЩЛКМ. Слайд 28). Из этого следует, что луч ОС разделит развернутый угол на два смежных угла. При этом, слева от луча ОС будет создан тупой угол, а справа – острый. На слайде 28, анимацией показано, что луч ОС создал два смежных угла: ∠AOC – тупой угол и ∠COB – острый угол.
- (ЩЛКМ. Слайд 28). Предположим, что луч ОС теперь находится там, где и должен находиться. По схеме видно, что развернутый угол состоит из суммы двух смежных углов:
∠АОВ=∠АОС + ∠СОВ = 3∠СОВ + ∠СОВ = 4∠СОВ.
- Из этого равенства, мы можем найти градусную меру угла СОВ:
∠СОВ = ∠АОВ : 4 = 180o : 4 = 45o.
- А теперь посмотрим, через какое значение проходит луч ОС.
- (ЩЛКМ. Слайд 28). Видим, что луч ОС проходит через значение 400 по внутренней шкале, а должен проходить через значение 45o.
 (ЩЛКМ. Слайд 28).
(ЩЛКМ. Слайд 28). - Значение угла АОВ можно вычислить, но можно значение этого угла найти на внешней шкале, т.к. луч ОС проходит через ее значение 135o. Таким образом, ∠АОС = ∠АОВ – ∠СОВ = 180o – 45o = 135o.
(Данное решение привожу с применением транспортира и анимированной схемы, т.к. это позволяет эффективно воздействовать на формирование образного мышления учащихся. Ученикам говорю и том, что вычислив одно значение, второе значение можно увидеть на противоположной шкале транспортира. Все это показано в предлагаемой презентации).
4. Решение примеров по изученной теме урокаУчитель: Выполняем задание №1649 на стр.251 учебника. (Слайд 29).
Ученики выполняют задание и делают записи в тетрадях. Один из учеников работает у доски.
Чтобы ученики могли проверить свои ответы, на слайд 29 создана анимация решения данного номера. Анимация является дополнительным способом воздействия на образное мышление учеников.
Учитель: Выполняем задание №1651 на стр.251 учебника. (Слайд 30).
Ученики выполняют задание, записывают результаты измерений в тетрадь.
Проверить правильность выполнения задания можно по слайду 30.
Учитель: Выполняем №1652 на стр.251 учебника. (Слайд 31).
В случае затруднения можно показать подготовленную анимацию на слайде 30.
5. Закрепление материалаСлайд 32.
- Как называется инструмент для измерения и построения углов?
- Назовите составные части транспортира.
- Что такое градус?
- Какие углы называются острыми углами?
- Какие углы называются тупыми углами?
- Чему равна градусная мера прямого угла?
- Чему равна градусная мера развернутого угла?
- Какой из углов, представленных на слайде 32, является: прямым, острым или тупым углом? Объясните данный ответ, используя интерактивные возможности слайда.
 Домашнее задание
Домашнее заданиеСтр.255, №1682, 1683; стр. 256, 1692(а).
определение, виды, как обозначают с примерами вычисления и решения
Содержание:
Определение: Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, и частью плоскости, которую они ограничивают.
Два угла называются равными, если их можно совместить наложением.
Биссектрисой угла называется луч, который выходит из вершины угла и делит его на два равных угла.
Определение. Развернутым углом называется угол, стороны которого являются дополнительными лучами.
На рисунке 56 луч АК — биссектриса угла ВАС и
На рисунке 57 угол ABC — развернутый, лучи ВА и ВС — дополнительные. Другая (незакрашенная) полуплоскость относительно прямой АС также задает развернутый угол ABC.
Углы измеряются в градусах, минутах, секундах.
Развернутый угол равен 180°; часть развернутого угла называется градусом и обозначается 1°; часть одного градуса называется минутой и обозначается 1′; часть минуты называется секундой и обозначается 1″.
Угол, равный 5 градусов 20 минут и 35 секунд, записывается так: 5°20’35».
Вместо «градусная мера угла равна 20°» часто говорят «угол равен 20°», вместо найти «градусную меру угла» говорят «найти угол».
Определения
Определение: Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, и частью плоскости, которую они ограничивают.
Определение: Угол, равный 90°, называется прямым; угол, меньший 90°, — острым; угол, больший 90°, но меньший 180°, — тупым; угол, равный 360°, называется полным (его стороны совпадают).
На рисунке 58 последовательно изображены: острый угол, равный 60°; прямой угол, равный 90°; тупой угол, равный 120°; угол, равный 270°; и полный угол, равный 360°.
Градусная мера угла является его важной характеристикой. Свойства градусной меры угла: любой угол имеет градусную меру, выраженную некоторым положительным числом; равным углам соответствуют равные градусные меры, а большему углу — большая градусная мера. И наоборот.
Аксиомы
Аксиома измерения углов. Если внутри угла из его вершины провести луч, то он разобьет данный угол на два угла, сумма градусных мер которых равна градусной мере данного угла.
Аксиома откладывания углов. От любого луча в данную полуплоскость можно отложить угол данной градусной меры, и притом только один.
На рисунке 59 луч AD проходит внутри угла ВАС. По аксиоме измерения углов Например, если из вершины развернутого угла АОВ (рис.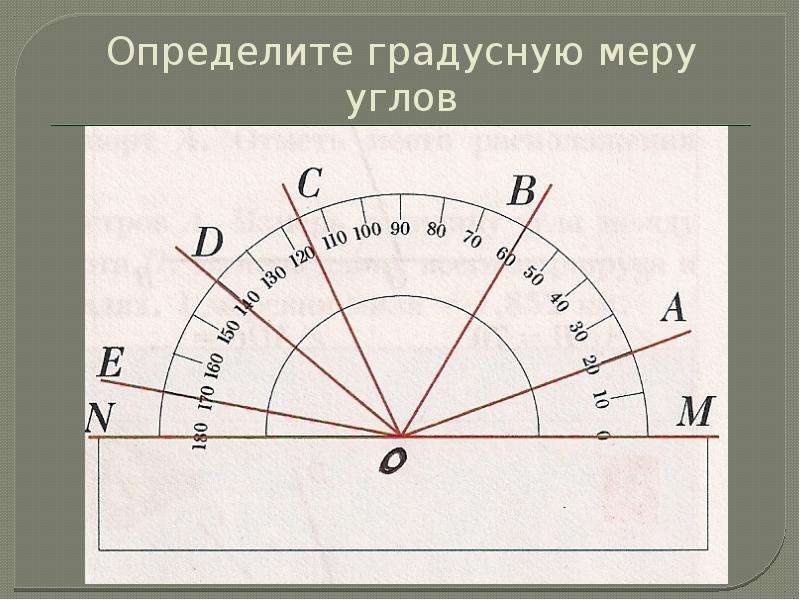 60) провести ЛУЧ ОС, который составит со стороной ОВ угол 50°, то со стороной OA луч ОС составит 180° — 50° = 130°.
60) провести ЛУЧ ОС, который составит со стороной ОВ угол 50°, то со стороной OA луч ОС составит 180° — 50° = 130°.
Два луча с общим началом задают на плоскости два угла. В дальнейшем будем рассматривать меньший из этих двух углов (если они неразвернутые). Такой угол меньше 180°.
Пример №1Внутри угла ВАС, равного 114°, из его вершины проведен луч АЕ. Угол ВАЕ в 2 раза больше угла ЕАС. Найти величину угла ВАЕ.
Решение:
Пусть Тогда (рис. 61).
По аксиоме измерения углов
Тогда
Ответ: 76о
Замечания. 1. Возможен другой способ записи решения, когда рядом с буквой пишут знак градуса: Тогда в уравнении знак градуса писать не нужно:
2. В дальнейшем при решении задач не будем ссылаться на аксиому измерения углов.
Пример №2Внутри угла проведены лучи BD и BF (рис. 62).
Найти величину угла DBF, если:
Решение:
Если сложить углы ABF и CBD, то получим угол ABC плюс угол DBF.
Отсюда
Ответ:
Пример №3Луч AD делит угол ВАС на два угла BAD и CAD. Доказать, что угол между биссектрисами АК и АЕ углов BAD и CAD равен половине угла ВАС (рис. 63).
Доказательство:
Так как АК иАЕ — биссектрисы, то Тогда
Следовательно, Что и требовалось доказать.
Замечание. В данной задаче мы доказали свойство: «Если внутри угла из его вершины провести луч, то угол между биссектрисами полученных углов равен половине данного угла».
Геометрия 3D
В пространстве при пересечении двух плоскостей образуются двугранные углы. Две полуплоскости с общей границей являются гранями такого двугранного угла, а их граница — его ребром. Измеряется двугранный угол величиной линейного угла, образованного двумя лучами, проведенными в каждой из полуплоскостей из точки на ребре двугранного угла перпендикулярно этому ребру. На рисунке 69 ZABC — линейный угол изображенного двугранного угла.
Геометрия 3D
В пространстве при пересечении двух плоскостей образуются двугранные углы. Две полуплоскости с общей границей являются гранями такого двугранного угла, а их граница — его ребром. Измеряется двугранный угол величиной линейного угла, образованного двумя лучами, проведенными в каждой из полуплоскостей из точки на ребре двугранного угла перпендикулярно этому ребру. На рисунке 69 — линейный угол изображенного двугранного угла.
Определение. Два угла называются смежными, если у них одна сторона общая, а две другие являются дополнительными лучами.
Если на рисунке 70 лучи OA и ОВ дополнительные, то углы АОС и ВОС — смежные.
Теорема (свойство смежных углов). Сумма смежных углов равна 180°.
Дано: — смежные.
Доказать:
Доказательство:
Из определения смежных углов следует, что лучи OA и ОВ являются дополнительными и поэтому образуют развернутый угол АОВ, равный 180°. Луч ОС проходит между сторонами этого угла, и по аксиоме измерения углов Поэтому . Теорема доказана.
Луч ОС проходит между сторонами этого угла, и по аксиоме измерения углов Поэтому . Теорема доказана.
Следствия.
- Если смежные углы равны, то каждый из них прямой.
- Если два угла равны, то равны и смежные с ними углы.
Замечание. Все теоремы курса геометрии 7—9 классов описывают свойства фигур на плоскости.
Определение. Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами к сторонам другого.
При пересечении двух прямых АС и DB в точке О (рис. 71) получим, что лучи OA и ОС, О В и OD — дополнительные. Поэтому углы AOD и BОС — вертикальные. Углы АОВ и DOC также вертикальные.
Теорема (свойство вертикальных углов). Вертикальные углы равны.
Дано: — вертикальные (рис. 72).
Доказать:
Доказательство:
Углы 1 и 3 смежные, так как лучи OA и OD — дополнительные по определению вертикальных углов. По свойству смежных углов Углы 2 и 3 также смежные,
По свойству смежных углов Углы 2 и 3 также смежные,
Так как
Теорема доказана.
Углом между двумя пересекающимися прямыми называется меньший из образованных ими углов. Если при пересечении прямых АВ и CD (рис. 73) то как вертикальные. Угол между прямыми АВ и CD равен 30°. Говорят, что прямые пересекаются под углом 30°.
При пересечении двух прямых образуются четыре угла (не считая развернутых). Если один из них 90°, то и остальные по 90° (докажите самостоятельно). Говорят, что прямые пересекаются под прямым углом.
Угол между параллельными прямыми считается равным 0°.
Пример №4Смежные углы относятся как 2:3. а) Найти величину каждого из углов, б) Определить, сколько процентов развернутого угла составляет меньший угол.
Решение:
а) Пусть — данные смежные углы (рис. 74). Согласно условию (градусную меру одной части принимаем за ). По свойству смежных углов
По свойству смежных углов
то есть
б) Меньшим является а 72° от 180° составляют
Ответ: 72°, 108°; 40 %.
Пример №5а) Найти угол между биссектрисами ОК и ОМ смежных углов ВОС и АОС (рис. 75), если б) Доказать, что биссектрисы смежных углов образуют прямой угол.
Решение:
а) Если
б) Так как ОМ и ОК — биссектрисы, то
Найдем градусную меру По свойству смежных углов Тогда . Что и требовалось доказать.
Замечание. Можно было сослаться на ключевую задачу 3* к § 5.
Пример №6Доказать, что биссектрисы вертикальных углов образуют развернутый угол.
Решение:
а) Пусть ОЕ и ОК — биссектрисы вертикальных углов АОС и BOD (рис. 76). Докажем, что — развернутый. Известно, что биссектриса делит угол пополам. Так как вертикальные углы равны, то равны и их половины. Поэтому
Так как вертикальные углы равны, то равны и их половины. Поэтому
б) так как лучи OA и ОВ дополнительные, и поэтому — развернутый. Заменив в последнем равенстве на равный ему получим Отсюда следует, что — развернутый.
Замечание. Из решения задачи следует свойство: если — развернутый и — вертикальные.
Градусная ⚠️ мера угла: прямого, развернутого, тупого, обозначение
Градусная мера угла — формулировка
Градусная мера, в первую очередь, делает возможным измерение углов в геометрии.
Это число – показатель того, сколько градусов, минут и секунд содержится в данном угле.
ПримечаниеОно всегда больше нуля.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Что отражает величина
Количество градусов, минут и секунд, которые находятся между сторонами угла.
Обозначение
С помощью символов градусов \((º)\), минут \((′)\) и секунд \((″)\).
В одном градусе содержится шестьдесят минут, в одной минуте — шестьдесят секунд.
Пример\(125º\) \(22′\) \(15″\) (сто двадцать пять градусов, двадцать две минуты, пятнадцать секунд).
ПримечаниеЕсли настолько точно, как показано выше определить меру невозможно, пользуются дробной мерой градуса. Например, \(123,5º\).
ПримерОбозначение на чертеже:
Источник: https://www.budu5.com/Мера прямого угла
Прямой всегда равен \(90º\). В него входит \(5400′\) или \(324000″\). Является половиной развернутого.
Источник: webmath.ruМера развернутого угла
Развернутый всегда равен \(180º\). Представляет собой прямую.
Источник: syl.ruМера тупого угла
Тупой всегда больше \(90º\), но меньше \(180º\).
Мера острого угла
Острый всегда меньше \(90º\).
ПримечаниеВыглядит как нечто с острым концом, способным «уколоть».
Источник: impariamoninsieme.comКак найти градусную меру
С помощью специального измерительного инструмента – транспортира. Он может быть сделан из разного материала (пластик, дерево, тонкий металл) и выглядеть по-разному.
Источник: infourok.ruРазница только во внешнем виде. Устроены инструменты одинаково. Состоят из:
- основания (часто со шкалой-линейкой),
- дуги (полукруга) с двумя шкалами с градусной сеткой.
Круглый транспортир имеет отличие в строении сетки: на нем указан полный круг в \(360°\).
Описание
Как производить измерения:
- найти в середине транспортира специальную метку (это может быть отверстие\штрих\точка и т.
 п.), она проходит через «0º» на сетке дуги;
п.), она проходит через «0º» на сетке дуги; - приложить инструмент этой отметкой к вершине угла, т.е. совместить «0º» с точкой вершины;
- повернуть так, чтобы основание инструмента совпадало с одной из сторон угла;
- следить, чтобы при повороте транспортира отметка «0º» не сходила с вершины;
- проводим мысленно дугу справа налево (снизу, от основания, вверх по дуге) до второй стороны угла;
- вторая сторона угла покажет на отметку с цифрой на шкале инструмента;
- это и будет градусная мера данного угла.
Если после того, как вы приложили центральную метку транспортира к вершине угла, одна из его сторон прошла через отметку «0º» на внешней шкале полукруга, то дальше измерение проводите только по внешней шкале. Если же сторона прошла через внутренний «0º», то пользуйтесь внутренней шкалой, на внешнюю уже смотреть не нужно.
Чтобы не сделать ошибку при измерении, воспользуйтесь образцом: https://yadi. sk/i/LVbtcivDBPzimw
sk/i/LVbtcivDBPzimw
Свойства углов
Градусная мера меньшего всегда меньше.
Если углы равны, то их градусные меры тоже равны (и наоборот: равные меры говорят о равенстве углов).
Ниже представлены основные свойства.
Мера больше нуля
Градусная мера любого угла всегда больше \(0º\).
Мера соответствует сумме градусных мер углов, разбиваемых лучом
Если угол разделен лучом на несколько углов, то его градусная мера будет равна сумме всех этих углов.
Отложение угла от луча
От любого луча можно построить только один угол с градусной мерой меньше \(180º\).
Примеры нахождения меры угла
Задача №1Луч ОС лежит внутри \(∠АОВ\). При этом \(∠АОС = 36º\), а \(∠ВОС = 18º\). Чему равен \(∠АОВ\)?
Решение
- Луч делит исходный угол на два.
- Значит, чтобы найти \(∠АОВ\), нужно сложить меры углов, полученных при проведении луча.

- \(36º+18º=54º.\)
Луч \(ОК\) делит \(∠АОВ\) на два угла. Один из них больше другого в два раза и равен \(60º\). Чему равен \(∠АОВ\)?
Здесь, как и в задаче выше, решение будет простое. Специальная формула не требуется.
Решение:
- \(∠AOK = 60º,\)
- Известно также, что второй — вдвое меньше него, значит, \(∠KOB = 60º:2 = 30º,\)
- Мы знаем что \(∠АОВ = ∠АОК+∠КОВ,\)
- Нам остается только выполнить сложение:\( 60º+30°= 90º\). Это и есть величина \(∠AOB.\)
Определение угла | Треугольники
Что такое угол? Введём определение угла.
Определение.
Угол — это геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки.
Лучи называются сторонами угла, а их общее начало — вершиной угла.
Например, вершина угла BAC — точка A, стороны — лучи AB и AC.
Знак угла — ∠ — представляет собой уменьшенное изображение угла.
Запись «∠ABC» читают как «угол ABC».
Угол можно назвать одной или тремя буквами. Если буква одна, то это — вершина угла. Если букв три, то вершина вершина должна стоять посередине, а по бокам — точки, лежащие на сторонах угла:
∠B или ∠ABC или ∠CBA.
Другой способ определить угол: по названию лучей — сторон угла.
∠(a; b) — угол, стороны которого — лучи a и b.
Обозначают угол дужкой.
Два угла называются равными, если они могут быть совмещены так, что совпадут их соответствующие стороны и вершины.
∠BAC=∠MNK.
Равные углы обозначают равным количеством дужек.
Единицы измерения углов — градусы и радианы.
1 градус (1º) равен 1/180 доле развёрнутого угла.
Градусную меру угла измеряют с помощью транспортира.
1 радиан — величина центрального угла, опирающегося на дугу окружности, равной её радиусу.
Наглядное представление об угле в 1 радиан можно получить, если отрезать кусок нити длиной, равной радиусу окружности, и приложить эту нить к окружности. Центральный угол, опирающийся на полученную дугу, — это и есть угол в один радиан:
Центральный угол, опирающийся на полученную дугу, — это и есть угол в один радиан:
∠ABC=1 радиану
1 радиан ≈ 57º, π радиан=180º.
Основные свойства измерения углов:
Каждый угол имеет определённую градусную меру, большую нуля.
Развёрнутый угол равен 180 градусам.
Градусная мера угла равна сумме градусных мер углов, на которые они разбиваются любым лучом, проходящим между его сторонами.
Иногда угол определяют как часть плоскости, заключённую между двумя лучами с общим началом.
В тех случаях, когда угол рассматривают как меру поворота луча вокруг его начала до заданного положения, величина угла может принимать любые значения, в зависимости от направления поворота как положительные, так и отрицательные.
Урок по теме: «Угол.Градусная мера угла».
Краткосрочный план урока по математике
Школа: КГУ ШГ №118 Дата: 11. 04.2018г.
04.2018г.
ФИО учителя: Курбанова Э.М.
Класс: 5 «Б» класс.
Количество присутствующих:
отсутствующих:
Тема урока:
Угол. Градусная мера угла
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу):
5.3.1.4
усвоить понятия угла и его градусной меры, обозначать и сравнивать углы;
5.3.1.5
различать виды углов (острый, прямой, тупой, развёрнутый, полный);
5.3.3.3
решать задачи на нахождение градусной меры угла, на сравнение углов;
Цели урока:
Формулируют определение угла;
Различают виды углов;
Обозначают и сравнивают углы.
Критерии оценивания:
Все: — Формулируют определение угла
— Различают виды углов
— Обозначают и сравнивают углы
Большинство:
— Решают задачи на нахождение градусной меры угла
Межпредметные
Связи
Взаимосвязь с предметами: геометрия, черчение, естествознание
Навыки
использования
ИКТ
На данном уроке учащиеся используют презентацию на интерактивной доске
Предварительные
Знания
Выполняют сложение и вычитание дробей с разными знаменателями;
Находят процент от данного числа, и число по его проценту.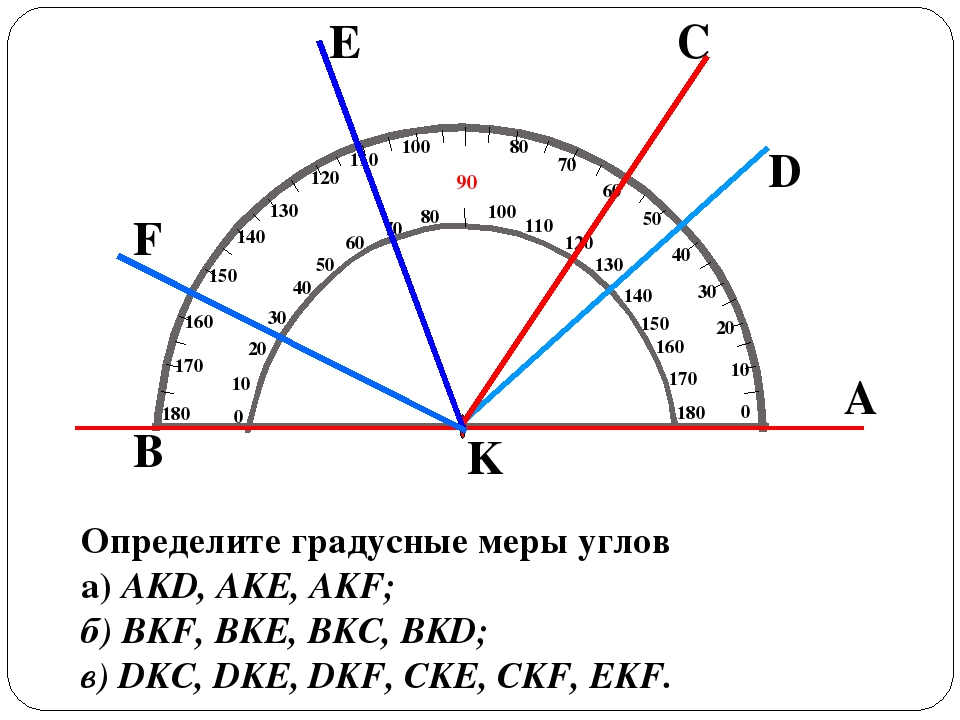
Ход урока
Этапы урока
Запланированная деятельность на уроке
Ресурсы
Начало урока
Организационный момент. Приветствует учеников. Для создания психологической атмосферы проводит игру «Мне в тебе нравится…».
Середина урока
Индивидуальная работа. Учитель раздает карточки.
Задание: Выполните действия с дробями. Расположите полученные числа в порядке убывания и вы получите то понятие, которое будет интересовать нас сегодня на уроке.
Ответ: угол.По методу «Снежный ком» изучают новый материал.
Ученики работают над текстом. Демонстрируют свои знания, по изученной теме: “Угол. Градусная мера угла”.
1-группа: Острый угол; Выполнение чертежа,
2-группа: Прямой угол; обозначение угла,
3-группа: Тупой угол; определение угла
4-группа: Развернутый угол.
Задание
. Исправьте ошибки в определениях.
Угол – это геометрическая фигура, состоящая из точки и двух лучей.
Градус – это часть развернутого угла.
Тупой угол меньше острого.
Прямой угол составляет половину от развернутого.
Задание 2. Не прибегая к измерениям, укажите угол, равный 900, 500,1400, 1800,
Рисунок 2.
Презентация
Учебник:
Рабочая тетрадь:
Ресурсы
Вывод: на рисунке изображены тупой, острый и прямой угол.
Задание 3
Вычислите величину угла.
Рисунок 3.
DAC =700
CAB = 600
Найти: DAB
Дано:
GEF =300
HEG В ТРИ РАЗА БОЛЬШЕ УГЛАGEF
Найти: HEF
Дано:
КМS =1500
KML =650
Найти: LMS
Задание 4
Задачи на часть от числа, число по части, проценты, связанные с понятием прямого угла, развернутого угла.
1. Чему равен угол, градусная мера которого составляет прямого угла?
2. Прямой угол составляет некоторого угла. Найдите этот угол.
3. Какую часть угол в 600 составляет от развернутого угла?
4. Сколько процентов составляет угол в 450 от развернутого угла
Конец урока
Подведение итогов урока. Проведение рефлексии урока.
Домашнее задание: №1187, №1189
Дифференциация
Каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?
Оценивание
Как Вы планируете проверить уровень усвоения материала учащимися?
Здоровье и соблюдение техники безопасности
Классификация: при формировании гетерогенной группы в начале урока
Задания: По уровням сложности.
Дифференциация по принципу углубления при закрепления изучаемого материала
Диалог и поддержка: при выполнения групповых и парных работ, консультация учащихся друг другу, помощь учителя по необходимости
Учащиеся в парах проводит взаимооценивание
Самооценивание с помощью шаблона правильных ответов
Формативное оценивание на протяжения всего урока
Ребята давайте немного подвигаемся. Проведение физминутки.
Проведение физминутки.
Значение, методы измерения градусов, градусы в радианы
Градус – это единица измерения угла. Углы обычно измеряются в радианах и градусах. В случае практической геометрии мы всегда используем градусы как единицу измерения угла. Градус обозначается знаком ° (символ градуса).
Определение градусов
Единица измерения угла в математике называется градусом. Градус угла измеряется с помощью инструмента, называемого транспортиром.Полный круг вращается на 360°, а углы можно измерять под разными углами, демонстрируя разные градусы, такие как 30°, 45°, 60° и так далее. Один оборот делится на 360 равных частей, и каждая часть называется градусом. Обозначим степень кружком °. Например, 180° означает 180 градусов.
градусов и радиан
Углы измеряются не только в градусах, но и в радианах. Радиан получается путем обертывания радиуса вокруг окружности. Один полный оборот против часовой стрелки в радианах равен 2π.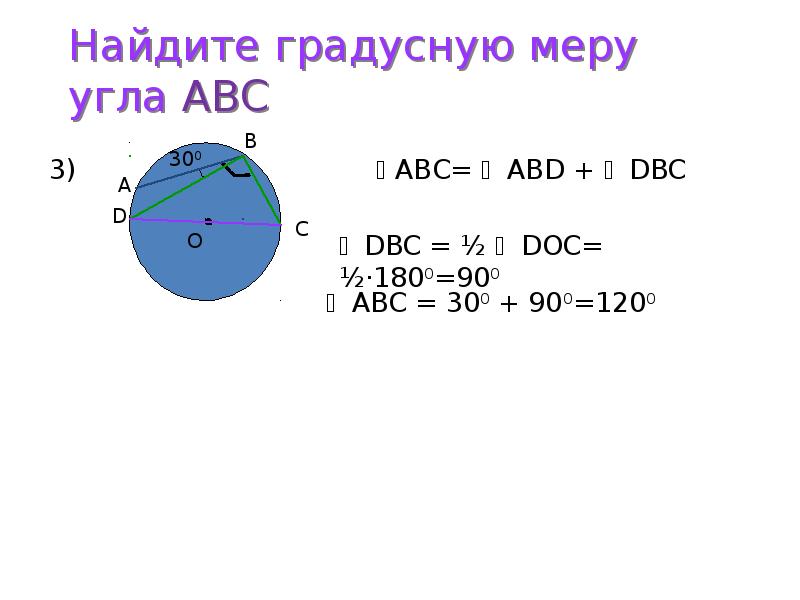 Мы можем преобразовать градусы в радианы и радианы в градусы, используя следующие две формулы:
Мы можем преобразовать градусы в радианы и радианы в градусы, используя следующие две формулы:
- Чтобы преобразовать радианы в градусы, используйте формулу [Градусы = Радианы × 180 / π]. Один радиан равен примерно 57,2958 градусам.
- Чтобы преобразовать градусы в радианы, используйте формулу [радианы = градусы × π / 180].
Ниже приведена таблица, показывающая эквивалентные значения в радианах для соответствующих градусов:
| Градусы | Радиан |
| 30° | №/6 |
| 45° | №/4 |
| 60° | п/3 |
| 90° | п/2 |
Измерение углов в градусах
Лучшим инструментом для измерения углов в градусах является транспортир.Изогнутый край транспортира разделен на 180 равных частей.
На транспортире два набора чисел:
- Один по часовой стрелке
- Другой против часовой стрелки
Если присмотреться, транспортир имеет градусы, отмеченные от 0° до 180° слева направо на внешнем краю и от 180° до 0° на внутреннем.
Внутреннее считывание и внешнее считывание дополняют друг друга.то есть они складываются, образуя угол 180 градусов.
Посмотрите на изображение выше, если измеренный угол находится слева от центра транспортира, мы будем ориентироваться на внешние показания транспортира. В этом случае ∠POR лежит слева, поэтому ∠POR = 80°.
Если измеренный угол находится на правой стороне транспортира, мы будем ориентироваться на внутренние показания транспортира. В этом случае ∠QOR лежит справа, поэтому , ∠QOR = 100°.
Вот еще один пример измерения угла в градусах. Попробуем измерить угол ∠AOB на рисунке ниже с помощью транспортира.
Шаг 1: Держите транспортир так, чтобы его середина совпадала с вершиной О данной фигуры. Точно совместите транспортир с лучом OB, как показано ниже.
Шаг 2: Начните чтение с отметки 0° в правом нижнем углу транспортира. Измерьте угол, используя внутренние показания на нижней дуге транспортира.
Измерьте угол, используя внутренние показания на нижней дуге транспортира.
Следовательно, ∠AOB = 37°.
Связанные статьи о степенях
Ознакомьтесь с этими интересными статьями о степенях. Нажмите, чтобы узнать больше!
Часто задаваемые вопросы о степенях
Что такое 1 градус в радианах?
1 градус = π/180 радиан
= 0,0174533 радиан
Как определить степень?
Градус, обычно обозначаемый ° (символ градуса), является мерой угла.Углы могут иметь разную меру или градус, например 30°, 90°, 55° и так далее. Для измерения степени угла воспользуемся транспортиром.
Какие инструменты используются для измерения углов?
Существует 5 типов инструментов для измерения углов:
- Транспортиры
- Угловой датчик
- Линейка для измерения нескольких углов
- Пробная площадь
- Синусоида
Сколько градусов в половине оборота?
Полуоборот означает выполнение прямого угла. Измерение прямого угла составляет 180°. Следовательно, в пол-оборота 180 градусов.
Измерение прямого угла составляет 180°. Следовательно, в пол-оборота 180 градусов.
Сколько градусов составляет полный оборот?
«Полный поворот» означает выполнение более полного угла. Полный угол равен 360°. Следовательно, в одном полном обороте 360 градусов.
Что такое степень по математической геометрии?
Градус — это единица измерения. При измерении любого угла мы используем символ градусов для его обозначения. Обозначается °. Например, один полный оборот составляет 360 градусов или (360 °).Один градус равен π180 радианам.
Какие различные степени углов мы видим в геометрии?
Существуют различные типы углов в зависимости от их степени в геометрии. Давайте посмотрим, что это такое:
- Прямой угол. Измерение прямого угла составляет 90 градусов (90 °).
- Тупой угол — измерение тупого угла больше 90° и меньше 180°
- Прямой угол — прямой угол равен 180°
- Угол рефлекса — измерение угла рефлекса больше 180° и меньше 360°.

радиан и градусы: определение и примеры — видео и расшифровка урока
Что такое степени?
Градусы используются для измерения направления и величины угла. Если вы смотрите на север, говорят, что вы находитесь на 0°. Если вы повернетесь лицом к югу в противоположном направлении, вы повернетесь на 180°.
Полный круг состоит из 360°.
Считается, что эта система измерения кругов была изобретена древними вавилонянами и основывалась на их шестидесятеричной системе счета.Эта система имеет 60 в качестве основы по сравнению с нашей текущей системой счета с 10 в качестве основы.
Большинство математических расчетов вплоть до геометрии используют градусы для измерения и вычисления углов. Есть много практических приложений в строительстве и архитектуре, которые используют градусные меры.
Что такое радианы?
Формальное определение радиана состоит в том, что радиан — это мера угла, который, будучи нарисован центральным углом окружности, пересекает дугу, длина которой равна длине радиуса окружности. Радианная мера полного круга равна 2π. Это может выглядеть еще более запутанно, чем 360°, но если вы доведете до конца математику, все действительно сработает. Если вы помните, уравнение для нахождения 90 174 длины окружности 90 175 окружности с радиусом (r) выглядит так: C = 2πr. Если r = 1, то C = 2π. По этой причине 2π равно одному полному обороту вокруг окружности, или 360°. Окружность с радиусом 1 называется единичной окружностью .
Радианная мера полного круга равна 2π. Это может выглядеть еще более запутанно, чем 360°, но если вы доведете до конца математику, все действительно сработает. Если вы помните, уравнение для нахождения 90 174 длины окружности 90 175 окружности с радиусом (r) выглядит так: C = 2πr. Если r = 1, то C = 2π. По этой причине 2π равно одному полному обороту вокруг окружности, или 360°. Окружность с радиусом 1 называется единичной окружностью .
Преобразование градусов в радианы
Уравнение для преобразования градусов в радианы: градусы = радианы x (180°/ π).А уравнение для преобразования радианов в градусы таково: радианы = (π/180°) x градусы.
Давайте сделаем пример:
Преобразуем 60 градусов в радианы.
Поскольку мы ищем радианы, форма уравнения, которая нам нужна, будет следующей: радианы = градусы x π/180
Подставим наши 60 градусов, чтобы получить: радианы = 60 x π/180
Это можно упростить до : радианы = π/3, что и является нашим ответом.
Вот еще один пример:
Преобразование 3π/4 радиана в градусы
На этот раз нам нужно уравнение: получаем уравнение: градусы = 3π/4 x 180/π.Два / π сокращаются, и у нас остаются градусы = 135 °.
Резюме урока
И градусы, и радианы — это способы измерения угла. Для математики более высокого уровня используются радиана , потому что они являются реальными числами и упрощают математику, потому что многие вычисления с использованием кругов включают π. Градусов , однако, легче визуализировать. Я бы предпочел, чтобы кто-нибудь сказал мне повернуться на 90° влево, чем повернуться влево на π/2 радиана.Однако при необходимости можно легко преобразовать одно в другое.
Измерение углов
Определения
В геометрии угол определяется как фигура, образованная двумя лучами, имеющими общий конец. Лучи называются сторонами угла, а общий конец — его вершиной.
В тригонометрии угол часто определяется с точки зрения поворота. Рассмотрим луч, который вращается вокруг своей конечной точки, образуя угол.Луч в начальном положении называется начальной стороной угла. Соответственно луч в конечном положении после поворота называется конечной стороной угла. Величина поворота от начальной стороны к конечной стороне определяет меру угла.
Рассмотрим луч, который вращается вокруг своей конечной точки, образуя угол.Луч в начальном положении называется начальной стороной угла. Соответственно луч в конечном положении после поворота называется конечной стороной угла. Величина поворота от начальной стороны к конечной стороне определяет меру угла.
Положительный угол — это угол, образованный вращением против часовой стрелки. Если угол создается вращением по часовой стрелке, он имеет отрицательную меру.
Существует два широко используемых способа измерения углов — в градусах и радианах.{\ простое \ простое} \]
Радианная мера угла
Радианная мера угла определяется как отношение дуги, которую он отсекает, к радиусу окружности с центром в вершине угла.
Рис. 3.Если \(\ell\) — длина дуги, а \(R\) — радиус окружности, то центральный угол \(\alpha\), стягивающий дугу, определяется в радианах как
Напомним, что длина окружности радиуса \(R\) равна \(2\pi R.\circ} = 60 \cdot \frac{\pi }{{180}} = \frac{\pi }{3}\,радиан. \]
\]
Пример 4
Дана окружность радиусом \(3.\). Найдите длину дуги, отсеченной центральным углом \(2\) радиан.
Раствор.
Длина дуги определяется по формуле \(\ell = \alpha R,\), где \(\alpha\) — центральный угол, выраженный в радианах, а \(R\) — радиус окружности. Подставляя известные значения, получаем
\[\ell = \alpha R = 2 \cdot 3 = 6.\]
См. решенные проблемы на стр. 2.
Шлюз
Veuillez réessayer данс quelques мгновения. Si le problème сохраняется, veuillez communiquer avec le service de soutien method de Alberta Education (доступно на английском языке).
| Телефон : | 780-427-5318 | |
| (Composer d’abord le 310-0000 pour obtenir une ligne sans frais) | ||
| Телекопьер: | 780-427-1179 | |
| Курьерский адрес: | cshelpdesk@gov. ab.ca ab.ca | |
Измерение
Пифагорейцы Теорема
Используйте Java апплет для построения доказательства теоремы Пифагора. |
Пи — греческая буква, обозначающая число, приблизительно равное
3.141592654. Пи — иррациональное число, поэтому указанное выше число не является
точно, но приблизительно. Чтобы увидеть число, представленное расширенным до большего числа знаков после запятой, щелкните здесь или здесь (две разные версии).
Архимед, великий древний математик, использовал метод, называемый «Исчерпание», чтобы попытаться найти значение для .Нам надлежит знать, что это за ценность представляет собой.
Проще говоря, представляет собой отношение длины окружности к диаметру. круга. Таким образом, = c/d. Метод «Исчерпания», используемый Архимеда, чтобы найти приближение, можно посмотреть на веб-сайте, доступ к которому можно получить, нажав здесь.
Мы тоже сделаем один…сейчас .
Углы и их измерение
Определение угла.
Угол состоит из двух полупрямых (лучей)
с общей начальной точкой, называемой вершиной. Мы согласны
что крайняя сторона получается поворотом начальной стороны против часовой стрелки на угол t. Угол
находится в стандартном положении с вершиной в начале координат и
начальная сторона вдоль положительной оси x. |
Угол положительной меры получается, когда
сторона терминала повернута против часовой стрелки и угол отрицательный
мера получается при вращении угла по часовой стрелке.Углы, полученные
различные повороты, имеющие одинаковые начальную и конечную стороны, называются котерминальными.
Измерение угла
Существует разница между углом (геометрическим объектом) и его мера (число). Однако правильно сказать, что «угол равен x единицам», так что наша работа не становится слишком утомительным.
Степень
Классической единицей измерения углов является градус.Полный оборот, чтобы конечная сторона лежит на начальной стороне под углом 360, поэтому 1 составляет 1/360 от одного полное вращение. Части угла измеряются в минутах и секундах.
В дальнейшем будут использоваться следующие символы:
= градусы
‘ = минуты 90 121 » = секунды
На основании определения степени (в предыдущем абзаце) следующие эквивалентности должно иметь смысл:
| 1 = 60′ | 1 = 60 дюймов |
Отсюда следует, что 1 = (60)(60)». = 3600″ = 3600″ | |
| (1/60) = 1′ | (1/60)’ = 1 дюйм |
| Отсюда следует, что 1″ = (1/60)(1/60) = (1/3600) | |
Теперь, используя конверсии на основе эквивалентностей, отмеченных в
таблице выше, мы можем изменить единицы измерения с градусов, минут и секунд на десятичные
эквиваленты:
| 42 25 48 |
| = 42 + 25 (1/60) + 48 (1/3600) |
| = 42 + (25/60) + (48/3600) |
| = 42 + .4167 + .0133 |
| = 42,4300 |
Радиан
Более удобной единицей измерения углов в приложениях является радиан.
| Рассмотрим круг радиусом 1 единица. Начните с точку ( 1,0 ) и отмерьте 1 единицу против часовой стрелки вдоль окружность круга.  Отметьте эту точку и соедините ее с исходной точкой, чтобы
составить конечную сторону угла.Этот угол равен 1 радиану. Отметьте эту точку и соедините ее с исходной точкой, чтобы
составить конечную сторону угла.Этот угол равен 1 радиану.
|
На окружности радиусом 1 единица (единичная окружность) угол 1 радиан отсекает дугу в 1 единицу на окружности окружности.
Длина окружности любого круга равна 2 (радиус).
2 радиана = 360 или
радианы = 180
Угол в радианах представляет собой отношение длины дуги на
Окружность равна длине начальной стороны угла, поэтому она не имеет размерных единиц.
Изменение единиц измерения между градусами и радианами. С использованием
эквивалентность
радианы = 180
мы можем записать это как отношение: радианы относятся к 180 как x радиан к t
Или математически говоря:
радиан = x радиан
180 т
Введите заданный угол (градусы или радианы) в пропорцию и найдите
неизвестный.
5.2: Углы — Математика LibreTexts
Поскольку многие приложения, использующие круги, также включают вращение круга, естественно ввести меру поворота или угла между двумя лучами (прямыми сегментами), исходящими из центра круга. . Измерение угла, с которым вы, скорее всего, знакомы, — это градусы, поэтому мы начнем с него.
Определение: мера угла
Мера угла — это мера между двумя пересекающимися линиями, отрезками или лучами, начинающаяся с начальной стороны и заканчивающаяся конечной стороной .{\circ}\).
Определение: стандартная позиция
При измерении углов на окружности, если не указано иное, мы измеряем углы в стандартном положении : начиная с положительной горизонтальной оси и с вращением против часовой стрелки.
Пример \(\PageIndex{1}\)
Назовите градусную меру угла, изображенного на окружности.
Раствор
Вертикальные и горизонтальные линии делят круг на четверти.{\circ}\).
Греческий язык
При представлении углов с помощью переменных традиционно используются греческие буквы. Вот список часто встречающихся греческих букв.
| \(\тета\) | \(varphi\) или \(\phi\) | \(\альфа\) | \(\бета\) | \(\гамма\) |
| тета | фи | альфа | бета | гамма |
Работа с углами в градусах
Обратите внимание, что, поскольку в одном обороте 360 градусов, угол больше 360 градусов будет означать более 1 полного оборота.Показанное на окружности результирующее направление, в котором конечные точки сторон этого угла будут такими же, как и для другого угла от 0 до 360 градусов. {\circ}\)
{\circ}\)
Раствор
Поскольку добавление или вычитание полного оборота, 360 градусов, приведет к углу с конечной стороной, указывающей в том же направлении, мы можем найти котерминальные углы, добавляя или вычитая 360 градусов.{\circ}\номер\]
Может быть полезно ознакомиться с часто встречающимися углами за один оборот окружности. Обычно встречаются углы, кратные 30, 45, 60 и 90 градусам. Эти значения показаны справа. Запоминание этих углов и понимание их свойств будет очень полезно, поскольку мы изучаем свойства, связанные с углами
.Углы в радианах
Хотя измерение углов в градусах может быть привычным делом, это часто усложняет дело, поскольку единицы измерения могут мешать вычислениям.По этой причине обычно используется другая мера углов. Эта мера основана на расстоянии вокруг окружности.
Определение: длина дуги
Длина дуги — это длина дуги, \(s\), вдоль окружности радиуса \(r\), стянутой (вытянутой) углом \(\theta\).
Это часть окружности между начальной и конечной сторонами угла.
Длина дуги, огибающей весь круг, называется окружностью круга.Длина окружности равна \(C=2\pi r\). Отношение длины окружности к радиусу дает константу \(2\pi\). Независимо от радиуса, это отношение всегда одинаково, так же как градусная мера угла не зависит от радиуса.
Чтобы развить эту идею, рассмотрим две окружности, одну с радиусом 2, а другую с радиусом 3. Вспомним, что длина окружности (периметр) окружности равна \(C=2\pi r\), где \(r\) – радиус окружности. Тогда меньший круг имеет окружность \(2\pi (2)=4\pi\), а больший — окружность\(2\pi (3)=6\pi\).{th}\) полной окружности, поэтому для меньшего круга длина дуги = \(\dfrac{1}{8} (4\pi )=\dfrac{1}{2} \pi\), а для больший круг, длина дуги или длина дуги = \(\dfrac{1}{8} (6\pi )=\dfrac{3}{4} \pi\).
Обратите внимание, что произойдет, если мы найдем отношение длины дуги к радиусу окружности:
Меньший круг: \(\dfrac{\dfrac{1}{2} \pi }{2} =\dfrac{1}{4} \pi\)
Большой круг: \(\dfrac{\dfrac{3}{4} \pi }{3} =\dfrac{1}{4} \pi\)
Отношение одинаковое независимо от радиуса круга – оно зависит только от угла. Это свойство позволяет нам определить меру угла на основе длины дуги.
Это свойство позволяет нам определить меру угла на основе длины дуги.
радиана
радиан мера угла представляет собой отношение длины дуги окружности, образуемой углом, к радиусу окружности.
Другими словами, если s — длина дуги окружности, а \(r) — радиус окружности, то
радиан мера\(=\dfrac{s}{r}\)
Если радиус окружности равен 1, то мера радиана соответствует длине дуги.\ circ \) = \ (\ dfrac {\ pi} {2} \) радиан
Пример \(\PageIndex{5}\)
Найдите в радианах меру одной трети полного оборота.
Раствор
Для любого круга длина дуги вдоль такого поворота будет составлять одну треть окружности, \(C=\dfrac{1}{3} (2\pi r)=\dfrac{2\pi r}{3}\ ). Радианная мера будет делением длины дуги на радиус:
\[\text{Радианы} = \dfrac{2\pi r}{3r} =\dfrac{2\pi }{3}\]
преобразование между радианами и градусами
1 градус = \(\dfrac{\pi }{180}\) радиан
или: чтобы преобразовать градусы в радианы, умножьте на \(\dfrac{\pi \text{радианы}}{180^{\circ}}\)
1 радиан = \(\dfrac{180}{\pi }\) градусов
или: чтобы преобразовать радианы в градусы, умножьте на \(\dfrac{180^{\circ}}{\pi \text{радианы}}\)
Преобразование радианов в градусы
Пример \(\PageIndex{6}\)
Преобразование \(\dfrac{\pi }{6}\) радиан в градусы. {\circ}\номер\]
{\circ}\номер\]
Точно так же, как мы перечислили все общие углы в градусах на окружности, мы должны также перечислить соответствующие значения в радианах для обычных мер окружности, соответствующих градусам, кратным 30, 45, 60 и 90 градусам. Как и в случае с измерениями градусов, было бы целесообразно запомнить их.
Мы можем работать с радианами угла так же, как мы работаем с градусами.
Пример \(\PageIndex{8}\)
Найдите угол \(\beta\), котерминальный углу \(\dfrac{19\pi }{4}\), где \(0\le \beta <2\pi\).
Раствор
При работе в градусах мы находили котерминальные углы, добавляя или вычитая 360 градусов, то есть полный оборот. Точно так же в радианах мы можем найти котерминальные углы, добавляя или вычитая полные обороты \(2\pi\) радиан.
\[\dfrac{19\pi }{4} -2\pi =\dfrac{19\pi }{4} -\dfrac{8\pi }{4} =\dfrac{11\pi }{4} \номер\]
Угол \(\dfrac{11\pi }{4}\) котерминальный, но не меньше \(2\pi\), поэтому мы вычитаем еще один поворот.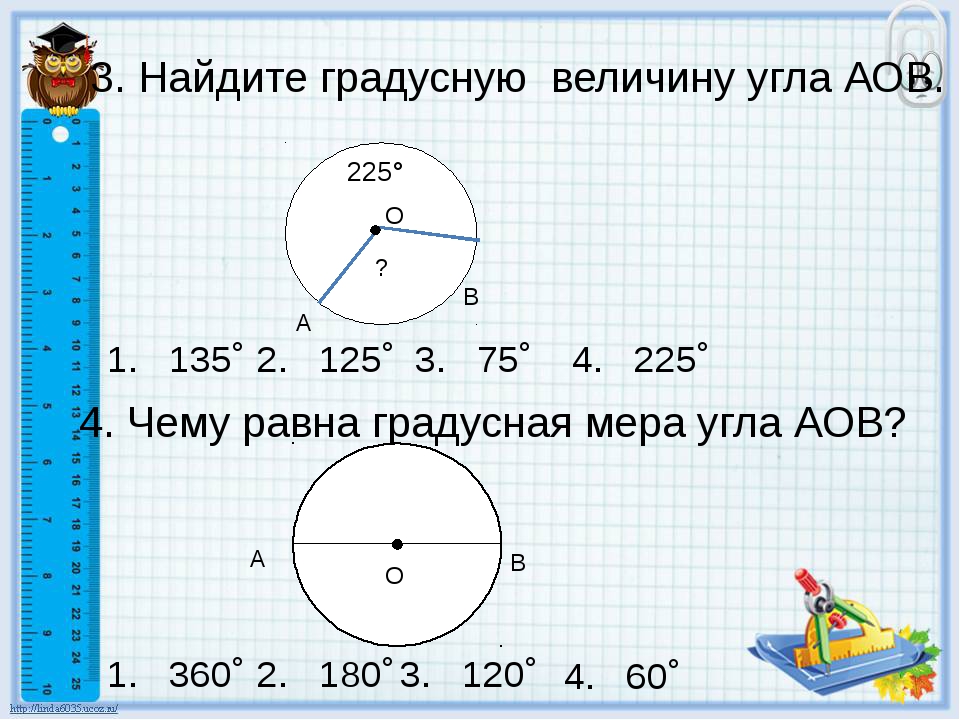
\[\dfrac{11\pi }{4} -2\pi =\dfrac{11\pi }{4} -\dfrac{8\pi }{4} =\dfrac{3\pi }{4} \номер\]
Угол \(\dfrac{3\pi }{4}\) совпадает с углом \(\dfrac{19\pi }{4}\).
Упражнение \(\PageIndex{4}\)
Найдите угол \(\phi\), котерминальный углу \(-\dfrac{17\pi }{6}\), где \(0\le \phi <2\pi\).
- Ответить
\[-\dfrac{17\pi }{6} +2\pi +2\pi =-\dfrac{17\pi }{6} +\dfrac{12\pi }{6} +\dfrac{12 \pi }{6} =\dfrac{7\pi }{6}\номер\]
Длина дуги и площадь сектора
Напомним, что мера угла в радианах определялась как отношение длины дуги окружности к радиусу окружности, \(\theta =\dfrac{s}{r}\).Из этого соотношения мы можем найти длину дуги вдоль окружности с заданным углом.
длина дуги на окружности
Длина дуги \(s\) вдоль окружности радиуса \(r\), опирающейся на угол \(\theta\) в радианах, равна
\[s=r\тета\]
Пример \(\PageIndex{9}\)
Меркурий вращается вокруг Солнца на расстоянии примерно 36 миллионов миль. {\circ}\) = \(\dfrac{215\pi }{180}\) радиан.{2}\]
{\circ}\) = \(\dfrac{215\pi }{180}\) радиан.{2}\]
Пример \(\PageIndex{10}\)
Автоматический разбрызгиватель для газонов распыляет на расстояние 20 футов при повороте на 30 градусов. Чему равна площадь сектора травяных поливов?
Раствор
Во-первых, нам нужно преобразовать угловую меру в радианы. Поскольку 30 градусов — это один из наших общих углов, в идеале вы уже должны знать эквивалентную меру радиана, но если нет, мы можем преобразовать:
30 градусов = \(30 \cdot \dfrac{\pi }{180} =\dfrac{\pi }{6}\) радиан.{2}\)
Упражнение \(\PageIndex{6}\)
При центральном круговом орошении большая ирригационная труба на колесах вращается вокруг центральной точки, как показано здесь (http://commons.wikimedia.org/wiki/Fi…_otech_002.JPG CC-BY-SA). Фермер имеет центральную поворотную систему с радиусом действия 400 метров. Если ограничения по воде позволяют ей поливать только 150 тысяч квадратных метров в день, какой угол она должна покрывать системой?
- Ответить
\(\dfrac{1}{2} \theta (400)^{2} =150 000\).
 {\circ}\)
{\circ}\)
Линейная и угловая скорость
Когда ваша машина едет по дороге, имеет смысл описать ее скорость в милях в час или метрах в секунду. Это меры скорости вдоль линии, также называемые линейной скоростью. Когда точка на окружности вращается, мы бы описали ее угловую скорость или скорость вращения в радианах в секунду, оборотах в минуту или градусах в час.
Определение: угловая и линейная скорость
Когда точка движется по окружности радиуса \(r\), ее угловая скорость, \(\omega\), может быть найдена как угловой поворот \(\theta\) в единицу времени, \(t\ ).
\[\omega =\dfrac{\theta}{t}\]
линейная скорость , \(v\), точки может быть найдена как пройденное расстояние, длина дуги \(s\), в единицу времени, \(t\).
\[v=\dfrac{s}{t}\]
Пример \(\PageIndex{11}\)
Водяное колесо совершает 1 оборот каждые 5 секунд. Найдите угловую скорость в радианах в секунду. (http://en.Wikipedia.org/wiki/File:R%…m%C3%BChle.svg CC-BY)
(http://en.Wikipedia.org/wiki/File:R%…m%C3%BChle.svg CC-BY)
Раствор
Колесо совершает 1 оборот = \(2\pi\) радиан за 5 секунд, поэтому угловая скорость будет \(\omega =\dfrac{2\pi }{5} \приблизительно 1.257\) радиан в секунду.
Объединив приведенные выше определения с уравнением длины дуги \(s=r\theta\), мы можем найти взаимосвязь между угловой и линейной скоростями. Уравнение угловой скорости может быть решено относительно \(\theta\), что дает \(\theta =\omega t\). Подстановка этого в уравнение длины дуги дает \(s=r\theta =r\omega t\).
Подставляя это в уравнение линейной скорости, получаем
\(v=\dfrac{s}{t} =\dfrac{r\omega t}{t} =r\omega\)
связь между линейной и угловой скоростью
Когда угловая скорость измеряется в радианах в единицу времени, линейная скорость и угловая скорость связаны уравнением
\[v=r\омега\]
Пример \(\PageIndex{12}\)
Велосипед имеет колеса диаметром 28 дюймов. Тахометр определяет, что колеса вращаются со скоростью 180 об/мин (оборотов в минуту). Найдите скорость, с которой велосипед движется по дороге.
Тахометр определяет, что колеса вращаются со скоростью 180 об/мин (оборотов в минуту). Найдите скорость, с которой велосипед движется по дороге.
Раствор
Здесь у нас есть угловая скорость, и нам нужно найти соответствующую линейную скорость, поскольку линейная скорость внешней стороны шин — это скорость, с которой велосипед движется по дороге.
Начнем с преобразования оборотов в минуту в радианы в минуту. Может быть полезно использовать единицы, чтобы сделать это преобразование
\[180\dfrac{\text{вращения}}{\text{минуты}} \cdot \dfrac{2\pi \text{радианы}}{\text{rotation}} =360\pi \dfrac{\text {радиан}}{\текст{минута}}\номер\]
Используя приведенную выше формулу вместе с радиусом колес, мы можем найти линейную скорость
\[v=(14 \text{дюймы})\left(360\pi \dfrac{\text{радианы}}{\text{минуты}} \right)=5040\pi \dfrac{\text{дюймы} }{\текст{минута}}\номер\]
Вам может быть интересно, куда делись «радианы» в этом последнем уравнении. Помните, что радианы — это безразмерная мера, поэтому их не обязательно включать.
Помните, что радианы — это безразмерная мера, поэтому их не обязательно включать.
Наконец, мы можем преобразовать эту линейную скорость в более привычное измерение, такое как мили в час.
\[5040\pi \dfrac{\text{дюймы}}{\text{минуты}} \cdot \dfrac{1 \text{футы}}{12 \text{дюймы}} \cdot \dfrac{1 \text {миля}}{5280 \text{футов}} \cdot \dfrac{60 \text{минут}}{1 \text{час}} =14,99\text{ миль в час (миль/ч)}\nonumber\]
Упражнение \(\PageIndex{7}\)
Спутник вращается вокруг Земли со скоростью 27 934 км/мин на высоте 242 км над землей.Найдите угловую скорость спутника, если радиус Земли равен 6378 км.
- Ответить
\(v\) = 27934. \(r\) = 6378+242=6620. \(\omega =\dfrac{v}{r} =\dfrac{27934}{6620} =4,2196\) радиан в час.
Важные темы этого раздела
- Градусная мера угла
- Радианная мера угла
- Преобразование градусов в радианы
- Общие углы в градусах и радианах
- Котерминальные уголки
- Длина дуги
- Площадь сектора
- Линейная и угловая скорость
Градус (угол) — Энциклопедия Нового Света
Один градус (отмечен красным).
- В этой статье описывается единица измерения угла.
A градус (полностью градус дуги , градус дуги или градус дуги ), обычно обозначаемый как ° (символ градуса), представляет собой измерение плоского угла, представляющее 1 ⁄ 360 полного оборота; один градус равен π/180 радиан. Когда этот угол относится к опорному меридиану, он указывает на положение вдоль большого круга сферы, такой как Земля (см. Географическая система координат), Марс или небесная сфера.
История
Окружность с равносторонней хордой (геометрия) (красная). Одна шестидесятая (1/60) этой дуги является градусом. Шесть таких аккордов замыкают круг. Выбор числа 360 в качестве числа градусов (, т. е. наименьших практических поддуг) в окружности, вероятно, был основан на том факте, что 360 — это приблизительное количество дней в году. Часто говорят, что его использование восходит к методам древних вавилонян. [1] Древние астрономы заметили, что звезды на небе, которые каждый день вращаются вокруг небесного полюса, как бы продвигаются по этому кругу примерно на одну 360-ю окружности, i.э., по одному градусу, каждый день. (Примитивные календари, такие как персидский календарь, использовали 360 дней в году.) Его применение для измерения углов в геометрии, возможно, можно проследить до Фалеса, который популяризировал геометрию среди греков и жил в Анатолии (современная западная Турция) среди людей, которые отношения с Египтом и Вавилоном.
[1] Древние астрономы заметили, что звезды на небе, которые каждый день вращаются вокруг небесного полюса, как бы продвигаются по этому кругу примерно на одну 360-ю окружности, i.э., по одному градусу, каждый день. (Примитивные календари, такие как персидский календарь, использовали 360 дней в году.) Его применение для измерения углов в геометрии, возможно, можно проследить до Фалеса, который популяризировал геометрию среди греков и жил в Анатолии (современная западная Турция) среди людей, которые отношения с Египтом и Вавилоном.
Самая ранняя тригонометрия, использовавшаяся вавилонскими астрономами и их греческими последователями, основывалась на хордах окружности. Хорда длины, равной радиусу, составляет натуральную базовую величину.Одна шестидесятая из них, если использовать их стандартное шестидесятеричное деление, составляла градус; а шесть таких аккордов замыкали полный круг.
Другая причина выбора числа 360 заключается в том, что оно легко делится: 360 имеет 24 делителя (включая 1 и 360), включая все числа от 1 до 10, кроме 7. Чтобы количество степеней в круге делилось на все число от 1 до 10, в окружности должно быть 2520 градусов, что является гораздо менее удобным числом.
Чтобы количество степеней в круге делилось на все число от 1 до 10, в окружности должно быть 2520 градусов, что является гораздо менее удобным числом.
- Делителями числа 360 являются 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180 и 360.
Индия
Деление круга на 360 частей произошло и в Древней Индии, о чем свидетельствует Ригведа:
- Двенадцать спиц, одно колесо, три пупка.
- Кто может это понять?
- На нем размещаются вместе
- триста шестьдесят подобных колышков.
- Они ничуть не трясутся.
- ( Диргхатама, Ригведа 1.164.48)
Подразделения
Для многих практических целей градус — это достаточно малый угол, чтобы целые градусы обеспечивали достаточную точность.Когда это не так, как в астрономии или для широты и долготы на Земле, градусы могут быть записаны с десятичными знаками, но обычно используется традиционное шестидесятеричное деление. Один градус делится на 60 минут (угловых), и одна минута на 60 секунд (угловых). Эти единицы измерения, также называемые угловыми минутами, и угловыми секундами, , соответственно представлены в виде одинарного и двойного штриха или, при необходимости, в виде одинарных и двойных кавычек: например, 40.1875 ° = 40 ° 11 ’15 дюймов (или 40 ° 11 ’15 дюймов).
Один градус делится на 60 минут (угловых), и одна минута на 60 секунд (угловых). Эти единицы измерения, также называемые угловыми минутами, и угловыми секундами, , соответственно представлены в виде одинарного и двойного штриха или, при необходимости, в виде одинарных и двойных кавычек: например, 40.1875 ° = 40 ° 11 ’15 дюймов (или 40 ° 11 ’15 дюймов).
Если требуется еще большая точность, обычно используются десятичные деления секунд, а не третей 1 ⁄ 60 секунд, четвертых 1 ⁄ 450 90 3 на. Эти (редко используемые) подразделения были отмечены написанием римской цифры для числа шестидесятых в верхнем индексе: 1 I для «штрих» (минута дуги), 1 II для секунды, 1 III для третий, 1 IV для четвертого и т.д.Отсюда и современные обозначения минуты и секунды дуги.
Альтернативные блоки
В большинстве математических работ, помимо практической геометрии, углы обычно измеряются в радианах, а не в градусах. Это происходит по разным причинам; например, тригонометрические функции имеют более простые и «естественные» свойства, когда их аргументы выражены в радианах. Эти соображения перевешивают удобную делимость числа 360. Один полный круг (360 °) равен 2 π радиан, поэтому 180 ° равен π радианам или, что то же самое, градус является математической константой ° = π ⁄ 180 .
Это происходит по разным причинам; например, тригонометрические функции имеют более простые и «естественные» свойства, когда их аргументы выражены в радианах. Эти соображения перевешивают удобную делимость числа 360. Один полный круг (360 °) равен 2 π радиан, поэтому 180 ° равен π радианам или, что то же самое, градус является математической константой ° = π ⁄ 180 .
С изобретением метрической системы, основанной на десятичных степенях, была предпринята попытка определить «десятичный градус» ( град или град ), чтобы количество десятичных градусов в прямом углу было 100 угольник, и было бы 400 угольник по кругу. Однако эта идея не получила большого распространения.
Угловой мил, который чаще всего используется в военных целях, имеет как минимум три конкретных варианта.
В компьютерных играх, изображающих трехмерный виртуальный мир, потребность в очень быстрых вычислениях привела к принятию двоичной системы с 256 градусами. В этой системе прямой угол равен 64 градусам, углы могут быть представлены одним байтом, а все тригонометрические функции реализованы в виде небольших интерполяционных таблиц. Эти единицы иногда называют «бинарными радианами» («брадами») или «бинарными градусами».
В этой системе прямой угол равен 64 градусам, углы могут быть представлены одним байтом, а все тригонометрические функции реализованы в виде небольших интерполяционных таблиц. Эти единицы иногда называют «бинарными радианами» («брадами») или «бинарными градусами».
См. также
Примечания
Ссылки
Ссылки ISBN поддерживают NWE за счет реферальных сборов
Внешние ссылки
Все ссылки получены 6 ноября 2017 г.
Кредиты
New World Encyclopedia писатели и редакторы переписали и дополнили статью Wikipedia в соответствии со стандартами New World Encyclopedia .Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства. Упоминание должно осуществляться в соответствии с условиями этой лицензии, которая может ссылаться как на авторов New World Encyclopedia , так и на самоотверженных добровольных участников Фонда Викимедиа.


 (ЩЛКМ. Слайд 28).
(ЩЛКМ. Слайд 28).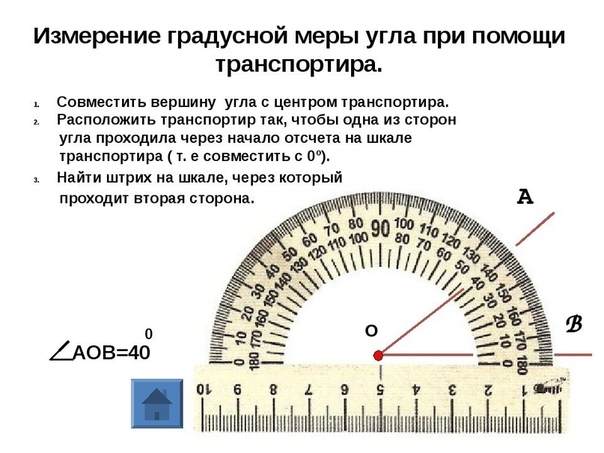 п.), она проходит через «0º» на сетке дуги;
п.), она проходит через «0º» на сетке дуги;

 {\circ}\)
{\circ}\)