Расстояние между точками от точки до плоскости
Этот случай совершенно аналогичен движению под действием постоянной силы тяжести. Работа зависит только от расстояния между перпендикулярными к направлению поля плоскостями, на которых лежат начальная и конечная точки перемещения. Если направление электрического поля условно считать направлением вниз , то работа силы зависит только от разности высот начальной и конечной точек перемещения. В частном случае, когда перемещение заряда происходит от одной обкладки конденсатора до другой, работа силы [c.126]Слуховая локализация источника звука зависит от расстояния между ушами. В обычных условиях человек определяет направление прихода звуковых волн в горизонтальной плоскости с точностью 3—4°. Если к ушам приставить раструбы с большим расстоянием между их отверстиями, то точность определения направления прихода звуковых волн может быть значительно повышена (такими звукоулавливателями пользовались до войны при определении местонахождения самолета).

Принимаемая в расчет стрела выпуклости днища (б,бо) представляет собой расстояние от наивысшей точки выпуклости днища до плоскости, проходящей через граничные точки между цилиндрической поверхностью днища и поверхностью сопряжения ее со сферой. [c.178]
Схождение колес, определенное как разность расстояний между наиболее близкими точками боковин правой и левой шин в горизонтальной плоскости, для автомобиля ГАЗ-53А должно быть от 1,5 до [c.217]
Результаты. Расчеты проводились при числе Маха набегающего потока перед каверной М] = 1,25 и числе Рейнольдса 10 , рассчитанном по ее глубине Н (принятой равной единице) и параметрам течения на входной границе АС. Толщина пограничного слоя 5 составляла 0,05. Температура невязкого потока задавалась равной 250 К, а поверхности — 300 К.
Для нахождения фронтальной проекции промежуточной точки (например, точки проводят между характерными точками 1 н 2 секущую плоскость Д—Д и определяют радиус Rд. Дальнейшие построения аналогичны построениям для нахождения 2у. Профильную проекцию 3w этой точки находят, отложив на профильной проекции по горизонтальной линии связи влево от оси симметрии детали отрезок, равный расстоянию от Зн до фронтальной плоскости симметрии.
Если прямая перпендикулярна к какой-либо плоскости (рис. 155,6), то расстояние от точки 3.0 прямой измеряется расстоянием между проекцией точки и точкой— проекцией прямой на этой плоскости. Если прямая занимает в системе V, Н общее положение, то, чтобы определить расстояние от точки до прямой способом перемены плоскостей проекций, надо ввести в систему V, Н еще две дополнительные плоскости.
[c.111]
Если прямая занимает в системе V, Н общее положение, то, чтобы определить расстояние от точки до прямой способом перемены плоскостей проекций, надо ввести в систему V, Н еще две дополнительные плоскости.
[c.111]
Расстояние между параллельными плоскостями измеряется длиной перпендикуляра, опуш енного из любой точки одной плоскости на другую. Таким образом, задача сводится к определению расстояния от точки до плоскости и может быть решена теми же способами (см. черт. 311—313). [c.110]
Два одинаковых физических маятника подвешены па параллельных горизонтальных осях, расположенных в одной горизонтальной плоскости, и связаны упругой пружиной, длина которой в ненапряженном состоянии равна расстоянию между осями маятников. Пренебрегая сопротивлением движению и массой пружины, определить частоты и отношения амплитуд главных колебаний системы при малых углах отклонения от равновесного положения. Вес каждого маятника Р радиус инерции его относительно оси, проходящей через центр масс параллельно осп подвеса, р жесткость пружины с, расстояния от центра масс маятника и от точки прикрепления пружины к маятникам до оси подвеса равны соответственно I и Н.
При вращении твердого тела вокруг неподвижной оси каждая его точка описывает окружность в плоскости, перпендикулярной к оси вращения. Радиус окружности равен расстоянию от точки до оси вращения. Положение некоторой точки М тела в пространстве можно однозначно охарактеризовать двугранным углом а между двумя плоскостями, проходящими через ось вращения. Одна из плоскостей неподвижна, а вторая содержит точку М и вращается. Величина скорости точки М при движении по окружности есть
Этап 3. Пусть имеются однородный шар радиуса Я и массы М и материальная точка массы т, расположенная от центра шара на расстоянии г. Разобьем шар плоскостями, перпендикулярными к прямой, соединяющей центр шара и точку т. Пусть V — одна из таких плоскостей. Расстояние от центра О шара до этой плоскости обозначим X. Будем считать х > О, когда плоскость V расположена между точками О и т, и а сечении шара плоскостью V получается круг радиуса I = у/а расстояние у от точки т до плоскости V дается равенством у — г — х. С точностью до малых второго порядка слой, вырезаемый из шара соседними плоскостями указанного разбиения, имеет массу
С точностью до малых второго порядка слой, вырезаемый из шара соседними плоскостями указанного разбиения, имеет массу
По каждой из трех пространственных осей координат следует иметь только одну главную базовую плоскость, от которой на каждом элементе пресс-формы отмечаются применяемые базовые плоскости. Размеры базовой плоскости должны быть возможно меньшими, тогда коробление ее будет минимальным и, следовательно, допуск на базовый размер будет меньшим. В случае невозможности получения общей базы для литья и механической обработки расстояние между этими базами следует брать минимальным, тогда допус на базовый размер будет наименьшим. Желательно, чтобы эти базовые поверхности были сторонами одной стенки, а еще лучше — находились в одной плоскости и желательно располагать базовую плоскость в центре литой детали. Тогда размеры от базы до самой удаленной точки литой детали, а следовательно и допуск на эти размеры, будут наименьшими. [c.134]
Равенство (5.
Азимут 7(, дефекта, измеряемый в градусах, соответствует углу между нормалью к сечению объекта и плоскостью падения волны при установке преобразователя в положение, при котором достигается максимальная амплитуда эхо-сигнала. Угол индикации Ду характеризуется углом поворота плоскости падения волны в одну сторону от положения, при котором был определен азимут, до некоторого крайнего положения при неизменном расстоянии от точки ввода луча до точки на проекции дефекта на контактную поверхность объекта (рис.
Тяжелая материальная точка, оставаясь на поверхности сферы радиуса а, притягивается пропорционально расстоянию неподвижной точкой В, находящейся на вертикали Oz и проходящей через центр О сферы расстояние OB = b. Даны значение л. притяжения на единицу расстояния, ускорение g силы тяжести, начальная скорость k движущейся точки, предполагаемая горизонтальной, и, наконец, начальное расстояние h от точки до горизонтальной плоскости Оху, проходящей через центр сферы. Требуется 1) найти границы, между которыми изменяется во время движения координата z точки 2) определить движение в частном случае, когда притяжение неподвижной точки В в центре сферы равно и противоположно весу.
На рис. 1.36 показано расположение атомов в сечении кристалла, в котором вдоль плоскости скольжения произведен незавершенный сдвиг, т. е. сдвиг, распространившийся не по всему сечению кристалла, а дошедший лишь до плоскости ОМ.
 В результате такого сдвига в верхней части решетки появляется лишняя атомная плоскость ОМ, которую называют экстраплоскостью. Соответственно атомный ряд 1, лежащий над плоскостью сдвига, содержит на один атом больше, чем ряд 2, расположенный ниже этой плоскости. Поэтому расстояние между атомами ряда 1 у точки О (центр дислокации) меньше нормального (решетка сжата), а расстояние между атомами ряда 2 больше нормального (решетка растянута). По мере перемещения от центра дислокации вправо и влево, вверх и вниз искажения решетки постепенно уменьшаются и на некотором расстоянии от О в кристалле восстанавливается нормальное расположение атомов. В направлении перпендикулярном плоскости чертежа, дислокация может проходить в виде линии (края плоскости ОМ) через весь кристалл. Такая дислокация называется краевой
[c.49]
В результате такого сдвига в верхней части решетки появляется лишняя атомная плоскость ОМ, которую называют экстраплоскостью. Соответственно атомный ряд 1, лежащий над плоскостью сдвига, содержит на один атом больше, чем ряд 2, расположенный ниже этой плоскости. Поэтому расстояние между атомами ряда 1 у точки О (центр дислокации) меньше нормального (решетка сжата), а расстояние между атомами ряда 2 больше нормального (решетка растянута). По мере перемещения от центра дислокации вправо и влево, вверх и вниз искажения решетки постепенно уменьшаются и на некотором расстоянии от О в кристалле восстанавливается нормальное расположение атомов. В направлении перпендикулярном плоскости чертежа, дислокация может проходить в виде линии (края плоскости ОМ) через весь кристалл. Такая дислокация называется краевой
[c.49]При использовании аппарата геометрически нелинейной теории упругости обнаруживается более точная картина деформации круглого цилиндра при чистом его кручении. Если торцы не закреплены против сближения, то первоначально прямолинейные продольные волокна в процессе кручения не испытывают растяжения. Но поскольку прямолинейная ось каждого из таких волокон превращается при кручении в равновеликую по длине винтовую кривую, концы последней должны располагаться в плоскостях, перпендикулярных оси цилиндра, расстояние между которыми меньше расстояния между плоскостями торцов до деформации. При сопоставлении деформации двух первоначально прямолинейных продольных волокон, находящихся на разных расстояниях от оси цилиндра, обнаруживается, что винтовые кривые, в которые превращаются оси этих волокон, имеют различные кривизны — большую у более удаленного от оси цилиндра волокна. Вследствие этого перемещения в направлении параллельном оси цилиндра точек торцов, находящихся на разных расстояниях от оси цилиндра, различны и торцы, строго говоря, перестают быть плоскими. Если же сближению торцов воспрепятствовать, то при кручении цилиндра первоначально прямолинейные продольные волокна испытывают растяжение.
Если торцы не закреплены против сближения, то первоначально прямолинейные продольные волокна в процессе кручения не испытывают растяжения. Но поскольку прямолинейная ось каждого из таких волокон превращается при кручении в равновеликую по длине винтовую кривую, концы последней должны располагаться в плоскостях, перпендикулярных оси цилиндра, расстояние между которыми меньше расстояния между плоскостями торцов до деформации. При сопоставлении деформации двух первоначально прямолинейных продольных волокон, находящихся на разных расстояниях от оси цилиндра, обнаруживается, что винтовые кривые, в которые превращаются оси этих волокон, имеют различные кривизны — большую у более удаленного от оси цилиндра волокна. Вследствие этого перемещения в направлении параллельном оси цилиндра точек торцов, находящихся на разных расстояниях от оси цилиндра, различны и торцы, строго говоря, перестают быть плоскими. Если же сближению торцов воспрепятствовать, то при кручении цилиндра первоначально прямолинейные продольные волокна испытывают растяжение.
L — расстояние между осями в начальный момент д — расстояние от точки пересечения траектории с секущей плоскостью (нормальной оси инструмента) до-оси инструмента. [c.184]
Пусть расстояние от точки М до оси фрезы в плоскости, касательной к основному цилиндру, будет п от оси фрезы до плоскости, проходящей через точку М и перпендикулярной к оси колеса, — расстояние 2 = а os 0, тогда угол между осью фрезы и осью симметрии впадины определяется из формулы а os а [c.402]
Примечание. В формулах приняты обозначения W — развиваемая сила зажима в кГ М — момент на рукоятке в кГ -см, I, h, U 1, —длины плеч прихвата в мм[ 1 — угол подъема кривой эксцентрика в град-, — угол трения между эксцентриком и опорной плоскостью г — расстояние от центра вращения эксцентрика до точки соприкосновения с опорной плоскостью в лш tg Ф = — коэффициент трения на оси эксцентрика е — эксцентрицитет в, мм-, 3 — угол поворота эксцентрика в град-, ф — угол трения в резьбовом соединении ft — коэффициент, учитывающий смещения точки приложения силы Q относительно оси / = /2=0,1— коэффициент трения q — сопротивление пружины в кГ Т1 — коэффициент, учитывающий трение в шарнирных соединениях и направлениях ф, — угол трения на скосе клипа tg ф, = ig ф = /
[c. 93]
93]
Отклонение направления линии зуба Др в точке Р может быть определено как угол между линией пересечения производящей поверхности с плоскостью Пд (штриховая линия) и проекцией на эту плоскость линии ее пересечения с плоскостью Т (сплошная линия). Для нахождения этого угла возьмем точку на линии зуба в плоскости Яо на образующей = k L, отстоящую на бесконечно малом расстоянии А/ от точки Р. Точка Р находится на линии зуба в плоскости Т на том же радиусе (сечение Б—Б). Ее расстояние от плоскости Яо с точностью до бесконечно малых величин высшего порядка равно А/ os р tg Y> а расстояние ее проекции на плоскость Я от точки Р равно A/tga tgY- Вследствие малости всех величин дуги РР и РРд можно считать прямыми. Поэтому искомый угол Др с точностью до бесконечно малых высшего порядка будет равен [c.94]
Определить расстояние от точки N до плоскости я (К) и др. Угол между линией действия вектора [c.168]
Так как л — расстояние от шарнирной опоры рамы до балансируемой плоскости коррекции, а Хд—ДО исключаемой, то их разность оказывается равной расстоянию между плоскостями коррекции. Подставим в выражение (19 ) х — Xq I и разделим левую и правую части на тг, далее раскрыв значения коэффициентов 272
[c.272]
Подставим в выражение (19 ) х — Xq I и разделим левую и правую части на тг, далее раскрыв значения коэффициентов 272
[c.272]
Схема угловых и линейных перемещений деталей прибора показана на рис. 203, на которой Ь — расстояние от оси поворота трз бки до плоскости пятки а — расстояние между осью микровинта и осью поворота трубки, равное 150 0,1 мн R, — радиус сферы микровинта и — линейное перемещение микровинта 8 — вертикальное перемещение точки контакта сферы в исходном положении после поворота трубки на угол а. [c.243]
О. микроскопа — важнейшая часть его оптич, системы, создающая увелич. изображение объекта наблюдения в передней фокальной плоскости окуляра. Масштаб изображения обратно пропорционален фокусному расстоянию О. и составляет примерно от 1,5 до 100 крат. Предел разрешения микроскопа е — мин. расстояние между центрами светящихся точек объекта, видимых раздельно, определяется дифракц. явлениями в О. и вычисляется по ф-ле е = 0,6 ХМ, где А — числовая апертура О. , равная произведению показателя преломления среды, находящейся между объектом и О., на синус апертурного угла. Для О, микроскопов 0,03 Л 1,4 диаметр поля изображения — от 18 мм до 32 мм. Простейшие О. микроскопов создают изображение, обладающее значит, кривизной, в результате чего при переходе от наблюдения центр, части поля к его краям необходима перефокусировка.
[c.392]
, равная произведению показателя преломления среды, находящейся между объектом и О., на синус апертурного угла. Для О, микроскопов 0,03 Л 1,4 диаметр поля изображения — от 18 мм до 32 мм. Простейшие О. микроскопов создают изображение, обладающее значит, кривизной, в результате чего при переходе от наблюдения центр, части поля к его краям необходима перефокусировка.
[c.392]
При повороте плоской кривой (меридиана) вокруг оси z, лежащей в этой плоскости (рис. 9.5.1), образуется срединная поверхность оболочки вращения. Точка М мервдиана при повороте описывает окружность (параллель). Положение точки на поверхности может быть задано угловыми координатами углом а между осью вращения и нормалью к меридиану углом (3, образуемым плоскостью меридиана с начальной плоскостью отсчета. На рис. 9.5.1 показаны угловые координаты точки поверхности М. На рис. 9.5.2 обозначены радиусы кривизн поверхности радиус R кривизны меридиана окружной радиус кривизны, который равен расстоянию по нормали от точки на поверхности до оси вращения.
 Длина дуги элемента вдоль меридиана dsi = R da., а вдоль параллели
[c.144]
Длина дуги элемента вдоль меридиана dsi = R da., а вдоль параллели
[c.144]Требуется определить расстояние от точки А до прямой /. Искомый отрезок АК должен быгь перпендикулярен к этой прямой, а так как в первых двух случаях I параллельна плоскости Oj, то на эту плоскость прямой угол между АК I проецируется без искажения. Но поскольку в первом случае /ХП], то отрезок АК, перпендикулярный /, окажется параллельным П,, и горизонтальная проекция его будет определять искомое расстояние. [c.55]
Как определить расстояние от точки до плоскости между плоскостями между параллельными и скрещивающимися прймыми [c.195]
Этап 2. Пусть в плоскости V расположен круговой однородный диск массы М2 и радиуса /. На оси, перпендикулярной к плоскости диска и проходящей через его центр, расположена материальная точка массы т. Начало отсчета поместим в центр диска. Расстояние от точки т до плоскости V обозначим у. Чтобы найти силовую функцию /2(2/), разобьем диск концентрическими окружностями. Пусть р — радиус такой окружности, в йр — ширина кольца между соседними окружностями. С точностью до малых второго порядка масса кольца Мх = 2жМ2р(1р/ жР). Искомая силовая функция получается суммированием силовых функций, соответствующих всем кольцам разбиения. Воспользуемся результатом первого этапа
[c.267]
Пусть р — радиус такой окружности, в йр — ширина кольца между соседними окружностями. С точностью до малых второго порядка масса кольца Мх = 2жМ2р(1р/ жР). Искомая силовая функция получается суммированием силовых функций, соответствующих всем кольцам разбиения. Воспользуемся результатом первого этапа
[c.267]
Вектор вз направим вдоль оси динамической симметрии. Предположим, что точка опоры О волчка о плоскость. дежит на оси симметрии волчка. Расстояние от точки опоры до центра масс равно I. Угол между векторами 63 и ез по-прежнему обозначим 9 (угол нутации). Радиус-вектор центра масс представим разложением по векторам абсолютного репера [c.501]
Проведем плоскость FD, перпендикулярную к направлению нормалей дифрагировавших волн. Распределение фаз, которое будет иметь место на этой плоскости, определяет соотношение фаз элементарных волн, собирающихся в точке Вф, ибо линза не вносит дополнительной разности фаз (таутохронизм, см. 20). Таким образом, достаточно определить разность хода, возникающую на пути от плоскости FE до плоскости FD. Из рис. 9.2 видно, что разность хода между волнами, идущими от элементарной зоны при точке F (край щели) и от какой-либо точки N (лежащей на расстоянии X от края щели), есть NP = хsin ф. Световое возмущение в точке Р плоскости FD запишется следующим образом
[c.176]
Таким образом, достаточно определить разность хода, возникающую на пути от плоскости FE до плоскости FD. Из рис. 9.2 видно, что разность хода между волнами, идущими от элементарной зоны при точке F (край щели) и от какой-либо точки N (лежащей на расстоянии X от края щели), есть NP = хsin ф. Световое возмущение в точке Р плоскости FD запишется следующим образом
[c.176]
После определения диаметров в намеченных сечениях разрабатывают конструкцию вала, устанавливают места посадки сопряженных G ними деталей (зубчатых или червячных колес, звездочек, шкивов, полумуфт и др.), расположения подшипников—все перечисленные действия воплощают в эскизную компоновку редуктора. Эскизная компоновка редуктора имеет целью установить положение редукторной и открытой передач относительно опор (подшипников), определить расстояние между средними плоскостями подшипников и расстояние от подшипников до открытой передачи, а также расстояние между точками приложения реакций подшипников (методику выполнения эскизной компоновки см. 7.1 в пособии [14]). На основании полученной расчетной схемы вы-чнсляют действующие на валы изгибающие н5 -. грузки, строят эпюры изгибающих и крутящих моментов (О построении эпюр см. в 9.2 второго раздела данной книги). На рис. 3.123, а в качестве примера показан ведомый вал червячного редуктора. На вал насажено червячное колесо диаметром dai на выходной конец вала насажена звездочка цепной передачи. Опорами вала являются радиально-упорные конические роликоподшипники. Выступающий конец вала имеет наименьший диаметр d диаметр цапф под подшипники d несколько больше. Диаметр участка вала под червячным колесом еще больше. Левый торец ступицы червячного колеса упирается в заплечики бурта, диаметр
[c.514]
7.1 в пособии [14]). На основании полученной расчетной схемы вы-чнсляют действующие на валы изгибающие н5 -. грузки, строят эпюры изгибающих и крутящих моментов (О построении эпюр см. в 9.2 второго раздела данной книги). На рис. 3.123, а в качестве примера показан ведомый вал червячного редуктора. На вал насажено червячное колесо диаметром dai на выходной конец вала насажена звездочка цепной передачи. Опорами вала являются радиально-упорные конические роликоподшипники. Выступающий конец вала имеет наименьший диаметр d диаметр цапф под подшипники d несколько больше. Диаметр участка вала под червячным колесом еще больше. Левый торец ступицы червячного колеса упирается в заплечики бурта, диаметр
[c.514]
Предположим теперь, что вдоль оси та на равных расстояниях d расположен ряд одинаковых краевых дислокаций (Ь, О, 0). Основываясь на результатах предыдущего параграфа, следует ожидать, что такое расположение будет устойчивым. В последующем мы вернемся к вопросу об устойчивости подобного расположения, пока что ограничимся соответствующим допущением. Если мы хотим рассматривать напряженное состояние в точках, отстоящих от оси Х2 на расстояние, достаточно большое по сравнению с расстоянием d между дислокациями, мы можем замег(ить дискретный ряд дислокаций непрерывным их распределением, слоем дислокаций. Представим себе, что на каждый бесконечно малый элемент dgj оси хг приходится краевая дислокация с вектором Бюргерса р На больших расстояниях от оси Х2 такой слой вызывает напряженное состояние, не отличающееся от напряженного состояния, вызванного рядом дислокаций на расстоянии d одна от другой, если р = b/d. Слой дислокаций может простираться неограниченно вдоль оси х или может быть расположен на части плоскости ц = О от = —L до Х2 = +L. Рассмотрим сначала случай бесконечной стенки. Вращение, вызванное краевой дислокацией (6, О, 0), проходящей через начало координат, дается формулой (14.4.4)
[c.478]
Если мы хотим рассматривать напряженное состояние в точках, отстоящих от оси Х2 на расстояние, достаточно большое по сравнению с расстоянием d между дислокациями, мы можем замег(ить дискретный ряд дислокаций непрерывным их распределением, слоем дислокаций. Представим себе, что на каждый бесконечно малый элемент dgj оси хг приходится краевая дислокация с вектором Бюргерса р На больших расстояниях от оси Х2 такой слой вызывает напряженное состояние, не отличающееся от напряженного состояния, вызванного рядом дислокаций на расстоянии d одна от другой, если р = b/d. Слой дислокаций может простираться неограниченно вдоль оси х или может быть расположен на части плоскости ц = О от = —L до Х2 = +L. Рассмотрим сначала случай бесконечной стенки. Вращение, вызванное краевой дислокацией (6, О, 0), проходящей через начало координат, дается формулой (14.4.4)
[c.478]
Если на стержень действуют внешние нагрузки, равнодействующая которых находится на оси стержня (осевая сила), то стержень продольно деформируется (осевое растяжение или сжатие). В результате деформации расстояния между точками разных поперечных сечений изменяются в зависимости от нагрузок и их распределения по длине стержня. Для достаточно длинных стержней на некотором удалении от концов стержня, к которым приложены внешние продольные силы, можно напряженно-деформированное состояние считать равномерным в пределах каждого отдельного поперечного сечения. Такое положение наблюдается уже на расстоянии порядка толщ,ины стержня от нагруженных концов, и с удалением от концов оно выполняется с более высокой точностью. На рис. 3.1 показаны два различных характера загружения концов стержня внешней осевой нагрузкой Fi = 2Fa- Штриховыми линиями показано очевидное деформированное состояние с изображением искривления поперечных сечений по мере изменения расстояния от нагруженных концов. На расстояниях порядка толщины (ширины) стержня плоские поперечные сечения практически не искривляются. Это одна из иллюстраций справедливости принципа Сен-Вепана, который утверждает, что статически эквивалентное преобразование внешних нагрузок на малой площади границы тела не влияет на распределение напряжений на некотором удалении от места приложения нагрузок.
В результате деформации расстояния между точками разных поперечных сечений изменяются в зависимости от нагрузок и их распределения по длине стержня. Для достаточно длинных стержней на некотором удалении от концов стержня, к которым приложены внешние продольные силы, можно напряженно-деформированное состояние считать равномерным в пределах каждого отдельного поперечного сечения. Такое положение наблюдается уже на расстоянии порядка толщ,ины стержня от нагруженных концов, и с удалением от концов оно выполняется с более высокой точностью. На рис. 3.1 показаны два различных характера загружения концов стержня внешней осевой нагрузкой Fi = 2Fa- Штриховыми линиями показано очевидное деформированное состояние с изображением искривления поперечных сечений по мере изменения расстояния от нагруженных концов. На расстояниях порядка толщины (ширины) стержня плоские поперечные сечения практически не искривляются. Это одна из иллюстраций справедливости принципа Сен-Вепана, который утверждает, что статически эквивалентное преобразование внешних нагрузок на малой площади границы тела не влияет на распределение напряжений на некотором удалении от места приложения нагрузок. Опираясь на этот принцип, примем гипотезу плоских сечений, которая состоит в следующем материальные, точки стержня, расположенные в плоскости поперечного сечения до деформирования, после деформирования располагаются в одной и той же плоскости поперечного сечения (гипотеза Бернулли), или, иначе, плоские до деформирования поперечные се-нЕНия бруса остаются плоскими и после деформирования.
[c.51]
Опираясь на этот принцип, примем гипотезу плоских сечений, которая состоит в следующем материальные, точки стержня, расположенные в плоскости поперечного сечения до деформирования, после деформирования располагаются в одной и той же плоскости поперечного сечения (гипотеза Бернулли), или, иначе, плоские до деформирования поперечные се-нЕНия бруса остаются плоскими и после деформирования.
[c.51]
Формулы для определения расстояния от точки до плоскости и от точки до прямой
Знание расстояния от точки до плоскости или до прямой позволяет вычислить объем и площадь поверхности фигур в пространстве. Расчет этого расстояния в геометрии осуществляется с использованием соответствующих уравнений для указанных геометрических объектов. В статье покажем, с помощью каких формул можно его определить.
Уравнения прямой и плоскости
Перед тем как приводить формулы для определения расстояния от точки до плоскости и до прямой, покажем, какими уравнениями описываются эти объекты.
Для определения точки используется набор координат в данной системе координатных осей. Здесь будем рассматривать только декартову прямоугольную систему, в которой оси имеют одинаковые единичные векторы и являются взаимно перпендикулярными. На плоскости произвольная точка описывается двумя координатами, в пространстве — тремя.
Для определения прямой используют разные типы уравнений. В соответствии с темой статьи, приведем лишь два из них, которые применяются в двумерном пространстве для задавания прямых.
Векторное уравнение. Оно имеет следующую форму записи:
(x; y) = (x0; y0 ) + λ*(a; b).
Первый член здесь представляет координаты известной точки, лежащей на прямой. Второй член — это координаты направляющего вектора, умноженные на произвольное число λ.
Уравнение общего вида. Его форма записи такая:
A*x + B*y + C = 0;
где A, B, C — некоторые коэффициенты.
Общее уравнение чаще используется для определения прямых на плоскости, однако для нахождения расстояния от точки до прямой на плоскости удобнее работать с векторным выражением.
Плоскость в трехмерном пространстве тоже можно записать несколькими математическими способами. Тем не менее чаще всего в задачах встречается уравнение общего вида, которое записывается так:
A*x + B*y + C*z + D = 0.
Преимуществом этой формы записи по отношению к остальным является то, что она в явном виде содержит координаты вектора, перпендикулярного плоскости. Этот вектор называется направляющим для нее, он совпадает с направлением нормали, а его координаты равны (A; B; C).
Заметим, что приведенное выражение совпадает с формой записи уравнения общего вида для прямой в двумерном пространстве, поэтому при решении задач стоит быть внимательным и не путать эти геометрические объекты.
Дистанция между точкой и прямой
Покажем, как можно вычислить расстояние между прямой и точкой в двумерном пространстве.
Пусть имеется некоторая точка Q(x1; y1) и прямая, заданная выражением:
(x; y) = (x0; y0 ) + λ*(a; b).
Под дистанцией между прямой и точкой понимают длину перпендикулярного этой прямой отрезка, опущенного на нее из точки Q.
Перед тем как вычислять это расстояние, следует подставить координаты Q в это равенство. Если они ему будут удовлетворять, значит Q принадлежит данной прямой, и соответствующее расстояние равно нулю. Если же координаты точки не приводят к соблюдению равенства, тогда расстояние между геометрическими объектами отлично от нуля. Его можно рассчитать по формуле:
d = |[PQ¯*u¯]|/|u¯|.
Здесь P — произвольная точка прямой, которая является началом вектора PQ¯. Вектор u¯ — это направляющий отрезок для прямой, то есть его координаты равны (a; b).
Использование этой формулы предполагает умение вычислять векторное произведение, стоящее в числителе.
Задача с точкой и прямой
Допустим, необходимо найти дистанцию между Q(-3; 1) и прямой, удовлетворяющей уравнению:
y = x -2.
Подставив координаты Q в выражение, можно убедиться, что Q на прямой не лежит. Применить приведенную в пункте выше формулу для d можно, если представить данное уравнение в векторном виде. Сделаем это следующим образом:
Применить приведенную в пункте выше формулу для d можно, если представить данное уравнение в векторном виде. Сделаем это следующим образом:
(x; y) = (x; x -2) =>
(x; y) = (x; x) + (0; -2) =>
(x; y) = x*(1; 5) + (0; -2) =>
(x; y) = (0; -2) + λ*(1; 5).
Теперь возьмем любую точку на этой прямой, например (0; -2), и построим вектор с началом в ней и концом в Q:
(-3; 1) — (0; -2) = (-3; 3).
Теперь применяем формулу для определения расстояния, получаем:
d = |[(-3; 3)*(1; 5)]|/|(1; 5)| = 18/√26 ≈ 3,53.
Расстояние от точки до плоскости
Как и в случае с прямой, под дистанцией между плоскостью и точкой в пространстве понимают длину отрезка, который из данной точки перпендикулярно опущен на плоскость и пересекает ее.
В пространстве точка задается тремя координатами. Если они равны (x1; y1; z1), тогда расстояние между плоскостью и этой точкой можно вычислить по формуле:
d = |A*x1 + B*y1 + C*z1 + D|/√(A2+B2+C2).
Отметим, что использование формулы позволяет найти только расстояние от плоскости до прямой. Чтобы найти координаты точки, в которой перпендикулярный отрезок пересекает плоскость, необходимо составить уравнение прямой, которой этот отрезок принадлежит, а затем найти общую точку для этой прямой и заданной плоскости.
Задача с плоскостью и точкой
Найдите расстояние от точки до плоскости, если известно, что точка имеет координаты (3; -1; 2), а плоскость задана выражением:
-y + 3*z = 0.
Чтобы воспользоваться соответствующей формулой, выпишем сначала коэффициенты для заданной плоскости. Поскольку переменная x и свободный член отсутствуют, то коэффициенты A и D равны нулю. Имеем:
A = 0; B = -1; C = 3; D = 0.
Легко показать, что эта плоскость проходит через начало координат, и ось x ей принадлежит.
Подставляем координаты точки и коэффициенты плоскости в формулу для дистанции d, получаем:
d = |0*3 + (-1)*(-1) + 2*3 + 0|/√(1 +9 ) = 7/√10 ≈ 2,21.
Заметим, что если изменить координату x точки, то расстояние d не изменится. Этот факт означает, что совокупность точек (x; -1; 2) образует прямую, параллельную заданной плоскости.
Расстояние от точки до прямой. Расстояние от точки до прямой на плоскости
Формула для вычисления расстояния от точки до прямой на плоскости
Если задано уравнение прямой Ax + By + C = 0, то расстояние от точки M(M x , M y) до прямой можно найти, используя следующую формулу
Примеры задач на вычисление расстояния от точки до прямой на плоскости
Пример 1.
Найти расстояние между прямой 3x + 4y — 6 = 0 и точкой M(-1, 3).
Решение. Подставим в формулу коэффициенты прямой и координаты точки
Ответ: расстояние от точки до прямой равно 0.6.
уравнение плоскости проходящей через точки перпендикулярно векторуОбщее уравнение плоскости
Ненулевой
вектор ,
перпендикулярный заданной плоскости,
называетсянормальным
вектором (или,
короче, нормалью )
для этой плоскости.
Пусть в координатном пространстве (в прямоугольной системе координат) заданы:
а) точка ;
б) ненулевой вектор (рис.4.8,а).
Требуется составить уравнение плоскости, проходящей через точку перпендикулярно векторуКонец доказательства.
Рассмотрим теперь различные типы уравнений прямой на плоскости.
1) Общее уравнение плоскости P .
Из вывода уравнения следует, что одновременно A , B и C не равны 0 (объясните почему).
Точка принадлежит плоскостиP только в том случае, когда ее координаты удовлетворяют уравнению плоскости. В зависимости от коэффициентов A , B , C и D плоскость P занимает то или иное положение:
‑ плоскость проходит через начало системы координат, ‑ плоскость не проходит через начало системы координат,
‑ плоскость параллельна оси X ,
X ,
‑ плоскость параллельна оси Y ,
‑ плоскость не параллельна оси Y ,
‑ плоскость параллельна оси Z ,
‑
плоскость
не параллельна оси Z .
Докажите эти утверждения самостоятельно.
Уравнение
(6) легко выводится из уравнения (5).
Действительно, пусть точка лежит
на плоскости P .
Тогда ее координаты удовлетворяют
уравнениюВычитая
из уравнения (5) уравнение (7) и группируя
слагаемые, получим уравнение (6). Рассмотрим
теперь два вектора с координатами соответственно.
Из формулы (6) следует, что их скалярное
произведение равно нулю. Следовательно,
вектор перпендикулярен
вектору Начало
и конец последнего вектора находятся
соответственно в точках которые
принадлежат плоскости P .
Следовательно, вектор перпендикулярен
плоскости P .
Расстояние от точкидо
плоскости P ,
общее уравнение которой определяется
по формулеДоказательство
этой формулы полностью аналогично
доказательству формулы расстояния
между точкой и прямой (см. рис. 2).
Рис.
2. К выводу формулы расстояния между
плоскостью и прямой.
Действительно, расстояние d между прямой и плоскостью равно
где ‑
точка лежащая на плоскости. Отсюда, как
и в лекции № 11, получается выше приведенная
формула. Две плоскости параллельны,
если параллельны их нормальные вектора.
Отсюда получаем условие параллельности
двух плоскостей‑
коэффициенты общих уравнений плоскостей .
Две плоскости перпендикулярны, если
перпендикулярны их нормальные вектора,
отсюда получаем условие перпендикулярности
двух плоскостей, если известны их общие
уравнения
Отсюда, как
и в лекции № 11, получается выше приведенная
формула. Две плоскости параллельны,
если параллельны их нормальные вектора.
Отсюда получаем условие параллельности
двух плоскостей‑
коэффициенты общих уравнений плоскостей .
Две плоскости перпендикулярны, если
перпендикулярны их нормальные вектора,
отсюда получаем условие перпендикулярности
двух плоскостей, если известны их общие
уравнения
Угол f между
двумя плоскостями равен углу между их
нормальными векторами (см. рис. 3) и может,
поэтому, быть вычислен по формуле
Определение
угла между плоскостями.
(11)
Расстояние от точки до плоскости и способы его нахождения
Расстояние от точки до плоскости – длина перпендикуляра, опущенного из точки на эту плоскость. Существует, по крайней мере, два способа найти расстояние от точки до плоскости:геометрический и алгебраический .
При
геометрическом способе нужно
сначала понять, как расположен
перпендикуляр из точки на плоскость:
может он лежит в какой –то удобной
плоскости, является высотой в какой-нибудь
удобном (или не очень) треугольнике, а
может этот перпендикуляр вообще является
высотой в какой-нибудь пирамиде.
После этого первого и самого сложного этапа задача распадается на несколько конкретных планиметрических задач (быть может, в разных плоскостях).
При алгебраическом способе для того, чтобы найти расстояние от точки до плоскости, нужно ввести систему координат, найти координаты точки и уравнение плоскости, и после этого применить формулу расстояния от точки до плоскости.
Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на прямую. В начертательной геометрии она определяется графическим путем по приведенному ниже алгоритму.
Алгоритм
- Прямую переводят в положение, в котором она будет параллельна какой-либо плоскости проекции. Для этого применяют методы преобразования ортогональных проекций.
- Из точки проводят перпендикуляр к прямой. В основе данного построения лежит теорема о проецировании прямого угла.
- Длина перпендикуляра определяется путем преобразования его проекций или с использованием способа прямоугольного треугольника.

На следующем рисунке представлен комплексный чертеж точки M и прямой b, заданной отрезком CD. Требуется найти расстояние между ними.
Согласно нашему алгоритму, первое, что необходимо сделать, это перевести прямую в положение, параллельное плоскости проекции. При этом важно понимать, что после проведенных преобразований фактическое расстояние между точкой и прямой не должно измениться. Именно поэтому здесь удобно использовать метод замены плоскостей , который не предполагает перемещение фигур в пространстве.
Результаты первого этапа построений показаны ниже. На рисунке видно, как параллельно b введена дополнительная фронтальная плоскость П 4 . В новой системе (П 1 , П 4) точки C»» 1 , D»» 1 , M»» 1 находятся на том же удалении от оси X 1 , что и C»», D»», M»» от оси X.
Выполняя вторую часть алгоритма, из M»» 1 опускаем перпендикуляр M»» 1 N»» 1 на прямую b»» 1 , поскольку прямой угол MND между b и MN проецируется на плоскость П 4 в натуральную величину. По линии связи определяем положение точки N» и проводим проекцию M»N» отрезка MN.
По линии связи определяем положение точки N» и проводим проекцию M»N» отрезка MN.
На заключительном этапе нужно определить величину отрезка MN по его проекциям M»N» и M»» 1 N»» 1 . Для этого строим прямоугольный треугольник M»» 1 N»» 1 N 0 , у которого катет N»» 1 N 0 равен разности (Y M 1 – Y N 1) удаления точек M» и N» от оси X 1 . Длина гипотенузы M»» 1 N 0 треугольника M»» 1 N»» 1 N 0 соответствует искомому расстоянию от M до b.
Второй способ решения
- Параллельно CD вводим новую фронтальную плоскость П 4 . Она пересекает П 1 по оси X 1 , причем X 1 ∥C»D». В соответствии с методом замены плоскостей определяем проекции точек C»» 1 , D»» 1 и M»» 1 , как это изображено на рисунке.
- Перпендикулярно C»» 1 D»» 1 строим дополнительную горизонтальную плоскость П 5 , на которую прямая b проецируется в точку C» 2 = b» 2 .
- Величина расстояния между точкой M и прямой b определяется длиной отрезка M» 2 C» 2 , обозначенного красным цветом.

Похожие задачи:
Данная статья рассказывает о теме « расстояния от точки до прямой», рассматриваются определения расстояния от точки к прямой с иллюстрированными примерами методом координат. Каждый блок теории в конце имеет показанные примеры решения подобных задач.
Yandex.RTB R-A-339285-1
Расстояние от точки до прямой находится через определение расстояния от точки до точки. Рассмотрим подробней.
Пусть имеется прямая a и точка М 1 , не принадлежащая заданной прямой. Через нее проведем прямую b , расположенную перпендикулярно относительно прямой a . Точка пересечения прямых возьмем за Н 1 . Получим, что М 1 Н 1 является перпендикуляром, который опустили из точки М 1 к прямой a .
Определение 1
Расстоянием от точки М 1 к прямой a называется расстояние между точками М 1 и Н 1 .
Бывают записи определения с фигурированием длины перпендикуляра.
Определение 2
Расстоянием от точки до прямой называют длину перпендикуляра, проведенного из данной точки к данной прямой.
Определения эквивалентны. Рассмотрим рисунок, приведенный ниже.
Известно, что расстояние от точки до прямой является наименьшим из всех возможных. Рассмотрим это на примере.
Если взять точку Q , лежащую на прямой a , не совпадающую с точкой М 1 , тогда получим, что отрезок М 1 Q называется наклонной, опущенной из М 1 к прямой a . Необходимо обозначить, что перпендикуляр из точки М 1 является меньше, чем любая другая наклонная, проведенная из точки к прямой.
Чтобы доказать это, рассмотрим треугольник М 1 Q 1 Н 1 , где М 1 Q 1 является гипотенузой. Известно, что ее длина всегда больше длины любого из катетов. Значим, имеем, что M 1 H 1
Исходные данные для нахождения от точки до прямой позволяют использовать несколько методов решения: через теорему Пифагора, определения синуса, косинуса, тангенса угла и другими. Большинство заданий такого типа решают в школе на уроках геометрии.
Когда при нахождении расстояния от точки до прямойможно ввести прямоугольную систему координат, то применяют метод координат. В данном пункте рассмотрим основных два метода нахождения искомого расстояния от заданной точки.
В данном пункте рассмотрим основных два метода нахождения искомого расстояния от заданной точки.
Первый способ подразумевает поиск расстояния как перпендикуляра, проведенного из М 1 к прямой a . Во втором способе используется нормальное уравнение прямой а для нахождения искомого расстояния.
Если на плоскости имеется точка с координатами M 1 (x 1 , y 1) , расположенная в прямоугольной системе координат, прямая a , а необходимо найти расстояние M 1 H 1 , можно произвести вычисление двумя способами. Рассмотрим их.
Первый способ
Если имеются координаты точки H 1 , равные x 2 , y 2 , тогда расстояние от точки до прямой вычисляется по координатам из формулы M 1 H 1 = (x 2 — x 1) 2 + (y 2 — y 1) 2 .
Теперь перейдем к нахождению координат точки Н 1 .
Известно, что прямая линия в О х у соответствует уравнению прямой на плоскости. Возьмем способ задания прямой a через написание общего уравнения прямой или уравнения с угловым коэффициентом. Составляем уравнение прямой, которая проходит через точку М 1 перпендикулярно заданной прямой a . Прямую обозначим буковой b . Н 1 является точкой пересечения прямых a и b , значит для определения координат необходимо воспользоваться статьей, в которой идет речь о координатах точек пересечения двух прямых.
Прямую обозначим буковой b . Н 1 является точкой пересечения прямых a и b , значит для определения координат необходимо воспользоваться статьей, в которой идет речь о координатах точек пересечения двух прямых.
Видно, что алгоритм нахождения расстояния от заданной точки M 1 (x 1 , y 1) до прямой a проводится согласно пунктам:
Определение 3
- нахождение общего уравнения прямой a , имеющее вид A 1 x + B 1 y + C 1 = 0 ,или уравнение с угловым коэффициентом, имеющее вид y = k 1 x + b 1 ;
- получение общего уравнения прямой b , имеющее вид A 2 x + B 2 y + C 2 = 0 или уравнение с угловым коэффициентом y = k 2 x + b 2 , если прямая b пересекает точку М 1 и является перпендикулярной к заданной прямой a ;
- определение координат x 2 , y 2 точки Н 1 , являющейся точкой пересечения a и b , для этого производится решение системы линейных уравнений A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 y + C 2 = 0 или y = k 1 x + b 1 y = k 2 x + b 2 ;
- вычисление искомого расстояния от точки до прямой, используя формулу M 1 H 1 = (x 2 — x 1) 2 + (y 2 — y 1) 2 .

Второй способ
Теорема способна помочь ответить на вопрос о нахождении расстояния от заданной точки дот заданной прямой на плоскости.
Теорема
Прямоугольная система координат имеет О х у имеет точку M 1 (x 1 , y 1) , из которой проведена прямая а к плоскости, задаваемая нормальным уравнением плоскости, имеющее вид cos α · x + cos β · y — p = 0 , равно по модулю значению, получаемому в левой части нормального уравнения прямой, вычисляемому при x = x 1 , y = y 1 , значит, что M 1 H 1 = cos α · x 1 + cos β · y 1 — p .
Доказательство
Прямой а соответствует нормальное уравнение плоскости, имеющее вид cos α · x + cos β · y — p = 0 , тогда n → = (cos α , cos β) считается нормальным вектором прямой a при расстоянии от начала координат до прямой a с p единицами. Необходимо изобразить все данные на рисунке, добавить точку с координатами M 1 (x 1 , y 1) , где радиус-вектор точки М 1 — O M 1 → = (x 1 , y 1) . Необходимо провести прямую от точки до прямой, которое обозначим M 1 H 1 . Необходимо показать проекции М 2 и Н 2 точек М 1 и Н 2 на прямую, проходящую через точку O с направляющим вектором вида n → = (cos α , cos β) , а числовую проекцию вектора обозначим как O M 1 → = (x 1 , y 1) к направлению n → = (cos α , cos β) как n p n → O M 1 → .
Необходимо показать проекции М 2 и Н 2 точек М 1 и Н 2 на прямую, проходящую через точку O с направляющим вектором вида n → = (cos α , cos β) , а числовую проекцию вектора обозначим как O M 1 → = (x 1 , y 1) к направлению n → = (cos α , cos β) как n p n → O M 1 → .
Вариации зависят от расположения самой точки М 1 . Рассмотрим на рисунке, приведенном ниже.
Результаты фиксируем при помощи формулы M 1 H 1 = n p n → O M → 1 — p . После чего приводим равенство к такому виду M 1 H 1 = cos α · x 1 + cos β · y 1 — p для того, чтобы получить n p n → O M → 1 = cos α · x 1 + cos β · y 1 .
Скалярное произведение векторов в результате дает преобразованную формулу вида n → , O M → 1 = n → · n p n → O M 1 → = 1 · n p n → O M 1 → = n p n → O M 1 → , которая является произведением в координатной форме вида n → , O M 1 → = cos α · x 1 + cos β · y 1 . Значит, получаем, что n p n → O M 1 → = cos α · x 1 + cos β · y 1 . Отсюда следует, что M 1 H 1 = n p n → O M 1 → — p = cos α · x 1 + cos β · y 1 — p . Теорема доказана.
Теорема доказана.
Получаем, что для нахождения расстояния от точки M 1 (x 1 , y 1) к прямой a на плоскости необходимо выполнить несколько действий:
Определение 4
- получение нормального уравнения прямой a cos α · x + cos β · y — p = 0 , при условии, что его нет в задании;
- вычисление выражения cos α · x 1 + cos β · y 1 — p , где полученное значение принимает M 1 H 1 .
Применим данные методы на решении задач с нахождением расстояния от точки до плоскости.
Пример 1
Найти расстояние от точки с координатами M 1 (- 1 , 2) к прямой 4 x — 3 y + 35 = 0 .
Решение
Применим первый способ для решения.
Для этого необходимо найти общее уравнение прямой b , которая проходит через заданную точку M 1 (- 1 , 2) , перпендикулярно прямой 4 x — 3 y + 35 = 0 . Из условия видно, что прямая b является перпендикулярной прямой a , тогда ее направляющий вектор имеет координаты, равные (4 , — 3) . Таким образом имеем возможность записать каноническое уравнение прямой b на плоскости, так как имеются координаты точки М 1 , принадлежит прямой b . Определим координаты направляющего вектора прямой b . Получим, что x — (- 1) 4 = y — 2 — 3 ⇔ x + 1 4 = y — 2 — 3 . Полученное каноническое уравнение необходимо преобразовать к общему. Тогда получаем, что
Определим координаты направляющего вектора прямой b . Получим, что x — (- 1) 4 = y — 2 — 3 ⇔ x + 1 4 = y — 2 — 3 . Полученное каноническое уравнение необходимо преобразовать к общему. Тогда получаем, что
x + 1 4 = y — 2 — 3 ⇔ — 3 · (x + 1) = 4 · (y — 2) ⇔ 3 x + 4 y — 5 = 0
Произведем нахождение координат точек пересечения прямых, которое примем за обозначение Н 1 . Преобразования выглядят таким образом:
4 x — 3 y + 35 = 0 3 x + 4 y — 5 = 0 ⇔ x = 3 4 y — 35 4 3 x + 4 y — 5 = 0 ⇔ x = 3 4 y — 35 4 3 · 3 4 y — 35 4 + 4 y — 5 = 0 ⇔ ⇔ x = 3 4 y — 35 4 y = 5 ⇔ x = 3 4 · 5 — 35 4 y = 5 ⇔ x = — 5 y = 5
Из выше написанного имеем, что координаты точки Н 1 равны (- 5 ; 5) .
Необходимо вычислить расстояние от точки М 1 к прямой a . Имеем, что координаты точек M 1 (- 1 , 2) и H 1 (- 5 , 5) , тогда подставляем в формулу для нахождения расстояния и получаем, что
M 1 H 1 = (- 5 — (- 1) 2 + (5 — 2) 2 = 25 = 5
Второй способ решения.
Для того, чтобы решить другим способом, необходимо получить нормальное уравнение прямой. Вычисляем значение нормирующего множителя и умножаем обе части уравнения 4 x — 3 y + 35 = 0 . Отсюда получим, что нормирующий множитель равен — 1 4 2 + (- 3) 2 = — 1 5 , а нормальное уравнение будет вида — 1 5 · 4 x — 3 y + 35 = — 1 5 · 0 ⇔ — 4 5 x + 3 5 y — 7 = 0 .
Вычисляем значение нормирующего множителя и умножаем обе части уравнения 4 x — 3 y + 35 = 0 . Отсюда получим, что нормирующий множитель равен — 1 4 2 + (- 3) 2 = — 1 5 , а нормальное уравнение будет вида — 1 5 · 4 x — 3 y + 35 = — 1 5 · 0 ⇔ — 4 5 x + 3 5 y — 7 = 0 .
По алгоритму вычисления необходимо получить нормальное уравнение прямой и вычислить его со значениями x = — 1 , y = 2 . Тогда получаем, что
4 5 · — 1 + 3 5 · 2 — 7 = — 5
Отсюда получаем, что расстояние от точки M 1 (- 1 , 2) к заданной прямой 4 x — 3 y + 35 = 0 имеет значение — 5 = 5 .
Ответ: 5 .
Видно, что в данном методе важно использование нормального уравнения прямой, так как такой способ является наиболее коротким. Но первый метод удобен тем, что последователен и логичен, хотя имеет больше пунктов вычисления.
Пример 2
На плоскости имеется прямоугольная система координат О х у с точкой M 1 (8 , 0) и прямой y = 1 2 x + 1 . Найти расстояние от заданной точки до прямой.
Решение
Решение первым способом подразумевает приведение заданного уравнения с угловым коэффициентом к уравнению общего вида. Для упрощения можно сделать иначе.
Если произведение угловых коэффициентов перпендикулярных прямых имеют значение — 1 , значит угловой коэффициент прямой перпендикулярной заданной y = 1 2 x + 1 имеет значение 2 . Теперь получим уравнение прямой, проходящее через точку с координатами M 1 (8 , 0) . Имеем, что y — 0 = — 2 · (x — 8) ⇔ y = — 2 x + 16 .
Переходим к нахождению координат точки Н 1 , то есть точкам пересечения y = — 2 x + 16 и y = 1 2 x + 1 . Составляем систему уравнений и получаем:
y = 1 2 x + 1 y = — 2 x + 16 ⇔ y = 1 2 x + 1 1 2 x + 1 = — 2 x + 16 ⇔ y = 1 2 x + 1 x = 6 ⇔ ⇔ y = 1 2 · 6 + 1 x = 6 = y = 4 x = 6 ⇒ H 1 (6 , 4)
Отсюда следует, что расстояние от точки с координатами M 1 (8 , 0) к прямой y = 1 2 x + 1 равно расстоянию от точки начала и точки конца с координатами M 1 (8 , 0) и H 1 (6 , 4) . Вычислим и получим, что M 1 H 1 = 6 — 8 2 + (4 — 0) 2 20 = 2 5 .
Вычислим и получим, что M 1 H 1 = 6 — 8 2 + (4 — 0) 2 20 = 2 5 .
Решение вторым способом заключается в переходе от уравнения с коэффициентом к нормальному его виду. То есть получим y = 1 2 x + 1 ⇔ 1 2 x — y + 1 = 0 , тогда значение нормирующего множителя будет — 1 1 2 2 + (- 1) 2 = — 2 5 . Отсюда следует, что нормальное уравнение прямой принимает вид — 2 5 · 1 2 x — y + 1 = — 2 5 · 0 ⇔ — 1 5 x + 2 5 y — 2 5 = 0 . Произведем вычисление от точки M 1 8 , 0 к прямой вида — 1 5 x + 2 5 y — 2 5 = 0 . Получаем:
M 1 H 1 = — 1 5 · 8 + 2 5 · 0 — 2 5 = — 10 5 = 2 5
Ответ: 2 5 .
Пример 3
Необходимо вычислить расстояние от точки с координатами M 1 (- 2 , 4) к прямым 2 x — 3 = 0 и y + 1 = 0 .
Решение
Получаем уравнение нормального вида прямой 2 x — 3 = 0:
2 x — 3 = 0 ⇔ 1 2 · 2 x — 3 = 1 2 · 0 ⇔ x — 3 2 = 0
После чего переходим к вычислению расстояния от точки M 1 — 2 , 4 к прямой x — 3 2 = 0 . Получаем:
M 1 H 1 = — 2 — 3 2 = 3 1 2
Уравнение прямой y + 1 = 0 имеет нормирующий множитель со значением равным -1. Это означает, что уравнение примет вид — y — 1 = 0 . Переходим к вычислению расстояния от точки M 1 (- 2 , 4) к прямой — y — 1 = 0 . Получим, что оно равняется — 4 — 1 = 5 .
Это означает, что уравнение примет вид — y — 1 = 0 . Переходим к вычислению расстояния от точки M 1 (- 2 , 4) к прямой — y — 1 = 0 . Получим, что оно равняется — 4 — 1 = 5 .
Ответ: 3 1 2 и 5 .
Подробно рассмотрим нахождение расстояния от заданной точки плоскости к координатным осям О х и О у.
В прямоугольной системе координат у оси О у имеется уравнение прямой, которое является неполным имеет вида х = 0 , а О х — y = 0 . Уравнения являются нормальными для осей координат, тогда необходимо найти расстояние от точки с координатами M 1 x 1 , y 1 до прямых. Это производится, исходя из формул M 1 H 1 = x 1 и M 1 H 1 = y 1 . Рассмотрим на рисунке, приведенном ниже.
Пример 4
Найти расстояние от точки M 1 (6 , — 7) до координатных прямых, расположенных в плоскости О х у.
Решение
Так как уравнение у = 0 относится к прямой О х, можно найти расстояние от M 1 с заданными координатами, до этой прямой, используя формулу. Получаем, что 6 = 6 .
Так как уравнение х = 0 относится к прямой О у, то можно найти расстояние от М 1 к этой прямой по формуле. Тогда получим, что — 7 = 7 .
Ответ: расстояние от М 1 к О х имеет значение 6 , а от М 1 к О у имеет значение 7 .
Когда в трехмерном пространстве имеем точку с координатами M 1 (x 1 , y 1 , z 1) , необходимо найти расстояние от точки A до прямой a .
Рассмотрим два способа, которые позволяют производить вычисление расстояние от точки до прямой a , расположенной в пространстве. Первый случай рассматривает расстояние от точки М 1 к прямой, где точка на прямой называется Н 1 и является основанием перпендикуляра, проведенного из точки М 1 на прямую a . Второй случай говорит о том, что точки этой плоскости необходимо искать в качестве высоты параллелограмма.
Первый способ
Из определения имеем, что расстояние от точки М 1 , расположенной на прямой а, является длиной перпендикуляра М 1 Н 1 , тогда получим, что при найденных координатах точки Н 1 , тогда найдем расстояние между M 1 (x 1 , y 1 , z 1) и H 1 (x 1 , y 1 , z 1) , исходя из формулы M 1 H 1 = x 2 — x 1 2 + y 2 — y 1 2 + z 2 — z 1 2 .
Получаем, что все решение идет к тому, чтобы найти координаты основания перпендикуляра, проведенного из М 1 на прямую a . Это производится следующим образом: Н 1 является точкой, где пересекаются прямая a с плоскостью, которая проходит через заданную точку.
Значит, алгоритм определения расстояния от точки M 1 (x 1 , y 1 , z 1) к прямой a пространства подразумевает несколько пунктов:
Определение 5
- составление уравнение плоскости χ в качестве уравнения плоскости, проходящего через заданную точку, находящуюся перпендикулярно прямой;
- определение координат (x 2 , y 2 , z 2) , принадлежавших точке Н 1 , которая является точкой пересечения прямой a и плоскости χ ;
- вычисление расстояния от точки до прямой при помощи формулы M 1 H 1 = x 2 — x 1 2 + y 2 — y 1 2 + z 2 — z 1 2 .
Второй способ
Из условия имеем прямую a , тогда можем определить направляющий вектор a → = a x , a y , a z с координатами x 3 , y 3 , z 3 и определенной точки М 3 , принадлежащей прямой a . При наличии координат точек M 1 (x 1 , y 1) и M 3 x 3 , y 3 , z 3 можно произвести вычисление M 3 M 1 → :
При наличии координат точек M 1 (x 1 , y 1) и M 3 x 3 , y 3 , z 3 можно произвести вычисление M 3 M 1 → :
M 3 M 1 → = (x 1 — x 3 , y 1 — y 3 , z 1 — z 3)
Следует отложить векторы a → = a x , a y , a z и M 3 M 1 → = x 1 — x 3 , y 1 — y 3 , z 1 — z 3 из точки М 3 , соединим и получим фигуру параллелограмма. М 1 Н 1 является высотой параллелограмма.
Рассмотрим на рисунке, приведенном ниже.
Имеем, что высота М 1 Н 1 является искомым расстоянием, тогда необходимо найти его по формуле. То есть ищем M 1 H 1 .
Обозначим площадь параллелограмма за букву S , находится по формуле, используя вектор a → = (a x , a y , a z) и M 3 M 1 → = x 1 — x 3 . y 1 — y 3 , z 1 — z 3 . Формула площади имеет вид S = a → × M 3 M 1 → . Также площадь фигуры равняется произведению длин его сторон на высоту, получим, что S = a → · M 1 H 1 с a → = a x 2 + a y 2 + a z 2 , являющимся длиной вектора a → = (a x , a y , a z) , являющейся равной стороне параллелограмма. Значит, M 1 H 1 является расстоянием от точки до прямой. Ее нахождение производится по формуле M 1 H 1 = a → × M 3 M 1 → a → .
Ее нахождение производится по формуле M 1 H 1 = a → × M 3 M 1 → a → .
Для нахождения расстояния от точки с координатами M 1 (x 1 , y 1 , z 1) до прямой a в пространстве, необходимо выполнить несколько пунктов алгоритма:
Определение 6
- определение направляющего вектора прямой a — a → = (a x , a y , a z) ;
- вычисление длины направляющего вектора a → = a x 2 + a y 2 + a z 2 ;
- получение координат x 3 , y 3 , z 3 , принадлежавших точке М 3 , находящейся на прямой а;
- вычисление координат вектора M 3 M 1 → ;
- нахождение векторного произведения векторов a → (a x , a y , a z) и M 3 M 1 → = x 1 — x 3 , y 1 — y 3 , z 1 — z 3 в качестве a → × M 3 M 1 → = i → j → k → a x a y a z x 1 — x 3 y 1 — y 3 z 1 — z 3 для получения длины по формуле a → × M 3 M 1 → ;
- вычисление расстояния от точки до прямой M 1 H 1 = a → × M 3 M 1 → a → .
Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве
Пример 5Найти расстояние от точки с координатами M 1 2 , — 4 , — 1 к прямой x + 1 2 = y — 1 = z + 5 5 .
Решение
Первый способ начинается с записи уравнения плоскости χ , проходящей через М 1 и перпендикулярно заданной точке. Получаем выражение вида:
2 · (x — 2) — 1 · (y — (- 4)) + 5 · (z — (- 1)) = 0 ⇔ 2 x — y + 5 z — 3 = 0
Нужно найти координаты точки H 1 , являющейся точкой пересечения с плоскостью χ к заданной по условию прямой. Следует переходить от канонического вида к пересекающемуся. Тогла получаем систему уравнений вида:
x + 1 2 = y — 1 = z + 5 5 ⇔ — 1 · (x + 1) = 2 · y 5 · (x + 1) = 2 · (z + 5) 5 · y = — 1 · (z + 5) ⇔ x + 2 y + 1 = 0 5 x — 2 z — 5 = 0 5 y + z + 5 = 0 ⇔ x + 2 y + 1 = 0 5 x — 2 z — 5 = 0
Необходимо вычислить систему x + 2 y + 1 = 0 5 x — 2 z — 5 = 0 2 x — y + 5 z — 3 = 0 ⇔ x + 2 y = — 1 5 x — 2 z = 5 2 x — y + 5 z = 3 по методу Крамера, тогда получаем, что:
∆ = 1 2 0 5 0 — 2 2 — 1 5 = — 60 ∆ x = — 1 2 0 5 0 — 2 3 — 1 5 = — 60 ⇔ x = ∆ x ∆ = — 60 — 60 = 1 ∆ y = 1 — 1 0 5 5 2 2 3 5 = 60 ⇒ y = ∆ y ∆ = 60 — 60 = — 1 ∆ z = 1 2 — 1 5 0 5 2 — 1 3 = 0 ⇒ z = ∆ z ∆ = 0 — 60 = 0
Отсюда имеем, что H 1 (1 , — 1 , 0) .
M 1 H 1 = 1 — 2 2 + — 1 — — 4 2 + 0 — — 1 2 = 11
Второй способ необходимо начать с поиска координат в каноническом уравнении. Для этого необходимо обратит внимание на знаменатели дроби. Тогда a → = 2 , — 1 , 5 является направляющим вектором прямой x + 1 2 = y — 1 = z + 5 5 . Необходимо вычислить длину по формуле a → = 2 2 + (- 1) 2 + 5 2 = 30 .
Понятно, что прямая x + 1 2 = y — 1 = z + 5 5 пересекает точку M 3 (- 1 , 0 , — 5) , отсюда имеем, что вектор с началом координат M 3 (- 1 , 0 , — 5) и его концом в точке M 1 2 , — 4 , — 1 является M 3 M 1 → = 3 , — 4 , 4 . Находим векторное произведение a → = (2 , — 1 , 5) и M 3 M 1 → = (3 , — 4 , 4) .
Мы получаем выражение вида a → × M 3 M 1 → = i → j → k → 2 — 1 5 3 — 4 4 = — 4 · i → + 15 · j → — 8 · k → + 20 · i → — 8 · j → = 16 · i → + 7 · j → — 5 · k →
получаем, что длина векторного произведения равняется a → × M 3 M 1 → = 16 2 + 7 2 + — 5 2 = 330 .
Имеются все данные для использования формулы вычисления расстояния от точки для прямлой, поэтому применим ее и получим:
M 1 H 1 = a → × M 3 M 1 → a → = 330 30 = 11
Ответ: 11 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Для вычисления расстояния от данной точки M до прямой L можно использовать разные способы. Например, если на прямой L взять произвольную точку M 0 , то можно определить ортогональную проекцию вектора M 0 M на направление нормального вектора прямой. Эта проекция с точностью до знака и есть нужное расстояние.
Другой способ вычисления расстояния от точки до прямой основан на использовании нормального уравнения прямой . Пусть прямая L задана нормальным уравнением (4.23). Если точка M(x; у) не лежит на прямой L, то ортогональная проекция пр n OM радиус-вектора точки M на направление единичного нормального вектора n прямой L равна скалярному произведению векторов OM
и n, т.е. x cosφ + у sinφ. Эта же проекция равна сумме расстояния p от начала координат до прямой и некоторой величины δ (рис. 4.10). Величина δ по абсолютной величине равна расстоянию от точки М до прямой. При этом δ > 0, если точки М и O находятся по разные стороны от прямой, и δ отклонением точки М от прямой.
При этом δ > 0, если точки М и O находятся по разные стороны от прямой, и δ отклонением точки М от прямой.
Отклонение δ для точки M(x; у) от прямой L вычисляется как разность проекции пр n OM и расстояния p от начала координат до прямой (см. рис. 4.10), т.е. δ = x cosφ + у sinφ — p.
По этой формуле можно получить и расстояние p(M, L) от точки M(x; у) до прямой L, заданной нормальным уравнением: p(M, L) = |δ | = |x cosφ + у sinφ — p|.
2 Два смежныхугла в сумме дают 180°
Учитывая приведенную выше процедуру преобразования общего уравнения прямой в ее нормальное уравнение, получаем формулу для расстояния от точки M(х; у) до прямой L, заданной своим общим уравнением:
Пример 4.8. Найдем общие уравнения высоты AH, медианы AM и биссектрисы AD треугольника ABC, выходящих из вершины A. Известны координаты вершин треугольника А(-1;- 3), B(7; 3), C(1;7).
Прежде всего уточним условие примера: под указанными уравнениями подразумевают уравнения прямых L AH , L AM и L AD , на которых расположены соответственно высота АН, медиана AM и биссектриса AD указанного треугольника (рис. 4.11).
4.11).
Чтобы найти уравнение прямой L AM , воспользуемся тем, что медиана делит противоположную сторону треугольника пополам. Найдя координаты (x 1 ; y 1) середины стороны BC x 1 = (7 + 1)/2 = 4, у 1 = (3 + 7)/2 = 5, записываем уравнение для L AM в виде уравнения прямой, проходящей через две точки, (x + 1)/(4 + 1) = (y + 3)/(5 + 3). После преобразований получаем общее уравнение медианы 8х — 5у — 7 = 0./p>
Чтобы найти уравнение высоты L AH , воспользуемся тем, что высота перпендикулярна про-тивоположной стороне треугольника. Следовательно, вектор BC перпендикулярен высоте AH и его можно выбрать в качестве нормального вектора прямой L AH . Уравнение этой прямой получаем из (4.15), подставляя координаты точки A и нормального вектора прямой L AH:
(-6)(х + 1) + 4(у + 3) = 0.
После преобразований получаем общее уравнение высоты 3x — 2у — 3 = 0.
Чтобы найти уравнение биссектрисы L AD , воспользуемся тем, что биссектриса AD принадлежит множеству тех точек N(х; у), которые равноудалены от прямых L AB и L AC . Уравнение этого множества имеет вид
Уравнение этого множества имеет вид
P(N, L AB) = P(N, L AC), (4.28)
и оно задает две прямые, проходящие через точку A и делящие углы между прямыми L AB и L AC пополам. Воспользовавшись уравнением прямой, проходящей через две точки, найдем общие уравнения прямых L AB и L AC:
L AB: (x + 1)/(7 + 1) = (y + 3)/(3 + 3), L AC: (x + 1)/(1 + 1) = (y + 3)/(7 + 3)
После преобразований получаем L AB: 3х — 4у — 9 = 0, L AC: 5х — у + 2 = 0. Уравнение (4.28) с помощью формулы (4.27) для вычисления расстояния от точки до прямой запишем в виде
Преобразуем его, раскрыв модули:
В итоге получим общие уравнения двух прямых
(3 ± 25/√26)x + (-4 ± 5/√26)y + (-9 ± 10/√26) = 0
Чтобы выбрать из них уравнение биссектрисы, учтем, что вершины B и C треугольника расположены по разные стороны от искомой прямой и поэтому подстановки их координат в левую часть общего уравнения прямой L AD должны давать значения с разными знаками. Выбираем уравнение, соответствующее верхнему знаку, т. е.
е.
(3 — 25/√26)x + (-4 + 5/√26)y + (-9 — 10/√26) = 0
Подстановка координат точки B в левую часть этого уравнения дает отрицательное значение, поскольку
(3 — 25/√26)7 + (-4 + 5/√26)3 + (-9 — 10/√26) = 21 — 12 — 9 + (-175 + 15 — 10)/√26 = -170/√26
и такой же знак получается для координат точки C, так как
(3 — 25/√26)1 + (-4 + 5/√26)7 + (-9 — 10/√26) = 3 — 28 — 9 + (-25 + 35 — 10)/√26 = -34
Следовательно, вершины B и C расположены по одну сторону прямой с выбранным уравнением, а потому уравнением биссектрисы является
(3 + 25/√26)х + (-4 — 5/√26)у + (-9 + 10/√26) = 0.
Расстояние от точки до плоскости
Вопросы занятия:
· расстояние от точки до плоскости;
· расстояние между параллельными плоскостями;
· расстояние между прямой и параллельной ей плоскостью;
·
расстояние
между скрещивающимися прямыми.
Материал урока.
Вы уже знаете, что расстоянием от точки до прямой называют длину перпендикуляра проведённого из данной точки к данной прямой. Ведь длина этого перпендикуляра наименьшая среди длин всевозможных отрезков, проведённых из данной точки к данной прямой.
Рассмотрим случай точки и плоскости.
Понятно, что если точка лежит в плоскости, то расстояние между ними равно нулю. Что же на счет случая, когда точка не лежит в плоскости?
Итак, точку с плоскостью можно соединить различными способами. Но среди всех возможных проведённых отрезков можно выделить один особенный. Тот, который перпендикулярен к данной плоскости.
Давайте рассмотрим отрезок перпендикулярный к плоскости и любой из оставшихся.
Если соединить точки пересечения данных отрезков с плоскостью, то тем самым получим треугольник, причём он будет являться прямоугольным.
Действительно,
если прямая перпендикулярна к плоскости, то она перпендикулярна к любой прямой
из этой плоскости.
Введём несколько новых понятий.
Запомните, отрезок AH называют перпендикуляром, проведённым из точки А к плоскости α, а точку H — основанием перпендикуляра.
Отрезок AM называю наклонной к плоскости, а точку M — основанием наклонной.
Отрезок HM называют проекцией наклонной на плоскость α.
Понятно, что гипотенуза всегда длиннее любого из катетов. Тогда можем сделать вывод, что перпендикуляр, проведённый из данной точки к плоскости, меньше любой наклонной, проведённой из той же точки к этой плоскости.
Тем самым можно утверждать, что расстоянием от точки А до плоскости α является длина перпендикуляра, проведённого из точки А к плоскости α.
Основываясь на этом определении, получим несколько замечаний. Первым рассмотрим расстояние между параллельными плоскостями.
Рассмотрим
параллельные плоскости α и β. В плоскости α отметим две
произвольные точки А и B.
И проведём перпендикуляры из этих точек к плоскости β.
В плоскости α отметим две
произвольные точки А и B.
И проведём перпендикуляры из этих точек к плоскости β.
Мы получили отрезки AA1 и BB1. Каждый из них перпендикулярен плоскости β, а значит, АА1 параллельно BB1.
Вам уже известно, что отрезки параллельных прямых, заключенных между параллельными плоскостями, равны.
Можно сказать, что если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости.
Запишем замечание. Расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называется расстоянием между параллельными плоскостями.
Хорошим примером может служить расстояние между плоскостями пола и потолка комнаты. Все точки потолка находятся на одинаковом расстоянии от пола, это расстояние и является высотой комнаты.
Рассмотрим
следующий случай, расстояние между прямой и параллельной ей плоскостью.
В данном случае на прямой нужно выбрать некоторую точку и провести перпендикуляр к плоскости. Ведь понятно, что все точки прямой равноудалены от данной плоскости.
Таким образом, можем записать, что расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.
Нам осталось рассмотреть две скрещивающиеся прямые. Ранее уже было доказано, что через одну из скрещивающихся прямых можно провести плоскость параллельную другой прямой и притом только одну. А определение расстояния между прямой и плоскостью нам уже известно.
Тогда можно сказать, что расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.
Решим несколько задач.
Доказательство.
Что
и требовалось доказать.
Решим ещё одну задачу.
Задача. перпендикуляр к плоскости, наклонные к плоскости . , см.
Найти расстояние между основаниями наклонных.
Решение.
Ответ. 3 см.
Подведём итоги нашего урока.
Сегодня мы ввели такие понятия, как «перпендикуляр к плоскости», «наклонная к плоскости», «основание перпендикуляра» и «основание наклонной», а также «проекция наклонной на плоскость».
В ходе решения задач мы доказали, что: если наклонные равны, то равны и их проекции; если проекции наклонных равны, то равны и наклонные; если наклонные не равны, то большая наклонная имеет большую проекцию.
Также мы сформулировали определение понятия расстояния от точки до плоскости.
Расстоянием от точки А до плоскости α является длина перпендикуляра, проведённого из точки А к плоскости α.
Опираясь
на это определение, мы сделали следующие замечания.
Расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называется расстоянием между параллельными плоскостями.
Расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.
Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.
Все определения и утверждения, с которыми вы познакомились на этом уроке, очень пригодятся в дальнейшем изучении стереометрии.
Нахождение расстояния от точки до плоскости. 11-й класс
Цели:
- обобщение и систематизация знаний и умений учащихся;
- развитие умений анализировать, сравнивать, делать выводы.
Оборудование:
- мультимедийный проектор;
- компьютер;
- листы с текстами задач
ХОД ЗАНЯТИЯ
I. Организационный момент
Организационный момент
II. Этап актуализации знаний (слайд 2)
Повторяем как определяется расстояние от точки до плоскости
III. Лекция (cлайды 3-15)
На занятии мы рассмотрим различные способы нахождения расстояния от точки до плоскости.
Первый метод: поэтапно-вычислительный
Расстояние от точки М до плоскости α:
– равно расстоянию до плоскости α от
произвольной точки Р, лежащей на прямой a,
которая проходит через точку М и параллельна
плоскости α;
– равно расстоянию до плоскости α от
произвольной точки Р, лежащей на плоскости β,
которая проходит через точку М и параллельна
плоскости α.
Решим следующие задачи:
№1. В кубе А…D1 найти расстояние от точки С1 до плоскости АВ1С.
Решение.
Осталось вычислить значение длины отрезка О1Н.
№2. В правильной шестиугольной призме А…F1, все ребра которой равны 1, найдите расстояние от точки А до плоскости DEA1.
Решение:
Следующий метод: метод объемов.
Если объем пирамиды АВСМ равен V, то
расстояние от точки М до плоскости α, содержащей ∆АВС вычисляется по формуле ρ(М; α) = ρ(М; АВС) =
При решении задач мы используем равенство
объемов одной фигуры, выраженные двумя
различными способами.
Решим следующую задачу:
№3. Ребро AD пирамиды DABC перпендикулярно плоскости основания АВС. Найдите расстояние от А до плоскости, проходящей через середины ребер АВ, АС и АD, если .
Ответ: 2
При решении задач координатным методом расстояние от точки М до плоскости α можно вычислить по формуле ρ(М; α) = , где М(х0; у0; z0), а плоскость задана уравнением ax + by + cz + d = 0
Решим следующую задачу:
№4. В единичном кубе A…D1 найдите
расстояние от точки А1 до плоскости ВDC1.
В единичном кубе A…D1 найдите
расстояние от точки А1 до плоскости ВDC1.
Решение.
Введем систему координат с началом в точке А ,
ось у пройдет по ребру АВ, ось х – по ребру АD, ось z
– по ребру АА1. Тогда координаты точек В
(0; 1; 0) D (1; 0; 0;) C1(1; 1; 1)
Составим уравнение плоскости, проходящей через
точки В, D, C1.
Тогда – dx – dy + dz + d = 0 x + y – z – 1= 0. Следовательно, ρ =
Ответ:
Следующий метод, который можно использовать при решении задач данного типа – метод опорных задач.
Применение данного метода состоит в применении известных опорных задач, которые формулируются как теоремы.
Решим следующую задачу:
№5. В единичном кубе А…D1
найдите расстояние от точки D1 до
плоскости АВ1С.
Рассмотрим применение векторного метода.
№6. В единичном кубе А…D1 найдите расстояние от точки А1 до плоскости ВDС1.
Итак, мы рассмотрели различные способы, которые можно использовать при решении данного типа задач. Выбор того или иного метода зависит от конкретной задачи и ваших предпочтений.
IV. Работа в группах
Попробуйте решить задачу разными способами.
№1. Ребро куба А…D1 равно . Найдите расстояние от вершины С до плоскости BDC1.
№2. В правильном тетраэдре АВСD с ребром найдите расстояние от точки А до плоскости BDC
№3. В правильной треугольной призме
АВСА1В1С1 все ребра которой
равны 1, найдите расстояние от А до плоскости
ВСА1.
№4. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от А до плоскости SCD.
V. Итог урока, домашнее задание, рефлексия
Расстояние между точкой и плоскостью
Расстояние между точкой и плоскостью — это длина перпендикуляра к плоскости, проходящего через данную точку. Другими словами, мы можем сказать, что расстояние между точкой и плоскостью — это длина вектора нормали, опущенного из данной точки на данную плоскость. Если мы хотим определить расстояние между точкой P с координатами (x o , y o , z o ) и данной плоскостью уравнением Ax + By + Cz = D, то расстояние между точкой P и данная плоскость задается формулой |Ax o + By o + Cz o + D|/√(A 2 + B 2 + C 2 ).
Что такое расстояние между точкой и плоскостью?
Расстояние между точкой и плоскостью — это кратчайшее перпендикулярное расстояние от точки до данной плоскости. Проще говоря, кратчайшее расстояние от точки до плоскости — это длина перпендикуляра, параллельного вектору нормали, опущенного из данной точки на данную плоскость. Давайте теперь посмотрим формулу для расстояния между точкой и плоскостью.
Проще говоря, кратчайшее расстояние от точки до плоскости — это длина перпендикуляра, параллельного вектору нормали, опущенного из данной точки на данную плоскость. Давайте теперь посмотрим формулу для расстояния между точкой и плоскостью.
Формула расстояния между точкой и плоскостью
Кратчайшее расстояние между точкой и плоскостью равно длине вектора нормали, который начинается в данной точке и касается плоскости.Рассмотрим точку P с координатами (x o , y o , z o ) и данную плоскость π с уравнением Ax + By + Cz = D. Тогда расстояние между точкой P и плоскостью π равно определяется выражением |Ax o + By o + Cz o + D|/√(A 2 + B 2 + C 2 ).
Расстояние между точкой и плоскостью Доказательство
Теперь, когда мы знаем формулу расстояния между точкой и плоскостью, выведем ее формулу, используя различные формулы трехмерной геометрии. Рассмотрим точку P с координатами (x o , y o , z o ) в трехмерном пространстве и плоскость с вектором нормали, скажем, v = (A, B, C) и точку Q с координатами (x 1 , y 1 , z 1 ) на плоскости. Тогда уравнение плоскости задается как A(x — x 1 ) + B(y — y 1 ) + C(z — z 1 ) = 0. Это уравнение можно переписать как Ax + By + Cz + (- Ax 1 — By 1 — Cz 1 ) = 0 ⇒ Ax + By + Cz + D = 0, где D = — (Ax 1 + By 1 + Cz 1 ).Отсюда имеем:
Рассмотрим точку P с координатами (x o , y o , z o ) в трехмерном пространстве и плоскость с вектором нормали, скажем, v = (A, B, C) и точку Q с координатами (x 1 , y 1 , z 1 ) на плоскости. Тогда уравнение плоскости задается как A(x — x 1 ) + B(y — y 1 ) + C(z — z 1 ) = 0. Это уравнение можно переписать как Ax + By + Cz + (- Ax 1 — By 1 — Cz 1 ) = 0 ⇒ Ax + By + Cz + D = 0, где D = — (Ax 1 + By 1 + Cz 1 ).Отсюда имеем:
- Уравнение плоскости: Ax + By + Cz + D = 0
- Точка P: (x o , y o , z o )
- Нормальный вектор: Ai + Bj + Ck
Пусть w вектор, соединяющий точки P(x o , y o , z o ) и Q(x 1 , y 1 , z 1 ). Тогда w = (x o — x 1 , y o — y 1 , z o — z 1 ). Теперь давайте вычислим единичный вектор нормали, т. Е. Вектор нормали с величиной, равной 1, который определяется делением вектора нормали v на его величину. Единичный вектор нормали определяется выражением
Теперь давайте вычислим единичный вектор нормали, т. Е. Вектор нормали с величиной, равной 1, который определяется делением вектора нормали v на его величину. Единичный вектор нормали определяется выражением
n = v/||v||
= (А, В, С)/√(А 2 + В 2 + С 2 )
Теперь расстояние между точкой P и данной плоскостью есть не что иное, как длина проекции вектора w на единичный вектор нормали n. Как известно, длина вектора n равна единице, расстояние от точки P до плоскости есть модуль скалярного произведения векторов w и n, т.е.д.,
Расстояние, d = |w.n|
= | (х o — х 1 , у o — у 1 , z o — z 1 ). [(A, B, C)/√(A 2 + B 2 + C 2 )] |
= |A(x o — x 1 ) + B(y o — y 1 ) + C(z o — z 1 )|/√1(708 + 90 90 В 2 + С 2 )
= | AX O + к O + CZ O — (AX 1 + на 1 + CZ 1 ) | / √ (A 2 + B 2 + C 2 )
= | Ax o + By o + Cz o + D |/√(A 2 + B 2 + C 2 ) [Поскольку D = — (Ax 90 6 90 0 60 1 90 + Cz 1 )]
Так как точка Q с координатами (x 1 , y 1 , z 1 ) является произвольной точкой на данной плоскости и D = — (Ax 1 + By 1 + Cz 6 1
5 ), поэтому формула остается неизменной для любой точки Q на плоскости и, следовательно, не зависит от точки Q, т.
 е.т. е. везде, где точка Q лежит на плоскости, формула для расстояния между точкой и плоскостью остается той же. Следовательно, расстояние между точкой P(x o , y o , z o ) и плоскостью π: Ax + By + Cz + D = 0 определяется выражением, d = |Ax o + By о + Cz о + D |/√(A 2 + B 2 + C 2 )
е.т. е. везде, где точка Q лежит на плоскости, формула для расстояния между точкой и плоскостью остается той же. Следовательно, расстояние между точкой P(x o , y o , z o ) и плоскостью π: Ax + By + Cz + D = 0 определяется выражением, d = |Ax o + By о + Cz о + D |/√(A 2 + B 2 + C 2 )Как применить формулу расстояния от точки до плоскости?
Мы вывели формулу расстояния от точки до плоскости, решим пример с помощью формулы, чтобы понять ее применение и определить расстояние между точкой и плоскостью.
Пример: Определить расстояние между точкой P = (1, 2, 5) и плоскостью π: 3x + 4y + z + 7 = 0
Решение: Мы знаем, что формула для расстояния между точкой и плоскостью: + С 2 )
Здесь, A = 3, B = 4, C = 1, D = 7, x o = 1, y o = 2, z o = 5
Подставляя значения в формулу, имеем
d = |Ax o + By o + Cz o + D |/√(A 2 + B 2 + C 2 )
= |3 × 1 + 4 × 2 + 1 × 5 + 7|/√(3 2 + 4 2 + 1 2 )
= |3 + 8 + 5|/√(9 + 16 + 1)
= |16|/√26
= 8√26/13 единиц
Важные замечания по расстоянию между точкой и плоскостью
- Расстояние между точкой и плоскостью Формула: |Ax o + By o + Cz o + D |/√(A 2 + B 2 + C 2 )
- Расстояние между точкой и плоскостью равно нулю, если данная точка лежит на данной плоскости.

Темы, связанные с расстоянием между точкой и плоскостью
Часто задаваемые вопросы о расстоянии между точкой и плоскостью
Что такое расстояние между точкой и плоскостью в геометрии?
Расстояние между точкой и плоскостью — это длина перпендикуляра к плоскости, проходящего через данную точку. Другими словами, расстояние между точкой и плоскостью есть кратчайшее перпендикулярное расстояние от точки до данной плоскости.
Какая формула для расстояния между точкой и плоскостью?
Расстояние между точкой P(x o , y o , z o ) и плоскостью π: Ax + By + Cz + D = 0 определяется выражением, d = |Ax o + By o + Cz или + D |/√(A 2 + B 2 + C 2 )
Как найти кратчайшее расстояние между точкой и плоскостью?
Чтобы найти кратчайшее расстояние между точкой и плоскостью, мы используем формулу d = |Ax o + By o + Cz o + D |/√(A 2 + B 2 + C 2 ), где (x o , y o , z o ) — заданная точка, Ax + By + Cz + D = 0 — уравнение данной плоскости.
Каково расстояние между точкой и плоскостью x-z?
Расстояние между точкой (x o , y o , z o ) и плоскостью x-z определяется координатой y, т. е. y o
Как найти кратчайшее расстояние от точки до плоскости?
Чтобы вычислить кратчайшее расстояние от точки до плоскости, мы рассматриваем длину вектора, параллельного вектору нормали к плоскости, которая опускается из данной точки на данную плоскость.
Каково расстояние между точкой и плоскостью, когда точка лежит на данной плоскости?
Расстояние между точкой и плоскостью равно нулю, если данная точка лежит на данной плоскости.
Расстояние между плоскостью и точкой
Иногда бывает важно найти расстояние $D$ между некоторой точкой $P_0$ и плоскостью в виде $ax + by + cz + d = 0$. Формула расстояния между плоскостью $\Pi: ax + by + cz + d = 0$ и точкой $P(x_0, y_0, z_0)$ выглядит следующим образом:
(1)\begin{align} D = \frac{\mid ax_0 + by_0 + cz_0 + d \mid}{\sqrt{a^2 + b^2 + c^2}} \end{align}
Теперь мы приступим к доказательству этой формулы. 2}}$.
2}}$.
- Доказательство: Пусть $Q(x_1, y_1, z_1)$ — любая точка на плоскости $\Pi$, а $P_0 = (x_0, y_0, z_0)$ — наша точка интереса. Пусть $\vec{QP_0} = (x_0 — x_1, y_0 — y_1, z_0 — z_1)$. Напомним, что эта плоскость может быть определена с помощью вектора, который перпендикулярен плоскости, известной как нормаль. Пусть $n = (a, b, c)$ — нормаль к нашей плоскости $\Pi$.
- Ортогональная проекция $\vec{QP_0}$ на $\vec{n}$ равна расстоянию между плоскостями $\Pi$ и $P_0$, как показано ниже:
- Отсюда следует, что $D = \| \mathrm{proj}_{\vec{n}} \vec{QP_{0}} \|$.2}} \\ D = \frac{\mid -8 +56 +36 + 5 \mid}{\sqrt{16 + 64 + 9}} \\ D = \frac{\mid 89 \mid}{\sqrt {89}} \\ D = \frac{89}{\sqrt{89}} \end{align}
5.3.1: Расстояние между точкой и плоскостью
Расстояние между определенной точкой и плоскостью важно для ряда различных действий.
Например, вышка для прыжков с тарзанки не была бы очень безопасной, если бы расстояние до земли не измерялось в точке непосредственно под башней, так как любой угол, отклоняющийся от прямой линии вниз, увеличил бы расстояние и привел бы к слишком длинному шнуру.
 !
!Программист компьютерных игр должен знать, как рассчитать расстояние между местоположением персонажа на экране и стенами вокруг него, чтобы сообщить игре, как определить, когда снаряд попадает в цель или когда персонаж попадает в стену.
Определение точки, ближайшей к исходной точке
Независимо от того, какова ориентация плоскости, всегда будет одна точка, расположенная ближе к началу координат, чем любая другая точка на плоскости. Это означает, что вектор положения для этой точки короче, чем для любой другой точки на плоскости. На приведенной ниже диаграмме показана двухмерная проекция плоскости, выделенная серым цветом, рядом с точкой, находящейся не на плоскости, черным цветом. Векторы положения в различные точки показаны на диаграмме.Вектор положения, отмеченный синим цветом, короче, чем векторы положения для других точек. Этот кратчайший вектор перпендикулярен к плоскости. Вы также можете видеть, что синяя линия — это векторная проекция любого оранжевого вектора на перпендикулярное направление.

Эта ортогональность (т. е. перпендикулярность) полезна для нас, поскольку означает, что вектор положения этой особой точки параллелен вектору нормали.Поэтому, если мы знаем уравнение для вектора нормали и вектор положения для любой точки на плоскости, мы можем определить положение точки на плоскости, ближайшей к началу координат, найдя проекцию вектора положения данной точки на нормаль направление.
Двугранный угол
Угол между двумя плоскостями называется двугранным углом . Угол между двумя плоскостями равен углу между их векторами нормали. Если мы хотим определить двугранный угол между двумя плоскостями, мы идентифицируем векторы нормалей к двум плоскостям, тогда мы можем использовать скалярное произведение двух векторов нормалей, чтобы определить угол между двумя нормалями, который также является двумя плоскостями.Напомним \(\ \vec{A} \times \vec{B}=|\vec{A}||\vec{B}| \cos \theta\).

Пример 1
Три точки \(\ P=(3,7,2), Q=(1,4,3)\) и \(\ R=(2,3,4)\) определяют плоскость. Определите точку на плоскости, ближайшую к началу координат.
Раствор
Сначала найдите векторы между двумя парами точек.
\(\ \begin{array}{l}
\overrightarrow{PQ}=\left\langle\left(Q_{x}-P_{x}\right),\left(Q_{y}-P_{y }\right),\left(Q_{z}-P_{z}\right)\right\rangle=\langle(1-3),(4-7),(3-2)\rangle=\langle- 2,-3,1\rangle \\
\overrightarrow{PR}=\left\langle\left(R_{x}-P_{x}\right),\left(R_{y}-P_{y}\ вправо),\влево(R_{z}-P_{z}\вправо)\вправо\rangle=\langle(2-3),(3-7),(4-2)\rangle=\langle-1, -4,2\rangle
\end{массив}\)Перекрестное произведение этих двух векторов перпендикулярно плоскости.
\(\ \begin{array}{l}
\overrightarrow{PQ} \times \overrightarrow{PR}=\left\langle\left(P Q_{y} P R_{z}-P Q_{z} P R_{y}\right),\left(P Q_{z} P R_{x}-P Q_{x} P R_{z}\right),\left(P Q_{x} P R_{y}- P Q_{y} P R_{x}\right)\right\rangle \\
\overrightarrow{PQ} \times \overrightarrow{PR}=\langle[(-3 \cdot 2)-(1 \cdot-4 )],[(1 \cdot-1)-(-2 \cdot 2)],[(-2 \cdot-4)-(-1 \cdot-3)]\rangle \\
\vec{n} =\overrightarrow{PQ} \times \overrightarrow{PR}=\langle[(-6)-(-4)],[(-1)-(-4)],[(8)-(3)]\ rangle=\langle-2,3,5\rangle
\end{массив}\)Точка на плоскости, ближайшая к началу координат, может быть найдена путем определения проекции вектора положения любой из этих трех точек на вектор нормали.
 {2}}}=\frac{\langle-2,3, 5\rangle}{\sqrt{38}}=\langle-0.32,0.49,0.81\rangle \\
{2}}}=\frac{\langle-2,3, 5\rangle}{\sqrt{38}}=\langle-0.32,0.49,0.81\rangle \\
\vec{P} \times \шляпа{n}=P_{x} \шляпа{n}_{x}+P_{y} \шляпа{n}_{y} +P_{z} \шляпа{n}_{z}=(3)(-0,32)+(7)(0,49)+(2)(0,81)= \\
-0,96+3,43+1,62=4,09 \\
(\vec{P} \times \шляпа{n}) \шляпа{n}=(4.09)\langle-0.32,0.49,0.81\rangle=\langle-1.3088,2.0041,3.3129\rangle
\end{массив }\)Следовательно, ближайшая к началу координат точка на плоскости (-1,3088, 2,0041, 3,3129).
Пример 2
Три точки \(\ P=(3,7,2), Q=(1,4,3)\) и \(\ R=(2,3,4)\) определяют плоскость.Определите двугранный угол между этой плоскостью и плоскостью xy.
Раствор
Как мы видели в примере выше, эти три точки определяют плоскость с вектором нормали \(\ \vec{n}=\langle-2,3,5\rangle\)
Нормалью к плоскости x-y является единичный вектор \(\ \hat{z}=\langle 0,0,1\rangle\). Чтобы найти угол между этими двумя векторами, мы используем тот факт, что \(\ \vec{A} \times \vec{B}=|\vec{A}||\vec{B}|\) и что \(\ \vec{A} \times \vec{B}=A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{z}\)
Сначала найдите числовое значение скалярного произведения:
\(\ \begin{array}{l}
\vec{n} \times \hat{z}=n_{x} z_{x}+n_{y} z_{y}+n_{z} z_{ z}=(-2 \cdot 0)+(3 \cdot 0)+(5 \cdot 1)=5 \\
|\vec{n}|=\sqrt{n_{x}^{2}+n_ {y}^{2}+n_{z}^{2}}=\sqrt{(-2)^{2}+(3)^{2}+(5)^{2}}=\sqrt{ 4+9+25}=\sqrt{38} \\
|\шляпа{z}|=\sqrt{z_{x}^{2}+z_{y}^{2}+z_{z}^{ 2}}=\sqrt{0^{2}+0^{2}+1^{2}}=1
\end{массив}\)Затем найдите косинусную версию скалярного произведения:
\(\ \vec{n} \times \hat{z}=\sqrt{38} \cos \theta\)
Теперь приравняйте два числа и найдите угол: θ
\(\ \begin{array}{l}
\vec{n} \times \hat{z}=5=\sqrt{38} \cos \theta \\
\theta=\cos ^{-1} \left(\frac{5}{\sqrt{38}}\right)=62. {\circ}
{\circ}
\end{массив}\)Пример 3
Определить дигидральный угол между двумя плоскостями 12 + 23 Y + 14 Z — 5 = 0 и 7 x + 3 y + г + 12 = 0,
Раствор
Двугранный угол определяется как угол между двумя плоскостями. Этот угол также равен углу между нормалями к двум плоскостям.В двух предыдущих задачах мы определили единичные векторы, перпендикулярные этим двум плоскостям \(\ \overrightarrow{n_{1}}=\left\langle\frac{12}{29.5}, \frac{23}{29.5 }, \frac{14}{29.5}\right\rangle\) и \(\ \overrightarrow{n_{2}}=\left\langle\frac{7}{\sqrt{59}}, \frac{3 }{\sqrt{59}}, \frac{1}{\sqrt{59}},\right\rangle\). Затем мы можем использовать скалярное произведение этих двух векторов нормалей, чтобы определить угол между ними. Скалярное произведение определяется как \(\ \vec{A} \times \vec{B}=A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{z}+ \ldots\) и как \(\ \vec{A} \times \vec{B}=|A||B| \cos \theta\).
 Во-первых, нам нужно найти компонентную версию скалярного произведения и величины двух векторов нормалей.
Во-первых, нам нужно найти компонентную версию скалярного произведения и величины двух векторов нормалей.\(\ \begin{array}{l}
\overrightarrow{n_{1}} \times \overrightarrow{n_{2}}=\overrightarrow{n_{1 x} n_{2 x}}+\overrightarrow{ n_{1 y} n_{2 y}}+\overrightarrow{n_{1 z} n_{2 z}}=\frac{12 \cdot 7}{29,5 \sqrt{59}}+\frac{23 \cdot 3}{29 \cdot 5 \sqrt{59}}+\frac{14 \cdot 1}{29,5 \sqrt{59}} \\
\overrightarrow{n_{1}} \times \overrightarrow{n_{2} }=\frac{12 \cdot 7}{29,5 \sqrt{59}}+\frac{23 \cdot 3}{29.{\circ}
\end{массив}\)Пример 4
Определить угол между плоскостью 2 x — 5 y + 8 — 10 = 0 и плоскостью y — z
Раствор
Двугранный угол определяется как угол между двумя плоскостями, а также равен углу между двумя единичными векторами нормали. В этом случае мы уже знаем единичный вектор нормали для плоскости y-z, \(\ \hat{x}=\langle 1,0,0\rangle\).
 {2}}}=\frac{\langle 2,-5,8\rangle}{\sqrt{4+25+64}}=\frac{\langle 2,-5,8\rangle}{9,64} = \left\langle\frac{2}{9.64}, \frac{-5}{9.64}, \frac{8}{9.64}\right\rangle\)
{2}}}=\frac{\langle 2,-5,8\rangle}{\sqrt{4+25+64}}=\frac{\langle 2,-5,8\rangle}{9,64} = \left\langle\frac{2}{9.64}, \frac{-5}{9.64}, \frac{8}{9.64}\right\rangle\)Угол между двумя плоскостями равен углу между двумя векторами нормалей.
Затем мы можем использовать скалярное произведение этих двух векторов нормалей, чтобы определить угол между ними. Скалярное произведение определяется как \(\ \vec{A} \times \vec{B}=A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{z}+ \ldots\) и как \(\ \vec{A} \times \vec{B}=|A||B| \cos \theta\).Во-первых, нам нужно найти компонентную версию скалярного произведения и величины двух векторов нормалей.
\(\ \overrightarrow{n_{1}} \times \overrightarrow{n_{2}}=\overrightarrow{n_{1 x}} \overrightarrow {n_{2 x}}+\overrightarrow{n_{1 y} } \overrightarrow{n_{2 y}}+\overrightarrow{n_{1 z}}\overrightarrow {n_{2 z}}=\frac{2 \cdot 1}{9,64}+\frac{-5 \cdot 0 {9,64}+\frac{8 \cdot 0}{9,64}=\frac{2}{9,64}=0,2074\)
Поскольку эти два вектора являются единичными, их величины равны 1.
 {\circ}
{\circ}
\end{массив}\)Пример 5
Три точки \(\ \vec{P}=\langle-2,3,4\rangle, \vec{Q}=\langle 5,-6,7\rangle\) и \(\ \vec{ R}=\langle 8,9,-1\rangle\) идентифицируют плоскость. Определить точку на плоскости, ближайшую к началу координат.
Раствор
Ближайшую к началу координат точку на плоскости можно найти, определив проекцию вектора положения одной из этих трех точек на вектор нормали. Помните, что векторная проекция одного вектора на направление другого задается скалярным произведением первого вектора на единичный вектор, определяющий направление второго вектора: \(\ (\vec{P} \times \hat{ п}) \шляпа{п}\).
Мы можем использовать векторы положения трех точек, чтобы определить два вектора внутри плоскости. Когда у нас есть эти два вектора, их векторное произведение будет определять направление нормали к плоскости. Сначала найдите два уравнения на плоскости:
\(\ \begin{array}{l}
\vec{A}=\vec{Q}-\vec{P}=\langle 5,-6,7\rangle-\langle-2,3,4 \rangle=\langle 7,-9,3\rangle \\
\vec{B}=\vec{R}-\vec{P}=\langle 8,9,-1\rangle-\langle-2, 3,4\rangle=\langle 10,6,-5\rangle
\end{массив}\)Теперь определите векторное произведение двух векторов
\(\ \begin{array}{l}
\vec{n}=\vec{A} \times \vec{B}=\left\langle\left(A_{y} B_{z}-A_{ z} B_{y}\right),\left(A_{z} B_{x}-A_{x} B_{z}\right),\left(A_{x} B_{y}-A_{y} B_{x}\right)\right\rangle \\
\vec{n}=\vec{A} \times \vec{B}=\langle(45-18),(30-(-35)), (42+90)\rangle \\
\vec{n}=\vec{A} \times \vec{B}=\langle 27,65,132\rangle
\end{массив}\)Теперь нам нужно определить единичный вектор, связанный с этим вектором нормали
\(\ \begin{array}{l}
\шляпа{n}=\frac{\vec{n}}{|\vec{n}|}=\frac{\left\langle n_{x}, n_{y}, n_{z}\right\rangle}{\sqrt{n_{x}^{2}+n_{y}^{2}+n_{z}^{2}}}=\frac{ \ langle 27,65,132\rangle}{\sqrt{27^{2}+(65)^{2}+(132)^{2}}}=\frac{\langle 27,65,132\rangle}{\sqrt {22378}} \\
\шляпа{n}=\frac{\vec{n}}{|\vec{n}|}=\langle 0. 181,0,435,0,882\rangle
181,0,435,0,882\rangle
\end{массив}\)Теперь мы определяем векторную прогрессию одного из трех векторов начального положения в направлении этого нормального единичного вектора: \(\ (\vec{P} \times \hat{n}) \hat{n}\). Помните, что скалярное произведение равно
.\(\ \begin{array}{l}
\vec{A} \times \vec{B}=A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{ z}+\ldots\\
(\vec{P} \times\hat{n}) \hat{n}=(-2(0,181)+3(0,435)+4(0,882))\langle 0,181,0,435 ,0,882\rangle \\
(\vec{P} \times \шляпа{n}) \шляпа{n}=(4.471)\langle 0,181,0,435,0,882\rangle \\
(\vec{P} \times \hat{n}) \hat{n}=(4,471)\langle 0,181,0,435,0,882\rangle=\langle 0,809 ,1.945,3.943\rangle
\end{массив}\)Пример 7
Определить точку на плоскости 7 x + 3 y + z + 12 = 0, ближайшую к началу координат.
Раствор
Точка на плоскости, ближайшая к началу координат, может быть найдена путем определения проекции вектора положения любой точки на плоскости на вектор нормали.
 {2}}} = \ frac {\ langle 7,3,1 \ rangle} {\ sqrt {49+ 9+1}}=\frac{\langle 7,3,1\rangle}{\sqrt{59}} = \left\langle\frac{7}{\sqrt{59}}, \frac{3}{ \sqrt{59}}, \frac{1}{\sqrt{59}}\right\rangle\)
{2}}} = \ frac {\ langle 7,3,1 \ rangle} {\ sqrt {49+ 9+1}}=\frac{\langle 7,3,1\rangle}{\sqrt{59}} = \left\langle\frac{7}{\sqrt{59}}, \frac{3}{ \sqrt{59}}, \frac{1}{\sqrt{59}}\right\rangle\)Нам также нужно знать положение точки на плоскости.Если мы запишем уравнение плоскости в форме точки пересечения, мы сможем определить вектор положения для осей x, y и z плоскости.
Уравнение \(\ 1=\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) должно выполняться для всех точек на плоскости. Поэтому мы должны сначала переставить 7 x +3 y + z + 12 = 0 в виде \(\ 1=\frac{x}{a}+\frac{y {b}+\frac{z}{c}\).
\(\ 7 x+3 y+z=-12 \text { становится } \frac{7}{-12} x+\frac{3}{-12} y+\frac{1}{-12} z= 1\)
Следовательно, \(\ a=\frac{-12}{7}, b=\frac{-12}{3}=-4\) и \(\ c=\frac{-12}{1} =-12\) , а векторы положения трех точек пересечения равны \(\ \vec{A}=\langle-1.714,0,0\rangle, \vec{B}=\langle 0,-4,0\rangle\) и \(\ \vec{C}=\langle 0,0,-12\rangle\).

Чтобы решить задачу, вычислите скалярное произведение.
\(\ (\vec{B} \times \шляпа{n}) \шляпа{n}=\left(B_{x} \шляпа{n}_{x}+B_{y} \шляпа{n} _{y}+B_{z} \шляпа{n}_{z}\справа) \шляпа{n} = \слева(0\слева(\frac{7}{\sqrt{59}}\справа)- 4\влево(\frac{3}{\sqrt{59}}\right)+0\влево(\frac{1}{\sqrt{59}}\right)\right)\left\langle\frac{7 }{\sqrt{59}}, \frac{3}{\sqrt{59}}, \frac{1}{\sqrt{59}}\right\rangle\)
\(\ (\vec{B} \times \hat{n}) \hat{n}=\frac{-12}{\sqrt{59}}\left\langle\frac{7}{\sqrt{ 59}}, \frac{3}{\sqrt{59}}, \frac{1}{\sqrt{59}}\right\rangle=\left\langle\frac{-84}{59}, \frac {-36}{59}, \frac{-12}{59}\right\rangle=\langle-1.424,-0,610,-0,203\угол\)
Видео-вопрос: нахождение расстояния между прямой и плоскостью
Стенограмма видео
Найдите перпендикулярное расстояние между вектором линии 𝐫, равным единице, двум, четырем плюс 𝑡, умноженному на минус два, один, четыре, и плоскому вектору 𝐫 точка два, ноль, единица равна единице.
Этот вопрос включает в себя определение перпендикулярного расстояния между прямой и плоскостью.
 При рассмотрении линии и плоскости на самом деле есть две основные возможности.Либо прямая параллельна плоскости, либо прямая пересекает плоскость. Если прямая пересекает плоскость, то кратчайшее расстояние в любой точке между прямой и плоскостью будет равно нулю. Поэтому нам нужно определить, пересекаются ли прямая и плоскость.
При рассмотрении линии и плоскости на самом деле есть две основные возможности.Либо прямая параллельна плоскости, либо прямая пересекает плоскость. Если прямая пересекает плоскость, то кратчайшее расстояние в любой точке между прямой и плоскостью будет равно нулю. Поэтому нам нужно определить, пересекаются ли прямая и плоскость.Мы можем взять уравнение прямой и изменить его так, чтобы вектор 𝐫 был равен единице минус два 𝑡, двум плюс 𝑡, четырем плюс четыре 𝑡. Теперь мы можем подставить этот вектор в уравнение плоскости. Вместо вектора 𝐫 у нас будет один минус два 𝑡, два плюс 𝑡, четыре плюс четыре 𝑡, из которых мы затем можем взять скалярное произведение с двумя, нулем, единицей.Находя сумму произведений соответствующих компонентов, мы имеем два умножить на один минус два 𝑡 плюс ноль умножить на два плюс 𝑡 плюс один умножить на четыре плюс четыре 𝑡 равно единице. Упрощая, у нас есть два минус четыре 𝑡 плюс четыре плюс четыре 𝑡 равно единице. Но когда мы еще больше упростим это, мы получим шесть слева и один справа.
 Это означает, что это не будет верно для любого значения 𝑡. А значит прямая и плоскость не пересекаются.
Это означает, что это не будет верно для любого значения 𝑡. А значит прямая и плоскость не пересекаются.Следовательно, мы можем сказать, что эта линия и плоскость должны быть параллельны.Расстояние между прямой и плоскостью можно найти, взяв точку на прямой и найдя перпендикулярное расстояние от этой точки до плоскости. Посмотрим, сможем ли мы найти точку, лежащую на прямой. Мы можем сделать это, взяв уравнение прямой и подставив любое значение 𝑡. Итак, давайте использовать 𝑡 равно нулю. Делая это, мы можем понять, что точка один, два, четыре должны лежать на прямой.
Теперь мы можем вспомнить и использовать формулу, чтобы найти перпендикулярное расстояние между точкой и плоскостью, заданной в векторной форме.Эта формула говорит нам, что расстояние по перпендикуляру, обозначенное прописной буквой 𝐷, между точкой 𝑥 под единицей, 𝑦 под единицей, 𝑧 под единицей и плоским вектором 𝐫 точка 𝑎, 𝑏, 𝑐 равно отрицательному 𝑑 задается как 𝐷 равно величине 𝑎𝑥 под единицы плюс 𝑏𝑦 меньшая единица плюс 𝑐𝑧 меньшая единица плюс 𝑑 на квадратный корень из 𝑎 в квадрате плюс 𝑏 в квадрате плюс 𝑐 в квадрате.

Когда мы подставляем множество значений в формулу, подобную этой, всегда стоит записать значения, которые мы будем использовать. Значения 𝑥 sub one, 𝑦 sub one и 𝑧 sub one исходят из точки, которую мы используем.Их соответственно один, два и четыре. Значения 𝑎, 𝑏, 𝑐 и 𝑑 исходят из уравнения плоскости. Итак, 𝑎 равно двум, 𝑏 равно нулю, а 𝑐 равно единице. Однако нам нужно быть более осторожными с термином 𝑑. Обратите внимание, что в этой форме, которую мы используем в формуле, у нас отрицательный знак 𝑑 в правой части. Так как значение в уравнении плоскости, которое нам дано, имеет единицу в правой части, то это означает, что значение 𝑑 должно быть отрицательным.
Итак, теперь мы готовы подставить эти значения в формулу для нахождения перпендикулярного расстояния.Итак, у нас есть 𝐷 равно величине, умноженной на два, умноженная на один, плюс ноль, умноженная на два, плюс один, умноженный на четыре, плюс минус один на квадратный корень из двух в квадрате плюс ноль в квадрате плюс один в квадрате.
 Когда мы упрощаем, у нас есть величина два плюс четыре минус один на квадратный корень из четырех плюс один. Числитель будет равен величине пяти, то есть пяти, а знаменатель — квадратному корню из пяти. Мы можем рационализировать этот знаменатель, умножив числитель и знаменатель на корень пять.Затем мы можем вычесть общий множитель из пяти, чтобы получить ответ, что перпендикулярное расстояние между данной линией и плоскостью составляет корень из пяти единиц длины.
Когда мы упрощаем, у нас есть величина два плюс четыре минус один на квадратный корень из четырех плюс один. Числитель будет равен величине пяти, то есть пяти, а знаменатель — квадратному корню из пяти. Мы можем рационализировать этот знаменатель, умножив числитель и знаменатель на корень пять.Затем мы можем вычесть общий множитель из пяти, чтобы получить ответ, что перпендикулярное расстояние между данной линией и плоскостью составляет корень из пяти единиц длины.Как найти расстояние между двумя плоскостями (видео и примеры)
Стены вашего класса, школы или дома, вероятно, расположены вертикально по отношению к полу и потолку. Это означает, что две стены в комнате, вероятно, параллельны друг другу. Если бы вы могли представить себе эти две стены, простирающиеся бесконечно в двух направлениях (в ширину и длину, а не в высоту), вы бы получили две плоскости на заданном расстоянии друг от друга.Расстояние между этими двумя плоскостями можно найти математически.
Содержание
- Расстояние между двумя параллельными плоскостями
- шага, чтобы найти расстояние между двумя плоскостями
- Формула расстояния между точкой и плоскостью
- Нахождение расстояния между двумя плоскостями
Расстояние между двумя параллельными плоскостями
Под расстоянием между двумя параллельными плоскостями понимается кратчайшее расстояние между их поверхностями.
 Подумай об этом; если плоскости не параллельны, в конце концов они должны пересечься.Если они пересекаются, то на этой линии пересечения между ними нет расстояния — 0 расстояния. Часть вашей детективной работы заключается в том, чтобы выяснить, параллельны ли две плоскости.
Подумай об этом; если плоскости не параллельны, в конце концов они должны пересечься.Если они пересекаются, то на этой линии пересечения между ними нет расстояния — 0 расстояния. Часть вашей детективной работы заключается в том, чтобы выяснить, параллельны ли две плоскости.шагов, чтобы найти расстояние между двумя плоскостями
Пять шагов следующие:
- Напишите уравнения в стандартном формате для обеих плоскостей
- Узнайте, параллельны ли две плоскости
- Определите коэффициенты a, b, c и d из одного уравнения плоскости
- Найти точку (x1, y1, z1) на другой плоскости
- Подставить a, b, c, d, x1, y1 и z1 в формулу расстояния
Просмотрев шаги, давайте пройдемся по ним.
Шаг 1: Напишите уравнения для плоскостей в стандартном формате, ax + by + cz + d = 0, с нижними индексами, обозначающими две плоскости, 1 и 2, в наших общих уравнениях:
a1x + b1y + c1z + d1 = 0
a2x + b2y + c2z + d2 = 0
Шаг 2: Они пересекаются или параллельны? Помните, если они параллельны, ваша работа выполнена! Расстояние равно 0.
 Сравните отношения трех идентифицированных точек каждой плоскости (a1a2, b1b2, c1c2). Две плоскости параллельны, если их отношения равны:
Сравните отношения трех идентифицированных точек каждой плоскости (a1a2, b1b2, c1c2). Две плоскости параллельны, если их отношения равны:a1a2 = b1b2 = c1c2
Шаг 3: Определите коэффициенты a, b, c и d в одном из уравнений плоскости.Просто посмотрите на одно уравнение и вытяните эти коэффициенты, поняв, что a1 — это a (если вы используете первую плоскость), b1 — это b и так далее.
Шаг 4: Укажите точку (x1, y1, z1) на другой плоскости. В нашей общей задаче мы используем вторую плоскость. Использование точки с двумя нулевыми значениями упрощает вашу работу: x = 0 = y, что дает вам:
a20 + b20 + c2z1 + d2 = 0
Решить для z1 (неизвестная третья точка):
c2z1 + d2 — d22 = 0 — d2 (вычесть d2 с обеих сторон)
c2z1 = 0 — d2
c2z1c2 = -d2c2 (разделите обе части на c2)
z1 = -d2c2
Наши три пункта теперь ясны:
x 1 = 0
y1 = 0
z1 = -d2c2
Не зацикливайтесь на переменных в нашем универсальном примере.
 У вас будут реальные числа в реальных уравнениях, что значительно упростит внешний вид этих уравнений.
У вас будут реальные числа в реальных уравнениях, что значительно упростит внешний вид этих уравнений.Шаг 5: Подставьте найденные значения в формулу расстояния. Вы нашли a, b, c и d на шаге 3 выше. Это коэффициенты уравнения одной плоскости. Вы нашли x1, y1 и z1 на шаге 4 выше. Это координаты точки на другой плоскости. Подставьте найденные значения в формулу расстояния точка-плоскость.
Формула расстояния точка-плоскость
D = ax1 + by1 + cz1 + da2 + b2 + c2
Нахождение расстояния между двумя плоскостями
Вот два уравнения для самолетов:
3x + 4y + 5z + 9 = 0
9x + 12y + 15z — 27 = 0
Пройдите пять шагов:
- Напишите уравнения в стандартном формате для обеих плоскостей — мы уже сделали это за вас!
- Узнайте, параллельны ли две плоскости:
- Определите коэффициенты a, b, c и d из уравнения одной плоскости:
- Найдите точку (x1, y1, z1) на другой плоскости, которая в данном случае является первой плоскостью:
- Подставьте a, b, c, d, x1, y1 и z1 в формулу расстояния:
39 = 412 = 515 = 13
Две плоскости параллельны.
Вместо того, чтобы повторять выбор из нашего общего примера, мы будем использовать второе уравнение, которое даст нам следующие значения:
а = 9
б = 12
с = 15
д = -27
Попробуйте использовать x = y = 0 для двух координат точки и решить для z1:
3x + 4y + 5z + 9 = 0
3(0) + 4(0) + 5(z1) + 9 = 0
5(z1) + 9 = 0
5(z1) + 9 — 9 = 0 -9 (вычесть d1 с обеих сторон)
5(z1) = -9
(5(z1))/5 = -9/5 (разделить обе части на c1)
z1 = -9/5 = -1.
 8
8Наши три точки на первой плоскости:
х = 0
г = 0
г = -9/5 = -1,8
Расстояние между нашими двумя самолетами примерно 2,54.
Следующий урок:
Формула расстояния
Как найти расстояние между двумя плоскостями — видео и расшифровка урока
Как найти расстояние между двумя плоскостями
Представьте себе стену.Стена – плоская поверхность. Если бы стена простиралась во всех направлениях до бесконечности, у нас было бы плоскостей . Стена обычно имеет вертикальную ориентацию, а плоскость может иметь любую ориентацию. Расстояние между двумя плоскостями является кратчайшим расстоянием между поверхностями плоскостей.
Найдем это расстояние!
Шаг 1: Напишите уравнения для каждой плоскости в стандартном формате.
Стандартный формат, который мы будем использовать: a x + b y + c z + d = 0.
 Для двух уравнений имеем следующее:
Для двух уравнений имеем следующее:Шаг 2: Определите, параллельны ли плоскости.
Если плоскости не параллельны, они в конечном итоге пересекутся, потому что каждая плоскость простирается до бесконечности во всех направлениях. Таким образом, если плоскости не параллельны, расстояние между плоскостями равно нулю, и мы можем остановить процесс нахождения расстояния. Чтобы узнать, параллельны ли плоскости, проверьте отношения a 1/ a 2, b 1/ b 2 и c 1/ c 2.
Плоскости параллельны, если эти отношения равны.
Если плоскости параллельны, переходим к следующему шагу.
Шаг 3: Из одного из уравнений плоскости определите коэффициенты
a , b , c и d .Эта часть очень проста.
 Допустим, мы выбрали первое уравнение плоскости. Затем
Допустим, мы выбрали первое уравнение плоскости. ЗатемШаг 4: Найдите точку (
x 1, y 1, z 1) на другой плоскости.Подойдет любая точка. Хороший выбор обычно состоит в том, чтобы позволить любой из двух координат быть равной нулю, а затем найти третью координату. Например, если x = y = 0, это означает следующее:
и решение для z 1 означает:
Таким образом,
- х 1 = 0
- у 1 = 0
- z 1 = — d 2/ c 2
Примечание. Эта часть может показаться сложной из-за множества буквенных переменных.На практике у нас есть цифры, и работа выглядит намного проще. Мы покажем это позже в разделе приложений.
Шаг 5: Подставьте в формулу расстояния и упростите.

Замените на A , B , C , C , D , Z 1, Z 1 и Z 1 в формулу для поиска расстояния, D, между двумя плоскостями.
Расстояние между точкой и линией
Пусть у нас есть общая линия ax+by+c=0ax + by + c = 0ax+by+c=0 с именем LLL.Эта линия имеет наклон −ab-\frac{a}{b}−ba. Пусть также есть общая точка P=(x0,y0)P=(x_0, y_0)P=(x0,y0). Расстояние между линией LLL и точкой PPP можно изобразить другой линией, перпендикулярной L;L;L; назовем это ТТТ. TTT будет иметь наклон ba\frac{b}{a}ab, так как он перпендикулярен LLL. Теперь, чтобы найти расстояние между точкой PPP и линией L,L,L, мы можем использовать небольшой геометрический трюк и иметь другую прямую, параллельную LLL, которая проходит через PPP; назовем это ССС. Точно так же у нас может быть другая линия, на этот раз параллельная TTT, которая проходит через начало координат (0,0)(0,0)(0,0); назовем это РРР.
Теперь, когда время рисования подошло к концу, пора работать.

Прежде всего, поскольку SSS проходит через PPP и имеет тот же наклон, что и LLL, его уравнение равно
.y−y0=−ab(x−x0) ⟹ y=−ax+ax0+by0b.y — y_0 = -\dfrac{a}{b}(x — x_0) \ подразумевает y = \dfrac{-ax + ax_0 + by_0}{b}.y−y0=−ba(x−x0)⟹y=b−ax+ax0+by0.
Строка RRR имеет уравнение
у=бакс. y = \dfrac{b}{a}x.y=abx.
Итак, линия SSS пересекается с линией RRR, когда
bax=−ax+ax0+by0b ⟹ x=a(ax0+by0)a2+b2.2}}. \end{выровнено} d=(− a2+b2ac−a2+b2a(ax0+by0))2+(– a2+b2bc−a2+b2b(ax0+by0))2 =(a2+b2)2[−a(ax0+by0+c)]2+[−b(ax0+by0+c)v]2=(a2+b2)2(a2+b2 )(ax0+by0+c)2=a2+b2(ax0+by0+c)2=a2+b2∣ax0+by0+c∣.
Знак абсолютного значения необходим, так как расстояние должно быть положительным значением. □_\квадрат□
Здесь мы приводим геометрическое доказательство.
Во-первых, мы проводим линию, параллельную LLL, которая проходит через PPP, которая имеет уравнение ax+by-(ax0+by0)=0ax+by-(ax_0+by_0)=0ax+by-(ax0+by0) =0.





 !
!
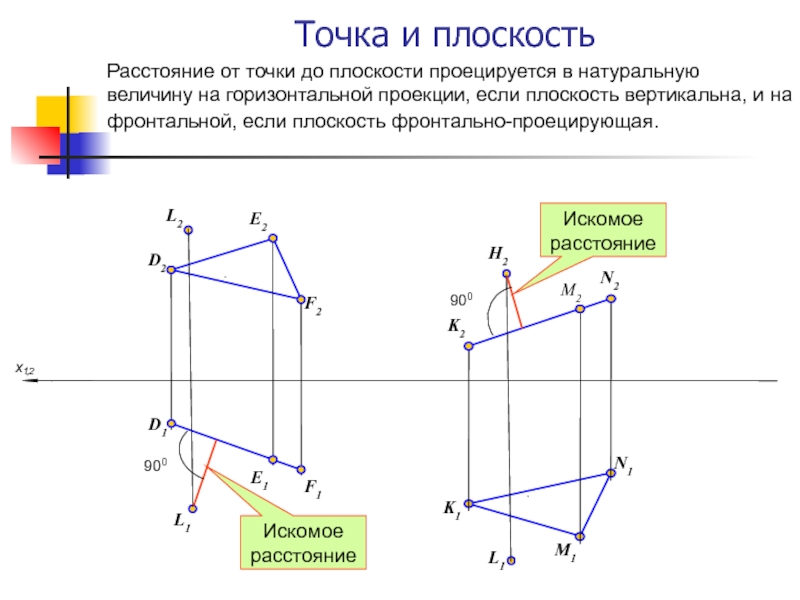
 {2}}}=\frac{\langle-2,3, 5\rangle}{\sqrt{38}}=\langle-0.32,0.49,0.81\rangle \\
{2}}}=\frac{\langle-2,3, 5\rangle}{\sqrt{38}}=\langle-0.32,0.49,0.81\rangle \\  {\circ}
{\circ}  Во-первых, нам нужно найти компонентную версию скалярного произведения и величины двух векторов нормалей.
Во-первых, нам нужно найти компонентную версию скалярного произведения и величины двух векторов нормалей. {2}}}=\frac{\langle 2,-5,8\rangle}{\sqrt{4+25+64}}=\frac{\langle 2,-5,8\rangle}{9,64} = \left\langle\frac{2}{9.64}, \frac{-5}{9.64}, \frac{8}{9.64}\right\rangle\)
{2}}}=\frac{\langle 2,-5,8\rangle}{\sqrt{4+25+64}}=\frac{\langle 2,-5,8\rangle}{9,64} = \left\langle\frac{2}{9.64}, \frac{-5}{9.64}, \frac{8}{9.64}\right\rangle\) {\circ}
{\circ}  181,0,435,0,882\rangle
181,0,435,0,882\rangle  {2}}} = \ frac {\ langle 7,3,1 \ rangle} {\ sqrt {49+ 9+1}}=\frac{\langle 7,3,1\rangle}{\sqrt{59}} = \left\langle\frac{7}{\sqrt{59}}, \frac{3}{ \sqrt{59}}, \frac{1}{\sqrt{59}}\right\rangle\)
{2}}} = \ frac {\ langle 7,3,1 \ rangle} {\ sqrt {49+ 9+1}}=\frac{\langle 7,3,1\rangle}{\sqrt{59}} = \left\langle\frac{7}{\sqrt{59}}, \frac{3}{ \sqrt{59}}, \frac{1}{\sqrt{59}}\right\rangle\)
 При рассмотрении линии и плоскости на самом деле есть две основные возможности.Либо прямая параллельна плоскости, либо прямая пересекает плоскость. Если прямая пересекает плоскость, то кратчайшее расстояние в любой точке между прямой и плоскостью будет равно нулю. Поэтому нам нужно определить, пересекаются ли прямая и плоскость.
При рассмотрении линии и плоскости на самом деле есть две основные возможности.Либо прямая параллельна плоскости, либо прямая пересекает плоскость. Если прямая пересекает плоскость, то кратчайшее расстояние в любой точке между прямой и плоскостью будет равно нулю. Поэтому нам нужно определить, пересекаются ли прямая и плоскость. Это означает, что это не будет верно для любого значения 𝑡. А значит прямая и плоскость не пересекаются.
Это означает, что это не будет верно для любого значения 𝑡. А значит прямая и плоскость не пересекаются.
 Когда мы упрощаем, у нас есть величина два плюс четыре минус один на квадратный корень из четырех плюс один. Числитель будет равен величине пяти, то есть пяти, а знаменатель — квадратному корню из пяти. Мы можем рационализировать этот знаменатель, умножив числитель и знаменатель на корень пять.Затем мы можем вычесть общий множитель из пяти, чтобы получить ответ, что перпендикулярное расстояние между данной линией и плоскостью составляет корень из пяти единиц длины.
Когда мы упрощаем, у нас есть величина два плюс четыре минус один на квадратный корень из четырех плюс один. Числитель будет равен величине пяти, то есть пяти, а знаменатель — квадратному корню из пяти. Мы можем рационализировать этот знаменатель, умножив числитель и знаменатель на корень пять.Затем мы можем вычесть общий множитель из пяти, чтобы получить ответ, что перпендикулярное расстояние между данной линией и плоскостью составляет корень из пяти единиц длины. Подумай об этом; если плоскости не параллельны, в конце концов они должны пересечься.Если они пересекаются, то на этой линии пересечения между ними нет расстояния — 0 расстояния. Часть вашей детективной работы заключается в том, чтобы выяснить, параллельны ли две плоскости.
Подумай об этом; если плоскости не параллельны, в конце концов они должны пересечься.Если они пересекаются, то на этой линии пересечения между ними нет расстояния — 0 расстояния. Часть вашей детективной работы заключается в том, чтобы выяснить, параллельны ли две плоскости. Сравните отношения трех идентифицированных точек каждой плоскости (a1a2, b1b2, c1c2). Две плоскости параллельны, если их отношения равны:
Сравните отношения трех идентифицированных точек каждой плоскости (a1a2, b1b2, c1c2). Две плоскости параллельны, если их отношения равны: У вас будут реальные числа в реальных уравнениях, что значительно упростит внешний вид этих уравнений.
У вас будут реальные числа в реальных уравнениях, что значительно упростит внешний вид этих уравнений. 8
8 Для двух уравнений имеем следующее:
Для двух уравнений имеем следующее: Допустим, мы выбрали первое уравнение плоскости. Затем
Допустим, мы выбрали первое уравнение плоскости. Затем

