Определить площадь – Калькулятор для расчета площади

Posted on by alexxlab

Содержание

Калькулятор для расчета площади

Данный онлайн-калькулятор позволяет рассчитать площадь различных геометрических фигур, таких как:

Для удобства расчетов вы можете выбрать единицу измерения (миллиметр, сантиметр, метр, километр, фут, ярд, дюйм, миля). Также полученный результат можно конвертировать в другую единицу измерения путем выбора её из выпадающего списка.


Полезные калькуляторы Конвертер единиц площади | Конвертер единиц длины

Расчет площади прямоугольника

Результат:

S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля

Расчет площади треугольника

Способ нахождения площади треугольника: По трем сторонамПо одной стороне и высоте, опущенной на эту сторонуПо двум сторонам и углу между ними

Вычислить

Результат:

S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля


Расчет площади круга

Рассчитать площадь круга, если известен:

Вычислить

Результат:

S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля

Расчет площади параллелограмма

Способ нахождения площади параллелограмма:
По основанию и высоте параллелограммаПо двум сторонам и углу между нимиПо двум диагоналям и углу между ними

Вычислить

Результат:

S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля

Расчет площади правильного многоугольника

Многоугольник с числом сторон n и длиной стороны аМногоугольник с числом сторон n, вписанный в окружность радиуса RМногоугольник с числом сторон n, описанный вокруг окружности радиуса r

Вычислить

Результат:

S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля

Расчет площади эллипса

Результат:

S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля


Расчет площади сектора круга

Рассчитать площадь сектора круга, если известен:

r=

ммсммкмфутярддюйммиля

 Расчет площади сектора круга (рисунок)

θ=

ммсммкмфутярддюйммиля

град.рад.
Вычислить

Результат:

S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля

Расчет площади трапеции

Способ нахождения площади трапеции: По двум основаниям a,b и высоте hПо двум основаниям a,b и боковым сторонам c,d

Результат:

S= 1111 кв.ммкв.смкв.мкв.кмкв.футкв.ярдкв.дюймкв.миля

Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры.

Метрические единицы измерения площади:   
Квадратный метр, производная единица системы СИ 1 м2 =1 са (сантиар)
Квадратный километр — 1 км2 = 1 000 000 м2
Гектар — 1 га = 10 000 м2
Ар (сотка) — 1 а =		 100 м2 (сотка как правило применяется для измерения земельных участков и равна 100 м2 или 10м х 10м)
Квадратный дециметр, 100 дм2 = 1 м2;
Квадратный сантиметр, 10 000 см2 =1 м2;
Квадратный миллиметр, 1 000 000 мм2 = 1 м2.

Данный онлайн-калькулятор удобен при расчете площадей помещений и земельных участков.

calc.by

Как узнать площадь комнаты в квадратных метрах

Можно поступить еще проще и просто все стороны помещения перемножить: потолок, пол, стены.

Перевод квадратных сантиметров в квадратные метры

Перед тем, как узнать сколько в комнате квадратных метров, очень важно разобраться в самих значениях, ведь когда идет расчет с сотнями сантиметров, их в любом случае необходимо переводить в метры. Делается это по следующей формуле, уже на известном примере: 160 см * 100 см – разница величин (в одном метре – 100 сантиметров), в итоге получается 16000 см2, которые нужно разделить на 10000 и получим = 1.60 м2.

Такими цифрами намного проще оперировать и запоминать. Тем более, что «квадратуру» помещения всегда измеряют именно в метрах. Для перевода необходимо подставлять следующие формулы:

  • 8000 см² / 10000 = 0,8 м²;
  • 34000 см² / 10000 = 3,4 м²;
  • 2400 см²/ 10000 = 0,24 м².

Все достаточно просто и не составит труда составить такие несложные арифметические вычисления, даже школьнику. Очень важно перед тем, как узнать квадратуру комнаты, провести максимально точные измерения, после чего приступить к расчетам.

Как посчитать площадь комнаты в квадратных метрах

Необходимость в расчете площади возникает зачастую только во время ремонтных работ, строительства или при смене мебели. Практически все строительные материалы (например напольное покрытие) исчисляется в квадратных метрах. Для правильного расчета количества материала, важно знать площадь пола. Зная ширину и длину комнаты, найти площадь не вызовет никаких сложностей.

Измерения

Перед тем как измерить комнату в квадратных метрах, необходим минимальный набор предметов:

  • калькулятор;
  • рулетка;
  • карандаш;
  • лист бумаги.

На бумаге необходимо сделать подробный план помещения. Каждая стена должна быть измерена с использованием рулетки.

Внимание! Очень важно делать измерения на уровне пола, ведь бывают случаи (особенно в старых домах), когда стены немного завалены в одну из сторон. Так как происходит измерение пола, необходимо измерять с максимальным прилеганием к стенам.

Вторым этапом является проставление полученных измерений на плане. Лучше всего сразу делать это в метрах, но точность каждого замера должна быть до 1 сантиметра. Это необходимо для того, чтобы при выборе необходимого количества материалов, удалось максимально точно подобрать метраж требуемого материала. Рулонные напольные покрытия продаются в погонных метрах.

Округлять можно только в случае небольшого увеличения, чтобы в случае непредвиденных обстоятельство, было достаточное количество материала.

Как высчитать квадратуру комнаты

Чтобы понять, как узнать общую площадь комнаты, необходимо воспользоваться простой формулой и перемножить показания длины на ширину. Как показано на рисунке длинная стена имеет длину в 7 метров а противоположная только 4. Выходит площадь пола будет равна 28 м2. Именно таким образом и находят квадратуру. Обязательно требуется помнить о небольшом запасе, который потребуется для подгонки и подрезки, причем чем сложнее будет вариант укладки, тем больше потребуется брать запас.

Зачастую комнаты не имеют ровной квадратной или прямоугольной формы.Поэтому, перед тем как узнать площадь комнаты в квадратных метрах, необходимо просто разбить комнату на несколько простых фигур (квадраты и прямоугольники) и после считают общую квадратуру. Так например для комнаты у которой форма буквы Г, достаточно разбить ее на 2 прямоугольника, отдельно посчитать площадь, а потом сложить.

Выглядит это все следующим образом:

  • вычисляем квадратуру большого прямоугольника: 5 умножаем на 4,35 и получаем 21,75 квадратных метров;
  • теперь по тому же принципу второй: 2,5 на 2,65 и получаем 6,625 квадратов;
  • далее суммируем общий результат 6,625 + 21,75 и получаем площадь комнаты в размере 28,375 квадратных метров.

Имея на руках полученный точный результат, можно немного округлить его в большую сторону и учитывать 28,4 квадратных метра.

В том случае, если комната имеет участок со срезанной стеной, как показано на картинке, тогда необходимо нарисовать прямоугольник таким образом, чтобы косая делила его на 2 треугольника. Тогда опять получается помещение по форме буквы Г. Далее можно вычислить площадь, по выше представленному методу.

Необходимо будет найти площадь трех прямоугольников. Недостающий участок – половина маленького прямоугольника. Достаточно будет просто найти его площадь и разделить на 2, после чего прибавить к остальным размерам.

Итак, для примера можно использовать следующие данные:

  • большой прямоугольник: 1,75 м *1,93 м = 3,3775 м². Чтобы было проще, возьмем 3,38 м²;
  • средний прямоугольник: 1,18 м * 0,57 м = 0,6726 м². Опять произведем округление до 0,67 м²;
  • самый маленький прямоугольник: 0,57 м *0,57 м = 0,3249 м2, доводим до 0,33 м²;
  • теперь осталось только сложить получившиеся значения и прибавить ½ маленького прямоугольника: 3,38 + 0,67 +0,33/2 = 3,38 + 0,67 +0,17 = 4,22 м².

Это наиболее удобная методика, которой может воспользоваться любой желающий. Достаточно только разбивать сложную фигуру на несколько простых. Несмотря на то, что измерений будет больше, такой метод не требует больших усилий и временных потерь, а все вычисления можно сделать буквально на коленке.

Площадь квартиры

Многие утверждают, что ремонт – процесс, который практически невозможно закончить, его можно только приостановить. Несмотря на это, чтобы не превратить незначительный ремонт в глобальный, очень важно правильно рассчитать все необходимые цифры и провести нужные расчеты, одним из которых является измерение квадратуры.

Теперь вы знаете, как найти площадь комнаты зная длину и ширину и после всех выполненных манипуляций, достаточно просто сложить полученные данные по комнатам, тогда можно получить квадратуру всей квартиры.

Такой процесс требуется для закупки материалов. Последним этапом будет только проработка плана, где будут указаны все длины, ширина оконных и дверных рам и т.д. Это необходимо например для укладки напольной плитки или ламината. Такая схема потребуется при укладке теплого пола.

Существуют и современные приложения на смартфон или сервисы в интернете, которые упростят эти моменты и помогут найти площадь.

j.etagi.com

Площадь прямоугольника. Онлайн-калькулятор

Онлайн-калькулятор площади прямоугольника поможет вам точно и быстро рассчитать или проверить расчеты по нахождению площади любого прямоугольника. Обычно площадь прямоугольника можно рассчитать двумя способами: через две стороны прямоугольника или через его диагонали. При первом способе расчета введите значения длин сторон a и b. При втором – длину диагоналей и значение угла между ними в градусах или радианах. Помимо ответа калькулятор покажет решение.

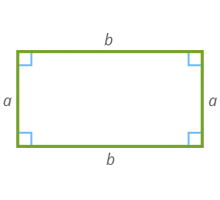
Расчет площади прямоугольника. Рисунок.

Способ расчета площади прямоугольника:

по двум сторонамчерез диагонали

Рассчитать



Прямоугольник – это геометрическая фигура, представляющая собой четырехугольник, у которого все углы прямые (90° ). Диагонали прямоугольника равны между собой.

Как найти площадь прямоугольника?

Существует несколько способов найти площадь прямоугольника. Самый простой способ, если известны стороны прямоугольника, то достаточно их перемножить. Если стороны не известны, а имеется величины диагоналей прямоугольника и угла между ними, то нужно воспользоваться формулой, приведенной ниже:

1) через две стороны

Формула площади прямоугольника. Расчет площади через две стороны. a, b – стороны

2) через диагонали и угол

Формула площади прямоугольника. Расчет площади через диагонали и угол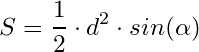. d – диагонали,
α – угол между диагоналями.

calc.by

Формулы площадей всех основных фигур

1. Формула площади равнобедренной трапеции через стороны и угол

Формула площади равнобедренной трапеции через стороны и угол

b — верхнее основание

a — нижнее основание

c — равные боковые стороны

α — угол при нижнем основании

 

Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны

 

Формула площади равнобедренной трапеции через стороны и угол, (S):

Формула площади равнобедренной трапеции через стороны и угол

Формула площади равнобедренной трапеции через стороны и угол

Формула площади равнобедренной трапеции через стороны и угол

 

 

2. Формула площади равнобокой трапеции через радиус вписанной окружности

Формула площади равнобокой трапеции через радиус вписанной окружности

R — радиус вписанной окружности

D — диаметр вписанной окружности

O — центр вписанной окружности

H — высота трапеции

α, β — углы трапеции

 

Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

Формула площади равнобокой трапеции через радиус вписанной окружности

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

площадь для вписанной окружности в равнобокую трапецию

 

 

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции

α, β — углы между диагоналями

 

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

Формула площади равнобедренной трапеции через диагонали и угол между ними

 

 

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

Формула площади равнобедренной трапеции через среднюю линию

m — средняя линия трапеции

c — боковая сторона

α, β — углы при основании

 

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

Формула площади равнобедренной трапеции через среднюю линию

 

 

5. Формула площади равнобедренной трапеции через основания и высоту

Формула площади равнобедренной трапеции через основания и высоту

b — верхнее основание

a — нижнее основание

h — высота трапеции

 

Формула площади равнобедренной трапеции через основания и высоту, (S):

Формула площади равнобедренной трапеции через основания и высоту

 

www-formula.ru

Как найти площадь геометрических фигур? – boeffblog.ru

Что такое площадь?

Площадь – характеристика замкнутой геометрической фигуры (круг, квадрат, треугольник и т.д.), которая показывает ее размер. Площадь измеряется в квадратных сантиметрах, метрах и т.д. Обозначается буквой S (square).

 

Как найти площадь треугольника?

1. Самая известная формула площади треугольника по стороне и высоте:

 

S =\displaystyle \bf{\frac{1}{2}} a · h

где a – длина основания, h  – высота треугольника, проведенная к основанию.

\displaystyle \bf{\frac{1}{2}}

Причем, основание не обязательно должно находиться снизу. Так тоже сойдет. \displaystyle \bf{\frac{1}{2}}

Если треугольник тупоугольный, то высота опускается на продолжение основания:

\displaystyle \bf{\frac{1}{2}}

Если треугольник прямоугольный, то основанием и высотой являются его катеты:

\displaystyle \bf{\frac{1}{2}}

 

2. Другая формула, которая является не менее полезной, но которую почему-то всегда забывают:

S = \displaystyle \bf{\frac{1}{2}}   a · b · sinα  

где a и b – две стороны треугольника,  sinα  – синус угла между этими сторонами.

\displaystyle \bf{\frac{1}{2}} \displaystyle \bf{\frac{1}{2}}

Главное условие – угол берется между двумя известными сторонами.

3. Формула площади по трем сторонам (формула Герона):

S = \displaystyle \bf{\sqrt{p(p - a)(p - b)(p - c)}}  

где a, b и с – стороны треугольника, а р – полупериметр. p = (a + b + c)/2.

\displaystyle \bf{\sqrt{p(p - a)(p - b)(p - c)}}

4. Формула площади треугольника через радиус описанной окружности:

S = \displaystyle \bf{\frac{a \cdot b \cdot c}{4R}}  

где a, b и с – стороны треугольника, а R – радиус описанной окружности.

\displaystyle \bf{\frac{a \cdot b \cdot c}{4R}}

5. Формула площади треугольника через радиус вписанной окружности:

S =p · r

где р – полупериметр треугольника, а r – радиус вписанной окружности.

\displaystyle \bf{\frac{a \cdot b \cdot c}{4R}}

Как найти площадь прямоугольника?

1. Площадь прямоугольника находится довольно-таки просто:

S = a · b

\displaystyle \bf{\frac{a \cdot b \cdot c}{4R}}

Никаких подвохов.

Как найти площадь квадрата?

1. Так как квадрат является прямоугольником, у которого все стороны равны, то к нему применяется такая же формула:

S = a · a = a2

\displaystyle \bf{\frac{a \cdot b \cdot c}{4R}}

 

2. Также площадь квадрата можно найти через его диагональ:

S = \displaystyle \bf{\frac{1}{2}}   d2

 

\displaystyle \bf{\frac{1}{2}}

Как найти площадь параллелограмма?

1. Площадь параллелограмма находится по формуле:

S = a · h

\displaystyle \bf{\frac{1}{2}}

Это связано с тем, что если от него отрезать прямоугольный треугольник справа и приставить его слева, получится прямоугольник:

\displaystyle \bf{\frac{1}{2}}

 

 

2. Также площадь параллелограмма можно найти через угол между двумя сторонами:

S = a · b · sinα

\displaystyle \bf{\frac{1}{2}}

 

Как найти площадь ромба?

Ромб по своей сути является параллелограммом, у которого все стороны равны. Поэтому для него применяются те же формулы площади.

 

1. Площадь ромба через высоту:

S = a · h

\displaystyle \bf{\frac{1}{2}}

2. Площадь ромба через угол между сторонами:

S = a · a sinα = a2 · sinα

\displaystyle \bf{\frac{1}{2}}

3. Площадь ромба через диагонали:

S = \displaystyle \bf{\frac{1}{2}}   d1 · d2

\displaystyle \bf{\frac{1}{2}}

Как найти площадь трапеции?

1. Площадь трапеции находится по следующей формуле:

S = \displaystyle \bf{\frac{a + b}{2}}   · h 

\displaystyle \bf{\frac{a + b}{2}}

Как найти площадь круга?

1. Площадь круга можно найти через радиус:

S = π r2 

\displaystyle \bf{\frac{a + b}{2}}

2. Площадь круга можно найти через диаметр:

S = πd2/4

\displaystyle \bf{\frac{a + b}{2}}

boeffblog.ru

Калькулятор расчета площади земельного участка неправильной формы

Инструкция для калькулятора расчета площади неправильного земельного участка

Данный онлайн калькулятор помогает произвести расчет, определение и вычисление площади земельного участка в онлайн режиме. Представленная программа способна правильно подсказать, как выполнить расчет площади земельных участков неправильной формы.

Важно! Важ участок должен приблизительно вписываться в окружность. Иначе расчеты будут не совсем точными.

Указываем все данные в метрах

A B, D A, C D, B C— Размер каждой стороны делянки.

Согласно введен данным, наша программа в онлайн режиме выполнить расчет и определить, площадь земельных угодий в квадратных метрах, сотках, акрах и гектарах.

Методика определения размеров участка ручным методом

Чтобы правильно выполнить расчет площади делянок, не нужно использовать сложные инструменты. Мы берем деревянные колышки или металлические прутья и устанавливаем их в углах нашего участка. Далее при помощи измерительной рулетки определяем ширину и длину делянки. Как правило, достаточно выполнить замер одной ширины и одной длины, для прямоугольных или равносторонних участков. Для примера, у нас получились следующие данные: ширина – 20 метров и длина – 40 метров.

Далее переходим к расчету площади делянки. При правильной форме участка, можно использовать геометрическую формулу определения площади (S) прямоугольника. Согласно этой формуле, нужно выполнить умножение ширины (20) на длину (40) , то есть произведение длин двух сторон. В нашем случае S=800 м².

После того, как мы определили нашу площадь, мы можем определить количество соток на земельном участке. Согласно общепринятым данным, в одной сотке – 100 м². Далее при помощи простой арифметики, мы разделим наш параметр S на 100. Готовый результат и станет равен размеру делянки в сотках. Для нашего примера, этот результат – 8. Таким образом, получаем, что площадь участка составляет восемь соток.

В том случае, когда территория угодий очень большая, то лучше всего выполнять все измерения в других единицах – в гектарах. Согласно общепринятым единицам измерения – 1 Га = 100 соток. К примеру, если наша земельная делянка согласно полученным измерениям составляем 10 000 м², то в этом случае его площадь равна 1 гектару или 100 соткам.

Если Ваш участок неправильной формы, то в этом случае количество соток напрямую зависит от площади. Именно по этой причине при помощи онлайн калькулятора Вы сможете правильно рассчитать параметр S делянки, и после этого разделив полученный результат на 100. Таким образом, Вы получите расчеты в сотках. Такой метод предоставляет возможность измерять делянки сложных форм, что весьма удобно.

Общие данные

Расчет площади земельных участков базируется на классических расчетах, которые выполняются согласно общепринятым геодезическим формулам.

Всего доступно несколько методов для расчета площади земельных угодий – механический (рассчитывается по плану при помощи мерных палеток), графический (определяется по проекту) и аналитический (при помощи формулы площади по измеренным линиям границ).

На сегодняшний день самым точным способом заслуженно считается – аналитический. Используя данный метод, ошибки при расчетах, как правило, появляются из-за погрешностей на местности измеренных линий. Данный способ является также и достаточно сложным, если границы криволинейные или количество углом на делянке больше десяти.

Немного проще по расчетам является графическим способ. Его лучше всего использовать в том случае, когда границы участка представлены в виде ломанной линии, с небольшим количеством поворотов.

И самый доступный и простой способ, и наиболее популярный, но и в тоже время самой большой погрешностью – механический способ. Используя данный метод, Вы сможете легко и быстро выполнить расчет площади земельных угодий простой или сложной формы.

Среди серьезных недостатков механического или графического способа, выделяют следующее, кроме погрешностей при измерении участка, при расчетах добавляется погрешность из-за деформации бумаги или погрешность при составлении планов.

o-builder.ru

Как посчитать площадь комнаты, стены, пола, потолка

Главная » Разное » Как посчитать квадратуру комнаты, стен, потолка, пола

Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты.  О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.  

Часто требуется посчитать площадь комнаты или ее объем

Часто требуется посчитать кубатуру комнаты, ее объем

Площадь комнаты в квадратных метрах

Содержание статьи

Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:

  • Рулетка. Лучше — с фиксатором, но подойдет и обычная.
  • Бумага и карандаш или ручка.
  • Калькулятор (или считайте в столбик или в уме).

Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.

Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.

Прямоугольная комната

Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).

Как высчитать площадь комнаты

Как высчитать площадь комнаты

Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м.  В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.

Помещение неправильной формы

Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).

Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.

Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.

Площадь комнаты сложной офрмы

Площадь комнаты сложной формы

Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):

  1. Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
  2. Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
  3. Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.

Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.

Как посчитать площадь комнаты неправильной формы

Как посчитать площадь комнаты неправильной формы

В этом случае порядок вычислений такой:

  1. Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
  2. Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
  3. Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
  4. Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.

Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.

Формулы расчета площади и периметра простых геометрических фигур

Формулы расчета площади и периметра простых геометрических фигур

Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.

Как рассчитать квадратуру стен

Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:

  • высота потолков;
  • высота и ширина дверных проемов;
  • высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.

Удобнее всего размеры наносить на план

Удобнее всего размеры наносить на план

Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.

  1. Стена с дверью:
    • 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
    • сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
    • стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
  2. Стена с окном:
    1. квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
    2. сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,75 кв.м.
    3. стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.

Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.

Объем комнаты

Формула расчета объема комнаты

Формула расчета объема комнаты

Для некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:

  • длинна — 5,6 м;
  • ширина — 3,2 м;
  • высота — 2,5 м.

Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м3. Итак, объем помещения 44,8 куба.

 

stroychik.ru

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *