Оптика — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Световые волны
К оглавлению…
Свет – это электромагнитные волны, длины волн которых лежат для среднего глаза человека в пределах от 400 до 760 нм. В этих пределах свет называется видимым. Свет с наибольшей длиной волны кажется нам красным, а с наименьшей – фиолетовым. Запомнить чередование цветов спектра легко с помощью поговорки «Каждый Охотник Желает Знать, Где Сидит Фазан». Первые буквы слов поговорки соответствуют первым буквам основных цветов спектра в порядке убывания длины волны (и соответственно возрастания частоты): «Красный – Оранжевый – Желтый – Зеленый – Голубой – Синий – Фиолетовый».
Электромагнитные волны (и, в частности, световые волны, или просто свет) – это распространяющееся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы электрической напряженности и магнитной индукции перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны. Световые волны, как и любые другие электромагнитные волны, распространяются в веществе с конечной скоростью, которая может быть рассчитана по формуле:
где: ε и μ – диэлектрическая и магнитная проницаемости вещества, ε0 и μ0
– электрическая и магнитная постоянные: ε0 = 8,85419·10–12 Ф/м, μ0 = 1,25664·10–6 Гн/м. Скорость света в вакууме (где ε = μ = 1) постоянна и равна с = 3∙108 м/с, она также может быть вычислена по формуле:
Скорость света в вакууме (где ε = μ = 1) постоянна и равна с = 3∙108 м/с, она также может быть вычислена по формуле:Скорость света в вакууме является одной из фундаментальных физических постоянных. Если свет распространяется в какой-либо среде, то скорость его распространения также выражается следующим соотношением:
где: n – показатель преломления вещества – физическая величина, показывающая во сколько раз скорость света в среде меньше чем в вакууме. Показатель преломления, как видно из предыдущих формул, может быть рассчитан следующим образом:
- Свет переносит энергию. При распространении световых волн возникает поток электромагнитной энергии.
- Световые волны испускаются в виде отдельных квантов электромагнитного излучения (фотонов) атомами или молекулами.
Кроме света существуют и другие виды электромагнитных волн. Далее они перечислены по уменьшению длины волны (и соответственно, по возрастанию частоты):
- Радиоволны;
- Инфракрасное излучение;
- Видимый свет;
- Ультрафиолетовое излучение;
- Рентгеновское излучение;
- Гамма-излучение.

Интерференция
К оглавлению…
Интерференция – одно из ярких проявлений волновой природы света. Оно связано с перераспределением световой энергии в пространстве при наложении так называемых когерентных волн, то есть волн, имеющих одинаковые частоты и постоянную разность фаз. Интенсивность света в области перекрытия пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра.
Для расчета интерференции используется понятие оптической длины пути. Пусть свет прошел расстояние L в среде с показанием преломления n. Тогда его оптическая длина пути рассчитывается по формуле:
Для интерференции необходимо наложение хотя бы двух лучей. Для них вычисляется оптическая разность хода (разность оптических длин) по следующей формуле:
Именно эта величина и определяет, что получится при интерференции: минимум или максимум. Запомните следующее: интерференционный максимум (светлая полоса) наблюдается в тех точках пространства, в которых выполняется следующее условие:
Запомните следующее: интерференционный максимум (светлая полоса) наблюдается в тех точках пространства, в которых выполняется следующее условие:
Разность фаз колебаний при этом составляет:
При m = 0 наблюдается максимум нулевого порядка, при m = ±1 максимум первого порядка и так далее. Интерференционный минимум (темная полоса) наблюдается при выполнении следующего условия:
Разность фаз колебаний при этом составляет:
При первом нечетном числе (единица) будет минимум первого порядка, при втором (тройка) минимум второго порядка и т.д. Минимума нулевого порядка не бывает.
Дифракция. Дифракционная решетка
К оглавлению…
Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий, размеры которых сопоставимы с длиной волны света (огибание светом препятствий). Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени (то есть быть там, где его быть не должно).
Дифракционные решетки представляют собой периодические структуры, выгравированные специальной делительной машиной на поверхности стеклянной или металлической пластинки. У хороших решеток параллельные друг другу штрихи имеют длину порядка 10 см, а на каждый миллиметр приходится до 2000 штрихов. При этом общая длина решетки достигает 10–15 см. Изготовление таких решеток требует применения самых высоких технологий. На практике применяются также и более грубые решетки с 50–100 штрихами на миллиметр, нанесенными на поверхность прозрачной пленки.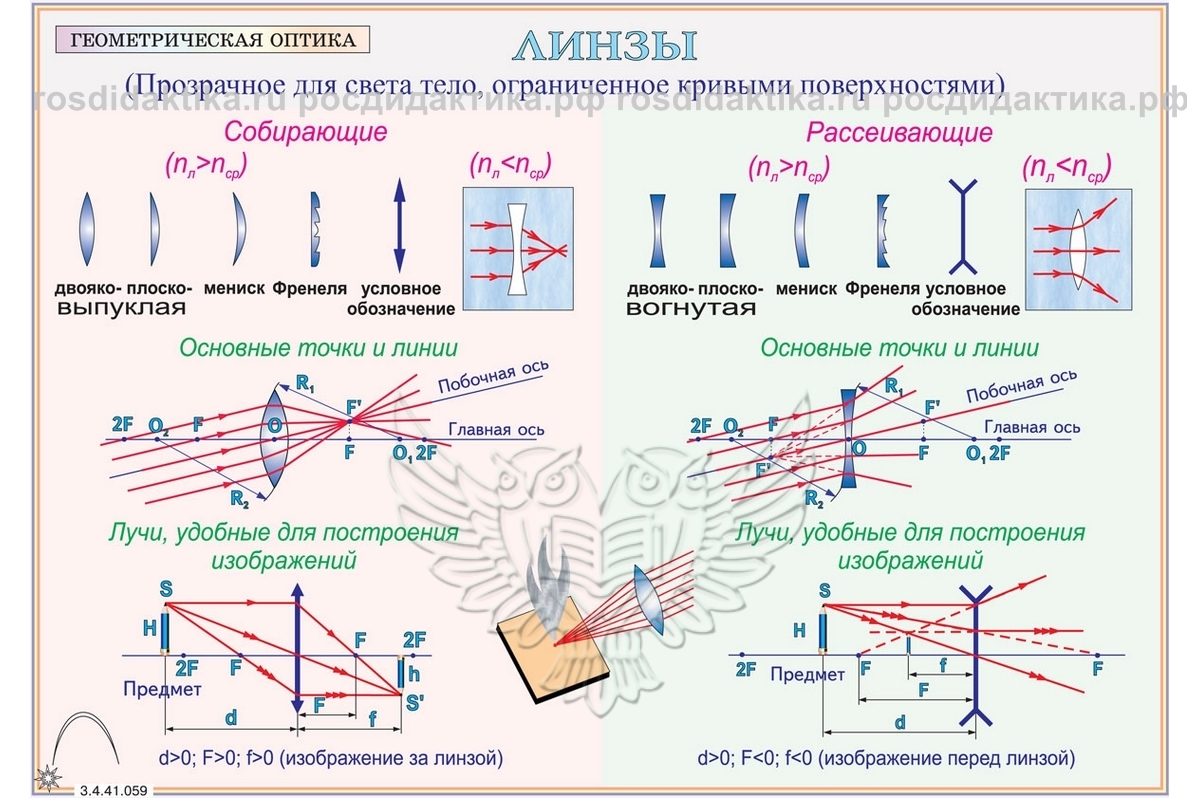
При нормальном падении света на дифракционную решетку в некоторых направлениях (помимо того, в котором изначально падал свет) наблюдаются максимумы. Для того, чтобы наблюдался интерференционный максимум, должно выполняться следующее условие:
где: d – период (или постоянная) решетки (расстояние между соседними штрихами), m – целое число, которое называется порядком дифракционного максимума. В тех точках экрана, для которых это условие выполнено, располагаются так называемые главные максимумы дифракционной картины.
Законы геометрической оптики
К оглавлению…
Геометрическая оптика – это раздел физики, в котором не учитываются волновые свойства света. Основные законы геометрической оптики были известны задолго до установления физической природы света.
Оптически однородная среда — это среда, во всем объеме которой показатель преломления остаётся неизменным.
Закон прямолинейного распространения света: в оптически однородной среде свет распространяется прямолинейно. Этот закон приводит к представлению о световом луче как о геометрической линии, вдоль которой распространяется свет. Следует отметить, что закон прямолинейного распространения света нарушается и понятие светового луча утрачивает смысл, если свет проходит через малые отверстия, размеры которых сравнимы с длиной волны (в этом случае наблюдается дифракция).
Этот закон приводит к представлению о световом луче как о геометрической линии, вдоль которой распространяется свет. Следует отметить, что закон прямолинейного распространения света нарушается и понятие светового луча утрачивает смысл, если свет проходит через малые отверстия, размеры которых сравнимы с длиной волны (в этом случае наблюдается дифракция).
На границе раздела двух прозрачных сред свет может частично отразиться так, что часть световой энергии будет распространяться после отражения по новому направлению, а частично пройти через границу и распространяться во второй среде.
Закон отражения света:
Закон преломления света (закон Снеллиуса): падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред, и определяется выражением:
Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред, и определяется выражением:
Закон преломления был экспериментально установлен голландским ученым В.Снеллиусом в 1621 году. Постоянную величину n21 называют относительным показателем преломления второй среды относительно первой. Показатель преломления среды относительно вакуума называют абсолютным показателем преломления.
Среду с большим значением абсолютного показателя называют оптически более плотной, а с меньшим – менее плотной. При переходе из менее плотной среды в более плотную луч «прижимается» к перпендикуляру, а при переходе из более плотной в менее плотную – «удаляется» от перпендикуляра. Единственный случай, когда луч не преломляется, это если угол падения равен 0 (то есть лучи перпендикулярны границе раздела сред).
При переходе света из оптически более плотной среды в оптически менее плотную n2 < n1 (например, из стекла в воздух) можно наблюдать явление полного внутреннего отражения, то есть исчезновение преломленного луча. Это явление наблюдается при углах падения, превышающих некоторый критический угол
Это явление наблюдается при углах падения, превышающих некоторый критический угол
Как только угол падения становиться больше предельного, то преломленный луч уже не просто идет вдоль границы, а он и вовсе не появляется, так как его синус теперь уж должен быть больше единицы, а такого не может быть.
Линзы
К оглавлению…
Линзой называется прозрачное тело, ограниченное двумя сферическими поверхностями. Если толщина самой линзы мала по сравнению с радиусами кривизны сферических поверхностей, то линзу называют тонкой.
Линзы бывают собирающими и рассеивающими. Если показатель преломления линзы больше, чем окружающей среды, то собирающая линза в середине толще, чем у краев, рассеивающая линза, наоборот, в средней части тоньше. Если показатель преломления линзы меньше, чем окружающей среды, то всё наоборот.
Если показатель преломления линзы больше, чем окружающей среды, то собирающая линза в середине толще, чем у краев, рассеивающая линза, наоборот, в средней части тоньше. Если показатель преломления линзы меньше, чем окружающей среды, то всё наоборот.
Прямая, проходящая через центры кривизны сферических поверхностей, называется главной оптической осью линзы. В случае тонких линз можно приближенно считать, что главная оптическая ось пересекается с линзой в одной точке, которую принято называть оптическим центром линзы. Луч света проходит через оптический центр линзы, не отклоняясь от первоначального направления. Все прямые, проходящие через оптический центр, называются побочными оптическими осями.
Если на линзу направить пучок лучей, параллельных главной оптической оси, то после прохождения через линзу лучи (или их продолжения) соберутся в одной точке F, которая называется главным фокусом линзы. У тонкой линзы имеются два главных фокуса, симметрично расположенных относительно линзы на главной оптической оси.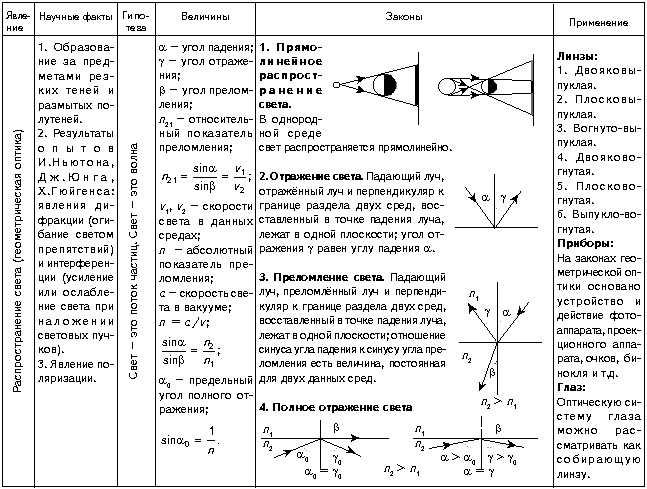 У собирающих линз фокусы действительные, у рассеивающих – мнимые. Расстояние между оптическим центром линзы O и главным фокусом F называется фокусным расстоянием. Оно обозначается той же буквой F.
У собирающих линз фокусы действительные, у рассеивающих – мнимые. Расстояние между оптическим центром линзы O и главным фокусом F называется фокусным расстоянием. Оно обозначается той же буквой F.
Правила построения хода луча в линзах
К оглавлению…
Формула линзы
К оглавлению…
Основное свойство линз – способность давать изображения предметов. Изображение – это точка пространства, где пересекаются лучи (или их продолжения), испущенные источником после преломления в линзе. Изображения бывают прямыми и перевернутыми, действительными (пересекаются сами лучи) и мнимыми (пересекаются продолжения лучей), увеличенными и уменьшенными.
Положение изображения и его характер можно определить с помощью геометрических построений. Для этого используют свойства некоторых стандартных лучей, ход которых известен. Это лучи, проходящие через оптический центр или один из фокусов линзы, а также лучи, параллельные главной или одной из побочных оптических осей.
Это лучи, проходящие через оптический центр или один из фокусов линзы, а также лучи, параллельные главной или одной из побочных оптических осей.
Для простоты можно запомнить, что изображение точки будет точкой. Изображение точки, лежащей на главной оптической оси, лежит на главной оптической оси. Изображение отрезка – отрезок. Если отрезок перпендикулярен главной оптической оси, то его изображение перпендикулярно главной оптической оси. А вот если отрезок наклонен к главной оптической оси под некоторым углом, то его изображение будет наклонено уже под некоторым другим углом.
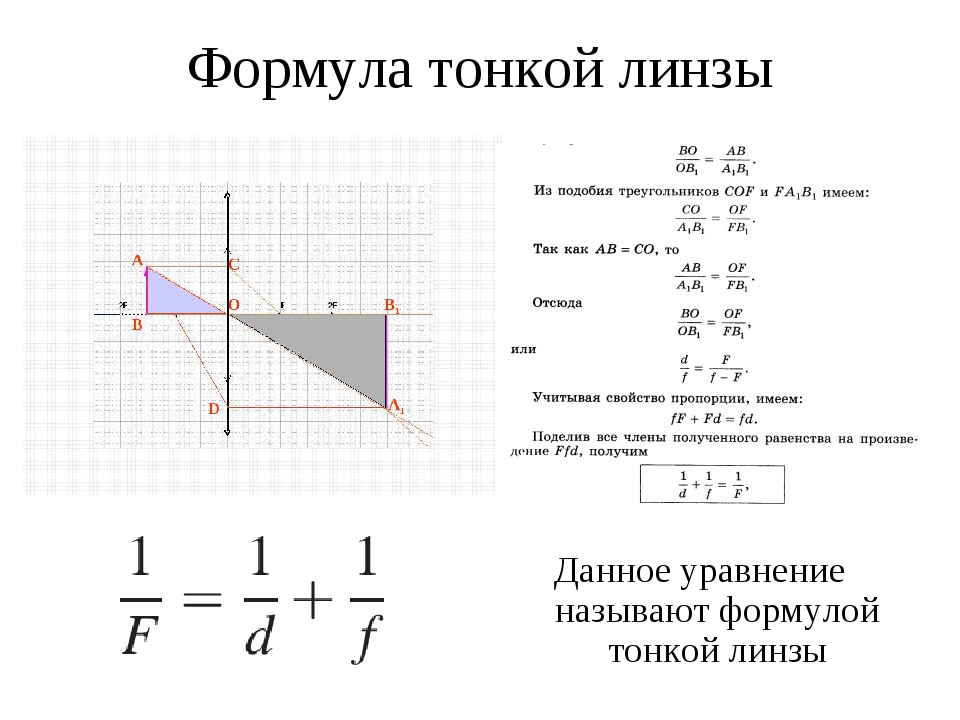
Изображения можно также рассчитать с помощью формулы тонкой линзы. Если кратчайшее расстояние от предмета до линзы обозначить через d, а кратчайшее расстояние от линзы до изображения через f, то формулу тонкой линзы можно записать в виде:
Величину D, обратную фокусному расстоянию. называют оптической силой линзы. Единица измерения оптической силы является 1 диоптрия (дптр). Диоптрия – оптическая сила линзы с фокусным расстоянием 1 м.
Диоптрия – оптическая сила линзы с фокусным расстоянием 1 м.
Фокусным расстояниям линз принято приписывать определенные знаки: для собирающей линзы F > 0, для рассеивающей F < 0. Оптическая сила рассеивающей линзы также отрицательна.
Величины d и f также подчиняются определенному правилу знаков: f > 0 – для действительных изображений; f < 0 – для мнимых изображений. Перед d знак «–» ставится только в том случае, когда на линзу падает сходящийся пучок лучей. Тогда их мысленно продлевают до пересечения за линзой, помещают туда воображаемый источник света, и определяют для него расстояние d.
В зависимости от положения предмета по отношению к линзе изменяются линейные размеры изображения. Линейным увеличением линзы Γ называют отношение линейных размеров изображения и предмета. Для линейного увеличения линзы существует формула:
Во многих оптических приборах свет последовательно проходит через две или несколько линз. Изображение предмета, даваемое первой линзой, служит предметом (действительным или мнимым) для второй линзы, которая строит второе изображение предмета и так далее.
Изображение предмета, даваемое первой линзой, служит предметом (действительным или мнимым) для второй линзы, которая строит второе изображение предмета и так далее.
Оптика — Основные формулы
1. Фотометрия и светотехника
1.1 Поток излучения
Φ — поток излучения,
W — энергия излучения,
t — время прохождения энергии излучения.
1.2 Сила света
I — сила света,
Φ — поток излучения,
Ω — телесный угол, через который проходит поток излучения.
1.3 Освещенность
E — освещенность,
Φ — поток излучения,
σ — площадь, через которую проходит поток излучения.
1.4 Яркость источника света
L — яркость источника света,
I — сила света,
σ — площадь видимой светящейся поверхности.
1.5 Коэффициент поглощения
α — коэффициент поглощения,
Φα — световой поток, поглощенный телом,
Φi — световой поток, падающий на тело.
1.6 Коэффициент отражения
ρ — коэффициент отражения,
Φρ — световой поток, отраженный телом,
Φi — световой поток, падающий на тело.
1.7 Коэффициент пропускания
τ — коэффициент пропускания,
Φτ — световой поток, пропущенный телом,
Φi — световой поток, падающий на тело.
2. Геометрическая оптика
2.1 Относительный показатель преломления
n — относительный показатель преломления для граничащих сред
n2 — абсолютный показатель преломления для второй среды,
n1 — абсолютный показатель преломления для первой среды.
2.2 Закон преломления света
i — угол отражения,
r — угол преломления,
n — относительный показатель преломления для граничащих сред.
2.3 Предельный угол полного внутреннего отражения
iпр — предельный угол полного внутреннего отражения,
n — относительный показатель преломления для граничащих сред.
2.4 Основная формула тонкой линзы
a — расстояние от источника света до линзы,
a’ — расстояние от линзы до изображения источника света,
f — фокусное расстояние линзы.
2.5 Основная формула сферического зеркала
a — расстояние от источника света до зеркала,
a’ — расстояние от зеркала до изображения источника света,
R — радиус кривизны зеркала,
f — фокусное расстояние зеркала.
2.6 Линейное увеличение
β — линейное увеличение линзы или зеркала,
h — высота источника света,
h’ — высота изображения источника света,
a — расстояние от источника света до линзы или зеркала,
a’ — расстояние от линзы или зеркала до изображения источника света.
2.7 Угловое увеличение
γ — угловое увеличение линзы или зеркала,
β — линейное увеличение линзы или зеркала.
2.8 Оптическая сила линзы
D — оптическая сила линзы,
f — фокусное расстояние.
2.9 Светосила линзы
E — светосила линзы,
d — диаметр линзы или диафрагмы, закрывающей линзу,
f — фокусное расстояние.
3. Оптические приборы
3.1 Увеличение лупы
N — увеличение лупы,
D — расстояние наилучшего видения человеческого глаза, обычно D=250 мм, при этом f также должно быть выражено в мм,
f — фокусное расстояние лупы.
3.2 Увеличение микроскопа
N — увеличение микроскопа,
N1 — увеличение окуляра микроскопа,
N2 — увеличение объектива микроскопа,
D — расстояние наилучшего видения человеческого глаза, обычно D=250 мм, при этом f также должно быть выражено в мм,
f — фокусное расстояние системы линз микроскопа: окуляра и объектива.
3.3 Увеличение зрительной (подзорной) трубы
N — увеличение зрительной (подзорной) трубы,
f1 — фокусное расстояние объектива,
f2 — фокусное расстояние окуляра.
Оптика: физика, 8 класс. Закон отражения: формула расчета
Сегодня мы расскажем о законе отражения света. Мы также выделим часть линейной оптики, к которой относится это явление.
Школа и свет
В первый класс дети идут с нетерпением. Им интересно, что значит учиться, их захватывает возня с учебниками и тетрадками. Но дисциплина – вещь строгая. Да и психологические законы замкнутой группы детей достаточно жестокие. Поэтому со школой более взрослые ученики ассоциируют только нежелание ходить туда. Тем не менее при креативном подходе к самим знаниям, можно изменить взгляд на мир уроков и дневников. Сегодня мы расскажем об одном важном понятии оптики. Физика 8 класса дает это явление как законы преломления и отражения света.
Волна и свет
Как ни странно это звучит, но свет – это волна. «В каких морях?» – спросят школьники. И мы ответим: «В электромагнитных». Начало этой сложной системе дает движущийся заряженный объект. В прямом смысле этого слова. Если экспериментатор наэлектризует кусочек янтаря и быстро побежит с ним, то в процессе движения возникнет очень слабое и очень короткое электромагнитное поле. Источником больших полей, которые пронизывают всю вселенную, являются в основном звезды. Солнце тоже объект с ненулевым зарядом, поэтому Земля буквально «купается» в созданных им частицах и электромагнитных полях. А свет – это квант электромагнитного поля, а значит, можно к нему применить закон отражения.
Отражение, преломление, поглощение
Итак, в чем же суть закона? В следующем:
- Если на гладкую поверхность падает пучок света, то он, нормаль к поверхности в точке падения и отраженный свет лежат в одной плоскости.
- Угол наклона падающего пучка к нормали равен углу наклона отраженного света.

Иногда учеников школы пугает непонятное слово «нормаль». Но оно совсем не страшное. Это всего лишь перпендикуляр к данной точке поверхности. И нормаль чаще всего воображаемая линия, ее надо додумывать для того, чтобы решить задачу.
Угол падения равен углу отражения
Чем вредна эта формулировка закона отражения света? 8 класс часто уменьшает количество слов в школьных правилах, чтобы лучше запомнить их. Но даже линейная оптика – предмет, в котором имеет значение вектор действия и распространения. То есть важны не только взаимные углы пучков света, но и направление их распространения. В данном случае важно не забывать, что для падающего, отраженного изображения и нормали к поверхности в точке падения есть только одна плоскость.
Виды отражения
Казалось бы, проще этого правила и быть не может. Но и здесь есть свои особенности:
- Встречаясь с диэлектриком, свет вызывает в его атомах колебания диэлектрической поляризации. Это приводит к тому, что каждая точка среды становится вторичным источником волн.
 Складываясь, они порождают отраженный, преломленный и рассеянный свет.
Складываясь, они порождают отраженный, преломленный и рассеянный свет. - Попадая на проводящий материал, электромагнитное излучение вызывает колебания электронов. Материал стремится скомпенсировать возникающий ток, отчего возникает почти полное отражение. Поэтому металл такой блестящий.
- Диффузное отражение возникает, когда поверхность имеет шероховатости. Их размер должен превышать длину волны падающего излучения. Однако может возникнуть ситуация, при которой коротковолновое фиолетовое излучение рассеивается, а длинноволновое красное отлично отражается.
- Внутреннее отражение. Если свет падает из более плотной среды в более разреженную (например, из воды в воздух), то при определенном угле весь пучок отражается обратно. Закон полного отражения связан с разностью показателей преломления света в среде. Его формула выражается так:
где j – угол, при котором наступает полное внутреннее отражение, а n2 и n1 – показатели преломления двух сред.
Что и когда отражается?
Помимо школьных уроков и скучных задач, закон отражения, формулу которого мы привели чуть выше, можно наблюдать и в других случаях:
- Когда волны звука отражаются от твердых поверхностей, они возвращаются обратно в виде эха. Именно из-за этого эффекта голоса детей звучат громче в закрытом дворе, чем на берегу реки. Пустая комната сразу после ремонта тоже дает эхо, а мебель, которую туда ставят потом, поглощает колебания воздуха.
- Разведывательные корабли пускают впереди себя волны ультразвука, по скорости отражения которых можно судить о рельефе дна.
- Радиоволны отражаются от самолетов, что и позволяет определить их местонахождение в воздухе.
- При медицинском исследовании ультразвук отражается от границы органов и дает специалистам возможность судить о происходящих внутри человека процессах, не разрезая ткани.
Зеркало и Китай
Однако не стоит думать, что отражение – это изобретение новейшее. Как только люди научились получать чистый металл (бронза), женщины тут же захотели знать, как они выглядят.
Как только люди научились получать чистый металл (бронза), женщины тут же захотели знать, как они выглядят.
Чтобы материал лучше отражал, его поверхность долго шлифовали вручную. А так как смотреться можно было только в одну сторону бронзового диска, другую украшали каким-нибудь рисунком.
В Древнем Китае некоторые мастера умели делать зеркала, тайна которых не разгадана до сих пор. Если солнечный зайчик от гладкой стороны такого предмета направить на белую стену или лист бумаги, то в круге света… проявится картинка, выгравированная на обратной стороне. Суть этого явления не смогли объяснить даже современные методы исследования. Предположения о том, как это происходит, такие:
- Рисунок вдавливается насквозь, потом одна сторона ошлифовывается, а разница в структуре металла остается.
- Медный расплав льется в подготовленный заранее шаблон, и более толстый слой металла (где у рисунка выпуклость) застывает в немного иной форме, чем тонкий элемент. Эта разница остается и после шлифовки.

- Гладкая сторона зеркала травится кислотой. После обработки разница в цвете незаметна, но при этом в ярком солнечном свете интенсивность отраженного изображения разная.
- На зеркальную часть предмета рисунок наносится медью другого сорта.
- Изображение вырезают на тыльной стороне зеркала, когда лицевая часть уже отшлифована до определенной степени. Давление воздействует на обе части предмета. Зеркальная сторона покрывается как бы серией микровыпуклостей, которые соответствуют рисунку. Еще одна шлифовка завершает работу, придавая созданным буграм и впадинам более гладкий вид.
Трудно поверить в то, что в век атомной спектроскопии и рентгеновского исследования материи еще существуют загадки, связанные с отражением, но факты – вещь упрямая.
Основные формулы и методические рекомендации по решению задач на законы геометрической оптики
В данной теме будут рассмотрены основные формулы и методические рекомендации по решению задач на оптику
Геометрическая
оптика изучает законы распространения света в прозрачных
средах, отражения света от зеркально-отражающих поверхностей, а также принципы
построения изображений при прохождении света в оптических системах без учёта
его волновых свойств.
Волновая оптика рассматривает волновые свойства света, такие как интерференция, дифракция, поляризационные эффекты и так далее (то есть, те оптические явления, которые выходят за рамки геометрической оптики).
Фотометрия производит количественные измерения характеристик поля излучения, таких как освещённость, световой поток, сила света и так далее. Эта наука является прикладной и используется в различных областях.
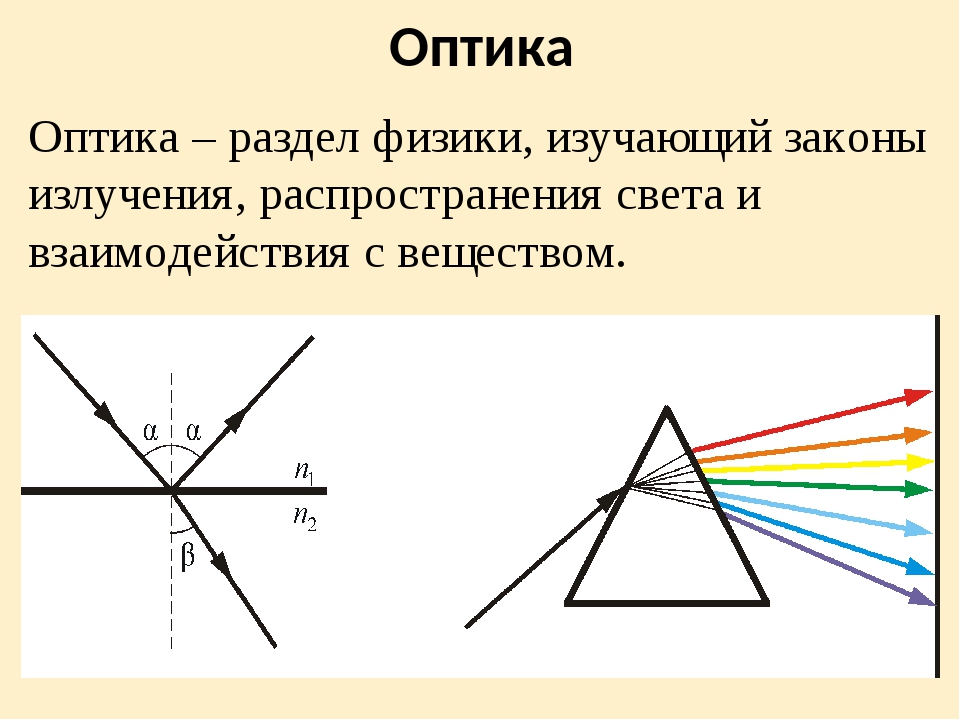
Изобразим на рисунке некоторую среду, на границу которой падает световой луч. Известно, что свет имеет способность преломляться и отражаться. Проведём перпендикуляр в точке падения и обозначим на чертеже необходимые углы.
Угол
a называется углом падения. Это угол
между падающим лучом и перпендикуляром, восстановленным в точку падения. Угол g
называется
углом отражения – это угол между отражённым лучом и перпендикуляром,
восстановленным в точку падения.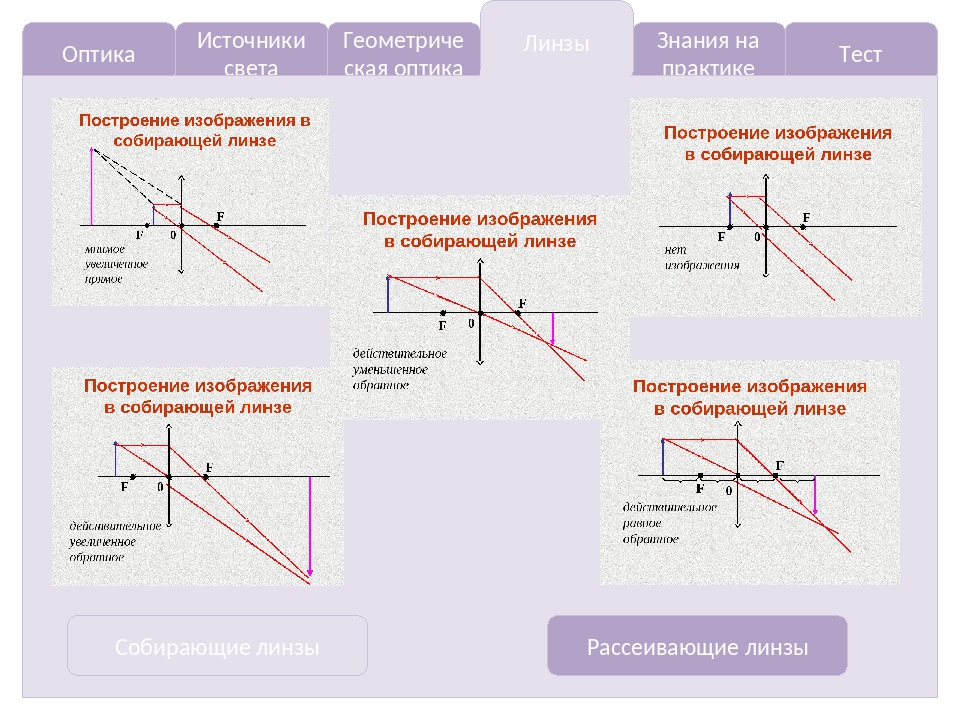 Угол b называется углом
преломления – это угол между преломлённым лучом и перпендикуляром,
восстановленным в точку падения.
Угол b называется углом
преломления – это угол между преломлённым лучом и перпендикуляром,
восстановленным в точку падения.
Линзой называется любое прозрачное тело, которое с обеих сторон ограничено сферическими поверхностями. Линзы бывают собирающими и рассеивающими. Собирающая (или выпуклая) линза – это линза, края которой тоньше, чем середина. Рассеивающая (или вогнутая) линза – это линза, края которой толще, чем середина.
На чертежах собирающие и рассеивающие линзы обозначаются специальным образом (так, как показано на рисунке).
Тонкая линза – это линза, толщина которой много меньше, чем радиусы кривизны сферических поверхностей, которыми она ограничена.
Проведём
линию, проходящую через центры сферических поверхностей, которыми ограничена
линза. Эта линия называется главной оптической осью (или просто
оптической осью). На этой линии лежит точка, которая называется оптическим
центром линзы. Это единственная точка линзы, проходя через
которую, свет не преломляется. Если линза симметрична и однородна, то её
оптический центр совпадает с геометрическим центром.
На этой линии лежит точка, которая называется оптическим
центром линзы. Это единственная точка линзы, проходя через
которую, свет не преломляется. Если линза симметрична и однородна, то её
оптический центр совпадает с геометрическим центром.
Рассмотрим несколько лучей, направленных на собирающую линзу параллельно оптической оси (чтобы упростить чертёж, мы изобразили всего два луча). После преломления эти лучи пересекутся в некоторой точке F, расположенной на главной оптической оси. Повторим ту же процедуру для рассеивающей линзы: направим на неё два луча параллельно оптической оси. После преломления получаются расходящиеся лучи, которые не пересекутся. Но если начертить продолжения этих лучей, то эти продолжения тоже пересекутся на главной оптической оси (только с другой стороны от линзы).
Полученные
точки F называются фокусами
линзы. В случае собирательной линзы фокус называется действительным, а в
случае рассеивающей линзы – мнимым.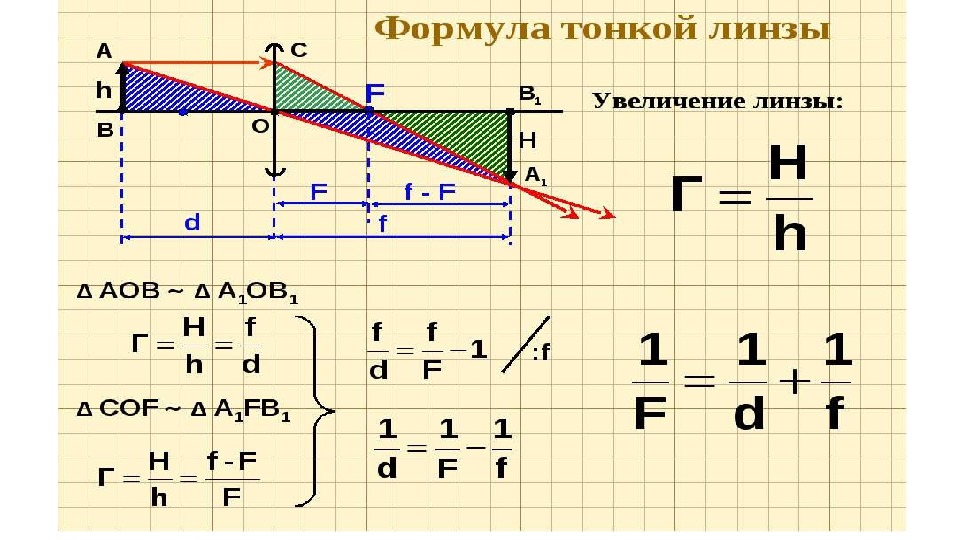 Расстояние между оптическим центром линзы и
её фокусом называется фокусным расстоянием. Фокусное расстояние
зависит от того, насколько сильно преломляются лучи, проходя через данную
линзу. Поэтому, вводится такая величина, как оптическая сила –
именно этой величиной характеризуется преломляющая способность линзы.
Расстояние между оптическим центром линзы и
её фокусом называется фокусным расстоянием. Фокусное расстояние
зависит от того, насколько сильно преломляются лучи, проходя через данную
линзу. Поэтому, вводится такая величина, как оптическая сила –
именно этой величиной характеризуется преломляющая способность линзы.
Рассмотрим некоторые понятия и величины, связанные с трёхгранной призмой.
При прохождении через такую призму, луч света отклоняется в сторону основания. Грани, через которые проходит луч света, называются преломляющими гранями призмы. Соответственно угол, образованный этими гранями, называется преломляющим. Угол между падающим лучом и лучом, выходящим из призмы, называется углом отклонения. Именно с углом отклонения связано большинство задач на ход лучей в призме.
Интерференция
света – это явление сложения двух и более когерентных волн, приводящее к
образованию в пространстве устойчивой картины чередующихся максимумов и
минимумов интенсивности света.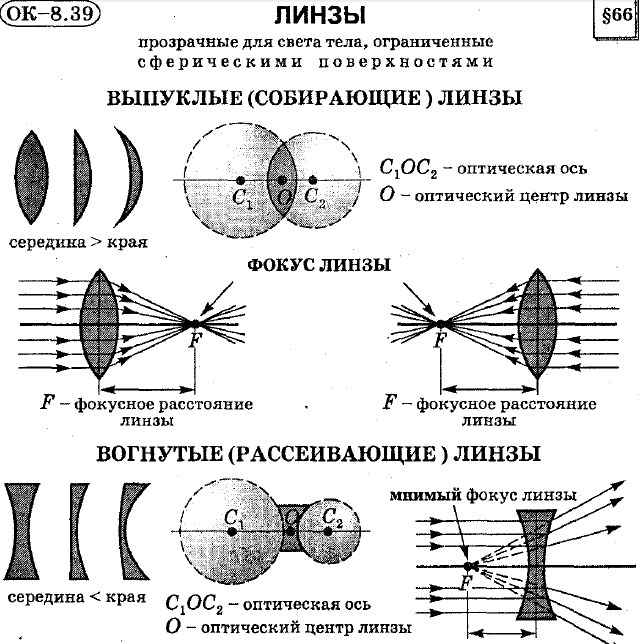
На рисунке показан простейший способ получения двух интерферирующих волн света.
Полученная картина чередования минимумов и максимумов называется интерференционной картиной. То есть, происходит перераспределение интенсивности света: в одних областях волны суммируются, а в других – погашают друг друга.
Дифракцией света называется совокупность оптических явлений, в результате которых происходит огибание волнами препятствий, размеры которых соизмеримы с длиной волны.
Если воспользоваться пластиной с круглым отверстием и направить в это отверстие луч света, то в центре светлого пятна получится тёмное пятнышко, и, наоборот, за непрозрачным диском тени будет находиться светлое пятно в центре тени.
На
основе явления дифракции был создан прибор, который называется дифракционной
решёткой. Он используется для разложения света в спектр и измерения
длины волны.
Рассмотрим самое обычное помещение, например, учебный класс. Иногда ученики говорят, что в классе светло или темно. Существует такая величина, как освещённость. Она равна отношению светового потока, падающего на поверхность к площади этой поверхности. Например, когда туча заслоняет солнце, то в классе становится темнее. Имеется ввиду, что освещённость класса уменьшилась, поскольку теперь меньший поток солнечных лучей приходится на ту же площадь. Световым потоком называется отношение полной энергии, выделенной источником света ко времени, в течение которого выделялась энергия.
Сила света – это величина световой энергии, переносимой в определённом направлении в единицу времени.
Рассмотрим
некоторые коэффициенты, определяющие оптические свойства различных тел. Коэффициент
поглощения – это соотношение поглощенного потока света с падающим
потоком. Часть падающего светового потока на стекло поглощается и только часть
проходит сквозь него. В противном случае, стекло бы не нагревалось под
солнечными лучами. Например, коэффициент поглощения у тел тёмного цвета больше,
чем коэффициент поглощения у тел светлого цвета, поэтому, тёмные тела быстрее
нагреваются на солнце.
В противном случае, стекло бы не нагревалось под
солнечными лучами. Например, коэффициент поглощения у тел тёмного цвета больше,
чем коэффициент поглощения у тел светлого цвета, поэтому, тёмные тела быстрее
нагреваются на солнце.
Коэффициент отражения – это соотношение отражённого потока света с падающим потоком. Известно, что часть солнечных лучей отражается от окна.
Коэффициент пропускания – это соотношение пропущенного потока света с падающим потоком. Этот коэффициент связан с двумя предыдущими коэффициентами. Чем больший световой поток тело отражает и поглощает, тем меньший световой поток оно пропускает.
Сведём в таблицу основные формулы геометрической оптики.
|
Формула |
Описание формулы |
|
Закон
отражения света, где a – угол падения, g
– угол отражения. |
|
|
Закон преломления света, где a – угол падения, b – угол преломления, и – скорости света в данных средах, а – относительный показатель преломления для данных двух сред |
|
|
Абсолютный показатель преломления среды, где с –скорость света в вакуумек |
|
|
Оптическая сила линзы, F – фокусное расстояние линзы. |
|
|
Формула тонкой линзы, d – расстояние от предмета до линзы, f – расстояние от линзы до изображения. |
|
|
Линейное увеличение |
|
|
Угол
отклонения луча призмой, –
угол падения на преломляющую грань призмы, –
угол выхода луча из призмы, –
преломляющий угол призмы. |
|
|
Угол отклонения луча призмой при падении света на преломляющую грань призмы под очень малым углом, n – относительный показатель преломления материала призмы. |
Сведём в таблицу основные формулы волновой оптикию
|
Формула |
Описание формулы |
|
Формула дифракционной решётки, где d – период дифракционной решетки, j – угол, определяющий направление распространения волн, l – длина волны, – определяет порядок спектра. |
|
|
Условие интерференционных максимумов |
|
|
Условие интерференционных минимумов |
Сведём
в таблицу основные формулы фотометрии.
|
Формула |
Описание формулы |
|
Полный световой поток от точечного источника с силой света I. |
|
|
Освещённость поверхности площадью S, где F – световой поток равномерно распределённый по всей поверхности. |
|
|
Освещенность поверхности, на которую падает световой поток под углом a. |
|
|
Коэффициент поглощения света, где Fa – световой поток, поглощенный телом, Fi – световой поток, падающий на тело. |
|
|
Коэффициент
отражения света, где Fr
– световой поток, отражённый телом. |
|
|
Коэффициент пропускания, где Ft– световой поток, пропущенный телом. |
Методические рекомендации по решению задач на законы отражения и преломления света.
1. Сделать наглядный чертёж, отметив на нём падающие, отражённые и/или преломлённые лучи, а также соответствующие углы.
2. При необходимости отметить на чертеже дополнительные углы (например, углы отклонения лучей).
3. Применить закон отражения и/или закон преломления света.
4. Используя теоремы и аксиомы геометрии, рассмотреть чертеж.
5. На основании применённых теорем и законов, составить систему уравнений и решить её относительно искомых величин.
Методические рекомендации по решению задач на линзы
1. Сделать
наглядный чертёж и построить изображение, требуемое для решения задачи.
Сделать
наглядный чертёж и построить изображение, требуемое для решения задачи.
2. В зависимости от условия задачи, применить формулу тонкой линзы, формулу линейного увеличения линзы или формулу для вычисления оптической силы линзы.
3. Записать в виде уравнений какие-либо дополнительные условия задачи (если таковые имеются).
4. На основании применённых законов и формул, составить систему уравнений и решить её относительно искомых величин.
Методические рекомендации по решению задач на призмы
1. Сделать наглядный чертёж, построив ход лучей в призме и указав не нём все необходимы углы.
2. Применить формулу для нахождения угла отклонения.
3. При необходимости использовать теоремы и аксиомы геометрии.
4.
На
основании применённых законов и формул, составить систему уравнений и решить её
относительно искомых величин.
Методические рекомендации по решению задач на интерференцию и дифракцию света
1. При необходимости сделать чертёж, соответствующий ситуации, описанной в задаче.
2. Применить условия интерференционных минимумов и максимумов.
3. При необходимости использовать формулу дифракционной решётки.
4. Записать в виде уравнений какие-либо дополнительные условия задачи (если таковые имеются).
5. На основании применённых теорем и законов, составить систему уравнений и решить её относительно искомых величин.
Методические рекомендации по решению элементарных задач на фотометрию
1. При необходимости сделать чертёж, соответствующий ситуации, описанной в задаче.
2. Применить формулы освещенности и/или светового потока.
3.
Записать
в виде уравнений какие-либо дополнительные условия задачи (если таковые
имеются).
4. На основании применённых теорем и законов, составить систему уравнений и решить её относительно искомых величин.
Примеры решения задач. Геометрическая оптика
Примеры решения задач. Геометрическая оптика
- Подробности
- Просмотров: 887
«Физика — 11 класс»
1.
Плоское зеркало повернули на угол α = 17° вокруг оси, лежащей в плоскости зеркала.
На какой угол β повернется отраженный от зеркала луч, если направление падающего луча осталось неизменным?
Р е ш е н и е.
Пусть φ — первоначальный угол падения луча.
По закону отражения угол отражения также равен φ, и, следовательно, угол между падающим лучом и отраженным лучом равен 2φ.
При повороте зеркала на угол α перпендикуляр I к зеркалу, восставленный в точке падения, также повернется на угол α и займет положение II.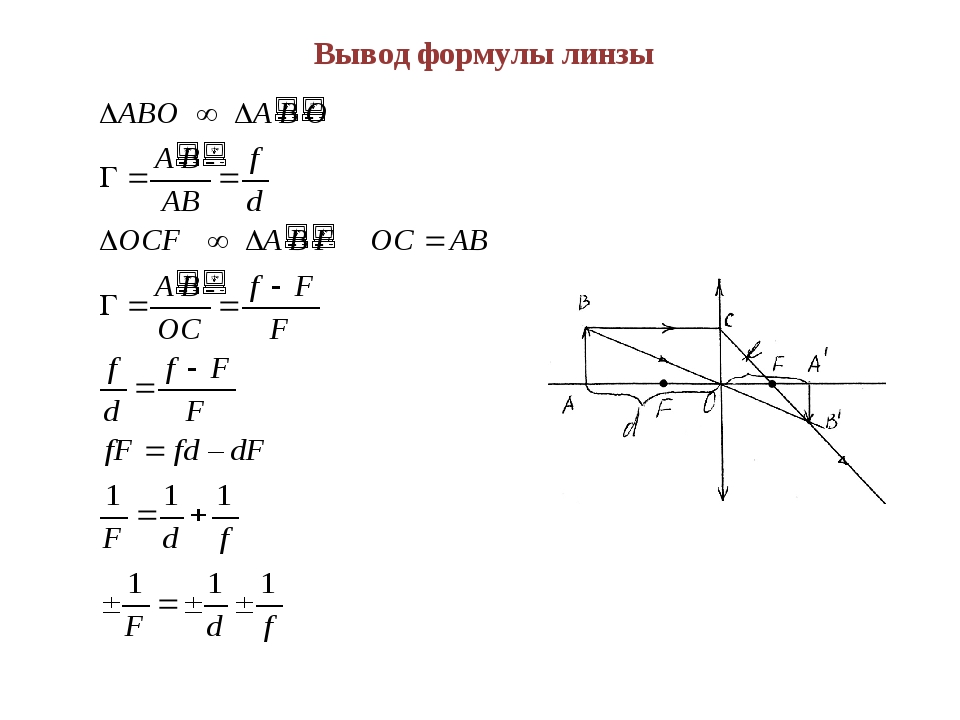
Значит, новый угол падения будет равен φ + α.
Таким же будет и новый угол отражения.
Поэтому угол, на который повернется отраженный луч β = (φ + α) + α — φ = 2α = 34°.
2.
Определите, на какой угол θ отклоняется световой луч от своего первоначального направления при переходе из воздуха в воду, если угол падения а = 75°.
Р е ш е н и е.
Из рисунка видно, что θ = α — β.
Согласно закону преломления
где n — показатель преломления воды.
Отсюда
Из таблицы синусов находим: β ≈ 46°33′.
Следовательноб
β ≈ 75° — 46°33′ = 28°27′.
3.
Начертите ход лучей сквозь треугольную стеклянную призму, основанием которой является равнобедренный прямоугольный треугольник.
Лучи падают на широкую грань перпендикулярно этой грани.
Показатель преломления стекла равен 1,5.
Р е ш е н и е.
Проходя через широкую грань, лучи не изменяют своего направления, так как угол падения равен нулю.
На узкой грани АВ лучи полностью отражаются, так как угол падения равен 45° и, следовательно, больше предельного угла полного отражения для стекла, равного 42°.
После полного отражения от левой грани лучи падают на правую грань, снова полностью отражаются и выходят из призмы по направлению, перпендикулярному широкой грани.
Таким образом, направление пучка света изменяется на 180°.
Такой ход лучей используется, например, в призматических биноклях.
4.
Определите, во сколько раз истинная глубина водоема больше кажущейся, если смотреть по вертикали вниз.
Р е ш е н и е.
Построим ход лучей, вышедших из точки S на дне водоема и попавших в глаз наблюдателя.
Так как наблюдение ведется по вертикали, один из лучей SA направим перпендикулярно поверхности воды, другой SB — под малым углом α к перпендикуляру, восставленному в точке В (при больших углах а лучи не попадут в глаз).
Точка S1 пересечения луча SA и продолжения преломленного луча SB — мнимое изображение точки S.
Угол ASB равен углу падения а (внутренние накрест лежащие углы), а угол AS1B равен углу преломления Р (соответственные углы при параллельных прямых).
Прямоугольные треугольники ASB и AS1B имеют общий катет АВ, который можно выразить через истинную глубину водоема SA = Н и через кажущуюся глубину S1A = h:
АВ = Н tg α = htg β.
где n — показатель преломления воды.
Следовательно,
Истинная глубина водоема больше кажущейся в n = 1,3 раза.
5.
На рисунке показано расположение главной оптической оси MN линзы, светящейся точки S и ее изображения S1.
Найдите построением оптический центр линзы и ее фокусы.
Определите, собирающей или рассеивающей является эта линза, действительным или мнимым является изображение.
Р е ш е н и е.
Луч, проходящий через оптический центр линзы, не отклоняется от своего направления.
Поэтому оптический центр О совпадает с точкой пересечения прямых SS1 и MN.
Проведем луч SK, параллельный главной оптической оси.
Преломленный луч KS1 пройдет через фокус.
Зная, что луч, падающий на линзу через фокус, после преломления идет параллельно главной оптической оси, находим другой фокус.
Линза является собирающей, а изображение — действительным.
6.
Изображение предмета имеет высоту Н = 2 см.
Какое фокусное расстояние F должна иметь линза, расположенная на расстоянии ƒ = 4 м от экрана, чтобы изображение данного предмета на экране имело высоту h = 1м?
Р е ш е н и е.
Из формулы линзы
находим фокусное расстояние:
Увеличение линзы можно выразить так:
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Формулы ⚠️ по физике 8 класс: список, пояснения по разделам
Формулы по физике за 8 класс: основные разделы
В 8 классе школьники на уроках физики изучают следующие разделы:
- Тепловые явления.

- Электрические явления.
- Электромагнитные явления.
- Световые явления.
Рассмотрим подробно основные законы и формулы каждого из разделов. Дадим все необходимые пояснения к ним.
Тепловые явления
ОпределениеЯвления, которые связаны с изменением температуры тела, приводящей к его нагреванию или охлаждению, называют тепловыми.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В качестве примера можно привести нагревание и охлаждение воздуха, таяние льда, плавление металлов и др.
Закон сохранения энергии
Закон сохранения энергии постулирует, что в природе не происходит возникновения или исчезновения энергии. Энергия существует всегда, просто она превращается из одного вида в другой, передается от одного тела другому, и при этом ее значение сохраняется.
Уравнение, иллюстрирующее закон сохранения механической энергии, выглядит так:
\(E_{k_1}+E_{p_1}=E_{k_2}+E_{p_2}\)
и означает следующее:
Сумма кинетической и потенциальной энергии тел, которые находятся в замкнутой системе и взаимодействуют между собой силами тяготения и упругости, остается постоянной.
В данном уравнении \(E_{k_1}\) и \(E_{k_2}\) — кинетическая энергия тела, \(E_{p_1}\) и \(E_{p_2}\) — потенциальная энергия тела.
Полная механическая энергия (E) будет определяться по формуле:
\(E=E_k+E_p\)
где \(E_k\) — кинетическая энергия, \(E_p\) — потенциальная.
Формула вычисления количества теплоты
Внутренняя энергия тела может изменяться двумя путями:
- за счет совершения работы;
- без совершения работы, за счет теплопередачи.
Энергия, которую получает или теряет тело при теплопередаче, называется количеством теплоты.
Определяется по формуле:
\(Q=c\times m\times\left(t_2-t_1\right)\)
где Q — количество теплоты, измеряемое в джоулях, c — удельная теплоемкость, m — масса тела, \(t_1\) — начальная, \(t_2\) — конечная температуры.
Формула вычисления количества теплоты при сгорании топлива
ОпределениеКоличеством теплоты при сгорании топлива называется величина, которая равняется количеству энергии, выделяемой при полном сгорании топлива.
Для определения количества теплоты при сгорании топлива необходимо знать удельную теплоту сгорания q — количество теплоты, которое выделяет 1 килограмм топлива при полном сгорании.
Формула выглядит так:
\(Q=q\times m\)
где Q — количество теплоты при сгорании топлива, измеряется в джоулях, m — масса топлива.
Количество теплоты плавления (кристаллизации)
ОпределениеКоличество теплоты плавления или кристаллизации — это физическая величина, которая показывает, какое количество теплоты необходимо для плавления тела при условии, что оно находится в условиях температуры плавления и нормальном атмосферном давлении.
Для определения количества теплоты плавления нужно знать удельную теплоту плавления (\lambda) — величину, показывающую, какое количество теплоты необходимо дать кристаллическому телу массой 1 кг, чтобы при температуре плавления полностью перевести его в жидкое состояние. 3}\).
3}\).
Вычисление относительной влажности воздуха
Определение 6
Относительная влажность воздуха \((\varphi)\) — это отношение абсолютной влажности воздуха (ρ) к плотности насыщенного водяного пара при той же температуре (\(ρ_0\)), выражается в процентах.
Насыщение водяного пара зависит от:
- температуры;
- количества водяных паров;
- давления.
Соответственно, относительную влажность воздуха можно вычислить при помощи формулы:
\(\varphi=\frac p{p_0}\times100\%\)
КПД тепловой машины
С помощью коэффициента полезного действия (КПД) двигателя определяют экономичность различных тепловых двигателей.
ОпределениеКПД называется отношение совершенной двигателем полезной работы к энергии, полученной от нагревателя.
КПД двигателя находят по формуле:
\(\eta=\frac{Q_1-Q_2}{Q_1}\times100\%\)
где \eta — КПД, выражается в процентах; \(Q_1\) — количество теплоты, полученное от нагревателя, \(Q_2\) — количество теплоты, отданное телом холодильнику.
Электрические явления
Раздел «Электрические явления» учебника 8-го класса рассматривает основные закономерности и параметры, характерные для работы электроцепей.
Закон Ома для участка цепи
В 1827 году немецкий физик Георг Ом вывел и доказал опытным путем зависимость силы тока от напряжения и сопротивления. Эта зависимость называется законом Ома и звучит так: сила тока на участке электрической цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна его сопротивлению.
Формула, отражающая эту зависимость, выглядит так:
\(I=\frac UR\)
где I — сила тока на участке цепи, измеряется в амперах, U — напряжение на участке электроцепи, R — сопротивление участка цепи.
Вычисление удельного сопротивления проводника
Зависимость сопротивления проводника от его размера и материала, из которого он изготовлен, впервые изучил Ом. Он доказал, что сопротивление прямо пропорционально длине проводника, обратно пропорционально площади его поперечного сечения и зависит от материала изготовления. 2 называют удельным сопротивлением вещества (p).
2 называют удельным сопротивлением вещества (p).
Сопротивление проводника определяем по формуле:
\(R=\frac{pl}S\)
где R — сопротивление проводника, измеряется в омах, l — длина проводника, S — площадь сечения.
Законы последовательного соединения проводников
Следующие закономерности справедливы для последовательно соединенных проводников в любом количестве:
\(I=I_1=I_2\)
\(U=U_1+U_2\)
\(R=R_1+R_2\)
где \(I_1, U_1, R_1\) — сила тока, напряжение и сопротивление на одном участке цепи, \(I_2, U_2, R_2\) — сила тока, напряжение и сопротивление на другом участке цепи.
Сила тока измеряется в амперах, напряжение — в вольтах, сопротивление — в омах.
Законы параллельного соединения проводников
Для параллельного соединения действуют следующие закономерности:
\(I=I_1+I_2\)
\(U=U_1=U_2\)
\(R=\frac{R_1\times R_2}{R_1+R_2}\)
где \(I_1, U_1, R_1\)1 — сила тока, напряжение и сопротивление первого участка цепи, \(I_2, U_2, R_2\) — сила тока, напряжение и сопротивление второго участка цепи.
Единицы измерения основных характеристик электроцепи одинаковые при последовательном и параллельном соединениях.
Вычисление величины заряда
ОпределениеЭлектрический заряд (q) — это физическая величина, которая описывает особенность частиц или тел выступать источником электромагнитных полей и участвовать в электромагнитном взаимодействии.
Измеряется в кулонах, вычисляется по формуле:
\(q=I\times t, \)
где I — сила, t — время прохождения тока.
Нахождение работы электрического тока
ОпределениеРабота электрического тока — это физическая величина, которая показывает, какая работа была совершена электрическим полем при перемещении зарядов по проводнику.
Работа электрического тока обозначается символом A, измеряется в джоулях, рассчитывается по формуле:
\(A=U\times I\times t\)
где I — сила тока в проводнике, U — напряжение на концах проводника, t — время протекания тока через проводник.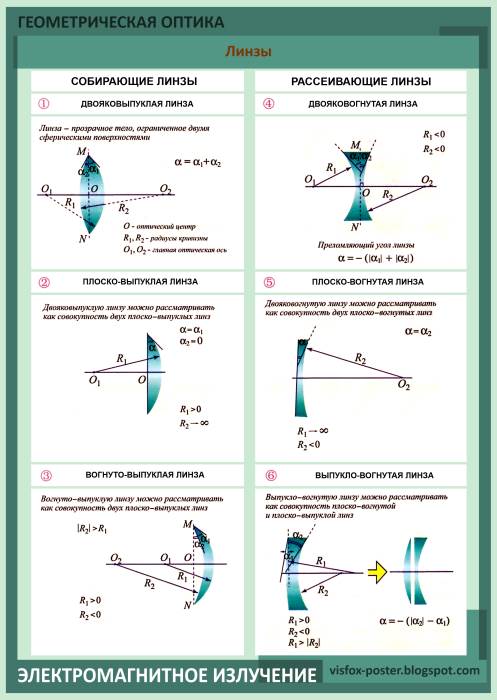 2\times R\times\Delta t\)
2\times R\times\Delta t\)
где Q — количество теплоты, выделяемое за время \((\Delta t)\), в течение которого ток течет в проводнике, измеряется в джоулях, I — сила тока в проводнике, R — сопротивление проводника.
Электромагнитные явления
Раздел «Электромагнитные явления» разбирает физические процессы, которые связаны с электрическим током и образующимся вокруг него магнитным полем.
Правило правой руки
ОпределениеЕсли обхватить проводник с током ладонью правой руки и направить большой палец, отставленный на 90 градусов по направлению силы тока в проводнике, оставшиеся четыре пальца покажут направление линий магнитного поля проводника.
Правило буравчика
Световые явления
В разделе «Световые явления» рассматривается свет, его источники и распространение в пространстве, а также основные физические законы, согласно которым свет распространяется в среде. Рассмотрим подробнее каждый из них.
Рассмотрим подробнее каждый из них.
Закон отражения света
Закон отражения света от зеркальной поверхности звучит так: падающий и отраженный лучи лежат в одной плоскости с перпендикуляром, который проведен к границе раздела двух сред в точке падения луча.
Угол падения alpha равен углу отражения \(\beta\):
\(<\alpha=<\beta\)
Закон преломления
ОпределениеПреломлением света называется изменение направления светового луча на границе сред при переходе его из одной среды в другую.
Законы преломления света:
- Лучи, падающий и отраженный, лежат в одной плоскости с перпендикуляром, который проведен к границе раздела двух сред в точке падения луча.
- Угол преломления может быть меньше или больше угла падения — в зависимости от того, из какой среды и в какую луч переходит.
Закон открыл в 1621 году голландский математик В. Снеллиус.
Вычисление абсолютного и относительного показателя преломления вещества
ОпределениеАбсолютный показатель преломления вещества (n) — это показатель преломления вещества относительно вакуума.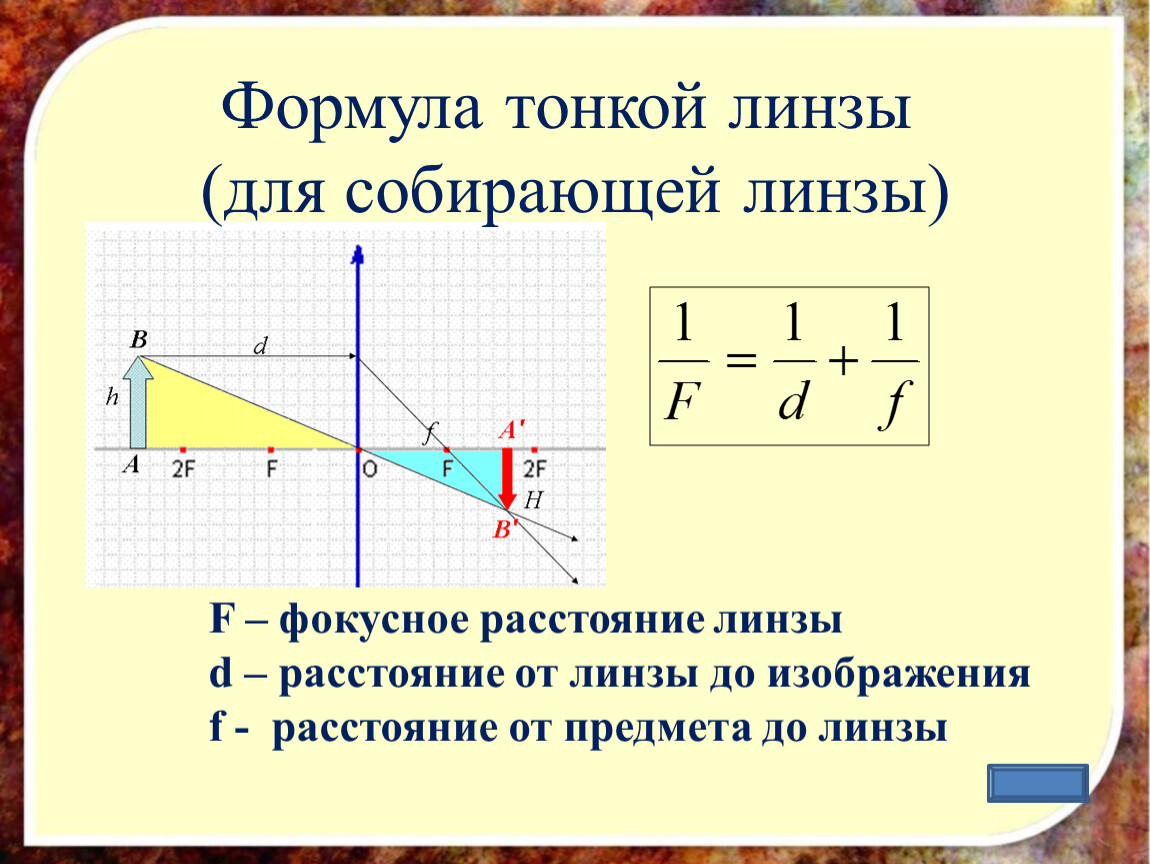
Он показывает, во сколько раз скорость света в вакууме больше, чем в среде.
Определяется по формуле:
\(n=\frac cv\)
где c — скорость света в вакууме, v — скорость света в данной среде.
Относительный показатель преломления вещества показывает, во сколько раз скорость света в первой среде отличается от скорости во второй среде.
Оптическая сила линзы
ОпределениеЛинзы — это прозрачные тела, созданные для управления световыми лучами с помощью изменения их направления, которые представляют собой ограниченные с двух сторон сферические поверхности.
Линзы характеризует величину, которую называют оптической силой линзы, измеряется в диоптриях (D).
Оптическая сила линзы обратно пропорциональна фокусному расстоянию линзы (F) и рассчитывается по формуле:
\(D=\frac1F\)
1 диоптрия — это оптическая сила линзы, фокусное расстояние которой составляет 1 м.
Примеры задач с решением
Рассмотрим варианты самых распространенных задач с решениями.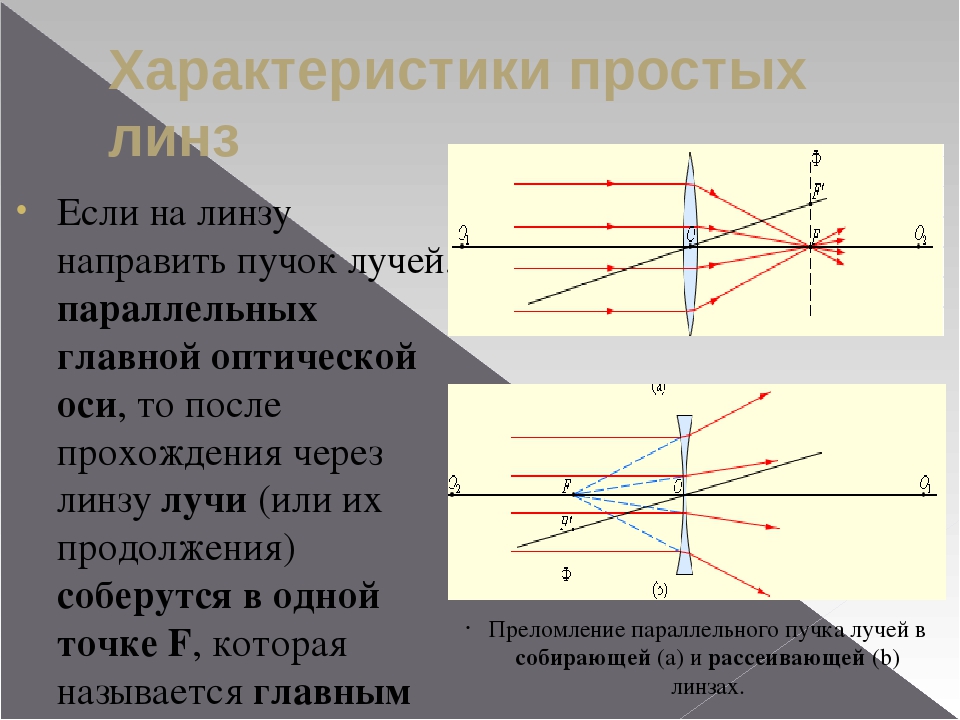 6 \)Дж.
6 \)Дж.
Задача на вычисление абсолютной влажности
Задача
Какой будет абсолютная влажность воздуха, если относительная влажность равна 50% при температуре 20 градусов?
Решение:
Смотрим в таблице, сколько пара может содержаться при температуре 20 градусов. Обнаруживаем значение 17 г. Так как у нас относительная влажность равна 50%, необходимо 17 / 2, получаем 8,5 г/м3. Абсолютная влажность равна 8,5 г/м3.
Задача на вычисление относительной влажности воздуха
Задача
Какой будет относительная влажность при том условии, что при температуре 30 градусов в воздухе содержалось 17 г воды?
Решение:
\(\varphi=17*100/30=56%\)
Задача на вычисление КПД тепловой машины
Задача
Какой КПД у теплового двигателя, который совершил полезную работу 70 кДж, если при полном сгорании топлива выделилась энергия 200 кДж?
Решение:
\(\eta=70/200*100%=35%\)
Задачи из раздела «Электрические явления»
Задача на вычисление удельного сопротивления проводника
Задача
Чему будет равно сопротивление проводника, в котором течет ток силой 600 мА при напряжении на концах 1,2 кВ?
Решение:
\(R=1200/0,6=200 Ом. 2/80*600=363000 \)Дж.
2/80*600=363000 \)Дж.
Для решения задач по правилам правой руки и буравчика, важно знать условные обозначения:
Задачи из раздела «Световые явления»
Задача на вычисление абсолютного показателя преломления вещества
Расчет оптической силы линзы
Задача
Какой будет оптическая сила линз объектива фотоаппарата, если его фокусное расстояние составляет 58 мм?
Решение:
58 мм=0,058 м.
\(D=1/0,058=17,24 дптр.\)
ФГОС комплект. Лабораторный комплект (набор) по оптике
Комплект учебного оборудования предназначен для проведения фронтальных лабораторных работ при изучении раздела «Оптика» школьного курса физики.
Конструкция защищена патентом РФ на изобретение 2227329Назначение
Комплект учебного оборудования позволяет выполнять не менее 21 лабораторной работы в соответствии с требованиями учебных программ
школьного курса физики, в том числе: измерения фокусного расстояния собирающей и рассеивающей линз, увеличения
лупы, длины световой волны с помощью дифракционной решетки, показателя преломления света, исследования явления
отражения света, формулы линзы, размеров изображений предметов, явлений дисперсии, преломления и полного
внутреннего отражения света, проводить сборку моделей трубы Кеплера, трубы Галилея, микроскопа, наблюдать
дифракцию и интерференцию света, дифракцию световой волны в круглом отверстии, проводить построение изображения
предмета в плоском зеркале, определять фокусное расстояние собирающей линзы, получать изображения с помощью
собирающей линзы.
Комплект поставки
| №п/п | Наименование | Кол-во |
| 1. | Пенал с крышкой и ложементом | 1 |
| 2. | Оптическая скамья | 1 |
| 3. | Источник света | 1 |
| 4. | Рейтер для рамок | 1 |
| 5. | Линза собирающая длиннофокусная с рейтером | 1 |
| 6. | Линза собирающая короткофокусная с рейтером | 1 |
| 7. | Линза рассеивающая с рейтером | 1 |
| 8. | Рамка с дифракционными решетками | 1 |
| 9. | Рамка с диафрагмой с отверстиями различной формы | 2 |
10. |
Пластина с параллельными гранями | 1 |
| 11. | Подставка | 1 |
| 12. | Булавка | 4 |
| 13. | Коврик | 1 |
| 14. | Провод соединительный | 2 |
| 15. | Экран | 1 |
| 16. | Зеркало | 1 |
Преимущества:
- не требует затемнения помещения, где проводятся опыты
- надежная фиксация оптических элементов
- компактная конструкция
- возможность использования при надомном обучении
- не содержит деталей и узлов с ограниченным ресурсом работы
Методическое обеспечение (не входит в базовую комплектацию):
Методики использования лабораторного комплекта в учебном процессе представлены в методических рекомендациях и электронном пособии на СD.
Печатное методическое пособие:
Электронное методическое пособие на CD:
Оказываем содействие в подготовке технических требований для тендерной документации.
Перечень лабораторных работ, выполняемых с помощью лабораторного комплекта
1. Исследование явления отражения света
2 Построение изображения предмета в плоском зеркале
3. Измерение фокусного расстояния собирающей линзы
4. Измерение оптической силы собирающей линзы
5. Определение фокусного расстояния собирающей линзы с использованием формулы линзы
6. Измерение фокусного расстояния рассеивающей линзы
7. Получение изображения с помощью собирающей линзы
8. Экспериментальное исследование формулы линзы
9. Исследование размеров изображений предметов даваемых линзами
10. Измерение увеличения лупы
11. Сборка модели трубы Кеплера
12. Сборка модели трубы Галилея
13.Сборка модели микроскопа
14. Исследование явления дисперсии
15. Наблюдение дифракции света
16. Наблюдение интерференции света
17. Измерение длины световой волны с помощью дифракционной решетки
18. Наблюдение дифракции световой волны на круглом отверстии
19. Исследование явления преломления света
20. Измерение показателя преломления вещества
21. Исследование явления полного внутреннего отражения света
Пример:
Формулы оптики
Призма полного внутреннего отражения (ПВО)
МДП зависит от чистого интерфейса стекло-воздух. Отражающие поверхности не должны содержать посторонних материалов. TIR также можно устранить, уменьшив угол падения выше критического значения. Для прямоугольной призмы индекса n лучи должны входить в грань призмы под углом θ:
θ 2-1) 1/2 -1)/√2)
В видимом диапазоне θ = 5,8° для БК 7 (n = 1,517) и 2. 6° для плавленого кварца (n = 1,46). Наконец, призмы увеличивают оптический путь. Хотя в лазерных приложениях эффекты минимальны, следует учитывать смещение фокуса и хроматические эффекты в расходящихся пучках.
6° для плавленого кварца (n = 1,46). Наконец, призмы увеличивают оптический путь. Хотя в лазерных приложениях эффекты минимальны, следует учитывать смещение фокуса и хроматические эффекты в расходящихся пучках.
Уравнения Френеля:
- i — падающая среда
- t — среда передачи
используйте закон Снеллиуса, чтобы найти θ t
Нормальная заболеваемость:
r = (n i -n t )/(n i + n t )
t = 2n i /(n i + n t )
Угол Брюстера:
θ β = арктангенс (n t /n i )
Отражается только s-поляризованный свет.
Полное внутреннее отражение (TIR):
θ TIR > arcsin (n t /n i )
n t i требуется для TIR
Коэффициенты отражения и передачи поля:
Коэффициенты отражения и пропускания поля определяются по формуле:
r = E r /E i t = E t /E i
Ненормальная заболеваемость:
R S = (N I COSOθ I -N T COSOθ T ) / (N I COSθ I + N T COSθ T )
R P = (N T COS θ I -N I COSθ T ) / N T COSOθ I + N I COSθ T )
t s = 2n i cosθ i /(n i cosθ i + n t cosθ t
)t p = 2n i cosθ i /(n t cosθ i + n i cosθ t )
Мощность отражения:
Коэффициенты отражения и передачи мощности обозначены прописными буквами:
R = r 2 T = t 2 (n t cosθ t )/(n i cosθ i )
Показатели преломления объясняют разные скорости света в двух средах; отношение косинусов корректирует различные площади поперечного сечения лучей по обеим сторонам границы.
Интенсивность (Вт/площадь) также должна быть скорректирована на этот коэффициент геометрического наклона:
I t = T x I i (cosθ i /cosθ t )
Сохранение энергии:
Р + Т = 1
Это соотношение справедливо как для компонентов p и s по отдельности, так и для полной мощности.
Поляризация
Для упрощения расчетов отражения и пропускания падающее электрическое поле разбивается на две плоскополяризованные составляющие.«Колесо» на рисунках ниже обозначает плоскость падения. В этой плоскости лежат нормаль к поверхности и все векторы распространения ( k i , k r , k t ).
Преломление и лучевая модель света
Диаграммы лучей можно использовать для определения местоположения, размера, ориентации и типа изображения, образованного объектами, помещенными в заданное место перед линзой. Использование этих диаграмм было продемонстрировано ранее в Уроке 5 как для собирающих, так и для рассеивающих линз.Лучевые диаграммы предоставляют полезную информацию об отношениях объект-изображение, но не могут предоставить информацию в количественной форме. Хотя лучевая диаграмма может помочь определить приблизительное местоположение и размер изображения, она не дает числовой информации о расстоянии до изображения и размере изображения. Чтобы получить этот тип числовой информации, необходимо использовать уравнение линзы и уравнение увеличения . Уравнение линзы выражает количественную зависимость между расстоянием до объекта (d o ), расстоянием до изображения (d i ) и фокусным расстоянием (f).Уравнение формулируется следующим образом:
Использование этих диаграмм было продемонстрировано ранее в Уроке 5 как для собирающих, так и для рассеивающих линз.Лучевые диаграммы предоставляют полезную информацию об отношениях объект-изображение, но не могут предоставить информацию в количественной форме. Хотя лучевая диаграмма может помочь определить приблизительное местоположение и размер изображения, она не дает числовой информации о расстоянии до изображения и размере изображения. Чтобы получить этот тип числовой информации, необходимо использовать уравнение линзы и уравнение увеличения . Уравнение линзы выражает количественную зависимость между расстоянием до объекта (d o ), расстоянием до изображения (d i ) и фокусным расстоянием (f).Уравнение формулируется следующим образом: Уравнение увеличения связывает отношение расстояния до изображения и расстояния до объекта с отношением высоты изображения (h i ) и высоты объекта (h o ). Уравнение увеличения сформулировано следующим образом:
Уравнение увеличения сформулировано следующим образом:
Эти два уравнения можно объединить, чтобы получить информацию о расстоянии до изображения и высоте изображения, если известно расстояние до объекта, высота объекта и фокусное расстояние.
Практические задачиВ качестве демонстрации эффективности уравнения линзы и уравнения увеличения рассмотрим следующую примерную задачу и ее решение.
Пример задачи №1
Лампа высотой 4,00 см расположена на расстоянии 45,7 см от двояковыпуклой линзы с фокусным расстоянием 15,2 см. Определите расстояние до изображения и размер изображения.
Как и все проблемы в физике, начните с идентификации известной информации.
| ч о = 4,00 см | д о = 45.7 см | f = 15,2 см |
Затем укажите неизвестные величины, которые вы хотите найти.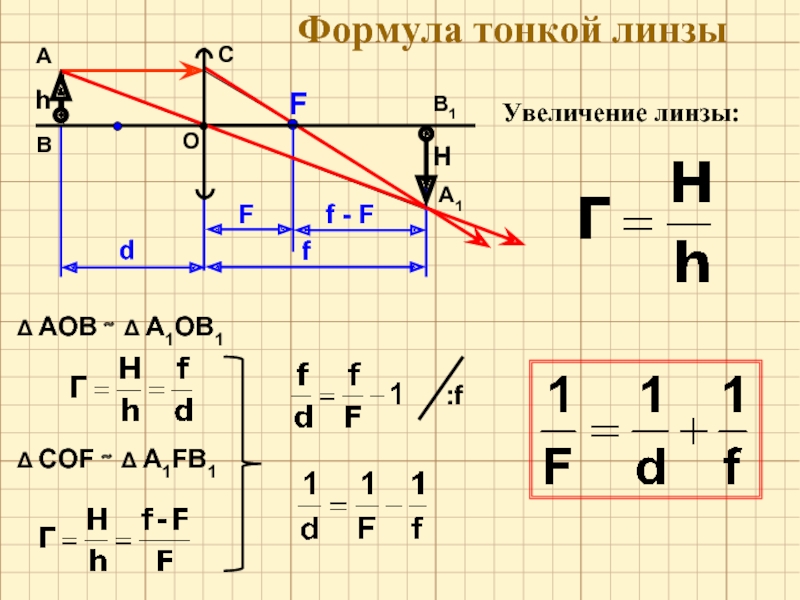
Для определения расстояния до изображения необходимо использовать уравнение линзы. Следующие строки представляют решение расстояния изображения; показаны замены и алгебраические шаги.
1/f = 1/do + 1/d i1/(15,2 см) = 1/(45,7 см) + 1/d i
0.0658 см -1 = 0,0219 см -1 + 1/d i
0,0439 см -1 = 1/d i
Численные значения в приведенном выше решении были округлены при записи, однако во всех расчетах использовались неокругленные числа. Окончательный ответ округляется до третьей значащей цифры.
Для определения высоты изображения необходимо уравнение увеличения. Поскольку три из четырех величин в уравнении (без учета M) известны, можно вычислить четвертую величину.Решение показано ниже.
h i /h o = — d i /d oч i /(4,00 см) = — (22,8 см)/(45,7 см)
ч i = — (4,00 см) • (22,8 см)/(45,7 см)
Отрицательные значения высоты изображения указывают на то, что изображение является перевернутым.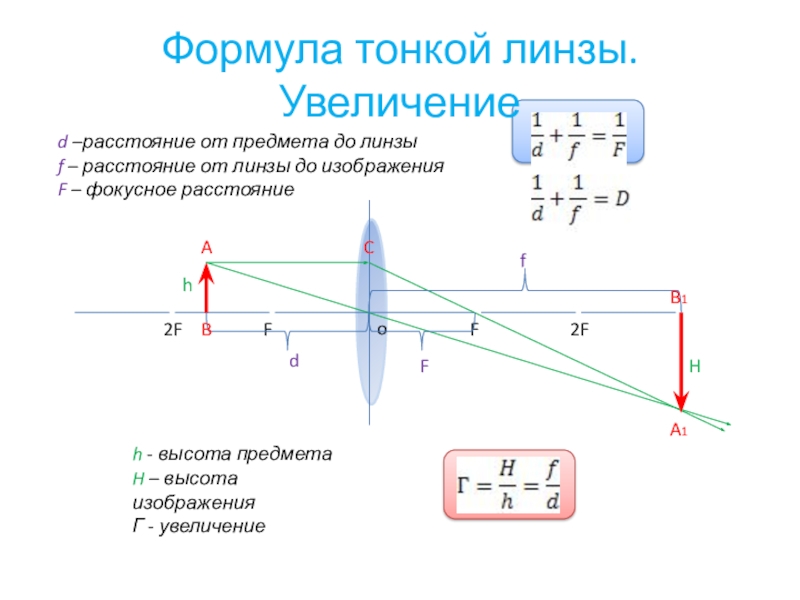 Как это часто бывает в физике, отрицательный или положительный знак перед числовым значением физической величины представляет информацию о направлении.В случае высоты изображения отрицательное значение всегда указывает на перевернутое изображение.
Как это часто бывает в физике, отрицательный или положительный знак перед числовым значением физической величины представляет информацию о направлении.В случае высоты изображения отрицательное значение всегда указывает на перевернутое изображение.
Из расчетов в этой задаче можно сделать вывод, что если предмет высотой 4,00 см поместить на расстоянии 45,7 см от двояковыпуклой линзы с фокусным расстоянием 15,2 см, то изображение будет перевернутым, высотой 1,99 см и расположенным на 22,8 см от объектива. Результаты этого расчета согласуются с принципами, обсуждавшимися ранее в этом уроке. В этом случае объект расположен на за точкой 2F (которая будет на расстоянии двух фокусных расстояний от линзы), а изображение расположено между точкой 2F и точкой фокуса.Это попадает в категорию Случая 1: Объект расположен на за 2F для собирающей линзы.
Теперь давайте попробуем второй пример задачи:
Пример задачи №2Лампа высотой 4,00 см помещена на расстоянии 8,30 см от двояковыпуклой линзы с фокусным расстоянием 15,2 см.(ПРИМЕЧАНИЕ: это тот же предмет и та же линза, только на этот раз предмет расположен ближе к линзе.) Определите расстояние до изображения и размер изображения.
Опять же, начните с идентификации известной информации.
| ч о = 4,00 см | д о = 8,3 см | f = 15,2 см |
Затем укажите неизвестные величины, которые вы хотите найти.
Для определения расстояния до изображения необходимо использовать уравнение линзы.Следующие строки представляют решение расстояния изображения; показаны замены и алгебраические шаги.
1/f = 1/do + 1/d i1/(15,2 см) = 1/(8,30 см) + 1/d i
0,0658 см -1 = 0,120 см -1 + 1/d i
-0,0547 см -1 = 1/d i
Численные значения в приведенном выше решении были округлены при записи, однако во всех расчетах использовались неокругленные числа. Окончательный ответ округляется до третьей значащей цифры.
Окончательный ответ округляется до третьей значащей цифры.
Для определения высоты изображения необходимо уравнение увеличения. Поскольку три из четырех величин в уравнении (без учета M) известны, можно вычислить четвертую величину. Решение показано ниже.
h i /h o = — d i /d oч i /(4,00 см) = — (-18,3 см)/(8,30 см)
ч i = — (4.00 см) • (-18,3 см)/(8,30 см)
Отрицательное значение расстояния до изображения указывает на то, что изображение является виртуальным изображением, расположенным со стороны объектива со стороны объекта. Опять же, отрицательный или положительный знак перед числовым значением физической величины представляет информацию о направлении. В случае расстояния до изображения отрицательное значение всегда означает, что изображение расположено на стороне объекта от линзы. Обратите также внимание, что высота изображения является положительным значением, что означает вертикальное изображение. Любое изображение, которое находится в вертикальном положении и расположено со стороны объекта от линзы, считается виртуальным изображением.
Любое изображение, которое находится в вертикальном положении и расположено со стороны объекта от линзы, считается виртуальным изображением.
Из расчетов во втором примере задачи можно сделать вывод, что если предмет высотой 4,00 см поместить на расстоянии 8,30 см от двояковыпуклой линзы с фокусным расстоянием 15,2 см, то изображение будет увеличенным, прямым, 8,81 см. высотой и расположен на расстоянии 18,3 см от линзы со стороны предмета. Результаты этого расчета согласуются с принципами, обсуждавшимися ранее в этом уроке.В этом случае объект находится перед фокусом (т. е. расстояние до объекта меньше фокусного расстояния), а изображение — за линзой. Это относится к категории случая 5: объект расположен перед F (для собирающей линзы).
Третья примерная задача относится к рассеивающей линзе.
Пример задачи №3Лампа высотой 4,00 см помещена на расстоянии 35,5 см от рассеивающей линзы с фокусным расстоянием -12.2 см. Определите расстояние до изображения и размер изображения.
Как и все проблемы в физике, начните с идентификации известной информации.
| ч о = 4,00 см | д о = 35,5 см | f = -12,2 см |
Затем укажите неизвестные величины, которые вы хотите найти.
Для определения расстояния до изображения необходимо использовать уравнение линзы.Следующие строки представляют решение расстояния изображения; показаны замены и алгебраические шаги.
1/f = 1/do + 1/d i1/(-12,2 см) = 1/(35,5 см) + 1/d i
-0,0820 см -1 = 0,0282 см -1 + 1/d i
-0,110 см -1 = 1/д i
Численные значения в приведенном выше решении были округлены при записи, однако во всех расчетах использовались неокругленные числа. Окончательный ответ округляется до третьей значащей цифры.
Окончательный ответ округляется до третьей значащей цифры.
Для определения высоты изображения необходимо уравнение увеличения. Поскольку три из четырех величин в уравнении (без учета M) известны, можно вычислить четвертую величину. Решение показано ниже.
h i /h o = — d i /d oч i /(4,00 см) = — (-9,08 см)/(35,5 см)
ч i = — (4.00 см) * (-9,08 см)/(35,5 см)
Отрицательные значения расстояния до изображения указывают на то, что изображение расположено на стороне объектива от объекта. Как уже упоминалось, отрицательный или положительный знак перед числовым значением физической величины представляет информацию о направлении. В случае расстояния до изображения отрицательное значение всегда указывает на существование мнимого изображения, расположенного со стороны объектива со стороны объекта. В случае высоты изображения положительное значение указывает на вертикальное изображение.
Из расчетов в этой задаче можно сделать вывод, что если предмет высотой 4,00 см поместить на расстоянии 35,5 см от рассеивающей линзы с фокусным расстоянием 12,2 см, то изображение будет прямым, высотой 1,02 см и расположенным на 9,08 см. от объектива со стороны объекта. Результаты этого расчета согласуются с принципами, обсуждавшимися ранее в этом уроке. Рассеивающие линзы всегда дают изображения, которые являются прямыми, виртуальными, уменьшенными в размере и расположенными со стороны предмета линзы.
Практика ведет к совершенству! Используйте виджет Find the Image Distance ниже, чтобы исследовать влияние фокусного расстояния и расстояния до объекта на расстояние до изображения. Просто введите фокусное расстояние и расстояние до объекта. Затем нажмите кнопку Calculate Image Distance , чтобы просмотреть результат. Используйте виджет как тренировочный инструмент.
Постоянная задача фотографов — создать изображение, на котором как можно больше сфокусировано на объекте.
 Цифровые камеры используют линзы для фокусировки изображения на сенсорной пластине на том же расстоянии от линзы. Тем не менее, в этом уроке мы узнали, что расстояние до изображения зависит от расстояния до объекта. Так как же фотограф может сфокусировать объекты в поле зрения, если они находятся на разном расстоянии от камеры? Это постоянная проблема для фотографов (будь то любители-энтузиасты или профессионалы), которые хотят контролировать, какая часть объекта находится в фокусе. Глубина резкости — это термин фотографа для описания расстояния от ближайшего до самого дальнего объекта в поле зрения, которые приемлемо сфокусированы на фотографии.Виджет Фотография и глубина резкости позволяет исследовать переменные, влияющие на глубину резкости.
Цифровые камеры используют линзы для фокусировки изображения на сенсорной пластине на том же расстоянии от линзы. Тем не менее, в этом уроке мы узнали, что расстояние до изображения зависит от расстояния до объекта. Так как же фотограф может сфокусировать объекты в поле зрения, если они находятся на разном расстоянии от камеры? Это постоянная проблема для фотографов (будь то любители-энтузиасты или профессионалы), которые хотят контролировать, какая часть объекта находится в фокусе. Глубина резкости — это термин фотографа для описания расстояния от ближайшего до самого дальнего объекта в поле зрения, которые приемлемо сфокусированы на фотографии.Виджет Фотография и глубина резкости позволяет исследовать переменные, влияющие на глубину резкости. f-stop или f-число объектива камеры связано с размером круглого отверстия или апертуры, через которую проходит свет на пути к цифровому датчику. Чем больше число f, тем меньше отверстие и тем меньше света попадает на сенсор. Кружок нерезкости связан с ограничением глаза для разрешения деталей изображения в пределах небольшой области.Для 35-мм камеры, изображения которой увеличены до размера отпечатка 5×7 дюймов, общепринятое значение кружка нерезкости составляет 0,0333 мм.
Кружок нерезкости связан с ограничением глаза для разрешения деталей изображения в пределах небольшой области.Для 35-мм камеры, изображения которой увеличены до размера отпечатка 5×7 дюймов, общепринятое значение кружка нерезкости составляет 0,0333 мм.
Условные обозначения
Условные обозначения для заданных величин в уравнении линзы и уравнениях увеличения следующие:
- f is + если линза представляет собой двойную выпуклую линзу (собирающую линзу)
- f is — если линза двояковыпуклая (рассеивающая линза)
- d i равно +, если изображение является реальным изображением и расположено на противоположной стороне линзы.
- d i is — если изображение является мнимым и расположено со стороны предмета в объективе.
- h i +, если изображение прямое (и, следовательно, также виртуальное)
- h i is — если изображение перевернутое (а значит, и реальное)
Подобно многим математическим задачам в физике, этот навык приобретается только в результате большой личной практики. Возможно, вы хотели бы потратить некоторое время, чтобы решить следующие задачи.
Возможно, вы хотели бы потратить некоторое время, чтобы решить следующие задачи.
Проверьте свое понимание
1. Определите расстояние до изображения и высоту изображения для объекта высотой 5 см, расположенного на расстоянии 45,0 см от двояковыпуклой линзы с фокусным расстоянием 15,0 см.
2. Определите расстояние до изображения и высоту изображения для объекта высотой 5 см, расположенного под номером 30.0 см от двояковыпуклой линзы с фокусным расстоянием 15,0 см.
3. Определите расстояние до изображения и высоту изображения для объекта высотой 5 см, расположенного на расстоянии 20,0 см от двояковыпуклой линзы с фокусным расстоянием 15,0 см.
4. Определите расстояние до изображения и высоту изображения для объекта высотой 5 см, расположенного на расстоянии 10,0 см от двояковыпуклой линзы с фокусным расстоянием 15.0 см.
5. Увеличенное перевернутое изображение расположено на расстоянии 32,0 см от двояковыпуклой линзы с фокусным расстоянием 12,0 см. Определите расстояние до объекта и скажите, является ли изображение реальным или виртуальным.
6. ZINGER : Перевернутое изображение увеличивается в 2 раза, когда объект находится на расстоянии 22 см от двояковыпуклой линзы.Определить расстояние до изображения и фокусное расстояние линзы.
ZINGER : Перевернутое изображение увеличивается в 2 раза, когда объект находится на расстоянии 22 см от двояковыпуклой линзы.Определить расстояние до изображения и фокусное расстояние линзы.
7. Двойная вогнутая линза имеет фокусное расстояние -10,8 см. Предмет находится на расстоянии 32,7 см от поверхности линзы. Определить расстояние до изображения.
8. Определите фокусное расстояние двояковыпуклой линзы, дающей изображение на расстоянии 16,0 см за линзой, когда объект имеет размер 28.5 см от объектива.
9. Монета диаметром 2,8 см находится на расстоянии 25,0 см от двояковыпуклой линзы с фокусным расстоянием -12,0 см. Определите расстояние изображения и диаметр изображения.
10. Фокус находится на расстоянии 20,0 см от двояковыпуклой линзы. Предмет находится на расстоянии 12 см от линзы. Определить расстояние до изображения.
Что такое оптика — Получить заметки, книги, формулы, уравнения для оптики
Вы когда-нибудь задумывались, как на небе образуется радуга? Магия этого приятного глазу явления заключается в понятиях Оптики. Оптика — это часть физики, изучающая поведение света и то, как он распространяется. Без света было бы невозможно получить знания о мире, представьте себе мир, где нет света, мы ничего не могли бы видеть, тогда у нас будет только 4 чувства и мы сможем наблюдать за окружающими нас предметами только их осязанием, запах, звук, который они производят, и их вкус.В нашей повседневной жизни мы находим множество применений оптической физики, например, выпуклое зеркало используется в автомобилях. Вогнутые зеркала используются в фокусных фонарях и телескопах. Точно так же оптические линзы используются для коррекции дефектов фокусировки глаза, таких как близорукость, дальнозоркость и т. д.
д.
Оптика также является очень важным разделом для различных вступительных экзаменов, включая доски. Поэтому очень важно усвоить концепции из этой главы, чтобы получить хорошие оценки. Изучая эту главу, вы также узнаете о различных оптических устройствах и их функциях, таких как телескоп, бинокль и микроскоп.
Темы для оптикиОбщие понятия, используемые в геометрической оптике, отражение света, отражение от сферической поверхности, преломление света и показатель преломления среды, закон преломления, одиночное преломление от плоской поверхности, смещение из-за стеклянной пластины, преломление от сферической поверхности, линза Теория, полное внутреннее отражение, преломление через призму, отклонение, оптические приборы
Обзор оптики
Мы обсуждали, что без света мы не сможем ничего видеть, но знаете ли вы, что свет — это всего лишь часть электромагнитного спектра с длиной волны от 4000 до 7000, то есть мы можем видеть только ограниченное количество электромагнитных излучений. Мы не можем видеть рентгеновские лучи, радиоволны, гамма-лучи и т. д., потому что их длина волны не воспринимается человеческим глазом. В этой главе вы сначала изучите отражение света от различных типов зеркал, таких как плоское зеркало, выпуклое и вогнутое зеркало. В этой главе вы познакомитесь с новыми терминами, поэтому давайте разберемся с некоторыми из них, которые являются очень простыми.
Мы не можем видеть рентгеновские лучи, радиоволны, гамма-лучи и т. д., потому что их длина волны не воспринимается человеческим глазом. В этой главе вы сначала изучите отражение света от различных типов зеркал, таких как плоское зеркало, выпуклое и вогнутое зеркало. В этой главе вы познакомитесь с новыми терминами, поэтому давайте разберемся с некоторыми из них, которые являются очень простыми.
Crack JEE 2021 с онлайн-программой подготовки к JEE/NEET
Начинай сейчасЦентр кривизны — Центр сферы, частью которой является зеркало.
Полюс — Центр зеркальной поверхности.
Основная ось — линия, соединяющая центр кривизны и полюс.
Главный фокус — это точка на главной оси зеркала или линзы, к которой сходятся параллельные лучи света или от которой они кажутся расходящимися после отражения или преломления.

Затем вы познакомитесь с преломлением света в различных типах сред и форм, таких как выпуклые и вогнутые линзы, стеклянные призмы и стеклянные пластины, жидкости и т. д.Преломление — это явление, возникающее при переходе луча света из одной среды в другую с изгибом или без него. Луч будет искривляться, если показатели преломления обеих сред будут отличаться друг от друга, и он входит в поверхность, образуя угол с нормалью. Вы, должно быть, слышали термин «показатель преломления», но каково значение этого слова? Таким образом, в основном скорость света в разных средах различна, а показатель преломления — это отношение света в двух разных средах.И эта разница возникает из-за того, что длина волны света меняется в разных средах. Характер искривления света зависит от формы среды. Например, выпуклая линза собирает свет, а вогнутая линза рассеивает свет.
Продолжая читать эту главу, вы познакомитесь с различными оптическими инструментами, в которых используется комбинация линз. Большинство основных оптических инструментов — это простой микроскоп и зрительная труба.
Большинство основных оптических инструментов — это простой микроскоп и зрительная труба.
Формулы для оптики
Формула зеркала :
Боковое или линейное увеличение в зеркале:
Формула линзы :
Боковое или линейное увеличение объектива:
Мощность линзы или зеркала (в диоптриях):
Формула производителя линз:
Как подготовиться к оптике
Оптика включает в себя множество новых терминов и формул, и из этой главы можно задать очень широкий круг вопросов.Для вас очень важно изучать темы и практиковать вопросы по одному шаблону. Было бы легко разделить эту главу на 3 части: первое отражение от зеркал, второе преломление через сферу, линзы, пластины и призму и третье оптическое оборудование. Сначала начните с вопросов, относящихся к определенному разделу, а затем, потренировавшись с большим количеством вопросов, попробуйте решить вопросы, включающие смешанную концепцию. Проходите пробные тесты всякий раз, когда вы уверены в каком-либо разделе.Кроме того, постарайтесь запомнить формулы, потому что много раз вы будете получать прямые вопросы, в которых будет использоваться формула. Как и в других главах, здесь вы также должны много практиковаться, чтобы лучше понять оптику.
Сначала начните с вопросов, относящихся к определенному разделу, а затем, потренировавшись с большим количеством вопросов, попробуйте решить вопросы, включающие смешанную концепцию. Проходите пробные тесты всякий раз, когда вы уверены в каком-либо разделе.Кроме того, постарайтесь запомнить формулы, потому что много раз вы будете получать прямые вопросы, в которых будет использоваться формула. Как и в других главах, здесь вы также должны много практиковаться, чтобы лучше понять оптику.
Примечания для оптики
Всегда помните об условности знаков при решении вопросов, связанных с зеркалом или линзой.
Запомните формулу после полного понимания концепции, в противном случае вы часто будете путаться в том, какая формула работает для какой задачи.
Для задач, связанных с несколькими оптическими поверхностями, всегда решайте однонаправленно и вычисляйте требуемые значения для предыдущей поверхности перед переходом к следующей поверхности.

- В книге
NCERT есть несколько очень хороших примеров для оптики, внимательно прочитайте их.
Общий совет: При отработке вопросов всегда пишите, какие количества даны в вопросе и что вам нужно найти.
Рекомендуемые книги по оптике
Вы можете начать с NCERT как для теории, так и для вопросов, это, безусловно, поможет вам построить свои концепции. После завершения книги NCERT решите вопросы из книги NCERT Exemplar, а для вопросов более продвинутого уровня вы можете либо следовать Концепциям физики Х.К. Верма, или Понимание физики, DC Pandey.
Примечания по главам физики для технических и медицинских экзаменов
Journal of Optics — IOPscience
Метаповерхности представляют собой тонкие двумерные слои метаматериала,
разрешать или препятствовать распространению электромагнитных волн в
желаемые направления. Например, метаповерхности
продемонстрировал необычные рассеивающие свойства падающего
плоские волны или для направления и модуляции поверхностных волн для получения
желаемые радиационные свойства. Эти свойства были использованы,
например, для создания инновационных беспроводных приемников и
передатчики. Кроме того, недавно были предложены метаповерхности.
ограничивать электромагнитные волны, тем самым избегая нежелательных
утечка энергии и повышение общей эффективности
электромагнитные приборы и устройства.Основные преимущества
метаповерхностей по отношению к существующей традиционной технологии
относятся их дешевизна, низкий уровень впитываемости по сравнению с
громоздкие метаматериалы и легкая интеграция из-за их тонкого
профиль. Благодаря этим преимуществам они являются перспективными кандидатами на
реальные решения для преодоления проблем, связанных со следующим
поколение передатчиков и приемников будущих высокоскоростных
системы связи, требующие высокой точности и эффективности
антенны, датчики, активные компоненты, фильтры и встроенные
технологии.
Например, метаповерхности
продемонстрировал необычные рассеивающие свойства падающего
плоские волны или для направления и модуляции поверхностных волн для получения
желаемые радиационные свойства. Эти свойства были использованы,
например, для создания инновационных беспроводных приемников и
передатчики. Кроме того, недавно были предложены метаповерхности.
ограничивать электромагнитные волны, тем самым избегая нежелательных
утечка энергии и повышение общей эффективности
электромагнитные приборы и устройства.Основные преимущества
метаповерхностей по отношению к существующей традиционной технологии
относятся их дешевизна, низкий уровень впитываемости по сравнению с
громоздкие метаматериалы и легкая интеграция из-за их тонкого
профиль. Благодаря этим преимуществам они являются перспективными кандидатами на
реальные решения для преодоления проблем, связанных со следующим
поколение передатчиков и приемников будущих высокоскоростных
системы связи, требующие высокой точности и эффективности
антенны, датчики, активные компоненты, фильтры и встроенные
технологии. Эта дорожная карта направлена на объединение
опыт видных исследователей в области метаповерхностей,
из которого объяснения физики, лежащей в основе необычайного
свойства этих структур должны быть предоставлены с точки зрения
разнообразные теоретические предпосылки. Другими целями этого начинания являются
подчеркнуть преимущества и ограничения метаповерхностей, т.к.
а также изложить рекомендации по их использованию в настоящем и будущем
электромагнитные устройства.
Эта дорожная карта направлена на объединение
опыт видных исследователей в области метаповерхностей,
из которого объяснения физики, лежащей в основе необычайного
свойства этих структур должны быть предоставлены с точки зрения
разнообразные теоретические предпосылки. Другими целями этого начинания являются
подчеркнуть преимущества и ограничения метаповерхностей, т.к.
а также изложить рекомендации по их использованию в настоящем и будущем
электромагнитные устройства.
Эта дорожная карта разделена на пять разделов:
1. Антенны на основе метаповерхности. В последние несколько лет метаповерхности показали возможности для продвинутых манипуляций с электромагнитные волны, открывая новые горизонты в дизайне антенны. В этом разделе авторы объясняют, как метаповерхности могут использоваться для настройки характеристик излучения антенн, их значительные преимущества по сравнению с обычными антеннами, и будущие задачи, которые необходимо решить.
2. Оптические метаповерхности. Хотя многие из присутствующих
демонстранты работают в микроволновом режиме, либо из-за
снижение затрат на производство и испытания или для удовлетворения
интерес коммуникационной или аэрокосмической промышленности, часть
потенциальное использование метаповерхностей находится в оптическом режиме.В
В этом разделе авторы обобщают классические приложения и
объяснить новые возможности оптических метаповерхностей, такие как
генерация сверхколебательных полей и сборщиков энергии.
Хотя многие из присутствующих
демонстранты работают в микроволновом режиме, либо из-за
снижение затрат на производство и испытания или для удовлетворения
интерес коммуникационной или аэрокосмической промышленности, часть
потенциальное использование метаповерхностей находится в оптическом режиме.В
В этом разделе авторы обобщают классические приложения и
объяснить новые возможности оптических метаповерхностей, такие как
генерация сверхколебательных полей и сборщиков энергии.
3. Реконфигурируемые и активные метаповерхности. Динамические метаповерхности
перспективные новые платформы для связи 5G, дистанционного зондирования
и радарные приложения. Внедрением активных элементов,
метаповерхности могут нарушить фундаментальные ограничения пассивного и
статические системы. В этом разделе у нас есть материалы, которые
описать проблемы и потенциальное использование активных компонентов в
метаповерхности, в том числе новые исследования не-Фостера, паритетного времени
симметричные и невзаимные метаповерхности.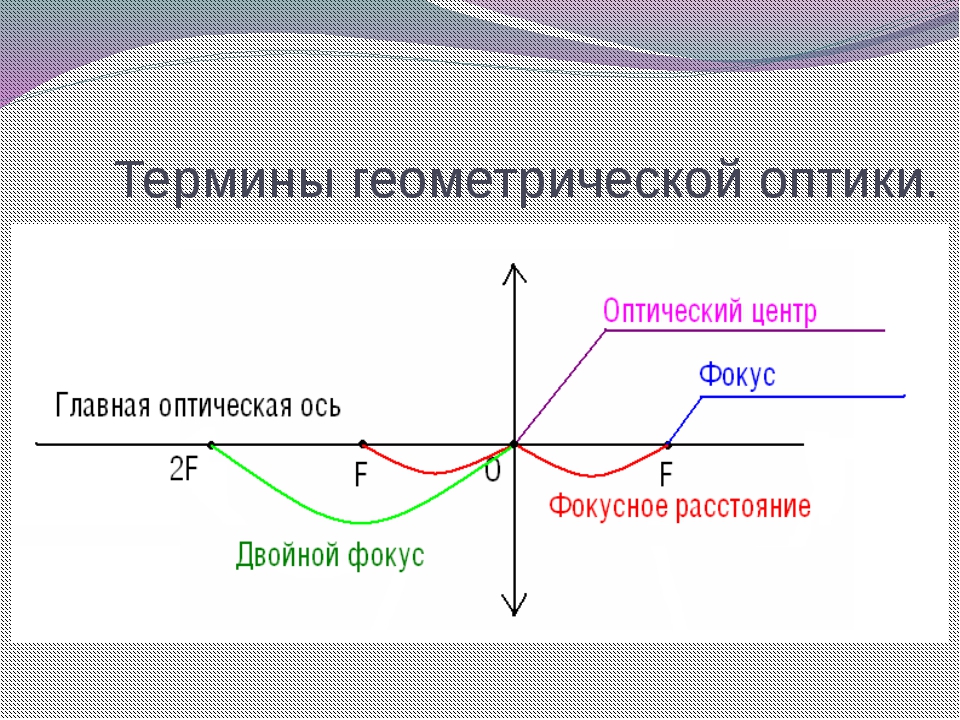
4. Метаповерхности с более высокой симметрией. Недавние исследования показали, что на свойства метаповерхностей влияет симметрии составляющих их элементов. Следовательно, по контролируя свойства этих составных элементов и их расположение, можно контролировать способ взаимодействия волн с метаповерхностью. В этом разделе авторы анализируют возможности комбинирования более чем одного слоя метаповерхности, создание более высокой симметрии, увеличение рабочей полосы пропускания плоские линзы или производство экономичных электромагнитных запрещенные зоны.
5. Численное и аналитическое моделирование метаповерхностей. В большинстве
Иногда метаповерхности представляют собой электрически большие объекты, которые
не могут быть смоделированы с помощью обычного программного обеспечения. Инструменты моделирования
которые позволяют инженерии свойств метаповерхности получить
желаемый ответ имеет важное значение в разработке практических
электромагнитные устройства. В этом разделе представлены последние достижения
и будущие проблемы в трех группах методов, которые
широко используется для анализа и синтеза метаповерхностей: схема
модели, аналитические решения и вычислительные методы.
В этом разделе представлены последние достижения
и будущие проблемы в трех группах методов, которые
широко используется для анализа и синтеза метаповерхностей: схема
модели, аналитические решения и вычислительные методы.
Ибн Аль-Хайтам: отец современной оптики
Ann Saudi Med. 2007 ноябрь-декабрь; 27(6): 464–467.
, MD * и, MD †Абдельгани Тбахи
* Отделение патологии и лабораторной медицины, больница Hôtel-Dieu Grace, Университет Западного Онтарио, Виндзор, Онтарио, Канада
Samir S. Amr
† Отделение патологии, Медицинский центр Дахрана, Организация медицинских услуг Саудовской Арамко, Дахран, Саудовская Аравия
* Отделение патологии и лабораторной медицины, больница Hôtel-Dieu Grace, Университет Западного Онтарио, Виндзор, Онтарио, Канада
† Отделение патологии, Медицинский центр Дахрана, Организация медицинских услуг Саудовской Арамко, Дахран, Саудовская Аравия
Автор, ответственный за переписку. Для корреспонденции и запросов на перепечатку: Абдельгани Тбахи, доктор медицинских наук, отделение патологии и лабораторной медицины, больница Hôtel-Dieu Grace, 1030 Ouellette Avenue, Windsor, ON-N9A 1E1, Канада, T: +1-519-973-4411, доб. 3579, [email protected]Эта статья была процитирована другими статьями в PMC.
Для корреспонденции и запросов на перепечатку: Абдельгани Тбахи, доктор медицинских наук, отделение патологии и лабораторной медицины, больница Hôtel-Dieu Grace, 1030 Ouellette Avenue, Windsor, ON-N9A 1E1, Канада, T: +1-519-973-4411, доб. 3579, [email protected]Эта статья была процитирована другими статьями в PMC.Арабский мусульманский ученый Абу Али аль-Хасан ибн аль-Хайсам, известный на западе как Альхасен или Альхазен, родился в 965 году в городе Басра на юге Ирака, поэтому он также известен как Аль-Басри. 1 Он получил образование в Басре и Багдаде и умер в Каире, Египет, в 1040 году. 2
Многие подробности жизни Ибн аль-Хайтама со временем были утеряны. Истории, связанные с его жизнью, часто противоречивы, в зависимости от рассказывающего их историка. Большая часть сведений о биографии Ибн аль-Хайсама взята из сочинений мусульманского историка тринадцатого века Ибн аль-Кифти (1172–1248). Первоначально Ибн аль-Хайтам прошел подготовку для работы на государственной службе и был назначен судьей Басры. Из-за наличия в то время различных религиозных течений с разнообразными и противоречивыми взглядами он разочаровался в религиоведении и решил посвятить свое время и силы изучению науки.Его познания в математике и физике стали легендарными, и он был хорошо известен в Ираке, Сирии и Египте. Он был приглашен Аль-Хакимом би-Амр Аллахом, фатимидским халифом Египта, чтобы помочь регулировать течение Нила во время наводнений. Аль-Хаким, шиит из секты исмаилитов, был известен как эксцентричный правитель, который издал несколько произвольных указов и законов, запрещающих употребление определенных продуктов, запрещающих женщинам покидать свои дома, убивающих всех собак и заставляющих людей работать. ночью и отдых днем.Он был довольно жестоким и убивал своих наставников и министров по прихоти. Когда Ибн аль-Хайтам понял во время своих полевых работ на Ниле, что его план по регулированию потока воды Нила путем строительства плотины к югу от Асуана нереален, он испугался за свою жизнь. Чтобы избежать потенциального смертельного гнева и гнева своего темпераментного и психически неуравновешенного покровителя, он симулировал безумие.
Из-за наличия в то время различных религиозных течений с разнообразными и противоречивыми взглядами он разочаровался в религиоведении и решил посвятить свое время и силы изучению науки.Его познания в математике и физике стали легендарными, и он был хорошо известен в Ираке, Сирии и Египте. Он был приглашен Аль-Хакимом би-Амр Аллахом, фатимидским халифом Египта, чтобы помочь регулировать течение Нила во время наводнений. Аль-Хаким, шиит из секты исмаилитов, был известен как эксцентричный правитель, который издал несколько произвольных указов и законов, запрещающих употребление определенных продуктов, запрещающих женщинам покидать свои дома, убивающих всех собак и заставляющих людей работать. ночью и отдых днем.Он был довольно жестоким и убивал своих наставников и министров по прихоти. Когда Ибн аль-Хайтам понял во время своих полевых работ на Ниле, что его план по регулированию потока воды Нила путем строительства плотины к югу от Асуана нереален, он испугался за свою жизнь. Чтобы избежать потенциального смертельного гнева и гнева своего темпераментного и психически неуравновешенного покровителя, он симулировал безумие. Он был лишен своего имущества и книг и находился под домашним арестом около 10 лет до момента смерти Аль-Хакима в 1021 году, когда он был убит при загадочных обстоятельствах.
Он был лишен своего имущества и книг и находился под домашним арестом около 10 лет до момента смерти Аль-Хакима в 1021 году, когда он был убит при загадочных обстоятельствах.
Исходное изображение, Схема глаз и связанных с ними нервов, из Китаб аль-Маназир (Книга оптики) Ибн аль-Хайтама, Стамбул, одиннадцатый век.
После освобождения из-под домашнего ареста он жил в здании с куполом (Кубба) недалеко от мечети Азхар в Каире, преподавал математику и физику, писал научные тексты и зарабатывал деньги копированием текстов. 3
Во время своего заключения он написал свой влиятельный «Китаб Аль Маназер» или Книгу Оптики, в дополнение к нескольким важным книгам и главам по физике, математике, технике, астрономии, медицине, психологии, анатомии. , зрительное восприятие и офтальмология.Он написал введение в научные методы. 4
Ибн аль-Хайтам был плодовитым автором. Он написал более 200 работ по широкому кругу вопросов, из которых известно не менее 96 его научных трудов, и до наших дней дошло около 50 из них.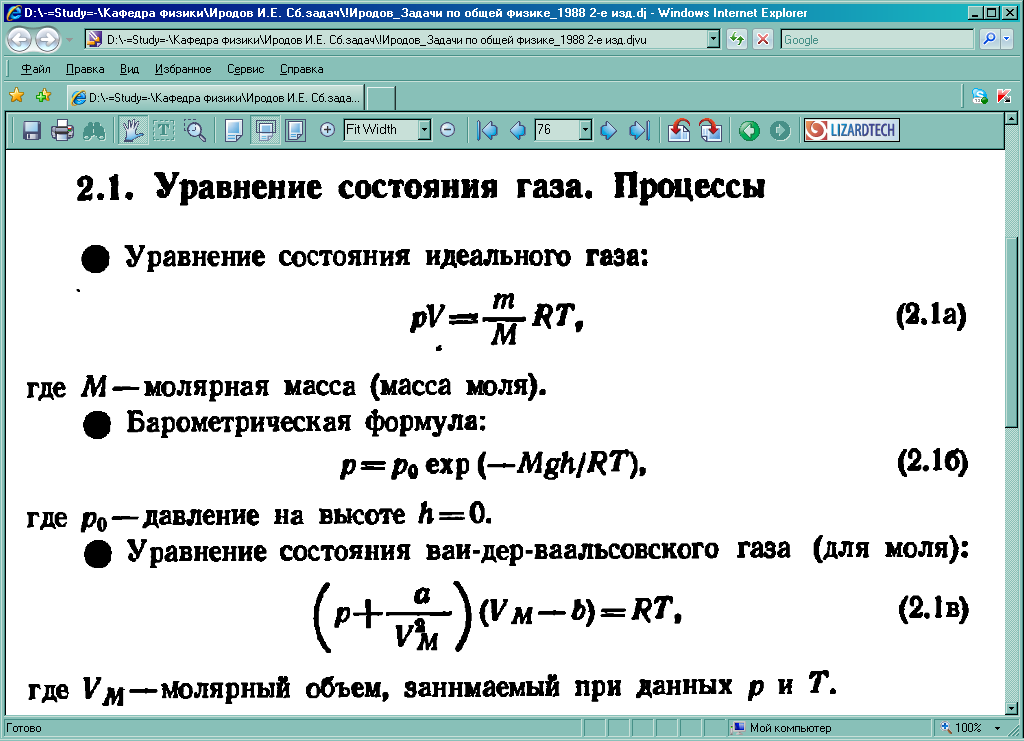 Почти половина его сохранившихся работ относится к математике, из них 23 — к астрономии, 14 — к оптике и несколько — к другим областям науки. 5 Не все его сохранившиеся работы изучены, но некоторые из наиболее важных описаны ниже.К ним относятся:
Почти половина его сохранившихся работ относится к математике, из них 23 — к астрономии, 14 — к оптике и несколько — к другим областям науки. 5 Не все его сохранившиеся работы изучены, но некоторые из наиболее важных описаны ниже.К ним относятся:
Kitab Al Manazer (Книга Оптика)
Risalah Fi Al-Dawa ‘ (трактат на свете)
Mizan Al-Hikmah (Баланс мудрости)
Maqalah Fi al-karaStun (трактат на центрах гравитации)
Risalah Fi Al-Makan (трактат на месте)
Al-Shukuk Al Batlamyus (сомнения относительно Ptolemy)
О конфигурации мира
Модель движения семи планет
Научный метод
между конкурирующими научными теориями и общим убеждением, что знание честно раскрывает природу.
 Исламская философия развивалась в средние века и играла ключевую роль в научных дебатах. Ключевыми фигурами в этих дебатах были ученые и философы. Ибн аль-Хайтам был весьма влиятельным в этом отношении. Важное наблюдение в его книге «Китаб аль-Маназер» привело его к предположению, что глаза воспринимают свет, отраженный от объектов, а не сами излучают свет, что противоречит современным убеждениям, в том числе убеждениям Птолемея и Евклида. То, как Ибн аль-Хайтам сочетал наблюдения и рациональные аргументы, оказало большое влияние на Роджера Бэкона и, в частности, на Джона Кеплера.Бэкон (1214–1296), монах-францисканец, работавший под руководством Гроссетеста, был вдохновлен трудами Ибн аль-Хайтама, который сохранил и дополнил предисловие Аристотеля.
Исламская философия развивалась в средние века и играла ключевую роль в научных дебатах. Ключевыми фигурами в этих дебатах были ученые и философы. Ибн аль-Хайтам был весьма влиятельным в этом отношении. Важное наблюдение в его книге «Китаб аль-Маназер» привело его к предположению, что глаза воспринимают свет, отраженный от объектов, а не сами излучают свет, что противоречит современным убеждениям, в том числе убеждениям Птолемея и Евклида. То, как Ибн аль-Хайтам сочетал наблюдения и рациональные аргументы, оказало большое влияние на Роджера Бэкона и, в частности, на Джона Кеплера.Бэкон (1214–1296), монах-францисканец, работавший под руководством Гроссетеста, был вдохновлен трудами Ибн аль-Хайтама, который сохранил и дополнил предисловие Аристотеля.Ибн аль-Хайтам разработал строгие экспериментальные методы контролируемой научной проверки для проверки теоретических гипотез и подтверждения индуктивных догадок. Научный метод Ибн аль-Хайтама был очень похож на современный научный метод и состоял из повторяющегося цикла наблюдений, гипотез, экспериментов и необходимости независимой проверки.
 5 , 6
5 , 6 Горини написал следующее о введении Ибн аль-Хайтама в научный метод: «По мнению большинства историков, аль-Хайтам был пионером современного научного метода. Своей книгой он изменил значение термина «оптика» и установил эксперименты как норму доказательства в этой области. Его исследования основывались не на абстрактных теориях, а на экспериментальных данных. Его эксперименты были систематическими и повторяемыми». 7
Физика и оптика
Теория света и зрения Ибн аль-Хайтама не идентична и не является прямым потомком ни одной из теорий, которые, как известно, ранее существовали в древности или в исламе. Первое реальное понимание действия линзы, в частности способности выпуклой формы создавать увеличенное изображение объекта, по-видимому, принадлежит Ибн аль-Хайсаму. 8 , 9 Только в конце 13 века были изобретены очки, представлявшие собой первое практическое использование увеличения в обществе.
 9 , 10 Ибн аль-Хайтам провел тщательное исследование прохождения света через различные среды и открыл законы преломления. Он также провел первые опыты по рассеиванию света на составляющие его цвета. Семитомный трактат Ибн аль-Хайтама по оптике, Kitab al-Manazer (Книга оптики), который он написал, находясь в заключении между 1011 и 1021 годами, считается одним из самых влиятельные книги, когда-либо написанные по физике, коренным образом изменили понимание света и зрения. 8 , 9
9 , 10 Ибн аль-Хайтам провел тщательное исследование прохождения света через различные среды и открыл законы преломления. Он также провел первые опыты по рассеиванию света на составляющие его цвета. Семитомный трактат Ибн аль-Хайтама по оптике, Kitab al-Manazer (Книга оптики), который он написал, находясь в заключении между 1011 и 1021 годами, считается одним из самых влиятельные книги, когда-либо написанные по физике, коренным образом изменили понимание света и зрения. 8 , 9 Строение глаза, Ибн аль-Хайтам, из Книги оптики.
Он подробно занимался теорией различных физических явлений, таких как тени, затмения, радуга, и размышлял о физической природе света. Он также попытался объяснить бинокулярное зрение и дал правильное объяснение кажущемуся увеличению размеров Солнца и Луны вблизи горизонта. Он известен первым использованием камеры-обскуры и камеры-обскуры. 11 Как указывалось выше, он противоречил теории зрения Птолемея и Евклида о том, что объекты воспринимаются лучами света, исходящими из глаз; согласно ему, лучи исходят из объекта зрения, а не из глаза.
 Благодаря этим обширным исследованиям в области оптики он считается отцом современной оптики.
Благодаря этим обширным исследованиям в области оптики он считается отцом современной оптики.В дополнение к Книге Оптики Ибн аль-Хайсам написал дополнение под названием «Рисала фи л-Дау» (Трактат о Свете). Это приложение содержало дальнейшие исследования свойств яркости и ее лучистого рассеивания через различные прозрачные и полупрозрачные среды.В своем трактате Мизан аль-Хикма (Равновесие мудрости) Ибн аль-Хайтам обсуждал плотность атмосферы и связывал ее с высотой. Он также изучал атмосферную рефракцию. Его оптические труды оказали влияние на многих западных интеллектуалов, таких как Роджер Бэкон, Джон Печам, Витело и Иоганн Кеплер. 11 , 12 , 13
Астрономия
Хотя он не считается одним из величайших арабских астрономов, его работы показывают, что он освоил методы Птолемея.Некоторые из этих работ также раскрывают его способность решать проблемы, привлекшие внимание арабских астрономов, такие как определение киблы (направления молитвы).
 Его критика птолемеевских планетарных моделей, представленная в Альмагесте и планетарных гипотезах , похоже, вдохновила исследования, которые привели к их замене нептолемеевскими аранжировками в Мараге 13 века и Дамаске 14 века. Этот астрономический труд был написан между 1025–1028 «Аль-Шукук ала Батламюс» , а затем переведен как Сомнения относительно Птолемея или Апории против Птолемея . 14 Он считал, что некоторые математические приемы, введенные Птолемеем в астрономию, особенно эквант, не удовлетворяют физическому требованию равномерного кругового движения. 14
Его критика птолемеевских планетарных моделей, представленная в Альмагесте и планетарных гипотезах , похоже, вдохновила исследования, которые привели к их замене нептолемеевскими аранжировками в Мараге 13 века и Дамаске 14 века. Этот астрономический труд был написан между 1025–1028 «Аль-Шукук ала Батламюс» , а затем переведен как Сомнения относительно Птолемея или Апории против Птолемея . 14 Он считал, что некоторые математические приемы, введенные Птолемеем в астрономию, особенно эквант, не удовлетворяют физическому требованию равномерного кругового движения. 14 На астрономов европейского Возрождения оказала влияние его работа «О конфигурации мира» , где он продолжал принимать физическую реальность геоцентрической модели Вселенной, представляя подробное описание физического строения небесных сфер: «Земля в целом есть круглая сфера, центр которой есть центр мира.Он неподвижен в своей [мировой] середине, неподвижен в ней и не движется ни в каком направлении и не движется ни с какой из разновидностей движения, но всегда покоится».
 15
15 Книга Ибн аль-Хайсама Модель движения каждой из семи планет , написанная в 1038 году, была важной книгой по астрономии. Сохранившаяся рукопись этой работы была обнаружена совсем недавно, и большая ее часть все еще отсутствует, поэтому работа еще не опубликована в наше время. Его реформа исключила космологию, поскольку он разработал систематическое изучение небесной кинематики, которое было полностью геометрическим.Это, в свою очередь, привело к инновационным разработкам в бесконечно малой геометрии. 16
Математика
В области математики Ибн аль-Хайтам опирался на математические работы Евклида и Табита ибн Курры и продолжал систематизировать исчисление бесконечно малых, конические сечения, теорию чисел и аналитическую геометрию после того, как связал алгебру с геометрией. Его вклад в математику был обширен. Он разработал аналитическую геометрию, установив связь между алгеброй и геометрией. Он изучал механику движения тела и был первым, кто утверждал, что тело движется постоянно, если внешняя сила не остановит его или не изменит направление его движения.
 Это поразительно похоже на первый закон движения, описанный столетия спустя Исааком Ньютоном.
Это поразительно похоже на первый закон движения, описанный столетия спустя Исааком Ньютоном.Его работа по катоптрике в Книга V Книги Оптики содержит важную проблему, известную как Проблема Альхазена . Он включает в себя рисование линий из двух точек на плоскости круга, встречающихся в точке на окружности и образующих равные углы с нормалью в этой точке. Это приводит к уравнению четвертой степени. В конечном итоге это привело Ибн аль-Хайтама к выводу самой ранней формулы суммы четвертых степеней; и, используя раннее доказательство с помощью математической индукции, он разработал метод определения общей формулы для суммы любых целых степеней.Это было фундаментальным для развития инфинитезимального и интегрального исчисления. 17
В геометрии Ибн аль-Хайтам разработал аналитическую геометрию, установив связь между алгеброй и геометрией. Ибн аль-Хайтам также открыл формулу сложения первых 100 натуральных чисел.
Его вклад в теорию чисел включает работу над совершенными числами.
 В своем «Анализе и синтезе» Ибн аль-Хайсам первым понял, что каждое четное совершенное число имеет форму 2 n -1 (2 n -1), где 2 n -1 является простым, но ему не удалось успешно доказать этот результат.Позднее, в 18 веке, это доказал Эйлер. 17
В своем «Анализе и синтезе» Ибн аль-Хайсам первым понял, что каждое четное совершенное число имеет форму 2 n -1 (2 n -1), где 2 n -1 является простым, но ему не удалось успешно доказать этот результат.Позднее, в 18 веке, это доказал Эйлер. 17 Медицина и психология
Ибн аль-Хайтам был первым, кто точно описал различные части глаза и дал научное объяснение процесса зрения. В медицине и офтальмологии Ибн аль-Хайтам добился важных успехов в глазной хирургии, впервые изучил и правильно объяснил процесс зрения и зрительного восприятия. 18 , 19 Он подробно описал различные части глаза и ввел представление о том, что предметы видятся лучами света, исходящими от предметов, а не глазами, как считалось в народе.«Зрение воспринимает свет и цвет, существующие на поверхности созерцаемого предмета. Зрение с необходимостью воспринимает все предметы через предполагаемые прямые линии, протянувшиеся между предметом и центральной точкой зрения».
 10
10 Некоторые считают Ибн аль-Хайтама основателем психофизики и экспериментальной психологии за его новаторскую работу по психологии визуального восприятия. 20
Философия
В философии Ибн аль-Хайтам считается пионером феноменологии.Он сформулировал связь между физическим и наблюдаемым миром и интуицией, психологией и психическими функциями. Его теории о знании и восприятии, связывающие области науки и религии, привели к философии существования, основанной на прямом наблюдении за реальностью с точки зрения наблюдателя. Большая часть его мыслей о феноменологии не получила дальнейшего развития до 20 века. 21 На самом деле, он хорошо известен тем, что сформулировал всеобъемлющую теорию познания. 22
Ибн аль-Хайтам, как говорят, был сторонником ашаритской школы исламского богословия и выступал против учений школы мутазилитов, хотя он, возможно, сам был сторонником мутазилитов в какой-то момент в его жизни.
Наконец, Ибн аль-Хайтам оказал влияние на многие научные дисциплины благодаря своей гениальной проницательности и новым и оригинальным наблюдениям.
 Без сомнения, он считается отцом-первооткрывателем современной оптики.
Без сомнения, он считается отцом-первооткрывателем современной оптики.ССЫЛКИ
1.Смит АМ. Теория визуального восприятия Альхасена: критическое издание с английским переводом и комментариями первых трех книг «О аспекте» Альхасена, средневековой латинской версии «Китаб аль-Маназир» Ибн аль-Хайтама. Том. 1. Филадельфия: Американское философское общество; [Google Академия]2. Хамарне С. Обзор Хакима Мохаммада Саида, Ибн аль-Хайтама. Исида. 1972; 63 (1): 118–119. [Google Академия]3. Сабра АИ. Ибн аль-Хайтам, Абу Али аль-Хасан ибн аль-Хасан. В: Гиллиспи Чарльз Коулстон, редактор.Справочник научной биографии. VI. Сыновья Чарльза Скрибнера; Нью-Йорк: 1974. С. 189–210. [Google Академия]4. Беттани Л. Ибн аль-Хайтам: ответ на мультикультурное преподавание науки? Физическое образование. 1995; 30: 247–252. [Google Академия]5. Стеффенс Б. Ибн аль-Хайтам: первый ученый. Издательство Морган Рейнольдс; Гринсборо, Северная Каролина: 2006. [Google Scholar]6. Эль-Бизри Н. Ибн аль-Хайтам или Альхазен. В: Мери Йозеф В., редактор. Средневековая исламская цивилизация: энциклопедия. II. Рутледж; Нью-Йорк, Лондон: 2006.стр. 343–345. [Google Академия]7. Горини Р. Аль-Хайтам, опытный человек: первые шаги в науке о видении. J Inter Soc по истории исламской медицины (JISHIM) 2003; 2 (4): 53–55. [Google Академия]8. Мудрый А. История использования микроскопа в хирургии уха. Ам Дж. Отол. 2000;21(6):877–886. [PubMed] [Google Scholar]9. Крисс ТС, Крисс ВМ. История операционного микроскопа: от лупы к микронейрохирургии. Нейрохирургия. 1998;42(4):899–907. [PubMed] [Google Scholar] 10. Кальдерон АЕ.Эволюция конструкции микроскопа от его изобретения до наших дней. Ам Дж. Сург Патол. 1983;7(1):95–102. [PubMed] [Google Scholar] 11. Уэйд Н.Дж., Фингер С. Глаз как оптический инструмент: от камеры-обскуры до перспективы Гельмгольца. Восприятие. 2001;30(10):1157–1177. [PubMed] [Google Scholar] 13. Лен В.Х., Ван дер Верф С. Атмосферная рефракция: история. Прил. опт. 2005;44(27):5624–5636. [PubMed] [Google Scholar] 14.
В: Мери Йозеф В., редактор. Средневековая исламская цивилизация: энциклопедия. II. Рутледж; Нью-Йорк, Лондон: 2006.стр. 343–345. [Google Академия]7. Горини Р. Аль-Хайтам, опытный человек: первые шаги в науке о видении. J Inter Soc по истории исламской медицины (JISHIM) 2003; 2 (4): 53–55. [Google Академия]8. Мудрый А. История использования микроскопа в хирургии уха. Ам Дж. Отол. 2000;21(6):877–886. [PubMed] [Google Scholar]9. Крисс ТС, Крисс ВМ. История операционного микроскопа: от лупы к микронейрохирургии. Нейрохирургия. 1998;42(4):899–907. [PubMed] [Google Scholar] 10. Кальдерон АЕ.Эволюция конструкции микроскопа от его изобретения до наших дней. Ам Дж. Сург Патол. 1983;7(1):95–102. [PubMed] [Google Scholar] 11. Уэйд Н.Дж., Фингер С. Глаз как оптический инструмент: от камеры-обскуры до перспективы Гельмгольца. Восприятие. 2001;30(10):1157–1177. [PubMed] [Google Scholar] 13. Лен В.Х., Ван дер Верф С. Атмосферная рефракция: история. Прил. опт. 2005;44(27):5624–5636. [PubMed] [Google Scholar] 14. Говард ИП. Забытые открытия Альхазена визуальных явлений. Восприятие.1996;25(10):1203–1217. [PubMed] [Google Scholar] 15. Кромби АС. Ожидание, моделирование и согласие в истории оптики: Часть I. Альхазен и средневековая традиция. Stud Hist Philos Sci. 1990;21(4):605–632. [PubMed] [Google Scholar] 16. Росс HE, Росс GM. Понимал ли Птолемей лунную иллюзию? Восприятие. 1976; 5 (4): 377–385. [PubMed] [Google Scholar] 17. Кадир А. Относительность: введение в специальную теорию. Мировое научное издательство; Сингапур: с. 1089. [Google Академия] 18. Рашид Р.Небесная кинематика Ибн аль-Хайтама. Арабская наука и философия. 2007;17(1):7–55. [Google Академия] 19. Кац В.Дж. Идеи исчисления в исламе и Индии. Математический журнал. 1995;68(3):163–174. [Google Академия] 20. Саад А., Азайзе Х., Саид О. Традиции и перспективы арабской фитотерапии. Обзор. Доказательный комплемент Alternat Med. 2005;2(4):475–479. [Бесплатная статья PMC] [PubMed] [Google Scholar]21. Arrington GE., Jr. Три араба: их влияние на офтальмологию: Хунаин ибн-Исхак, Разес, Альхазен.
Говард ИП. Забытые открытия Альхазена визуальных явлений. Восприятие.1996;25(10):1203–1217. [PubMed] [Google Scholar] 15. Кромби АС. Ожидание, моделирование и согласие в истории оптики: Часть I. Альхазен и средневековая традиция. Stud Hist Philos Sci. 1990;21(4):605–632. [PubMed] [Google Scholar] 16. Росс HE, Росс GM. Понимал ли Птолемей лунную иллюзию? Восприятие. 1976; 5 (4): 377–385. [PubMed] [Google Scholar] 17. Кадир А. Относительность: введение в специальную теорию. Мировое научное издательство; Сингапур: с. 1089. [Google Академия] 18. Рашид Р.Небесная кинематика Ибн аль-Хайтама. Арабская наука и философия. 2007;17(1):7–55. [Google Академия] 19. Кац В.Дж. Идеи исчисления в исламе и Индии. Математический журнал. 1995;68(3):163–174. [Google Академия] 20. Саад А., Азайзе Х., Саид О. Традиции и перспективы арабской фитотерапии. Обзор. Доказательный комплемент Alternat Med. 2005;2(4):475–479. [Бесплатная статья PMC] [PubMed] [Google Scholar]21. Arrington GE., Jr. Три араба: их влияние на офтальмологию: Хунаин ибн-Исхак, Разес, Альхазен. Int Rec Med Gen Pract Clin. 1959;172(6):337–338. [PubMed] [Google Scholar] 22. Халифа О. Кто является основоположником психофизики и экспериментальной психологии? Am J Islamic Social Sciences (AJISS) 1999;16(2) [Google Scholar]
Int Rec Med Gen Pract Clin. 1959;172(6):337–338. [PubMed] [Google Scholar] 22. Халифа О. Кто является основоположником психофизики и экспериментальной психологии? Am J Islamic Social Sciences (AJISS) 1999;16(2) [Google Scholar]1.2 Закон отражения. Университетская физика, том 3
Цели обучения
К концу этого раздела вы сможете:
- Объясните отражение света от полированных и шероховатых поверхностей
- Описать принцип и применение уголковых отражателей
Всякий раз, когда мы смотрим в зеркало или щуримся на солнечный свет, отражающийся от озера, мы видим отражение.Когда вы смотрите на лист белой бумаги, вы видите рассеянный от него свет. Большие телескопы используют отражение для формирования изображения звезд и других астрономических объектов.
Закон отражения гласит, что угол отражения равен углу падения, или
Закон отражения проиллюстрирован на рис. 1.5, где также показано, как измеряются угол падения и угол отражения относительно перпендикуляра к поверхности в точке падения луча света.
Фигура 1,5 Закон отражения гласит, что угол отражения равен углу падения — θr=θi.θr=θi. Углы измеряются относительно перпендикуляра к поверхности в точке падения луча на поверхность.
Мы ожидаем увидеть отражения от гладких поверхностей, но на рис. 1.6 показано, как шероховатая поверхность отражает свет. Поскольку свет падает на разные части поверхности под разными углами, он отражается в разных направлениях или рассеивается.Рассеянный свет — это то, что позволяет нам видеть лист бумаги под любым углом, как показано на рис. 1.7(а). Люди, одежда, листья и стены имеют шероховатую поверхность и видны со всех сторон. Зеркало, с другой стороны, имеет гладкую поверхность (по сравнению с длиной волны света) и отражает свет под определенными углами, как показано на рис. 1.7(b). Когда Луна отражается от озера, как показано на рис. 1.7(с), имеет место комбинация этих эффектов.
Фигура 1,6 Свет рассеивается, когда отражается от шероховатой поверхности.
 Здесь падает много параллельных лучей, но они отражаются под разными углами, потому что поверхность шероховатая.
Здесь падает много параллельных лучей, но они отражаются под разными углами, потому что поверхность шероховатая.Фигура 1,7 а) Когда лист бумаги освещается многими параллельными падающими лучами, его можно увидеть под разными углами, потому что его поверхность шероховатая и рассеивает свет. б) Зеркало, освещенное множеством параллельных лучей, отражает их только в одном направлении, потому что его поверхность очень гладкая. Только наблюдатель под определенным углом видит отраженный свет.(c) Лунный свет распространяется, когда он отражается от озера, потому что поверхность блестящая, но неровная. (кредит c: модификация работы Диего Торреса Сильвестра)
Когда вы видите себя в зеркале, кажется, что изображение на самом деле находится за зеркалом (рис. 1.8). Мы видим свет, исходящий из направления, определяемого законом отражения. Углы таковы, что изображение находится точно на том же расстоянии за зеркалом, на каком вы стоите перед зеркалом. Если зеркало висит на стене комнаты, все изображения в нем находятся за зеркалом, из-за чего комната может казаться больше.
 Хотя эти зеркальные отражения заставляют предметы казаться там, где их быть не может (например, за сплошной стеной), изображения не являются плодом вашего воображения. Зеркальные изображения можно фотографировать и снимать на видео с помощью инструментов, и они выглядят так же, как и наши глаза (которые сами по себе являются оптическими инструментами). Точный способ, которым изображения формируются зеркалами и линзами, обсуждается в следующей главе о геометрической оптике и формировании изображений.
Хотя эти зеркальные отражения заставляют предметы казаться там, где их быть не может (например, за сплошной стеной), изображения не являются плодом вашего воображения. Зеркальные изображения можно фотографировать и снимать на видео с помощью инструментов, и они выглядят так же, как и наши глаза (которые сами по себе являются оптическими инструментами). Точный способ, которым изображения формируются зеркалами и линзами, обсуждается в следующей главе о геометрической оптике и формировании изображений.Фигура 1,8 а) Ваше отражение в зеркале находится за зеркалом.Два показанных луча падают на зеркало под правильным углом, чтобы отразиться в глазах человека. Кажется, что изображение находится за зеркалом на том же расстоянии, что и (b), если бы вы смотрели на своего близнеца прямо, без зеркала.
Угловые отражатели (ретроотражатели)
Луч света, падающий на предмет, состоящий из двух взаимно перпендикулярных отражающих поверхностей, отражается обратно точно параллельно тому направлению, откуда он пришел (рис.
 9). Это верно, когда отражающие поверхности перпендикулярны, и не зависит от угла падения. (Доказательство см. [ссылка] в конце этого раздела.) Такой объект называется угловым отражателем, поскольку свет отражается от его внутреннего угла. Угловые отражатели — это подкласс ретрорефлекторов, все из которых отражают лучи обратно в том направлении, откуда они пришли. Хотя геометрия доказательства намного сложнее, угловые отражатели также могут быть построены с тремя взаимно перпендикулярными отражающими поверхностями и полезны в трехмерных приложениях.
9). Это верно, когда отражающие поверхности перпендикулярны, и не зависит от угла падения. (Доказательство см. [ссылка] в конце этого раздела.) Такой объект называется угловым отражателем, поскольку свет отражается от его внутреннего угла. Угловые отражатели — это подкласс ретрорефлекторов, все из которых отражают лучи обратно в том направлении, откуда они пришли. Хотя геометрия доказательства намного сложнее, угловые отражатели также могут быть построены с тремя взаимно перпендикулярными отражающими поверхностями и полезны в трехмерных приложениях.Фигура 1,9 Луч света, падающий на две взаимно перпендикулярные отражающие поверхности, отражается обратно точно параллельно тому направлению, откуда он пришел.
Многие недорогие отражатели на велосипедах, автомобилях и предупреждающих знаках имеют угловые отражатели, предназначенные для отражения света в том направлении, откуда он исходит. Вместо того, чтобы просто отражать свет под широким углом, световозвращение обеспечивает хорошую видимость, если наблюдатель и источник света расположены вместе, например, водитель автомобиля и фары.
 Астронавты Аполлона разместили на Луне настоящий уголковый отражатель (рис. 1.10). Лазерные сигналы с Земли могут отражаться от этого углового отражателя, чтобы измерять постепенно увеличивающееся расстояние до Луны на несколько сантиметров в год.
Астронавты Аполлона разместили на Луне настоящий уголковый отражатель (рис. 1.10). Лазерные сигналы с Земли могут отражаться от этого углового отражателя, чтобы измерять постепенно увеличивающееся расстояние до Луны на несколько сантиметров в год.Фигура 1.10 (а) Астронавты разместили на Луне уголковый отражатель, чтобы измерить ее постепенно увеличивающееся орбитальное расстояние. (b) Яркие пятна на этих велосипедных отражателях являются отражением вспышки камеры, которая сделала этот снимок темной ночью.(кредит a: модификация работы НАСА; кредит b: модификация работы «Julo»/Wikimedia Commons)
Работающие по тому же принципу, что и эти оптические отражатели, угловые отражатели обычно используются в качестве радиолокационных отражателей (рис. 1.11) для радиочастотных приложений. В большинстве случаев небольшие лодки из стекловолокна или дерева слабо отражают радиоволны, излучаемые радиолокационными системами. Чтобы сделать эти лодки видимыми для радаров (например, чтобы избежать столкновений), к лодкам прикрепляют радиолокационные отражатели, обычно на возвышенностях.

Фигура 1.11 Радиолокационный отражатель, установленный на парусной лодке, относится к типу уголковых отражателей. (кредит: Тим Ширман-Чейз)
В качестве контрпримера, если вы заинтересованы в создании самолета-невидимки, отражения радара должны быть сведены к минимуму, чтобы избежать обнаружения. Таким образом, одним из соображений дизайна будет избегать создания углов 90 ° 90 ° в планере.
CBSE Notes Class 12 Physics Ray Optics
Физико-лучевая оптика класса 12 – Получите здесь примечания по физике лучевой оптики класса 12.Кандидаты, которые стремятся получить класс 12 с хорошим баллом, могут проверить эту статью для примечаний. Это возможно только в том случае, если у вас есть лучший учебный материал по физике CBSE Class 12 и продуманный план подготовки. Чтобы помочь вам в этом, мы здесь с примечаниями. Надеюсь, что эти заметки помогут вам понять важные темы и запомнить ключевые моменты экзамена. Ниже мы предоставили заметки по физике для 12 класса по теме Лучевая оптика.

- 8 Класс: 12-й
- Тема:
- Тема:
- 8 Тема:
- 8 Тема:
Ray Optics- 8 Ресурс:
Примечания - Тема:
CBSE Notes Class 12 Ray Ray Optics
Подписаться на последние обновления
Кандидатам, претендующим на 12-й класс, рекомендуется пересмотреть примечания к этому посту.С помощью Notes кандидаты могут планировать свою стратегию для конкретного более слабого раздела предмета и усердно учиться. Итак, продолжайте и ознакомьтесь с важными примечаниями для класса 12 Physics Ray Optics.
Легкий
Свет — это форма энергетических глаз. Источники света бывают трех типов: тепловые и люминесцентные.
Фотометрия — это отрасль измерения световой энергии.
Характеристики света
Световые волны — это электромагнитные волны, природа которых поперечная.Скорость света в вакууме 3 х 10 8 мс, но в разных средах она различна.

Скорость и длина волны света изменяются при переходе из одной среды в другую, но его частота остается неизменной.
Важные условия
(i) Светящиеся объекты Объекты, излучающие собственный свет, называются светящимися объектами, например, солнце, другие звезды, масляная лампа и т. д.
(ii) Несветящиеся предметы Предметы, которые не излучают собственного света, но становятся видимыми благодаря отражению падающего на них света, называются несветящимися предметами, т.е.г., луна, стол, стул. деревья и т. д.
(iii) Луч света Прямая линия, проведенная в направлении распространения света, называется лучом света.
(iv) Луч света Пучок смежных световых лучей называется лучом света.
(v) Изображение Если луч света, идущий от предмета, после отражения или преломления встречается или кажется встречающимся в какой-то точке, то эта точка называется изображением предмета.

(vi) Реальное изображение Изображение, полученное при реальной встрече световых лучей, называется реальным изображением.
Реальное изображение может быть получено на экране. Реальное изображение перевернуто.
(vii) Виртуальное изображение Изображение, полученное, когда световые лучи на самом деле не встречаются, а только кажутся встречающимися, называется виртуальным изображением.
Отражение света
Отражение лучей света обратно в ту же среду при попадании на хорошо отполированную поверхность, такую как зеркало, называется отражением света.Законы отражения
Есть два закона отражения.
(i) Падающий луч, отраженный луч и нормаль к точке падения лежат в одной плоскости.
(ii) Угол падения (i) всегда равен углу отражения (r).
Типы отражения
(i) Регулярное отражение Когда параллельный пучок отраженных световых лучей получается для параллельного пучка падающих световых лучей после отражения от плоскости, отражающее отражение, называется регулярным отражением.

(ii) Неравномерное или рассеянное отражение Когда непараллельный пучок отраженных световых лучей получается для параллельного пучка падающих световых лучей после отражения от поверхности, то такой тип отражения называется нерегулярным или рассеянным отражением.
Зеркало
Гладкая и хорошо отполированная отражающая поверхность называется зеркалом.
(i) Плоское зеркало Хорошо отполированная плоская поверхность называется плоским зеркалом.
Различные свойства изображения, формируемого плоским зеркалом
Размер изображения = Размер объекта
Увеличение == Единство
Расстояние изображения == Расстояние объекта
Плоское зеркало может формировать как мнимое, так и реальное изображение.
Человек может видеть свое полное изображение в зеркале в половину человеческого роста.
Когда два плоских зеркала удерживаются под углом θ, количество изображений объекта, помещенного между ними, определяется следующим образом:
(a) n = [(360°/θ) – 1], где 360°/θ — целое число.

(b) n = целая часть 360°/θ, когда 360° не является целым числом.
[Плоское зеркало может формировать реальное изображение, когда луч света, падающий на зеркало, сходится. Дети во время игры формируют изображение солнца в виде стены полосой плоского зеркала.]
В калейдоскопе и перископе используется принцип формирования изображения плоским зеркалом.
Если, удерживая объект неподвижным, плоское зеркало повернуть в своей плоскости на угол θ, то отраженный луч повернется в том же направлении на угол 2 θ.
Фокусное расстояние, как и радиус кривизны плоского зеркала, равны бесконечности. Сила плоского зеркала равна нулю.
Изображение, образованное плоским зеркалом, мнимое, прямое, перевернутое вбок, того же размера, что и предмет, и на том же расстоянии, что и предмет от зеркала.
(ii) Сферическое зеркало Хорошо отполированная криволинейная поверхность, отражающая поверхность которой представляет собой вырезанную часть впадины на стеклянном шаре, называется сферическим зеркалом.
 Зеркала сферические двух типов
Зеркала сферические двух типов(a) Вогнутое зеркало Сферическое зеркало, изогнутая поверхность которого является отражающей поверхностью, называется вогнутым зеркалом.
(b) C Выпуклое зеркало Сферическое зеркало, выпуклая поверхность которого является отражающей поверхностью, называется выпуклым зеркалом.
Некоторые термины, относящиеся к сферическим зеркалам, приведены ниже(i) Центр кривизны Это центр сферы, частью которой является зеркало или линза.
(ii) Радиус кривизны (R) Радиус полой сферы, частью которой является зеркало, называется радиусом кривизны.
(iii) Полюс Центральная точка сферического зеркала называется его полюсом (P).
(iv) Фокус Когда параллельный пучок световых лучей падает на сферическое зеркало, то после отражения он встречается или кажется сходящимся в точке на главной оси, которая называется фокусом сферического зеркала.

(v) Фокусное расстояние Расстояние между полюсом и фокусом называется фокусным расстоянием (f).
Отношение между фокусным расстоянием и радиусом кривизны определяется как
f=R/2
Сила зеркала определяется как P = 1/f (метр)
(vi) Формула зеркала 1/f = 1/v + 1/u
.
Линейное увеличение
Отношение высоты изображения (1), образованного зеркалом, к высоте объекта (O) называется линейным увеличением (м).
Линейное увеличение (м) = I/O = -v/u
Площадное и осевое увеличение
Отношение площади изображения к площади объекта называется площадным увеличением.
Условные обозначения для сферических зеркал
- Все расстояния измеряются от полюса зеркала.
- Расстояния, измеренные в направлении падающих световых лучей, считаются положительными.
- Расстояния, измеренные в направлении, противоположном падающим световым лучам, считаются отрицательными.

- Расстояния, измеренные над главной осью, положительны.
- Расстояния, измеренные ниже главной оси, отрицательны.
Боковой вариант
В изображении, сформированном плоским зеркалом, правая сторона объекта выглядит как левая и наоборот.Это явление называется боковой инверсией.
При помещении предмета между полюсом и фокусом вогнутого зеркала формируется его мнимое, вертикальное и увеличенное изображение.
Выпуклое зеркало формирует мнимое прямое и уменьшенное изображение для всех состояний объекта.
Фокусное расстояние вогнутого зеркала принимается отрицательным, а выпуклого зеркала принимается положительным.
Преломление света
Отклонение световых лучей от своего пути при переходе из одной прозрачной среды в другую прозрачную среду называется преломлением света.
Причина рефракции
Скорость света различна в разных средах.

Законы преломления
(i) Падающий луч, преломленный луч и нормаль к точке падения лежат в одной плоскости.
(ii) Отношение синуса угла падения к синусу угла преломления является постоянным для пары двух сред,
, где 1 &mu 2 называется показателем преломления второй среды по отношению к первой среде.
Этот закон также называют законом Снелла.
Показатель преломления
Отношение скорости света в вакууме (с) к скорости света в любой среде (u) называется показателем преломления среды.
Показатель преломления среды,
мк = c/v
Показатель преломления воды =4/3 = 1,33; Показатель преломления стекла = 3/2 = 1,50·
Когда свет отражается более плотной средой, создается разность фаз π радиан, разность хода λ/2 или разность времени T/2.Это известно как закон Стокса. Расстояние x, пройденное светом в среде с показателем преломления μ, равно расстоянию (&mux), пройденному в вакууме.

Время, за которое свет проходит толщину x времени = µx/c, где c = скорость света в вакууме.
Относительный показатель преломления
Показатель преломления второй среды по отношению к первой среде
Формула Коши
Критический угол
Угол падения в более плотной среде, при котором угол преломления в более разреженной среде становится равным 90°.называется критическим углом (С).
Критический угол для алмаза = 24°
Критический угол для стекла = 42° :
Критический угол для воды = 48° :
Показатель преломления более плотной среды μ = 1/sin C
Полное внутреннее отражение (ПВО)
Когда луч света, идущий от более плотной среды к более разреженной среде, падает на границу раздела под углом падения, превышающим критический угол, тогда
луч света отражается обратно в более плотную среду.Это явление называется МДП.Критический угол увеличивается с температурой.

Показатель преломления максимален для фиолетового цвета света и минимален для красного цвета света. т. е. μ v > μ R , следовательно, критический угол максимален для красного цвета света и минимален для фиолетового цвета света, т. е. C v < C R
Полное внутреннее отражение возникает, если угол падения в более плотной среде превышает критический угол.
Мираж — это оптическая иллюзия, наблюдаемая в пустынях и на дорогах в жаркий день, когда воздух у земли более шумный и, следовательно, более разреженный, чем воздух над головой.
Оптические волокна
также основаны на явлении полного внутреннего отражения. Оптические волокна состоят из нескольких тысяч очень длинных и качественных волокон из стекла или кварца. Диаметр каждого волокна порядка 10-4 см при показателе преломления материала порядка 1,5. Оптические волокна используются для передачи и приема электрических сигналов путем преобразования их сначала в световые сигналы.

Для преломления на выпуклой или вогнутой сферической поверхностигде μ = показатель преломления, u = расстояние до объекта, v = расстояние до изображения и R = радиус кривизны сферической поверхности
Линза
Линза — однородная прозрачная среда, ограниченная двумя сферическими или одной сферической и одной плоской поверхностями.
Выпуклая линза
Линза, которая тоньше по краям и толще в середине, называется выпуклой или собирающей линзой.
Вогнутая линза
Линза, которая утолщается по краям и тоньше посередине, называется вогнутой или рассеивающей линзой.
Формула объектива
1/f = 1/v – 1/u
где f = фокусное расстояние объектива, U = расстояние до объекта, U = расстояние до изображения.Формула производителя линз
1/f=(μ – 1) (1/R 1 – 1/R 2 ), где μ = показатель преломления материала линзы, а R 1 и R 2 — радиусы кривизны линзы.

Мощность линзы
Обратная величина фокусного расстояния линзы, когда она измеряется в метрах, называется оптической силой линзы.
Сила линзы, (P) = 1/f(метр)
Единицей измерения является диоптрия (D).
Оптическая сила выпуклой (собирающей) линзы положительна, а вогнутой (рассеивающей) линзы — отрицательна.
Фокусное расстояние комбинации линз
(i) Когда линзы соприкасаются 1/F – 1/f 1 + 1/f 2
Мощность комбинации P = P 1 + P 2
(ii) Когда линзы находятся на расстоянии d
1/F = 1/F 1 + 1/F 2 – D/F 1 F 1
Мощность комбинации
P = P 1 + P 2 – dP 1 P 2Линейное увеличение
м = ввод/вывод = v/u
Для объекта небольшого размера, расположенного линейно вдоль главной оси, его осевое (продольное) увеличение равно
Осевое увеличение = – dv/du = (v/u) 2
=(f/f+u) 2 = (f-v/f) 2Фокусное расстояние выпуклой линзы методом смещения
Фокусное расстояние выпуклой линзы f = (a 2 – d 2 ) / 4a
, где a = расстояние между стержнем изображения и стержнем объекта, а
d = расстояние между двумя положениями линзы.
Расстояние между двумя штифтами должно быть более чем в четыре раза больше фокусного расстояния выпуклой линзы, т. е. a > 4f.
Высота объекта O = √I 1 I 2
Обрезка линзы
(i) Если симметричную выпуклую линзу с фокусным расстоянием f разрезать вдоль ее оптической оси на две части, то фокусное расстояние каждой части (плосковыпуклая линза) равно 2f. Однако, если две части соединены, как показано на рисунке, фокусное расстояние комбинации снова равно f.
(ii) Если симметричную выпуклую линзу с фокусным расстоянием f разрезать вдоль главной оси на две части, то фокусное расстояние каждой части останется неизменным как f. Если эти две части соединяются изогнутыми концами с одной стороны, фокусное расстояние комбинации составляет f/2. Но при соединении двух частей в противоположном направлении чистое фокусное расстояние становится равным
.Призма
Призма представляет собой однородную прозрачную среду, заключенную между двумя преломляющими поверхностями, наклоненными под углом.

Угол отклонения
Угол, образуемый между направлением падающего светового луча и выходящего из призмы светового луча, называется углом отклонения (δ).
Формула призмы
Показатель преломления материала призмы
Рассеивание света
Расщепление белого света на составляющие его цвета в последовательности VIBGYOR при прохождении через призму. называется дисперсией света.
Показатель преломления μ v > μ R , поэтому фиолетовый цвет отклоняется больше всего, а красный — меньше всего. т. е. δ v > δ R .
Угловая дисперсия
Угол между направлением выхода фиолетового и красного лучей света из призмы называется угловой дисперсией.
Угловая дисперсия
(θ) δ v – δ R = (μ v – μ R A
, где δ v и δ R — угол отклонения.

Дисперсионная способность
W = θ/δ Y = (μ v – μ R ) / (μ Y – 1)
, где μ Y = (μ v + μ R ) / 2 — средний показатель преломления.
Человеческий глаз
Глаз человека — оптический прибор, формирующий реальное изображение предметов на сетчатке глаза.
цвета сетчатки содержат сотни колбочек и палочек, которые отражают свет и интенсивность света соответственно.
Цилиарные мышцы изменяют фокусное расстояние хрусталика глаза. Эта сила глаза называется силой аккомодации глаза.
Различные дефекты зрения человеческого глаза описаны ниже
(i) Близорукость или близорукость Это дефект зрения, из-за которого человек может ясно видеть близлежащие предметы, но не может ясно видеть удаленные предметы.
При этом дефекте дальняя точка глаза смещается от бесконечности к ближнему.

Этот дефект можно устранить с помощью вогнутой линзы подходящего увеличения.
(ii) Гиперметропия или дальнозоркость При этом дефекте человек может ясно видеть удаленные объекты, но не может четко видеть близкие объекты.
При этом дефекте ближняя точка глаза смещается от глаза.
Этот дефект можно устранить с помощью выпуклой линзы подходящего увеличения.
(iii) Астигматизм При этом дефекте человек не может одновременно фокусироваться на горизонтальных и вертикальных линиях на одном и том же расстоянии.
Этот дефект можно устранить, используя подходящие цилиндрические линзы.
(iv) Дальтонизм При этом дефекте человек различает несколько цветов. человек не может. Причина этого дефекта — отсутствие нескольких цветов. колбочек, чувствительных к
Этот дефект не может быть устранен.
(v) Катаракта В этом дефекте.на роговице развивается непрозрачная белая пленка, из-за которой человек теряет зрение частично или полностью.

Этот дефект можно устранить, удалив мембрану хирургическим путем.
Камера
Фотокамера состоит из светонепроницаемой коробки, на одном конце которой установлена система собирающих линз. На другом конце бокса, противоположном линзовой системе, закреплена светочувствительная пленка. Реальное перевернутое изображение объекта формируется на пленке системой линз.
Число f для камеры: Число f представляет размер апертуры.
число f = фокусное расстояние объектива (F) / диаметр объектива (d)
Обычно 2, 2,8, 4, 5,6, 8, 11, 22, 32 — это числа f.
Количество света (L), попадающего в камеру, прямо пропорционально площади (A) апертуры, т. е.
L ∝A∝ d 2
Яркость изображения ∝ (d2/f2)
, где d = диаметр линзы и F = фокусное расстояние линзы.
Время экспозиции – это время, в течение которого свет падает на фотопленку.
Простой микроскоп
Используется для наблюдения увеличенных изображений объектов.
 Он состоит из собирающей линзы с малым фокусным расстоянием.
Он состоит из собирающей линзы с малым фокусным расстоянием.Увеличение мощности
(i) Когда окончательное изображение формируется на расстоянии не менее четкого зрения (D), тогда M=1+d/f
где f= фокусное расстояние объектива.
(ii) Когда окончательное изображение формируется на бесконечности, тогда M = D/f
Составной микроскоп
Это комбинация двух выпуклых линз, называемых объективом, и окуляра, разделенных расстоянием.Обе линзы имеют малые фокусные расстояния, но f o < f e , где f o и f e — фокусные расстояния объектива и окуляра соответственно
Увеличение мощности
M = v o / u o {1 + (D/f o )
Где v o = расстояние изображения, формируемого линзой объектива и
u o = расстояние объекта от объектива(ii) Когда окончательное изображение формируется на бесконечности, тогда
M = v o /u o . Д/ф и
Д/ф и Астрономический телескоп
Это также комбинация двух линз, называемых объективом и окуляром, разделенных расстоянием. Он используется для наблюдения четких изображений небесных тел, таких как звезды, планеты и т. д.
Увеличение мощности
(i) Когда окончательное изображение формируется на расстоянии не менее четкого зрения (D), тогда M = f o /f e {1+ (D/f e )}, где f o и f и — фокусные расстояния объектива и окуляра соответственно.
Длина зрительной трубы (L) = (f o + u e )
, где u e = расстояние от объекта до окуляра.
(ii) Когда окончательное изображение формируется на бесконечности, тогда M = f o /f e
Длина зрительной трубы (L) = f o + f e
Для большого увеличения телескопа f o должно быть большим, а f e маленьким.

Для большого увеличения микроскопа; f o < f e должно быть маленьким.
Разрешающая способность
Способность оптического прибора давать отдельные и четкие изображения двух близко расположенных объектов называется его разрешающей способностью.
Предел разрешения
Минимальное расстояние между двумя близко расположенными объектами, которое может быть точно разрешено прибором, называется его пределом разрешения (d).
Разрешающая способность микроскопа = 1/d = 2 мк sin θ / λ
, где d = предел разрешения, λ = длина волны используемого света.
μ = показатель преломления среды между объектами и линзой объектива, а θ = половина угла конуса.Разрешающая способность телескопа = 1/dθ = d/1,22 λ
где dθ = предел разрешения, A = длина волны используемого света и
d = диаметр апертуры объективаАберрация линз
Изображение, формируемое объективом, имеет следующие два основных недостатка:
(i) Спберическая аберрация Аберрация линзы, из-за которой лучи, проходящие через линзу, не фокусируются в одну точку, а изображение точечного объекта, расположенного на оси, размыто.
 называется сферической аберрацией.
называется сферической аберрацией.Можно уменьшить с помощью
- линзы с большим фокусным расстоянием
- плосковыпуклые линзы
- скрещенные линзы
- линзы, сочетающие выпуклую и вогнутую линзы
(ii) Хроматическая аберрация Изображение белого объекта, образованное линзой, обычно окрашено и размыто. Этот дефект изображения, создаваемого объективом, называется хроматической аберрацией.
Рассеяние света
Когда свет проходит через среду, в которой взвешены частицы, размер которых порядка длины волны света, то свет, ударяясь об эти частицы, отклоняется в разные стороны.Эти явления называются рассеянием света.
По лорду Рэлею интенсивность рассеянного света
I ∝ 1/λ 4
Следовательно, красный цвет света рассеивается меньше всего, а фиолетовый цвет света рассеивается больше всего.
Примеры рассеяния света из повседневной жизни
- Синий цвет неба.

- Красный цвет сигналов опасности. /
- Черный цвет неба при отсутствии атмосферы, здесь
- Красный цвет времени восхода и захода солнца.
- Человеческий глаз наиболее чувствителен к желтому цвету
Класс 12 Ключевые моменты, важные вопросы и практические документы
Надеюсь, эти заметки помогли вам в подготовке к школьным экзаменам. Кандидаты также могут ознакомиться с ключевыми моментами, важными вопросами и практическими работами по различным предметам для класса 12 на хинди и английском языках по ссылке ниже.
Решения NCERT класса 12
Кандидаты, которые учатся в классе 12, также могут проверить решения NCERT для класса 12 здесь.Это поможет кандидатам узнать решения по всем темам, охватываемым 12-м классом. Кандидаты могут щелкнуть по теме мудрой ссылки, чтобы получить то же самое. Подробные ответы на вопросы учебников NCERT по главам 12 предоставляются с целью помочь учащимся сравнить свои ответы с примерами ответов.

Пробный тест/практика класса 12
Пробный тест— это тренировочный тест или, можно сказать, план основного экзамена. Прежде чем появиться на основном экзамене, кандидаты должны пройти пробный тест, так как это помогает студентам учиться на своих ошибках.С помощью пробного теста/практики класса 12 кандидаты также могут получить представление о схеме и схеме выставления оценок на этом экзамене. Ради кандидатов мы предоставляем ссылки на пробный тест / практику класса 12 ниже.
Образцовые вопросы класса 12
Образцовые вопросы Класс 12 – очень важный ресурс для учащихся, готовящихся к экзамену. Здесь мы предоставили примеры решений задач вместе с примерами задач NCERT класса 12. Вопросы из очень важных тем рассматриваются в примерах вопросов для класса 12.
Физика 12 класс Заметки по химии Математические заметки Заметки по биологии
Чтобы быстрее получать оповещения об экзаменах и о вакансиях в государственных органах Индии, присоединяйтесь к нашему каналу Telegram.



 Складываясь, они порождают отраженный, преломленный и рассеянный свет.
Складываясь, они порождают отраженный, преломленный и рассеянный свет.




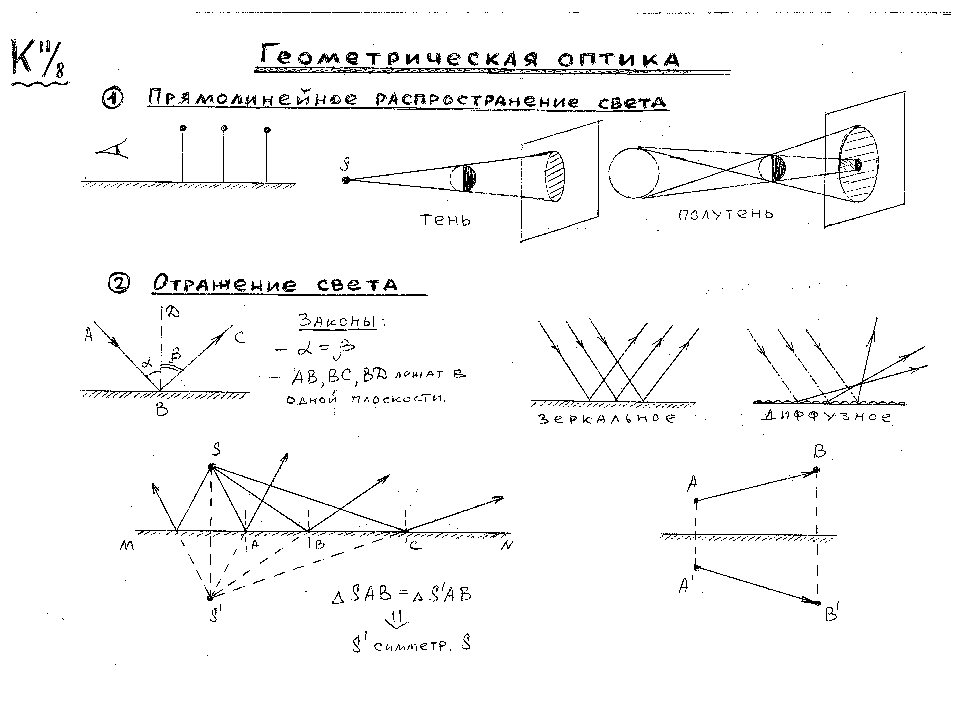 Сборка модели микроскопа
Сборка модели микроскопа (ПРИМЕЧАНИЕ: это тот же предмет и та же линза, только на этот раз предмет расположен ближе к линзе.) Определите расстояние до изображения и размер изображения.
(ПРИМЕЧАНИЕ: это тот же предмет и та же линза, только на этот раз предмет расположен ближе к линзе.) Определите расстояние до изображения и размер изображения. 2 см. Определите расстояние до изображения и размер изображения.
2 см. Определите расстояние до изображения и размер изображения.

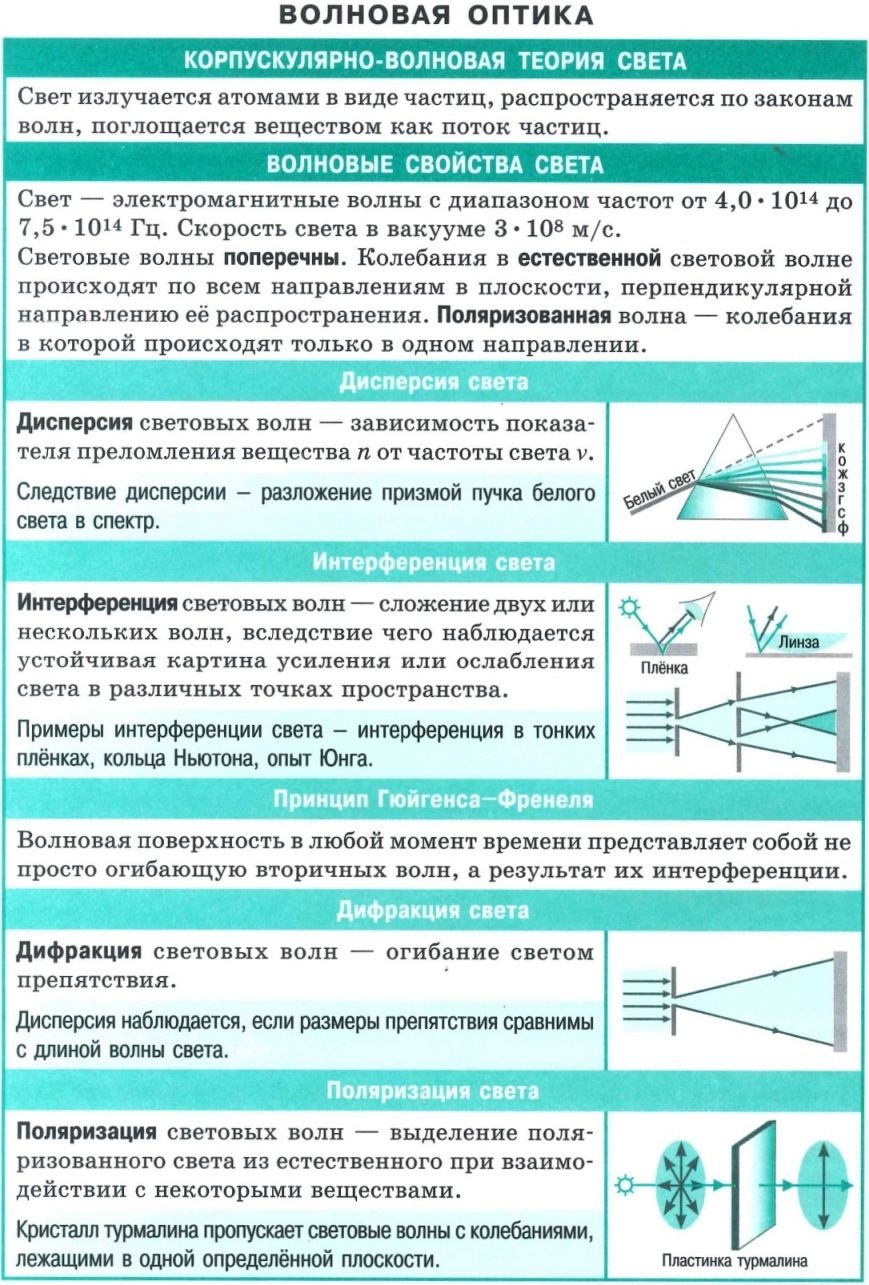 Исламская философия развивалась в средние века и играла ключевую роль в научных дебатах. Ключевыми фигурами в этих дебатах были ученые и философы. Ибн аль-Хайтам был весьма влиятельным в этом отношении. Важное наблюдение в его книге «Китаб аль-Маназер» привело его к предположению, что глаза воспринимают свет, отраженный от объектов, а не сами излучают свет, что противоречит современным убеждениям, в том числе убеждениям Птолемея и Евклида. То, как Ибн аль-Хайтам сочетал наблюдения и рациональные аргументы, оказало большое влияние на Роджера Бэкона и, в частности, на Джона Кеплера.Бэкон (1214–1296), монах-францисканец, работавший под руководством Гроссетеста, был вдохновлен трудами Ибн аль-Хайтама, который сохранил и дополнил предисловие Аристотеля.
Исламская философия развивалась в средние века и играла ключевую роль в научных дебатах. Ключевыми фигурами в этих дебатах были ученые и философы. Ибн аль-Хайтам был весьма влиятельным в этом отношении. Важное наблюдение в его книге «Китаб аль-Маназер» привело его к предположению, что глаза воспринимают свет, отраженный от объектов, а не сами излучают свет, что противоречит современным убеждениям, в том числе убеждениям Птолемея и Евклида. То, как Ибн аль-Хайтам сочетал наблюдения и рациональные аргументы, оказало большое влияние на Роджера Бэкона и, в частности, на Джона Кеплера.Бэкон (1214–1296), монах-францисканец, работавший под руководством Гроссетеста, был вдохновлен трудами Ибн аль-Хайтама, который сохранил и дополнил предисловие Аристотеля. 5 , 6
5 , 6  9 , 10 Ибн аль-Хайтам провел тщательное исследование прохождения света через различные среды и открыл законы преломления. Он также провел первые опыты по рассеиванию света на составляющие его цвета. Семитомный трактат Ибн аль-Хайтама по оптике, Kitab al-Manazer (Книга оптики), который он написал, находясь в заключении между 1011 и 1021 годами, считается одним из самых влиятельные книги, когда-либо написанные по физике, коренным образом изменили понимание света и зрения. 8 , 9
9 , 10 Ибн аль-Хайтам провел тщательное исследование прохождения света через различные среды и открыл законы преломления. Он также провел первые опыты по рассеиванию света на составляющие его цвета. Семитомный трактат Ибн аль-Хайтама по оптике, Kitab al-Manazer (Книга оптики), который он написал, находясь в заключении между 1011 и 1021 годами, считается одним из самых влиятельные книги, когда-либо написанные по физике, коренным образом изменили понимание света и зрения. 8 , 9  Благодаря этим обширным исследованиям в области оптики он считается отцом современной оптики.
Благодаря этим обширным исследованиям в области оптики он считается отцом современной оптики. Его критика птолемеевских планетарных моделей, представленная в Альмагесте и планетарных гипотезах , похоже, вдохновила исследования, которые привели к их замене нептолемеевскими аранжировками в Мараге 13 века и Дамаске 14 века. Этот астрономический труд был написан между 1025–1028 «Аль-Шукук ала Батламюс» , а затем переведен как Сомнения относительно Птолемея или Апории против Птолемея . 14 Он считал, что некоторые математические приемы, введенные Птолемеем в астрономию, особенно эквант, не удовлетворяют физическому требованию равномерного кругового движения. 14
Его критика птолемеевских планетарных моделей, представленная в Альмагесте и планетарных гипотезах , похоже, вдохновила исследования, которые привели к их замене нептолемеевскими аранжировками в Мараге 13 века и Дамаске 14 века. Этот астрономический труд был написан между 1025–1028 «Аль-Шукук ала Батламюс» , а затем переведен как Сомнения относительно Птолемея или Апории против Птолемея . 14 Он считал, что некоторые математические приемы, введенные Птолемеем в астрономию, особенно эквант, не удовлетворяют физическому требованию равномерного кругового движения. 14  15
15 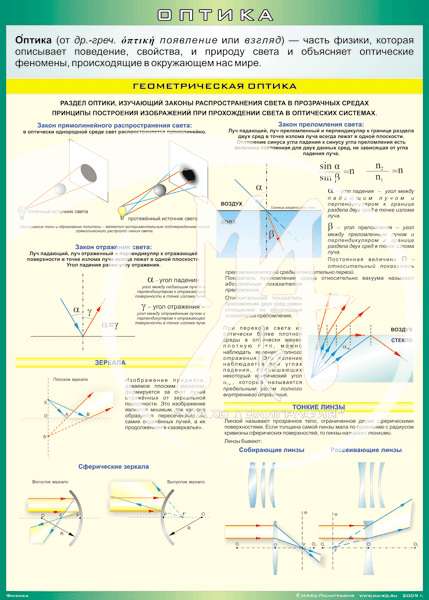 Это поразительно похоже на первый закон движения, описанный столетия спустя Исааком Ньютоном.
Это поразительно похоже на первый закон движения, описанный столетия спустя Исааком Ньютоном. В своем «Анализе и синтезе» Ибн аль-Хайсам первым понял, что каждое четное совершенное число имеет форму 2 n -1 (2 n -1), где 2 n -1 является простым, но ему не удалось успешно доказать этот результат.Позднее, в 18 веке, это доказал Эйлер. 17
В своем «Анализе и синтезе» Ибн аль-Хайсам первым понял, что каждое четное совершенное число имеет форму 2 n -1 (2 n -1), где 2 n -1 является простым, но ему не удалось успешно доказать этот результат.Позднее, в 18 веке, это доказал Эйлер. 17 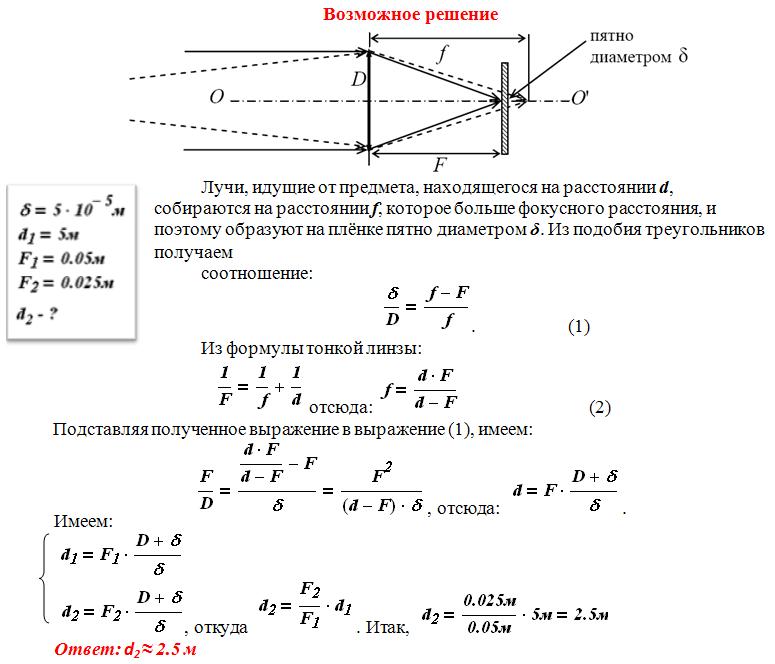 10
10  Без сомнения, он считается отцом-первооткрывателем современной оптики.
Без сомнения, он считается отцом-первооткрывателем современной оптики. В: Мери Йозеф В., редактор. Средневековая исламская цивилизация: энциклопедия. II. Рутледж; Нью-Йорк, Лондон: 2006.стр. 343–345. [Google Академия]7. Горини Р. Аль-Хайтам, опытный человек: первые шаги в науке о видении. J Inter Soc по истории исламской медицины (JISHIM) 2003; 2 (4): 53–55. [Google Академия]8. Мудрый А. История использования микроскопа в хирургии уха. Ам Дж. Отол. 2000;21(6):877–886. [PubMed] [Google Scholar]9. Крисс ТС, Крисс ВМ. История операционного микроскопа: от лупы к микронейрохирургии. Нейрохирургия. 1998;42(4):899–907. [PubMed] [Google Scholar] 10. Кальдерон АЕ.Эволюция конструкции микроскопа от его изобретения до наших дней. Ам Дж. Сург Патол. 1983;7(1):95–102. [PubMed] [Google Scholar] 11. Уэйд Н.Дж., Фингер С. Глаз как оптический инструмент: от камеры-обскуры до перспективы Гельмгольца. Восприятие. 2001;30(10):1157–1177. [PubMed] [Google Scholar] 13. Лен В.Х., Ван дер Верф С. Атмосферная рефракция: история. Прил. опт. 2005;44(27):5624–5636. [PubMed] [Google Scholar] 14.
В: Мери Йозеф В., редактор. Средневековая исламская цивилизация: энциклопедия. II. Рутледж; Нью-Йорк, Лондон: 2006.стр. 343–345. [Google Академия]7. Горини Р. Аль-Хайтам, опытный человек: первые шаги в науке о видении. J Inter Soc по истории исламской медицины (JISHIM) 2003; 2 (4): 53–55. [Google Академия]8. Мудрый А. История использования микроскопа в хирургии уха. Ам Дж. Отол. 2000;21(6):877–886. [PubMed] [Google Scholar]9. Крисс ТС, Крисс ВМ. История операционного микроскопа: от лупы к микронейрохирургии. Нейрохирургия. 1998;42(4):899–907. [PubMed] [Google Scholar] 10. Кальдерон АЕ.Эволюция конструкции микроскопа от его изобретения до наших дней. Ам Дж. Сург Патол. 1983;7(1):95–102. [PubMed] [Google Scholar] 11. Уэйд Н.Дж., Фингер С. Глаз как оптический инструмент: от камеры-обскуры до перспективы Гельмгольца. Восприятие. 2001;30(10):1157–1177. [PubMed] [Google Scholar] 13. Лен В.Х., Ван дер Верф С. Атмосферная рефракция: история. Прил. опт. 2005;44(27):5624–5636. [PubMed] [Google Scholar] 14.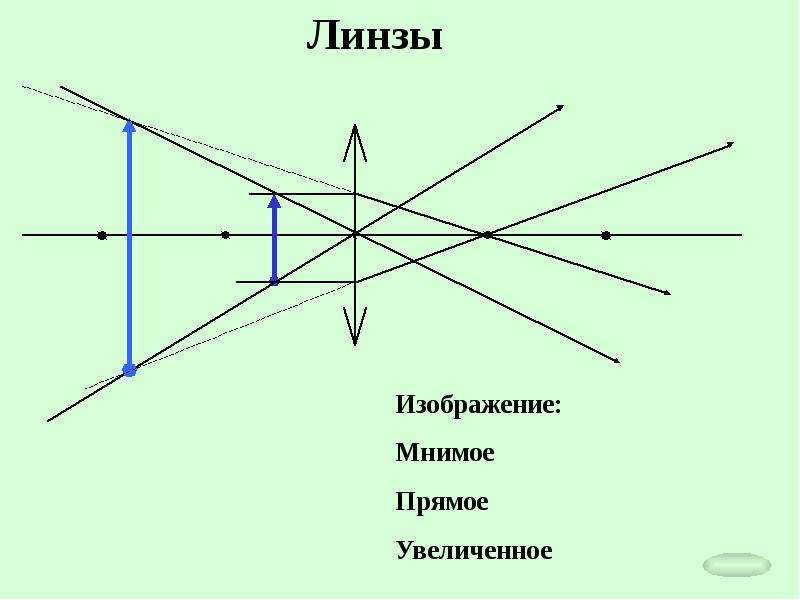 Говард ИП. Забытые открытия Альхазена визуальных явлений. Восприятие.1996;25(10):1203–1217. [PubMed] [Google Scholar] 15. Кромби АС. Ожидание, моделирование и согласие в истории оптики: Часть I. Альхазен и средневековая традиция. Stud Hist Philos Sci. 1990;21(4):605–632. [PubMed] [Google Scholar] 16. Росс HE, Росс GM. Понимал ли Птолемей лунную иллюзию? Восприятие. 1976; 5 (4): 377–385. [PubMed] [Google Scholar] 17. Кадир А. Относительность: введение в специальную теорию. Мировое научное издательство; Сингапур: с. 1089. [Google Академия] 18. Рашид Р.Небесная кинематика Ибн аль-Хайтама. Арабская наука и философия. 2007;17(1):7–55. [Google Академия] 19. Кац В.Дж. Идеи исчисления в исламе и Индии. Математический журнал. 1995;68(3):163–174. [Google Академия] 20. Саад А., Азайзе Х., Саид О. Традиции и перспективы арабской фитотерапии. Обзор. Доказательный комплемент Alternat Med. 2005;2(4):475–479. [Бесплатная статья PMC] [PubMed] [Google Scholar]21. Arrington GE., Jr. Три араба: их влияние на офтальмологию: Хунаин ибн-Исхак, Разес, Альхазен.
Говард ИП. Забытые открытия Альхазена визуальных явлений. Восприятие.1996;25(10):1203–1217. [PubMed] [Google Scholar] 15. Кромби АС. Ожидание, моделирование и согласие в истории оптики: Часть I. Альхазен и средневековая традиция. Stud Hist Philos Sci. 1990;21(4):605–632. [PubMed] [Google Scholar] 16. Росс HE, Росс GM. Понимал ли Птолемей лунную иллюзию? Восприятие. 1976; 5 (4): 377–385. [PubMed] [Google Scholar] 17. Кадир А. Относительность: введение в специальную теорию. Мировое научное издательство; Сингапур: с. 1089. [Google Академия] 18. Рашид Р.Небесная кинематика Ибн аль-Хайтама. Арабская наука и философия. 2007;17(1):7–55. [Google Академия] 19. Кац В.Дж. Идеи исчисления в исламе и Индии. Математический журнал. 1995;68(3):163–174. [Google Академия] 20. Саад А., Азайзе Х., Саид О. Традиции и перспективы арабской фитотерапии. Обзор. Доказательный комплемент Alternat Med. 2005;2(4):475–479. [Бесплатная статья PMC] [PubMed] [Google Scholar]21. Arrington GE., Jr. Три араба: их влияние на офтальмологию: Хунаин ибн-Исхак, Разес, Альхазен. Int Rec Med Gen Pract Clin. 1959;172(6):337–338. [PubMed] [Google Scholar] 22. Халифа О. Кто является основоположником психофизики и экспериментальной психологии? Am J Islamic Social Sciences (AJISS) 1999;16(2) [Google Scholar]
Int Rec Med Gen Pract Clin. 1959;172(6):337–338. [PubMed] [Google Scholar] 22. Халифа О. Кто является основоположником психофизики и экспериментальной психологии? Am J Islamic Social Sciences (AJISS) 1999;16(2) [Google Scholar]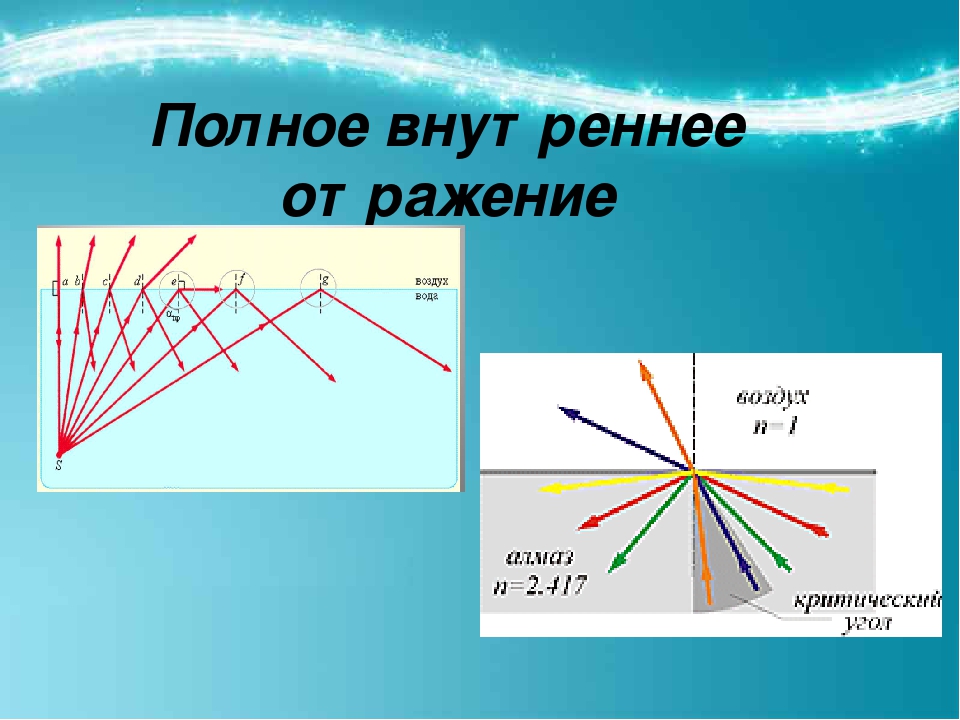
 Здесь падает много параллельных лучей, но они отражаются под разными углами, потому что поверхность шероховатая.
Здесь падает много параллельных лучей, но они отражаются под разными углами, потому что поверхность шероховатая. Хотя эти зеркальные отражения заставляют предметы казаться там, где их быть не может (например, за сплошной стеной), изображения не являются плодом вашего воображения. Зеркальные изображения можно фотографировать и снимать на видео с помощью инструментов, и они выглядят так же, как и наши глаза (которые сами по себе являются оптическими инструментами). Точный способ, которым изображения формируются зеркалами и линзами, обсуждается в следующей главе о геометрической оптике и формировании изображений.
Хотя эти зеркальные отражения заставляют предметы казаться там, где их быть не может (например, за сплошной стеной), изображения не являются плодом вашего воображения. Зеркальные изображения можно фотографировать и снимать на видео с помощью инструментов, и они выглядят так же, как и наши глаза (которые сами по себе являются оптическими инструментами). Точный способ, которым изображения формируются зеркалами и линзами, обсуждается в следующей главе о геометрической оптике и формировании изображений. 9). Это верно, когда отражающие поверхности перпендикулярны, и не зависит от угла падения. (Доказательство см. [ссылка] в конце этого раздела.) Такой объект называется угловым отражателем, поскольку свет отражается от его внутреннего угла. Угловые отражатели — это подкласс ретрорефлекторов, все из которых отражают лучи обратно в том направлении, откуда они пришли. Хотя геометрия доказательства намного сложнее, угловые отражатели также могут быть построены с тремя взаимно перпендикулярными отражающими поверхностями и полезны в трехмерных приложениях.
9). Это верно, когда отражающие поверхности перпендикулярны, и не зависит от угла падения. (Доказательство см. [ссылка] в конце этого раздела.) Такой объект называется угловым отражателем, поскольку свет отражается от его внутреннего угла. Угловые отражатели — это подкласс ретрорефлекторов, все из которых отражают лучи обратно в том направлении, откуда они пришли. Хотя геометрия доказательства намного сложнее, угловые отражатели также могут быть построены с тремя взаимно перпендикулярными отражающими поверхностями и полезны в трехмерных приложениях. Астронавты Аполлона разместили на Луне настоящий уголковый отражатель (рис. 1.10). Лазерные сигналы с Земли могут отражаться от этого углового отражателя, чтобы измерять постепенно увеличивающееся расстояние до Луны на несколько сантиметров в год.
Астронавты Аполлона разместили на Луне настоящий уголковый отражатель (рис. 1.10). Лазерные сигналы с Земли могут отражаться от этого углового отражателя, чтобы измерять постепенно увеличивающееся расстояние до Луны на несколько сантиметров в год.



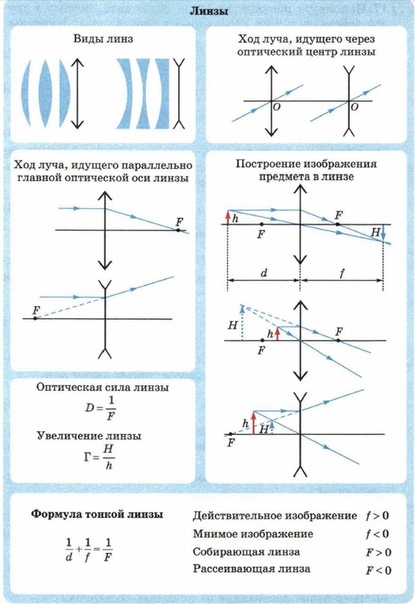

 Зеркала сферические двух типов
Зеркала сферические двух типов











 Он состоит из собирающей линзы с малым фокусным расстоянием.
Он состоит из собирающей линзы с малым фокусным расстоянием. Д/ф и
Д/ф и 
 называется сферической аберрацией.
называется сферической аберрацией.