Древнегреческий ученый определил размеры земли. Кто такой Эратосфен? Биография, открытия ученого
Древние египтяне заметили, что во время летнего солнцестояния солнце освещает дно глубоких колодцев в сиене (ныне Асуан), а в Александрии — нет. У Эратосфена Киренского (276 год до н. э. -194 год до н. э.
) появилась гениальная идея — использовать этот факт для измерения окружности и радиуса земли. В день летнего солнцестояния в Александрии он использовал скафис — чашу с длинной иглой, при помощи которого можно было определить под каким углом солнце находится на небе.
Итак, после измерения угол оказался 7 градусов 12 минут, то есть 1/50 окружности. Стало быть сиена отстоит от александрии на 1/50 окружности земли. Расстояние между городами считалось равным 5, 000 стадиям, следовательно окружность земли равнялась 250, 000 стадиям, а радиус тогда 39, 790 стадиев.
Неизвестно каким стадием пользовался Эратосфен. Лишь в том случае, если греческим (178 метров), то его радиус земли равнялся 7, 082 км, если египетским, то 6, 287 км.
Люди давным-давно догадывались, что Земля, на которой они обитают, похожа на шар. Одним из первых высказал мысль о шарообразности Земли древнегреческий математик и философ Пифагор (ок. 570—500 до н. э.). Величайший мыслитель древности Аристотель, наблюдая лунные затмения, подметил, что край земной тени, падающей на Луну, всегда имеет круглую форму. Это и позволило ему с уверенностью судить о том, что наша Земля шарообразна. Теперь же, благодаря достижениям космической техники, все мы (и не раз) имели возможность любоваться красотой земного шара по снимкам, сделанным из космоса.
Уменьшенным подобием Земли, ее миниатюрной моделью является глобус. Чтобы узнать длину окружности глобуса, достаточно обернуть его питью, а затем определить длину этой нити. По огромную Землю с мерной лептой по меридиану или экватору не обойдешь. Да и в каком бы направлении мы ни стали ее измерять, па пути обязательно появятся непреодолимые препятствия — высокие горы, непроходимые болота, глубокие моря и океаны…
А можно ли узнать размеры Земли, не измеряя всей ее окружности? Конечно, можно.
Известно, что в окружности 360 градусов. Поэтому, чтобы узнать длину окружности, в принципе достаточно измерить точно длину одного градусаи результат измерения умножить на 360.
Первое измерение Земли таким способом произвел древнегреческий ученый Эратосфен (ок. 276—194 до и. э.), живший в египетском городе Александрии, па берегу Средиземного моря.
С юга в Александрию приходили караваны верблюдов. От сопровождавших их людей Эратосфен узнал, что в городе Сиене (нынешнем Асуане) в день летнего солнцестояния Солнце в иол-день находится над головой. Предметы в это время не дают никакой тени, а солнечные лучи проникают даже в самые глубокие колодцы. Стало быть, Солнце достигает зенита.
Путем астрономических наблюдений Эратосфен установил, что в этот же самый день в Александрии Солнце отстоит от зенита на 7,2 градуса, что составляет ровно 1/50 часть окружности. (В самом деле: 360: 7,2 = 50.) Теперь, чтобы узнать, чему равна окружность Земли, оставалось измерить расстояние между городами и умножить его па 50. Но измерить это расстояние, пролегающее по пустыне, Эратосфену было не под силу. Не могли измерить его и проводники торговых караванов. Они лишь знали, сколько времени тратят их верблюды на один переход, и считали, что от Сиены до Александрии 5000 египетских стадий. Значит, вся окружность Земли: 5000 x 50 = 250 000 стадий.
Но измерить это расстояние, пролегающее по пустыне, Эратосфену было не под силу. Не могли измерить его и проводники торговых караванов. Они лишь знали, сколько времени тратят их верблюды на один переход, и считали, что от Сиены до Александрии 5000 египетских стадий. Значит, вся окружность Земли: 5000 x 50 = 250 000 стадий.
К сожалению, мы не знаем точно длину египетской стадии. По некоторым данным, она равна 174,5 м, что дает для земной окружности 43 625 км. Известно, что радиус в 6,28 раза меньше длины окружности. Получалось, что радиус Земли, но Эратосфену,— 6943 км. Вот так более двадцати двух веков тому назад впервые были определены размеры земного шара.
По современным данным, средний радиус Земли составляет 6371 км. По почему средний? Ведь если Земля — шар, то идее земные радиусы должны быть одинаковыми. Об этом мы расскажем дальше.
Способ точного измерения больших расстояний впервые предложил голландский географ и математик Вилдеброрд Сиеллиус (1580-1626).
Представим себе, что необходимо измерить расстояние между точками А и Б, удаленными одна от другой на сотни километров. Решение этой задачи следует начать с построения на местности так называемой опорной геодезической сети. В простейшем варианте она создается в виде цепочки треугольников. Вершины их выбираются на возвышенных местах, где сооружаются так называемые геодезические знаки в виде специальных пирамид, и обязательно так, чтобы из каждого пункта были видны направления на все соседние пункты. А еще эти пирамиды должны быть удобны для работы: для установки угломерного инструмента — теодолита — и измерения всех углов в треугольниках этой сети. Кроме того, в одном из треугольников измеряется одна сторона, которая пролегает по ровной и открытой местности, удобной для линейных измерений. В результате получается сеть треугольников с известными углами и исходной стороной — базисом. Затем следуют вычисления.
Решение этой задачи следует начать с построения на местности так называемой опорной геодезической сети. В простейшем варианте она создается в виде цепочки треугольников. Вершины их выбираются на возвышенных местах, где сооружаются так называемые геодезические знаки в виде специальных пирамид, и обязательно так, чтобы из каждого пункта были видны направления на все соседние пункты. А еще эти пирамиды должны быть удобны для работы: для установки угломерного инструмента — теодолита — и измерения всех углов в треугольниках этой сети. Кроме того, в одном из треугольников измеряется одна сторона, которая пролегает по ровной и открытой местности, удобной для линейных измерений. В результате получается сеть треугольников с известными углами и исходной стороной — базисом. Затем следуют вычисления.
Решение наминается с треугольника, содержащего базис. По стороне и углам вычисляются две другие стороны первого треугольника. Но одна из его сторон является одновременно стороной смежного с ним треугольника. Она служит исходной для вычисления сторон второго треугольника и так далее. В конце концов находятся стороны последнего треугольника и вычисляется искомое расстояние — дуга меридиана АБ.
Она служит исходной для вычисления сторон второго треугольника и так далее. В конце концов находятся стороны последнего треугольника и вычисляется искомое расстояние — дуга меридиана АБ.
Геодезическая сеть обязательно опирается на астрономические пункты А и Б. Методом астрономических наблюдений звезд определяются их географические координаты (широты и долготы) и азимуты (направления на местные предметы).
Теперь, когда известна протяженность дуги меридиана АБ, а также ее выражение в градусной мере (как разность широт астропунктов А и Б), не составит особого труда вычислить длину дуги 1 градуса меридиана путем простого деления первой величины на вторую.
Этот способ измерения больших расстояний на земной поверхности получил название триангуляции — от латинского слова «триапгулюм», что значит «треугольник». Он оказался удобным для определения размеров Земли.
Изучением размеров нашей планеты и формы се поверхности занимается наука геодезия, что в переводе с греческого означает «землеизмерение».
Самое грандиозное градусное измерение XIX века возглавил основатель Пулковской обсерватории В. Я. Струве.
Под руководством Струве русские геодезисты совместно с норвежскими измерили дугу» простиравшуюся от Дуная по западным областям России в Финляндию и Норвегию до побережья Северного Ледовитого океана. Общая протяженность этой дуги превысила 2800 км! В ней было заключено более 25 градусов, что составляет почти 1/14 часть земной окружности. В историю науки она -вошла под названием «дуги Струве». Автору этой книги в послевоенные годы довелось работать на наблюдениях (измерениях углов) на пунктах государственной триангуляции, примыкавших непосредственно к знаменитой «дуге».
Градусные измерения показали, что паша Земля не является в точности шаром, а похожа на эллипсоид, то есть она сжата у полюсов. У эллипсоида все меридианы представляют собой эллипсы, а экватор и параллели — окружности.
Чем длиннее измеряемые дуги меридианов и параллелей, тем точнее можно вычислить радиус Земли и определить ее сжатие.
Отечественные геодезисты промерили государственную триангуляционную сеть почти на половине территории СССР. Это позволило советскому ученому Ф. Н. Красовскому (1878-1948) более точно определить размеры и форму Земли. Эллипсоид Красовского: экваториальный радиус — 6378,245 км, полярный радиус — 6356,863 км. Сжатие планеты — 1/298,3, то есть на такую часть полярный радиус Земли короче экваториального (в линейной мере — 21,382 км).
Представим себе, что па глобусе с поперечником 30 см решили изобразить сжатие земного шара. Тогда полярную ось глобуса пришлось бы укоротить на 1 мм. Это так мало, что совершенно незаметно для глаза. Вот так и Земля с большого расстояния кажется совершенно круглой. Такой ее наблюдают космонавты.
Изучая форму Земли, ученые прийти к выводу, что она сжата не только вдоль оси вращения. Экваториальное сечение земного шара в проекции на плоскость дает кривую, которая тоже отличается от правильной окружности, правда совсем немного — на сотни метров. Все это свидетельствует о том, что фигура у нашей планеты более сложная, чем казалось раньше.
Все это свидетельствует о том, что фигура у нашей планеты более сложная, чем казалось раньше.
Теперь уже совершенно ясно, что Земля не является правильным геометрическим телом, то есть эллипсоидом. К тому же поверхность нашей планеты далеко не гладкая. На ней есть возвышенности и высокие горные хребты. Правда, суши почти в три раза меньше, чем воды. Что же в таком случае мы должны подразумевать подземной поверхностью?
Как известно, океаны и моря, сообщаясь друг с другом, образуют на Земле обширную водную гладь. Поэтому ученые условились принимать за поверхность планеты поверхность Мирового океана, находящегося в спокойном состоянии.
А как поступать в районах континентов? Что там считать поверхностью Земли? Тоже поверхность Мирового океана, мысленно продолженную под всеми материками и островами.
Вот эта фигура, ограниченная поверхностью среднего уровня Мирового океана, была названа геоидом. От поверхности геоида и ведется отсчет всех известных «высот над уровнем моря». Слово «геоид», или «землеподобный», специально придумало для названия фигуры Земли. В геометрии такой фигуры не существует. Близок по форме к геоиду геометрически правильный эллипсоид.
Слово «геоид», или «землеподобный», специально придумало для названия фигуры Земли. В геометрии такой фигуры не существует. Близок по форме к геоиду геометрически правильный эллипсоид.
4 октября 1957 года с запуском в нашей стране первого искусственного спутника Земли человечество вступило в космическую эру. 11ачалось активное исследование околоземного пространства. При этом выяснилось, что спутники очень полезны и для познания самой Земли. Даже в области геодезии они сказали свое «веское слово».
Как известно, классическим методом изучения геометрических характеристик Земли является триангуляция. Но раньше геодезические сети развивали лишь в пределах материков, а между собой они не были связаны. Ведь на морях и океанах триангуляцию не построишь. Поэтому расстояния между материками были определены менее точно. За счет этого снижалась точность определения размеров самой Земли.
С запуском спутников геодезисты сразу поняли: появились «визирные цели» на большой высоте. Теперь можно будет измерить большие расстояния.
Идея метода космической триангуляции проста. Синхронные (одновременные) наблюдения спутника из нескольких отдаленных пунктов земной поверхности позволяют привести их геодезические координаты к единой системе. Так были связаны воедино триангуляции, построенные на разных материках, а заодно были уточнены размеры Земли: экваториальный радиус — 6378,160 км, полярный радиус — 6356,777 км. Величина сжатия — 1/298,25, то есть почти такая же, как у эллипсоида Красовского. Разница между экваториальным и полярным диаметрами Земли достигает 42 км 766 м.
Если бы наша планета была правильным шаром, а массы внутри нее распределены равномерно, то спутник мог бы двигаться вокруг Земли по круговой орбите. Но отклонение формы Земли от шарообразной и неоднородность ее недр приводят к тому, что над различными точками земной поверхности сила притяжения неодинаковая. Изменяется сила притяжения Земли — изменяется орбита спутника. И все, даже малейшие изменения в движении спутника с низкой орбитой — то результат гравитационного воздействия на него той или иной земной выпуклости или и падины, над которой он пролетает.
Оказалось, что наша планета имеет еще и слегка грушевидную форму. Ее Северный полюс приподнят над плоскостью экватора па 16 м, а Южный — примерно на столько же опущен (как бы вдавлен). Вот и получается, что в сечении по меридиану фигура Земли напоминает грушу. Она чуть-чуть вытянута к северу и приплюснута у Южного полюса. Налицо полярная асимметрия: Се пер нос полушарие нетождественно Южному. Так на основании спутниковых данных было получено самое точное представление об истинной форме Земли. Как видим, фигура нашей планеты заметно отклоняется от геометрически правильной формы шара, а также от фигуры эллипсоида вращения.
Шарообразность Земли позволяет определить ее размеры способом, который впервые применил греческий ученый Эратосфен. Идея Эратосфена заключается в следующем. На одном и том же географическом меридиане земного шара выберем две точки \(O_{1}\) и \(O_{2}\). Обозначим длину дуги меридиана \(O_{1}O_{2}\) через \(l\), а ее угловое значение через \(n\) (в градусах). Тогда длина дуги 1° меридиана \(l_{0}\) будет равна: \ а длина всей окружности меридиана: \ где \(R\) — радиус земного шара. Отсюда \(R = \frac{180° · l}{πn}\).
Тогда длина дуги 1° меридиана \(l_{0}\) будет равна: \ а длина всей окружности меридиана: \ где \(R\) — радиус земного шара. Отсюда \(R = \frac{180° · l}{πn}\).
Длина дуги меридиана между выбранными на земной поверхности точками \(O_{1}\) и \(O_{2}\) в градусах равна разности географических широт этих точек, т. е. \(n = Δφ = φ_{1} — φ_{2}\).
Для определения величины \(n\) Эратосфен использовал то обстоятельство, что города Сиена и Александрия расположены на одном меридиане и расстояние между ними известно. С помощью простого прибора, который ученый назвал «скафис», было установлено, что если в Сиене в полдень дня летнего солнцестояния Солнце освещает дно глубоких колодцев (находится в зените), то в это же время в Александрии Солнце отстоит от вертикали на \(\frac{1}{50}\) долю окружности (7,2°). Таким образом, определив величину длины дуги \(l\) и угол \(n\), Эратосфен подсчитал, что длина земной окружности составляет 252 тыс. стадиев (стадий примерно равен 180 м). Учитывая грубость измерительных приборов того времени и ненадежность исходных данных, результат измерений был весьма удовлетворительным (действительная средняя длина меридиана Земли равна 40 008 км).
Точное измерение расстояния \(l\) между точками \(O_{1}\) и \(O_{2}\) затруднено из-за естественных препятствий (гор, рек, лесов и т. п.).
Поэтому длина дуги \(l\) определяется путем вычислений, требующих измерения только сравнительно небольшого расстояния — базиса и ряда углов. Этот метод разработан в геодезии и называется триангуляцией (лат. triangulum — треугольник).
Суть его состоит в следующем. По обе стороны дуги \(O_{1}O_{2}\), длину которой необходимо определить, выбирается несколько точек \(A\), \(B\), \(C\), … на взаимных расстояниях до 50 км, с таким расчетом, чтобы из каждой точки были видны по меньшей мере две другие точки.
Во всех точках устанавливаются геодезические сигналы в виде вышек пирамидальной формы высотой от 6 до 55 м в зависимости от условий местности. Наверху каждой вышки имеется площадка для размещения наблюдателя и установки угломерного инструмента — теодолита. Расстояние между какими-либо двумя соседними точками, например \(O_{1}\) и \(A\), выбирается на совершенно ровной поверхности и принимается за базис триангуляционной сети. Длину базиса очень тщательно измеряют специальными мерными лентами.
Длину базиса очень тщательно измеряют специальными мерными лентами.
Измеренные углы в треугольниках и длина базиса позволяют по тригонометрическим формулам вычислить стороны треугольников, а по ним длину дуги \(O_{1}O_{2}\) с учетом ее кривизны.
В России с 1816 по 1855 г. под руководством В. Я. Струве была измерена дуга меридиана длиной 2800 км. В 30-е гг. ХХ века высокоточные градусные измерения были проведены в СССР под руководством профессора Ф. Н. Красовского. Протяженность базиса в то время выбиралась небольшой, от 6 до 10 км. Позже, благодаря использованию свето- и радиолокации, длина базиса была увеличена до 30 км. Точность измерений дуги меридиана повысилась до +2 мм на каждые 10 км длины.
Триангуляционные измерения показали, что длина дуги 1° меридиана не одинакова под разными широтами: около экватора она равна 110,6 км, а около полюсов — 111,7 км, т. е. увеличивается к полюсам.
Истинная форма Земли не может быть представлена ни одним из известных геометрических тел. Поэтому в геодезии и гравиметрии форму Земли считают геоидом , т. е. телом с поверхностью, близкой к поверхности спокойного океана и продолженной под материками.
Поэтому в геодезии и гравиметрии форму Земли считают геоидом , т. е. телом с поверхностью, близкой к поверхности спокойного океана и продолженной под материками.
В настоящее время созданы триангуляционные сети со сложной радиолокационной аппаратурой, установленной на наземных пунктах, и с отражателями на геодезических искусственных спутниках Земли, что позволяет точно вычислять расстояния между пунктами. Значительный вклад в развитие космической геодезии внес уроженец Беларуси — известный геодезист, гидрограф и астроном И. Д. Жонголович. На основе изучения динамики движения искусственных спутников Земли И. Д. Жонголович уточнил сжатие нашей планеты и несимметричность Северного и Южного полушарий.
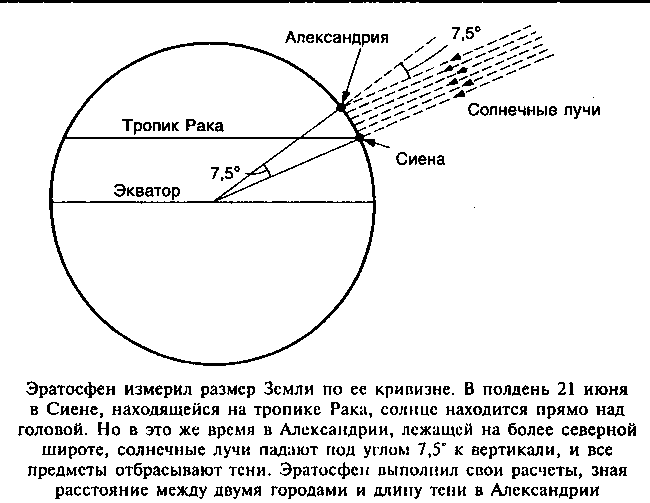
Совершая путешествия из г. Александрии на юг, в г. Сиену (теперь Асуан), люди замечали, что там летом в тот день, когда солнце бывает всего выше на небе (день летнего солнцестояния — 21 или 22 июня), в полдень оно освещает дно глубоких колодцев, т. е. бывает как раз над головой, в зените. Вертикально стоящие столбы в этот момент не дают тени. В Александрии же и в этот день солнце в полдень не доходит до зенита, не освещает дна колодцев, предметы дают тень.
Вертикально стоящие столбы в этот момент не дают тени. В Александрии же и в этот день солнце в полдень не доходит до зенита, не освещает дна колодцев, предметы дают тень.
Эратосфен измерил, насколько полуденное солнце в Александрии отклонено от зенита, и получил величину, равную 7°12′, что составляет 1/50 окружности. Это ему удалось сделать при помощи прибора, называемого скафисом. Скафис представлял собой чашу в форме полушария. В центре ее отвесно укреплялась
Слева — определение высоты солнца скафисом. В центре — схема направления солнечных лучей: в Сиене они падают вертикально, в Александрии — под углом в 7°12′. Справа — направление солнечного луча в Сиене в момент летнего солнцестояния.
Скафис — древний прибор для определения высоты солнца над горизонтом (в разрезе).
игла. Тень от иглы падала на внутреннюю поверхность скафиса. Для измерения отклонения солнца от зенита (в градусах) на внутренней поверхности скафиса проводились окружности, помеченные цифрами. Если, например, тень доходила до окружности, помеченной цифрой 50, солнце стояло на 50° ниже зенита. Построив чертеж, Эратосфен совершенно правильно заключил, что Александрия отстоит от Сиены на 1/50 окружности Земли. Чтобы узнать окружность Земли, оставалось измерить расстояние между Александрией и Сиеной и умножить его на 50. Это расстояние было определено по числу дней, которое тратили караваны верблюдов на переход между городами. В единицах того времени оно равнялось 5 тыс. стадий. Если 1/50 окружности Земли равняется 5000 стадий, то вся окружность Земли равна 5000х50 = 250 000 стадий. В переводе на наши меры это расстояние приблизительно равно 39 500 км. Зная длину окружности, можно вычислить и величину радиуса Земли. Радиус всякой окружности в 6,283 раза меньше ее длины. Поэтому средний радиус Земли, по Эратосфену, оказался равным круглому числу — 6290 км, а диаметр — 12 580 км. Так Эратосфен нашел приблизительно размеры Земли, близкие к тем, которые определены точными приборами в наше время.
Если, например, тень доходила до окружности, помеченной цифрой 50, солнце стояло на 50° ниже зенита. Построив чертеж, Эратосфен совершенно правильно заключил, что Александрия отстоит от Сиены на 1/50 окружности Земли. Чтобы узнать окружность Земли, оставалось измерить расстояние между Александрией и Сиеной и умножить его на 50. Это расстояние было определено по числу дней, которое тратили караваны верблюдов на переход между городами. В единицах того времени оно равнялось 5 тыс. стадий. Если 1/50 окружности Земли равняется 5000 стадий, то вся окружность Земли равна 5000х50 = 250 000 стадий. В переводе на наши меры это расстояние приблизительно равно 39 500 км. Зная длину окружности, можно вычислить и величину радиуса Земли. Радиус всякой окружности в 6,283 раза меньше ее длины. Поэтому средний радиус Земли, по Эратосфену, оказался равным круглому числу — 6290 км, а диаметр — 12 580 км. Так Эратосфен нашел приблизительно размеры Земли, близкие к тем, которые определены точными приборами в наше время.
Как проверялась информация о форме и величине земли
После Эратосфена Киренского на протяжении многих столетий никто из ученых не пытался вновь измерить земную окружность. В XVII в. был изобретен надежный способ измерения больших расстояний на поверхности Земли — способ триангуляции (названный так от латинского слова «триангулюм» — треугольник). Этот способ удобен тем, что встречающиеся на пути препятствия — леса, реки, болота и т. п.- не мешают точному измерению больших расстояний. Измерение производится следующим образом: непосредственно на поверхности Земли очень точно измеряют расстояние между двумя близко расположенными точками А и В, из которых видны удаленные высокие предметы — холмы, башни, колокольни и т. п. Если из А и В через зрительную трубу можно разглядеть предмет, находящийся в точке С, то нетрудно измерить в точке А угол между направлениями АВ и АС, а в точке В — угол между ВА и ВС.
После этого по измеренной стороне АВ и двум углам при вершинах А и В можно построить треугольник АBС и, следовательно, найти длины сторон АС и ВС, т. е. расстояния от А до С и от В до С. Такое построение можно выполнить на бумаге, уменьшив все размеры в несколько раз или с помощью вычисления по правилам тригонометрии. Зная расстояние от В до С и наводя из этих точек зрительную трубу измерительного инструмента (теодолита) на предмет в какой-либо новой точке D, тем же путем измеряют расстояния от В до D и от С до D. Продолжая измерения, как бы покрывают часть поверхности Земли сетью треугольников: ABC, BCD и т. д. В каждом из них можно последовательно определить все стороны и углы (см. рис.).
После того как измерена сторона АВ первого треугольника (базис), все дело сводится к измерению углов между двумя направлениями. Построив сеть треугольников, можно вычислить по правилам тригонометрии расстояние от вершины одного треугольника до вершины любого другого, как бы далеко друг от друга они ни находились. Так решается вопрос об измерении больших расстояний на поверхности Земли. Практическое применение способа триангуляции — дело далеко не простое. Эту работу могут выполнять только опытные наблюдатели, вооруженные очень точными угломерными инструментами. Обычно для наблюдений приходится сооружать специальные вышки. Работы такого рода поручаются особым экспедициям, которые продолжаются по нескольку месяцев и даже лет.
Так решается вопрос об измерении больших расстояний на поверхности Земли. Практическое применение способа триангуляции — дело далеко не простое. Эту работу могут выполнять только опытные наблюдатели, вооруженные очень точными угломерными инструментами. Обычно для наблюдений приходится сооружать специальные вышки. Работы такого рода поручаются особым экспедициям, которые продолжаются по нескольку месяцев и даже лет.
Способ триангуляции помог ученым уточнить знания о форме и величине Земли. Произошло это при следующих обстоятельствах.
Знаменитый английский ученый Ньютон (1643-1727) высказал мнение, что Земля не может иметь форму точного шара, потому что она вращается вокруг своей оси. Все частицы Земли находятся под влиянием центробежной силы (силы инерции), которая особенно велика
Если нам нужно измерить расстояние от А до D (при этом точку В не видно из точки А), то мы измеряем базис АВ и в треугольнике AВС измеряем углы, прилегающие к базису (a и b). По одной стороне и прилегающим к ней двум углам определяем расстояние АС и BС. Далее из точки С мы с помощью зрительной трубы измерительного инструмента находим точку D, видимую из точки С и точки B. В треугольнике CUB нам известна сторона СВ. Остается измерить прилегающие к пей углы, а затем определить расстояние DB. Зная расстояния DB u AB и угол между этими линиями, можно определить расстояние от А до D.
Далее из точки С мы с помощью зрительной трубы измерительного инструмента находим точку D, видимую из точки С и точки B. В треугольнике CUB нам известна сторона СВ. Остается измерить прилегающие к пей углы, а затем определить расстояние DB. Зная расстояния DB u AB и угол между этими линиями, можно определить расстояние от А до D.
Схема триангуляции: АB — базис; BE — измеряемое расстояние.
у экватора и отсутствует у полюсов. Центробежная сила у экватора действует против силы тяжести и ослабляет ее. Равновесие между силой тяжести и центробежной силой было достигнуто тогда, когда земной шар у экватора «раздулся», а у полюсов «сплющился» и постепенно приобрел форму мандарина, или, выражаясь научным языком, сфероида. Интересное открытие, сделанное в то же время, подтвердило предположение Ньютона.
В 1672 г. один французский астроном установил, что если точные часы перевезти из Парижа в Кайенну (в Южной Америке, вблизи экватора), то они начинают отставать на 2,5 минуты в сутки. Это отставание происходит потому, что маятник часов около экватора качается медленнее. Стало очевидно, что сила тяжести, которая заставляет маятник качаться, в Кайенне меньше, чем в Париже. Ньютон объяснил это тем, что на экваторе поверхность Земли находится дальше от ее центра, чем в Париже.
Это отставание происходит потому, что маятник часов около экватора качается медленнее. Стало очевидно, что сила тяжести, которая заставляет маятник качаться, в Кайенне меньше, чем в Париже. Ньютон объяснил это тем, что на экваторе поверхность Земли находится дальше от ее центра, чем в Париже.
Французская академия наук решила проверить правильность рассуждений Ньютона. Если Земля имеет форму мандарина, то дуга меридиана размером в 1° должна удлиняться при приближении к полюсам. Оставалось при помощи триангуляции измерить длину дуги в 1° на разном расстоянии от экватора. Измерить дугу на севере и на юге Франции поручили директору Парижской обсерватории Джованни Кассини. Однако южная дуга у него получилась длиннее северной. Казалось, что Ньютон не прав: Земля не сплюснута, как мандарин, а вытянута подобно лимону.
Но Ньютон не отказался от своих выводов и уверял, что Кассини ошибся при измерениях. Между сторонниками теории «мандарина» и «лимона» разгорелся ученый спор, который длился 50 лет. После смерти Джованни Кассини его сын Жак, также директор Парижской обсерватории, чтобы защитить мнение своего отца, написал книгу, где доказывал, что по законам механики Земля должна быть вытянута, как лимон. Чтобы окончательно решить этот спор, Французская академия наук снарядила в 1735 г. одну экспедицию к экватору, другую — к северному полярному кругу.
После смерти Джованни Кассини его сын Жак, также директор Парижской обсерватории, чтобы защитить мнение своего отца, написал книгу, где доказывал, что по законам механики Земля должна быть вытянута, как лимон. Чтобы окончательно решить этот спор, Французская академия наук снарядила в 1735 г. одну экспедицию к экватору, другую — к северному полярному кругу.
Южная экспедиция проводила измерения в Перу. Для измерения была выбрана дуга меридиана длиной около 3° (330 км). Она пересекала экватор и проходила через ряд горных долин и высочайших горных хребтов Америки.
Работа экспедиции продолжалась восемь лет и была сопряжена с большими трудностями и опасностями. Однако ученые выполнили свою задачу: градус меридиана у экватора был измерен с очень большой точностью.
Северная экспедиция работала в Лапландии (так до начала XX в. называлась северная часть Скандинавского и западная часть Кольского полуостровов).
После сравнения результатов работы экспедиций выяснилось, что полярный градус длиннее экваториального.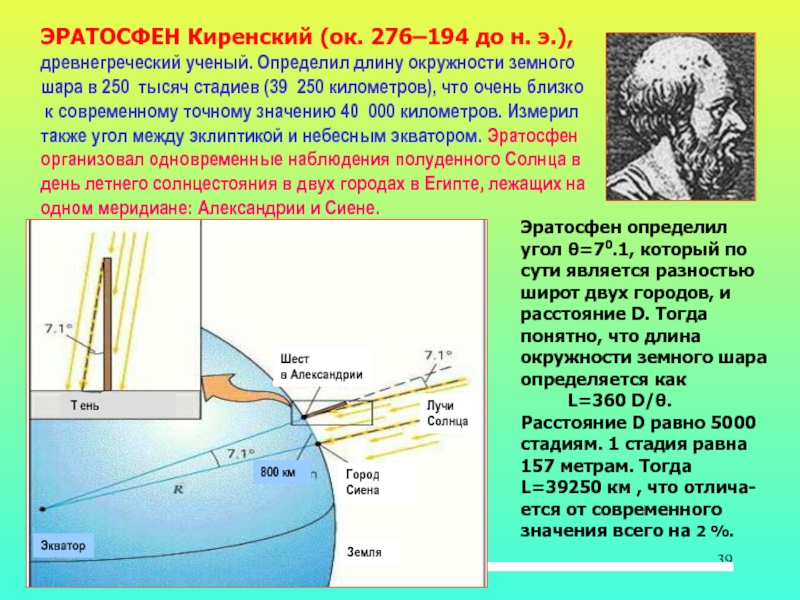 Следовательно, Кассини действительно ошибался, а Ньютон был прав, утверждая, что Земля имеет форму мандарина. Так кончился этот затянувшийся спор, и ученые признали правильность утверждений Ньютона.
Следовательно, Кассини действительно ошибался, а Ньютон был прав, утверждая, что Земля имеет форму мандарина. Так кончился этот затянувшийся спор, и ученые признали правильность утверждений Ньютона.
В наше время существует особая наука — геодезия, которая занимается определением величины Земли при помощи точнейших измерений ее поверхности. Данные этих измерений позволили достаточно точно определить действительную фигуру Земли.
Геодезические работы по измерению Земли проводились и проводятся в различных странах. Такие работы выполнены и в нашей стране. Еще в прошлом веке русскими геодезистами была проделана очень точная работа по измерению «русско-скандинавской дуги меридиана» протяжением более 25°, т. е. длиной почти в 3 тыс. км. Ее назвали «дугой Струве» в честь основателя Пулковской обсерватории (под Ленинградом) Василия Яковлевича Струве, который задумал эту огромную работу и руководил ею.
Градусные измерения имеют большое практическое значение прежде всего для составления точных карт. Как на карте, так и на глобусе вы видите сеть меридианов — кругов, идущих через полюсы, и параллелей — кругов, параллельных плоскости земного экватора. Карта Земли не могла быть составлена без длительной и кропотливой работы геодезистов, определявших шаг за шагом на протяжении многих лет положение разных мест на земной поверхности и затем наносивших полученные результаты на сеть меридианов и параллелей. Чтобы иметь точные карты, требовалось знать действительную форму Земли.
Как на карте, так и на глобусе вы видите сеть меридианов — кругов, идущих через полюсы, и параллелей — кругов, параллельных плоскости земного экватора. Карта Земли не могла быть составлена без длительной и кропотливой работы геодезистов, определявших шаг за шагом на протяжении многих лет положение разных мест на земной поверхности и затем наносивших полученные результаты на сеть меридианов и параллелей. Чтобы иметь точные карты, требовалось знать действительную форму Земли.
Результаты измерений Струве и его сотрудников оказались очень важным вкладом в эту работу.
Впоследствии другие геодезисты с большой точностью измерили длины дуг меридианов и параллелей в разных местах земной поверхности. По этим дугам при помощи вычислений удалось определить длину поперечников Земли в плоскости экватора (экваториальный диаметр) и в направлении земной оси (полярный диаметр). Оказалось, что экваториальный диаметр длиннее полярного примерно на 42,8 км. Это еще раз подтвердило, что Земля сжата с полюсов. По последним данным советских ученых, полярная ось на 1/298,3 короче экваториальной.
По последним данным советских ученых, полярная ось на 1/298,3 короче экваториальной.
Допустим, мы хотели бы изобразить отклонение формы Земли от шара на глобусе с поперечником в 1 м. Если шар по экватору имеет поперечник точно 1 м, то его полярная ось должна быть всего лишь на 3,35 мм короче! Это столь малая величина, что на глаз ее нельзя обнаружить. Форма Земли, таким образом, очень мало отличается от шара.
Можно подумать, что неровности земной поверхности, и особенно горные вершины, высочайшая из которых Джомолунгма (Эверест) достигает почти 9 км, должны сильно искажать форму Земли. Однако это не так. В масштабе глобуса диаметром в 1 м девятикилометровая гора изобразится в виде прилипшей к нему песчинки диаметром около 3/4 мм. Разве только на ощупь, да и то с трудом, можно обнаружить этот выступ. А с той высоты, на которой летают наши корабли-спутники, его можно различить разве по черному пятнышку тени, отбрасываемой им при низком стоянии Солнца.
В наше время размеры и форма Земли очень точно определены учеными Ф. Н. Красовским, А. А. Изотовым и др. Вот числа, показывающие размер земного шара по измерениям этих ученых: длина экваториального диаметра — 12 756,5 км, длина полярного диаметра — 12 713,7 км.
Изучение пути, пройденного искусственными спутниками Земли, позволит определить величину силы тяжести в разных местах над поверхностью земного шара с такой точностью, которой нельзя было достигнуть никаким другим способом. Это в свою очередь позволит внести дальнейшее уточнение в наши знания о размерах и форме Земли.
Постепенное изменение формы земли
Однако, как удалось выяснить при помощи все тех же космических наблюдений и сделанных на их базе специальных вычислений, геоид имеет сложный вид вследствие вращения Земли и неравномерного распределения масс в земной коре, но достаточно хорошо (с точностью до нескольких сотен метров) представляется эллипсоидом вращения, имеющим полярное сжатие 1:293,3 (эллипсоид Красовского).
Тем не менее до самого недавнего времени считалось вполне установленным фактом, что этот небольшой дефект медленно, но верно нивелируется из-за так называемого процесса восстановления гравитационного (изостатического) равновесия, начавшегося примерно восемнадцать тысяч лет назад. Но совсем недавно Земля опять начала сплющиваться.
Геомагнитные измерения, которые с конца 70-х годов стали неотъемлемым атрибутом научно-исследовательских программ спутникового наблюдения, стабильно фиксировали выравнивание гравитационного поля планеты. В общем, с точки зрения мейнстримовских геофизических теорий гравитационная динамика Земли представлялась вполне прогнозируемой, хотя, разумеется, как внутри мейнстрима, так и за его рамками существовали многочисленные гипотезы, по-разному интерпретирующие средне- и долгосрочные перспективы этого процесса, а равно и то, что происходило в прошлой жизни нашей планеты. Довольно большой популярностью пользуется сегодня, скажем, так называемая пульсационная гипотеза, согласно которой Земля периодически то сжимается, то расширяется; есть сторонники и у «контракционной» гипотезы, постулирующей, что в долгосрочном плане размеры Земли будут уменьшаться. Нет единства у геофизиков и по части того, в какой фазе находится сегодня процесс послеледникового восстановления гравитационного равновесия: большинство специалистов полагают, что он довольно близок к завершению, но имеются и теории, утверждающие, что до его конца еще далеко или что он уже прекратился.
Нет единства у геофизиков и по части того, в какой фазе находится сегодня процесс послеледникового восстановления гравитационного равновесия: большинство специалистов полагают, что он довольно близок к завершению, но имеются и теории, утверждающие, что до его конца еще далеко или что он уже прекратился.
Тем не менее, несмотря на обилие разночтений, до конца 90-х годов прошлого века у ученых все-таки не было сколько-нибудь веских причин сомневаться в том, что процесс послеледникового гравитационного выравнивания живет и здравствует. Конец научному благодушию пришел довольно внезапно: потратив несколько лет на проверку и перепроверку результатов, полученных с девяти различных спутников, двое американских ученых, Кристофер Кокс из компании Raytheon и Бенджамен Чао, геофизик Годдардовского центра управления космическими полетами NASA, пришли к удивительному выводу: начиная с 1998 года, «экваториальный охват» Земли (или, как окрестили эту размерность многие западные СМИ, ее «толщина») вновь стал увеличиваться.
Зловещая роль течений океана.
Статья Кокса и Чао, в которой декларируется «обнаружение крупномасштабного перераспределения массы Земли», была опубликована в журнале Science в начале августа 2002 года. Как отмечают авторы исследования, «длительные наблюдения за поведением гравитационного поля Земли показали, что у выравнивавшего его послеледникового эффекта в последние несколько лет неожиданно возник более мощный противник, примерно вдвое превосходящий его по силе гравитационного воздействия».
Благодаря этому «таинственному противнику» Земля вновь, как и в последнюю «эпоху Великого Обледенения», начала сплющиваться, то есть с 1998 года в районе экватора происходит нарастание массы вещества, тогда как из полярных зон идет его отток.
Прямых измерительных методик, позволяющих обнаружить этот феномен, у земных геофизиков пока нет, поэтому в своей работе им приходится пользоваться косвенными данными, прежде всего результатами сверхточных лазерных замеров изменений траекторий орбит спутников, происходящих под влиянием колебаний гравитационного поля Земли. Соответственно, говоря о «наблюдаемых перемещениях масс земного вещества», ученые исходят из предположения о том, что именно они ответственны за эти локальные гравитационные колебания. Первые попытки объяснения этого странного явления и предприняты Коксом и Чао.
Соответственно, говоря о «наблюдаемых перемещениях масс земного вещества», ученые исходят из предположения о том, что именно они ответственны за эти локальные гравитационные колебания. Первые попытки объяснения этого странного явления и предприняты Коксом и Чао.
Версия о каких-либо подземных явлениях, например перетекании вещества в земной магме или ядре, выглядит, по мнению авторов статьи, довольно сомнительной: для того, чтобы подобные процессы возымели хоть сколько-нибудь значимый гравитационный эффект, якобы требуется куда более длительное время, чем смехотворные по научным меркам четыре года. В качестве возможных причин, обусловивших утолщение Земли по экватору, они называют три основных: океаническое воздействие, таяние полярных и высокогорных льдов и некие «процессы в атмосфере». Впрочем, последняя группа факторов ими также сразу отметается — регулярные замеры веса атмосферного столба не дают никаких оснований для подозрений в причастности тех или иных воздушных явлений к возникновению обнаруженного гравитационного феномена.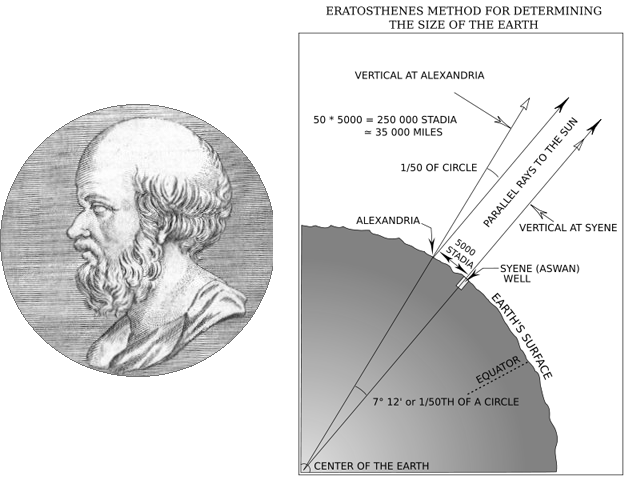
Далеко не столь однозначной представляется Коксу и Чао гипотеза о возможном влиянии на экваториальное вздутие процесса таяния льда в арктической и антарктической зонах. Этот процесс как важнейший элемент пресловутого глобального потепления мирового климата, безусловно, в той или иной степени может быть ответственен за перенос значительных масс вещества (прежде всего воды) от полюсов к экватору, но сделанные американскими исследователями теоретические расчеты показывают: для того, чтобы он оказался определяющим фактором (в частности, «перекрыл» последствия тысячелетнего «роста положительного рельефа»), размерность ежегодно растапливаемой с 1997 года «виртуальной глыбы льда» должна была бы составлять 10х10х5 километров! Никаких эмпирических свидетельств того, что процесс таяния льда в Арктике и Антарктике за последние годы мог принять подобные масштабы, у геофизиков и метеорологов не имеется. Согласно самым оптимистическим оценкам, совокупный объем растаявших льдин как минимум на порядок меньше этого «суперайсберга», следовательно, даже если он и оказал какое-то влияние на прирост экваториальной массы Земли, едва ли это влияние могло быть столь существенным.
В качестве наиболее вероятной причины, обусловившей внезапное изменение гравитационного поля Земли, Кокс и Чао рассматривают сегодня океаническое воздействие, то есть все тот же перенос больших объемов водной массы Мирового океана от полюсов к экватору, который, однако, связан не столько с быстрым таянием льда, сколько с некими не вполне объяснимыми резкими флуктуациями океанических течений, происходящими в последние годы. Причем, как полагают специалисты, главный кандидат на роль возмутителя гравитационного спокойствия — Тихий океан, точнее, циклические перемещения огромных водных масс из его северных регионов в южные.
Если данная гипотеза окажется верной, человечество в весьма скором будущем может столкнуться с очень серьезными изменениями мирового климата: зловещая роль океанических течений хорошо известна всем мало-мальски знакомым с основами современной метеорологии (чего стоит один Эль-Ниньо). Правда, вполне логичным выглядит и предположение, что внезапное разбухание Земли по экватору — следствие уже идущей полным ходом климатической революции. Но, по большому счету, толком разобраться по свежим следам в этом клубке причинно-следственных взаимосвязей пока едва ли представляется возможным.
Но, по большому счету, толком разобраться по свежим следам в этом клубке причинно-следственных взаимосвязей пока едва ли представляется возможным.
Очевидную нехватку понимания происходящих «гравитационных безобразий» прекрасно иллюстрирует небольшой фрагмент интервью самого Кристофера Кокса корреспонденту службы новостей журнала Nature Тому Кларку: «По моему мнению, сейчас можно с высокой степенью определенности (здесь и далее выделено нами. — ‘Эксперт’) говорить лишь об одном: ‘проблемы с весом’ нашей планеты, вероятно, носят временный характер и не являются прямым результатом человеческой деятельности». Однако, продолжая эту словесную эквилибристику, американский ученый тут же еще раз предусмотрительно оговаривается: «Постровидимому, рано или поздно все вернется ‘к норме’, но, возможно, мы заблуждаемся на сей счет».
Главная → Юридическая консультация → Терминология → Единицы измерения площади
Единицы измерения площади земельных участков
Принятая в России система измерения площадей земельных участков
- 1 сотка = 10 метров х 10 метров = 100 кв.
 м
м - 1 гектар = 1 га = 100 метров х 100 метров = 10000 кв.м = 100 соток
- 1 квадратный километр = 1 кв.км = 1000 метров х 1000 метров = 1 млн. кв.м =100 га = 10 000 соток
Обратные единицы
- 1 кв.м = 0,01 сотки = 0,0001 га = 0,000001 кв.км
- 1 сотка = 0,01 га = 0,0001 кв.км
Таблица перевода единиц измерения площади
| Единицы измерения площади | 1 кв. км. | 1 Гектар | 1 Акр | 1 Сотка | 1 кв.м. |
| 1 кв. км. | 1 | 100 | 247.1 | 10.000 | 1.000.000 |
| 1 гектар | 0.01 | 1 | 2.47 | 100 | 10.000 |
| 1 акр | 0.004 | 0.405 | 1 | 40.47 | 4046.9 |
| 1 сотка | 0.0001 | 0.01 | 0.025 | 1 | 100 |
1 кв. м. м. | 0.000001 | 0.0001 | 0.00025 | 0.01 | 1 |
единица площади в метрической системе мер, применяемая для измерений земельных участков.
Сокращённое обозначение: русское га, международное ha.
1 га равен площади квадрата со стороной 100 м.
Наименование «гектары» образовано добавлением приставки «гекто…» к наименованию единицы площади «ар»:
1 га = 100 ар = 100 м х 100 м = 10 000 м2
единица площади в метрической системе мер, равна площади квадрата со стороной в 10 м, то есть:
- 1 ар = 10 м х 10 м = 100 м2.
- 1 десятина = 1,09254 га.
земельная мера, применяемая в ряде стран, использующих английскую систему мер (Великобритания, США, Канада, Австралия и др.).
1 акр = 4840 кв.ярдов = 4046,86 м2
Наиболее употребительная в практике земельная мера гектар — сокращенное обозначение га:
1 га = 100 ар = 10 000 м2
В России гектар является основной единицей измерения площади земли, особенно сельскохозяйственной.
На территории России единица «гектар» была введена в практику после Октябрьской революции, вместо десятины.
Старинные русские единицы измерения площадей
Площадь земельных участков для ИЖС, ЛПХ обычно указывают в сотках
Одна сотка — это площадь участка размером 10 х 10 метров, которая составляет 100 квадратных метров, и поэтому называется соткой.
Вот несколько характерных примеров размеров, которые может иметь земельный участок площадью 15 соток:
В будущем, если вы вдруг забудете, как найти площадь прямоугольного земельного участка, то вспоминайте очень старый анекдот, когда дедушка спрашивает у пятиклассника как найти площадь Ленина, а тот отвечает: «Нужно ширину Ленина умножить на длину Ленина «)))
Полезно ознакомиться и с этим
- Для тех, кого интересует возможность увеличения площади земельных участков для ИЖС, ЛПХ, садоводства, огродничества, находящихся в собственности, полезно ознакомиться с порядком оформления прирезок.

- С 1 января 2018 года в кадастровом паспорте должны быть зафиксированы точные границы участка, поскольку купить, продать, заложить или подарить землю без точного описания границ будет попросту невозможно. Так регламентировано поправками к Земельному кодексу. А тотальная ревизия границ по инициативе муниципалитетов началась с 1 июня 2015 г.
- С 1 марта 2015 года вступил в силу новый Федеральный закон «О внесении изменений в Земельный кодекс РФ и отдельные законодательные акты РФ» (N 171-ФЗ «от 23.06.2014 в соответствии с которым, частности, упрощена процедура выкупа земельных участков у муниципалитетов& Ознакомиться с основными положениями закона можно здесь.
- В отношении регистрации домов, бань, гаражей и других построек на земельных участках, находящихся в собственности граждан, улучшит ситуацию новая дачная амнистия.
Люди давным-давно догадывались, что Земля, на которой они обитают, похожа на шар. Одним из первых высказал мысль о шарообразности Земли древнегреческий математик и философ Пифагор (ок. 570—500 до н. э.). Величайший мыслитель древности Аристотель, наблюдая лунные затмения, подметил, что край земной тени, падающей на Луну, всегда имеет круглую форму. Это и позволило ему с уверенностью судить о том, что наша Земля шарообразна. Теперь же, благодаря достижениям космической техники, все мы (и не раз) имели возможность любоваться красотой земного шара по снимкам, сделанным из космоса.
570—500 до н. э.). Величайший мыслитель древности Аристотель, наблюдая лунные затмения, подметил, что край земной тени, падающей на Луну, всегда имеет круглую форму. Это и позволило ему с уверенностью судить о том, что наша Земля шарообразна. Теперь же, благодаря достижениям космической техники, все мы (и не раз) имели возможность любоваться красотой земного шара по снимкам, сделанным из космоса.
Уменьшенным подобием Земли, ее миниатюрной моделью является глобус. Чтобы узнать длину окружности глобуса, достаточно обернуть его питью, а затем определить длину этой нити. По огромную Землю с мерной лептой по меридиану или экватору не обойдешь. Да и в каком бы направлении мы ни стали ее измерять, па пути обязательно появятся непреодолимые препятствия — высокие горы, непроходимые болота, глубокие моря и океаны…
А можно ли узнать размеры Земли, не измеряя всей ее окружности? Конечно, можно.
Известно, что в окружности 360 градусов. Поэтому, чтобы узнать длину окружности, в принципе достаточно измерить точно длину одного градуса и результат измерения умножить на 360.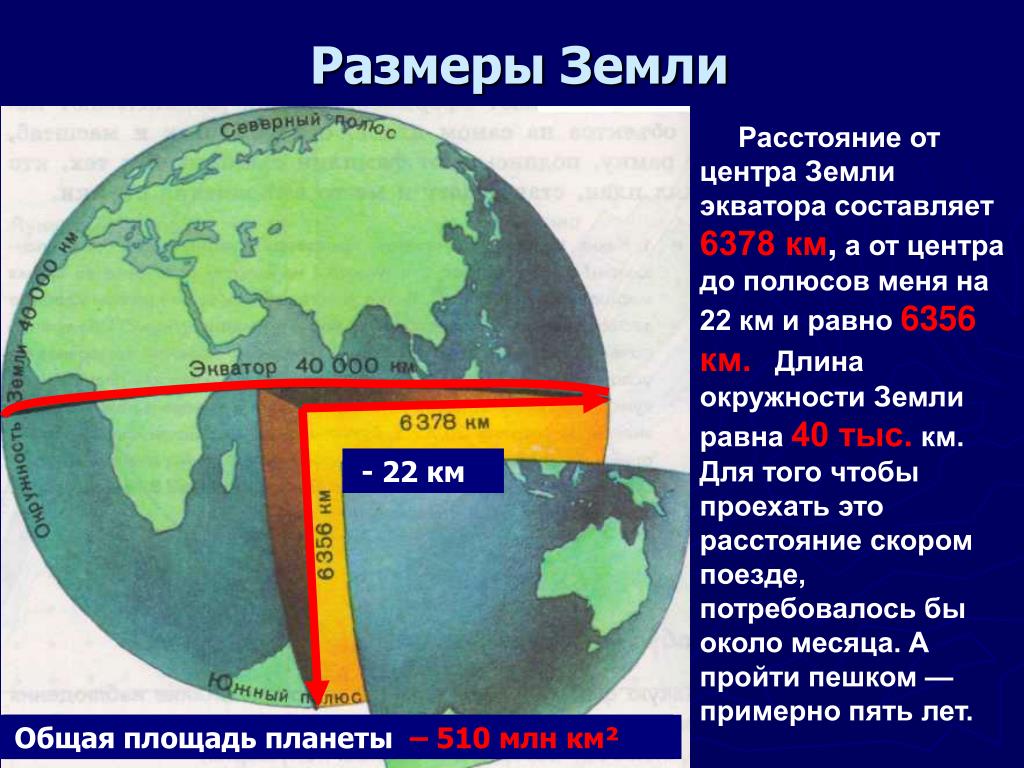
Первое измерение Земли таким способом произвел древнегреческий ученый Эратосфен (ок. 276—194 до и. э.), живший в египетском городе Александрии, па берегу Средиземного моря.
С юга в Александрию приходили караваны верблюдов. От сопровождавших их людей Эратосфен узнал, что в городе Сиене (нынешнем Асуане) в день летнего солнцестояния Солнце в иол-день находится над головой. Предметы в это время не дают никакой тени, а солнечные лучи проникают даже в самые глубокие колодцы. Стало быть, Солнце достигает зенита.
Путем астрономических наблюдений Эратосфен установил, что в этот же самый день в Александрии Солнце отстоит от зенита на 7,2 градуса, что составляет ровно 1/50 часть окружности. (В самом деле: 360: 7,2 = 50.) Теперь, чтобы узнать, чему равна окружность Земли, оставалось измерить расстояние между городами и умножить его па 50. Но измерить это расстояние, пролегающее по пустыне, Эратосфену было не под силу. Не могли измерить его и проводники торговых караванов. Они лишь знали, сколько времени тратят их верблюды на один переход, и считали, что от Сиены до Александрии 5000 египетских стадий.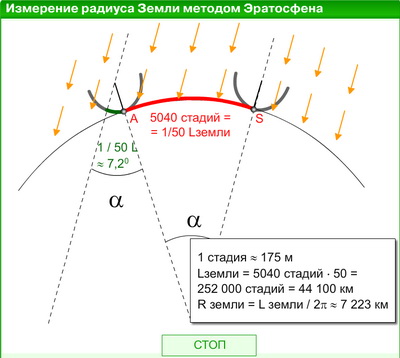 Значит, вся окружность Земли: 5000 x 50 = 250 000 стадий.
Значит, вся окружность Земли: 5000 x 50 = 250 000 стадий.
К сожалению, мы не знаем точно длину египетской стадии. По некоторым данным, она равна 174,5 м, что дает для земной окружности 43 625 км. Известно, что радиус в 6,28 раза меньше длины окружности. Получалось, что радиус Земли, но Эратосфену,— 6943 км. Вот так более двадцати двух веков тому назад впервые были определены размеры земного шара.
По современным данным, средний радиус Земли составляет 6371 км. По почему средний? Ведь если Земля — шар, то идее земные радиусы должны быть одинаковыми. Об этом мы расскажем дальше.
Способ точного измерения больших расстояний впервые предложил голландский географ и математик Вилдеброрд Сиеллиус (1580-1626).
Представим себе, что необходимо измерить расстояние между точками А и Б, удаленными одна от другой на сотни километров. Решение этой задачи следует начать с построения на местности так называемой опорной геодезической сети. В простейшем варианте она создается в виде цепочки треугольников.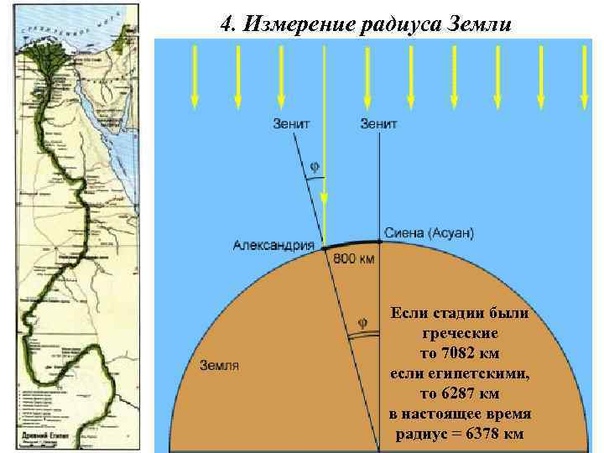 Вершины их выбираются на возвышенных местах, где сооружаются так называемые геодезические знаки в виде специальных пирамид, и обязательно так, чтобы из каждого пункта были видны направления на все соседние пункты. А еще эти пирамиды должны быть удобны для работы: для установки угломерного инструмента — теодолита — и измерения всех углов в треугольниках этой сети. Кроме того, в одном из треугольников измеряется одна сторона, которая пролегает по ровной и открытой местности, удобной для линейных измерений. В результате получается сеть треугольников с известными углами и исходной стороной — базисом. Затем следуют вычисления.
Вершины их выбираются на возвышенных местах, где сооружаются так называемые геодезические знаки в виде специальных пирамид, и обязательно так, чтобы из каждого пункта были видны направления на все соседние пункты. А еще эти пирамиды должны быть удобны для работы: для установки угломерного инструмента — теодолита — и измерения всех углов в треугольниках этой сети. Кроме того, в одном из треугольников измеряется одна сторона, которая пролегает по ровной и открытой местности, удобной для линейных измерений. В результате получается сеть треугольников с известными углами и исходной стороной — базисом. Затем следуют вычисления.
Решение наминается с треугольника, содержащего базис. По стороне и углам вычисляются две другие стороны первого треугольника. Но одна из его сторон является одновременно стороной смежного с ним треугольника. Она служит исходной для вычисления сторон второго треугольника и так далее. В конце концов находятся стороны последнего треугольника и вычисляется искомое расстояние — дуга меридиана АБ.
Геодезическая сеть обязательно опирается на астрономические пункты А и Б. Методом астрономических наблюдений звезд определяются их географические координаты (широты и долготы) и азимуты (направления на местные предметы).
Теперь, когда известна протяженность дуги меридиана АБ, а также ее выражение в градусной мере (как разность широт астропунктов А и Б), не составит особого труда вычислить длину дуги 1 градуса меридиана путем простого деления первой величины на вторую.
Этот способ измерения больших расстояний на земной поверхности получил название триангуляции — от латинского слова «триапгулюм», что значит «треугольник». Он оказался удобным для определения размеров Земли.
Изучением размеров нашей планеты и формы се поверхности занимается наука геодезия, что в переводе с греческого означает «землеизмерение». Ее зарождение следует отнести к Эратосфсну. Но собственно научная геодезия началась с триангуляции, впервые предложенной Сиеллиусом.
Самое грандиозное градусное измерение XIX века возглавил основатель Пулковской обсерватории В. Я. Струве. Под руководством Струве русские геодезисты совместно с норвежскими измерили дугу» простиравшуюся от Дуная по западным областям России в Финляндию и Норвегию до побережья Северного Ледовитого океана. Общая протяженность этой дуги превысила 2800 км! В ней было заключено более 25 градусов, что составляет почти 1/14 часть земной окружности. В историю науки она -вошла под названием «дуги Струве». Автору этой книги в послевоенные годы довелось работать на наблюдениях (измерениях углов) на пунктах государственной триангуляции, примыкавших непосредственно к знаменитой «дуге».
Я. Струве. Под руководством Струве русские геодезисты совместно с норвежскими измерили дугу» простиравшуюся от Дуная по западным областям России в Финляндию и Норвегию до побережья Северного Ледовитого океана. Общая протяженность этой дуги превысила 2800 км! В ней было заключено более 25 градусов, что составляет почти 1/14 часть земной окружности. В историю науки она -вошла под названием «дуги Струве». Автору этой книги в послевоенные годы довелось работать на наблюдениях (измерениях углов) на пунктах государственной триангуляции, примыкавших непосредственно к знаменитой «дуге».
Градусные измерения показали, что паша Земля не является в точности шаром, а похожа на эллипсоид, то есть она сжата у полюсов. У эллипсоида все меридианы представляют собой эллипсы, а экватор и параллели — окружности.
Чем длиннее измеряемые дуги меридианов и параллелей, тем точнее можно вычислить радиус Земли и определить ее сжатие.
Отечественные геодезисты промерили государственную триангуляционную сеть почти на половине территории СССР. Это позволило советскому ученому Ф. Н. Красовскому (1878-1948) более точно определить размеры и форму Земли. Эллипсоид Красовского: экваториальный радиус — 6378,245 км, полярный радиус — 6356,863 км. Сжатие планеты — 1/298,3, то есть на такую часть полярный радиус Земли короче экваториального (в линейной мере — 21,382 км).
Это позволило советскому ученому Ф. Н. Красовскому (1878-1948) более точно определить размеры и форму Земли. Эллипсоид Красовского: экваториальный радиус — 6378,245 км, полярный радиус — 6356,863 км. Сжатие планеты — 1/298,3, то есть на такую часть полярный радиус Земли короче экваториального (в линейной мере — 21,382 км).
Представим себе, что па глобусе с поперечником 30 см решили изобразить сжатие земного шара. Тогда полярную ось глобуса пришлось бы укоротить на 1 мм. Это так мало, что совершенно незаметно для глаза. Вот так и Земля с большого расстояния кажется совершенно круглой. Такой ее наблюдают космонавты.
Изучая форму Земли, ученые прийти к выводу, что она сжата не только вдоль оси вращения. Экваториальное сечение земного шара в проекции на плоскость дает кривую, которая тоже отличается от правильной окружности, правда совсем немного — на сотни метров. Все это свидетельствует о том, что фигура у нашей планеты более сложная, чем казалось раньше.
Теперь уже совершенно ясно, что Земля не является правильным геометрическим телом, то есть эллипсоидом. К тому же поверхность нашей планеты далеко не гладкая. На ней есть возвышенности и высокие горные хребты. Правда, суши почти в три раза меньше, чем воды. Что же в таком случае мы должны подразумевать подземной поверхностью?
К тому же поверхность нашей планеты далеко не гладкая. На ней есть возвышенности и высокие горные хребты. Правда, суши почти в три раза меньше, чем воды. Что же в таком случае мы должны подразумевать подземной поверхностью?
Как известно, океаны и моря, сообщаясь друг с другом, образуют на Земле обширную водную гладь. Поэтому ученые условились принимать за поверхность планеты поверхность Мирового океана, находящегося в спокойном состоянии.
А как поступать в районах континентов? Что там считать поверхностью Земли? Тоже поверхность Мирового океана, мысленно продолженную под всеми материками и островами.
Вот эта фигура, ограниченная поверхностью среднего уровня Мирового океана, была названа геоидом. От поверхности геоида и ведется отсчет всех известных «высот над уровнем моря». Слово «геоид», или «землеподобный», специально придумало для названия фигуры Земли. В геометрии такой фигуры не существует. Близок по форме к геоиду геометрически правильный эллипсоид.
4 октября 1957 года с запуском в нашей стране первого искусственного спутника Земли человечество вступило в космическую эру. 11ачалось активное исследование околоземного пространства. При этом выяснилось, что спутники очень полезны и для познания самой Земли. Даже в области геодезии они сказали свое «веское слово».
11ачалось активное исследование околоземного пространства. При этом выяснилось, что спутники очень полезны и для познания самой Земли. Даже в области геодезии они сказали свое «веское слово».
Как известно, классическим методом изучения геометрических характеристик Земли является триангуляция. Но раньше геодезические сети развивали лишь в пределах материков, а между собой они не были связаны. Ведь на морях и океанах триангуляцию не построишь. Поэтому расстояния между материками были определены менее точно. За счет этого снижалась точность определения размеров самой Земли.
С запуском спутников геодезисты сразу поняли: появились «визирные цели» на большой высоте. Теперь можно будет измерить большие расстояния.
Идея метода космической триангуляции проста. Синхронные (одновременные) наблюдения спутника из нескольких отдаленных пунктов земной поверхности позволяют привести их геодезические координаты к единой системе. Так были связаны воедино триангуляции, построенные на разных материках, а заодно были уточнены размеры Земли: экваториальный радиус — 6378,160 км, полярный радиус — 6356,777 км. Величина сжатия — 1/298,25, то есть почти такая же, как у эллипсоида Красовского. Разница между экваториальным и полярным диаметрами Земли достигает 42 км 766 м.
Величина сжатия — 1/298,25, то есть почти такая же, как у эллипсоида Красовского. Разница между экваториальным и полярным диаметрами Земли достигает 42 км 766 м.
Если бы наша планета была правильным шаром, а массы внутри нее распределены равномерно, то спутник мог бы двигаться вокруг Земли по круговой орбите. Но отклонение формы Земли от шарообразной и неоднородность ее недр приводят к тому, что над различными точками земной поверхности сила притяжения неодинаковая. Изменяется сила притяжения Земли — изменяется орбита спутника. И все, даже малейшие изменения в движении спутника с низкой орбитой — то результат гравитационного воздействия на него той или иной земной выпуклости или и падины, над которой он пролетает.
Оказалось, что наша планета имеет еще и слегка грушевидную форму. Ее Северный полюс приподнят над плоскостью экватора па 16 м, а Южный — примерно на столько же опущен (как бы вдавлен). Вот и получается, что в сечении по меридиану фигура Земли напоминает грушу. Она чуть-чуть вытянута к северу и приплюснута у Южного полюса. Налицо полярная асимметрия: Се пер нос полушарие нетождественно Южному. Так на основании спутниковых данных было получено самое точное представление об истинной форме Земли. Как видим, фигура нашей планеты заметно отклоняется от геометрически правильной формы шара, а также от фигуры эллипсоида вращения.
Налицо полярная асимметрия: Се пер нос полушарие нетождественно Южному. Так на основании спутниковых данных было получено самое точное представление об истинной форме Земли. Как видим, фигура нашей планеты заметно отклоняется от геометрически правильной формы шара, а также от фигуры эллипсоида вращения.
Впервые измерения размера Земли выполнил александрийский ученый Эратосфен еще в III веке до нашей эры, причем сумел получить удивительно точные результаты. Как это было сделано?
Эратосфену было известно, что в день летнего солнцестояния в городе Сиене Солнце в полдень находится точно в зените, освещая дно глубоких колодцев. Действительно, этот город расположен на линии северного тропика. В этот день Эратосфен измерил высоту Солнца в Александрии и нашел, что оно отстоит от зенита на 1/50 часть окружности. Расстояние между этими городами было известно и составляло 5000 стадиев. Следовательно, вся окружность земного шара имеет длину в 50 раз большую — 250000 стадиев или 39600 километров. Возможно, реальная точность измерений была несколько ниже и результат лишь случайно оказался настолько близок к реальности, но факт остается фактом — более точное значение смогли получить лишь в XVIII веке…
Возможно, реальная точность измерений была несколько ниже и результат лишь случайно оказался настолько близок к реальности, но факт остается фактом — более точное значение смогли получить лишь в XVIII веке…
(Это значение — 40 000 км. И не стоит удивляться такой круглой цифре — дело в том, что именно по результатам этих измерений было принято определение километра, как 1/40000 части длины меридиана. Позже значение длины меридиана не раз уточнялось, но длину эталона метра уже не меняли, поэтому сейчас цифры не такие «красивые»)
Мы можем повторить этот опыт великого ученого. В общем, нам не нужно, чтобы Солнце находилось в зените в одном из пунктов наблюдений, нам даже не нужно проводить измерения в один день — нам нужно только вычислить разность широт, определенных по высоте Солнца. Другой вопрос, что если мы будем определять склонение Солнца приближенно, как описано ранее, это внесет дополнительные погрешности. Поэтому, если из стремления к чистоте эксперимента не пользоваться современными астрономическими таблицами и вычислительной техникой, измерения действительно лучше производить вблизи дня солнцестояния — в это время склонение его очень мало изменяется в течение нескольких дней. Так что если мы путешествуем с 20 по 25 июня мы можем вполне обойтись сравнением высот Солнца.
Так что если мы путешествуем с 20 по 25 июня мы можем вполне обойтись сравнением высот Солнца.
Δφ/360 = L/2πR 0
R 0 = L*360/2πΔφ , где
R 0 — радиус Земли
Δφ=(z 1 -z 2) — разность географических широт пунктов наблюдения или разность высот Солнца
L — расстояние между пунктами наблюдений
(Кстати, все тот же Эратосфен определил и склонение Солнца в день солнцестояния как 11/166 окружности, или 23.855° — тоже весьма достойная точность!)
Второе условие получения более-менее точного результата — достаточно большое и точно известное расстояние между пунктами наблюдений, расположенными примерно на одной долготе. Конечно, бессмысленно измерять это расстояние по карте — при этом мы уже неявно используем ту величину, которую только собираемся определить, а вот измерения по одометру автомобиля будут вполне честным способом.
Я когда-то пытался проделать этот эксперимент, определяя высоты Cолнца в Минске и расположенном в 100 км южнее Слуцке, но такое расстояние между городами слишком мало для получения хоть сколько-нибудь приемлемого результата — ведь высоты Солнца отличались менее чем на 1 градус, что сравнимо с точностью измерений с помощью гномона. Намного лучше было бы использовать пары Киев-Одесса или даже Витебск-Одесса, Москва-Елец или Москва-Ростов-на-Дону.
Намного лучше было бы использовать пары Киев-Одесса или даже Витебск-Одесса, Москва-Елец или Москва-Ростов-на-Дону.
Интересно, кто-то еще считает гномон несерьезным инструментом?
ЭРАТОСФЕН
Киренский
(ок.276-194 до н.э.)
древнегреческий ученый. Родился в Кирене (Северная Африка). Образование получил в Александрии и в Афинах. Служил воспитателем наследного принца при дворе Птолемея III Эвергета, около 225 г. до н. э. начал заведовать Александрийской библиотекой. Заложил основы математической географии, впервые измерил дугу меридиана. С большой точностью определил наклон эклиптики, составил каталог 675 неподвижных звезд. Заложил основы научной хронологии, предложил вводить лишний день в календарь каждые 4 года. Труды по математике (теория чисел), астрономии, филологии, философии, музыке. Сохранились лишь отрывки.
Жан Эффель, «Сотворение мира»
-И какая стройная! Если считать в миллионах сантиметров, ее талия — 40!
Теперь вы знаете, что в сказочной Вселенной наших далеких предков Земля даже не напоминала шар. Жители Древнего Вавилона представляли ее в виде острова в океане. Египтянам она виделась вытянутой с севера на юг долиной, в центре которой был Египет. А древние китайцы одно время изображали Землю в виде прямоугольника… Вы улыбаетесь, представляя себе такую Землю, но часто ли вы задумывались о том, как люди догадались, что Земля — не безграничная плоскость или диск, плавающий в океане? Когда я спрашивал об этом ребят, то одни говорили, что о шарообразности Земли люди узнали после первых кругосветных путешествий, а другие вспоминали, что при появлении из-за горизонта корабля мы сначала видим мачты, а потом палубу. Доказывают ли такие и некоторые подобные им примеры, что Земля — шар? Вряд ли. Ведь объехать можно и вокруг… чемодана, а верхние части корабля появлялись бы и в том случае, если бы Земля имела форму полушария или была похожа, скажем, на… бревно. Подумайте об этом и постарайтесь изобразить сказанное на своих рисунках. Тогда вы поймете: приведенные примеры свидетельствуют лишь о том, что Земля изолирована в пространстве и, возможно, шарообразна.
Жители Древнего Вавилона представляли ее в виде острова в океане. Египтянам она виделась вытянутой с севера на юг долиной, в центре которой был Египет. А древние китайцы одно время изображали Землю в виде прямоугольника… Вы улыбаетесь, представляя себе такую Землю, но часто ли вы задумывались о том, как люди догадались, что Земля — не безграничная плоскость или диск, плавающий в океане? Когда я спрашивал об этом ребят, то одни говорили, что о шарообразности Земли люди узнали после первых кругосветных путешествий, а другие вспоминали, что при появлении из-за горизонта корабля мы сначала видим мачты, а потом палубу. Доказывают ли такие и некоторые подобные им примеры, что Земля — шар? Вряд ли. Ведь объехать можно и вокруг… чемодана, а верхние части корабля появлялись бы и в том случае, если бы Земля имела форму полушария или была похожа, скажем, на… бревно. Подумайте об этом и постарайтесь изобразить сказанное на своих рисунках. Тогда вы поймете: приведенные примеры свидетельствуют лишь о том, что Земля изолирована в пространстве и, возможно, шарообразна.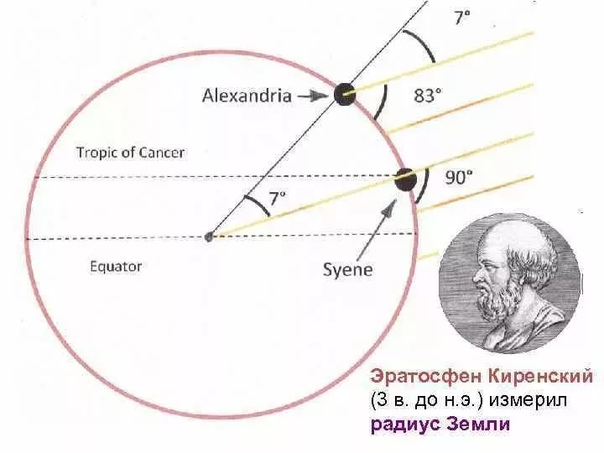
Как же узнали, что Земля — шар? Помогла, как я уже вам рассказал, Луна, а точнее — лунные затмения, во время которых на Луне всегда видна круглая тень Земли. Устройте небольшой «театр теней»: освещайте в темной комнате предметы разной формы (треугольник, тарелку, картофелину, мяч и т. д.) и замечайте, какая тень от них получается на экране или просто на стене. Убедитесь, что только мячик всегда образует на экране тень в виде круга. Итак, Луна помогла людям узнать, что Земля — это шар. К такому выводу ученые в Древней Греции (например, великий Аристотель) пришли еще в IV веке до нашей эры. Но еще очень долго «здравый смысл» человека не мог смириться с тем, что люди обитают на шаре. Даже представить себе не могли, как можно жить на «другой стороне» шара, ведь находящимся там «антиподам» пришлось бы все время ходить вниз головой… Но где бы ни находился человек на земном шаре, всюду брошенный вверх камень будет под действием силы притяжения Земли падать вниз, то есть на земную поверхность, а если бы было возможно, то и к центру Земли. На самом деле, людям, конечно, нигде, кроме цирков и спортивных залов, не приходится ходить вверх ногами и вниз головой. Они в любом месте Земли ходят нормально: земная поверхность у них под ногами, а небо над головой.
На самом деле, людям, конечно, нигде, кроме цирков и спортивных залов, не приходится ходить вверх ногами и вниз головой. Они в любом месте Земли ходят нормально: земная поверхность у них под ногами, а небо над головой.
Около 250 года до нашей эры греческий ученый Эратосфен впервые довольно точно измерил земной шар. Эратосфен жил в Египте в городе Александрия. Он догадался сравнить высоту Солнца (или его угловое расстояние от точки над головой, зенита, которое так и называется — зенитное расстояние ) в один и тот же момент времени в двух городах — Александрии (на севере Египта) и Сиене (ныне Асуан, на юге Египта). Эратосфену было известно, что в день летнего солнцестояния (22 июня) Солнце в полдень освещает дно глубоких колодцев. Следовательно, в это время Солнце находится в зените. Но в Александрии в этот момент Солнце не бывает в зените, а отстоит от него на 7,2°. Такой результат Эратосфен получил, изменяя зенитное расстояние Солнца с помощью своего несложного угломерного инструмента — скафиса. Это просто вертикальный шест — гномон, укрепленный на дне чаши (полусферы). Скафис устанавливают так, чтобы гномон принимал строго вертикальное положение (направлен в зенит) Освещенный солнцем шест отбрасывает тень на разделенную на градусы внутреннюю поверхность скафиса. Так вот в полдень 22 июня в Сиене гномон тень не отбрасывает (Солнце в зените, его зенитное расстояние равно 0°), а в Александрии тень от гномона, как видно по шкале скафиса, отмечала деление 7,2°. Во времена Эратосфена расстояние от Александрии до Сиена считали равным 5000 греческих стадий (примерно 800 км). Зная все это, Эратосфен сопоставил дугу в 7,2° со всей окружностью в 360° градусов, а расстояние 5000 стадий — со всей окружностью земного шара (обозначим ее буквой X) в километрах. Тогда из пропорции
Это просто вертикальный шест — гномон, укрепленный на дне чаши (полусферы). Скафис устанавливают так, чтобы гномон принимал строго вертикальное положение (направлен в зенит) Освещенный солнцем шест отбрасывает тень на разделенную на градусы внутреннюю поверхность скафиса. Так вот в полдень 22 июня в Сиене гномон тень не отбрасывает (Солнце в зените, его зенитное расстояние равно 0°), а в Александрии тень от гномона, как видно по шкале скафиса, отмечала деление 7,2°. Во времена Эратосфена расстояние от Александрии до Сиена считали равным 5000 греческих стадий (примерно 800 км). Зная все это, Эратосфен сопоставил дугу в 7,2° со всей окружностью в 360° градусов, а расстояние 5000 стадий — со всей окружностью земного шара (обозначим ее буквой X) в километрах. Тогда из пропорции
получилось, что Х = 250 000 стадий, или примерно 40 000 км (представьте себе, это так и есть!).
Если вам известно, что длина окружности равна 2πR, где R — радиус окружности (а π ~ 3,14), зная длину окружности земного шара, легко найти его радиус (R):
Замечательно, что Эратосфену удалось очень точно измерить Землю (ведь и сегодня считают, что средний радиус Земли 6371 км! ).
Но почему здесь упомянут средний радиус Земли, разве у шара не все радиусы одинаковы? Дело в том, что фигура Земли отличается от шара. Об этом ученые стали догадываться еще в XVIII веке, но какова в действительности Земля — сжата она у полюсов или у экватора — выяснить было трудно. Чтобы разобраться в этом, Французской академии наук пришлось снарядить две экспедиции. В 1735 году одна из них отправилась проводить астрономические и геодезические работы в Перу и занималась этим в экваториальном районе Земли около 10 лет, а другая, лапландская, трудилась в 1736-1737 годах вблизи Северного полярного круга. В результате выяснилось, что длина дуги одного градуса меридиана неодинакова у полюсов Земли и у ее экватора. Градус меридиана оказался у экватора длиннее, чем в высоких широтах (111,9 км и 110,6 км). Так может быть лишь в том случае, если Земля сжата у полюсов и представляет собой не шар, а тело, близкое по форме к сфероиду. У сфероида полярный радиус меньше экваториального (у земного сфероида полярный радиус короче экваториального почти на 21 км ).
Полезно знать, что великий Исаак Ньютон (1643-1727) предвосхитил результаты экспедиций: он сделал правильный вывод о том, что Земля сжата, потому наша планета вращается вокруг оси. Вообще, чем быстрее вращается планета, тем больше должно быть ее сжатие. Поэтому, например, сжатие Юпитера больше, чем Земли (Юпитер успевает сделать оборот вокруг оси по отношению к звездам за 9 ч 50 мин, а Земля только за 23 ч 56 мин).
И еще. Истинная фигура Земли очень сложна и отличается не только от шара, но и от сфероида вращения. Правда, в данном случае речь идет о разнице не в километры, а…метры! Подобным тщательным уточнением фигуры Земли ученые занимаются по сей день, используя для этой цели специально проводимые наблюдения с искусственных спутников Земли. Так что вполне возможно, что в решении задачи, за которую давным-давно взялся Эратосфен, когда-нибудь и вам придется принять участие. Это очень нужное людям дело.
Какой же лучше всего запомнить вам фигуру нашей планеты? Думаю, что пока достаточно, если вы будете представлять Землю в виде шара с надетым на него «дополнительным поясом», своего рода «нашлепкой» на область экватора. Такое искажение фигуры Земли, превращающее ее из шара в сфероид, имеет немалые последствия. В частности, из-за притяжения Луной «дополнительного пояса» земная ось примерно за 26 000 лет описывает в пространстве конус. Это движение земной оси называется прецессионным. В результате роль Полярной звезды, которая сейчас принадлежит α Малой Медведицы, поочередно играют некоторые другие звезды (ею в будущем станет, например, α Лиры — Вега). Кроме того, из-за такого (прецессионного ) движения земной оси знаки Зодиака все больше и больше не совпадают с соответствующими созвездиями. Другими словами, через 2000 лет после эпохи Птолемея «знак Рака», например, уже не совпадает с «созвездием Рака» и т. д. Впрочем, современные астрологи стараются не обращать на это внимания…
Такое искажение фигуры Земли, превращающее ее из шара в сфероид, имеет немалые последствия. В частности, из-за притяжения Луной «дополнительного пояса» земная ось примерно за 26 000 лет описывает в пространстве конус. Это движение земной оси называется прецессионным. В результате роль Полярной звезды, которая сейчас принадлежит α Малой Медведицы, поочередно играют некоторые другие звезды (ею в будущем станет, например, α Лиры — Вега). Кроме того, из-за такого (прецессионного ) движения земной оси знаки Зодиака все больше и больше не совпадают с соответствующими созвездиями. Другими словами, через 2000 лет после эпохи Птолемея «знак Рака», например, уже не совпадает с «созвездием Рака» и т. д. Впрочем, современные астрологи стараются не обращать на это внимания…
Постараюсь не только ответить на вопрос, но и описать метод измерения, который, на мой взгляд, весьма оригинален. В общем, надеюсь, получится интересно, а главное — познавательно.
Как Эратосфен измерил окружность Земли
Сегодня с этим справится, пожалуй, любой школьник, но тогда, более 2000 лет назад, это было сделать практически невозможно. Более того, в те времена большинство полагало, что мир представляет собой плоский диск, с края которого можно свалиться в бездну. Однако ученый, живший в Александрии, навсегда вошел в историю как первый, кому удалось вычислить размеры нашей планеты. Но как он это сделал, ведь в его арсенале не было практически никаких специальных приборов? Он использовал те данные, которыми располагали египтяне, а именно — тот факт, что в день летнего солнцестояния лучи светила достигают дна самых глубоких колодцев города Сиена. При этом, в Александрии такое явление не наблюдается. Итак, в 240 году до н.э., ученый использовал обычную чашу с иголкой, чтобы понять, каков угол светила в небе. Далее были произведены следующие расчеты:
Более того, в те времена большинство полагало, что мир представляет собой плоский диск, с края которого можно свалиться в бездну. Однако ученый, живший в Александрии, навсегда вошел в историю как первый, кому удалось вычислить размеры нашей планеты. Но как он это сделал, ведь в его арсенале не было практически никаких специальных приборов? Он использовал те данные, которыми располагали египтяне, а именно — тот факт, что в день летнего солнцестояния лучи светила достигают дна самых глубоких колодцев города Сиена. При этом, в Александрии такое явление не наблюдается. Итак, в 240 году до н.э., ученый использовал обычную чашу с иголкой, чтобы понять, каков угол светила в небе. Далее были произведены следующие расчеты:
- в Сиене полдень — тень абсолютно отсутствует, то есть, угол равен 0°;
- в Александрии, что расположена почти в 5000 стадиев (около 800 км), угол составил 7° 12′ — стало быть, 1/50 окружности;
- после расчетов было установлено, что окружность составляет не менее 250 тысяч стадий или почти 40 тысяч км.

Как видно, с учетом небольшой погрешности, результат соответствует действительности. В общем, очевидно, что Эратосфен для своего времени оказался великолепным ученым.
Как измеряют Землю сегодня
В наши дни существует специальная наука — геодезия, которая и занимается решением подобных задач. Специалисты применяют множество приборов для вычисления угловых расстояний. Например, для определения точной формы планеты сопоставляют колебания силы тяжести на разных участках, а для определения углов используют спутники.
Аппарат является как бы вершиной треугольника, естественно, воображаемого, а остальные углы опираются на разные участки поверхности Земли.
Окружность Земли
Окружность Земли – это расстояние вокруг Земли . Измеренная вокруг экватора , это 40 075,017 км (24 901,461 мили). Окружность, измеренная вокруг полюсов , составляет 40 007,863 км (24 859,734 мили). [1]
Измерение окружности Земли было важно для навигации с древних времен. Первые известные научные измерения и расчеты были сделаны Эратосфеном , который достиг большой степени точности в своих вычислениях. [2] Если рассматривать Землю как сферу , то определение окружности Земли будет ее самым важным измерением. [3] Земля отклоняется от сферической примерно на 0,3%, что характеризуется сплющиванием .
Первые известные научные измерения и расчеты были сделаны Эратосфеном , который достиг большой степени точности в своих вычислениях. [2] Если рассматривать Землю как сферу , то определение окружности Земли будет ее самым важным измерением. [3] Земля отклоняется от сферической примерно на 0,3%, что характеризуется сплющиванием .
В наше время окружность Земли использовалась для определения основных единиц измерения длины: морской мили в семнадцатом веке и метра в восемнадцатом. Полярная окружность Земли очень близка к 21 600 морских миль, потому что морская миля предназначалась для выражения одной минуты широты (см. дугу меридиана ), что составляет 21 600 частей полярной окружности (то есть 60 минут × 360 градусов). Полярная окружность также близка к 40 000 километров, потому что метр изначально был определен как одна 10-миллионная (то есть километр равен одной 10-тысячной) дуги от полюса до экватора ( четверть меридиана ).). Физическая длина каждой единицы измерения осталась близкой к тому, что было определено в то время, но точность измерения окружности с тех пор улучшилась.
Измерение окружности Земли является наиболее известным среди результатов, полученных Эратосфеном [4] , который оценил длину меридиана в 252 000 стадий с погрешностью реального значения от -2,4% до +0,8% (при условии, что значение для стадиона между 155 и 160 метрами). [2] Эратосфен описал свою технику в книге под названием « О мере Земли », которая не сохранилась.
Метод Эратосфена для вычисления окружности Земли был утерян; сохранилась упрощенная версия, описанная Клеомедом для популяризации открытия. [5] Клеомед предлагает своему читателю рассмотреть два египетских города, Александрию и Сиену , современный Ассуан :
При предыдущих предположениях, пишет Клеомед, можно измерить угол возвышения Солнца в полдень летнего солнцестояния в Александрии, используя вертикальный стержень ( гномон ) известной длины и измерив длину его тени на земле; тогда можно вычислить угол солнечных лучей, который, как он утверждает, составляет около 7°, или 1/50 окружности круга. Если принять Землю за шар, окружность Земли будет в пятьдесят раз больше расстояния между Александрией и Сиеной, то есть 250 000 стадий. Поскольку 1 египетский стадион равен примерно 157,7 метрам, [7] результат составляет примерно 39 425 км, что на 1,5% меньше, чем реальная длина окружности, равная 40 008 км.
Если принять Землю за шар, окружность Земли будет в пятьдесят раз больше расстояния между Александрией и Сиеной, то есть 250 000 стадий. Поскольку 1 египетский стадион равен примерно 157,7 метрам, [7] результат составляет примерно 39 425 км, что на 1,5% меньше, чем реальная длина окружности, равная 40 008 км.
Измерение окружности Земли в соответствии с упрощенной версией Клеомеда, основанной на приближении, согласно которому Сиена находится на тропике Рака и на том же меридиане, что и Александрия . Диаграмма, показывающая, как аль-Бируни смог рассчитать окружность Земли по высшей и низшей точкам в одном и том же месте.
Глава 4 Измерение Земли. Том 38. Измерение мира. Календари, меры длины и математика
Глава 4
Измерение Земли
Изучение движения небесных тел помогло определить единицы измерения времени, однако человека также интересовали очертания и размеры мира, в котором он жил, и он захотел измерить Землю. Птолемей не только внес вклад в измерение небес, но и стал непререкаемым авторитетом во всем, что касалось измерения Земли, описав в своей «Географии» весь известный мир своего времени. В XV–XVI веках, с открытием новых территорий, европейцы расширили границы привычного мира и внесли в труд Птолемея поправки. В конце XVII века были произведены более тщательные измерения размеров Земли при помощи триангуляции. Так были заложены основы геодезии. Относительно формы Земли существовало две точки зрения: согласно первой, Земля была сплюснута у полюсов, согласно второй — у экватора. Разногласия сторонников этих двух точек зрения вылились в бурную полемику, и было принято решение найти истину, измерив длину дуги меридиана величиной в один градус. Измерения должны были произвести две экспедиции в двух точках, максимально отстоящих по широте друг от друга.
В XV–XVI веках, с открытием новых территорий, европейцы расширили границы привычного мира и внесли в труд Птолемея поправки. В конце XVII века были произведены более тщательные измерения размеров Земли при помощи триангуляции. Так были заложены основы геодезии. Относительно формы Земли существовало две точки зрения: согласно первой, Земля была сплюснута у полюсов, согласно второй — у экватора. Разногласия сторонников этих двух точек зрения вылились в бурную полемику, и было принято решение найти истину, измерив длину дуги меридиана величиной в один градус. Измерения должны были произвести две экспедиции в двух точках, максимально отстоящих по широте друг от друга.
Первые представления о форме и размерах Земли
В древности большинство людей верило, что обитаемая Земля плоская — по крайней мере, она выглядела именно так, если не принимать в расчет неровности рельефа. Однако древнегреческие философы начали рассматривать иные гипотезы. Анаксимандру приписывается концепция, согласно которой Земля имела цилиндрическую форму, была вытянута в длину и располагалась в центре небесной сферы. Согласно этой концепции, обитаемым был лишь верхний диск цилиндрической Земли. Считается, что Анаксимандр составил карту Земли, которую позднее исправил и усовершенствовал Гекатей Милетский (ок. 550 г. до н. э. — ок. 476 г. до н. э.). На этой карте были изображены известные на тот момент области Европы, Азии и Африки, расположенные на диске, окруженном рекой-океаном. В центральной части диска располагалась Греция.
Согласно этой концепции, обитаемым был лишь верхний диск цилиндрической Земли. Считается, что Анаксимандр составил карту Земли, которую позднее исправил и усовершенствовал Гекатей Милетский (ок. 550 г. до н. э. — ок. 476 г. до н. э.). На этой карте были изображены известные на тот момент области Европы, Азии и Африки, расположенные на диске, окруженном рекой-океаном. В центральной части диска располагалась Греция.
Хотя в точности оценить величину древних единиц измерения всегда непросто, считается, что диаметр диска, изображенного на карте Гекатея, составлял примерно 8000 километров.
Карта Гекатея I в. до н. э.
Если Земля была плоской, то имела ли она конец? Гекатей, по всей видимости, считал, что да. Но почему тогда океан, окружавший сушу, не переливался через края? Быть может, он упирался в некую стену, где небо соединялось с морем? Как Земля удерживалась на месте? Как видите, гипотеза о плоской форме Земли вызывала множество непростых вопросов. Древние греки предположили, что Земля имеет форму сферы, и привели убедительные доводы в поддержку этой гипотезы — об этом мы уже рассказали в главе 2. Но как греческие мыслители определили размеры Земли?
Древние греки предположили, что Земля имеет форму сферы, и привели убедительные доводы в поддержку этой гипотезы — об этом мы уже рассказали в главе 2. Но как греческие мыслители определили размеры Земли?
* * *
ДОВОДЫ АРИСТОТЕЛЯ В ПОЛЬЗУ СФЕРИЧЕСКОЙ ФОРМЫ ЗЕМЛИ
Аристотель привел ряд доводов против того, что Земля плоская. К примеру, он указал, что высота звезд над горизонтом меняется в зависимости отточки наблюдения. Так, путешественник, идущий на юг, видел, что созвездия поднимались все выше над горизонтом. Это означало, что горизонт на юге образовывал определенный угол с горизонтом, который видел наблюдатель на севере. Следовательно, Земля не могла быть плоской. Аналогично, тень, отбрасываемая Землей на Луну во время частичных лунных затмений, всегда имела круглую границу вне зависимости от высоты Луны над горизонтом. Какое тело, кроме сферы, могло отбрасывать круглую тень во всех направлениях?
* * *
Измерение размеров сферической Земли. Эратосфен
Эратосфен
В эллинистический период Александрия стала научным центром греческой цивилизации благодаря двум важнейшим учреждениям — музею и библиотеке. Именно там впервые была вычислена длина окружности Земли. Сделал это греческий мудрец, математик и географ Эратосфен Киренский (276 г. до н. э. — 194 г. до н. э.).
Будучи главой Александрийской библиотеки, он имел доступ ко множеству различных данных, записанных на папирусах. Эратосфен знал, что в городе Сиена (ныне — Асуан), расположенном к югу от Александрии, в полдень по местному времени в день летнего солнцестояния солнечные лучи достигают дна глубоких колодцев, а вертикальные шесты не отбрасывают тени. В это же время в Александрии гномон отбрасывал тень.
Гравюра с изображением древней Александрийской библиотеки.
Эратосфен предположил: так как Солнце находится на большом расстоянии, его лучи падают на Землю параллельно. Если Земля плоская, как в те времена по-прежнему считали многие, то одинаковые предметы в один и тот же день и час должны отбрасывать одинаковую тень вне зависимости от того, где они находятся. Но тени предметов отличались, следовательно, Земля не была плоской. В полдень в день летнего солнцестояния в Александрии Эратосфен при помощи гномона измерил угол, на который солнечные лучи отстоят от вертикали. Этот угол составил 1/50 окружности (7°12?). Предположив, что Земля имеет форму сферы (360°), а Александрия расположена к северу от Сиены на том же меридиане, путем простых рассуждений (см. рисунок) он определил, что центральный угол между двумя радиусами Земли, соответствующими Сиене и Александрии, также составляет 1/50 окружности (7°12?).
Но тени предметов отличались, следовательно, Земля не была плоской. В полдень в день летнего солнцестояния в Александрии Эратосфен при помощи гномона измерил угол, на который солнечные лучи отстоят от вертикали. Этот угол составил 1/50 окружности (7°12?). Предположив, что Земля имеет форму сферы (360°), а Александрия расположена к северу от Сиены на том же меридиане, путем простых рассуждений (см. рисунок) он определил, что центральный угол между двумя радиусами Земли, соответствующими Сиене и Александрии, также составляет 1/50 окружности (7°12?).
Схема рассуждений Эратосфена.
Эратосфен знал, что расстояние между этими городами равнялось 5000 стадиев (примерно 800 километров), и определил длину окружности Земли с помощью простой пропорции. Длина окружности Земли должна была превышать расстояние между Александрией и Сиеной в 50 раз, то есть составлять 250 тысяч стадиев. Он округлил результат вычислений и принял один градус равным 70 стадиев, таким образом, общая длина земной окружности составила 252 тысячи стадиев.
К сожалению, нам неизвестно, какой была точная длина стадия, использованного Эратосфеном в расчетах. Греческий стадий примерно равен 185 м — в этом случае длина земной окружности составляет 46620 км (на 16,3 % больше, чем на самом деле). Но если предположить, что ученый использовал египетский стадий, который равнялся 157,5 м, то его результат равен 39690 км (в этом случае ошибка составляет менее 2 %).
Рассуждения Эратосфена были безошибочны, однако следует сделать небольшое замечание относительно точности проведенных им измерений: Сиена не расположена на одном меридиане с Александрией, а Солнце видится с Земли как диск, расположенный на конечном расстоянии, поэтому его нельзя считать бесконечно удаленным точечным источником света. Кроме того, в древности измерение расстояний по суше было ненадежным и становилось источником ошибок. Если учесть погрешности во всех данных, которые применил Эратосфен в вычислениях, то станет очевидно, что полученный им результат был на удивление точным.
Карты Земли: широта и долгота, географическое положение и картографические проекции
Птолемей работал в Александрии на несколько веков позже Эратосфена. В своей «Географии» он, применив строгие научные методы, описал весь известный древним грекам мир. Птолемей изложил математические методы составления точных карт при помощи различных проекций, а также указал географические координаты почти 10 тысяч точек известного в то время мира. При нанесении этих точек на карту он построил сетку параллелей и меридианов и применил такие понятия, как широта и долгота. Нулевой меридиан на карте Птолемея располагался возле Канарских островов, нулевая параллель — вблизи экватора. Северную оконечность обитаемого мира он расположил на параллели острова Туле.
По всей видимости, размеры Земли, использованные Птолемеем, были меньше реальных: он предполагал, что длина дуги экватора величиной в один градус составляет примерно 80 километров, таким образом, длина земной окружности была чуть меньше 30 тысяч километров.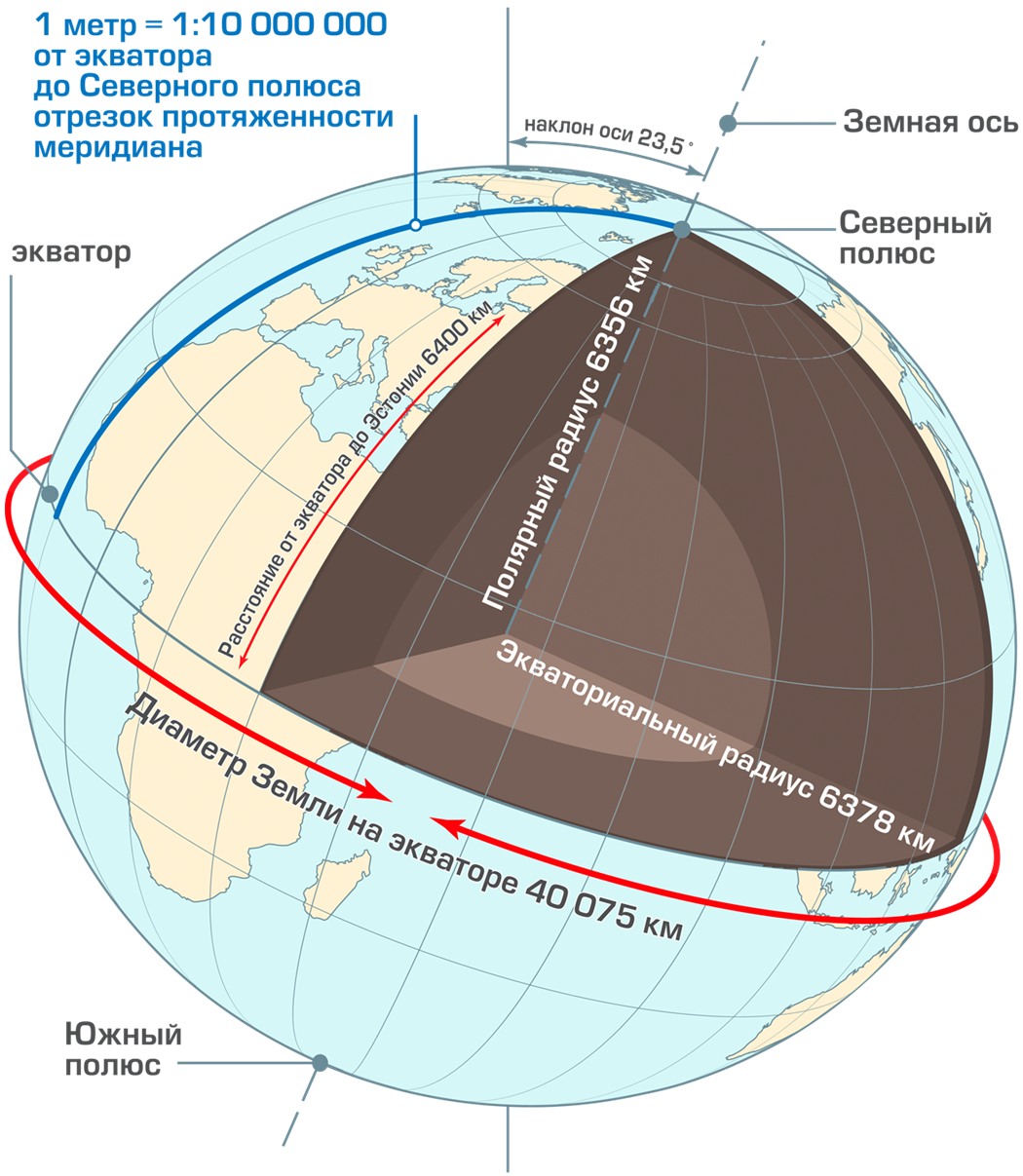 Птолемей пользовался огромным авторитетом в эпоху Возрождения, и только благодаря этому моряки осмелились пересечь океан в поисках новых земель.
Птолемей пользовался огромным авторитетом в эпоху Возрождения, и только благодаря этому моряки осмелились пересечь океан в поисках новых земель.
Задача о представлении криволинейной поверхности на плоскости решается математическими методами. В этом смысле Птолемей также внес значимый вклад в картографию. Считается, что еще до него Гиппарх разделил земную окружность на 360° и построил сетку параллелей и меридианов. Гиппарх изучал способы изображения сферической поверхности на плоской карте и, по мнению некоторых ученых, применил для решения этой задачи стереографическую проекцию. Большое влияние на Птолемея оказал географ и картограф Марин Тирский (ок. 60 — ок. 130), который первым принял меридиан Канарских островов за нулевой, а параллель Родоса — за начало отсчета широты. По всей видимости, он же предложил использовать цилиндрическую проекцию для составления карт.
Чтобы изобразить поверхность Земли на плоскости, Птолемей разработал коническую и псевдоконическую проекции. С их помощью ему удалось изобразить на одной плоскости разные участки земной поверхности в разном масштабе. В своей конической проекции он представил параллели в виде концентрических дуг окружностей, меридианы — в виде прямых линий, сходящихся в фокусе, который совпадал с Северным полюсом. Во второй, псевдоконической проекции Птолемея меридианы также изображались кривыми линиями, сходившимися в полюсе, за счет чего ему удалось изобразить больший участок земной поверхности с меньшими искажениями.
С их помощью ему удалось изобразить на одной плоскости разные участки земной поверхности в разном масштабе. В своей конической проекции он представил параллели в виде концентрических дуг окружностей, меридианы — в виде прямых линий, сходящихся в фокусе, который совпадал с Северным полюсом. Во второй, псевдоконической проекции Птолемея меридианы также изображались кривыми линиями, сходившимися в полюсе, за счет чего ему удалось изобразить больший участок земной поверхности с меньшими искажениями.
Коническая проекция Птолемея, приведенная в его «Географии» («Geographicae enarrationis libri octo»), изданной в Лионе и Вене в 1541 году.
Коническая проекция Птолемея использовалась вплоть до XV века, пока границы известного мира существенно не расширились. С новыми открытиями для составления карт мира этой проекции оказалось недостаточно, и она стала применяться только в картах отдельных регионов.
Ни в одной картографической проекции земного шара нельзя одновременно сохранить и площади, и углы, но можно обеспечить сохранение площадей и углов с различной точностью в зависимости от типа проекции — в частности, в проекциях, предположительно созданных Гиппархом, Марином и Птолемеем.
В стереографической проекции произвольной точке сферы А, отличной от полюса Р (фокус проекции), ставится в соответствие точка плоскости, определяемая как точка пересечения прямой РА и плоскости. И напротив, каждой точке плоскости В соответствует единственная точка А, отличная от Р, которая определяется как точка пересечения сферы с прямой РВ. Птолемей объясняет эту проекцию в своей «Планисфере» и использует ее для изображения небесной сферы на плоскости. Позднее эту проекцию применили арабы при изготовлении астролябий — инструментов для определения положения звезд на небосводе.
Стереографическая проекция.
В цилиндрической проекции поверхность земного шара проецируется на цилиндр, касающийся его в точке, лежащей на экваторе. Полученная карта отличается малыми искажениями возле экватора и огромными искажениями в приполярных областях. Эта проекция сохраняет углы, но не площади — они увеличиваются по мере удаления от экватора и приближения к любому из двух полюсов.
В конической проекции точки земного шара проецируются на конус, при этом в качестве фокуса выбирается один из полюсов. Приполярные области в этой проекции искажаются, но полушарие, в котором расположен полюс, выбранный в качестве фокуса, будет изображено с высокой точностью. На карте, построенной в конической проекции, искажения вдоль параллели касания невелики и возрастают по мере удаления от нее.
Арабы переняли у греков значительную часть культурного багажа, но в том, что касалось картографии и задач определения местоположения, были практичнее греков: они пересматривали и исправляли картографические данные по мере исследования новых земель. В конце XIII века крупные центры картографии находились в Средиземноморье — в Генуе, Венеции и Пальма-де-Мальорке, где изготавливались морские карты, а исследования носили ярко выраженный прикладной характер. С появлением компаса в Европе при создании морских карт стали применяться расчеты, связывавшие координаты корабля с расстояниями до различных портов.
Эти карты, в которых основное внимание уделялось морским путям, называются портуланами. В них отражены форма побережий, береговой рельеф, устья рек, направления ветров и так далее. В XIV–XV веках было изготовлено значительное количество таких карт.
Лучший из портуланов, изготовленный на Мальорке, — «Каталанский атлас» Авраама Крескеса 1375 года. На иллюстрации изображена копия этой карты, выполненная в XIX веке.
XVI век стал вершиной мореплавания: менее чем за 100 лет было открыто столько новых земель, что площадь известного мира удвоилась. Карты Земли совершенствовались, и впервые удалось получить прямое доказательство сферической формы Земли: Фернан Магеллан (1480–1521) и Хуан Себастьян Элькано (1476–1526) совершили кругосветное путешествие. И вскоре вновь встал вопрос об измерении земного шара.
* * *
ПЕРВОЕ ПРЯМОЕ ДОКАЗАТЕЛЬСТВО СФЕРИЧЕСКОЙ ФОРМЫ ЗЕМЛИ
Первое кругосветное путешествие (1519–1522), ставшее прямым доказательством сферической формы Земли, начал Фернан Магеллан, а закончил Хуан Себастьян Элькано. Магеллан возглавил экспедицию из пяти кораблей, которые отправились в плавание из города Санлукарде-Баррамеда в испанской провинции Кадис 20 сентября 1519 года. Мореплаватель пересек Атлантику и достиг побережья Бразилии близ Рио-де-Жанейро. Затем он проследовал в направлении реки Ла-Плата и далее на юг, к Патагонии. Там Магеллан открыл пролив, который теперь носит его имя, и провел по нему свои корабли. Его команде пришлось перенести много невзгод, но экспедиция пересекла Тихий океан, открыла остров Гуам в архипелаге Марианские острова и в марте 1521 года достигла Филиппин. Там же, на Филиппинах, 27 апреля 1521 года Фернан Магеллан скончался. После его смерти экспедицию возглавил Хуан Себастьян Элькано. Отправившись в путь от Молуккских островов, он пересек Индийский океан, обогнул Африку и прибыл в Санлукар-де-Баррамеда 6 сентября 1522 года на корабле «Виктория». Так завершилось первое кругосветное путешествие.
Магеллан возглавил экспедицию из пяти кораблей, которые отправились в плавание из города Санлукарде-Баррамеда в испанской провинции Кадис 20 сентября 1519 года. Мореплаватель пересек Атлантику и достиг побережья Бразилии близ Рио-де-Жанейро. Затем он проследовал в направлении реки Ла-Плата и далее на юг, к Патагонии. Там Магеллан открыл пролив, который теперь носит его имя, и провел по нему свои корабли. Его команде пришлось перенести много невзгод, но экспедиция пересекла Тихий океан, открыла остров Гуам в архипелаге Марианские острова и в марте 1521 года достигла Филиппин. Там же, на Филиппинах, 27 апреля 1521 года Фернан Магеллан скончался. После его смерти экспедицию возглавил Хуан Себастьян Элькано. Отправившись в путь от Молуккских островов, он пересек Индийский океан, обогнул Африку и прибыл в Санлукар-де-Баррамеда 6 сентября 1522 года на корабле «Виктория». Так завершилось первое кругосветное путешествие.
* * *
Измерение дуг меридианов посредством триангуляции
В 1669–1670 годах французский астроном аббат Жан Пикар стал первым, кому удалось вычислить размер Земли с достаточно высокой точностью. Для этого он применил принципы триангуляции и воспользовался методом лейденского астронома, математика и профессора Виллеброрда Снелла (1580–1626). Снелл спланировал и провел измерения в 1615 году, а в 1617 году описал свои методы в книге Eratosthenes Batavus («Голландский Эратосфен»), заложив тем самым основы геодезии. Его метод измерения окружности Земли заключался в определении длины дуги меридиана посредством триангуляции.
Для этого он применил принципы триангуляции и воспользовался методом лейденского астронома, математика и профессора Виллеброрда Снелла (1580–1626). Снелл спланировал и провел измерения в 1615 году, а в 1617 году описал свои методы в книге Eratosthenes Batavus («Голландский Эратосфен»), заложив тем самым основы геодезии. Его метод измерения окружности Земли заключался в определении длины дуги меридиана посредством триангуляции.
С точки зрения геометрии триангуляция заключается в использовании треугольников и их тригонометрических свойств для вычисления неизвестных параметров (сторон и углов) на основе известных. В геодезии триангуляцией называется метод, позволяющий определить размеры Земли, покрыв ее поверхность сетью смежных треугольников. Измерения при триангуляции начинаются с грамотного выбора вершин треугольника и определения точной длины одной из сторон треугольника.
Далее из вершин этой стороны производятся измерения углов треугольника. Полученный треугольник станет первым в сети треугольников, которая в конечном итоге охватит дугу меридиана.
Гениальный писатель Жюль Верн (1828–1905) в своем романе «Приключения троих русских и троих англичан в Южной Африке» четко описывает последовательность действий при триангуляции:
«Чтобы лучше понять, что представляет собой геодезическая операция, называемая триангуляцией, позаимствуем следующие геометрические построения из учебника «Новые уроки космографии» г-на А. Гарсе, преподавателя математики лицея Генриха IV. С помощью прилагаемого здесь рисунка эта любопытная процедура будет легко понята:
«Пусть АВ — меридиан, длину которого требуется найти. Тщательно измеряем основание (базис) АС, идущий от оконечности А меридиана до первой позиции С. Затем по обеим сторонам этого меридиана избираем дополнительные позиции D, E, F, G, Н, I и так далее, каждая из которых позволяет видеть соседнюю позицию, и измеряем с помощью теодолита углы каждого из треугольников ACD, CDE, EDF и так далее, которые они образуют между собой.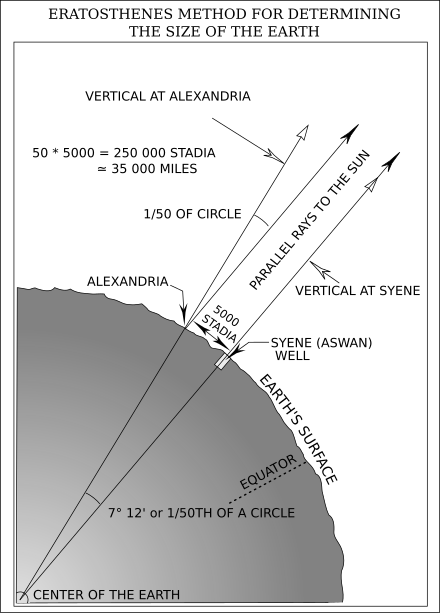 Эта первая операция позволяет определить параметры различных треугольников, ибо в первом известна длина АС и углы и можно вычислить сторону CD; во втором — сторона CD и углы, и легко подсчитывается сторона DE; в третьем — известна сторона DE и углы и можно получить сторону EF и так далее. Затем определяем наклон меридиана относительно основания АС, для чего измеряем угол MAC. Таким образом, в треугольнике ACM известны сторона АС и прилегающие к ней углы и можно вычислить первый отрезок AM меридиана. Аналогично вычисляются угол М и сторона СМ; таким образом, в треугольнике MDN оказывается известной сторона DM = CD — СМ и прилегающие к ней углы, и можно подсчитать второй отрезок MN меридиана, угол N и сторону DN. Таким образом, в треугольнике NEP становится известна сторона EN = DE — DN и прилегающие к ней углы и можно определить третий отрезок NP меридиана, и так далее.
Эта первая операция позволяет определить параметры различных треугольников, ибо в первом известна длина АС и углы и можно вычислить сторону CD; во втором — сторона CD и углы, и легко подсчитывается сторона DE; в третьем — известна сторона DE и углы и можно получить сторону EF и так далее. Затем определяем наклон меридиана относительно основания АС, для чего измеряем угол MAC. Таким образом, в треугольнике ACM известны сторона АС и прилегающие к ней углы и можно вычислить первый отрезок AM меридиана. Аналогично вычисляются угол М и сторона СМ; таким образом, в треугольнике MDN оказывается известной сторона DM = CD — СМ и прилегающие к ней углы, и можно подсчитать второй отрезок MN меридиана, угол N и сторону DN. Таким образом, в треугольнике NEP становится известна сторона EN = DE — DN и прилегающие к ней углы и можно определить третий отрезок NP меридиана, и так далее. Понятно, что таким образом получается по частям общая длина оси АВ»[3].
Понятно, что таким образом получается по частям общая длина оси АВ»[3].
Таким образом, для проведения триангуляции необходимо как можно точнее определить длину стороны треугольника, которую мы будем называть основанием, так как от результата этого измерения (на практике оно оказывается самым сложным и трудоемким) зависят все остальные расчеты. Основание должно быть как можно длиннее, чтобы свести к минимуму возможные ошибки. Из обоих концов основания производятся измерения углов, которые основание образует с двумя другими сторонами треугольника. Эти две стороны сходятся в грамотно выбранной третьей вершине. Так определяется первый треугольник сети.
Зная два угла и сторону (основание) треугольника, мы при помощи тригонометрических методов можем без труда вычислить третий угол и две оставшиеся стороны. Так мы полностью определим треугольник и сможем выбрать любую из трех его сторон в качестве основания второго, смежного треугольника. Если мы последовательно будем добавлять к сети все новые и новые смежные треугольники, то в конечном итоге сеть триангуляции охватит две крайние точки дуги меридиана, которую мы хотим измерить, и мы определим астрономическую широту и долготу этих точек.
Далее по известной длине основания необходимо найти длину его горизонтальной проекции. В общем случае вершины треугольника необязательно находятся на одной высоте, поэтому их следует спроецировать на горизонтальную плоскость или контрольную поверхность. Снелл нашел способ внести в формулы триангуляции поправки, учитывающие кривизну Земли.
Основой для систематического использования современных сетей триангуляции стали результаты первых измерений, выполненных Снеллом, а также рассчитанное им расстояние между городами Алкмар и Берген-оп-Зом в Нидерландах. Эти города находились приблизительно на одном меридиане и отстояли друг от друга на один градус долготы. В качестве длины основания Снелл выбрал расстояние от своего дома до башни местной церкви. Он построил сеть из 33 треугольников и измерил их углы при помощи квадранта размером 2×2 метра. Проведя измерения, он определил, что расстояние между городами составляет 117 449 ярдов (107,393 км). Фактическое расстояние между этими городами составляет примерно 111 км.
Применив методы Снелла, Пикар измерил расстояние, соответствующее одному градусу долготы парижского меридиана. Он построил сеть из тринадцати треугольников, начиная из города Мальвуазен близ Парижа до часовой башни городка Сур дон близ Амьена. Основание сети треугольников было измерено по поверхности Земли, а углы треугольников измерялись из точек, расположенных на башнях, колокольнях или иных возвышениях, откуда можно было увидеть вершины соседних треугольников.
Пикар впервые применил при измерениях квадрант, дополненный зрительной трубой, а также сконструировал собственные измерительные инструменты. Он использовал подвижные квадранты, дополненные зрительными трубами, а также микрометр французского астронома Адриена Озу, обеспечивший точность измерений в несколько угловых секунд. Принцип действия микрометра основан на перемещении винта, при котором небольшие расстояния, слишком малые для прямых измерений, откладываются на измерительной шкале. При триангуляции требовалось определить разницу в высоте между точками наблюдения, а также их высоту относительно плоскости отсчета. Пикару удалось произвести нивелирование с точностью порядка 1 сантиметра на километр.
Пикару удалось произвести нивелирование с точностью порядка 1 сантиметра на километр.
* * *
ЖАН ПИКАР (1620–1682)
Французский астроном Жан Пикар, получивший образование в иезуитской школе Ла-Флеш, работал вместе с Пьером Гассенди, преподавателем математики в парижском Коллеж Рояль (ныне Коллеж де Франс). В 1655 году, после смерти Гассенди, Пикар стал преподавателем астрономии в этом учебном заведении, а в 1666 — членом недавно созданной Французской академии наук. Он сконструировал микрометр — прибор для измерения диаметров небесных тел (Солнца, Луны и планет). В 1667 году Пикар дополнил квадрант зрительной трубой, сделав его намного удобнее для наблюдений. Исследователь значительно повысил точность измерений Земли, применив метод триангуляции Снелла, а также использовал научные методы при составлении карт. В 1671 году совместно с датским астрономом Оле Рёмером в обсерватории Ураниборг он наблюдал около 140 затмений спутника Юпитера Ио. На основе полученных данных Рёмер получил первую количественную оценку скорости света.
На основе полученных данных Рёмер получил первую количественную оценку скорости света.
* * *
Целью Пикара было определить, сколько туазов (так называлась использованная им единица длины) составляла длина прямой линии между Мальвуазеном и Сурдоном, а также их разницу в широте, отсчитанную вдоль окружности меридиана. Таким образом, требовалось произвести два измерения: геодезическое (в туазах) и астрономическое (в градусах, минутах и секундах).
Он тщательно измерил длину прямой дороги между Вильжюифом и Жювизисюр-Орж (она составила 5663 туаза), а остальные результаты получил посредством триангуляции. В качестве единицы измерения он использовал туаз Шатле, или парижский туаз (позднее, в конце XVIII века, он был принят равным 1,949 м). По результатам измерений длина дуги меридиана величиной в один градус составила 57 060 туазов.
Благодаря высокой точности измерительных инструментов и усовершенствованиям, которые внес Пикар, считается, что именно он первым дал достаточно точную оценку радиуса Земли. Он получил, что один градус широты равен 110,46 км, что соответствует радиусу Земли в 6328,9 км (сегодня экваториальный радиус Земли оценивается в 6378,1 км, полярный радиус — в 6356,8 км, средний радиус — в 6371 км). Данные Пикара применил Исаак Ньютон при создании своей теории тяготения.
Он получил, что один градус широты равен 110,46 км, что соответствует радиусу Земли в 6328,9 км (сегодня экваториальный радиус Земли оценивается в 6378,1 км, полярный радиус — в 6356,8 км, средний радиус — в 6371 км). Данные Пикара применил Исаак Ньютон при создании своей теории тяготения.
Пять треугольников из сети триангуляции Пикара.
После Пикара измерения длины вдоль парижского меридиана посредством триангуляции провели Джованни Доменико Кассини (1625–1712), глава Парижской обсерватории, и его сын Жак Кассини (1677–1756), сменивший отца на его посту. Жак Кассини измерил длину дуги меридиана между Дюнкерком и Перпиньяном и опубликовал результаты в 1720 году. Позднее, в 1733–1740 годах, вместе с сыном, Цезарем Франсуа Кассини, он впервые построил сеть триангуляции, которая охватила всю страну. В 1745 году благодаря его труду появилась первая точная карта Франции.
Позднее в других странах также были построены сети триангуляции. К примеру, проект триангуляции Великобритании под названием Principal Triangulation of Great Britain был начат в 1783 году, а полностью завершен лишь в середине XIX века.
К примеру, проект триангуляции Великобритании под названием Principal Triangulation of Great Britain был начат в 1783 году, а полностью завершен лишь в середине XIX века.
Первый проект по составлению точной карты Испании предложил Хорхе Хуан в 1751 году, однако первые листы Национальной топографической карты Испании увидели свет лишь в 1875 году.
Определение местоположения и ориентирование.
Навигация и задача о долготе
Чтобы определить положение точки на плоскости, можно использовать декартову систему координат с перпендикулярными осями: осью абсцисс (х) и осью ординат (у). Пара значений (х, у) однозначно определяет единственную точку плоскости. Аналогично, чтобы точно определить положение любой точки на поверхности Земли (будем считать ее сферической), достаточно знать два числа — широту и долготу (географические координаты точки). В этом случае роль осей координат будут играть экватор и большой круг, проходящий через полюса, то есть меридиан, выбранный в качестве базового (меридиан 0°).
Широта точки на поверхности Земли — это угловое расстояние между экватором и этой точкой, измеренное из центра нашей планеты вдоль меридиана, проходящего через эту точку. Широта измеряется в градусах, минутах и секундах и находится на интервале от 0° до 90°. Кроме того, указывается, в каком полушарии, Северном или Южном, находится точка, к примеру 41°24?14? северной широты (с.ш.). Следовательно, все точки, расположенные на одной параллели Земли (окружности круга, параллельного экватору), имеют одинаковую широту.
Широту можно вычислить астрономическими методами. Простейший метод для Северного полушария состоял в том, чтобы найти на небе Полярную звезду (Северный полюс мира) и измерить угол между визирной линией и горизонтальной плоскостью, на которой находится наблюдатель. Полученный угол и будет искомой широтой. В Южном полушарии следует действовать аналогичным образом, выбрав для наблюдений Южный крест. Существуют и другие методы определения широты днем — к примеру, можно измерить высоту Солнца над горизонтом в полдень и применить таблицы, где указано положение Солнца относительно эклиптики в день наблюдений.
Широта и долгота точки Р на сфере.
Долгота — это значение угла между нулевым меридианом (точнее, полумеридианом), выбранным в качестве начала отсчета (0°), и меридианом, проходящим через данную точку. Этот угол измеряется из центра Земли вдоль экватора. Значения долготы лежат на интервале от 0° до 180°. Кроме того, указывается, в каком направлении от нулевого меридиана была измерена долгота — к востоку или к западу, например, 2°14?50? западной долготы (з.д.). Следовательно, все точки, расположенные на одном полумеридиане между двумя полюсами Земли, имеют одинаковую долготу.
Широта и долгота отсчитываются от экватора и меридиана, выбранного в качестве начала отсчета (такой меридиан называется нулевым, его долгота равна 0°).
Сегодня нулевым меридианом обычно считается Гринвичский, но до него в качестве нулевых использовались многие другие меридианы.
Как мы уже говорили, определить широту корабля в море несложно. Также относительно просто узнать долготу корабля, если с него видна земля. Но если он находится в открытом море, то определение долготы связано с серьезными трудностями.
Также относительно просто узнать долготу корабля, если с него видна земля. Но если он находится в открытом море, то определение долготы связано с серьезными трудностями.
Эта задача обрела огромное значение после открытия Америки Христофором Колумбом. В то время долгота вычислялась приближенно, на основе расстояния, пройденного кораблем с запада на восток или наоборот. Чтобы определить скорость корабля, моряки использовали лаг, который представлял собой свободно вращающуюся катушку с намотанной на нее веревкой. На веревке через равные промежутки были завязаны узлы, а на ее конце закреплялся груз. Моряк выбрасывал лаг за корму, и когда о его руку ударялся первый узел, он давал команду, и другой моряк начинал отсчет времени при помощи песочных часов. Когда весь песок пересыпался из верхнего сосуда часов в нижний, второй моряк сообщал об этом первому, и тот указывал число ушедших за борт узлов, например, «три с половиной узла» или «шесть узлов с четвертью». Скорость судов до сих пор измеряется в узлах.
Разумеется, столь примитивный метод определения долготы сопровождался значительными ошибками, которые приводили к катастрофическим последствиям. Поэтому в XVII — начале XVIII века задача определения долготы стала стратегическим приоритетом для всех держав, имевших интересы за океаном.
Теоретически вычисление долготы можно свести к определению разницы во времени между точкой отсчета (портом отплытия или нулевым меридианом) и точкой, в которой находится корабль. Когда солнце проходит через меридиан наблюдателя (то есть меридиан корабля), то, зная точное время в точке отсчета, можно определить долготу корабля, то есть угловое расстояние до точки отсчета, а следовательно, и до нулевого меридиана. Этот метод действует благодаря тому, что разницу во времени между двумя меридианами можно пересчитать в градусы долготы. Так как Земля совершает полный оборот в 360° за 24 часа, за 1 час она поворачивается на 1/24 оборота, то есть на 13°. Если за час, то есть за 60 минут, Земля поворачивается на 13°, то разница в 4 минуты соответствует одному градусу долготы.
Следовательно, долготу можно вычислить, определив разницу во времени между двумя точками при помощи наблюдений и астрономических измерений. Была высказана идея об определении долготы по результатам наблюдений затмений, но этот метод не слишком пригоден в открытом море, да и затмения наблюдались редко.
* * *
НАБЛЮДЕНИЕ ЗАТМЕНИЙ ДЛЯ ВЫЧИСЛЕНИЯ ДОЛГОТЫ
Допустим, что нам известно, в какое время затмение будет наблюдаться в определенном месте (на суше, в обсерватории и так далее), при этом мы находимся в открытом море. Если мы определим, когда наблюдалось затмение по местному времени, то сможем вычислить долготу места, в котором находимся. Для использования этого метода нам потребуются таблицы, где указано, в какое время произойдет затмение в определенной точке (разумеется, мы не сможем обойтись без математических расчетов). В XVI веке определять долготу по наблюдениям затмений было удобно на суше, но не в открытом море — зафиксировать измерительные приборы из-за качки было очень сложно, а главное, что затмения наблюдались редко: в год происходит от двух до пяти солнечных затмений. Если же учитывать и лунные, то в год набирается не менее двух и не более семи затмений, в среднем — четыре. За весь XX век наблюдалось 375 затмений: 228 солнечных и 147 лунных. И без того редкие затмения еще и не всегда видны: наблюдениям могут помешать неблагоприятные погодные условия.
Если же учитывать и лунные, то в год набирается не менее двух и не более семи затмений, в среднем — четыре. За весь XX век наблюдалось 375 затмений: 228 солнечных и 147 лунных. И без того редкие затмения еще и не всегда видны: наблюдениям могут помешать неблагоприятные погодные условия.
* * *
С недостаточной частотой затмений удалось справиться благодаря открытию Галилеем спутников Юпитера в 1610 году. Луны Юпитера при вращении вокруг него скрываются из вида и появляются вновь. Эти затмения наблюдаются несколько тысяч раз в год, и их время можно точно предсказать. Этот метод действительно можно было бы применять для определения долготы, но в открытом море мешала качка, а также наблюдения можно было производить только ночью, в ясную погоду и лишь в определенное время года.
Задача определения долготы в открытом море довольно долго оставалась нерешенной. Определить местное время на корабле можно было по Солнцу. Но как узнать время в точке отсчета, не располагая достаточно точными часами? Точность хода маятниковых часов снижалась, среди прочих факторов, и из-за качки корабля, кроме того, период колебаний маятника на разных широтах отличался, и в результате часы спешили или опаздывали. Корабельные часы не могли сохранять время в порту отплытия, это было причиной существенных ошибок при определении долготы.
Корабельные часы не могли сохранять время в порту отплытия, это было причиной существенных ошибок при определении долготы.
В 1714 году Британский парламент предложил огромную премию размером в 20 тысяч фунтов стерлингов тому, кто сможет представить метод или инструмент, позволяющий определять долготу корабля в открытом море. Премия досталась английскому часовщику Джону Гаррисону (1693–1776), который после нескольких десятилетий работы смог изготовить очень точный хронометр. В 1761 году для проверки хронометр был погружен на корабль, направлявшийся на Ямайку. Хронометр проработал 147 дней, и по возвращении в Англию отклонение составило всего 1 минуту 34 секунды. Задача определения долготы была решена. Сегодня определить точное положение корабля можно благодаря системе GPS, о которой мы поговорим в главе 6.
Несферическая Земля. Научные экспедиции в вице-королевство Перу и Лапландию
При измерениях Земли, в том числе при измерениях Пикара, считалось, что она имеет форму идеальной сферы. Спустя несколько лет после опыта Пикара, в 1671–1673 годах, французский астроном Жан Рише (1630–1696), ассистент Джованни Доменико Кассини, совершил путешествие в Кайенну во Французской Гвиане, где сделал важное открытие: он обратил внимание, что в Кайенне колебания маятника были медленнее, чем в Париже, и первым понял, что сила тяготения Земли в разных ее частях отличается. Он сделал верный вывод: изменение силы тяготения объяснялось тем, что Кайенна находилась дальше от центра Земли, чем Париж. Когда новость об открытии достигла Европы, она вызвала большое оживление среди членов Французской академии наук. По возвращении на родину Рише приступил к изготовлению маятника, который отсчитывал бы секунды — иными словами, период колебаний маятника в Париже должен был составлять ровно одну секунду. Такие же маятники были изготовлены и в других частях земли, и оказалось, что длина маятника в зависимости от широты менялась. Согласно известным в то время теориям все указывало на то, что если сила, с которой Земля притягивает к себе маятник, в разных точках отличается, то Земля не может иметь форму идеальной сферы.
Спустя несколько лет после опыта Пикара, в 1671–1673 годах, французский астроном Жан Рише (1630–1696), ассистент Джованни Доменико Кассини, совершил путешествие в Кайенну во Французской Гвиане, где сделал важное открытие: он обратил внимание, что в Кайенне колебания маятника были медленнее, чем в Париже, и первым понял, что сила тяготения Земли в разных ее частях отличается. Он сделал верный вывод: изменение силы тяготения объяснялось тем, что Кайенна находилась дальше от центра Земли, чем Париж. Когда новость об открытии достигла Европы, она вызвала большое оживление среди членов Французской академии наук. По возвращении на родину Рише приступил к изготовлению маятника, который отсчитывал бы секунды — иными словами, период колебаний маятника в Париже должен был составлять ровно одну секунду. Такие же маятники были изготовлены и в других частях земли, и оказалось, что длина маятника в зависимости от широты менялась. Согласно известным в то время теориям все указывало на то, что если сила, с которой Земля притягивает к себе маятник, в разных точках отличается, то Земля не может иметь форму идеальной сферы.
Ньютон принял во внимание результаты Рише в своих знаменитых «Математических началах натуральной философии», опубликованных в 1687 году, в которых излагались основы механики. Он предложил математическое описание формы Земли, связав его со своей гениальной теорией тяготения. Ньютон рассмотрел нашу планету как однородное жидкое тело вращения и сделал вывод: Земля должна быть сплюснутой у полюсов. По его мнению, Земля была сплюснутой на 1/230. Иными словами, если предположить, что поперечное сечение Земли — эллипс, то его большая ось будет длиннее малой оси на 1/230-ю.
В 1720 году во Франции был опубликован труд Жака Кассини «О размере и форме Земли», где опровергалась гипотеза Ньютона. Кассини подкрепил свою точку зрения результатами собственных астрономических наблюдений и геодезических измерений меридиана Коллиур — Париж — Дюнкерк (впрочем, некоторые члены Французской академии наук считали эти измерения не вполне точными).
Кассини назвал доводы Ньютона спекулятивными и указал, что Земля представляет собой эллипсоид, сплюснутый у экватора.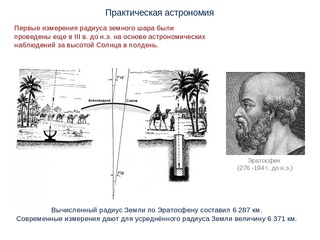 На что больше похожа Земля — на арбуз или дыню? Развернулась полемика, в которую оказались вовлечены ученые из Лондонского королевского общества и Французской академии наук. В результате дискуссия стала рассматриваться как противостояние французской и английской науки.
На что больше похожа Земля — на арбуз или дыню? Развернулась полемика, в которую оказались вовлечены ученые из Лондонского королевского общества и Французской академии наук. В результате дискуссия стала рассматриваться как противостояние французской и английской науки.
Чтобы положить конец спорам, Французской академией наук было принято решение измерить длину дуги меридиана, соответствующей центральному углу в один градус, в максимально далеких друг от друга точках. Для этого были организованы две научные экспедиции из астрономов, математиков, натуралистов и других ученых. Первая экспедиция, возглавляемая Пьером Луи Моро де Мопертюи (1698–1739), отправилась в Лапландию. Ее членами были Пьер Шарль Ле Моннье, Алекси Клод Клеро, Шарль Этьенн Луи Камю, швед Андерс Цельсий и аббат Утье. Вторую экспедицию, которая направилась в вице-королевство Перу, на территорию современного Эквадора, возглавлял астроном Луи Годен (1704–1760).
Участниками экспедиции стали географ Шарль Мари де ла Кондамин, астроном и гидрограф Пьер Бугер, ботаник Антуан Лоран де Жюссьё и испанцы Хорхе Хуан и Антонио де Ульоа. Креольский ученый Педро Висенте Мальдонадо присоединился к экспедиции в Гуаякиле. Также в экспедицию вошли часовщик Уго, инженер и рисовальщик Моренвилль, капитан фрегата Купле, хирург и ботаник Сеньерг, мастер по изготовлению инструментов Годен де Одонне, племянник Луи Годена, картограф и военный инженер Верген.
В то время вице-королевство Перу, расположенное в экваториальных Андах, было испанской территорией, поэтому участникам экспедиции пришлось просить разрешения испанской короны. Разрешение было дано с условием, что к экспедиции присоединятся два юных одаренных офицера Кадисской академии гардемаринов — Хорхе Хуан и Антонио де Ульоа.
Участники экспедиции в Лапландию (1736–1737) благодаря способностям и проницательности математика Клеро получили нужные результаты относительно быстро.
При обустройстве наблюдательных пунктов им помогали шведские военные. Ученые проводили триангуляцию во время длинных летних дней и охватили расстояние в 100 километров между городами Киттис и Торнео. Астрономические измерения производились весной и осенью, когда ночи были уже достаточно длинными и в то же время не слишком холодными. Основание триангуляции было измерено по замерзшему руслу реки. Итоговый результат измерений, проведенных членами экспедиции Мопертюи, был таков: на средней широте 66°20? длина дуги меридиана величиной в один градус равнялась 37 438 туазам. Если сравнить этот результат с результатом измерений Пикара, проведенных близ Парижа на широте около 48° (57060 туазов), то станет очевидно, что Земля представляет собой сфероид, сплюснутый у полюсов.
Ученые проводили триангуляцию во время длинных летних дней и охватили расстояние в 100 километров между городами Киттис и Торнео. Астрономические измерения производились весной и осенью, когда ночи были уже достаточно длинными и в то же время не слишком холодными. Основание триангуляции было измерено по замерзшему руслу реки. Итоговый результат измерений, проведенных членами экспедиции Мопертюи, был таков: на средней широте 66°20? длина дуги меридиана величиной в один градус равнялась 37 438 туазам. Если сравнить этот результат с результатом измерений Пикара, проведенных близ Парижа на широте около 48° (57060 туазов), то станет очевидно, что Земля представляет собой сфероид, сплюснутый у полюсов.
Гониометрические измерения при триангуляции. Иллюстрация к роману Жюля Верна «Приключения троих русских и троих англичан в Южной Африке».
Экспедиция в Америку, в свою очередь, растянулась на десять лет и превратилась в настоящую эпопею. Участники отправились в путь из Ла-Рошели весной 1735 года и прибыли в Кито год спустя. Им пришлось столкнуться с самыми разными проблемами: помимо постоянных ученых споров, членам экспедиции мешали суровый климат, сложный рельеф, многочисленные финансовые неурядицы, а в 1741 году им и вовсе пришлось разделиться на две группы. Измерения и триангуляция были особенно сложными ввиду особенностей рельефа Анд и большой высоты, превышавшей 4 тысячи метров. Ученые решили построить масштабную триангуляцию из 43 треугольников, чтобы охватить отрезок протяженностью в 354 километра и измерить дугу меридиана величиной не в 1°, а в 3°. Бугер (1749) определил, что длина дуги меридиана величиной в один градус равна 56763 туаза, а Хуан и Ульоа (1748), равно как и ла Кондамин (1751) получили результат в 56768 туазов. Если вспомнить аналогию с арбузом или дыней, которую предложил Вольтер, то можно сказать, что Земля представляет собой скорее арбуз. Результаты измерений и математических расчетов, казалось, подтвердили правоту Ньютона.
Им пришлось столкнуться с самыми разными проблемами: помимо постоянных ученых споров, членам экспедиции мешали суровый климат, сложный рельеф, многочисленные финансовые неурядицы, а в 1741 году им и вовсе пришлось разделиться на две группы. Измерения и триангуляция были особенно сложными ввиду особенностей рельефа Анд и большой высоты, превышавшей 4 тысячи метров. Ученые решили построить масштабную триангуляцию из 43 треугольников, чтобы охватить отрезок протяженностью в 354 километра и измерить дугу меридиана величиной не в 1°, а в 3°. Бугер (1749) определил, что длина дуги меридиана величиной в один градус равна 56763 туаза, а Хуан и Ульоа (1748), равно как и ла Кондамин (1751) получили результат в 56768 туазов. Если вспомнить аналогию с арбузом или дыней, которую предложил Вольтер, то можно сказать, что Земля представляет собой скорее арбуз. Результаты измерений и математических расчетов, казалось, подтвердили правоту Ньютона.
* * *
ХОРХЕ ХУАН И КОРОЛЕВСКАЯ ОБСЕРВАТОРИЯ В САН-ФЕРНАНДО (КАДИС)
Испанский мореплаватель Хорхе Хуан и Сантасилья (1713–1773), участвовавший в экспедиции по измерению дуги меридиана на экваторе, внес весомый вклад в развитие испанской науки в XVIII веке. Следы его трудов сохранились до наших дней — он, среди прочего, основал Королевскую обсерваторию в Сан-Фернандо (Кадис) в 1757 году. Современный Королевский институт и обсерватория военно-морских сил — не только сердце астрономических и геодезических исследований, но и научно-исследовательский и культурный центр, находящийся в ведении испанской армии. Сотрудники центра занимаются вычислением эфемерид, определением точного времени, публикуют морские астрономические ежегодники и результаты метеорологических, сейсмических и магнитных наблюдений. Институт отвечает за определение официального испанского времени (всемирное координированное время, или UTC) и за хранение эталонов официальных единиц измерения Испании.
Следы его трудов сохранились до наших дней — он, среди прочего, основал Королевскую обсерваторию в Сан-Фернандо (Кадис) в 1757 году. Современный Королевский институт и обсерватория военно-морских сил — не только сердце астрономических и геодезических исследований, но и научно-исследовательский и культурный центр, находящийся в ведении испанской армии. Сотрудники центра занимаются вычислением эфемерид, определением точного времени, публикуют морские астрономические ежегодники и результаты метеорологических, сейсмических и магнитных наблюдений. Институт отвечает за определение официального испанского времени (всемирное координированное время, или UTC) и за хранение эталонов официальных единиц измерения Испании.
Хорхе Хуан и Сантасилья. Морской музей Мадрида.
Протяженность земли по экватору в километрах. Каковы величины диаметра и экватора Земли
Экватор в переводе с латыни означает «уравнивать» . Принято считать, что экватор — это условная окружность, делящая земной шар на северное и южное полушария, и самая длинная окружность (или параллель) Земли, перпендикулярная ее оси вращения.
Принято считать, что экватор — это условная окружность, делящая земной шар на северное и южное полушария, и самая длинная окружность (или параллель) Земли, перпендикулярная ее оси вращения.
Экватор является отправной точкой для определения координат любого места на планете. Без него невозможно бы было определить точное положение в пространстве любых географических объектов или это было крайне затруднительно.
Всем давно известно, что если быть академически точным, то Земля на самом деле представляет собой не сферу, а геоид. Геоид — тело, по своим пропорциям напоминающее сферу, однако ей не являющееся. И действительно, в самой высокой точке планеты высота составляет 8 848 м (гора Эверест) и в самой низкой — 10 994 м (Марианская впадина) относительно уровня моря.
То есть если учитывать все перепады высот, то любой расчет вызовет массу проблем. Поэтому в международном сообществе для простоты расчетов нашу планету принято считать сферой. В том числе экватор считается окружностью, хоть и на самом деле ею не является.
Согласно международному стандарту WGS-84 радиус Земли составляет 6 378 137 м . Согласно другому стандарту IAU-1976 и IAU-2000 радиус Земли равен 6 378 140 м. Разница в три метра связана с разницей в подходах и способах расчета. Тем не менее, длина экватора составляет 40 075 км, какой бы из стандартов мы ни взяли, поскольку после вычисления длины окружности по формуле l=2πR разница будет только во втором знаке после запятой.
Первые попытки подсчитать длину экватора были предприняты еще в Древней Греции Эратосфеном . Хотя, собственно, если брать известный на тот момент мир, он считал не экватор, а радиус Земли в районе Европы, который привязан к длине окружности через 2πR. В те времена еще не существовало научного понятия о Земле как планете.
Чтоб не вдаваться в подробности эксперимента, объясним его суть. Эратосфен определил, что в момент, когда в городе Сиена (ныне Асуан) Солнце находится в зените и освещает дно колодца, в этот же момент времени в Александрии оно «отстает» примерно на 7 градусов и не освещает дно колодца. Что, в свою очередь, примерно составляет 1/50 часть окружности. Теперь, зная расстояние от Сиены до Александрии (оно составляло около 5000 стадиев), можно было определить длину окружности.
Что, в свою очередь, примерно составляет 1/50 часть окружности. Теперь, зная расстояние от Сиены до Александрии (оно составляло около 5000 стадиев), можно было определить длину окружности.
Тем неожиданнее являются результаты расчетов. Эратосфен считал протяженность экватора в 252 000 стадиев. Но так как за свою жизнь он прожил и в Александрии (Египет) и в Афинах (Греция), историки и географы до сих пор не могут с уверенностью сказать, какими именно стадиями пользовался при расчетах Эратосфен. Если греческими, то по Эратосфену радиус составлял 7 082 км, если египетскими — 6 287 км. Какой бы результат вы ни взяли для своего времени, это был невероятно точный расчет радиуса.
Позже попытки рассчитать длину экватора были приняты многими европейскими учеными. Впервые о возможном усреднении радиуса для удобства вычислений при расчетах заговорил голландец Снеллиус . В XVII веке он предложил рассчитывать радиус без учета естественных преград. В XVIII веке Франция (первая из стран) перешла на метрическую систему измерения.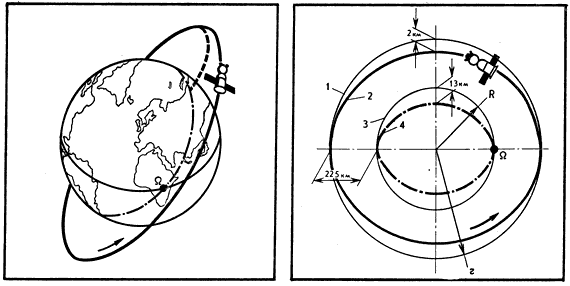 Причем при расчете эталона длины французские ученые привязывались именно к радиусу Земли.
Причем при расчете эталона длины французские ученые привязывались именно к радиусу Земли.
Расчет был привязан к длине математического маятника, полупериод колебания которого составляет одну секунду. Для своего времени идея была прорывная. Однако при путешествиях к южным широтам, французский картограф Жан Рише заметил, что период колебания увеличился. Причина была в том, что Земля представляет собой геоид и сила тяжести ближе к экватору падает.
Исследования в России
В Российской империи также проводились исследования по определению формы, длины и других параметров Земли. Пожалуй, самым крупным и важным из них был проект «Русской дуги» или «Дуги Струве» под руководством Фридриха Георга Вильгельма Струве (Василия Яковлевича Струве). Для проведения измерений было построено 265 триангуляционных пункта, представлявших собой 258 треугольников с общей стороной. Длина дуги составляла 2820 км, что является 1/14 окружности Земного шара. Дуга на тот момент проходила через территорию Норвегии, Швеции и Российской империи. Финансировалось исследование лично императором Александром I, а далее и Николаем I.
Финансировалось исследование лично императором Александром I, а далее и Николаем I.
Данный проект был первым из измерений Земли, который точно определил ее форму и параметры. При измерении параметров Земли спутниковыми методами в XX веке погрешность измерений Струве составила 2 см.
В Советском Союзе геодезическая школа также предпринимала попытки расчета параметров эллипсоида Земли. В 1940 году благодаря работам А.Н. Изотова и Ф.Н. Красовского был рассчитан и принят как стандарт для геодезических работ в СССР эллипсоид Красовского, определяющий все основные параметры эллипсоида Земли. По Красовскому приняты следующие параметры:
- Малый радиус Земли (полярный радиус) составляет 6 356,863 км.
- Большой радиус (экваториальный) 6 378,245 км.
- Длина экватора составляет 40 075,696 км.
- Площадь поверхности Земли 510 083 058 км2.
Эти факты будет интересно знать:
- Длину в 40 075 км в среднем за два года проезжает автомобиль в России.

- Скорость вращения Земли на экваторе составляет 465 метров в секунду, что быстрее скорости звука. С этим связано предпочтение запуска космических кораблей ближе к экватору. При старте ракета уже движется со сверхзвуковой скоростью относительно Земли. Это значительно экономит топливо.
- Единственным ледником на экваторе является шапка вулкана Каямба в Эквадоре.
- При перемещении с полюса на экватор предметы и тела теряют 0,53% своей массы. Это связано с удалением от центра масс Земли.
- Еще ни одному путешественнику не удалось пройти вдоль земной части экватора.
- В Бразилии в городе Макапа есть футбольный стадион, посередине которого проходит линия экватора.
Видео
Массу полезной информации о Земле вы узнаете из этого видео.
> > > Сколько километров займет путь вокруг Земли?
Облететь вокруг Земли : расстояние в километрах для облета вокруг третьей планеты Солнечной системы, сфероидальная форма, округлость, длина экватора и меридиан.
Наша планета расположена на третьей позиции по приближенности от Солнца и считается самой большой из планет земной группы. Ее радиус – 6371 км, так что перед нами большой дом. Но можно ли измерить ее от конца в конец? Если вы решите полностью ее обойти, то сколько километров придется пропутешествовать, чтобы вернуться в изначальную точку? То есть, какова окружность Земли? Если коротко, то чуть больше 40075 км. Но в реальности все сложнее.
Напомним, что форма планеты играет большую роль при вычислении ее размеров. Земля – приплюснутый сфероид. Если бы это была идеальная сфера, то вы бы могли отправиться в любую сторону и пройти единую дистанцию.
В нашем случае форма планеты Земля выпуклая на экваториальной линии, к чему привело быстрое осевое вращение. Ее охват в талии на 47 км превышает объем на полюсах.
В сферичность начали верить еще во времена Древней Греции. Особенно сильно на этом настаивал Пифагор. Все началось с активной торговли между странами. Стали отмечать, что некоторые звезды можно было наблюдать в разных местах, а удаленные на горизонте объекты намекали на планетарную изогнутость. Можете рассмотреть форму и внешний вид Земли на фото из космоса.
Можете рассмотреть форму и внешний вид Земли на фото из космоса.
В 240 г. до н. э. Эрасофен решил измерить земную окружность при помощи отслеживания углов теней, созданных Солнцем. При помощи тригонометрических вычислений он привел показатели с погрешностью в 2-20%.
В 17-м веке мы могли похвастаться более качественными приборами, и идея идеальной сферы начала рушиться. Впервые именно Исаак Ньютон предположил, что планета должна быть шире в экваториальной линии. Мы смогли подтвердить его идеи с появлением космических аппаратов на орбите и получением фото из космоса.
Экваториальный и меридиональный путь вокруг Земли
Сплюснутая сферичность отображается в экваториальной и меридиональной окружностях. Если вычисляем по экватору, то получим 40075.017 км, а вот между полюсами – 40007.86 км.
Это касается и вычисления радиуса. Если вы берете за основу показатели от центра к экваториальной линии, то радиус – 6378.1 км, а от центра к полюсу – 6356.8 км. Кажется, что разница не велика. Но это все же вычеркивает нашу планету со списков кандидатов в идеальные сферы. Теперь вы знаете все об окружности Земли, ее размерах и форме.
Кажется, что разница не велика. Но это все же вычеркивает нашу планету со списков кандидатов в идеальные сферы. Теперь вы знаете все об окружности Земли, ее размерах и форме.
На две половины. В связи с этим неудивительно, что люди задаются вопросом: что же такое экватор? Экватор — это условная линия, которая точно пересекает поверхность нашей Земли такой плоскостью, которая считается перпендикулярной к оси вращения планеты и проходит прямо через ее центр. С латыни слово «aequator» переводится как «уравнитель». Эта линия — условное начало для отсчета географической широты, равной на экваторе 0 град.
Длина экватора составляет 40 075, 676 км, остальные линии (параллели) всегда меньше его длины. На протяжении всей его линии день постоянно равен ночи. Именно экватор делит нашу планету на два полушария, Южное и Северное. Два раза в год, в дни осеннего и весеннего равноденствия, солнце над ним находится в зените. приходится на 20-21 марта, а осеннее — на 23 сентября. В эти находится прямо над головой, и предметы не отбрасывают тени.
Длина экватора учеными высчитана по формуле 2πR, несмотря на то, что Земля имеет не шарообразную форму, а вытянута в виде эллипса (шара, сплюснутого у полюсов). Тем не менее, радиус нашей планеты условно принят за радиус шара. Длина земли по экватору составляет самую длинную линию, опоясывающую Землю. Интересный факт заключается в том, что она пересекает 14 государств.
Если двигаться от в сторону востока, то экватор пересекает такие государства, как Сан-Томе и Принсипи в Атлантическом океане, затем Габон, Конго, Кения, Уганда, Сомали в Африке. Двигаясь по Индийскому океану, он проходит через Мальдивские острова и Индонезию. В Тихом океане экватор пересекает Кирибати и острова Бейкер, принадлежащие США, далее — Эквадор, Колумбию и Бразилию, которые находятся на южноамериканском континенте. Эти страны являются самыми жаркими на планете.
Длина экватора впервые была высчитана древнегреческим ученым Эратосфеном, который был не только великим математиком, географом, поэтом, но и астрономом. Измеряя время, в течение которого солнечные лучи достигали дна колодца, ученый смог вычислить радиус земного шара и узнать, какова длина экватора. Эти вычисления весьма приблизительны, но они многое дали последующим поколениям ученых для более точного вычисления длины этой воображаемой линии. Эратосфен Киренский появился на свет в 276 году до н.э. и умер в 194 году до н.э.
Измеряя время, в течение которого солнечные лучи достигали дна колодца, ученый смог вычислить радиус земного шара и узнать, какова длина экватора. Эти вычисления весьма приблизительны, но они многое дали последующим поколениям ученых для более точного вычисления длины этой воображаемой линии. Эратосфен Киренский появился на свет в 276 году до н.э. и умер в 194 году до н.э.
Это был один из величайших ученых древнего мира. Он родился в греческом городе Кирены и по приглашению царя Птолемея III Эвергета заведовал Александрийской библиотекой. Умер этот великий ученый от голода, в страшной нищете, но вошел в историю, как проницательный исследователь с неординарным подходом к науке. Длина экватора по Эратосфену равнялась 252 тысячам стадий, что составляет 39 690 км. Создатель математической и физической географии, Эратосфен сделал великие открытия во многих областях. Современному человеку очень трудно понять, как ученый, не имея никаких приборов, высчитал, какова длина экватора, с погрешностью всего в 386 километров.
Многие ученые-математики и астрономы впоследствии тоже пытались высчитать длину экватора. Голландец Снеллиус в начале XVII века предложил рассчитывать это значение без учета встречающихся преград. В XVIII веке такими вычислениями серьезно занимались ученые из Франции. Россияне тоже не остались в стороне и внесли свой вклад в науку, который позволил определить, какова же длина земли по экватору. Директор В.Я.Струве провел эти измерения в градусах в период с 1822 по 1852 годы, а в 1941 году советский ученый-геодезист Ф.Н. Красовский смог высчитать длину земного эллипса, от которой отталкиваются современные ученые всего мира, так как она признана эталоном.
Поэтому я расскажу о том, какие величины имеет земной диаметр и экватор. Учитывая, как я говорил раннее, что земная форма не идеально шарообразная, принято считать экватор окружностью. На экваторе диаметр равен 12 тысячам 756 километрам, а на полюсах, естественно, чуть меньше — на 43 километра. Например, в 2007 году выяснилось, что с 2000 года диаметр планеты стал меньше на пять миллиметров.
Окружность Земли по экватору 40000 км, а сколько км будет если мерить через полюса?
Именно благодаря вращению образовалась выпуклость вокруг экватора. Исходя из предпосылки, что Земля имеет форму шара, а окружность равна 360 градусам, находим расстояние (хорду) между двумя точками, расположенными на расстоянии градуса и умножаем на 360. Просто? Длина экватора учеными высчитана по формуле 2πR, несмотря на то, что Земля имеет не шарообразную форму, а вытянута в виде эллипса (шара, сплюснутого у полюсов).
Какая длина экватора Земли?
40 075 километров — такова длина экватора. Экватор делит поверхность земного шара на Северное и Южное полушария и служит началом отсчёта географической широты. Это воображаемая линия, которая проходит по поверхности Земли в плоскости, проходящей через ее центр и перпендикулярной оси вращения планеты. Однако достижение границы между Северным и Южным полушариями все равно не позволило определить, чему равна длина экватора. Измеряя время, в течение которого солнечные лучи достигали дна колодца, ученый смог вычислить радиус земного шара и узнать, какова длина экватора.
В результате внутренних процессов в недрах планеты происходит постепенное разогревание ядра и выделение водорода. Данная теория, кроме всего прочего, дает возможность объяснить и массовое вымирание за короткий промежуток времени многих видов древних животных, так называемое триасовое побоище. Так что со временем длина экватора будет увеличиваться.
Чему равна окружность Земли в километрах — как посчитали эту величину? Какова длина окружности земли по экваториальной линии или по меридиану? Это круговая линия, опоясывающая планету и проходящая через её центр. Экватор перпендикулярен оси земного вращения. Учёный измерил угол и обнаружил, что его величина составляет 1/50 часть от целой окружности, равняемой 360 градусам. Выяснилось, что на экваторе градус имеет меньшую длину. Таким образом выяснили, что окружность Земли полярная меньше окружности по экватору на 21,4 километра.
Какой размер имеет окружность Земли
Кто из нас на память назовет, сколько километров содержит окружность Земли по экватору? Кто в курсе, когда и каким образом была впервые измерена длина земной окружности? Измерив данный угол с помощью астрономических инструментов, ученый установил, что он составляет 1/50 часть полной окружности. Таким образом, достаточно знать хорду угла в 1 градус (т. е. расстояние между точками на поверхности Земли, лежащими на лучах с угловым расстоянием между ними в 1 градус).
Таким образом, достаточно знать хорду угла в 1 градус (т. е. расстояние между точками на поверхности Земли, лежащими на лучах с угловым расстоянием между ними в 1 градус).
Линия экватора перпендикулярна оси вращения нашей планеты и находится на равном расстоянии от обоих полюсов. Это помогло ему вычислить длину радиуса Земли и, соответственно, экватора благодаря формуле длины окружности. К тому же в других статьях Эратосфен вычислил Экватор с помощью угла наклона тень когда Солнце освещало дно колодца!! 1. Линия, проходящая по поверхности Земли (экватор), не может проходить и через центр Земли, как у вас написано.
Эратосфен будто бы измерял углы с точностью до угловых секунд и разница широт Александрии составила у него 7° 6,7′, то есть 7х60=420+6,7=426,7 морских миль (угловых минут). Непонятно какой стадий использован Эратосфеном для измерения расстояний и т.п. Первый угол опирается на дугу от конца тени гномона до его основания, а второй — на дугу с центром в центре Земли, проведённую от Сиены до Александрии. Эти дуги подобны между собой, поскольку на них опираются равные углы. И какое отношение имеет дуга на чаше к своему кругу, такое же отношение имеет и дуга от Сиены до Александрии.
Эти дуги подобны между собой, поскольку на них опираются равные углы. И какое отношение имеет дуга на чаше к своему кругу, такое же отношение имеет и дуга от Сиены до Александрии.
Измерение окружности Земли
Вот простой способ измерения окружности (и диаметр) Земли, который скорее всего был использован древними астрономами. Идеальным выбором была бы Звезда, которая близко расположена к небесной оси Северного полюса (с указанием центра оси вращения Земли). Угловой диаметр Луны и Солнца почти одинаковы: 0,5 градуса. Если один из наших астрономов делал это измерение от места расположения в точке(A) возле Гизы (30 0 С), звезда Мицар должна была появиться около 41 градусов над местным горизонтом.
Общая протяженность этой дуги превысила 2800 км. Она охватывала более 25 градусов, что составляет почти 1/14 часть земной окружности. Теоремы Клеро устанавливают связь между формой Земли, ее вращением и распределением силы тяжести на ее поверхности, тем самым были заложены основы нового направления науки — гравиметрии. Геоид — условная поверхность равного потенциала (поверхность равновесия), совпадающая с поверхностью свободно покоящейся воды в открытом океане. Очевидно, что рельеф литосферы в океанах располагается ниже поверхности геоида, а на материках — выше (говорят: «высота над уровнем моря»).
Геоид — условная поверхность равного потенциала (поверхность равновесия), совпадающая с поверхностью свободно покоящейся воды в открытом океане. Очевидно, что рельеф литосферы в океанах располагается ниже поверхности геоида, а на материках — выше (говорят: «высота над уровнем моря»).
Еще совсем недавно, в 1862 г., немецкий ученый П. Иоселиани, определяя «глубину толстоты земного шара», получил 4536,8 км, что в 11/2 раза меньше действительной величины. Трудно поверить, но еще в 1876 г. в Петербурге была издана брошюра под названием: «Земля неподвижна, популярная лекция, доказывающая, что земной шар не вращается ни около оси, ни около Солнца. В 1841 г. немецкий астроном Ф. Бессель, используя градусные измерения, вычислил радиус Земли и ее сжатие у полюсов, т. е. получил цифры, характеризующие основные элементы земного эллипсоида. Приходится считать также, что северное и южное полушария, как показал русский ученый А. А. Иванов, не вполне симметричны относительно плоскости экватора.
По своим размерам она превосходит только Меркурий, Марс и Плутон. Когда к Солнцу обращена область вокруг Северного полюса, в Северном полушарии лето, а в Южном — зима. Когда к Солнцу обращена область вокруг Южного полюса — наоборот. Мередиан–половина окружности, соответствует _______градусам и ________», категории «география».
Конечно, в результате подобных изучений Эратосфен вычислил приближенную длину радиуса Земли, а значит и экватора. Для вычисления земного экватора необходимо знать радиус планеты. На экваторе широта равна нулю. Длина экватора – это одна из основных характеристик любой планеты.
Магнитное поле Земли в первом приближении представляет собой диполь, полюсы которого расположены рядом с географическими полюсами планеты.
21,3 километра — настолько экватор дальше от центра Земли, чем ее полюса. Из-за вращения земной шар сплюснут с полюсов на 1/298 диаметра. 35 786 километров — на такой высоте над экватором расположена геостационарная орбита, на которой «висят» спутники связи. Сигнал со скоростью света идет туда-обратно всего четверть секунды.
Сигнал со скоростью света идет туда-обратно всего четверть секунды.
Из-за наклона земной оси высота Солнца над горизонтом в течение года изменяется. Для Земли радиус сферы Хилла (сфера влияния земной гравитации) равен примерно 1,5 млн км[комм. 5]. Это максимальное расстояние, на котором влияние гравитации Земли больше, чем влияние гравитации других планет и Солнца.
Для измерения зенитного расстояния Солнца Эратосфен использовал в качестве угломерного прибора солнечные часы — скафис. Солнца составляет 47 градусов 42 минуты.
Иными словами, метр был определен как 1/10, 000000 расстояния от экватора Земли до Северного полюса измеряется по поверхности окружности (эллипсоида) Земли через долготу Парижа.
465 метров в секунду — скорость вращения Земли на экваторе. 33 острова пересекает экватор. Но что такое Экватор? Длина экватора земли — 40 075,696 км. Не так уж и много, если задуматься. Длина земли по экватору рассчитывается достаточно просто. 40 075 километров — такова длина экватора. Проведя серию сложных экспериментов и расчетов, он определил, что длина экватора Земли составляет 252 000 стадий.
Проведя серию сложных экспериментов и расчетов, он определил, что длина экватора Земли составляет 252 000 стадий.
Экватор делит поверхность земного шара на Северное и Южное полушария и служит началом отсчёта географической широты. Города, расположенные на широте экватора — Мбандака (ДРК), Мбарара (Уганда), Кисуму и Накуру в Кении, а также города Понтианак в Индонезии и Макапа в Бразилии.
17 из них принадлежат Индонезии (причём два находятся в озере на острове Калимантан), 9 расположены в устье Амазонки в Южной Америке, 5 — в африканском озере Виктория. За неимением письменных источников современные историки не могут с точностью сказать, что думал о строении Земли человек неолита.
И в одном из древнеиндийских текстов была отражена теория, согласно которой плоская Земля покоится на трех гигантских китах, а киты плавают в океане. Это воображаемая линия, которая проходит по поверхности Земли в плоскости, проходящей через ее центр и перпендикулярной оси вращения планеты. Пройдя через Геркулесовы Столбы (Гибралтарский пролив), они вышли в Атлантический океан, пересекли экватор и обогнули Африку.
Однако достижение границы между Северным и Южным полушариями все равно не позволило определить, чему равна длина экватора. Последовали громкие открытия новых земель и морских путей: Америка, водный путь в Индию, Австралия. Так как Эратосфен жил и работал в Александрии, стадии он использовал египетские.
Шли годы, века. Совершенствовались измерительные приборы и методики. Человечество вышло в космос и смогло создать подробнейшие карты земной поверхности. А теперь попробуем ответить на вопрос о том, в чем причина расхождения в значениях длины экватора у современных ученых и Эратосфена. А если экватор просто стал длиннее? Он вступил в реакцию с железом и никелем, из которых состоит ядро Земли, в результате чего образовались гидриды этих элементов.
Два раза в год, в дни осеннего и весеннего равноденствия, солнце над ним находится в зените. В Тихом океане экватор пересекает Кирибати и острова Бейкер, принадлежащие США, далее – Эквадор, Колумбию и Бразилию, которые находятся на южноамериканском континенте.
Длина экватора впервые была высчитана древнегреческим ученым Эратосфеном, который был не только великим математиком, географом, поэтом, но и астрономом. Измеряя время, в течение которого солнечные лучи достигали дна колодца, ученый смог вычислить радиус земного шара и узнать, какова длина экватора.
Какая длина экватора Земли?
Современному человеку очень трудно понять, как ученый, не имея никаких приборов, высчитал, какова длина экватора, с погрешностью всего в 386 километров. В XVIII веке такими вычислениями серьезно занимались ученые из Франции. Буквально это означает, что Земля имеет форму Земли, присущую исключительно ей. Наша планета как бы сплюснута с полюсов.
Окружность Земли по экватору 40000 км, а сколько км будет если мерить через полюса?
Именно благодаря вращению образовалась выпуклость вокруг экватора. Так называется воображаемая линия, которая делит Землю на два полушария – северное и южное, словно опоясывая ее. Слово произошло от латинского aequo, означающего «делаю равным».
Кстати, день и ночь на экваторе всегда длятся одинаково! При современных скоростях и средствах передвижения каждый из нас наверняка не раз обогнул землю (достаточно посмотреть на показания автомобильных приборов). Какова длина экватора сумел вычислить еще древнегреческий ученый Эратосфен. Исходя из предпосылки, что Земля имеет форму шара, а окружность равна 360 градусам, находим расстояние (хорду) между двумя точками, расположенными на расстоянии градуса и умножаем на 360. Просто?
Длина экватора учеными высчитана по формуле 2πR, несмотря на то, что Земля имеет не шарообразную форму, а вытянута в виде эллипса (шара, сплюснутого у полюсов). Многие ученые-математики и астрономы впоследствии тоже пытались высчитать длину экватора. Россияне тоже не остались в стороне и внесли свой вклад в науку, который позволил определить, какова же длина земли по экватору.
Как измерили Землю — Сайт Александра Таранова
Впервые
довольно точно измерил величину земного шара Эратосфен Киренский (ок. 276-194 до
н.э.) – древнегреческий математик, астроном и географ из египетского города
Александрия. Он, как и Аристотель, считал, что Земля шар.
276-194 до
н.э.) – древнегреческий математик, астроном и географ из египетского города
Александрия. Он, как и Аристотель, считал, что Земля шар.
Эратосфен
узнал, что в день летнего солнцестояния в Сиене (теперь Асуан), расположенной
южнее Александрии, солнце освещало в полдень дно глубоких колодцев, т.е.
находилось в зените. В тот же полдень в Александрии, по измерениям Эратосфена,
Солнце отстояло от зенита на 7°12′, что составляет 1/50 долю окружности. Отсюда
Эратосфён заключил, что такую же долю окружности Земли составляет расстояние от
Сиены до Александрии. Измерить это расстояние в те времена можно было только по
числу дней, которое тратили караваны верблюдов на переход между этими городами.
Оно составило 5.000 греческих стадий. И если 1/50 окружности Земли равняется
5.000 стадий, то вся окружность Земли должна быть в 50 раз больше, т.е.
5.000х50=250.000 стадий. К сожалению, точная длина древнегреческой стадии теперь
неизвестна, но, по-видимому, она была близка к 160 м. Таким образом, по
определению Эратосфена, окружность Земли приблизительно равна
40.000
км, что очень близко к современным расчётам.
К сожалению, точная длина древнегреческой стадии теперь
неизвестна, но, по-видимому, она была близка к 160 м. Таким образом, по
определению Эратосфена, окружность Земли приблизительно равна
40.000
км, что очень близко к современным расчётам.
Конечно, здесь был элемент случайности. На самом деле расчёт Эратосфена был очень грубым главным образом потому, что он не знал точного расстояния от Сиены до Александрии. Но идея расчёта была совершенно правильной. Она применяется поныне и заключается в следующем. На Земле измеряется расстояние в несколько сотен километров по прямой, проще всего по меридиану.
В конечных
точках этой длины проводятся астрономические наблюдения, например, Солнца в
полдень или звёзд в соответствующей части неба. Так определяют, скольким
градусам, т.е. 360 долям окружности, соответствует эта длина. Элементарными
расчетами легко получить длину дуги 1°. А если умножить длину одного градуса на
360, то получим всю длину земной окружности, равной 2Пи*R, где R – радиус земного шара, в
круглых числах равный 6370
км.
Таким образом, измерение величины земного шара сводится к определению длины одного градуса на Земле. Такая операция называется градусным измерением. В наше время в этот способ внесены многие усовершенствования, главным образом в измерение больших расстояний на земной поверхности.
Многочисленные исследования были проведены учёными разных эпох, прежде чем удалось уточнить длину дуги одного градуса Земли. Трудности были связаны с отсутствием специальных астрономических инструментов, при помощи которых можно было бы с большой точностью определить разницу в географической широте двух мест на земном шаре. Ещё труднее было измерять большие расстояния с нужной точностью.
Эратосфен знал расстояние
между Сиеной (Н) и Александрией (К) и полагал, что они лежат на одном меридиане.
Ему удалось заметить, что, когда в Сиене Солнце стоит прямо над головой
(отражается в воде глубоких колодцев), в Александрии его лучи отклоняются от
отвеса на 7°12′, т. е. на 1/50 окружности. По углу между радиусами Земли и хорде
он вычислил длину окружности Земли.
е. на 1/50 окружности. По углу между радиусами Земли и хорде
он вычислил длину окружности Земли.
В начале
XVII в. голландский географ Снеллиус
предложил способ расчёта, при котором точному измерению больших расстояний не
мешают встречающиеся на пути водные преграды, леса, горы, долины, овраги. Из
геометрии известно, что можно построить треугольник по стороне и двум прилежащим
к ней углам, а по формулам тригонометрии – вычислить длину двух других сторон.
Поэтому для измерения большого расстояния, например между пунктами А и Д,
выбирают ряд точек так, чтобы из каждой были видны 3-4 соседние. Это могут быть
вершины гор или возвышенностей, высокие здания или же сооружённые с этой целью
специальные вышки, так называемые геодезические сигналы. В этих точках с помощью
угломерных инструментов – теодолитов – измеряют углы между направлениями на
соседние точки. В полученном ряде треугольников остается измерить длину лишь
одной какой-нибудь стороны. Она называется базисом, что означает «основание».
Базис длиной около 10
км выбирают в наиболее удобной местности, без крутых
склонов и других препятствий. Измерение базиса – сложный и трудоёмкий процесс.
Зная длину базиса и углы в соответствующем треугольнике, вычисляют длину двух
других сторон, которые входят в состав соседних треугольников. Таким образом,
двигаясь дальше, можно шаг за шагом найти величины всех других треугольников и в
конечном итоге определить расстояние АД. Именно так решается вопрос об измерении
больших расстояний на поверхности Земли.
Она называется базисом, что означает «основание».
Базис длиной около 10
км выбирают в наиболее удобной местности, без крутых
склонов и других препятствий. Измерение базиса – сложный и трудоёмкий процесс.
Зная длину базиса и углы в соответствующем треугольнике, вычисляют длину двух
других сторон, которые входят в состав соседних треугольников. Таким образом,
двигаясь дальше, можно шаг за шагом найти величины всех других треугольников и в
конечном итоге определить расстояние АД. Именно так решается вопрос об измерении
больших расстояний на поверхности Земли.
Вся эта
операция называется триангуляцией (от латинского «триангулум» – треугольник).
Вершины треугольников, или триангуляционные пункты, служат ещё и для важной
практической цели: поскольку их взаимное положение известно с большой точностью,
они используются при топографических съёмках для составления подробных
географических карт. Способ триангуляции очень помог учёным уточнить
представления о форме и величине Земли.
Уже в
первой половине XVIII в. французскими учёными была сделана попытка уточнить при
помощи триангуляции длину 1° меридиана. Было найдено, что длина 1° меридиана
несколько увеличивается с севера к югу. Это послужило основанием для
предположения о том, что Земля не правильный шар, а слегка вытянутый в
направлении полюсов. Но это противоречило теоретическому выводу Ньютона,
утверждавшему, что Земля должна быть растянута в направлении экватора и сжата у
полюсов вследствие наибольшей центробежной силы на экваторе при вращении Земли.
Чтобы решить этот спорный вопрос, Французская Академия наук снарядила две
экспедиции: одну – к Северному полярному кругу, в Финляндию и Швецию, другую – в
Перу, к экватору. Экспедиции работали в очень трудных условиях несколько лет.
После сравнения результатов работы экспедиций выяснилось: чем ближе к экватору,
тем длина градуса меридиана заметно короче по сравнению с умеренными широтами,
т. е. ближе к полюсу. Таким образом, было доказано, что Земля действительно
немного сплюснута у полюсов: полярный радиус Земли приблизительно на
21 км
короче экваториального. Может показаться, что в таком случае более короткому
радиусу должна соответствовать и меньшая длина градуса. Но оказывается, что
градусное измерение дает не длину радиуса Земли, т.е. не расстояние её
поверхности от центра, а так называемый радиус кривизны, определяющий, насколько
круто в данном месте изгибается земная поверхность. Действительно, поверхность
Земли у полюсов менее выпуклая, чем у экватора, как это преувеличенно показано
на рисунке. Заметим, что фигура Земли определяется поверхностью океанов, т.е.
уровнем моря, от которого отсчитываются все высоты. Эта поверхность очень близка
к поверхности вращения эллипса вокруг малой оси, поэтому тело Земли принято
считать эллипсоидом.
е. ближе к полюсу. Таким образом, было доказано, что Земля действительно
немного сплюснута у полюсов: полярный радиус Земли приблизительно на
21 км
короче экваториального. Может показаться, что в таком случае более короткому
радиусу должна соответствовать и меньшая длина градуса. Но оказывается, что
градусное измерение дает не длину радиуса Земли, т.е. не расстояние её
поверхности от центра, а так называемый радиус кривизны, определяющий, насколько
круто в данном месте изгибается земная поверхность. Действительно, поверхность
Земли у полюсов менее выпуклая, чем у экватора, как это преувеличенно показано
на рисунке. Заметим, что фигура Земли определяется поверхностью океанов, т.е.
уровнем моря, от которого отсчитываются все высоты. Эта поверхность очень близка
к поверхности вращения эллипса вокруг малой оси, поэтому тело Земли принято
считать эллипсоидом.
Если нам нужно измерить
расстояние от А до Д, когда точки Д не видно из точки А, то мы измеряем базис АВ
и в треугольнике АСВ – углы, прилегающие к базису. По одной стороне и прилегающим к ней углам определяем расстояния АС и ВС. Далее
из точки С мы с помощью зрительной трубы измерительного инструмента находим
точку Д, видимую из точек В и С. В треугольнике СДВ нам известна сторона СВ.
Остается измерить прилегающие к ней углы, а затем определить расстояние ДВ. Зная
расстояние ДВ и АВ и угол между этими линиями, можно определить расстояние от А
до Д.
По одной стороне и прилегающим к ней углам определяем расстояния АС и ВС. Далее
из точки С мы с помощью зрительной трубы измерительного инструмента находим
точку Д, видимую из точек В и С. В треугольнике СДВ нам известна сторона СВ.
Остается измерить прилегающие к ней углы, а затем определить расстояние ДВ. Зная
расстояние ДВ и АВ и угол между этими линиями, можно определить расстояние от А
до Д.
В конце
XVIII в. специальная французская экспедиция стремилась установить новую
естественную единицу длины, из природы. За эту единицу – метр – решено было
принять одну десятимиллионную часть четверти меридиана, т.е. расстояния от
экватора до полюса. В таком случае вся окружность Земли по меридиану точно
равнялась бы 40.000
км. Последующие, более точные измерения показали, что
принятая в 1799
г. и ныне применяемая в качестве эталона длина метра
примерно на 0,2
мм короче той, которая соответствовала первоначальному
(связанному с размерами Земли) замыслу французских учёных, поэтому фактическая
полная длина меридиана на 8,55 км больше, чем должна бы быть по
расчётам.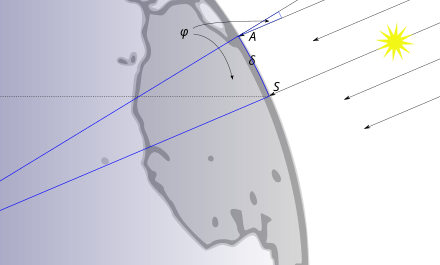
В России замечательное по точности градусное измерение было проведено в 1822-1852 гг. под руководством выдающегося астронома, основателя и первого директора Пулковской обсерватории (под Ленинградом) В.Я.Струве.
Были измерены дуги меридиана общей длиной 2800 км от северных берегов Норвегии до Дуная. В триангуляцию вошло 258 треугольников. Это измерение имело большое практическое значение для составления точных карт.
В настоящее время почти все страны мира покрыты триангуляционной сетью. Геодезисты с большой точностью измерили длины дуг меридианов в разных местах земной поверхности. Результаты произведённых измерений позволили достаточно точно определить действительную фигуру Земли.
В 1941 г. советский геодезист Ф.Н.Красовский вывел из многих измерений размеры земного эллипсоида, принятые у нас за стандартные.
Какое расстояние экватора. Чему равна окружность Земли в километрах — как посчитали эту величину
© Владимир Каланов,
сайт
«Знания-сила».
Земля… Такая милая, родная для всего человечества планета. Много ли мы знаем о ней? Да, много. А много ли того, чего мы не знаем о ней? Очень много, больше того, что знаем. Тайны свои планета наша раскрывает совсем неохотно. В значительной степени это потому, что тайны планеты Земля, так сказать, не только её личные, но это тайны и космические, тайны Вселенной.
Как космическое тело Земля является планетой, вращающейся вокруг Солнца вместе с другими планетами (Меркурий, Венера, Марс, Юпитер, Сатурн, Уран, Нептун, Плутон).
Основные параметры планеты ЗемляСреднее расстояние от Земли до Солнца — 149597870 км.
Среднее расстояние от Земли до Луны — 384400 км.
Время полного оборота
Земли вокруг своей оси (звёздные сутки) — 23 часа 56 мин. 4,09 сек.
Период обращения Земли вокруг Солнца (тропический год) — 365,25 суток
Средняя
скорость движения Земли по орбите — 29,76 км/сек.
Масса 6 000 000 000 000 млрд. тонн.
Большая полуось (экваториальный радиус), а — 6378,2 км.
Малая полуось (полярный радиус), в — 6356,9 км.
Сжатие с=(а-в)/а — 1: 298,3
Средний радиус Земли, принимаемой за шар — 6371,2 км.
Длина меридиана — 40008,6 км.
Длина экватора — 40075,7 км.
(диаметр экватора — 12756 км.)
Поверхность Земли — 510 100 000 кв.км.
Средняя высота суши над уровнем океана — 875 м.
Средняя глубина мирового
океана — 3800 м.
Наибольшая высота суши над уровнем океана — 8848 м. (гора Эверест)
Наибольшая глубина мирового океана — 11022 м. (Марианская впадина)
| Поверхность земного шара | Северное полушарие | Южное полушарие | Земля в целом | |||
| млн. кв.км | % | млн. кв.км | % | млн. кв.км | % | |
| Суша | 100 | 39 | 49 | 19 | 149 | 29 |
| Вода | 155 | 61 | 206 | 81 | 361 | 71 |
| Всего | 255 | 100 | 255 | 100 | 510 | 100 |
*)
Данные взяты из Малого атласа мира, издательство Москва, 1980.
Из этих данных следует давно общепризнанный факт, что Земля незначительно сжата у полюсо́в. Однако имеются данные о том, что Земля имеет дынеобра́зную форму, т.е. сжата по экватору так, что по вертикальной оси она на несколько десятков километров больше, чем по экваториальной оси. Но эту гипотезу учёных Калифорнийского технологического института мы не рассматриваем и приводим здесь исключительно для све́дения любителей экзотики.
Какова́ же действительная форма Земли по современным представлениям официальной науки? Из приведенных данных (Малый а́тлас мира) следует, что Земля — это шар с отклонениями от математически точной формы. Назвать Землю эллипсоидом рука не поднимается: слишком крохотная для размеров Земли разница между большой и малой осями эллипсоида. Поэтому в науке форму Земли называют геоидом. Это надо понимать так, что Земля имеет форму Земли.
Правда, для людей, которые изо дня в день наблюдают окружающие их предметы и явления природы и не задумываются над их сущностью, причинами и,
тем более, происхождением, абсолютно всё равно, какую форму имеет планета Земля. Они не видят потрясающую красоту и великую мудрость окружающего мира, у них не
возникают вопросы о том, почему так всё устроено на Земле, и не возникает желания узнать что-нибудь о планете, на которой они живут. Их интересы
ограничиваются кругом повседневных житейских забот. Таких людей много, они рядом с нами. Сразу хочу заявить: наш рассказ не для них. Наш рассказ для тех
людей, которых интересует всё о Земле: её происхождение и возраст, её красота и богатство, её уникальность как космического тела и как ме́ста возникновения жизни
и пребывания нашей человеческой цивилизации. Наш рассказ для людей, которых не просто интересует, а глубоко волнует будущее Земли, её экологии, всей её
биосферы, а, значит, и будущее человечества.
Они не видят потрясающую красоту и великую мудрость окружающего мира, у них не
возникают вопросы о том, почему так всё устроено на Земле, и не возникает желания узнать что-нибудь о планете, на которой они живут. Их интересы
ограничиваются кругом повседневных житейских забот. Таких людей много, они рядом с нами. Сразу хочу заявить: наш рассказ не для них. Наш рассказ для тех
людей, которых интересует всё о Земле: её происхождение и возраст, её красота и богатство, её уникальность как космического тела и как ме́ста возникновения жизни
и пребывания нашей человеческой цивилизации. Наш рассказ для людей, которых не просто интересует, а глубоко волнует будущее Земли, её экологии, всей её
биосферы, а, значит, и будущее человечества.
В начале нашего рассказа о Земле и геосферах необходимо сказать о том, как произошла Земля. Вопрос о происхождении Земли очень сложен,
ибо речь тут может идти о происхождении всей солнечной системы и даже всей галактики, именуемой Млечным путём. На эту тему существует много научных гипотез
и просто предположений. Достаточно упомянуть о гипотезе так называемого Большого взрыва. Сразу отметим, что какой-то единой стройной теории происхождения
Вселенной и Солнечной системы до сих пор не существует. Различные гипотезы, выдвигаемые разными научными школами и отдельными учёными, часто противоречат
друг другу.
Можно остановиться, например, на такой гипотезе возникновения Солнечной системы и Земли:
Достаточно упомянуть о гипотезе так называемого Большого взрыва. Сразу отметим, что какой-то единой стройной теории происхождения
Вселенной и Солнечной системы до сих пор не существует. Различные гипотезы, выдвигаемые разными научными школами и отдельными учёными, часто противоречат
друг другу.
Можно остановиться, например, на такой гипотезе возникновения Солнечной системы и Земли:
Образование Солнца и планет солнечной системы. и планеты образовались около пяти миллиардов лет назад из громадного космического газопылево́го облака (1). Это облако имело приплюснутую, чечевицеобразную форму — форму диска. Ученые полагают, что и этот диск, и Солнце образовались из одной и той же вращающейся массы межзвездного газа — протосолнечной туманности. Наименее изучена самая ранняя стадия происхождения Солнечной системы — выделение протосолнечной туманности из гигантского родительского молекулярного облака, принадлежащего Галактике.
Под действием гравитационных сил притяжения облако начало́ сжима́ться, и образовался вращающийся диск из веществ, основная часть которых
собралась в центре (2). Центральное ядро уменьшалось, притягивая к себе все больше материи, и в какой-то момент в его недрах под действием огромного
давления сжатия пошла ядерная реакция (3) — зажглась звезда, возникло Солнце. Остальное вещество сбивалось в меньшие образования из камней и сгустков газа —
так образовались планеты. Солнечная система приняла современный вид (4).
Центральное ядро уменьшалось, притягивая к себе все больше материи, и в какой-то момент в его недрах под действием огромного
давления сжатия пошла ядерная реакция (3) — зажглась звезда, возникло Солнце. Остальное вещество сбивалось в меньшие образования из камней и сгустков газа —
так образовались планеты. Солнечная система приняла современный вид (4).
На начальной стадии своего формирования Солнце было очень горячим, что явилось причиной испарения в космос большой части лёгких летучих
веществ (преимущественно водорода и гелия), которые находились в области, где формировалась Земля. Другими словами, протопланетная туманность вокруг
Солнца разделилась на две различные по составу и температуре части: ближайшая к Солнцу содержала меньше легких элементов и имела достаточное насыщение тяжелыми
элементами, в отличие от более удаленной, обедненной тяжелыми элементами и состоящей преимущественно из легких газов. В более отдаленных и холодных
областях будущей Солнечной системы, легкие вещества могли конденсироваться, образуя под действием гравитации гигантские газообразные планеты — «газовые
планеты-гиганты», такие как и .
Под действием гравитационных сил материя солнечной туманности аккумулировалась также и во внутренней части туманности — здесь происходило образование Земли и других планет земной группы. Но из-за огромной температуры материя находилась в расплавленном состоянии; более плотные вещества, такие, как железо, никель и их соединения, устремились к центру планеты, тогда как более легкие, например, силикаты разных металлов, из которых впоследствии образовались скальные породы, остались на поверхности. Такой процесс получил название гравитационной дифференциации. По окончании этого процесса температура на Земле постепенно понизилась настолько, что начался процесс затвердения.
Следует отметить, что этот сценарий — только один из теоретических сценариев образования Земли. Например, в 40-х годах XX века
академик О.Ю. Шмидт выдвинул ставшую общепринятой гипотезу об образовании Земли и других планет из холодных твёрдых допланетных тел — планетезималей.
Планетезима́ль (от англ. planet
— планета и
infinitesimal
— бесконечно малый ) — тело, представляющее собой промежуточную ступень формирования планеты из протопланетного газово-пылевого
облака. Более детально основные моменты теорий образования планет мы рассмотрим в отдельной главе, посвященной происхождению Солнечной системы.
Более детально основные моменты теорий образования планет мы рассмотрим в отдельной главе, посвященной происхождению Солнечной системы.
Уважаемые посетители!
У вас отключена работа JavaScript . Включите пожалуйста скрипты в браузере, и вам откроется полный функционал сайта!Экватор — это воображаемая круговая линия, которая опоясывает весь земной шар и проходит через центр Земли.
Линия экватора перпендикулярна оси вращения нашей планеты и находится на равном расстоянии от обоих полюсов.
Экватор: что это и зачем он нужен?
Итак, экватор — это воображаемая линия. Зачем серьезным ученым понадобилось воображать какие-то линии, очерчивающие Землю? Затем, что экватор, как и меридианы, параллели и прочие разделители планеты, которые существуют только в воображении и на бумаге, дают возможность производить подсчеты, ориентироваться в море, на суше и в воздухе, определять месторасположение различных объектов и т.д.
Экватор делит Землю на Северное и Южное полушария и служит началом отсчета географической широты: широта экватора равна 0 градусов. Он помогает ориентироваться в климатических поясах планеты. Приэкваториальная часть Земли получает самое большое количество солнечных лучей. Соответственно, чем дальше территории расположены от экваториальной линии и чем ближе они к полюсам, тем меньше солнца им достается.
Он помогает ориентироваться в климатических поясах планеты. Приэкваториальная часть Земли получает самое большое количество солнечных лучей. Соответственно, чем дальше территории расположены от экваториальной линии и чем ближе они к полюсам, тем меньше солнца им достается.
Приэкваториальная область — это вечное лето, где воздух всегда горячий и очень влажный из-за постоянных испарений. На экваторе день всегда равен ночи. Солнце бывает в зените — светит вертикально вниз — только на экваторе и только дважды в год (в те дни, на которые приходятся дни равноденствий в большинстве географических поясов Земли).
Экватор проходит через 14 государств. Города, расположенные непосредственно на линии: Макапа (Бразилия), Кито (Эквадор), Накуру и Кисуму (Кения), Понтинак (остров Калиманта, Индонезия), Мбандака (Республика Конго), Кампала (столица Уганды).
Длина экватора
Экватор является самой длинной параллелью Земли. Его длина составляет 40.075 км. Первым, кто смог приблизительно вычислить протяженность экватора, был Эратосфен — древнегреческий астроном и математик. Для этого он измерял время, в течение которого солнечные лучи достигали дна глубокого колодца. Это помогло ему вычислить длину радиуса Земли и, соответственно, экватора благодаря формуле длины окружности.
Для этого он измерял время, в течение которого солнечные лучи достигали дна глубокого колодца. Это помогло ему вычислить длину радиуса Земли и, соответственно, экватора благодаря формуле длины окружности.
Следует отметить, что Земля не является идеальной окружностью, поэтому радиус ее в разных частях немого отличается. К примеру, радиус на экваторе равен 6378,25 км, а радиус на полюсах — 6356,86 км. Поэтому для решения задач по вычислению длины экватора радиус принимают равным 6371 км.
Длина экватора является одной из ключевых метрических характеристик нашей планеты. Ее используют для вычислений не только в географии и геодезии, но в астрономии и астрологии.
Земля круглая — это общеизвестно. А что мы еще знаем о ее форме и размерах? Кто из нас на память назовет, сколько километров содержит окружность Земли по экватору? А по меридиану? Кто в курсе, когда и каким образом была впервые измерена длина земной окружности? Между тем, эти факты чрезвычайно интересны.
Впервые окружность Земли была измерена по имени Эратосфен, жившим в городе Сиена. В то время ученые уже знали, что Земля по форме представляет собой шар. Наблюдая за небесным светилом в разное время суток, Эратосфен обратил внимание, что в одно и то же время солнце, будучи наблюдаемым из Сиены, располагается точно в зените, при этом в Александрии в тот же день и час отклоняется на некий угол.
Наблюдения проводились ежегодно в Измерив данный угол с помощью астрономических инструментов, ученый установил, что он составляет 1/50 часть полной окружности.
Как известно, полная окружность равняется 360 градусам. Таким образом, достаточно знать хорду угла в 1 градус (т. е. расстояние между точками на поверхности Земли, лежащими на лучах с угловым расстоянием между ними в 1 градус). Затем полученную величину следует умножить на 360.
Взяв за длину хорды расстояние между городами Александрией и Сиеной (5 тысяч египетских стадий) и предполагая, что эти города лежат на одном меридиане, Эратосфен произвел необходимые вычисления и назвал цифру, которой равнялась окружность Земли — 252 тысячи египетских стадий.
Для того времени это измерение было достаточно точным, ведь надежных методов измерения расстояния между городами не существовало, и путь от Сиены до Александрии измерялся скоростью движения каравана верблюдов.
Впоследствии ученые разных стран многократно измеряли и уточняли величину, которую составляет длина окружности Земли. В 17 веке голландский ученый по фамилии Сибелиус придумал способ измерять расстояния с помощью первых теодолитов — специальных геодезических приборов. Данный способ был назван триангуляцией и основан на построении большого количества треугольников с измерением базиса каждого из них.
Способ триангуляции применяется и поныне, вся земная поверхность виртуально поделена и расчерчена на большие треугольники.
Российские ученые тоже внесли свой вклад в эти исследования. В 19 веке окружность Земли измерялась в руководил исследованием В. Я. Струве.
До середины 17 века Землю считали шаром правильной формы. Но позже были накоплены некоторые факты, свидетельствующие об уменьшении силы земного притяжения от экватора к полюсу. Ученые ожесточенно дискутировали о причинах этого, самой правдоподобной была признана теория о сжатии Земли с полюсов.
Ученые ожесточенно дискутировали о причинах этого, самой правдоподобной была признана теория о сжатии Земли с полюсов.
Для проверки этой гипотезы Французской академией были организованы две независимые экспедиции (в 1735 и 1736 годах), которые измеряли длину экваториального и полярного градуса соответственно в Перу и в Лапландии. На экваторе градус, как выяснилось, короче!
Впоследствии другие, более точные измерения подтвердили, что полярная окружность Земли короче экваториальной на 21,4 км.
В настоящее время произведены высокоточные измерения с помощью новейших методов исследований и современных приборов. В нашей стране официально утверждены данные, полученные советскими учеными Изотовым А. А. и Красовским Ф. Н. Согласно этим исследованиям, длина окружности нашей планеты по экватору — 40075,7 километров, по меридиану — 40008,55 км. Экваториальный радиус земного шара (т. н. большая полуось) равняется 6378245 метрам, полярный (малая полуось) — 6356863 метрам.
510 миллионов кв. 21 тонн. Из них около 7 % приходится на долю водных ресурсов.
21 тонн. Из них около 7 % приходится на долю водных ресурсов.
Всем известно, что планета Земля обладает круглой формой. Но какие размеры имеет планета, мало кто сможет сказать. Какова длина окружности земли по экваториальной линии или по меридиану? Чему равен диаметр Земли? Постараемся ответить на эти вопросы максимально подробно.
Прежде всего рассмотрим основные понятия , с которыми мы столкнёмся при ответе на вопрос о длине окружности Земли.
Что называют экватором? Это круговая линия, опоясывающая планету и проходящая через её центр. Экватор перпендикулярен оси земного вращения. Он удалён одинаково от одного и другого полюса. Экватор разделяет планету на два полушария, называемые Северным и Южным. Он играет большую роль в определении климатических поясов на планете. Чем ближе к экватору, тем климат жарче, ведь этим территориям достаётся больше солнечного света.
Что такое меридианы? Это такие линии, которые разделяют весь земной шар . Всего их 360, то есть каждая доля между ними равняется одному градусу. Меридианы пролегают через полюса планеты. По меридианам считают географическую долготу. Отсчёт начинается от нулевого меридиана, который также именуют Гринвичским, поскольку он пролегает через Гринвичскую обсерваторию в Англии. Долготу называют восточной или западной — в зависимости от того, в каком направлении идёт отсчёт.
Меридианы пролегают через полюса планеты. По меридианам считают географическую долготу. Отсчёт начинается от нулевого меридиана, который также именуют Гринвичским, поскольку он пролегает через Гринвичскую обсерваторию в Англии. Долготу называют восточной или западной — в зависимости от того, в каком направлении идёт отсчёт.
В древние времена
Впервые окружность Земли измерили ещё в Древней Греции. Это был математик Эратосфен из города Сиены. В то время уже было известно , что планета обладает шаровидной формой. Эратосфен наблюдал за Солнцем и заметил, что светило в одно и то же время суток при наблюдении из Сиены расположено точно в зените, а в Александрии оно имеет угол отклонения.
Эти измерения производились Эратосфеном в день солнцестояния в летний период . Учёный измерил угол и обнаружил, что его величина составляет 1/50 часть от целой окружности, равняемой 360 градусам. Зная хорду угла в один градус, её нужно умножить на 360. Затем Эратосфен взял в качестве длины хорды интервал между двумя городами (Сиеной и Александрией), предположил, что они находятся на одном меридиане, произвёл расчёты и назвал цифру 252 тысячи стадий.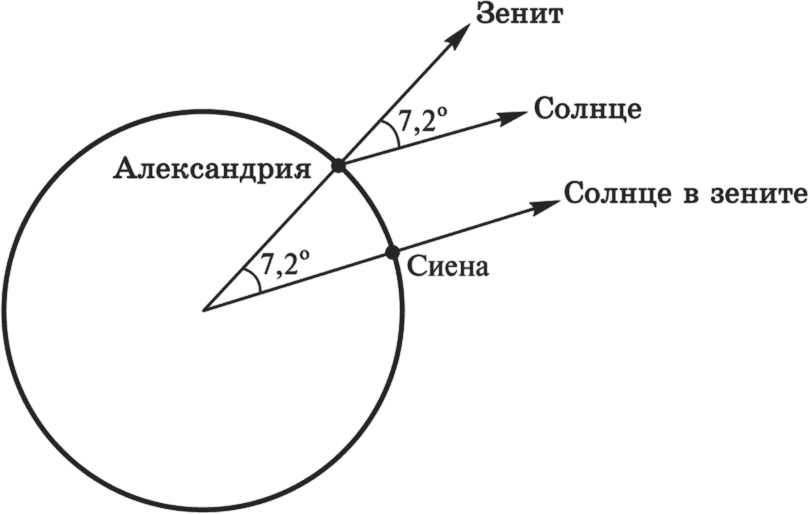 Это число и означало окружность Земли.
Это число и означало окружность Земли.
Для того времени подобные измерения считались точными, ведь никаких способов измерить величину окружности Земли более точно, не существовало. Современные учёные признаются, что величина, посчитанная Эратосфеном, получилась довольно точной, несмотря на то, что:
- эти два города — Сиена и Александрия не расположены на одном меридиане;
- древний учёный получил цифру, исходя из дней пути верблюдов, а ведь ходили они не по идеально прямой линии;
- неизвестно, какой прибор применял учёный для измерения углов;
- непонятно, чему равнялся стадий, используемый Эратосфеном.
Тем не менее, учёные до сих пор придерживаются мнения о точности и уникальности метода Эратосфена, впервые измерившего диаметр Земли.
В Средние века
В XVII веке учёный из Голландии по имени Сибелиус изобрёл метод расчёта расстояний с помощью теодолитов. Это специальные приборы для измерения углов , используемые в геодезии. Метод Сибелиуса назвали триангуляцией, он заключался в построении треугольников и измерении их базисов.
Метод Сибелиуса назвали триангуляцией, он заключался в построении треугольников и измерении их базисов.
Триангуляция практикуется и в наши дни. Учёные условно поделили всю поверхность земного шара на треугольные участки.
Российские исследования
Учёные из России в XIX веке также внесли свой вклад в вопрос измерения длины экватора. Исследования велись в Пулковской обсерватории. Руководил процессом В. Я Струве.
Если ранее Землю считали шаром идеальной формы, то позднее накопились факты, согласно которым сила земного притяжения уменьшалась от экватора к полюсам. Учёные пытались дать объяснение этому явлению . Было несколько теорий. Самой популярной из них считалась теория о сжатии Земли со стороны того и другого полюса.
Чтобы проверить верность гипотезы, Французская академия организовала экспедиции в 1735 и 1736 годах. В результате учёные измерили длину экваториального и полярного градуса в двух точках земного шара — в Перу и Лапландии. Выяснилось, что на экваторе градус имеет меньшую длину. 21 тонн. Доля воды в этой величине составляет 7%.
21 тонн. Доля воды в этой величине составляет 7%.
Видео
Посмотрите интересный эксперимент, демонстрирующий, каким способом Эратосфену удалось высчитать окружность Земли.
А. Соколовский
Геометрия (древнегреческий: Гео -” земля “,-Metron” измерение “) первоначальное значение слова было- измерение Земли. Сегодня, геометрия имеет более широкий смысл: это раздел математики, занимающийся вопросами форм, размера, относительное положение в пространстве и свойства пространства. Геометрия возникла независимо в ряде ранних культур, как дисциплина практического знания, касающаяся длины, площади, объема, с элементами формальной математической науки.
Современные единицы измерения длиныСовременные единицы измерения, связанные с размерами нашей планеты.
МетрПервоначально метр был разработан, чтобы быть одной десятимиллионной (1/10, 000000) квадранта, расстояние между экватором и Северным полюсом. Иными словами, метр был определен как 1/10, 000000 расстояния от экватора Земли до Северного полюса измеряется по поверхности окружности (эллипсоида) Земли через долготу Парижа.
Используя данное значение, окружность идеально круглой Земле должна быть точно 40.000, 000 метров (или 40000 км). Но так как форма Земного шара не идеальная окружность а больше похожа на эллипсоид, то на сегодня официальная величина окружности Земли по линии долготы является 40,007.86 км.
Морская миляМорская миля в основе окружности планеты Земля. Если вы разделите окружность Земли на 360 градусов, а затем разделить каждый градус на 60 минут, вы получите 21600 минут дуги.
1 морская миля определяется как 1 минута дуги (окружности Земли). Эта единица измерения используется всеми странами для воздушных и морских перевозок. Использование 40,007.86 км по официальным данным окружности нашей планеты, мы получим значение морских миль в километры: 1,852 км (40,007.86 / 21600)
Древние единицы измерения показывают, что наши предки были в состоянии измерить размеры нашей планеты с идеальной точностью …
Измерение окружности ЗемлиВот простой способ измерения окружности (и диаметр) Земли, который скорее всего был использован древними астрономами .
Этот метод основан на понимании, что Земля, как Солнце и Луна, так же округлой формы и, что звезды находятся очень далеко от нашей планеты (за исключением Солнца), и они, вращаются вокруг определенной точки над северным горизонтом (Северный полюс).
Съемки на длинных выдержках показывают видимое движение звезд вокруг северного полюса.
Процесс измерения следует проводить в местах с хорошей видимостью неба, например, пустынной местности, в отдалении от населенных пунктов.
В одну ночь, 2 астронома в двух разных местах (А и Б), разделенных известным расстоянием (так будет легко измерить окружность Земли зная расстояние между точками расположенных в сотнях километрах друг от друга) , будут измерять угол над горизонтом (с помощью астролябии с отвесом дающим вертикальную линию) определенной звезды на её местоположение на ночном небе над горизонтом.
Идеальным выбором была бы Звезда , которая близко расположена к небесной оси Северного полюса (с указанием центра оси вращения Земли). В наши дни Полярная звезда будет лучшим выбором, однако тысячи лет назад, из-за прецессии (вращения оси Земли), Полярная звезда не находилась в районе Северного полюса (см. изображение ниже).
В наши дни Полярная звезда будет лучшим выбором, однако тысячи лет назад, из-за прецессии (вращения оси Земли), Полярная звезда не находилась в районе Северного полюса (см. изображение ниже).
Прецессия- вращение оси Земли а течении 26 000 лет
Несмотря на то, что Полярная звезда, находится в пределах северного полюса в половине окружности , это не всегда было так. Ось вращения Земли претерпевает медленные колебания, в течении 26 000 лет, известное как прецессия, вокруг перпендикуляра к ее орбите вокруг Солнца, в результате чего положение вращательного полюса неба, вокруг которой все звезды движутся, постоянно меняется. Примерно во времена греческого поэта Гомера, звезда Kochab была звездой северного полюса. До неё, звездой северного полюса, была звезда Thuban, которая почти точно была на полюсе в 2700 г. до н.э. Она занимала лучшее положение, близкое к идеальному, чем звезда Kochab, примерно до 1900 г. до н.э., и поэтому являлась Полярной звездой во времена древних египтян . Другие яркие звезды, в том числе Alderamin, были в своё время полярными звёздами, и будут снова в отдаленном будущем. Звезда которая в настоящее время находится ближе к Южному полюсу является Sigma Octantis, которая едва видна невооруженным глазом и находится в 1 º 3 ‘от полюса (хотя она была ближе, на 45′ всего столетие назад). [Энциклопедия Науки ]
Другие яркие звезды, в том числе Alderamin, были в своё время полярными звёздами, и будут снова в отдаленном будущем. Звезда которая в настоящее время находится ближе к Южному полюсу является Sigma Octantis, которая едва видна невооруженным глазом и находится в 1 º 3 ‘от полюса (хотя она была ближе, на 45′ всего столетие назад). [Энциклопедия Науки ]
Тщательное наблюдение за ночным небом позволит выбрать яркую звезду с наиболее подходящими параметрами для сравнения местоположения звезды с измеренными параметрами той же звезды с другого места.
Нажмите, чтобы увеличить
Например, в 2600 г. до н.э. (см. изображение выше) в Египте возле плато Гизы, когда звезды Мицар и Kochab (которые вращаются каждую ночь вокруг Северного полюса) будут совпадать с вертикальной линией (отмечено линией отвеса),звезда Мицар (легко измерить высоту) будет идеальной звездой для сравнения её высоты в разных точках (А и B).
Так как звезды в космосе находятся слишком далеко от Земли используя эффект параллакса можно, зная расстояние между точками наблюдения D (база) и угол смещения α в радианах, определить расстояние до объекта:
для малых углов:
эффект параллакса: (смещение или разница в видимом положении объекта рассматривается по двум различным точкам наблюдения), единственной причиной изменения измеренного угла северной звезды является кривизна окружности Земли.
Угловой диаметр Луны и Солнца почти одинаковы: 0,5 градуса.
Наши древние астрономы / Священнослужители, жрецы / могли производить измерения положения северной звезды с точностью до 1 градуса. Используя такой измерительный прибор для измерения угла (астролябия), калиброванной в градусах, он мог получить достаточно точные результаты (возможно с 0,25% степенью точности).
Если один из наших астрономов делал это измерение от места расположения в точке(A) возле Гизы (30 0 С), звезда Мицар должна была появиться около 41 градусов над местным горизонтом. Если второй астроном был расположен в 120 морских милях к югу от *точки (А) (* измеряется в древних единицах длины, конечно), он бы заметил, что высота одного и того же объекта (звезды) 39 градусов (на 2 градуса ниже, чем высота измеряется в месте расположения).
Эти 2 простых измерений позволили бы древним астрономам произвести расчет окружности Земли с достаточно высокой точностью:
(360/2) * 120 морских миль = 21600 морских миль, откуда диаметр Земли может быть оценен как: 21600 морских миль / (22/7)(древние египетские оценки Pi) = = 6873 морских миль = 12728 км
Примечание: современные и точные данные: Окружность Земли между Северным и Южным полюсами:
21,602. 6 морских миль = 24,859.82 миль (40008 км) Диаметр Земли на экваторе:6,887.7 морских миль = 7,926.28 км (12,756.1 км)
6 морских миль = 24,859.82 миль (40008 км) Диаметр Земли на экваторе:6,887.7 морских миль = 7,926.28 км (12,756.1 км)
Экватор — это воображаемая круговая линия, которая опоясывает весь земной шар и проходит через центр Земли.
Линия экватора перпендикулярна оси вращения нашей планеты и находится на равном расстоянии от обоих полюсов.
Экватор: что это и зачем он нужен?
Итак, экватор — это воображаемая линия. Зачем серьезным ученым понадобилось воображать какие-то линии, очерчивающие Землю? Затем, что экватор, как и меридианы, параллели и прочие разделители планеты, которые существуют только в воображении и на бумаге, дают возможность производить подсчеты, ориентироваться в море, на суше и в воздухе, определять месторасположение различных объектов и т.д.
Экватор делит Землю на Северное и Южное полушария и служит началом отсчета географической широты: широта экватора равна 0 градусов. Он помогает ориентироваться в климатических поясах планеты. Приэкваториальная часть Земли получает самое большое количество солнечных лучей. Соответственно, чем дальше территории расположены от экваториальной линии и чем ближе они к полюсам, тем меньше солнца им достается.
Приэкваториальная часть Земли получает самое большое количество солнечных лучей. Соответственно, чем дальше территории расположены от экваториальной линии и чем ближе они к полюсам, тем меньше солнца им достается.
Приэкваториальная область — это вечное лето, где воздух всегда горячий и очень влажный из-за постоянных испарений. На экваторе день всегда равен ночи. Солнце бывает в зените — светит вертикально вниз — только на экваторе и только дважды в год (в те дни, на которые приходятся дни равноденствий в большинстве географических поясов Земли).
Экватор проходит через 14 государств. Города, расположенные непосредственно на линии: Макапа (Бразилия), Кито (Эквадор), Накуру и Кисуму (Кения), Понтинак (остров Калиманта, Индонезия), Мбандака (Республика Конго), Кампала (столица Уганды).
Длина экватора
Экватор является самой длинной параллелью Земли. Его длина составляет 40.075 км. Первым, кто смог приблизительно вычислить протяженность экватора, был Эратосфен — древнегреческий астроном и математик. Для этого он измерял время, в течение которого солнечные лучи достигали дна глубокого колодца. Это помогло ему вычислить длину радиуса Земли и, соответственно, экватора благодаря формуле длины окружности.
Для этого он измерял время, в течение которого солнечные лучи достигали дна глубокого колодца. Это помогло ему вычислить длину радиуса Земли и, соответственно, экватора благодаря формуле длины окружности.
Следует отметить, что Земля не является идеальной окружностью, поэтому радиус ее в разных частях немого отличается. К примеру, радиус на экваторе равен 6378,25 км, а радиус на полюсах — 6356,86 км. Поэтому для решения задач по вычислению длины экватора радиус принимают равным 6371 км.
Длина экватора является одной из ключевых метрических характеристик нашей планеты. Ее используют для вычислений не только в географии и геодезии, но в астрономии и астрологии.
Где проходит и что такое экватор, какую имеет продолжительность и зачем ученым вообще нужно было придумывать эту воображаемую линию. Обо всем этом поговорим подробнее.
Вконтакте
Определение понятия
Экватором называют условную линию, которая проходит ровно по центру нашей планеты.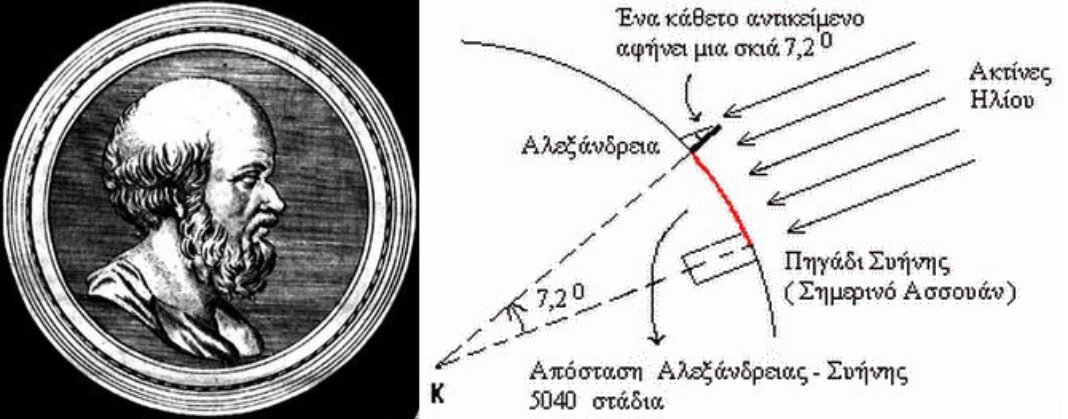 Географическая широта экватора — 0 градусов. Он служит точкой отсчета и дает возможность ученым проводить различные расчеты, о которых речь пойдет ниже. Экватор делит земной шар на две абсолютно равные части.
Географическая широта экватора — 0 градусов. Он служит точкой отсчета и дает возможность ученым проводить различные расчеты, о которых речь пойдет ниже. Экватор делит земной шар на две абсолютно равные части.
Важно! На территориях, по которым проходит экватор, ночь всегда равна дню, без отклонения даже на долю секунды.
Экваториальная зона получает наибольшее количество ультрафиолетовых лучей. Следовательно, чем дальше находится точка от условной линии, тем меньше тепла и света к ней поступает. Именно поэтому в районе условной линии зарегистрированы самые высокие температурные показатели.
Назначение
Для ведения различных расчетов ученым необходимо обозначить особые разделители планеты, которыми служат экватор, параллели и меридианы.
Эти условные линии позволяют определять положение различных объектов, дают возможность самолетам ориентироваться в , а кораблям — на .
Кроме того, именно эта полоса позволяет ученым разделать всю территорию планеты на климатические зоны или же пояса.
На самом деле длина окружности по экватору – это ключевая метрическая характеристика, которая берется к расчету. Она помогает не только в таких науках, как геодезия или элементарная география, но и в астрологии и астрономии.
На экваторе в данный момент расположены территории четырнадцати государств. Политическая карта мира постоянно меняется: страны появляются и исчезают, их границы могут расширяться либо сужаться. О каких государствах идет речь:
- Бразилия,
- Эквадор,
- Индонезия,
- Мальдивы и другие страны.
Какова длина окружности Земли по экватору
По самым точным подсчетам длина экватора в расчете на километры составляет 40075 км. А вот длина экватора Земли в милях достигает 24901 милю.
Что касается такого понятия, как радиус, то он бывает полярным и экваториальным. Размеры первого в километрах достигают 6356, а второго – 6378 км
Все территории, находящиеся в непосредственной близости к данной воображаемой линии, обладают теплым и влажным климатом.
Не случайно в этих районах жизнь просто бурлит. Именно здесь сосредоточено наибольшее разнообразие видов растений и животных.
Экваториальные леса считаются самыми густыми в мире, а некоторые из них и вовсе непроходимыми дебрями, даже с учетом всех современных научных достижений.
Осадки в экваториальной зоне практически ежедневные и очень обильные. Именно потому, все что находится и растет здесь, сияет самыми разнообразными красками.
На планете существует вулкан под названием Вольф. Так вот, дело в том, что он на данный момент действующий и что интересно, находится по обе стороны условной линии.
Внимание! Средняя годовая температура в данной зоне достигает 25-30 градусов по Цельсию.
Высокая температура круглый год делает страны, которые находятся в этом регионе, идеальным местом для отдыха для туристов. Особенно это касается популярных курортов, расположенных на Мальдивах, куда ежегодно приезжают миллионы отдыхающих со всех уголков мира.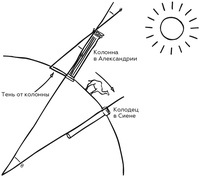
Важно! На экваторе расположен ледник. Он находиться на высоте 4690 метров на склоне вулкана под названием Каямбе.
Это удивительное место, особенно для . Дело в том, что скорость вращения Земли на этой условной линии достигает более 460 метров в секунду.
Скорость звука при этом достигает всего 330 метров в секунду. Следовательно, любые космические аппараты, которые запускаются отсюда, уже как бы стартуют со сверхзвуковой скоростью.
Мы рассказали о том, какова протяженность экватора, какую роль он отыгрывает в современной жизни человека. Целых три страны названы в его часть.
Экватор проходит. Точная длина экватора земли
> > > Сколько километров займет путь вокруг Земли?
Облететь вокруг Земли : расстояние в километрах для облета вокруг третьей планеты Солнечной системы, сфероидальная форма, округлость, длина экватора и меридиан.
Наша планета расположена на третьей позиции по приближенности от Солнца и считается самой большой из планет земной группы. Ее радиус – 6371 км, так что перед нами большой дом. Но можно ли измерить ее от конца в конец? Если вы решите полностью ее обойти, то сколько километров придется пропутешествовать, чтобы вернуться в изначальную точку? То есть, какова окружность Земли? Если коротко, то чуть больше 40075 км. Но в реальности все сложнее.
Ее радиус – 6371 км, так что перед нами большой дом. Но можно ли измерить ее от конца в конец? Если вы решите полностью ее обойти, то сколько километров придется пропутешествовать, чтобы вернуться в изначальную точку? То есть, какова окружность Земли? Если коротко, то чуть больше 40075 км. Но в реальности все сложнее.
Напомним, что форма планеты играет большую роль при вычислении ее размеров. Земля – приплюснутый сфероид. Если бы это была идеальная сфера, то вы бы могли отправиться в любую сторону и пройти единую дистанцию.
В нашем случае форма планеты Земля выпуклая на экваториальной линии, к чему привело быстрое осевое вращение. Ее охват в талии на 47 км превышает объем на полюсах.
В сферичность начали верить еще во времена Древней Греции. Особенно сильно на этом настаивал Пифагор. Все началось с активной торговли между странами. Стали отмечать, что некоторые звезды можно было наблюдать в разных местах, а удаленные на горизонте объекты намекали на планетарную изогнутость. Можете рассмотреть форму и внешний вид Земли на фото из космоса.
Можете рассмотреть форму и внешний вид Земли на фото из космоса.
В 240 г. до н. э. Эрасофен решил измерить земную окружность при помощи отслеживания углов теней, созданных Солнцем. При помощи тригонометрических вычислений он привел показатели с погрешностью в 2-20%.
В 17-м веке мы могли похвастаться более качественными приборами, и идея идеальной сферы начала рушиться. Впервые именно Исаак Ньютон предположил, что планета должна быть шире в экваториальной линии. Мы смогли подтвердить его идеи с появлением космических аппаратов на орбите и получением фото из космоса.
Экваториальный и меридиональный путь вокруг Земли
Сплюснутая сферичность отображается в экваториальной и меридиональной окружностях. Если вычисляем по экватору, то получим 40075.017 км, а вот между полюсами – 40007.86 км.
Это касается и вычисления радиуса. Если вы берете за основу показатели от центра к экваториальной линии, то радиус – 6378.1 км, а от центра к полюсу – 6356.8 км. Кажется, что разница не велика. Но это все же вычеркивает нашу планету со списков кандидатов в идеальные сферы. Теперь вы знаете все об окружности Земли, ее размерах и форме.
Кажется, что разница не велика. Но это все же вычеркивает нашу планету со списков кандидатов в идеальные сферы. Теперь вы знаете все об окружности Земли, ее размерах и форме.
Теперь вы знаете, что в сказочной Вселенной наших далеких предков Земля даже не напоминала шар. Жители Древнего Вавилона представляли ее в виде острова в океане. Египтянам она виделась вытянутой с севера на юг долиной, в центре которой был Египет. А древние китайцы одно время изображали Землю в виде прямоугольника… Вы улыбаетесь, представляя себе такую Землю, но часто ли вы задумывались о том, как люди догадались, что Земля — не безграничная плоскость или диск, плавающий в океане? Когда я спрашивал об этом ребят, то одни говорили, что о шарообразности Земли люди узнали после первых кругосветных путешествий, а другие вспоминали, что при появлении из-за горизонта корабля мы сначала видим мачты, а потом палубу. Доказывают ли такие и некоторые подобные им примеры, что Земля — шар? Вряд ли. Ведь объехать можно и вокруг. .. чемодана, а верхние части корабля появлялись бы и в том случае, если бы Земля имела форму полушария или была похожа, скажем, на… бревно. Подумайте об этом и постарайтесь изобразить сказанное на своих рисунках. Тогда вы поймете: приведенные примеры свидетельствуют лишь о том, что Земля изолирована в пространстве и, возможно, шарообразна.
.. чемодана, а верхние части корабля появлялись бы и в том случае, если бы Земля имела форму полушария или была похожа, скажем, на… бревно. Подумайте об этом и постарайтесь изобразить сказанное на своих рисунках. Тогда вы поймете: приведенные примеры свидетельствуют лишь о том, что Земля изолирована в пространстве и, возможно, шарообразна.
Как же узнали, что Земля — шар? Помогла, как я уже вам рассказал, Луна, а точнее — лунные затмения, во время которых на Луне всегда видна круглая тень Земли. Устройте небольшой «театр теней»: освещайте в темной комнате предметы разной формы (треугольник, тарелку, картофелину, мяч и т. д.) и замечайте, какая тень от них получается на экране или просто на стене. Убедитесь, что только мячик всегда образует на экране тень в виде круга. Итак, Луна помогла людям узнать, что Земля — это шар. К такому выводу ученые в Древней Греции (например, великий Аристотель) пришли еще в IV веке до нашей эры. Но еще очень долго «здравый смысл» человека не мог смириться с тем, что люди обитают на шаре. Даже представить себе не могли, как можно жить на «другой стороне» шара, ведь находящимся там «антиподам» пришлось бы все время ходить вниз головой… Но где бы ни находился человек на земном шаре, всюду брошенный вверх камень будет под действием силы притяжения Земли падать вниз, то есть на земную поверхность, а если бы было возможно, то и к центру Земли. На самом деле, людям, конечно, нигде, кроме цирков и спортивных залов, не приходится ходить вверх ногами и вниз головой. Они в любом месте Земли ходят нормально: земная поверхность у них под ногами, а небо над головой.
Даже представить себе не могли, как можно жить на «другой стороне» шара, ведь находящимся там «антиподам» пришлось бы все время ходить вниз головой… Но где бы ни находился человек на земном шаре, всюду брошенный вверх камень будет под действием силы притяжения Земли падать вниз, то есть на земную поверхность, а если бы было возможно, то и к центру Земли. На самом деле, людям, конечно, нигде, кроме цирков и спортивных залов, не приходится ходить вверх ногами и вниз головой. Они в любом месте Земли ходят нормально: земная поверхность у них под ногами, а небо над головой.
Около 250 года до нашей эры греческий ученый Эратосфен впервые довольно точно измерил земной шар. Эратосфен жил в Египте в городе Александрия. Он догадался сравнить высоту Солнца (или его угловое расстояние от точки над головой, зенита, которое так и называется — зенитное расстояние ) в один и тот же момент времени в двух городах — Александрии (на севере Египта) и Сиене (ныне Асуан, на юге Египта). Эратосфену было известно, что в день летнего солнцестояния (22 июня) Солнце в полдень освещает дно глубоких колодцев. Следовательно, в это время Солнце находится в зените. Но в Александрии в этот момент Солнце не бывает в зените, а отстоит от него на 7,2°. Такой результат Эратосфен получил, изменяя зенитное расстояние Солнца с помощью своего несложного угломерного инструмента — скафиса. Это просто вертикальный шест — гномон, укрепленный на дне чаши (полусферы). Скафис устанавливают так, чтобы гномон принимал строго вертикальное положение (направлен в зенит) Освещенный солнцем шест отбрасывает тень на разделенную на градусы внутреннюю поверхность скафиса. Так вот в полдень 22 июня в Сиене гномон тень не отбрасывает (Солнце в зените, его зенитное расстояние равно 0°), а в Александрии тень от гномона, как видно по шкале скафиса, отмечала деление 7,2°. Во времена Эратосфена расстояние от Александрии до Сиена считали равным 5000 греческих стадий (примерно 800 км). Зная все это, Эратосфен сопоставил дугу в 7,2° со всей окружностью в 360° градусов, а расстояние 5000 стадий — со всей окружностью земного шара (обозначим ее буквой X) в километрах. Тогда из пропорции
получилось, что Х = 250 000 стадий, или примерно 40 000 км (представьте себе, это так и есть!).
Если вам известно, что длина окружности равна 2πR, где R — радиус окружности (а π ~ 3,14), зная длину окружности земного шара, легко найти его радиус (R):
Замечательно, что Эратосфену удалось очень точно измерить Землю (ведь и сегодня считают, что средний радиус Земли 6371 км! ).
Но почему здесь упомянут средний радиус Земли, разве у шара не все радиусы одинаковы? Дело в том, что фигура Земли отличается от шара. Об этом ученые стали догадываться еще в XVIII веке, но какова в действительности Земля — сжата она у полюсов или у экватора — выяснить было трудно. Чтобы разобраться в этом, Французской академии наук пришлось снарядить две экспедиции. В 1735 году одна из них отправилась проводить астрономические и геодезические работы в Перу и занималась этим в экваториальном районе Земли около 10 лет, а другая, лапландская, трудилась в 1736-1737 годах вблизи Северного полярного круга. В результате выяснилось, что длина дуги одного градуса меридиана неодинакова у полюсов Земли и у ее экватора. Градус меридиана оказался у экватора длиннее, чем в высоких широтах (111,9 км и 110,6 км). Так может быть лишь в том случае, если Земля сжата у полюсов и представляет собой не шар, а тело, близкое по форме к сфероиду. У сфероида полярный радиус меньше экваториального (у земного сфероида полярный радиус короче экваториального почти на 21 км ).
Полезно знать, что великий Исаак Ньютон (1643-1727) предвосхитил результаты экспедиций: он сделал правильный вывод о том, что Земля сжата, потому наша планета вращается вокруг оси. Вообще, чем быстрее вращается планета, тем больше должно быть ее сжатие. Поэтому, например, сжатие Юпитера больше, чем Земли (Юпитер успевает сделать оборот вокруг оси по отношению к звездам за 9 ч 50 мин, а Земля только за 23 ч 56 мин).
И еще. Истинная фигура Земли очень сложна и отличается не только от шара, но и от сфероида вращения. Правда, в данном случае речь идет о разнице не в километры, а…метры! Подобным тщательным уточнением фигуры Земли ученые занимаются по сей день, используя для этой цели специально проводимые наблюдения с искусственных спутников Земли. Так что вполне возможно, что в решении задачи, за которую давным-давно взялся Эратосфен, когда-нибудь и вам придется принять участие. Это очень нужное людям дело.
Какой же лучше всего запомнить вам фигуру нашей планеты? Думаю, что пока достаточно, если вы будете представлять Землю в виде шара с надетым на него «дополнительным поясом», своего рода «нашлепкой» на область экватора. Такое искажение фигуры Земли, превращающее ее из шара в сфероид, имеет немалые последствия. В частности, из-за притяжения Луной «дополнительного пояса» земная ось примерно за 26 000 лет описывает в пространстве конус. Это движение земной оси называется прецессионным. В результате роль Полярной звезды, которая сейчас принадлежит α Малой Медведицы, поочередно играют некоторые другие звезды (ею в будущем станет, например, α Лиры — Вега). Кроме того, из-за такого (прецессионного ) движения земной оси знаки Зодиака все больше и больше не совпадают с соответствующими созвездиями. Другими словами, через 2000 лет после эпохи Птолемея «знак Рака», например, уже не совпадает с «созвездием Рака» и т. д. Впрочем, современные астрологи стараются не обращать на это внимания…
Всем известно, что планета Земля обладает круглой формой. Но какие размеры имеет планета, мало кто сможет сказать. Какова длина окружности земли по экваториальной линии или по меридиану? Чему равен диаметр Земли? Постараемся ответить на эти вопросы максимально подробно.
Прежде всего рассмотрим основные понятия , с которыми мы столкнёмся при ответе на вопрос о длине окружности Земли.
Что называют экватором? Это круговая линия, опоясывающая планету и проходящая через её центр. Экватор перпендикулярен оси земного вращения. Он удалён одинаково от одного и другого полюса. Экватор разделяет планету на два полушария, называемые Северным и Южным. Он играет большую роль в определении климатических поясов на планете. Чем ближе к экватору, тем климат жарче, ведь этим территориям достаётся больше солнечного света.
Что такое меридианы? Это такие линии, которые разделяют весь земной шар . Всего их 360, то есть каждая доля между ними равняется одному градусу. Меридианы пролегают через полюса планеты. По меридианам считают географическую долготу. Отсчёт начинается от нулевого меридиана, который также именуют Гринвичским, поскольку он пролегает через Гринвичскую обсерваторию в Англии. Долготу называют восточной или западной — в зависимости от того, в каком направлении идёт отсчёт.
В древние времена
Впервые окружность Земли измерили ещё в Древней Греции. Это был математик Эратосфен из города Сиены. В то время уже было известно , что планета обладает шаровидной формой. Эратосфен наблюдал за Солнцем и заметил, что светило в одно и то же время суток при наблюдении из Сиены расположено точно в зените, а в Александрии оно имеет угол отклонения.
Эти измерения производились Эратосфеном в день солнцестояния в летний период . Учёный измерил угол и обнаружил, что его величина составляет 1/50 часть от целой окружности, равняемой 360 градусам. Зная хорду угла в один градус, её нужно умножить на 360. Затем Эратосфен взял в качестве длины хорды интервал между двумя городами (Сиеной и Александрией), предположил, что они находятся на одном меридиане, произвёл расчёты и назвал цифру 252 тысячи стадий. Это число и означало окружность Земли.
Для того времени подобные измерения считались точными, ведь никаких способов измерить величину окружности Земли более точно, не существовало. Современные учёные признаются, что величина, посчитанная Эратосфеном, получилась довольно точной, несмотря на то, что:
- эти два города — Сиена и Александрия не расположены на одном меридиане;
- древний учёный получил цифру, исходя из дней пути верблюдов, а ведь ходили они не по идеально прямой линии;
- неизвестно, какой прибор применял учёный для измерения углов;
- непонятно, чему равнялся стадий, используемый Эратосфеном.
Тем не менее, учёные до сих пор придерживаются мнения о точности и уникальности метода Эратосфена, впервые измерившего диаметр Земли.
В Средние века
В XVII веке учёный из Голландии по имени Сибелиус изобрёл метод расчёта расстояний с помощью теодолитов. Это специальные приборы для измерения углов , используемые в геодезии. Метод Сибелиуса назвали триангуляцией, он заключался в построении треугольников и измерении их базисов.
Триангуляция практикуется и в наши дни. Учёные условно поделили всю поверхность земного шара на треугольные участки.
Российские исследования
Учёные из России в XIX веке также внесли свой вклад в вопрос измерения длины экватора. Исследования велись в Пулковской обсерватории. Руководил процессом В. Я Струве.
Если ранее Землю считали шаром идеальной формы, то позднее накопились факты, согласно которым сила земного притяжения уменьшалась от экватора к полюсам. Учёные пытались дать объяснение этому явлению . Было несколько теорий. Самой популярной из них считалась теория о сжатии Земли со стороны того и другого полюса.
Чтобы проверить верность гипотезы, Французская академия организовала экспедиции в 1735 и 1736 годах. В результате учёные измерили длину экваториального и полярного градуса в двух точках земного шара — в Перу и Лапландии. Выяснилось, что на экваторе градус имеет меньшую длину. Таким образом выяснили, что окружность Земли полярная меньше окружности по экватору на 21,4 километра.
В наши дни, после безошибочных и точных исследований было установлено, что длина окружности Земли по экватору равна 40075,7 км, а по меридиану – 40008,55 км.
Также известно, что:
- большая полуось Земли (радиус планеты по экватору) равен 6378245 метрам;
- полярный радиус, то есть малая полуось, — 6356863 метрам.
Учёные посчитали площадь поверхности Земли и определили цифру 510 миллионов кв. км. Суша занимает 29% от этой площади. Объем голубой планеты составляет 1083 миллиарда куб.21 тонн. Доля воды в этой величине составляет 7%.
Видео
Посмотрите интересный эксперимент, демонстрирующий, каким способом Эратосфену удалось высчитать окружность Земли.
А. Соколовский
Геометрия (древнегреческий: Гео -” земля “,-Metron” измерение “) первоначальное значение слова было- измерение Земли. Сегодня, геометрия имеет более широкий смысл: это раздел математики, занимающийся вопросами форм, размера, относительное положение в пространстве и свойства пространства. Геометрия возникла независимо в ряде ранних культур, как дисциплина практического знания, касающаяся длины, площади, объема, с элементами формальной математической науки.
Современные единицы измерения длиныСовременные единицы измерения, связанные с размерами нашей планеты.
МетрПервоначально метр был разработан, чтобы быть одной десятимиллионной (1/10, 000000) квадранта, расстояние между экватором и Северным полюсом. Иными словами, метр был определен как 1/10, 000000 расстояния от экватора Земли до Северного полюса измеряется по поверхности окружности (эллипсоида) Земли через долготу Парижа.
Используя данное значение, окружность идеально круглой Земле должна быть точно 40.000, 000 метров (или 40000 км). Но так как форма Земного шара не идеальная окружность а больше похожа на эллипсоид, то на сегодня официальная величина окружности Земли по линии долготы является 40,007.86 км.
Морская миляМорская миля в основе окружности планеты Земля. Если вы разделите окружность Земли на 360 градусов, а затем разделить каждый градус на 60 минут, вы получите 21600 минут дуги.
1 морская миля определяется как 1 минута дуги (окружности Земли). Эта единица измерения используется всеми странами для воздушных и морских перевозок. Использование 40,007.86 км по официальным данным окружности нашей планеты, мы получим значение морских миль в километры: 1,852 км (40,007.86 / 21600)
Древние единицы измерения показывают, что наши предки были в состоянии измерить размеры нашей планеты с идеальной точностью …
Измерение окружности ЗемлиВот простой способ измерения окружности (и диаметр) Земли, который скорее всего был использован древними астрономами .
Этот метод основан на понимании, что Земля, как Солнце и Луна, так же округлой формы и, что звезды находятся очень далеко от нашей планеты (за исключением Солнца), и они, вращаются вокруг определенной точки над северным горизонтом (Северный полюс).
Съемки на длинных выдержках показывают видимое движение звезд вокруг северного полюса.
Процесс измерения следует проводить в местах с хорошей видимостью неба, например, пустынной местности, в отдалении от населенных пунктов.
В одну ночь, 2 астронома в двух разных местах (А и Б), разделенных известным расстоянием (так будет легко измерить окружность Земли зная расстояние между точками расположенных в сотнях километрах друг от друга) , будут измерять угол над горизонтом (с помощью астролябии с отвесом дающим вертикальную линию) определенной звезды на её местоположение на ночном небе над горизонтом.
Идеальным выбором была бы Звезда , которая близко расположена к небесной оси Северного полюса (с указанием центра оси вращения Земли). В наши дни Полярная звезда будет лучшим выбором, однако тысячи лет назад, из-за прецессии (вращения оси Земли), Полярная звезда не находилась в районе Северного полюса (см. изображение ниже).
Прецессия- вращение оси Земли а течении 26 000 лет
Несмотря на то, что Полярная звезда, находится в пределах северного полюса в половине окружности , это не всегда было так. Ось вращения Земли претерпевает медленные колебания, в течении 26 000 лет, известное как прецессия, вокруг перпендикуляра к ее орбите вокруг Солнца, в результате чего положение вращательного полюса неба, вокруг которой все звезды движутся, постоянно меняется. Примерно во времена греческого поэта Гомера, звезда Kochab была звездой северного полюса. До неё, звездой северного полюса, была звезда Thuban, которая почти точно была на полюсе в 2700 г. до н.э. Она занимала лучшее положение, близкое к идеальному, чем звезда Kochab, примерно до 1900 г. до н.э., и поэтому являлась Полярной звездой во времена древних египтян . Другие яркие звезды, в том числе Alderamin, были в своё время полярными звёздами, и будут снова в отдаленном будущем. Звезда которая в настоящее время находится ближе к Южному полюсу является Sigma Octantis, которая едва видна невооруженным глазом и находится в 1 º 3 ‘от полюса (хотя она была ближе, на 45′ всего столетие назад). [Энциклопедия Науки ]
Тщательное наблюдение за ночным небом позволит выбрать яркую звезду с наиболее подходящими параметрами для сравнения местоположения звезды с измеренными параметрами той же звезды с другого места.
Нажмите, чтобы увеличить
Например, в 2600 г. до н.э. (см. изображение выше) в Египте возле плато Гизы, когда звезды Мицар и Kochab (которые вращаются каждую ночь вокруг Северного полюса) будут совпадать с вертикальной линией (отмечено линией отвеса),звезда Мицар (легко измерить высоту) будет идеальной звездой для сравнения её высоты в разных точках (А и B).
Так как звезды в космосе находятся слишком далеко от Земли используя эффект параллакса можно, зная расстояние между точками наблюдения D (база) и угол смещения α в радианах, определить расстояние до объекта:
для малых углов:
эффект параллакса: (смещение или разница в видимом положении объекта рассматривается по двум различным точкам наблюдения), единственной причиной изменения измеренного угла северной звезды является кривизна окружности Земли.
Угловой диаметр Луны и Солнца почти одинаковы: 0,5 градуса.
Наши древние астрономы / Священнослужители, жрецы / могли производить измерения положения северной звезды с точностью до 1 градуса. Используя такой измерительный прибор для измерения угла (астролябия), калиброванной в градусах, он мог получить достаточно точные результаты (возможно с 0,25% степенью точности).
Если один из наших астрономов делал это измерение от места расположения в точке(A) возле Гизы (30 0 С), звезда Мицар должна была появиться около 41 градусов над местным горизонтом. Если второй астроном был расположен в 120 морских милях к югу от *точки (А) (* измеряется в древних единицах длины, конечно), он бы заметил, что высота одного и того же объекта (звезды) 39 градусов (на 2 градуса ниже, чем высота измеряется в месте расположения).
Эти 2 простых измерений позволили бы древним астрономам произвести расчет окружности Земли с достаточно высокой точностью:
(360/2) * 120 морских миль = 21600 морских миль, откуда диаметр Земли может быть оценен как: 21600 морских миль / (22/7)(древние египетские оценки Pi) = = 6873 морских миль = 12728 км
Примечание: современные и точные данные: Окружность Земли между Северным и Южным полюсами:
21,602.6 морских миль = 24,859.82 миль (40008 км) Диаметр Земли на экваторе:6,887.7 морских миль = 7,926.28 км (12,756.1 км)
Экватор — это воображаемая круговая линия, которая опоясывает весь земной шар и проходит через центр Земли.
Линия экватора перпендикулярна оси вращения нашей планеты и находится на равном расстоянии от обоих полюсов.
Экватор: что это и зачем он нужен?
Итак, экватор — это воображаемая линия. Зачем серьезным ученым понадобилось воображать какие-то линии, очерчивающие Землю? Затем, что экватор, как и меридианы, параллели и прочие разделители планеты, которые существуют только в воображении и на бумаге, дают возможность производить подсчеты, ориентироваться в море, на суше и в воздухе, определять месторасположение различных объектов и т.д.
Экватор делит Землю на Северное и Южное полушария и служит началом отсчета географической широты: широта экватора равна 0 градусов. Он помогает ориентироваться в климатических поясах планеты. Приэкваториальная часть Земли получает самое большое количество солнечных лучей. Соответственно, чем дальше территории расположены от экваториальной линии и чем ближе они к полюсам, тем меньше солнца им достается.
Приэкваториальная область — это вечное лето, где воздух всегда горячий и очень влажный из-за постоянных испарений. На экваторе день всегда равен ночи. Солнце бывает в зените — светит вертикально вниз — только на экваторе и только дважды в год (в те дни, на которые приходятся дни равноденствий в большинстве географических поясов Земли).
Экватор проходит через 14 государств. Города, расположенные непосредственно на линии: Макапа (Бразилия), Кито (Эквадор), Накуру и Кисуму (Кения), Понтинак (остров Калиманта, Индонезия), Мбандака (Республика Конго), Кампала (столица Уганды).
Длина экватора
Экватор является самой длинной параллелью Земли. Его длина составляет 40.075 км. Первым, кто смог приблизительно вычислить протяженность экватора, был Эратосфен — древнегреческий астроном и математик. Для этого он измерял время, в течение которого солнечные лучи достигали дна глубокого колодца. Это помогло ему вычислить длину радиуса Земли и, соответственно, экватора благодаря формуле длины окружности.
Следует отметить, что Земля не является идеальной окружностью, поэтому радиус ее в разных частях немого отличается. К примеру, радиус на экваторе равен 6378,25 км, а радиус на полюсах — 6356,86 км. Поэтому для решения задач по вычислению длины экватора радиус принимают равным 6371 км.
Длина экватора является одной из ключевых метрических характеристик нашей планеты. Ее используют для вычислений не только в географии и геодезии, но в астрономии и астрологии.
— (лат., от aequus равный). Воображаемая линия, проводимая чрез центр земного шара и делящая его на два полушария: северное и южное; равноденственная линия. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ЭКВАТОР… … Словарь иностранных слов русского языка
экватор — а, м. equateur <лат. aequator уравнитель. 1. Воображаемая линия, проходящая вокруг земного шара на равном расстоянии от обоих полюсов и делящая земной шар (или небесную сферу) на Северное и Южное полушарие. БАС 1. Я под экватором, под… … Исторический словарь галлицизмов русского языка
ЭКВАТОР, название особых воображаемых окружностей. Земной экватор располагается посередине между северным и южным полюсами и делит земной шар на Северное и Южное полушария; он является нулевой линией, от которой отсчитывается географическая… … Научно-технический энциклопедический словарь
ЭКВАТОР, экватора, муж. (лат. aequator, букв. уравнитель). 1. Воображаемый круг, делящий земной шар или небесную сферу на два разных полушария южное и северное (геогр., астр.). Земной экватор. Небесный экватор. 2. Всякий срединный круг на шаре,… … Толковый словарь Ушакова
Действующее вещество ›› Амлодипин* + Лизиноприл* (Amlodipine* + Lisinopril*) Латинское название Ekvator АТХ: ›› C09BB АПФ ингибиторы в комбинации с блокаторами кальциевых каналов Фармакологические группы: Ингибиторы АПФ в комбинациях ›› Блокаторы … Словарь медицинских препаратов
Ягодицы, жопа, туалет, меридиан, живот, задница, зад Словарь русских синонимов. экватор сущ., кол во синонимов: 9 жара (23) живот … Словарь синонимов
— (от позднелатинского aequator уравнитель) (географическое), линия сечения земной поверхности плоскостью, проходящей через центр Земли, перпендикулярно оси ее вращения. Разделяет Северное и Южное полушария. Начало отсчета географической широты.… … Современная энциклопедия
— (от позднелат. aequator уравнитель) (в географии) линия сечения земной поверхности плоскостью, проходящей через центр Земли, перпендикулярно оси ее вращения. Делит земной шар на Сев. и Юж. полушария. Служит началом счета широты географической.… … Большой Энциклопедический словарь
ЭКВАТОР, а, м. Воображаемая линия пересечения земной поверхности плоскостью, проходящей через центр Земли, перпендикулярно к земной оси, делящая земной шар на Северное и Южное полушария. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949… … Толковый словарь Ожегова
М лат. равноденник, денственник; круг, подотвесный к оси мира и деляший мнимую небесную твердь и землю нашу на две равные половины: северную и южную; то небесный, а это земной равноденник, под которым дни и ночи всегда равны, а широта места нуль … Толковый словарь Даля
Небесный большой круг небесной сферы, которого плоскостьперпендикулярна к линии, соединяющей полюсы сферы, и параллельнаплоскости земного Э. Служит основной плоскостью для счета склонений ипрямых восхождений светил … Энциклопедия Брокгауза и Ефрона
Книги
- Экватор , Тавареш М.. «Экватор» — роман грандиозного драматизма и бешеной страстности, а его внешняя неспешность и подробность лишь еще более акцентируют неудержимое движение главного героя, молодого дипломата…
Земля круглая — это общеизвестно. А что мы еще знаем о ее форме и размерах? Кто из нас на память назовет, сколько километров содержит окружность Земли по экватору? А по меридиану? Кто в курсе, когда и каким образом была впервые измерена длина земной окружности? Между тем, эти факты чрезвычайно интересны.
Впервые окружность Земли была измерена по имени Эратосфен, жившим в городе Сиена. В то время ученые уже знали, что Земля по форме представляет собой шар. Наблюдая за небесным светилом в разное время суток, Эратосфен обратил внимание, что в одно и то же время солнце, будучи наблюдаемым из Сиены, располагается точно в зените, при этом в Александрии в тот же день и час отклоняется на некий угол.
Наблюдения проводились ежегодно в Измерив данный угол с помощью астрономических инструментов, ученый установил, что он составляет 1/50 часть полной окружности.
Как известно, полная окружность равняется 360 градусам. Таким образом, достаточно знать хорду угла в 1 градус (т. е. расстояние между точками на поверхности Земли, лежащими на лучах с угловым расстоянием между ними в 1 градус). Затем полученную величину следует умножить на 360.
Взяв за длину хорды расстояние между городами Александрией и Сиеной (5 тысяч египетских стадий) и предполагая, что эти города лежат на одном меридиане, Эратосфен произвел необходимые вычисления и назвал цифру, которой равнялась окружность Земли — 252 тысячи египетских стадий.
Для того времени это измерение было достаточно точным, ведь надежных методов измерения расстояния между городами не существовало, и путь от Сиены до Александрии измерялся скоростью движения каравана верблюдов.
Впоследствии ученые разных стран многократно измеряли и уточняли величину, которую составляет длина окружности Земли. В 17 веке голландский ученый по фамилии Сибелиус придумал способ измерять расстояния с помощью первых теодолитов — специальных геодезических приборов. Данный способ был назван триангуляцией и основан на построении большого количества треугольников с измерением базиса каждого из них.
Способ триангуляции применяется и поныне, вся земная поверхность виртуально поделена и расчерчена на большие треугольники.
Российские ученые тоже внесли свой вклад в эти исследования. В 19 веке окружность Земли измерялась в руководил исследованием В. Я. Струве.
До середины 17 века Землю считали шаром правильной формы. Но позже были накоплены некоторые факты, свидетельствующие об уменьшении силы земного притяжения от экватора к полюсу. Ученые ожесточенно дискутировали о причинах этого, самой правдоподобной была признана теория о сжатии Земли с полюсов.
Для проверки этой гипотезы Французской академией были организованы две независимые экспедиции (в 1735 и 1736 годах), которые измеряли длину экваториального и полярного градуса соответственно в Перу и в Лапландии.21 тонн. Из них около 7 % приходится на долю водных ресурсов.
| Кем был Эратосфен? Эратосфен (276 г. до н.э. – 194 г. до н.э.) был греческим математиком, географом и астрономом. Он родился в Кирене (ныне Ливия) и умер в Птолемеевской Александрии. Он известен тем, что разработал систему карт, основанную на линиях широты и долготы, и вычислил размер Земли. Эратосфен учился в Александрии и несколько лет в Афинах. В 236 г. до н.э. он был назначен Птолемеем III Эвергетом I библиотекарем Александрийской библиотеки.Он сделал несколько важных вкладов в математику и науку и был хорошим другом Архимеда. Около 255 г. до н.э. он изобрел армиллярную сферу (астрономический инструмент для определения положения на небе), которая широко использовалась до изобретения оррерия в 18 веке. Около 200 г. до н.э. считается, что Эратосфен придумал или принял слово «география», описательное исследование Земли. Другие работы Эратосфена включают:
Детали своего метода он опубликовал в работе Об измерении Земли , которая, к сожалению, была утеряна.О его методе мы знаем косвенно от других авторов. Прежде чем мы начнем несколько определений: Тропик Рака — это один из пяти основных кругов широты, которые отмечают на картах Земли. Тропик Рака в настоящее время находится на широте 23° 26′ 22″ к северу от экватора. Местный полдень — это время, когда солнце находится высоко в небе и может сильно отличаться от 12:00 на часах. Солнцестояние — это астрономическое событие, которое происходит два раза в год, когда наклон оси Земли наиболее наклонен к Солнцу или от него.В северном полушарии максимальное наклонение к солнцу приходится на 21 июня (летнее солнцестояние), а максимальное наклонение в сторону — на 21 декабря (зимнее солнцестояние). Для южного полушария зимнее и летнее солнцестояние чередуются. Для нашего эксперимента важен тот факт, что в день летнего солнцестояния, в полдень по местному времени, солнечные лучи проходят прямо над головой (под прямым углом к земле) на Тропике Рака. Очень интересно, что измерение расстояния между Александрией и Сиеной основано на предполагаемой средней скорости каравана верблюдов, прошедшего это расстояние(!).Верблюды прошли это расстояние много раз, чтобы получить среднюю оценку расстояния. Правда ли это, не ясно. Эратосфен измерил в свой местный полдень в Александрии угол возвышения солнца в день летнего солнцестояния (21 июня). Эратосфен использовал местный полдень и никакое другое время суток, поскольку в местный полдень все соответствующие места и солнечные лучи помещаются в одну и ту же воображаемую плоскость, что позволяет использовать простую геометрию для его расчетов.Чтобы повторить эксперимент Эратосфена, вам придется сделать то же самое. Сначала рассчитайте местный полдень, потому что он может сильно отличаться от 12:00 на часах. Есть несколько способов вычислить его точное появление. По сути, местный полдень находится на полпути между восходом и закатом. Вы можете узнать время восхода и захода солнца на 21 июня в местной газете или по этой ссылке: http://aa.usno.navy.mil…, которая также рассчитывает местный полдень (проход солнца). Вы также можете получить его самостоятельно, используя солнечные часы или узнать, когда тень самая короткая около полудня. 21 июня установите вертикальную прямую палку или шест около 1 метра с помощью столярного уровня и измерьте длину тени, которую он отбрасывает в местный полдень. С помощью простой тригонометрии вы можете получить угол возвышения солнца. Вы также можете получить угол без тригонометрии, пропорционально нарисовав палку и тень и измерив их транспортиром. Вы можете сравнить свои результаты с веб-приложением, например: http://www.jgiesen.de/azimuth, но будьте осторожны, чтобы использовать его правильно (вставьте правильный часовой пояс, местный полдень, координаты, дату и убедитесь, что выпадающее меню указывает на высоту). После того, как вы получите угол возвышения солнца, очень легко вычислить зенитный угол, вычитая его из 90°, как это делал Эратосфен. Теперь вам нужно будет измерить расстояние от вашего местоположения до линии широты Тропика Рака — не верблюжьими караванами, конечно, способом Эратосфена. Вы можете использовать карту относительно крупного масштаба, но учтите, что карты имеют тенденцию искажать расстояние, и лучший вариант — использовать глобус.Расстояние от вашего местоположения до Тропика Рака следует измерять с севера на юг. Другими словами, линия расстояния должна пересекать Тропик Рака под прямым углом. Для этого также есть веб-калькуляторы: https://web.archive.org…. Теперь легко вычислить окружность Земли по следующей формуле: Точно так же вы можете провести этот эксперимент в день зимнего солнцестояния, которое происходит примерно 21 декабря, но вам придется измерять расстояние от тропика Козерога, а не от тропика Рака, потому что в этот день солнце достигает своего наивысшего градуса. возвышения на тропике Козерога (23° 26′ 22″ к югу от экватора). Также можно провести этот эксперимент с двумя равноденствиями, которые происходят 20 марта и 23 сентября каждого года, когда солнце пересекает экватор в местный полдень в эти дни, и солнечные лучи проходят прямо над экватором под прямым углом. наземь. Но вместо того, чтобы измерять расстояние от Тропика Рака или Тропика Козерога, вам придется измерять его от экватора. Есть еще один вариант, и вы можете провести этот эксперимент в любой другой день года, в полдень по местному времени, но у вас должен быть напарник, расположенный на вашей долготе и желающий измерить высоту солнца в это же время.Имейте в виду, что вам придется быть немного осторожным, правильно обращаясь с углами солнца, полученными в этом случае. В любой день солнце достигает своего наивысшего положения в полдень на некоторой широте. Отсюда ясно, что если два рассматриваемых места расположены на одной стороне этой широты (к северу или югу), то тени будут отбрасываться в одном направлении и полученные углы следует вычесть друг из друга, тогда как если места расположены на разных сторонах этой широты тени будут отбрасываться в разные стороны (на юг или на север) и углы должны складываться. Дополнительная литература СсылкиПроект «Полдень» — Технологический институт Стивенса Как измерить размер Земли — Астрономия в режиме онлайн Эратосфен находит диаметр Земли! — Деннис П. Донован, Университет Райса Эратосфен из Кирены — Майкл Лаханас Измерение размера Земли — Д. Трапп, т.е. физика Диаметр Земли по Эратосфену — Джон Х. Линхард Эратосфен из Кирены — MacTutor Модель о Оценка Эратосфеном радиуса и окружности Земли (Java-апплет) Древние измерения окружности Земли — Ливио К.Стеккини Книги Библиотекарь, измеривший Землю, Кэтрин Ласки, Кевин Хоукс Книги                     |
Эратосфен вычисляет окружность Земли
ОбзорИзмерение расстояния становилось все более важным для древних и классических цивилизаций по мере расширения их территориальных и культурных горизонтов.Используя элегантные математические рассуждения и ограниченные эмпирические измерения, примерно в 240 г. до н. э. Эратосфен из Кирены (276–194 гг. до н. э.) точно измерил окружность Земли. Этот подвиг был больше, чем просто научное достижение. Расчет Эратосфена и другие подобные ему внесли свой вклад в область геодезии (изучение формы и размера Земли) и помогли стимулировать последующие исследования и расширение. По иронии судьбы, столетия спустя греческий математик и астроном Клавдий Птолемей отверг математические расчеты Эратосфена, которые, в сочетании с другими допущенными им математическими ошибками, дали математическую оценку меньшей Земли, которая, хотя и была ошибочной, сделала более протяженной морские путешествия и исследования кажутся более осуществимыми.
ИсторияЭратосфен, служивший при Птолемее III и обучавший Птолемея IV, был третьим библиотекарем в Великой библиотеке в Александрии. Этот пост имел большое значение, потому что библиотека была местом обучения и учебы в древнем мире. Например, с кораблей, заходящих в порт Александрии, были скопированы их письменные документы для включения в библиотеку. С годами коллекция библиотеки разрослась до сотен тысяч папирусов и свитков, содержащих большую часть интеллектуального богатства древнего мира.
Помимо управления сбором, чтением и расшифровкой документов, Эратосфен изучал и писал на многие темы. Хотя все его сочинения и расчеты утеряны, мы знаем из работ других греческих ученых, что Эратосфен изучал фундаментальные понятия и определения арифметики и геометрии. Одним из его открытий было «решето Эратосфена» — метод определения простых чисел, который используется до сих пор. Эратосфен также составил звездный каталог, в который вошли сотни звезд, разработал удивительно современный календарь и попытался установить дату исторических событий, начиная с осады Трои.Его способности были настолько разнообразны, что современники, по-видимому, называли его «бета» — вторая буква греческого алфавита — подразумевая, что он хорошо разбирался в слишком многих научных дисциплинах, чтобы быть лучшим в любой из них.
Эратосфен наиболее известен своим удивительно точным и гениальным вычислением окружности Земли. Хотя его собственные заметки о методе вычислений были утеряны, есть дразнящие ссылки на них в работах Страбона и других ученых, в том числе в «Синагоге » Паппа или «Собрание », сборнике и кратком изложении работ по математике. физике, астрономии и географии, изданной в третьем веке до нашей эры.д. Помимо точной оценки окружности Земли, основанной на наблюдаемых различиях в положении Солнца в зените, Эратосфен также сделал удивительно точное измерение наклона земной оси.
limpactОчевидно, вдохновленный наблюдениями в свитках, которые он просматривал как библиотекарь, Эратосфен заметил тонкие различия в описаниях теней, отбрасываемых полуденным летним солнцем. В частности, он прочитал о наблюдении, сделанном недалеко от Сиены (недалеко от современного Асуана, Египет), что в полдень в день летнего солнцестояния Солнце светило прямо в глубокий колодец и что вертикальные столбы не отбрасывали тени.Напротив, Эратосфен заметил, что в Александрии в тот же день полуденное Солнце отбрасывало тень на обе колонны и палку, воткнутую в землю.
Основываясь на своих исследованиях астрономии и геометрии, Эратосфен предположил, что Солнце находилось на таком большом расстоянии, что его лучи были практически параллельны Земле к тому времени, когда они достигли ее. Хотя расчетные расстояния до Солнца и Луны, подтвержденные измерениями и оценками, сделанными во время лунных затмений, были слишком малы, предположения Эратосфена оказались в основном верными.Предполагая параллельное падение световых лучей, ему нужно было определить разницу между углами теней, отбрасываемых на Сиену и Александрию в одно и то же время в один и тот же день. Кроме того, ему нужно было рассчитать расстояние между двумя городами.
С точки зрения современной науки кажется интуитивно понятным, что Эратосфен пытался определить точные значения углов и расстояний, необходимых для выполнения его вычислений. Однако в древнем мире этот тип объективной науки сильно отличался от господствующей научной традиции, которая придерживалась более философского или математического подхода к проблемам.Более того, вера Эратосфена в то, что Земля круглая, сама по себе вызывала споры.
Для выполнения своих расчетов Эратосфен определил угловую разницу между тенями в Сиене и Александрии примерно в 7°. Он определил расстояние до Сиены примерно в 500 миль (805 км), возможно, как утверждают некоторые легенды, заплатив бегуну за то, чтобы он прошел его. Эратосфен рассудил, что отношение угловой разности теней к числу градусов в окружности (360°) должно равняться отношению расстояния к окружности Земли.Полученная оценка, около 25 000 миль (40 234 км), удивительно точна.
В своих вычислениях Эратосфен измерил расстояние в стадий, единиц измерения, основанных на греческом беге, или стадий. Эти юниты варьировались от места к месту в древнем мире. Эратосфен почти наверняка использовал аттический стадион, который был основан на одном контуре трассы на афинском стадионе, 606 футов 10 дюймов (185 м) или чуть более десятой мили. Используя эту меру, Эратосфен смог вычислить окружность, которая отличается всего на несколько процентов от современного значения в 24 902 мили (40 076 км) на экваторе.Необходимо указать, что это окружность на экваторе , потому что Земля на самом деле представляет собой сплюснутую (слегка сжатую) сферу с выпуклостью посередине, что делает окружность на экваторе больше, чем если бы она была измерена вокруг полюсов. .
Теории и расчеты Эратосфена были опубликованы в его Географии, названии, которое отражает первое известное использование термина, что означает «писать о Земле». Хотя его расчеты оспаривались в его время, они позволили разработать карты и глобусы, которые оставались одними из самых точных на протяжении более тысячи лет.Это, в свою очередь, вызвало интерес к географии и геодезии и стимулировало региональные морские исследования с использованием только самых примитивных навигационных инструментов. Более того, работа Эратосфена помогла укрепить веру в круглую Землю и продвинула раннюю теорию о том, что относительная теплота или прохлада климата местности определяется ее расстоянием от экватора. География также поддерживал концепцию антиподов — неоткрытых земель и народов на «другой стороне» мира.
Работа Эратосфена, возможно, вдохновила греческого астронома и географа Клавдия Птолемея на собственное определение окружности Земли во втором веке нашей эры.д. К сожалению, он отверг расчеты Эратосфена и заменил ошибочными значениями географа Посидония (130-50 гг. до н. э.). В этой системе градус покрывал то, что теперь равнялось бы примерно 50 милям (80 км), вместо более точной оценки Эратосфена примерно в 70 миль (113 км) на градус на экваторе. Хотя Птолемей пошел дальше Эратосфена в своих расчетах, измерив движение теней за различные промежутки времени, его неточные предположения и измерения исказили его окончательные значения до менее точных и гораздо меньших размеров окружности, примерно 16 000 миль (25 750 км).
Птолемей опубликовал эти неточные числа в своем Альмагесте, , написанном около н.э. 150 и оставался самым влиятельным в мире трудом по астрономии и географии на протяжении всего Средневековья. Широко разрекламированная ошибка Птолемея о том, что Земля меньше, в конечном счете, возможность выжить при переходе на запад в Индию кажется более вероятной. Хотя этот пункт оспаривается многими учеными, ошибка Птолемея, возможно, сыграла свою роль в решении Колумба искать западный путь в Индию.
К. ЛИ ЛЕРНЕР
Дополнительная литератураКлагетт, Маршалл. Греческая наука в древности. Абеляр-Шуман, Нью-Йорк, 1955.
Дутка, Дж. «Пересмотр измерения Земли Эратосфеном». Архив истории точных наук 46(1), 1993:1. 55-66.
Фаулер, Д. Х. Математика Академии Платона: новая реконструкция . Оксфорд: Clarendon Press; Нью-Йорк: Издательство Оксфордского университета, 1987.
Гольдштейн, Б.Р. «Эратосфен об измерении Земли». Historia Mathematica 11 (4), 1984: 411-416.
Хит, Т. Л. История греческой математики. Oxford: The Clarendon Press, 1921.
Наука и ее времена: понимание социальной значимости научных открытий
Окружность Земли, Эратосфен, астрономия, солнцестояния, равноденствия, широта, наука и математика
Эратосфенаг. Эратосфен, греческий географ (около 276–194 гг. до н. э.), сделал удивительно точную оценку окружности Земли.
В большой библиотеке в Александрии, Египет, он прочитал, что существует глубокий вертикальный колодец недалеко от Сиены, на юге Египта, который полностью освещается до дна колодца солнцем в полдень раз в году: летнее солнцестояние . Эратосфен понял, что если солнце находится прямо над головой, его лучи будут падать прямо в колодец и освещать дно.
Солнцестояние — это один из двух периодов в году: Летнее Солнцестояние и Зимнее Солнцестояние .Солнцестояние 90 228 – 90 227, когда солнце находится в самой высокой или самой низкой точке неба в полдень. Что составляет самые длинные и самые короткие дни (примерно 22 июня и 20 декабря). Вызвано тем, что движение Солнца является самым длинным или самым коротким путем по небу.
Тропик Рака находится к северу от экватора на 23,4372° широты. Это широта, на которой один раз в год солнце находится прямо над головой в -й день летнего солнцестояния -го года.
Тропик Козерога находится к югу от экватора на -23.4372° широты. Это широта, на которой один раз в год солнце находится прямо над головой в -й день зимнего солнцестояния -го года.
Равноденствие — это день (два раза в год), когда Солнце пересекает небесный экватор, когда день и ночь имеют одинаковую продолжительность (примерно 22 сентября и 20 марта) .
Эратосфен понял движение Солнца по небу. Он знал, что в Александрии, Египет, солнце не было прямо над головой в полдень 90 227 летнего солнцестояния 90 228, потому что вертикальные объекты отбрасывали там тень.Он знал, что Александрия находилась в 5000 стадиях почти прямо к северу от Сиены в Египте. И он достаточно хорошо разбирался в геометрии, чтобы использовать эту информацию для расчета окружности Земли.
Предположения :
- Он предполагал : Земля была круглой (извините Колумб).
- Солнечные лучи шли по прямой. и
- Лучи в обоих местах были практически параллельны.
Данные :
Он установил вертикальный столб в Александрии и измерил угол его тени в день летнего солнцестояния (7.2 градуса), когда колодец в Сиене был полностью освещен солнцем, что означало, что солнце находилось над колодцем вертикально.
Рассуждение :
- Из геометрии Эратосфен знал, что угол тени в Сиене равен углу в центре земли между Сиеной и Александрией. Прямые, пересекающие параллельные прямые, будут иметь одинаковые углы.
- Дуга угла такого размера была, следовательно, 1/50 окружности (360° / 7,2° ≈ 50). На основе предположения о круглой земле на 360°.
- Расстояние между Сиеной и Александрией было 5000 стадий.
- Итак, он умножил 5000 на 50, чтобы найти окружность Земли.
- Его результат, 250 000 стадий (около 46 250 км), довольно близок к современным измерениям (40 075 км на экваторе).
Источник Исследование Земли , AGI, 1970, глава 3, с. 66.
Формула, использованная Эратосфеном :
(360°/угол тени вертикального стержня) * расстояние от Сиены до Александрии = Окружность Земли
Формула, по которой можно рассчитать длину окружности Земли .
(360°/угол тени вертикального стержня) * расстояние от Сиены = Окружность Земли
Сиена расположена на Тропике Рака (23,5° северной широты) или рядом с ним, где Солнце будет находиться над головой в день летнего солнцестояния.
- Солнце находится прямо над тропиком Рака (23,5° северной широты) в день летнего солнцестояния,
- Над головой над тропиком Козерога (23,5° южной широты) в день зимнего солнцестояния
- Над головой на экваторе (0° северной широты) в дни весеннего и осеннего равноденствий.
Используйте эти идеи, чтобы определить окружность Земли.
- В день летнего солнцестояния поместите вертикальную палочку в земля.
- Когда солнце достигает своей высшей вертикали согласие на день (солнечный полдень, поэтому длина тени будет самой короткой), измерьте угол тени (угол тени вертикальной палочки).
(360° / угол тени вертикального джойстика) * расстояние от тропика Рака = окружность Земли
В день равноденствия вертикаль лучи солнца проходят прямо над экватором.Как бы вы рассчитали окружность Земли, используя тот же метод, во время равноденствия?
Как насчет того, чтобы поделиться измерением угла тени с другими глобус. Свяжитесь с другими, которые захотят собрать те же данные и обменяйте его, возможно, используя следующий формат.
Дата измерения ____________
Ваше измерение угла тени ____________ градусов
Ваше местонахождение город ____________________________________
Страна вашего местонахождения ________________________________
Ваша широта _________________________________________
Ваша долгота __________________________________________
Если у вас есть разные наборы данных, скомпилируйте их и сравните различные места и ракурсы.
Оригинальная идея Джима Мейнке (сентябрь 1994 г.) Лейквуд Средняя школа в Кливленде.
Заметки доктора Роберта Суитленда
[Домашняя страница: thehob.net]
Измерение окружности Земли с помощью тени
Ключевые понятия
Математика
Геометрия
Окружность
Уголки
Экватор Земли
Введение
Если бы вы хотели измерить окружность Земли, какой длины должна была бы быть ваша рулетка? Вам нужно будет пройти весь мир, чтобы найти ответ? Как вы думаете, вы можете сделать это с помощью всего лишь метра в одном месте? Попробуйте этот проект, чтобы узнать!
Однако, прежде чем вы начнете, важно отметить, что этот проект будет работать только в течение двух недель после весеннего или осеннего равноденствия (обычно около 20 марта и 23 сентября соответственно).
Фон
Какова окружность Земли? В век современных технологий ученым может показаться, что на этот вопрос легко ответить с помощью таких инструментов, как спутники и GPS, а вам будет еще проще найти ответ в Интернете. Может показаться, что вы не сможете измерить окружность нашей планеты, используя только линейку. Однако греческий математик Эратосфен смог оценить окружность Земли более 2000 лет назад без помощи каких-либо современных технологий.Как? Он использовал немного знаний о геометрии!
В то время Эратосфен находился в городе Александрии в Египте. Он читал, что в городе под названием Сиена к югу от Александрии в определенный день года в полдень на дне глубокого колодца было видно отражение солнца. Это означало, что солнце должно быть прямо над головой. (Другой способ думать об этом состоит в том, что совершенно вертикальные объекты не будут отбрасывать тени.) В тот же день в Александрии вертикальный объект действительно отбрасывал тень. Используя геометрию, он вычислил окружность Земли, основываясь на нескольких фактах, которые знал (и на одном не знал):
.- Он знал, что в окружности 360 градусов.
- Он мог измерить угол тени, отбрасываемой высоким объектом в Александрии.
- Он знал сухопутное расстояние между Александрией и Сиеной. (Два города были достаточно близко, чтобы расстояние можно было измерить пешком.)
- Единственная неизвестная величина в уравнении — это окружность Земли!
Результирующее уравнение:
Угол тени в Александрии / 360 градусов = Расстояние между Александрией и Сиеной/ Окружность Земли
В этом проекте вы сделаете этот расчет самостоятельно, измерив угол, образованный тенью метра в вашем местоположении.Вам нужно будет выполнить тест в дни осеннего или весеннего равноденствия, когда солнце находится прямо над головой на экваторе Земли. Затем вы можете найти расстояние между вашим городом и экватором и использовать то же уравнение, которое Эратосфен использовал для расчета окружности Земли. Как вы думаете, насколько ваш результат будет близок к «реальному» значению?
Существует геометрическое правило об углах, образованных прямой, пересекающей две параллельные прямые. Эратосфен предположил, что Солнце было достаточно далеко от нашей планеты, чтобы его лучи были фактически параллельны, когда они достигли Земли.Это подсказало ему, что угол тени, измеренный им в Александрии, равен углу между Александрией и Сиеной, измеренному в центре Земли. Если это звучит запутанно, не волнуйтесь! Гораздо легче визуализировать с картинкой. См. ссылки в разделе «Дополнительно для изучения» для некоторых полезных диаграмм и более подробного объяснения используемой геометрии.
Материалы
- Солнечный день в дни весеннего или осеннего равноденствия или вблизи них (около 20 марта или 23 сентября соответственно)
- Плоская, ровная площадка, которая будет находиться под прямыми солнечными лучами около полудня
- Измерительный стержень
- Вызовите добровольца и помогите держать измерительную рейку, пока вы проводите измерения (Или, если вы проводите тест в одиночку, вы можете использовать ведро с песком или грязью, чтобы вставить один конец измерительной рейки, чтобы держать ее в вертикальном положении.)
- Палка или камень, чтобы отметить местонахождение тени
- Калькулятор
- Транспортир
- Длинная веревка
- Дополнительно: отвес (вы можете сделать его, привязав небольшой груз к концу веревки) или столбик уровня, чтобы убедиться, что измерительная рейка стоит вертикально
Подготовка
- Посмотрите местный прогноз погоды за несколько дней и выберите день, когда около полудня будет преимущественно солнечно.(У вас есть окно в несколько недель, чтобы выполнить этот проект, так что не расстраивайтесь, если окажется пасмурно! Вы можете попробовать еще раз.)
- Найдите время восхода и захода солнца для этого дня в местной газете или на веб-сайте календаря, погоды или астрономии. Вам нужно будет рассчитать «солнечный полдень», время ровно посередине между восходом и заходом солнца, когда солнце будет прямо над головой. Вероятно, это будет не ровно 12 часов дня.
- Выйдите на улицу и подготовьте свои материалы примерно за 10 минут до солнечного полудня, чтобы все было готово.
Процедура
- Установите измерительную рейку вертикально на открытом солнечном месте незадолго до полудня.
- Если у вас есть волонтер, попросите его подержать измерительную линейку. В противном случае закопайте один конец измерительной линейки в ведро с песком или землей, чтобы она оставалась в вертикальном положении.
- Если у вас есть уровень или отвес, используйте его, чтобы убедиться, что измерительная рейка стоит строго вертикально. В противном случае сделайте все возможное, чтобы увидеть это на глаз.
- В солнечный полдень отметьте конец тени измерительной линейки на земле палкой или камнем.
- Проведите воображаемую линию между вершиной измерительной линейки и кончиком ее тени. Ваша цель состоит в том, чтобы измерить угол между этой линией и измерительной линейкой. Попросите вашего добровольца натянуть кусок веревки между верхушкой измерительной линейки и концом ее тени.
- С помощью транспортира измерьте угол между струной и измерительной линейкой в градусах. Запишите этот угол.
- Посмотрите расстояние между вашим городом и экватором.
- Рассчитайте окружность Земли, используя это уравнение:
Окружность = 360 x расстояние между вашим городом и экватором / измеренный угол тени
- Какое значение вы получите? Насколько близко ваш ответ к истинной окружности Земли (см. раздел «Наблюдения и результаты»)?
- Дополнительно: Попробуйте повторить тест в разные дни до, во время и после равноденствия; или в разное время до, в и после солнечного полудня. Насколько изменится точность вашего ответа?
- Дополнительно: Попросите друга или члена семьи в другом городе пройти тест в тот же день и сравнить свои результаты. Вы получаете тот же ответ?
Наблюдения и результаты
В 200 г. до н.э. Эратосфен оценил окружность Земли примерно в 46 250 километров (28 735 миль). Сегодня мы знаем, что окружность нашей планеты составляет примерно 40 000 километров (24 850 миль).Неплохо для оценки более чем 2000-летней давности, сделанной без использования современных технологий! В зависимости от погрешности ваших измерений — например, от точного дня и времени проведения теста, от того, насколько точно вы смогли измерить угол или длину тени и насколько точно вы измерили расстояние между вашим городом и экватором — вы должны быть в состоянии рассчитать значение, довольно близкое к 40 000 километров (в пределах нескольких сотен или, может быть, нескольких тысяч). Все не выходя из собственного двора!
Еще для изучения
Вычисление окружности Земли, от Science Buddies
Урок: измерение окружности Земли, от eGFI
Углы, параллельные линии и сечения, от Math Planet
Научные занятия для всех возрастов!, от Science Buddies
Это задание было предложено вам в сотрудничестве с Science Buddies
История жеод: Учебное пособие по глобальному позиционированию
На протяжении всей истории ученые и философы спорили о форме Земли.К 500 г. до н.э. большинство ученых думали, что Земля имеет полностью сферическую форму. Греческий философ Аристотель (384-322 до н.э.) считается первым человеком, который попытался вычислить размер Земли, определив ее окружность (длину вокруг экватора). измерение, равное примерно 600 футам). С одной милей, равной 5280 футов, Аристотель рассчитал, что расстояние вокруг Земли составляет около 45 500 миль.
Около 250 г. до н.э.э., другой греческий философ, Эратосфен, измерил окружность Земли, используя следующее уравнение:
(360° ÷ θ) х (с)
В этом расчете (s) — это расстояние между двумя точками, лежащими на севере и юге друг от друга на поверхности Земли. Если бы вы провели линию от каждой из этих точек к центру Земли, угол, образованный между ними, был бы равен θ.
На этой иллюстрации показано, как Эратосфен вычислил окружность Земли.В полдень летнего солнцестояния Эратосфен измерил длину тени, отбрасываемой колонной известной высоты в Александрии. С этими двумя длинами он мог найти угол между ними (θ). Если бы длина тени и высота колонны (h) были пропорциональны расстоянию между Александрией и Сиеной (s = 4400 стадий) и радиусу Земли, то, вычислив угол на колонне (θ), он вычислял тот же самый угол, образованный в центре Земли (θ). Уравнение, которое он использовал для определения окружности Земли [(360° ÷ θ) x (s)], отражает эту теорию.
Очевидно, что Эратосфен не мог добраться до центра Земли, поэтому он получил измерение угла с помощью лучей солнца. В полдень самого длинного дня в году, летнего солнцестояния, солнце светило прямо в глубокий колодец в Сиене (ныне Асуан, Египет), не отбрасывая тени.
В то же время в Александрии, Египет, он обнаружил, что солнце отбрасывает тень, равную примерно 1/50 окружности или 7,12°. Эратосфен объединил это измерение с расстоянием между Сиеной и Александрией, составляющим около 4400 стадий.
Если мы подставим эти числа в приведенное выше уравнение, мы получим: (360°÷ 7,12°), что равно 50; а 50 х 4400 равняется 220 000 стадий, или около 25 000 миль. Принятое измерение окружности Земли сегодня составляет около 24 855 миль. Учитывая простые инструменты и технологии, которые были в распоряжении Эратосфена более 2000 лет назад, его расчеты были весьма замечательными.
Расчеты Эратосфена основывались на двух предположениях. Во-первых, Сиена лежала на Тропике Рака.Второе предположение заключалось в том, что Александрия лежала к северу от Сиены точно на той же линии долготы (линия меридиана). В полдень во время летнего солнцестояния лучи солнца всегда светят прямо перпендикулярно поверхности Земли, но только на тропик Рака. Если Александрия находилась точно к северу от Сиены, то Эратосфен мог бы утверждать, что ключевые измерения, которые он использовал — длина тени колонны в Александрии и расстояние между Александрией и Сиеной — были географически правильными.
По мере развития технологий ученые и геодезисты начали использовать различные методы измерения расстояния. В 16—17 вв. стала широко применяться триангуляция. Триангуляция — это метод определения положения фиксированной точки путем измерения углов к ней от двух других фиксированных точек, находящихся на известном расстоянии друг от друга. Триангуляция легла в основу многих национальных обследований. К концу 19 века основные сети триангуляции охватывали Соединенные Штаты, Индию, Великобританию и большую часть Европы.
«Во второй половине 17 века были основаны Королевское общество в Лондоне и Королевская академия наук в Париже. Вскоре они вступили в битву за определение формы Земли. Французы утверждали, что Земля была вытянутой или имела форму яйца. Англичане, используя универсальную теорию гравитации сэра Исаака Ньютона и знание того, что Земля вращается вокруг своей оси, думали, что Земля сплющена или сплющена у полюсов. Чтобы доказать свою идею, Академия в Париже организовала две экспедиции, одну в Перу (ныне Эквадор) на экваторе, а другую на границу Швеции и Финляндии в северном полушарии.Их цель состояла в том, чтобы измерить кривизну Земли с севера на юг на широте каждого места и определить, чье представление о форме Земли было правильным. Усилия Академии доказали, что Ньютон был прав. Земля сплющена в форме сплющенного шара.
За последние 100 лет геодезия и ее приложения значительно продвинулись вперед. 20-й век принес космические технологии, сделавшие геодезические измерения чрезвычайно точными. Сегодня спутники NAVSTAR Global Positioning System позволяют ученым измерять изменения земной поверхности с точностью до сантиметра.
Представление о форме Земли резко изменилось с течением времени по мере развития науки и техники.
Со времен древней мифологии ученые и философы спорят о форме Земли. Примерно с 500 г. до н.э. идея о том, что Земля представляет собой идеальную сферу, доминировала в большинстве научных представлений, даже несмотря на то, что концепция плоской Земли могла сохраняться в некоторых регионах еще тысячелетие. Примерно в конце 17 века идея о том, что Земля является идеальной сферой, превратилась в радикально новую идею: что Земля является несовершенной сферой.Этот новый способ мышления первоначально был разделен на две основные школы мысли. Одни считали, что Земля имеет форму яйца (вытянутого). Другой считал, что Земля сплющена у полюсов (сплющена). Было продемонстрировано, что современная концепция в основном сжатой Земли верна и породила множество теоретических вариаций за последние сто лет по мере развития геодезии.
Как рассчитать окружность Земли (шаг за шагом)
Еще в 240 г. до н. э. грек по имени Эратосфен вычислил окружность Земли.Сегодня мы знаем, как измерить окружность многих вещей, в том числе земли, с помощью многих современных инструментов, но Эратосфен делал это с помощью колодца, солнца и палки.
[все примечания к рисункам предполагают, что вы не делаете анимацию, что, честно говоря, объяснило бы все лучше, чем рисунки]
Содержание
- Земля представляет собой сплюснутый сфероид
- Установка космологической сцены
- Параллельные линии
- Окружность
- Соответствующие углы
Земля представляет собой сплюснутый сфероид
Умные и образованные люди древнего мира знали, что земля круглая.Они знали, что это сфера, а сегодня мы знаем, что это сжатая сфера, сплюснутый сфероид . Он сдавлен из-за сильного гравитационного притяжения Солнца, из-за чего он слегка выпячивается на экваторе.
Эратосфен, главный библиотекарь великой Александрийской библиотеки, имел в своем распоряжении практически все знания мира того времени. Он знал, что земля круглая, но , а не знал ее размер. Он понятия не имел, какова окружность Земли.
Представьте, что вы главный библиотекарь величайшей библиотеки на планете, и посетитель библиотеки задает вам простой вопрос:
[вставить картинку обмена]
- Посетитель библиотеки: «Какова окружность Земли?»
- Эратосфен: «Не знаю.»
Он не знал, но, как любой хороший математик и ученый, намеревался выяснить это, используя имеющиеся у него ресурсы.
Установка космологической сцены
Наше Солнце находится очень далеко от Земли, в среднем 149 600 000 км.Земля настолько мала по сравнению с Солнцем — примерно 109 земных шаров могут поместиться поперек поверхности (диаметра) Солнца — что солнечные лучи падают на землю почти параллельно друг другу. Земля занимает лишь небольшую часть окружности Солнца.
[вставить рисунок крошечной земли и большого солнца на противоположных сторонах экрана, показывающий параллельные солнечные лучи, падающие на землю]
Это означает, что солнечные лучи, падающие на дом Эратосфена в Александрии, параллельны солнечным лучам, падающим на Сиену, город далеко на юге, который сегодня мы называем Асуаном.
Поколения внимательных египетских землеустроителей знали, что Сиена находится на расстоянии 5000 стадий — древние единицы измерения, эквивалентные 804 километрам или 500 милям — к югу от Александрии. Эратосфен тоже это знал.
[вставьте мультяшный рисунок земли, показывающий расстояние от Александрии до Сиены, обозначенное как 804 км/500 миль]
Параллельные линии
В Сиене был глубокий, широкий колодец. В местный полдень каждого летнего солнцестояния (самый длинный день на Земле и самая короткая ночь) солнечные лучи шли прямо в колодец, а это означало, что Сиена идеально выровнялась с этими параллельными солнечными лучами.В колодце не появилось тени.
[приложить чертеж колодца в поперечном разрезе, в который падают солнечные лучи]
Эратосфен хорошо знал о Сиене, и он также знал солнце в Александрии, 804 км или 500 миль. на севере был , а не , идеально выровненный с параллельными лучами солнца в местный полдень в день летнего солнцестояния.
Что-либо торчащее из земли в Александрии — как палка — отбрасывало тень в то же мгновение, когда палка в Сиене отбрасывала не тень.
[вставить рисунок палки в земле в Александрии, отбрасывающей тень]
Если бы Эратосфен мог точно измерить угол тени палки, вбитой перпендикулярно в александрийскую землю, он мог бы использовать только две части информации для вычисления окружности земли:
- Угол тени палки в Александрии в день летнего солнцестояния
- Расстояние от Александрии до Сиены
Окружность
Окружность — это расстояние по окружности или сфере.Дуга — это часть или часть окружности круга или сферы. Один полный оборот вокруг Земли (один оборот) составляет 360°, поэтому любая дуга круга или сферы представляет собой дробную часть 360°.
человек в 240 г. до н. э. умел измерять окружность. Они знали формулу длины окружности сферы 2πr. Они знали о центральных углах и дугах.
Расстояние от Александрии до Сиены является одной из таких дуг, измеримой и известной долей общей окружности Земли.
Соответствующие углы
Эратосфен знал, что расстояние от Александрии до Сиены на сферической земле составляет дугу окружности, а это означает, что два города образуют центральный угол в центре земли, который мы будем называть 𝜃:
[вставьте чертеж земли в разрезе с центральным углом 𝜃, Александрия — точка A, центр земли — точка B, а Сиена — точка C]
Это сделало линию от недоступного центра Земли, С, до Александрии, А, поперечной параллельных солнечных лучей.
Секущая — это линия, пересекающая другие прямые, а в случае параллельных прямых секущей образует соответствующих углов . Какой угол он образует на одной параллельной линии, такой же угол он создает и на другой.
Это сделало угол тени палки в Александрии в день летнего солнцестояния соответствующим углу центрального угла 𝜃 в недоступном центре земли.
Если бы он мог точно измерить угол тени палки в Александрии в местный полдень в день летнего солнцестояния, у Эратосфена были бы обе части информации, необходимые для вычисления окружности Земли.
[справочная диаграмма с https://ourplnt.com/how-eratosthenes-calculated-earth-circumference/eratosthenes-calculation-earth-circumference/ предоставлена для ясности и вдохновения]
Эратосфен провел измерения и обнаружил, что угол равен 7,2°, что означает, что центральный угол 𝜃 также равен 7,2°. Этот угол, 7,2°, составляет 1/50 полного круга:
.Итак, если 804 км или 500 миль. (или 5000 стадий для Эратосфена) равняется 1/50, умножение дает вам длину окружности Земли:
- 500 миль.х 50 = 25 000 миль.
- 804 км х 50 = 40 200 км
- И для любого из вас, древних греков, 5000 стадий x 50 = 250 000 стадий
Земля, как мы уже говорили, представляет собой сплюснутый сфероид, поэтому геодезисты (ученые, которые измеряют землю и ее положение в пространстве) измерили и вычислили среднюю длину окружности Земли как 40 075 км или 24 901 милю.
Эратосфен, около 2200 лет назад, отклонился всего на 125 км или 101 милю. И он сделал это, имея лишь небольшие познания в географии и математике, колодец и палку.
Следующий урок:
Вписанный угол
19 июня 240 г. до н.э.: Земля круглая, и она такая большая
Современная иллюстрация показывает, как Эратосфен вычислил окружность Земли.
Предоставлено NOAA Ocean Service Education __240 г. до н.э.: __греческий астроном, географ, математик и библиотекарь Эратосфен вычислил окружность Земли. Его данные были грубыми, но он был не за горами.
Эратосфен был разносторонним парнем, человеком эпохи Возрождения за столетия до Возрождения.Некоторые современники называли его Пентаталосом, чемпионом во множестве навыков. Широта его знаний сделала его естественным кандидатом на должность библиотекаря Александрийской библиотеки в Египте, величайшего хранилища классических знаний.
Его недоброжелатели, однако, высмеивали Эратосфена как мастера на все руки и ничего не умеющего. Его называли Бета, потому что он был вторым во всех категориях.
Зависть? Возможно. Он изобрел решето Эратосфена, алгоритм для нахождения простых чисел, который до сих пор используется в измененной форме.Он начертил русло Нила от моря до Хартума и правильно предсказал, что исток великой животворящей реки будет находиться в больших горных озерах.
Эратосфен знал, что в полдень в день летнего солнцестояния солнце было замечено прямо над головой в Сиене (современный Асуан): его можно было увидеть со дна глубокого колодца, и солнечные часы не отбрасывали тени . Тем не менее, к северу, в Александрии, солнечные часы отбрасывали тень даже в полдень солнцестояния, потому что там солнце не было прямо над головой.Следовательно, Земля должна быть круглой, как это уже принято было считать астрономами того времени.
Более того, если предположить, что солнце находится достаточно далеко, чтобы отбрасывать параллельные лучи на Сиену и Александрию, можно было бы вычислить окружность Земли. Эратосфен вычислил, что тень в Александрии составляет 1/50 полного круга в 360 градусов. Затем он оценил расстояние между двумя точками и умножил его на 50, чтобы получить длину окружности.
Конечно, его размеры немного отличались.Александрия находилась не строго к северу от Сиены, а на 2 градуса долготы от нее. Сиена находилась не точно на Тропике Рака, а в 39 минутах широты к северу от него. Расстояние между городами было оценочным. Земля не идеальная сфера, а сплюснутый у полюсов сфероид.
И сегодня мы не знаем точного размера единицы измерения, которую использовал Эратосфен, когда он пришел к окончательной цифре в 252 000 стадий. (Мы знаем, что он знал, что это всего лишь грубая оценка, потому что он увеличил свое первоначальное число в 250 000 на 2 000 — или на 0.8 процентов — чтобы оно делилось на 60 или 360 для простоты вычислений.)
Итак, насколько велики 252 000 стадий? В зависимости от того, какому классическому источнику вы доверяете, это где-то между 24 663 и 27 967 милями. Принятая сегодня цифра экваториальной окружности составляет 24 902 мили. Чертовски хорошо для парня без современных инструментов измерения.
Эратосфен пошел дальше и вычислил наклон земной оси с точностью до градуса. Он также определил продолжительность года как 365¼ дней. Он предложил, чтобы каждый четвертый год в календаре был високосный день, и два века спустя эту идею подхватил Юлий Цезарь.
Школьные сказки в сторону, задолго до Колумба было известно, что Земля круглая и даже приблизительно большая. Но он просто не был широко известен в массах Европы 15-го века. Одна из причин заключается в том, что собственная библиотека Эратосфена в Александрии была уничтожена, и не было полной резервной копии ее данных.
Источник: Картографические изображения, другие29, 45 г.
 м
м