Отношение чисел | СПАДИЛО.РУ 👈

---

Отношения чисел: определение, свойства, виды

---

Определение

Отношением пары чисел называют результат их деления одно на другое. То есть понятия частного и отношения являются синонимами, обозначая одно и то же понятие. При этом число, которое делят, называют предыдущим членом, а число, на которое осуществляется деление, – последующим.

Для обозначения отношения чисел используется знак деления «:» либо черта дроби.

Общая форма записи отношения чисел: a : b или, соответственно,  . В таких записях a – предыдущий член отношения, b – последующий. Обязательное условие для всякого отношения: .

Пример №1:

3:2

Здесь 3 и 4 – предыдущие члены отношений, 2 и 9 – последующие.

Свойства отношений

Свойство №1. Членами всякого отношения могут быть как целые, так и дробные, рациональные или другие числа.

Примеры отношений, члены которых являются целыми числами, приведены выше (см. Пример №1).

Пример №2. Отношения, члены которого дробные числа:

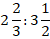
0,6:4,08

Свойство №2. Если члены отношения умножить (либо разделить) на одно и то же число, то его значение не изменится. Это свойство называют основным для отношений чисел.

Пример №3:

 

Деление членов отношения на одно и то же число называют сокращением отношения.

Это свойство нередко используется для перехода от нецелых членов отношения к целым, что более удобно для расчетов.

Свойство №3. В отношении могут участвовать и более 2-х членов. Так, в прикладных задачах нередко используются пропорциональные величины, значения которых выражаются как раз через их отношения. Количество членов при этом может быть произвольным и равняться трем, четырем и так далее. В общем виде такие отношения записываются как  a:b:c:d:…n и читаются так: «величины относятся между собой как a, b, c…»

Пример №4. Имеется треугольник, длины сторон которого относятся как 3:4:5.

Пример №5. Даны 4 пропорциональных числа, которые относятся между собой как 1:2:4:5.

В задачах, в которых приведены такого рода отношения, обычно вводится коэффициент пропорциональности и, используя свойства объекта, для которого они приведены, и (или) данные из условия, по заданному отношению находят абсолютные значения величин для этого объекта. При этом под абсолютными величинами понимают величины, выраженные в конкретных единицах измерения – кг, км и так далее.

Процентное отношение

Процентное отношение – это характерное и одно из наиболее распространенных направлений прикладного использования отношения чисел. Обозначение процентного отношения – % (процент). 1 % – это сотая часть от целого.

Процентное отношение основывается на обычном отношении, которое множат на 100. Процентное отношение показывает часть объекта (величины) в сравнении с его 100 частями, которые принимаются за целое.

Математическая запись:

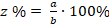
Где a – часть целого, выраженная в единицах измерения, b – значение целого, выраженное в тех же единицах, z – количество процентов, которое составляет данная часть от целого.

Пример №6. На книжной полке 80 книг. Сколько процентов от этого количества составляют 36 книг?

Обозначим искомую величину через х. Тогда получаем:

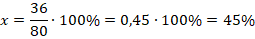
Пример №7. Фермер посеял пшеницу на 2 га, что составляет 80 % от всех его посевных площадей. Какова общая посевная площадь, которой он располагает?

Обозначим искомую величину через х. Составим процентное отношение на основании данных задачи:

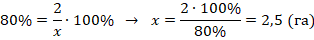
Нередко вместо понятия процентного отношения используют понятие долей. В этом случае целое абстрактно принимается за 1, а понятие процента не используется. Доля (часть) от данного целого в такой ситуации – это всегда будет величина, меньшая 1. Для определения доли (части) от целого используется обычное отношение:

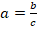Где b – часть от целого, c – величина целого, a – доля, которую b составляет от c.

Специальной единицы измерения доля не имеет и измеряется просто в единицах.

Пример №8. Какую долю тиража изданной книги удалось продать писателю, если тираж составляет 10 тысяч экземпляров, а приобретено было 6830 книг?

Обозначим искомую величину через х. Составим отношение и найдем х:

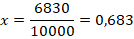
Переход от долей к процентам предельно прост: достаточно умножить долю на 100. Так, в предыдущем примере 0,683 по отношению к общему тиражу составит .

Пример №9. С 1 га планировалось собрать 40 тонн картофеля. Реальная урожайность составила 0,7 от планируемой. Сколько тонн картофеля собрали?

Обозначим искомую величину через х. Составим выражение для расчета реальной урожайности и найдем х:

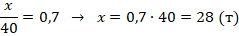
Пропорция

Пропорцией называют равенство двух числовых отношений. В общем виде такое равенство записывают как

, где a и d называют крайними членами пропорции, b и c – средними. Прочтение пропорции: отношение a к b равно отношению c к d, или a относится к b как c к d, или a во столько раз больше b во сколько больше d.

Пример №9. Примеры конкретных пропорций:

При решении практических задач с использованием отношений в виде пропорции чаще всего от деления переходят к умножению ее членов. Для этого используют основное ее свойство.

Основное свойство пропорции: произведение ее крайних членов равно произведению средних.

Математически это свойство записывается так:

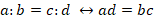
Пример №10.

Если провести дальнейшие вычисления, то в итоге мы должны прийти к равенству чисел слева и справа. А именно:

 

Отсюда следует важная особенность: основное свойство применяют для проверки истинности составленной пропорции. Если в результате числовых преобразований получено верное равенство, то это означает, что исходные 4 числа действительно могут составить пропорцию.

Когда один из членов пропорции неизвестен и требуется найти его, то применяют правило: для вычисления неизвестного крайнего (среднего) члена перемножают средние (крайние) и делят полученное произведение на известный крайний (средний) член.

Математически это выражается так:

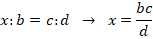
То есть для определения неизвестного члена перемножают пару соответствующих известных и делят их на тот известный член, который не имеет известной пары.

Пример №11. Дана пропорция:

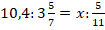
Требуется найти х.

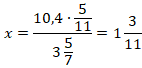
Пример 12. Дана пропорция:

Необходимо найти х.

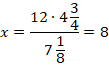
Скачать PDFРаспечатать

Отношения

Для решения практических задач человеку часто приходится сравнивать разные значения одной и той же величины – массы, расстояния, времени, скорости, стоимости, объёма, площади и т.д.

Для сравнения чисел и величин существуют, как вы знаете, два способа:

1-ый: вычисление разности и 2-ой: вычисление частного.

Оба этих способа используют часто при решении практических задач, но служат они для разных целей. К делению прибегают в тех случаях, когда хотят получить качественную оценку или относительную оценку той или иной ситуации.

Задача

На экране изображены два отрезка. Отрезок AB длиной 15 см и отрезок CD, длина которого 6 см. Во сколько раз отрезок АВ больше или длиннее отрезка CD?

Решение:

Вторая задача: на экране изображены эти же два отрезка. Отрезок AB длиной 15 см и отрезок CD, длина которого 6 см. Но поставим вопрос по-другому: какую часть отрезок CD составляет от отрезка АВ?

Решение:

Обе рассмотренные задачи решаются делением, и ответ даётся в виде частного. В таких случаях частное двух чисел называют их отношением

.

Определение

Частное двух не равных нулю чисел (или двух величин) называют отношением.

Сами эти числа (величины) называют членами отношения.

Иными словами, отношение двух чисел – это другое название их частного. Отношение чисел записывают с помощью знака деления, а также с помощью черты обыкновенной дроби.

Частные чисел читают так:

Напомним, что отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого.

Черта дроби используется для записи отношения и тогда, когда его члены не являются натуральными числами.

Задача

Рост дяди Степы 2 м 10 см, а рост мальчика Васи – 105 см. Во сколько раз дядя степа выше мальчика Васи?

Решение:

Но ведь дробную черту мы использовали для записи дробей! А сейчас записана не дробь. Верно. Но вы давно знаете, что при записи деления натуральных чисел вместо знака деления можно использовать дробную черту. Так вот, договариваются о том же и при записи деления любых чисел.

Итак, если а и b – любые числа, то

Сделаем важное замечание:

Если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения.

Отношение величин одного наименования (длин, скоростей, стоимостей и т.д., выраженных одинаковыми единицами измерения) есть число. Такие величины называют однородными.

Отношение величин разных наименований (пути и времени, стоимости товара и его количества, массы тела и его объема и т.д.) есть новая величина.

Вот, например, в предыдущей задаче мы находили во сколько раз дядя Степа выше мальчика Васи.

Рост Васи и рост дяди Степы – это однородные величины, т.е. длина. Поэтому отношение их роста выраженно натуральным числом.

А теперь давайте разберёмся, почему отношение разноимённых величин – это новая величина.

Задача

Муравей за 20 секунд пробегает 240 сантиметров. Определите скорость движения муравья.

Решение:

Отметим, что обозначения км/ч, м/с и т.п. приняты именно потому, что расстояние делят на время. Их обычно записывают с наклонной чертой.

В виде отношений определяются и другие величины:

Из основного свойства частного следует свойство отношения.

Давайте вспомним основное свойство частного:

если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Следовательно, получаем свойство отношения:

отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.

Пример

Мы с вами убедились, что свойство отношения действует. Мы умножили числитель и знаменатель дроби на одно и то же число, само же отношение не изменилось.

Итоги       

Итак, сегодня на уроке мы узнали, что частное двух не равных нулю чисел (или двух величин) называют отношением.

Сами эти числа (величины) называют членами отношения.

Если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения.

И свойство отношения: отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.

6.1. Отношение   математика-повторение

I. Частное двух чисел называют отношением этих чисел. 

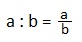
так с помощью букв записывают отношение чисел a и b, причем, а – предыдущий член, b – последующий член. (Напоминание: дробная черта означает знак деления).

Примеры. 

1) Найти отношения: а) 9 : 5; б) 0,21 : 0,3; в) 51 : 7.

Решение. Выполняем деление.

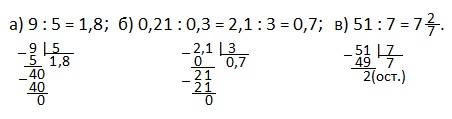
2) Найти неизвестные члены отношений: а) х : 6 = 24; б) 35 : х = 0,07.

Решение.

а) х : 6 = 24.  Делимое равно х, делитель равен 6, частное равно 24. Чтобы найти неизвестное делимое, нужно частное умножить на делитель. 

х = 24 · 6;

х = 144.

б) 35 : х = 0,07.  Делимое равно 35, делитель равен х, частное равно 0,07. Чтобы найти неизвестный делитель, нужно делимое разделить на частное.

х = 35 : 0,07;

х = 3500 : 7;

х= 500.

 II. Если члены данного отношения переставить местами, то получившееся отношение называют обратным для данного отношения. 

 III. Отношение не изменится, если оба члена отношения умножить или разделить на одно и то же число, отличное от нуля.

В самом деле, отношение означает деление.

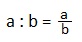
Члены отношения — это числитель и знаменатель обыкновенной дроби.

А мы знаем основное свойство обыкновенной дроби: значение дроби не изменится, если ее числитель и знаменатель умножить или разделить на одно и то же натуральное число. 

Примеры.

3) Сократите отношение: а) 80 : 5; б) 42 : 45.

а) 80 : 5. Разделим оба члена этого отношения на 5. Тогда вместо числа 80 получим число 16 (80:5=16), а вместо числа 5 получим число 1 (5:5=1). Запишем: 80 : 5 = 16 : 1.  Читают: восемьдесят так относится к пяти, как шестнадцать относится к единице.

б) 42 : 45. Каждый член этого отношения разделим на 3,

тогда получим равенство: 42 : 45 = 14 : 15. Читают: сорок два так относится к сорока пяти, как четырнадцать относится к пятнадцати.

 

8 признаков, по которым можно отличить кризис в отношениях от окончательного разрыва

Ребята, мы вкладываем душу в AdMe.ru. Cпасибо за то,
что открываете эту красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте

Часто после серьезной ссоры у многих из нас в голове мелькает: «А может, пора расстаться?» На самом деле безоблачные отношения бывают только в мультфильмах про диснеевских принцесс, а периодические разногласия между двумя любящими людьми — норма. Поэтому, вместо того чтобы необдуманно разрывать связь с любимым, стоит сначала понять, конец ли это отношений или всего лишь очередной нелегкий период, который скоро закончится.

AdMe.ru разобрался, как отличить кризис от окончательного разрыва и спасти отношения в сложный период.

1. Желание быть одному

• Кризис: Желание иногда побыть одному в тишине или пойти погулять с друзьями без своей половинки абсолютно нормально, и это всегда идет на пользу отношениям. Психологи даже советуют парам, которые постоянно проводят время вместе или работают в одном офисе, делать небольшие паузы и посвящать время самому себе, успевая соскучиться.
• Конец: Вы и так проводите много времени порознь, однако при мысли о скорой командировке партнера вы начинаете невольно улыбаться. И если вы с нетерпением ожидаете момента, когда он уедет на работу или пойдет на встречу с друзьями, чтобы не видеться еще несколько часов, несмотря на регулярные разлуки, то это верный признак конца.

2. Вы не скучаете по партнеру

• Кризис: Пары сталкиваются с тем, что время от времени им начинает надоедать общество друг друга. Рутина и быт без отдыха могут вывести из себя кого угодно. Часто только из-за усталости мы срываемся на близких и мечтаем спрятаться в лесу, чтобы нас никто не трогал. В такие периоды можно поймать себя на мысли, что партнер надоел, и начать видеть в нем сплошные недостатки. Однако в этих ситуациях помогает полноценный отдых, встречи с друзьями порознь или небольшое путешествие.
• Конец: Вы кричите от радости, когда ваша половинка уехала, ведь вам так хорошо одной или с друзьями. А как только вы понимаете, что партнер скоро вернется, настроение портится. Вы забываете писать друг другу милые «Как дела?» или «Скучаю», так как есть дела или люди намного интереснее ваших отношений. Возможно, пришло время расстаться.

3. Нет совместных планов на будущее

• Кризис: Всегда сложно найти компромисс, особенно если в отношениях две сильные личности и каждый настаивает на своем. Часто это приводит к ссорам. Однако споры из-за планов с целью найти решение проблемы или вариант, который устраивает обоих, говорят о том, что вы небезразличны друг другу. Именно общие мечты и идеи удерживают двух любящих людей вместе во время ссор или кризисов.
• Конец: Партнер рассказывает друзьям: «Я планирую найти работу в другом городе через год и переехать», а вы впервые слышите об этом? Да и вы вряд ли можете представить себя с этим человеком через 10–15 лет. Возможно, вы даже перестали спорить из-за каких-то проектов или целей, так как обоим безразлично мнение друг друга, или никогда этих планов и не строили. Тогда имеет ли смысл продолжать эти отношения?

4. Ссор становится все больше

• Кризис: Ссоры двух любящих людей — это нормально. Все мы испытываем эмоции, иногда у всех пар бывают конфликты. И даже если после серьезной ссоры вы хлопнули дверью или уехали к родителям, то стоит подождать некоторое время, успокоиться, затем обсудить проблему, найти решение и продолжить отношения с близким человеком. В некоторых парах разногласия случаются довольно часто просто потому, что оба партнера очень эмоциональные. Однако это не означает, что пришло время расстаться навсегда.
• Конец: Если вы начали ссориться практически каждый день и без серьезных поводов, стоит задуматься. И если страстные выяснения отношений, заканчивающиеся бурным примирением, превратились в рутинные перебранки, а вы не реагируете на происходящее и у вас нет страха потерять человека, то, возможно, вам предстоит все обдумать и принять окончательное решение. Отношения — это в первую очередь радость, а не постоянные конфликты.

6 методов » Наша Психология

Мы все знаем, что для создания здоровых отношений и истинной любви, необходима отдача обоих партнеров. А когда у вас что-то не получается, и возникают сложности с партнером, тогда вы должны понимать, как решать проблемы в отношениях. Любовь нужно регулярно подпитывать и поддерживать ее, тем самым пробуждая в трудные времена. Хотя, многие верят в идею родственной души. Когда вы находите человека, с которым ваша любовь будет легкой, а отношения счастливыми и беззаботными. Но, на самом деле, проблемы могут возникать, казалось бы, в идеальных отношениях. Поэтому, на каком бы этапе вы не находились, важно понимать, как находить решения этих проблем, при этом не расставаясь с любимым человеком.

То, как вы решаете проблемы в отношениях, формирует историю вашей любви. Когда вы и партнер сталкиваетесь с глубоким конфликтом, вам нужно ответить на несколько вопросов. Вы действительно пытаетесь что-то исправить? Что именно вы делаете для решения возникших проблем? Работают ли ваши методы? Возможно, вам необходимо найти другие пути решения проблем? Давайте рассмотрим несколько способов, как это можно сделать.

Содержание статьи

Практические советы, как решать проблемы в отношениях

---

1. Открыто поговорите друг с другом

Одним из первых инструментов, который вы можете использовать, чтобы избежать расставания — являются ваши слова. Открытое общение — это самый полезный инструмент для решения проблем в отношениях. Вы должны уважительно и откровенно поговорить с партнером, и внимательно выслушать его точку зрения. Искренний разговор покажет вам пути решения проблем. Поэтому не стесняйтесь говорить о всем, что вас волнует, и чем вы недовольны. В конце разговора старайтесь найти компромисс, и ни в коем случае не переводите ваше общение в конфликт.

Поговорите лучше о том, почему вы решили быть вместе. Что вас привлекло друг в друге в самом начале отношений. Вспомните первые встречи, и то время, когда вы только познакомились, и как хорошо вам тогда было. Разве вы не хотите вернуть эти теплые и радостные чувства?

2. Избавьтесь от рутины в отношениях

Одним из ключевых факторов, который негативно сказывается на отношениях, является рутина. Мужчины и женщины перестают прилагать усилия, чтобы как-то разнообразить свои отношения, и не привносят новые идеи. Они проживают каждый день, как обычно, и ничего не меняют в своей жизни. Мужчина может каждый вечер после работы смотреть телевизор или сидеть за компьютером. А жена в свою очередь, болтать с подружками по телефону, либо посещать спортзал.

Даже если пара не осознает этого, выполнение таких рутинных действий будет иметь негативные последствия в долгосрочной перспективе. Они сами ограничивают свои возможности и не способствуют развитию отношений. Из-за этого возникают обиды, ссоры и конфликты. Они принимают друг друга как должное. Поэтому, прежде чем кричать: «мне это надоело, я ухожу от тебя!». Попробуйте внести изменения в вашу жизни, и начать делать что-то новое вместе. Начните делать короткие поездки на выходные в те места, где вы никогда не были раньше. Посетите кафе или ресторан, в котором еще не были. Возьмите несколько уроков бального танца вместе. Тем самым добавьте немного свежести в отношения. Суть состоит в том, чтобы увидеть партнера в новом свете. В таком случае, вы не будете думать, как решать проблемы в отношениях. Вы поймете, что вокруг вас существует множество интересных вещей, которые могут разнообразить вашу жизнь.

3. Слушайте своего партнера

Вы не сможете понять, как решать проблемы в отношениях, если не будете слушать своего партнера. Ведь на самом деле неприятно чувствовать, что партнер не обращает на вас внимания. Он этим проявляет неуважение, и не дает вам возможности высказаться. Поэтому, когда он что-то говорит, покажите, что вы действительно слушаете его, используя технику активного слушания. Когда он закончил говорить, перефразируйте то, что он сказал, своими словами. Если с чем-то не согласны, не скрывайте этого, и выскажите свое мнение. Это поможет предотвратить возможные недоразумения и недопонимания в будущем. Также покажет партнеру, что вы его уважаете, и для вас действительно важно все то, что он говорит.

4. Не проявляйте презрения к партнеру

Из всех негативных вещей, которые вы можете сделать или сказать во время конфликта, худшим может быть только презрение. Оно довольно часто приводит к серьезным проблемам в отношениях. Презрительные замечания, которые унижают вашего партнера, также к этому относятся. Это может включать в себя сарказм, обзывания или невербальное поведение. Такое, как закатывание глаз или ухмылка. Такое поведение крайне неуважительно, и подразумевает, что вы испытываете отвращение к партнеру.

5. Не поддавайтесь негативу

Может быть сложно не реагировать на плохое поведение человека. Но снисходительное отношение к нему только усугубит ситуацию, и не поможет решать проблемы в отношениях. Ведь когда пары проявляют негатив друг к другу, обмениваются оскорблениями и презрительными замечаниями, они этим только обостряют конфликт. Вам необходимо с пониманием относится к партнеру, и стараться быть более смиренными в отношениях с ним. Если вы будете регулярно указывать на его недостатки, в какой-то момент он не выдержит и прекратит с вами отношения.

6. Сделайте перерыв в отношениях

Давайте представим, что у вас есть давние трудности в отношениях. Вы старались что-то сделать, разговаривали друг с другом, пытались найти пути решения проблем, но так и не достигли результата. В данном случае, вы можете просто отдохнуть друг от друга. Многие пары, которые проводили сознательное время отдельно друг от друга, утверждают, что это самая здоровая вещь, которую они когда-либо делали, чтобы спасти свои отношения. Поговорите об этом с партнером, если вы решите, что перерыв будет хорошей идеей, важно, чтобы вы обговорили определенные правила, которых будете придерживаться в течение этого периода. Они должны включать в себя:

• Дату окончания перерыва. Это конкретная дата, когда вы двое должны оценить полезность временного разрыва отношений, и решить, стоит ли вам оставаться в отношениях;
• Разрешаете ли вы партнеру заводить новые отношения во время этого перерыва?
• Как будет выглядеть ваше общение во время перерыва? Может быть лучше вовсе не общаться, чтобы дать возможность скучать друг по другу.

Разумно используйте время вдали друг от друга. Встретьтесь со своими друзьями или родственниками, которых давно не видели. Займитесь новым видом спорта или найдите новое хобби. Занимайтесь тем, что вам нравится и приносит удовольствие. Будьте немного эгоистичны, вам необходимо сосредоточиться только на себе и на своих чувствах. Этот перерыв позволит осознать ваши чувства к партнеру, когда его долгое время не будет рядом.

Заставьте отношения работать

Один из лучших советов, как решать проблемы в отношениях — это понимать, что любовь — это не сказка. И если вы хотите ощущать счастье и гармонию в отношениях, тогда должны для этого что-нибудь делать. В вашей жизни могут возникать различные сложности, которые будут негативно сказываться на отношениях. Так что это вполне нормально, если между вами будут возникать незначительные конфликты. Только вам необходимо решать их в дружеской обстановке, не прибегая к расставанию. И только когда вы использовали все методы, и они не дали никакого результата. Только тогда стоит задумываться о разрыве.

Понравилась статья? Поделитесь в соц. сетях или оставьте комментарий!

---

Об авторе

Milena

Пишу для вас на самые актуальные и востребованные темы. Следите за нашим ресурсом, будет много полезных статей. Добавляйте сайт в закладки и делитесь с друзьями.

Соотношение — Википедия

У этого термина существуют и другие значения, см. Отношение.

Соотношение в математике (отношение, пропорция) — это взаимосвязь между двумя числами одного рода^[1] (предметами, действиями, явлениями, свойствами (признаками), понятиями, объектами, например, людьми (студентами), чайными ложками, единицами чего-либо одинаковой размерности), обычно выражаемое как «a к b» или a:b{\displaystyle a:b}, а иногда выражаемое арифметически как безразмерное отношение (результат деления) двух чисел^[2], непосредственно отображающее, сколько раз первое число содержит второе (не обязательно целое).^[3]

Проще говоря, соотношение показывает для каждого количества чего-то одного сколько есть чего-то другого. Например, предположим, что у кого-то есть 8 апельсинов и 6 лимонов в вазе для фруктов, соотношение апельсинов и лимонов составит 4:3 (что эквивалентно 8:6), а соотношение лимонов и апельсинов составит 3:4. Кроме того, количество апельсинов относительно общего количества фруктов составит 4:7 (что эквивалентно 8:14). Соотношение 4:7 можно преобразовать в дробь 4/7, показывающую, какую долю от общего числа фруктов составляют апельсины.

Соотношение чисел A и B можно представить как:^[2]

Числа A и B в данном контексте иногда называют членами (terms), где A — антецедент, а B — консеквент.

Пропорция, выражающая равенство соотношений A:B и C:D, записывается как A:B=C:D или A:B::C:D. Читается:

A относится к B как C относится к D.

И в данном случае, A, B, C, D называются членами пропорции. A и D — крайние члены пропорции, а B и C — средние члены. Равенство трёх и более соотношений называется непрерывной пропорцией (continued proportion, ряд отношений).^[2]

Иногда в соотношениях три и более членов. Например, размеры предмета с сечением два к четырём и длиной десять сантиметров составят 2:4:10.

Невозможно проследить истоки концепции соотношения, поскольку идеи, из которых она развилась, должны были быть известны дописьменным культурам. Например, идея того, что одна деревня вдвое больше другой, настолько базовая, что была бы понятна даже в доисторическом обществе.^[4]

Для обозначения отношения греки использовали термин др.-греч. λόγος, которое латиняне передавали как ratio («разумное основание»; как в слове «рациональный») или как proportio. (Рациональное число можно представить как результат отношения двух целых чисел.) Более современная интерпретация евклидова значения ближе к «вычисление» или «расчёт».^[3]Боэций («Основы арифметики», «Основы музыки», начало VI в.) использовал слово proportio (наряду с ratio, comparatio и habitudo) для обозначения отношения и proportionalitas (перевод др.-греч. ἀναλογία) для обозначения пропорции (отношения отношений)^[5]. Такое терминоупотребление (в связи с широчайшей распространённостью «Арифметики» и «Музыки» Боэция) практиковалось и в Средние века.

Евклид объединил в «Началах» результаты из более ранних источников. Пифагорейцы развили теорию соотношения и пропорции в приложении к числам^[6]. Пифагорейская концепция числа включая лишь то, что сейчас называют рациональными числами, что навело сомнения на применимость теории в геометрии, где, как также обнаружили пифагорейцы, существуют несоизмеримые размеры, соответствующие иррациональным числам. Открытие теории отношений, не предполагавшей соизмеримость, вероятно, принадлежит Евдоксу Книдскому. В Книге VII «Начал» приведена и более ранняя теория отношений соизмеримых величин^[7].

Существование нескольких теорий выглядит ненужным усложнением для современного взгляда, поскольку соотношения, во многом, определяются результатом деления. Однако, это довольно недавнее открытие, что можно увидеть на примере того, что современные учебники по геометрии до сих пор используют различную терминологию для соотношений (ratio) и результатов деления (quotient, частное). Причин для этого две. Во-первых, существовало вышеупомянутое нежелание признавать иррациональные числа как истинные числа. Во-вторых, нехватка широко используемых символов (обозначений) для замены уже устоявшейся терминологии соотношений задержало полное принятие дробей как альтернативы вплоть до XVI века.^[8]

Определения Евклида[править | править код]

В книге V «Начал» Евклида 18 определений, касающихся соотношений^[9]. Кроме того, Евклид использует идеи, которые были в настолько широком употреблении, что он не даёт им определений. Первые два определения гласят, что часть количества есть другое количество, которое «измеряет» его, и наоборот, кратное для количества есть другое количество, измеряемое им. В современных терминах, это означает, что кратное для количества есть это количество, умноженное на целое число, большее единицы, а часть количества (то есть делитель) при умножении на число, большее единицы, даёт то количество.

Эвклид не даёт определения слова «измерять». Тем не менее, можно предположить, что, если количество принимается за единицу измерения, а другое количество представлено как общее количество таких единиц измерения, то первое количество измеряет второе. Заметим, эти определения повторяются почти слово в слово как определения 3 и 5 в книге VII.

Определение 3 разъясняет, что такое соотношение в общем смысле. Оно не является математически строгим и некоторые исследователи приписывают его редакторам, а не самому Евклиду.^[10] Евклид определяет соотношение между двумя количествами одного вида, например двух отрезков или двух площадей, но не соотношение длины к площади. Определение 4 указывает это ещё более строго. Оно утверждает, что соотношение между двумя количествами существует, если есть кратное для каждого, превышающее другое. В современных терминах: соотношение между количествами p и q существует, если существуют целые числа m и n такие, что mp>q и nq>p. Это условие известно как аксиома Архимеда.

Определение 5 наиболее сложное и трудное для понимания. Оно объясняет, что означает равенство для двух соотношений. Сегодня можно просто заявить, что соотношения равны, если равны результаты деления членов, но Евклид не признавал существование результатов деления для несоизмеримых величин, поэтому для него такое определение было бы бессмысленным. Поэтому требовалось более тонкое определение для случая количеств, не измеряющих друг друга напрямую. Хотя может быть невозможно присвоить соотношению рациональное значение, но вполне возможно сравнить соотношение с рациональным числом. А именно, для двух количеств p и q, а также рационального числа m/n, мы можем сказать, что соотношение p к q меньше, равно или больше m/n, когда np меньше, равно или больше mq, соответственно. Евклидово определение равенства можно сформулировать так: два соотношения равны, когда они одинаково себя ведут, будучи одновременно меньше, равны или больше любого рационального числа. В современной нотации это выглядит так: для данных количеств p, q, r и s выполняется p:q::r:s, если для любых положительных целых чисел m и n выполняется отношение np<mq, np=mq, np>mq в соответствии с nr<ms, nr=ms, nr>ms. Есть примечательное сходство между этим определением и теорией Дедекиндова сечения, используемого в современной теории иррациональных чисел^[11].

Определение 6 гласит, что количества с одинаковым соотношением пропорциональны или состоят в пропорции. Евклид использует греческое слово ἀναλόγον (analogon), с тем же корнем, что и λόγος, от которого произошло слово «аналог».

Определение 7 объясняет, что значит для соотношения быть меньше или больше другого, и основывается на идеях из определения 5. В современной нотации: для данных количеств p, q, r и s выполняется p:q>r:s, если существуют положительные целые числа m и n такие, что np>mq и nr≤ms.

Как и в случае с определением 3, определение 8 некоторыми исследователями рассматривается как позднее включение редакторов. Оно гласит, что три члена p, q и r находятся в пропорции, если p:q::q:r. Это расширяется на 4 члена p, q, r и s как p:q::q:r::r:s и т. д. Последовательности, обладающие таким свойством, что соотношения последовательных членов равны, называются геометрическими прогрессиями. Определения 9 и 10 применяют это, говоря, что, если p, q и r состоят в пропорции, то p:r есть двойное отношение (duplicate ratio, отношение квадратов) для p:q, а если p, q, r и s находятся в пропорции, то p:s есть тройное отношение (triplicate ratio, отношение кубов) для p:q. Если p, q и r находятся в пропорции, то q называется средним пропорциональным (или геометрическим средним) для p и r. Подобным образом, если p, q, r и s находятся в пропорции, то q и r называют средними пропорциональными для p и s.

Процентное соотношение[править | править код]

Если умножить все количества в соотношении на одно и то же число, то соотношение не изменится. Например, соотношение 3:2 есть то же самое, что 12:8. Обычно члены пропорции уменьшают до наименьшего общего знаменателя либо выражают их в долях ста (процент). Иногда для удобства сравнения соотношения представляют в виде n:1 или 1:n.

Если смесь содержит вещества A, B, C и D в соотношении 5:9:4:2, то в ней 5 частей A приходится на каждые 9 частей B, 4 части C и 2 части D. Поскольку 5+9+4+2=20, то всего смесь содержит 5/20 A (5 частей из 20), 9/20 B, 4/20 C и 2/20 D. Если эти числа, деленные на общую сумму, умножить на 100, то получаем проценты: 25 % A, 45 % B, 20 % C и 10 % D (эквивалентно написанию соотношения в виде 25:45:20:10).

Если два или более количества, состоящих в пропорциональном соотношении, являются всеми количествами, задействованными в конкретной ситуации, например, два яблока и три апельсина в корзине, в которой нет других фруктов, то можно сказать, что «целое» содержит пять частей, состоящих из двух частей яблок и трёх частей апельсинов. В данном случае, 25{\displaystyle {\tfrac {2}{5}}}, или 40 % целого, — это яблоки, а 35{\displaystyle {\tfrac {3}{5}}}, или 60 % целого, — это апельсины. Такое сравнение определённого количества с «целым» иногда называют пропорцией. Пропорции иногда выражают в процентах, как указано выше.

Другие применения[править | править код]

• Соотношения часто используются для простых растворов в химии и биологии (степень разбавления).
• Шансы выигрыша в играх выражают в виде соотношения.
• Возможны соотношения количеств, измеряемых в разных единицах измерения.

1. ↑ Wentworth, p. 55
2. ↑ ^{1 2 3} New International Encyclopedia
3. ↑ ^{1 2} Penny Cyclopedia, p. 307
4. ↑ Smith, p. 477
5. ↑ А. М. С. Боэций. Основы музыки / Подготовка текста, перевод с латинского и комментарий С. Н. Лебедева. М.: Научно-издательский центр «Московская консерватория», 2012, pp. xxxiv-xxxv, 276.
6. ↑ Heath, 1908, p. 112.
7. ↑ Heath, 1908, p. 113.
8. ↑ Smith, p. 480
9. ↑ Heath, 1908, reference for section.
10. ↑ «Geometry, Euclidean» Encyclopædia Britannica Eleventh Edition p682.
11. ↑ Heath, 1908, p. 125.

• Отношение // Большая Советская энциклопедия (в 30 т.) / А. М. Прохоров (гл. ред.). — 3-е изд. — М: Сов. энциклопедия, 1974. — Т. XVIII. — С. 629. — 632 с.
• Отношение, в математике // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
• «Ratio» The Penny Cyclopædia vol. 19, The Society for the Diffusion of Useful Knowledge (1841) Charles Knight and Co., London pp. 307ff
• «Proportion» New International Encyclopedia, Vol. 19 2nd ed. (1916) Dodd Mead & Co. pp270-271
• «Ratio and Proportion» Fundamentals of practical mathematics, George Wentworth, David Eugene Smith, Herbert Druery Harper (1922) Ginn and Co. pp. 55ff
• The thirteen books of Euclid’s Elements, vol 2 / trans. Sir Thomas Little Heath. — Cambridge Univ. Press, 1908. — P. 112ff.
• D.E. Smith, History of Mathematics, vol 2 Dover (1958) pp. 477ff

бинарные отношения калькулятор онлайн

Вы искали бинарные отношения калькулятор онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и бинарные отношения онлайн калькулятор, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «бинарные отношения калькулятор онлайн».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как бинарные отношения калькулятор онлайн,бинарные отношения онлайн калькулятор,доказать равенство множеств онлайн,калькулятор множеств,калькулятор множеств онлайн,калькулятор множества онлайн,калькулятор онлайн множества,калькулятор онлайн множество,множеств онлайн калькулятор,множества калькулятор онлайн,множества онлайн,множества онлайн калькулятор,множества онлайн решение,множества решение онлайн,множество калькулятор онлайн,множество онлайн калькулятор,найти объединение множеств онлайн,онлайн калькулятор множеств,онлайн калькулятор множества,онлайн калькулятор множество,онлайн множества,онлайн решение множеств,онлайн решение множества,операции над множествами онлайн калькулятор,решение множеств онлайн,решение множеств онлайн калькулятор,решение множества онлайн,решение онлайн множеств,решение онлайн множества. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и бинарные отношения калькулятор онлайн. Просто введите задачу в окошко и нажмите «решить» здесь (например, доказать равенство множеств онлайн).

Где можно решить любую задачу по математике, а так же бинарные отношения калькулятор онлайн Онлайн?

Решить задачу бинарные отношения калькулятор онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.