Урок 3: Фигуры — 100urokov.ru
План урока:
Что такое точка?
Что такое прямая?
Что такое луч?
Что такое отрезок?
Что такое вершины и стороны угла?
Что такое окружность?
Что такое круг?
Минутка истории
Что такое точка?
Как только маленький ребенок берет в ручки карандаш, он уже замечательно умеет рисовать геометрическую фигуру. Какую? – удивитесь вы. Это точка.
Точка – наименьшая, простейшая фигура геометрии, никак не измеряется.
И строить её умеет даже маленький ребенок.

Обозначать точки в математике, принято большими буквами латиницы.
Произносится:точка А, точка В, точка С.
Следующее понятие, которое мы рассмотрим, знакомо каждому с самого детства. Нет ничего проще, чем нарисовать прямую линию. Многие успешно рисовали их на новых обоях, мебели. А оказывается – она одна из основных фигур геометрии.
Что такое прямая?

Прямая – масса точек, находящихся на общей, бесконечной линии. Обозначается прописными буквами латиницы.
Произносится: прямая а.
Через выбранные 2 точки можно провести одну-единственную прямую!
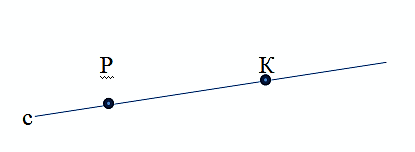
Через точки Р, К, проводится только 1 прямая.
Все очень просто!
Теперь предлагаю нарисовать солнышко.

(Источник)
Давайте рассмотрим его поподробнее. Солнышко состоит из круга, лучиков. Вот мы подошли к следующему понятию геометрии.
Что такое луч?
Каждый лучик имеет начало, продолжается бесконечно, как одноименная фигура.
Луч – это часть прямой, ограниченная начальной точкой с одной стороны. Лучи обозначают заглавными и строчными буквами латиницы.

Точкой А прямая поделена на два луча: луч А, луч АС (в начале ставится символ начала луча).

(Источник)
Для рассмотрения следующего понятия, вспомним мультфильм «38
попугаев». Серию, где друзья пытались измерить удава. Если рассматривать удава с математической точки зрения, тов математике его бы обозначили, отрезком.
Что такое отрезок?
Давайте схематично изобразим удава. Сначала отметим две точки – голова и хвост (начало и конец). После соединим эти точки.

Получается, что схематично изображая удава, начертили еще одну геометрическую фигуру, которая называется отрезком. Давайте сформулируем определение:
Отрезок–это фигура на прямой, ограниченная двумя точками. Точки называются концами отрезка и обозначаются заглавными буквами латиницы.

Произносится: отрезок ТМ.
Если при наложении концы отрезков совпадают, то такие отрезки называют равными.

Значит, АВ=КМ
А что такое единичный отрезок, где используется?
Давайте вернемся к мультфильму. Вспомните момент, когда удава очень волновал его рост (длина). Друзья не растерялись, нашли способ его измерять. Сначала его измеряли обезьянками, потом слонами, наконец, попугаями.

(Источник)
Но каждый раз длина удава была разной только потому, что друзья очень отличались своими размерами. При измерении длины удава, каждый друг выступил в роли единичного отрезка, величины, в которой измерялся предмет (в слонах, обезьянах, попугаях). Так как попугай имел самый маленький размер, то длина удава в попугаях оказалась самой большой – 38 попугаев. Сформулируем определение:
Единичный отрезок – выбранная единица для измерения чего-либо.
Возьмем линейку длиной 20 см. На ней можно увидеть штрихи, делящие линейку на одинаковые кусочки, которые называют делениями. Из них состоит шкала. За единицу измерения принят отрезок длиной 1 см (единичный), и таких единиц измерения на линейке 20 штук.

(Источник)
Для изучения следующего понятия необходимо схематически начертить линейку. Для этого чертим луч, указываем направление луча стрелочкой, наносимделения:

Точка В, с соответствующимчисловым значением 0. Следующая точка С, с числовым значением 1. Получается, отрезок ВС считается единичным, его длина принимается за единицу измерения. Все имеющиеся точки расположены на расстоянии единичного отрезка.
Луч с нанесенным единичным отрезком, направлением, называют координатным лучом, координатной прямой.
Каждая точка на координатном луче имеет соответствующее числовое значение – координату точки.
Точке Р соответствует числовое значение 5.
Обозначается на письме: Р (5).
Произносится: координата точки Р – 5
Постарайтесь запомнить эти понятия, чтобы избежать трудностей с определением координат точек!
Фигура, которую мы рассмотрим, состоит из точки, лучей.
Давайте отметим начало двух лучей точкой.

Полученная фигура называется углом.
Угол– геометрическая фигура, состоящая из точки и выходящих из неё лучей.
Что такое вершина и стороны угла?
Точка называется вершиной угла, лучи– сторонами угла. Обозначают строчными, заглавными буквами латиницы (отметив на сторонах дополнительные точки). Для письменного обозначенияиспользуется специальный знак ∠.

Записывается, читается:∠β – угол бета,∠BAС – угол BAС.
Углы равны, если при наложении они совпадают.

Мы наложили ∠BAС на ∠ β,при совмещении, у них совпали (полностью совместились) вершины, стороны углов. Значит ∠BAС=∠ β.
Бывают случаи, когда източки выходят два луча в противоположные стороны, образуя при этом прямую линию. Например:

Полученная фигура называется развернутым углом.
Развернутый угол – фигура, стороны которой, дополняя друг друга, создают прямую линию. Градусная мера угласоставляет 180 ˚.
Все углы принято измерять градусами. Градус–единица измерения углов, составляет 1/180 часть развернутого угла. Для письменного обозначения градуса используется специальный символ – ˚.
Получается, что∠ α=180 ˚.
Читается как: градусная мера развернутого угла альфа равна 180 градусам.
Если такой угол разделить пополам, то получим 2 равнозначных угла.

Рассмотрим развернутый ∠ВАС. Луч АО делит ∠ВАС пополам, чтобы узнать градусную меру полученных углов, необходимо градусную меру развернутого угла, поделить пополам (180:2=90). Получается, что ∠ОАС и ∠ВАО имеют градусную меру равную 90 ˚, называются прямыми углами.
Прямым углом называют половину развернутого угла, градусная мера которого составляет 90 ˚
Ну, а теперь, можете попросить у родителей чашку горячего чая. Ведь для изучения следующего определения, будем использовать вкусный, ароматный бублик.

(Источник)
Бублик – лакомство, знакомое с самого детства. Но вряд ли кто-то из вас задумывался какую форму имеет любимая выпечка? Если рассматриватьс геометрической точки зрения, то бублик представляетзамкнутую линию теста, все точки которой лежат на одинаковом расстоянии от центра изделия. В геометрии такая фигура называется окружностью.
Что такое окружность?
Окружность – это замкнутая линия, все точки которой находятся на одинаковом расстоянии от выбранной точки О. Точка О называется центром окружности.

Точка О является центром окружности.
Все очень просто!
Снова возвращаемся к бубликам. Многие бабушки, мамы делают бублики вкуснее, наполняя всевозможными начинками.

(Источник)
Нас интересует бублик с начинкой,как геометрическая фигура. Если рассматривать всю область внутри бублика, учитывая сам бублик, то получается фигура, которую называют кругом.
Что такое круг?
Круг – это область внутри окружности, учитывающая саму окружность.

Точка О называется центром круга.
Если центр окружности соединить отрезком с точкой окружности, то получим радиус. Радиус принято обозначать буквой латиницы–R.
Рассмотрим на примере что такое радиус: отрезок ОВ соединяет центр окружности и точку, лежащую на окружности, поэтому онявляется радиусом. ОВ=R.

Протяженность от центра до любой точки окружности одинакова, все радиусы одной окружности равны. ОС=ОВ=R.
Если отрезком, проведенным через центр окружности соединить две точки окружности, то получим диаметр окружности.
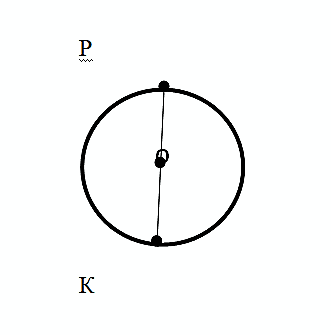
Диаметр окружности – это длина отрезка РК, диаметр обозначается буквой латиницы – D. Значит, РК= D.
На рисунке видно, что диаметр состоит из двух радиусов, то есть D=R+R=2R.
И последнее, часть окружности между любыми точками окружности, называется дугой окружности.
Минутка истории
В древней Греции существовали две идеальные фигуры – окружность, круг. Все точки окружности одинаковые между собой, это позволяет окружности самостоятельно совершать движение. Именно это свойство положило начало изобретения колеса. К огромному сожалению, изобретатель остался неизвестным. А модель колеса с того времени практически не изменилась.
Известно, что первые колеса появились в Месопотамии в 3000гг. до н.э. и использовались для изготовления гончарных изделий и колес для движения телег.
Почему так много внимания уделяется обычной геометрической фигуре? – спросите вы.
Давайте представим, что колесо просто не создано, его нет! А значит, нет совершенно никакого транспорта, не работают фабрики и заводы, не существуют механизмы. Человечество не двигается вперед. Жизнь остановилась!
Такое даже представить страшно!
Обложка урока взята с источника.
100urokov.ru
Онлайн урок: Отрезок. Длина отрезка по предмету Математика 5 класс
Каждый отрезок имеет определенную длину, значение которой является числом.
Длина в геометрии — это величина, которая характеризует протяженность.
Длина отрезка — это расстояние между концами отрезка.
Так как каждый отрезок имеет длину, отрезки можно измерять и сравнивать.
Существует несколько способов сравнения отрезков.
1. Приблизительный способ сравнения.
Данный способ сравнения применяют только в том случае, когда длины отрезков явно отличаются.
Пример: Даны два отрезка АВ и ЕР
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Очевидно, что отрезок АВ длиннее отрезка ЕР, значит, АВ > ЕР
2. Совмещение отрезков — более точный способ сравнения отрезков.
Метод заключается в следующем: совмещаются два отрезка друг с другом так, чтобы совпали их концы с одной стороны.
По расположению других концов относительно друг друга можно оценить какой из отрезков длиннее, а какой короче.
Если при наложении отрезков друг на друга длины отрезков совпадут, то отрезки равны (отрезки в этом случае будут равными фигурами).
Если при наложении отрезков друг на друга один из отрезков будет составлять часть второго, то первый отрезок является короче второго (т.е. длина первого меньше длины второго).
Пример: Даны два отрезка АВ и ОЕ
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Сравним данные отрезки методом совмещения отрезков.
Совместим левый конец А отрезка АВ и левый конец О отрезка ОЕ.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Можно заметить, что отрезок ОЕ составляет часть отрезка АВ.
Значит, отрезок ОЕ короче отрезка АВ.
Данный метод удобен, если есть возможность перемещать отрезки, совмещать один с другим.
3. Сравнение отрезков с помощью измерителя.
Если нет возможности перемещать сравниваемые отрезки, то можно использовать промежуточный измеритель.
В математике для этих целей используют специальный чертежный инструмент, который называется циркулем.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Чтобы сравнить отрезки с помощью циркуля, необходимо совместить концы отрезка с ножками циркуля.
Не меняя раствор циркуля, приложить его ко второму отрезку и сравнить.
- Если ножки циркуля совпадают с концами сравниваемого отрезка, то отрезки считаются равными.
- Если отрезок выходит за пределы расставленных ножек циркуля, то он больше исходного отрезка.
- Если же отрезок находится между концами измерителя, то сравниваемый отрезок меньше исходного.
Если нет возможности сравнить отрезки наложением и нет циркуля под рукой, то в качестве измерителя можно использовать нитку.
В таком случае нужно нитку приложить к исходному отрезку, на нитке по отрезку сделать замер, затем нитку приложить ко второму отрезку, оценить расположение замера на нитке по отношению к исследуемому отрезку, сделать вывод.
Пример:
Пусть даны три отрезка СD, АЕ, BG
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Сравним эти отрезки с помощью циркуля.
Соединим ножки циркуля с концами С и D отрезка СD.
Приложим циркуль с заданным раствором к отрезку АЕ.
Концы измерителя совпали с точками отрезка АЕ, значит, отрезки CD и AE равны: (CD = AE).
Приложим циркуль с заданным раствором к отрезку BG.
Отрезок выходит за концы измерителя, т.е. является частью отрезка BG, следовательно, отрезок BG длиннее отрезка СD: (BG > СD).
Все рассмотренные способы сравнения длины отрезков проводят без определения значения длины сравниваемых отрезков.
4. Существует еще один способ сравнения длины отрезков путем измерения их длинны.
Для этого необходимо сначала измерить длину каждого отрезка, далее сравнить полученные значения их длины и сделать вывод.
Большим будет являться тот отрезок, длина которого больше.
Соответственно, если длины измеряемых отрезков равны, то и отрезки равны.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Многоугольником называется фигура, ограниченная замкнутой ломаной линией, звенья которой не пересекаются.
Отрезки (звенья) ломаной линии называют сторонами многоугольника.
Общие точки двух отрезков (сторон) многоугольника называют его вершинами.
Каждая пара сторон многоугольника, сходящиеся в одной точке, образуют углы многоугольника.
Количество сторон и количество углов в многоугольнике совпадают.
Вершины, стороны и углы многоугольника обозначаются аналогично ломаной линии.
Многоугольник принято обозначать и называть по его вершинам, начиная с любой вершины и называя их последовательно, в любом порядке.
Рассмотрим пример:
На рисунке изображен многоугольник АBCDEF.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Вершины многоугольника АBCDEF: А, B, C, D, Е, F.
Стороны многоугольника АBCDEF: AB, BC, CD, DE, EF, FA.
Любые многоугольники можно сравнить: два многоугольника называются равными, если они совпадают при наложении.
Зная длину каждой стороны многоугольника, можно найти периметр этого многоугольника.
Периметр многоугольника — это сумма длин всех сторон.
Периметр многоугольника принято обозначать заглавной латинской буквой Р
Найдем периметр многоугольника АBCDEF (изображенного на рисунке):
РАВСDEF = AB+ BC+ CD+ DE+ EF+ FA = 2 см + 3 см + 2 см + 2 см + 3 см + 2 см = 14 см.
Существует огромное множество различных видов многоугольников.
Обычно многоугольники различают по числу сторон и углов.
Например: пятиугольник имеет 5 углов и 5 сторон, шестиугольник — 6 углов и 6 сторон.
Многоугольник с наименьшим числом вершин, сторон и углов называют треугольником.
Треугольник — плоская геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки.
Треугольник часто обозначают символом «Δ» и тремя заглавными латинскими буквами, которые обозначают его вершины.
Рассмотрим пример:
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
На рисунке изображен треугольник АBC (Δ АBC).
А, В, С — вершины треугольника АBC.
Отрезки AB, BC, АC— стороны треугольника АBC.
Периметр треугольника- это сумма длин трех его сторон.
Найдем периметр треугольника АBC (изображенного на рисунке):
РАВС = AB+ BC+ АС = 4 см + 6 см + 3 см = 13 см.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
ladle.ru
Геометрические фигуры, изучаемые в школе
Государственное бюджетное профессиональное образовательное учреждение
Ростовской области
«Волгодонский педагогический колледж»
(ГБПОУ РО «ВПК»)
Реферат
Тема: «Геометрические фигуры, изучаемые в начальной школе»
Выполнила: студентка группы ПНК-2
Чуракова К.С.
Проверила: Пасечник Г.Н.
г.Волгодонск
2016
Содержание
1.Введение(стр.3)
2. Геометрические понятия и фигуры, изучаемые в начальной школе(стр.4)
3.Вывод(стр.10)
Введение
В программе традиционной начальной школы геометрический материал является составной частью курса математики. Он не выделяется в самостоятельный раздел, а включается в программу каждого года обучения.
Одной из основных задач изучения геометрического содержания в курсе математики начальной школы является развитие пространственного воображения у ребенка, умения наблюдать, сравнивать, обобщать, анализировать и абстрагировать. Второй важной задачей является формирование у ребенка практических умений измерения и построения геометрических фигур с помощью циркуля, угольника и линейки.
Обязательный минимум содержания образования по математике содержит следующий перечень понятий геометрического характера:
Точка.
Линии: прямые, кривые.
Отрезок.
Угол.
Прямой угол.
Многоугольники: треугольник, прямоугольник, квадрат.
Вершины и стороны многоугольника.
Окружность и круг.
Куб.
Шар.
Измерение длин.
Измерение площади.
Вычисление площади прямоугольника.
Геометрические понятия и фигуры, изучаемые в начальной школе
Точка
Точка — это основная и самая простая геометрическая фигура.
В геометрии точка обозначается заглавной латинской буквой или цифрой. Многие латинские буквы по написанию похожи на английские буквы.
Прямая
Прямая — это самая простая геометрическая фигура, которая не имеет ни начала, ни конца.
Слова «не имеет ни начала, ни конца» говорят о том, что прямая бесконечна.
Через две точки можно провести единственную прямую.
Две прямые могут пересекаться только в одной точке.
Через одну точку можно провести бесконечное множество прямых.
Способы обозначения прямых
Прямая a.
Двумя заглавными латинскими буквами в том случае, если этими буквами обозначены точки, расположенные на прямой.

Прямая АB.
Луч
Луч — это часть прямой линии, которая расположена по одну сторону от какой-либо точки. У луча есть начало, но нет конца.
Способы обозначения лучей
Луч c.
Двумя заглавными латинскими буквами в том случае, когда первая точка — начало луча, а вторая точка лежит на луче.
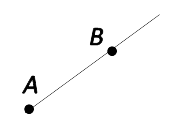
Луч AB.
Отрезок
Отрезок — это часть прямой линии, которая ограничена двумя точками (концами отрезка). У отрезка есть и начало, и конец.
Основное свойство отрезка — это его длина.
Длина отрезка — это расстояние между его концами.
В математике отрезок обозначается заглавными латинскими буквами.
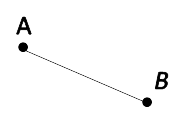
Отрезок AB.
Ломаная
Ломаная — это геометрическая фигура, состоящая из точек, которые соединены отрезками.
Вершины ломаной — это точки, в которых соединяются отрезки, образующие ломаную.
Звенья ломаной — это отрезки ломаной.
В математике ломаная обозначается заглавными латинскими буквами.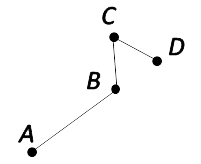
Ломаная ABCD.
Вершины ломаной — A, B, C, D.
Звенья ломаной — AB, BC, CD.
Угол
Угол — это геометрическая фигура, которая состоит из двух лучей и вершины.
Вершина угла — это точка, в которой два луча берут начало.
Стороны угла — это лучи, которые образуют угол.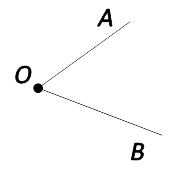
Например:
Вершина угла — точка O.
Стороны угла — OA и OB.
Для обозначения угла в тексте используется символ:
 AOB
AOB
Способы обозначения углов
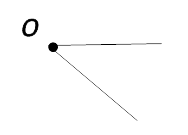 Угол:
Угол:  O
O
Тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.

Угол:  AOD
AOD
Называть угол можно с любого края, но НЕ с вершины.
Угол с рисунка имеет два названия:  AOD и
AOD и DOA.
DOA.
Угол:  fn
fn
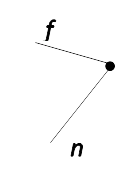
Единица измерения углов — градусы. Углы измеряют с помощью специального прибора — транспортира.
Для обозначения градусов в тексте используется символ: °
50 градусов обозначаются так: 50°
Виды углов
Прямоугольник
Прямоугольник — это фигура, которая имеет четыре стороны и четыре прямых угла.
У прямоугольника противоположные стороны равны.
В геометрии прямоугольник обозначают четырьмя заглавными латинскими буквами.
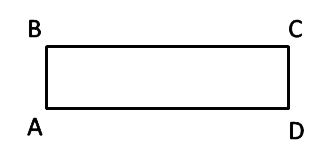
Противоположные стороны прямоугольника ABCD: AB = CD, BC = DA.
Углы:  ABC =
ABC =  BCD =
BCD =  CDA =
CDA =  DAB = 90° — все углы прямые.
DAB = 90° — все углы прямые.
Квадрат
Квадрат — это прямоугольник, у которого все стороны равны.
В геометрии квадрат, также как и прямоугольник, обозначают четырьмя большими латинскими буквами.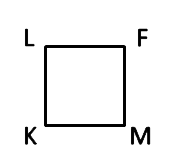
Стороны квадрата KLFM: KL = LF = FM = MK.
Углы:  KLF =
KLF =  LFM =
LFM =  FMK =
FMK =  MKL = 90° — все углы прямые.
MKL = 90° — все углы прямые.
Треугольник
Треугольник — это геометрическая фигура, которая имеет три стороны и три угла (вершины треугольника).
Треугольник обозначается тремя заглавными латинскими буквами, перед которыми ставится знак:  .
. 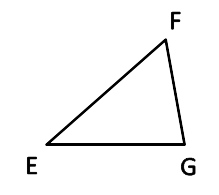
Треугольник EFG —  EFG.
EFG.
Виды треугольников
Многоугольник
Многоугольники — это геометрические фигуры различной формы.
Вершины многоугольника — это точки, соединяющие отрезки, из которых состоит многоугольник.
Стороны многоугольника — это отрезки, из которых состоит многоугольник.
Многоугольник ELNFK.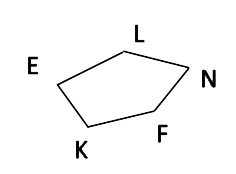
Вершины многоугольника — E, L, F, N, K.
Стороны многоугольника — EL, LN, NF, FK, KE.
Окружность. Круг
Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой находятся на одинаковом расстоянии от центра.
Круг — это геометрическая фигура, которая ограничена окружностью.
Окружность — это граница круга.
Радиус круга — это расстояние от центра окружности до любой её точки.
Диаметр круга — это отрезок, который соединяет две точки окружности и проходит через её центр.
Диаметр круга равен двум его радиусам.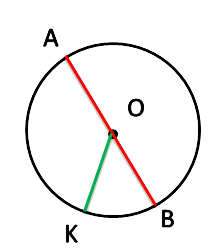
Точка O — центр круга.
AB — диаметр круга.
OK — радиус круга.
АB = 2 OK.
Точка. Линия — кривая и прямая. Отрезок. Ломаная. Звенья ломаной. Вершина ломаной. Замкнутая и незамкнутая ломаная. Многоугольники. Треугольники и четырехугольники.
Геометрические понятия, с которыми знакомятся в 3 классе:
Периметр многоугольника. Площадь прямоугольника. Круг. Окружность. Радиус. Диаметр. Треугольники равносторонние, равнобедренные и разносторонние.
Вывод
Особое содержание геометрического материала, включенного в программу и реализованного в системе тщательно отобранных задач, направлено на формирование достаточно полной системы геометрический представлений (включающей образы геометрических фигур, их элементов, отношений между фигурами, их элементами).
На этой основе формируются пространственные представления и воображение, развивается речь и мышление учащихся, организуется целенаправленная работа по формированию важных практических навыков.
infourok.ru
Урок математики в 1-м классе по теме «Отрезок»
Тема: Отрезок
Цель: познакомить с новой геометрической фигурой – отрезком, его признаками, учить сравнивать отрезки.
I. Оргмомент.
II. Повторение
– Какие геометрические фигуры знаете? Расскажите.
– О каких фигурах можно сказать, что их 2, 3, 1?
– Сколько всего фигур?
– Сколько синих?
– Сколько не красных?
Как думаете, мы уже все геометрические фигуры изучили?
III. Знакомство с новым материалом.
Сегодня мы познакомимся с новой геометрической фигурой и её признаками. Какая это фигура, вы догадаетесь, когда послушаете сказку.
Мне нужны 2 помощника (держат бумажную модель прямой).
– Какую геометрическую фигуру я изобразила с помощью узкой полоски бумаги?
Сказка.
Однажды Карандаш отправился гулять по прямой линии. Устал. Где начало? Где конец? Присел отдохнуть. Нарисовал точку и пошел дальше, напевая: без конца и края
Линия прямая.
Хоть сто лет по ней идти
Не найти конца пути.
Снова устал. Присел отдохнуть. Нарисовал ещё одну точку. А тут ножницы: чик-чик.
Лучи и отрезок вывешиваются на доску.
– Крайние фигуры вам знакомы?
(Лучи)
– А как получили эту фигуру? (отрезок)
(Отрезали от прямой линии.)
– Кто догадался, как её назвали?
(Отрезок) Открываю на доске название темы урока.
IV. Объявление целей урока.
Об отрезке мы и будем сегодня говорить, узнаем его признаки и будем учиться сравнивать отрезки разной длины.
– Отрезок – это прямая линия?
(Часть прямой)
– Чем отрезок отличается от луча? Ведь луч тоже часть прямой линии?
(У луча только начало, у отрезка и начало и конец)
Молодцы. И для названия отрезка используют не одну, а две буквы.
Обозначаю буквами отрезок на доске. На доске плакат с некоторыми буквами латинского алфавита: А (а), В(бэ).С(цэ), Д(дэ), М(эм), К(ка).
– А что одинакового у отрезка, луча, прямой? Как их чертят?
(По линейке)
V. Закрепление.
Мы научимся чертить отрезки различной длины и располагать их на плоскости тетрадного листа, используя текст задания № 117, как руководство к действию.
Дети открывают тетради. Задание читает хорошо читающий ученик. Выполняем задание (дети в тетради, учитель на доске).
— Поставь в тетради 2 точки и соедини их по линейке. У тебя получился отрезок..Концы отрезка обозначают буквами.
– Подумай, сколько отрезков можно провести через две точки?
VI. Физпауза.
VII. Визуальное сравнение отрезков.
А вот в задании 118 три пары точек соединены тремя отрезками.
На доске такой же чертеж
– Что можно о них сказать?
(Отрезки разной длины, МК – самый длинный, СД – самый короткий)
– Докажите.
Сравниваем, проводя пунктирную линию, чтобы увидеть равные отрезки.
Вывод: если отрезки начинаются на одном уровне – легко сравнить их длину визуально.
VIII. Работа в парах.
Вы получили лист. на котором 2 отрезка.
– Какой из них длиннее? Короче? Легко сравнить?
(Нет, на глаз сравнить трудно, можно ошибиться)
Возьмите прозрачную пленку и подумайте, как используя её сравнить отрезки?
Намечаем план действий:
1. Приложить пленку к отрезку,
2. Обозначить на пленке начало и конец.
3. Соединить точки с помощью линейки.
4. Приложить полученный отрезок к другому отрезку и сравнить.
Работа в парах, вывод: АВ – длиннее, МК – короче.
IX. Физпауза.
X. Работа по вариантам в тетрадях на печатной основе.
Задание для I варианта — № 46 – построить отрезок на луче ОВ, который будет длиннее данного,
Задание для II варианта — № 47 – построить отрезок на луче ОВ, который будет короче данного.
Перед началом работы в тетради обсуждаем, что сначала нужно “увидеть” отрезок, равный данному, затем ребята показывают с помощью рук, что двигаясь вправо, отрезок увеличивается, влево – становится короче.
Проверка по чертежу на доске с помощью магнитов. Несколько ребят показывают, где они поставили точки.
Выясняем, в какой части луча работали ребята I варианта, в какой – II вариант.
Проверьте свои работы. Самопроверка.
XI. Итог урока.
– Что нового узнали на уроке?
– Чем отрезок отличается от прямой линии и от луча?
– А что у них одинакового?
– Как думаете, а в жизни нам пригодится умение чертить и сравнивать длину отрезков?
Об этом мы с вами поговорим на следующем уроке математики.
urok.1sept.ru
Ломаная геометрическая фигура: звенья, вершины и длина, разновидности
 Ломаной называется особая разновидность геометрической фигуры, которая составлена из нескольких отрезков. Эти отрезки последовательно соединены между собой своими концами. Конец каждого отрезка, за исключением последнего, является начальной точкой следующего. Смежные отрезки не должны находиться на одной прямой линии.
Ломаной называется особая разновидность геометрической фигуры, которая составлена из нескольких отрезков. Эти отрезки последовательно соединены между собой своими концами. Конец каждого отрезка, за исключением последнего, является начальной точкой следующего. Смежные отрезки не должны находиться на одной прямой линии.
Существует и другое определение того, что такое ломаная фигура. Согласно ему это геометрический объект, который представляет собой непрямую линию и состоит из череды отрезков, последовательно соединенных между собой. Эти отрезки могут образовывать углы различной величины. Даже если угол между ними будет минимальным, он все равно будет ломать линию и ее уже можно считать ломаной. В этом и заключается ее основное отличие от прямой.
Это интересно: разность чисел что это, как ее найти?
Ломаную линию следует отличать от кривой. Основное отличие заключается в том, что отрезки ломаной являются прямыми линиями, а отрезки кривой — нет. Эти понятия подробно объяснит школьная программа по математике за 8 класс.
Звенья, вершины и длина
Чтобы полностью усвоить сущность и свойства этого понятия, рассмотрим, что такое звенья ломаной линии в математике, а также что представляют собой ее вершины и длина:
 Отдельные отрезки, составляющие такую линию, называются ее звеньями. Каждая такая линия может состоять как минимум из двух звеньев. Максимальное количество звеньев при этом не ограничено.
Отдельные отрезки, составляющие такую линию, называются ее звеньями. Каждая такая линия может состоять как минимум из двух звеньев. Максимальное количество звеньев при этом не ограничено.- Точки соединения концов этих отрезков называются вершинами.
- Если концы ломаной соединяются в одной точке, такая фигура носит название замкнутой. Ее звенья могут иметь взаимные пересечения.
- Если же звенья одной замкнутой линии не пересекаются между собой, она называется многоугольником.
- Геометрическое понятие длины ломаной включает в себя сумму длин всех ее звеньев.
Интересно знать: что такое выпуклый четырехугольник, его особенности и признаки.
Обозначение ее составляется из заглавных латинских букв, которые стоят на вершинах:
- Каждая вершина на рисунке обозначается одной буквой (например: A, B, C, D или E).
- Звено принято обозначать двумя буквами (концы соответствующего отрезка, например: AB, BC, CD, DE).
В целом такую совокупность принято называть ABCDE или EDCBA.
Обратите внимание: что такое луч в геометрии.
Разновидности
В геометрии принято различать несколько разновидностей по структуре:
- Замкнутые самопересекающиеся.
- Незамкнутые самопересекающиеся.
- Замкнутые без самопересечений.
- Незамкнутые без самопересечений.
Как уже было описано выше, замкнутая непересекающаяся фигура получила название многоугольника.
Если звенья фигуры имеют пересечения между собой — она называется самопересекающейся.
Многоугольники
Многоугольник — это геометрическая фигура, которая характеризуется количеством углов и звеньев. Углы составлены парами звеньев замкнутой ломаной, сходящимися в одной точке. Звенья называются еще сторонами многоугольника. Общие точки двух отрезков называют вершинами многоугольника.
 Количество звеньев или сторон в каждом многоугольнике соответствует количеству углов в нем же. Замкнутая ломаная из трех отрезков называется треугольником. Ломаная из четырех звеньев получила название четырехугольника. Фигура из пяти отрезков — пятиугольник и т. д.
Количество звеньев или сторон в каждом многоугольнике соответствует количеству углов в нем же. Замкнутая ломаная из трех отрезков называется треугольником. Ломаная из четырех звеньев получила название четырехугольника. Фигура из пяти отрезков — пятиугольник и т. д.
Часть плоскости, которая ограничена замкнутой ломаной, называется плоским многоугольником. Другое ее название — многоугольная область.
Свойства
Ниже приведены основные свойства, общие для всех многоугольников:
- Если вершины многоугольника служат концами одной стороны, их называют соседними. Если же вершины не прилежат к одной стороне, они несоседние.
- Наименьшее количество сторон у многоугольника равняется трем. Однако треугольники, находясь рядом друг с другом, могут образовывать новые фигуры.
- Если отрезок соединяет между собой несоседние вершины, он носит название диагонали.
- Если фигура лежит относительно одной прямой в любой полуплоскости, она называется выпуклой. При этом прямая содержит в себе одну сторону фигуры и сама принадлежит полуплоскости.
- Угол, смежный внутреннему углу многоугольника при некоторой вершине, называется внешним.
- Если все стороны и углы многоугольника равны, он называется правильным.
Треугольники
Треугольником в математике принято называть плоскую геометрическую фигуру, которая состоит из трех точек, не располагающихся на одной прямой. Эти точки соединены тремя отрезками.
Точки представляют собой вершины или треугольника, а отрезки — его стороны. Возле каждой из вершин образуется угол треугольника. Таким образом эта фигура имеет три угла, что видно из ее названия.
Различают следующие виды треугольников:
- Равносторонние — все стороны их равны по длине.
- Разносторонние — все стороны различаются по длине.
- Равнобедренные — две стороны из трех имеют одинаковую длину.
- Остроугольные — если все углы острые.
- Прямоугольные — если имеется прямой угол.
- Тупоугольные — если есть один тупой угол.
Четырехугольники
Плоская геометрическая фигура, имеющая четыре угла и четыре стороны, называется четырехугольником.
Если все углы у четырехугольника прямые — это прямоугольник.
Правильный четырехугольник носит название квадрата.
Существуют и другие разновидности четырехугольников — ромб, трапеция, параллелограмм и пр. Все они подчиняются общим правилам, описанным выше.
tvercult.ru
Точка. Линия. Луч. Отрезок. Кривая.
План урока
Предмет: МатематикаСквозная тема: «Моя школа»
Раздел3: Элементы геометрии
Подраздел 3.1.: Геометрические фигуры и их классификация
Класс: 1
Тема урока
Геометрические фигуры: Точка. Линия. Луч. Отрезок. Кривая.
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)
1.3.1.1 распознавать и называть геометрические фигуры: точка, прямая, кривая, замкнутая и незамкнутая линии, луч, отрезок, угол.
Цель урока
Учащиеся смогут распознавать точку, линии, прямую, отрезок , кривую, луч, угол;
выявлять различия геометрических фигур.
Критерии оценивания
Смогут определять, перечислять геометрические фигуры;
Выбирать данную геометрическую фигуру из всех фигур;
сравнивать фигуры, выделять основные признаки, классифицировать фигуры.
Языковые цели
Учащиеся могут:
обсуждать и объяснять геометрические фигуры в соответствии с их признаками, выделять ее среди других фигур
Предметная лексика . Ключевые слова и фразы: луч, прямая, точка, замкнутая, кривая, незамкнутая, ломаная, отрезок, начало, конец
Вопросы для обсуждения:
Обсуждение:
• Почему следует группировать их вместе?
• Какие общие признаки имеют эти фигуры?
• Где вы использовали подобные фигуры?
Можете ли вы сказать, почему…? Это линия называется замкнутой?
Воспитание ценностей
Воспитание коммуникативных возможностей (уважения, взаимопомощи, сотрудничества; труд и творчество воспитание осуществляется через все приемы и методы, используемые на уроке.
Межпредметные связи
Обучение грамоте, художественный труд, геометрия
Предыдущие
знания
перерабатывают полученную информацию: сравнивают и группируют плоские геометрические фигуры.
Ход урока
Запланированные этапы урока
Виды упражнений, запланированных на уроке
Ресурсы
Начало урока
1-9 мин.
Создание коллаборативной среды. Метод «Четыре стихии»

2.1. Деление на группы
Дома заранее учащимся предлагалось разукрасить картинки. Если я скажу «солнце» — вы подтягиваетесь к солнышку . Если я скажу «радуга» — вы вытягиваете руки к друг другу и создаете радугу. Если скажу «ветер» — вы поднимаетесь на носочки и дуете вверх. Если я скажу «дождь» — вы вращаете руками топаете ногами. Далее распределяются по группам
1группа-солнце это будут названия групп
2группа-радуга
3группа-ветер
4 группа-дождь.
– формируются группы по 5 человека)
Эти знаки являются в каждой группе своим обозначением для ФО.
ФО добавляются условные обозначения на каждый правильный ответ. (В конце урока ведется подсчет каждой группы. Выигрывает группа, получившая большее количество знаков).
2.2 стратегия «Предположение»)
В группах на столах лежат конверты, в которых геометрические фигуры:
-Как вы думаете о чем будем говорить?
Выход на тему урока
2.3Прием «Что лишнее?» Д/О
( учащимся предлагаются предложения для ответов
………..является…………..в то время как……….., потому что…………. Все лишние фигуры по предложения детей вывешиваются на доску.
Ф/О-«»

Середина урока
35 мин
Ф.О. первая группа показывает прямые-остальные группы сверяются. Если правильно то берут условный знак.
2гр.кривые линии
3гр замкнутые
4гр лучи. Остается одна карточка с отрезком
Ф.О. за ответ на вопрос – условный знак
Критерии успеха
Проблемная ситуация. Учитель: Сегодня на уроке проведем исследование, совершим маленькие «открытия» и, надеюсь, по окончанию урока проверим наши ответы- предположения.
Пожелание успеха на уроке.
3.Стратения «Предположение»
—Как вы думаете, о чем будем говорить сегодня на уроке?
Выход на тему урока
Проблемная ситуация. Учитель: Сегодня на уроке мы будем наблюдать за такими линиями, займёмся исследованием, совершим маленькие «открытия» и, надеюсь, ответим на многие ваши вопросы

Мы с вами отправимся в Шишкину школу. В гости к Шунечке
Просматривают мультфильм до момента (поселилась точка)
Работают индивидуально.
-Давайте вы тоже поселите себе точку на ламинированные листы. И мы нарисуете друзей своим точкам.(вр 2,35с)
Выполним просьбу точки, добавьте ей много, много друзей. (2,45сек). — Сколько у вас получилось точек? (Множество).
Подружите их между собой ( вр 3,54с)
— Какие линии у вас получились? (Кривые).
— Почему они называются кривыми?
(Они неровные, проводятся от руки).
— Ровную линию провести очень трудно. Какой инструмент понадобиться , чтобы провести прямую линию.
Я люблю прямоту, я сама прямая.
Сделать ровную черту всем я помогаю.
Что-нибудь без меня начертить сумей-ка.
Угадайте-ка, друзья, кто же я ?… (Линейка)
Исследование
А как мы с вами можем показать, что мы дружные?
В группе дети берутся за руки.
Постройте прямую. /дети выстраиваются в линии.
Сколько у нас получилось прямых?/4/
Предложите , каким образом мы можем превратиться в одну линию? / встать в одну линию/
Постараться построиться ровно, прямо (но в кабинете не хватит места и линия будет кривая) Дети в руках держат нить или веревку.
Наша линия соответствует выполненному заданию?/нет/ Почему? Как мы ее тогда можем назвать? Дети дают название – кривая.
Разыгрывает учитель. Где будет мое место?/ учитель встает либо с одного конца прямой, либо с другого конца прямой. Показывает начало отрезка. Кто назовет- что теперь у нас получилось?/луч/ Что же мне делать,- Не могу же я вечно гулять по прямой.
Кто догадался, каким способом нам вернуться на свои группы и превратиться обратно в отрезки./ разъединиться/ Позвать на помощь ножницы,
Тут, откуда ни возьмись появились ножницы, щёлкнули раз, щёлкнули два, и разрезали прямую.
Это отрезок, — сказали ножницы, теперь ты на отрезке прямой. Что необходимо для построения прямой? Чем нужно было пользоваться? Знакомство с линейкой.
Дети возвращаются на свои места и выполняют следующее задание, Как интересно, что же получилось из прямой, которую мы с вами построили?/луч, кривая, замкнутая, отрезок/
Вывод. Возвращаемся к началу нашего урока , когда мы выбирали геометрические фигуры. Проверим наши ответы. Дети делают выводы.
Стадия осмысления.
Формирвание новых знаний. Практическая работа 1. Прием «Шкатулка»
В группы предлагается детям продукты и предметы из повседневной жизни
( трубочки, макароны, спагетти, гречка, горох, лапша, ватные палочки, пластилин, тесьма. Используя активный словарь, расположенным на классной доске. Распределить данный материал, по соответствующим группам.
2 . сквозная тема «Моя школа»
В классе, где мы можем наблюдать наши изученные геометрические фигуры?
З. межпредметная связь.
На уроке обучению грамоте?
Значок /сигнал светофор/
Стадия осмысления.
Формирвание новых знаний. Практическая работа.
— А в какую группу поместить оставшуюся карточку? Назовите ее отличия?
Кто знает как называется такая фигура?( отрезок)
Какой вывод можно сделать? Линии бывают прямые и кривые, замкнутые, незамкнутые, ломаные.
Ребята, посмотрите, как проведены линии? Прямые ли линии?(кривые) Почему не получились?
—
—
Рабочий лист 46 «Учись строить линии, лучи и точки», с. 48.
Предложите учащимся рассмотреть иллюстрацию в тетради, задание детям найти на рисунке точки, замкнутые и незамкнутые линии.
Ответы
Закрепите понятие о разных видах линий: прямых и кривых. Сделайте вывод о том, что для изображения прямых линий следует пользоваться линейкой и остро заточенным карандашом.
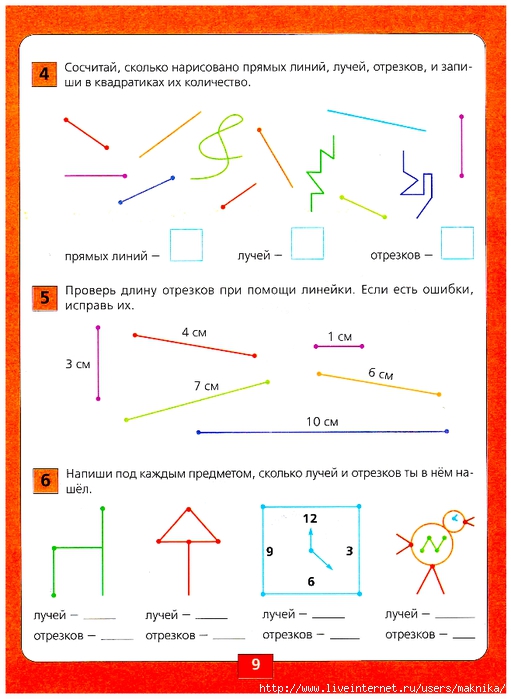
Физминутка
Точка-двигаются по одному
Луч- строят луч
Прямая линия – идут в колонне друг за другом
Кривая – извиваются змейкой и т.д.
Попробуй. Предложите школьникам выполнить задание в парах, используя ламинированные листы и маркеры. Предоставьте им возможность в парах построить две точки и провести через них линию. Обратите внимание на то, что линия должна быть прямая.
Реши. Задание направлено на отработку умения называть линии. Сообщите ребятам, что для обозначения линий в математике можно использовать строчные буквы латинского алфавита.
Стадия осмысления Работа в группе:
1.гр.: найди и назови геом. фигуры на картинке и при помощи пластилина раскатать различные виды линий
2гр.: Найдите подобные геометрические фигуры среди окружающих предметов в классе.
Преобразуйте лучи в отрезки, точки в лучи. Кто больше составит картинок из геом.фигур
3гр.: 1.Из окружающего нас мира приведите примеры какие предметы могут быть в виде прямой, отрезка, луча.
2.Как можно больше нарисовать предметов из геом.фигур
Оценивание группами: карточки с буквами Д, С (достиг, стремится)
Формативное оценивание учителем (похвала, у каждой группы условный знак за правильные ответы)
умеют распознавать геометрические фигуры: прямая линия, кривая линия, луч, различать прямые и кривые линии, чертить прямые линии при помощи линейки.
Ресурсы:Образов. сайт «Шишкина школа»
цветные фломастеры
маркерная доска или листы формата A3;
ламинированные дощечки для учащихся;
электронная
;
Составляется активный словарь урока./ карточки с названием геометрических фигур/ постепенно вывешиваются на доску
Учебник:
Точка. Линия. Луч, с. 48—49.
На классной доске формируется словарь:
Точка.
луч.
прямая.
замкнутая.
кривая
Рабочая тетрадь:
Рабочий лист 45 «Точка. Линия. Луч», с. 47. Рабочий лист 46 «Учись строить линии, лучи и точки», с. 48.
Конец урока
10 мин.
Рефлексия (
прием-4 стихии)
Рисунки солнышек: солнышко улыбающееся – урок понравился, все понятно;
Солнышко слегка хмурое: есть затруднения, на уроке было интересно;
Солнышко закрыто тучками: ничего не понятно, урок не понравился.
Формативное оценивание учителем (похвала)
Самооценивание: подсчет значков у каждой группы

Задание
Соотнесите название с изображением фигуры (или укажите номер фигуры в
соответствии с названием
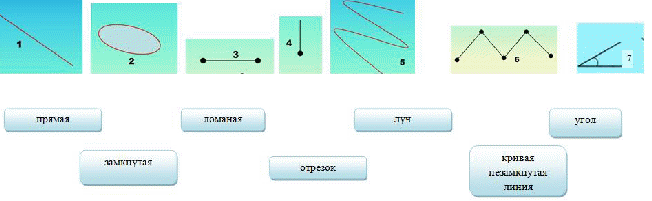
Дескриптор: Обучающийся
— определяет отрезок;
— определяет прямую линию;
— определяет ломаную линию;
— определяет луч;
— определяет угол;
— определяет замкнутую линию;
— определяет кривую незамкнут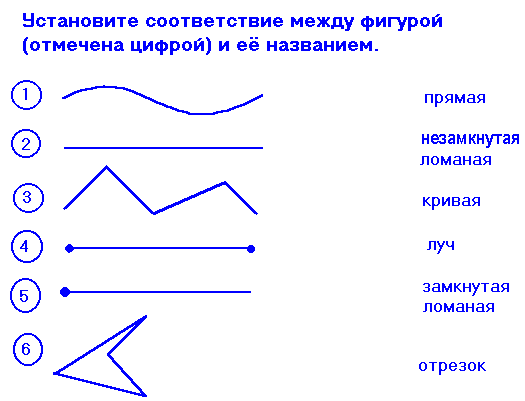 ую линию.
ую линию.
infourok.ru
Многоугольник — определение и основные понятия, виды и свойства фигур
Многоугольником называется геометрическая фигура, которая со всех сторон ограничена замкнутой ломаной линией. При этом количество звеньев ломаной не должно быть меньше трех. Каждая пара отрезков ломаной имеет общую точку и образует углы. Количество углов совместно с количеством отрезков ломаной являются основными характеристиками многоугольника. В каждом многоугольнике количество звеньев ограничивающей замкнутой ломаной совпадает с количеством углов.
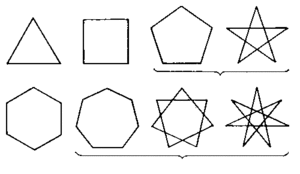
Сторонами в геометрии принято называть звенья ломаной линии, которая ограничивает геометрический объект. Вершинами называют точки соприкосновения двух соседних сторон, по количеству которых получают свои названия многоугольники.
Если замкнутая ломаная состоит из трех отрезков, она носит название треугольника; соответственно, из четырех отрезков — четырехугольником, из пяти — пятиугольником и пр.
Для обозначения треугольника или четырехугольника пользуются заглавными латинскими буквами, обозначающими его вершины. Буквы называют по порядку — по часовой стрелке или против нее.
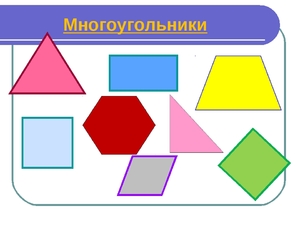
Основные понятия
Описывая определение многоугольника, следует учитывать некоторые смежные геометрические понятия:
- Если вершины являются концами одной стороны, они называются соседними.
- Если отрезок соединяет между собой несоседние вершины, то он имеет название диагонали. У треугольника не может быть диагоналей.
- Внутренний угол — это угол при одной из вершин, который образован двумя его сторонами, сходящимися в этой точке. Он всегда располагается во внутренней области геометрической фигуры. Если многоугольник невыпуклый, его размер может превосходить 180 градусов.
- Внешний угол при определенной вершине — это угол смежный с внутренним при ней же. Иными словами, внешним углом можно считать разность между 180° и величиной внутреннего угла.
- Сумма величин всех отрезков носит название периметра.
- Если все стороны и все углы равны — он носит название правильного. Правильными могут быть только выпуклые.
Как уже упоминалось выше, названия многоугольных геометрических строятся исходя из количества вершин. Если у фигуры их количество равняется n, она носит название n-угольника:
- Многоугольник называется плоским, если ограничивает конечную часть плоскости. Эта геометрическая фигура может быть вписанной в окружность или описанной вокруг окружности.
- Выпуклым называется n-угольник, который соответствует одному из условий, приведенных ниже.
- Фигура расположена по одну сторону от прямой линии, которая соединяет две соседних вершины.
- Эта фигура служит общей частью или пересечением нескольких полуплоскостей.
- Диагонали располагаются внутри многоугольника.
- Если концы отрезка располагаются в точках, которые принадлежат многоугольнику, весь отрезок принадлежит ему.
- Фигура может называться правильной, если у нее все отрезки и все углы равны. Примерами могут служить квадрат, равносторонний треугольник или правильный пятиугольник.
- Если n-угольник невыпуклый, все стороны и углы его равны, а вершины совпали с таковыми правильного n-угольника, он называется звездчатым. У таких фигур могут иметься самопересечения. Примерами могут служить пентаграмма или гексаграмма.
- Треугольник или четырехугольник называется вписанным в окружность, когда все его вершины располагаются внутри одной окружности. Если же стороны этой фигуры имеют точки соприкосновения с окружностью, это многоугольник описанным около некоторой окружности.
Любой выпуклый n-угольник можно поделить на треугольники. При этом количество треугольников бывает меньше количества сторон на 2.

Виды фигур
Треугольник
Это многоугольник с тремя вершинами и тремя отрезками, соединяющими их. При этом точки соединения отрезков не лежат на одной прямой.
Точки соединения отрезков — это вершины треугольника. Сами отрезки называются сторонами треугольника. Общая сумма внутренних углов каждого треугольника равняется 180°.
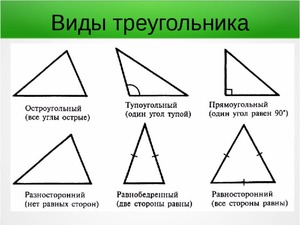
По соотношениям между сторонами все треугольники можно подразделять на несколько видов:
- Равносторонние — у которых длина всех отрезков одинаковая.
- Равнобедренные — треугольники, у которых равны два отрезка из трех.
- Разносторонние — если длина всех отрезков разная.
Кроме того, принято различать следующие треугольники:
- Остроугольные.
- Прямоугольные.
- Тупоугольные.
Четырехугольник
Четырехугольником называется плоская фигура, имеющая 4 вершины и 4 отрезка, которые их последовательно соединяют.
- Если все углы четырехугольника прямые — эта фигура называется прямоугольником.
- Прямоугольник, у которого все стороны имеют одинаковую величину, называется квадратом.
- Четырехугольник, все стороны которого равны, называется ромбом.
На одной прямой не может находиться сразу три вершины четырехугольника.
Видео
Дополнительную информацию о многоугольниках вы найдете в этом видео.
liveposts.ru

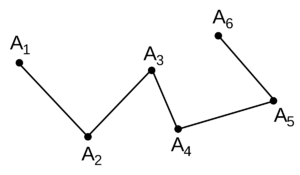 Отдельные отрезки, составляющие такую линию, называются ее звеньями. Каждая такая линия может состоять как минимум из двух звеньев. Максимальное количество звеньев при этом не ограничено.
Отдельные отрезки, составляющие такую линию, называются ее звеньями. Каждая такая линия может состоять как минимум из двух звеньев. Максимальное количество звеньев при этом не ограничено.