Что такое параметр

 

Анна Малкова (автор книги для подготовки к ЕГЭ, ведущая годового Онлайн-курса подготовки к ЕГЭ на 100 баллов, руководитель компании «ЕГЭ-студия» (Курсы ЕГЭ))

Приветствую будущих студентов!

Я заметила, что на своем YouTube- канале я разбирала несколько задач с параметрами, но так и не рассказала, что такое параметр.

А что же это?

Толковый словарь русского языка, куда полезно иногда заглядывать, дает следующее определение: «Параметр – это величина, характеризующая какое-нибудь основное свойство устройства, системы, явления или процесса». Что же это значит? Давайте разберемся.

Вот ракете выводит космический корабль в околоземное пространство. Если спутник запустить с первой космической скоростью, приближенно равной 7,9 км/с, он выйдет на круговую орбиту. Первый искусственный спутник Земли, СССР, 1957 год. Вторая космическая скорость, приближенно равная 11,2 км/с, и космический корабль преодолевает поле тяжести Земли. Третья космическая скорость, приближенно 16,7 км/с, дает космическому кораблю возможность выйти за пределы Солнечной системы и преодолеть гравитационное притяжение Земли и Солнца. Например, такой космический корабль, который назывался «Вояджер-1», был запущен в 1977 году, и в 2012 году вышел за пределы Солнечной системы, и теперь будет вечно бороздить просторы космоса. Этот корабль передал на Землю сигналы и снимки отдаленных планет. Кроме аппаратуры, он несет на своем борту золотой диск. На этом диске записаны звуковые и видеосигналы. Например, схема излучения атома водорода, местоположение Солнца, человек и его строение, земные пейзажи, шум моря, звук шагов, песни птиц, приветствие на разных языках, музыка, даже грузинский хор; плач ребенка, голос мамы, которая его успокаивает. Это подарок неизвестным существам от маленького, затерянного во Вселенной, мира нашей планеты. И может быть когда-нибудь они обнаружат этот корабль, расшифруют наше послание и узнают о нас.

Значит скорость космического корабля – это параметр, от которого зависит его дальнейшая траектория и судьба, и конечно, это не единственный параметр. При запуске космического корабля таких параметров десятки и сотни.

Реальные задачи науки и техники используют функции не одной, а многих переменных: и первые-вторые, и энные производные этих функций.

А что же будет если какой-то параметр рассчитан неправильно?

Помните, как появилось выражение «Кажется, что-то пошло не так»? Эти слова вырвались у комментатора, который вел прямую трансляцию о запуске космического корабля, и через несколько секунд после старта увидел, что ракета, вместо того, чтобы устремиться к звездам, по параболе направилась к Земле.

Но, конечно, мы начнем не со сложных функций многих переменных, а с чего-то очень-очень простого.

На картинке мы видим параболу и ее формулу, С – это параметр. На что он влияет? Посмотрите, здесь С равно 0, и парабола проходит через начало координат. С равно 2, и парабола поднимается на 2 вверх по вертикале. С равно – 3, и парабола опускается по вертикале на 3 единицы.

Значит параметр – это такая переменная в уравнении, которая может принимать разные значения, и при разных значениях этой переменной мы получаем разные уравнения.

В заданиях ЕГЭ у вас есть задачи с параметром. Это задача №18 профильного раздела.

И сейчас я покажу самую простую иллюстративную задачу. Проще тех, которые будут на ЕГЭ, но зато ее можно красиво нарисовать.

При каком значении параметра с уравнение, которое вы видите на экране имеет ровно 6 корней?

Давайте нарисуем график левой части этого уравнения. Начнем с графика функции. Сначала сдвигаем его на 2 вправо. Затем вычитаем 3, график сдвигается на 3 единицы вниз. Снова берем модуль от получившегося выражения. Все, что было ниже оси абсцисс, переворачивается вверх. Далее все, что получилось, мы сдвигаем на 1 единицу вниз. И снова берем модуль. Все, что было ниже абсцисс, переворачивается вверх. И получаем график функции, похожий на Кавказские горы.

При каком же значении параметра с это уравнение имеет ровно 6 корней? Проведем горизонтальную прямую. Следовательно, с равно 1.

Это была самая простая задача с параметром. Чтобы научиться решать такие задачи, нужно отлично знать графики основных элементарных функций, преобразование графиков, базовые элементы для решения задач с параметрами и еще множество приемов и секретов.

Подписывайтесь на мой канал и переходите по ссылкам в описании!

С Вами Анна Малкова!

Задачи с параметрами. Использование четности функций.

Материал для повторения:

Четные и нечетные функции
Что такое параметр. Простые задачи с параметром.

Графический метод в решении задач с параметрами.

Встречались ли вам в задаче 18 Профильного ЕГЭ по математике страшные-престрашные уравнения с параметрами? Такие, на которые смотришь – и вообще не понимаешь, что делать?

Есть множество «инструментов» для решения задач с параметрами — методов, приемов, больших и маленьких секретов. Конечно, эти приемы лучше не изобретать на экзамене, а изучить заранее.

Например, использование четности функций, входящих в уравнение.

1. Найдите все значения a, при каждом из которых уравнение имеет единственный корень

Откроем секрет. Есть два универсальных способа для решения задач с параметрами. Вот они:

1) Если задачу с параметром можно решить графически — решаем графически.

2) Если в задаче с параметром можно сделать замену переменной — делаем замену переменной.

Второй из этих полезных советов — как раз для нашей задачи. Сделаем замену . Получим:

Конечно, можно решать уравнение графически, построив графики левой и правой его частей. Однако у этого способа есть недостаток: как мы узнаем, пересекаются ли графики в одной точке, или у них еще есть точки касания? Все равно без аналитического исследования не обойтись.

Поэтому выберем другой способ. Обозначим функции в левой и правой частях уравнения как f(x) и g(x):

Заметим, что f(x) и g(x) — четные относительно х, так как их области определения симметричны относительно нуля и , .

Значит, если — корень уравнения, то и
— тоже его корень. Поэтому единственное решение может быть только если . В этом и состоит идея решения таких задач.

Обратите внимание, как аккуратно мы сформулировали: «единственное решение может быть только если ». Ведь может быть еще и такой случай, что — один из корней уравнения, и при этом есть еще решения. Тогда общее количество решений уравнения нечетно.

Давайте подставим в уравнение и посмотрим, что получится.

. Решив это уравнение, получим:

, или , или .

Каждое из найденных значений параметра надо проверить. Подставим их по очереди в исходное уравнение и найдем, сколько решений оно будет иметь при каждом таком b.

1) . При этом .

У этого уравнения три решения:

, или , или . Такое значение параметра нам не подходит.

2)

Уравнение решается методом интервалов для модулей (ССЫЛКА). На числовой прямой отмечаем точки -2 и 2 и решаем уравнение на каждом промежутке.

Получим единственное решение . Нам это подходит. При этом .

При уравнение получится таким же. Эта ветвь решения дает в результате:

.

Ответ: -9,-5

Это была простая задача. А вот следующая… Только не пугаться! Мы справимся!

2. При каких значениях параметра a система имеет единственное решение

Найти это значение a. Найти решение.

Перед нами система из двух уравнений, в которой есть две переменные

х и у, а также параметр а.

Решать такую систему, выражая, например, у через х и подставляя во второе уравнение? — Страшно даже думать об этом!

Для начала запишем ОДЗ — область допустимых значений системы.

ОДЗ:

Заметим, что все функции, входящие в уравнения системы, четны относительно х. А вот это уже что-то. Это значит, что если — решения, то
– тоже решение. Единственное решение возможно, если .

Подставим в уравнения системы.

Получим:

, отсюда , следовательно

1)Если , то

Получаем:

– единственное решение, так как .

Подставив в уравнения, из первого уравнения получили, что .

2) Если , то

– 3 решения. Это нам не подходит.

Ответ: . При этом система имеет единственное решение .

«Базовые элементы» для решения задач с параметрами

В задачах с параметрами Профильного ЕГЭ по математике вам встретятся не только графики функций (в школьном смысле этого слова), но и множества точек на плоскости.

Вот несколько уравнений и неравенств, задающих окружность, круг, ромбик, отрезок. Заметим, что окружность или ромбик, хотя и задаются уравнениями, не являются графиками функций в школьном смысле этого слова. Чтобы лучше почувствовать эту разницу, повторите тему «Что такое функция».

Задачи с параметрами на ЕГЭ по математике считаются одними из самых сложных. Однако на самом деле они похожи на конструктор, где вы собираете решение из готовых элементов. Чтобы уверенно решать задачи с параметрами, необходимо отлично знать 5 типов элементарных функций и их графики. Преобразования графиков функций. И вот эти базовые элементы:

1. Уравнение задает окружность с центром в начале координат и радиусом

2. Уравнение задает окружность с центром в точке (a;b) и радиусом

3. Неравенство задает круг вместе с границей.

4. Уравнение задает верхнюю полуокружность с центром в начале координат и радиусом

5. Уравнение задает нижнюю полуокружность с центром в начале координат и радиусом

6. Уравнение задает верхнюю полуокружность центром в точке и радиусом

7. Уравнение при положительных и задает ромбик, симметричный относительно начала координат.

8. Уравнение (сумма модулей) задает график следующего вида:

9. Расстояние между точками и находится по формуле:

Координаты середины М отрезка АВ находятся по формуле:

Уравнение отрезка концы отрезка и

В левой части уравнения сумма расстояний от точки P с координатами до точек и В правой расстояние между точками и

Пара чисел соответствует координатам любой точки этого отрезка.

Кратко это можно записать так: Это значит, что точка P лежит на отрезке

Статья о задачах с параметрами в школьном курсе математики

Задачи с параметром в школьном курсе математики 8-го класса

Задачи с параметрами играют важную роль в формировании логического мышления и математической культуры учащихся. Они имеют принципиально исследовательский характер, и с этим связаны как методическое значение таких задач, так и трудности выработки навыков их решения. Важность понятия параметра связана с тем, что, как правило, именно в терминах параметров происходит описание свойств математических объектов: функций, уравнений, неравенств. Под параметрами мы понимаем входящие в алгебраические выражения величины, численные значения которых явно не заданы, однако считаются принадлежащими определенным числовым множествам. Учащимся 8 класса известны линейная функция и ее частный случай – прямая пропорциональность:

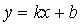
(параметры 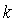и 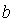определяют расположение графика функции на плоскости и точки пересечения с осями), а также линейное и квадратное уравнение и соответствующие неравенства:

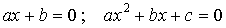
(параметры , 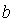и определяют, вообще говоря, не только существование и количество корней, но и степень уравнения).

Решение задач с параметрами требует исследования, даже если это слово не упомянуто в формулировке задачи. Недостаточно механического применения формул, необходимо понимание закономерностей, навыки анализа конкретного случая на основе известных общих свойств объекта, системность и последовательность в решении, умение объединить рассматриваемые частные случаи в единый результат. Этим обусловлены трудности, возникающие у учащихся при решении таких задач, и этим же объясняется справедливое включение задач с параметрами в экзаменационные работы в школе и на вступительных экзаменах в вузы.

Таким образом, очевидна необходимость отработки приемов решения различных задач с параметрами. Ниже приводится система упражнений по решению и исследованию квадратных уравнений и неравенств с одним параметром в курсе 8 класса.

 Квадратные уравнения с параметром

1. При каких значениях уравнение 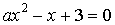имеет единственное решение?

Решение.

Ошибочно считать данное уравнение квадратным. На самом деле это уравнение степени не выше второй. Исходя из этого соображения, рассмотрим следующие случаи:

а) 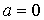. При этом уравнение принимает вид 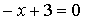, откуда 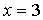, т.е. решение единственно.

б) 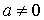, тогда 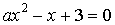– квадратное уравнение, дискриминант 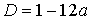. Для того, чтобы уравнение имело единственное решение, нужно, чтобы 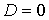, откуда .

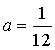Ответ: 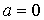или .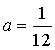

2. При каких значениях уравнение 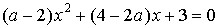имеет единственное решение?

Решение.

1) При 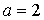исходное уравнение не имеет решения.

2) 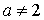, тогда данное уравнение является квадратным и принимает вид 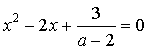. Искомые значения параметра – это корни дискриминанта, который обращается в нуль при .

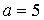Ответ: .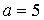

3. При каких значениях уравнение 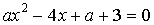имеет более одного корня?

Решение.

1) При 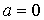уравнение имеет единственный корень .

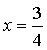2) При 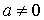исходное уравнение, будучи квадратным, имеет два корня, если его дискриминант положителен, т.е. 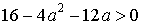. Решая неравенство, получаем 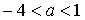. Из этого промежутка следует исключить число нуль.

Ответ: 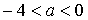или .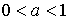

4. При каких значениях уравнения и 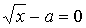равносильны?

Решение.

1) При 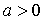: имеет два различных корня, 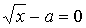имеет один корень. Равносильности нет.

2) При 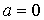решения уравнений совпадают.

3) При ни первое, ни второе уравнения решений не имеют. Как известно, такие уравнения считаются равносильными.

Ответ: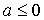

.

5. При каких значениях 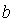уравнения 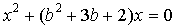и 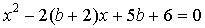равносильны?

6. При каких значениях параметра уравнение имеет одно решение?

7. При каких значениях 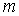ровно один из корней уравнения равен нулю?

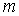8. При каких значениях корни уравнения равны по модулю, но противоположны по знаку: 9. При каких значениях 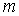оба корня уравнения равны нулю?

а) 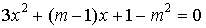; б)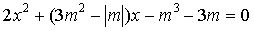

10. Решите уравнения:

I.

II. III. IV. V. 11. При каких значениях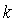 произведение корней квадратного уравнения равно нулю?

12. При каких значениях 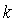сумма корней квадратного уравнения 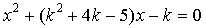равна нулю?

13. В уравнении 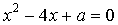сумма квадратов корней равна 16. Найти .

14. В уравнении 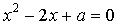квадрат разности корней равен 16. Найти .

15. При каких значениях сумма корней уравнения 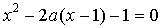равна сумме квадратов корней?

16. При каком значении параметра 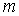сумма квадратов корней уравнения 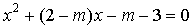наименьшая?

17. При каком значении параметра 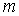сумма квадратов корней уравнения наибольшая?

18. При каких значениях параметра один из корней квадратного уравнения 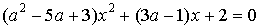в два раза больше другого?

19. Известно, что корни уравнения 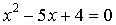на 1 меньше корней уравнения 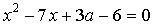. Найдите и корни каждого из уравнений.

20. Найдите наименьшее целое значение , при котором уравнение 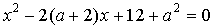имеет два различных действительных корня.

21. При каких значениях уравнение 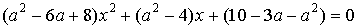имеет более двух корней?

22. При каких значениях уравнение 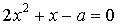имеет хотя бы один общий корень с уравнением ?

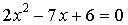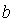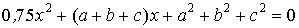23. При каком соотношении между , , уравнение имеет один корень? Может ли данное уравнение иметь два действительных различных корня?

24. При каком значении параметра уравнение 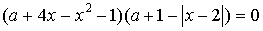имеет три корня?

 Неравенства с параметром

1. Решите неравенство, где – параметр:

2. Найдите все значения , при которых квадратное уравнение имеет два действительных различных корня: 3. Найдите все значения , при которых квадратное уравнение не имеет действительных корней: 4. При каких значениях уравнение 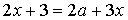имеет положительное решение?

5. При каких значениях уравнение 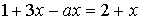имеет отрицательное решение?

6. При каких значениях уравнение 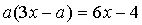имеет одно положительное решение?

7. При каких значениях уравнение имеет решения, удовлетворяющее условию ?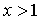

8. При каких значениях система неравенств имеет хотя бы одно решение:

а)

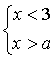
б)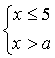

в)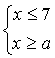

г)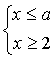

9. При каких значениях система неравенств не имеет решений:

а)

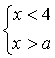
б)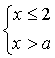

в)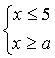

г)

10. При каких значениях система неравенств имеет хотя бы одно решение?

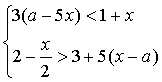
11. При каких значениях уравнение 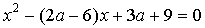имеет корни разных знаков?

12. При каких значениях уравнение 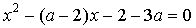имеет корн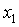и и 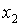такие, что ?

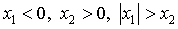13. Найдите все значения , при которых корни уравнения 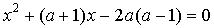меньше, чем 1.

14. Найдите все значения , при которых один из корней уравнения 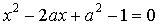меньше 1, а другой больше 1.

15. При каких значениях система уравнений

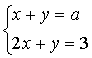
имеет решение ?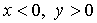

16. При каких значениях система уравнений

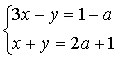
имеет решение ?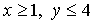

17. Для каждого решите неравенство:

I.

II. III. IV.

Задание 18. Задача с параметрами

Задание 18 Профильного ЕГЭ по математике — это уравнение, система уравнений или неравенство с параметром. Или несколькими параметрами.

Конечно, за один день научиться решать такие задачи невозможно. И все-таки мы немного расскажем о том, как научиться решать задачи с параметрами. С чего начать. И какие вообще есть методы решения задач с параметрами.

Начнем с хорошей новости. Задача 18 (с параметром) оценивается в целых 4 первичных балла ЕГЭ, которые отлично пересчитываются в тестовые.

Если вы полны решимости получить на ЕГЭ заветные 4 первичных балла за задачу 18 (с параметром), не стоит начинать с реальных экзаменационных задач. Ведь мы хотим получить результат, а не разочарование! Поэтому сначала необходимо повторить следующие темы:

1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».

2. Преобразование графиков функций.

3. Построение графиков функций.

4. Базовые элементы для решения задач с параметрами. Да, мы будем рисовать не только привычные функции. Но еще и окружности, ромбики, полуплоскости и всевозможные их комбинации.

5. Что такое параметр. Простые задачи с параметрами.

Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому.

Читайте статью, смотрите видеокурс. И помните, что графический метод — хороший, но не единственный.

Потому что, кроме него, есть и другие:

— Квадратные уравнения и неравенства с параметрами

— Задачи с параметрами. Условия касания

— Метод оценки в задачах с параметрами

— Использование четности функций в задачах с параметрами

И не думайте, что это все возможные методы решения задач с параметрами. Их намного больше! Мы дали ссылки на те, которые встречаются чаще всего в задачах ЕГЭ.

Несколько мудрых советов о том, как и зачем решать задачи с параметрами.

1. Чтобы на ЕГЭ уверенно справиться с заданием 18, нужно решить не менее 50 задач с параметрами.

2. Настанет момент, когда вы увидите, что задача с параметром похожи на конструктор, где вы собираете решение из знакомых элементов.

3. Два самых главных секрета решения задач с параметрами. Готовы узнать? Вот они:

— Если в задаче с параметром можно сделать замену переменной — сделайте замену.

— Если задачу с параметром можно решить графически — решите графически.

4. Сколько бы вы ни занимались задачами с параметрами, каким бы отличником ни стали — всегда найдется задача, над которой вы задумаетесь. Вот такая, например:

Задача 1. При каких значениях a системы  и равносильны?

Две системы уравнений с двумя переменными называются равносильными, если они имеют одни и те же решения, или обе системы не имеют решений.

1) При — системы равносильны, так как обе не имеют решений

2) При — второе уравнение имеет решение которое является решением первой системы.

3) При 

Система уравнений

Уравнение задает окружность с центром в начале координат и радиусом

Решениями системы

являются две точки, в которых прямая пересекает окружность, заданную уравнением

А вот уравнение задает семейство параллельных прямых

Мы хотим, чтобы две системы были равносильны, то есть чтобы окружность, заданная уравнением , пересекала только одну из этого семейства прямых, а именно прямую , и не имела общих точек с другими прямыми из этого семейства.

Меняя параметр а, мы можем менять радиус окружности. Мы хотим, чтобы окружность радиуса не имела общих точек с прямыми, параллельными прямой , то есть лежала ниже прямой, проходящей через точку А на рисунке, и выше прямой, проходящей через точку В.

Когда же происходит касание в точках A и B?

В случае касания радиус окружности Мы легко находим это из треугольника прямоугольного треугольника СОА, где О — начало координат.

Значит, в случае касания , а если — касания не происходит.

Объединяя случаи, получим, что системы равносильны, если

Легко? Если справились — вот еще одна интересная задача:

Задача 2. При каких значениях параметра a найдется такое значение параметра , что система уравнений  имеет ровно три различных решения?

Вот решение этой задачи.

Лучше всего осваивать эту непростую тему на нашем Онлайн-курсе подготовки к ЕГЭ на 100 баллов. Или на интенсивах ЕГЭ-Студии в Москве. Удачи, друзья!