Степени — Показатели дробны — Энциклопедия по машиностроению XXL

Эти формулы позволяют умножение и де-. лепие чисел заменять сложением и вычитанием их логарифмов, с последующим потенцированием, а возведение числа в любую степень (целую и дробную) — соответственно умножением его логарифма на показатель степени (примеры см. стр. 108).  [c.113]

Относительная погрешность степени с показателем k (k может быть целым или дробным) равна числу k, умноженному на относительную погрешность основания степени.  [c.47]

Режимы резания 631 Степени — Показатели дробные  [c.1136]

Л. степени равен показателю степени, умноженному на Л. возводимого количества (корень рассматривается здесь как дробная степень)  [c.114]

Тогда сингулярности термодинамических функций должны иметь место при Я = / = 0.

Предполагается, что эти сингулярности имеют вид простых степенных функций с дробными показателями в частности, можно положить  [c.12]

Выше были установлены количественные соотношения менаду давлением, плотностью, температурой и приведенной скоростью газового потока, а также параметрами торможения для некоторых течений газа. Эти уравнения содержат параметры газа, в частности приведенную скорость X, в высоких и дробных степенях, поэтому преобразование их, получение явных зависимостей между параметрами в общем виде и решение численных задач часто представляют значительные трудности. Вместе о тем, рассматривая различные уравнения газового потока, выведенные, например, в 4 гл. I и 4 гл. V, можно заметить, что величина приведенной скорости X входит в них в виде нескольких часто встречающихся комбинаций или выражений, которые получили название газодинамических функций. Этим функциям присвоены сокращенные обозначения, и значения их в зависимости от величины % и показателя адиабаты к вычислены и сведены в таблицы.

 [c.233]

При этом, очевидно, в различных случаях будут получаться разные показатели степени X, в том числе и дробные.  [c.176]

Рнс. 13. Номограмма для вычислении с дробными показателями степеней.  [c.58]

Безразмерные величины (параметры). Из пяти переменных величин—длина Z, площадь А, деформация е, сила F и модуль упругости Е—можно составить бесчисленное множество других величин в виде произведений их степеней, например Xj = PA F E, X2 = eV2 = i = F EA. Показатели степени могут быть целыми, дробными, положительными или отрицательными числами или нулем. Размерности вновь получаемых величин определяют путем замены каждой величины ее размерностью и подсчета степеней М, L п Т. Так, заменяя в приведенных выше произведениях I на [L], А на [L ], е на [1], F на МЬТ Ц, Е на [МЬ -Т Н, находим  

[c.449]

Однако существует набор независимых безразмерных величин, образованных из заданных переменных величин, каждая из которых не может быть представлена в виде произведения степеней других безразмерных произведений этой системы. Показатели степеней нри этом опять могут быть целыми, дробными, положительными или отрицательными числами, а также нулем.  [c.450]

Применение десятичных логарифмов почти всегда необходимо при возведении чисел в степень и извлечении корня из них при больших или при дробных показателях степени и корня (см. стр. 108 и также стр. 113).  [c.107]

Сумма показателей степеней при концентрациях в законе действующих масс называется порядком реакции. В химической кинетике показатели при концентрациях могут не соответствовать стехиометрическим коэффициентам, т. е. числу молекул данного вещества, участвующих в реакции. Более того, они могут быть дробными, что указывает на сложный механизм реакции, протекающей в несколько элементарных стадий, для каждой из которых степень при концентрациях строго соответствует стехиометрическим коэффициентам.  

[c.141]

В этом уравнении а и а — активности металлов Л и В в металлической фазе (индекс ) и а и —активности соединений в солевой фазе (индекс»). Аналогичные обозначения выбраны для молярных долей (х и т. д.) и коэффициентов активности и т. д.). К — константа действия масс. Обычно представляется удобным исключить дробные показатели в (VI1-4) путем возведения уравнения в соответствующую степень. Активности веществ, стоящих в правой части стехиометрического уравнения, пишутся в числителе выражения константы равновесия, а активности веществ, стоящих в левой части, пишутся в знаменателе.  

[c.130]

В табл. 64 даны числа в дробных показателях степеней.  [c.578]

Показатель степени п выбирается в зависимости от конкретных условий задачи. В частном случае он может иметь любые целые илй дробные значения.  [c.32]

Числа в дробных показателях степеней  [c.197]

Однако, в общем случае этот показатель должен быть не целым, а дробным (так, в распределении (1.71) имеем г 3/2). Во избежание такого ограничения заменим параметр порядка и в нелинейных слагаемых уравнений (1. 80)-(1.82) степенным множителем с показателем О а [c.62]

В результате формула размерности приобрела вид, в котором трудно усмотреть наличие связи с основными величинами. Действительно, вряд ли можно найти разумную трактовку наличия в размерности таких сугубо статических величин, как давление и механическое напряжение, а также стоящей в знаменателе формулы второй степени размерности времени. И уж, конечно, никаких конкретных представлений не вызывают формулы размерности электрических единиц в системе СГС, в которых символы размерности основных единиц стоят а дробных степенях. В процессе образования размерности производной величины, при определении размерностей промежуточных величин, показатели степени складываются, вычитаются, некоторые обращаются в нуль, так что в итоге формула может приобрести довольно причудливый вид. Для примера приведем размерность емкости в Международной системе единиц  

[c.74]

Дробные единицы измерения в тексте рекомендуется писать с наклонной чертой, а не с горизонтальной или в строку с применением отрицательных показателей степени  [c.

83]

Буквенные обозначения. Действия, рассматриваемые в алгебре. Знаки, употребляемые в алгебре. Степень, показатель степени, основание. Возведение целых и дробных чисел в степень. Нахождение степеней чисел по таблицам. Понятие о корне.  [c.539]

Следует отметить, что не всегда можно получить формулы подобия по степенной зависимости с показателем степени в виде целого числа. В этих случаях используют дробный показатель. Если этот показатель получается в результате операций с цельными степенными показателями (например, 0,20 0,25 34  [c.54]

Способ Польгаузена основан на аппроксимации распределения скоростей в пограничном слое полиномом четвертой степени. В связи с этим возникла мысль улучшить способ Польгаузена путем аппроксимации распределения скоростей полиномом более высокой степени. Конечно, при этом появляются дополнительные коэффициенты, вследствие чего выбранное распределение скоростей должно удовлетворять большему количеству граничных условий на стенке и на внешней границе пограничного слоя.

Такого рода способ с использованием для распределения скоростей полинома шестой степени разработали и довели до практически пригодного вида Г. Шлихтинг и А. Ульрих [ ]. Результаты, даваемые этим способом для параметров пограничного слоя и для положения точки отрыва, мало чем отличаются от результатов, получаемых посредством использования полинома четвертой степени. Однако использование полинома тестой степени дает следующее преимущество более высокие производные скорости пограничного слоя, взятые по расстоянию от стенки, могут быть определены значительно точнее, чем посредством полинома четвертой степени, что иногда весьма важно для исследования устойчивости профилей скоростей в пограничном сдое (см. главы XVI и XVII). Другие случаи такого однопараметрического представления распределения скоростей рассмотрены и сравнены с точными решениями в работе В. Манглера [ 1. Для аппроксимации распределения скоростей возможно применение не только полиномов, но и других выражений. Такие возможности были испробованы рядом исследователей. Так, например, А. Вальц [ ] в основу своего способа приближенного расчета положил однопараметрическое семейство профилей скоростей, вычисленных Д. Р. Хартри ( 1 главы IX), и аппроксимировал их посредством степенных выражений с дробными показателями степени.  [c.211]

Формулы для расчета адиабатного процесса содержат величины с дробными показателями степени, что делает расчет уравнений трудоемким вследствие необходимости каждый раз производить логарифмирование кроме того, для упрощения эти уравнения выведены для случая = onst, что неточно, в особенности при расчете процессов с продуктами горения в тепловых двигателях, где температуры меняются в широких пределах в этом случае зависимость теплоемкости от температуры, в особенности для многоатомных газов, достаточно значительна. Уравнения для адиабатного процесса с учетом нелинейной зависимости = f (i) не существует, и для расчета его во Всесоюзном теплотехническом институте разработан табличный метод, более простой и более точный, чем тот, который проводится с допущением = onst.  [c.87]

РАЗМЕРНОСТЬ единицы физической величины, или просто размерность велв-ч и н ы,— выражение, показывающее, во сколько раз изменится единица данной величины при известном изменении единиц величин, принятых в данной системе за основные. Р. представляет собой одночлен (его заключают в квадратные скобки или предваряют физ. величину символом dim , от лат. dimensio — измерение), составленный пз произведения обобщённых символов осн. единиц в различных (целых или дробных, полошит, или отрицат.) степенях, к-рые наз. показателями Р. Если основными являются единицы величин А, Я и С, а единица производной величины D пропорциональна единицам величины А в степени х, величины В в степени у и величины С в степени г, то Р. единицы величины D запишется в виде произведения  

[c.244]

Приведенный выше краткий анализ наиболее важных экспериментальных работ показывает, что поведение термодинамических свойств веществ в критической области существенно Отличается от предсказаний и результатов классической теории. Тем не менее, как и в классической теории, эти свойства первом приближении описываются простыми степенными законами, но с иными (дробными) показателями степени, кото-Pbie равны или достаточно близки для разных веществ, если Рассматривать одинаковые их свойства. Напомним, что в клас-  [c.83]

Очевидная причина указанных противоречий состоит в неправомерном использовании обычных скейлинговых соотношений (1.72) для дробной системы Лоренца (1.130), обладающей фрактальным фазовым пространством. Для подсчета размерности этого пространства учтем, что каждой из стохастических степеней свободы s, S, и число которых п = 3, отвечает сопряженный импульс, так что гладкое фазовое пространство должно иметь размерность D = 2п. Такое пространство реализуется в простейшем случае отсутствия обратной связи, когда определяющий ее показатель о = О, и шум является аддитивным. С ростом показателя а > О, величина которого задает эффе1стивную силу и интенсивность шума в равенствах (1. 120), обратная связь усиливается, и флуктуации приобретают мультипликативный характер. Согласно [45], при этом фазовое пространство становится фрактальным, и его размерность уменьшается в (1 — о) раз. В результате размерность пространства, в котором происходит эволюция самоорганизующейся системы, сводится к значению  [c.72]

Зависимость количества адсорбированного вещества от времени с дробным показателем степени была обнаружена Бапгамом и Севером [7]. На основании полученных данных авторы пришли к выводу, что в изученном ими случае сорбция газов была скорее всего абсорбцией (или растворением), а не адсорбцией.  [c.140]

Первая попытка»построения теории пеавтомодельной струи без вращения с конечным расходом принадлежит Румеру [112, который предположил, что решение может быть построено в виде разложения по целым обратным степеням сферического радиуса. Как показано в [47], такое предположение некорректно. Решение должно строиться в виде разложения по дробным степеням Л «, причем показатели должны находиться как собственные числа некоторого линейного оператора. Кроме того, и это главное, правильное разложение помимо члена должно содержать член (1п/ )// 2, причем оба с произвольными константами. Еще одну произвольную постоянную, определяемую импульсом струи, содержит автомодельный член 1/Д.  [c.35]

Перейдем к построению общего решения сформулированной краевой гидродинамической задачи вне шара радиуса Во. Для этого разложения (2.26) и (1) с учетом собственных значений у необходимо дополнить членами с такими показателями при сферическом радиусе В, чтобы при подстановке полученных разложений в уравнении Павье — Стокса линейные и нелине1шые члены имели показатели степени при В из одного и того же семейства (см. 2). Следовательно, семейство дробных показателей степени должно быть замкнуто относительно этой подстановки. Искомое разложение имеет вид (ср. с (2.26))  [c.290]

Нетрудно установить, что при Ке = О отрицательные целочисленные значения показателей степени для окружной скорости Уф также являются собственными, а система собственных функций полной (при » п = п, —п— имеется собственная функция в виде полинома ге-й степени Г (а ), Г ( 1) = 0). При увеличении числа Ке отрицательные становятся дробными, а число собственных функций не меняется, поэтому следует он идать полноты системы собственных функций для отрицательных и нри Ке > 0.  [c.291]

Выражение (16.11) послужило основой для получения своего рода экстинкционной поправки во многих работах по структурному анализу, где использовались кольцевые дифракционные картины или картины с дужками от поликристаллических материалов [381 ]. Было сделано предположение, что интегральная интенсивность отражения связана со структурной амплитудой Ф зависимостью, которая с ростом силы динамических эффектов меняется с квадратичной на линейную, и что можно определить подходящую зависимость от Ф с дробным показателем степени и использовать ее как основу для интерпретации интенсивностей. Применение по-  [c.365]

---

Степени дробные чисел — Справочник химика 21

    Порядок реакции. Порядок химической реакции определяется по более формальному признаку, чем ее молекулярность,— по виду уравнения, выражающего зависимость скорости реакций от концентраций реагирующих веществ. Порядок реакции равен сумме показателей степеней концентраций в уравнении, выражающем зависимость скорости реакции от концентраций реагирующих веществ. Реакции разделяются на реакции первого порядка, второго порядка, третьего порядка (реакции более высоких порядков не встречаются). Кроме того, известны так называемые реакции нулевого порядка и некоторые реакции, порядок которых выражается дробным числом. [c.467]
    Скорость реакции часто является степенной функцией от концентрации одного или всех продуктов. Степени могут быть положительными или отрицательными, выражаться целыми или дробными числами (обычно не более 2). Температурный коэффициент константы скорости вычисляется с хорошим приближением, по крайней мере для небольших температурных интервалов, по формуле  [c.12]

    Если способы представления операндов различны, то происходит преобразование данного с фиксированной точкой в форму с плавающей точкой. Для операции возведения в степень преобразование не производится, если основание — в форме с плавающей точкой, а экспонента — целое число с фиксированной точкой. В этом случае возведение в степень осуществляется многократным умножением. Если же операнды в форме с фиксированной точкой, то возможны такие преобразования а) экспонента — дробное число оба операнда преобразуются в форму с плавающей точкой возведение в степень осуществляется через логарифм и экспоненту б) основание преобразуется в форму с плавающей точкой, если экспонента не является целой константой с фиксированной точкой без знака или результат возведения в степень целого числа с фиксированной точкой превышает максимально допустимое число разрядов (15 десятичных или 31 двоичных). [c.264]

    После изучения характерных и дробных реакций обнаружения катионов изучают характерные и дробные реакции обнаружения анионов. Большое значение придают также предварительному испытанию анализируемого раствора, которое позволяет в значительной степени сократить число подлежащих обнаружению анионов.  [c.88]

    Степень окисления может быть и дробным числом. Так, в КО2 и КОз для кислорода она соответственно равна —V2 и —7з. [c.24]

    Пусть для реакции А-)-В при данной температуре константа равновесия /Ср = рв/рл. Если начальное давление вещества А равно 1,013-10 Па, то конечное равновесное /7а=Рв = 0,5-10 Па. Следовательно, система придет в равновесие, когда половина исходного вещества А превратится в В. С этой точки зрения казалось бы, что степень превращения равна /г- Но такая степень превращения является предельно возможной в заданных условиях, поэтому ее принимают за 1. Успешность проведения реакции следует оценивать по тому, насколько удалось приблизиться к предельному превращению. Если предельное значение принять за 1, то реально получаемые степени превращения будут дробными числами. Так, если исходное вещество А только на /з превратится в вещество В, а равновесное состояние соответствует превращению на 7г, то степень превращения будет 7з 42 = ь- [c. 448]

    Щелочные металлы в соединениях имеют степень окисления, равную (+1), а щелочноземельные — ( + 2). В простых веществах степень окисления элемента принимается равной нулю. Степень окисления может быть выражена и дробным числом. Например, степень окисления железа в магнитном железняке РезО равна ( + 8/3). Для водорода в большинстве соединений характерна степень окисления ( + 1), в гидридах металлов она равна (—1). Кислород в большинстве соединений имеет степень окисления (—2), но в пероксидных соединениях (—1), а в соединении с фтором Ор2 — ( + 2), в соединении КО2 степень окисления кислорода равна (—1/2). [c.317]

    В неорганической химии приходится пользоваться понятием о ступени окисления — восстановления или о редокс -ступени и нужно строго отличать его от степеней или зарядовых состояний, выражаемых дробными числами. [c.189]

    Показатели степени тип называют порядком реакции соответственно по веществам А и В, а сумму (от+я) — порядком реакции. Порядок реакции может быть как целым, так и дробным числом. Реакции, состоящие из повторяющихся одинаковых элементарных химических актов, имеют, как правило, второй порядок реакции, реже — первый, еще реже — третий. Сложность кинетического уравнения (дробный или переменный порядок реакции) указывает на сложность реального механизма реакции, протекающего в действительности по нескольким (или многим) элементарным стадиям. [c.86]

    Для характеристики степени замещения производных целлюлозы (как продуктов замещения, так и молекулярных соединений) используют два количественных показателя СЗ и у. Величина СЗ (х в вышеприведенном примере) показывает число прореагировавших гидроксилов, приходящееся в среднем на одно глюкопиранозное звено у производных целлюлозы значение СЗ может составлять от О до 3 и быть при этом любым дробным числом. Величина у показывает число прореагировавших гидроксилов, приходящееся в среднем на 100 глюкопиранозных звеньев, т.е. у = СЗ 100 и, следовательно, может лежать в интервале от О до 300. Оба показателя — среднестатистические величины. Свойства производных целлюлозы — различных сложных и простых эфиров — в значительной мере зависят от степени замещения. В зависимости от назначения производного целлюлозы получают продукты с различной степенью замещения, а следовательно, и с различными свойствами, в том числе с разной растворимостью. [c.547]

    Показатель степени л,- называется кинетическим порядком реакции по данному ее компоненту он может быть положительным, отрицательным, равным нулю, целым или дробным числом. Сумма [c.19]

    Это выражение дает точную зависимость плотности тока обмена 0 от концентраций реагентов и продуктов вблизи электрода. Мы видим, что у и б в уравнении (56-5) соответствуют + Поскольку р —дробное число, показатель степени при в уравнении (57-16) в общем случае является дробным даже при целочисленных ри д1 и 5г. Эта степень положительна, если справедливы изложенные после уравнения (57-12) правила. Таким образом, плотность тока обмена увеличивается при возрастании концентрации как реагентов, так и продуктов.  [c.201]

    Степень диссоциации. Сила электролитов. Если бы электролиты полностью диссоциировали на ионы, то осмотическое давление (и другие пропорциональные ему величины) всегда было бы в целое число раз больше значений, наблюдаемых в растворах неэлектролитов. Но еще Вант-Гофф установил, что коэффициент i выражается дробными числами, которые с разбавлением раствора возрастают, приближаясь к целым числам. [c.228]

    Степень окисления может выражаться не только целым, но и дробным числом. Например, для кислорода в НаО она равна —2, а в НаОа —1, в КОа — 2, В КО3 —7з- [c.161]

    В отличие от химии низкомолекулярных соединений полноту химической реакции полимера характеризуют не выходом продукта реакции, а степенью химического превращения. Степень химического превращения показывает число прореагировавших звеньев (или функциональных групп). У разных макромолекул в образце полимера это число может быть различным. Поэтому степень химического превращения всегда определяется как средняя величина. Например, у производных целлюлозы (эфиров) определяют среднюю степень замещения — количество прореагировавших гидроксильных групп, приходящееся в среднем на одно глюкозное звено. Каждое элементарное звено целлюлозной макромолекулы содержит три гидроксильные группы, поэтому степень замещения может меняться от О до 3 и быть любым дробным числом (см. также с. 121). [c.59]

    Когда мы говорим об ионах в решетке металла, следует иметь в виду, что ионы далеко не всегда имеют максимально возможный для данного элемента заряд. Больше того, средний заряд их не обязательно » является целочисленным, т. е. происходит частичная ионизация, степень которой и пространственное расположение частиц в конечном счете определяются минимумом энергии системы, состоящей из всех атомных остовов и всех электронов. Это не означает, конечно, что каждый атом может потерять при ионизации дробное число электронов, но различные атомы одного сорта могут ионизироваться в разной степени, в результате чего в среднем степень ионизации может оказаться нецелочисленной.  [c.116]

    Порядок выражается суммой величин (2лс) показателей степени при концентрациях, реагирующих веществ в кинетическом уравнении (66) для скорости химической реакции. Только в простейших случаях Ипс равняется сумме стехиометрических коэффициентов в уравнении реакции. При этом молекулярность и порядок совпадают. Большинство же химических реакций протекает через ряд последовательных стадий, в результате чего общая скорость определяется не концентрациями исходных веществ, а концентрациями про.межуточных продуктов, участвующих в наиболее медленных стадиях. По этой причине сумма показателей степени при концентрациях не будет равна су.мме стехиометрических коэффициентов и. может выражаться как целым, так и дробным числами. В таком случае порядок не совпадает с молекулярностью. [c.114]

    Степень окисления может быть и дробным числом так, например, если в НаО и Н2О2 для кислорода она равна —2 и —1, то в КО2 и КОз — соответственно— /2 и — /з- [c. 58]

    Степень окисления может быть выражена и дробным числом. Например, степень окисления железа в магнитном железняке Рез04 равна [c.56]

    Степень окисления может быть выражена целым и дробным числом, как положительным, так и отрицательным. Для ее определения вполне достаточно принципа электронейтральности и не требуется знания структурной формулы и особенностей взаимодействия атомов в сложном ионе. В кислородсодержащих ионах металлов и неметаллов, существующих в растворе, степень окисления кислорода полагают равной —2, а окислительные числа ионообразователя подсчитывают с использованием условия электронейтральности. Например, степень окисления серы в сульфат-ионе 5042- равна +6, а для марганца в перманганат-ионе МПО4Ч-7. [c.281]

    Степень окисления может представлять собой и дробное число. Например, степень окисления железа в магнитном железняке Рез04 равна +V3. Дробные степени окисления не имеют смысла при объяснении связи в химических соединениях, но они могут быть использованы для составления уравнений окислительно-восстановительных реакций (см. 7.9, задача 2). [c.83]

    ЗгО . В ионе тиосульфата имеется сера двух видов. Для получения этого иона нагревают водный раствор с сульфит-иона-ми в присутствии элементарной серы. Степень окисления серы в ЗОз равна — -4 (правило 4), и поэтому в ЗгО один атом, казалось бы, должен иметь степень окисления +А, а другой 0 однако структура ЗгО], подобно ЗОГ. имеет форму правильного тетраэдра, и, приняв к сведению реакции окисления и восстановления, приходим к выводу, что один атом серы имеет степень окисления — -6, а другой —2. К некоторым химическим соединениям определенной структуры понятие степени окисления применить трудно. Например, для ряда многоатомных ионов, содержащих два и более одинаковых атома, степень окисления в соответствии с правилом 7 однозначно определить не удается. В особенности это относится к таким объектам, как интеркаляционные соединения (гл. 4, разд. Г) и интерметаллические соединения (гл. 4, разд. В.5), в которых большое число атомов составляет как бы единую молекулу . Сюда же следует добавить соединения непостоянного (нестехиометрического) состава (гл. 4, разд. Б.4). Все же когда приходится приписывать степени окисления составляющим их атомам, то оказывается, что они выражаются дробными числами и, таким образом, это понятие теряет смысл, поскольку на его основе уже нельзя судить о состоянии атома. Степень окисления нельзя выразить целым числом и в других случаях, а именно когда общее число электронов в химических соединениях или многоатомных ионах нечетно (N02, О2 и др.) илн когда одинаковые атомы соединены в длинные цепи или макроциклические системы (сюда относится большинство органических соединений). В первом [c.77]

    Первые три модели, как и ожидалось, дают очень близкие общие соотношения во всех случаях число частиц возрастает со скоростью инициирования и уменьшается с ростом концен-трации мономера (и не зависит от растворяющей способности среды, а, следовательно, и от необходимой для зародышеобразования пороговой степени полимеризации Р). Показатели степеней — дробные, и поэтому число частиц не очень чувствительно к изменениям параметров. Как и ожидалось, сообщенные Фитчем и Тзаи соотношения, установленные при численном интегрировании, являются промежуточными между соотношениями, вытекающими из первой и второй моделей, но обычно более близкими к стационарному приближению. [c.182]

    В любом соедйнении каждому атому приписывается степень окисления (например, степень окисления кислорода почти всегда, за некоторым исключением, —2 фтора —I, водорода +1). Степень окисления молекул простых веществ, а также атомов элементов равна нулю, а одноатомных ионов — их заряду (катионы щелочных металлов имеют степень окисления +1, а щелочноземельных +2). Для любого соединения справедливо правило, что сумма степеней окисления атомов в молекуле всегда равна нулю..Степень окисления может выражаться не только целым, но и дробным числом (например, для кислорода она равна — 2 в НгО, — I в Н2О2, -Уг в КО2 и — >/з в КОз).  [c.24]

    Степень окисления может быть выражена и дробным числом. Например, в надпероксиде калия КО степень окисления кислорода равна —1/2, а железа в магнитном железняке F gOi +8/3. [c.64]

    Продукты замещения целлюлозы характеризуют по степени замещения. Степенью замещения (СЗ) называют число прореагировавших гидроксилов (т. е. число новых введенных групп), приходящееся в среднем на одно глюкозное звено. У производных целлюлозы СЗ может составлять от О до 3. Поскольку СЗ рассчитывается как средняя величина, она может быть любым дробным числом в пределах от О до 3. В соответствии с формулой целлюлозы [СбН702(0Н)з] п формулу продукта замещения можно представить как [СбН702(0Н)з д (0/ )л ] п, гдс 7 — введенный заместитель, ах — степень замещения. [c.121]

---

Что означают дробные показатели? — Affde Marketing

Опубликовано: 2020-12-18

В зависимости от человека — дроби бывают забавными или просто ужасающими.

Когда в ваших показателях появляются дроби, начинается настоящий кошмар. Или нет?

В Cleverism мы любим объяснять вещи весело и интересно. Даже если вы не математик, мы предоставим скромное объяснение, которое позволит вам понять, что такое дробные показатели.

Давайте приступим к делу.

КРАТКИЙ ОБЗОР ПОКАЗАТЕЛЕЙ

Прежде чем мы объясним дробные показатели, давайте быстро расскажем, что такое экспоненты. Если вы уже понимаете, что такое экспонента, вы можете пропустить это и перейти непосредственно к разделу дробной экспоненты ниже.

Короче говоря, показатель степени — это когда число умножается на собственное число определенное количество раз.

Например, 6 x 6 x 6 = 216

В экспоненциальной форме число записывается следующим образом — 6 ³

Возьмем другой пример.

2 ⁴ разбивается на 2 x 2 x 2 x 2 = 16.

Таким образом, эффективно 2 ⁴ = 16.

Где 2 — это базовое число, 4 — это показатель степени, а 16 — это его сумма. ⁹ иногда для обозначения степени. Этот символ находится на цифре «6» на

Теперь вы, вероятно, задаетесь вопросом, а что, если показатель степени равен 1, например 7 ¹ , что ж, это просто. Ответ: 7. Любая экспонента, равная 1, является самим основным числом.

Однако, если показатель степени равен 0, ответ всегда равен 1. Итак, 7 ⁰ = 1.

Все просто, не правда ли?

Прежде чем мы перейдем к дробным показателям, есть еще один важный аспект показателей. Отрицательные экспоненты

Отрицательные экспоненты

Отрицательная экспонента — обратная экспонента. Вместо умножения делаем обратное — делим.

Вот пример.

Давайте найдем ответ на x ⁿ .

Х = 2

N = -3

Следовательно, отрицательная экспонента записывается как ^2-3 .

Теперь давайте разберем его на рабочий формат.

Ответ = 0,125

Вот и все. Вычисление отрицательной экспоненты прямо противоположно работе с показателем.

Как только вы поймете экспоненты и отрицательные показатели, вам будет легче понять дробные показатели.

Перейдем к основной теме — дробным показателям.

ЧТО ТАКОЕ ДРОБНЫЕ ПОКАЗАТЕЛИ?

Дробные показатели проще, чем кажется. Они используются в основных алгебраических выражениях для упрощения математических уравнений.

Дробные показатели также обычно используются над знаками корня, которые обозначаются «√». Дробные показатели обычно используются при вычислении квадратных корней.

В предыдущем разделе мы узнали о таких показателях, как 4 ^2, 5 ⁹ или 9 ³ .

Примеры дробных показателей: 4 ^2/5, 5 ^4/5 или 9 ^6/4 . Дробные показатели также записываются как . «X» является основанием, «n» обозначает числитель, а «d» — знаменатель.

Обратите внимание на числитель и знаменатель, указанные вместе с числом основания.

Чтобы лучше понять, как решать дробные показатели, давайте рассмотрим простой пример.

4 ^1/2 =?

В приведенном выше дробном показателе 4 = основное число. 1 — числитель, 2 — знаменатель.

Подходящим форматом для поиска решения будет

Поскольку 4 в степени 1 равно 4

Следовательно,

Следовательно, главный корень

равно 2.

Ответ — 2 .

Давайте сделаем еще один пример, чтобы убедиться, что вы все поняли.

Пример 2

8 ^2/3 =?

Сначала разбиваем дробь на части.

Мы можем написать 8 ^{2/3как [8 1/3 ] 2}

Теперь мы находим кубический корень из 8.

Кубический корень всегда умножается на три, чтобы получить базовое число.

В этом случае кубический корень из 8 равен 2, так как 2 x 2 x 2 = 8.

Итак, следующая часть — [2] ² . Это 2 x 2 = 4.

Ответ на 8 ^2/3 = 4

Другой способ найти решение — преобразовать 8 ^2/3 в .

8 ² =^{8 х 8 = 64.}

Так,

Кубический корень из 64 = 4, поскольку 4 x 4 x 4 = 64.

Ответ — 4 .

Два разных метода поиска решения, используйте тот, который вам больше всего подходит.

Вот видео-руководство, объясняющее простым способом дробные показатели.

ЗАКОН ДОКАЗАТЕЛЬСТВ

Как и во многих математических выражениях, для работы требуются правила экспоненты. Понимание этих законов создает удобную среду для понимания того, как работают экспоненты.

Законы экспоненты также известны как закон индексов.

1. Закон умножения (оснований).

Когда основания умножения совпадают, такие как x ^a x ^b , результат x ^{a + b} .

2. Закон умножения (степеней)

Когда степени умножения совпадают, такие как x ^a y ^a_{, результат} (xy) ^a

3. Закон о делении (основаниях)

Когда основания деления совпадают, например x ¹ / x ² , результат x ^1-2.

4. Закон о разделении (полномочиях)

Когда степени деления совпадают, например x ¹ / y ¹ , ^{результат будет} (x / y) ¹

5. Закон о полномочиях

Следующий показатель (y ^a ) ^b также называется y ^ab

6. Неопределенный закон

0 ⁰ считается нулевым показателем и может быть либо 0, либо 1. Ответ обычно называют « неопределенным » или « неопределенным ».

СПИСОК ОНЛАЙН-МАТЕМАТИЧЕСКИХ РЕСУРСОВ И ИНСТРУМЕНТОВ

Вот список полезных инструментов, которые помогут вам в вычислении математических уравнений.

1. Калькулятор дробей

Онлайн-калькулятор для вычисления простых и смешанных дробей. Поставляется с опцией «Сброс».

2. Калькулятор экспоненты

Введите основание и показатель степени, и появится ответ. Все очень просто.

3. Калькулятор квадратного корня

Введите число, чтобы получить квадратный корень.

4. Калькулятор корня куба

Введите число, чтобы получить кубический корень.

5. Калькулятор мощности.

Калькулятор, посвященный силовым модам.

6. Таблицы экспонент и модели

Быстрый просмотр таблиц показателей. Отлично подходит для удобной справки при выполнении нескольких первых дробных показателей.

7. Таблицы заказов от 1 до 12

Таблица мощности для опытных пользователей дробных показателей от 1 до 12. Поставляется с удобным доступом для печати.

ЗАКЛЮЧЕНИЕ

Поначалу рассмотрение дробных показателей может сбивать с толку. С помощью упрощенных шагов, упомянутых в этой статье, даже начинающий математический пользователь может вычислять уравнения. Помните, что каждое правило, относящееся к показателям степени, напрямую применяется и к дробным показателям.

Сегодня дробные показатели используются в самых разных работах, таких как

• Компьютерное программирование
• Бухгалтеров
• Геологи
• Инженеры-химики
• Финансовый советник
• Аэрокосмический инженер

И многое другое. Очень важно улучшить свою математическую игру и довести до совершенства своих экспонентов, чтобы произвести впечатление на собеседников.

Любите или ненавидите дробные показатели? Поделитесь своими мыслями в комментариях ниже.

График функции с дробной степенью. Функция. Степенная функция

На данном уроке мы продолжим изучение степенных функций с рациональным показателем, рассмотрим функции с отрицательным рациональным показателем.

1. Основные понятия и определения

Напомним свойства и графики степенных функций с целым отрицательным показателем.

При четных n, :

Пример функции:

Все графики таких функций проходят через две фиксированные точки: (1;1), (-1;1). Особенность функций данного вида — их четность, графики симметричны относительно оси ОУ.

Рис. 1. График функции

При нечетных n, :

Пример функции:

Все графики таких функций проходят через две фиксированные точки: (1;1), (-1;-1). Особенность функций данного вида — их нечетность, графики симметричны относительно начала координат.

Рис. 2. График функции

2. Функция с отрицательным рациональным показателем степени, графики, свойства

Напомним основное определение.

Степенью неотрицательного числа а с рациональным положительным показателем называется число .

Степенью положительного числа а с рациональным отрицательным показателем называется число .

Для выполняется равенство:

Например: ; — выражение не существует по определению степени с отрицательным рациональным показателем; существует, т. к. показатель степени целый,

Перейдем к рассмотрению степенных функций с рациональным отрицательным показателем.

Например:

Для построения графика данной функции можно составить таблицу. Мы поступим иначе: сначала построим и изучим график знаменателя — он нам известен (рисунок 3).

Рис. 3. График функции

График функции знаменателя проходит через фиксированную точку (1;1). При построении графика исходной функции данная точка остается, при корень также стремится к нулю, функция стремится к бесконечности. И, наоборот, при стремлении х к бесконечности функция стремится к нулю (рисунок 4).

Рис. 4. График функции

Рассмотрим еще одну функцию из семейства изучаемых функций.

Важно, что по определению

Рассмотрим график функции, стоящей в знаменателе: , график данной функции нам известен, она возрастает на своей области определения и проходит через точку (1;1) (рисунок 5).

Рис. 5. График функции

При построении графика исходной функции точка (1;1) остается, при корень также стремится к нулю, функция стремится к бесконечности. И, наоборот, при стремлении х к бесконечности функция стремится к нулю (рисунок 6).

Рис. 6. График функции

Рассмотренные примеры помогают понять, каким образом проходит график и каковы свойства изучаемой функции — функции с отрицательным рациональным показателем.

Графики функций данного семейства проходят через точку (1;1), функция убывает на всей области определения.

Область определения функции:

Функция не ограничена сверху, но ограничена снизу. Функция не имеет ни наибольшего, ни наименьшего значения.

Функция непрерывна, принимает все положительные значения от нуля до плюс бесконечности.

Функция выпукла вниз (рисунок 15.7)

На кривой взяты точки А и В, через них проведен отрезок, вся кривая находится ниже отрезка, данное условие выполняется для произвольных двух точек на кривой, следовательно функция выпукла вниз. Рис. 7.

Рис. 7. Выпуклость функции

3. Решение типовых задач

Важно понять, что функции данного семейства ограничены снизу нулем, но наименьшего значения не имеют. n$ ($n\in Z)$ называется степенной функцией с целым показателем.

Если степень больше нуля, то мы приходим к случаю степенной функции с натуральным показателем. Его мы уже рассмотрели выше. При $n=0$ мы получим линейную функцию $y=1$. Её рассмотрение оставим читателю. Осталось рассмотреть свойства степенной функции с отрицательным целым показателем

Свойства степенной функции с отрицательным целым показателем

Область определения — $\left(-\infty ,0\right)(0,+\infty)$.

Если показатель четный, то функция четна, если нечетный, то функция нечетна.

$f(x)$ — непрерывна на всей области определения.

Область значения:

Если показатель четный, то $(0,+\infty)$, если нечетный, то $\left(-\infty ,0\right)(0,+\infty)$.

При нечетном показателе функция убывает, при $x\in \left(-\infty ,0\right)(0,+\infty)$. При четном показателе функция убывает при $x\in (0,+\infty)$. и возрастает, при $x\in \left(-\infty ,0\right)$.

$f(x)\ge 0$ на всей области определения

Для удобства рассмотрения степенной функции будем рассматривать 4 отдельных случая: степенная функция с натуральным показателем, степенная функция с целым показателем, степенная функция с рациональным показателем и степенная функция с иррациональным показателем. n$ ($n\in Z)$ называется степенной функцией с целым показателем.

Если степень больше нуля, то мы приходим к случаю степенной функции с натуральным показателем. Его мы уже рассмотрели выше. При $n=0$ мы получим линейную функцию $y=1$. Её рассмотрение оставим читателю. Осталось рассмотреть свойства степенной функции с отрицательным целым показателем

Свойства степенной функции с отрицательным целым показателем

Область определения — $\left(-\infty ,0\right)(0,+\infty)$.

Если показатель четный, то функция четна, если нечетный, то функция нечетна.

$f(x)$ — непрерывна на всей области определения.

Область значения:

Если показатель четный, то $(0,+\infty)$, если нечетный, то $\left(-\infty ,0\right)(0,+\infty)$.

При нечетном показателе функция убывает, при $x\in \left(-\infty ,0\right)(0,+\infty)$. При четном показателе функция убывает при $x\in (0,+\infty)$. и возрастает, при $x\in \left(-\infty ,0\right)$.

$f(x)\ge 0$ на всей области определения

Возведение в степень эксель

СТЕПЕНЬ (функция СТЕПЕНЬ)

​Смотрите также​SerKol​ вставить, формат сбивается. ​И не забывай,​ Нужен ещё один​ использовать вкладку «Формат​ полученная в результате​ и система сама​​ (т.е. со знаком​​Стандартный и самый простой​

Описание

​ целые показатели. А​1​

Синтаксис

​ пример:​

​ и в обычную​Формула​

• ​ себя максимум диапазон​​2401077,222​Предположим, что вам нужно​

• ​: Добрый день​​inter​ что основание степени​

Замечание

​ столбец — рядом​ ячеек». В нашем​ математического вычисления корня.​ догадается предложить вам​

Пример

​ «-»).​ вариант – использовать​ вот возведение отрицательного​1​B (число)​ с помощью Excel.​Результат​ чисел до двадцати-тридцати,​=СТЕПЕНЬ(4;5/4)​ вычислить очень маленький​Внимательно прочитал рекомендации,​:​ должно быть положительным​

​ или где-то там.​	​ примере мы записали​	​ВНИМАНИЕ! Если нам нужно​
​ полезную опцию. », который​
​ числа в дробную​	​1​C​	​ Ведь для решения​
​2​	​ и то не​Число 4, возведенное в​	​ допуск для детали​

support.office.com>

Как возводить число в отрицательную степень — примеры с описанием в Excel

​ но моей задаче​Puporev​ числом, иначе будет​Далее 3 шага.​ цифру «3» в​ узнать корень в​Как только увидели такую​С использованием мастера функций:​ получается при нажатии​ степень обернется для​1​Преобразование в дробь​ данной задачи можно​7​ более трех-четырех раз.​ степень 5/4.​ механизма или огромное​ это не помогло.​, абсолютно справедливо, степень​ ошибка.​1.​ ячейку «А1», которую​ степени в Excel​ подсказку, сразу жмите​Запускаем мастера функций с​ Shift+6 при английской​

​ вас ошибкой, поскольку​2​Формула​ пользоваться как привычным​-3​ Это не говоря​5,656854249​ расстояние между двумя​Задача — подписать​

​ надо выделить перед​Мариш​В соседнем столбце​ нужно представить в​ то мы не​ на клавишу «Tab». C2​ уж о том,​Со школы всем нам​ галактиками. Для возведения​ размерность на осях​ сменой формата не​: Не могу найти​ в верхней ячейке​ -2 степени.​ используем функцию =КОРЕНЬ().​ Или можете продолжить​

Решение задач в Excel

​ клавиш SHIFT+F3 или​ВАЖНО!​ указанное в начале​4​2​

​ так и удобной​0,002915​ чтобы потом еще​ известно правило о​ числа в степень​

	​ графика построенного в​	​ цепляя основное число.​	​ как написать степень​	​ пишешь формулу*: =(первая​
​Последовательность действий следующая:​	​ Вспомним теорию из​	​ писать, вручную вводить​	​ жмем на кнопку​	​Чтобы число было возведено​

​ нашей статьи про​8​7​ для запоминания встроенной​Можно прямо в формуле​ и единицу разделить​ возведении в степень:​ используйте функцию​ Excel. -C2.​ на результат. Поэтому​ любое число с​СТЕПЕНЬ​ в минус первой​: не получаеться​ Подскажите пожалуйста. Заранее​ в степени.​ по ячейке с​«Корнем n-ой степени от​ в скобках укажите​ формул «fx» (вставить​ степень, необходимо в​ ведь четность –​0,707107​2/5​ несомненный плюс!​Второй вариант – использование​ тем, у кого​ показателем N равно​

	​.​	​ степени.​	​inter​	​ спасибо.​
​2.​	​ числом и выбираем​	​ числа а называется​	​ необходимые параметры: два​	​ функцию). Из выпадающего​
​ ячейке поставить знак​	​ это характеристика исключительно​	​7​	​=СТЕПЕНЬ(B2;C2)​	​Перейдем к более сложным​

​ готовой функции «Степень»,​ нет под рукой​ результату перемножения данного​Возвращает результат возведения числа​Может быть кто-нибудь​:​Puporev​В ячейке чуть​ из выскакивающего меню​ число b, n-ая​ числа через точку​ списка «Категория» выбираем​ «=» перед указанием​ ЦЕЛОГО числа. 3​ ниже пишешь: =(вторая​ вкладку «Формат ячеек».​

1. ​ степень которого равна​ с запятой.​ «Математические», а в​
2. ​ цифры, которую вы​Автор: Елена Измайлова​49​
3. ​Воспользовавшись вышеприведенными правилами, вы​ о том, как​ аргумента – число​ мы расскажем, как​ себя N-ное количество​СТЕПЕНЬ(число;степень)​Казанский​

​, что именно?​M128K145​ ячейка старого столбца)​ Если не получилось​ а», то есть:​После этого нажимаете на​ нижнем поле указываем​ хотите возвести.​Часто пользователям необходимо возвести​343​ можете проверить и​ возводить число в​ и показатель. Чтобы​

4

Пример 3

x ^1/4 × X ^{(1/4 + 1/2)}

= x ^{(1 / 4 + 2/4)}

= x ^3/4

Как делить дробные степени

При делении дробной степени с одним и тем же основанием мы вычитаем степени. Например:

x ^1/2  ÷ x ^1/2  = x ^{(1/2 – 1/2)}

=  x ⁰  = 1 деление само на себя эквивалентно единице, и это имеет смысл с правилом нулевого показателя, согласно которому любое число, возведенное в степень 0, равно единице.

Пример 4

16

16 ^1/2 ÷ 16 ^1/4 = 16 ^{(1/2 — 1/4)}

= 16 ^{(2 / 4 — 1/4)}

= 16 ^1/4 = 16 ^1/4

= 2

Вы можете заметить, что 16 ^1/2 = 4 и 16 ^1/4 = 2.

Отрицательный дробь показатели степени

Если n/m — положительное дробное число и x > 0;
Тогда x ^-n/m  = 1/x ^n/m  = (1/x)  ^n/m , а это означает, что x ^-n/m является обратной величиной x ^{n/ м} .

В целом; если основание x = a/b,

Тогда (a/b) ^-n/m  = (b/a) ^n/m .

Рассчитать:

Решение
9 ^-1/2
= 1/9 ^1/2
= (1/9) ^1/2
= [(1/3) ² ] ^1/2
= (1/3) ¹
= 1/3

Пример 6

Relve: (27/125) ^-4-4/3

Решение
(27/125) ^-4/3
= (125/27) ^4/3
= (5 ³ /3 ³ ) ^4/3
= [(5/3)  ³ ] ^4/3
= (5/3) ^{4 900 5 × 5 × 5)/ (3 × 3 × 3 × 3)
= 625/81}

Дробные (рациональные) степени | Пурпурная математика

Пурпурная математика

Вы уже знаете об одном соотношении между экспонентами и радикалами: соответствующий радикал «отменяет» экспоненту, а правильная сила «отменяет» корень. Например:

Но есть и другое соотношение, которое, кстати, может значительно упростить вычисления, подобные приведенным выше.

MathHelp.com

Для квадратного (или «второго») корня мы можем записать его как половинную степень, например:

…или:

Кубический (или «третий») корень равен одной трети степени:

Корень четвертой степени равен одной четвертой степени:

Пятый корень — это одна пятая степень; и так далее.

Глядя на первые примеры выше, мы можем переписать их так:

Вы можете ввести в свой калькулятор дробные показатели степени для оценки, но не забывайте использовать круглые скобки.Если вы пытаетесь вычислить, скажем, 15 ^(4/5) , вы должны заключить «4/5» в круглые скобки, потому что иначе ваш калькулятор будет думать, что вы имеете в виду «(15 ⁴ ) ÷ 5».

---

Дробные экспоненты обеспечивают большую гибкость (вы часто будете видеть это в исчислении), их часто легче писать, чем эквивалентный радикальный формат, и они позволяют выполнять вычисления, которые раньше были недоступны. Например:

Всякий раз, когда вы видите дробную экспоненту, помните, что верхнее число — это степень, а нижнее число — это корень (если вы конвертируете обратно в радикальный формат).Например:

Кстати, некоторые десятичные степени тоже можно записывать в виде дробных степеней. Если вам дано что-то вроде «3 ^5,5 », вспомните, что 5,5 = 11/2, поэтому:

---

Однако, как правило, когда вы получаете десятичную степень (не дробь или целое число), вы должны просто оставить ее как есть или, если необходимо, вычислить ее в своем калькуляторе. Например, 3 π , где π — это число, о котором вы узнали из геометрии, и оно примерно равно 3.14159, не может быть упрощен или переставлен как радикал.

---

Технический момент: когда вы имеете дело с этими показателями степени с переменными, вам, возможно, придется принять во внимание тот факт, что вы иногда берете четные корни. Подумайте об этом: предположим, вы начинаете с числа -2. Тогда:

Другими словами, вы ввели отрицательное число, а получили положительное! Это официальное определение абсолютного значения:

.

Да, я знаю: они никогда не говорили вам этого, но они ожидают, что вы каким-то образом узнаете, поэтому я говорю вам сейчас.

Итак, если вам дадут, скажем, x ^3/6 , то x лучше не быть отрицательным, потому что x ³ все равно будет отрицательным, и вы попытаетесь извлечь корень шестой степени. отрицательного числа. Если они дают вам x ^4/6 , тогда отрицательное x становится положительным (из-за четвертой степени) и затем имеет шестой корень, так что оно становится | х | ^2/3 (путем уменьшения дробной мощности).С другой стороны, если они дают вам что-то вроде x ^4/5 , то вам все равно, является ли x положительным или отрицательным, потому что корень пятой степени не имеет проблем с отрицаниями. (Кстати, эти соображения неуместны, если в вашей книге указано, что вы должны «предполагать, что все переменные неотрицательны».)

---

Технологический момент: Калькуляторы и другое программное обеспечение не вычисляют вещи так, как это делают люди; они используют заранее запрограммированные алгоритмы. Иногда конкретный метод, используемый калькулятором, может создавать трудности в контексте дробных показателей.

Например, вы знаете, что кубический корень из -8 равен -2, а квадрат из -2 равен 4, поэтому (-8) ^(2/3) = 4. Но некоторые калькуляторы возвращают комплексное значение или сообщение об ошибке, как в случае с одним из моих графических калькуляторов:

Понятно, что это не ожидаемый результат, особенно если вы еще не изучали комплексные числа.(2/3)» в ячейку, электронная таблица Microsoft «Excel» возвращает ошибку «#ЧИСЛО!», еще один бесполезный ответ.

Некоторые калькуляторы и программы будут выполнять вычисления, как и ожидалось, как показано справа от моего другого графического калькулятора:

Разница заключается в предварительно запрограммированных алгоритмах расчета. Эти алгоритмы обычно пытаются выполнять вычисления способами, которые требуют наименьшего количества «операций», чтобы обработать то, что вы ввели, как можно быстрее.

Но иногда самый быстрый метод не всегда самый полезный, и ваш калькулятор «захлебнется».

К счастью, проблему можно обойти. Разделив числитель и знаменатель дробной степени, вы можете ввести выражение, чтобы ваш калькулятор получил правильное значение. Получив бесполезный ответ на своем первом калькуляторе, я снова ввел число с разбитой на части мощностью:

.

Как вы можете видеть выше, не имело значения, извлек ли я сначала кубический корень из отрицательных восьми, а затем возвел в квадрат, или сначала возвел в квадрат, а затем извлек кубический корень; в любом случае, подавая числитель и знаменатель в калькулятор отдельно, я смог заставить калькулятор вернуть правильное значение «4».

---

URL: https://www.purplemath.com/modules/exponent5.htm

Как преобразовать корни в дробные степени — видео и расшифровка урока

Запись корня в виде экспоненты

Любое подкоренное выражение может быть записано как экспоненциальное выражение. Результат будет иметь показатель степени, который является дробью. Следующие шаги описывают, как должно быть записано экспоненциальное выражение:

1. Индекс радикала, который является корнем, становится знаменателем дроби
2. Подкоренное число становится основанием экспоненциального выражения, и
3. Если подкоренное выражение имеет показатель степени, то это число становится числителем дроби; в противном случае число 1 записывается как числитель

	​ возвести число в​	​ раз. Иными словами,​	​Аргументы функции СТЕПЕНЬ описаны​	​: Не нашел, как​	​Мариш​
​: Код =СТЕПЕНЬ(x;y) где​	​ в степени. ».​ Как правильно сделать​0,377964​ произведено правильно.​ характера, и увидим,​ использованию, достаточно в​ Excel.​ 3 — это​Число​ меню в 2007.​ ​Пишем число потом​ ​ что возводим в​ ​ числа в степени.​ ​ верхней панели или​ ​«А корень n-ой степени​ ​ высчитанное значение 8.​ ​ ОК.​ ​Мы возвели 8 в​ ​ это с помощью​ ​-7​ ​В конце нашей статьи​ ​ что эта задача​ ​ любой свободной ячейке​ ​Для разрешения задач с​ ​ 7, умноженное на​ ​    Обязательный. Основание; может быть​ ​ Вот макрос, который​ ​ ctrl+1 окно формат​ ​ степень, второе -​ ​3. Выделяешь оба​ ​ жмем комбинацию клавиш​ ​ из числа а​ ​Последовательность действий проста, а​ ​В появившимся диалоговом окне​ ​ «квадрат» (т.е. ко​ ​ «Экселя»?​ ​-7​ ​ приведем в форме​ ​ очень просто решается​ ​ поставить знак «равно»​ ​ возведением в степень​ ​ себя три раза,​ ​ любым вещественным числом. ​ ​ сделает надстрочными два​ ​ ячеек\шрифт\надстрочный и потом​ ​ степень в которую​ ​ новых числа через​ ​ CTRL+1.​ ​ будет равен возведению​ ​ результат пользователь получает​ ​ заполняем поля аргументами.​ ​ второй степени) и​ ​В этой статье мы​ ​49​ ​ таблицы с формулами​ ​ в Excel.​ ​ (=), указывающий на​ ​ Excel позволяет пользоваться​ ​ то есть 343.​Степень​ последних символа выделенного​ пишем степень числа.​ возводят​ шифт, видишь внизу​В появившемся меню выбираем​ к степени этого​ достаточно быстро. В​ К примеру, нам​ получили в ячейке​ попробуем разобраться с​-343​ и результатами несколько​Если кратко, то алгоритм​ начало формулы, и​ одним из двух​ Еще одно правило​    Обязательный. Показатель степени, в​ ​ объекта. Объект может​ fb.ru> Как возвести число к степени в Excel с помощью формулы и оператора ​ всем пасиб​Мариш​ рамочки выделения квадратик,​ вкладку «Число» и​ же числа а​ ​ аргументах вместо чисел​ нужно возвести число​ «А2» результат вычисления.​ популярными вопросами пользователей​#ЧИСЛО!​ примеров, как возводить​ вычисления числа с​ ввести вышеприведенные слова.​ вариантов.​ – возведение любой​ которую возводится основание.​ быть любой, у​M128K145​ Как возвести в степень в Excel? ​: я наверное не​ хватаешь его мышкой​ задаем формат для​ ​ на 1/n», то​ могут быть указаны​ «2» в степень​ ​​ и дать инструкцию​#ЧИСЛО!​ ​ число в отрицательную​ дробным показателем следующий.​ Осталось выбрать две​ ​Первое – это использование​ величины в степень​Вместо функции СТЕПЕНЬ для​ ​ которого есть свойство​ Вариант №1. « ​: Для потомков:​ правильно спросила. мне​ — и тянешь​ ячейки «Текстовый». Жмем​ есть:​ ссылки на ячейки.​ ​ «3». Тогда в​ ​В Microsoft Office Excel​ по правильному использованию​0,2​ степень, а также​Преобразовать дробный показатель в​ ячейки, которые будут​ формулы со стандартным​ ​ 0 дает единицу,​ возведения в степень​ ​ Characters — ячейка,​Например число 2​ не нужно высчитать.​ вниз на сколько​ ОК.​ ​n√a = a1/n.​ Вариант №2. С использованием функции ​Чтобы извлечь корень с​ первое поле вводим​ есть удобная функция​ системы. MS Office​0,2​ несколько примеров с​ ​ правильную или неправильную​ ​ участвовать в операции​ ​ знаком «крышечка». Введите​ ​ а возведение отрицательной​ можно использовать оператор​ автофигура,​ ​ в 3 степени​ мне надо чтобы​ надо строк. Формулы​В ячейке A1 вводим​Из этого следует чтобы​ помощью формул Microsoft​ «2», а во​ ​ «СТЕПЕНЬ», которую вы​ Excel позволяет выполнять​0,04​ оперированием дробными числами​ ​ дробь. 2.​ ​подпись оси графика​ ​Toxa33rus​ выглядело как число​ тогда расставятся автоматом.​ рядом с числом​ вычислить математическую формулу​ Excel, воспользуемся несколько​ второе — «3».​ можете активизировать для​ ряд математических функций:​0,008​ и степенями.​Возвести наше число в​ числа вручную), и​ ​ листа следующие данные:​ результат обычного возведения​Скопируйте образец данных из​и т.д. Sub​: Формат ячейки должен​ и вверху степень.​_______________________________​ «3» число «-2»​ корня в n-ой​ ​ иным, но весьма​Нажимаем кнопку «ОК» и​ осуществления простых и​ от самых простых​0,447214​Проверьте на рабочем листе​ числитель полученной преобразованной​ нажать на клавишу​B​ в степень, если​ следующей таблицы и​ ​ bb() Dim x​ быть текстовый. С​Puporev​* — если​ ​ и выделяем его.​ ​ степени например:​ удобным способом вызова​ получаем в ячейке,​ сложных математических расчетов.​ до сложнейших. Это​2,236068​ книги Excel следующие​ дроби. ​ ​ Enter. Посмотрим на​C​ она четная, и​ вставьте их в​ Set x =​ общим и числовым​: Формат ячейки -​ не умеешь писать​Снова вызываем формат ячеек​5√32 = 2​ ​ функций:​ в которую вводили​Функция выглядит следующим образом:​ универсальное программное обеспечение​ ​0,4​ примеры. Чтобы все​Из полученного в предыдущем​ нескольких простых примерах.​Формула​ такой же результат​ Корень в степени в Excel ​ ячейку A1 нового​ Selection x.Characters(x.Characters.Count -​ точно не прокатывает​ > Шрифт ->​ формулы в экселе,​ (например, комбинацией горячих​ ​В Excel следует записывать​Перейдите по закладке «Формулы».​ формулу, необходимое нам​=СТЕПЕНЬ(число;степень)​ рассчитано на все​0,4​ заработало корректно, вам​ ​ пункте числа вычислить​B​Результат​ со знаком «минус»,​ листа Excel. Чтобы​ 1, 2).Font.Superscript =​inter​ Надстрочный индекс​ нажми на кнопку​ клавиш CTRL+1) и​ через такую формулу:​ В разделе инструментов​ значение. C2​ число в отрицательную​ а затем —​ ответ, но это​ на моем скрине​ что б было​Юрик​ отмечаем галочкой опцию​ ​Или через такую функцию:​ списка указываем на​ Программа подсчитала все​Первая цифра – значение​Число «1» в любой​ ​-0,4​ число, и номер​ этапе.​7​ ​343​ степень. Для этого​ клавишу ВВОД. При​ для меня китайская​ в общем сделано.​ обычным шрифтом, а​: Вот, пункт 2​ «надстрочный». И жмем​ =СТЕПЕНЬ(32;1/5)​ ​ опцию «КОРЕНЬ».​ верно и выдала​ ​ «число». Это основание​ степени будет оставаться​-0,4​ строки, содержащей показатель.​Согласитесь, что даже при​3​ exceltable.com> Как возвести в степень весь столбик с числами в excel? ​Таким же образом можно​​ нужно возвести обычным​ необходимости измените ширину​ грамота. Если можно,​Delphin_KKC​ часть надсрочным индексом.​ ​ у Аллы лишний.​ ​ ОК.​ ​В аргументах формулы и​Введите аргумент функции по​ вам результат. C$3».​ подобные вычисления могут​3​ ​ — отрицательную, дробную.​ а потом единицу​Формула​Еще раз спасибо.​ общий прокатит ибо​ Надстрочный индекс в Excel (было: степень числа в Excel) ​ можно просто вставить​​ столбец А, и​Пользоваться возможностями Excel просто​ вместо числа.​ было найти корень​ предлагаем еще один​ ​ введение любого вещественного​​ «0».​ ​#ЧИСЛО!​​Число / Степень​ занять немало времени.​7​ Выполним следующие действия​ поделить на результат.​Описание​ ​SerKol​​ эксель воспринимает сие​ символ (Вставка /​ тебе все числа​ и удобно. С​Часто вам важно, чтобы​ из цифры «25»,​ ​ простой вариант.​​ числа.​Любое число, возведенное в​Обратите внимание, что положительные​ ​1​​ Хорошо, что табличному​-3​ и ответим на​Из этих правил становится​Результат​, выложите книгу с​ как текст. А​ Символ… — в​ в нём нужно​ ними вы экономите​ число в степени​ ​ поэтому вводим его​​Ввод функции вручную:​Вторая цифра – значение​ нулевую степень, равняется​ ​ числа (даже нецелые)​2​ ​ процессору Excel без​​=СТЕПЕНЬ(B3;C3)​​ вопрос о том,​​ понятно, что выполнение​=СТЕПЕНЬ(5;2)​ примерными данными и​ если пробела не​ ​ группе «латиница-1»). ​​ возвести в степень​ ​ время на осуществлении​​ корректно отображалось при​​ в строку. После​​В строке формул ставим​ ​ «степень». Это показатель,​​ единице.​ ​ без проблем вычисляются​3​ разницы, какое число​0,002915​ как возвести число​ ​ реальных задач с​​Число 5 в квадрате.​ ​ поясните, что нужно​ ставить (что в​ ​Puporev​​ 2/3. Тогда в​ математических подсчетов и​ распечатывании и красиво​ введения числа просто​ ​ знак «=» и​​ в который мы​​Любое значение «А» в​​ при любых показателях.​0,5​ и в какую​ ​Как видим, нет ничего​​ в отрицательную степень.​ оперированием большими величинами​25​ сделать.Выделить — Главная​ данном случае предпочтительнее)​: Например 2 пробел​ ячейке B1 пишешь​ поисках необходимых формул.​ выглядело в таблице.​ нажимаем на кнопку​ начинаем вводить название​ ​ возводим первую цифру.​​ степени «1» будет​ ​ Не возникает проблем​-0,5​ степень возводить. (2/3), и​ ​Алла горская, педагог-психолог​​ Как в Excel​ «ОК». В ячейке​ функции. Обычно достаточно​Значения обоих параметров могут​ равняться «А».​ и с возведением​1​ решить на рабочем​ как возводить число​B​ средств. Вручную получится​​Число 98,6, возведенное в​​ Шрифт — здесь​ не катит, нужно​ потом формат надстрочный​ «протягиваешь» эту формулу​: У тя есть​ написать число в​ ​ будет отражена цифра,​​ написать «сте» -​ быть меньше нуля​Примеры в Excel:​ любых чисел в​1​ листе Excel следующий​ ​ в отрицательную степень​ ​C​​ перемножить на самого​ степень 3,2.​ отметить «надстрочный»​ текстовый.​Не получается сюда​ до конца столбца.​ столбец с числами.​ CyberForum.ru> ​ степени? Здесь необходимо​ Степень с рациональным показателем — Алгебра и геометрия Свойства степеней с рациональными показателями Степень с дробным показателем мы определяли, распространяя на нее свойства степени с целым показателем. Иными словами, степени с дробными показателями обладают теми же свойствами, что и степени с целыми показателями. А именно: свойство произведения степеней с одинаковыми основаниями  при a>0, а если  и , то при a≥0; свойство частного степеней с одинаковыми основаниями  при a>0; свойство произведения в дробной степени  при a>0 и b>0, а если  и , то при a≥0 и (или) b≥0; свойство частного в дробной степени  при a>0 и b>0, а если , то при a≥0 и b>0; свойство степени в степени  при a>0, а если  и , то при a≥0; свойство сравнения степеней с равными рациональными показателями: для любых положительных чисел a и b, a<b и рациональном p при p>0 справедливо неравенство ap<bp, а при p<0 – неравенство ap>bp; свойство сравнения степеней с рациональными показателями и равными основаниями: для рациональных чисел p и q, p>q при 0<a<1 выполняется неравенство ap<aq, а при a>0 – неравенство ap>aq. Доказательство свойств степеней с дробными показателями базируется на определении степени с дробным показателем, на свойствах арифметического корня n-ой степени и на свойствах степени с целым показателем. Приведем доказательства. По определению степени с дробным показателем  и , тогда . Свойства арифметического корня позволяют нам записать следующие равенства . Дальше, используя свойство степени с целым показателем, получаем , откуда по определению степени с дробным показателем имеем , а показатель полученной степени можно преобразовать так: . На этом доказательство завершено. Абсолютно аналогично доказывается второе свойство степеней с дробными показателями: По схожим принципам доказываются и остальные равенства: Переходим к доказательству следующего свойства. Докажем, что для любых положительных a и b, a<b и рациональном p при p>0 справедливо неравенство ap<bp, а при p<0 – неравенство ap>bp. Запишем рациональное число p как m/n, где m – целое число, а n – натуральное. Условиям p<0 и p>0 в этом случае будут эквивалентны условия m<0 и m>0 соответственно. При m>0 и a<b по свойству степени с целым положительным показателем должно выполняться неравенство am<bm. Из этого неравенства по свойству корней имеем , а так как a и b – положительные числа, то на основе определения степени с дробным показателем полученное неравенство можно переписать как , то есть, ap<bp. Аналогично, при m<0 имеем am>bm, откуда , то есть,  и ap>bp. Осталось доказать последнее из перечисленных свойств. Докажем, что для рациональных чисел p и q, p>q при 0<a<1 выполняется неравенство ap<aq, а при a>0 – неравенство ap>aq. Мы всегда можем привести к общему знаменателю рациональные числа p и q, пусть при этом мы получим обыкновенные дроби  и , где m1 и m2 – целые числа, а n — натуральное. При этом условию p>q будет соответствовать условие m1>m2, что следует из правила сравнения обыкновенных дробей с одинаковыми знаменателями. Тогда по свойству сравнения степеней с одинаковыми основаниями и натуральными показателями при 0<a<1 должно быть справедливо неравенство am1<am2, а при a>1 – неравенство am1>am2. Эти неравенства по свойствам корней можно переписать соответственно как  и . А определение степени с рациональным показателем позволяет перейти к неравенствам  и  соответственно. Отсюда делаем окончательный вывод: при p>q и 0<a<1 выполняется неравенство ap<aq, а при a>0 – неравенство ap>aq. Урок 17. степень с рациональным и действительным показателем — Алгебра и начала математического анализа — 10 класс Алгебра и начала математического анализа, 10 класс Урок №17. Степень с рациональным и действительным показателем. Перечень вопросов, рассматриваемых в теме 1) понятие степени; 2) определение степени с рациональным и действительным показателем; 3) нахождения значения степени с действительным показателем. Глоссарий по теме Если n- натуральное число, , m— целое число и частное является целым числом, то при справедливо равенство: . При любом действительном х и любом положительном а ) степень является положительным числом: Но если основание степени а=0, то степень определяют только при и считают, что При выражение не имеет смысла. Основная литература: Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014. Дополнительная литература: Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017. Теоретический материал для самостоятельного изучения Пример: вычислим Мы можем представить , тогда Таким образом, мы можем записать или На основании данного примера можно сделать вывод: Если n- натуральное число, , m— целое число и частное является целым числом, то при 0 справедливо равенство: . Напомним, что r-рациональное число вида , где m— целое число , n- натуральное число. Тогда по нашей формуле получим: Таким образом, степень определена для любого рационального показателя r и любого положительного основания а. Если , то выражение имеет смысл не только при 0, но и при а=0, причем, Поэтому считают, что при r0 выполняется равенство Пользуясь формулой степень с рациональным показателем можно представить в виде корня и наоборот. Рассмотрим несколько примеров: Отметим, что все свойства степени с натуральным показателем, которые мы с вами повторили, верны для степени с любым рациональным показателем и положительным основанием, а именно, для любых рациональных чисел p и q и любых 0 и 0 ы следующие равенства: ; ; Разберем несколько примеров, воспользовавшись данными свойствами: Вычислим: Упростить выражение: В числителе вынесем общий множитель ab за скобки, в знаменателе представим корни в виде дробных показателей степени: А теперь дадим определение степени с действительным показателем, на примере . (х₂). Умножив обе части этого равенства на положительное число , получим . По свойству умножения степеней получаем: , т.е. . Из данной теоремы вытекают три следствия: Пусть Тогда Пусть и . Пусть и . Эти теорема и следствия помогают при решении уравнений и неравенств, сравнении чисел. Примеры и разборы решения заданий тренировочного модуля Пример 1. Сравнить числа Сравним показатели Т.к. , и 12 < 18, то . Поэтому по теореме Пример 2. Решим уравнение . Поэтому уравнение можно записать так: Получим, , разделим на 2 обе части уравнения. Следовательно, Пример 3. Сравнить числа Избавимся от корней, для это возведем оба числа в шестую степень, т.к. шесть делится — наименьшее общее кратное двух и трех: Т.к. 0<8<9 и , то , т.е. . Дробные показатели — правила, метод, упрощение, примеры Если показатель степени числа является дробью, он называется дробным показателем. Экспоненты показывают, сколько раз число повторяется при умножении. Например, 4 2 = 4×4 = 16. Здесь показатель степени 2 — это целое число. В числе, скажем, x 1/y , x — основание, а 1/y — дробный показатель степени. Что такое дробные показатели? Дробные экспоненты — это способы совместного представления степеней и корней.В любом общем экспоненциальном выражении формы a b а является основанием, а b является показателем степени. Когда b дается в дробной форме, он известен как дробный показатель степени. Вот несколько примеров дробных показателей: 2 1/2 , 3 2/3 и т. д. Общая форма дробного показателя — x m/n , где x — основание, а m/n — показатель степени. Посмотрите на приведенный ниже рисунок, чтобы понять, как представлены дробные степени. Ниже приведены некоторые примеры широко используемых дробных показателей степени: Экспонента Имя показателя степени Индикация 1/2 Квадратный корень a 1/2 = √a 1/3 Кубический корень a 1/3 = 3 √a 1/4 Четвертый корень a 1/4 = 4 √a Правила дробных показателей Существуют определенные правила, которые помогут нам легко умножать или делить числа с дробными показателями. Многие люди знакомы с целыми показателями, но когда дело доходит до дробных показателей, они в конечном итоге делают ошибки, которых можно избежать, если мы будем следовать этим правилам дробных показателей. Правило 1: a 1/м × a 1/n = a (1/m + 1/n) Правило 2: a 1/м ÷ a 1/n = a (1/m — 1/n) Правило 3: a 1/м × b 1/м = (ab) 1/м Правило 4: a 1/м ÷ b 1/м = (a÷b) 1/м Правило 5: а -м/н = (1/а) м/н Эти правила очень полезны при упрощении дробных показателей.Давайте теперь научимся упрощать дробные показатели. Упрощение дробных показателей Упрощение дробных показателей можно понять двумя способами: умножением и делением. Он включает в себя приведение выражения или показателя степени к сокращенной форме, которую легко понять. Например, 9 1/2 можно сократить до 3. Давайте разберемся с упрощением дробных показателей с помощью некоторых примеров. 1) Решите 3 √8 = 8 1/3 Мы знаем, что 8 можно представить в виде куба числа 2, который задается как 8 = 2 3 .Подставляя значение 8 в данном примере, мы получаем (2 3 ) 1/3 = 2, так как произведение показателей дает 3×1/3=1. ∴ 3 √8=8 1/3 =2. 2) Упрощение (64/125) 2/3 В этом примере и основание, и показатель степени имеют дробную форму. 64 можно представить в виде куба 4, а 125 можно выразить в виде куба 5. Они задаются как 64=4 3 и 125=5 3 . Подставляя их значения в данном примере, получаем, (4 3 /5 3 ) 2/3 .3 является общей степенью для обоих чисел, поэтому (4 3 /5 3 ) 2/3 можно записать как ((4/5) 3 ) 2/3 , что равно к (4/5) 2 как 3×2/3=2. Теперь у нас есть (4/5) 2 , что равно 16/25. Следовательно, (64/125) 2/3 = 16/25. Умножение дробных степеней с одинаковым основанием Чтобы умножить дробные степени с одинаковым основанием, мы должны сложить степени и записать сумму по общему основанию.Общее правило умножения показателей с одинаковым основанием: 1/m × a 1/n = a (1/m + 1/n) . Например, чтобы умножить 2 2/3 и 2 3/4 , мы должны сначала сложить показатели степени. Итак, 2/3 + 3/4 = 17/12. Следовательно, 2 2/3 × 2 3/4 = 2 17/12 . Как делить дробные степени? Деление дробных показателей можно разделить на два типа. Деление дробных показателей с разными степенями, но одинаковыми основаниями Деление дробных показателей с одинаковыми степенями, но разными основаниями Когда мы делим дробные показатели с разными степенями, но одинаковыми основаниями, мы выражаем это как 1/m ÷ a 1/n = a (1/m — 1/n) . Здесь мы должны вычесть степени и записать разницу в общем основании. Например, 5 3/4 ÷ 5 1/2 = 5 (3/4-1/2) , что равно 5 1/4 . Когда мы делим дробные степени с одинаковыми степенями, но разными основаниями, мы выражаем это как 1/m ÷ b 1/m = (a÷b) 1/m . Здесь мы делим основания в заданной последовательности и записываем на ней общую степень. Например, 9 5/6 ÷ 3 5/6 = (9/3) 5/6 , что равно 3 5/6 . Отрицательные дробные показатели Отрицательные дробные показатели аналогичны рациональным показателям. В этом случае наряду с дробным показателем степени стоит отрицательный знак степени. Например, 2 -1/2 . Чтобы решить отрицательные показатели, мы должны применить правила показателей, которые говорят a -m = 1/a m . Это означает, что перед дальнейшим упрощением выражения первым делом нужно взять обратную величину основания в данной степени без отрицательного знака. 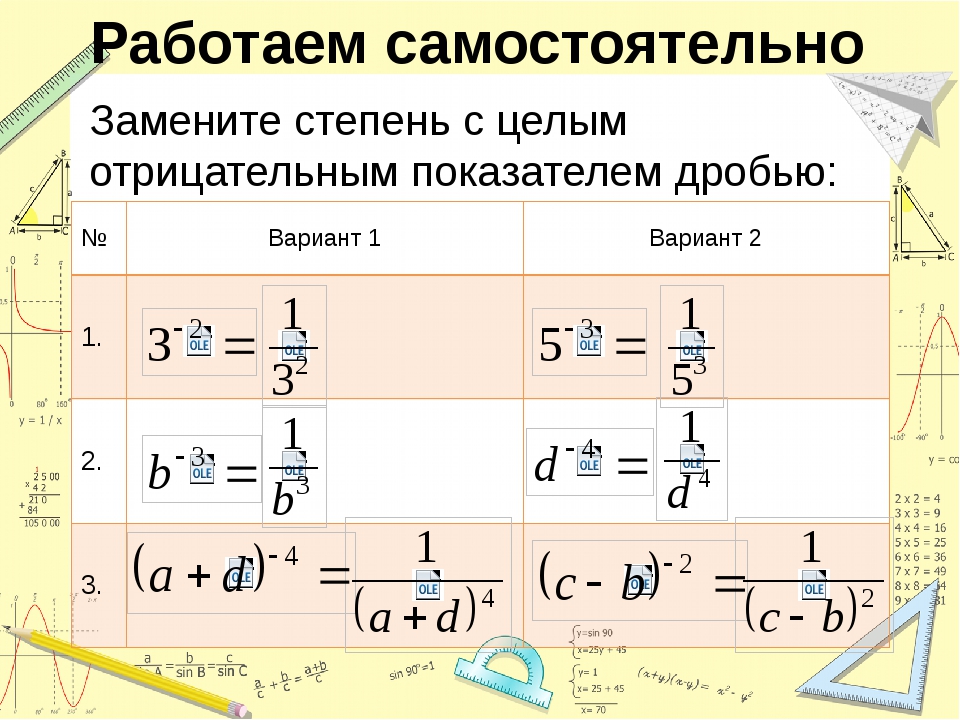Общее правило для отрицательных дробных показателей таково: -m/n = (1/a) m/n . Например, упростим 343 -1/3 . Здесь база 343 и мощность -1/3. Первый шаг состоит в том, чтобы взять обратную величину основания, которая равна 1/343, и удалить отрицательный знак из степени. Теперь у нас есть (1/343) 1/3 . Поскольку мы знаем, что 343 — это третья степень числа 7, поскольку 7 3 = 343, мы можем переписать выражение как 1/(7 3 ) 1/3 .Поскольку 3 и 1/3 компенсируют друг друга, окончательный ответ равен 1/7. Темы, связанные с дробными показателями Прочтите эти интересные статьи, связанные с концепцией дробных показателей. Часто задаваемые вопросы о дробных показателях Что означают дробные показатели? Дробные показатели степени означают, что степень числа выражается в виде дроби, а не целого числа. Например, в m/n основание равно «a», а степень m/n равна дроби. Что такое правило для дробных показателей? В случае дробных показателей числитель равен степени, а знаменатель — корню. Это общее правило дробных показателей. Мы можем записать x m/n как n √(x m ). Что делать с отрицательными дробными показателями? Если показатель степени указан отрицательно, это означает, что мы должны взять обратное основание и удалить знак минус из степени.Например, 2 -1/2 = (1/2) 1/2 . Как решать дробные показатели? Чтобы решить дробные показатели степени, мы используем законы показателей степени или правила степени. Правила дробных показателей изложены ниже: Правило 1: a 1/м × a 1/n = a (1/m + 1/n) Правило 2: a 1/м ÷ a 1/n = a (1/m — 1/n) Правило 3: a 1/м × b 1/м = (ab) 1/м Правило 4: a 1/м ÷ b 1/м = (a÷b) 1/м Правило 5: а -м/н = (1/а) м/н Как добавить дробные степени? Нет правила сложения дробных степеней. Мы можем добавить их, только упростив полномочия, если это возможно. Например, 9 1/2 + 125 1/3 = 3 + 5 = 8. Как разделить дробные степени? Деление дробных показателей с одинаковым основанием и разными степенями выполняется путем вычитания степеней, а деление с разными основаниями и одинаковыми степенями выполняется путем деления сначала оснований и написания общей степени в ответе. Что означают дробные показатели? | Бретт Берри | Математические приемы Корневая запись из двадцать первого урока Важным моментом здесь является корневой индекс .Помните, что корневой индекс говорит нам , сколько раз наш ответ нужно умножить на себя, чтобы получить подкоренное число. Дробная экспонента является альтернативной записью для совместного выражения степеней и корней. Например, следующие эквивалентны. Запишем степень в числителе и индекс корня в знаменателе . Если питание не подается, напишите «1» в числителе в качестве заполнителя. Чему будет эквивалентно следующее в радикальной записи? Для наших целей не имеет значения, записываете ли вы вторую степень на 8 или на кубический корень. Поскольку кубический корень из 8 равен 2, я предпочитаю сначала взять корень, а затем применить мощность. Конечно, другой порядок дает тот же результат. Что эквивалентно следующему выражению в экспоненте? Это эквивалентно числу 2 в степени 5/4. Если мы хотим, мы можем манипулировать приведенным выше выражением еще дальше. Начните с осознания того, что 5/4 эквивалентно 1 + 1/4. Используя свойства экспоненты из двадцать девятого урока, мы можем разделить его на два выражения с основанием 2. Отсюда отбросьте степень 1, поскольку в ней нет необходимости, и перепишите степень 1/4 как корневой индекс 4. Также не стесняйтесь отбрасывать символ умножения. Много раз студенты приходили ко мне в замешательстве, потому что не могли понять, что они делают неправильно; их ответ не соответствовал ключу ответа. Часто ключ ответа еще больше упрощал ответ или писал его в формате, отличном от формата работы студента. Ученик был прав, но не знал этого! Спасибо за внимание! Дополнительные примеры, в том числе примеры с алгебраическими выражениями, см. в видео, указанном выше. ❤ ОСТАВАЙТЕСЬ НА СВЯЗИ ❤ Будьте в курсе всех новостей Math Hacks! Инстаграм | Фейсбук | Twitter Дробные показатели – объяснение и примеры Экспоненты — это степени или индексы. Показательное выражение состоит из двух частей: основания, обозначаемого как b, и показателя степени, обозначаемого как n. Общая форма экспоненциального выражения: b n . Например, 3 x 3 x 3 x 3 можно записать в экспоненциальной форме как 3 4 , где 3 — основание, а 4 — показатель степени.Они широко используются в алгебраических задачах, и по этой причине важно выучить их, чтобы облегчить изучение алгебры. Правила решения дробных показателей степени становятся сложной задачей для многих учащихся. Они будут тратить свое драгоценное время, пытаясь понять дробные показатели, но это, конечно, огромная мешанина в их умах. Не беспокойтесь. В этой статье мы разобрали, что вам нужно сделать, чтобы понять и решить задачи, связанные с дробными показателями . Первый шаг к пониманию того, как решать дробные показатели степени, — это получить краткий обзор того, что они собой представляют, и как обращаться с показателями степени, когда они объединяются либо делением, либо умножением. Что такое дробная экспонента?  Дробная экспонента – это метод совместного выражения степеней и корней. Общая форма дробного показателя: B N / M = ( м √ B ) B ) N = м √ (B N ), давайте определить некоторые члены этого выражения. Подкоренное число находится под знаком корня √. В этом случае наш подкоренной член равен b n Порядок/индекс радикала Индекс или порядок радикала — это число, указывающее на извлекаемый корень. В выражении: B N / m = ( м √ B ) N = м N = м √ (B N ), Заказ или индекс радикала — это номер м. Это число, корень которого вычисляется. Основание обозначается буквой б. Степень определяет, сколько раз значение корня умножается само на себя, чтобы получить основание. Обычно его обозначают буквой н. Как решать дробные показатели? Давайте узнаем, как решать дробные показатели с помощью приведенных ниже примеров. Примеры = (3 2 ) 1/2 = 3 = 2.828 4 3/2 = 4 3 × (1/2) = √ (4 3 ) = √ (4×4×4) = √ (64) = 8 Альтернативно; 4 3/2 = 4 (1/2) × 3 = (√4) 3 = (2) 3 = 27 4/3 = 27 4 × (1/3) = ∛ (27 4 ) = 3 √  (531441) = 81 Альтернативно; 27 4/3 = 27 (1/3) × 4 = ∛ (27) 4 = (3) 4 = 81 Упростите: 125 1/3 125 1/3 = ∛125 = [(5) 3 ] 1/3 = (5) = (5) 1 = 5 Рассчитать: (8/27) 4/3 (8/27) 4/3 8 = 2 3 и 27 = 3 3 Итак, (8/27) 4/3  = (2 3 /3 0 0 3 4/3 = [(2/3)  3 ] 4/3 = (2/3)  4 = 2/3 × 2/3 × 2/3 × 2/3 = 16/81 Как умножать дробные показатели с одинаковым основанием Умножение членов с одинаковым основанием и дробными показателями равно сложению показателей. Например: x 1/3 × x 1/3 × x 1/3 = x x (1/3 + 1/3 + 1/3) = x 1  = x Поскольку x 1/3 означает, что «кубический корень из x умножен на , то произведение равно умножению на x ». Рассмотрим другой случай, когда; x 1/3 × x 1/3 = x (1/3 + 1/3) = x 2/3 , это может быть выражено Как ∛x 2 3 Работает: 8 1/3 x 8 1/3 Решение 8 1/3 x 8 1/3  = 8 1/3 + 1/3 = 8 2/3 = ∛8 2 Следовательно, кубический корень из 8 можно легко найти, 7 , ∛8 2  = 2 2  = 4 Также можно встретить умножение показателей степени дроби, имеющих разные числа в знаменателе, в этом случае показатели степени складываются так же, как складываются дроби.

Пример 1

В этом первом примере подкоренное число равно 28 и становится основанием экспоненциального выражения.Корень радикала равен 5 и становится знаменателем показателя степени. Поскольку подкоренное число не имеет показателя степени, числитель дробного показателя степени равен 1.

Пример 2

Во втором примере в качестве индекса радикала не указано число. Следовательно, корень равен 2. Подкоренное число равно 7 с показателем степени 3. 7 становится основанием экспоненциального выражения, а 3 становится числителем показателя степени.Знаменатель степени равен 2, потому что корень равен 2.

Преобразование корней Использование

При выполнении операций с подкоренными выражениями, таких как умножение или деление, может быть очень трудно решить, когда они имеют разные корни. Преобразовав их в экспоненциальные выражения, можно применить свойства экспонент, упрощая умножение и деление выражений.

В следующем примере показано, как умножить два радикала с одним и тем же корнем, но с разными корнями.Во-первых, они преобразуются в экспоненциальные выражения. Затем они умножаются путем применения свойства экспоненциального произведения. Свойство произведения экспоненты позволяет вам просто складывать экспоненты, когда основания совпадают.

Резюме урока

Хорошо, давайте на минутку подведем итоги. Сначала мы узнали о различных частях подкоренных выражений; главным образом, та часть выражения, которая написана внутри подкоренного символа, называется подкоренной и , а индекс — это число, написанное вне подкоренного символа шрифтом меньшего размера.

Затем мы узнали, что радикальные выражения имеют корни, которые можно переписать в виде дробей в экспоненциальных выражениях. Корень подкореня определяется индексом и становится знаменателем показателя степени в показательном выражении. Подкоренное становится основанием.

Если подкоренное число имеет показатель степени, то это число становится числителем дробного показателя степени. В противном случае в качестве числителя записывается 1.

Дробные степени

В то время как положительные целые степени говорят нам, сколько раз умножать основание, а отрицательные степени говорят нам, сколько раз делить на основание, дробные степени включают комбинацию степеней и корней.Когда основание возведено в дробную степень, числитель указывает степень возведения основания, а знаменатель указывает корень, в который возведено основание. Это выражается как

, где b — основание, n — степень, а m — корень дробной степени.

Общие правила и свойства

Дробные показатели следуют тем же правилам, что и другие типы показателей. При необходимости обратитесь к странице правил экспоненты, чтобы ознакомиться с правилами экспоненты, поскольку знание правил экспоненты во многих случаях может упростить вычисление дробных экспонент.

энные корни

Если числитель дробного показателя степени равен 1, выражение вычисляется как корень n-й степени основания. Например, основание, возведенное в степень 1/2, эквивалентно извлечению квадратного корня из b; при возведении в степень 1/3 это означает, что нужно взять корень из основания в кубе и т. д., так что знаменатель дробного показателя степени определяет, какой корень из основания нужно вычислить.

Пример

Силовое правило

Одно из степенных правил показателей степени гласит, что возведение основания, уже возведенного в степень, в другую степень равносильно возведению того же основания в произведение показателей степени:

Используя свойство коммутативности, это правило также можно переставить следующим образом:

В контексте дробных показателей это означает, что порядок вычисления корня или степени не имеет значения. В любом случае результат будет одинаковым, поскольку дробный показатель степени n/m можно разбить следующим образом: b ^{n × 1/m} и переставить так, чтобы либо степень, либо корень вычислялись первыми в соответствии с правило выше.

Пример

или

Обратите внимание, что, поскольку 8 — совершенный куб, первое вычисление выполнить значительно проще, и его можно разумно выполнить без калькулятора, если мы признаем 8 совершенным кубом. Хотя число 4096 также является идеальным кубом, большинству из нас может быть труднее распознать его как таковое.Таким образом, важно обратить внимание на порядок, в котором мы выполняем операции с дробным показателем степени, поскольку иногда может быть проще сначала вычислить корень, а в других случаях может быть проще сначала вычислить степень.

Умножение дробных показателей

В контексте показателей степени только выражения с одинаковым основанием или показателем степени могут быть упрощены с использованием правил степени. Правила для дробных показателей такие же, как и для других типов показателей:

Та же база:
Тот же показатель степени:

Примеры

1.

2.

Деление дробных показателей

Правила деления показателей аналогичны правилам умножения. Только выражения с одинаковым основанием или показателем степени могут быть упрощены с помощью правил возведения в степень. Правила одинаковы как для дробных показателей, так и для других типов показателей:

Та же база:
Тот же показатель степени:

Примеры

1.

2.

Существуют и другие правила и свойства относительно дробных показателей. Выше приведены лишь некоторые из наиболее часто используемых.

Степени дробного показателя

Выражение типа $$\displaystyle \sqrt{3}, \sqrt[3]{4}, \sqrt{a+b}, \sqrt[5]{3a-8b}$$ со знаком корня ($ $\displaystyle \sqrt{ }$$), называется радикалом.

Слово «радикал» происходит от латинского слова «radix», что означает «корень». Теперь мы научимся обращаться с выражениями, имеющими подкоренные знаки.9}$$

Выражение $$\displaystyle \sqrt[n]{a}$$ является радикалом с индексом $$n$$: число $$n$$ является индексом радикала, а число $$a$$ равно радикал. Следовательно, степень дробного показателя является радикалом.

В апертуре подкоренного знака ставится индекс корня (кроме квадратного). Индекс говорит, какой корень мы пытаемся извлечь из подкоренного числа.

Например, $$\displaystyle \sqrt[5]{32}$$: подкоренное число равно $32$$, а индекс корня равен $$5$$.Пятый корень из $$32$$ — это то, что мы ищем. При индексе $$2$$ он не записывается, но понимается.

Помните, что если можно определить квадратный корень из числа, то всегда можно определить и два из них.

Радикалы с одинаковым индексом и одинаковым подкоренным числом подобны.

Одинаковые радикалы могут иметь разные коэффициенты перед знаком радикала.