Все формулы динамики по физике: Ошибка: 404 Материал не найден — Детская игровая комната «Волшебный лес»

Posted on 25.03.197315.01.2022 by alexxlab

Содержание

Основные законы Динамики. Законы Ньютона — первый, второй, третий. Принцип относительности Галилея. Закон всемирного тяготения. Сила тяжести. Силы упругости. Вес. Силы трения — покоя, скольжения, качения + трение в жидкостях и газах.

Таблицы DPVA.ru — Инженерный Справочник

Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Основные законы Динамики. Законы Ньютона — первый, второй, третий. Принцип относительности Галилея. Закон всемирного тяготения. Сила тяжести. Силы упругости. Вес. Силы трения — покоя, скольжения, качения + трение в жидкостях и газах.

Основные законы Динамики. Законы Ньютона — первый, второй, третий. Принцип относительности

Галилея. Закон всемирного тяготения. Сила тяжести. Силы упругости. Вес.
Силы трения — покоя, скольжения, качения + трение в жидкостях и газах.

Законы Ньютона, основные законы динамики:
Первый закон Ньютона:
Вариант1. Существуют такие системы отсчета, называемые инерциальными, относительно которых тело движется прямолинейно и равномерно или покоится, если на него не действует сила, или действие внешних сил взаимно скомпенсировано. Вариант2. Существуют такие системы отсчета, называемые инерциальными, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной (в т. ч. равной 0) , если на него не действуют другие тела (или действие других тел взаимно компенсируется)
Второй закон Ньютона:
Сила, действующая на тело равна произведению массы тела на сообщаемое этому телу этой силой ускорение Под «силой» понимается равнодействующая всех сил:
Третий закон Ньютона.
Вариант 1. Тела действуют друг на друга с силами, направленными вдоль одной и той-же прямой, равными по модулю и противоположными по направлению Вариант 2. Действие равно противодействию
Принцип относительности Галилея:
Все механические процессы протекают одинаково во всех инерциальных системах отсчета:
Закон всемирного тяготения:
где: — это гравитационная постоянная
Силы в механике. Сила тяжести, сила упругости, сила трения:
Гравитационные силы (сила притяжения = сила тяжести):
Сила тяжести — сила, с которой Земля притягивает тело, находящееся на ее поверхности или на некотором расстоянии от поверхности. Определяется законом всемирного тяготения. Вблизи поверхности Земли и на ее поверхности сила тяжести: — где: -ускорение свободного падения
Силы упругости, закон Гука, сила реакции опоры, вес:
Силы упругости — силы, возникающие при деформации (изменении объема или формы) тела. Строго говоря, имеется в виду упругая деформация, т.е. такая, которая после снятия нагрузки — исчезает, хотя , бывает, понятие используют и при неупругой (невозвратной) деформации.

Сила реакции опоры : Вес тела (Р) — Сила, с которой тело действует на опору или подвес:
Силы трения, трение покоя, трение скольжения, трение качения, трение в жидкостях и газах:


1. Трение покоя = силе, приложенной к телу 2. Трение скольжения — относительно постоянная величина, после начала движения 3.Трение качения, вполне корректный подход 4 Трение в жидкостях и газах — очень упрощенный подход. Трение прямо пропорционально скорости только на малых скоростях, в маловязких жидкостях и т.д.

Поиск в инженерном справочнике DPVA. Введите свой запрос:

Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.

Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers

Консультации и техническая
поддержка сайта: Zavarka Team

Проект является некоммерческим.

Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Задачи ⚠️ по динамике с решениями: основы, как научиться, методы

Физика — серьезная наука, которая состоит из нескольких крупных разделов и множества менее объемных подразделов. Проще всего с каждым из них знакомиться отдельно, чтобы избежать путаницы в голове. В этой статье подробно поговорим о динамике.

Что такое динамика в физике

Динамика в физике — это раздел механики, который изучает взаимодействие тел и причины возникновения/изменения движения.

Источник: prezentacii.org

Динамика, которая опирается на законы Ньютона, называется классической. Этот раздел изучает движение объектов со скоростями в пределах от миллиметров в секунду до километров в секунду.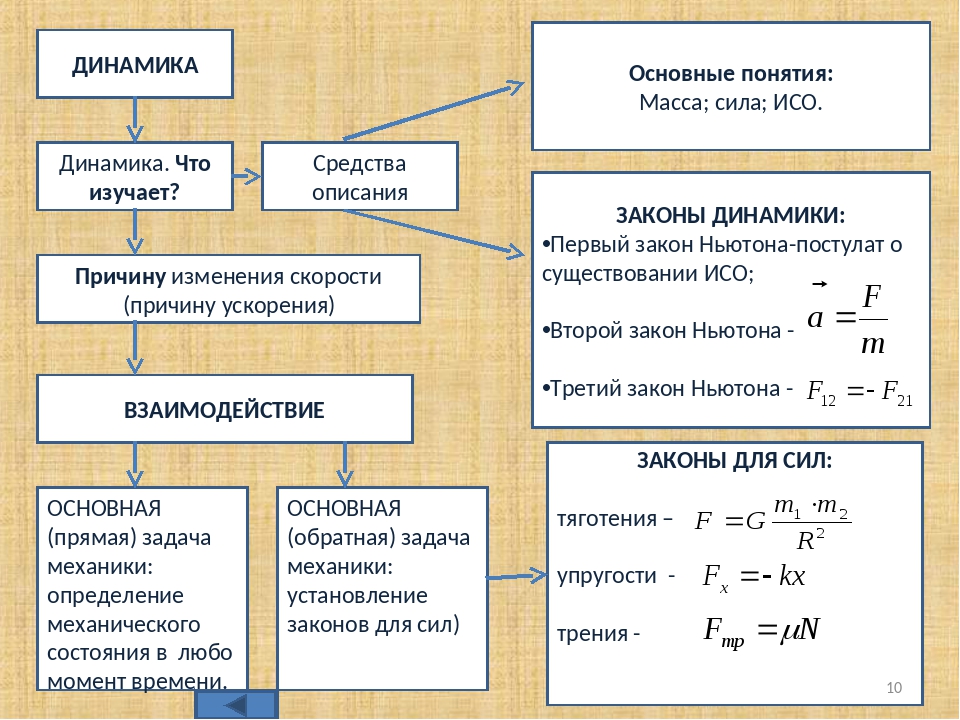 В классической механике причинами движения всегда выступают силы. Законы динамики изучают также:

движение упруго и пластически деформируемых тел;
жидкостей;

газов.

Не все виды движения можно описать законами динамики. Например, движение элементарных частиц при скоростях, близких к скорости света, подчиняется другим физическим законам.

В ходе изучения динамики конкретных объектов, возникли специальные дисциплины:

баллистика;
небесная механика;
динамика корабля и самолёта и др.

Основные понятия и определение

Классическая механика изучает такие понятия, как:

масса;
энергия;
импульс;
момент импульса;
сила;
равнодействующая сила и др.

Масса

— это скалярная физическая величина, которая является характеристикой такого свойства объекта, как инертность, и определяет количество вещества в теле.

Энергия — это количественная мера, характеризующая движение и взаимодействие объектов, а также их способность воздействовать на окружающий мир.

Импульс — это векторная физическая величина, измеряющая механическое движение тела, которая рассчитывается по формуле: \vec p=m\times\vec v

Момент импульса — это количественная характеристика вращательного движения.

Сила — это векторная величина, которая является причиной изменения скорости тела или его деформации, а также количественной мерой взаимодействия тел.

Любая сила в физике характеризуется 3 параметрами:

точкой приложения;
направлением;
численным значением или модулем.

Линией действия силы

называют прямую, вдоль которой эта сила действует.

Равнодействующая сила — это сила, которая оказывает на тело такое же действие, как все другие вместе взятые силы, воздействующие на него. Величина рассчитывается по формуле:

\(\vec F=\vec F_1+\vec F_2+\vec F_3 \)

В том случае, когда объект находится в состоянии покоя, равнодействующая всех сил, действующих на него, равна нулю.

В динамике встречаются следующие виды сил:

Тяжести. Приложена к центру массы тела и направлена вертикально вниз (всегда перпендикулярно горизонту). Рассчитывается по формуле: \(F=m\times g\) где \(m\) — масса тела, \(g\) — ускорение свободного падения.
Трения. Приложена к поверхности касания тела и опоры и направлена в противоположную сторону той, куда направлены другие силы, действующие на тело. Вычисляется по формуле: \(F=\mu\times N\), где \(\mu\) — коэффициент трения, \(N\) — сила реакции опоры.

Сопротивления. Возникает при движении тела в газе или жидкости, всегда направлена против скорости движения.
Реакции опоры. Действует на тело со стороны опоры, направлена перпендикулярно от нее.
Натяжения нити. Направлена от тела вдоль нити.
Упругости. Возникает при деформации тела, направлена против деформации. Вычисляется она согласно закону Гука по формуле: \(F=k\times\Delta l\), где \(k\) — коэффициент упругости, \(\Delta l\) — удлинение тела при деформации.

Основные законы динамики, формулы

Законы, на которых строится динамика, были впервые сформулированы Исааком Ньютоном в 1687 году. Именно поэтому их чаще всего и называют законами Ньютона.

Источник: infourok.ru

Законы Ньютона верны только для описания движений, которые происходят в инерциальных системах отсчета (ИСО). Инерциальной называют такую систему отсчета, в которой тела двигаются равномерно и прямолинейно.

Первый закон Ньютона

Согласно первому закона Ньютона, тело остается в покое или равномерно прямолинейно движется, если на него не действуют никакие силы или равнодействующая всех сил равна нулю.

Инерцией называется способность тел сохранять скорость движения при отсутствии воздействия на него других объектов. Иногда первый закон Ньютона называют еще законом инерции.

Второй закон Ньютона

Второй закон Ньютона считается основным законом динамики и представляет собой формулу нахождения ускорения: ускорение, которое приобретает тело, прямо пропорционально равнодействующей сил (F), воздействующих на тело и обратно пропорционально массе (\(m\)) этого тела:

\(\vec a=\frac{\vec F}m\)

Когд на тело действуют сразу несколько сил, под силой в этом уравнении подразумевается равнодействующая всех сил.

Третий закон Ньютона

Третий закон Ньютона гласит: тела воздействуют друг на друга с силами, которые равны по модулю и противоположны по направлению, лежат на одной прямой и имеют одну физическую природу:

\(\vec F=-\vec F\)

Данные силы не могут уравновесить друг друга, так как приложены к разным телам. По этой же причине их нельзя складывать.

Методы решения задач, алгоритм

Как правило, все задачи из раздела динамики решаются с использованием законов Исаака Ньютона.

Для того, чтобы существенно упростить процесс решения задач по динамике, нужно:

Внимательно прочитать условие задачи, разобраться, какие силы воздействуют на тела, указанные в задании.
Нарисовать рисунок, на котором изобразить все векторные силы и указать их направление.
Выбрать систему отсчета: одну координатную ось направить по направлению ускорения рассматриваемого тела, другую — перпендикулярно ускорению.
Вспомнить второй закон Ньютона: \(\vec F_1+\vec F_2+\vec F_3=m\times \vec a\)
Записать скалярную форму уравнения, учитывая, что силы, которые направлены против выбранных осей координат, будут иметь отрицательные значения. Получится такая система уравнений: \(\left\{\begin{array}{l}F_{1x}+F_{2x}+F_{3x}=m\times a_x\\F_{1y}+F_{2y}+F_{3y}=m\times a_y\end{array}\right. 2, F=?\)
Находим силу по формуле, иллюстрирующей второй закон Ньютона: \(F=m\times a.\)
Подставляем числовые данные в формулу и получаем ответ: \(12 Н.\)

Задача №2:

Источник: infourok.ru

Задачи по динамике вращательного движения с решениями

Решение задач на вращательное движение производится при помощи законов Ньютона, также важно помнить основное уравнение динамики вращательного движения:

\(\vec M=J\times\vec\epsilon\)

где \(M\) — момент силы, которая действует на тело, \(J\) — инерция, \(\epsilon\) — угловое ускорение.

Задача:

Источник: zen.yandex.md

Задачи по физике могут изрядно испортить настроение, если предмет не нравится, а суть его остается неясной. В таком случае за помощью можно обратиться к образовательному сервису Феникс.Хелп. Наши специалисты с легкостью разбираются в любых темах.

Глава 3.

Динамика

Задачи на динамику часто входят в задания единого государственного экзамене по физике. Для решения этих задач необходимо понимать смысл законов Ньютона, уметь применять их в простейших ситуациях и знать свойства ряда сил: тяжести, трения, упругости и нескольких других.

Первый закон Ньютона определяет такие системы отсчета, в которых тело, не испытывающее воздействий со стороны других тел (сил), движется прямолинейно и равномерно. Такие системы отсчета называются инерциальными, а движение в отсутствии сил — движением по инерции.

Согласно второму закону Ньютона ускорение тела относительно инерциальных систем отсчета определяется из уравнения

(3.1)

где — масса тела, — векторная сумма сил, действующих на тело (эту сумму часто называют равнодействующей или результирующей силой).

Третий закон Ньютона утверждает, что всегда существует взаимное действие тел друг на друга, причем силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению.

Чтобы использовать уравнение (3.1) для нахождения ускорений тел необходимо задать законы для действующих на них сил. Рассмотрим ряд сил, с которыми приходится сталкиваться в школьном курсе физики.

На любое тело, находящееся вблизи поверхности Земли действует сила притяжения со стороны Земли, которая называется силой тяжести. Эта сила пропорциональна массе тела и может быть записана в виде

(3.2)

где — вектор ускорения свободного падения, величина которого равна м/с² (в расчетах часто используют значение м/с² ).

При соприкосновении тел возникают контактные взаимодействия. Сила, перпендикулярная поверхности и возникающая при контакте тела с этой поверхностью, называется силой нормальной реакции поверхности. При скольжении тела по поверхности или при попытке его сдвинуть возникает сила, параллельная поверхности, и препятствующая движению тела. Эта сила называется силой трения (сила трения подробно рассматривается в следующей главе).

Если тело растягивает или сжимает пружину, на тело со стороны пружины действует сила, которая называется силой упругости. Свойства силы упругости определяются законом Гука, в котором утверждается, что сила упругости пропорциональна удлинению пружины

(3.3)

Здесь — длина деформированной пружины, — длина этой пружины в недеформированном состоянии, — коэффициент пропорциональности, который называется коэффициентом жесткости (или просто жесткостью) пружины.

При движении тела в воздухе, воде или в другой среде на тело со стороны этой среды действует сила сопротивления, величина которой при небольших скоростях тела пропорциональна его скорости

(3.4)

Здесь — скорость тела, — коэффициент пропорциональности, зависящий от свойств среды и геометрии тела. Для больших скоростей сила сопротивления определяется формулой . Направлена сила сопротивления противоположно скорости тела и тормозит его движение.

Рассмотрим теперь задачи.

В задаче 3.1.1 из второго закона Ньютона (3.1) заключаем, что данное тело движется равноускоренно 0,5 м/с² (ответ 4).

Единицей силы является «Ньютон», который определяется посредством второго закона Ньютона (3.1): 1 Ньютон (1 Н) — это сила, которая телу массой 1 кг сообщает ускорение 1 м/с² (ответ 3).

В задаче 3.1.3 только один из четырех предложенных ответов говорит о связи силы с ускорением (ответ 3). Остальные варианты ответов говорят о связи силы и скорости, поэтому они не верны. Аналогичный вопрос (но поставленный графически) предлагается в задаче 3.1.4 Согласно второму закону Ньютона вектор результирующей силы направлен так же, как и вектор ускорения тела (ответ 3), а не как вектор скорости и тем более не как вектор суммы или разности скорости и ускорения (эти векторы вообще нельзя складывать, т. к. они имеют разные размерности).

Несколько следующих задач посвящены простейшим вычислениям на основе второго закона Ньютона. В задаче 3.1.5 второй закон Ньютона в проекциях на вертикальную ось для тела, движущегося вместе с лифтом (т.е. с таким же ускорением) дает

где – сила реакции, действующая на тело со стороны пола (см. рисунок). Отсюда находимо силу реакции

(ответ 2).

Основная идея решения задачи 3.1.6 заключается в том, чтобы из данных кинематических характеристик движения (пути и времени) найти ускорение тела, а затем из второго закона Ньютона — силу. Из закона равноускоренного движения находим, что ускорение тела равно м/с². Поэтому Н (правильный ответ — 3).

В задаче 3.1.7 нужно найти силу, которая сообщает телу массой ускорение, направленное вертикально вверх и вдвое превосходящее по величине ускорение свободного падения. Поскольку на рассматриваемое тело действуют только искомая сила и сила тяжести (см. рисунок), второй закон Ньютона для этого тела в проекциях на вертикальную ось дает

Поскольку , из этой формулы находим, что (ответ 3).

В задаче 3.1.8 второй закон Ньютона в проекциях на горизонтальную ось дает

(см. рисунок). Отсюда находим, что м/с² (ответ 1).

В задаче 3.1.9 проверяется понимание школьником векторного характера второго закона Ньютона. Из закона (3.1) следует, что величина ускорения тела определяется величиной (модулем) равнодействующей силы:

Находя величину равнодействующей силы

получим м/с² (ответ 4).

Равнодействующей двух сил называется их векторная сумма. Из закона векторного сложения заключаем, что величина суммы векторов не может превосходить суммы величин векторов-слагаемых, и обязательно больше их разности. Поэтому величина равнодействующей сил 30 и 10 Н в задаче 3.1.10 не может равняться 19 Н (ответ 3).

По третьему закону Ньютона силы, с которыми мальчики в задаче 3.2.1 действуют друг на друга, равны. Поэтому массы и ускорения мальчиков связаны соотношением . Отсюда находим ускорение второго мальчика м/с² (ответ 2).

Поскольку силы, действующие на канат из задачи 3.2.2 со стороны обеих команд, уравновешивают друг друга, ускорение каната равно нулю. Очевидно, что и любая часть каната, и в частности, его часть от первой команды до какой-то средней точки также будет в равновесии. А поскольку на эту часть каната действуют только сила со стороны одной из команд и сила со стороны другой части каната (сила натяжения), то условие равновесия этой части каната дает , откуда заключаем, что = 5000 Н (ответ 1).

Силы, о которых говорится в третьем законе Ньютона (силы действия и противодействия) приложены к разным телам. В задаче 3.2.3 одна из них действует со стороны Земли на тело (сила тяжести), и, следовательно, вторая должна действовать со стороны тела на Землю — это сила притяжения Земли к телу (ответ 3).

Если бы лифт в задаче 3.2.4 покоился, то вместе с ним покоилось бы и тело, и, следовательно, сила реакции пола равнялась бы силе тяжести. По третьему закону Ньютона с такой же силой и тело действовало бы на пол. Т.е. в этом случае выполнялось бы равенство =20 Н. Здесь же =10 Н, что означает, что сила тяжести больше силы реакции, и, следовательно, тело вместе с лифтом движется вниз. Применяя второй закон Ньютона к телу, найдем его ускорение, которое равно ускорению лифта: м/с², направлено вертикально вниз (ответ 1).

Весы измеряют силу, с которой лежащее на весах тело действует на них (или они на тело). Поэтому показания весов в задаче 3. 2.5 будут наибольшими, если наибольшей является сила реакции. А эта сила увеличивается по сравнению с силой тяжести, если лифт имеет ускорение, направленное вверх. Поэтому правильный ответ в этой задаче — 2.

Умение использовать условия равновесия тел (и понимание ситуаций, когда это можно делать) часто проверяется в заданиях единого государственного экзамена по физике. Например, в задаче 3.2.6 тело находится в равновесии на пружине. Ясно, что в этом положении сила тяжести уравновешивается силой упругости. Используя закон Гука (3.3) для силы упругости и приравнивая силу упругости силе тяжести, получим , где — жесткость пружины, — ее удлинение (ответ 1).

При падении тела на вертикально стоящую пружину (задача 3.2.7) оно движется следующим образом. До контакта с пружиной тело движется с ускорением . После контакта на тело кроме силы тяжести действует сила упругости, направленная вертикально вверх. При этом пока укорочение пружины не достигло величины , сила упругости меньше силы тяжести, и по второму закону Ньютона ускорение тела направлено вертикально вниз. Поэтому скорость тела при таких значениях укорочения пружины продолжает увеличиваться. Начиная с того момента, когда укорочение пружины станет больше значения , суммарная сила, действующая на тело, будет направлена вверх, и, следовательно, скорость тела будет уменьшаться. Поэтому максимальной скорость тела будет на высоте от поверхности (ответ 2).

Поскольку нити в задаче 3.2.8 нерастяжимы, все тела имеют одинаковые ускорения. Сила натяжения первой нити сообщает его четырем одинаковым телам, сила натяжения четвертой нити — одному такому телу. Поэтому из второго закона Ньютона заключаем, что последняя в четыре раза меньше первой (правильный ответ — 4).

Из формулы (3.4) для силы сопротивления следует, что свободно падающее тело движется в среде следующим образом (задача 3.2.9). При малых скоростях сила сопротивления мала по сравнению с силой тяжести, поэтому тело имеет ускорение, близкое к ускорению свободного падения, и его скорость возрастает временем. При этом возрастает и сила сопротивления среды, которая при некоторой скорости тела сравнивается с силой тяжести. А поскольку эти силы противоположны, ускорение тела становится равным нулю, и тело движется с постоянной скоростью (ответ 1).

Поскольку тело в задаче 3.2.10 падает с большой высоты, оно успевает разогнаться до такой скорости, что сила сопротивления воздуха равна по величине силе тяжести, и тело движется с постоянной скоростью (см. предыдущую задачу). После отражения от поверхности скорость тела меняет свое направление на противоположное, а ее величина остается такой же (сразу после удара). А поскольку сила сопротивления определяется скоростью, то величина силы сопротивления также не меняется, а ее направление меняется на противоположное. Поэтому после удара сумма сил сопротивления и тяжести равна , и, следовательно, ускорение тела равно (ответ 3).

Формулы по кинематике, динамике, законам сохранения, молекулярной физике, электричеству, магнетизму, оптике.

Тест Формулы по кинематике, динамике, законам сохранения, молекулярной физике, электричеству, магнетизму, оптике. Тест — курсы по физике Skip navigation

Элементы математики

действия с векторами

выражение неизвестной

Физические величины

Единицы измерения

внесистемные единицы

Постоянные величины в физике

плотность вещества

предел прочности, модуль Юнга

скорость звука

удельная теплота

диэлектрическая проницаемость

удельное сопротивление

электрохимический эквивалент

Формулы
I. Механика

Кинематика

равномерное движение

относительность движения

неравномерное движение

равноускоренное движение

ускорение свободного падения

графики движения

движение по окружности

параболическое движение

Динамика

закон тяготения

законы Ньютона

силы в природе

равнодействующая сила

Законы сохранения

импульс тела, импульс силы

закон сохранения импульса

работа и мощность

кинетическая и потенциальная энергии

закон сохранения энергии

Статика

плечо и момент силы

условия равновесия

центр тяжести, центр масс

Колебания и волны

колебательное движение

гармонические колебания

маятники

превращение энергии при колебаниях

упругие волны

звуковые волны
II. Молекулярная физика

Молекулярная физика

основные положения мкт

давление

основное уравнение мкт, температура

уравнение идеального газа

изопроцессы

свойства жидкостей*

свойства твердых тел

Термодинамика

количество теплоты

работа, внутренняя энергия

первый закон термодинамики

второй закон термодинамики

тепловые двигатели
III. Основы электродинамики

Электричество

электрический заряд

закон Кулона

напряженность поля

потенциал и работа поля

диэлектрики, проводники

электроемкость, конденсаторы

энергия конденсатора

Электрический ток

электрический ток, сила и плотность

закон Ома для участка цепи

работа и мощность тока

закон Ома для замкнутой цепи

электрический ток в различных средах

электрические явления

Магнетизм

магнитное поле

сила Ампера

сила Лоренца

Электромагнетизм

магнитный поток

закон электромагнитной индукции

самоиндукция, энергия поля

электромагнитные колебания

электромагнитные волны

переменный ток

трансформатор*
IV. Оптика

Волновая оптика

свет как электромагнитные волны

интерференция

дифракция

Геометрическая оптика

законы распространения света

линзы, оптические приборы
V. Теория относительности

Теория относительности

постулаты теории относительности
VI. Квантовая физика

Световые кванты

фотон

фотоэффект

квантовые постулаты Бора

излучение и поглощение света

Атомное ядро

энергия связи ядра

ядерные реакции

закон радиоактивного распада

элементарные частицы и их свойства

Современная физика*

физика элементарных частиц

мир внутри атомного ядра

время расщепляем на мгновения

нанотехнологии и нанофизика

вещество в экстремальных состояниях

Закрыть
Динамика — Образовательный сайт Казахстана
Сила — это векторная величина, характеризующая действие одного тела на другое и сообщающая ускорение или деформацию последнему.
Масса тела — это мера его инертности и гравитации.
Инертность (бездействие) характеризует способность тел сохранять свое предыдущее состояние.
Первый закон Ньютона
Второй закон Ньютона
Второй закон Ньютона
в проекциях на оси ОХ, ОУ, OZ:
F_x = ma_x; F_y — ma_y; F_z = ma_z
Основное уравнение динамики
Третий закон Ньютона
Наклонная плоскость
Рис. 16
В вектором виде:
в скалярном виде в проекциях на оси:
Движение тела в лифте
Рис. 17
Движение по выпуклому и вогнутому мостам
Рис. 18
Закон всемирного тяготения
Вес тела на высоте
Вес тела при опускании в шахту
Закон Гука
Напряжение материала
Относительная деформация
Виды деформации:
продольного растяжения;
продольного сжатия;
всестороннего сжатия;
поперечного изгиба
продольного изгиба;
сдвига;
кручения.
Рис. 19
Импульс тела
Импульс силы
Сила трения
Закон сохранения импульса
Второй закон Ньютона
Рис. 20
В векторной форме (рис. 20):
в скалярной форме с учетом знаков проекций на выбранную ось ОХ:
m₁V₁ — m₂V₂ = (m₁ +m₂)v
Первая космическая скорость
Вторая космическая скорость
Движение спутника будет:
если v < v₁ — тело упадет на Землю;
если — становится искусственным спутником Земли и движется в случае равенства v = v₁ no окружности, а в случае v > v₁ — по эллипсу;
если — тело преодолевает земное тяготение и уходит в космическое пространство по параболе или гиперболе (V >V_II)
Механическая работа
Мощность
Работа положительна, если < а между векторами силы F и перемещения s равен нулю => cos = 1 => А — Fs > О
Работа отрицательна, если < =180° => cos = -1 => А= — Fs < 0:
работа силы трения всегда отрицательна
Рис. 21
Работа численно равна площади под графиком зависимости между силой и перемещением
Работа равна нулю, если < = 90° => cos = 0 => A_mg = 0 => Работа силы тяжести при горизонтальном перемещении тела равна О
Консервативными называются силы, работа которых не зависит от вида траектории, а определяется только начальным и конечным положениями тела.
Работа консервативных сил по замкнутому контуру равна нулю.
Потенциальная энергия
Закон сохранения механической энергии
E = E_k + E_n = const
Кинетическая энергия
КПД
применение законов Ньютона в работе / Хабр
В этой статье Джеймс Клир (James Clear), расскажет, как использовать законы Ньютона для повышения продуктивности в повседневной жизни.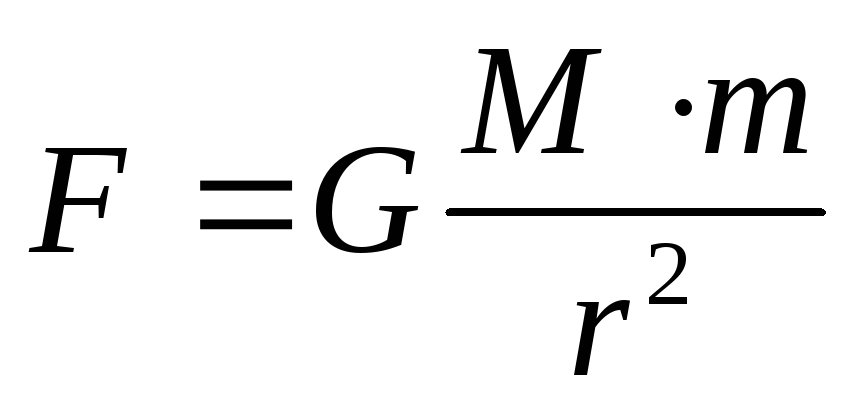
В 1687 году Исаак Ньютон опубликовал свою революционную книгу «Математические принципы естественной философии», в которой изложил три закона динамики. Таким образом, Ньютон заложил основы классической механики и изменил взгляды человечества на физику и науку в целом.
Но большинство людей не догадывается, что три закона динамики Ньютона можно по аналогии использовать и для повышения продуктивности, упрощения рабочего процесса и улучшения своей жизни.
Позвольте мне такую аналогию назвать законами продуктивности Ньютона.
Первый закон продуктивности Ньютона

Первый закон динамики:
Тело остается в состоянии покоя или продолжает движение с постоянной скоростью, если на него не действует внешняя сила (т.е. движущееся тело стремится продолжать движение, а покоящееся — оставаться в состоянии покоя).
Инертность — фундаментальный закон вселенной. Первый закон Ньютона применим и к продуктивности. Тело в состоянии покоя стремится оставаться в покое.
Хорошая новость? Закон работает и по-другому. Движущееся тело стремится продолжать движение. В отношении продуктивности это означает только одно: Самое важное — найти способ начать. Начав, продолжать движение гораздо легче.
Итак, какой же наилучший способ начать, когда находишься во власти инертности?
По своему опыту могу сказать, что проверенным методом начать работу является правило двух минут.
Вот как звучит правило двух минут в применении к продуктивности: Чтобы преодолеть инертность, найдите способ приступить к выполнению задачи в течение менее двух минут.
Обратите внимание, что речь не идет о завершении работы. Фактически, не нужно даже непосредственно работать. Но благодаря первому закону Ньютона, вы часто будете замечать, что, начав эту небольшую часть задания в течение двух минут, продолжать работать будет гораздо легче.
Приведу несколько примеров…
Возможно, прямо сейчас вам не хочется отправляться на пробежку. Но если вы обуете кроссовки и наполните водой бутылку, этого небольшого стартового действия будет достаточно, чтобы заставить вас выйти из дома.

Возможно, прямо сейчас вы смотрите на пустой экран и не можете заставить себя начать писать отчет. Но если в течение двух минут вы напишете какие-то случайные предложения, то может оказаться, что необходимые фразы начнут сами рождаться под вашими пальцами.

Возможно, прямо сейчас вам нужно выполнить творческое задание, а вы не можете заставить себя хоть что-то нарисовать. Но если вы начертите на листе бумаги случайную линию, а затем превратите ее в собаку, то сможете ощутить, как начинается прилив творческих сил.

Мотивация часто приходит после старта. Найдите способ начать с малого. Движущееся тело стремится продолжать движение.
Второй закон продуктивности Ньютона

Второй закон динамики:
F=ma. Векторная сумма сил, действующих на тело, равна произведению массы этого тела и вектора ускорения этого тела (т. е. сила равна произведению массы и ускорения).
Давайте рассмотрим составляющие этого уравнения и то, как оно может быть применено к продуктивности.
В данном уравнении надо обратить внимание на один важный момент. Сила F — векторная величина. Вектор характеризуется величиной (сколько работы вы выполняете) и направлением (куда направлена эта работа). Другими словами, если вы хотите придать телу ускорение в определенном направлении, то имеет значение, как величина прилагаемого усилия, так и направление этого усилия.
Знаете что? В жизни все происходит точно так же.
Если вы хотите быть продуктивны, это зависит не только от того, насколько напряженно вы трудитесь (величина), но также от того, куда вы прилагаете усилия (направление). Это справедливо как для крупных, значимых дел нашей жизни, так и для небольших повседневных задач.
Например, одни и те же способности можно приложить в различных направлениях и получить абсолютно разные результаты.
Проще говоря, у вас есть только определенное количество сил, которое вы можете вложить в вашу работу, и направление приложения сил так же важно, как и то, насколько напряженно вы трудитесь.
Третий закон продуктивности Ньютона

Третий закон динамики:
Если одно тело воздействует на второе, то второе тело тоже воздействует на первое с силой, равной по величине, но противоположной по направлению (т.е. силы равны и противоположны по направлению).
У каждого из нас есть средняя скорость, с которой мы работаем в повседневной жизни. Наш обычный уровень продуктивности и эффективности обычно является балансом производительных и непроизводительных сил, согласно формуле Ньютона — равных по величине и противоположных по направлению.
В нашей жизни есть производительные усилия — концентрация, позитив и мотивация. Есть также усилия непроизводительные — стресс, недосыпание и попытки заниматься одновременно слишком многими делами.
Если мы хотим стать более эффективными и продуктивным, у нас есть два варианта.
Первый: добавить производительных усилий. Это вариант «продавливания». Мы пересиливаем себя, выпиваем дополнительную чашку кофе и работаем еще напряженней. Именно для этого люди принимают препараты, помогающие им сконцентрироваться, или смотрят мотивирующие видео, чтобы «накачать» себя. Все это — попытки повысить свои производительные силы и превозмочь непроизводительные.
Очевидно, что делать это можно лишь пока ты не выгоришь до конца, но на коротком отрезке времени стратегия «продавливания» может дать хороший результат.
Второй вариант: устранить силы противодействия. Упростите себе жизнь, научитесь говорить «нет», смените обстановку, сократите количество взятых на себя обязанностей или каким-либо другим способом устраните силы, которые вас сдерживают.
Если вы уменьшаете непроизводительные силы в своей жизни, ваша продуктивность возрастает естественным образом. Это как если бы вы чудесным образом избавились от руки, которая вас тянет назад. (Как я люблю говорить: если бы вы устранили все факторы, мешающие вам стать продуктивным, вам не потребовались бы советы по повышению продуктивности.)
Большинство людей старается «продавить» и силой проложить себе путь через препятствия. Недостаток этой стратегии заключается в том, что по-прежнему приходится иметь дело с другими силами. Я считаю, что гораздо меньше стресса предполагает вариант, при котором мы устраняем противодействующие силы и даем возможность нашей продуктивности расти естественным образом.
Законы продуктивности Ньютона
Законы динамики Ньютона, в значительной степени, проливают свет на то, как быть продуктивным.

Движущееся тело стремится продолжать движение. Найдите способ приступить к делу в течение не более двух минут.

Вопрос не только в том, чтобы напряженно работать, но также в том, чтобы работать над правильными вещами. Ваши силы ограниченны, направление их приложения также важно.

Продуктивность является балансом противоположных сил. Если вы хотите быть более продуктивным, вы можете либо «продавить» препятствия, либо устранить силы противодействия. Второй вариант менее стрессовый.

P.S. Рекомендуем ещё одну статью по теме –
14 советов, как сделать 2015 год самым продуктивным.
Автор перевода — Давиденко Вячеслав, основатель компании MBA Consult
Алгоритм решения задач по Динамике
Умение решать задачи на законы Ньютона — является одним из показателей того, что учащийся знает и понимает физику. Тем более, что динамические задачи встречаются не только в «Механике», но и в других разделах физики (например задачи на равновесие и движение частицы в электрическом поле или движение заряженной частицы в магнитном поле).
А для того, чтобы решать задачи, всего-то надо знать алгоритм решения задач по Динамике.
И самые простые, и более сложные задачи решаются с использованием этого алгоритма, приведенного ниже.
Сам алгоритм сопровождается пояснительными рисунками (для большей наглядности).
Алгоритм решения задач по динамике.
1. Сделать рисунок, на котором изобразить тело (систему тел), о котором идет речь в задаче, и указать направление вектора скорости (если движение равномерное) или направление вектора ускорения (если движение равноускоренное или равнозамедленное) для тела (системы тел).
Тело на горизонтали Тело на наклонной плоскости Cвязанные тела

2. Указать все силы, действующие на тело (систему тел).
3. Записать уравнение Ньютона (уравнение динамики) в векторной форме (векторная сумма сил, действующих на тело равна равнодействующей ma). Если речь идет о связанных телах, то уравнения Ньютона записываются для каждого тела.
4. Выбрать удобное направление координатных осей (для связанных тел направление координатных осей может отличаться).
5. Спроецировать векторное(-ые) уравнение(-я) на координатные оси.
6. Записать дополнительные кинематические уравнения, если это необходимо и формулы для определения сил.
7. Составить систему уравнений, выделить неизвестные и решить систему получившихся уравнений относительно неизвестных величин.
Большое количество задач, решенных с помощью этого алгоритма, Вы можете найти на нашем сайте.
Вы можете оставить комментарий, или поставить трэкбек со своего сайта.
Написать комментарий
Динамика – Гиперучебник по физике
Обсуждение
Почему существует эта страница?
Это не страница о каком-то фундаментальном принципе физики. Это страница о решении определенного (и распространенного) вида задач в механике.
Неофициально динамика — это изучение сил и движения. Говоря более формально, динамика — это раздел механики, изучающий влияние сил на движение объектов. Напротив, статика изучает силы без движения; или, более формально, раздел механики, который имеет дело с силами при отсутствии изменений в движении.Динамика подразумевает изменение. Статика подразумевает неизменность. Важное изменение — это ускорение.
Цель этого раздела этой книги — служить хранилищем проблем динамики. Ускорение в каждой задаче будет ненулевым в одном направлении. Это справедливо только для этого раздела. Идея состоит в том, чтобы увидеть, каково это решать такие проблемы, чтобы вы могли распознать их, когда они всплывут позже.
Увеличить
Чистая сила
Возьмите первый закон движения Ньютона и разбейте его на две части.«Объект в состоянии покоя имеет тенденцию оставаться в покое, а объект в движении имеет тенденцию продолжать движение с постоянной скоростью…». В этом длинном главном предложении живет статика. «Если только не действует чистая внешняя сила». В этом коротком придаточном предложении мы находим динамику.
Слово net во фразе net force означает общий, комбинированный или общий. Это то, что вы получаете, когда учтены все обстоятельства. Слово net связано со словом аккуратный. Поиск чистого значения — это что-то вроде очистки математического беспорядка (или, по крайней мере, уменьшения беспорядка).Это можно записать как ∑ F (используя греческую букву сигма для обозначения суммы и полужирный шрифт, чтобы указать, что силы являются векторами) или как F _net (используя подстрочное слово net, чтобы символ читался как устный). язык и курсив, чтобы указать, что знание величины силы часто имеет значение) или другие варианты, подобные этим.
Сила является векторной величиной, а это значит, что направление имеет значение. Используйте положительные значения для сил, направленных в предпочтительном направлении, и отрицательные значения для сил, направленных в противоположном направлении.Если проблема двумерная, выберите два предпочтительных направления под прямым углом — например, вверх и вправо. Выберите предпочтительные направления, которые сделают вашу жизнь проще. Законам физики все равно, назовете ли вы правое положительное или левое положительное. Пространство в математическом смысле изотропно . Он измеряет одинаково во всех направлениях.
Второй закон движения Ньютона описывает, как связаны результирующая сила, масса и ускорение. По сути, результирующая сила вызывает ускорение, а масса сопротивляется ему.Лучший способ написать это не словами, а символами. Что-то вроде этого…
∑ F = м a или F _нетто = мА
Теперь вы готовы начать следующий этап обучения.
Например,
Возьмем обычный пример обычного велосипеда, который без каких-либо исключений крутит педали по обычной ровной дороге обычным образом.Какие силы действуют на велосипед и наездника (вместе в целом)?
Начните с очевидного. Все имеет вес и весовые точки вниз. Велосипед находится на твердой поверхности, поэтому нормальная сила направлена по нормали к этой поверхности. Поверхность ровная, поэтому нормальное направление вверх. Всадник крутит педали. Это означает, что есть какая-то сила, толкающая велосипед вперед. Я не хочу чрезмерно анализировать ситуацию, так что давайте просто назовем эту силу push .Даже правильно накачанные шины сопротивляются качению, ось может нуждаться в смазке, а может и не нуждаться в ней, а воздух, безусловно, притягивает движущееся тело. Давайте упростим жизнь и назовем все эти силы вместе трением . Всадник толкает велосипед вперед, а трение толкает его назад.
Мы готовы сделать свободную диаграмму тела. Нарисуйте прямоугольник, изображающий велосипед и всадника. Нарисуйте четыре стрелки, выходящие из центра коробки, чтобы обозначить четыре силы, действующие на велосипед и наездника. Хотя это и не всегда необходимо, следует попытаться нарисовать стрелки с длиной, соответствующей относительной величине сил.Длинные стрелы для сильных сил. Короткие для слабаков.
Начни с легкой пары — вес и нормал. В этом сценарии ничего не происходит в вертикальном направлении. Дорога ровная, и всадник не выполняет трюк. Вес и норма нейтрализуют друг друга. Нарисуйте одну стрелку вниз, а другую вверх и придайте им одинаковую длину.
Закончите чуть менее легкой парой — толчок и трение. Нечто — это , происходящее в горизонтальном направлении. Движение происходит в горизонтальном направлении.Велосипед куда-то едет. Это должно быть хорошо для чего-то. Разве не должно?
Извините, но нет. Движение не главное. Изменение в движении – вот что важно. Велосипед ускоряется или движется с постоянной скоростью? Ускорение делает ситуацию динамичной. Отсутствие ускорения делает его статичным. Направление чистой силы определяет ускорение. Сила, направленная в направлении чистой силы, будет большей из двух.
Если велосипед набирает скорость, значит, велосипедист толкает велосипед вперед больше, чем трение толкает его назад.Если велосипед движется с постоянной скоростью, то толчок и трение равны. Если велосипед тормозит, то сила трения побеждает силу, толкающую велосипед вперед.
Вот несколько рисунков, иллюстрирующих то, что я только что сказал.
Вот набор уравнений, которые показывают то, что я только что сказал. Мне нравится использовать вверх и вправо как положительные направления, но это не закон физики. Это просто предпочтение.

вертикально
∑ Ф _у = 0
С − Ш = 0
Н = Вт

горизонтально
∑ F _x = мА
P — f = мА

↙ ↓ ↘
ускорение
П > ф
и > 0
постоянная скорость
П = f
и = 0
замедление
П < ф
и < 0
Иди и решай проблемы.
Обернутые (деформированные) координаты
два тела, соединенные нитью
Часто используемые уравнения — Гиперучебник по физике
Часто используемые уравнения — Гиперучебник по физике
обсуждение
резюме
практика
проблемы
ресурсов
Артикул
механика, теплофизика, волны и оптика, электричество и магнетизм, современная физика
механика
18 Уравнения движения1)
V = V ₀ + на S = S _{0 S ₀ + V ₀ T + ½ на ²6 2 V
6 2 = V ₀ ₀
6 2
7 + 2 A ( S — S ₀)
V = ½ ( v + v ₀)}
8 Уравнения)

Ω = Ω ₀ + α T θ = θ ₀ + Ω ₀ T + ½α T ² ²
Ω ² = Ω ₀ ² + 2α (θ — θ ₀)
Ω = ½ (Ω + Ω ₀)

τ = rF sin θ τ = r × F
Теплофизика
c. оп 90 319
+
КС _{реальное} = В _С
В _Н — В _С
КС _{идеальным} = Т _С
Т _Н — Т _С
Волны и оптика
9004 5
доплеровский эффект
F _о = λ _с = с ± об _о
F _с λ _o c ∓ v _s
F с
Δ F ≈ Δλ ≈ Δ v
λ
Электричество и магнетизм

+
закон Фарадея 90 319
∮ Е · г сек = — ∂Φ _в
∂ т
∇ × Е = — ∂ B
∂ т
закона Ампера
9 + μ ₀ I 9006 3
∮ B · г S = μ ₀ ε ₀ ∂φ _E

∂ т
∇ × B = μ ₀ ε ₀ ∂ Е + μ ₀ J
∂ t
Современная физика
релятивистская k. е. +
90 750
К = ⎛
⎜
⎝ 1 — 1 ⎞
⎟
⎠ MC ²
√ (1 — об ²/ с ²)
К = (γ — 1) MC ²
Шрёдингеровский уравнение
I ℏ ∂ ∂ ψ ( R , T ) = — ℏ ² ∇ ² ψ ( R , T ) + U ( R ) ψ ( R , T )
∂T 2 м
9 E ψ ( R ) = − 9005 2 ℏ ² 9 ∇ ² ψ ( R ) + u ( R ) ψ ( R ) 2 м Механика физика, волны и оптика, электричество и магнетизм, современная физика
обсуждение
резюме
практика
проблемы
ресурсов
Ни одно состояние не является постоянным.
Механика
Кинематика
Движение
Расстояние и перемещение
Скорость и скорость
Ускорение
Уравнения движения
Свободное падение
Графики движения
Кинематика и исчисление
Кинематика в двух измерениях
Снаряды
Параметрические уравнения
Динамика I: Сила
Силы
Сила и масса
Действие-реакция
Вес
Динамика
Статика
Трение
Силы в двух измерениях
Центростремительная сила
Системы отсчета
Энергия
Работа
Энергия
Кинетическая энергия
Потенциальная энергия
Сохранение энергии
Мощность
Простые машины
Динамика II: Импульс
Импульс и импульс
Сохранение импульса
Импульс и энергия
Импульс в двух измерениях
Вращательное движение
Вращательная кинематика
Инерция вращения
Вращательная динамика
Вращательная статика
Угловой момент
Энергия вращения
Прокатка
Вращение в двух измерениях
сила Кориолиса
Планетарное движение
Геоцентризм
Гелиоцентризм
Всемирная гравитация
Орбитальная механика I
Гравитационная потенциальная энергия
Орбитальная механика II
Гравитация вытянутых тел
Периодическое движение
Пружины
Простой гармонический осциллятор
Маятники
Резонанс
Эластичность
Жидкости
Плотность
Давление
Плавучесть
Поток жидкости
Вязкость
Аэродинамическое сопротивление
Режимы течения
Теплофизика
Тепло и температура
Температура
Тепловое расширение
Атомная природа материи
Газовые законы
Кинетико-молекулярная теория
Фазы
Калориметрия
Явное тепло
Скрытая теплота
Химическая потенциальная энергия
Теплопередача
Проводка
Конвекция
Радиация
Термодинамика
Тепло и работа
Диаграммы давление-объем
Двигатели
Холодильники
Энергия и энтропия
Абсолютный ноль
Волны и оптика
Волновые явления
Природа волн
Периодические волны
Интерференция и наложение
Интерфейсы и барьеры
Звук
Природа звука
Интенсивность
Эффект Доплера (звук)
Ударные волны
Дифракция и интерференция (звук)
Стоячие волны
бьет
Музыка и шум
Физическая оптика
Природа света
Поляризация
Эффект Доплера (свет)
Черенковское излучение
Дифракция и интерференция (свет)
Тонкопленочная интерференция
Цвет
Геометрическая оптика
Отражение
Преломление
Сферические зеркала
Сферические линзы
Аберрация
Электричество и магнетизм
Электростатика
Электрический заряд
Закон Кулона
Электрическое поле
Электрический потенциал
Закон Гаусса
Проводники
Электростатические приложения
Конденсаторы
Диэлектрики
Батареи
Электрический ток
Электрический ток
Электрическое сопротивление
Электроэнергия
Цепи постоянного тока
Резисторы в цепях
Батареи в цепях
Конденсаторы в цепях
Правила Кирхгофа
Магнитостатика
Магнетизм
Электромагнетизм
Закон Ампера
Электромагнитная сила
Магнитодинамика
Электромагнитная индукция
Закон Фарадея
Закон Ленца
Индуктивность
Цепи переменного тока
Переменный ток
RC-цепи
Цепи РЛ
LC-цепи
Электромагнитные волны
Уравнения Максвелла
Электромагнитные волны
Электромагнитный спектр
Современная физика
Относительность
Пространство-время
Масса-энергия
Общая теория относительности
кванта
Излучение черного тела
Фотоэлектрический эффект
Рентген
Антивещество
Волновая механика
Волны материи
Атомные модели
Полупроводники
Конденсированные вещества
Ядерная физика
Изотопы
Радиоактивный распад
Период полураспада
Энергия связи
Деление
Фьюжн
Нуклеосинтез
Ядерное оружие
Радиобиология
Физика элементарных частиц
Квантовая электродинамика
Квантовая хромодинамика
Квантовая динамика вкуса
Стандартная модель
Помимо стандартной модели
Фонды
Единицы
Международная система единиц
Гауссова система единиц
Британско-американская система единиц
Разные единицы
Время
Преобразование единиц измерения
Измерение
Значащие цифры
Порядок величины
Графики
Графическое представление данных
Линейная регрессия
Изогнутый фитинг
Исчисление
Векторов
Тригонометрия
Сложение и вычитание векторов
Векторное разрешение и компоненты
Умножение на вектор
Ссылка
Специальные символы
Часто используемые уравнения
Физические константы
Астрономические данные
Периодическая таблица элементов
Люди в физике
Задняя часть
Предисловие
Об этой книге
Связаться с автором
Гленнелерт. сша
Беханс
Инстаграм
Твиттер
Ютуб
Аффилированные веб-сайты
гипертекстовая книга.com
midwoodscience.org
Веб-сайт кабинета физики
Законы движения Ньютона: обзор набора задач
Этот набор из 30 задач нацелен на вашу способность различать массу и вес, определять результирующую силу по значениям отдельных сил, связывать ускорение с результирующей силой и массой, анализировать физические ситуации, рисовать диаграмму свободного тела и решать задачи. неизвестная величина (ускорение или значение отдельной силы), а также объединить анализ второго закона Ньютона с кинематикой для решения неизвестной величины (кинематической величины или значения силы).Задачи варьируются по сложности от очень простых и прямолинейных до очень сложных и сложных. Более сложные задачи обозначены цветом синих задач .
Масса против веса
Этот набор из 30 задач нацелен на вашу способность различать массу и вес, определять результирующую силу по значениям отдельных сил, связывать ускорение с результирующей силой и массой, анализировать физические ситуации, рисовать диаграмму свободного тела и решать задачи. неизвестная величина (ускорение или значение индивидуальной силы), aMass — величина, зависящая от количества материи, присутствующей в объекте; обычно выражается в килограммах.Будучи количеством материи, которой обладает объект, масса не зависит от его местоположения во Вселенной. С другой стороны, вес — это сила тяжести, с которой Земля притягивает объект к себе. Поскольку гравитационные силы меняются в зависимости от местоположения, вес объекта на поверхности Земли отличается от его веса на Луне. Будучи силой, вес чаще всего выражается в метрических единицах, таких как ньютоны. Каждое место во Вселенной характеризуется постоянной гравитационного поля, представленной символом g (иногда называемой ускорением свободного падения).Вес (или F _грав ) и масса ( m ) связаны уравнением:
F _грав = м • г
Второй закон Ньютона
Второй закон Ньютона гласит, что ускорение ( a ), испытываемое объектом, прямо пропорционально суммарной силе ( F _net ), действующей на объект, и обратно пропорционально массе объекта.В форме уравнения можно сказать, что a = F _нетто / m . Чистая сила представляет собой векторную сумму всех отдельных значений силы. Если величина и направление отдельных сил известны, то эти силы можно сложить в виде векторов для определения результирующей силы. Следует обратить внимание на векторный характер силы. Направление важно. Силу подъема и силу опускания можно добавить, присвоив прижимной силе отрицательное значение, а поднимающей силе положительное значение. Аналогичным образом можно добавить силу, направленную вправо, и силу, направленную влево, присвоив силе, направленной влево, отрицательное значение, а силе, направленной вправо, — положительное значение.
Уравнение a = F _net /m можно использовать и как формулу для решения задач, и как руководство к размышлению. При использовании уравнения в качестве формулы для решения задач важно, чтобы числовые значения двух из трех переменных в уравнении были известны, чтобы найти неизвестную величину. При использовании уравнения в качестве руководства к мышлению необходимо учитывать прямые и обратные отношения между ускорением, результирующей силой и массой. Двукратное или трехкратное увеличение результирующей силы вызовет такое же изменение ускорения, удвоив или утроив его значение.Двукратное или трехкратное увеличение массы вызовет обратное изменение ускорения, уменьшая его значение в два или три раза.
Бесплатные диаграммы тела
Диаграммы свободного тела представляют силы, действующие на объект в данный момент времени. Отдельные силы, действующие на объект, представлены векторными стрелками. Направление стрелок указывает направление силы, а приблизительная длина стрелки представляет относительную величину силы.Силы маркируются в соответствии с их типом. Диаграмма свободного тела может быть полезным подспорьем в процессе решения проблем. Он обеспечивает визуальное представление сил, действующих на объект. Если величины всех отдельных сил известны, диаграмму можно использовать для определения результирующей силы. А если известны ускорение и масса, то можно рассчитать результирующую силу и использовать диаграмму для определения значения одной неизвестной силы.
Коэффициент трения
Объект, который движется (или событие, пытающееся двигаться) по поверхности, сталкивается с силой трения.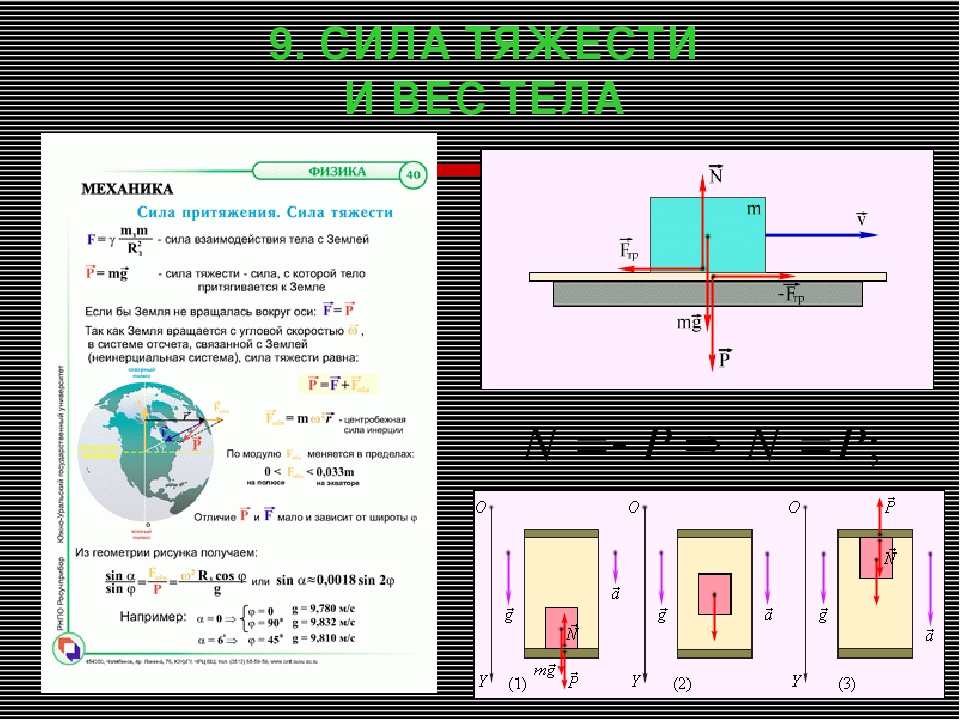 Сила трения возникает из-за того, что две поверхности плотно прижимаются друг к другу, вызывая силы межмолекулярного притяжения между молекулами с разными поверхностями. Таким образом, трение зависит от природы двух поверхностей и от степени их прижатия друг к другу. Силу трения можно рассчитать по уравнению:
F _трение = µ• F _норма
Символ µ (произносится как «мяу») обозначает коэффициент трения и будет разным для разных поверхностей.
Сочетание законов Ньютона и кинематических уравнений
Кинематика относится к описанию движения объекта и фокусируется на вопросах, как далеко?, как быстро?, сколько времени? и с каким ускорением? Чтобы помочь ответить на такие вопросы, четыре кинематических уравнения были представлены в блоке одномерной кинематики. Четыре уравнения перечислены ниже.
d = v _о • t + 0.5 • а • т ²
v _f = v _o + a • t
v _f ² = v _o ² + 2 • a • d
d = (v _o + v _f )/ 2 • t
где
d = рабочий объем
т = время
а = ускорение
v _o = исходная или начальная скорость
v _f = конечная скорость
Законы Ньютона и кинематика имеют один общий вопрос: с каким ускорением? Ускорение (a) уравнения F _net = m•a равно ускорению кинематических уравнений. Таким образом, общие задачи включают:
использование кинематической информации для определения ускорения, а затем использование ускорения в анализе законов Ньютона, или
использование информации о силе и массе для определения значения ускорения, а затем использование ускорения в кинематическом анализе.
При анализе задачи по физике разумно идентифицировать известные величины и организовать их либо как кинематические величины, либо как величины типа F-m-a.
Привычки эффективного решателя проблем
Эффективный решатель проблем по привычке подходит к задаче физики таким образом, который отражает набор дисциплинированных привычек. Хотя не каждый эффективный решатель проблем использует один и тот же подход, у всех у них есть общие привычки. Эти привычки кратко описаны здесь. Эффективное решение проблем…
….внимательно читает задачу и создает мысленную картину физической ситуации. При необходимости они рисуют простую диаграмму физической ситуации, чтобы визуализировать ее.
… организованно идентифицирует известные и неизвестные величины, часто записывая их на самой диаграмме. Они приравнивают заданные значения к символам, используемым для представления соответствующей величины (например, v _o = 0 м/с, a = 2,67 м/с/с, v _f = ???).
…строит стратегию решения для неизвестной величины; стратегия обычно сосредоточена вокруг использования физических уравнений и сильно зависит от понимания принципов физики.
… определяет подходящие формулы для использования, часто записывая их. Там, где это необходимо, они выполняют необходимое преобразование величин в соответствующие единицы.
…выполняет замены и алгебраические манипуляции, чтобы найти неизвестную величину.
Подробнее…
Дополнительные материалы для чтения/учебные пособия:
Следующие страницы из учебного пособия The Physics Classroom могут помочь вам в понимании концепций и математики, связанных с этими задачами.
Набор задач по законам движения Ньютона
Просмотр набора задач
Решения с аудиоуправлением по законам движения Ньютона
Посмотреть решение проблемы с аудиогидом:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30
Динамика поступательного движения
Единицы СИ и физические константы

Динамика поступательного движения исследует поступательное движение объектов и изучает влияние сил на движение
Здесь (все блоки см. здесь):
м масса объекта
– вектор скорости
.
– вектор линейного ускорения
.
– вектор линейного импульса
.
– вектор силы
.
Общие формулы и определение
Определение массы: масса, м, вещества или тела – скалярная величина, определяющая его инерционные и гравитационные свойства.Единицей массы является килограмм, 1 кг , определяемый эталоном массы как удельный платино-иридиевый цилиндр
Линейный импульс является вектором, умноженным на
Force is vector fefined by
Результирующая сила или результирующая сила из n сил, приложенных к объекту, определяется векторной суммой
Правило многоугольника для чистой силы для случая n = 3
Некоторые силы в механике
Гравитационная сила
где g ускорение свободного падения
Сила трения
где:
— коэффициент трения
Н нормальная составляющая полной силы, действующей на объект с поверхности
Усилие пружины
где:
k жесткость пружины
x _o длина нерастянутой пружины
x длины пружины, растянутой под действием силы F
Законы движения Ньютона в инерциальных системах отсчета
Инерциальная система отсчета — это система отсчета, которая находится в состоянии покоя или движется с постоянной скоростью, которая подчиняется Первому закону Ньютона
Первый закон Ньютона
Если тогда , то объект находится в равномерном движении или покоится
Второй закон Ньютона:
— для общего случая
— для постоянной массы
Третий закон Ньютона
где: сила, приложенная к массе m ₁, приложенная массой m ₂ , и сила, приложенная к массе m ₂, приложенная массой m ₁ , показанная на диаграмме ниже
Закон сохранения количества движения
Полный импульс системы из n частиц определяется векторной суммой
где — импульс i -й частицы с массой и скоростью
Закон сохранения количества движения
Если тогда
где является результирующей силой всех внешних сил, приложенных к системе частиц
.
Полностью неупругое столкновение — это столкновение, после которого объекты движутся вместе как одно тело
Скорость после неупругого столкновения
Полностью упругое столкновение — это столкновение, при котором полная механическая энергия сохраняется при столкновении
Столкновение для однонаправленного движения:
Скорости объектов после столкновения:
где коэффициент реституции
Для полностью упругого столкновения
Для полностью неупругого столкновения
Теорема об импульсе-импульсе
Импульс силы
где средняя сила, действующая на объект в течение интервала времени, заданного интегралом
Теорема об импульсе-импульсе

где и — начальный и конечный импульсы объекта соответственно
Движение центра масс системы частиц
Вектор положения центра масс n частиц:
где:
и – масса и радиус-вектор положения i -й частицы
— полная масса системы частиц
Вектор скорости центра масс
Второй закон Ньютона для движения центра масс
где является результирующей силой всех внешних сил, приложенных к системе частиц
.
Пропульсивное движение объекта с переменной массой

Где:
м текущая масса объекта
– текущая скорость объекта
.
это доверие (или реактивная сила)
— скорость выбрасываемой массы относительно объекта
Сила тяги
где — скорость изменения массы м
Уравнение движения объекта с переменной массой
Текущая скорость объекта массой м пуск из состояния покоя с исходной массой

Модуль 2: Динамика | Пособие для начинающих по физике для 11 класса
Нужно ли немного подтолкнуть ваши годовые оценки по физике? Не волнуйтесь! В этом руководстве мы собираемся дать вам обзор динамики 11-го класса, чтобы вы могли придать своим результатам необходимый импульс!
Год 11 Динамика
В этой статье мы рассмотрим следующие темы Dynamics:
Что такое динамика?
В модуле 1 вы изучали кинематику: описание движения без учета того, что вызвало или изменило движение. Динамика представляет собой другую половину механики, где мы узнаем, как силы приводят к движению и влияют на него, и анализируем взаимодействия между объектами.
В этой теме есть ряд новых понятий, величин и отношений. Убедитесь, что вы понимаете определения каждого из них, а также уравнения, которые их связывают.

Динамика Тема 1: Силы и законы Ньютона
Возможно, самым большим вкладом Исаака Ньютона в науку была его формулировка классической механики.Он провел широкий спектр физических наблюдений и показал, что их можно объяснить тремя фундаментальными законами:
Объект остается в покое или движется с постоянной скоростью, если на него не действует результирующая внешняя сила.
Ускорение объекта равно сумме внешней силы, действующей на объект, деленной на массу объекта: \(\vec{a}=\frac{\vec{F}_{net}}{m}\)
Для каждой силы действия существует равная и противоположная сила противодействия.
Вы узнаете некоторые термины, используемые в законах кинематики – скорость и ускорение .Ньютон утверждал, что ускорение может происходить только в результате ненулевой результирующей силы, действующей на массу. Так что же такое сила?
Сила — это любой толчок или притяжение, действующий на объект, и измеряется в ньютонах (Н). Некоторые из них легко идентифицировать, например, силу, которую ваши руки прилагают к мячу, когда вы его бросаете. Другими примерами сил являются трение и сопротивление воздуха или даже невидимая сила гравитации, притягивающая вас обратно к поверхности Земли, когда вы прыгаете. Независимо от того, какой тип силы задействован, три закона Ньютона всегда верны.
Когда вы будете изучать динамику, вы увидите, что происходит, когда силы применяются к отдельным объектам или даже к сложным системам объектов, таким как изображенная здесь машина Этвуда.
Схема машины Atwood

Две силы, которые мы можем рассчитать с помощью уравнений, — это вес и трение.
Вес — это сила, действующая на объект из-за гравитации Земли, и определяется как \(w=mg\). \(g\) представляет силу гравитационного поля и равен \(9.{-1}\).
Величина трения, испытываемая объектом, зависит от затронутых поверхностей и от того, насколько сильно объект давит на эту поверхность. Сила трения равна \(F=µN\), где \(µ\) называется коэффициентом трения, а \(N\) — нормальной силой. Трение будет статическим , если объект не движется, удерживая объект на месте против приложенной силы. Если объект движется, он испытывает кинетическое трение, которое сопротивляется движению объекта.Часто коэффициент трения для этих двух типов будет разным.
Нужна помощь в сдаче экзамена по физике?

Динамика Тема 2: Работа, энергия и мощность
Как только мы поймем силы, мы сможем начать использовать родственную концепцию работы. В физике работа выполняется, когда сила прикладывается к некоторому перемещению. Он рассчитывается по формуле \(W=Fs \cos⁡θ\), где \(θ\) — угол между вектором силы и вектором смещения, а единицей измерения являются джоули (Дж).Из-за зависимости \(\cos⁡θ\) работа может быть положительной, нулевой или отрицательной в зависимости от направления векторов.
Результатом выполнения работы является передача энергии из одного места в другое или из одной формы в другую. Выполнение положительной работы над объектом увеличивает его энергию, тогда как отрицательная работа уменьшает его энергию.
Вы будете знать некоторые основы энергии из Junior Science. В частности, вы узнаете о сохранении энергии: ее можно передавать между объектами или в разные формы, но никогда не создавать и не уничтожать.2\) — это энергия, которой объект обладает благодаря своему движению.
Гравитационная потенциальная энергия \(U=mgh\) – это энергия, которой объект обладает благодаря своему положению в гравитационном поле.
Гравитация сама по себе может совершать работу над объектом, или внешняя сила может совершать работу против гравитации. Когда гравитация работает, любые потери потенциальной энергии преобразуются в кинетическую энергию и наоборот.
Еще одно родственное понятие – мощность, измеряемая в ваттах (джоулях в секунду). Это скорость выполнения работы (или изменения энергии) с течением времени.
\(P=\frac{W}{t}\)
Более медленное выполнение той же задачи требует меньше энергии.
Динамика Тема 3: Импульс и импульс
Движущийся объект имеет количество, называемое импульсом , вычисляемым по формуле \(\vec{p}=m\vec{v}\). Это мера того, насколько сложно было бы остановить объект. Возвращаясь к Первому закону Ньютона, мы можем сказать, что импульс объекта остается неизменным, если на него не действует чистая внешняя сила. Обратите внимание, что это векторная величина — направление имеет значение!
Произведение силы на время, в течение которого она действует, называется импульсом , \(I = F\Delta t\), и эта величина равна изменению импульса.
Этот курс в основном имел дело с одиночными объектами, на которые воздействуют силы, и иногда на соединенные объекты с внутренними силами. Понятия импульса и импульса позволяют нам расширить наше понимание до столкновений — взаимодействий, при которых два объекта прилагают силы друг к другу в течение коротких периодов времени, изменяя движение обоих.
Когда два объекта А и В сталкиваются, силы, которые они прикладывают друг к другу, равны и противоположны — следствие третьего закона Ньютона.В результате, в то время как A и B испытают изменение импульса, их суммарный импульс останется неизменным до и после столкновения! Если мы используем соглашение о том, что \(\vec{u}\) представляет собой начальную скорость, а \(\vec{v}\) представляет конечную скорость, то:
\(m_A \vec{u}_A+m_B \vec{u}_B=m_A \vec{v}_A+m_B \vec{v}_B\)
Столкновение может быть упругим , в этом случае также сохраняется кинетическая энергия, или неупругим , и в этом случае часть кинетической энергии преобразуется в другие формы, такие как тепло и звук.

Нужно вернуть импульс к отметкам по физике?
Матричные семестровые курсы по физике для 11-го года обучения доказали свою эффективность в улучшении результатов учащихся. Выучить больше!

© Matrix Education и www.matrix.edu.au, 2022. Несанкционированное использование и/или копирование этого материала без письменного разрешения автора и/или владельца этого сайта строго запрещено.Выдержки и ссылки могут быть использованы при условии, что Matrix Education и www.matrix.edu.au полностью и четко указаны с соответствующим и конкретным указанием на исходный контент.
Физика — Линейная динамика — Законы Ньютона
На этой странице мы будем рассматривать только линейное движение, затем на других страницах перейдем к рассмотрению более общего случая, включающего вращение.
Чтобы не было вращательного движения, мы могли бы либо предположить, что объект рассматриваемое является частицей (его масса сосредоточена в одной точке). или мы могли бы предположить, что любые силы, действующие на объект, действуют на его центр масс.
Законы Ньютона
Законы Ньютона обычно излагаются в той или иной форме, подобной следующей.
Первый закон. Объект, находящийся в состоянии покоя, остается в состоянии покоя, если на него не воздействуют внешние сила. Движущийся объект продолжает двигаться с постоянной скоростью, если только действует внешняя сила.
Второй закон. Ускорение объекта направлено в сторону сетки. на него действует внешняя сила.Он пропорционален чистой внешней силе, и обратно пропорциональна массе объекта.
Третий закон — Силы всегда встречаются в равных и противоположных парах. Если объект А действует на объект B с такой же, но противоположной силой Б на объекте А.
Эти законы определены для линейного движения, а не для вращательного движения. Эйлер определили аналогичные законы для вращающихся объектов, но прежде чем мы перейдем к разработке общих законы для объекта как с линейным, так и с угловым движением, я думаю, это важно чтобы быть очень ясно о наших предположениях.
Итак, на этой странице мы будем рассматривать только линейное движение. Чтобы было вращательного движения, мы могли бы либо предположить, что рассматриваемый объект является частицей (его масса сосредоточена в одной точке). или мы могли бы предположить что любые силы, действующие на объект, действуют на его центр масс.
Соотношение между силой и ускорением количественно выражается в секундах Ньютона. закон, который говорит, что ускорение равно:
Пропорционально чистой внешней силе.
Обратно пропорциональна его массе.
В направлении силы.
Итак, если правильно подобрать единицы измерения, то:
F=ма
где:
символ
описание
тип
шт.
Ф чистая сила вектор кг м/с ²
м масса скаляр кг
и ускорение вектор м/с ²
Альтернативная форма этого уравнения состоит в том, что Сила представляет собой скорость изменения импульса, или интегрирование обеих частей дает: импульс — это линейный интеграл от сила.
Я думаю, что важно очень четко понимать предположения и условия с этим уравнением. Это может показаться педантичным, но когда мы переходим к случаю, когда объект вращается, тогда все становится сложнее и менее инициативно. Таким образом, остальная часть этой страницы предназначена для того, чтобы наше понимание было максимально ясным.
Инерция и внешние силы
F в приведенном выше уравнении представляет собой результирующую внешнюю силу, другими словами, вектор сумма всех внешних сил. Этой внешней силе соответствует равная и противоположной «внутренней» или «инерционной» силе (как и следует из третьего закона). Этот силу инерции можно рассматривать как сопротивление массы случайному изменению скорости. Эту силу инерции, естественно, не следует включать в уравнение F=ma (иначе результирующая сила всегда будет равна нулю), но это, например, «реальная» сила, это окажет влияние на другие объекты и может быть задействовано, когда мы рассматриваем вращения.Например, попробуйте ускорить большую массу (не против силы тяжести) и вы можете почувствовать силу инерции, противодействующую ускорению.
Векторная форма уравнения
До сих пор мы измеряли силу и ускорение в направлении, они действуют. Когда мы делаем это, мы можем работать в одном измерении и использовать скаляры для всех величин.
Когда мы моделируем физику в нашей программе, мы можем работать в некоторых координатах система, которая может быть не выровнена по направлению силы и ускорения. Чтобы избежать постоянной смены систем координат, вместо этого мы можем представить ньютоны второй закон в терминах векторов.
Итак, уравнение принимает вид:
=м
Где: m скаляр и , являются векторами (векторами, указанными стрелкой выше).
Альтернативное обозначение
.
При умножении вектора на скаляр просто умножайте каждый член вектора скаляром следующим образом:
Итак, мы говорим, что масса действует пропорционально одинаково в каждом измерении. одинаково.
Нам не нужно использовать для этого матричное представление, но если мы хотим использовать матричное обозначения по другим причинам, мы можем легко сделать это следующим образом:
Хотя реальный мир имеет 3 измерения (по крайней мере, в ньютоновских терминах), мы можем ограничивать движение двумя измерениями, например бильярдным столом (ну, это не совсем так, но вы понимаете, о чем я, можете ли вы придумать пример получше?). Поэтому, если мы работаем в двух измерениях, нам нужно использовать только двумерные векторы.
Относительные и абсолютные величины
Некоторые величины всегда относительны, то есть для того, чтобы их измерить должны выбрать произвольную нулевую точку. Другие величины, такие как ускорение абсолютны, потому что мы не можем выбрать нулевое значение, если наша система отсчета Если точка отсчета ускоряется, то законы Ньютона не действуют внутри этой системы отсчета. ссылки.
Ньютоновская физика Эйнштейновская физика
время родственник родственник
расстояние родственник родственник
скорость родственник абсолютный
ускорение абсолютный абсолютный
Система отсчета.
Система отсчета похожа на ориентацию для нашей системы координат. Мы можем выбрать для наблюдения и измерения величины в любой декартовой системе координат при условии, что оси взаимно перпендикулярны. Одна система отсчета может двигаться относительно другого.
Например, мы можем измерить движение человека, идущего в поезде, в системе отсчета поезда или в системе отсчета земли, или в системе отсчета какого-то совершенно другого объекта, движущегося по поверхность земли.
Получается, что законы Ньютона соблюдаются вне зависимости от системы отсчета из которого мы наблюдаем, при условии, что:
Мы последовательны, мы не можем смешивать, скажем, измерения скорости в одной системе отсчета с ускорением, измеренным в другой системе отсчета, не принимая эту в учетную запись.
Законы Ньютона не обязательно применимы при наблюдении из вращающейся системы отсчета, например, неподвижный объект, на который не действуют никакие силы, может показаться вращаться вокруг вращающейся системы отсчета.
Две системы отсчета не ускоряются относительно друг друга.
Итак, когда мы продолжим обсуждение ротации, мы должны быть очень осторожны.
В приведенной ниже структуре программирования сохраняется смена системы отсчета. в структуре «преобразования».
У нас может быть иерархия вложенных систем отсчета, в приведенном выше примере, земля движется относительно солнца, солнце движется относительно… и так на.
В этих вложенных системах отсчета может помочь упростить проблемы, если мы сможем разработать правила, позволяющие переводить количества вверх и вниз по иерархии следующим образом:
Масса — изменение системы отсчета
Масса не должна изменяться при просмотре в разных системах отсчета
Force — изменение системы отсчета
Сила не должна изменяться при условии, что две системы отсчета не движутся относительно друг друга, или если они движутся, то они движутся вместе с постоянная относительная линейная скорость. Если система отсчета ускоряется, то силу необходимо пересчитать из суммы местных ускорений объектов и ускорение локальной системы отсчета. Затем умножьте это вместе ускорение массой.
F абс. =Fl + F’ = m * al + m * ar
где:
символ
описание
тип
шт.
Фл Сила в местных координатах. вектор кг м/с ²
Ф’ дополнительная составляющая силы из-за ускорения системы отсчета. вектор кг м/с ²
м масса скаляр кг
и ускорение в местных координатах. вектор м/с ²
ар ускорение системы отсчета. вектор м/с ²
Ускорение — изменение системы отсчета
Ускорение, измеренное в системе отсчета над местной, равно сумма местного ускорения объектов и местного ускорения систему отсчета относительно системы отсчета над ней.
аа = ал + ар
Скорость — изменение системы отсчета
Скорость, измеренная в системе отсчета выше локальной, равна сумма локальной скорости объектов и скорости локальной системы отсчета относительно системы отсчета над ним.
ва = вл + вр
Позиция — изменение системы отсчета
Позиция, измеренная в системе отсчета над местной, является сумма локального положения объектов и положения локальной системы отсчета относительно системы отсчета над ним.
па = пл + пр
Структура программирования
Структура преобразования содержит относительное положение объекта, это означает что любые структуры внутри этого могут быть определены в локальных координатах и инерционный каркас объекта.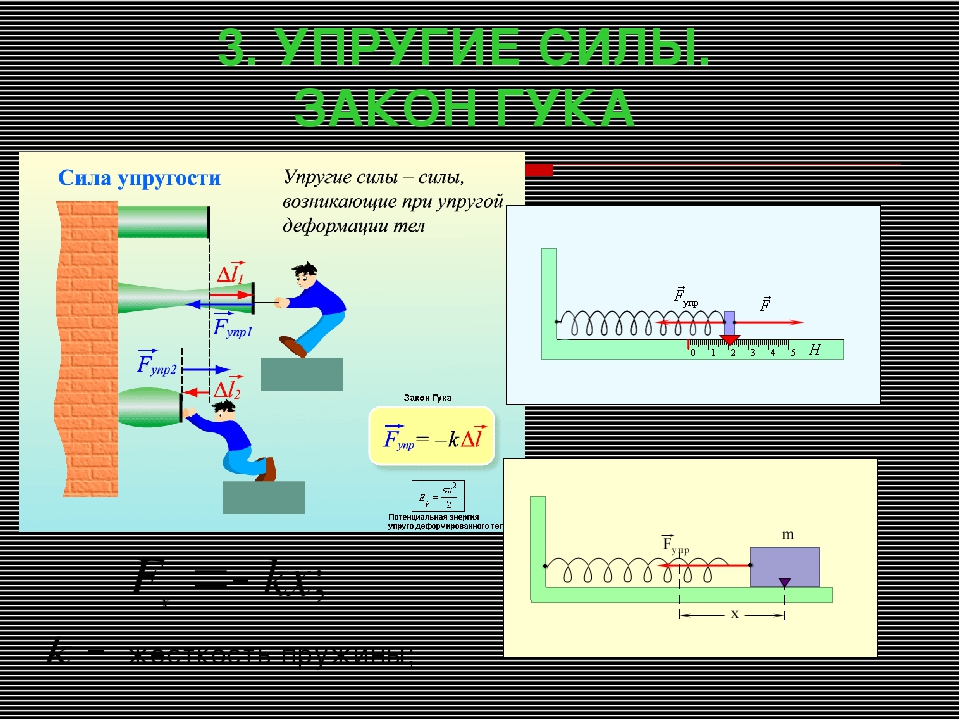
Каждый объект содержит свои собственные динамические данные, такие как информация о массе и кинематике.
Где хранить скорость и ускорение? Это кажется естественным для он должен храниться в данных кинематики для объекта, поскольку он специфичен для этого объект. Однако эти величины измеряются в приведенной выше системе отсчета. объекта (они были бы равны нулю относительно самого себя). Поэтому я думаю, что лучше всего удерживать его в структуре данных кинематики, но помнить, что это относительно к системе отсчета над ним.
Из третьего закона мы знаем, что силы всегда действуют парами, поэтому нам нужно удерживать силы в отдельной структуре, связанной с двумя объектами. Этот гарантирует, что величина силы должна быть сохранена только один раз. Строго гравитация также должна быть связана с двумя объектами, точно так же, как контакт силы, однако в случае гравитации другим объектом обычно является земля, поэтому, вероятно, более эффективно рассматривать это как частный случай. Я не уверен необходимо сохранить силу инерции, так как ее можно вычислить из m * a, однако, вероятно, полезно иметь его, когда мы делаем вычисления чтобы в поступательной динамике сначала отработать все силы, потом работать из ускорений от этого.
Для такой симуляции нескольких объектов, как эта, мы могли бы начать с поиска для объекта, внешние силы которого можно определить, в приведенном выше примере ни один из объектов не является независимым.Таким образом, нам, возможно, придется настроить набор уравнений определить силу инерции, действующую на каждый объект, через силы, действующие на другие объекты.
Что такое Сила?
На этой странице не объясняется, что такое сила, я не уверен, что кто-нибудь знает? Все мы пытаемся построить математическую модель для определения его эффектов. Мы мы не можем видеть силу, хотя, если мы становимся частью системы, мы можем чувствовать ее по прижимаясь к объекту. Таким образом, мы можем получить некоторое интуитивное представление о силе, но когда мы смотрим на систему извне, мы можем видеть не только силы, но и их эффекты. Так здесь нас интересует моделирование только измеримых эффектов.

Физика 101 Формулы
Физика 101 Формулы
Кинематика
v _пр. = Д х / Дт и _пр. = D v / Dt
v = v ₀ + в х = х ₀ + v ₀ t + ¹ / ₂ на ² v ² = v ₀ ² + 2aDx
g=9.81 м/с ² = 32,2 фута/с ² (около Поверхность земли)
Динамика
S F = м а F _г = Gm ₁ м ₂ / R ² F _г = мг (у поверхности Земли)
f _{с, макс} = m _s F _N            Гравитационная постоянная, G = 6,7 x 10 ^-11 Н·м ² /кг ²
f _k = m _k F _N a _c = v ² / R = w ² R
Работа и энергия
Вт _Ж = FScos(q) KE = ¹ / ₂ mv ²       W _NET = ДКЭ = KE _f — KE _i
W _NC = DE = Е _ф — Е _я = (КЕ _ф + ПЭ _ф ) — (KE _i + PE _i )
W _грав = -мгДи PE _грав = мгг
Импульс и Импульс
Импульс I = F _ave Dt = D p Ф _пр Дт = Д р = м v _f — м в _я Ф _пр.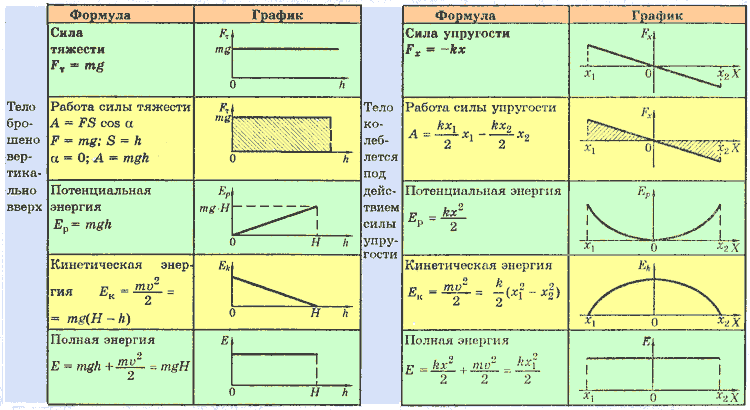 = D p /Dt
S F _доб Dt= D P _всего = P _{всего, конечного} — P _{всего, исходного} (импульс сохраняется, если S F _доб = 0)
Х _см = (m ₁ x ₁ + m ₂ x ₂ )/ (m ₁ +m ₂ ) )
Кинематика вращения
w = ш ₀ + в д = д ₀ + ш ₀ т + ¹ / ₂ в ²        w ² = ш ₀ ² + 2aDq
v _T = wR a _T = aR   ( поэтому для качения без проскальзывания v = wR    a = aR )
Вращательный Статика и динамика
t = Пт грех q
St = 0 и SF=0 (статический равновесие)
St = Ia
I = Smr ²    (для совокупность точечных частиц)
I = ¹ / ₂ MR ² (сплошной диск или цилиндр)   I = ² / ₅ MR ² (сплошная сфера)   I = ² / ₃ MR ² (полая сфера)
I = MR ² (обруч или полый цилиндр) I = ¹ /12 ML ² (однородный стержень по центру)
Вт = tq    (работа сделано с помощью крутящего момента)
L = I с S т _доб Дт = Д Л (угловой момент сохраняется, если S t _ext = 0)
KE _rot = ¹ / ₂ Iw ² =L ² /2I KE _всего =KE _транс + КЭ _гниль = ¹ / ₂ мв ² + ¹ / ₂ Iw ²
Простая гармоника Движение
Закон Гука: F _s = -kx
W _{пружина} = ¹ / ₂ kx _i ² — ¹ / ₂ kx _f ² PE _{пружина} = ¹ / ₂ kx ²
x(t) = Acos (масса) или   x(t) = Asin(wt)
v(t) = -Awsin(wt)   или   v(t) = AWcos (масса)
a(t) = -Aw ² cos(wt)   или   a(t) = -Aw ² sin(wt)
w ² = k/m, T = 2p/w, f = 1/T
x _max = A        v _max = wA    a _max = w ² A
Для простого маятника w ² = г/л

Жидкости
P ₂ = P ₁ + rg(y ₁ -y ₂ ) изменение в давление с глубиной
Плавучий сила F _B = rgV _дис = вес вытесненной жидкости
Поток скорость Q = v ₁ A ₁ = v ₂ A ₂ Уравнение непрерывности (область круга A = PR ²)
P ₁ + ^{1 + ¹}
/₂ RV ₁
6 2 + R ₂ = P ₂ +
6 1
7/₂ рв ₂ ² + рги ₂ уравнение Бернулли
r _вода = 1000 кг/м ³    1 м ³ = 1000 литров
r = M/V 1 атм. = 1,01 х 10 ⁵ Па
Температура и нагрев
температура:
по Цельсию (T _C ) до Фаренгейты (T _F) преобразование: T _C = (5/9) * (T _F -32)
Цельсия (T _C) в Кельвин (T _K ) преобразование: T _K = T _C +273
DL = АЛ ₀ ДТ ДВ = бВ ₀ ДТ тепловой расширение
a _{алюминий} = 23 x10 ^— ⁶ и a _сталь = 12 x10 ^— ⁶ (линейное расширение коэффициенты)
Q = зависит от cMDT теплоемкость
c _вода = 4186 Дж/кг/ ^o C   c _лед = 2000 Дж/кг/ ^o C
c _{алюминий} = 900 Дж/кг/ ^o C c _сталь = 450 Дж/кг/ ^o C
Q = L _f M скрытая теплота плавления           Q = L _v M   скрытая теплота парообразования
L _f,вода = 33. 5 х 10 ⁴ Дж/кг     л _v,вода = 22,6 x 10 ⁵ Дж/кг
Q = kADTt/л проводимость
k _сталь = 14 Дж/с/м/ ^o C     k _{алюминий} = 240 Дж/с/м/ ^o C (тепловой проводимости)
Q = ЕСТ ⁴ В Излучение (S = 5,67×10 ^— ⁸ J / S / M ^O K ⁴ K ⁴)
P _NET = ESA (T ⁴ -T ₀ ⁴ ) (площадь поверхности сферы A = 4pr ² )
Идеальный газ и Кинетическая теория
N _A =6.022 х 10 ²³ молекул/моль        Масса углерода-12 = 12.000u
PV = nRT = Nk _B T R = 8,31 Дж/моль/К      k _B = R/N _A = 1,38 x 10 ^— ²³ J/K
KE _ave = ³ / ₂ k _B T = ¹ / ₂ mv _rms ² U = ³ / ₂ Nk _B T (внутренняя энергия одноатомный идеальный газ)
v _{среднеквадратичное значение} ²    = 3k _B Т/м = 3RT/M (M = молярная масса = кг/моль)
Термодинамика
Q = DU + W (1-й закон)
U = ( ³ / ₂ )nRT (внутренний энергия одноатомного газа для фиксированного n)
С _В = (³ / ₂ )nR = 12. 5 Дж/ ^o Кл/моль (удельная теплоемкость при постоянном объеме для одноатомный газ)
К _Х = Q _С + W (тепловая машина или холодильник)
e = W/Q _H = 1 — Q _C /Q _H e _max = 1 — T _C /T _H (двигатель Карно)
Q _C /Q _H = T _C /T _H    когда КПД максимальный (2-й закон)
Вт = PDV (работа, совершаемая при расширении газа)
Гармонические волны
v = l / T = l f
v ² = F/(m/L) для волны на строка
v ² = 1.4k _B т/м за звук
v = c = 3 x 10 ⁸ м/с для электромагнитные волны (свет, микроволны и т. д.)
I = P / (4пр ² ) (интенсивность звука)
Звуковые волны
громкость: β=(10 дБ) log ₁₀ (I/I ₀ ), где I ₀ = 10 ^-12 Вт/м ²
(эффект Доплера)
.