Задача 1. Построить графики функций y=|x| y=|x-1|.
Решение. Сравним его с графиком функции y=|x|.При положительных x имеем |x|=x. Значит, для положительных значений аргумента график y=|x| совпадает с графиком y=x, то есть эта часть графика является лучём, выходящим из начала координат под углом 45 градусов к оси абсцисс. При x< 0 имеем |x|= -x; значит, для отрицательных x график y=|x| совпадает с биссектрисой второго координатного угла.
Впрочем, вторую половину графика (для отрицательных X) легко получить из первой, если заметить, что функция y=|x| — чётная, так как |-a|=|a|. Значит, график функции y=|x| симметричен относительно оси Oy, и вторую половину графика можно приобрести, отразив относительно оси ординат часть, начерченную для положительных x. Получается график:
y=|x|
Для построения берём точки (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2).
Теперь график y=|x-1|.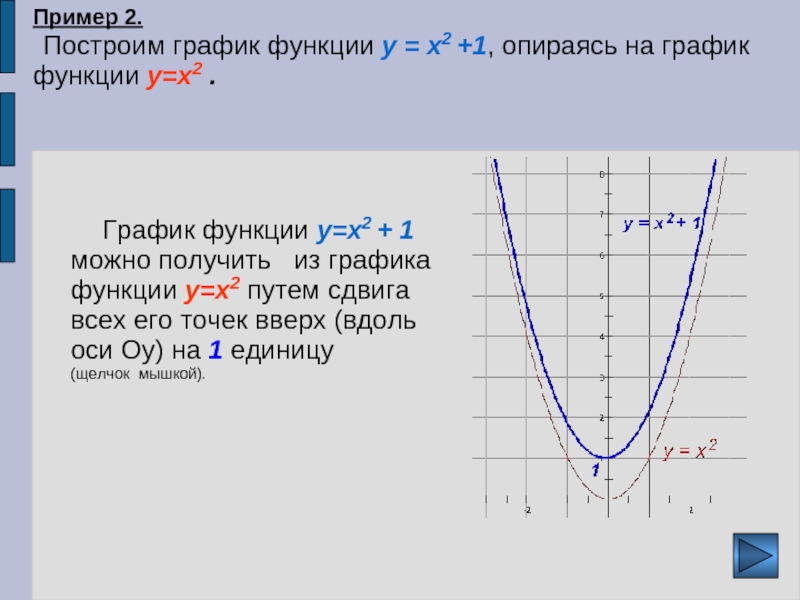
Построим графики:
y=|x-1|
Для построения берём точки (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1).
Это была простенькая задачка. Теперь то, что многих приводит в ужас.
Задача 2. Постройте график функции y=3*|x-4| — x + |x+1|.
Решение. Найдем точки, в которых подмодульные выражения обращаются в нуль, т.е. так называемые «критические» точки функции. Такими точками будут х=-1 и х=4. В этих точках подмодульные выражения могут изменить знак.
Пусть x<-1. Тогда х+1<0, |x+1|=-x-1; x-4<0, |x-4|=-x+4; Следовательно y= 3(-х+4)-х+(-х-1)= -5х+11.
 2 — |x| — 3|
2 — |x| — 3|Итак, всем спасибо! Теперь мы получили ту базу знаний, необходимую для построения графиков со знаком модуля! А то его так все боятся.
Вот ссылка, которая поможет вам проверить ваши построения:
Построение совмещенных графиков в Microsoft Office Excel-2007.
Практическая работа
Построение совмещенных графиков в Microsoft Office Excel-2007
Для построения графиков функций Y(X) в Microsoft Office Excel используется тип диаграммы Точечная:
Для этого требуется два ряда значений: Х и Y значения, которые должны быть соответственно расположены в левом и правом столбцах.
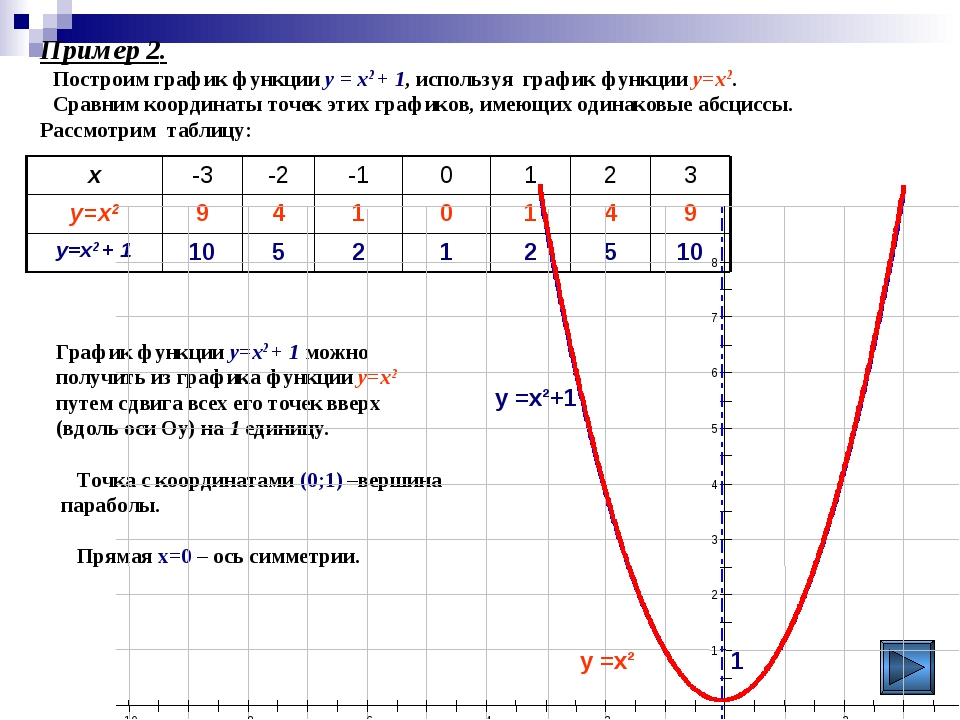
ЗАДАНИЕ 1: Построить графики функций y1= x 2 и y2= x 3 на интервале [- 3 ; 3] с шагом 0,5.
Алгоритм выполнения задания:
Заполнить таблицу значений:
Выделить таблицу и указать тип диаграммы Точечная .
Выбрать формат точечной диаграммы с гладкими кривыми.
-
В Макете указать название диаграммы «Графики», дать название осей: X и Y
Должен получиться график:
P.S. В версии 97-2003 для получения графика, представленного на рисунке надо провести редактирование.
ЗАДАНИЕ 2: Построить графики функций y1= x 2 -1, y2= x 2+1 и y=К·(y1/ y2)на интервале [- 3 ; 3] с шагом 0,3.
Проведите исследование, поменяйте значение К.
ЗАДАНИЕ 4: Построить графики функций y1= , y2= на интервале [- 0,5 ; 9] с шагом 0,5.
ЗАДАНИЕ 5: Построить графики функций y1=, y2= на интервале [- 5 ; -0,5] с шагом 0,5.
ЗАДАНИЕ 6: Построить графики функций y1= , y2= на интервале [0,5 ; 5] с шагом 0,5.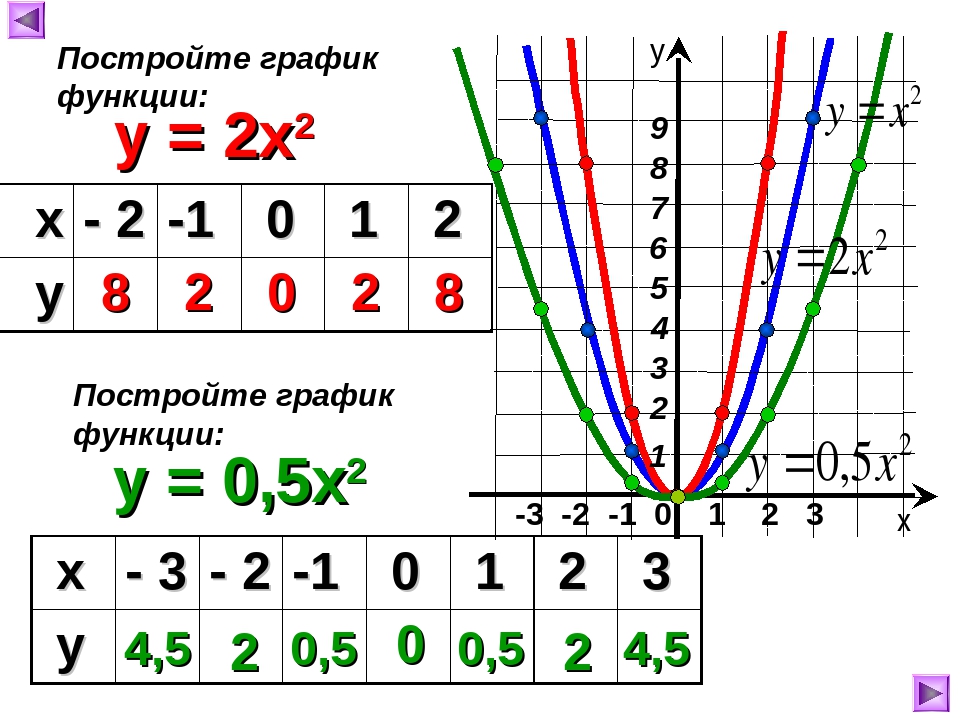 {2}} f{\left (x \right )} = Вторая производная
{2}} f{\left (x \right )} = Вторая производная
6 \left(2 x + 1\right) = 0.
Решаем это уравнение.
Корни этого уравнения
x_{1} = — \frac{1}{2}
Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках [-1/2, oo)Выпуклая на промежутках (-oo, -1/2]8. Искомый график функции дан в приложении.
|
ЛИНЕЙНАЯ ФУНКЦИЯ
y = kx + b, где k,b — действительные числа Частные случаи линейной функции:
Взаимное расположение графиков линейных функций:
СВОЙСТВА ЛИНЕЙНОЙ ФУНКЦИИ y = kx + b
если k = 0, b > 0, то y > 0 при x R если k = 0, b y x R если k = 0, b = 0, то y = 0 при x R
Рассмотрим построение графика линейной функции по двум точкам:
Функция y = 3x + 2 строиться по двум точкам (x1;b) и (x2;b+k), при x1=0, а x2=1. График функции y = kx + b можно получить из графика y = x в три этапа:
|
Grand Theft Auto V: Premium Edition
Grand Theft Auto V: Premium Edition
В издание Grand Theft Auto V: Premium Edition входят сюжетный режим Grand Theft Auto V, бесплатный доступ к постоянно развивающемуся миру Grand Theft Auto Online и все ранее выпущенные материалы и обновления, в том числе «Судный день», «Торговля оружием», «Контрабандисты», «Байкеры» и многое другое. Вы также получите стартовый набор «Преступная организация» — самый быстрый способ основать собственную криминальную империю в Grand Theft Auto Online.
GRAND THEFT AUTO V
Чтобы провести серию дерзких ограблений и выжить в большом неприветливом городе, уличному ловчиле, вышедшему на пенсию грабителю банков и вселяющему ужас психопату приходится работать с самыми оторванными и безумными преступниками, шоуменами и госслужащими Западного побережья.
GRAND THEFT AUTO ONLINE
Вас ждёт открытый, постоянно развивающийся мир, где вы можете по сети строить криминальную карьеру в Лос-Сантосе и округе Блэйн самими разными способами.
СТАРТОВЫЙ НАБОР «ПРЕСТУПНАЯ ОРГАНИЗАЦИЯ»
Стартовый набор «Преступная организация» — самый быстрый способ для новых игроков построить собственную криминальную империю в GTA Online. В набор вошли самые интересные и популярные материалы стоимостью более 10 000 000 долларов GTA, а также денежный бонус в размере 1 000 000 долларов GTA.
ВСТАНЬТЕ ВО ГЛАВЕ КРИМИНАЛЬНОЙ ИМПЕРИИ
Вы сможете запускать бизнес-проекты из своего офиса в западном здании Maze Bank, создавать мощное оружие в подземном бункере и штамповать фальшивые банкноты в собственной печатной мастерской.
ЦЕЛАЯ ПОДБОРКА МОЩНЫХ ТРАНСПОРТНЫХ СРЕДСТВ
К вашим услугам 10 образцов высококлассных транспортных средств, в том числе суперкар, мотоциклы, Dune FAV с оружием, вертолёт и раллийный автомобиль. Также вы получите в своё распоряжение недвижимость, в том числе гараж на 10 машин, где сможете разместить свой растущий автопарк.
ОРУЖИЕ, ОДЕЖДА И ТАТУИРОВКИ
Вы получите доступ к укороченному гранатомёту, высокоточной винтовке и укороченной винтовке, а также каскадёрским костюмам, байкерским татуировкам и не только.
2-мерный график — график MATLAB
Формат для datetime меток делений, заданных как пара, разделенная запятыми
состоящий из 'DatetimeTickFormat' и символа
вектор или строка, содержащая формат даты. Используйте буквы A-Z и a-z для создания
нестандартный формат. Эти буквы соответствуют стандарту языка разметки данных локали (LDML) Unicode ® для дат.Ты
может включать буквенные символы, отличные от ASCII, такие как дефис, пробел или
двоеточие для разделения полей.
Если вы не укажете значение для 'DatetimeTickFormat' ,
затем график автоматически оптимизирует и обновляет
метки в виде галочки на основе пределов оси.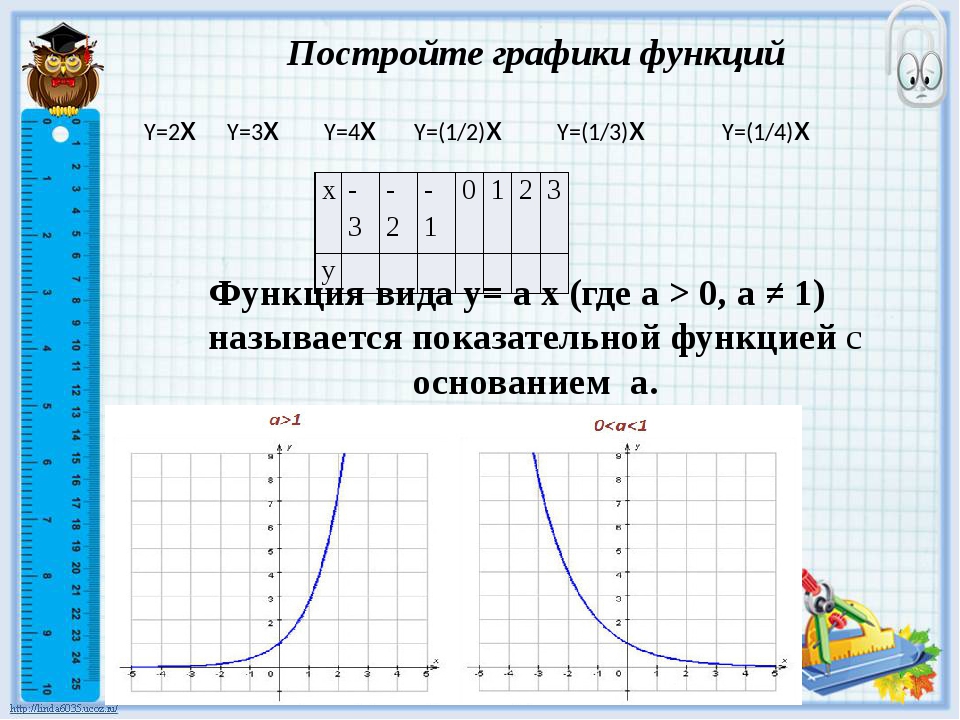
Пример: Отображается 'DatetimeTickFormat', 'eeee, MMMM d, yyyy HH: mm: ss' дата и время, например суббота, апрель
19, 2014 21:41:06 .
В следующей таблице показаны несколько распространенных форматов отображения и примеры форматированного вывода для даты, суббота, 19 апреля, 2014 г., 21:41:06 в Нью-Йорке.
Значение DatetimeTickFormat | Пример |
|---|---|
'yyyy-MM-dd' | 2014-04-19 |
'dd / MM / гггг ' | 19.04.2014 |
' дд.MM.yyyy ' | 19.04.2014 |
' yyyy 年 MM 月 dd 日 ' | 2014 年 04 月 19 日 |
' MMMM d, yyyy ' 19 апреля 2014 г. | |
'eeee, MMMM d, yyyy HH: mm: ss' | Суббота, 19 апреля 2014 г. |
'MMMM d, yyyy ЧЧ: мм: сс Z ' | 19 апреля 2014 г. 21:41:06 -0400 |
Полный список допустимых буквенных идентификаторов см. В свойстве Format .
для массивов datetime.
DatetimeTickFormat не является свойством линии диаграммы.
Вы должны установить формат галочки, используя аргумент пары имя-значение, когда
создание сюжета. Или установите формат с помощью функций xtickformat и ytickformat .
Свойство TickLabelFormat объекта datetime
линейка хранит формат.
Построение линейного уравнения с помощью таблицы значений
Построение графика линейного уравнения
Линейное уравнение — это уравнение, которое имеет две переменные, которые при отображении на графике дают нам прямую линию.Вы, наверное, знаете, как читать график линейного уравнения, но как нам нарисовать линейное уравнение на координатной плоскости? Оказывается, на самом деле это не так уж и сложно! Первый шаг — научиться составлять таблицу значений.
Что такое таблица значений
Когда нам нужно построить линейное уравнение, вы начнете с создания таблицы значений. Таблица значений, как следует из названия, представляет собой графический способ определения значений, которые будут использоваться для создания вашего графика.Это место, где вы можете записать ответы, которые вы получите, когда найдете значения x и y. Вам нужно будет использовать как минимум 2 набора точек для построения линейного уравнения, но обычно вы делаете больше в таблице значений.
Таблица значений состоит из двух столбцов. В одном столбце перечислены значения x, а в одном столбце — соответствующие значения y. Давайте перейдем к выяснению того, как эту таблицу можно использовать для построения графиков линейных уравнений.
Построение линейных уравнений с помощью таблицы значений
Когда у вас есть пустая таблица значений и линейное уравнение, которое вы хотите построить графиком, вы можете взять любое значение x на оси x по вашему выбору, чтобы начать с таблицы. Допустим, вы берете число 3. Подставьте его в линейное уравнение, чтобы увидеть, что вы получите, когда решите относительно y по оси y. Представим, что у вас -5. Запишите оба этих числа в свою таблицу: 3 в столбце со значениями x и -5 в столбце для значений y.
Допустим, вы берете число 3. Подставьте его в линейное уравнение, чтобы увидеть, что вы получите, когда решите относительно y по оси y. Представим, что у вас -5. Запишите оба этих числа в свою таблицу: 3 в столбце со значениями x и -5 в столбце для значений y.
Выберите другое значение x, с которым вы хотите работать, и снова решите относительно y. Повторите столько раз, сколько хотите, чтобы выработать наборы значений для включения в вашу таблицу. Когда у вас есть сумма, которая вас устраивает или которую требует ваш вопрос, вы можете затем взять эти значения x и y и нанести их в виде координат на график, чтобы отобразить точки на линейном уравнении!
Примеры задач
Вопрос 1:
График следующей функции с использованием таблицы значений
у = 3х — 1
Раствор:
Сначала создайте таблицу значений для уравнения.Используйте x, чтобы найти y. Вы можете использовать разные значения, но ваш график будет одинаковым независимо от того, какие значения вы используете.
Для x = -2
у = 3 (-2) — 1
г = -6 — 1
г = -7
Для x = -1
у = 3 (-1) — 1
г = -3 — 1
г = -4
Для x = 0
у = 3 (0) — 1
г = 0 — 1
г = -1
Для x = 1
у = 3 (1) — 1
г = 3 — 1
г = 2
Для x = 2
у = 3 (2) — 1
г = 6 — 1
г = 5
Теперь у нас есть полная таблица значений
Заполненная таблица значений x и yТеперь мы можем нанести упорядоченные пары на сетку
Построение данныхЗатем соедините точки прямой линией, и готово!
Связывание данных по прямойВопрос 2:
Изобразите следующую функцию, используя таблицу значений:
2x + 4y = 8
Раствор:
Во-первых, мы хотим упростить уравнение
2x + 4y = 8
х + 2у = 4
2у = -x + 4
y = −12 \ frac {-1} {2} 2−1 x + 2
Теперь у нас есть уравнение в форме пересечения наклона.
Затем создайте таблицу значений для уравнения. Используйте x, чтобы найти y.
Таблица x решает относительно yДля x = -2
y = −12 \ frac {-1} {2} 2−1 (-2) + 2
г = 1 + 2
г = 3
Для x = -1
y = −12 \ frac {-1} {2} 2−1 (-1) + 2
у = 0,5 + 2
г = 2,5
Для x = 0
y = −12 \ frac {-1} {2} 2−1 (0) + 2
у = 0 + 2
г = 2
Для x = 1
y = −12 \ frac {-1} {2} 2−1 (1) + 2
у = -0.5 + 2
г = 1,5
Для x = 2
y = −12 \ frac {-1} {2} 2−1 (2) + 2
г = -1 + 2
г = 1
Теперь у нас есть полная таблица значений
Таблица заполненных данныхМы можем нанести упорядоченные пары на сетку.
Координаты, построенные с использованием таблицы данныхЗатем соедините точки прямой линией, и готово!
Свяжите данные вместе прямой линией Хотите проверить свой ответ, чтобы увидеть, насколько точен ваш график? Вот для справки онлайн-калькулятор. 2-5, что соответствует значениям x -8 и -10, затем нанесите вершину и отражения этих точек на оси симметрии.
2-5, что соответствует значениям x -8 и -10, затем нанесите вершину и отражения этих точек на оси симметрии.
Это уравнение со степенью x 2 , парабола.
f (x) = 1 / 2 (x + 6) 2 — 5
Нам нужно построить точки и нарисовать кривую.
Я думаю, что также полезно знать форму вершины параболы , y = a (x — h) 2 + k с вершиной на (h, k) .Но здесь не обязательно искать запрошенные баллы.
для x = -8
y = 1 / 2 (-8 + 6) 2 -5 = 1 / 2 (-2) 2 -5 = -3
(-8, -3)
для x = -10
y = 1 / 2 (-10 + 6) 2 -5 = 1 / 2 (-4 ) 2 — 5 = 3
(-10, 3)
член x равен нулю, когда x = -6
y = 1 / 2 (-6 + 6) 2 — 5 = 1 / 2 (0) 2 — 5 = -5
вершина находится в точке (-6, -5)
Парабола симметрична с прохождением оси симметрии через вершину .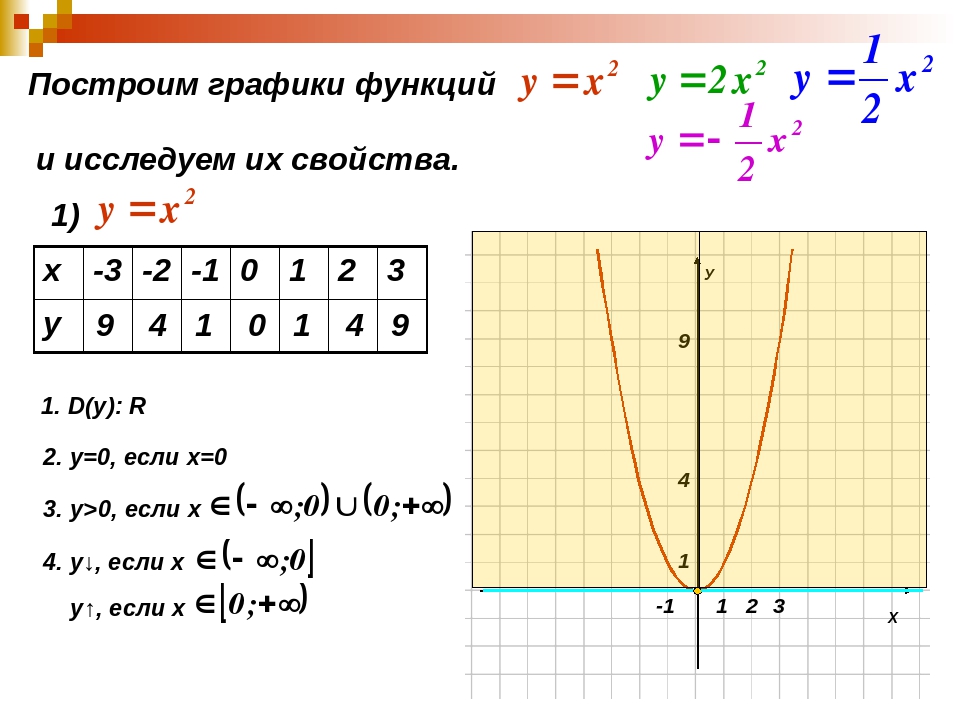 Эта прямая вертикальная с уравнением x = -6. Возможно, вам будет полезно его нарисовать.
Эта прямая вертикальная с уравнением x = -6. Возможно, вам будет полезно его нарисовать.
Если ось симметрии вертикальна (x = что-то), тогда значение y отраженной точки остается неизменным, изменяется только значение x.
для (-10, 3) это на 4 единицы слева от оси (x = -6), поэтому отраженная точка будет на 4 единицы вправо (x = -2), поэтому точка будет ( -2,3).
для (-8, -3) это на 2 единицы слева от оси (x = -6), поэтому отраженная точка будет на 2 единицы вправо (x = -4), поэтому точка будет (-4, -3).
Теперь у вас есть ось симметрии, вершина и две дополнительные точки с каждой стороны кривой. Теперь вы сможете нарисовать красивую параболу.
Функции и линейные уравнения (Алгебра 2, Как построить график функций и линейных уравнений) — Mathplanet
Если мы в следующем уравнении y = x + 7 присвоим значение x, уравнение даст нам значение для y.
Пример
$$ y = x + 7 $$
$$ если \; х = 2 \; затем
долларов США$$ y = 2 + 7 = 9 $$
Если бы мы присвоили x другое значение, уравнение дало бы нам другое значение y. Вместо этого мы могли бы присвоить значение y и решить уравнение, чтобы найти совпадающее значение x.
Вместо этого мы могли бы присвоить значение y и решить уравнение, чтобы найти совпадающее значение x.
В нашем уравнении y = x + 7 у нас есть две переменные, x и y. Переменная, которой мы присваиваем значение, мы называем независимой переменной, а другая переменная является зависимой переменной, поскольку ее значение зависит от независимой переменной. В нашем примере выше x — независимая переменная, а y — зависимая переменная.
Функция — это уравнение, которое имеет только один ответ для y для каждого x.Функция назначает ровно один выход каждому входу указанного типа.
Обычно функцию называют f (x) или g (x) вместо y. f (2) означает, что мы должны найти значение нашей функции, когда x равно 2.
Пример
$$ f (x) = x + 7 $$
$$ если \; х = 2 \; затем
долларов США$$ f (2) = 2 + 7 = 9 $$
Функция является линейной, если ее можно определить с помощью
.$$ f (x) = mx + b $$
f (x) — значение функции.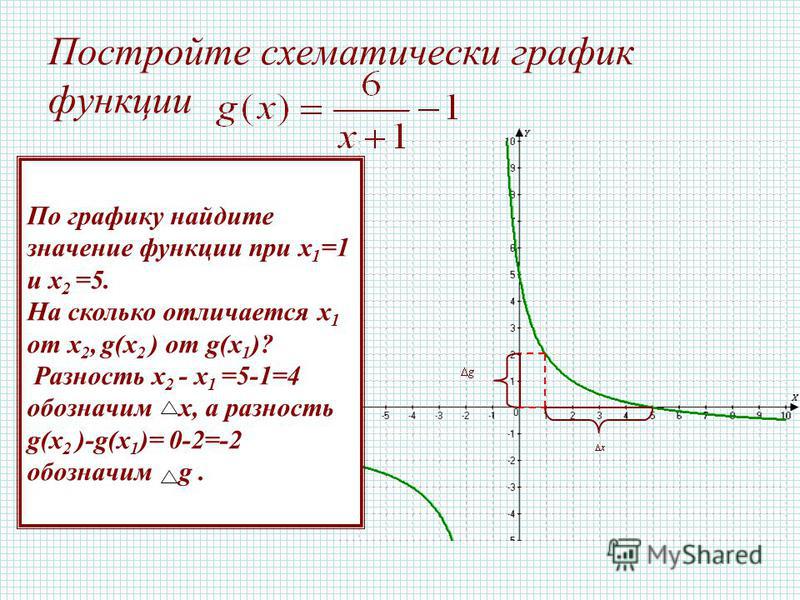
м — наклон линии.
b — значение функции, когда x равно нулю, или координата y точки, в которой линия пересекает ось y в координатной плоскости.
x — значение координаты x.
Эта форма называется формой пересечения наклона. Если m (наклон) отрицательный, значение функции уменьшается с увеличением x и наоборот, если наклон положительный.
Уравнение, такое как y = x + 7 , является линейным, и существует бесконечное количество упорядоченных пар x и y, которые удовлетворяют этому уравнению.
Наклон m здесь равен 1, а наш b (точка пересечения с y) равен 7.
Наклон прямой, проходящей через точки (x1, y1) и (x2, y2), равен
$$ m = \ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}} $$
$$ x_ {2} \ neq x_ {1} $$
Если двум линейным уравнениям задан один и тот же наклон, это означает, что они параллельны, а если произведение двух наклонов m1 * m2 = -1, два линейных уравнения называются перпендикулярными.
Видеоурок
Если x равен -1, какое значение имеет f (x), когда f (x) = 3x + 5?
Построение графиков линейных уравнений — MathBootCamps
Есть три способа построения графиков линейных уравнений: (1) вы можете найти две точки, (2) вы можете использовать точку пересечения по оси Y и наклон или (3) использовать точки пересечения по оси x и y.В следующем руководстве мы рассмотрим все три. Построение графиков линейных уравнений не должно быть трудным и даже увлекательным, если у вас есть эти методы!
реклама
Метод 1. Использование двух точек для построения линейного уравнения
График любого линейного уравнения, такого как \ (y = 3x + 2 \) или \ (y = -x + 9 \), представляет собой линию, и для ее определения нужны только две точки. Идея этого метода состоит в том, чтобы найти две точки на линии, выбирая значения \ (x \).
Пример
Изобразите линейное уравнение:
\ (y = \ dfrac {1} {3} x — 2 \)
Решение
Чтобы найти две точки на линии, выберите любые два значения \ (x \), с которыми будет легко работать, а затем найдите соответствующее значение \ (y \). Двумя простыми значениями здесь будут 0 и 3 (поскольку 3 заменяется на 3 в дроби).
Пусть \ (x = 0 \):
\ (\ begin {align} y & = \ dfrac {1} {3} x — 2 \\ & = \ dfrac {1} {3} (0) — 2 \\ & = -2 \ end {align} \ )
Итак, одна точка на прямой равна \ ((x, y) = (0, –2) \).
Пусть \ (x = 3 \):
\ (\ begin {align} y & = \ dfrac {1} {3} x — 2 \\ & = \ dfrac {1} {3} (3) — 2 \\ & = 1 — 2 \\ & = — 1 \ end {align} \)
Итак, еще одна точка на прямой — это \ ((x, y) = (3, –1) \).
Когда у вас есть две точки, вы можете построить их, а затем нарисовать линию. Лучше всего использовать линейку или что-то подобное, чтобы убедиться, что вы нарисовали график как можно лучше.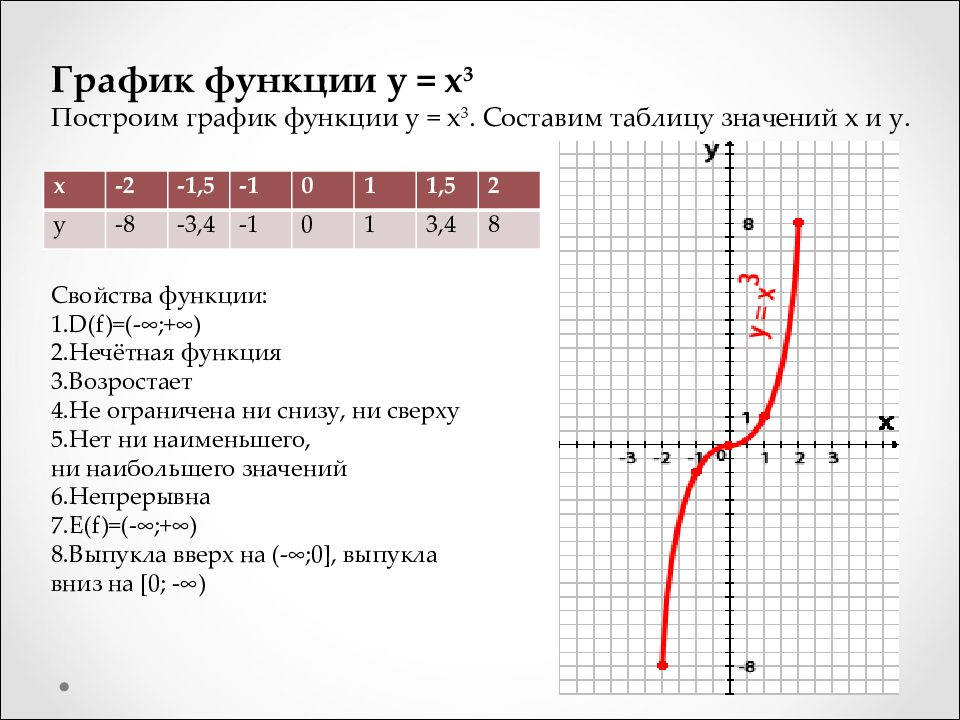
СОВЕТ: Возможно, вам будет полезно найти три или четыре точки на графике, чтобы вы могли нарисовать его более точно.Для этого просто выберите больше значений x, чтобы найти точки!
Метод 2: Используйте наклон и точку пересечения оси Y
Линейное уравнение, записанное в форме \ (y = mx + b \), называется записанным в форме углового пересечения. Эта форма показывает наклон \ (m \) и точку пересечения оси y \ (b \) графика. Знание этих двух значений позволит вам быстро нарисовать график линейного уравнения, как вы можете видеть в примере ниже.
Пример
Изобразите линейное уравнение:
\ (y = \ dfrac {2} {3} x + 4 \)
Решение
Поскольку это уравнение имеет форму \ (y = mx + b \), вы знаете, что:
- Наклон:
\ (m = \ dfrac {2} {3} \) - Отсечка по оси Y:
\ (b = 4 \)
Давайте сначала посмотрим на точку пересечения оси y.
Пересечение оси y — это точка, в которой график пересекает ось y (вертикальная ось). Итак, вы можете изобразить эту точку как:
Итак, вы можете изобразить эту точку как:
Теперь рассмотрим наклон. Наклон можно рассматривать как скорость изменения: он представляет собой изменение \ (y \) по сравнению с изменением \ (x \). Иногда это называется «подъем за пробегом».
\ (\ text {slope} = \ dfrac {\ text {rise}} {\ text {run}} = \ dfrac {\ text {изменение in} y} {\ text {изменение in} x} \)
Для этого примера:
\ (\ text {slope} = \ dfrac {2} {3} = \ dfrac {\ text {change in} y} {\ text {change in} x} \)
Это можно перевести на:
\ (\ dfrac {2} {3} = \ dfrac {\ text {на 2 единицы вверх}} {\ text {на каждые 3 единицы вправо}} \)
Следовательно, чтобы найти другую точку на линии, начните с точки пересечения оси Y и пройдите на 3 единицы вправо и на 2 единицы вверх.Сделайте это еще раз, и вы найдете другую точку. Фактически, вы можете продолжать делать это, чтобы найти столько точек, сколько, по вашему мнению, вам понадобится для построения хорошего графика.
Соедините точки, и у вас есть график вашей линейной функции!
Этот метод построения графиков линейных уравнений может применяться, даже если наклон отрицательный или если наклон не дробный, даже если это не так. Следующий пример покажет вам, как это работает!
Пример
Изобразите линейное уравнение:
\ (y = -2x + 1 \)
Решение
Отсечка по оси Y здесь равна 1, поэтому сначала постройте эту точку.
Наклон –2. Хотя это не дробь, ее можно рассматривать как единицу, если принять знаменатель равным 1.
\ (\ text {slope} = -2 = \ dfrac {-2} {1} \)
Другими словами:
\ (\ dfrac {-2} {1} = \ dfrac {\ text {на две единицы вниз}} {\ text {на каждую 1 единицу вправо}} \)
Теперь это можно применить для поиска точек на графике.
Наконец, соедините точки, чтобы нарисовать график линейного уравнения.
СОВЕТ: Если наклон дан в десятичной форме, посмотрите, можно ли преобразовать его в дробь, чтобы применить этот метод.
В противном случае лучше всего подойдет способ 1.
Метод 3. Использование пересечений по осям x и y
При построении графиков линейных уравнений, представленных в форме \ (y = mx + b \), проще всего применить метод 2. Но иногда линейные уравнения задаются в стандартной форме: \ (Ax + By = C \) , где \ (A \), \ (B \) и \ (C \) — положительные или отрицательные целые числа. В этом случае использование точки пересечения по осям x и y может быть самым быстрым подходом.
Пример
Постройте линейное уравнение:
\ (- 3x + 2y = 6 \)
Решение
Чтобы найти точку пересечения с осью x, то есть точку, в которой график пересекает ось x, положим \ (y = 0 \) и решим относительно \ (x \):
\ (\ begin {align} -3x + 2y & = 6 \\ -3x + 2 (0) & = 6 \\ — 3x & = 6 \\ x & = -2 \ end {align} \)
Чтобы найти точку пересечения оси Y, то есть точку, в которой график пересекает ось Y, положим \ (x = 0 \) и решим относительно \ (y \):
\ (\ begin {align} -3 (0) + 2y & = 6 \\ 2y & = 6 \\ y & = 3 \ end {align} \)
Это дает вам две точки на линии, которые вы можете построить, а затем соединить для построения графика линейного уравнения.
Чтобы узнать больше о x-перехватах и y-перехватах, ознакомьтесь со статьями Understanding x-intercepts и Understanding y-intercepts.
реклама
Резюме
Есть много возможных подходов к построению графиков линейных уравнений. Три распространенных подхода:
- Точки поиска:
выберите простые значения \ (x \) и найдите соответствующие значения \ (y \). Постройте эти точки и используйте их, чтобы построить линию. - Использование наклона и точки пересечения по оси Y:
используйте концепцию «превышения высоты над пробегом» и точку пересечения по оси Y, чтобы найти точки на графике. Этот метод особенно полезен, если линия имеет форму пересечения наклона. - Использование пересечений по осям x и y:
пусть \ (x = 0 \) и \ (y = 0 \) найдут точки пересечения на графике. Затем используйте эти точки для построения линии. Этот метод полезен, когда линейное уравнение имеет стандартную форму.
Какой метод вы используете, зависит от формы имеющегося у вас линейного уравнения и от того, какой метод вам удобнее всего.Несмотря ни на что, вы всегда можете найти очки, если застрянете.
Подпишитесь на нашу рассылку новостей!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.
Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!
СвязанныеГрафические логарифмические функции
Функция у знак равно бревно б Икс является обратной функцией экспоненциальная функция у знак равно б Икс .
Рассмотрим функцию у знак равно 3 Икс . Это можно изобразить как:
График обратной функции любой функции — это отражение графика функции относительно линии
у
знак равно
Икс
. Итак, график логарифмической функции
у
знак равно
бревно
3
(
Икс
)
что является обратной функцией
у
знак равно
3
Икс
является отражением приведенного выше графика относительно линии
у
знак равно
Икс
.
Итак, график логарифмической функции
у
знак равно
бревно
3
(
Икс
)
что является обратной функцией
у
знак равно
3
Икс
является отражением приведенного выше графика относительно линии
у
знак равно
Икс
.
Икс 1 9 1 3 1 3 9 27 81 год у знак равно бревно 3 Икс — 2 — 1 0 1 2 3 4
Область определения функции — это набор всех положительных действительных чисел.
Если база не записана, предположим, что журнал является базовым. 10
.
10
.
Икс 1 1000 1 100 1 10 1 10 100 1000 у знак равно бревно Икс — 3 — 2 — 1 0 1 2 3
Логарифмическая функция,
у
знак равно
бревно
б
(
Икс
)
, можно сдвинуть
k
единиц по вертикали и
час
единиц по горизонтали с уравнением
у
знак равно
бревно
б
(
Икс
+
час
)
+
k
.
Вертикальный сдвиг
Если k > 0 , график сдвинется вверх.
Если k < 0 , график сместится вниз.
Горизонтальный сдвиг
Если час > 0 , график сдвинется влево.
Если час < 0 , график сдвинется вправо.
Рассмотрим логарифмическую функцию у знак равно [ бревно 2 ( Икс + 1 ) — 3 ] . Это можно получить, переведя родительский граф у знак равно бревно 2 ( Икс ) Пару раз.
Рассмотрим график функции
у
знак равно
бревно
2
(
Икс
)
.
С час знак равно 1 , у знак равно [ бревно 2 ( Икс + 1 ) ] перевод у знак равно бревно 2 ( Икс ) на одну единицу влево.
В настоящее время,
k
знак равно
—
3
.График
у
знак равно
[
бревно
2
(
Икс
+
1
)
]
будет перемещен
3
единицы вниз, чтобы получить
у
знак равно
[
бревно
2
(
Икс
+
1
)
]
—
3
.
Вы можете вспомнить, что логарифмические функции определены только для положительных действительных чисел.Это связано с тем, что для отрицательных значений соответствующее экспоненциальное уравнение не имеет решения. Например, 3 Икс знак равно — 1 не имеет реального решения, поэтому бревно 3 ( — 1 ) не определено.
Итак, как насчет такой функции, как у знак равно бревно 4 ( — Икс ) ?
Это определено только для отрицательных значений Икс .
Найдите значения функции для нескольких отрицательных значений Икс . Для упрощения расчета вы можете использовать экспоненциальную форму уравнения, 4 у знак равно — Икс .
Икс — 1 — 2 — 4 — 8 — 16 — 32 у знак равно бревно 4 ( — Икс ) или 4 у знак равно — Икс 0 1 2 1 1 1 2 2 2 1 2
Постройте точки и соедините их плавной кривой.
Вы можете видеть, что график является отражением графика функции у знак равно бревно 4 ( Икс ) о у -ось.
1,4 Смены и расширения
Многие функции в приложениях построены из простых функций с помощью вставка констант в разные места. Важно понимать влияние таких констант на внешний вид графика.2 $. Это $ y = x-4 $, линия с наклоном 1, а не смещенная парабола.
Вертикальные смещения. Если мы заменим $ y $ на $ y-D $, то график
поднимается на $ D $ единиц. (Если значение $ D $ отрицательное, это означает, что график
перемещается вниз на $ | D | $ единиц.) Если формула записана в виде
$ y = f (x) $, и если $ y $ заменить на $ y-D $, чтобы получить $ y-D = f (x) $, мы можем
эквивалентно переместите $ D $ на другую часть уравнения и напишите
$ y = f (x) + D $. Таким образом, можно сформулировать такой принцип: , чтобы получить
график $ y = f (x) + D $, возьмите график $ y = f (x) $ и переместите его на $ D $ единиц вверх.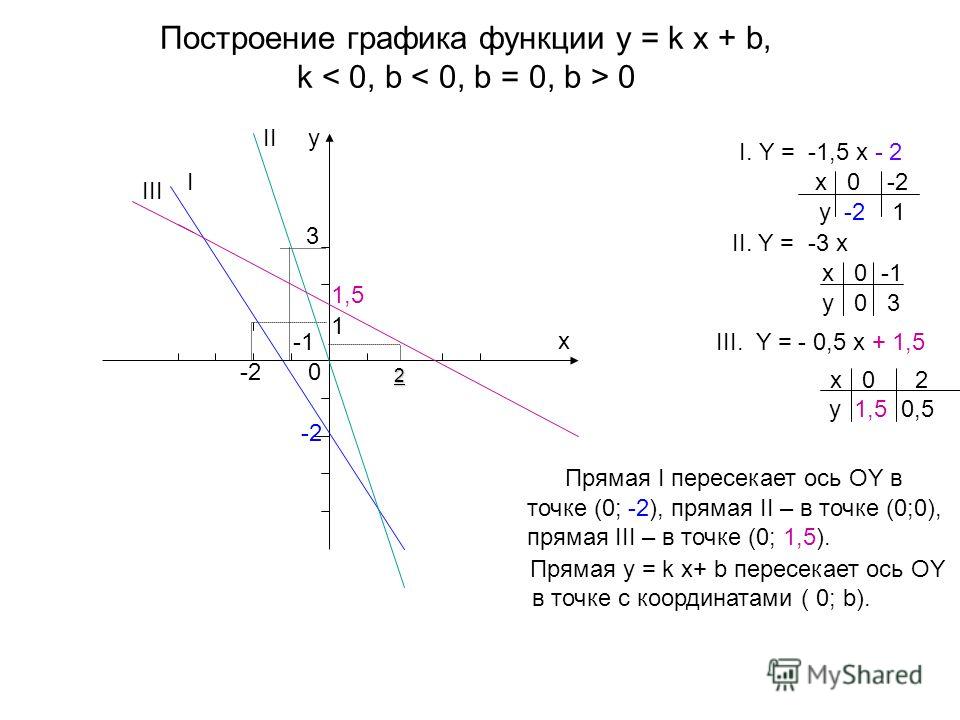 2 $ — круг перемещается на $ C $ в
вправо и $ D $ вверх, получая окружность радиуса $ r $
с центром в точке $ (C, D) $. Это говорит нам, как писать
уравнение любой окружности, не обязательно с центром в начале координат.
$ \ квадрат $
2 $ — круг перемещается на $ C $ в
вправо и $ D $ вверх, получая окружность радиуса $ r $
с центром в точке $ (C, D) $. Это говорит нам, как писать
уравнение любой окружности, не обязательно с центром в начале координат.
$ \ квадрат $
Позже мы захотим использовать еще два принципа, касающихся эффектов константы внешнего вида графика функции.
Горизонтальное расширение. Если $ x $ заменяется на $ x / A $ в формуле и $ A> 1 $, то влияние на график будет следующим: расширить его в $ A $ раз в направлении $ x $ (от $ y $ -ось). Если $ A $ находится в диапазоне от 0 до 1, то влияние на график будет уменьшаться в 1 доллар / австралийский доллар. (по направлению к оси $ y $). Мы используем слово «расширяться» для обозначения расширения или сжатия.
Например, заменив $ x $ на
$ x / 0,5 = x / (1/2) = 2x $ имеет эффект сужения к оси $ y $ в несколько раз.
из 2. Если значение $ A $ отрицательное, мы расширяемся в $ | A | $ раз, а затем
переверните ось $ y $. Таким образом, замена $ x $ на $ -x $ имеет эффект
получение зеркального отображения графа относительно оси $ y $.За
Например, функция $ y = \ sqrt {-x} $, имеющая домен
$ \ {x \ in \ R \ mid x \ le 0 \} $, получается
взяв график $ \ sqrt {x} $ и перевернув его вокруг оси $ y $ в
второй квадрант.
Таким образом, замена $ x $ на $ -x $ имеет эффект
получение зеркального отображения графа относительно оси $ y $.За
Например, функция $ y = \ sqrt {-x} $, имеющая домен
$ \ {x \ in \ R \ mid x \ le 0 \} $, получается
взяв график $ \ sqrt {x} $ и перевернув его вокруг оси $ y $ в
второй квадрант.
Вертикальное расширение. Если $ y $ заменяется на $ y / B $ в формуле и $ B> 0 $, тогда граф расширится в $ B $ раз в вертикальное направление. Как и раньше, это расширение или сокращение в зависимости от того, больше или меньше $ B $ единицы.Обратите внимание, что если у нас есть функция $ y = f (x) $, замена $ y $ на $ y / B $ эквивалентна умножению функции на справа от $ B $: $ y = Bf (x) $. Эффект на графике — расширение изображения. от оси $ x $ в $ B $ раз, если $ B> 1 $, чтобы сжать его в направлении ось $ x $ с коэффициентом 1 / B $, если $ 0
Пример 1.4.2 (Эллипсы)
Базовый пример двух принципов расширения дается эллипсом большой полуоси $ a $ и малой полуоси $ b $ . 2 = 1 $ — и расширяется в раз
$ a $ по горизонтали и в $ b $ по вертикали.2} = 1.
$$
$ \ квадрат $
2 = 1 $ — и расширяется в раз
$ a $ по горизонтали и в $ b $ по вертикали.2} = 1.
$$
$ \ квадрат $
Наконец, если мы хотим проанализировать функцию, которая включает в себя оба сдвигов и дилатаций, обычно проще всего работать с сначала дилатации, а затем сдвиги. Например, если мы хотим расширить функцию в $ A $ раз в направлении $ x $, а затем сдвинем $ C $ вправо, мы сделаем это, заменив сначала $ x $ на $ x / A $ а затем на $ (x-C) $ в формуле. В качестве примера предположим, что после расширения нашей единичной окружности на $ a $ в направлении $ x $ и на $ b $ в направлении $ y $, чтобы получить эллипс в последнем абзаце, мы затем хотел сместить его на расстояние $ h $ вправо и на расстояние $ k $ вверх, чтобы центрироваться в точке $ (h, k) $.2} + 2 $
График $ f (x) $ показан ниже. Нарисуйте графики следующих функций.
Пример 1.4.13 $ \ ds y = f (x-1) $
Пример 1.4.14 $ \ ds y = 1 + f (x + 2) $
Пример 1.4.
 Теперь проведем через данные точки прямую:
Если k 0, b 0, можно выбрать точки (0;b) и (-b/k;0) на осях координат:
Например: y = 2x + 2
Если x1 = 0, то y1 = 2;
Через точки (0,2) и (-1;0) проведем прямую:
Если коэффициент перед х дробный, удобно выбирать х1 и х2 так, чтобы у1 и у2 были целыми.
y = — 1/3x + 2
Если x1 = 3, то y1 = 1;
Если x1 = -3, то y2 = 3;
Через точки (3;1) и (-3;3) провести прямую.
Теперь проведем через данные точки прямую:
Если k 0, b 0, можно выбрать точки (0;b) и (-b/k;0) на осях координат:
Например: y = 2x + 2
Если x1 = 0, то y1 = 2;
Через точки (0,2) и (-1;0) проведем прямую:
Если коэффициент перед х дробный, удобно выбирать х1 и х2 так, чтобы у1 и у2 были целыми.
y = — 1/3x + 2
Если x1 = 3, то y1 = 1;
Если x1 = -3, то y2 = 3;
Через точки (3;1) и (-3;3) провести прямую.
 Построить график функции y = x
Построить график функции y = x 21:41:06
21:41:06  В противном случае лучше всего подойдет способ 1.
В противном случае лучше всего подойдет способ 1.