Окружность / Основы геометрии / Справочник по математике для начальной школы

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Основы геометрии
5. Окружность

Приступаем к изучению окружности и круга. Вспомним замкнутые и незамкнутые линии. Познакомимся с центром окружности, радиусом и диаметром и научимся определять радиус при известном диаметре и диаметр при известном радиусе.

Окружность и овал

Для начала рассмотрим рисунок и найдём окружность:

---

Теперь рассмотрим сходства и различия этих геометрических фигур:

	Овал	Окружность
Сходства	Центр в точке О  Есть точки A,B,C,D
Различия	В овале отрезки от точки O до крайней линии разные, а в окружности – все отрезки одинаковые.

Правило:

Окружность – это замкнутая кривая линия с точкой О в середине, которая называется центром.

Расстояния от центра до линии окружности одинаковые.

Начертить окружность можно при помощи циркуля:

А овал рисуют от руки:

---

Окружность и круг

Если заполнить пространство внутри окружности, то получим круг.

 

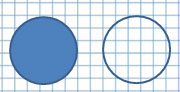
Круг – это часть плоскости, ограниченная окружностью.

---

Диаметр и радиус

Если соединить центр окружности с линией окружности, получим радиус, например,  OC, OA и OD.

---

Радиус – длина отрезка, соединяющего центр окружности с любой точкой, лежащей на окружности. Радиус составляет половину диаметра.

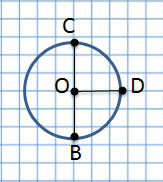
Если отрезок проходит через центр и соединяет две точки на окружности – это диаметр.

Диаметр – это длина отрезка, проходящего через центр окружности и соединяющего две точки на этой окружности.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Круг. Шар. Овал

Треугольники

Многоугольники

Угол. Виды углов

Обозначение геометрических фигур буквами

Периметр многоугольника

Площадь фигуры

Основы геометрии

Правило встречается в следующих упражнениях:

3 класс

Страница 94, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 95, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 96, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 97, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 106, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 18, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 59, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 67, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 69, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 39. Вариант 2. № 5, Моро, Волкова, Проверочные работы

4 класс

Страница 53, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 78, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 83, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 21, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 22, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

---

© budu5.com, 2020

Пользовательское соглашение

Copyright

Вписанная окружность — Википедия

Материал из Википедии — свободной энциклопедии

Окружность, вписанная в многоугольник ABCDE

Окружность называют вписанной в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех его сторон.

• Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех внутренних углов данного многоугольника пересекаются в одной точке, которая и является центром вписанной окружности.

• Радиус вписанной в многоугольник окружности равен отношению его площади S{\displaystyle S} к его полупериметру p{\displaystyle p}

r=Sp{\displaystyle r={\frac {S}{p}}}

Окружность, вписанная в треугольник со сторонами a, b, c.

Свойства вписанной окружности:

• В каждый треугольник можно вписать окружность, притом только одну.
• Центр I{\displaystyle I} вписанной окружности равноудалён от всех сторон и является точкой пересечения биссектрис треугольника.
• Радиус r{\displaystyle r} вписанной в треугольник окружности равен:

r=(−a+b+c)(a−b+c)(a+b−c)4(a+b+c);{\displaystyle r={\sqrt {\frac {(-a+b+c)(a-b+c)(a+b-c)}{4(a+b+c)}}};}

1r=1ha+1hb+1hc{\displaystyle {\frac {1}{r}}={\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}}

где a,b,c{\displaystyle a,b,c} — стороны треугольника, ha,hb,hc{\displaystyle h_{a},h_{b},h_{c}} — высоты, проведённые к соответствующим сторонам^[1];

r=Sp=(p−a)(p−b)(p−c)p{\displaystyle r={\frac {S}{p}}={\sqrt {\frac {(p-a)(p-b)(p-c)}{p}}}}

где S{\displaystyle S} — площадь треугольника, а p{\displaystyle p} — его полупериметр.

r=p−actg⁡(α/2)=p−bctg⁡(β/2)=p−cctg⁡(γ/2){\displaystyle r={\frac {p-a}{\operatorname {ctg} (\alpha /2)}}={\frac {p-b}{\operatorname {ctg} (\beta /2)}}={\frac {p-c}{\operatorname {ctg} (\gamma /2)}}}, p{\displaystyle p} — полупериметр треугольника (Теорема котангенсов).

• Если AB{\displaystyle AB} — основание равнобедренного треугольника △ABC{\displaystyle \triangle ABC}, то окружность, касающаяся сторон угла ∠ACB{\displaystyle \angle ACB} в точках A{\displaystyle A} и B{\displaystyle B}, проходит через центр вписанной окружности треугольника △ABC{\displaystyle \triangle ABC}.
• Теорема Эйлера: R2−2Rr=|OI|2{\displaystyle R^{2}-2Rr=|OI|^{2}}, где R{\displaystyle R} — радиус описанной вокруг треугольника окружности, r{\displaystyle r} — радиус вписанной в него окружности, O{\displaystyle O} — центр описанной окружности, I{\displaystyle I} — центр вписанной окружности.
• Если прямая, проходящая через точку I параллельно стороне AB{\displaystyle AB}, пересекает стороны BC{\displaystyle BC} и CA{\displaystyle CA} в точках A1{\displaystyle A_{1}} и B1{\displaystyle B_{1}}, то A1B1=A1B+AB1{\displaystyle A_{1}B_{1}=A_{1}B+AB_{1}}.
• Если точки касания вписанной в треугольник T{\displaystyle T} окружности соединить отрезками, то получится треугольник T1{\displaystyle T_{1}} со свойствами:
• Радиус вписанной в прямоугольный треугольник с катетами a, b и гипотенузой c окружности равен a+b−c2=aba+b+c{\displaystyle {\frac {a+b-c}{2}}={\frac {ab}{a+b+c}}}.
• Расстояние от вершины С треугольника до точки, в которой вписанная окружность касается стороны, равно d=a+b−c2=p−c{\displaystyle d={\frac {a+b-c}{2}}=p-c}.
• Расстояние от вершины C до центра вписанной окружности равно lc=rsin⁡(γ2){\displaystyle l_{c}={\frac {r}{\sin({\frac {\gamma }{2}})}}}, где r{\displaystyle r} — радиус вписанной окружности, а γ — угол вершины C.
• Расстояние от вершины C до центра вписанной окружности может также быть найдено по формулам lc=(p−c)2+r2{\displaystyle l_{c}={\sqrt {(p-c)^{2}+r^{2}}}} и lc=ab−4Rr{\displaystyle l_{c}={\sqrt {ab-4Rr}}}
• Теорема о трезубце или теорема трилистника: Если D — точка пересечения биссектрисы угла A с описанной окружностью треугольника ABC, I и J — соответственно центры вписанной и вневписанной окружности, касающейся стороны BC, тогда |DI|=|DB|=|DC|=|DJ|{\displaystyle |DI|=|DB|=|DC|=|DJ|}.
• Лемма Веррьера^[2]: пусть окружность V{\displaystyle V} касается сторон AB{\displaystyle AB}, AC{\displaystyle AC} и дуги BC{\displaystyle BC} описанной окружности треугольника ABC{\displaystyle ABC}. Тогда точки касания окружности V{\displaystyle V} со сторонами и центр вписанной окружности треугольника ABC{\displaystyle ABC} лежат на одной прямой.

Связь вписанной и описанной окружностей[править | править код]

• Формула Эйлера: Если d{\displaystyle d} — расстояние между центрами вписанной и описанной окружностей, а их радиусы равны r{\displaystyle r} и R{\displaystyle R} соответственно, то d2=R2−2Rr{\displaystyle d^{2}=R^{2}-2Rr}.
• Формулы для отношения и произведения радиусов:

rR=4S2pabc=cos⁡α+cos⁡β+cos⁡γ−1;{\displaystyle {\frac {r}{R}}={\frac {4S^{2}}{pabc}}=\cos \alpha +\cos \beta +\cos \gamma -1;}^[3]

2Rr=abca+b+c{\displaystyle 2Rr={\frac {abc}{a+b+c}}},

rR=4sin⁡α2sin⁡β2sin⁡γ2=cos⁡α+cos⁡β+cos⁡γ−1{\displaystyle {\frac {r}{R}}=4\sin {\frac {\alpha }{2}}\sin {\frac {\beta }{2}}\sin {\frac {\gamma }{2}}=\cos \alpha +\cos \beta +\cos \gamma -1}

где p{\displaystyle p} — полупериметр треугольника, S{\displaystyle S} — его площадь.

• Перпендикуляры, восставленные к сторонам треугольника в точках касания вневписанных окружностей, пересекаются в одной точке. Эта точка симметрична центру вписанной окружности относительно центра описанной окружности^[4].

• Для треугольника можно построить полувписанную окружность, или окружность Варьера. Это окружность, касающаяся двух сторон треугольника и его описанной окружности внутренним образом. Отрезки, соединяющие вершины треугольника и соответствующие точки касания окружностей Веррьера с описанной окружностью, пересекаются в одной точке. Эта точка служит центром гомотетии с положительным коэффициентом, переводящей описанную окружность во вписанную.
• Центр вписанной окружности лежит на отрезке, соединяющем точки касания сторон треугольника и полувписанной окружности.

Полувписанная окружность и центр гомотетии G для вписанной и описанной окружностей с радиусами соответственно r и R

• Описанный четырёхугольник, если у него нет самопересечений («простой»), должен быть выпуклым.
• Некоторые (но не все) четырёхугольники имеют вписанную окружность. Они называются описанными четырёхугольниками. Среди свойств этих четырёхугольников наиболее важным является то, что суммы противоположных сторон равны. Это утверждение называется теоремой Пито.
• Иными словами, в выпуклый четырёхугольник ABCD можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны: AB+CD=BC+AD{\displaystyle AB+CD=BC+AD}.

• Во всяком описанном четырёхугольнике две середины диагоналей и центр вписанной окружности лежат на одной прямой (теорема Ньютона). На ней же лежит середина отрезка с концами в точках пересечения продолжений противоположных сторон четырёхугольника (если они не параллельны). Эта прямая называется прямой Гаусса. На рисунке она зелёная, диагонали красные, отрезок с концами в точках пересечения продолжений противоположных сторон четырёхугольника тоже красный.
• Центр описанной около четырёхугольника окружности — точка пересечения высот треугольника с вершинами в точке пересечения диагоналей и точках пересечения противоположных сторон (теорема Брокара).

Вписанная окружность для сферического треугольника — это окружность, касающаяся всех его сторон.

• Тангенс радиуса^[5] вписанной в сферический треугольник окружности равен^[6]:73-74

tg⁡r=sin⁡(p−a)sin⁡(p−b)sin⁡(p−c)sin⁡p{\displaystyle \operatorname {tg} r={\sqrt {\frac {\sin(p-a)\sin(p-b)\sin(p-c)}{\sin p}}}}

• Вписанная в сферический треугольник окружность принадлежит сфере. Радиус, проведенный из центра сферы через центр вписанной окружности пересечет сферу в точке пересечения биссектрис углов (дуг больших кругов сферы, делящих углы пополам) сферического треугольника^[6]:20-21.

1. ↑ Altshiller-Court, 1925, p. 79.
2. ↑ Ефремов Д. Новая геометрия треугольника. — Одесса, 1902. — С. 130. — 334 с.
3. ↑ Longuet-Higgins, Michael S., «On the ratio of the inradius to the circumradius of a triangle», Mathematical Gazette 87, March 2003, 119—120.
4. ↑ Мякишев А. Г. Элементы геометрии треугольника. Серия: «Библиотека „Математическое просвещение“». М.: МЦНМО, 2002. c. 11, п. 5
5. ↑ Здесь радиус окружности измеряется по сфере, то есть представляет собой градусную меру дуги большого круга, соединяющей точку пересечения радиуса сферы, проведенного из центра сферы через центр окружности, со сферой и точку касания окружностью стороны треугольника.
6. ↑ ^{1 2} Степанов Н. Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — 154 с.

Как решать задания на окружность? – boeffblog.ru

В этой теме я хотел бы рассказать об основных понятиях, которые необходимо знать при решении заданий на окружность.

Но для начала давайте разберемся с понятиями круг и окружность.

Окружность – линия, каждая точка которой равноудалена от центра.

Круг – часть плоскости, которая лежит внутри окружности.

Другими словами, окружность – это контур круга (то, что мы рисуем циркулем). Круг – та часть листа бумаги, которая остается внутри.

 

---

1. Вся окружность составляет 360°.

Это означает, что если окружность разбита на несколько дуг (дуга – часть окружности), то их сумма всегда равна 360°.

Например, в этом задании необходимо найти длину дуги АВ. 

Так как сумма всех дуг равна 360°, то АВ + АС + ВС = 360. Причем две из них (АС и ВС) известны. Поэтому мы можем легко найти дугу АВ: 360 – 130 – 115.

---

2. Площадь круга находится по формуле: S = πr² (π = 3.14, r – радиус круга). Радиус – это отрезок, который соединяет центр окружности и точку, лежащую на окружности.

Най­ди­те площадь круга радиусом 4. (В от­ве­те укажите площадь, деленную на π.)

А вот здесь и главная подсказка “деленную на π“. Значит при нахождении площади не нужно подставлять 3,14.

S = π·4² = 16π. В ответ запишем только 16.

---

3. Все радиусы в одной окружности равны. Все диаметры в одной окружности равны.

Я думаю это и так понятно.

---

4. Центральный угол равен дуге, на которую он опирается.

Центральный угол

 

 

---

5. Вписанный угол равен половине дуги, на которую он опирается.

Вписанный угол

---

6. Вписанные углы, которые опираются на одну и ту же дугу равны.

Угол АВС равен углу АМС, так как они опираются на одну дугу АС.

---

7. Гипотенуза прямоугольного треугольника является диаметром, описанной около него окружности.

Это связано с тем, что угол В = 90°. При этом он является вписанным углом. Вписанный угол в 2 раза меньше дуги АС, на которую он опирается. Поэтому дуга АС = 180°, а это половина окружности. То есть АС – диаметр.

---

8. Радиус, проведенный из точки касания, всегда лежит под углом 90° к касательной.

Из точки А проведены две касательные к окружности – АВ и АС. Радиус ОВ будет перпендикулярен касательной АВ, а радиус ОС – перпендикулярен касательной АС.

---

9. Если окружность вписана в некоторый угол х, то центральный угол окружности, который опирается на те же точки находится как 180° – х.

Окружность вписана в угол А = 95°, который касается ее в точках В и С. Центральный угол ВОС будет равен 180 – 95 = 85°.

---

10. Если окружность вписана в некоторый угол х, то вписанный угол окружности, который опирается на те же точки находится как (180° – х)/2.

Окружность вписана в угол А = 70°, который касается ее в точках В и С. Вписанный угол ВМС будет равен (180 – 70)2 = 55°.

 

---

 

 

Эти правила помогут Вам решить практически все задания на тему Окружностей.

Деление окружности, или Геометрия для чайников

Приветствую всех мастеров и мастериц!

Очень многие из нас, учась в школе, думали, что очень многие предметы школьной программы в жизни нам никогда не понадобятся. Я так думала про геометрию. Однако жизнь сложилась так, что именно геометрия мне оказалась и нужна.

Одной из основных сложностей при создании круглого орнаменты является его симметричность. Иногда хочется, чтобу у нас был точный 8-ми гранник, иногда 5-ти конечная звезда, а иногда нужен 7-ми конечный цветок.

Эту глобальную проблему симметричного деления окружности на равное количество частей можно решить просто при помощи циркуля, линейки, листа бумаги и геометрии.

Деление окружности на 3 равных сектора.

Для начала нам понадобиться сама окружность. Рисуем ее при помощи циркуля

Выбираем на поверхности окружности любую точку, отмечаем ее карандашиком. Далее циркулем отмеряем радиус нашей окружности (кто забыл — это расстояние от центра окружности до любой ее точки)

Ставим наш циркуль с набранным радиусом в точку, которую мы на окружности отметили и проводим дугу до пересечения с нашей основной окружностью.

Через точку на окружности и центр окружность проводим линию до пересечения с гранью.

Таким образом мы получили 3 точки на нашей окружности.

Теперь из центра проводим линии, соединяя центр с этими точками и у нас образовались 3 одинаковых сектора.

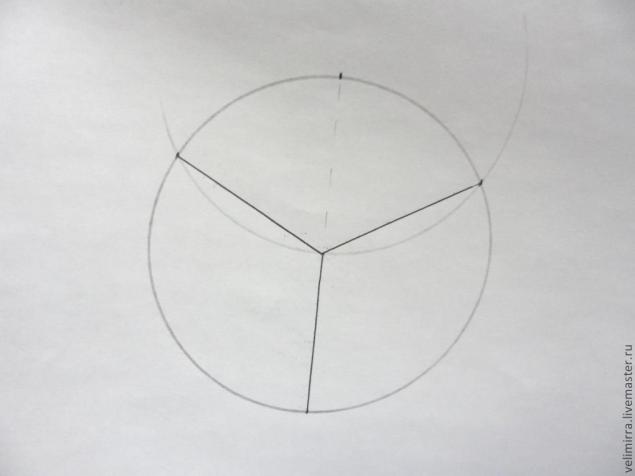
Деление окружности на 4 равных сектора.

Начинаем опять с окружности, необходимого нам диаметра. Назову ее окружность 1.

Через центр окружности 1 проводим линию до пересечения с обеими сторонами окружности 1.

Из центра окружность 1 при помощи циркуля рисуем окружность больше диаметра — окружность 2.

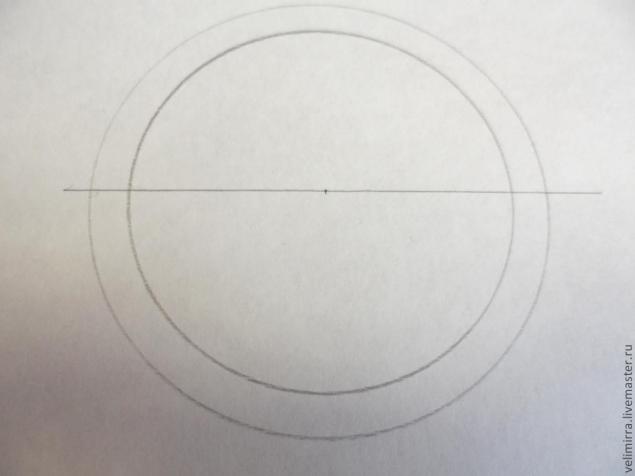
Ставим ножку циркуля в точку на пересечении наше прямой линии и окружности 2 и из нее проводим дугу. Расстояние от точки на окружности до дуги равно диаметру окружности 1. (диаметр = 2 радиусам). Ту же процедуру повторяем с точкой на другой стороны окружности.

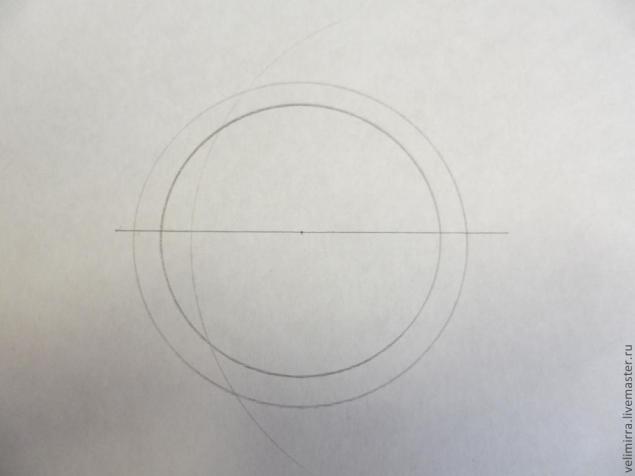
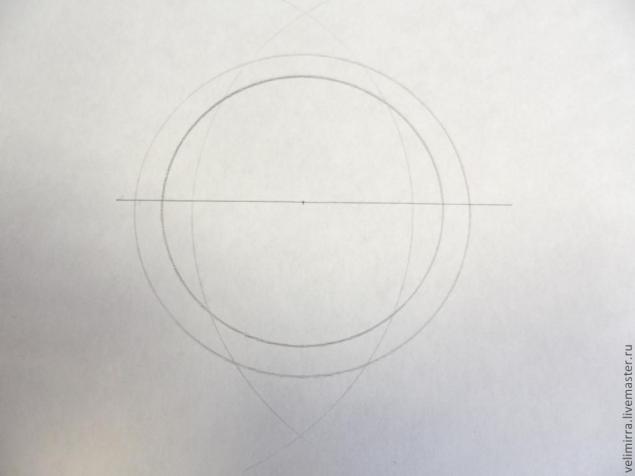
У нас есть 2 новые точки, появившиеся на пересечении дуг. Соединяем их и получаем окружность, разбитую на 4 ровных сектора.

Деление окружности на 5 равных секторов.

Начало работы с делением окружности на 5 частей очень схожа с делением окружности на 4 части, поэтому я начну уже с разделенного круга на 4 части.

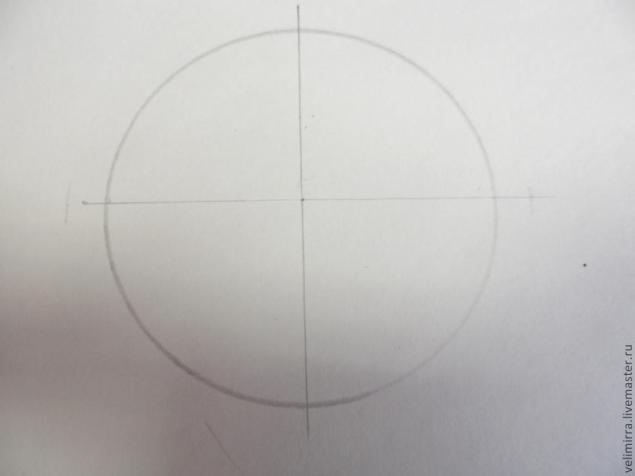
Циркулем набираем радиус нашей окружности и ставим ножку в одну из имеющихся у нас точек. В моем случае это левая точка. Проводим дугу до пересечения ее с основной линии окружности.

Соединяем получившиеся точки при помощи линейки и находим новую точку пересечения (точка Н)

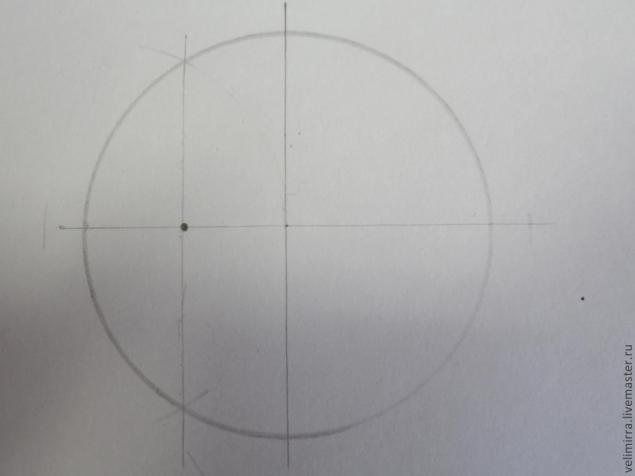
Циркулем набираем расстояние от верхний точки на окружности до точки Н. Ставим ножку в точку Н и проводим дугу и получаем еще одну точку (точка М)

Ставим ножку циркуля в верхнюю точку окружности и набираем расстояние до точки М.

Ставим ножку циркуля в верхнюю точку и откладываем набранное нами расстояние на нашей окружности.

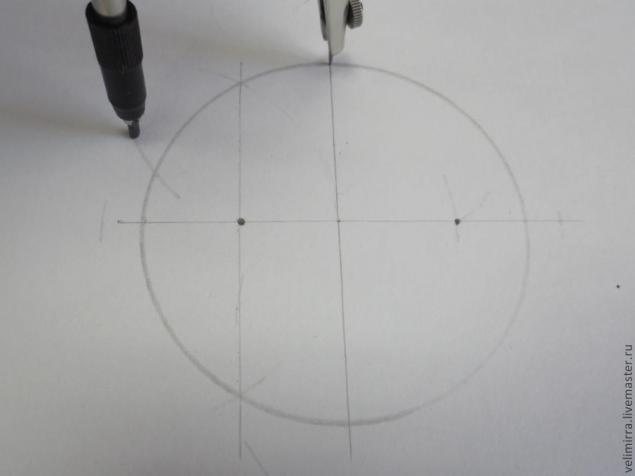
Ставим циркуль в получившуюся точку и еще раз откладываем это расстояние. Таким же образом ставим еще 2 точки.

У нас получилось 4 отложенных точки и 1 верхняя точка окружности. Соединяем центр окружности с этими точками и получаем 5 равных секторов.

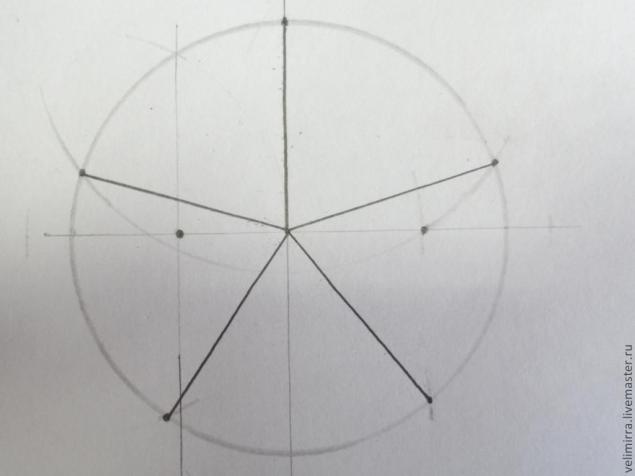
Деление окружности на 6 равных секторов.

Нам снова нужна окружность.

Берем любую точку на этой окружности, ставим в нее ножку циркуля с набранным расстоянием радиуса и проводим дугу до пересечения с нашей окружностью.

Далее соединяем выбранную нами точку с центром окружности и находим еще одну точку с противоположной стороны.

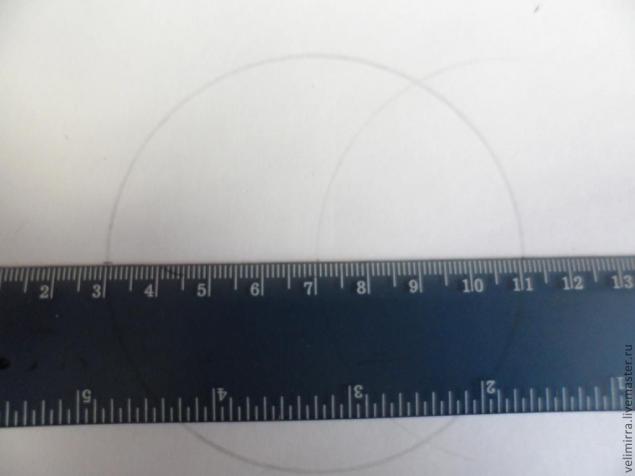
Из этой точки таким же расстоянием проводим еще одну дугу.

Мы получили 6 точек — 2 мы шали при помощи дуг, 1- наша выбранная и 1 найденная при помощи линейки. Соединяем их с центром и получаем 6 равных секторов.

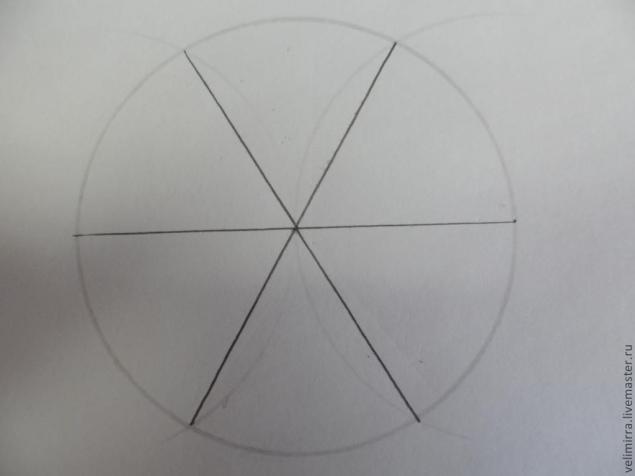
Деление окружности на 7 равных секторов.

Чтобы не повторяться и не описывать уже знакомые алгоритмы, берем за основу момент нахождения точки Н для разбития окружности на 5 частей.

Отмеряем циркулем расстояние от точки Н до точки на окружности.

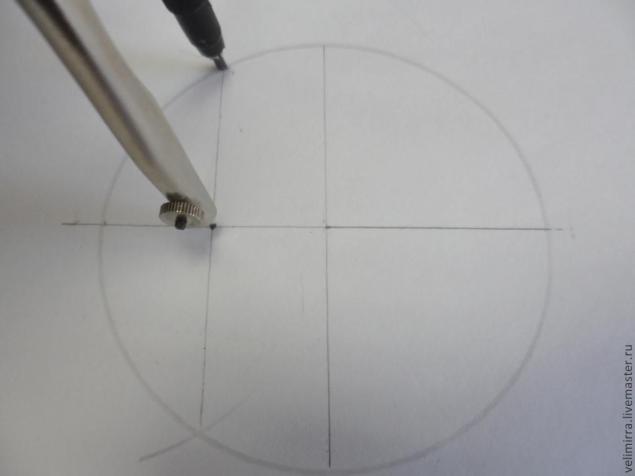
Ставим ножку циркуля в верхнюю точку и набранным на циркуле расстоянием откладываем точки, аналогично как мы делали в случае разбивки окружности на 5 частей

Соединяем наши новые точки с центром и получаем 7 равных секторов.

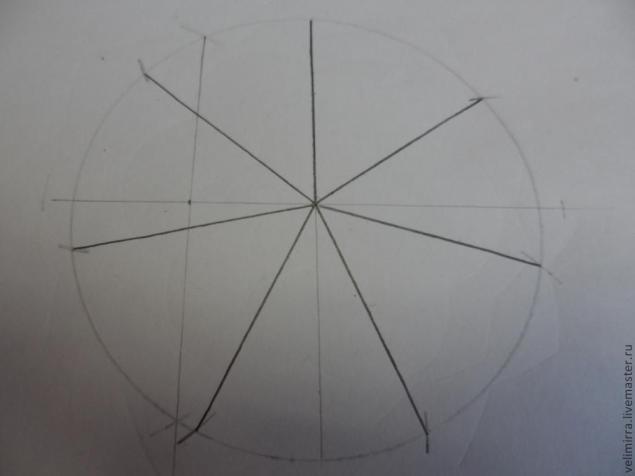
Используя эти простые приемы можно создавать геометрические орнаменты различной сложности

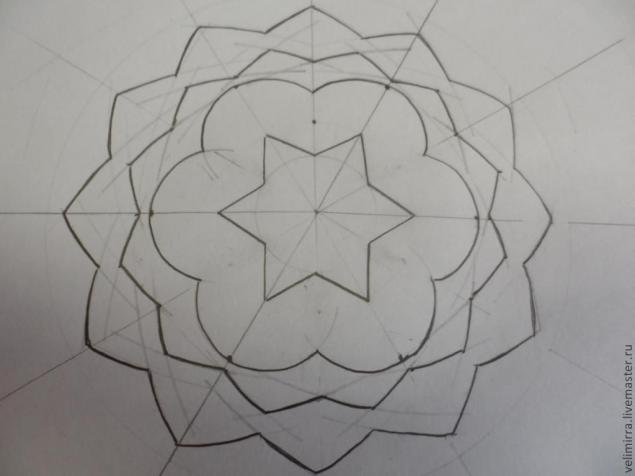
Надеюсь мой МК окажется кому-то полезным.

Удачи в создании шедеворов.

Ваша Velimira

Окружность. Как построить окружность? Формула окружности.

Как построить окружность?

Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.

Радиусом называется любой отрезок соединяющей точку окружности с ее центром.

Чтобы построить окружность необходимо знать уравнение окружности:

(х – а)² + (у – b)² = R ²

Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.

И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:

Пример №1:
(х – 1)² + (у – 2)² = 4²

Найдем центр окружности:
х – 1=0
x=1

у – 2=0
y=2

Центр окружности будет находится в точке (1;2)

Найдем радиус окружности:
R ²=4
R ²=2²
R=2

Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.

Пример №2:
х² + (у + 1)² =1

Можно представить уравнение окружности ввиде:
(х-0)² + (у + 1)² =1²

Найдем центр окружности:
х=0

у + 1=0
y=–1

Центр окружности будет находится в точке (0;–1)

Найдем радиус окружности:
R ²=1
R ²=1²
R=1

Построим окружность.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Радикальная ось двух окружностей — Википедия

Материал из Википедии — свободной энциклопедии

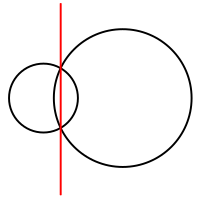Радикальная ось двух пересекающихся окружностей

Радика́льная ось двух окружностей — геометрическое место точек, степени которых относительно двух заданных окружностей равны. Иными словами, равны длины четырёх касательных, проведенных к двум данным окружностям из любой точки M данного геометрического места точек.

Радикальная ось двух окружностей существует тогда и только тогда, когда окружности неконцентрические, и может быть определена как для окружностей, так и для точек (окружностей нулевого радиуса) и мнимых окружностей (мнимого радиуса).

• Радикальная ось является прямой. Поскольку степень точки относительно окружности равна x2+y2+Ax+By+C,{\displaystyle x^{2}+y^{2}+Ax+By+C,} где коэффициенты A, B и C определяются через координаты центра и радиус окружности, то, приравняв степени точки относительно двух окружностей, получим x2+y2+A1x+B1y+C1=x2+y2+A2x+B2y+C2⇔(A1−A2)x+(B1−B2)y+(C1−C2)=0,{\displaystyle x^{2}+y^{2}+A_{1}x+B_{1}y+C_{1}=x^{2}+y^{2}+A_{2}x+B_{2}y+C_{2}\Leftrightarrow (A_{1}-A_{2})x+(B_{1}-B_{2})y+(C_{1}-C_{2})=0,} а это уравнение прямой. Существует также доказательство этого факта с использованием только геометрических методов.
• Радикальная ось перпендикулярна линии центров, что следует из симметричности обеих окружностей относительно линии центров.
• Если P — точка на радикальной оси, то длины касательных из точки P к обеим окружностям равны — это следует из того, что степень точки равна квадрату длины отрезка касательной. В частности, радикальная ось делит пополам отрезки общих касательных.

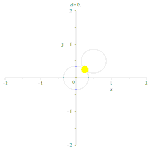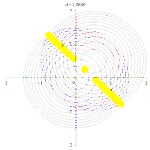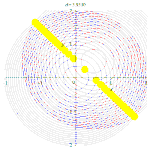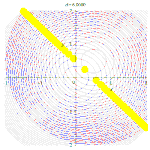Расширяющиеся окружности точек степени d относительно каждой из двух начальных окружностей и точки, принадлежащие радикальной оси (жёлтые).

• Если окружности пересекаются в двух точках, то их радикальной осью будет прямая, проходящая через эти точки, если они касаются внешним образом — то радикальной осью будет общая внутренняя касательная, если внутренним — то общая касательная (единственная).

Построение радикальной оси двух окружностей

• Если прямые, содержащие хорды AB{\displaystyle AB} и CD{\displaystyle CD} первой и второй окружности соответственно пересекаются на радикальной оси, то четырёхугольник ABCD{\displaystyle ABCD} вписанный. Это несложно доказать: пусть P{\displaystyle P} — точка пересечения. По свойству степени точки, она равна PA⋅PB,{\displaystyle PA\cdot PB,} а так как P лежит на радикальной оси, то она равна и PC⋅PD.{\displaystyle PC\cdot PD.} Так как PA⋅PB=PC⋅PD,{\displaystyle PA\cdot PB=PC\cdot PD,} то точки A,B,C{\displaystyle A,B,C} и D{\displaystyle D} лежат на одной окружности. Верно и обратное: если две окружности пересечь третьей так, что AB{\displaystyle AB} — общая хорда первой и третьей, а CD{\displaystyle CD} — общая хорда второй и третьей, то прямые AB и CD пересекутся на радикальной оси первых двух окружностей, причём в так называемом радикальном центре трёх окружностей (см. ниже). На этом свойстве основано построение радикальной оси циркулем и линейкой: построим окружность, пересекающую две данные в четырёх точках, а затем опустим из их радикального центра перпендикуляр на линию центров.

Радикальный центр трёх окружностей

• Радикальные оси трёх окружностей с неколлинеарными центрами пересекаются в одной точке, называемой радикальным центром. Пусть Ω1,Ω2,Ω3{\displaystyle \Omega _{1},\Omega _{2},\Omega _{3}} — окружности, а P{\displaystyle P} — точка пересечения радикальной оси окружностей Ω1{\displaystyle \Omega _{1}} и Ω2{\displaystyle \Omega _{2}} с радикальной осью окружностей Ω2{\displaystyle \Omega _{2}} и Ω3{\displaystyle \Omega _{3}}. Если P(ω,A){\displaystyle {\mathfrak {P}}(\omega ,A)} — степень точки A{\displaystyle A} относительно окружности ω,{\displaystyle \omega ,} то по определению радикальной оси P(Ω1,P)=P(Ω2,P)=P(Ω3,P),{\displaystyle {\mathfrak {P}}(\Omega _{1},P)={\mathfrak {P}}(\Omega _{2},P)={\mathfrak {P}}(\Omega _{3},P),} и точка P{\displaystyle P} лежит на радикальной оси окружностей Ω1{\displaystyle \Omega _{1}} и Ω3.{\displaystyle \Omega _{3}.}
• Геометрическое место центров окружностей, ортогональных двум данным, есть их радикальная ось с исключённой общей хордой (если она есть).
• Антигомологические хорды^{[уточнить]} двух окружностей пересекаются на их радикальной оси.
• Пусть ABCD{\displaystyle ABCD} — четырёхугольник, прямые AB{\displaystyle AB} и CD{\displaystyle CD} пересекаются в точке F{\displaystyle F}, BC{\displaystyle BC} и AD{\displaystyle AD} — в E{\displaystyle E}. Тогда окружности, построенные на отрезках AC{\displaystyle AC}, BD{\displaystyle BD} и EF{\displaystyle EF}, как на диаметрах, имеют общую радикальную ось, на которой лежат точки пересечения высот треугольников ABE{\displaystyle ABE}, CDE{\displaystyle CDE}, BCF{\displaystyle BCF} и ADF{\displaystyle ADF} (прямая Обера — Штейнера).

• Две окружности, пересекающиеся под прямым углом, называются ортогональными. Окружности можно считать ортогональными, если они образуют прямой угол друг с другом.
• Две пересекающиеся в точках A и B окружности с центрами O и O’ называются ортогональными, если являются прямыми углы OAO’ и OBO’ . Именно это условие гарантирует прямой угол между окружностями. В этом случае перпендикулярны радиусы (нормали) двух окружностей, проведенные в точку их пересечения. Следовательно, перпендикулярны и касательные двух окружностей, проведенные в точку их пересечения. Касательная окружности перпендикулярна радиусу (нормали), проведенному в точку касания. Обычно угол между кривыми — это угол между их касательными, проведенными в точке их пересечения.
• Возможно другое дополнительное условие. Пусть две пересекающиеся в точках A и B окружности имеют середины пресекающихся дуг в точках C и D, то есть дуга AС равна дуге СB, дуга AD равна дуге DB. Тогда эти окружности называются ортогональными, если являются прямыми углы СAD и СBD.

Следствия из свойств радикальной оси[править | править код]

• На прямой, проходящей через точки касания двух вневписанных окружностей треугольника с его сторонами, эти вневписанные окружности высекают равные отрезки.
• Диагонали описанного около окружности шестиугольника, соединяющие противоположные вершины, пересекаются в одной точке (теорема Брианшона для окружности).

Круг и окружность

Цели:

• Познакомить детей с новым понятием – круг. Помочь детям освоить признаки круга.
• Дать понятие “окружности”, определить место положения окружности по отношению к кругу.
• Освоить с детьми работу с циркулем-помощником.
• Развивать умение логически мыслить, воображение и творческие способности детей.
• Воспитывать интерес к предмету и умение оценивать свой труд.

Оборудование: Бумага, циркули, карандаш, металлическая крышка для консервирования с резинкой, шаблоны треугольника, квадрата, пятиугольника, смайлики, клей, ножницы.

Ход урока

1. Организационный момент.

Долгожданный дан звонок,
Начинается урок.

Возьмём с собой на урок улыбки и хорошее настроение. Посмотрим, какое оно у вас.

Игра.

У меня два солнышка – грустное и радостное.

Хлопните в ладоши те, у кого грустное настроение. А у кого радостное?

Надеюсь, у кого настроение грустное, станет радостным, а у кого хорошее – станет ещё лучше. Пожелаем друг другу удачи и улыбнёмся. Покажите свои ладошки, потрите их, погладьте себя по голове и скажите: “Какой я замечательный!”

На уроке вас ждут открытия: у кого-то они будут большие, у кого-то маленькие, но у каждого они свои.

2. Повторение изученного материала.

Прежде чем, приступить к новому материалу давайте, повторим то, что нам известно.

Игра “Угадай фигуру”

В конверте фигуры (треугольник, квадрат, пятиугольник). Один ученик описывает фигуру, не называя её, а другие должны отгадать.

Три вершинки, три угла,
Три сторонки – вот и я! (треугольник)

Он давно знаком со мной,
Каждый угол в нём прямой.
Все четыре стороны
Одинаковой длины.
Вам его представить рад,
А зовут его.. (квадрат)

3. Изучение нового материала.

Сегодня мы с вами снова отправимся в страну Геометрию с нашими старыми знакомыми — Линейкой, Карандашом и Резинкой. Они идут по улице и видят, что жители Геометрии рассматривают на стене дома такую картинку:

 — Ну, это я знаю, — сказал Карандаш. – Это кривые.

— Красивый рисунок, хороший мастер его делал, - говорит Линейка, — смотри, Карандаш, здесь есть одна кривая удивительной формы: вся такая одинаково плавная, гладкая..

— Про какую кривую говорит Линейка? Каким инструментом можно начертить такую правильную, всю одинаково плавную кривую?

(Дети называют циркуль. Если не называют, сюжет знакомит их с этим инструментом.)

— Кто же нарисовал эту замечательную кривую? – спросил Карандаш.

— Это мастер Циркуль, — ответили ему жители Геометрии.

Познакомились наши друзья с Циркулем. Спрашивает Линейка:

— Как вам удаётся такие плавные линии рисовать?

— А вот так, — говорит Циркуль. – Встаю на острую ножку и кручусь на ней, как балерина. Р-раз!

Учитель берёт большой циркуль и быстро чертит на доске окружность.

— О, какая красивая линия! – говорит Карандаш. – Что это?

— Это окружность,- говорит Циркуль. – Линию, которую рисует мой грифель называют словом окружность. Если вы начертите окружность на бумаге и вырежете её, то эта линия останется на границе выреза. А то, что останется у вас в руках, называется круг. (Учитель показывает бумажный круг.)

Окружность – это граница круга.

Пока Циркуль объяснял Линейке, что такое окружность, карандаш наклонился и что-то поднял с тротуара.

— Смотрите! – закричал он. – У меня есть и окружность, и круг.

— И показал всем вот это. (Учитель показывает детям металлическую крышку для консервирования и вынимает из неё круглую резинку).

— Ребята, что здесь окружность, а что — круг?

— Я знаю, как легко запомнить, чем отличается окружность от круга, — говорит Карандаш. – Резинка, иди сюда, прыгай!

Карандаш подставил Резинке то, что держал в одной руке. Резинка весело прыгнула. Но когда Карандаш предложил ей прыгнуть сквозь предмет в другой руке, Резинка обиделась и сказала:

— Ты что, карандаш, думаешь, ты один запомнил разницу между окружностью и кругом?

— Сквозь что прыгнула Резинка? (Сквозь окружность. Сквозь круг прыгнуть нельзя: он сплошной.)

— А что вы ещё умеете, мастер Циркуль? – спросила Линейка.

— О, я могу многое, ответил Циркуль, — смотрите!

(Учитель показывает несколько красивых орнаментов и аппликаций, выполненных с помощью циркуля.)

— Ой, как сложно! – говорит карандаш. – Я, наверное, не смогу так.

— Это совсем не сложно, говорит мастер Циркуль, - и я этому научу очень быстро. Самое главное – научиться правильно, держать меня в руках.

Физкультминутка

Раз, два, три, четыре, пять (шаги на месте)!
Все умеем мы считать (хлопки в ладоши),
Отдыхать умеем тоже (прыжки на месте).
Руки за спину положим (руки за спину),
Голову поднимем выше (поднять голову выше)
И легко-легко подышим (глубокий вдох-выдох).
Подтянитесь на носочках столько раз,
Ровно столько, сколько пальцев (показали, сколько пальцев на руках)
На руке у вас (поднимаемся на носочках 10 раз).

Практическая работа

Возьмите в руки циркуль, рассмотрите его, найдите и потрогайте остриё, на котором циркуль “крутится”, найдите “хвостик”, подвигайте “ноги”.

— Какая ножка циркуля стоит в центре окружности – игла или грифель?

(Центр учитель отмечает и показывает на чертеже.)

— Какой ножкой циркуль рисует? (Грифелем.)

— Ноги циркуля двигаются. Что надо сделать, чтобы нарисовать большую окружность, развести их или сдвинуть ближе?

— Попробуйте нарисовать самую большую окружность, какая поместится на вашем листе.

— А теперь самую маленькую, какая у вас только получится ( на том же листе в любом месте, можно внутри большой).

Физкультминутка для глаз

• Плотно сомкните веки на 5 секунд, затем широко откройте их на такое же время, не морща при этом лоб. Повторите 3-4 раза.
• Сосредоточьте взгляд на отдалённом предмете, затем переведите его на кончик носа. Повторите 4-6 раз.
• Делайте медленные круговые движения глазами, будто следите за большим колесом, вращающимся 2 раза в одну сторону и 2 раза в другую сторону. Повторите 2-4 раза.
• Посмотрите на верхний левый угол стены вашей комнаты, переведите взгляд на кончик носа, а затем на верхний правый угол стены и снова на кончик носа. Повторите 5-6 раз.

Игра “Сложи круг”

Из разных деталей сложить круг. Работа выполняется индивидуально. Ребятам предлагается 5 наборов с разными вариантами сборки (в конвертах).

Практическое задание по изготовлению аппликации “Снеговик”.

На листе цветной бумаги дети делают аппликацию “Снеговик”. Используются шаблоны кругов, ведро, метлу, нос, пуговицы, глаза дорисовывают фломастером.

4. Домашнее задание.

Дома доделать аппликацию, оформить снеговика, доделать фон (сделать ночь или день)

5. Итог урока. Рефлексия.

• Что нового вы узнали сегодня?
• Какие открытия вы сделали для себя?

Отгадайте загадки.

Нет углов у меня,
И похож на блюдце я,
На тарелку, и на крышку,
На кольцо, на колесо.
Кто же я такой, друзья? (круг)

У круга есть одна подруга,
Знакома всем её наружность.
Она идёт по краю круга
И называется… (окружность)

У вас на партах фигуры.

— я хорошо понял, что такое круг и окружность

— я не всё понял, у меня были ошибки

— я не понял, что такое круг и окружность

Учащимся предлагается выбрать символ и оценить свою деятельность. Дети сами вывешивают свои символы на магнитную доску.

Использованная литература.

1. Истомина Н.Б. Наглядная геометрия. Тетрадь по математике. 2-й класс. М.: ЛИНКА-ПРЕСС, 2008.
2. Газета “Начальная школа” издательский дом “Первое сентября” № 27-28 июль, 2004
3. Житомирский В.Г., Шеврин Л.Н. Путешествие по стране Геометрии. – М.: Педагогика, 1991.
4. Жильцова Т.В., Обухова Л.А. Поурочные разработки по наглядной геометрии: 1 – 4 класс. – М.: ВАКО, 2004.