Методы решения квадратных уравнений. Формула Виета для квадратного уравнения
Квадратные уравнения часто появляются в ряде задач по математике и физике, поэтому уметь их решать должен каждый школьник. В этой статье подробно рассматриваются основные методы решения уравнений квадратных, а также приводятся примеры их использования.
Какое уравнение называется квадратным
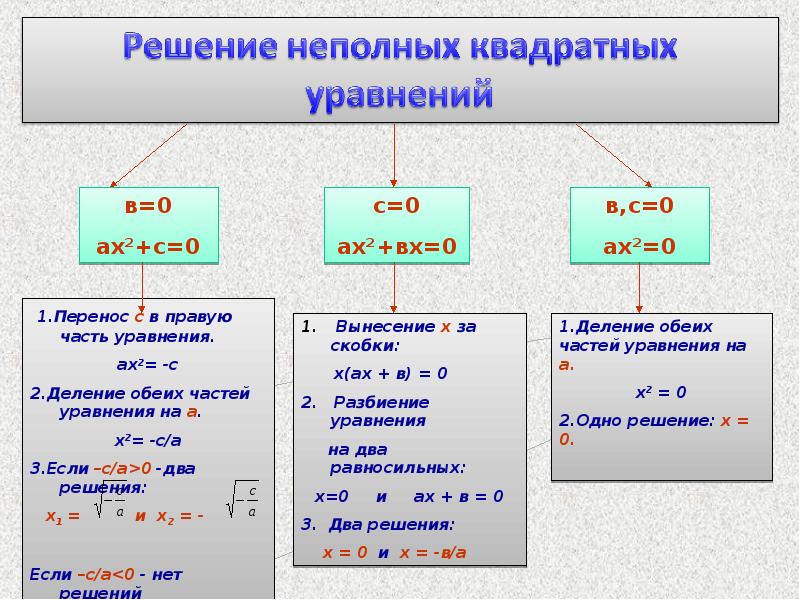
В первую очередь ответим на вопрос этого пункта, чтобы лучше понимать, о чем пойдет речь в статье. Итак, уравнение квадратное имеет следующий общий вид: c + b*x+a*x2=0, где a, b, c — некоторые числа, которые называются коэффициентами. Здесь a≠0 — это обязательное условие, в противном случае указанное уравнение вырождается в линейное. Остальные коэффициенты (b, c) могут принимать абсолютно любые значения, включая ноль. Так, выражения типа a*x2=0, где b=0 и c=0 или c+a*x2=0,где b=0, или b*x+a*x2=0, где c=0 — это тоже уравнения квадратные, которые называют неполными, поскольку в них либо линейный коэффициент b равен нулю, либо нулевым является свободный член c, либо они оба зануляются.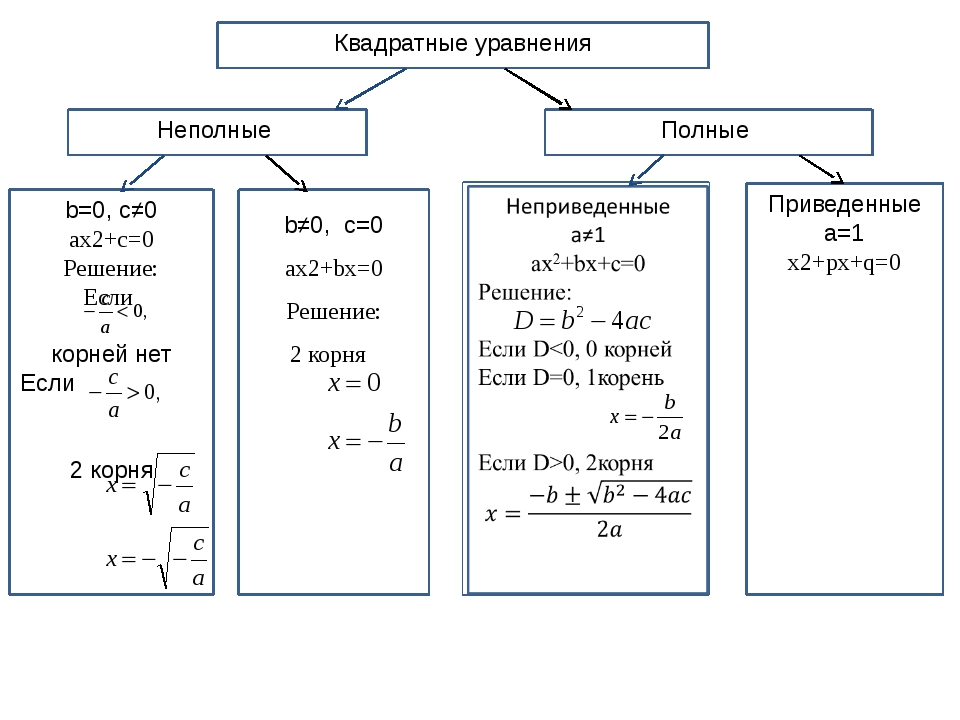
Уравнение, в котором a=1, называют приведенным, то есть оно вид имеет: x2 + с/a + (b/a)*x =0.
Решение квадратного уравнения заключается в нахождении таких значений x, которые удовлетворяют его равенству. Эти значения называются корнями. Поскольку рассматриваемое уравнение — это выражение второй степени, то это означает, что максимальное число его корней не может превышать двух.
Какие методы решения уравнений квадратных существуют
В общем случае существует 4 метода решения. Ниже перечисляются их названия:
- Разложение на множители.
- Дополнение до квадрата.
- Использование известной формулы (через дискриминант).
- Способ решения геометрический.
Как понятно из приведенного списка, первые три метода являются алгебраическими, поэтому они используются чаще, чем последний, который предполагает построение графика функции.
Существует еще один способ решения по теореме Виета уравнений квадратных. Его можно было бы включить 5-м в список выше, однако, это не сделано, поскольку теорема Виета является простым следствием 3-го метода.
Далее в статье рассмотрим подробнее названные способы решения, а также приведем примеры их использования для нахождения корней конкретных уравнений.
Метод №1. Разложение на множители
Для этого метода в математике квадратных уравнений существует красивое название: факторизация. Суть этого способа заключается в следующем: необходимо квадратное уравнение представить в виде произведения двух членов (выражений), которое должно равняться нулю. После такого представления можно воспользоваться свойством произведения, которое будет равно нулю только тогда, когда один или несколько (все) его членов являются нулевыми.
Теперь рассмотрим последовательность конкретных действий, которые нужно выполнить, чтобы найти корни уравнения:
- Перебросить все члены в одну часть выражения (например, в левую) так, чтобы в другой его части (правой) остался только 0.
- Представить сумму членов в одной части равенства в виде произведения двух линейных уравнений.
- Приравнять каждое из линейных выражений к нулю и решить их.

Как видно, алгоритм факторизации является достаточно простым, тем не менее, у большинства школьников возникают трудности во время реализации 2-го пункта, поэтому поясним его подробнее.
Чтобы догадаться, какие 2-а линейных выражения при умножении их друг на друга дадут искомое квадратное уравнение, необходимо запомнить два простых правила:
- Линейные коэффициенты двух линейных выражений при умножении их друг на друга должны давать первый коэффициент квадратного уравнения, то есть число a.
- Свободные члены линейных выражений при их произведении должны давать число c искомого уравнения.
После того, как подобраны все числа множителей, следует выполнить их перемножение, и если они дают искомое уравнение, тогда переходить к пункту 3 в изложенном выше алгоритме, в противном случае следует изменить множители, но делать это нужно так, чтобы приведенные правила всегда выполнялись.
Пример решения методом факторизации
Покажем наглядно, как алгоритм решения уравнения квадратного составить и найти неизвестные корни.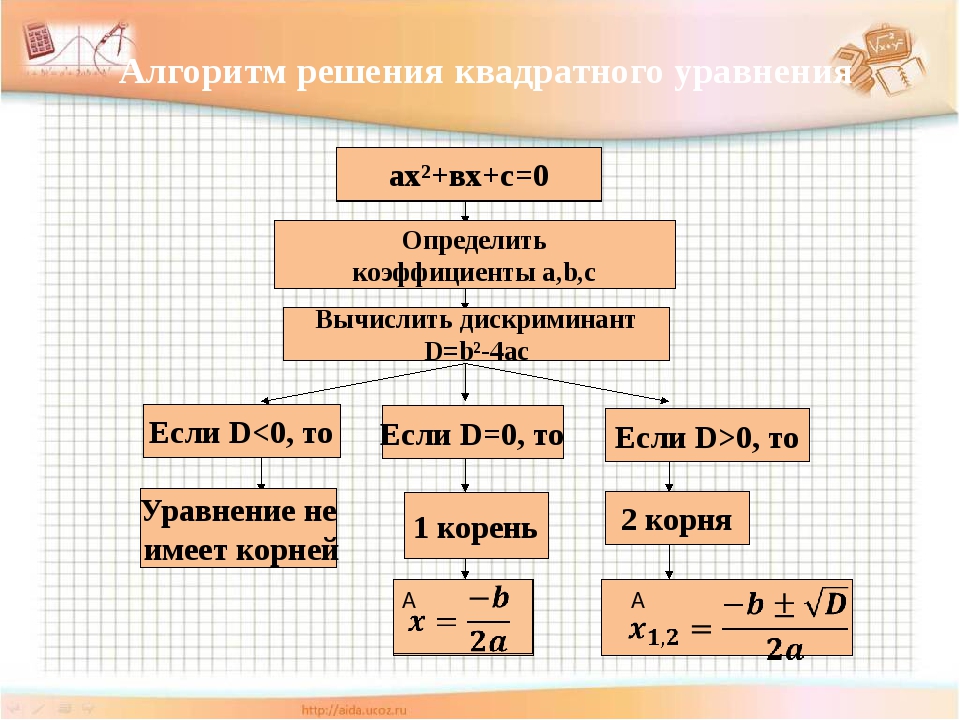 Пусть дано произвольное выражение, например, 2*x-5+ x2-2*x2 = x2+2+x2+1. Перейдем к его решению, соблюдая последовательность пунктов от 1-го до 3-х, которые изложены в предыдущем пункте статьи.
Пусть дано произвольное выражение, например, 2*x-5+ x2-2*x2 = x2+2+x2+1. Перейдем к его решению, соблюдая последовательность пунктов от 1-го до 3-х, которые изложены в предыдущем пункте статьи.
Пункт 1. Перенесем все члены в левую часть и выстроим их в классической последовательности для квадратного уравнения. Имеем следующее равенство: 2*x+(-8)+x2=0.
Пункт 2. Разбиваем на произведение линейных уравнений. Поскольку a=1, а с=-8, то подберем, например, такое произведение (x-2)*(x+4). Оно удовлетворяет изложенным в пункте выше правилам поиска предполагаемых множителей. Если раскрыть скобки, то получим: -8+2*x+x2, то есть получается точно такое же выражение, как в левой части уравнения. Это означает, что мы правильно угадали множители, и можно переходить к 3-му пункту алгоритма.
Пункт 3. Приравниваем каждый множитель нулю, получаем: x=-4 и x=2.
Если возникают какие-либо сомнения в полученном результате, то рекомендуется выполнить проверку, подставляя найденные корни в исходное уравнение. В данном случае имеем: 2*2+22-8=0 и 2*(-4)+(-4)2-8=0. Корни найдены правильно.
В данном случае имеем: 2*2+22-8=0 и 2*(-4)+(-4)2-8=0. Корни найдены правильно.
Таким образом, методом факторизации мы нашли, что заданное уравнение два корня различных имеет: 2 и -4.
Метод №2. Дополнение до полного квадрата
В алгебре уравнений квадратных метод множителей не всегда может использоваться, поскольку в случае дробных значений коэффициентов квадратного уравнения возникают сложности в реализации пункта 2 алгоритма.
Метод полного квадрата, в свою очередь, является универсальным и может применяться для квадратных уравнений любого типа. Суть его заключается в выполнении следующих операций:
- Члены уравнения, содержащие коэффициенты a и b, необходимо перебросить в одну часть равенства, а свободный член c — в другую.
- Далее, следует части равенства (правую и левую) разделить на коэффициент a, то есть представить уравнение в приведенном виде (a=1).
- Сумму членов с коэффициентами a и b представить в виде квадрата линейного уравнения.
 Поскольку a=1, то линейный коэффициент будет равен 1, что касается свободного члена уравнения линейного, то он равен должен быть половине линейного коэффициента приведенного уравнения квадратного. После того, как составлен квадрат линейного выражения, необходимо в правую часть равенства, где находится свободный член, добавить соответствующее число, которое получается при раскрытии квадрата.
Поскольку a=1, то линейный коэффициент будет равен 1, что касается свободного члена уравнения линейного, то он равен должен быть половине линейного коэффициента приведенного уравнения квадратного. После того, как составлен квадрат линейного выражения, необходимо в правую часть равенства, где находится свободный член, добавить соответствующее число, которое получается при раскрытии квадрата. - Взять квадратный корень со знаками «+» и «-» и решить полученное уже уравнение линейное.
Описанный алгоритм может на первый взгляд быть воспринят, как достаточно сложный, однако, на практике его реализовать проще, чем метод факторизации.
Пример решения с помощью дополнения до полного квадрата
Приведем пример уравнения квадратного для тренировки его решения методом изложенным в предыдущем пункте. Пусть дано уравнение квадратное -10 — 6*x+ x2 = 0. Начинаем решать его, следуя описанному выше алгоритму.
Пункт 1. Используем метод переброски при решении уравнений квадратных, получаем: — 6*x+ x2 = 10.
Пункт 2. Приведенный вид этого уравнения получается путем деления на число 5 каждого его члена (если равенства обе части поделить или умножить на одинаковое число, то равенство сохранится). В результате преобразований получим: x2 — 6/ x = 2.
Пункт 3. Половина от коэффициента — 6/5 равна -6/10 = -3/5, используем это число для составления полного квадрата, получаем: (-3/5+x)2. Раскроем его и полученный свободный член следует вычесть из части равенства левой, чтобы удовлетворить исходному виду квадратного уравнения, что эквивалентно его добавлению в правую часть. В итоге получаем: (-3/5+x)2 = 59/25.
Пункт 4. Вычисляем квадратный корень с положительным и отрицательным знаками и находим корни: x = 3/5±√59/5 = (3±√59)/5. Два найденных корня имеют значения: x1 = (√59+3)/5 и x1 = (3-√59)/5.
Поскольку проведенные вычисления связаны с корнями, то велика вероятность допустить ошибку. Поэтому рекомендуется проверить правильность корней x2 и x1. Получаем для x1: ((3+√59)/5)2-6*(3+√59)/5 — 10 = (9+59+6*√59)/5 — 18/5 — 6*√59/5-10 = 68/5-68/5 = 0. Подставляем теперь x2: ((3-√59)/5)2-6*(3-√59)/5 — 10 = (9+59-6*√59)/5 — 18/5 + 6*√59/5-10 = 68/5-68/5 = 0.
Получаем для x1: ((3+√59)/5)2-6*(3+√59)/5 — 10 = (9+59+6*√59)/5 — 18/5 — 6*√59/5-10 = 68/5-68/5 = 0. Подставляем теперь x2: ((3-√59)/5)2-6*(3-√59)/5 — 10 = (9+59-6*√59)/5 — 18/5 + 6*√59/5-10 = 68/5-68/5 = 0.
Таким образом, мы показали, что найденные корни уравнения являются истинными.
Метод №3. Применение известной формулы
Этот метод решения уравнений квадратных является, пожалуй, самым простым, поскольку он заключается в подставлении коэффициентов в известную формулу. Для его использования не нужно задумываться о составлении алгоритмов решения, достаточно запомнить только одну формулу. Она приведена на рисунке выше.
В этой формуле подкоренное выражение (b2— a*c) называется дискриминантом (D). От его значения зависит то, какие корни получатся. Возможны 3-и случая:
- D>0, тогда уравнение корня два имеет действительных и разных.
- D=0, тогда получается корень один, который можно вычислить из выражения x = -b/(a*2).

- D<0, тогда получается два различных мнимых корня, которые представляются в виде комплексных чисел. Например, число 3- i является комплексным, при этом мнимая единица i удовлетворяет свойству: i2=-1.
Пример решения через вычисление дискриминанта
Приведем пример уравнения квадратного для тренировки использования приведенной выше формулы. Найдем корни для -3*x2-6+3*x+ x = 0. Для начала вычислим значение дискриминанта, получаем: D = b2— a*c = 72— (-3)*(-6) = -23.
Поскольку получен D<0, значит, корни рассматриваемого уравнения являются числами комплексными. Найдем их, подставив найденное значение D в приведенную в предыдущем пункте формулу (она также представлена на фото выше). Получим: x = 7/6±√(-23)/(-6) = (7±i*√23)/6.
Метод №4. Использование графика функции
Он также называется графическим методом решения уравнений квадратных. Следует сказать, что применяется он, как правило, не для количественного, а для качественного анализа рассматриваемого уравнения.
Суть метода заключается в построении графика функции квадратичной y = f(x), который представляет собой параболу. Затем, необходимо определить, в каких точках пересекает ось абсцисс (X) парабола, они и будут корнями соответствующего уравнения.
Чтобы сказать, будет ли парабола пересекать ось X, достаточно знать положение ее минимума (максимума) и направление ее ветвей (они могут либо возрастать, либо убывать). Следует запомнить два свойства этой кривой:
- Если a>0 — параболы ветви направлены вверх, наоборот, если a<0, то они идут вниз.
- Координата минимума (максимума) параболы всегда равна x = -b/(2*a).
Например, необходимо определить, имеет ли корни уравнение — x+ x2+10 = 0. Соответствующая парабола будет направлена вверх, поскольку a=5>0. Ее экстремум имеет координаты: x=4/10=2/5, y=- 2/5+ (2/5)2+10 = 9,2. Поскольку минимум кривой лежит над осью абсцисс (y=9,2), то она не пересекает последнюю ни при каких значениях x. То есть действительных корней приведенное уравнение не имеет.
То есть действительных корней приведенное уравнение не имеет.
Теорема Виета
Как выше было отмечено, эта теорема является следствием метода №3, который основан на применении формулы с дискриминантом. Суть теоремы Виета заключается в том, что она позволяет связать в равенство коэффициенты уравнения и его корни. Получим соответствующие равенства.
Воспользуемся формулой для вычисления корней через дискриминант. Сложим два корня, получаем: x1+x2 = -b/a. Теперь умножим корни друг на друга: x1*x2, после ряда упрощений получается число c/a.
Таким образом, для решения уравнений квадратных по теореме Виета можно использовать полученных два равенства. Если все три коэффициента уравнения известны, тогда корни можно найти путем решения соответствующей системы из этих двух уравнений.
Пример использования теоремы Виета
Необходимо составить квадратное уравнение, если известно, что оно имеет вид x2+c = -b*x и корни его равны 3 и -4.
Поскольку в рассматриваемом уравнении a=1, то формулы Виета будут иметь вид: x2+x1 =-b и x2*x1= с. Подставляя известные значения корней, получаем: b = 1 и c = -12. В итоге восстановленное уравнение квадратное приведенное будет вид иметь: x2-12 = -1*x. Можно подставить в него значение корней и убедиться, что равенство выполняется.
Обратное применение Виета теоремы, то есть вычисление корней по известному виду уравнения, позволяет для небольших целых чисел a, b и c быстро (интуитивно) находить решения.
10 способов решения квадратных уравнений
10 способоврешения
квадратных
уравнений
Выполнила: Толстова Софья, 8 «А»
Школа-интернат №9 ОАО «РЖД»
История развития
квадратных уравнений
Квадратные уравнения в Древнем Вавилоне
Необходимость решать уравнения не только первой, но и второй степени ёщё в
древности была вызвана потребностью решать задачи, связанные с нахождением
площадей земельных участков и с земляными работами военного характера, а
также с развитием астрономии и самой математики.
 Квадратные уравнения
Квадратные уравненияумели решать около 2000 лет до нашей веры вавилоняне. Применяя современную
алгебраическую запись, можно сказать, что в их клинописных
текстах встречаются, кроме неполных, и такие, например, полные квадратные
уравнения:
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает с
современным, однако неизвестно, каким образом дошли вавилоняне до этого
задачи с решениями, изложенными в виде рецептов, без указаний относительно
того, каким образом они были найдены. Несмотря на высокий уровень развития
алгебры в Вавилонии, в клинописных текстах отсутствуют понятие отрицательного
числа и общие методы решения квадратных уравнений.
Как составлял и решал Диофант
квадратные уравнения
«Найти два числа, зная, что их сумма равна 20, а
произведение 96»
Диофант рассуждает следующим образом: из условия
задачи вытекает, что искомые числа не равны, т.
 к.
к.если бы они равны, то их произведение равнялось
бы не 96, а 100. Таким образом, одно из них будет
больше половины их суммы , т.е. 10+X , другое же
меньше, т.е. 10-X.
Разность между ними 2Х
Отсюда Х=2. Одно из искомых чисел равно 12, другое
8. Решение Х = -2 для Диофанта не существует, так
как греческая математика знала только
положительные числа.
УРАВНЕНИЕ:
или же:
Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются и в астрономическом трактате
«Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом
Ариабхаттой. Другой индийский ученый, Брахмагупта, изложил общее правило
решения квадратных уравнений, приведенных к единой канонической форме:
ax²+bx=c, a>0
Одна из задач знаменитого индийского
Соответствующее задачи уравнение:
математика XІІ века Бхаскары
Обезьянок резвых стая
Всласть поевши, развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась.

А двенадцать по лианам…
Стали прыгать повисая…
Сколько было обезьянок
Баскара пишет под видом:
Дополнил левую часть до квадрата,
Квадратные уравнения в Древней Азии
х2 +10 х = 39
Вот как решал это уравнение среднеазиатский ученый ал-Хорезми:
Он писал : «Правило таково:
раздвои число корней,
х=2х·5
получите в этой задаче пять,
5
умножь на это равное ему, будет двадцать пять,
5·5=25
прибавь это к тридцати девяти,
25+39
будет шестьдесят четыре,
64
извлеки из этого корень, будет восемь,
8
и вычти из этого половину числа корней, т.е.пять,
8-5
останется
3
это будет корень квадрата , который ты искал.»
А второй корень ? Второй корень не находили, так как отрицательные числа
не были известны.
Квадратные уравнения в Европе XIII-XVII вв.
Общее правило решения квадратных уравнений,
приведенных к единому каноническому виду
х2+вх+с=0 , было сформулировано в Европе лишь в
1544 г.
 Штифелем.
Штифелем..
Формулы решения квадратных уравнений
в Европе были впервые изложены в 1202
г. итальянским математиком
Леонардом Фибоначчи.
Вывод формулы решения квадратного
уравнения в общем виде имеется у Виета,
однако Виет признавал только
положительные корни. Лишь в 17 в.
благодаря трудам Декарта, Ньютона и
других ученых способ решения квадратных
уравнений принимает современный вид
О теореме Виета
Теорема, выражающая связь между коэффициентами квадратного уравнения и его
корнями, носящая имя Виета, была им сформулирована впервые в 1591 г. Следующим
образом: «Если B+D, умноженное на А-А , равно BD, то А равно В и равно D».
Чтобы понять Виета, следует помнить, что А, как и всякая гласная буква , означало у него
неизвестное (наше х), гласные же B,D- кэффициенты при неизвестном.
На языке современной алгебры вышеприведенная формулировка Виета означает:
x2+px+q=0 имеет действительные корни, то
их сумма равна -p, а произведение равно q,
то есть
x1 + x2 = -p ,
x1 x2 = q
(сумма корней приведенного квадратного
уравнения равна второму коэффициенту,
взятому с противоположным знаком, а
произведение корней равно свободному
члену).
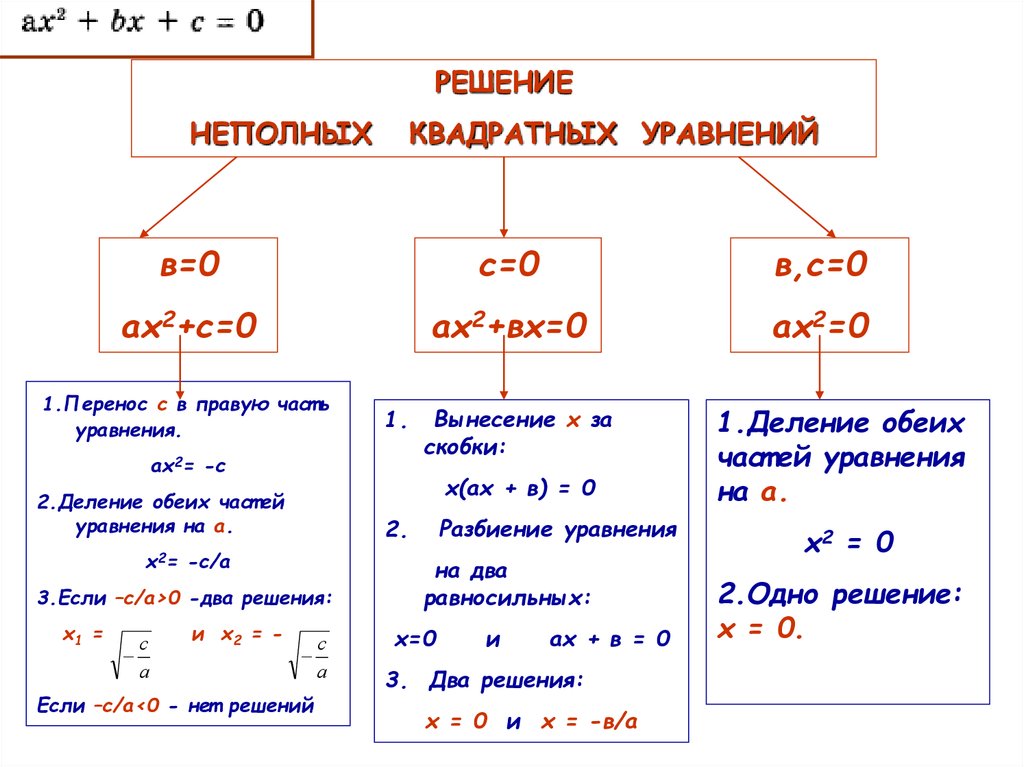
9. Метод разложения на множители
Цель:привести квадратное уравнение общего вида к виду:
А(х)·В(х)=0,
где А(х) и В(х) – многочлены относительно х.
Способы:
Пример:
Вынесение общего множителя за скобки;
Использование формул сокращенного умножения;
Способ группировки.
Метод выделения полного квадрата
Решим уравнение:
х2 + 6х — 7 = 0.
х2 + 6х -7 = 0.
(х +3)2 – 16 = 0.
(х +3)2 = 16.
х +3 = 4; х + 3 = -4.
х = 1, х =-7.
Ответ: 1; -7.
(a + b)2 = a2 + 2ab + b2,
(a — b)2 = a2 — 2ab + b2.
Решение квадратных уравнений по формуле
Выражение
называют дискриминантом квадратного уравнения.
Корни квадратного уравнения:
Если D>0,
Если D
Если D
Нет корней
Решение уравнений с помощью теоремы Виета
2
x
и
х
–
корни
уравнения
x
px q 0
если 1 2
то
x1 x 2 p
x1 x 2 q
( D 0)
Например:
Х2 + 3Х – 10 = 0
Х1·Х2 = – 10, значит корни имеют разные
знаки
Х1 + Х2 = – 3, значит больший по модулю
корень — отрицательный
Подбором находим корни: Х1 = – 5, Х2 = 2
Решение уравнений способом «переброски»
Решите уравнение: 2х2 — 11х +15 = 0.

Перебросим коэффициент 2 к свободному члену
у2 — 11у +30= 0.
D>0, по теореме, обратной теореме Виета,
получаем корни: 5;6,
далее возвращаемся к корням исходного уравнения: 2,5; 3.
Свойства коэффициентов квадратного уравнения
Если в квадратном уравнении a+b+c=0,
то один из корней равен 1, а
второй по теореме Виета равен
Если в квадратном уравнении a+c=b,
то один из корней равен (-1),
а второй по теореме Виета равен
Пример:
137х2 + 20х – 157 = 0.
a = 137, b = 20, c = -157.
a + b+ c = 137 + 20 – 157 =0.
x1 = 1,
Ответ: 1;
Второй коэффициент — четный
Графический способ решения квадратного уравнения
Не используя формул квадратное уравнение можно решить графическим
x2 x 1 0.
способом. Решим уравнение
Для этого построим два графика:
1)y=x2
2)y=x+1
X
-3
-2
-1
0
1
2
3
X
-1
0
1
Y
9
4
1
0
1
4
9
Y
0
1
2
Абсциссы точек пересечения графиков и
будет корнями уравнения.

Если графики пересекаются в двух точках, то
уравнение имеет два корня.
Если графики пересекаются в одной точке, то
уравнение имеет один корень.
Если графики не пересекаются, то уравнение
корней не имеет.
Ответ: x 0.6; x 2.6
Решение квадратных уравнений с помощью
циркуля и линейки
Корни квадратного уравнения ах2 + bх + с = 0 (а ≠ 0) можно рассматривать
как абсциссы точек пересечения окружности с центром Q (- ;
),
проходящей через точку A(О; 1), и оси Ох .
Решение квадратных уравнений с помощью номограммы
Это старый и незаслуженно забытый способ решения квадратных уравнений,
помещенный на с.83 «Четырехзначные математические таблицы» Брадис В.М.
Таблица XXII. Номограмма для
решения уравнения
Эта номограмма позволяет, не решая
квадратного уравнения, по его
коэффициентам определить корни
уравнения.
Для уравнения
Геометрический способ решения квадратных уравнений
В древности, когда геометрия была более развита, чем алгебра, квадратные
уравнения решали не алгебраически, а геометрически.

А вот, например, как древние греки решали уравнение:
или
Выражения
и
геометрически предоставляют собой один
и тот же квадрат, а исходное уравнение
одно и тоже уравнение.
Откуда и получаем что
, или
Заключение
• данные приёмы решения заслуживают внимания,
поскольку они не все отражены в школьных учебниках
математики;
• овладение данными приёмами поможет учащимся
экономить время и эффективно решать уравнения;
• потребность в быстром решении обусловлена применением
тестовой системы вступительных экзаменов;
Квадратные уравнения
1. Квадратные уравнения в Древнем Вавилоне.
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.
Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
X2 + X = ?; X2 — X = 14,5
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
2. Как составлял и решал Диофант квадратные уравнения.
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
Задача 11. «Найти два числа, зная, что их сумма равна 20, а произведение — 96»
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т.е. 10 + х, другое же меньше, т.е. 10 — х. Разность между ними 2х.
Отсюда уравнение:
(10 + х)(10 — х) = 96
или же:
100 — х2 = 96
х2 — 4 = 0 (1)
Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.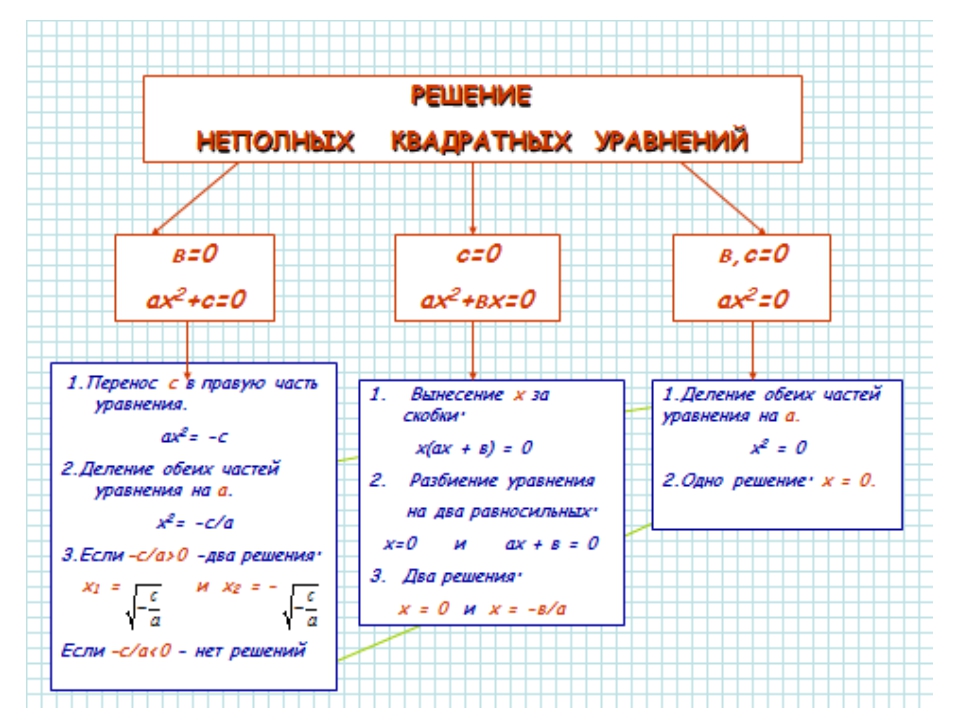
Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения
у(20 — у) = 96,
у2 — 20у + 96 = 0. (2)
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения (1).
3. Квадратные уравнения в Индии.
Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученный, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
ах2 + bх = с, а > 0. (1)
В уравнении (1) коэфиценты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
Задача 13.
«Обезьянок резвых стая А двенадцать по лианам…
Власть поевши, развлекалась. Стали прыгать, повисая…
Их в квадрате часть восьмая Сколько ж было обезьянок,
На поляне забавлялась. Ты скажи мне, в этой стае?»
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений (рис. 3).
формула корней, примеры. Приведенные и неприведенные квадратные уравнения
Рассмотрим квадратное уравнение
ах 2 + bх + с = 0, где а? 0.
Умножая обе его части на а, получаем уравнение
а 2 х 2 + аbх + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению
у 2 + by + ас = 0,
равносильно данному. Его корни у 1 и у 2 найдем с помощью теоремы Виета.
Окончательно получаем х 1 = у 1 /а и х 1 = у 2 /а. При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
* Пример.
Решим уравнение 2х 2 — 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у 2 — 11у + 30 = 0.
Согласно теореме Виета
у 1 = 5 х 1 = 5/2 x 1 = 2,5
у 2 = 6 x 2 = 6/2 x 2 = 3.
Ответ: 2,5; 3.
А. Пусть дано квадратное уравнение ах 2 + bх + с = 0, где а? 0.
1) Если, а+ b + с = 0 (т. е. сумма коэффициентов равна нулю), то х 1 = 1,
е. сумма коэффициентов равна нулю), то х 1 = 1,
Доказательство. Разделим обе части уравнения на а? 0, получим приведенное квадратное уравнение
x 2 + b/a * x + c/a = 0.
Согласно теореме Виета
x 1 + x 2 = — b/a,
x 1 x 2 = 1* c/a.
По условию а — b + с = 0, откуда b = а + с. Таким образом,
x 1 + x 2 = — а + b/a= -1 — c/a,
x 1 x 2 = — 1* (- c/a),
т.е. х 1 = -1 и х 2 = c/a, что м требовалось доказать.
- * Примеры.
- 1) Решим уравнение 345х 2 — 137х — 208 = 0.
Решение. Так как а + b + с = 0 (345 — 137 — 208 = 0), то
х 1 = 1, х 2 = c/a = -208/345.
Ответ: 1; -208/345.
2) Решим уравнение 132х 2 — 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 — 247 + 115 = 0), то
х 1 = 1, х 2 = c/a = 115/132.
Ответ: 1; 115/132.
Б. Если второй коэффициент b = 2k — четное число, то формулу корней
* Пример.
Решим уравнение 3х2 — 14х + 16 = 0.
Решение. Имеем: а = 3, b = — 14, с = 16, k = — 7;
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .
Эту формулу надо знать наизусть.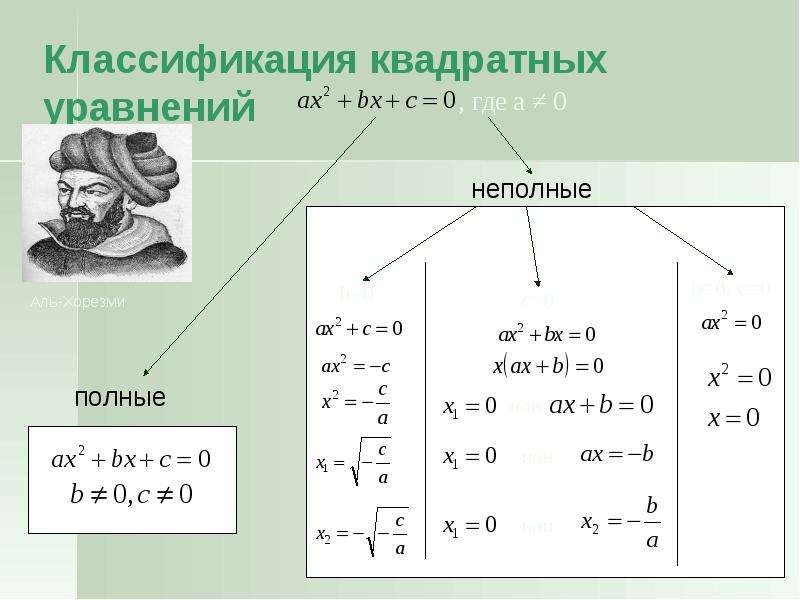 Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x 2 + 9x = 0;
- x 2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c
/a
) ≥ 0. Вывод:
Вывод:
- Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c /a )
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобкуПроизведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Виды квадратных уравнений
Что такое квадратное уравнение? Как оно выглядит? В термине квадратное уравнение ключевым словом является «квадратное». Оно означает, что в уравнении обязательно должен присутствовать икс в квадрате. Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и просто число (свободный член). И не должно быть иксов в степени, больше двойки.
Говоря математическим языком, квадратное уравнение — это уравнение вида:
Здесь a, b и с – какие-то числа. b и c – совсем любые, а а – любое, кроме нуля. Например:
b и c – совсем любые, а а – любое, кроме нуля. Например:
Здесь а =1; b = 3; c = -4
Здесь а =2; b = -0,5; c = 2,2
Здесь а =-3; b = 6; c = -18
Ну, вы поняли…
В этих квадратных уравнениях слева присутствует полный набор членов. Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.
Такие квадратные уравнения называются полными.
А если b = 0, что у нас получится? У нас пропадёт икс в первой степени. От умножения на ноль такое случается.) Получается, например:
5х 2 -25 = 0,
2х 2 -6х=0,
-х 2 +4х=0
И т.п. А если уж оба коэффицента, b и c равны нулю, то всё ещё проще:
2х 2 =0,
-0,3х 2 =0
Такие уравнения, где чего-то не хватает, называются неполными квадратными уравнениями. Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.
Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.
Кстати, почему а не может быть равно нулю? А вы подставьте вместо а нолик.) У нас исчезнет икс в квадрате! Уравнение станет линейным. И решается уже совсем иначе…
Вот и все главные виды квадратных уравнений. Полные и неполные.
Решение квадратных уравнений.
Решение полных квадратных уравнений.
Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:
Если уравнение вам дано уже в таком виде — первый этап делать не нужно.) Главное — правильно определить все коэффициенты, а , b и c .
Формула для нахождения корней квадратного уравнения выглядит так:
Выражение под знаком корня называется дискриминант . Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с . Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:
Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:
а =1; b = 3; c = -4. Вот и записываем:
Пример практически решён:
Это ответ.
Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…
Самые распространённые ошибки – путаница со знаками значений a, b и с . Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !
Предположим, надо вот такой примерчик решить:
Здесь a = -6; b = -5; c = -1
Допустим, вы знаете, что ответы у вас редко с первого раза получаются.
Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится . Вот и пишем подробно, со всеми скобочками и знаками:
А количество ошибок резко сократится . Вот и пишем подробно, со всеми скобочками и знаками:
Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!
Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:
Узнали?) Да! Это неполные квадратные уравнения .
Решение неполных квадратных уравнений.
Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с .
Сообразили? В первом примере a = 1; b = -4; а c ? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0 ! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с , а b !
Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с , а b !
Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.
И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х 1 = 0 , х 2 = 4 .
Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку, х 1 — то, что меньше, а х 2 — то, что больше.
Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:
Остаётся корень извлечь из 9, и всё. Получится:
Тоже два корня. х 1 = -3 , х 2 = 3 .
Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…
Дискриминант. Формула дискриминанта.
Волшебное слово дискриминант ! Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:
Выражение под знаком корня называется дискриминантом. Обычно дискриминант обозначается буквой D . Формула дискриминанта:
Обычно дискриминант обозначается буквой D . Формула дискриминанта:
D = b 2 — 4ac
И чем же примечательно это выражение? Почему оно заслужило специальное название? В чём смысл дискриминанта? Ведь -b, или 2a в этой формуле специально никак не называют… Буквы и буквы.
Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.
1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.
2. Дискриминант равен нулю. Тогда у вас получится одно решение. Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых . Но, в упрощённом варианте, принято говорить об одном решении.
3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.
Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.
Честно говоря, при простом решении квадратных уравнений, понятие дискриминанта не особо-то и требуется. Подставляем в формулу значения коэффициентов, да считаем. Там всё само собой получается, и два корня, и один, и ни одного. Однако, при решении более сложных заданий, без знания смысла и формулы дискриминанта не обойтись. Особенно — в уравнениях с параметрами. Такие уравнения — высший пилотаж на ГИА и ЕГЭ!)
Итак, как решать квадратные уравнения через дискриминант вы вспомнили. Или научились, что тоже неплохо.) Умеете правильно определять a, b и с . Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?
А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности. … За которые потом бывает больно и обидно…
… За которые потом бывает больно и обидно…
Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:
Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:
И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:
А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.
Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку.
Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку.
Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b , который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.
Приём третий . Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…
При работе с дробями ошибки, почему-то так и лезут…
Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.
Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:
Вот и всё! Решать – одно удовольствие!
Итак, подытожим тему.
Практические советы:
1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .
2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.
3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.
4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!
Теперь можно и порешать.)
Решить уравнения:
8х 2 — 6x + 1 = 0
х 2 + 3x + 8 = 0
х 2 — 4x + 4 = 0
(х+1) 2 + x + 1 = (x+1)(x+2)
Ответы (в беспорядке):
х 1 = 0
х 2 = 5
х 1,2 = 2
х 1 = 2
х 2 = -0,5
х — любое число
х 1 = -3
х 2 = 3
решений нет
х 1 = 0,25
х 2 = 0,5
Всё сходится? Отлично! Квадратные уравнения — не ваша головная боль. Первые три получились, а остальные — нет? Тогда проблема не в квадратных уравнениях. Проблема в тождественных преобразованиях уравнений. Прогуляйтесь по ссылке, это полезно.
Первые три получились, а остальные — нет? Тогда проблема не в квадратных уравнениях. Проблема в тождественных преобразованиях уравнений. Прогуляйтесь по ссылке, это полезно.
Не совсем получается? Или совсем не получается? Тогда вам в помощь Раздел 555. Там все эти примеры разобраны по косточкам. Показаны главные ошибки в решении. Рассказывается, разумеется, и о применении тождественных преобразований в решении различных уравнений. Очень помогает!
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Неполное квадратное уравнение отличаются от классических (полных) уравнений тем, что его множители или свободный член равны нулю. Графиком таких функций являются параболы. В зависимости от общего вида их делят на 3 группы. Принципы решения для всех типов уравнений одинаковы.
Принципы решения для всех типов уравнений одинаковы.
Ничего сложного в определении типа неполного многочлена нет. Рассмотреть основные отличия лучше всего на наглядных примерах:
- Если b = 0, то уравнение имеет вид ax 2 + c = 0.
- Если c = 0, то решать следует выражение ax 2 + bx = 0.
- Если b = 0 и c = 0, то многочлен превращается в равенство типа ax 2 = 0.
Последний случай является скорее теоретической возможностью и никогда не встречается в заданиях для проверки знаний, так как единственно верное значение переменной x в выражении – это ноль. В дальнейшем будет рассмотрены способы и примеры решения неполных квадратных уравнений 1) и 2) видов.
Общий алгоритм поиска переменных и примеры с решением
Не зависимо от разновидности уравнения алгоритм решения сводится к следующим шагам:
- Привести выражение к удобному для поиска корней виду.
- Произвести вычисления.
- Записать ответ.
Решать неполные уравнения проще всего, разложив на множители левую часть и оставив ноль в правой. Таким образом, формула неполного квадратного уравнения для поиска корней сводится к вычислению значения x для каждого из множителей.
Таким образом, формула неполного квадратного уравнения для поиска корней сводится к вычислению значения x для каждого из множителей.
Научиться способам решения можно только лишь на практике, поэтому рассмотрим конкретный пример нахождения корней неполного уравнения:
Как видно, в данном случае b = 0. Разложим левую часть на множители и получим выражение:
4(x – 0,5) ⋅ (x + 0,5) = 0.
Очевидно, что произведение равно нулю, когда хотя бы один из множителей равен нулю. Подобным требованиям отвечают значения переменной x1 = 0,5 и (или) x2 = -0,5.
Для того, чтобы легко и быстро справляться с задачей разложения квадратного трехчлена на множители, следует запомнить следующую формулу:
Если в выражении отсутствует свободный член, задача многократно упрощается. Достаточно будет всего лишь найти и вынести за скобки общий знаменатель. Для наглядности рассмотрим пример, как решать неполные квадратные уравнения вида ax2 + bx = 0.
Вынесем переменную x за скобки и получим следующее выражение:
x ⋅ (x + 3) = 0.
Руководствуясь логикой, приходим к выводу, что x1 = 0, а x2 = -3.
Традиционный способ решения и неполные квадратные уравнения
Что же будет, если применить формулу дискриминанта и попытаться найти корни многочлена, при коэффициентах равных нулю? Возьмем пример из сборника типовых заданий для ЕГЭ по математики 2017 года, решим его с помощью стандартных формул и методом разложения на множители.
7x 2 – 3x = 0.
Рассчитаем значение дискриминант: D = (-3)2 – 4 ⋅ (-7) ⋅ 0 = 9. Получается, многочлен имеет два корня:
Теперь, решим уравнение разложением на множители и сравним результаты.
X ⋅ (7x + 3) = 0,
2) 7x + 3 = 0,
7x = -3,
x = -.
Как видно, оба метода дают одинаковый результат, но решить уравнение вторым способ получилось гораздо проще и быстрее.
Теорема Виета
А что же делать с полюбившейся теоремой Виета? Можно ли применять данный метод при неполном трехчлене? Попробуем разобраться в аспектах приведения неполных уравнений к классическому виду ax2 + bx + c = 0.
На самом деле применять теорему Виета в данном случае возможно. Необходимо лишь привести выражение к общему виду, заменив недостающие члены нулем.
Например, при b = 0 и a = 1, дабы исключить вероятность путаницы следует записать задание в виде: ax2 + 0 + c = 0. Тогда отношение суммы и произведения корней и множителей многочлена можно выразить следующим образом:
Теоретические выкладки помогают ознакомиться с сутью вопроса, и всегда требуют отработки навыка при решении конкретных задач. Снова обратимся к справочнику типовых заданий для ЕГЭ и найдем подходящий пример:
Запишем выражение в удобном для применения теоремы Виета виде:
x 2 + 0 – 16 = 0.
Следующим шагом составим систему условий:
Очевидно, что корнями квадратного многочлена будут x 1 = 4 и x 2 = -4.
Теперь, потренируемся приводить уравнение к общему виду. Возьмем следующий пример: 1/4× x 2 – 1 = 0
Для того, чтобы применить к выражению теорему Виета необходимо избавиться от дроби. Перемножим левую и правую части на 4, и посмотрим на результат: x2– 4 = 0. Полученное равенство готово для решения теоремой Виета, но гораздо проще и быстрее получить ответ просто перенеся с = 4 в правую часть уравнения: x2 = 4.
Перемножим левую и правую части на 4, и посмотрим на результат: x2– 4 = 0. Полученное равенство готово для решения теоремой Виета, но гораздо проще и быстрее получить ответ просто перенеся с = 4 в правую часть уравнения: x2 = 4.
Подводя итог, следует сказать, что лучшим способом решения неполных уравнений является разложения на множители, является самым простым и быстрым методом. При возникновении затруднений в процессе поиска корней можно обратиться к традиционному методу нахождения корней через дискриминант.
В данной статье мы рассмотрим решение неполных квадратных уравнений.
Но сначала повторим какие уравнения называются квадратными. Уравнение вида ах 2 + bх + с = 0, где х – переменная, а коэффициенты а, b и с некоторые числа, причем а ≠ 0, называется квадратным . Как мы видим коэффициент при х 2 не равен нулю, а следовательно коэффициенты при х или свободный член могут равняться нулю, в этом случае мы и получаем неполное квадратное уравнение.
Неполные квадратные уравнения бывают трех видов :
1) Если b = 0, с ≠ 0, то ах 2 + с = 0;
2) Если b ≠ 0, с = 0, то ах 2 + bх = 0;
3) Если b= 0, с = 0, то ах 2 = 0.
- Давайте разберемся как решаются уравнения вида ах 2 + с = 0.
Чтобы решить уравнение перенесем свободный член с в правую часть уравнения, получим
ах 2 = ‒с. Так как а ≠ 0, то разделим обе части уравнения на а, тогда х 2 = ‒с/а.
Если ‒с/а > 0 , то уравнение имеет два корня
x = ±√(–c/a) .
Если же ‒c/a
Давайте попробуем разобраться на примерах, как решать такие уравнения.
Пример 1 . Решите уравнение 2х 2 ‒ 32 = 0.
Ответ: х 1 = ‒ 4, х 2 = 4.
Пример 2 . Решите уравнение 2х 2 + 8 = 0.
Ответ: уравнение решений не имеет.
- Разберемся как же решаются уравнения вида ах 2 + bх = 0.
Чтобы решить уравнение ах 2 + bх = 0, разложим его на множители, то есть вынесем за скобки х, получим х(ах + b) = 0. Произведение равно нулю, если хотя бы один из множителей равен нулю. Тогда или х = 0, или ах + b = 0. Решая уравнение ах + b = 0, получим ах = ‒ b, откуда х = ‒ b/a. Уравнение вида ах 2 + bх = 0, всегда имеет два корня х 1 = 0 и х 2 = ‒ b/a. Посмотрите как выглядит на схеме решение уравнений этого вида.
Уравнение вида ах 2 + bх = 0, всегда имеет два корня х 1 = 0 и х 2 = ‒ b/a. Посмотрите как выглядит на схеме решение уравнений этого вида.
Закрепим наши знания на конкретном примере.
Пример 3 . Решить уравнение 3х 2 ‒ 12х = 0.
х(3х ‒ 12) = 0
х= 0 или 3х – 12 = 0
Ответ: х 1 = 0, х 2 = 4.
- Уравнения третьего вида ах 2 = 0 решаются очень просто.
Если ах 2 = 0, то х 2 = 0. Уравнение имеет два равных корня х 1 = 0, х 2 = 0.
Для наглядности рассмотрим схему.
Убедимся при решении примера 4, что уравнения этого вида решаются очень просто.
Пример 4. Решить уравнение 7х 2 = 0.
Ответ: х 1, 2 = 0.
Не всегда сразу понятно какой вид неполного квадратного уравнения нам предстоит решить. Рассмотрим следующий пример.
Пример 5. Решить уравнение
Умножим обе части уравнения на общий знаменатель, то есть на 30
Сократим
5(5х 2 + 9) – 6(4х 2 – 9) = 90.
Раскроем скобки
25х 2 + 45 – 24х 2 + 54 = 90.
Приведем подобные
Перенесем 99 из левой части уравнения в правую, изменив знак на противоположный
Ответ: корней нет.
Мы разобрали как решаются неполные квадратные уравнения. Надеюсь, теперь у вас не будет сложностей с подобными заданиями. Будьте внимательны при определении вида неполного квадратного уравнения, тогда у вас все получится.
Если у вас появились вопросы по данной теме, записывайтесь на мои уроки , мы вместе решим возникшие проблемы.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Из истории квадратных уравнений. История развития квадратных уравнений
1.1. Из истории возникновения квадратных уравнений
Алгебра возникла в связи с решением разнообразных задач при помощи уравнений. Обычно в задачах требуется найти одну или несколько неизвестных, зная при этом результаты некоторых действий, произведенных над искомыми и данными величинами.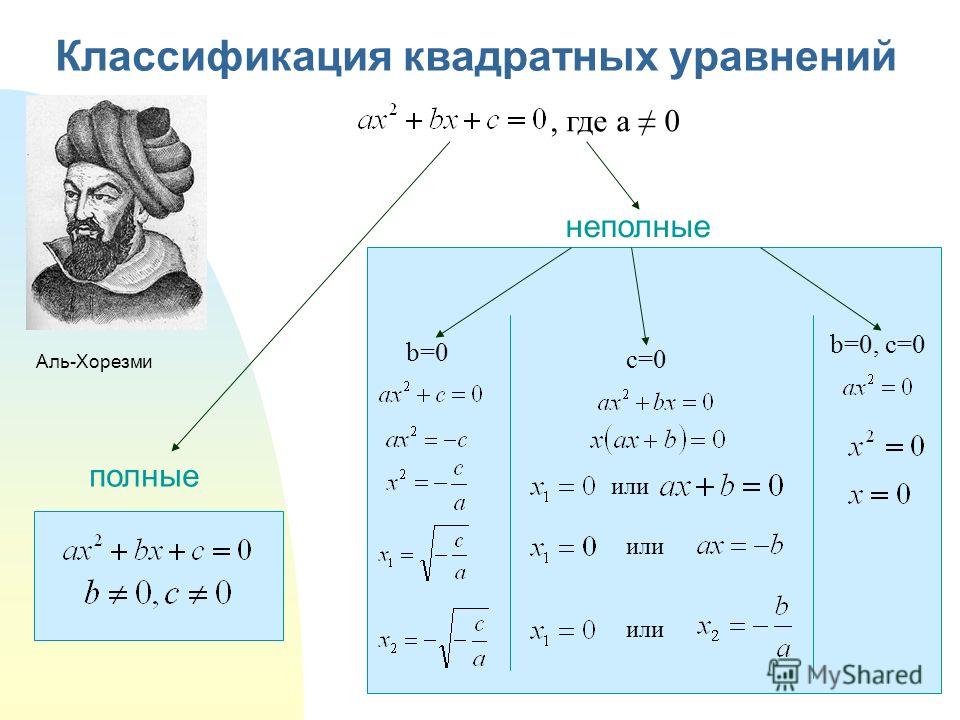 Такие задачи сводятся к решению одного или системы нескольких уравнений, к нахождению искомых с помощью алгебраических действий над данными величинами. В алгебре изучаются общие свойства действий над величинами.
Такие задачи сводятся к решению одного или системы нескольких уравнений, к нахождению искомых с помощью алгебраических действий над данными величинами. В алгебре изучаются общие свойства действий над величинами.
Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне.
Квадратные уравнения в Древнем Вавилоне
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
Задача 2. «Найти два числа, зная, что их сумма равна 20, а произведение — 96».
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 + х. Другое же меньше, т. е. 10 — х. Разность между ними 2х. Отсюда уравнение:
е. 10 + х. Другое же меньше, т. е. 10 — х. Разность между ними 2х. Отсюда уравнение:
(10+x)(10-x) =96,
Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = — 2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Если решить эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то можно прийти к решению уравнения:
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения.
Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
ax 2 + bх = с, а> 0. (1)
В уравнении (1) коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
Правило Брахмагупты по существу совпадает с нашим.
В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
Решение Бхаскары свидетельствует о том, что автор знал о двузначности корней квадратных уравнений.
Соответствующее задаче 3 уравнение:
Бхаскара пишет под видом:
x 2 — 64x = — 768
и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 32 2 , получая затем:
x 2 — б4х + 32 2 = -768 + 1024,
(х — 32) 2 = 256,
x 1 = 16, x 2 = 48.
Квадратные уравнения у Аль-Хорезми
В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
Автор насчитывает 6 видов уравнений, выражая их следующим образом:
1) «Квадраты равны корням», т. е. ах 2 = bх.
2) «Квадраты равны числу», т. е. ах 2 = с.
3) «Корни равны числу», т. е. ах = с.
4) «Квадраты и числа равны корням», т. е. ах 2 + с = bх.
5) «Квадраты и корни равны числу», т. е. ах 2 + bх =с.
6) «Корни и числа равны квадратам», т. е. bх + с == ах 2 .
Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения.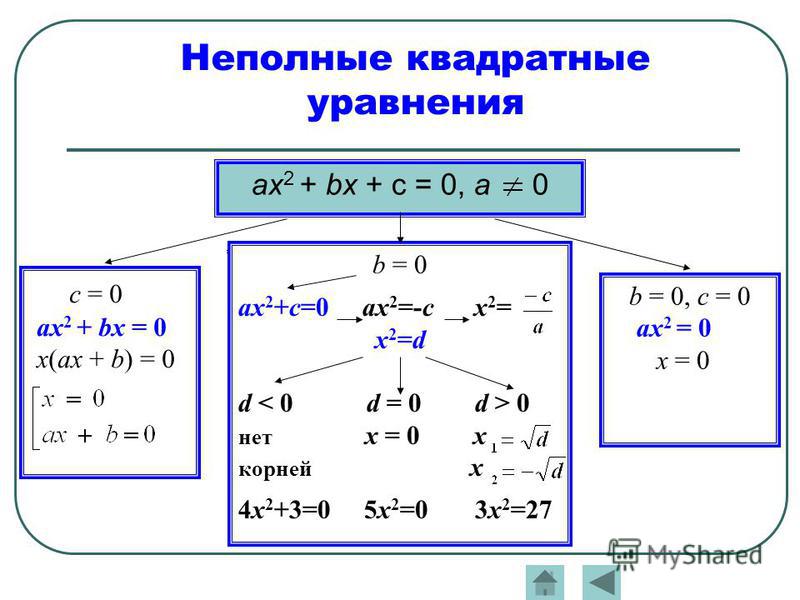 При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
Приведем пример.
Задача 4. «Квадрат и число 21 равны 10 корням. Найти корень» (подразумевается корень уравнения х 2 + 21 = 10х).
Решение: раздели пополам число корней, получишь 5, умножь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат Аль-Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.
Квадратные уравнения в Европе XII-XVII в.
Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел.
Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV-XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду x 2 + bх = с при всевозможных комбинациях знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М.Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид..
Истоки алгебраических методов решения практических задач связаны с наукой древнего мира. Как известно из истории математики, значительная часть задач математического характера, решаемых египетскими, шумерскими, вавилонскими писцами-вычислителями (XX-VI вв. до н. э.), имела расчетный характер. Однако уже тогда время от времени возникали задачи, в которых искомое значение величины задавалось некоторыми косвенными условиями, требующими, с нашей современной точки зрения, составления уравнения или системы уравнений. Первоначально для решения таких задач применялись арифметические методы. В дальнейшем начали формироваться начатки алгебраических представлений. Например, вавилонские вычислители умели решать задачи, сводящиеся с точки зрения современной классификации к уравнениям второй степени. Был создан метод решения текстовых задач, послуживший в дальнейшем основой для выделения алгебраического компонента и его независимого изучения.
до н. э.), имела расчетный характер. Однако уже тогда время от времени возникали задачи, в которых искомое значение величины задавалось некоторыми косвенными условиями, требующими, с нашей современной точки зрения, составления уравнения или системы уравнений. Первоначально для решения таких задач применялись арифметические методы. В дальнейшем начали формироваться начатки алгебраических представлений. Например, вавилонские вычислители умели решать задачи, сводящиеся с точки зрения современной классификации к уравнениям второй степени. Был создан метод решения текстовых задач, послуживший в дальнейшем основой для выделения алгебраического компонента и его независимого изучения.
Это изучение осуществлялось уже в другую эпоху сначала арабскими математиками (VI-Х вв. н. э.), выделившими характерные действия, посредством которых уравнения приводились к стандартному виду приведение подобных членов, перенос членов из одной части уравнения в другую с переменой знака. А затем европейскими математиками Возрождения, в итоге длительного поиска создавшими язык современной алгебры, использование букв, введение символов арифметических операций, скобок и т. д. На рубеже XVI-XVII вв. алгебра как специфическая часть математики, обладающая своим предметом, методом, областями приложения, была уже сформирована. Дальнейшее ее развитие, вплоть до нашего времени, состояло в совершенствовании методов, расширении области приложений, уточнении понятий и связей их с понятиями других разделов математики.
д. На рубеже XVI-XVII вв. алгебра как специфическая часть математики, обладающая своим предметом, методом, областями приложения, была уже сформирована. Дальнейшее ее развитие, вплоть до нашего времени, состояло в совершенствовании методов, расширении области приложений, уточнении понятий и связей их с понятиями других разделов математики.
Итак, ввиду важности и обширности материала, связанного с понятием уравнения, его изучение в современной методике математики связано с тремя главными областями своего возникновения и функционирования.
ВВЕДЕНИЕ
Уравнения в школьном курсе алгебры
занимают ведущее место. На их изучение
отводится времени больше, чем на любую
другую тему школьного курса математики.
Сила теории уравнений в том, что она не
только имеет теоретическое значение
для познания естественных законов, но
и служит конкретным практическим целям.
Большинство задач о пространственных
формах и количественных отношениях
реального мира сводится к решению
различных видов уравнений. Овладевая
способами их решения, люди находят
ответы на различные вопросы из науки и
техники (транспорт, сельское хозяйство,
промышленность, связь и т. д.). Так же для
формирования умения решать уравнения
большое значение имеет самостоятельная
работа учащегося при обучении решения
уравнений. При изучении любой темы
уравнения могут быть использованы как
эффективное средство закрепления,
углубления, повторения и расширения
теоретических знаний, для развития
творческой математической деятельности
учащихся .
Овладевая
способами их решения, люди находят
ответы на различные вопросы из науки и
техники (транспорт, сельское хозяйство,
промышленность, связь и т. д.). Так же для
формирования умения решать уравнения
большое значение имеет самостоятельная
работа учащегося при обучении решения
уравнений. При изучении любой темы
уравнения могут быть использованы как
эффективное средство закрепления,
углубления, повторения и расширения
теоретических знаний, для развития
творческой математической деятельности
учащихся .
В
современном мире уравнения широко
используются в различных разделах
математики, в решении важных прикладных
задач. Для этой темы характерна большая
глубина изложения и богатство
устанавливаемых с ее помощью связей в
обучении, логическая обоснованность
изложения. Поэтому она занимает
исключительное положение в линии
уравнений. К изучению темы «Квадратные
трехчлены» учащиеся приступают, уже
накопив определенный опыт, владея
достаточно большим запасом алгебраических
и общематематических представлений,
понятий, умений. В значительной мере
именно на материале данной темы необходимо
осуществлять синтез материала,
относящегося к уравнениям, реализовывать
принципы историзма, доступности.
В значительной мере
именно на материале данной темы необходимо
осуществлять синтез материала,
относящегося к уравнениям, реализовывать
принципы историзма, доступности.
Актуальность темы состоит в необходимости реализовывать принципы историзма и недостаточности материала для реализации этого по теме «Решение квадратных уравнений».
Проблема исследования : выявление исторического материала для обучения решению квадратных уравнений.
Цель работы : формирование представлений о работе над квадратными уравнениями на уроках математики, подбор комплекса уроков с элементами историзма по теме «Квадратные уравнения».
Объект исследования : решение квадратных уравнений в 8 классе с использованием элементов историзма.
Предмет исследования : квадратные уравнения и разработки уроков по обучению решения квадратных уравнений с использованием исторических материалов.
Задачи :
выполнить анализ научно-методической литературы по проблеме исследования;
проанализировать школьные учебники и выделить в них место обучения решению квадратных уравнений;
подобрать комплекс
уроков по решению квадратных уравнений
с использованием исторических
материалов.
Методы исследования :
анализ литературы по теме «Решение квадратных уравнений»;
наблюдение за учащимися во время урока на тему «Решение квадратных уравнений»;
подбор материала: уроков по теме «Решение квадратных уравнений» с использованием исторической справки.
Алгебра возникла в связи с решением разнообразных задач при помощи уравнений. Обычно в задачах требуется найти одну или несколько неизвестных, зная при этом результаты некоторых действий, произведенных над искомыми и данными величинами. Такие задачи сводятся к решению одного или системы нескольких уравнений, к нахождению искомых с помощью алгебраических действий над данными величинами. В алгебре изучаются общие свойства действий над величинами.
Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне.
Квадратные уравнения в Древнем Вавилоне
Необходимость
решать уравнения не только первой, но
и второй степени еще в древности была
вызвана потребностью решать задачи,
связанные с нахождением площадей
земельных участков и с земляными работами
военного характера, а также с развитием
астрономии и самой математики. Квадратные
уравнения умели решать около
2000 лет до
нашей эры вавилоняне. Применяя современную
алгебраическую запись, можно сказать,
что в их клинописных текстах встречаются,
кроме неполных, и такие, например, полные
квадратные уравнения:
Квадратные
уравнения умели решать около
2000 лет до
нашей эры вавилоняне. Применяя современную
алгебраическую запись, можно сказать,
что в их клинописных текстах встречаются,
кроме неполных, и такие, например, полные
квадратные уравнения:
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении
уравнений Диофант для упрощения решения
умело выбирает неизвестные.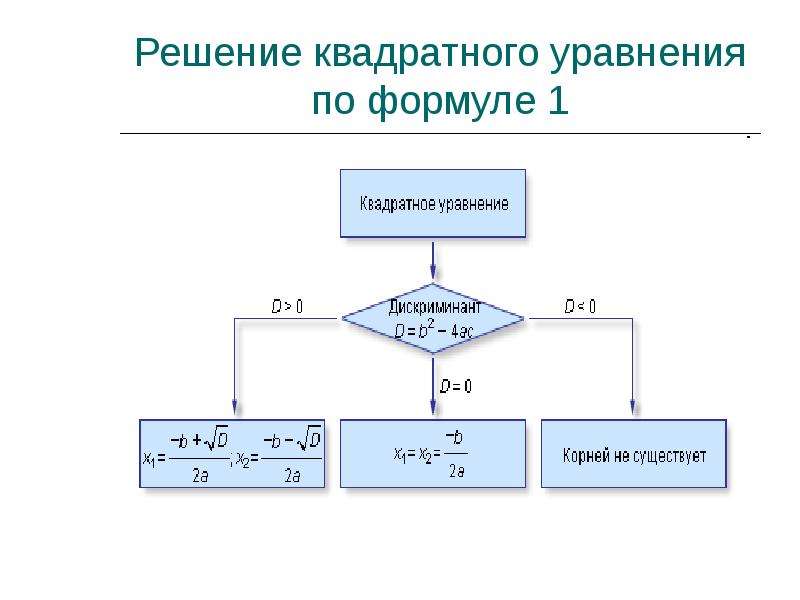
Вот, к примеру, одна из его задач.
Задача 2. «Найти два числа, зная, что их сумма равна 20, а произведение – 96».
Диофант
рассуждает следующим образом: из условия
задачи вытекает, что искомые числа не
равны, так как если бы они были равны,
то их произведение равнялось бы не
96, а
100. Таким
образом, одно из них будет больше половины
их суммы, т. е.
.
Другое же меньше, т. е.
.
Разность между ними
.
Отсюда уравнение:
Отсюда
.
Одно из искомых чисел равно
12, другое
8. Решение
для Диофанта не существует, так как
греческая математика знала только
положительные числа.
Если решить эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то можно прийти к решению уравнения:
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения.
Квадратные уравнения в Индии
Задачи
на квадратные уравнения встречаются
уже в астрономическом трактате
«Ариабхаттиам», составленном в
499 г. индийским математиком и астрономом
Ариабхаттой. Другой индийский ученый,
Брахмагупта
(VII в.),
изложил общее правило решения квадратных
уравнений, приведенных к единой
канонической форме:
индийским математиком и астрономом
Ариабхаттой. Другой индийский ученый,
Брахмагупта
(VII в.),
изложил общее правило решения квадратных
уравнений, приведенных к единой
канонической форме:
(1)
В уравнении (1) коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
Решение Бхаскары свидетельствует о том, что автор знал о двузначности корней квадратных уравнений.
Соответствующее задаче 3 уравнение:
Бхаскара пишет под видом:
и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 322, получая затем:
Квадратные уравнения у Аль-Хорезми
В
алгебраическом трактате Аль-Хорезми
дается классификация линейных и
квадратных уравнений.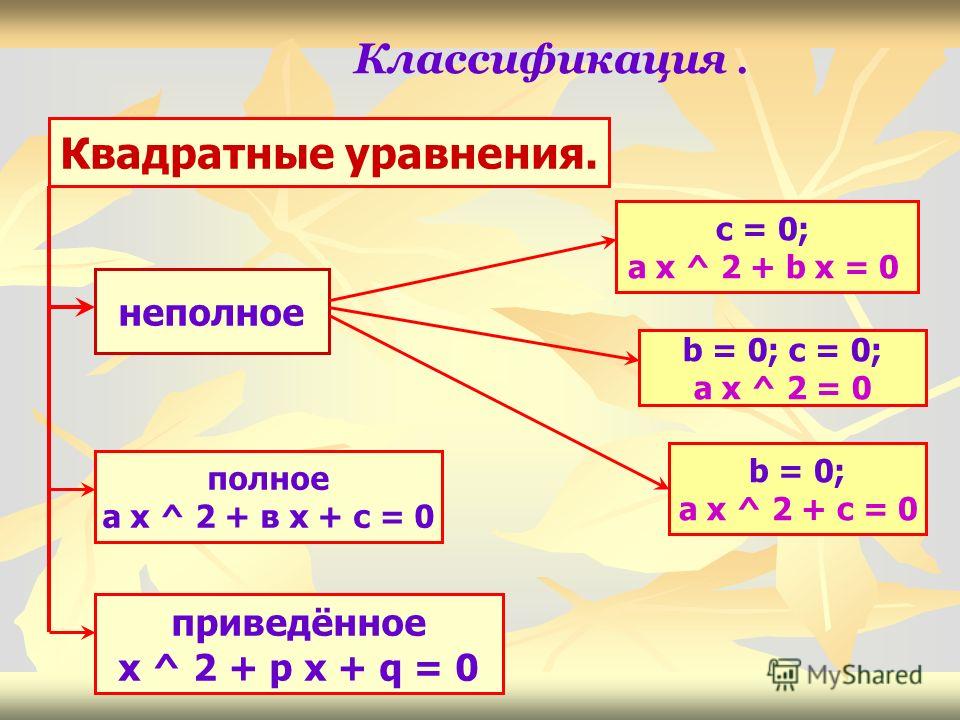 Автор насчитывает
6 видов
уравнений, выражая их следующим образом:
Автор насчитывает
6 видов
уравнений, выражая их следующим образом:
Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
Приведем пример.
Задача
4. «Квадрат
и число
21 равны
10 корням.
Найти корень» (подразумевается корень
уравнения
).
Решение: раздели пополам число корней, получишь 5, умножь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат Аль-Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения .
Квадратные уравнения в Европе XII — XVII в.
Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел.
Эта
книга способствовала распространению
алгебраических знаний не только в
Италии, но и в Германии, Франции и других
странах Европы. Многие задачи из этой
книги переходили почти во все европейские
учебники XIV-XVII
вв. Общее правило решения квадратных
уравнений, приведенных к единому
каноническому виду
Общее правило решения квадратных
уравнений, приведенных к единому
каноническому виду
при всевозможных комбинациях знаков и
коэффициентовb,
c,
было сформулировано в Европе в 1544 г. М.
Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид .
Истоки
алгебраических методов решения
практических задач связаны с наукой
древнего мира. Как известно из истории
математики, значительная часть задач
математического характера, решаемых
египетскими, шумерскими, вавилонскими
писцами-вычислителями
(XX-VI вв.
до н. э.), имела расчетный характер. Однако
уже тогда время от времени возникали
задачи, в которых искомое значение
величины задавалось некоторыми косвенными
условиями, требующими, с нашей современной
точки зрения, составления уравнения
или системы уравнений. Первоначально
для решения таких задач применялись
арифметические методы. В дальнейшем
начали формироваться начатки алгебраических
представлений. Например, вавилонские
вычислители умели решать задачи,
сводящиеся с точки зрения современной
классификации к уравнениям второй
степени. Был создан метод решения
текстовых задач, послуживший в дальнейшем
основой для выделения алгебраического
компонента и его независимого изучения.
Первоначально
для решения таких задач применялись
арифметические методы. В дальнейшем
начали формироваться начатки алгебраических
представлений. Например, вавилонские
вычислители умели решать задачи,
сводящиеся с точки зрения современной
классификации к уравнениям второй
степени. Был создан метод решения
текстовых задач, послуживший в дальнейшем
основой для выделения алгебраического
компонента и его независимого изучения.
Это
изучение осуществлялось уже в другую
эпоху сначала арабскими математиками
(VI-Х вв.
н. э.), выделившими характерные действия,
посредством которых уравнения приводились
к стандартному виду приведение подобных
членов, перенос членов из одной части
уравнения в другую с переменой знака.
А затем европейскими математиками
Возрождения, в итоге длительного поиска
создавшими язык современной алгебры,
использование букв, введение символов
арифметических операций, скобок и т. д.
На рубеже
XVI-XVII вв.
алгебра как специфическая часть
математики, обладающая своим предметом,
методом, областями приложения, была уже
сформирована. Дальнейшее ее развитие,
вплоть до нашего времени, состояло в
совершенствовании методов, расширении
области приложений, уточнении понятий
и связей их с понятиями других разделов
математики.
Дальнейшее ее развитие,
вплоть до нашего времени, состояло в
совершенствовании методов, расширении
области приложений, уточнении понятий
и связей их с понятиями других разделов
математики.
Итак, ввиду важности и обширности материала, связанного с понятием уравнения, его изучение в современной методике математики связано с тремя главными областями своего возникновения и функционирования.
Ковальчук Кирилл
Проект «Квадратные уравнения через века и страны» знакомит учащихся с учеными математики, открытия которых являются основой научно-технического прогресса, развивает интерес к математике как к предмету на основе знакомства с историческим материалом, расширяет кругозор учащихся, стимулирует их познавательную активность и творчество.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Проектная работа ученика 8 класса МОУ СОШ №17 с. Борисовка Ковальчука Кирилла Руководитель Мулюкова Г.В.
Борисовка Ковальчука Кирилла Руководитель Мулюкова Г.В.
Квадратные уравнения через века и страны
Цель проекта: Познакомить учащихся с учеными математики, открытия которых являются основой научно-технического прогресса. Показать значимость работ ученых для развития геометрии и физики.??????????? Наглядно продемонстрировать применение научных открытий в жизни. Развивать интерес к математике как к предмету на основе знакомства с историческим материалом. Расширять кругозор учащихся, стимулировать их познавательную активность и творчество
Необходимость решать уравнения не только первой степени, но и второй ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков, с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Правила решения этих уравнений, изложенные в вавилонских текстах, совпадает по существу с современными, но в этих текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
. (ок. 365 — 300 г. до н.э.) — древнегреческий математик, автор первых дошедших до нас теоретических трактатов по математике. Евклид, или Эвклид
Евклид Начала Там, где с морем Сливается Нил, В древнем жарком краю Пирамид Математик греческий жил — Многознающий, Мудрый Эвклид. Геометрию он изучал, Геометрии он обучал. Написал он великий труд. Эту книгу «Начала» зовут.
Евклид 3 век до н.э. Евклид решал квадратные уравнения, применяя геометрический способ. Вот одна из задач из древнегреческого трактата: «Имеется город с границей в виде квадрата со стороной неизвестного размера, в центре каждой стороны находятся ворота. На расстоянии 20бу(1бу=1,6м) от северных ворот стоит столб. Если пройти от южных ворот 14бу прямо, затем повернуть на запад и пройти еще 1775бу, то можно увидеть столб. Спрашивается: какова сторона границы города? »
Чтобы определить неизвестную сторону квадрата, получаем квадратное уравнение x ² +(k+l)x-2kd =0 . В данном случае уравнение имеет вид x ² +34x-71000=0 , откуда х=250бу l x d k
Квадратные уравнения в Индии Задачи на квадратные уравнения встречаются и в астрономическом трактате « Ариабхаттиам », составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта, изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме: ax ² +bx=c , a>0 В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи».
индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта, изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме: ax ² +bx=c , a>0 В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи».
Одна из задач знаменитого индийского математика XІІ века Бхаскары Обезьянок резвых стая Всласть поевши, развлекалась. Их в квадрате часть восьмая На поляне забавлялась. А двенадцать по лианам… Стали прыгать повисая… Сколько было обезьянок Ты скажи мне, в этой стае?.
Решение. () 2 +12 = х, х 2 — 64х +768 = 0, а =1, в = -64, с = 768, тогда Д = (-64) 2 -4·1·768 = 1024 > 0. Х 1 , 2 = , х 1 = 48, х 2 = 16. Ответ.Обезьян было 16 или 48. Давайте решим её.
Формула корней квадратного уравнения « переоткрывалась » неоднократно. Один из первых дошедших до наших дней выводов этой формулы принадлежит индийскому математику Брахмагупте. Среднеазиатский ученый ал-Хорезми в трактате « Китаб аль-джерб валь-мукабала » получил эту формулу методом выделения полного квадрата.
Один из первых дошедших до наших дней выводов этой формулы принадлежит индийскому математику Брахмагупте. Среднеазиатский ученый ал-Хорезми в трактате « Китаб аль-джерб валь-мукабала » получил эту формулу методом выделения полного квадрата.
Как же решал ал-Хорезми это уравнение. Он писал: «Правило таково: раздвои число корней, х=2х · 5 получите в этой задаче пять, 5 умножь на это равное ему, будет двадцать пять, 5 · 5=25 прибавь это к тридцати девяти, 25+39 будет шестьдесят четыре, 64 извлеки из этого корень, будет восемь, 8 и вычти из этого половину числа корней, т.е.пять, 8- 5 останется три- это и 3 Будет корень квадрата, который ты искал.» А второй корень? Второй корень не находили, так как отрицательные числа не были известны. х 2 +10 х = 39
Квадратные уравнения в Европе 13-17вв. Формулы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Этот объемистый труд, в котором отражено влияние математики как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники 16-17вв. и частично 18.
Автор разработал самостоятельно некоторые новые алгебраические решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники 16-17вв. и частично 18.
Франсуа Виет – крупнейший математик 16 века
До Ф. Виета решение квадратного уравнения выполнялось по своим правилам в виде очень длинных словесных рассуждений и описаний, довольно громоздких действий. Даже само уравнение не могли записать, для этого требовалось довольно длинное и сложное словесное описание. Он ввел термин «коэффициент». Предложил искомые величины обозначать гласными, а данные – согласными. Благодаря символике Виета можно записать квадратное уравнение в виде: ax 2 + bx + c =0 . Теорема: Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. Несмотря на то, что эта теорема называется «Теорема Виета», она была известна и до него, а он только преобразовал ее в современный вид. Виета называют «отцом алгебры»
Несмотря на то, что эта теорема называется «Теорема Виета», она была известна и до него, а он только преобразовал ее в современный вид. Виета называют «отцом алгебры»
Человечество прошло длительный путь от незнания к знанию, непрерывно заменяя на этом пути неполное и несовершенное знание все более полным и совершенным. Заключительное слово
Нас, живущих в начале XXI века, влечет старина. В своих предках мы замечаем прежде всего то, чего им не хватает с современной точки зрения, и обычно не замечаем того, что нам самим не хватает по сравнению с ними.
Не будем и мы забывать о них…
СПАСИБО ЗА внимание!
HTML-версии работы пока нет.
Подобные документы
История развития формул корней квадратных уравнений. Квадратные уравнения в Древнем Вавилоне. Решение квадратных уравнений Диофантом. Квадратные уравнения в Индии, в Хорезмии и в Европе XIII — XVII вв. Теорема Виета, современная алгебраическая запись.
контрольная работа , добавлен 27. 11.2010
11.2010
История квадратных уравнений: уравнения в Древнем Вавилоне и Индии. Формулы четного коэффициента при х. Квадратные уравнения частного характера. Теорема Виета для многочленов высших степеней. Исследование биквадратных уравнений. Сущность формулы Кордано.
реферат , добавлен 09.05.2009
Выведение формулы решения квадратного уравнения в истории математики. Сравнительный анализ технологий различных способов решения уравнений второй степени, примеры их применения. Краткая теория решения квадратных уравнений, составление задачника.
реферат , добавлен 18.12.2012
Значение математики в нашей жизни. История возникновения счета. Развитие методов вычислительной математики в настоящее время. Использование математики в других науках, роль математического моделирования. Состояние математического образования в России.
статья , добавлен 05.01.2010
Греческая математика. Средние века и Возрождение. Начало современной математики. Современная математика. В основе математики лежит не логика, а здравая интуиция. Проблемы оснований математики являются философскими.
В основе математики лежит не логика, а здравая интуиция. Проблемы оснований математики являются философскими.
реферат , добавлен 06.09.2006
История развития математической науки в Европе VI-XIV вв., ее представители и достижения. Развитие математики эпохи Возрождения. Создание буквенного исчисления, деятельность Франсуа Виета. Усовершенствование вычислений в конце XVI – начале XVI вв.
презентация , добавлен 20.09.2015
Обзор развития европейской математики в XVII-XVIII вв. Неравномерность развития европейской науки. Аналитическая геометрия. Создание математического анализа. Научная школа Лейбница. Общая характеристика науки в XVIII в. Направления развития математики.
презентация , добавлен 20.09.2015
Период зарождения математики (до VII-V вв. до н.э.). Время математики постоянных величин (VII-V вв. до н.э. – XVII в. н.э.). Математика переменных величин (XVII-XIX вв.). Современный период развития математики. Особенности компьютерной математики.
презентация , добавлен 20.09.2015
Достижения древнегреческих математиков, живших в период между VI веком до н.э. и V веком н.э. Особенности начального периода развития математики. Роль пифагорейской школы в развитии математики: Платон, Евдокс, Зенон, Демокрит, Евклид, Архимед, Аполлоний.
контрольная работа , добавлен 17.09.2010
История становления математики как науки. Период элементарной математики. Период создания математики переменных величин. Создание аналитической геометрии, дифференциального и интегрельного исчисления. Развитие математики в России в XVIII-XIX столетиях.
Представители различных цивилизаций: Древнего Египта, Древнего Вавилона, Древней Греции, Древней Индии, Древнего Китая, Средневекового Востока, Европы овладели приемами решения квадратных уравнений.
Впервые квадратное уравнение сумели решить математики Древнего Египта. В одном из математических папирусов содержится задача:
«Найти стороны поля, имеющего форму прямоугольника, если его площадь 12, а – длины равны ширине». «Длина поля равна 4», – указано в папирусе.
«Длина поля равна 4», – указано в папирусе.
Прошли тысячелетия, в алгебру вошли отрицательные числа. Решая уравнение х²= 16, мы получаем два числа: 4, –4.
Разумеется, в задаче египтян мы приняли бы X = 4, так как длина поля может быть только положительной величиной.
Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Правило решения квадратных уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом вавилоняне «дошли до этого». Но почти во всех найденных папирусах и клинописных текстах приводятся только задачи с решениями. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: «Смотри!», «Делай так!», «Ты правильно нашел!».
Греческий математик Диофант составлял и решал квадратные уравнения. В его «Арифметике» нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
Задачи на составление квадратных уравнений встречаются уже в астрономическом трактате «Ариа-бхатиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой.
Другой индийский ученый Брахмагупта (VII в.) изложил общее правило решения квадратных уравнений вида ах² + bх = с.
В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг по поводу таких соревнований говорится следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары:
Обезьянок резвых стая
Всласть поевши, развлекалась.
Их в квадрате часть восьмая на поляне забавлялась.
А двенадцать по лианам… стали прыгать, повисая…
Сколько ж было обезьянок,
Ты скажи мне, в этой стае?
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений.
Наиболее древние из дошедших до нас китайских математических текстов относятся к концу I в. до н.э. Во II в. до н.э. была написана «Математика в девяти книгах». Позднее, в VII в., она вошла в сборник «Десять классических трактатов», который изучали в течение многих столетий. В трактате «Математика в девяти книгах» объясняется, как извлечь квадратный корень с помощью формулы квадрата суммы двух чисел.
Метод получил название «тянь-юань» (буквально – «небесный элемент») – так китайцы обозначали неизвестную величину.
Первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово «аль-джебр»– со временем превратилось в хорошо знакомое всем слово «алгебра», а само сочинение аль-Хорезми стало отправной точкой в становлении науки о решении уравнений. В алгебраическом трактате аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает шесть видов уравнений, выражая их следующим образом:
-квадраты равны корням , то есть ах² = bх;
-квадраты равны числу , то есть ах² = с;
-корни равны числу , то есть ах = с;
-квадраты и числа равны корням , то есть ах²+ с = bх;
-квадраты и корни равны числу , то есть ах² + bх = с;
-корни и числа равны квадратам , то есть bх + с = ах²;
Трактат аль-Хорезми является первой дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.
Формулы решения квадратных уравнений по образцу аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Автор самостоятельно разработал некоторые новые алгебраические примеры решения задач и первым в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» были включены почти во все европейские учебники XVI-XVII в. и частично XVIII в.
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х² + bх = с, при всевозможных комбинациях знаков коэффициентов b и с было сформулировано в Европе лишь в 1544 г. М.Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако он также признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают помимо положительных и отрицательные корни. Лишь в XVII в., благодаря трудам Жирара, Декарта, Ньютона и других ученых, способ решения квадратных уравнений принимает современный вид.
Лишь в XVII в., благодаря трудам Жирара, Декарта, Ньютона и других ученых, способ решения квадратных уравнений принимает современный вид.
Решение квадратных уравнений через k. Как решать квадратные уравнения? Дискриминант
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D
= 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
Наконец, если D
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x 2 + 9x = 0;
- x 2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b
= 0, тогда получим неполное квадратное уравнение вида ax
2 + c
= 0. Немного преобразуем его:
Пусть b
= 0, тогда получим неполное квадратное уравнение вида ax
2 + c
= 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c /a )
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобкуПроизведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.
С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».
Какие же квадратные уравнения называются полными? Это уравнения вида ах 2 + b x + c = 0 , где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.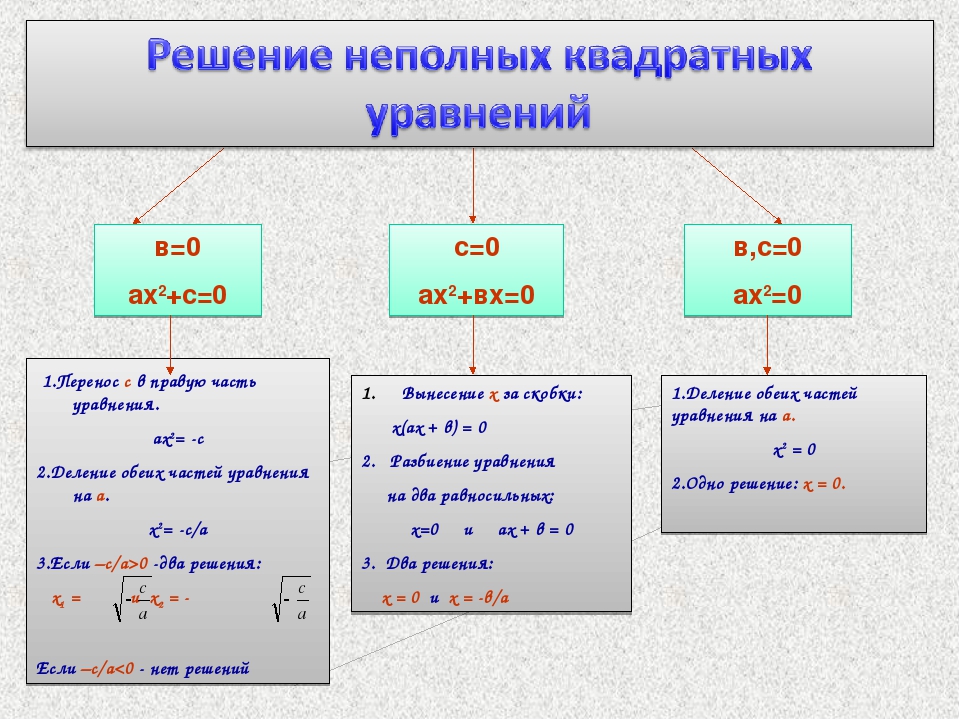
D = b 2 – 4ас.
В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.
Если дискриминант отрицательное число (D
Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),
тогда х 1 = (-b — √D)/2a , и х 2 = (-b + √D)/2a .
Например. Решить уравнение х 2 – 4х + 4= 0.
D = 4 2 – 4 · 4 = 0
x = (- (-4))/2 = 2
Ответ: 2.
Решить уравнение 2х 2 + х + 3 = 0.
D = 1 2 – 4 · 2 · 3 = – 23
Ответ: корней нет .
Решить уравнение 2х 2 + 5х – 7 = 0 .
D = 5 2 – 4 · 2 · (–7) = 81
х 1 = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5
х 2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1
Ответ: – 3,5 ; 1 .
Итак представим решение полных квадратных уравнений схемой на рисунке1.
По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида
ах 2 + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х 2 = 0, ошибочно можно решить, что
Например, в записи уравнения х + 3 + 2х 2 = 0, ошибочно можно решить, что
а = 1, b = 3 и с = 2. Тогда
D = 3 2 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).
Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах 2 , затем с меньшим – bx , а затем свободный член с.
При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.
Полное квадратное уравнение называется приведенным, если коэффициент при х 2 равен единице и уравнение примет вид х 2 + px + q = 0 . Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а , стоящий при х 2 .
Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а , стоящий при х 2 .
На рисунке 3 приведена схема решения приведенных квадратных
уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.
Пример. Решить уравнение
3х 2 + 6х – 6 = 0.
Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.
D = 6 2 – 4 · 3 · (– 6) = 36 + 72 = 108
√D = √108 = √(36 · 3) = 6√3
х 1 = (-6 — 6√3)/(2 · 3) = (6 (-1- √(3)))/6 = –1 – √3
х 2 = (-6 + 6√3)/(2 · 3) = (6 (-1+ √(3)))/6 = –1 + √3
Ответ: –1 – √3; –1 + √3
Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам, приведенным на схеме рисунка D 1 = 3 2 – 3 · (– 6) = 9 + 18 = 27
√(D 1) = √27 = √(9 · 3) = 3√3
х 1 = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3
х 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3
Ответ: –1 – √3; –1 + √3 . Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x 2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного
Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x 2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного
уравнения рисунок 3.
D 2 = 2 2 – 4 · (– 2) = 4 + 8 = 12
√(D 2) = √12 = √(4 · 3) = 2√3
х 1 = (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3
х 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3
Ответ: –1 – √3; –1 + √3.
Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Библиографическое описание: Гасанов А. Р., Курамшин А. А., Ельков А. А., Шильненков Н. В., Уланов Д. Д., Шмелева О. В. Способы решения квадратных уравнений // Юный ученый. 2016. №6. 1. С. 17-20..02.2019).
1. С. 17-20..02.2019).
Наш проект посвящен способам решения квадратных уравнений. Цель проекта: научиться решать квадратные уравнения способами, не входящими в школьную программу. Задача: найти все возможные способы решения квадратных уравнений и научиться их использовать самим и познакомить одноклассников с этими способами.
Что же такое «квадратные уравнения»?
Квадратное уравнение — уравнение вида ax 2 + bx + c = 0 , где a , b , c — некоторые числа (a ≠ 0 ), x — неизвестное.
Числа a, b,c называются коэффициентами квадратного уравнения.
- a называется первым коэффициентом;
- b называется вторым коэффициентом;
- c — свободным членом.
А кто же первый «изобрёл» квадратные уравнения?
Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне. Найденные древние вавилонские глиняные таблички, датированные где-то между 1800 и 1600 годами до н. э., являются самыми ранними свидетельствами об изучении квадратных уравнений. На этих же табличках изложены методы решения некоторых типов квадратных уравнений.
э., являются самыми ранними свидетельствами об изучении квадратных уравнений. На этих же табличках изложены методы решения некоторых типов квадратных уравнений.
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
Вавилонские математики примерно с IV века до н. э. использовали метод дополнения квадрата для решения уравнений с положительными корнями. Около 300 года до н.э. Эвклид придумал более общий геометрический метод решения. Первым математиком, который нашел решения уравнения с отрицательными корнями в виде алгебраической формулы, был индийский ученый Брахмагупта (Индия, VII столетие нашей эры).
э. использовали метод дополнения квадрата для решения уравнений с положительными корнями. Около 300 года до н.э. Эвклид придумал более общий геометрический метод решения. Первым математиком, который нашел решения уравнения с отрицательными корнями в виде алгебраической формулы, был индийский ученый Брахмагупта (Индия, VII столетие нашей эры).
Брахмагупта изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
ax2 + bх = с, а>0
В этом уравнении коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
Автор насчитывает 6 видов уравнений, выражая их следующим образом:
1) «Квадраты равны корням», т. е. ах2 = bх.
2) «Квадраты равны числу», т. е. ах2 = с.
3) «Корни равны числу», т. е. ах2 = с.
4) «Квадраты и числа равны корням», т. е. ах2 + с = bх.
5) «Квадраты и корни равны числу», т. е. ах2 + bх =с.
6) «Корни и числа равны квадратам», т. е. bх + с == ах2.
Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи . Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел.
Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV-XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду x2 + bх = с при всевозможных комбинациях знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М. Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья,Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
Итальянские математики Тарталья,Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
Рассмотрим несколько способов решения квадратных уравнений.
Стандартные способы решения квадратных уравнений из школьной программы:
- Разложение левой части уравнения на множители.
- Метод выделения полного квадрата.
- Решение квадратных уравнений по формуле.
- Графическое решение квадратного уравнения.
- Решение уравнений с использованием теоремы Виета.
Остановимся подробнее на решение приведенных и не приведенных квадратных уравнений по теореме Виета.
Напомним, что для решения приведенных квадратных уравнений достаточно найти два числа такие, произведение которых равно свободному члену, а сумма — второму коэффициенту с противоположным знаком.
Пример. x 2 -5x+6=0
Нужно найти числа, произведение которых равно 6, а сумма 5. Такими числами будут 3 и 2.
Ответ: x 1 =2, x 2 =3.
Но можно использовать этот способ и для уравнений с первым коэффициентом не равным единице.
Пример. 3x 2 +2x-5=0
Берём первый коэффициент и умножаем его на свободный член: x 2 +2x-15=0
Корнями этого уравнения будут числа, произведение которых равно — 15, а сумма равна — 2. Эти числа — 5 и 3. Чтобы найти корни исходного уравнения, полученные корни делим на первый коэффициент.
Ответ: x 1 =-5/3, x 2 =1
6. Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение ах 2 + bх + с = 0, где а≠0.
Умножая обе его части на а, получаем уравнение а 2 х 2 + аbх + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению у 2 + by + ас = 0, равносильному данному. Его корни у 1 и у 2 найдем с помощью теоремы Виета.
Его корни у 1 и у 2 найдем с помощью теоремы Виета.
Окончательно получаем х 1 = у 1 /а и х 2 = у 2 /а.
При этом способе коэффициент a умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Пример. 2х 2 — 11х + 15 = 0.
«Перебросим» коэффициент 2 к свободному члену и сделав замену получим уравнение у 2 — 11у + 30 = 0.
Согласно обратной теореме Виета
у 1 = 5, х 1 = 5/2, х 1 =2,5 ;у 2 = 6, x 2 = 6/2, x 2 = 3.
Ответ: х 1 =2,5; х 2 = 3.
7. Свойства коэффициентов квадратного уравнения.
Пусть дано квадратное уравнение ах 2 + bх + с = 0, а ≠ 0.
1. Если a+ b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то х 1 = 1.
2. Если а — b + с = 0, или b = а + с, то х 1 = — 1.
Если а — b + с = 0, или b = а + с, то х 1 = — 1.
Пример. 345х 2 — 137х — 208 = 0.
Так как а + b + с = 0 (345 — 137 — 208 = 0), то х 1 = 1, х 2 = -208/345.
Ответ: х 1 =1; х 2 = -208/345 .
Пример. 132х 2 + 247х + 115 = 0
Т.к. a-b+с = 0 (132 — 247 +115=0), то х 1 = — 1, х 2 = — 115/132
Ответ: х 1 = — 1; х 2 =- 115/132
Существуют и другие свойства коэффициентов квадратного уравнения. но ихиспользование более сложное.
8. Решение квадратных уравнений с помощью номограммы.
Рис 1. Номограмма
Это старый и в настоящее время забытый способ решения квадратных уравнений, помещенный на с.83 сборника: Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990.
Таблица XXII. Номограмма для решения уравнения z 2 + pz + q = 0 . Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
Криволинейная шкала номограммы построена по формулам (рис. 1):
Полагая ОС = р, ED = q, ОЕ = а (все в см), из рис.1 подобия треугольников САН и CDF получим пропорцию
откуда после подстановок и упрощений вытекает уравнение z 2 + pz + q = 0, причем буква z означает метку любой точки криволинейной шкалы.
Рис. 2 Решение квадратных уравнения с помощью номограммы
Примеры.
1) Для уравнения z 2 — 9z + 8 = 0 номограмма дает корни z 1 = 8,0 и z 2 = 1,0
Ответ:8,0; 1,0.
2) Решим с помощью номограммы уравнение
2z 2 — 9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение z 2 — 4,5z + 1 = 0.
Номограмма дает корни z 1 = 4 и z 2 = 0,5.
Ответ: 4; 0,5.
9. Геометрический способ решения квадратных уравнений.
Пример. х 2 + 10х = 39.
В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39».
Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5x. Полученную фигуру дополняют затем до нового квадрата АВСD, достраивая в углах четыре равных квадрата, сторона каждого из них 2,5, а площадь 6,25
Рис. 3 Графический способ решения уравнения х 2 + 10х = 39
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4∙2,5x = 10х) и четырех пристроенных квадратов (6,25∙ 4 = 25) , т.е. S = х 2 + 10х = 25. Заменяя х 2 + 10х числом 39, получим что S = 39+ 25 = 64, откуда следует, что сторона квадрата АВСD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим
10. Решение уравнений с использованием теоремы Безу.
Теорема Безу. Остаток от деления многочлена P(x) на двучлен x — α равен P(α) (т. е. значению P(x) при x = α).
е. значению P(x) при x = α).
Если число α является корнем многочлена P(x), то этот многочлен делится на x -α без остатка.
Пример. х²-4х+3=0
Р(x)= х²-4х+3, α: ±1,±3, α =1, 1-4+3=0. Разделим Р(x) на (х-1):(х²-4х+3)/(х-1)=х-3
х²-4х+3=(х-1)(х-3), (х-1)(х-3)=0
х-1=0; х=1, или х-3=0, х=3; Ответ: х 1 =2, х 2 =3.
Вывод: Умение быстро и рационально решать квадратные уравнения просто необходимо для решения более сложных уравнений, например, дробно-рациональных уравнений, уравнений высших степеней, биквадратных уравнений, а в старшей школе тригонометрических, показательных и логарифмических уравнений. Изучив все найденные способы решения квадратных уравнений, мы можем посоветовать одноклассникам, кроме стандартных способов, решение способом переброски (6) и решение уравнений по свойству коэффициентов (7), так как они являются более доступными для понимания.
Литература:
- Брадис В.
 М. Четырехзначные математические таблицы. — М., Просвещение, 1990.
М. Четырехзначные математические таблицы. — М., Просвещение, 1990. - Алгебра 8 класс: учебник для 8 кл. общеобразоват. учреждений Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. под ред. С. А. Теляковского 15-е изд., дораб. — М.: Просвещение, 2015
- https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%BD%D0%BE%D0%B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5
- Глейзер Г.И. История математики в школе. Пособие для учителей. / Под ред. В.Н. Молодшего. — М.: Просвещение, 1964.
Квадратные уравнения часто появляются во время решения различных задач физики и математики. В данной статье мы рассмотрим, как решать эти равенства универсальным способом «через дискриминант». Примеры использования полученных знаний также даются в статье.
О каких уравнениях пойдет речь?
На рисунке ниже изображена формула, в которой x — неизвестная переменная, а латинские символы a, b, c представляют собой некоторые известные числа.
Каждый из этих символов называется коэффициентом. Как можно заметить, число «a» стоит перед переменной x, возведенной в квадрат. Это максимальная степень представленного выражения, поэтому оно называется квадратным уравнением. Часто используют другое его название: уравнение второго порядка. Само значение a — это квадратный коэффициент (стоящий при переменной в квадрате), b — это линейный коэффициент (он находится рядом с переменной, возведенной в первую степень), наконец, число c — свободный член.
Отметим, что вид уравнения, который изображен на рисунке выше, является общим классическим квадратным выражением. Помимо него существуют другие уравнения второго порядка, в которых коэффициенты b, c могут быть нулевыми.
Когда ставят задачу решить рассматриваемое равенство, то это означает, что такие значения переменной x нужно найти, которые бы ему удовлетворяли. Здесь первым делом нужно запомнить следующую вещь: поскольку максимальная степень икса — это 2, то данный тип выражений не может иметь больше, чем 2 решения. Это означает, что если при решении уравнения были найдены 2 значения x, которые ему удовлетворяют, то можно быть уверенным, что не существует никакого 3-го числа, подставляя которое вместо x, равенство также бы являлось истиной. Решения уравнения в математике называют его корнями.
Это означает, что если при решении уравнения были найдены 2 значения x, которые ему удовлетворяют, то можно быть уверенным, что не существует никакого 3-го числа, подставляя которое вместо x, равенство также бы являлось истиной. Решения уравнения в математике называют его корнями.
Способы решения уравнений второго порядка
Решения уравнений этого типа требует знания некоторой теории о них. В школьном курсе алгебры рассматривают 4 различных метода решения. Перечислим их:
- с помощью факторизации;
- используя формулу для полного квадрата;
- применяя график соответствующей квадратичной функции;
- используя уравнение дискриминанта.
Плюс первого метода заключается в его простоте, однако, он не для всех уравнений может применяться. Второй способ является универсальным, однако несколько громоздким. Третий метод отличается своей наглядностью, но он не всегда удобен и применим. И, наконец, использование уравнения дискриминанта — это универсальный и достаточно простой способ нахождения корней абсолютно любого уравнения второго порядка. Поэтому в статье рассмотрим только его.
Поэтому в статье рассмотрим только его.
Формула для получения корней уравнения
Обратимся к общему виду квадратного уравнения. Запишем его: a*x²+ b*x + c =0. Перед тем как пользоваться способом его решения «через дискриминант», следует приводить равенство всегда к записанному виду. То есть оно должно состоять из трех слагаемых (или меньше, если b или c равен 0).
Например, если имеется выражение: x²-9*x+8 = -5*x+7*x², то сначала следует перенести все его члены в одну сторону равенства и сложить слагаемые, содержащие переменную x в одинаковых степенях.
В данном случае эта операция приведет к следующему выражению: -6*x²-4*x+8=0, которое эквивалентно уравнению 6*x²+4*x-8=0 (здесь левую и правую части равенства мы умножили на -1).
В примере выше a = 6, b=4, c=-8. Заметим, что все члены рассматриваемого равенства всегда суммируются между собой, поэтому если появляется знак «-«, то это означает, что отрицательным является соответствующий коэффициент, как число c в данном случае.
Разобрав этот момент, перейдем теперь к самой формуле, которая дает возможность получения корней квадратного уравнения. Она имеет вид, который представлен на фото ниже.
Как видно из этого выражения, оно позволяет получать два корня (следует обратить внимание на знак «±»). Для этого в него достаточно подставить коэффициенты b, c, и a.
Понятие о дискриминанте
В предыдущем пункте была приведена формула, которая позволяет быстро решить любое уравнение второго порядка. В ней подкоренное выражение называют дискриминантом, то есть D = b²-4*a*c.
Почему эту часть формулы выделяют, и она даже имеет собственное название? Дело в том, что дискриминант связывает в единое выражение все три коэффициента уравнения. Последний факт означает, что он полностью несет информацию о корнях, которую можно выразить следующим списком:
- D>0: равенство имеет 2 различных решения, причем оба они представляют собой действительные числа.
- D=0: у уравнения всего один корень, и он является действительным числом.

Задача на определение дискриминанта
Приведем простой пример, как найти дискриминант. Пусть дано такое равенство: 2*x² — 4+5*x-9*x² = 3*x-5*x²+7.
Приведем его к стандартному виду, получаем: (2*x²-9*x²+5*x²) + (5*x-3*x) + (- 4-7) = 0, откуда приходим к равенству: -2*x²+2*x-11 = 0. Здесь a=-2, b=2, c=-11.
Теперь можно воспользоваться названной формулой для дискриминанта: D = 2² — 4*(-2)*(-11) = -84. Полученное число является ответом на поставленную задачу. Поскольку в примере дискриминант меньше нуля, то можно сказать, что данное квадратное уравнение не имеет действительных корней. Его решением будут только числа комплексного типа.
Пример неравенства через дискриминант
Решим задачи несколько иного типа: дано равенство -3*x²-6*x+c = 0. Необходимо найти такие значения c, для которых D>0.
В данном случае известно лишь 2 из 3 коэффициентов, поэтому рассчитать точное значение дискриминанта не получится, однако известно, что он является положительным. Последний факт используем при составлении неравенства: D= (-6)²-4*(-3)*c>0 => 36+12*c>0. Решение полученного неравенства приводит к результату: c>-3.
Последний факт используем при составлении неравенства: D= (-6)²-4*(-3)*c>0 => 36+12*c>0. Решение полученного неравенства приводит к результату: c>-3.
Проверим полученное число. Для этого вычислим D для 2 случаев: c=-2 и c=-4. Число -2 удовлетворяет полученному результату (-2>-3), соответствующий дискриминант будет иметь значение: D = 12>0. В свою очередь, число -4 не удовлетворяет неравенству (-4Таким образом, любые числа c, которые больше -3, будут удовлетворять условию.
Пример решения уравнения
Приведем задачу, которая заключается не только в нахождении дискриминанта, но и в решении уравнения. Необходимо найти корни для равенства -2*x²+7-9*x = 0.
В этом примере дискриминант равен следующему значению: D = 81-4*(-2)*7= 137. Тогда корни уравнения определятся так: x = (9±√137)/(-4). Это точные значения корней, если вычислить приближенно корень, тогда получатся числа: x = -5,176 и x = 0,676.
Геометрическая задача
Решим задачу, которая потребует не только умения вычислять дискриминант, но и применения навыков абстрактного мышления и знания, как составлять квадратные уравнения.
У Боба было пуховое одеяло размером 5 x 4 метра. Мальчик захотел пришить к нему по всему периметру сплошную полосу из красивой ткани. Какой толщины будет эта полоса, если известно, что у Боба имеется 10 м² ткани.
Пусть полоса будет иметь толщину x м, тогда площадь ткани по длинной стороне одеяла составит (5+2*x)*x, а поскольку длинных сторон 2, то имеем: 2*x*(5+2*x). По короткой стороне площадь пришитой ткани составит 4*x, так как этих сторон 2, то получаем значение 8*x. Отметим, что к длинной стороне было добавлено значение 2*x, поскольку длина одеяла увеличилась на это число. Общая пришитая к одеялу площадь ткани равна 10 м². Поэтому получаем равенство: 2*x*(5+2*x) + 8*x = 10 => 4*x²+18*x-10 = 0.
Для этого примера дискриминант равен: D = 18²-4*4*(-10) = 484. Его корень равен 22. Воспользовавшись формулой, находим искомые корни: x = (-18±22)/(2*4) = (-5; 0,5). Очевидно, что из двух корней подходит по условию задачи только число 0,5.
Таким образом, полоса из ткани, которую пришьет Боб к своему одеялу, будет иметь ширину 50 см.
», то есть уравнения первой степени. В этом уроке мы разберем, что называют квадратным уравнением и как его решать.
Что называют квадратным уравнением
Важно!
Степень уравнения определяют по наибольшей степени, в которой стоит неизвестное.
Если максимальная степень, в которой стоит неизвестное — «2 », значит, перед вами квадратное уравнение.
Примеры квадратных уравнений
- 5x 2 − 14x + 17 = 0
- −x 2 + x + = 0
- x 2 + 0,25x = 0
- x 2 − 8 = 0
Важно! Общий вид квадратного уравнения выглядит так:
A x 2 + b x + c = 0
«a », «b » и «c » — заданные числа.- «a » — первый или старший коэффициент;
- «b » — второй коэффициент;
- «c » — свободный член.
Чтобы найти «a », «b » и «c » нужно сравнить свое уравнение с общим видом квадратного уравнения «ax 2 + bx + c = 0 ».
Давайте потренируемся определять
коэффициенты «a
», «b
»
и «c
» в квадратных уравнениях.
| Уравнение | Коэффициенты |
|---|---|
| |
| x 2 − 8 = 0 |
Как решать квадратные уравнения
В отличии от линейных уравнений для решения квадратных уравнений используется специальная формула для нахождения корней .
Запомните!
Чтобы решить квадратное уравнение нужно:
- привести квадратное уравнение к общему виду «ax 2 + bx + c = 0 ». То есть в правой части должен остаться только «0 »;
- использовать формулу для корней:
Давайте на примере разберем, как применять формулу для нахождения корней квадратного уравнения. Решим квадратное уравнение.
X 2 − 3x − 4 = 0
Уравнение «
x 2 − 3x − 4 = 0
» уже приведено к общему виду «ax 2 + bx + c = 0
» и не требует дополнительных упрощений. Для его решения нам достаточно применить формулу нахождения корней квадратного уравнения .
Для его решения нам достаточно применить формулу нахождения корней квадратного уравнения .
Определим коэффициенты «a », «b » и «c » для этого уравнения.
x 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =
С её помощью решается любое квадратное уравнение.
В формуле «x 1;2 =
» часто заменяют подкоренное выражение
«b 2 − 4ac
» на букву «D
» и называют
дискриминантом
. Более подробно понятие дискриминанта рассматривается в уроке
«Что такое дискриминант ».
Рассмотрим другой пример квадратного уравнения.
x 2 + 9 + x = 7x
В данном виде определить коэффициенты «a », «b » и «c » довольно сложно. Давайте вначале приведем уравнение к общему виду «ax 2 + bx + c = 0 ».
X 2 + 9 + x = 7x
x 2 + 9 + x − 7x = 0
x 2 + 9 − 6x = 0
x 2 − 6x + 9 = 0
Теперь можно использовать формулу для корней.
X 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =
x =
x = 3
Ответ: x = 3
Бывают случаи, когда в квадратных уравнениях нет корней. Такая ситуация возникает, когда в формуле под корнем
оказывается отрицательное число.
Такая ситуация возникает, когда в формуле под корнем
оказывается отрицательное число.
Решение квадратных уравнений методом переброски
Метод переброски.
Рассмотрим метод, который позволяет решать подавляющее большинство полных квадратных уравнений устно, аналогично решению приведенных квадратных уравнений с помощью теоремы Виета.
Рассмотрим полное квадратное уравнение
ax2 + bx + c = 0; (1)
Для его решения мы вначале используем формулу дискриминанта:
D = b2 – 4ac и если D > 0, то с помощью формул корней полного квадратного уравнения находим x1 и x2:
x1,2 = (—b ± √D) / 2a.
Теперь рассмотрим другое полное приведенное квадратное уравнение
y2 + by + ac = 0. (2)
Первый коэффициент у этого уравнения равен 1, а второй коэффициент равен b и совпадает со вторым коэффициентом уравнения (1). Свободный член уравнения (2) равен ac и получен как произведение первого коэффициента и свободного члена уравнения (1) (то есть можно сказать, что a «перебросилось» к c).
Свободный член уравнения (2) равен ac и получен как произведение первого коэффициента и свободного члена уравнения (1) (то есть можно сказать, что a «перебросилось» к c).
Найдем дискриминант и корни квадратного уравнения (2): D = b2 – 4ac, т.о. он полностью совпадает с дискриминантом уравнения (1).
Корни уравнения (2): y1,2 = (—b ± √D) / 2.
Если теперь корни x1,2 сравнить с корнями y1,2, то легко видеть, что корни уравнения (1) можно получить из корней уравнения (2) делением на a.
Теперь рассмотрим примеры, в которых очень удобно пользоваться приведенным выше методом «переброски».
Пример 1.
Решить уравнение 6x2 – 7x – 3 = 0.
Решение.
Выполним «переброску» и решим новое уравнение с помощью теоремы Виета:
y2 – 7y – 3 · 6 = 0;
y2 – 7y – 18 = 0.
По теореме Виета y1 = 9; y2 = —2.
Теперь вернемся к переменной x. Для этого разделим полученные результаты y1,2 на первый коэффициент исходного уравнения, т.е. на 6. Получим:
x1 = 9/6; x2 = —2/6.
После сокращения будем иметь x1 = 1,5; x2 = —1/3.
Ответ: -1/3; 1,5.
Пример 2.
Решить уравнение 4x2 – 1 7x – 15 = 0.
Решение.
Так как метод «переброски» предназначен для устного решения квадратных уравнений, то при определенном навыке несложно найти числа, сумма которых равна 17, а произведение —60 (ведь после «переброски» свободный член будет равен 4 · (—15) = —60).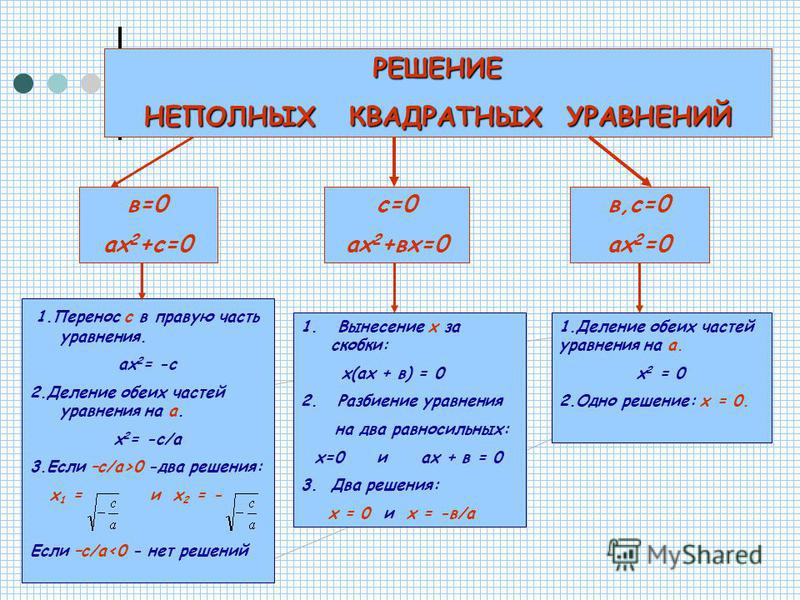 Это будут числа 20 и —3. Таким образом, получим корни:
Это будут числа 20 и —3. Таким образом, получим корни:
x1 = 20/4; x2 = —3/4.
Сократив полученные корни будем иметь x1 = 5; x2 = —3/4.
Ответ: -3/4; 5.
Пример 3.
Решить уравнение 4271x2 – 4272x + 1 = 0.
Решение.
По рассматриваемому методу нам необходимо найти числа, сумма которых равна 4272, а произведение 4271 (после «переброски» свободный член равен 1 · 4271 = 4271). Это будут числа 4271 и 1. Тогда получим:
x1 = 4271/4271; x2 = 1/4271.
А после сокращения будем иметь корни x1 = 1; x2 = 1/4271.
Ответ: 1; 1/4271.
Пример 4.
Найти корни уравнения sin4 · x2 – (sin4 + cos4) · x + cos4 = 0.
Решение.
Воспользуемся методом переброски и перепишем данное уравнение следующим образом:
y2 – (sin4 + cos4) · y + sin4 · cos4 = 0.
Теперь решим полученное уравнение с помощью теоремы Виета, т.е. найдем числа, сумма которых равна
sin4 + cos4, а произведение равно sin4 · cos4.
Очевидно, что искомые числа: sin4 и cos4. Значит y1 = sin4 и y2 = cos4. Теперь найдем корни исходного уравнения. Для этого полученные корни y1,2 поделим на первый коэффициент исходного уравнения, т.е. на sin4. Будем иметь
x1 = sin4 / sin4; x2 = cos4 / sin4. Упростив получим, что x1 = 1; x2 = ctg4.
Ответ: 1; ctg4.
Пример 5.
Решить уравнение √3x2 – 5x – √12 = 0.
Решение.
По методу «переброски» будем работать не с исходным, а с новым квадратным уравнением:
y2 – 5y – √12 · √3 = 0;
y2 – 5y – 6 = 0.
Находим числа, сумма которых равна 5, а произведение равно —6.
Легко видеть, что это будут числа 6 и —1. Тогда исходное уравнение будет иметь корни:
x1 = 6/√3; x2 = —1/√3.
В знаменателе уберем иррациональность. Получим:
x1 = 2√3; x2 = —√3/3.
Ответ: 2√3; -√3/3.
Рассмотренный метод очень эффективен при решении задач, он позволяет устно решать подавляющее большинство полных квадратных уравнений, а не тратить время на вычисление дискриминанта.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
2 — 4 ac , называется дискриминантом и может использоваться для определения количества и типа решений квадратного уравнения, не выполняя всю работу по поиску фактических решений.
Кроме того, если дискриминант отрицателен, мы получим два невещественных решения (комплексные решения). Если дискриминант представляет собой полный квадрат, то уравнение будет иметь рациональные решения.
Используйте Дискриминант, чтобы определить число и введите решения .
Решить .
Слова «проблемы» в этой главе должны показаться вам знакомыми. Настройки аналогичны, но обычно приводят к квадратным уравнениям. Вы можете использовать квадратичную формулу или любой другой метод, изученный до сих пор, чтобы решить их.
youtube.com/embed/Qss4C_euxf4″/>
Геометрическая задача : Площадь квадрата равна 32 квадратных фута.Найдите длину каждой стороны квадрата.
Геометрическая задача м: площадь круга квадратных сантиметров. Найдите длину диаметра.
Геометрическая задача : Длина прямоугольника в 2 раза меньше его ширины, чем в 3 раза. Найдите площадь прямоугольника, если его площадь равна 65 квадратных метров.
Ti p: Не забудьте указать в ответе правильные единицы измерения. Большинство инструкторов снимут несколько баллов, если вы пренебрежете единицами измерения.
Геометрическая задача : Основание треугольника в два раза больше его высоты. Найдите длину основания и высоту, если площадь треугольника 25 квадратных дюймов.

Теорема Пифагора Задача : Длины катетов прямоугольного треугольника равны 6 дюймам и 8 дюймам.Найдите длину гипотенузы.
Теорема Пифагора Задача : Основание 10-футовой лестницы расположено в 4 футах от стены и прислонено к ней. Определите высоту лестницы.
Теорема Пифагора. Задача . Экран компьютера имеет размеры 14,5 на 11 дюймов. Найдите длину диагонали.
Теорема Пифагора Задача : Если Джо проехал 100 миль на юг и 50 миль на запад до пляжа, то как далеко он находится от дома?
Если объект запускается с высоты s футов с начальной скоростью футов в секунду, его высота определяется следующей формулой.
youtube.com/embed/smKNGgasjYQ»/>
Проблема со снарядом : Объект брошен с земли с начальной скоростью 32 фута в секунду. Через какое время объект вернется на землю?
Проблема со снарядом : Объект запускается с вершины 32-футового здания с начальной скоростью 128 футов в секунду. Сколько времени потребуется, чтобы достичь земли?
Проблема со снарядом : Объект запускается с уровня земли со скоростью 128 футов в секунду.Сколько времени потребуется, чтобы достичь высоты 256 футов?
Вспомните формулы для расчета рабочей силы из главы 7.
Проблема со скоростью работы : сыну Джо обычно требуется на 2 часа больше времени, работая в одиночку, чтобы выполнить еженедельную работу во дворе.
 Если Джо и его сын делают работу вместе, это занимает 1 1/2 часа. Сколько времени потребуется Джо, чтобы работать во дворе в одиночку?
Если Джо и его сын делают работу вместе, это занимает 1 1/2 часа. Сколько времени потребуется Джо, чтобы работать во дворе в одиночку? Примеры видео на YouTube :
Решение квадратных уравнений с использованием свойства квадратного корня — Элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Решение квадратных уравнений формы с использованием свойства квадратного корня
- Решение квадратных уравнений формы с использованием свойства квадратного корня
Прежде чем начать, пройдите этот тест на готовность.
- Упрощение: .
Если вы пропустили эту проблему, просмотрите (рисунок). - Упрощение: .
Если вы пропустили эту проблему, просмотрите (рисунок). - Коэффициент: .
Если вы пропустили эту проблему, просмотрите (рисунок).
Квадратные уравнения – это уравнения вида , где . Они отличаются от линейных уравнений наличием члена с переменной, возведенной во вторую степень. Мы используем разные методы для решения квадратных уравнений, чем линейные уравнения, потому что простое сложение, вычитание, умножение и деление членов не изолирует переменную.
Они отличаются от линейных уравнений наличием члена с переменной, возведенной во вторую степень. Мы используем разные методы для решения квадратных уравнений, чем линейные уравнения, потому что простое сложение, вычитание, умножение и деление членов не изолирует переменную.
Мы видели, что некоторые квадратные уравнения можно решить с помощью факторизации. В этой главе мы будем использовать три других метода для решения квадратных уравнений.
Решение квадратных уравнений вида
x 2 = k с использованием свойства квадратного корняМы уже решили некоторые квадратные уравнения методом факторизации. Давайте рассмотрим, как мы использовали факторинг для решения квадратного уравнения.
Мы можем легко использовать факторинг, чтобы найти решения подобных уравнений, таких как и , потому что 16 и 25 являются полными квадратами.Но что происходит, когда у нас есть такое уравнение? Поскольку 7 не является полным квадратом, мы не можем решить уравнение с помощью факторизации.
Все эти уравнения имеют форму .
Мы определили квадратный корень числа следующим образом:
Это ведет к свойству квадратного корня.
Свойство квадратного корня
Если , и , то .
Обратите внимание, что свойство «Квадратный корень» дает два решения уравнения вида : главный квадратный корень из и его противоположность.Мы также можем записать решение в виде .
Теперь мы снова решим уравнение, на этот раз используя свойство квадратного корня.
Что происходит, когда константа не является точным квадратом? Давайте воспользуемся свойством квадратного корня, чтобы решить уравнение.
Решить: .
Решение
Решить: .
Решить: .
Как решить квадратное уравнение формы, используя свойство квадратного корняРешить: .
Решить: .
Решить: .
Решите квадратное уравнение, используя свойство Square Root.
- Выделить квадратичный член и сделать его коэффициент равным единице.
- Использовать свойство квадратного корня.
- Упрости радикал.
- Проверьте решения.
Чтобы использовать свойство «Квадратный корень», коэффициент переменного члена должен быть равен 1. В следующем примере мы должны разделить обе части уравнения на 5, прежде чем использовать свойство «Квадратный корень».
Решить: .
Решить: .
Решить: .
Свойство квадратного корня начиналось с утверждения «Если , и ». Что будет, если? Это будет иметь место в следующем примере.
Решить: .
Решение
Решить: .
Решить: .
Помните, сначала мы выделяем квадратный член, а затем приравниваем коэффициент к единице.
Решить: .
Решить: .
Решить: .
В решениях некоторых уравнений в радикалах могут быть дроби. Когда это происходит, мы должны рационализировать знаменатель.
Когда это происходит, мы должны рационализировать знаменатель.
Решить: .
Решение
Решить: .
Решить: .
Решение квадратных уравнений вида
a ( x − h ) 2 = k с использованием свойства квадратного корняМы также можем использовать свойство Square Root для решения уравнения типа .Мы будем рассматривать весь бином как квадратичный член.
Решить: .
Решить: .
Решить: .
Решить: .
Решить: .
Решить: .
Помните, когда мы извлекаем квадратный корень из дроби, мы можем извлечь квадратный корень из числителя и знаменателя отдельно.
Решить:
Решение
Решить:
Решить:
Мы начнем решение следующего примера с выделения бинома.
Решить: .
Решение
Решить: .
Решить: .
Решить: .
Решение
Решить: .
Решить: .
Левые части уравнений в следующих двух примерах не имеют вида . Но они представляют собой совершенные квадратные трехчлены, поэтому мы приведем их к нужному нам виду.
Решить: .
Решение
Левая часть уравнения представляет собой совершенный квадратный трехчлен. Мы учтем это в первую очередь.
Решить: .
Решить: .
Решить: .
Решение
Опять же, мы замечаем, что левая часть уравнения представляет собой совершенный квадратный трехчлен. Мы учтем это в первую очередь.
Решить: .
Решить: .
Ключевые понятия
- Свойство квадратного корня
Если , и , то .
Практика делает совершенным
Решение квадратных уравнений вида Использование свойства квадратного корня
В следующих упражнениях решите следующие квадратные уравнения.
Решение квадратных уравнений вида Использование свойства квадратного корня
В следующих упражнениях решите следующие квадратные уравнения.
Смешанная практика
В следующих упражнениях решите, используя свойство Square Root.
Математика на каждый день
У Паолы достаточно мульчи, чтобы покрыть 48 квадратных футов.Она хочет использовать его, чтобы сделать три квадратных огорода одинакового размера. Решите уравнение, чтобы найти длину каждой стороны сада.
Кэти рисует чертежи дома, который она проектирует. Она хочет иметь в гостиной четыре квадратных окна одинакового размера общей площадью 64 квадратных фута. Решив уравнение, найти длину сторон окон.
Письменные упражнения
Объясните, почему уравнение не имеет решения.
Объясните, почему уравнение имеет два решения.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.
ⓑ Если большинство ваших чеков:
…уверенно: Поздравляем! Вы достигли целей в этом разделе. Подумайте об учебных навыках, которые вы использовали, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы обрести уверенность в своих способностях делать эти вещи? Быть конкретными.
…с некоторой помощью: Это нужно решать быстро, потому что темы, которые вы не осваиваете, становятся выбоинами на вашем пути к успеху.В математике каждая тема основывается на предыдущей работе. Прежде чем двигаться дальше, важно убедиться, что у вас есть прочная основа. Кого можно попросить о помощи? Ваши одноклассники и преподаватель являются хорошими ресурсами.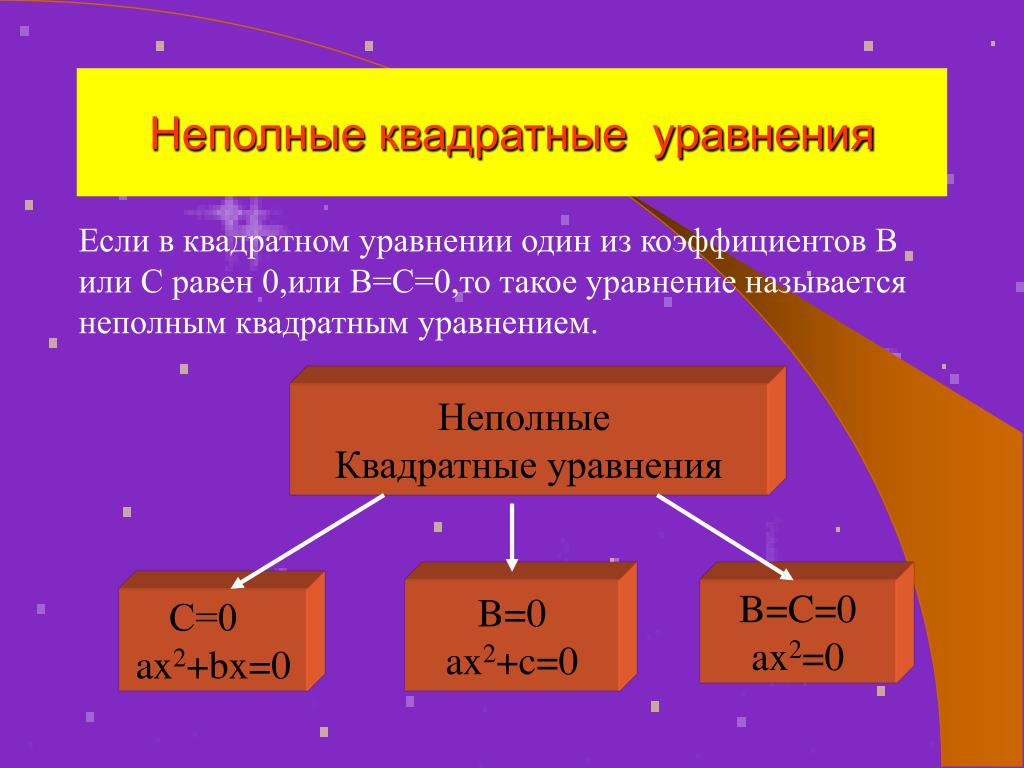 Есть ли в кампусе место, где есть репетиторы по математике? Можно ли улучшить свои учебные навыки?
Есть ли в кампусе место, где есть репетиторы по математике? Можно ли улучшить свои учебные навыки?
… нет, не понимаю! Это предупреждающий знак, и вы не должны его игнорировать. Вы должны немедленно обратиться за помощью, иначе вы быстро будете поражены. Как можно скорее обратитесь к инструктору, чтобы обсудить вашу ситуацию.Вместе вы можете придумать план, как получить необходимую вам помощь.
Принятие решения о том, какой метод использовать при решении квадратных уравнений
Принятие решения о том, какой метод использовать при решении квадратных уравнений Как решить, какой метод использовать при решении квадратных уравненийПри решении квадратного уравнения выполните следующие действия. (в этом порядке), чтобы выбрать метод:
- Попробуйте сначала решить уравнение факторингом. Быть уверенным
что ваше уравнение находится в стандартной форме (ax 2 +bx+c=0) до того, как вы
начать свою попытку факторинга.
 Не тратьте много времени на попытки
фактор вашего уравнения; если вы не можете учесть это менее чем за 60 секунд,
перейти к другому методу.
Не тратьте много времени на попытки
фактор вашего уравнения; если вы не можете учесть это менее чем за 60 секунд,
перейти к другому методу. - Затем посмотрите на сторону уравнения, содержащую переменную. Является ли эта сторона полным квадратом? Если да, то можно решить уравнение извлекая квадратный корень из обеих частей уравнения. Не забывайте чтобы включить знак ± в уравнение после того, как вы извлекли квадратный корень.
- Далее, если коэффициент квадрата члена равен 1 и коэффициент линейного (среднего) члена четный, завершающий квадрат это хороший метод для использования.
- Наконец, квадратичная формула будет работать на любом квадратичном уравнение. Однако, если использование формулы приводит к неловко большим числа под знаком радикала, может быть лучше использовать другой метод решения выбор.
Пример 1: Решить x 2 + 4 = 4x
Сначала приведем уравнение к стандартной форме, чтобы мы могли попробуй решить разложением:
х 2 — 4х + 4 = 0
(х — 2)(х — 2) = 0
х — 2 = 0 | х — 2 = 0
х = 2 | х = 2
Таким образом, решение этого уравнения, найденное с помощью факторизации,
х = 2.
Пример 2: Решить (2x — 2) 2 = -4
Часть уравнения, содержащая переменную (значение левая сторона) является полным квадратом, поэтому мы возьмем квадратный корень из обеих сторон решить уравнение.
(2x — 2) 2 = -4
2x — 2 = ± 2i
2х = 2 ± 2i
х = 1 ± i
Обратите внимание, что знак ±
была подставлена в уравнение в том месте, где был извлечен квадратный корень.
Пример 3: Решить x 2 + 6x — 11 = 0
Это уравнение неразложимо, и сторона, содержащая
переменная не является полным квадратом. Но так как коэффициент
x 2 равно 1, а коэффициент при x четный, завершая
Square будет подходящим методом. Чтобы найти число, которое необходимо
добавить к обеим частям уравнения, чтобы завершить квадрат, взять
коэффициент члена x, разделите его на 2, затем возведите это число в квадрат.В
в этой задаче 6 = 2 равно 3, а 3 2 равно 9, поэтому мы добавим 9 к обеим частям уравнения, как только мы изолируем
переменные термины.
х 2 + 6х — 11 = 0
х 2 + 6х = 11
х 2 + 6х +9 = 11 + 9
(х + 3) 2 = 20
Пример 4: Решите 2x 2 — x + 5 = 0
Это уравнение неразложимо, левая часть не идеальный квадрат, а коэффициенты x 2 и x условия не сделает заполнение квадрата удобным.Это оставляет квадратное формула как лучший метод для решения этого уравнения. Мы будем использовать a=2, b=-1, и с=5.
По-Шен Лох | Квадратичный метод: подробное объяснение
В последнее время я систематически думал о том, как объяснить школьные математические понятия более вдумчиво и интересно, создавая уроки Daily Challenge . Однажды ночью в сентябре 2019 года, во время мозгового штурма различных способов осмысления квадратичной формулы, я с удивлением придумал простой метод исключения догадок и проверок из факторинга, которого я никогда раньше не видел.
Альтернативный метод решения квадратных уравнений
- Если найти и с суммой и произведением, то и они все корни
- Сумма двух чисел равна
- Их произведение равно
- Квадратный корень всегда дает
- и все корни
Известные сотни лет назад (Виэт)
Известные тысячи лет назад (вавилоняне, греки)
Отдельные этапы этого метода были отдельно открыты древними математиками.Комбинацию этих шагов мог придумать каждый, но после того, как эта веб-страница была выпущена в открытый доступ, единственной предыдущей ссылкой на аналогичный последовательный метод решения квадратных уравнений была хорошая статья учителя математики Джона Сэвиджа. , опубликованный в The Mathematics Teacher в 1989 году. Его подход совпадал почти во всех расчетах с педагогической разницей в выборе знака, но имел разницу в логике, поскольку (возможно, из-за дружелюбного стиля письма, который оставляет некоторую логику для интерпретация) он, по-видимому, использует дополнительный (верный, но значительно более продвинутый) факт, что каждое квадратичное число может быть разложено на два линейных множителя или имеет некоторые обратные направления импликации, которые технически неверны. В частности, мой подход к избеганию дополнительного предположения в «Завершении квадрата» не был достигнут методом Сэвиджа. На соответствующей рабочей странице сравнивается метод, описанный Сэвиджем, с методом, который предложил я. Поскольку я до сих пор не видел ни одной ранее существовавшей книги или статьи, в которой этот тип метода излагается таким образом, чтобы он подходил для начинающих (избегая углубленных знаний) и четко и последовательно обосновывал все шаги, я решил поделиться им, чтобы предоставить версия, на которую можно безопасно ссылаться.
В частности, мой подход к избеганию дополнительного предположения в «Завершении квадрата» не был достигнут методом Сэвиджа. На соответствующей рабочей странице сравнивается метод, описанный Сэвиджем, с методом, который предложил я. Поскольку я до сих пор не видел ни одной ранее существовавшей книги или статьи, в которой этот тип метода излагается таким образом, чтобы он подходил для начинающих (избегая углубленных знаний) и четко и последовательно обосновывал все шаги, я решил поделиться им, чтобы предоставить версия, на которую можно безопасно ссылаться.
Объяснение квадратичного метода на примере
Приведенная ниже презентация основана на подходе, изложенном в моей первоначально опубликованной статье, но идет дальше. Он использует мое соглашение о знаках и мои собственные логические шаги (в отличие от версии Сэвиджа), чтобы быть логически обоснованным, а также потому, что я думаю, что мой выбор полезен для понимания более глубокой связи между квадратичным уравнением и его решениями. Он также показывает чистое сведение задачи от решения стандартного квадратичного уравнения к классической задаче, решаемой вавилонянами и греками.Это видео представляет собой самостоятельный практический урок, в котором рассматривается множество примеров с объяснением каждого логического шага. Обсуждение текста ниже идет немного глубже и включает комментарии, которые могут быть полезны учителям.
Он также показывает чистое сведение задачи от решения стандартного квадратичного уравнения к классической задаче, решаемой вавилонянами и греками.Это видео представляет собой самостоятельный практический урок, в котором рассматривается множество примеров с объяснением каждого логического шага. Обсуждение текста ниже идет немного глубже и включает комментарии, которые могут быть полезны учителям.
Повторение: Умножение и неумножение
Начнем с обзора фактов, которым обычно учат вводить квадратные уравнения. Во-первых, мы используем распределительное правило для умножения (также называемое FOIL):
Ключевой вывод состоит в том, что in получается из сложения вместе and, а the получается из умножения вместе and.
Вот еще один пример:
Так как у нас были и И, то члены И сокращаются, что дает нам разницу в квадратах. Это пригодится позже.
Причина, по которой полезно знать, что происходит при умножении, заключается в том, что если мы можем сделать это в обратном порядке, мы сможем решать квадратные уравнения. Например, предположим, что мы хотим найти все такие, что мы уже знаем, что это то же самое (имеет точно такие же решения), как и единственный способ умножить два числа на ноль, если одно (или оба) равны нулю.(Формальное обоснование этого свойства нулевого произведения использует основную аксиому, что вы можете делить на любое ненулевое число: предположим для противоречия, что и то, и другое не равно нулю. Тогда, разделив обе части уравнения на, мы получим противоречие.)
Итак, Работают именно те, где(что есть) или(что есть). Обратите внимание, что решения — это числа, из которых мы вычитаем, т. е. не и, а и. Важно, что это все решения.
Обзор: Настройка для факторинга
Давайте попробуем обратный процесс для примера. Было бы здорово, если бы мы могли разложить его на нечто подобное. Студенты еще не узнали, что всегда можно найти такую факторизацию, но наш подход также докажет им, что это всегда возможно! Согласно предыдущему разделу, если нам удалось разложить на множители, то все, что окажется в этих пробелах, будет решениями.Но что будет работать в этих пустых местах? Два числа, у которых есть сумма и произведение. Наиболее часто изучаемый метод состоит в том, чтобы найти эти числа путем угадывания и проверки. Это может разочаровать, особенно когда есть отрицательные числа, которые нужно попробовать, и когда у продукта есть много возможных разложений на множители (имеет массу возможностей).
Студенты еще не узнали, что всегда можно найти такую факторизацию, но наш подход также докажет им, что это всегда возможно! Согласно предыдущему разделу, если нам удалось разложить на множители, то все, что окажется в этих пробелах, будет решениями.Но что будет работать в этих пустых местах? Два числа, у которых есть сумма и произведение. Наиболее часто изучаемый метод состоит в том, чтобы найти эти числа путем угадывания и проверки. Это может разочаровать, особенно когда есть отрицательные числа, которые нужно попробовать, и когда у продукта есть много возможных разложений на множители (имеет массу возможностей).
Как указано в соответствующей работе, версия Сэвиджа имеет аналогичные вычисления, за исключением того, что он ищет факторизацию в математически эквивалентной форме. Затем числа в пробелах являются отрицательными значениями решений, поэтому после нахождения факторизации Сэвидж отрицает числа в качестве последнего шага.С образовательной точки зрения, я думаю, что немного выгоднее чисто свести стандартную квадратичную задачу к задаче на сумму и произведение (без необходимости возвращаться и помнить об отрицании в конце), потому что тогда можно получить представление о прямая связь между коэффициентами и суммой и произведением корней.
Чтобы сделать это еще более естественным для новичка, я бы посоветовал ввести понятие факторинга с начальным примером, который имеет отрицательный коэффициент, так что факторизация уже естественна и удобна.Кроме того, тогда еще более прозрачно наблюдать за решениями через свойство нулевого произведения, потому что не требуется никакого отрицания.
Проницательность: Факторинг без угадывания
Вот способ определения чисел, который работает без каких-либо угадываний! Сумма двух чисел равна их среднему значению. Таким образом, мы можем попытаться найти числа, которые плюс некоторая сумма и минус та же сумма. Все, что нам нужно сделать, это выяснить, существует ли такое, что работает как два числа и может существовать.
При поиске двух чисел формы и они автоматически суммируются.Итак, нам просто нужно их умножить на. Мы хотим выяснить, существует ли такое, которое удовлетворяет: Мы уже видели подобный шаблон, где у нас есть сумма двух чисел, умноженная на их разность. Ответ всегда разность их квадратов! Итак, переписав левую часть в эквивалентной форме, мы хотим выяснить, существует ли такое, что это интересно! Есть одиночка, а все остальное просто число! Это означает, что мы можем закончить поиск валидности, следуя своему чутью, вместо того, чтобы требовать каких-либо новых методов.Мы хотим: что мы можем получить от Итак, выбор существует! (В качестве альтернативы мы могли бы выбрать, но это в конечном итоге дало бы тот же результат.) Следовательно, прослеживая логику вверх, мы знаем, что и обязательно будут два числа, у которых есть сумма и произведение. Тот факт, что эти числа удовлетворяют отношениям суммы и произведения, означает, что факторизация существует, а это также означает, что мы нашли полный набор решений: или.
Ответ всегда разность их квадратов! Итак, переписав левую часть в эквивалентной форме, мы хотим выяснить, существует ли такое, что это интересно! Есть одиночка, а все остальное просто число! Это означает, что мы можем закончить поиск валидности, следуя своему чутью, вместо того, чтобы требовать каких-либо новых методов.Мы хотим: что мы можем получить от Итак, выбор существует! (В качестве альтернативы мы могли бы выбрать, но это в конечном итоге дало бы тот же результат.) Следовательно, прослеживая логику вверх, мы знаем, что и обязательно будут два числа, у которых есть сумма и произведение. Тот факт, что эти числа удовлетворяют отношениям суммы и произведения, означает, что факторизация существует, а это также означает, что мы нашли полный набор решений: или.
Обратите внимание, что в этом подходе нам нужно только существование одного конкретного числа, квадрат которого равен другому конкретному числу.В этом примере очевидно, что это число, квадрат которого равен . Когда у нас есть одно такое число, мы уже можем следовать нашим логическим шагам и вывести полный набор решений исходного квадратичного уравнения. Напротив, на соответствующем шаге завершения квадрата нам потребуется полный список всех чисел, которые возводятся в квадрат. Понятно, что и должно быть в списке, но сложнее ответить, почему это полный список (особенно когда в качестве вариантов разрешены комплексные числа).Эта деталь обсуждается более подробно здесь.
Напротив, на соответствующем шаге завершения квадрата нам потребуется полный список всех чисел, которые возводятся в квадрат. Понятно, что и должно быть в списке, но сложнее ответить, почему это полный список (особенно когда в качестве вариантов разрешены комплексные числа).Эта деталь обсуждается более подробно здесь.
Как я уже отмечал в своей полной статье, хотя я (как и многие другие) самостоятельно придумал способ нахождения двух чисел по их сумме и произведению, вавилоняне и греки уже знали этот трюк за тысячи лет до этого. Однако математика была недостаточно развита, чтобы они могли использовать этот трюк самостоятельно для решения общих квадратных уравнений. В частности, они не работали с полиномиальным факторингом или отрицательными числами (не говоря уже о недействительных комплексных числах).Для более подробного обсуждения посетите соответствующую рабочую страницу.
Пример использования: квадратное число, которое нельзя легко разложить на множители
Теперь, когда угадывание исключено, мы можем решить любое квадратное число с помощью этого метода.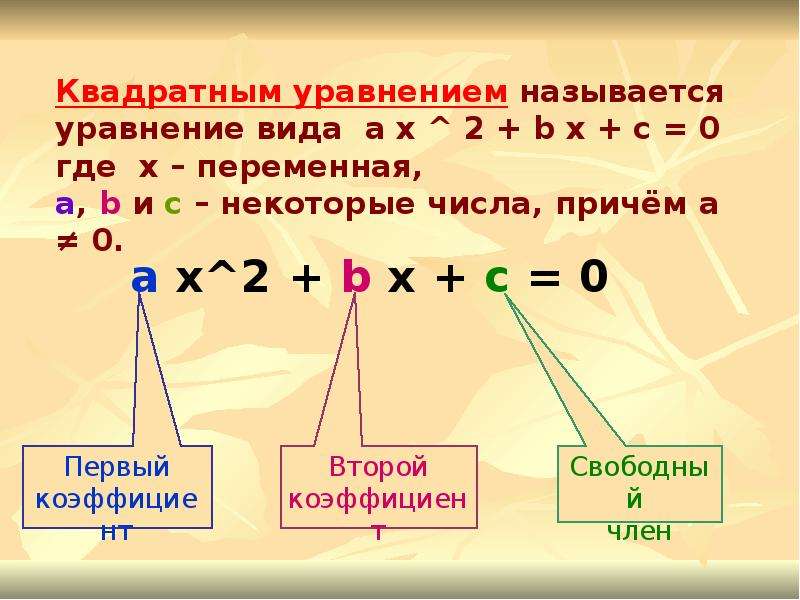 Рассмотрим этот пример: Во-первых, давайте очистим его, умножив обе части на, чтобы получить уравнение, набор решений которого идентичен: Как и раньше, , если мы можем найти два числа с суммой и произведением, тогда факторизация будет существовать, и эти два числа будут решения.Разделив сумму пополам, чтобы получить среднее значение, мы видим, что все будет готово, если мы сможем найти что-то такое, что числа вида и дают произведение. Эти два уравнения эквивалентны друг другу: мы можем удовлетворить уравнению дна, выбрав. Важно отметить, что математическое изобретение комплексных чисел позволяет нам извлекать квадратный корень из отрицательного числа, так что у нас есть правильный выбор. (Именно поэтому нам не нужна Основная теорема алгебры, и фактически именно поэтому этот подход доказывает эту теорему для многочленов степени 2.) Значит, действительно есть два числа с суммой и произведением, и они естьи, которые есть. Тот факт, что эти числа удовлетворяют отношениям суммы и произведения, означает, что факторизация существует, и поэтому мы нашли решения: Мы решили задачу, и нам вообще не понадобилось использовать заученную формулу! Этот метод работает для любого квадратного уравнения, не требует запоминания, и каждый шаг имеет простое математическое обоснование.
Рассмотрим этот пример: Во-первых, давайте очистим его, умножив обе части на, чтобы получить уравнение, набор решений которого идентичен: Как и раньше, , если мы можем найти два числа с суммой и произведением, тогда факторизация будет существовать, и эти два числа будут решения.Разделив сумму пополам, чтобы получить среднее значение, мы видим, что все будет готово, если мы сможем найти что-то такое, что числа вида и дают произведение. Эти два уравнения эквивалентны друг другу: мы можем удовлетворить уравнению дна, выбрав. Важно отметить, что математическое изобретение комплексных чисел позволяет нам извлекать квадратный корень из отрицательного числа, так что у нас есть правильный выбор. (Именно поэтому нам не нужна Основная теорема алгебры, и фактически именно поэтому этот подход доказывает эту теорему для многочленов степени 2.) Значит, действительно есть два числа с суммой и произведением, и они естьи, которые есть. Тот факт, что эти числа удовлетворяют отношениям суммы и произведения, означает, что факторизация существует, и поэтому мы нашли решения: Мы решили задачу, и нам вообще не понадобилось использовать заученную формулу! Этот метод работает для любого квадратного уравнения, не требует запоминания, и каждый шаг имеет простое математическое обоснование.
Доказательство квадратичной формулы
Если кто-то хочет вывести квадратную формулу, этот метод также предоставляет альтернативное простое доказательство.
Для общего квадратного уравнения вышеизложенное показывает, что достаточно найти два числа с суммой и произведением, после чего факторизация будет существовать, и они будут корнями. Итак, мы хотели бы выяснить, существует ли такое, что эти два числа будут работать. Они автоматически суммируются. Их произведение точно тогда, когда выполняются эти два эквивалентных уравнения: Поскольку квадратный корень всегда существует (распространяясь на комплексные числа, если необходимо), выбирая квадратный корень из for, мы можем удовлетворить последнее уравнение.Таким образом, у этих двух чисел есть сумма и произведение, и все они являются решениями.
Вышеприведенной формулы уже достаточно для решения любого квадратного уравнения, потому что вы можете умножить или разделить обе части на число так, что ничего не будет впереди. Однако просто для того, чтобы убедиться, что эта формула та самая, которую все привыкли запоминать (что уже не нужно, в свете нашего метода), мы можем показать, как получить формулу для самого общего квадратного уравнения при . Нам просто нужно сначала разделить на, чтобы получить эквивалентное уравнение. Затем, подставив информацию для и для в решения выше, мы получим, что решения таковы:
Однако просто для того, чтобы убедиться, что эта формула та самая, которую все привыкли запоминать (что уже не нужно, в свете нашего метода), мы можем показать, как получить формулу для самого общего квадратного уравнения при . Нам просто нужно сначала разделить на, чтобы получить эквивалентное уравнение. Затем, подставив информацию для и для в решения выше, мы получим, что решения таковы:
Резюме
Этот метод состоит из двух основных шагов, начиная с общего квадратного уравнения в стандартной форме.
- Из-за полиномиального разложения, если мы можем найти два числа с суммой и произведением, то это полный набор решений.
- Используйте древний вавилонско-греческий трюк (распространенный на комплексные числа), чтобы найти эти два числа в любых обстоятельствах.
Для того чтобы эти шаги были математически обоснованными как завершенный метод, важно, чтобы при любых обстоятельствах на шаге 2 были найдены два числа для использования в шаге 1, даже если они не являются действительными комплексными числами. Поэтому маловероятно, что математики до Кардано (~ 1500 г. н.э.) могли сделать это полностью.
Поэтому маловероятно, что математики до Кардано (~ 1500 г. н.э.) могли сделать это полностью.
Оба шага по отдельности хорошо известны. Оглядываясь назад, можно сказать, что их комбинация для формирования полного и последовательного метода решения общих квадратных уравнений проста и очевидна. Таким образом, основной вклад этого метода заключается в том, чтобы указать на что-то полезное, что скрывалось у всех на виду.
Исторические математические рукописи
Исследуя новизну этого подхода, я наткнулся на несколько древних математических работ.Благодаря Интернету теперь каждый может увидеть и оценить творчество первых математиков.
Решение квадратных уравнений путем заполнения квадрата — видео и расшифровка урока
Шаги
Допустим, вы пытаетесь найти решение этой задачи:
Приравняем y к 0 и приступим к поиску решений. Если вы не можете легко разложить это квадратное уравнение на множители, вы можете использовать метод под названием , завершающий квадрат . В этом методе вы манипулируете своим уравнением, так что в итоге вы получаете одну часть в квадрате, которая равна числу. Таким образом, вы можете легко найти два решения.
В этом методе вы манипулируете своим уравнением, так что в итоге вы получаете одну часть в квадрате, которая равна числу. Таким образом, вы можете легко найти два решения.
Давайте посмотрим, как решить квадратное уравнение, дополнив квадрат.
Шаг 1: Установите уравнение равным 0.
Всякий раз, когда задача требует от вас найти решения или x -пересечений, это означает, что вам нужно установить уравнение равным 0 (т.е. установить y = 0) .
Шаг 2: Переместите одну константу на другую сторону.
Вам нужны только ваши переменные слева и ваши числа справа. В нашем примере это означает, что мы перемещаем восьмерку на другую сторону. Мы можем сделать это, добавив его к обеим сторонам, так как он вычитается. Помните, что при перемещении терминов с одной стороны на другую вы всегда выполняете противоположную или обратную операцию.
Шаг 3: Разделите на коэффициент квадрата члена, если он есть.
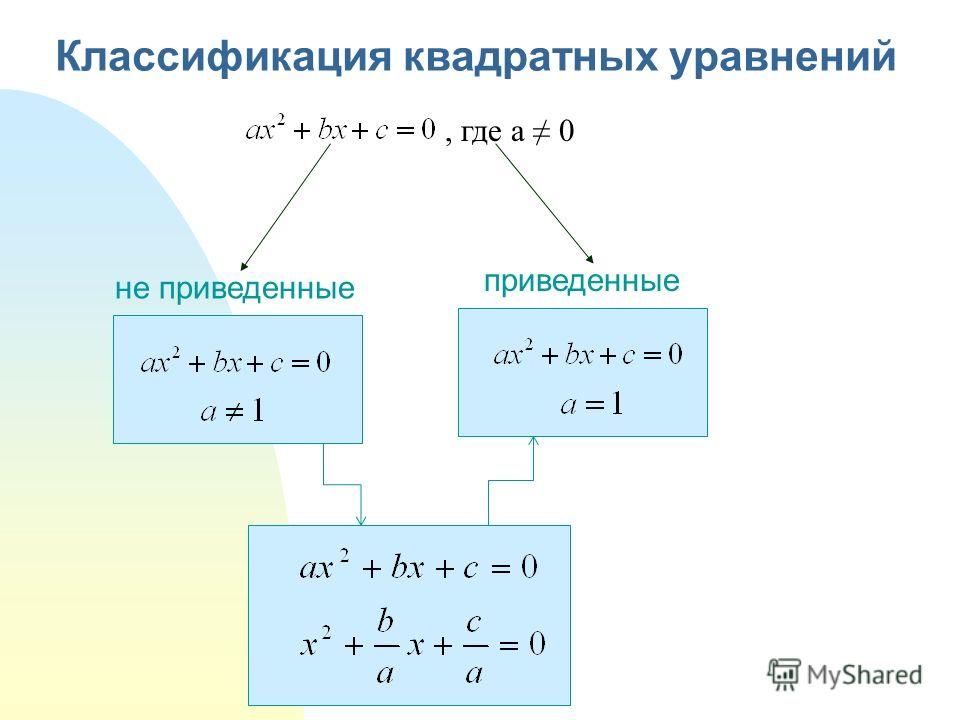
Вы хотите, чтобы ваш возведенный в квадрат член был именно таким: ваша переменная возведена в квадрат, и никакие другие константы не умножаются на нее.В нашем примере наш квадратный член умножается на 3, поэтому нам нужно разделить обе части на 3.
Шаг 4: Возьмите коэффициент вашего единственного члена размером
x , пополам, включая его знак, а затем прибавьте квадрат этого числа к обеим частям.Этот шаг немного сложен. Вы возьмете коэффициент члена x , затем разделите его на 2. Затем возведете это число в квадрат и прибавите его к обеим частям.Так, для нашего примера коэффициент терма x равен 4/3. Разделив его на 2, получим 4/6 или 2/3. Затем возведем 2/3 в квадрат и прибавим к обеим сторонам. Вот что мы получаем:
Шаг 5: Преобразуйте в квадратную форму и объедините одинаковые члены.
Теперь, когда вы вычислили квадрат коэффициента члена x , вы можете преобразовать уравнение в квадратную форму. Вы будете использовать то, что, как вы нашли, составляет половину коэффициента члена x .Вы также добавите похожие термины вместе в правой части уравнения. Для нашей задачи получаем:
Вы будете использовать то, что, как вы нашли, составляет половину коэффициента члена x .Вы также добавите похожие термины вместе в правой части уравнения. Для нашей задачи получаем:
Шаг 6: Извлеките квадратный корень из обеих сторон.
Следующим шагом в решении уравнения является извлечение квадратного корня из обеих частей. Это отменит ваш квадрат. Вот что мы получаем для нашей задачи:
Помните, что когда вы извлекаете квадратный корень из числа, у вас будет как положительная, так и отрицательная составляющая.
Шаг 7: Найдите переменную.
Поскольку у вас есть положительная и отрицательная часть, вам нужно решить два уравнения. Для нашей задачи вам нужно решить два уравнения, одно для положительной части, а другое для отрицательной:
Чтобы найти решения, найдите свою переменную, изолировав ее.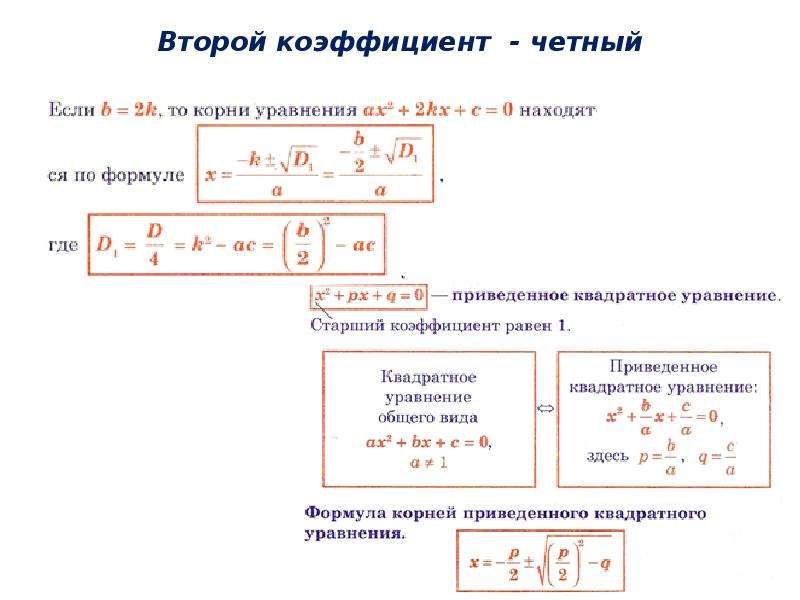 Для нашей задачи нам нужно вычесть 2/3 из обеих сторон, чтобы найти наши решения.
Для нашей задачи нам нужно вычесть 2/3 из обеих сторон, чтобы найти наши решения.
«Удивительный» трюк профессора упрощает решение квадратных уравнений
Квадратное уравнение на протяжении тысячелетий разочаровывало студентов-математиков.Но профессор математики из Университета Карнеги-Меллона в Питтсбурге, возможно, придумал лучший способ ее решения.
«Когда я наткнулся на это, я был просто в шоке», — сказал профессор По-Шен Лох.
Квадраты, которые вводятся на уроках элементарной алгебры, часто всплывают в физике и технике при расчете траекторий, даже в спорте. Если бы во время просмотра Суперкубка вы захотели оценить, как далеко по воздуху прошел пас, брошенный Патриком Махоумсом, вы бы решили квадратное уравнение.Уравнения также используются в расчетах максимизации прибыли, что является ключевым фактором для всех, кто хочет добиться успеха в бизнесе.
Доктор Ло не открыл ничего совершенно нового. Действительно, его метод смешивает идеи, восходящие к вавилонянам тысячи лет назад. Но не так преподносят эту тему современные учебники по алгебре.
Но не так преподносят эту тему современные учебники по алгебре.
«Узнать, что есть трюк тысячелетней давности, который можно импортировать сюда, меня поразило», — сказал доктор Лох. «Я хотел поделиться этим как можно шире.”
Доктор Ло является наставником некоторых из лучших учеников средней школы страны по математике в качестве тренера команды математической олимпиады США. Но он также хочет улучшить преподавание всех студентов по математике.
«Все считают, что я работаю только с олимпиадниками, — говорит доктор Лох, основатель образовательного веб-сайта Expii. «Это не правда. Моя страсть — все».
Несколько месяцев назад д-р Ло разместил в Интернете статью с описанием своего метода, и учителя уже опробовали его в своих классах.
«Я был очень удивлен, что большинство из них поняли это», — сказал Бобсон Вонг, учитель математики в средней школе Бэйсайд в Квинсе, штат Нью-Йорк, который использовал этот подход на уроке алгебры, где многие ученики боятся математики.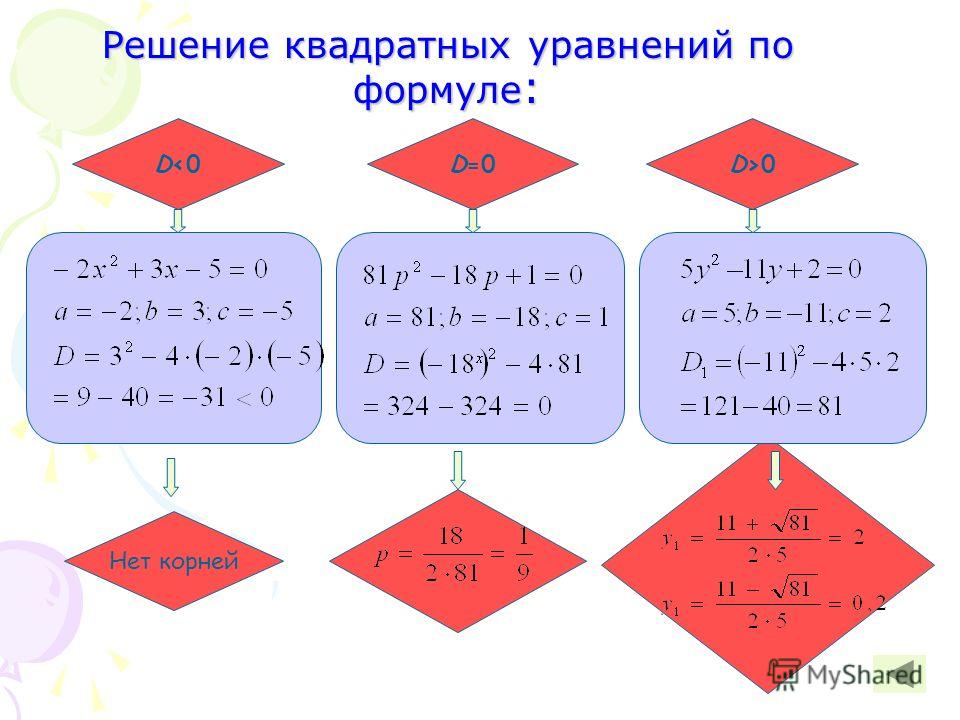 «Они смогли сделать это самостоятельно».
«Они смогли сделать это самостоятельно».
Всплеск педагогических дискуссий о квадратных уравнениях подчеркивает способность Интернета быстро распространять новые идеи обучения.
«Это инновации в образовании, которые реализуются в правильном направлении», — сказал Майкл Дрискилл, главный операционный директор Math for America, организации, которая награждает лучших учителей и предоставляет им форумы для обмена идеями.(Мистер Вонг — один из тех, кого программа «Математика для Америки» назначила главным учителем.)
Мистер Дрискилл сказал, что доктор Ло не заявлял, что у него есть что-то определенно лучшее, а вместо этого: «Он показал это учителям». и спросил: «Это работает в классе?»
Квадратичные уравнения и параболы 101
Во-первых, краткий обзор квадратных уравнений и парабол.
Что в настоящее время изучают студенты алгебры
Перед тем, как учащиеся знакомятся с квадратной формулой, их учат более простому методу решения определенных уравнений. Для простоты рассмотрим уравнение, в котором a = 1.
Для простоты рассмотрим уравнение, в котором a = 1.
Возможно, вы помните, как учитель просил вас разложить на множители набор символов. То есть, вы надеялись найти два номера R и S такого, что
x ² — 4 x — 5 = ( r — r ) ( S ) = 0Умножение ( x – r )( x – s ) дает x ² – ( r + s ) x + rs.
Ключ состоит в том, чтобы найти r и s так, чтобы сумма r и s равнялась 4 (то есть r + s = 4)
6 и 902 6 с дает –5 ( r × с = –5). Если они существуют, то r и s — два и только два решения. Выяснение факторов, которые работают, в основном методом проб и ошибок. «Тот факт, что вам внезапно приходится переключаться в режим угадывания, заставляет вас чувствовать, что, возможно, математика сбивает с толку или не является систематической», — говорит доктор. — сказал Лох.
— сказал Лох.
Угадывание также становится громоздким для квадратичных вычислений с большими числами и хорошо работает только для задач, ответы на которые придуманы целыми числами.
Метод доктора Ло исключает эту игру в догадки. Но многих студентов, изучающих алгебру, беспорядок алгебраических символов все еще сбивает с толку. Итак, мистер Вонг говорит им нарисовать параболу.
«Если вы нарисуете это в виде графика, детям будет намного легче понять, что происходит», — сказал он.
Как работает новый метод
Этот альтернативный метод решения квадратных уравнений использует тот факт, что параболы симметричны.
Тот же метод работает и для уравнений, которые не поддаются простой факторизации.
Вот когда студенты обращаются к квадратной формуле. Но они часто неправильно его помнят — обычный вывод немного запутан, включая технику, называемую «заполнение квадрата», — и получают неправильные ответы.
Метод доктора Ло позволяет людям вычислять ответы, не запоминая точную формулу. (Это также дает более простое доказательство).— сказал Лох.
(Это также дает более простое доказательство).— сказал Лох.
Г-н Вонг сказал, что версия доктора Ло проще для студентов, потому что она «предоставляет один метод для решения всех видов квадратных уравнений».
Техника с древними корнями
Доктор Ло погрузился в историю математики и обнаружил, что вавилоняне и греки обладали одним и тем же пониманием, хотя их понимание было ограниченным, поскольку их математика ограничивалась положительными числами. Это уже потом люди придумали понятия отрицательных чисел, нуля и еще более эзотерические понятия вроде мнимых чисел — квадратных корней из отрицательных чисел.
Он даже узнал, что учитель математики в Садбери, Канада, по имени Джон Сэвидж придумал аналогичный подход 30 лет назад. В статье г-на Сэвиджа в журнале «Учитель математики» в 1989 г. изложена почти та же процедура, хотя доктор Ло дополнил некоторые логические нюансы, объясняя, почему она работает.
«Честно говоря, я не могу точно вспомнить, где именно произошел момент озарения», — сказал г-н Сэвидж в телефонном интервью. Но это казалось улучшением по сравнению с обычным способом преподавания предмета.
Но это казалось улучшением по сравнению с обычным способом преподавания предмета.
Он продолжал использовать этот подход, как и некоторые другие учителя, которых он знал. Но интернет все еще был в зачаточном состоянии, и идея исчезла.
«Это так и не прижилось», — сказал мистер Сэвидж. «Оглядываясь назад, я должен был подтолкнуть его немного больше. Я думаю, что это намного проще, чем традиционный способ».
Г-н Сэвидж сказал, что он был взволнован, увидев возрождение той же идеи спустя 22 года после его ухода на пенсию. «Мне было очень интересно прочитать это сейчас», — сказал он о статье доктора Ло. «Довольно интересно, что он в основном пришел к той же идее.”
Квадратные уравнения — Квадратные уравнения Как решить
Льюис МулатероGetty Images
- Математик из Университета Карнеги-Меллона разработал более простой способ решения квадратных уравнений.
- Математик надеется, что этот метод поможет ученикам избежать заучивания тупых формул .

- Его секрет в том, что он объединяет два корня вместе, а не хранит их как отдельные значения.
Математик вывел более простой способ решения задач квадратного уравнения, согласно обзору технологий Массачусетского технологического института .
➗ Вы любите сложные математические задачи. И мы тоже. Давайте решим их вместе.
Квадратные уравнения — это многочлены, включающие x², и учителя используют их, чтобы научить учащихся находить два решения одновременно. Новый процесс, разработанный доктором По-Шеном Ло из Университета Карнеги-Меллона, обходит традиционные методы, такие как завершение квадрата, и превращает поиск корней в более простую задачу, включающую меньшее количество шагов и более интуитивную.
Вот объяснительное видео доктора Ло:
Этот контент импортирован с YouTube. Вы можете найти тот же контент в другом формате или найти дополнительную информацию на их веб-сайте.
Квадратные уравнения попадают в интересную дырку от бублика в образовании. Учащиеся изучают их, начиная с уроков алгебры или предварительной алгебры, но они представляют собой набитые с ложки примеры, которые работают очень легко и с целыми решениями. То же самое происходит с теоремой Пифагора, где в школе большинство примеров заканчиваются решением пифагорейских троек , небольшого набора целочисленных значений, которые четко работают в теореме Пифагора.
Этот контент импортирован из {embed-name}. Вы можете найти тот же контент в другом формате или найти дополнительную информацию на их веб-сайте.
Квадратные уравнения представляют собой многочлены, то есть цепочки математических выражений. Выражение типа «x + 4» является многочленом. Они могут иметь одну или несколько переменных в любой комбинации, и их величина определяется степенью, в которой переменные приведены. Таким образом, x + 4 — это выражение, описывающее прямую линию, а (x + 4)² — это кривая.
Поскольку линия пересекает какую-либо конкретную широту или долготу только один раз, ее решением является только одно значение. Если у вас есть x², это означает два корневых значения в форме круга или дуги, которые образуют два пересечения.
Росс Мантл
Метод доктора Ло, которым он также подробно поделился на своем веб-сайте, использует идею двух корней каждого квадратного уравнения, чтобы упростить способ вывода этих корней. Он понял, что может описать два корня квадратного уравнения следующим образом: если их объединить, они усредняются до определенного значения, затем появляется значение z, которое показывает любое дополнительное неизвестное значение.Вместо того, чтобы искать два отдельных, разных значения, мы ищем для начала два идентичных значения. Это упрощает арифметическую часть умножения формулы.
Популярная механика
«Обычно, когда мы решаем задачу факторинга, мы пытаемся найти два числа, которые умножаются на 12 и в сумме дают 8», — сказал доктор Лох. Эти два числа являются решением квадратного уравнения, но ученикам требуется много времени, чтобы решить их, поскольку они часто используют подход «угадай и проверь».
Эти два числа являются решением квадратного уравнения, но ученикам требуется много времени, чтобы решить их, поскольку они часто используют подход «угадай и проверь».
Вместо того, чтобы разложить на множители произведение 12, Ло начинает с суммы 8. . Таким образом, числа могут быть представлены как 4–u и 4+u.
Когда вы умножаете, средние члены сокращаются, и вы получаете уравнение 16–u2 = 12. При решении для u вы увидите, что положительные и отрицательные 2 работают, и когда вы подставите эти целые числа обратно в уравнения 4–u и 4+u вы получаете два решения, 2 и 6, которые решают исходное полиномиальное уравнение.
Это быстрее, чем классический метод фольгирования, используемый в квадратичной формуле, и не требует угадывания. — Кортни Линдер
Доктор Ло считает, что учащиеся могут освоить этот метод более интуитивно, отчасти потому, что не требуется специальной, отдельной формулы. Если учащиеся могут запомнить некоторые простые обобщения о корнях, они могут решить, куда двигаться дальше.
Решите эти сложные головоломки
Кубик Рубика SpeedRipper
Кубик Рубика уже 40 лет сводит людей с ума.Попробуйте решить ее самостоятельно или научитесь решать ее с помощью математики.
Трехмерная игра-головоломка Kanoodle
Образовательные идеи amazon.com$16,49
Всего 12 деталей, но всего 200 задач. Kanoodle поставит в тупик как детей, так и взрослых двухмерными и трехмерными головоломками.
Саграда Настольная игра
Взлом игр Амазонка.комВ одной из лучших настольных игр-головоломок года вы и еще три игрока пытаетесь создать витражи для храма Святого Семейства.
Трехмерная игра-головоломка Dimension
Темза и Космос amazon.com39,95 долларов США
В этой динамичной трехмерной игре-головоломке нужно сочетать сообразительность, логику и удачу, чтобы собрать сферы и заработать как можно больше очков.
Это по-прежнему сложно, но менее сложно, особенно если доктор Ло прав в том, что это облегчит понимание учащимися того, как работают квадратные уравнения и как они вписываются в математику. Понимание их является ключом к начальным идеям предварительного исчисления, например.
Понимание их является ключом к начальным идеям предварительного исчисления, например.
Квадратичный метод не так прост, если не считать готовых примеров для классной комнаты. Реальные примеры и приложения беспорядочны, с уродливыми корнями из десятичных дробей или иррациональных чисел.Будучи студентом, трудно понять, что вы нашли правильный ответ. Новый метод доктора Лоха предназначен для реальной жизни, но он также надеется, что он также поможет студентам почувствовать, что они лучше понимают квадратичную формулу.
Многие студенты, изучающие математику, с трудом преодолевают пропасть в понимании между простыми примерами в классе и собственным применением идей, и доктор Ло хочет построить для них лучший мост.
Смотрите сейчас:
Кэролайн Делберт Кэролайн Делберт — писатель, редактор книг, исследователь и заядлый читатель. Этот контент создается и поддерживается третьей стороной и импортируется на эту страницу, чтобы помочь пользователям указать свои адреса электронной почты.

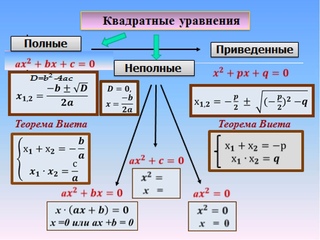 Поскольку a=1, то линейный коэффициент будет равен 1, что касается свободного члена уравнения линейного, то он равен должен быть половине линейного коэффициента приведенного уравнения квадратного. После того, как составлен квадрат линейного выражения, необходимо в правую часть равенства, где находится свободный член, добавить соответствующее число, которое получается при раскрытии квадрата.
Поскольку a=1, то линейный коэффициент будет равен 1, что касается свободного члена уравнения линейного, то он равен должен быть половине линейного коэффициента приведенного уравнения квадратного. После того, как составлен квадрат линейного выражения, необходимо в правую часть равенства, где находится свободный член, добавить соответствующее число, которое получается при раскрытии квадрата.


 М. Четырехзначные математические таблицы. — М., Просвещение, 1990.
М. Четырехзначные математические таблицы. — М., Просвещение, 1990.
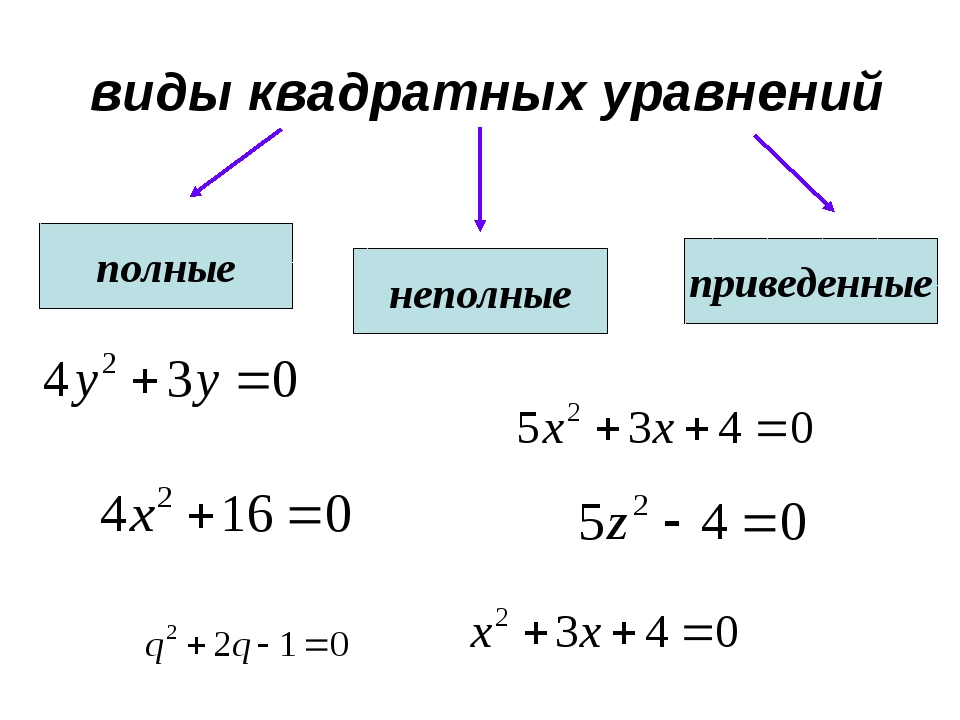
 Не тратьте много времени на попытки
фактор вашего уравнения; если вы не можете учесть это менее чем за 60 секунд,
перейти к другому методу.
Не тратьте много времени на попытки
фактор вашего уравнения; если вы не можете учесть это менее чем за 60 секунд,
перейти к другому методу.