Подобие треугольников. Визуальный гид (ЕГЭ — 2021)

P.S. Последний бесценный совет!

Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут. Почему? Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!

Теперь самое главное.

Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем большинство твоих сверстников. Проблема в том, что этого может не хватить…

Для чего?

Для успешной сдачи ЕГЭ и поступления в ВУЗ мечты на бюджет и, самое главное, для жизни. Я не буду тебя ни в чем убеждать, просто скажу одну вещь…  Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. 

Это статистика.  Но и это не главное.

Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…

Но думай сам…

Что нужно, чтобы сдать наверняка ЕГЭ, поступить в ВУЗ мечты и быть в конечном итоге… более счастливым? Две вещи.

Первое, тебе нужно набить руку, решая задачи

На экзамене у тебя не будут спрашивать теорию. Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.  “Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.

Второе, заниматься по системе  — иначе у тебя уйдет много времени и ты, что-нибудь пропустишь.

И сейчас будет честная реклама наших курсов подготовки к ЕГЭ, потому что они решают обе эти проблемы.

Тебе же понятен этот учебник? Так вот наши курсы такие же понятные как этот учебник.  

Потому что их подготовил и ведет автор этого учебника Алексей Шевчук. 

Он буквально разжевывает все на вебинарах. Вы решаете задачи. Много задач. У вас будет проверка домашки и марафон «Год за месяц» в мае, чтобы «упаковать» ваши знания и улучшить результат на 20-30%.

Курсы очень бюджетные: от 2000 до 3990 тыс/мес за 12 двухчасовых занятий с Алексеем. 

Кликайте по этим кнопкам и читайте условия, там все очень подробно описано:

Презентация на тему: «2,3 признаки подобия треугольников».

библиотека
материалов

Содержание слайдов

Номер слайда 1

Номер слайда 2

A B С BC II AD. Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос Запишите равенство отношений соответствующих сторон. COB AOD по 1 признаку подобия D BC AD = BO OD OC OA = O 4 12 21 21 4 12 x x x 21 = 4 12

Номер слайда 3

A B P Трапеция АDPC. Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос Запишите равенство отношений соответствующих сторон. BDP BAC по 1 признаку C DP AC = BP BC BD BA = D 8 21 8 4 x x x 21 = 8 12 12 12 21

Номер слайда 4

A B P Найдите пары подобных треугольников и докажите их подобие. Найдите АВ и РС. Блиц-опрос BDP BAC по 1 признаку C D 6 10 4 5 8 8 12 2 Справимся без пропорции

Номер слайда 5

докажем, что и применим 1 признак подобия треугольников А С В В1 С1 А1 II признак подобия треугольников. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны. ABC А1В1С1 Доказать: Доказательство: Дано: ABC, А1В1С1,

Номер слайда 6

А С В В1 С1 А1 С2 2 1 Рассмотрим у которого 1= А1, 2= В1. ABC2, ABC2 А1В1С1 по двум углам Тогда по условию АС = АС2 1).

Номер слайда 7

А С В В1 С1 А1 С2 2 1 2). ABC = АВС2 по двум сторонам и углу между ними В = 2, 2= В1 = В1 В

Номер слайда 8

Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос A B С 7см Е К F 400 400 8см 3,5см 4см 4 8 = 3,5 7 Верно FEK AВС по 2 признаку

Номер слайда 9

Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос Р Q R 3см В С А 400 400 3см 5см 5см 5 3 = 5 3 Верно ABC PQR по 2 признаку

Номер слайда 10

Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос A B C 10см M L K 700 400 10см 5см 5см 5 10 = 5 10 Верно KML ABC по 2 признаку 400

Номер слайда 11

Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос A B C 8см M L K 10см 4см 3см 6 3 = 8 4 Верно KML ABC по 2 признаку 6см

Номер слайда 12

Найдите пары подобных треугольников и докажите их подобие.

A B C 92см 3 69 = 4 92 Верно KML ABC по 2 признаку M L K 69 115см 5см 4см 3

Номер слайда 13

Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос AВС РВD по 2 признаку 3 12 = 5 20 Верно A B P C D 5 3 12 20 Найти

Номер слайда 14

A B С Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос AОD COD по 2 признаку D O 4 5 15 12 4 12 = 5 15 Верно 21 ? 7

Номер слайда 15

Площадь треугольника МОС на 8 см2 меньше площади треугольника КОР. Найти площадь треугольника ОКР, если КО=15см, ОР=12см, ОМ=5см, ОС=4см. C M О K P 5 x x-8 4 12 15 4 12 = 5 15 Верно MCO PKO по 2 признаку Запишите теорему об отношении площадей подобных треугольников SMCO SKPO = k2 x-8 x = 1 9 MO OK SMCO SKPO = 2 x x-8 5 15

Номер слайда 16

докажем, что и применим 2 признак подобия треугольников А С В В1 С1 А1 III признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны. ABC А1В1С1 Доказать: Доказательство: Дано: ABC, А1В1С1,

Номер слайда 17

А С В В1 С1 А1 С2 2 1 Рассмотрим у которого 1= А1, 2= В1. ABC2, ABC2 А1В1С1 по двум углам Тогда по условию АС = АС2 1). ВС = ВС2

Номер слайда 18

1= А1 А1 А А С В В1 С1 А1 С2 2 1 2). ABC = АВС2 по трем сторонам А = 1, =

Номер слайда 19

A B C Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос D E F 3см 3см 3см 5см 5см 5см 3 5 = 3 5 Верно DEF ABC по 3 признаку = 3 5 Докажите по 1 признаку подобия, по 2 признаку.

Номер слайда 20

A B C Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос D E F 4см 8см 6см 6см 9см 12см 6 4 = 9 6 Верно DEF ABC по 3 признаку = 12 8

Номер слайда 21

Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос A B C 6см M L K 8см 3см 4см 4 8 = 4 8 Верно KML ABC по 3 признаку 4см 8см = 3 6

Номер слайда 22

Доказать: КМ II BL Блиц-опрос A B C 6 M L K 10 7 3 7 14 = 5 10 Верно KMA LBC по 3 признаку 5 14 = 3 6 Найти

Номер слайда 23

A B С Найдите пары подобных треугольников и докажите их подобие. Найдите угол ВАD. D 15 14 550 21 10 9 1 3 800 10 15 = 14 21 Верно АСD ABC по 3 признаку = 14 9 1 3 800 550

Номер слайда 24

9 6 D N К 18см С В А 13,5см 6см 6 9 = 12 18 Верно DNK ABC по 3 признаку 12см = 9 13,5 В треугольниках АВС и DNK известны стороны. SDNK=36cм2. Найдите площадь треугольника АВС. 9см 9см Запишите теорему об отношении площадей подобных треугольников SABC SDNK = k2 x 36 = 4 9 AB DN SABC SDNK = 2 36 x x

Номер слайда 25

2 2 ADСD – параллелограмм. OF BC AB = 2см, BF = 5см, ВС = 9см. Найдите BЕ. B ЕFB NFA по 1 признаку A F N С D 9 BE AN = BF AF FE FN = 5 x 7 Е 7 O 9-x x 5 9-x 9-x x 9-x = 5 7

Номер слайда 26

A B С АВСD – параллелограмм. РАВСD=45см, ВN AD, BF CD, BN : BF = 2 : 3 Найти AB и AD. Запишите равенство отношений соответствующих сторон. ABN CBF по 1 признаку N BA CB = BN BF AN CF = F D 22,5-x x 22,5-x = 2 3 2 3 x x 22,5-x pАВСD=45:2=22,5(см)

Номер слайда 27

В треугольнике АВС DF II BC, AD = 3 cм, DB = 1см. SADF=27cм2. Найдите площадь треугольника АВС. 4 4 В А F Запишите теорему об отношении площадей подобных треугольников АDF ABC по 1 признаку C SADF SABC = k2 D 1 27 x = 9 16 3 3 AD AB SADF SABC = 2 27 х х

Средняя линия треугольника, теория в ЕГЭ по математике

\[{\Large{\text{Подобие треугольников}}}\]

Определения

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
(стороны называются сходственными, если они лежат напротив равных углов).

 

Коэффициент подобия (подобных) треугольников – это число, равное отношению сходственных сторон этих треугольников.

 

Определение

Периметр треугольника – это сумма длин всех его сторон.

 

Теорема

Отношение периметров двух подобных треугольников равно коэффициенту подобия.

 

Доказательство

Рассмотрим треугольники \(ABC\) и \(A_1B_1C_1\) со сторонами \(a,b,c\) и \(a_1, b_1, c_1\) соответственно (см. рисунок выше).

 

Тогда \(P_{ABC}=a+b+c=ka_1+kb_1+kc_1=k(a_1+b_1+c_1)=k\cdot P_{A_1B_1C_1}\)

 

Теорема

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

 

Доказательство

Пусть треугольники \(ABC\) и \(A_1B_1C_1\) подобны, причём \(\dfrac{AB}{A_1B_1} = \dfrac{AC}{A_1C_1} = \dfrac{BC}{B_1C_1} = k\). Обозначим буквами \(S\) и \(S_1\) площади этих треугольников соответственно.

 

Так как \(\angle A = \angle A_1\), то \(\dfrac{S}{S_1} = \dfrac{AB\cdot AC}{A_1B_1\cdot A_1C_1}\) (по теореме об отношении площадей треугольников, имеющих по равному углу).

 

Так как \(\dfrac{AB}{A_1B_1} = \dfrac{AC}{A_1C_1} = k\), то \(\dfrac{S}{S_1} = \dfrac{AB}{A_1B_1}\cdot\dfrac{AC}{A_1C_1} = k\cdot k = k^2\), что и требовалось доказать. \circ — \angle A_1 — \angle B_1 = \angle C_1\), то есть углы треугольника \(ABC\) соответственно равны углам треугольника \(A_1B_1C_1\).

 

Так как \(\angle A = \angle A_1\) и \(\angle B = \angle B_1\), то \(\dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac{AB\cdot AC}{A_1B_1\cdot A_1C_1}\) и \(\dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac{AB\cdot BC}{A_1B_1\cdot B_1C_1}\).

 

Из этих равенств следует, что \(\dfrac{AC}{A_1C_1} = \dfrac{BC}{B_1C_1}\).

 

Аналогично доказывается, что \(\dfrac{AC}{A_1C_1} = \dfrac{AB}{A_1B_1}\) (используя равенства \(\angle B = \angle B_1\), \(\angle C = \angle C_1\)).

 

В итоге, стороны треугольника \(ABC\) пропорциональны сходственным сторонам треугольника \(A_1B_1C_1\), что и требовалось доказать.

 

Теорема (второй признак подобия треугольников)

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

 

Доказательство

Рассмотрим два треугольника \(ABC\) и \(A’B’C’\), таких что \(\dfrac{AB}{A’B’}=\dfrac{AC}{A’C’}\), \(\angle BAC = \angle A’\). Докажем, что треугольники \(ABC\) и \(A’B’C’\) – подобны. Учитывая первый признак подобия треугольников, достаточно показать, что \(\angle B = \angle B’\).

 

Рассмотрим треугольник \(ABC»\), у которого \(\angle 1 = \angle A’\), \(\angle 2 = \angle B’\). Треугольники \(ABC»\) и \(A’B’C’\) подобны по первому признаку подобия треугольников, тогда \(\dfrac{AB}{A’B’} = \dfrac{AC»}{A’C’}\).

 

С другой стороны, по условию \(\dfrac{AB}{A’B’} = \dfrac{AC}{A’C’}\). Из последних двух равенств следует, что \(AC = AC»\).

 

Треугольники \(ABC\) и \(ABC»\) равны по двум сторонам и углу между ними, следовательно, \(\angle B = \angle 2 = \angle B’\).

 

Теорема (третий признак подобия треугольников)

Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

 

Доказательство

Пусть стороны треугольников \(ABC\) и \(A’B’C’\) пропорциональны: \(\dfrac{AB}{A’B’} = \dfrac{AC}{A’C’} = \dfrac{BC}{B’C’}\). Докажем, что треугольники \(ABC\) и \(A’B’C’\) подобны.

 

Для этого, учитывая второй признак подобия треугольников, достаточно доказать, что \(\angle BAC = \angle A’\).

 

Рассмотрим треугольник \(ABC»\), у которого \(\angle 1 = \angle A’\), \(\angle 2 = \angle B’\).

 

Треугольники \(ABC»\) и \(A’B’C’\) подобны по первому признаку подобия треугольников, следовательно, \(\dfrac{AB}{A’B’} = \dfrac{BC»}{B’C’} = \dfrac{C»A}{C’A’}\).

 

Из последней цепочки равенств и условия \(\dfrac{AB}{A’B’} = \dfrac{AC}{A’C’} = \dfrac{BC}{B’C’}\) вытекает, что \(BC = BC»\), \(CA = C»A\).

 

Треугольники \(ABC\) и \(ABC»\) равны по трем сторонам, следовательно, \(\angle BAC = \angle 1 = \angle A’\).

 

\[{\Large{\text{Теорема Фалеса}}}\]

Теорема

Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.

 

Доказательство

Докажем сначала лемму: Если в \(\triangle OBB_1\) через середину \(A\) стороны \(OB\) проведена прямая \(a\parallel BB_1\), то она пересечет сторону \(OB_1\) также в середине.

 

Через точку \(B_1\) проведем \(l\parallel OB\). Пусть \(l\cap a=K\). Тогда \(ABB_1K\) — параллелограмм, следовательно, \(B_1K=AB=OA\) и \(\angle A_1KB_1=\angle ABB_1=\angle OAA_1\); \(\angle AA_1O=\angle KA_1B_1\) как вертикальные. Значит, по второму признаку \(\triangle OAA_1=\triangle B_1KA_1 \Rightarrow OA_1=A_1B_1\). Лемма доказана.

 

Перейдем к доказательству теоремы. Пусть \(OA=AB=BC\), \(a\parallel b\parallel c\) и нужно доказать, что \(OA_1=A_1B_1=B_1C_1\).

 

Таким образом, по данной лемме \(OA_1=A_1B_1\). Докажем, что \(A_1B_1=B_1C_1\). Проведем через точку \(B_1\) прямую \(d\parallel OC\), причем пусть \(d\cap a=D_1, d\cap c=D_2\). Тогда \(ABB_1D_1, BCD_2B_1\) — параллелограммы, следовательно, \(D_1B_1=AB=BC=B_1D_2\). Таким образом, \(\angle A_1B_1D_1=\angle C_1B_1D_2\) как вертикальные, \(\angle A_1D_1B_1=\angle C_1D_2B_1\) как накрест лежащие, и, значит, по второму признаку \(\triangle A_1B_1D_1=\triangle C_1B_1D_2 \Rightarrow A_1B_1=B_1C_1\).

 

Теорема Фалеса

Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.

 

Доказательство

Пусть параллельные прямые \(p\parallel q\parallel r\parallel s\) разбили одну из прямых на отрезки \(a, b, c, d\). Тогда вторую прямую эти прямые должны разбить на отрезки \(ka, kb, kc, kd\) соответственно, где \(k\) – некоторое число, тот самый коэффициент пропорциональности отрезков.

 

Проведем через точку \(A_1\) прямую \(p\parallel OD\) (\(ABB_2A_1\) — параллелограмм, следовательно, \(AB=A_1B_2\)). Тогда \(\triangle OAA_1 \sim \triangle A_1B_1B_2\) по двум углам. Следовательно, \(\dfrac{OA}{A_1B_2}=\dfrac{OA_1}{A_1B_1} \Rightarrow A_1B_1=kb\).

Аналогично проведем через \(B_1\) прямую \(q\parallel OD \Rightarrow \triangle OBB_1\sim \triangle B_1C_1C_2 \Rightarrow B_1C_1=kc\) и т. д.

 

\[{\Large{\text{Средняя линия треугольника}}}\]

Определение

Средняя линия треугольника – это отрезок, соединяющий середины любых двух сторон треугольника.

 

Теорема

Средняя линия треугольника параллельна третьей стороне и равна ее половине.

 

Доказательство

1) Параллельность средней линию основанию следует из доказанной выше леммы.

 

2) Докажем, что \(MN=\dfrac12 AC\).

 

Через точку \(N\) проведем прямую параллельно \(AB\). Пусть эта прямая пересекла сторону \(AC\) в точке \(K\). Тогда \(AMNK\) — параллелограмм (\(AM\parallel NK, MN\parallel AK\) по предыдущему пункту). Значит, \(MN=AK\).

 

Т.к. \(NK\parallel AB\) и \(N\) – середина \(BC\), то по теореме Фалеса \(K\) – середина \(AC\). Следовательно, \(MN=AK=KC=\dfrac12 AC\).

 

Следствие

Средняя линия треугольника отсекает от него треугольник, подобный данному с коэффициентом \(\frac12\).

Признаки равенства треугольников. Признаки равенства прямоугольных треугольников. Признаки подобия треугольников. Признаки подобия прямоугольных треугольников.

	Навигация по справочнику TehTab.ru:  главная страница  / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.  / / Признаки равенства треугольников. Признаки равенства прямоугольных треугольников. Признаки подобия треугольников. Признаки подобия прямоугольных треугольников. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников. Признаки подобия треугольников. Признаки подобия прямоугольных треугольников. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников. Признаки подобия треугольников. Признаки подобия прямоугольных треугольников. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников. Признаки подобия треугольников. Признаки подобия прямоугольных треугольников.
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу.
TehTab.ru Реклама, сотрудничество: [email protected]	Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями.

8 класс. Геометрия. Подобные треугольники. Признаки подобия треугольников. — Второй и третий признаки подобия треугольников.

Комментарии преподавателя

По­доб­ны­ми на­зы­ва­ют­ся такие тре­уголь­ни­ки, у ко­то­рых углы со­от­вет­ствен­но равны, а сто­ро­ны од­но­го со­от­вет­ствен­но про­пор­ци­о­наль­ны сто­ро­нам дру­го­го тре­уголь­ни­ка (см. рис. 1).

 

Рис. 1. По­доб­ные тре­уголь­ни­ки 

От­но­ше­ние длин сто­рон од­но­го тре­уголь­ни­ка к сход­ствен­ным сто­ро­нам дру­го­го на­зы­ва­ет­ся ко­эф­фи­ци­ен­том по­до­бия (): .

Пер­вый при­знак по­до­бия тре­уголь­ни­ков

Если два угла од­но­го тре­уголь­ни­ка со­от­вет­ствен­но равны двум углам дру­го­го, то такие тре­уголь­ни­ки по­доб­ны (см. рис. 2). 

 

Рис. 2. Пер­вый при­знак по­до­бия тре­уголь­ни­ков

Если две сто­ро­ны од­но­го тре­уголь­ни­ка про­пор­ци­о­наль­ны двум дру­гим сто­ро­нам дру­го­го тре­уголь­ни­ка, а углы, за­клю­чён­ные между этими сто­ро­на­ми, равны, то такие тре­уголь­ни­ки по­доб­ны.

Дано: ;  ; ;  (см. рис. 3).

До­ка­зать: по­до­бие дан­ных тре­уголь­ни­ков  . 

 

Рис. 3. Ил­лю­стра­ция к до­ка­за­тель­ству

До­ка­за­тель­ство

Со­глас­но пер­во­му при­зна­ку по­до­бия тре­уголь­ни­ков, тре­уголь­ни­ки по­доб­ны, если два угла од­но­го со­от­вет­ствен­но равны двум углам дру­го­го. По­это­му для до­ка­за­тель­ства того, что , необ­хо­ди­мо до­ка­зать, что угол  равен углу  (угол  равен углу  по усло­вию).

По­стро­им тре­уголь­ник  (см. рис. 4), у ко­то­ро­го , а . Со­глас­но пер­во­му при­зна­ку по­до­бия тре­уголь­ни­ков  (при­знак по­до­бия по двум углам). 

 

Рис. 4. Ил­лю­стра­ция к до­ка­за­тель­ству

Из по­до­бия этих тре­уголь­ни­ков сле­ду­ет, что сто­ро­на  от­но­сит­ся к сто­роне  как сто­ро­на  от­но­сит­ся к сто­роне :

Из усло­вия из­вест­но, что . Сле­до­ва­тель­но, . Таким об­ра­зом, .

По­лу­ча­ем, что тре­уголь­ни­ки  и  равны, так как у них равны две сто­ро­ны и угол между ними ( – общая сто­ро­на,  и , по­сколь­ку  и ).

От­сю­да сле­ду­ет, что , а так как , то .

У тре­уголь­ни­ков  и : , а . Со­глас­но пер­во­му при­зна­ку по­до­бия тре­уголь­ни­ков эти тре­уголь­ни­ки по­доб­ны: . Что и тре­бо­ва­лось до­ка­зать.

По дан­ным ри­сун­ка 5 найти длину x, до­ка­зать, что .

 

Рис. 5. Ил­лю­стра­ция к за­да­че

Ре­ше­ние

1) Рас­смот­рим два тре­уголь­ни­ка с общей вер­ши­ной  и : , так как они вер­ти­каль­ные.

При­ле­га­ю­щие сто­ро­ны у этих тре­уголь­ни­ков про­пор­ци­о­наль­ны: .

Сле­до­ва­тель­но, эти тре­уголь­ни­ки по­доб­ны (), со­глас­но вто­ро­му при­зна­ку по­до­бия. Ко­эф­фи­ци­ент по­до­бия равен 2. С по­мо­щью него опре­де­лим длину .

2) Так как , то все углы у них равны.  – эти углы яв­ля­ют­ся на­крест ле­жа­щи­ми при пе­ре­се­че­нии пря­мых  и  се­ку­щей . Таким об­ра­зом, , что и тре­бо­ва­лось до­ка­зать.

Ответ: па­рал­лель­ность пря­мых  и  до­ка­за­на; .

По дан­ным ри­сун­ка найти длину , от­ме­тить рав­ные углы и до­ка­зать, что  (см. рис. 6).

Рис. 6. Ил­лю­стра­ция к за­да­че

Ре­ше­ние

1)  яв­ля­ет­ся общим для тре­уголь­ни­ков  и . К дан­но­му углу при­ле­га­ют сто­ро­на  и сто­ро­на  тре­уголь­ни­ка , а также сто­ро­на  и сто­ро­на  тре­уголь­ни­ка .

Видно, что .

Сле­до­ва­тель­но, , со­глас­но вто­ро­му при­зна­ку по­до­бия тре­уголь­ни­ков (общий угол и про­пор­ци­о­наль­ность при­ле­жа­щих сто­рон).

2) Ко­эф­фи­ци­ент по­до­бия у этих тре­уголь­ни­ков равен 3, по­это­му можно опре­де­лить сто­ро­ну : 

3) Сто­ро­ны  и  яв­ля­ют­ся сход­ствен­ны­ми, сле­до­ва­тель­но, они лежат на­про­тив рав­ных углов: .

Сто­ро­ны  и  также яв­ля­ют­ся сход­ствен­ны­ми, сле­до­ва­тель­но, .

От­ме­тим рав­ные углы на ри­сун­ке (см. рис. 7). 

Рис. 7. Ил­лю­стра­ция к за­да­че

Ответ: ; ; ; .

Найти длину , от­ме­тить рав­ные углы и до­ка­зать, что  (см. рис. 8). 

Рис. 8. Ил­лю­стра­ция к за­да­че

Ре­ше­ние

1)  яв­ля­ет­ся общим для тре­уголь­ни­ков  и . К дан­но­му углу при­ле­га­ют сто­ро­на  и сто­ро­на  тре­уголь­ни­ка , а также сто­ро­на  и сто­ро­на  тре­уголь­ни­ка .

Видно, что .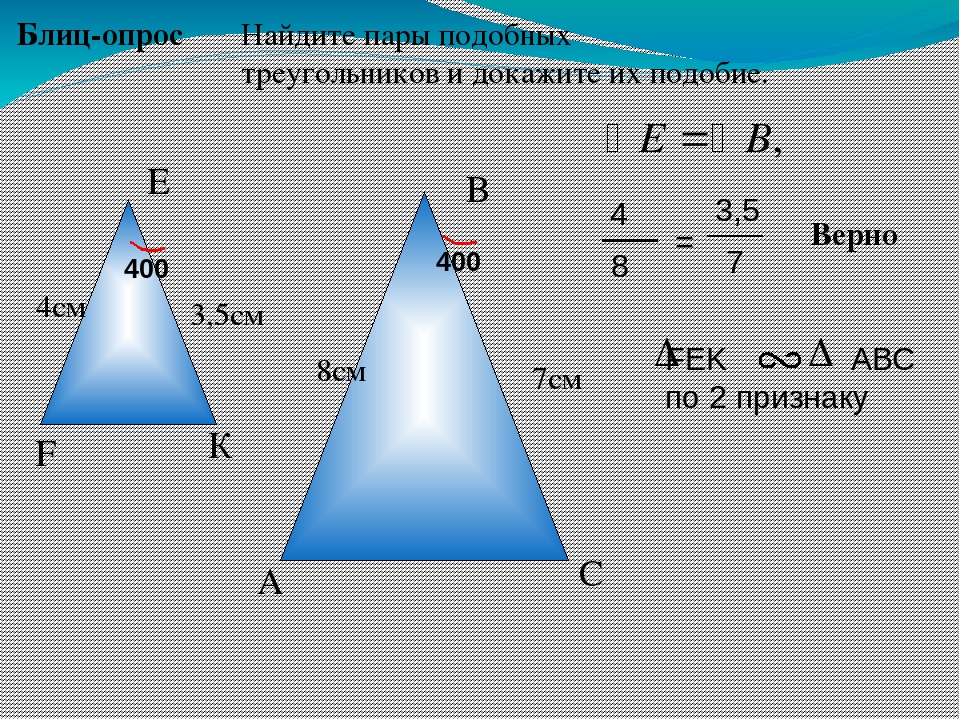

Сто­ро­ны тре­уголь­ни­ков, при­ле­жа­щие к , про­пор­ци­о­наль­ные, сле­до­ва­тель­но, , со­глас­но вто­ро­му при­зна­ку по­до­бия тре­уголь­ни­ков.

2) Сто­ро­ны  и  яв­ля­ют­ся сход­ствен­ны­ми, сле­до­ва­тель­но, они лежат на­про­тив рав­ных углов: .

Сто­ро­ны  и  также яв­ля­ют­ся сход­ствен­ны­ми, сле­до­ва­тель­но, .

От­ме­тим рав­ные углы на ри­сун­ке (см. рис. 9). 

Рис. 9. Ил­лю­стра­ция к за­да­че

3) , так как эти пря­мые пе­ре­се­ка­ют­ся се­ку­щей  и при этом со­от­вет­ствен­ные углы равны ().

4) Ко­эф­фи­ци­ент по­до­бия у тре­уголь­ни­ков  и  равен 3, по­это­му можно опре­де­лить сто­ро­ну : .

Ответ: ; ; ; па­рал­лель­ность пря­мых  и  до­ка­за­на.

 

До­маш­нее за­да­ние

1. За­да­чи 557, 559- Ата­на­сян Л. С., Бу­ту­зов В. Ф., Ка­дом­цев С. Б. Гео­мет­рия, 7-9 клас­сы  (Ис­точ­ник).
2. ; ; ;  (см. рис. 10). Найти  и . 
    
   Рис. 10. Ил­лю­стра­ция к за­да­че
3. В тре­уголь­ни­ке  точка  лежит на сто­роне , , , . До­ка­жи­те, что  (см. рис. 11). 
    
   Рис. 11. Ил­лю­стра­ция к за­да­че

Третий признак подобия треугольников

                                                                    

Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.

Если AB:DE=BC:EF=AC:DF, то ΔABC∼ΔDEF.

Третий признак подобия треугольников довольно редко используется в решении задач, а доказательство его аналогично доказательству второго признака, поэтому приводить его не будем.

 

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/8-klass/podobnye-treugolniki/vtoroy-priznak-podobiya-treugolnikov

http://www.yaklass.ru/p/geometria/8-klass/podobnye-treugolniki-9236/priznaki-podobiia-treugolnikov-9525/re-45c7d7dc-5837-418c-81eb-add8501d2c98

http://www. youtube.com/watch?v=1Nwv-LUoukI

http://www.youtube.com/watch?v=riotZSjYscE

http://sportstill.ru/post/imgs/56278bf1d7dd8.jpg

http://mypresentation.ru/documents/140277b244f0b9b2f8abf04e3274041f/img2.jpg

http://www.tutoronline.ru/blog/podobie-treugolnikov-chast-2

http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/101-test-po-geometrii-8-klass-tema-priznaki-podobiya-treugolnikov-variant-1.html

http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/102-test-po-geometrii-8-klass-tema-priznaki-podobiya-treugolnikov-variant-2.html

http://rushkolnik.ru/tw_files2/urls_3/891/d-890061/890061_html_m5ff065f.jpg

http://cs1-48v4.vk-cdn.net/p24/3551abddfac0c8.mp3?extra=amJxaBk9gfTT0lPmsOEwb8Rn_T2twbNJh2OUazYT-T9cSSu4_1787ibMzOu6ytv1rZKrpdEq7XnWZN1f-bjAuKyWIFf7mzw

Доказательство признаков подобия треугольников

☰

Доказательство первого признака подобия треугольников

Первый признак подобия треугольников утверждает, что если у треугольников две стороны соответственно пропорциональны, а углы между ними равны, то такие треугольники подобны.

Рассмотрим треугольники ABC и DEF, у которых DE = kAB, EF = kBC и ∠B = ∠E.

Чтобы доказать подобие данных треугольников, требуется доказать, что DF = kAC, так как подобие треугольников определяется по трем пропорциональным сторонам.

Найдем стороны AC и DF по теореме косинусов (квадрат стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон, умноженному на косинус угла между ними):

AC² = AB² + BC² – 2 · AB · BC · cos B
DF² = DE² + EF² – 2 · DE · EF · cos E

Так как ∠B = ∠E и AB = kDE, BC = kEF, то мы можем выразить квадрат стороны DF через угол и стороны треугольника ABC:

DF² = (kAB)² + (kBC)² – 2 · kAB · kBC · cos B

Вынесем k² за скобку:

DF² = k²(AB² + BC² – 2 · AB · BC · cos B)

Выражение в скобках равно ранее выраженному через теорему косинусов квадрату стороны AC. Поэтому можно записать так:

DF² = k²AC²

Отсюда получаем, что DF = kAC, что и требовалось доказать. Таким образом, если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника и углы между этими сторонами каждого треугольника равны, то оказываются соответственно пропорциональными и третьи их стороны, а, следовательно, такие треугольника подобны.

Доказательство второго признака подобия треугольников

Второй признак подобия треугольников определяет подобие по наличию двух соответственно равных углов.

Пусть даны треугольники ABC и DEF, у которых ∠A = ∠D, ∠B = ∠E.

Если эти треугольники подобны, то их стороны будут пропорциональны друг другу, т. е. будут соблюдаться равенства AB = kDE, BC = kEF, AB = kDF.

Если в одном треугольнике два угла соответственно равны двум углам в другом треугольнике, то равными будут и третьи углы этих треугольников, т. к. сумма углов любого треугольника равна 180°.

Как известно, у подобных треугольников углы соответственно равны. Т. е. если треугольники подобны, то их углы соответственно равны. Однако нельзя однозначно утверждать обратное: если углы соответственно равны, то треугольники подобны. Ведь можно предположить, что существую треугольники с соответственно равными углами, но у которых стороны не пропорциональны, а значит, такие треугольники не являются подобными.

Согласно теореме синусов, сторона треугольника равна произведению диаметра описанной окружности на синус противолежащего угла.

Если диаметр описанной около треугольника ABC окружности равен d, то мы можем выразить стороны этого треугольника так:

AB = d sin C, BC = d sin A, AC = d sin B

Если диаметр описанной около треугольника DEF окружности равен d₁, то получим:

DE = d₁ sin F, EF = d₁ sin D, DF = d₁ sin E

Так как углы A, B и C соответственно равны углам D, E и F, то мы можем заменить одни на другие.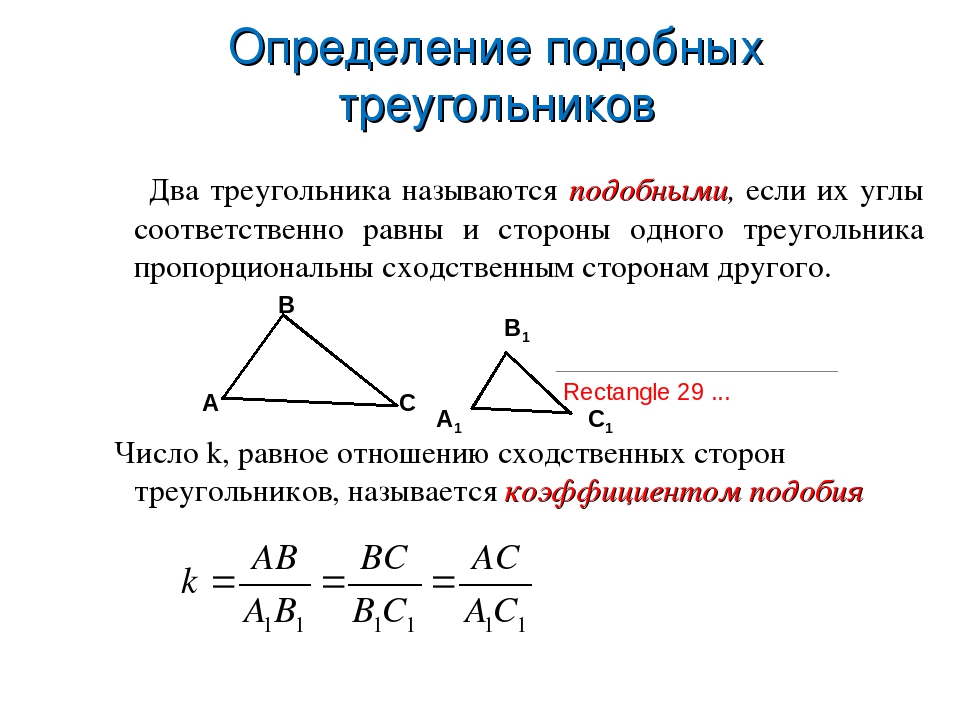 Сделаем это для сторон треугольника DEF:

DE = d₁ sin C, EF = d₁ sin A, DF = d₁ sin B

Найдем отношения сторон одного треугольника к соответствующим сторонам другого:

AB/DE = (d sin С) / (d₁ sin С) = d/d₁
BC/EF = (d sin A) / (d₁ sin A) = d/d₁
AC/DF = (d sin B) / (d₁ sin B) = d/d₁

То есть все три отношения равны одному и тому же значению (d/d₁), а значит, равны между собой; т. е.

AB/DE = BC/EF = AC/DF

Таким образом, стороны одного треугольника пропорциональны сторонам другого треугольника. Значит, треугольники подобны.

Третий признак подобия треугольников

Нередко выделяют третий признак подобия треугольников: если все стороны одного треугольника соответственно пропорциональны сторонам другого, то такие треугольники подобны. Однако само определение подобных треугольников нередко ограничивается именно этим признаком, а равенство углов подобных треугольников доказывается в виде теоремы (Углы подобных треугольников).

Для 8 класса «Признаки подобия треугольников» (геометрия)

Слайды и текст этой презентации

Слайд 1

«Подобие треугольников. Признаки подобия треугольников»
Пономарева Юлия Васильевна, учитель математики МБОУ Каменно-Балковская СОШ

Слайд 2

Содержание:
Пропорциональные отрезки. Определение подобных треугольников. Отношение площадей подобных треугольников. Первый признак подобия треугольников. Второй признак подобия треугольников. Третий признак подобия треугольников.

Слайд 3

Пропорциональные отрезки.
Отношением отрезков АВ и CD называется отношение их длин, т. е. АВ. CD Говорят, что отрезки АВ и CD пропор-циональны отрезкам А1В1 и C1D1, если АВ = CD. А1В1 C1D1 Например, отрезки АВ и CD, длины которых равны 2 см и 1 см, пропорциональны отрезкам А1В1 и C1D1, длины которых равны 3 см и 1,5 см.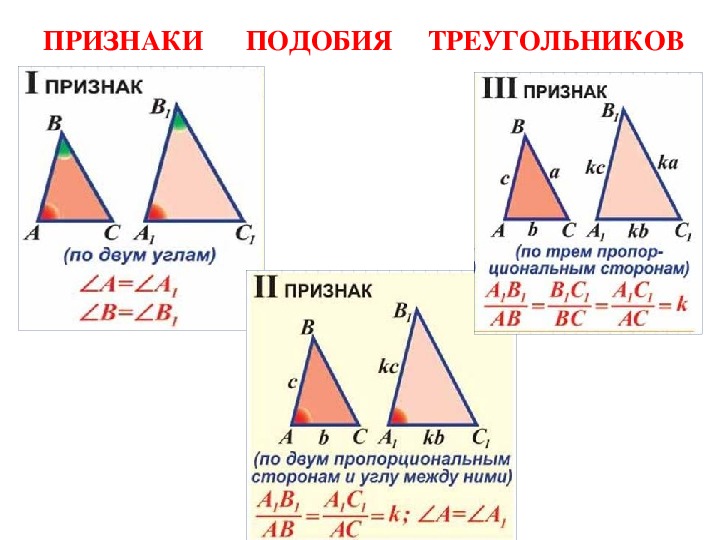 В самом деле, АВ = CD = 2. А1В1 C1D1 3

Слайд 4

Определение подобных треугольников.
Пусть у двух треугольников АВС и А1В1С1 соответствующие углы равны. В этом случае стороны АВ и А1В1, ВС и В1С1, СА и С1А1 называются сходственными. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
АВ ВС СА А1В1 В1С1 С1А1
k
Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия.

Слайд 5

Отношение площадей подобных треугольников.
Теорема: Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Дано:  АВС ~  А1В1С1. Коэффициент подобия равен k.
Доказать: S = S1
k²
Доказательство: Пусть площадь  АВС равна S, а площадь  А1В1С1 равна S1. Так как
то
(по теореме об отношении площадей треугольников, имеющих по равному углу). Так как
поэтому
Теорема доказана.

Слайд 6

Первый признак подобия треугольников.
Теорема: Если два угла одного треугольника соответственно равны двум углам другого , то такие треугольники подобны.
Дано:  АВС,  А1В1С1.
Доказать:  АВС ~  А1В1С1.
Доказательство: по теореме о сумме углов треугольника
и, значит,
Таким образом, углы  АВС
соответственно равны углам  А1В1С1. Докажем, что стороны АВС пропорциональны сходственным сторонам А1В1С1.
Т.к.
то
Из этих равенств следует, что
Аналогично, используя равенства
получаем
Итак, стороны  АВС пропорциональны сходственным сторонам  А1В1С1. Теорема доказана.

Слайд 7

Второй признак подобия треугольников.
Теорема: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Дано:  АВС,  А1В1С1,, у которых
Доказать:  АВС ~  А1В1С1.
Доказательство: Достаточно доказать, что
Рассмотрим  АВС2, у которого
Треугольники АВС2 и А1В1С1 подобны по первому признаку подобия треугольников, поэтому
С другой стороны, по условию
Из этих двух равенств получаем АС = АС2.
 АВС и  АВС2 равны по двум сторонам и углу между ними (АВ – общая сторона, АС=АС2 и )
Отсюда следует, что
а так, как
Теорема доказана.

Слайд 8

Третий признак подобия треугольников.
Теорема: Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Дано:  АВС,  А1В1С1,, у которых
Доказать:  АВС ~  А1В1С1.
Доказательство: Достаточно доказать, что
Рассмотрим  АВС2, у которого
Треугольники АВС2 и А1В1С1 подобны по первому признаку подобия треугольников, поэтому
Сравнивая эти равенства с равенствами, которые записаны в дано, получаем:
 АВС=  АВС2 по трем сторонам.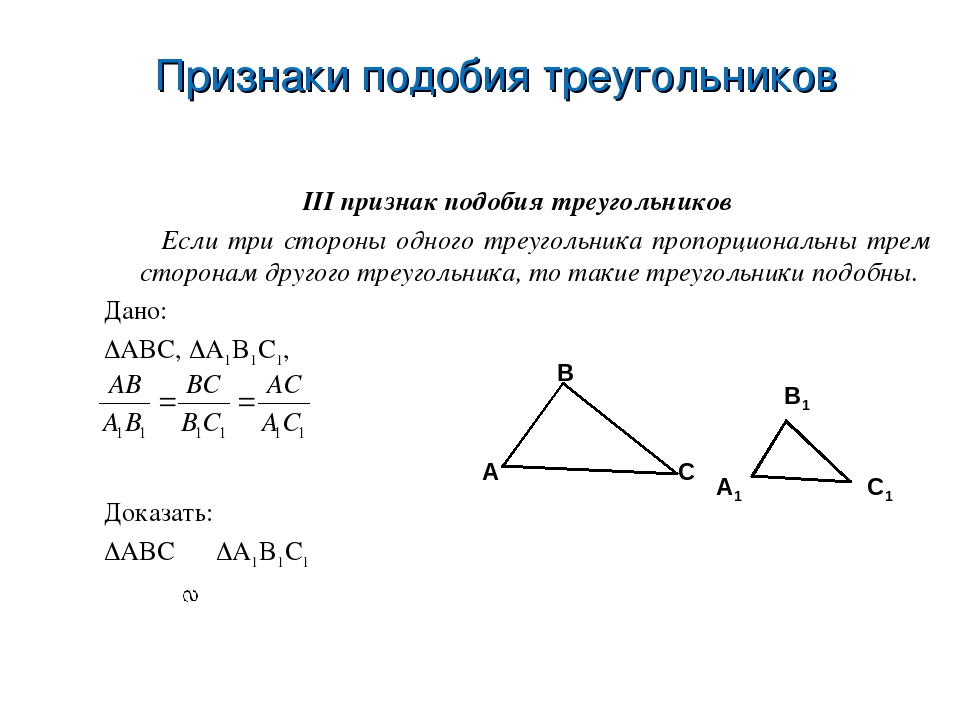 Отсюда следует, что
Теорема доказана.
а так как

похожих треугольников — объяснение и примеры

Теперь, когда мы закончили с конгруэнтными треугольниками, мы можем перейти к другому подобному виду концепции, который называется подобных треугольника.

В этой статье мы узнаем о похожих треугольниках, особенностях подобных треугольников, о том, как использовать постулаты и теоремы для определения похожих треугольников и, наконец, как решать похожие задачи о треугольниках.

Что такое похожие треугольники?

Понятия «одинаковые треугольники» и «равные треугольники» — это два разных термина, которые тесно связаны. Подобные треугольники — это два или более треугольника одинаковой формы, равных пар соответствующих углов и одинакового отношения соответствующих сторон.

Иллюстрация подобных треугольников:

Рассмотрим три треугольника ниже. if:

1. Соотношение соответствующих сторон равно.

AB / PQ = AC / PR = BC = QR, AB / XY = AC / XZ = BC / YZ

1. ∠ A = ∠ P = ∠X, ∠B = ∠Q = ∠Y, ∠C = ∠R = ∠Z

Следовательно, ΔABC ~ ΔPQR ~ ΔXYZ

Сравнение похожих треугольников и конгруэнтных треугольников

Характеристики	Конгруэнтные треугольники	Похожие треугольники	Похожие треугольники размер	одинаковый размер и форма	Та же форма, но другой размер
Символ	≅	~
Соответствующие длины сторон	Отношение соответствующих сторон в конгруэнтных треугольниках всегда равно постоянное число 1.	Соотношение всех соответствующих сторон в подобных треугольниках согласовано.
Соответствующие углы	Все соответствующие углы равны	Каждая пара соответствующих углов равна.

Как определить похожие треугольники?

Мы можем доказать сходство в треугольниках, применяя аналогичные теоремы о треугольниках. Это постулаты или правила, используемые для проверки похожих треугольников.

Есть три правила для проверки похожих треугольников , и они включают: правило AA, правило SAS или правило SSS.

Правило угла-угла (AA):
Согласно правилу AA, два треугольника считаются подобными, если два угла в одном конкретном треугольнике равны двум углам другого треугольника.

Правило стороны-угла-стороны (SAS):
Правило SAS гласит, что два треугольника подобны, если соотношение их соответствующих двух сторон равно, а также угол, образованный двумя сторонами, равен.

Правило стороны-стороны-стороны (SSS):
Два треугольника похожи, если все соответствующие три стороны данных треугольников находятся в одинаковой пропорции.

Как решать похожие треугольники?

Существует двух типов одинаковых задач треугольника ; это проблемы, которые требуют от вас доказательства того, что данный набор треугольников подобен, и те, которые требуют, чтобы вы вычислили недостающие углы и длины сторон подобных треугольников.

Давайте посмотрим на следующие примеры:

Пример 1

Проверьте, похожи ли следующие треугольники

Решение

Сумма внутренних углов в треугольнике = 180 °

Следовательно, учитывая Δ PQR

P + ∠Q + ∠R = 180 °

60 ° + 70 ° + ∠R = 180 °

130 ° + ∠R = 180 °

Вычтем обе стороны на 130 °.

∠ R = 50 °

Рассмотрим Δ XYZ

∠X + ∠Y + ∠Z = 180 °

∠60 ° + ∠Y + ∠50 ° = 180 °

∠ 110 ° + ∠Y = 180 °

Вычтем обе стороны на 110 °

∠ Y = 70 °

Отсюда;

• По правилу угла-угла (AA) ΔPQR ~ ΔXYZ.
• ∠Q = ∠ Y = 70 ° и ∠Z = ∠ R = 50 °

Пример 2

Найдите значение x в следующих треугольниках, если ΔWXY ~ ΔPOR.

Решение

Учитывая, что два треугольника подобны, тогда;

WY / QR = WX / PR

30/15 = 36 / x

Перекрестное умножение

30x = 15 * 36

Разделите обе стороны на 30.

x = (15 * 36) / 30

x = 18

Следовательно, PR = 18

Давайте проверим, равны ли пропорции соответствующих двух сторон треугольников.

WY / QR = WX / PR

30/15 = 36/18

2 = 2 (RHS = LHS)

Пример 3

Проверьте, похожи ли два треугольника, показанные ниже, и рассчитайте значение k.

Решение

В соответствии с правилом SAS, два треугольника подобны.

Доказательство:
8/4 = 20/10 (LHS = RHS)

2 = 2

Теперь вычислите значение k

12 / k = 8/4

12 / k = 2

Умножьте оба стороны на k.

12 = 2k

Разделите обе части на 2

12/2 = 2k / 2

k = 6.

Пример 4

Определите значение x на следующей диаграмме.

Решение

Пусть треугольник ABD и ECD похожи на треугольники.

Примените правило стороны-угла-стороны (SAS), где A = 90 градусов.

AE / EC = BD / CD

x / 1,8 = (24 + 12) / 12

x / 1,8 = 36/12

Перекрестное умножение

12x = 36 * 1,8

Разделите обе стороны на 12.

x = (36 * 1,8) / 12

= 5,4

Следовательно, значение x составляет 5,4 мм.

Предыдущий урок | Главная страница | Следующий урок

Как определить, похожи ли треугольники

Два треугольника похожи, если имеют:

• все их углы равны
• соответствующие стороны находятся в одинаковом соотношении

Но нам не нужно знать все три стороны и все три угла. .. двух-трех из шести обычно хватает.

Есть три способа определить, похожи ли два треугольника: AA , SAS и SSS :

AA

AA означает «угол, угол» и означает, что два угла треугольников равны.

Если два треугольника имеют два равных угла, треугольники подобны.

Пример: эти два треугольника похожи:

Если два их угла равны, то третий угол также должен быть равен, потому что углы треугольника всегда складываются, чтобы получить 180 °.

В данном случае недостающий угол составляет 180 ° — (72 ° + 35 °) = 73 °

Таким образом, AA можно также назвать AAA (потому что, когда два угла равны, все три угла должны быть равны).

SAS

SAS означает «сторона, угол, сторона» и означает, что у нас есть два треугольника, где:

• соотношение между двумя сторонами такое же, как соотношение между двумя другими сторонами
• , и мы также знаем, что включенные углы равны.

Если два треугольника имеют две пары сторон с одинаковым соотношением, и включенные углы также равны, то треугольники подобны.

Пример:

В этом примере мы видим, что:

• одна пара сторон находится в соотношении 21: 14 = 3: 2
• другая пара сторон находится в соотношении 15: 10 = 3: 2
• между ними угол совпадения 75 °

Итак, информации достаточно, чтобы сказать нам, что два треугольника похожи на .

Использование тригонометрии

Мы также можем использовать тригонометрию для вычисления двух других сторон, используя закон косинусов:

Продолжение примера

В треугольнике ABC:

• a ² = b ² + c ² — 2bc cos A
• a ² = 21 ² + 15 ² — 2 × 21 × 15 × Cos75 °
• a ² = 441 + 225 — 630 × 0.2588 …
• а ² = 666 — 163,055 . ..
• a ² = 502,944 …
• Итак, a = √502.94 = 22.426 …

В треугольнике XYZ:

• x ² = y ² + z ² — 2yz cos X
• x ² = 14 ² + 10 ² — 2 × 14 × 10 × Cos75 °
• x ² = 196 + 100 — 280 × 0,2588 …
• x ² = 296 — 72,469 …
• х ² = 223.530 …
• Итак, x = √223,530 … = 14,950 …

Теперь давайте проверим соотношение этих двух сторон:

a: x = 22,426 …: 14,950 … = 3: 2

такое же соотношение, как и раньше!

Примечание: мы также можем использовать закон синусов, чтобы показать, что два других угла равны.

ССС

SSS означает «сторона, сторона, сторона» и означает, что у нас есть два треугольника со всеми тремя парами соответствующих сторон в одинаковом соотношении.

Если два треугольника имеют три пары сторон с одинаковым соотношением, то треугольники подобны.

Пример:

В этом примере соотношение сторон:

• a: x = 6: 7,5 = 12: 15 = 4: 5
• б: у = 8: 10 = 4: 5
• с: z = 4: 5

Эти отношения равны, поэтому два треугольника подобны.

Использование тригонометрии

Используя тригонометрию, мы можем показать, что два треугольника имеют равные углы, используя закон косинусов в каждом треугольнике:

В треугольнике ABC:

• cos A = (b ² + c ² — a ² ) / 2bc
• cos A = (8 ² + 4 ² -6 ² ) / (2 × 8 × 4)
• cos A = (64 + 16 — 36) / 64
• cos A = 44/64
• cos A = 0.6875
• Угол A = 46,6 °

В треугольнике XYZ:

• cos X = (y ² + z ² — x ² ) / 2yz
• cos X = (10 ² + 5 ² — 7,5 ² ) / (2 × 10 × 5)
• cos X = (100 + 25 — 56,25) / 100
• cos X = 68,75 / 100
• cos X = 0,6875
• Угол X = 46,6 °

Значит, углы A и X равны!

Аналогичным образом мы можем показать, что углы B и Y равны, а углы C и Z равны.

теорем о подобных треугольниках

1. Теорема о боковом разветвлении

Если ADE — это любой треугольник и BC нарисована параллельно DE, то AB BD = AC CE

Чтобы показать, что это так, проведите линию BF параллельно AE, чтобы получился параллелограмм BCEF:

Треугольники ABC и BDF имеют одинаковые углы и поэтому похожи (Почему? См. Раздел под названием AA на странице Как определить, похожи ли треугольники.)

• Сторона AB соответствует стороне BD, а сторона AC соответствует стороне BF.
• Итак, AB / BD = AC / BF
• Но BF = CE
• Итак, AB / BD = AC / CE

Теорема о биссектрисе угла

Если ABC — любой треугольник и AD делит пополам (разрезает пополам) угол BAC, то AB BD = AC DC

Чтобы показать, что это правда, мы можем обозначить треугольник следующим образом:

• Угол BAD = Угол DAC = x °
• Угол ADB = y °
• Угловой АЦП = (180 − y) °

Умножаем обе стороны на AB: sin (x) AB BD = sin (y) 1

Разделите обе части на sin (x): AB BD = sin (y) sin (x)

По закону синусов в треугольнике ACD: sin (x) DC = sin (180 − y) AC

Умножить обе стороны на переменный ток: sin (x) AC DC = sin (180 − y) 1

Разделите обе части на sin (x): AC DC = sin (180 − y) sin (x)

Но sin (180 − y) = sin (y) : AC DC = sin (y) sin (x)

Оба AB BD и AC DC равны sin (y) sin (x) , поэтому:

AB BD = AC DC

В частности, если треугольник ABC равнобедренный, то треугольники ABD и ACD являются конгруэнтными треугольниками

И тот же результат верен:

AB BD = AC DC

3. Площадь и сходство

Если два одинаковых треугольника имеют стороны в соотношении x: y,

, то их площади находятся в соотношении x ² : y ²

Пример:

Эти два треугольника похожи со сторонами в соотношении 2: 1 (стороны одного в два раза длиннее другого):

Что можно сказать об их районах?

Ответ прост, если мы просто проведем еще три линии:

Мы видим, что маленький треугольник вписывается в большой треугольник четыре раза по .

Итак, когда длина в два раза больше, чем на , площадь будет в в четыре раза больше, чем в

.

Значит соотношение их площадей 4: 1

Мы также можем записать 4: 1 как 2 ² : 1

Общий случай:

Треугольники ABC и PQR похожи и имеют соотношение сторон x: y

Мы можем найти площади, используя эту формулу из раздела Площадь треугольника:

Площадь ABC = 1 2 bc sin (A)

Площадь PQR = 1 2 qr sin (P)

И мы знаем, что длины треугольников находятся в соотношении x: y

q / b = y / x, поэтому: q = by / x

и r / c = y / x, поэтому r = cy / x

Кроме того, поскольку треугольники похожи, углы A и P одинаковы:

A = P

Теперь мы можем сделать некоторые вычисления:

Площадь треугольника PQR : 1 2 qr sin (P)

Вставьте «q = by / x», «r = cy / x» и «P = A»: 1 2 (by) (cy) sin (A) (x) (x)

Упростить: 1 2 bcy ² sin (A) x ²

Переупорядочить: y ² x ² × 1 2 bc sin (A)

То есть: y ² x ² × Площадь треугольника ABC

Итак, получаем соотношение:

Площадь треугольника ABC: Площадь треугольника PQR = x ² : y ²

похожих треугольников — математический открытый справочник

подобных треугольников — математический открытый справочник

Определение: треугольники похожи, если имеют одинаковую форму, но могут быть разных размеров.
(Они все еще похожи, даже если один повернут или является зеркальным отображением другого).

Попробуй Перетащите любую оранжевую точку в вершину любого треугольника. Оба треугольника изменят форму и останутся похожими друг на друга.

Треугольники похожи, если они имеют одинаковую форму, но не обязательно одинакового размера. Вы можете думать об этом как о «увеличении» или «уменьшении», увеличивая или уменьшая треугольник, но сохраняя его основную форму. На рисунке выше, когда вы перетаскиваете любую вершину на треугольнике PQR, другой треугольник принимает ту же форму, но в два раза меньше.В формальных обозначениях мы можем написать

который читается как « Треугольник PQR подобен треугольнику P’Q’R ‘». Буква с небольшой вертикальной чертой после нее, например P ‘, читается как « P prime ».

Свойства подобных треугольников

1. Соответствующие углы совпадают (одинаковая величина)

   Итак, на рисунке выше, угол P = P ‘, Q = Q’ и R = R ‘.

2. Соответствующие стороны находятся в одинаковой пропорции.

   Выше PQ вдвое превышает длину P’Q ‘.Следовательно, остальные пары сторон также находятся в той же пропорции. PR вдвое больше P’R ‘, а RQ вдвое больше R’Q’. Формально в двух одинаковых треугольниках PQR и P’Q’R ‘:

Вращение

Один треугольник можно вращать, но пока они одинаковой формы, треугольники остаются похожими. На рисунке ниже треугольник PQR похож на P’Q’R ‘, хотя последний повернут. по часовой стрелке 90 °.

В этом конкретном примере треугольники одинакового размера, поэтому они также конгруэнтный.

Отражение

Один треугольник может быть зеркальным отражением другого, но до тех пор, пока они имеют одинаковую форму, треугольники остаются похожими. Он может отражаться в любом направлении: вверх, вниз, влево, вправо. На рисунке ниже треугольник PQR является зеркальным отображением P’Q’R ‘, но по-прежнему считается похожим на него.

Как определить, похожи ли треугольники

Любой треугольник определяется шестью мерками (три стороны, три угла). Но вам не нужно знать их все, чтобы показать, что два треугольника похожи.Подойдут разные группы по три человека. Треугольники подобны, если:

1. AAA (угол угол угол)
   Все три пары соответствующих углов одинаковы.
   См. Подобные треугольники AAA.
2. SSS в одинаковой пропорции (боковая сторона)
   Все три пары соответствующих сторон имеют одинаковую пропорцию
   См. Подобные треугольники SSS.
3. SAS (сторона бокового угла)
   Две пары сторон в одинаковой пропорции и равный внутренний угол.
   См. Подобные треугольники SAS.

Подобные треугольники могут иметь общие части

Два треугольника могут быть похожими, даже если у них есть общие элементы. На рисунке ниже больший треугольник PQR аналогичен меньшему STR. S и T — середины PR и QR соответственно. Они разделяют вершину R и часть сторон PR и QR. Они похожи по принципу ААА, поскольку соответствующие углы в каждом треугольнике одинаковы.

Другие похожие темы

Подобные полигоны

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

похожих треугольников

Два треугольники как говорят аналогичный если их соответствующие углы равны конгруэнтный и соответствующие стороны лежат в пропорция . Другими словами, похожие треугольники имеют одинаковую форму, но не обязательно одного размера.

Треугольники конгруэнтный если к тому же их соответствующие стороны имеют одинаковую длину.

Длины сторон двух одинаковых треугольников пропорциональны. То есть, если Δ U V W похоже на Δ Икс Y Z , то имеет место следующее уравнение:

U V Икс Y знак равно U W Икс Z знак равно V W Y Z

Это обычное отношение называется масштаб .

Символ ∼ используется для обозначения сходства.

Пример:

Δ U V W ∼ Δ Икс Y Z . Если U V знак равно 3 , V W знак равно 4 , U W знак равно 5 и Икс Y знак равно 12 , найти Икс Z и Y Z .

Нарисуйте фигуру, чтобы облегчить себе визуализацию.

Запишите пропорцию. Убедитесь, что соответствующие стороны указаны правильно.

3 12 знак равно 5 Икс Z знак равно 4 Y Z

Коэффициент масштабирования здесь 3 12 знак равно 1 4 .

Решение этих уравнений дает Икс Z знак равно 20 и Y Z знак равно 16 .

Понятия подобия и масштабного коэффициента могут быть распространены на другие фигуры помимо треугольников.

похожих треугольников — доказательство, определение и теоремы (видео)

Подобные треугольники (определение, доказательство и теоремы)

Сходство в математике не означает того же, что сходство в повседневной жизни. Подобные треугольники — это треугольники одинаковой формы, но с разными размерами сторон.

1. Определение похожих треугольников

Проверка треугольников аналогично

Теоремы подобия треугольника

Определение похожих треугольников

Мороженое с шоколадной крошкой и мороженое с шоколадной крошкой похожи, но не одинаковы.Это повседневное употребление слова «подобный», но не то, как мы используем его в математике.

В геометрии две формы похожи , если они одинаковой формы, но разных размеров. У вас может получиться квадрат со сторонами 21 см и квадрат со сторонами 14 см; они были бы похожи. Равносторонний треугольник со сторонами 21 см и квадрат со сторонами 14 см не похожи друг на друга, потому что это разные формы.

Подобные треугольники легко идентифицировать, потому что к треугольникам можно применить три теоремы.Эти три теоремы, известные как Угол — Угол (AA) , Сторона — Угол — Сторона (SAS) и Сторона — Сторона — Сторона (SSS) , являются надежными методами определения подобия в треугольниках.

1. Угол — Угол (AA)
2. Сторона — Угол — Сторона (SAS)
3. Сторона — Сторона — Сторона (SSS)

Соответствующие углы

В геометрии соответствие означает, что конкретная часть одного многоугольника точно соответствует аналогичной части другого.Даже если два треугольника ориентированы по-разному друг от друга, если вы можете повернуть их таким же образом и увидеть, что их углы одинаковы, вы можете сказать, что эти углы совпадают.

Три теоремы подобия в треугольниках зависят от соответствующих частей. Вы смотрите на один угол одного треугольника и сравниваете его с таким же углом положения другого треугольника.

Пропорции

Сходство связано с пропорцией. Треугольники легко оценить на предмет пропорциональных изменений, которые делают их похожими.Их сравнительные стороны пропорциональны друг другу; их соответствующие углы идентичны.

Вы можете установить отношения для сравнения длин сторон двух треугольников. Если отношения совпадают, соответствующие стороны подобны друг другу.

Уголок в комплекте

Включенный угол относится к углу между двумя парами соответствующих сторон. Вы не можете сравнить две стороны двух треугольников, а затем перепрыгнуть на угол, который не находится между этими двумя сторонами.

Проверка аналогичных треугольников

Вот два конгруэнтных треугольника. Чтобы облегчить вам жизнь, мы сделали их оба равносторонними треугольниками.

△ FOX сравнивается с △ HEN. Обратите внимание, что ∠O на △ FOX соответствует ∠E на △ HEN. Оба ∠O и ∠E — это , включая углы между сторонами FO и OX на △ FOX и сторонами HE и EN на HEN.

Side FO конгруэнтен боковому HE; сторона OX конгруэнтна стороне EN, а ∠O и ∠E — входящие конгруэнтные углы.

Два равносторонних треугольника одинаковы, за исключением букв.Они одинакового размера, поэтому представляют собой одинаковых треугольника . Если бы они оба были равносторонними треугольниками, но сторона EN была бы вдвое длиннее стороны HE, это были бы подобных треугольника .

Теоремы подобия треугольника

Угол-угол (AA) Теорема

Угол-угол (AA) говорит, что два треугольника подобны, если у них есть две пары соответствующих углов, которые совпадают. Два треугольника могут быть на больше, чем на , чем аналогичные; они могли быть идентичными.Для AA все, что вам нужно сделать, это сравнить две пары соответствующих углов.

Примерка Угол-Угол

Вот два разносторонних треугольника △ JAM и △ OUT. Мы уже отметили два внутренних угла каждого треугольника с помощью сокращения геометрии для сравнения: маленьких косых черт. Одна косая черта для внутреннего A и такая же косая черта для внутреннего U означает, что они совпадают. Обратите внимание, что ∠M совпадает с ∠T, потому что на каждом из них есть две маленькие косые черты.

Поскольку ∠A конгруэнтно ∠U, а ∠M конгруэнтно ∠T, теперь у нас есть две пары конгруэнтных углов, поэтому теорема AA утверждает, что эти два треугольника подобны.

Уловки торговли

Следите за уловками из учебников, онлайн-заданий и учителей математики. Иногда треугольники ориентированы по-разному, когда вы смотрите на них. Возможно, вам придется повернуть один треугольник, чтобы увидеть, сможете ли вы найти две пары соответствующих углов.

Еще одна проблема: два угла измеряются и идентифицируются на одном треугольнике, но два разных угла измеряются и идентифицируются на другом.

Поскольку у каждого треугольника есть только три внутренних угла, по одному каждому из идентифицированных углов должен быть конгруэнтным.Вычитая измеренные идентифицированные углы каждого треугольника из 180 °, вы можете узнать меру недостающего угла. Затем вы можете сравнить любые два соответствующих угла для сравнения.

Боковой угол-сторона (SAS) Теорема

Вторая теорема требует точного порядка: сторона, затем включенный угол, затем следующая сторона. Теорема Side-Angle-Side (SAS) гласит, что если две стороны одного треугольника пропорциональны двум соответствующим сторонам другого треугольника, и их соответствующие включенные углы совпадают, эти два треугольника подобны.

Попытка бокового угла

Вот два треугольника, расположенных бок о бок и ориентированных одинаково. △ RAP и △ EMO определили стороны размером 37 дюймов на △ RAP и 111 дюймов на EMO, а также стороны 17 на △ RAP и 51 дюйм на EMO. Обратите внимание, что угол между обозначенными измеренными сторонами одинаков для обоих треугольников: 47 °.

Отношение 37/111 такое же, как соотношение 17/51? Да; два соотношения пропорциональны, поскольку каждое из них упрощается до 1/3.Эти два треугольника схожи с одинаковым углом между ними.

Теорема Сторона-Сторона-Сторона (SSS)

Последняя теорема — Side-Side-Side или SSS . Эта теорема утверждает, что если два треугольника имеют пропорциональные стороны, они подобны. Это может показаться большим скачком, игнорирующим их углы, но подумайте об этом: единственный способ построить треугольник со сторонами, пропорциональными сторонам другого треугольника, — это скопировать углы.

Попытка сторона-сторона-сторона

Вот два треугольника: △ FLO и △ HIT.Обратите внимание, мы не определили внутренние углы. Стороны △ FLO имеют длину 15, 20 и 25 см. Стороны △ HIT имеют длину 30, 40 и 50 см.

Вам необходимо установить отношения соответствующих сторон и оценить их:

1530 = 12

2040 = 12

2550 = 12

Все они имеют одинаковое соотношение при упрощении. Их всех 12. Итак, даже не зная внутренних углов, мы знаем, что эти два треугольника похожи, потому что их стороны пропорциональны друг другу.

Краткое содержание урока

Теперь, когда вы изучили этот урок, вы можете определять и идентифицировать похожие фигуры, и вы можете описать требования к треугольникам, чтобы они были похожими (они должны иметь либо две конгруэнтные пары соответствующих углов, либо две пропорциональные соответствующие стороны с включенными соответствующими угол конгруэнтный, или все соответствующие стороны пропорциональны).

Вы также можете применить три теоремы подобия треугольников, известные как Угол — Угол (AA), Сторона — Угол — Сторона (SAS) или Сторона — Сторона — Сторона (SSS), чтобы определить, похожи ли два треугольника.

Следующий урок:

Постулаты конгруэнтности треугольника

Что такое теоремы подобия треугольника?

Подобные треугольники имеют одинаковую форму, но не обязательно одного размера. Когда треугольники похожи, они обладают многими одинаковыми свойствами и характеристиками. Теоремы подобия треугольников определяют условия, при которых два треугольника подобны, и имеют дело со сторонами и углами каждого треугольника. Как только определенная комбинация углов и сторон удовлетворяет теоремам, вы можете считать треугольники похожими.

TL; DR (слишком длинный; не читал)

Существуют три теоремы подобия треугольников, которые определяют, при каких условиях треугольники похожи:

• Если два угла одинаковы, третий угол одинаков и треугольники похожи.
  
• Если три стороны имеют одинаковые пропорции, треугольники подобны.
• Если две стороны имеют одинаковые пропорции и угол наклона одинаковый, треугольники подобны.

Теоремы AA, AAA и угол-угол

Если два из углов двух треугольников совпадают, треугольники аналогичны.Это становится ясно из наблюдения, что сумма трех углов треугольника должна составлять 180 градусов. Если известны два угла, третий можно найти, вычтя два известных угла из 180. Если три угла двух треугольников одинаковы, треугольники имеют одинаковую форму и похожи.

SSS или теорема сторона-сторона-сторона

Если все три стороны двух треугольников одинаковы, они не только похожи, но и совпадают или идентичны. Для подобных треугольников три стороны двух треугольников должны быть пропорциональными.Например, если один треугольник имеет стороны 3, 5 и 6 дюймов, а второй треугольник имеет стороны 9, 15 и 18 дюймов, каждая из сторон большего треугольника в три раза больше длины одной из сторон меньшего. треугольник. Стороны пропорциональны друг другу, а треугольники похожи.

Теорема SAS или стороны-угла-стороны

Два треугольника подобны, если две из сторон двух треугольников пропорциональны, а угол наклона, или угол между сторонами, одинаков.Например, если две стороны треугольника составляют 2 и 3 дюйма, а стороны другого треугольника — 4 и 6 дюймов, стороны пропорциональны, но треугольники могут не быть похожими, потому что две третьи стороны могут быть любой длины.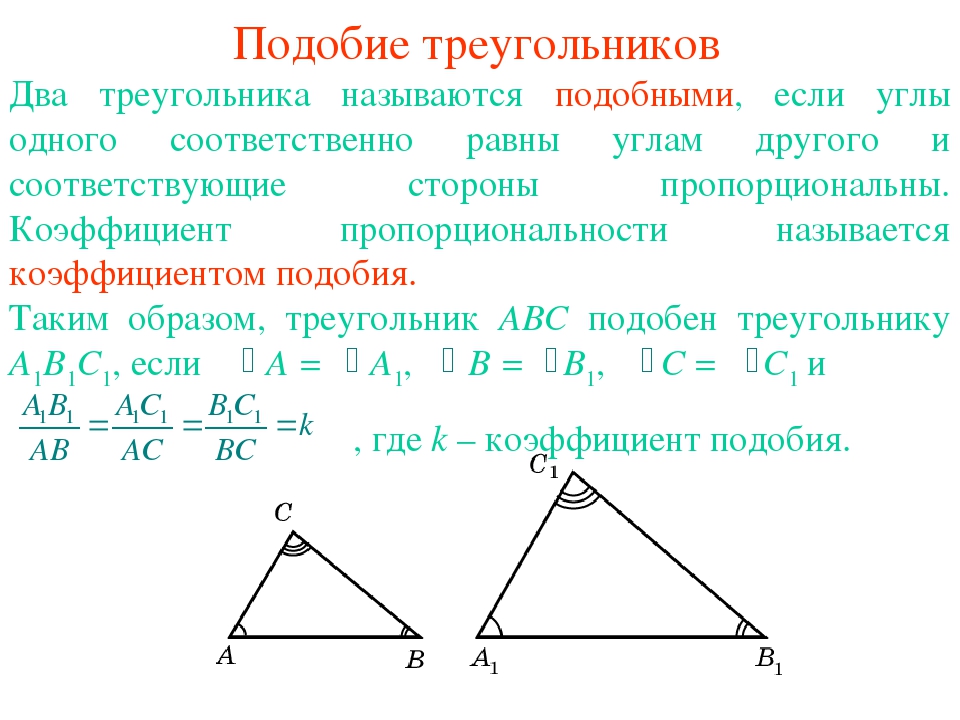 Если включенный угол одинаков, тогда все три стороны треугольников пропорциональны, а треугольники подобны.

Другие возможные комбинации угла и стороны

Если одна из трех теорем подобия треугольника выполняется для двух треугольников, треугольники подобны.Но есть и другие возможные комбинации бокового угла, которые могут гарантировать, а могут и не гарантировать сходство.

Для конфигураций, известных как угол-угол-сторона (AAS), угол-сторона-угол (ASA) или сторона-угол-угол (SAA), не имеет значения, насколько велики стороны; треугольники всегда будут похожи. Эти конфигурации сводятся к теореме угол-угол AA, что означает, что все три угла одинаковы, а треугольники похожи.

Однако конфигурации стороны-стороны-угла или угла-стороны-стороны не гарантируют сходства.(Не путайте стороны-стороны-угол с боковым-углом-стороной; «стороны» и «углы» в каждом названии относятся к порядку, в котором вы встречаете стороны и углы.