Как решить проблемы с математикой

Основные идеи

• Трудности в изучении математики знакомы многим детям.
• Их способности ни при чем: освоить эту науку мешают психологические причины.
• Красота и логика — только они помогут понять и полюбить этот предмет.

«Только и учим, что эту математику! — жалуется Ирина, мама 11-летней Алисы. — Дочь вроде бы формулы знает, а все равно спотыкается на каждом шагу. Иногда сложную задачу решит, а простую нет. Контрольные — это ужас для всей семьи. Ребенок весь на нервах, у нас с мужем головная боль. Никогда не знаешь, напишет она на четыре или двойку принесет. Занимаемся все выходные, и никакого прогресса!»

Я очень хорошо понимаю Алису. Помню, какую тоску навевали на меня в школе все эти уравнения, функции и тангенсы. Даже нелюбимые химия и физика были мне ближе: я могла хоть как-то соотнести их с собственным опытом. Но «а плюс b разделить на с» были бесконечно далеки от моей жизни.

Нас с Алисой нельзя назвать исключением. В каждом классе встречаются дети, для которых математика — сплошное мучение. А их родители мучаются вопросами, как к этому относиться и чем они могут помочь.

Нужна ли детям математика?

Проблемы эти есть повсюду. В прошлом году газета The New York Times начала дискуссию на тему, нужна ли детям алгебра, если каждый четвертый ученик в США не заканчивает школу из-за проблем с этим предметом.

А во Франции министр образования и науки Клод Аллегрэ, сам ученый-геофизик, всерьез обсуждал вопрос об отмене преподавания математики в школе, поскольку многие дети не справляются даже с элементарными задачами.

Так нужна ли математика всем детям? «Моей дочке — нет, она гуманитарий, как и я, пойдет на филфак, — уверена 36-летняя Марина. — Нам главное, чтобы по литературе, русскому, истории были пятерки, а по математике — лишь бы не двойка».

«Это мучительный вопрос: насколько глубоко нужно знать математику тем, кому она вроде бы не нужна? — размышляет писатель и математик Леонид Костюков. — Но кто такие гуманитарии? На одну десятую — люди искусства, и на девять десятых — люди культуры.

Людям искусства (художнику, поэту, актеру) математика, наверное, для творчества не обязательна. Но людям культуры — историку, филологу, редактору, издателю, журналисту — никак не обойтись без системного мышления. А именно математика воспитывает, дисциплинирует ум».

Курс математики устроен невероятно изящно, красиво, логично. Учить надо очень мало, гораздо больше нужно понимать

Я впервые задумалась, не напрасно ли пренебрегала математикой, когда стала писать диссертацию. Тема была сугубо филологической — но каких же мучений мне стоило упорядочить весь огромный фактический материал и убедительно обосновать свою концепцию! Логическое мышление — вот с чем была проблема. Но раз я все же справилась с диссертацией, то, может, я не так безнадежна по части логики, как когда-то казалось мне и моим родителям?

Самый сложный предмет?

Если у ребенка возникают трудности с математикой, у нас всегда есть наготове ответ: значит, нет математических способностей. И на этом мы как бы закрываем тему: на нет и суда нет. Другими словами, мы легко соглашаемся: математика так трудна, что справиться с ней могут не все. И мы утешаемся тем, что по другим дисциплинам наш ребенок вполне (или прекрасно) успевает.

Леонид Костюков, опытный репетитор, уверен, что преподает один из самых легких предметов: «Курс математики устроен невероятно изящно, красиво, логично. Учить надо очень мало, гораздо больше нужно понимать. Если я не помню формулу, но помню, откуда она следует, — я могу ее быстро вывести. Ни в каких других школьных науках такой возможности нет».

По его мнению, если ребенок успевает по другим предметам, нет никаких причин, чтобы он не справился с математикой. «Если у него, например, хорошо идет английский, значит, с логикой у него все в порядке, потому что английский язык устроен очень логично. Более того, объективно он сложней, чем язык школьной математики. Значит, этот ребенок должен успевать и в математике». Так почему же на практике это не так?

Когда проблемы нарастают как снежный ком

«Математика дает наиболее чистое и непосредственное переживание истины», — полагал немецкий физик, лауреат Нобелевской премии Макс Лауэ в книге «Страницы жизни Ландау». И в каждом классе найдутся дети, которым знакомо это переживание, которые испытывают наслаждение, например, от красивого решения задачи. Что отличает школьников, хорошо успевающих по математике?

«Как правило, это дети активные, любопытные, готовые рисковать, их не пугают проблемные ситуации, они любят делать открытия, — рассказывает детский психолог Елена Морозова. — А дети, которые боятся математики, зачастую не рассчитывают на себя, они слишком зависят от мнения родителей (учителей, одноклассников), не уверены в себе, легко верят в то, что они несообразительны.

Любая задача приводит такого ребенка в ступор: ему страшно само ожидание, что вот сейчас будет трудно и он окажется несостоятелен. Страх может стать причиной неудач и с другими предметами».

Он нарастает постепенно, как снежный ком. Например, напоминает детский психолог, в первых классах не все дети еще хорошо читают «и условие задачи могут просто не понять. Кроме того, у них еще не развито абстрактное мышление, им трудно представить себе картинку: вот поезд выходит из пункта А, а вот другой — из пункта Б, вот здесь они встречаются. И ребенок заведомо отказывается вникать в задачу: не буду даже и пытаться что-то с этим сделать».

То, что упущено в начальных классах, скажется потом, как ни в одном другом предмете. Именно потому, что в математике все логически связано.

Проблемы с математикой связаны не с интеллектуальными способностями, а с чем-то внутри ребенка, что мешает ему понимать учителя

«Если по литературе я пропустил Грибоедова, это не помешает мне изучать Тургенева, — замечает Леонид Костюков. — Но если что-то упустил по алгебре, то у меня начнутся системные проблемы. Другие предметы представляют собой определенный набор тем. Математика же, по большому счету, — это развитие одной темы. А ведь иной раз оказывается, что не все старшие школьники твердо знают даже таблицу умножения».

Причина не в математике

«У нее плохие отношения с учителем», «над ним смеются одноклассники», «она переживает, что отец ушел из семьи» — причин для неуспеваемости по любому предмету может быть много. Но существуют ли причины, которые вызывают трудности именно с математикой?

Педагог-психолог Анн Сьети уверена: математические понятия способны пробудить самые глубокие переживания. «Условие», «требуется», «доказать», «необходимо, но недостаточно» — все эти слова могут бессознательно ассоциироваться с внутренними проблемами.

«Чего стоит только пресловутый «икс» — неизвестный, за которым таится неведомо что, — говорит она. — Или другой пример: одна из моих учениц не ставила скобки в уравнениях, забывая отделить одни числа от других. А потом выяснилось, что дома ей трудно оставаться одной в своей комнате — то есть воспринимать себя отдельно от других членов семьи. Проблемы ребенка с математикой связаны не с его интеллектуальными способностями, а с чем-то внутри него, что мешает ему ясно мыслить и понимать учителя».

Вот откуда столько тревожных эмоций, которые блокируют разум.

Не выучить, а понять

Признаем: очень часто школьные неудачи выводят родителей из себя. Мы злимся, возмущаемся и критикуем ребенка, который «не старается», «не хочет понять» и вообще «плохо соображает». А эксперты единодушны: главная задача родителей прямо противоположная — уменьшить его напряжение и переживания. «Ребенка вообще не надо фиксировать на неудачах, — подчеркивает Елена Морозова. — Лучше сказать: да, это пока не получается, давай подумаем, как тебе помочь».

Нужно не вдалбливать, а последовательно подводить ребенка к самостоятельному решению

Однако это не значит «помочь выучить», как думают иногда родители. «Математику нужно понимать, почувствовать ее цельность, единство. Если просто зубрить, это будет лишь крайне утомительной и, главное, бессмысленной тренировкой для памяти», — предупреждает Леонид Костюков.

«Нужно не вдалбливать, а последовательно подводить ребенка к самостоятельному решению, — продолжает Елена Морозова. — И когда происходит этот инсайт, ребенок изумляется: «Надо же, я смог!» Получилось раз, другой, третий — и постепенно он начинает увлекаться, чувствовать свою состоятельность. Конечно, лучше всего здесь поможет специалист — учитель, которого можно попросить о дополнительных занятиях, или опытный репетитор. Но и сами родители могут попробовать совершить эти открытия вместе с ребенком».

Не обязательно после этого ученик станет блистать на уроках и приносить пятерки. Хотя оценки и становятся лучше, если на них не зацикливаться, отмечает Анн Сьети: «В конце концов, у каждого свои цели. Для одного важно не оказаться худшим в классе. А другой мечтает стать ветеринаром. Главное, чтобы дети начали чувствовать себя лучше, избавившись от тревоги и страха, и стали получать удовольствие от занятий математикой».

«Нужно преподавать математику как особую теорию красоты» 

Александр Лобок, психолог, автор книги «Другая математика»

Psychologies: Почему у многих детей математика вызывает скуку, страх, отвращение?

Александр Лобок: Это означает только одно: она принципиально неправильно для этого ребенка преподается в школе. Множество детей переживают унижение математикой. Долгие школьные годы они испытывают чувство своей непроходимой математической тупости, а учитель поддерживает это чувство либо в щадящей форме («Что поделаешь, у него гуманитарные мозги!»), либо в циничной и злобной («Ну ты тупой!»).

Многие учителя убеждены, что математические способности — «от Бога» и что причина «невменяемости» миллионов детей, не понимающих математику, в их природной ограниченности. Тогда как задача школы — помочь каждому ребенку почувствовать математический азарт и желание заниматься. Если этот интерес и любовь возникнут, ребенок будет гораздо более успешен — в том числе и в традиционном математическом обучении.

Чаще всего проблемы возникают у детей гуманитарного склада. Как в них пробудить этот азарт?

Для детей-гуманитариев важно почувствовать смысл. А традиционная школьная программа довольно часто предлагает математику как набор абстрактной «цифири», даже не пытаясь объяснить ученикам, что математика — это прежде всего философия, позволяющая совершенно по-новому взглянуть на окружающий мир. Если же детям открыть дверцу в смыслы того, чем занимается математика, — у них появляется азарт и интерес.

Например, когда объясняешь и показываешь, что математика — это такое особое волшебство, которое позволяет обсчитать весь мир. И значит, найти что-то фундаментально общее во всем мире. Например, все можно взвесить, измерить — на этом основании сравнить мальчика Петю, его любимую кошку и папин автомобиль. И вообще, оказывается, сравнить можно все во Вселенной!

А еще дети не подозревают, что математика наполнена внутренней красотой, — им тоже об этом никто не рассказывает. А ведь любая последовательность орнаментов или игра архитектурных форм — это математика. И если детям преподавать математику как особую теорию красоты, это очень может их зацепить.

Значит ли это, что освоить школьный курс математики по силам каждому ребенку?

В том виде, в каком он сегодня существует, — разумеется, нет. Да это и не нужно. А вот постигнуть эстетические и философские основания математики — это по силам и нужно всем. Благодаря этому интерес к математике — причем к самой традиционной — возникает у каждого ребенка. В том числе у тех, кто всю жизнь этот предмет ненавидел и считал себя неспособным.

Но что же делать родителям, чьи дети учатся в традиционной школе и не справляются с математикой?

Это всегда глубоко индивидуальная проблема. Но общая рекомендация может быть такой: надо найти такого педагога, который по-настоящему увлечен и математикой, и детьми.

Читайте также

www.psychologies.ru

Что делать, если у ребенка проблемы с математикой

Сталкивались ли вы с тем, что ребенок не может решить задачу или правильно сосчитать пример?

Если да и такая проблема возникала однократно или вы с ней сталкиваетесь редко, то возможно ребенок просто отвлекся или переутомился.

В таком случае обычно не нужно предпринимать никаких дополнительных мер, а просто простить ребенку его вычислительную ошибку.

Однако если ребенку трудно дается математика и он постоянно допускает ошибки в счете, то бездействие может быть чревато усилением проблемы.

В этой статье мы поговорим о том, какие проблемы с изучением математики могут возникать у детей и как их решать.

Трудности в дошкольном возрасте (6-7 лет), на которые нужно обратить внимание

• Если ребенку трудно считать до 100
• Имеет трудности в определении числа, которое следует за названным и перед названным числом
• Имеет проблемы с пониманием того, что число может быть использовано для описания количества входящих в него объектов, например, не знает, что 5 может быть использовано для группы из 5 пальцев, 5 бананов и 5 кошек
• Имеет трудности с распознаванием и записи чисел до 20
• Пропускает числа при подсчете, не может считать десятками
• Не может распознавать образы и не может сортировать предметы по размеру, форме или цвету

Проблемы в начальной школе

• Трудности в подсчете с заданным шагом (+2,+3,+10) Например: 2, 4, 6, 8…
• Невозможность мысленно рассчитать сложение и вычитание в пределах 20 с переходом через 10 (13-8, 9+6)
• Сложность распознавания основных математических знаков, таких как плюс или минус
• Сложность распознавания дестяков и единиц числа
• Не понимает понятие «больше чем» или «меньше»
• С трудом запоминает основные математические факты, такие как 5 + 5 = 10, 14 это 7 и 7 (состав числа)
• Не делает связь между связанными фактами математики (5 + 5 = 10, значит 10 — 5 = 5)
• Имеет проблемы с распознаванием графического образа цифры
• Использует пальцы, чтобы подсчитать, вместо того, чтобы посчитать в уме
• Испытывает затруднения записывать цифры аккуратно в колонках при решении математических задач
• Не может назвать, что в правой части примера
• Избегает игры, которые включают стратегию, как шашки или судоку
• Имеет трудности с использованием математики в реальной жизни, в том числе в таких вещах, как определение сдачи в магазине или подсчет, что можно купить на определенную сумму денег
• Имеет проблемы с пониманием диаграмм

Если вы увидели некоторые из этих признаков у вашего ребенка в течение шести месяцев, это обозначает, что нужно не закрывать глаза на трудности ребенка, а предпринять шаги для того, чтобы помочь ребенку сформировать вычислительные навыки.

Вы можете точно не знать, что вызывает проблемы с математикой у ребенка, но есть шаги, которые вы можете предпринять уже сейчас, чтобы сделать процесс обучения легче.

Что может вызвать проблемы с математикой?

Для того, чтобы производить вычисления человек должен обладать рядом навыков: абстрактное мышление, хорошая память, уметь оценивать количество объектов, а также иметь способность к критическому мышлению.

Существует специальный термин, который используют при диагностировании расстройства счета.

Дискалькулия (от греч. dys + лат. calculo – считать, вычислять) – любое расстройство счета. Иногда имеется в виду только нарушение развития способности считать. Часто является самостоятельным недугом, а не побочным следствием других нейрологических и психологических проблем. В основе дискалькулии лежит неспособность оценивать количество объектов с первого взгляда (то есть без пересчёта). За эту функцию в мозге отвечает внутритеменная борозда теменной доли.

Исследования показывают, дискалькулией страдают от 7 до 14 процентов людей.

Это проявляется следующим образом:

• Неспособность к быстрому распознаванию количества предметов в поле зрения.
• Присутствие высоких сложностей при вычислении с помощью цифр. Например, человек, страдающий дискалькулией, не сможет понять, почему 59 + 13 = 72.
• Наличие сложностей с абстрактным счётом времени.

Дискалькулия не является признаком низкого интеллекта.

Люди, имеющие дискалькулию, часто становятся поэтами, художниками, скульпторами, и, следовательно, не имеют проблем в изучении языков или других сферах.

Однако, дети с дискалькулией имеют психологические трудности с математикой и в целом с обучением в школе. Они настолько обеспокоены тем, что им снова предстоит считать и делать по истине трудное для них дело, что это снижает их производительность на уроках и математических тестах, снижает самооценку.

Как вы можете помочь ребенку с математикой?

Если ваш ребенок испытывает проблемы с математикой, то вы многое можете сделать. Зная, что проблема существует, вы и учитель можете найти наиболее эффективные способы формирования математических навыков без снижения самооценки ребенка.

Вот некоторые шаги , которые вы можете предпринять:

Поговорите с учителем вашего ребенка.

Это отличный первый шаг к выяснить , почему ваш ребенок испытывает проблемы с математикой. Вы можете обратиться к учителю , чтобы получить список навыков , которым ребенок должен научиться к концу учебного года.

Это может дать вам ощущение того , что нужно не так многому научиться, как вы можете думать изначально.

Учитель может попробовать различные стратегии , чтобы помочь ребенку сформировать математические навыки и понять концепции математических действий.

Используйте визуализацию для математических действий.

Превратите абстрактную математику на бумаге в увлекательное манипулирование объектами. Например, для того, чтобы научить ребенка знакам «больше-меньше» используйте сказку о вороне.

Играйте в математику.

Ребенок не должен бояться вычислений. Попросите ребенка помочь вам сортировать белье и пары вверх носки. Или же отмерить ингридиенты для приготовления пищи или оценить стоимость покупок в магазине .

Объясняйте ребенку ПОЧЕМУ используется тот или иной математический знак и термин.

Пусть даже ваше объяснение не всегда будет научным.

Например, для того, чтобы объяснить ребенку уравнения, возьмите обычную кружку, напишите на дне кружки «х» и переверните ее вверх дном. Закройте одно из чисел и спросите ребенка, что под кружкой?

Скажите, что кружка спрятала (или съела) одно число. Какое?

Повышайте самооценку ребенка.

Трудности с математикой могут повлиять на вашего ребенка, на общую самооценку и общение со сверстниками.

Помогите своему ребенку признать его сильные стороны и опираться на них. Напомните, что вы им очень гордитесь и любите.

Рисуйте математику.

Используйте карандаш и ручку для того, чтобы оживить задачи и нарисовать небольшой мультик по сюжету задачи.

Покажите ребенку, как умножают в Азии, для того, чтобы он мог с легкостью справиться с умножением.

 

Общайтесь с другими родителями.

Это поможет вам понять , что вы не единственная семья, которая столкнулась с данными трудностями.

Наша группа и этот блог может помочь вам найти родителей, чьи дети так же испытывают трудности с математикой.

Это отличный способ пообщаться, найти единомышленников, обменяться идеями и стратегиями.

Попробуйте разные стратегии.

Есть упражнения и игры, которыми в домашних условиях вы можете помочь ребенку полюбить математику и помочь ребенку сформировать математические навыки.

Поиск и опробирование разных стратегий является лучшим способом, чтобы получить поддержать ребенка в обучении.

Чем больше вы знаете, тем лучше вы будете помогать ребенку формировать свои математические навыки и укрепите доверие ребенка к вам.

Учитесь техникам эффективного обучения

Для этого мы создали новый утренний тренинг «Научите ребенка быстро считать в уме»

Который состоится во вторник, 14 марта, в 6.00 по мск

На нем мы разберем

• Разберете что нужно делать, чтобы ребенок умел считать в уме
• Изучите технику «Яйца» для обучения счету с переходом через десяток
• Изучите технику «Рожки» для быстрого счета в пределах 100
• Узнаете как объяснить и быстро выучить состав числа (9 это 8 и 1, 7 и 2, 6 и 3 и т.д.)
• Узнаете что делать, если ребенок постоянно ошибается в счете?
• Узнаете как научить не путать «увеличь на/увеличь в, уменьши на/уменьши в»
• Получите игры и упражнения, которые помогут ребенку сформировать навыки счета
• Узнаете игру «Кузнечик» для развития мозга
• Получите графические помогаторы для помощи ребенку по математике
• Узнаете приемы письменных вычислений
• Разберете сложение и вычитание больших чисел

Регистрируйтесь на бесплатный тренинг и за 1 утро решите вопрос с счетом раз и навсегда

Зарегистрироваться на тренинг бесплатно>>

Вам понравилась статья? Сохраните себе на стену, чтобы не потерять

Похожее

gladtolearn.ru

Урок 7. Устранение проблем с математикой

В этом уроке мы постараемся рассмотреть не столько проблемы с технической стороной усвоения математических знаний, сколько проблемы более глобального, можно сказать, психологического характера. И причин тому несколько:

• Во-первых, представленный раздел нашего курса посвящен обучению счету детей преимущественно дошкольного и младшего школьного возраста.
• Во-вторых, о многих технических проблемах уже шла речь в первых уроках данного раздела, и мы дали предостаточно информации на тему того, как избежать самых распространенных ошибок, из-за которых и возникают технические проблемы.
• В-третьих, психологический аспект важен потому, что уже в младшем возрасте можно проследить, возникают ли у ребенка трудности с усвоением материала, испытывает ли он тягу к математическим знаниям, к чему больше тяготеет – к гуманитарным или точным наукам.

Беря это во внимание, мы решили, что поговорить о трудностях с математикой с точки зрения педагогики и психологии будет вполне уместно. Несмотря на то, что практической информации, как таковой, в уроке минимум, в общем и целом эти знания непременно пригодятся вам на практике. Причем полезны они будут не только во время ваших занятий с ребенком, но и в перспективе – когда он пойдет в школу, начнет делать уроки, быть может, выбирать программу с углубленным изучением каких-то предметов.

Итак, давайте приступим.

Содержание:

1

Трудности с математикой

Изучая математику, с проблемами сталкивается огромное количество детей. Если числа, таблица умножения и простейшие вычисления даются всем, то формулы, доказательства теорем и тригонометрические функции может осилить не каждый. Однако от уроков и школьной программы деваться некуда, а это значит, что познавать азы необходимо. Чего же может не хватать детям, чтобы подружиться с царицей наук?

Множеству родителей знакомы проблемы их детей с алгеброй и геометрией. Уроки делаются всем семейством, а сам процесс нередко сопровождается истериками, нервами, стрессами и усталостью, отчего математика становится настоящим бичом, а уроки – серьезным испытанием на прочность. В итоге мамы и папы ломают голову над тем, какую помощь оказать ребенку: и чтобы предмет давался легче, и чтобы каждая неудовлетворительная оценка в тетрадке не становилась причиной для плохого настроения или – что часто случается – слез.

Математику можно смело назвать одним из самых спорных предметов в школьной программе, и среди выпускников всегда можно найти тех, у кого одни пятерки по всем дисциплинами, но только не по математике. Родители же в свою очередь относятся к такого рода проблемам по-разному. Одни уверены в том, что математика очень важна, а потому чуть ли не силой заставляют свое чадо грызть гранит науки, даже если он действительно не по зубам. Другие, видя в ребенке проявления гуманитарного склада ума, считают, что главное – это успехи в литературе, русском и иностранных языках, истории и т.д., а с математикой – да бог с ней, с этой математикой.

Но следует ли сводить на нет важность этого предмета, даже если в малыше уже с ранних лет наружу пытается выбраться творческая натура? К категории творческих людей можно отнести писателей, поэтов, художников, а также историков, журналистов и редакторов. Но если, например, художнику или писателю математика на самом деле нужна постольку-поскольку, то в таких профессиях, как журналист, историк или редактор она все-таки пригождается. Математика – это основа системного мышления, и во многих областях жизнедеятельности человека без нее не обойтись.

Когда у детей возникают трудности с математикой, родители часто говорят: «Ну не понимает он (или она) этого предмета, нет у него предрасположенности к нему». В итоге не остается ничего, кроме того чтобы без ропота принять сложность математики. «Зато остальные предметы даются ребенку прекрасно!». Однако, по мнению опытных педагогов и профессиональных репетиторов по математике (например, Леонида Костюкова) этот предмет может быть значительно проще остальных. Фишка в том, что математика – наука последовательная, и нет никакой необходимости заучивать бесчисленное количество дат, терминов и понятий. Все, что требуется от ученика – это понять математику.

Кроме того, если ребенок хорошо осваивает языки, каких бы то ни было проблем с освоением математики у него просто быть не должно. Большая часть иностранных языков построена на вполне логичной и понятной структуре, а школьная программа по изучению английского языка гораздо сложнее программы по изучению математики. Картинка, согласитесь, рисуется довольно приятная, но почему на деле все не так?

2

Психология «отношений» ребенка и математики

Профессиональные психологи (к примеру, детский психолог Елена Морозова) указывают на то, что между детьми, хорошо соображающими в технических дисциплинах, и остальными детьми есть некоторые психологические отличия. По большому счету, дети, любящие математику, характеризуются любопытством, готовностью пойти на риск, настойчивостью, отсутствием страха перед трудностями. А те, у кого с математикой «ни то, ни се», часто отличаются неуверенностью в себе, зависимостью от мнения родителей и других окружающих людей, боязнью трудностей, а также убежденностью в том, что они не так сообразительны, как остальные. Потому-то и решение трудных математических задач вызывает серьезные затруднения.

Вышеназванные различия формируются еще в детском садике и начальных классах школы. Одни дети умеют хорошо читать, а другие что-то невнятно мямлят. Одни знают таблицу умножения, а другие с трудом складывают «17» и «15». Одни при счете перебирают пальчики, а другие с успехом демонстрируют абстрактно-образное мышление. Одним не стоит никакого труда представить, как первый поезд выходит из пункта A, а второй – из пункта B, и встречаются они в точке C, а для других это – фантастика.

Все это во множестве случаев является следствием отсутствия фундамента математической дисциплины, по причине чего ребенку гораздо легче вообще запустить математику, нежели постараться в ней разобраться.

Любая запущенная математическая трудность лишь усугубляет проблемы в будущем. А в литературе, например, подобные проблемы отсутствуют, т.к. если ученик не читал «Отцы и дети» И. С. Тургенева, это совсем не мешает ему прочитать «Войну и мир» Л. Н. Толстого. С математикой же такое не прокатит, ведь из-за какой-то теоремы, непонятой в пятом классе, начнутся проблемы в последующих классах.

Но, по мнению все тех же психологов, отсутствие успеха в изучении математики может быть связано не только со способностями, но и с эмоциональными особенностями детей. Во-первых, и сами родители не всегда проявляют чудеса педагогики и воспитания, занимаясь ранним развитием своих подопечных, а во-вторых, не каждый учитель – Учитель с большой буквы. Особенности воспитания и стиль преподавания играют огромную роль и накладывают свой отпечаток. В частности, если ребенку часто дают понять, что он чего-то не соображает, отстает, не способен понять «прописных истин», на положительные результаты обучения рассчитывать не стоит.

3

Есть ли у родителей выход?

Нет совершенно никаких сомнений в том, что детские трудности с математикой, особенно когда они наблюдаются в старшем дошкольном и младшем школьном возрасте, воспринимаются родителями отнюдь не радостно. Но критика и злость по отношению к ребенку нисколько не облегчают ситуацию. И, опять же, психологи в этом вопросе сходятся – родители ни в коем случае не должны нагнетать обстановку, а, наоборот, должны стараться снимать напряжение, вызванное математикой. Нельзя фокусировать внимание ребенка на неудачах и отсутствии успеха. Если что-то не получается, это вполне можно исправить.

Не заставляйте ребенка зазубривать через силу основы предмета. С математикой ваша маленькая драгоценность сможет справиться только в том случае, если вы сможете донести целостность этой дисциплины. Старайтесь подводить свое чадо к самостоятельным решениям, как можно доступнее объясняя моменты, мешающие ему понять и увидеть – как решается пример, задача или уравнение. Если же желание научить ребенка основам математики есть, а возможности заниматься с ним самим по каким-то причинам нет, есть смысл прибегнуть к услугам репетитора. Но он должен не только разбираться в своем предмете, но и иметь опыт работы с детьми.

Но давайте резюмируем все вышесказанное, чтобы разложить все по полочкам.

4

Почему возникают проблемы с математикой

Не забывайте, что в этом уроке мы обсуждаем проблемы с математикой с психологической точки зрения. Исходя из этого, основными причинами таких проблем являются:

• Сложность восприятия, когда, например, у ребенка есть предрасположенность к гуманитарным дисциплинам, а математика преподносится родителем или учителем абстрактно. Большое упущение – если познавательная активность не стимулируется, а о значении и значимости математики в контексте жизненной полезности ничего не говорится.
• Неуверенность ребенка в своих силах, зависимость от мнения окружающих. Освоение математики и решение задач в этом случае служит дополнительным источником стресса. Вопрос ребенка самому себе о том, сможет ли он решить задачу, становится навязчивой боязнью неудачи.
• Психологические барьеры, вызываемые такими терминами, как «доказать», «неизвестное», «требуется» и т.п. С учетом особенностей воспитания каждое из этих понятий способно активизировать негативные внутренние переживания, в том числе и неосознаваемые.

Имейте в виду, что эти причины относятся к основным. Разбирая математические трудности ребенка, нужно брать в расчет наличие индивидуальных психологических проблем, зачастую совершенно не связанных с интеллектуальным потенциалом.

5

Что делать родителям

Подходя к вопросу решения проблем с математикой профессионально, следует прибегать к следующим методам:

• Экспериментируйте – пытайтесь доносить до ребенка информацию, освещая философскую, эстетическую и практическую стороны дисциплины.
• Снижайте напряжение ребенка и старайтесь делать так, чтобы он как можно меньше переживал по поводу трудностей с освоением математики (и чтобы меньше переживал вообще).
• Не концентрируйтесь на проблемах ребенка и его ошибках, и не фокусируйте на них его внимание. Указывайте на то, что если что-то не получается, то это всего-навсего временно, и скоро все будет замечательно.
• Оказывайте ребенку всяческую помощь в понимании математики, а не просто давайте ему задание заучивать или запоминать. Если что-то вам не под силу, используйте помощь репетитора.
• Давайте ребенку только такие подсказки, которые будут наталкивать его на поиск самостоятельного решения, и никогда не решайте за своего ребенка.
• Используйте в качестве мотиваторов поощрение и похвалу. Это будет способствовать развитию в ребенке уверенности в себе и снижению тревожности.
• Оценки не являются самоцелью. Намного важнее, чтобы ребенок получал от изучения математики удовольствие.

Проблемы у детей с математикой – это не нечто из ряда вон выходящее; они есть всегда и везде. Например, несколько лет назад, американское издание New York Times (выпуск от 28 июля 2014 года) поднимало вопрос о том, нужна ли вообще ученикам алгебра, если каждый четвертый американский школьник не может получить аттестат из-за «неприятностей» с математикой. А министр образования и науки Франции Клод Аллегрэ, будучи сам ученым-физиком, дискутировал на тему исключения математики из школьной программы, ссылаясь на то, что множество детей не способны решить даже элементарные задачи. Однако дисциплина все так же остается одной из главных в школе, а для многих – и в жизни.

Но помните, что умение считать, знание таблицы умножения, хорошие оценки и т.д. – все это прекрасно, но у ребенка могут быть свои потребности и цели. Если один хочет стать новым Пифагором, то для другого важно, чтобы его любили, ценили и принимали таким, какой он есть, а также чтобы математика не вызывала у него страхов и тревог, даже если он чего-то недопонимает. Так что успех вашего чада – в ваших руках. Используйте это ему во благо.

Предпоследний урок блока по обучению детей счету посвящен теме привития ребенку любви к математике. Из него вы узнаете, что делают многие родители, чтобы отбить у малыша всякую охоту осваивать математические основы, и что следует предпринимать, чтобы этого избежать, и чтобы интерес к этой науке возрастал с каждым днем.

Проверьте свои знания

Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.

Кирилл Ногалес

4brain.ru

Почему школьники не понимают математику? Топ-5 причин

К репетиторам TutorOnline очень часто обращаются родители с просьбой помочь ребёнку с математикой, т.к. «он совсем её не понимает». Тысячи школьники по всей России, и не только, сталкиваются с одной и той же проблемой. Но почему? Основываясь на 6-летнем опыте работы, мы выделили ТОП-5 причин. 

5) «Гуманитарий». Наименее популярной, но всё же часто встречающейся, причиной проблем с математикой является ярлык, который был безосновательно повешен на ребёнка учителем или родителями. Обычно это происходит после первых же ситуаций, когда ребёнок получает 5 по русскому и 2-3 по математике. «Наверное, ты гуманитарий, тебе видишь как сложно даётся математика, а язык — легко». И даже если это просто совпадение, у ребёнка начинает работать психологическая установка, что математика для него сложно, а гуманитарные предметы — легко. Поэтому совет всем учителям и родителям: не убивайте в ребёнке математика словом. Поддерживайте, придайте уверенности в силах, но не вешайте ярлык. 
4) «А зачем мне математика?» Есть тип учеников, которые сознательно «отключаются» на уроках по математике, не слушают учителя, потому что искренне не видят в этом никакой пользы для себя. Правда, к экзаменам приходится наверствывать такие объёмы информации, что школьники буквально ненавидят потом математику всю жизнь.  Чтобы этого не происходило, постарайтесь привести ребёнку действительно актуальные примеры, где  математика нужна. Это может быть что угодно: от расчета угла, под которым следуют бить по мячу в футболе, до возможности рассчитать свой бюджет так, чтобы скопить на ноутбук мечты. В конце концов, незнание математики может сказаться на результатах ЕГЭ так, что не удастся поступить на профессию мечты.
3) «Не хватило времени на математику». В таких случаях проблемы с математикой начинаются у перегруженных учеников: кружок по рисованию, шахматы, футбольный клуб, олимпиада по английскому, поездка на соревнования. Успеть бы поспать, тут не до математики. Но, как мы понимаем, эту проблему легко решить, нормализовав график ребёнка и взяв пару занятий с репетитором по проблемным темам.  

2) «Пропустил». Это самый классический пример, когда появляются пробелы. Пропуская занятия по болезни, ученик рискует заработать несколько серьёзных пробелов. И здесь важно вовремя их устранить. Как показывает практика, если скопить 5-6 таких пропущенных блоков, потом тратится очень много времени и сил, чтобы по кирпичикам восстановить знания. Лучше решать проблему сразу. Если дела идут на поправку, но ребёнок всё еще числится на больничном, возьмите пару занятий с онлайн-репетитором. Ученику не придётся никуда ехать, достаточно в удобное время связаться с репетитором и разобрать тему, которые одноклассники проходили в школе. Так и на контрольных всё будет в порядке! 

1) «Учитель в школе плохо объясняет». К сожалению, такие случаи действительно нередки и не все хорошие математики способны понятно объяснить предмет детям. Но так же случается, что учитель объясняет неплохо и половина класса сразу же схватывает тему. А некоторым ученикам требуется более подробное объяснение, но в силу нехватки времени и требований школьной программы, учитель «бежит» дальше, пытаясь успеть объяснить остальное. 

Если ученики долгое время просто смиряются с таким положением дел и ничего не делают, то со временем перед математикой формируется какой-то страх и нежелание слушать («Зачем, если опять ничего не пойму?»).  Поэтому здесь важно найти своего репетитора, который объясняет на понятном ученику языке каждую тему и способен заинтересовать. 

Как видим, не ни одного случая, когда нет решения проблемы, все причины можно обойти и освоить предмет на отлично! Важно лишь сделать шаг на пути к этому. А таким шагом может стать запись на бесплатное вводное занятие к онлайн-репетитору по математике, на котором учитель выявит все пробелы и сможет предложить план занятий!:) 

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

дискалькулия и проблемы с математикой

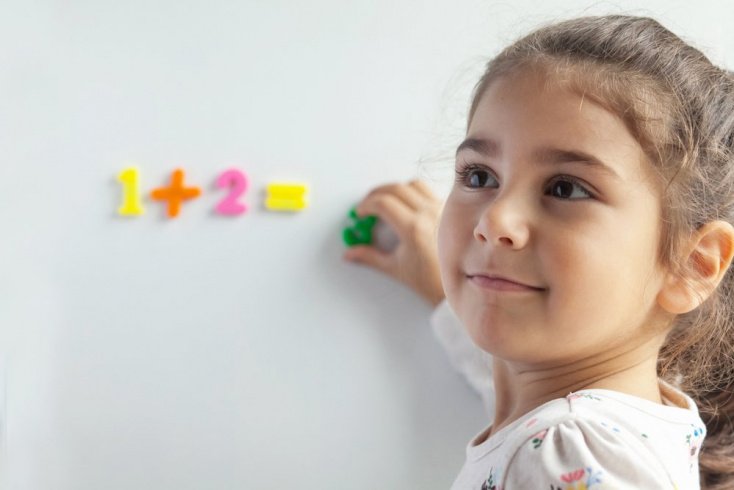
Если не брать во внимание проблемы образования, то истинная дискалькулия диагностируется в среднем у 7% учеников начальной школы. Исследования доказывают, что распространенность у нарушения способности к счету такая же, как и у дислексии, способности к чтению. Дискалькулию даже порой называют «математической дислексией», но это – совершенно другое состояние.

Дискалькулия нередко связана с СДВГ, синдромом дефицита внимания и гиперактивности. До 60% детей с СДВГ имеют также и «математическое нарушение».

У детей с дискалькулией нарушается процесс счета. Они могут считать на пальцах или использовать наглядные материалы намного дольше своих сверстников. Им сложно посмотреть на стол и сразу понять, сколько на нем яблок – 3 или 5. А тем временем ученые доказали, что дети второго года жизни, не зная счета, умеют отлично «считать» до трех: после демонстрации трех кубиков в коробке и выдачи двух они знают, что там остался еще кубик, даже если коробка закрыта. Даже новорожденные способны различать множества – где один предмет, где два, где три.

Умение что-то подсчитывать без основ математики – свойство нашего мозга. Им в ограниченных пределах владеют не только человекообразные, но даже птицы и насекомые. Они «считают» количество ягод на кустах, определяя, где их больше, цветы на полянках, а пчелы понимают, что такое ноль.

Близнецовый анализ доказал: способности к арифметике на треть определяются генами, а не условиями развития и обучения. Более того, они наследуются отдельно от способностей читать или запоминать слова, имена, названия. Так что для способности к подсчетам у нас явно есть отдельная часть мозга.

При дискалькулии теряется «смысл» чисел: мозг не понимает связи между числом и количеством. По мнению психологов, первоосновой способности к арифметике является автоматическое умение с одного взгляда определять количество предметов. Так, взрослый в норме оценивает количество до 5 предметов, а когда их больше, может быстро, не подсчитывая, понимать, где именно больше, а где меньше предметов. Дискалькулия нарушает такую способность. К примеру, чтобы понять, какая из двух игральных карт «старше» (если на них нет цифр), человеку с дискалькулией придется считать, сколько на них значков.

Еще одна выявленная связь нарушений счета и других отклонений – это неспособность различать свои пальцы. Именно их использует ребенок, начинающий осваивать счет, сравнивая количество пальцев и предметов.

Но есть нарушение под названием синдром Герштмана или пальцевая агнозия, при которой человек буквально путается в пальцах, не может найти его по названию или по образцу, показанному учителем на своей руке. Это нарушение связано с дефектом теменной доли.

При травме в теменной доле могут избирательно теряться арифметические навыки, и это доказано уже больше века назад. При помощи МРТ специалисты уже выяснили, что «орган арифметики» в человеческом мозге – это участок теменной коры под названием «внутритеменная борозда». И у людей с дискалькулией она короче среднего.

Не только этот участок нужен для уроков математики: важна префронтальная кора для внимания, рабочей памяти и способности рассуждать; угловая извилина левой теменной доли, чтобы вспоминать факты; веретеновидная извилина височной доли, чтобы различать числа, символы, слова. У ребенка с дискалькулией внутритеменная борозда во время занятий арифметикой работает не так активно, как должна бы, и объем серого вещества там меньше. Но причина не только в этом: нейронные связи между данной бороздой и остальными компонентами тоже развиты слабее.

medaboutme.ru

Это нужно знать родителям, если у их ребенка проблемы с математикой

Некоторые дети плохо разбираются в математике, в то время как другие испытывают неприятное чувство, которое называют математическим беспокойством. В таком случае учеба не приносит радость, и дети ощущают своеобразный внутренний прессинг или желание добиться успеха в математике, однако эти эмоции практически парализуют их.

Серьезные дисфункции

И все же у некоторых школьников существуют более серьезные проблемы с математикой, чем описанные выше. У таких детей может быть дискалькулия, математическая дисфункция, иногда называемая математической дислексией. Выдающиеся ученые и эксперты, разбирающиеся в вопросах когнитивной нейробиологии, говорят, что такие патологии довольно часто встречаются у современных школьников.

Итак, как узнать, имеет ваш ребенок дискалькулию или нет? Ниже приведены основные признаки, которые вам необходимо знать и которые помогут определить наличие тех или иных особенностей у вашего чада в зависимости от его возраста.

Дошкольники

Вас должно насторожить, если:

• Ребенок не может сосчитать и пропускает числа. В то же время дети его возраста помнят эти цифры в правильном порядке.
• Ребенок не понимает смысла подсчета. Как это видно на примере? Вы просите принести шесть машинок, он просто передает вам несколько игрушек, но не считает их количество.
• Он изо всех сил старается расставить предметы по образцу – от самого маленького к большому или от самого высокого к низкому. Однако это не всегда получается.
• У ребенка проблемы в понимании взаимосвязи между символом и словом. Например, он не может соединить в уме цифру «7» и слово «семь».
• У него не получается связать число с предметами. Например, ему сложно понять, что число 3 используется по отношению к группам разнообразных вещей, таких как 3 куклы, 3 автомобиля или 3 человека.

Школьники

Эти особенности вашего ребенка должны насторожить:

• Ребенку тяжело понять и запомнить общепринятые математические факты, такие как 1 + 3 = 4.

• Он использует пальцы для подсчета, вместо того чтобы решить элементарные задачки в уме или же на бумаге.
• Ребенку необходимо приложить много сил, чтобы распознать математические знаки, такие как “плюс” и “минус”. Ему не всегда получается правильно использовать их в решении примеров.
• Ребенку сложно осознать такие математические термины, как “больше” и “меньше”.
• Он неправильно располагает цифры, может поместить символы в другой клеточке или же поменять их местами.
• Ребенку сложно решить элементарный пример без вычисления: 3 + 26 — 26. Также он не осознает, что от перестановки мест слагаемых сумма не меняется.
• У него уходит много времени на то, чтобы изучить условия задачи и придумать к ней план ее решения.
• Ребенок плохо ориентируется в подсчете очков, когда играет в спортивные игры или участвует в других соревнованиях.
• Он с трудом понимает, что такое стоимость товаров, и такие понятия, как цена и сдача, для него сложны.
• Он старается избегать ситуаций, в которых требуется понимание чисел. Это могут быть игры, предполагающие проведение различных подсчетов.
• Школьнику сложно понять информацию относительно составления диаграмм и различных графиков.
• Ребенку сложно определить, сколько жидкости в бутылке или же сколько ложек сахара нужно положить в стакан чая.
• Ребенок испытывает неловкость, когда речь заходит о таких понятиях, как скорость, расстояние, направление. Сталкиваясь с данными терминами на практике, он теряется.
• Школьнику сложно решить задачу разными способами. Например, вместо того чтобы добавить длину и ширину прямоугольника и умножить сумму на два, он начинает поочередно прибавлять каждую сторону.

Что делать?

Если вы полагаете, что у вашего ребенка дискалькулия, не паникуйте. Поговорите с учителем, обратитесь за помощью к директору школы. Возможно, педагоги станут уделять больше внимания обучению вашего чада и перестанут слишком занижать ему оценки.

Как бы там ни было, если вы понимаете, почему у вашего ребенка проблемы по математике, это поможет вам оказать ему квалифицированную помощь. Заверяйте его в своей любви и с добротой помогайте ориентироваться в арифметических науках.

Тогда ребенок получит необходимые навыки, которые понадобятся ему во взрослой жизни. Ведь математика, а точнее умение считать, — это важная составляющая повседневности.

Нашли нарушение? Пожаловаться на содержание

fb.ru

Задачи современной математики, которые до сих пор не решены

На протяжении веков лучшие умы человечества решали одну математическую задачу за другой, однако есть несколько, не поддавшихся до сих пор никому. За нахождение алгоритма их решения некоторые фонды и компании готовы заплатить большие деньги.

Василий Парфенов

1 октября 2019 14:00

Гипотеза Коллатца

Другие названия: гипотеза 3n+1, сиракузская проблема, числа-градины. Если взять любое натуральное число n и совершить с ним следующие преобразования, рано или поздно всегда получится единица. Четное n нужно разделить надвое, а нечетное — умножить на 3 и прибавить единицу. Для числа 3 последовательность будет такой: 3×3+1=10, 10:2=5, 5×3+1=16, 16:2=8, 8:2=4, 4:2=2, 2:2=1. Очевидно, что если продолжить преобразование с единицы, то начнется цикл 1,4,2. Достаточно быстро количество шагов в вычислениях начинает превышать сто и на решение каждой новой последовательности требуется все больше ресурсов.

Небольшой прогресс в решении этой задачи почти вековой давности наметился буквально в прошлом месяце. Однако знаменитый американской математик Терренс Тао лишь ближе всех подошел к нему, но ответа все равно пока не нашел. Гипотеза Коллатца является фундаментом такой математической дисциплины, как «Динамические системы», которая, в свою очередь, важна для множества других прикладных наук, например, химии и биологии. Сиракузская проблема выглядит, как простой безобидный вопрос, но именно это делает ее особенной. Почему ее так сложно решить?

Проблема Гольдбаха (бинарная)

Еще одна задачка, формулировка которой выглядит проще пареной репы — любое четное число (больше 2) можно представить в виде суммы двух простых. И это краеугольный камень современной математики. Данное утверждение легко проверяется в уме для небольших значений: 18=13+5, 42=23+19. Причем рассматривая последнее, можно достаточно быстро понять всю глубину проблемы, ведь 42 представляется и как 37+5 и 11+31, а еще как 13+29 и 19+23. Для чисел больше тысячи количество пар слагаемых становится просто огромным. Это очень важно в криптографии, но даже самые мощные суперкомпьютеры не могут перебирать все значения до бесконечности, поэтому нужно какое-то четкое доказательство для всех натуральных чисел.

Проблема была сформулирована Кристианом Гольдбахом в его переписке с другим величайшим светилом математики Леонардом Эйлером в 1742 году. Сам Кристиан ставил вопрос несколько проще: «каждое нечетное число, больше 5, можно представить в виде суммы трех простых чисел». В 2013 году перуанский математик Харальд Хельфготт нашел окончательное решение этого варианта. Однако предложенное Эйлером следствие этого утверждения, которое и назвали «бинарной проблемой Гольдбаха», до сих пор не поддается никому.

Гипотеза о числах-близнецах

Близнецами называются такие простые числа, которые отличаются всего на 2. Например, 11 и 13, а также 5 и 3 или 599 и 601. Если бесконечность ряда простых чисел была доказана множество раз начиная с античности, то бесконечность чисел-близнецов находится под вопросом. Начиная с 2, среди простых чисел нет четных, а начиная с 3 — делящихся на три. Соответственно, если вычесть из ряда все, подходящие под «правила деления», то количество возможных близнецов становится все меньше. Единственный модуль для формулы нахождения таких чисел — 6, а формула выглядит следующим образом: 6n±1.

Как и всегда в математике, если проблема не решается «в лоб», к ней подходят с другого конца. Например, в 2013 году было доказано, что количество простых чисел, отличающихся на 70 миллионов, бесконечно. Тогда же, с разницей менее чем в месяц, значение разницы было улучшено до 59 470 640, а затем и вовсе на порядок — до 4 982 086. На данный момент существуют теоретические обоснования бесконечности пар простых чисел с разницей в 12 и 6, однако доказанной является лишь разность в 246. Как и прочие проблемы такого рода, гипотеза о числах-близнецах особенно важна для криптографии.

Гипотеза Римана

Если кратко, то Бернхард Риман предположил, что распределение простых чисел по множеству всех натуральных чисел не подчиняется каким-либо законам. Но их количество на заданном участке числового ряда коррелирует с распределением определенных значений на графике дзета-функции. Она расположена выше и для каждого s дает бесконечное количество слагаемых. Например, когда в качестве s подставляется 2, то в результате получается уже решенная «базельская задача» — ряд обратных квадратов (1 + ¼ + 1/9 + 1/16 + …).

Одна из «проблем тысячелетия», за решение которой назначен приз в миллион долларов, а также вхождение в пантеон «богов» современной математики. На деле, доказательство этой гипотезы настолько сильно толкнет вперед теорию чисел, что это событие по праву будет называться историческим. Многие вычисления и утверждения в математике строятся на предположении о том, что «гипотеза Римана» верна, и до сих пор никого не подводили. Немецкий математик сформулировал знаменитую задачу 160 лет назад, и с тех пор к ее решению подступались неисчислимое количество раз, однако прогресс очень скромен.

Гипотеза Берча и Суиннертон-Дайера

Еще одна «задача тысячелетия», за решение которой Институт Клэя одарит миллионом долларов. Не-математику достаточно трудно хотя бы в общих чертах сформулировать и понять, в чем же суть гипотезы. Берч и Свиннертон-Дайер предположили определенные свойства эллиптических кривых. Идея заключалась в том, что ранг кривой можно определить зная порядок нуля дзета-функции. Как говорится, ничего не понятно, но очень интересно.

Эллиптическими кривыми называются такие линии на графике, которые описываются, на первый взгляд, безобидными уравнениями вида y²=x³+ax+b. Некоторые их свойства чрезвычайно важны для алгебры и теории чисел, а решение данной задачи может серьезно продвинуть науку вперед. Наибольший прогресс был достигнут в 1977 году коллективом математиков из Англии и США, которые смогли найти доказательство гипотезы Берча и Суиннертон-Дайера для одного из частных случаев.

Проблема плотной упаковки равных сфер

Это даже не одна, а целая категория схожих проблем. Причем мы сталкиваемся с ними ежедневно, например, когда хотим разложить фрукты на полке в холодильнике или как можно плотнее расставить бутылки на полке. С математической точки зрения необходимо найти среднее количество контактов («поцелуев», также называется контактным числом) каждой сферы с остальными. На данный момент есть точные решения для размерностей 1−4 и 8.

Под размерностью или измерением понимается количество линий, вдоль которых размещаются шары. В реальной жизни больше третьей размерности не встречается, однако математика оперирует и гипотетическими значениями. Решение этой задачи может серьезно продвинуть не только теорию чисел и геометрию вперед, но также поможет в химии, информатике и физике.

Проблема развязывания

И снова каждый день встречающаяся проблема. Казалось бы, что сложного — узел развязать? Тем не менее, вычисление минимального времени, необходимого для этой задачи является еще одним краеугольным камнем математики. Трудность в том, что мы знаем, вычислить алгоритм развязывания можно, но его сложность может быть такой, что даже самый мощный суперкомпьютер будет считать слишком долго.

Первые шаги на пути решения этой задачи были сделаны в 2011 году американским математиком Грегом Купербергом. В его работе развязывание узла из 139 вершин было сокращено со 108 часов до 10 минут. Результат впечатляющий, но это лишь частный случай. На данный момент существует несколько десятков алгоритмов разной степени эффективности, однако ни один из них не является универсальным. Среди применений этой области математики — биология, в частности, процессы сворачивания белков.

Самый большой кардинал

Какая бесконечность самая большая? На первый взгляд бредовый вопрос, но так и есть — все бесконечности разные по размеру. А точнее, по мощности, ведь именно так различают множества чисел в математике. Под мощностью понимается общее количество элементов множества. Например, самая маленькая бесконечность — натуральные числа (1, 2, 3, …), потому что она включает в себя только целые положительные числа. Ответа на этот вопрос пока нет и математики постоянно находят все более мощные множества.

Мощность множества характеризуется его кардинальным числом или просто кардиналом. Существует целая онлайн-энциклопедия бесконечностей и примечательных «конечностей», названная в честь Георга Кантора. Этот немецкий математик первым обнаружил, что неисчислимые множества могут быть больше или меньше друг друга. Более того, он смог доказать разницу в мощностях различных бесконечностей.

Что не так с суммой числа π и e?

Является ли сумма этих двух иррациональных чисел алгебраическим числом? Мы оперируем этими константами сотни лет, но так и не узнали о них все. Алгебраическое число — корень многочлена с целыми коэффициентами. На первый взгляд кажется, что все вещественные числа алгебраичны, но нет, наоборот. Большинство чисел трансцендентны, то есть не являются алгебраическими. Более того, все вещественные трансцедентные числа иррациональны (например, π и e), но вот их сумма может быть любой.

Если от предыдущего абзаца у читателя не заболела голова, то вот продолжение загадки — а что с πe, π/e и π-e? Также неизвестно, а знать это наверняка довольно важно для теории чисел. Трансцедентность числа доказал в конце XIX века Фердинанд фон Линдеман вместе с невозможностью решения задачи квадратуры круга. С тех пор значимых подвижек в решении вопроса не было.

Является ли γ рациональной?

Вот еще одна проблема, которую очень легко написать, но трудно решить. Является ли постоянная Эйлера-Маскерони иррациональной или нет? Рациональные числа можно записать в виде p/q, где p и q — целые числа. Таким образом, 42 и -11/3 являются рациональными, а и √2 — нет. Формула выше позволяет вычислить постоянную, которая является пределом разности между частичной суммой гармонического ряда и натуральным логарифмом числа. За определение ее рациональности миллион долларов, конечно, не светит, зато вполне можно рассчитывать на кресло профессора в Оксфорде.

Значение γ было вычислено до нескольких тысяч знаков после запятой, первые четыре из которых — 0,5772. Она достаточно широко используется в математике, в том числе вместе с другим числом Эйлера — e. Согласно теории цепных дробей, если постоянная Эйлера-Маскерони является рациональной дробью, то ее знаменатель должен быть больше 10 в 242 080 степени.

www.popmech.ru