Правило сложения степеней: Сложение, вычитание, умножение, и деление степеней. — Детская игровая комната «Волшебный лес»

Posted on 17.07.197618.02.2022 by alexxlab

Содержание

Как решать выражения со степенями и дробями. Сложение, вычитание, умножение, и деление степеней

Разделы: Математика

Тип урока: урок обобщения и систематизации знаний

Цели:

обучающие – повторить определение степени, правила умножения и деления степеней, возведения степени в степень, закрепить умения решения примеров, содержащих степени,

развивающие – развитие логического мышления учащихся, интереса к изучаемому материалу,

воспитывающие – воспитание ответственного отношения к учебе, культуры общения, чувства коллективизма.

Оборудование: компьютер, мультимедийный проектор, интерактивная доска, презентация “Степени” для устного счета, карточки с заданиями, раздаточный материал.

План урока:

Организационный момент.

Повторение правил

Устный счет.

Историческая справка.

Работа у доски.

Физкультминутка.

Работа на интерактивной доске.

Самостоятельная работа.

Домашнее задание.

Подведение итогов урока.

Ход урока

I. Организационный момент

Сообщение темы и целей урока.

На предыдущих уроках вы открыли для себя удивительный мир степеней, научились умножать и делить степени, возводить их в степень. Сегодня мы должны закрепить полученные знания при решении примеров.

II. Повторение правил (устно)

Дайте определение степени с натуральным показателем? (Степенью числа а с натуральным показателем, большим 1, называется произведение n множителей, каждый из которых равен а .)
Как умножить две степени? (Чтобы умножить степени с одинаковыми основаниями, надо основание оставить тем же, а показатели сложить.)
Как разделить степень на степень? (Чтобы разделить степени с одинаковыми основаниями, надо основание оставить тем же, а показатели вычесть.)
Как возвести произведение в степень? (Чтобы возвести произведение в степень, надо каждый множитель возвести в эту степень)

Как возвести степень в степень? (Чтобы возвести степень в степень, надо основание оставить тем же, а показатели перемножить)

III. Устный счет (по мультимедиа)

IV. Историческая справка

Все задачи из папируса Ахмеса, который записан около 1650 года до н. э. связаны с практикой строительства, размежеванием земельных наделов и т. п. Задачи сгруппированы по тематике. По преимуществу это задачи на нахождение площадей треугольника, четырёхугольников и круга, разнообразные действия с целыми числами и дробями, пропорциональное деление, нахождение отношений, здесь присутствует и возведение в разные степени, решение уравнений первой и второй степени с одним неизвестным.

Полностью отсутствуют какие бы то ни было объяснения или доказательства. Искомый результат либо даётся прямо, либо приводится краткий алгоритм его вычисления. Такой способ изложения, типичный для науки стран древнего Востока, наводит на мысль о том, что математика там развивалась путём обобщений и догадок, не образующих никакой общей теории. Тем не менее, в папирусе есть целый ряд свидетельств того, что египетские математики умели извлекать корни и возводить в степень, решать уравнения, и даже владели зачатками алгебры.

V. Работа у доски

Найдите значение выражения рациональным способом:

Вычислите значение выражения:

VI. Физкультминутка

для глаз
для шеи
для рук
для туловища
для ног

VII. Решение задач (с показом на интерактивной доске)

Является ли корень уравнения положительным числом?

xn--i1abbnckbmcl9fb.xn--p1ai

Формулы степеней и корней.

Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.

Число c является n -ной степенью числа a когда:

Операции со степенями.

1. Умножая степени с одинаковым основанием их показатели складываются:

2. В делении степеней с одинаковым основанием их показатели вычитаются:

3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:

(abc…) n = a n · b n · c n …

4. Степень дроби равняется отношению степеней делимого и делителя:

5. Возводя степень в степень, показатели степеней перемножают:

Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.

Операции с корнями.

1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:

2. Корень из отношения равен отношению делимого и делителя корней:

3. При возведении корня в степень довольно возвести в эту степень подкоренное число:

4. Если увеличить степень корня в n раз и в тоже время возвести в n -ую степень подкоренное число, то значение корня не поменяется:

5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:

Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:

Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m 4:a 7 = a 4 — 7 = a -3 .

Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.

Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.

Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n –ой степени из m -ой степени этого числа а :

Формулы степеней.

6. a — n = — деление степеней;

7. — деление степеней;

8. a 1/n = ;

Степени правила действия со степенями

1. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей (с тем же показателем):

(abc…) n = a n b n c n …

Пример 1. (7 2 10) 2 = 7 2 2 2 10 2 = 49 4 100 = 19600. Пример 2. (x 2 –a 2) 3 = [(x +a)(x — a)] 3 =(x +a) 3 (x — a) 3

Практически более важно обратное преобразование:

т. е. произведение одинаковых степеней нескольких величин равно той же степени произведения этих величин.

Пример 3. Пример 4. (a +b) 2 (a 2 – ab +b 2) 2 =[(a +b)(a 2 – ab +b 2)] 2 =(a 3 +b 3) 2

2. Степень частного (дроби) равна частному от деления той же степени делимого на ту же степень делителя:

Пример 5. Пример 6.

Обратное преобразование:. Пример 7.. Пример 8..

3. При умножении степеней с одинаковыми основаниями показатели степеней складываются:

Пример 9.2 2 2 5 =2 2+5 =2 7 =128. Пример 10. (a – 4c +x) 2 (a – 4c +x) 3 =(a – 4c + x) 5 .

4. При делении степеней с одинаковыми основаниями показатель степени делителя вычитается из показателя степени делимого

Пример 11. 12 5:12 3 =12 5-3 =12 2 =144. Пример 12. (x-y) 3:(x-y) 2 =x-y.

5. При возведении степени в степень показатели степеней перемножаются:

Пример 13. (2 3) 2 =2 6 =64. Пример 14.

www.maths.yfa1.ru

Степени и корни

Операции со степенями и корнями. Степень с отрицательным ,

нулевым и дробным показателем. О выражениях, не имеющих смысла.

Операции со степенями.

1. При умножении степеней с одинаковым основанием их показатели складываются:

a m · a n = a m + n .

2. При делении степеней с одинаковым основанием их показатели вычитаются .

3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.

4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):

(a / b ) n = a n / b n .

5. При возведении степени в степень их показатели перемножаются:

Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.

П р и м е р. (2 · 3 · 5 / 15) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .

Операции с корнями. Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).

1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:

2. Корень из отношения равен отношению корней делимого и делителя:

3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:

4. Если увеличить степень корня в m раз и одновременно возвести в m -ую степень подкоренное число, то значение корня не изменится:

5. Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:

Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным , нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.

Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:

Т еперь формула a m : a n = a m — n может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .

П р и м е р. a 4: a 7 = a 4 — 7 = a — 3 .

Если мы хотим, чтобы формула a m : a n = a m — n была справедлива при m = n , нам необходимо определение нулевой степени.

Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.

П р и м е р ы. 2 0 = 1, (– 5) 0 = 1, (– 3 / 5) 0 = 1.

Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а:

О выражениях, не имеющих смысла. Есть несколько таких выражений.

где a ≠ 0 , не существует.

В самом деле, если предположить, что x – некоторое число, то в соответствии с определением операции деления имеем: a = 0· x , т.e. a = 0, что противоречит условию: a ≠ 0

— любое число.

В самом деле, если предположить, что это выражение равно некоторому числу x , то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x , что и требовалось доказать.

0 0 — любое число.

Р е ш е н и е. Рассмотрим три основных случая:

1) x = 0 – это значение не удовлетворяет данному уравнению

2) при x > 0 получаем: x / x = 1, т. e. 1 = 1, откуда следует,

что x – любое число; но принимая во внимание, что в

нашем случае x > 0 , ответом является x > 0 ;

Свойства степени

Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.

Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.

Свойство № 1

При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.

a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.

Данное свойство степеней также действует на произведение трёх и более степеней.

Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17
Представить в виде степени.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15

Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями . Оно не относится к их сложению.

Нельзя заменять сумму (3 3 + 3 2) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2) = (27 + 9) = 36 , а 3 5 = 243

Свойство № 2

При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.

Записать частное в виде степени
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2
Вычислить.

11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
Пример. Решить уравнение. Используем свойство частного степеней.
3 8: t = 3 4

Ответ: t = 3 4 = 81

Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.

Пример. Упростить выражение.
4 5m + 6 · 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5

Пример. Найти значение выражения, используя свойства степени.

2 11 − 5 = 2 6 = 64

Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.

Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4

Свойство № 3

Возведение степени в степень

При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.

(a n) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.

Пример.
(a 4) 6 = a 4 · 6 = a 24

Пример. Представить 3 20 в виде степени с основанием 3 2 .

По свойству возведения степени в степень известно, что при возведении в степень показатели перемножаются, значит:

Свойства 4

Степень произведения

При возведении степени в степень произведения в эту степень возводится каждый множитель и результаты перемножаются.

(a · b) n = a n · b n , где « a », « b » — любые рациональные числа; « n » — любое натуральное число.

Пример 1.
(6 · a 2 · b 3 · c) 2 = 6 2 · a 2 · 2 · b 3 · 2 · с 1 · 2 = 36 a 4 · b 6 · с 2
Пример 2.
(−x 2 · y) 6 = ((−1) 6 · x 2 · 6 · y 1 · 6) = x 12 · y 6

Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.

(a n · b n)= (a · b) n

То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.

Пример. Вычислить.
2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000
Пример. Вычислить.
0,5 16 · 2 16 = (0,5 · 2) 16 = 1

В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.

Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216

Пример возведения в степень десятичной дроби.

4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4

Свойства 5

Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.

(a: b) n = a n: b n , где « a », « b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.

Пример. Представить выражение в виде частного степеней.
(5: 3) 12 = 5 12: 3 12

Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.

Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .

Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .

Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.

Так, сумма 2a 2 и 3a 2 равна 5a 2 .

Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.

Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.

Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .

Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.

Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .

Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.

Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6

Умножение степеней

Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.

Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.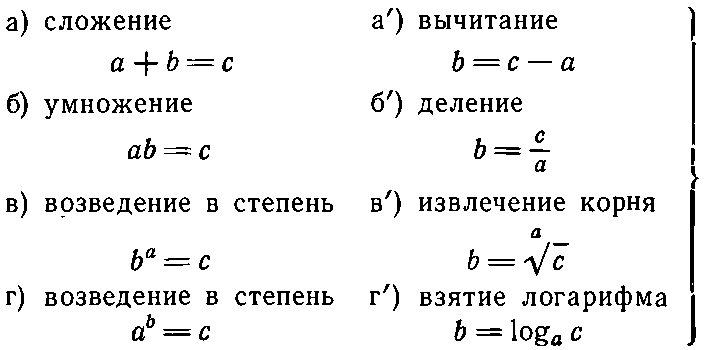

Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y

Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .

Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.

Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .

Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.

Так, a n .a m = a m+n .

Для a n , a берётся как множитель столько раз, сколько равна степень n;

И a m , берётся как множитель столько раз, сколько равна степень m;

Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.

Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .

Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1

Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).

Это правило справедливо и для чисел, показатели степени которых — отрицательные .

1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.

2. y -n .y -m = y -n-m .

3. a -n .a m = a m-n .

Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть

Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.

Если умножается сумма и разница двух чисел, возведённых в квадрат , результат будет равен сумме или разнице этих чисел в четвёртой степени.

Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .

Деление степеней

Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби.

Таким образом a 3 b 2 делённое на b 2 , равно a 3 . 5}$. Ответ: $\frac{2x}{1}$ или 2x.

3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .

4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .

5. Умножьте (a 3 + b)/b 4 на (a — b)/3.

6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).

7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .

8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.

9. Разделите (h 3 — 1)/d 4 на (d n + 1)/h.

Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.

Yandex.RTB R-A-339285-1

Что представляют собой степенные выражения?

В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.

Определение 1

Степенное выражение – это выражение, которое содержит степени.

Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.

Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 3 2 , 7 5 + 1 , (2 + 1) 5 , (− 0 , 1) 4 , 2 2 3 3 , 3 · a 2 − a + a 2 , x 3 − 1 , (a 2) 3 . А также степени с нулевым показателем: 5 0 , (a + 1) 0 , 3 + 5 2 − 3 , 2 0 . И степени с целыми отрицательными степенями: (0 , 5) 2 + (0 , 5) — 2 2 .

Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 264 1 4 — 3 · 3 · 3 1 2 , 2 3 , 5 · 2 — 2 2 — 1 , 5 , 1 a 1 4 · a 1 2 — 2 · a — 1 6 · b 1 2 , x π · x 1 — π , 2 3 3 + 5 .

В качестве показателя может выступать переменная 3 x — 54 — 7 · 3 x — 58 или логарифм x 2 · l g x − 5 · x l g x .

С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.

Основные виды преобразований степенных выражений

В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.

Пример 1

Вычислите значение степенного выражения 2 3 · (4 2 − 12) .

Решение

Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 2 3 · (4 2 − 12) = 2 3 · (16 − 12) = 2 3 · 4 .

Нам остается заменить степень 2 3 ее значением 8 и вычислить произведение 8 · 4 = 32 . Вот наш ответ.

Ответ: 2 3 · (4 2 − 12) = 32 .

Пример 2

Упростите выражение со степенями 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 .

Решение

Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .

Ответ: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .

Пример 3

Представьте выражение со степенями 9 — b 3 · π — 1 2 в виде произведения.

Решение

Представим число 9 как степень 3 2 и применим формулу сокращенного умножения:

9 — b 3 · π — 1 2 = 3 2 — b 3 · π — 1 2 = = 3 — b 3 · π — 1 3 + b 3 · π — 1

Ответ: 9 — b 3 · π — 1 2 = 3 — b 3 · π — 1 3 + b 3 · π — 1 .

А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений.

Работа с основанием и показателем степени

Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, (2 + 0 , 3 · 7) 5 − 3 , 7 и . Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.

Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.

Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, (2 + 0 , 3 · 7) 5 − 3 , 7 можно выполнить действия для перехода к степени 4 , 1 1 , 3 . Раскрыв скобки, мы можем привести подобные слагаемые в основании степени (a · (a + 1) − a 2) 2 · (x + 1) и получить степенное выражение более простого вида a 2 · (x + 1) .

Использование свойств степеней

Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s — произвольные действительные числа:

Определение 2

a r · a s = a r + s ;
a r: a s = a r − s ;
(a · b) r = a r · b r ;
(a: b) r = a r: b r ;
(a r) s = a r · s .

В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство a m · a n = a m + n , где m и n – натуральные числа, то оно будет верно для любых значений a , как положительных, так и отрицательных, а также для a = 0 .

Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.

При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».

Пример 4

Представьте выражение a 2 , 5 · (a 2) − 3: a − 5 , 5 в виде степени с основанием a .

Решение

Для начала используем свойство возведения в степень и преобразуем по нему второй множитель (a 2) − 3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:

a 2 , 5 · a − 6: a − 5 , 5 = a 2 , 5 − 6: a − 5 , 5 = a − 3 , 5: a − 5 , 5 = a − 3 , 5 − (− 5 , 5) = a 2 .

Ответ: a 2 , 5 · (a 2) − 3: a − 5 , 5 = a 2 .

Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.

Пример 5

Найти значение степенного выражения 3 1 3 · 7 1 3 · 21 2 3 .

Решение

Если мы применим равенство (a · b) r = a r · b r , справа налево, то получим произведение вида 3 · 7 1 3 · 21 2 3 и дальше 21 1 3 · 21 2 3 . Сложим показатели при умножении степеней с одинаковыми основаниями: 21 1 3 · 21 2 3 = 21 1 3 + 2 3 = 21 1 = 21 .

Есть еще один способ провести преобразования:

3 1 3 · 7 1 3 · 21 2 3 = 3 1 3 · 7 1 3 · (3 · 7) 2 3 = 3 1 3 · 7 1 3 · 3 2 3 · 7 2 3 = = 3 1 3 · 3 2 3 · 7 1 3 · 7 2 3 = 3 1 3 + 2 3 · 7 1 3 + 2 3 = 3 1 · 7 1 = 21

Ответ: 3 1 3 · 7 1 3 · 21 2 3 = 3 1 · 7 1 = 21

Пример 6

Дано степенное выражение a 1 , 5 − a 0 , 5 − 6 , введите новую переменную t = a 0 , 5 .

Решение

Представим степень a 1 , 5 как a 0 , 5 · 3 . Используем свойство степени в степени (a r) s = a r · s справа налево и получим (a 0 , 5) 3: a 1 , 5 − a 0 , 5 − 6 = (a 0 , 5) 3 − a 0 , 5 − 6 . В полученное выражение можно без проблем вводить новую переменную t = a 0 , 5 : получаем t 3 − t − 6 .

Ответ: t 3 − t − 6 .

Преобразование дробей, содержащих степени

Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.

Пример 7

Упростить степенное выражение 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 .

Решение

Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:

3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = 3 · 5 2 3 · 5 1 3 — 3 · 5 2 3 · 5 — 2 3 — 2 — x 2 = = 3 · 5 2 3 + 1 3 — 3 · 5 2 3 + — 2 3 — 2 — x 2 = 3 · 5 1 — 3 · 5 0 — 2 — x 2

Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12 — 2 — x 2 = — 12 2 + x 2

Ответ: 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = — 12 2 + x 2

Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.

Пример 8

Приведите дроби к новому знаменателю: а) a + 1 a 0 , 7 к знаменателю a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 к знаменателю x + 8 · y 1 2 .

Решение

а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a 0 , 7 · a 0 , 3 = a 0 , 7 + 0 , 3 = a , следовательно, в качестве дополнительного множителя мы возьмем a 0 , 3 . Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a 0 , 3 не обращается в нуль.

Выполним умножение числителя и знаменателя дроби на a 0 , 3 :

a + 1 a 0 , 7 = a + 1 · a 0 , 3 a 0 , 7 · a 0 , 3 = a + 1 · a 0 , 3 a

б) Обратим внимание на знаменатель:

x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 2 — x 1 3 · 2 · y 1 6 + 2 · y 1 6 2

Умножим это выражение на x 1 3 + 2 · y 1 6 , получим сумму кубов x 1 3 и 2 · y 1 6 , т. е. x + 8 · y 1 2 . Это наш новый знаменатель, к которому нам надо привести исходную дробь.

Так мы нашли дополнительный множитель x 1 3 + 2 · y 1 6 . На области допустимых значений переменных x и y выражение x 1 3 + 2 · y 1 6 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 + 2 · y 1 6 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 3 + 2 · y 1 6 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2

Ответ: а) a + 1 a 0 , 7 = a + 1 · a 0 , 3 a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2 .

Пример 9

Сократите дробь: а) 30 · x 3 · (x 0 , 5 + 1) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 , б) a 1 4 — b 1 4 a 1 2 — b 1 2 .

Решение

а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15 . Также мы можем произвести сокращение на x 0 , 5 + 1 и на x + 2 · x 1 1 3 — 5 3 .

Получаем:

30 · x 3 · (x 0 , 5 + 1) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · (x 0 , 5 + 1)

б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:

a 1 4 — b 1 4 a 1 2 — b 1 2 = a 1 4 — b 1 4 a 1 4 2 — b 1 2 2 = = a 1 4 — b 1 4 a 1 4 + b 1 4 · a 1 4 — b 1 4 = 1 a 1 4 + b 1 4

Ответ: а) 30 · x 3 · (x 0 , 5 + 1) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · (x 0 , 5 + 1) , б) a 1 4 — b 1 4 a 1 2 — b 1 2 = 1 a 1 4 + b 1 4 .

К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.

Пример 10

Выполните действия x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 .

Решение

Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю:

x 1 2 — 1 · x 1 2 + 1

Вычтем числители:

x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = = x 1 2 + 1 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 — x 1 2 — 1 · x 1 2 — 1 x 1 2 + 1 · x 1 2 — 1 · 1 x 1 2 = = x 1 2 + 1 2 — x 1 2 — 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = x 1 2 2 + 2 · x 1 2 + 1 — x 1 2 2 — 2 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2

Теперь умножаем дроби:

4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · x 1 2

Произведем сокращение на степень x 1 2 , получим 4 x 1 2 — 1 · x 1 2 + 1 .

Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4 x 1 2 — 1 · x 1 2 + 1 = 4 x 1 2 2 — 1 2 = 4 x — 1 .

Ответ: x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = 4 x — 1

Пример 11

Упростите степенное выражение x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 .
Решение

Мы можем произвести сокращение дроби на (x 2 , 7 + 1) 2 . Получаем дробь x 3 4 x — 5 8 · x 2 , 7 + 1 .

Продолжим преобразования степеней икса x 3 4 x — 5 8 · 1 x 2 , 7 + 1 . Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x 3 4 x — 5 8 · 1 x 2 , 7 + 1 = x 3 4 — — 5 8 · 1 x 2 , 7 + 1 = x 1 1 8 · 1 x 2 , 7 + 1 .

Переходим от последнего произведения к дроби x 1 3 8 x 2 , 7 + 1 .

Ответ: x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 = x 1 3 8 x 2 , 7 + 1 .

Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение (x + 1) — 0 , 2 3 · x — 1 можно заменить на x 3 · (x + 1) 0 , 2 .

Преобразование выражений с корнями и степенями

В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.

Пример 12

Представьте выражение x 1 9 · x · x 3 6 в виде степени.

Решение

Область допустимых значений переменной x определяется двумя неравенствами x ≥ 0 и x · x 3 ≥ 0 , которые задают множество [ 0 , + ∞) .

На этом множестве мы имеем право перейти от корней к степеням:

x 1 9 · x · x 3 6 = x 1 9 · x · x 1 3 1 6

Используя свойства степеней, упростим полученное степенное выражение.

x 1 9 · x · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 · 1 3 · 6 = = x 1 9 · x 1 6 · x 1 18 = x 1 9 + 1 6 + 1 18 = x 1 3

Ответ: x 1 9 · x · x 3 6 = x 1 3 .

Преобразование степеней с переменными в показателе

Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 5 2 · x + 1 − 3 · 5 x · 7 x − 14 · 7 2 · x − 1 = 0 .

Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:

5 2 · x · 5 1 − 3 · 5 x · 7 x − 14 · 7 2 · x · 7 − 1 = 0 , 5 · 5 2 · x − 3 · 5 x · 7 x − 2 · 7 2 · x = 0 .

Теперь поделим обе части равенства на 7 2 · x . Это выражение на ОДЗ переменной x принимает только положительные значения:

5 · 5 — 3 · 5 x · 7 x — 2 · 7 2 · x 7 2 · x = 0 7 2 · x , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 2 · x — 2 · 7 2 · x 7 2 · x = 0 , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 x · 7 x — 2 · 7 2 · x 7 2 · x = 0

Сократим дроби со степенями, получим: 5 · 5 2 · x 7 2 · x — 3 · 5 x 7 x — 2 = 0 .

Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5 · 5 7 2 · x — 3 · 5 7 x — 2 = 0 , которое равносильно 5 · 5 7 x 2 — 3 · 5 7 x — 2 = 0 .

Введем новую переменную t = 5 7 x , что сводит решение исходного показательного уравнения к решению квадратного уравнения 5 · t 2 − 3 · t − 2 = 0 .

Преобразование выражений со степенями и логарифмами

Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 1 4 1 — 5 · log 2 3 или log 3 27 9 + 5 (1 — log 3 5) · log 5 3 . Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Тип урока: урок обобщения и систематизации знаний

Цели:

обучающие – повторить определение степени, правила умножения и деления степеней, возведения степени в степень, закрепить умения решения примеров, содержащих степени,
развивающие – развитие логического мышления учащихся, интереса к изучаемому материалу,
воспитывающие – воспитание ответственного отношения к учебе, культуры общения, чувства коллективизма.

План урока:

Организационный момент.
Повторение правил
Устный счет.
Историческая справка.
Работа у доски.
Физкультминутка.
Работа на интерактивной доске.
Самостоятельная работа.
Домашнее задание.
Подведение итогов урока.

Ход урока

I. Организационный момент

Сообщение темы и целей урока.

II. Повторение правил (устно)

Дайте определение степени с натуральным показателем? (Степенью числа а с натуральным показателем, большим 1, называется произведениеn множителей, каждый из которых равен а . )
Как умножить две степени? (Чтобы умножить степени с одинаковыми основаниями, надо основание оставить тем же, а показатели сложить.)
Как разделить степень на степень? (Чтобы разделить степени с одинаковыми основаниями, надо основание оставить тем же, а показатели вычесть.)
Как возвести произведение в степень? (Чтобы возвести произведение в степень, надо каждый множитель возвести в эту степень)
Как возвести степень в степень? (Чтобы возвести степень в степень, надо основание оставить тем же, а показатели перемножить)

III. Устный счет (по мультимедиа)

IV. Историческая справка

V. Работа у доски

Найдите значение выражения рациональным способом:

Вычислите значение выражения:

VI. Физкультминутка

для глаз
для шеи
для рук
для туловища
для ног

VII. Решение задач (с показом на интерактивной доске)

Является ли корень уравнения положительным числом?

а) 3x + (-0,1) 7 = (-0,496) 4 (x > 0)

б) (10,381) 5 = (-0,012) 3 — 2x (x

VIII. Самостоятельная работа

IX. Домашнее задание

Х. Подведение итогов урока

Анализ результатов, объявление оценок.

Полученные знания о степенях мы будем применять при решении уравнений, задач в старших классах, также они часто встречаются в ЕГЭ.

Число c является n -ной степенью числа a когда:

Операции со степенями.

1. Умножая степени с одинаковым основанием их показатели складываются:

a m ·a n = a m + n .

2. В делении степеней с одинаковым основанием их показатели вычитаются:

(abc…) n = a n · b n · c n …

4. Степень дроби равняется отношению степеней делимого и делителя:

(a/b) n = a n /b n .

5. Возводя степень в степень, показатели степеней перемножают:

(a m) n = a m n .

Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.

Например . (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4 .

Операции с корнями.

1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:

2. Корень из отношения равен отношению делимого и делителя корней:

3. При возведении корня в степень довольно возвести в эту степень подкоренное число:

Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:

Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m n .

Например . a 4:a 7 = a 4 — 7 = a -3 .

Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.

Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.

Например . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.

Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n -ой степени из m -ой степени этого числа а .

Свойства степеней при сложении. Основные свойства степеней. Примеры на умножение степеней с одинаковыми показателями

Каждая арифметическая операция порою становится слишком громоздкой для записи и её стараются упростить. Когда-то так было и с операцией сложения. Людям было необходимо проводить многократное однотипное сложение, например, посчитать стоимость ста персидских ковров, стоимость которого составляет 3 золотые монеты за каждый. 3. В остальном, когда различные основания и показатели, произвести полное умножение нельзя. Иногда можно частично упростить или прибегнуть к помощи вычислительной техники.

Число c является n -ной степенью числа a когда:

Операции со степенями.

1. Умножая степени с одинаковым основанием их показатели складываются:

a m ·a n = a m + n .

2. В делении степеней с одинаковым основанием их показатели вычитаются:

(abc…) n = a n · b n · c n …

4. Степень дроби равняется отношению степеней делимого и делителя:

(a/b) n = a n /b n .

5. Возводя степень в степень, показатели степеней перемножают:

(a m) n = a m n .

Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.

Например . (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4 .

Операции с корнями.

1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:

2. Корень из отношения равен отношению делимого и делителя корней:

3. При возведении корня в степень довольно возвести в эту степень подкоренное число:

Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m n .

Например . a 4:a 7 = a 4 — 7 = a -3 .

Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.

Например . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.

Операции со степенями и корнями. Степень с отрицательным ,

нулевым и дробным показателем. О выражениях, не имеющих смысла.

Операции со степенями.

1. При умножении степеней с одинаковым основанием их показатели складываются :

a m · a n = a m + n .

2. При делении степеней с одинаковым основанием их показатели вычитаются .

3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.

( abc … ) n = a n · b n · c n …

4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):

( a / b ) n = a n / b n .

5. При возведении степени в степень их показатели перемножаются:

(a m ) n = a m n .

Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.

П р и м е р. (2 · 3 · 5 / 15) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .

1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:

2. Корень из отношения равен отношению корней делимого и делителя:

3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:

П р и м е р . a 4 : a 7 = a 4 — 7 = a — 3 .

Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.

П р и м е р ы. 2 0 = 1, (– 5) 0 = 1, (– 3 / 5) 0 = 1.

О выражениях, не имеющих смысла. Есть несколько таких выражений. любое число.

Случай 3.

0 0 — любое число.

Действительно,

Р е ш е н и е. Рассмотрим три основных случая:

1) x = 0 – это значение не удовлетворяет данному уравнению

(Почему?).

2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует,

что x – любое число; но принимая во внимание, что в

Нашем случае x > 0 , ответом является x > 0 ;

3) при x x / x = 1, т. e . –1 = 1, следовательно,

В этом случае нет решения.

Таким образом, x > 0.

Как умножать степени? Какие степени можно перемножить, а какие — нет? Как число умножить на степень?

В алгебре найти произведение степеней можно в двух случаях:

1) если степени имеют одинаковые основания;

2) если степени имеют одинаковые показатели.

При умножении степеней с одинаковыми основаниями надо основание оставить прежним, а показатели — сложить:

При умножении степеней с одинаковыми показателями общий показатель можно вынести за скобки:

Рассмотрим, как умножать степени, на конкретных примерах.

Единицу в показателе степени не пишут, но при умножении степеней — учитывают:

При умножении количество степеней может быть любое. Следует помнить, что перед буквой знак умножения можно не писать:

В выражениях возведение в степень выполняется в первую очередь.

Если нужно число умножить на степень, сначала следует выполнить возведение в степень, а уже потом — умножение:

www.algebraclass.ru

Сложение, вычитание, умножение, и деление степеней

Сложение и вычитание степеней

Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .

Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.

Так, сумма 2a 2 и 3a 2 равна 5a 2 .

Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.

Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .

Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.

Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .

Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6

Умножение степеней

Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.

Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y

Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .

Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.

Так, a n .a m = a m+n .

Для a n , a берётся как множитель столько раз, сколько равна степень n;

И a m , берётся как множитель столько раз, сколько равна степень m;

Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.

Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .

Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1

Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).

Это правило справедливо и для чисел, показатели степени которых — отрицательные .

1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.

2. y -n .y -m = y -n-m .

3. a -n .a m = a m-n .

Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть

Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.

Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .

Деление степеней

Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби.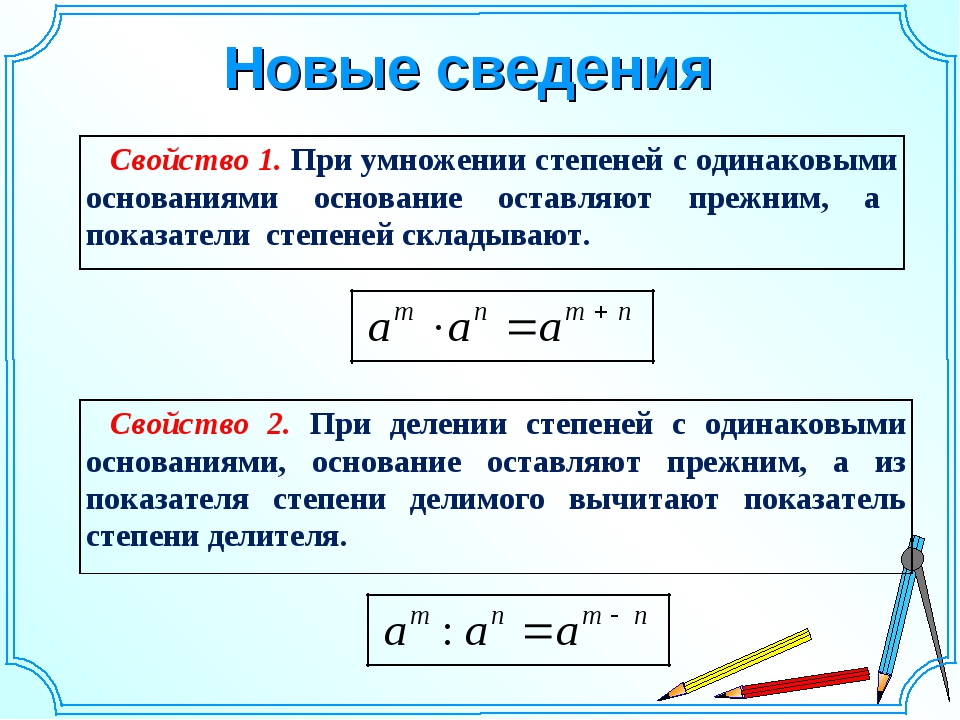 3$

Необходимо очень хорошо усвоить умножение и деление степеней, так как такие операции очень широко применяются в алгебре.

Примеры решения примеров с дробями, содержащими числа со степенями

1. Уменьшите показатели степеней в $\frac $ Ответ: $\frac $.

2. Уменьшите показатели степеней в $\frac $. Ответ: $\frac $ или 2x.

5. Умножьте (a 3 + b)/b 4 на (a — b)/3.

6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).

7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .

8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.

Свойства степени

Свойство № 1

Произведение степеней

a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.

Данное свойство степеней также действует на произведение трёх и более степеней.

Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15

Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17

Представить в виде степени.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15

Нельзя заменять сумму (3 3 + 3 2) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2) = (27 + 9) = 36 , а 3 5 = 243

Свойство № 2

Частное степеней

Записать частное в виде степени
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2

Вычислить.

11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
Пример. Решить уравнение. Используем свойство частного степеней.
3 8: t = 3 4

Ответ: t = 3 4 = 81

Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.

Пример. Найти значение выражения, используя свойства степени.

2 11 − 5 = 2 6 = 64

Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.

Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4

Свойство № 3

Возведение степени в степень

(a n) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.

Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.

(a n · b n)= (a · b) n

Пример. Вычислить.
2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000

Пример. Вычислить.
0,5 16 · 2 16 = (0,5 · 2) 16 = 1

Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216

Пример возведения в степень десятичной дроби.

4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4

Свойства 5

Степень частного (дроби)

(a: b) n = a n: b n , где « a », « b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.

Пример. Представить выражение в виде частного степеней.
(5: 3) 12 = 5 12: 3 12

Степени и корни

Операции со степенями и корнями. Степень с отрицательным ,

нулевым и дробным показателем. О выражениях, не имеющих смысла.

Операции со степенями.

1. При умножении степеней с одинаковым основанием их показатели складываются:

a m · a n = a m + n .

2. При делении степеней с одинаковым основанием их показатели вычитаются .

3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.

4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):

(a / b ) n = a n / b n .

5. При возведении степени в степень их показатели перемножаются:

Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.

П р и м е р. (2 · 3 · 5 / 15) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .

1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:

2. Корень из отношения равен отношению корней делимого и делителя:

3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:

П р и м е р. a 4: a 7 = a 4 — 7 = a — 3 .

Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.

П р и м е р ы. 2 0 = 1, (– 5) 0 = 1, (– 3 / 5) 0 = 1.

О выражениях, не имеющих смысла.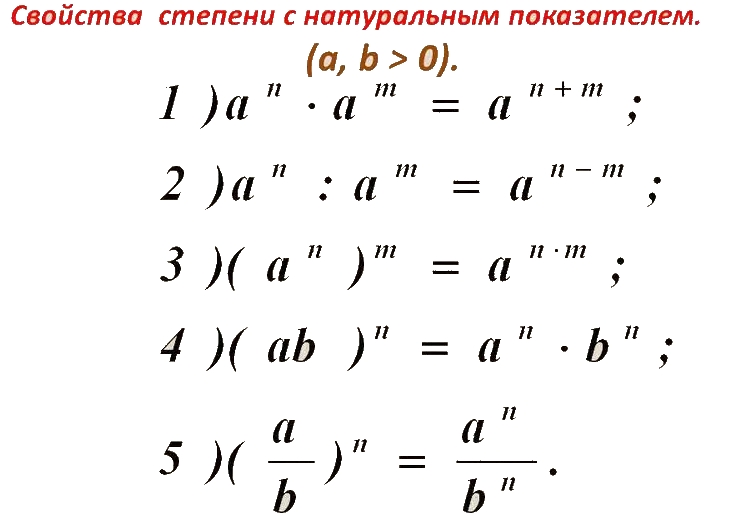 Есть несколько таких выражений.

где a ≠ 0 , не существует.

— любое число.

0 0 — любое число.

Р е ш е н и е. Рассмотрим три основных случая:

1) x = 0 – это значение не удовлетворяет данному уравнению

2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует,

что x – любое число; но принимая во внимание, что в

нашем случае x > 0 , ответом является x > 0 ;

Правила умножения степеней с разным основанием

СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ,

СТЕПЕННАЯ ФУНКЦИЯ IV

§ 69. Умножение и деление степеней с одинаковыми основаниями

Теорема 1. Чтобы перемножить степени с одинаковыми основаниями, достаточно показатели степеней сложить, а основание оставить прежним , то есть

Доказательство. По определению степени

2 2 2 3 = 2 5 = 32; (-3) (-3) 3 = (-3) 4 = 81.

Мы рассмотрели произведение двух степеней. На самом же деле доказанное свойство верно для любого числа степеней с одинаковыми основаниями.

Теорема 2. Чтобы разделить степени с одинаковыми основаниями, когда показатель делимого больше показателя делителя, достаточно из показателя делимого вычесть показатель делителя, а основание оставить прежним, то есть при т > п

(a =/= 0)

Доказательство. Напомним, что частным от деления одного числа на другое называется число, которое при умножении на делитель дает делимое. Поэтому доказать формулу , где a =/= 0, это все равно, что доказать формулу

Если т > п , то число т — п будет натуральным; следовательно, по теореме 1

Теорема 2 доказана.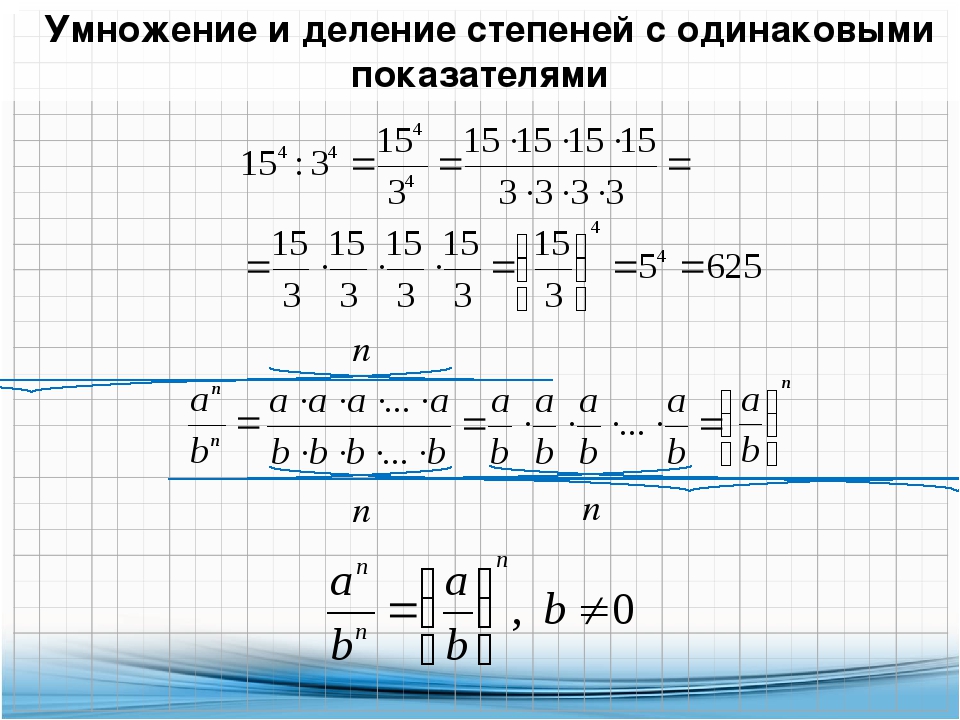

Следует обратить внимание на то, что формула

доказана нами лишь в предположении, что т > п . Поэтому из доказанного пока нельзя делать, например, таких выводов:

К тому же степени с отрицательными показателями нами еще не рассматривались и мы пока что не знаем, какой смысл можно придать выражению 3 — 2 .

Теорема 3. Чтобы возвести степень в степень, достаточно перемножить показатели, оставив основание степени прежним , то есть

Доказательство. Используя определение степени и теорему 1 этого параграфа, получаем:

что и требовалось доказать.

Например, (2 3) 2 = 2 6 = 64;

518 (Устно.) Определить х из уравнений:

1) 2 2 2 2 3 2 4 2 5 2 6 = 2 x ; 3) 4 2 4 4 4 6 4 8 4 10 = 2 x ;

2) 3 3 3 3 5 3 7 3 9 = 3 x ; 4) 1 / 5 1 / 25 1 / 125 1 / 625 = 1 / 5 x .

519. (У с т н о. ) Упростить:

520. (У с т н о.) Упростить:

521. Данные выражения представить в виде степеней с одинаковыми основаниями:

1) 32 и 64; 3) 8 5 и 16 3 ; 5) 4 100 и 32 50 ;

2) -1000 и 100; 4) -27 и -243; 6) 81 75 8 200 и 3 600 4 150 .

Что могут степени . Математика для мам и пап: Домашка без мучений

Сколько песчинок понадобится, чтобы заполнить песком всю наблюдаемую Вселенную? Глупый вопрос, ведь такого количества песчинок, чтобы заполнить Вселенную, просто не существует (откуда бы взялся весь этот песок?), но дети обожают глупые вопросы. А у этого к тому же есть ответ, который тоже звучит глупо: для этого потребовался бы миллион миллиардов миллиардов триллионов квадриллионов пентиллионов гекстиллионов песчинок… умноженный на три! Или, если записать это привычным способом как три с 90 нулями:

3 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000.

Это длинное число, и писать его утомительно, но математики, к счастью, придумали для него более короткий способ записи. Данное гигантское число можно записать так: 3 ? 1090. Число 90, записанное вверху маленькими цифрами, называется показателем степени, или экспонентой, а еще иногда его называют (осторожно, сейчас появится страшное слово) логарифмом (по основанию 10).

Большинство родителей припомнят, что слышали что-то о логарифмах в школе, но вряд ли они смогут сколько-нибудь подробно рассказать о том, как те устроены и работают. В лучшем случае мамы и папы скажут, что такое и как выглядят логарифмы. Но на самом деле идеи, которые стоят за этим понятием, вполне можно донести до десятилетнего ребенка.

Для начала напомните сыну или дочери о том, что площадь квадрата со стороной 10 равна 10 ? 10, или «10 в квадрате». Кратко это можно записать как 102 (что имеет смысл, поскольку число 10 в полной записи повторяется дважды).

Поэтому не удивительно и понятно с точки зрения здравого смысла, что 10 ? 10 ? 10 записывается как 103.

А теперь зададимся вопросом: сколько будет 102 ? 103? Если расписать это подробно, получится 10 ? 10 ? 10 ?10 ? 10, или 100 000, но в краткой записи это будет 105. Вы заметили, что маленькие числа в обоих сомножителях (3 и 2) просто сложились и дали такое же маленькое число 5 в ответе?

Всегда ли работает такое сложение? Чему, как вы полагаете, равно 102 ? 104? Если правило сложения работает, то в ответе должно получиться 106, поскольку 2 + 4 = 6 – и быстрая проверка показывает, что это верный ответ (100 ? 10 000 = 1 000 000, или миллион).

Таким образом, при помощи логарифмов можно без труда превратить умножение в сложение. И это работает при любом основании. То есть 32 ? 34 = 36 (2 + 4 = 6). Если записать полностью, то получится, что мы 3 ? 3 (9) умножаем на 3 ? 3 ? 3 ? 3 (81), и получается 3 ? 3 ? 3 ? 3 ? 3 ? 3 (729). Это оказывается весьма полезным, когда числа становятся слишком большими для калькулятора. Так что теперь вы можете уверенно сказать, что 179 ? 174 равно 1713, хотя при попытке проверить это утверждение при помощи электроники вы, вероятно, получите лишь сообщение об ошибке.

Далее. Если ваш ребенок готов признать, что такое правило сложения – штука хорошая и удобная и что правило это, судя по всему, работает всегда, вы можете воспользоваться ситуацией и расширить идею о применении степеней. Что такое 30? Большинство детей (да и большинство взрослых), скорее всего, скажет, что это нуль, но если вы усвоили, что правило сложения работает всегда, то 30 должно равняться 1. Почему? Посмотрите, скажем, на пример 30 ? 32. Согласно правилу сложения степеней 0 + 2 = 2, так что ответ должен равняться 32 или, иными словами, 30 ? 9 = 9… что означает, что 30 должно равняться 1. Более того, по этому правилу любое число в нулевой степени равняется 1!

Здесь не обойтись без некоторого осмысления, поэтому стоит остановиться и дать мальчику или девочке время освоиться с новыми идеями. Но на всякий случай – если вам или вашему ребенку не терпится двигаться дальше – добавим, что правило сложения степеней работает также для дробей и отрицательных чисел. К примеру, 101/2 – это квадратный корень из 10 (примерно 3,16), потому что 101/2 ? 101/2 = 101. А что с отрицательными числами? 10–1 равно 0,1, или одной десятой, потому что 10–1 ? 101 = 100 = 1. Очень хорошо, хватит!!!

Все это весьма серьезные идеи, и вполне возможно, что для многих ребят некоторые из них окажутся слишком серьезными. Но не забывайте, что очень большие числа, как правило, завораживают детей. Тот факт, что для записи числа, при помощи которого можно выразить размер Вселенной, достаточно всего трех или четырех цифр (к примеру, 1091), – интересная математическая загадка, которой имеет смысл поделиться.

Степень с натуральным показателем. Действия со степенями

1.	Основное свойство дроби. Сокращение дробей (интерактивное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 1,37 Мб)
2.	Основное свойство дроби. Сокращение дробей (интерактивное задание) Направлено на усвоение учащимися знаний по данной теме.	Тип: П
		Скачать (архив, 1,17 Мб)
3.	Сокращение дроби (интерактивное задание) Направлено на усвоение учащимися знаний по данной теме.	Тип: П
		Скачать (архив, 1,17 Мб)
4.	Сложение и вычитание дробей с разными знаменателями (схема, интерактивное задание) Демонстрирует правило сложения дробей с разными знаменателями и способствует первичному закреплению материала.	Тип: И
		Скачать (архив, 1,07 Мб)
5.	Сложение и вычитание дробей с разными знаменателями (интерактивное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 1,18 Мб)
6.	Решение текстовых задач (интерактивное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 1,19 Мб)
7.	Сложение и вычитание дробей с разными знаменателями (интерактивное задание) Направлено на усвоение учащимися знаний по данной теме.	Тип: П
		Скачать (архив, 1,24 Мб)
8.	Умножение дробей (интерактивное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 1,18 Мб)
9.	Нахождение числа, обратного данной дроби (интерактивное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 1,17 Мб)
10.	Умножение дробей (интерактивное задание) Направлено на усвоение учащимися знаний по данной теме.	Тип: П
		Скачать (архив, 1,18 Мб)
11.	Умножение дробей (интерактивное задание) Направлено на усвоение учащимися знаний по данной теме.	Тип: П
		Скачать (архив, 1,17 Мб)
12.	Деление дробей (интерактивное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 1,16 Мб)
13.	Деление дробей (интерактивное задание) Направлено на усвоение учащимися знаний по данной теме.	Тип: П
		Скачать (архив, 1,19 Мб)
14.	Нахождение дроби от числа. Нахождение числа по его дроби (интерактивное задание) Направлено на усвоение учащимися знаний по данной теме.	Тип: П
		Скачать (архив, 1,18 Мб)
15.	Нахождение дроби от числа. Нахождение числа по его дроби (интерактивное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 1,16 Мб)
16.	Нахождение дроби от числа. Нахождение числа по его дроби (интерактивное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 1,16 Мб)
17.	Нахождение дроби от числа. Нахождение числа по его дроби (интерактивное задание) Направлено на усвоение учащимися знаний по данной теме.	Тип: П
		Скачать (архив, 1,17 Мб)
18.	Решение текстовых задач (интерактивное задание) Направлено на усвоение учащимися знаний по данной теме.	Тип: П
		Скачать (архив, 1,20 Мб)
19.	Действия с обыкновенными и десятичными дробями (интерактивное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 1,17 Мб)
20.	Свойства некоторых обыкновенных дробей (интерактивное задание) Направлено на усвоение учащимися знаний по данной теме.	Тип: П
		Скачать (архив, 1,17 Мб)
21.	Основное свойство дроби. Сокращение дробей (интерактивное иллюстрированное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 375 Кб)
22.	Основное свойство дроби. Сокращение дробей (интерактивное иллюстрированное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: П
		Скачать (архив, 375 Кб)
23.	Сложение и вычитание дробей с разными знаменателями (интерактивное иллюстрированное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 383 Кб)
24.	Умножение дробей (интерактивное иллюстрированное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 383 Кб)
25.	Нахождение дроби от числа. Нахождение числа по его дроби (интерактивное иллюстрированное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 397 Кб)
26.	Действия с обыкновенными и десятичными дробями (интерактивное иллюстрированное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 425 Кб)
27.	Одночлены (определение, интерактивное задание) Знакомит учащихся с понятием одночленов и способствует первичному закреплению материала.	Тип: И
		Скачать (архив, 496 Кб)
28.	Одночлены (интерактивное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 1,17 Мб)
29.	Одночлены (интерактивное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 1,16 Мб)
30.	Сокращение дроби (интерактивное задание) Направлено на усвоение учащимися знаний по данной теме.	Тип: П
		Скачать (архив, 1,18 Мб)
31.	Сокращение дроби (интерактивное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 2,00 Мб)
32.	Сокращение дроби (интерактивное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 1,17 Мб)
33.	Сокращение дроби (интерактивное задание) Направлено на усвоение учащимися знаний по данной теме.	Тип: П
		Скачать (архив, 1,15 Мб)
34.	Сокращение дроби (интерактивное задание) Направлено на усвоение учащимися знаний по данной теме.	Тип: П
		Скачать (архив, 1,17 Мб)
35.	Сокращение дроби (интерактивное задание) Направлено на усвоение учащимися знаний по данной теме.	Тип: П
		Скачать (архив, 1,17 Мб)
36.	Сокращение дроби (интерактивное задание) Направлено на проверку усвоения учащимися знаний по данной теме.	Тип: К
		Скачать (архив, 1,20 Мб)
37.	Сокращение дроби (интерактивное задание) Направлено на усвоение учащимися знаний по данной теме.	Тип: П
		Скачать (архив, 1,37 Мб)

Правила сложения и вычитания. — Инженерный справочник DPVA.ru / Технический справочник ДПВА / Таблицы для инженеров (ex DPVA-info)

Правила сложения и вычитания.

1. От перемены мест слагаемых сумма не изменится (коммутативное свойство сложения)

Пример:

13+25=38, можно записать как: 25+13=38

2. Результат сложения не изменится, если соседние слагаемые заменить их суммой (ассоциативное свойство сложения).

Пример:

10+13+3+5=31 можно записать как: 23+3+5=31; 26+5=31; 23+8=31 и т.д.

3. Единицы складываются с единицами, десятки с десятками и т.д.

Пример:

34+11=45 (3 десяка плюс еще 1 десяток; 4 единицы плюс 1 единица).

4. Единицы вычитаются из единиц, десятки из десятков и т.д.

Пример:

53-12=41 (3 единицы минус 2 единицы; 5 десятков минус 1 десяток)

примечание: 10 единиц составляют один десяток. Это надо помнить при вычитании, т.к. если количество единиц у вычитаемого больше, чем у уменьшаемого, то мы можем «занять» один десяток у уменьшаемого.

Пример:

41-12=29 (Для того чтобы и 1 вычесть 2, мы сначала должны «занять» единицу у десятков, получаем 11-2=9; помним, что у уменьшаемого остается на 1 десяток меньше, следовательно, остается 3 десятка и от него отнимается 1 десяток. Ответ 29).

5. Если из суммы двух слагаемых вычесть одно из них, то получится второе слагаемое.

Это значит, что сложение можно проверить с помощью вычитания.

Пример:

42+7=49

Для проверки из суммы вычитают одно из слагаемых: 49-7=42 или 49-42=7

Примечание:

Если в результате вычитания вы не получили одно из слагаемых, значит в вашем сложении была допущена ошибка.

6. Если к разности прибавить вычитаемое, то получится уменьшаемое.

Это значит, что вычитание можно проверить сложением.

Пример:

69-50=19

Для проверки к разности прибавим вычитаемое: 19+50=69.

Примечание:

Если в результате описанной выше процедуры вы не получили уменшьшаемое, значит в вашем вычитании была допущена ошибка.

Многочлены, или полиномы | Математика, которая мне нравится

Определение. Множество элементов называется полем, если для этих элементов определены действия: сложение и умножение и выполняются свойства

относительно сложения:

1) коммутативность ;
2) ассоциативность ;
3) существование нуля: ;
4) существование противоположного элемента: ;

относительно умножения:

5) коммутативность ;

6) ассоциативность ;
7) существование единицы ;
8 ) для любого ненулевого элемента существование обратного .

относительно сложения и умножения:

9) дистрибутивность (распределительный закон) ;
10) в поле должно существовать хотя бы два элемента .

Определение. Множество элементов называется кольцом, если для всех его элементов определены операции сложения и умножения, и выполняются свойства:\\

относительно сложения:

1) коммутативность ;
2) ассоциативность ;
3) существование нуля: ;
4) существование противоположного элемента: ;
относительно сложения и умножения:

5) дистрибутивность (распределительный закон) — правосторонний распределительный закон.

5′) дистрибутивность (распределительный закон) — левосторонний распределительный закон.

Поскольку коммутативности умножения не требуется, то распределительных закона два.

Кольцо называется коммутативным, если есть коммутативность умножения, ассоциативным, если ассоциативность, унитарным (или кольцом с единицей), если в нем есть .

Определение. Многочленом (полиномом) называется выражение вида

где — элементы некоторого поля , — буква, — коэффициенты полинома, — старший коэффициент.

Если , то число называется степенью многочлена. Степень нулевого многочлена не будем считать равной какому-либо конкретному числу, но будем считать, что она меньше степени любого ненулевого многочлена.

Обозначение. — степень многочлена .

Условимся считать, что многочлен не меняется, если приписать к нему слагаемое .

Пусть и — многочлены над одним и тем же полем, пусть

Будем говорить, что , если и .

Пример (метод неопределенных коэффициентов). Требуется найти значения такие, чтобы выполнялось равенство

Отсюда .

Можно определить обычным образом сумму, разность, произведение многочленов и доказать, что при этом выполняются обычные законы действий.

Свойства степени многочлена

1) ,
2) .

Задачи.

1) Найдите все значения параметров и такие, что многочлены и равны, если

2) Найдите все значения параметров такие, что при всех выполняется равенство

3) Найдите все значения параметров и такие, что многочлен является кубом двучлена .

4) Найдите многочлен третьей степени со старшим коэффициентом единицей и такой, что .

%d0%bf%d1%80%d0%b0%d0%b2%d0%b8%d0%bb%d0%be%20%d1%81%d0%bb%d0%be%d0%b6%d0%b5%d0%bd%d0%b8%d1%8f — с русского на все языки

Все языкиРусскийАнглийскийИспанский────────Айнский языкАканАлбанскийАлтайскийАрабскийАрагонскийАрмянскийАрумынскийАстурийскийАфрикаансБагобоБаскскийБашкирскийБелорусскийБолгарскийБурятскийВаллийскийВарайскийВенгерскийВепсскийВерхнелужицкийВьетнамскийГаитянскийГреческийГрузинскийГуараниГэльскийДатскийДолганскийДревнерусский языкИвритИдишИнгушскийИндонезийскийИнупиакИрландскийИсландскийИтальянскийЙорубаКазахскийКарачаевскийКаталанскийКвеньяКечуаКиргизскийКитайскийКлингонскийКомиКомиКорейскийКриКрымскотатарскийКумыкскийКурдскийКхмерскийЛатинскийЛатышскийЛингалаЛитовскийЛюксембургскийМайяМакедонскийМалайскийМаньчжурскийМаориМарийскийМикенскийМокшанскийМонгольскийНауатльНемецкийНидерландскийНогайскийНорвежскийОрокскийОсетинскийОсманскийПалиПапьяментоПенджабскийПерсидскийПольскийПортугальскийРумынский, МолдавскийСанскритСеверносаамскийСербскийСефардскийСилезскийСловацкийСловенскийСуахилиТагальскийТаджикскийТайскийТатарскийТвиТибетскийТофаларскийТувинскийТурецкийТуркменскийУдмуртскийУзбекскийУйгурскийУкраинскийУрдуУрумскийФарерскийФинскийФранцузскийХиндиХорватскийЦерковнославянский (Старославянский)ЧеркесскийЧерокиЧеченскийЧешскийЧувашскийШайенскогоШведскийШорскийШумерскийЭвенкийскийЭльзасскийЭрзянскийЭсперантоЭстонскийЮпийскийЯкутскийЯпонский

Все языкиРусскийАнглийскийИспанский────────АлтайскийАрабскийАрмянскийБаскскийБашкирскийБелорусскийВенгерскийВепсскийВодскийГреческийДатскийИвритИдишИжорскийИнгушскийИндонезийскийИсландскийИтальянскийКазахскийКарачаевскийКитайскийКорейскийКрымскотатарскийКумыкскийЛатинскийЛатышскийЛитовскийМарийскийМокшанскийМонгольскийНемецкийНидерландскийНорвежскийОсетинскийПерсидскийПольскийПортугальскийСловацкийСловенскийСуахилиТаджикскийТайскийТатарскийТурецкийТуркменскийУдмуртскийУзбекскийУйгурскийУкраинскийУрумскийФинскийФранцузскийЦерковнославянский (Старославянский)ЧеченскийЧешскийЧувашскийШведскийШорскийЭвенкийскийЭрзянскийЭсперантоЭстонскийЯкутскийЯпонский

Правило сложения в вероятности

Если А а также Б являются двумя событиями в вероятностном эксперименте, то вероятность того, что одно из этих событий произойдет, равна:

п ( А или Б ) знак равно п ( А ) + п ( Б ) − п ( А а также Б )

Это может быть представлено в виде Диаграмма Венна так как:

п ( А ∪ Б ) знак равно п ( А ) + п ( Б ) − п ( А ∩ Б )

Если А а также Б два взаимоисключающие события , п ( А ∩ Б ) знак равно 0 . Тогда вероятность того, что произойдет одно из событий, равна: п ( А или Б ) знак равно п ( А ) + п ( Б )

Это можно представить на диаграмме Венна как:

п ( А ∪ Б ) знак равно п ( А ) + п ( Б )

Пример:

Если вы достанете одну карту из обычной колоды, какова вероятность того, что это туз или пика?

Позволять Икс быть событием выбора туза и Д быть событие выбора пики.

п ( Икс ) знак равно 4 52

п ( Д ) знак равно 13 52

Эти два события не исключают друг друга, так как есть один благоприятный исход, при котором карта может быть как тузом, так и пикой.

п ( Икс а также Д ) знак равно 1 52

п ( Икс или Д ) знак равно 4 52 + 13 52 − 1 52 знак равно 16 52 знак равно 4 13

БЕСПЛАТНЫЙ пошаговый урок по правилу сложения вероятностей с интерактивными упражнениями

Изучение правила сложения вероятностей и сложения вероятностей с примерами задач и интерактивными упражнениями

Эксперимент: бросается одна шестигранная игральная кость. Какова вероятность того, что выпадет 2 или 5?

Возможности:

1. Выпавшее число может быть 2.

2. Выпавшее число может быть 5.

События: Эти события являются взаимоисключающими, поскольку они не могут происходить одновременно.

Вероятности: как найти вероятности этих взаимоисключающих событий? Нам нужно правило, чтобы вести нас.

Правило добавления 1: Когда два события, A и B, являются взаимоисключающими, вероятность того, что произойдет A или B, равна сумме вероятностей каждого события.

Р(А или В) = Р(А) + Р(В)

Давайте воспользуемся этим правилом сложения, чтобы найти вероятность эксперимента 1.

Эксперимент 1. Бросается одна шестигранная игральная кость. Какова вероятность того, что выпадет 2 или 5?

Вероятности:

Эксперимент 2. Спиннер имеет 4 равных сектора желтого, синего, зеленого и красного цветов. Какова вероятность приземлиться на красное или синее после вращения этого блесны?

Вероятность:

Эксперимент 3. В стеклянной банке находятся 1 красный, 3 зеленых, 2 синих и 4 желтых шарика.Если из банки наугад выбрать один шарик, какова вероятность того, что он будет желтым или зеленым?

Вероятность:

Р (желтый)	=	4
		10

P (зеленый)	=	3
		10

P (желтый или зеленый)	=	P(желтый)	+	P (зеленый)

	=	4	+	3
		10		10

	=	7
		10

В каждом из трех приведенных выше экспериментов события являются взаимоисключающими. Давайте рассмотрим некоторые эксперименты, в которых события не исключают друг друга.

Эксперимент 4. Из стандартной колоды из 52 игральных карт случайным образом выбирается одна карта. Какова вероятность выбора короля или трефы?

Вероятность:

P (король или трефа)	=	П(король)	+	P(клуб)	—	P(король треф)

	=	4	+	13	—	1
		52		52		52

	=	16
		52

	=	4
		13

В эксперименте 4 события не исключают друг друга. Сложение приводит к тому, что король треф считается дважды, поэтому его вероятность необходимо вычесть. Когда два события не являются взаимоисключающими, необходимо использовать другое правило сложения.

Дополнительное правило 2: Если два события, A и B, не являются взаимоисключающими, вероятность того, что произойдет A или B, составляет:

Р(А или В) = Р(А) + Р(В) — Р(А и В)

В приведенном выше правиле P(A и B) относится к перекрытию двух событий. Применим это правило к некоторым другим экспериментам.

Эксперимент 5. В математическом классе из 30 учеников 17 мальчиков и 13 девочек. В модульном тесте 4 мальчика и 5 девочек получили оценку «А». Если ученица выбрана случайным образом из класса, какова вероятность того, что она выберет девочку или отличницу?

Вероятности: P(девушка или A) = P(девушка) + P(A) — P(девушка и A)

=	13	+	9	—	5
	30		30		30

=	17
	30

Эксперимент 6: В канун Нового года вероятность того, что человек попадет в автомобильную аварию, равна 0. 09. Вероятность того, что человек будет управлять автомобилем в состоянии алкогольного опьянения, равна 0,32, а вероятность того, что человек попадет в автомобильную аварию в состоянии алкогольного опьянения, равна 0,15. Какова вероятность того, что человек за рулем в состоянии алкогольного опьянения или попадет в автомобильную аварию?

Вероятность:

P (в состоянии алкогольного опьянения или в результате несчастного случая)	=	П(в состоянии алкогольного опьянения)	+	П(авария)	—	P(пьянство и несчастный случай)

	=	0. 32	+	0,09	—	0,15
	=	0,26

Резюме: Чтобы найти вероятность события A или B, мы должны сначала определить, являются ли события взаимоисключающими или нет. Затем мы можем применить соответствующее правило добавления:

Правило сложения 1: Если два события, A и B, являются взаимоисключающими, вероятность того, что произойдет A или B, равна сумме вероятностей каждого события.

Р(А или В) = Р(А) + Р(В)

Правило добавления 2: Если два события, A и B, не являются взаимоисключающими, между этими событиями есть некоторое совпадение. Вероятность того, что произойдет A или B, представляет собой сумму вероятности каждого события за вычетом вероятности совпадения.

Р(А или В) = Р(А) + Р(В) — Р(А и В)

Упражнения

Указания: Прочитайте каждый вопрос ниже. Выберите свой ответ, нажав на его кнопку. Обратная связь по вашему ответу представлена в ОКНО РЕЗУЛЬТАТЫ.Если вы ошиблись, выберите другую кнопку.

1.	День недели выбирается случайным образом. Какова вероятность того, что вы выберете понедельник или вторник?

2.	В зоомагазине есть 6 щенков, 9 котят, 4 песчанки и 7 попугаев. Если домашнее животное выбрано наугад, какова вероятность того, что вы выберете щенка или попугая?

3.	Вероятность того, что у подростка из Нью-Йорка будет скейтборд, равна 0,37, велосипеда — 0,81, а того и другого — 0,36. Если наугад выбрать подростка из Нью-Йорка, какова вероятность того, что у него есть скейтборд или велосипед?

4.	Случайным образом выбирается число от 1 до 10.Какова вероятность выбрать 5 или четное число?

5.	Брошен один шестигранный кубик. Какова вероятность того, что выпадет число больше 3 или четное число?

Правило сложения для вероятностей – обзор, расчет, пример

Что такое правило сложения для вероятностей?

При наличии нескольких событий правило сложения вероятностей используется для вычисления вероятности того, что хотя бы одно из событий произойдет.Вероятность можно определить как раздел математики, который количественно определяет достоверность или неопределенность события или набора событий.

Связанные понятия

Прежде чем понять правило сложения, важно понять несколько простых понятий:

Пример пространства : Это множество всех возможных событий. Например, при подбрасывании монеты выборочное пространство равно {Орел, Решка}, потому что орёл и решка — это все возможные результаты.
Событие : В вероятности событие определяется как конкретный результат.Например, подбрасывание монеты и выпадение орла — это событие.
Взаимоисключающие события : Это такие события, при которых одно не может произойти. Опять же, в примере с монетой, если выпадает орел, мы не можем выпасть решкой. Следовательно, это два взаимоисключающих события.
Взаимно исчерпывающие события : События, которые вместе охватывают все пространство выборки. В случае подбрасывания монеты получение орла и получение решки взаимно исчерпывают друг друга, поскольку все пространство выборки равно {Орел, Решка}.
Независимые события : События, происходящие независимо друг от друга. Например, при подбрасывании двух монет результат второй монеты не зависит от результата первой монеты.

Формула вычислить вероятность двух событий A и B дается:

, где:

p (A ∪ B) — вероятность того, что либо A или B бывает
P(A) – Вероятность события A
P(B) – Вероятность события B
P(A ∩ B) – Вероятность того, что A и B произойдут вместе

Следующая Venn Диаграмма иллюстрирует, как и почему работает формула:

Как показано выше, мы вычитаем член P(AB), потому что он будет учитываться дважды при сложении P(A) и P(B).

Расчет P(A ∩ B)

Вероятность того, что события A и B произойдут – P(A ∩ B) – может быть легко вычислена, если события независимы друг от друга, путем умножения двух вероятностей P(A ) и P(B), как показано ниже:

Если A и B являются независимыми событиями, то:

событий, или иным образом трудно определить.

Взаимоисключающие события

В случае взаимоисключающих событийВзаимоисключающие событияВ статистике и теории вероятностей два события считаются взаимоисключающими, если они не могут произойти одновременно. Простейший пример взаимоисключающих событий: вероятность того, что оба события произойдут одновременно, равна нулю по определению, потому что, если одно событие произойдет, другое не может произойти. Следовательно, для взаимоисключающих событий A и B имеется:

Обратите внимание на тот факт, что взаимоисключающие события не являются независимыми, потому что если обе вероятности P(A) и P(B) ненулевые, то P(AB) = P(A) * P(B) не может быть нулем. Фактически, по самому своему определению взаимоисключающих событий они зависят от того, не произойдет ли другое событие. Схема ниже иллюстрирует концепцию:

Числовой пример

Давайте перейдем к числовому примеру, который иллюстрирует концепцию. Предположим, два независимых события, A и B. Пусть P(A) = 0,6 и P(B) = 0,4. Тогда P(A ∪ B) определяется как:

P(A ∩ B) = P(A) * P(B) = 0,6 * 0,4 = 0,24

P(A ∪ B) = P(A) + Р(В) – Р(АВ) = 0.6 + 0,4 – 0,24 = 0,76

Следовательно, P(A ∪ B) равно 76% .

Производные правила

Правило сложения вероятностей дает некоторые другие правила, которые можно использовать для расчета других вероятностей.

взаимоисключающие события

для взаимоисключающих событий, совместная вероятность P (A ∪ B) = 0. Следовательно, мы получаем:

Вероятность для ровно одного из двух событий

ровно одного из двух событий можно рассчитать, просто изменив правило сложения следующим образом: Бизнес-аналитика и аналитик данных (BIDA)™ От Power BI до SQL и машинного обучения — сертификация бизнес-аналитики CFI (BIDA) поможет вам освоить свои аналитические сверхспособности. программа сертификации, разработанная, чтобы помочь каждому стать финансовым аналитиком мирового уровня. Для продвижения по карьерной лестнице вам будут полезны следующие дополнительные ресурсы CFI:

Зависимые события и независимые события Зависимые события и независимые события В математике, особенно в статистике, события часто классифицируются как зависимые или независимые. Как правило, наличие или отсутствие
Теория игрТеория игрТеория игр представляет собой математическую основу, разработанную для решения проблем с конфликтующими или сотрудничающими сторонами, способными принимать рациональные решения.
Количественный анализКоличественный анализКоличественный анализ — это процесс сбора и оценки измеримых и проверяемых данных для понимания поведения и эффективности бизнеса.
Правило общей вероятностиПравило полной вероятностиПравило общей вероятности (также известное как закон полной вероятности) является фундаментальным правилом в статистике, относящимся к

8.

2: Взаимоисключающие события и правило сложения

Цели обучения

В этом разделе вы научитесь:

Определение составных событий с использованием объединения, пересечения и дополнения.
Идентифицировать взаимоисключающие события
Используйте правило сложения для расчета вероятности объединения событий.

В прошлой главе мы научились находить объединение, пересечение и дополнение множества. Теперь мы будем использовать эти операции над множествами для описания событий.

Объединение двух событий E и F, E $\cup$ F, представляет собой множество исходов, которые находятся в E или в F или в обоих.
Пересечение двух событий E и F, E $\cap$ F, представляет собой множество исходов, которые находятся как в E, так и в F.{c}\right)=\frac{n-k}{n}=1-\frac{k}{n}=1-P(E) \nonumber\]
Особый интерес для нас представляют события, исходы которых не пересекаются. Мы называем эти события взаимоисключающими.
Два события E и F называются взаимоисключающими , если они не пересекаются: E $\cap$ F = $\varnothing$.
Далее мы определим, являются ли данная пара событий взаимоисключающими.
Пример $\PageIndex{1}$
Карта вытягивается из стандартной колоды.Определите, являются ли приведенные ниже пары событий взаимоисключающими.
E = {Вытянутая карта — туз}
F = {Вытянутая карта — сердце}
Раствор
Очевидно, что туз червей принадлежит обоим наборам. Это
\[\mathrm{E} \cap \mathrm{F}=\{\text {Туз червей}\} \neq \varnothing \nonumber\]
Следовательно, события E и F не исключают друг друга.
Пример $\PageIndex{2}$
Брошены две игральные кости.Определите, являются ли приведенные ниже пары событий взаимоисключающими.
G = {Сумма граней равна шести}
H = {Один кубик показывает четыре}
Раствор
Для наглядности перечислим элементы обоих наборов.
G = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)} и H = {(2, 4), (4, 2)}
Ясно, что G $\cap$ H = {(2, 4), (4, 2)} $\neq \varnothing$.
Следовательно, эти два набора не исключают друг друга.
Пример $\PageIndex{3}$
В семье трое детей.Определите, являются ли следующие пары событий взаимоисключающими.
M = {В семье есть хотя бы один мальчик}
N = {В семье все девочки}
Раствор
Хотя ответ может быть ясен, мы перечисляем оба набора.
M = {BBB, BBG, BGB, BGG, GBB, GBG, GGB} и N = {GGG}
Ясно, что M $\cap$ N = $\varnothing$
Таким образом, события M и N исключают друг друга.
Теперь мы рассмотрим задачи на объединение двух событий.
При наличии двух событий, E, F, определение вероятности E $\cup$ F равносильно нахождению вероятности того, что произойдет E, или произойдет F, или произойдет и то, и другое.
Пример $\PageIndex{4}$
Если подбросить игральную кость, какова вероятность того, что выпадет четное число или число больше четырех?
Раствор
Пусть E будет событием, когда число, выпавшее на кубике, является четным числом, и пусть F будет событием, когда выпавшее число больше четырех.
Демонстрационное пространство S = {1, 2, 3, 4, 5, 6}. Событие E = {2, 4, 6} и событие F = {5, 6}
Нам нужно найти P(E $\cup$ F).
Поскольку P(E) = 3/6, а P(F) = 2/6, учащийся может сказать P(E $\cup$ F) = 3/6 + 2/6. Это будет неверно, потому что элемент 6, который есть и в E, и в F, подсчитывался дважды, один раз как элемент E и один раз как элемент F. Другими словами, множество E $\cup$ F имеет только четыре элемента, а не пять: множество E $\cup$ F = { 2,4,5,6 }
Следовательно, P(E $\cup$ F) = 4/6, а не 5/6.
Это можно проиллюстрировать диаграммой Венна. Мы воспользуемся диаграммой Венна, чтобы повторно изучить пример $\PageIndex{4}$ и вывести вероятностное правило, которое мы можем использовать для расчета вероятностей объединений событий.
Пример пространства S, события E и F и E $\cap$ F перечислены ниже.
\[\mathrm{S}=\{1,2,3,4,5,6\}, \mathrm{E}=\{2,4,6\}, \mathrm{F}=\{5 ,6\}, \text { и } \mathrm{E} \cap \mathrm{F}=\{6\} \nonumber. \]
На приведенном выше рисунке показаны S, E, F и E $\cap$ F.
Нахождение вероятности того, что E $\cup$ F, равнозначно нахождению вероятности того, что произойдет E, или произойдет F, или произойдет и то, и другое.
Если мы подсчитаем количество элементов n(E) в E и добавим к нему количество элементов n(F) в F, точки как в E, так и в F будут подсчитаны дважды, один раз как элементы E и один раз как элементы числа F. Теперь, если мы вычтем из суммы n(E) + n(F) число n(E $\cap$ F), мы удалим двусмысленность и получим правильный ответ. Так что, как правило,
\[\mathrm{n}(\mathrm{E} \cup \mathrm{F})=\mathrm{n}(\mathrm{E})+\mathrm{n}(\mathrm{F})-\ mathrm{n}(\mathrm{E} \cap \mathrm{F}) \nonumber\]
Разделив все уравнение на n(S), мы получим
\[\ frac{\ mathrm {n} (\ mathrm {E} \ cup \ mathrm {F})} {\ mathrm {n} (\ mathrm {S})} = \ frac {\ mathrm {n} ( \ mathrm {E})} {\ mathrm {n} (\ mathrm {S})} + \ frac {\ mathrm {n} (\ mathrm {F})} {\ mathrm {n} (\ mathrm {S} )} — \ frac {\ mathrm {n} (\ mathrm {E} \ cap \ mathrm {F})} {\ mathrm {n} (\ mathrm {S})} \ nonumber \]
Поскольку вероятность события равна количеству элементов в этом событии, деленному на количество всех возможных исходов, мы имеем
\[\mathrm{P}(\mathrm{E} \cup \mathrm{F})=\mathrm{P}(\mathrm{E})+\mathrm{P}(\mathrm{F})-\ mathrm{P}(\mathrm{E} \cap \mathrm{F}) \nonumber\]
Применяя вышеописанное для примера $\PageIndex{4}$, мы получаем
\[\mathrm{P}(\mathrm{E} \cup \mathrm{F})=3 / 6+2 / 6-1 / 6=4 / 6 \nonumber\]
Это потому, что, когда мы добавляем P(E) и P(F), мы добавляем P(E $\cap$ F) дважды. Следовательно, мы должны вычесть P(E $\cap$ F) один раз.
Это дает нам общую формулу, называемую Правилом сложения , для нахождения вероятности объединения двух событий. Поскольку событие E $\cup$ F — это событие, в котором произойдет E, ИЛИ произойдет F, ИЛИ произойдет и то, и другое, мы иногда называем это правилом сложения для событий OR. В нем указано
Правило добавления
\[\mathbf{P}(\mathbf{E} \cup \mathbf{F})=\mathbf{P}(\mathbf{E})+\mathbf{P}(\mathbf{F})-\ mathbf{P}(\mathbf{E} \cap \mathbf{F}) \nonumber\]
Если и только если два события $\mathrm{E}$ и $\mathrm{F}$ являются взаимоисключающими, тогда $\mathrm{E} \cap \mathrm{F}=\varnothing $ и $\mathrm{P}(\mathrm{E} \cap \mathrm{F})=0$, и мы получаем $\mathrm{P}(\mathrm{E} \cup \mathrm{ F})=\mathrm{P}(\mathrm{E})+\mathrm{P}(\mathrm{F})$
Пример $\PageIndex{5}$
Если из колоды вытянута карта, используйте правило сложения, чтобы найти вероятность получения туза или червы.
Раствор
Пусть событие A — туз, а событие H — черва.
Поскольку в колоде четыре туза и тринадцать червей,
Р(А) = 4/52 и Р(Н) = 13/52.
Кроме того, поскольку пересечение двух событий состоит только из одной карты, туза червей, теперь у нас есть:
P(A $\cap$H) = 1/52
Нам нужно найти P(A $\cup$ H):
\begin{align}
\mathrm{P}(\mathrm{A} \cup \mathrm{H}) &=\mathrm{P}(\mathrm{A})+\mathrm{P}(\mathrm{ H})-\mathrm{P}(\mathrm{A} \cap \mathrm{H}) \\
&=4/52+13/52-1/52=16/52
\end{выровнено}
Пример $\PageIndex{6}$
Два игральных кубика брошены, и события F и T следующие:
F = {Сумма костей равна четырем} и T = {По крайней мере, на одном кубике выпала тройка}
Найти P(F $\cup$ T).
Раствор
Перечислим F и T и F $\cap$ T следующим образом:
Ф = {(1, 3), (2, 2), (3, 1)}
Т = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1, 3), (2, 3 ), (4, 3), (5, 3), (6, 3)}
F $\cap$ T = {(1, 3), (3, 1)}
Поскольку P(F $\cup$ T) = P(F) + P(T) — P(F $\cap$ T)
Имеем P(F $\чашка$ T) = 3/36 + 11/36 — 2/36 = 12/36.
Пример $\PageIndex{7}$
Мистер Вашингтон ищет преподавателя математики в своем любимом общественном колледже в Купертино.Его трудоустройство зависит от двух условий: утвердит ли правление должность и выберет ли его комитет по найму. Вероятность того, что совет утвердит эту должность, составляет 80%, а вероятность того, что комитет по найму выберет его, составляет 70%. Если существует 90-процентная вероятность того, что будет выполнено хотя бы одно из двух условий — одобрение совета директоров или его избрание, — какова вероятность того, что г-н Вашингтон будет принят на работу?
Раствор
Пусть A — событие, когда правление одобряет позицию, а S — событие, когда Mr.Вашингтон выбирается. У нас есть,
P(A) = 0,80, P(S) = 0,70 и P(A $\cup$ S) = 0,90.
Нам нужно найти P(A $\cap$ S).
Формула сложения утверждает, что
\[P(A \чашка S)=P(A)+P(S)-P(A \cap S) \номер\]
Подставляя известные значения, получаем
\[. 90=.80+.70-P(\mathrm{A} \cap \mathrm{S}) \номер\]
Следовательно, P(A $\cap$ S) = 0,60.
Пример $\PageIndex{8}$
Вероятность того, что в эти выходные будет холодно, равна .6, вероятность того, что будет дождь, равна 0,7, а вероятность того, что будет и холодно, и дождливо, равна 0,5. Какова вероятность того, что не будет ни холода, ни дождя?
Раствор
Пусть C — событие, что выходные будут холодными, а R — событие, что будет дождь. Нам дано, что
\[\mathrm{P}(\mathrm{C})=.6, \quad \mathrm{P}(\mathrm{R})=.7, \quad \mathrm{P}(\mathrm{C} \cap \mathrm{R})=.5 \номер\]
Сначала мы находим P(C $\cup$ R), используя правило сложения.{c}\right)=1-P(C \cup R)=1-.8=.2 \nonnumber\]
Подведем итоги этого раздела, перечислив важные правила.
Резюме
Правило сложения
Для двух событий $\mathrm{E}$ и $\mathrm{F}$, $\mathrm{P}(\mathrm{E} \cup \mathrm{F})=\mathrm{P }(\mathrm{E})+\mathrm{P}(\mathrm{F})-\mathrm{P}(\mathrm{E} \cap \mathrm{F})$
Правило добавления для взаимоисключающих событий
Если два события $\mathrm{E}$ и $\mathrm{F}$ являются взаимоисключающими, то $\mathrm{P}(\mathrm{E} \cup \mathrm{F})= \mathrm{P}(\mathrm{E})+\mathrm{P}(\mathrm{F})$
Правило дополнения
Если $\mathrm{E}^c$ является дополнением к событию $\mathrm{E}$, то $\mathrm{P}(\mathrm{E}^c) = 1 — \mathrm {P}(\mathrm{E})$
Что такое правило сложения для лимитов? — Определение и обзор — Видео и стенограмма урока
Формула правила сложения
Формула правила сложения, показанная здесь, показывает, как применять ее во всех ситуациях, когда у вас есть функции, являющиеся суммой меньших функций.
Правило добавления лимитов.
Как и многие вещи в математике, эта формула имеет ограничение или условие, при которых она будет работать. Вне этого условия формула не будет работать.
Условие правила добавления
Что это за условие? Дело в том, что должны существовать пределы меньших разделенных функций. Если их нет, то вы не можете использовать это правило, потому что оно вам не поможет.Например, предположим, что мы хотим получить предел следующей функции:
Нахождение предела большей функции.
Правило сложения гласит, что мы можем разбить эту большую функцию на пределы меньших функций следующим образом:
Применение правила сложения.
С этим проще работать, потому что мы знаем, как найти пределы самих меньших функций, а не большей функции в целом.
Применение правила добавления
Теперь давайте посмотрим, как применить это правило к проблемам ограничения. Допустим, мы пытаемся найти предел следующей функции:
Нахождение предела другой большей функции.
Правило сложения говорит нам, что мы можем разделить эту функцию на две меньшие функции, прежде чем брать предел.
Применение правила сложения.
Делая это, мы видим, что для меньших функций легко найти пределы.Мы видим, что это полиномы, поэтому мы можем подключить наш предел x непосредственно к меньшим функциям, чтобы найти их предел.
Оценка лимита.
Как мы видим, это дает нам (1)2 + 3(1). Поскольку это становится 3 + 1, это достаточно просто, верно? Итак, после выполнения этих основных вычислений мы видим, что наш ответ для этого предела равен 4.
Однако, если у нас есть проблема, подобная следующей, мы не сможем использовать правило сложения для пределов:
Можем ли мы применить здесь правило сложения?
Мы не можем использовать правило сложения для этой функции, потому что эта функция не является суммой меньших функций.У нас есть только один член в этой функции, который оказывается дробью многочленов. Мы должны использовать другие инструменты, чтобы оценить этот предел.
Итоги урока
Хорошо, давайте теперь повторим. В этом уроке мы впервые вспомнили, что предел — это значение, к которому приближается функция по мере приближения к определенной точке. Мы видели, что в математических символах это выглядело так:
. Определение предела.
И это в основном говорит о том, что когда вы берете предел f( x ) по мере того, как он приближается к c , он либо приближается, либо становится значением L .
Как мы также узнали, правило сложения для пределов говорит нам, что мы можем разделить большие функции, которые являются суммой меньших функций, на меньшие функции и взять предел каждой из этих функций, чтобы найти предел большей функции. . Однако, как мы узнали, это работает только в том случае, если у этих меньших функций действительно есть предел.
Раздел 5.2: Правила добавления и дополнения
Цели
К концу этого урока вы сможете…
1. использовать правило сложения для непересекающихся событий
2. используйте Общее правило добавления
3. использовать правило дополнения
Чтобы получить краткий обзор этого раздела, посмотрите этот краткий видеообзор:

Дополнительное правило для непересекающихся событий
В этой главе у нас будет довольно много правил о вероятности, но мы начнем с малого. Первая ситуация, которую мы хотим рассмотреть, — это когда два события не имеют общих исходов. Мы называем подобные события непересекающимися. события .
Два события являются непересекающимися , если у них нет общих исходов. (Также обычно известный как взаимоисключающих событий.)
Еще в 1881 году Джон Венн разработал отличный способ визуализации наборов. Как это часто бывает случай в математике, диаграммы взяли его имя и с тех пор его имя — Венн диаграммы.Поскольку события представляют собой наборы исходов, хорошо работает визуализация вероятности. также. Вот пример диаграммы Венна, показывающий два непересекающихся результата: Е и Ф.
Продолжим немного дальше и расставим точки на графике вот так — для обозначения результатов.
Глядя на рисунок, мы ясно видим, что P(E) = 5/15 = 1/3, так как в E 5 исходов, а всего исходов 15. Точно так же P (F) также равно 1/3.
Далее мы хотим рассмотреть все события, которые находятся либо в E, либо в F. вероятности, мы называем это событие E или F . Итак, в нашем примере P(E или F) = 10/15 = 2/3.
Но это было видно только на картинке! Просто посчитайте точки, которые Е и добавить к нему количество точек в F.
В общем, можем создать правило. Мы назовем это…
Правило сложения для непересекающихся событий
Если E и F непересекающиеся (взаимно исключающие) события, то
P(E или F) = P(E) + P(F)
Пример 1
ОК — время для примера. Давайте воспользуемся примером из предыдущего раздела о семья с тремя детьми, и определим следующие события:
E = в семье ровно два мальчика
F = в семье ровно один мальчик
Опишите событие «Е или F» и найдите его вероятность.
[показать ответ]
«E или F» — это событие, когда в семье один или два мальчика.
Ясно, что оба эти события не могут произойти одновременно. одновременно, поэтому они не пересекаются. Вероятность того, что в семье либо один, либо два мальчика тогда:
P(E или F) = P(E) + P(F) = 3/8 + 3/8 = 6/8 = 3/4
Конечно, часто бывают случаи, когда два события имеют исходы в общее, поэтому нам понадобится более надежное правило для этого случая.

Общее правило добавления
Что произойдет, если два события с по имеют общие исходы? Хорошо, давайте рассмотрим пример ниже. В этом случае P(E) = 4/10 = 2/5, и P(F) = 5/10 = 1/2, но P(E или F) не равно 9/10. Вы видите, почему?
Ключевым здесь являются два результата в середине, где E и F перекрываются. Официально мы называем этот регион событием E и F .Это все исходы, которые есть в и E и F. В нашем визуальном пример:
В этом случае, чтобы найти P(E или F), нам нужно сложить результаты в E с результатами в F, а затем вычесть дубликатов, которые мы подсчитано, что находится в E и F. Мы называем это общим дополнением Правило .
Общее правило добавления
P(E или F) = P(E) + P(F) — P(E и F)
Давайте попробуем пару быстрых примеров.
Пример 2
Рассмотрим колоду стандартных игральных карт.
Предположим, мы вытягиваем одну карту из колоды наугад и определяем следующее событий:
E = вытянутая карта туз
F = вытянутая карта — король
Используйте эти определения, чтобы найти P(E или F).
[показать ответ]
Хорошо, так как E и F не имеют общих исходов, мы можем использовать правило сложения для непересекающихся событий:
P(E или F) = P(E) + P(F) = 4/52 + 4/52 = 8/52 = 2/13
Пример 3
Рассматривая колоду игральных карт, одна из которых вытягивается наугад.Предположим, мы определяем следующие события:
F = вытянутая карта — король
G = вытянутая карта — сердце
Используйте эти определения, чтобы найти P(F или G).
[показать ответ]
В отличие от предыдущего примера, события F и G, и имеют общий результат — король червей — поэтому нам нужно использовать общий Правило сложения:
P(E или F)
= P(E) + P(F) — P(E и F)
= 4/52 + 13/52 — 1/52
= 16/52 = 4/13
Итак, ключевая идея и разница между этими двумя примерами — когда вы находка
P(E или F), обязательно ищите исходы, общие для E и F.
Правило дополнения
Я думаю, что лучший способ представить последнюю идею в этом разделе — это рассмотреть пример. Давайте снова посмотрим на колоду стандартных игральных карт:
.
А давайте определим событие E = взята карта меньше короля. Если я спрошу тебя чтобы найти P(E), вы не будете их подсчитывать. (Вы не собирались, были ты?!) Нет — ты скажешь, что карт всего 52, а королей 4, поэтому должно быть на 48 карт меньше, чем у короля.Итак, P(E) = 48/52 = 12/13.
Идея, которую вы уже используете, называется дополнением . (Это дополнение, с e . Не комплимент, как в «Мой, ты выглядишь красиво сегодня!»)
Дополнение E , обозначенное E ^c , представляет собой все результаты в выборочном пространстве, которые нет в Е.
Таким образом, дополнение E равно всему, кроме результатов. в Э.На самом деле, в некоторых текстах это написано как «не E».
Чем полезно дополнение? На самом деле вы уже использовали ключевую идею в приведенном выше примере. Давайте посмотри на а Диаграмма Венна.
Из раздела 5.1 мы знаем, что P(S) = 1. Ясно, что E и E ^c не пересекаются, поэтому
P(E или E ^c ) = P(E) + P(E ^c ) . Объединив эти два факта, получаем:
Правило дополнения
P(E) + P(E ^c ) = 1
Имейте это в виду, когда рассматриваете достаточно сложное событие.Иногда гораздо проще найти вероятность дополнения.

Правила умножения, сложения и полной вероятности
Правило умножения основано на условной вероятности.
P(A|B) = P(AB)/P(B), P(B) ≠ 0
, где P(AB) = совместная вероятность события A и B = вероятность того, что оба события A и B произойдут вместе
P(A|B) = условная вероятность события A, основанная на возникновении события B или вероятности события A при заданном B
Мы знаем, что P(A|B) — это вероятность события A при условии, что событие B произошло. Поскольку событие B уже произошло, то вероятность A при данном B будет равна вероятности возникновения обоих событий вместе, деленной на вероятность возникновения события B.
Аналогично, P(B|A) = P(BA)/P(A) = P(AB)/P(A), P(A) ≠ 0
Правило сложения для вероятностей помогает в расчете вероятности возникновения события A или B.
Р(А или В) = Р(А) + Р(В) — Р(АВ)
Когда мы добавляем P(A) и P(B), то P(AB) добавляется дважды.Итак, мы вычитаем его, чтобы получить P(A или B)
.
Для взаимоисключающих событий P(AB) = 0, так как эти события никогда не могут произойти вместе.
Следовательно, P(A или B) для взаимоисключающих событий = P(A) + P(B)
Правило полной вероятности помогает в расчете безусловной вероятности события. Предположим, что событие A = Вероятность увеличения цены акции. Предположим, что есть четыре события, влияющие на вероятность повышения цены акции.Эти четыре события должны быть взаимоисключающими, а также исчерпывающими, чтобы вычислить общую вероятность события А. Давайте определим эти четыре события и их соответствующие безусловные вероятности.
Событие A = Увеличение цены акции
Событие A ₁ = Процентная ставка < 3 процентов
Событие A ₂ = 3 процента ≤ процентная ставка < 5 процентов
Событие A ₃ = 5 процентов ≤ процентная ставка < 7 процентов
Событие A ₄ = Процентная ставка ≥ 7 процентов
Р(А ₁ ) = 0.20, Р(А ₂ ) = 0,25, Р(А ₃ ) = 0,40, Р(А ₄ ) = 0,15
Кроме того, P(A|A ₁ ) = 0,90, P(A|A ₂ ) = 0,70, P(A|A ₃ ) = 0,40, P(A|A ₄ ) = 0,10
, где P(A|A ₁ ) — вероятность события A при условии, что произошло событие B, и так далее.
Теперь по правилу полной вероятности
P(A) = P(AA ₁ ) + P(AA ₂ ) + P(AA ₃ ) + … ..+ P(AA _n )
, потому что A всегда встречается с одним из A ₁ , A ₂ ,. …, A _n
P(A) = P(A|A ₁ )*P(A ₁ ) + P(A|A ₂ )*P(A ₂ ) + …. + P(A |A _n )*P(A _n )
, потому что P(AA ₁ ) = P(A|A ₁ )*P(A ₁ )
Итак, вероятность события А = 0,90*0,20 + 0,70*0,25 + 0.40*0,40 + 0,10*0,15 = 0,18 + 0,175 + 0,16 + 0,015 = 0,53 = 53 процента .
Предыдущий LOS: Условные и безусловные вероятности
Следующий LOS: Совместная вероятность
.