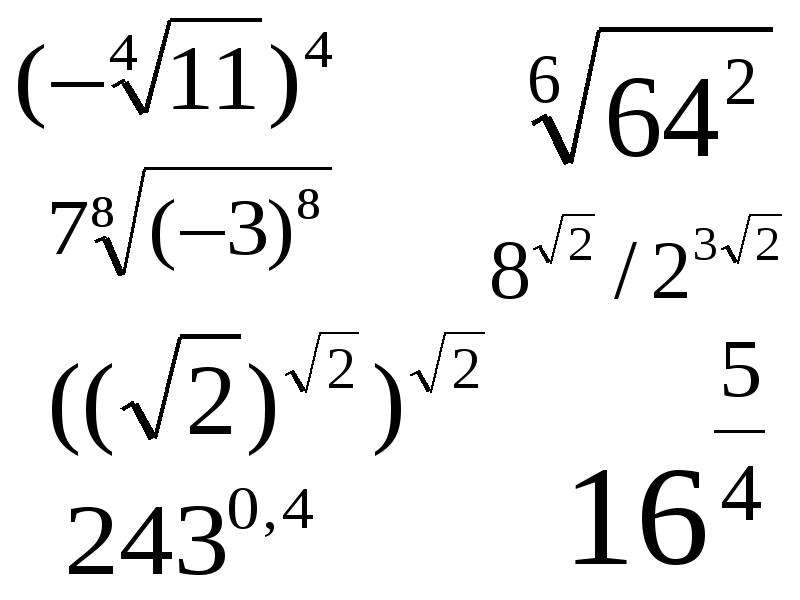Корень n -й степени его свойства
Корень n-й степени, его свойства.
Арифметическим корнем n-й степени из числа а называют неотрицательное число , n-я
степень которого равна а.
Обозначается арифметический корень n-й степени из числа а
,
где n- показатель корня,
а- подкоренное выражение.
Знак называют еще радикалом.
Арифметический корень второй степени называется корнем квадратным и обозначается √,
арифметический корень третьей степени называется кубическим корнем о обозначается
Например :
а) и 2≥0;
б) и 3≥0;
в)
Из определения арифметического корня n-й степени следует, что при четом n подкоренное выражение должно быть больше или равно нулю, а значит и значение такого корня тоже неотрицательно, например:
арифметический
корень 4-й степени из числа -81 не существует,
так как ни одно число в четвертой степени
не даст -81 ( при возведении в четную
степень значение выражения всегда
неотрицательно).
При нечетном показателе корня подкоренное выражение может быть отрицательным, и тогда минус может быть вынесен за знак коня.
Например:
Уравнение хn=а.
Уравнение хn=а при нечетном n имеет единственное решение х=.
Например : х3=-125;
х=;
х=-;
х=-5.
Для наглядности сделаем проверку:
(-5)3=-125;
-125=-125- верно.
Ответ : х=-5.
Уравнение хn=а при четном n имеет и положительном а имеет два корня
х=±.
Например:
х 4=16;
х1=; х2=-;
х1=2; х2=-2.
Можно убедиться при проверке, что 24=16 и (-2)4=16.
Ответ : ±2.
Иногда нужно применить такое свойство арифметического корня n-й степени:
|х|, если n четно;
х, если n нечетно.
х, если х≥0;
Вспомним, что |х|= -х, если х<0.
Например :
.
Так как <0, следовательно
.
Основные свойства корней.
Для арифметического корня n-й степени, как и для квадратного корня, существуют операции внесения множителя под знак корня и вынесение множителя из-под знака корня.
Например :
2.
Из примера видно, что для внесения множителя под знак корня n-й степени его нужно
возвести в n-ю степень. Нужно помнить, что под знак с четным показателем мы имеем право внести только положительный множитель, например:
Аналогично производится вынесение множителя из-под знака корня , например:
а)
б)
в)
Примеры решения упражнений:
№1
Вычислить:
а) ; б); в) г)
Решение:
а) =-; б) =2;
в) = ; г)
№2
Решить уравнение:
а)х 6=5;
б) х3=5;
в) 0,01х3+10=0.
Решение:
а) х6=5;
так как 6- четное число, то уравнение имеет два корня
Ответ: .
б) х3=5;
так как 3-нечетное число, то уравнение имеет один корень.
.
Ответ:
в) 0,01х3+10=0;
0,01х3=-10;
х3=;
х3=;
х3=-10
х3=-1000;
х=
х=-
х= -10.
Ответ :-10.
№3
Вычислить:
а); б) ; в); в).
Решение:
а) =
б)
в)
г)
№4
Упростите выражение:
а); б) если х>0;
в)если
к>0 ; г)
:.
Решение:
а) =
так как 3- нечетное число, получим
а2вс4.
Ответ: а2вс4.
б) =
Так как 4-нечетное число, то получим
Так как х>0 по условию, то
у4≥0 (так как 4-четное число), следовательно ,
аналогично рассуждая, получим .
Итого получим:
Ответ:
в) ==;
так как к>0, то к6>0, следовательно .
Итого получим:
.
Ответ: .
г) :=
Задания для самостоятельного решения .
№1
Вычислить:
а) б) ; в) ; г) .
№2
Решите уравнение:
а) х3=64;
б)х4— 81=0; в)
16х4-1=0; г)12.
№3
Вычислить:
№4
Упростите выражение:
а) б); в); г)
д) : е)
№5
Вынесите множитель из-под знака корня.
а) б)
Корень n-й степени с примерами решения
Содержание:
Перейдем к изучению корней степени п для произвольного натурального числа
Определение:
Пусть называется такое число степень которого равна .
Таким образом, утверждение « — корень -й степени из » означает, что .
Корень 3-й степени называется также кубическим.
Например, кубический корень из числа — это число , так как . Кубический корень из числа — это число , так как .
Корень 7-й степени из числа 128 — это число 2, так как . Корень 7-й степени из числа -128 — это число -2, так как . Корень 7-й степени из числа 0 — это 0, так как .
Во множестве действительных чисел существует единственный корень нечетной степени п из любого числа . Этот корень обозначается
Например, .
Утверждение о существовании корня нечетной степени из любого числа мы принимаем без доказательства. Согласно определению, когда п нечетное, то при любом значении а верно равенство
Например,
Заметим, что 0 — это единственное число, -я степень которого равна 0. Поэтому при любом натуральном существует единственный корень -й степени из 0 — это число 0, т.
Примерами корней четной степени могут служить квадратные корни: -7 и 7 — квадратные корни из 49, а -15 и 15 — из 225. Рассмотрим еще несколько примеров. Корни 4-й степени из числа 81 — это числа 3 и -3, так как и . Корни 6-й степени из числа 64 — это числа 2 и -2, так как и .
Во множестве действительных чисел существует ровно два корня четной степени п из любого положительного числа а, их модули равны, а знаки противоположны. Положительный корень обозначается
Например,
Утверждение о существовании корня четной степени из любого положительного числа мы принимаем без доказательства. Согласно определению, когда четное, то при любом положительном, значении а верно равенство
Например, .
Не существует такого числа, 4-я степень которого равна -81. Поэтому корня 4-й степени из числа -81 не существует. И вообще, поскольку не существует такого числа, четная степень которого была бы отрицательной, то не существует корня четной степени из отрицательного числа.
Определение:
Неотрицательный корень -й степени из числа называется арифметическим корнем -й степени из .
При четном символом обозначается только арифметический корень -й степени из числа (при чтении записи слово «арифметический» обычно пропускают).
Выражение, стоящее под знаком корня, называется подкоренным выражением.
Извлечь корень -й степени из числа — это значит найти значение выражения
Так как корня четной степени из отрицательного числа не существует, то выражение при четном и отрицательном не имеет смысла.
Например, не имеют смысла выражения
Как мы установили, при любом значении , при котором выражение имеет смысл, верно равенство
(1)
Поэтому равенство (1) является тождеством.
В конце XV в. бакалавр Парижского университета Н. Шюке внес усовершенствования в алгебраическую символику. В частности, знаком корня служил символ (от латинского слова radix — корень).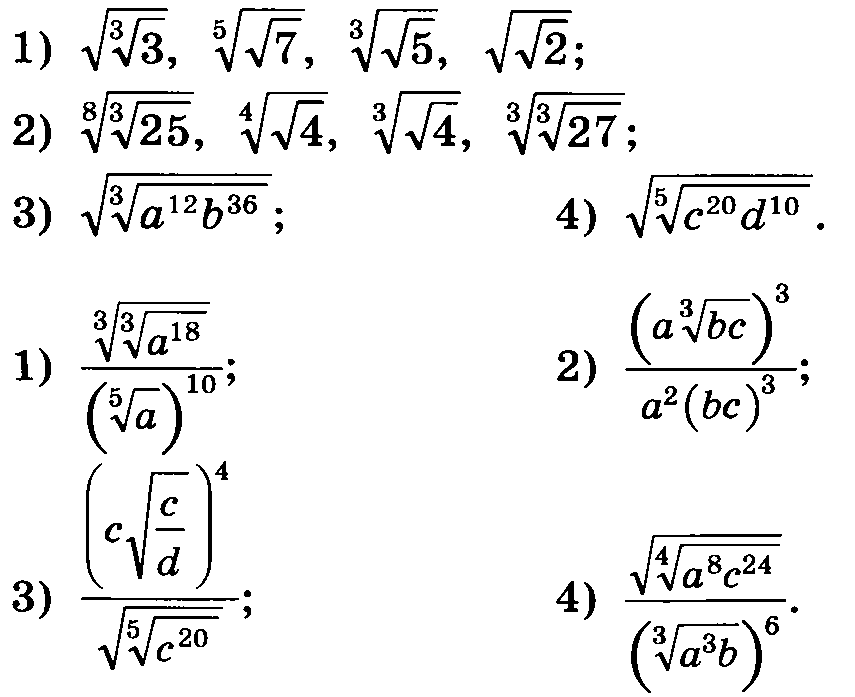 Так, выражение в символике Шюке имело вид
Так, выражение в символике Шюке имело вид
Знак корня в современном виде был предложен в 1525 г. чешским математиком К. Рудольфом. Его учебник алгебры переиздавался до 1615 г., и по нему учился знаменитый математик Л. Эйлер.
Знак еще называют радикалом.
Определение корня n-й степениКорнем степени из числа называется число, степень которого равна .
Например, корнем степени из числа является , потому что . Корнем степени из числа является и , потому что и .
Если нечетное число, то для любого числа существует единственное действительное число, степень которого равна .
Если четное число, то при существуют два действительных числа, степень которых равна . Эти числа являются взаимно противоположными.
Если четное число, при не имеет действительного корня.
Арифметическим корнем степени из числа называется неотрицательное число, степень которого равна . Обозначается и читается так: «корень степени из числа ». Число называется подкоренным числом или подкоренным выражением, — показателем корня. При отрицательный корень четной степени из числа обозначается
Число называется подкоренным числом или подкоренным выражением, — показателем корня. При отрицательный корень четной степени из числа обозначается
Корень нечетной степени из отрицательного числа можно выразить через арифметический корень той же степени. Например,
Если , то
Если нечетное число, то выражение имеет смысл для любого
Если четное число, то выражение имеет смысл только при
При всех значениях имеющего смысл выражения , справедливо
Если нечетное число, Если четное число, то
Пример 1:
Если , то
Пример 2:
Примеры:
- Уравнение с нечетной степенью имеет единственный действительный корень:
- Уравнение не имеет действительных корней, т.к. степень с четным показателем не равна отрицательному числу.
- Уравнение имеет два действительных корня:
Свойство 1.
Если и то,
Корень степени из произведения неотрицательных сомножителей равен произведению корней степени сомножителей.
Пример:
Свойство 2.
Если и то,
Корень из дроби степени с неотрицательным числителем и положительным знаменателем равен отношению корней степени числителя и знаменателя.
Пример:
Свойство 3.
Если — натуральные числа и , то
Пример:
Свойство 4.
Если — натуральные числа и , то
Действительно, при выражения и имеют смысл и их значения неотрицательны. Т.к. то,
Пример:
Свойство 5.
Если натуральные числа и то, . Если показатель корня и показатель степени подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится. Действительно, согласно свойству 4,
Пример:
Пример: Вычислите значение выражения
Вынесение множителя из-под знака контроляПримеры:
Примеры с решением
Пример №1Верно ли, что:
а) б)
Решение:
а) По определению арифметический корень -й степени из неотрицательного числа (—четное число) является неотрицательным числом, -я степень которого равна подкоренному выражению .
Поскольку , то равенство неверное. Верно равенство
б) По определению корень -й степени из числа ( — нечетное число) является числом, -я степень которого равна подкоренному выражению .
Поскольку — верное равенство, то равенство верное.
Пример №2Решить уравнение:
Решение:
а) Решением этого уравнения является такое значение , 3-я степень которого равна 7, т. е. по определению кубического корня имеем:
б) Решением этого уравнения является такое значение х, 4-я степень которого равна 5, т. е. (по определению) — это корень 4-й степени из числа 5. Но из положительного числа 5 существуют два корня четвертой степени, которые равны по модулю и имеют противоположные знаки. Поскольку положительный корень обозначают , то второй корень равен , т. е.
Ответ:
В тетради решение уравнения б) (аналогично и а)) можно записать так:
Решение:
Ответ:
Пример №3Решить уравнение:
Решение:
а) Число 8 — четное, значит, данное равенство является тождеством при , поэтому каждое неотрицательное значение х является решением (корнем) уравнения
б) Число 13 — нечетное, значит, данное равенство является тождеством при любом значении , поэтому решением уравнения является любое действительное число, a R — множество всех его корней.
Ответ:
Пример №4Решить уравнение:
Решение:
Обозначим , тогда получим уравнение
Корни этого уравнения
Таким образом, имеем
откуда (поясните, почему уравнение не имеет корней).
Ответ:
Корень n-ой степени. Тождественные преобразования.
Корень n-ой степени. Тождественные преобразования.
Определение 1. Корнем n-ой степени (nN,n>1) из числа a называется такое число b, n-ая степень которого равна a, то есть bn=a.
Определение 2. Арифметическим корнем n—ой степени (nN,n>1) из числа a называется неотрицательное число b, n-ая степень которого равна a.
Обозначение:.
Свойства корня n –ой степени:
Способы разложения на множители:
Применение формул сокращенного умножения.
Вынесение общего множителя за скобки.
Способ группировки.
Выделение полного квадрата.
Метод неопределённых коэффициентов.
Примеры.
.
Ответ:
Упрощая выражения вида , есть смысл представить выражение в виде квадрата двучлена.
Примеры.
Пусть выражение равно x , тогда
=x3,
Так как , то значение равно 1.
Ответ:1.
х≥0,
0 1
Х
Если 0≤х<1, то
Если х≥1, то
Ответ: х, если 0≤х<1, 1/x, если х≥1.
Задания для устной работы.
1. Найдите значение выражения:
2. При каких значениях переменной имеет смысл выражение:
3. Найдите значение выражения:
4.Вынесите множитель из-под знака корня:
5. Внесите множитель под знак корня:
Внесите множитель под знак корня:
6. Упростите выражение:
7. При каких значениях а верно равенство:
Задания для самоподготовки.
Преобразования выражений, содержащих корень n-ой степени.
Ⅰ.Вычислите:
Ⅱ. Представьте выражение в виде степени с рациональным показателем:
Ⅲ.Упростите выражение:
Ⅳ. Упростите выражение и найдите его значение при b=0,0025
Ⅴ.Известно,что
Во сколько раз а больше b, если оба числа положительные?
Ответы:
I.1)0; 2)9; 3)2; 4)22; 5)19; 6); 7)15; 8);10)2,5; 11) ; ;; 19)-6; 20)-2.
II.
III. 1)3; 2)1; 3); 4)х-1; 5)-1; 6); 7); 8); 11).
IV.-0,05;
V. в 2 раза.
Арифметический корень в математике с примерами решения и образцами выполнения
Если а есть положительное рациональное число, представляющее собой точный квадрат, то арифметический квадратный корень из него есть положительное рациональное число. Например:
Если положительное рациональное число Q не представляет собой точного квадрата, то арифметический квадратный корень из него есть положительное иррациональное число. Например:
суть числа иррациональные.
Сказанное относительно арифметического квадратного корня распространяется соответствующим образом на кубические корни и на корни любой степени. Например:
Корни суть числа иррациональные.
Действительные корни нечетных степеней из отрицательного числа суть числа отрицательные. Например:
Действительных корней четной степени из отрицательных чисел не существует.
Например, не существует такого действительного числа q, чтобы равенство
было справедливым.
В самом деле, будет положительным числом и тогда, когда q положительно, и тогда, когда q отрицательно.
Поэтому т. е. символ не представляет собой никакого действительного числа.
Арифметические корни из степенейОчевидно, что
Правило. Если подкоренное выражение представляет степень положительного числа а и при этом показатель этой степени делится на показатель корня, то арифметический корень будет равен степени, основанием которой служит а, а показателем — частное от деления показателя степени, стоящей под корнем, на показатель корня.
Например,
Действительно,
Примеры:
О выражении
Если а > 0, то
Если же а < 0, то
Во всех случаях
Например,
О выражении
Из определения следует, что
Действительно, пусть
Тогда
Подставляя вместо q равное ему выражение получим
что и требовалось доказать.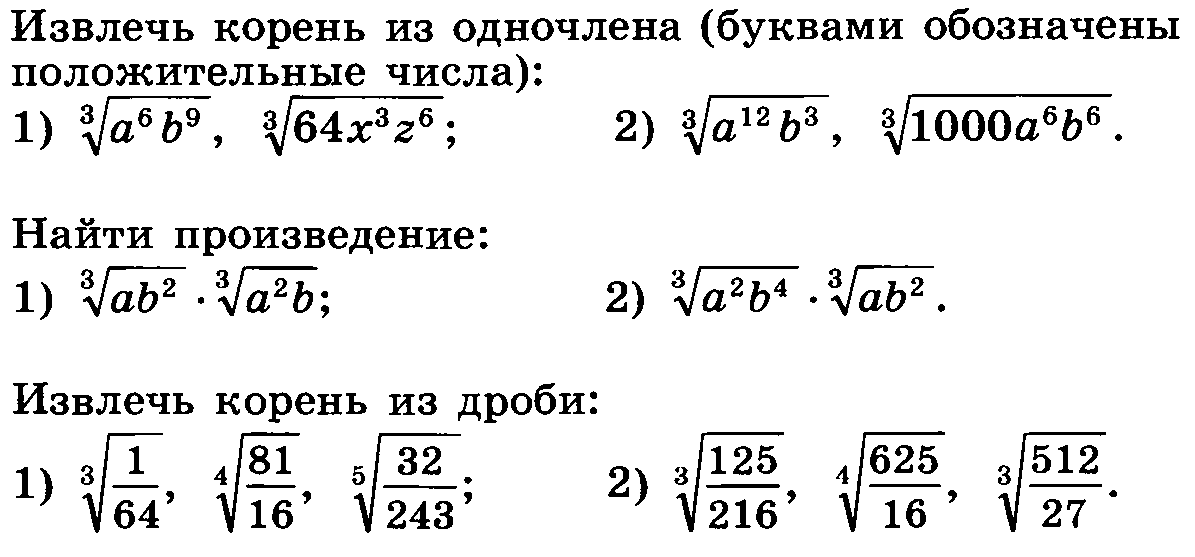
Примеры:
Основное свойство арифметического корня
Вспомогательные предложенияПрежде чем формулировать и доказывать основное свойство арифметического корня, докажем несколько вспомогательных предложений.
Определение:
Если М и N два различных действительных числа, то М> N, если разность М— N есть число положительное.
Предложение 1-е.
Если А > В и m>0, то Am>Вm.
Доказательство:
Разность Am — Вm можно записать в виде
По условию А — В > 0 и m > 0, следовательно, разность Am — Вm есть число положительное, а это и значит, что Am > Вm. Как раз это и требовалось доказать.
Предложение 2-е.
Если а > b и с > d и при этом все числа а, b, с, d положительные, то
Доказательство:
Из того, что а > b и с > 0 следует ас > bc. Из того, что
Из того, что
с > d и b > О следует bc > bd. Из того, что ас>bс и bc>bd следует, что ac>bd, что и требовалось доказать.
Предложение 3-е.
Если х > у и при этом числа х, у— положительные, то > (n — целое положительное число).
Доказательство:
Из того, что х > у и х>0 следует
Из того, что х > у и у > 0 следует
Из того, что и следует
Продолжая аналогичные рассуждения, получим:
что и требовалось доказать.
Предложение 4-е.
Если и числа х и у положительные, то х = у.
Доказательство. Предположим, что х> у, тогда что противоречит условию. Предположим, что у > х, тогда что также противоречит условию. Значит, не может быть, чтобы числа х к у были бы различными. Как раз это и требовалось доказать.
Как раз это и требовалось доказать.
Примечание:
Из равенства не всегда следует равенство х = у. Например, равенство является верным, хотя числа+ 5 и — 5 не равны друг другу.
Формулировка основного свойства арифметического корняАрифметическое значение корня не изменится, если показатель корня умножить на натуральное число, а подкоренное выражение возвысить в степень этого же натурального числа, т. е.
(q и р — натуральные числа и Q 0).
Доказательство:
Очевидно, что (см. стр. 270). Также очевидно, что
Две величины, порознь равные третьей, равны между собой. Поэтому
Но так как числа — положительны, то
что и требовалось доказать.
Примеры:
Основное свойство арифметического корня позволяет нам сокращать показатель корня в тех случаях, когда это возможно.
Примеры:
Основное свойство арифметического корня позволяет нам приводить к общему показателю корни, имеющие разные показатели.
Примеры:
Корни можно заменить соответственно следующими корнями
Корни можно заменить соответственно корнями
Корни можно заменить соответственно корнями
Корни можно заменить соответственно корнями
Чтобы определить, какое из двух чисел, например, или больше, приведем эти корни к общему показателю:
Ясно, что
Действия над арифметическими корнями
УмножениеПроизведение корней, имеющих одинаковые показатели, равно корню с тем же показателем из произведения подкоренных выражений перемножаемых корней, т. е.
(n — число натуральное, а и b — числа положительные).
Доказательство:
Очевидно, что
Tакже очевидно, что
Две величины, порознь равные третьей, равны между собой. Поэтому
Поэтому
Но так как числа положительные, то
что и требовалось доказать.
Совершенно аналогичным путем можно доказать правила для других действий.
Другие действия(Правило деления корней, имеющих одинаковые показатели.)
(Правило возведения корня в степень.)
(Правило извлечения корня из корня.)
Учащемуся предлагается самостоятельно сформулировать и доказать каждое из трех последних правил.
Примечание:
Обратим внимание на то, что равенство
справедливо лишь при условии, что а > 0. (При не будет действительным числом.)
Примеры:
Правило. Чтобы перемножить или разделить корни, имеющие разные показатели, необходимо привести эти корни предварительно к общему показателю.
Примеры:
Запишем равенство в обратном порядке:
Отсюда правило: корень из произведения равен произведению корней из сомножителей.
Пример:
Аналогично
Пример:
Некоторые важные преобразования
Вывод множителей из-под знака корняПусть а и b — положительные числа. Тогда
Рассмотрим выражение
Пусть при делении числа m на n получается в частном k, а в остатке r. Тогда и мы получим
Пусть a — отрицательное число, а b — положительное. Тогда
Итак, если подкоренное выражение разлагается на такие множители, что из некоторых можно извлечь точный корень, то такие множители по извлечении из них корня могут быть выведены из-под знака корня в качестве множителей.
Введение под знак корняПусть а и b — положительные числа. Тогда
Пусть а — отрицательное число, а b — положительное. Тогда
Тогда
Пусть а и b — положительные числа. Тогда
Устранение иррациональности в знаменателе дробиУстранить иррациональность в знаменателе дроби — это значит преобразовать дробь, знаменатель которой содержит корни, к новой дроби, знаменатель которой корней не содержит.
Мы рассмотрим лишь некоторые частные случаи такого преобразования.
а) Случай, когда знаменатель есть корень.
б) Случай, когда знаменатель есть сумма или разность, содержащая квадратные корни.
в) Случай, когда знаменатель есть сумма или разность, содержащая кубические корни.
Устранение иррациональности в числителе дробиУстранить иррациональность в числителе дроби — это значит преобразовать дробь, числитель которой содержит корни, к новой дроби, числитель которой корней не содержат.
Эта операция производится аналогично тому, как и операции, указанные в предыдущем пункте. Например:
Нормальный вид корня
Корень считается приведенным к нормальному виду, если:
1) возможные множители вынесены за знак корня;
2) подкоренное выражение приведено к целому виду;
3) показатель корня и показатель степени подкоренного выражения сделаны взаимно простыми.
Примеры:
Подобные корни и их приведение
Корни называются подобными, если после приведения их к нормальному виду окажутся одинаковыми как их подкоренные выражения, так и показатели корней.
Примеры:
Корни — подобны.
Действительно,
Корни — подобны. Действительно,
Корни подобны. Действительно,
Приведение подобных корнейПримеры:
При извлечении корня из суммы нельзя производить извлечение корней из слагаемых, т. е. нельзя писать
е. нельзя писать
Например:
Отсюда видно, что
Преобразование сложного корня
Выражения вида
называются сложными корнями.
Теорема:
Если а > 0, b > 0 и то верны формулы
Докажем справедливость первой формулы. Очевидно, что
С другой стороны,
Две величины, порознь равные третьей, равны между собой. Поэтому
Основания этих квадратов положительны, а поэтому
что и требовалось доказать.
Совершенно так же доказывается и вторая формула.
Доказанные формулы представляют особый интерес в том случае, когда разность представляет собой точный квадрат. В этом случае сложный корень представляется в виде суммы или разности двух несложных корней. Например:
Замечание:
Корни иногда называют радикалами.
есть радикал n-й степени. Символ eсть знак радикала n-й степени.
Символ eсть знак радикала n-й степени.
Корнем n-й степени из числа а называется всякое число х, n-я степень которого равна а.
Правило нахождения всех значений корня n-й степени из любого числа изложено в гл. «Комплексные числа».
В настоящей главе мы изучали лишь арифметические значения корней.
О возможности нахождения арифметического корня с любой степенью точности
Мы покажем сейчас, что элементарным способом можно находить значение любого арифметического корня с любой степенью точности. Сущность этого способа раскроем на примере хотя бы
Пусть требуется найти Сначала среди чисел 1,0; 1,1; 1,2; 1,3; 1,4; 1,5; 1,6; 1,7; 1,8; 1,9; 2,0 найдем два таких рядом стоящих числа, чтобы куб левого был меньше 2, а куб правого — больше 2.
Очевидно, что Поэтому
Далее Значит,
Наконец, Значит,
Теперь можно сказать, что 1,2 будет приближенным значением с недостатком, а 1,3 с избытком, с точностью до .
Чтобы получить приближенные значения с точностью до , надо испытать числа
Этот процесс можно продолжить как угодно далеко и таким путем получить значение с любой степенью точности.
Изложенный элементарный способ имеет принципиальное значение, но не практическое. Практически пользоваться этим способом крайне неудобно, так как он слишком громоздок. Принципиальное же значение этого способа заключается в том, что он убеждает нас в возможности отыскания значений любого арифметического корня с любой степенью точности.
Для практического же вычисления значений любых арифметических корней существуют другие более удобные способы. Один из этих способов мы встретим в главе «Логарифмы».
Для нахождения приближенных значений часто встречающихся величин можно пользоваться готовыми таблицами. Пример подобной таблицы приведен ниже.
Таблица квадратов, кубов, корней квадратных, корней кубических и обратных величин
Такого рода таблицы, значительно более полные и с более высокой степенью точности, даны, например, в книге Барлоу: «Таблицы квадратов, кубов, корней квадратных, корней кубических и обратных величин».
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Корни квадратного уравнения — Формула, Калькулятор, Примеры
Корни квадратного уравнения ax 2 + bx + c = 0 не что иное, как решения квадратного уравнения. т. е. они являются значениями переменной (x), которая удовлетворяет уравнению. Корни квадратичной функции — это x-координаты x-перехватов функции. Поскольку степень квадратного уравнения равна 2, оно может иметь максимум 2 корня. Мы можем найти корни квадратных уравнений, используя различные методы.
т. е. они являются значениями переменной (x), которая удовлетворяет уравнению. Корни квадратичной функции — это x-координаты x-перехватов функции. Поскольку степень квадратного уравнения равна 2, оно может иметь максимум 2 корня. Мы можем найти корни квадратных уравнений, используя различные методы.
- Факторинг (по возможности)
- Квадратичная формула
- Завершение квадрата
- График (используется для поиска только действительных корней)
Давайте узнаем больше о корнях квадратного уравнения, а также о дискриминанте, природе корней, сумме корней, произведении корней и многом другом вместе с некоторыми примерами.
Корни квадратного уравнения
корней квадратного уравнения — это значения переменной, которые удовлетворяют уравнению. Они также известны как «решения» или «нули» квадратного уравнения. Например, корнями квадратного уравнения x 2 — 7x + 10 = 0 являются x = 2 и x = 5, поскольку они удовлетворяют уравнению. то есть
то есть
- при x = 2, 2 2 — 7(2) + 10 = 4 — 14 + 10 = 0.
- при x = 5, 5 2 — 7(5) + 10 = 25 — 35 + 10 = 0.
Но как найти корни общего квадратного уравнения ax 2 + bx + c = 0? Попробуем решить его относительно x, заполнив квадрат.
топор 2 + Ьх = — с
Деление обеих сторон на «а»,
х 2 + (б/а) х = — в/а
Здесь коэффициент x равен b/a. Половина его равна b/(2a). Его площадь равна b 2 /4a 2 . Добавление b 2 /4a 2 с обеих сторон,
x 2 + (b/a) x + b 2 /4a 2 = (b 2 /4a 2 ) — (c/a)
[ x + (b/2a) ] 2 = (b 2 — 4ac) / 4a 2 (с использованием формулы (a + b)²)
Извлечение квадратного корня с обеих сторон,
х + (b/2a) = ±√ (b² — 4ac) / 4a²
х + (b/2a) = ±√ (b² — 4ac) / 2a
Вычитание b/2a с обеих сторон,
х = (-b/2a) ±√ (b² — 4ac) / 2a (или)
х = (-b ± √ (b² — 4ac))/2a
Это известно как квадратная формула , и ее можно использовать для нахождения любого типа корней квадратного уравнения.
Как найти корни квадратного уравнения?
Процесс нахождения корней квадратных уравнений известен как «решение квадратных уравнений». В предыдущем разделе мы видели, что корни квадратного уравнения можно найти с помощью квадратной формулы. Наряду с этим методом у нас есть несколько других методов нахождения корней квадратного уравнения. Чтобы узнать об этих методах подробно, нажмите здесь. Давайте обсудим каждый из этих методов здесь, решая пример нахождения корней квадратного уравнения x 2 — 7x + 10 = 0 (о котором упоминалось в предыдущем разделе) в каждом случае.Обратите внимание, что в каждом из этих методов уравнение должно иметь стандартный вид ax 2 + bx + c = 0,
.Нахождение корней квадратного уравнения с помощью факторинга
- Фактор левой части.
(х — 2) (х — 5) = 0 - Установите каждый из этих коэффициентов равным нулю и решите.
х — 2 = 0, х — 5 = 0
х = 2, х = 5.
Нахождение корней квадратного уравнения по квадратичной формуле
- Найдите значения a, b и c, сравнив данное уравнение с ax 2 + bx + c = 0.
Тогда a = 1, b = -7 и c = 10 - Подставьте их в квадратную формулу и упростите.
х = [-(-7) ± √((-7)² — 4(1)(10))] / (2(1))
= [ 7 ± √(49 — 40) ] / 2
= [ 7 ± √(9) ] / 2
= [ 7 ± 3 ] / 2
= (7 + 3) / 2, (7 — 3) / 2
= 10/2, 4/2
= 5, 2
Следовательно, х = 2, х = 5.
Нахождение корней квадратного уравнения путем заполнения квадрата
- Заполните квадрат с левой стороны.
(х — (7/2) ) 2 = 9/4 - Решите, извлекая квадратный корень из обеих сторон.
х — 7/2 = ± 3/2
х — 7/2 = 3/2, х — 7/2 = -3/2
х = 10/2, х = 4/2
х = 5, х = 2
Нахождение корней квадратного уравнения с помощью графика
- Постройте график левой части вручную или с помощью графического калькулятора (GDC).

График показан ниже. - Найдите точки пересечения, которые являются не чем иным, как корнями квадратного уравнения.
Следовательно, корни квадратного уравнения равны x = 2 и x = 5 .
Мы можем заметить, что корни квадратного уравнения x 2 — 7x + 10 = 0 равны x = 2 и x = 5 в каждом из методов. Среди этих методов метод факторинга работает только тогда, когда квадратное уравнение факторизуемо; и мы не можем найти комплексные корни квадратного уравнения с помощью графического метода. Таким образом, лучшие методы, которые всегда работают для нахождения корней, — это квадратичная формула и методы завершения квадрата.
Природа корней квадратного уравнения
Природа корней квадратного уравнения говорит о том, «сколько корней имеет уравнение?» и «какой тип корней имеет уравнение?». Квадратное уравнение может иметь:
- два действительных и разных корня
- два сложных корня
- два действительных и равных корня (это означает только один действительный корень)
Например, в приведенном выше примере корни квадратного уравнения x 2 — 7x + 10 = 0 равны x = 2 и x = 5, где 2 и 5 — два разных действительных числа. и поэтому мы можем сказать, что уравнение имеет два действительных и различных корня. Но чтобы найти природу корней, нам на самом деле не нужно решать уравнение. Мы можем определить природу корней, используя дискриминант . Дискриминант квадратного уравнения ax 2 + bx + c = 0 равен D = b 2 — 4ac .
и поэтому мы можем сказать, что уравнение имеет два действительных и различных корня. Но чтобы найти природу корней, нам на самом деле не нужно решать уравнение. Мы можем определить природу корней, используя дискриминант . Дискриминант квадратного уравнения ax 2 + bx + c = 0 равен D = b 2 — 4ac .
Квадратичная формула x = (-b ± √ (b² — 4ac))/2a. Таким образом, это можно записать как x = (-b ± √ D )/2a. Поскольку дискриминант D находится в квадратном корне, мы можем определить природу корней в зависимости от того, является ли D положительным, отрицательным или нулевым.
Природа корней при D > 0
Тогда приведенная выше формула принимает вид
.
х = (-b ± √ положительное число)/2a
и это дает нам два действительных и разных корня. Таким образом, квадратное уравнение имеет два действительных и различных корня, когда b 2 — 4ac > 0,
Природа корней при D
< 0 Тогда приведенная выше формула принимает вид
. х = (-b ± √ отрицательное число)/2a
х = (-b ± √ отрицательное число)/2a
и это дает нам два комплексных корня (которые различны), поскольку квадратный корень из отрицательного числа является комплексным числом.Таким образом, квадратное уравнение имеет два комплексных корня при b 2 — 4ac < 0,
Примечание. Квадратное уравнение не может иметь один комплексный корень. Сложные корни всегда встречаются парами. т. е. если a + bi — корень, то a — bi тоже корень.
Природа корней при D = 0
Тогда приведенная выше формула принимает вид
.
х = (-b ± √ 0)/2a = -b/2a
и, следовательно, уравнение имеет только один действительный корень. Таким образом, квадратное уравнение имеет только один действительный корень (или два равных корня -b/2a и -b/2a), когда b 2 — 4ac = 0.
Сумма и произведение корней квадратного уравнения
Мы видели, что корнями квадратного уравнения x 2 — 7x + 10 = 0 являются x = 2 и x = 5.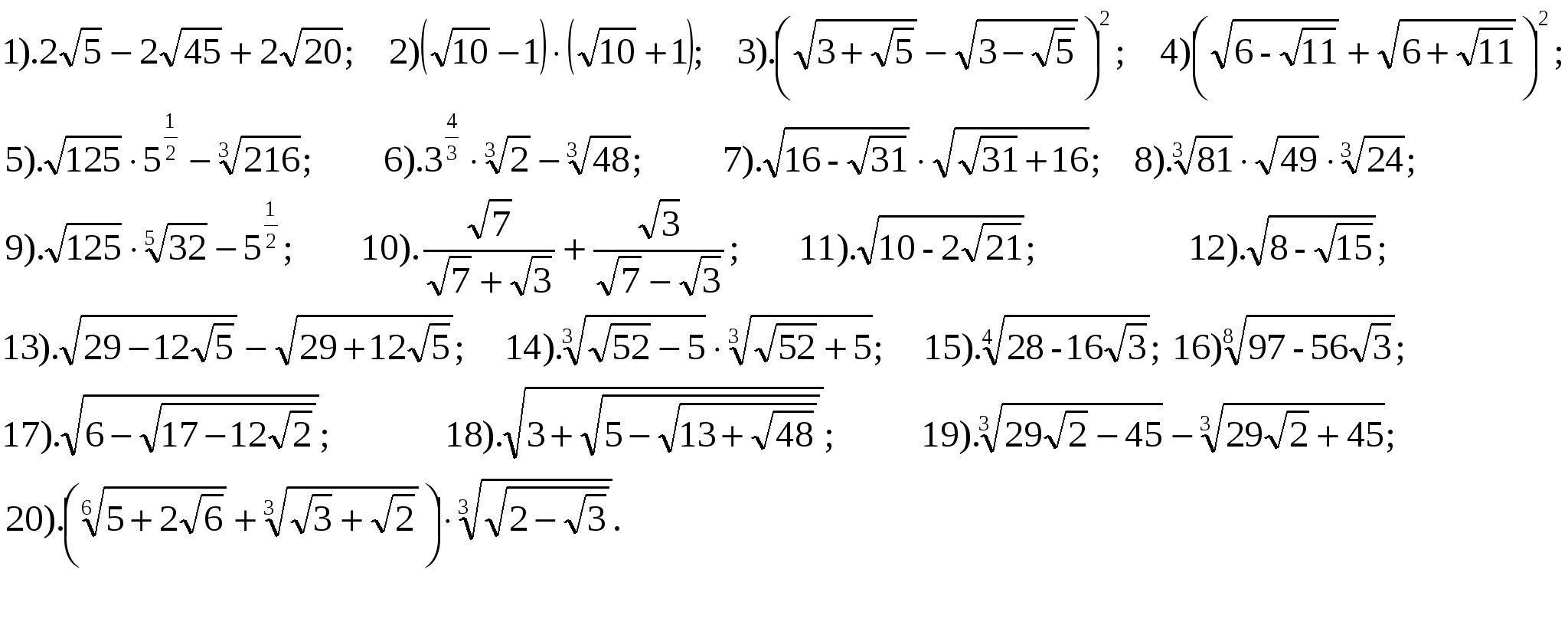 Таким образом, сумма его корней = 2 + 5 = 7, а произведение его корней = 2 × 5 = 10. Но сумму и произведение корней квадратного уравнения ax 2 + bx + c = 0 можно найти без фактического вычисления корней. Давайте посмотрим, как.
Таким образом, сумма его корней = 2 + 5 = 7, а произведение его корней = 2 × 5 = 10. Но сумму и произведение корней квадратного уравнения ax 2 + bx + c = 0 можно найти без фактического вычисления корней. Давайте посмотрим, как.
Мы знаем, что корнями квадратного уравнения ax 2 + bx + c = 0 по квадратной формуле являются (-b + √ (b² — 4ac))/2a и (-b — √ (b² — 4ac))/ 2а.Обозначим их через x₁ и x₂ соответственно.
Сумма корней квадратного уравнения
Сумма корней = x₁ + x₂
= (-b + √ (b² — 4ac))/2a + (-b — √ (b² — 4ac))/2a
= -б/2а — б/2а
= -2б/2а
= -б/а
Следовательно, сумма корней квадратного уравнения ax 2 + bx + c = 0 равна -b/a.
Для уравнения x 2 — 7x + 10 = 0, сумма корней = -(-7)/1 = 7 (что было суммой фактических корней 2 и 5).
Произведение корней квадратного уравнения
Произведение корней = x₁ · x₂
= (-b + √ (b² — 4ac))/2a · (-b — √ (b² — 4ac))/2a
= (-b/2a) 2 — (√b² — 4ac / 2a) 2 (по формуле a² — b²)
= б 2 / 4а 2 — (б 2 — 4ас) / 4а 2
= б 2 / 4а 2 — б 2 / 4а 2 + 4ас / 4а 2
= 4ас / 4а 2
= к/к
Следовательно, произведение корней квадратного уравнения ax 2 + bx + c = 0 равно c/a.
Для уравнения x 2 — 7x + 10 = 0, произведение корней = 10/1 = 10 (которое было произведением фактических корней 2 и 5).
Важные формулы, относящиеся к корням квадратных уравнений:
Для квадратного уравнения ax 2 + bx + c = 0,
- Корни вычисляются по формуле x = (-b ± √ (b² — 4ac))/2a.
- Дискриминант, D = b 2 — 4ac.
Если D > 0, то уравнение имеет два действительных и различных корня.
Если D < 0, уравнение имеет два комплексных корня.
Если D = 0, уравнение имеет только один действительный корень. - Сумма корней = -b/a
- Произведение корней = c/a
Темы, относящиеся к корням квадратных уравнений:
Часто задаваемые вопросы о корнях квадратного уравнения
Что такое корни квадратного уравнения?
Корни квадратного уравнения ax 2 + bx + c = 0 — это значения переменной (x), которые удовлетворяют уравнению. Например, корни уравнения x 2 + 5x + 6 = 0 равны -2 и -3.
Например, корни уравнения x 2 + 5x + 6 = 0 равны -2 и -3.
Как найти корни квадратного уравнения?
Корни квадратного уравнения ax 2 + bx + c = 0 можно найти с помощью квадратной формулы x = (-b ± √ (b² — 4ac))/2a. В качестве альтернативы, если квадратное выражение можно разложить на множители, мы можем разложить его на множители и установить множители равными нулю, чтобы найти корни.
Какие три типа корней корней квадратного уравнения?
Квадратное уравнение ax 2 + bx + c = 0 может иметь:
- два действительных и различных корня, когда b 2 — 4ac > 0.
- два сложных корня при b 2 — 4ac < 0,
- два действительных и равных корня при b 2 — 4ac = 0.
Как определить природу корней квадратного уравнения?
Характер корней квадратного уравнения ax 2 + bx + c = 0 определяется его дискриминантом D = b 2 — 4ac.
- Если D > 0, уравнение имеет два действительных и различных корня.
- Если D < 0, уравнение имеет два комплексных корня.
- Если D = 0, уравнение имеет два равных действительных корня.
Как найти корни квадратного уравнения, заполнив квадрат?
Чтобы найти корни квадратного уравнения ax 2 + bx + c = 0, заполнив квадрат, сначала заполните квадрат с левой стороны. Затем найдите x, извлекая квадратный корень с обеих сторон.
Как найти корни квадратного уравнения с помощью квадратной формулы?
Квадратная формула говорит, что корни квадратного уравнения ax 2 + bx + c = 0 равны x = (-b ± √ (b² — 4ac))/2a.Чтобы решить любое квадратное уравнение, приведите к стандартной форме ax 2 + bx + c = 0, найдите значения a, b и c, подставьте их в квадратную формулу и упростите.
Могут ли оба корня квадратного уравнения быть нулями?
Да, оба корня квадратного уравнения могут быть нулями. Например, два корня квадратного уравнения x 2 = 0 равны 0 и 0,
Например, два корня квадратного уравнения x 2 = 0 равны 0 и 0,
Как найти корни квадратного уравнения с помощью факторинга?
Чтобы найти корни квадратного уравнения ax 2 + bx + c = 0, разложите его левую часть на множители, приравняйте каждый из множителей к нулю и решите.
Как найти сумму и произведение корней квадратного уравнения?
Для любого квадратного уравнения ax 2 + bx + c = 0,
- сумма корней = -b/a
- произведение корней = c/a
График функций квадратного корня и кубического корня — видео и расшифровка урока
Преобразования функций
Обратите внимание, что две упомянутые нами неосновные функции являются алгебраическими функциями основных функций.Эти алгебраические вариации соответствуют перемещению графика функции различными способами и называются преобразованиями.
Существует четыре типа преобразований.
Горизонтальный
Смещает график влево или вправо. Это соответствует добавлению или вычитанию числа c из x в функции. Если мы складываем c , мы сдвигаем график c единиц влево, а если мы вычитаем c , то мы сдвигаем график c единиц вправо.
Это соответствует добавлению или вычитанию числа c из x в функции. Если мы складываем c , мы сдвигаем график c единиц влево, а если мы вычитаем c , то мы сдвигаем график c единиц вправо.
Пример: 3, добавленная к x в y = 2√( x + 3), соответствует смещению графика y = √( x ) на 3 единицы влево.
Растягивание/сжатие
Растягивает или сжимает график по вертикали или горизонтали. Это соответствует умножению всей функции на число c или просто переменной x на число c . Если мы умножим всю функцию на c , то мы растянем график по вертикали в c раз, если c > 1, и сожмем график по вертикали в c раз, если 0 < c < 1.Если мы умножим только переменную x на c , то мы растянем график по горизонтали в c раз, если 0 < c < 1, и мы сожмем график по горизонтали в c раз, если c > 1.
Пример: 2, умноженное на √( x ) в y = 2√( x + 3) соответствует растяжению графика y 9056 x 90 по вертикали с коэффициентом 2.
Отражение
Отражает график по осям x или y .Это соответствует умножению на минус. Если мы умножим всю функцию на минус, то мы отразим график по оси x , а если мы умножим только переменную x на минус, то мы отразим график по оси y .
Пример: Отрицательное значение в y = -3√( x ) — 4 соответствует отображению графика y = 3√( x ) по оси x .
По вертикали
Смещает график вверх или вниз.Это соответствует добавлению или вычитанию числа c из функции. Если к функции добавить c , то мы сдвинем график вверх на c единиц. Если из функции вычесть c , то мы сдвинем график вниз на c единиц.
Пример: вычитание 4 из y = -3√( x ) — 4 соответствует смещению графика y = 3√( x ) вниз на 4 единицы.
Графики с преобразованиями
Чтобы построить графики неосновных функций квадратного корня и кубического корня, мы можем использовать следующие шаги:
- Определите алгебраические операции с соответствующими преобразованиями.
- Возьмите график базовой функции через эти преобразования в порядке горизонтали, отражения, растяжения/сжатия и вертикали.
Давайте воспользуемся этими шагами и преобразованиями для построения графика неосновных функций, о которых мы упоминали ранее. Во-первых, рассмотрим y = 2√( x + 3). Первый шаг состоит в том, чтобы идентифицировать алгебраические операции с соответствующими преобразованиями. Как вы помните, мы делали это в примерах горизонтальных трансформаций и трансформаций растяжения/сжатия.
Теперь мы просто возьмем базовый граф y = √( x ) через эти преобразования.
Не так уж сложно, не так ли? Давайте посмотрим на пример с кубическим корнем: y = -3√( x ) — 4. Во-первых, мы идентифицируем наши преобразования, которые мы сделали в примере с отражением и вертикальном примере.
Во-первых, мы идентифицируем наши преобразования, которые мы сделали в примере с отражением и вертикальном примере.
Теперь мы просто возьмем базовый граф y = 3√( x ) через эти преобразования.
Та-да! У нас есть наш график!
Итоги урока
Хорошо, давайте на минутку повторим, что мы узнали. Функция квадратного корня — это функция с переменной под квадратным корнем. Точно так же функция корня куба — это функция с переменной под корнем куба. Самыми основными из этих функций являются √( x ) и 3√( x ) соответственно, и мы можем легко построить график этих основных функций, нанеся несколько точек и соединив их.
Небазовые функции квадратного и кубического корня представляют собой алгебраические манипуляции с базовыми функциями. Эти алгебраические операции соответствуют графическим преобразованиям, и мы можем использовать эти преобразования для построения графиков этих неосновных функций квадратного корня и кубического корня. Преобразования включают следующее:
Преобразования включают следующее:
- Горизонтальное , которое сдвигает график влево или вправо
- Растягивание/сжатие , которое растягивает или сжимает график по вертикали или горизонтали
- Reflection , который отражает график по осям x или y
- Вертикальный , который сдвигает график вверх или вниз
Зная эти преобразования, мы можем графически изобразить функции квадратного и кубического корня, выполнив следующие два шага:
- Определите алгебраические операции с соответствующими преобразованиями.
- Возьмите график базовой функции через эти преобразования в порядке горизонталь, отражение, растяжение/сжатие, вертикаль.
Это делает построение графиков неосновных функций квадратного корня и кубического корня почти таким же простым, как построение графика основных функций, и это здорово, поскольку эти неосновные функции часто встречаются в различных областях математики, а также в реальных приложениях.
тестов статистической значимости
тестов статистической значимостиPPA 696 МЕТОДЫ ИССЛЕДОВАНИЯ
ТЕСТЫ НА ЗНАЧИМОСТЬ
Что такое тесты на значимостьшагов в тестировании для статистики Значение
1) Сформулируйте исследовательскую гипотезу
2) Сформулируйте нулевую гипотезу
3) Ошибки типа I и типа II
Выберите вероятность уровня ошибки (альфа-уровень)
4) Тест хи-квадрат
Вычислить хи-квадрат
степеней свободы
Распределительные столы
Интерпретация результатов
5) Т-тест
Рассчитать Т-тест
степеней свободы
Распределительные столы
Интерпретация результатов
Отчетные тесты статистических Значение
Заключительные комментарии Что такое тесты значимости
- Возникают два вопроса о любых гипотетических отношениях. между двумя переменными:
- 1) какова вероятность того, что связь существует;
- 2) если да, то насколько сильна связь

Тесты на статистическую значимость используются для решения вопрос: какова вероятность того, что то, что мы думаем, является отношением между двумя переменными на самом деле просто случайность?
Если мы выбрали много образцов из одной и той же популяции, найдем ли мы такое же отношение между этими двумя переменными в каждый образец? Если бы мы могли провести перепись населения, разве мы найти, что эта связь существует в популяции, из которой выборка был нарисован? Или наша находка обусловлена только случайностью?
Тесты на статистическую значимость говорят нам, что Вероятность состоит в том, что отношения, которые, как мы думаем, мы обнаружили, обусловлены только к случайному.Они говорят нам, какова вероятность того, что мы ошибемся, если предположим, что обнаружили, что связь существует.
Мы никогда не можем быть на 100 % уверены, что отношения
существует между двумя переменными. Слишком много источников ошибок, чтобы
например, ошибка выборки, предвзятость исследователя, проблемы с
надежность и валидность, простые ошибки и т. д.
д.
Но, используя теорию вероятностей и нормальную кривую, мы можем оценить вероятность ошибиться, если предположим, что наш вывод отношения верны.Если вероятность ошибиться мала, то мы говорим, что наше наблюдение взаимосвязи является статистически значимым найти.
Статистическая значимость означает наличие хорошего шанс, что мы правы, находя, что связь существует между две переменные. Но статистическая значимость не то же самое, что практическая значение. Мы можем получить статистически значимый результат, но последствия этого вывода могут не иметь практического применения.Исследователь необходимо всегда проверять как статистическую, так и практическую значимость любых результатов исследования.
Например, мы можем обнаружить, что статистически
значимая связь между возрастом гражданина и удовлетворенностью
услуги городского отдыха. Возможно, пожилые граждане на 5% менее удовлетворены
чем более молодые граждане с городскими рекреационными услугами. Но 5% большой
достаточная разница для беспокойства?
Но 5% большой
достаточная разница для беспокойства?
Часто, когда различия небольшие, но статистически
значителен, это связано с очень большим размером выборки; в образце меньшего размера
размер, различия не были бы достаточными, чтобы быть статистически значимыми.
2) Сформулируйте нулевую гипотезу
3) Выберите уровень вероятности ошибки (альфа-уровень)
4) Выберите и рассчитайте критерий статистической значимости
5) Интерпретация результатов
1) Сформулировать исследовательскую гипотезу
- Гипотеза исследования утверждает ожидаемую взаимосвязь между двумя переменными.Он может быть изложен в общих чертах или может включать размеры направления и величины. Например,
- Общее: продолжительность программы профессионального обучения связана со ставкой
трудоустройства стажеров.

- Направление: Чем дольше программа обучения, тем выше скорость работы размещение стажеров.
- Масштабы: более длительные программы обучения позволят в два раза большему числу слушателей задания в виде более коротких программ.
- Общее: на оплату помощника выпускника влияет пол.
- Направление: Помощникам выпускников-мужчинам платят больше, чем выпускникам-женщинам помощники.
- Величина: ассистенты выпускников получают менее 75% от зарплаты мужчин. ассистенты выпускников оплачиваются.
2) Сформулируйте нулевую гипотезу 90 714
- Нулевая гипотеза обычно утверждает, что связи нет между двумя переменными.Например,
- Нет никакой связи между продолжительностью программы профессионального обучения и уровень трудоустройства стажеров.
- Зарплата помощника выпускника не зависит от пола.
- Нулевая гипотеза может также утверждать, что отношение
предложенная в исследовании гипотеза не соответствует действительности.
 Например,
Например,
- В более длительных программах обучения будет задействовано такое же или меньшее количество слушателей. задания в виде более коротких программ.
- Помощникам выпускников-женщин платят не менее 75% от зарплаты выпускников-мужчин. помощники оплачиваются.
3) ОШИБКИ ТИПА I И ТИПА II
Даже в самом лучшем исследовательском проекте всегда есть вероятность (надеюсь, небольшая) того, что исследователь совершит ошибку относительно связи между двумя переменными. Есть два возможных ошибки или ошибки.
Первая называется ошибкой типа I.Это происходит, когда исследователь предполагает, что связь существует, когда на самом деле доказательства в том, что это не так. При ошибке типа I исследователь должен принять нулевую гипотезу и отклонить исследовательскую гипотезу, но происходит обратное. Вероятность совершения ошибки первого рода называется альфа.
Вторая ошибка называется ошибкой второго рода. Это происходит когда исследователь предполагает, что отношения не существует, когда в на самом деле доказательство того, что это так.При ошибке типа II исследователь должен отвергнуть нулевую гипотезу и принять гипотезу исследования, но происходит наоборот. Вероятность совершения ошибки II рода называется бета.
Как правило, снижение вероятности совершения ошибка типа I увеличивает вероятность совершения ошибки типа II и наоборот, уменьшая вероятность совершения ошибки второго рода. увеличивает вероятность совершения ошибки первого рода.
Исследователи обычно стараются свести к минимуму ошибки типа I,
потому что, когда исследователь предполагает, что отношения существуют, когда на самом деле
нет, все может быть хуже, чем раньше. При ошибках II рода исследователь
упускает возможность подтвердить, что отношения существуют, но не
хуже, чем раньше.
При ошибках II рода исследователь
упускает возможность подтвердить, что отношения существуют, но не
хуже, чем раньше.
- В этом примере, какой тип ошибки вы бы предпочли совершить?
- Гипотеза исследования: Эль-Ниньо снизил урожайность сельскохозяйственных культур в графстве X, в результате чего он имеет право на государственную помощь при стихийных бедствиях.
- Нулевая гипотеза: Эль-Ниньо не снизил урожайность в графстве X, что делает он не имеет права на государственную помощь при стихийных бедствиях.
Если совершена ошибка типа II, то округ
считается непригодным для оказания помощи при стихийных бедствиях, хотя на самом деле имеет право
(нулевая гипотеза должна быть принята, но она отвергнута). Правительство
могут не тратить средства на помощь при стихийных бедствиях, когда это необходимо, и фермеры могут уйти
в банкротство.
Правительство
могут не тратить средства на помощь при стихийных бедствиях, когда это необходимо, и фермеры могут уйти
в банкротство.
- В этом примере, какой тип ошибки вы бы предпочли совершить?
- Гипотеза исследования: новый препарат лучше лечит сердечные приступы, чем старый наркотик
- Нулевая гипотеза: новый препарат лечит сердечные приступы не лучше, чем старый наркотик
Если совершена ошибка типа II, то новый препарат
предполагается не лучше, когда оно действительно лучше (нулевая гипотеза
следует отвергнуть, но он принимается). Людей нельзя лечить
новый препарат, хотя им было бы лучше, чем со старым.
ВЫБЕРИТЕ ВЕРОЯТНОСТЬ УРОВНЯ ОШИБКИ (АЛЬФА-УРОВЕНЬ)
Исследователи обычно указывают вероятность совершения ошибка типа I, которую они готовы принять, т. е.е., значение альфа.
В социальных науках большинство исследователей выбирают альфа = 0,05. Это означает
что они готовы принять вероятность 5% сделать Тип I
ошибка предположения, что связь между двумя переменными существует, когда она
на самом деле нет. Однако в исследованиях, связанных с общественным здравоохранением, альфа-
0,01 не является чем-то необычным. Исследователи не хотят иметь вероятность
ошибаться более чем в 0,1% случаев, или один раз из тысячи.
е.е., значение альфа.
В социальных науках большинство исследователей выбирают альфа = 0,05. Это означает
что они готовы принять вероятность 5% сделать Тип I
ошибка предположения, что связь между двумя переменными существует, когда она
на самом деле нет. Однако в исследованиях, связанных с общественным здравоохранением, альфа-
0,01 не является чем-то необычным. Исследователи не хотят иметь вероятность
ошибаться более чем в 0,1% случаев, или один раз из тысячи. Если связь между двумя переменными
сильная (согласно оценке с помощью показателя ассоциации) и выбранный уровень
для альфы.05, то средние или малые размеры выборки обнаружат его. В виде
однако отношения становятся слабее и/или по мере того, как уровень альфы становится меньше,
потребуются большие размеры выборки, чтобы исследование достигло статистической
значение.
4) Тест хи-квадрат
Для номинальных и порядковых данных используется хи-квадрат. тест на статистическую значимость. Например, мы предполагаем, что существует представляет собой взаимосвязь между типом посещаемой учебной программы и успешность трудоустройства стажеров. Мы собираем следующие данные:
Мы собираем следующие данные: | Посещенный вид обучения: | Номер посещающего обучение |
| Профессиональное образование | 200 |
| Обучение навыкам работы | 250 |
| Итого | 450 |
| Устроились на работу? | Количество стажеров |
| Да | 300 |
| № | 150 |
| Итого | 450 |
Для расчета хи-квадрата таблица, показывающая сустав необходимо распределение двух переменных:
Таблица 1.Трудоустройство по типу обучения (наблюдаемые частоты)
Устроен на работу? | Тип обучения | ||
| Профессиональный Образование | Рабочие навыки Обучение | Всего | |
| Да | 175 | 125 | 300 |
| № | 25 | 125 | 150 |
| Всего | 200 | 250 | 450 |
Хи-квадрат вычисляется путем рассмотрения различных
части стола. «Ячейками» таблицы являются квадраты посередине.
таблицы, содержащей полностью закрытые числа. Клетки
содержат частоты, возникающие при совместном распределении двух
переменные. Частоты, которые мы действительно находим в данных, называются
«наблюдаемые» частоты.
«Ячейками» таблицы являются квадраты посередине.
таблицы, содержащей полностью закрытые числа. Клетки
содержат частоты, возникающие при совместном распределении двух
переменные. Частоты, которые мы действительно находим в данных, называются
«наблюдаемые» частоты.
В этой таблице ячейки содержат частоты для стажеров профессионального образования, устроившихся на работу (n=175) и не устроившихся устроиться на работу (n=25), а частота стажеров профессиональных навыков, получивших работающие (n=125) и не устроившиеся на работу (n=125).
Столбцы и строки «Всего» таблицы показывают предельные частоты. Предельные частоты – это частоты, которые мы бы нашли, если бы рассматривали каждую переменную отдельно. Например, мы видим в колонке «Всего» 300 человек, которые получили работу и 150 человек, которые этого не сделали. В строке «Всего» мы видим, что было 200 человек на профессиональном обучении и 250 человек на профессиональных навыках обучение.
Наконец, общее количество наблюдений
во всей таблице, названной Н. В этой таблице N=450.
В этой таблице N=450.
Вычислить хи-квадрат
1) отображать наблюдаемые частоты для каждой ячейки2) рассчитать ожидаемые частоты для каждой ячейки
3) рассчитать для каждой ячейки ожидаемую минус наблюдаемую частоту в квадрате, деленное на ожидаемую частоту
4) все результаты по всем ячейкам
Чтобы найти значение хи-квадрат, мы сначала предполагаем что нет никакой связи между типом посещаемой программы обучения и был ли стажер принят на работу.Если мы посмотрим на итог столбца, мы видим, что 300 из 450 человек нашли работу, или 66,7% от общего числа людей на учебе нашел работу. Мы также видим, что 150 из 450 человек не найти работу, или 33,3% от общего числа обучающихся не нашли работу.
Если между типом участие в программе и успех в поиске работы, то можно было бы ожидать 66,7% слушателей обоих видов программ обучения устроились на работу, а 33,3% обоих типов учебных программ, чтобы не получить работу.
Первое, что делает Хи-квадрат, это вычисляет
«ожидаемые» частоты для каждой ячейки. Ожидаемая частота – это частота
которые мы ожидали бы увидеть в каждой ячейке, если бы не было связи
между типом программы обучения и трудоустройством.
Ожидаемая частота – это частота
которые мы ожидали бы увидеть в каждой ячейке, если бы не было связи
между типом программы обучения и трудоустройством.
Способ расчета ожидаемой частоты ячеек состоит в том, чтобы умножить сумму столбца для этой ячейки на сумму строки для этой ячейке и разделить на общее количество наблюдений для всей таблицы.
Для ячейки в верхнем левом углу умножьте 200 на 300 и разделите
на 450=133,3
Для ячейки в нижнем левом углу умножьте 200 на 150 и разделите
на 450=66,7
Для ячейки в верхнем правом углу умножьте 250 на 300 и разделите
на 450=166,7
Для ячейки в нижнем правом углу умножьте 250 на 150 и разделите
на 450=83,3
Таблица 2. Трудоустройство по типу обучения (ожидаемая периодичность)
Устроен на работу? | Тип обучения | ||
| Профессиональный Образование | Рабочие навыки Обучение | Всего | |
| Да | 133. 3 3 | 166,7 | 300 |
| № | 66,7 | 83,3 | 150 |
| Всего | 200 | 250 | 450 |
В этой таблице показано распределение «ожидаемых» частот, то есть частоты ячеек, которые мы ожидали бы найти, если бы не было связи между видом обучения и трудоустройством.
Обратите внимание, что хи-квадрат ненадежен, если какая-либо ячейка в таблице непредвиденных обстоятельств имеет ожидаемую частоту менее 5.
Чтобы рассчитать хи-квадрат, нам нужно сравнить исходный,
наблюдаемые частоты с новыми, ожидаемыми частотами. Для каждой ячейки,
производим следующие расчеты:
а) Вычесть значение наблюдаемой частоты из значения
ожидаемая частота
б) возвести результат в квадрат
в) результат разделить на значение ожидаемой частоты
Для каждой ячейки выше,
| ф д — ф о | (ф и — ф или ) 2 | [(ф е — ф o ) 2 ] / ф е | Результат |
(133. 3 — 175) 3 — 175) | (133,3 — 175) 2 | [(133,3 — 175) 2 ] / 133,3 | 13.04 |
| (66,7–25) | (66,7 — 25) 2 | [(66,7–25) 2 ] / 66,7 | 26.07 |
| (166,7 — 125) | (166,7–125) 2 | [(166,7 — 125) 2 ] / 166.7 | 10,43 |
| (83,3 — 125) | (83,3 — 125) 2 | [(83,3 — 135) 2 ] / 83,3 | 20,88 |
Чтобы вычислить значение хи-квадрат, сложите результаты для каждой ячейки — итого = 70,42.
СТЕПЕНИ СВОБОДЫ
Мы не можем интерпретировать значение статистики хи-квадрат. сам по себе.Вместо этого мы должны поместить его в контекст. Теоретически значение статистики хи-квадрат
нормально распределяется; то есть значение статистики хи-квадрат
выглядит как нормальная (колоколообразная) кривая. Таким образом, мы можем использовать свойства
нормальной кривой для интерпретации значения, полученного в результате нашего расчета
статистики Хи-квадрат.
Таким образом, мы можем использовать свойства
нормальной кривой для интерпретации значения, полученного в результате нашего расчета
статистики Хи-квадрат.
Если значение, которое мы получаем для хи-квадрата, достаточно велико, то можно сказать, что это указывает на уровень статистической значимости при котором можно предположить, что связь между двумя переменными существует.
Однако достаточно ли велико значение, зависит на двух вещах: размере таблицы непредвиденных обстоятельств, из которой Хи-квадрат статистика рассчитана; и уровень альфы, который мы выбрали.
Чем больше размер таблицы непредвиденных обстоятельств, тем больше значение хи-квадрат должно быть, чтобы достичь статистического значимость при прочих равных условиях. Аналогично, чем строже уровень альфы, тем больше должно быть значение Chi Square, для достижения статистической значимости при прочих равных условиях.
Термин «степени свободы» используется для обозначения
размер таблицы непредвиденных обстоятельств, на которой значение хи-квадрат
статистика подсчитана. Степени свободы рассчитываются как
произведение (количество строк в таблице минус 1) умножить на (количество
столбцов в таблице минус ).
Степени свободы рассчитываются как
произведение (количество строк в таблице минус 1) умножить на (количество
столбцов в таблице минус ).
- Для таблицы с двумя строками ячеек и двумя столбцами ячеек формула это:
- df = (2 — 1) х (2 — 1) = (1) х (1) = 1
- Для таблицы с двумя строками ячеек и тремя столбцами ячеек формула это:
- df = (3 — 1) х (2 — 1) = (2) х (1) = 2
- Для таблицы с тремя строками ячеек и тремя столбцами ячеек формула это:
- df = (3 — 1) х (3 — 1) = (2) х (2) = 4

При сообщении об уровне альфа-канала обычно
сообщается как «меньше» некоторого уровня с использованием знака «меньше чем» или <. Таким образом, сообщается как p<0,05 или p<0,01; если вы не
сообщая точное значение p, например, p=.04 или р=0,22.
РАСПРЕДЕЛИТЕЛЬНЫЕ СТОЛЫ
Как только мы получим рассчитанное значение хи-квадрата статистика, и степени свободы для таблицы непредвиденных обстоятельств, и желаемый уровень для альфы, мы можем найти нормальное распределение для Чи Квадрат в столе. В текстах статистики доступно множество таблиц для этой цели.В таблице найдите степени свободы (обычно перечислены в столбце внизу страницы).Далее находим нужный уровень альфы (обычно перечисляются в строке вверху страницы). Найди пересечение степеней свободы и уровня альфа, и что значение, которому вычисленный хи-квадрат должен быть равен или превышать, чтобы достичь Статистическая значимость.
Например, для df=2 и p=0,05 хи-квадрат должен
равен или превышает 5,99, чтобы указать, что отношения между двумя
переменных, вероятно, не случайно. Для df=4 и p=.05, площадь Чи
должен быть равен или превышать 9,49.
Для df=4 и p=.05, площадь Чи
должен быть равен или превышать 9,49.
ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ
Если вычисленное значение хи-квадрата равно или превышает значение, указанное в таблице для данного уровня альфы и градусов свободы, то исследователь может предположить, что наблюдаемая связь между двумя переменными существует (при заданном уровне вероятности ошибки, или альфа), и отклонить нулевую гипотезу. Это дает поддержку к исследовательской гипотезе. Вычисленное значение хи-квадрат на заданном уровне
альфа и с заданной степенью свободы, является типом измерения «годен-не годен».
Это не похоже на меру ассоциации, которая может варьироваться от 0,0 до (плюс
или минус) 1,0, и которые можно интерпретировать в любой точке распределения.
Либо вычисленное значение хи-квадрата достигает требуемого уровня для
статистической значимости или нет.
- Важно отметить, что Хи-квадрат, как и другие тесты на статистическую значение:
- 1) не указывает на силу связи между двумя переменными
- 2) не указывает направление связи между двумя переменными
- 3) не указывает на вероятность ошибки первого рода
- 4) не учитывает достоверность и достоверность исследования
- 5) не предоставляет абсолютных, убедительных доказательств родства
- 1) сформулировать исследовательскую гипотезу:
- Существует взаимосвязь между типом посещаемой учебной программы и успех трудоустройства стажеров
- 2) сформулировать нулевую гипотезу:
- Нет никакой связи между типом посещаемой программы обучения и успешность трудоустройства стажеров
- 3) рассчитать тест на статистическую значимость
- Хи-квадрат=70.
 42
42 - 4) рассчитать степени свободы таблицы непредвиденных обстоятельств
- дф=1
- 5) выбираем уровень альфы
- р=0,05
- 6) найдите значение хи-квадрата в таблице при p=0,05 и df=1 .
- Хи-квадрат=3,84
- 7) интерпретировать результат
- Вычисленное значение хи-квадрата (70,42) превышает значение в таблице. для р=.05 и df=1 (хи-квадрат=3,84). Следовательно, мы можем отказаться от нуля гипотезу (с 5% вероятностью ошибки) и принять гипотезу исследования что существует взаимосвязь между типом пройденной учебной программы и успешность трудоустройства стажеров.
Резюмируя приведенный выше пример:
Использование T-тестов
- Т-тесты — это тесты на статистическую значимость, которые используются с данными об интервалах и уровнях отношения. Т-тесты могут быть использованы в нескольких различные виды статистических тестов:
- 1) проверить, есть ли различия между двумя группами на одном и том же переменная, основанная на среднем (среднем) значении этой переменной для каждой группы; например, учащиеся частных школ получают более высокие баллы на тесте SAT чем учащиеся государственных школ?
- 2) чтобы проверить, является ли среднее (среднее) значение группы больше или меньше, чем
какой-то стандарт; например, это средняя скорость автомобилей на автомагистралях в г.
 Калифорния выше 65 миль в час?
Калифорния выше 65 миль в час? - 3) проверить, имеют ли одна и та же группа разные средние (средние) баллы по разные переменные; например, те же клерки более продуктивны на Компьютеры IBM или Macintosh?
Чтобы вычислить значение t,
а) сформулировать исследовательскую гипотезу;б) сформулировать нулевую гипотезу;
c) указать, будет ли t-критерий односторонним или двусторонним тест на значимость
г) выберите уровень альфы
д) рассчитать т
Чтобы вычислить значение t,
- а) сформулировать исследовательскую гипотезу;
- Средняя заработная плата ассистентов выпускников-мужчин выше средней зарплата ассистентов женского пола в CSULB.
- б) сформулировать нулевую гипотезу;
- Нет разницы в средней зарплате выпускника мужского и женского пола помощники в CSULB.
- в) выбрать уровень альфы
- выберите значение альфа-канала, например, p=0,05, p=0,01 или p=0,001
Как и другие статистические данные, t-критерий имеет распределение
которое приближается к нормальному распределению, особенно если размер выборки
больше 30. Зная свойства нормальной кривой, мы
может ли он сказать нам, как далеко от среднего значения распределения наши вычисленные
t-счет.
Зная свойства нормальной кривой, мы
может ли он сказать нам, как далеко от среднего значения распределения наши вычисленные
t-счет.
Нормальная кривая имеет среднее значение, равное нулю, со стандартным отклонением, равным единице. Т-показатель может падать по нормальной кривой либо выше, либо ниже среднего; то есть либо плюс либо минус какой-то стандартный единицы отклонения от среднего.
Значение t должно быть далеко от среднего, чтобы достичь статистической значимости.То есть он должен сильно отличаться от значение среднего распределения, что-то, что имеет только низкий вероятность случайного возникновения, если нет связи между две переменные. Если мы выбрали значение p=0,05 для альфы, мы смотрим для значения t, попадающего в крайние 5% распределения.
Если у нас есть гипотеза, утверждающая ожидаемое
направление результатов, например, что заработная плата аспиранта-мужчины
выше, чем зарплата ассистента-женщины, то мы ожидаем, что рассчитанная
t-показатель попадает только в один конец нормального распределения. Мы ожидаем
расчетный t-показатель попадает в крайние 5% распределения.
Мы ожидаем
расчетный t-показатель попадает в крайние 5% распределения.
Если у нас есть гипотеза, которая утверждает только что есть некоторая разница между двумя группами, но не указывается, какая ожидается, что группа будет иметь более высокий балл, чем рассчитанный t-показатель может попасть в любой конец нормального распределения. Например, наша гипотеза Возможно, мы ожидаем найти разницу между средней заработной платой мужчин и женщин-выпускников-ассистентов (но мы не знаем, какие будет выше, а что ниже).
Для гипотезы, которая не указывает направления, нам нужно
использовать «двусторонний» t-критерий. То есть мы должны искать значение t, которое
попадает в любой из крайних концов («хвостов») распределения.
Но поскольку t может попасть в любой хвост, если мы выберем p = 0,05 для альфа, мы
должны разделить 5% на две части по 2-1/2% каждая. Итак, двусторонний тест
требует, чтобы t принимало более экстремальное значение, чтобы достичь статистической значимости
чем односторонний тест t.
д) рассчитать т
T-показатель рассчитывается путем сравнения среднего значение некоторой переменной, полученное для двух групп; расчет также включает дисперсия каждой группы и количество наблюдений в каждой группе. Например,
Таблица 3. Заработная плата ассистентов выпускников мужского и женского пола в CSULB
| Помощники выпускников мужского пола | Ассистент женского пола | |
| Количество наблюдений | 403 | 132 |
| Среднее | 17 095 долларов | 14 885 долларов |
| Стандарт Отклонение | 6329 | 4676 |
| Разница | 40045241 | 21864976 |
Для расчета t,
1) вычесть среднее значение второй группы из среднего значения первой
группа
2) рассчитать для каждой группы дисперсию, деленную на количество
наблюдения минус 1
3) сложите вместе результаты, полученные для каждой группы на втором шаге
4) извлеките квадратный корень из результатов третьего шага
5) разделить результаты первого шага на результаты четвертого шага
Например,
- 1) вычесть среднее значение второй группы из среднего значения первой группы
- 17095-14885=2210
- 2) рассчитать для каждой группы дисперсию, деленную на количество наблюдений минус 1
- Помощники выпускников мужского пола:
- [40056241 / (403-1)] = [40056241 / (402)] = 99642
- Ассистент женского пола:
- [21864976 / (132-1)] = [21864976 / (131)] = 166908
- 3) сложите результаты, полученные для каждой группы на втором шаге, вместе
- 99642+166908=266550
- 4) извлеките квадратный корень из результатов третьего шага
- квадратный корень из 266550=516.
 28
28 - 5) разделить результаты первого шага на результаты четвертого шага
- 2210/516,28=4,28
f) рассчитать степени свободы
г) ищите значение в таблице
h) интерпретировать значение t
Степени свободы
- Степени свободы для t-теста рассчитываются путем сложения количество наблюдений для каждой группы, а затем вычитание числа два (потому что есть две группы).Например, (403 + 132 — 2) = 533
Раздача Т
Значения t печатаются в таблицах в большинстве статистик. тексты. Значения степеней свободы перечислены в столбце вниз стороне, а значения альфа (значение p) перечислены в строке поперек вершина. Существуют разные таблицы для односторонних и двусторонних тестов. т.- Найдите правильную таблицу количества решек. потом
найти пересечение степеней свободы и значения альфа
в таблице.Это значение является значением, которое должен иметь рассчитанный t-показатель.
 равны или превышают, чтобы указать статистическую значимость.
равны или превышают, чтобы указать статистическую значимость.
- Для одностороннего теста t с df = 533 и p = 0,05 t должно быть равно или превышать 1.645.
- Для двустороннего теста t с df = 533 и p = 0,05 t должно быть равно или превышать 1.960.
Интерпретировать значение t
Если вычисленный t-показатель равен или превышает значение t, указанных в таблице, то исследователь может сделать вывод, что существует является статистически значимой вероятностью того, что связь между две переменные существуют и не случайны, и отвергают нуль гипотеза.Это подтверждает гипотезу исследования.В этом примере вычисленный t-показатель 4,28 превышает табличное значение t, поэтому мы можем отвергнуть нулевую гипотезу об отсутствии связи между полом аспиранта и оплатой аспиранта, и вместо этого принять гипотезу исследования и сделать вывод о наличии связи между полом аспиранта и оплатой аспиранта.
Помните, однако, что это только одна статистика,
на основе только одной выборки в один момент времени из одного исследовательского проекта. Это не абсолютное, окончательное доказательство того, что связь существует, а скорее
подтверждение исследовательской гипотезы. Это только одно доказательство,
которые необходимо учитывать наряду со многими другими доказательствами в отношении
тот же предмет.
Это не абсолютное, окончательное доказательство того, что связь существует, а скорее
подтверждение исследовательской гипотезы. Это только одно доказательство,
которые необходимо учитывать наряду со многими другими доказательствами в отношении
тот же предмет.
ОТЧЕТНЫЕ ИСПЫТАНИЯ СТАТИСТИЧЕСКИХ ЗНАЧЕНИЕ
- В отчетах об исследованиях тесты статистической значимости сообщается тремя способами. Во-первых, результаты теста могут быть сообщены в текстовом обсуждении результатов.Включая:
- 1) гипотеза
- 2) используемая тестовая статистика и ее значение
- 3) степеней свободы
- 4) значение для альфа (p-значение)
- Например,
- Работники организаций с неавторитарным управлением Было обнаружено, что стили имеют более высокий уровень удовлетворенности работой, чем рабочие. в организациях с авторитарным стилем управления (Квадрат Хи=50.57, df=4, p<0,05).
- Средняя заработная плата ассистентов-выпускников-мужчин выше, чем у
ассистенты выпускников (t = 4,28, df = 533, p <0,05).

- Различий в показателях трудоустройства между профессиональными образованиями выявлено не было. программы и программы рабочих навыков (хи-квадрат=1,2, df=1, p>0,05).
Второй способ сообщения результатов испытаний для статистической значимости должен сообщить тест и его значение, градусы свободы и p-значение в нижней части таблицы непредвиденных обстоятельств или распечатки показать данные, на которых основывались расчеты.
Таблица 1. Трудоустройство по типу обучения (наблюдаемая частота)
Устроен на работу? | Тип обучения | ||
| Профессиональный Образование | Рабочие навыки Обучение | Всего | |
| Да | 175 | 125 | 300 |
| № | 25 | 125 | 150 |
| Всего | 200 | 250 | 450 |
 42, df=1, p<0,05
42, df=1, p<0,05 Таблица 3. Заработная плата ассистентов выпускников мужского и женского пола в CSULB
| Помощники выпускников мужского пола | Ассистент женского пола | |
| Количество наблюдений | 403 | 132 |
| Среднее | 17 095 долларов | 14 885 долларов |
| Стандарт Отклонение | 6329 | 4676 |
| Разница | 40045241 | 21864976 |
Третий способ отчета о тестах статистической значимости
заключается в том, чтобы включить их в таблицы, отображающие результаты расширенного анализа
данных, включая ряд переменных. Например, вот некоторые
результаты исследования пожилых латиноамериканских женщин в Эль-Пасо, Техас, и Лонг-Бич,
Калифорния.
Например, вот некоторые
результаты исследования пожилых латиноамериканских женщин в Эль-Пасо, Техас, и Лонг-Бич,
Калифорния.
Таблица 4. Характеристики участников семинара в возрасте 40 лет и старше
| Характеристики | Эль-Пасо (N=83) | Лонг-Бич (N=131) | значение т |
| Средний возраст | 60.5 лет | 68,7 лет | 2,1* |
| Этническая самоидентификация Американец мексиканского происхождения | 97,2 | 89,7 | 0,9 |
| Выбор языка Только испанский | 68,5 | 52. | 3,2** |
**t значимо при p<0,01
Заключительные комментарии
Тесты на статистическую значимость используются для оценки вероятность того, что взаимосвязь, наблюдаемая в данных, имела место только случайно; вероятность того, что переменные действительно не связаны между собой Население. Их можно использовать для фильтрации бесперспективных гипотез.Тесты на статистическую значимость используются, потому что они представляют собой общий критерий, который может быть понят очень многими людей, и они сообщают важную информацию об исследовательском проекте которые можно сравнить с результатами других проектов.
Однако они не гарантируют, что исследование
был тщательно разработан и выполнен. На самом деле тесты на статистическую значимость
может ввести в заблуждение, потому что это точные цифры.Но у них нет отношений
к практической значимости результатов исследования.
Наконец, всегда нужно использовать меры ассоциации вместе с тестами на статистическую значимость. Последние оценивают вероятность того, что отношения существуют; в то время как первые оценивают сила (а иногда и направление) отношений. У каждого есть свой использовать, и лучше всего их использовать вместе.
Что такое энный корень?
Что такое n-й корень числа?
«Корень n-й степени» числа — это число, которое умножается само на себя «n» раз, чтобы получить начальное значение.
-й корень представлен символом n √ . Чтобы найти n-й корень числа, мы должны найти это число, умножение которого на n раз само по себе дает число, для которого мы должны найти n-й корень.
Следовательно, число, умноженное само на себя n раз, является корнем n-й степени данного числа.
Здесь n может быть любым числом 2, 3, 4, 5 …… и т. д.
Объяснение степени n-го корня в алгебре
Например, Найдите корень n-й степени из «а» или можете сказать: найти n √a
Это просто (1/n) -й корень числа, такой же, как квадратный корень, тогда это 1/2 корня и кубический корень, тогда это 1/3 корня. Следовательно, n-й корень может быть представлен как 1/n экспоненциально.
Следовательно, n-й корень может быть представлен как 1/n экспоненциально.
В показателях мы можем представить это как n √a = a 1/n
2 nd корень квадратный √y x √y = y 1/2 x y 1/2 = y
3 rd корень кубический ∛y x ∛y x ∛y = y 1/3 x y 1/3 x y 1/3 = y
n th корень является n-м корнем. n √y x n √y x n √y x…… n √y (n раз) = y
Вместо использования 4 th , 5 th и т. д.как правило, мы можем использовать n th .
Использование корня n th является общим способом записи корней, это может быть 2 nd root (квадратный корень), 3 rd root (кубический корень), 4 th root, 5 th root и т.д.
| Примеры корня | Имя корня | Уравнение |
|---|---|---|
| Второй корень | Квадратный корень | √y x √y = y1/2 x y1/2 = y |
| Корень 3-й степени | Кубический корень | ∛y x ∛y x ∛y = y1/3 x y1/3 x y1/3 = y |
| n-й корень | n-й корень | n√y x n√y x n√y x…… n√y (n раз) = y |
n-й корень Пример
Как найти энный корень числа
Пример: Найдите «n» в этом вопросе.
п √32 = 2
Решение: Значение n √32 равно 2. Итак, мы должны разложить 32 на множители 2.
32 = 2 × 2 × 2 × 2 × 2
п √32 = 2
n √2 × 2 × 2 × 2×2 = 2
2 умножается здесь 5 раз, чтобы получить 32.
Следовательно, значение n равно 5.
n
th Корневые свойстваКак умножать и делить корневые функции n-й степени.
Свойства умножения и деления
Как складывать и вычитать корневые функции n-й степени.
Свойства сложения и вычитания
Связь между корнями и показателями Корень с одной стороны от равенства до «=» может быть заменен на показатель степени с другой стороны от равенства с «=».
Если = n √y, то x = y n .
Например: n √81 = 3
, значит, 81 = 3 4 .
энный корень единства
Корень n-й степени из единицы — это комплексное число, которое равно 1, если его возвести в степень положительного целого числа. (1/12)
(1/12)
N-й корень — объяснение, символ, метод нахождения, свойства и часто задаваемые вопросы Здесь n — положительное целое число, иногда называемое степенью корня.Корень степени 2 известен как квадратный корень, а корень степени 3 известен как кубический корень. Корни более высокой степени также упоминаются с использованием обычных чисел, таких как корень четвертой степени, корень пятой степени, корень двадцатой степени и т. Д. Вычисление корня n-й степени является извлечением корня.
Например, 4 — это квадратный корень из 2, так как 22 = 4, а −2 — это также квадратный корень из 4, так как (−2)2 = 4.
\[\sqrt{x} \times \ sqrt{x} = x\] Здесь квадратный корень используется дважды при умножении, чтобы получить исходное значение.
\[\sqrt[3]{x} \times \sqrt[3]{x} = x\] Здесь кубический корень используется трижды при умножении для получения исходного значения.
\[\sqrt[n]{x} \times \sqrt[n]{x} . . . \sqrt[n]{x} = x\] Здесь n-й корень используется n раз при умножении, чтобы получить исходное значение.
(Изображение будет загружено в ближайшее время)
Определение N-го корня
Напомним, что k является квадратным корнем из y тогда и только тогда, когда k² = y. Точно так же k является кубическим корнем из y тогда и только тогда, когда k³ = y. Например, 5 — это кубический корень из 125, потому что 5³ = 125.Давайте разберемся с определением n-го корня с помощью этой концепции.
Пусть n — целое число больше 1, тогда y является корнем n-й степени x тогда и только тогда, когда yⁿ = x.
Например, -1/2 — это корень 5-й степени из -1/32, как (-1/2)⁵ = -1/32. Корню n не присваивается никаких специальных имен, кроме квадратного корня (где n = 2) и кубического корня (где n = 3). Другие корни n-й степени известны как корень четвертой степени, корень пятой степени и так далее.
Символ N-го корня
Символ, используемый для представления n-го корня: \[\sqrt[n]{x}\].Это радикальный символ, используемый для квадратного корня с маленькой буквой n для определения корня n-й степени.
В выражении \[\sqrt[n]{x}\] n называется индексом, а x называется подкоренным числом.
Как найти корень N-й степени числа?
Корень числа n-й степени можно вычислить с помощью метода Ньютона. Давайте разберемся, как найти n-й корень числа «A», используя метод Ньютона.
Начните с начального предположения x 0 , а затем повторите, используя рекуррентное соотношение.{n-1}}\].
Например, чтобы найти корень четвертой степени из 16, обратите внимание, что 2⁴ = 16 и, следовательно, x = 2, n = 4 и y = 2 в приведенной выше формуле. Это дает:
\[\sqrt[5]{34} = \sqrt[5]{32 + 2} \приблизительно 2 + \frac{2}{5,16} = 2,025\]. Погрешность аппроксимации составляет всего около 0,03%.
Когда существует N-й корень?
В вещественной системе счисления
Если n — четное целое число, корень n-й степени из x существует всякий раз, когда x положителен и для всех x. {x/y}\]
{x/y}\]
В каждом положительном действительном числе есть ровно один положительный корень n-й степени.{2} = -1\]
По правилу \[\sqrt[n]{x} \sqrt[n]{y} = \sqrt[n]{xy}\], строго справедливо для не- только отрицательные вещественные подкоренные числа, его использование приводит к неравенству на шаге 1 выше.
Факты, которые необходимо запомнить
Корень n-й степени из 0 равен 0 для всех положительных целых чисел n, так как 0 n равно 0.
Корень n-й степени из 1 играет важную роль в различных областях математики, таких как теория чисел, теория уравнений и т. д.{6}}\]
Шаг 4: 2xy 2
Корни с более высоким индексом | Пурпурная математика
Пурпурная математика
Операции с кубическими корнями, корнями четвертой степени и другими корнями с более высоким индексом работают аналогично квадратным корням, хотя в некоторых местах нам нужно немного расширить наше мышление.
Упрощение терминов с более высоким индексом Я объясню, как мы идем.
Я объясню, как мы идем.На предыдущих страницах мы упростили квадратные корни, убрав из радикала все множители, встречающиеся в наборах по два.Для второго корня нам нужна была вторая копия.
Для корней с более высоким индексом мышление такое же. Если у нас есть кубический корень, мы можем убрать любой множитель, который встречается в наборах по три; в четвертом корне мы убираем любой множитель, который встречается в наборах из четырех; в пятом корне мы убираем любой множитель, который встречается в наборах из пяти; и так далее. Например:
Справка по математике.ком
Упростить
Раньше я мог извлечь из квадратного корня все, что у меня было в двух экземплярах.
 Точно так же теперь я могу извлечь из четвертого корня все, что у меня есть в четырех экземплярах. Так как 16 = 2 4 , то:
Точно так же теперь я могу извлечь из четвертого корня все, что у меня есть в четырех экземплярах. Так как 16 = 2 4 , то:Упростить кубический корень:
Я извлекаю кубический корень. Затем я могу вытащить из радикала любой фактор, который встречается три раза.Так как 8 = 2 3 , то этот радикал полностью упростится.
Упростить кубический корень:
Мой первый шаг — это полностью разложить на множители:
54 = 2 · 27 = 2 · (3 · 3 · 3)
У меня есть три копии числа 3, поэтому я могу извлечь число 3 из кубического корня, оставив число 2 внутри.

Упростить:
Опять же, я начинаю с факторинга:
48 = 3 · 16 = 3 · 2 · 2 · 2 · 2
У меня есть четыре копии множителя 2, но это кубический корень, поэтому я могу вытащить двойку только для трех из этих копий.3 и четвертая 2 останутся внутри корня.
Упростить:
Я знаю, что 27 = 3 3 , поэтому кубический корень упростится до целого числа. Тогда я закончу умножением.
Упростить:
Внутри этого радикала мне дали переменные, но процесс работает так же, как и всегда.
 Я беру корень пятой степени, поэтому я могу вытащить из корня все, для чего у меня есть пять копий.
Я беру корень пятой степени, поэтому я могу вытащить из корня все, для чего у меня есть пять копий.32 равно 2 5 , так что это получится из радикала. x 10 = ( x 2 ) 5 , поэтому получится x 2 . y 6 = ( y 5 )( y 1 ), так что я смогу вытащить y , оставив внутри корня 6 y
.И Z 7 = ( Z 5 ) ( Z 2 ), поэтому я смогу вытащить Z , оставив Z 2 внутри.Моя работа выглядит так:
Примечание. Когда вы упрощаете подкоренные выражения с переменными, если радикал представляет собой корень с четным индексом (например, квадратный корень или корень из четвертой степени), они, вероятно, укажут, что вы должны «предполагать, что все переменные неотрицательны».
 (или «положительно»).Это делается для того, чтобы не принимать во внимание, нужны ли в вашем ответе столбцы абсолютных значений. Если вы не уверены, о чем я говорю, проверьте здесь.
(или «положительно»).Это делается для того, чтобы не принимать во внимание, нужны ли в вашем ответе столбцы абсолютных значений. Если вы не уверены, о чем я говорю, проверьте здесь.
Умножение корней с более высоким индексомУпростите выражение кубического корня:
Это умножение работает так же, как умножение квадратных корней, в том смысле, что произведение двух одинаковых корней с более высоким индексом может быть преобразовано в корень с более высоким индексом произведения.Затем упрощаю обычным образом.
Упростите продукт:
В данном случае мне дали произведение корней четвертой степени. Я могу превратить произведение радикалов в радикал произведения.
 Тогда я могу упростить.
Тогда я могу упростить.
Добавление корней с более высоким индексомУпростить:
Оба члена в этом выражении являются кубическими корнями, но я могу объединить их, только если они являются кубическими корнями одного и того же значения.Сейчас это не так. Так что я сначала упрощу радикалы, а потом посмотрю, смогу ли я пойти дальше.
Замечу, что 8 = 2 3 и 64 = 4 3 , так что я действительно смогу полностью упростить радикалы.
Упростить:
Второй радикал я никак не могу упростить.Но я могу упростить первый радикал, потому что 81 = 3 4 = (3 3 )(3).
 Таким образом, я получу сумму двух третьих корней из трех, которые я могу объединить.
Таким образом, я получу сумму двух третьих корней из трех, которые я могу объединить.
Деление корней с более высоким индексомУпростить кубический корень:
Знаменатель представляет собой куб, то есть 27 = 3 3 , поэтому я могу легко упростить и получить «рациональный» знаменатель:
Упростить кубический корень:
Это похоже на предыдущее упражнение, но здесь в числителе стоит куб (то есть 27).Я не могу правильно упростить это выражение, потому что я не могу упростить радикал в знаменателе до целых чисел:
Чтобы рационализировать знаменатель, содержащий квадратный корень, мне понадобились две копии любых множителей внутри радикала.
 Для кубического корня мне понадобится три копии. Вот что я умножу на эту дробь.
Для кубического корня мне понадобится три копии. Вот что я умножу на эту дробь.У меня один экземпляр с делителем 5 в знаменателе.Я умножу сверху и снизу на кубический корень из 25, что даст две дополнительные копии 5, которые мне нужны, чтобы рационализировать знаменатель.
Возможно, это окончательное выражение ненамного «проще» исходного выражения. В этом контексте «упростить» означает «рационализировать знаменатель». Часто «правильный» ответ будет ненамного, если вообще «проще», чем то, с чего вы начали.
Упростить:
Поскольку 72 = 8 × 9 = (2 × 2 × 2) × (3 × 3), у меня есть только три двойки и две тройки. Другими словами, при нынешнем состоянии дроби мне не хватит ни одного из множителей знаменателя, чтобы избавиться от радикала.

Чтобы извлечь что-либо из корня четвертой степени, мне потребуется по четыре копии каждого множителя.Для радикала этого знаменателя мне понадобятся еще две тройки и еще одна двойка. Итак, я умножу верхнюю и нижнюю части на корень четвертой степени из 3 · 3 · 2 = 18.
Вы можете использовать приведенный ниже виджет Mathway, чтобы попрактиковаться в работе с выражениями с более высоким индексом. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/radicals6.htm
Рациональный тест корней — ChiliMath
Тест на рациональные корни (также известный как теорема о рациональных нулях) позволяет нам найти все возможные рациональные корни многочлена.
 Предположим, что a является корнем многочлена P\left( x \right), что означает, что P\left( a \right) = 0. Другими словами, если мы подставим a в многочлен P\left( x \right) и получим нуль , 0 означает, что входное значение является корнем функции.
Предположим, что a является корнем многочлена P\left( x \right), что означает, что P\left( a \right) = 0. Другими словами, если мы подставим a в многочлен P\left( x \right) и получим нуль , 0 означает, что входное значение является корнем функции.Но как нам найти возможный список рациональных корней? Вот как это работает в двух словах!
Ключевые идеи Rational Roots Test
Предположим, у нас есть многочлен P\left( x \right) с целыми коэффициентами и ненулевым постоянным членом:
Тогда каждый рациональный корень P\left( x \right) имеет вид:
Лучший способ изучить этот метод — взглянуть на несколько примеров!
Примеры поиска рациональных корней полинома с помощью теста рациональных корней
Пример 1: Найдите рациональные корни приведенного ниже многочлена, используя тест рациональных корней.
Нахождение рациональных корней (также известных как рациональные нули) многочлена аналогично нахождению рациональных точек пересечения по оси x.

- Начните с определения постоянного члена a 0 и старшего коэффициента a n .
- Определите положительные и отрицательные факторы каждого из них.
Факторы постоянного члена, {a_0} = 6\,\,:\,\, \pm \,\left( {1,2,3,6} \right)
Факторы старшего члена, {a_n} = 3\,\,:\,\, \pm \,\left( {1,3} \right)
- Запишите список возможных рациональных корней, найдя {p \over q}, которое представляет собой просто отношение множителей постоянного члена и старшего члена .Убедитесь, что вы отслеживаете возможные комбинации.
Вот как я это делаю . Я беру каждый числитель и делю его на все знаменатели. Затем я перехожу к следующему числителю и снова делю на все знаменатели. Я продолжаю повторять этот процесс, пока не пройду все числители. Это гарантирует, что мы рассмотрели все возможные комбинации.

БОЛЬШОЕ Внимание : После того, как вы запишете все комбинации, упростите дроби, чтобы избавиться от дубликатов.
Итак, это числа без дубликатов , которые мы будем проверять как возможные корни. У нас есть двенадцать (12) возможных кандидатов для проверки.
- Помните, что если a является корнем многочлена P\left( x \right), то P\left( a \right) = 0. Теперь проверим каждое число.
- Следовательно, рациональные корни многочлена
это
Вот график полинома, показывающий, где он пересекает или касается оси x.На самом деле это x-пересечения многочлена.
Пример 2: Найдите рациональные корни приведенного ниже полинома, используя тест рациональных корней.
Постоянный член равен a 0 = –2 и его возможные множители равны p = ± 1, ± 2. Для старшего коэффициента имеем a n = 4 и его множители равны q = ± 1, ± 2, ± 4.




 Например,
Например, 42
42 Калифорния выше 65 миль в час?
Калифорния выше 65 миль в час? 28
28 равны или превышают, чтобы указать статистическую значимость.
равны или превышают, чтобы указать статистическую значимость.
 3
3 Я объясню, как мы идем.
Я объясню, как мы идем. Точно так же теперь я могу извлечь из четвертого корня все, что у меня есть в четырех экземплярах. Так как 16 = 2 4 , то:
Точно так же теперь я могу извлечь из четвертого корня все, что у меня есть в четырех экземплярах. Так как 16 = 2 4 , то:
 Я беру корень пятой степени, поэтому я могу вытащить из корня все, для чего у меня есть пять копий.
Я беру корень пятой степени, поэтому я могу вытащить из корня все, для чего у меня есть пять копий. (или «положительно»).Это делается для того, чтобы не принимать во внимание, нужны ли в вашем ответе столбцы абсолютных значений. Если вы не уверены, о чем я говорю, проверьте здесь.
(или «положительно»).Это делается для того, чтобы не принимать во внимание, нужны ли в вашем ответе столбцы абсолютных значений. Если вы не уверены, о чем я говорю, проверьте здесь. Тогда я могу упростить.
Тогда я могу упростить. Таким образом, я получу сумму двух третьих корней из трех, которые я могу объединить.
Таким образом, я получу сумму двух третьих корней из трех, которые я могу объединить. Для кубического корня мне понадобится три копии. Вот что я умножу на эту дробь.
Для кубического корня мне понадобится три копии. Вот что я умножу на эту дробь.
 Предположим, что a является корнем многочлена P\left( x \right), что означает, что P\left( a \right) = 0. Другими словами, если мы подставим a в многочлен P\left( x \right) и получим нуль , 0 означает, что входное значение является корнем функции.
Предположим, что a является корнем многочлена P\left( x \right), что означает, что P\left( a \right) = 0. Другими словами, если мы подставим a в многочлен P\left( x \right) и получим нуль , 0 означает, что входное значение является корнем функции.