Тема решение квадратных уравнений по формуле алгебра 8 класс

Тема: Решение квадратных уравнений по формуле. Алгебра, 8 класс.

Учитель математики: Башарова Ольга Геннадьевна

Цель урока: Вывести формулу для вычисления корней квадратного уравнения с четным вторым коэффициентом и способствовать усвоению этой формулы в ходе выполнения упражнений.

Урок изучения нового материала и первичного закрепления новых знаний.

Ход урока: 1) Оргмомент.

2) Проверка д/з

№ 434(4) 1учащийся на доске выполняет решение.

№ 434(2;6) самопроверка по слайду. (Приложение, слайд 2,3)

3 учащихся получают карточки с заданиями.

Образец задания на карточке: а) Вычислите дискриминант квадратного уравнения:

5х²-3х-1=0

б) Решите квадратное уравнение: 3х²-х-2=0

-х²+5х=0

Как называется последнее уравнение?

3) Актуализация опорных знаний:

-Как называются уравнения, решения которых вы выполняли дома?

-Какие уравнения называются квадратными? Приведите примеры.

-Назовите формулу дискриминанта.

-Назовите формулу корней квадратного уравнения.

-Как корни квадратного уравнения зависят от дискриминанта?

У вас на партах лежат распечатанные таблицы. Посмотрите внимательно на задание и заполните свои таблицы.

Сравните ваше решение со слайдом. (Слайд 4)

Кто безошибочно определил количество корней квадратного уравнения?

4) Создание проблемной ситуации:

Решите уравнение: 4х²-36х+77=0

Почему решение заняло довольно много времени? (Большие коэффициенты).

Что же делать? Можно ли как-нибудь решение сделать проще? Оказывается да, но при одном условии, что второй коэффициент — четное число.

5) Выход из проблемной ситуации:

Запишем тему урока: решение квадратных уравнений с четным вторым коэффициентом.

Итак, выведем формулу вычисления корней квадратного уравнения с четным вторым коэффициентом.

Назовите формулу квадратного уравнения. (Слайд 5)

Какова формула четного числа? (в=2m, где m-целое число).

Значит, наше уравнение приобретает вид ах²+2mх+с=0. Найдем его дискриминант Д=4m²-4ас=4(m²-ас). Знак произведения 4(m²-ас) зависит от знака выражения m²-ас. Следовательно, вывод о числе корней уравнения можно сделать по знаку выражения m²-ас. Назовем его сокращенным дискриминантом и обозначим Д

1=m²-ас.

Если дискриминант является положительным числом, то по общей формуле корней квадратного уравнения получим: _1,2=

Если в=2m, то Подставим значение m в формулу:

, где

Решим теперь наше уравнение по новой формуле: 4х²-36х+77=0 (Слайд 6)

Упростилось решение?

6) Закрепление пройденного материала:

а) Совместное выполнение задания по учебнику №444(1,3)

б) Расположите полученные корни всех уравнений по возрастанию и, воспользовавшись ключом в таблице, расшифруйте имя ученого. Решаем эти уравнения по формуле, с которой познакомились сегодня. (Слайд 7,8)

7) Рефлексия:

— Как называется формула, с которой вы сегодня познакомились?

-Назовите ее.
— Когда можно ее использовать?

— Назовите формулу сокращенного дискриминанта.

8) Подведение итогов. Выставление отметок.

Д/з: 1 группа: №444(2,4), 435(2,3) (Слайд 9)

2 группа: №435(2,3), 3х²+13х=2х²-х-49, (х+6)²=8(3х+8)

Для всех: уравнение №3 из последнего задания решить еще 2-мя способами.

Решение квадратных уравнений с помощью дискриминанта.

Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.

С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».

Какие же квадратные уравнения называются полными? Это уравнения вида ах² + b x + c = 0, где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.

D = b² – 4ас .

В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.

Если дискриминант отрицательное число (D < 0),то корней нет.

Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),

тогда х₁ = (-b — √D)/2a ,  и  х₂ = (-b + √D)/2a .

Например. Решить уравнение х² – 4х + 4= 0.

D = 4² – 4 · 4 = 0

x = (- (-4))/2 = 2

Ответ: 2.

Решить уравнение 2х² + х + 3 = 0.

D = 1² – 4 · 2 · 3 = – 23

Ответ: корней нет.

Решить уравнение 2х² + 5х – 7 = 0.

D = 5² – 4 · 2 · (–7) = 81

х₁ = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5

х₂ = (-5 + √81)/(2·2) = (-5 + 9)/4=1

Ответ: – 3,5 ; 1.

Итак представим решение полных квадратных уравнений схемой на рисунке1. 

По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида

ах² + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х² = 0, ошибочно можно решить, что

а = 1, b = 3 и с = 2. Тогда

D = 3² – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).

Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть

ах², затем с меньшим  – bx, а затем свободный член с.

При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2. 

Полное квадратное уравнение называется приведенным, если коэффициент при х² равен единице и уравнение примет вид х² + px + q = 0. Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент

а, стоящий при х².

На рисунке 3 приведена схема решения приведенных квадратных уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.

Пример. Решить уравнение

3х² + 6х – 6 = 0.

Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.

D = 6² – 4 · 3 · (– 6) = 36 + 72 = 108

√D = √108 = √(36 · 3) = 6√3

х₁ = (-6 — 6√3 )/(2 · 3) = (6 ( -1- √(3)))/6 = –1 – √3

х₂ = (-6 + 6√3 )/(2 · 3) = (6 ( -1+ √(3)))/6 = –1 + √3

Ответ: –1 – √3; –1 + √3

Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам , приведенным на схеме рисунка D

1 = 3² – 3 · (– 6) = 9 + 18 = 27

√(D₁) = √27 = √(9 · 3) = 3√3

х₁ = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3

х₂ = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3

Ответ: –1 – √3; –1 + √3. Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x² + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного уравнения рисунок 3.

D₂ = 2² – 4 · (– 2) = 4 + 8 = 12

√(D₂) = √12 = √(4 · 3) = 2√3

х₁= (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3

х₂= (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3

Ответ: –1 – √3; –1 + √3.

Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Презентация для урока алгебры в 8 классе на тему: «Квадратные уравнения»

Муниципальное образовательное учреждение основная школа № 4

Сысоева Анна Николаевна , учитель математики МОУ ОШ №4

Фролово, 2017г.

• Определение квадратного уравнения
• Решение квадратного уравнения
• Виды квадратных уравнений
• Примеры решения неполных квадратных уравнений
• Дискриминант
• Формулы корней квадратного уравнения
• Пример решения квадратного уравнения по формулам
• Ресурсы

Квадратным уравнением называют уравнение вида

ax 2 + bx + c = 0,

где a , b , c – любые действительные числа, причем a  0.

а

b

с

а – старший коэффициент;

b – второй коэффициент;

с – свободный член.

Корнем квадратного уравнения ax 2 + bx + c = 0 называют всякое значение переменной х, при котором квадратный трехчлен ax 2 + bx + c обращается в нуль.

Решить квадратное уравнение — значит найти все его корни или установить, что корней нет.

Полным квадратным уравнением называют уравнение вида а x 2 + bx + c = 0 , у которого коэффициенты b и с отличны от 0.

3х 2 + 5х – 7 = 0

-6х 2 + 5х – 7 = 0

7 + 4х 2 — 3х = 0

-16х — 3х 2 – 8 = 0

Приведенным квадратным уравнением называют уравнение вида x 2 + bx + c = 0 , у которого старший коэффициент равен 1 (а = 1).

х 2 + 5х – 7 = 0

7х + х 2 – 3 = 0

5 + х 2 – 2х= 0

Неполным квадратным уравнением называют уравнение вида а x 2 + bx = 0 или а x 2 + c = 0 , в котором присутствуют не все слагаемые.

7х 2 – 14 = 0

4х 2 – 12х = 0

27 + 3х 2 = 0

9х + 2х 2 = 0

7х 2 – 14 = 0

7х 2 – 14х = 0

7х 2 = 14

7х(х – 14) = 0

х 2 = 14 : 7

7х = 0 или х – 14 = 0

х 2 = 2

х = 0 : 7

х = 14

х = 0

х = ±

Ответ: 0; 14

Ответ:

Дискриминантом квадратного уравнения а x 2 + bx + c = 0 называют величину, которая обозначается буквой D и находится по формуле b 2 – 4ac .

Дискриминант служит для определения количества корней квадратного уравнения.

0, то квадратное уравнение имеет два корня «

• Если D = 0, то квадратное уравнение имеет один корень

• Если D 0, то квадратное уравнение имеет два корня

0, значит уравнение имеет 2 корня 3 . Найдем корни уравнения, используя формулу х = х 2 = = 1 х 1 = = — 2,5 — 2,5 и 1 – корни уравнения 4. Ответ: — 2,5; 1 . «

2х 2 + 3х – 5 = 0

• Найдем дискриминант D :

D = b ² – 4ac , где a = 2, b = 3, c = — 5

Подставив значения a, b, c в формулу , получим

D = 3 2 – 4 · 2 · (- 5) = 49

2. Определим число корней уравнения:

D 0, значит уравнение имеет 2 корня

3 . Найдем корни уравнения, используя формулу

х =

х 2 =

= 1

х 1 =

= — 2,5

— 2,5 и 1 – корни уравнения

4. Ответ: — 2,5; 1 .

0, 2 корня   3.   х =   х 1 = = 1   х 2 = = — 2,5 — 2,5 и 1 – корни уравнения   Ответ: — 2,5; 1. Найти дискриминант Определить число корней уравнения Найти корни уравнения по формулам Записать ответ «

2х 2 + 3х – 5 = 0

  1.   D = b – 4ac ,

D = 3 ² – 4 · 2 · (- 5) = 49

  2.   D 0, 2 корня

  3.   х =

  х 1 = = 1

  х 2 = = — 2,5

— 2,5 и 1 – корни уравнения

  Ответ: — 2,5; 1.

• Найти дискриминант
• Определить число корней уравнения
• Найти корни уравнения по формулам
• Записать ответ

Теляковский С.А. Алгебра. 8 класс: Учебник для общеобразовательных

учреждений. – 17 изд., доработ. – М.: Просвещение, 200810.

Дискриминанты — Алгебра II

Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже. Если университетские наставники примут меры в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права. Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.

Чтобы подать уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \ достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем а ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.

Отправьте жалобу нашему назначенному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

 

1.5: Квадратные уравнения с комплексными корнями

В разделе \(1.3,\) мы рассмотрели решение квадратных уравнений, имеющих два действительных корня. {2}-4 a c,\), часто называемая дискриминантом), всегда была положительным числом.{2}-4(1)(3)}}{2 * 1} \\
=\frac{6 \pm \sqrt{36-12}}{2} \\
=\frac{6 \pm \ sqrt{24}}{2} \\
=\frac{6 \pm 4.899}{2}
\end{массив}
\]
\begin{массив}{ll}
\приблизительно \frac{6+4.899 {2} & \приблизительно \frac{6-4.899}{2} \\
\приблизительно \frac{10.899}{2} & \приблизительно \frac{1.101}{2} \\
\приблизительно 5.449 & \приблизительно 0,551
\end{массив}

Когда мы прибавили и вычли квадратный корень из 24 из 6 в квадратной формуле, это дало два ответа, и они были действительными, потому что квадратный корень из 24 является действительным.{2}-4(1)(12)}}{2 * 1} \\
=\frac{6 \pm \sqrt{36-48}}{2} \\
=\frac{6 \pm \ sqrt{-12}}{2} \\
=\frac{6}{2} \pm \frac{6 \cdot 464 i}{2} \\
\приблизительно 3 \pm 1,732 i
\end{array }

Здесь дискриминант отрицателен, что приводит к двум комплекснозначным ответам. Если уравнение имеет действительные коэффициенты, комплексные корни всегда будут сопряженными парами. {2}-\) \(6 x +12\) полностью перемещает график от оси \(x\).{2}\)
11) \(\quad (x+5)(x-6)=(2 x-1)(x-4)\)
12) \(\quad (3 x-4)( х+2)=(2 х-5)(х+5)\)

Ответить

1) \(\quad x \приблизительно 1,758,-0,758\)
3) \(\quad x \приблизительно 0,344,-1,744\)
5) \(\quad x \приблизительно 0,1 \overline{6} \pm 0,373 i\)
7) \(\quad x \приблизительно-0,5 \pm 1,204 i\)
9) \(\quad x \приблизительно 0,286 \pm 0,881 i\)
11) \(\quad x \приблизительно 4 \pm 4,243 i\)

Квадратные уравнения — Полный курс алгебры

37

Стандартная форма квадратного уравнения

A корень квадратного числа

Решение факторингом

Раздел 2 :

Заполнение квадрата

Квадратичная формула

Дискриминант

Доказательство квадратичной формулы

Раздел 3 :

График   y = квадратичный:  парабола

КВАДРАТ — это многочлен, старший показатель которого равен 2.

ах ² + бх + с .

Коэффициент x ² называется старшим коэффициентом.

Вопрос 1. Какова стандартная форма квадратного уравнения ?

ах ² + Ьх + с = 0.

Квадратичный слева. 0 находится справа.

Вопрос 2.Что мы понимаем под корнем квадратного?

Решение квадратного уравнения.

Например, корни этого квадратного числа —

x ² + 2 x − 8

— это решения

х ² + 2 х — 8 = 0,

Чтобы найти корни, мы можем разложить квадратное число как

.

( х + 4)( х — 2).

Теперь, если   x = −4, то первый множитель будет равен 0. (Урок 2.) В то время как, если   x  = 2, второй множитель будет равен 0.  Но если какой-либо множитель равен 0, то весь продукт будет 0.  Поэтому, если x  = −4 или 2, то

х ² + 2 х — 8 = 0,

−4  или  2 являются решениями квадратного уравнения. Они являются корнями этого квадратного числа.

И наоборот, если корни a или b скажем, то квадратное число можно разложить как

( х — а )( х — б ).

Корень квадратного числа также называют нулем. Потому что, как мы увидим, в каждом корне значение графа равно 0. (См. Тему 7 Предварительного исчисления, Вопрос 2.)

Вопрос 3. Сколько корней имеет квадратное уравнение?

Всегда два. Потому что квадратное число (по крайней мере, со старшим коэффициентом 1) всегда можно разложить на множители как ( x − a ) ( x − b ), а a , b — это два корня.

Другими словами, когда старший коэффициент равен 1, корень имеет знак, противоположный числу в множителе.
Если ( x + q ) является множителем, то   x = − q  является корнем.

− · + · = 0,

Задача 1.    Если квадратное число можно разложить как ( x + 3)( x − 1), то какие два корня?

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите кнопку «Обновить» («Reload»).
Сначала решай задачу сам!

−3 или 1,

Мы говорим «или», потому что x может принимать только одно значение за раз.

Вопрос 4. Что мы понимаем под двойным корнем?

Два корня равны. Множители будут ( x − a )( x − a ), так что два корня равны a , a .

Например, этот квадратичный

x ² − 12 x + 36

можно разложить как

( х — 6)( х — 6).

Если x = 6, то каждый множитель будет равен 0, и, следовательно, квадратичный будет 0. 6 называется двойным корнем.

Когда квадратное число будет иметь двойной корень? Когда квадратное число является совершенным квадратным трехчленом.

Пример 1. Решите для x : 2 x ² + 9 x − 5,

Решение . Это квадратичное число факторизуется следующим образом:

2 х ² + 9 х — 5 = (2 х — 1)( х + 5).

Урок 17.

Теперь легко увидеть, что второй множитель будет равен 0, когда x = −5.

Что касается значения x , то получится

2 х − 1	=	0,
мы должны решить это маленькое уравнение.Урок 9.			=	1
x	=	1 2

Решения:

Задача 2.   Как возможно, что произведение двух множителей ab = 0?

Решение факторингом

Проблема 3.Найдите корни каждого квадратного уравнения, разложив его на множители.

а)	x ² − 3 x + 2		б)	x ² + 7 x + 12
	( х — 1)( х — 2)			( х + 3)( х + 4)
	x = 1 или 2.			x = −3 или −4.

Опять же, мы используем союз «или», потому что x принимает только одно значение за раз.

в)	x ² + 3 x − 10		г)	х ² − х − 30
	( х + 5)( х — 2)			( х + 5)( х — 6)
	x = −5 или 2.			x = −5 или 6.

д)	2 x ² + 7 x + 3				е)	3 x ² + x − 2
	(2 х + 1)( х + 3)					(3 х — 2)( х + 1)
	х = —	1 2	или −3.			х =	2 3	или −1.

г)	x ² + 12 x + 36		ч)	x ² − 2 x + 1
	( х + 6)²			( х — 1)²
	х = -6, -6.			х = 1, 1.
	Двойной корень.			Двойной корень.

Пример 2.   c   =  0.   Решите это квадратное уравнение:

ax ² + bx   =  0

Решение . Поскольку постоянного члена нет: c   = 0,   x является общим делителем:

		х ( а х + б)	=	0.
	Отсюда следует:
х			=	0
		или
х			=	—	б а	.

Это два корня.

Задача 4.   Найти корни каждого квадратного числа.

а)	x ² − 5 x		б)	x ² + x
	х ( х — 5)			х ( х + 1)
	x = 0 или 5.			x = 0 или −1.

в)	3 x ² + 4 x			г)	2 x ² − x
	х (3 х + 4)				x (2 x − 1)
	x = 0 или −	4 3			x = 0 или ½

Пример 3. b   =  0. Решите это квадратное уравнение:

ax ² − c   =  0,

Решение . В случае, когда среднего члена нет, мы можем написать:

	топор ²	=	с .
	Отсюда следует:
	х ²	=	в в
	х	=	, согласно Уроку 26.

Однако, если форма представляет собой разность двух квадратов —

x ² − 16

— тогда мы можем разложить его как:

( х + 4)( х -4).

Корни равны ±4.

На самом деле, если квадратное число равно

х ² − с ,

, тогда мы могли бы разложить его как:

( х + )( х — ),

, так что корни равны ±.

Задача 5.   Найти корни каждого квадратного числа.

а)	x ² − 3		б)	x ² − 25		в)	x ² − 10
	х ² = 3			( х + 5)( х — 5)			( х + )( х — )
	х = ±.			х = ±5.			х = ±.

Пример 4.   Решите это квадратное уравнение:

x ²	=	х + 20.
Решение . Сначала перепишем уравнение в стандартной форме, переставив все члены влево:
x ² − x − 20	=	0
( x + 4)( x − 5)	=	0
x	=	−4 или 5.

Итак, уравнение решено, когда x изолированы слева.

x = ± не является решением.

Задача 6.   Решите каждое уравнение для x .

а)	x ²  = 5 x − 6		б)	x ² + 12  = 8 x
	х ² — 5 х + 6 = 0			х ² − 8 х + 12 = 0
	( х — 2)( х — 3) = 0			( х — 2)( х — 6) = 0
	x = 2 или 3.			x = 2 или 6.
в)	3 x ² + x  = 10		г)	2 x ²  =  x
	3 х ² + х — 10 = 0			2 х ² − х = 0
	(3 ​​ х — 5)( х + 2) = 0			х (2 х — 1) = 0
	x = 5/3 или − 2.			x = 0 или 1/2.

Пример 5.   Решите уравнение

.

3 −

5 2

х − 3 х ²

=

0

Решение . Это уравнение можно привести к стандартной форме, изменив все знаки в обеих частях.0 не изменится. У нас есть стандартная форма:

3 x ² +

5 2

х − 3

=

0

Далее мы можем избавиться от дроби, умножив обе части на 2. Опять же, 0 не изменится.

6 x ² + 5 x − 6	=	0
(3 ​​ x − 2)(2 x + 3)	=	0.

Корни

2 3

или −

3 2

.

Задача 7.   Решите для x .

а)

3 −

11  2

x − 5 x ²

=  0

б)

4 +

11  3

x − 5 x ²

=  0

5 x ² +	11  2	х − 3	=  0		5 x ² −	11  3	х − 4	=  0
10 x ² + 11 x − 6			=  0		15 x ² − 11 x − 12			=  0
(5 x − 2 )(2 x + 3)			=  0		(3 х — 4)(5 х + 3)			=  0

Корни

2 5

или −

3 2

.

Корни

4 3

или −

3 5

.

в)	− х ² − х + 20	= 0		г)	− х ² + 3 х + 18	= 0
	х ² + х − 20	= 0			x ² − 3 x − 18	= 0
	( х + 5)( х — 4)	= 0.			( х — 6)( х + 3)	= 0,
	x = −5 или 4.				x = 6 или −3.

Раздел 2: Заполнение квадрата

Содержание | Дом

---

Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.

---

Copyright © 2021 Лоуренс Спектор

Вопросы или комментарии?

Электронная почта: [email protected]

10.3 Решение квадратных уравнений с помощью квадратной формулы — Элементарная алгебра 2e

Цели обучения

К концу этого раздела вы сможете:

• Решать квадратные уравнения с помощью квадратной формулы
• Использование дискриминанта для предсказания числа решений квадратного уравнения
• Определите наиболее подходящий метод решения квадратного уравнения

Будьте готовы 10.7

Прежде чем начать, пройдите этот тест на готовность.

Упростить: −20−510−20−510.
Если вы пропустили эту проблему, просмотрите пример 1.74.

Будьте готовы 10.8

Упрощение: 4+1214+121.
Если вы пропустили эту проблему, просмотрите пример 9.29.

Будьте готовы 10.9

Упрощение: 128128.
Если вы пропустили эту проблему, просмотрите пример 9.12.

Когда мы решали квадратные уравнения в последнем разделе, дополняя квадрат, мы каждый раз делали одни и те же шаги.К концу набора упражнений вы, возможно, задавались вопросом: «А нет ли более простого способа сделать это?» Ответ «да». В этом разделе мы выведем и используем формулу, чтобы найти решение Квадратное уравнение.

Мы уже видели, как решить формулу для определенной переменной «вообще», так что мы должны были бы сделать алгебраические шаги только один раз, а затем использовать новую формулу, чтобы найти значение конкретной переменной. Теперь мы пройдем этапы завершения квадрата в целом, чтобы решить квадратное уравнение для x .Может оказаться полезным взглянуть на один из примеров в конце последнего раздела, где мы решали уравнение вида видеть их с номерами, а также «в целом».

Начнем со стандартной формы квадратного уравнения
и решим его для x , заполнив квадрат.

ax2+bx+c=0a≠0ax2+bx+c=0a≠0
Изолируйте переменные термины с одной стороны.	ax2+bx=-cax2+bx=-c
Сделайте ведущий коэффициент 1, разделив на a.	ax2a+bax=-caax2a+bax=-ca
Упрощение.	x2+bax=-cax2+bax=-ca
Чтобы завершить квадрат, найдите (12·ba)2(12·ba)2 и прибавьте его к обеим частям уравнения. (12ba)2=b24a2(12ba)2=b24a2	x2+bax+b24a2=-ca+b24a2x2+bax+b24a2=-ca+b24a2
Левая сторона представляет собой идеальный квадрат, разложите его на множители.	(x+b2a)2=-ca+b24a2(x+b2a)2=-ca+b24a2
Найдите общий знаменатель правой части и запишите эквивалентных дробей с общим знаменателем.	(x+b2a)2=b24a2−c·4aa·4a(x+b2a)2=b24a2−c·4aa·4a
Упрощение.	(x+b2a)2=b24a2−4ac4a2(x+b2a)2=b24a2−4ac4a2
Объединить в одну фракцию.	(x+b2a)2=b2−4ac4a2(x+b2a)2=b2−4ac4a2
Используйте свойство квадратного корня.	х+b2a=±b2−4ac4a2x+b2a=±b2−4ac4a2
Упрощение.	х+b2a=±b2−4ac2ax+b2a=±b2−4ac2a
Добавьте -b2a-b2a к обеим частям уравнения.	х=-b2a±b2-4ac2ax=-b2a±b2-4ac2a
Объедините термины справа.	х=-b±b2-4ac2ax=-b±b2-4ac2a

Это последнее уравнение является квадратичной формулой.

Квадратичная формула

Решения квадратного уравнения вида ax2+bx+c=0ax2+bx+c=0, a≠0a≠0 находятся по формуле:

х=-b±b2-4ac2ax=-b±b2-4ac2a

Чтобы использовать квадратичную формулу, мы подставляем значения a,b,ca,b,c в выражение в правой части формулы.Затем мы делаем всю математику, чтобы упростить выражение. Результат дает решение(я) квадратного уравнения.

Пример 10.28

Как решить квадратное уравнение с помощью квадратичной формулы

Решите 2×2+9x-5=02×2+9x-5=0 с помощью квадратичной формулы.

Попробуйте 10,55

Решите 3y2−5y+2=03y2−5y+2=0 с помощью квадратичной формулы.

Попробуйте 10.56

Решите 4z2+2z−6=04z2+2z−6=0 с помощью квадратичной формулы.

How To

Решите квадратное уравнение, используя квадратную формулу.

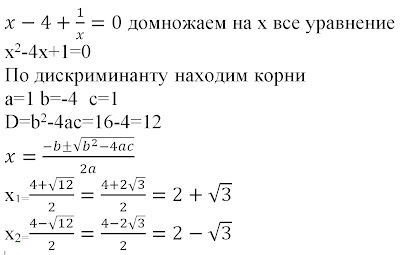
1. Шаг 1. Запишите квадратную формулу в стандартной форме. Определите значения aa, bb и cc.
2. Шаг 2. Напишите квадратную формулу. Затем подставьте значения aa, bb и c.c.
3. Шаг 3. Упрощение.
4. Шаг 4. Проверьте решения.

Если вы произносите формулу, когда пишете ее в каждой задаче, вы быстро ее запомните. И помните, квадратная формула — это уравнение.Убедитесь, что вы начинаете с «x=x=».

Пример 10.29

Решите x2−6x+5=0x2−6x+5=0 с помощью квадратичной формулы.

Попробуйте 10,57

Решите a2−2a−15=0a2−2a−15=0 с помощью квадратичной формулы.

Попробуйте 10,58

Решите b2+10b+24=0b2+10b+24=0 с помощью квадратичной формулы.

Когда мы решали квадратные уравнения, используя свойство квадратного корня, мы иногда получали ответы, содержащие радикалы. Это может произойти и при использовании квадратичной формулы.Если мы получаем радикал в качестве решения, окончательный ответ должен иметь радикал в его упрощенной форме.

Пример 10.30

Решите 4y2−5y−3=04y2−5y−3=0 с помощью квадратичной формулы.

Решение

Мы можем использовать квадратную формулу для решения переменной в квадратном уравнении, независимо от того, называется ли она « x ».

Попробуйте 10,59

Решите 2p2+8p+5=02p2+8p+5=0 с помощью квадратичной формулы.

Попробуйте 10.60

Решите 5q2−11q+3=05q2−11q+3=0 с помощью квадратичной формулы.

Пример 10.31

Решите 2×2+10x+11=02×2+10x+11=0 с помощью квадратичной формулы.

Попробуйте 10.61

Решите 3m2+12m+7=03m2+12m+7=0 с помощью квадратичной формулы.

Попробуйте 10.62

Решите 5n2+4n−4=05n2+4n−4=0 с помощью квадратичной формулы.

Мы не можем извлечь квадратный корень из отрицательного числа. Итак, когда мы подставляем aa, bb и cc в квадратную формулу, если величина внутри радикала отрицательна, квадратное уравнение не имеет реального решения. Мы увидим это в следующем примере.

Пример 10.32

Решите 3p2+2p+9=03p2+2p+9=0 с помощью квадратичной формулы.

Попробуйте 10,63

Решите 4a2−3a+8=04a2−3a+8=0 с помощью квадратичной формулы.

Попробуйте 10,64

Решите 5b2+2b+4=05b2+2b+4=0 с помощью квадратичной формулы.

Все квадратные уравнения, которые мы решали до сих пор в этом разделе, были записаны в стандартной форме: ax2+bx+c=0ax2+bx+c=0. Иногда нам нужно будет выполнить некоторую алгебру, чтобы привести уравнение к стандартной форме, прежде чем мы сможем использовать квадратную формулу.

Пример 10.33

Решите x(x+6)+4=0x(x+6)+4=0 с помощью квадратичной формулы.

Попробуйте 10,65

Решите x(x+2)−5=0x(x+2)−5=0 с помощью квадратичной формулы.

Попробуйте 10,66

Решите y(3y−1)−2=0y(3y−1)−2=0 с помощью квадратичной формулы.

Когда мы решали линейные уравнения, если в уравнении было слишком много дробей, мы «очищали дроби», умножая обе части уравнения на ЖК-дисплее. Это дало нам эквивалентное уравнение — без дробей — для решения.Мы можем использовать ту же стратегию с квадратными уравнениями.

Пример 10.34

Решите 12u2+23u=1312u2+23u=13 с помощью квадратичной формулы.

Попробуйте 10,67

Решите 14c2−13c=11214c2−13c=112 с помощью квадратичной формулы.

Попробуйте 10,68

Решите 19d2−12d=−1219d2−12d=−12 с помощью квадратичной формулы.

Подумайте об уравнении (x−3)2=0(x−3)2=0. Из принципа нулевых продуктов мы знаем, что это уравнение имеет только одно решение: x=3x=3.

В следующем примере мы увидим, как использование квадратичной формулы для решения уравнения с полным квадратом также дает только одно решение.

Пример 10.35

Решите 4×2−20x=−254×2−20x=−25 с помощью квадратичной формулы.

Решение

Знаете ли вы, что 4×2−20x+254×2−20x+25 — это правильный квадрат?

Попробуйте 10,69

Решите r2+10r+25=0r2+10r+25=0 с помощью квадратичной формулы.

Попробуйте 10.70

Решите 25t2−40t=−1625t2−40t=−16 с помощью квадратичной формулы.

Использование дискриминанта для прогнозирования количества решений квадратного уравнения

Когда мы решали квадратные уравнения в предыдущих примерах, иногда мы получали два решения, иногда одно решение, иногда никаких действительных решений. Есть ли способ предсказать количество решений квадратного уравнения без фактического решения уравнения?

Да, количество внутри радикала квадратной формулы позволяет нам легко определить количество решений.Эта величина называется дискриминантом.

Дискриминант

В квадратной формуле x=−b±b2−4ac2ax=−b±b2−4ac2a величина b2−4acb2−4ac называется дискриминантом.

Давайте посмотрим на дискриминант уравнений в примере 10.28, примере 10.32 и примере 10.35, а также на количество решений этих квадратных уравнений.

1 «>

	Квадратное уравнение (в стандартной форме)	Дискриминант b2-4acb2-4ac	Знак дискриминанта	Количество действительных решений
Пример 10.28	2×2+9x-5=02×2+9x-5=0	92−4·2(−5)=12192−4·2(−5)=121	+	2
Пример 10. 35	4×2-20x+25=04×2-20x+25=0	(-20)2-4·4·25=0(-20)2-4·4·25=0	0	1
Пример 10.32	3п2+2п+9=03п2+2п+9=0	22−4·3·9=−10422−4·3·9=−104	—	0

Когда дискриминант положителен (x=−b±+2a)(x=−b±+2a), квадратное уравнение имеет два решения .

Когда дискриминант равен нулю (x=−b±02a)(x=−b±02a) квадратное уравнение имеет одно решение .

Когда дискриминант отрицательный (x=-b±-2a)(x=-b±-2a), квадратное уравнение не имеет действительных решений .

How To

Используйте дискриминант b2−4acb2−4ac для определения количества решений квадратного уравнения.

Для квадратного уравнения вида ax2+bx+c=0ax2+bx+c=0, a≠0a≠0,

• если b2−4ac>0b2−4ac>0, уравнение имеет два решения.
• , если b2−4ac=0b2−4ac=0, уравнение имеет одно решение.
• , если b2−4ac<0b2−4ac<0, уравнение не имеет действительных решений.

Пример 10.36

Определить количество решений каждого квадратного уравнения:

ⓐ 2v2−3v+6=02v2−3v+6=0 ⓑ 3×2+7x−9=03×2+7x−9=0 ⓒ 5n2+n+4=05n2+n+4=0 ⓓ 9y2−6y+1= 09y2−6y+1=0

Решение

Чтобы определить количество решений каждого квадратного уравнения, посмотрим на его дискриминант.

ⓐ

	2v2−3v+6=02v2−3v+6=0
Уравнение в стандартной форме, идентифицируйте a , b , c .	а=2,б=-3,в=6а=2,б=-3,в=6
Запишите дискриминант.	б2-4асб2-4ас
Замените значения на , b , c .	(3)2−4·2·6(3)2−4·2·6
Упрощение.	9−48−399−48−39
Поскольку дискриминант отрицательный, у уравнения нет действительных решений.

ⓑ

	3×2+7x-9=03×2+7x-9=0
Уравнение в стандартной форме, идентифицируйте a , b , c .	а=3,б=7,в=-9а=3,б=7,в=-9
Запишите дискриминант.	б2-4асб2-4ас
Замените значения на , b , c .	(7)2−4·3·(−9)(7)2−4·3·(−9)
Упрощение.	49+10815749+108157
Поскольку дискриминант положительный, у уравнения есть два решения.

ⓒ

	5n2+n+4=05n2+n+4=0
Уравнение в стандартной форме, идентифицируйте a , b , c .	а=5,б=1,в=4а=5,б=1,в=4
Запишите дискриминант.	б2-4асб2-4ас
Замените значения на , b , c .	(1)2−4·5·4(1)2−4·5·4
Упрощение.	1-80-791-80-79
Поскольку дискриминант отрицательный, у уравнения нет действительных решений.

ⓓ

	9y2−6y+1=09y2−6y+1=0
Уравнение в стандартной форме, идентифицируйте a , b , c .	а=9,б=-6,в=1а=9,б=-6,в=1
Запишите дискриминант.	б2-4асб2-4ас
Замените значения на , b , c .	(-6)2-4·9·1(-6)2-4·9·1
Упрощение.	36−36036−360
Поскольку дискриминант равен 0, уравнение имеет одно решение.

Попробуйте 10.71

Определить количество решений каждого квадратного уравнения:

ⓐ 8m2−3m+6=08m2−3m+6=0 ⓑ 5z2+6z−2=05z2+6z−2=0 ⓒ 9w2+24w+16=09w2+24w+16=0 ⓓ 9u2−2u+4= 09u2−2u+4=0

Попробуйте 10.72

Определить количество решений каждого квадратного уравнения:

ⓐ b2+7b−13=0b2+7b−13=0 ⓑ 5a2−6a+10=05a2−6a+10=0 ⓒ 4r2−20r+25=04r2−20r+25=0 ⓓ 7t2−11t+3= 07t2−11t+3=0

Определите наиболее подходящий метод для решения квадратного уравнения

Мы использовали четыре метода решения квадратных уравнений:

• Факторинг
• Свойство квадратного корня
• Завершение квадрата
• Квадратичная формула

Вы можете решить любое квадратное уравнение, используя квадратную формулу, но это не всегда самый простой метод.

How To

Определите наиболее подходящий метод решения квадратного уравнения.

1. Шаг 1. Сначала попробуйте Факторинг . Если квадратичные факторы легко, этот метод очень быстро.
2. Шаг 2. Далее попробуйте свойство квадратного корня . Если уравнение соответствует форме ax2=kax2=k или a(x−h)2=ka(x−h)2=k, его можно легко решить, используя свойство квадратного корня.
3. Шаг 3. Используйте квадратичную формулу . Любое квадратное уравнение можно решить с помощью квадратной формулы.

Как насчет способа заполнения квадрата? Большинство людей считают этот метод громоздким и предпочитают его не использовать. Нам нужно было включить его в эту главу, потому что мы завершили квадрат в целом, чтобы вывести квадратную формулу. Вы также будете использовать процесс заполнения квадрата в других областях алгебры.

Пример 10.37

Определите наиболее подходящий метод для решения каждого квадратного уравнения:

ⓐ 5z2=175z2=17 ⓑ 4×2−12x+9=04×2−12x+9=0 ⓒ 8u2+6u=118u2+6u=11

Решение

ⓐ 5z2=175z2=17

Поскольку уравнение находится в виде ax2=kax2=k, наиболее подходящим методом является использование свойства Square Root.

ⓑ 4×2−12x+9=04×2−12x+9=0

Мы понимаем, что левая часть уравнения представляет собой точный квадратный трехчлен, поэтому факторинг будет наиболее подходящим методом.

ⓒ 8u2+6u=118u2+6u=11

Приведите уравнение к стандартной форме. 8u2+6u−11=08u2+6u−11=0

Хотя нашей первой мыслью может быть попытка факторинга, размышления обо всех возможностях проб и ошибок приводят нас к выбору квадратичной формулы как наиболее подходящего метода

Попробуйте 10.73

Определите наиболее подходящий метод для решения каждого квадратного уравнения:

ⓐ x2+6x+8=0x2+6x+8=0 ⓑ (n−3)2=16(n−3)2=16 ⓒ 5p2−6p=95p2−6p=9

Попробуйте 10,74

Определите наиболее подходящий метод для решения каждого квадратного уравнения:

ⓐ 8a2+3a−9=08a2+3a−9=0 ⓑ 4b2+4b+1=04b2+4b+1=0 ⓒ 5c2=1255c2=125

Раздел 10.

3 Упражнения

Практика ведет к совершенству

Решение квадратных уравнений с помощью квадратичной формулы

В следующих упражнениях решите с помощью квадратичной формулы.

105.

r2-8r-33=0r2-8r-33=0

113.

v(v+5)−10=0v(v+5)−10=0

114.

3w(w−2)−8=03w(w−2)−8=0

118.

25d2−60d+36=025d2−60d+36=0

121.

р2-6р-27=0р2-6р-27=0

129.

2×2+12x-3=02×2+12x-3=0

Использование дискриминанта для прогнозирования количества решений квадратного уравнения

В следующих упражнениях определите количество решений каждого квадратного уравнения.

131.

1. ⓐ 4×2−5x+16=04×2−5x+16=0
2. ⓑ 36у2+36у+9=036у2+36у+9=0
3. ⓒ 6м2+3м-5=06м2+3м-5=0
4. ⓓ 18n2−7n+3=018n2−7n+3=0

132.

1. ⓐ 9v2−15v+25=09v2−15v+25=0
2. ⓑ 100w2+60w+9=0100w2+60w+9=0
3. ⓒ 5c2+7c−10=05c2+7c−10=0
4. ⓓ 15d2−4d+8=015d2−4d+8=0

133.

1. ⓐ r2+12r+36=0r2+12r+36=0
2. ⓑ 8t2−11t+5=08t2−11t+5=0
3. ⓒ 4u2−12u+9=04u2−12u+9=0
4. ⓓ 3v2−5v−1=03v2−5v−1=0

134.

1. ⓐ 25p2+10p+1=025p2+10p+1=0
2. ⓑ 7q2-3q-6=07q2-3q-6=0
3. ⓒ 7у2+2у+8=07у2+2у+8=0
4. ⓓ 25z2−60z+36=025z2−60z+36=0

Определение наиболее подходящего метода решения квадратного уравнения

В следующих упражнениях определите наиболее подходящий метод (факторинг, вычисление квадратного корня или квадратную формулу) для решения каждого квадратного уравнения. Не решить.

135.

ⓐ x2−5x−24=0x2−5x−24=0 ⓑ (y+5)2=12(y+5)2=12 ⓒ 14m2+3m=1114m2+3m=11

136.

ⓐ (8v+3)2=81(8v+3)2=81 ⓑ w2-9w-22=0w2-9w-22=0 ⓒ 4n2-10=64n2-10=6

137.

ⓐ 6a2+14=206a2+14=20 ⓑ (x−14)2=516(x−14)2=516 ⓒ y2−2y=8y2−2y=8

138.

ⓐ 8b2+15b=48b2+15b=4 ⓑ 59v2−23v=159v2−23v=1 ⓒ (w+43)2=29(w+43)2=29

Математика на каждый день

139.

Ракета запускается прямо с корабля в море. Решите уравнение 16(t2-13t+40)=016(t2-13t+40)=0 для tt, количества секунд, которое потребуется для того, чтобы вспышка находилась на высоте 640 футов.

140.

Архитектор проектирует вестибюль отеля. Она хочет иметь треугольное окно, выходящее в атриум, с шириной окна на 6 футов больше, чем высота. Из-за ограничений по энергопотреблению площадь окна должна составлять 140 квадратных футов. Решите уравнение 12h3+3h=14012h3+3h=140 для hh, высоты окна.

Письменные упражнения

141.

Решите уравнение x2+10x=200×2+10x=200
ⓐ, заполнив квадрат
ⓑ с помощью квадратичной формулы
ⓒ Какой метод вы предпочитаете? Почему?

142.

Решите уравнение 12y2+23y=2412y2+23y=24
ⓐ, заполнив квадрат
ⓑ с помощью квадратичной формулы
ⓒ Какой метод вы предпочитаете? Почему?

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.

ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?

Квадратичная формула: обзор, объяснение и примеры

Прелесть квадратной формулы в том, что она всегда подходит для решения квадратных уравнений.

Точно так же, как мы знаем, что завтра утром взойдет солнце, мы знаем, что квадратичная формула даст решения (действительные и мнимые) наших квадратных уравнений. Если вы ищете немного больше красоты (и гораздо меньше стирания) при решении квадратичных уравнений, продолжайте читать, чтобы просмотреть квадратную формулу, понять вывод квадратной формулы и увидеть примеры того, как использовать квадратичную формулу!

Квадратная формула : надежна как восход солнца !

Вернуться к оглавлению

Что такое квадратичная формула?

Давайте начнем с полной квадратичной формулы ниже:

Квадратичная формула: x = \dfrac{-b \pm \sqrt{b^2 — 4ac}}{2a}

Буквы a, b и c происходят из стандартная форма квадратного уравнения:

Стандартная форма квадратного уравнения: y=ax^2+bx+c

Коэффициент перед x^2 равен a, коэффициент перед x равен b, а коэффициент без переменной равен c.

Вы можете узнать больше о стандартной форме и других формах квадратных уравнений в нашей обзорной статье о формах квадратных уравнений.

История квадратичной формулы

Ранняя история

Решение квадратных уравнений не является современным достижением. На самом деле древние вавилоняне составляли квадрат для решения квадратных уравнений задолго до того, как появилось слово «алгебра», согласно Хакворту и Хауленду в тексте «Введение в математику колледжа: история вещественных чисел».

Представьте, что вы решаете квадратные уравнения на счетах вместо того, чтобы доставать калькулятор. Согласно Mathnasium, не только вавилоняне, но и китайцы решали квадратные уравнения, дополняя квадрат с помощью этих инструментов.

В 700 году нашей эры Брахмагупта, математик из Индии, разработал общее решение квадратного уравнения, но только в 1100 году нашей эры известное нам сегодня решение было разработано другим математиком из Индии по имени Бхаскара, как утверждалось. по Матназиуму.

Хакворт и Хауленд сообщили нам, что до тех пор, пока не существовала индуистская математика, математика, разработанная в Индии, числа не выглядели так, как мы их знаем, с системой счисления с основанием 10. Другими словами, одновременно с этими разработками в области решения квадратных уравнений в математике произошло много других разработок. Знаменитые древние математики, такие как Пифагор, не понимали существования таких чисел, как \sqrt{2} или \pi. На самом деле, как сообщил нам Mathnasium, распознавание Бхаскарой двух решений квадратного корня из числа помогло ему решать квадратные уравнения.Britannica сообщает нам, что Бхаскара также смог аппроксимировать значение \pi как 3,141666.

Более поздняя история

Мухаммад Аль-Хорезми, «отец алгебры»

Согласно Mathnasium, в период между Брахмагуптой и Бхаскарой арабский математик Аль-Хорезми также решал квадратные уравнения. Он написал текст под названием «Аль-джабр валь мукабала», из которого, согласно Хакворту и Хауленду, мы получили слово «алгебра». Хакворт и Хауленд также сообщили нам, что в своем тексте Аль-Хорезми объясняет с помощью конкретных шагов, как решать уравнения, в том числе квадратные уравнения.В эпоху Возрождения, примерно в 1545 году нашей эры, Джироламо Кардано основывался на работах Аль-Хорезми, как утверждает Матназиум, включая воображаемые решения. В то время как работы Кардано включают мнимые числа, Аль-Хорезми не включал даже отрицательных решений, согласно Хэкворку и Хауленду.

Наконец, в 1637 году Рене Декарт включил квадратичную формулу в том виде, в каком мы ее знаем сегодня, в свой труд «Геометрия», как сообщает Mathnasium.

Вывод квадратичной формулы

Мы можем вывести квадратную формулу, заполнив квадрат стандартной формы квадратного уравнения.2 — 4ас}}{2а}

Потребовалось немного работы, но теперь у нас есть доказано квадратичная формула будет работать во всех случаях!

Если вы хотите увидеть этот процесс в наглядной форме, ниже приведено короткое видео от ютубера patrickJMT, показывающее, как вывести квадратную формулу:

Вернуться к оглавлению

Когда использовать квадратичную формулу

Иногда, пытаясь решить квадратное уравнение с помощью факторизации, мы натыкаемся на препятствие.Не каждое квадратное уравнение факторизуемо.

Хорошая новость о квадратной формуле заключается в том, что вы всегда можете ее использовать! Не существует квадратных уравнений, для которых квадратная формула не дает решения. Даже в тех случаях, когда нет реальных решений, квадратичная формула все равно дает решения! Ознакомьтесь с нашим разделом ниже о дискриминанте, чтобы узнать больше о том, как квадратичная формула всегда дает подходящие решения.

Однако, когда квадратное уравнение факторизуемо, факторинг часто является более эффективным методом решения уравнений. 2-x+9 равны

\dfrac{1}{14} + \dfrac{i \sqrt{251}}{14} и \dfrac{1}{14} — \dfrac{i \sqrt{251}}{14}.

Вернуться к оглавлению

Бесплатный рабочий лист квадратичной формулы

Учителя математики: вы ищете простой в использовании рабочий лист с квадратичными формулами, который включает краткие заметки и некоторые основные практические задачи?

Предварительный просмотр таблицы квадратичных формул:

Что такое дискриминант квадратного уравнения?

Теперь, когда мы решили уравнения по квадратной формуле, определение дискриминанта покажется простым! Дискриминант — это часть квадратной формулы.2 — 4ac}}{2a}

• Если дискриминант положительный , это означает, что мы извлекаем квадратный корень из положительного числа. У нас будет положительное и отрицательное реальное решение. Это уравнение будет иметь два действительных решения или точки пересечения.

• Если дискриминант равен нулю , мы берем квадратный корень из нуля, который равен нулю. Добавление нуля и вычитание нуля дают одно и то же значение, поэтому уравнение будет иметь только одну точку пересечения по оси x.

• Наконец, если дискриминант отрицательный , мы извлекаем квадратный корень из отрицательного числа. У этого уравнения не будет действительных решений, а только два мнимых решения, потому что i=\sqrt{-1}.

В этой таблице показано, как использовать дискриминант для определения количества и типа решений в квадратном уравнении:

дискриминант	Количество решений для уравнения
положительные	два реальных решения
отрицательный	два воображаемых решения
ноль	один реальный раствор

возврат к оглавлению

БЫСТРЫЙ СОВЕТ.

Дискриминанты и факторинг

Вы также можете использовать дискриминант, чтобы определить, являются ли уравнения факторизуемыми.2}-4\цвет{красный}{(1)}\цвет{зеленый}{(9)}

36-36

0

Мы знаем, что 0=0. Дискриминант со значением , равным 0 , говорит нам, что уравнение имеет только одну точку пересечения по оси . Мы можем увидеть, как функция попала в x, построив график этого квадратного уравнения.

Более визуальный ученик? Посмотрите прекрасное видео с пояснением ниже о том, как найти дискриминант квадратного числа:

Вернуться к оглавлению

5 лучших песен с квадратичными формулами

Что может быть лучше для запоминания формулы, чем прослушивание раздражающей песни? Да, есть несколько приятных песен, но песня, которая будет играть в вашей голове, даже когда вы захотите, чтобы она остановилась, лучше всего поможет вам запомнить формулу. Вот несколько отличных вариантов для вас!

1. Набрав более трех миллионов просмотров, мы должны были начать с полностью оригинальной песни о квадратичной формуле.
2. Вот еще одна оригинальная версия песни о квадратичной формуле — предупреждение: она может застрять у вас в голове.
3. Вот отличная кавер-версия песни One Direction с использованием квадратичной формулы.
4. Хотя этот рэп может и не заставит формулу застрять у вас в голове, он делает обзор трех методов решения квадратных уравнений!
5. Чтобы завершить наш список, еще одна обложка.Припев в этой версии — действительно приятный способ пропеть квадратичную формулу (начинается с 1:00).

Свободная практика с квадратичной формулой

Для бесплатных практических вопросов, посвященных квадратичной формуле, изучите практический курс Albert’s Algebra 1! Все вопросы Альберта включают объяснения решений и способы избежать распространенных ошибок. Учителя математики: прочитайте наше подробное руководство о том, как преподавать квадратные уравнения, включая стратегии, примеры из жизни и необходимые навыки учащихся.

Кроме того, лицензированные учителя Альберта могут назначить учащимся этот короткий тест по алгебре 1, посвященный решению квадратных уравнений.

Наконец, ознакомьтесь с другими нашими подробными обзорными руководствами по алгебре 1, чтобы узнать больше о квадратичных вычислениях.

7.3 Классификация квадратичных решений – промежуточная алгебра

Цели обучения

• Квадратные уравнения с комплексными решениями
  • Использование формулы квадратного уравнения для решения квадратных уравнений с комплексными решениями
  • Соедините комплексные решения с графиком квадратичной функции, не пересекающей ось x.
• Дискриминант
  • Определение дискриминанта и его использование для классификации решений квадратных уравнений

В этом уроке мы объединим концепции решения квадратных уравнений и комплексных чисел, чтобы обрабатывать квадратные уравнения, не имеющие действительных решений. Вы также узнаете о полезном свойстве квадратной формулы, которое может помочь вам узнать, имеет ли квадратное уравнение действительные или комплексные решения.

Заполняя квадрат или используя квадратную формулу, мы видели три разных результата для квадратных уравнений: обычно было два решения из-за «плюс-минус» природы квадратного корня, но иногда было только одно решение, потому что мы заканчивали с «плюс-минус ноль», и иногда у нас не было реальных решений, потому что нам нужен был квадратный корень из отрицательного числа.2+3х+6=0\)

Используя квадратную формулу для решения этого уравнения, мы сначала идентифицируем \(a\), \(b\) и \(c\).

\(а = 2, Ь = 3, с = 6\)

Мы можем подставить \(a\), \(b\) и \(c\) в квадратичную формулу и упростить, чтобы получить следующий результат:

\(\displaystyle x=-\frac{3}{4}+\frac{\sqrt{-39}}{4}, \;\;\;\;\; x=-\frac{3}{ 4}-\frac{\sqrt{-39}}{4}\)

До этого момента мы бы сказали, что \(\sqrt{-39}\) не определено для действительных чисел и определено, что это уравнение не имеет решений. Но теперь, когда мы определили квадратный корень из отрицательного числа, мы также можем определить решение этого уравнения следующим образом.

\(x=-\frac{3}{4}+\frac{\sqrt{39}}{4}i, x=-\frac{3}{4}-\frac{\sqrt{39}} {4}и\)

В этом разделе мы будем практиковаться в упрощении и записи решений сложных квадратных уравнений. Затем мы представим метод классификации того, будет ли решение(я) квадратного уравнения комплексным, и сколько будет решений.

В нашем первом примере мы рассмотрим процесс решения квадратного уравнения с комплексными решениями.{2}-\left(4\right)\cdot \left(1\right)\cdot \left(2\right)}}{2\cdot 1} \\
&=\frac{-1}{2 } \pm \frac{\sqrt{1 — 8}}{2} \\
&=\frac{-1}{2} \pm \frac{\sqrt{-7}}{2} \\\
&=\frac{-1}{2} \pm \frac{\sqrt{7}}{2}i\hfill \end{align*}\)

Теперь мы можем разделить ответ на два решения:

Решениями уравнения являются \(x=\frac{-1}{2}+\frac{\sqrt{7}}{2}i\) и \(x=\frac{-1}{2} — \ гидроразрыва {\ sqrt {7}} {2} я \).

В следующем видео показан еще один пример использования формулы квадратного уравнения для поиска решений квадратного уравнения, имеющего комплексные решения.{2}-4ac<0\), то число под радикалом будет отрицательным. Поскольку вы не можете найти квадратный корень из отрицательного числа, используя действительные числа, реальных решений нет. Однако вы можете использовать мнимые числа. Тогда у вас будет два сложных решения: одно путем добавления мнимого квадратного корня, а другое путем его вычитания.

В таблице ниже значения дискриминанта соотносятся с решениями квадратного уравнения.

{2}-4ac\).{2}}-4ac\). Он определяет количество и тип решений квадратного уравнения. Если дискриминант положительный, то существует 2 действительных решения. Если он равен 0, существует 1 реальное повторяющееся решение. Если дискриминант отрицателен, есть 2 комплексных решения (но нет действительных решений).

Понимание дискриминанта в квадратной формуле

Квадратное уравнение в алгебре — это уравнение, в котором наибольшая степень неизвестной переменной равна 2. Вы пишете квадратные уравнения, используя следующую формулу: ax² + bx + c = 0

Некоторые быстрые примеры квадратных уравнений включают:

• 2x² + 5x – 8 = 0
• 7x² + 9 = 0
• xx² – 26 = 3x

В этой конкретной статье я покажу вам, как дискриминант влияет на решения квадратных уравнений.Дискриминант квадратной формулы — часть квадратной формулы, определяющая тип корня в квадратном уравнении (мнимый, вещественный, сингулярный).

Решения квадратного уравнения

Решениями квадратного уравнения являются значения неизвестной переменной, которые делают уравнение верным. Существует четыре стандартных способа нахождения корней квадратного уравнения.

Метод факторизации

Этот метод применим, если вы можете разложить на множители коэффициенты квадратного уравнения как av + bx + c = a( rx + n )( px + m ) = 0 .Где n и m — корни квадратного уравнения.

Квадратный метод

Этот метод полезен, когда вы не можете разложить на множители коэффициенты квадратного уравнения, как показано выше. При завершении метода квадратов квадратное уравнение выражается в виде

• ax² + bx + c = x2 + (b/a)x + (c/a) = 0
• x² + (b/a)x + (c/a) = (x +½b)2 + (c/a) – (b²/4) = 0
• (x +½b)2 = (b²/4) – (c/a)

Решение x дает корни квадратного уравнения.

Квадратичная формула

Вы получите формулу квадрата, выполнив метод квадрата. Если квадратное уравнение задано как ax² + bx + c , то корни квадратного уравнения задаются как x = (-b+-(b²–4ac )1/2 )/2a .

Графический метод

В этом методе вы строите квадратное уравнение, а точки, в которых график пересекает ось x, являются корнями уравнения.

Однако в рамках этой темы мы сосредоточимся на квадратичной формуле.

Дискриминант квадратичной формулы

Вы можете решить все квадратные уравнения, используя метод квадратных формул. Из-за его универсальности мы называем его всемогущей формулой. Вы можете найти корни квадратного уравнения, используя x = (-b +- (b² – 4ac)1/2)/2a .

Член b² – 4ac под квадратным корнем определяет корни квадратного уравнения и является дискриминантом квадратного уравнения. Дискриминант может иметь три возможных исхода.

b² - 4ac > 0

Это происходит, когда b ²  больше 4ac. Если это так, вы получите два действительных корня квадратного уравнения. Это верно, потому что квадратный корень из любого положительного числа является положительным числом. Если вы построите график квадратного уравнения, он будет пересекать ось x в двух точках.

б² – 4ас = 0

Это происходит, когда b² равно 4ac. Когда это ваш результат, у квадратного уравнения есть только один действительный корень.Квадратный корень из нуля равен нулю. Если вы построите график квадратного уравнения, он будет касаться оси x только в одной точке.

(б² - 4ас) = 0

Это происходит, когда b ² меньше 4ac. Это работа для мнимых корней. Корни мнимые, так как квадратный корень из отрицательного числа является мнимым числом. График такого квадратного уравнения не будет касаться оси x.

Проиллюстрируем различные случаи, когда дискриминант определяет корни квадратных уравнений.

Пример 1

Найдите корни следующих квадратных уравнений:

1. х² + 7х + 3 = 0
2. 3x² – 13x – 12 = 0
3. 6y² + 10y = 0

Поскольку мы хотим продемонстрировать, как дискриминант влияет на корни квадратного уравнения, мы воспользуемся формульным методом для решения вышеуказанных задач.

Квадратная формула: x = (-b + -(b² - 4ac)1 / 2) / 2a

Уравнение 1

х² + 7х + 3 = 0

а = 1, b = 7 и с = 3

Подставьте значения коэффициентов a, b и c в квадратную формулу.

• (-7 +- (72 – 4*1*3)1/2)/(2*1)

Дискриминант здесь равен ( 72 – 4 * 1 * 3 ) и достигает 37. Поскольку 37 больше 0, это означает, что у нас есть два действительных корня. Давайте решим и получим корни!

• (-7 +- (72 – 4*1*3)1/2)/(2*1)
• (-7 +- 371/2)/(2*1)
• (-7 +- 6,08)/(2*1)

Корни

• (-7 + 6.08)/(2*1) и (-7 – 6,08)/(2*1)
• -0,46 и -6,54

Корни x² + 7x + 3 = 0 равны -0,46 и -6,54

Уравнение 2

3x² – 13x – 12 = 0

а = 3 , б = -13 и с = -12

После подстановки значений a, b и c в формулу имеем

• (-(-13) +- (-132 – 4*3*-12)1/2)/(2*3)
• (13 +- (313)1/2)/(2*3)
• ( 13 +- 17. 69)/(2*3)

Корни

• (13 + 17,69) / (2 * 3) и (13 – 17,69) / (2 * 3)
• 5,11 и -0,78

Корни 3x2 – 13x – 12 = 0 равны 5,11 и -0,78

Уравнение 3

6y² + 10y = 0

а = 6 , б = 10 и с = 0

Коэффициент c равен нулю, поэтому он не фигурировал в вопросе.

После подстановки значений a, b и c в квадратичную формулу получаем следующее:

• (-10 +- (102 – 4 * 6 * 0)1/2) / (2 * 6)
•   (-10 +- (102)1/2)/(2 * 6)

Корни следующие:

• (-10 + 10)/12 и (-10–10)/12
• 0 и -1.67

Во всех вопросах дискриминант был больше 0. Все корни вещественные и парные.

Пример 2

Ваше квадратное уравнение 2x2 + 4x + 2 = 0 .

а = 2 , б = 4 и с = 2

Подставьте значения коэффициентов для a, b и c в квадратное уравнение.

• (-4 +- (42 – 4 * 2 * 2 )1/2) / 2 * 2
• (-4 +- 0) / 4

Корни

• (-4 + 0)/4 или (-4 – 0)/4
• -1 и -1

Корень квадратного уравнения равен -1.В этом примере дискриминант равен 0, и мы получили только один корень.

Пример 3

Найдите корни числа 3x2 + 2x + 7 = 0 .

а = 3 , б = 2 и с = 7

Введите значения a, b и c в квадратную формулу.

• (-2 +- (22 – 4 * 3 * 7 )1/2) / 2 * 2
• (-2 +- (-80)1/2)/4
• (-2 +- 8,9j) / 4

Корни

• (-2 + 8.9j)/4 и (-2 – 8,9j)/4
• Дальнейшее упрощение корней невозможно.

Корни здесь мнимые. Они содержат мнимую переменную j, которую мы определяем как (-1)1/2 или квадратный корень из -1. Мы пришли к мнимым корням, потому что дискриминант был меньше нуля.