Законы сохранения | Репетитор по физике
Алгоритм решения задач на закон сохранения импульса:
- Записать краткое условие задачи.
- Перевести единицы измерения в систему СИ.
- Выбрать систему отсчёта.
- Считать систему тел замкнутой.
- Нарисовать тела до взаимодействия и после, учитывая упругий удар или неупругий, указывая направления их скоростей.
- Выбрать оси координат.
- Записать Закон сохранения импульса в векторной форме.
- Спроецировать Закон сохранения импульса на оси координат.
- Решить систему уравнений.
- Оценить полученный результат.
Проверьте свои знания, пройдя Тренировочный тест по Законам Сохранения
Примеры решения задач
С2. Свинцовый шар массой 500 г, движущийся со скоростью 0, 6 м/с, сталкивается с неподвижным шаром из воска массой 100 г, после чего оба шара движутся вместе. Определите кинетическую энергию шаров после удара.
Решение: В инерциальной системе отсчёта, связанной с Землёй, считая систему тел замкнутой.
Закон сохранения импульса:
Проекция на ось Х:
m1v0 = (m1 + m2) v ;
Ответ: Е= 0,075 Дж
Закон сохранения энергии.
Алгоритм решения задач на закон сохранения энергии:
- Записать краткое условие задачи.
- Перевести единицы измерения в систему СИ.
- Выбрать систему отсчёта.
- Определить начальное и конечное положения тел, а так же, если необходимо, то промежуточные положения, о которых идёт речь в задаче.
- Выбрать нулевой уровень потенциальной энергии.
- Если на тела действуют только потенциальные силы, записать закон сохранения механической энергии: Е1= Е2. Если в системе тел действуют также и непотенциальные силы, то закон сохранения энергии записать в следующем виде: ΔЕ = Е2 — Е1 = А , где А А — работа непотенциальных сил.
- Выразить неизвестное.
- Произвести расчёт численного значения и единиц измерения.
- Оценить полученный результат.
С2. Два пластилиновых шарика массами по 50 г движутся с одинаковыми по модулю скоростями 0,8 м/с, направленными под углом 90˚ друг к другу. Какая часть энергии перейдёт в тепло при абсолютно неупругом ударе?
Решение:
В инерциальной системе отсчёта, считая систему
замкнутой. Закон сохранения импульса:
Энергия системы до удара: Е1 = m1v12/2 + m2v22/2 ; E1 = 0,032 Дж
Энергия системы после удара: Е2 = (m1+m2) v2/2 ; E2
= 0,016 ДжКоличество теплоты, выделенное при ударе:
Q = E1— E2 ; Q = 0,016 Дж
Часть энергии, перешедшая в тепло после удара: Q/E1= 0,5
Ответ: 50%
Типичные ошибки в задачах на применение законов сохранения энергии, а также энергии и импульса:
- Неверное представление об импульсе и его изменении, носящих векторный характер.
- При неупругом столкновения не выполняется закон сохранения механической энергии. В этом случае следует применять закон сохранения импульса.
- Работа равнодействующей всех сил равна изменению кинетической энергии, произошедшему под действием этой силы.
- При выборе ответа полагаться только на физические законы, а не на интуицию.
- Применение закона сохранения энергии в совокупности с анализом графиков.
2.2.4. Закон сохранения импульса. Совместное применение законов сохранения импульса и механической энергии
1. Закон сохранения импульса
 ,
,
то
есть суммарный импульс замкнутой системы
тел 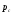 сохраняется постоянным.
сохраняется постоянным.
2. Закон сохранения импульса для системы из двух тел
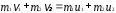 ,
,
где 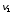
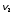 – скорости тел в короткий момент до
взаимодействия;
– скорости тел в короткий момент до
взаимодействия;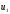 и
и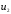 – скорости тех же тел после взаимодействия.
– скорости тех же тел после взаимодействия.3. Применение законов сохранения энергии и импульса к прямому центральному удару шаров:
а) неупругий удар
— закон сохранения импульса
 ,
,
— скорость шаров после неупругого удара
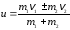 ,
,
знак “минус” соответствует движению шаров навстречу;
б) упругий удар
скорости упругих шаров после удара
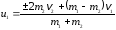 ,
,
 ,
,
где 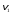 и
и – скорости шаров до удара,
– скорости шаров до удара,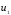 и
и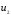 – после удара.
– после удара.
Примеры решения задач
Задача 1
Человек массой 60 кг стоит на тележке массой 30 кг. Определить скорость тележки, если человек будет двигаться по ней с относительной скоростью 3 м/с. Трением между тележкой и дорогой пренебречь.
Дано: | Решение: |
m1 = 60 кг m2 = 30 кг
| Систему человек – тележка можно считать замкнутой, так как сила тяжести уравновешивается силой нормальной реакции тележки. До взаимодействия суммарный импульс человек – тележка был равен нулю. |
u = ? |
При
движении человека его скорость
относительно Земли будет равна 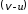 ,
а импульс человека
,
а импульс человека
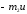 .
.Запишем закон сохранения импульса в проекции на ось X в системе отсчета относительно Земли
 .
.
Отсюда 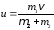 .
.
Проведём вычисление u:
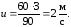
Задача 2
Пуля массой 10 г, летящая горизонтально со скоростью 400 м/с, попадает в мешок с песком массой 4 кг, висящий на длинной нерастяжимой нити и застревает в нем. Найти высоту, на которую поднимется мешок после попадания в него пули.
Дано: | Решение: |
m1= 10 г = 10-2 кг; v1 = 400 м/с; m2= 4 кг; v2 = 0 | Решение задачи основано на использовании двух законов: закона сохранения энергии и закона сохранения импульса. После попадания пули мешок с песком движется вместе с застрявшей в нем пулей со скоростью u. |
h = ? |
На основе закона сохранения энергии запишем:
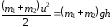
Для определения скорости совместного движения мешка и пули используем закон сохранения импульса. Запишем его в проекции на ось Х:
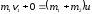 ,
(2)
,
(2)
откуда
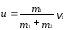 .
(3)
.
(3)
Подставим выражение (3) в формулу (1) и тогда высота h равна
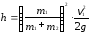 .
(4)
.
(4)
Выполним вычисления по формуле (4)
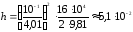 м
= 5,1 см.
м
= 5,1 см.
Алгоритм решения задач на законы сохранения импульса и энергии.
Выберите систему тел.
Выберите 2 (или больше) состояний этой системы до и после взаимодействия.
Запишите выражение для импульса или энергии системы этих состояний.
Уясните, является ли эта система замкнутой.
Выберите систему отсчёта.
Найдите изменение импульса или энергии.
Приравняйте выражение а) 0, если система замкнута; б) импульсу (работе) внешних сил, если система не замкнута.
Найдите неизвестную величину.
Примеры решения задач.
С
 тоящий
на льду человек массой 60 кг ловит мяч
массой 0,5 кг, который летит горизонтально
со скоростью 20 м/с. С какой скоростью
человек начнет скользить по льду?
тоящий
на льду человек массой 60 кг ловит мяч
массой 0,5 кг, который летит горизонтально
со скоростью 20 м/с. С какой скоростью
человек начнет скользить по льду?
Решение: Запишем закон сохранения импульса в
проекциях на ось ОХ:  .Ответ:
0,165 м/с.
.Ответ:
0,165 м/с.
2. Какую работу нужно совершить для равномерного перемещения по горизонтальной поверхности на расстояние 500 м тела массой 200 кг? Считать, что направление действующей силы совпадает с направлением движения, а коэффициент трения равен 0,02.
Решение: 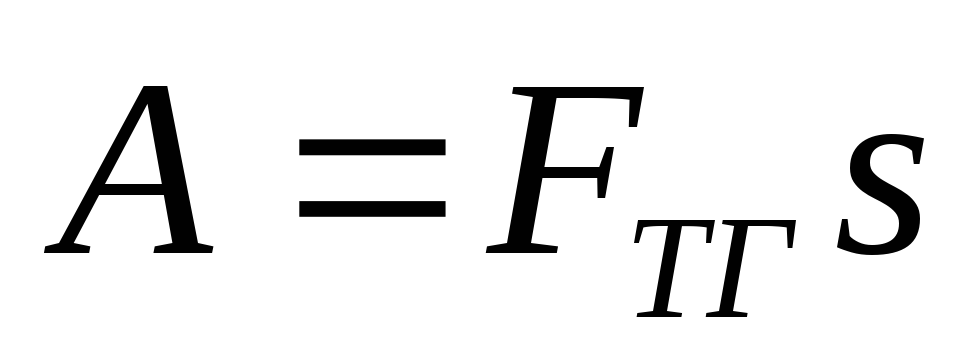 ,
т.к. движение равномерное, то
,
т.к. движение равномерное, то .Ответ:
2.104Дж.
.Ответ:
2.104Дж.
3. Тело массой 0,5 кг, брошенное вертикально вверх со скоростью 20 м/с, поднялось на высоту 15 м. Определите работу силы сопротивления воздуха.
Решение: При подъёме тела на максимальную высоту
кинетическая энергия расходуется на
преодоление сил сопротивления и переход
в потенциальную энергию: 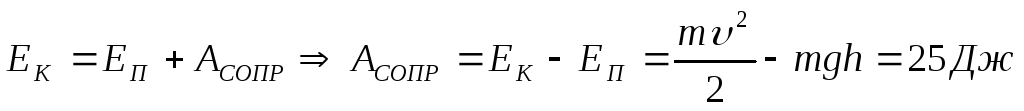 .Ответ: 25Дж
.Ответ: 25Дж
Колебания и волны.
Колебаниями в механике называют движение тела, которое точно или приблизительно точно повторяется через одинаковые промежутки времени.
Механическим колебаниями называются такие движения тел, при которых через равные интервалы времени координаты движущегося тела, его скорость и ускорение принимают исходные значения.
Механические колебания, которые происходят под действием силы, пропорциональной смещению и направленной противоположно ему, являются гармоническими колебаниями.
Свободными называются колебания, которые после возбуждения происходят без внешних воздействий.
Вынужденными называются колебания, совершаемые телом под действием внешней, периодически изменяющейся силы.
Условия возникновения свободных колебаний:
система должна находиться вблизи положения устойчивого равновесия;
силы трения или силы сопротивления должны быть достаточно малыми.
Резонанс – это явление резкого возрастания амплитуды вынужденных колебаний при совпадении частоты колебаний вынужденной силы и собственной частоты колебательной системы.
Основные величины, характеризующие колебательное движение:
Период колебаний
– минимальный интервал времени, через
который происходит повторение движения.  – обозначение
периода колебаний,
– обозначение
периода колебаний, (секунда) – единица измерения;
(секунда) – единица измерения; ,
где
,
где – время,
– время, – число
колебаний.
– число
колебаний.
Частота колебаний – это число колебаний в единицу времени.
 –обозначение
частоты, 1 Гц (герц) =1 с-1 – единица
измерения.
–обозначение
частоты, 1 Гц (герц) =1 с-1 – единица
измерения.  ,
,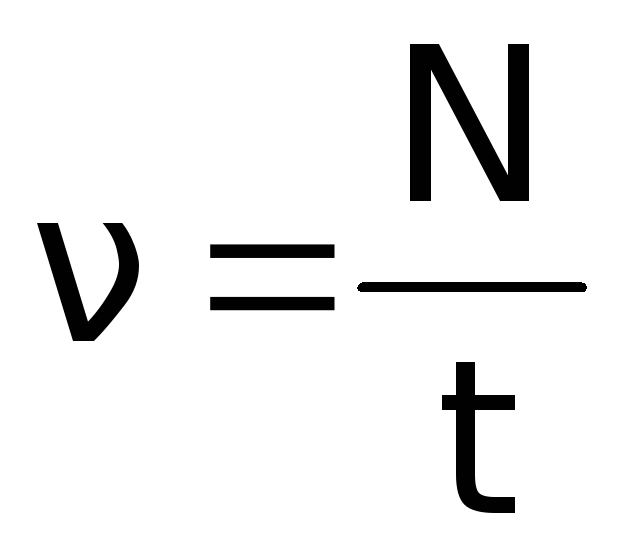 .
.
Один
оборот по окружности называют циклом.
Циклическая частота колебаний есть число колебаний,
совершаемых за 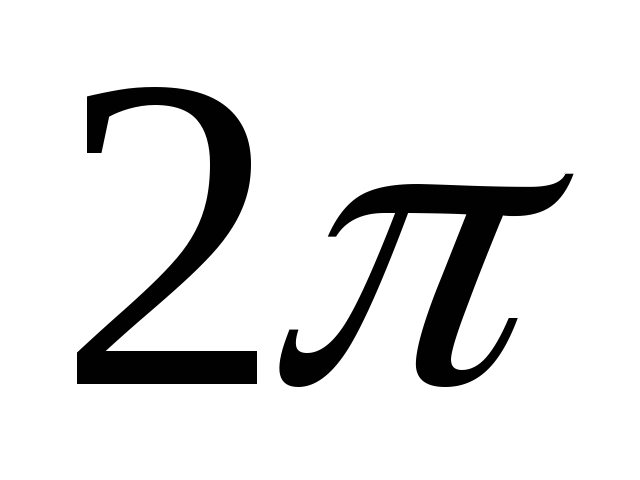 секунд.
секунд. –
обозначение циклической частоты
–
обозначение циклической частоты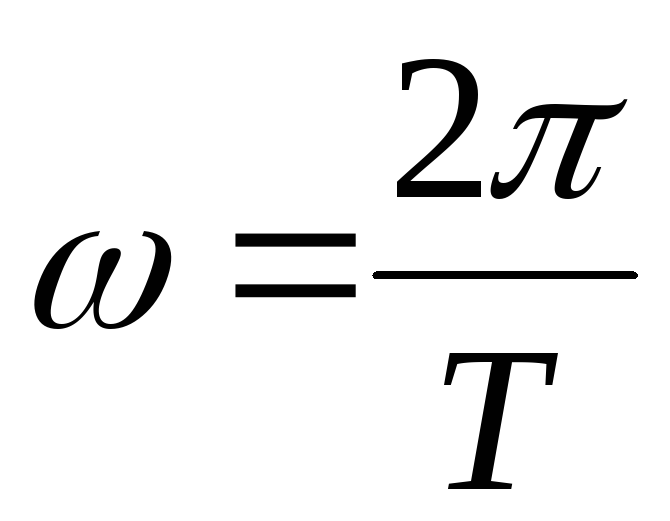 ,
, .
.
X – смещение (м) – произвольное отклонение тела от положения равновесия.
А мплитудой
колебанияА (м) называется наибольшее по модулю
смещение тела от положения равновесия.
мплитудой
колебанияА (м) называется наибольшее по модулю
смещение тела от положения равновесия.
Графическое представление:
Гармонические колебания описываются формулами:
 ,
где
,
где 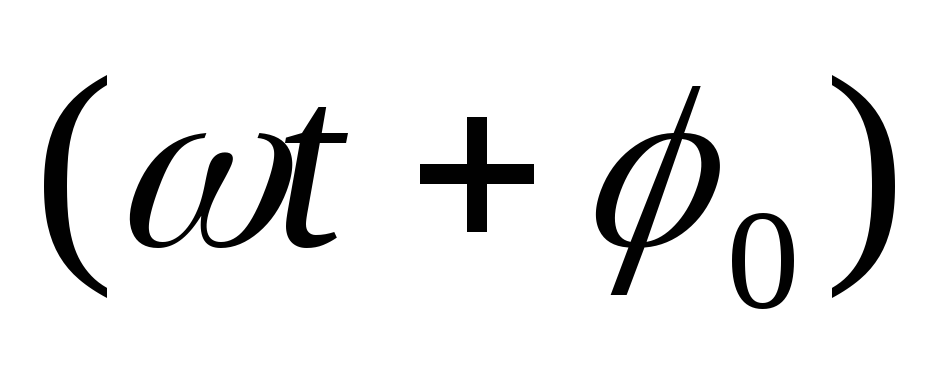 – фаза
колебаний,
– фаза
колебаний, – начальная
фаза.
– начальная
фаза.
Полная
механическая энергия системы равна сумме кинетической и
потенциальной энергии: .
.
В
состоянии наибольшего отклонения тела
от положения равновесия: 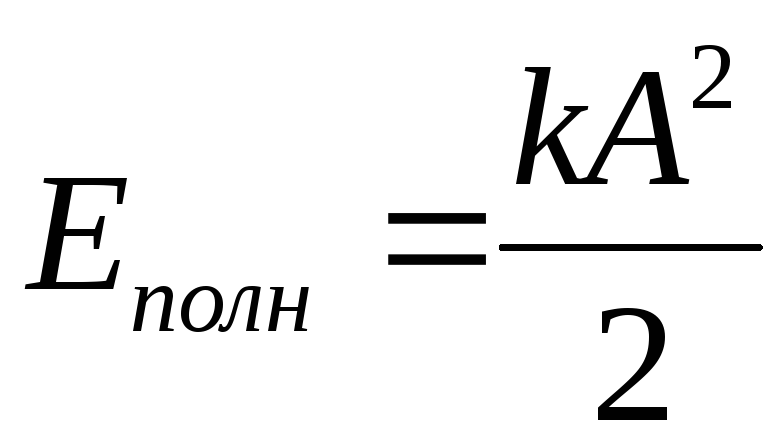 .
.
В
положении равновесия: 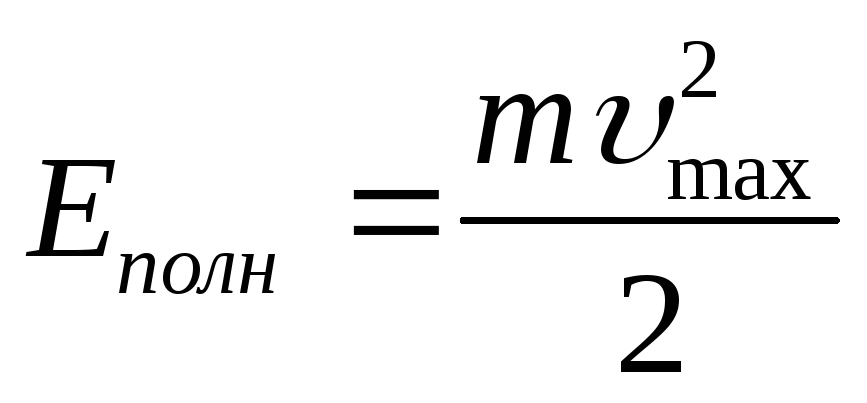 .
.
Математическим маятником называют материальную точку, подвешенную на длинной, невесомой, нерастяжимой нити.
Основные законы математического маятника:
Период математического маятника не зависит от массы груза.
Период математического маятника не зависит от амплитуды колебаний.
 ,
где
,
где – длина
нити маятника,g–
ускорение свободного падения.
– длина
нити маятника,g–
ускорение свободного падения.
Пружинный маятник – это простейшая колебательная система, состоящая из груза, прикрепленного к пружине.
Период пружинного
маятника зависит только от массы груза
и жесткости пружины. ,
где
,
где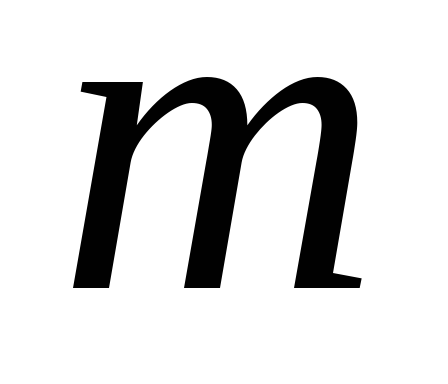 – масса груза;
– масса груза;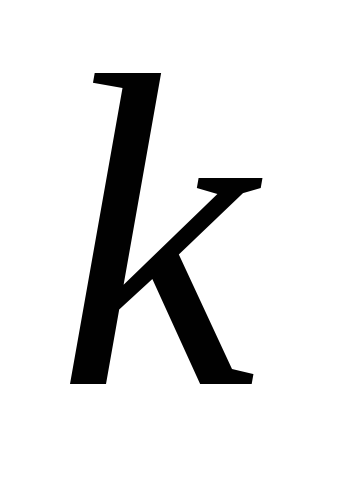 – жесткость
пружины.
– жесткость
пружины.
Закон сохранения импульса
Рассмотрим теперь простой пример: любая совокупность взаимодействующих тел может называться системой тел. Например, рюкзак и несущий его путник являются системой тел. На эти тела системы действуют внешние и внутренние силы.

Внутренние силы — это силы, возникающие в результате взаимодействия тел системы.
Внешние силы — это силы, возникающие в результате взаимодействия тел системы с телами, не принадлежащими этой системе.
Например, рюкзак давит на плечи путника своим весом — это пример внутренней силы. Также, на путника действует сила трения или сила сопротивления воздуха — это пример действия внешних сил. Запишем теперь импульсы тел системы, используя другую формулировку второго закона Ньютона:


Чтобы найти импульс системы нужно сложить импульсы каждого тела системы:

А теперь, обратите внимание, что равнодействующая сила, складывается из действия внешних и внутренних сил на каждое тело системы. Но, по третьему закону Ньютона, тела действуют друг на друга с силами, равными по модулю и противоположными по направлению. Иными словами, сумма внутренних сил системы всегда равна нулю:

Таким образом, мы выяснили, что изменить импульс системы тел могут только внешние силы. Отсюда вытекает формулировка закона сохранения импульса: если сумма внешних сил равна нулю, то импульс системы тел сохраняется (то есть остается неизменным):

где  —
начальные скорости тел, а
—
начальные скорости тел, а  —
конечные скорости тел.
—
конечные скорости тел.
Эта формулировка закона сохранения импульса справедлива для системы, включающей в себя любое количество тел.
Все вы прекрасно знаете, что если столкнуть два мячика, направив их по одной прямой, то они обязательно, отскочат в разные стороны. Если мы предположим, что их массы равны, то можно с уверенностью утверждать, что скорости мячей будут равны по модулю и противоположны по направлению. Конечно, вы можете сказать, что мячи очень скоро остановятся, а, значит, потеряют свой импульс. Дело в том, что и на тот, и на другой мяч будет действовать сила трения, которая является внешней силой и способна изменить импульс системы. Если же мы предположим, что трение отсутствует, то мячи так и будут катиться с полученными скоростями, пока действие каких-либо других внешних сил не изменит их скорость.
Давайте рассмотрим частные случаи закона сохранения импульса для двух тел (поскольку в ближайшее время мы чаще всего будем рассматривать системы из двух тел). Существуют так называемые, абсолютно упругие и абсолютно неупругие удары.
При абсолютно неупругом ударе два тела сцепляются и продолжают движение как одно тело.
Абсолютно упругим ударом называется такой удар, при котором деформацией тел можно пренебречь (то есть сохраняется кинетическая энергия системы).
Ярким примером демонстрации закона сохранения импульса является механическая система, получившая название «колыбель Ньютона».

В этой системе силы трения практически отсутствуют, поэтому, требуется достаточно длительное время, чтобы шарики остановились. Удары этих шаров вполне можно считать абсолютно упругими.
Примеры решения задач.
Задача 1. Из пушки массой 600 кг произвели выстрел, после чего, пушка откатилась назад со скоростью 4 м/с. Учитывая, что ствол пушки расположен горизонтально, какова скорость снаряда, массой 50 кг?

Задача 2. Груженая тележка массой 100 кг, едет со скоростью 6 м/с. Впереди неё в том же направлении катится вторая тележка со скоростью 1 м/с. После абсолютно неупругого удара скорость груженой тележки равна 5 м/с. Найдите массу второй тележки.
В первую очередь, обратите внимание, что мы рассматриваем абсолютно неупругий удар. То есть, после столкновения две тележки продолжили катиться как одно тело. А это значит, что скорость первой тележки, конечно же, равна скорости второй тележки.

Решение задач на закон сохранения импульса

Решение задач
«Закон сохранения импульса»

Цель урока:
- Научится применять теоретические знания при решении задач на закон сохранения импульса.
- Рассмотреть примеры задач которые могут быть на ОГЭ по физике
- Проверить уровень усвоения тем «Импульс тела» и «Закон сохранения импульса тел»

Проверяем домашнее задание
- Величина, равная ________________ массы тела на его скорость, называется ______________________________.
- Вектор скорости и импульса движущегося тела имеют __________ направление
- За единицу импульса принимают _____________.
- Если два или несколько тел взаимодействуют только между собой, то эти тела образуют ___________________.
- Закон _______________________ заключается в том, что векторная сумма импульсов тел, образующих замкнутую систему, _________________ с течением времени при любых движениях и взаимодействиях этих тел.
- Для замкнутой системы, состоящей из двух тел, закон сохранения импульса записывается в таком виде ________________________________________.
- Поясните, что означает каждый символ в этом уравнении:_____________________________________________

Проверяем
- Величина, равная произведению массы тела на его скорость, называется импульсом тела
- Вектор скорости и импульса движущегося тела имеют одинаковое направление
- За единицу импульса принимают
- Если два или несколько тел взаимодействуют только между собой, то эти тела образуют замкнутую систему
- Закон сохранения импульса заключается в том, что векторная сумма импульсов тел, образующих замкнутую систему, не меняется с течением времени при любых движениях и взаимодействиях этих тел
- Для замкнутой системы, состоящей из двух тел, закон сохранения импульса записывается в таком виде Р / 1 +Р / 2 =Р 1 +Р 2 или m 1 V / 1 +m 2 V / 2 =m 1 V 1 +m 2 V 2

Решение задач
Задача № 1

Задача № 2

Задача № 3

Домашнее задание
§ 21, 23
Спасибо
за
урок !





Продолжим повторение теории!
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела
Теорема о кинетической энергии тела: работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии
A = E k2 – Е k1
Потенциальная энергия тела в поле силы тяжести равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень
E p = mgh
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией

Продолжим повторение теории!
Закон сохранения энергии в механических процессах:
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной
А – кинетическая энергия шара;
В – потенциальная энергия шара;
С – полная механическая энергия шара.

Рассмотрим другие примеры
Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда неизвестны действующие силы. Примером такого рода задач является ударное взаимодействие тел.
Ударом (соударением, столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения.
Часто используются две модели ударного взаимодействия –
и абсолютно неупругий удар .
абсолютно упругий удар

Образовательный портал «Мой университет» — www.moi-universitet.ru
Факультет «Реформа образования» — www . edu — reforma . ru
Неупругие и упругие соударения
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.

Рассмотрим пример
На основе законов механики математически точно описывается «поведение» бильярдных шаров, столкновения которых друг с другом и со стенками бильярдного стола можно считать абсолютно упругими.
При этом соударения могут быть центральными и нецентральными
Центральное соударение
Нецентральное соударение

Переходим к практике
Задача . Под каким углом могут разлететься два тела одинаковой массы после упругого нецентрального столкновения?
Построим диаграмму импульсов
Применим закон сохранения импульса в векторном виде с учётом равенства масс:
По закону сохранения энергии при равных массах:
Первое из этих равенств означает, что векторы скоростей образуют треугольник, а второе – что для этого треугольника справедлива теорема Пифагора, то есть он прямоугольный. Искомый угол – это угол между катетами, т.е. он равен 90° .

Повторим теорию!
для упругого взаимодействия
для неупругого взаимодействия
Решение задач на закон сохранения импульса

Решение задач по теме: «Закон сохранения импульса»

Повторение
1. Что называют импульсом тела?
2. Назовите единицу импульса тела
в системе СИ?
3. Система каких тел называется
замкнутой?
4. Какие силы называются внутренними,
внешними?
5. Сформулируйте закон сохранения
импульса.

Важно знать!!!
- Закон сохранения импульса

Реши задачи устно.
1.Из двух тел различной массы, движущихся с
одинаковыми скоростями, импульс которого
больше?
2. Из двух тел равной массы , движущихся
с различными скоростями, импульс какого
больше?
3. Чему равен импульс вороны, сидящей
на заборе?
v 2
v 1

Реши задачи устно.
4. Определите знаки проекций импульсов тел.
5. Машина массой 2т движется со скоростью
10 м/с. Каков импульс машины?
o
x

Реши задачи.
1. Мальчик массой 50 кг изменил свою скорость, с 2 м/с до 3 м/с за 10 с. Какая сила действовала на мальчика?
2. Сани массой 200 кг под действием силы 400 Н за 5 с изменили скорость с 3 м/с до 8 м/с. Найти импульс силы, импульс саней в начале и в конце движения.

Важно знать!!!
Алгоритм решения задач на ЗСИ
- Сделать рисунок, на котором обозначить направления оси координат, векторов
скорости тел до и после взаимодействия
2) Записать в векторном виде закон сохранения импульса
3) Записать закон сохранения импульса в проекции на ось координат
4) Из полученного уравнения выразить неизвестную величину и найти её значение

Рассмотрим пример
решения задачи.
Снаряд массой 100кг , летящий горизонтально вдоль железнодорожного пути со скоростью 500 м/с , попадает в вагон с песком массой 10т и застревает в нем. Какую скорость получит вагон , если он двигался со скоростью 36км/ч в направлении, противоположном движению снаряда?

Запишите ЗСИ в векторном виде.
Запишите ЗСИ в проекции на ось Оx.
Из полученного уравнения выразите скорость вагона после попадания в него снаряда.
Ответ: 5 м/с.

Задачи.
1.Вагон массой 20 т , движущийся со скоростью
0,3 м/с , нагоняет вагон массой 30 т , движущийся со скоростью 0,2 м/с . Какова скорость вагонов после того, как сработает сцепка?
2.Какую скорость приобретёт лежащее на льду чугунное ядро, если пуля, летящая горизонтально со скоростью 500 м/с , отскочит от него и будет двигаться в противоположном направлении со скоростью 400 м/с ? Масса пули 10 г , масса ядра 25 кг .

Домашнее задание.
1.Выучить алгоритм решения задач.
2. С лодки общей массой 200 кг, движущейся со скоростью 1 м/с, выпал груз массой 100 кг. Какой стала скорость лодки?
Решение задач на закон сохранения импульса

Решение задач по теме: «Закон сохранения импульса»

Повторение
1. Что называют импульсом тела?
2. Назовите единицу импульса тела
в системе СИ?
3. Система каких тел называется
замкнутой?
4. Какие силы называются внутренними,
внешними?
5. Сформулируйте закон сохранения
импульса.

Важно знать!!!
- Закон сохранения импульса

Реши задачи устно.
1.Из двух тел различной массы, движущихся с
одинаковыми скоростями, импульс которого
больше?
2. Из двух тел равной массы , движущихся
с различными скоростями, импульс какого
больше?
3. Чему равен импульс вороны, сидящей
на заборе?
v 2
v 1

Реши задачи устно.
4. Определите знаки проекций импульсов тел.
5. Машина массой 2т движется со скоростью
10 м/с. Каков импульс машины?
o
x

Реши задачи.
1. Мальчик массой 50 кг изменил свою скорость, с 2 м/с до 3 м/с за 10 с. Какая сила действовала на мальчика?
2. Сани массой 200 кг под действием силы 400 Н за 5 с изменили скорость с 3 м/с до 8 м/с. Найти импульс силы, импульс саней в начале и в конце движения.

Важно знать!!!
Алгоритм решения задач на ЗСИ
- Сделать рисунок, на котором обозначить направления оси координат, векторов
скорости тел до и после взаимодействия
2) Записать в векторном виде закон сохранения импульса
3) Записать закон сохранения импульса в проекции на ось координат
4) Из полученного уравнения выразить неизвестную величину и найти её значение

Рассмотрим пример
решения задачи.
Снаряд массой 100кг , летящий горизонтально вдоль железнодорожного пути со скоростью 500 м/с , попадает в вагон с песком массой 10т и застревает в нем. Какую скорость получит вагон , если он двигался со скоростью 36км/ч в направлении, противоположном движению снаряда?

Запишите ЗСИ в векторном виде.
Запишите ЗСИ в проекции на ось Оx.
Из полученного уравнения выразите скорость вагона после попадания в него снаряда.
Ответ: 5 м/с.

Задачи.
1.Вагон массой 20 т , движущийся со скоростью
0,3 м/с , нагоняет вагон массой 30 т , движущийся со скоростью 0,2 м/с . Какова скорость вагонов после того, как сработает сцепка?
2.Какую скорость приобретёт лежащее на льду чугунное ядро, если пуля, летящая горизонтально со скоростью 500 м/с , отскочит от него и будет двигаться в противоположном направлении со скоростью 400 м/с ? Масса пули 10 г , масса ядра 25 кг .

Домашнее задание.
1.Выучить алгоритм решения задач.
2. С лодки общей массой 200 кг, движущейся со скоростью 1 м/с, выпал груз массой 100 кг. Какой стала скорость лодки?
 =
3 м/с
=
3 м/с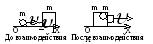 тоящий
на льду человек массой 60 кг ловит мяч
массой 0,5 кг, который летит горизонтально
со скоростью 20 м/с. С какой скоростью
человек начнет скользить по льду?
тоящий
на льду человек массой 60 кг ловит мяч
массой 0,5 кг, который летит горизонтально
со скоростью 20 м/с. С какой скоростью
человек начнет скользить по льду?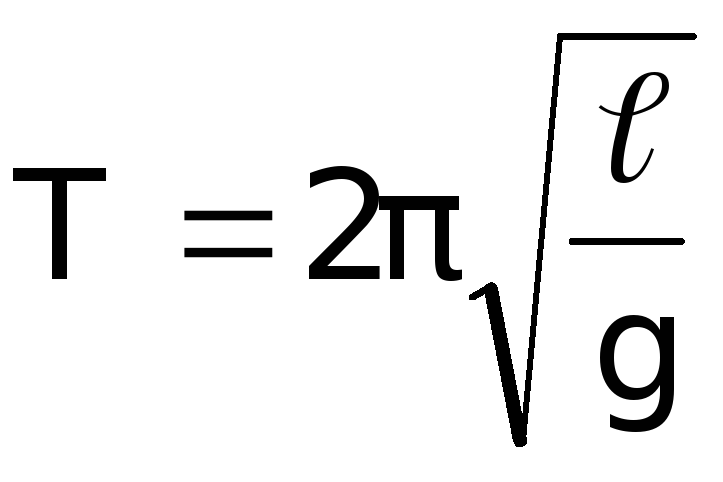 ,
где
,
где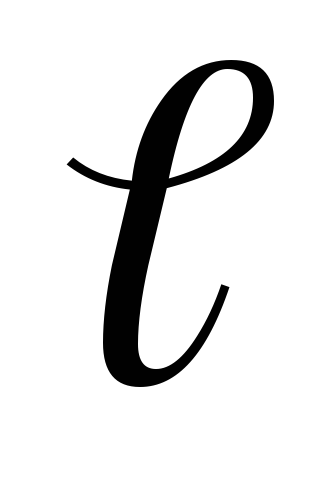 – длина
нити маятника,g–
ускорение свободного падения.
– длина
нити маятника,g–
ускорение свободного падения.