Урок математики в 5-м классе по теме «Степень числа. Квадрат и куб числа»

Цели и задачи урока:

1. Ввести понятие степени числа, основания степени и показателя степени, закрепить понятие возведения в степень на решении заданий.
2. Развивать внимание, логическое мышление, математическую речь.
3. Воспитание культуры речи, усидчивости.

Оборудование:

• компьютер,
• мультимедийный проектор,
• экран,
• презентация “Возведение в степень квадрат и куб числа”.

Ход урока

1. Организационный момент.

2. Актуализация знаний: (слайд)

Упростить выражение:

• 25х + 15 х;
• 12у – 3у;
• 9k + 9k – 4k;
• 80c-35c-14c;
• 8d+d-9d;
• 163 + 37v + 18v

Решить уравнение:

• 7х+2х = 918;
• 5а-3а = 222;
• 18у – 13у – 5 = 35

Проверьте порядок действий:

       1      3           2         4
508 * 609 — (22313 + 345) : 69

     4      6     5     2      3     1
34 * 45 + 56 — 78 * 356 : 56 * 4

3. Объяснение нового материала: (слайд)

Вы знаете, что сумму равных слагаемых заменяют произведением,

например:

5+5+5+5+5+5+5+5+5+5= 5*10 это короче и удобней.

А есть ли способ, чтобы заменить произведение равных сомножителей?

Как, например, произведение 5*5*5*5*5*5*5*5*5*5 записать короче?

Такой способ есть 5*5*5*5*5*5*5*5*5*5=5¹⁰

5¹⁰ — читают: “пять в десятой степени”

5 – основание степени

10 – показатель степени, который показывает, сколько множителей было в произведении

В математике произведение одинаковых множителей называется – возведением в степень.

4. Закрепление: (слайд)

А)Записать в тетрадь произведения в виде степени и вычислить:

3*3*3*3=3⁴=81

5*5*5=5³=125

2*2*2*2*2*2=2⁶=64

Б) Устно: (слайд)

Назовите основание и показатель степени:

3⁴; 5³;2⁶; 6¹

Если показатель степени равен 1, то что это значит?

Первая степень любого числа равна этому числу.

5. Объяснение нового материала: (слайд)

Квадрат и куб числа а² и а³

Вторая и третья степени числа имеют особые названия.
Вторую степень называют – Квадратом этого числа.
Квадрат числа 2 равен 4,
Квадрат числа 3 равен 9.
Запись 2² читают: “Два в квадрате”.

А почему такое название – квадрат?

Ведь у нас никаких геометрических фигур здесь не появилось.
Фигура сейчас появится. И именно квадрат. Рассмотрим квадрат со стороной 2 см. его площадь равна 2*2=2²(кв.см)
Рассмотрим шахматную доску. У нее 8 строк (горизонталей) и 8 столбцов (вертикалей).
Клетки этой таблицы-доски называют полями.

Сколько у нее полей? Ответ: 8*8=8²=64

Третью степень называют – Кубом этого числа.
Запись 2³ читают: “Два в кубе”.

Рассмотрим куб, ребро которого имеет длину 2 см, видно, что он сложен из восьми кубиков с ребром 1 см.

Но 8 как раз и равно 2*2*2=2³

6. Работа с учебником.

№ 653 (выполняет у доски ученик)

7. Закрепление

А) запишите выражение с помощью символов степени и вычислите его значение:

• 10*10*10
• 6*6*6
• 4*4+8*8
• 2*2*2+3*3

Б) вычислите: 11²; 9³; 34¹; 13²; 4³.

В) Вопросы: Что называется возведением в степень?
Произведение одинаковых множителей называется – возведением в степень.

• На примере поясните, какое число называется степенью, основанием степени, показателем степени?
• Дано число. Чему равна его первая степень?
  Первая степень числа равна самому числу.
• Что такое квадрат данного числа ?Куб данного числа?
• Дан куб со стороной а см (а – натуральное число). Из скольких кубиков с ребром 1 см он сложен?
  Из а кубиков.
• Верно ли равенство? 15*3=15³
  Равенство неверное, т.к. 15³ =15*15*15

7. Домашнее задание:

8.Итог урока:

1. Что нового вы узнали на уроке?
2. Какие трудности были у вас на уроке?
3. Что понравилось на уроке?

urok.1sept.ru

Степень числа 5 класс Как найти степень

Степень числа 5 класс

Как найти степень числа. • Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение. Так, вместо произведения шести одинаковых множителей 4 • 4 • 4 • 4 пишут 46 и произносят «четыре в шестой степени». 4 • 4 • 4 • 4 = 46

Выражение 4 в степени 6 • 4 — основание степени; • 6 — показатель степени.

• В общем виде степень с основанием «a» и показателем «n» записывается с помощью выражения:

Запомните! • Запись an читается так: «а в степени n» или «n-ая степень числа a». • Исключение составляют записи: • a 2 — её можно произносить как «а в квадрате»; • a 3 — её можно произносить как «а в кубе».

Степенью числа «a» с натуральным показателем «n», бóльшим 1, называется произведение «n» одинаковых множителей, каждый из которых равен числу «a».

• Конечно, выражения выше можно читать и по определению степени: • a 2 — «а во второй степени»; • a 3 — «а в третьей степени».

• Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0). • • Степенью числа «а» с показателем n = 1 является само это число: a 1 = a • Любое число в нулевой степени равно единице. a 0 = 1 • Ноль в любой натуральной степени равен нулю. 0 n = 0 • Единица в любой степени равна 1. 1 n = 1

• Выражение 00 (ноль в нулевой степени) считают лишённым смыслом. • (-32)ст0 = 1 • 0 ст253 = 0 • 1 ст4 = 1 • При решении примеров нужно помнить, что возведением в степень называется нахождение значения степени.

• При решении примеров нужно помнить, что возведением в степень называется нахождение значения степени. • Пример. Возвести в степень. • 5 ст3 = 5 • 5 = 125 • 2. 5 ст2 = 2. 5 • 2. 5 = 6. 25

Возведение в степень отрицательного числа 5 класс

Запомните! • Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.

• При возведении в степень положительного числа получается положительное число. • При возведении нуля в натуральную степень получается ноль.

• При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел. • Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.

• Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.

Запомните! • Отрицательное число, возведённое в чётную степень, есть число положительное. • Отрицательное число, возведённое в нечётную степень, число отрицательное. • Квадрат любого числа есть положительное число или нуль, то есть: a 2 ≥ 0 при любом a.

Пример 2 • (- 3)ст2 = 2 • (- 3) = 2 • 9 = 18 — 5 • (- 2)ст3 = — 5 • (- 8) = 40

• При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (5)ст4 и -5 ст4 это разные выражения. Результаты возведения в степень данных выражений будут разные.

• Вычислить (- 5)ст4 означает найти значение четвёртой степени отрицательного числа. • (- 5)ст4 = (- 5) • (- 5) = 625

• В то время как найти -5 ст4 означает, что пример нужно решать в 2 действия: • Возвести в четвёртую степень положительное число 5. 5 ст4 = 5 • 5 • 5 = 625 • Поставить перед полученным результатом знак «минус» (то есть выполнить действие вычитание). -5 ст4 = — 625

Обратите внимание! • • • Вычислить: — 6 ст2 — (- 1)ст4 6 ст2 = 6 • 6 = 36 -6 ст2 = — 36 (- 1)ст4 = (- 1) • (- 1) = 1 — (- 1)ст4 = — 1 — 36 — 1 = — 37

Порядок действий в примерах со степенями. 5 класс

• Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

Запомните! • В выражениях со степенями, не содержащими скобки, сначала выполняют вовзведение в степень, затем умножение и деление, а в конце сложение и вычитание. • Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

Пример • Вычислить:

• Для облегчения решения примеров полезно знать и пользоваться таблицей степеней.

Спасибо за внимание!

present5.com

Тест по математике: Степень числа (Мерзляк, 5 класс) — пройти тест онлайн — игра — вопросы с ответами

Мой результат

Выбрав правильный на ваш взгляд вариант ответа, жмите на кнопку «Проверить». Если хотите сразу увидеть правильные ответы, ищите под вопросами ссылку «Посмотреть правильные ответы»

1. 

Верно ли равенство 2⁴ = 4²?

2. 

В выражении 8³² число 32 называют:

3. 

В выражении 32⁸ число 8 называют:

4. 

Вычислите значение выражения 0,1³ + 0,2².

5. 

Как правильно записать на математическом языке: число 12,5 умножить на разность квадратов 16 и 4,5?

6. 

Вычислите значение степени 1^а, если а = 20.

7. 

В конце ХХ века население Москвы составляло примерно 88 · 10⁵ человек. Сколько всего человек проживало в Москве в это время?

8. 

Как правильно записать в виде степени произведение 0,8 · 0,8 · 0,8 · 0,8?

9. 

Упростите выражение 4 · 10³ · х · х · х.

10. 

По формуле S = а² вычислите площадь квадрата с длиной стороны 0,008 км.

kupidonia.ru

Методическая разработка по алгебре (5 класс) на тему: разработка урока для 5 класса «Степень числа»

Разработка урока математики по теме: «Степень числа». 5 класс.

Тема: « Степень числа»

Тип урока: Урок усвоения новых знаний.

Цели урока:

Знать: определение степени; понятия – « основание степени », « показатель степени ».

Уметь: находить числовое значение степени, определять порядок действий и находить значения числовых выражений, содержащих степень.

Структура урока:

1. Организационный.

2. Актуализация знаний и умений.

3. Постановка цели урока.

4. Усвоение нового материала. (Адаптивная технология. Самостоятельная деятельность учащихся под руководством учителя. Парная, групповая, индивидуальная  форма работы.)

5. Подведение итогов урока.

6. Информация о домашнем задании.

Ход урока.

1. Актуализация темы. Постановка цели урока.

На доске написаны примеры. Каким действием можно заменить сумму, чтобы получить верное равенство? (ответ детей)

4+4=                                                                            4*4=

5+5+5=                                                                        5*5*5=

3+3+3+3=                                                                    3*3*3*3=

2+2+2+2+2=                                                                2*2*2*2*2=

Посмотрим на другой столбец примеров. Что можно заметить в них? Есть ли способ замены произведения другим действием? (дискуссия  детей). Выход на тему и цель урока: «Степень числа». Включение учащихся в самостоятельную работу по алгоритму.

2. Изучение нового материала.

Алгоритм работы.

І. Работа в парах.

1.Прочитайте п.7 учебника (один ученик читает, другой слушает):

                        1 вариант: стр.69 и два абзаца стр.70.

                        2 вариант: с третьего абзаца стр. 70.

Взаимопередача  темы.

2.Выучите определение степени на стр.70.

3.Устно ответьте на вопросы: (работа в парах)

              — Какое выражение называется степенью?

              — Как обозначают основание степени?

              — Как обозначают показатель степени?

              — Что показывает основание степени?

              — Что показывает показатель степени?

ІІ. Фронтальная работа.

(на доску поместить Схему 1 – отработка понятий: степень, основание степени, показатель степени, которыми учащиеся овладевали, работая в парах. Составление опорной записи.)

 Схема 1

СТЕПЕНЬ  ЧИСЛА

an  — cтепень

a – основание степени

n – показатель степени

ІІІ. Работа в парах. Первичный контроль усвоения понятий. (Приложение 1. Тест 1.)

1.Выполните ТЕСТ  1. Оцените работу.

2.Проверьте друг друга с помощью ключа на доске. Оцените работу.

ІV. Фронтальная работа.

Возвращение и выполнение недорешенных примеров (второй столбец).

Замена произведения степенью. ( На доску поместить схему 2. Отработка понятий: степень, основание степени, показатель степени на примерах.

Выполнение преобразования выражений, содержащих степени, на основе определения; задания на порядок действий в выражении, содержащем степень).

Схема 2

ПРИМЕР:

8 3 – степень

8 – основание степени

3 – показатель степени

8 3 = 8 * 8 * 8 = 512

10 * 5 2 = 10 * 25 = 250

( 10 * 5 )2 = 50 2 = 2500

V. Индивидуальная работа. Первичный контроль: усвоение знаний 1 уровня. (Приложение 2. Тест 2.)

1.Выполните ТЕСТ 2.. Оцените работу.

2.Проверьте правильность решения по ключу у учителя. Оцените работу. (Если есть вопросы обратитесь к учителю).

VІ. Индивидуальная работа. Вторичный контроль: усвоение знаний 2 уровня. (Приложение 3. Тест 3.)

1.Выполните ТЕСТ 3. Оцените работу.

2.Проверьте правильность решения по ключу у учителя. Оцените работу. (Если есть вопросы обратитесь к учителю).

VІІ. Индивидуальная работа. Вторичный контроль: усвоение знаний 3 уровня.

(Приложение 4. Тест 4.)

1. Выполните ТЕСТ 4. Оцените работу.

2. Проверьте правильность решения по ключу у учителя. Оцените работу. (Если есть вопросы обратитесь к учителю).

3.Сдайте работу учителю.

4.Выполните устную контрольную работу (Схема  3). Результаты запишите в тетрадь (сверить ответ).

Схема 3

УСТНАЯ КОНТРОЛЬНАЯ РАБОТА

Какая самая яркая звезда на зимнем ночном небе в северном полушарии?

*23           +32           :72              *43                 -82                       +51

Возможные ответы: Вега – 3; Венера – 2; Сириус – 5; Альтаир – 6.

VІІІ. Самостоятельная работа на три уровня самооценки.

                 1 вариант                                                             2 вариант

                                                1 уровень

1. Запишите в виде степени:

а) 3*3                                                                         а) 4*4*4

б) 10*10*10                                                               б) 2*2*2*2

в) 1*1*1*1*1*1*1                                                     в) 5*5

2. Вычислите:

а) 53                                                                             а) 43

б) 132                                                                           б) 122

в) 304                                                                           в) 204

                                                 2 уровень

1. Вычислите:

а) 5*103                                                                       а) 33*10

б)  3*22                                                                        б) 4*22

в) (3*2)2                                                                       в) (2*4)2

2. Сравните числа:

а) 23 и 32                                                                       а) 34 и 43

б) 42 и 32                                                                       б) 62 и 53

в) 43 и 53                                                                       в) 34 и 24

 

                                               3 уровень

1. Определите показатель степени числа и запишите его вместо звездочки:

а) 8* = 512                                                                 а) 3* = 81

б) 2* = 64                                                                   б) 7* = 343

в) 6* = 1296                                                               в) 5* = 3125

2. Упростите запись, используя степень:

а) 2*2*2*5                                                                  а) 8*3*3

б) (2*5)*(2*5)*(2*5)                                                  б) 17*5*5*5*17

в) 13*6*6*6*6*13                                                      в) (5*3)*(5*3)*(5*3)*(5*3)     

                         

ІХ. Резервный материал. Работа в группах. Решение занимательной развивающей задачи с использованием степени.

Играем в математическое лото. Приложение 5.

Х. Рефлексия. Подведение итогов урока.

ХІ. Задание на дом.

В рабочих тетрадях выполнить № 75; 76; 77.

Приложение 1

Тест 1.

Заполни пропуски.

Выражение вида______ называется степенью, где ____________- это основание степени, а _____________- это показатель степени.

Основание степени – это ________________________________________, а показатель равен _____________________________________________________________________.

Примеры:

1. В выражении 64         число __________ основание степени, число ___________________ — показатель степени.

2. У степени _____________ основание равно 2, а показатель равен 5.

Приложение 2

Тест 2.

 Запишите в виде степени.

1. 2*2*2

а)   23                       б)   8                 в) 32                    г) 6

2. 100*100

а) 10000                 б)  100 2             в)  200               г) 2 100

3. 5*5*5*5*5*5

а)  5 6                       б)  15625          в)  30                 г) 6 5

                                                                                                                                       Приложение 3

Тест 3.

 Вычислите:

1. 7 2                                                                             4. 4*10 2

а) 49           б) 14           в) 56                                    а) 400          б) 1600               в)160

2. 90 2                                                                          5. 0*10 3

а) 180         б) 8100       в) 810                                  а) 1000        б) 0                     в) 10

3. 20 3                                                                          6. 1*10 3

а) 80           б) 600         в) 8000                                а) 10            б) 100                 в) 1000

Приложение 4

Тест 4.

 Вычислите:

1. 6*2 3                                                                       4. (4+5) 2

а) 48           б) 1728       в) 36                                    а) 81            б) 18                   в) 41

2. 27 : 3 2                                                                    5. (13- 5) 2

а) 81           б) 3             в) 4                                      а) 16            б) 64                   в) 144

3. 250 : 5 3                                                                  6. 10 + 5 2

а) 1250       б) 150         в) 2                                      а) 30            б) 35                   в) 20

Приложение 5

Математическое лото

А  51                                                 М  33                                               И  ( 2+1 )2

Ц  62                                                Д  72                                                Н  2 + 12

К  23                                                Г  82                                                 С  ( 5 – 4 )3

Т  42                                                Е  01                                                 Х  5 * 22

В  22                                                Р  52                                                 О  ( 5 * 2 )2

Ключ.

Тест 1.

Выражение вида an  называется степенью, где a – это основание степени, n – это показатель степени.

Основание степени – это повторяющийся множитель, а показатель равен числу одинаковых множителей.

Примеры:

1.В выражении 6 4 число 6 – основание степени, число 4 – показатель степени.

2. У степени 2 5 основание равно 2, а показатель равен 5.

Тест 2.

Тест 3.

Тест 4.

Самостоятельная работа

                                             

                                        1 вариант                                             2 вариант   

Уровень	№ задания	а	б	в	а	б	в
1	1	32	103	17	43	24	52
	2	125	169	810000	64	144	160000
2	1	5000	12	36	270	16	64
	2	меньше	меньше	меньше	больше	меньше	больше
3	1	3	6	4	4	3	5
	2	23 *5	(2*5)3	132*64	8*32	172*53	(5*3)4

Математическое лото

«В математике нет царских дорог»

Литература:

1.Дорофеев Г.В. и др. Математика: Учебник для 5 кл., Москва «Просвещение», 1996.

2. Дорофеев Г.В. и др. Дидактические материалы для 5 кл., Москва «Просвещение», 2001.

3. Бунимович Е.А. и др. Математика: Рабочая тетрадь для 5 кл., Москва «Просвещение»,2001.

nsportal.ru

Урок математики в 5 классе «Степень числа»

МОБУ ООШ с. Новые Балыклы

Открытый урок по математике

«Степень числа.

Квадрат и куб числа.»

5 класс

Учитель Батыркаева Л.А.

2013-2014 учебный год

Урок математики в 5-м классе по теме

«Степень числа. Квадрат и куб числа»

Цели и задачи урока:

1. Ввести понятие степени числа, основания степени и показателя степени, закрепить понятие возведения в степень на решении заданий.

2. Развивать внимание, логическое мышление, математическую речь.

3. Воспитание культуры речи, усидчивости.

Оборудование:

Ход урока

1. Организационный момент.

2. Актуализация знаний: (слайд)

Упростить выражение:

• 25х + 15 х;

• 12у – 3у;

• 9k + 9k – 4k;

• 80c-35c-14c;

• 8d+d-9d;

• 163 + 37v + 18v

Проверьте порядок действий:

       1      3           2         4
508 * 609 — (22313 + 345) : 69

     4      6     5     2      3     1
34 * 45 + 56 — 78 * 356 : 56 * 4

3. Объяснение нового материала: (слайд)

Вы знаете, что сумму равных слагаемых заменяют произведением,

например:

5+5+5+5+5+5+5+5+5+5= 5*10 это короче и удобней.

А есть ли способ, чтобы заменить произведение равных сомножителей?

Как, например, произведение 5*5*5*5*5*5*5*5*5*5 записать короче?

Такой способ есть 5*5*5*5*5*5*5*5*5*5=5¹⁰

5¹⁰ — читают: “пять в десятой степени”

5 – основание степени

10 – показатель степени, который показывает, сколько множителей было в произведении

В математике произведение одинаковых множителей называется – возведением в степень.

4. Закрепление: (слайд)

А)Записать в тетрадь произведения в виде степени и вычислить:

3*3*3*3=3⁴=81

5*5*5=5³=125

2*2*2*2*2*2=2⁶=64

Б) Устно: (слайд)

Назовите основание и показатель степени:

3⁴; 5³;2⁶; 6¹

Если показатель степени равен 1, то что это значит?

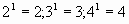
Первая степень любого числа равна этому числу.

5. Объяснение нового материала: (слайд)

Квадрат и куб числа а² и а³

Вторая и третья степени числа имеют особые названия.
Вторую степень называют – Квадратом этого числа.
Квадрат числа 2 равен 4,
Квадрат числа 3 равен 9.
Запись 2² читают: “Два в квадрате”.

А почему такое название – квадрат?
Ведь у нас никаких геометрических фигур здесь не появилось.
Фигура сейчас появится. И именно квадрат. Рассмотрим квадрат со стороной 2 см. его площадь равна 2*2=2²(кв.см)
Рассмотрим шахматную доску. У нее 8 строк (горизонталей) и 8 столбцов (вертикалей).
Клетки этой таблицы-доски называют полями.

Сколько у нее полей? Ответ: 8*8=8²=64

Третью степень называют – Кубом этого числа.
Запись 2³ читают: “Два в кубе”.

Рассмотрим куб, ребро которого имеет длину 2 см, видно, что он сложен из восьми кубиков с ребром 1 см.

Но 8 как раз и равно 2*2*2=2³

6. Работа с учебником.

№ 653 (выполняет у доски ученик)

7. Закрепление

А) запишите выражение с помощью символов степени и вычислите его значение:

• 10*10*10

• 6*6*6

• 4*4+8*8

• 2*2*2+3*3

Б) вычислите: 11²; 9³; 34¹; 13²; 4³.

В) тест

• 1. Куб числа – это:

• А) произведение трех одинаковых чисел

• Б) сумма трех одинаковых чисел

• В) сумма двух чисел

• 2. Числовое значение выражения 6² равно:

• А) 12, Б) 36, В) 8.

• 3. Числовое значение выражения 8³ равно:

• А) 24, Б) 64, В) 512.

• 4. Выражение 5 + 5 + 5 означает

• А) 5³, Б) 5 + 3, В) 5 · 3.

• 5. С какими геометрическими фигурами ассоциируются слова: а) квадрат, б) куб

• А) Б) В) Г)

8. Домашнее задание:

9.Итог урока:

1. Что нового вы узнали на уроке?

2. Какие трудности были у вас на уроке?

3. Что понравилось на уроке?

infourok.ru

Степень числа. 5-й класс

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели урока:

Образовательные:

• ознакомить учащихся с действием возведения в степень,
• дать понятия квадрат и куб числа,
• научить формулировать определение квадрата и куба числа,
• научить возводить числа в степень, в квадрат и куб,
• научить находить значения числовых выражений, содержащих вторую и третью степень натурального числа.

Развивающие:

• развивать логическое мышление,
• развивать информационную и учебно-познавательную компетенции учащихся,
• развивать умение сравнивать, обобщать, делать выводы,
• развивать интерес к предмету посредством показа межпредметных связей.

Воспитательные:

• воспитывать аккуратность в записях,
• целеустремленность,
• воспитывать интерес к родному краю, использую связь между математическими вычислениями и интересными страницами из Красной книги Московской области.

Структура урока:

1. Актуализация знаний.
   1. Мобилизующее начало и сообщение плана урока.
   2. Диктант
   3. Мотивация изучения нового материала.
   4. Постановка учебных задач.
2. Формирование новых знаний и способов действий.
   1. Введения понятия степени, квадрат и куб числа.
   2. Диктант с целью отработки умения записи степени.
   3. Физкультминутка с целью отработки понятий основание и показатель степени.
3. Применение знаний, формирование навыков. Путешествие по страницам Красной книги Московской области.
   1. Домашнее задание.
   2. Решение задач в тетради (с последующей проверкой у доски) с целью отработки умений представлять в виде степени произведения и установления соответствий между получившимися показателями и растениями, занесенными в Красную книгу.
   3. Подведение итога урока.

Ход урока

I. Организационный момент урока

1 слайд

Отгадайте такую загадку: 2 слайд

Он давно знакомый мой,
Каждый угол в нём прямой.
Все четыре стороны одинаковой длины
Вам его представить рад.
Как зовут его? (Квадрат).

Это слово мы с вами встретим еще на уроке.

II. Актуализация знаний учащихся, через изучение их субъектного опыта. Подведение к проблеме.

– Начать наш урок я хотела бы с выяснения вопроса: “Встречался кто-нибудь из вас в повседневной жизни со словом “степень”?

– Да

– Давайте приведём примеры словосочетаний из жизни, в которых оно используется и попытаемся с их помощью разобраться, что же в жизни означает слово “степень”. (Ученая степень, степень прилагательного, степень точности, степень сравнения, …)

– Каким же близким по смыслу словом можно заменить слово “степень”?

– А где мы можем уточнить его значение?

(в толковом словаре стр. 198)

Степень – это мера, сравнительная величина; уровень чего-нибудь. Слово “степень” находит широкое применение и в математике

III. Постановка проблемы.

– Давайте выясним, меняется ли его смысловая нагрузка в математике или остаётся той же.

IV. Пути исследования поставленной проблемы. Сообщение темы урока.

– Что же нам для этого нужно сделать?

1. Разобраться с понятием степени в математике
2. Выяснить, зачем она понадобилась людям?

– Запишите в тетрадях тему сегодняшнего урока: «Степень числа»

V. Исследовательская работа.

– Вы знаете, что все новые понятия в любой науке возникают из потребностей человека. Давайте попытаемся представить себе, как бы могло возникнуть понятие степени в математике, и разберёмся, зачем оно понадобилось людям.

Для этого напишем диктант. Задание: вычислить значение произведения

4 слайд

Проверим результаты. (появляются ответы)

Какое действие мы выполняли в каждом примере? (умножение)

Что особенного в каждом из этих примеров? (все множители одинаковы)

Какие примеры вы уже встречали, запись которых можно сократить? (сложение одинаковых слагаемых) .

5 слайд

Так вот ребята умножение одинаковых множителей в математике имеет свою особенную краткую запись и особое название.

Степень числа. Вводятся понятия: степень, основание, показатель.

6 слайд

Что же показывает показатель (сколько множителей было в произведении), что показывает основание (какое число умножается).

В математике произведение одинаковых множителей называется возведением в степень.

А что значит, если показатель степени равен 1. Это значит

21 = 2, 31 = 3, 4 1 = 4

Первая степень любого числа равна этому числу.

А теперь давайте послушаем сообщение учащихся на тему «История возникновения степени» (Приложение 1)

VI . Закрепление знаний.

Спасибо ребятам за сообщение. Сейчас мы потренируемся записывать степени. В тетради запишите произведение в виде степени (только ответ).

Слайд с заданиями 7. А теперь давайте проверим (появляются ответы). Вы согласны с ответами на доске. Ребята находят ошибку. Появляется правильный ответ.

Есть степени числа, которые имеют особое название.

Вторая и третья степени числа имеют особые названия.

Вторую степень называют квадратом. Третью степень – кубом.

А сейчас Физкультминутка

Я называю основание или показатель степени. Например, степень , 5 – это основание. Если вы со мной согласны, то киваете головой, если не согласны, то хлопаете в ладоши, если не знаете – пожимаете плечами.

Молодцы.

А сейчас послушаем сообщение ребят о великом советском математике.

(Приложение 2)

8 слайд

А почему такое название степени – квадрат. Ведь у нас никаких геометрических фигур не получается. Ребята выдвигают гипотезы.

Фигура сейчас появится и именно квадрат.

Рассмотрим квадрат со стороной 2 см. Его площадь равна 2 ∙ 2 = 2² = 4 (см²)

Вот поэтому такое особое краткое название для второй степени.

Итак, ребята мы с вами вооружились новыми знаниями. И теперь мы можем выполнять задания учебника. Но прежде запишем домашнее задание.

9 слайд.

Выполняя задания в тетради. Мы будем путешествовать по страницам Красной книги Московской области . А значит нашего родного края.

После того как вы выполните задание номера, надо прочитать название птицы, занесенной в Красную книгу.

К данным заданиям есть ключ (связь между полученными ответами и буквами). В результате получается название птицы, занесенной в Красную книгу. Слайд 9, 10, 11. После того как ребята отгадают слово, учащиеся рассказывают об отгаданной птице (презентации о птицах ребята готовят заранее, не понимая зачем птицы на уроке математики. Таким образом, интерес у учащихся к уроку повышается).

(Приложение 3, Приложение 4, Приложение 5) Сообщения учащихся находятся в Приложении 6.

Итак, ребята, мы с вами совершили небольшое путешествие по Красной книги Московской области.

По страницам Красной книги
Очень бережно ступай,
Ты животных и растений
Никогда не обижай!
Математику-науку
Вместе с ними изучай.

А какие математические знания нам в этом помогли. Вопросы:

1. На любом примере поясните, какое число называется степенью, основание степени, показателем степени?
2. Чему равна первая степень любого числа?
3. Что такое квадрат данного числа?
4. Что такое куб данного числа?

В заключении урока проведем небольшой тест. Выберете правильный ответ и запишите его в тетради. Сверьте свой ответ с ответом вашего соседа. Поставьте оценку за урок себе сами.

11 слайд

Спасибо за урок.

urok.1sept.ru

Примеры задач со степенями — СПИШИ У АНТОШКИ

1. Найдите такое натуральное число n такое, что 3ⁿ=729

Решение:

Возьмем число 3 и будем домножать его на 3 до тех пор, пока не получим 729: 3⋅3=9, 9⋅3=27 27⋅3=81, 81⋅3=243, 249⋅3 = 729  значит 729=3⋅3⋅3⋅3⋅3⋅3=3⁶⇒n=6.

Можно посмотреть таблицу основных степеней

2.Вычислите 2²²⁺²⋅2.

Решение:

2²²⁺²⋅2=2²²⁺²⁺¹=2⁴⁺²⁺¹=2⁷=2⋅2⋅2⋅2⋅2⋅2⋅2=128.

3. Вычислите 

2 ⁴⁰

4 ²⁰  

2 ⁴⁰ =  2 ⁴⁰ =   2 ⁴⁰

4 ²⁰     2 ^2*20  2 ⁴⁰

4. Как известно, в компьютерах объем памяти измеряется в байтах, килобайтах, мегабайтах и гигабайтах. Причем, чтобы получить один мегабайт памяти необходимо взять один килобайт памяти и увеличить количество памяти вдвое и со вновь получившейся памятью необходимо вновь произвести такую же процедуру — увеличение памяти вдвое, и, проведя таких процедур ровно 10, мы получим количество памяти, равное одному мегабайту. Так сколько же килобайтов в одном мегабайте?

Решение задачи

Для нахождения искомого числа достаточно умножить исходное количество килобайт на 2 столько раз, сколько раз мы применяем процедуру. Исходное количество килобайт по условию это 1, а количество применений процедур — 10, значит искомое число есть 2⋅2⋅2…⋅2 = 2¹⁰ = 1024.

5.  Решите уравнение: (5-x)² — x(2,5+x) = 0

(5-x)² — x(2,5+x) = 0

25 — 10х +  x² — 2,5x — x² = 0

 — 10x²  — 2,5х + 25 = 0

-12,5х = 25

х = 2

6. Решите уравнение: (х-4)² + (х+9)²  = 2х²

(х-4)² + (х+9)² = 2х²

Расскроем скобки

(х-4)(х-4) + (х+9)(х+9)  = 2х²

х² — 8х + 16 + х² + 18х + 81  = 2х²

2х² — 2х²   + 97 + 10х = 0

10х =  -97

х = -9,7

7. Упростите выражение:

(а²*а²)² :  а⁷

(а²*а²)² : а⁷ = а⁴*а⁴ : а⁷= а

 

spishy-u-antoshki.ru