Признаки делимости на 2,3,4,5,6,7,8 и 9. Примеры решения задач.
Что такое делимость?
«Делимость» означает, что при делении одного числа на другое результатом должно быть целое число с нулевым остатком. Под признаком делимости понимают правило, позволяющие быстро определить, является ли число кратным заданному числу.
Пример:
\(6:3 =2; \) \(6\) делится на \(3\), так как результат \(2\) — целое число, а остаток равен \(0\).
\(7:3=2,333…\) \(7\) не делится на \(3\) так как результат \(2,333…\) не является целым числом.
Признаки делимости чисел от \(1\) до \(10\).
Признак делимости на \(1\)
Каждое целое число делится на \(1\)
Признак делимости на \(2\)
Последняя цифра должна быть четной — \(0,2,4,6,8\).
Пример : \(3456\) делится на \(2\) так как последняя цифра \(6\) — четное число.
\(343423\) не делится на \(2\), так как последняя цифра \(3\) нечетная.
Все четные числа делятся на \(2\).
Признак делимости на \(3\)
Сумма цифр в данном числе должна быть кратна \(3\). Это простой способ найти числа кратные \(3\).
\(3789\) делится на \(3\), так как сумма \(3+7+8+9=27\) делится на \(3\).
\(43266737\) не делится на \(3\) – сумма цифр \(4+3+2+6+6+7+3+7=38\) не делится на \(3\).
Признак делимости на \(4\)
Число, образованное последними двумя цифрами в данном числе, должно быть кратно \(4\).
Пример: \(23746228\) делится на \(4\) если \(28\) делится на \(4\).
\(674235642\) не делится на \(4\), так как \(4\) не кратно \(42\).
Признаки делимости на \(5\)
Последняя цифра должна быть \(0\) или \(5\).
Пример: \(42340\) делится на \(5\) так как \(0\) — последняя цифра.
\(672234\) не делится на \(5\) так как \(4\) последняя цифра.
Признак делимости на \(6\)
Число должно быть кратным \(2\) и \(3\).
\(7563894\) делится на \(6\) — последняя цифра \(4\) делится на \(2\) и сумма цифр \(7+5+6+3+8+9+4=42\) делится на \(3\).
\(567423\) не делится на \(6\) — последняя цифра \(3\), поэтому не делится на \(2\). Даже не нужно проверять на \(3\).
Признаки делимости на \(7\)
Дважды умноженная последняя цифра отнимается от оставшихся цифр в данном числе, результат должен быть кратным \(7\).
- \(343\) делится на 7 так как \(34-(2*3)=28\), \(28\) делится на \(7\).
2. \(345343\) \(3\) — последняя цифра. Вычитаем \(2*3\) из \(34534\).
\(34534-(2*3)=34528\) число слишком большое.
\(3452-(2*8)-3436\) число слишком большое.
\(343-(2*6)=331\) повторяем снова
\(33-(2*1)=31,31\)не делится на \(7\).
\(345343\) не делится на \(7\).
Признак делимости на \(8\)
Число, образованное последними тремя цифрами в данном числе, должно быть кратно \(8\).
Пример:\(234568:8-568\) делится на \(8\).
\(4568742\)не делится на \(8\) , так как \(8\) не кратно \(742\)
Признак делимости на \(9\)
Сумма цифр в данном числе должна быть кратна \(9\).
\(456786:9 -\) если сумма \( 4+5+6+7+8+6=36\) делится на \(9\).
\(87956:9-\) сумма \(8+7+9+5+6=25\)не делится на 9.
Признак делимости на \(10\)
Последняя цифра должна быть \(0\).
Пример: \(456780\) делится на \(10\) — если последняя цифра равна \(0\).
\(78521\) не делится на \(10\) – последняя цифра \(1\).
Если число \(S\) делится на два числа \(a\) и \(b\), где \(a,b\) — простые числа , то \(S\) делится на \(a*b\), где \(a\) и \(b\) простые числа.
\(24\) делится на \(2\) и \(3\) и следовательно и на \(6\).
\(36\) делится на \(2 \) и \(4\), но не делится на \(8\), так как \(4\) не простое число.
Если число \(N\) делится на другое число \(M\), то \(N\) также делится на множители \(M\).
Например:
- \(72:12=6\)
- \(72\) также делится на \(2,3,4,6\) так как \(12\) кратно \(2,3,4,6\).
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуКазанский федеральный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов.
Криворожский педагогический университет
Проведенных занятий:
Дистанционно (Скайп)
Репетитор 5-9 классов. Ещё с детства я знала, что стану учителем математики. Ведь ни один предмет, кроме математики не развивает настолько хорошо логику, мозг. Математика учит находить закономерность, анализировать, делать выводы. При решении задач привожу примеры из жизни. Научу вашего ребенка не зазубривать, а понимать материал.
Ещё с детства я знала, что стану учителем математики. Ведь ни один предмет, кроме математики не развивает настолько хорошо логику, мозг. Математика учит находить закономерность, анализировать, делать выводы. При решении задач привожу примеры из жизни. Научу вашего ребенка не зазубривать, а понимать материал.
Репетитор по математике
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-8 классов. Я люблю математику, поскольку математическое мышление помогает вникать в суть вещей и решать повседневные задачи. Математика тренирует память и развивает ум. С радостью помогу ученикам закрепить школьные знания и узнать новое. Научу правильно задавать вопросы, рассуждать и самостоятельно искать решение задач.
Я люблю математику, поскольку математическое мышление помогает вникать в суть вещей и решать повседневные задачи. Математика тренирует память и развивает ум. С радостью помогу ученикам закрепить школьные знания и узнать новое. Научу правильно задавать вопросы, рассуждать и самостоятельно искать решение задач.
Похожие статьи
| Признак делимости на 2 | Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2, то есть является чётной. |
| Признак делимости на 3 | Число делится на 3 тогда и только тогда, когда сумма его всех цифр делится на 3. |
| Признак делимости на 4 | Число делится на 4 только тогда, когда две его последние цифры – нули или составляют число, которое делится на 4. |
| Признак делимости на 5 | Число делится на 5 тогда и только тогда, когда последняя цифра делится на 5, т. е. если она 0 или 5. |
| Признак делимости на 6 | Число делится на 6 тогда, когда оно делится и на 2, и на 3 (то есть если оно четное и сумма его цифр делится на 3). Другой признак делимости: число делится на 6 тогда и только тогда, когда учетверённое число десятков, сложенное с числом единиц делится на 6. |
| Признак делимости на 7 | Признак 1. число делится на 7 тогда и только тогда, когда утроенное число десятков, сложенное с числом единиц, делится на 7. Признак 2. число делится на 7 тогда и только тогда, когда модуль алгебраической суммы чисел, образующих нечётные группы по три цифры (начиная с единиц), взятых со знаком «+», и чётных со знаком «-» делится на 7. |
| Признак делимости на 8 | Число делится на 8 тогда и только тогда, когда число, образованное тремя его последними цифрами, делится на 8. Трёхзначное число делится на 8 тогда и только тогда, когда число единиц, сложенное с удвоенным числом десятков и учетверённым числом сотен, делится на 8. Трёхзначное число делится на 8 тогда и только тогда, когда число единиц, сложенное с удвоенным числом десятков и учетверённым числом сотен, делится на 8. |
| Признак делимости на 9 | Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9. |
| Признак делимости на 10 | Число делится на 10 тогда и только тогда, когда оно оканчивается на нуль. |
| Признаки делимости на 11 | Признак 1: число делится на 11 тогда и только тогда, когда модуль разности между суммой цифр, занимающих нечётные позиции, и суммой цифр, занимающих чётные места делится на 11. Признак 2: число делится на 11 тогда и только тогда, когда на 11 делится сумма чисел, образующих группы по две цифры (начиная с единиц). |
| Признак делимости на 13 | Число делится на 13 если сумма числа десятков с учетверенным числом единиц делится на 13. |
| Признак делимости на 17 | Число делится на 17 если модуль разности числа десятков и пятикратного числа единиц делится на 17. |
| Признак делимости на 19 | Число делится на 19 тогда и только тогда, когда число десятков, сложенное с удвоенным числом единиц, делится на 19. |
| Признак делимости на 20 | Число делится на 20 тогда и только тогда, когда число, образованное двумя последними цифрами, делится на 20. |
| Признаки делимости на 23 | Признак 1: число делится на 23 тогда и только тогда, когда число сотен, сложенное с утроенным числом, образованным двумя последними цифрами, делится на 23. Признак 2: число делится на 23 тогда и только тогда, когда число десятков, сложенное с семикратным числом единиц, делится на 23. Признак 3: число делится на 23 тогда и только тогда, когда число сотен, сложенное с семикратным числом десятков и утроенным числом единиц, делится на 23. |
| Признак делимости на 25 | Число делится на 25 тогда и только тогда, когда две его последние цифры составляют число, которое делится на 25. |
| Признак делимости на 27 | Число делится на 27 тогда и только тогда, когда на 27 делится сумма чисел, образующих группы по три цифры (начиная с единиц). |
| Признак делимости на 29 | Число делится на 29 тогда и только тогда, когда число десятков, сложенное с утроенным числом единиц, делится на 29. |
| Признак делимости на 30 | Число делится на 30 тогда и только тогда, когда оно заканчивается на 0 и сумма всех цифр делится на 3. |
| Признак делимости на 31 | Число делится на 31 тогда и только тогда, когда модуль разности числа десятков и утроенного числа единиц делится на 31. |
| Признак делимости на 37 | Признак 1: число делится на 37 тогда и только тогда, когда при разбивании числа на группы по три цифры (начиная с единиц) сумма этих групп кратна 37. Признак 2: число делится на 37 тогда и только тогда, когда на 37 делится модуль утроенного числа сотен, сложенного с учетверённым числом десятков, за вычетом числа единиц, умноженного на семь. Признак 3: число делится на 37 тогда и только тогда, когда на 37 делится модуль суммы числа сотен с числом единиц, умноженного на десять, за вычетом числа десятков, умноженного на 11.  |
| Признак делимости на 41 | Признак 1: число делится на 41 тогда и только тогда, когда модуль разности числа десятков и четырёхкратного числа единиц делится на 41. Признак 2: чтобы проверить, делится ли число на 41, его следует справа налево разбить на грани по 5 цифр в каждой. Затем в каждой грани первую справа цифру умножить на 1, вторую цифру умножить на 10, третью — на 18, четвёртую — на 16, пятую — на 37 и все полученные произведения сложить. Если результат будет делиться на 41, тогда и только тогда само число будет делиться на 41. |
| Признак делимости на 50 | Число делится на 50 тогда и только тогда, когда число, образованное двумя его младшими десятичными цифрами, делится на 50. |
| Признак делимости на 59 | Число делится на 59 тогда и только тогда, когда число десятков, сложенное с числом единиц, умноженное на 6, делится на 59. |
| Признак делимости на 79 | Число делится на 79 тогда и только тогда, когда число десятков, сложенное с числом единиц, умноженное на 8, делится на 79. |
| Признак делимости на 99 | Число делится на 99 тогда и только тогда, когда на 99 делится сумма чисел, образующих группы по две цифры (начиная с единиц). |
| Признак делимости на 101 | Число делится на 101 тогда и только тогда, когда модуль алгебраической суммы чисел, образующих нечётные группы по две цифры (начиная с единиц), взятых со знаком «+», и чётных со знаком «-» делится на 101. |
Признаки делимости | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Числа от 2 до 10 имеют признаки делимости, позволяющие определить, если число делится на них без остатка.
Как определить делится ли число на 2: последняя цифра числа должна быть четной. Пример: 1864 делится на 2, так как 4 – четная цифра; 2593 не делится на 2, так как 3 – нечетная цифра.
Как определить делится ли число на 3: сумма всех цифр в числе должна делиться на 3. Пример: 243 делится на 3, так как 2+4+3=9 и 9 делится на 3 без остатка; 760 не делится на 3, так как 7+6+0=13 и 13 не делится на три полностью.
Как определить делится ли число на 4: две последние цифры в числе должны делиться на 4 (00 принимается за 100). Пример: 87524 делится на 4, так как последние цифры 24 делятся 4; 6500 делится на 4, так как последние цифры – 00, а 100 делится на 4; 59431 не делится на 4, так как 31 не делится на 4 без остатка.
Как определить делится ли число на 5: последняя цифра числа должна быть 0 или 5. Пример: 58 не делится на 5, так как последняя цифра 8; 1580 делится на 5, так как последняя цифра числа – 0.
Как определить делится ли число на 6: число должно делится одновременно на 2 и на 3, согласно вышеописанным признакам. Пример: 81 не делится на 6, так как оно делится на 3, но не делится на 2; 100 не делится на 6, так как оно делится на 2, но не делится на 3; 72 делится на 6, так как оно делится и на 2, и на 3.
Как определить делится ли число на 7: число десятков, умноженное на 3, в сумме с числом единиц должно делиться на 7. Пример: 511 делится на 7, так как 51*3+1=154 и 154 делится на 7; 635 не делится на 7, так как 63*3+5=194 и 194 не делится на 7.
Как определить делится ли число на 8: последние три цифры числа должны делится на 8 (000 берутся за 1000, которая делится на 8). Пример: 86240 делится на 8, так как 240 делится на 8; 56343 не делится на 8, так как 343 не делится на 8.
Как определить делится ли число на 9: сумма всех цифр в числе должна быть кратна 9. Пример: 243 делится на 9 без остатка, так как 2+4+3=9 и 9 делится на 9; 5081 не делится на 9, так как 5+0+8+1=14 и 14 не делится на 9
Как определить, что число делится на 10: последняя цифра числа должна быть 0. Пример: 1530 делится на 10, так как последняя цифра 0; 6572 не делится на 10, так как последняя цифра 2.
Признак делимости — это… Что такое Признак делимости?
При́знак дели́мости — правило, позволяющее сравнительно быстро определить, является ли число кратным заранее заданному без необходимости выполнять фактическое деление. Как правило, основано на действиях с частью цифр из записи числа в позиционной системе счисления (обычно десятичной).
Существуют несколько простых правил, позволяющих найти малые делители числа в десятичной системе счисления:
Признак делимости на 2
Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2, то есть является чётной.
Признак делимости на 3
Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3 (так как все числа вида 10n при делении на 3 дают в остатке единицу).
Признак делимости на 4
Число делится на 4 тогда и только тогда, когда число из двух последних его цифр (оно может быть двузначным, однозначным или нулём) делится на 4.
Признак делимости на 5
Число делится на 5 тогда и только тогда, когда последняя цифра делится на 5 (то есть равна 0 или 5).
Признак делимости на 6
Число делится на 6 тогда и только тогда, когда оно делится и на 2, и на 3.
Признак делимости на 7
Число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7 (например, 364 делится на 7, так как 36 — (2 × 4) = 28 делится на 7).
Либо использовать модификацию признака деления на 1001=10³+1, которое само делится на 7:
Для того, чтобы натуральное число делилось на 7 необходимо и достаточно, чтобы алгебраическая сумма чисел, образующих нечётные группы по три цифры (начиная с единиц) взятых со знаком «+» и чётных со знаком «-» делилась на семь.
Ещё один признак — берём первую цифру, умножаем на 3, прибавляем следующую (здесь можно взять остаток от деления на 7 от получившегося числа). И далее — сначала: умножаем на 3, прибавляем следующую… Для 364: 3 * 3 + 6 = 15. Остаток — 1. Далее 1 * 3 + 4 = 7.
Признак делимости на 8
Число делится на 8 тогда и только тогда, когда три его последние цифры — нули или образуют число, которое делится на 8.
Признак делимости на 9
Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.
Признак делимости на 10
Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль.
Признак делимости на 11
Число делится на 11 тогда и только тогда, когда сумма цифр с чередующимися знаками равна 0 или делится на 11 (то есть 182 919 делится на 11, так как 1 — 8 + 2 — 9 + 1 — 9 = −22 делится на 11) — следствие факта, что все числа вида 10n при делении на 11 дают в остатке (-1)n.
Признак делимости на 12
Число делится на 12 тогда и только тогда, когда оно делится на 3 и на 4.
Признак делимости на 13
Число делится на 13 тогда и только тогда, когда число его десятков, сложенное с учетверённым числом единиц, кратно 13 (например, 845 делится на 13, так как 84 + (4 × 5) = 104 делится на 13).
Признак делимости на 14
Число делится на 14 тогда и только тогда, когда оно делится на 2 и на 7.
Признак делимости на 15
Число делится на 15 тогда и только тогда, когда оно делится на 3 и на 5.
Признак делимости на 17
Число делится на 17 тогда и только тогда, когда число его десятков, сложенное с увеличенным в 12 раз числом единиц, кратно 17 (например, 29053→2905+36=2941→294+12=306→30+72=102→10+24=34. Поскольку 34 делится на 17, то и 29053 делится на 17). Признак не всегда удобен, но имеет определенное значение в математике. Есть способ немного проще — число делится на 17 тогда и только тогда, когда разность между числом его десятков и упятерённым числом единиц кратна 17 (например, 32952→3295-10=3285→328-25=303→30-15=15; поскольку 15 не делится на 17, то и 32952 не делится на 17)
Признак делимости на 19
Число делится на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, кратно 19 (например, 646 делится на 19, так как 64 + (6 × 2) = 76 делится на 19).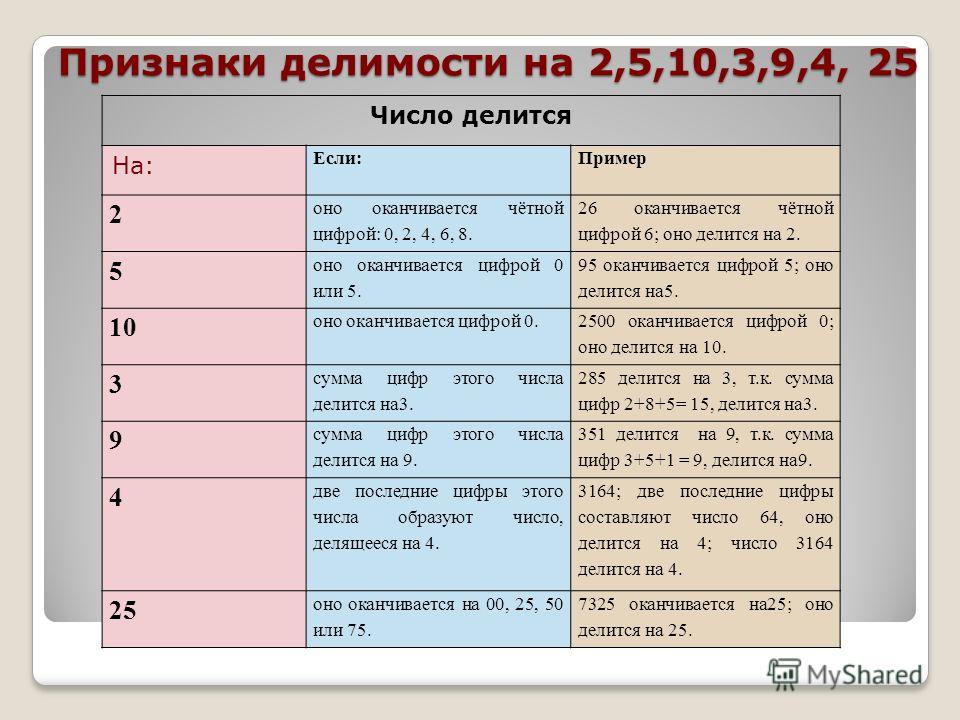
Признак делимости на 23
Число делится на 23 тогда и только тогда, когда число его сотен, сложенное с утроенным числом десятков и единиц, кратно 23 (например, 28842 делится на 23, так как 288 + (3 * 42) = 414; продолжаем: 4 + (3 * 14) = 46 — очевидно, делится на 23).
Признак делимости на 25
Число делится на 25 тогда и только тогда, когда две его последние цифры делятся на 25 (то есть образуют 00, 25, 50 или 75).
Признак делимости на 99
Разобьем число на группы по 2 цифры справа налево (в самой левой группе может быть одна цифра) и найдем сумму этих групп, считая их двузначными числами. Эта сумма делится на 99 тогда и только тогда, когда само число делится на 99.
Признак делимости на 101
Разобьем число на группы по 2 цифры справа налево (в самой левой группе может быть одна цифра) и найдем сумму этих групп с переменными знаками, считая их двузначными числами. Эта сумма делится на 101 тогда и только тогда, когда само число делится на 101. Например, 590547 делится на 101, так как 59-05+47=101 делится на 101).
Например, 590547 делится на 101, так как 59-05+47=101 делится на 101).
Признак делимости на 2
nЧисло делится на n-ю степень двойки тогда и только тогда, когда число, образованное его последними n цифрами, делится на ту же степень.
Признак делимости на 5
nЧисло делится на n-ю степень пятёрки тогда и только тогда, когда число, образованное его последними n цифрами, делится на ту же степень.
Признак делимости на 10
n − 1Разобьем число на группы по n цифр справа налево (в самой левой группе может быть от 1 до n цифр) и найдем сумму этих групп, считая их n-значными числами. Эта сумма делится на 10n − 1 тогда и только тогда, когда само число делится на 10n − 1.
Признак делимости на 10
nЧисло делится на n-ю степень десятки тогда и только тогда, когда n его последних цифр — нули.
Признак делимости на 10
n + 1Разобьем число на группы по n цифр справа налево (в самой левой группе может быть от 1 до n цифр) и найдем сумму этих групп с переменными знаками, считая их n-числами. Эта сумма делится на 10n + 1 тогда и только тогда, когда само число делится на 10n + 1.
Эта сумма делится на 10n + 1 тогда и только тогда, когда само число делится на 10n + 1.
См. также
- Признак Паскаля — универсальный признак делимости, позволяющий для любых целых a и b определить, делится ли a на b. Точнее, он позволяет вывести почти все из выше приведённых признаков.
Ссылки
Wikimedia Foundation. 2010.
Делимость чисел: делитель, признаки, примеры
Делитель числа
Пусть a и b – целые числа.
Число b называется делителем числа a, если существует такое целое число c, что выполняется равенство: a = b $\cdot$ с.
В этом случае говорят, что a делится на b нацело или a кратно b.
Также говорят о делимости a на b.
Записывают: a ⋮ b
Например, множество всех целых делителей числа 12:
$$ A = \{n | 12 ⋮ n,n \in \Bbb Z\} $$
$$ A = \{ \pm 1; \pm 2; \pm 3; \pm 4; \pm 6; \pm 12 \} $$
Если число a имеет два взаимно простых делителя b и c, то произведение bc также является делителем для a:
$$(a ⋮ b и a ⋮ c) \iff a ⋮ bc; b, c — взаимно \quad простые$$
Например:
Число 105 делится на 3 и на 5. Значит, оно также делится на 15, т.е. 105 ⋮ 15
Значит, оно также делится на 15, т.е. 105 ⋮ 15
Число 231 делится на 7 и на 11. Значит, оно также делится на 77, т.е. 231 ⋮ 77
Признаки делимости
Чтобы определить делимость без самого деления, существует набор методов «экспресс-анализа», которые называют признаками делимости.
Двузначные грани числа – разбиение числа на группы по 2 цифры, считая справа налево. Например: 1|23|45|67.
Трёхзначные грани числа – разбиение числа на группы по 3 цифры, считая справа налево. Например: 1|234|567.
Знакопеременная сумма граней – каждая грань входит со знаком +/-, последняя с +.
Делитель | Признак делимости | Пример | |
2 | Число заканчивается чётной цифрой {0;2;4;6;8} | 1028 | |
3 | Сумма цифр числа делится на 3 | 1029 1+2+9 = 12 | |
4 | Число, составленное из двух последних цифр, делится на 4 | 1028 28:4 = 7 | |
5 | Число заканчивается на 0 или 5 | 1025 | |
7 | Число, полученное вычитанием удвоенной последней цифры из исходного числа с отброшенной последней цифрой, делится на 7 | 1491 149-2 = 147 147:7 = 21 | |
Знакопеременная сумма 3-значных граней числа делится на 7 | 1|491 -1+491 = 490 490:7 = 70 | ||
8 | Число, составленное из трёх последних цифр, делится на 8 | 1736 736:8 = 92 | |
9 | Сумма цифр числа делится на 9 | 1026 1+2+6 = 9 | |
10 | Число заканчивается на 0 | 1030 | |
11 | Сумма цифр на нечётных позициях и сумма цифр на нечётных позициях либо равны, либо отличаются на число, кратное 11 | 1408 (1+0)-(4+8) = -11 | |
Знакопеременная сумма цифр делится на 11 или равна 0 | -1+4+8 = 11 | ||
13 | Число, полученное добавлением учетверенной последней цифры к исходному числу с отброшенной последней цифрой, делится на 13 | 1131 113+4 $\cdot$ 1 = 117 11+4 $\cdot$ 7 = 39 39:13 = 3 | |
Знакопеременная сумма 3-значных граней числа делится на 13 | 1|131 -1+131 = 130 130:13 = 10 | ||
17 | Число, полученное добавлением последней цифры, умноженной на 12, к исходному числу с отброшенной последней цифрой, делится на 17 | 1479 147+12 $\cdot$ 9 = 255 25+12 $\cdot$ 5 = 85 85:17 = 5 | |
Число, полученное вычитанием последней цифры, умноженной на 5, к исходному числу с отброшенной последней цифрой, делится на 17 | 1479 147-5 $\cdot$ 9 = 102 10-5 $\cdot$ 2 = 0 | ||
19 | Число, полученное добавлением удвоенной последней цифры из исходного числа с отброшенной последней цифрой, делится на 19 | 1273 127+2 $\cdot$ 3 = 133 13+2 $\cdot$ 3 = 19 19:19 = 1 | |
23 | Число, полученное добавлением утроенного числа из двух последних цифр с числом сотен, делится на 23. | n последних цифр числа – нули | 21000 делится на 1000 |
Примеры
Пример 1. Число 15464*543 делится на 3. Какие цифры могут стоять на месте звёздочки?
Обозначим цифру на месте звёздочки x. Сумма всех цифр:
1+5+4+6+4+x+5+4+3 = 32+x
Сумма должна делиться на 3:
Ответ: {1;4;7}
Пример 2. Число 14*6* делится на 45. Какое это число?
45 = 9 $\cdot$ 5. Значит, данное число делится на 9 и на 5.
Делимость на 9 требует сумму цифр, кратную 9: 1+4+x+6+y = 9k
Делимость на 5 даёт y = 0 или y = 5.
Получаем, учитывая, что x,y – цифры:
$$ {\left\{ \begin{array}{c} y = 0 \\ 1+4+x+6+0 = 9k \end{array} \right.} \Rightarrow 11+x = 9k \Rightarrow x = 7 $$
$$ {\left\{ \begin{array}{c} y = 5 \\ 1+4+x+6+0 = 9k \end{array} \right.} \Rightarrow 16+x = 9k \Rightarrow x = 2 $$
Ответ: 14760 или 14265
Пример 3. В течение месяца три воскресенья пришлись на чётные числа. {2020} + 8 = 10000…08 $$
{2020} + 8 = 10000…08 $$
Сумма цифр данного числа 1+8 = 9 – делится на 9.
Значит, само число также делится на 9.
Ответ: да
Свойства делимости чисел
Признак делимости на 2
Чётное число – это число, которое делится на 2.
Нечётное число – не делится на 2.
Число делится на два, в том случае если его последняя цифра является чётной или нуль. Во всех остальных случаях – не делится.
Число 52 738 делится на 2, так как у него последняя цифра 8 которая является чётной.
Число 7691 не делится на 2, так как цифра 1 находящаяся в конце нечетная.
Число 1250 делится на 2, так как цифра, которая находится в конце нуль.
Признак делимости на 4
Число делится на 4, при условии, если две последние его цифры нули либо образуют число, которое делится на 4. В остальных случаях – не делится.
В остальных случаях – не делится.
Число 31 800 делится на 4, так как в его окончании находятся два нуля.
Число 325 734 не делится на 4, так как крайние две цифры дают число 34, которое не делится на 4.
Число 15 608 делится на 4, так как две конечные цифры 0 и 8 дают число 8, которое делится на 4.
Признак делимости на 8
Число делится на 8, в случае, когда три последние цифры его нули или формируют число, делящееся на 8. В остальных случаях – не делится.
Число 225 000 делится на 8, так как оканчивается тремя нулями.
Число 180 004 не делится на 8, так как три крайние цифры дают число 4, которое не делится на 8.
Число 112 120 делится на 8 так как три цифры находящиеся в конце дают число 120, которое делится на 8.
Можно указать аналогичные признаки и делимости на 16, 32, 64 и т. п., но это не будет иметь практического значения.
Признаки делимости на 3 и на 9
На число 3 делятся числа, сумма составляющих цифр которых делится на 3.
На число 9 делятся числа, сумма составляющих цифр которых делится на 9.
Число 17 835 делится на 3 и не может быть разделено на 9, так как сумма его цифровых значений 1 + 7 + 8 + 3 + 5 = 24 может быть разделено на 3 и не делится на 9.
Число 106 499 не может быть разделено ни на 3, ни на 9, так как составляющие его цифры в сумме даёт число 29 которое не делится как на 3, так и на 9.
Число 52 632 может быть разделено на 9, так как сумма цифр входящих его состав 18 которое делится на 9.
Признак делимости на 6
Число делится на 6, когда оно может быть разделено одновременно на 2 и на 3. В противном случае – не делится.
Число 126 может быть разделено на 6, в виду того, что оно делится и на 2 и на 3.
Признак делимости на 5
На 5 делятся те числа, у которых последняя цифра 0 или 5. Другие – не делятся.
Число 240 может быть разделено на 5, так как последняя цифра 0.
Число 554 не делится на 5, так как последняя цифра 4.
Признак делимости на 25
На 25 можно разделит только те числа, у которых две крайние цифры нули либо формируют число, которое может быть разделено на 25, например числа оканчивающиеся на 00, 25, 50 или 75. Другие — не делятся.
Другие — не делятся.
Число 7150 можно разделить на 25, так как оканчивается на 50.
Число 4855 не получится разделить на 25.
Признаки делимости на 10, 100 и 1000
Числа делятся на 10, когда последняя цифра является нулём.
Числа делятся на 100, если две последние цифры этих чисел нули.
Числа делятся на 1000, если три конечные цифры у них нули.
8200 можно разделить на 10 и на 100.
542 000 можно разделить на 10, 100 и 1000.
Признак делимости на 11
На 11 можно разделить только те числа, у которых сумма цифр, находящихся на нечётных местах, или равна сумме цифр, находящихся на чётных местах, либо отличны от нее на число, которое делится на 11.
103 785 можно разделить на 11, так как 1 + 3 + 8 = 12 и 0 + 7 + 5 = 12
9 163 627 можно разделить на 11, так как при вычитании из 28 числа 6 получается 22, которое делится на 11. (
( 9 + 6 + 6 + 7 = 28 ) ( 1 + 3 + 2 = 6 )
461 025 не может разделено на 11, в виду того что числа 7 и 11 взаимно не ровны, а их разность 4 на 11 не разделить. ( 11 – 7 = 4 ),( 4 + 1 + 2 = 7 ), ( 6 + 0 + 5 = 11).
Существуют признаки делимости так же и на другие числа, но эти признаки гораздо сложнее.
Признаки делимости
В некоторых случаях, для того, чтобы узнать делится ли какое-либо натуральное число m на натуральное число n без остатка, не обязательно делить данные числа. Достаточно знать некоторые признаки делимости. Существует две теоремы о делимости и пять признаков делимости.
Теорема о делимости произведения: если в данном произведении хоть один из сомножителей можно поделить на определенное число, то и все произведение будет делиться на это же число.
Теорема о делимости суммы: если каждое слагаемое определенной суммы делится на данное число, то и вся сумма будет делиться на это же число. Однако не стоит думать, что если слагаемые не делятся на какое-либо определенное число, то и сумма делиться на него не будет. Взять, к примеру, 19+37, в сумме данные числа дают число 56, которое делится на 4, но ведь ни 19, ни 37 на 4 не делятся.
Признаки делимости
Признак делимости на 2. Число, делящееся на 2, называется четным, не делящееся — нечетным. Число делится на 2, если его последняя цифра четная или нуль. В остальных случаях не делится (2, 4, 16, 20, 3172…).
Признак делимости на 4. Число делится на 4, если две последние его цифры нули или образуют число, делящееся на 4. В остальных случаях не делится (4, 8, 24, 1200, 23516,…).
Признак делимости на 8. Число делится на 8, если три последние цифры нули или образуют число, делящееся на 8. В остальных случаях не делится (8, 16, 88, 1000, 47128,…).
В остальных случаях не делится (8, 16, 88, 1000, 47128,…).
Признак делимости на 3 и на 9. На 3 делятся только те числа, у которых сумма цифр делится на 3; на 9 — только те, у которых сумма цифр делится на 9 (3, 6, 27, 123, 3321,… и 9, 18, 81, 729, 218493,…).
Признак делимости на 6. Число делится на 6, если оно делится одновременно на 2 и на 3. В остальных случаях не делится (6, 12, 36, 216, 66342,…).
Признак делимости на 5. На 5 делятся числа, последняя цифра которых 0 или 5. Другие не делятся (5, 15, 30, 420, 12345,…).
Признак делимости на 25. На 25 делятся числа, две последние цифры которых нули или образуют число, делящееся на 25 (т.е числа, оканчивающиеся на 00, 25, 50 или 75). Другие числа не делятся (25, 75, 200, 625, 25850,…).
Признак делимости на 10, 100 и 1000. На 10 делятся только те числа, последняя цифра которых нуль, на 100 — только те числа, у которых две последние цифры нули, на 1000 — только те, у которых три последние цифры нули (10, 20, 300, 4020, 505010,. .., 100, 200, 1100, 51500,…, 1000, 3000, 55000, 439000,…).
.., 100, 200, 1100, 51500,…, 1000, 3000, 55000, 439000,…).
Признак делимости на 11. На 11 делятся только те числа, у которых сумма цифр, занимающих нечетные места, либо равна сумме цифр, занимающих четные места, либо отличаются от нее на число, делящееся на 11 (11, 22, 132, 616, 5786,…).
Что делимо? — Определение, факты и пример
Давайте узнаем!
Что значит делимое?
В математике говорят, что число делится на другое число, если остаток равен 0.Правила делимости — это набор общих правил, которые часто используются, чтобы определить, делится ли число без остатка на другое число.
| Правила делимости | Пример |
| 2: Если число четное или заканчивается на 0,2,4, 6 или 8, оно делится на 2. | |
3: Если сумма всех цифр делится на три, число делится на 3. | |
| 4: Если число, образованное двумя последними цифрами, делится на 4, число делится на 4. | |
| 5: Если последняя цифра — 0 или 5, число делится на 5. | |
| 6: Если число делится и на три, и на два, оно делится на 6. | |
| 7: Если разница последней цифры удвоена, а остальные цифры делятся на семь, число делится на 7. | |
| 8: Если последние три цифры числа делятся на 8, число делится на 8. | |
| 9: Если сумма цифр делится на девять, число делится на 9. | |
| 10: Если последняя цифра числа 0, она делится на 10. |
Интересные факты
|
Давайте споем!
Полезно знать правила делимости,
С ними деление не так уж и медленно!
Каждый раз проверять конечные цифры или их сумму,
Чтобы проверить их делимость на 2, 3, 5, 10 или 9!
Давай сделаем это!
Вместо того, чтобы раздавать детям листы с разделением, дайте им чистый лист бумаги и карандаш.Напишите числа на маленьких листочках бумаги, положите их в таз, а затем попросите их взять кусочки чисел из миски и используйте правила делимости чисел от 2 до 10, чтобы проверить делимость чисел.
Связанный математический словарь
Правила делимости (тесты)
Легко проверить, можно ли точно разделить одно число на другое
делится на
«Делится на» означает «при делении одного числа на другое получается целое число»
Примеры:
14 — это , делимое на 7, потому что 14 ÷ 7 = 2 точно
15 — это , а не , делимое на 7, потому что 15 ÷ 7 = 2 1 7 (результат , а не целое число)
0 — это , делимое на 7, потому что 0 ÷ 7 = 0 ровно (0 — целое число)
«Может быть разделено на» и «может быть разделено на» означает одно и то же.
Правила делимости
Эти правила позволяют проверить, делится ли одно число на другое, без необходимости выполнять слишком много вычислений!
Пример: делится ли 723 на 3?
Можно попробовать разделить 723 на 3
Или используйте правило «3»: 7 + 2 + 3 = 12, а 12 ÷ 3 = 4 точно Да
Примечание. Ноль делится на на любое число (кроме самого себя), поэтому мы получаем «да» на все эти тесты.
1
Любое целое число (не дробное) делится на 1
2
Последняя цифра четная (0,2,4,6,8)
12 8 Есть
12 9 №
3
Сумма цифр делится на 3
381 (3 + 8 + 1 = 12 и 12 ÷ 3 = 4) Да
217 (2 + 1 + 7 = 10 и 10 ÷ 3 = 3 1 / 3 ) №
Это правило можно повторить при необходимости:
99996 (9 + 9 + 9 + 9 + 6 = 42, затем 4 + 2 = 6) Да
4
Последние 2 цифры делятся на 4
13 12 равно (12 ÷ 4 = 3) Да
70 19 не равно (19 ÷ 4 = 4 3 / 4 ) Нет
Быстрая проверка (полезная для небольших чисел) состоит в том, чтобы уменьшить число вдвое, и результатом будет целое число.
12/2 = 6, 6/2 = 3, 3 — целое число. Есть
30/2 = 15, 15/2 = 7,5, что не является целым числом. №
5
Последняя цифра 0 или 5
17 5 Есть
80 9 №
6
Четно и делится на 3 (проходит как правило 2, так и правило 3 выше)
114 (четно, и 1 + 1 + 4 = 6 и 6 ÷ 3 = 2) Да
308 (четно, но 3 + 0 + 8 = 11 и 11 ÷ 3 = 3 2 / 3 ) Нет
7
Удвойте последнюю цифру и вычтите ее из числа, образованного другими цифрами.Результат должен делиться на 7. (Мы можем снова применить это правило к этому ответу)
672 (Двойное 2 равно 4, 67−4 = 63 и 63 ÷ 7 = 9) Да
105 (Двойная 5 равна 10, 10−10 = 0, а 0 делится на 7) Да
905 (Двойное 5 равно 10, 90−10 = 80 и 80 ÷ 7 = 11 3 / 7 ) Нет
8
Последние три цифры делятся на 8
109 816 (816 ÷ 8 = 102) Есть
216 302 (302 ÷ 8 = 37 3 / 4 ) №
Быстрая проверка — это трижды уменьшить вдвое, и результат все равно будет целым числом:
816/2 = 408, 408/2 = 204, 204/2 = 102 Да
302/2 = 151, 151/2 = 75. 5 №
5 №
9
Сумма цифр делится на 9
(Примечание: это правило можно повторить при необходимости)
1629 (1 + 6 + 2 + 9 = 18, и снова 1 + 8 = 9) Да
2013 (2 + 0 + 1 + 3 = 6) №
10
Число заканчивается на 0
22 0 Есть
22 1 №
11
Сложить и вычесть цифры поочередно (добавить цифру, вычесть следующую цифру, добавить следующую цифру и т. Д.).Затем проверьте, делится ли этот ответ на 11.
1 3 6 4 (+ 1−3 + 6−4 = 0 ) Да
9 1 3 (+ 9−1 + 3 = 11 ) Есть
3 7 2 9 (+ 3−7 + 2−9 = −11 ) Да
9 8 7 (+ 9-8 + 7 = 8 ) №
12
Число делится на 3 и 4 (он проходит как правило 3, так и правило 4 выше)
648
( По 3? 6 + 4 + 8 = 18 и 18 ÷ 3 = 6 Да)
(По 4? 48 ÷ 4 = 12 Да)
Оба пройдены, поэтому Да
524
( По 3? 5 + 2 + 4 = 11, 11 ÷ 3 = 3 2 / 3 Нет)
(Нет необходимости проверять по 4) Нет
Есть еще много всего! Существуют не только тесты на делимость для больших чисел, но и другие тесты для чисел, которые мы показали.
Факторы могут быть полезны
Факторы— это числа, которые вы умножаете, чтобы получить другое число:
Это может быть полезно, потому что:
Когда одно число делится на другое число …
… тогда также делится на каждый из множителей этого числа.
Пример: если число делится на 6, оно также делится на 2 и 3
Пример: если число делится на 12, оно также делится на 2, 3, 4 и 6.
Другое правило для 11
- Вычтите последнюю цифру из числа, образованного другими цифрами.
- Если это число делится на 11, то и исходное число тоже.
При необходимости можно повторить
Пример: 286
28-6 равно 22, из которых делится на на 11, поэтому 286 делится на 11
Пример: 14641
- 1464-1 это 1463
- 146-3 из 143
- 14-3 равно 11, из которых делится на и делится на 11, поэтому 14641 делится на 11
1625, 1626, 1627, 1628, 2689, 3599, 3600, 3601, 3602, 5007
Правил делимости для 2, 3, 4, 5, 6, 9 и 10
Число a делится на число b, если остаток a \ div b равен нулю (0). Например, 15, разделенное на 3, равно 5, что означает, что его остаток равен нулю. Затем мы говорим, что 15 делится на 3.
Например, 15, разделенное на 3, равно 5, что означает, что его остаток равен нулю. Затем мы говорим, что 15 делится на 3.
На другом уроке мы обсудили правила делимости для 7, 11 и 12. На этот раз мы рассмотрим правила или тесты делимости для 2 , 3 , 4 , 5 , 6 , 9 и 10 . Поверьте, вы сможете выучить их очень быстро, потому что вы можете не знать, что у вас уже есть базовое и интуитивное понимание этого.Например, очевидно, что все четные числа делятся на 2. Это в значительной степени правило делимости для 2 . Цель этого урока по правилам делимости — формализовать то, что вы уже знаете.
Правила делимости помогают нам определить, делится ли одно число на другое без прохождения фактического процесса деления, такого как метод деления в столбик. Если рассматриваемые числа достаточно малы численно, нам может не понадобиться использовать правила для проверки делимости. Однако для чисел, значения которых достаточно велики, мы хотим иметь некоторые правила, которые служили бы «ярлыками», чтобы помочь нам выяснить, действительно ли они делятся друг на друга.
Однако для чисел, значения которых достаточно велики, мы хотим иметь некоторые правила, которые служили бы «ярлыками», чтобы помочь нам выяснить, действительно ли они делятся друг на друга.
Правила делимости чисел 2, 3, 4, 5, 6, 9 и 10
Число делится на 2, если последняя цифра числа 0, 2, 4, 6 или 8.
Пример 1. Делится ли число 246 на 2?
Решение: поскольку последняя цифра числа 246 заканчивается на 6, это означает, что оно делится на 2.
Пример 2. Какие из чисел 100, 514, 309 и 768 делятся на 2?
Решение: если мы рассмотрим все четыре числа, только число 309 не оканчивается на 0, 2, 4, 6 или 8. Мы можем сделать вывод, что все числа выше, кроме 309, делятся на 2.
Число делится на 3, если сумма цифр числа делится на 3.
Пример 1. Делится ли число 111 на 3?
Решение: Давайте сложим цифры числа 111. У нас есть 1 + 1 + 1 = 3. Поскольку сумма цифр делится на 3, следовательно, число 111 также делится на 3.
У нас есть 1 + 1 + 1 = 3. Поскольку сумма цифр делится на 3, следовательно, число 111 также делится на 3.
Пример 2. Какое из двух чисел 522 и 713 делится на 3?
Решение: сумма цифр 522 (5 + 2 + 2 = 9) равна 9, что делится на 3. Таким образом, 522 делится на 3. Однако в числе 713 сумма цифр 11 равна сумме цифр. не делится на 3, поэтому 713 не делится на 3. Следовательно, только 522 делится на 3.
Число делится на 4, если последние две цифры числа делятся на 4.
Пример 1: Какое единственное число в приведенном ниже наборе делится на 4?
{945, 736, 118, 429}
Решение: Обратите внимание на последние две цифры четырех чисел в наборе. Обратите внимание, что 736 — единственное число, в котором две последние цифры (36) делятся на 4. Мы можем заключить, что 736 — единственное число в наборе, которое делится на 4.
Пример 2: Верно или неверно. Число 5,554 делится на 4.
Решение: Последние две цифры числа 5,554 равны 54, что не делится на 4. Это означает, что данное число НЕ делится на 4, поэтому ответ будет ложным .
Число делится на 5, если последняя цифра числа 0 или 5.
Пример 1: Множественный выбор. Какое число делится на 5.
А) 68
Б) 71
С) 20
Г) 44
Решение: чтобы число делилось на 5, последняя цифра числа должна быть либо 0, либо 5.Перебирая варианты, можно сказать, что только число 20 делится на 5, поэтому ответ — вариант C .
Пример 2. Выберите все числа, которые делятся на 5.
А) 27
Б) 105
С) 556
Г) 343
E) 600
Решение: И 105, и 600 делятся на 5, потому что они либо оканчиваются на 0, либо на 5. Таким образом, варианты B и E являются правильными ответами.
Таким образом, варианты B и E являются правильными ответами.
Число делится на 6, если число делится как на 2, так и на 3.
Пример 1. Делится ли число 255 на 6?
Решение: чтобы число 255 делилось на 6, оно должно делиться на 2 и 3. Давайте сначала проверим, делится ли оно на 2. Обратите внимание, что 255 не является четным числом (любое число, оканчивающееся на 0, 2, 4, 6 или 8), что делает его неделимым. 2. Дальнейшая проверка не требуется. Теперь мы можем сделать вывод, что это число не делится на 6.Ответ: NO .
Пример 2: Делится ли число 4,608 на 6?
Решение: Число является четным числом, поэтому оно делится на 2. Теперь проверим, делится ли оно на 3. Давайте сделаем это, сложив все цифры 4608, что составляет 4 + 6+ 0 + 8 = 18. Очевидно, что число сумма цифр делится на 3, потому что 18 ÷ 3 = 6. Поскольку число 4 608 делится на 2 и 3, оно также должно делиться на 6. Ответ: ДА .
Ответ: ДА .
Число делится на 9, если сумма цифр делится на 9.
Пример 1. Делится ли число 1764 на 9?
Решение: Чтобы число делилось на 9, сумма его цифр также должна делиться на 9. Для числа 1,764 мы получаем 1 + 7 + 6 + 4 = 18. Так как сумма цифр равна 18 и равна делится на 9, следовательно, 1764 должно делиться на 9.
Пример 2. Выберите все числа, которые делятся на 9.
А) 7,065
Б) 3,512
С) 8,874
Г) 22,778
E) 48069
Решение: Давайте сложим цифры каждого числа и проверим, делится ли его сумма на 9.
- Для 7,065, 7 + 0 + 6 + 5 = 18, что делится на 9.
- Для 3,512, 3 + 5 + 1 + 2 = 11, что составляет НЕ , делимое на 9.
- Для 8,874, 8 + 8 + 7 + 4 = 27, что делится на 9.
- Для 22,778, 2 + 2 + 7 + 7 + 8 = 26, что составляет НЕ , делимое на 9.

- Для 48,069, 4 + 8 + 0 + 6 + 9 = 27, что делится на 9.
Следовательно, варианты A , C и E делятся на 9.
Число делится на 10, если последняя цифра числа равна 0.
Все числа 20, 40, 50, 170 и 990 делятся на 10, потому что их последняя цифра равна нулю, 0. С другой стороны, числа 21, 34, 127 и 468 не делятся на 10, поскольку они не делятся. заканчиваются нулем.
Возможно, вас заинтересует:
Правила делимости для 7, 11 и 12
Тест на делимость на 13 (а также 7 и 11)
Есть простые правила, по которым можно определить, делится ли число на 2, 3, 4, 5 и 6.
- Число делится на 2, если его последняя цифра делится на 2.
- Число делится на 3, если сумма его цифр делится на 3.
- Число делится на 4, если число, образованное его двумя последними цифрами, делится на 4.

- Число делится на 5, если его последняя цифра делится на 5.
- Число делится на 6, если оно делится на 2 и на 3.
Есть правило делимости на 7, но оно немного шаткое.Давайте продолжим.
- Число делится на 8, если число, образованное его последними тремя цифрами, делится на 8.
- Число делится на 9, если сумма его цифр делится на 9.
- Число делится на 10, если его последняя цифра равна 0.
Есть правило делимости на 11. Это немного сложно, хотя и не так сложно, как правило для 7. Я описываю правило для 11 в предпоследнем абзаце.
Число делится на 12, если оно делится на 3 и 4.(Здесь важно, что 3 и 4 являются взаимно простыми числами. Неверно, например, что число делится на 12, если оно делится на 2 и 6.)
Но что вы будете делать, когда вам исполнится 13?
Проверка делимости на 7, 11 и 13
Мы собираемся убить трех зайцев одним выстрелом , представив правило проверки делимости на 13, которое также дает новые правила проверки делимости на 7 и 11. Итак, если вы пытаетесь разложить число на множители вручную, это даст возможность проверить сразу три простых числа.
Итак, если вы пытаетесь разложить число на множители вручную, это даст возможность проверить сразу три простых числа.
Чтобы проверить делимость на 7, 11 и 13, запишите свое число цифрами, сгруппированными в тройки, как обычно. Например,
11 037 989
Тогда представьте каждую группу как отдельное число — например, 11, 37 и 989 — и возьмите переменную сумму, начиная со знака + на последнем члене.
989 — 37 + 11
Исходное число делится на 7 (или 11 или 13), если эта переменная сумма делится на 7 (или 11 или 13 соответственно).
Альтернативная сумма в нашем примере — 963, что явно равно 9 * 107 и не делится на 7, 11 или 13.Следовательно, 11 037 989 не делятся на 7, 11 или 13.
Вот еще пример. Начнем с
4 894 498 518
Переменная сумма
518 — 498 + 894 — 4 = 910
Сумма требует немного работы, но меньше работы, чем деление 10-значного числа на 7, 11 и 13.
Сумма 910 делится на 7 * 13 * 10, поэтому она делится на 7 и 13, но не на 11. Это говорит о том, что 4 894 498 518 делится на 7 и 13, но не на 11.
Это говорит о том, что 4 894 498 518 делится на 7 и 13, но не на 11.
Почему это работает
Суть метода в том, что 7 * 11 * 13 = 1001.Если я вычитаю из числа, кратное 1001, я не изменяю его делимость на 7, 11 или 13. Более того, я не меняю его остаток на 7, 11 или 13.
Шаги в методе сводятся к сложению или вычитанию кратных 1001 и делению на 1000. Первое не изменяет остаток на 7, 11 или 13, но последний умножает остаток на -1, следовательно, получается переменная сумма. (1000 соответствует -1 mod 7, mod 11 и mod 13.) См. Более формальные аргументы в сноске [1].
Таким образом, с помощью этого метода мы можем не только проверить делимость на 7, 11 и 13, мы также можем найти остатки на 7, 11 и 13. Исходное число и чередующаяся сумма совпадают по модулю 1001, поэтому они совпадают. мод 7, мод 11 и мод 13.
В нашем первом примере n = 11 037 989, а переменная сумма составила m = 963. Остаток при делении m на 7 равен 4, поэтому остаток при делении n на 7 также равен 4. То есть m конгруэнтно 4 mod 7, и поэтому n конгруэнтно 4 mod 7.Точно так же m конгруэнтно 6 mod 11, и поэтому n конгруэнтно 6 mod 11. И, наконец, m конгруэнтно 1 mod 13, поэтому n конгруэнтно 1 mod 13.
То есть m конгруэнтно 4 mod 7, и поэтому n конгруэнтно 4 mod 7.Точно так же m конгруэнтно 6 mod 11, и поэтому n конгруэнтно 6 mod 11. И, наконец, m конгруэнтно 1 mod 13, поэтому n конгруэнтно 1 mod 13.
Похожие сообщения
[1] Ключевой расчет:
Искусство решения проблем
Эти правила делимости помогают определить, когда положительные целые числа делятся на определенные другие целые числа. Все эти правила применяются для base-10 , только для — у других баз есть свои собственные, разные версии этих правил.
Видео о делимости
https://youtu.be/bIipw2XSMgU
Основы
Правило делимости на 2 и степени 2
Число делится на тогда и только тогда, когда последние цифры числа делятся на. Таким образом, в частности, число делится на 2 тогда и только тогда, когда его цифра единиц делится на 2, то есть если число заканчивается на 0, 2, 4, 6 или 8.
Доказательство
Правило делимости на 3 и 9
Число делится на 3 или 9 тогда и только тогда, когда сумма его цифр делится на 3 или 9 соответственно.Обратите внимание, что это не , а работает для более высоких степеней 3. Например, сумма цифр 1899 делится на 27, но 1899 сам не делится на 27.
Доказательство
Правило делимости на 5 и степени 5
Число делится на тогда и только тогда, когда последние цифры делятся на эту степень 5.
Доказательство
Правило делимости для 7
Правило 1: Разделите числа на трехзначные числа справа (). Альтернативная сумма () делится на 7 тогда и только тогда, когда делится на 7.
Доказательство
Правило 2: усеките последнюю цифру, удвойте эту цифру и вычтите ее из остальной части числа (или наоборот). делится на 7 тогда и только тогда, когда результат делится на 7.
Доказательство
Правило 3: «Хвостовая делимость». Примечание. Это только говорит вам, делится ли он, а НЕ остаток. Возьмите число, скажем, 12345. Посмотрите на последнюю цифру и прибавьте или вычтите число, кратное 7, чтобы оно стало равным нулю. В этом случае мы получаем 12380 или 12310 (оба приемлемы; я использую первый).Отрежьте конечные 0 и повторите. 1238 — 28 ==> 1210 ==> 121 — 21 ==> 100 ==> 1 НЕТ. В целом работает с числами, которые взаимно просты с основанием (и отлично работает в двоичном формате). Вот тот, который работает. 12348 — 28 ==> 12320 ==> 1232 +28 ==> 1260 ==> 126 + 14 ==> 14 УРА!
Возьмите число, скажем, 12345. Посмотрите на последнюю цифру и прибавьте или вычтите число, кратное 7, чтобы оно стало равным нулю. В этом случае мы получаем 12380 или 12310 (оба приемлемы; я использую первый).Отрежьте конечные 0 и повторите. 1238 — 28 ==> 1210 ==> 121 — 21 ==> 100 ==> 1 НЕТ. В целом работает с числами, которые взаимно просты с основанием (и отлично работает в двоичном формате). Вот тот, который работает. 12348 — 28 ==> 12320 ==> 1232 +28 ==> 1260 ==> 126 + 14 ==> 14 УРА!
Правило делимости 10 и степени 10
Если число является степенью 10, определите его как степень 10. Показатель степени — это количество нулей, которые должны быть в конце числа, чтобы оно делилось на эту степень 10.
Пример: Чтобы число делилось на 1 000 000, в конце должно быть 6 нулей, потому что.
Правило делимости для 11
Число делится на 11 тогда и только тогда, когда чередующаяся сумма цифр делится на 11.
Доказательство
Общее правило для композитов
Число делится на, где разложение на простые множители равно, если число делится на каждое из.
Пример
Для примера мы проверим, делится ли 55682168544 на 36.
Разложение 36 на простые множители. Таким образом, мы должны проверить делимость на 4 и 9, чтобы увидеть, делится ли оно на 36.
- Поскольку последние две цифры, 44 числа, делятся на 4, то же самое и все число.
- Чтобы проверить делимость на 9, мы смотрим, делится ли сумма цифр на 9. Сумма цифр равна 54, что делится на 9.
Таким образом, число делится как на 4, так и на 9 и должен делиться на 36.
Продвинутый
Общее правило для простых чисел
Для каждого простого числа, кроме 2 и 5, существует правило, аналогичное правилу 2 для делимости на 7.Для общего простого числа существует такое число, что целое число делится на тогда и только тогда, когда усечение последней цифры, ее умножение на и вычитание из оставшегося числа дает результат, делящийся на. Правило делимости 2 на 7 говорит, что для,. Правило делимости 11 эквивалентно выбору. Правило делимости 3 эквивалентно выбору. Эти правила также можно найти при соответствующих условиях в системах счисления, отличных от 10. Также обратите внимание, что эти правила существуют в двух формах: если заменяется на, то вычитание может быть заменено сложением.Мы видим один пример этого в правиле делимости 13: мы могли бы умножить на 9 и вычесть, а не умножать на 4 и складывать.
Правило делимости 3 эквивалентно выбору. Эти правила также можно найти при соответствующих условиях в системах счисления, отличных от 10. Также обратите внимание, что эти правила существуют в двух формах: если заменяется на, то вычитание может быть заменено сложением.Мы видим один пример этого в правиле делимости 13: мы могли бы умножить на 9 и вычесть, а не умножать на 4 и складывать.
Правило делимости для 13
Правило 1. Обрежьте последнюю цифру, умножьте ее на 4 и прибавьте к остальной части числа. Результат делится на 13 тогда и только тогда, когда исходное число делится на 13. Этот процесс можно повторить для больших чисел, как со вторым правилом делимости для 7.
Доказательство
Правило 2: Разделите числа на трехзначные числа справа ().Альтернативная сумма () делится на 13 тогда и только тогда, когда делится на 13.
Доказательство
Правило делимости для 17
Усечь последнюю цифру, умножить ее на 5 и вычесть из оставшегося первого числа. Число делится тогда и только тогда, когда результат делится. Процесс можно повторить для любого числа.
Число делится тогда и только тогда, когда результат делится. Процесс можно повторить для любого числа.
Доказательство
Правило делимости для 19
Усечь последнюю цифру, умножить ее на 2 и прибавить к оставшемуся начальному числу.Число делится тогда и только тогда, когда результат делится. Это также можно повторить для больших чисел.
Доказательство
Правило делимости для 29
Обрезать последнюю цифру, умножить ее на 3 и прибавить к оставшемуся начальному числу. Число делится тогда и только тогда, когда результат делится. Это также можно повторить для больших чисел.
Доказательство
Правило делимости для 49
Почему 49? Для вынимания надоедливости из корня.
Полезно до 23:00.Округлите число до ближайшего 50, позвоните по нему и вычтите исходное число, позвоните по этому номеру. Если, он делится на 49.
Примеры:
49. Округлить:. Разница: . ? Да!
1501. Округлить:. Разница: . ? Нет!
? Нет!
1470. Округлить:. Разница: . ? Да!
Доказательство
Проблемы
Ресурсы
Книги
Классы
См. Также
Как узнать, делится ли число на 4?
В этом посте мы узнаем критерии делимости числа 4 и поймем, как они работают.
Критерии делимости числа 4 — это правила, позволяющие узнать, можно ли разделить число на 4. Их легко выучить, и их объяснения легко понять.
Как узнать, делится ли число на 4?
Если число можно выразить путем умножения другого числа на 4, оно делится на 4.
Вам необходимо знать несколько свойств умножения: ассоциативное и распределительное. Если вы не совсем понимаете их, вы можете просмотреть их в этом посте.
Критерии деления одно- и двузначных чисел на 4
Во-первых, мы собираемся узнать, как определить, соответствует ли одно- или двузначное число критерию делимости на 4. Легко: это когда мы делим и видим, что остаток равен нулю.
Например: делится ли 24 на 4?
Да, потому что когда мы делим 24 на 4, частное равно 6, а остаток равен 0.
24 = 6 х 4
Критерии деления трех- и четырехзначных чисел на 4
Для того, чтобы трех- или четырехзначное число делилось на 4, оно должно удовлетворять одному из двух условий:
- Последние две цифры равны нулю .
- Последние две цифры делятся на 4.
Например: делятся ли 500 и 339 на 4?
500 делится на четыре, потому что его последние две цифры равны нулю.
339 не делится на четыре, потому что 39 (его последние две цифры) — нет.
Применение известных нам правил, чтобы увидеть, соблюдаются они или нет, помогает нам определить, делится ли число на четыре. Но мы не знаем рассуждений, давайте продолжим и попробуем разобраться.
Разъяснение критериев деления числа на 4
Как возможно, что два простых правила могут сказать нам, соответствует ли число критерию делимости на 4? Откуда берутся эти правила?
Причина очень проста, и мы собираемся объяснить ее в три этапа.
Мы начинаем с наименьшего возможного числа, которое имеет ноль в качестве последних двух цифр, 100. Если мы разделим 100 на 4, получится 25, а остаток — 0. 100 делится на 4 .
100 = 25 х 4
- Числа больше 100 с нулем в последних двух цифрах.
Все числа, последние две цифры которых содержат ноль, можно выразить умножением другого числа на 100. Мы выберем одно, например, 4300.
4,300 = 43 х 100
Так как мы знаем, что 100 делится на четыре, мы также можем сказать, что 4300 делится. Вот математическое объяснение:
4300 = 43 x 100 = 43 x (25 x 4) = (43 x 25) x 4 = 1075 x 4
Мы можем использовать ту же операцию для любого числа, имеющего эти характеристики. Таким образом, мы обнаруживаем первое правило: любое число, которое имеет ноль в качестве последних двух цифр, делится на 4.
Для всех остальных чисел, тех, которые больше ста и тех, у которых нет нуля в последних двух цифрах, мы можем применить процесс, аналогичный упомянутому ранее. Их можно выразить как сумму числа с нулем в последних двух цифрах и еще одного числа. Возьмем случайное число, например 6 548.
Их можно выразить как сумму числа с нулем в последних двух цифрах и еще одного числа. Возьмем случайное число, например 6 548.
6,548 = 6,500 + 48
Так как мы знаем, что 6500 делится на 4, мы не должны забывать проверить, делится ли 48 тоже. Ну да, две последние цифры делятся на 4.
48 = 12 х 4
Итак, мы можем выразить это следующим образом:
6548 = 6500 + 48 = (65 х 100) + 48 =
= (65 х 25 х 4) + (12 х 4) = (1,625 х 4) + (12 х 4) =
= (1,625 + 12) х 4 = 1,637 х 4
Вот как мы понимаем второе правило: любое число делится на 4, если его последние две цифры делятся на 4.
Заключение
Нам не нужно проходить все этапы этого процесса каждый раз, когда нам нужно знать, делится ли число на четыре. Мы узнали необходимые критерии для деления числа на 4, но понимание этого помогает понять, почему эти критерии существуют, и если однажды мы забудем какой-либо из них… Я уверен, что мы вспомним, откуда они взялись!
Чтобы по-настоящему понять критерии, которые мы узнали о делении на 4, возможно, вы хотели бы обновить, как делить на 3-значное число.
Если вы хотите узнать больше о материалах по начальной математике, зарегистрируйтесь в Smartick и попробуйте бесплатно.
Подробнее:
Развлечение — любимый способ обучения нашего мозга
Дайан Акерман
Smartick — увлекательный способ изучения математики- 15 веселых минут в день
- Адаптируется к уровню вашего ребенка
- Миллионы учеников с 2009 года
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Правила делимости — методы и примеры
Деление — это одна из четырех основных операций, при которой число распределяется на равные части. Это математический метод, при котором число делится на более мелкие группы, или метод распределения количеств на равные части. Обозначается несколькими символами: косой чертой, горизонтальной чертой и знаком деления.
Деление — это операция, обратная умножению. Например, умножение 5 на 2 дает 10.Вы можете получить любой из множителей 2 и 5, разделив 10 на любое из чисел.
Что такое правило делимости?
Правила делимости были разработаны, чтобы упростить и ускорить процесс деления . Понимание правил делимости от 1 до 20 — важный навык в математике, поскольку он позволяет лучше решать задачи.
Например, правило делимости числа 9 определенно скажет нам, делится ли число на 9, независимо от того, насколько большим может показаться число.
Вы можете легко запомнить правила делимости для чисел, таких как 2, 3, 4 и 5. Но правила делимости для 7, 11 и 13 немного сложны, и по этой причине необходимо тщательно их понимать. .
Правила делимости
Как следует из названия, правила или тесты делимости — это процедуры, используемые для проверки того, делится ли число на другое число, без обязательного выполнения фактического деления. Число делится на другое число, если результат или частное — целое число, а остаток равен нулю.
Поскольку не все числа полностью делятся на другие числа, правила делимости на самом деле являются сокращениями для определения действительного делителя числа просто путем изучения цифр, составляющих число.
Давайте теперь рассмотрим эти правила делимости для разных чисел.
Проверка делимости 1 не имеет условий для чисел. Все числа делятся на 1, независимо от их размера. Когда любое число делится на 1, результатом является само число.Например, 5/1 = 5 и 100000/1 = 100000.
Число делится на 2, если последняя цифра числа равна 2, 4, 6, 8 или 0.
Например: 102/2 = 51, 54/2 = 27, 66/2 = 33, 28/2 = 14 и 20/2 = 10
Тест делимости для 3 утверждает, что число полностью делится на 3, если цифры числа делятся на 3 или кратно 3.
Например, рассмотрим два числа, 308 и 207:
Чтобы проверить, делится ли 308 на 3 или нет, найдите сумму цифр.
3 + 0 + 8 = 11. Так как сумма равна 11, что не делится на 3, то 308 также не делится на 3.
Проверьте 207, суммируя его цифры: 2 + 0 + 7 = 9, так как 9 делится на 3, то 207 также делится на 3.
Тест делимости для 4 утверждает, что число делится на 4, если последние две цифры числа делятся на 4,
Например: Рассмотрим два числа , 2508 и 2506.
Последние цифры числа 2508 — 08. Поскольку 08 делится на 4, то число 2508 также делится на 4.
2506 не делится на 4, потому что две последние цифры, 06, не делятся на 4.
Все числа с последней цифрой 0 или 5 делятся на 5. Например, 100/5 = 20, 205 / 5 = 41.
Число делится на 6, если его последняя цифра является четным числом или нулем, а сумма цифр кратна 3.
Например, 270 делится на 2, потому что последняя цифра равна 0
Сумма цифр: 2 + 7 + 0 = 9, что также делится на 3.
Следовательно, 270 делится на 6.
Проверка делимости 7 объясняется в следующем алгоритме
Рассмотрим число 1073. Чтобы проверить, делится ли число на 7 или нет?
Удалите число 3 и умножьте его на 2, получится 6. Вычтите 6 из оставшегося числа 107, поэтому 107 — 6 = 101.
Вычтите 6 из оставшегося числа 107, поэтому 107 — 6 = 101.
Повторите процесс. У нас 1 x 2 = 2, а оставшееся число 10-2 = 8. Поскольку 8 не делится на 7, следовательно, число 1073 также не делится на 7.
Тест делимости для 8 утверждает, что число равно делится на 8, если его последние три цифры делятся на 8.
Проверка делимости числа 9 аналогична проверке делимости числа 3. Если сумма цифр числа делится на 9, то число также делится на 9.
Пример: в таком числе, как 78532, сумма цифр равна: 7 + 8 + 5 + 3 + 2 = 25. Поскольку 25 не делится на 9, число 78532 также не делится на 9. Рассматривая другой случай числа: 686997, сумма цифр равна: 6 + 8 + 6 + 9 + 9 + 7 = 45. Поскольку сумма делится на 9, то число 686997 делится на 9.
Правило делимости 10 гласит, что любое число, последняя цифра которого равна нулю, означает число I, делимое на 10.
Например, числа: 30, 50, 8000, 20 33000 делятся на 10.
- Правила делимости для 11
Это правило гласит, что число делится на 11, если разница суммы альтернативных цифр делится на 11.
Например, чтобы проверить, делится ли число 2143 на 11 или нет, процедура:
Сумма альтернативных цифр каждой группы: 2 + 4 = 6 и 1+ 3 = 4
Следовательно, 6-4 = 2, и поэтому число не делится на 11.Следовательно, 2143 не делится на 11.
- Правила делимости для 13
Чтобы проверить, делится ли число на 13, повторное добавление последней цифры к оставшемуся числу выполняется 4 раза, пока не получится двузначное число. прибыл. Если двузначное число делится на 13, то целое число также делится на 13.
Например:
2795 → 279 + (5 x 4) → 279 + (20) → 299 → 29 + (9 х 4) → 29 + 36 → 65.
В этом случае оказывается, что двузначным числом является 65, которое делится на 13, следовательно, число 2795 также делится на 13.
Практические вопросы1. Какие из следующих чисел делятся на 2, 5 и 10?
а. 149
г. 19400
с. 720345
г. 125370
эл.
 n$
n$ Например, число, делимое на 6, также будет делиться на 2 и 3.
Например, число, делимое на 6, также будет делиться на 2 и 3.
