Что важнее признаки равенства треугольника или подобие треугольников

Представление

Учащиеся 7 и 8 класса приняли участие в создание проект «Что важнее признаки равенства треугольника или подобие треугольников»

Краткое описание работы.

Проект «Что важнее признаки равенства треугольника или подобие треугольников» представлен в номинации учебных проектов «Сделаем мир лучше» в создании проекта приняли участие учащиеся 7-8 класса. У каждого было свое задание защитить свои утверждения.

Цель работы:

Определить понятие необходимости изучения признаков равенства и подобие треугольников в жизни человека, и связь их с другими предметами.

Задачи исследовательской работы:

1. Формирование умение проектно-исследовательской деятельности.

2. Оценить важность исследуемого объекта.

3. Объяснение возникновения признаков равенства и дальнейшего появления подобия треугольников.

4. Развитие умения использовать дополнительные источники (интернет ресурсы. Справочники. Энциклопедии.)

5. Подготовить презентацию с картинками и дискуссию по теме: что важнее признаки равенства треугольника и подобие треугольников.

6. Показ презентация для 8-9 классов под девизом «Зачем нам признаки равенства треугольников и подобие, и какую роль они играю в жизни человека»

Муниципальное бюджетное общеобразовательное учреждение

«Орловская средняя общеобразовательная школа

Городищенского района Волгоградской области»

Районный конкурс

социальных и

учебных проектов

«Сделаем мир лучше!»

«Что важнее признаки равенства треугольника или

подобие треугольников»

Выполнили обучающиеся

7 класса

Кривогузова Мария

Карагичева Ирина

8класса

Киселева Юлия

Руководитель проекта:

Захарова

Луиза Александровна

2015

Паспорт исследователя-проектировщика

№

п/п

Этапы работы над проектом (исследованием)

Деятельность ученика

Деятельность учителя

Выявление проблемы.

Почему заинтересовала эта проблема.

Обсуждение с учителем темы проекта, что важнее признаки равенства треугольника или подобие треугольников.

Обсуждение с учащимися темы проблемы проекта.

Определение цели и задач проекта.

Цель работы: выявить закономерность и зависимость рассматриваемых вопросов.

Определить понятие необходимости изучения признаков равенства треугольников и их подобие в жизни человека, и связь его с другими предметами.

Задачи:

1. Формирование и умение проектно-исследовательской деятельности.

2. Оценить важность исследуемого объекта.

3. Объяснение возникновения признаков равенства и подобия треугольников.

4. Проанализировать как человеком они могут применятся в жизни.

5. Развитие умения использовать дополнительные источники: Интернет ресурсы. Справочники. Энциклопедии

6. Приготовить картинки по разделам проекта.

7. Провести презентации в 8-9 классах «Что важнее признаки равенства треугольника или подобие треугольников»

Помощь в постановке цели и определение задач.

Планирование самостоятельной деятельности.

Выработка плана действий.

Как можно это сделать?

Определение основных методов исследования.

1. Работа с учебниками, энциклопедией и интернет ресурсами.

2. Отобрать нужный материал по разделам: строительство, искусство, военное дело.

3. Сделать вывод: зачем нужно признаки равенства и подобие треугольников.

4. Создать презентацию «Что важнее признаки равенства треугольника или подобие треугольников» и ее защиту.

Познакомить обучающегося с разными средствами и приёмами познавательной, исследовательской деятельности.

Использование исследовательских методов. Сбор информации.

Проведение исследования:

1. Поиск и обработка необходимой информации.

2. Работа с различными источниками.

3. Подбор рисунков.

4. Создание презентации.

Наблюдения, совет, помощь в работе с компьютерными программами.

Оформление конечных результатов.

Оформление защиты:

1. План защиты по рубрикам.

2. Составление презентации.

3. Оформление страницы «Зачем нам признаки равенства и подобия треугольников?»

Знакомство с готовой работой.

Учитель помогает оформить проект «Путешествие в прошлое.»

Презентация своего исследования.

Участие в мероприятиях:

На уроках геометрии 8-9 классах во II полугодии.

Оценивание.

Вывод.

Участники сами анализируют свое творение. Дают своей работе самооценку.

Учащиеся класса высказывают свое мнение «Зачем нам признаки равенства и подобия треугольников?»

Самое главное заинтересовать обучающихся в изучение «Признаков равенства и подобия треугольников».

Участие в оценке путём коллективного обсуждения и самооценок.

Содержание.

1. Вступление. Актуальность проекта.

2. Историческая справка:

   1. Подобия.

   2. Признаки равенства треугольников.

3. Признаки равенства и подобия треугольников.

   1. Равенства треугольников по стороне и двум углам.

   2. Подобие треугольников по двум углам.

   3. Равенство треугольников по двум сторонам и углу между ними.

   4. Подобие треугольников по пропорциональности двух сторон одного треугольника к другому и равенству угла между ними.

   5. Жесткий треугольник.

   6. Подобие пропорциональности трех сторон одного треугольника к другому.

   7. Признак равенства треугольников по трем углам.

4. Заключение:

   1. Вывод.

   2. Применение на практике.

   3. Применение при возведение зданий.

5. Защита проекта.

Вступление

Меня зовут Кривогузова Мария, я ученица 7 класса будут вам представлять признаки равенства треугольников и их историю.

Меня зовут Киселева Юлия, я ученица 8 класса буду вам представлять признаки подобия треугольников их историю возникновения и необходимость их изучать.

Основной целью нашего исследования является определить важность изучения данных утверждений.

Для начала мы решили провести опрос в более старших классов. Вопросы с вариантами ответа были таковыми:

1. Что важнее равенство треугольников или подобие треугольников?

1. Равенство треугольников;

2. Подобие треугольников;

3. Важны оба утверждения.

2. Пригодились ли вам признаки равенства треугольников и подобие треугольников при дальнейшем изучении геометрии?

1. Да;

2. Нет.

3. Как вы думаете, где больше пригодится вам этот изученный материал?

1. Я думаю, что мне это пригодится при учебе в высшем учебном заведении;

2. Я изучал(а) для того чтобы в будущем не выглядеть тупым перед своими детьми.

3. Мне это совсем не как не нужно.

Поэтому мы сами решили выяснить, что важнее равенство или подобие треугольников, и как они применимы в жизни человека.

Актуальность.

Треугольник является центральной фигурой всей геометрии. При решении задач используют его самые разнообразные свойства. Свойства треугольника широко применяют на практике. Например, в архитектуре; при разработке чертежа здания, при планировке будущих квартир; в промышленности: при проектировании различны деталей, при изготовлении стройматериалов, при строительстве морских и авиа судов; в навигации: для проложения правильного и максимально точного маршрута; в астрологии и астрономии, одним словом просто необходимо знать треугольник и все его свойства. Одно из важнейших свойств для пары треугольников, устанавливать их равенство или подобие. Существует ряд задач на тему установления равенства двух треугольников, а также множество задач на подобие треугольников.

Историческая справка подобия треугольников

Искусство изображать предметы на плоскости с Древних времён привлекает к себе внимание человека, люди рисовали на скалах, стенах, сосудах и прочих предметах быта, различные орнаменты, растения, животных. Люди стремились к тому, чтобы изображение правильно отображало естественную форму предмета.

Учение о подобии фигур на основе теории отношений и пропорций было создано в Древней Греции в 5-4 веках до нашей эры и существует и развивается до сих пор. Например, очень много детских игрушек подобным предметам взрослого мира, обувь и одежда одного фасона выпускается различных размеров. Эти примеры можно продолжать и дальше. В конце концов, все люди подобны друг другу и как утверждает Библия, создал их бог по своему образу и подобию.

Историческая справка о признаках равенства треугольников:

Признаки равенства треугольников имели издавна важнейшее значение в геометрии, так как доказательства многочисленных теорем сводилось к доказательству равенства тех или иных треугольников. Доказательством признаков равенства треугольников занимались еще пифагорейцы. По словам Прокла, Евдем Родосский приписывает Фалесу Милетскому доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников).

Равенство треугольников по стороне и двум прилежащим углам.

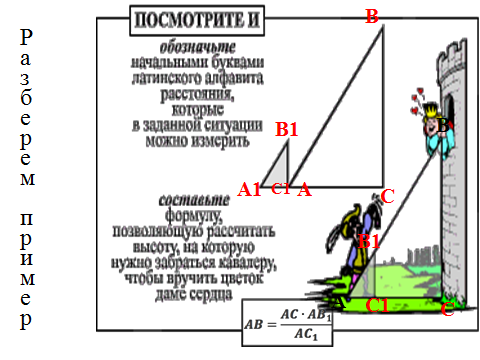
Эту теорему Фалес использовал для определения расстояния от берега до морских кораблей. Каким способом пользовался при этом Фалес, точно не известно. Предполагают, что его способ состоял в следующем: пусть A – точка берега, B – корабль на море. Для определения расстояния AB восстанавливают на берегу перпендикуляр произвольной длины AC  AB; в противоположном направлении восстанавливают CE AC так, чтобы точки D (середина AC), B и E находились на одной прямой. Тогда CE будет равна искомому расстоянию AB. Доказательство основывается на втором признаке равенства треугольников (DC = DA;  С = A;  EDС = BDA как вертикальные).

Признак подобия треугольников по двум углам.

Но так не удобно решать задачу для этого можно воспользоваться первым признаком подобия треугольников. И как не странно его создатель также Фалес Милетский

Давайте представим картину такую

Мы с вами в Египте сейчас оказались.

Стоим и смотрим на пирамиду большую

Её высотою большой восхищаясь.

И тут сам фараон задачу нам ставит

Измерить нам надо высоту пирамиды.

Как же рулетку к ней приставить

Ведь конца её даже не видно.

Но всё-таки задачу можно решить

Вспомнив подобие треугольников.

Фалес Милетский нам предложил

Пример преподавший для школьников.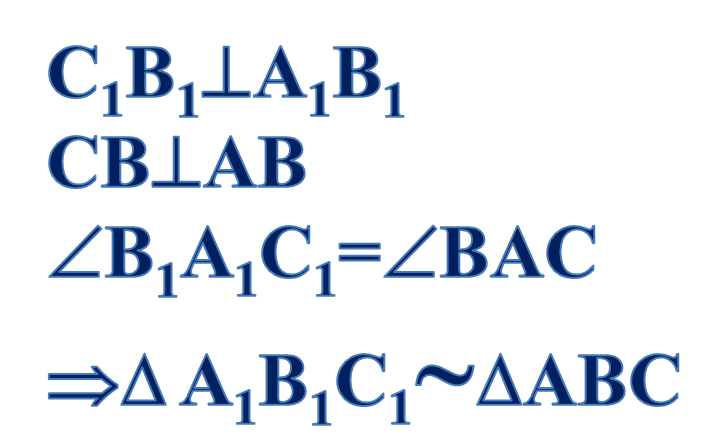

Он подождал пока тень его

Точно совпадет с его ростом.

Как оказалось немного терпения

Задача решилась легко и просто.

В этот миг теорему применив

Высота пирамиды равна её тени.

Знай про подобие треугольников

И применяй её в жизни без лени.

Используя этот признак подобия мы можем измерить высоту любой башни и не только высоту, а спроектировать на чертежах любую постройку.

Равенства треугольников по двум сторонам и углу между ними.

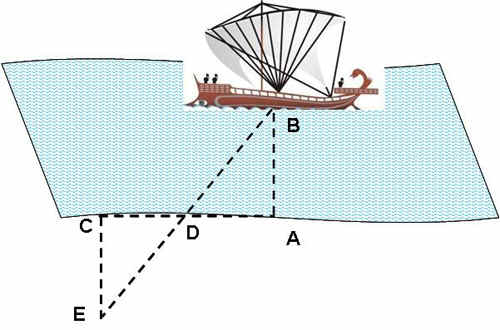
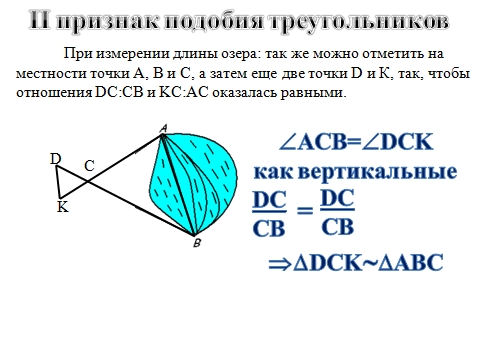
Для исследования этого признака я решила взять практическую задачу на вычисление длины озера.

При измерении длины озера отметили на местности точки А, В и С, а затем еще две точки D и К, так, чтобы точка С оказалась серединой отрезков АК и ВD. Измерив DК, получили 500 м и сделали вывод, что длина озера равна 500м.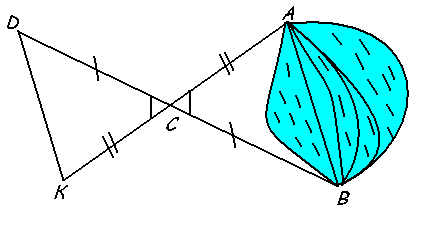

Сколько же нужно много свободного пространства чтобы сделать эти измерения, а не легче ли применить второй признак подобия треугольников.

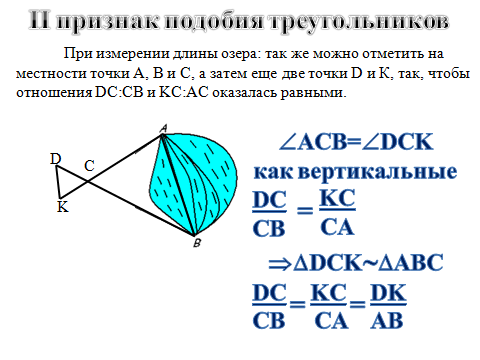
Подобия треугольника по пропорциональности двух сторон одного треугольника к другому и равенству угла между ними.

При измерении длины озера: так же можно отметить на местности точки А, В и С, а затем еще две точки D и К, так, чтобы отношения DC:CB и KC:AC оказалась равными.

Равенства треугольников по трем сторонам. Жесткий треугольник

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Из третьего признака равенства треугольников следует, что треугольник — жёсткая фигура. Потому, что: можно представим себе две рейки, (рис 1) у которых два конца скреплены гвоздем. Такая конструкция не является жёсткой однако сдвигая или раздвигая свободные концы реек, мы можем менять угол между ними. Теперь возьмем ещё одну рейку и скрепим её концы со свободными концами первых двух реек.(рис 2) Полученная конструкция — треугольник — будет уже жёсткой. В ней нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному. Но это невозможно, так как новый треугольник должен быть равен исходному по третьему признаку равенства треугольников.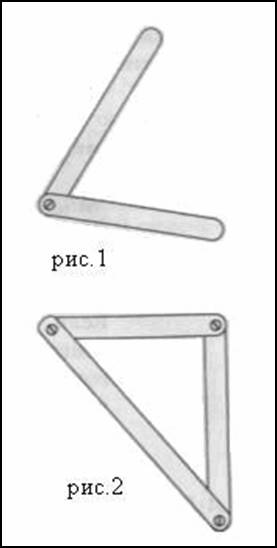

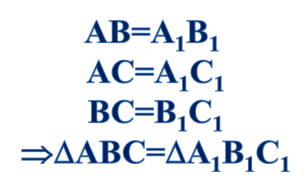
Если все три стороны

треугольников равны,

То давно понятно всем

Что равны они совсем.

Подобие треугольников пропорциональности трех сторон одного треугольника к другому.

Если жесткий треугольник мы решим увеличить или уменьшить в несколько раз, то увечится или уменьшится в это число раз каждая его сторона, и тем самым получим третий признак подобия треугольника «Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны».

Если три стороны треугольника одного

Пропорциональны трём сторонам другого,

То эти треугольники будут абсолютно подобны

Даже если один маленький, а другой огромный.

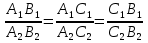
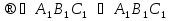
Равенства треугольников по трем углам.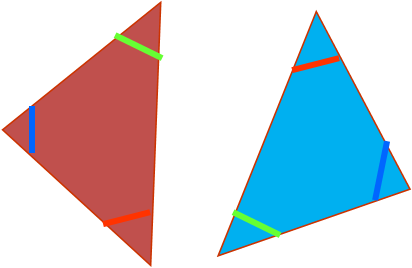

Был такой великий русский философ математик Николай Лобачевский, который доказал четвертый признак равенства треугольников. «Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники равны»

Такого признака равенства треугольников нет. Это часть определение подобия треугольника. «Если углы одного соответственно равны углам другого и соответствующие стороны пропорциональны».

Вывод.

Наш спор был долгим и упорным что важнее: признаки равенства треугольников или подобия. Мы сделали следующий вывод – если бы не было признаков равенства треугольников, то не было бы и подобия. Такой вывод помог сделать нам древнегреческий филосов и математик Фалес Милетский, который доказал не толькоодин из признаки равенства треугольников, но а также один из основных признаков подобие.

«Природа формулирует свои законы языком математики» Г.Галилей.

В наше время чтобы измерить высоту здание, найти расстояние мы не обходимся без гениальных идей Фалеса Милетского.

Прежде чем построить здание делают его уменьшенный макет, а уж потом его возводят в реальные размеры.

Защита проекта:

Уроки геометрии 8, 9, 10, 11 класс.

«Природа формулирует свои законы языком математики»  Г.Галилей

Защита проекта на конкурсе «Сделаем мир лучше»

Используемые источники в написание проекта.

1. Энциклопедия «Аванта» по математике. 2004 г

2. «Википедия» свободная энциклопедия. http://ru.wikipedia.org/wiki/Заглавная_страница

3. http://to-name.ru/biography/biografii.htm

4. Глейзер Г.И. «История математики в школе 7-8 классах», Просвещение 1982 г.

5. http://nytva.taba.ru/page1291435753/fest/542212_OF_IV-6_Priznaki_ravenstva_treugolnikov_Geometriya_7_klass.html

6. ГусеваТ.М. Признаки подобия треугольников.- М.// Первое сентября, приложение«Математика», 1999, №28

7. Автор всех стихо Сусь Р.С.

Первый признак подобия треугольников. Видеоурок. Геометрия 8 Класс

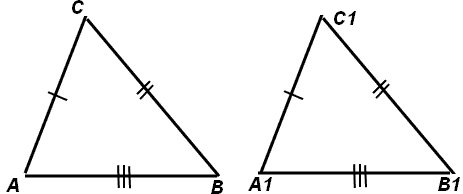
Подобными называются такие треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника (см. рис. 1).

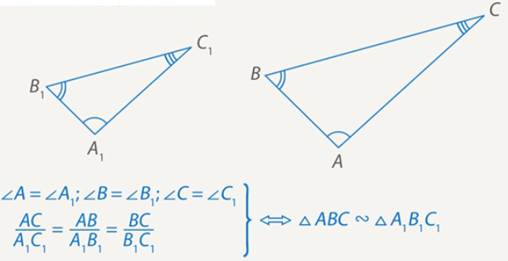
Рис. 1. Подобные треугольники

Отношение длин сторон одного треугольника к сходственным сторонам другого называется коэффициентом подобия (): .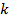

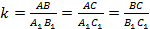На практике для установления подобия треугольников достаточно проверить некоторые равенства (см. рис. 1). Комбинации этих равенств называются признаками подобия треугольников. Таким образом, признаки подобия треугольников – это геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.

На данном уроке мы рассмотрим первый признак подобия треугольников.

Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

Доказательство первого признака подобия треугольников

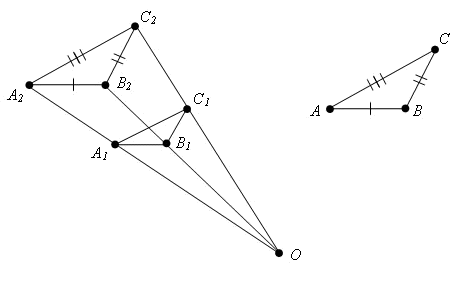
Дано: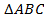; ; 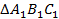;  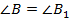(см. рис. 2).

Доказать: подобие данных треугольников .

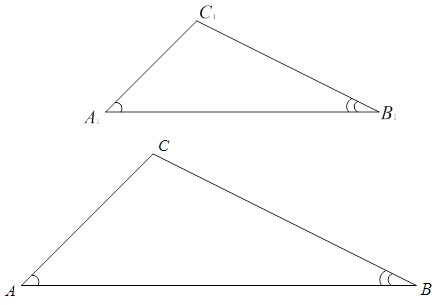
Рис. 2. Иллюстрация к доказательству

Доказательство

Для доказательства подобия данных треугольников необходимо установить равенство соответствующих углов и равенство отношений соответствующих сторон, то есть: ; ; .

1) Из теоремы о сумме углов треугольника известно, что сумма внутренних углов треугольника равна

Признаки равенства треугольников. Признаки равенства прямоугольных треугольников. Признаки подобия треугольников. Признаки подобия прямоугольных треугольников.

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.  / / Признаки равенства треугольников. Признаки равенства прямоугольных треугольников. Признаки подобия треугольников. Признаки подобия прямоугольных треугольников. Поделиться:    Признаки равенства треугольников. Признаки равенства прямоугольных треугольников. Признаки подобия треугольников. Признаки подобия прямоугольных треугольников. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников. Признаки подобия треугольников. Признаки подобия прямоугольных треугольников. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников. Признаки подобия треугольников. Признаки подобия прямоугольных треугольников. Поиск в инженерном справочнике DPVA. Введите свой запрос:

Признаки подобия и равенства треугольников. Свойства подобных треугольников

Треугольник является самой простой замкнутой фигурой на плоскости. При изучении школьного курса геометрии рассмотрению его свойств уделяют особое внимание. В данной статье раскроем вопрос признаков подобия и равенства треугольников.

Какие треугольники называются подобными, а какие равными?

Логично предположить, что две рассматриваемые фигуры будут равны между собой, если они имеют все одинаковые углы и длины сторон. Что касается подобия, то здесь дело обстоит немного сложнее. Два треугольника будут подобны тогда, когда каждый угол одного будет равен соответствующему углу другого, а стороны, лежащие напротив равных углов обеих фигур, будут пропорциональны. Ниже изображен рисунок, на котором представлены два подобных треугольника.

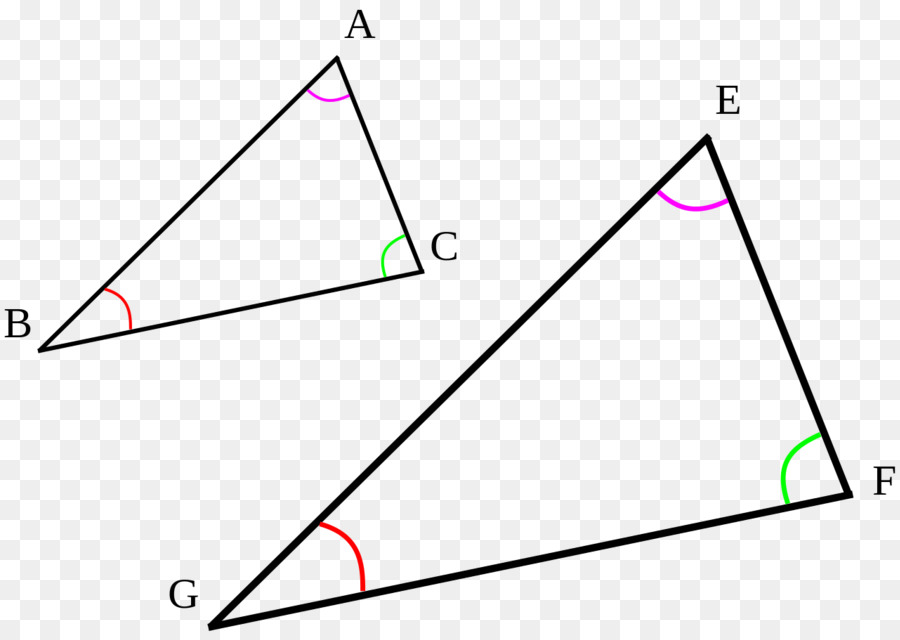
Используя этот рисунок, запишем в виде математических равенств данное выше определение: B = G, A = E, C = F, BA / GE = AC / EF = BC / GF = r, здесь одна латинская буква означает угол, а две буквы — длину стороны. Величина r носит название коэффициента подобия. Понятно, что если r = 1, то имеют место не только подобные, но и равные треугольники.

Признаки подобия

Говоря о свойствах и признаках подобия и равенства треугольников, следует перечислить три основных критерия, по которым можно определить, являются ли рассматриваемые фигуры подобными или нет.

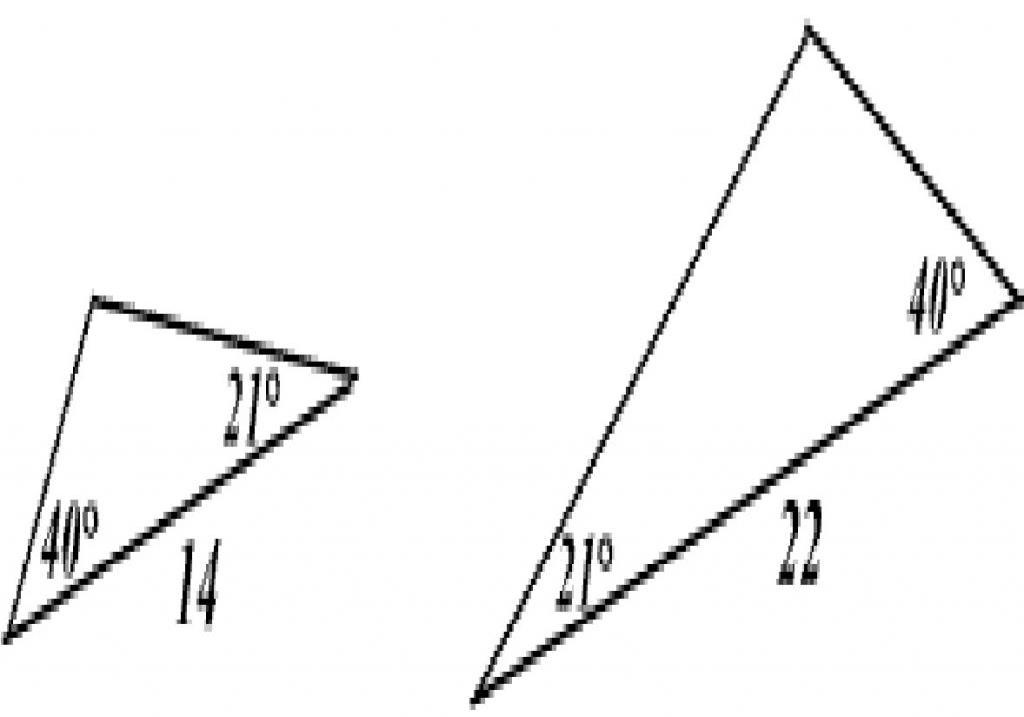
Итак, две фигуры будут подобными между собой, если выполняется одно из следующих условий:

1. Их два угла равны. Поскольку сумма углов треугольника эквивалентна 180^o, то равенство первых двух из них автоматически означает, что одинаковыми будут и третьи. Используя рисунок выше, этот признак можно записать так: если B = G и A = E, то ABC и GEF являются подобными. Если же в этом случае будут равными хотя бы по одной стороне обоих фигур, тогда можно говорить о полной эквивалентности треугольников.
2. Две стороны пропорциональны и углы между ними одинаковые. Например, BA / GE = AC / EF и A = E, тогда GEF и ABC будут подобными. Заметим, что углы A и E лежат между соответствующими пропорциональными сторонами.
3. Все три стороны взаимно пропорциональны. Излагая математическим языком, получаем: BA / GE = AC / EF = BC / GF = r, тогда рассматриваемые фигуры тоже являются подобными.

Отметим еще раз, что для доказательства подобия достаточно привести какой-либо один из представленных признаков. Логично, что все остальные будут выполняться также.

Прямоугольные треугольники: когда они подобны, а когда равны?

Говоря о признаках равенства и подобия прямоугольных треугольников, следует отметить сразу, что у каждого из них по одному углу уже равны (90^o).

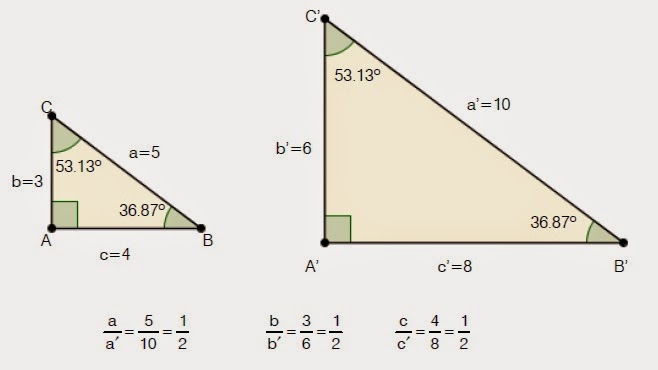
Последний факт приводит к следующей формулировке изложенных выше критериев подобия:

1. Если в двух треугольниках прямоугольных равен всего один угол, который не является прямым, то такие фигуры подобны между собой.
2. Если катеты пропорциональны между собой, тогда фигуры тоже будут подобны, поскольку угол между катетами является прямым.
3. Наконец, пропорциональности всего двух любых сторон для обоих прямоугольных треугольников достаточно для доказательства их подобия. Причина этого заключается в том, что стороны данных фигур связаны между собой теоремой Пифагора, поэтому пропорциональность 2-х из них приводит к пропорциональности с аналогичным коэффициентом подобия и для третьих сторон.

Что касается равенства треугольников с прямыми углами, то здесь просто запомнить: если два каких-либо элемента (прямой угол не считается) обеих фигур равны, то равны и сами фигуры. Например, этими двумя элементами могут быть острый угол и катет, катет и гипотенуза или гипотенуза и острый угол.

Свойства треугольников подобных

Из рассмотренных признаков подобия и равенства треугольников свойства можно выделить такие:

1. Периметры этих фигур относятся друг к другу как коэффициент подобия, то есть P₁ / P₂ = r, где P₁ и P₂ — периметры 1-го и 2-го треугольников, соответственно.
2. Площади подобных фигур относятся как квадрат коэффициента подобия, то есть: S₁ / S₂ = r², где S₁ и S₂ — площади 1-го и 2-го треугольников, соответственно.

Оба эти свойства можно доказать самостоятельно. Суть доказательства сводится к применению математической записи подобия между сторонами фигур. Здесь приведем лишь доказательство 1-го свойства.

Пусть a, b, c — длины сторон одного треугольника и a’, b’, c’ — стороны второго. Поскольку фигуры подобны, то можно записать: a = r * a’, b = r * b’, c = r * c’. Теперь эти выражения подставим в отношении их периметров, получим: P₁ / P₂ = (a + b + c) / (a’ + b’ + c’) = (r * a’ + r * b’ + r*c’) / (a’ + b’ + c’) = r(a’ + b’ + c’) / (a’ + b’ + c’) = r.

Пример решения задачи

Признаки подобия и равенства треугольников можно использовать для решения различных геометрических задач. Ниже приводится один из примеров.

Имеются два треугольника. У одного из них стороны равны 7,6 см, 4,18 см и 6,65 см, а у другого 3,5 см, 2,2 см и 4 см. Необходимо определить, подобны ли эти фигуры.

Поскольку даны значения трех сторон, то можно сразу проверить 3-й критерий подобия. Сложность здесь состоит в том, что нужно понять, между какими сторонами брать отношения. Тут следует воспользоваться простыми логическими рассуждениями: коэффициенты подобия могут быть равными, если делить самую маленькую сторону одного треугольника на аналогичную для другого и так далее. Поэтому имеем: 4,18 / 2,2 = 1,9; 6,65 / 3,5 = 1,9; 7,6 / 4 = 1,9. Проверив отношение всех сторон, можно с уверенностью сказать, что треугольники являются подобными, поскольку выполняется 3-й критерий.

Треугольник — Википедия

Треуго́льник (в евклидовом пространстве) — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Часть плоскости, ограниченная сторонами, называется внутренностью треугольника: нередко треугольник рассматривается вместе со своей внутренностью (например, для определения понятия площади)^[1].

Стороны треугольника образуют в вершинах треугольника три угла, поэтому треугольник можно также определить как многоугольник, у которого имеется ровно три угла^[2]. Треугольник является одной из важнейших геометрических фигур, повсеместно используемых в науке и технике, поэтому исследование его свойств проводилось начиная с глубокой древности.

Понятие треугольника допускает различные обобщения. Можно определить это понятие в неевклидовой геометрии (например, на сфере): на таких поверхностях треугольник определяется как три точки, соединённые геодезическими линиями. В n{\displaystyle n}-мерной геометрии аналогом треугольника является n{\displaystyle n}-й мерный симплекс.

Иногда рассматривают вырожденный треугольник, три вершины которого лежат на одной прямой. Если не оговорено иное, треугольник в данной статье предполагается невырожденным.

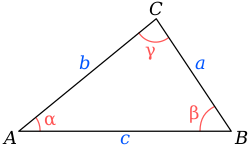Стандартные обозначения

Вершины, стороны, углы[править | править код]

Традиционно вершины треугольника обозначаются заглавными буквами латинского алфавита: A,B,C{\displaystyle A,B,C}, а противолежащие им стороны — теми же строчными буквами (см. рисунок). Треугольник с вершинами A{\displaystyle A}, B{\displaystyle B} и C{\displaystyle C} обозначается как ΔABC{\displaystyle \Delta ABC}. Стороны можно также обозначать буквами ограничивающих их вершин: AB=c{\displaystyle AB=c}, BC=a{\displaystyle BC=a}, CA=b{\displaystyle CA=b}.

Треугольник ΔABC{\displaystyle \Delta ABC} имеет следующие углы:

Величины углов при соответствующих вершинах традиционно обозначаются греческими буквами (α{\displaystyle \alpha }, β{\displaystyle \beta }, γ{\displaystyle \gamma }).

Внешним углом DCA{\displaystyle DCA} плоского треугольника ABC{\displaystyle ABC} при данной вершине C{\displaystyle C} называется угол, смежный внутреннему углу ACB{\displaystyle ACB} треугольника при этой вершине (см. рис.). Если внутренний угол при данной вершине треугольника образован двумя сторонами, выходящими из данной вершины, то внешний угол треугольника образован одной стороной, выходящей из данной вершины и продолжением другой стороны, выходящей из той же вершины. Внешний угол может принимать значения от 0{\displaystyle 0} до 180∘{\displaystyle 180^{\circ }}.

Периметром треугольника называют сумму длин трёх его сторон, а половину этой величины называют полупериметром.

Классификация треугольников[править | править код]

По величине углов[править | править код]

Поскольку в евклидовой геометрии сумма углов треугольника равна 180∘{\displaystyle 180^{\circ }}, то не менее двух углов в треугольнике должны быть острыми (меньшими 90∘{\displaystyle 90^{\circ }}). Выделяют следующие виды треугольников^[2].

• Если все углы треугольника острые, то треугольник называется остроугольным.
• Если один из углов треугольника прямой (равен 90∘{\displaystyle 90^{\circ }}), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
• Если один из углов треугольника тупой (больше 90∘{\displaystyle 90^{\circ }}), то треугольник называется ‘тупоугольным.’Остальные два угла, очевидно, острые (треугольников с двумя тупыми или прямыми углами быть не может).

По числу равных сторон[править | править код]

• Разносторонним называется треугольник, у которого все три стороны не равны.
• Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны.
• Равносторонним или правильным называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают. Равносторонний треугольник является частным случаем равнобедренного треугольника.

Медианы, высоты, биссектрисы[править | править код]

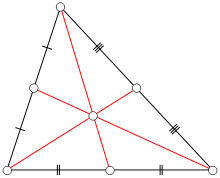Медианы в треугольнике

Медианой треугольника, проведённой из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны (основанием медианы). Все три медианы треугольника пересекаются в одной точке. Эта точка пересечения называется центроидом или центром тяжести треугольника. Последнее название связано с тем, что у треугольника, сделанного из однородного материала, центр тяжести находится в точке пересечения медиан. Центроид делит каждую медиану в отношении 1:2, считая от основания медианы. Треугольник с вершинами в серединах медиан называется срединным треугольником. Основания медиан данного треугольника образуют так называемый дополнительный треугольник. Длину медианы mc,{\displaystyle m_{c},} опущенной на сторону c,{\displaystyle c,} можно найти по формулам:

mc=122(a2+b2)−c2=12a2+b2+2abcos⁡γ;{\displaystyle m_{c}={1 \over 2}{\sqrt {2(a^{2}+b^{2})-c^{2}}}={1 \over 2}{\sqrt {a^{2}+b^{2}+2ab\cos \gamma }};}      для других медиан аналогично.

• Высота в треугольниках различного типа

• 

  Высоты пересекаются в ортоцентре

Высотой треугольника, проведённой из данной вершины, называется перпендикуляр, опущенный из этой вершины на противоположную сторону или её продолжение. Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника. Треугольник с вершинами в основаниях высот называется ортотреугольником.

Длину высоты hc{\displaystyle h_{c}}, опущенной на сторону c{\displaystyle c}, можно найти по формулам:

hc=bsin⁡α=asin⁡β{\displaystyle h_{c}=b\sin \alpha =a\sin \beta };      для других высот аналогично.

Длины высот, опущенных на стороны. можно также найти по формулам:^[3]:p.64

hc=ab2R,ha=bc2R,hb=ca2R{\displaystyle h_{c}={\frac {ab}{2R}},\quad h_{a}={\frac {bc}{2R}},\quad h_{b}={\frac {ca}{2R}}}.

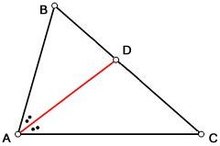Биссектриса AD{\displaystyle AD} делит пополам угол A{\displaystyle A}

Биссектрисой (биссéктором) треугольника, проведённой из данной вершины, называют отрезок, соединяющий эту вершину с точкой на противоположной стороне и делящий угол при данной вершине пополам. Биссектрисы треугольника пересекаются в одной точке, и эта точка совпадает с центром вписанной окружности (инцентром).

Если треугольник разносторонний (не равнобедренный), то биссектриса, проведённая из любой его вершины, лежит между медианой и высотой, проведёнными из той же вершины. Ещё одно важное свойство биссектрисы: она делит противоположную сторону на части, пропорциональные прилегающим к ней сторонам^[4].

Длину биссектрисы lc{\displaystyle l_{c}}, опущенной на сторону c{\displaystyle c}, можно найти по одной из формул:

lc=ab(a+b+c)(a+b−c)a+b=2abp(p−c)a+b{\displaystyle l_{c}={\frac {\sqrt {ab(a+b+c)(a+b-c)}}{a+b}}={\frac {2{\sqrt {abp(p-c)}}}{a+b}}}, где p{\displaystyle p} — полупериметр.

lc=2abcos⁡γ2a+b{\displaystyle l_{c}={\frac {2ab\cos {\frac {\gamma }{2}}}{a+b}}}.

lc=hccos⁡α−β2{\displaystyle l_{c}={\frac {h_{c}}{\cos {\frac {\alpha -\beta }{2}}}}};     здесь hc{\displaystyle h_{c}} — высота.

Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают. Верно и обратное: если биссектриса, медиана и высота, проведённые из одной вершины, совпадают, то треугольник равнобедренный.

Описанная и вписанная окружности[править | править код]

Треугольник АВС и его окружности: вписанная (синяя), описанная (красная) и три вневписанные (зелёные)

Описанная окружность (см. рис. справа) — окружность, проходящая через все три вершины треугольника. Описанная окружность всегда единственна, её центр совпадает с точкой пересечения перпендикуляров к сторонам треугольника, проведённых через середины сторон. В тупоугольном треугольнике этот центр лежит вне треугольника^[4].

Вписанная окружность (см. рис. справа) — окружность, касающаяся всех трёх сторон треугольника. Она единственна. Центр вписанной окружности называется инцентром, он совпадает с точкой пересечения биссектрис треугольника.

Следующие формулы позволяют вычислить радиусы описанной R{\displaystyle R} и вписанной r{\displaystyle r} окружностей.

r=Sp,{\displaystyle r={S \over p},} где S{\displaystyle S} — площадь треугольника, p{\displaystyle p} — его полупериметр.

r=(−a+b+c)(a−b+c)(a+b−c)4(a+b+c){\displaystyle r={\sqrt {\frac {(-a+b+c)(a-b+c)(a+b-c)}{4(a+b+c)}}}}

R=a2sin⁡α=b2sin⁡β=c2sin⁡γ{\displaystyle R={\frac {a}{2\sin \alpha }}={\frac {b}{2\sin \beta }}={\frac {c}{2\sin \gamma }}}

R=abc4S=abc4p(p−a)(p−b)(p−c){\displaystyle R={\frac {abc}{4S}}={\frac {abc}{4{\sqrt {p(p-a)(p-b)(p-c)}}}}},

1r=1ha+1hb+1hc{\displaystyle {\frac {1}{r}}={\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}}

где ha{\displaystyle h_{a}} и т. д. — высоты, проведённые к соответствующим сторонам;^[3]:p.79

Ещё два полезных соотношения:

rR=4S2pabc=cos⁡α+cos⁡β+cos⁡γ−1;{\displaystyle {\frac {r}{R}}={\frac {4S^{2}}{pabc}}=\cos \alpha +\cos \beta +\cos \gamma -1;}^[5]

2Rr=abca+b+c{\displaystyle 2Rr={\frac {abc}{a+b+c}}}.

Существует также формула Карно^[6]:

R+r=ka+kb+kc=12(dA+dB+dC){\displaystyle R+r=k_{a}+k_{b}+k_{c}={\frac {1}{2}}(d_{A}+d_{B}+d_{C})},

где ka{\displaystyle k_{a}}, kb{\displaystyle k_{b}}, kc{\displaystyle k_{c}} — расстояния от центра описанной окружности соответственно до сторон a{\displaystyle a}, b{\displaystyle b}, c{\displaystyle c} треугольника, dA{\displaystyle d_{A}}, dB{\displaystyle d_{B}}, dC{\displaystyle d_{C}} — расстояния от ортоцентра соответственно до вершин A{\displaystyle A}, B{\displaystyle B}, C{\displaystyle C} треугольника.

Расстояние от центра описанной окружности например до стороны a{\displaystyle a} треугольника равно:

ka=a/(2tg⁡A){\displaystyle k_{a}=a/(2\operatorname {tg} A)};

расстояние от ортоцентра например до вершины A{\displaystyle A} треугольника равно:

dA=a/tg⁡A{\displaystyle d_{A}=a/\operatorname {tg} A}.

Равенство по двум сторонам и углу между ними Равенство по стороне и двум прилежащим углам