Пропорциональность в композиции.Правило золотого сечения
Композиция в интерьере или в целом архитектурном объекте состоит из частей, взаимосвязанных друг с другом и с целым. При этом,части как правило, имеют различную величину. Эта взаимосвязь выражается через пропорциональные отношения частей между собой и их отношение к целому.
Пропорции — один из важнейших методов достижения выразительности и гармонии.Пропорции в архитектуре часто привязываются к параметрам человека. Все сооружения служат человеку и должны быть ему соразмерны. В древние времена части человеческого тела стали естественной основой всех единиц измерения. И сейчас все размеры мы сравниваем с человеческим ростом, это важно и с точки зрения эргономики и психологии. Один из самых известных способов пропорционирования это правило Золотого сечения
Золотое сечение- это гармоническая пропорция, которая удовлетворяет следующему соотношению:
(А:Б)=А:(А+Б) и (А+Б)=С
Деления отрезка на части по принципу Золотого сечения
Малая часть отрезка А, так относится к средней части Б, как Б относится к сумме А+Б
Если приравнять С к 1, то получим такое соотношение
(0,382:0,618)=0,618:(0,382+0,618) и (0,382+0,618)=1
Отношение между числами 0,382 и 0,618 соответствует Золотому сечению
Только это отношение 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.Чтобы создавать наиболее гармоничные отношения между частями композиции желательно приводить их пропорциональные размеры к золотому сечению
. Для этого необходимо использовать коэффициенты 0,618 и 1,618.Например, в декоративных целях необходимо разделить стену высотой 2,7 метра по правилу золотого сечения на 2 части. Для этого 2,7 умножим на 0,618 получим 1,6686 теперь из общей высоты 2,7 вычтем 1,6686 получим 1,0314. Таким образом стену высотой 2,7 метра делим на части 1,6686 м. и 1,0314 м.
Ряд Фибоначчи
С историей золотого сечения связано и имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:, который удовлетворяет Золотому сечению
0 — 0 — 1 — 2 — 3 — 5 — 8 — 13 — 21 — 34 и т.д.
Сумма двух предшествующих чисел равна последующему в ряду числу. Отношение соседних чисел в ряду приближено к Золотому сечению.
Этот ряд чисел называют рядом Фибоначчи. Воспользовавшись рядом Фибоначчи мы можем получить пропорцию для деления.предмета на гармоничные части. Например, для отрезка длиной 5 идеальной пропорцией будет деление его на части равные 2 и 3, для отрезка 8 это 3 и 5 и т.д.
Золотой прямоугольник
Прямоугольник, стороны которого находятся в золотом отношении, называют золотым прямоугольником. Из определения золотых прямоугольников следует, что все они подобны. Если от золотого прямоугольника отрезать квадрат со стороной, равной меньшей стороне прямоугольника, то снова получим золотой прямоугольник меньших размеров
Примеры золотого сечения в архитектуре
Парфенон в Афинах (V в. до н.э.) имеет 8 колонн по коротким сторонам и 17 по длинным..Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада.
Известный русский архитектор М.Ф. Казаков тоже широко использовал в своем творчестве золотое сечение. Его можно обнаружить, например, в архитектуре здания бывшего Сената в Кремле.
По проекту М.Ф.Казакова в Москве была построена Голицынская больница, которая в настоящее время называется Первой клинической больницей им. Н.И.Пирогова (Ленинский просп., д. 8).Как использовать пропорциональность в интерьере
Возникает вопрос- а что дает на практике знание закона золотого сечения и гармоничной пропорции. Вот некоторые приемы, использующие эти знания.
- Например, для отделки стен мы хотим использовать деревянные панели. При этом будем обшивать стену не на всю высоту, а частично.Чтобы панели смотрелись гармонично, можно использовать два варианта обшивки стены. Вначале замеряйте высоту стены и умножьте её значение на 0,618 ( «золотое число»). Запишите полученное значение. Теперь из общей высоты стены вычтите его.. В результате мы имеем два значения высот для обшивки панелями стены. Первое = высота стены умноженная на 0,618, а второе равно высота стены минус высота, умноженная на 0,618.
- Этот же прием можно использовать и при оклеивании стен обоями. Разделив стену по высоте на бордюр,фриз и основное полотно обоев.
- Пропорциональность можно использовать при зонировании пространства. Для этого можно разбить стену вертикалью на части по правилу золотого сечения и отделывать полученные сегменты стены разными материалами или разным цветом.
.
- Пропорциональность можно использовать при выборе мебели в интерьер. например высота шкафа и стоящего рядом рядом дивана будут смотреться гармонично если соотношение их размеров будут приближены к «магическому числу» 0,618. То есть высота дивана должна быть приблизительно равна высоте шкафа умноженной на 0,618
- По пропорции можно подбирать размер декоративных элементов на плоскости. Например панно или гобелен на стене или ковер на полу.
- Ну и так далее, проявляйте творчество и все получится!
Кроме этого приема композиции в интерьере, вы можете ознакомиться с видеосюжетом Правила Дизайна Баланс и Порядок в котором автор рассказывает о многих композиционных приемах, применяемых в современном дизайне интерьера
ПРОПОРЦИИ И ПРОПОРЦИОНИРОВАНИЕ
⇐ ПредыдущаяСтр 14 из 17Следующая ⇒В математической пропорции А:В=С:Д=…=К каждый из членов тесно связан определенными соотношениями с остальными. Отсюда и возникает строгая согласованность входящих в пропорцию отдельных членов, возникает их взаимосвязь и их взаимообусловленность. И это обстоятельство широко используется не только и архитектуре и дизайне, но и во всех видах художественной деятельности, в которых так или иначе можно вести речь о соотношении каких-то элементов, соотношении каких-то линейных или объемных величин.
Как образуется самая элементарная пропорция? Из математики известно, что если взять две подобные фигуры, то соотношение аналогичных элементов в этих фигурах дает пропорциональный ряд.
Пропорционирование
– это использование с целью получения искомой целостности предмета закономерных соотношений различных величин или частей предмета между собойКогда говорят о пропорциях применительно к художественной деятельности, то имеют в виду прежде всего сопоставление вертикальных и горизонтальных элементов в пределах определенной плоскости. Сложный предмет обычно заключают в какую-то простую фигуру-схему, скажем, параллелепипед, основные линейные величины которого и должны соотноситься, создавать какой-то определенный пропорциональный ряд. В этом и заключается их соразмерность.
Сочетание различных геометрически подобных элементов дает различные виды пропорциональных отношений (рис. 5.21). Это прежде всего арифметические пропорции типа Н2 – Н1=Н3 – Н2 и т.д. и геометрические пропорции, или пропорции, которые иногда называются непрерывными, когда один из членов одного ряда обязательно повторяется в другом: Н1:Н2=Н2:Н3 и т. д.. Н2 является здесь средней пропорциональной величиной.
Существуют, таким образом, различные виды пропорциональных отношений, начиная от самых простых арифметических пропорций и кончая довольно сложными геометрическими пропорциями. Ихочень много, но вес они являются результатом подобия различных типов геометрических фигур, т. е. сочетания каких-то трех линейных величин этих фигур.
Немного особняком стоит геометрическая пропорция, которая получила название «золотого сечения». Золотое число Ф=1,6180339… которое называется еще Золотым сечением или Золотой пропорцией, возникающей как результат решения геометрической задачи о делении отрезка в крайнем и среднем отношении, то есть делении отрезка на две неравные части таким образом, чтобы отношение большей части к меньшей равнялось бы отношению всего отрезка к большей части (математический анализ позволяет вычислить иррациональную величину Ф с помощью выражения (1+√5)/2).
В эпоху итальянского Возрождения золотая пропорция возводится в ранг главного эстетического принципа. Леонардо да Винчи именует ее «Setio autea». Лука Пачели в 1509 году пишет сочинение о золотой пропорции, названной им «божественной». По словам Иоанна Кеплера: «Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора, а другое – деление отрезка в крайнем и среднем отношении… Первое можно сравнить с мерой золота, а второе же больше напоминает драгоценный камень». Немецкий ученый Цейзит в 1580 году в своих «Эстетических исследованиях» обнаруживает проявление золотой пропорции в соотношении частей человеческого тела, животных, в эллинских храмах, ботанике, музыке (рис. 5.22).
Греки в своих скульптурах, отражающих совершенство творения, придерживались божественной пропорции. Места сочленения отдельных элементов скелета человека и животных являются точками деления целого в пропорции золотого сечения. Этот факт имеет и чисто механическое объяснение: оптимальным образом работает шарнирная пара, элементы которой находятся в пропорции золотого сечения. Пропорцией Ф определяется принцип строения живого организма, она является той универсальной мерой, позволяющей по установленным размерам одной известной части восстанавливать размеры следующей части и т.д.
 |  |
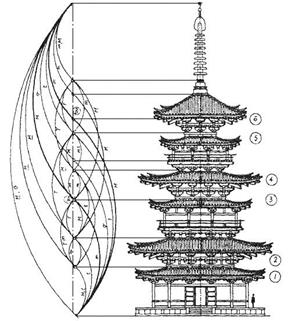Рис. 5.22 Проявление золотой пропорции в строении храма и строении человеческого тела.
С помощью спирали золотого сечения представляется возможно решение таких задач, как квадратура круга и построение квадрата с периметром, равным длине окружности. Исследованию Золотого сечения в средневековой науке посвящено сочинение «Liber abacci», знаменитого итальянского математика Леонардо из Пизы, который известен более под именем Фибоначчи (Fibonacci – сокращенное filius Bonacci, сын Боначчи). Эта книга, написанная в 1202 г., дошла до нас во втором своем варианте, который относится к 1228 г. Сообщаемый в «Liber abacci» материал поясняется на большом числе задач, в том числе и знаменитая задача о кроликах: «пара кроликов через месяц производит на свет другую пару, а потомство они дают со второго месяца после своего рождения. Итак, через месяц будет две пары, через два месяца – три пары, а через четыре месяца – пять, так как к паре, рожденной первой парой добавятся первые дети от второй пары…». Продолжая процесс, мы и получим количество пар кроликов по месяцам: 1, 1, 2, 3, 5, 8, 13, 21, 35, 56… – эти числа и представляют ряд, названный по имени автора задачи (ряд Фибоначчи[12]). Цифры этого ряда образуются как сумма двух предыдущих чисел. Их отношения 3/5,5/8,8/13 и т. д. близки к ряду золотого сечения. В образовании пропорции могут участвовать различные математические отношения, использующие ряды как целых, так и иррациональных чисел. Используются иррациональные отношения, и частности, образованные на числах ряда √5 (пентагональная система), √3 и √2.
Если говорить о натуральном ряде чисел, то можно представить себе такое рациональное их сочетание в единой модульной системе (расчленение тех же прямоугольников), которое строится на подобии их элементов и соотношения которых являются кратными (1:2, 1:3 и т.д.), т.е. основаны на натуральных числах. Иррациональные числа √2или 1,414; √3 или 1,732; √5 или 2, 236, обычноникогда в чистом виде не используются.
Используются или отношения, образованные иррациональными числами, или сочетание целых чисел с иррациональными.
Графическое построение геометрических фигур, в которых имеет место сочетание целых чисел с иррациональными, производится довольно просто. Берется основание квадрата, потом его диагональ – соотношение диагонали квадрата с целым числом дает √2; потом диагональ этой фигуры, еще раз положенная в основание, – сочетание опять с единицей квадрата дает соотношение √3; следующая диагональ этого прямоугольника, опять превращенная в основание, в соотношении дает √5 (рис.3.33).Таким образом, полученные прямоугольники есть соотношение единицы √2, √3 , √4 и √5. Это сочетание, в свою очередь, образует отношение золотого сечения.
Дизайнеру необходимо не только знать принципы построения пропорций, но и уметь правильно использовать их для гармонизации формы предмета. Использование пропорциональных соотношений является очень сильным средством для получения целостной формы, так как создает твердую соразмерность отдельных линейных и объемных частей изделия. Но пропорциональность служит и решению главных, функциональных задач. Простой пример – стол. Если это стол. за которым сидят со всех сторон, то, наверное, удобнее всего квадрат. Если это письменный стол, за которым сидит один человек, то квадратная форма вряд ли целесообразна, то есть пропорции этого стола связаны с его функцией.
Можно выделить два приема пропорционирования промышленных изделий: соподчинение и расчленение (рис.5.23).
Соподчинение используется тогда, когда к какому-то элементу пристраивается другой, который находится в смысле соразмерности в подчинении к этому основному элементу. Расчленение используется тогда, когда имеется какой-то объект (самый простой случай – прямоугольник) и эту основную форму или плоскость надо разбить на более мелкие элементы.
В дизайне основным является прием расчленения, потому что дизайнер имеет дело обычно сначала с общими габаритами вещи и уже внутри них ищет соотношение отдельных элементов между собой.
Однако соблюдение пропорций еще не гарантирует качества композиции. Важно найти гармоническое согласование, связи пропорционирования с другими средствами композиции.
Пропорциональные отношения могут оказывать непосредственное влияние на композицию, так как соподчинение элементов формы во многом зависит от размерных отношений. Так, пропорции выражают связи формы и конструкции, т.е. обусловливают тектонику и характер объемно-пространственной структуры. С пропорциями связаны такие важнейшие качества, как статичность и динамичность формы, ее зрительная устойчивость. На пропорциональных отношениях могут строиться контраст и нюанс соотносимых величин, ритм и метрический повтор.
Таким образом, нет и не может быть какой-то пропорции, которая всегда хороша. Не всякое математическое соотношение, не всякая пропорция имеет художественную ценность и не каждая пропорция, даже имеющая художественное значение для одного случая, приемлема для другого.
Правильно найденные пропорции способствуют не только достижению гармоничной формы, но и улучшению функциональных и конструктивных показателей изделия. Поэтому при проектировании технических объектов поиск системы пропорций необходимо вести уже на ранних этапах работы.
МАСШТАБ И МАСШТАБНОСТЬ
Под масштабностьюпредметного мира понимается соразмерность или относительное соответствие формы предмета размерам человека, соответствие размеров предмета действительно необходимым.
Важным условием достижения гармоничности композиции является нахождение правильной масштабности.
Масштабом характеризуется любая вещь, но не каждая может быть масштабной. Дизайнеру масштаб нужен для того, чтобы сделать вещь соразмерной человеку и окружающей среде.
Ощущения масштаба связаны с представлениями о целесообразности и удобстве пользования изделием. Выявление масштабности обусловливается соответствием формы предмета его назначению, конструкции, материалам, а также правильным использованием других средств гармонизации, в первую очередь пропорционирования.
Масштаб любого сооружения или технического объекта не определяется его величиной. Маленькое здание или предмет могут иметь крупный масштаб, а большие – наоборот мелкий. Поэтому при проектировании здания рядом с фасадом архитектор изображает фигуру человека в масштабе чертежа. Она служит для соотнесения с ней всех элементов здания. К сожалению, технические объекты далеко не всегда соотносятся с размерами человека. Правда, масштаб механизмов задается техническими условиями, кинематикой, конструкцией. Однако для технических объектов имеется немало средств достижения масштабности.
Масштабность изделию придают элементы, которые позволяют соотнести его с размерами человека. Прямое влияние на масштабность оказывают все те размеры, которые связаны с человеком, определяют удобство пользования. В архитектуре это размеры дверных проемов, лестничных ступеней и т. п. В вещах и предметах это элементы, также связанные определенным образом с размерами человеческого тела: высота стола, стула, размер сиденья. величина различных ручек, рукояток, переключателей и т. п.
 |  |
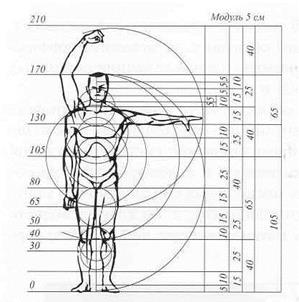| Рис. 5.24 Модулор Ле Корбюзье | Рис. 5.25 Антропометрическая система АСМОС В.А.Пахомова |
Технические и бытовые объекты часто наделяются многократно повторяющимися элементами, что обусловливает необходимость применять в практике проектирования систему модульной координации на основе соизмеримого с человеком пропорционального ряда. С целью увязки масштабных соотношений с модулем и пропорциональными отношениями, а также с размерами человека Ле Корбюзье создал математическую шкалу «Модулор» применительно к росту человека 1829 мм (рис.5.24), который для нашей страны является завышенным. В.А.Пахомовым (Ленинградский филиал ВНИИТЭ) разработана антропометрическая модульная система АСМОС (рис.5.25),основанная на модуле 5 см и выраженная рядом Фибоначчи. В этой системе числовые ряды составлены для роста человека 1700 мм.
Использование модульной системы позволяет унифицировать и увязывать размеры оборудования с размерами человека и помещений.
КОНТРАСТ, НЮАНС И ТОЖДЕСТВО
Иногда среди средств, используемых для достижения соразмерности, называют еще два средства, а именно контрастные и нюансные соотношения.
Контраст как средство композиции имеет сильные и слабые стороны. Сильные заключаются в том, что формы, построенные на контрастах, всегда выразительны и хорошо запоминаются. При слишком резком контрасте композиционная связь элементов может разрушиться, а форма зрительно распасться на части. Таким образом, применение контраста еще не гарантирует гармонии формы. Необходимым условием достижения гармонии является соблюдение меры контраста, а также создание плавных переходов между контрастирующими элементами.
В композиции различных изделий роль контраста неодинакова. В тех случаях, когда контраст обусловлен объективно, он может стать главным средством организации формы. Если применение его необязательно, он привлекается как вспомогательное средство.
Использование контраста в производственной среде, как правило, обусловливается необходимостью создания оптимальных условий для работы. Чрезмерная сила контрастов, так же как и их отсутствие, вызывает преждевременное утомление работающего человека. В связи с этим степень контраста должна проверяться не только с позиций художественного подхода, но и эргономики.
При работе над композицией важное значение имеет выбор оптимальных цветовых отношений. Предельные цветовые Контрасты могут привести к нарушению целостности формы. Это относится не только к организации производственной среды, но и к проектированию технических изделий и изделий культурно-бытового назначения.
 |  |
Рис. 5.26 Подобие. Контраст. Нюанс. Л. Егорова[13]
Под контрастомпонимается противопоставление, резкое различие между однородными свойствами. Так, низкое может противопоставляться высокому, Приемы использования контраста в технике можно разделить на две большие группы: 1) обусловленные объективно, т.е. тектоникой или объёмно-пространственной структурой; эффект использования таких контрастов достигается лишь при тесном контакте инженера и дизайнера еще на ранних этапах проектирования; 2) в значительной мере зависящие от дизайнера, например контрасты в отделочных материалах, обработкеповерхностей, окраске. декоративных элементах и т.д. В композиции одного изделия могут одновременно совмещаться оба приема использования контрастов.
В композиции контраст неразрывно связан с нюансом (рис. 5.26). Если контраст не дополняется тонкими нюансными переходами, он может не только огрубить форму, но и разрушить ее целостность. легкое – тяжелому, светлое — темному, сложное – простому и т.д.
Нюанс – это последовательный переход. например, от тяжелого к легкому, от темного к светлому, от большого к малому, от простого к сложному и т.д. Если нюанс усиливать, он может перейти в контраст. Если же его сильно ослабить, он окажется зрительно неразличимым, т.е. станет тождеством. Следовательно, нюансировка – самое тонкое из всех средств композиции, а ее использование представляет сложную задачу и требует от дизайнера высокой квалификации. Если контраст часто обусловливается функцией или конструкцией изделия, то нюанс не определяет ни то, ни другое. Он связан с художественным осмыслением формы, материала, цвета и в значительной степени зависит от индивидуальности дизайнера.
Нюансировка играет особенно важную роль при конструировании изделий бытового назначения. Необходима она при работе над композицией малых форм, а также при проектировании крупных технических изделий. Нюансировка формы во многом связана с технологией производства изделия и свойствами применяемых материалов. Дизайнер должен тонко чувствовать особенности материала и уметь правильно их использовать. Нюансозначает отклонение, небольшие, слабо выраженные различия свойств.
Нюанс проявляется в пропорциях, ритме, цвете, пластике, декоре, фактуре поверхности и т.д. Формы, построенные на нюансах, всегда спокойны и раскрываются не сразу (в отличие от форм, построенных на контрастах). Поэтому в работе над формой одного изделия могут использоваться многие нюансы. На них порой строится даже вся композиция изделия. Особенно велика роль нюанса при разработке интерьеров в которых всегда необходимо связывать отдельные элементы.
Тождество используется в тех случаях, когда имеют место повторы одинаковых элементов, поэтому оно связано с такими средствами композиции, которые основаны на повторах.
ТЕНИ И ПЛАСТИКА
Пластика формы характеризуетособенности объёмно-пространственной структуры, определяет ее рельефность, насыщенность тенями и светом.
Пластичная форма имеет мягкие переходы образующих линий, а при недостатке этих свойств она становится сухой и аскетичной.
Свет и тени не являются компонентами формы изделия, так как зависят от освещения и места расположения источника света. В то же время характер распределения света и теней, их глубина определяются особенностями объемно-пространственной структуры, ее пластического решения. В силу этого свет и тени в известной степени можно считать самостоятельным средством организации формы изделий. Светотеневая структура может определять целостность композиции, выявлять строй формы и другие ее качества.
Если форма элементарно проста, возможности использовать свет и тени незначительны. Поэтому дизайнер иногда специально усложняет форму, чтобы сделать ее более пластичной, полнее использовать взаимодействие теней со светом и такими приемами обеспечить интересную композицию.
Пластика и тени тесно связаны, при этом светотеневая структура зависит от пластического решения формы, т.е. от того, что материально определяет поверхность. Поэтому тени как средство композиции рассматриваются не независимо, а вместе с пластикой.
Роль теней и света в композиции не всегда одинакова. Например, когда простая форма организована крупными плоскостями, приобретают значение легкие тени, которые членят объем. Они контрастируют с большими освещенными поверхностями и придают объему графическую остроту и выразительность. Если же форма сложная и часть элементов ее находится в зоне глубоких теней, основная роль в композиции принадлежит правильно организованному свету.
Пластика и светотеневая структура имеют особенно важное значение при достижении целостности малых и миниатюрных форм. В данном случае эти средства композиции наряду с нюансом становятся важнее всех остальных. При этом они тесно между собой переплетаются.
ЦВЕТ
Важные характеристики поверхности материальной формы предмета связаны также с ее цветом, фактурой (внешней структурой поверхности) и текстурой (своеобразным рисунком, отражающим структуру покрывающего поверхность материала).
Цвет — это одно из самых субъективных средств композиции. Поэтому цветовое решение предмета зависит лишь от интуиции и вкуса дизайнера. Но этого недостаточно, если проектируются сложные машины, насыщенный интерьер или когда необходимо учитывать психофизиологическое восприятие цвета. Поэтому выбор цветового решения зависит от назначения изделий и условий их эксплуатации. Так, цвет станков, машин, приборов во многом определяется эргономическими требованиями. При цветовом решении изделий культурно-бытового назначения возрастает роль создания гармоничного ансамбля всего жилого интерьера.
Особенности восприятия цвета и применения его в промышленном дизайне показаны в гл.4.3.
Цвет всегда должен быть увязан с объемно-пространственной структурой предмета, со всеми средствами соразмерности, а через них, естественно, и с его функцией, обеспечивающейся тем или иным техническим (конструктивным) решением. С помощью цвета можно акцентировать и, наоборот, ослабить влияние на композицию тех или иных элементов структуры, тех или иных членений и деталей, можно скорректировать пропорции или тектоническое решение, увеличить образность веши, изменив общий характер восприятия формы.
Подводя общий итог, можно сказать, что правильное построение объёмно-пространственной структуры и нахождение тектонических характеристик сооружения или предмета позволяют создать целостную вещь, отдельные элементы которой находятся в известном единстве с содержанием, и это создает ощущение или уравновешенности, устойчивости и главенствования, или, наоборот, динамичности и подчиненности, в соответствии с се назначением и реальным использованием. В отличие от этого, соразмерность вещи и ее пластическая отработка позволяют идти дальше по пути придания ей наибольшей выразительности, характеризующей принадлежность этой вещи к определенной культуре, к определенной предметной среде, к конкретному потребителю с его конкретными требованиями к свойствам вещи, ее внешнему виду и возможностям ее использования.
§5 Пропорции. Основы рисунка для учащихся 5-8 классов
Мы признаем определенные пропорциональные отношения в построении фигуры человека, его окружения, архитектуры, как нечто должное. Эмоциональное начало художественного творчества проверяется точной наукой. Выдающиеся мастера былых эпох постоянно стремились проверить алгеброй гармонию, впрочем, математика античности, средневековья и Возрождения была лишена сухости и абстрактности.
Когда мы знакомимся с историей искусства, любуемся совершенными произведениями, например античной статуей или храмом, картинами Леонардо да Винчи, Рафаэля, Энгра, то нас поражает удивительная гармония, присущая им, которая во многом определяется таким эстетическим качеством, как пропорциональность целого и деталей. Слово «пропорция» в переводе с латыни обозначает «соотношение», «соразмерность». Сравнивая предметы, окружающие нас, по величине, высоте, ширине, объему мы можем сказать, что одни из них длинные, а другие короткие, высокие и низкие, широкие и узкие, большие и маленькие и т. д. Устанавливая соотношение между предметами и между частями формы отдельного предмета, мы выясняем их пропорциональные характеристики.
Пропорциями называются размерные соотношения элементов или частей формы между собой, а также между различными объектами.
75. Измерение высоты (а) и ширины (б)
Проверять пропорции можно с помощью обычного карандаша или кисточки, при этом держать их следует на вытянутой руке.
76. Определение пропорций
Для удобства определения пропорций методом визирования можно прищурить один глаз. С помощью длины карандаша уточняют также степень наклона всей формы.
Пропорция – это гармонизация формы художественного произведения, пропорциональность – ее эстетическое качество. Соразмерность частей образует красоту формы. В основе определения пропорций лежит метод сравнения. Все эти свойства лежат и в основе грамотного рисунка. В художественной практике существует известный метод определения пропорций, называемый визированием.
Однако никакие механические способы определения пропорций не могут заменить развитого глазомера. Именно эту способность необходимо развивать в себе тренировкой.
Рисуя, нужно помнить, что мы изображаем предметы несколько меньшими их натуральной величины, поэтому необходимо придерживаться единого масштаба для определения пропорций всех объектов изображения, составляющих композицию. Таким образом, выдержать пропорции в рисунке – значит добиться соотношения величин всех частей предмета к целому в пределах выбранного формата листа.
Поиск пропорций в изображении фигуры человека является сложной задачей. Обратимся к истории, посмотрев, как решали ее художники разных эпох и разных культур.
77. Композиция пропорций человека в Древнем Египте
Единицей измерения фигуры у древнеегипетских художников служила длина среднего пальца руки, вытянутой вдоль бедра.
В Древнем Египте для изображения человеческой фигуры был разработан специальный канон – то есть такая система пропорций человеческой фигуры, которая делила изображение на части и позволяла по части определить целое и по одной части тела определить другую. Известно, что египтяне положили в основу деления фигуры 21 1/4 части. В это число входили 19 равных частей разделения самой фигуры, а 2 1/4 части приходились на изображение традиционного головного убора (ил. 77), Египтяне пользовались и специальными сетками-таблицами, которые наносили на поверхность каменной плиты или стены для создания рельефа или росписи (ил. 34а).
На сохранившихся и дошедших до нас памятниках можно видеть, что горизонтальные и вертикальные линии делят рисунок в определенных местах, что соответствует членению фигур на части. Были установлены также определенные размеры для изображения сидящих фигур и изображения разных богов в соответствии с их иерархическим старшинством (одни должны быть выше, другие немного ниже). Детей изображали как взрослых, но значительно меньшими по размеру. Художнику необходимо было знать установленные каноном нормы и научиться вписывать в них изображения, пользуясь сеткой-таблицей. Единая система обучения и строгое соблюдение выработанных норм позволяли выполнять части одного произведения разными мастерами. Когда такие части составляли в единую композицию, то они точно сходились и не было нарушения пропорций.
Вся история учения о пропорциях связана с поисками законов гармонии и красоты. В Древней Греции систему идеальных пропорций человеческой фигуры создал скульптор Поликлет в V веке до н. э. Его теоретическое сочинение на эту тему называлось «Канон», а выражением в скульптуре этой системы явилась его статуя «Дорифор», что означает копьеносец. Мастер изобразил атлета-юношу, победителя в соревнованиях по метанию копья, в момент, когда после одержанной победы он совершает круг почета по стадиону и его приветствуют восторженные зрители.
Открытие пропорций, полагают, принадлежит к заслугам древневосточной математики, античная же традиция связывает его с именем выдающегося философа и математика Пифагора, жившего в VI веке до н. э. Универсальный принцип гармонии и красоты в пропорциях получил название «золотое сечение», которое олицетворяло равновесие знания, чувств и силы. Золотое сечение возникает при делении отрезка на две неравные части таким образом, при котором весь отрезок относится к большей его части, как большая к меньшей (0,618).
78. ПОЛИКЛЕТ. Дорифор
Поликлет создал новые членения пропорций человеческой фигуры, однако точных сведений о том, что именно было выбрано за единицу меры – величина ладони, ступни или высота головы,- не сохранилось.
79. С. БОТТИЧЕЛЛИ. Канон пропорций
80. МИКЕЛАНДЖЕЛО. Пропорции фигуры человека
Знакомство с золотым сечением сыграло немалую роль в работе античных архитекторов, скульпторов и живописцев. Обучающимся рисунку будет интересно узнать правило, наглядно прослеживающееся в древнегреческих статуях: при делении туловища человека в соответствии с золотым сечением легко найти уровень пупа и локтя, при повторном делении двух отрезков в противоположных направлениях определяется высота колена и нижний уровень шеи.
Примерами использования золотого сечения может быть античная голова Афродиты и любое из произведений художника Рафаэля. В поисках гармонии художники интуитивно всегда следовали этому принципу и в той или иной мере приближались к идеальным соотношениям, но теоретически принцип золотого сечения был сформулирован в эпоху Возрождения. Леонардо да Винчи, изучавший и глубоко анализировавший опыт древних, разрабатывая правила изображения человеческой фигуры, пытался на основе литературных сведений восстановить так называемый «квадрат древних». Он выполнил рисунок, в котором показана пропорциональная закономерность в соотношении частей тела человека.
Над выработкой канонов пропорций трудились такие знаменитые мастера эпохи Возрождения, как С. Боттичелли и Микеланджело. Проблема поиска системы идеальных пропорций остается актуальной и для художников и архитекторов XX века. Французский зодчий Jle Корбюзье в 1947 году разработал «Модулор» – систему деления человеческой фигуры на согласованные в золотом сечении отрезки от ступни до талии, от талии до затылка и от затылка до верха пальцев поднятой руки. На этой основе была создана школа модулей для архитектурного проектирования и дизайна.
Античное искусство установило идеальные пропорции и для головы человека, согласно которым она по вертикали от темени до конца подбородка делится на две равные части линией глазных впадин (ил. 83). Каждую из этих половин можно, в свою очередь, разделить на две равные части: верхнюю – линией волос, а нижнюю – основанием носа. Получается четыре равные части. Расстояние между глазами принимается равным ширине крыльев носа.
81. ЛЕОНАРДО ДА ВИНЧИ. «Квадрат древних»
82. ЛЕ КОРБЮЗЬЕ. Модулор
Расстояние от бровей до основания носа определяет величину ушей. В действительности редко встречаются у людей такие идеальные пропорции, но знать их необходимо, чтобы видеть отклонения от нормы и лучше понимать индивидуальные пропорции живой натуры.
Пока общая форма головы не решена, не найдены ее пропорции, нельзя переходить к отделке деталей. Портретное сходство зависит во многом от правильно выдержанных общих пропорций.
Следует помнить, что при определении пропорций лучше сравнивать отношения нескольких деталей на рисунке с соотношениями таких же деталей в натуре.
Переходя к эмоциональной характеристике портретируемого, полезно изучить схемы лица при различных психологических состояниях на ил. 84.
83. Пропорции головы
84. Схематическая таблица сокращения мускулов лица при различных психологических состояниях (по М. Дювалю): 1 – спокойствие, 2 – печаль, 3 – радость, 4 – боль, 5 – смех, 6 – плач, 7 – презрение, 8 – внимание, 9 – размышление
Посмотрите, как с помощью самых простых средств, всего лишь опуская или приподнимая уголки губ, брови или веки, можно передать печаль, радость, боль, смех, презрение, внимание и т. д. (ил. 84-85).
85. Лица в различном эмоциональном состоянии
Поделитесь на страничкеСледующая глава >
Какие бывают пропорции в одежде
Гармония в образе зависит не столько от цвета или фасона, сколько от правильно подобранных пропорций в одежде для каждого конкретного человека.Пропорции — это соотношение отдельных предметов гардероба между собой.
Чтобы разделить образ на составляющие, необходим какой-то разграничитель. Чаще всего им становятся хорошо различимые горизонтальные линии — нижний край изделия, пояс или ремень, конструктивные швы, элементы декора.
Каждый раз, когда мы визуально разделяем образ на составляющие, мы невольно сравниваем их между собой по размеру занимаемой площади или размеру цветовых пятен, то есть подсознательно составляем из них пропорцию.
В этой статье:
Формула стиля: 10 лайфхаков от Ксении Штиль
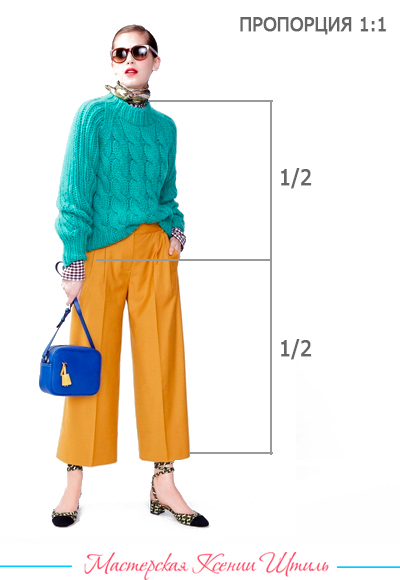
Подобная пропорция
Подобная пропорция (1:1) — одинаковые по размеру части костюма делят фигуру пополам.
Такая пропорция вызывает ощущение статичности и покоя. Часто используется при изготовлении домашней и повседневной одежды.
Подобную пропорцию можно создать как на базе юбки, так и на базе брюк или шорт. Важно, чтобы верхняя часть визуально равнялась нижней.
Гармонические пропорции
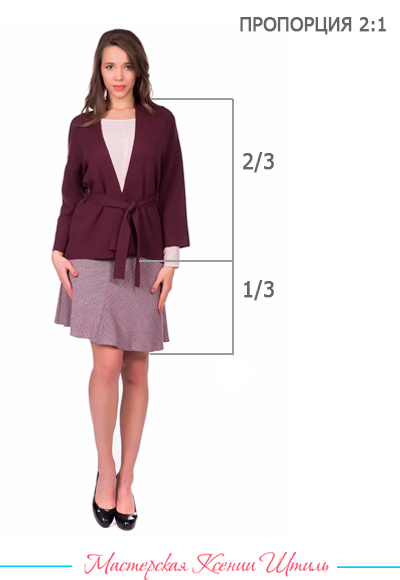
Гармонические пропорции (1:2, 1:3) — наиболее гармоничные из всех пропорций, основанные на принципе «золотого сечения». Контраст в таких пропорциях присутствует, но он невелик.
Чаще всего гармонические пропорции используются при пошиве деловой одежды.
Гармонические пропорции подходят всем людям. Важно лишь правильно определить, какая часть будет больше (верх или низ), исходя из телосложения.
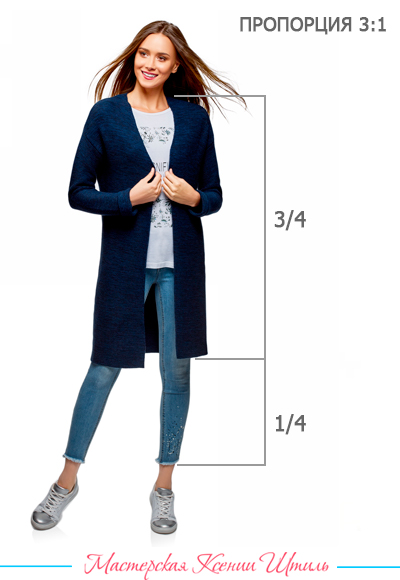
Контрастные пропорции
Контрастные пропорции (1:4, 1:5, 1:6 и т.д.) — соотношение больших и малых частей в образе выражено очень ясно и четко. Налицо ощутимый контраст.
Контрастные пропорции — это всегда динамика и выразительность, активное начало. Поэтому их часто используют в спортивной моде (динамика) и в вечерней моде (выразительность).
Однако использование контрастных пропорций в одежде меняет представление о реальных размерах фигуры.
Как определить идеальную длину в одежде? Золотая пропорция в одежде
В человеке все должно быть гармонично: и тело, и костюм. Эту гармонию наш глаз способен определять интуитивно, и, кажется, что такая гармония иррациональна и ничем не может быть объяснима, кроме обычного человеческого чувства прекрасного. Но на самом деле всем правит ее величество Математика. И в основе гармоничных пропорций заложена точная математическая формула золотого сечения, согласно которой гармоничным считается деление чего-либо в соотношении 62% и 38%. И эта пропорция может быть применима как к отдельным предметам гардероба и их длинам, так и к деталям, членениям и даже отделке.В этой статье:
Формула стиля: 10 лайфхаков от Ксении Штиль
Золотая пропорция в одежде
Давайте рассмотрим практическое применение золотой пропорции в одежде. Для удобства расчетов мы будем использовать формулу не в процентом соотношении, а в виде дробей: 3/8 (что примерно соответствует 38%) и 5/8 (что примерно соответствует 62%).
Предположим, Вы захотели обновить гардероб и купить новый костюм для работы, состоящий из жакета и юбки. Но Вы не знаете, какой длины должен быть Ваш жакет, и какова идеальная длина юбки именно для Вас? Как их рассчитать? Давайте сделаем это вместе. Пля правильных расчетов нам необходимо лишь знать предполагаемую длину костюма и положение талии: является ли она у Вас завышенной, заниженной или пропорциональной.
Как определить положение талии
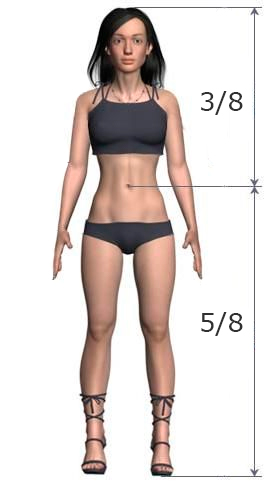Определить положение талии очень просто. Вам небходимо измерить расстояние от пола до талии. Талия — это самое узкое место на Вашем туловище. Как правило, она расположена на несколько сантиметров выше пупка.
Встаньте возле стены, отметьте линию талии карандашом на стене и измерьте получившееся расстояние до пола с помощью рулетки.
Линия талии считается пропорциональной, если она делит фигуру человека в пропорции золотого сечения, т.е. 3/8 от верха (или 5/8 от пола). К примеру, при росте 170 см талия пропорциональна, если находится на расстоянии 106 см от пола (170/8*5). Допускается погрешность в 2см.
Если получившееся у Вас число меньше (более чем на 2 см), то есть талия расположена чуть ниже, чем в идеальной фигуре, то такая талия считается заниженной. Если получившееся число больше (более чем на 2 см), то есть талия расположена выше, чем в идеальной фигуре, то такая талия считается завышенной.
Формула расчета идеальной длины в одежде
Итак, когда Вы точно определили положение талии (пропорциональная, завышенная или заниженная), давайте приступим к непосредственным вычислениям Ваших идеальных длин для костюма, состоящего из жакета и юбки. Но сначала надо определиться с предполагаемой длиной костюма. С помощью сантиметровой ленты измерьте расстояние от предполагаемого воротника до области колен. Это и будет длина Вашего костюма.
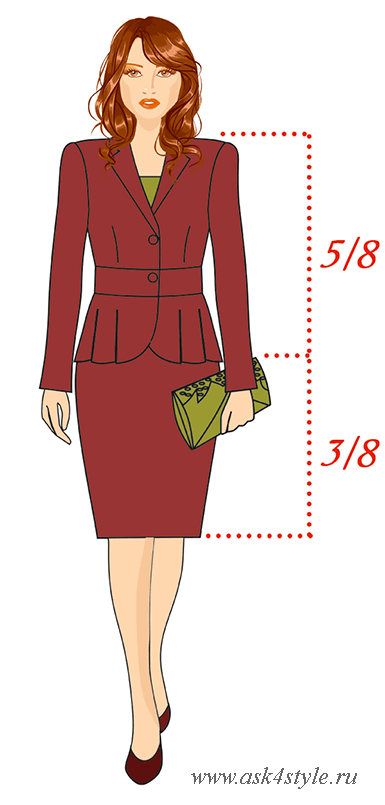Теперь необходимо решить, какая часть будет бОльшей в Вашем костюме — жакет или юбка, т.е. что из них будет 3/8, а что 5/8. И вопрос этот не праздный, зависит не от Ваших предпочтений в одежде, а как раз от линии талии. При пропорциональной талии Вы можете выбрать любой вариант.
Если Ваша талия завышена, то Вам рекомендованы те фасоны жакетов, которые «ставят» талию на свое место, т.е. несколько удлиненные. При завышенной талии можно порекомендовать жакету отвести бОльшую часть, т.е. 5/8, а юбке — 3/8.
Формула расчета длины для завышенной линии талии будет выглядеть так:
- » Для жакета: Длина костюма /8 *5
- » Для видимой части юбки: Длина костюма /8 *3
При заниженной талии фасоны жакетов должны способствовать «подъему» талии на место, т.е. быть несколько укороченными. Таким женщинам можно порекомендовать взять для жакета меньшую часть, т.е. 3/8, а для юбки -5/8.
Формула расчета длины для заниженной линии талии будет выглядеть так:
- » Для жакета: Длина костюма /8 *3
- » Для видимой части юбки: Длина костюма /8 *5
С помощью теории золотого сечения и золотой пропорции можно определять не только длину отдельных предметов гардероба, но и лучшее расположение конструктивных линий, элементов декора и т.д. К примеру, длину рукава по отношению к длине жакета, глубину V-образного выреза по отношению к общей длине изделия, ширину баски на юбке по отношению к общей длине юбки и т.д. Здесь все зависит только от Вашего воображения!
7 ошибок в стиле после 30 лет..
Практикум со стилистом
Ваша идеальная пропорция в одежде
При составлении любого ансамбля одежды первое, с чего необходимо начинать, — это правильный выбор пропорций.
Пропорции — это соотношение отдельных предметов гардероба между собой. Выбор самой гармоничной пропорции для каждого конкретного человека зависит от его типа фигуры, роста и положения талии.
Скачайте Альбом рекомендаций по типу фигуры:
А ЧТО ВЫ ДУМАЕТЕ ПО ЭТОЙ ТЕМЕ?
Пропорциональность — это… Что такое Пропорциональность?
Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.[1].
Пример
Масса керосина пропорциональна его объёму: 2 л керосина имеют массу 1,6 кг, 5 л имеют массу 4 кг, 7 л имеют массу 5,6 кг. Отношение массы к объёму всегда будет равно плотности:
- 1,6 / 2 = 0,8;
- 4 / 5 = 0,8;
- 5,6 / 7 = 0,8 и т. д.
Коэффициент пропорциональности
Неизменное отношение пропорциональных величин называется коэффициентом пропорциональности. Коэффициент пропорциональности показывает, сколько единиц одной величины приходится на единицу другой[1].
Символ
Математический символ ‘∝’ используется для указания пропорциональности двух величин. Пример, A ∝ B.
В юникоде для отображения используется символ U+221D.
Прямая пропорциональность
Прямая пропорциональность — функциональная зависимость, при которой некоторая величина зависит от другой величины таким образом, что их отношение остаётся постоянным. Иначе говоря, эти переменные изменяются пропорционально, в равных долях, то есть, если аргумент изменился в два раза в каком-либо направлении, то и функция изменяется тоже в два раза в том же направлении.
Математически прямая пропорциональность записывается в виде формулы:
Графиком прямой пропорциональности является прямая линия, проходящая через начало координат.
Обратная пропорциональность
Обра́тная пропорциона́льность — это функциональная зависимость, при которой увеличение независимой величины(аргумента) вызывает пропорциональное уменьшение зависимой величины(функции).
Свойства функции:
См. также
Источники
- ↑ 1 2 М. Я. Выгодский «Справочник по элементарной математике», М., 1974