Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Арифметика

Пропорции, члены пропорции. Основное свойство пропорции

      Частное от деления числа   a   на число   b   называют отношением числа   a   к числу   b.

      Число   a   называют предыдущим членом отношения, число   b   – последующим членом отношения.

      Пропорцией называют равенство двух отношений:

.

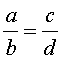      Иногда пропорцию записывают так:

a : b = c : d .

      И в одной, и во второй формах записи пропорции числа   a   и   d   называют крайними членами пропорции, а числа   b   и   c   – средними членами пропорции.

      Для любой пропорции справедливо следующее равенство, которое называют основным свойством пропорции:

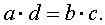
      Словесно это равенство можно сформулировать так: произведение крайних членов пропорции равно произведению средних членов пропорции.

      Для того, чтобы доказать основное свойство пропорции, умножим пропорцию на выражение   .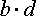

      В результате получим:

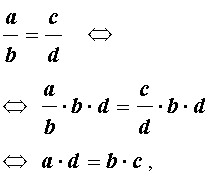
что и требовалось доказать.

      Основное свойство пропорции позволяет по трем любым известным членам пропорции найти четвертый неизвестный член пропорции. Покажем это на двух примерах.

      Пример 1. Найти неизвестный член пропорции   x ,   если

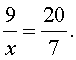
      Решение. Воспользовавшись основным свойством пропорции, получаем:

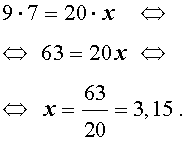
      Ответ:   3,15 .

      Пример 2. Найти неизвестный член пропорции   x ,   если

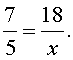
      Решение. Воспользовавшись основным свойством пропорции, получаем:

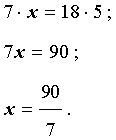
      Ответ: .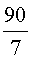

      Из основного свойства пропорции легко вытекают также свойства пропорции, которые называют перестановкой членов пропорции. Эти свойства формулируются так: если

.

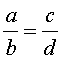то

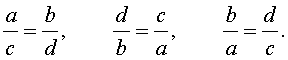
Производные пропорции

      Справедливы также свойства пропорции, которые называют производными пропорциями. Эти свойства формулируются так: если

,

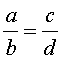то

      В качестве примера докажем первое из указанных свойств (остальные свойства доказываются аналогично). Для этого к обеим частям пропорции

.

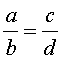достаточно прибавить 1. В результате получаем,

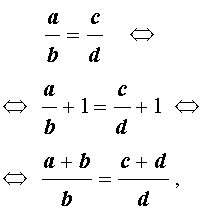
что и требовалось.

      Замечание. Последнее из свойств пропорций является наиболее общим и может быть доказано, например, с помощью основного свойства пропорции.

Свойства равных отношений

      Если выполнено соотношение

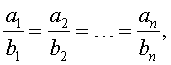
то выполнено и соотношение

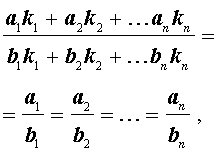
где

k₁ ,  k₂ , … k_n

– произвольные числа, которые не могут все одновременно равняться нулю.

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

www.resolventa.ru

Пропорции (Вольфсон Г.И.). Видеоурок. Математика 6 Класс

Слово «пропорция» происходит от латинского корня и означает «соразмерность». Люди часто используют его в повседневной жизни. Говорят, например, о пропорциях человеческого тела или о пропорциях в кулинарии. Сегодня мы узнаем, что вкладывают в это слово математики.

Рассмотрим два отношения. Мы помним, что отношение – это частное двух чисел.

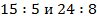
Заметим, что и в первом и во втором случае значение частного равно трем. Перед нами два равных отношения. Запишем равенство.

Пятнадцать так относится к пяти, как двадцать четыре к восьми. Такое равенство и называют пропорцией. Иногда это равенство записывают в виде равенства обыкновенных дробей.

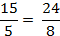
Сформулируем определение: равенство двух отношений называют пропорцией.

С помощью букв пропорцию можно записать:

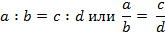
Отношение a к b равно отношению c к d. Иногда пропорцию читают по-другому: «a так относится к b, как c относитсяк d». Участвующие в пропорции числа называют членами пропорции. Считают, что все члены отличны от нуля.

Числа a и d называют крайним членами пропорции, а числа b и c– средними членами. Действительно, в первом варианте записи числа

b и c находятся посередине, а числа a и d с краю.

В рассмотренной ранее пропорции 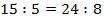найдем произведение ее средних и крайних членов.

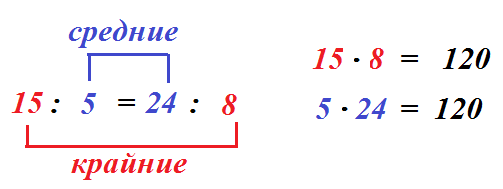
Заметим, что два полученных произведения равны.

Сформулируем основное свойство пропорции в общем виде.

В верной пропорции произведение крайних членов равно произведению средних.

Верно и обратное утверждение.

Если произведение крайних членов равно произведению средних членов пропорции, то пропорцияверна.

Найдем неизвестный член пропорции, то есть решим пропорцию.

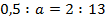
Числа 0,5 и 13 – это крайние члены; числа aи 2 – это средние члены. Воспользуемся основным свойством пропорции.

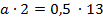
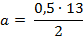
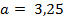
Решим пропорцию.

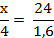
Используя основное свойство пропорции, получи

interneturok.ru

Пропорция. Основное свойство пропорции. Математика, 6 класс: уроки, тесты, задания.

1.	Запись пропорции по словесному описанию Сложность: лёгкое	1
2.	Выбор отношений, равных данному отношению Сложность: лёгкое	2
3.	Верные пропорции (целые числа) Сложность: лёгкое	2
4.	Истинность пропорции Сложность: лёгкое	1
5.	Крайние или средние члены пропорции Сложность: лёгкое	1
6.	Вычисление неизвестного члена пропорции 1 Сложность: среднее	2
7.	Вычисление неизвестного члена пропорции 2 Сложность: среднее	2
8.	Истинность пропорции Сложность: среднее	2
9.	Выбор отношений для составления пропорции Сложность: среднее	2
10.	Основное свойство пропорции (десятичные дроби) Сложность: среднее	2
11.	Уравнение (десятичные дроби) Сложность: среднее	2
12.	Уравнение (десятичные дроби и смешанное число) Сложность: среднее	2
13.	Составление пропорции Сложность: среднее	2
14.	Уравнение (обыкновенные дроби) Сложность: среднее	3
15.	Неизвестное число (смешанные числа и обыкновенная дробь) Сложность: сложное	5
16.	Составление пропорций (буквы) Сложность: сложное	3
17.	Неизвестное четвёртое число Сложность: сложное	6

www.yaklass.ru

Урок математики в 6-м классе. Тема: Пропорция

Тип урока: Урок изучения и первичного закрепления новых знаний.

Форма урока: Урок-исследование.

Цели урока:

• активизировать познавательную деятельность учащихся;
• познакомить учащихся с понятиями: пропорция, члены пропорции; верная и неверная пропорции;
• познакомить учащихся с основным свойством пропорции и сформировать навык по определению верной пропорции.

Оборудование:

1. Маршрутный лист (МР) (приложение 1)

В маршрутных листах указаны баллы, которые можно получить за решение заданий. При выставлении баллов учащийся учитывает правильность своего решения, скорость решения (самопроверка и взаимопроверка с помощью презентации). В строке “Дополнительные баллы” выставляются баллы за ответы на дополнительные вопросы, за помощь учителю в организации проверки других учащихся, а также за “отгадывание” темы урока.

2. Конверты с карточками (приложение 2)

Карточки разрезаются и в конвертах раздаются учащимся (один конверт на парту).

3. Карточки для магнитной доски (рисунок 1, рисунок 2, рисунок 3)

В ходе урока данные карточки вывешиваются на магнитную доску.

4. Ребусы (рисунок 4, рисунок 5, рисунок 6, рисунок 7).

Ребусы, составленные учащимися старших классов (кроме ребуса “Пропорция” — этот ребус взят из урока, представленного на ФПИ учителем Козак Татьяной Ивановной, МОУ СОШ №20 пгт Прогресс Амурской области) расположены на доске, учащимся предлагается разгадать их после урока.

Техническое оснащение урока – компьютер, проектор для демонстрации презентации, экран. Компьютерная презентация в Microsoft PowerPoint (приложение 4).

I. Организация начала урока

Здравствуйте! Проверьте, пожалуйста, наличие раздаточного материала у вас на парте, наличие красного и синего карандаша, а также свою готовность к уроку.

II. Сообщение темы , цели и задач урока.

Сегодня на уроке мы продолжаем изучение большого раздела курса математики. Мы закончили изучение темы (какой? — “Отношение”). Теперь мы приступаем к изучению новой темы в этом разделе. А узнать тему урока нам помогут несколько примеров. На титульном листе вашего маршрутного листа вам необходимо заполнить таблицу, устно решив примеры и, тогда, вы узнаете тему сегодняшнего урока. СЛАЙД 1

Итак, тема сегодняшнего урока Пропорция. СЛАЙД 2

Зная тему урока, попробуйте составить план урока. Что вы должны узнать сегодня на уроке? Что вы хотите узнать? Чему хотите научиться на уроке?

Составим план, который будем дополнять по ходу урока. (учащиеся называют два первых и два последних пункта плана, остальные заполняются в течение урока, по мере “открытия” новых знаний; план урока записывается на доске)

— повторение (вопросы, связанные с отношением)

— определение пропорции

-ЧЛЕНЫ ПРОПОРЦИИ

— ВЕРНЫЕ и НЕВЕРНЫЕ ПРОПОРЦИИ

— ОСНОВНОЕ СВОЙСТВО ПРОПОРЦИИ

— применение в математике

— применение в жизни

Два последних пункта мы сможем разобрать на следующих уроках, по ходу изучения темы.

III. Актуализация знаний учащихся. Подготовка к активной учебно-познавательной деятельности на основном этапе урока.

Обсудите вопросы, связанные с темой “Отношение”, с соседом по парте.

— Кто готов задать вопросы, связанные с прошлой темой? (блицопрос) МР1

— Что такое отношение?

— Как можно записать отношение?

— На какие вопросы отвечает отношение?

— Как можно записать отношение двух чисел?

— Чем можно заменить знак делания?

— Как вы думаете, зачем мы повторили эти понятия?

— Они помогут нам при изучении новой темы.

Возьмите конверты и составьте отношения а к b и c к d двумя способами. (всего 4 отношения) РАБОТА В ПАРАХ.

МР2 Перед вами несколько отношений. Найдите значение этих выражений. СЛАЙД 3

4 : 0,5=
=
5 : 10 =
=
8 : 1 =
2,5 : 5 =

Сгруппируйте отношения по определенному признаку и составьте соответствующие равенства.

IV. Усвоение новых знаний.

СЛАЙД 3

4 : 0,5 = 8 : 1

=

5 : 10 = 2,5 : 5

— По какому признаку вы сгруппировали данные отношения?

— Их значения равны.

— Полученные равенства называются пропорцией.

Подумайте и дайте определение пропорции.

ПОДСКАЗКА – пропорция – это … НА ЭКРАНЕ (равенство)

— равенство …ЧЕГО (отношений)

— скольких отношений? (двух).

Кто уверен в своем мнении, запишите определение в маршрутный лист. МР3

Кто готов выйти к доске и составить определение пропорции? (приложение 3)

ОПРЕДЕЛЕНИЕ (на магнитной доске): Пропорция – равенство двух отношений.

Посмотрим на толкование слова пропорция в словаре русского языка Ожегова С.И. СЛАЙД 4: “Пропорция — определенное соотношение частей между собой, соразмерность. В математике – равенство двух отношений”.

Вы сформулировали определение пропорции также как в словаре русского языка!

Подумайте, с каким математическим термином созвучно слово “пропорция”? (проценты). Как переводится термин “процент”? ( от ста). Значит, “про” переводится как “от”. Какая часть слова осталась? (“порция”). Где вы встречались с этим словом? (в кулинарии) Что оно означает? (размер)

Слово пропорция произошло от латинского слова proportio – соразмерность. (этимологический словарь). СЛАЙД 4

Используя определение пропорции, составьте пропорции, используя знак деления и дробную черту. (РАБОТА В ПАРАХ, конверты).

В маршрутных листах запишите пропорцию, используя буквы a,b,c,d. МР4

a : b = c : d

или

=

А сейчас мы узнаем, как называются числа, из которых состоит пропорция.

Числа a, b, c, d называются членами пропорции

Назовите первый и последний член пропорции? (а и с)

А как обычно (в жизни) называют первого и последнего? (крайние)

Значит, члены a и b называются …? ( крайними)

А где находятся члены с и d? ( в середине)

И как называются члены с и d? (средними)

Красным цветом выделим какие члены? (крайние)

Синим

цветом (средние) члены.

СЛАЙД 6

средние члены

Вернемся к плану урока – есть чем его дополнить? (крайние и средние члены пропорции)

V. Первичное закрепление знаний

МР5 Заполните таблицу:

Пропорция	=	72 : 9 = 16 : 2	a : b = c : d
Крайние члены	3; 20	72; 2
Средние члены	4; 15	9; 16
Произведение крайних членов	60	144
Произведение средних членов	60	144

Какой вывод можно сделать? Запишите вывод в маршрутном листе. (В пропорции произведение крайних членов равно произведению средних) СЛАЙД 8

МР6 Перед вами пять равенств. Все ли они являются пропорциями?

Подчеркните пропорции.

= ; 7 + 11 = 36 : 2; 72 : 9 = 16 : 2; = 20 : 4; 5 • 40 = 100 • 2

СЛАЙД 7 Встаньте, кто закончил.

Все уверены в том, что здесь три пропорции? Ведь в последнем равенстве произведение крайних членов не равно произведению средних. Вернемся к определению пропорции (Пропорция – равенство двух отношений). Третье равенство является равенством двух отношений? (является). По определению это пропорция? (да). А произведение крайних членов равно произведению средних? (нет). Значит, это пропорция…? (неправильная). Такая пропорция называется неверной. Значит, бывают пропорции неверные и …? (верные). Сформулируйте основное свойство пропорции, используя полученные знания. (В верной пропорции произведение крайних членов равно произведению средних).

VI. Закрепление знаний.

Заполните с таблицу.

Верная пропорция Неверная пропорция

= 72 : 9 = 16 : 2

= 20 : 4

А как еще можно определить верная пропорция или неверная? (найти значение отношений)

В дальнейшем мы будет говорить о верных пропорциях.

Вернемся к плану урока. Что можно добавить? (пропорции верные и неверные)

МР7 Используя буквы В и Н отметьте верные и неверные пропорции.

VII. Обобщение и систематизация.

МР8 Используя основное свойство пропорции, составьте верную пропорцию из следующих чисел: 4, 5, 12, 15. Сколько верных пропорций можно составить?

1 : 3 = 5 : 15

3 : 1 = 15 : 5

1 : 5 = 3 : 15

5 : 1 = 15 : 3

СЛАЙД 9

*Составьте верные пропорции, используя буквы a, b, c, d (необязательное задание)

а : b = c : d

b : а = d : c

а : c = b : d

c : а = d : b

VIII. Контроль и самопроверка знаний

МР9 Математический диктант

1. Запишите пропорцию: Число 18 так относится к 4, как 27 относится к 6.
2. Запишите пропорцию: Отношение трех к пяти равно отношению двух к семи.
3. Запишите средние члены пропорции: 1,5 : 2 = 4,5 : 6
4. Запишите крайние члены пропорции: 2/1,9 = 3/2,8
5. Верна ли пропорция в п.3
6. Верна ли пропорция в п.4
7. Верно ли высказывание: Корень уравнения 20/5 = х/0,5 число 2
8. Верно ли высказывание: Из любых четырех натуральных чисел можно составить пропорцию?

СЛАЙД 10. Взаимопроверка

IX. Подведение итогов урока.

Обратитесь к плану урока.

Что вы узнали сегодня на уроке? (что такое пропорция, из чего состоит пропорция, пропорции бывают верными и неверными, основное свойство пропорции, …)

Чему вы научились сегодня на уроке? (определять крайние и средние члены пропорции, выяснять является пропорция верной или неверной, …)

Какие еще вопросы можно задать по итогам урока?

— Сколько верных пропорций можно составить из данной верной пропорции?

— Как можно определить является пропорция верной или неверной?

Вспомним последнее задание математического диктанта.

Из любых четырех натуральных чисел можно составить пропорцию. Правильный ответ ДА. Составить пропорцию можно, но она не обязательно будет верной.

Из фразы “Из любых четырех натуральных чисел можно составить пропорцию” исключите одно слово, чтобы это высказывание стало неверным. (натуральных). Почему? (Число 0 не может являться членом пропорции). Из любых четырех чисел можно составить пропорцию

В данную фразу “Из любых четырех натуральных чисел можно составить пропорцию” вставьте одно слово, чтобы высказывание стало неверным (верную). Из любых четырех натуральных чисел можно составить верную пропорцию.

Подсчитайте количество баллов, которые вы заработали на уроке и выставите оценку.

X. Информация о домашнем задании и инструктаж по его выполнению

Математика – 6, Виленкин Н.Я. и др. 6-е издание

П.21, №№ 760, 781, 782, 783 (а)

urok.1sept.ru

Пропорция

Если у двух отношений одинаковое частное, то их можно соединить знаком равенства, тогда это равенство будет уже пропорцией.

Определение, Равенство двух отношений называется пропорцией.

Пропорции можно записывать в виде частного двух натуральных чисел, обыкновенными дробями, численно и буквенно. Например:
2 : 3 = 8 : 12;

Буквенная запись пропорции a : b = c : d — это общий
вид пропорции, где:

a и d — это крайние члены пропорции;

b и c — это средние члены пропорции.

Основное свойство пропорции: a * d = b * c

Правило . Произведение средних членов истинной пропорции равно произведению ее крайних членов.

Правило. Средние и крайние члены пропорции можно менять местами, от этого пропорция не изменится.

Например, для истинной пропорции a : b = c : d верно: a * d = b * c

Истинными будут и пропорции a : b = b : d, d : b = c : a, d : c = b : a.

В пропорции один из ее членов можно заменить буквой (обозначить буквой неизвестный член пропорции).

Например: 2 : 3 = x : 12 или x : 3 = 8 : 12.

В первом примере неизвестен средний член пропорции, а во втором — ее крайний член.

Пропорция с одним неизвестным часто встречается в решении задач (значение неизвестного — это ответ на вопрос задачи). Вычислить любой член пропорции можно по следующем правилу.

Правило . Неизвестный крайний член пропорции равен частному произведения средних членов пропорции и известного крайнего члена.

Неизвестный средний член пропорции равен частному произведения крайних членов пропорции и известного среднего члена.

Определение неизвестного члена пропорции :

x : b = c : d, x = (b * c) : d
a : b = c : x, x = (b * c) : a
a : x = c : d, x = (a * d) : c
a : b = x : d, x = (a * d) : b

shkolo.ru

Пропорции

Один кусок верёвки имеет длину  6 м, а другой – 3 м. Для того, чтобы узнать, во сколько раз длина первого куска больше длины второго куска, необходимо длину первого куска разделить на длину второго: 6 : 3 = 2. Первый кусок в 2 раза длиннее другого. Эти же куски верёвки можно измерить в сантиметрах. Тогда
600 : 300 = 2. Частные 6 : 3 и 600 : 300 равны одному и тому же числу 2. Они равны друг другу:

6 : 3 = 600 : 300.

Частное чисел 6 и 3 называют иначе отношением 6 к 3. Отношение двух положительных чисел показывает, во сколько раз одно число больше другого.

Равенство двух отношений называют пропорцией.

С помощью букв пропорцию можно записать так:

a : b = с : d или a / b = с / d.

Эти записи читают так: « а, делённое на b, равно с, делённому на d», или «отношение а к b равно отношению с r d», или «а относится к b, как с относится к d».

В пропорции  a : b = с : d числа a и b называют крайними членами пропорции, а числа с и d – средними членами пропорции.

Пропорция 4,8 : 1,2 = 8,4 : 2,1 верна. Потому что значениями её левой и правой частей является одно и то же число 4. Найдём произведение крайних и произведение средних членов данной пропорции:

4,8 ∙ 2,1 = 10,08;

1,2 ∙ 8,4 = 10,08.

В любой верной пропорции произведение крайних членов равно произведению средних членов. Это свойство называют основным свойством пропорции.

Пусть пропорция a : b = с : d верна. Если значение левой части этой пропорции равно k, то значение правой части равно k:

a : b = k  и с : d = k.

Отсюда а = b ∙ k и с = d ∙ k.

Рассмотрим произведение крайних и средних членов пропорции:

a ∙ d = (b ∙ k) ∙ d =  b ∙ k ∙ d;

b ∙ c = b ∙ (d ∙ k) = b ∙ k ∙ d.

Отсюда видно, что произведение крайних членов пропорции равно произведению её средних членов:

Если  a : b = с : d, то ad = bc.

С помощью пропорций можно решать многие задачи.

Задача 1.

За 3,5 кг сливочного масла заплатили  336 р. Сколько необходимо заплатить за 2,5 кг сливочного масла?

Решение.

Пусть 2,5 кг сливочного масла стоят х р. Цену масла можно найти двумя способами: разделить 336 р. на 3,5 кг или разделить х на 2,5 кг. В обоих случаях должен получиться один и тот же результат. Получаем пропорцию:

336 : 3,5 = х : 2,5.

По основному свойству пропорции

336 ∙ 2,5 = 3,5 ∙ х.

Значит, х = 240 р.

Ответ: за 2,5 кг сливочного масла необходимо заплатить 240 р.

Задача 2.

В лыжной секции занимаются 90 учащихся. Среди них 36 девочек. Какой процент участников секции составляют девочки?

Решение.

Пусть девочки составляют х % участников секции. Тогда один процент участников можно найти двумя способами: разделить 90 на 100 или 36 на х. Получаем пропорцию:

90 : 100 = 36 : х.

После решения пропорции х = 100 ∙ 36 : 90 = 40 получаем ответ.

Ответ: девочки составляют 40 % участников секции.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Что такое пропорция | Математика

Здесь мы рассмотрим, что такое пропорция, как называются члены пропорции и основное свойство пропорции.

Определение пропорции:

Пропорция — это равенство двух отношений.

С помощью букв пропорцию записывают так:

   

или

   

Читают: «a относится к b как c относится к d» или «отношение a к b равно отношению c к d».

Числа a и d называют крайними членами пропорции, числа b и c — средними членами пропорции:

Примеры пропорций:

1) 4,8:1,6=3,6:1,2

Здесь 4,8 и 1,2 — крайние члены пропорции, 1,6 и 3,6 — средние члены пропорции.

   

Здесь 2,1 и 6 — крайние члены пропорция, 8,4 и 1,5 — средние члены пропорции.

Основное свойство пропорции:

Произведение крайних членов пропорции равно произведению ее средних членов.

   

   

Отсюда следует, что

   

Таким образом, если в пропорции поменять местами крайние члены или средние члены, то получим новые верные пропорции.

Пропорция- это равенство.  Если это равенство содержит переменную, значение которой надо найти, то оно является уравнением. Как решать пропорции, мы рассмотрим в следующий раз.
Кроме того,  пропорции используются для решения некоторых задач. В частности,  пропорции существенно облегчают решение задач на проценты.  Позже мы рассмотрим также решение задач с помощью пропорций.

www.for6cl.uznateshe.ru