Прямая и обратная пропорциональные зависимости. 6 класс
1. Прямая и обратная пропорциональные зависимости
2. Повторим!!!
Что такое пропорция?Прочитайте пропорцию х:а=у:в.
Назовите ее крайние члены; средние
члены.
Сформулируйте основное свойство
пропорции.
Какие перестановки членов
пропорции снова приводят к верным
пропорциям?
3. Устно решить задачи!!!
1)Найдите неизвестный членпропорции 5:х=4:12.
2)Верна ли пропорция: 12:0,2=30:0,5?
3)Автобус был в пути 2 ч и проехал
120 км. Какой путь проедет
автобус за 4 ч, если будет ехать с
той же скоростью?
4)Как зависит путь от времени
движения автобуса?
4. Устно решить задачи!!!
5)Станок за 2 часа изготавливает 28деталей. Сколько деталей
изготовит станок за 4 часа?
6)Как зависит количество деталей
от времени работы станка?
Такие величины, как время движения
автобуса и его путь, как время работы
станка и число изготовленных деталей,
называют прямо пропорциональными
величинами.
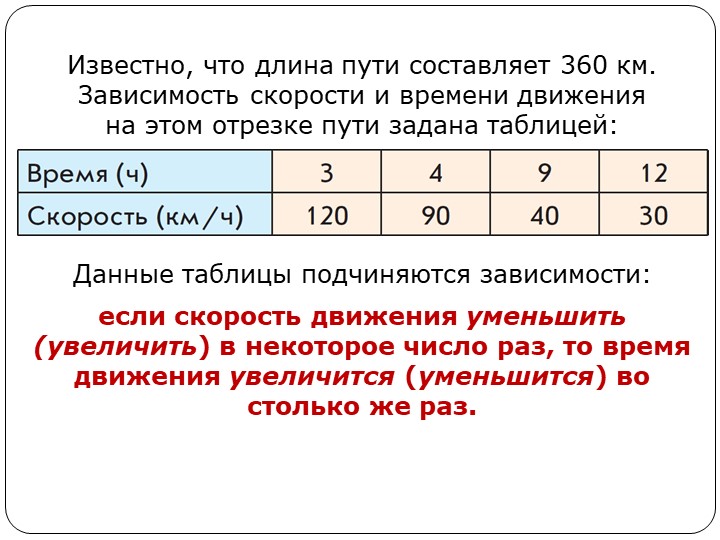
5. Прямо пропорциональные величины
Две величины называют прямопропорциональными, если при
увеличении (уменьшении) одной из них
в несколько раз другая увеличивается
(уменьшается) во столько же раз.
Если две величины прямо
пропорциональны, то отношения
соответствующих значений этих
величин равны.
6. Прямо пропорциональные величины
Задача 1. За 3,2 кг товара заплатили115,2 р. Сколько следует заплатить за
1,5 кг этого товара?
Решение:
Количество
товара
1 покупка
3,2 кг
1,5 кг
2 покупка
3,2:1,5=115,2:х
х=1,5∙115,2:3,2
х=54
Стоимость
товара
115,2 р.
х р.
Ответ: следует
заплатить 54 р.
7. Устно решить задачи!!!
7)Путь из города А в город В поезд соскоростью 40 км/ч проходит за 12 ч.
Сколько времени потребуется поезду
на преодоление этого же пути, если
его скорость увеличить вдвое?
8)Как изменилось время в зависимости
от скорости?
Во сколько раз увеличится скорость движения,
во столько же раз уменьшится время движения.

Такие величины, как время и скорость,
называют обратно пропорциональными
величинами.
8. Обратно пропорциональные величины
Две величины называют обратнопропорциональными, если при
увеличении (уменьшении) одной из них
в несколько раз другая уменьшается
(увеличивается) во столько же раз.
Если две величины обратно
пропорциональны, то отношение
значений одной величины равно
обратному отношению
соответствующих значений другой
величины.
9. Обратно пропорциональные величины
Задача 2. Два прямоугольника имеютодинаковую площадь. Длина первого
прямоугольника 3,6 м, а ширина 2,4 м. Длина
второго прямоугольника 4,8 м. Найдите
ширину второго прямоугольника.
Решение:
Длина
Ширина
1 прямоугольник
3,6 м
2,4 м
4,8 м
х м
2 прямоугольник
х=3,6∙2,4:4,8
х =1,8
Ответ: ширина — 1,8 м.
10. Не пропорциональные величины
Не всякие две величины являютсяпрямо пропорциональными или
обратно пропорциональными.

Например: рост ребенка
увеличивается при увеличении его
возраста, но эти величины не
являются пропорциональными, так
как при удвоении возраста рост
ребенка не удваивается.
11. Решение задач
Учебник:12. Итог урока
Две величины называют прямо пропорциональными,если при увеличении (уменьшении) одной из них в
несколько раз другая увеличивается (уменьшается) во
столько же раз.
Если две величины прямо пропорциональны, то
отношения соответствующих значений этих величин
равны.
Две величины называют обратно пропорциональными,
если при увеличении (уменьшении) одной из них в
несколько раз другая уменьшается (увеличивается) во
столько же раз.
Если две величины обратно пропорциональны, то
отношение значений одной величины равно обратному
отношению соответствующих значений другой
величины.
13. ДОМА
6 класс . презентация и конспект урока. Прямая и обратная пропорциональность
6 класс
УРОК № 12. Глава 1. Отношения, пропорции, проценты (26 часов)
Глава 1. Отношения, пропорции, проценты (26 часов)
Тема. Прямая и обратная пропорциональность. С/р № 3.
Цель. Проверить знания учащихся по теме «Пропорции». Дать определение прямо пропорциональных и обратно пропорциональных величин. Научится решать задачи по данной теме.
Ход урока.
Организационный момент.
Проверка домашнего задания.
Самостоятельная работа по теме «Пропорции». (10 min)
Вариант 1. Вариант 1.
Решить пропорцию: Решить пропорцию:
1) , 1) ,
, ,
. Ответ: . . Ответ: .
2) , 2) ,
, ,
. Ответ: . . Ответ: .
3) , 3) ,
, ,
, ,
. Ответ: . . Ответ: .
Объяснение нового материала.
Прямая и обратная пропорциональность.
Мультимедийная доска. Электронное приложение. Каталог. Анимация. Расход электроэнергии в квартире. (1 мин 31 секунды)
(Слайд 2). Пусть ручка стоит 3 р. (это цена). Тогда легко рассчитать стоимость двух, трех и т.д. ручек по формуле: .
Заметим, что с увеличением количества ручек в несколько раз их стоимость увеличивается во столько же раз.Говорят, что стоимость покупки прямо пропорциональна количеству купленных ручек.
(Слайд 3). Определение. Две величины называются прямо пропорциональными , если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
(Слайд 4). Примеры прямо пропорциональных величин:
1. Периметр квадрата и длина стороны квадрата – прямо пропорциональные величины. .
2. Если скорость движения постоянна, то пройденный путь и время движения – прямо пропорциональные величины.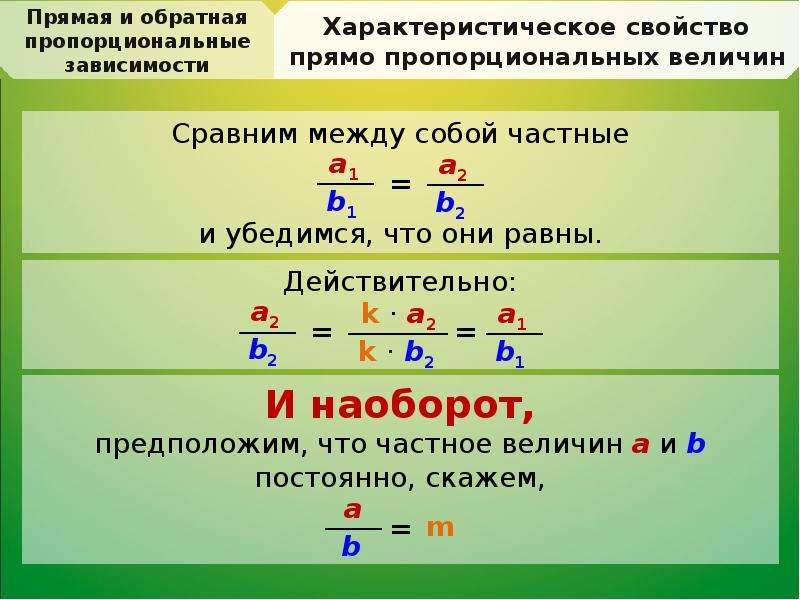 .
.
3. Если производительность труда постоянна, то объём выполненных работ и время – прямо пропорциональные величины. .
4. Выручка кассы кинотеатра прямо пропорциональна количеству проданных билетов при одинаковой цене. И т.д.
(Слайд 5). Задача 1. За 5 тетрадей в клетку заплатили 40 р. Сколько заплатят за 12 таких же тетрадей?
Кол-во Стоимость
5 тетрадей – 40 р. Прямая пропорциональность
12 тетрадей – х р.
Решение.
Т.к. величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
,
,
.
96 р. заплатят за 12 тетрадей. Ответ: 96 р.
(Слайд 6). Хотят купить на 120 р. несколько одинаковых книг. Тогда легко рассчитать количество книг по 10 р., 20 р., 30 р. 40 р. и т.д. по формуле: .
Заметим, что с увеличением цены книги в несколько раз их количество уменьшается во столько же раз.
Говорят, что количество купленных книг обратно пропорционально их цене.
(Слайд 7). Определение. Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Если величины обратно пропорциональны, то отношение значений одной величины равно обратному отношению значений другой величины.
(Слайд 8). Примеры обратно пропорциональных величин:
1. Если пройденный путь постоянен, то скорость движения и время движения – обратно пропорциональные величины. .
2. Если производительность труда постоянна, то объём выполненных работ и время – обратно пропорциональные величины. .
(Слайд 9). Задача 2. 6 рабочих выполнят работу за 5 часов. За какое время справятся с этой работой 3 рабочих?
Кол-во Время
6 рабочих – 5 ч Обратная пропорциональность
3 рабочих – х ч
Решение.
Т.к. величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
,
,
.
За 10 ч справятся с этой работой 3 рабочих. Ответ: 10 ч.
Алгоритм решения задач.
Составить краткую запись и определить вид пропорциональности. (Одноименные величины записываются друг под другом)
Составить пропорцию.
Если две величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
Если две величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Найти неизвестный член пропорции.
Проанализировать полученный результат и записать ответ.

Решение упражнений.
Уч.с.21 № 75(а). В 100 г раствора содержится 4 г соли. Сколько соли содержится в 300 г этого раствора?
Р-р Соль
100 г – 4 г Прямая пропорциональность
300 г – х г
Решение.
Т.к. величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
,
,
.
12 г соли содержится в 300 г этого раствора. Ответ: 12 г.
Уч.с.22 № 88. Некоторую работу 6 человек сделают за 18 дней. За сколько дней сделают эту же работу 9 человек, работающие так же успешно, как и первые?
Кол-во Время
6 человек – 18 дн. Обратная пропорциональность
9 человек – х дн.
Решение.
Т.к. величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
,
,
.
За 12 дней сделают эту же работу 9 человек. Ответ: 12 дней.
Уч.с.22 № 83. Один килограмм металлолома заменяет кг богатой железом руды. Сколько руды заменяют 4 т металлолома?
Металлолом Руда
1 кг – кг Прямая пропорциональность
4 т – х кг
Решение.
Т.к. величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
1) 4 т = 4000 кг;
2) ,
,
.
10 000 кг руды заменяют 4 т металлолома. Ответ: 10 000 кг.
Уч.с.22 № 84(а). Автомобилист заметил, что со скоростью 60 км/ч он проехал мост через реку за 40 с. На обратном пути он проехал этот же мост за 30 с. Определите скорость автомобиля на обратном пути?
v t
60 км/ч – 40 с Обратная пропорциональность
х км/ч – 30 с
Решение.
Т.к. величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
,
,
.
80 км/ч скорость автомобиля на обратном пути. Ответ: 80 км/ч.
Подведение итогов урока
Домашнее задание. § 1.5 (выучить теорию). № 73, 75(б), 77(а), 84(б).
Урок математики в 6-м классе по теме «Прямая и обратная пропорциональные зависимости»
Цели урока:
1. Образовательная:
- в результате урока учащиеся закрепляют понятия прямой и обратной пропорциональных зависимостей.
2. Развивающая:
- учащиеся развивают мышление, внимание, память, умение анализировать, сопоставлять, сравнивать.
3. Воспитательная:
- учащиеся развивают коммуникативные навыки.

Тип урока: урок применения знаний.
Используемые технологии обучения: КСО, работа в группах.
Оборудование: компьютер, мультимедийный проектор.
Ход урока
I. Организационный момент.
II. Мотивация учебной деятельности учащихся.
Урок начинается со слов учителя:
— Тема нашего урока «Прямая и обратная пропорциональные зависимости». Попробуйте сформулировать, каждый для себя цель урока.
Учащиеся формулируют цели. Далее обобщая всё что сказали учащиеся учитель делает вывод:
— Итак, на предыдущих уроках мы рассматривали прямую пропорциональную
зависимость величин, обратную пропорциональную зависимость величин. Сегодня на
уроке мы будем решать разные задачи, анализируя условия которых находить прямую
или обратную пропорциональные зависимости величин, составлять пропорции.
Повторим основное свойство пропорций. А следующий урок, завершающий по данной
теме, т. е. урок – контрольная работа.
е. урок – контрольная работа.
(см. Презентацию) Демонстрируется слайд 1
III. Устная работа.
Вопросы:
- Какие величины называют прямо пропорциональными?
- Какие величины называют обратно пропорциональными?
Далее учащиеся работают в тетрадях на печатной основе №1 (ТПО №1), выполняют № 110 на странице 58.
Учащиеся, работая индивидуально, отмечают знаком «+» верные высказывания:
- Периметр квадрата и длина стороны квадрата – прямо пропорциональные величины.
- Длина стороны квадрата и площадь квадрата – прямо пропорциональные величины.
- Если скорость движения постоянна, то пройденный путь и время движения – прямо пропорциональные величины.
- Выручка кассы кинотеатра обратно пропорциональна количеству проданных билетов.
- Выручка кассы кинотеатра прямо пропорциональна количеству проданных билетов,
проданных по одной и той же цене.

- При постоянной цене стоимость товара и его масса – обратно пропорциональные величины.
- Если площадь прямоугольника постоянная величина, то его длина и ширина – обратно пропорциональные величины.
Затем учащиеся обмениваются тетрадями и проверяют верно ли выполнено задание, слушая комментарии одноклассников к каждой ситуации.
IV. Применение знаний (этап обобщения знаний).
Демонстрируется слайд 2
а) На пошив 9 рубашек ушло 18,9 м ткани. Сколько метров уйдёт на пошив 12 таких рубашек?
б) 6 одинаковых труб заполняют бассейн за 24 минуты. За сколько минут заполнят бассейн 9 таких труб?
в) Бригада из 8 рабочих выполняет задание за 12 дней. Сколько рабочих сможет выполнить это задание за 8 дней, работая с той же производительностью?
г) Из 9,6 кг помидоров получают 4 л томатного соуса. Сколько литров соуса можно получить из 84 кг помидоров?
Учащиеся работают по вариантам, ответы записывают на листе бумаги, указав
номер варианта.
I вариант. Запишите буквы, под которыми задачи содержат обратно пропорциональные величины.
II вариант. Запишите буквы, под которыми задачи содержат прямо пропорциональные величины.
- Обсуди свой ответ с соседом по варианту.
- Обсуди свой ответ с соседом по парте.
- Составь пропорции для решения задач.
| I вариант | II вариант | |
| в) и г) | а) и б) |
- Обменяйтесь работами с соседом по парте и проверьте ответы.
Демонстрируется слайд 3
|
|
|
|
|
- Передай ТПО №1, вложив в неё свой листочек, учителю.

Далее учащиеся решают задачи, выясняя в каждой, какими являются величины: прямо пропорциональными или обратно пропорциональными.
№ 361 («Математика 6» авт. Н.Б. Истомина)
Учащиеся читают задачу. По ходу анализа условия задачи учащимся у доски, демонстрируется слайд 4. Затем ученик на доске, а остальные дети в тетрадях, записывают решение задачи.
Задача:
28 строчек – 144 страницы
32 строчки – х страниц
Решение:
Ответ: 126 страниц.
Демонстрируется слайд 5 (самостоятельная работа учащихся):
Задача:
На чертеже, масштаб которого 1 : 6, деталь имеет длину 18, 9 см . Какую длину будет иметь эта деталь на чертеже, масштаб которого 1 : 9?
Задание (проговаривает учитель): По рисунку выясните, какие это величины. Составьте пропорцию и решите её.
М 1 : 6 – 18, 9 см
М 1 : 9 – x см
Решение:
Ответ: 12,6 см.
Решение этой задачи комментирует с места один из учащихся класса, остальные проверяют решение по своим тетрадям, по мере необходимости исправляют ошибки.
Следующая задача № 363 («Математика 6» авт. Н.Б. Истомина).
Учащиеся записывают не краткую запись условия, а составляют схему, анализируя условие задачи (фронтальная работа).
Демонстрируется слайд 6
Затем, ученик у доски составляет пропорцию и решает её.
Решение:
Ответ: 10 часов.
Далее учащиеся работают в группах (в группу объединяются учащиеся двух соседних парт). Демонстрируется слайд 7
Задача:
Из пункта А в пункт В выехали одновременно мотоциклист со скоростью 56 км/ч и велосипедист, скорость которого 14 км/ч. Мотоциклист через 30 минут прибыл в пункт В. Кто был дольше в пути: мотоциклист или велосипедист и на сколько?
Учащиеся анализируют и решают задачу в группах, затем представитель группы,
которая решила задачу первой, объясняет решение.
Решение:
Ответ: мотоциклист на 1,5 часа был в пути дольше.
Демонстрируется слайд 8
Задание (проговаривает учитель): Составьте по рисункам задачу, величины в которой находятся в обратно пропорциональной зависимости, и решите её.
Учащиеся после выполнения этого задания сдают тетради учителю.
V. Итог урока подводят дети, отвечая на вопрос учителя: «Какой алгоритм решения задач можно сформулировать»?
Учащиеся в ходе фронтальной работы формулируют алгоритм.
Демонстрируется слайд 9
Алгоритм решения задач на прямую и обратную пропорциональные зависимости:
- неизвестное число обозначить буквой x;
- записать условие задачи;
- установить вид зависимости между величинами;
- прямую пропорциональную зависимость обозначить одинаково направленными стрелками, а обратную пропорциональную зависимость – противоположно направленными стрелками;
- записать пропорцию;
- найти её неизвестный член.

Распечатанный заранее алгоритм после фронтальной работы выдаётся каждому ученику.
Сообщение учителем оценок за урок.
После проверки, сданных тетрадей и ТПО №1, каждый ученик получит оценку.
VI. Домашнее задание: № 354; № 355; № 362.
Презентация «Прямая и обратная пропорциональность»
библиотека
материалов
Содержание слайдов
Номер слайда 1
№ 53 (а, б), 54 (а, б),57. Проверка домашней работы:
Номер слайда 2
№ 53 (а, б)а) х=𝟐·𝟑𝟕, х=𝟔𝟕. б) х=𝟐·𝟑𝟓, х=𝟔𝟓.
б) х=𝟐·𝟑𝟓, х=𝟔𝟓.
Номер слайда 3
№ 54 (а, б)а) х=𝟕·𝟔𝟖, х=𝟐𝟏𝟒. б) х=𝟏𝟎·𝟏𝟑𝟏𝟓, х=𝟐𝟔𝟑.
Номер слайда 4
№ 57а) х=𝟏𝟐·𝟑𝟓, х=𝟑𝟏𝟎. б) х=𝟐𝟑·𝟑𝟒, х=𝟏𝟐.
б) х=𝟐𝟑·𝟑𝟒, х=𝟏𝟐.
Номер слайда 5
№ 57в) х=𝟓·𝟕𝟏𝟐, х=𝟕𝟎. г) х=𝟏𝟑·𝟔𝟖, х=𝟏𝟒.
Номер слайда 6
Математический диктант: Верно ли, что:1) Отношение двух чисел — это произведение одного из них на другое?2)Верное равенство двух отношений называют пропорцией?3)Произведение крайних членов пропорции равно сумме её средних членов? 4)Найти неизвестный член пропорции – это значит решить пропорцию?618. 09.2019
09.2019
Номер слайда 7
Верно ли, что:5)В пропорции m:n=p:q числа m и q называют средними, а числа n и p называют крайними членами пропорции?6)Является пропорцией данное равенство: 8:10=4:5?7)Можно составить пропорцию из чисел 4, 9, 12 и 27?8)Пройденный путь пропорционален времени движения когда скорость постоянна?9)Рост человека пропорционален его возрасту? Математический диктант:
Номер слайда 8
Проверь себя : 1 2 3 4 5 6 7 8 9- + — + — + + + -89 правильных ответов – «5»7 – 8 правильных ответов – «4»4 – 5 правильных ответов – «3»
Номер слайда 9
Устно: Что называется отношением двух чисел?Что называется отношением двух величин?Что такое пропорция?Что показывает отношение двух чисел? Что значит решить пропорцию?Основное свойство пропорции.
Номер слайда 10
1. Если нам известно,что скорость автомобиля составляет 60 км/ч,то мы можем рассчитать пройденноеим расстояние за любой отрезок времени:{3 B4 B98 B0-60 AC-42 C2-AFA5-B58 CD77 FA1 E5}Время, ч123456 Путь, км{3 B4 B98 B0-60 AC-42 C2-AFA5-B58 CD77 FA1 E5}Время, ч123456 Путь, км60{3 B4 B98 B0-60 AC-42 C2-AFA5-B58 CD77 FA1 E5}Время, ч123456 Путь, км60120{3 B4 B98 B0-60 AC-42 C2-AFA5-B58 CD77 FA1 E5}Время, ч123456 Путь, км60120180{3 B4 B98 B0-60 AC-42 C2-AFA5-B58 CD77 FA1 E5}Время, ч123456 Путь, км60120180240{3 B4 B98 B0-60 AC-42 C2-AFA5-B58 CD77 FA1 E5}Время, ч123456 Путь, км60120180240300{3 B4 B98 B0-60 AC-42 C2-AFA5-B58 CD77 FA1 E5}Время, ч123456 Путь, км60120180240300360 Какой вывод можно сделать по данным этой таблицы?Если время увеличить (уменьшить)в некоторое число раз,то и расстояние увеличится (уменьшится)в это же число раз.
Номер слайда 11
2. На 120 р. необходимо купить несколько одинаковых книг. Сколько книг можно купить, если цена каждой 10 р., 20 р., 30 р., 40 р.?Решение: С=10 р., к=12 книг;С=20 р., к=6 книг;С=30 р., к=4 книги;С=40 р., к=3 книги. Какой вывод можно сделать из данного решения?Если стоимость увеличить (уменьшить)в некоторое число раз,то и количество книг уменьшится (увеличится) в это же число раз.
Номер слайда 12
Прямая и обратная пропорциональность18. 09.2019«Всякая задача кажется очень простой, после того, как вам ее растолкуют» Шерлок Холмс.
09.2019«Всякая задача кажется очень простой, после того, как вам ее растолкуют» Шерлок Холмс.
Номер слайда 13
Цель урока:ввести новые понятия прямой и обратной пропорциональных зависимостей; научиться решать задачи, с использованием прямой и обратной пропорциональными зависимостями.
Номер слайда 14
Определение прямой и обратной пропорциональности. Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается(уменьшается) во столько же раз. Вел. 1 — Вел 2 Вел 1. — Вел 2. Вел. 1 — Вел 2 Вел 1. — Вел 2.
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается(уменьшается) во столько же раз. Вел. 1 — Вел 2 Вел 1. — Вел 2. Вел. 1 — Вел 2 Вел 1. — Вел 2.
Номер слайда 15
Определение прямой и обратной пропорциональности. Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз. Вел. 1 — Вел 2 Вел 1. — Вел 2.
Номер слайда 16
Работа по учебнику: стр. 21№72 Время Расстояние Пусть x км расстояние. 6 ч 480 км 2 ч x км. Решение: x = x = 160 (км) Ответ: 160 км. =
21№72 Время Расстояние Пусть x км расстояние. 6 ч 480 км 2 ч x км. Решение: x = x = 160 (км) Ответ: 160 км. =
Номер слайда 17
Работа по учебнику: стр. 22№82(а) Время Скорость Пусть x ч время. 8 ч 60 км/ч x ч 80 км/ч. Решение:=x =X = 6 (ч) Ответ: 6 ч.
Номер слайда 18
Алгоритм решения задач:1. Записать краткое условие задачи. (одноименные величины ставятся одна под другой).2. Определить к какому виду относится пропорция.3. Составить пропорцию.3а) При прямой пропорциональности, величины записываются не меняя порядка.3б) При обратной пропорциональности, величины меняют местами (у одной величины).4. Найти неизвестный член пропорции.5. Ответить на вопрос задачи.6. Записать ответ.
Записать краткое условие задачи. (одноименные величины ставятся одна под другой).2. Определить к какому виду относится пропорция.3. Составить пропорцию.3а) При прямой пропорциональности, величины записываются не меняя порядка.3б) При обратной пропорциональности, величины меняют местами (у одной величины).4. Найти неизвестный член пропорции.5. Ответить на вопрос задачи.6. Записать ответ.
Номер слайда 19
Учебник: стр. 20№62, 63, 65. Устно:
Номер слайда 20
Работа в парах:№74 Вишня Сахарный Пусть x кг масса вишни. песок 6кг 4 кг x кг 12 кг = x = x = 18 (кг). Ответ: 18 кг.
песок 6кг 4 кг x кг 12 кг = x = x = 18 (кг). Ответ: 18 кг.
Номер слайда 21
Работа в парах№77(а)Количество Количество Пусть x дней работа маляров дней 10 маляров. 5 8 10 x = x = x = 4 (дн). Ответ: 4 дня.
Номер слайда 22
Рефлексия. Урок понравился, я работал (ла) активно, отвечал (ла) на все вопросы правильно. Остались вопросы, я стеснялся (ась) отвечать на уроке, был (а) не уверен (а) в ответе. Урок не понравился, было много не понятного.
Урок понравился, я работал (ла) активно, отвечал (ла) на все вопросы правильно. Остались вопросы, я стеснялся (ась) отвечать на уроке, был (а) не уверен (а) в ответе. Урок не понравился, было много не понятного.
Номер слайда 23
Домашнее задание:1)п.1.5 (правила), №74, №76.2)Дополнительное задание: №79, №80.3)Творческое задание: Найдите в учебнике, справочной литературе или Интернете, как решали задачи на прямую и обратную пропорциональности во времена Л. Ф. Магницкого. Придумайте задачу и решите её этим способом.
Номер слайда 24
Вы можете использовать данное оформление для создания своих презентаций, но в своей презентации вы должны указать источник шаблона: Ранько Елена Алексеевна учитель начальных классов МАОУ лицей №21 г. Иваново. Сайт: http://elenaranko.ucoz.ru/
Иваново. Сайт: http://elenaranko.ucoz.ru/
Номер слайда 25
Интернет – ресурсы:http://www.mamusik.ru//upload/userimages/kpwoktwyzvbpodhaalxho.jpeg фонhttp://s1.pic4you.ru/allimage/y2012/10-26/12216/2601759.png книгиhttp://mosaica.ru/sites/default/files/news/preview/2009/07/27/1_sent.jpg колокольчикhttp://img-fotki.yandex.ru/get/6409/131624064.235/0_906e7_8c51635e_XLосенний букетhttp://s3.uploads.ru/5o8gm.pngрамка
Обратно пропорциональный – объяснение и примеры
Что означает обратно пропорциональный?
В повседневной жизни мы часто сталкиваемся с ситуациями, когда на изменение значений одной величины влияет изменение значений другой величины.
Например, , сирена приближающейся пожарной машины или машины скорой помощи становится тем громче, чем машина приближается к вам, и тише, чем дальше. Вы заметили, что чем меньше расстояние между вами и транспортным средством, тем громче сирена и чем больше расстояние, тем тише становится сирена.Этот тип ситуации упоминается как обратная пропорция или иногда косвенная пропорция.
Прямая и косвенная пропорция — это два понятия, с которыми мы все знакомы, только, может быть, не на математическом уровне. Прямая и обратная пропорции используются, чтобы показать, как две величины связаны друг с другом.
В этой статье мы узнаем об обратной и косвенной пропорции и о том, как эти понятия важны в реальных жизненных ситуациях. но прежде чем мы начнем, давайте напомним себе о концепции прямой пропорциональности.
Прямая пропорция
Две переменные a и b называются прямо пропорциональными, если увеличение одной переменной приводит к увеличению другой переменной, и наоборот. Это означает, что в прямой зависимости отношение соответствующих значений переменных остается постоянным. В этом случае, если значения b; b 1 , b 2 соответствует значениям a; а 1 , а 2 соответственно, то их отношение постоянно;
Это означает, что в прямой зависимости отношение соответствующих значений переменных остается постоянным. В этом случае, если значения b; b 1 , b 2 соответствует значениям a; а 1 , а 2 соответственно, то их отношение постоянно;
a 1/ /b 1 = a 2 /b 2
Прямая пропорция представлена знаком пропорциональности «∝» в виде a ∝ b.Формула прямой вариации:
a/b = k
, где k называется константой пропорциональности.
Обратная пропорция
В отличие от прямой зависимости, где одна величина прямо пропорциональна изменению другой величины, в обратной пропорции увеличение одной переменной вызывает уменьшение другой переменной, и наоборот. Две переменные a и b называются обратно пропорциональными, если; а∝1/б. В этом случае увеличение переменной b вызывает уменьшение значения переменной a.Точно так же уменьшение переменной b вызывает увеличение значения переменной a.
Формула косвенной пропорциональности
Если переменная a обратно пропорциональна переменной b, то это может быть представлено в формуле:
a∝1/b
ab = k; где k — постоянная пропорциональности.
Чтобы составить уравнение обратной пропорциональности, необходимо выполнить следующие шаги:
- Запишите пропорциональную зависимость
- Запишите уравнение, используя пропорциональную константу
- Теперь найдите значение константы, используя заданные значения
- Подставьте значение константы в уравнении.
Реальные примеры концепции обратной пропорциональности
- Время, затрачиваемое определенным числом рабочих на выполнение части работы, обратно пропорционально количеству занятых рабочих. Это означает, что чем меньше рабочих, тем больше времени требуется для завершения работы, и наоборот.
- Скорость движущегося судна, такого как поезд, транспортное средство или корабль, изменяется обратно пропорционально времени, затрачиваемому на преодоление определенного расстояния.
 Чем выше скорость, тем меньше времени уходит на преодоление расстояния.
Чем выше скорость, тем меньше времени уходит на преодоление расстояния.
Пример 1
35 рабочих собирают кофе на плантации за 8 дней. Сколько времени потребуется 20 рабочим, чтобы собрать кофе на одной плантации?
Решение
- 35 рабочих собирают кофе за 8 дней
Продолжительность, затрачиваемая одним рабочим = (35 × 8) дней
- Теперь рассчитайте продолжительность, затрачиваемую 20 рабочими
= 14 дней
Следовательно, 20 рабочих займут 14 дней.
Пример 2
6 коз или 8 овец пасутся за 28 дней. За какое время 9 коз и 2 овцы будут пастись на одном поле?
Решение
6 коз = 8 овец
⇒ 1 коза = 8/6 овец
⇒ 9 коз ≡ (8/6 × 9) овец = 12 овец
⇒ (9 коз + 2 овцы) ≡ (12 овец + 2 овец) = 14 овец
Теперь 8 овец => 28 дней
Одна овца будет пастись через (28 × 8) дней
⇒ 14 овец возьмут (28 × 8)/14 дней
= 16 дней
Следовательно, 9 коз и 2 овцы будут пастись на поле 16 дней.
Пример 3
Девять кранов могут наполнить резервуар за четыре часа. За какое время один и тот же резервуар наполнится двенадцатью кранами с одинаковым расходом?
Решение
Пусть отношения;
x 1 / x 2 / x 2 y 2/ y 1
⇒ 9 000 × = 12/4
x = 3
Следовательно, 12 кран займет 3 часа для заполнения бака .
Скорость, отношение и пропорциональное рассуждение
6 класс: Рассуждение о скорости, соотношении и пропорциональности
Рейтинг:
https:// www.georgiastandards.org/CommonCore/Common%20Core%20Frameworks/CCGPS_Math_6_6thGrade_Unit2SE.pdf
Общие базовые стандарты
Стандарты содержания
6.RP.1 — Понимать концепцию отношения и использовать язык отношений для описания отношений отношений между двумя величинами.
6.RP.2 — Понимать концепцию удельной ставки a/b, связанную с отношением a:b, где b ≠ 0, и использовать формулировку ставок в контексте соотношения отношения.
6.RP.3 — Используйте рассуждения об отношении и скорости для решения реальных и математических задач, например, рассуждая о таблицах эквивалентных отношений, ленточных диаграммах, линейных диаграммах с двойным числом или уравнениях.
6.RP.3a — Составьте таблицы эквивалентных отношений, связывающих величины с целыми числами, найдите недостающие значения в таблицах и нанесите пары значений на координатную плоскость. Используйте таблицы для сравнения коэффициентов.
6.RP.3b — Решение проблем с расценками за единицу, в том числе связанных с ценообразованием за единицу и постоянной скоростью.
6.RP.3c — Найти процент от количества как ставку на 100; решать задачи на нахождение целого по заданной части и процентам.
6.RP.3d — Использовать соотношение для преобразования единиц измерения; правильно манипулировать и преобразовывать единицы при умножении или делении величин.
Стандарты математической практики
MP.1 Понимать проблемы и настойчиво решать их.
MP.2 Рассуждайте абстрактно и количественно.
MP.3 Создавать жизнеспособные аргументы и критиковать рассуждения других.
MP.4 Модель с математикой.
Описание блока
Этот модуль «Оценка, отношение и пропорциональные рассуждения с использованием эквивалентных дробей» от Министерства энергетики Джорджии представляет собой набор из 6 заданий, охватывающих основные концепции отношений и ставок с использованием эквивалентных дробей. Общий блок рассчитан на 3 — 4 недели. В этом блоке учащиеся получат более глубокое понимание пропорциональных рассуждений, понимая, что отношение — это сравнение двух чисел или величин.Студенты будут развивать и использовать мультипликативное мышление и находить проценты, используя тот же процесс для решения ставок и пропорций. Наконец, учащиеся будут решать реальные задачи, связанные с единицами измерения, которые необходимо преобразовать.
Предостережения
Учителя штата Коннектикут должны знать, что модуль не полностью охватывает область 6.RP.3a, используя таблицы соотношений и ленточные диаграммы для решения задач. В состав блока не входят следующие компоненты:
- дифференциация или поддержка для учащихся, работающих выше/ниже уровня своего класса, изучающих английский язык или учащихся с ограниченными возможностями.
- использование технологий или средств массовой информации.
- явные связи между стандартами математической практики в модуле и содержанием.
- структур для реализации и выполнения задач производительности. Инструктивных заметок нет (ключи ответов, рубрики, образцы работ учащихся).
Обоснование выбора
В этом модуле рассматривается одна из основных областей применения этого класса. Стандарты, рассматриваемые в каждой задаче, указаны в начале задачи; есть свидетельство строгости и согласованности в области отношений и пропорциональных рассуждений. Строгие задачи актуальны и заставляют задуматься; они способствуют контекстуальному пониманию стандартов.
Строгие задачи актуальны и заставляют задуматься; они способствуют контекстуальному пониманию стандартов.
6 класс | Математика | Iowa Core
В 6-м классе учебное время должно быть сосредоточено на четырех важнейших областях: (1) подключение отношения и скорости к целочисленному умножению и делению и использование понятий отношения и скорости для решения задач; (2) завершение понимания деления дробей и расширение понятия числа на систему рациональных чисел, включающую отрицательные числа; (3) написание, интерпретация и использование выражений и уравнений; и (4) развитие понимания статистического мышления.
- Учащиеся используют рассуждения об умножении и делении для решения задач на отношения и оценки величин. Рассматривая эквивалентные отношения и коэффициенты как производные от пар строк (или столбцов) в таблице умножения и расширяя их, а также анализируя простые рисунки, показывающие относительный размер величин, учащиеся связывают свое понимание умножения и деления с отношениями и коэффициентами.
 . Таким образом, учащиеся расширяют круг задач, для решения которых они могут использовать умножение и деление, а также связывают соотношения и дроби.Студенты решают широкий спектр задач, связанных с отношениями и коэффициентами.
. Таким образом, учащиеся расширяют круг задач, для решения которых они могут использовать умножение и деление, а также связывают соотношения и дроби.Студенты решают широкий спектр задач, связанных с отношениями и коэффициентами.
- Учащиеся используют значения дробей, значения умножения и деления, а также взаимосвязь между умножением и делением, чтобы понять и объяснить, почему процедуры деления дробей имеют смысл. Учащиеся используют эти операции для решения задач. Учащиеся расширяют свое прежнее понимание числа и порядка чисел на полную систему рациональных чисел, которая включает в себя отрицательные рациональные числа и, в частности, отрицательные целые числа.Они рассуждают о порядке и абсолютном значении рациональных чисел и о расположении точек во всех четырех квадрантах координатной плоскости.
- Учащиеся понимают, как использовать переменные в математических выражениях. Они пишут выражения и уравнения, соответствующие заданным ситуациям, оценивают выражения и используют выражения и формулы для решения задач.
 Учащиеся понимают, что выражения в разных формах могут быть эквивалентны, и они используют свойства операций для перезаписи выражений в эквивалентных формах.Учащиеся знают, что решениями уравнения являются значения переменных, которые делают уравнение верным. Учащиеся используют свойства операций и идею сохранения равенства обеих частей уравнения для решения простых одношаговых уравнений. Учащиеся составляют и анализируют таблицы, например, таблицы величин, находящихся в эквивалентных соотношениях, и используют уравнения (например, 3 x = y ) для описания взаимосвязей между величинами.
Учащиеся понимают, что выражения в разных формах могут быть эквивалентны, и они используют свойства операций для перезаписи выражений в эквивалентных формах.Учащиеся знают, что решениями уравнения являются значения переменных, которые делают уравнение верным. Учащиеся используют свойства операций и идею сохранения равенства обеих частей уравнения для решения простых одношаговых уравнений. Учащиеся составляют и анализируют таблицы, например, таблицы величин, находящихся в эквивалентных соотношениях, и используют уравнения (например, 3 x = y ) для описания взаимосвязей между величинами.
- Опираясь на свое понимание числа и закрепляя его, учащиеся начинают развивать свои способности к статистическому мышлению.Учащиеся понимают, что распределение данных может не иметь определенного центра и что разные способы измерения центра дают разные значения. Медиана измеряет центр в том смысле, что это примерно среднее значение. Средние показатели центрируются в том смысле, что это значение, которое приняла бы каждая точка данных, если бы сумма значений данных была перераспределена поровну, а также в том смысле, что это точка баланса.
 Учащиеся признают, что показатель изменчивости (межквартильный размах или среднее абсолютное отклонение) также может быть полезен для обобщения данных, поскольку два совершенно разных набора данных могут иметь одно и то же среднее значение и медиану, но различаться по своей изменчивости.Учащиеся учатся описывать и обобщать наборы числовых данных, выявляя кластеры, пики, пробелы и симметрию с учетом контекста, в котором данные были собраны.
Учащиеся признают, что показатель изменчивости (межквартильный размах или среднее абсолютное отклонение) также может быть полезен для обобщения данных, поскольку два совершенно разных набора данных могут иметь одно и то же среднее значение и медиану, но различаться по своей изменчивости.Учащиеся учатся описывать и обобщать наборы числовых данных, выявляя кластеры, пики, пробелы и симметрию с учетом контекста, в котором данные были собраны.Учащиеся 6-го класса также дополняют свою работу с площадью в начальной школе, рассуждая о взаимосвязях между формами для определения площади, площади поверхности и объема. Они находят площади прямоугольных треугольников, других треугольников и специальных четырехугольников, разлагая эти фигуры, переставляя или удаляя части и связывая фигуры с прямоугольниками.Используя эти методы, учащиеся обсуждают, разрабатывают и обосновывают формулы площадей треугольников и параллелограммов. Учащиеся находят площади многоугольников и площади поверхностей призм и пирамид, разлагая их на части, площадь которых они могут определить.
 Они рассуждают о прямоугольных призмах с дробными длинами сторон, чтобы распространить формулы для объема прямоугольной призмы на дробные длины сторон. Готовятся к работе над чертежами и конструкциями в масштабе 7 класса, рисуя многоугольники в координатной плоскости.
Они рассуждают о прямоугольных призмах с дробными длинами сторон, чтобы распространить формулы для объема прямоугольной призмы на дробные длины сторон. Готовятся к работе над чертежами и конструкциями в масштабе 7 класса, рисуя многоугольники в координатной плоскости.
Правило 3: прямое и обратное
В сегодняшней статье мы будем работать над пропорциями . На этот раз мы рассмотрим способ решения прямой и обратной пропорции: правило 3 .
Что такое правило 3?
Правило 3 — это операция, которая помогает нам быстро решать как прямые, так и обратные пропорции словесных задач.
Чтобы использовать правило 3, нам нужны три значения: два пропорциональных друг другу и третье.Оттуда мы вычислим четвертое значение .
Прямое правило 3
Начнем с рассмотрения того, как применить в случае прямых пропорций .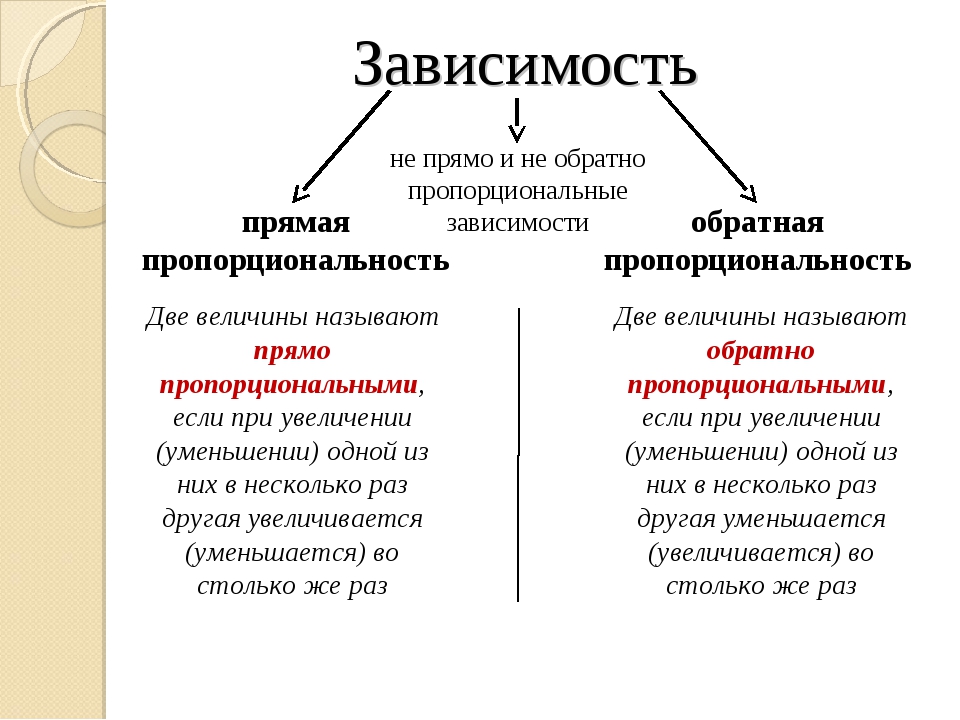
Мы поместим 3 значения (которые мы назовем «a» , «b» и «c» ) и неизвестное значение, которое мы хотим вычислить ( «x» ) в таблице. Далее применим следующую формулу:
В качестве примера решим следующую задачу:
По прибытии в отель персонал дал нам карту с указанием достопримечательностей города и сказал, что 5 сантиметров на карте соответствуют 600 метрам в действительности.Сегодня мы хотим отправиться в парк, который находится в 8 сантиметрах от отеля на карте. Как далеко от отеля парк?
Давайте составим таблицу с 3 значениями и неизвестным значением («x»), и мы найдем «x» с помощью только что изученной формулы .
Сантиметры на карте Метры в реальности
Ответ: Парк находится в 960 метрах от отеля.
Обратное правило 3
Теперь посмотрим, как применить правило 3 в случае обратных пропорций .
Мы поместим 3 значения и неизвестное значение в таблицу , так же, как мы сделали в предыдущем случае, , но мы применим другую формулу:
Давайте рассмотрим пример:
Вчера 2 грузовика перевезли товар из порта на склад.Сегодня 3 грузовика того же размера, что и вчера, должны будут совершить 6 рейсов, чтобы перевезти такое же количество товаров со склада в торговый центр. Сколько рейсов грузовики сделали вчера?
Мы помещаем значения в таблицу и применяем формулу для обратного правила 3 :
Грузовые автомобили Необходимые поездки
Ответ: Вчера 2 грузовика совершили 9 рейсов.
Что вы думаете об этом посте? Разве не легко применить правило 3 к пропорциональным задачам со словами!
Вы можете узнать больше о прямой и обратной пропорции из этого предыдущего поста в нашем блоге: Правило трех задач.
Помните, что с помощью Smartick вы сможете практиковать упражнений, решать задачи с пропорциями слов и и многое другое! Попробуйте бесплатно!
Узнать больше:
Веселье — любимый способ обучения нашего мозга
Дайан Акерман
Smartick — увлекательный способ изучения математики- 15 минут веселья в день
- Адаптируется к уровню вашего ребенка
- Миллионы учеников с 2009 года
Группа создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.
Математика 6 класс
1. Учащиеся свяжут отношение и скорость с умножением и делением целых чисел и будут использовать понятия отношения и скорости для решения задач.
Учащиеся свяжут отношение и скорость с умножением и делением целых чисел и будут использовать понятия отношения и скорости для решения задач.
2. Учащиеся завершат понимание деления дробей и распространят понятие числа на систему рациональных чисел, которая включает отрицательные числа.
3. Учащиеся будут писать, интерпретировать и использовать выражения и уравнения.
4. Учащиеся разовьют понимание статистического мышления.
Больше заниматься математикой дома
Две важные цели для всех учащихся: 1) научиться ценить математику и 2) стать уверенными в своих способностях заниматься математикой. Родители могут помочь детям развить склонность к математике, воспитывая их естественное любопытство и оказывая им поддержку и поддержку.
Математика повсюду, но многие дети ее не видят. Ищите способы отметить и закрепить математические навыки дома. Например:
Например:
· рассказывайте о том, как вы используете математику на работе или дома
· вовлекайте детей в задачи, требующие вычисления, измерения, оценки, построения, выполнения указаний, решения проблем и рассуждений
5 · ищите занятия, которые требуют от детей использования их математических навыков, таких как построение масштабных моделей, приготовление пищи, планирование поездок и игра в логические игры
Ищите игры и занятия, которые учат и/или укрепляют математику и мышление.Например, ищите игры, которые:
· Требовать и развивать навыки с психическими вычислениями и оценками
· Требовать, чтобы игроки использовали свои математические навыки
· Влиять на разработку стратегий
· Требовать игроки должны думать о вероятности наступления определенных событий
· требуется использование навыков пространственной визуализации
· требуется логическое мышление
Когда вы видите статьи, содержащие данные, которые могут заинтересовать ваших детей (г. , спортивная статистика, данные о подростковом курении, факты о стихийных бедствиях), поделитесь ими и расскажите, что означают цифры.
, спортивная статистика, данные о подростковом курении, факты о стихийных бедствиях), поделитесь ими и расскажите, что означают цифры.
Поделитесь своими стратегиями и методами решения проблем, стратегиями умственных вычислений и стратегиями оценки. Пусть ваши дети научат вас чему-нибудь. Поработайте над одной и той же проблемой, а затем сравните стратегии и ответы.
Предложите своим детям объяснить, что они узнали на уроке математики, или пусть они научат этому вас. Это дает детям возможность прояснить свое мышление, попрактиковаться в новых навыках и попрактиковаться в математическом общении.
Если у ваших детей есть доступ к технологиям, ищите программное обеспечение и приложения, которые укрепляют и обучают математическим понятиям. Помогите своим детям научиться пользоваться математическими утилитами, такими как электронные таблицы и графические программы.
6 класс Обзор
Соотношение и пропорциональные отношения
· Понимание понятий соотношения для решения задач на соотношение.
· Словарь
o Отношение – сравнение двух величин, выраженных как 3/5, 3:5 или 3 к 5.
o Удельная ставка – ставка с одним из чисел равна 1 или количество 1.
o Проценты – из 100. o Прибыль – сумма, на которую доходы превышают расходы.
Система счисления
· Применить и расширить прежнее понимание умножения и деления для деления дробей на дроби
· Применить и расширить предыдущее понимание чисел на систему рациональных чисел.
· Словарь
o Множитель – одно или несколько целых чисел, которые перемножаются для получения произведения.
o Множитель – произведение данного целого числа на другое целое число.
o Простое число — число, имеющее ровно два делителя, единицу и само себя.
o Составной – число с более чем двумя делителями.
o Разложение на простые множители – произведение простых чисел, возможно, с некоторыми повторениями, в результате чего получается желаемое число. БЫВШИЙ. 27 = 3 x 3 x 3 или 30 = 2 x 3 x 5
o Квадратное число – число, являющееся результатом произведения числа, умноженного само на себя.
o Наименьшее общее кратное (НОК) – наименьшее кратное, общее для двух или более чисел.
o Наибольший общий множитель (GCF) – наибольший множитель, общий для двух или более чисел.
o Экспонента — небольшое выпуклое число, указывающее, сколько раз используется коэффициент.
o Повторяющаяся десятичная дробь – десятичная дробь с шаблоном фиксированного числа цифр, который повторяется вечно.
o Конечная десятичная дробь – десятичная дробь, которая заканчивается или завершается.
Выражения и уравнения
· Применить и расширить прежнее понимание арифметики на алгебраические выражения.
· Рассуждайте и решайте уравнения и выражения с одной переменной.
· Представление и анализ количественных взаимосвязей между зависимыми и независимыми переменными.
· Словарь
o Распределительное свойство – математическое свойство, используемое для перезаписи выражений, включающих сложение и умножение. БЫВШИЙ. 4(5 + x) = 4(5) + 4(x) = 20 + 4x
o Порядок операций – установленное соглашение на проведение расчетов с одной или несколькими операциями. ( Скобки, Экспоненты, Умножение/деление (движение слева направо), сложение/вычитание (движение слева направо)
o Эквивалент – равенство по значению
o Неравенство – Утверждение, которое сравнивает две величины. <, >, < и > используются для выражения неравенства.
<, >, < и > используются для выражения неравенства.
o Выражение – математическая фраза, содержащая числа, переменные и символы операций.
o Переменная – величина, которая может изменяться, часто обозначается буквой
o Коэффициент – число, которое умножается на переменную в уравнении или выражении.
Геометрия
· Решайте реальные и математические задачи, связанные с площадью, площадью поверхности и объемом.
· Словарь
o Площадь – мера площади поверхности, ограниченной границей фигуры, количества квадратных единиц в фигуре.
o Периметр – мера расстояния вокруг двумерной фигуры.
o Объем – объем пространства, занимаемый трехмерной фигурой, количество единичных кубов, вписывающихся в фигуру.
o Площадь поверхности – площадь, необходимая для покрытия трехмерной формы.
o Координаты X и Y – числа в паре координат, используемые для определения точки на координатном графике.
Статистика и вероятность
· Развить понимание статистической изменчивости.
· Обобщить и описать распределения.
· Словарь
o Среднее – значение, полученное при объединении всех данных и последующем их равномерном распределении (среднее)
o Mode – число, которое встречается чаще всего в заданном наборе данных.
o Диапазон – разница между максимальным и минимальным значением в распределении.
o Линейный график – способ организации данных вдоль числовой строки, где X (или другие символы) над числом показывают, как часто упоминается каждое значение.
o Таблица частот —
o Коробчатая диаграмма – отображение, показывающее распределение значений в наборе данных, разделенных на 4 группы одинакового размера, составленные из сводки данных из 5 чисел (минимальное значение, нижний квартиль, медиана, верхний квартиль и максимальное значение)
o Верхний квартиль — медиана данных слева от медианы.
o Нижний квартиль – медиана данных справа от медианы.
o Выброс — значение, которое находится далеко от центра распределения данных и не похоже на другие значения.
М/Д Математика 6 класс — 1205010
Неравенство в тематических парках: часть 2:Следуйте за Джамалом, который представляет алгебраические неравенства на числовой прямой во время посещения тематического парка со своей семьей в этом интерактивном руководстве.
Это вторая часть серии статей о неравенствах, состоящей из двух частей. Нажмите ЗДЕСЬ , чтобы открыть часть 1.
Тип: Оригинальное учебное пособие для учащихся
Неравенство в тематических парках: часть 1: Следуйте за Джамалом, когда он переводит письменные описания тематического парка в алгебраические неравенства в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Алгебраические выражения Часть 2: Умножение и деление:Помогите Оскару перевести письменные описания умножения и деления в алгебраические выражения с помощью этого интерактивного руководства.
Это часть 2 из 3. Нажмите ниже, чтобы открыть другие руководства из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Часть 3 тома: Отсутствующие размеры: Помогите Синди найти недостающее измерение прямоугольной призмы в ее работе службы доставки с помощью этого интерактивного руководства.
Это третья часть из трех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Том Часть 2:Следуйте за Синди, пока она исследует кубы с дробными единицами измерения и находит объем прямоугольных призм с рациональными размерами в этом интерактивном учебном пособии.
Это вторая часть из трех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Том Часть 1: Следуйте за Синди, когда она узнает о формулах объема для создания ящиков в этом интерактивном руководстве.
Это первая часть из трех частей.Нажмите ниже, чтобы открыть другие руководства из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Эквивалентные соотношения:Помогите Лили определить и создать эквивалентные коэффициенты в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Рациональные числа на Аляске: Следуйте за Маттео, пока он исследует противоположные числа, положительные и отрицательные рациональные числа и ноль в контексте реального мира, планируя и отправляясь в круиз по Аляске, в этом интерактивном учебном пособии.
Тип: Оригинальное учебное пособие для учащихся
Математические модели и социальное дистанцирование:Из этого интерактивного руководства вы узнаете, как математические модели могут показать, почему социальное дистанцирование во время эпидемии или пандемии важно.
Тип: Оригинальное учебное пособие для учащихся
Плавание через вычитание десятичных знаков: Выполните вычитание десятичных дробей до тысячных, используя стандартный алгоритм, в этом интерактивном учебном пособии.
Тип: Оригинальное учебное пособие для учащихся
Добавить еще одну начинку: Добавление десятичных знаков:Из этого интерактивного руководства научитесь добавлять десятичные дроби к тысячным, используя стандартный алгоритм в магазине мороженого.
Тип: Оригинальное учебное пособие для учащихся
Балансировка машины: Используйте модели для решения проблем с равновесием на космической станции в этом интерактивном учебном пособии по математике и естественным наукам.
Тип: Оригинальное учебное пособие для учащихся
Замки, катапульты и данные: гистограммы, часть 2:Узнайте, как интерпретировать гистограммы для анализа данных и помочь изобретателю предсказать дальность действия катапульты во второй части этой серии интерактивных руководств.В частности, вы научитесь описывать форму и распространение распределений данных.
Нажмите ЗДЕСЬ , чтобы открыть часть 1.
Тип: Оригинальное учебное пособие для учащихся
Замки, катапульты и данные: гистограммы, часть 1: Из этого интерактивного руководства вы узнаете, как создать гистограмму для отображения непрерывных данных о снарядах, запущенных катапультой.
Это первая часть из двух частей. Нажмите ЗДЕСЬ , чтобы открыть часть 2.
Тип: Оригинальное учебное пособие для учащихся
Ферма MacCoder, часть 4: повторяющиеся циклы:Изучите компьютерное кодирование на ферме, используя операторы IF и повторяющиеся циклы для вычисления математических выражений.В этом интерактивном руководстве вы также решите задачи, связанные с неравенством.
Щелкните ниже, чтобы ознакомиться с другими руководствами из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Ферма MacCoder, часть 3: операторы if: Изучение компьютерного кодирования на ферме с использованием операторов отношения и операторов IF для оценки выражений. В этом интерактивном руководстве вы также решите задачи, связанные с неравенством.
В этом интерактивном руководстве вы также решите задачи, связанные с неравенством.
Щелкните ниже, чтобы ознакомиться с другими руководствами из этой серии.
Тип: Оригинальное учебное пособие для учащихся
MacCoder’s Farm, часть 2: Заявления об условиях:Изучите компьютерное кодирование на ферме, используя условия и операторы ЕСЛИ в этом интерактивном руководстве.Вы также получите возможность применить порядок операций при использовании кодирования для решения проблем.
Щелкните ниже, чтобы ознакомиться с другими руководствами из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Ферма MacCoder, часть 1: объявление переменных: Изучите компьютерное кодирование на ферме, объявив и инициализировав переменные в этом интерактивном руководстве. Вы также получите возможность попрактиковаться в своих навыках длинного дивизиона.
Вы также получите возможность попрактиковаться в своих навыках длинного дивизиона.
Тип: Оригинальное учебное пособие для учащихся
Движущееся БЕЗУМИЕ:Узнайте, как рассчитать и интерпретировать среднее абсолютное отклонение (MAD) наборов данных в этом интерактивном учебном пособии по статистике на тему путешествий.
Тип: Оригинальное учебное пособие для учащихся
Что на ланч?: Узнайте, как формируются аргументы с утверждениями, причинами и доказательствами. В этом интерактивном руководстве вы прочитаете несколько коротких речей студентов, которые надеются быть избранными президентом школьного совета.Мы проследим утверждение, сделанное каждым студентом, а также причины и доказательства, которые они используют в его поддержку.
В этом интерактивном руководстве вы прочитаете несколько коротких речей студентов, которые надеются быть избранными президентом школьного совета.Мы проследим утверждение, сделанное каждым студентом, а также причины и доказательства, которые они используют в его поддержку.
Тип: Оригинальное учебное пособие для учащихся
Это может быть зоопарк данных!:Узнайте, как рассчитать и интерпретировать среднее значение, медиану, моду и диапазон наборов данных из зоопарка в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Соотношение помощников шеф-повара: В этом интерактивном учебном пособии вы будете организовывать информацию в виде таблицы и записывать отношения, эквивалентные заданному отношению, чтобы решать реальные и математические задачи.
Тип: Оригинальное учебное пособие для учащихся
Куда делись все скраб-джей?:Изучите ограничивающие факторы экосистемы Флориды и опишите, как эти ограничивающие факторы влияют на одну местную популяцию — флоридскую кустарниковую сойку — с помощью этого интерактивного учебного пособия.
Тип: Оригинальное учебное пособие для учащихся
По горячим следам: Узнайте, как температура влияет на скорость химических реакций, с помощью этого интерактивного руководства.
Тип: Оригинальное учебное пособие для учащихся
Да или нет ГМО?:Узнайте, что такое генная инженерия и некоторые области применения этой технологии.В этом интерактивном руководстве вы получите представление о некоторых преимуществах и потенциальных недостатках генной инженерии. В конце концов, вы сможете критически относиться к генной инженерии и написать аргумент, описывающий вашу собственную точку зрения на ее влияние.
Тип: Оригинальное учебное пособие для учащихся
Гольф: где отрицательные числа — это хорошо: Узнайте, как создавать и использовать числовые линии с положительными и отрицательными числами, отображать положительные и отрицательные числа, находить их расстояние от нуля, находить число, противоположное числу, используя числовую прямую и знаки, и распознавать, что ноль является своей собственной противоположностью с помощью этого интерактивного, учебник на тему гольфа.
Тип: Оригинальное учебное пособие для учащихся
Решение уравнений: одна и та же переменная, обе стороны, одно решение:В этой игре-вызове вам предстоит решать уравнения с переменными с обеих сторон.Каждое уравнение имеет действительное решение. Используйте кнопку «Научи меня», чтобы просмотреть содержимое перед испытанием. После испытания просмотрите проблемы по мере необходимости. Попробуйте еще раз, чтобы ответить на все контрольные вопросы правильно! Наборы вопросов меняются в зависимости от игры, поэтому не стесняйтесь играть в игру несколько раз по мере необходимости! Удачи!
Тип: обучающая игра
Ice Ice Maybe: игра по оценке операций:
Эта веселая интерактивная игра помогает тренировать навыки оценивания, используя различные операции по выбору, включая сложение, вычитание, умножение, деление, использование десятичных дробей, дробей и процентов.
Различные уровни сложности делают эту игру подходящей для разных возрастов и уровней способностей.
Сложение/ Вычитание: Сложение и вычитание целых чисел, сложение и вычитание десятичных дробей.
Умножение/Деление: Умножение и сложение целых чисел.
Проценты: Определите процент от целого числа.
Дроби: Умножение и деление целого числа на дробь, а также применение свойств операций.
Тип: обучающая игра
Цветочная сила: игра в упорядочение рациональных чисел:
Это веселая интерактивная игра, которая помогает учащимся практиковаться в упорядочивании рациональных чисел, включая десятичные дроби, дроби и проценты. Вы сажаете и собираете цветы за деньги. Позвольте пчелам опылять, и вы сможете умножить свой урожай и денежные вознаграждения!
Вы сажаете и собираете цветы за деньги. Позвольте пчелам опылять, и вы сможете умножить свой урожай и денежные вознаграждения!
Тип: обучающая игра
Фракция Викторина:Проверьте свои навыки фракции, отвечая на вопросы на этом сайте.В этом тесте вам предлагается упростить дроби, преобразовать дроби в десятичные числа и проценты, а также ответить на вопросы по алгебре, связанные с дробями. Вы даже можете выбрать уровень сложности, типы вопросов и ограничение по времени.
Тип: обучающая игра
Временная викторина по алгебре: В этом задании на время учащиеся решают линейные уравнения (одно- и двухшаговые) или квадратные уравнения различной сложности в зависимости от выбранных начальных условий. Это задание позволяет учащимся практиковаться в решении уравнений, в то время как задание записывает их баллы, чтобы они могли отслеживать свой прогресс. Это задание включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Это задание позволяет учащимся практиковаться в решении уравнений, в то время как задание записывает их баллы, чтобы они могли отслеживать свой прогресс. Это задание включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Тип: обучающая игра
Алгебра четыре: В этом упражнении два ученика играют в смоделированную игру «Соедини четыре», но чтобы разместить фигуру на доске, они должны правильно решить алгебраическое уравнение.Эта деятельность позволяет учащимся практиковаться в решении уравнений различной сложности: одношаговых, двухшаговых или квадратных уравнений и использовании дистрибутивного свойства при желании. Это задание включает в себя дополнительные материалы, в том числе справочную информацию по изучаемым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Это задание включает в себя дополнительные материалы, в том числе справочную информацию по изучаемым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Тип: обучающая игра
Лабиринт игры:В этом упражнении учащиеся вводят координаты, чтобы проложить путь к месту назначения, минуя мины.Это задание позволяет учащимся изучить декартовы координаты и плоскость декартовых координат. Это задание включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Тип: обучающая игра
Улыбки: В этом онлайн-задаче на решение задач учащиеся применяют алгебраические рассуждения, чтобы определить «стоимость» отдельных типов лиц из суммы хмурых, улыбчивых и нейтральных лиц. На этой странице представлены три иллюстрированные задачи, связанные с решением систем уравнений, а также советы по обдумыванию проблемы, решения и других подобных задач.
На этой странице представлены три иллюстрированные задачи, связанные с решением систем уравнений, а также советы по обдумыванию проблемы, решения и других подобных задач.
Тип: Задача решения проблем
Треугольные столы:Студентов просят использовать диаграмму или таблицу, чтобы написать алгебраическое выражение и использовать выражение для решения задач.
Тип: Задача решения проблем
Копейки в рай: Цель этого задания — дать учащимся условия для исследования больших чисел и измерений. Студенты должны бегло преобразовать единицы с очень большими числами, чтобы успешно выполнить это задание.Общее количество пенни, отчеканенных либо за один год, либо за последнее столетие, феноменально велико, и его трудно понять. Один из способов оценить, насколько велико это число, — это рассмотреть, как далеко могли бы добраться все эти пенни, если бы мы могли сложить их одну поверх другой: это еще одно феноменально большое число, но то, насколько оно велико, может стать неожиданностью. .
Студенты должны бегло преобразовать единицы с очень большими числами, чтобы успешно выполнить это задание.Общее количество пенни, отчеканенных либо за один год, либо за последнее столетие, феноменально велико, и его трудно понять. Один из способов оценить, насколько велико это число, — это рассмотреть, как далеко могли бы добраться все эти пенни, если бы мы могли сложить их одну поверх другой: это еще одно феноменально большое число, но то, насколько оно велико, может стать неожиданностью. .
Тип: Задача решения проблем
Периметр прямоугольника 1: В этом задании дается словесное описание вычисления периметра прямоугольника и предлагается учащимся найти выражение для этого периметра.Затем они должны использовать выражение для оценки периметра для конкретных значений двух переменных.
Тип: Задача решения проблем
Периметр прямоугольника 2:Учащихся просят определить, эквивалентны ли данные выражения.
Тип: Задача решения проблем
Периметр прямоугольника 3:Цель этого задания — попросить учащихся написать выражения и подумать, что означает эквивалентность двух выражений.
Тип: Задача решения проблем
Предложение Джинни: Учащихся просят исследовать, а затем написать выражение с показателем степени. Цель этой задачи — представить идею экспоненциального роста, а затем связать этот рост с выражениями, включающими показатели степени. Это хорошо иллюстрирует, как быстро растут экспоненциальные выражения.
Цель этой задачи — представить идею экспоненциального роста, а затем связать этот рост с выражениями, включающими показатели степени. Это хорошо иллюстрирует, как быстро растут экспоненциальные выражения.
Тип: Задача решения проблем
Ваза Кендалла — Налог:В этой задаче учащемуся предлагается найти 3% налога с продаж на вазу стоимостью 450 долларов.
Тип: Задача решения проблем
Анна в Вашингтоне: Цель этого задания — дать учащимся возможность решить сложную многоступенчатую процентную задачу, к которой можно подойти несколькими способами. Студентов просят найти стоимость еды до вычета налогов и дать чаевые, если известна общая стоимость еды. Задача может иллюстрировать несколько стандартов в зависимости от предварительных знаний учащихся и подхода, используемого для решения проблемы.
Студентов просят найти стоимость еды до вычета налогов и дать чаевые, если известна общая стоимость еды. Задача может иллюстрировать несколько стандартов в зависимости от предварительных знаний учащихся и подхода, используемого для решения проблемы.
Тип: Задача решения проблем
Основание и высота:Учащихся просят определить и проиллюстрировать все возможные описания основания и высоты заданного треугольника.
Тип: Задача решения проблем
Здание Христо: Учащихся просят нарисовать масштабную модель здания и найти соответствующие объем и площадь поверхности модели и здания, которые представляют собой прямоугольные призмы.
Тип: Задача решения проблем
Покраска амбара:Студентов просят использовать предоставленную информацию, чтобы определить стоимость покраски амбара.
Тип: Задача решения проблем
Добавление нескольких: Цель этого задания — лучше понять факторы и общие факторы.Студенты должны использовать распределительное свойство, чтобы показать, что сумма двух чисел, имеющих общий делитель, также кратна общему делителю.
Тип: Задача решения проблем
Миля Хай:Учащихся просят рассуждать и объяснять положение двух мест относительно уровня моря.
Тип: Задача решения проблем
Билеты в кино: Цель этого задания состоит в том, чтобы учащиеся решили задачи с десятичными знаками в контексте концепции, поддерживающей финансовую грамотность, а именно инфляции.Инфляция – это устойчивый рост среднего уровня цен. В этом задании учащихся просят сравнить покупательную способность 20 долларов в 1987 и 2012 годах, по крайней мере, в отношении билетов в кино.
Тип: Задача решения проблем
Приготовление горячего какао, вариант 1:Учащихся просят решить задачу на деление дроби, используя как визуальную модель, так и стандартный алгоритм в реальном контексте.
Тип: Задача решения проблем
Преобразование квадратных единиц: Целью этой задачи является преобразование квадратных единиц. Используйте предоставленную информацию, чтобы ответить на поставленные вопросы. Поскольку в этом задании учащимся предлагается подвергнуть критике рассуждения Джады, оно дает возможность поработать над Стандартом для математической практики — конструировать жизнеспособные аргументы и критиковать рассуждения других.
Используйте предоставленную информацию, чтобы ответить на поставленные вопросы. Поскольку в этом задании учащимся предлагается подвергнуть критике рассуждения Джады, оно дает возможность поработать над Стандартом для математической практики — конструировать жизнеспособные аргументы и критиковать рассуждения других.
Тип: Задача решения проблем
Деньги Джима и Джесси:Студентов просят использовать соотношение, чтобы определить, сколько денег было у Джима и Джесси в начале их путешествия.
Тип: Задача решения проблем
Камера безопасности: Учащихся просят определить процент площади магазина, охваченной камерой слежения. Затем студентов просят определить «лучшее» место для размещения камеры и подтвердить свой ответ.
Затем студентов просят определить «лучшее» место для размещения камеры и подтвердить свой ответ.
Тип: Задача решения проблем
Распродажа рубашки:Используйте предоставленную информацию, чтобы узнать первоначальную цену рубашки Селины.Есть несколько разных способов решить эту проблему; показаны два подхода.
Тип: Задача решения проблем
Голосование за три, вариант 1: Эта задача является пятой в серии из семи задач на отношения. На первый взгляд может показаться, что проблема выходит за рамки , что ограничивает себя «описанием соотношения между двумя величинами». Однако, несмотря на то, что есть три количества (количество голосов каждого кандидата), они учитываются только два одновременно.
На первый взгляд может показаться, что проблема выходит за рамки , что ограничивает себя «описанием соотношения между двумя величинами». Однако, несмотря на то, что есть три количества (количество голосов каждого кандидата), они учитываются только два одновременно.
Тип: Задача решения проблем
Голосование за три, вариант 2:Это шестая задача из семи, в которых используется контекст выборов в классе.Хотя он по-прежнему имеет дело с простыми отношениями и легко управляемыми числами, математика, связанная с отношениями, становится все более сложной. В этой задаче учащимся предлагается определить разницу голосов, полученных двумя из трех кандидатов.
Тип: Задача решения проблем
Голосование за три, вариант 3: Это последняя задача из семи в серии о соотношениях, установленных в контексте школьных выборов. Поскольку количество избирателей неизвестно, проблема достаточно абстрактна и требует глубокого понимания соотношений и их связи с дробями.
Поскольку количество избирателей неизвестно, проблема достаточно абстрактна и требует глубокого понимания соотношений и их связи с дробями.
Тип: Задача решения проблем
Голосование за двоих, вариант 3:Эта задача является третьей в серии задач, поставленных в контексте выбора класса.Учащимся дается соотношение и общее количество избирателей, и их просят определить разницу между выигрышным количеством полученных голосов и количеством голосов, необходимых для победы.
Тип: Задача решения проблем
Голосование за двоих, Вариант 1: Это первая и самая основная задача в серии из семи задач, поставленных в контексте выборов в классе. Учащимся дается соотношение и общее количество избирателей, и их просят определить количество голосов, полученных каждым кандидатом.
Учащимся дается соотношение и общее количество избирателей, и их просят определить количество голосов, полученных каждым кандидатом.
Тип: Задача решения проблем
Голосование за двоих, вариант 2:Это второе из серии заданий, поставленных в контексте выборов в классе.Это требует, чтобы студенты понимали, что такое отношения, и применяли их в контексте. В простой версии этого вопроса просто спрашивалось, сколько голосов получает каждый. У этого есть дополнительный шаг запроса разницы между голосами.
Тип: Задача решения проблем
Голосование за двоих, Вариант 4: Это четвертое задание из серии о соотношениях, установленных в контексте выборов в классе. Учитывая только соотношение, студентов просят определить дробную разницу между полученными и требуемыми голосами.
Учитывая только соотношение, студентов просят определить дробную разницу между полученными и требуемыми голосами.
Тип: Задача решения проблем
Коллегия выборщиков:Учащимся предоставляется контекст и точечный график, а также им задается ряд вопросов, касающихся формы, центра и распространения данных.
Тип: Задача решения проблем
Кнопки: Статистические вопросы: Учащимся дается контекст и ряд вопросов, и их просят определить, является ли каждый вопрос статистическим, и представить свое обоснование. Студентам предлагается составить оригинальный статистический вопрос для заданного контекста.
Студентам предлагается составить оригинальный статистический вопрос для заданного контекста.
Тип: Задача решения проблем
Вес щенка:Используя предоставленную информацию, создайте соответствующий графический дисплей и ответьте на вопросы, касающиеся формы, центра и изменчивости.
Тип: Задача решения проблем
Расстояния по числовой прямой 2: Цель этого задания состоит в том, чтобы укрепить понимание учащимися рациональных чисел как точек на числовой прямой и дать им наглядное представление о том, что сумма числа и его обратная сумма (обычно называемая его «противоположностью») равен нулю.
Тип: Задача решения проблем
Приготовление горячего какао, вариант 2:Ученикам задают ряд вопросов с дробями и целыми числами в контексте рецепта. Студентам предлагается решить задачу, используя как визуальную модель, так и стандартный алгоритм.
Тип: Задача решения проблем
Бег в школу, Вариант 3: Учащихся просят решить задачу на расстояние с использованием дробей. Цель этого задания — помочь учащимся расширить свое понимание деления целых чисел на деление дробей, и, учитывая используемые простые числа, оно наиболее подходит для учащихся, только изучающих деление дробей, поскольку оно легко поддается графическому решению.
Тип: Задача решения проблем
Ставить цели:Целью этого задания является решение учащимися задач на умножение и деление десятичных дробей в реальном контексте постановки финансовых целей.Основное внимание в задании уделяется моделированию и пониманию концепции постановки финансовых целей, поэтому свободное владение вычислениями позволит учащимся сосредоточиться на других аспектах задания.
Тип: Задача решения проблем
Цветочный магазин: Студентов просят решить реальную задачу на общие кратные.
Тип: Задача решения проблем
Пробка:Учащихся просят использовать дроби, чтобы определить, сколько часов потребуется машине, чтобы проехать заданное расстояние.
Тип: Задача решения проблем
Кредиты на видеоигры:Студентов просят использовать дроби, чтобы определить, как долго можно играть в видеоигру.
Тип: Задача решения проблем
Обмен валют: Цель этого задания — заставить учащихся конвертировать несколько валют, чтобы решить задачу. Аббревиатура CDN для Канады может показаться студентам запутанной.Учителям может потребоваться объяснить тот факт, что деньги в Канаде также называются долларами, поэтому, чтобы различать их, мы называем их канадскими долларами.
Аббревиатура CDN для Канады может показаться студентам запутанной.Учителям может потребоваться объяснить тот факт, что деньги в Канаде также называются долларами, поэтому, чтобы различать их, мы называем их канадскими долларами.
Тип: Задача решения проблем
Дом Даны:Используйте предоставленную информацию, чтобы узнать, какой процент участка Даны не будет покрыт домом.
Тип: Задача решения проблем
Обмен данными: В этом задании учащимся предлагается решить реальную задачу, связанную с единицами измерения (данные за единицу времени), используя единицы измерения, о которых многие подростки и подростки слышали, но не знают определения. Хотя используемые вычисления не особенно сложны, единицы измерения будут абстрактными для многих учащихся. Первое решение больше основано на рассуждениях о значении умножения и деления, а второе решение использует единицы измерения, помогающие отслеживать шаги в процессе решения.
Хотя используемые вычисления не особенно сложны, единицы измерения будут абстрактными для многих учащихся. Первое решение больше основано на рассуждениях о значении умножения и деления, а второе решение использует единицы измерения, помогающие отслеживать шаги в процессе решения.
Тип: Задача решения проблем
Встреча друзей на велосипедах:Учащихся просят использовать знания о скоростях и соотношениях, чтобы ответить на ряд вопросов, касающихся времени, расстояния и скорости.
Тип: Задача решения проблем
Игры на перемене: Учащихся просят написать полные предложения, чтобы описать соотношения для контекста.
Тип: Задача решения проблем
Сравнение температур:Цель этого задания состоит в том, чтобы учащиеся сравнили числа со знаком в контексте реального мира.
Тип: Задача решения проблем
Стратегия дивизиона Дэна: Цель этого задания — помочь учащимся изучить значение дробного деления и связать его с тем, что они знают о делении целых чисел.Учащимся предлагается объяснить, почему частное двух дробей с общими знаменателями равно частному числителей этих дробей.
Тип: Задача решения проблем
Питьевой сок, Вариант 2:Это задание основано на задании пятого класса на умножение дробей «Пить сок.» В этой задаче используется тот же контекст, но задается соответствующая задача деления «Количество групп неизвестно». См. «Питьевой сок, вариант 3» для версии «Размер группы неизвестен».
Тип: Задача решения проблем
Питьевой сок, вариант 3: Учащихся просят решить задачу на деление дробей с помощью визуальной модели и стандартного алгоритма.
Тип: Задача решения проблем
Сколько _______ в. . . ?:Это учебное задание требует, чтобы учащиеся смоделировали каждую задачу с помощью некоторого типа манипуляций с дробями или рисунков.Это могут быть шаблонные блоки, полоски, сделанные учащимися или учителями, или серийно выпускаемые дроби. Как минимум, учащиеся должны нарисовать каждую из них. Вышеупомянутые задачи предназначены для развития, требующего более глубокого понимания значения дробей по мере их прохождения учащимися.
Тип: Задача решения проблем
Целые числа в числовой строке 2: Цель этого задания — помочь учащимся лучше понять взаимное расположение и значения положительных и отрицательных чисел.
Тип: Задача решения проблем
В Майами теплее:Целью этого задания является применение учащимися своих знаний о целых числах в реальном контексте.
Тип: Задача решения проблем
Закуски Джейдена:Учащихся просят складывать или вычитать десятичные дроби для решения задач в контексте.
Тип: Задача решения проблем
Трудный день: Учащихся просят написать и решить уравнение с одной переменной, чтобы ответить на реальный вопрос.
Тип: Задача решения проблем
Продажа шоколадных батончиков:В этом задании учащиеся используют различные представления для анализа взаимосвязи между двумя величинами и решения реальной проблемы.Представленная ситуация дает хорошую возможность установить связи между информацией, предоставленной таблицами, графиками и уравнениями. В последней части задачи числа достаточно велики, поэтому использование формулы является наиболее эффективным способом решения задачи; однако творческое использование таблицы или графика также сработает.
Тип: Задача решения проблем
Расстояние до школы: В этом задании учащимся предлагается найти эквивалентные выражения, визуализируя знакомую деятельность, связанную с расстоянием. Данное решение показывает некоторые возможные эквивалентные выражения, но возможны многие варианты.
Данное решение показывает некоторые возможные эквивалентные выражения, но возможны многие варианты.
Тип: Задача решения проблем
Эквивалентные выражения:Учащихся просят использовать свойства операций для сопоставления эквивалентных выражений и написать эквивалентные выражения для любых выражений, не имеющих соответствия.
Тип: Задача решения проблем
Назначение пожарного: В этом задании учащихся просят написать уравнение для решения реальной задачи.
Тип: Задача решения проблем
Рыбацкие приключения 1:Учащихся просят написать и изобразить на графике два неравенства, описанных в контексте: одно дискретное и одно непрерывное.
Тип: Задача решения проблем
Бревенчатая поездка:Студентов просят решить неравенство, чтобы ответить на реальный вопрос.
Тип: Задача решения проблем
Утренняя прогулка: Студентов просят написать уравнение с одной переменной, чтобы найти пройденное расстояние.
Тип: Задача решения проблем
Прыгающая блоха:Цель этого задания — помочь учащимся понять абсолютное значение числа как его расстояние от 0 на числовой прямой. Контекст нереалистичен и не должен быть таковым; это мысленный эксперимент, который помогает учащимся сосредоточиться на относительном положении чисел на числовой прямой.
Тип: Задача решения проблем
Продажа манго: Учащихся просят определить, подходят ли два разных соотношения для одного и того же контекста.
Тип: Задача решения проблем
Смешивание бетона:Учитывая соотношение, учащихся просят определить, сколько каждого ингредиента необходимо для изготовления бетона.
Тип: Задача решения проблем
Перекрывающиеся квадраты: Эта задача обеспечивает интересный геометрический контекст для работы над понятием процента. Предусмотрены два различных метода анализа геометрии: первый размещает два квадрата рядом друг с другом, а затем перемещает один так, чтобы они перекрывались. Второе решение устанавливает уравнение для нахождения перекрытия с точки зрения заданной информации, которое отражает математические идеи, описанные в кластере MAFS.6.EE.2 — Обоснование и решение уравнений и неравенств с одной переменной.
Второе решение устанавливает уравнение для нахождения перекрытия с точки зрения заданной информации, которое отражает математические идеи, описанные в кластере MAFS.6.EE.2 — Обоснование и решение уравнений и неравенств с одной переменной.
Тип: Задача решения проблем
Цена за фунт и фунты за доллар:Учащихся просят использовать данное соотношение, чтобы определить, верны ли две разные интерпретации этого соотношения, и определить максимальное количество, которое можно купить в заданном контексте.
Тип: Задача решения проблем
Бег с постоянной скоростью: Учащимся предлагается применить знания об отношениях, чтобы ответить на несколько вопросов, касающихся скорости, расстояния и времени.
Тип: Задача решения проблем
Формы распределения:В этом видео вы потренируетесь описывать форму распределений как скошенную влево, скошенную вправо или симметричную.
Тип: Учебник
Силы нуля: Учащиеся узнают, что ненулевые числа в нулевой степени равны единице. Они также узнают, что ноль в любой положительной степени равен нулю.
Тип: Учебник
Построение коробчатого графика:В этом видеоролике показано, как построить блочную диаграмму, ранее известную как блочная диаграмма с усами.
Тип: Учебник
Нахождение площади путем разложения фигуры: В этом учебном пособии показано, как можно определить площадь неправильной геометрической формы путем разложения на знакомые формы меньшего размера.
Тип: Учебник
Объем прямоугольной призмы: дробные кубы:В этом видеоролике вы узнаете о другом способе нахождения объема прямоугольной призмы, включающем в себя деление ее на дробные кубы, нахождение объема единицы, а затем умножение этой площади на количество кубов, входящих в прямоугольную призму.
Тип: Учебник
Четырехугольник на координатной плоскости: В этом примере учащимся сообщают координаты вершин и просят построить полученный многоугольник, а именно четырехугольник.
Тип: Учебник
Гистограммы:Узнайте, как создавать гистограммы, которые суммируют данные, сортируя их по группам.
Тип: Учебник
Решение одношаговых уравнений с использованием деления: Чтобы найти значение переменной, вы должны получить его только в одной части уравнения. Для этого вам нужно что-то сделать с ОБЕИМИ сторонами уравнения.
Для этого вам нужно что-то сделать с ОБЕИМИ сторонами уравнения.
Тип: Учебник
Что такое переменная?: Основное внимание здесь уделяется пониманию того, что переменная — это просто символ, который может представлять различные значения в выражении.
Тип: Учебник
Координатная плоскость:Учащиеся начертят упорядоченную пару по осям x (горизонтальная) и y (вертикальная) оси координатной плоскости.
Тип: Учебник
Наименьший общий множитель: В этом видеоролике демонстрируется метод разложения простых чисел для нахождения lcm (наименьшего общего кратного).
Тип: Учебник
Координатная плоскость:Учащиеся познакомятся с координатной плоскостью.
Тип: Учебник
Сравнение абсолютных значений: В этом руководстве вы будете сравнивать абсолютное значение чисел, используя понятия больше (>), меньше (<) и равно (=).
Тип: Учебник
Сортировка значений в числовой строке:В этом видеоролике демонстрируется сортировка значений, включая абсолютное значение, от наименьшего к наибольшему с использованием числовой строки.
Тип: Учебник
Порядок действий : Проработайте сложный пример порядка операций только с положительными числами.
Тип: Учебник
Порядок действий :В этом видео показано, как вычислять выражения с показателями степени, используя порядок операций.
Тип: Учебник
Площадь трапеции: Трапеция – это тип четырехугольника с одним набором параллельных сторон.Здесь мы объясним, как найти его площадь.
Тип: Учебник
Нулевая сила:Узнайте, почему число, возведенное в нулевую степень, равно 1.
Тип: Учебник
Площадь треугольника на сетке:Мы сможем найти площадь треугольника в координатной сетке.В этом уроке приведена формула площади треугольника.
Тип: Учебник
Периметр и площадь: Учащиеся изучат основы нахождения периметра и площади квадратов и прямоугольников.
Тип: Учебник
Вычитание десятичных знаков 2:В этом уроке мы покажем вычитание цифр до тысячных.
Тип: Учебник
Проблема соотношения слов: В этом видео коэффициент задается, а затем применяется для решения проблемы.
Тип: Учебник
Нахождение процента:В видео мы находим проценты, когда дана часть и целое.
Тип: Учебник
Как оценить выражение с помощью замены: В этом примере у нас есть формула для преобразования температуры Цельсия в Фаренгейта. Давайте заменим переменную значением (температура по Цельсию), чтобы получить градусы в градусах Фаренгейта. Большая проблема, чтобы практиковать с нами!
Давайте заменим переменную значением (температура по Цельсию), чтобы получить градусы в градусах Фаренгейта. Большая проблема, чтобы практиковать с нами!
Тип: Учебник
Значение процента:В этом видео показано, что на самом деле означают проценты, если смотреть на сетку 10 на 10.
Тип: Учебник
Что такое переменная?: Здесь мы сосредоточимся на том, чтобы понять, что переменная — это просто буква или символ (обычно строчная буква), который может представлять различные значения в выражении. Мы получили это. Просто смотрю.
Мы получили это. Просто смотрю.
Тип: Учебник
Распределительное свойство и ментальная математика:Свойство распределения указывает, что операторы сложения или вычитания в круглых скобках могут быть отдельно умножены на значение вне круглых скобок.В этом уроке учащиеся изучат распределительное свойство, которое очень полезно при математических вычислениях в уме и решении уравнений.
Тип: Учебник
Декартова система координат: Декартова система координат, образованная декартовым произведением действительной числовой прямой на саму себя, позволяет визуализировать алгебраические уравнения в виде геометрических фигур в двух или трех измерениях. Хотя это руководство включает в себя основы системы координат, оно также включает в себя идеи, выходящие за рамки стандартов пятого класса. Скорее всего, это видео понравится только продвинутым пятиклассникам.
Хотя это руководство включает в себя основы системы координат, оно также включает в себя идеи, выходящие за рамки стандартов пятого класса. Скорее всего, это видео понравится только продвинутым пятиклассникам.
Тип: Учебник
Предварительная алгебра — дроби и рациональные числа:Первыми дробями, использовавшимися древними цивилизациями, были «единичные дроби».Позже были добавлены числители, отличные от единицы, что привело к созданию «общих дробей», которые стали нашими современными дробями. Вместе дроби и целые числа образуют «рациональные числа».
Тип: Учебник
Предварительная алгебра — целые числа, целые числа и числовая линия: Системы счисления эволюционировали от натуральных «счетных» чисел к целым числам (с добавлением нуля), к целым числам (с добавлением отрицательных чисел) и далее. Эти системы счисления легко понять, используя числовую линию.
Эти системы счисления легко понять, используя числовую линию.
Тип: Учебник
Добавление целых чисел:Учащиеся смогут увидеть примеры сложения целых чисел во время просмотра короткого видео и попрактиковаться в сложении целых чисел с помощью онлайн-викторины.
Тип: Учебник
Линейные уравнения с одной переменной: Этот урок знакомит учащихся с линейными уравнениями с одной переменной, показывает, как решать их, используя свойства равенства сложения, вычитания, умножения и деления, и позволяет учащимся определить, является ли значение решением, существует ли бесконечно много решений или вообще никакого решения. Сайт содержит объяснение уравнений и линейных уравнений, способы решения уравнений в целом и стратегию решения линейных уравнений. Урок также объясняет противоречие (уравнение без решения) и тождество (уравнение с бесконечными решениями). В конце есть пять практических задач для студентов, чтобы проверить свои знания со ссылками на ответы и объяснениями того, как эти ответы были найдены. Также упоминаются дополнительные ресурсы.
Сайт содержит объяснение уравнений и линейных уравнений, способы решения уравнений в целом и стратегию решения линейных уравнений. Урок также объясняет противоречие (уравнение без решения) и тождество (уравнение с бесконечными решениями). В конце есть пять практических задач для студентов, чтобы проверить свои знания со ссылками на ответы и объяснениями того, как эти ответы были найдены. Также упоминаются дополнительные ресурсы.
Тип: Учебник
Основные аддитивные цвета: Этот ресурс помогает пользователю изучить три основных цвета, которые являются фундаментальными для человеческого зрения, изучить различные цвета в видимом спектре, наблюдать за результирующими цветами при добавлении двух цветов и узнать, что такое белый свет. Сочетание текста и виртуальных манипуляторов позволяет пользователю исследовать эти концепции несколькими способами.
Сочетание текста и виртуальных манипуляторов позволяет пользователю исследовать эти концепции несколькими способами.
Тип: Учебник
Основные субтрактивные цвета:Пользователь изучит три основных субтрактивных цвета в видимом спектре, исследует результирующие цвета, когда два субтрактивных цвета взаимодействуют друг с другом, и исследует образование черного цвета.
Тип: Учебник
Преобразование единиц скорости: На этом уроке учащиеся будут просматривать видеоролик Академии Хана, в котором показано, как преобразовывать отношения с использованием единиц измерения скорости.
Тип: Учебник
Умножение дробей:В видео рассказывается, как умножать дроби и формулировать ответ в минимальных выражениях.
Тип: Учебник
Порядок числовых выражений:Видео демонстрирует преобразование заданных чисел в общий формат (в виде десятичных дробей), чтобы их можно было сравнивать и упорядочивать.
Тип: Учебник
Простые уравнения: Введение в решение уравнения умножения с одной переменной вида px = q.
Тип: Учебник
Смеси:В этом онлайн-упражнении учащиеся применяют свое понимание пропорциональных отношений, добавляя круги, цветные или нет, к двум разным стопкам, а затем объединяют стопки, чтобы получить требуемый процент цветных кружков.Студенты могут играть в четырех режимах: исследование, неизвестная часть, неизвестное целое или неизвестный процент. Это задание также включает дополнительные материалы на вкладках над апплетом, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Тип: виртуальный манипулятор
Коробка Сюжет: В этом упражнении учащиеся используют предустановленные данные или вводят свои собственные данные, которые будут представлены в блочной диаграмме. Это упражнение позволяет учащимся исследовать как отдельные, так и расположенные рядом диаграммы различных данных. Это задание включает в себя дополнительные материалы, в том числе справочную информацию по изучаемым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Это упражнение позволяет учащимся исследовать как отдельные, так и расположенные рядом диаграммы различных данных. Это задание включает в себя дополнительные материалы, в том числе справочную информацию по изучаемым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Тип: виртуальный манипулятор
Расширенный графировщик данных:Это онлайн-утилита для построения графиков, которую можно использовать для создания коробчатых диаграмм, пузырьковых диаграмм, диаграмм рассеяния, гистограмм и диаграмм «стебли и листья».
Тип: виртуальный манипулятор
Коробчатый плоттер: Пользователи выбирают набор данных или вводят свои собственные данные для создания ящичковой диаграммы.
Тип: виртуальный манипулятор
Баланс панорамирования — Числа:Этот инструмент помогает учащимся лучше понять, что равенство — это отношения, а не оперативная команда «найти ответ».» Апплет имеет функцию балансировки чашек, которая позволяет учащемуся вводить каждую половину уравнения в чаши, которые реагируют на значение числового выражения путем повышения, понижения или балансировки.
Тип: виртуальный манипулятор
Инструмент гистограммы: Этот виртуальный манипулятивный инструмент гистограммы может помочь в анализе распределения набора данных. Он имеет 6 предустановленных наборов данных и функцию добавления собственных данных для анализа.
Он имеет 6 предустановленных наборов данных и функцию добавления собственных данных для анализа.
Тип: виртуальный манипулятор
Викторина по порядку операций:В этом упражнении учащиеся учатся решать алгебраические выражения, используя порядок операций.Апплет записывает их баллы, чтобы учащийся мог отслеживать свой прогресс. Эта деятельность позволяет учащимся практиковать применение порядка операций при решении задач. Это задание включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Тип: виртуальный манипулятор
Гистограмма: В этом упражнении учащиеся могут создавать и просматривать гистограммы, используя существующие наборы данных или введенные исходные данные. Учащиеся могут настроить размер интервала с помощью ползунка, а также другие шкалы на графике. Это задание позволяет учащимся изучить гистограммы как способ представления данных, а также понятия среднего значения, стандартного отклонения и масштаба. Это задание включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Учащиеся могут настроить размер интервала с помощью ползунка, а также другие шкалы на графике. Это задание позволяет учащимся изучить гистограммы как способ представления данных, а также понятия среднего значения, стандартного отклонения и масштаба. Это задание включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Тип: виртуальный манипулятор
.





 Чем выше скорость, тем меньше времени уходит на преодоление расстояния.
Чем выше скорость, тем меньше времени уходит на преодоление расстояния. . Таким образом, учащиеся расширяют круг задач, для решения которых они могут использовать умножение и деление, а также связывают соотношения и дроби.Студенты решают широкий спектр задач, связанных с отношениями и коэффициентами.
. Таким образом, учащиеся расширяют круг задач, для решения которых они могут использовать умножение и деление, а также связывают соотношения и дроби.Студенты решают широкий спектр задач, связанных с отношениями и коэффициентами. 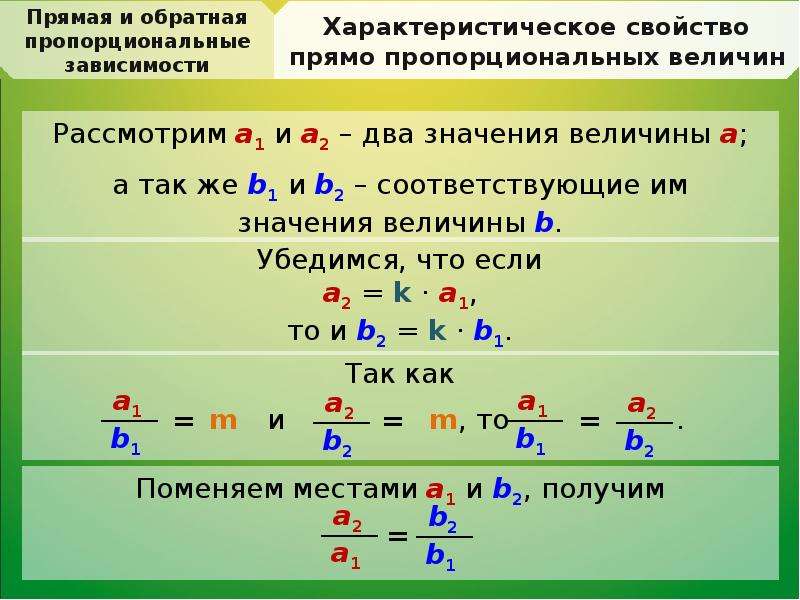 Учащиеся понимают, что выражения в разных формах могут быть эквивалентны, и они используют свойства операций для перезаписи выражений в эквивалентных формах.Учащиеся знают, что решениями уравнения являются значения переменных, которые делают уравнение верным. Учащиеся используют свойства операций и идею сохранения равенства обеих частей уравнения для решения простых одношаговых уравнений. Учащиеся составляют и анализируют таблицы, например, таблицы величин, находящихся в эквивалентных соотношениях, и используют уравнения (например, 3 x = y ) для описания взаимосвязей между величинами.
Учащиеся понимают, что выражения в разных формах могут быть эквивалентны, и они используют свойства операций для перезаписи выражений в эквивалентных формах.Учащиеся знают, что решениями уравнения являются значения переменных, которые делают уравнение верным. Учащиеся используют свойства операций и идею сохранения равенства обеих частей уравнения для решения простых одношаговых уравнений. Учащиеся составляют и анализируют таблицы, например, таблицы величин, находящихся в эквивалентных соотношениях, и используют уравнения (например, 3 x = y ) для описания взаимосвязей между величинами.  Учащиеся признают, что показатель изменчивости (межквартильный размах или среднее абсолютное отклонение) также может быть полезен для обобщения данных, поскольку два совершенно разных набора данных могут иметь одно и то же среднее значение и медиану, но различаться по своей изменчивости.Учащиеся учатся описывать и обобщать наборы числовых данных, выявляя кластеры, пики, пробелы и симметрию с учетом контекста, в котором данные были собраны.
Учащиеся признают, что показатель изменчивости (межквартильный размах или среднее абсолютное отклонение) также может быть полезен для обобщения данных, поскольку два совершенно разных набора данных могут иметь одно и то же среднее значение и медиану, но различаться по своей изменчивости.Учащиеся учатся описывать и обобщать наборы числовых данных, выявляя кластеры, пики, пробелы и симметрию с учетом контекста, в котором данные были собраны. Они рассуждают о прямоугольных призмах с дробными длинами сторон, чтобы распространить формулы для объема прямоугольной призмы на дробные длины сторон. Готовятся к работе над чертежами и конструкциями в масштабе 7 класса, рисуя многоугольники в координатной плоскости.
Они рассуждают о прямоугольных призмах с дробными длинами сторон, чтобы распространить формулы для объема прямоугольной призмы на дробные длины сторон. Готовятся к работе над чертежами и конструкциями в масштабе 7 класса, рисуя многоугольники в координатной плоскости.