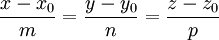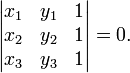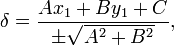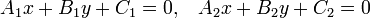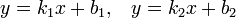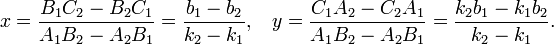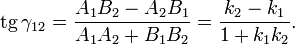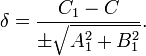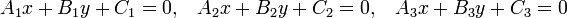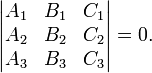Точка, линия, прямая, луч, отрезок, ломанная
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
ABCточка 1, точка 2, точка 3
123Можно нарисовать на листке бумаги три точки "А" и предложить ребёнку провести линию через две точки "А". Но как понять через какие? AAA
Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
abcЛиния может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
aпрямая линия AB
BAПрямые могут быть
- пересекающимися, если имеют общую точку. Две прямые могут пересекаться только в одной точке.
- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча A A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
aлуч AB
BAЛучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
CBAОтрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками
Через одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
BAпрямая линия AB
BAОт прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ BA✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
BAЗадача: где прямая, луч, отрезок, кривая?
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
ABCDE646212752Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее, а у какой больше вершин? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
ABCDEF120605812298141Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т.д.
треугольники
четырёхугольники: квадрат, прямоугольник, дельтоид, ромб, параллелограмм, трапеция
пятиугольники
shpargalkablog.ru
Прямая линия — это… Что такое Прямая линия?
Прямая — одно из основных понятий геометрии.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.
Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.
Аналитически прямая задаётся уравнением (в трёхмерном пространстве — системой уравнений) первой степени.
- Через любые две несовпадающие точки можно провести единственную прямую.
- Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются параллельными.
- В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:
- Прямая линия — алгебраическая линия первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).
Уравнения прямой на плоскости
 Способы задания прямой:
Способы задания прямой: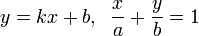 или
или 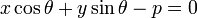
Общее уравнение прямой линии на плоскости в декартовых координатах:
где A и B одновременно не равны нулю. При C = 0 прямая проходит через начало координат.
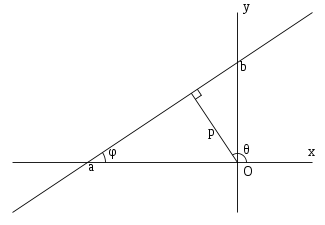
Уравнение прямой с угловым коэффициентом. Прямая линия, пересекающая ось Oy в точке 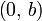 и образующая угол φ с положительным направлением оси
и образующая угол φ с положительным направлением оси
Коэффициент k называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси Oy.
Уравнение прямой в отрезках. Прямая линия, пересекающая ось Ox в точке 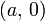 и ось Oy в точке
и ось Oy в точке 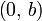 :
:
В этом виде невозможно представить прямую, проходящую через начало координат.
Нормальное уравнение прямой:
где p — длина перепендикуляра, опущенного на прямую из начала координат, а θ — угол (измеренный в положительном направлении) между положительным направлением оси Ox и направлением этого перпендикуляра. Если p = 0, то прямая проходит через начало координат, а угол 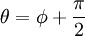 задаёт угол наклона прямой.
задаёт угол наклона прямой.
Если прямая задана общим уравнением Ax + By + C = 0, то отрезки a и b, отсекаемые ею на осях, угловой коэффициент k, расстояние прямой от начала координат p, cosθ и sinθ выражаются через коэффициенты A, B и C следующим образом:
Во избежание неопределённости знак перед радикалом выбирается так, чтобы соблюдалось условие p > 0. В этом случае cosθ и sinθ являются направляющими косинусами положительной нормали прямой — перпендикуляра, опущенного из начала координат на прямую. Если C = 0, то прямая проходит через начало координат и выбор положительного напрвления произволен.
Уравнение прямой, проходящей через две заданные несовподающие точки 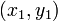 и
и 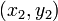
или
или в общем виде
Параметрические уравнения прямой могут быть записаны в виде:
где t — производный параметр, при этом
Уравнение прямой в полярных координатах ρ и φ:
или
Тангенциальное уравнение прямой на плоскости:
- ξx + ηy = 1
Числа ξ и η называются её тангенциальными, линейными или плюккеровыми координатами.
Уравнения прямой в пространстве
Каноническое уравнение прямой в пространстве:
- Пусть M(x0,y0,z0) — точка, лежащая на прямой, и
 — вектор, ей коллинеарный. Тогда уравнение прямой имеет вид:
— вектор, ей коллинеарный. Тогда уравнение прямой имеет вид: 
Взаимное расположение точек и прямых
Три точки 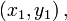
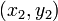 и
и 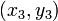 лежат на одной прямой тогда и только тогда, если выполняется условие
лежат на одной прямой тогда и только тогда, если выполняется условие
Отклонение точки 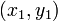 от прямой Ax + By + C = 0 может быть найдено по формуле
от прямой Ax + By + C = 0 может быть найдено по формуле
где знак перед радикалом противоположен знаку C. Отклонение по модулю равно расстоянию между точкой и прямой; оно положительно, если точка и начало координат лежат по разные стороны от прямой, и отрицательно, если по одну сторону.
Взаимное расположение нескольких прямых
Две прямые, заданные уравнениями
или
пересекаются в точке
Угол γ12 между пересекающимися прямыми определяется формулой
При этом под γ12 понимается угол, на который надо повернуть первую прямую (заданную параметрамиA1, B1, C1, k1 и b1) вокруг точки пересечения против часовой стрелки до первого совмещения со второй прямой.
Эти прямые параллельны, если A1B2 − A2B1 = 0 или k1 = k2, и перпендикулярны, если A1A2 + B1B2 = 0 или 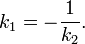
Любую прямую, паралельную A1x + B1y + C1 = 0, можно выразить уравнением A1x + B1y + C = 0. При этом расстояние между ними будет равно
Если знак перед радикалом противоположен C1, то δ будет положительным, когда вторая прямая и начало координат лежат по разные стороны от первой прямой.
Для того, чтобы три прямые
пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие
См. также
Ссылки
Wikimedia Foundation. 2010.
dic.academic.ru
Прямая — это… Что такое Прямая?
Прямая — одно из основных понятий геометрии, то есть точного универсального определения не имеет.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.
Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.
Аналитически прямая задаётся уравнением (в трёхмерном пространстве — системой уравнений) первой степени.
- Через любые две несовпадающие точки можно провести единственную прямую.
- Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются параллельными.
- В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:
- Прямая линия — алгебраическая линия первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).
Уравнения прямой на плоскости
 Способы задания прямой:
Способы задания прямой:или .
Общее уравнение прямой
Общее уравнение прямой линии на плоскости в декартовых координатах:
где , и — произвольные постоянные, причем постоянные и не равны нулю одновременно. Вектор с координатами точки называется нормальным вектором, он перпендикулярен прямой.
При прямая проходит через начало координат. Также уравнение можно переписать в виде
Уравнение прямой с угловым коэффициентом
Уравнение прямой линии, пересекающей ось в точке и образующей угол с положительным направлением оси :
Коэффициент называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси
Получение уравнения прямой в отрезкахУравнение прямой в отрезках
Уравнение прямой линии, пересекающей ось в точке и ось в точке :
В этом виде невозможно представить прямую, проходящую через начало координат.
Нормальное уравнение прямой
где — длина перпендикуляра, опущенного на прямую из начала координат, а — угол (измеренный в положительном направлении) между положительным направлением оси и направлением этого перпендикуляра. Если , то прямая проходит через начало координат, а угол задаёт угол наклона прямой.
Вывод нормального уравнения прямой
Если прямая задана общим уравнением то отрезки и отсекаемые ею на осях, угловой коэффициент расстояние прямой от начала координат и выражаются через коэффициенты , и следующим образом:
Во избежание неопределённости знак перед радикалом выбирается так, чтобы соблюдалось условие В этом случае и являются направляющими косинусами положительной нормали прямой — перпендикуляра, опущенного из начала координат на прямую. Если то прямая проходит через начало координат и выбор положительного направления произволен.
Уравнение прямой, проходящей через две заданные несовпадающие точки
Если заданы две несовпадающие точки с координатами и , то прямая, проходящая через них, задаётся уравнением
или
или в общем виде
Векторное параметрическое уравнение прямой
Векторное параметрическое уравнение прямой задается вектором конец которого лежит на прямой, и направляющим вектором прямой Параметр пробегает все действительные значения.
Параметрические уравнения прямой
Параметрические уравнения прямой могут быть записаны в виде:
где — производный параметр, — координаты и направляющего вектора прямой. При этом
Смысл параметра аналогичен параметру в векторно-параметрическом уравнении.
Каноническое уравнение прямой
Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:
где — координаты и направляющего вектора прямой, и координаты точки, принадлежащей прямой.
Уравнение прямой в полярных координатах
Уравнение прямой в полярных координатах и :
или
Тангенциальное уравнение прямой
Тангенциальное уравнение прямой на плоскости:
Числа и называются её тангенциальными, линейными или плюккеровыми координатами.
Уравнения прямой в пространстве
Векторное параметрическое уравнение прямой в пространстве:
где — радиус-вектор некоторой фиксированной точки лежащей на прямой, — ненулевой вектор, коллинеарный этой прямой (называемый её направляющим вектором), — радиус-вектор произвольной точки прямой.
Параметрические уравнения прямой в пространстве:
где — координаты некоторой фиксированной точки лежащей на прямой; — координаты вектора, коллинеарного этой прямой.
Каноническое уравнение прямой в пространстве:
где — координаты некоторой фиксированной точки лежащей на прямой; — координаты вектора, коллинеарного этой прямой.
Общее векторное уравнение прямой[уточнить] в пространстве:
- Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями:
- и
то уравнение прямой можно задать системой этих уравнений:
Векторное уравнение прямой в пространстве[1]:196-199:
- Уравнение прямой в пространстве можно записать в виде векторного произведения радиуса-вектора произвольной точки этой прямой на фиксированный направляющий вектор прямой :
где фиксированный вектор , ортогональный вектору , можно найти, подставляя в это уравнение радиус-вектор какой-нибудь одной известной точки прямой.
Взаимное расположение точек и прямых на плоскости
Три точки , и лежат на одной прямой тогда и только тогда, когда выполняется условие
Отклонение точки от прямой может быть найдено по формуле
где знак перед радикалом противоположен знаку Отклонение по модулю равно расстоянию между точкой и прямой; оно положительно, если точка и начало координат лежат по разные стороны от прямой, и отрицательно, если по одну сторону.
В пространстве расстояние от точки до прямой, заданной параметрическим уравнением
можно найти как минимальное расстояние от заданной точки до произвольной точки прямой. Коэффициент этой точки может быть найден по формуле
Взаимное расположение нескольких прямых на плоскости
Две прямые, заданные уравнениями
или
пересекаются в точке
Угол между пересекающимися прямыми определяется формулой
При этом под понимается угол, на который надо повернуть первую прямую (заданную параметрами , , , и ) вокруг точки пересечения против часовой стрелки до первого совмещения со второй прямой.
Эти прямые параллельны, если или , и перпендикулярны, если или .
Любую прямую, параллельную прямой с уравнением можно выразить уравнением При этом расстояние между этими прямыми будет равно
Если знак перед радикалом противоположен то будет положительным, когда вторая прямая и начало координат лежат по разные стороны от первой прямой.
Для того, чтобы три прямые
пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие
Если и , то прямые и перпендикулярны.
См. также
Примечания
Ссылки
dic.academic.ru
ПРЯМАЯ ЛИНИЯ — это… Что такое ПРЯМАЯ ЛИНИЯ?
прямая линия — ▲ линия ↑ прямая (линия) прямая линия линия нулевой кривизны; самая простая линия; линия, имеющая одно направление на всем своем протяжении; изображение линейной функции; линия 1 го порядка: две прямые линии могут пересечься между собой не более… … Идеографический словарь русского языка
ПРЯМАЯ ЛИНИЯ — одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий … Большой Энциклопедический словарь
ПРЯМАЯ ЛИНИЯ — (1) одно из основных понятий геометрии, принятое за аксиому: «через любые две точки проходит прямая и притом только одна»; (2) П. л. в аналитической геометрии алгебраическая линия первого порядка, уравнение которой у = ах + b, где а угловой… … Большая политехническая энциклопедия
Прямая линия — ПРЯМАЯ ЛИНИЯ, простейшая линия в евклидовой геометрии (определяющая кратчайший путь между своими двумя точками). … Иллюстрированный энциклопедический словарь
ПРЯМАЯ ЛИНИЯ — «ПРЯМАЯ ЛИНИЯ», СССР, киностудия ИМ. М.ГОРЬКОГО, 1967, ч/б, 92 мин. Психологическая драма. Молодой московский физик Белов работает в области атомных испытаний в секретном НИИ. После успешной сдачи проекта, в котором он принимал самое активное… … Энциклопедия кино
прямая линия — Означает либо электрическую линию, связывающую изолированное место производства с изолированным потребителем, либо электрическую линию, связывающую производителя электроэнергии непосредственно с предприятием, занимающимся поставками… … Справочник технического переводчика
Прямая линия — Изображение прямых в прямоугольной системе координат Прямая одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется… … Википедия
прямая линия
прямая линия — 06.01.136 прямая линия [ forward link]: Передача информации от устройства считывания/опроса к радиочастотной метке. Примечание Альтернативный термин «линия вниз». Сравнить с терминологической статьей «линия вверх». Источник … Словарь-справочник терминов нормативно-технической документации
прямая линия — tiesė statusas T sritis fizika atitikmenys: angl. right line; straight line vok. Gerade, f; gerade Linie, f rus. прямая, f; прямая линия, f pranc. droite, f; ligne droite, f … Fizikos terminų žodynas
dic.academic.ru
ПРЯМАЯ ЛИНИЯ — это… Что такое ПРЯМАЯ ЛИНИЯ?
прямая линия — ▲ линия ↑ прямая (линия) прямая линия линия нулевой кривизны; самая простая линия; линия, имеющая одно направление на всем своем протяжении; изображение линейной функции; линия 1 го порядка: две прямые линии могут пересечься между собой не более… … Идеографический словарь русского языка
ПРЯМАЯ ЛИНИЯ — (1) одно из основных понятий геометрии, принятое за аксиому: «через любые две точки проходит прямая и притом только одна»; (2) П. л. в аналитической геометрии алгебраическая линия первого порядка, уравнение которой у = ах + b, где а угловой… … Большая политехническая энциклопедия
ПРЯМАЯ ЛИНИЯ — ПРЯМАЯ линия, простейшая линия в евклидовой геометрии (определяющая кратчайший путь между своими двумя точками) … Современная энциклопедия
Прямая линия — ПРЯМАЯ ЛИНИЯ, простейшая линия в евклидовой геометрии (определяющая кратчайший путь между своими двумя точками). … Иллюстрированный энциклопедический словарь
ПРЯМАЯ ЛИНИЯ — «ПРЯМАЯ ЛИНИЯ», СССР, киностудия ИМ. М.ГОРЬКОГО, 1967, ч/б, 92 мин. Психологическая драма. Молодой московский физик Белов работает в области атомных испытаний в секретном НИИ. После успешной сдачи проекта, в котором он принимал самое активное… … Энциклопедия кино
прямая линия — Означает либо электрическую линию, связывающую изолированное место производства с изолированным потребителем, либо электрическую линию, связывающую производителя электроэнергии непосредственно с предприятием, занимающимся поставками… … Справочник технического переводчика
Прямая линия — Изображение прямых в прямоугольной системе координат Прямая одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется… … Википедия
прямая линия — одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий. * * * ПРЯМАЯ ЛИНИЯ ПРЯМАЯ ЛИНИЯ, одно из основных понятий геометрии. При систематическом изложении геометрии… … Энциклопедический словарь
прямая линия — 06.01.136 прямая линия [ forward link]: Передача информации от устройства считывания/опроса к радиочастотной метке. Примечание Альтернативный термин «линия вниз». Сравнить с терминологической статьей «линия вверх». Источник … Словарь-справочник терминов нормативно-технической документации
прямая линия — tiesė statusas T sritis fizika atitikmenys: angl. right line; straight line vok. Gerade, f; gerade Linie, f rus. прямая, f; прямая линия, f pranc. droite, f; ligne droite, f … Fizikos terminų žodynas
dic.academic.ru
Прямая линия — это… Что такое Прямая линия?
прямая линия — ▲ линия ↑ прямая (линия) прямая линия линия нулевой кривизны; самая простая линия; линия, имеющая одно направление на всем своем протяжении; изображение линейной функции; линия 1 го порядка: две прямые линии могут пересечься между собой не более… … Идеографический словарь русского языка
ПРЯМАЯ ЛИНИЯ — одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий … Большой Энциклопедический словарь
ПРЯМАЯ ЛИНИЯ — (1) одно из основных понятий геометрии, принятое за аксиому: «через любые две точки проходит прямая и притом только одна»; (2) П. л. в аналитической геометрии алгебраическая линия первого порядка, уравнение которой у = ах + b, где а угловой… … Большая политехническая энциклопедия
ПРЯМАЯ ЛИНИЯ — ПРЯМАЯ линия, простейшая линия в евклидовой геометрии (определяющая кратчайший путь между своими двумя точками) … Современная энциклопедия
Прямая линия — ПРЯМАЯ ЛИНИЯ, простейшая линия в евклидовой геометрии (определяющая кратчайший путь между своими двумя точками). … Иллюстрированный энциклопедический словарь
ПРЯМАЯ ЛИНИЯ — «ПРЯМАЯ ЛИНИЯ», СССР, киностудия ИМ. М.ГОРЬКОГО, 1967, ч/б, 92 мин. Психологическая драма. Молодой московский физик Белов работает в области атомных испытаний в секретном НИИ. После успешной сдачи проекта, в котором он принимал самое активное… … Энциклопедия кино
прямая линия — Означает либо электрическую линию, связывающую изолированное место производства с изолированным потребителем, либо электрическую линию, связывающую производителя электроэнергии непосредственно с предприятием, занимающимся поставками… … Справочник технического переводчика
Прямая линия — Изображение прямых в прямоугольной системе координат Прямая одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется… … Википедия
прямая линия — одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий. * * * ПРЯМАЯ ЛИНИЯ ПРЯМАЯ ЛИНИЯ, одно из основных понятий геометрии. При систематическом изложении геометрии… … Энциклопедический словарь
прямая линия — 06.01.136 прямая линия [ forward link]: Передача информации от устройства считывания/опроса к радиочастотной метке. Примечание Альтернативный термин «линия вниз». Сравнить с терминологической статьей «линия вверх». Источник … Словарь-справочник терминов нормативно-технической документации
прямая линия — tiesė statusas T sritis fizika atitikmenys: angl. right line; straight line vok. Gerade, f; gerade Linie, f rus. прямая, f; прямая линия, f pranc. droite, f; ligne droite, f … Fizikos terminų žodynas
dic.academic.ru
Точка. Кривая. Прямая линия / Виды линий / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Виды линий
- Точка. Кривая. Прямая линия
Точка



Прямая линия

Прямая линия не имеет ни начала, ни конца.
Прямую линию можно продолжить. Она бесконечна.
Через 2 точки можно провести только одну прямую.
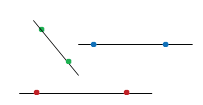
Через 1 точку можно провести много прямых линий.
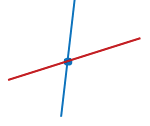

Расстояние между двумя точками
Поставим две точки на одинаковом расстоянии друг от друга и проведём между ними ломаную линию и прямую линию. Посчитаем расстояние между точками по количеству клеточек.

Вывод: Самое короткое расстояние между двумя точками — это прямая.
Кривая

Через 1 точку можно провести много кривых линий.

Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Отрезок. Луч
Ломаная линия
Длиннее. Короче. Уже. Шире. Одинаковые по длине и ширине
Виды линий
Правило встречается в следующих упражнениях:
1 класс
Страница 40, Моро, Волкова, Степанова, Учебник, 1 часть
Страница 41, Моро, Волкова, Степанова, Учебник, 1 часть
Страница 15, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 84, Моро, Волкова, Степанова, Учебник, 2 часть
Страница 13, Моро, Волкова, Рабочая тетрадь, 2 часть
2 класс
Страница 28, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 92, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 23, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
3 класс
Страница 15, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
4 класс
Страница 57, Моро, Волкова, Рабочая тетрадь, 1 часть
© budu5.com, 2019
Пользовательское соглашение
Copyright
budu5.com
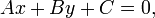
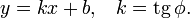
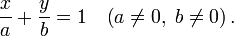
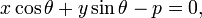
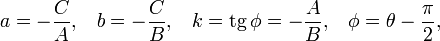
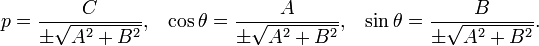
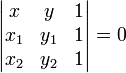
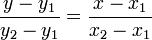
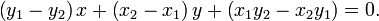
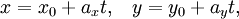
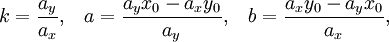
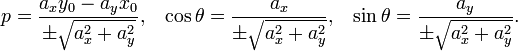
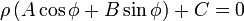
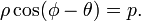
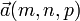 — вектор, ей коллинеарный. Тогда уравнение прямой имеет вид:
— вектор, ей коллинеарный. Тогда уравнение прямой имеет вид: